Problema 683. ( Laboratorio Virtual del Triángulo con Cabri)
Construir un triángulo rectángulo con el baricentro en la circunferencia inscrita.
Barroso, R. (2013): Comunicación personal.
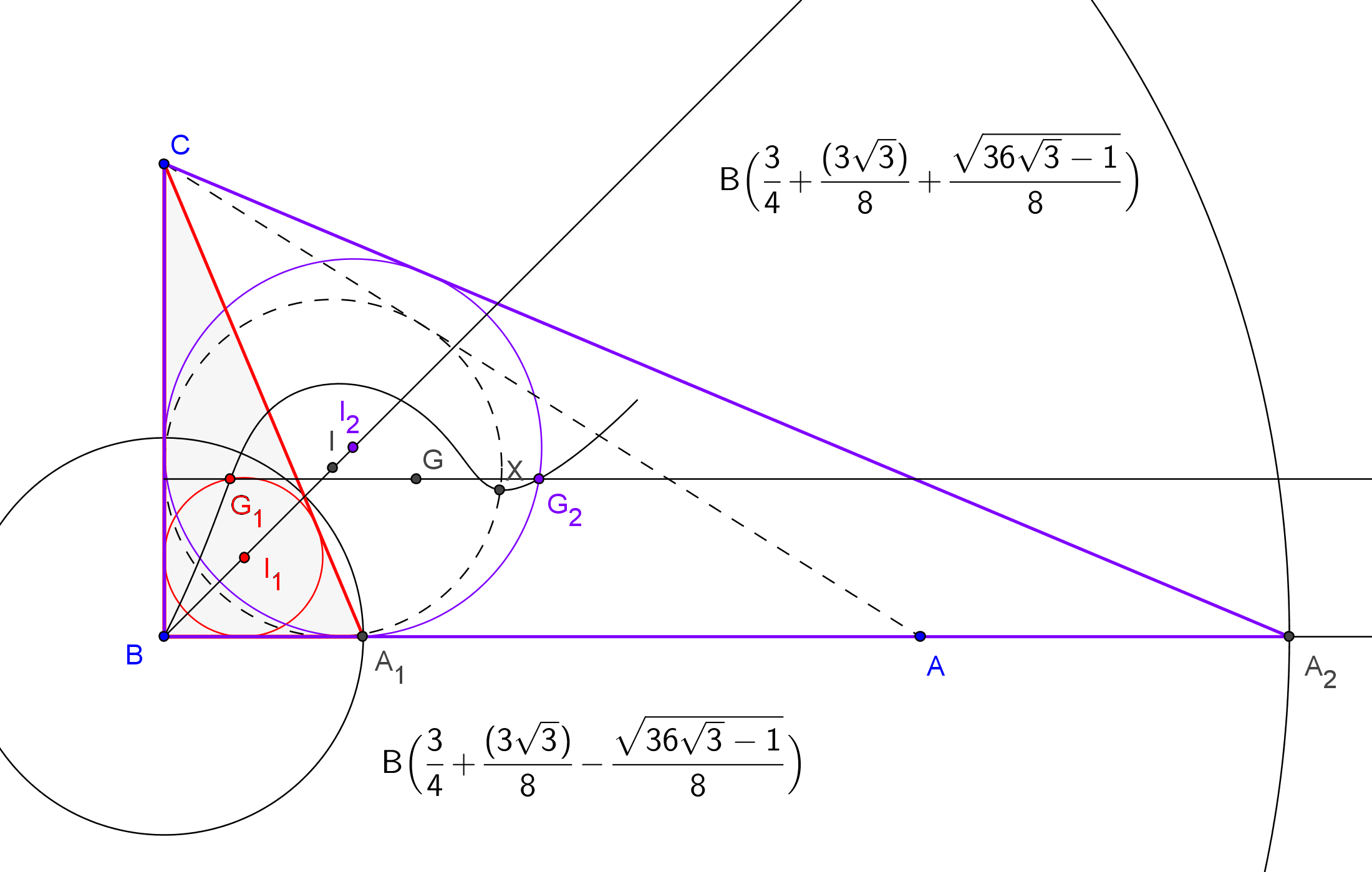
Vamos a construir el triángulo ABC, rectángulo en el vértice B y en el que suponemos dado la longitud a del lado BC (sin que con esto el problema pierda generalidad; incluso podemos tomar la cantidad a como unidad de medida).
La circunferencia inscrita en un triángulo ABC tiene por ecuación baricéntrica:
a²yz + b²zx +c²xy -
(1/4)(x + y + z)((b+c-a)²x + (c+a-b)²y + (a+b-c)²z)=0
Si imponemos que el baricentro G(1:1:1) esté en esta circunferencia y b^2 =a^2+c^2 (ABC triángulo rectángulo), de la ecuación anterior resulta que debemos resolver el sistema de ecuaciones, en las variables b y c:
3ab + 3ac + 3bc - 5a² - 5c² = 0, b² = a²+c².
Tomando a=1 (nueva unidad de medida), se tiene que:
![3/4 + (3*Sqrt[3])/8 - Sqrt[ 36*Sqrt[3]-1]/8](../imagenes/RB683Formula.png)
Longitudes que pueden ser construidas con regla y compás.
|
Angel Montesdeoca, 1 Mayo 2013, Creado con GeoGebra
|