Let Ia(ra), Ib(rb), Ic(rc) be excircles of the ABC. There are four circles tangent to Ib(rb), Ic(rc) and passing through Ia.
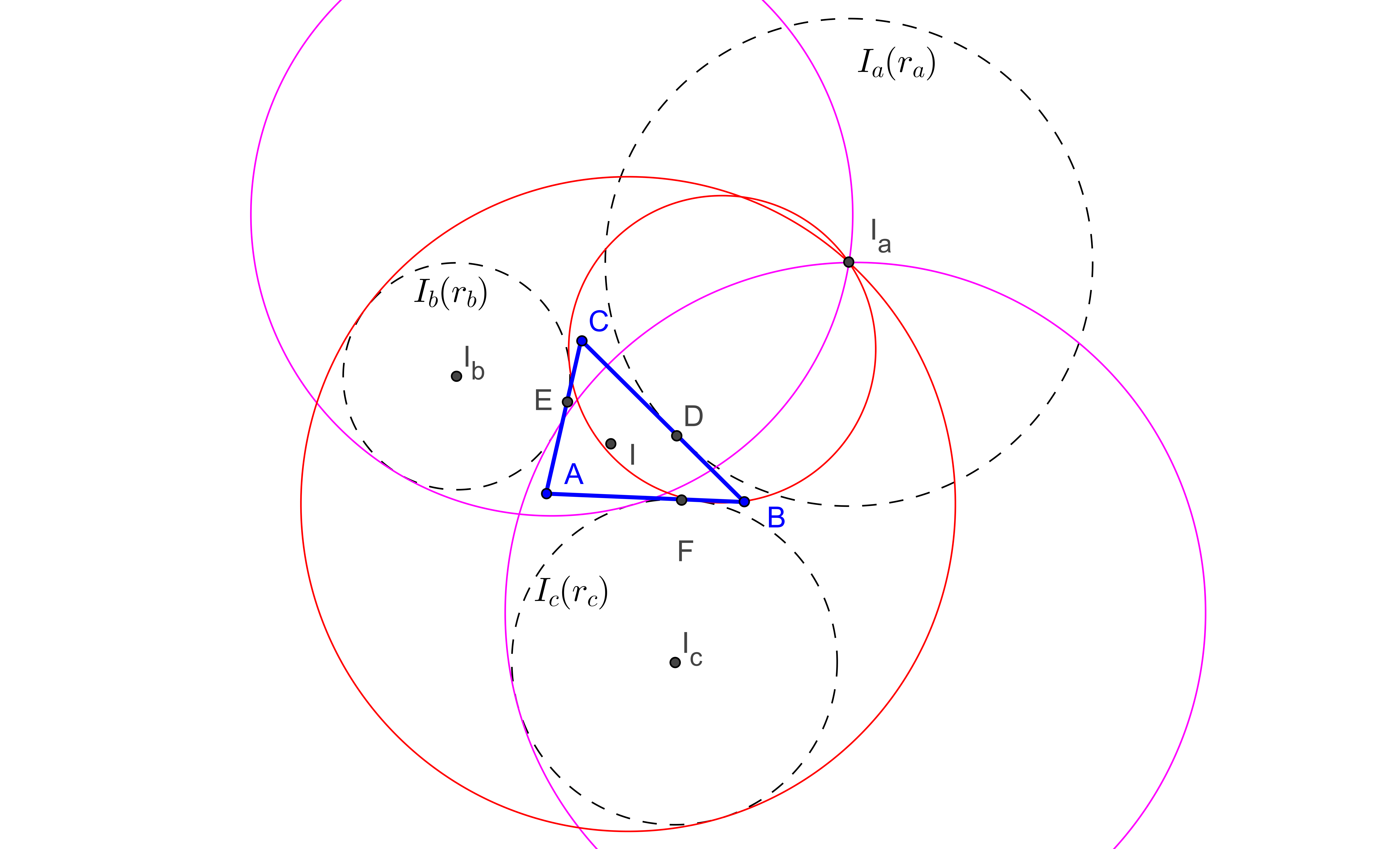
Let (S_a) the circle touching Ib(rb), Ic(rc) externally, and da the line passing through the points of contact of (S_a) with Ib(rb) and Ic(rc)
Similary construct db and dc. Let A_1B_1C_! be the triangle bounded by the lines da, db and dc. Then the triangles ABC and A_1B_1C_1 are perspective.
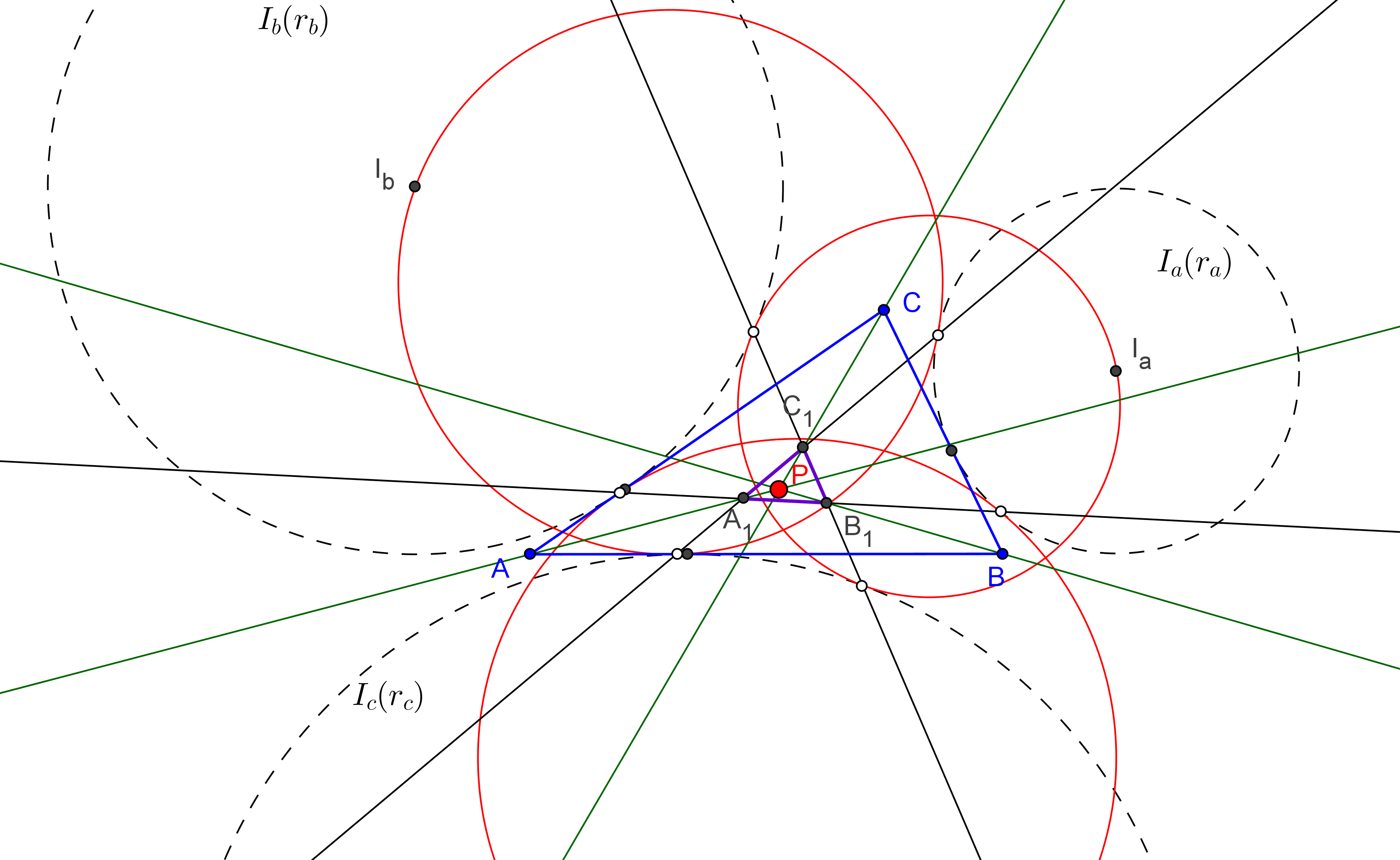
Let (T_a) the circle touching Ib(rb), Ic(rc) internally, and da the line passing through the points of contact of (T_a) with Ib(rb) and Ic(rc)
Similary construct db and dc. Let A_2B_2C_2 be the triangle bounded by the lines da, db and dc. Then the triangles ABC and A_2B_2C_2 are perspective.
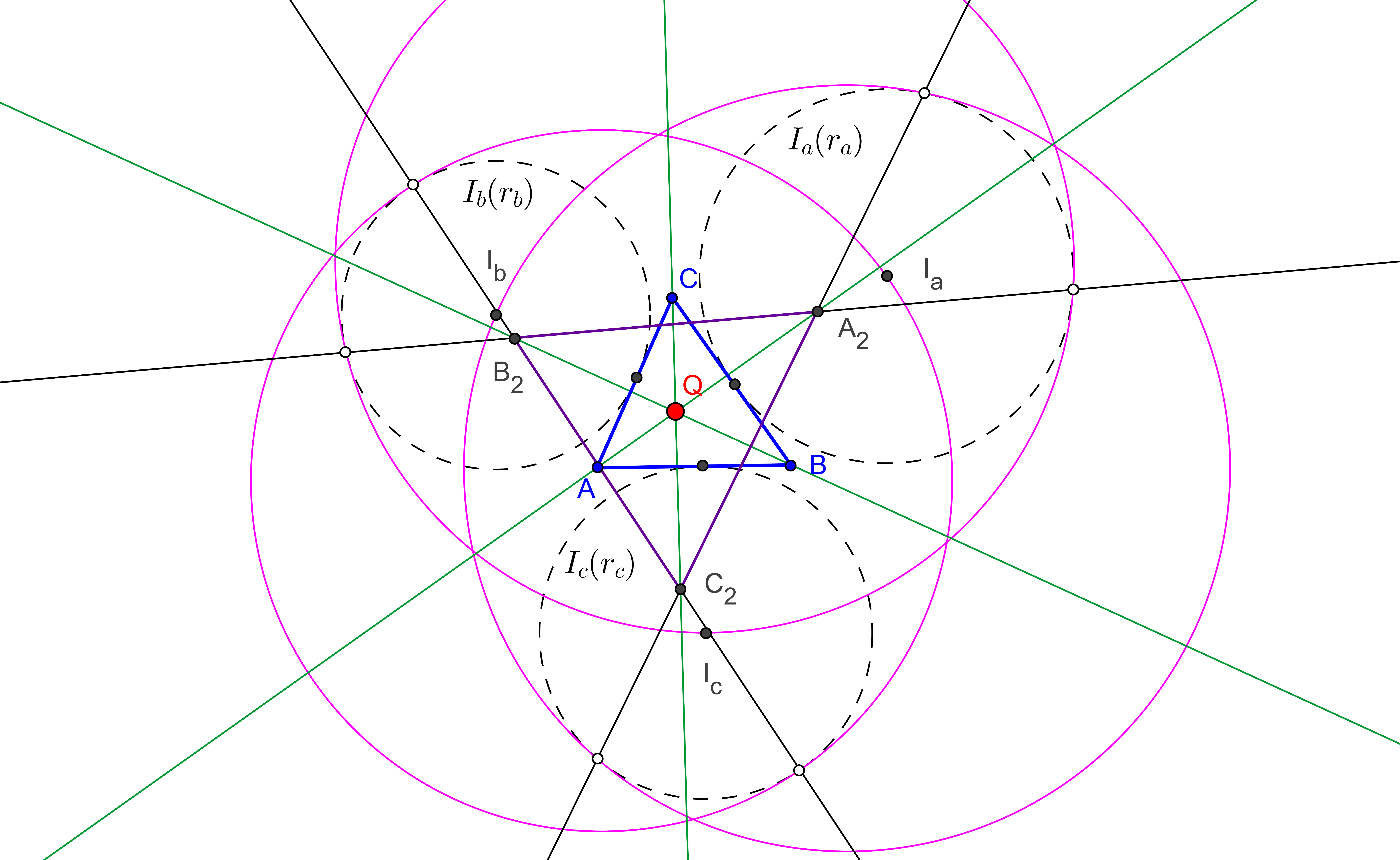
Angel Montesdeoca



