Bicentric pairs associated with the IO line


  A triangle ABC is given, with incenter I = X1 and circumcenter O = X3, and let X be a point with pedal triangle DEF.
 The interior bisector at A intersects the XE and XF lines at Ab and Ac, respectively.
 The interior bisector at B intersects the lines XF and XD at Bc and Ba, respectively.
 And the inner bisector at C intersects the lines XD and XE at Ca and Cb, respectively.
  The circles 𝒫 = (AcBaCb) and 𝒰 = (AbBcCa) pass through I if and only if X lies on the perpendiculars by I to the sidelines of ABC or on the line IO.

HG090421.png


  Let us take the point X on the line IO,

( Barycentric equation of IO:
b c (b - c)(-a + b + c) x - a c(a - c)(a - b + c) y + a b(a - b)(a + b - c) z = 0.
Triangle centers Xi on IO:
i ∈ {1, 3, 35, 36, 40, 46, 55, 56, 57, 65, 165, 171, 241, 260, 354, 484, 517, 559, 940, 942, 980, 982, 986, 988, 999, 1038, 1040, 1060, 1062, 1082, 1155, 1159, 1214, 1319, 1381, 1382, 1385, 1388, 1402, 1403, 1420, 1429, 1454, 1460, 1466, 1467, 1470, 1482, 1617, 1622, 1697, 1715, 1735, 1754, 1758, 1764, 1771, 1936, 2061, 2077, 2078, 2093, 2095, 2098, 2099, 2223, 2283, 2352, 2446, 2447, 2448, 2449, 2556, 2557, 2564, 2565, 2572, 2573, 2646, 2662, 3057, 3072, 3075, 3245, 3256, 3295, 3303, 3304, 3333, 3336, 3337, 3338, 3339, 3340, 3359, 3361, 3428, 3503, 3513, 3514, 3550, 3576, 3579, 3587, 3601, 3612, 3660, 3666, 3670, 3675, 3677, 3744, 3745, 3746, 3748, 3749, 3750, 3931, 3953, 3976, 3999, 4003, 4038, 4424, 4689, 4694, 4860, 4883, 5010, 5045, 5048, 5049, 5061, 5078, 5091, 5119, 5122, 5126, 5128, 5131, 5137, 5143, 5172, 5173, 5183, 5193, 5204, 5217, 5221, 5228, 5255, 5264, 5266, 5269, 5285, 5329, 5337, 5347, 5348, 5363, 5425, 5482, 5535, 5536, 5537, 5538, 5563, 5570, 5584, 5597, 5598, 5662, 5697, 5706, 5707, 5708, 5709, 5710, 5711, 5885, 5902, 5903, 5908, 5919, 6244, 6282, 6583, 6766, 6767, 6769, 7011, 7070, 7146, 7280, 7373, 7688, 7742, 7957, 7962, 7964, 7982, 7987, 7991, 7994, 8069, 8071, 8148, 8158, 8162, 8163, 8171, 8186, 8187, 8193, 8251, 8270, 8273, 8726, 8758, 8924, 9120, 9364, 9371, 9441, 9627, 9630, 9659, 9672, 9819, 9940, 9957, 10202, 10222, 10225, 10246, 10247, 10252, 10253, 10267, 10268, 10269, 10270, 10273, 10284, 10306, 10310, 10319, 10383, 10388, 10389, 10434, 10439, 10441, 10470, 10473, 10474, 10475, 10476, 10480, 10500, 10508, 10618, 10679, 10680, 10831, 10832, 10856, 10857, 10882, 10902, 10965, 10966, 10980, 11009, 11010, 11011, 11012, 11014, 11018, 11021, 11224, 11227, 11248, 11249, 11252, 11253, 11278, 11280, 11366, 11367, 11407, 11492, 11493, 11507, 11508, 11509, 11510, 11518, 11521, 11529, 11531, 11567, 11575, 11822, 11823, 11849, 11873, 11874, 11875, 11876, 11877, 11878, 11879, 11880, 11881, 11882, 11883, 11884, 12000, 12001, 12009, 12410, 12435, 12458, 12459, 12555, 12702, 12703, 12704, 12915, 13145, 13151, 13370, 13373, 13384, 13388, 13389, 13462, 13528, 13600, 13601, 13624, 13750, 13751, 14000, 14110, 14115, 14122, 14131, 14132, 14792, 14793, 14794, 14795, 14796, 14797, 14798, 14799, 14800, 14801, 14802, 14803, 14804, 14882, 15016, 15177, 15178, 15803, 15804, 15931, 15932, 15934, 15941, 16189, 16191, 16192, 16193, 16200, 16201, 16202, 16203, 16204, 16205, 16206, 16207, 16208, 16209, 16215, 16216, 16217, 16218, 16541, 16678, 16687, 16763, 16778, 16877, 16878, 17102, 17437, 17502, 17591, 17592, 17593, 17594, 17595, 17596, 17597, 17598, 17599, 17600, 17601, 17603, 17609, 17642, 17699, 17700, 17715, 17716, 17798, 18115, 18193, 18201, 18208, 18280, 18330, 18398, 18421, 18443, 18447, 18453, 18455, 18758, 18788, 18838, 18839, 18856, 18857, 18955, 18956, 18967, 19758, 19761, 19765, 19782, 20182, 20254, 20323, 20358, 20359, 20367, 20368, 20764, 20788, 20789, 20790, 20878, 21010, 21164, 21334, 21842, 22341, 22765, 22766, 22767, 22768, 22770, 23171, 23207, 23340, 23703, 23832, 23853, 23890, 23960, 23961, 23981, 24299, 24301, 24310, 24464, 24468, 24474, 24806, 24926, 24927, 24928, 24929, 25405, 25413, 25414, 25415, 26086, 26087, 26285, 26286, 26287, 26290, 26291, 26296, 26297, 26319, 26320, 26351, 26352, 26357, 26358, 26365, 26366, 26380, 26393, 26395, 26398, 26399, 26400, 26401, 26402, 26404, 26417, 26419, 26422, 26423, 26424, 26425, 26426, 26437, 26903, 26904, 26908, 27247, 30274, 30282, 30323, 30337, 30343, 30350, 30389, 30392, 30502, 30503, 31393, 31498, 31508, 31511, 31515, 31662, 31663, 31666, 31778, 31779, 31780, 31781, 31785, 31786, 31787, 31788, 31792, 31793, 31794, 31797, 31798, 31849, 32167, 32612, 32613, 32622, 32623, 32636, 32760, 33176, 33177, 33178, 33179, 33281, 33574, 33596, 33649, 33657, 33658, 33795, 33862, 33925, 34339, 34345, 34346, 34471, 34486, 34489, 34556, 34557, 34560, 34561, 34583, 34592, 34593, 34871, 34879, 34880, 34881, 34890, 34891, 34923, 35000, 35004, 35010, 35014, 35046, 35059, 35202, 35238, 35239, 35242, 35244, 35245, 35251, 35252, 35390, 35445, 35448, 35457, 35459, 35460, 35461, 35597, 35612, 35620, 35621, 35631, 35645, 36152, 36274, 36279, 36946, 37080, 37520, 37521, 37522, 37523, 37524, 37525, 37526, 37527, 37528, 37529, 37530, 37531, 37532, 37533, 37534, 37535, 37536, 37537, 37538, 37539, 37540, 37541, 37542, 37543, 37544, 37545, 37546, 37547, 37548, 37549, 37550, 37551, 37552, 37553, 37554, 37555, 37556, 37557, 37558, 37559, 37560, 37561, 37562, 37563, 37564, 37565, 37566, 37567, 37568, 37569, 37570, 37571, 37572, 37573, 37574, 37575, 37576, 37577, 37578, 37579, 37580, 37581, 37582, 37583, 37584, 37585, 37586, 37587, 37588, 37589, 37590, 37591, 37592, 37593, 37594, 37595, 37596, 37597, 37598, 37599, 37600, 37601, 37602, 37603, 37604, 37605, 37606, 37607, 37608, 37609, 37610, 37611, 37612, 37613, 37614, 37615, 37616, 37617, 37618, 37619, 37620, 37621, 37622, 37623, 37624, 37625, 37772, 37773, 38013, 38014, 38284, 38285, 38286, 38287, 38288, 38289, 38290, 38291, 38474, 38483, 39271, 39550, 39578, 39598, 40245, 40255, 40292, 40293, 40294, 40295, 40296, 40910, 40946, 40959} )

then the centers P and U of the circles 𝒫 and 𝒰 are a bicentric par. The line PU is perpendicular to IK, so its point at infinity is X(3309), (X(3309) = ideal point of PU(44), X(3309) = bicentric difference of PU(44)). The midpoint of PU coincides with the midpoint of IX.

Xn
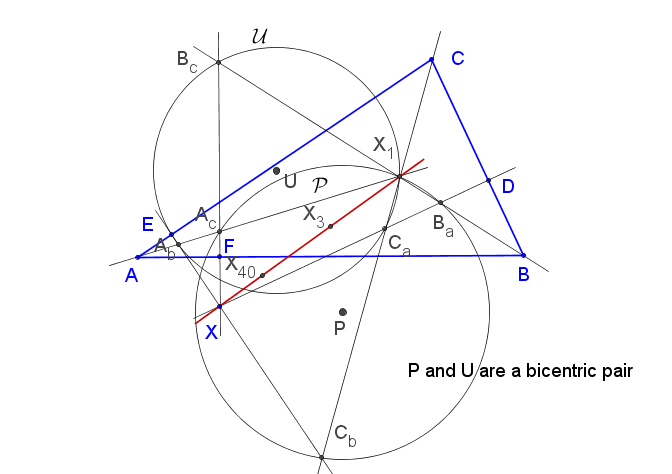
on IO		 bicentric par (barycentic)
3 a (a^3 + b^2 (b - c) - a^2 c + a b (-2 b + c)): :
35a (a^3 - 2 a b^2 + b^2 (b - c) - a^2 c): :
36a (a - b) (a^2 + a (b - c) + b (-b + c)): :
40a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + c^2)) : :  P(44) = 1st Laemmel Point
46a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + 2 b c + c^2)): :
55a (a^3 + b^2 (b - c) - a^2 c - a b (2 b + c)): :
56a (a^3 + b^2 (b - c) - a^2 c + a b (-2 b + 3 c)): :
57a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + 4 b c + c^2)): :
65a (a^2 b + (b - c) c^2 + a (-b^2 + b c + c^2)): :
165a (3 a^3 + 3 b^3 + a^2 (b - 3 c) - 3 b^2 c + b c^2 - c^3 + a (-7 b^2 + 2 b c + c^2)): :
171a (a^3 + a^2 b + b (b^2 + c^2) + a (-b^2 + 2 b c + c^2)): :
241a (a^4 (b + 2 c) + a^3 (b^2 - b c - 3 c^2) + (b - c)^2 c (2 b^2 + b c + c^2) + a^2 (-5 b^3 + 2 b^2 c + 2 b c^2 + c^3) + a (3 b^4 - 5 b^3 c + 4 b^2 c^2 - b c^3 - c^4)): :
354a (a^2 b + (b - c) c^2 + a (-b^2 + 5 b c + c^2)): :
484a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + b c + c^2)): :
517a (a^2 b + (b - c) c^2 - a (b^2 + b c - c^2)): :
559a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + b Sqrt[-3 a^4 - 3 (b^2 - c^2)^2 + 6 a^2 (b^2 + c^2)] + c Sqrt[-3 a^4 - 3 (b^2 - c^2)^2 + 6 a^2 (b^2 + c^2)] + a (-3 b^2 + 4 b c + c^2 + Sqrt[-3 a^4 - 3 (b^2 - c^2)^2 + 6 a^2 (b^2 + c^2)])): :
940a (a^3 + a^2 (2 b + c) + a c (5 b + 2 c) + b (b^2 + b c + 2 c^2)): :
942a (a^2 b + (b - c) c^2 + a (-b^2 + 3 b c + c^2)): :
980a (b c^2 (2 b^2 + b c + c^2) + a^3 (b^2 + 2 b c + 2 c^2) + a c (4 b^3 + 2 b^2 c + 2 b c^2 + c^3) + a^2 (3 b^3 + 3 b^2 c + 2 b c^2 + c^3)): :
982a (2 a b (b - c) + a^2 c + c (b^2 + c^2)): :
986a (2 a b^2 + a^2 c + b^2 c + c^3): :
988a (a^3 + b^3 - 3 b^2 c - b c^2 - c^3 - a^2 (b + 3 c) - a (5 b^2 - 2 b c + c^2)): :
999a (a^3 + b^2 (b - c) - a^2 c + a b (-2 b + 5 c)): :
1038a (a^6 + 4 a b^3 (b - c) c - 4 a^3 b c^2 + (b^2 - c^2)^2 (b^2 + c^2) - a^4 (b^2 - 4 b c + c^2) - a^2 (b^4 + 8 b^3 c - 6 b^2 c^2 + c^4)): :
1040a (a^6 + 4 a^3 b c^2 + 4 a b^3 c (-b + c) + (b^2 - c^2)^2 (b^2 + c^2) - a^4 (b^2 + 4 b c + c^2) - a^2 (b^4 - 8 b^3 c + 2 b^2 c^2 + c^4)): :
1060a (a^6 - a^4 (b - c)^2 + 2 a b^3 (b - c) c - 2 a^3 b c^2 + (b^2 - c^2)^2 (b^2 + c^2) - a^2 (b^4 + 4 b^3 c - 4 b^2 c^2 + c^4)): :
1062a (a^6 + 2 a^3 b c^2 + 2 a b^3 c (-b + c) - a^4 (b + c)^2 + (b^2 - c^2)^2 (b^2 + c^2) - a^2 (b^4 - 4 b^3 c + c^4)): :
1082-(a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 - b Sqrt[-3 a^4 - 3 (b^2 - c^2)^2 + 6 a^2 (b^2 + c^2)] - c Sqrt[-3 a^4 - 3 (b^2 - c^2)^2 + 6 a^2 (b^2 + c^2)] + a (-3 b^2 + 4 b c + c^2 - Sqrt[-3 a^4 - 3 (b^2 - c^2)^2 + 6 a^2 (b^2 + c^2)]))): :
1155a (2 a^3 + 2 b^3 + a^2 (b - 2 c) - 2 b^2 c + b c^2 - c^3 + a (-5 b^2 + 3 b c + c^2)): :
1159a (a^3 + b^3 - b^2 c - 4 b c^2 + 4 c^3 - a^2 (4 b + c) + a (2 b^2 - 3 b c - 4 c^2)): :
1214a (-2 a^2 b^3 (b + c) + a^5 (b + 2 c) + a^4 (2 b^2 - c^2) - 2 a^3 (2 b^3 + c^3) + a b (3 b^4 - 2 b^3 c - 2 b^2 c^2 + 2 b c^3 - c^4) + c (2 b^5 - b^4 c - 2 b^3 c^2 + c^5)): :
1319a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 - 5 b c + c^2)): :
1385a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 - 3 b c + c^2)): :
1388a (3 a^3 + 3 b^3 - 3 b^2 c - 2 b c^2 + 2 c^3 - a^2 (2 b + 3 c) + a (-4 b^2 + 7 b c - 2 c^2)): :
1402a (a^5 (b + c) + a^4 b (b + c) + b^3 c (b^2 - c^2) - a^3 (2 b^3 - 2 b c^2 + c^3) + a^2 b (-b^3 + b c^2 + c^3) + a b (b^4 - b^3 c + b c^3 + c^4)): :
1403a (a^4 b^2 + a^5 (b + c) + b^3 c (b^2 - c^2) - a^2 b^2 (b^2 - 3 b c + 3 c^2) - a^3 (2 b^3 + b^2 c - 3 b c^2 + c^3) + a (b^5 - 2 b^4 c + b^3 c^2 + 2 b c^4)): :
1420a (3 a^3 + 3 b^3 - 3 b^2 c - b c^2 + c^3 - a^2 (b + 3 c) - a (5 b^2 - 8 b c + c^2)): :
1429a (a^5 + a^4 b - 2 a^3 b (b - c) - 2 a^2 c (b^2 + c^2) + b (b^4 - 2 b c^3 + c^4) + a (-b^4 + 2 b^3 c - 2 b^2 c^2 + 2 b c^3 + c^4)): :
1454a (a^6 - 2 a^5 c + a^4 (-5 b^2 + 4 b c + c^2) + a^3 (4 b^3 - 6 b c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 8 b^3 c + 4 b^2 c^2 - c^4) - 2 a (2 b^5 - 4 b^4 c + b^3 c^2 + 2 b^2 c^3 - c^5)): :
1460a (a^6 + a^5 b + b^6 - a^4 b (b - 4 c) - b^2 c^4 + 2 a^3 b c (b + c) - a^2 (b^4 + 4 b^3 c - 4 b^2 c^2 - 4 b c^3 + c^4) + a b (-b^4 + 2 b^3 c + 2 b c^3 + c^4)): :
1466a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c - 3 b c^2 + c^3) + a^2 (b^4 - 12 b^3 c + 14 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 8 b^3 c + 4 b^2 c^2 + c^4)): :
1467a (a^6 - 2 a^5 (b + c) - a^4 (b + c)^2 + (b - c)^4 (b + c)^2 + 4 a^3 (b^3 - b^2 c + b c^2 + c^3) - a^2 (b^4 - 12 b^3 c + 14 b^2 c^2 + 4 b c^3 + c^4) - 2 a (b^5 + b^4 c - 2 b^3 c^2 + 2 b^2 c^3 - 3 b c^4 + c^5)): :
1470a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - 3 b c^2 + c^3) + a^2 (b^4 - 10 b^3 c + 12 b^2 c^2 - c^4) + a b (-3 b^4 + 8 b^3 c - 4 b^2 c^2 - 2 b c^3 + c^4)): :
1482a (a^3 + b^3 - b^2 c + a (3 b - 2 c) c - 2 b c^2 + 2 c^3 - a^2 (2 b + c)): :
1617a (a^6 - 3 a^4 b^2 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + c^3) + a^2 (b^4 + 2 b^3 c - 6 b^2 c^2 - c^4) + a b (-3 b^4 + 2 b^3 c + 2 b^2 c^2 - 2 b c^3 + c^4)): :
1622a (a^9 + b^2 (b - c)^3 (b + c)^4 + a^8 (2 b + c) - 3 a^7 (b^2 + b c + c^2) - a^6 (7 b^3 + 2 b^2 c - 4 b c^2 + 3 c^3) - a b (b - c)^2 c (7 b^4 + 8 b^3 c + 2 b^2 c^2 - c^4) + a^5 (3 b^4 + 7 b^3 c + 8 b^2 c^2 - b c^3 + 3 c^4) - a^2 (b - c)^2 (5 b^5 + 4 b^4 c - 3 b^3 c^2 - b^2 c^3 + 2 b c^4 + c^5) + a^4 (9 b^5 - 6 b^4 c - 7 b^3 c^2 - b^2 c^3 - 6 b c^4 + 3 c^5) - a^3 (b^6 - 3 b^5 c + 11 b^4 c^2 - 10 b^3 c^3 + 3 b^2 c^4 - 3 b c^5 + c^6)): :
1697a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 - 4 b c + c^2)): :
1715a (a^8 (b + c) + a^7 (b^2 - 2 b c - c^2) + b (b - c)^3 c (b + c)^2 (b^2 + c^2) - a^6 (5 b^3 + 2 b^2 c - 4 b c^2 + c^3) + a^5 (-b^4 + 6 b^3 c - 2 b^2 c^2 - 2 b c^3 + c^4) - a^2 (b - c)^3 (3 b^4 + 3 b^3 c + 2 b^2 c^2 + 3 b c^3 + c^4) + a^4 (7 b^5 - 6 b^4 c - b^3 c^2 + 5 b^2 c^3 - 4 b c^4 - c^5) + a (b - c)^2 (b^6 - 4 b^5 c - 5 b^4 c^2 + b^2 c^4 - c^6) + a^3 (-b^6 + 2 b^5 c - b^4 c^2 - 4 b^3 c^3 + b^2 c^4 + 2 b c^5 + c^6)): :
1735a (a^5 c - a^3 b (2 b^2 + b c - 3 c^2) + a^4 (2 b^2 - 2 b c - c^2) + a (b - c)^3 (2 b^2 + 2 b c + c^2) - a^2 b (2 b^3 - 5 b^2 c + 2 b c^2 + c^3) + c (b^5 - b^4 c - b c^4 + c^5)): :
1754a (a^6 - 3 a^4 b^2 - a^5 c + a^3 b (2 b^2 - b c - c^2) + a^2 (b^4 + b^3 c - b c^3 - c^4) + b (b^5 - b^4 c - b c^4 + c^5) + a (-2 b^5 + 2 b^4 c + b^3 c^2 - 3 b^2 c^3 + b c^4 + c^5)): :
1758a (a^6 - a^5 (b + 3 c) + a^4 (-5 b^2 + 3 b c + c^2) + 2 a^3 (3 b^3 - 2 b c^2 + c^3) + a^2 (3 b^4 - 4 b^3 c + 2 b^2 c^2 - c^4) + (b - c)^2 (b^4 - b^3 c - 2 b^2 c^2 - b c^3 - c^4) + a (-5 b^5 + 7 b^4 c - 4 b^2 c^3 + b c^4 + c^5)): :
1764a (2 a^4 b^2 + a^5 (b + c) - a^3 b (2 b^2 + b c - 3 c^2) - a^2 b (2 b^3 + b^2 c + 4 b c^2 - c^3) + b c (b^4 - c^4) + a (b^5 - 4 b^4 c - b^3 c^2 + b^2 c^3 - c^5)): :
1771a (a^6 - a^5 c + a^4 b (-3 b + 2 c) + a^3 b (2 b^2 + b c - 3 c^2) - a (b - c)^3 (2 b^2 + 2 b c + c^2) + a^2 (b^4 - 5 b^3 c + 4 b^2 c^2 + b c^3 - c^4) + b (b^5 - b^4 c - b c^4 + c^5)): :
1936a (a^6 - a^5 c + a^4 b (-3 b + c) + 2 a^3 (b^3 - b c^2) + a^2 (b^4 - 2 b^3 c + 4 b^2 c^2 - c^4) + a (-2 b^5 + 3 b^4 c - 2 b^2 c^3 + c^5) + b (b^5 - b^4 c - b c^4 + c^5)): :
2077a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 5 c) - a b^2 (3 b^3 - 7 b^2 c + 3 b c^2 + c^3) + a^3 (4 b^3 + b^2 c - 5 b c^2 + 2 c^3) + a^2 (b^4 - 9 b^3 c + 6 b^2 c^2 + b c^3 - c^4)): :
2078a (a^6 + a^4 b (-3 b + c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a b^2 (-3 b^3 + 3 b^2 c + b c^2 - c^3) + a^3 (4 b^3 + b^2 c - b c^2 + 2 c^3) + a^2 (b^4 - b^3 c - 2 b^2 c^2 + b c^3 - c^4)): :
2093a (a^3 + b^3 + a^2 (3 b - c) - b^2 c + 3 b c^2 - 3 c^3 + a (-5 b^2 + 2 b c + 3 c^2)): :
2095a (a^6 + a^5 (b - 2 c) + a^4 (-7 b^2 + 4 b c + 2 c^2) + a^3 (4 b^3 - 8 b c^2 - 2 c^3) + (b - c)^3 (b^3 + b^2 c + 2 b c^2 + 2 c^3) + a^2 (5 b^4 - 10 b^3 c + 10 b^2 c^2 - c^4) - a (5 b^5 - 10 b^4 c + 2 b^3 c^2 + 6 b^2 c^3 + b c^4 - 4 c^5)): :
2098a (a^3 + b^3 - b^2 c + a (5 b - 2 c) c - 2 b c^2 + 2 c^3 - a^2 (2 b + c)): :
2099a (a^3 + b^3 - b^2 c + a (b - 2 c) c - 2 b c^2 + 2 c^3 - a^2 (2 b + c)): :
2223a (a^3 (b - c) c + b^3 (b - c) c + a^4 (b + c) - a^2 b^2 (2 b + c) + a b (b^3 - b^2 c + c^3)): :
2283-(a (a^7 (b + c) + b^3 (b - c)^3 c (b + c) - a^6 (b^2 + b c + 2 c^2) - 3 a^5 (b^3 - b c^2) + a^4 (4 b^4 + 2 b^3 c + b^2 c^2 - 5 b c^3 + 2 c^4) + a b (b - c)^2 (b^4 - b^3 c + 2 b^2 c^2 + 2 b c^3 + 2 c^4) + a^3 (b^5 - 6 b^4 c + 2 b^2 c^3 + 2 b c^4 - c^5) + a^2 (-3 b^6 + 6 b^5 c - 5 b^4 c^2 + 4 b^3 c^3 - 2 b c^5))): :
2352a (a^5 (b + c) + a^4 b (b + 2 c) + b^3 c (b^2 - c^2) - a^3 (2 b^3 - b c^2 + c^3) - a^2 (b^4 + 2 b^3 c - b c^3) + a b (b^4 - b^2 c^2 + b c^3 + c^4)): :
2446-(a (a^2 b + b c^2 - c^3 - a (b^2 + b c - c^2) - 2 Sqrt[a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 - 3 b c + c^2))])): :
2447a (a^2 b + b c^2 - c^3 - a (b^2 + b c - c^2) + 2 Sqrt[a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 - 3 b c + c^2))]): :
2564a (a^3 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + b^2 (b - c) Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] - a^2 c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + a b (-2 c Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 2 b Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])): :
2565a (a^3 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + b^2 (b - c) Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] - a^2 c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + a b (2 c Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 2 b Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])): :
2572a (a^7 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + a^5 (5 c^2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + b^2 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 12 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a^4 (b c^2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 5 c^3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b^3 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - b^2 c (5 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a^2 (5 b^5 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b c^4 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b^3 c^2 (2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 3 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - c^5 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - b^4 c (5 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + 2 b^2 c^3 (-4 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 3 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + (b - c) (5 b^4 c^2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b^2 c^4 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + c^6 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^6 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a^6 (b (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - c (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a^3 (4 b^3 c Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 b c^3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b^2 c^2 (-2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + c^4 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^4 (-7 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 10 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a (4 b^3 c^3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b^5 c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + 2 b c^5 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + c^6 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - 3 b^2 c^4 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^4 c^2 (-7 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 8 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - b^6 (3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 10 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]))): :
2573-(a (a^7 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + a^6 (-(b Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)]) + c Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] - 4 c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - a^2 (5 b^5 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b c^4 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b^4 c (-5 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + c^5 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + 2 b^3 c^2 (2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 3 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) - 2 b^2 c^3 (4 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 3 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + (b - c) (-5 b^4 c^2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b^2 c^4 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + c^6 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^6 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a (-4 b^3 c^3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b^5 c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + 2 b c^5 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + b^6 (3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 10 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + 3 b^2 c^4 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 4 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + c^6 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^4 c^2 (7 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 8 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a^3 (-4 b^3 c Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 4 b c^3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 b^2 c^2 (2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + c^4 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^4 (7 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 10 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) - a^5 (5 c^2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 2 b c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)] + b^2 (Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 12 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])) + a^4 (-(b c^2 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)]) + 5 c^3 Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + b^3 (-Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] + 2 Sqrt[b^2 c^2 + a^2 (b^2 + c^2)]) + b^2 (5 c Sqrt[a^4 + b^4 - b^2 c^2 + c^4 - a^2 (b^2 + c^2)] - 2 c Sqrt[b^2 c^2 + a^2 (b^2 + c^2)])))): :
2646a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 - b c + c^2)): :
2662a (-(a^9 b c (b + 3 c)) + b^2 c^2 (b^2 - c^2)^4 - 4 a^3 b (b - c)^2 c (b + c)^3 (b^2 - b c + c^2) + a^10 (b^2 + 3 b c + c^2) + 4 a^7 b c (b^3 + c^3) + a b (b - c)^3 c (b + c)^2 (3 b^4 + 2 b^2 c^2 - c^4) - 4 a^4 (b^2 - c^2)^2 (b^4 - 2 b^3 c + 3 b^2 c^2 - b c^3 + c^4) - a^8 (4 b^4 + 8 b^3 c - 3 b^2 c^2 + 4 b c^3 + 4 c^4) + a^2 (b - c)^3 (b + c)^2 (b^5 - 4 b^4 c + b^3 c^2 - 5 b^2 c^3 - c^5) + 2 a^5 b c (-b^5 + 3 b^4 c - 2 b^3 c^2 - 2 b^2 c^3 + b c^4 + c^5) + 2 a^6 (3 b^6 + b^5 c - 2 b^4 c^2 + 6 b^3 c^3 - 2 b^2 c^4 - b c^5 + 3 c^6)): :
3057-(a (a^2 b + (b - c) c^2 + a (-b^2 - 3 b c + c^2))): :
3072a (a^6 - a^5 c + a^4 b (-3 b + c) + 2 a^3 (b^3 - b c^2) + a^2 (b^4 - 2 b^3 c - c^4) + a (-2 b^5 + 3 b^4 c - 2 b^2 c^3 + c^5) + b (b^5 - b^4 c - b c^4 + c^5)): :
3075a (a^6 - 3 a^4 b (b - c) - a^5 c + 2 a^3 (b^3 - 2 b c^2) + a^2 (b^4 - 6 b^3 c + 6 b^2 c^2 - c^4) + a (-2 b^5 + 5 b^4 c - 2 b^3 c^2 - 2 b^2 c^3 + c^5) + b (b^5 - b^4 c - b c^4 + c^5)): :
3245a (a^3 + b^3 + a^2 (2 b - c) - b^2 c + 2 b c^2 - 2 c^3 + a (-4 b^2 + 2 c^2)): :
3256a (a^6 - 3 a^4 b (b - c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 + 3 b^2 c - 3 b c^2 + 2 c^3) + a b (-3 b^4 + 5 b^3 c - b^2 c^2 + b c^3 - 2 c^4) + a^2 (b^4 - 7 b^3 c + 6 b^2 c^2 + 3 b c^3 - c^4)): :
3295a (a^3 + b^2 (b - c) - a^2 c - a b (2 b + 3 c)): :
3303a (a^3 + b^2 (b - c) - a^2 c - a b (2 b + 5 c)): :
3304a (a^3 + b^2 (b - c) - a^2 c + a b (-2 b + 7 c)): :
3333a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + 8 b c + c^2)): :
3336a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + 3 b c + c^2)): :
3337a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + 5 b c + c^2)): :
3338a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 + 6 b c + c^2)): :
3339-(a (a^3 + b^3 + a^2 (3 b - c) - b^2 c + 3 b c^2 - 3 c^3 + a (-5 b^2 + 6 b c + 3 c^2))): :
3340-(a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 - 3 c^2))): :
3359a (a^6 - 2 a^5 c + 4 a^3 b (b^2 + b c - 2 c^2) + a^4 (-5 b^2 + 6 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 16 b^3 c + 6 b^2 c^2 + 4 b c^3 - c^4) - 2 a (2 b^5 - 5 b^4 c + 2 b^3 c^2 + 2 b c^4 - c^5)): :
3361a (3 a^3 + 3 b^3 + a^2 (b - 3 c) - 3 b^2 c + b c^2 - c^3 + a (-7 b^2 + 10 b c + c^2)): :
3428a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - b^2 c - b c^2 + c^3) + a^2 (b^4 + 6 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 4 b^3 c - 4 b c^3 + 3 c^4)): :
3503a (a^5 (b^2 + b c + c^2) + a^4 (b^3 - b^2 c + b c^2 - c^3) + b^2 c^2 (b^3 - b^2 c + b c^2 - c^3) + a b c (b^4 - 3 b^3 c + 2 b^2 c^2 + b c^3 + c^4) + a^3 (-3 b^4 + 2 b^3 c - b^2 c^2 + 2 b c^3 + c^4) + a^2 (b^5 - b^4 c + 3 b^3 c^2 - 3 b^2 c^3 + b c^4 - c^5)): :
3513a (a^4 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] - a^3 Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + a (3 b^2 - 4 b c - c^2) Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] - a^2 (2 b^2 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + b Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + c (2 c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] - Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)])) - (b - c) (-(b^3 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)]) + b c^2 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + b^2 (-(c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)]) + Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)]) + c^2 (c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)]))): :
3514-(a (a^4 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + a^3 Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + a (-3 b^2 + 4 b c + c^2) Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + (b - c) (b^3 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] - b c^2 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + c^2 (-(c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)]) + Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)]) + b^2 (c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)])) + a^2 (-2 b^2 Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + b Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] - c (2 c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] + Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)])))): :
3550a (2 a^3 + a^2 (b - c) + b (2 b^2 - b c + c^2) + a (-3 b^2 + b c + c^2)): :
3576a (3 a^3 + 3 b^3 - 3 b^2 c - b c^2 + c^3 - a^2 (b + 3 c) - a (5 b^2 - 4 b c + c^2)): :
3579a (2 a^3 + 2 b^3 + a^2 (b - 2 c) - 2 b^2 c + b c^2 - c^3 + a (-5 b^2 + b c + c^2)): :
3587a (a^6 - 2 a^5 c + 4 a^3 b (b^2 + c^2) + a^4 (-5 b^2 - 6 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 + 12 b^3 c - 2 b^2 c^2 - c^4) - 2 a (2 b^5 + b^4 c - 4 b^3 c^2 + 2 b^2 c^3 - c^5)): :
3601-(a (3 a^3 + 3 b^3 - 3 b^2 c - b c^2 + c^3 - a^2 (b + 3 c) - a (5 b^2 + c^2))): :
3612-(a (3 a^3 + 3 b^3 - 3 b^2 c - b c^2 + c^3 - a^2 (b + 3 c) - a (5 b^2 - 2 b c + c^2))): :
3660-(a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (4 b + c) + a^4 (-2 b^2 + 6 b c + c^2) + 2 a^2 b^2 (b^2 - 7 b c + 8 c^2) - a (b^5 - 8 b^4 c + 6 b^3 c^2 + 2 b^2 c^3 + b c^4 - 2 c^5))): :
3666a (a^2 (b + 2 c) + c (2 b^2 + b c + c^2) + a (3 b^2 + b c + c^2)): :
3670a (a b (2 b - c) + a^2 c + c (b^2 + c^2)): :
3675a (a^4 c + a^3 (b^2 - 2 b c - 2 c^2) + a^2 (-3 b^3 + 3 b^2 c + 2 b c^2 + c^3) + a (2 b^4 - 4 b^3 c + 4 b^2 c^2 - 2 b c^3 - c^4) + c (b^4 - 2 b^3 c + b^2 c^2 - b c^3 + c^4)): :
3677a (a^3 + b^3 + 3 b^2 c + b c^2 + 3 c^3 + a^2 (b + 3 c) + a (5 b^2 - 4 b c + c^2)): :
3744a (2 a^3 + a^2 b + 2 b^3 + b c^2 + c^3 - a (b^2 + b c - c^2)): :
3745a (2 a^3 + 2 b^3 + 2 b^2 c + 3 b c^2 + c^3 + a^2 (3 b + 2 c) + a (b^2 + 5 b c + 3 c^2)): :
3746a (a^3 + b^2 (b - c) - a^2 c - 2 a b (b + c)): :
3748a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 + 7 b c + c^2)): :
3749a (3 a^3 + 3 b^3 + a^2 (b - c) - b^2 c + b c^2 + c^3 + a (-3 b^2 - 2 b c + c^2)): :
3750a (a^3 - a^2 (b + 2 c) + b (b^2 - 2 b c - c^2) - a (3 b^2 + 4 b c + c^2)): :
3931a (a^2 (b + 2 c) + c (2 b^2 + b c + c^2) + a (3 b^2 + 3 b c + c^2)): :
3953a (a b (2 b - 3 c) + a^2 c + c (b^2 + c^2)): :
3976a (2 a b (b - 2 c) + a^2 c + c (b^2 + c^2)): :
3999-(a (a^2 (b - 2 c) + c (-2 b^2 + b c - 3 c^2) + a (-5 b^2 + 9 b c + c^2))): :
4003a (a^2 (b + 4 c) + a (7 b^2 - 3 b c + c^2) + c (4 b^2 + b c + 3 c^2)): :
4038a (a^3 + a^2 (3 b + 2 c) + b (b^2 + 2 b c + 3 c^2) + a (b^2 + 8 b c + 3 c^2)): :
4424a (a^2 c + a b (2 b + c) + c (b^2 + c^2)): :
4689a (-2 a^3 - 2 b^3 + 4 b^2 c + b c^2 + c^3 + a^2 (b + 4 c) + a (7 b^2 + 3 b c + c^2)): :
4694a (a b (2 b - 5 c) + a^2 c + c (b^2 + c^2)): :
4860-(a (a^3 + b^3 + a^2 (2 b - c) - b^2 c + 2 b c^2 - 2 c^3 + a (-4 b^2 + 9 b c + 2 c^2))): :
4883-(a (a^2 (3 b + 2 c) + c (2 b^2 + 3 b c - c^2) + a (b^2 + 11 b c + 3 c^2))): :
5010a (2 a^3 + 2 b^2 (b - c) - 2 a^2 c + a b (-4 b + c)): :
5045-(a (a^2 b + (b - c) c^2 + a (-b^2 + 7 b c + c^2))): :
5048a (2 a^3 + 2 b^3 - 2 b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + 2 c) - a (b^2 - 7 b c + 3 c^2)): :
5049a (a^2 b + (b - c) c^2 + a (-b^2 + 11 b c + c^2)): :
5061a (a^6 + a^5 b - 2 a^4 b (b - 2 c) - a^3 c^2 (2 b + c) + a^2 c (-6 b^3 + 3 b^2 c + b c^2 - c^3) + b (b^5 - b^2 c^3 - b c^4 + c^5) + a (-b^5 + 4 b^4 c - 2 b^3 c^2 - b^2 c^3 + b c^4 + c^5)): :
5078a (a^6 + a^5 b + b^6 - a^4 b (b - 3 c) + a^3 b c^2 - b^2 c^4 - a^2 (b^4 + 4 b^3 c + b^2 c^2 - 2 b c^3 + c^4) + a (-b^5 + b^4 c - b^3 c^2 + b c^4)): :
5091a (a^5 - a^4 c + a^3 (-2 b^2 + b c + c^2) + a^2 (2 b^3 - b^2 c - 2 c^3) + b (b^4 - b^3 c + b^2 c^2 - 2 b c^3 + c^4) + a (-2 b^4 + 3 b^3 c - 2 b^2 c^2 + b c^3 + c^4)): :
5119-(a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 - 2 b c + c^2))): :
5122-(a (4 a^3 + 4 b^3 + a^2 (b - 4 c) - 4 b^2 c + b c^2 - c^3 + a (-9 b^2 + 7 b c + c^2))): :
5126a (4 a^3 + 4 b^3 - 4 b^2 c - b c^2 + c^3 - a^2 (b + 4 c) - a (7 b^2 - 9 b c + c^2)): :
5128-(a (3 a^3 + 3 a^2 (b - c) + a (-9 b^2 + 4 b c + 3 c^2) + 3 (b^3 - b^2 c + b c^2 - c^3))): :
5131-(a (3 a^3 + 3 b^3 + a^2 (b - 3 c) - 3 b^2 c + b c^2 - c^3 + a (-7 b^2 + 5 b c + c^2))): :
5137a (a^6 + a^5 b - 2 a^4 b (b - c) - a^3 c (b^2 + c^2) - a^2 c (b^3 + c^3) + b (b^5 - b^2 c^3 - b c^4 + c^5) + a (-b^5 + 2 b^4 c - 2 b^2 c^3 + 2 b c^4 + c^5)): :
5143a (a^4 b^2 + a^5 (b + c) + b^3 c (b^2 - c^2) - a^2 b^2 (b^2 - b c + c^2) - a^3 (2 b^3 + b^2 c - 2 b c^2 + c^3) + a b (b^4 - 2 b^3 c + c^4)): :
5172a (a^6 - 3 a^4 b (b - c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 - 3 b c^2 + 2 c^3) + a^2 (b^4 - 4 b^3 c + 3 b^2 c^2 - c^4) + a b (-3 b^4 + 5 b^3 c - b^2 c^2 - 2 b c^3 + c^4)): :
5173a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 + 2 b c + c^2) - 2 a^3 c (2 b^2 + 2 b c + c^2) + 2 a^2 (b^4 - b^3 c - 2 b c^3) - a (b^5 - 4 b^4 c + 2 b^3 c^2 + 6 b^2 c^3 - 3 b c^4 - 2 c^5)): :
5183-(a (2 a^3 + 2 b^3 + a^2 (3 b - 2 c) - 2 b^2 c + 3 b c^2 - 3 c^3 + a (-7 b^2 + b c + 3 c^2))): :
5193a (a^6 - 3 a^4 b (b - 3 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 - 3 b^2 c - 9 b c^2 + 2 c^3) + a^2 (b^4 - 13 b^3 c + 18 b^2 c^2 - 3 b c^3 - c^4) + a b (-3 b^4 + 11 b^3 c - 7 b^2 c^2 - 5 b c^3 + 4 c^4)): :
5204-(a (3 a^3 + 3 b^2 (b - c) - 3 a^2 c + a b (-6 b + 5 c))): :
5217-(a (3 a^3 + 3 b^2 (b - c) - 3 a^2 c + a b (-6 b + c))): :
5221-(a (a^3 + b^3 + a^2 (2 b - c) - b^2 c + 2 b c^2 - 2 c^3 + a (-4 b^2 + 5 b c + 2 c^2))): :
5228-(a (a^5 - a^4 c + a^3 (-3 b^2 + b c + c^2) + b (b - c)^2 (b^2 + b c + 2 c^2) + a^2 (3 b^3 - 4 b^2 c - 4 b c^2 - 3 c^3) + a (-2 b^4 + 5 b^3 c - 6 b^2 c^2 + b c^3 + 2 c^4))): :
5255a (a^3 + a^2 b - a b^2 + b^3 + a c^2 + b c^2): :
5264a (a^3 + a^2 b + b (b^2 + c^2) + a (-b^2 + b c + c^2)): :
5266a (2 a^3 + a^2 b + 2 b^3 + b c^2 + c^3 + a (-b^2 + b c + c^2)): :
5269a (3 a^3 + 3 b^3 + b^2 c + 3 b c^2 + c^3 + a^2 (3 b + c) + a (-b^2 + 4 b c + 3 c^2)): :
5285-(a (a^6 + a^5 b + b^6 - b^2 c^4 + a^4 b (-b + c) + a^3 b c (-b + c) - a b^2 (b^3 + b^2 c + b c^2 + c^3) - a^2 (b^4 + 3 b^3 c - b c^3 + c^4))): :
5329-(a (a^2 - b^2 + c^2) (a^4 + a^3 b + a^2 (2 b - c) c + a b (b^2 + c^2) - b^2 (b^2 + c^2))): :
5337a (a^5 - a^2 b (b - 2 c) c + a^4 (2 b + c) + a^3 c (3 b + c) + a c (b^3 + 3 b c^2 + c^3) + b (b^4 + b^3 c + b^2 c^2 + c^4)): :
5347-(a (a^6 + a^5 b + b^6 + 3 a^3 b c^2 - b^2 c^4 + a^4 b (-b + c) - a^2 (b^4 - b^2 c^2 - 2 b c^3 + c^4) + a (-b^5 - b^4 c + b^3 c^2 + b c^4))): :
5348-(a (a^6 - a^5 c + a^4 b (-3 b + 2 c) + a^3 (2 b^3 - 3 b c^2) + a^2 (b^4 - 4 b^3 c + 3 b^2 c^2 - c^4) + a (-2 b^5 + 4 b^4 c - b^3 c^2 - 2 b^2 c^3 + c^5) + b (b^5 - b^4 c - b c^4 + c^5))): :
5363-(a (a^6 + a^5 b + b^6 - a^4 b (b - 3 c) - b^2 c^4 + a^3 b c (b + 2 c) - a^2 (b^4 + 3 b^3 c - 2 b^2 c^2 - 3 b c^3 + c^4) + a b (-b^4 + b^3 c + b c^3 + c^4))): :
5425a (a^3 + b^3 - b^2 c - 2 b c^2 + 2 c^3 - 2 a c (b + c) - a^2 (2 b + c)): :
5482a (a^4 b (b - 3 c) + a^3 c^2 (5 b + c) + b c^3 (b^2 - c^2) + a^2 b (-b^3 + 6 b^2 c - 4 b c^2 + c^3) + a c (-5 b^4 + 3 b^3 c + b^2 c^2 - c^4)): :
5535a (a^6 - 2 a^5 c + a^3 b (4 b^2 + b c - 5 c^2) + a^4 (-5 b^2 + 3 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 7 b^3 c + 6 b^2 c^2 + b c^3 - c^4) - a (4 b^5 - 7 b^4 c + b^3 c^2 + 3 b^2 c^3 + b c^4 - 2 c^5)): :
5536a (a^6 - 2 a^5 c + a^3 b (4 b^2 - b c - 5 c^2) + a^4 (-5 b^2 + 3 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 5 b^3 c + 8 b^2 c^2 - b c^3 - c^4) + a (-4 b^5 + 7 b^4 c - b^3 c^2 - 5 b^2 c^3 + b c^4 + 2 c^5)): :
5537a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 5 c) + a^3 (4 b^3 + 3 b^2 c - 5 b c^2 + 2 c^3) + a b (-3 b^4 + 7 b^3 c - 3 b^2 c^2 + b c^3 - 2 c^4) + a^2 (b^4 - 11 b^3 c + 4 b^2 c^2 + 3 b c^3 - c^4)): :
5538a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 - 7 b c + c^2) + a^3 (4 b^3 - b^2 c - 5 b c^2 + 4 c^3) - a^2 (b^4 + 9 b^3 c - 8 b^2 c^2 + b c^3 + c^4) - a (2 b^5 - 7 b^4 c + 5 b^3 c^2 + b^2 c^3 - 3 b c^4 + 2 c^5)): :
5563-(a (a^3 - 2 a b (b - 2 c) + b^2 (b - c) - a^2 c)): :
5570a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (2 b + c) + a^4 (-2 b^2 + 2 b c + c^2) + 2 a^2 b^2 (b^2 - 3 b c + 4 c^2) - a (b - c)^2 (b^3 - 2 b^2 c - 3 b c^2 - 2 c^3)): :
5584-(a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - a^4 b (3 b + 2 c) + 2 a^3 (2 b^3 - b^2 c + b c^2 + c^3) + a^2 (b^4 + 8 b^3 c + 2 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 4 b^2 c^2 - 4 b c^3 + 3 c^4))): :
5597a (a^3 - 2 a b^2 + b^3 - a^2 c - a b c - b^2 c + Sqrt[2] Sqrt[-(a b c (a + b + c) (a^2 + (b - c)^2 - 2 a (b + c)))]): :
5598a (a^3 - 2 a b^2 + b^3 - a^2 c - a b c - b^2 c - Sqrt[2] Sqrt[-(a b c (a + b + c) (a^2 + (b - c)^2 - 2 a (b + c)))]): :
5662a (a^6 (b^2 + b c + 2 c^2) + a^5 (2 b^3 - 2 b^2 c - 5 b c^2 - c^3) + a^4 (-4 b^4 - b^3 c + b^2 c^2 + 6 b c^3 - 2 c^4) + a (b - c)^2 c (3 b^4 - b^3 c - b^2 c^2 + c^4) - a^3 b (2 b^4 - 7 b^3 c + 2 b c^3 + c^4) + a^2 b^2 (3 b^4 - 8 b^3 c + 7 b^2 c^2 - 4 b c^3 + 2 c^4) + b c^2 (2 b^5 - b^4 c - 2 b^3 c^2 + c^5)): :
5697-(a (a^2 b + (b - c) c^2 + a (-b^2 - 2 b c + c^2))): :
5706a (a^6 + a^5 b - 3 a^4 b^2 - 2 a^3 c (b^2 + b c + c^2) + a^2 (b^4 - 2 b^2 c^2 - 2 b c^3 - c^4) + b (b^5 - 2 b^2 c^3 - b c^4 + 2 c^5) + a (-b^5 + 2 b^4 c - 4 b^2 c^3 + b c^4 + 2 c^5)): :
5707a (a^6 + a^5 b - 2 a^3 c (b + c)^2 + a^4 b (-3 b + 2 c) + a^2 (b^4 - 4 b^3 c - 2 b c^3 - c^4) + b (b^5 - 2 b^2 c^3 - b c^4 + 2 c^5) + a (-b^5 + 4 b^4 c - 2 b^3 c^2 - 4 b^2 c^3 + b c^4 + 2 c^5)): :
5708a (a^3 + b^3 + a^2 (2 b - c) - b^2 c + 2 b c^2 - 2 c^3 + a (-4 b^2 + 7 b c + 2 c^2)): :
5709a (a^6 - 2 a^5 c + a^4 (-5 b^2 + 2 b c + c^2) + 4 a^3 (b^3 - b c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 4 b^3 c + 6 b^2 c^2 - c^4) + a (-4 b^5 + 6 b^4 c - 4 b^2 c^3 + 2 c^5)): :
5710a (a^3 + a^2 (2 b + c) + a c (b + 2 c) + b (b^2 + b c + 2 c^2)): :
5711a (a^3 + a^2 (2 b + c) + a c (3 b + 2 c) + b (b^2 + b c + 2 c^2)): :
5885a (a^5 b + (b - c)^3 c^2 (b + c) + a^3 c (b^2 - 4 b c - 2 c^2) + a^4 (-2 b^2 + 2 b c + c^2) + a^2 b (2 b^3 - 7 b^2 c + 3 b c^2 + c^3) - a (b^5 - 4 b^4 c + 2 b^3 c^2 + b^2 c^3 + 2 b c^4 - 2 c^5)): :
5902a (a^2 b + (b - c) c^2 + a (-b^2 + 2 b c + c^2)): :
5903a (a^2 b + (b - c) c^2 + a (-b^2 + c^2)): :
5908a (a^8 b + (b - c)^3 c^2 (b + c)^4 + a^7 (b^2 - 3 b c + c^2) + a^6 (-3 b^3 - 2 b^2 c + 8 b c^2 + c^3) - a^5 (3 b^4 - 15 b^3 c + 12 b^2 c^2 + 5 b c^3 + 3 c^4) + a^3 (b - c)^2 (3 b^4 + b^3 c + 16 b^2 c^2 + 9 b c^3 + 3 c^4) + a^4 (3 b^5 - 12 b^4 c - 3 b^3 c^2 + 19 b^2 c^3 - 4 b c^4 - 3 c^5) - a^2 (b - c)^2 (b^5 - 12 b^4 c - 3 b^3 c^2 + 3 b^2 c^3 - 2 b c^4 - 3 c^5) - a (b - c)^2 (b^6 + 9 b^5 c + 7 b^4 c^2 + 2 b^3 c^3 - b^2 c^4 - 3 b c^5 + c^6)): :
5919-(a (a^2 b + (b - c) c^2 + a (-b^2 - 7 b c + c^2))): :
6244a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 8 c) + 2 a^3 (2 b^3 + 2 b^2 c - 4 b c^2 + c^3) + a b (-3 b^4 + 10 b^3 c - 6 b^2 c^2 + 2 b c^3 - 3 c^4) + a^2 (b^4 - 18 b^3 c + 6 b^2 c^2 + 4 b c^3 - c^4)): :
6282a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 - 10 b c + c^2) + 4 a^3 (b^3 - 2 b c^2 + c^3) - a^2 (b^4 + 16 b^3 c - 10 b^2 c^2 + c^4) - 2 a (b^5 - 5 b^4 c + 4 b^3 c^2 - b c^4 + c^5)): :
6583-(a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 + 2 b c + c^2) - a^3 c (b^2 + 4 b c + 2 c^2) + a^2 b (2 b^3 - 5 b^2 c + 5 b c^2 - c^3) - a (b^5 - 4 b^4 c + 2 b^3 c^2 + 3 b^2 c^3 - 2 c^5))): :
6766-(a (a^6 - 2 a^5 c + 4 a^3 b (b^2 - 3 b c - c^2) + a^4 (-5 b^2 + 2 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 + 8 b^3 c + 18 b^2 c^2 - 12 b c^3 - c^4) + 2 a (-2 b^5 + 3 b^4 c - 8 b^2 c^3 + 6 b c^4 + c^5))): :
6767a (a^3 + b^2 (b - c) - a^2 c - a b (2 b + 7 c)): :
6769a (-a^6 + 2 a^5 (b + c) - (b - c)^4 (b + c)^2 + a^4 (b^2 - 6 b c + c^2) - 4 a^3 (b^3 + b^2 c - b c^2 + c^3) + a^2 (b^4 + 12 b^3 c - 2 b^2 c^2 - 4 b c^3 + c^4) + 2 a (b^5 - 3 b^4 c + 2 b^3 c^2 - 2 b^2 c^3 + b c^4 + c^5)): :
7011-(a (a^9 + b^2 (b - c)^3 (b + c)^4 + a^8 (2 b + c) + a^7 (-3 b^2 + b c - 3 c^2) - a^6 (7 b^3 + 2 b^2 c - 4 b c^2 + 3 c^3) - a b (b - c)^2 c (3 b^4 - 6 b^2 c^2 - 8 b c^3 - 5 c^4) + a^5 (3 b^4 + 3 b^3 c - 5 b c^3 + 3 c^4) - a^2 (b - c)^2 (5 b^5 + 4 b^4 c + 5 b^3 c^2 + 7 b^2 c^3 + 2 b c^4 + c^5) + a^4 (9 b^5 - 6 b^4 c + b^3 c^2 + 7 b^2 c^3 - 6 b c^4 + 3 c^5) - a^3 (b^6 + b^5 c + 3 b^4 c^2 - 2 b^3 c^3 - 5 b^2 c^4 + b c^5 + c^6))): :
7070a (3 a^6 + 4 a^3 b^3 - 2 a^5 c - a^4 (7 b^2 + 2 b c + c^2) + a^2 (b^4 + 4 b^3 c + 6 b^2 c^2 - 3 c^4) + (b - c)^2 (3 b^4 + 4 b^3 c + 4 b^2 c^2 + 4 b c^3 + c^4) + 2 a (-2 b^5 + b^4 c + 2 b^3 c^2 - 2 b^2 c^3 + c^5)): :
7146a (a^4 c - 2 a^3 c (b + c) - 2 a^2 b (b^2 + c^2) + 2 a (b^4 - b^3 c - b c^3) + c (b^4 - 2 b^3 c + c^4)): :
7280-(a (2 a^3 + 2 b^2 (b - c) - 2 a^2 c + a b (-4 b + 3 c))): :
7373a (a^3 + b^2 (b - c) - a^2 c + a b (-2 b + 9 c)): :
7688-(a (a^6 + b^2 (b - c)^3 (b + c) - a^4 b (3 b + c) - a^5 (b + 2 c) + a^3 (4 b^3 - b^2 c + b c^2 + 2 c^3) + a^2 (b^4 + 5 b^3 c + 2 b^2 c^2 - b c^3 - c^4) + a b (-3 b^4 + b^3 c + 3 b^2 c^2 - 3 b c^3 + 2 c^4))): :
7742-(a (a^6 - 3 a^4 b^2 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + c^3) + a^2 (b^4 + 2 b^3 c - 2 b^2 c^2 - c^4) + a b (-3 b^4 + 2 b^3 c + 2 b^2 c^2 - 2 b c^3 + c^4))): :
7957a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 - 4 b c + c^2) - 2 a^3 c (b^2 - b c + c^2) + 2 a^2 (b^4 + 4 b^3 c - b c^3) + a (-b^5 - 2 b^4 c + 4 b^3 c^2 - 4 b^2 c^3 + b c^4 + 2 c^5)): :
7962-(a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 + 8 b c - 3 c^2))): :
7964a (2 a^6 - a^5 (b + 4 c) + a^4 (-8 b^2 - 4 b c + c^2) + 2 a^3 (4 b^3 - b^2 c + b c^2 + c^3) + (b - c)^3 (2 b^3 + 2 b^2 c + b c^2 + c^3) + 2 a^2 (2 b^4 + 6 b^3 c + 2 b^2 c^2 - b c^3 - c^4) + a (-7 b^5 + 2 b^4 c + 8 b^3 c^2 - 8 b^2 c^3 + 3 b c^4 + 2 c^5)): :
7982-(a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 + 4 b c - 3 c^2))): :
7987-(a (5 a^3 + 5 b^3 - 5 b^2 c - b c^2 + c^3 - a (-3 b + c)^2 - a^2 (b + 5 c))): :
7991-(a (a^3 + b^3 + a^2 (3 b - c) - b^2 c + 3 b c^2 - 3 c^3 + a (-5 b^2 - 2 b c + 3 c^2))): :
7994a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 - 10 b c + c^2) + 4 a^3 (b^3 + 2 b^2 c - 2 b c^2 + c^3) - a^2 (b^4 + 24 b^3 c - 2 b^2 c^2 - 8 b c^3 + c^4) - 2 a (b^5 - 5 b^4 c + 4 b^3 c^2 - 4 b^2 c^3 + 3 b c^4 + c^5)): :
8069a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) - a b (b - c)^2 (3 b^2 - c^2) + 2 a^3 (2 b^3 - 2 b c^2 + c^3) + a^2 (b^4 - 6 b^3 c + 2 b^2 c^2 - c^4)): :
8071a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) - a b (b - c)^2 (3 b^2 - c^2) + 2 a^3 (2 b^3 - 2 b c^2 + c^3) + a^2 (b^4 - 6 b^3 c + 10 b^2 c^2 - c^4)): :
8148a (a^3 + b^3 - b^2 c - 4 b c^2 + 4 c^3 - a^2 (4 b + c) + a (2 b^2 + 5 b c - 4 c^2)): :
8158a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 - 4 b^2 c - 2 b c^2 + c^3) + a^2 (b^4 + 2 b^3 c + 14 b^2 c^2 - 8 b c^3 - c^4) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 - 10 b c^3 + 9 c^4)): :
8162a (a^3 + b^2 (b - c) - a^2 c - a b (2 b + 13 c)): :
8163a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 10 c) + 2 a^3 (2 b^3 - 7 b^2 c - 5 b c^2 + c^3) + a^2 (b^4 - 4 b^3 c + 42 b^2 c^2 - 14 b c^3 - c^4) + a b (-3 b^4 + 12 b^3 c - 8 b^2 c^2 - 16 b c^3 + 15 c^4)): :
8171a (3 a^6 + 3 b^2 (b - c)^3 (b + c) - 3 a^5 (b + 2 c) + a^4 b (-9 b + 4 c) + 2 a^3 (6 b^3 - 2 b c^2 + 3 c^3) + a^2 (3 b^4 - 2 b^3 c - 22 b^2 c^2 - 3 c^4) + a b (-9 b^4 + 10 b^3 c + 2 b^2 c^2 - 6 b c^3 + 3 c^4)): :
8186a (2 a^3 - 4 a b^2 + 2 b^3 - 2 a^2 c - 2 a b c - 2 b^2 c + Sqrt[2] Sqrt[-(a b c (a + b + c) (a^2 + (b - c)^2 - 2 a (b + c)))]): :
8187a (2 a^3 - 4 a b^2 + 2 b^3 - 2 a^2 c - 2 a b c - 2 b^2 c - Sqrt[2] Sqrt[-(a b c (a + b + c) (a^2 + (b - c)^2 - 2 a (b + c)))]): :
8193a (a^6 + a^5 b - a^4 b^2 + b^6 - b^2 c^4 + 2 a^3 b c (-b + c) - a b (b^4 + 2 b^3 c + 2 b c^3 - c^4) - a^2 (b^4 + c^4)): :
8251a (a^9 + a^8 (b - c) + 2 a^7 b (-2 b + c) - 2 a^6 b c (b + 2 c) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3)^2 + 2 a^5 (b^4 - 3 b^3 c + 2 b^2 c^2 - c^4) + 2 a^2 b^2 c (-3 b^4 + 2 b^3 c + 2 b^2 c^2 - 2 b c^3 + c^4) + 2 a^3 b (2 b^5 + b^4 c - 2 b^3 c^2 + 2 b^2 c^3 + 2 b c^4 - c^5) + 2 a^4 (-b^5 + 5 b^4 c + b c^4 + c^5) + a (-3 b^8 + 2 b^7 c + 6 b^4 c^4 - 2 b^3 c^5 - 4 b^2 c^6 + c^8)): :
8270a (a^6 - a^4 (b - c)^2 + 2 a^3 b (b - c) c + (b^2 - c^2)^2 (b^2 + c^2) + 2 a b c (b^3 - b^2 c + b c^2 - c^3) - a^2 (b^4 + 6 b^3 c - 2 b^2 c^2 - 2 b c^3 + c^4)): :
8273a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - 3 a^4 b (b + 2 c) + 2 a^3 (2 b^3 + b^2 c + 3 b c^2 + c^3) + a^2 (b^4 + 12 b^3 c - 6 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 + 4 b^3 c - 8 b^2 c^2 + c^4)): :
8726a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 + 6 b c + c^2) + 4 a^3 (b^3 + 2 b c^2 + c^3) - a^2 (b^4 - 16 b^3 c + 6 b^2 c^2 + c^4) - 2 a (b^5 + 3 b^4 c - 4 b^3 c^2 - b c^4 + c^5)): :
8758a (a^5 (b + 2 c) + a^4 (2 b^2 - 2 b c - c^2) + 2 a^2 b^2 (-b^2 + b c + c^2) - 2 a^3 (2 b^3 - b c^2 + c^3) + a b (3 b^4 - 4 b^3 c + 2 b c^3 - c^4) + c (2 b^5 - b^4 c - 2 b^3 c^2 + c^5)): :
8924-(a (a^5 (b^2 - b c + c^2) + a^4 (b^3 - b^2 c + b c^2 - c^3) + b^2 c^2 (b^3 - b^2 c + b c^2 - c^3) - a b c (b^4 + 3 b^3 c - 2 b^2 c^2 - b c^3 + c^4) + a^3 (-3 b^4 + 2 b^3 c - b^2 c^2 + 2 b c^3 + c^4) + a^2 (b^5 - b^4 c + 3 b^3 c^2 - 3 b^2 c^3 + b c^4 - c^5))): :
9120a (a^12 + 8 a^9 b (b - c) c + a^10 (-6 b^2 + 8 b c - 6 c^2) + (b^2 - c^2)^6 + 8 a b (b - c)^3 c (b^3 + b^2 c + b c^2 + c^3)^2 + a^8 (15 b^4 - 32 b^3 c + 18 b^2 c^2 + 15 c^4) + a^4 (b^2 - c^2)^2 (15 b^4 + 32 b^3 c + 18 b^2 c^2 + 15 c^4) - 16 a^5 b c (b^5 - b^4 c + b c^4 - c^5) - 2 a^2 (b^2 - c^2)^2 (3 b^6 + 12 b^5 c - 3 b^4 c^2 + 8 b^3 c^3 - 3 b^2 c^4 - 4 b c^5 + 3 c^6) - 4 a^6 (5 b^6 - 4 b^5 c + 3 b^4 c^2 - 8 b^3 c^3 + 3 b^2 c^4 + 4 b c^5 + 5 c^6)): :
9364a (a^6 - a^5 c + a^4 b (-3 b + 5 c) + 2 a^3 b (b^2 + b c - 3 c^2) + a^2 (b^4 - 12 b^3 c + 10 b^2 c^2 + 2 b c^3 - c^4) + a (-2 b^5 + 7 b^4 c - 4 b^3 c^2 - 2 b c^4 + c^5) + b (b^5 - b^4 c - b c^4 + c^5)): :
9371a (a^5 (b + 2 c) + a^4 (2 b^2 - 6 b c - c^2) - 2 a^3 (2 b^3 + b^2 c - 3 b c^2 + c^3) - 2 a^2 b (b^3 - 6 b^2 c + 2 b c^2 + c^3) + a b (3 b^4 - 8 b^3 c + 4 b^2 c^2 + c^4) + c (2 b^5 - b^4 c - 2 b^3 c^2 + c^5)): :
9441a (a^5 - a^4 (b + 2 c) - 2 a^3 (b^2 - c^2) + b (b - c)^2 (b^2 + c^2) + a^2 (4 b^3 - 2 c^3) + a (-3 b^4 + 4 b^3 c - 2 b^2 c^2 + c^4)): :
9627a (a^6 + a^3 b c^2 + a b^3 c (-b + c) + (b^2 - c^2)^2 (b^2 + c^2) - a^4 (b^2 + b c + c^2) - a^2 (b^4 - 2 b^3 c - 3 b^2 c^2 + c^4)): :
9630a (a^6 + a^3 b c^2 + a b^3 c (-b + c) + (b^2 - c^2)^2 (b^2 + c^2) - a^4 (b^2 + b c + c^2) - a^2 (b^4 - 2 b^3 c + b^2 c^2 + c^4)): :
9659a (a^9 - a^8 c + b^2 (b - c)^3 (b + c)^2 (b^2 + c^2) - a^7 (3 b^2 - b c + c^2) - a b (b^2 - c^2)^2 (2 b^3 - b^2 c + 2 b c^2 - c^3) + a^6 (b^3 + c^3) + a^5 (b^4 - b^3 c + 2 b^2 c^2 - b c^3 - c^4) + a^4 (-b^5 + 2 b^4 c - b^3 c^2 + b^2 c^3 + c^5) + a^3 (3 b^6 - b^5 c - b^4 c^2 + 4 b^3 c^3 + b^2 c^4 - b c^5 + c^6) - a^2 (b^7 - b^4 c^3 + b^3 c^4 - 2 b^2 c^5 + c^7)): :
9672a (a^9 - a^8 c + b^2 (b - c)^3 (b + c)^2 (b^2 + c^2) - a^7 (3 b^2 - b c + c^2) - a b (b^2 - c^2)^2 (2 b^3 - b^2 c + 2 b c^2 - c^3) + a^6 (b^3 + c^3) + a^5 (b^4 - b^3 c + 2 b^2 c^2 - b c^3 - c^4) + a^4 (-b^5 + 2 b^4 c - b^3 c^2 + b^2 c^3 + c^5) + a^3 (3 b^6 - b^5 c - b^4 c^2 - 4 b^3 c^3 + b^2 c^4 - b c^5 + c^6) - a^2 (b^7 - b^4 c^3 + b^3 c^4 - 2 b^2 c^5 + c^7)): :
9819a (a^3 + b^3 + a^2 (3 b - c) - b^2 c + 3 b c^2 - 3 c^3 + a (-5 b^2 - 10 b c + 3 c^2)): :
9940-(a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (4 b + c) + a^4 (-2 b^2 + 6 b c + c^2) + 2 a^2 b^2 (b^2 - 7 b c + 4 c^2) - a (b^5 - 8 b^4 c + 6 b^3 c^2 + 2 b^2 c^3 + b c^4 - 2 c^5))): :
9957a (a^2 b + (b - c) c^2 + a (-b^2 - 5 b c + c^2)): :
10202a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (3 b + c) + a^4 (-2 b^2 + 4 b c + c^2) + 2 a^2 b^2 (b^2 - 5 b c + 3 c^2) - a (b^5 - 6 b^4 c + 4 b^3 c^2 + 2 b^2 c^3 + b c^4 - 2 c^5)): :
10222a (2 a^3 + 2 b^3 - 2 b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + 2 c) - a (b^2 - 5 b c + 3 c^2)): :
10225a (2 a^6 - a^5 (b + 4 c) + a^4 (-8 b^2 + 8 b c + c^2) + (b - c)^3 (2 b^3 + 2 b^2 c + b c^2 + c^3) + a^3 (8 b^3 + 3 b^2 c - 10 b c^2 + 2 c^3) + a^2 (4 b^4 - 17 b^3 c + 11 b^2 c^2 + 3 b c^3 - 2 c^4) - a (7 b^5 - 14 b^4 c + 4 b^3 c^2 + 3 b^2 c^3 + 2 b c^4 - 2 c^5)): :
10246a (3 a^3 + 3 b^3 - 3 b^2 c - 2 b c^2 + 2 c^3 - a^2 (2 b + 3 c) + a (-4 b^2 + 5 b c - 2 c^2)): :
10247a (3 a^3 + 3 b^3 - 3 b^2 c - 4 b c^2 + 4 c^3 - a^2 (4 b + 3 c) + a (-2 b^2 + 7 b c - 4 c^2)): :
10267a (a^6 - 3 a^4 b^2 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c + c^3) + a^2 (b^4 + 2 b c^3 - c^4) + a (-3 b^5 + 2 b^4 c + 2 b^3 c^2 - b c^4)): :
10268a (3 a^6 - 2 a^5 (b + 3 c) + a^4 (-11 b^2 + 2 b c + c^2) + 4 a^3 (3 b^3 + b^2 c - b c^2 + c^3) + (b - c)^3 (3 b^3 + 3 b^2 c + b c^2 + c^3) + a^2 (5 b^4 - 4 b^3 c + 6 b^2 c^2 + 4 b c^3 - 3 c^4) - 2 a (5 b^5 - 5 b^4 c - 2 b^3 c^2 + 2 b^2 c^3 + b c^4 - c^5)): :
10269a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 8 c) + 2 a^3 (2 b^3 - b^2 c - 4 b c^2 + c^3) + a^2 (b^4 - 12 b^3 c + 12 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 10 b^3 c - 6 b^2 c^2 - 4 b c^3 + 3 c^4)): :
10270a (3 a^6 - 2 a^5 (b + 3 c) + a^4 (-11 b^2 + 18 b c + c^2) + 4 a^3 (3 b^3 + b^2 c - 5 b c^2 + c^3) + (b - c)^3 (3 b^3 + 3 b^2 c + b c^2 + c^3) + a^2 (5 b^4 - 36 b^3 c + 22 b^2 c^2 + 4 b c^3 - 3 c^4) - 2 a (5 b^5 - 13 b^4 c + 6 b^3 c^2 + 2 b^2 c^3 + b c^4 - c^5)): :
10273a (3 a^5 b + 3 (b - c)^3 c^2 (b + c) + a^4 (-6 b^2 + 3 c^2) - 2 a^3 c (-4 b^2 + 3 b c + 3 c^2) + 2 a^2 b (3 b^3 - 7 b^2 c - b c^2 + 4 c^3) + a (-3 b^5 + 6 b^4 c + 2 b^2 c^3 - 11 b c^4 + 6 c^5)): :
10284a (a^5 b + (b - c)^3 c^2 (b + c) + a^3 c (7 b^2 + 2 b c - 2 c^2) + a^4 (-2 b^2 - 4 b c + c^2) + a^2 b (2 b^3 - b^2 c - 9 b c^2 + 7 c^3) - a (b^5 + 2 b^4 c - 4 b^3 c^2 - 5 b^2 c^3 + 8 b c^4 - 2 c^5)): :
10306a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 + 2 b^2 c - 2 b c^2 + c^3) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 + 2 b c^3 - 3 c^4) + a^2 (b^4 - 10 b^3 c + 2 b^2 c^2 + 4 b c^3 - c^4)): :
10310a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c - 3 b c^2 + c^3) + a^2 (b^4 - 12 b^3 c + 6 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 8 b^3 c + 4 b^2 c^2 + c^4)): :
10319a (a^6 + 2 a^5 b - 4 a^3 b^2 c + (b^2 - c^2) (b^2 + c^2)^2 + a^4 (-b^2 + 4 b c + c^2) - 2 a b (b^4 + 2 b^2 c^2 + 2 b c^3 - c^4) - a^2 (b^4 + 8 b^3 c + 6 b^2 c^2 + c^4)): :
10383a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 + 10 b c + c^2) + 4 a^3 (b^3 + b^2 c + 3 b c^2 + c^3) - a^2 (b^4 - 20 b^3 c - 2 b^2 c^2 - 4 b c^3 + c^4) - 2 a (b^5 + 5 b^4 c - 6 b^3 c^2 - 2 b^2 c^3 + b c^4 + c^5)): :
10388a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 - 6 b c + c^2) + 4 a^3 (b^3 + b^2 c - b c^2 + c^3) - a^2 (b^4 + 12 b^3 c + 14 b^2 c^2 - 4 b c^3 + c^4) - 2 a (b^5 - 3 b^4 c + 2 b^3 c^2 - 2 b^2 c^3 + b c^4 + c^5)): :
10389a (3 a^3 + 3 b^3 - 3 b^2 c - b c^2 + c^3 - a^2 (b + 3 c) - a (5 b^2 + 8 b c + c^2)): :
10434a (2 a^5 (b + c) + a^4 b (2 b + c) + 2 b^3 c (b^2 - c^2) + a^3 (-4 b^3 - 3 b^2 c + b c^2 - 2 c^3) - a^2 b (2 b^3 + 3 b^2 c + 4 b c^2 + c^3) + a b (2 b^4 - 3 b^3 c - 3 b^2 c^2 - b c^3 + c^4)): :
10439a (a^4 b (2 b - c) + 2 b c^3 (b^2 - c^2) + a^3 c (b^2 + 5 b c + 2 c^2) + a^2 b (-2 b^3 + b^2 c - 4 b c^2 + 3 c^3) + a c (-5 b^4 + b^3 c + 3 b^2 c^2 - b c^3 - 2 c^4)): :
10441a (a^4 b^2 + a^3 c^2 (2 b + c) + b c^3 (b^2 - c^2) - a^2 b (b^3 + b c^2 - c^3) - a (2 b^4 c - b^2 c^3 + c^5)): :
10470a (2 a^4 b^2 + 3 a^5 (b + c) + a^3 (-6 b^3 - 3 b^2 c + b c^2 - 4 c^3) - a^2 b (2 b^3 + 3 b^2 c + 8 b c^2 + c^3) + b c (3 b^4 - 4 b^2 c^2 + c^4) + a (3 b^5 - 4 b^4 c - 3 b^3 c^2 - b^2 c^3 + c^5)): :
10473a (a^4 b^2 + b c^3 (b^2 - c^2) + a^3 c (2 b^2 + 4 b c + c^2) + a^2 b (-b^3 + 2 b^2 c + b c^2 + 3 c^3) - a c (2 b^4 - 2 b^3 c - 3 b^2 c^2 + c^4)): :
10474a (a^5 (b + c) - a^4 b (b + c) + a^2 b (b^3 - 2 b^2 c - 5 b c^2 - 3 c^3) - a^3 (2 b^3 + 2 b^2 c + 4 b c^2 + 3 c^3) + b c (b^4 - 3 b^2 c^2 + 2 c^4) + a (b^5 + b^4 c - 2 b^3 c^2 - 3 b^2 c^3 - b c^4 + 2 c^5)): :
10475a (a^4 b (b - c) + a^5 (b + c) + b^3 c (b^2 - c^2) - a^2 b (b^3 - 2 b^2 c + 3 b c^2 - 3 c^3) - a^3 (2 b^3 - 2 b^2 c - 4 b c^2 + c^3) + a b (b^4 - 3 b^3 c + 2 b^2 c^2 + 3 b c^3 - c^4)): :
10476a (a^4 b (2 b - c) + a^5 (b + c) - 2 a^3 (b^3 - 2 b c^2) - 2 a^2 b (b^3 + 3 b c^2 - c^3) + b c (b^4 - c^4) + a (b^5 - 5 b^4 c + 2 b^2 c^3 - b c^4 - c^5)): :
10480a (a^4 b^2 + b c^3 (b^2 - c^2) + a^3 (-2 b^2 c + c^3) - a^2 b (b^3 + 2 b^2 c + 3 b c^2 + c^3) - a c (2 b^4 + 2 b^3 c + b^2 c^2 + c^4)): :
10508-(a (-(a Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)]) - b Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] - c Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + (a^2 b + (b - c) c^2 + a (-b^2 - 7 b c + c^2)) Cos[A/2] + (a^2 b + (b - c) c^2 + a (-b^2 - 7 b c + c^2)) Cos[B/2] + a^2 b Cos[C/2] - a b^2 Cos[C/2] - 7 a b c Cos[C/2] + a c^2 Cos[C/2] + b c^2 Cos[C/2] - c^3 Cos[C/2])): :
10618a (a^5 (7 b + 8 c) + a^4 (2 b^2 + 2 b c - c^2) + (b - c)^2 c (8 b^3 + 15 b^2 c + 8 b c^2 + c^3) - a^2 b (2 b^3 + 9 b^2 c + 15 b c^2 + 9 c^3) - a^3 (16 b^3 + 9 b^2 c + 8 b c^2 + 14 c^3) + a (9 b^5 - 10 b^3 c^2 - 7 b^2 c^3 + 2 b c^4 + 6 c^5)): :
10679a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + 2 b^2 c - b c^2 + c^3) + a b (-3 b^4 + 4 b^3 c + 2 b c^3 - 3 c^4) + a^2 (b^4 - 6 b^3 c + 4 b c^3 - c^4)): :
10680a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - 2 b^2 c - 3 b c^2 + c^3) + a^2 (b^4 - 6 b^3 c + 12 b^2 c^2 - 4 b c^3 - c^4) + a b (-3 b^4 + 8 b^3 c - 4 b^2 c^2 - 6 b c^3 + 5 c^4)): :
10831a (a^9 - a^8 c + b^2 (b - c)^3 (b + c)^2 (b^2 + c^2) - a^7 (3 b^2 - b c + c^2) - a b (b^2 - c^2)^2 (2 b^3 - b^2 c + 2 b c^2 - c^3) + a^6 (b^3 + c^3) + a^5 (b^4 - b^3 c - b c^3 - c^4) + a^4 (-b^5 + 2 b^4 c - b^3 c^2 + 3 b^2 c^3 + c^5) + a^3 (3 b^6 - b^5 c + 3 b^4 c^2 + 6 b^3 c^3 + b^2 c^4 - b c^5 + c^6) - a^2 (b^7 + 2 b^5 c^2 - 3 b^4 c^3 + b^3 c^4 - 2 b^2 c^5 + c^7)): :
10832a (a^9 - a^8 c + b^2 (b - c)^3 (b + c)^2 (b^2 + c^2) - a^7 (3 b^2 - b c + c^2) - a b (b^2 - c^2)^2 (2 b^3 - b^2 c + 2 b c^2 - c^3) + a^6 (b^3 + c^3) + a^5 (b^4 - b^3 c - b c^3 - c^4) + a^4 (-b^5 + 2 b^4 c - b^3 c^2 + 3 b^2 c^3 + c^5) + a^3 (3 b^6 - b^5 c + 3 b^4 c^2 - 10 b^3 c^3 + b^2 c^4 - b c^5 + c^6) - a^2 (b^7 + 2 b^5 c^2 - 3 b^4 c^3 + b^3 c^4 - 2 b^2 c^5 + c^7)): :
10856a (a^6 + b^6 + 6 b^5 c - b^4 c^2 - 4 b^3 c^3 - b^2 c^4 - 2 b c^5 + c^6 + 6 a^5 (b + c) + a^4 (7 b^2 + 2 b c - c^2) - 4 a^3 (3 b^3 + 2 b^2 c - 2 b c^2 + c^3) - a^2 (9 b^4 + 8 b^3 c + 22 b^2 c^2 + c^4) + 2 a (3 b^5 - 7 b^4 c - 4 b^3 c^2 + b c^4 - c^5)): :
10857a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 + 14 b c + c^2) + 4 a^3 (b^3 + 4 b c^2 + c^3) - a^2 (b^4 - 32 b^3 c + 14 b^2 c^2 + c^4) - 2 a (b^5 + 7 b^4 c - 8 b^3 c^2 - b c^4 + c^5)): :
10882a (a^4 b (2 b - c) + 2 a^5 (b + c) + 2 b^3 c (b^2 - c^2) - a^2 b (2 b^3 + b^2 c + 8 b c^2 - c^3) - a^3 (4 b^3 + b^2 c - 3 b c^2 + 2 c^3) + a b (2 b^4 - 5 b^3 c - b^2 c^2 + b c^3 - c^4)): :
10902a (a^6 + a^4 b (-3 b + c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a b^2 (-3 b^3 + 3 b^2 c + b c^2 - c^3) + a^3 (4 b^3 + b^2 c - b c^2 + 2 c^3) + a^2 (b^4 - b^3 c + 2 b^2 c^2 + b c^3 - c^4)): :
10965a (a^6 - 3 a^4 b^2 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + 3 b^2 c + c^3) + a b (-3 b^4 + 2 b^3 c + 2 b^2 c^2 + 4 b c^3 - 5 c^4) + a^2 (b^4 - 4 b^3 c - 8 b^2 c^2 + 6 b c^3 - c^4)): :
10966a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 - b^2 c - 2 b c^2 + c^3) + a^2 (b^4 - 4 b^3 c + 12 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 - 4 b c^3 + 3 c^4)): :
10980a (a^3 + b^3 + a^2 (3 b - c) - b^2 c + 3 b c^2 - 3 c^3 + a (-5 b^2 + 14 b c + 3 c^2)): :
11009a (a^3 + b^3 - b^2 c + 2 a (b - c) c - 2 b c^2 + 2 c^3 - a^2 (2 b + c)): :
11010a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 - b c + c^2)): :
11011a (2 a^3 + 2 b^3 - 2 b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + 2 c) - a (b^2 - 3 b c + 3 c^2)): :
11012a (a^6 - 3 a^4 b (b - c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 - b^2 c - 3 b c^2 + 2 c^3) - a b (3 b^4 - 5 b^3 c + b^2 c^2 + 3 b c^3 - 2 c^4) + a^2 (b^4 - 3 b^3 c + 6 b^2 c^2 - b c^3 - c^4)): :
11014a (a^6 - 2 a^5 (b + c) + (b - c)^4 (b + c)^2 - a^4 (b^2 - 5 b c + c^2) + a^3 (4 b^3 - 5 b^2 c - 3 b c^2 + 4 c^3) - a^2 (b^4 + b^3 c - 10 b^2 c^2 + 5 b c^3 + c^4) - a (2 b^5 - 5 b^4 c + 3 b^3 c^2 + 5 b^2 c^3 - 7 b c^4 + 2 c^5)): :
11018a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (2 b^2 + 4 b c + c^2) + a^4 (-2 b^2 + 6 b c + c^2) - a (b - c)^2 (b^3 - 6 b^2 c - 7 b c^2 - 2 c^3) + 2 a^2 b (b^3 - 5 b^2 c - 2 b c^2 - 2 c^3)): :
11021a (a^4 b (2 b + c) + 2 b c^3 (b^2 - c^2) + a^3 c (7 b^2 + 11 b c + 2 c^2) + a^2 b (-2 b^3 + 7 b^2 c + 8 b c^2 + 9 c^3) + a c (-3 b^4 + 7 b^3 c + 9 b^2 c^2 + b c^3 - 2 c^4)): :
11224a (3 a^3 + 3 b^3 - 3 b^2 c - 7 b c^2 + 7 c^3 - a^2 (7 b + 3 c) + a (b^2 + 10 b c - 7 c^2)): :
11227a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (6 b + c) + a^4 (-2 b^2 + 10 b c + c^2) + 2 a^2 b^2 (b^2 - 11 b c + 6 c^2) - a (b^5 - 12 b^4 c + 10 b^3 c^2 + 2 b^2 c^3 + b c^4 - 2 c^5)): :
11248a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 + b^2 c - 2 b c^2 + c^3) + a^2 (b^4 - 8 b^3 c + 4 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 6 b^3 c + 2 b^2 c^2 + c^4)): :
11249a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 - b^2 c - 2 b c^2 + c^3) + a^2 (b^4 - 4 b^3 c + 8 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 - 4 b c^3 + 3 c^4)): :
11278a (2 a^3 + 2 b^3 - 2 b^2 c - 5 b c^2 + 5 c^3 - a^2 (5 b + 2 c) + a (b^2 + 7 b c - 5 c^2)): :
11280a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 + 3 b c - 3 c^2)): :
11366-(a (a^3 + b^3 - a^2 c - b^2 c - a b (2 b + c) + 2 Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
11367-(a (a^3 + b^3 - a^2 c - b^2 c - a b (2 b + c) - 2 Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
11407a (a^6 + 2 a^5 (b - c) + a^4 (-9 b^2 + 26 b c + 3 c^2) + 4 a^3 (b^3 - 8 b c^2 - c^3) + (b - c)^3 (b^3 + b^2 c + 3 b c^2 + 3 c^3) + a^2 (7 b^4 - 56 b^3 c + 34 b^2 c^2 - c^4) - 2 a (3 b^5 - 17 b^4 c + 12 b^3 c^2 + 4 b^2 c^3 + b c^4 - 3 c^5)): :
11507-(a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c - b c^2 + c^3) + a^2 (b^4 - 4 b^3 c + 6 b^2 c^2 + 2 b c^3 - c^4) - a (3 b^5 - 4 b^4 c + b c^4))): :
11508a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c - b c^2 + c^3) + a^2 (b^4 - 4 b^3 c - 2 b^2 c^2 + 2 b c^3 - c^4) - a (3 b^5 - 4 b^4 c + b c^4)): :
11509-(a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 + b^2 c - 2 b c^2 + c^3) + a^2 (b^4 - 8 b^3 c + 8 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 6 b^3 c + 2 b^2 c^2 + c^4))): :
11510a (a^6 - 3 a^4 b^2 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c + c^3) + a^2 (b^4 - 4 b^2 c^2 + 2 b c^3 - c^4) + a (-3 b^5 + 2 b^4 c + 2 b^3 c^2 - b c^4)): :
11518a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 - 8 b c - 3 c^2)): :
11521a (a^5 (b + c) - 2 a^4 b (b + c) + a^3 (-2 b^3 + b^2 c - 3 b c^2 - 4 c^3) + a^2 b (2 b^3 + b^2 c - 4 b c^2 - c^3) + b c (b^4 - 4 b^2 c^2 + 3 c^4) + a (b^5 + 2 b^4 c + b^3 c^2 - b^2 c^3 - 2 b c^4 + 3 c^5)): :
11529-(a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 - 4 b c - 3 c^2))): :
11531-(a (a^3 + b^3 - b^2 c - 5 b c^2 + 5 c^3 - a^2 (5 b + c) + a (3 b^2 + 6 b c - 5 c^2))): :
11567a (2 a^6 - 4 a^5 (b + c) + 2 (b - c)^4 (b + c)^2 - 2 a^4 (b^2 - 6 b c + c^2) + a^3 (8 b^3 - 7 b^2 c - 8 b c^2 + 8 c^3) - a^2 (2 b^4 + 9 b^3 c - 19 b^2 c^2 + 7 b c^3 + 2 c^4) - a (4 b^5 - 12 b^4 c + 8 b^3 c^2 + 7 b^2 c^3 - 11 b c^4 + 4 c^5)): :
11575a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (-2 b^2 + 8 b c + c^2) + a^4 (-2 b^2 + 14 b c + c^2) + 2 a^2 b (b^3 - 17 b^2 c + 14 b c^2 + 2 c^3) - a (b^5 - 16 b^4 c + 14 b^3 c^2 - 2 b^2 c^3 + 5 b c^4 - 2 c^5)): :
11849a (a^6 - 3 a^4 b (b - c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 + 2 b^2 c - 3 b c^2 + 2 c^3) + a^2 (b^4 - 6 b^3 c + 3 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 5 b^3 c + b^2 c^2 + c^4)): :
11877-(a (a^6 + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^3 (4 b^3 + 2 b^2 c - 2 b c^2 + 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-b^4 + 4 b^3 c - 2 b^2 c^2 - 2 b c^3 + c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a (3 b^5 - 4 b^4 c + b c^4 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]))): :
11878a (a^6 + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^3 (-4 b^3 - 2 b^2 c + 2 b c^2 - 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (b^4 - 4 b^3 c + 2 b^2 c^2 + 2 b c^3 - c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (-3 b^5 + 4 b^4 c - b c^4 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
11879-(a (a^6 + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^3 (4 b^3 + 2 b^2 c - 2 b c^2 + 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-b^4 + 4 b^3 c - 2 b^2 c^2 - 2 b c^3 + c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a (3 b^5 - 4 b^4 c + b c^4 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - 4 Sqrt[2] b c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]))): :
11880a (a^6 + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^3 (-4 b^3 - 2 b^2 c + 2 b c^2 - 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (b^4 - 4 b^3 c + 2 b^2 c^2 + 2 b c^3 - c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (-3 b^5 + 4 b^4 c + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - b (c^4 + 4 Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]))): :
11881a (a^6 - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + (b - c)^2 (b + c) (b^3 - b^2 c + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^3 (4 b^3 + 2 b^2 c - 4 b c^2 + 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-b^4 + 8 b^3 c - 2 b c^3 + c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a (3 b^5 - 6 b^4 c + 2 b^3 c^2 + b c^4 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
11882a (a^6 - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + (b - c)^2 (b + c) (b^3 - b^2 c - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^3 (-4 b^3 - 2 b^2 c + 4 b c^2 - 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (b^4 - 8 b^3 c + 2 b c^3 - c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (-3 b^5 + 6 b^4 c - 2 b^3 c^2 - b c^4 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
11883a (a^6 - 3 a^4 b^2 - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^3 (4 b^3 + 2 b^2 c + 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-b^4 - 4 b^2 c^2 - 2 b c^3 + c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a (3 b^5 - 2 b^4 c - 2 b^3 c^2 + b c^4 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - 4 Sqrt[2] b c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
11884a (a^6 - 3 a^4 b^2 - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^3 (-4 b^3 - 2 b^2 c - 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (b^4 + 4 b^2 c^2 + 2 b c^3 - c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (-3 b^5 + 2 b^4 c + 2 b^3 c^2 + Sqrt[2] b^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c^2 Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - b (c^4 + 4 Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]))): :
12000a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - a^4 b (3 b + 2 c) + 2 a^3 (2 b^3 + 4 b^2 c + b c^2 + c^3) + a b (-3 b^4 + 4 b^2 c^2 + 6 b c^3 - 7 c^4) + a^2 (b^4 - 2 b^3 c - 8 b^2 c^2 + 8 b c^3 - c^4)): :
12001a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 10 c) + 2 a^3 (2 b^3 - 4 b^2 c - 5 b c^2 + c^3) + a^2 (b^4 - 10 b^3 c + 20 b^2 c^2 - 8 b c^3 - c^4) + a b (-3 b^4 + 12 b^3 c - 8 b^2 c^2 - 10 b c^3 + 9 c^4)): :
12009a (3 a^5 b + 3 (b - c)^3 c^2 (b + c) + a^4 (-6 b^2 + 10 b c + 3 c^2) - a^3 c (b^2 + 16 b c + 6 c^2) + a^2 b (6 b^3 - 25 b^2 c + 17 b c^2 - c^3) - a (3 b^5 - 16 b^4 c + 10 b^3 c^2 + 7 b^2 c^3 + 2 b c^4 - 6 c^5)): :
12410a (a^6 + a^5 b - a^4 b^2 + b^6 - b^2 c^4 + 2 a^3 b c (-b + c) - a b (b^4 + 2 b^3 c + 2 b c^3 - c^4) - a^2 (b^4 - 4 b^2 c^2 + c^4)): :
12435-(a (a^4 b (2 b + c) + 2 b c^3 (b^2 - c^2) + a^3 c (-b^2 + 3 b c + 2 c^2) + a^2 (-2 b^4 - b^3 c + b c^3) + a c (-3 b^4 - b^3 c + b^2 c^2 + b c^3 - 2 c^4))): :
12555a (a^6 + b^6 - 2 b^5 c - b^4 c^2 - 4 b^3 c^3 - b^2 c^4 + 6 b c^5 + c^6 - 2 a^5 (b + c) - a^4 (9 b^2 - 2 b c + c^2) + 4 a^3 (b^3 - 4 b c^2 - c^3) + a^2 (7 b^4 + 10 b^2 c^2 - 8 b c^3 - c^4) - 2 a (b^5 - 9 b^4 c + 4 b^2 c^3 - b c^4 - 3 c^5)): :
12702-(a (a^3 + b^3 + a^2 (2 b - c) - b^2 c + 2 b c^2 - 2 c^3 - a (4 b^2 + b c - 2 c^2))): :
12703-(a (a^6 - 2 a^5 c + 2 a^3 b (2 b^2 + 5 b c - c^2) + a^4 (-5 b^2 + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 10 b^3 c - 6 b^2 c^2 + 10 b c^3 - c^4) + 2 a (-2 b^5 + 2 b^4 c + b^3 c^2 + 3 b^2 c^3 - 5 b c^4 + c^5))): :
12704-(a (a^6 - 2 a^5 c + 2 a^3 b (2 b^2 - b c - 3 c^2) + a^4 (-5 b^2 + 4 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 6 b^3 c + 10 b^2 c^2 - 2 b c^3 - c^4) + 2 a (-2 b^5 + 4 b^4 c - b^3 c^2 - 3 b^2 c^3 + b c^4 + c^5))): :
12915a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (2 b + c) + a^4 (-2 b^2 + 2 b c + c^2) + 2 a^2 b^2 (b^2 - 3 b c + 10 c^2) - a (b - c)^2 (b^3 - 2 b^2 c - 3 b c^2 - 2 c^3)): :
13145a (a^5 b + (b - c)^3 c^2 (b + c) + a^3 c (3 b^2 - 4 b c - 2 c^2) + a^4 (-2 b^2 + 2 b c + c^2) + a^2 b (2 b^3 - 9 b^2 c + b c^2 + 3 c^3) + a (-b^5 + 4 b^4 c - 2 b^3 c^2 + b^2 c^3 - 4 b c^4 + 2 c^5)): :
13151a (2 a^6 - a^5 (3 b + 4 c) - a^4 (4 b^2 + c^2) + 2 a^2 c (3 b^3 + b^2 c - c^3) + (b - c)^3 (2 b^3 + 2 b^2 c - b c^2 - c^3) + 2 a^3 (4 b^3 + b c^2 + 3 c^3) + a (-5 b^5 + 2 b^4 c + 4 b^3 c^2 - 2 b^2 c^3 + 3 b c^4 - 2 c^5)): :
13370a (a^6 - 3 a^4 b (b - 3 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 - b^2 c - 9 b c^2 + 2 c^3) + a^2 (b^4 - 15 b^3 c + 20 b^2 c^2 - b c^3 - c^4) + a b (-3 b^4 + 11 b^3 c - 7 b^2 c^2 - 3 b c^3 + 2 c^4)): :
13373a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (b^2 + 4 b c + c^2) + a^4 (-2 b^2 + 6 b c + c^2) + 2 a^2 b (b^3 - 6 b^2 c + 5 b c^2 - c^3) + a (-b^5 + 8 b^4 c - 6 b^3 c^2 - 4 b^2 c^3 + b c^4 + 2 c^5)): :
13384a (5 a^3 + 5 b^3 - 5 b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + 5 c) + a (-7 b^2 + 4 b c - 3 c^2)): :
13388a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 - b Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] - c Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + a (-3 b^2 + 4 b c + c^2 - Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)])): :
13389a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + b Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + c Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)] + a (-3 b^2 + 4 b c + c^2 + Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)])): :
13462a (5 a^3 + 5 b^3 - 5 b^2 c - b c^2 + c^3 - a^2 (b + 5 c) - a (9 b^2 - 14 b c + c^2)): :
13528a (2 a^6 - a^5 (b + 4 c) + a^4 (-8 b^2 + 8 b c + c^2) + 2 a^3 (4 b^3 + 3 b^2 c - 5 b c^2 + c^3) + (b - c)^3 (2 b^3 + 2 b^2 c + b c^2 + c^3) + a^2 (4 b^4 - 20 b^3 c + 8 b^2 c^2 + 6 b c^3 - 2 c^4) + a (-7 b^5 + 14 b^4 c - 4 b^3 c^2 - 5 b c^4 + 2 c^5)): :
13600a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 - 6 b c + c^2) - 2 a^3 c (-6 b^2 - 2 b c + c^2) + 2 a^2 b (b^3 - b^2 c - 8 b c^2 + 6 c^3) - a (b^5 + 4 b^4 c - 6 b^3 c^2 - 10 b^2 c^3 + 13 b c^4 - 2 c^5)): :
13601a (a^5 b + 2 a^2 b (b - 2 c)^2 (b + c) + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 - 2 b c + c^2) + a^3 (8 b^2 c - 2 c^3) + a (-b^5 + 2 b^3 c^2 + 6 b^2 c^3 - 9 b c^4 + 2 c^5)): :
13624a (4 a^3 + 4 b^3 - 4 b^2 c - b c^2 + c^3 - a^2 (b + 4 c) - a (7 b^2 - 5 b c + c^2)): :
13750a (a^5 b + 2 a^2 b^3 (b - 3 c) + (b - c)^3 c^2 (b + c) - 2 a^3 c^2 (2 b + c) + a^4 (-2 b^2 + 2 b c + c^2) - a (b - c)^2 (b^3 - 2 b^2 c - 3 b c^2 - 2 c^3)): :
13751a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 + 4 b c + c^2) - a^3 c (b^2 + 6 b c + 2 c^2) + a^2 b (2 b^3 - 9 b^2 c + 9 b c^2 - c^3) - a (b^5 - 6 b^4 c + 4 b^3 c^2 + 3 b^2 c^3 - 2 c^5)): :
14000a (4 a^6 - a^5 (b + 10 c) + a^4 (-22 b^2 + 26 b c + 5 c^2) + a^3 (20 b^3 + 11 b^2 c - 34 b c^2 + 2 c^3) + (b - c)^2 (4 b^4 - 2 b^3 c - 3 b^2 c^2 - 2 b c^3 - 5 c^4) + a^2 (14 b^4 - 61 b^3 c + 39 b^2 c^2 + 11 b c^3 - 4 c^4) - a (19 b^5 - 44 b^4 c + 16 b^3 c^2 + 7 b^2 c^3 + 10 b c^4 - 8 c^5)): :
14110a (a^5 b + (b - c)^3 c^2 (b + c) + 2 a^3 c (b^2 + b c - c^2) + a^4 (-2 b^2 - 4 b c + c^2) + 2 a^2 b (b^3 + 2 b^2 c - 2 b c^2 + c^3) - a (b^5 + 2 b^4 c - 4 b^3 c^2 + 3 b c^4 - 2 c^5)): :
14115a (a^7 b (b - 3 c) + b (b - c)^3 c^3 (b + c)^2 + a^6 (-b^3 + 8 b c^2 + c^3) - a^5 (2 b^4 - 15 b^3 c + 20 b^2 c^2 + 4 b c^3 + c^4) + a^4 (2 b^5 - 14 b^4 c + 25 b^2 c^3 - 3 b c^4 - 2 c^5) + a^3 (b^6 - 7 b^5 c + 34 b^4 c^2 - 36 b^3 c^3 + b^2 c^4 + 3 b c^5 + 2 c^6) + a^2 (-b^7 + 14 b^6 c - 30 b^5 c^2 + 11 b^4 c^3 + 13 b^3 c^4 - 4 b^2 c^5 - 4 b c^6 + c^7) - a c (5 b^7 - 8 b^6 c + 3 b^4 c^3 - b^3 c^4 + 4 b^2 c^5 - 4 b c^6 + c^7)): :
14122a (2 a^6 + 2 b^6 - 4 b^5 c + b^4 c^2 + b^3 c^3 - 2 b^2 c^4 + 3 b c^5 - c^6 - a^5 (b + 4 c) + a^4 (-9 b^2 + 13 b c + c^2) + a^3 (8 b^3 + 5 b^2 c - 19 b c^2 + c^3) + a^2 (5 b^4 - 33 b^3 c + 31 b^2 c^2 + 4 b c^3 - 2 c^4) - a (7 b^5 - 21 b^4 c + 11 b^3 c^2 + 2 b^2 c^3 + 6 b c^4 - 3 c^5)): :
14131a (a^4 b (b - 7 c) + a^3 c^2 (9 b + c) + b c^3 (b^2 - c^2) + a^2 b (-b^3 + 14 b^2 c - 8 b c^2 + c^3) + a c (-9 b^4 + 7 b^3 c + b^2 c^2 - c^4)): :
14132a (a^8 b + (b - c)^3 c^2 (b + c)^4 + a^7 (b^2 + b c + c^2) + a^6 (-3 b^3 - b^2 c + 2 b c^2 + c^3) - a^5 (3 b^4 + 3 b^3 c + 2 b^2 c^2 + 2 b c^3 + 3 c^4) + a^4 (3 b^5 - 3 b^3 c^2 + b^2 c^3 - 6 b c^4 - 3 c^5) - a (b - c)^2 (b^6 + 5 b^5 c + 5 b^4 c^2 - b^3 c^3 - 3 b^2 c^4 + c^6) + a^3 (3 b^6 + 5 b^5 c - 5 b^4 c^2 - 4 b^3 c^3 + b^2 c^4 - b c^5 + 3 c^6) - a^2 (b^7 - b^6 c - 2 b^5 c^2 + b^4 c^3 + 3 b^3 c^4 + 5 b^2 c^5 - 4 b c^6 - 3 c^7)): :
14792a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) - a b (b - c)^2 (3 b^2 - c^2) + 2 a^3 (2 b^3 - 2 b c^2 + c^3) + a^2 (b^4 - 6 b^3 c + 7 b^2 c^2 - c^4)): :
14793a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) - a b (b - c)^2 (3 b^2 - c^2) + 2 a^3 (2 b^3 - 2 b c^2 + c^3) + a^2 (b^4 - 6 b^3 c + 8 b^2 c^2 - c^4)): :
14794a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - b c^2 + c^3) + a^2 (b^4 - 2 b^3 c + 5 b^2 c^2 - c^4) + a b (-3 b^4 + 4 b^3 c - 2 b c^3 + c^4)): :
14795a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + a^2 (b - c)^2 (b^2 - b c - c^2) - a b^2 (3 b^3 - 4 b^2 c + c^3) + a^3 (4 b^3 + b^2 c - 2 b c^2 + 2 c^3)): :
14796a (a^3 + b^2 (b - c) - a^2 c - a b (2 b + Sqrt[2] c)): :
14797a (a^3 + b^2 (b - c) - a^2 c + a b (-2 b + Sqrt[2] c)): :
14798a (a^6 + a^4 b (-3 b + c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a b^2 (-3 b^3 + 3 b^2 c + b c^2 - c^3) + a^3 (4 b^3 + b^2 c - b c^2 + 2 c^3) + a^2 (b^4 - b^3 c + b c^3 - c^4)): :
14799a (a^6 - 3 a^4 b^2 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - a b^2 (3 b^3 - 2 b^2 c - 2 b c^2 + c^3) + a^3 (4 b^3 + b^2 c + 2 c^3) + a^2 (b^4 + b^3 c + 2 b^2 c^2 + b c^3 - c^4)): :
14800a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 - b^2 c - 6 b c^2 + 2 c^3) + a^2 (b^4 - 9 b^3 c + 8 b^2 c^2 - b c^3 - c^4) + a b (-3 b^4 + 8 b^3 c - 4 b^2 c^2 - 3 b c^3 + 2 c^4)): :
14801a (a^12 + b^2 (b - c)^7 (b + c)^3 - a^11 (3 b + 4 c) + a^10 (-2 b^2 - 2 (-10 + Sqrt[2]) b c + 3 c^2) + a^9 (15 b^3 + (-19 + 3 Sqrt[2]) b^2 c + 3 (-13 + 2 Sqrt[2]) b c^2 + 8 c^3) - a b (b - c)^5 (b + c)^2 (5 b^3 + (-11 + 2 Sqrt[2]) b^2 c + b c^2 + (2 + Sqrt[2]) c^3) - a^8 (9 b^4 + (53 - 9 Sqrt[2]) b^3 c + 3 (-36 + 7 Sqrt[2]) b^2 c^2 + 3 (-1 + Sqrt[2]) b c^3 + 14 c^4) - a^7 b (22 b^4 + (-115 + 19 Sqrt[2]) b^3 c + 33 b^2 c^2 - 4 (-37 + 9 Sqrt[2]) b c^3 + (-73 + 7 Sqrt[2]) c^4) + a^2 (b - c)^3 (b + c) (6 b^6 + (-43 + 9 Sqrt[2]) b^5 c + (58 - 15 Sqrt[2]) b^4 c^2 + 2 b^3 c^3 - (20 + 3 Sqrt[2]) b^2 c^4 + (5 + 3 Sqrt[2]) b c^5 + c^6) + a^6 (28 b^6 - (17 + 3 Sqrt[2]) b^5 c + 3 (-79 + 23 Sqrt[2]) b^4 c^2 + 2 (145 - 31 Sqrt[2]) b^3 c^3 - (20 + 9 Sqrt[2]) b^2 c^4 + 3 (-23 + 3 Sqrt[2]) b c^5 + 14 c^6) + a^5 (6 b^7 + (-131 + 27 Sqrt[2]) b^6 c + 18 (17 - 4 Sqrt[2]) b^5 c^2 - 6 (7 + 3 Sqrt[2]) b^4 c^3 + (-285 + 77 Sqrt[2]) b^3 c^4 - 6 (-31 + 4 Sqrt[2]) b^2 c^5 - 3 (5 + Sqrt[2]) b c^6 - 8 c^7) + a^3 (b - c) (9 b^8 + (22 - 9 Sqrt[2]) b^7 c + (-173 + 51 Sqrt[2]) b^6 c^2 + (177 - 41 Sqrt[2]) b^5 c^3 + 6 (11 - 4 Sqrt[2]) b^4 c^4 + 12 (-11 + Sqrt[2]) b^3 c^5 + (28 + 9 Sqrt[2]) b^2 c^6 + (14 - 3 Sqrt[2]) b c^7 - 4 c^8) - a^4 (25 b^8 + (-109 + 13 Sqrt[2]) b^7 c + 3 (7 + 5 Sqrt[2]) b^6 c^2 + 2 (177 - 56 Sqrt[2]) b^5 c^3 + (-392 + 79 Sqrt[2]) b^4 c^4 + 6 (7 + 3 Sqrt[2]) b^3 c^5 + (115 - 21 Sqrt[2]) b^2 c^6 + (-49 + Sqrt[2]) b c^7 + 3 c^8)): :
14802a (a^12 + b^2 (b - c)^7 (b + c)^3 - a^11 (3 b + 4 c) + a^10 (-2 b^2 + 2 (10 + Sqrt[2]) b c + 3 c^2) + a^9 (15 b^3 - (19 + 3 Sqrt[2]) b^2 c - 3 (13 + 2 Sqrt[2]) b c^2 + 8 c^3) - a b (b - c)^5 (b + c)^2 (5 b^3 - (11 + 2 Sqrt[2]) b^2 c + b c^2 - (-2 + Sqrt[2]) c^3) + a^8 (-9 b^4 - (53 + 9 Sqrt[2]) b^3 c + 3 (36 + 7 Sqrt[2]) b^2 c^2 + 3 (1 + Sqrt[2]) b c^3 - 14 c^4) + a^7 b (-22 b^4 + (115 + 19 Sqrt[2]) b^3 c - 33 b^2 c^2 - 4 (37 + 9 Sqrt[2]) b c^3 + (73 + 7 Sqrt[2]) c^4) + a^2 (b - c)^3 (b + c) (6 b^6 - (43 + 9 Sqrt[2]) b^5 c + (58 + 15 Sqrt[2]) b^4 c^2 + 2 b^3 c^3 + (-20 + 3 Sqrt[2]) b^2 c^4 + (5 - 3 Sqrt[2]) b c^5 + c^6) + a^6 (28 b^6 + (-17 + 3 Sqrt[2]) b^5 c - 3 (79 + 23 Sqrt[2]) b^4 c^2 + 2 (145 + 31 Sqrt[2]) b^3 c^3 + (-20 + 9 Sqrt[2]) b^2 c^4 - 3 (23 + 3 Sqrt[2]) b c^5 + 14 c^6) + a^5 (6 b^7 - (131 + 27 Sqrt[2]) b^6 c + 18 (17 + 4 Sqrt[2]) b^5 c^2 + 6 (-7 + 3 Sqrt[2]) b^4 c^3 - (285 + 77 Sqrt[2]) b^3 c^4 + 6 (31 + 4 Sqrt[2]) b^2 c^5 + 3 (-5 + Sqrt[2]) b c^6 - 8 c^7) + a^3 (b - c) (9 b^8 + (22 + 9 Sqrt[2]) b^7 c - (173 + 51 Sqrt[2]) b^6 c^2 + (177 + 41 Sqrt[2]) b^5 c^3 + 6 (11 + 4 Sqrt[2]) b^4 c^4 - 12 (11 + Sqrt[2]) b^3 c^5 + (28 - 9 Sqrt[2]) b^2 c^6 + (14 + 3 Sqrt[2]) b c^7 - 4 c^8) + a^4 (-25 b^8 + (109 + 13 Sqrt[2]) b^7 c + 3 (-7 + 5 Sqrt[2]) b^6 c^2 - 2 (177 + 56 Sqrt[2]) b^5 c^3 + (392 + 79 Sqrt[2]) b^4 c^4 + 6 (-7 + 3 Sqrt[2]) b^3 c^5 - (115 + 21 Sqrt[2]) b^2 c^6 + (49 + Sqrt[2]) b c^7 - 3 c^8)): :
14803a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 7 c) + a^3 (4 b^3 - b^2 c - 7 b c^2 + 2 c^3) + a^2 (b^4 - 11 b^3 c + 8 b^2 c^2 - b c^3 - c^4) + a b (-3 b^4 + 9 b^3 c - 5 b^2 c^2 - 3 b c^3 + 2 c^4)): :
14804a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + a^3 (4 b^3 - b^2 c - 4 b c^2 + 2 c^3) + a^2 (b^4 - 5 b^3 c + 4 b^2 c^2 - b c^3 - c^4) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 - 3 b c^3 + 2 c^4)): :
14882a (a^6 - 3 a^4 b (b - c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^3 (4 b^3 + 2 b^2 c - 3 b c^2 + 2 c^3) + a^2 (b^4 - 6 b^3 c + 5 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 5 b^3 c + b^2 c^2 + c^4)): :
15016a (a^5 b + (b - c)^3 c^2 (b + c) + a^3 c (b^2 - 5 b c - 2 c^2) + a^4 (-2 b^2 + 3 b c + c^2) + a^2 b (2 b^3 - 9 b^2 c + 4 b c^2 + c^3) - a (b^5 - 5 b^4 c + 3 b^3 c^2 + b^2 c^3 + 2 b c^4 - 2 c^5)): :
15177a (a^9 - a^8 c + b^2 (b - c)^3 (b + c)^2 (b^2 + c^2) - a^7 (3 b^2 - b c + c^2) - a b (b^2 - c^2)^2 (2 b^3 - b^2 c + 2 b c^2 - c^3) + a^6 (b^3 + c^3) + a^5 (b^4 - b^3 c + 2 b^2 c^2 - b c^3 - c^4) + a^4 (-b^5 + 2 b^4 c - 3 b^3 c^2 + b^2 c^3 + c^5) + a^3 (3 b^6 - b^5 c + b^4 c^2 + 2 b^3 c^3 - b^2 c^4 - b c^5 + c^6) - a^2 (b^7 - b^4 c^3 + 3 b^3 c^4 - 4 b^2 c^5 + c^7)): :
15178a (4 a^3 + 4 b^3 - 4 b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + 4 c) + a (-5 b^2 + 7 b c - 3 c^2)): :
15803a (3 a^3 + 3 b^3 + a^2 (b - 3 c) - 3 b^2 c + b c^2 - c^3 + a (-7 b^2 + 6 b c + c^2)): :
15804a (a^9 + b^2 (b - c)^5 (b + c)^2 - a^8 (2 b + 3 c) - a b (b - c)^3 (b + c)^2 (4 b^2 - b c + c^2) + a^7 (-3 b^2 + b c + c^2) + a^6 (9 b^3 + 6 b^2 c + 4 b c^2 + 5 c^3) - a^5 (b^4 - 3 b^3 c + 16 b^2 c^2 + b c^3 + 5 c^4) - a^4 (11 b^5 + 6 b^4 c + 11 b^3 c^2 - 15 b^2 c^3 + 2 b c^4 + c^5) + a^3 (7 b^6 - 9 b^5 c + 41 b^4 c^2 - 46 b^3 c^3 - 11 b^2 c^4 - b c^5 + 3 c^6) + a^2 (3 b^7 + 6 b^6 c - 26 b^5 c^2 + 15 b^4 c^3 - 9 b^3 c^4 + 12 b^2 c^5 - c^7)): :
15931a (a^6 + b^2 (b - c)^3 (b + c) - a^4 b (3 b + c) - a^5 (b + 2 c) + a b^2 (-3 b^3 + b^2 c + 3 b c^2 - c^3) + a^3 (4 b^3 + b^2 c + b c^2 + 2 c^3) + a^2 (b^4 + 3 b^3 c + b c^3 - c^4)): :
15932a (a^6 - 2 a^5 c + a^3 b (4 b^2 - b c - 5 c^2) + a^4 (-5 b^2 + 3 b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 5 b^3 c - b c^3 - c^4) + a (-4 b^5 + 7 b^4 c - b^3 c^2 - 5 b^2 c^3 + b c^4 + 2 c^5)): :
15934a (a^3 + b^3 - b^2 c - 2 b c^2 + 2 c^3 - a^2 (2 b + c) - a c (5 b + 2 c)): :
15941a (a^9 + a^8 (b - c) - 2 a^7 b (2 b + c) + 2 a^6 b c (b + 2 c) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3)^2 + 2 a^5 (b^4 + 3 b^3 c + 2 b^2 c^2 - c^4) + 2 a^2 b^2 c (3 b^4 - 2 b^3 c - 2 b^2 c^2 + 2 b c^3 - c^4) - 2 a^4 (b^5 + 3 b^4 c + 3 b c^4 - c^5) + 2 a^3 b (2 b^5 - b^4 c - 6 b^3 c^2 - 2 b^2 c^3 + 2 b c^4 + c^5) + a (-3 b^8 - 2 b^7 c + 8 b^6 c^2 - 2 b^4 c^4 + 2 b^3 c^5 - 4 b^2 c^6 + c^8)): :
16189a (5 a^3 + 5 b^3 - 5 b^2 c - 9 b c^2 + 9 c^3 - a^2 (9 b + 5 c) - a (b^2 - 14 b c + 9 c^2)): :
16191a (9 a^3 + 9 b^3 - 9 b^2 c - 17 b c^2 + 17 c^3 - a^2 (17 b + 9 c) - a (b^2 - 26 b c + 17 c^2)): :
16192a (7 a^3 + 7 b^3 + a^2 (b - 7 c) - 7 b^2 c + b c^2 - c^3 + a (-15 b^2 + 6 b c + c^2)): :
16193a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (2 b^2 + 4 b c + c^2) + a^4 (-2 b^2 + 6 b c + c^2) - a (b - c)^2 (b^3 - 6 b^2 c - 7 b c^2 - 2 c^3) + 2 a^2 b (b^3 - 5 b^2 c + 2 b c^2 - 2 c^3)): :
16200a (3 a^3 + 3 b^3 - 3 b^2 c - 5 b c^2 + 5 c^3 - a^2 (5 b + 3 c) - a (b^2 - 8 b c + 5 c^2)): :
16201a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (2 b^2 + 4 b c + c^2) + a^4 (-2 b^2 + 6 b c + c^2) + 2 a^2 b (b^3 - 5 b^2 c - 10 b c^2 - 2 c^3) - a (b - c)^2 (b^3 - 6 b^2 c - 7 b c^2 - 2 c^3)): :
16202a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - a^4 b (3 b + 2 c) + 2 a^3 (2 b^3 + 2 b^2 c + b c^2 + c^3) + a b (-3 b^4 + 4 b^2 c^2 + 2 b c^3 - 3 c^4) + a^2 (b^4 + 2 b^3 c - 4 b^2 c^2 + 4 b c^3 - c^4)): :
16203a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 10 c) + 2 a^3 (2 b^3 - 2 b^2 c - 5 b c^2 + c^3) + a^2 (b^4 - 14 b^3 c + 16 b^2 c^2 - 4 b c^3 - c^4) + a b (-3 b^4 + 12 b^3 c - 8 b^2 c^2 - 6 b c^3 + 5 c^4)): :
16204a (5 a^6 - 2 a^5 (7 b + 5 c) + 3 a^4 (b^2 + 10 b c - 3 c^2) + (b - c)^3 (5 b^3 + 5 b^2 c - 9 b c^2 - 9 c^3) + 4 a^3 (5 b^3 - 5 b^2 c - 3 b c^2 + 7 c^3) - a^2 (13 b^4 + 12 b^3 c - 42 b^2 c^2 + 20 b c^3 + 5 c^4) - 2 a (3 b^5 - 11 b^4 c + 10 b^3 c^2 + 6 b^2 c^3 - 17 b c^4 + 9 c^5)): :
16205a (5 a^6 - 2 a^5 (7 b + 5 c) + a^4 (3 b^2 + 46 b c - 9 c^2) + (b - c)^3 (5 b^3 + 5 b^2 c - 9 b c^2 - 9 c^3) + 4 a^3 (5 b^3 - 13 b^2 c - 7 b c^2 + 7 c^3) - a^2 (13 b^4 + 12 b^3 c - 90 b^2 c^2 + 52 b c^3 + 5 c^4) - 2 a (3 b^5 - 19 b^4 c + 18 b^3 c^2 + 22 b^2 c^3 - 33 b c^4 + 9 c^5)): :
16206a (5 a^6 - 2 a^5 (7 b + 5 c) + a^4 (3 b^2 + 32 b c - 9 c^2) + (b - c)^3 (5 b^3 + 5 b^2 c - 9 b c^2 - 9 c^3) + 2 a^3 (10 b^3 - 11 b^2 c - 7 b c^2 + 14 c^3) - a^2 (13 b^4 + 14 b^3 c - 46 b^2 c^2 + 22 b c^3 + 5 c^4) - 2 a (3 b^5 - 12 b^4 c + 11 b^3 c^2 + 7 b^2 c^3 - 18 b c^4 + 9 c^5)): :
16207a (5 a^6 - 2 a^5 (7 b + 5 c) + a^4 (3 b^2 + 44 b c - 9 c^2) + (b - c)^3 (5 b^3 + 5 b^2 c - 9 b c^2 - 9 c^3) + a^3 (20 b^3 - 50 b^2 c - 26 b c^2 + 28 c^3) - a^2 (13 b^4 + 10 b^3 c - 86 b^2 c^2 + 50 b c^3 + 5 c^4) - 2 a (3 b^5 - 18 b^4 c + 17 b^3 c^2 + 21 b^2 c^3 - 32 b c^4 + 9 c^5)): :
16208a (3 a^6 - 2 a^5 (b + 3 c) + a^4 (-11 b^2 + c^2) + (b - c)^3 (3 b^3 + 3 b^2 c + b c^2 + c^3) + 2 a^3 (6 b^3 + 3 b^2 c - b c^2 + 2 c^3) + a^2 (5 b^4 - 2 b^3 c + 2 b^2 c^2 + 6 b c^3 - 3 c^4) - 2 a (5 b^5 - 4 b^4 c - 3 b^3 c^2 + b^2 c^3 + 2 b c^4 - c^5)): :
16209a (3 a^6 - 2 a^5 (b + 3 c) + a^4 (-11 b^2 + 20 b c + c^2) + (b - c)^3 (3 b^3 + 3 b^2 c + b c^2 + c^3) + 2 a^3 (6 b^3 + b^2 c - 11 b c^2 + 2 c^3) + a^2 (5 b^4 - 38 b^3 c + 26 b^2 c^2 + 2 b c^3 - 3 c^4) - 2 a (5 b^5 - 14 b^4 c + 7 b^3 c^2 + 3 b^2 c^3 - c^5)): :
16215a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (2 b^2 + 4 b c + c^2) + a^4 (-2 b^2 + 6 b c + c^2) - a (b - c)^2 (b^3 - 6 b^2 c - 7 b c^2 - 2 c^3) + 2 a^2 b (b^3 - 5 b^2 c + 14 b c^2 - 2 c^3)): :
16216a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (3 b^2 + 4 b c + c^2) + a^4 (-2 b^2 + 6 b c + c^2) + 2 a^2 b (b^3 - 4 b^2 c - 9 b c^2 - 3 c^3) - a (b^5 - 8 b^4 c + 6 b^3 c^2 + 8 b^2 c^3 - 5 b c^4 - 2 c^5)): :
16217a (a^8 b + (b - c)^5 c^2 (b + c)^2 + a^7 (-3 b^2 + 5 b c + c^2) + a^6 (b^3 - 8 b^2 c - 16 b c^2 - 3 c^3) + a^5 (5 b^4 - 13 b^3 c + 8 b^2 c^2 + b c^3 + c^4) + a^2 (b - c)^2 (3 b^5 - 14 b^4 c - 21 b^3 c^2 - 17 b^2 c^3 - 10 b c^4 - c^5) - a (b - c)^3 (b^5 - 6 b^4 c - 7 b^3 c^2 + 5 b^2 c^3 + 8 b c^4 + 3 c^5) + a^4 (-5 b^5 + 28 b^4 c + 13 b^3 c^2 - b^2 c^3 + 20 b c^4 + 5 c^5) - a^3 (b^6 + b^5 c + 3 b^4 c^2 + 30 b^3 c^3 - 13 b^2 c^4 + 5 b c^5 + 5 c^6)): :
16218a (a^8 b + (b - c)^5 c^2 (b + c)^2 + a^7 (-3 b^2 + 5 b c + c^2) + a^6 (b^3 - 4 b^2 c - 16 b c^2 - 3 c^3) + a^5 (5 b^4 - 21 b^3 c + 32 b^2 c^2 + 5 b c^3 + c^4) + a^2 (b - c)^2 (3 b^5 - 18 b^4 c + 3 b^3 c^2 + 11 b^2 c^3 - 2 b c^4 - c^5) - a (b - c)^3 (b^5 - 6 b^4 c - 7 b^3 c^2 + b^2 c^3 + 4 b c^4 + 3 c^5) + a^4 (-5 b^5 + 28 b^4 c - 3 b^3 c^2 - 33 b^2 c^3 + 12 b c^4 + 5 c^5) - a^3 (b^6 - 7 b^5 c + 43 b^4 c^2 - 82 b^3 c^3 + 3 b^2 c^4 + 5 b c^5 + 5 c^6)): :
16541a (a^9 - a^8 c + b^2 (b - c)^3 (b + c)^2 (b^2 + c^2) - a^2 (b - c)^2 (b + c)^3 (b^2 - b c + c^2) - a^7 (3 b^2 - b c + c^2) - a b (b^2 - c^2)^2 (2 b^3 - b^2 c + 2 b c^2 - c^3) + a^6 (b^3 + c^3) + a^5 (b^4 - b^3 c + 4 b^2 c^2 - b c^3 - c^4) - a^4 (b^5 - 2 b^4 c + b^3 c^2 + b^2 c^3 - c^5) + a^3 (3 b^6 - b^5 c - 5 b^4 c^2 - 14 b^3 c^3 + b^2 c^4 - b c^5 + c^6)): :
16678a (a^5 (b + c) + a^4 b (b + c) - a^2 b^3 (b + 3 c) + a b^3 (b^2 - b c - 2 c^2) + b^3 c (b^2 - c^2) - a^3 (2 b^3 + b^2 c + c^3)): :
16687a (a^5 (b + c) + a^4 b (b + 3 c) + b^3 c (b^2 - c^2) + a^3 (-2 b^3 + b^2 c + 2 b c^2 - c^3) - a^2 (b^4 + b^3 c - 2 b c^3) + a b (b^4 + b^3 c + 2 b c^3 + 2 c^4)): :
16763a (a^6 - 2 a^5 c + a^4 (-5 b^2 + 6 b c + c^2) + 4 a^3 (b^3 - 2 b c^2) - 2 a (b - c)^2 (2 b^3 - b^2 c - 2 b c^2 - c^3) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 12 b^3 c + 7 b^2 c^2 - c^4)): :
16778a (2 a^5 (b + c) + a^4 b (2 b + 3 c) + 2 b^3 c (b^2 - c^2) + a b (b - c)^2 (2 b^2 + 3 b c + c^2) - a^3 (4 b^3 + b^2 c - b c^2 + 2 c^3) + a^2 (-2 b^4 - 5 b^3 c + b c^3)): :
16877a (a^7 (b + c) + a^6 b (b + c) + a b^4 (b - c)^2 (b + c) + a^4 b c^2 (b + 3 c) + a^5 (-b^3 + b c^2) - a^2 b^3 (b^3 + 2 b^2 c + b c^2 + 2 c^3) + b^3 c (b^4 - c^4) - a^3 (b^5 + 2 b^3 c^2 - 2 b c^4 + c^5)): :
16878a (2 a^5 (b + c) + a^4 b (2 b + 3 c) + 2 b^3 c (b^2 - c^2) + a^3 (-4 b^3 + b^2 c + 3 b c^2 - 2 c^3) + a^2 b (-2 b^3 - 3 b^2 c + 6 b c^2 + 3 c^3) + a b (2 b^4 - b^3 c - b^2 c^2 + 3 b c^3 + c^4)): :
17102a (a^5 (b + 2 c) + a b (b - c)^2 (3 b^2 - c^2) + a^4 (2 b^2 - 4 b c - c^2) - 2 a^2 b^2 (b^2 - 3 b c + 2 c^2) - 2 a^3 (2 b^3 - 2 b c^2 + c^3) + c (2 b^5 - b^4 c - 2 b^3 c^2 + c^5)): :
17437a (a^6 - 2 a^5 c + a^4 (-5 b^2 + 6 b c + c^2) + 4 a^3 (b^3 - 2 b c^2) - 2 a (b - c)^2 (2 b^3 - b^2 c - 2 b c^2 - c^3) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 12 b^3 c + 14 b^2 c^2 - c^4)): :
17502a (6 a^3 + 6 b^3 - 6 b^2 c - b c^2 + c^3 - a^2 (b + 6 c) - a (11 b^2 - 7 b c + c^2)): :
17591a (a^2 (b + 3 c) + a (5 b^2 - b c + c^2) + c (3 b^2 + b c + 2 c^2)): :
17592a (a^2 (2 b + 3 c) + 2 a (2 b^2 + 2 b c + c^2) + c (3 b^2 + 2 b c + c^2)): :
17593a (a^3 + b^3 - 4 b^2 c - b c^2 - 2 c^3 - a^2 (b + 4 c) - a (7 b^2 + c^2)): :
17594a (a^3 + b^3 - 3 b^2 c - b c^2 - c^3 - a^2 (b + 3 c) - a (5 b^2 + 2 b c + c^2)): :
17595a (a^3 + b^3 - 3 a^2 c - 3 b^2 c - 2 c^3 + 3 a b (-2 b + c)): :
17596a (a^3 + b^3 - 2 a^2 c - 2 b^2 c - c^3 + a b (-4 b + c)): :
17597a (a^3 + b^3 + a b (2 b - 5 c) + a^2 c + b^2 c + 2 c^3): :
17598a (a^3 + b^3 + 2 b^2 c + b c^2 + 2 c^3 + a^2 (b + 2 c) + a (3 b^2 - 2 b c + c^2)): :
17599a (a^3 + b^3 + 3 b^2 c + 2 b c^2 + 2 c^3 + a^2 (2 b + 3 c) + a (4 b^2 + b c + 2 c^2)): :
17600a (a^3 + b^3 + 4 b^2 c + 3 b c^2 + 2 c^3 + a^2 (3 b + 4 c) + a (5 b^2 + 4 b c + 3 c^2)): :
17601a (2 a^3 - 6 a b^2 + 2 b^3 - 3 a^2 c - 3 b^2 c - c^3): :
17603a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (b^2 + 5 b c + c^2) + a^4 (-2 b^2 + 8 b c + c^2) + 2 a^2 b (b^3 - 8 b^2 c + 2 b c^2 - c^3) + a (-b^5 + 10 b^4 c - 8 b^3 c^2 - 4 b^2 c^3 + b c^4 + 2 c^5)): :
17609a (a^2 b + (b - c) c^2 + a (-b^2 + 9 b c + c^2)): :
17642a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 + c^2) - 2 a^3 c (b^2 + b c + c^2) + 2 a^2 b (b^3 + 6 b c^2 - c^3) + a (-b^5 + 2 b^4 c - 4 b^2 c^3 + b c^4 + 2 c^5)): :
17699a (a^6 - 2 a^5 c + a^4 (-5 b^2 + 6 b c + c^2) + 4 a^3 (b^3 - 2 b c^2) - 2 a (b - c)^2 (2 b^3 - b^2 c - 2 b c^2 - c^3) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 12 b^3 c - 2 b^2 c^2 - c^4)): :
17700a (a^6 - 2 a^5 c + a^4 (-5 b^2 + 6 b c + c^2) + 4 a^3 (b^3 - 2 b c^2) - 2 a (b - c)^2 (2 b^3 - b^2 c - 2 b c^2 - c^3) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - 12 b^3 c + 6 b^2 c^2 - c^4)): :
17715a (2 a^3 + 2 b^3 - a^2 c - b^2 c + c^3 - 2 a b (b + 2 c)): :
17716a (2 a^3 + 2 b^3 + b^2 c + 2 b c^2 + c^3 + 2 a c (b + c) + a^2 (2 b + c)): :
17798a (a^5 + a^4 b + b^5 - b^2 c^3 + a^3 b (-b + c) - a^2 (b^3 + b^2 c - 2 b c^2 + c^3) - a (b^4 + b^3 c - b c^3)): :
18115-(a (a^8 c + a^7 (b^2 - 2 b c - 2 c^2) + (b - c)^3 c (b + c)^2 (b^3 - b^2 c - c^3) - a^6 (3 b^3 - 4 b c^2 + c^3) + a^5 c (6 b^3 - 4 b^2 c - b c^2 + 3 c^3) + a^4 b (6 b^4 - 8 b^3 c - b^2 c^2 + 5 b c^3 - 3 c^4) + a^3 b (-3 b^5 + 7 b^3 c^2 - 5 b^2 c^3 - 2 b c^4 + 2 c^5) + a (b - c)^2 (2 b^6 + 3 b^3 c^3 + b^2 c^4 - b c^5 - c^6) - a^2 (3 b^7 - 6 b^6 c + 4 b^5 c^2 + b^4 c^3 - 4 b^3 c^4 + b^2 c^5 + c^7))): :
18193a (a^3 + b^3 + a^2 (b - 3 c) - 3 b^2 c + b c^2 - 3 c^3 + a (-7 b^2 + 8 b c + c^2)): :
18201a (a^3 + b^3 + a^2 (b - 2 c) - 2 b^2 c + b c^2 - 2 c^3 + a (-5 b^2 + 6 b c + c^2)): :
18208-(a (a^4 c + a^3 (b^2 - 2 b c - c^2) + a b (2 b^3 - 2 b^2 c + b c^2 - 2 c^3) + a^2 (-b^3 + b^2 c - b c^2 + c^3) + c (b^4 - b^3 c + b^2 c^2 + c^4))): :
18280a (a^12 + a^11 b - a b (b - c)^5 (b + c)^4 (b + 2 c) + a^10 (-6 b^2 + b c - 5 c^2) + b^2 (b^2 - c^2)^5 - a^9 b (5 b^2 + b c + 2 c^2) + a^7 b (10 b^4 + 4 b^3 c + b^2 c^2 + 6 b c^3 - 2 c^4) + a^8 (15 b^4 - 4 b^3 c + 14 b^2 c^2 - 4 b c^3 + 10 c^4) + a^6 (-20 b^6 + 6 b^5 c - 7 b^4 c^2 + 7 b^3 c^3 - 8 b^2 c^4 + 6 b c^5 - 10 c^6) + a^3 b (b + c)^2 (5 b^6 - 6 b^5 c - 6 b^4 c^2 + 15 b^3 c^3 - 19 b^2 c^4 + 18 b c^5 - 7 c^6) + a^5 b (-10 b^6 - 6 b^5 c + 8 b^4 c^2 - 7 b^3 c^3 + 3 b^2 c^4 - 8 b c^5 + 8 c^6) - a^2 (b - c)^3 (6 b^7 + 17 b^6 c + 19 b^5 c^2 + 14 b^4 c^3 + 10 b^3 c^4 + 3 b^2 c^5 - 2 b c^6 - c^7) + a^4 (15 b^8 - 4 b^7 c - 11 b^6 c^2 - b^5 c^3 + b^3 c^5 - 5 b^2 c^6 - 4 b c^7 + 5 c^8)): :
18330a (a^7 b^2 + b (b - c)^3 c^3 (b + c)^2 + a^6 (-b^3 - 2 b^2 c + 2 b c^2 + c^3) - a^5 (2 b^4 - 4 b^3 c + 3 b^2 c^2 + 3 b c^3 + c^4) + a^4 (2 b^5 - 2 b^4 c - 2 b^3 c^2 + 6 b^2 c^3 + b c^4 - 2 c^5) - a (b - c)^2 c (2 b^5 + 2 b^4 c + b^3 c^2 - b^2 c^3 - b c^4 + c^5) + a^3 (b^6 - 2 b^5 c + 6 b^4 c^2 - 5 b^3 c^3 - b^2 c^4 + 2 c^6) + a^2 (-b^7 + 4 b^6 c - 5 b^5 c^2 + 3 b^3 c^4 - 2 b c^6 + c^7)): :
18398a (a^2 b + (b - c) c^2 + a (-b^2 + 4 b c + c^2)): :
18421a (a^3 + b^3 - b^2 c - 5 b c^2 + 5 c^3 - a^2 (5 b + c) + a (3 b^2 - 2 b c - 5 c^2)): :
18443a (a^6 - 2 a^5 (b + c) - a^4 (b + c)^2 + (b - c)^4 (b + c)^2 + 4 a^3 (b^3 + b c^2 + c^3) - a^2 (b^4 - 8 b^3 c + 2 b^2 c^2 + c^4) - 2 a (b^5 + b^4 c - 2 b^3 c^2 - b c^4 + c^5)): :
18447a (a^6 + a b^3 (b - c) c - a^3 b c^2 + (b^2 - c^2)^2 (b^2 + c^2) - a^4 (b^2 - b c + c^2) - a^2 (b^4 + 2 b^3 c - 3 b^2 c^2 + c^4)): :
18453a (a^9 + a^8 (b - c) + a^7 b (-4 b + c) - a^6 b c (b + 2 c) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3)^2 + a^5 (2 b^4 - 3 b^3 c + 4 b^2 c^2 - 2 c^4) + a^2 b^2 c (-3 b^4 + 2 b^3 c + 2 b^2 c^2 - 2 b c^3 + c^4) + a^3 b (4 b^5 + b^4 c - 6 b^3 c^2 + 2 b^2 c^3 + 4 b c^4 - c^5) + a^4 (-2 b^5 + 6 b^4 c + 2 c^5) + a (-3 b^8 + b^7 c + 2 b^6 c^2 + 4 b^4 c^4 - b^3 c^5 - 4 b^2 c^6 + c^8)): :
18455a (a^6 + a^3 b c^2 + a b^3 c (-b + c) + (b^2 - c^2)^2 (b^2 + c^2) - a^4 (b^2 + b c + c^2) - a^2 (b^4 - 2 b^3 c - b^2 c^2 + c^4)): :
18758a (a^4 (b - c) c^2 + b^4 (b - c) c^2 + a^5 (b^2 + c^2) + a b^2 c^2 (-b^2 + b c + c^2) + a^3 (-2 b^4 + b^3 c + b c^3) + a^2 b (b^4 + 2 b^2 c^2 - b c^3 + c^4)): :
18788a (a^5 + b^5 - 2 a^4 c - 2 b^4 c + 3 b^3 c^2 - b^2 c^3 - c^5 + a^3 (-b^2 + b c + 3 c^2) + a^2 (3 b^3 - 2 b^2 c + 2 b c^2 - c^3) + a b (-4 b^3 + b^2 c - 2 b c^2 + c^3)): :
18838a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 + 2 b c + c^2) - 2 a^3 c (-b^2 + 2 b c + c^2) + 2 a^2 b (b^3 - 4 b^2 c + 3 b c^2 + c^3) - a (b^5 - 4 b^4 c + 2 b^3 c^2 + 3 b c^4 - 2 c^5)): :
18839a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (b + c)^2 + a^4 (-2 b^2 + 2 b c + c^2) + 2 a^2 b (b^3 - 2 b^2 c + 5 b c^2 - c^3) + a (-b^5 + 4 b^4 c - 2 b^3 c^2 - 4 b^2 c^3 + b c^4 + 2 c^5)): :
18856a (a^8 b + (b - c)^5 c^2 (b + c)^2 + a^7 (-3 b^2 + 5 b c + c^2) + a^6 (b^3 - 16 b c^2 - 3 c^3) + a^5 (5 b^4 - 29 b^3 c + 32 b^2 c^2 + 9 b c^3 + c^4) - a (b - c)^3 (b^5 - 6 b^4 c - 7 b^3 c^2 - 3 b^2 c^3 + 3 c^5) + a^4 (-5 b^5 + 28 b^4 c + 9 b^3 c^2 - 41 b^2 c^3 + 4 b c^4 + 5 c^5) - a^3 (b^6 - 15 b^5 c + 63 b^4 c^2 - 46 b^3 c^3 - 9 b^2 c^4 + 5 b c^5 + 5 c^6) + a^2 (3 b^7 - 28 b^6 c + 50 b^5 c^2 - 13 b^4 c^3 - 17 b^3 c^4 - 2 b^2 c^5 + 8 b c^6 - c^7)): :
18857a (4 a^6 - a^5 (5 b + 8 c) - a^4 (10 b^2 - 22 b c + c^2) + (b - c)^3 (4 b^3 + 4 b^2 c - b c^2 - c^3) + 2 a^3 (8 b^3 - 3 b^2 c - 10 b c^2 + 5 c^3) + 2 a^2 (b^4 - 14 b^3 c + 17 b^2 c^2 - 3 b c^3 - 2 c^4) - a (11 b^5 - 28 b^4 c + 14 b^3 c^2 + 12 b^2 c^3 - 11 b c^4 + 2 c^5)): :
18967a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 8 c) + 2 a^3 (2 b^3 - 3 b^2 c - 4 b c^2 + c^3) + a^2 (b^4 - 8 b^3 c + 12 b^2 c^2 - 6 b c^3 - c^4) + a b (-3 b^4 + 10 b^3 c - 6 b^2 c^2 - 8 b c^3 + 7 c^4)): :
19758a (a^5 - a^4 c - 3 a^3 (b^2 + b c + c^2) - a^2 (5 b^3 + 8 b^2 c + 4 b c^2 + 3 c^3) + b (b^4 - b^3 c - 3 b^2 c^2 - 3 b c^3 - 2 c^4) - a (2 b^4 + 7 b^3 c + 6 b^2 c^2 + 3 b c^3 + 2 c^4)): :
19761a (a^5 + a^4 (4 b + 3 c) + a^3 (b^2 + 5 b c + c^2) + a^2 (-b^3 + 4 b c^2 + c^3) + b (b^4 + 3 b^3 c + b^2 c^2 + b c^3 + 2 c^4) + a (2 b^4 + b^3 c + 2 b^2 c^2 + 5 b c^3 + 2 c^4)): :
19765a (a^3 - a^2 (2 b + 3 c) + b (b^2 - 3 b c - 2 c^2) - a (4 b^2 + 3 b c + 2 c^2)): :
19782a (a^6 - a^4 b^2 - a^5 (b + 2 c) + 4 a^3 (b^3 + b c^2 + c^3) - a^2 (b^4 - 2 b^3 c - 2 b c^3 + c^4) + b (b^5 - 2 b^4 c + 4 b^2 c^3 - b c^4 - 2 c^5) + a (-3 b^5 - 2 b^4 c + 2 b^3 c^2 + b c^4 - 2 c^5)): :
20182a (a^3 + b^3 + 5 b^2 c + 4 b c^2 + 2 c^3 + a^2 (4 b + 5 c) + a (6 b^2 + 7 b c + 4 c^2)): :
20254-(a (a^5 c + a^4 (b^2 - 2 b c - c^2) + a^2 b^2 (-b^2 + 3 b c + c^2) + a^3 (-2 b^3 + b^2 c + b c^2 - c^3) + a b (2 b^4 - 2 b^3 c + b^2 c^2 + 2 b c^3 - c^4) + c (b^5 - b^4 c - b^3 c^2 + c^5))): :
20323a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 - 9 b c + c^2)): :
20358a (a^3 b (b - c) + b (b - c) c^3 - a c (3 b^3 - 2 b^2 c + b c^2 + c^3) + a^2 (-b^3 + b^2 c + 2 b c^2 + c^3)): :
20359a (a^4 b (b - 3 c) + b c^3 (b^2 - c^2) + a^3 c (-b^2 + 3 b c + c^2) - a^2 b^2 (b^2 - 3 b c + 3 c^2) - a c (5 b^4 - b^3 c + b c^3 + c^4)): :
20367a (a^4 (b + c) + a^3 (b^2 - c^2) + b c (b^3 - b^2 c + b c^2 - c^3) + a^2 (-3 b^3 + 2 b c^2 + c^3) + a (b^4 - 4 b^3 c + 2 b^2 c^2 - c^4)): :
20368a (a^4 b (2 b - 3 c) + a^5 (b + c) - 2 a^3 b (b^2 + b c - 3 c^2) - 2 a^2 b^2 (b^2 - 3 b c + 3 c^2) + b c (b^4 - c^4) + a (b^5 - 7 b^4 c + 2 b^3 c^2 + b c^4 - c^5)): :
20764a (-(a^7 c^2) + a^8 (b + c) + b^3 (b - c)^3 c (b + c)^2 - a^6 (4 b^3 + b^2 c - 2 b c^2 + 2 c^3) - a^2 b^2 (b - c)^2 (2 b^3 + b^2 c + 2 b c^2 + 3 c^3) + a^5 (b^4 + 2 b^3 c - 2 b^2 c^2 - 2 b c^3 + 2 c^4) + a^4 (5 b^5 - 4 b^4 c + b^3 c^2 + 4 b^2 c^3 - 3 b c^4 + c^5) + a b (b - c)^2 (b^5 + b^3 c^2 + 4 b^2 c^3 + 4 b c^4 + 2 c^5) + a^3 (-2 b^6 + b^4 c^2 + 2 b^2 c^4 - c^6)): :
20788a (b^2 (b - c) c^4 (b + c)^2 + a^6 (b^3 - b c^2) + a^5 (b^4 + b^3 c + 3 b^2 c^2 + 3 b c^3 + c^4) + a^4 (-b^5 + 2 b^4 c + 3 b^3 c^2 + 4 b^2 c^3 + 6 b c^4 + c^5) - a b c^2 (3 b^5 + b^4 c - 4 b^3 c^2 - b^2 c^3 + 3 b c^4 + 2 c^5) - a^3 (b^6 + 3 b^5 c + 3 b^4 c^2 - 5 b^3 c^3 - 5 b^2 c^4 - b c^5 + c^6) - a^2 c (4 b^6 + 3 b^5 c - 3 b^3 c^3 + 3 b c^5 + c^6)): :
20789a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 - 10 b c + c^2) - 2 a^3 c (-6 b^2 - 4 b c + c^2) - a (b - c)^2 (b^3 + 10 b^2 c + 9 b c^2 - 2 c^3) + 2 a^2 b (b^3 + 3 b^2 c - 18 b c^2 + 6 c^3)): :
20790a (a^5 b + (b - c)^3 c^2 (b + c) - 2 a^3 c (6 b^2 + 8 b c + c^2) + a^4 (-2 b^2 + 14 b c + c^2) + 2 a^2 b (b^3 - 9 b^2 c - 18 b c^2 - 6 c^3) - a (b - c)^2 (b^3 - 14 b^2 c - 15 b c^2 - 2 c^3)): :
20878a (a^5 b^2 (b - c) + b^4 c^2 (b^2 - c^2) + a^6 (b^2 + c^2) + a b^3 c^2 (-2 b^2 - b c + c^2) + a^2 b^2 (b^4 - b^3 c + 2 b c^3 - 2 c^4) - a^4 (2 b^4 + 2 b^2 c^2 - b c^3 + c^4) + a^3 (-b^5 + 4 b^3 c^2 + b c^4)): :
21010a (b^3 (b - c) c + a^3 (2 b - c) c + a^4 (b + c) + a^2 b (-2 b^2 + b c + 2 c^2) + a b (b^3 + 2 b c^2 + 2 c^3)): :
21164a (3 a^6 - 2 a^5 (b + 3 c) + a^4 (-11 b^2 + 22 b c + c^2) + 4 a^3 (3 b^3 - 6 b c^2 + c^3) + (b - c)^3 (3 b^3 + 3 b^2 c + b c^2 + c^3) + a^2 (5 b^4 - 40 b^3 c + 30 b^2 c^2 - 3 c^4) - 2 a (5 b^5 - 15 b^4 c + 8 b^3 c^2 + 4 b^2 c^3 - b c^4 - c^5)): :
21334a (a^4 b (b - c) + b c^3 (b^2 - c^2) + a^3 c (-b^2 + b c + c^2) - a^2 b^2 (b^2 + b c + 5 c^2) - a c (3 b^4 + b^3 c + b c^3 + c^4)): :
21842a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 - 4 b c + c^2)): :
22341a (a^8 (b + c) - a^7 c (b + c) + b^3 (b - c)^3 c (b + c)^2 - a^6 (4 b^3 + b^2 c - 2 b c^2 + 2 c^3) - a^2 b^2 (b - c)^2 (2 b^3 + b^2 c + 2 b c^2 + 3 c^3) + a^5 (b^4 + 3 b^3 c - 2 b^2 c^2 - b c^3 + 2 c^4) + a^4 (5 b^5 - 4 b^4 c + b^3 c^2 + 4 b^2 c^3 - 3 b c^4 + c^5) + a b (b - c)^2 (b^5 - b^4 c - b^3 c^2 + 2 b^2 c^3 + 2 b c^4 + c^5) + a^3 (-2 b^6 + b^5 c + b^4 c^2 - 2 b^3 c^3 + 2 b^2 c^4 + b c^5 - c^6)): :
22765a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 5 c) + a^3 (4 b^3 - 2 b^2 c - 5 b c^2 + 2 c^3) + a^2 (b^4 - 6 b^3 c + 9 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 7 b^3 c - 3 b^2 c^2 - 4 b c^3 + 3 c^4)): :
22766a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - a b (b - c)^2 (3 b^2 - 2 b c - 3 c^2) + 2 a^3 (2 b^3 - b^2 c - 3 b c^2 + c^3) + a^2 (b^4 - 8 b^3 c + 6 b^2 c^2 - 2 b c^3 - c^4)): :
22767a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) - a b (b - c)^2 (3 b^2 - 2 b c - 3 c^2) + 2 a^3 (2 b^3 - b^2 c - 3 b c^2 + c^3) + a^2 (b^4 - 8 b^3 c + 14 b^2 c^2 - 2 b c^3 - c^4)): :
22768a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 8 c) + 2 a^3 (2 b^3 - b^2 c - 4 b c^2 + c^3) + a^2 (b^4 - 12 b^3 c + 8 b^2 c^2 - 2 b c^3 - c^4) + a b (-3 b^4 + 10 b^3 c - 6 b^2 c^2 - 4 b c^3 + 3 c^4)): :
22770a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + 2 a^3 (2 b^3 - 2 b^2 c - 2 b c^2 + c^3) + a^2 (b^4 - 2 b^3 c + 10 b^2 c^2 - 4 b c^3 - c^4) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 - 6 b c^3 + 5 c^4)): :
23171a (a^7 (b - c) c + a^8 (b + c) + b^3 (b - c)^3 c (b + c)^2 - 2 a^6 (2 b^3 + b^2 c + c^3) + a^5 (b^4 - b^3 c - 2 b^2 c^2 - 2 b c^3 + 2 c^4) - 2 a^2 b^2 (b^5 - b^2 c^3 - b c^4 + c^5) + a^4 (5 b^5 + b^3 c^2 + 4 b^2 c^3 - b c^4 + c^5) + a^3 (-2 b^6 + b^5 c + 3 b^4 c^2 + 2 b^3 c^3 + 2 b^2 c^4 - b c^5 - c^6) + a (b^8 - b^7 c + 2 b^5 c^3 - b^4 c^4 - 3 b^3 c^5 + 2 b c^7)): :
23207a (a^7 (b - c) c + a^8 (b + c) + b^3 (b - c)^3 c (b + c)^2 - a^2 b^2 (b + c)^3 (2 b^2 - 3 b c + c^2) + a b (b^2 - c^2)^2 (b^3 - b^2 c + c^3) - a^6 (4 b^3 + 3 b^2 c + 2 b c^2 + 2 c^3) + a^5 (b^4 - 3 b^3 c - 2 b^2 c^2 - b c^3 + 2 c^4) + a^4 (5 b^5 + 4 b^4 c + b^3 c^2 + 4 b^2 c^3 + b c^4 + c^5) - a^3 (2 b^6 - 3 b^5 c - 5 b^4 c^2 - 2 b^3 c^3 - 2 b^2 c^4 + b c^5 + c^6)): :
23340a (a^5 b + (b - c)^3 c^2 (b + c) + 2 a^3 c (4 b^2 + b c - c^2) + a^4 (-2 b^2 - 4 b c + c^2) + 2 a^2 b (b^3 - b^2 c - 5 b c^2 + 4 c^3) - a (b^5 + 2 b^4 c - 4 b^3 c^2 - 6 b^2 c^3 + 9 b c^4 - 2 c^5)): :
23703a (2 a^6 - 6 a^4 b (b - c) - a^5 (b + 3 c) + b (b - c)^2 (2 b^3 + b^2 c + c^3) + a^3 (6 b^3 + 3 b^2 c - 7 b c^2 + 2 c^3) + a^2 (2 b^4 - 13 b^3 c + 8 b^2 c^2 + 3 b c^3 - 2 c^4) + a (-5 b^5 + 10 b^4 c - 3 b^3 c^2 - b^2 c^3 - 2 b c^4 + c^5)): :
23832a (a^4 b (b - 5 c) + a^5 (b + c) + b^3 c (b^2 - c^2) - a^3 (2 b^3 + 3 b^2 c - 6 b c^2 + c^3) - a^2 b (b^3 - 11 b^2 c + 4 b c^2 + 2 c^3) + a b (b^4 - 7 b^3 c + 4 b^2 c^2 - 2 b c^3 + 2 c^4)): :
23853a (a^4 b^2 + a^5 (b + c) + b^3 c (b^2 - c^2) + a b^3 (b^2 - 2 b c - c^2) - a^2 b^2 (b^2 + b c - c^2) - a^3 (2 b^3 + b^2 c - b c^2 + c^3)): :
23890a (2 a^7 - a^6 (b + 3 c) + a^4 b (6 b^2 + b c - 3 c^2) - a^5 (7 b^2 - 8 b c + c^2) + b (b - c)^3 (2 b^3 + 3 b^2 c + 2 b c^2 - c^3) - a (b - c)^2 (5 b^4 - 2 b^3 c - 6 b^2 c^2 - 6 b c^3 - c^4) + 2 a^3 (b^4 - 4 b^3 c + 3 b^2 c^2 - 4 b c^3 + 3 c^4) + a^2 (b^5 - 7 b^4 c + 2 b^3 c^2 + 10 b^2 c^3 - b c^4 - 5 c^5)): :
23960a (2 a^6 - 2 a^5 (3 b + 2 c) + 2 a^4 (b^2 + 9 b c - 2 c^2) + 2 (b - c)^3 (b^3 + b^2 c - 2 b c^2 - 2 c^3) + a^3 (8 b^3 - 19 b^2 c - 10 b c^2 + 12 c^3) - a^2 (6 b^4 + 5 b^3 c - 33 b^2 c^2 + 19 b c^3 + 2 c^4) - a (2 b^5 - 14 b^4 c + 14 b^3 c^2 + 15 b^2 c^3 - 25 b c^4 + 8 c^5)): :
23961-(a (2 a^6 + 2 b^2 (b - c)^3 (b + c) - 2 a^5 (b + 2 c) + 2 a^4 b (-3 b + 5 c) + a^3 (8 b^3 - b^2 c - 10 b c^2 + 4 c^3) + a^2 (2 b^4 - 15 b^3 c + 15 b^2 c^2 - b c^3 - 2 c^4) + a b (-6 b^4 + 14 b^3 c - 6 b^2 c^2 - 5 b c^3 + 3 c^4))): :
23981a (a^8 (b + c) + b^3 (b - c)^3 c (b + c)^2 - a^7 c (3 b + c) - 2 a^6 (2 b^3 - 3 b c^2 + c^3) - 2 a^2 b (b - c)^2 (b^4 - 3 b^3 c + 2 b c^3 + c^4) + a^5 (b^4 + 11 b^3 c - 8 b^2 c^2 - 2 b c^3 + 2 c^4) + a^4 (5 b^5 - 12 b^4 c - 3 b^3 c^2 + 12 b^2 c^3 - 5 b c^4 + c^5) + a b (b - c)^2 (b^5 - 3 b^4 c - b^3 c^2 + 3 b^2 c^3 + 2 b c^4 + 2 c^5) - a^3 (2 b^6 + 3 b^5 c - 15 b^4 c^2 + 10 b^3 c^3 + 2 b^2 c^4 - 3 b c^5 + c^6)): :
24299a (2 a^6 - a^4 (-2 b + c)^2 - a^5 (3 b + 4 c) + (b - c)^3 (2 b^3 + 2 b^2 c - b c^2 - c^3) - 2 a^2 c (b^3 - 3 b^2 c + c^3) + a^3 (8 b^3 - 2 b c^2 + 6 c^3) + a (-5 b^5 + 6 b^4 c - 2 b^2 c^3 + 3 b c^4 - 2 c^5)): :
24301-(a (2 a^9 - a^8 (b + 2 c) + a^7 (-5 b^2 + 3 b c - 3 c^2) + 3 a^6 (b^3 + c^3) + (b - c)^3 (b + c)^2 (2 b^4 + b^2 c^2 - c^4) + a^5 (b^4 - 3 b^3 c + 4 b^2 c^2 - 3 b c^3 - c^4) - a (b^2 - c^2)^2 (3 b^4 - 3 b^3 c + 4 b^2 c^2 - 3 b c^3 + c^4) + a^4 (-b^5 + 4 b^4 c - 3 b^3 c^2 + b^2 c^3 + 2 b c^4 + c^5) + a^3 (5 b^6 - 3 b^5 c + b^4 c^2 + 2 b^3 c^3 - b^2 c^4 - 3 b c^5 + 3 c^6) + a^2 (-3 b^7 + 2 b^5 c^2 + b^4 c^3 - 3 b^3 c^4 + 6 b^2 c^5 - 3 c^7))): :
24310a (a^5 (b + c) + a^4 b (2 b + c) - 2 a^3 (b^3 - b c^2) - 2 a^2 (b^4 + 2 b^3 c - b c^3) + b c (b^4 - c^4) + a (b^5 - 3 b^4 c - 2 b^3 c^2 + 2 b^2 c^3 - b c^4 - c^5)): :
24464-(a (a^3 c^2 + a^2 b^2 (2 b + c) + b c^2 (b^2 + c^2) + a (2 b^3 c + c^4))): :
24468a (a^6 - 2 a^5 c + a^3 b (4 b^2 - b c - 3 c^2) + a^4 (-5 b^2 + b c + c^2) + (b - c)^3 (b^3 + b^2 c + b c^2 + c^3) + a^2 (3 b^4 - b^3 c + 6 b^2 c^2 - b c^3 - c^4) + a (-4 b^5 + 5 b^4 c + b^3 c^2 - 5 b^2 c^3 + b c^4 + 2 c^5)): :
24474a (a^5 b - 2 a^3 c^2 (b + c) + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 + c^2) + 2 a^2 b^2 (b^2 - b c + c^2) - a (b^5 - 2 b^4 c + 2 b^2 c^3 + b c^4 - 2 c^5)): :
24806a (-(a^4 b c) + a^5 (b + c) + b c (b^2 - c^2)^2 - 2 a^2 b c (b^2 + b c - c^2) - 2 a^3 (b^3 - b^2 c + c^3) + a (b^5 - b^4 c + 2 b^2 c^3 - 3 b c^4 + c^5)): :
24926a (3 a^3 + 3 b^3 - 3 b^2 c - 2 b c^2 + 2 c^3 - a^2 (2 b + 3 c) - 2 a (2 b^2 - 2 b c + c^2)): :
24927a (2 a^6 - a^5 (3 b + 4 c) - a^4 (4 b^2 - 16 b c + c^2) + (b - c)^3 (2 b^3 + 2 b^2 c - b c^2 - c^3) - 2 a^2 c (9 b^3 - 13 b^2 c + 4 b c^2 + c^3) + 2 a^3 (4 b^3 - 4 b^2 c - 7 b c^2 + 3 c^3) - a (5 b^5 - 18 b^4 c + 12 b^3 c^2 + 10 b^2 c^3 - 11 b c^4 + 2 c^5)): :
24928a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 - 7 b c + c^2)): :
24929a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 + b c + c^2)): :
25405a (4 a^3 + 4 b^3 - 4 b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + 4 c) + a (-5 b^2 + 11 b c - 3 c^2)): :
25413a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 - b c + c^2) - a^3 c (-4 b^2 + b c + 2 c^2) + a^2 b (2 b^3 - 4 b^2 c - 3 b c^2 + 4 c^3) + a (-b^5 + b^4 c + b^3 c^2 + 2 b^2 c^3 - 5 b c^4 + 2 c^5)): :
25414-(a (a^5 b + (b - c)^3 c^2 (b + c) + a^4 (-2 b^2 - 2 b c + c^2) + a^3 (5 b^2 c - 2 c^3) + a^2 b (2 b^3 - 3 b^2 c - 7 b c^2 + 5 c^3) + a (-b^5 + 2 b^3 c^2 + 3 b^2 c^3 - 6 b c^4 + 2 c^5))): :
25415a (a^3 + b^3 - b^2 c - 3 b c^2 + 3 c^3 - a^2 (3 b + c) + a (b^2 + 2 b c - 3 c^2)): :
26086a (2 a^6 + 2 b^2 (b - c)^3 (b + c) - 2 a^5 (b + 2 c) + a^4 (-6 b^2 + 8 b c) + a^3 (8 b^3 + b^2 c - 8 b c^2 + 4 c^3) + a^2 (2 b^4 - 13 b^3 c + 11 b^2 c^2 + b c^3 - 2 c^4) + a b (-6 b^4 + 12 b^3 c - 4 b^2 c^2 - 3 b c^3 + c^4)): :
26087a (2 a^6 - 4 a^5 (b + c) + 2 (b - c)^4 (b + c)^2 - 2 a^4 (b^2 - 6 b c + c^2) + a^3 (8 b^3 - 9 b^2 c - 8 b c^2 + 8 c^3) - a^2 (2 b^4 + 7 b^3 c - 21 b^2 c^2 + 9 b c^3 + 2 c^4) - a (4 b^5 - 12 b^4 c + 8 b^3 c^2 + 9 b^2 c^3 - 13 b c^4 + 4 c^5)): :
26285a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) - a b^2 (3 b^3 - 6 b^2 c + 2 b c^2 + c^3) + a^3 (4 b^3 + b^2 c - 4 b c^2 + 2 c^3) + a^2 (b^4 - 7 b^3 c + 5 b^2 c^2 + b c^3 - c^4)): :
26286a (a^6 + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + a^4 b (-3 b + 4 c) + a^3 (4 b^3 - b^2 c - 4 b c^2 + 2 c^3) + a^2 (b^4 - 5 b^3 c + 7 b^2 c^2 - b c^3 - c^4) + a b (-3 b^4 + 6 b^3 c - 2 b^2 c^2 - 3 b c^3 + 2 c^4)): :
26287a (2 a^6 - a^5 (3 b + 4 c) - a^4 (4 b^2 - 10 b c + c^2) + (b - c)^3 (2 b^3 + 2 b^2 c - b c^2 - c^3) - a^2 c (11 b^3 - 15 b^2 c + 3 b c^2 + 2 c^3) + a^3 (8 b^3 - 3 b^2 c - 8 b c^2 + 6 c^3) - a (5 b^5 - 12 b^4 c + 6 b^3 c^2 + 5 b^2 c^3 - 6 b c^4 + 2 c^5)): :
26290a (a^6 + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^3 (-4 b^3 + 2 b^2 c + 2 b c^2 - 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (b - c) (-3 b^4 + b^3 c + b^2 c^2 - 3 b c^3 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (b^4 + 6 b^2 c^2 - 2 b c^3 - c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26291a (a^6 + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + (b - c)^2 (b + c) (b^3 - b^2 c + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^3 (4 b^3 - 2 b^2 c - 2 b c^2 + 2 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a (b - c) (3 b^4 - b^3 c - b^2 c^2 + 3 b c^3 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-b^4 - 6 b^2 c^2 + 2 b c^3 + c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26296a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 - 2 b c + c^2) + 2 Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26297a (a^3 + b^3 + a^2 (b - c) - b^2 c + b c^2 - c^3 + a (-3 b^2 - 2 b c + c^2) - 2 Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26319a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - b^2 c - b c^2 + c^3) + a^2 (b^4 + 6 b^2 c^2 - 2 b c^3 - c^4) - a b (3 b^4 - 4 b^3 c + 4 b c^3 - 3 c^4 + 2 Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26320a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - b^2 c - b c^2 + c^3) + a^2 (b^4 + 6 b^2 c^2 - 2 b c^3 - c^4) - a b (3 b^4 - 4 b^3 c + 4 b c^3 - 3 c^4 - 2 Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26351a (2 a^4 b c + Sqrt[2] (b - c)^2 (b + c) Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + a^3 (-2 b c^2 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (b - c) (2 b^3 c - Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (4 b^3 c + 2 b^2 c^2 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26352a (2 a^4 b c - Sqrt[2] (b - c)^2 (b + c) Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - a^3 (2 b c^2 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (b - c) (2 b^3 c + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (-4 b^3 c - 2 b^2 c^2 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26357a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - b c^2 + c^3) + a^2 (b^4 - 2 b^3 c + 8 b^2 c^2 - c^4) + a b (-3 b^4 + 4 b^3 c - 2 b c^3 + c^4)): :
26358a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + 2 b^2 c - b c^2 + c^3) + a b (-3 b^4 + 4 b^3 c + 2 b c^3 - 3 c^4) + a^2 (b^4 - 6 b^3 c - 4 b^2 c^2 + 4 b c^3 - c^4)): :
26365a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 + b c + c^2) + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26366a (2 a^3 + 2 b^3 - 2 b^2 c - b c^2 + c^3 - a^2 (b + 2 c) - a (3 b^2 + b c + c^2) - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26380a (2 a^4 b c - Sqrt[2] (b - c)^2 (b + c) Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - a^3 (4 b^2 c + 2 b c^2 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (b - c) (2 b^3 c - 4 b c^3 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (2 b^2 c^2 - 4 b c^3 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26393a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c - b c^2 + c^3) + a^2 (b^4 - 4 b^3 c + 2 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 4 b^3 c + c^4 - 2 Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26395a (a^3 + b^3 - b^2 c + a (b - 2 c) c - 2 b c^2 + 2 c^3 - a^2 (2 b + c) - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26398a (2 a^6 - 2 a^5 (b + 2 c) + a^4 (-6 b^2 + 4 b c) + (b - c)^2 (b + c) (2 b^3 - 2 b^2 c + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^3 (8 b^3 + 2 b^2 c - 4 b c^2 + 4 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a (b - c) (6 b^4 - 2 b^3 c - 2 b^2 c^2 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-2 b^4 + 6 b^3 c - 6 b^2 c^2 - 2 b c^3 + 2 c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26399a (a^3 + b^3 - a^2 c - b^2 c + a b (-2 b + c) + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26401a (a^3 + b^3 - a^2 c - b^2 c + a b (-2 b + 3 c) + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26404a (2 a^4 b c + Sqrt[2] (b - c)^2 (b + c) Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + a^3 (-4 b^2 c - 2 b c^2 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^2 (-2 b^2 c^2 + 4 b c^3 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (b - c) (2 b^3 c + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - b (4 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]))): :
26417a (a^6 + b^2 (b - c)^3 (b + c) + a^4 b (-3 b + 2 c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 + b^2 c - b c^2 + c^3) + a^2 (b^4 - 4 b^3 c + 2 b^2 c^2 + 2 b c^3 - c^4) - a b (3 b^4 - 4 b^3 c + c^4 + 2 Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26419a (a^3 + b^3 - b^2 c + a (b - 2 c) c - 2 b c^2 + 2 c^3 - a^2 (2 b + c) + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26422a (2 a^6 - 2 a^5 (b + 2 c) + a^4 (-6 b^2 + 4 b c) + (b - c)^2 (b + c) (2 b^3 - 2 b^2 c - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) - a^3 (-8 b^3 - 2 b^2 c + 4 b c^2 - 4 c^3 + Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a (b - c) (-6 b^4 + 2 b^3 c + 2 b^2 c^2 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] - Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]) + a^2 (2 b^4 - 6 b^3 c + 6 b^2 c^2 + 2 b c^3 - 2 c^4 + Sqrt[2] b Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))] + Sqrt[2] c Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))])): :
26423a (a^3 + b^3 - a^2 c - b^2 c + a b (-2 b + c) - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26425a (a^3 + b^3 - a^2 c - b^2 c + a b (-2 b + 3 c) - Sqrt[2] Sqrt[-(a b c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) - a (b^2 + 6 b c + c^2)))]): :
26437a (a^6 - 3 a^4 b (b - 2 c) + b^2 (b - c)^3 (b + c) - a^5 (b + 2 c) + 2 a^3 (2 b^3 - 2 b^2 c - 3 b c^2 + c^3) + a^2 (b^4 - 6 b^3 c + 8 b^2 c^2 - 4 b c^3 - c^4) + a b (-3 b^4 + 8 b^3 c - 4 b^2 c^2 - 6 b c^3 + 5 c^4)): :
26903a (2 b^4 (b - c)^5 c^2 (b + c)^4 - 2 a^12 c (b^2 + c^2) - 2 a^3 b^2 (b^2 - c^2)^4 (2 b^2 + c^2) + a^13 (2 b^2 + b c + 2 c^2) + 2 a^2 b^2 (b^2 - c^2)^4 (b^3 - b^2 c + b c^2 - 2 c^3) + a b c (b^2 - c^2)^4 (b^4 - 4 b^3 c + 4 b^2 c^2 + c^4) - 2 a^11 (6 b^4 + 5 b^2 c^2 + 4 c^4) + 2 a^10 (b^5 + 3 b^4 c + b^3 c^2 + 2 b^2 c^3 + 4 c^5) - 2 a^4 (b - c)^3 (b + c)^2 (4 b^6 + b^5 c + 7 b^4 c^2 + 4 b^2 c^4 - b c^5 - c^6) + a^5 (b^2 - c^2)^2 (18 b^6 - 9 b^5 c + 22 b^4 c^2 - 18 b^3 c^3 + 14 b^2 c^4 - 9 b c^5 + 2 c^6) + a^9 (28 b^6 - 9 b^5 c + 16 b^4 c^2 + 20 b^2 c^4 - 9 b c^5 + 12 c^6) - 2 a^8 (4 b^7 + 2 b^6 c + 3 b^5 c^2 - b^4 c^3 + 4 b^3 c^4 - 2 b^2 c^5 + 6 c^7) - 4 a^7 (8 b^8 - 4 b^7 c + b^6 c^2 + 5 b^2 c^6 - 4 b c^7 + 2 c^8) + 4 a^6 (3 b^9 - b^8 c + b^7 c^2 - 2 b^6 c^3 + b^5 c^4 - 3 b^4 c^5 + 3 b^3 c^6 - 4 b^2 c^7 + 2 c^9)): :
26904a (2 b^4 (b - c)^5 c^2 (b + c)^4 - 2 a^12 c (b^2 + c^2) + a^13 (2 b^2 - b c + 2 c^2) - 2 a^3 b (b^2 - c^2)^4 (2 b^3 - 2 b^2 c + b c^2 - 2 c^3) + 2 a^2 b^2 (b^2 - c^2)^4 (b^3 - b^2 c + b c^2 - 2 c^3) - a b c (b^2 - c^2)^4 (b^4 + 4 b^3 c + c^4) - 2 a^11 (6 b^4 - 2 b^3 c + 5 b^2 c^2 - 2 b c^3 + 4 c^4) + 2 a^10 (b^5 + 3 b^4 c + b^3 c^2 + 2 b^2 c^3 + 4 c^5) - 2 a^4 (b - c)^3 (b + c)^2 (4 b^6 + b^5 c + 7 b^4 c^2 + 4 b^2 c^4 - b c^5 - c^6) + a^5 (b^2 - c^2)^2 (18 b^6 - 7 b^5 c + 22 b^4 c^2 - 6 b^3 c^3 + 14 b^2 c^4 - 7 b c^5 + 2 c^6) + a^9 (28 b^6 - 7 b^5 c + 16 b^4 c^2 - 12 b^3 c^3 + 20 b^2 c^4 - 7 b c^5 + 12 c^6) - 2 a^8 (4 b^7 + 2 b^6 c + 3 b^5 c^2 - b^4 c^3 + 4 b^3 c^4 - 2 b^2 c^5 + 6 c^7) - 4 a^7 (8 b^8 - 2 b^7 c + b^6 c^2 - 2 b^5 c^3 - 2 b^3 c^5 + 5 b^2 c^6 - 2 b c^7 + 2 c^8) + 4 a^6 (3 b^9 - b^8 c + b^7 c^2 - 2 b^6 c^3 + b^5 c^4 - 3 b^4 c^5 + 3 b^3 c^6 - 4 b^2 c^7 + 2 c^9)): :
26908a (-2 a^12 c^3 + 2 b^4 (b - c)^5 c^2 (b + c)^4 + a^13 (2 b^2 + b c + 2 c^2) + 2 a^2 b^2 (b^2 - c^2)^4 (b^3 - 2 b^2 c - b c^2 - c^3) + a b c (b^2 - c^2)^4 (b^4 - 4 b^3 c - 2 b^2 c^2 - c^4) - 2 a^11 (6 b^4 + 4 b^3 c + 5 b^2 c^2 + 3 b c^3 + 4 c^4) - 2 a^3 b (b^2 - c^2)^3 (2 b^5 + 4 b^4 c - b^3 c^2 + 3 b^2 c^3 - b c^4 + c^5) + 2 a^10 (b^5 - 2 b^4 c - b^3 c^2 - b^2 c^3 + 4 c^5) + a^9 (28 b^6 + 23 b^5 c + 16 b^4 c^2 + 18 b^3 c^3 + 20 b^2 c^4 + 13 b c^5 + 12 c^6) + 2 a^8 (-4 b^7 + 8 b^6 c + 5 b^5 c^2 + 5 b^4 c^3 + 4 b^3 c^4 + 4 b^2 c^5 - 6 c^7) - 2 a^4 (b^2 - c^2)^2 (4 b^7 - 8 b^6 c - 2 b^5 c^2 - 5 b^4 c^3 - 4 b^3 c^4 - 2 b^2 c^5 + c^7) - 4 a^7 (8 b^8 + 8 b^7 c + b^6 c^2 + 3 b^5 c^3 + 2 b^3 c^5 + 5 b^2 c^6 + 3 b c^7 + 2 c^8) + 4 a^6 (3 b^9 - 6 b^8 c - 5 b^7 c^2 + b^6 c^3 - 3 b^5 c^4 - 2 b^4 c^5 - 3 b^3 c^6 - 3 b^2 c^7 + 2 c^9) + a^5 (18 b^10 + 23 b^9 c - 14 b^8 c^2 - 12 b^7 c^3 - 12 b^6 c^4 - 10 b^5 c^5 - 4 b^4 c^6 - 4 b^3 c^7 + 10 b^2 c^8 + 3 b c^9 + 2 c^10)): :


Angel Montesdeoca, April, 2021