Construcción de cónicas

(Última actualización: )

Rut Almeida
Elvira Espinosa
Elisa Guzmán
Angel Montesdeoca
José Agustín Noda

Nota

Para prescindir de JAVA, se han sustituido los "applet" por "script".
Angel Montesdeoca
12 de diciembre del 2015

Notaciones

En una cónica se designa por:

2a: longitud del eje focal (segmento)	h, h₁,h₂: asíntotas de una hipérbola
2b: longitud del eje secundario (segmento)	I, I₁, I₂: puntos del infinito de una cónica
A, A': vértices del eje focal	O: centro
B, B': vértices del eje secundario	p: distancia del foco al vértice en un parábola (parámetro)
2c: distancia focal	P, P₁,P₂,...: puntos en la cónica
C: cónica en general	Pi: punto imaginario
c_p ó c_p : circunferencia principal	p_Q ó p_Q: polar de un punto Q respecto a una cónica
c_F ó c_F : circunferencia focal del foco F	S, S', S₁, S₂: simétricos de los focos, respecto a una tangente
C_e ó C_e: elipse	t, t₁,t₂,...: tangentes a la cónica
C_h ó C_h: hipérbola	t_P ó t_P: tangente en P
C_p ó C_p: parábola
d: directriz	—— Otras notaciones ——
D, D', D₁, D₂: punto de intersección del eje focal con la directriz corresponiente a los focos F, F', F₁, F₂	ρ: cierta razón entre magnitudes
e ó ε: excentricidad	π_δQ ó π_δQ : Proyección ortogonal del punto Q sobre la recta δ
e1 ó e₁ : eje focal (recta) o bien vector en la dirección del eje principal	M∈c_F : Punto en un objeto
e2 ó e₂ : eje secundario (recta)	Q(r) : Circunferencia de centro Q y radio r
ek ó e_k : uno de los ejes (recta), k=1 ó k=2	Q(MN) : Circunferencia de centro Q y radio la longitud del segmento MN
F, F', F₁, F₂: focos	x : Para indicar que el dato dado de la cónica no se puede expresar de forma clara con las notaciones usadas aquí.

Elementos de una cónica

Introducción

Apolonio (262-190 A.C.) estudió las cónicas y encontró las propiedades que las definían.

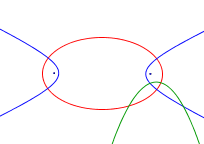
Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas:

Las elipses son las curvas que se obtiene cortando una superficie cónica con un plano que no es paralelo a ninguna de sus generatrices.
Las hipérbolas son las curvas que se obtiene al cortar una superficie cónica con un plano que es paralelo a dos de sus generatrices.
Las parábolas son las curvas que se obtienen al cortar una superficie cónica con un plano paralelo a una sola generatriz.
Debido a estas caracterizaciones a las cónicas se llaman a veces secciones cónicas.

En el siglo XVI el filósofo y matemático René Descartes (1596-1650) relacionó las curvas con ecuaciones relativas a un sistema de coordenadas; es lo que se conoce como Geometría Analítica. En la Geometría Analítica las cónicas se pueden representar por ecuaciones algebraicas de segundo grado y, recíprocamente, todas las ecuación de segundo grado en dos variables representa sección cónica. El astrónomo alemán Johannes Kepler (1570-1630) descubrió que las órbitas de los planetas alrededor del Sol son elipses con el Sol en uno de sus focos. Para La Tierra, la excentricidad es 0.017 y los demás planetas varían desde 0.004 de Neptuno a 0.250 de Plutón. El matemático y físico inglés Isaac Newton (1642-1727) demostró que la órbita de un cuerpo alrededor de una fuerza de tipo gravitatorio es siempre una cónica.

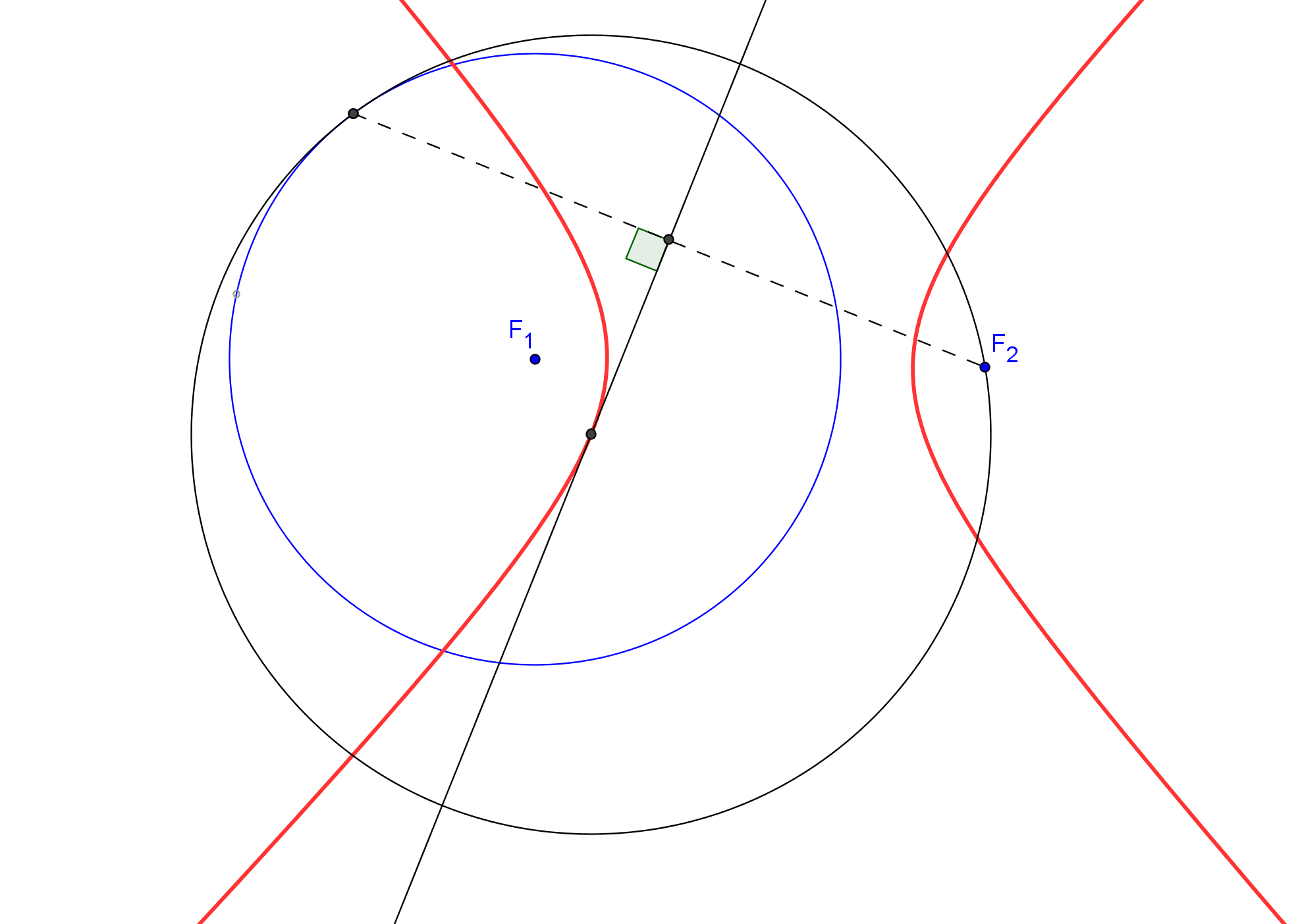
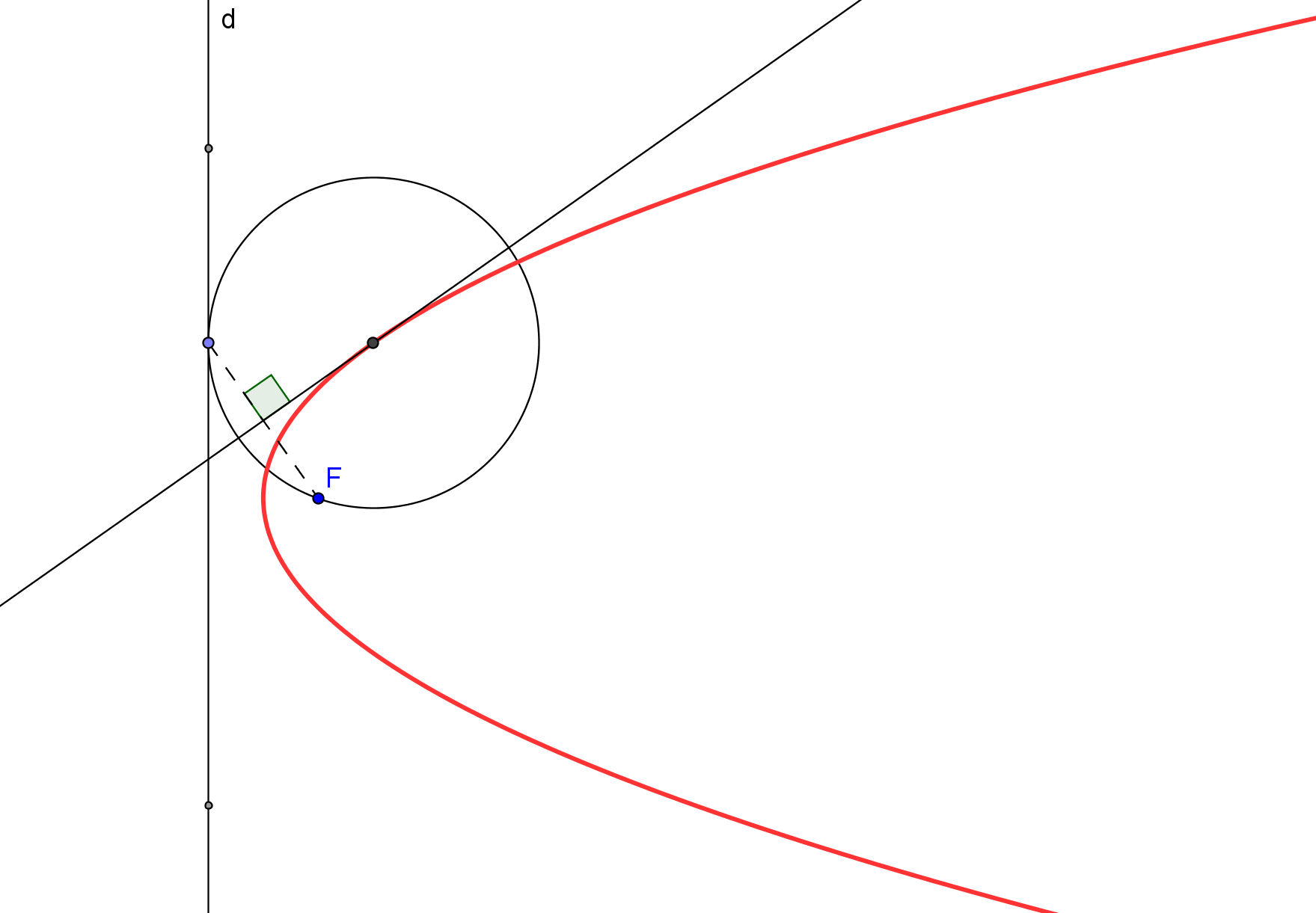
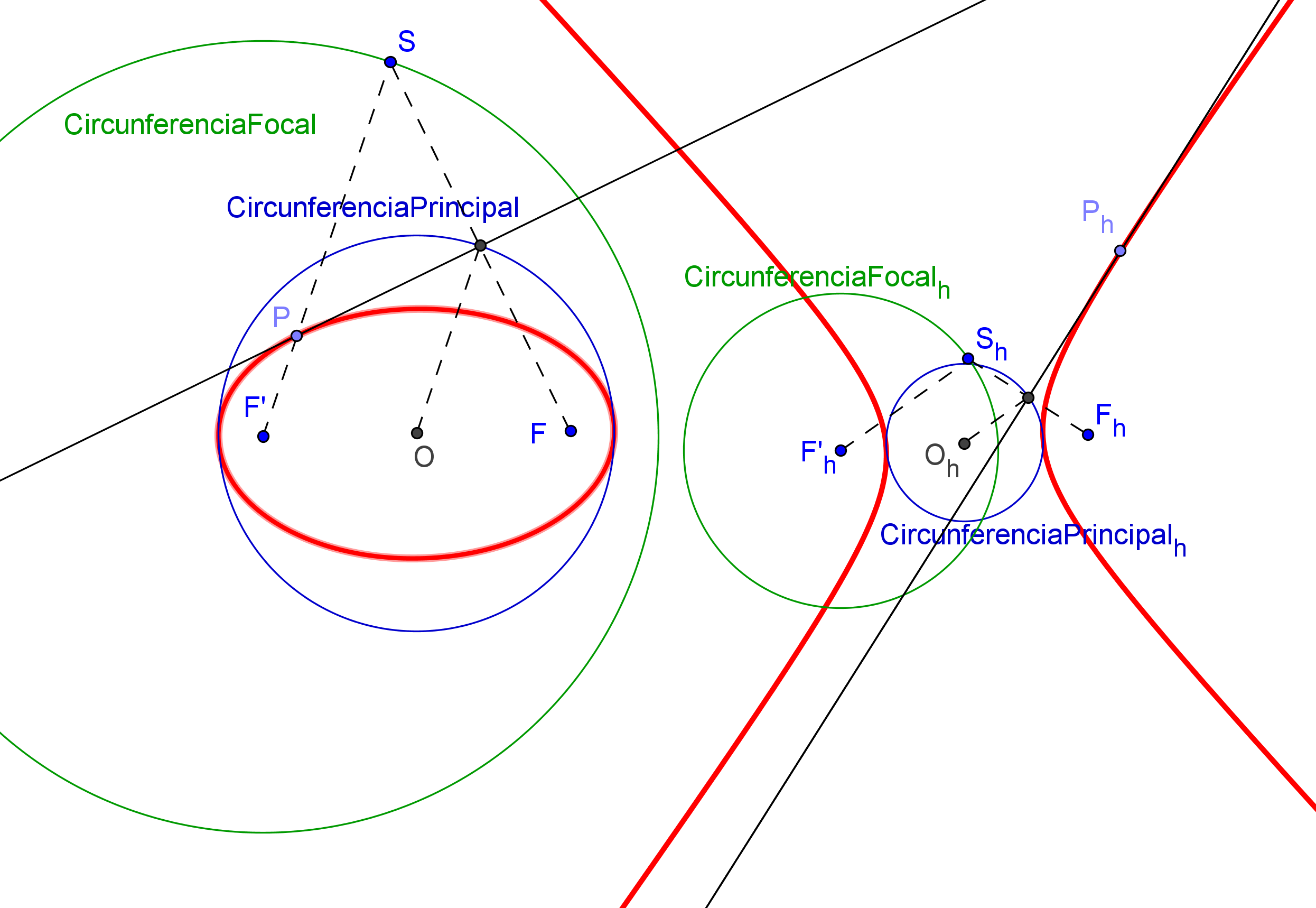
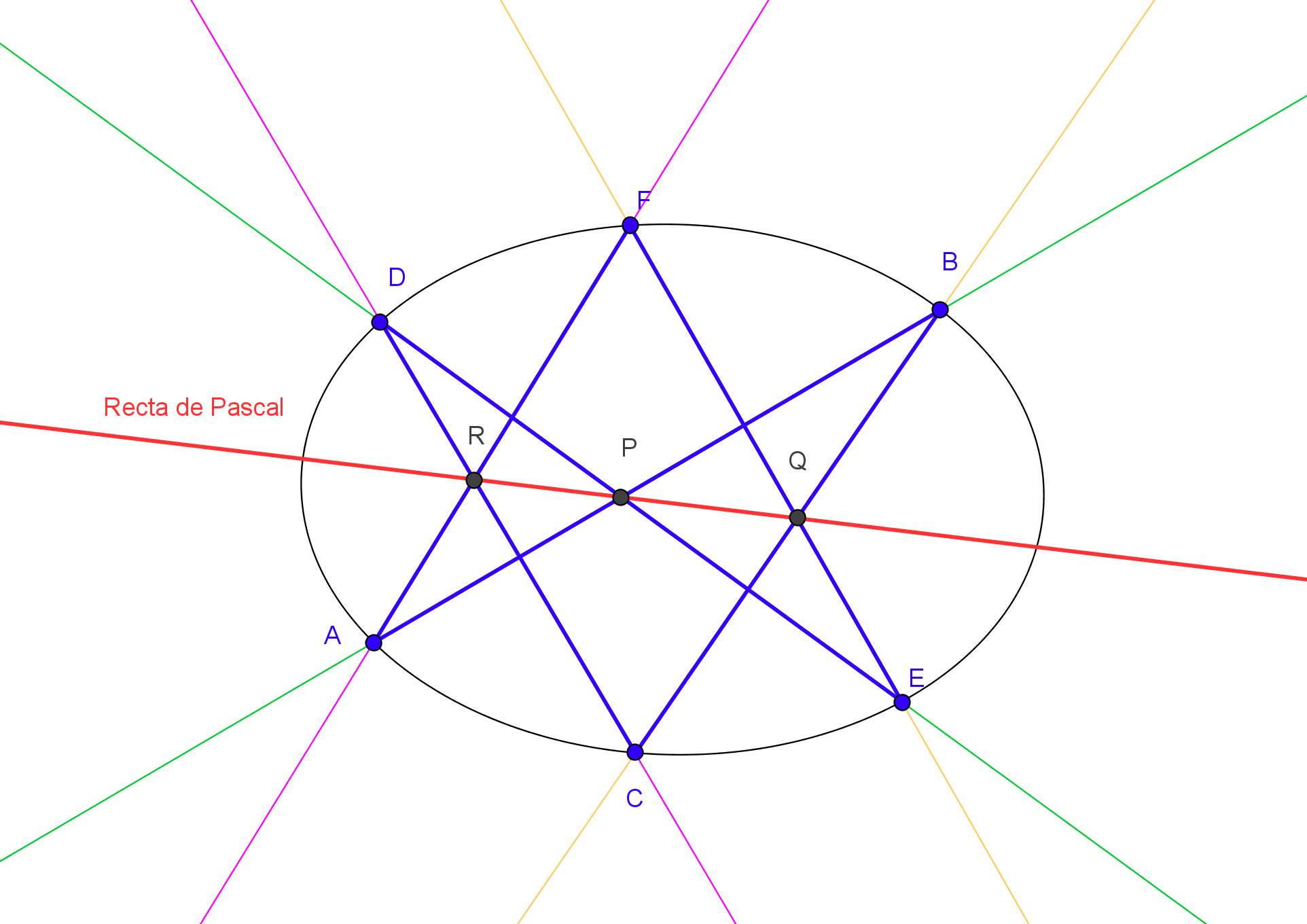
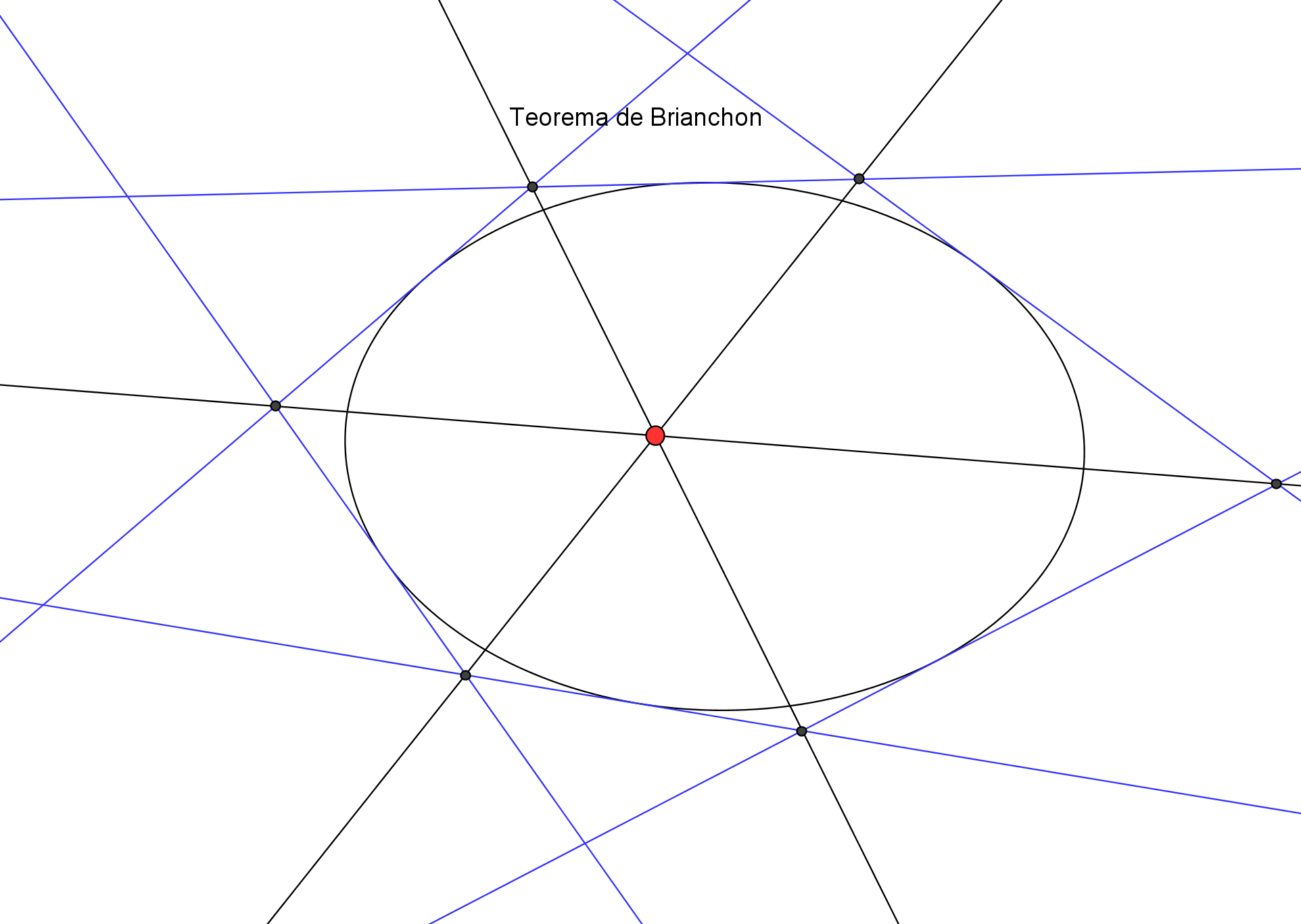
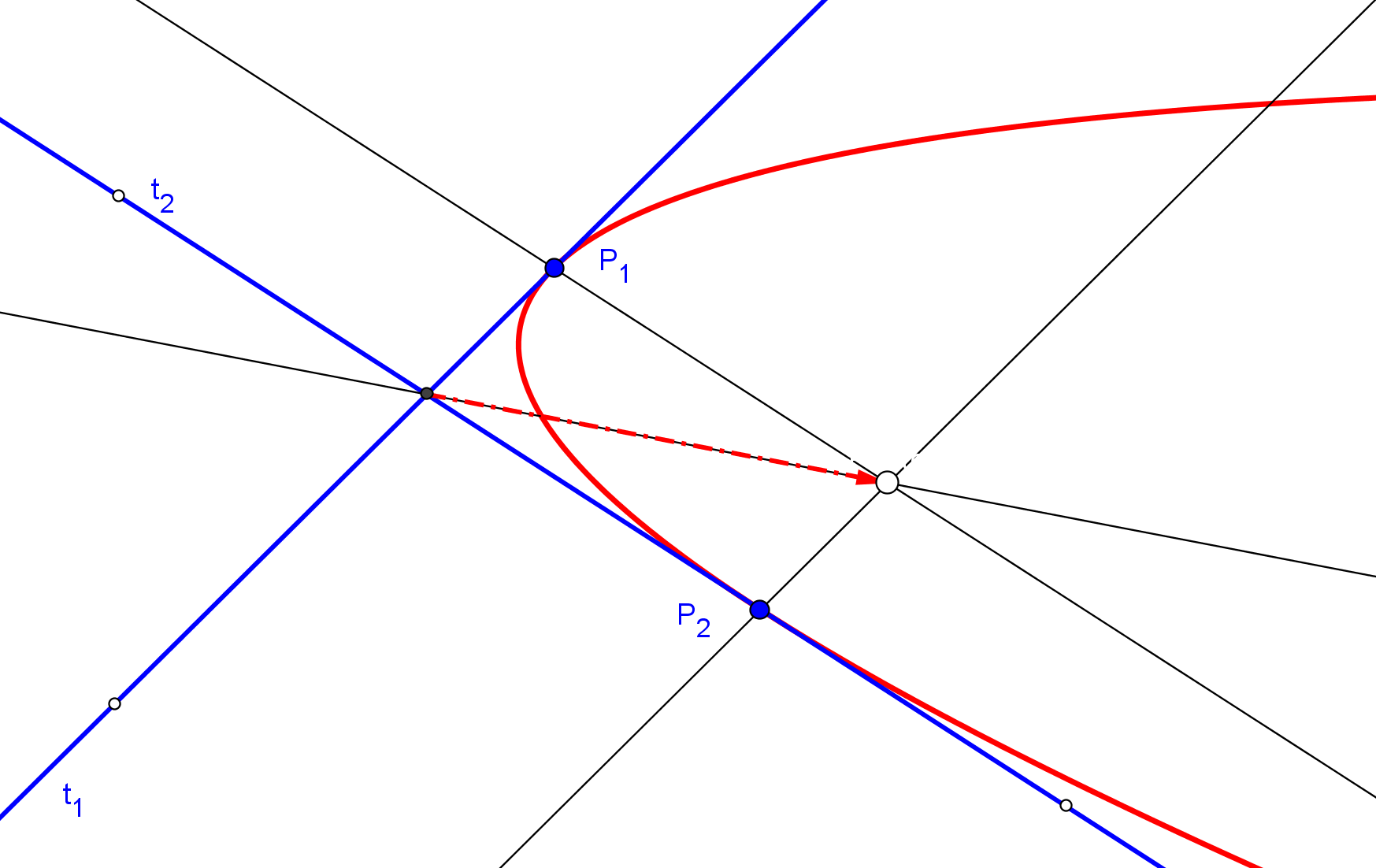
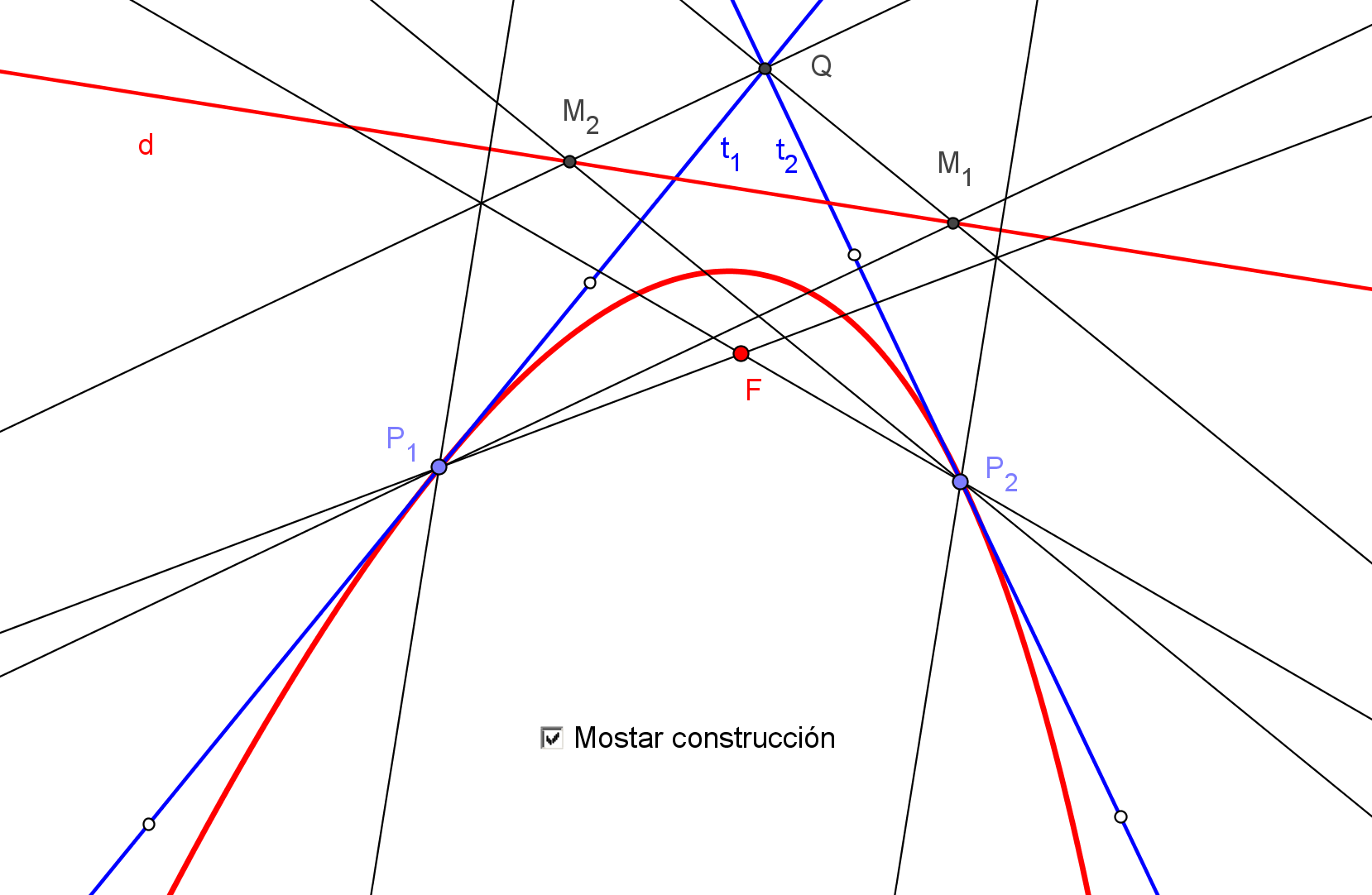
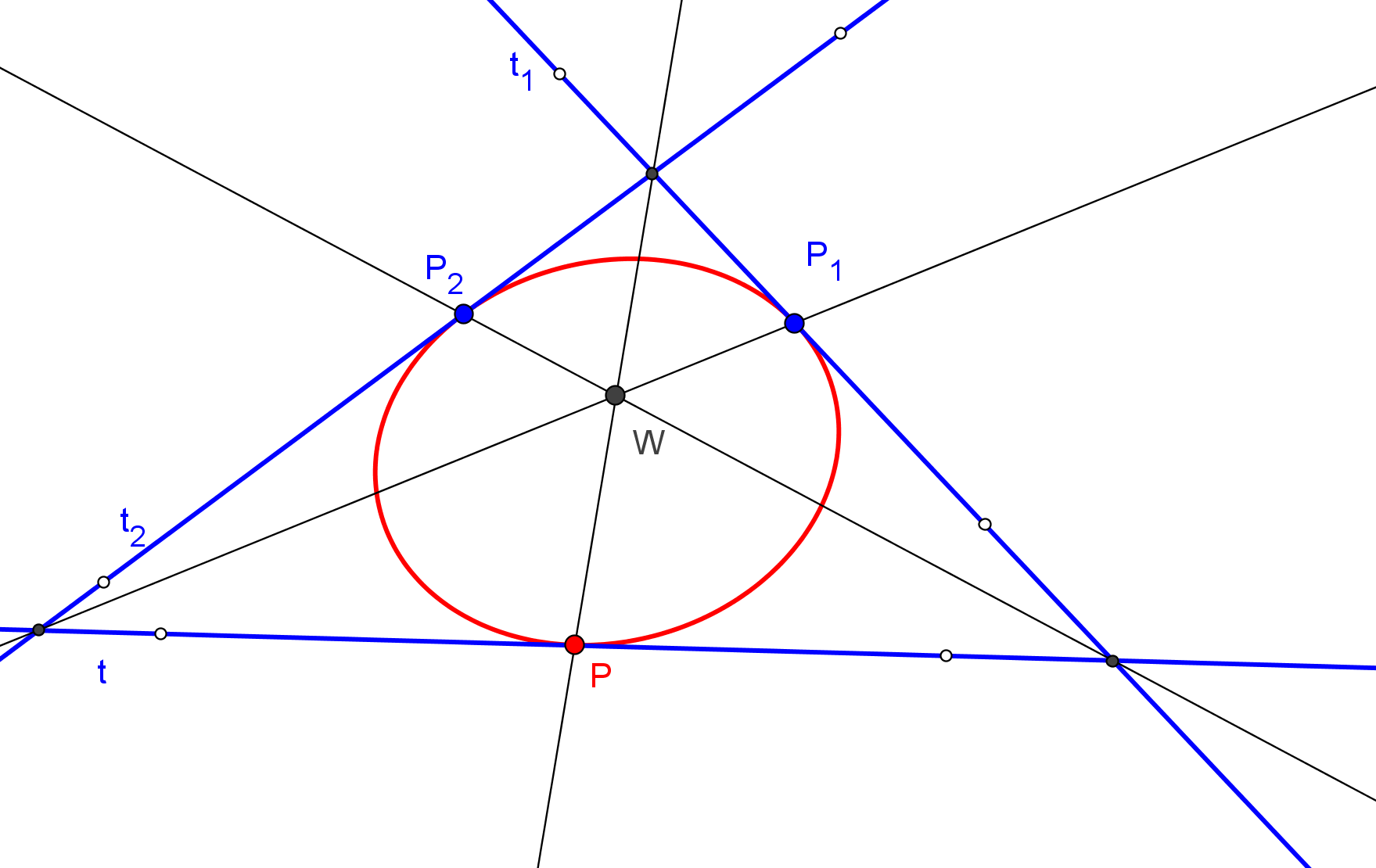
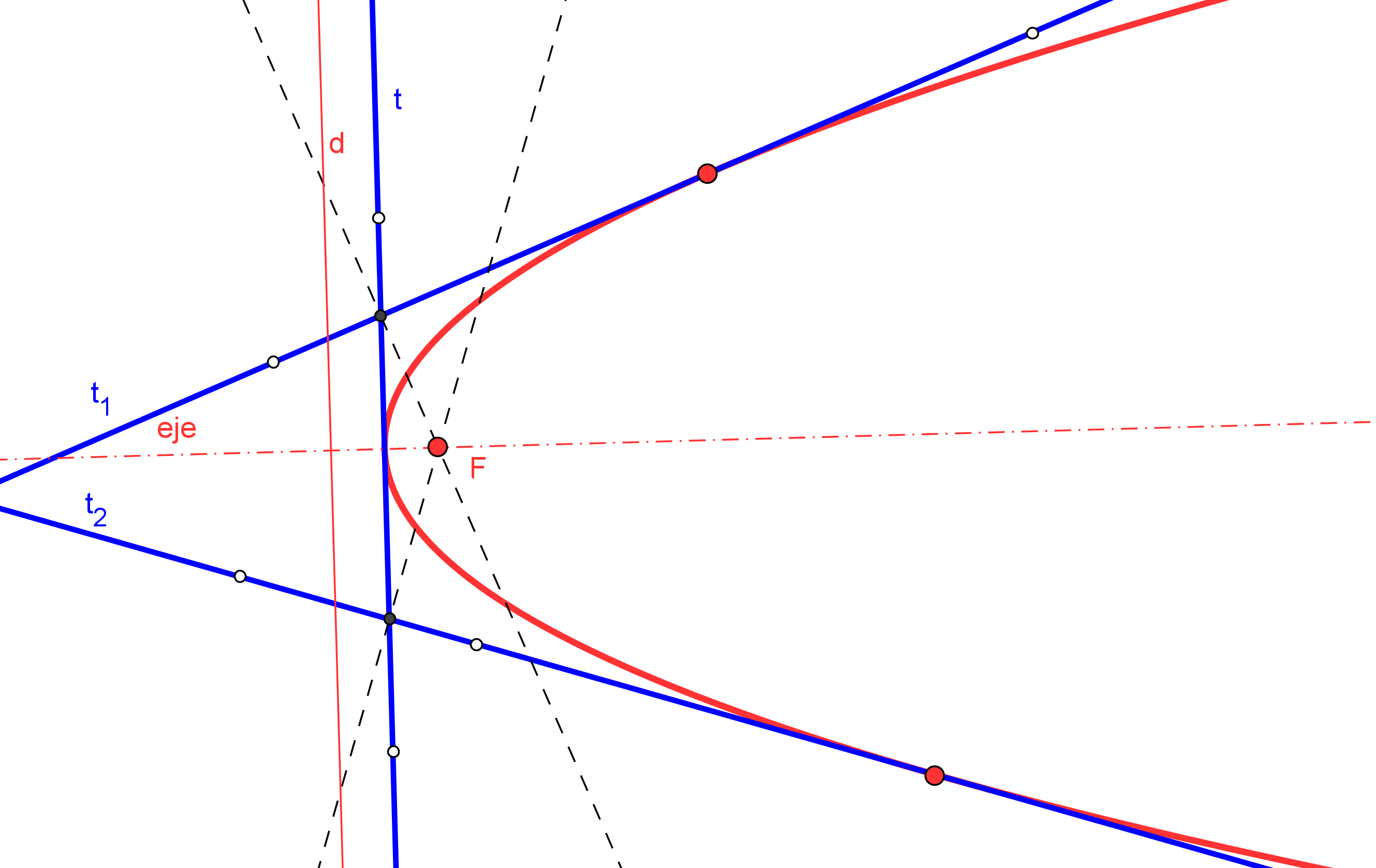
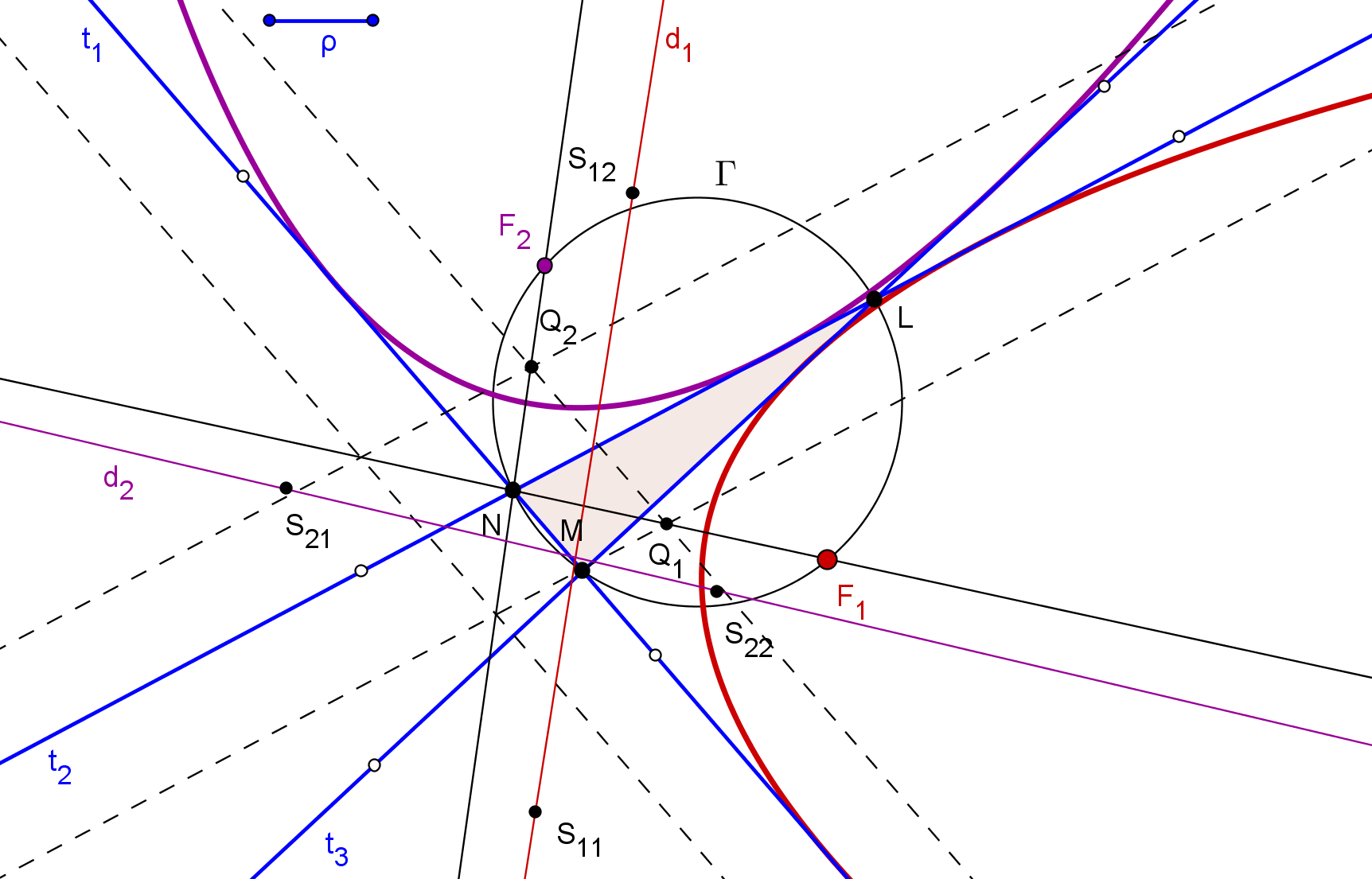
Existe una caracterización proyectiva de las cónicas, debida a Steiner, como el lugar geométrico de los puntos de intersección de pares de rayos homólogos en una proyectividad entre haces.

Definiciones

Una elipse es el lugar geométrico de los puntos P cuya suma de distancias a dos puntos fijos, F y F' llamados focos, es constante (igual a 2a).
Una hipérbola es el lugar geométrico de los puntos P cuya diferencias de distancias (en valor absoluto) a dos puntos fijos, F y F' llamados focos, es constante (igual a 2a).
Una parábola es el lugar geométrico de los puntos equidistantes de un punto, llamado foco, y de una recta d, llamada directriz.

La excentricidad es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. Es el cociente entre las distancias de cualquiera de sus puntos al foco y a la directriz (e=c/a).
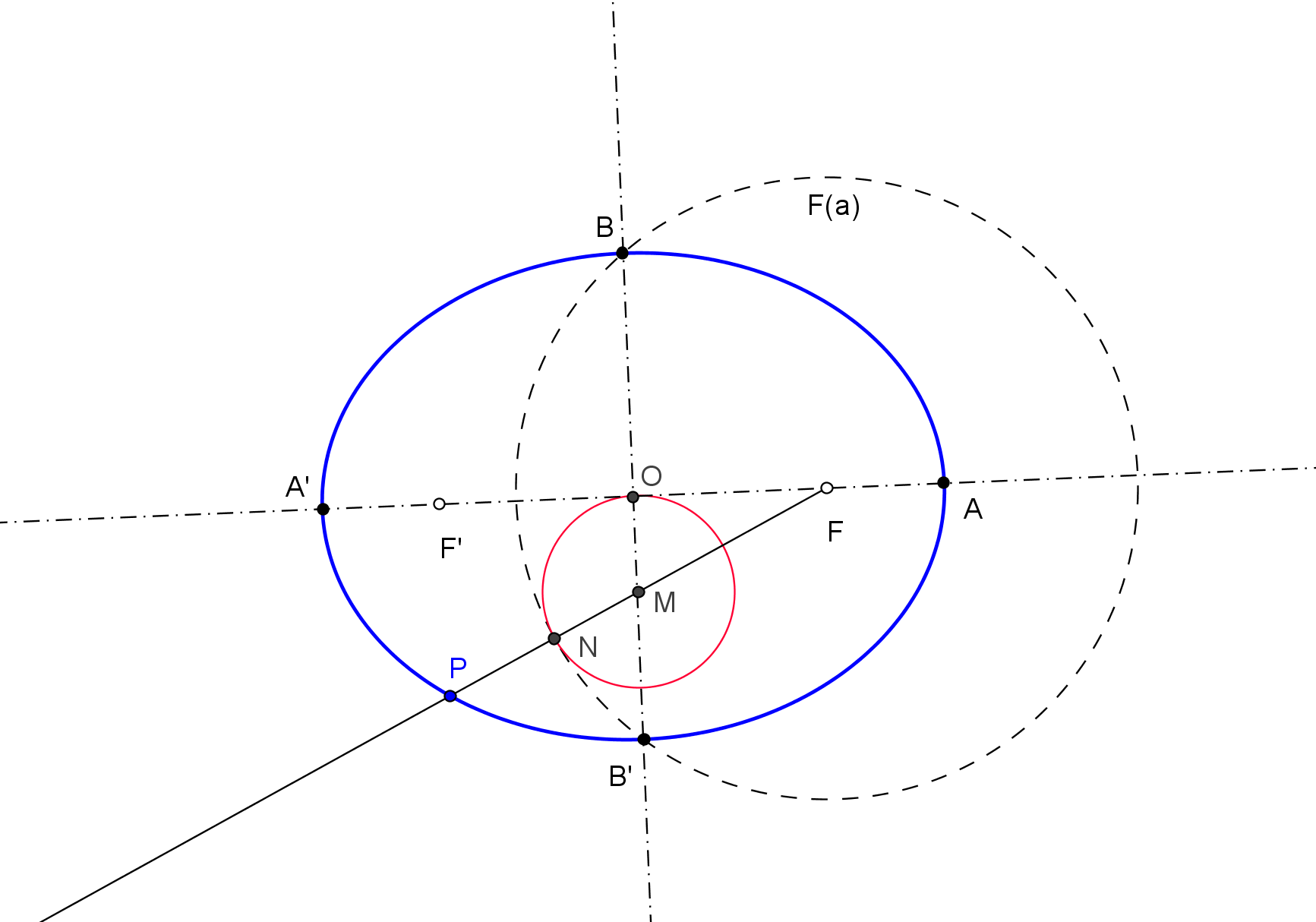
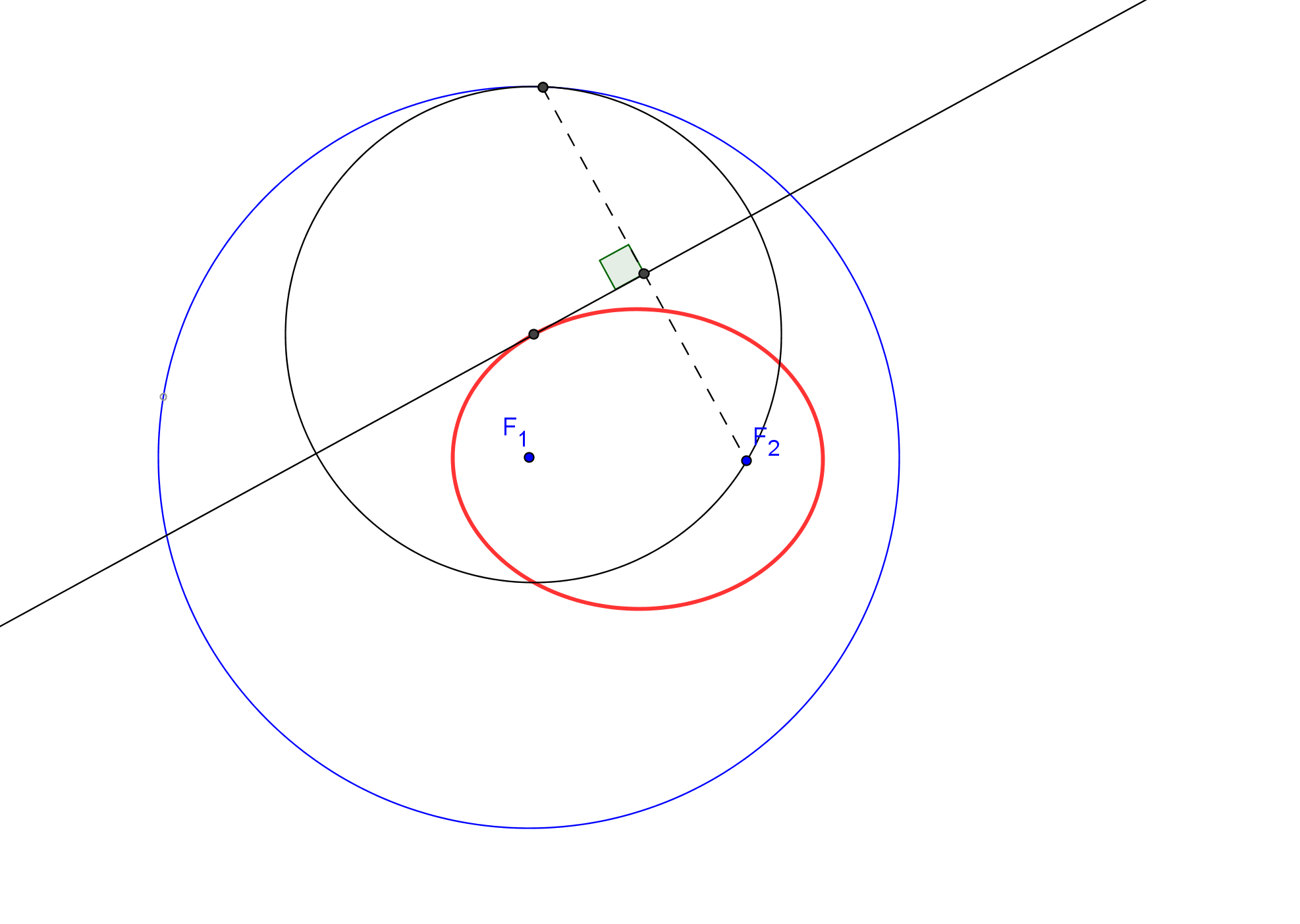
En una elipse o hipérbola, la circunferencia con centro O, el de la cónica, y radio la semilongitud del eje focal, a, se denomina circunferencia principal, y es tangente a la cónica en sus vértices.
En una elipse o hipérbola, la circunferencia con centro en un foco y radio la longitud del eje focal, 2a, se denomina circunferencia focal, relativa a dicho foco.

Propiedades de cónicas

El simétrico de un foco respecto de toda tangente a una elipse o hipérbola está sobre la circunferencia focal con centro el otro foco.
El simétrico del foco de una parábola respecto de toda tangente, está en la directriz.
El segmento de tangente a una cónica comprendido entre el punto de contacto y una directriz, se ve desde el foco correspondiente según un ángulo recto.
Dados dos puntos P₁ y P₂ y una recta d, el lugar geométrico de los focos de las cónicas con directriz correspondiente d y que pasan por P₁ y P₂, es la circunferencia de Apolonio de P₁ y P₂ y razón k=MP₁ ⁄ MP₂, siendo M el punto en el que la recta P₁P₂ corta a d.
En una elipse, sea F un foco, P un punto sobre ella y designamos por M el punto medio de FP, entonces la circunferencia de centro en M y tangente a la circunferencia F(a), de centro en F y radio a (longitud del semieje focal), pasa por el centro O de la elipse. (Mostrar/Ocultar figura)

En una hipérbola, la paralela al eje focal por uno de sus puntos P, corta a las asíntotas en los puntos M (el más cercano a P) y en N ( el más alejado de P), entonces una cualquiera de las semicircunferencias de diámetro PN y la recta perpendicular al eje focal por el punto M se cortan en en un punto Q, tal que PQ=a (longitud del semieeje focal).
En una parábola, la tangente t en un punto P corta a la tangente t_A, en su vértice A, en el punto medio de AQ, siendo Q la proyección ortogonal de P sobre t_A.
Más en general, en una parábola, la tangente t en un punto arbitrario corta a la tangente t_P (en P) en el punto medio M de PQ, siendo Q el punto de intersección de t_P con la recta paralela al eje por el punto de tangencia de t.
Las tangentes trazada desde un punto a una cónica son rectas isogonales de las rectas que unen dicho punto con los focos.
Toda parábola inscrita en un triángulo tiene su foco en la circunferencia circunscrita al triángulo.
Una elipse es el lugar geométrico de los centros de las circunferencias que pasan por un punto fijo (foco) y tangentes interiormente a una crcunferencia fija (circunferencia focal del otro foco). (Mostrar/Ocultar figura)

Una hipérbola es el lugar geométrico de los centros de las circunferencias que pasan por un punto fijo (foco) y tangentes exteriormente a una fija (circunferencia focal del otro foco). (Mostrar/Ocultar figura)

Una parábola es el lugar geométrico de los centros de las circunferencias tangentes a una recta fija (directriz) y que pasan por un punto exterior (foco). (Mostrar/Ocultar figura)

El lugar geométrico de las proyecciones ortogonales de un foco sobre las tangentes a una elipse o hipérbola es la circunferencia principal. (Mostrar/Ocultar figura)

Circunferencias principal y focal de la elipse e hipérbola

El lugar geométrico de las proyecciones ortogonales de un foco sobre las tangentes a una parábola es la tangente en el vértice.
Una cónica es el lugar geométrico de los puntos del plano tales que la razón de sus distancias a un punto fijo, llamado foco, y a una recta fija, llamada directriz es constante. Esta constante se llama excentricidad.

La polar de un foco es la directriz correspondiente.
Teorema de Pascal: "Si un hexágono se encuentra inscrito en una cónica, los tres puntos en los que se intersecan los lados opuestos están sobre una recta, denominada la recta de Pascal". (Mostrar/Ocultar figura)

Teorema de Brianchon: "Si un hexágono se encuentra circunscrito en una cónica, las tres rectas que unen vértices opuestos se intersecan en un punto, denominado punto de Brianchon". (Mostrar/Ocultar figura)

Referencias

Romeo Barbieri.- Dibujo Técnico (http://www.zonabarbieri.com/indexProbgeneral.html) (Consultada 24-05-2012)
Michel Bataille.- A Unified Construction of Conics. The Mathematical Gazette, Vol. 86, No. 507, Nov., 2002 (pp.408-414) (http://www.jstor.org/stable/10.2307/3621132)
Quim Castellsaguer.- Todo Triágulos Web (Construcciones) (http://www.xtec.cat/~qcastell/ttw/ttwesp/portada.html) (Consultada 24-05-2012)
Antonio Castilla.- TRAZOIDE. Dibujo técnico, geometría y CAD. (http://trazoide.com/forum/index.php) (Consultada 24-05-2012)
Philippe Chevanne.- MATHS en folie. Recueil de divertissements mathématiques (http://mathafou.free.fr/themes/coniques.html) (Consultada 24-05-2012)
Roger Cuppens.- Faire de la Géomètrie Supérieure en jount avec Cabri-Géomètre II (2 tomes). Brochures de APMEP. Paris (http://www.apmep.asso.fr)
Michael Fox.- Constructions for Sketchpad (http://mysite.mweb.co.za/residents/profmd/constructions.pdf) (Consultada 27-06-2012)
Geometrikon.- A collection of Topics in Geometry (created with the Dynamic Geometry application EucliDraw). (http://www.math.uoc.gr/~pamfilos/eGallery/Gallery.html) (Consultada 4-09-2012).
Ignacio Larrosa Cañestro.- Secciones conicas con Cabri 3D y GeoGebra. (http://www.xente.mundo-r.com/ilarrosa/GeoGebra/index_conicas.html) (Consultada 24-05-2012)
Pedro Puig Adam.- Curso de Geometría Métrica (2 vols.). Biblioteca Matemática S.L. Madrid 1973.
Paris Pamfilos.- A Gallery of Conics by Five Elements. Forum Geometricorum Volume 14 (2014) 295–348. (http://forumgeom.fau.edu/FG2014volume14/FG201431.pdf) (Consultada 28-10-2014)
B. M. WOODS.- The construction of conics under given conditions. AMM Volume 21 Nº 6 (Jun. 1914) pp. 73-180. (https://www.jstor.org/stable/pdf/2971797.pdf) (Consultada 22-04-2020)

C O N S T R U C C I O N E S D E C Ó N I C A S

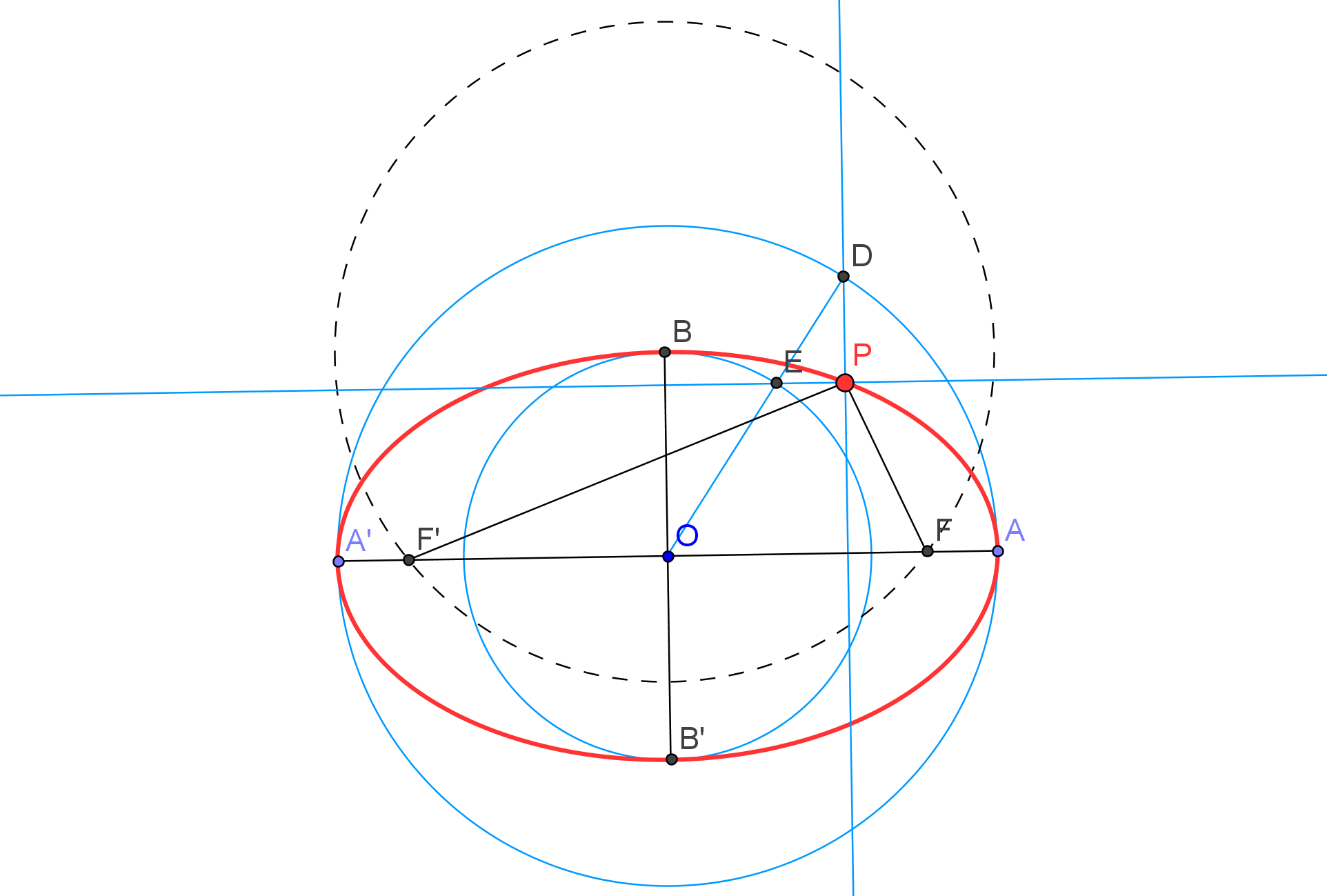
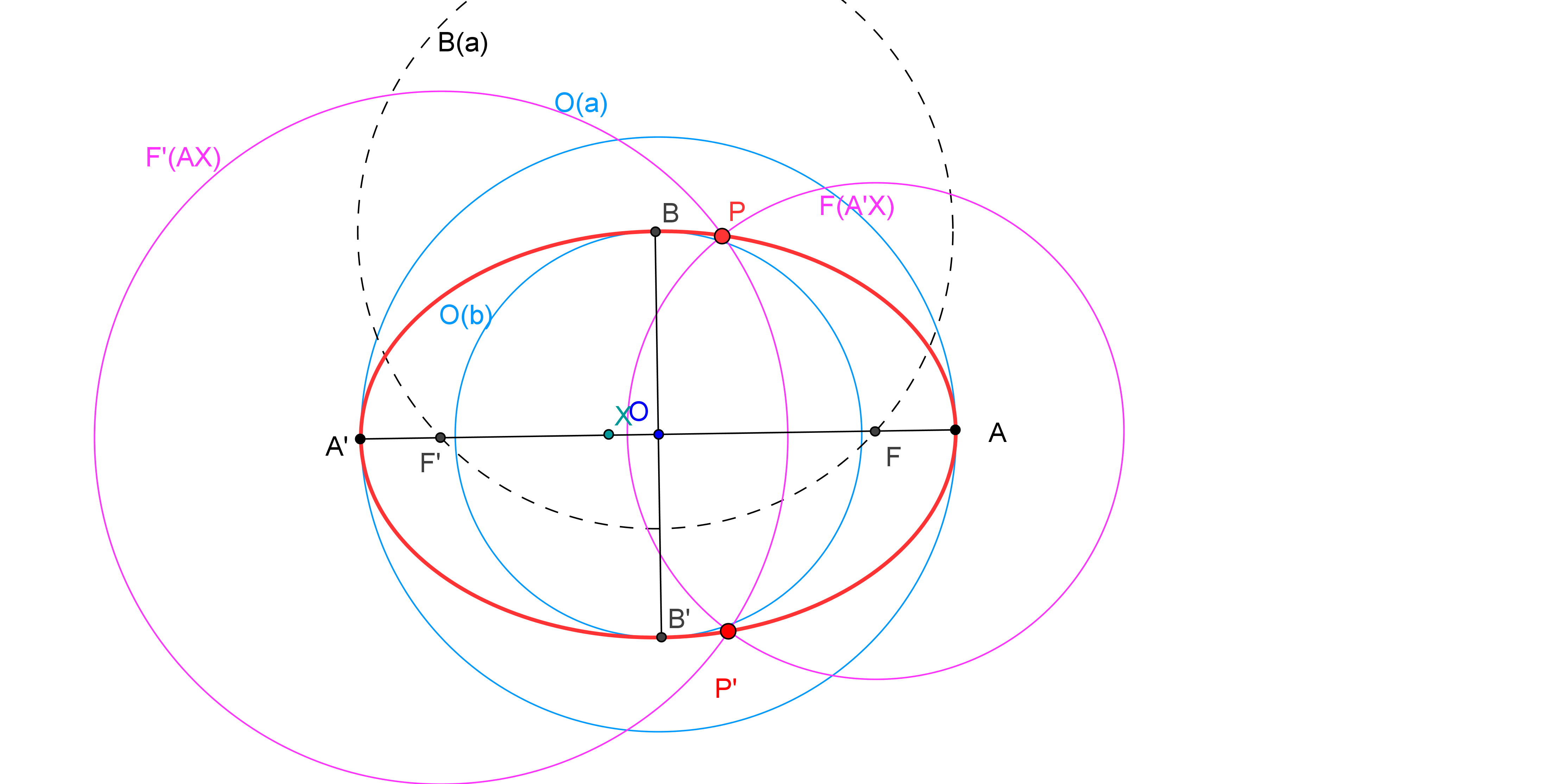
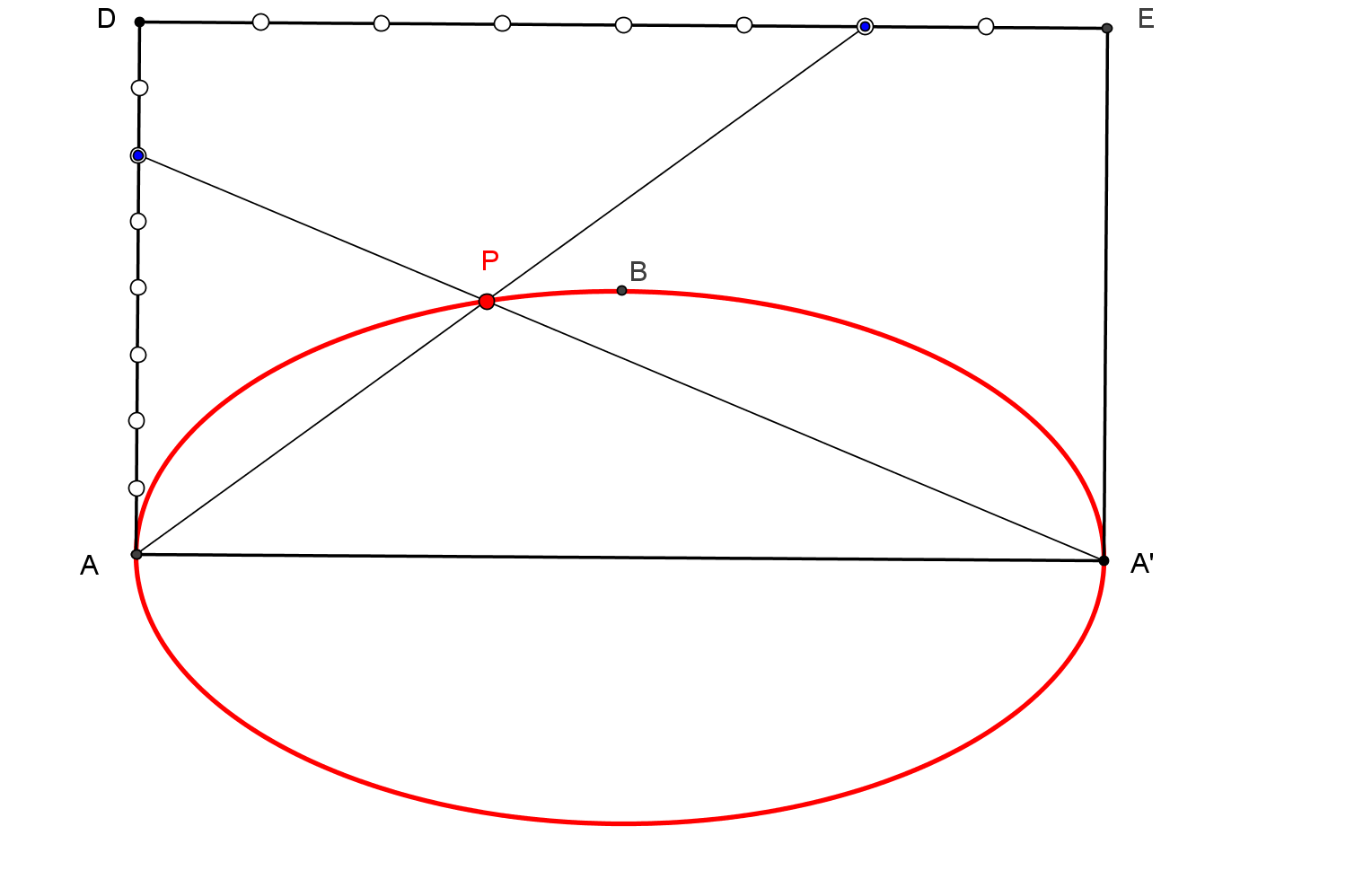
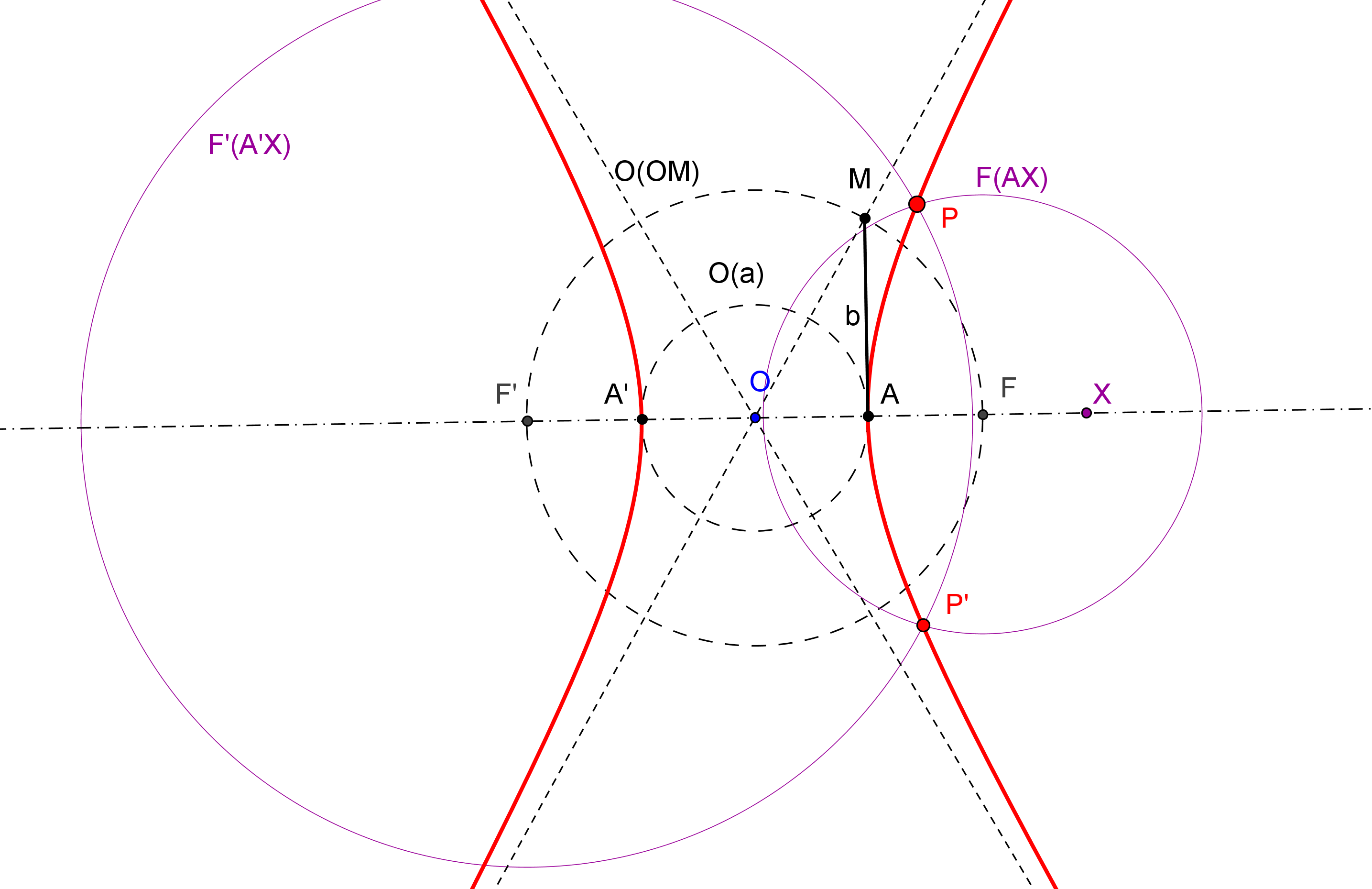
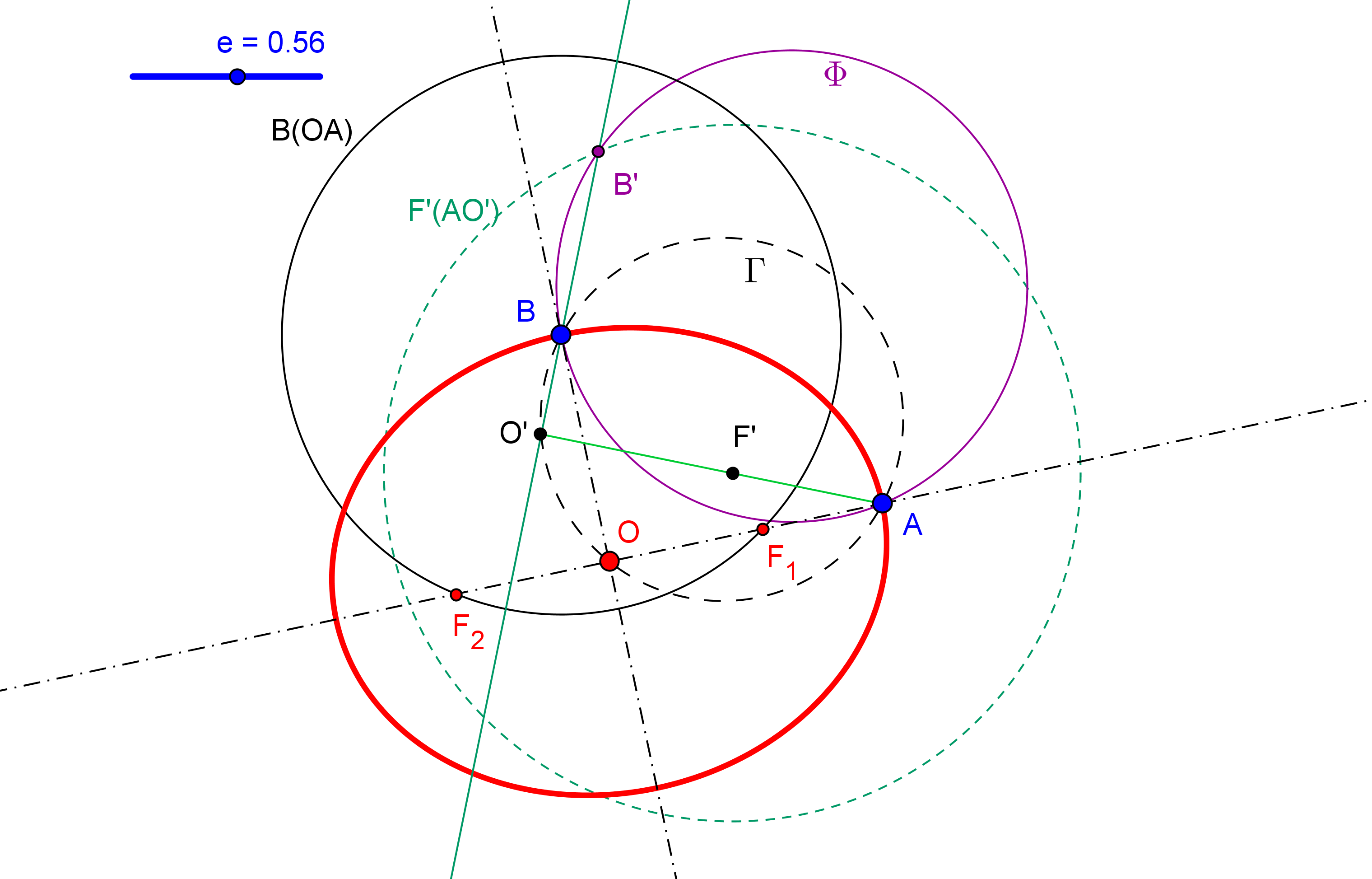
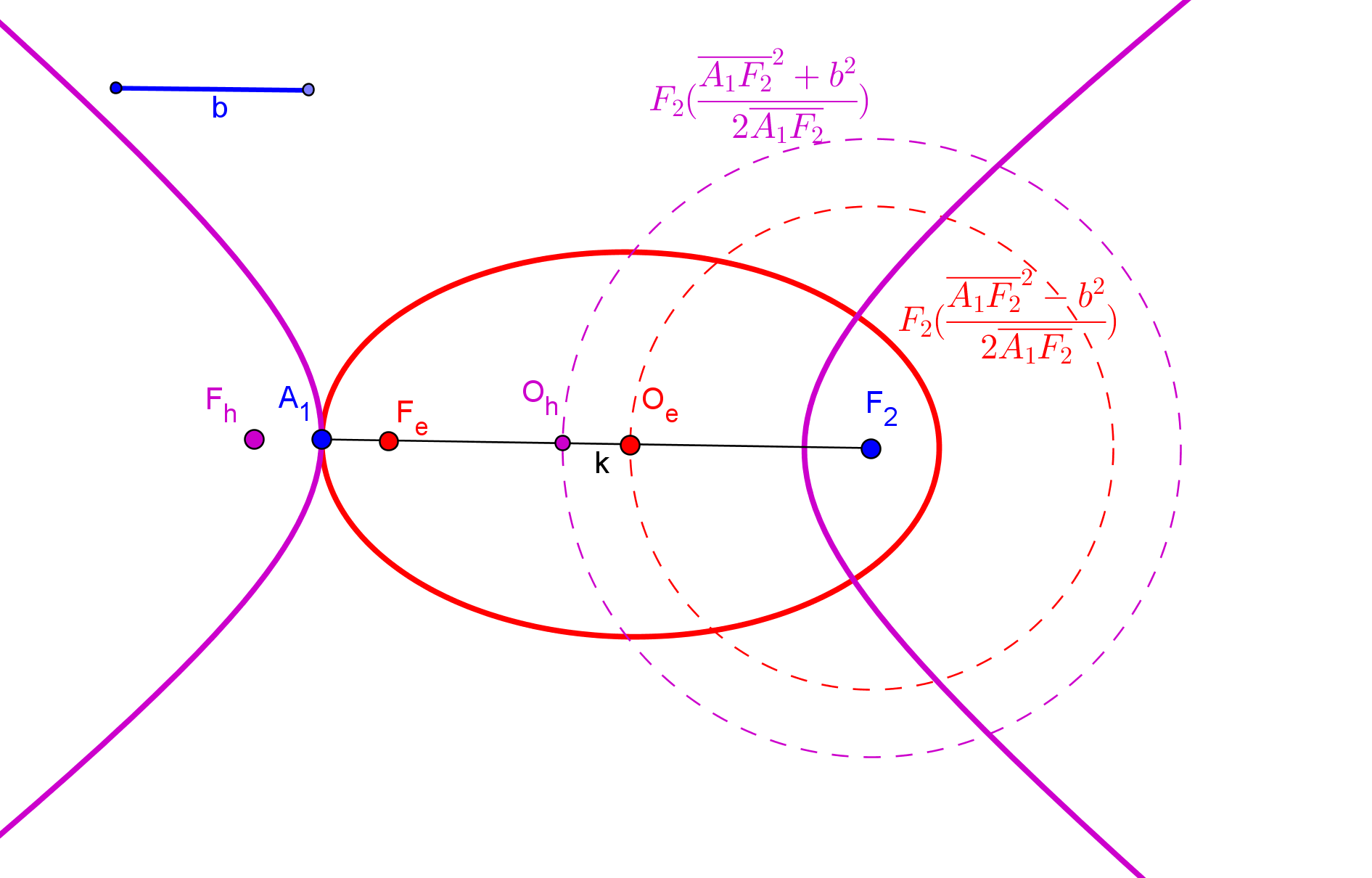
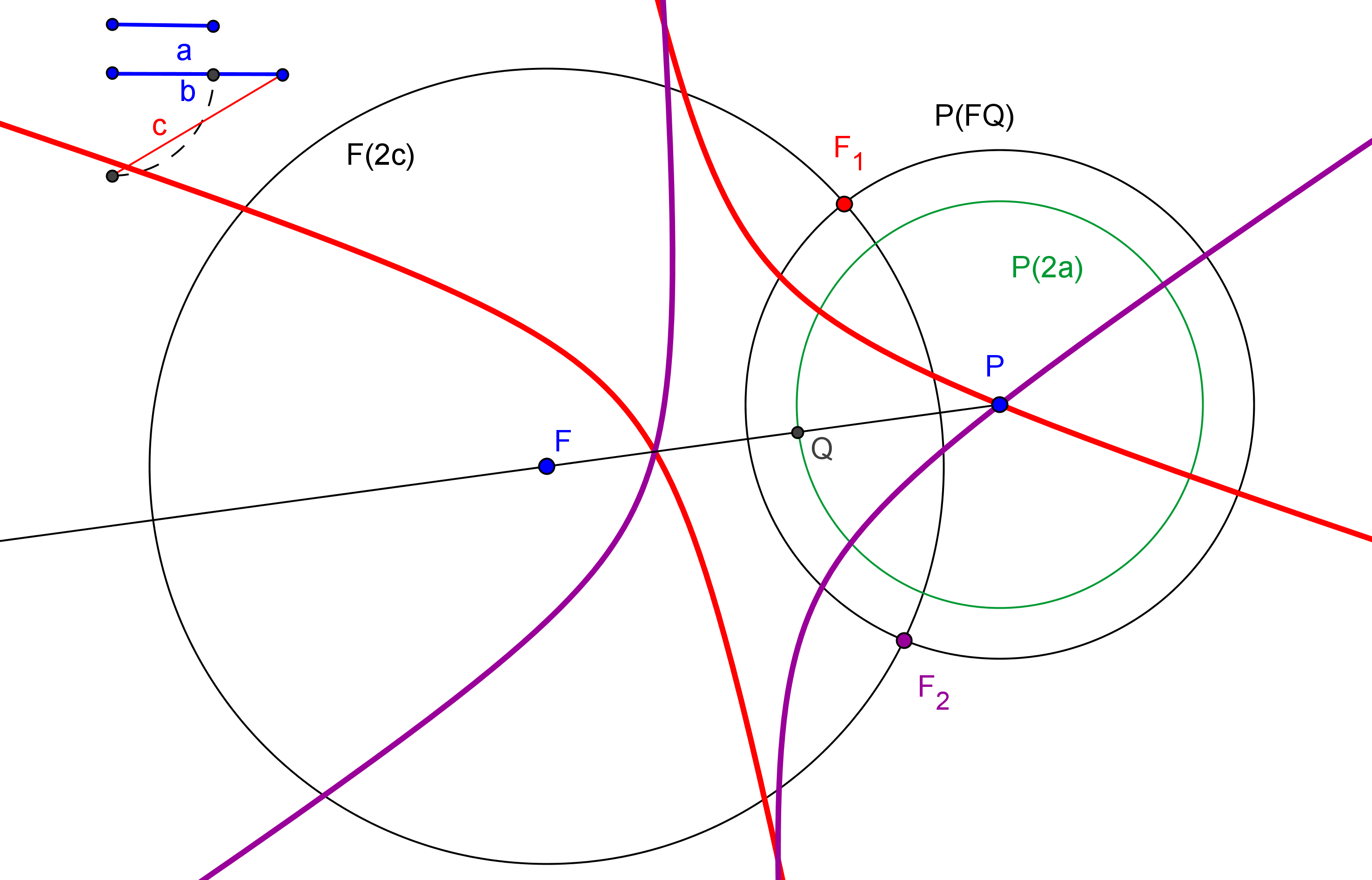
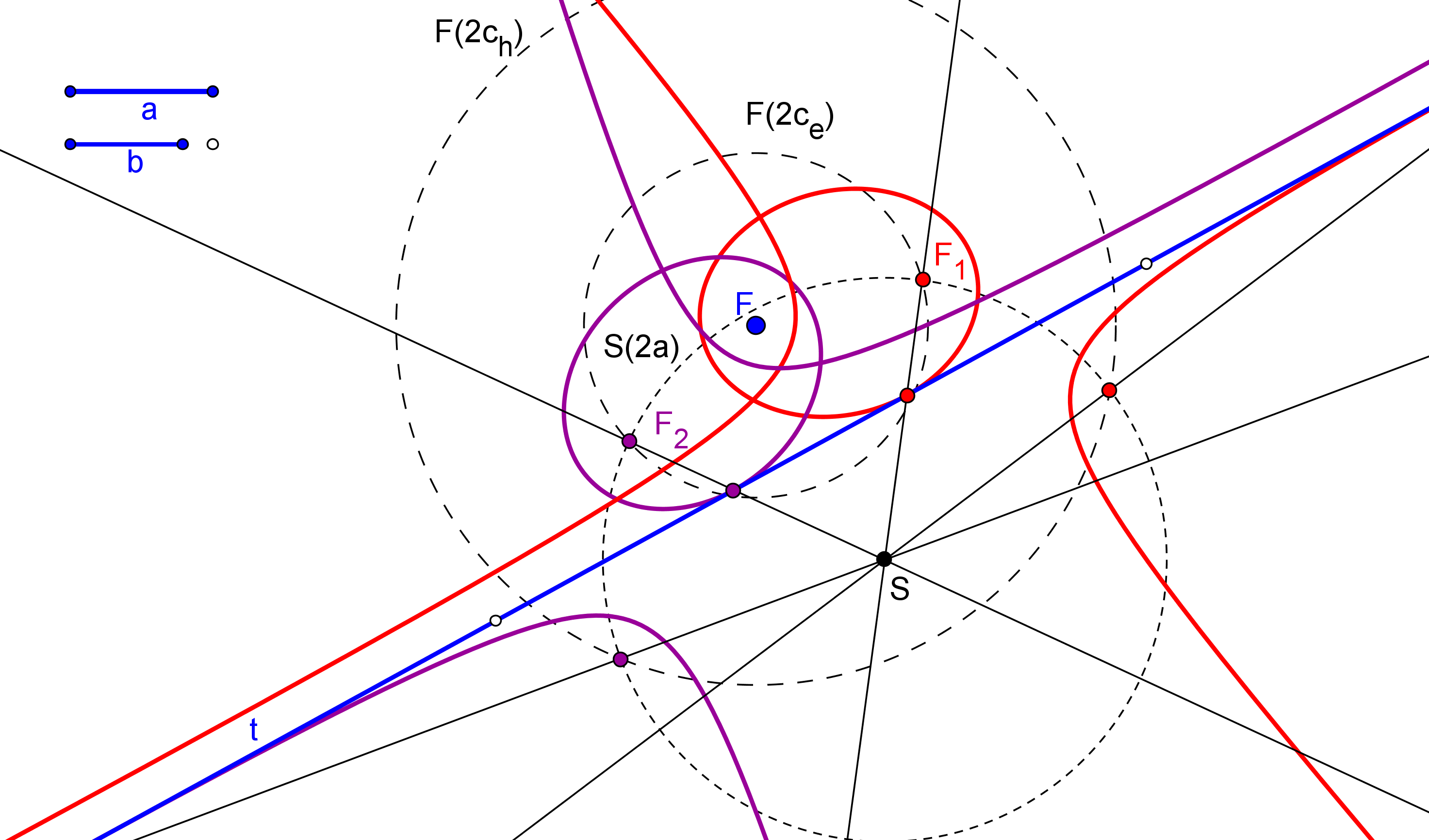
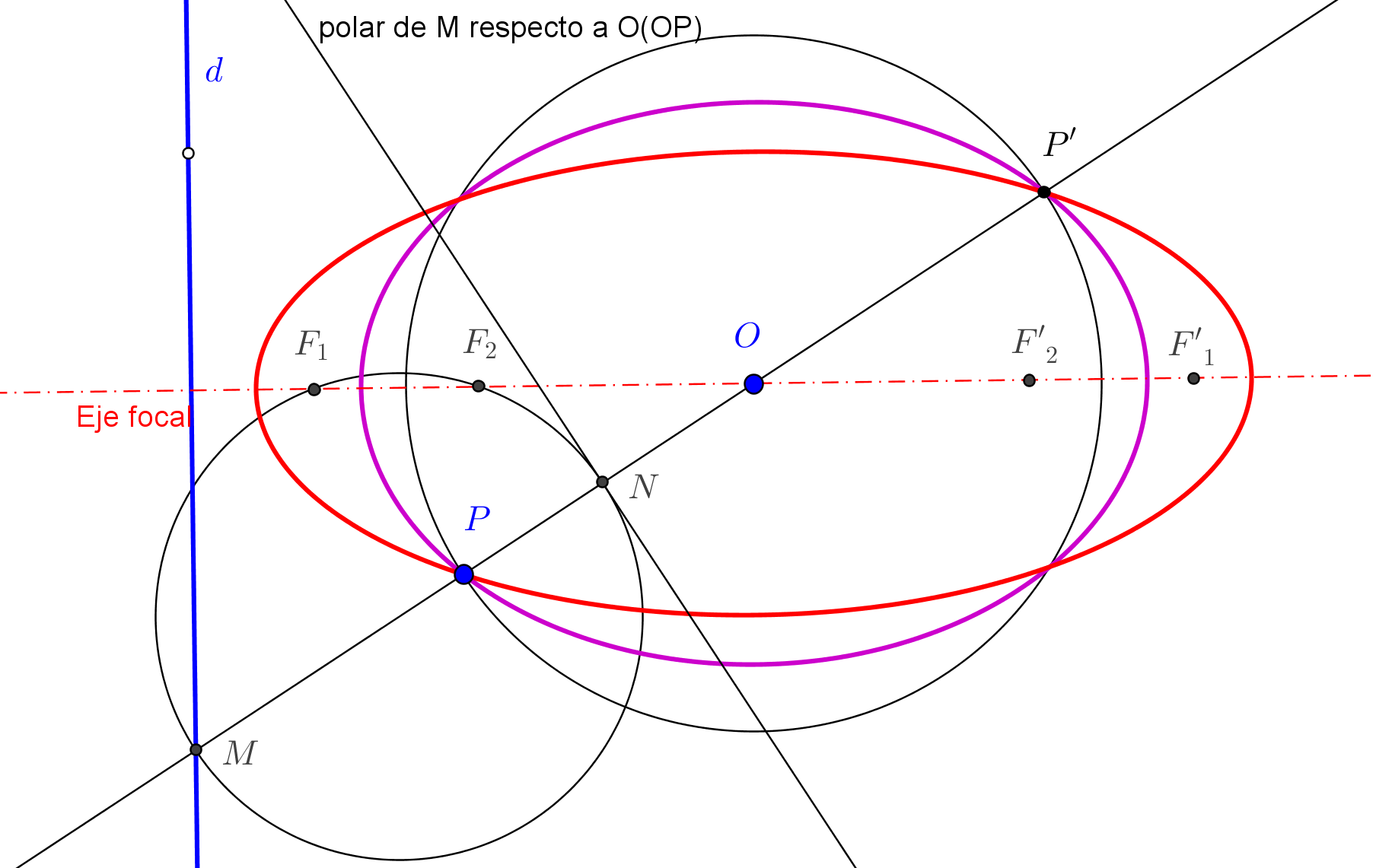
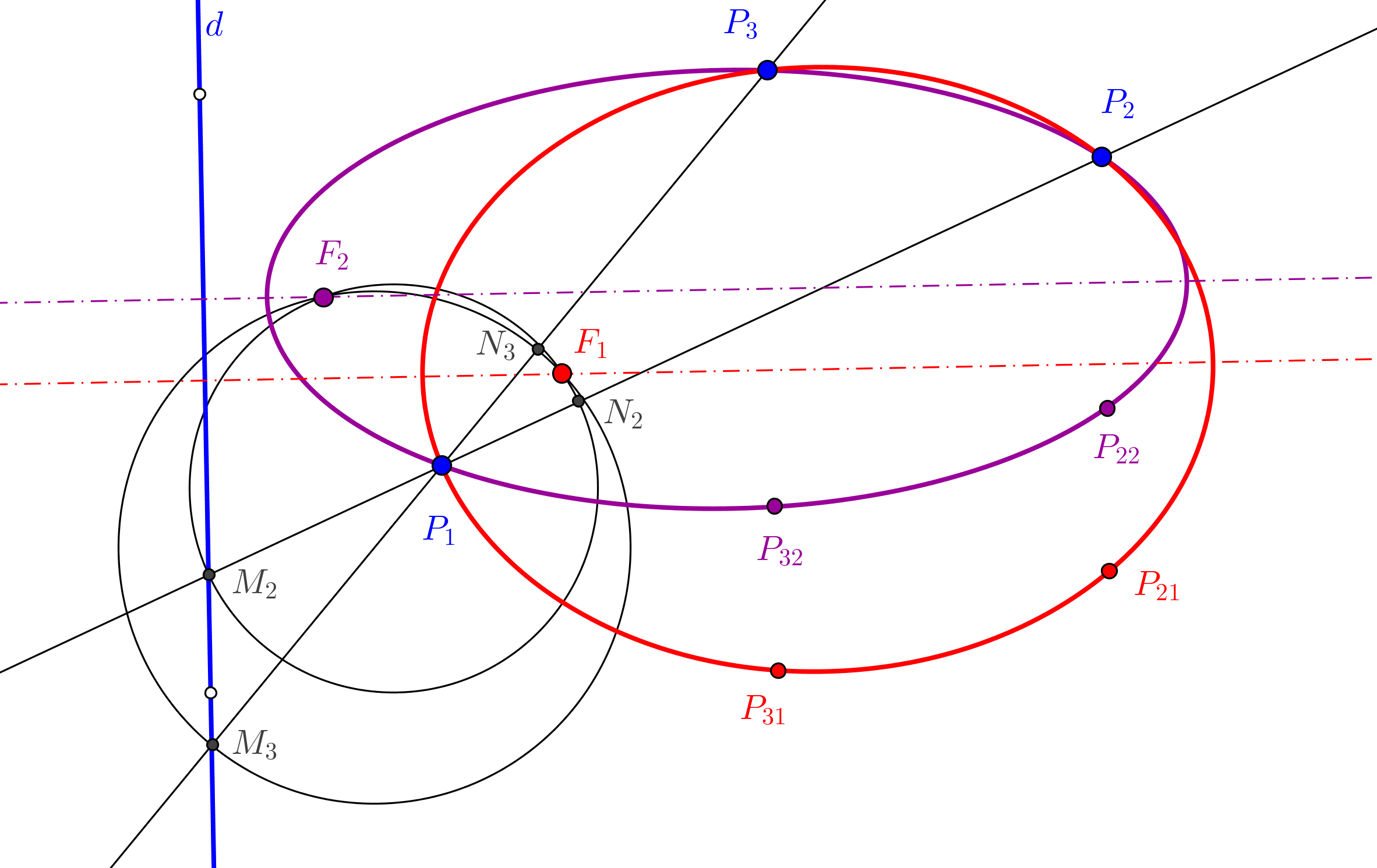
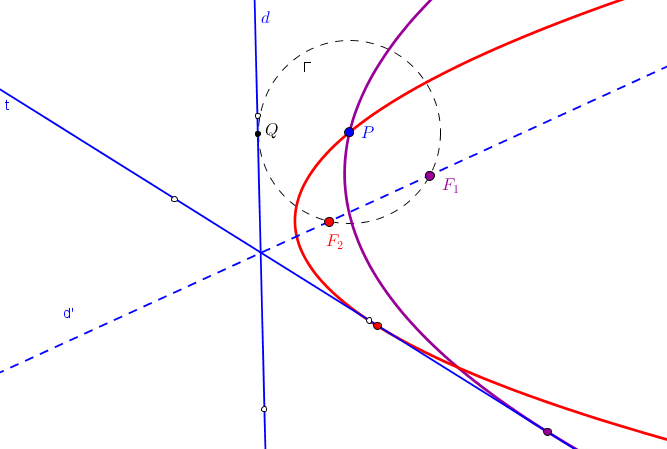
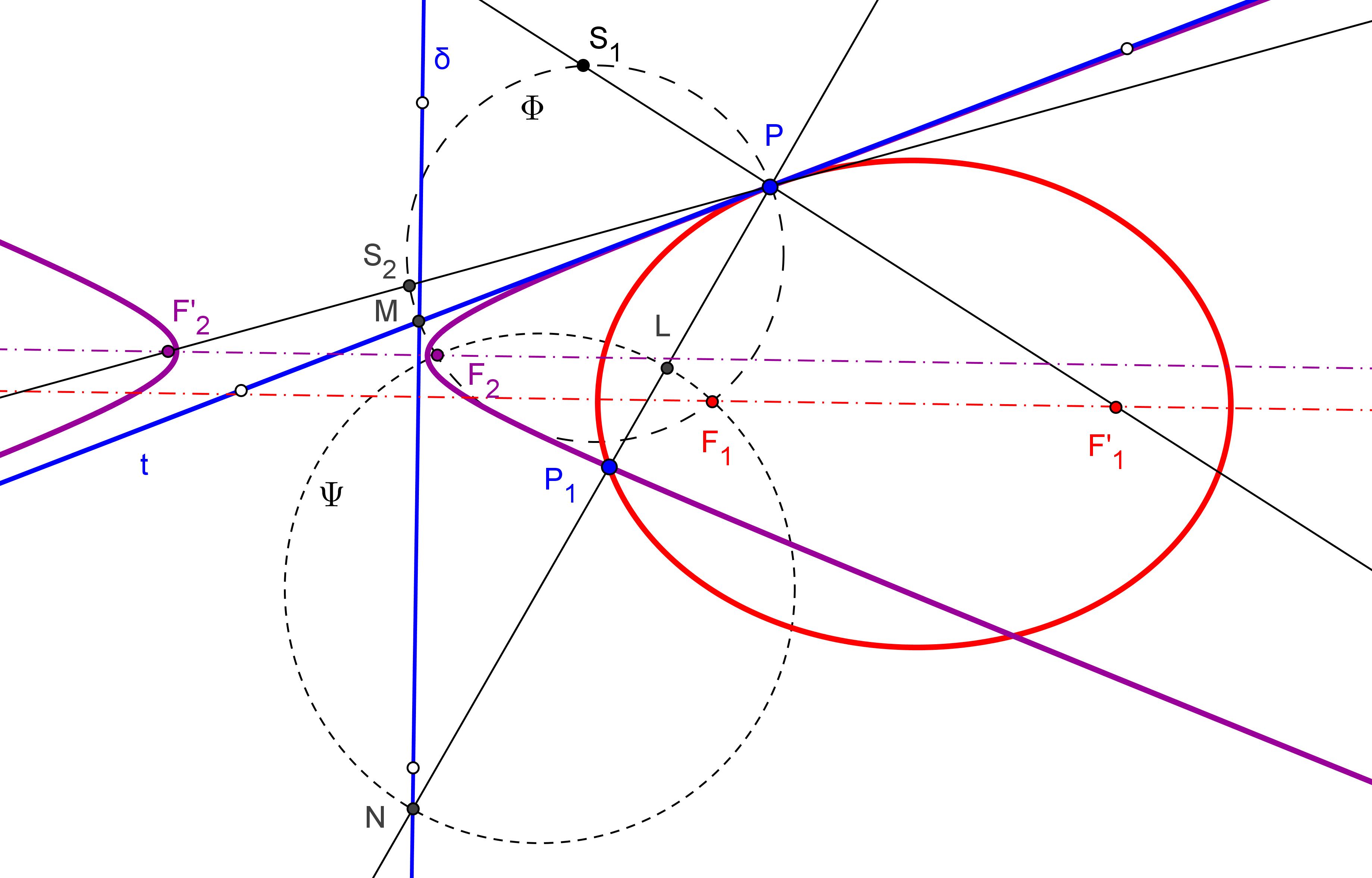
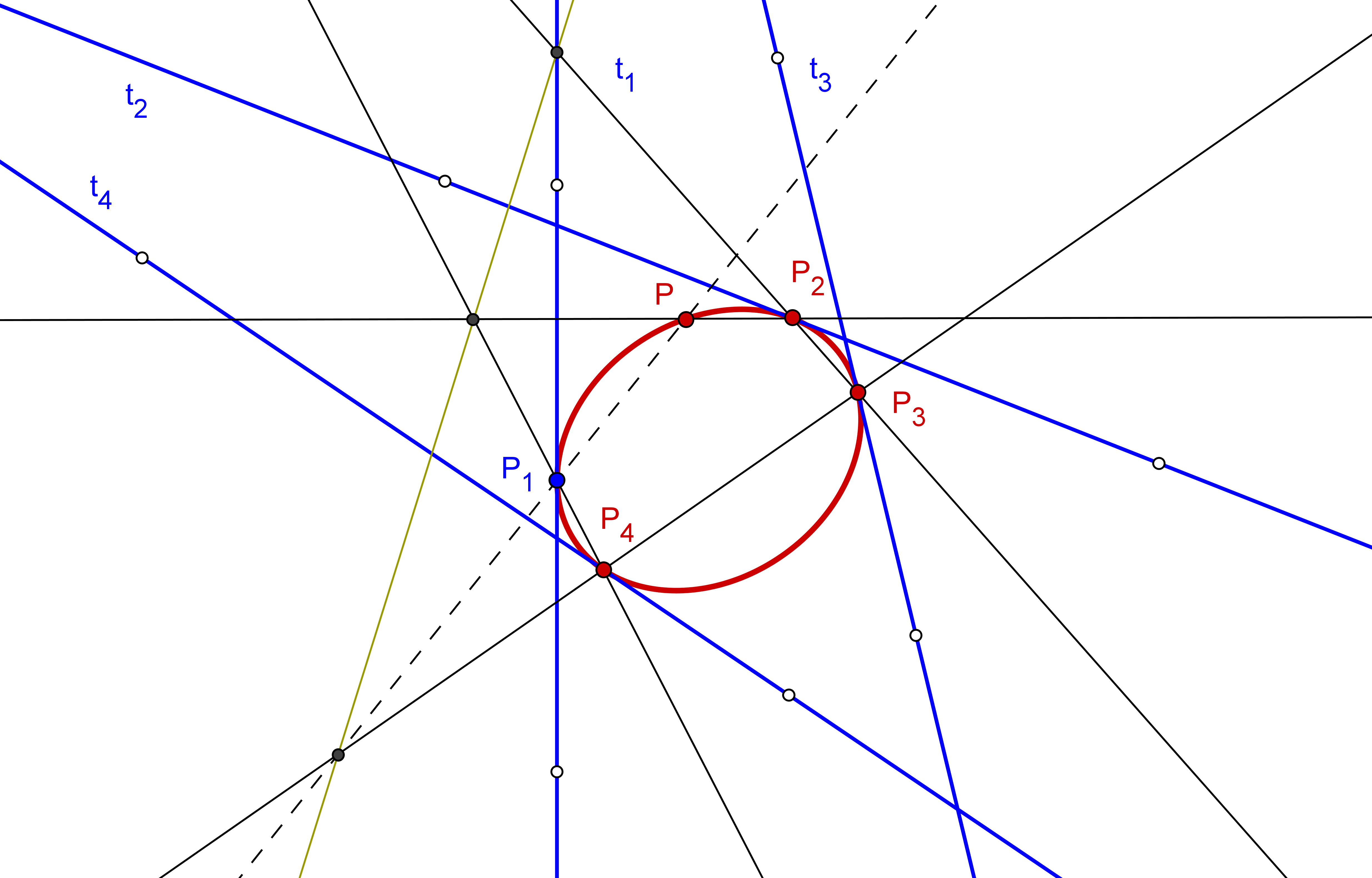
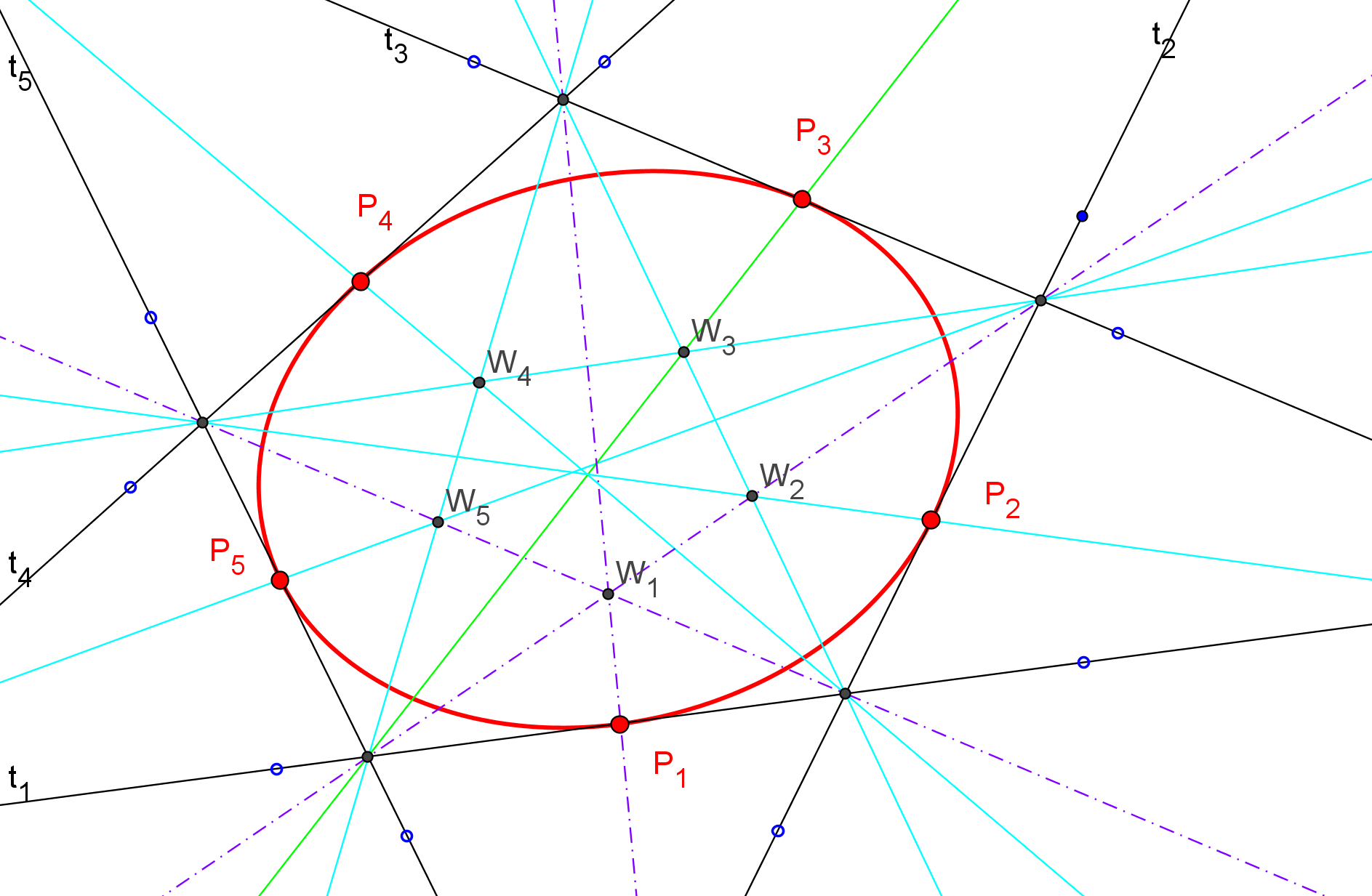
Para considerar que una cónica puede ser construida debemos conocer CINCO PUNTOS o bien SUS FOCOS y UN PUNTO. Así, si usamos GeoGebra, podemos utilizar las herramientas de construcción de cónicas que dispone por defecto:

Las construcciones solo se deben basar en operaciones con regla y compás, es decir, están solo permitidas estas cinco:

Trazar una recta uniendo dos puntos.

Trazar un punto mediante la intersección de dos rectas.

Trazar una circunferencia conociendo el centro y el radio.

Trazar un punto mediante la intersección de recta y circunferencia.

Trazar un punto mediante la intersección de dos circunferencias.

Construcción de cónicas

Nota

Notaciones

Introducción

Definiciones

Propiedades de cónicas

Referencias

C O N S T R U C C I O N E S D E C Ó N I C A S

document.write(vAAe) (AAe)

document.write(vAAt) (AAt)

document.write(vabC_e1) (abCe(1))

document.write(vabC_e2) (abCe(2))

document.write(vabC_e3) (abCe(3))

document.write(vabC_h) (abCh)

document.write(vABe) (ABe)

document.write(vA_1bF_2); (A1bF2)

document.write(vabFPC_e) abFPCe

document.write(vabFPC_h) (abFPCh)

document.write(vabFt) (abFt)

document.write(vAbO); (AbO)

document.write(vac); (ac)

document.write(vacFt) (acFt)

document.write(vAdP) (AdP)

document.write(vae_1Ft) (ae1Ft)

document.write(vae_1h); (ae1h)

document.write(vae_1hP); (ae1hP)

document.write(vAe_1PC_p) (Ae1PCp)

document.write(vAe_1tC_p) (Ae1tCp)

document.write(vaFFC_h); (aFFCh)

document.write(vaFh) (aFh)

document.write(vaFPPC_e); (aFPPCe)

document.write(vaFPPC_h) (aFPPCh)

document.write(vAFt) (AFt)

document.write(vaFt_P) (aFtP)

document.write(vaFtt); (aFtt)

document.write(vaOtt) (aOtt)

document.write(vBBe) (BBe)

document.write(vBBt) (BBt)

document.write(vBdO) (BdO)

document.write(vbe_1Ft) (be1Ft)

document.write(vBFP) (BFP)

document.write(vbhh) (bhh)

document.write(vcFt_P); (cFtP)

document.write(vcFtt) (cFtt)

document.write(vc_ptt) (cptt)

document.write(vddPP) (ddPP)

document.write(vdeF) (deF)

document.write(vdeF2) (deF(2))

document.write(vdeF3); (deF(3))

document.write(vdFC_p1) (dFCp(1))

document.write(vdFC_p2) (dFCp(2))

document.write(vdFt) (dFt)

document.write(vdFxC_h); (dFh⊥h)

document.write(vdOP) (dOP)

document.write(vdPPP) (dPPP)

document.write(vdPtC_p) (dPtCp)

document.write(vdPt_P) (dPtP)

document.write(vdttC_p) (dttCp)

document.write(ve_1FPPalineados) (e1FPPalineados)

document.write(ve_1FtC_p) (e1FtCp)

document.write(ve_khP); (ekhP)

document.write(ve_1PPC_p); (e1PPCp)

document.write(ve1tMMc_p) (e1tMM∈cp)

document.write(ve1t_PC_p) (e1tPCp)

document.write(vFFP); (FFP)

document.write(vFFt) (FFt)

document.write(vFht) (Fht)

document.write(vFPPC_p) (FPPCp)

document.write(vFPPP) (FPPP)

document.write(vFPPt) (FPPt)

document.write(vFPQdC_p); (FPQ∈dCp)

document.write(vFPtC_p) (FPtCp)

document.write(vFPtt) (FPtt)

document.write(vFSp_tF) (FSπtF)

document.write(vFt_PC_p) (FtPCp)

document.write(vFttC_p) (FttCp)

document.write(vFtt_P) (FttP)

document.write(vFttt) (Fttt)

document.write(vFxxC_e); (FxxCe)

document.write(vhhP) (hhP)

(AAe)

(AAt)

(abC_e(1))

(abC_e(2))

(abC_e(3))

(abC_h)

(ABe)

(A₁bF₂)

abFPC_e

(abFPC_h)

(abFt)

(AbO)

(ac)

(acFt)

(AdP)

(ae₁Ft)

(ae₁h)

(ae₁hP)

(Ae₁PC_p)

(Ae₁tC_p)

(aFFC_h)

(aFh)

(aFPPC_e)

(aFPPC_h)

(AFt)

(aFt_P)

(aFtt)

(aOtt)

(BBe)

(BBt)

(BdO)

(be₁Ft)

(BFP)

(bhh)

(cFt_P)

(cFtt)

(c_ptt)

(ddPP)

(deF)

(deF(2))

(deF(3))

(dFC_p(1))

(dFC_p(2))

(dFt)

(dFh⊥h)

(dOP)

(dPPP)

(dPtC_p)

(dPt_P)

(dttC_p)

(e₁FPPalineados)

(e₁FtC_p)

(e_khP)

(e₁PPC_p)

(e₁tMM∈c_p)

(e₁t_PC_p)

(FFP)

(FFt)

(Fht)

(FPPC_p)

(FPPP)

(FPPt)

(FPQ∈dC_p)

(FPtC_p)

(FPtt)

(FSπ_tF)

(Ft_PC_p)

(FttC_p)

(Ftt_P)

(Fttt)

(FxxC_e)

(hhP)

(hhP(2))

(hht)

(hIPP)

(hIp_Q)

(hOt_P)

(hPPP)

(IIPPP)

(IIPt_P)