Construcciones:
(las letras indican elementos cono-
cidos de la cónica)
 |
 |
Rut Almeida Elvira Espinosa Elisa Guzmán Angel Montesdeoca José Agustín Noda |
|
![]()
Fue el matemático griego Apolonio (262-190 A.C.) de Perga el primero en estudiar detalladamente las curvas cónicas y encontrar la propiedades que las definían.
Apolonio descubrió que las cónicas se podían clasificar en tres tipos a los que dio el nombre de: elipses, hipérbolas y parábolas:
Las elipses son las curvas que se obtiene cortando una superficie cónica con un plano que no es paralelo a ninguna de sus generatrices.
Las hipérbolas son las curvas que se obtiene al cortar una superficie cónica con un plano que es paralelo a dos de sus generatrices.
Las parábolas son las curvas que se obtienen al cortar una superficie cónica con un plano paralelo a una sola generatriz.
Debido a estas caracterizaciones a las curvas cónicas se llaman a veces secciones cónicas.
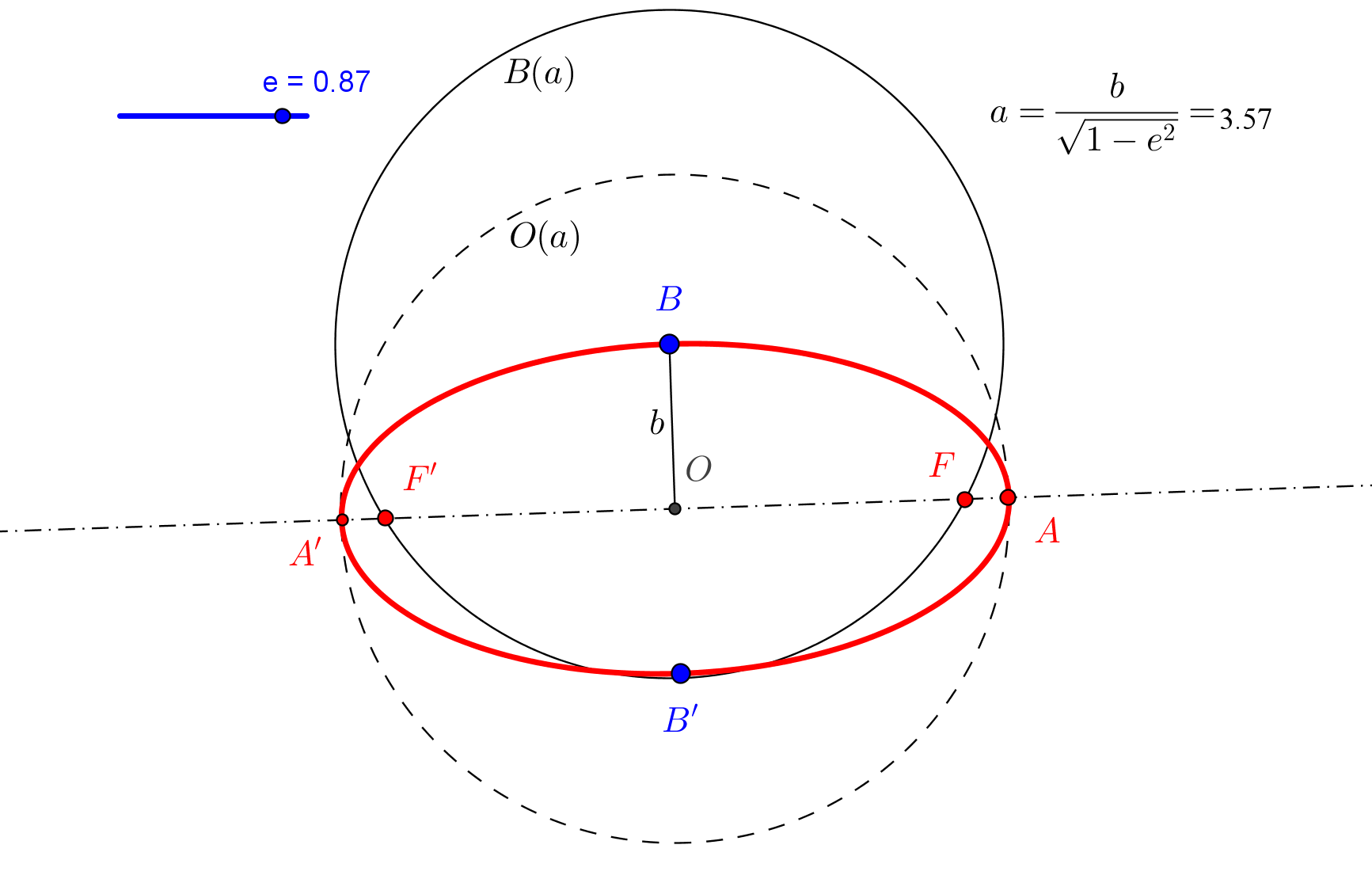
En el siglo XVI el filósofo y matemático René Descartes (1596-1650) relacionó las curvas con ecuaciones relativas a un sistema de coordenadas; es lo que se conoce como Geometría Analítica. En la Geometría Analítica las cónicas se pueden representar por ecuaciones algebraicas de segundo grado y, recíprocamente, todas las ecuación de segundo grado en dos variables representa sección cónica. El astrónomo alemán Johannes Kepler (1570-1630) descubrió que las órbitas de los planetas alrededor del Sol son elipses con el Sol en uno de sus focos. Para La Tierra, la excentricidad es 0.017 y los demás planetas varían desde 0.004 de Neptuno a 0.250 de Plutón. El matemático y físico inglés Isaac Newton (1642-1727) demostró que la órbita de un cuerpo alrededor de una fuerza de tipo gravitatorio es siempre una cónica.
Existe una caracterización proyectiva de las cónicas, debida a Steiner, como el lugar geométrico de los puntos de intersección de pares de rayos homólogos en una proyectividad entre haces.
![]()
![]()
![]()
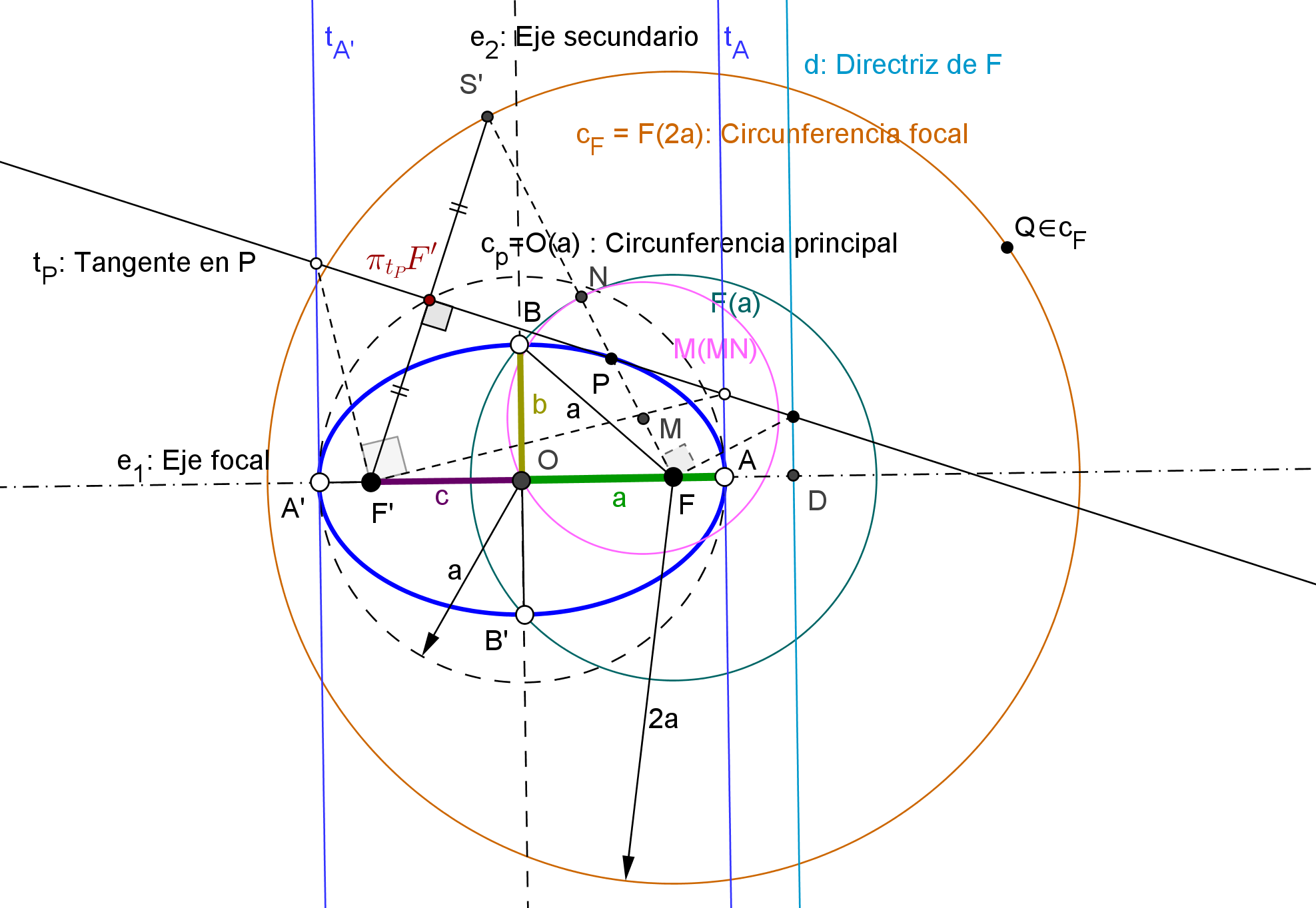
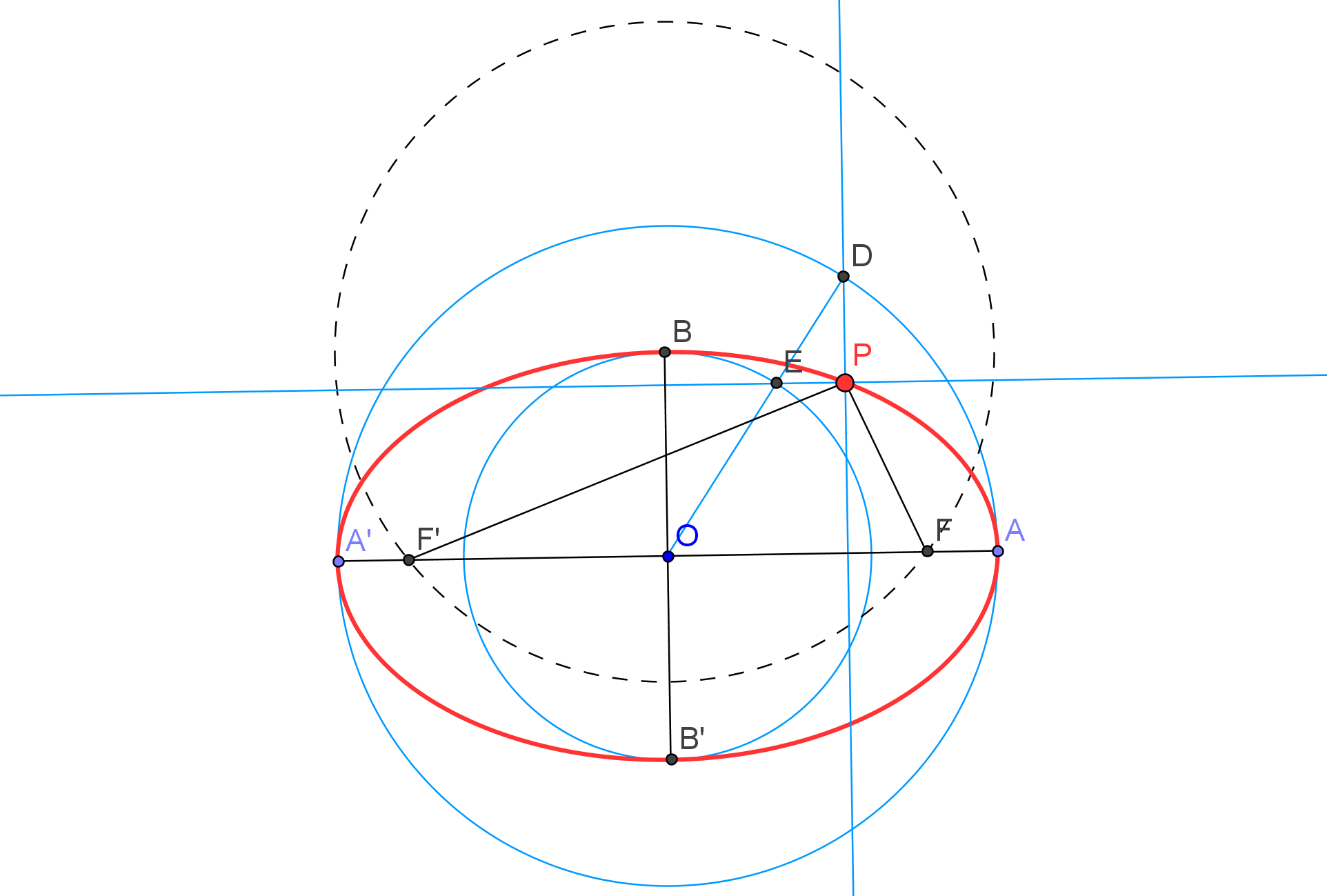
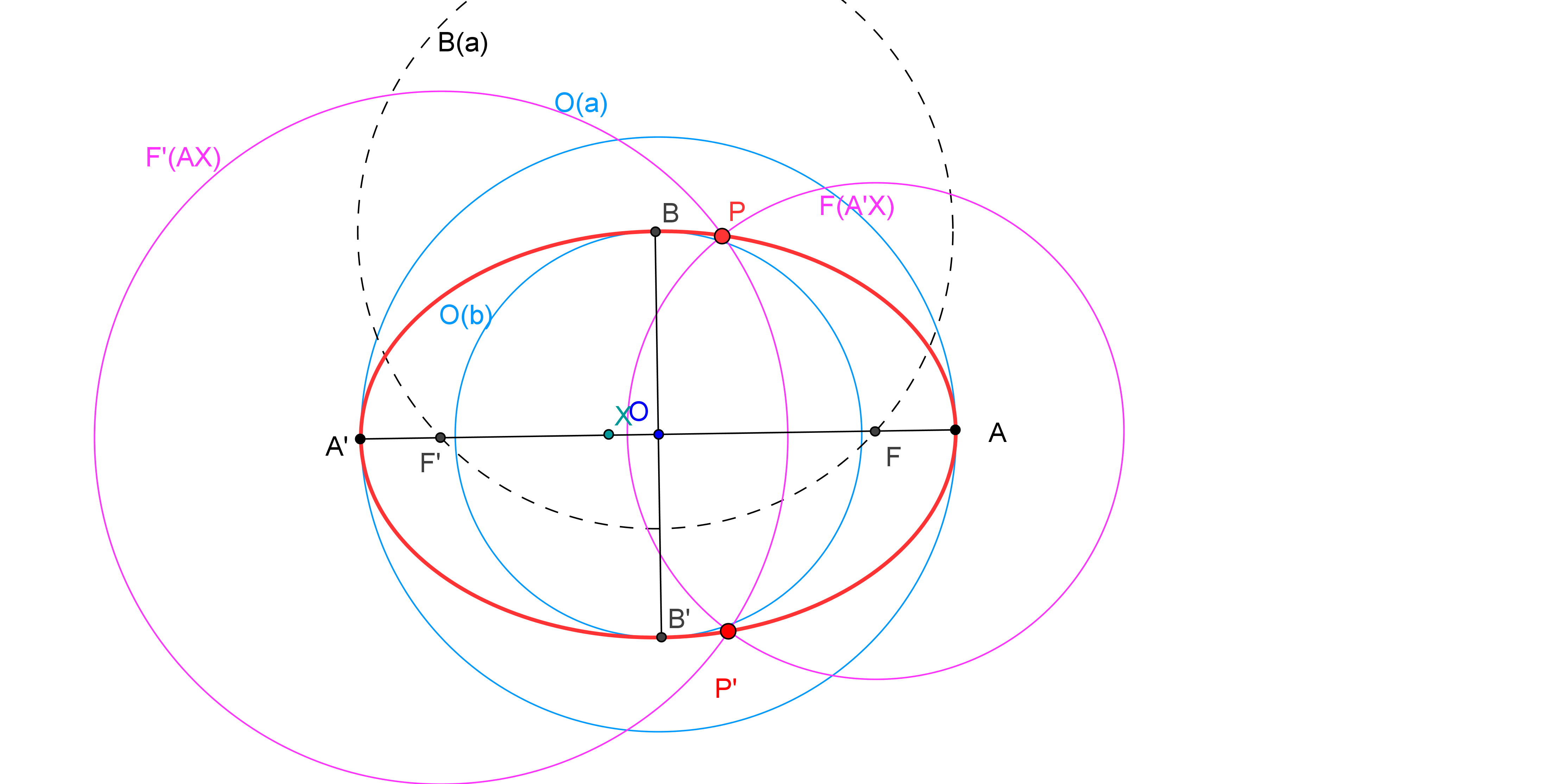
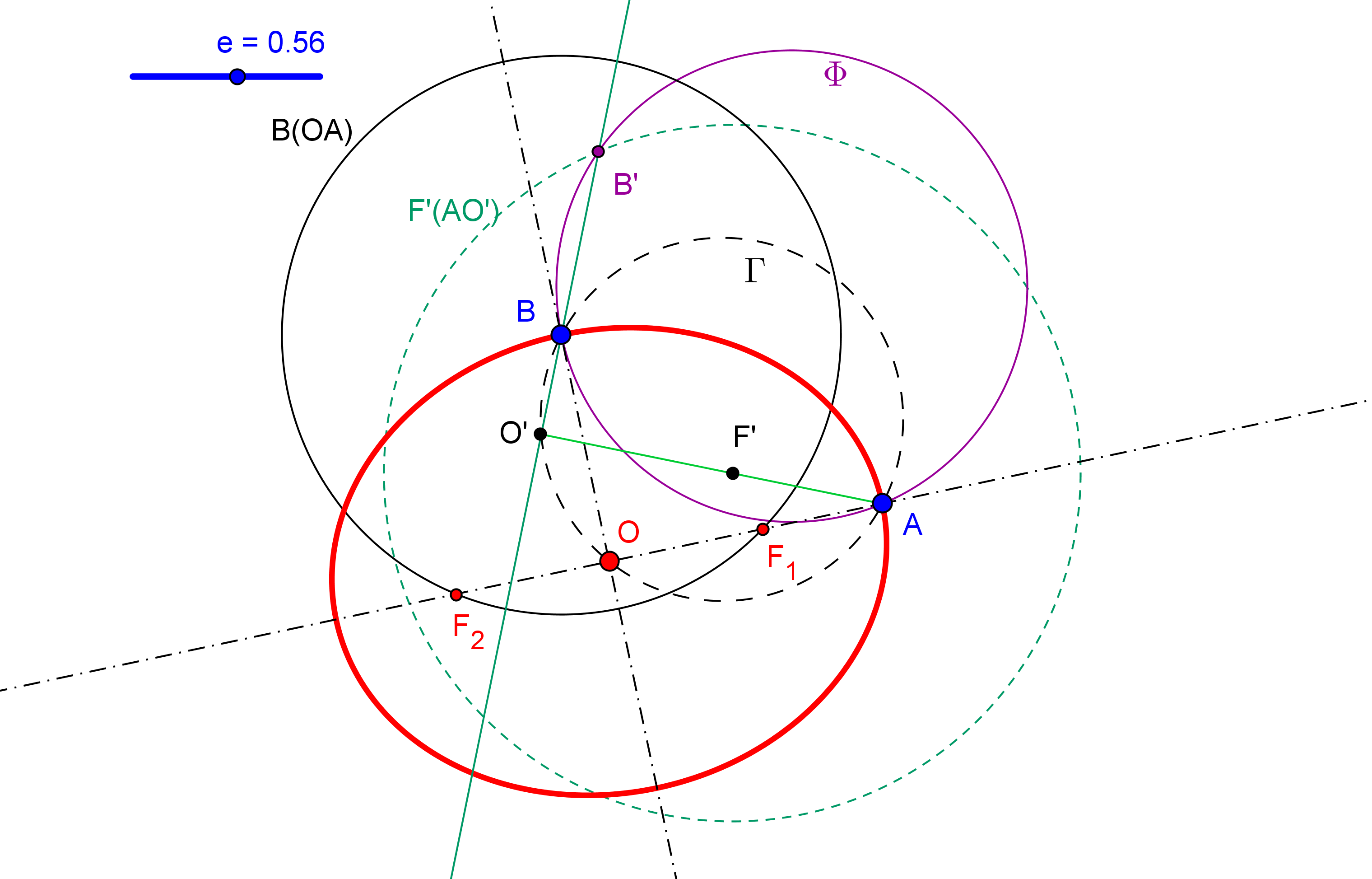
Para considerar que una cónica puede ser construida debemos conocer CINCO PUNTOS o bien SUS FOCOS y UN PUNTO. Así, si usamos GeoGebra, podemos utilizar las herramientas de construción de cónicas que dispone por defecto:



Las construciones solo se deben basar en operaciones con regla y compás, es decir, están solo permitidas estas cinco:
| Trazar una recta uniendo dos puntos. |
| Trazar un punto mediante la intersección de dos rectas. |
| Trazar una circunferencia conociendo el centro y el radio. |
| Tazar un punto mediante la intersección de recta y circunferencia. |
| Trazar un punto mediante la intersección de dos circunferencias. |
![]()
( Mostrar/Ocultar figura)
![]()
![]()
( Mostrar/Ocultar figura)
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)

![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)

![]()
( Mostrar/Ocultar figura)
![]()
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
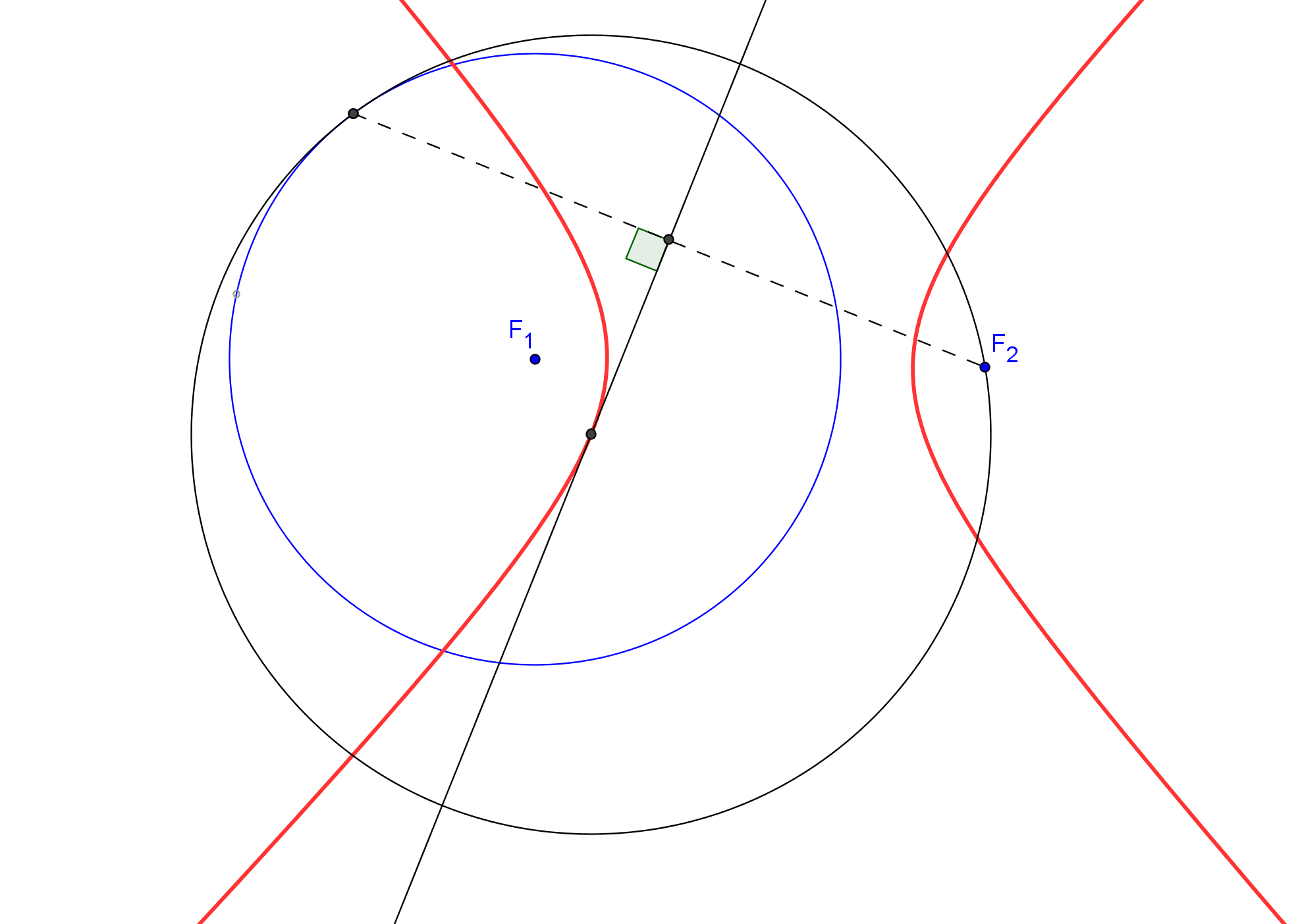
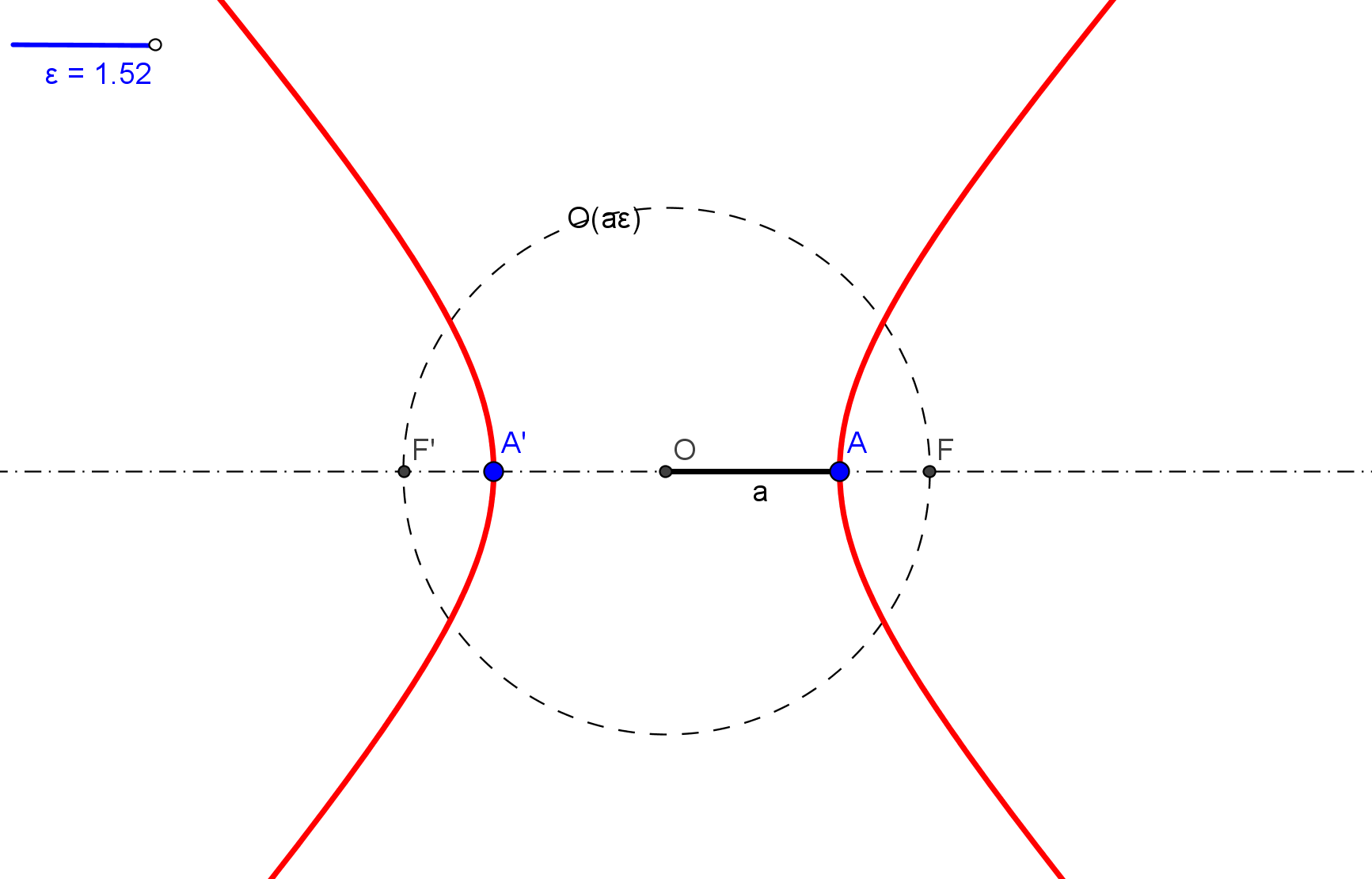
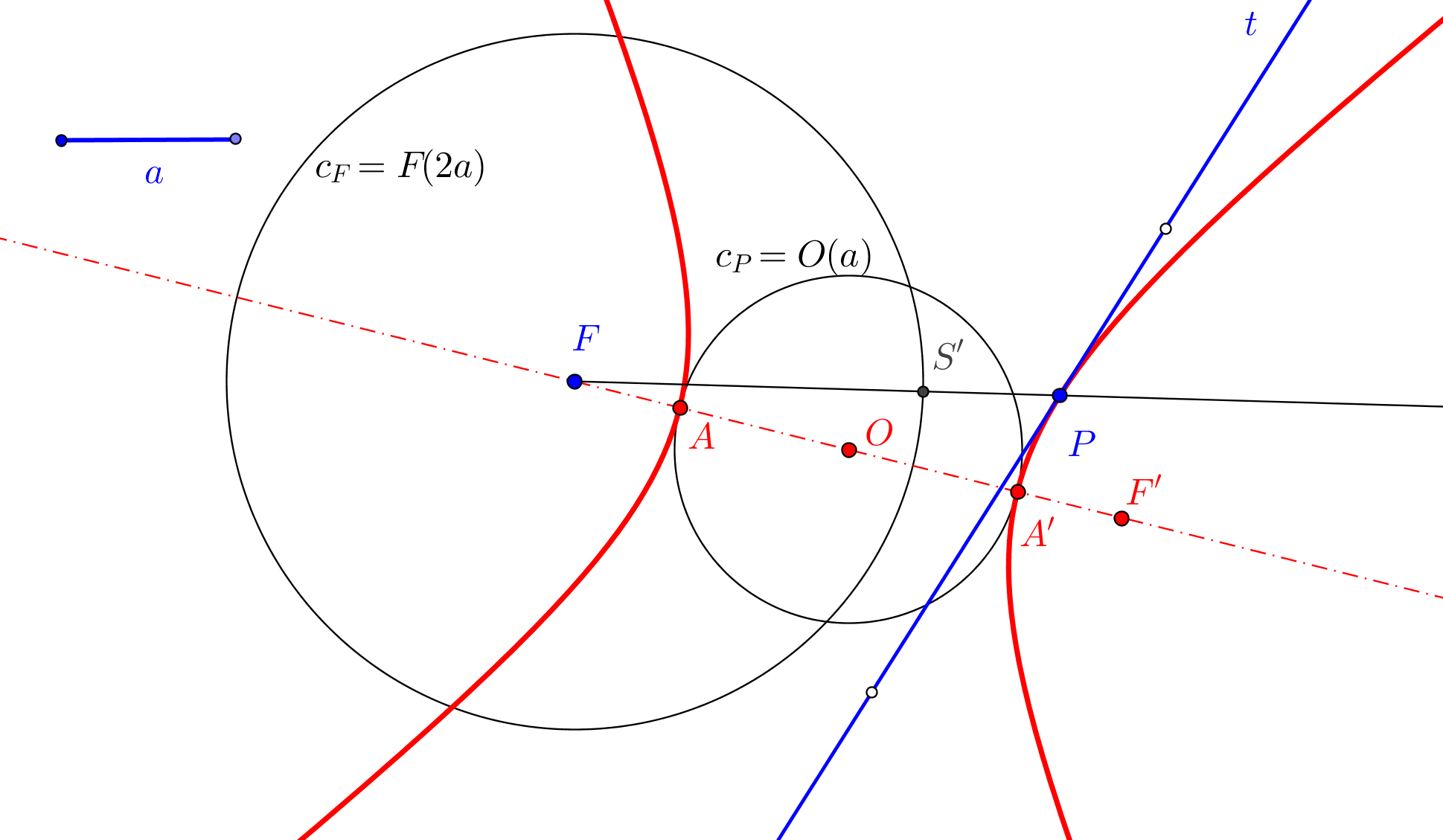
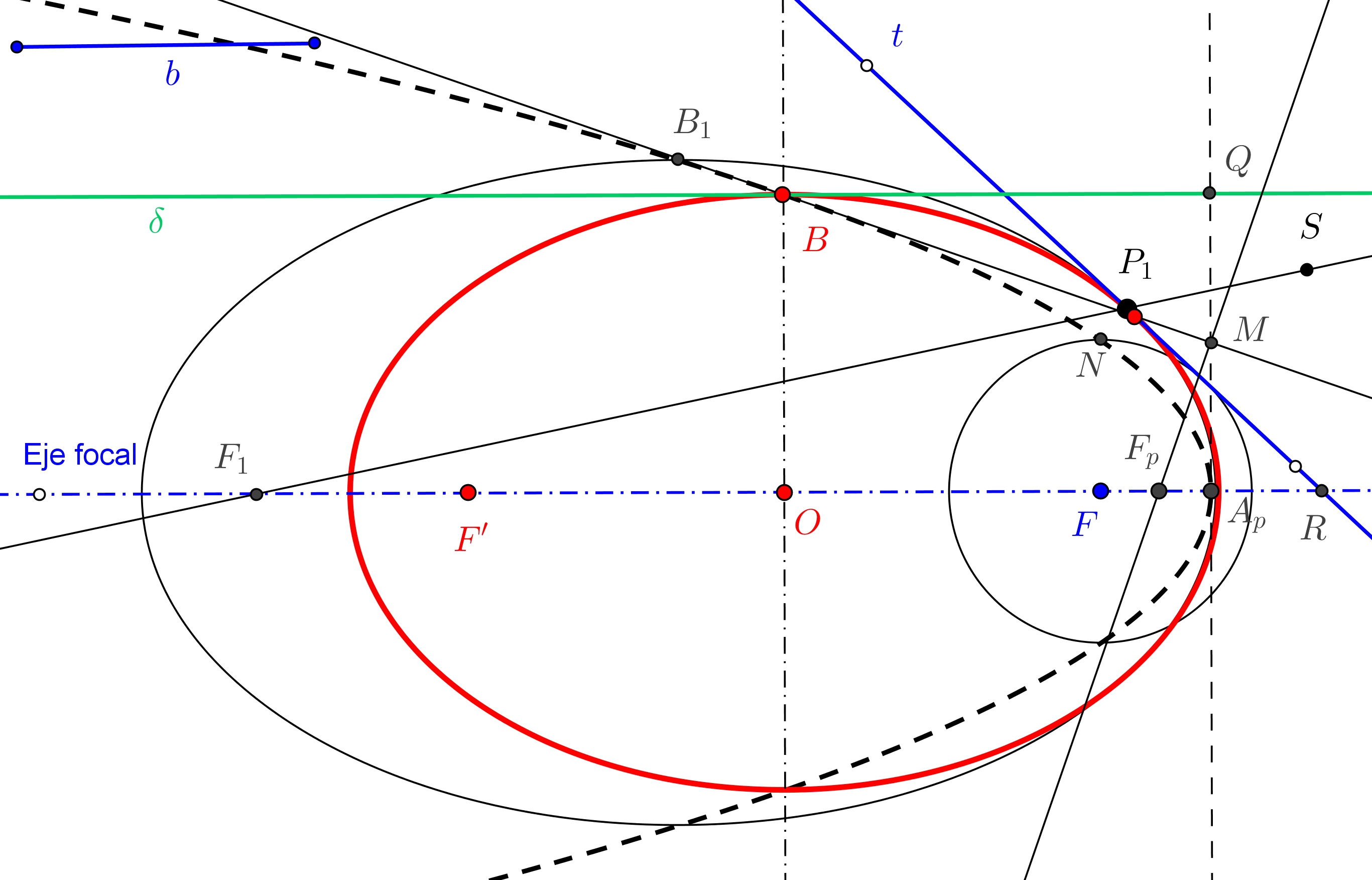
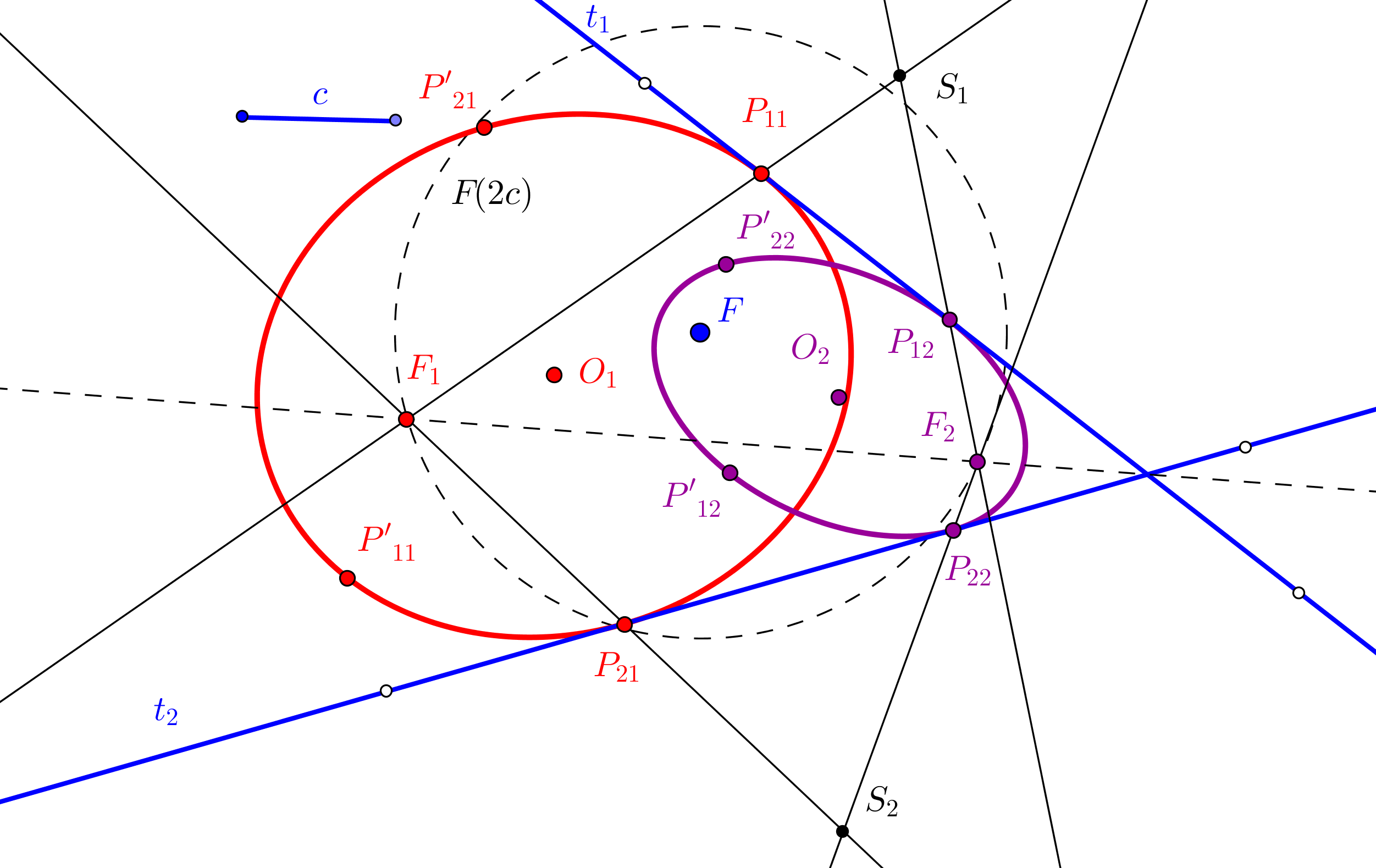
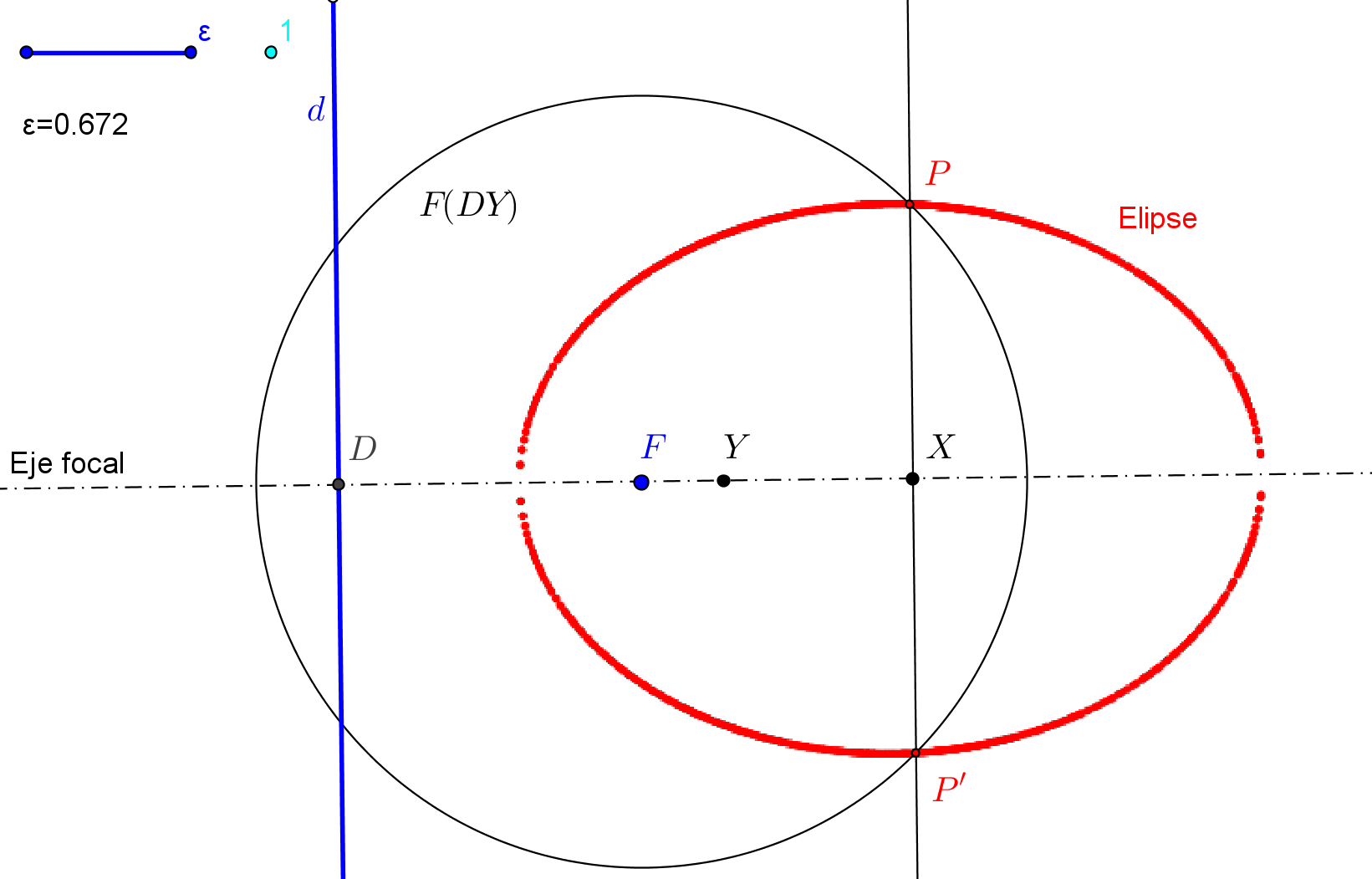
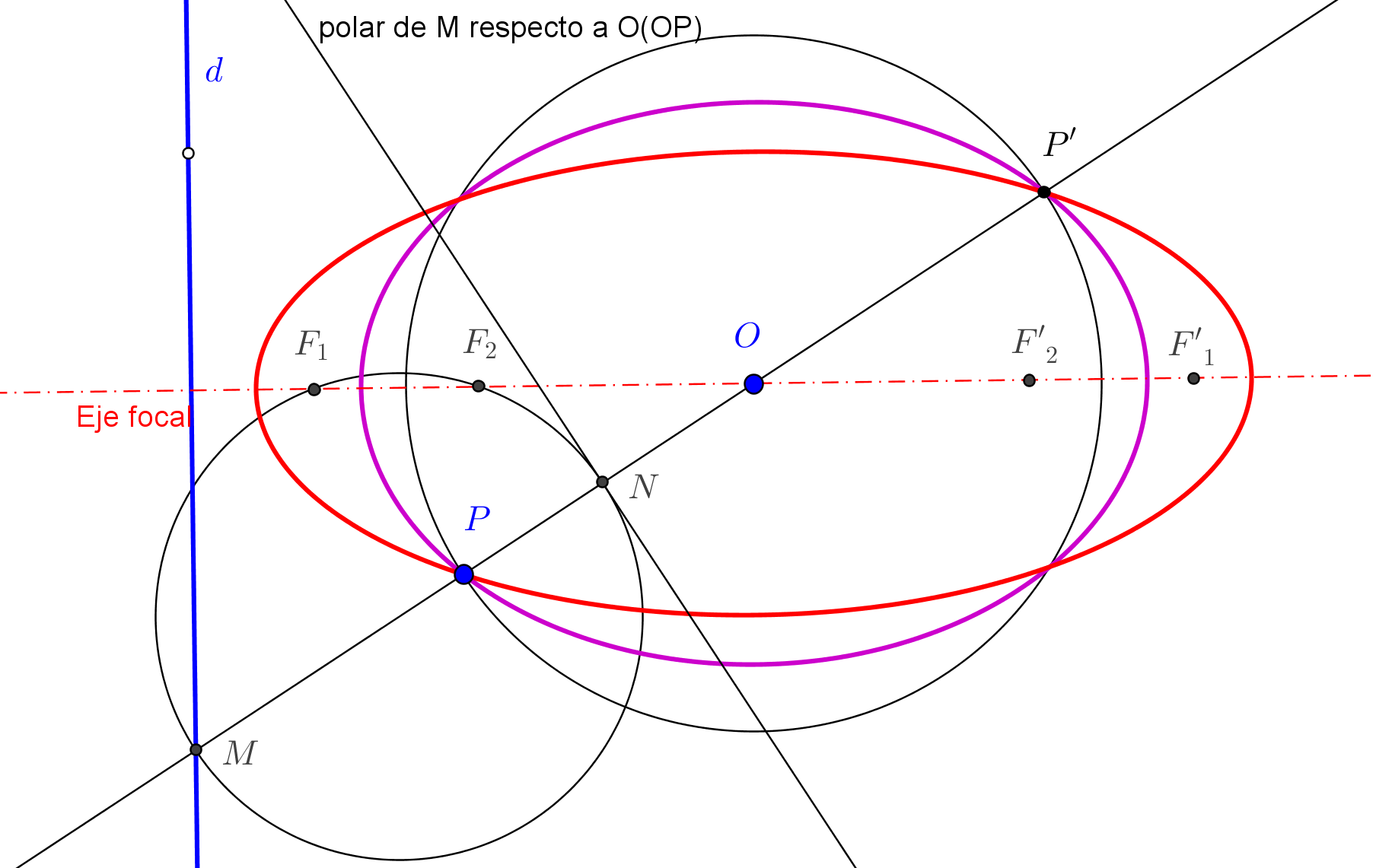
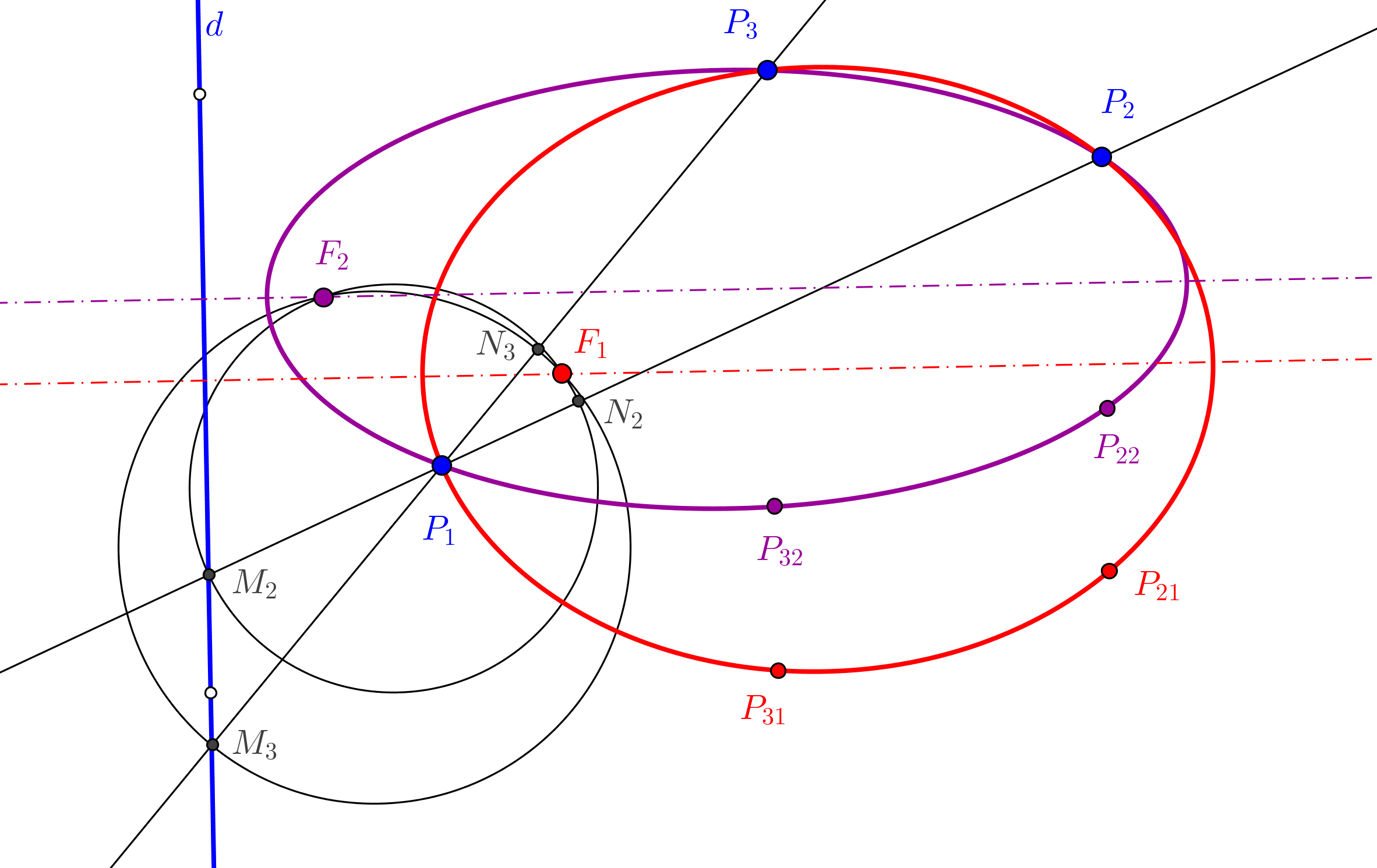
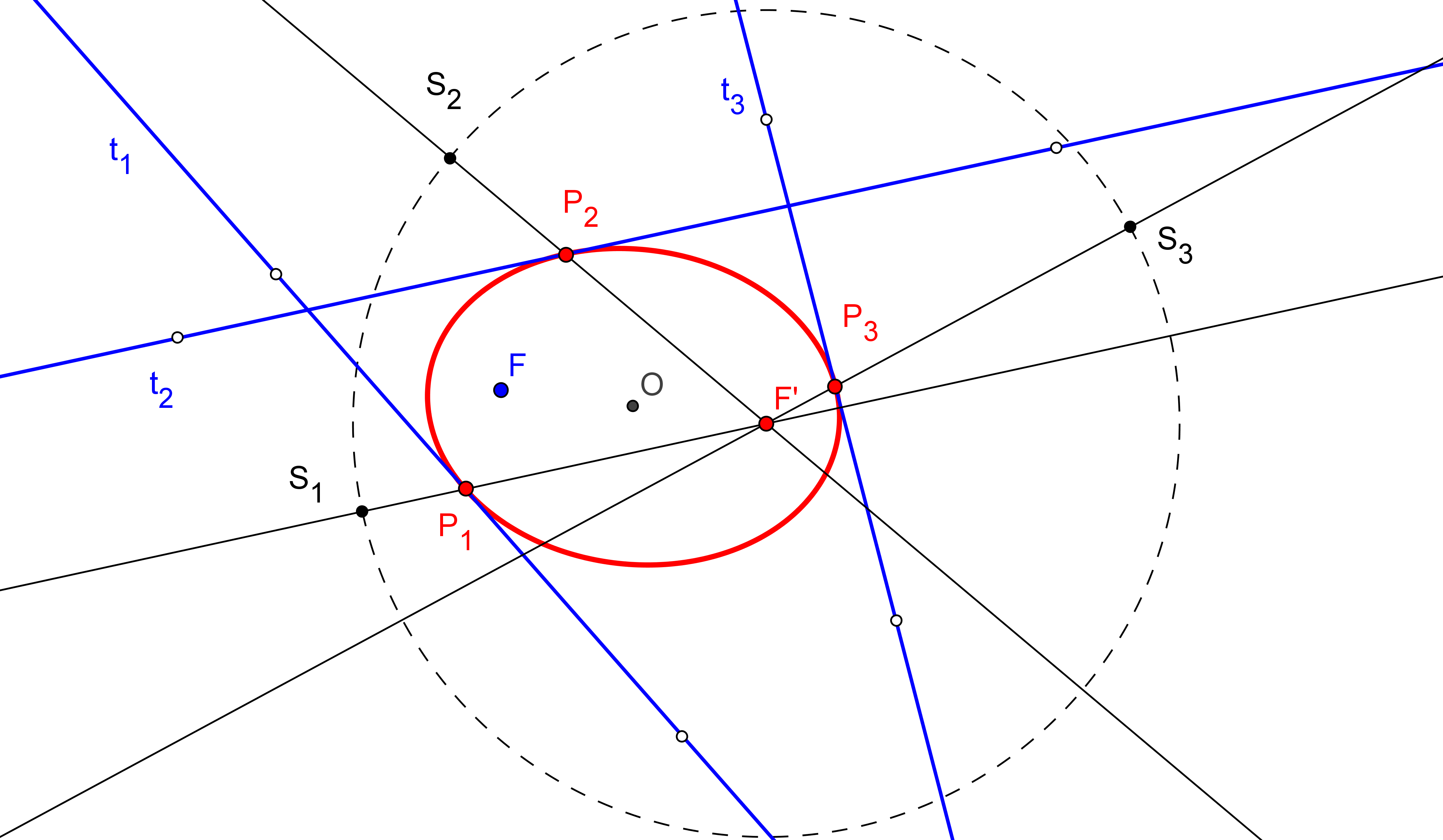
--- El foco ha de estar en la circunferencia Γ de centro P y tangente a la directriz dada d.
--- Además, el simétrico del foco, respecto a la tangente t, ha de estar en la directriz d.
1. Trazamos la circunferencia Γ de centro en el punto P dado y que es tangente a d.
2. Hallamos la simétrica de Γ respecto a t. Sean S1 y S2 los puntos de intersección de Γ con la directriz d.
3. Determinamos los simétricos de los puntos S1 y S2, respecto a t. Los puntos obtenidos son los focos F1 y F2 de las parábolas buscadas.
--- Si la circunferencia Γ corta a la directriz d en dos puntos, existen dos parábolas; si d es tangente a Γ hay una sola parábola; y si d es exterior a Γ, no hay solución.
( Mostrar/Ocultar figura)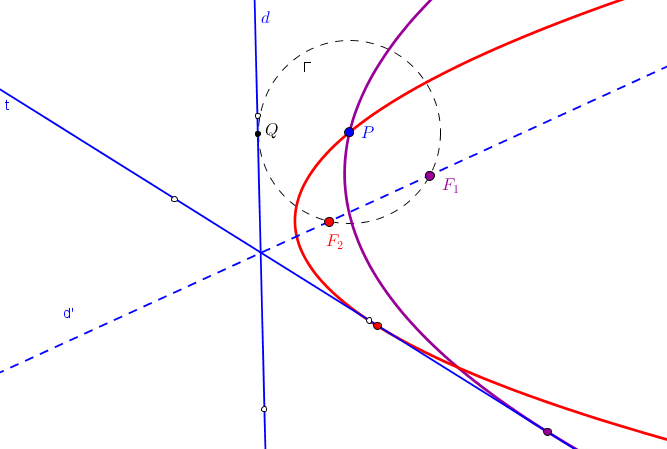
![]()
( Mostrar/Ocultar figura)
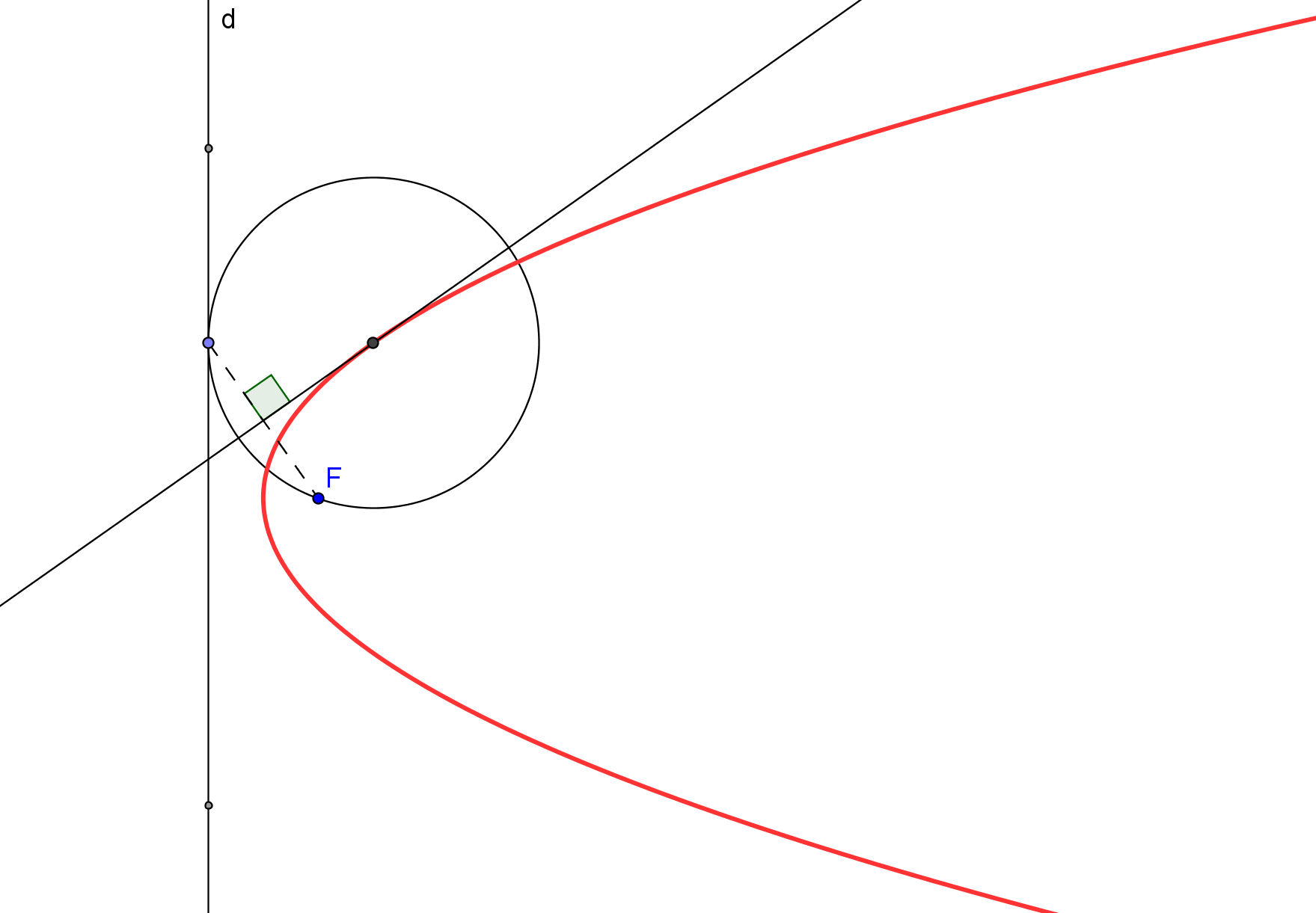
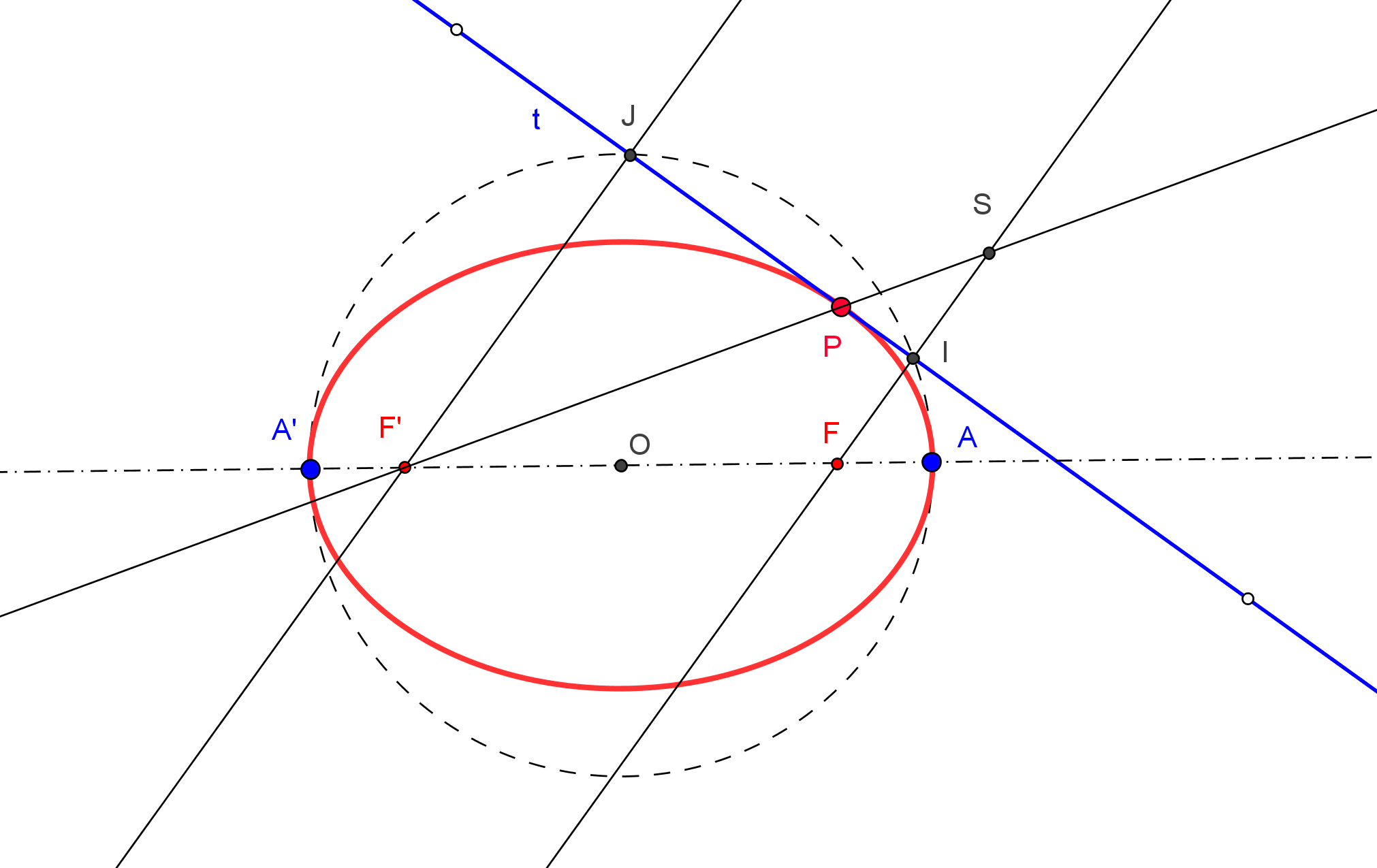
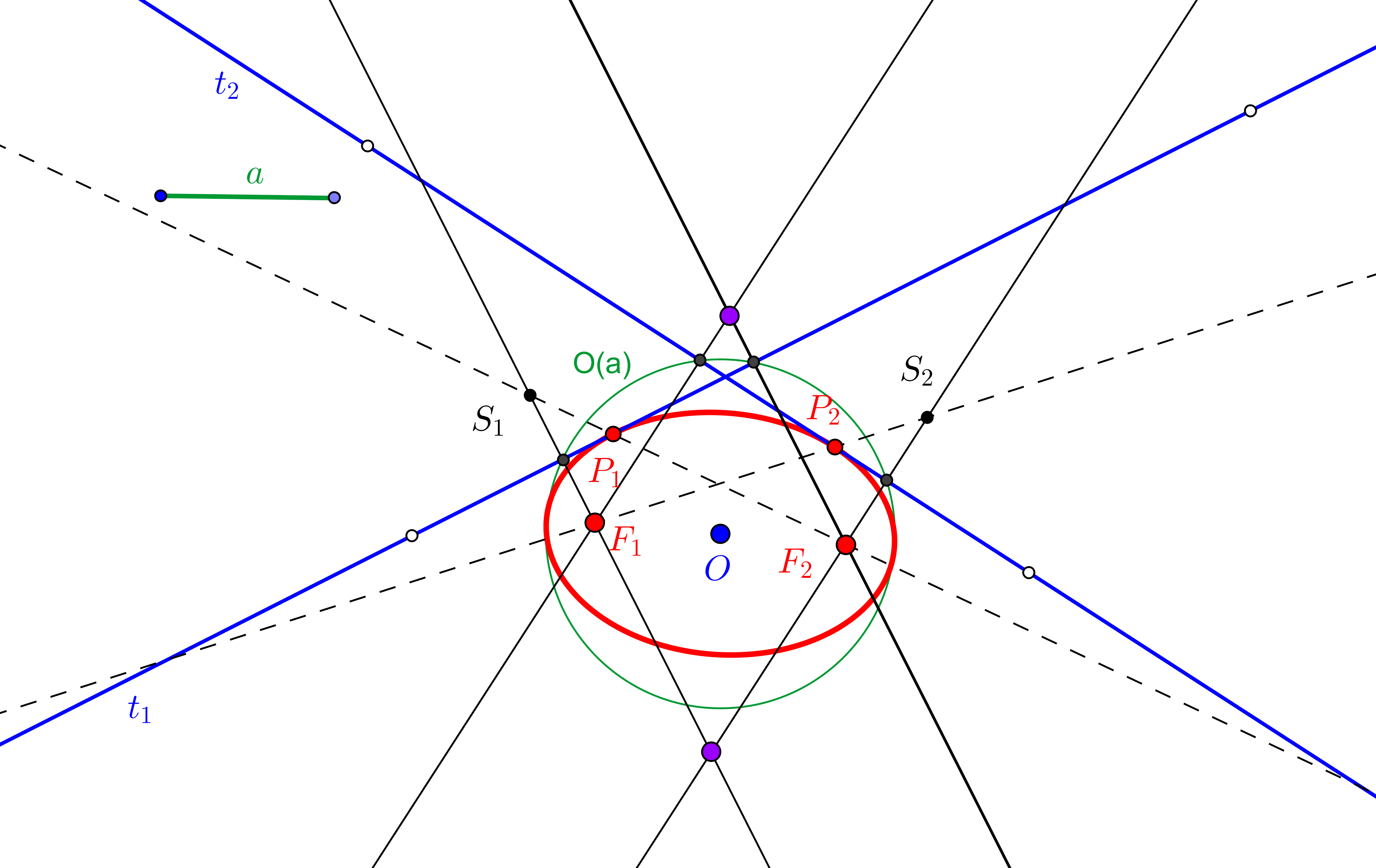
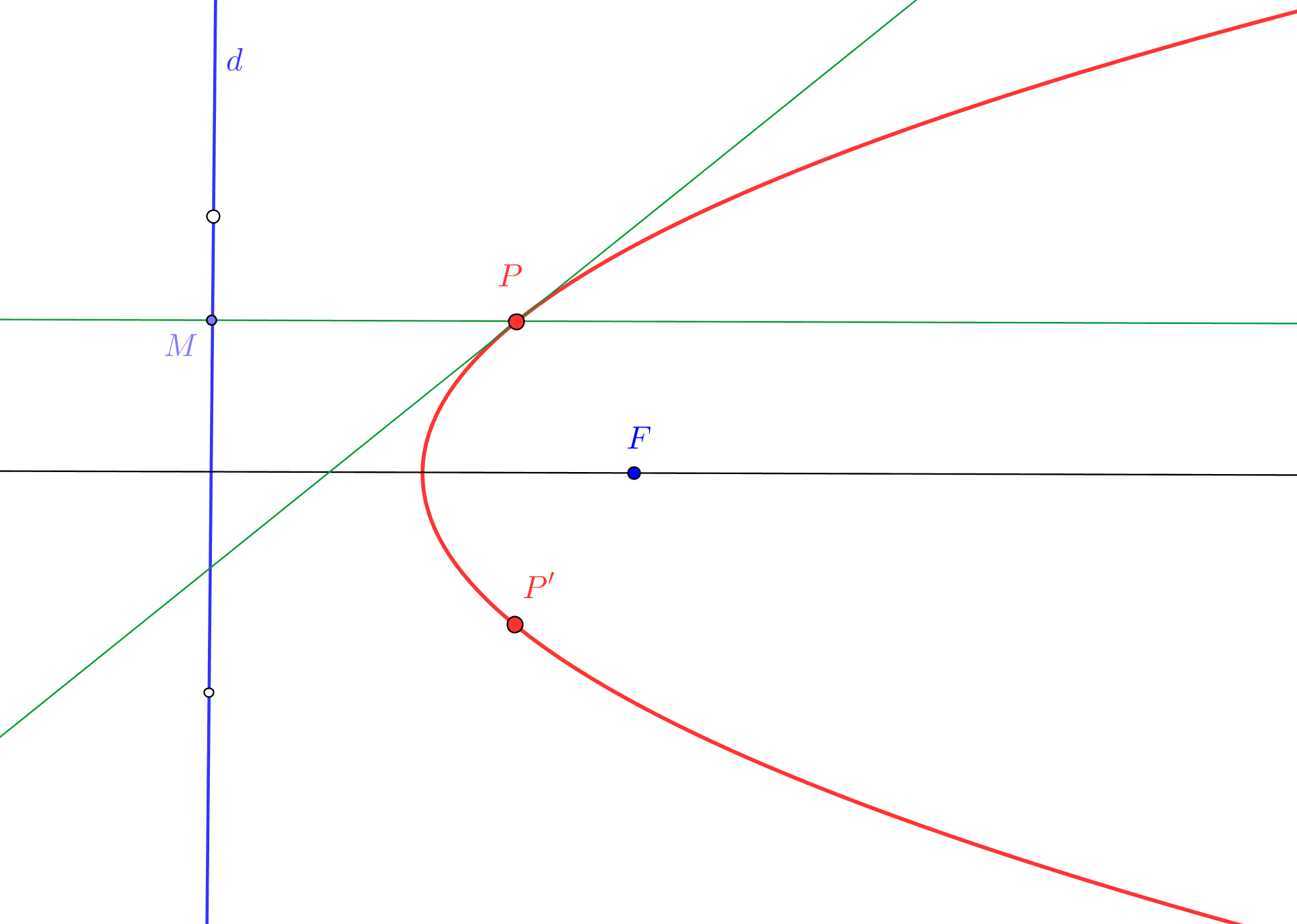
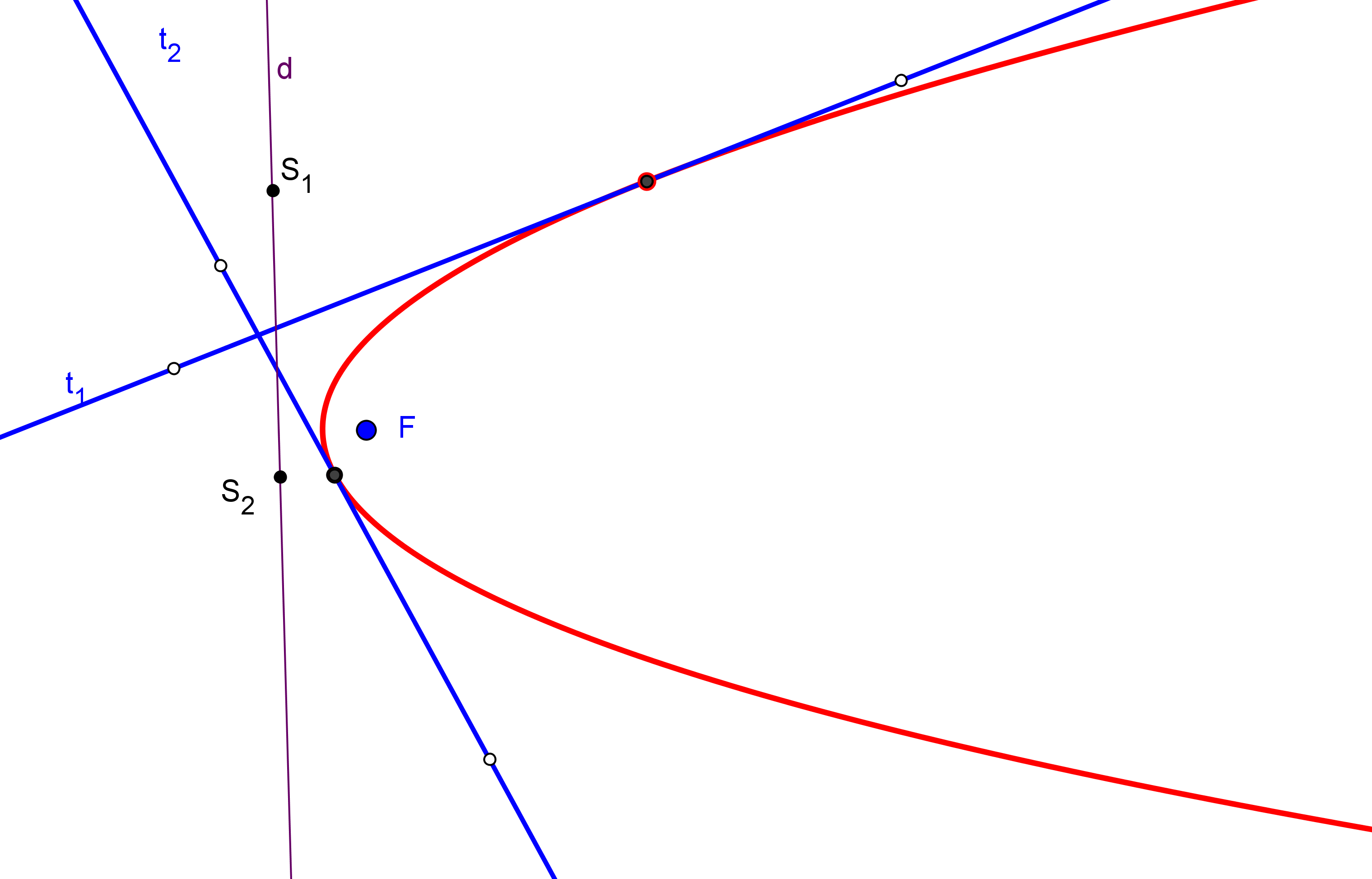
--- Usaremos que, en parábola, el simétrico del foco, respecto a una tangente, queda en la directriz.
--- Así, la recta simétrica de la directriz, respecto a una tangente, pasa por el foco.
1. Trazamos las simétricas de la directriz d, respecto a cada una de las tangentes dadas t1 y t>sub>2; ambas se cortan en el foco F.
2. Se conoce el foco F y la directriz d y podemos proceder como en el caso "Parábola dado el foco y la directriz".
( Mostrar/Ocultar figura)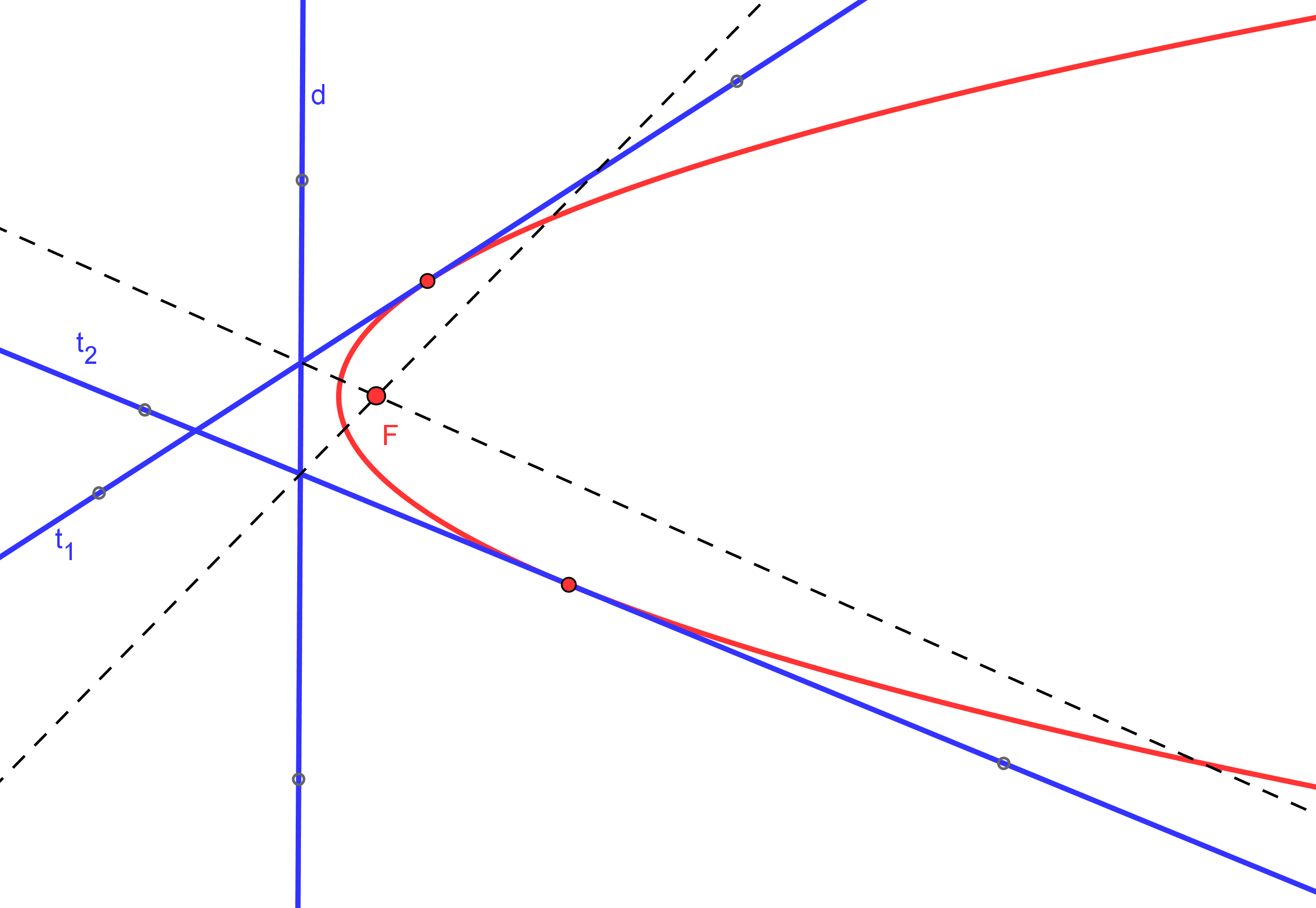
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
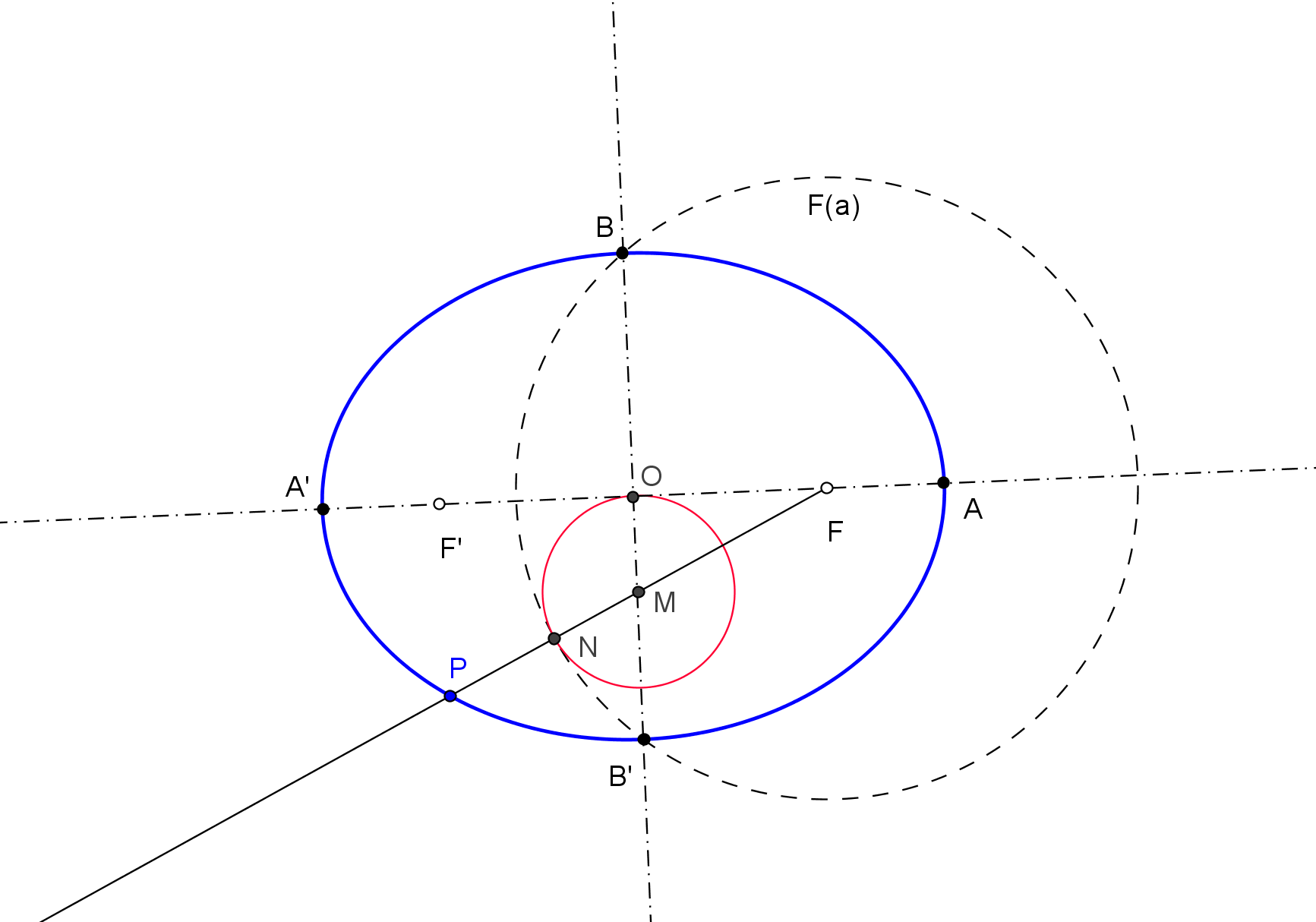
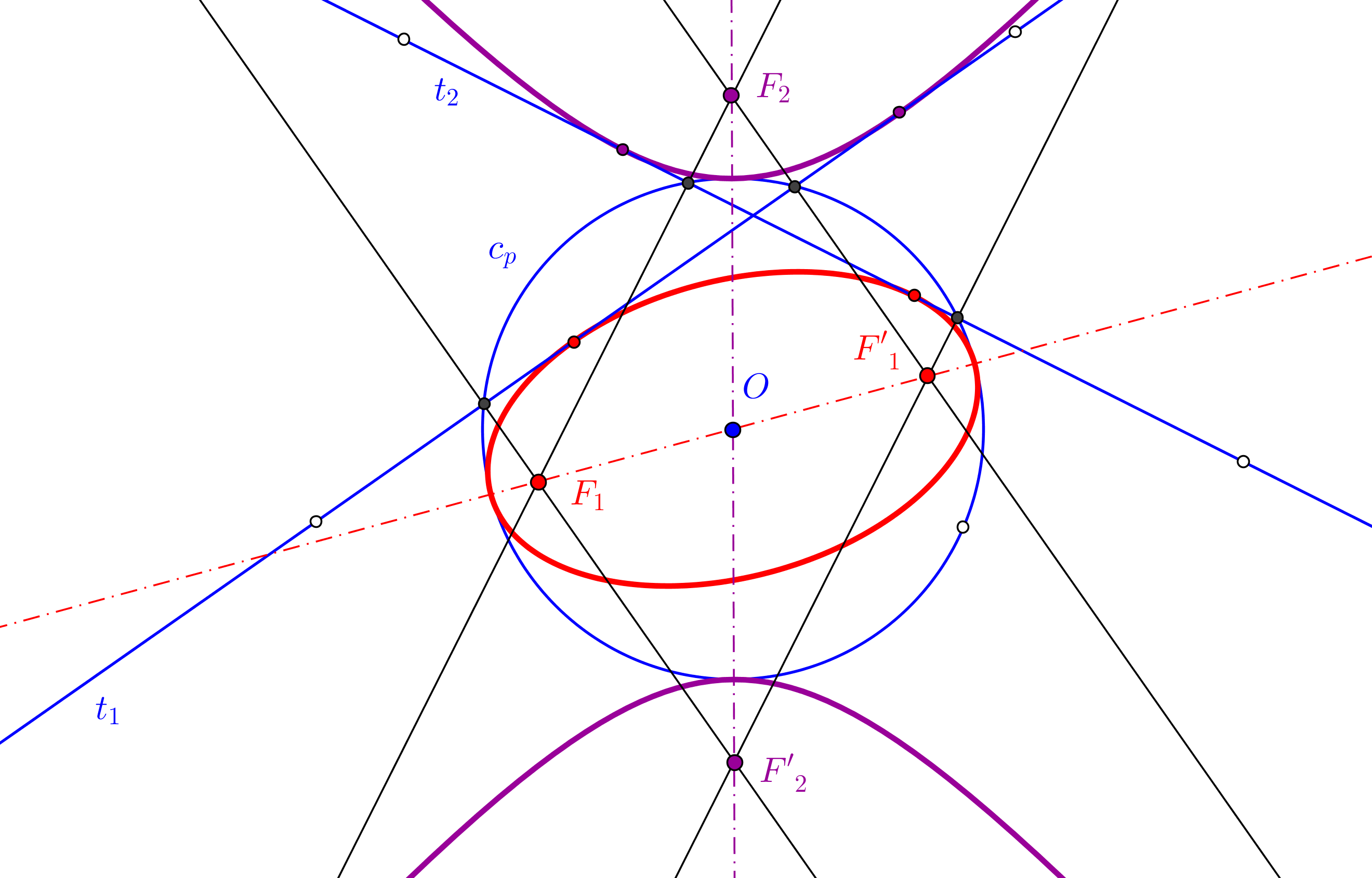
1. Se construyen los simétricos St y Sh de F, respeto a la tangente t y a la asíntota h, respectivamente.
2. El otro foco F' ha de estar en la mediatriz de StSh y también en la recta que pasa por Sh y por el punto de tangencia de la asíntota (en el infinito), es decir, en la paralela por Sh a la asíntota h.
3. El punto de intersección P de la tangente t con la recta StF' pertenece a la hipérbola.
( Mostrar/Ocultar figura)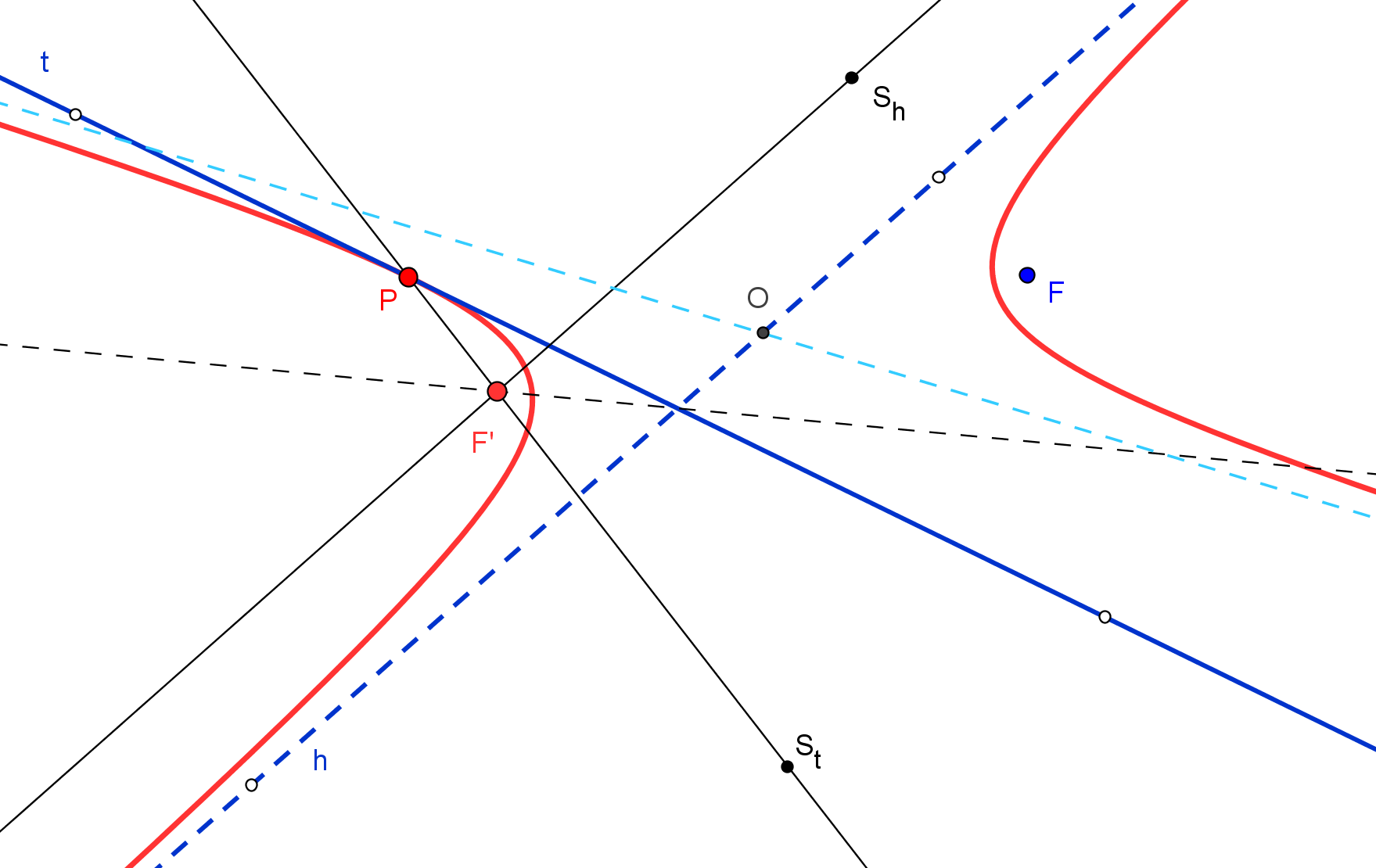
![]()
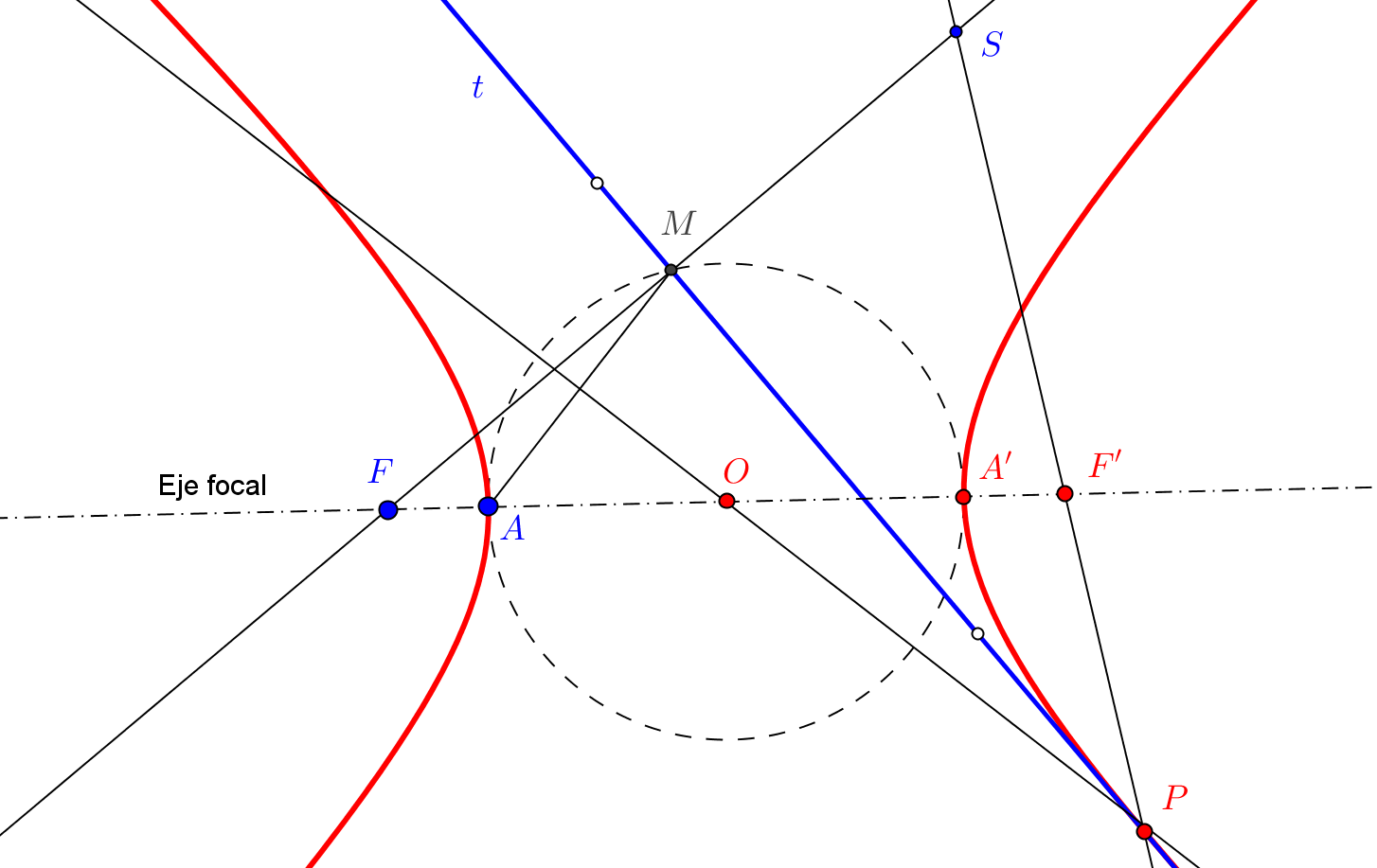
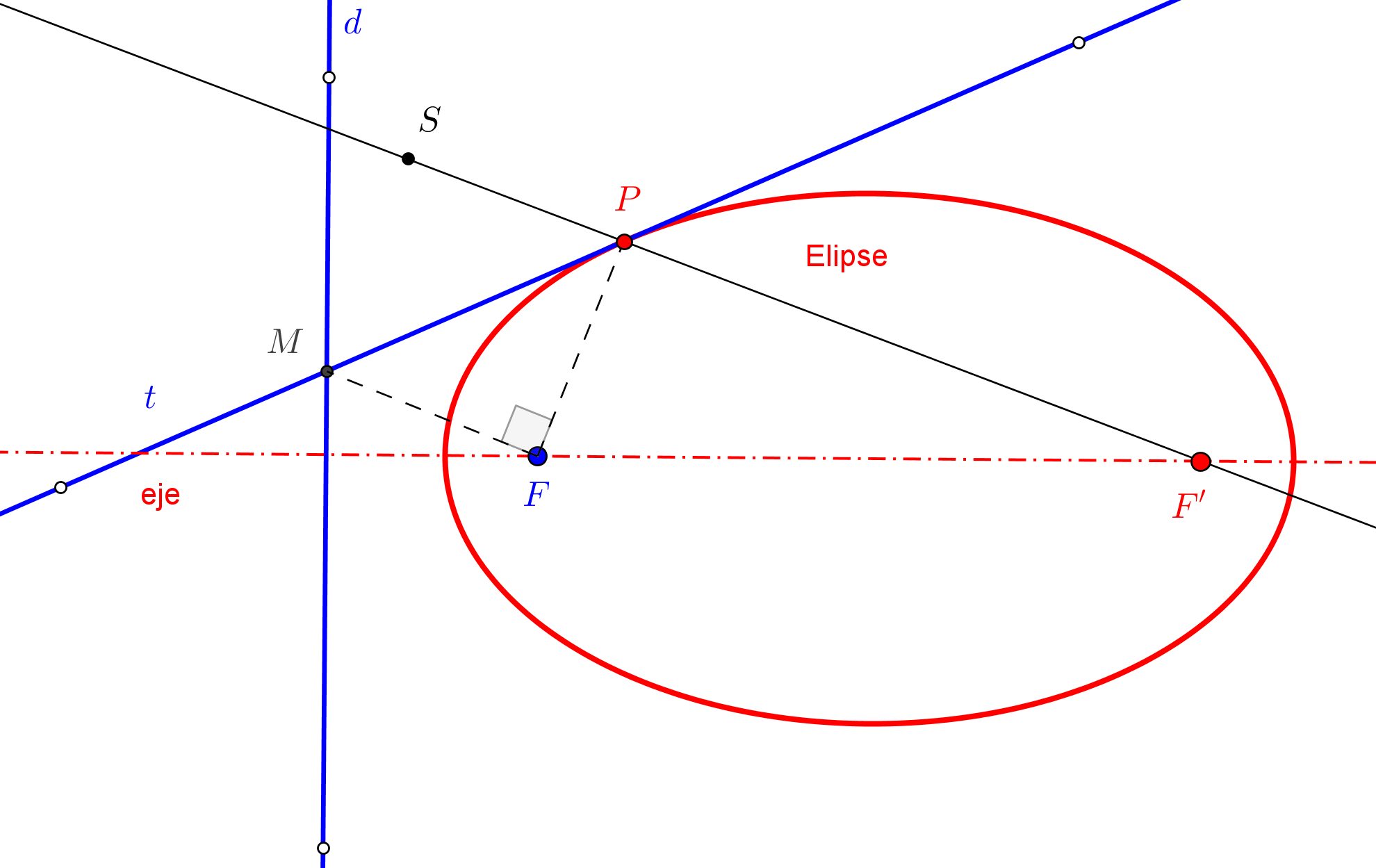
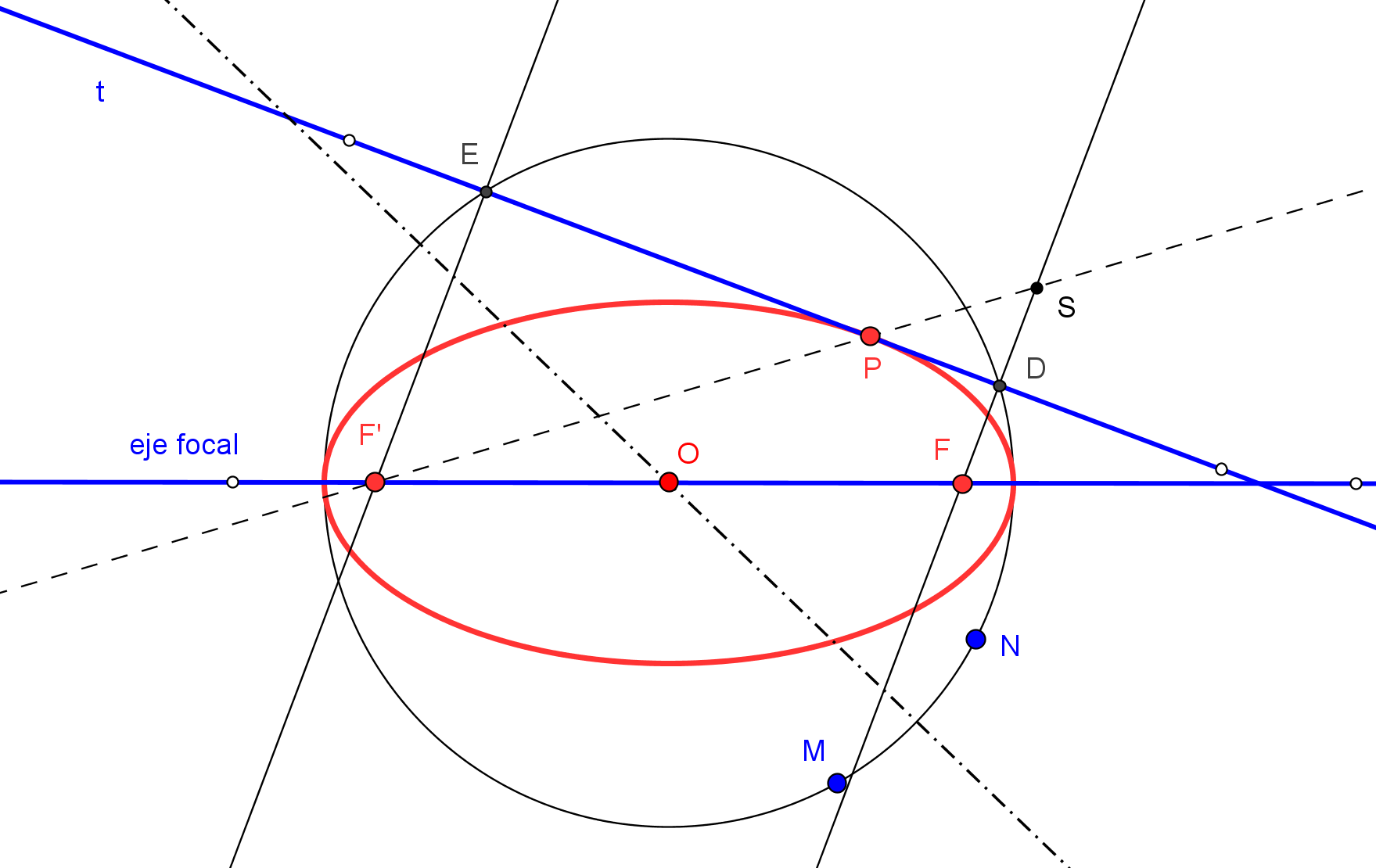
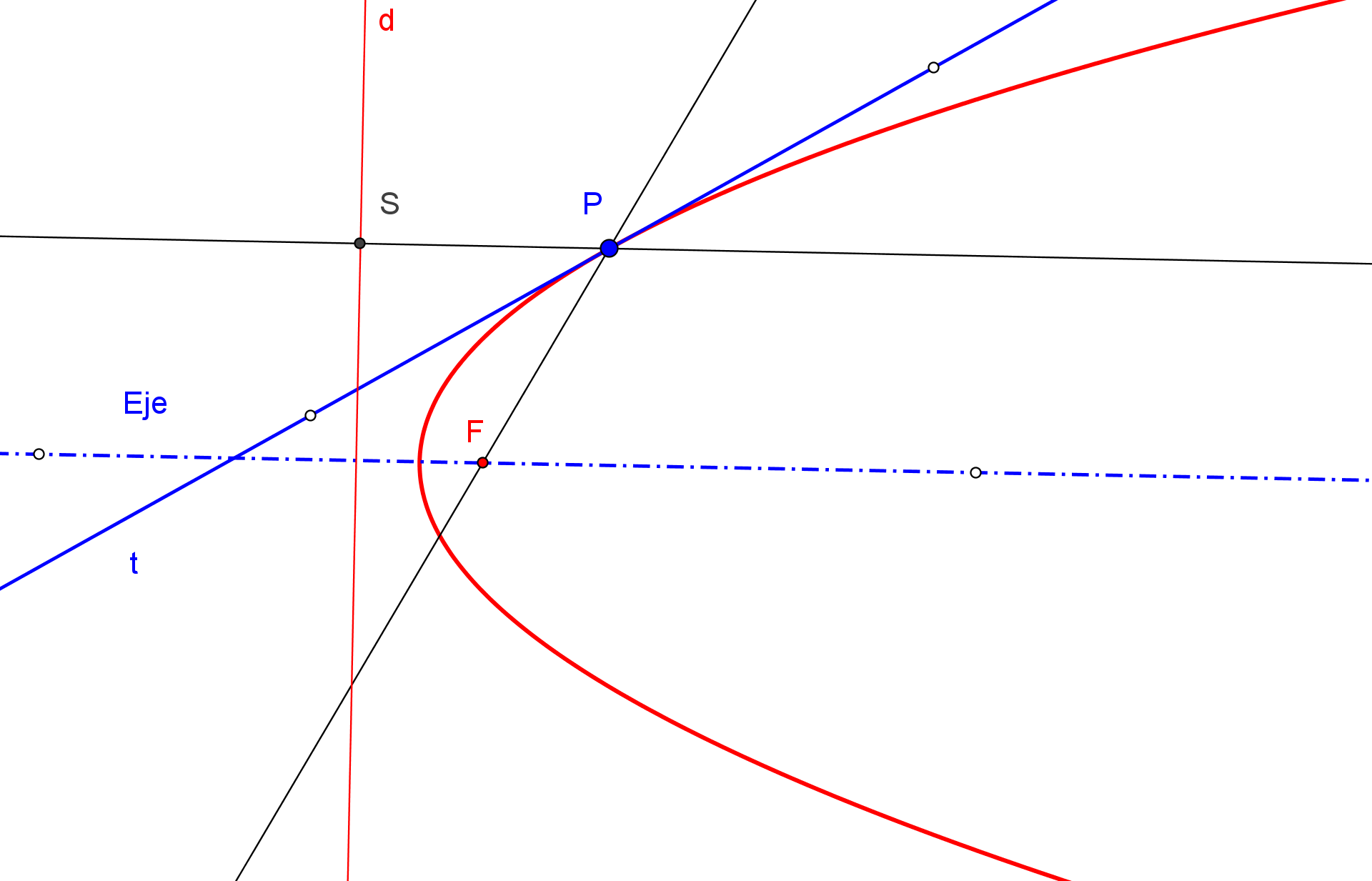
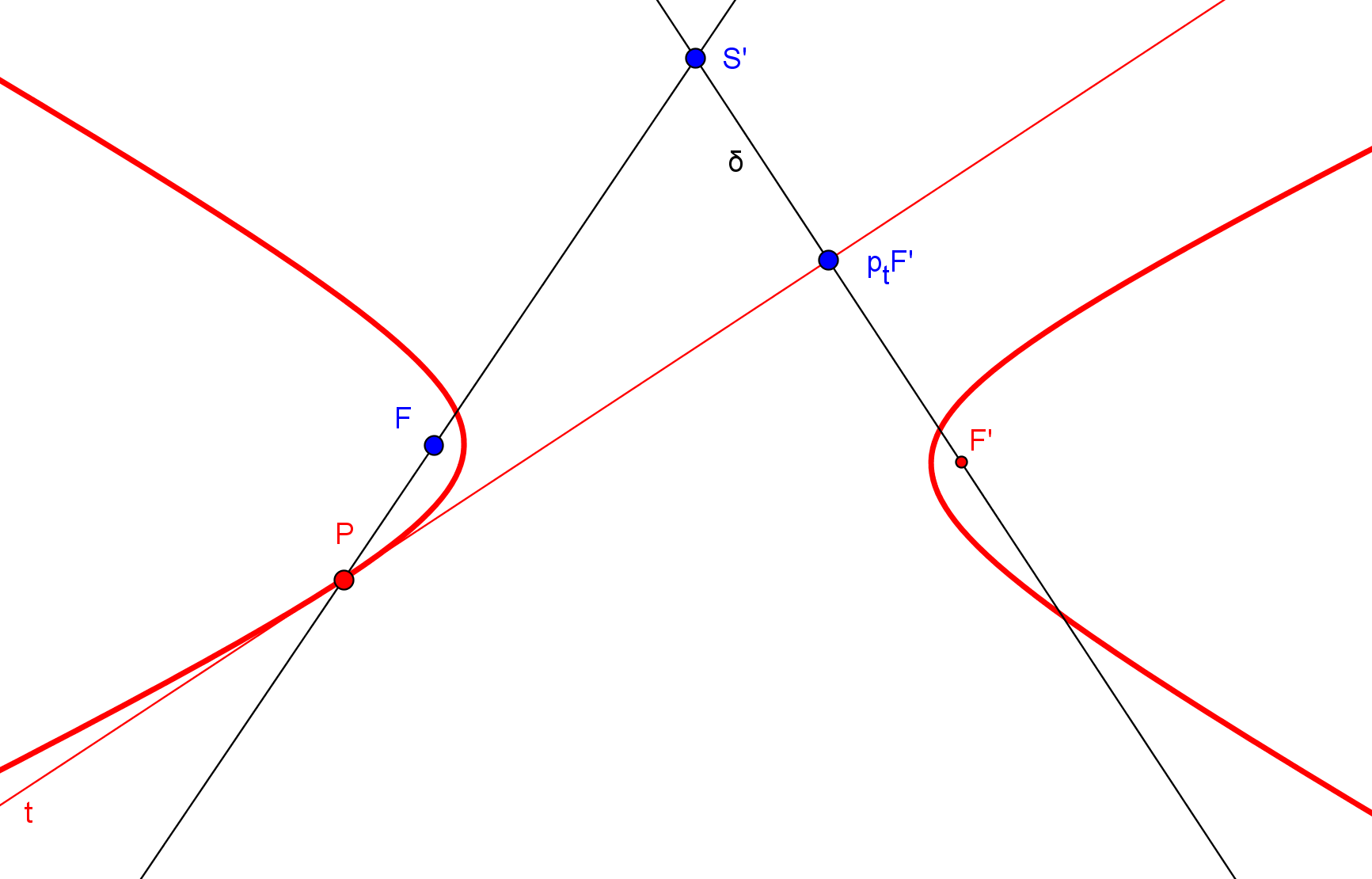
1. Se construye el simétrico S, respeto a la tangente t, de un foco F.
2. Trazamos la recta que pasa por S y el otro foco F'.
3. El punto de intersección P de la tangente t con la recta SF' pertenece a la cónica.
( Mostrar/Ocultar figura)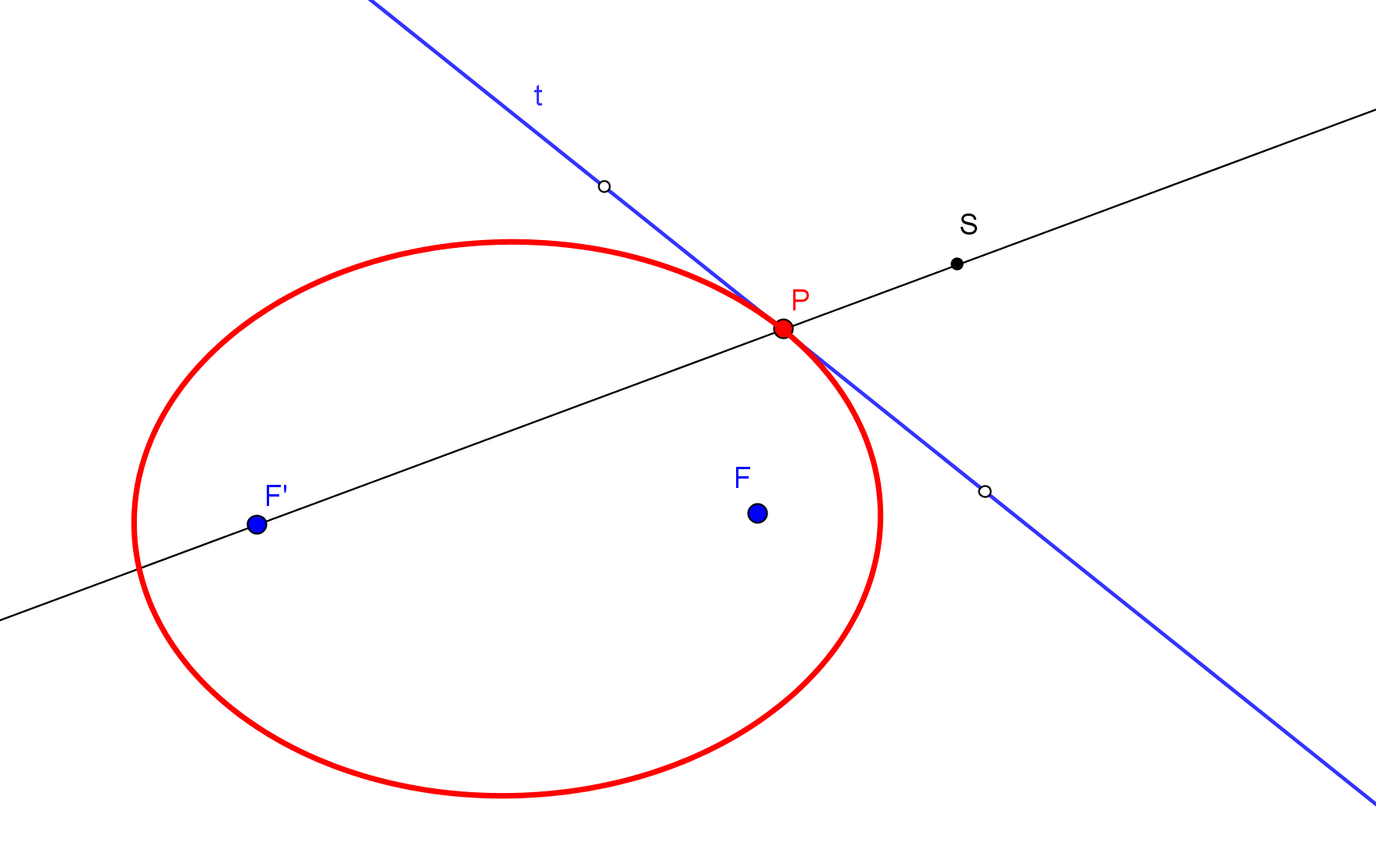
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
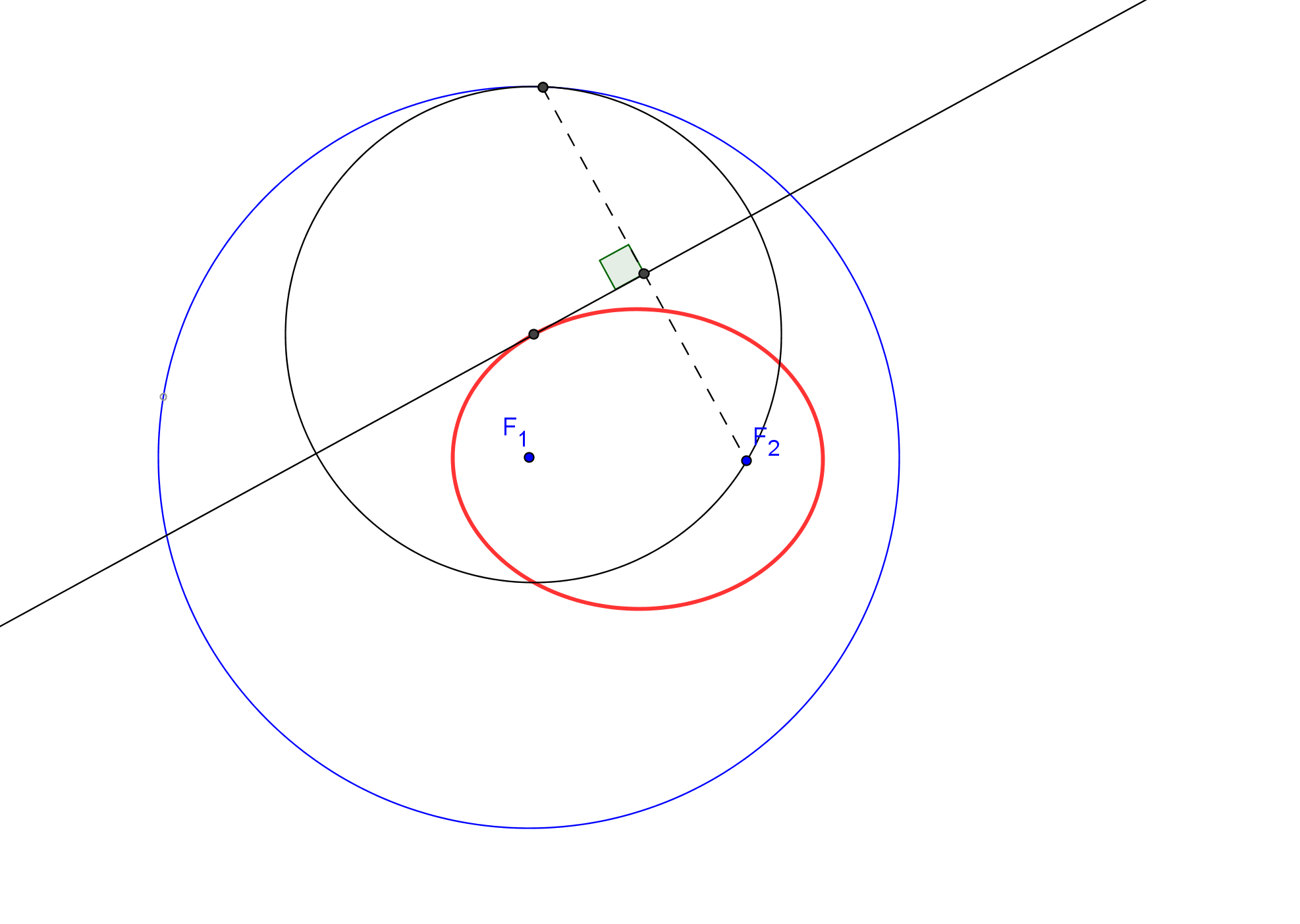
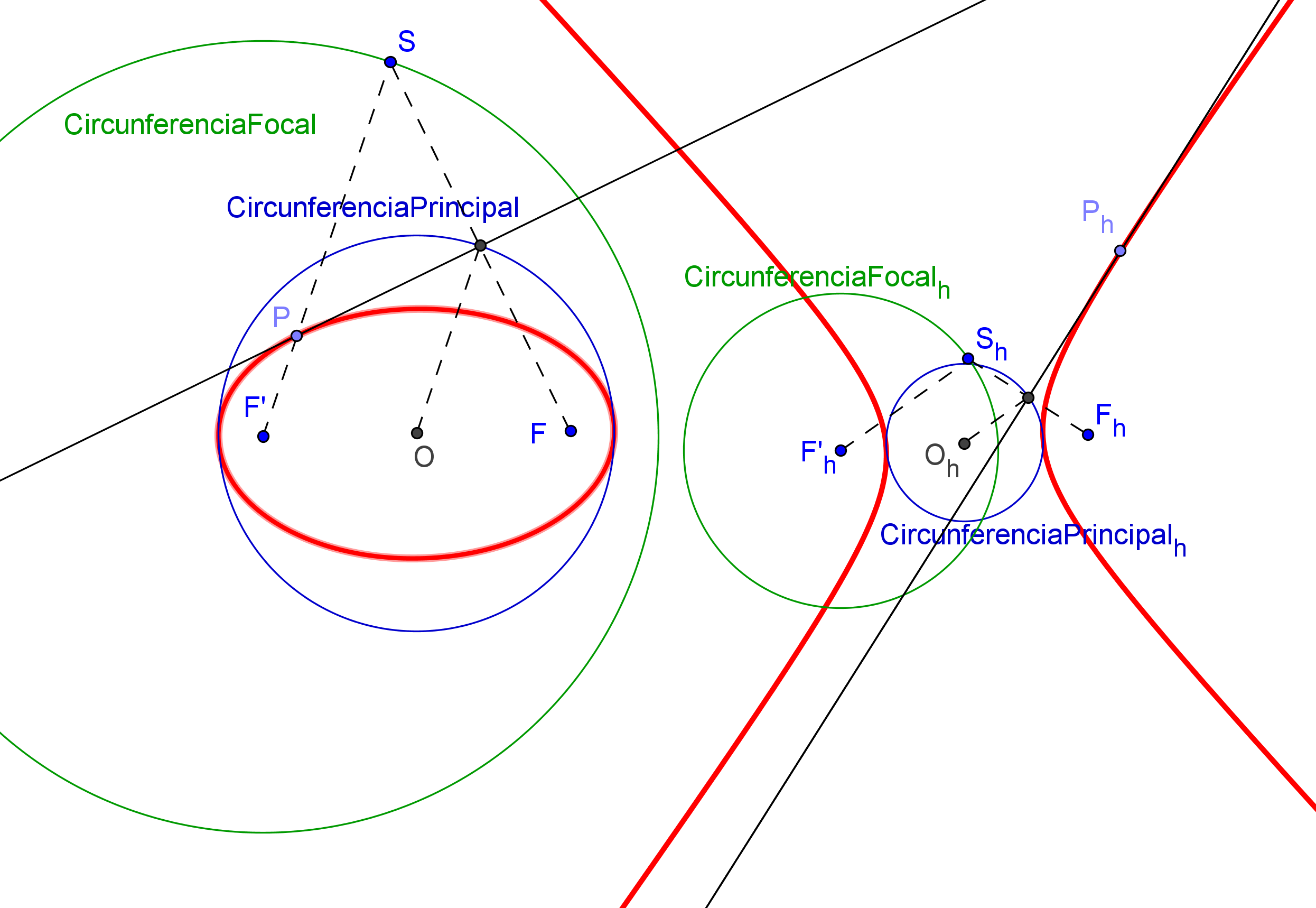
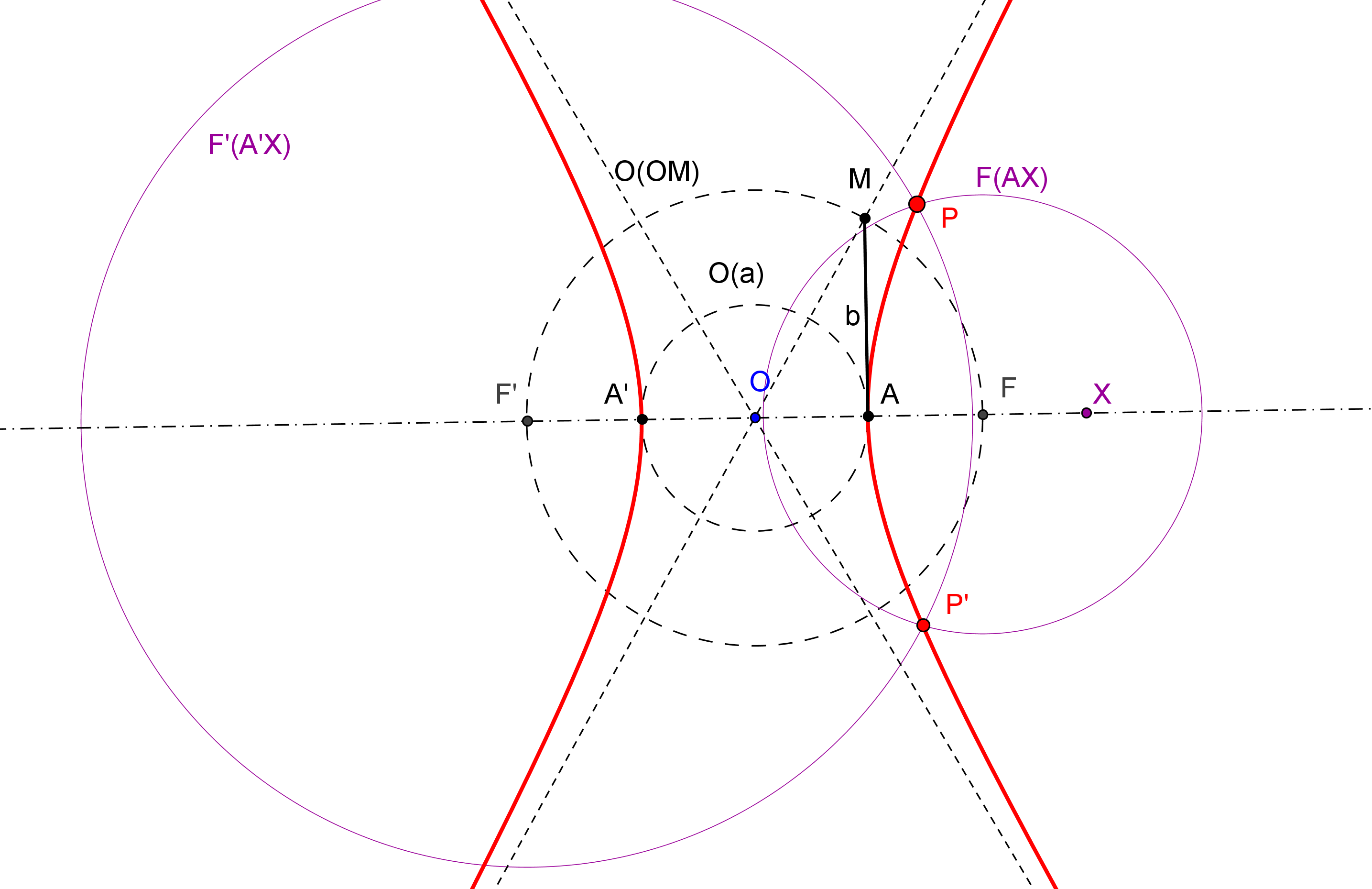
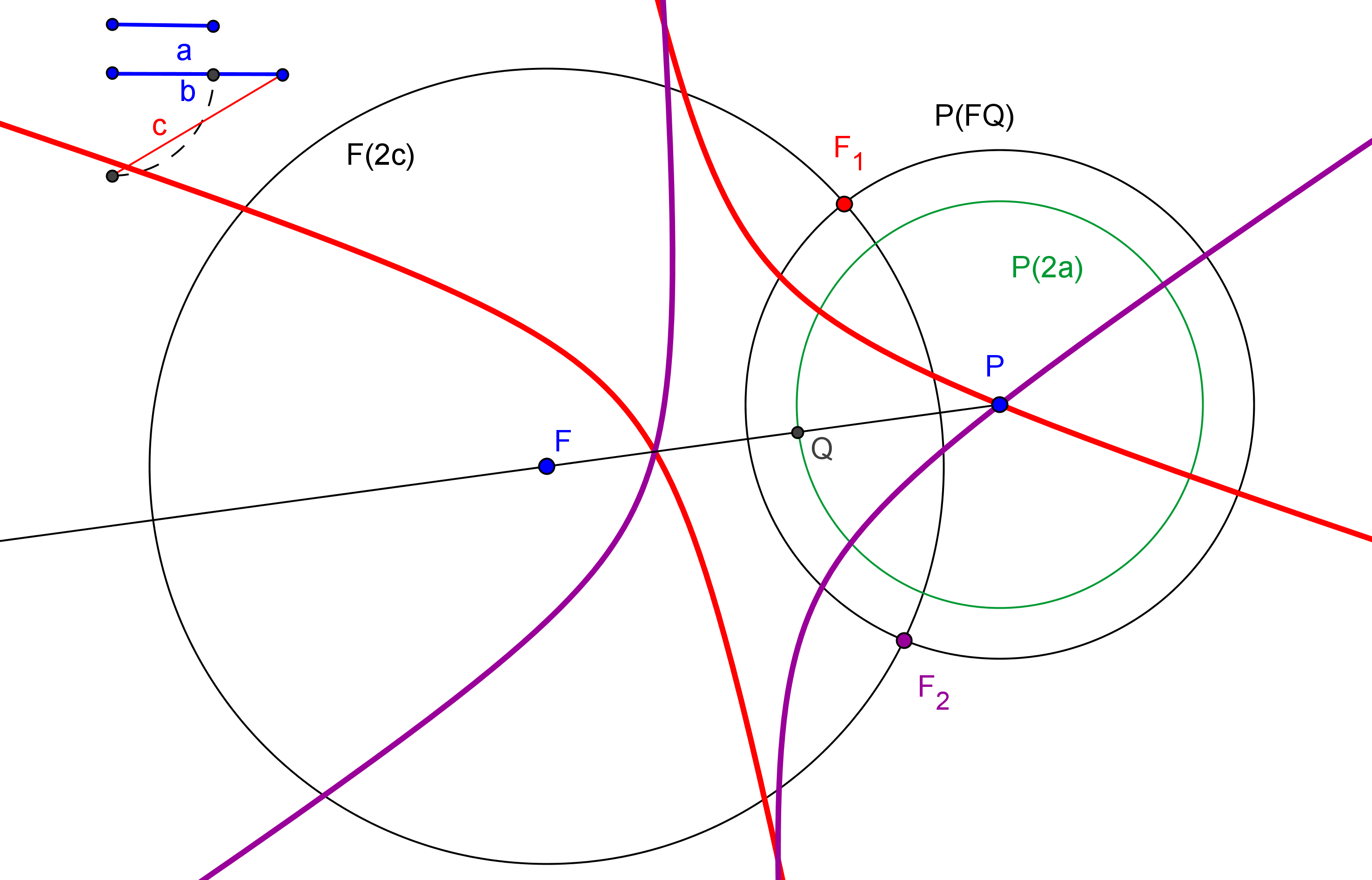
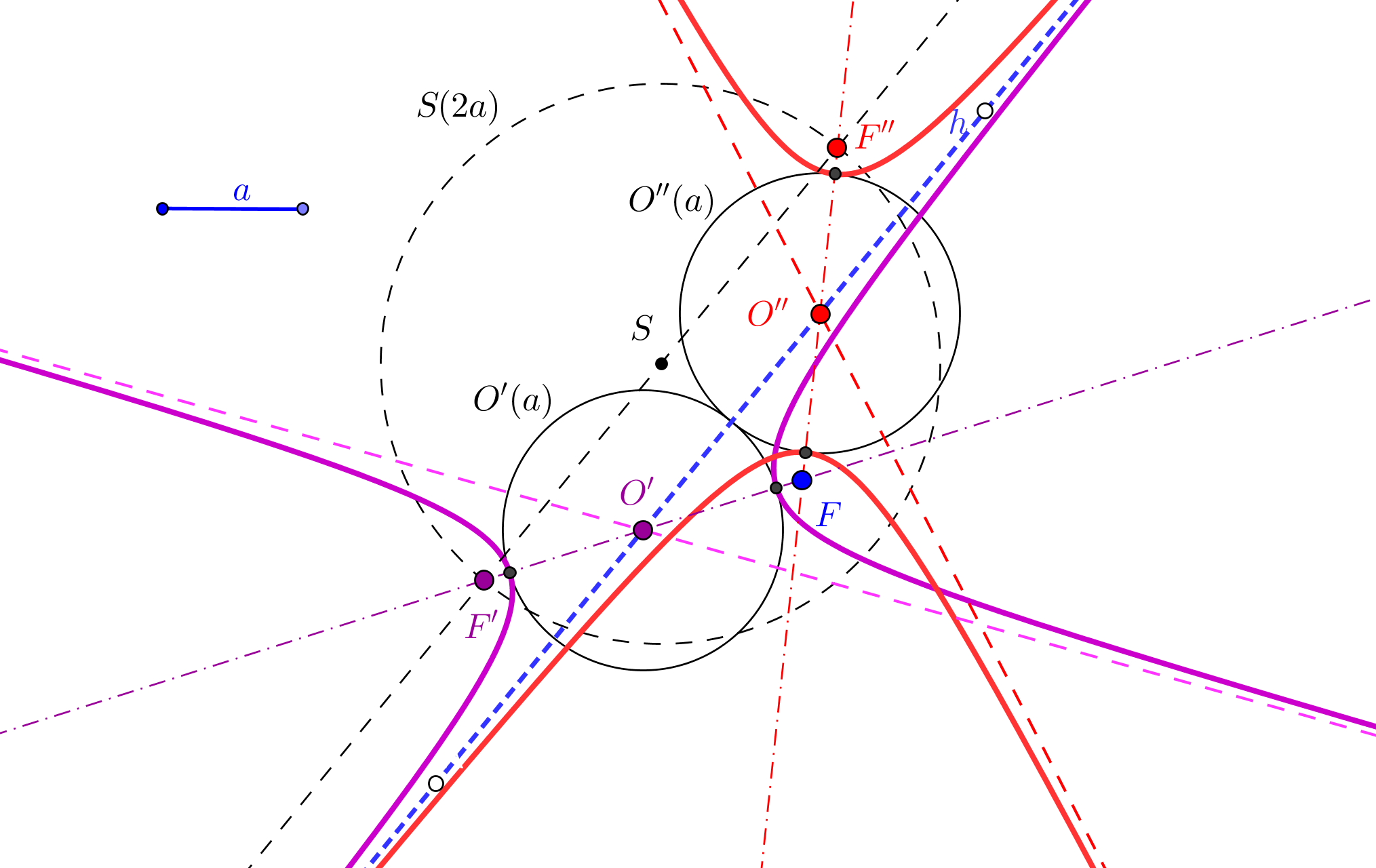
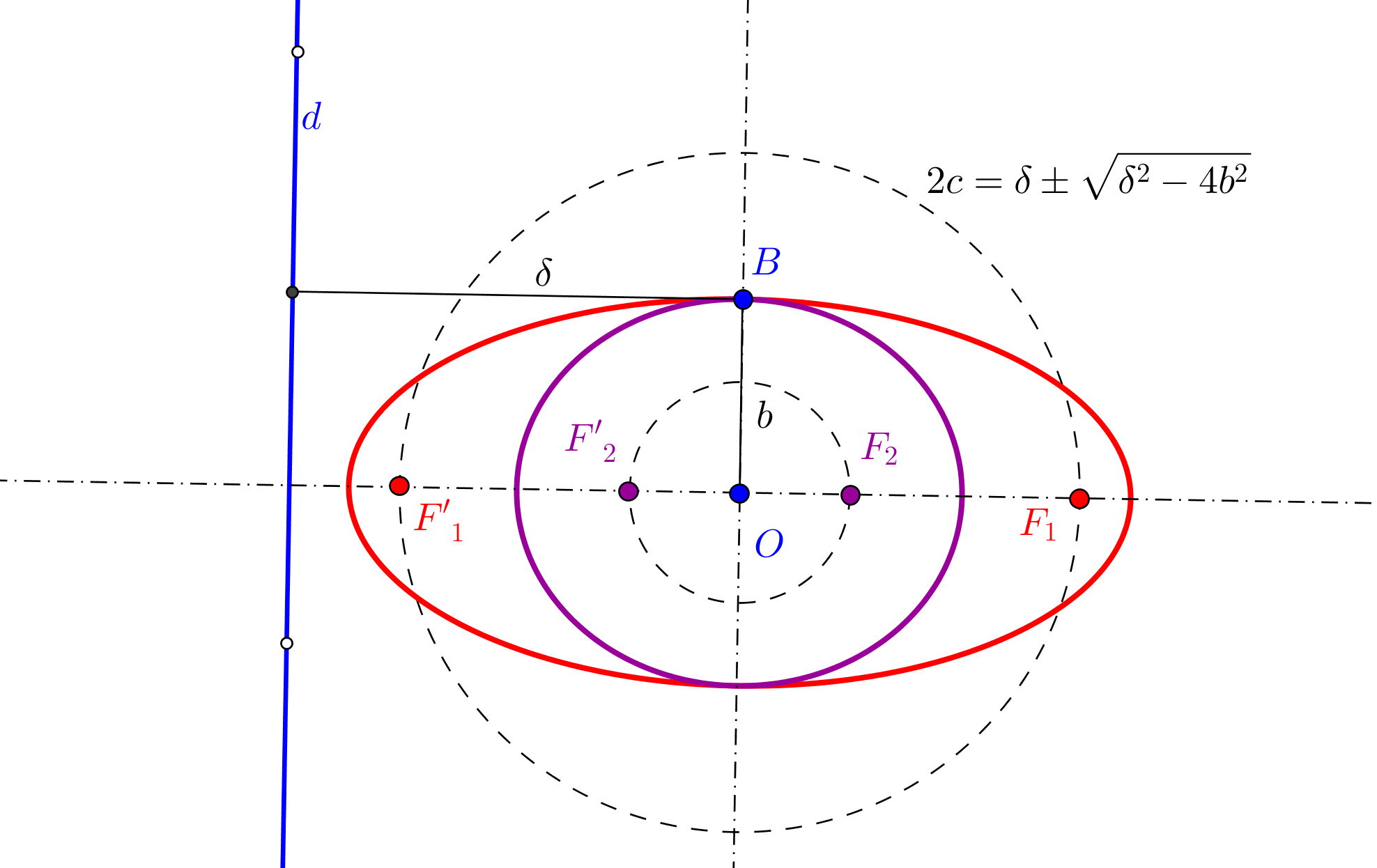
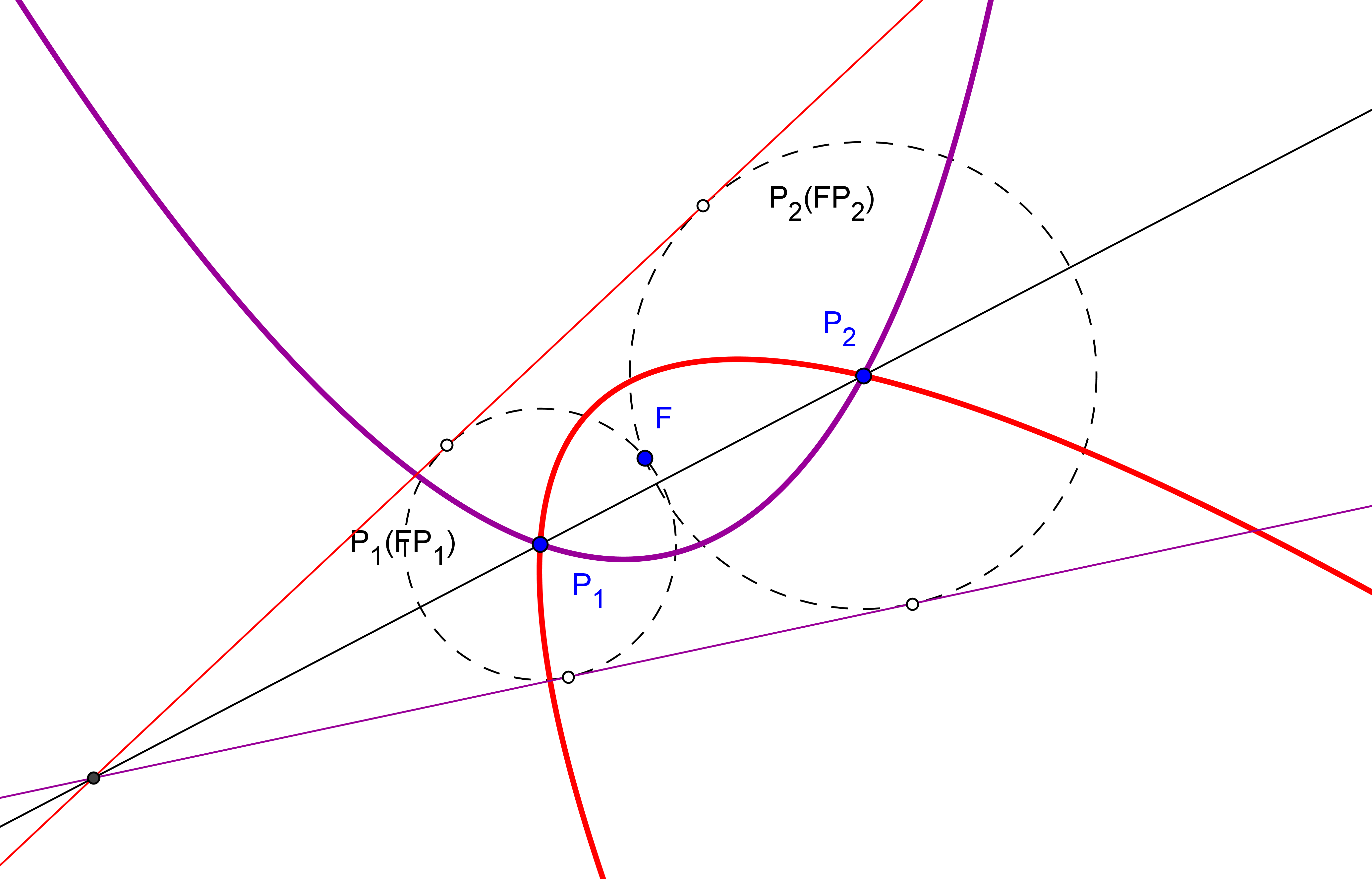
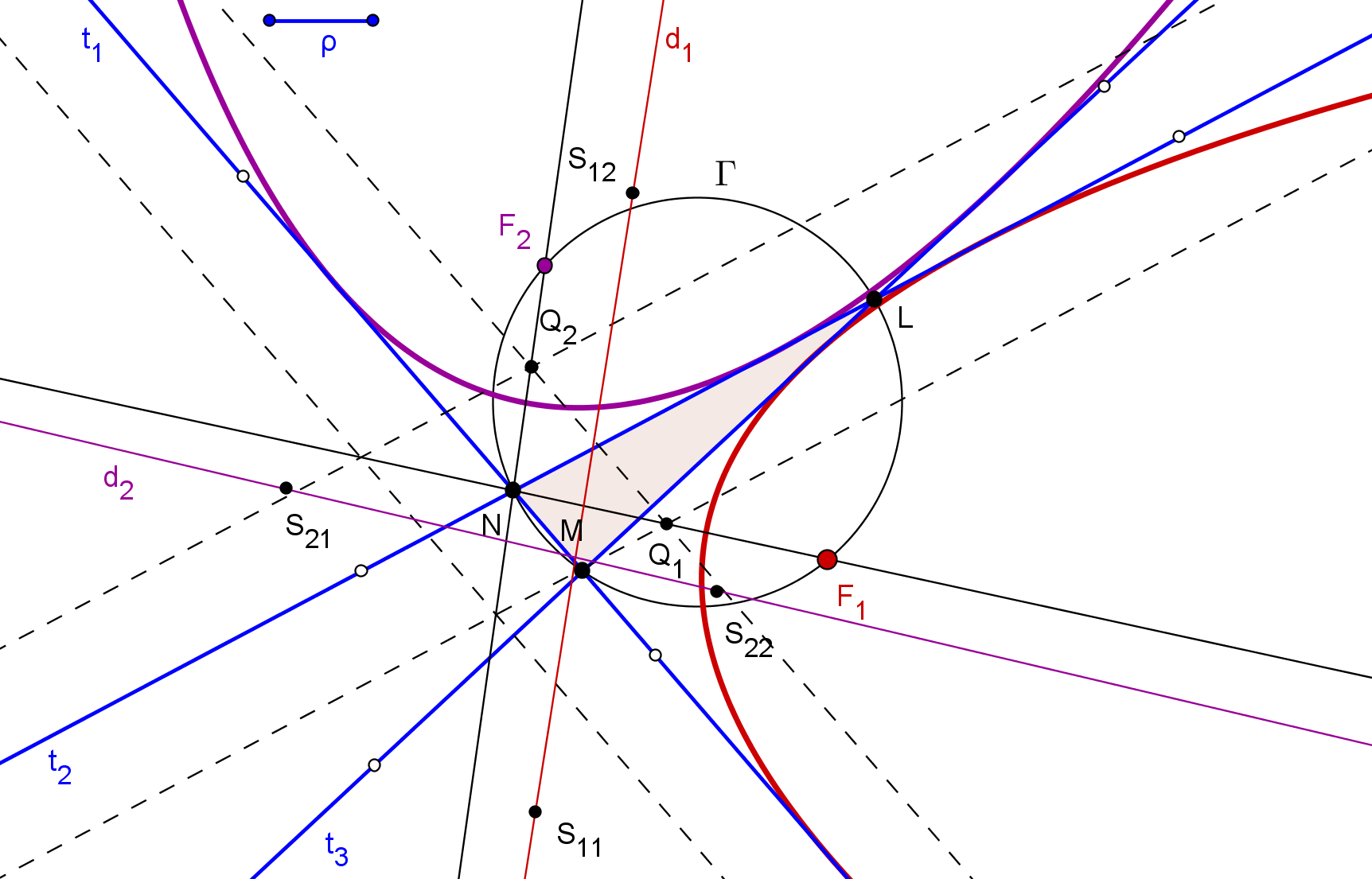
-- Las circunferencias P1(P1F) y P2(P2F), de centros P1 y P2, respectivamente, y que pasa por el foco F, son tangentes a la circunferencia focal relativa al otro foco, que pasa por el punto simétrico del foco F respecto a la tangente dada t.
1. Se construyen los simétrico S, respeto a la tangente t, del foco dado F.
2.
Se traza cada una de las circunferencias que pasan por S y son tangentes a las circunferencias P1(P1F) y P2(P2F) (Problema de Apolonio Pcc: Circunferencia que pasa por un punto y es tangente a dos circunferencias. ![]() ). El centro de cada una es el otro foco de la cónica pedida.
). El centro de cada una es el otro foco de la cónica pedida.
-- Si las circunferencias P1(P1F) y P2(P2F) son ambas exteriores a una de la circunferencia obtenida, la cónica de focos en F y en el cento de esta circunferencia, y que pasa por P1 (también por P2), es una hipérbola.
-- Si las circunferencias P1(P1F) y P2(P2F) son ambas interiores a una de la circunferencia obtenida, la cónica de focos en F y en el cento de esta circunferencia, y que pasa por P1 (también por P2), es una elipse.
3. La cónica buscada será parábola cuando una recta tangente común a las circunferencias P1(P1F) y P2(P2F) pasa por S, dejando estas dos circunferencias en un mismo semiplano respecto a tal tangente común (que es la directriz de la parábola).
( Mostrar/Ocultar figura)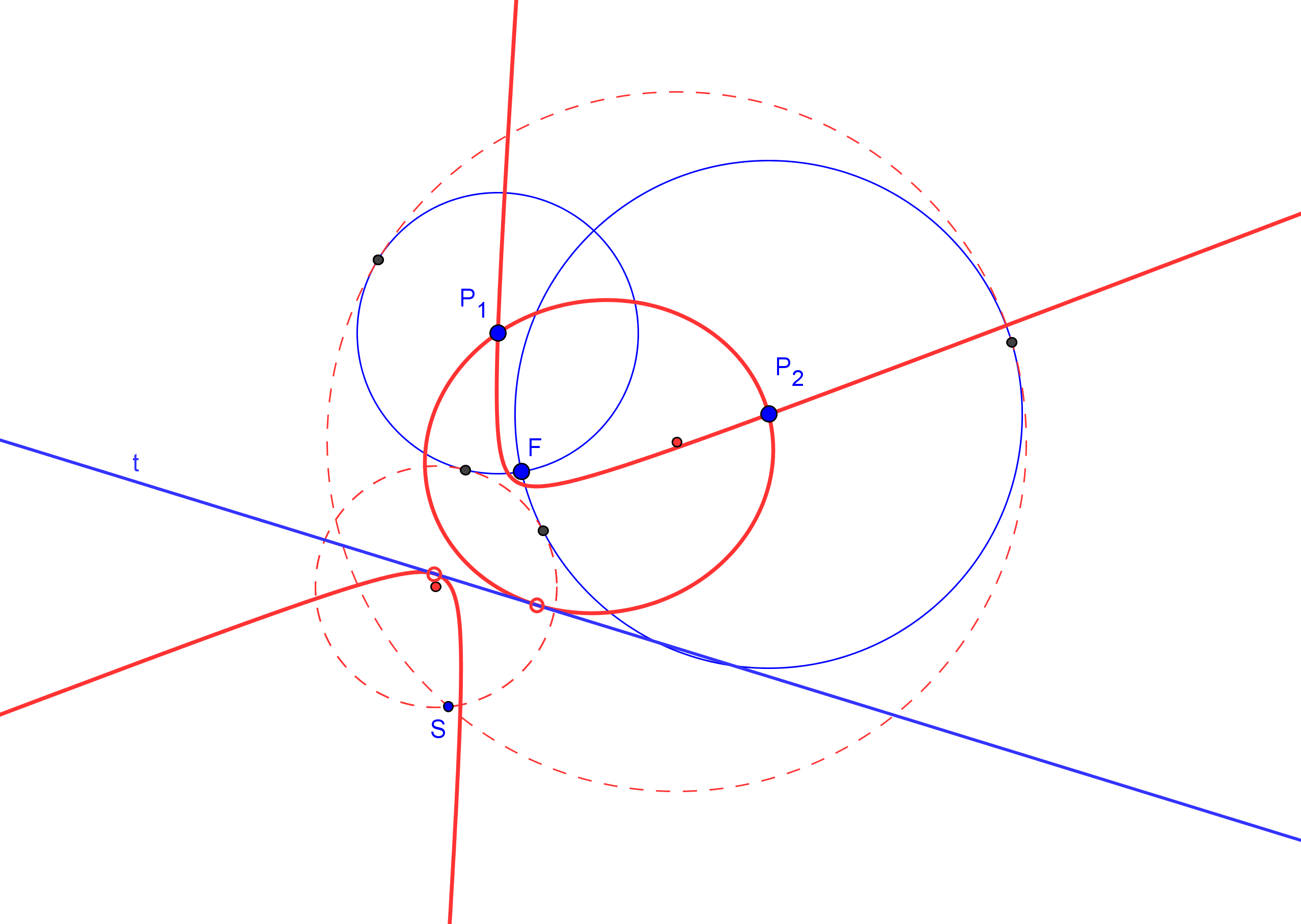
![]()
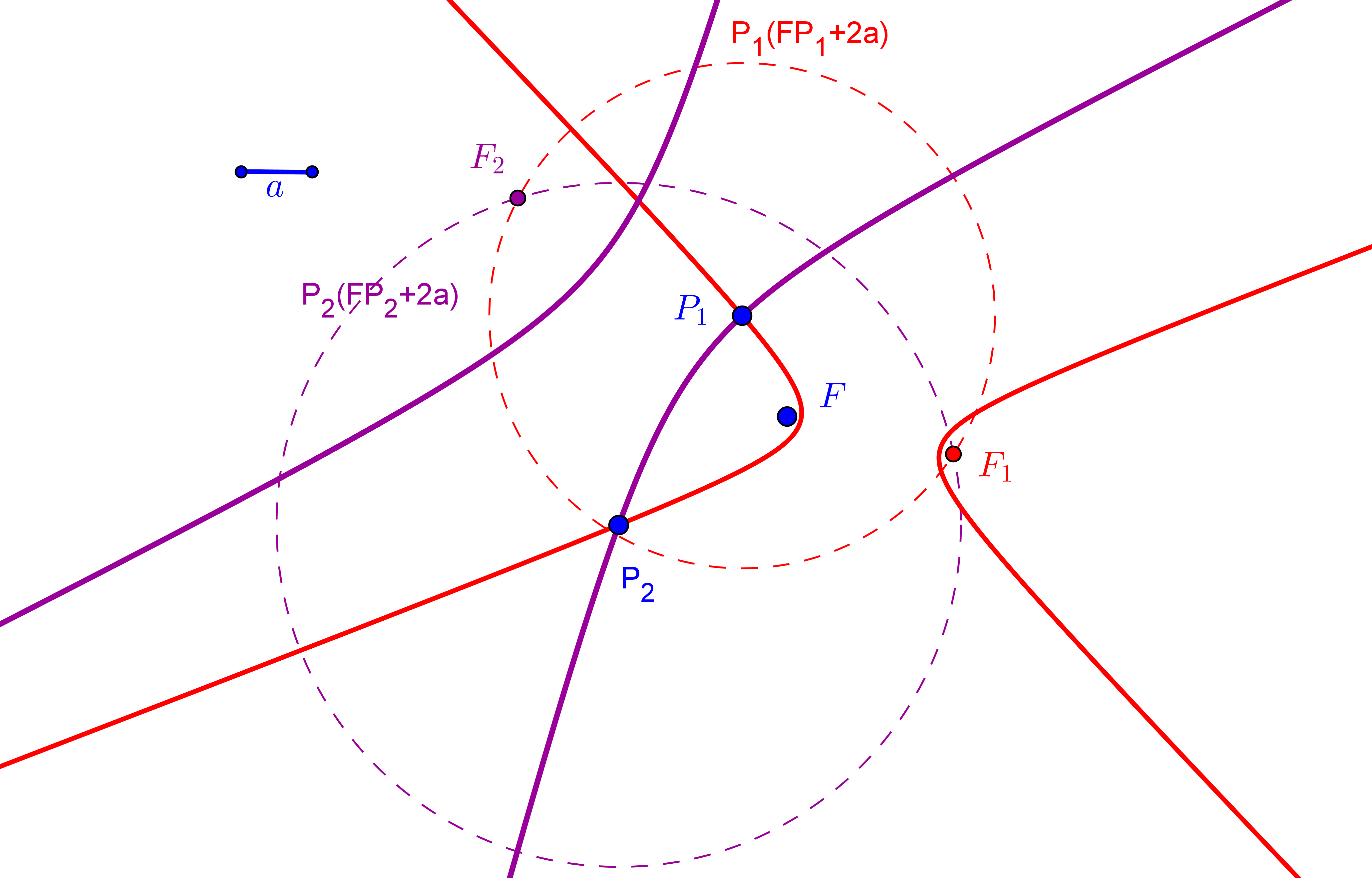
-- La circunferencia P(PF), de centro P y que pasa por el foco F, es tangente a la circunferencia focal relativa al otro foco, que pasa por los puntos simétricos, S1 y S2, del foco F respecto a las tangentes dadas t1 y t2.
1. Se construyen los simétrico S1 y S2, respeto a las tangentes t1 y t2, del foco dado F.
2.
Se trazan las circunferencias que pasan por S1 y S2 y son tangentes a la circunferencia P(PF) (Problema de Apolonio PPc: Circunferencia que pasa por dos puntos y es
tangente a una circunferencia. ![]() ). Sean I y J los puntos de tangencia.
). Sean I y J los puntos de tangencia.
3. Si la circunferencia P(PF) es exterior a la circunferencia que pasa por S1 y S2 e I, la cónica de focos en F y en el cento FI de la circunferencia S1S2I y que pasa por P, es una hipérbola. Ocurre que (FI I P)<0 ó 1<(FI I P).
4. Si la circunferencia P(PF) es interior a la circunferencia que pasa por S1 y S2 y J, la cónica de focos en F y en el cento FJ de la circunferencia S1S2J y que pasa por P, es una elipse. Ocurre que 0<(FI J P)<1.
5. La cónica buscada será parábola cuando la circunferencia P(PF) es tangente a la recta S1S2, es decir, cuando la distancia de P a F y dicha recta sean iguales.
( Mostrar/Ocultar figura)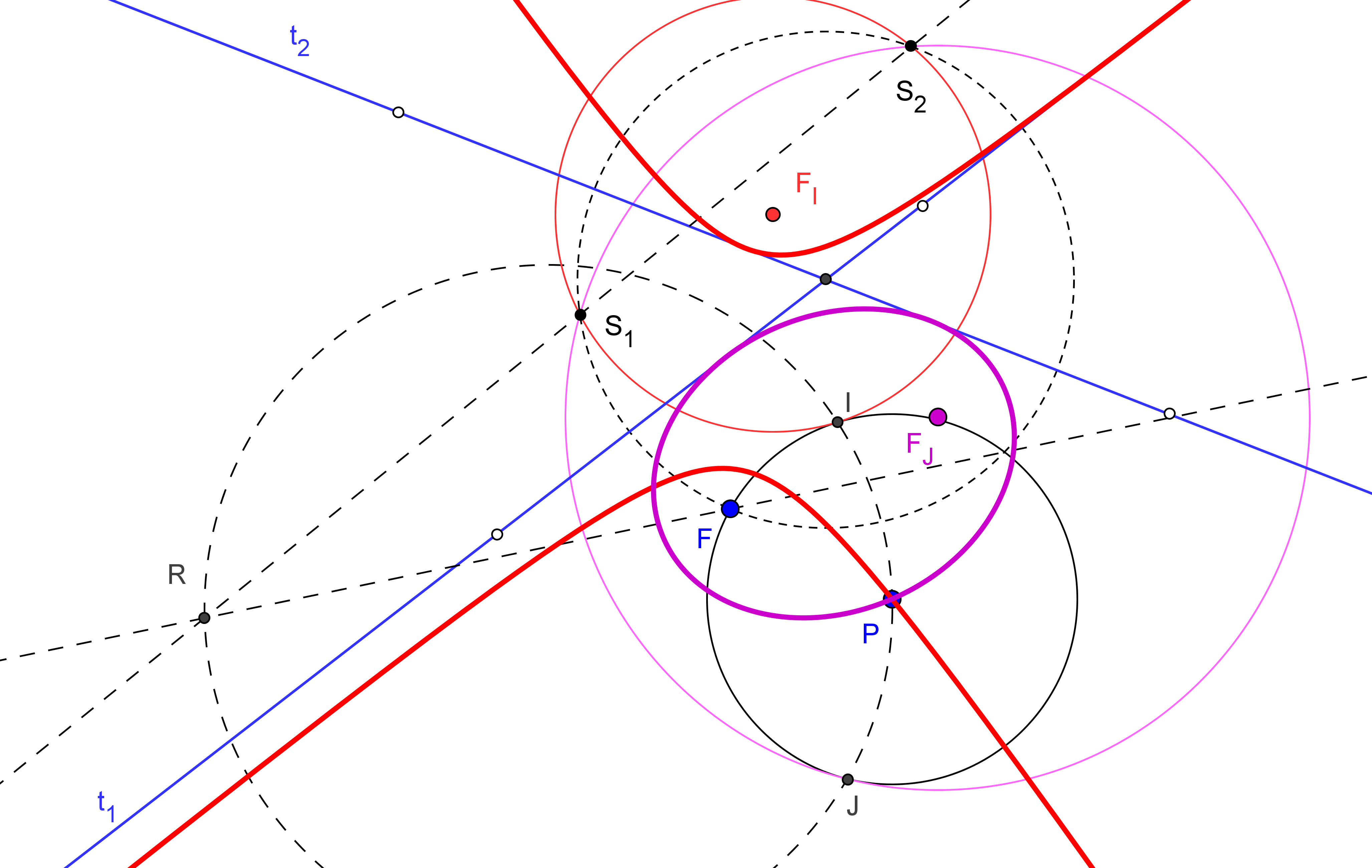
![]()
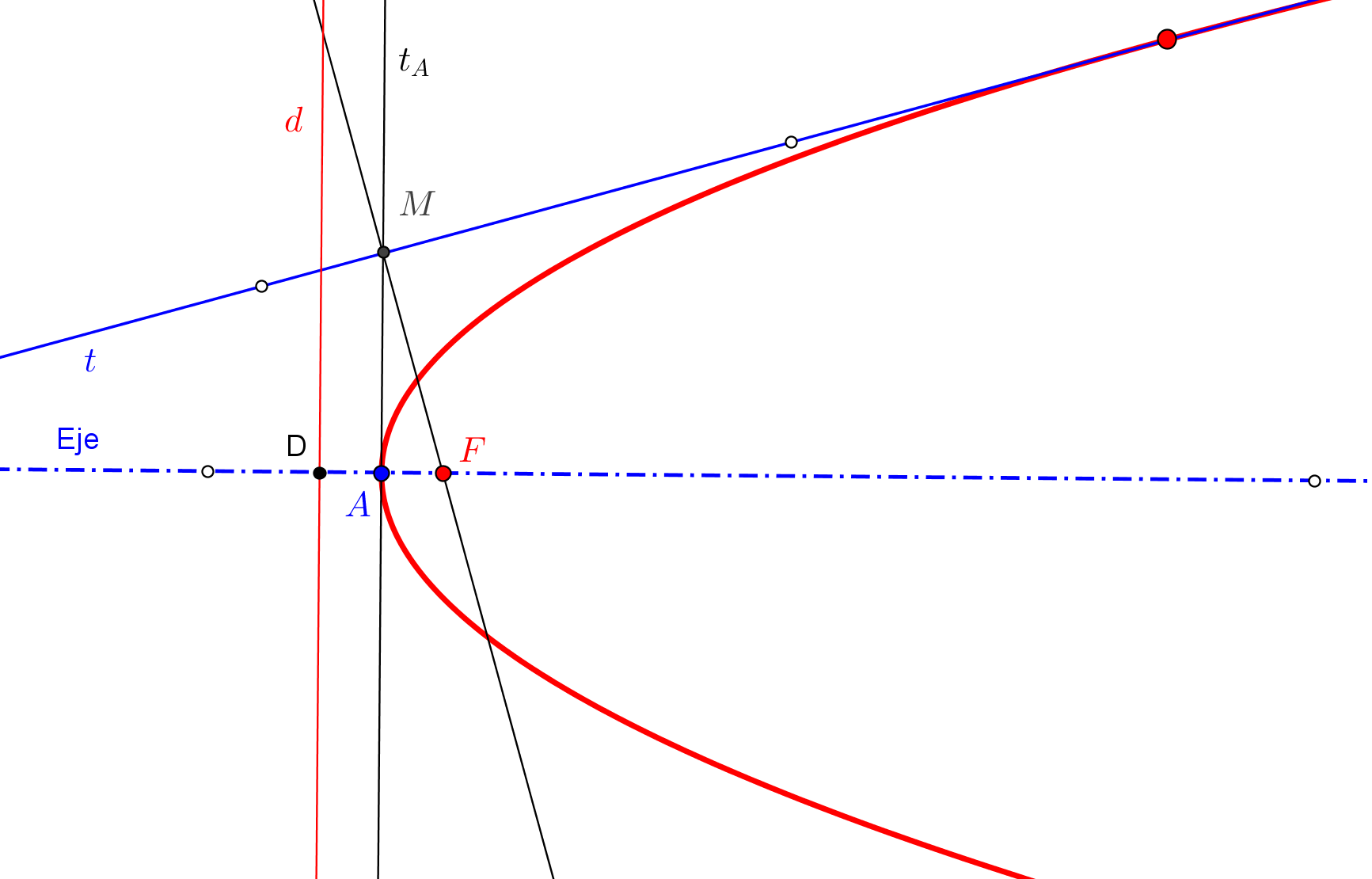
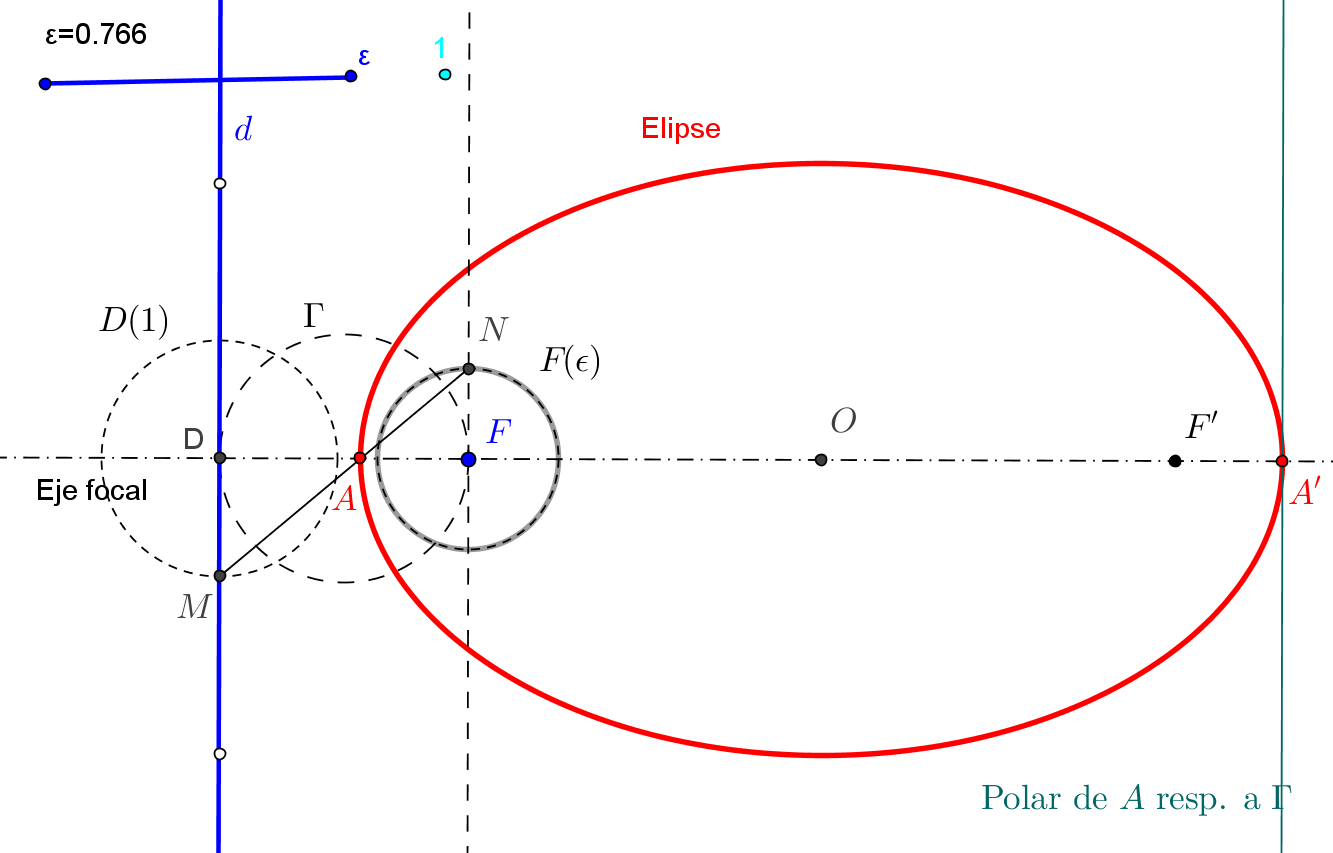
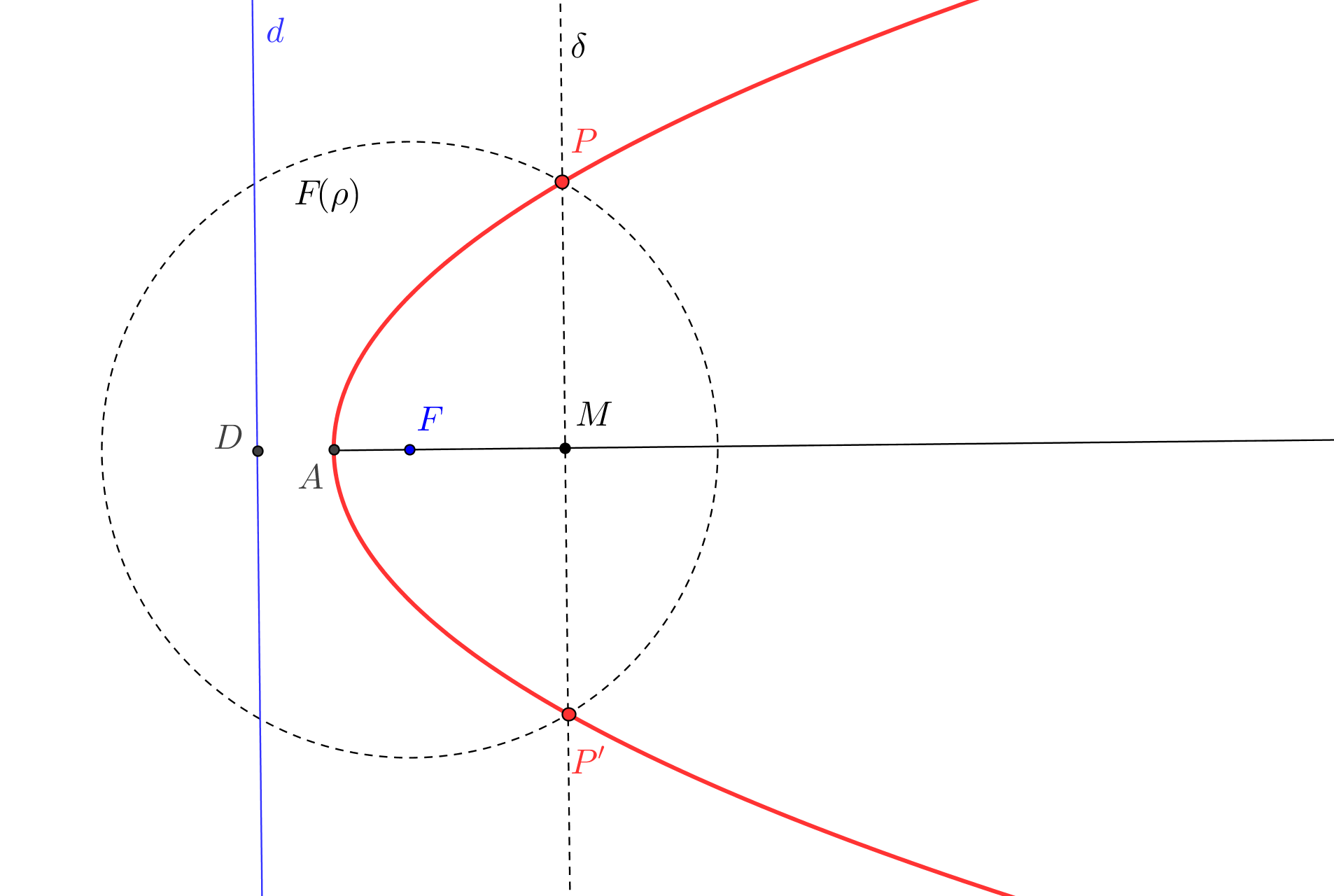
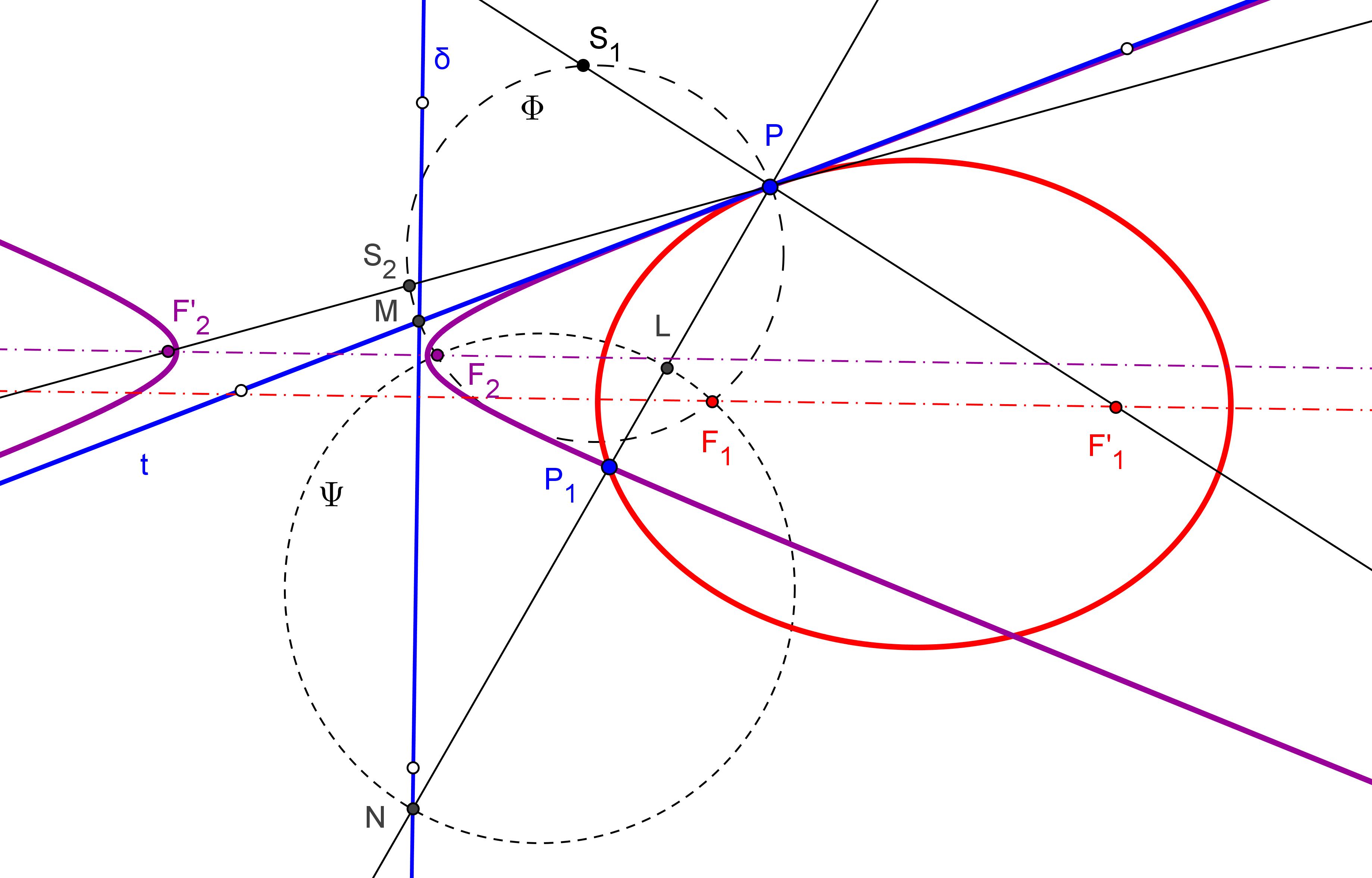
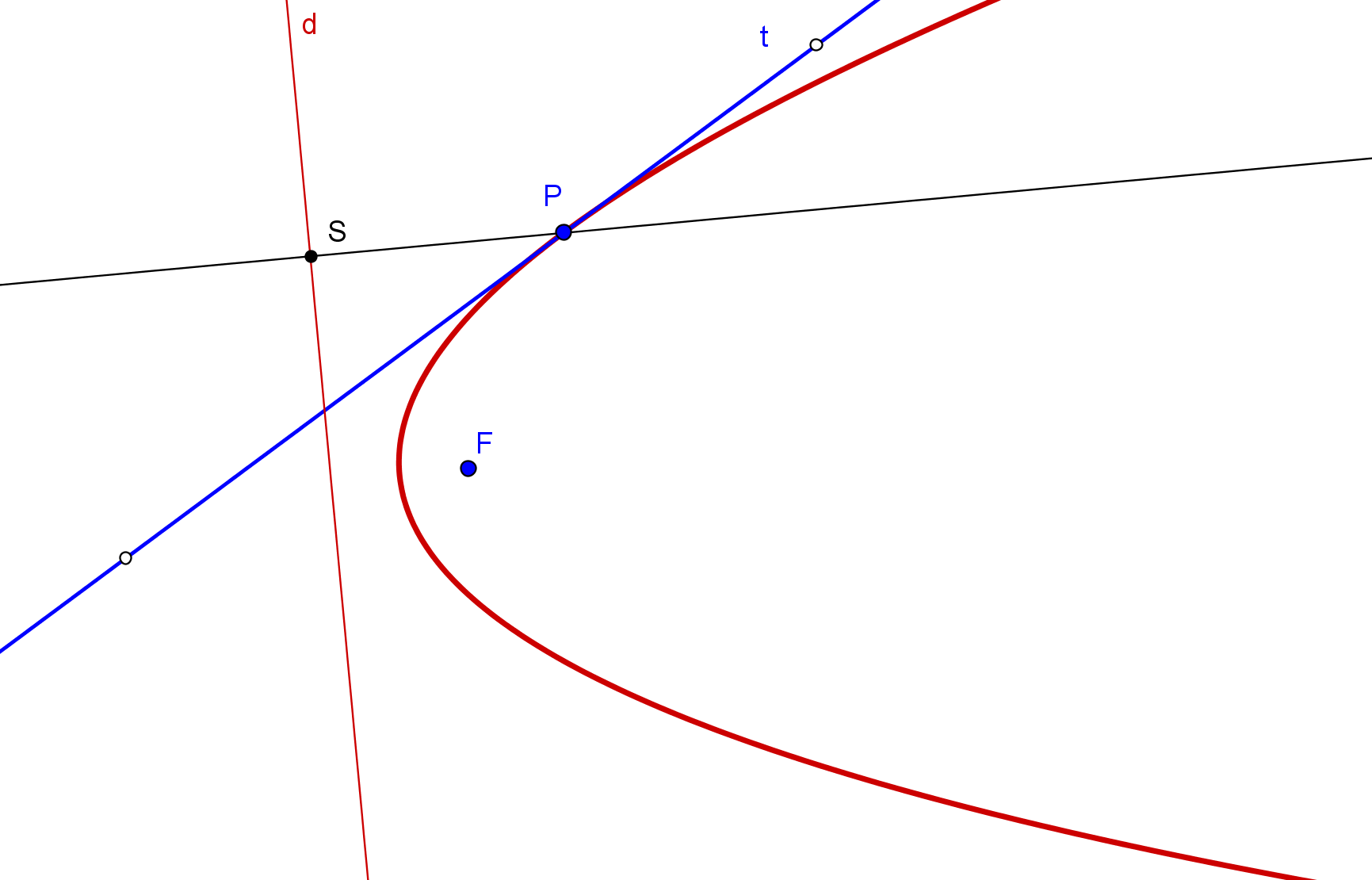
1. Se construye el simétrico S (que estará en la directriz) del foco F, respecto a la tangente t.
-- La circunferencia P(PF), de centro P y radio PF, ha de ser tangente a la directriz.
2. Las tangentes a la circunferencia P(PF) desde S son las directrices d1 y d2 de las parábolas solución.
-- Si S es exterior a la circunferencia P(PF), hay dos parábolas; si S está sobre P(PF), hay una sola parábola; y si S es interior a P(PF) no hay solución.
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
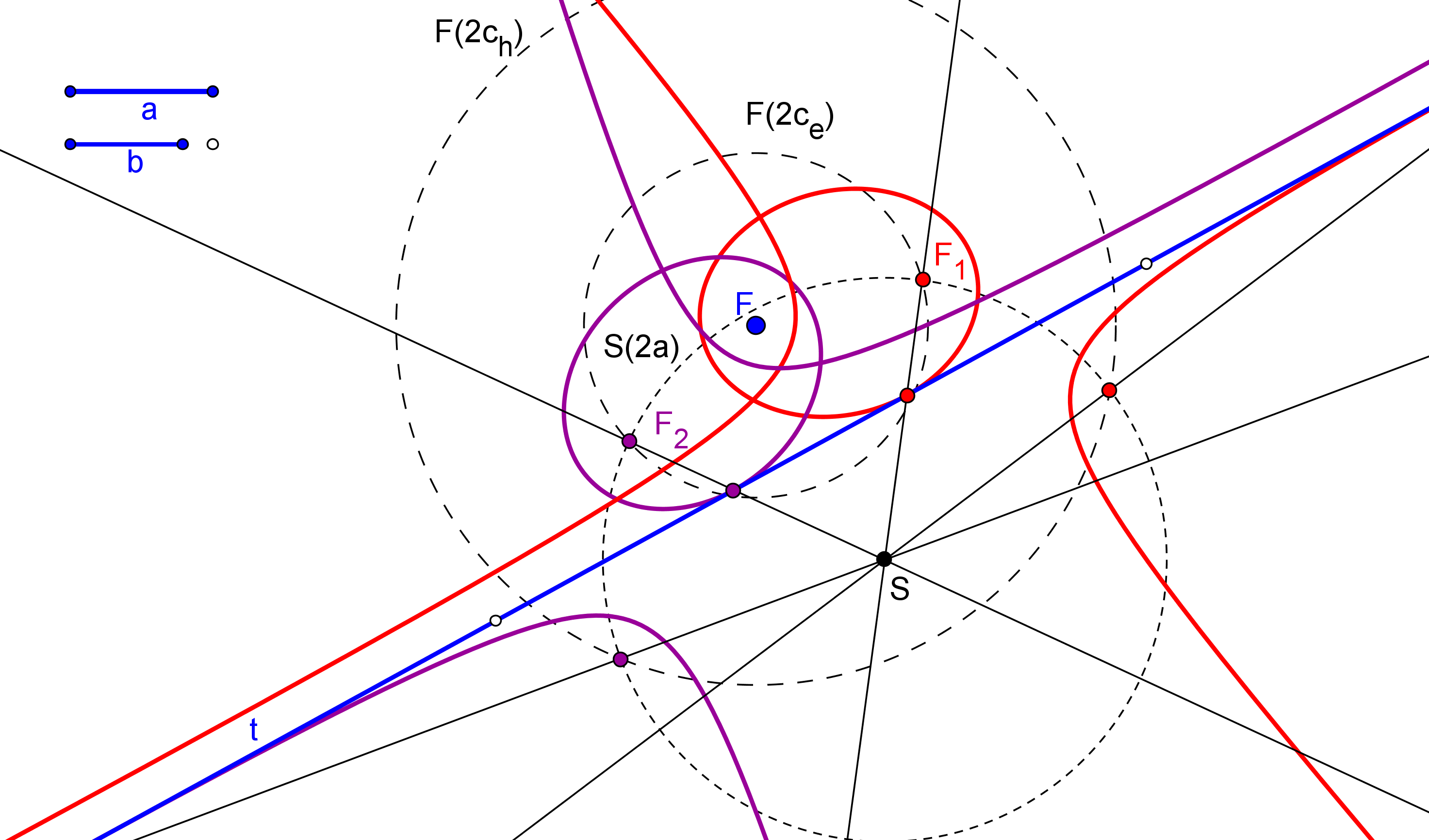
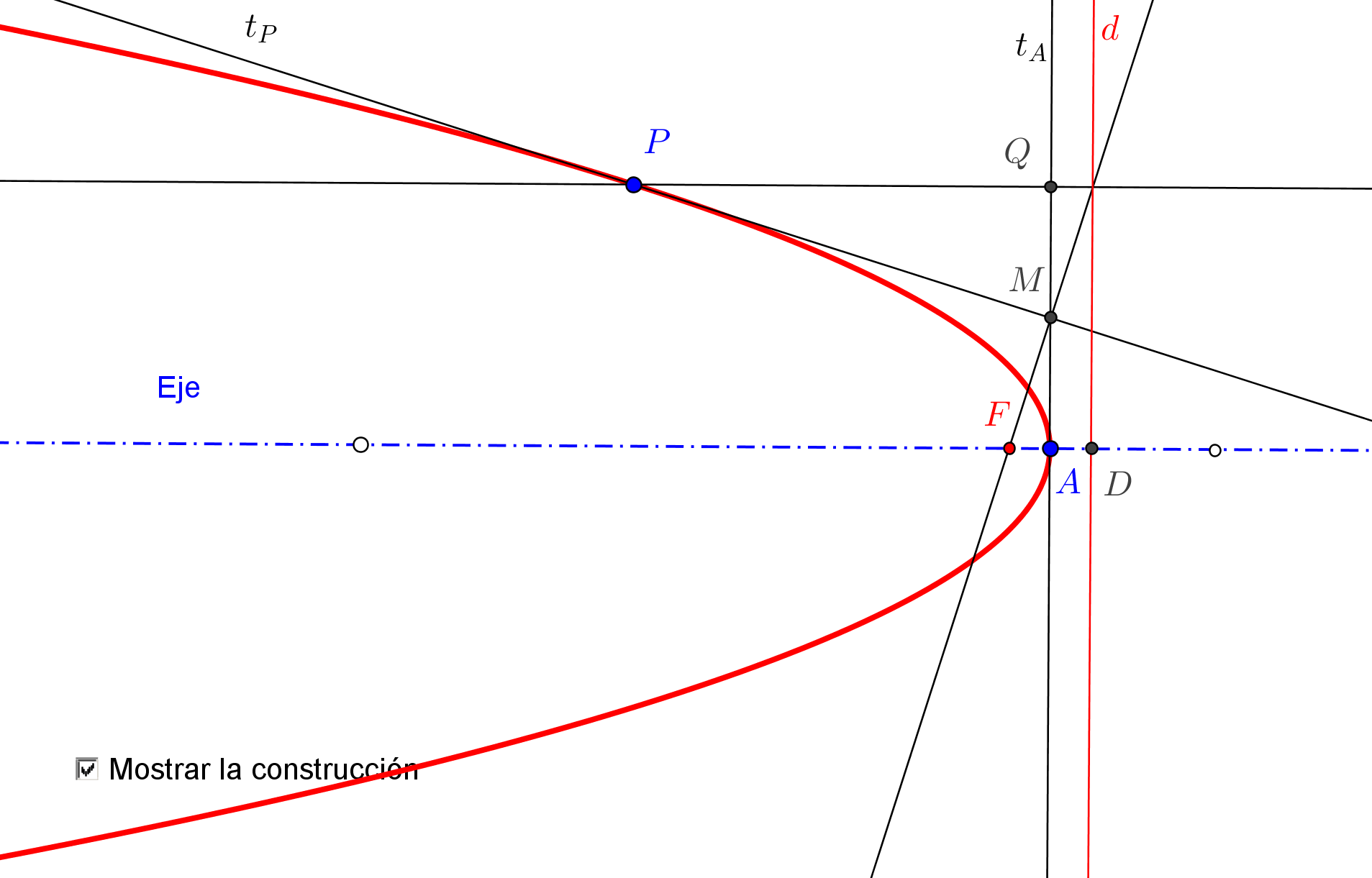
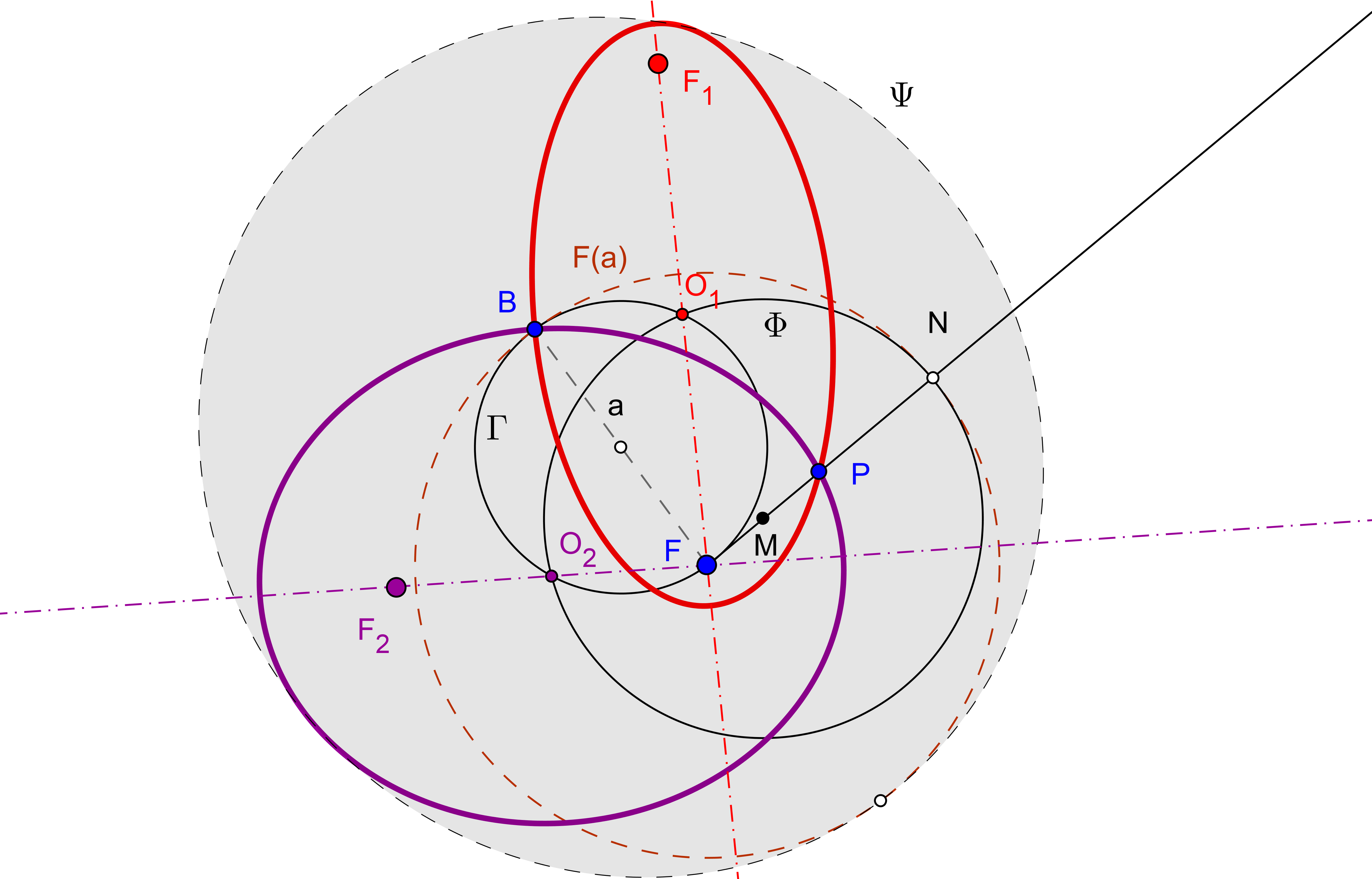
1. Se construyen los simétrico S1 y S2 del foco F, respeto a las tangentes t y tP, respectivamente.
2. La circunferencia P(PF), de centro P y radio PF, es tangente a la circunferencia focal del otro foco F2, en el punto S2. Luego, el centro de ésta, F2, es el punto de intersección de la mediatriz de S1S2 con la recta PS2.
-- La cónica es elipse si la circunferencia P(PF) es tangente por el interior a la circunferencia focal de F2, es decir, si 0<(S2 S2 P)<1.
-- La cónica es hipérbola si la circunferencia P(PF) es tangente por el exterior a la circunferencia focal de F2, es decir, si (S2 S2 P)<0 ó 1<(S2 S2 P).
-- La cónica es parábola si la mediatriz de S1S2 y la recta PS2 son paralelas. (En GeoGebra: Definido[RazónSimple[S2, S2, P]] es "falso").
( Mostrar/Ocultar figura)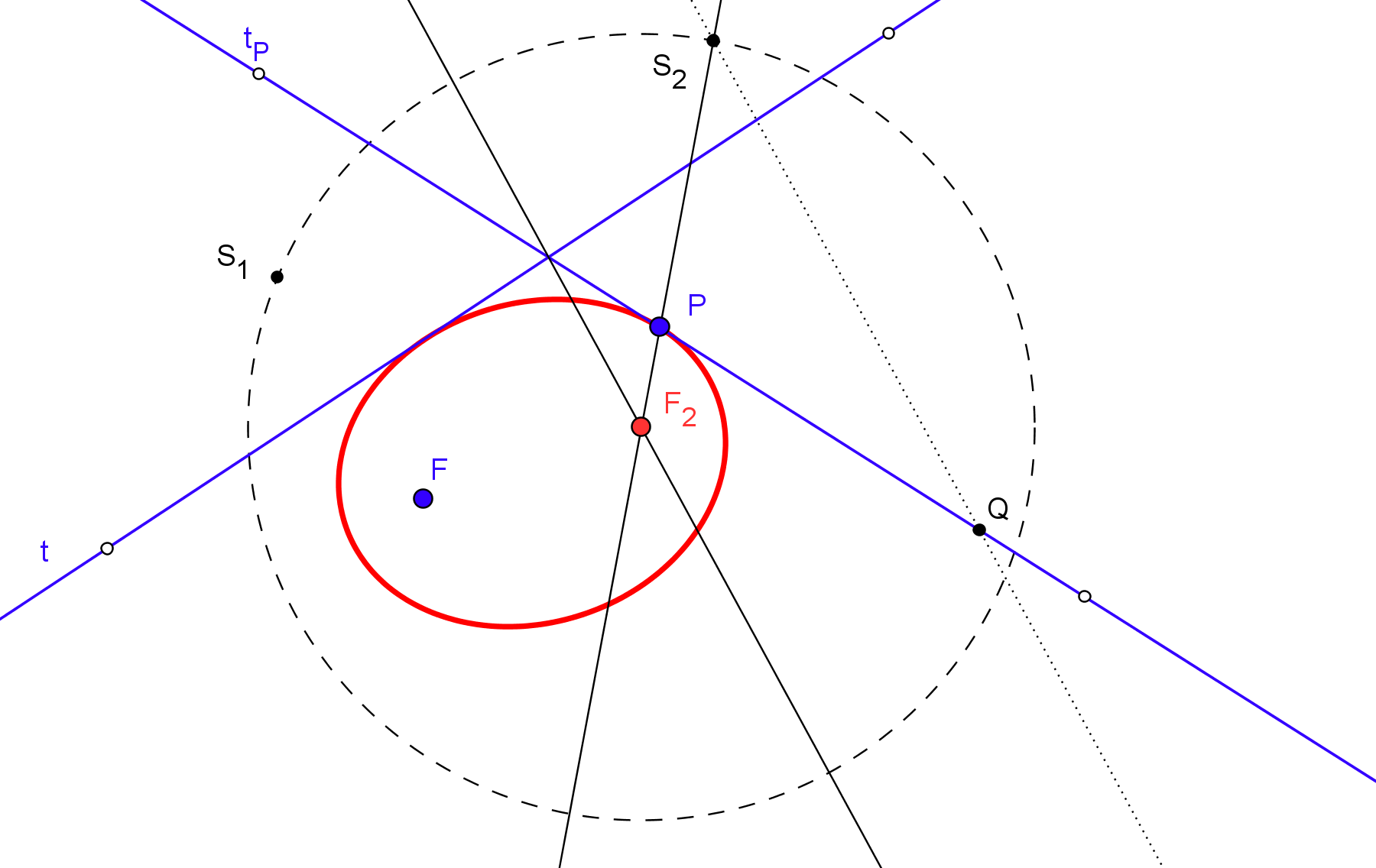
![]()
( Mostrar/Ocultar figura)
![]()
( Mostrar/Ocultar figura)
![]()
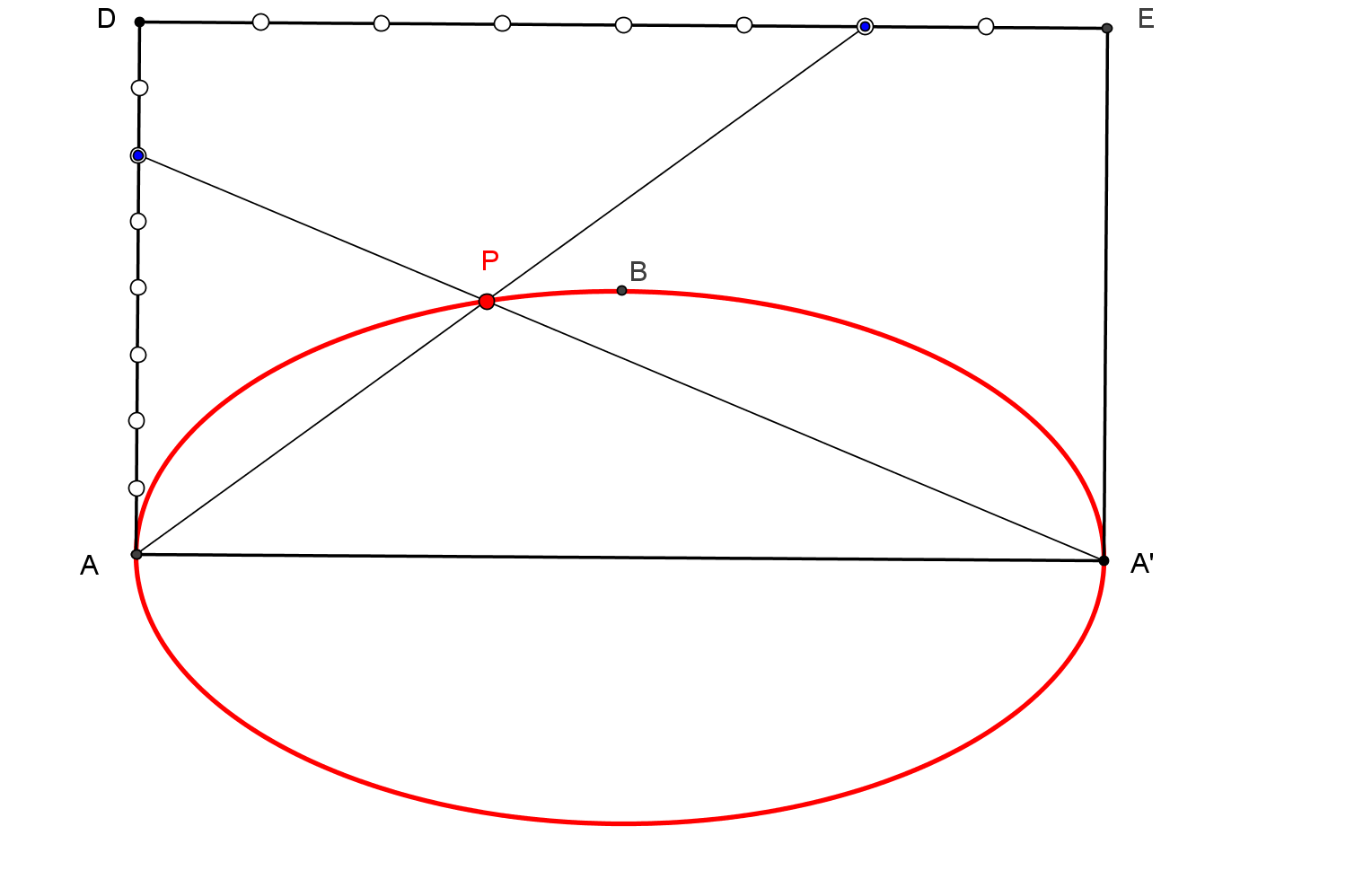
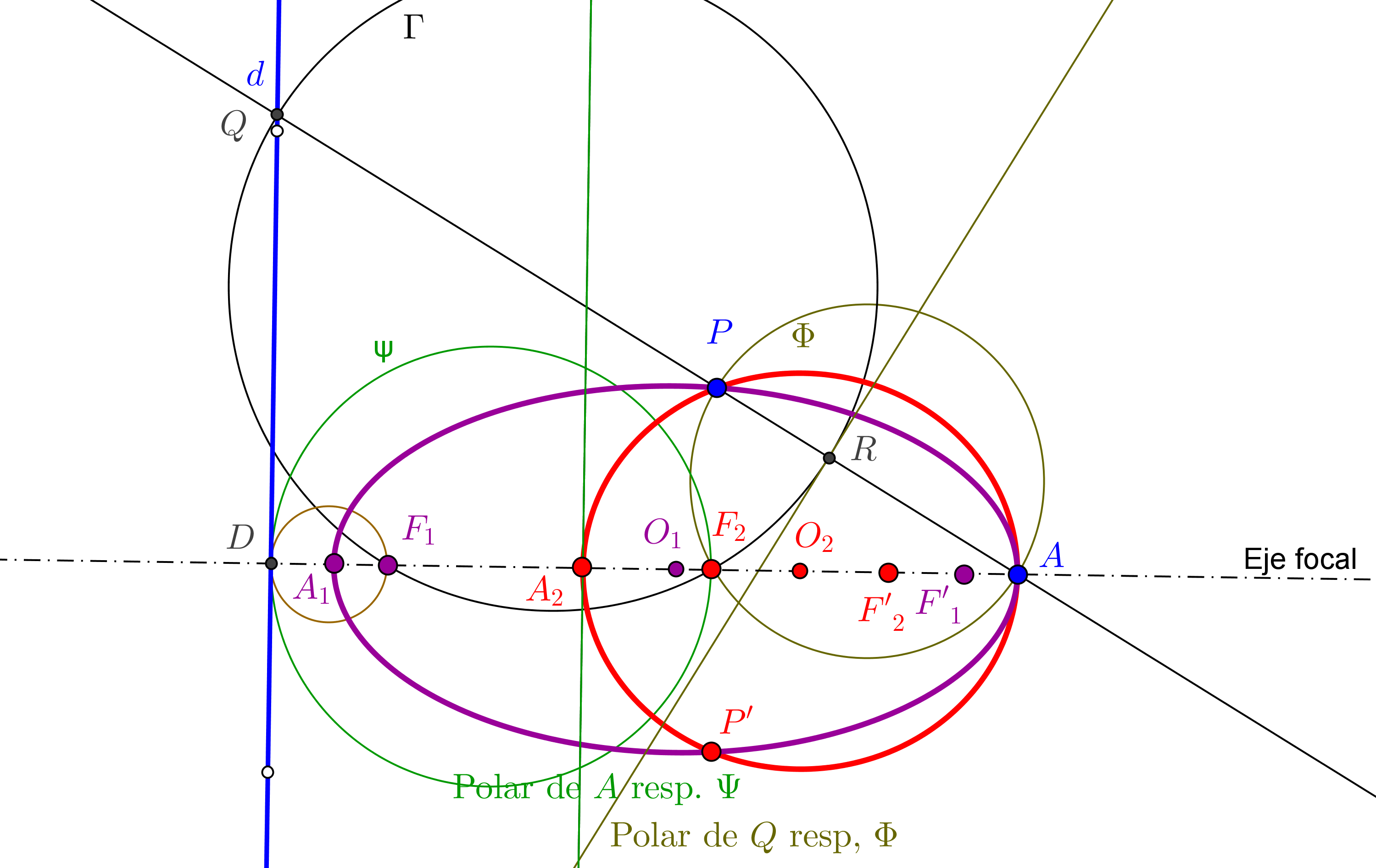
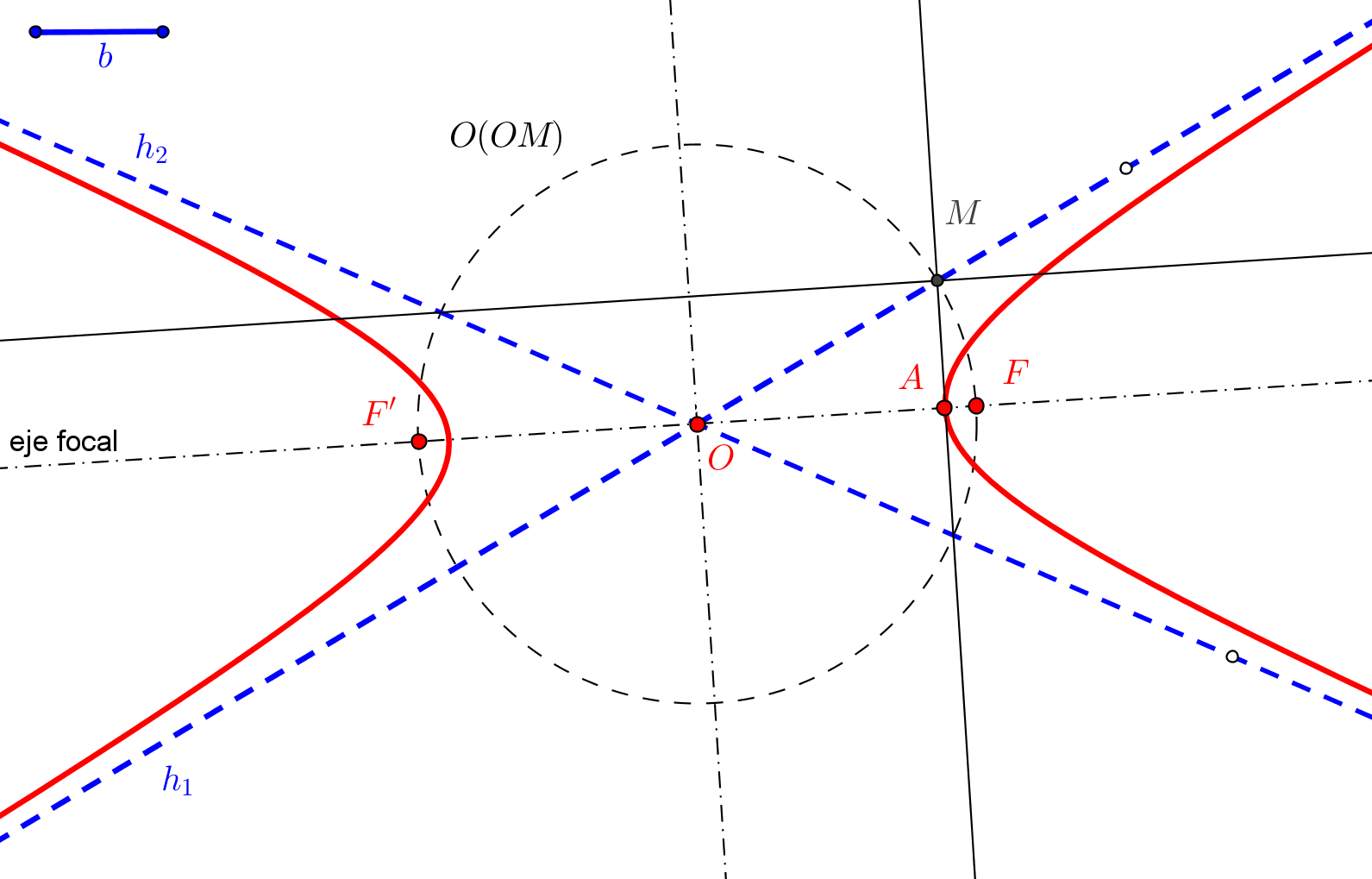
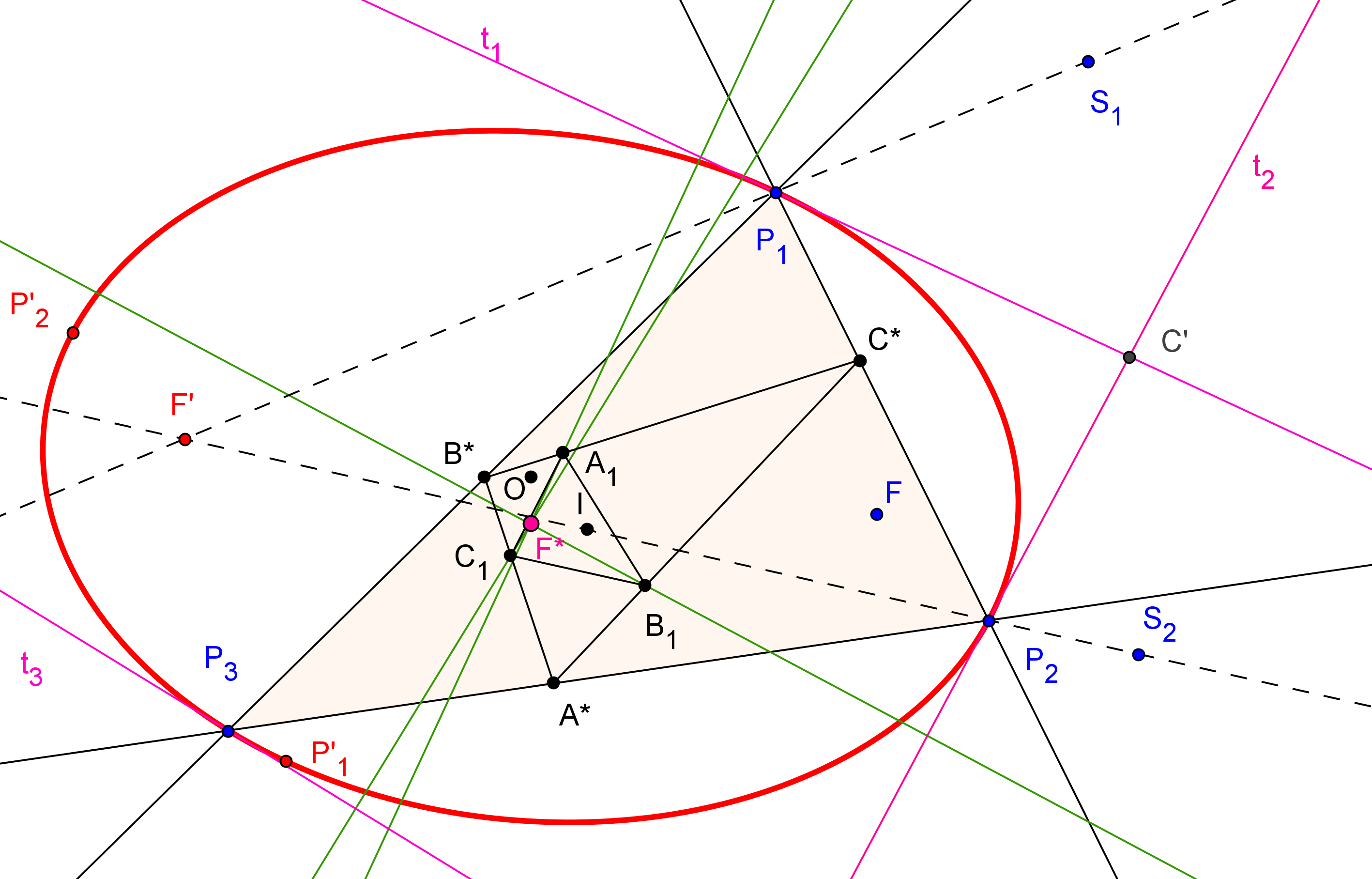
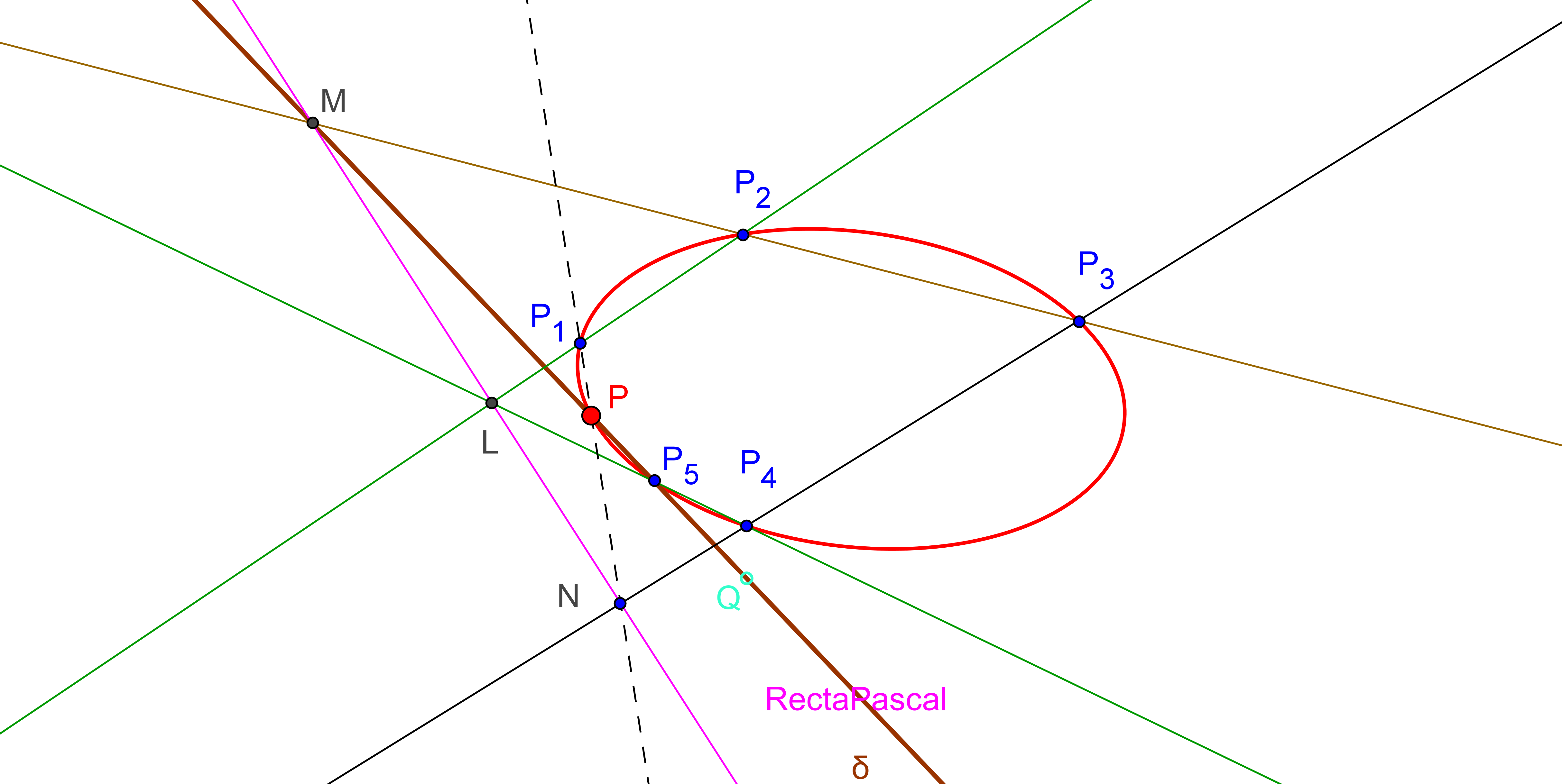
-- Utilizamos el caso límite del Teorema de Pascal para hallar el otro punto de la hipérbola de una recta que pase por P.
1. Pertenece a la hipérbola el punto P' simétrico de P respecto su centro O, intersección de las dos asíntotas.
--- Consideramos el pentágono inscrito en la hipérbola a construir con vértices en P, punto del infinito de h1, punto del infinito de h2, P' y P1 (a determinar, sobre una recta δ que pase por P y que no contenga a ninguno de los puntos anteriores). A este pentágono junto con la asíntota h1 (tangente en el infinito a la hipérbola) le aplicamos el Teorema de Pascal.
2. Trazamos la Recta de Pascal que pasa por δ∩h1 y por el punto de intersección de la paralela a h1 por P' con la paralela a h2 por P.
--- Como la recta del infinito y la recta P'P1 se han de cortar en la recta de Pascal:
3. Se traza la paralela a la recta de Pascal por P', y donde corte a δ es el nuevo punto P1 de la hipérbola.
4. Pertenece a la hipérbola el punto P'1 simétrico de P respecto su centro O.
5. Un punto más P2 de la hipérbola se obtiene partiendo de otra recta, distinta de δ, que pase por P, y e intercambiando las asíntotas, es decir, ahora la tangente (en el infinito) que tomamos es la hipérbola h2
( Mostrar/Ocultar figura)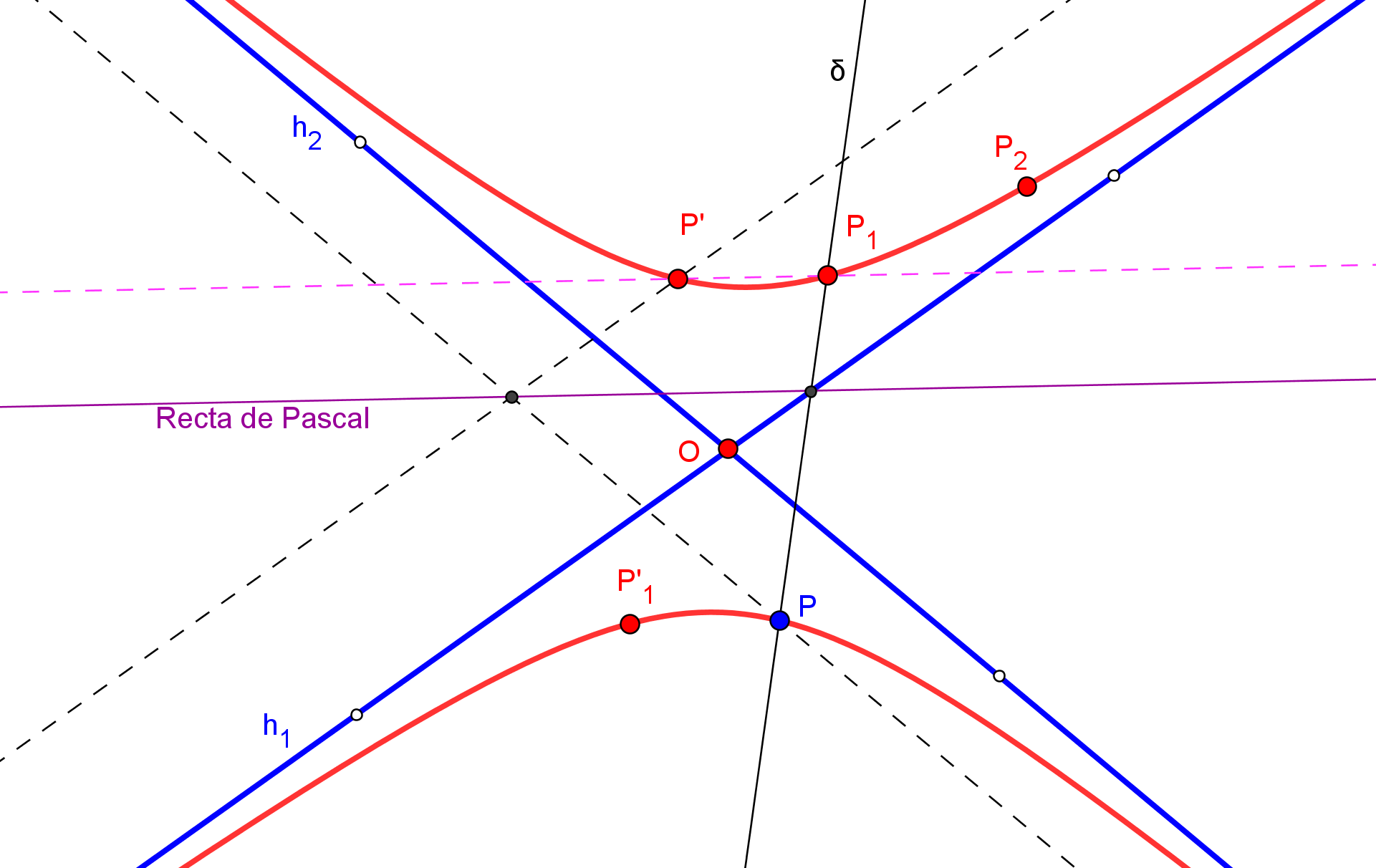
![]()
( Mostrar/Ocultar figura)
![]()
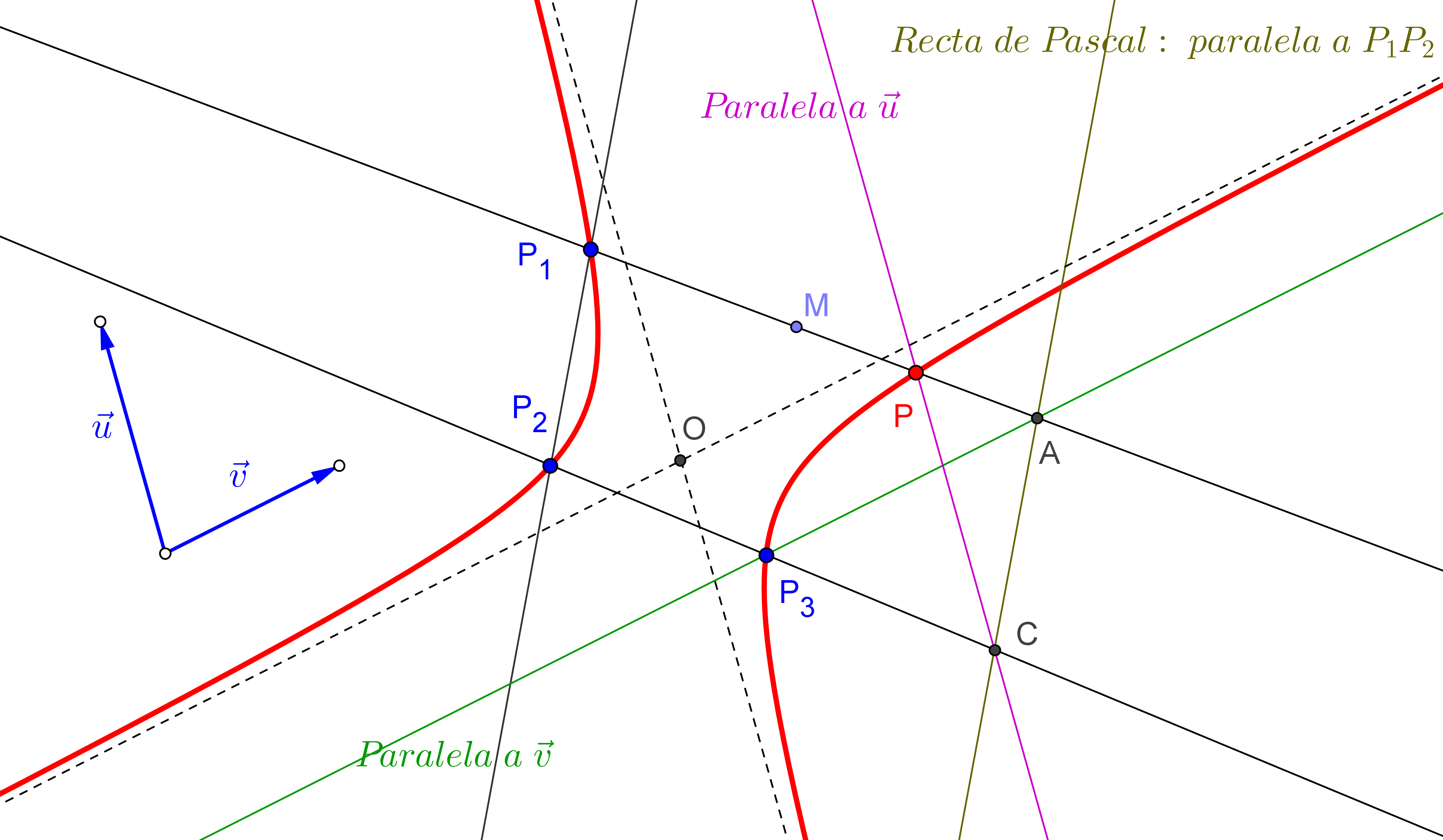
-- Utilizamos un caso límite del Teorema de Pascal para hallar la tangente en uno de sus puntos. Luego construimos la "Parábola: dado la dirección del eje, un punto y una tangente con su punto de tangencia" (IPt_PC_p).
--- Designamos por t1 la tangente (a determinar) en el punto P1. Consideramos el hexágono determinado por las seis rectas t1, P1P2, P2P3, la paralela por P3 al eje, la recta del infinito y la paralela por P1 al eje..
1. La recta de Pascal es la recta paralela a P1P2 por el punto de intersección de la recta P2P3 con la paralela al eje por P1.
2. La tangente t1 en P1, pasa por el punto de intersección de la recta de Pascal con la paralela al eje por P3.
( Mostrar/Ocultar figura)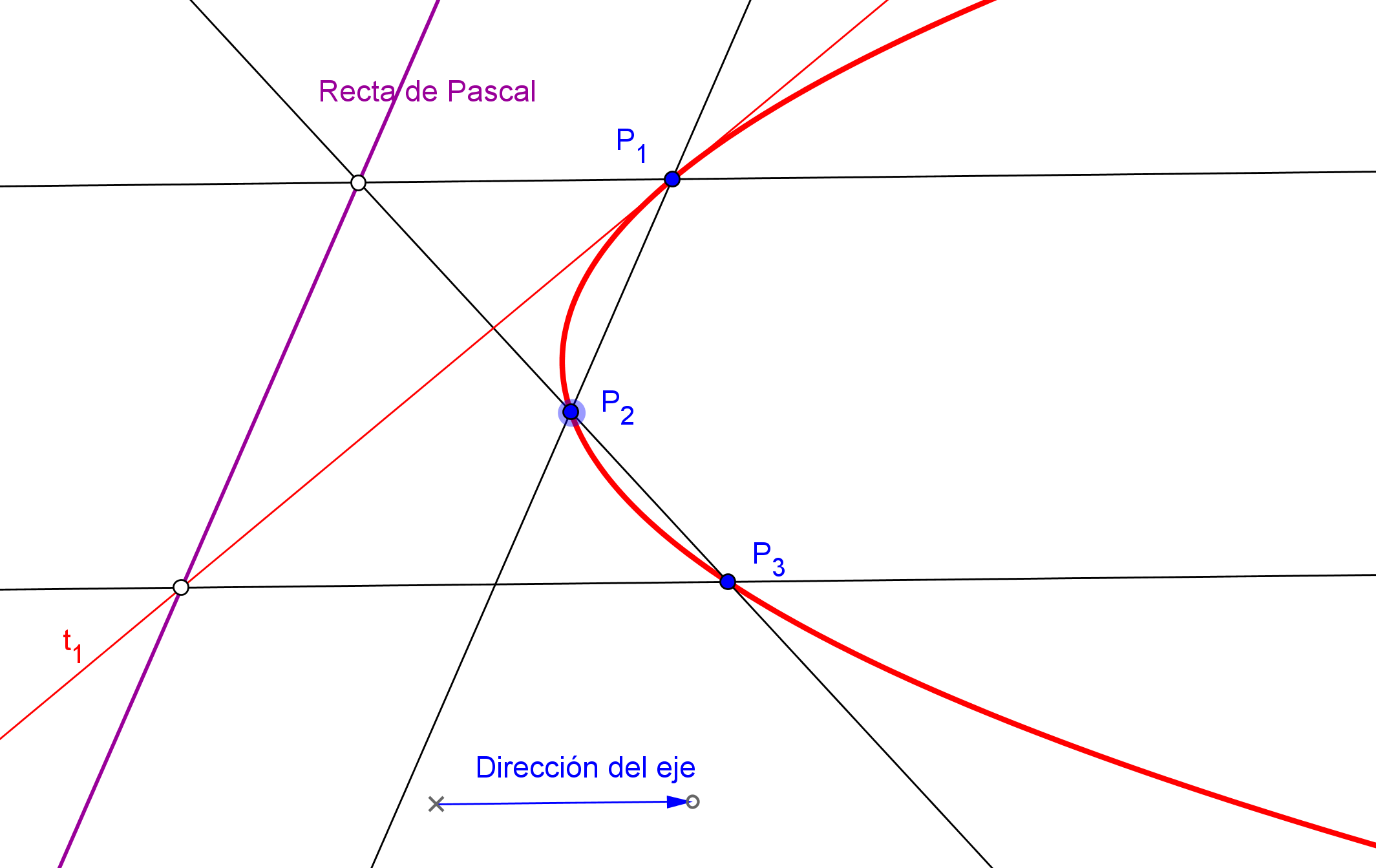
![]()
-- Podemos encontar el otro punto X de intersección con la parábola de una recta δ, que pasa por P1 (no paralela a la dirección del eje y que no pasa por P), utilizando un caso límite del Teorema de Pascal, aplicado a los puntos I (punto del infinito del eje), P, P1, X, a la tangente tP y a la recta del infinto:
1. La recta de Pascal está determinada por el punto de intersección de δ con la paralela al eje por P, y por el punto de intersección de tP con la recta paralela al eje por P1.
2. El punto X es la intersección de la recta δ con la paralela a la recta de Pascal por P.
--- Variando la recta δ, obtenemos otros puntos de pa parábola.
( Mostrar/Ocultar figura)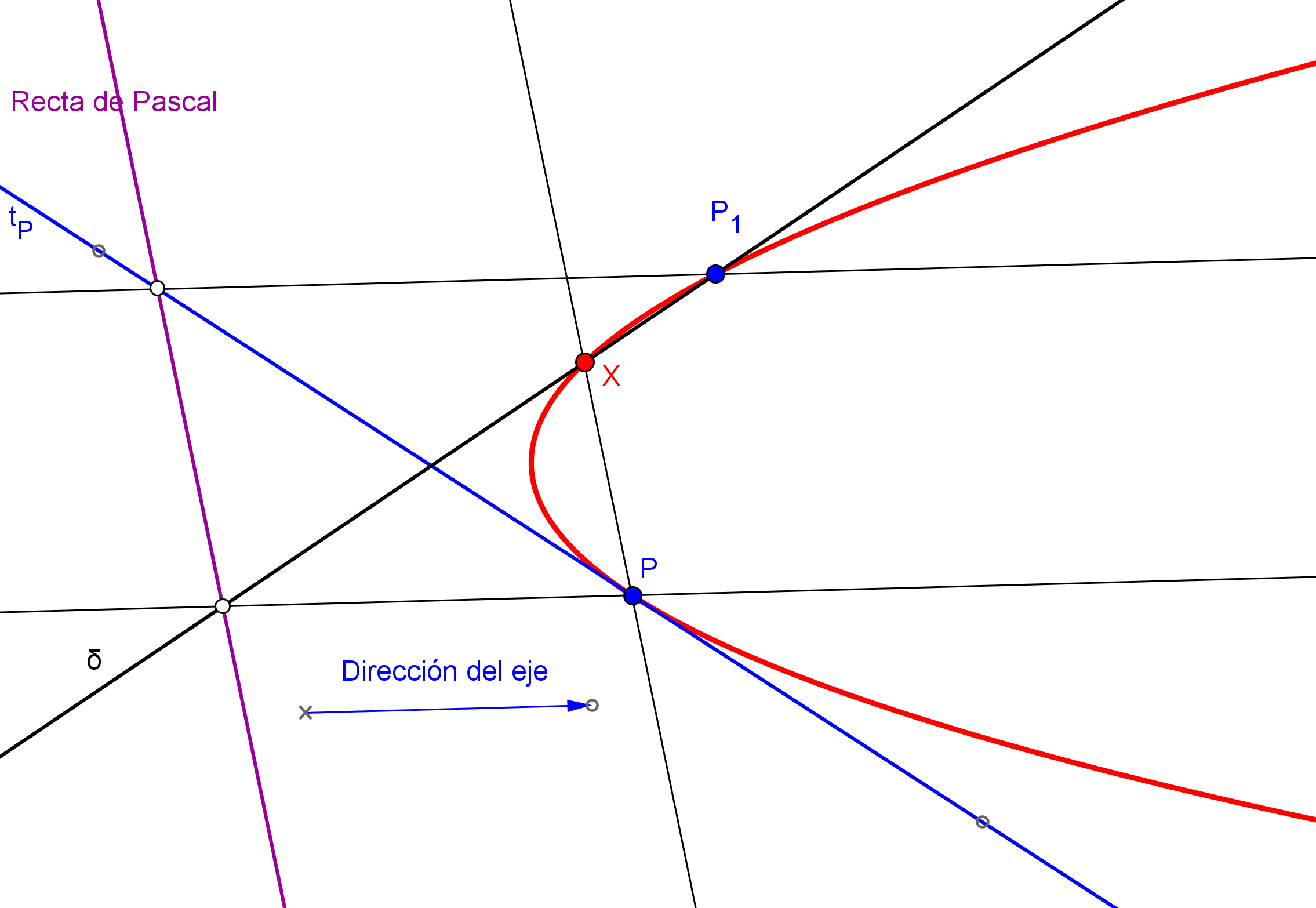
![]()
---
Utilizaremos el Teorema de Pascal:
---
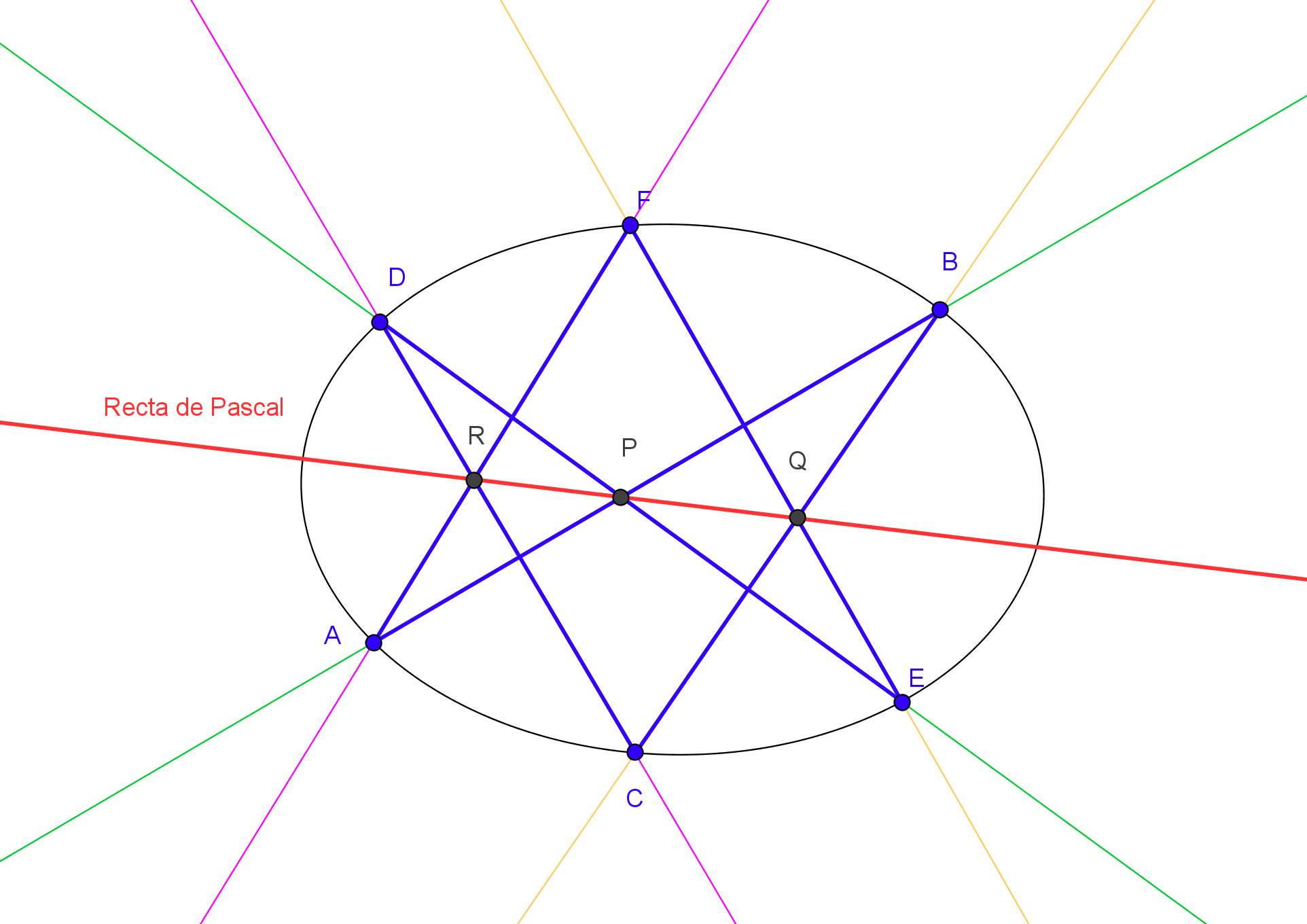
Dados cinco puntos P1, P2, P3, P4 y P5 de una cónica, si P es el otro punto en la cónica de intersección con una recta δ que pasa por P5, los puntos P, P1, P2, P3, P4 y P5 determinan un hexágono inscrito en ella, cuya recta de Pascal pasa por:
1.
El punto L de intersección de los lados opuestos P1P2 y P4P5.
2.
El punto M de intersección de los lados opuestos P2P3 y δ.
3.
Determinamos ahora el punto N de intersección del lado P3P4 con la recta de Pascal, LM.
4.
El punto P buscado es la intersección de la recta δ con la recta NP1.
"Si un hexágono se encuentra inscrito en una cónica, los tres puntos en los que se intersecan los lados opuestos están sobre una recta, denominada la recta de Pascal".
![]()
---
Utilizaremos el Teorema de Pascal
---
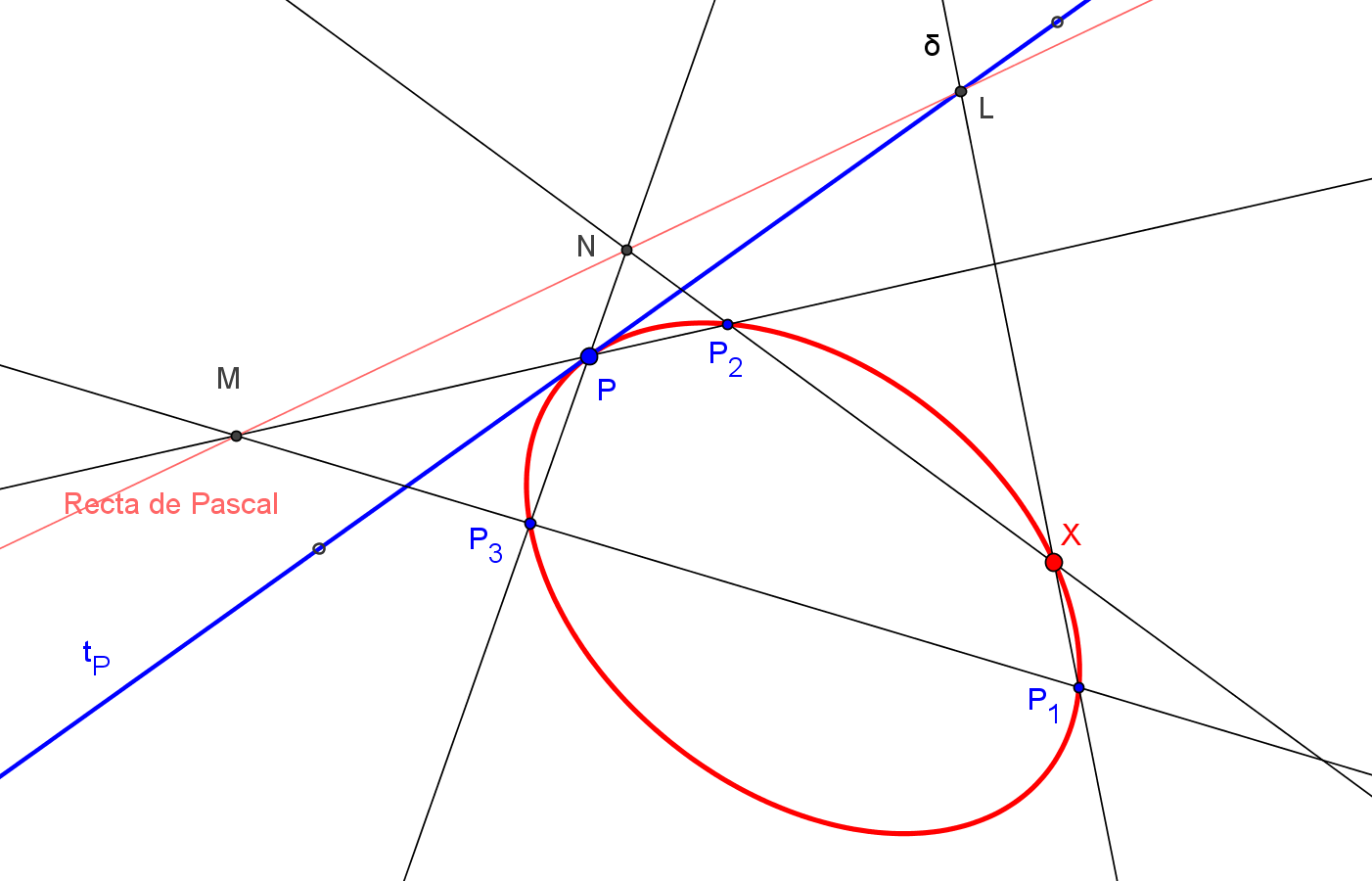
Dados cuatro puntos P, P1, P2 y P3 de una cónica, si P es el punto de tangencia de la tangente dada t, sea δ una recta que pasa por P1 (no pasando por ninguno de los puntos P, P2, P3 y P4). Vamos a construir el segundo punto X de intersección de la recta l con la cónica a determinar. Para ello consideremos el caso limite del Teorema de Pascal, cuando dos lados consecutivos coinciden en la tangente en punto de la cónica.
1.
El punto L de intersección de los lados opuestos δ y tP.
2.
El punto M de intersección de los lados opuestos PP2 y P1P3.
3.
Determinamos ahora el punto N de intersección del lado PP3 con la recta de Pascal, LM.
4.
El punto X buscado es la intersección de la recta δ con la recta NP2.
![]()
--- Dadas cuatro tangentes t1, t2, t3 y t4 de una parábola, designamos por t5 la recta del infinito que es tangente a la parábola. Determinar el punto de tangencia P5 de la recta del infinito, es determinar la dirección de su eje.
1. La recta paralela a t3 y que pasa t1∩t2 y la recta paralela a t2 y que pasa por t3∩t4 se cortan en el punto de Brianchon W5.
2. La recta que une t1∩t4 con W5 tiene la dirección del eje de la parábola.
3. Los puntos de tangencia P1 y P4 con las tangentes t1 y t4 se determinan como en el caso ttttt .
4. Las rectas paralelas al eje por P1 y P4 se reflejan en las respectivas tangentes en dos rectas que se cortan en el foco F de la parábola.
5. La reflexión del foco F en las tangentes t1 y t4 dan dos puntos P1 y P4 de la directriz ( dFCp(1) ).
( Mostrar/Ocultar figura)
![]()
--- Usaremos que la proyección ortogonal del foco de una parábola sobre una tangente está en la tangente en su vértice.
1. Por los puntos de intersección de la tangente en el vértice t, con cada una de las otras tangentes dadas, t1 y t2, se trazan las perpendiculares a cada una de las tangentes t1 y t2.
2. El punto de intersección de tales perpendiculares es el foco F de la parábola buscada.
3. La paralela a la tangente en el vértice t, por el simétrico de F respecto a t, es la directriz de la parábola. ( dFCp(1) ).
( Mostrar/Ocultar figura)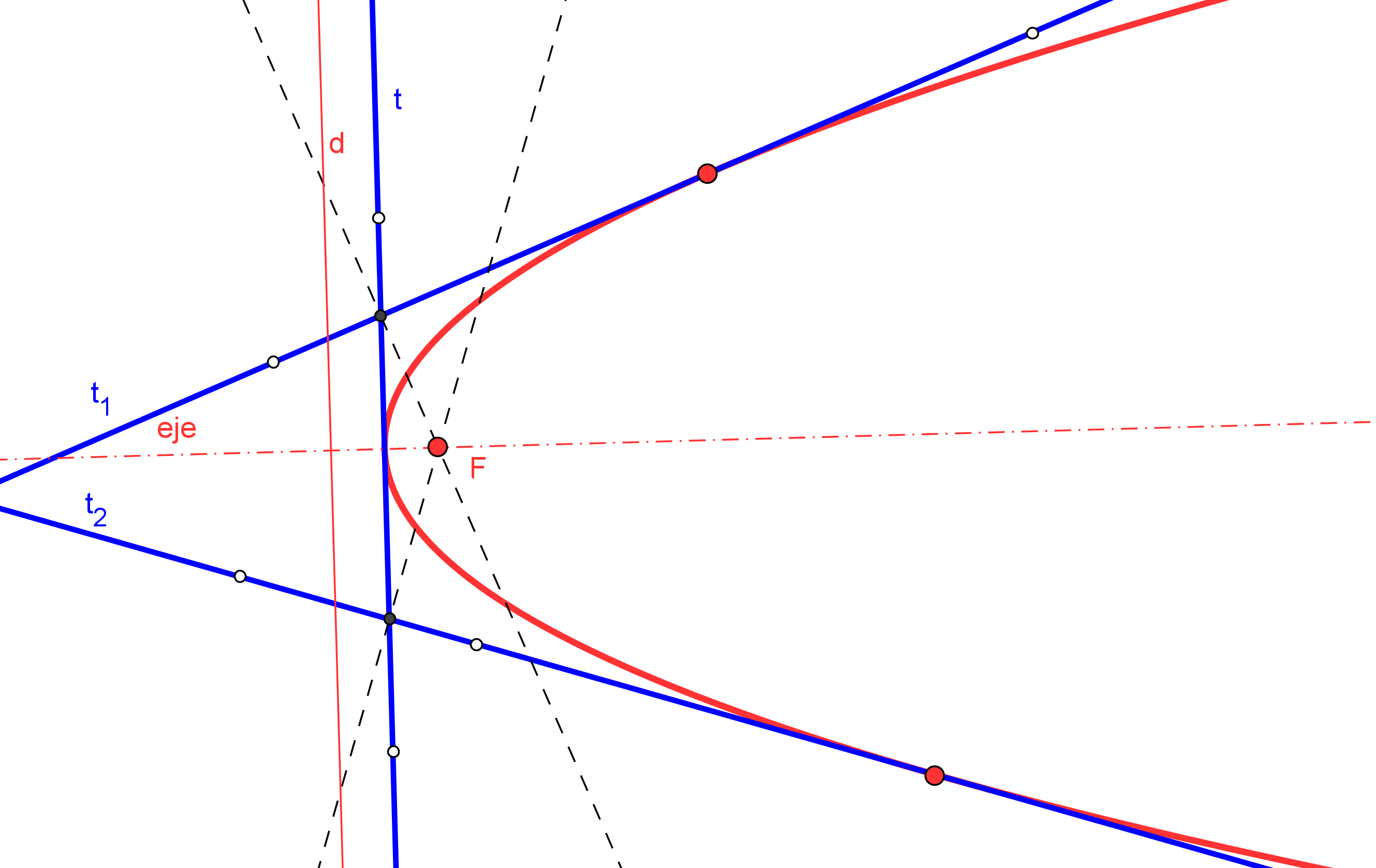
![]()
( Mostrar/Ocultar figura)
![]()
--- Usaremos un caso límite del Teorema de Brianchon, para determinar los puntos de tangencia de las restantes tangentes.
1. La recta que unen los puntos tP∩t1 y t2∩t3 corta a la recta que pasa por P y t1∩t2 en el punto de Brianchon.
2. La recta que pasa por el punto de Brianchon y por tP∩t3, corta a la tangente t1 en su punto de tangencia T1.
3. Similarmente se obtienen los puntos de tangencia T2 y T3 de la tangentes t2 y t3, respectivamente.
4. Ya podemos acudir a la construcción de "Cónica: dado cuatro puntos y la tangente en uno de ellos" , T1, T2 T3 y la tangente tP en P.
( Mostrar/Ocultar figura)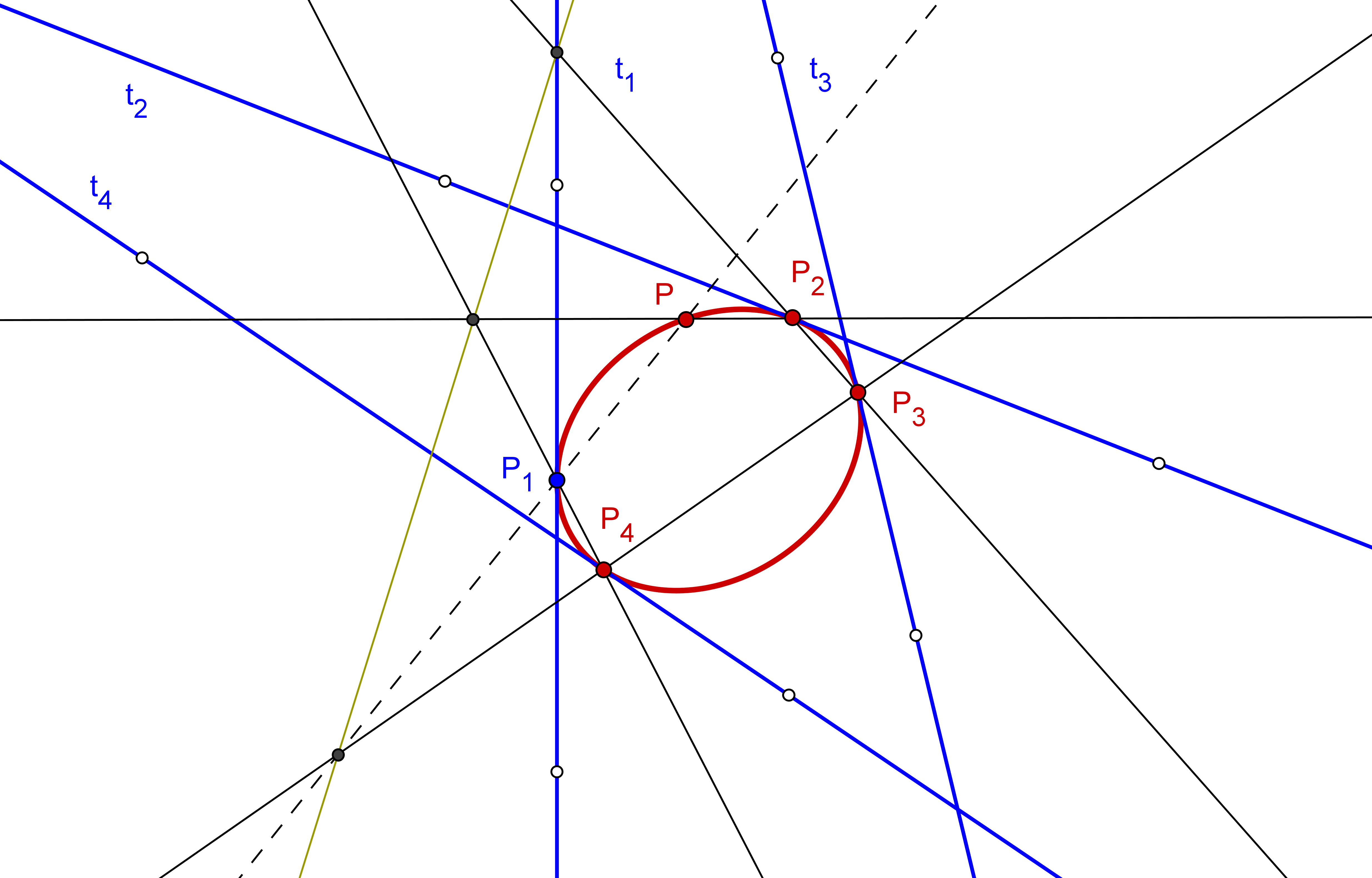
![]()
---
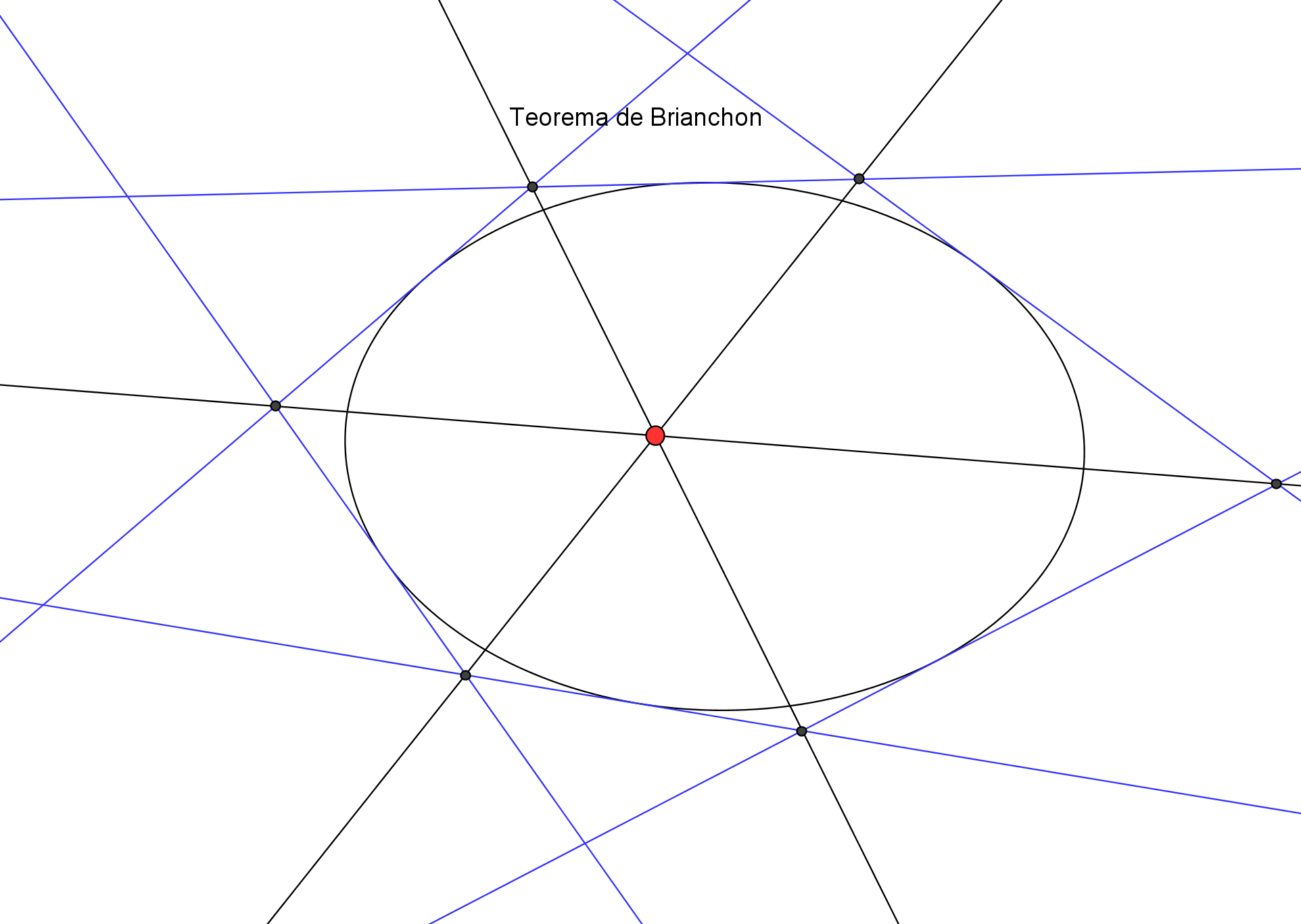
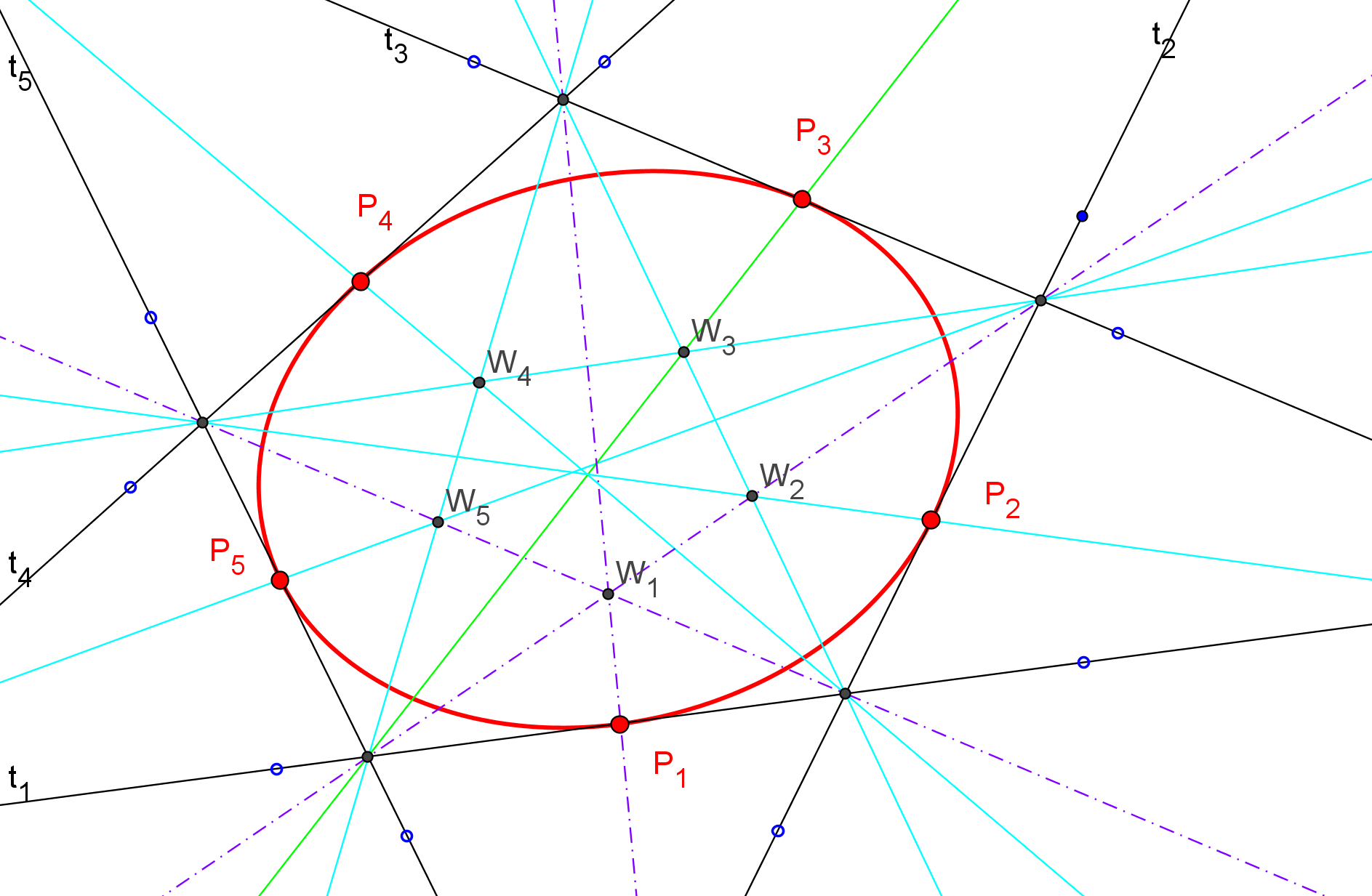
Utilizaremos el Teorema de Brianchon:
---
Dadas cinco tangentes t1, t2, t3, t4 y t5 de una cónica, para determinar el punto de tangencia P1 de la recta t1 con la cónica, utilizamos una situación límite del teorema de Brianchon cuando el hexágono circunscrito se reduce a una pentágono, sustituyendo dos lados consecutivos por una tangente y el vértice donde se cortan dichos lados pasa a ser el punto de tangencia:
1.
La recta que une t1∩t2 con t4∩t5 y la recta que une t5∩t1 con t2∩t3 se cortan en el punto de Brianchon W1.
2.
La recta que une t3∩t4 con W1 corta a la tangente t1 en el punto de tangencia P1.
3.
El mismo procedimiento nos permite encontrar los puntos de tangencia de las tangentes restantes.
4.
Conocidos cinco puntos de la cónica podemos determinar otros puntos, según el caso PPPPP .
"Si un hexágono se encuentra circunscrito en una cónica, las tres rectas que unen vértices opuestos se intersecan en un punto, denominado punto de Brianchon".
![]()
---
Utilizaremos el Teorema de Brianchon, para el caso del hexágono circunscrito a la parábola, formado por las rectas t1, P1P2, t2, la recta paralela al eje por P2, la recta del infinito y la recta paralela al eje por P1.
1.
Obtenemos el punto de Brianchon, de intersección de la paralela a t2 por P1, con la paralela a t1 por P2.
2.
La dirección del eje de la parábola es la de la recta que une el punto de Brianchon con el de intersección de las tangentes t1 y t2.
3.
Ya podemos determinar la "Parábola: dado la dirección del eje, un punto y una tangente con su punto de tangencia" (IPt_PC_p).

![]()