

Hechos Geométricos en el Triángulo
(2013)
(2014)
(2015)
|
Cómo es el enlace a un Hecho Geométrico correspondiente a un día concreto: http://amontes.webs.ull.es/otrashtm/HGT2016.htm#HGddmmaa EJEMPLO: Viernes, 1 de enero del 2016 http://amontes.webs.ull.es/otrashtm/HGT2016.htm#HG010116 |
A' (p+(p+q+r)k:q:r), B' (p:q+(p+q+r)m:r), C' (p:q:r+(p+q+r)n),
La ecuación de la cónica (Ca) que pasa por U, B, C, B',C' es:
(n q (-q u+p v) w+m (r v (-r u+p w)+n (p+q+r) (-r u v-q u w+p v w)))x^2 +
(-p u (n (q u-p v)+m (r u+n (p+q+r) u-p w)))y z +
(n q u (q u-p v)+m (n q (p+q+r) u^2+p v (r u-p w)))z x +
(n p (q u-p v) w+m r u (r u+n (p+q+r) u-p w))x y =0.
Ab =
(n (((1+3 k+2 k^2) p^2+k (3+4 k) p r+2 k^2 r^2) v^2+2 q^2 (u^2-k u v+k^2 v^2)+q v (2 k r (-u+2 k v)+p (-(3+2 k) u+k (3+4 k) v)))+k (-2 (p+k p+k r) v+q (u-2 k v)) (-r v+q w) : q v (n (((-1+k) p+k r) v+q (u+k v))+k (r v-q w)) : n q (q u-p v) w+k r v (r v+n (p+q+r) v-q w)),
Ac=
(k (r v-q w) (2 (p+k p+k q) w-r (u-2 k w))-m (((1+3 k+2 k^2) p^2+k (3+4 k) p q+2 k^2 q^2) w^2+2 r^2 (u^2-k u w+k^2 w^2)+r w (2 k q (-u+2 k w)+p (-(3+2 k) u+k (3+4 k) w))) : k q w (r v-q w)-m (r^2 u v+k q (p+q) w^2+r w (-p v+k q w)) : -r w (k (-r v+q w)+m (((-1+k) p+k q) w+r (u+k w)))).
V =(((1+m) n q u+m (1+n) r u-p (-m n u+n v+m w)) / ((1+m) n u w q ^2+m (1+n) u v r^2 +m n u(q (p+r)w+(p+q) r v )-p (m r+n q+m n(p+q+r))v w) : ... : ...).
Este punto también está sobre la cónica (Ca).
Σ kmnpqrxyz [k x (r (r + k (p + q + r))y^2+ q (q + k (p + q + r))z^2)]
- 2((1+k) m n p^2+k (1+m) n q^2+k m (1+n)r^2+k (1+m+n+2 m n)q r+m (1+k+n+2 k n)r p+n(1+k+m+2 k m) p q)xyz=0.
Theorem 7. If a cubic C is of type nK, but not of type cK, then there is a unique desmic structure which defines C as a Grassmann cubic.
• Si P es el ortocentro y A'B'C' es el (triángulo ceviano del ortocentro)
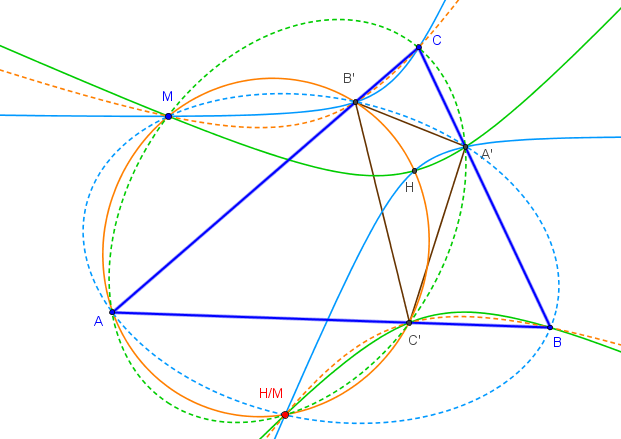
Sea A', (respectivamente B', C') los pies de las alturas desde el vértice A (respectivamente B, C) en un triángulo ABC.Sea H su ortocentro y sea M un punto arbitrario del plano. Demostrar que las seis cónicas que continenen a los puntos MABA'B', MBCB'C', MCAC'A', MHCA'B', MHAB'C' y MHBC'A' tienen en común otro punto además de M.
Dou, J. (1986): Problema E3172. American Mathematical Monthly (Vol 93, nº 9, Nov. pg 733)
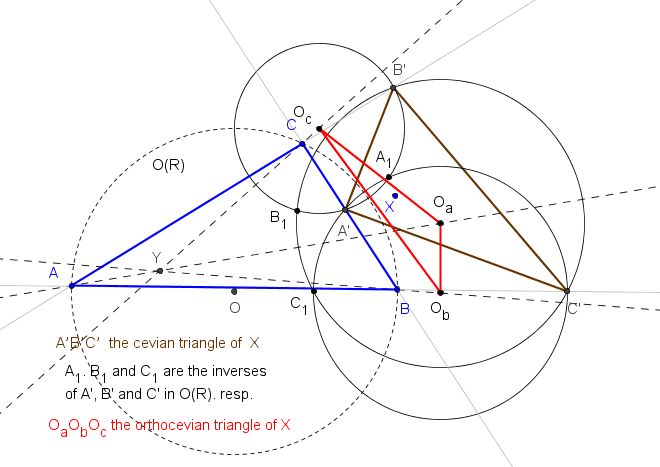
V = (p^2(c^2v+b^2w)+a^2 (-qru+prv+pqw) : q^2(a^2w+c^2u)+b^2(-rpv+qpw+qru) : r^2(b^2u+a^2v)+c^2(-pqw+rqu+rpv).
Cuando P=I es el incentro, V es el punto medio del incentro y el cociente ceviano U*/I, del de U y el incentro.x(c^2 (a^4 - b^2c^2)y^2+ b^2 (a^4 - b^2c^2)z^2)+ ... =0.
p w (-r u + p w)y^2 -p v (-q u + p v)z^2 -r v (q u - p v)z x+ q w (r u - p w)x y=0,
que pasa por P/Q (u (-q r u + p r v + p q w) : v (q r u - p r v + p q w) : w (q r u + p r v - p q w)).-q r v w x^2 + u (q r u - p r v - p q w)y z + p q v w z x + p r v w x y=0.
que también pasa por P/Q. Lo mismo ocurre con las dos cónicas restantes.La recta PQ vuelve a cortar al cónica que pasa por los puntos Q, B, C, Pb, Pc en el punto Qa = (-q r u + p r v + p q w : q^2 w : r^2 v). Análogamente, se obtienen los puntos Qb = (-p^2 w : p r v-q r u+p q w :-r^2 u) y Qc = (p^2 v : q^2 u : q r u+p r v-p q w).
Ab = (-p u (-q r u+p r v+p q w) : q (p v (r u-2 p w)+q u (-r u+p w)) : -2 p^2 r v w),
Ac = (p u (-q r u+p r v+p q w) : 2 p^2 q v w : r (q u (r u-p w)+p v (-r u+2 p w))).
q^2 r^2 v w (p^3 r^2 v^3 (r u-4 p w)+q^3 u (r u-p w)^2 (r u+p w)+p^2 q r v^2 (-r^2 u^2-p r u w+8 p^2 w^2)-p q^2 v (r^3 u^3+2 p r^2 u^2 w+p^2 r u w^2+4 p^3 w^3)) x^2+2 p^2 q r u (-2 q^4 u w^2 (r u-p w)^2+p^2 r^3 v^4 (-2 r u+p w)-p q r^2 v^3 (-4 r^2 u^2+p r u w+p^2 w^2)-q^2 r v^2 (2 r^3 u^3+9 p r^2 u^2 w-14 p^2 r u w^2+p^3 w^3)+q^3 v w (9 r^3 u^3-9 p r^2 u^2 w-p^2 r u w^2+p^3 w^3)) y z+... =0.
Q = (u^2-v w : v^2-w u : w^2-u v).
Éste es el punto de intersección de la recta PX2: (v - w)x+(w-u)y+(u-v)z=0 y la polar de P respecto a ℰ: (v + w)x+(w+u)y+(u+v)z=0.
![]()
b^2 x^3 y-c^2 x^2 y^2+a^2 x y^3+c^2 x^3 z-a^2 x^2 y z-b^2 x y^2 z+c^2 y^3 z-b^2 x^2 z^2-c^2 x y z^2-a^2 y^2 z^2+a^2 x z^3+b^2 y z^3 = 0.
W = ((a^2+b^2-2 c^2) (a^2-2 b^2+c^2) (a^6+5 a^2 b^2 c^2-2 a^4 (b^2+c^2)-b^2 c^2 (b^2+c^2)):...:...),
que tiene números de búsqueda en (2.16868078347488, 3.61405138663714, 0.137699314170263) y está sobre las rectas XiXj s.e.u.o., para los índices {i,j}: {2,99}, {385,691}, {538,892}, {690,895}, {8267,8877}.U = (a^2/((b^2-c^2)(-a^6-5 a^2 b^2 c^2+2 a^4 (b^2+c^2)+b^2 c^2 (b^2+c^2)) ):...:...),
que tiene números de búsqueda en (-0.142868687501235, 0.234812353161126, 3.54404147779648).a Bea, por su "cumple"
Oa = (-2 a^2 (a^2-b^2-c^2) : -a^4-3 b^4+4 b^2 c^2-c^4+2 a^2 (2 b^2+c^2) : -a^4-b^4+4 b^2 c^2-3 c^4+2 a^2 (b^2+2 c^2))
Na = (-2 a^4-3 (b^2-c^2)^2+5 a^2 (b^2+c^2) : -a^4+c^2 (b^2-c^2)+a^2 (b^2+2 c^2) : -a^4-b^4+b^2 c^2+a^2 (2 b^2+c^2))
O1 =
(4 a^8-(b^2-c^2)^4-8 a^6 (b^2+c^2)+2 a^2 (b^2-c^2)^2 (b^2+c^2)+3 a^4 (b^4+c^4):
2 a^8-(b^2-c^2)^3 (2 b^2-c^2)-a^6 (7 b^2+5 c^2)+a^4 (6 b^4+4 b^2 c^2+3 c^4)+a^2 (b^6-2 b^2 c^4+c^6) :
2 a^8-(b^2-2 c^2) (b^2-c^2)^3-a^6 (5 b^2+7 c^2)+a^4 (3 b^4+4 b^2 c^2+6 c^4)+a^2 (b^6-2 b^4 c^2+c^6)).
(2 a^6-6 a^4 (b^2+c^2)+a^2 (6 b^4+b^2 c^2+6 c^4)-2 (b^2-c^2)^2 (b^2+c^2))x+ ⋯ =0,
cuyo punto del infinito es X523, en la dirección de la perpendicular a la recta de Euler.W = (4 a^10-10 a^8 (b^2+c^2)+2 a^6 (2 b^4+7 b^2 c^2+2 c^4)-a^2 (b^2-c^2)^2 (8 b^4+3 b^2 c^2+8 c^4)-a^4 (-8 b^6+11 b^4 c^2+11 b^2 c^4-8 c^6)+2 (b^2-c^2)^4 (b^2+c^2):...:...),
que tiene números de búsqueda en (2.43812614140663, 1.56217438018609, 1.43387015343711).The Parry point is one of the two intersections of the Parry circle and the circumcircle of a triangle (the other is the focus of the Kiepert parabola, which is Kimberling center X110. The Parry point is Kimberling center X111.
The Parry circle is the circle passing through the and the triangle centroid of a triangle.
A' = (2 (-a^4+b^4-b^2 c^2+c^4) : -a^2 (a^2-2 b^2+c^2) : -a^2 (a^2+b^2-2 c^2)).
La simétrica de la recta AA', respecto a la bisectirz en A, vuelve a cortar a la circunfeencia circunscrita en el punto de Parry, (a^2/(b^2+c^2-2a^2) : b^2/(c^2+a^2-2b^2) : c^2/(a^2+b^2-2c^2)).El lugar geométrico de los puntos P tales que los triángulos NaNbNc y el pedal de P son perspectivos es la .
El lugar geométrico de los centros de perspectividad es la
hipérbola
((3 a^12 b^6 c^2-7 a^10 b^8 c^2+10 a^6 b^12 c^2-5 a^4 b^14 c^2-3 a^2 b^16 c^2+2 b^18 c^2-6 a^12 b^4 c^4+7 a^10 b^6 c^4+19 a^8 b^8 c^4-34 a^6 b^10 c^4+4 a^4 b^12 c^4+19 a^2 b^14 c^4-9 b^16 c^4+3 a^12 b^2 c^6+7 a^10 b^4 c^6-38 a^8 b^6 c^6+24 a^6 b^8 c^6+29 a^4 b^10 c^6-39 a^2 b^12 c^6+14 b^14 c^6-7 a^10 b^2 c^8+19 a^8 b^4 c^8+24 a^6 b^6 c^8-56 a^4 b^8 c^8+23 a^2 b^10 c^8-7 b^12 c^8-34 a^6 b^4 c^10+29 a^4 b^6 c^10+23 a^2 b^8 c^10+10 a^6 b^2 c^12+4 a^4 b^4 c^12-39 a^2 b^6 c^12-7 b^8 c^12-5 a^4 b^2 c^14+19 a^2 b^4 c^14+14 b^6 c^14-3 a^2 b^2 c^16-9 b^4 c^16+2 b^2 c^18) x^2+(a^16 b^2 c^2+5 a^14 b^4 c^2-21 a^12 b^6 c^2+15 a^10 b^8 c^2+15 a^8 b^10 c^2-21 a^6 b^12 c^2+5 a^4 b^14 c^2+a^2 b^16 c^2-a^16 c^4-9 a^14 b^2 c^4+14 a^12 b^4 c^4+33 a^10 b^6 c^4-74 a^8 b^8 c^4+33 a^6 b^10 c^4+14 a^4 b^12 c^4-9 a^2 b^14 c^4-b^16 c^4+4 a^14 c^6+10 a^12 b^2 c^6-62 a^10 b^4 c^6+48 a^8 b^6 c^6+48 a^6 b^8 c^6-62 a^4 b^10 c^6+10 a^2 b^12 c^6+4 b^14 c^6-3 a^12 c^8+24 a^10 b^2 c^8+39 a^8 b^4 c^8-112 a^6 b^6 c^8+39 a^4 b^8 c^8+24 a^2 b^10 c^8-3 b^12 c^8-10 a^10 c^10-53 a^8 b^2 c^10+45 a^6 b^4 c^10+45 a^4 b^6 c^10-53 a^2 b^8 c^10-10 b^10 c^10+25 a^8 c^12+31 a^6 b^2 c^12-48 a^4 b^4 c^12+31 a^2 b^6 c^12+25 b^8 c^12-24 a^6 c^14-4 a^4 b^2 c^14-4 a^2 b^4 c^14-24 b^6 c^14+11 a^4 c^16+2 a^2 b^2 c^16+11 b^4 c^16-2 a^2 c^18-2 b^2 c^18) x y+(2 a^18 c^2-3 a^16 b^2 c^2-5 a^14 b^4 c^2+10 a^12 b^6 c^2-7 a^8 b^10 c^2+3 a^6 b^12 c^2-9 a^16 c^4+19 a^14 b^2 c^4+4 a^12 b^4 c^4-34 a^10 b^6 c^4+19 a^8 b^8 c^4+7 a^6 b^10 c^4-6 a^4 b^12 c^4+14 a^14 c^6-39 a^12 b^2 c^6+29 a^10 b^4 c^6+24 a^8 b^6 c^6-38 a^6 b^8 c^6+7 a^4 b^10 c^6+3 a^2 b^12 c^6-7 a^12 c^8+23 a^10 b^2 c^8-56 a^8 b^4 c^8+24 a^6 b^6 c^8+19 a^4 b^8 c^8-7 a^2 b^10 c^8+23 a^8 b^2 c^10+29 a^6 b^4 c^10-34 a^4 b^6 c^10-7 a^8 c^12-39 a^6 b^2 c^12+4 a^4 b^4 c^12+10 a^2 b^6 c^12+14 a^6 c^14+19 a^4 b^2 c^14-5 a^2 b^4 c^14-9 a^4 c^16-3 a^2 b^2 c^16+2 a^2 c^18) y^2+(-a^16 b^4+4 a^14 b^6-3 a^12 b^8-10 a^10 b^10+25 a^8 b^12-24 a^6 b^14+11 a^4 b^16-2 a^2 b^18+a^16 b^2 c^2-9 a^14 b^4 c^2+10 a^12 b^6 c^2+24 a^10 b^8 c^2-53 a^8 b^10 c^2+31 a^6 b^12 c^2-4 a^4 b^14 c^2+2 a^2 b^16 c^2-2 b^18 c^2+5 a^14 b^2 c^4+14 a^12 b^4 c^4-62 a^10 b^6 c^4+39 a^8 b^8 c^4+45 a^6 b^10 c^4-48 a^4 b^12 c^4-4 a^2 b^14 c^4+11 b^16 c^4-21 a^12 b^2 c^6+33 a^10 b^4 c^6+48 a^8 b^6 c^6-112 a^6 b^8 c^6+45 a^4 b^10 c^6+31 a^2 b^12 c^6-24 b^14 c^6+15 a^10 b^2 c^8-74 a^8 b^4 c^8+48 a^6 b^6 c^8+39 a^4 b^8 c^8-53 a^2 b^10 c^8+25 b^12 c^8+15 a^8 b^2 c^10+33 a^6 b^4 c^10-62 a^4 b^6 c^10+24 a^2 b^8 c^10-10 b^10 c^10-21 a^6 b^2 c^12+14 a^4 b^4 c^12+10 a^2 b^6 c^12-3 b^8 c^12+5 a^4 b^2 c^14-9 a^2 b^4 c^14+4 b^6 c^14+a^2 b^2 c^16-b^4 c^16) x z+(-2 a^18 b^2+11 a^16 b^4-24 a^14 b^6+25 a^12 b^8-10 a^10 b^10-3 a^8 b^12+4 a^6 b^14-a^4 b^16-2 a^18 c^2+2 a^16 b^2 c^2-4 a^14 b^4 c^2+31 a^12 b^6 c^2-53 a^10 b^8 c^2+24 a^8 b^10 c^2+10 a^6 b^12 c^2-9 a^4 b^14 c^2+a^2 b^16 c^2+11 a^16 c^4-4 a^14 b^2 c^4-48 a^12 b^4 c^4+45 a^10 b^6 c^4+39 a^8 b^8 c^4-62 a^6 b^10 c^4+14 a^4 b^12 c^4+5 a^2 b^14 c^4-24 a^14 c^6+31 a^12 b^2 c^6+45 a^10 b^4 c^6-112 a^8 b^6 c^6+48 a^6 b^8 c^6+33 a^4 b^10 c^6-21 a^2 b^12 c^6+25 a^12 c^8-53 a^10 b^2 c^8+39 a^8 b^4 c^8+48 a^6 b^6 c^8-74 a^4 b^8 c^8+15 a^2 b^10 c^8-10 a^10 c^10+24 a^8 b^2 c^10-62 a^6 b^4 c^10+33 a^4 b^6 c^10+15 a^2 b^8 c^10-3 a^8 c^12+10 a^6 b^2 c^12+14 a^4 b^4 c^12-21 a^2 b^6 c^12+4 a^6 c^14-9 a^4 b^2 c^14+5 a^2 b^4 c^14-a^4 c^16+a^2 b^2 c^16) y z+(2 a^18 b^2-9 a^16 b^4+14 a^14 b^6-7 a^12 b^8-7 a^8 b^12+14 a^6 b^14-9 a^4 b^16+2 a^2 b^18-3 a^16 b^2 c^2+19 a^14 b^4 c^2-39 a^12 b^6 c^2+23 a^10 b^8 c^2+23 a^8 b^10 c^2-39 a^6 b^12 c^2+19 a^4 b^14 c^2-3 a^2 b^16 c^2-5 a^14 b^2 c^4+4 a^12 b^4 c^4+29 a^10 b^6 c^4-56 a^8 b^8 c^4+29 a^6 b^10 c^4+4 a^4 b^12 c^4-5 a^2 b^14 c^4+10 a^12 b^2 c^6-34 a^10 b^4 c^6+24 a^8 b^6 c^6+24 a^6 b^8 c^6-34 a^4 b^10 c^6+10 a^2 b^12 c^6+19 a^8 b^4 c^8-38 a^6 b^6 c^8+19 a^4 b^8 c^8-7 a^8 b^2 c^10+7 a^6 b^4 c^10+7 a^4 b^6 c^10-7 a^2 b^8 c^10+3 a^6 b^2 c^12-6 a^4 b^4 c^12+3 a^2 b^6 c^12) z^2=0)
ℋ, que pasa a través del circuncentro, centro de la circunferencia de los nueve puntos y X5663 (punto del infinito de la recta de Euler del ).
W = ((a^2-b^2-c^2) (-2a^8+2 a^6 (b^2+c^2)+a^4 (b^4-4 b^2 c^2+c^4)-(b^2-c^2)^4):...:...),
que tiene números de búsqueda en (1.22023184857025, 1.04347413196238, -1.28558909839099).La parábola ℘ es tangente a la recta de Euler en el ortocentro, pasa por X6225 ( de X64), por X6759 (inverso de X6760 en la circunferencia circunscrita) y el punto del infinito es X2777 (conjugado isogonal de la reflexión de X1304 en el circuncentro).
Let A'B'C' be the reflection of the of the circumcenter in the of the circumcenter. The lines AA', BB', CC' concur in X(6760).
(1/((b^2-c^2)^2 ): 1/((c^2-a^2)^2 SB^3):1/((a^2-b^2)^2 SC^3)),
que tiene números de búsqueda en (-0.0299591539722006, -0.0449445061606283, 3.68560721108275) y está sobre las rectas XiXj s.e.u.o., para los índices {i,j}: {30,250}, {107,523}, {450,3260}, {648,8057}, {1503,1559}, {1971,1990}, {2404,2409}, {6524,9214}.Sea P un punto sobre la de ABC y Ma, Mb, Mc los puntos medios de PNa, PNb, PNc, resp.
El circuncentro Q del triángulo MaMbMc está sobre la recta de Euler de ABC si y solo si D está sobre una
quíntica
(a^6 c^2 x^3 y^2-3 a^4 b^2 c^2 x^3 y^2+3 a^2 b^4 c^2 x^3 y^2-b^6 c^2 x^3 y^2-a^4 c^4 x^3 y^2+a^2 b^2 c^4 x^3 y^2-a^2 c^6 x^3 y^2+c^8 x^3 y^2+a^6 c^2 x^2 y^3-3 a^4 b^2 c^2 x^2 y^3+3 a^2 b^4 c^2 x^2 y^3-b^6 c^2 x^2 y^3-a^2 b^2 c^4 x^2 y^3+b^4 c^4 x^2 y^3+b^2 c^6 x^2 y^3-c^8 x^2 y^3+3 a^2 b^4 c^2 x^3 y z-3 b^6 c^2 x^3 y z-3 a^2 b^2 c^4 x^3 y z+3 b^2 c^6 x^3 y z+2 a^6 c^2 x^2 y^2 z-2 b^6 c^2 x^2 y^2 z-4 a^4 c^4 x^2 y^2 z+4 b^4 c^4 x^2 y^2 z+2 a^2 c^6 x^2 y^2 z-2 b^2 c^6 x^2 y^2 z+3 a^6 c^2 x y^3 z-3 a^4 b^2 c^2 x y^3 z+3 a^2 b^2 c^4 x y^3 z-3 a^2 c^6 x y^3 z-a^6 b^2 x^3 z^2+a^4 b^4 x^3 z^2+a^2 b^6 x^3 z^2-b^8 x^3 z^2+3 a^4 b^2 c^2 x^3 z^2-a^2 b^4 c^2 x^3 z^2-3 a^2 b^2 c^4 x^3 z^2+b^2 c^6 x^3 z^2-2 a^6 b^2 x^2 y z^2+4 a^4 b^4 x^2 y z^2-2 a^2 b^6 x^2 y z^2+2 b^6 c^2 x^2 y z^2-4 b^4 c^4 x^2 y z^2+2 b^2 c^6 x^2 y z^2+2 a^6 b^2 x y^2 z^2-4 a^4 b^4 x y^2 z^2+2 a^2 b^6 x y^2 z^2-2 a^6 c^2 x y^2 z^2+4 a^4 c^4 x y^2 z^2-2 a^2 c^6 x y^2 z^2+a^8 y^3 z^2-a^6 b^2 y^3 z^2-a^4 b^4 y^3 z^2+a^2 b^6 y^3 z^2+a^4 b^2 c^2 y^3 z^2-3 a^2 b^4 c^2 y^3 z^2+3 a^2 b^2 c^4 y^3 z^2-a^2 c^6 y^3 z^2-a^6 b^2 x^2 z^3+b^8 x^2 z^3+3 a^4 b^2 c^2 x^2 z^3+a^2 b^4 c^2 x^2 z^3-b^6 c^2 x^2 z^3-3 a^2 b^2 c^4 x^2 z^3-b^4 c^4 x^2 z^3+b^2 c^6 x^2 z^3-3 a^6 b^2 x y z^3+3 a^2 b^6 x y z^3+3 a^4 b^2 c^2 x y z^3-3 a^2 b^4 c^2 x y z^3-a^8 y^2 z^3+a^2 b^6 y^2 z^3+a^6 c^2 y^2 z^3-a^4 b^2 c^2 y^2 z^3-3 a^2 b^4 c^2 y^2 z^3+a^4 c^4 y^2 z^3+3 a^2 b^2 c^4 y^2 z^3-a^2 c^6 y^2 z^3 = 0)
que pasa a través de A, B, C (dobles), los vértices del triángulo ceviano de X265, X1, X4, X5, X30, X1113, X1114, X1138. Su asíntota real es la parelela a la recta de Euler por X1138.
X(4), orthocenter, is the point of concurrence of the altitudes of ABC.
X(5), nine-point center, is the center of the nine-point circle.
X(30) is the point of intersection of the Euler line and the line at infinity.
Let P = X(74), H = X(4), H' =H-of-BCP, H'' = H-of-CAP, and H''' = H-of ABP. Then X(265) is the circumcenter of the cyclic quadrilateral HH'H''H'''. (Randy Hutson, 9/23/2011)
X(1113) and X(1114) are the points of intersection of the Euler line and the circumcircle.
There are only two points X such that the pedal triangle of X is similar to the cevian triangle of X. They are X(4) and X(1138). (Jean-Pierre Ehrmann, 1/4/03)
Na = (-(b^2-c^2)^2 p^2+a^2 p (c^2 (p+q-r)+b^2 (p-q+r))+a^4 (2 q r+p (q+r)):
-(b^2-c^2) p (b^2 (q+r)-c^2 (p+q+r))-a^4 (p^2+q r+p (2 q+r))+a^2 (b^2 (p^2+3 p q-q r)+c^2 (2 p^2+3 p q+2 p r+q r)):
-(b^2-c^2) p (-c^2 (q+r)+b^2 (p+q+r))-a^4 (p^2+q r+p (q+2 r))+a^2 (c^2 (p^2+3 p r-q r)+b^2 (2 p^2+2 p q+3 p r+q r))).
Ma =
((b^2-c^2)^2 p (5 p+2 (q+r))+a^4 (2 p^2-6 q r-p (q+r))-a^2 p (c^2 (7 p+7 q+r)+b^2 (7 p+q+7 r))+3 ((b^2-c^2)^2 p^2+a^4 (2 p^2-2 q r+p (q+r))-a^2 p (c^2 (3 p+3 q+r)+b^2 (3 p+q+3 r))) t :
a^4 (5 p^2+8 p q+5 p r+3 q r)-a^2 (b^2 (7 p^2+13 p q+4 p r-3 q r)+c^2 (10 p^2+13 p q+10 p r+3 q r))+(b^2-c^2) p (-5 c^2 (p+q+r)+b^2 (2 p+5 (q+r)))+3 (a^4 (p^2+q r+p (2 q+r))-a^2 (b^2 (3 p^2+5 p q+2 p r-q r)+c^2 (2 p^2+3 p q+2 p r+q r))+(b^2-c^2) p (-c^2 (p+q+r)+b^2 (2 p+3 (q+r)))) t:
a^4 (5 p^2+5 p q+8 p r+3 q r)-a^2 (c^2 (7 p^2+4 p q+13 p r-3 q r)+b^2 (10 p^2+10 p q+13 p r+3 q r))+(b^2-c^2) p (5 b^2 (p+q+r)-c^2 (2 p+5 (q+r)))+3 (a^4 (p^2+q r+p (q+2 r))-a^2 (c^2 (3 p^2+2 p q+5 p r-q r)+b^2 (2 p^2+2 p q+3 p r+q r))+(b^2-c^2) p (b^2 (p+q+r)-c^2 (2 p+3 (q+r)))) t)
(a^4 q^2 r^2 (2 p+q+r)+a^2 p (b^2 r (p^2 (q-r)+q^2 (q+r)+p (2 q^2+2 q r-r^2))+c^2 q (p^2 (-q+r)+r^2 (q+r)+p (-q^2+2 q r+2 r^2)))-p (b^4 r (p^2 q+q (q+r)^2+p (2 q^2+3 q r+r^2))+c^4 q (p^2 r+r (q+r)^2+p (q^2+3 q r+2 r^2))-b^2 c^2 (2 q r (q+r)^2+p^2 (q^2+4 q r+r^2)+p (q^3+5 q^2 r+5 q r^2+r^3))):...:...)
Por consiguiente, el centro Q de la circunferencia circunscrita al triángulo MaMbMc está sobre la recta de Euler si D(p:q:r) está sobre la quíntica:
Na =
(-2 a^8+(b^2-c^2)^4+4 a^6 (b^2+c^2)-2 a^2 (b^2-c^2)^2 (b^2+c^2)-a^4 (b^4-4 b^2 c^2+c^4) :
(a^4+(b^2-c^2)^2-a^2 (b^2+2 c^2)) (a^4+b^4-3 b^2 c^2+2 c^4-a^2 (2 b^2+3 c^2)) :
(a^4+(b^2-c^2)^2-a^2 (2 b^2+c^2)) (a^4+2 b^4-3 b^2 c^2+c^4-a^2 (3 b^2+2 c^2))).
At =
(-2a^4-a^2(b^2+c^2)(-4+t)+(b^2-c^2)^2(-2+t) : (a^4-b^2c^2+c^4-a^2(b^2+2c^2))t : (a^4+b^4-b^2c^2-a^2(2b^2+c^2))t),
Bt =
(-(-(b^2-c^2)^2+a^2(b^2+c^2))t : a^2(-b^2(-4+t)-2c^2(-2+t))-(b^2-c^2)(2b^2+c^2(-2+t))+a^4(-2+t) : (a^4+b^4-b^2c^2-a^2(2b^2+c^2))t),
Ct =
(-(-(b^2-c^2)^2+a^2(b^2+c^2))t : (a^4-b^2c^2+c^4-a^2(b^2+2c^2))t : a^2(-c^2(-4+t)-2b^2(-2+t))+(b^2-c^2)(2c^2+b^2(-2+t))+a^4(-2+t)).
2 a^16 (-1+t)+a^14 (b^2+c^2) (16-13 t+t^2)
-a^12 (2 b^2 c^2 (38-25 t+3 t^2)+b^4 (56-37 t+5 t^2)+c^4 (56-37 t+5 t^2))
+a^10 (b^2+c^2) (-4 b^2 c^2 (-3+t)+b^4 (114-65 t+11 t^2)+c^4 (114-65 t+11 t^2))
-a^8 (6 b^4 c^4 (-3+t)^2+5 b^8 (30-17 t+3 t^2)+5 c^8 (30-17 t+3 t^2)+2 b^6 c^2 (24-13 t+3 t^2)+2 b^2 c^6 (24-13 t+3 t^2))
+3 a^6 (b^2+c^2) (3 b^4 c^4 (28-19 t+3 t^2)-2 b^6 c^2 (43-25 t+4 t^2)-2 b^2 c^6 (43-25 t+4 t^2)+b^8 (44-29 t+5 t^2)+c^8 (44-29 t+5 t^2))
-a^4 (b^2-c^2)^2 (2 b^6 c^2 (-29+3 t)+2 b^2 c^6 (-29+3 t)+3 b^4 c^4 (-18-3 t+t^2)+b^8 (76-63 t+11 t^2)+c^8 (76-63 t+11 t^2))
+a^2 (b^2-c^2)^4 (b^2+c^2) (-2 b^2 c^2 (29-13 t+2 t^2)+b^4 (26-27 t+5 t^2)+c^4 (26-27 t+5 t^2))
-(b^2-c^2)^6 (2 b^2 c^2 (-5+t)+b^4 (4-5 t+t^2)+c^4 (4-5 t+t^2))
(b^2-c^2)(2(^2-3S^2)(SB SC-3S^2)x^2+
(a^8-6 a^6 (b^2+c^2)+3 a^4 (4 b^4+3 b^2 c^2+4 c^4)+a^2 (-10 b^6+7 b^4 c^2+7 b^2 c^4-10 c^6)+(b^2-c^2)^2 (3 b^4-4 b^2 c^2+3 c^4))y z)+ ⋯ = 0.
((b^2-c^2)(5a^8-14a^6(b^2+c^2)+a^4(14b^4+b^2c^2+14c^4)+a^2(-6b^6+3b^4c^2+3b^2c^4-6c^6)+(b^2-c^2)^2(b^4+c^4)):...:...),
que tiene números de búsqueda en (0.288632328111871, -1.20215426516882, 4.33971020635731).{X3, X468= 3X2 + X23 },
{X67, (a^2 (-b^6+2 a^2 b^2 c^2+2 b^4 c^2+2 b^2 c^4-c^6+a^4 (b^2+c^2)):...:...)},
que tiene coordenadas trilineales exactas en el triángulo de (0.938855731419020, -0.0243852962146813, 3.22422858017038).{X187, ((8 a^2-b^2-c^2) (3 a^4-4 b^4+10 b^2 c^2-4 c^4-a^2 (b^2+c^2)) :...:...)},
que tiene coordenadas trilineales exactas en el triángulo de (-0.0486401258368504, -2.40922095926275, 5.33103597332175). La asíntota real tiene punto del infinito :(4 a^8-5 a^6 (b^2+c^2)-2 (b^4-c^4)^2-2 a^4 (b^4-3 b^2 c^2+c^4)+a^2 (5 b^6-3 b^4 c^2-3 b^2 c^4+5 c^6) :...:...)},
que tiene coordenadas trilineales exactas en el triángulo de (1.61888280407429, 0.898880431224801, -1.36947851580530). El punto T correspondiente a este punto es X1843.
Ha = (0 : a^2+b^2-c^2 : a^2-b^2+c^2),
Oa = (-2a^2(-(b^2-c^2)^2+a^2(b^2+c^2)) : (a^2-b^2-c^2)(a^4-2a^2c^2+(b^2-c^2)^2) : (a^2-b^2-c^2)(a^4-2a^2b^2+(b^2-c^2)^2)).
P = (SBSC(S²+SBSC) (3SA(S²+SBSC)+b²S²B+c²S²C) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de (-2.7032638423341250, 1.8214747911479623, 3.6273037075746168).(a^6-3a^4(b^2+c^2)+a^2(3b^4+4b^2c^2+3c^4) -b^6-b^4c^2-b^2c^4-c^6)x^2 + 2a^2(a^4+(b^2-c^2)^2-2a^2(b^2+c^2))y z + ... = 0.
El centro de esta cónica es:D = ((a^2(b^2+c^2)-(b^2-c^2)^2) (2a^8-5a^6(b^2+c^2)+a^4(5b^4+2b^2c^2+5c^4)-3a^2(b^2-c^2)^2(b^2+c^2)+(b^2-c^2)^4) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de (-1.8862860827434219, 0.59575460944049869, 4.0988125597148440).(b^2 (p+q) (b^2 p+a^2 q) r^3-c^4 p q^3 (p+r)-c^2 q r (b^2 p (p-q-r) (q-r)+a^2 q^2 (p+r))) x+r (a^4 q (p+q) r (p+r)-(b^2-c^2) p^2 (b^2 (p+q) r-c^2 q (p+r))+a^2 p (c^2 q (p+q-r) (p+r)+b^2 (p+q) r (p-q+r))) y-q (a^4 q (p+q) r (p+r)-(b^2-c^2) p^2 (b^2 (p+q) r-c^2 q (p+r))+a^2 p (c^2 q (p+q-r) (p+r)+b^2 (p+q) r (p-q+r))) z = 0.
Las rectas A'Oa, B'Ob y C'Oc son concurrentes si el punto P está sobre la circunferencia circunscrita o sobre la séptica de ecuación:-c^4 x^4 y^3+c^4 x^3 y^4+a^2 c^2 x^4 y^2 z-c^4 x^4 y^2 z-2 a^2 c^2 x^3 y^3 z+2 b^2 c^2 x^3 y^3 z-b^2 c^2 x^2 y^4 z+c^4 x^2 y^4 z-a^2 b^2 x^4 y z^2+b^4 x^4 y z^2-a^2 b^2 x^3 y^2 z^2+b^4 x^3 y^2 z^2+a^2 c^2 x^3 y^2 z^2-c^4 x^3 y^2 z^2-a^4 x^2 y^3 z^2+a^2 b^2 x^2 y^3 z^2-b^2 c^2 x^2 y^3 z^2+c^4 x^2 y^3 z^2-a^4 x y^4 z^2+a^2 b^2 x y^4 z^2+b^4 x^4 z^3+2 a^2 b^2 x^3 y z^3-2 b^2 c^2 x^3 y z^3+a^4 x^2 y^2 z^3-b^4 x^2 y^2 z^3-a^2 c^2 x^2 y^2 z^3+b^2 c^2 x^2 y^2 z^3-2 a^2 b^2 x y^3 z^3+2 a^2 c^2 x y^3 z^3-a^4 y^4 z^3-b^4 x^3 z^4-b^4 x^2 y z^4+b^2 c^2 x^2 y z^4+a^4 x y^2 z^4-a^2 c^2 x y^2 z^4+a^4 y^3 z^4 = 0.
∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗
Sean P1 y P2 los puntos, sobre la circunferencia circunscrita, que dan como centro de perspectividad X3167. El polo de la recta P1P2, respecto a la circunferencia circunscrita, es X9723.
Oa =
(a^4 q (p+q) r (p+r)-(b^2-c^2) p^2 (b^2 (p+q) r-c^2 q (p+r))+a^2 p (c^2 q (p+q-r) (p+r)+b^2 (p+q) r (p-q+r)):
-b^2 ((p+q) (b^2 p+a^2 q) r^2-c^2 p q (p q+r^2)):
-c^2 (c^2 p q^2 (p+r)+r (a^2 q^2 (p+r)-b^2 p (q^2+p r))))
Q = (a^2 (b^2 (-1+t)-c^2 t) (b^2 (-1+t)-(c^2+2 a^2 (-1+t)) t) : b^2 (c^2+a^2 (-1+t)) (2 b^2 (-1+t)-(c^2+a^2 (-1+t)) t) : c^2 (-b^2+a^2 t) (-b^2 (-1+t)+(2 c^2+a^2 (-1+t)) t)),
que describe la cúbica:(-a^2 b^2 c^2+3 b^4 c^2+3 b^2 c^4) x^3+(3 a^4 c^2-3 a^2 b^2 c^2+6 b^4 c^2-15 a^2 c^4-12 b^2 c^4+18 c^6) x^2 y+(6 a^4 c^2-3 a^2 b^2 c^2+3 b^4 c^2-12 a^2 c^4-15 b^2 c^4+18 c^6) x y^2+(3 a^4 c^2-a^2 b^2 c^2+3 a^2 c^4) y^3+(3 a^4 b^2-15 a^2 b^4+18 b^6-3 a^2 b^2 c^2-12 b^4 c^2+6 b^2 c^4) x^2 z+(-9 a^6+15 a^4 b^2+15 a^2 b^4-9 b^6+15 a^4 c^2-60 a^2 b^2 c^2+15 b^4 c^2+15 a^2 c^4+15 b^2 c^4-9 c^6) x y z+(18 a^6-15 a^4 b^2+3 a^2 b^4-12 a^4 c^2-3 a^2 b^2 c^2+6 a^2 c^4) y^2 z+(6 a^4 b^2-12 a^2 b^4+18 b^6-3 a^2 b^2 c^2-15 b^4 c^2+3 b^2 c^4) x z^2+(18 a^6-12 a^4 b^2+6 a^2 b^4-15 a^4 c^2-3 a^2 b^2 c^2+3 a^2 c^4) y z^2+(3 a^4 b^2+3 a^2 b^4-a^2 b^2 c^2) z^3 = 0,
con punto singular X3167, cociente ceviano del simediano y el circuncentro:(a^2(a^2-b^2-c^2)(3a^2-b^2-c^2) : b^2(-a^2+b^2-c^2)(-a^2+3b^2-c^2) : c^2(-a^2-b^2+c^2)(-a^2-b^2+3c^2)).
Los puntos P1 y P2 (sobre la circunferencia circunscrita) para los cuales los centros de perspectividad Q coinciden en X3167, se obtienen para los valores:t1,2 = ((a^2+b^2-c^2) (a^4+b^4-2 a^2 c^2-2 b^2 c^2+c^4)) ±Sqrt[((a^3-a^2 b-a b^2+b^3+a^2 c+b^2 c-a c^2-b c^2-c^3) (a^3+a^2 b-a b^2-b^3+a^2 c+b^2 c-a c^2+b c^2-c^3) (a^3-a^2 b-a b^2+b^3-a^2 c-b^2 c-a c^2-b c^2+c^3) (a^3+a^2 b-a b^2-b^3-a^2 c-b^2 c-a c^2+b c^2+c^3)]) /(2 (a^6-a^4 b^2+2 a^2 b^4-a^4 c^2-4 a^2 b^2 c^2+2 a^2 c^4)).
La recta P1P2 (que pasa por los centros X3566, X6562, X6563, X9131) es la polar de X9723, respecto a la circunferencia circunscrita.X9723 = (a^2(-a^6 + 3a^4(b^2+c^2)-a^2(3b^4+4b^2c^2+3c^4) +b^6+b^4c^2+b^2c^4+c^6) : ... : ...).
| vw((qr-vw)x^2 - 2u(p-u)yz) + ⋯ = 0. | (1) |
(x':y:z')=(a^2(c^2y+b^2z) : b^2(c^2x+a^2z) : c^2(b^2x+a^2y)),
que usamos para poner las coordenadas, en la nueva referencia, de los vértices del triángulo de Fuhrmann en la forma D'(p:v:w), E'(u:q:w), F'(u:v:r); donde (u:v:w) son las coordenadas del circuncentro.
D' = (
(a^2(a^2-b^2-b c-c^2)(a^2+b^2+c^2)(-b^2c^2(-a^2+b^2-c^2)-b^2c^2(-a^2-b^2+c^2))+(-a^4-(b+c)^2(b^2-b c+c^2)+a^2(2b^2+b c+2c^2))(c^2(-a^2b^2(a^2-b^2-c^2)-a^2b^2(-a^2+b^2-c^2))+b^2(-a^2c^2(a^2-b^2-c^2)-a^2c^2(-a^2-b^2+c^2))+a^2(-b^2c^2(-a^2+b^2-c^2)-b^2c^2(-a^2-b^2+c^2))))/((a^2-b^2-b c-c^2)(a^2+b^2+c^2)):
b^2(-a^2c^2(a^2-b^2-c^2)-a^2c^2(-a^2-b^2+c^2)):
c^2(-a^2b^2(a^2-b^2-c^2)-a^2b^2(-a^2+b^2-c^2))).
b^2c^2((2a^5 -3a^3(b^2+c^2) -a^2(b-c)^2(b+c) +a(b^4+b^3c+b c^3+c^4) + (b-c)^2(b+c)^3 )x^2 - 2a^2(a^3+a^2(b+c)-a(b^2+b c+c^2)-(b-c)^2(b+c))y z) + ⋯ = 0.
Cuyo centro es X8614:(a^2(a^5+a^4(b+c)+a^3(-2b^2+b c-2c^2) -2a^2(b^3+c^3) +a(b-c)^2(b^2+b c+c^2) +b^5-b^4c-b c^4+c^5) : ... : ...).
(a^6-a^4 (b^2+c^2)-a^2 (b^4-7 b^2 c^2+c^4)+b^6-3 b^4 c^2-3 b^2 c^4+c^6)x^2 +2 (a^6+a^4 (b^2+c^2)-(b^2-c^2)^2 (b^2+c^2)-a^2 (b^4+b^2 c^2+c^4))y z+...=0.
(a^10-2 a^8 (b^2+c^2)+a^6 (b^4+5 b^2 c^2+c^4)+a^4 (b^6-9 b^4 c^2-9 b^2 c^4+c^6)-a^2 (b^2+c^2)^2 (2 b^4-5 b^2 c^2+2 c^4)+(b^2+c^2)^3 (b^4-b^2 c^2+c^4))x^2 + 2 (a^10-3 a^8 (b^2+c^2)+a^6 (-4 b^4+2 b^2 c^2-4 c^4)+4 a^4 (b^6+c^6)+3 a^2 (b^8-b^6 c^2+b^4 c^4-b^2 c^6+c^8)-(b^2-c^2)^2 (b^6+c^6))y z+...=0.
El centro de estas cónicas es X9465 y tienen los mismos ejes.
X9465 es la tripolar, con respecto al triángulo circunmedial, del .Las rectas BcCb, CaAc y AbBa forman un triángulo DEF homotético a ABC con centro de homotecia en X33.
Ab = (-a(a+b-c) : b(a-b+ c): - c(a+b-c)), Ac = (-a(a-b+c) : b(-a+b-c) : c(a+b-c)).
D = (a(a^3+a(b-c)^2-a^2(b+c)-(b-c)^2(b+c)) : b(a^3+a^2(-b+c)-(b-c)^2(b+c)+a(b^2-c^2)) : c(a^3+a^2(b-c)-(b-c)^2(b+c)+a(-b^2+c^2))).
El centro de homotecia de los triángulos ABC y DEF es X33:(a(b+c-a)/SA : b(c+a-b)/SB : c(a+b-c)/SC).
La razón de homotecia es k=2rR/((r+2R)^2-s^2), donde r y R son los radios de las circunferencias inscrita y circunscrita, y s el semiperímetro de ABC.GENERALIZACIÓN
El triángulo DEF es no degenerado y perspectivo con ABC si y solo so P está sobre la cúbica de Thomson.
Ab = (u(c^2(2u-w)+(-a^2+b^2)w) : w((a^2-c^2)v+b^2(-2u+v)) : -w((a^2-b^2)w+c^2(-2u+w))),
Ac = (u(b^2(2u-v)+(-a^2+c^2)v) : -v((a^2-c^2)v+b^2(-2u+v)) : v((a^2-b^2)w+c^2(-2u+w))).
Q = (3a^4-(b^2-c^2)^2 - 2a^2(b^2+c^2))/((a^8 - 4a^6(b^2+c^2) + a^4(6b^4-4b^2c^2+6c^4) - 4a^2(b^2-c^2)^2(b^2+c^2) + (b^2-c^2)^2(b^4+ 6b^2c^2+c^4)) SA) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de (-0.9850917925434449, -2.046976200144293, 5.512459601642787).
Si P=X6
Q = (a^2SA/(b^4+c^4-a^4) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (1.658309789942009, 2.092830820411105, 1.426407857034225).
Si P=X9
Q = (a(b+c-a)/(a^2-2a(b+c)+b^2+c^2) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (13.73266187994108, -3.371858943735532, -0.3631232708638266).
Las rectas BcCb, CaAc y AbBa son concurrentes si y solo si P está sobre la nK(X6,X20,?), de parámetro k=a^6+b^6+c^6 -a^4 b^2-a^2 b^4-a^4 c^2-b^4 c^2-a^2 c^4-b^2 c^4 +10 a^2 b^2 c^2.
Esta cúbica isogonal interseca a los lados de ABC en puntos de la del punto de De Longschamps, X20.
Las rectas DOa, EOb y FOc concurren en un punto T de la circunferencia circunscrita.
Si se hace la misma construcción con el P* de P, se obtiene el mismo punto T sobre la circunferencia circunscrita.( a^2/(q r a^2 (q SB-r SC)+p a^2 (q^2 c^2-r^2 b^2)+p^2 (q c^2 SC-r SB b^2)):...:...).
Las rectas AA', BB' y CC' concurren en un punto en la , que es el del centro del triángulo X3830.
Las coordenadas baricéntricas de A' son:A' = (2 a^2 (2 a^4-4 a^2 b^2+2 b^4-4 a^2 c^2+5 b^2 c^2+2 c^4),-b^2 (4 a^4-8 a^2 b^2+4 b^4+a^2 c^2+b^2 c^2-5 c^4),-c^2 (4 a^4+a^2 b^2-5 b^4-8 a^2 c^2+b^2 c^2+4 c^4)).
Y las del punto de intersección de las rectas AA', BB' y CC' son:(a^2/(5a^4-a^2 (b^2+c^2)-4(b^2-c^2)^2) : ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de (-9.8296135126341636, -10.673202666890961, 15.566549487893889); es el conjugado isogonal de X3830.Las rectas AA'', BB'' y CC'' concurren en un punto en a hipérbola de Jerabek , que es el conjugado isogonal del centro del triángulo X3843.
Las coordenadas del punto de intersección de las rectas AA'', BB'' y CC'' son:(a^2/(3a^4+a^2(b^2+c^2)-4(b^2-c^2)^2) : ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de (-3.1848229499019600, -4.0459412294420152, 7.9116190022451404); es el conjugado isogonal de X3843.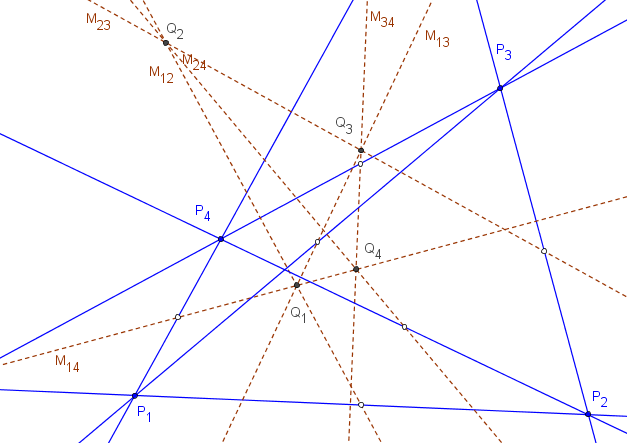
A1 = (SC^2(u+v)w+SB^2v(u+w)+2SBSC(u+v)(u+w)+a^2SAu(u+v+w) :
(SBv+SC(u+v))(SAu-SCw) : (SAu-SBv)(SCw+SB(u+w))).
P1 = (a^2SAu+SBSC(2u+v+w) : b^2SBv+SCSA(u+2v+w) : c^2SCw+SASB(u+v+2w)).
P1 es el punto medio P y el ortocentro.
Consideremos la transformación afín ΦP1 que transforma ABC en (la imagen del baricento de ABC es el baricentroEl punto fijo FP (propio) de la transformación afín ΦP1 es el centro de la hipérbola ℋ(P), equilátera circunscrita a ABC que pasa por P.
FP =(u(b^2w(u+v)-c^2v(u+w))(a^2(v-w)-(b^2-c^2)(v+w)) : ... : ... ).
Para todo punto Q, sobre la hipérbola ℋ(P), se tiene que FQ=FP.(c^2uv+b^2uw+a^2vw)^2/ (vw(u+v)(u+w)a^4+wu(u+v)(v+w)b^4+uv(u+w)(v+w)c^4-2uvw((u+v)a^2b^2+(v+w)b^2c^2+(u+w)c^2a^2).
Los puntos Ab, Ac, Bc, Ba, Ca y Cb están en una misma cónica C(P).
Si las coordenadas baricéntricas de P respecto a ABC son (u:v:w), la ecuación de la cóncica C(P) es:
(b+c-a)^2(a(u+v-w)+c(v+w-u)-b(u+v+w))(a(u-v+w)+b(v+w-u)-c(u+v+w))x^2
- 2(b+c-a)(a+b-c)(a-b+c)u(a(u-v-w)-c(u+v-w)-b(u-v+w))yz + ⋯ = 0.
El triángulo A'B'C' es perspectivo con los triángulos ABC y DEF.
El centro de perspectividad Q de A'B'C' y DEF es:Q = (u(a(v+w)-(b-c)(v-w)) : v(b(w+u)-(c-a)(w-u)) : w(c(u+v)-(a-b)(u-v))).
El centro de perspectividad R de A'B'C' y ABC es:R = ((b+c-a)u^2 : (c+a-b)v^2 : (a+b-c)w^2).
Los puntos P, Q y R están alinedados en la recta de ecuación:vw(a(v-w)-(b-c)(v+w))x + wu(b(w-u)-(c-a)(w+u))y + uv(c(u-v)-(a-b)(u+v))z = 0.
Cuando el punto P recorre la circunfercencia circunscrita, el punto Q está sobre la recta que pasa por los centros del triángulo X3309 y X4897, de ecuación:(b+c-a)(a^3 - a^2(b+c) + a(b^2+c^2) - (b-c)^2(b+c))x + ⋯ = 0.
((2 a^2-(b-c)^2-a (b+c))/(b+c-a)^2 : ... : ...).
que tiene coordenadas trilineales exactas en el triángulo de (-0.071782871224331350, -0.093494041398146657, 3.7385216819020182).((a^2-(b-c)^2) (5 a^2-2 (b-c)^2-3 a (b+c)): ... : ...).
que tiene coordenadas trilineales exactas en el triángulo de (-1.4401136495962944, -1.2759716637283297, 5.1886973181484356).Los puntos Oa, Ob y Oc están, respectivamente, sobre las tangentes en A, B y C a la circunferencia circunscrita y están alineados.
Si L=(u:v:w), en coordenadas baricéntricas respecto a ABC,
Ab = (2a^2v;0:(b^2-c^2)(v-w)+a^2(v+w)),
Ac = (2a^2w:(b^2-c^2)(v-w)-a^2(v+w):0),
Oa = (a^2(a^2(v-w)-(b^2-c^2)(v+w)):-b^2((b^2-c^2)(v-w)-a^2(v+w)):-c^2(-(b^2-c^2)(v-w)+a^2(v+w))).
M = (a^2/((b^2-c^2)(v-w)-a^2(v+w)) : ... : ... ).
El punto N, de intersección de las rectas l y m, es:N = (a^2(a^2-b^2-c^2)u(c^2v(u-w)+b^2(-u+v)w) : ... : ... ).
El lugar geométrico del punto M, cuando L se mueve sobre una recta d, es una cónica circunscrita C(d) a ABC.
C(d): a^2 (SBSC p - SCSA q - SASB r) y z + ⋯ = 0.
Q = (a^2/(a^4(p-q-r)(q-r) + 2 a^2(q+r)(c^2q-b^2r) - (b^2-c^2)(b^2(p(q-r)-(q+r)^2)-c^2(p(q-r)+(q+r)^2)))) : ... : ... ).
Lugar geométrico del perspector P de C(d), cuando d es la tripolar de un punto D que se mueve sobre la recta de Euler, es la cónica diagonal:
b^4c^4(b^2-c^2)x^2+c^4a^4(c^2-a^2)y^2+a^4b^4(a^2-b^2)z^2=0
Esta cónica es φX31(Q066), la transfomada de la cuártica de Stammler (Q066) mediante la de polo X31(a^3:b^3:c^3). El centro de esta cónica diagonal es X1576 y pasa por los puntos X6, X31, X48, X154, X1613, X2578, X2579, X5638, X5639.
El punto Q queda sobre la circunferencia circunscrita si y solo si la recta d es la tripolar de un punto D, sobre la recta de Euler.
Si el punto D recorre la circunferencia circunscrita, el lugar geométrico del punto Q es la cuártica con puntos dobles en los vértices de ABC, que pasa por el baricentro, circuncentro, y los puntos donde la recta de Euler corta a la circunferencia circunscrita, de ecuación:
(b^2-c^2)y z(b^2c^2S^2x^2+a^4SA^2y z) + ⋯ = 0.
El lugar geométrico de los centros de las cónicas C(d), cuando el tripolo de d recorre la circunferencia circunscrita, es la C(X2,X54).
El centro de C(X2,X54) es X6689, baricentro de {A, B, C, X54}.
El lugar geométrico del punto N, cuando L se mueve sobre la circunferencia circunscrita, es la cúbica cK(#X6,X25)=nK(X32,X25,X6):
a^2SBSCx(c^2y-b^2z)^2 + ⋯ = 0.
b^2c^2(b^2c^2(b^2-c^2)^2SA^2x^2 + 2a^4SB SC(a^4-a^2b^2-a^2c^2-b^2c^2)y z + ⋯ = 0.
a^2y z(b^2c^2SA x^2-a^2 SB SC y z) + ⋯ = 0.
El centro de perspectividad de ABC, A'B'C' es el simediano, X6.
El centro de perspectividad de ABC, DEF es X3445.
El centro de perspectividad de A'B'C', DEF es X3052
A' = (-a^2:b^2:c^2), B' = (a^2:-b^2:c^2), C' = (a^2:b^2:-c^2).
A1 = (a(b-c):b^2:-c^2), B1 = (-a^2:b(c-a):c^2), A1 = (a^2,-b^2:c(a-b)).
Estos puntos están alineados, por tanto, la recta que los contiene es el eje de perspectividad de los triángulos A'B'C' y DEF, formado por las rectas A'A1, B'B1, C'C1.
D = (a^2(a+b+c):b^2(a+b-3c):c^2(a-3b+c)),
E = (a^2(a+b-3c):b^2(a+b+c):c^2(-3a+b+c)),
F = (a^2(a-3b+c):b^2(-3a+b+c):c^2(a+b+c)).
(a^2(b-c)((b-c)^2-a^2) : b^2(c-a)((c-a)^2-b^2) : c^2(a-b)((a-b)^2-c^2))
que tiene coordenadas trilineales exactas en el triángulo de (0.34496092029735371, -1.4488358652488856, 4.4844919638655982).Los puntos Ac, Ab, Ba, Bc, Cb y Ca están sobre una misma cónica y el lugar geometrico de su centro es la cuártica de ecuación baricéntrica:
| (a c^2-b c^2)x^3 y+(-2a c^2+2b c^2)x^2y^2+(a c^2-b c^2)x y^3+(-a b^2+b^2c)x^3z+(-a^2b+a^2c)x^2y z+(a b^2-b^2 c)x y^2 z+(a^2b-a^2c)y^3z+(2a b^2-2b^2c)x^2z^2+(-a c^2+b c^2)x y z^2+(-2a^2b+2a^2c)y^2z^2+(-a b^2+b^2c) x z^3+(a^2 b-a^2 c)y z^3=0. | (1) |
Ab(b-k:0:k), Ac(c-k:k:0), Bc(k:c-k:0), Ba(0:k:a-k), Ca(0:a-k:k), Cb(k:0:b-k).
Ecuación de la cónica que pasa por estos seis puntos:(b-k)(c-k)((a-k)kx^2 - (a^2-2ak+2k^2)yz) + ⋯ = 0.
Su centro D:D = (a^2(b-k)(c-k)(a^2(b-k)(c-k)+k(b c^2+b^2(c-k)-c^2k)+a(-b c^2+c^2k+b^2(-c+k))) : b^2(a-k)(-c+k)(a^2(b-k)(c-k)-a(b-c)(b(c-k)-c k)+(b-c)k(b(c-k)-c k)) : c^2(a-k)(-b+k)(a^2(b-k)(c-k)+a(b-c)(b(c-k)-c k)-(b-c)k(b(c-k)-c k))).
Al variar k, este punto describe la cuártica de ecuación (1), que pasa por los vertices de ABC, por los puntos medios (dobles) de los lados y por los centros del triángulo X3 (circuncentro), X9 ("Mittenpunkt"), X478, X6626, X9470.Las rectas que contienen las bases de los triángulo isósceles AAcAb, BBaBc y CCbCa, forman un triángulo A'B'C' perspectivo con ABC, con centro de perspectividad F sobre la .
Las coordenadas de F son:F = (1/(a b+(-a-b+c) k) : 1/(b c+(a-b-c)k) : 1/(a c+(-a+b-c)k)).
Eliminando k y λ en λ(x:y:z)=F, resulta al ecuación de la hipérbola:(a^2b-ab^2+b^2c-bc^2)xy + (a^2b-ab^2-a^2c+ac^2)xz + (-a^2c+b^2c+ac^2-bc^2)yz = 0.
Los triángulos ABC y A'B'C' son perspectivos si y solo si P está sobre la circunferencia circunscrita, sobre la cúbica K018 (ortopivotal cúbica O(X6)), o sobre una séxtica tricircular.
Si P(u:v:w), en coordenadas baricénticas, tenemos las ecuaciones de las circunferencias:
(Ba):
a^2yz+b^2zx+c^2xy+(x+y+z)(-c^2x-(-c^2u^2+b^2uw-c^2uw+a^2vw)z/(w(u+v+w)))=0,
(Ca):
a^2yz+b^2zx+c^2xy+(x+y+z)(-b^2x-(-b^2u^2-b^2uv+c^2uv+a^2vw)y/(v(u+v+w)))=0.
A' = (-(b^2u+a^2v)^2w^2+c^4u^2v(u+w)+c^2u w(b^2u+a^2v)(u-v+w))(-b^2u(u+v)+v(c^2u+a^2w)) :
b^2v(u+v+w)((b^2u+a^2v)w-c^2u(u+w))^2 : c^2w(u+v+w)(b^2u(u+v)-v(c^2u+a^2w))^2).
a^2u(
2v^3w^3(c^2(u^2+u(-3v+w)+2v(v+w))+b^2(u^2+u(v-3w)+2w(v+w)))a^6
-v^2w^2(b^4(u^4+2u^3(v-2w)-8uw^2(v+w)+2w^2(v+w)^2+u^2(v^2-4vw+3w^2))+
c^4(u^4-8u v^2(v+w)+2v^2(v+w)^2+u^3(-4v+2w)+u^2(3v^2-4v w+w^2))+
2b^2c^2(-u^3(v+w)+u^2(v^2+10v w+w^2)+2u(v-w)^2(v+w)+2v w(v+w)^2))a^4
2v w(-b^6u w(u^4+u^3(2v-w)+u^2v(v-w)-2u w^2(v+w)+2w^2(v+w)^2)-
c^6u v(u^4-u^3(v-2w)+u^2w(-v+w)-2u v^2(v+w)+2v^2(v+w)^2)+
b^4c^2(u^4v(v+3w)+u^3(2v^3+2v^2w-7vw^2-2w^3) +
u^2(v^4-v^3w+3v^2w^2+4v w^3-w^4)-u w^2(2v-w)(v+w)^2+v w^2(v+w)^3) +
b^2c^4(u^4w(3v+w)+u^3(2w^3+2v w^2-7v^2w-2v^3) +
u^2(w^4-v w^3+3v^2w^2+4v^3w-v^4)+u v^2(v-2w)(v+w)^2+v^2w(v+w)^3))a^2
-c^8u^2v^2(u^4+2u^3w+u^2w^2+2v^2(v+w)^2)
-b^8u^2w^2(u^4+2u^3v+u^2v^2+2w^2(v+w)^2) +
2b^2c^6u v(u v^3(v+w)^2+v^2w(v+w)^3+u^4w(2v+w)+u^3w^2(3v+2w)+u^2(v^4+4v^3w+3v^2w^2+v w^3+w^4)) +
2b^6c^2u w(u w^3(v+w)^2+v w^2(v+w)^3+u^4v(v+2w)+u^3v^2(2v+3w)+u^2(v^4+v^3w+3v^2w^2+4v w^3+w^4)) -
b^4c^4(v^2w^2(v+w)^4+u^2(v+w)^2(v^4+4v^2w^2+w^4)+
u^4(v^4+6v^3w+13v^2w^2+6v w^3+w^4)+
2u^3(v^5+4v^4w+3v^3w^2+3v^2w^3+4v w^4+w^5)).
{74,1494}, {98,290}, {99,670}, {100,668}, {101,190}, {105,2481}, {106,903}, {107,6528}, {109,664}, {110,99}, {111,671}, {112,648}, {691,892}, {699,3225}, {727,3226}, {729,3228}, {739,3227}, {813,4562}, {825,4586}, {827,4577}, {842,5641}, {898,889}, {901,4555}, {919,666}, {934,4569}, {1379,6190}, {1380,6189}, {2291,1121}, {2715,2966}, {4588,4597}, {6551,6635}, {8687,6648}, {8701,6540}, {9136,9487}, {9150,886}
(b^2-c^2)x(c^2y^2+b^2z^2)+··· = 0.
Esta cúbica pasa por los centros del triángulo X2, X6, X13, X14, X15, X16, X111, X368, X524. Su asíntota pasa por X9146 y tiene la dirección del punto X524 ( del , X111), es la imagen de la rectas que pasa por el baricentro y simediano mediante la homotecia de centro X111 y razón 2.
(a^2(a^16 - 4a^14(b^2+c^2) + a^12(-14b^4+29b^2c^2-14c^4) +
a^10(-7b^6+87b^4c^2+87b^2c^4-7c^6) +
a^8(b^8-59b^6c^2-489b^4c^4-59b^2c^6+c^8) -
2a^6(5b^10+40b^8c^2-301b^6c^4-301b^4c^6+40b^2c^8+5c^10) +
a^4(-8b^12+141b^10 c^2+285b^8c^4-1753b^6c^6+285b^4c^8+141b^2c^10-8c^12) +
a^2(5b^14+53b^12c^2-714b^10c^4+868b^8c^6+868b^6c^8-714b^4c^10+53b^2c^12+5c^14) +
(b^2+c^2)^2(4b^12-63b^10c^2+315b^8c^4-532b^6c^6+315b^4c^8-63b^2c^10+4c^12)) : ... : ...)
{X2,X2482*}, {X6, X2482}, {X111, X671= X187*}, {X524, X187=X671*}.
La cúbica K018 es el lugar geométrico de los puntos tales que los puntos Ba, Ca, Cb, Ab, Ac, Bc están en una misma cónica.
u(3v^2w^2a^4
-v w((b^2+c^2)u^2+2(b^2+c^2)v w+u(b^2v-3c^2v-3b^2w+c^2w)+2(c^2v^2+b^2w^2))a^2
+b^2c^2v w(v+w)^2-u^3(c^4v+b^4w)-u^2(-b^2c^2v^2+b^4v w-5b^2c^2v w+c^4v w-b^2c^2w^2)-u(v+w)(-b^2c^2v^2+2c^4v^2+2b^4w^2-b^2c^2w^2))
{X2,X671}, {X6, X524}, {X111, X671}, {X524, X534}.
| a^2 c^4 x^4 y^2-c^6 x^4 y^2+a^2 c^4 x^3 y^3+b^2 c^4 x^3 y^3+b^2 c^4 x^2 y^4-c^6 x^2 y^4-b^4 c^2 x^4 y z-b^2 c^4 x^4 y z+a^4 c^2 x^3 y^2 z-4 a^2 b^2 c^2 x^3 y^2 z+4 b^2 c^4 x^3 y^2 z-c^6 x^3 y^2 z-4 a^2 b^2 c^2 x^2 y^3 z+b^4 c^2 x^2 y^3 z+4 a^2 c^4 x^2 y^3 z-c^6 x^2 y^3 z-a^4 c^2 x y^4 z-a^2 c^4 x y^4 z+a^2 b^4 x^4 z^2-b^6 x^4 z^2+a^4 b^2 x^3 y z^2-b^6 x^3 y z^2-4 a^2 b^2 c^2 x^3 y z^2+4 b^4 c^2 x^3 y z^2-a^6 x y^3 z^2+a^2 b^4 x y^3 z^2+4 a^4 c^2 x y^3 z^2-4 a^2 b^2 c^2 x y^3 z^2-a^6 y^4 z^2+a^4 b^2 y^4 z^2+a^2 b^4 x^3 z^3+b^4 c^2 x^3 z^3+4 a^2 b^4 x^2 y z^3-b^6 x^2 y z^3-4 a^2 b^2 c^2 x^2 y z^3+b^2 c^4 x^2 y z^3-a^6 x y^2 z^3+4 a^4 b^2 x y^2 z^3-4 a^2 b^2 c^2 x y^2 z^3+a^2 c^4 x y^2 z^3+a^4 b^2 y^3 z^3+a^4 c^2 y^3 z^3-b^6 x^2 z^4+b^4 c^2 x^2 z^4-a^4 b^2 x y z^4-a^2 b^4 x y z^4-a^6 y^2 z^4+a^4 c^2 y^2 z^4=0, | (1) |
Los seis puntos Db, Dc, Ec, Ea, Fa y Fb están en una misma cónica si y solo si el punto P está sobre la séxtica tricircular (1) o sobre la cuártica bicircular, que pasa por A, B, C (dobles) y por el ortocentro, de ecuación:
c^4 x^3 y - a^2 b^2 x^3 z + b^4 x^3 z - 2 a^2 b^2 x^2 y z + 2 b^4 x^2 y z + 2 a^2 c^2 x^2 y z - 3 b^2 c^2 x^2 y z + c^4 x^2 y z - a^2 b^2 x y^2 z + b^4 x y^2 z - b^2 c^2 x y^2 z - a^2 b^2 x^2 z^2 + b^4 x^2 z^2 - b^2 c^2 x^2 z^2 + a^4 x y z^2 - 3 a^2 b^2 x y z^2 + 2 b^4 x y z^2 + 2 a^2 c^2 x y z^2 - 2 b^2 c^2 x y z^2 + b^4 x z^3 - b^2 c^2 x z^3 + a^4 y z^3=0.f(a,b,c) = a/[a2vwyz - ux(bw + cv)(bz + cy)].
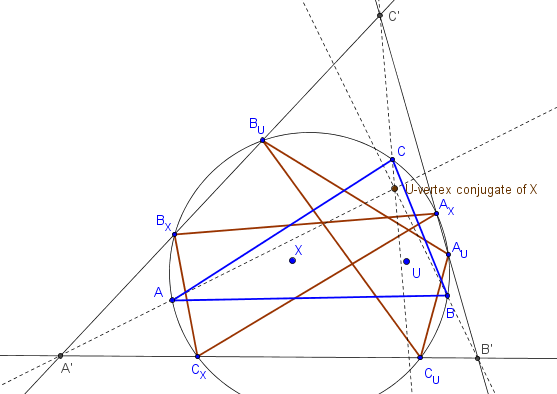
The U-vertex conjugate of X is the point
f(a,b,c) : f(b,c,a) : f(c,a,b).
For a geometric interpretation, let T be the vertex triangle of the circumcevian triangles, AUBUCU and AXBXCX, of U and X; viz., the sidelines of T are AUAX, BUBX, CUCX. Then T is perspective to ABC, and the perspector is the U-vertex conjugate of X.
La del triángulo ABC corta a los lados TbTc, TcTa y TaTb del en los puntos D, E y F, respectivamente. Las rectas DTa, ETb, FTc forman un con ABC, con centro de perspectividad en X3447.
Consideremos una situación más general: Sea la cónica circunscrita al triángulo ABC con centro en un punto P, de coordenadas baricéntricas (u:v:w),u(-u+v+w)yz+v(u-v+w)zx+w(u+v-w)xy=0.
Las tangentes en los vértices de ABC forman un triángulo de vértices:
Ta = (u(u-v-w):v(u-v+w):w(u+v-w)),
Tb = (u(-u+v+w):v(-u+v-w):w(u+v-w)),
Ta = (u(-u+v+w):v(u-v+w):w(-u-v+w)).
D = ((-2a^2v^2+b^2u(u+v-w))w^2+c^2uv^2(u-v+w) : v(u-v+w)(c^2v^2-b^2w^2) : -(u+v-w)w(c^2v^2-b^2w^2)),
E = (-u(u-v-w)(c^2u^2-a^2w^2) : (-2b^2u^2+a^2v(u+v-w)) w^2+c^2u^2v(-u+v+w) : -(u+v-w)w(c^2u^2-a^2w^2)),
F = (-u(b^2u^2-a^2v^2)(u-v-w) : -v(b^2u^2-a^2v^2)(u-v+w) : -2c^2u^2v^2+w(a^2v^2(u-v+w)+b^2u^2(-u+v+w))).
Q = ((u-v-w)/(b^2 c^2 v w u^4+2 (c^2 v^2-b^2 w^2) (c^2 v-b^2 w)u^3+-(2 c^4 v^4+2 b^4 w^4+v w (c^2 (a^2-b^2+c^2) v^2-4 b^2 c^2 v w+b^2 (a^2+b^2-c^2) w^2))u^2+2 a^2 u v w(v-w) (c^2 v^2-b^2 w^2)-a^2 v w (c^2 v^4-(a^2+b^2+c^2) v^2 w^2+b^2 w^4)) : ... : ...).
El centro de perspectividad de A'B'C' y (tripolo de la rectas PP* respecto a ) es:R = (u^2 (u-v-w) (2 c^4 u^3 v^3-2 c^4 u^2 v^4+b^2 c^2 u^4 v w-2 b^2 c^2 u^3 v^2 w-a^2 c^2 u^2 v^3 w+b^2 c^2 u^2 v^3 w-c^4 u^2 v^3 w+2 a^2 c^2 u v^4 w-a^2 c^2 v^5 w-2 b^2 c^2 u^3 v w^2+4 b^2 c^2 u^2 v^2 w^2-2 a^2 c^2 u v^3 w^2+2 b^4 u^3 w^3-a^2 b^2 u^2 v w^3-b^4 u^2 v w^3+b^2 c^2 u^2 v w^3-2 a^2 b^2 u v^2 w^3+a^4 v^3 w^3+a^2 b^2 v^3 w^3+a^2 c^2 v^3 w^3-2 b^4 u^2 w^4+2 a^2 b^2 u v w^4-a^2 b^2 v w^5) : ... : ...)
(a^2/(a^6 - a^4(b^2+c^2) + a^2(b^4-b^2c^2+c^4) - (b^2-c^2)^2(b^2+c^2)) : .. : ..)
R = X(7669) = trilinear pole, with respect to the tangential triangle, of the Euler line.(1/(a^4-a^2(b^2+c^2)-b^4+3b^2c^2-c^4) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (8.7692667109160826, 0.47500701016217498, -0.73554039170454939).(a^2(b^2+c^2-a^2)/(a^6-a^4(b^2+c^2)+a^2(b^4-b^2c^2+c^4)-(b^2-c^2)^2(b^2+c^2)) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (3.1091488118738361, 1.5496489138331613, 1.1328388591581123).El triángulo A'B'C' es circunceviano de un punto Q si y sólo si P está sobre la circunscrita con centro en X10 (). El punto Q queda sobre la recta conjugada isogonal de esta elipse.
A'(a(av+b(v+w))(aw+c(v+w)) : b(cv-bw)(av+b(v+w)) : -c(cv-b w)(aw+c(v+w))).
Los triángulos ABC y A'B'C' son perspectivos si sólo si las coordenadas de P satisfacen a la ecuación:a(b+c)y z +b(c+a)z x + c(a+b)x y = 0,
elipse circunscrita de centro en X10(b+c:c+a:a+b).El punto Q es el conjugado isogonal del antipodal de P en esta elipse.
(a(2a-b-c)/(b+c) : b(2b-c-a)/(c+a) : c(2c-a-b)/(a+b))
que tiene coordenadas trilineales exactas en el triángulo de ETC (-3.3973055373431202, -0.39337222011341392, 5.4809862669135673).(a(a^4-a^2(b^2+c^2)-a(b-c)^2(b+c)+b^2c^2) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (4.4144065118861021, -14.063868306264553, 11.339770303835484).(a^2(b-c)(a^4-a^3(b+c)-a^2(b^2-b c+c^2)+a(b-c)^2 (b+c)-b c(b^2+c^2)) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (53.398656858579238, -99.786306412977542, 48.077958063855336).(a(a(b-c)^2+a^2(b+c)-b c(b+c)) : ... : ...)
que tiene coordenadas trilineales exactas en el triángulo de ETC (-4.3575843225451956, 1.2871156539902179, 4.7607771780120108).En la cónica circunscrita a un triángulo ABC que pasa por un punto D, de coordenadas baricéntricas (u:v:w), y por el P=G/D están los puntos Fd y Fp de primeras cordenadas, u(u-v-w)/(v+w-3u) y u/(3u^2-2u(v+w)-(v-w)^2), respectivamente.
Las polares at, bt y ct de At, Bt y Ct respecto a la cónica cs(D) forman un triángulo A'B'C' perspectivo con ABC y con .
Cuando t varía, el lugar geométrico del centro de perspectividad Qd de ABC y A'B'C' es la cónica c(Q) circunscrita a ABC y que pasa por P y D; y el lugar geométrico del centro de perspectividad Rd de y A'B'C' es la cónica c(R) circunscrita a y que pasa por P y D.
La recta QdRd por un punto fijo Fd, sobre la cónica circunscrita c(Q).
c(P): u(-u+v+w)yz + v(u-v+w)zx + w(u+v-w)xy = 0.
La cónica que pasa por los seis puntos Ba, Ca, Cb, Ab, Ac, Bc es:cs(D): 2vw(u-v-w)x² + u(u²-v²+6vw-w²)yz + ···· = 0.
At = ((1+t)u^2-(v-w)^2-tu(v+w) : tv(u-v+w) : tw(u+v-w)),
Bt = (tu(-u+v+w) : -u^2+(v-w)(v+tv+w)+u(-tv+2 w) : tw(u+v-w)),
Ct = (tu(-u+v+w) : tv(u-v+w) : -u^2+u(2v-tw)-(v-w)(v+w+tw)).
Qd = (u/((3+2t)u^5-(7+4t)u^4(v+w) + 2u^3(v^2+2(3+6t+2t^2)vw+w^2) + 2u^2(v+w)((3+2t)v^2+(3+2t)w^2-6v(w+2tw)) - u(v-w)^2((5+2t)v^2+2(3+2t+4t^2)vw+(5+2t)w^2) + (v-w)^4(v+w)): ... : ...).
El centro de perspectiviad de y el triángulo A'B'C' es:Rd = (u(u^4 - 4u^3(v+w) + u^2(6v^2-4(-1+t+t^2)vw+6w^2) - 4u(v+w)(v^2-(1+t^2)vw+w^2) +(v-w)^2(v^2+w^2+2v(w+2tw))) : ... : ...).
La recta QdRd, para cualquier t, pasa por:Fd = (u(u-v-w)/(v+w-3u) : v(v-w-u)/(w+u-3v) : w(w-u-v)/(u+v-3w)).
Fp = (u/(3u^2-2u(v+w)-(v-w)^2) : v/(3v^2-2v(w+u)-(w-u)^2) : w/(3w^2-2w(u+v)-(u-v)^2) ).
• Las rectas QdQp, RdRp y FdFp son paralelas a la recta DP.QdRd∩QpRp, QdRp∩QpRd, FdQp∩FpQd, FdRp∩FpRd,
están en la recta (pasa por el baricentro de ABC) que une los centros Q0 y R0 de las cónicas c(Q) y c(R).Q0R0 : (v-w)(v^2+w^2-u(v+w))x + (w-u)(w^2+u^2-v(w+u))y + (u-v)(u^2+v^2-w(u+v))z = 0.
Caso del punto D sobre la elipse inscrita de Steiner
Σx(x²(y-z)² - y²z²)=0
Esta curva tiene puntos dobles tangenciales en los vértices de ABC, con tangentes las medianas. Las asíntotas son las imágenes de los lados BC, CA, AB en las homotecias de razón 3/2 y centros en A, B, C, respectivamnete. Las asíntotas vuelven a cortar a la curva en puntos sobre la elipse imagen de la mediante la homotecia de centro el baricentro y razón √23/5.(2a^4-(b^2-c^2)^2-a^2(b^2+c^2))/(5a^8-5a^6(b^2+c^2) + a^4(-6b^4+17b^2c^2-6c^4)+ 7a^2(b^2-c^2)^2(b^2+c^2)-(b^2-c^2)^2(b^4+7b^2c^2+c^4))
que tiene coordenadas trilineales exactas en el triángulo de ETC (0.44454930701495823, 4.7005898780480680, 0.18123334771342822).
NOTA. El sombreado del triángulo mixtilineal de esta figura está realizado con GeoGebra:
camino={Segmento[A,B], ArcoCircunferencia[X_3,B,C],Segmento[C,A]}
M=Punto[camino]
N un punto en plano
N=M
LugarGeométrico[N,M]
Este lugar geométrico se puede sombrear cambiando sus propiedades.
Los triángulos ABC y son perspectivos y el centro de pespectividad es X1407.
En coordenadas baricéntricas:Aa=(-a(a+b-c)(a-b+c):2b^2(a+b-c):2c^2(a-b+c)), Ab=(a+b-c:0:2c), Ab=(-a+b-c:-2b:0).
La matriz M asociada a la homografía que transforma A ↦ Aa, B ↦ Ab, C ↦ Ac, y el baricentro de ABC en el baricentro, Ga=(a(3a^2-5(b-c)^2-2a(b+c)) : 2b(a^2-3b^2+5b c-2c^2-a(2b+c)) : 2c(a^2-2b^2+5b c-3c^2-a(b+2c))), de AaAbAc, es:| a (a+b-c) (a-b+c) | (a-b+c) (a^2-2 (b-c)^2-a (b+c)) | (a+b-c) (a^2-2 (b-c)^2-a (b+c)) |
| -2 b^2 (a+b-c) | -2 b (-a^2+2 (b-c)^2+a (b+c)) | 0 |
| -2 c^2 (a-b+c) | 0 | -2 c (-a^2+2 (b-c)^2+a (b+c)) |
Fa =(-(a+b-c)(a-b+c)(a^2-2(b-c)^2-a(b+c)) : 2b^2(a+b-c)^2 : 2c^2(a-b+c)^2).
Procediendo cíclicamente se obtienen los puntos fijos Fb y Fc, relativos a las otras dos circunferencia de Mannhein de ABC.(a^2/(-a+b+c)^2 : b^2/(a-b+c)^2 : c^2/(a+b-c)^2).
El punto fijo (no situado en la recta del infinito) de la transformación afín que transforma los vértices de ABC en los de es:
F = (a^2(a^2-a(b+c)-2(b-c)^2) : b^2(b^2-b(c+a)-2(c-a)^2) : c^2(c^2-c(a+b)-2(a-b)^2))
que tiene coordenadas trilineales exactas en el triángulo de (1.3328099951365518, 2.9363470205352157, 0.99266577762774432).Los triángulos ABC y son inversamente semejantes.
(a^2 b^2 c^2u^2+a^2 (a^4-2 a^2 (b^2+c^2)+b^4+c^4)+...)/(4 a^2 b^2 c^2 (u+v+w)^2),
donde ... indica suma cíclica. Esta expresión es simétrica, por lo que coincide con los cuadrados de las razones entre las longitudes de los otros dos pares de lados; así, expresa el cuadrado de la razón de semejanza entre los triángulos y ABC.σP((x:y:z))=(a^2 b^2 c^2 (v+w) x+a^2 (b^2 c^2 u+c^2(a^2+b^2-c^2)v y+a^2 (b^2 c^2 u+b^2(a^2-b^2+c^2) w) z: ... : ...)
El punto fijo, corresponde a la raíz λ=-2 a^2 b^2 c^2 (u+v+w) del polinomio característico p(λ)=|M-λI| (M matriz asociada a la semejanza), es:F=(b^2 c^2 u^2+c^2(a^2+b^2-c^2)v^2+b^2(a^2-b^2+c^2)w^2+(-a+b+c)(a-b+c)(a+b-c)(a+b+c)v w+3b^2c^2w u+3b^2c^2u v:...:...)
A continuación se da una lista conteniendo pares {P,F}={X(i),X(j)} de centros del triángulo que figuran actualmente es , expresados por su número de orden {i,j}:(b^2-c^2)(b^2 c^2 (a^2 (b^2+c^2)-(b^2-c^2)^2)x^2+a^2 (a^2-b^2-c^2) (a^4-2 a^2 (b^2+c^2)+b^4-3 b^2 c^2+c^4)y z) + ... =0.
La conjugada isogonal de esta hipérbola es una cuártica con puntos dobles en los vértices de ABC, pasando por X4, X5, X54, X1113, X1114, X7608.a^6 c^2 x^2 y^2-3 a^4 b^2 c^2 x^2 y^2+3 a^2 b^4 c^2 x^2 y^2-b^6 c^2 x^2 y^2-a^4 c^4 x^2 y^2+b^4 c^4 x^2 y^2-a^6 b^2 x^2 y z+3 a^4 b^4 x^2 y z-3 a^2 b^6 x^2 y z+b^8 x^2 y z+a^6 c^2 x^2 y z+2 a^2 b^4 c^2 x^2 y z-3 b^6 c^2 x^2 y z-3 a^4 c^4 x^2 y z-2 a^2 b^2 c^4 x^2 y z+3 a^2 c^6 x^2 y z+3 b^2 c^6 x^2 y z-c^8 x^2 y z-a^8 x y^2 z+3 a^6 b^2 x y^2 z-3 a^4 b^4 x y^2 z+a^2 b^6 x y^2 z+3 a^6 c^2 x y^2 z-2 a^4 b^2 c^2 x y^2 z-b^6 c^2 x y^2 z+2 a^2 b^2 c^4 x y^2 z+3 b^4 c^4 x y^2 z-3 a^2 c^6 x y^2 z-3 b^2 c^6 x y^2 z+c^8 x y^2 z-a^6 b^2 x^2 z^2+a^4 b^4 x^2 z^2+3 a^4 b^2 c^2 x^2 z^2-3 a^2 b^2 c^4 x^2 z^2-b^4 c^4 x^2 z^2+b^2 c^6 x^2 z^2+a^8 x y z^2-3 a^6 b^2 x y z^2+3 a^2 b^6 x y z^2-b^8 x y z^2-3 a^6 c^2 x y z^2+2 a^4 b^2 c^2 x y z^2-2 a^2 b^4 c^2 x y z^2+3 b^6 c^2 x y z^2+3 a^4 c^4 x y z^2-3 b^4 c^4 x y z^2-a^2 c^6 x y z^2+b^2 c^6 x y z^2-a^4 b^4 y^2 z^2+a^2 b^6 y^2 z^2-3 a^2 b^4 c^2 y^2 z^2+a^4 c^4 y^2 z^2+3 a^2 b^2 c^4 y^2 z^2-a^2 c^6 y^2 z^2 = 0.
b^2(a-b-c)(3a-b-c)c^2x^2 - a^2(a^4-2a^2(b^2+b c+c^2)+(b-c)^2(b^2+6b c+c^2)+2a b c(b+c))yz+ ... = 0.
Sea P el cuarto punto de intersección de Γ y (C), entonces la polar de P respecto a O(IO) es la recta de Sherman, tangente a la circunferencia inscrita en X3326.
D' = (a^2 (a^2-4 b c+a (b+c)) : -b (a^2 (b-2 c)-2 b^2 c+2 c^3+a b (b+c)) : -c (a^2 (-2 b+c)+a c (b+c)+2 b (b^2-c^2)))
E' = (-a (a^2 (b-2 c)-2 b^2 c+2 c^3+a b (b+c)) : b^2 (a (b-4 c)+b (b+c)) : c (-2 a^3-b c (b+c)+a (2 b^2-b c+2 c^2)))
F' = (-a (a^2 (-2 b+c)+a c (b+c)+2 b (b^2-c^2)) : b (-2 a^3-b c (b+c)+a (2 b^2-b c+2 c^2)) : c^2 (a (-4 b+c)+c (b+c)))
P = (a(a+b-c)(a-b+c)(a^7-a^5(b^2+5b c+c^2)+5a^4b c(b+c)-a^3(b^4-b^3c+4b^2c^2-b c^3+c^4) -3a^2bc(b-c)^2(b+c) + a(b^2-c^2)^2(b^2+4b c+c^2)-2bc(b-c)^2(b+c)^3) : ... : ... ).
que tiene coordenadas trilineales exactas en el triángulo de (-0.87107795515190942, 0.27156053351460059, 3.8546970149289984).(a-b)(a-c)(a^6+a^2(b-c)^4-a^5(b+c)+2a^3(b-c)^2(b+c)-a(b-c)^4(b+c)+a^4(-2b^2+5b c-2c^2)-b c(b^2-c^2)^2) x + ... =0.
In memoriam de Marta (serían 40)
Special Isocubics in the Triangle Plane §8 Conico-pivotal (unicursal) isocubics or cK, J.P.Ehrmann and B.Gibert.
Isocúbicas cónico-pivotales cK(#Q,X2)
Otra descripción de las isocúbicas cónico-pivotales cK(#Q,X2)
Isocúbicas cónico-pivotales cK(#Q,X2) y transversales isotómicas
Las rectas AA', BB', CC' concurren en un punto D sobre la cónica circunscrita a ABC de centro F.
d: (g(t-1)+ht)x + (f+h-ft)y - (g+ft)z = 0.
Se tiene que:A' (2f : g-f t : h+f(t-1), B' (g-f t : -2g t : g(t-1)-h t), C' (h+f(t-1) : g(t-1)-h t : 2h(t-1)).
Las rectas AA', BB', CC' concurren enD ((g-f t)(-f+h+f t) : (g-f t)(-g+g t-h t) : (f-h-f t)(g-g t+h t)).
El lugar geométrico del punto D, cuando la rectas d gira alrededor de F, es la cónica C(F/G), circunscrita a ABC con centro en F, de ecuación:C(F/G): f(-f+g+h)yz + g(f-g+h)zx + h(f+g-h)xy= 0.
La ecuación de la tangente a esta cónica en D es:tD: f(f-g-h)(g(t-1)-h t)²x - g(f-g+h)(h+f(t-1))²y - h(f+g-h)(g-f t)²z = 0.
Si determinamos el punto M1=d∩tD y luego su reflexión en F, obtenemos:M (f(f-g-h)(-h+f(t-1))(g+f t)(g(t-1)-h t) : g(f-g+h)(h+f(t-1))(g+f t)(g(t-1)+h t) : -h(f+g-h)(-h+f(t-1))(-g+f t)(g(t-1)+h t)).
El lugar geométrico del punto M, cuando la rectas d gira alrededor de F, es la cK(#F,P)=nK(F²,P,F), de polo Ω=F² ( de F) y raíz P el F²- de F:
| f(f+g-h)(f-g+h)x(h²y²+g²z²) + g(f+g-h)(-f+g+h)y(h²x²+f² z²) + h(f-g+h)(-f+g+h)z(g²x²+f²y²) + 2fgh(f²+g²+h²-2f g-2f h-2g h)x y z = 0. | (1) |
(C): g²h²(f-g-h)²(g-h)²x² + 2f²gh(f+g-h)(f-g+h)(f²-fg-fh-gh)yz + ··· = 0.
Esta cónica se puede construir a partir de cinco tangentes tomadas entre los lados del FaFbFb de F y las rectas AU, BV, CW, donde U, V, W son las intersecciones de la de P con las rectas BC, CA, AB.En este tipo de isocúbicas cónico pivotales, cK(#F,crossdiv(F²,F)), la polar de F respecto a la cónica pivotal coincide con la tripolar del F★F² de F y F², es decir, la polar de F respecto a la cónica circunscrita de F².
El F²-isoconjugado M* de M puede ser construido como el segundo punto común de las tres cónicas que pasan, respectivamente, por los puntos {B,Fb,C,Fc,M}, {C,Fc,A,Fa,M}, {A,Fa,B,Fb,M}.
(ADGEOM #3180)
.png)
.png)
Las rectas BaCa, CbAb, y AcBc forman un triángulo A'B'C' perspectivo con ABC, con centro de perspectividad X9311.
D(0 : a+b-c : a-b+c), E(a+b-c : 0 : -a+b+c), F(a-b+c : -a+b+c : 0).
Ba (a+b-c : 0 : a-b+c), Ca (a-b+c : a+b-c : 0).
A' (-a^3(b+c)+a(b-c)^2(b+c)+a^2(b^2+c^2)-(b-c)^2(b^2+c^2) : (-a+b+c)^2(2ab-ac-bc+c^2) : -(-a+b+c)^2(a(b-2c)+b(-b+c))).
Finalmente, las rectas AA', BB' y CC' concurren en X9311:(1/(a^2-a(b+c)+2bc) : 1/(b^2-b(c+a)+2ca) : 1/(c^2-c(a+b)+2ab)).
Los triángulos ABC y XYZ son perspectivos y el centro de perspectividad es X6049.
El centro X6049 (de coordenadas baricéntricas ((3a-b-c)²/(b+c-a):...:...) ) ha sido descrito (Agosto, 2014) por Nikolaos Dergiades (Forum Geometricorum Volume 14 (2014) 163–171, Proposition 6.Antirhombi) y en Hechos Geométricos en el Triángulo (2013).El de A'B'C' respecto a γ ( de γ respecto a A'B'C') es:
W = ((3a-b-c)^2(3a^2-6a(b+ c)+7b^2-2b c+7c^2)/(b+c-a) : ... : ...),
que tiene coordenadas trilineales exactas en el : (0.36807387978126350, 0.93622894549490614, 2.8226257289734763).El triángulo de contacto interior DEF es persepctivo con A'B'C', el centro de perspectividad es:
Q = ((5a-3(b+c))(3a-b-c)/(a-b-c) : (5b-3(c+a))(3b-c-a)/(b-c-a) : (5c-3(a+b))(3c-a-b)/(c-a-b)),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (0.29654535253632161, -0.21087669513693981, 3.6497889542931890).X6049 = 2rX145+(4R-9r)Q,
donde R y r son los radios de las circunferencias circunscrita e inscrita a ABC, respectivamente.
Special Isocubics in the Triangle Plane §8 Conico-pivotal (unicursal) isocubics or cK, J.P.Ehrmann and B.Gibert.
Isocúbicas cónico-pivotales cK(#Q,X2)
Otra descripción de las isocúbicas cónico-pivotales cK(#Q,X2)
Isocúbicas cónico-pivotales cK(#Q,X2) y transversales isotómicas
Propiedades de la cúbica nodal de Tucker
"The tripolar centroid and the Tucker nodal cubic"
La cúbica nodal de Tucker como lugar geométrico
f(M) = ((v - w) / (v + w) : (w - u) / (w + u) : (u - v) / (u + v)).
f transforms the line at infinity and the Steiner circum-ellipse into K015 which gives a lot of points on K015 with rather simple coordinates. Very few of these points are listed in ETC.Los triángulos ABC y son perspectivos si y solo si P esta sobre la cónica circunscrita de Steiner o sobre la recta del infinito. El centro de perspectividad queda sobre la cúbica nodal de Tucker.
Sean (u:v:w) las coordenadas baricéntricas de un punto P en el plano de un triángulo ABC, la ecuación de una recta d que pasa por P la podemos poner de la forma:d: (v - t v - t w) x + (t-1) u y + t u z=0.
Esta recta corta al lado B'C' del triángulo antimedial A'B'C' en el punto de coordenadas (u:v-t(v+w):-v+t(v+w)). La reflexión de este punto en A, nos da el punto (u:-v+t(v+w):(1-t)v-tw), donde la transversal isotómica d' corta a B'C'. Procediendo análogamente, se obtienen las coordenadas de los puntos de intersección de d' con los los restantes lados del triángulo antimedial y con ello, deducir la ecuación de d':d': ((-1 + t) v + t w) ((-1 + 2 t) u + (-1 + t) v + t w) x + (-1 + t) u (-u + (-1 + t) v + t w) y + t u (u + (-1 + t) v + t w) z=0,
El punto Q=d∩d' es:((t-1) t u^2 : t ((t-1) v + t w) (-v + t (u + v + w)) : (1 - t) ((-1 + t) v + t w) ((t-1) u + (t-1) v + t w))
El lugar geométrico de este punto, cuando la recta d gira alrededor de P, es la cúbica nK(P²,X2,P):x (w^2 y^2+v^2 z^2)+y (w^2 x^2+u^2 z^2)+z(v^2 x^2+u^2 y^2) -2 (uv+uw+vw) x y z=0.
La envolvente de las rectas d' es la cónica-pivotal (CP) inscrita en el triángulo antimedial (descrita en Special Isocubics in the Triangle Plane §8.1, J.P.Ehrmann and B.Gibert.):(v-w)^2x^2 - 2(u^2+3u(v+w)+vw)yz+... =0,
x (w^2 x y+w^2 y^2+v^2 x z-2 v w y z+v^2 z^2)=0,
en la recta BC y una hipérbola (Ha). La cónica-pivotal es ahora:(Ca): (v^2 -2 v w +w^2) x^2+w^2 y^2+v^2 z^2-6 v w x y-2 w^2 x y-2 v^2 x z-6 v w x z-2 v w y z=0.
El haz de cónicas generado por (Ha) y (Ca) tiene las cónicas degeneradas:x (v^2 x - 2 v w x + w^2 x - 6 v w y - 3 w^2 y - 3 v^2 z - 6 v w z)=0, (v x-w x-3 w y+3 v z)^2=0.
Es, por tanto, una haz bitangente con puntos de tangencia Pa(0:v:w) yA1 = (9vw(v+w) : v(2v^2-vw-w^2) : w(-v^2-vw+2w^2)).
Procedienco cíclicamente, se definen los puntos:B1 = (u(-w^2-wu+2u^2) : 9wu(w+u) : w(2w^2-wu-u^2)), C1 = (u(2u^2-uv-v^2) : v(-u^2-uv+2v^2) : 9uv(u+v)).
Para que los triángulos ABC y sean perspectivos es necesario y suficiente que que P esté en la recta el infinito o sobre la elipse circunscrita de Steiner. El centro de perspectividad es:ψ(P)=Q = (u(4u^2 - 4u(v+w) - 2v^2-vw-2w^2) : v(4v^2 - 4v(w+u) - 2w^2-wu-2u^2) : w(4w^2 - 4w(u+v) - 2u^2-uv-2v^2)).
Con la condición u+v+w=0 o uv+vw+wu=0.
ψ(P) = ((-1 + τ) τ (-1 + 2 τ) : (-2 + τ) (-1 + τ) : -τ (1 + τ)).
ψ(P•) = (-(-2 + τ) (1 + τ) : -τ (1 + τ) (-1 + 2 τ) : (-2 + τ) (-1 + τ) (-1 + 2 τ)).
x(y^2+ z^2) + y(x^2+z^2)+ z(x^2+y^2)- 6xyz = 0.
En cada una de las siguientes ternas de centros en , el primer elemento está sobre la elipse circunscrita de Steiner, el segundo está en la recta de infinto y el tercero es la imagen de los dos primeros, mediante ψ:{99, 524, 5468}, {648, 30, 4240}, {671, 523, 5466}, {903, 514, 6548}.
Usando la notación, gX = conjugdo isogonal de X, tX = conjugado isotomico de X, kX = segundo punto de intersección de la recta XK con la circunferencia circunscrita (donde K es el simediano y X está sobre la circunferencia circunscrita), se tiene que:
Si P está sobre la elipse circunscrita de Steiner, entonces f(P)=f(tP)=ψ(P)=ψ(gkgtP),
Si P está sobre la recta del infinito, entonces ψ(P)=ψ(tgkgP)=f(tgkgP)=f(gkgP).
Special Isocubics in the Triangle Plane §8 Conico-pivotal (unicursal) isocubics or cK, J.P.Ehrmann and B.Gibert.
Isocúbicas cónico-pivotales cK(#Q,X2)
Otra descripción de las isocúbicas cónico-pivotales cK(#Q,X2)
El lugar geométrico de los puntos de intersección de las rectas d y d' es la cónico-pivotal nK(P2,X2,P)=cK(#P,X2).
La envolvente de las rectas d' es la cónica pivotal de la cúbica cK(#Q,X2) (envolvente de las rectas QQ*, donde Q* es el P-isoconjugado de Q), inscrita al triángulo antimedial de ecuación:
(a^2/(u(c^2v+b^2w) - a^2vw) : b^2/(v(a^2w+c^2u) - b^2uv) : c^2/(w(b^2u+a^2v) - c^2uv)),
y el eje de perspectividad es:a^2v^2w^2x + b^2w^2u^2y + c^2u^2v^2z = 0.
Por lo que, el lugar geométrico de los puntos P tales que los ejes de perspectividad de ABC y A'B'C' pasan por un punto fijo Q(p:q:r) es la cuárticaa^2py^2z^2 + b^2qz^2x^2 + c^2rx^2y^2 = 0.
El lugar geométrico del punto P, tal que el eje de perspectividad del triángulo tangencial de su triángulo circunceviano y del triángulo de referencia, tiene la dirección del del foco de la , es la cuártica de Stammler (Q066).
El conjugado isogonal del foco de la parábola de Kiepert es el punto (en la recta del infinito) de coordenadas baricéntricas (b^2-c^2:c^2-a^2:a^2-b^2). Por lo que se tratra de la cuártica de Stammler:a^2(b^2-c^2)y^2z^2 + b^2(c^2-a^2)z^2x^2 + c^2(a^2-b^2)x^2y^2 = 0.
Más sobre la cúartica de Stammler:
La cúbica cónico-pivotal cK(#X6,X25) y otras curvas
Cuártica de Stammler e hipérbola de Jerabek
Cuárticas tipo Stammler
Otra caracterización de la cuártica de Stammler
Caracterización de la cuártica de Stammler
Q = (a^2/(a^2vw-u(SBv+SCw)) : b^2/(b^2wu-v(SCw+SAu)) : c^2/(c^2uv-w(SAu+SBv)) )
Cuando P se mueve sobre la cicunferencia circunscrita, la envolvente de las rectas PQ es una elipse, bitangente a Γ en puntos de la recta de Euler.
La ecuación de la cónica envolvente es:(1/(a^2SA+4b^2c^2) : 1/(b^2SB+4c^2a^2) : 1/(c^2SC+4a^2b^2),
que tiene coordenadas trilineales exactas en el : (0.71334292374542307, 0.94937443683429287, 2.6541700608319811).t' = (2c^2 ((a^2-b^2) 2SC-a^2 (a^2-3 b^2-c^2) t))/(a^2 (c^2 (a^2+3 b^2-c^2)+2(b^2-c^2)2SC t)),
por lo que P ↦ Q es una proyectividad sobre la circunferencia circunscrita a ABC.
En coordenadas baricéntricas respecto a ABC, el lugar geométrico de los puntos P tales que las rectas d, e, f son concurrentes consta de:
Φ: (b^2+c^2-a^2)x^2+(c^2+a^2-b^2)y^2+(a^2+b^2-c^2)z^2=0,
Q066: a^2(b^2-c^2)y^2z^2 + b^2(c^2-a^2)z^2x^2 + c^2(a^2-b^2)x^2y^2 = 0.
Más sobre la cúartica de Stammler:
La cúbica cónico-pivotal cK(#X6,X25) y otras curvas
Cuártica de Stammler como lugar geométrico
Cuárticas tipo Stammler
Otra caracterización de la cuártica de Stammler
Caracterización de la cuártica de Stammler
P' (u(v+w)/(v+w-2u):v(u+w)/(u+w-2v):w(u+v)/(u+v-2w)).
C(Q): x(y+z)p/(y+z-2x) + y(z+x)q/(z+x-2y) + z(x+y)r/(x+y-2z) = 0.
En particular, el punto P' está en la recta del infinito si P describe la cúbica nodal de Tucker (K015)x(y^2+z^2) + y(z^2+x^2) + z(x^2+ y^2) - 6xyz=0,
o bien P está en al recta del infinito, entonces P=P'.Las tipolares de dos puntos, L y L•, conjugados isotómicos sobre K015 se cortan en un punto T, sobre la .
Tomando rectas por el baricentro (punto aislado de K015) podemos expresar un punto L sobre esta cúbica por:L ((t-1)t : t(1-5t+6t^2) : 2-9t+13t^2-6t^3).
Y su conjugado isotómico:L• ( (2t-1)(3t-2)(3t-1) : (t-1)(3t-2) : t(1-3t) ).
las tripolates de L y L• se cortan en:T ( (1-2 t)^2 : (1-3 t)^2 (-1+t)^2 : (2-3 t)^2 t^2 ),
que es un punto genérico de la elipse inscrita de Steiner, x^2+y^2+z^2-2 x y-2 x z-2 y z=0.
Más sobre la cúbica nodal de Tucker:
"The tripolar centroid and the Tucker nodal cubic"
La cúbica nodal de Tucker como lugar geométrico
Otra descripción de las isocúbicas cónico-pivotales cK(#Q,X2)
Special Isocubics in the Triangle Plane §8.1, J.P.Ehrmann and B.Gibert.
Isocúbicas cónico-pivotales cK(#Q,X2)
Isocúbicas cónico-pivotales cK(#Q,X2) y transversales isotómicas
El lugar geométrico del punto Q, cuando L gira alrededor de U, es la isocúbica cónico-pivotal nK(U²,G,U), con polo el cuadrado baricéntrico de U, raíz el baricentro y parámetro k=-2(uv+uw+vw).
Si tomamos, sobre la recta L: px+qy+rz=0, un punto:P=((q-r)(qr+t) : (r-p)(pr+t) : (p-q)(pq+t))
el punto Pa es:Pa = (-qr(q-r)(qr+t) : pr(p-r)(pq-q^2+qr+t) : -pq(p-q)(pr+qr-r^2+t)).
Y el punto Q de concurrencia de las rectas que pasan por Pa, Pb, Pc y son paralelas, respectivamente, a AP, BP, CP (que queda sobre L) es:Q = (qr(r-q) : rp(p-r) : pq(q-p))
Cuando la recta L gira alrededor de un punto U(u:v:w) el lugar geométrico de Q es la cúbica:x(w^2y^2+v^2z^2)+y(u^2z^2+w^2x^2)+z(v^2x^2+u^2y^2) - 2(uv+uw+vw)xyz=0.
En recuerdo a Marta (hace 17)
u((a^4-(b^2-c^2)^2)u+2b^2(-a^2+b^2-c^2)v+2c^2(-a^2-b^2+c^2)w) + λ((-a^2-b^2+c^2)u+2b^2v-2c^2w)((-a^2+b^2-c^2)u-2b^2v+2c^2w)=0.
Esta ecuación es satisfecha por la polar (2(b+c)^2:a^2+b^2+2bc-3c^2:a^2-3b^2+2bc+c^2) de A respecto a la circunferencia 4(a^2yz+b^2xz+c^2xy)-(x+y+z)((b+c)^2x+a^2y+a^2z)=0, de diámetro DU. Esto permite determinar λ=(-a^2+b^2+c^2-2bc)/(2a^2), por lo que la ecuación tangencial de (U'a) es:SBSC(a^2+(b-c)^2)u^2 + b^4(a+b-c)(a-b+c)v^2 + (a+b-c)c^4(a-b+c)w^2 - 2b^2c^2(a+b-c)(a-b+c)v w - c^2(a^4+b^4-c^4+2bc(c^2-b^2))w u - b^2(a^4-b^4+c^4+2bc(b^2-c^2))u v=0.
La ecuación puntual de (U'a) es la que tiene como matriz asociada la adjunta de la matriz asociada a su ecuación tangencial:c²(b-c)²y² + b²(b-c)²z² - (a4 -(b²+c²)²+2bc(b²+c²))yz - 2b²(a+b-c)(a-b+c)zx - 2c²(a+b-c)(a-b+c)xy=0.
γ′u: (c+bt-ct)^2(a^2yz+b^2xz+c^2xy) - (x+y+z)(b^2c^2x + (a^2c^2-2a^2c^2t+a^2c^2t^2)y+ (a^2b^2t^2z))=0
La polar de A respecto a γ′u es:pa: -2b^2c^2x + c^2(t-1)(-a^2(t-1)+(b-c)(b+c+(b-c)t))y + b^2t(c^2(t-2)-2bc(t-1)-a^2t+b^2t)z=0.
Eliminado "t" entre esta ecuación y la que resulta de derivarla respecto a "t", se llega a la misma ecuación obtenida anteriormente para (U'a).c²(b+c)²y² + b²(b+c)²z² - (a4-(b²+c²)²-2bc(b²+c²))yz - 2b²(a-b-c)(a+b+c)zx - 2(a-b-c)c²(a+b+c)xy=0.
El triangulo , delimitado por las rectas da, dc y dc, es homotético a ABC con centro de homotecia X12, centro de homotecia interior de la circunferencia inscrita y la . La razón de homotecia de los triángulos ABC y es (3r-R)/r.
Una de las dos cónicas degeneradas del haz (Ua)+λΓ=0 se obtiene para λ=a^2, y es (c^2y+b^2z)(a^2x-(b+c)^2(2x+y+z))=0.El triangulo , delimitado por las rectas d'a, d'c y d'c, es homotético a ABC con centro de homotecia X11, . La razón de homotecia de los triángulos ABC y es (3r+R)/r.
Una de las dos cónicas degeneradas del haz (U'a)+λΓ=0 se obtiene para λ=a^2, y es (c^2y+b^2z)(a^2x-(b-c)^2(2x+y+z))=0.(3a^4-3a^3(b+c) - 2a^2(b^2-3bc+c^2) + 3a(b-c)^2(b+c) - (b^2-c^2)^2 : ··· : ···. ).
que tiene coordenadas trilineales exactas en el triángulo de ETC: (3.9651820451012903, 5.7071388701250661, -2.1405156797643391).
Sean un triángulo ABC y un punto F sobre la .
El lugar geométrico de los puntos P tales que la circunferencia circunscrita a su pasa por F consta de la hipérbola equilátera H(F), circunscrita a ABC con centro en F, y de una cuártica Q(F).
c(P):
(a^2vw(u+v)(u+w)-u(v+w)(b^2w(u+v)+c^2v(u+w)))x^2/(2u(u+v)(u+w)(v+w)) +
((c^2v^2+b^2w^2+(a^2-b^2-c^2)vw)u^2 +
uvw(a^2(v+w)-(b^2-c^2)(v-w)) + a^2v^2w^2)yz/(2vw(u+v)(u+w)) + ... =0.
Un punto genérico F de la circunferencia de Euler se puede expresar, en términos de un parámetro t, como:
F = ( (b^4+c^4-a^2(b^2+c^2)-2(b^2-c^2)t) (2a^4+(b-c)^2(b+c)^2-a^2(b^2+c^2)+2(b^2-c^2)t) : ... : ... ).
La condición analítica para que la circunferencia c(P) pase por F es que las coordenadas de P satisfagan a una de las ecuaciones:
H(F) :
(2a^4+(b^2-c^2)^2-a^2(b^2+c^2)+2(b^2-c^2)t)yz + ... =0,
Q(F) :
a^2(a^2(b^2+c^2)-b^4-c^4+2(b^2-c^2)t)y^2z^2 +
... = 0.
b^2c^2(a^2(b^2+c^2)-b^4-c^4+2(b^2-c^2)t)x^2+ ... =0,
que pertenece al haz de cónicas que pasan por el simediano y por los vértices de su triángulo anticeviano. Entre las que se encuentra la , conjugada isogonal de la cuártica de Stammler.
Más sobre la cúartica de Stammler:
La cúbica cónico-pivotal cK(#X6,X25) y otras curvas
Cuártica de Stammler como lugar geométrico
Cuártica de Stammler e hipérbola de Jerabek
Otra caracterización de la cuártica de Stammler
Caracterización de la cuártica de Stammler
a Aye, por su "cumple"
Pa (-2(a^2(b^2w-c^2v)-(b^2-c^2)(c^2v+b^2w)) : -(a^2-b^2-c^2)((a^2-c^2)v-b^2(v+2w)) : (a^2-b^2-c^2)((a^2-b^2)w-c^2(2v+w)) ).
Procediendo cíclicamente sobre los lados de ABC se definen similarmente los puntos Pb y Pc y las correspondientes rectas Lb y Lc donde están.La: SAx -c^2y-b^2z=0, Lb: -c^2x+SBy -a^2z=0, Lc: -b^2x-a^2y+SCz=0.
Denotemos por A'B'C' el triángulo delimitado por las rectas La, Lb y Lc. Este triángulo está descrito por Randy Hutson en X7610 de ETC, por una vía distinta.A' (3a^4+(b^2-c^2)^2 : -2(c^2(b^2-c^2)+a^2(2b^2+c^2)) : -2(-b^4+b^2c^2+a^2(b^2+2c^2))), ...
Los triángulos ABC y A'B'C' tienen el mismo baricentro y la de A'B'C' pasa por el simediano.
El triángulo A'B'C' es perspectivo con:
•
El triángulo de referencia ABC y el centro de perspectividad es X262:
(sinA sec(A-ω) : sinB sec(B-ω) : sinC sec(C-ω) ) ≡
(1/(a^4-a^2(b^2+c^2)-2b^2c^2) : ... : ...).
•
El triángulo medial y el centro de perspectividad es
X7710:
((a^4+2a^2(b^2+c^2)-3b^4-2b^2c^2-3c^4) (3a^4+b^4-2b^2c^2+c^4) : ... : ...).
•
El triángulo antimedial y el centro de perspectividad es:
(3a^8+12a^6(b^2+c^2)-2a^4(13b^4+16b^2c^2+13c^4)+4a^2(5b^6+b^4c^2+b^2c^4+5c^6) - (b^2-c^2)^2(9b^4+2b^2c^2+9c^4) : ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (0.54080603485835454, -6.8259465626679512, 8.1167170092044894).
•
El triángulo tangencial y el centro de perspectividad es:
(3a^8 - 3a^6(b^2+c^2) + a^4(5b^4+2b^2c^2+5c^4) - 5a^2(b^2-c^2)^2(b^2+c^2) - 4b^2c^2(b^2-c^2)^2: ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (-17.666044325016434, -22.653598907634627, 27.477484183354398).
•
El triángulo órtico y el centro de perspectividad es:
((3a^4 + (b^2-c^2)^2)(a^4 - 4a^2(b^2+c^2)+3b^4-2b^2c^2+3c^4 ): ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (-2.3130635454920857, -2.0081191696445738, 6.0984686203500467).
•
El triángulo de reflexión y el centro de perspectividad es:
(3a^8- 12a^6(b^2+c^2) + 2a^4(7b^4+b^2c^2+7c^4) - 8a^2(b^2-c^2)^2(b^2+c^2) + (b^2-c^2)^2(3b^4-4b^2c^2+3c^4) : ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (-5.9040620654651642, -4.7407532933726518, 9.6476761767647522).
•
El primer triángulo de Brocard y el centro de perspectividad es:
( a^8(16b^4+31b^2c^2+16c^4)- 4a^6(5b^6+4b^4c^2+4b^2c^4+5c^6) + a^4(8b^8-26b^6c^2-36b^4c^4-26b^2c^6+8c^8) - 4a^2(b^2-c^2)^2(b^6-2b^4c^2-2b^2c^4+c^6) -b^2c^2(b^2-c^2)^2(5b^4-2b^2c^2+5c^4): ... : ...),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (17.319173814766243, 18.906284810428768, -17.441766762896880).El triángulo pedal en A'B'C' del baricentro de ABC es persepctivo con el triángulo órtico, con centro de perspectividad X427 ( del ).
Los puntos Pa, Pb y Pc están alineados si y solo si P está sobre la o sobre la .
Cuando P recorre la recta de Euler, la recta PaPbPc envuelve la de A'B'C'.
Cuando P está en la elipse circunscrita de Steiner, la recta PaPbPc pasa por el ortocentro.
(a^4(b^4+14b^2c^2+c^4) -
2a^2(b^6+7b^4c^2+7b^2c^4+c^6) + b^8+14b^4c^4+c^8)x^2+
2(a^8-a^6(b^2+c^2) +
a^4(-5b^4+11b^2c^2-5c^4)+
5a^2(b^2-c^2)^2(b^2+c^2) - b^2c^2(b^2-c^2)^2)y z+... =0,
El lugar geométrico del punto Q. cuando P se mueve sobre δ es una cónica C(δ).
Existen dos rectas δ1 y δ2 (si el ángulo en A es agudo) pasando por A, para las cuales las cónicas C(δ1) y C(δ2) son parábolas.
((a^2+b^2-c^2)x + 2a^2y) ((a^2+b^2-c^2)(t-1)x-2a^2tz) - 2λx^2 = 0.
La ecuación de la cónica C(δ) de este haz que pasa por el punto Qa que corresponde a P=A es:C(δ): 2b^2(t-1)x^2 - 2a^2tyz - (a^2+b^2-c^2)tzx + (a^2+b^2-c^2)(t-1)xy = 0.
Estas cónicas son parábolas para:t = ((b^2-c^2)^2+a^2(2a^2-b^2-3 c^2) ± 2√2 aS√-a^2+b^2+c^2)/ (2((b^2-c^2)^2+2a^2(a^2-b^2-c^2))).
Estos valores son reales sólo cuando el ángulo en A es agudo.
D1 = (0 : 2a^4+(b^2-c^2)^2-a^2(b^2+3c^2) -
4aS√SA :
2a^4+(b^2-c^2)^2-a^2(3b^2+c^2)+ 4aS√SA),
D2 = (0 : 2a^4+(b^2-c^2)^2-a^2(b^2+3c^2) +
4aS√SA :
2a^4+(b^2-c^2)^2-a^2(3b^2+c^2) - 4aS√SA)
Si el triángulo ABC es acutángulo, los puntos D1, D2, E1, E2, F1 y F2, están definidos y quedan en una misma cónica, de ecuación:
(a^2-b^2-c^2)^2x^2 -
2((b^2-c^2)^2+a^2(3a^2-4b^2-4c^2))yz + ... = 0.
( a^6(b^2+c^2) - a^4(3b^4-2b^2c^2+3c^4) + 3a^2(b^2-c^2)^2(b^2+c^2) - (b^2-c^2)^4 : ... : ... ),
que tiene coordenadas trilineales exactas en el triángulo de ETC: (1.168138920150068, 2.209129060254948, 1.572126400123230).S=(u (SB v + SC (u + v)) : -u (SA u + SC (u + v)) : (SB v + SC (u + v)) w))
Eliminando u,v,w entre las ecuaciones
(x, y, z) = (u (SB v + SC (u + v)), -u (SA u + SC (u + v)), (SB v +
SC (u + v)) w),
u + v + w = 0
SA x^2 - SB x y - SC x z - SB y z - SC y z=0.
En general, a la recta x+qy+rz=0 le corresponde la cónica:(q SA - p SC + q SC) x^2 + (-p SB - p SC + q SC) x y - r SC x z + (-r SB - r SC) y z=0.
Las polares de P respecto a D(a), E(b), F(c), resp, son concurrentes en un punto Q si y solo si P está sobre la isocúbica no pivotal Φ de polo X32, raíz el baricentro y parámetro k=S²(-5+2csc²ω).
Si (u:v:w) son las coordenadas baricéntricas de P en el triángulo de referencia ABC, la polar de P respecto a la circunferencia D(a) es:pa: (((b^2-c^2)^2-2a^2(b^2+c^2))u + a^4(5u+4(v+w)))x + 4a^4(u+v+ w)y + 4a^4(u+v+w)z=0.
Por permutación cíclica se deducen las ecuaciones de las polares pb y pc de P, respecto a las circunferencia E(b) y F(e), respectivamente.-(4u(c^4v^2+b^4w^2)+4v(a^4v^2+c^4u^2)+4w(b^4w^2+a^4v^2)+5(a^4+b^4+c^4)-2(b^2c^2+c^2a^2+a^2b^2))/(4S^2uvw)
Por lo que las polares pa, pb y pc son concurrentes si P queda en la isocúbica no pivotal nK(X32,X2,?) de parámetro k=S²(-5+2csc²ω), de la que no se conocen centros del triángulo sobre ella, de ecuación:x(c^4y^2+b^4z^2)+ y(a^4z^2+c^4x^2)+z(b^4z^2+a^4y^2)+S²(-5+2csc²ω)xyz=0.