================= Encyclopedia Triangle Centers ETC. Clark Kimberling ================
-
X(40) = BEVAN POINT
Barycentrics a (a^3 + a^2 (b + c) - (b - c)^2 (b + c) - a (b + c)^2) : :
Let I = X(1) and P = X(40), and let
DEF = pedal triangle of P,
Ab = AI∩PE, and define Bc and Ca cyclically,
Ac = AI∩PF, and define Ba and Cb cyclically.
The centers of the circles {{Ab, Bc, Ca}} and {{Ac, Ba, Cb}} are the bicentric pair PU(44). (Angel Montesdeoca, April 12, 2021)
-
X(57) ISOGONAL CONJUGATE OF X(9)
Barycentrics a/(b + c - a) : b/(c + a - b) : c/(a + b - c)
Let Va, Vb, Vc be the antipodes of V=X(40) in the circles (VBC), (VCA), (VAB), respectively. The lines AVa, BVb, CVc concur in X(57). (Angel Montesdeoca, October 14, 2019). See
Antipodales del punto de Bevan y el centro X(57)
Let DEF be the intouch triangle. Let Ia be the internal bisector of angle BAC, and let D' be the point, other than D, where the line through D parallel to Ia meets the incircle. Let A' be the point, other than A, where AD' meets the incircle. Let La be the radical axis of the circumcircles of triangles A'BF and A'CE, and define Lb and Lc cyclically. The lines La, Lb, Lc concur in X(57). See X(57) and HG211219. (Angel Montesdeoca, December 21, 2019)
-
X(101) = Ψ(INCENTER, SYMMEDIAN POINT)
Barycentrics a2/(b - c) : b2/(c - a) : c2/(a - b)
X(101) = (r 2 + 6rR + 8R2 +
s2)*X(1) - 6R(r + 4R)*X(2) - 2(r2 + 4rR -
s2)*X(3) (Peter Moses, April 2, 2013)
Let IaIbIc be the excentral triangle. The Brocard axes of BCIa, CAIb, ABIc concur in X(101). (Randy Hutson, February 10, 2016)
X(101) = intersection of Lemoine axes of 1st & 2nd Montesdeoca bisector triangles.
-
X(175) = ISOPERIMETRIC POINT and X(176) = EQUAL DETOUR POINT
Barycentrics (a + b - c)*(a - b + c)*(a*(a - b - c) + S) : :
and
Barycentrics (a + b - c)*(a - b + c)*(a*(a - b - c) - S) : :
In the plane of a triangle ABC, let
Oa = circle with diameter BC
C' = the point, other than B, where Oa meets AB
B' = the point, other than C, where Oa meets AC
Ub = B-mixtilinear incircle of BCC'
Uc = C-mixtilinear incircle of CBB'
Ab = touchpoint of Ub and BC; define Bc and Ca cyclically
Ac = touchpoint of Uc and BC; define Ba and Cb cyclically
The points Ab, Ac, Ba, Ba, Cb, Cb line on a conic, of which the center is X(176). A barycentric equation for this conic follows:
2 (a-b-c) (a^2-b^2-c^2) (a^2 (b+c)-(b-c)^2 (b+c)+2 a S) x^2 - ((a+b-c) (a-b+c) (3 a^4-2 a^3 (b+c)-3 (b^2-c^2)^2+2 a (b+c) (b^2+c^2))+2 (a^4-3 (b^2-c^2)^2+2 a^2 (b^2+c^2)) S) y z + (cyclic) = 0.
See X(175) and X(176). Continuing, let
Vb = B-mixtilinear excircle of BCC'
Vc = C-mixtilinear excircle of CBB'
A'b = touchpoint of Vb and BC; define B'c and C'a cyclically
A'c = touchpoint of Vc and BC; define B'a and C'b cyclically
The points A'b, A'c, B'a, B'c, C'a, C'b line on a conic, of which the center is X(175). A barycentric equation for this conic follows:
(a+b-c) (a-b+c) (2 (a-b-c) (2 a^3 b c+a^4 (b+c)-2 a b c (b+c)^2+(b-c)^2 (b+c)^3-2 a^2 (b^3+b^2 c+b c^2+c^3)+2 (a^3-2 b c (b+c)-a (b+c)^2) S) x^2 + (3 a^6-4 a^5 (b+c)-4 a (b-c)^2 (b+c)^3-3 (b-c)^2 (b+c)^4+a^2 (b+c)^2 (9 b^2+2 b c+9 c^2)-a^4 (9 b^2+14 b c+9 c^2)+8 a^3 (b^3+b^2 c+b c^2+c^3)-2 (a^4+6 a^3 (b+c)-4 a^2 (b+c)^2+3 (b^2-c^2)^2-2 a (3 b^3+7 b^2 c+7 b c^2+3 c^3)) S) y z) + (cyclic) = 0. (Angel Montesdeoca, September 9, 2022)
See HG050922. X(175) y X(176) centros de cónicas con los mismos puntos en el infinito que la cónica circunscrita de perspector el punto de Gergonne.
-
X(195) = X(5)-CEVA CONJUGATE OF X(3)
Barycentrics 4 cos 2A + cot²2A - cot A cot ω : :( (M. Iliev, 5/13/07)
a^2(a^8 + b^8 + c^8 - 4a^6(b^2 + c^2) + a^4(6b^4 + 6c^4 + 5b^2c^2) - a^2(4b^6 + 4c^6 - b^4c^2 - b^2c^4) - 2b^2c^2(b^4 + c^4 - b^2c^2)) : : : :
Hyacinthos #24180
Re: N, O, diameters, radical axes, reflections
Antreas Hatzipolakis
Aug 28, 2016
[APH]:
Let ABC be a triangle.
Denote:
Ab, Ac = the orthogonal projections of A on NB, NC, resp.
(Oab), (Oac) = the circles with diameters AAb,AAc, resp.
Similarly (Obc), (Oba) and (Oca), (Ocb)
R1 = the radibal axis of (Oab), (Oac)
R2 = the radical axis of (Obc), (Oba)
R3 = the radical axis of (Oca), (Ocb)
The reflections of R1, R2, R3 in BC, CA, AB, resp. are concurrent.
[Angel Montesdeoca]:
The reflections of R1, R2, R3 in BC, CA, AB, resp. are concurrent. at
X(195) = X(5)-CEVA CONJUGATE OF X(3)
-
X(221) = X(1)-CEVA CONJUGATE OF X(56)
Barycentrics a^2 (a^5+a^4 (b+c)-2 a^3 (b^2+c^2)-2 a^2 (b-c)^2 (b+c)+a (b^2-c^2)^2+(b-c)^4 (b+c)) : :
Let I = X(1) = incenter, and A'B'C' = medial triangle. Let Ab = AC∩IA', and define Bc and Ca cyclically. Let Ac = AB∩IA', and define Ba and Cb cyclically. Let Oa be the circumcircle of AAbAc, and define Ob and O cyclically. Then X(221) is the radical center of Oa, Ob, Oc. (Angel Montesdeoca, April 27, 2021)
X(221) como centro radical.
-
X(223) = X(2)-CEVA CONJUGATE OF X(57)
Barycentrics a (a + b - c) (a - b + c) (a^3 + a^2 (b + c) - (b - c)^2 (b + c) -
a (b + c)^2) : :
Let Va, Vb, Vc be the antipodes of V=X(40) in the circles (VBC), (VCA), (VAB), respectively. The triangle VaVbVc is here named the Bevan antipodal triangle (Hyacinthos #29638). The point X(223) is the unique finite fixed point of the affine transformation that maps the reference triangle ABC onto VaVbVc. (Angel Montesdeoca, October 15, 2019). See Antipodales del punto de Bevan y el centro X(57).
The construction of the triangle VaVbVc can be generalized for an arbitrary point P (instead of V=X(40)), and is, in fact, the antipedal triangle of P (Randy Hutson, message in Anopolis Group). Thus, "Bevan antipodal triangle" = antipedal triangle of X(40). (Angel Montesdeoca, October 16, 2019)
-
X(402) = ZEEMAN-GOSSARD PERSPECTOR
Barycentrics p(a,b,c)y(a,b,c) : :
p(a,b,c) = 2a4 - a2b2 - a2c2 - (b2 - c2)2
y(a,b,c) = a8 - a6(b2 + c2) + a4(2b2 - c2)(2c2 - b2) + [(b2 - c2)2][3a2(b2 + c2) - b4 - c4 - 3b2c2]
(From Angel Montesdeoca, November 25, 2020) Let P be a variable point on the Euler line and Q its isotomic conjugate. Let TP and TQ be the cevian triangles of P and Q, respectively. Let F be the finite fixed point of the affine transformation that carries TP onto TQ. The envelope of the line PF is a hyperbola (H) with center X(402), an asymptote of the Euler line. A barycentric equation for (H) follows:
cyclic sum [(-b^4+c^4+a^2 (b^2-c^2))^4 (-2 a^4+(b^2-c^2)^2+a^2 (b^2+c^2))^2x^2-2 (a^2-b^2)^2 (a^2-c^2)^2 (a^4-(b^2-c^2)^2)^2 (a^8-a^6 (b^2+c^2)+5 a^2 (b^2-c^2)^2 (b^2+c^2)+a^4 (-3 b^4+7 b^2 c^2-3 c^4)-(b^2-c^2)^2 (2 b^4+5 b^2 c^2+2 c^4))y z ] = 0.
-
X(427) = COMPLEMENT OF X(22)
Barycentrics tan A + tan ω : :
(a^2+b^2-c^2) (a^2-b^2+c^2) (b^2+c^2) : :
Let A'B'C' be the circummedial triangle. Let A" be the pole, wrt the polar circle, of line B'C', and define B" and C" cyclically. The lines AA", BB", CC" concur in X(427). Moreover, X(427) is the Euler line intercept of radical axis of nine-point circle and every circle with center on orthic axis that is orthogonal to nine-point circle, and X(427) is the point in which the extended trapezoid legs (P(4),P(4)-Ceva conjugate of U(4)) and (U(4),U(4)-Ceva conjugate of P(4)) meet. Also, X(427) is the QA-P38 center (Montesdeoca-Hutson Point) of quadrangle ABCX(2). (Randy Hutson, October 13, 2015)
-
X(845) = X(165)X(166) ∩ X(173)X(503)
Let Ia, Ib, Ic be the excenters of a triangle ABC. Let A' be the Clawson point of IaBC, and define B' and C' cyclically. The lines AA', BB', CC' concur in X(845). (Angel Montesdeoca, August 12, 2018)
-
X(900) = CROSSDIFFERENCE OF X(6) AND X(101)
Barycentrics (b - c)(b + c - 2a) : :
Let Ua be the line through X(80) perpendicular to the line AX(80), and define Ub and Uc cyclically. Let Va be the reflection of BC in Ua, and define Vb and Vc cyclically. The lines Va, Vb, Vc are parallel, and they concur in X(900). (Angel Montesdeoca, June 30, 2017)
(Una descripción del punto X(900) )
-
X(933) = X(4)-CROSS CONJUGATE OF X(250)
Barycentrics a^2((a^2-b^2)^2-(a^2+b^2) c^2) (a^4-b^2 c^2+c^4-a^2 (b^2+2 c^2))/((b^2-c^2) (-a^2+b^2+c^2)) : :
Let P be a point on the circumcircle, and let
(Oab) = circle through A tangent to line BC at B
(Oac) = circle through A tangent to line BC at C
Ba = point other than A where the line PB meets (Oab)
Ca = point other than A where the line PC meets (Oac)
Hab = orthocenter of APBa
Hac = orthocenter of APCa
Define Hbc and Hca cyclically, and define Hba and Hcb cyclically. The points Hab, Hac, Hbc, Hba, Hca, Hcb lies on a hyperbola with center = midpoint(P and H), where H = X(4), the orthocenter. This hyperbola is rectangular if and only if P = X(933). This note is related to a problem posed in 2017 Olympiad of Rusanovsky Lyceum in Kyiv, Ukraine , IX-X Team p9. For details, see
El centro X(933) y una hipérbola rectangular. (Angel Montesdeoca, July 3, 2021)
-
X(953) = ISOGONAL CONJUGATE OF X(952)
Barycentrics a2/(2a4 - 2a3(b + c) - a2(b2 - 4bc + c2) + (2a - b - c)(b - c)(b2 - c2)) : :
X(953) = Miquel point of the sidelines of ABC and the Sherman line. (Angel Montesdeoca, July 24, 2019)
See HG250719
-
X(962) = LONGUET-HIGGINS POINT
Barycentrics a^4 + 2a^3(b + c) - 4a^2bc - (b + c)(b - c)^2(2a + b + c) : :
Let I = X(1) and H = X(4) in a triangle ABC. Let Lb be the perpendicular to B at I, and let Lc be the perpendicular to CI at I. Let Ab = Lb∩AH and Ac = Lc∩AH. Let U be the circle (I, Ab, Ac). Let Mb be the point, other than I, where BI meets U, and let Mc be the point, other than I, where CI meets U. Let ℓa be the line MbMc, and define ℓb and ℓc cyclically. The lines ℓa, ℓb, ℓc concur in X(962). (Angel Montesdeoca, March 12, 2020). See Otra construcción del punto de Longuet-Higgins
-
X(974) = 2nd EHRMANN POINT
Barycentrics a^2 (a^2-b^2-c^2) (a^10 b^2-3 a^8 b^4+2 a^6 b^6+2 a^4 b^8-3 a^2 b^10+b^12+a^10 c^2+2 a^8 b^2 c^2-a^6 b^4 c^2-11 a^4 b^6 c^2+12 a^2 b^8 c^2-3 b^10 c^2-3 a^8 c^4-a^6 b^2 c^4+18 a^4 b^4 c^4-9 a^2 b^6 c^4+3 b^8 c^4+2 a^6 c^6-11 a^4 b^2 c^6-9 a^2 b^4 c^6-2 b^6 c^6+2 a^4 c^8+12 a^2 b^2 c^8+3 b^4 c^8-3 a^2 c^10-3 b^2 c^10+c^12) : :
The pedal triangles of circumcenter and orthocenter with respect to orthic and medial triangles, respectively, are perspective, with perspector X(974). (Angel Montesdeoca, August 29, 2019)
El centro X(974) y triángulos pedales.
-
X(1001) = MIDPOINT OF X(1) AND X(9)
Barycentrics a(a^2-a(b+c)-2bc) : :
Let A' be the line through X(1) parallel to line BC. Let AB = A'∩AB and AC = A'∩AC. Define BC and CA cyclically, and define BA and CB cyclically. The six points AB, BC, CA, AB, BC, CA lie on a conic whose center is X(1001). (Angel Montesdeoca, April 27, 2016)
(Hechos Geométricos en el Triángulo (2016) )
-
X(1083) = MIDPOINT OF X(105) AND X(644)
Trilinears a4 - a3(b + c) - a2bc + 2abc(b + c) - bc(b2 + c2): :
X(1083) = X(112)-of-1st-Montesdeoca-bisector-triangle
X(1083) = X(112)-of-2nd-Montesdeoca-bisector-triangle
X(1083) = similicenter of 1st and 2nd Montesdeoca bisector triangles
-
X(1125) = COMPLEMENT OF X(10)
Barycentrics 2a+b+c : a+2b+c : a+b+2c
Hyacinthos #24185 Re: I, NPC, Concurrent Euler lines
Antreas Hatzipolakis
Aug 28, 2016
[APH]:
Let ABC be a triangle.
Denote:
Na, Nb, Nc = the NPC centers of IBC, ICA, IAB, resp.
Aa, Ab, Ac = the orthogonal projections of Na on IA, IB, IC, resp.
Ba, Bb, Bc = the orthogonal projections of Nb on IA, IB, IC, resp.
Ca, Cb, Cc = the orthogonal projections of Nc on IA,IB, IC, resp.
The Euler lines of AaAbAc, BaBbBc, CaCbCc are concurrent.
[Angel Montesdeoca]:
The Euler lines of AaAbAc, BaBbBc, CaCbCc are concurrent. at
X(1125)= the centroid of {A,B,C,X(1)} (Darij Grinberg, 12/28/02)
-
X(1141) = GIBERT POINT
Barycentrics ( (SA SB+S^2)(SA SC+S^2))/(b^2c^2-4SA^2) :...:...)
See
Hyacinthos #24187 Re: O, NPC, Euler lines, parallelogic
Antreas Hatzipolakis Message 2 of 2 , Aug 29, 2016
[APH]:
Let ABC be a triangle.
Denote:
Na, Nb, Nc = the NPC centers of OBC, OCA, OAB, resp.
Aa, Ab, Ac = the orthogonal projections of Na on OA, OB, OC, resp.
Ba, Bb, Bc = the orthogonal projections of Nb on OA, OB, OC, resp.
Ca, Cb, Cc = the orthogonal projections of Nc on OA, OB, OC, resp.
The Euler lines of AaAbAc, BaBbBc, CaCbCc bound a triangle A*B*C*.
ABC, A*B*C* are parallelogic.
The parallelogic center (ABC, A*B*C*) lies on the circumcircle.
[Angel Montesdeoca]:
The parallelogic center (ABC, A*B*C*) is X(1141) = Gibert point
X(1141) was first noted (Hyacinthos #1498, September 25, 2000) by Bernard Gibert as a point of intersection of the circumcircle and certain cubic.
-
X(1156) = ISOGONAL CONJUGATE OF X(1155)
Barycentrics af(a,b,c) : bf(b,c,a) : cf(c,a,b)
where
f(a,b,c) = 1/[(b - c)2 + a(b + c - 2a)]
Let Bc be the reflection of B in the internal angle bisector of angle C, and let Cb be the reflection of C in the internal angle bisector of angle B. Let Γa be the circle that passes through A, Bc, Cb. Let A' be the pole of BC, with respect to Γa and define B 'and C' cyclically. Then X(1156) is the perspector of A'B'C' and ABC, and X(35445) is the perspector of A'B'C' and the excentral triangle. (Angel Montesdeoca, January 13, 2021)
See HG120121.
-
X(1177) = 1st SARAGOSSA POINT OF X(67)
Trilinears f(a,b,c)
: f(b,c,a) : f(c,a,b), where f(a,b,c) = a/(b6 +
c6 - a4b2 - a4c2
+ 2a2b2c2 - b4c2
- b2c4) (M. Iliev,
5/25/07)
See Angel Montesdeoca, Hyacinthos #21528, 2/12/2013
[Antreas Hatzipolakis]:
3. Let OaObOc be the medial triangle [pedal tr. of O], (N1),(N2),(N3)
the reflections of the NPC (N) in the perp. bisectors
OOa,OOb,OOc, resp. and and A'B'C' the triangle bounded by the radical
axes of ((O),(N1)), ((O),(N2)), ((O),(N3)), resp.
The triangles ABC, A'B'C' are perspective.
Perspector?
[Angel Montesdeoca]:
The triangles ABC, A'B'C' are perspective.
Perspector: X(1177) = 1st SARAGOSSA POINT OF X(67) (M.Iliev, 5/25/07)
-
X(1320) = ISOGONAL CONJUGATE OF X(1319)
Barycentrics a(b + c - a)/ (b + c - 2a) : :
Let DEF be the intouch triangle. Let Ha be the orthocenter of IBC. Let
A1 be the point, other than A, where AI meets the circumcircle. Let ta be the tangent to the circle (DHaA1) at Ha, and define tb and tc cyclically. The lines ta, tb , tc concur in X(1320). (Angel Montesdeoca, September 3, 2020)
Conjugado isogonal del punto Bevan-Schröder
-
X(1380) = 2nd BROCARD-AXIS INTERCEPT OF CIRCUMCIRCLE
Barycentrics a^6-a^2 b^2 c^2-a^4 Sqrt[a^4+b^4-b^2 c^2+c^4-a^2 (b^2+c^2)] : :
In the plane of a triangle ABC, let
F1 = X(39162) and F2 = X(39163); these points are the foci of the Steiner inellipse;
L1 = trilinear polar of F1
L2 = trilinear polar of F1
A1 = L1∩BC, and define B1 and C1 cyclically
A2 = L2∩BC, and define B2 and C2 cyclically
The seven circle (ABC), (AB1C1), (BC1A1), (CA1B1), (AB2C2), (BC2A2), (CA1B2) concur in X(1380).
See X(1380)
(Angel Montesdeoca, February 18, 2023).
-
X(1384) = 2nd GRINBERG HOMOTHETIC CENTER
Barycentrics a^2(b^2 + c^2 - 5a^2) :
Let DEF be the circumsymmedial triangle and let (Oa) be the circle tangent at D to circumcircle and with center Oa=AH∩OD. Define (Ob) and (Oc) cyclically. The radical center of the circles (Oa), (Ob), (Oc) is X(1384). (Angel Montesdeoca, October 2, 2018) HG300918
-
X(1441) = X(313)-BETH CONJUGATE OF X(313)
Barycentrics b c (b + c)/(a - b - c) : :
In the plane of a triangle ABC, let
I = incenter = X(1)
O = circumcenter = X(3)
DEF = cevian triangle of I
Lb = line through B perpendicular to AI
Lc = line through C perpendicular to AI
Ab = Lb∩AO
Ac = Lc∩AO
Oa = circumcircle of DAbAc
A' = the point of intersection, other than D of Oa and AI, and define B' and C' cyclically. Then X(1441) = finite fixed point of the affine transformation that carries ABC onto A'B'C'. (Angel Montesdeoca, May 30, 2023)
See HG300523
-
X(1493) = NAPOLEON CROSSSUM
Barycentrics sin A(3 sin²A - cos²A)(3 sin B sin C - cos B cos C) : :
Hyacinthos #24179
24179Re: N, NPC, radical axes, reflections
Antreas Hatzipolakis
Aug 28,2016
[APH]:
Let ABC be a triangle.
Denote:
Ab, Ac = the orthogonal projections of A on NB, NC, resp.
(Nab), (Nac) = the NPCs of AAbN, AAcN, resp.
Similarly (Nbc), (Nba) and (Nca), (Ncb)
R1 = the radibal axis of (Nab), (Nac)
R2 = the radical axis of (Nbc), (Nba)
R3 = the radical axis of (Nca), (Ncb)
The reflections of R1, R2, R3 in BC, CA, AB, resp. are concurrent.
[Angel Montesdeoca]:
The reflections of R1, R2, R3 in BC, CA, AB, resp. are concurrent at
X(1493) = NAPOLEON CROSSSUM
-
X(1576) = ISOGONAL CONJUGATE OF X(850)
Barycentrics a4/(b2 - c2) : b4/(c2 - a2) : c4/(a2 - b2)
X(1576) is the center of the conic transform of the Stammler quartic (Q066 in Bernard Gibert' catalogue) by X(31)-isoconjugation. This conic is given by the barycentric equation b^4c^4(b^2-c^2)x^2+c^4a^4(c^2-a^2)y^2+a^4b^4(a^2-b^2)z^2 = 0, and it passes through the following triangle centers: X(6), X(31), X(48), X(154), X(1613), X(2578), X(2579), X(5638), X(5639). (Angel Montesdeoca, May 7, 2016)
-
X(1593) = POINT CEBALRAI
Barycentrics a^2 (a^4 + b^4 + c^4 - 2 a^2 b^2 - 2 a^2 c^2 + 6 b^2 c^2)/(a^2 - b^2 - c^2) : :
In the plane of a triangle ABC, let
Γ= circumcircle
DEF = medial triangle
(A) = circle that passes through E,F, and that intersects Γ in two antipodal points
A' = center of (A), and define B' and C' cyclically.
Then the triangles ABC and A'B'C' are homothetic, and their homothetic center is X(1593). (Angel Montesdeoca, February 14, 2023)
See X(1593) centro de homotecia
-
X(1650) = TRIPOLAR CENTROID OF X(525)
Barycentrics (-b^4 + c^4 + a^2 (b^2 - c^2))^2 (2 a^4 - (b^2 - c^2)^2 -
a^2 (b^2 + c^2)) : :
Let W be the circumconic with center X(1650). One of the asymptotes of W is the Euler line. The other is in the direction of X(9033). Also, X(9033) is the infinity point of the isotomic line of the Euler line. For a sketch, click X(9033). (Angel Montesdeoca, April 19, 2016)
-
X(2052) = ISOGONAL CONJUGATE OF X(577)
Barycentrics sec²A : :
Let A'B'C' be the orthic triangle of a triangle ABC, and let
O(A) = circle with center A and radius AA', and define O(B) and O(C) cyclically
p(A) = polar of X(4) wrt O(A), and define p(B) and p(C) cyclically
A'' = p(B)∩p(C), and define B'' and C'' cyclically.
Then A''B''C'' is homothetic to ABC, and the center of homothety is X(2052). (Angel Montesdeoca, September 30, 2016)
-
X(2163) = X(2)-ISOCONJUGATE OF X(45)
Let IaIbIc be the excentral triangle of a triangle ABC. Let A2 and A3 be the points where the perpendicular bisector of BC meets the internal angle bisector of angle ABC and the internal angle bisector of angle BCA, respectively. Let A'2 and A'3 be the points where the perpendicular bisector of BC meets the external angle bisector of angle ABC and the external angle bisector of angle BCA, respectively. Let Oab, Oac be the circumcenters of triangles IbA2A'3, IcA3A'2, respectively. Define Obc, Oba, Oca, Ocb cyclically. Then the triangle having sidelines OabOac, ObcOba, OcaOcb is perspective to ABC, and the perspector is X(2163). See Angel Montesdeoca, HG090218: El centro del triángulo X(2163).
-
-
X(2185) = X(2)-ISOCONJUGATE OF X(181)
Barycentrics a (a + b)^2 (a - b - c) (a + c)^2 : :
Let DEF be the cevian triangle of the incenter. Let OA be the circumcircle of AEF. Let T1 be the line tangent to OA at E, and let T2 be the line tangent to OA at F. Let AB = T1∩BC and AC = T2∩BC, and let A' be the radical center of the circumcircles of AEF, BFAB, CAAC.. Define B' and C' cyclically. The lines AA', BB', CC' concur in X(2185). (Angel Montesdeoca, January 4, 2021)
See Una construcción del X(2185)
X(2217) = X(2)-ISOCONJUGATE OF X(573)
Contribution by Angel Montesdeoca, September 10, 2017:
In the plane of a triangle ABC, let
O = X(3) = circumcenter
U(O,q) = circle with center O and radius q
A'B'C' = excentral triangle
A*B*C* = polar triangle of A'B'C' with respect to U(O,q).
There exists a unique q such that the lines AA*, BB*, CC* concur, and the point of concurrence is X(2217).
Moreover, the radius and a barycentric equation for U(O,q) are given as follows:
q^2 = R(r+R) = (a b c (2 a b c+(a+b-c) (a-b+c)(-a+b+c)))/(2 (a+b-c) (a-b+c) (-a+b+c) (a+b+c));
abc(x^2+y^2+z^2) + 2a (a+b) (a+c)y z + 2b(b+c)(b+a)z x + 2c(c+a)(c+b)x y = 0.
(Hechos Geométricos en el Triángulo (2017) )
-
X(2222) = X(2)-ISOCONJUGATE OF X(654)
Let A'B'C' be the excentral triangle in the plane of a triangle ABC. Let
A'' = X(110)-of-A'BC, and define B'' and C'' cyclically
(Oa) = circle with diameter AA'', and define (Ob) and (Oc) cyclically
The circles (Oa), (Ob), (Oc), and the circumcircle concur in X(2222). (Angel Montesdeoca, September 12, 2016)
(Hechos Geométricos en el Triángulo (2016) )
-
X(2292) = X(2)-ISOCONJUGATE OF X(1169)
Let FaFbFc be the Fuhrmann triangle, and AbBcCa and AcBaCb be the 1st and 2nd Montesdeoca bisector triangles. X(2292) is the radical center of the circumcircles of FaAbAc, FbBcBa, FcCaCb. (Randy Hutson, December 2, 2017)
-
X(2334) = X(2)-ISOCONJUGATE OF X(1449)
Barycentrics a^2/(3a + b + c) : b^2/(3b + c + a) : c^2/(3c + a + b)
Let A'B'C' = circumcevian triangle of X(1), and let
Oa = center of A-mixtilinear incircle
Ta = touchpoint of A-mixtilinear incircle and circumcircle
A1 = circumcenter of A'OaTa, and define B1 and C1 cyclically.
Then AA1, BB1, CC1 concur in X(2334).
(Angel Montesdeoca, November 29, 2018)
El centro del triángulo X(2334)
Let DEF be the cevian triangle of X(8), and let A5 is the QA-P5 center (Isotomic Center) of AEFX(8) (see Chris van Tienhoven, Quadrangle points and other objects). Let B5 be the QA-P5 center of BFDX(8) and C5 the QA-P5 center of CDEX(8). Then the triangles ABC and A5B5C5 are perspective, and X(2334) is their perspector. (Angel Montesdeoca, March 20, 2019).
El centro del triángulo X(2334), otra propiedad
In the plane of a triangle ABFC, let
DEF = cevian triangle of X(1);
Γ = circumcircle;
Aa = pole of EF wrt Γ
T1 and T2 = lines through Aa tangent to BC;
Ab and Ac = T1∩BC and T2∩BC;
Define Bc and Ca cyclically, and define Ba and Cb cyclically.
The six points Ab, Ac, Bc, Ba, Ca, Cb lie on a conic, 𝒞, given by the barycentric equation
b^2 c^2x^2+a^2 c^2y^2+a^2 b^2z^2+a^2 (a^2+b^2+c^2+2 a (b+c))yz+b^2 (a^2+2 a b+(b+c)^2)zx+c^2 (a^2+2 a c+(b+c)^2)xy= 0.
The polars of Aa, Bb, Cc with respect to 𝒞 form a perspective triangle to ABC, and the perspector is X(2334). (Angel Montesdeoca, November 27, 2022)
Triángulos con perspectriz el eje de Lemoine
-
X(2646) = SUM OF PU(80)
Barycentrics a (a - b - c) (2 a^2 - (b - c)^2 + a (b + c)) : :
In the place of a triangle ABC, let I = X(1) = incenter, and let
A'B'C' = intouch triangle;
Ma = midpoint of segment AI;
La = MaA', and define Lb and Lc cyclically;
Ra = reflection of La in AI, and define Bb and Rc cyclically.
The lines Ra, Rb, Rc concur in X(2646). (Angel Montesdeoca, October 9, 2021)
See Antreas Hatzipolakis and Angel Montesdeoca, Euclid 2662.
-
X(2883) = COMPLEMENTARY CONJUGATE OF X(4)
Barycentrics (3a^4 - 2a^2(b^2 + c^2) - (b^2 - c^2)^2)*(a^4(b^2 + c^2) - 2a^2(b^2 - c^2)^2 + (b^2 - c^2)^2(b^2 + c^2)) : :
In the plane of a triangle ABC, let
H = X(4);
L = X(20);
Ab = AL∩BH;
Ac = AL∩CH;
U = line through Ab parallel to AC;
V = line through Ac parallel to AB;
A1 = U∩V;
A2 = U∩BC;
A3 = V∩BC;
O = circle {{A1, A2, A3}};
A' = pole of BC wrt O, and define B' and C' cyclically.
Then A'B'C' = reflection of ABC in X(2883). (Angel Montesdeoca, July 30, 2021)
El complemento del conjugado isogonal del punto de De Longchamps.
-
X(2904) = ORTHIC-ISOGONAL CONJUGATE OF X(24)
Let O be the circumcircle of a triangle ABC. Let
A' = perpendicular bisector of segment OA, and define B' and C' cyclically
A'' = B'∩C', and define B'' and C'' cyclically
A* = reflection of A* in BC, and define B* and C* cyclically.
Then A*B*C* is perspective to the orthic triangle of ABC, and the perspector is X(2904). (Angel Montesdeoca, November 12, 2016).
(Hechos Geométricos en el Triángulo (2016) )
Let P be an arbitrary point of the circumcircle , O, and let S(P) be the Simson-Wallace line of P, and P' the reflection of P in S(P). The locus of P' as P ranges through O is a bicircular circumquartic that meets the sidelines of ABC in 6 points other than A, B, C. The 6 points lie on a conic, here called the Montesdeoca conic, M. The center of M is X(2904), and the perspector of M is X(14111). Let u = SA, v = SB, w = SC, f(a,b,c) = u2(S2 - v2)(S2 - w2), g(a,b,c) = 2vw(u2 - S2)(S2 + vw). A barycentric equation for M is
f(a,b,c)x2 + f(b,c,a)y2 + (f,c,a,b)z2 + g(a,b,c)yz + g(b,c,a)zx + g(c,b,a)xy = 0.
See HG121017 and X(2904).
-
X(2963) = BARYCENTRIC PRODUCT X(17)*X(18)
Barycentrics 1/(a^4 + b^4 + c^4 - 2 a^2 b^2 - 2 a^2 c^2 - b^2 c^2) : :
Let Q be the pedal curve (a limaçon of Pascal) of the circle with center X(7728) and radius |OH|, with respect to X(265). Let A'B'C' be the triangle formed by the tangents at A,B,C to Q. Then the triangles ABC and A'B'C' are perspective, and their perspector is X(2963). Moreover, X(21975) is the only finite fixed point of the affine transformation that maps a triangle ABC onto A'B'C'. See X(21975). (Angel Montesdeoca, September 10, 2019). See HG080919.
-
X(3052) = INTERSECTION X(31)X(42)∩X(32)X(220)
Barycentrics a^2(3a - b - c) : :
Let A'B'C' be the tangential triangle of ABC, and let L be the line through X(1) parallel to BC. Let A'' = L∩B'C', and define B'' and C'' cyclically. Let A* = B'B''∩C'C'', and define B* and C* cyclically. The lines AA*, BB*, CC* concur in X(3445), and the lines A'A*, B'B*, C'C* concur in X(3052). (Angel Montesdeoca, April 29, 2016)
Hechos Geométricos en el Triángulo (2016). Los puntos X(3052) y X(3445) como centros de perspectividad.
-
X(3345) = ISOGONAL CONJUGATE OF X(1490)
Barycentrics a (a^12-6 a^10 (b-c)^2+(b-c)^8 (b+c)^4+5 a^8 (b-c)^2 (3 b^2+2 b c+3 c^2)+3 a^4 (b-c)^2 (b+c)^4 (5 b^2-2 b c+5 c^2)-2 a^2 (b-c)^2 (b+c)^4 (3 b^4-4 b^3 c+10 b^2 c^2-4 b c^3+3 c^4)-4 a^6 (b-c)^2 (5 b^4+12 b^3 c+18 b^2 c^2+12 b c^3+5 c^4)) : :
Let ABC be a triangle with incenter I = X(1), De Longchamps point L = X(20), and Bevan point Be = X(40). Let DEF = cevian triangle of L. Let A' = ABe∩ID, and define B' and C' cyclically. The triangles ABC and A'B'C' are orthologic. The center of orthology of ABC with respect to A'B'C' is X(3345) and the center of orthology of A'B'C' with respect to ABC is X(9121). (Angel Montesdeoca, October 3, 2023 *)
-
X(3346) = ISOGONAL CONJUGATE OF X(1498)
Let M be a point on the slideline BC of triangle ABC. Let (AM) be the circle with diameter AM. Let Mb be the point, other than A, in (AM)∩AC, and let Mc be the point, other than A, in (AM)∩AB. Let Tb be the line tangent to (AM) at Mb, and let Tc be the line tangent to (AM) at Mc. As M varies on BC, the locus of Tb∩Tc is a line, La. Define Lb and Lc cyclically. Let A' = Lb∩Lc, and define B' and C' cyclically. The triangle A'B'C' is perspective to ABCF, and the perspector is X(3346). (Angel Montesdeoca, November 11, 2017)
See also ejtr2224 (10 de Junio del 2008).
Una propiedad del centro X(3346) (11 de noviembre del 2017)
-
X(3445) = X(56)-VERTEX CONJUGATE OF X(56)
Barycentrics a^2/(3a - b - c) : b^2/(3b - c - a) : c^2/(3c - a - b)
Let A'B'C' be the tangential triangle of ABC, and let L be the line through X(1) parallel to BC. Let A'' = L∩B'C', and define B'' and C'' cyclically. Let A* = B'B''∩C'C'', and define B* and C* cyclically. The lines AA*, BB*, CC* concur in X(3445); also, the lines A'A*, B'B*, C'C* concur in X(3052). (Angel Montesdeoca, April 29, 2016)
Hechos Geométricos en el Triángulo (2016). Los puntos X(3052) y X(3445) como centros de perspectividad.
-
X(3447) = X(523)-VERTEX CONJUGATE OF X(523)
Let E be the Euler line and TATBTC the tangential triangle of ABC. Let DA = E∩TBTC, and define DB and DC cyclically. Let A' = DBTB∩DCTC, and define B' and C' cyclically. Then A'B'C' is perspective to ABC, and the perspector is X(3447). For a sketch, click X(3447)andX(7669). (Angel Montesdeoca, April 22, 2016)
Hechos Geométricos en el Triángulo (2016). Una caracterización geométrica de X(3447).
-
X(3513) = 1st DILATION CENTER
Barycentrics a (a + b - c) (a - b + c) (a Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] - b Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] - c Sqrt[-a^2 - (b - c)^2 + 2 a (b + c)] - Sqrt[-a^4 - (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)]) : :
In the plane of a triangle ABC, let P be a point on the line X(1)X(3), and let DEF = intouch triangle. Let RA = reflection of AP in EF, and define RB and RC cyclically. The lines RA, RB, RC concur in a point, P', that lies on a rectangular hyperbola that circumscribes DEF. Let P'' = DEF-isogonal conjugate of P'. The mapping P -> P'' is a projective transformation of the line X(1)X(3), and its fixed points are X(3513) and X(3514). (Angel Montesdeoca, April 17, 2021).
Hechos Geométricos en el Triángulo (2021). Los centros X(3513) y X(3514) como puntos dobles de una proyectividad
-
X(3521) = ISOGONAL CONJUGATE OF X(3520)
Barycentrics a/(4 cos A + sec A) : :
Let Pa be the isotomic conjugate of X(1105) with respect to the triangle AX(3)X(4), and define Pb and Pc cyclically. Then PaPbPc and ABC are perspective at X(3521). (Angel Montesdeoca, September 23, 2018) HG220918
-
X(3532) = INTERSECTION OF LINES X(6,1204) AND X(64,1620)
Barycentrics a^2/(5 a^4 - 2 a^2 (b^2 + c^2)- 3 (b^2 - c^2)^2) : :
Let DEF be the cevian triangle of X(69) and A' the center of the circle that passes through D and through points where the line EF cuts to the circumcircle, and define B' and C' cyclically. The lines AA', BB', CC' concur in X(3532). (Angel Montesdeoca, October 30, 2019). Una propiedad del centro X(3532)
-
X(3627) = H-1(X(3); M,-1/2)
Barycentrics a2(b2 + c2 - 4a2) + 3(b2 - c2)2 : :
Let ABC be a triangle and Γa a variable circle passing through A and the midpoint of side BC. Let Ab and Ac be the points, other than A, in which the circle Γa meets AC and AB, respectively. Let A' be the vertex of parallelogram with vertices A, Ab, A', Ac. When Γa varies, the locus of A' is a line ℓa. Define ℓb and ℓc cyclically. The triangle formed by the lines ℓa, ℓb, ℓc is orthologic to ABC with orthology center X(3627) . The reciprocal orthologic center of these triangles is X(3). See X(3627). (Angel Montesdeoca, July 13, 2022)
See HG130722
-
X(3628) = H-1(X(5); M, 2)
X(3628) is the centroid of the set {A', B', C', X(5)}, where A'B'C' is the medial triangle; more generally, H-1(X; M, 2) is the centroid of the set {A', B', C', X}. (Angel Montesdeoca, 12/20/2011)
(Encyclopedia of Triangle Centers )
-
X(3683) = X(3219)com(EXTOUCH TRIANGLE)
Barycentrics a(-a + b + c)(2a + b + c)
In the plane of a triangle ABC, let
A'B'C' = circumcevian triangle of X(1);
DEF = cevian triangle of X(10);
La = line tfhrough D perpendicular to BC;
A'' = La∩AA', and define B'' and C'' cyclically.
Then X(36;83) is the finite fixed point of the affine transformation that carries A'B'C' onto A''B''C'. (Angel Montesdeoca, November 21, 2022)
X(3683) punto fijo de una transformación afín (21/11/2022)
-
X(3817) = X(2)com(3rd EULER TRIANGLE)
Let A'B'C' be the circumcevian triangle of X(1). Let L1 be the Simson line of A', and define L2 and L3 cyclically. Let A'' = L2∩L3, and define B'' and C'' cyclically. Then X(3817) = X(2)-of-A''B''C''. (Angel Montesdeoca, June 28, 1017)
(Encyclopedia of Triangle Centers )
-
X(4012) = X(269)com(EXTOUCH TRIANGLE)
Barycentrics (b + c - a)3(a2 + b2 + c2 - 2bc) : :
Let DEF be the extouch triangle of ABC. Let Ha be the hyperbola with foci E and F, passing through A, and define Hb and Hc cyclically. These three hyperbolas have two common points, U and V. Let Pa be the pole of the line UV with respect to Ha, and define Pb and Pc cyclically. Then DEF and PaPBPc are perspective at X(4012). (Angel Montesdeoca, September 23, 2018) HG150918
-
X(4292) = INTERSECTION OF LINES X(1)X(7) AND X(4)X(57)
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = b4 + c4 - 2a4 -
a3b - a3c + a2b2 +
a2c2 - 2a2bc + ab3 +
ac3 - ab2c - abc2 -
2b2c2
A construction of X(4292) is given by Antreas Hatipolakis and Angel Montesdeoca at Hyacinthos 24046 (Aug 16, 2016).
[APH]:
Let ABC be a triangle and A'B'C' the pedal triangle of I.
Denote:
A"B"C" = the pedal triangle of the orthocenter H' of A'B'C' wrt the triangle A'B'C'
(ie A"BC" = the orthic triangle of A'B'C')
Ab, Ac = the orthogonal projections of A" on AC, AB, resp.
(Nab), (Nac) = the NPCs of AbA"B', AcA"C', resp.
(Nbc), (Nba) = the NPCs of BcB"C', BaB"A', resp.
(Nca), (Ncb) = the NPCs of CaC"A', CbC"B', resp.
S1 = the radical axis of (Nba), (Nca).
S2 = the radical axis of (Ncb), (Nab)
S3 = the radical axis of (Nac), (Nbc)
1. S1, S2, S3 are concurrent.
2. the parallels to S1, S2, S3 through A, B, C, resp. are concurrent at H.
3. the parallels to S1, S2, S3 through A', B', C', resp. are concurrent at I.
4. the parallels to S1, S2, S3 through A",B",C", resp. are concurrent.
This is equivalent to:
The triangles ABC and the orthic triangle of the pedal triangle of I are orthologic.
[Angel Montesdeoca]:
1. S1, S2, S3 are concurrent at X(354)
4. the parallels to S1, S2, S3 through A",B",C", resp. are concurrent at X(4292)
-
X(4319) = INTERSECTION OF LINES X(1)X(7) AND X(19)X(25)
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a(b + c -a)2(a2 + b2 + c2 - 2bc)
X(4319) is the point of concurrence of three lines associated with Soddy hyperbolas; see Angel Montesdeoca's construction at Hyacinthos 21290 (Nov 12, 2012)
(Paul Yiu, Introduction to the Geometry of the Triangle, 2002; 12.4 The Soddy hyperbolas, p. 143)
Given triangle ABC, consider the hyperbola passing through A, and with foci at B and C. We shall call this the A-Soddy hyperbola of the triangle.
The equation of A-Soddy hyperbola is
(Fa): (c+a-b)(a+b-c)(y^2+z^2)-2(a^2+(b-c)^2)y z+4(b-c)c x y -4b(b-c)z x=0.
The perspector of a (Fa): Pa = ( SB SC : - b c SC : -b c SB ).
The polar of Pa with respect to (Fa) is is the line "da":
2b(b-c)cx + (a^2+(b-c)^2)cy - b(a^2+(b-c)^2)z=0.
Similarly define the lines "db" and "dc"; then the lines da, db and dc are concurrent at the triangle center X(4319).
-
X(4350) = INTERSECTION OF LINES X(1)X(7) AND X(41)X(57)
Barycentrics a(a^2 + b^2 + c^2 - 2a b - 2a c)/(b + c - a)^2 ::
In the plane of a triangle ABC, let
I = X(1) = incenter;
DEF = intouch triangle;
(O) = circumcircle;
A' = the point, other than A, where the circle {{A,I,D}} meets (O), and define B' and C' cyclically;
Oa = center of the circle {{B',E,F,C'}}, and define Ob and Oc cyclically;
Oaa = A-extraversion of Oa, and define Obb and Occ cyclically;
T = affine transfomation that maps ABC onto OaObOc;
TT = affine transformation that maps ABC onto OaaObbOcc.
Then X(4350) = finite fixed point of T, and X(5250) = finite fixed point of TT. (Angel Montesdeoca, December 29, 2023)
See HG261223
-
X(4432) = X(44)com[T(a,c)]
Barycentrics (b + c - 2a)(a2 - bc) : :
X(4432) is the intersection of the orthic axes of the 1st & 2nd Montesdeoca bisector triangles. (Randy Hutson, December 2, 2017)
-
X(4674) = X(3952)com[T(-a, a + c)]
Barycentrics a(b + c)(b + c - 2a) : :
Let A'B'C' be the cevian triangle, and let A"B"C" be the circumcevian triangle of X(1). The four points of intersection of the circumcircles of BA'I, CA'I with the side lines A"C", A"B", respectively, lie on a circle Oa; define Ob and Oc cyclically. Then the triangles ABC and OaObOc are orthologic, with orthology centers the X(3) and X(4674). (Angel Montesdeoca, April 14, 2019).
HG130519
-
X(4846) = ISOGONAL CONJUGATE OF X(378)
Barycentrics (b2 + c2 - a2)/(a4 + b4 + c4 - 2a2b2 - 2a2c2 + 4b2c2) : :
X(4846) is the Segovia point of the circumcevian triangle of the circumcenter. (Antreas Hatzipolakis, January 23 2012; Hyacinthos #20737; see Segovia Point, continued.)
Let A'B'C' be the translation of ABC by the vector X(4)X(3). Let MA be the midpoint of the (possibly nonreal) points in which the circumcircle of ABC meets the line B'C', and define MB and MC cyclically. The triangle MAMBMC is perspective to ABC, and the perspector is X(4846). If you have GeoGebra, you can view X(4846). (Angel Montesdeoca, May 20, 2018)
-
X(4882) = X(1058)com[INVERSE(nT(a, c - a)]
Barycentrics a(b + c - a)(b^2 + c^2 - a^2 + 6b c) :
Consider any triangle ABC. Let A-excircle ωA of ABC is tangent to BC at A'. Similarly define ωB, ωC, B', C'. Consider two tangent lines ℓa, ℓa' from A' to ωB, ωC which are different from BC. Similarly define ℓb, ℓb', ℓc, ℓc'. Then ℓa, ℓa', ℓb, ℓb', ℓc, ℓc' form a hexagon which has an incircle.
The center of the incircle of the hexagon is X(4882). (Angel Montesdeoca, October 2, 2018). HG021018
-
X(5000) = WALSMITH POINT
Barycentrics 2 (a^6-a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)-a^2 (b^4-3 b^2 c^2+c^4)) (-2 a^4+2 a^2 b^2-b^4+2 a^2 c^2+2 b^2 c^2-c^4+(b^2-c^2)^2-((2 a^4-(b^2-c^2)^2-a^2 (b^2+c^2)) (-a^6+a^4 b^2+a^2 b^4-b^6+a^4 c^2-6 a^2 b^2 c^2+b^4 c^2+a^2 c^4+b^2 c^4-c^6+Sqrt[(a^2-b^2-c^2) (a^2+b^2-c^2) (a^2-b^2+c^2) (a^2+b^2+c^2) (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))]))/(2 (a^6-a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)-a^2 (b^4-3 b^2 c^2+c^4)))) : :
In the plane of a triangle ABC, let P be a point on the Euler line and P' = isogonal conjugate of P, and let DEF = medial triangle. Let ℓa = reflection of AP' in EF, and define ℓb and ℓc cyclically. The lines ℓa, ℓb, ℓc concur in a point, P", that lies on the Euler line. The mapping P ↦ P'' is a projective transformation of the Euler line, and its fixed points are X(5000) and X(5001).
If P=X(3) + t X(4), then P"= 4 t SA SB SC X(3) + (a^2 b^2 c^2 + 4 t SA SB SC) X(4).
The fixed points are obtained for t = (2 SA SB SC ± S Sqrt[2 (a^2+b^2+c^2) SA SB SC])/(4 SA SB SC). (Angel Montesdeoca, April 19, 2021)
Proyectividad sobre la recta de Euler y los centros X(5000) y X(5001)
-
X(5024) = INVERSE-IN-1st-BROCARD-CIRCLE OF X(1384)
Let A'B'C' be the circumcevian triangle of the symmedian point (Lemoine point), X(6). The sidelines BC, CA, AB meet the sidelines of B'C', C'A', A'B' in 9 points, of which 6 do not lie on the trilinear polar of K; barycentrics for the 6 points are 0 : b2 : 2c2, 0 : 2b2 : c2, 2a2 : 0 : c2, a2 : 0 : 2c2, a2 : 2b2 : 0, 2a2 : b2 : 0. The 6 points lie on a conic with center X(5024) and equation
2(b4c4x2 + c4a4y2 + a4b4z2) -5a2b2c2(a2yz + b2zx + c2xy) = 0.
Moreover, the center of the conic tangent to the 6 lines BC, CA, AB, B'C', C'A', A'B' is X(39), and an equation for this conic is
b4c4x2 + c4a4y2 + a4b4z2 -2a2b2c2(a2yz + b2zx + c2xy) = 0.
(From Angel Montesdeoca, March 28, 2013)
(Encyclopedia of Triangle Centers )
-
X(5048) = INVERSE-IN-INCIRCLE OF X(3057)
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a(b + c - a)(3b2 + 3c2 - 2a2 + ab + ac - 6bc)
X(5048) = (R - 3r)*X(1) + r*X(3)
Let I be the incenter of a triangle ABC, let NA be the nine-point circle of the triangle IBC, and define NB and NC cyclically. Let RA be the reflection of NA in the line AI, and define RB and RC cyclically. Then X(5048) is the radical center of the circles RA, RB, RC. (Angel Montesdeoca, Hyacinthos #22502, July 7, 2014.)
X(5048) lies on these lines:
{1, 3}, {8, 1392}, {11, 519}, {33, 1878}, {78, 3893}, {145, 1837}, {210, 3872}, {495, 4870}, {497, 3241}, {513, 4162}, {515, 1317}, {535, 3058}, {950, 3635}, {960, 4861}, {1318, 1320}, {1387, 1737}, {1391, 1870}, {1478, 3656}, {1836, 3476}, {2170, 2348}, {2269, 3723}, {3021, 3328}, {3318, 3319}, {3486, 3623}, {3655, 4302}, {3683, 3877}, {3693, 4919}, {3711, 4915}
(Encyclopedia of Triangle Centers )
-
X(5173) = INVERSE-IN-INCIRCLE OF X(2078)
Barycentrics a(a + b - c)(a - b + c)(a2b + a2c - 2ab2 - 2ac2 - 2abc + b3 - b2c - bc2 + c3) : :
Let AaBaCa be the intouch triangle, so that the lines BI and CI intersect BbCc at Ba and Ca, respectively. Let A1A2A3 be the intouch triangle of AaBaCa. Define B1B2B3 and C1C2C3 cyclically. Let da be the radical axis of (A1B3C2) and (A1A2A3). Let ea be the radical axis of (A1B3C2) and (AaBbCc). Define db, dc and eb, ec cyclically. Then the triangles A'B'C' and A"B"C" formed by the lines da, db, dc and the lines ea, eb, ec, respectively, are homothetic and the homothetic center is X(5173).
(Angel Montesdeoca, April 1, 2020)
See X(1000) como centro de perspectividad.
-
X(5250) = INTERSECTION OF LINES X(1)X(21) AND X(2)X(40)
Barycentrics a(b + c - a)(a^2 + b^2 + c^2 + 2a b + 2a c) : :
In the plane of a triangle ABC, let
I = X(1) = incenter;
DEF = intouch triangle;
(O) = circumcircle;
A' = the point, other than A, where the circle {{A,I,D}} meets (O), and define B' and C' cyclically;
Oa = center of the circle {{B',E,F,C'}}, and define Ob and Oc cyclically;
Oaa = A-extraversion of Oa, and define Obb and Occ cyclically;
T = affine transfomation that maps ABC onto OaObOc;
TT = affine transformation that maps ABC onto OaaObbOcc.
Then X(4350) = finite fixed point of T, and X(5250) = finite fixed point of TT. (Angel Montesdeoca, December 29, 2023)
See HG261223
-
X(5450) = 3rd HATZIPOLAKIS-MOSES POINT
Barycentrics a (a^6-2 a^4 (b-c)^2-a^5 (b+c)-b c (b^2-c^2)^2+a^2 (b-c)^2 (b^2-b c+c^2)-a (b-c)^2 (b^3+c^3)+a^3 (2 b^3-b^2 c-b c^2+2 c^3)),b (-a^5 (b+c)+b (b-c)^3 (b+c)^2+a^4 b (b+2 c)-a^2 b (2 b^3+b^2 c-4 b c^2+c^3)+a^3 (2 b^3-3 b^2 c-b c^2+2 c^3)-a (b^5-4 b^4 c+b^3 c^2+3 b^2 c^3-2 b c^4+c^5)) : :
Let M be the isogonal conjugate of the trilinear polar of X(57) with respect to the circumcevian triangle of X(1). Then M is a conic, and its center is X(5450). (Angel Montesdeoca, August 9, 2019)
-
X(5466) = TRILINEAR POLE OF LINE X(115)X(523)
Barycentrics b2 - c2)/(b2 +
c2 - 2a2 : :
In the plane of a triangle ABC, let
Γ= circumcircle;
D = line tangent to Γ at A;
Ta = D∩BC;
Oab = center of the circle through Ta that is tangent to Γ at B;
Oac = center of the circle through Ta that is tangent to Γ at C;
Ab = orthogonal projection of Oab onto AC;
Ac = orthogonal projection of Oac onto AB;
A' = AbAc∩BC, and define B' and C' cyclically.
The lines AA', BB', CC' concur in X(5466). See X(5466) (Angel Montesdeoca, August 21, 2022)
See Angel Montesdeoca, HG180822.
-
X(5482) = 1st HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a5b2 + a5c2 - 2a5b2c2 + a3b3 + a3c3 + a3b2c + a3bc2 + a2b4 + a2c4 - 3a2b3c - 3a2bc3 - ab5 - ac5 - ab4c - abc4 - bc(b2 - c2)2 (Angel Montesdeoca, May 13, 2013)
X(5482) = 3*X(549) - X(970)
X(5482) = (R - 2r)*X(140) - R*X(143)
Let ABC be a triangle and let A'B'C' be the cevian triangle of the incenter, X(1). Let R be the radical center of the circles (A', |A'B|, {B',|B'C|), (C', |C'A|), and let S be the radical center of the circles (A',|A'C|), (B',|B'A|), (C',|C'B|). X(5482) is the midpoint of the segment RS. (Antreas Hatzipolakis, May 4, 2013)
X(5482) is the {X(3),X(1764)}-harmonic conjugate of X(3579) (Peter Moses, May 13, 2013)
For the construction and generalizations, see Hechos Geométricos en el Triángulo.
X(5482) lies on these lines: {1,3}, {140,143}, {549,970}
(Encyclopedia of Triangle Centers )
-
X(5494) = 2nd HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a[a9 - a8(b + c) - a7( b - c)2 + a6(2b3 - b2c - bc2 + 2c3) - a5(3b4 + b3c - 7b2c2 + bc3 + 3c4) + 4a4bc(b - c)2(b + c) + a3(b2 - c2)2(5b2 - 4bc + 5c2) - a2(b - c)2(2b5 + 5b4c + b3c2 + b2c3 + 5bc4 + 2c5) - a(b2 - c2)2(2b4 - 3b3c + 5b2c2 - 3bc3 + 2c4) + (b - c)4(b + c)3(b2 + c2)] (Angel Montesdeoca, May 25, 2013)
X(5494) = (2r + R)*X(110) - 4(r + R)X(1385)
X(5494) = 2R*X(65) + (2r + R)*X(74)
Let ABC be a triangle and let A'B'C' be the cevian triangle of the incenter, X(1). Let AB be the reflection of A' in line BB', and define BC and CA cyclically. Let AC be the reflection of A' in line CC', and define BA and CB cyclically. Let L be the Euler line of ABC, let LA be the Euler line of AABAC, and define LB and LC cyclically. Let MA be the reflection of LA in AA', and define MB and MC cyclically. The lines MA, MB, MC concur in X(5494). Moreover, the four Euler lines L, LA, LB, LC are parallel, concurring in X(30). (Antreas Hatzipolakis, May 25, 2013)
For the construction and discussion, see Hechos Geométricos en el Triángulo.
X(5494) lies on these lines: {1,2779},{21,104},{36,1725},{65,74},{125,860}
(Encyclopedia of Triangle Centers )
-
X(5495) = 3rd HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a2[a7(b + c) - a6(b2 + c2) - a5(3b3 + 2b2c + 2bc2 + 3c3) + a4(3b4 - b3c + 4b2c2 - bc3 + 3c4) + a3(3b5 + b4c + 2b3c2 + 2b2c3 + bc4 + 3c5) - a2(3b6 - 2b5c - 2bc5 + 3c6) - a(b7 - b4c3 - b3c4 + c7) + (b2 - c2)2(b4 - b3c - bc3 - b2c2 + c4)] (Angel Montesdeoca, May 28, 2013)
Let ABC be a triangle and let A'B'C' be the cevian triangle of the incenter, X(1). Let LA be the line through A' perpendicular to line AA', and define LB add LC cyclically. Let
UA = reflection of LA in AA'
UB = reflection of LA in BB'
UC = reflection of LA in CC'
VA = reflection of LB in AA'
VB = reflection of LB in BB'
VC = reflection of LB in CC'
WA = reflection of LC in AA'
WB = reflection of LC in BB'
WC = reflection of LC in CC'
TA = triangle formed by the lines in UA, UB, UC
TB = triangle formed by the lines in VA, VB, VC
TC = triangle formed by the lines in WA, WB, WC
OA = circumcenter of TA, OB = circumcenter of TA, OC = circumcenter of TA, O = X(3) = circumcenter of ABC. The points O, OA, OB, OC are concyclic. The center of their circle is X(5495). (Antreas Hatzipolakis, May 28, 2013)
For the construction and discussion, see Concyclic Circumcenters.
X(5495) lies on these lines: (pending)
(Encyclopedia of Triangle Centers )
-
X(5496) = 4th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a(b + c)[a5 - 2a3(b2 + c2) - a2bc(b+c) + a(b4 - b2c2 + c4) + bc(b + c)(b - c)2 (Angel Montesdeoca, May 29, 2013)
Let ABC be a triangle and let A'B'C' be the cevian triangle of the incenter, X(1). Let LA be the line through A' perpendicular to line AA', and define LB add LC cyclically. Using the notation at X(5495), let MA be the line parallel to UA through B', and define MB and MC cyclically. Let A'' = MB∩MC, and define B'' and C'' cyclically. Let OA = circumcenter of A''B'C', and define OB and OC cyclically. Then the points X(1), OA, OB, OC are concyclic, and the center of their circle is X(5496). (Antreas Hatzipolakis, May 29, 2013)
For a discussion, see Concurrent Circles.
X(5496) lies on these lines: (pending)
(Encyclopedia of Triangle Centers )
-
X(5497) = 5th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a7 - a6(b + c) - a5(b + c)2 + a4(2b3 + b2c + bc2 + 2c3) - a2(b4 - b3c - 3b2c2 - bc3 + c4) + abc(b2 + c2)(b2 - c2)2 (Angel Montesdeoca, May 29, 2013)
Let ABC be a triangle and let A'B'C' be the cevian triangle of the incenter, X(1). The circles OA, OB, OC defined at X(5496) concur in X(5497). (Antreas Hatzipolakis, May 29, 2013)
For a discussion, see Hechos Geométricos en el Triángulo.
X(5497) lies on these lines: (pending)
(Encyclopedia of Triangle Centers )
-
X(5498) = 6th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = 2a10 - 5a8(b2 + c2) + 2a6(b4 + 5b2c2 + c4) + a4(4b6 - 5b4c2 - 5b2c4 + 4c6) - a2(b2 - c2)2(4b4 + 5b2c2 + 4c4) + (b2 - c2)sup>4(b2 + c2)
(Angel Montesdeoca, May 30, 2013)
Let ABC be a triangle, let NA be the nine-point center of the triangle BCO, where O = X(3), and define NB and NC cyclically. The nine-point center of the triangle NANBNC is X(5498), which lies on the Euler line of ABC. (Antreas Hatzipolakis, May 30, 2013)
X(5498) lies on these lines: (2,3}, (more pending)
(Encyclopedia of Triangle Centers )
-
X(5499) = 7th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a5(b2 + 4bc + c2) - a4(b3 + b2c - bc2 + c3) + a3(2b4 + 3b3c + 3bc3 + 2c4) + 2a2(b5 - b3c2 - b2c3 + c5) + a(b2 - c2)2(b2 - bc + c2) - (b - c)4(b + c)3 (Angel Montesdeoca, May 30, 2013)
Let IA be the A-excenter of a triangle ABC and let NA be the nine-point center of IABC. Define NB and NC cyclically. The circumcenter of NANBNC is X(5499), which lies on the Euler line of ABC. (Antreas Hatzipolakis, May 30, 2013)
X(5499) lies on these lines: (2,3}, (more pending)
(Encyclopedia of Triangle Centers )
-
X(5500) = 8th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) =
2a22
- 15a20(b2 + c2)
+ 6a18(8b4 + 13b2c2 + 8c4)
- a16(81b6 + 52b4c2 + 152b2c4 + 81c6)
+ a14(64b8 + 111b6c2 + 128b4c4 + 111b2c6 + 64c8)
+ a12(14b10 + 29b8c2 + 36b6c4 + 36b4c6 + 29b2c8 + 14c10)
- a10(84b^12 + 67b10c2 + 56b8c4 + 48b6c6 + 56b4c8 + 67b2c10 + 84c12)
+ a8(82b14 - 23b12c2 - 31b10c4 - 19b8c6 - 19b6c8 - 31b4c10 - 23b2c12+ 82c14)
- a6(b2 - c2)2(34b12 + 11b10c2 - 30b8c4 - 35b6c6 - 30b4c8 + 11b2c10 + 34c12)
+ a4(b2- c2)4(b10 - 2b8c2 - 22b6c4 - 22b4c6 - 2b2c8+ c10)
+ a2(b2 - c2)6(4b8 + 5b6c2 + 8b4c4 + 5b2c6 + 4c8)
- (b2 - c2)8(b6 + b4c2 + b2c4 + c6) (Angel Montesdeoca, May 30, 2013)
Let A'B'C' be the antipedal triangle of the nine-point center, N = X(5) of a triangle ABC. Let NA be the nine-point center of NB'C', and define NB and NC cyclically. The nine-point center of NANBNC is X(5500), which lies on the Euler line of ABC. (Antreas Hatzipolakis, May 30, 2013)
X(5500) lies on these lines: (2,3}, (more pending)
(Encyclopedia of Triangle Centers )
-
X(5501) = 9th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) =
-2a^16+ 9a^14(b^2+c^2)-
a^10(b^6+b^4c^2+b^2c^4+c^6)+
a^8(25b^8+10b^6c^2+8b^4c^4+10b^2c^6+25c^8) +
a^6(-33b^10+31b^8c^2+11b^6c^4+11b^4c^6+31b^2c^8-33c^10)+
a^4(b^2-c^2)^2(21b^8-20b^6c^2-25b^4c^4-20b^2c^6+21c^8)-
a^2(b^2-c^2)^4(7b^6-13b^4c^2-13b^2c^4+7c^6)+
(b^2-c^2)^6(b^4-4b^2c^2+c^4)-a^12(13b^4+18b^2c^2+13c^4) (Angel Montesdeoca, June 2, 2013)
Let N be a the nine-point center of triangle ABC. Let NA be the nine-point center of NBC, and define NB and NC cyclically. The circumcenter of NANBNC is X(5501), which lies on the Euler line of ABC. (Antreas Hatzipolakis, June 2, 2013)
See For a discussion, see Hechos Geométricos en el Triángulo.
X(5501) lies on these lines: {2,3}, {137,8254}
(Encyclopedia of Triangle Centers )
(
Mostrar/Ocultar figura )
-
X(5502) = 10th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) =
a2(a2 - b2)[a2 - c2)(a6 - a4(b2 + c2) + a2(a2 -b2)(a2 - c2) + 3(b2 - c2)2(b2 + c2)] (Angel Montesdeoca, June 3, 2013)
Let L be the Euler line of a triangle ABC. Let LA be the reflection of L in line BC, and define LB and LC cyclically. Let A' = L∩BC, and define B' and C' cyclically. The circles whose diameters are the segments AA', BB', CC' are coaxial. Let D be their coaxial axis (the line X(4)X(74)); let DA be the reflection of D in line BC, and define DB and DC cyclically. Let HA = LB∩DC, and define HB and HC cyclically. Let MA = LC∩DB, and define MB and MC cyclically. The triangles HAHBHC and MAMBMC are perspective, and their perspector is X(5502). (Antreas Hatzipolakis, June 3, 2013)
See For a discussion, see Hechos Geométricos en el Triángulo.
X(5502) lies on these lines: {3,64}, {110, 351}
(Encyclopedia of Triangle Centers )
-
X(5540) = GIBERT-BUREK-MOSES CONCURRENT CIRCLES IMAGE OF X(101)
The 1st and 2nd Montesdeoca bisector triangles and inversely similar to the excentral triangle. Let s1 and s2 be the similarity mappings. Then there is a unique point X such that s1(X) = s2(X), and X = X(5540). See HGT2017 and AdvGeom3769
-
X(5559) = GARCIA-FEUERBACH POINT GF(5/3)
Barycentrics 1/[(a + b + c)(b + c - a) - (b2 + c2 - a2)(5/3)] : :
Let Pa be the isotomic conjugate of X(1222) with respect to AX1)X(8), and define Pb and Pc cyclically. Then ABC and PaPbPc are perspective at X(5559). (Angel Montesdeoca, September 23, 2018). See HG220918
-
X(5618) = 1st MONTESDEOCA EQUILATERAL TRIANGLES POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = 1/[(b2 - c2)(271/2b2c2SA + S(S2 + 9SASA)
Let AP, BP, CP be the cevians of a point P in the plane of a triangle ABC. Let AB be a point on BP and AC a point on CP such that the triangle AABAC is equilateral. The lines ABAC, BCBA, CBCA concur in X(5618). Moreover, the centers of the three equilateral triangles are collinear with P; denote their line by L(P). If P is on the circumcircle of ABC, then L(P) passes through X(110). (Angel Montesdeoca, November 3, 2013)
For the construction and generalizations, see Hechos Geométricos en el Triángulo.
X(5618) lies on the circumcircle and these lines: {13,74}, {115,2378}, {1989,2380}
(Encyclopedia of Triangle Centers )
-
X(5619) = 2nd MONTESDEOCA EQUILATERAL TRIANGLES POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = = 1/[(b2 - c2)(271/2b2c2SA - S(S2 + 9SASA)
The negative Montesdeoca equilateral triangles for a point P are constructed as follows: in the construction of the positive Montesdeoca equilateral triangles atX(5618), replace the rotation angles (30, -60, -60) by (-30, 60, 60). Barycentrics for X(5619) are obtained from those of X(5618) by replacing S by - S. (Peter Moses, November 8, 2013)
If you have The Geometer's Sketchpad, you can view Montesdeoca Equilateral Triangles.
X(5619) lies on the circumcircle and these lines: {14,74}, {115,2379}, {1989,2381}
(Encyclopedia of Triangle Centers )
-
X(5620) = ISOGONAL CONJUGATE OF X(5127)
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = (b + c)[a6 - a4(b2 + c2) - a2(b4 + c4 - 3b2c2) - 2abc(b + c)(b - c)2 + (b + c)2(b - c)4]
X(5620) = R*X(65) - (2r + R)*X(1365)
Let A'B'C' be the excentral triangle of ABC. Let NA be the nine-point center of A'BC, and let OA be the circumcircle of NABC. Define OB and OC cyclically. The circles OA, OB, OC concur in X(5620). (Angel Montesdoca, Anapolis #1120, November 2013: see Concurrent Circumcircles)
X(5620) lies on these lines:
{1,149},{10,1109},{36,759},{37,115},{65,1365},{162,1838},{267,3336},{897,1738},{1054,1247},{1737,2166},{2218,2915}
X(5620) = isogonal conjugate of X(5127)
(Encyclopedia of Triangle Centers )
-
X(5627) = YIU REFLECTION POINT
Barycentrics g(a,b,c) : g(b,c,a): g(c,a,b), where g(a,b,c)
= 1/[(a2SA -
2SBSC)(S2 -
3SASA)]
Let P = X(110) and A1A2, B1B2, C1C2 be the diameters of the circumcircle of ABC, parallel to AP, BP, CP, respectively. The Simson-Wallace lines of the points A1 and A2 intersect orthogonally in Pa, on the nine-point circle. The points Pb and Pc are defined similarly. The triangles ABC and PaPbPc are perspective and inversely similar; the perspector is X(5627). (Angel Montesdeoca, October 21, 2018)
HG201018
-
X(5643) = H(2) ON THE THOMSON-GIBERT-MOSES HYPERBOLA
Barycentrics f(A,B,C) : f(B,C,A) : f(C,A,B),
where f(A,B,C) = a2(13S2 +
7S2A + 2SBSC)
(Peter Moses, June 9, 2014)
X(5643) is the only point whose polar conic in the Napoleon
cubic (K005) is a circle. (Bernard Gibert, June 22,
2014)
Let A' be the centroid of the A-altimedial triangle, and define B'
and C' cyclically; then X(5643) is the center of similitude of ABC and
A'B'C'. (Randy Hutson, July 7, 2014)
X(5643) is the only finite fixed point of the affine transformation that maps a triangle ABC onto the pedal triangle of X(5). (Angel Montesdeoca, August 19, 2016).
-
X(5691) = DE LONGCHAMPS POINT OF OUTER GARCIA TRIANGLE
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = 3 a^4- a^3 (b + c) - a^2 (b - c)^2 + a (b - c)^2 (b + c) - 2 (b^2 - c^2)^2
(Angel Montesdeoca, January 21, 2015)
Let I = X(1) and O = X(3). Let A'' be the reflection of I in line AO and let IA be the reflection of A'' in line AI. Define IB and IC cyclically. Then ABC and IAIB IC are orthologic triangles, and X(5691) is the ABC-orthology center of IAIB IC. (Angel Montesdeoca, January 21, 2015)
-
X(5702) = CENTER OF MONTESDEOCA CONIC
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = SBSC(5a2SA - SBSC)
Let ABC be a triangle, let PA be the polar of A with respect to the circle with diameter BC, and define PB and PC cyclically. Let AB = PA∩AB and AC = PA∩AC, and define BC, CA, BA, and CB cyclically. The six points AB, AC, BC, BA, CA, CB lie on, and define, the Montesdeoca conic. (Angel Montesdeoca, June 23, 2014)
A barycentric equation for the Montesdeoca conic is found from AB = SC : 0 : 2SA and AC = SB : 2SA : 0 to be as follows:
2(S2Ax2 + S2By2 + S2Cz2) - 5(SBSCyz + SCSAzx + SASBxy) = 0 (Peter Moses, June 23, 2014)
The Montesdeoca conic is the anticevian-intersection conic when P = X(4); this conic is defined by Francisco J. Garcia Capitán ( The Anticevian Intersection Conic and Hyacinthos #20547 (December 19, 2011). Also, the perspector of the Montesdeoca conic is X(4).
X(5702) lies on these lines:
{4,6},{297,5032},{340,1992},{376,3284},{468,5304},{578,3183},{631,5158},{3163,3545}
(Encyclopedia of Triangle Centers )
-
X(5836) = INTERSECTION OF LINES X(5)X(10) AND X(7)X(8)
Barycentrics f(a,b,c) : f(b,c,a) :
f(c,a,b), where f(a,b,c) = a*(a^2*b - b^3 + a^2*c - 2*a*b*c + 3*b^2*c + 3*b*c^2 - c^3)
A construction of X(5836) is given by Antreas Hatipolakis and Angel Montesdeoca at Hyacinthos #24129. (Aug 23, 2016)
[APH]:
Let ABC be a triangle and A'B'C' the pedal triangle of I.
Denote:
A"B"C" = the orthic triangle of A'B'C'
Ab, Ac = the orthogonal projections of A on B'B", C'C", resp.
L1 = the Euler line of AAbAc. Similarly L2, L3
1. L1, L2, L3 are concurrent.
The parallels to L1, L2, L3 through:
2.1. A, B, C, resp.
2.2. A', B',C', resp.
2.3. A",B", C", resp.
are concurrent.
[Angel Montesdeoca]:
*** 1. L1, L2, L3 are concurrent. at X(5836)
*** 2.1. The parallels to L1, L2, L3 through A, B, C, resp.are concurrent. at X(8) = Nagel point
*** 2.2. The parallels to L1, L2, L3 through A', B', C', resp.are concurrent. at X(145) = anticomplement of Nagel point
*** 2.3. The parallels to L1, L2, L3 through A", B" C", resp.are concurrent. at X(10106) = 29th Hatzipolakis-Montesdeoca Point.
-
X(6042) = PERSPECTOR OF MONTESDEOCA-HUNG TRIANGLE AND ABC
Barycentrics f(a,b,c) : f(b,c,a) :
f(c,a,b), where f(a,b,c) = a(b + c)2(b2 +
c2 + ab + ac)2
Let (Ap) be the Apollonius circle, and let (KA),
(KB), (KC) be the circles described at X(5973) in
association with the Hung-Feuerbach circle at X(5974). Let
LA be the radical axis of (Ap) and (KA), and
define LB and LC cyclically. The lines
LA, LB, (LC form a triangle T (here
named the Montesdeoca-Hung triangle) that is perspective to ABC, and
the perspector is X(6042). (Tran Quang Hung, ADGEOM #1506; Angel
Montesdeoca, ADGEOM #1525, August 24, 2014)
-
X(6043) = PERSPECTOR OF MONTESDEOCA-HUNG TRIANGLE AND EXCENTRAL TRIANGLE
Barycentrics f(a,b,c) : f(b,c,a) :
f(c,a,b), where f(a,b,c) = a(a + b)(a + c)(a3 + ab2 + ac2 + 3abc - b2c - bc2)
Continuing from X(6042), the triangle T is perspective to the excentral triangle, and the perspector is X(6043). (Peter Moses, August 24, 2014)
-
X(6048) = CENTER OF MOSES HULL CIRCLE
Barycentrics f(a,b,c) : f(b,c,a) :
f(c,a,b), where f(a,b,c) = a(a2b + a2c + ab2 + ac2 + abc - 3b2c - 3bc2)
Let (Ia), (Ib), (Ic) be the excircles of ABC, and let (AP) be the classical Apollonius circle (e.g., TCCT, p. 102). Let (Ja) be the circle internally tangent to (Ia) and externally tangent to (Ib) and (Ic), and define (Jb) and Jc) cyclically. Let (J) be the circle internally tangent to (Ja), (Jb), (Jc). Then X(6048) = center of (J). See ADGEOM #1541 and Problema de Apolonio relativo a las circunferencias exinscritas. (Angel Montesdeoca, February 25, 2017)
-
X(6094) = 11th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = (a^4+5 a^2 b^2+b^4-4 a^2 c^2-4 b^2 c^2+c^4) (a^4-4 a^2 b^2+b^4+5 a^2 c^2-4 b^2 c^2+c^4)
Suppose that P = p : q : r (barycentrics) and P* are a pair of isogonal conjugate points in the plane of a triangle ABC. Let A'B'C' be the pedal triangle of P and A''B''C'' the pedal triangle of P*. Let A* be the reflection of A' in line B''C'', and define B* and C* cyclically. In Hyacinthos (October 3, 2014), Antreas Hatzipolakis asks for the locus of P for which the circumcircles of A*BC, B*CA, C*AB concur. Angel Montesceoca responds that the three circumcircles concur for all choices of P. He further notes that if P is not on the circumcircle and not on the line at infinity, then the point Q of conurrence of the three circles has barycentrics Q(a,b,c,p,q,r) : Q(b,c,a,q,r,p) : Q(c,a,b,r,p,q) given by
Q(a,b,c,p,q,r) = (q + r)/[a4qr(p + q)(p + r) - 2a2(q + r)(r + p)(p + q)(c2q + b2r) + p(q + r)(b4r(p + q) + c4q(q + r) + 2b2c2(q2 + r2 + pq + qr + rp))]
Writing Q as Q(P), the occurrence of (i,j) in the following list means that Q(X(i)) = X(j): (1,5620), (2,6094), (3, 1263), (8, 6095), (20, 265), (69, 6096), (1138, 1138). In particular, Q(X(2)) = X(6094).
X(6094) lies on these lines: {6,543},{263,2854}
X(6094) = isogonal conjugate of X(352)
-
X(6095) = 12th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a (a^3-a^2 b-a b^2+b^3-2 a^2 c+7 a b c-2 b^2 c-2 a c^2-2 b c^2+c^3) (a^3-2 a^2 b-2 a b^2+b^3-a^2 c+7 a b c-2 b^2 c-a c^2-2 b c^2+c^3)
X(6095) = Q(X(8)); see X(6094).
X(6095) lies on these lines: {1,121}, {56,2802}, {106,1739}
-
X(6096) = 13th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a (a^3-a^2 b-a b^2+b^3-2 a^2 c+7 a b c-2 b^2 c-2 a c^2-2 b c^2+c^3) (a^3-2 a^2 b-2 a b^2+b^3-a^2 c+7 a b c-2 b^2 c-a c^2-2 b c^2+c^3)
X(6096) = Q(X(69)); see X(6094).
X(6096) lies on these lines: (pending)
X(6096) = isogonal conjugate of X(5913)
-
X(6097) = 14th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = (a^2 (a^2 - b^2 - b c - c^2) (a^5 (b + c) - 2 a^3 (b^3 + c^3) - a^2 b c (b^2 + c^2) + a (b^5 - b^4 c - b c^4 + c^5)+ b c (b^2 - c^2)^2)
X(6097) = (r2 + 2rR - R2 + s2)*X(3) + R2*X(4)
barycentrics, Peter Moses, October 3, 2014; combo, Angel Montesdoca, October 3, 2014
Let ABC be a triangle and A'B'C' the cevian triangle of X(1). Let OAB be the circumcenter of ABA', and define OBC and OCA cyclically; let OAC be the circumcenter of ACA', and define OBA and OCB cyclically. Let OA be the circumcenter of triangle AOABOAC, and define OB and OC cyclically. Hatzipolakis proposed, and Montesdeoca proved, that the Euler lines concur, in X(186), and that the orthocenter of triangle OAOBOC, which is X(6097), lies on the Euler line. See Anthrakitis (October 3, 2014)
X(6097) lies on these lines: {2,3},{35,500},{55,5453},{511,5495},{3724,5492}
-
X(6098) = 15th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a (a^2 - b^2 + b c - c^2)
(a^2 (b + c) - 2 a b c - b^3 + b^2 c + b c^2 - c^3) / ((b^2 + c^2 - a^2) (a^6 - a^4 (b^2 - b c + c^2) - a^3 b c (b + c) - a^2 (b^4 - b^3 c - 2 b^2 c^2 - b c^3 + c^4) + a b (b - c)^2 c (b + c) + (b - c)^4 (b + c)^2))
Let A'B'C' be the antipedal triangle of the incenter. Let A'' = X(1986)-of-A'BC, and define B'' and C'' cyclically. Let OA be the circumcenter of A'BC, and define OB and OC cyclically. The circumcircles of the four triangles A''B''C'', A''BC, AB''C, ABC'' concur in X(6098). See Hyacinthos 22617, October 8, 2014.
X(6098) lies on these lines: (pending)
-
X(6099) = 16th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a^2/((b - c) (a^3 b - a^2 b^2 - a b^3 + b^4 + a^3 c + a b^2 c - a^2 c^2 + a b c^2 - 2 b^2 c^2 - a c^3 + c^4))
Let A'B'C' be the antipedal triangle of the incenter. Let A'' = X(1986)-of-A'BC, and define B'' and C'' cyclically. Let OA be the circumcenter of A'BC, and define OB and OC cyclically. The circumcircles of the four triangles ABC, AB''C'', A''BC'', A"B''C concur in X(6099). The lines OAA'', OBB'', OCC'' also concur in X(6099). See Hyacinthos 22617, October 8, 2014.
Let T be the triangle whose sidelines are the reflections of the line X(3)X(11) in the sidelines of ABC. Then T is perspective to ABC, and X(6099) is the perpsector. (Randy Hutson, October 16, 2014)
X(6099) lies on these lines: (pending)
-
X(6100) = 17th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a (a^14 (b + c) - 2 a^13 (b + c)^2 - (b - c)^6 (b + c)^5 (b^2 + c^2)^2 + a^12 (-3 b^3 + 5 b^2 c + 5 b c^2 - 3 c^3) + 2 a^11 (b + c)^2 (4 b^2 - 5 b c + 4 c^2) + a^10 (b^5 - 21 b^4 c + b^3 c^2 + b^2 c^3 - 21 b c^4 + c^5) - 10 a^9 (b^2 - c^2)^2 (b^2 - b c + c^2) + a^8 (5 b^7 + 15 b^6 c - 21 b^5 c^2 + 21 b^4 c^3 + 21 b^3 c^4 - 21 b^2 c^5 + 15 b c^6 + 5 c^7) + 2 a^7 b c (-10 b^6 + 7 b^5 c + 4 b^4 c^2 - 18 b^3 c^3 + 4 b^2 c^4 + 7 b c^5 - 10 c^6) + a^6 (-5 b^9 + 15 b^8 c + 4 b^7 c^2 - 32 b^6 c^3 + 22 b^5 c^4 + 22 b^4 c^5 - 32 b^3 c^6 + 4 b^2 c^7 + 15 b c^8 - 5 c^9) + 2 a^5 (b - c)^2 (5 b^8 + 10 b^7 c - b^6 c^2 + 4 b^5 c^3 + 14 b^4 c^4 + 4 b^3 c^5 - b^2 c^6 + 10 b c^7 + 5 c^8) - a^4 (b - c)^2 (b^9 + 23 b^8 c + 16 b^7 c^2 + 28 b^5 c^4 + 28 b^4 c^5 + 16 b^2 c^7 + 23 b c^8 + c^9) - 2 a^3 (b^2 - c^2)^2 (4 b^8 - 7 b^7 c + b^6 c^2 + 5 b^5 c^3 - 12 b^4 c^4 + 5 b^3 c^5 + b^2 c^6 - 7 b c^7 + 4 c^8) + a^2 (b - c)^4 (b + c)^3 (3 b^6 + 8 b^5 c - 4 b^4 c^2 +
18 b^3 c^3 - 4 b^2 c^4 + 8 b c^5 + 3 c^6) + 2 a (b^2 - c^2)^4 (b^6 - 3 b^5 c + 4 b^4 c^2 - 6 b^3 c^3 + 4 b^2 c^4 - 3 b c^5 + c^6))
Let A'B'C' be the antipedal triangle of the incenter. Let A'' = X(1986)-of-A'BC, and define B'' and C'' cyclically. Let OA be the circumcenter of A'BC, and define OB and OC cyclically. The points A'', B'', C'', X(6098) lie on a circle, of which the center is X(6100). See Hyacinthos 22617, October 8, 2014.
X(6100) lies on these lines: (pending)
-
X(6101) = 18th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a^2 (a^6 (b^2 + c^2) - a^4 (3b^4 + 4b^2 c^2 + 3c^4) + a^2(3b^6 + 2b^4 c^2 + 2b^2 c^4 + 3c^6) - b^8 + b^6 c^2 + b^2 c^6 - c^8)
Let AB be the reflection of A in line OB, where O = circumcenter of ABC, and define
BC and CA cyclically. Let AC be the reflection of A in line OC, and define BA and CB cyclically. Let A' be the nine-point center of triangle AABAC, and define B' and C' cyclically. The circumcircles of the four triangles A'B'C', A'BC, AB'C, ABC' concur in X(6101). (Also, the circumcircles of the four triangles ABC, AB'C', A'BC', A'B'C concur in X(930)). See Hyacinthos 22624, October 10, 2014.
X(6101) lies on these lines:
{2,143},{3,54},{4,2889},{5,141},{20,5663},{22,156},{26,394},{30,5562},{49,323},{51,3628},{52,140},{67,68},{110,2937},{155,1350},{185,548},{389,549},{546,5891},{568,631},{632,3819},{1092,1511},{1147,5944},{1656,3060},{2392,5694},{2781,5609},{3313,3564},{3526,3567},{3627,5907},{5070,5640}
X(6101) = reflection of X(i) in X(j) for these (i,j): (5,1216), (52,140), (185,548), (389,5447), (3627,5907), (5946,3917)
X(6101) = anticomplement of X(143)
X(6101) = {X(i),X(j)}-harmonic conjugate of X(k) for these (i,j,k): (3,195,5012), (52,140,5946), (52,3917,140), (389,5447,549), (1092,1658,1511), (3819,5462,632)
-
X(6102) = 19th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = a^2(a^6(b^2+c^2)-
3a^4(b^4+c^4)+a^2(3b^6-2b^4c^2-2b^2c^4+3c^6)-b^8+b^6c^2+b^2c^6-c^8
Let AB be the reflection of A in line OB, where O = circumcenter of ABC, and define
BC and CA cyclically. Let AC be the reflection of A in line OC, and define BA and CB cyclically. Let A' be the nine-point center of triangle AABAC, and define B' and C' cyclically. Then X(6102) is the ABC-orthology center of A'B'C' on the circumcircle of A'B'C'. (Also, X(1141) is the ABC-orthology center of ABC on the circumcircle of ABC.) See Hyacinthos 22628 and Hechos Geometricos 121014, October 12, 2014.
Let NA be the reflection of X(5) in the A-altitude, and define NB and NC cyclically. Then X(6102) is the orthocenter of NANBNC. Let A'B'C' be the reflection triangle. Let A'' be the trilinear pole, with respect to A'B'C', of the line BC, and define B'' and C'' cyclically. Let A* be the trilinear pole, with respect to A'B'C', of line B''C'', and define B* and C* cyclically. The lines A'A*, B'B*,C'C* concur in X(6102), and the lines A'A'', B'B'', C'C'' concur in X(382). (Randy Hutson, October 16, 2014)
X(6102) lies on these lines:
{3,54},{4,94},{5,389},{24,156},{26,1181},{30,52},{49,186},{51,546},{140,5562},{155,2929},{184,1658},{381,3567},{382,3060},{511,550},{549,1216},{567,1199},{576,2781},{632,5892},{974,1204},{1147,1511},{1614,2070},{1994,3520},{3530,3917},{3627,5446},{3628,5891},{3851,5640}
X(6102) = midpoint of X(i) and X(j) for these (i,j): (52,185), (3,5889)
X(6102) = reflection of X(i) in X(j) for these (i,j): (4,143), (5,389), (5562,140), (3627,5446), (5876,5), (5907,5462)
X(6102) = X(5)-of-circumorthic-triangle
X(6102) = {X(i),X(j)}-harmonic conjugate of X(k) for these (i,j,k): (4,568,143), (5,389,5946), (184,1658,5944), (389,5907,5462), (5462,5907,5), (5876,5946,5), (5889,5890,3)
-
X(6126) = X(1)-CEVA CONJUGATE OF X(36)
Barycentrics f(a,b,c) : f(b,c,a) : f(c,a,b), where f(a,b,c) = (a^2 (a^5 + a^4(b+c) - 2a^3(b^2+c^2) - a^2(2b^3-b*c(b+c)+2c^3)+ a(b^4+b^2c^2+c^4) + (b-c)^2(b^3+c^3))
X(6126) is the point QA-P41 ('Involutary Conjugate of QA-P4') of the quadrangle ABCX(1). X(6126)-of-orthocentroidal-triangle = X(1). These properties and others are presented in Hyacinthos messages 21651 and 22707-22710 by S. Topor, A. Montesdeoca, R. Hutson, and A. Hatzipolakis; see 22710)
-
X(6177) = CEVAPOINT OF THE REAL FOCI OF THE STEINER INELLIPSE
Barycentrics g(a,b,c) : g(b,c,a) : g(c,a,b), where g(a,b,c) = a4 + b4 + c4 - a2b2 - a2c2 + (b2 + c2)(a4 + b4 + c4 - a2b2 - a2c2 - b2c2) 1/2
In the plane of a triangle ABC, let
F1 and F2 be the real foci of the Steiner inellipse
A1 = AF1∩BC
A2 = AF2∩BC
Ga = conic tangent to AF1 at A1, to AF2 at A2, and to F1F2
Ta = Ga∩F1F2
Ao = center of Ga, and define Bo and Co cyclically
The lines AAo, BBo, CCo concur in X(14633), and the lines ATa, BTb, CTc concur in X(6177). See X(6177) and X(14633). (Angel Montesdeoca, July 21, 2023)
-
X(6188) = DAO (a,b,c,R) PERSPECTOR
Barycentrics 1 /[a^8 - 4 a^6 (b^2 + c^2) + (b^2 - c^2)^2 (b^4 + 6 b^2 c^2 + c^4) + a^4 (6 b^4 - 3 b^2 c^2 + 6 c^4) + a^2 (-4 b^6 + 3 b^4 c^2 + 3 b^2 c^4 - 4 c^6)]
Let rA be a positive valued function of a,b,c, and define rB and rC cyclically. Let (A) denote the circle with center A and radius rA, and define (B) and (C) cyclically. Let P be the radical center of (A), (B), (C). Let rP be a positive valued function of a,b,c, let LA be the radical axis of (A), (B), (P), and define LB and LC cyclically. Let A' = LB∩LC, and define B' and C' cyclically. Then the lines AA', BB', CC" concur in a point, D. Moreover, the six points A, B, C, X(4), P, D lie on a hyperbola. (Dao Thanh Oai, ADGEOM 893, November 26, 2013)
The hyperbola is here called the Dao (rA,rB,rC,rP) hyperbola. The triangle A'B'C' is the Dao (rA,rB,rC,rP) triangle, and the perspector D of ABC and A'B'C' is the Dao (rA,rB,rC,rP) perspector.
For details and examples, including coordinates and equations, see Angel Montesdeoca's presentation at Hechos Geometricos.
-
X(6240) = CIRCUMORTHIC-TRIANGLE-ORTHOLOGIC CENTER OF MACBEATH TRIANGLE
Barycentrics (a^2+b^2-c^2) (a^2-b^2+c^2) (2 a^6-3 a^4 b^2+b^6-3 a^4 c^2+2 a^2 b^2 c^2-b^4 c^2-b^2 c^4+c^6) : :
Let MaMbMc = medial triangle and DEF = circumorthic triangle. Let (Oa) be the circle with center A that passes through E and F (and X(4)). Let E' be the point, other than E, in which (Oa) meets EMa, and let F' be the point, other than F, in which (Oa) meets FMa. Let A' = EF'∩FE', and define B' and C' cyclically. The lines A'DF, B'E, C'F concur in X(6240). (Angel Montesdeoca, September 25, 2020)
El centro del triángulo X(6340) como centro de perspectividad
-
X(6288) = JOHNSON-TRIANGLE-ORTHOLOGIC CENTER OF REFLECTION TRIANGLE
Barycentrics a^10-2 a^8 b^2+a^6 b^4-a^4 b^6+2 a^2 b^8-b^10-2 a^8 c^2+3 a^6 b^2 c^2-2 a^4 b^4 c^2-2 a^2 b^6 c^2+3 b^8 c^2+a^6 c^4-2 a^4 b^2 c^4-2 b^6 c^4-a^4 c^6-2 a^2 b^2 c^6-2 b^4 c^6+2 a^2 c^8+3 b^2 c^8-c^10 : :
Let (Ha) be the hyperbola having diameter X(3)X(4), passing through A, with an asymptote parallel to the internal bisector of angle A. Let A' be the reflecttion of A in X(5), and let Ta be the tangent to (Ha) at A'. Define Tb and Tc cyclically. The lines Ta, Tb, Tc concur in X(6288). See X(6288). (Angel Montesdeoca, December 9, 2019) HGT
-
X(6525) = SS(a → SBSC) of X(55)
Barycentrics [3a^4 - 2a^2b^2 - 2a^2c^2 - (b^2 - c^2)^2]/(b^2 + c^2 - a^2)^2 : :
Let DEF be the orthic triangle and D' the midpoint of AD . Let A' be the reflection of A in D'X(3), Let La be the perpendicular bisector of A'D, and define Lb and Lc cyclically. Let A" = Lb∩Lc, B"= Lc∩La, C" = La∩Lb. The lines DA", EB", FC" concur in X(6525). (Angel Montesdeoca, August 21, 2019).
HG210819.
-
X(6595) = (ABC-1st-SCHIFFLER) CYCLOLOGIC CENTER
Barycentrics a (a^9+a^7 (-6 b^2+7 b c-6 c^2)-(b-c)^4 (b+c)^3 (2 b^2+5 b c+2 c^2)+a^6 (2 b^3-3 b^2 c-3 b c^2+2 c^3)+a (b^2-c^2)^2 (3 b^4-b^3 c+2 b^2 c^2-b c^3+3 c^4)+a^5 (12 b^4-15 b^3 c+13 b^2 c^2-15 b c^3+12 c^4)+a^4 (-6 b^5+3 b^4 c+5 b^3 c^2+5 b^2 c^3+3 b c^4-6 c^5)+a^3 (-10 b^6+9 b^5 c-3 b^4 c^2+5 b^3 c^3-3 b^2 c^4+9 b c^5-10 c^6)+a^2 (6 b^7+3 b^6 c-11 b^5 c^2+b^4 c^3+b^3 c^4-11 b^2 c^5+3 b c^6+6 c^7)) : :
Let I = X(1), the incenter of a triangle ABC. Let LA be the Euler line of triangle IBC, and define LB and LC cyclically. These lines concur in S = X(21), the Schiffler point of ABC. Let C2 be the point, other than S, of intersection of the line LB and the circle (C, |CS|). Let B3 be the point, other than S, of intersection of the line LC and the circle (B, |BS|). Let O1 be the circumcenter of SC2B3, and define O2 and O3 cyclically. The triangle O1O2O3 is here named the 1st Schiffler triangle. The triangles ABC and O1O2O3 are cyclologic, and X(6595) is the (ABC, O1O2O3)-cyclologic center. See X(6596)-X(6599) and Hyacinthos #23098 and Hyacinthos #23101. (S. Kirikami, A. Hatzipolakis and A.Montesdeoca, February 4-5, 2015)
-
X(6596) = (1st SCHIFFLER, 2nd SCHIFFLER) CYCLOLOGIC CENTER
Barycentrics a (a^9 + 10 a^7 b c - 3 a^8 (b + c) + (b - c)^6 (b + c)^3 - a (b - c)^4 (b + c)^2 (3 b^2 - 2 b c + 3 c^2) + a^6 (8 b^3 - 6 b^2 c - 6 b c^2 + 8 c^3) - a^5 (6 b^4 + 12 b^3 c - 13 b^2 c^2 + 12 b c^3 + 6 c^4) - a^4 (6 b^5 - 18 b^4 c + 7 b^3 c^2 + 7 b^2 c^3 - 18 b c^4 + 6 c^5) - a^2 b c (6 b^5 - 13 b^4 c + 11 b^3 c^2 + 11 b^2 c^3 - 13 b c^4 + 6 c^5) + a^3 (8 b^6 - 6 b^5 c - 9 b^4 c^2 + 26 b^3 c^3 - 9 b^2 c^4 - 6 b c^5 + 8 c^6)) : :
Continuing from X(6595), let W = X(3065). Let C'2 be the point, other than S, of intersection of the Euler line of the triangle WCA and the circle (C, |CS|). Let B'3 be the point, other than S, of intersection of the Euler line of the triangle WAB and the circle (B, |BS|). Let O'1 be the circumcenter of SC2B3, and define O'2 and O'3 cyclically. The triangle O'1O'2O'3 is here named the 2nd Schiffler triangle.The triangles ABC,
O1O2O3, and O'1O'2O'3 and pairwise cyclologic:
X(6595) = (ABC, O1O2O3)-cyclologic center
X(3065) = (O1O2O3, ABC)-cyclologic center
X(1320) = (ABC, O'1O'2O'3)-cyclologic center
X(1) = (O'1O'2O'3, ABC)-cyclologic center
X(6596) = (O1O2O3, O'1O'2O'3)-cyclologic center
X(6597) = (O'1O'2O'3, O1O2O3)-cyclologic center
The points O'1, O'2, O'3 lie on the Feuerbach hyperbola. (Randy Hutson, September 14, 2016)
See Hyacinthos #23101. (S. Kirikami, A. Hatzipolakis and A.Montesdeoca, February 4-5, 2015)
-
X(6599) = (2nd SCHIFFLER, 1st SCHIFFLER)-ORTHOLOGIC CENTER
Barycentrics a^13 - 2 a^12 (b + c) - (b - c)^8 (b + c)^5 + a^11 (-3 b^2 + 5 b c - 3 c^2) + 2 a (b - c)^6 (b + c)^4 (b^2 - b c + c^2) - a^8 (b + c) (3 b^2 - 2 b c + 3 c^2)^2 + a^10 (7 b^3 + 2 b^2 c + 2 b c^2 + 7 c^3) + a^2 (b - c)^4 (b + c)^3 (3 b^4 - 3 b^3 c - 5 b^2 c^2 - 3 b c^3 + 3 c^4) + a^9 (4 b^4 - 14 b^3 c + 15 b^2 c^2 - 14 b c^3 + 4 c^4) -
3 a^7 (2 b^6 - 6 b^5 c + 6 b^4 c^2 - 7 b^3 c^3 + 6 b^2 c^4 - 6 b c^5 + 2 c^6) - a^4 (b + c)^3 (4 b^6 - 16 b^5 c + 26 b^4 c^2 - 27 b^3 c^3 + 26 b^2 c^4 - 16 b c^5 + 4 c^6) - a^3 (b^2 - c^2)^2 (7 b^6 - 17 b^5 c + 11 b^4 c^2 - 6 b^3 c^3 + 11 b^2 c^4 - 17 b c^5 + 7 c^6) + a^6 (6 b^7 - 4 b^6 c + 7 b^5 c^2 + 4 b^4 c^3 + 4 b^3 c^4 + 7 b^2 c^5 - 4 b c^6 + 6 c^7) +
a^5 (9 b^8 - 20 b^7 c + 3 b^6 c^2 + 3 b^5 c^3 + 6 b^4 c^4 + 3 b^3 c^5 + 3 b^2 c^6 - 20 b c^7 + 9 c^8) : :
In addition to the notes at X(6596), Angel Montesdeoca notes in Hyacinthos 23101 that the following 15 points lie on the Feuerbach hyperbola: O1, O2, O3, O'1, O'2, O'3, the cyclologic ceners X(1), X(1320), X(3065), X(6595)-X(6599), and S.
-
X(7004) = PERSPECTOR OF ABC AND THE EXTRA-TRIANGLE OF X(201)
Barycentrics a(b - c)2(b + c - a)(b2 + c2 - a2) : :
In the plane of a triangle ABC, let
P = X(80) = reflection of X(1) in X(11);
R1 = reflection of AB in CP;
R2 = reflection of AC in BP;
A' = R1∩R2, and define B' and C' cyclically;
T = the affine transformation that carries ABC onto A'B'C'.
Then X(7004) = the finite fixed point of T. The fixed lines of T are parallel to the asymptotes of the Jerabek hyperbola. (Angel Montesdeoca, March 14, 2024)
See Afinidad con puntos fijos X(7004) y los del infinito de la hipérbola de Jerabek
-
X(7100) = PERSPECTOR OF ABC AND THE EXTRA-TRIANGLE OF X(1807)
Barycentrics sin(A) / (2 + sec(A)) : :
Let I be the incenter of triangle ABC. Let LB be the line through I perpendiculat to AC, and let
AB = LB∩BC and BA = LB∩BA. Define BC and CA cyclically, and define CB and AC cyclically. Let
A' be the circumcenter of IABAC, and define B' and C' cyclically. The triangle A'B'C' is perspective to ABC, and the perspector is X(7100). (Angel Montesdeoca, June 11, 2016)
-
X(7319) = PERSPECTOR OF ABC AND THE EXTRA-TRIANGLE OF X(5556)
Barycentrics 1 / [3(b^2 + c^2 - a^2) - 2bc] : : : :
Let DEF be the extouch triangle of ABC. Let D' be the point, other than A, in which the line AD meets the A-excircle, and define E' and F' cyclically. Let La be the line tangent to the A-excircle at D', and define Lb and Lc cyclically. Let A' = Lb∩Lc, and define B' and C' cyclically. Then A'B'C' is perspective to ABC, and the perspector is X(7319). (Angel Montesdeoca, July 14, 2018)
-
X(7494) = {X(2),X(22)}-HARMONIC CONJUGATE OF X(4)
Barycentrics (b^2 + c^2 - a^2)(3a^4 - b^4 - c^4 + 2a^2b^2 + 2a^2c^2 + 2b^2c^2) : :
Let DEF = medial triangle and D'E'F' = circummedial triangle. Let Γ = circumcircle, and let Ab be the point, other than E', in which the line E'F intersects Γ. Define Bc and Ca cyclically. Let Ac be the point, other than F', in which the line F'E intersects Γ. Let Oa be the center of the conic tangent to the five lines BC, AE', AF', BAb, CAc, and define Ob and Oc cyclically. The finite fixed point of the affine transformation that carries ABC onto OaObOC is X(7494). (Angel Montesdeoca, May 3, 2020)
HG020520.
-
X(7619) = X(5)-OF-McCAY-TRIANGLE
Barycentrics 8 a^4-14 a^2 b^2+5 b^4-14 a^2 c^2-8 b^2 c^2+5 c^4 : :
X(7619) = (1 + 20 sin²ω)*X(2) + (-1 + 4 sin²ω)*X(99)
Let G be the centroid of a triangle ABC, and
Oa = circumcenter of GBC, and define Ob and Oc cyclically
Na = nine-point center of GObOc, and define Nb and Nc cyclically
L = Euler line of NaNbNc
L' = Euler line of McCay triangle
Then X(7619) = L∩L'. See Angel Montesdeoca, X(7619) and Hyacinthos #24690. (October 25, 2016)
-
X(7666) = GIUGIUC CENTER OF SIMILITUDE
Trilinears (4 + 6 cos 2A) cos(B - C) - 16 cos A - 9 cos 3A : : (César Lozada)
Barycentrics a^2 (9 a^8 - 24 a^6 (b^2 + c^2) + a^4 (18 b^4 + 37 b^2 c^2 + 18 c^4) - 15 a^2 b^2 c^2 (b^2 + c^2) - (b^2 - c^2)^2 (3 b^4 + 4 b^2 c^2 + 3 c^4)) : : (Angel Montesdeoca)
Let OA = reflection of X(3) in line AX(4), let HA = reflection of X(4) in OA, let MA = midpoint of segment OAHA, and define MB and MC cyclically. Then MAMBMC is similar to ABC, and the center of similitude is X(7666). See Hyacinthos 23263 and 23277.
(Triángulos inversamente semejantes)
-
X(7669) = POLE OF X(115)X(125) WITH RESPECT TO THE CIRCUMCIRCLE
For a sketch, click X(3447)andX(7669). (Angel Montesdeoca, April 22, 2016)
-
X(7740) = MIDPOINT OF X(3) AND X(5502)
Barycentrics ((-a^2+b^2+c^2)^2-b^2*c^2)*(2*a^10-2*(b^2+c^2)*a^8-(5*b^4-12*b^2*c^2+5*c^4)*a^6+7*(b^4-c^4)*(b^2-c^2)*a^4-(b^2-c^2)^2*(b^4+8*b^2*c^2+c^4)*a^2-(b^4-c^4)*(b^2-c^2)^3)*a^2 : :
X(7740) = center of the circle D = {{X(3), X(110), X(4240}}. Dao Thanh Oai finds seven other points on D, as follows. Let A' = (Euler line)∩BC, and define B' and C' cyclically. The points X(3)-of-AB'C', X(3)-of-A'BC', X(3)-of-A'B'C, X(110)-of-AB'C', X(110)-of-A'BC', X(110)-of-A'B'C all lie on D. Let P be the paralogic triangle whose perspectrix is the Euler line of ABC. Then X(3)-of-P lies on D. See ADGEOM 2342 (February 2015) and Centro X(5502) (A. Montesdeoca. Hechos Geométricos en el Triángulo).
-
X(7971) = ORTHOLOGIC CENTER OF THESE TRIANGLES: 5th MIXTILINEAR AND EXTOUCH
Barycentrics a (a^6-4 a^5 (b+c)+a^4 (b^2+6 b c+c^2)+8 a^3 (b-c)^2 (b+c)-a^2 (b-c)^2 (5 b^2+14 b c+5 c^2-4 a (b-c)^4 (b+c)+(b^2-c^2)^2 (3 b^2-2 b c+3 c^2))) : :
Let A' = reflection of A in X(1), and define B' and C' cyclically. Let A" be the orthogonal projection of A' on BC. Let Ta be the tangent at A' to the circle (IA'A"), and define Tb and Tc cyclically. The lines Ta, Tb, Tc concur in X(7971). (Angel Montedeoca, April 20, 2020) HG200420
-
X(8041) = DANNEELS POINT OF X(4576)
Barycentrics a^2(b^2 + c^2)^2 : :
In the plane of a triangle ABC, let
G = centroid = X(2);
DEF = cevian triangle of X(6);
TA = line tangent to circumcircle at A;
LAB = line through B parallel to AG;
LAC = line through C parallel to AG;
A2 = TA∩LAB;
A3 = TA∩LAC;
Ab = DA2∩AG;
Ac = DA3∩AG;
A' = {Ab,Ac}-harmonic conjugate of A, and define B' and C' cyclically.
The finite fixed point of the affine transformation that carries ABC onto A'B'C' is X(8041). See
X(8041) (Angel Montesdeoca, February 23, 2021) and HG200221
-
X(8051) = CYCLOCEVIAN CONJUGATE OF X(7319)
Barycentrics 1/((-a+b+c) (a^2+2 a b+b^2+2 a c-6 b c+c^2)) : :
Let Na be the Nagel point. The incircle intersects ANa at two points, the closer of which to the vertex A is denoted by A1 and the other by A2. Define B1, C1 and B2, C2 cyclically. X(8051) is the trilinear pole of the perspectrix of the triangles A1B1C1 and A2B2C2, line X(3667)X(3669). (Angel Montesdeoca, November 17, 2021)
-
X(8105) = X(2)-CEVA CONJUGATE OF X(1313)
Barycentrics (b^2-c^2) (2 a^4-a^2 b^2-b^4-a^2 c^2+2 b^2 c^2-c^4 + a^2 (a^2-b^2-c^2) J) : : , where J = |OH|/R
Let MaMbMc = medial triangle and HaHbHc = orthic triangle. Let A' = reflection of A in X(3), and let A'' be the point, other than A', where the line A'Ma meets the circumcircle. Define B'' and C'' cyclically. The points D=BC∩HbHc, E=CA∩HcHa, F=AB∩HaHb, D'=B"C"∩MbMc, E'=C"A"∩McMa, F'=A"B"∩MaMb lie on orthic axis (common perspectrix of ABC and HaHbHc, MaMbMc and A"B"C" ). The fixed points of the projectivity that maps D, E, F onto D', E', F', respectively, are X(8105) and X(8106). (Angel Montesdeoca, May 17, 2019)
Proyectividad sobre el eje órtico.
-
X(8160) = CENTER OF THE OUTER MONTESDEOCA-LEMOINE CIRCLE
Barycentrics a^2(a^6(b^2+c^2)+2a^4(b^2+c^2)^2-a^2(4b^6+7b^4c^2+7b^2c^4+4c^6)+b^8-3b^6c^2-2b^4c^4-3b^2c^6+c^8 + 4S^3(2a^2-b^2-c^2) csc ω) : :
X(8160) = 3 X[3] - X[1671] = 3 X[1670] + X[1671] = 2 X[1671] - 3 X[8161] = 2 X[1670] + X[8161]
Let ABC be a triangle, and let A'B'C' be the cevian triangle of X(6). Let U be the line through A' parallel to AB, and let V be the line through A' parallel to AC. Let U = U∩BC and V' = V∩AB. The 4 points B, C, U', V' lie on a circle, (O)A. Define (O)B and (O)C cyclically. Let M be the circle tangent to (O)A, (O)B, (O)C that encompasses them; call M the outer Montesdeoca-Lemoine circle. Let M' be the circle tangent to (O)A, (O)B, (O)C that is encompassed by each of them; call M' the inner Montesdeoca-Lemoine circle. Then X(8160) is the center of M, and X(8161) is the center of M'. The contact points of M with (O)A, (O)B, (O)C are the vertices of a triangle perspective to ABC, with perspector X(1343). Likewise, the contact points of M' with (O)A, (O)B, (O)C are the vertices of a triangle perspective to ABC, with perspector X(1342). (Based on notes from Angel Montesdeoca, October 2, 2015)
The points X(8160) and X(8161) are labeled Z1 and Z2, respectively, in this sketch:
Hechos Geométricos 02/10/2015.
X(8160) lies on these lines: {3,6}, {30,5404}, {35,3238}, {36,3237}, {140,5403}, {1676,6683}, {2546,7786}
X(8160) = midpoint of X(3) and X(1670)
X(8160) = reflection of X(8161) in X(3)
X(8160) = {X(i),X(j)}-harmonic conjugate of X(k) for these (i,j,k): (3,1343,5092), (39,5092,8161)
-
X(8161) = CENTER OF THE INNER MONTESDEOCA-LEMOINE CIRCLE
Barycentrics a^2(a^6(b^2+c^2)+2a^4(b^2+c^2)^2-a^2(4b^6+7b^4c^2+7b^2c^4+4c^6)+b^8-3b^6c^2-2b^4c^4-3b^2c^6-c^8 - 4S^3(2a^2-b^2-c^2) csc ω) : :
X(8161) = 3 X[3] - X[1670] = X[1670] + 3 X[1671] = 2 X[1670] - 3 X[8160] = 2 X[1671] + X[8160]
See X(8160).
X(8161) lies on these lines: {3,6}, {30,5403}, {35,3237}, {36,3238}, {140,5404}, {1677,6683}, {2547,7786}
X(8161) = midpoint of X(3) and X(1671)
X(8161) = reflection of X(8160) in X(3)
X(8161) = {X(i),X(j)}-harmonic conjugate of X(k) for these (i,j,k): (3,1342,5092), (39,5092,8160)
-
X(8183) = MONTESDEOCA DEGENERATE CONICS POINT
Barycentrics: a - a1/3b1/3c1/3 : b - a1/3b1/3c1/3 : c - a1/3b1/3c1/3
(Contributed by Angel Montesceoca, Ocftober 9, 2015)
Hechos Geométricos 09/10/2015.
Let ABC be a triangle and k a real number. Let BA on line AB and CA on line AC be points such that BACA is parallel to BC at distance |kr(A)|, where r(A) is the inradius of triangle ABACA. Points CB, AB, AC, BC are defined cyclically. The six points BA, CA, CB, AB, AC, BC lie on a conic, with barycentric equation
0 = cyclic sum of kbc(a + b + c)x2 - a(a2 + b2 + c2 + 2bc + 2ca + 2ab + bck2)yz
The 4 degenerate real conics are given by these values of k: -(a + b + c)/a, -(a + b + c)/b, -(a + b + c)/c, and -(a + b + c)a-1/3b-1/3c-1/3. The 4 singular points of degenerate conics (i.e., points of intersection of the pairs of lines comprising each degenerate conic) are X(8183) and
bc - a2 : ba - bc : ca - cb
ab - ac : ac - b2 : cb - ca
ac - ab : bc - ba : ba - c2
These last three points are collinear on the trilinear pole of X(86).
-
X(8770) = BARYCENTRIC PRODUCT OF PU(128)
Barycentrics a^2 (a^2 + b^2 - 3 c^2) (a^2 - 3 b^2 + c^2) : :
Let A'B'C' be the tangential triangle and L the orthic axis. Let A'' = L∩B'C', and define B'' and C'' cyclically. Let Ta be the line, other than B'C', through A'' tangent to the circumcircle, and define Tb and Tc cyclically. Let A* = Tb∩Tc, and define B* and C* cyclically. Then A*B*C* is perspective to ABC, and the perspector is X(8770). (Angel Montesdeoca, July 17, 2019).
-
X(9033) = CROSSDIFFERENCE OF X(6) AND X(2781)
Barycentrics (b^2 - c^2)*(-a^2 + b^2 + c^2)*(-2*a^4 + a^2*b^2 + b^4 + a^2*c^2 - 2*b^2*c^2 + c^4) : :
Let W be the circumconic with center X(1650). One of the asymptotes of W is the Euler line. The other is in the direction of X(9033). For a sketch, click X(9033). (Angel Montesdeoca, April 19, 2016)
-
X(9121) = (1,84,1498)-(4,3,20)-(1490,40,64)-LOUD POINT OF THE DARBOUX CUBIC
Barycentrics a (a^9+a^8 (b+c)+(b-c)^6 (b+c)^3+a (b-c)^2 (b+c)^6-4 a^7 (b^2-b c+c^2)-4 a^2 (b-c)^2 (b+c)^3 (b^2-b c+c^2)-4 a^3 (b^2-c^2)^2 (b^2+b c+c^2)+2 a^4 (b+c)^3 (3 b^2-4 b c+3 c^2)+2 a^5 (b-c)^2 (3 b^2+4 b c+3 c^2)-4 a^6 (b^3+2 b^2 c+2 b c^2+c^3)) : :
Let ABC be a triangle with incenter I = X(1), De Longchamps point L = X(20), and Bevan point Be = X(40). Let DEF = cevian triangle of L. Let A' = ABe∩ID, and define B' and C' cyclically. The triangles ABC and A'B'C' are orthologic. The center of orthology of ABC with respect to A'B'C' is X(3345) and the center of orthology of A'B'C' with respect to ABC is X(9121). (Angel Montesdeoca, October 3, 2023 *)
-
X(9311) = CEVAPOINT OF PU(47)
Barycentrics 1/(a^2-(b+c)*a+2*b*c) : :
X(9311) is the trilinear pole of line X(2254)X(3667), which is the radical axis of incircle and excircles radical circle, and also the polar of X(1) wrt {circumcircle, nine-point circle}-inverter. (Randy Hutson, February 10, 2016)
Let DEF be the intouch triangle of triangle ABC. Let L be the line through D parallel to CA, and let CA = L∩AB, and define AB and BC cyclically. Let L' be the line through D parallel to AB, and let BA = L'∩CA, and define CB and AC cyclically. Let A'B'C' be the triangle having sidelines BACA, CBAB, ACBC. Then A'B'C' is perspective to ABC, and the perspector is X(9311). Click here for a sketch showing X(9311). (Angel Montesdeoca, March 20, 2016.)
-
X(9581) = EXSIMILCENTER OF THESE CIRCLES: BEVAN AND 2ND JOHNSON-YFF
Barycentrics (a^3+(b-c)^2*a+2*(b^2-c^2)*(b-c))*(a-b-c) : :
Let
(I) = incircle;
T = a point on (I);
t = line tangent to (I) at T;
T1 and T2 = points of intersection of t and the nine-point circle;
t1 = line through T1 tangent to (I);
t2 = line through T2 tangent to (I).
The locus of t1∩t2 as T varies on (I) is a conic, Γ, with center X(50443).
The center of the reciprocal polar of Γ wrt (I) is X(9581).
The center of the reciprocal polar of (I) wrt Γ is X(50444).
If you have Geogebra, you can view X(9581)
(Angel Montesdeoca, June 8, 2022)
See Angel Montesdeoca, HG060622.
-
X(9969) = ORTHOLOGIC CENTER OF THESE TRIANGLES: MIDHEIGHT TO 1ST EHRMANN
Barycentrics a^2*((b^2+c^2)*(a^4-(b^2-c^2)^2)+2*a^2*b^2*c^2) : :
In the plane of a triangle ABC, let
Γ = circumcircle of ABC
TaTbTc = tangential triangle of ABC
DEF = cevian triangle of X(1176)
Ab = the point, other than B, of intersection of circles Γ and (BDT)
Ac = the point, other than C, of intersection of circles Γ and (CDT)
La = AbAc, and define Lb and Lc cyclically
A' = Lb∩Lc, and define B' and C' cyclically
Then A'B'C' is perspective to ABC, and the perspector is X(9969). (Angel Montesdeoca, February 10, 2021)
See El centro X(9969) y el triángulo ceviano del 1º punto Saragossa del conjugado isogonal del punto de Exeter
-
X(10018) = 20th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics (a^2+b^2-c^2) (a^2-b^2+c^2) (2 a^6-5 a^4 b^2+4 a^2 b^4-b^6-5 a^4 c^2+2 a^2 b^2 c^2+b^4 c^2+4 a^2 c^4+b^2 c^4-c^6) : :
Centers X(10018)-X(10021) lie on the Euler line. For constructions and properties, see Hyacinthos messages beginning with 23422 (May 30, 2016). See also X(6102).
-
X(10019) = 21st HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics (a^2+b^2-c^2) (a^2-b^2+c^2) (2 a^6+a^4 b^2-8 a^2 b^4+5 b^6+a^4 c^2+8 a^2 b^2 c^2-5 b^4 c^2-8 a^2 c^4-5 b^2 c^4+5 c^6) : :
Centers X(10018)-X(10021) lie on the Euler line. For constructions and properties, see Hyacinthos messages beginning with 23422 (May 30, 2016).
-
X(10020) = 22nd HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 2 a^10-5 a^8 b^2+2 a^6 b^4+4 a^4 b^6-4 a^2 b^8+b^10-5 a^8 c^2+4 a^6 b^2 c^2-2 a^4 b^4 c^2+6 a^2 b^6 c^2-3 b^8 c^2+2 a^6 c^4-2 a^4 b^2 c^4-4 a^2 b^4 c^4+2 b^6 c^4+4 a^4 c^6+6 a^2 b^2 c^6+2 b^4 c^6-4 a^2 c^8-3 b^2 c^8+c^10 : :
Centers X(10018)-X(10021) lie on the Euler line. For constructions and properties, see Hyacinthos messages beginning with 23422, especially 23429
-
X(10021) = 23rd HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 2 a^7-2 a^6 b-5 a^5 b^2+5 a^4 b^3+4 a^3 b^4-4 a^2 b^5-a b^6+b^7-2 a^6 c+2 a^5 b c+a^4 b^2 c+a^3 b^3 c+2 a^2 b^4 c-3 a b^5 c-b^6 c-5 a^5 c^2+a^4 b c^2+4 a^3 b^2 c^2+2 a^2 b^3 c^2+a b^4 c^2-3 b^5 c^2+5 a^4 c^3+a^3 b c^3+2 a^2 b^2 c^3+6 a b^3 c^3+3 b^4 c^3+4 a^3 c^4+2 a^2 b c^4+a b^2 c^4+3 b^3 c^4-4 a^2 c^5-3 a b c^5-3 b^2 c^5-a c^6-b c^6+c^7 : :
Centers X(10018)-X(10021) lie on the Euler line. For constructions and properties, see Hyacinthos messages beginning with 23422, especially 23436
-
X(10032) = X(8)X(30)∩X(21)X(551)
Barycentrics (7a^3-a^2(b+c)-a(4b^2+b c+4c^2)-2(b-c)^2(b+c) : :
X(10032) = 5 X[21] - 4 X[551] = 5 X[79] - 8 X[3634] = 7 X[3624] - 10 X[3647] = X[8] + 5 X[3648] = X[8] - 10 X[3650] = X[3648] + 2 X[3650]
Let Ia be the A-excenter of a triangle ABC, and define Ib and Ic cyclically. Let A' = reflection of Ia in BC, and define B' and C' cyclically. Let A'' = reflection of IA in A', and define B'' and C'' cyclically. The Euler lines of A''BC, B''CA,C''AB concur in X(10032). (Tran Quang Hung and Angel Montesdeoca, July 19, 2016: Hyacinthos 23831)
X(10032) lies on these lines:
{8,30}, {21,551}, {79,3634}, {191,6175}, {527,2346}, {553,5284}, {1281,6054}, {2796,4921}, {2975,3656}, {3624,3647}
X(10032) = reflection of X(6175) in X(9)
-
X(10033) = 24th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 4 a^8+a^4 (4 b^4+7 b^2 c^2+4 c^4)-2 a^2 (3 b^6-5 b^4 c^2-5 b^2 c^4+3 c^6)-(b^2-c^2)^2 (2 b^4+7 b^2 c^2+2 c^4) : :
Let ABC be a triangle and A'B'C' the cevian triangle of the centroid, G, and let
Oa = circumcenter of GB'C'; define Ob and Oc cyclically
Oab = circumcenter of AB'G; define Obc and Oca cyclically
Oac = circumcenter of AC'G; define Oba and Ocb cyclically
Ga = centroid of OaObOc; define Gb and Gc cyclically
Na = nine-point center of GB'C'; define Nb and Nc cyclically
Nab = nine-point center of AB'G; define Nbc and Nca cyclically
Nac = nine-point center of AC'G; define Nba and Ncb cyclically
The triangles GaGbGc, G1G2G3 are perspective, and their perspector is X(10033). Let Ea be the Euler line of OaOabOac, and define Eb and Ec cyclically; then Ea, Eb, Ec are parallel, and they concur in X(524). Let Fa be the Euler line of NaNabNac, and define Fb and Fc cyclically. Let A'' = Fb∩Fc, and define B'' and C'' cyclically. Then the triangles ABC and A''B''C'' are parallelogic, and the parallelogic center of ABC with respect to A''B''C'' is X(6094), the 11th Hatzipolakis-Montesdeoca point, and the parallelogic center of A''B''C'' with respect to ABC is X(10034). (Antreas Hatzipolakis and Angel Montesdeoca, August 1, 2016; see Hyacinthos 23907)
X(10033) lies on these lines:
{2,1495}, {4,3849}, {30,7697}, {98,381}, {114,8592}, {183,3830}, {262,542}, {3545,7694}, {3839,9753}, {3845,9993}, {5066,7792}, {6054,9830}, {8370,9873}
-
X(10034) = 25th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 10 a^12-33 a^10 (b^2+c^2)-6 a^8 (11 b^4-34 b^2 c^2+11 c^4)+a^6 (221 b^6-108 b^4 c^2-108 b^2 c^4+221 c^6)-3 a^4 (41 b^8-112 b^6 c^2+288 b^4 c^4-112 b^2 c^6+41 c^8)-6 a^2 (5 b^10-28 b^8 c^2+8 b^6 c^4+8 b^4 c^6-28 b^2 c^8+5 c^10)+13 b^12-81 b^10 c^2+153 b^8 c^4-154 b^6 c^6+153 b^4 c^8-81 b^2 c^10+13 c^12 : :
Let A''B''C'' be as at X(10035). The parallelogic center of A''B''C'' with respect to ABC is X(10034). (Antreas Hatzipolakis and Angel Montesdeoca, August 1, 2016; see Hyacinthos 23907)
-
X(10035) = 26th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 2 a^9 (b+c)+b c (b^2-c^2)^4-2 a^8 (b^2+c^2)+a (b-c)^4 (b+c)^3 (b^2+b c+c^2)-a^7 (7 b^3+b^2 c+b c^2+7 c^3)+2 a^2 (b^2-c^2)^2 (b^4-2 b^3 c-2 b c^3+c^4)+a^6 (6 b^4-2 b^3 c+8 b^2 c^2-2 b c^3+6 c^4)-a^3 (b-c)^2 (5 b^5+7 b^4 c+6 b^3 c^2+6 b^2 c^3+7 b c^4+5 c^5)+a^5 (9 b^5-4 b^4 c+b^3 c^2+b^2 c^3-4 b c^4+9 c^5)-a^4 (6 b^6-5 b^5 c+2 b^4 c^2+6 b^3 c^3+2 b^2 c^4-5 b c^5+6 c^6) : :
Let ABC be a triangle and A'B'C' the cevian triangle of the incenter, I, and let
Oa = circumcenter of IB'C'; define Ob and Oc cyclically
Oab = circumcenter of AB'I; define Obc and Oca cyclically
Oac = circumcenter of AC'I; define Oba and Ocb cyclically
Ga = centroid of OaObOc; define Gb and Gc cyclically
Na = nine-point center of IB'C'; define Nb and Nc cyclically
Nab = nine-point center of AB'I; define Nbc and Nca cyclically
Nac = nine-point center of AC'I; define Nba and Ncb cyclically
Let Ea be the Euler line of NaNabNac, and define Eb and Ec cyclically; then Ea, Eb, Ec concur in X(10035). Let Fa be the Euler line of OaOabOac, and define Fb and Fc cyclically; the lines Fa, Fb, Fc are parallel, and they meet in X(517). (Antreas Hatzipolakis and Angel Montesdeoca, August 1, 2016; see Hyacinthos 23914)
X(10035) lies on these lines:
{11,500}, {30,1319}, {496,5495}, {511,6713}, {549,4271}, {952,5453}
-
X(10036) = 27th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 4 a^8 b c-2 a^9 (b+c)+b c (b^2-c^2)^4-12 a^6 b c (b^2+c^2)-6 a^2 b c (b^2-c^2)^2 (b^2+c^2)-a (b-c)^4 (b+c)^3 (b^2+3 b c+c^2)+a^7 (7 b^3+5 b^2 c+5 b c^2+7 c^3)+5 a^3 (b-c)^2 (b^5+3 b^4 c+2 b^3 c^2+2 b^2 c^3+3 b c^4+c^5)-a^5 (9 b^5+6 b^4 c-5 b^3 c^2-5 b^2 c^3+6 b c^4+9 c^5)-a^4 (-13 b^5 c+6 b^3 c^3-13 b c^5) : :
Let ABC be a triangle and A'B'C' the cevian triangle of the incenter, I. Continuing from X(10035), let Pa be the line through A' parallel to Ea, and define Pb and Pc cyclically. Then Pa,Pb,Pc concur in X(10036). (Antreas Hatzipolakis and Angel Montesdeoca, August 1, 2016; see Hyacinthos 23914)
X(10036) lies on these lines:
{11,8143}, {115,119}, {952,5492}, {1317,2771}
X(10105) = 28th HATZIPOLAKIS-MONTESDEOCA POINT
-
Barycentrics a (a^7 b^2-3 a^5 b^4+3 a^3 b^6-a b^8-2 a^7 b c-6 a^6 b^2 c+3 a^5 b^3 c+13 a^4 b^4 c-8 a^2 b^6 c-a b^7 c+b^8 c+a^7 c^2-6 a^6 b c^2-16 a^5 b^2 c^2+9 a^4 b^3 c^2+15 a^3 b^4 c^2-2 a^2 b^5 c^2-b^7 c^2+3 a^5 b c^3+9 a^4 b^2 c^3+12 a^3 b^3 c^3+10 a^2 b^4 c^3+a b^5 c^3-3 b^6 c^3-3 a^5 c^4+13 a^4 b c^4+15 a^3 b^2 c^4+10 a^2 b^3 c^4+2 a b^4 c^4+3 b^5 c^4-2 a^2 b^2 c^5+a b^3 c^5+3 b^4 c^5+3 a^3 c^6-8 a^2 b c^6-3 b^3 c^6-a b c^7-b^2 c^7-a c^8+b c^8) : :
Let I be the incenter of a triangle ABC, and
A'B'C' = intouch triangle (the pedal triangle of I)
A''B''C'' = cevian triangle of I
Ab = orthogonal projection of A'' on IB, and define Bc and Ca cyclically
Ac = orthogonal projection of A'' on IC, and define Ba and Cb cyclically
A'b = orthogonal projection of A'' on IB', and define B'c and C'a cyclically
A'c = orthogonal projection of A'' on IC', and define B'a and C'b cyclically
(Nab) = nine-point cricle of A''AbA'b, and define (Nbc) and (Nca) cyclically
(Nac) = nine-point cricle of A''AcA'c, and define (Nba) and (Ncb) cyclically
Ra = radical axis of (Nab) and (Nac) = perpendicular bisector of segment NabNac.
The lines Ra, Rb, Rc concur in X(10105). Also, the parallels to Ra, Rb, Rc through A', B', C, respectively, concur in X(942); and the parallels to Ra, Rb, Rc through A'', B'', C'', respectively, concur in X(500). (Antreas Hatzipolakis and Angel Montesdeoca, August 8, 2016; see Hyacinthos 23972)
-
X(10106) = 29th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 2 a^4-a^3 (b+c)+a (b-c)^2 (b+c)-(b^2-c^2)^2-a^2 (b^2-6 b c+c^2) : :
X(10106) = (2R - r)*X(1) + r*X(4)
Let I be the incenter of a triangle ABC, and
A'B'C' = intouch triangle (the pedal triangle of I)
H' = X(4)-of-A'B'C'
Ab = orthogonal projection of A on H'B', and define Bc and Ca cyclically
Ac = orthogonal projection of A on H'C', and define Ba and Cb cyclically
La = Euler line of AAbAc, and define Lb and Lc cyclically
Pa = line through A'' parallel to La, and define Pb and Pc cyclically
The lines La, Lb, Lc concur in X(10106). Let
Qa = line through A parallel to La, and define Qb and Qc cyclically
Ra = line through A' parallel to La, and define Rb and Rc cyclically
The lines La, Lb, Lc concur in X(5836), the midpoint of X(8) and X(65). The lines Qa, Qb, Qc concur in X(8), and the lines Ra, Rb, Rc concur in X(145). (Antreas Hatzipolakis and Angel Montesdeoca, August 9, 2016; see Hyacinthos 23990)
-
X(10107) = 30th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics a(3a^2(b+c)-2a b c-3b^3+5b c(b+c)-3c^3) : :
X(10107) = 3(4R + r)*X(7) + (4R-3r)*X(8)
Let I be the incenter of a triangle ABC, and
A'B'C' = intouch triangle (the pedal triangle of I)
H' = X(4)-of-A'B'C'
Ab = orthogonal projection of A on H'B', and define Bc and Ca cyclically
Ac = orthogonal projection of A on H'C', and define Ba and Cb cyclically
La = Euler line of AAbAc, and define Lb and Lc cyclically
Ia = excenter of ABC, and define Ib and Ic cyclically
Pa = orthogonal projection of Ia on BC, and define Pb and Pc cyclically
A* = midpoint of AbAc, and define B* and C* cyclically
Qa = line through A* parallel to La, and define Qb and Qc cyclically
The lines Qa, Qb, Qc concur in X(10107). Let
Qa = line through Ia parallel to La, and define Qb and Qc cyclically
The lines Qa, Qb, Qc concur in X(2136), which is the X(145)-Ceva conjugate of X(1).
(Antreas Hatzipolakis and Angel Montesdeoca, August 10, 2016; see Hyacinthos 23998)
-
X(10108) = 31st HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics a (a^4 (b-c)^2-a^2 (b^4+7 b^3 c+16 b^2 c^2+7 b c^3+c^4)-a (b^5+b^4 c+8 b^3 c^2+8 b^2 c^3+b c^4+c^5)+b c (b^2-c^2)^2+a^3 (b^3-7 b^2 c-7 b c^2+c^3)) : :
Let I be the incenter of a triangle ABC, and
A'B'C' = cevian triangle of X(I)
Ab = orthogonal projection of A' on BB', and define Bc and Ca cyclically
Ac = orthogonal projection of A' on CC', and define Ba and Cb cyclically
Abc = orthogonal projection of Ab on CC', and define Bca and Cab cyclically
Acb = orthogonal projection of Ac on BB', and define Bac and Cba cyclically
La = Euler line of IAbcAcb, and define Lb and Lc cyclically
The lines La, Lb, Lc concur in X(10108). (Antreas Hatzipolakis and Angel Montesdeoca, August 10, 2016; see Hyacinthos 23949)
-
X(10122) = 32nd HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics a (a^4 (b-c)^2-a^5 (b+c)+(b^2-c^2)^2 (b^2-b c+c^2)-a (b-c)^2 (b^3+4 b^2 c+4 b c^2+c^3)+a^3 (2 b^3+3 b^2 c+3 b c^2+2 c^3)+a^2 (-2 b^4+3 b^3 c+6 b^2 c^2+3 b c^3-2 c^4)) : :
X(10122) = (r+2R)*X(1) - r*X(21) = (r+4R)*X(7) - (r+2R)*X(79)
Let ABC be a triangle, and let
A'b = orthogonal projection of A on the external bisector of angle ABC
A'c = orthogonal projection of A on the external bisector of angle ACB
Ea = Euler line of AA'bA'c, and define Eb and Ec cyclically
Ia = A-excenter of ABC, and define Ib and Ic cyclically
A'B'C' = intouch triangle (the pedal triangle of the incenter)
A'' = orthogonal projection of IA on B'C', and define B'' and C'' cyclically
Pa = line through A'' parallel to Ea, and define Pb and Pc cyclically
A''' = orthogonal projections of A' on IbIc, and define B''' and C''' cyclically
Qa = line through A''' parallel to Ea, and define Qb and Qc cyclically
The lines Pa, Pb, Pc concur in X(10122). The lines Qa, Qb, Qc concur in X(10123). The lines Ea, Eb, Ec concur in X(442). (Antreas Hatzipolakis and Angel Montesdeoca, August 14, 2016. See Hyacinthos 24025 and Hyacinthos 24015.
-
X(10123) = 33rd HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 2 a^7-a^6 (b+c)-(b-c)^4 (b+c)^3+5 a b c (b^2-c^2)^2+a^3 (b+c)^2 (2 b^2-3 b c+2 c^2)-a^5 (4 b^2+6 b c+4 c^2)+a^4 (b^3-4 b^2 c-4 b c^2+c^3)+a^2 (b-c)^2 (b^3+6 b^2 c+6 b c^2+c^3) : :
X(10123) = (r+3R)*X(21) - (r+4R)*X(142) = (2r+R)*X(35) - (2r+5R)*X(79)
For a construction and references, see X(10122).
-
X(10124) = 34th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 10 a^4-17 a^2 (b^2+c^2)+7 (b^2-c^2)^2 : :
X(10124) = 5X(3) + 7X(5) = 7X(2) + X(3)
Let O be the circumcenter and N the nine-point center of a triangle ABC. Let
Ma = midpoint of OA, and define Mb and Mc cyclically
Aa = orthogonal projection of Ma on NA, and define Bb and Cc cyclically
Ba = orthogonal projection of Mb on NA, and define Cb and Ac cyclically
Ca = orthogonal projection of Mc on NA, and define Cb and Ac cyclically
M1 = midpoint of NA, and define M2 and M3 cyclically
A1 = orthogonal projection of M1 on OA, and define A2 and A3 cyclically
B1 = orthogonal projection of M2 on OA, and define B2 and B3 cyclically
C1 = orthogonal projection of M3 on OA, and define C2 and C3 cyclically
Oa = circumcenter of AaAbAc, and define Ob and Oc cyclically
O1 = circumcenter of A1A2A3, and define O2 and O3 cyclically
La = Euler line of OaO2O3, and define Lb and Lc cyclically
L1 = Euler line of O1ObOC, and define L2 and L3 cyclically
Then L1, L2, L3 concur in X(10124), which lies on the Euler line, and La, Lb, Lc concur in X(140). (Antreas Hatzipolakis and Angel Montesdeoca, August 14, 2016. See Hyacinthos 24036.
-
X(10189) = CENTER OF THE CENTROIDAL CONIC OF THE SCHRÖTER TRIANGLE
Barycentrics (3*a^4-3*(b^2+c^2)*a^2-b^4+5*b^2*c^2-c^4)*(b^2-c^2) : :
Let ABC be a triangle, P a point, DEF the cevian triangle of P, and A'B'C' the Schröeter triangle. As P moves on GK, the centroids of the triangles DB'C', EC'A', FA'C' are aligned' and their line envelops a conic having center X(10189). This conic is given by the barycentric equation
(a^2-b^2) (a^2-c^2)((a^2-b^2) (a^2-c^2) (4 a^4-4 a^2 (b^2+c^2)+9 b^4-14 b^2 c^2+9 c^4) x^2-6 (b^2-c^2)^2 (3 a^4-3 a^2 (b^2+c^2)+2 b^4-b^2 c^2+2 c^4) y z) + cyclic sum =0.
See Angel Montesdeoca HG131223. (December 15, 2023.)
-
X(10203) = X(5)-OF-ANTIPEDAL-TRIANGLE OF X(54)
Barycentrics a^2 (a^14-4 a^12 (b^2+c^2)-4 a^8 b^2 c^2 (b^2+c^2)-b^2 c^2 (b^2-c^2)^4 (b^2+c^2)+a^10 (5 b^4+8 b^2 c^2+5 c^4)-a^2 (b^2-c^2)^2 (b^8-5 b^6 c^2-7 b^4 c^4-5 b^2 c^6+c^8)-5 a^6 (b^8-b^6 c^2-b^4 c^4-b^2 c^6+c^8)+a^4 (4 b^10-11 b^8 c^2-5 b^6 c^4-5 b^4 c^6-11 b^2 c^8+4 c^10)) : :
X(10203) = 4R²X(3) - |OH²|2X(54)
X(10203) is the nine-point center of the antipedal triangle of the Kosnita point. (Tran Quang Hung and Angel Montesdeoca, August 31, 2016; see Hyacinthos #24193):
[Tran Quang Hung]:
1. The centroid of antipedal triangle of symmedian point of a triangle lies on Euler line of this triangle.
2. The NPC center of the antipedal triangle of Kosnita point of a triangle lies on the line connecting this Kosnita point and the circumcenter of this triangle.
3. The Euler line of triangle ABC bisects the segment connecting symmedian point L of ABC and symmedian point of antipedal triangle of L with respect to ABC.
4. The line connecting the NPC center of the antipedal triangle of N of a triangle passes through circumcenter of this triangle.
[Antreas Hatzipolakis]:
Questions:
Which are the points 1,2,3 and which is the NPC of the antipedal triangle of N of 4?
[Angel montesdeoca]:
*** 1. The centroid of antipedal triangle of symmedian point of a triangle is the circumcenter
*** 2. The NPC center of the antipedal triangle of Kosnita point of a triangle is W2 = 4R^2 X(3)- |OH|^2 X(54)
W2 = ( a^2 (a^14-4 a^12 (b^2+c^2)-4 a^8 b^2 c^2 (b^2+c^2)-b^2 c^2 (b^2-c^2)^4 (b^2+c^2)+a^10 (5 b^4+8 b^2 c^2+5 c^4)-a^2 (b^2-c^2)^2 (b^8-5 b^6 c^2-7 b^4 c^4-5 b^2 c^6+c^8)-5 a^6 (b^8-b^6 c^2-b^4 c^4-b^2 c^6+c^8)+a^4 (4 b^10-11 b^8 c^2-5 b^6 c^4-5 b^4 c^6-11 b^2 c^8+4 c^10)) : ... : ...),
with (6-9-13)-search numbers (253.269435013061,-86. 4545432539761,-53. 3997755790604).
*** 3. The Euler line of triangle ABC bisects the segment connecting symmedian point L of ABC and symmedian point of antipedal triangle of L with respect to ABC at
W3 = (a^2 (a^8-b^8+12 a^4 b^2 c^2-7 b^6 c^2+24 b^4 c^4-7 b^2 c^6-c^8-4 a^6 (b^2+c^2)+a^2 (4 b^6+3 b^4 c^2+3 b^2 c^4+4 c^6)) : ... : ... ),
with (6-9-13)-search numbers (3.22662598230530,2. 34859413859511,0. 525502701816087 )
On lines: {2,3}, {6235,9871}, {8546,9830}
*** The NPC of the antipedal triangle of N of 4. is W4 on Euler line of ABC:
W4 = (2 a^16-13 a^14 (b^2+c^2)-(b^2-c^2)^6 (b^4+c^4)+a^12 (37 b^4+50 b^2 c^2+37 c^4)+3 a^2 (b^2-c^2)^4 (b^6+b^4 c^2+b^2 c^4+c^6)-a^10 (59 b^6+71 b^4 c^2+71 b^2 c^4+59 c^6)+a^4 (b^2-c^2)^2 (3 b^8-4 b^6 c^2-7 b^4 c^4-4 b^2 c^6+3 c^8)+a^8 (55 b^8+34 b^6 c^2+32 b^4 c^4+34 b^2 c^6+55 c^8)+a^6 (-27 b^10+13 b^8 c^2+5 b^6 c^4+5 b^4 c^6+13 b^2 c^8-27 c^10) : ... :... ),
with (6-9-13)-search numbers (14.263493810476143237204984, )
On lines: {2,3}, {252,1263}
-
X(10204) = MIDPOINT OF X(6) AND X(6)-OF-ANTIPEDAL-TRIANGLE OF X(6)
Barycentrics a^2 (a^8-b^8+12 a^4 b^2 c^2-7 b^6 c^2+24 b^4 c^4-7 b^2 c^6-c^8-4 a^6 (b^2+c^2)+a^2 (4 b^6+3 b^4 c^2+3 b^2 c^4+4 c^6)) : :
In the plane of a triangle ABC, let
K = X(6)
K' = X(6)-of-antipedial-triangle of X(6)
X(10204) = midpoint of K and K'. X(10204) lies on the Euler line of ABC. (Tran Quang Hung and Angel Montesdeoca, August 31, 2016; see Hyacinthos #24193).
-
X(10205) = (Name pending)
Barycentrics (2 a^16-13 a^14 (b^2+c^2)-(b^2-c^2)^6 (b^4+c^4)+a^12 (37 b^4+50 b^2 c^2+37 c^4)+3 a^2 (b^2-c^2)^4 (b^6+b^4 c^2+b^2 c^4+c^6)-a^10 (59 b^6+71 b^4 c^2+71 b^2 c^4+59 c^6)+a^4 (b^2-c^2)^2 (3 b^8-4 b^6 c^2-7 b^4 c^4-4 b^2 c^6+3 c^8)+a^8 (55 b^8+34 b^6 c^2+32 b^4 c^4+34 b^2 c^6+55 c^8)+a^6 (-27 b^10+13 b^8 c^2+5 b^6 c^4+5 b^4 c^6+13 b^2 c^8-27 c^10) : :
In the plane of a triangle ABC, let
N = X(5)
X(10205) = X(5)-of-antipedial-triangle of X(5)-of-[triangle, pending]; X(10205) lies on the Euler line of ABC. (Tran Quang Hung and Angel Montesdeoca, August 31, 2016; see Hyacinthos #24193).
X(10205) lies on these lines: {2,3}, {252,1263}
X(10205) = anticomplement of X(5501).
-
X(10206) = HUNG-MONTESDEOCA RADICAL CENTER
Barycentrics a (a^2 (b+c)+2 a b c-(b-c)^2 (b+c)) (a^6-2 a^5 (b+c)-a^4 (b^2+3 b c+c^2)+4 a^3 (b^3+b^2 c+b c^2+c^3)-a^2 (b+c)^2 (b^2-6 b c+c^2)-2 a (b-c)^2 (b+c)^3+(b^2-c^2)^2 (b^2-b c+c^2)) : :
In the plane of a triangle ABC, let
HaHbHc = orthic triangle.
Ja = incenter of AHbHc, and define Jb and Jc cyclically
Ab = JbJc∩CA, and define Bc and Ca cyclically
Ac = JcJa∩BA, and define Ba and Cb cyclically
The points Jb,Jc,Ca,Ba lie on a circle, (Oa); define (Ob) and (Oc) cyclically.
X(10206) = radical center of (Oa), (Ob), (Oc); X(10206) lies on the Euler line of OaObOc.
Let Go = X(5902) = X(2)-of-OaObOc and Ho = X(4)-of-OaObOc.
X(10206) = 3[(r + 2R)2 - s2]Go + 2s2Ho.
(Tran Quang Hung and Angel Montesdeoca, August 31, 2016; see Hyacinthos #24219).
-
X(10207) = HUNG-MONTESDEOCA PERSPECTOR
Barycentrics a (2 a^7 (b^2+b c+c^2) +7 a^6 b c (b+c)-2 a^5 (3 b^4+3 b^3 c-b^2 c^2+3 b c^3+3 c^4) -a^4 b c (15 b^3+17 b^2 c+17 b c^2+15 c^3)+2 a^3 (b+c)^2 (3 b^4-3 b^3 c-4 b^2 c^2-3 bc^3+3 c^4)+9 a^2 b (b-c)^2 c (b+c)^3-2 a (b^2-c^2)^2 (b^4+b^3 c-3 b^2 c^2+bc^3+c^4)-b (b-c)^4 c (b+c)^3) : :
In the plane of a triangle ABC, let
HaHbHc = orthic triangle
Ja = incenter of AHbHc, and define Jb and Jc cyclically
Ab = JbJc∩CA, and define Bc and Ca cyclically
Ac = JcJa∩BA, and define Ba and Cb cyclically
The points Jb,Jc,Ca,Ba lie on a circle, (Oa); define (Ob) and (Oc) cyclically.
The triangles JaJbJc and OaObOc are perspective, and their perspector is X(10207); see X(10206). (Tran Quang Hung and Angel Montesdeoca, August 31, 2016; see Hyacinthos #24219).
-
X(10208) = 1st HUNG-MONTESDEOCA-MOSES
Barycentrics (2 a^7 (b+c)^3-(b-c)^4 (b+c)^6-2 a (b-c)^4 (b+c)^3 (b^2+3 b c+c^2)+a^8 (b^2+6 b c+c^2)-2 a^5 (b+c)^3 (3 b^2-b c+3 c^2)+2 a^3 (b-c)^2 (b+c)^3 (3 b^2+4 b c+3 c^2)-a^4 b^2 c^2 (11 b^2+18 b c+11 c^2)-2 a^6 (b^4+5 b^3 c+4 b^2 c^2+5 b c^3+c^4)+a^2 (b^2-c^2)^2 (2 b^4+6 b^3 c+19 b^2 c^2+6 b c^3+2 c^4) : :
X(10208) = 3 X[5947] - 2 X[5953]
In the plane of a triangle ABC, let
FaFbFc = Feuerbach triangle.
U = projection of A on line FbFc, and define V and W cyclically
The lines UFa, VFb, WFc concur in X(10208); see Hyacinthos #23529).
-
X(10209) = 2nd HUNG-MONTESDEOCA-MOSES POINT
Barycentrics a^11 (b-c)^2-(b-c)^6 (b+c)^7-a (b-c)^4 (b+c)^6 (b^2-7 b c+c^2)+a^10 (b^3-5 b^2 c-5 b c^2+c^3)-a^9 (5 b^4+5 b^3 c+12 b^2 c^2+5 b c^3+5 c^4)+a^8 (-5 b^5+b^4 c+b c^4-5 c^5)+a^3 (b^2-c^2)^2 (5 b^6-4 b^5 c-42 b^4 c^2-59 b^3 c^3-42 b^2 c^4-4 b c^5+5 c^6)+a^2 (b-c)^2 (b+c)^3 (5 b^6+12 b^5 c-8 b^4 c^2-26 b^3 c^3-8 b^2 c^4+12 b c^5+5 c^6)+a^7 (10 b^6+22 b^5 c+25 b^4 c^2+14 b^3 c^3+25 b^2 c^4+22 b c^5+10 c^6)+a^6 (10 b^7+28 b^6 c+45 b^5 c^2+33 b^4 c^3+33 b^3 c^4+45 b^2 c^5+28 b c^6+10 c^7)+a^5 (-10 b^8-16 b^7 c+22 b^6 c^2+57 b^5 c^3+54 b^4 c^4+57 b^3 c^5+22 b^2 c^6-16 b c^7-10 c^8)-2 a^4 (5 b^9+20 b^8 c+20 b^7 c^2-14 b^6 c^3-41 b^5 c^4-41 b^4 c^5-14 b^3 c^6+20 b^2 c^7+20 b c^8+5 c^9) : :
X(10209) = 2 X[442] - 3 X[5947]
In the plane of a triangle ABC, let
FaFbFc = Feuerbach triangle.
U = AFbFc-isogonal conjugates of Fa, and define V and W cyclically
The lines UFa, VFb, WFc concur in X(10209); see Hyacinthos #23530. The construction was originally posted in ADGEOM #1550 by Tran Quang Hung, 9/1/2014.
-
X(10212) = 35th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics -6 a^10 + 13 a^8 (b^2 + c^2) - (b^2 - c^2)^4 (b^2 + c^2) - 2 a^6 (b^4 + 13 b^2 c^2 + c^4) + a^2 (b^2 - c^2)^2 (8 b^4 + 13 b^2 c^2 + 8 c^4) + a^4 (-12 b^6 + 13 b^4 c^2 + 13 b^2 c^4 - 12 c^6) : :
Let O be the circumcenter of a triangle ABC, and let
Na = X(5)-of-OBC, and define Nb and Nc cyclically
Aa = orthogonal projection of Na on OA, and define Ab and Ac cyclically
Ba = orthogonal projection of Nb on OA, and define OB and OC cyclically
Ca = orthogonal projection of Nc on OA, and define OB and OC cyclically
Oa = circumcenter of AaAbAc, and define Ob and Oc cyclically.
X(10212) = X(5)-of-OaObOc; X(10212) lies on the Euler line of ABC. (Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos #24189)
-
X(10213) = 36th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics (a^2-b^2-c^2) (2 a^20-11 a^18 (b^2+c^2)-(b^2-c^2)^8 (b^4+b^2 c^2+c^4)+a^16 (25 b^4+42 b^2 c^2+25 c^4)+a^2 (b^2-c^2)^6 (8 b^6+7 b^4 c^2+7 b^2 c^4+8 c^6)-a^14 (29 b^6+61 b^4 c^2+61 b^2 c^4+29 c^6)+6 a^12 (2 b^8+7 b^6 c^2+9 b^4 c^4+7 b^2 c^6+2 c^8)-a^4 (b^2-c^2)^4 (26 b^8+12 b^6 c^2+13 b^4 c^4+12 b^2 c^6+26 c^8)-a^8 (b^2-c^2)^2 (44 b^8+31 b^6 c^2+35 b^4 c^4+31 b^2 c^6+44 c^8)+a^10 (19 b^10-26 b^8 c^2-20 b^6 c^4-20 b^4 c^6-26 b^2 c^8+19 c^10)+a^6 (b^2-c^2)^2 (45 b^10-11 b^8 c^2+9 b^6 c^4+9 b^4 c^6-11 b^2 c^8+45 c^10)) : :
In the plane of a triangle ABC, let
O = circumcenter, X(3)
N = nine-point center, X(5)
Na = N-of-OBC, and define Nb and Nc cyclically
Aa = orthogonal projection of Na on OA, and define Ab and Ac cyclically
Ba = orthogonal projection of Nb on OA, and define OB and OC cyclically
Ca = orthogonal projection of Nc on OA, and define OB and OC cyclically
Ea = Euler line of AaAbAc, and define Eb and Ec cyclically
A' = Eb∩Ec, and define B' and C' cyclically
Then ABC and A'B'C' are parallelogic, and
X(10213) = (A'B'C',ABC)-parallelogic center
X(1141) = (ABC,A'B'C')-parallelogic center.
(Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos #24183).
-
X(10221) = HATZIPOLAKIS-MONTESDEOCA-EULER-PEDAL POINT
Barycentrics a2/3b2/3c2/3SBSC - a2SA(SASBSC)1/3 : :
X(10221) = -2(SASBSC)1/3*X(3) + a2/3b2/3c2/3*X(4)
Suppose that W is a triangle center on the Euler line of a triangle ABC. Let A'B'C' be the pedal triangle of W. Then W(ABC) = W(A'B'C') if and only if W = X(10221). (Regarding the notation, recall that a triangle center is a function defined on a set of triangles, so that the notation W(T) is analogous to the notation f(x); i.e., W-of-T.) (Antreas Hatzipolakis and Angel Montesdeoca, September 13, 2016.) See 24354 and
HG100916
X(10221) lies on these lines: {2,3}
-
X(10223) = 37th HATZIPOLAKIS-MONTESDEOCA POINT
Barycentrics 2 a^14 b^2-9 a^12 b^4+15 a^10 b^6-10 a^8 b^8+3 a^4 b^12-a^2 b^14+2 a^14 c^2-6 a^12 b^2 c^2+5 a^10 b^4 c^2-3 a^8 b^6 c^2+10 a^6 b^8 c^2-14 a^4 b^10 c^2+7 a^2 b^12 c^2-b^14 c^2-9 a^12 c^4+5 a^10 b^2 c^4+2 a^8 b^4 c^4-8 a^6 b^6 c^4+19 a^4 b^8 c^4-15 a^2 b^10 c^4+6 b^12 c^4+15 a^10 c^6-3 a^8 b^2 c^6-8 a^6 b^4 c^6-16 a^4 b^6 c^6+9 a^2 b^8 c^6-15 b^10 c^6-10 a^8 c^8+10 a^6 b^2 c^8+19 a^4 b^4 c^8+9 a^2 b^6 c^8+20 b^8 c^8-14 a^4 b^2 c^10-15 a^2 b^4 c^10-15 b^6 c^10+3 a^4 c^12+7 a^2 b^2 c^12+6 b^4 c^12-a^2 c^14-b^2 c^14 : :
Let A'B'C' be the pedal triangle of a point P in the plane of a triangle ABC. Let
A'' = reflection of A' in the Euler line, and define B'' and C'' cyclically
Na = X(5)-of-A''B''C'', and define Nb and Nc cyclically
The locus of P such that Na, Nb, Nc are collinear is the union of the cubic K187 and a circum-quintic that passes through X(74) and X(1304). If P = X(4), the line NaNbNc meets the Euler line in X(10223). (Antreas Hatzipolakis and Angel Montesdeoca, September 14, 2016). See
Hyacinthos #24377).
-
X(10227) = HUNG-MONTESDEOCA-EULER POINT
Barycentrics 2 a^28 -19 a^26 (b^2+c^2)+a^24 (77 b^4+142 b^2 c^2+77 c^4) -2 a^22 (83 b^6+215 b^4 c^2+215 b^2 c^4+83 c^6)+4 a^20 (44 b^8+161 b^6 c^2+221 b^4 c^4+161 b^2 c^6+44 c^8)+a^18 (11 b^10-421 b^8 c^2-744 b^6 c^4-744 b^4 c^6-421 b^2 c^8+11 c^10)+a^16 (-297 b^12-22 b^10 c^2+91 b^8 c^4+144 b^6 c^6+91 b^4 c^8-22 b^2 c^10-297 c^12)+2 a^14 (198 b^14+54 b^12 c^2+95 b^10 c^4+75 b^8 c^6+75 b^6 c^8+95 b^4 c^10+54 b^2 c^12+198 c^14)-2 a^12 (99 b^16-20 b^14 c^2+41 b^12 c^4-6 b^10 c^6+3 b^8 c^8-6 b^6 c^10+41 b^4 c^12-20 b^2 c^14+99 c^16)-a^10 (77 b^18-131 b^16 c^2+82 b^14 c^4+42 b^12 c^6+29 b^10 c^8+29 b^8 c^10+42 b^6 c^12+82 b^4 c^14-131 b^2 c^16+77 c^18)+a^8 (b^2-c^2)^2 (187 b^16-120 b^14 c^2+82 b^12 c^4+56 b^10 c^6+87 b^8 c^8+56 b^6 c^10+82 b^4 c^12-120 b^2 c^14+187 c^16)-2 a^6 (b^2-c^2)^4 (67 b^14-5 b^12 c^2+26 b^10 c^4+22 b^8 c^6+22 b^6 c^8+26 b^4 c^10-5 b^2 c^12+67 c^14)+2 a^4 (b^2-c^2)^6 (26 b^12+6 b^10 c^2+5 b^8 c^4+5 b^4 c^8+6 b^2 c^10+26 c^12)-a^2 (b^2-c^2)^8 (11 b^10+3 b^8 c^2-6 b^6 c^4-6 b^4 c^6+3 b^2 c^8+11 c^10)+(b^2-c^2)^12 (b^2+c^2)^2 ) ) : :
Let N be the nine-point center of a triangle ABC. Let A'B'C' be the circumcevian triangle of N, and let A''B''C'' be the pedal triangle of N with respect to A'B'C'. The Euler lines of AB''C'', B'C''A'', C'A''B'' concur in X(10227). (Tran Quang Hung and Angel Montesdeoca, September 14, 2016). See
Hyacinthos #24387).
-
X(10228) = HUNG-MONTESDEOCA CENTER OF SIMILITUDE
Barycentrics
a^2 (a^26-8 a^24 (b^2+c^2)+28 a^22 (b^2+c^2)^2-6 a^20 (9 b^6+28 b^4 c^2+28 b^2c^4+9 c^6)+a^18 (53 b^8+277 b^6 c^2+406 b^4 c^4+277 b^2 c^6+53 c^8)+a^16 (6 b^10-273 b^8 c^2-499 b^6 c^4-499 b^4 c^6-273 b^2 c^8+6 c^10)+a^14 (-96 b^12+184 b^10 c^2+307 b^8 c^4+386 b^6 c^6+307 b^4 c^8+184 b^2 c^10-96 c^12)+2 a^12 (66 b^14-56 b^12 c^2-9 b^10 c^4-38 b^8 c^6-38 b^6 c^8-9 b^4 c^10-56 b^2 c^12+66 c^14) -a^10 (69 b^16+6 b^14 c^2+97 b^12 c^4+43 b^10 c^6+5 b^8 c^8+43 b^6 c^10+97 b^4 c^12+6 b^2 c^14+69 c^16)-a^8 (28 b^18-238 b^16 c^2+176 b^14 c^4-11 b^12c^6+63b^10 c^8+63 b^8 c^10-11 b^6 c^12+176 b^4 c^14-238 b^2 c^16+28 c^18)+a^6 (b^2-c^2)^2 (68 b^16-256 b^14 c^2+89 b^12 c^4+65 b^10 c^6+97 b^8 c^8+65 b^6 c^10+89 b^4 c^12-256 b^2 c^14+68 c^16)-a^4 (b^2-c^2)^4 (46 b^14-120 b^12 c^2+26 b^10 c^4+73 b^8 c^6+73 b^6 c^8+26 b^4 c^10-120 b^2 c^12+46 c^14) +a^2 (b^2-c^2)^6 (15 b^12-29 b^10 c^2+16 b^8 c^4+32 b^6 c^6+16 b^4 c^8-29 b^2 c^10+15 c^12)-(b^2-c^2)^8 (2 b^10-3 b^8 c^2+5 b^6 c^4+5 b^4 c^6-3 b^2 c^8+2 c^10) ) : :
Let N be the nine-point center of a triangle ABC. Let A'B'C' be the circumcevian triangle of N, and let A''B''C'' be the pedal triangle of N with respect to A'B'C'. The triangle A''B''C'' is similar to ABC, and the center of similitude is X(10228). (Tran Quang Hung and Angel Montesdeoca, September 14, 2016). See
Hyacinthos #24387).
-
X(10282) = X(3)X(64)∩X(51)X(54)
Barycentrics a^2 (2 a^8-5 a^6 (b^2+c^2)+a^4 (3 b^4+4 b^2 c^2+3 c^4)+a^2 (b^2-c^2)^2 (b^2+c^2)-(b^2-c^2)^2 (b^4+c^4)) : :
X(10282) = 5 X(3) - X(64)
Let O be the circumcenter of a triangle ABC, and let
Oa = circumcenter of OBC, and define Ob and OC cyclically
N1 = nine-point center of OObOC, and define N2 and N3 cyclically.
Then ABC and N1N2N3 are orthologic triangles, and X(10282) = (N1N2N3,ABC)-orthologic center, and X(74) = (ABC,N1N2N3)-othologic center. X(10282) lies on the circumcircle of N1N2N3. See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos #24665.
-
X(10284) = X(1)X(3)∩X(5)X(2802)
Barycentrics a (a^5 (b+c) -a^4 (b^2+6 b c+c^2) -a^3 (2 (b^3+c^3)-7 bc(b+c)) +2 a^2 (b^4+2 b^3 c-7 b^2 c^2+2 b c^3+c^4)+a (b-c)^2 (b^3-6 b c(b+c)+c^3)-(b-c)^4 (b+c)^2) : :
Let A1B1C1 be the intouch triangle of a triangle ABC, and let
A2 = reflection of A1 in X(1), and define B2 and C2 cyclically
A3 = reflection of A in A2, and define B3 and C3 cyclically.
Then X(10284) = nine-point center of A3B3C3. See Tran Quang Hung and Angel Montesdeoca, Hyacinthos #24438.
-
X(10287) = X(3)X(2575)∩X(5)X(523)
Barycentrics a^2 (b^4 (a^2-b^2) (-a^2+b^2-a c-c^2) (-a^2+b^2+a c-c^2) (-a^4+2 a^2 b^2-b^4-a^2 c^2-b^2 c^2+2 c^4+c^2 (-a^2-b^2+c^2) J)-c^4 (-a^2+c^2) (-a^2-a b-b^2+c^2) (-a^2+a b-b^2+c^2) (-a^4-a^2 b^2+2 b^4+2 a^2 c^2-b^2 c^2-c^4+b^2 (-a^2+b^2-c^2) J)) : : , where J = |OH|/R (Peter Moses, October 23, 2016)
Let H be the orthocenter of a triangle ABC. Let La be the Euler line of AHX(1113), and define Lb and Lc cyclically. The lines La, Lb, Lc concur in X(10287). See X(10288) and Seiichi Kirikami and Angel Montesdeoca, 24541 and 24545.
-
X(10288) = X(3)X(2574)∩X(5)X(523)
Barycentrics a^2 (b^4 (a^2-b^2) (-a^2+b^2-a c-c^2) (-a^2+b^2+a c-c^2) (-a^4+2 a^2 b^2-b^4-a^2 c^2-b^2 c^2+2 c^4-c^2 (-a^2-b^2+c^2) J)-c^4 (-a^2+c^2) (-a^2-a b-b^2+c^2) (-a^2+a b-b^2+c^2) (-a^4-a^2 b^2+2 b^4+2 a^2 c^2-b^2 c^2-c^4-b^2 (-a^2+b^2-c^2) J)) : : , where J = |OH|/R (Peter Moses, October 23, 2016)
Let H be the orthocenter of a triangle ABC. Let La be the Euler line of AHX(1114), and define Lb and Lc cyclically. The lines La, Lb, Lc concur in X(10288).
See X(10287) and Seiichi Kirikami and Angel Montesdeoca, 24541 and 24545.
-
X(10293) = PERSPECTOR OF ABC AND MID-TRIANGLE OF ORTHOCENTROIDAL AND ANTI-ORTHOCENTROIDAL TRIANGLES
Barycentrics 1/[a^8 - 2a^6(b^2 + c^2) + 11a^4b^2c^2 + 2a^2(b^2 + c^2)(b^4 - 4b^2c^2 + c^4) - (b^2 - c^2)^2(b^4 + 5b^2c^2 + c^4)] : :
Let ABC be a triangle and HaHbHc the orthic triangle. The segment AHa has two trisectors; let A' be the trisector closer to A. Let (Ha) be the (rectangular) hyperbola through A, A', X(6), with asymptotes parallel to those of the Jerabek hyperbola. Let Ao be the center of (Ha), and define Bo and Co cyclically. The lines AAo, BBo, CCo concur in X(10293). Let Ta be the line through A tangent to (Ha), and define Tb and Tc cyclically. The lines Ta, Tb, Tc concur in X(3426). (Angel Montesdeoca, January 1, 2017)
An equation for the hyperbola (Ha), in barycentrics:
(2S^2-3SB SC) (c^2y^2-b^2z^2) + S^2(b^2-c^2)y z - b^2(2S^2-3SA SB)z x + c^2(2S^2-3SA SC)x y = 0. (Angel Montesdeoca, January 1, 2017)
-
X(10618) = (name pending)
Barycentrics (a (7a^5(b+c)+a^4(b^2+4b c+c^2)-a^3(14b^3+9b^2c+9b c^2+14c^3)-2a^2(b^4+5b^3c+7b^2c^2+5b c^3+c^4)+a(b-c)^2(7b^3+16b^2c+16b c^2+7c^3)+(b^2-c^2)^2(b^2+6b c+c^2)) : :
X(10618) = (2r^2+5rR+4s^2)*X(1) + r(2r+3R)*X(3)
Let I be the incenter of a triangle ABC, and let A'B'C' be the cevian triangle of I.
Let
Na = nine-point center of IB'C', and define Nb and Nc cyclically
N1 = nine-point center of INbNc, and define N2 and N3 cyclically.
X(10618) = nine-point center of N1N2N3. See Tran Quang Hung and Angel Montesdeoca, July 19, 2016: Hyacinthos 24692. )
-
X(10628) = INFINITY POINT OF X(54)X(74)
Barycentrics a^2 (a^12 (b^2+c^2) - 2 a^10 (2 b^4+b^2 c^2+2 c^4) + a^8 (5 b^6+2 b^4 c^2+2 b^2 c^4+5 c^6) + a^6 (-5 b^6 c^2+4 b^4 c^4-5 b^2 c^6) - a^4 (b^2-c^2)^2 (5 b^6+2 b^4 c^2+2 b^2 c^4+5 c^6) + a^2 (b^2-c^2)^2 (4 b^8+3 b^6 c^2+3 b^2 c^6+4 c^8) - (b^2-c^2)^4 (b^2+c^2)^3) : :
Let H = X(4) be the orthocenter of a triangle ABC, and suppose that t > 0. Let
A' = the point on line AH such that |A'A|/|A'H| = t, and define B' and C' cyclically
Ab = orthogonal projection of A' on AB, and define Bc and Ca cyclically
Ac = orthogonal project of A' on AC, and define Ba and Cb cyclically
Ea = Euler line of A'AbAc, and define Eb and Ec cyclically
E'a = Euler line of AAbAc, and define E'b and E'c cyclically.
The lines Ea, Eb, Ec concur in a point whose locus as t varies is the line W =X(4)X(54). The lines E'a, E'b, E'c concur in a point whose locuse as t varies is the line W' = X(4)X(74). The lines W and W' are parallel, and X(10628) is their point of intersection on the line at infinity. See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24703.
-
X(10683) = (name pending)
Barycentrics 2 a^10 + 4 a^9 (b+c) + a^8 (-9 b^2+2 b c-9 c^2) - 2 a^7 (8 b^3+7 b^2 c+7 b c^2+8 c^3) + a^6 (10 b^4-7 b^3 c-7 b c^3+10 c^4) + a^5 (24 b^5+15 b^4 c+11 b^3 c^2+11 b^2 c^3+15 b c^4+24 c^5) + 2 a^4 (2 b^6+6 b^5 c+3 b^4 c^2+6b^3 c^3+3 b^2 c^4+6 b c^5+2 c^6) - 2 a^3 (b-c)^2 (8 b^5+18 b^4 c+21 b^3 c^2+21 b^2 c^3+18 b c^4+8 c^5) - a^2 (b^2-c^2)^2 (12 b^4+11 b^3 c+6 b^2 c^2+11 b c^3+12 c^4) + a (b-c)^4 (b+c)^3 (4 b^2+3 b c+4 c^2) + (b^2-c^2)^4 (5 b^2+4 b c+5 c^2) : :
X(10683) = (3r^2+17rR+24R^2-7s^2)*X[2] - (r^2+5rR+6R^2-s^2)*X[3]
Let ABC be a triangle, and let
Fa = A-Feuerbach point, and define Fb and Fc cyclically
Oa = circumcenter of AFbFc, and define Ob and Oc cyclically.
Then X(10683) = centroid of OaObOc, and X(10683) lies on Euler line of triangle ABC. See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 24711 and Hyacinthos 24719.
-
X(10684) = (name pending)
Barycentrics a^10 (b^2+c^2) - a^8 (2 b^4+b^2 c^2+2 c^4) + a^6 (b^6+b^4c^2+b^2 c^4+c^6) - a^4 b^2 c^2 (b^4-b^2 c^2+c^4) + b^4 c^4 (b^2-c^2)^2 : :
Let ABC be a triangle with two Brocard points Ω1 and Ω2
A1B1C1 is cevian triangle of Ω1 and Ω1* is isogonal conjugate of Br1 wrt A1B1C1.
A2B2C2 is cevian triangle of Ω2 and Ω2* is isogonal conjugate of Ω2 wrt A2B2C2.
Then the lines Ω1Ω1* and Ω2Ω2* intersect on Euler of ABC.
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 24712.
-
X(10685) = (name pending)
Barycentrics a^10 (b^2+c^2) - a^8 (3 b^4+b^2 c^2+3 c^4) + 2 a^6 (b^6+b^4 c^2+b^2 c^4+c^6) + a^4 (-2 b^6 c^2+b^4 c^4-2 b^2 c^6) - a^2 b^2 c^2 (b^2-c^2)^2 (b^2+c^2)b^4 c^4 (b^2-c^2)^2 : :
Let ABC be a triangle with two Brocard points Ω1 and Ω2
A1B1C1 is anticevian triangle of Ω1 and Ω1* is isogonal conjugate of Ω1 wrt A1B1C1.
A2B2C2 is anticevian triangle of Ω2 and Ω2* is isogonal conjugate of Ω12 wrt A2B2C2.
Then the lines Ω1Ω1* andΩ2Ω2* intersect on Euler of ABC.
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 24717.
-
X(10688) = X(30)X(6344)∩X(265)X(6000)
Barycentrics (b^10-3 b^8 c^2+2 b^6 c^4+2 b^4 c^6-3 b^2 c^8+c^10+(-2 b^8+6 b^6 c^2-8 b^4 c^4+6 b^2 c^6-2 c^8) a^2+(-b^6-2 b^4 c^2-2 b^2 c^4-c^6) a^4+(5 b^4+3 b^2 c^2+5 c^4) a^6+(-4 b^2-4 c^2) a^8+a^10) / (a^2(4SA^2-b^2c^2) : :
Let ABC be a triangle with orthocenter H and circumcenter O, and let
da = reflection of Euler line of triangle AOH in line OH, and define db and dc cyclically
A' = db∩dc, and define B' and C' cyclically.
The triangle A'B'C' is perspective to ABC, and the perspector is X(10688). See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 24745.
-
X(10694) = EULER INTERCEPT OF X(880)X(1502)
Barycentrics b^4 c^4 (b^2-c^2)^2+2 b^2 c^2 (b^2-c^2)^2 (b^2+c^2) a^2+b^2 c^2 (b^4+b^2 c^2+c^4) a^4-(b^6+b^4 c^2+b^2 c^4+c^6)a^6-b^2 c^2 a^8+(b^2+c^2) a^10 : :
In the plane of a triangle ABC, let
Ω1 = 1st Brocard point
Ω2 = 2nd Brocard point
Ω1* = Orion transform of &Omega1
Ω2* = Orion transform of &Omega2.
X(10694) = Ω1Ω1*∩Ω2Ω2*, and X(10694) lies on the Euler line of ABC. (Orion transform is define just before X(2055).) See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 24769.
-
X(10980) = {X(10655),X(10656)}-HARMONIC CONJUGATE OF X(3062)
Barycentrics a( a^2 + 2a(b + c) - 3(b - c)^2) : :
Let MaMbMc be the medial triangle of the intouch triangle DEF. Let Γa be the circle, other than the circle with diameter ID, tangent to the incircle and passing through Mb and Mc. Define Γb and Γc cyclically. X(10980) is the radical center of Γa, Γb and Γc. (Angel Montesdeoca, October 2, 2020).
Ver HG031020
-
X(11008) = REFLECTION OF X(69) IN X(193)
Barycentrics 7 a^2-3 (b^2+c^2) : :
X(11008) = 9 X[2] - 10 X[6], 6 X[2] - 5 X[69], 4 X[6] - 3 X[69], 7 X[69] - 8 X[141], 7 X[6] - 6 X[141], 4 X[141] - 7 X[193], 3 X[2] - 5 X[193], 2 X[6] - 3 X[193], 19 X[6] - 18 X[597], 19 X[193] - 12 X[597], 11 X[69] - 12 X[599], 11 X[2] - 10 X[599], 11 X[6] - 9 X[599], 11 X[193] - 6 X[599]
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24817 (November 16, 2016).
-
X(11016) = (name pending)
Barycentrics a^16-3 a^14 b^2-a^12 b^4+14 a^10 b^6-20 a^8 b^8+9 a^6 b^10+3 a^4 b^12-4 a^2 b^14+b^16-3 a^14 c^2+16 a^10 b^4 c^2-10 a^8 b^6 c^2-18 a^6 b^8 c^2+17 a^4 b^10 c^2+a^2 b^12 c^2-3 b^14 c^2-a^12 c^4+16 a^10 b^2 c^4-3 a^8 b^4 c^4-18 a^6 b^6 c^4-13 a^4 b^8 c^4+21 a^2 b^10 c^4-2 b^12 c^4+14 a^10 c^6-10 a^8 b^2 c^6-18 a^6 b^4 c^6-14 a^4 b^6 c^6-18 a^2 b^8 c^6+19 b^10 c^6-20 a^8 c^8-18 a^6 b^2 c^8-13 a^4 b^4 c^8-18 a^2 b^6 c^8-30 b^8 c^8+9 a^6 c^10+17 a^4 b^2 c^10+21 a^2 b^4 c^10+19 b^6 c^10+3 a^4 c^12+a^2 b^2 c^12-2 b^4 c^12-4 a^2 c^14-3 b^2 c^14+c^16 : :
In the plane of a triangle ABC, let N = X(5) = nine-point center, ) = X(3) = circumcenter, and
Na = nine-point center of NBC, and define Nb and Nc cyclically
Oa = reflection of O in BC, and define Ob and Oc cyclically
Then NaNbNc are OaObOc are perspective, and X(11016) is their perspector. See Antreas Hatzipolakis, Peter Moses, and Angel Montesdeoca, Hyacinthos 24853 (November 21, 2016).)
-
X(11538) = X(324)X(9381)∩X(1370,10155)
Barycentrics (b^2-c^2)^6-4 (b^2-c^2)^4 (b^2+c^2) a^2+(5 b^8-2 b^6 c^2-7 b^4 c^4-2 b^2 c^6+5 c^8) a^4-4 b^2 c^2 (b^2+c^2) a^6+(-5 b^4-4 b^2 c^2-5 c^4) a^8+4 (b^2+c^2)a^10-a^12 : :
In the plane of a triangle ABC, let O = X(3) = circumcenter, N = X(5) = nine-point center, and
A' = reflection of O in BC, and define B' and C' cyclically
Nab = N(AOB'), and define Nbc and Nca cyclically
Nac = N(AOC'), and define Nba and Ncb cyclically
Oa = O(ANabNac), and define Ob and Oc cyclically
The triangles ABC and OaObOc are orthologic, and
X(11538) = ABC-to-OaObOc orthologic center; and X(5) = OaObOc-to-ABC orthologic center. See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24908
(Nov. 29, 2016)
-
X(11539) = MIDPOINT OF X(2) AND X(5054)
Barycentrics 8a^4-13a^2 (b^2+c^2)+5 (b^2-c^2)^2 : :
In the plane of a triangle ABC, let G = X(2) = centroid, and
A'B'C' = cevian triangle of G; i,e., A'B'C' = medial triangle
A''B''C'' = pedal triangle of G
Ma = midpoint of AA', and define Mb and Mc cyclically
P = a point (as a function) on the Euler line of ABC
Pa = P(A''MbMc), and define Pb and Pc cyclically
The triangles ABC and PaPbPc are orthologic.
X(11539) = PaPbPc-to-ABC orthologic center, for P = X(2)
X(11540) = PaPbPc-to-ABC orthologic center, for P = X(3)
X(4) = PaPbPc-to-ABC orthologic center, for P = X(11541)
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24914
(Nov 30, 2016).
-
X(11540) = MIDPOINT OF X(140) AND X(10124)
Barycentrics 22 a^4-35 a^2 (b^2+c^2)+13 (b^2-c^2)^2 : :
See X(11539) and Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24914 Hyacinthos 24914
(Nov 30, 2016).
-
X(11541) = (name pending)
Barycentrics 17 a^4 - 8 a^2 (b^2 + c^2)- 9 (b^2 - c^2)^2 : :
X(11541) = 8 X(3) - 9 X(4)
See X(11539) and Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24914
(Nov 30, 2016).
-
X(11548) = EULER INTERCEPT OF X(230)X(233)
Barycentrics (2 a^6-3 a^4 (b^2+c^2)-2 a^2 (b^4+4 b^2 c^2+c^4)+3 (b^2-c^2)^2 (b^2+c^2) : :
In the plane of a triangle ABC, let H = X(4) = orthocenter, and let
A'B'C' = pedal triangle of H; i.e., A'B'C' = orthic triangle
Ab = orthogonal projection of A' on HB, and define Bc and Ca cyclically
Ac = orthogonal projection of A' on HC, and define Ba and Cb cyclically
Na = nine-point cneter of A'AbAc, and define Nb and Nc cyclically
Oa = nine-point circle of A'AbAc, and define Ob and Oc cyclically
Qa = reflection of Qa in BC, and define Qb and Qc cyclically
X(11548) = radical center of Qa, Qb, Qc, a point on the Euler line of ABC. See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 24935 (Dec 3, 2016).
-
X(11567) = X(1)X(3)∩X(3244)X(10265)
Barycentrics (2 a^6-3 a^4 (b^2+c^2)-2 a^2 (b^4+4 b^2 c^2+c^4)+3 (b^2-c^2)^2 (b^2+c^2) : :
X(11567) = (R+4r) X[1] - R X[3]
In the plane of a triangle ABC, let I = X(1) = incenter, and let
A'B'C' = pedal triangle of I
Na = X(5)-of-IBC, and define Nb and Nc cyclically,
Then X(11567) = radical center of the circles (A', A'Na), (B', B'Nb), (C', C'Nc). See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 25041 (Dec 24, 2016).
-
X(11567) = X(11576) = X(4)X(93)∩X(25)X(54)
Trilinears a^2 (a^12 (b^2+c^2)-4 a^10 (b^2+c^2)^2+5 a^8 (b^6+2 b^4 c^2+2 b^2 c^4+c^6)+2 a^6 b^2 c^2 (b^2-c^2)^2+-a^4 (b^2-c^2)^2 (5 b^6+11 b^4 c^2+11 b^2 c^4+5 c^6)+2 a^2 (b^2-c^2)^4 (2 b^4+3 b^2 c^2+2 c^4)-(b^2-c^2)^4 (b^6-2 b^4 c^2-2 b^2 c^4+c^6)) : :
In the plane of a triangle ABC, let H = X(4) = orthocenter, and let
HaHbHc = orthic triangle = pedal triangle of H
Ab = orthogonal projection of Ha on HHb, and define Bc and Ca cyclically
Ac = orthogonal projection of Ha on HHc, and define Ba and Cb cyclically
A2 = orthogonal projection of A on HaAb, and define B2 and C2 cyclically
A3 = orthogonal projection of A on HaAc, and define B3 and C3 cyclically
A'B'C' = pedal triangle of H with respect to the triangle HaHbHc
A'' = orthogonal projection of A on HbHc, and define B'' and C'' cyclically
La = Euler line of AA2A3, and define Lb and Lc cyclically
Pa = line through A' parallel to La, and define Pb and Pc cyclically
Qa = line through A'' parallel to La, and define Qb and Qc cyclically.
The lines Pa, Pb, Pc concur in X(11576). The lines Qa, Qb, Qc concur in A(11577). See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos
25068 (Dec 29, 2016).
-
X(11577) = X6)X(24)∩X(185)X(550)(name pending)
Barycentrics (a^2 (-a^12 (b^2+c^2) +4 a^10 (b^4+3 b^2 c^2+c^4)-a^8 (5 b^6+26 b^4 c^2+26 b^2 c^4+5 c^6)+20 a^6 b^2 c^2 (b^4+b^2 c^2+c^4)+a^4 (b^2-c^2)^2 (5 b^6+b^4 c^2+b^2 c^4+5 c^6)-4 a^2 (b^2-c^2)^2 (b^8+b^4 c^4+c^8)+(b^2-c^2)^4 (b^6+c^6)) : :
See X(11576) and Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos
25068 (Dec 29, 2016).
-
X(11578) = (name pending)
Barycentrics (a-b-c)/(a^4-2 a^2 (b^2-b c+c^2)+b^4-2 b^3 c+10 b^2 c^2-2 b c^3+c^4) : :
In the plane of a triangle ABC, let
(Ia) = A-excircle, and define (Ib) and (Ic) cyclically
A' = (Ia)∩BC, and define B' and C' cyclically, so that A'B'C' = excentral triangle
Ta = line B'Ab, tangent to (Ia), and define Tb and Tc cyclically
{Ua, Va} = lines through B' tangent to (Ia), and define {Ub, Vb} and {Uc,Vc} cyclically
{Ab,Ac} = {Ua,Va}∩(Ia), and define {Bc, Ba} and {Ca, Cb} cyclically
Wa = BcBa∩CaAb, and define Wb and Wc cyclically.
The triangle WaWbWc is perspective to A'B'C' at X(11578), and the perpendicular bisectors of AbAc, BcBa, CaCb concur in X(4882). See Tran Quang Hung and Angel Montesdeoca, Hyacinthos
25070 (Dec 30, 2016).
-
X(12048) = X(3)X(6)∩X(237)X(8881)
Barycentrics a^2 (SA+S Cot[w]^2 (Cot[w]-Csc[w])) : :
See Angel Montedeoca, Hechos Geométricos en el Triángulo (2015) and Circunferencias de Apolonio.
-
X(12049) = X(3)X(6)∩X(237)X(8880)
Barycentrics a^2 (SA+S Cot[w]^2 (Cot[w]+Csc[w])) : :
See Angel Montedeoca, Hechos Geométricos en el Triángulo (2015) and Circunferencias de Apolonio.
-
X(12050) = X(3)X(6)∩X(1501)X(8880)
Barycentrics = a^2 (SA+S (Csc[w]+Tan[w])) : :
See Angel Montedeoca, Hechos Geométricos en el Triángulo (2015) and Circunferencias de Apolonio.
-
X(12051) = X(3)X(6)∩(1501)X(8881)
Barycentrics = a^2 (SA-S (Csc[w]+Tan[w])) : :
See Angel Montedeoca, Hechos Geométricos en el Triángulo (2015) and Circunferencias de Apolonio.
-
X(12053) = X(1)X(4)∩X(10)X(11)
Barycentrics a^3 (b+c)+a^2 (b^2-6 b c+c^2)-a (b-c)^2 (b+c)-(b^2-c^2)^2: :
The line AX(8) meets the incircle in two points, A' and A'', where A' is the point closer to A. Let σ be the affine transformation that carries A'B'C' onto A''B''C''. The finite fixed point of σ is X(12053). (Angel Montesdeoca, July 5, 2021). Ver Hechos Geométrico del Triángulo
-
X(12053) = X(1)X(4)∩X(10)X(11)
Barycentrics a^3 (b+c)+a^2 (b^2-6 b c+c^2)-a (b-c)^2 (b+c)-(b^2-c^2)^2 : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 25502 .
Let ABC be a triangle and A'B'C' the pedal triangle of I.
Denote:
A", B", C" = the reflections of I in BC, CA, AB, resp.
A'''B'''C''' = the orthic triangle of A"B"C"
Ma, Mb, Mc = the midpoints of the altitudes A"A''', B"B''', C"C''', resp.
R1 = the radical axis of the circles (Mb, MbB'), (Mc, McC')
R2 = the radical axis of the circles (Mc, McC'), (Ma, MaA')
R3 = the radical axis of the circles (Ma, MaA'), (Mb, MaB')
[the radical center of the circles is the point they concur at = the NPC center of A"B"C"]
Ra, Rb, Rc = the reflections of R1, R2, R3 in IA, IB, IC, resp.
A*B*C* = the triangle bounded by Ra,Rb,Rc
ABC, A*B*C* are parallelogic.
The parallelogic center (ABC, A*B*C*) lies on the OI line of ABC [ = Euler line of A"B"C"]
The parallelogic center (ABC, A*B*C*) is X(56)
The parallelogic center (A*B*C*, ABC) is X(12053) = (r-2R) X(1) + r X(4)
-
X(12054) = X(3)X(6)∩X(30)X(83)
Barycentrics a^2 (a^6+a^4 b^2-2 a^2 b^4+a^4 c^2-5 a^2 b^2 c^2-3 b^4 c^2-2 a^2 c^4-3 b^2 c^4) : :
See Angel Montedeoca, Hechos Geométricos en el Triángulo (2015) , where circles Oa, Ob, Oc are defined. Let A' be the point, other than A, in which the circles Ob and Oc intersect. Define B' and C' cyclically. Then X(12054) = X(3)-of-A'B'C'. (Peter Moses, February 25, 2017)
-
X(12055) = X(3)X(6)∩X(99)X(3589)
Barycentrics a^2 (a^4-2 a^2 b^2-2 b^4-2 a^2 c^2-5 b^2 c^2-2 c^4) : :
See Angel Montedeoca, Hechos Geométricos en el Triángulo (2015), where circles Oa, Ob, Oc are defined. Let A' be the point, other than A, in which the circles Ob and Oc intersect. Define B' and C' cyclically. Then X(12055) = X(6)-of-A'B'C'. (Peter Moses, February 25, 2017)
-
X(12079) = X(30)X(74)∩X(125)X(523)
Barycentrics (b^2-c^2)^2/(2*a^4-(b^2+c^2)*a^2-(b^2-c^2)^2) : :
Let MaMbMc = medial triangle. Let (𝒫a) be the parabola, tangent to Euler line, to NMa, and to the line BC at its vertex, so that its directrix, da, is parallel to BC. Define the lines db and dc cyclically. Let T be the triangle bounded by the lines da, db, dc. Then T is homothetic to ABC, and the center of homothety is X(12079). For a construction, see Paris Pamfilos, A Gallery of Conics by Five Elements, Forum Geometricorum 14 (2014) 295-348, paragraph 13.3, page 346: construct a conic tangent to the line at infinity, i.e. a parabola, tangent to three lines a, b, c and passing through [D], i.e. with given axis-direction. (Angel Montesdeoca, March 1, 2022) See HG010322
-
X(13160) = POINT BEID 42
Barycentrics (a^8 (b^2+c^2)-4 a^4 b^2 c^2 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)-2 a^6 (b^4-b^2 c^2+c^4)+2 a^2 (b^8-b^6 c^2-b^2 c^6+c^8) : ... : ..
In the plane of a triangle ABC, let
DEF = circummedial triangle,
HaHbHc = orthic triangle,
Γa = circumcircle of EFHa,
Γb = circumcircle of FDHb,
Γc = circumcircle of DEHb,
U = circle tangent to and encompassing Γa, Γb, Γc.
Then X(13160) = center of U. See X(13160) (Angel Montesdeoca, March 25, 2020)
X(13160) como centro de una circunferencia de Apolonio.
https://faculty.evansville.edu/ck6/encyclopedia/X13160.png
-
X(13291) = PARALLELOGIC CENTER OF THESE TRIANGLES: 2nd PARRY TO 1st HYACINTH
Barycentrics (2*a^10-4*(b^2+c^2)*a^8+2*(b^4+4*b^2*c^2+c^4)*a^6-(b^2+c^2)^3*a^4+2*(b^4-b^2*c^2+c^4)^2*a^2-(b^6+c^6)*(b^2-c^2)^2)*(b^2-c^2) : :
Let A* be the intersection of the lies through X(110) perpendicular to BC, and define B* and C* cyclically. Then
X(13291) is the centroid of the degenerate triangle A*B*C*. (Angel Montesdeoca, November 1, 2021). See X(13291).
See Antreas Hatzipolakis and Angel Montesdeoca, euclid 2948.
-
X(13351) = CROSSSUM OF X(6) AND X(1656)
Barycentrics a^2 (a^4 b^2-2 a^2 b^4+b^6+a^4 c^2-3 a^2 b^2 c^2-b^4 c^2-2 a^2 c^4-b^2 c^4+c^6) : :
In the plane of a triangle ABC, let
DEF = circum-orthic triangle;
Ab = center of circle (BFO), and define Bc and Ca cyclically;
Ac = center of circle (CEO), and define Ba and Cb cyclically;
A' = BAc∩CAb, and define B' and C' cyclically;
T = the affine transformation that carries ABC onto A'B'C'.
Then X(13351) = the finite fixed point of T. (Angel Montesdeoca, March 4, 2024)
See El centro X(13351) como punto fijo de una transformación afín.
-
X(13419) = POINT BEID 75
Barycentrics 2 a^10-4 a^8 b^2+a^6 b^4+a^4 b^6+a^2 b^8-b^10-4 a^8 c^2-a^4 b^4 c^2+2 a^2 b^6 c^2+3 b^8 c^2+a^6 c^4-a^4 b^2 c^4-6 a^2 b^4 c^4-2 b^6 c^4+a^4 c^6+2 a^2 b^2 c^6-2 b^4 c^6+a^2 c^8+3 b^2 c^8-c^10 : :
Let P be a point on the circumcircle and D a point on the line BC. Let U and V be the reflections of D in PB and PC respectively. The envelope of lines UV when D moves on BC is a parabola with focus P and directrix da. The envelope of da when P moves on circumcircle is a circle (Oa). Define (Ob), (Oc) cyclically. The radical center of the circles (Oa), (Ob), (Oc) is X(13419); see Euclid #611 (Angel Montesdeoca, February 6, 2020)
-
X(13624) = X(1)X(3)∩X(30)X(1125)
Barycentrics a(4*a^3-(b+c)*a^2-2*(2*b^2-b*c+ 2*c^2)*a+(b^2-c^2)*(b-c)) : :
Let DEF be the cevian triangle of I=X(1) and A"B"C" the 2nd circumperp triangle. Let Db, Dc be the circumcenters of ABD, ACD. The lines through X(3) parallel to DDb, DDc intersects the lines through I perpendicular to IB, IC at Ab, Ac respectively. Let (A") be the circle with center centered at A" and tangent to line AbAc, and define (B"), (C") cyclically. X(13624) is the radical center of (A"), (B"), (C"). (Angel Montesdeoca, November 7, 2019) El centro X(13624) como centro radical
-
X(13867) = POINT BEID 149
Barycentrics a (a^5 (b+c) -a^4 (b^2+14 b c+c^2) +a (b-c)^2 (b^3-9 b^2 c-9 b c^2+c^3) -2 a^3 (b^3-5 b^2 c-5 b c^2+c^3) +2 a^2 (b^4+4 b^3 c+14 b^2 c^2+4 b c^3+c^4) -(b^2-c^2)^2 (b^2-6 b c+c^2)) : :
Let ABC be a triangle and A'B'C',IaIbIc the pedal, antipedal triangles of I, resp.
Denote:
A",B",C" = the antipodes of A', B', C', in the incircle, resp.
If Ra is the the radical center of incircle and circumcircle of IA"Ia, and define Rb, Rc cyclically.
Ra, Rb , Rc concur in a point in X(13867).
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 26354 (Jul 14, 2017).
-
X(13881) = ORTHOLOGIC CENTER OF THESE TRIANGLES: 3rd TRI-SQUARES TO 4th TRI-SQUARES
Barycentrics a^4-(b^2+c^2)*a^2+2*(b^2-c^2)^2 : :
Let DEF be the orthic triangle. Let Ab be the point in which the line through B perpendicular to AB meets the perpendicular bisector of segment BD . Let Ac be the point in which the line through C perpendicular to AC meets the perpendicular bisector of segment CD. Define Bc, Ba, Ca, Cb cyclically. The six ponts Ab, Ac, Bc, Ba, Ca, Cb lie on a conic with center X(13881). A barycentric equation for this conic follows:
0 = cyclic sum of (b^2+c^2-a^2)(5 a^4-12 a^2 (b^2+c^2)+7 b^4+2 b^2 c^2+7 c^4)x^2- 2 (11a^6-13 a^4 (b^2+c^2)+a^2 (b^2-c^2)^2+(b^2-c^2)^2 (b^2+c^2))y z. (Angel Montesdeoca, December 23, 2018)
El punto X(13881) como centro de una cónica.
-
X(14221) = REFLECTION OF X(316) IN X(3260)
Barycentrics (a^2-b^2) (a^2-c^2) (a^6 b^2-a^4 b^4-a^2 b^6+b^8+a^6 c^2-2 a^4 b^2 c^2+2 a^2 b^4 c^2-3 b^6 c^2-a^4 c^4+2 a^2 b^2 c^4+4 b^4 c^4-a^2 c^6-3 b^2 c^6+c^8) : :
Let P=X(110) be the focus of Kiepert parabola, and ℓ1. ℓ2 perpendicular lines through P, that intersect the sidelines BC, CA, AB at points A1 and A2, B1 and B2, C1 and C2, respectively . Let Abc = A1C2 ∩ A2B1 and Acb = A1B2 ∩ A2C1. When the lines ℓ1 and ℓ2 rotate around P, the points Abc and Acb lie on the same conic C(A), through B and C. Let Ao be its center. The conics C(B), C(C) and and their centers Bo and Co are defined cyclically. Then the lines AAo , BBo and CCo concur in X(14221). (See HG060721). (Angel Montesdeoca, July 13, 2021)
-
X(14249) = X(3)X(107)∩X(4)X(51)
Barycentrics b^2*c^2*(-a^2 + b^2 - c^2)^2*(a^2 + b^2 - c^2)^2*(-3*a^4 + 2*a^2*b^2 + b^4 + 2*a^2*c^2 - 2*b^2*c^2 + c^4) : :
Let DEF be the Euler triangle of ABC. Let La be the line through D perpendicular to OD, and define Lb, Lc, cyclically. Let A'B'C' be the triangle formed by the lines La, Lb, Lc. The point X(14249) is the unique finite fixed point of the affine transformation that maps the reference triangle ABC onto A'B'C'. (Angel Montesdeoca, July 5, 2022)
See Angel Montesdeoca, HG040722.
-
X(14356) = X(2)X(476)∩X(5)X(523)
Barycentrics (a^2 - a*b + b^2 - c^2)*(a^2 + a*b + b^2 - c^2)*(a^2 - b^2 - a*c + c^2)*(a^2 - b^2 + a*c + c^2)*(a^2*b^2 - b^4 + a^2*c^2 - c^4) : :
Let ABC be a triangle with anticomplementary triangle A'B'C'. Let DEF and D'E'F' be the cevian triangles of Steiner point and its isotomic conjugate, respectively. Let Ao, Bo, Co be the circumcenters of triangles A'DD', B'EE', C'FF', respectively. Then the triangles ABC and AoBoCo are perspective and the perspector is X(14356). (Angel Montesdeoca, July 18, 2022)
HG160722.
-
X(14491) = NGUYEN-MOSES IMAGE OF X(381)
Barycentrics a^2*(2*a^4 - 7*a^2*b^2 + 5*b^4 - 4*a^2*c^2 - 7*b^2*c^2 + 2*c^4)*(2*a^4 - 4*a^2*b^2 + 2*b^4 - 7*a^2*c^2 - 7*b^2*c^2 + 5*c^4) : :
From Angel Montesdeoca, February 28, 2020:
Let ℰa be the ellipse with major axis the segment BC and length of the minor axis a/Sqrt[3]. Let La be the polar of A wrt ℰa, and define Lb and Lc cyclically. Let A' = Lb∩Lc, B' = Lc∩La, C' = La∩Lb. The lines AA', BB', CC' concur in X(14491).
A barycentric equation for the ellipse ℰa:
2 a4 x2+a4 x y+a4 x z+2 a4 y z-3 a2 b2 x2-a2 b2 x y+a2 b2 x z-3 a2 c2 x2+a2 c2 x y-a2 c2 x z+b4 x2-2 b2 c2 x2+c4 x2=0.
-
X(14633) = MIDPOINT OF X(2029) AND X(2039)
Barycentrics 2*a^4 + b^4 + c^4 + (2*a^2 + b^2 + c^2)*Sqrt(a^4 - a^2*b^2 + b^4 - a^2*c^2 - b^2*c^2 + c^4) : :
In the plane of a triangle ABC, let
F1 and F2 be the real foci of the Steiner inellipse
A1 = AF1∩BC
A2 = AF2∩BC
Ga = conic tangent to AF1 at A1, to AF2 at A2, and to F1F2
Ta = Ga∩F1F2
Ao = center of Ga, and define Bo and Co cyclically
The lines AAo, BBo, CCo concur in X(14633), and the lines ATa, BTb, CTc concur in X(6177). See X(6177) and X(14633). (Angel Montesdeoca, July 21, 2023)
-
X(14683) = SINGULAR FOCUS OF THE CUBIC K753
Barycentrics 3*a^6 - 3*a^4*b^2 + a^2*b^4 - b^6 - 3*a^4*c^2 + a^2*b^2*c^2 + b^4*c^2 + a^2*c^4 + b^2*c^4 - c^6 : :
Let T the Steiner triangle, E the Euler line of ABC, and P the parabola inscribed in T with directrix E. The focus of P is X(14683). (Angel Montesdeoca, February 14, 2020) (HG100220)
-
X(15109) = X(3)X(6)∩X(115)X(2963)
Barycentrics a^8-3 a^6 (b^2+c^2+3 a^4 (b^4+b^2 c^2+c^4))-a^2 (b^2-c^2)^2 (b^2+c^2) : :
In the plane of a triangle ABC, let
Lab = reflection of AB in the perpendicular bisector of AC
Lab = reflection of AC in the perpendicular bisector of AB
A' = Lab ∩ Lac
A'' = the point, other than A', of intersection of the circle having diameter AA' and the circle {{A',B,C}}; define B'' and C'' cyclically.
Then X(15109) is the finite fixed point of the affine transformation that takes ABC onto A''B''C''. Moreover, the lines AA'',BB'',CC'' concur in the Kosnita point, X(54). (Angel Montesdeoca, April 21, 2023)
See X(15109) punto fijo de una transformación afín
-
X(15316) = ISOGONAL CONJUGATE OF X(3542)
Barycentrics a^2 (a^2 - b^2 - c^2)/(a^6 -
3 a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2) +
a^2 (3 b^4 - 2 b^2 c^2 + 3 c^4)) : :
Let DEF be the anticevian triangle of X(3), and let h be the affine transformation that carries ABC onto DEF. For any line ℒ through X(3), let ℒ' be the image of ℒ under h, and let U = ℒ∩ℒ'. Then as ℒ rotates around X(3), the line h(U)h-1(U) pass through X(15316). See X(15316). (Angel Montesdeoca, March 7, 2021)
-
X(15692) = X(2) + 4 X(3)
Barycentrics 13*a^4 - 14*a^2*b^2 + b^4 - 14*a^2*c^2 - 2*b^2*c^2 + c^4 : :
Given a triangle ABC and a point P, let c(P) be the circumconic having perspector P, and let A' be the center of the conic that passes through P and is tangent to c(P) at B and C. Define points B' and C' cyclically. The triangles ABC and A'B'C' are orthologic if and only P is on the sextic (passing through X(2), X(6)) having this barycentric equation:
Cyclic sum [ y z(17(b^2-c^2) x^4- ((15a^2+31b^2-19c^2) y-(15a^2-19b^2+31c ^2) z)x^3+ a^2(y+z)(y-z)^3) ]= 0.
If P is the centroid then the orthologic center of A'B'C' with respect to ABC is X(15692). The reciprocal orthologic center is X(4). If P is the symmedian then the orthologic center of ABC with respect to A'B'C' is X(18535). The reciprocal orthologic center is X(3). (Angel Montesdeoca, December 12, 2022)
See X(15692) y X(18535) centros ortológicos
-
X(15805) = MIDPOINT OF X(3) AND X(3527)
Barycentrics a^2 (a^8-4 a^6 b^2+6 a^4 b^4-4 a^2 b^6+b^8-4 a^6 c^2-4 a^4 b^2 c^2+16 a^2 b^4 c^2-8 b^6 c^2+6 a^4 c^4+16 a^2 b^2 c^4+14 b^4 c^4-4 a^2 c^6-8 b^2 c^6+c^8) : :
In the plane of a triangle ABC, let
DEF = orthic triangle of ABC
(O) = circle with center D and pass-thorugh point A
A2 = (O)∩AB
A3 = (O)∩AC
(Oa) = circle through B, C, A2, A3
A' = center of (Oa), and define B' and C' cyclically
Then X(15805) is the finite fixed point of the affine transformation that carries ABC onto A'B'C'. (Angel Montesdeoca, December 3, 2022)
See Angel Montesdeoca, X(15805) punto fijo de una transformación afín.
-
X(16186) = X(3)X(49)∩X(122)X(125)
Barycentrics a^2(b^2-c^2)^2SA(3SA^2-S^2) : :
Sean TaTbTc el triángulo tangencial,
A' la intersección de la reflexión de AB en TaTc con a la reflexión de AC en TaTb,
B' la intersección de la reflexión de BC en TbTa con a la reflexión de BA en TbTc, y
C' la intersección de la reflexión de CA en TcTb con a la reflexión de CB en TcTa.
El punto fijo (propio) de la transformación afín que aplica ABC en A'B'C' es X(16186)
See Angel Montesdeoca, HG010218.
-
X(16187) = X(2)X(98)∩X(3)X(5646)
Barycentrics a^2(a^4-a^2(b^2+c^2)+10b^2c^2) : :
Dado un triángulo ABC con simediano K,
la antiparalela
a BC, respecto a AB y a AC, corta en Ba y Ca a AC y AB, respectivamente;
la antiparalela a CA, respecto a BC y a BA, corta en Cb y Ab a BA y BC, respectivamente;
la antiparalela a AB, respecto a CA y a CB, corta en Ac y Bc a CB y CA, respectivamente.
El baricentro PG
de AbBcCa y el baricentro UG
de AbBcCa, forman un par bicéntrico.
La 'crosssum' de PG y UG es X(16187).
See Angel Montesdeoca, HG050218.
-
X(16188) = COMPLEMENT OF X(842)
Barycentrics 2a^12(b^2+c^2)- 4a^10(b^2+c^2)^2+ a^8(b^6+11b^4c^2+11b^2c^4+c^6)+ 2a^6(b^8-5b^6c^2-5b^2c^6+c^8)- a^4(2b^10-7b^8c^2+3b^6c^4+3b^4c^6-7b^2c^8+ 2c^10)+ 2a^2(b^12-3b^10c^2+2b^8c^4+2b^4c^8-3b^2c^10+c^12)-(b^2-c^2)^4(b^6+c^6) : :
See Angel Montesdeoca, HG120218.
-
X(16236) = X(1)X(631)∩X(7)X(519)
Barycentrics (a-2b-2c)(5a-b-c)/(b+c-a) : :
See Angel Montesdeoca, HG200218.
Dado un triángulo ABC, sean DEF el triángulo de contacto interior, D', E' y F', los puntos donde las rectas AD, BE y CF vuelven a cortar a la circunferencia inscrita a ABC.
Las rectas pa, pb y pc son las perpendiculares por D', E' y F' a AD, BE y CF, respetivamente. Sea A2B2C2 el triángulo delimitado por las rectas pa, pb y pc.
El centro de perspectividad de DEF y A2B2C2 es X(16236).
-
X(17749) = MOSES (0, 1, 1, -1, 0, -2, 0, 0, 0) POINT
Barycentrics a*(a^2*b + a*b^2 + a^2*c - a*b*c - 2*b^2*c + a*c^2 - 2*b*c^2) : :
Let MaMbMc, DEF, and A'B'C' be the medial, intouch and 1st circumperp triangles, respectively. Let D', E' and F' be the orthogonal projections of Ma, Mb and Mc on EF, FD and DE, respectively. Then A'B'C' and D'E'F' are bilogic and the orthology center of A'B'C' with respect to D'E'F' is X(17749). The reciprocal orthologic center is X(10). (Angel Montesdeoca, October 29, 2019). X(17749) como centro ortológico
-
X(18221) = PERSPECTOR OF THESE TRIANGLES: 1st ZANIAH AND 5th MIXTILINEAR
Barycentrics 3*a^4-8*(b+c)*a^3-2*(b^2+4*b*c+c^2)*a^2+8*(b^2-c^2)*(b-c)*a-(b^2-c^2)^2 : :
Let A'B'C' be the intouch triangle and let A"B"C" be the Euler triangle of A'B'C'. The finite fixed point of the affine transformation that carries ABC onto A''B''C'' is X(18221), i.e. X(18221) = ATFF(ABC, A"B"C"); see the preamble just before X(10129)). (Angel Montesdeoca, March 25, 2022).
See El centro X(18221) como punto fijo de una transformación afín
-
X(18279) = X(4)X(74)∩?X(5)X(523)
Barycentrics a^14 (b^2+c^2)-3 a^12 (b^4+c^4)-(b^2-c^2)^6 (b^4+3 b^2 c^2+c^4)+a^10 (b^6+2 b^4 c^2+2 b^2 c^4+c^6)+a^2 (b^2-c^2)^4 (3 b^6-b^4 c^2-b^2 c^4+3 c^6)-a^6 (b^2-c^2)^2 (5 b^6+4 b^4 c^2+4 b^2 c^4+5 c^6)-a^8 (-5 b^8+12 b^6 c^2-12 b^4 c^4+12 b^2 c^6-5 c^8)-a^4 (b^2-c^2)^2 (b^8-11 b^6 c^2+10 b^4 c^4-11 b^2 c^6+c^8) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 27613. Hyacinthos 27613 .
Let ABC be a triangle,
N is the NPC center,
A'B'C' is the pedal triangle of N.
The Hatzipolakis axes of the triangles AB'C', BC'A' and CA'B' bound a triangle
A''B''C''.
Then the circumcenter of the triangle A''B''C'' is X(18279), lies on the Euler line of ABC.
-
X(18280) = (name pending))
Barycentrics a^2 (a^11+a^10 (b+c) + a^9 (-5 b^2+b c-5 c^2) - a^8 (5 b^3+4 b^2 c+4 b c^2+5 c^3) +a^7 (10 b^4-4 b^3 c+11 b^2 c^2-4 b c^3+10 c^4) + a^6 (10 b^5+6 b^4 c+9 b^3 c^2+9 b^2 c^3+6 b c^4+10 c^5) + a^5 (-10 b^6+6 b^5 c-4 b^4 c^2+9 b^3 c^3-4 b^2 c^4+6 b c^5-10 c^6) - a^4 (10 b^7+4 b^6 c+2 b^5 c^2+5 b^4 c^3+5 b^3 c^4+2 b^2 c^5+4 b c^6+10 c^7) + a^3 (5 b^8-4 b^7 c-5 b^6 c^2-b^5 c^3+2 b^4 c^4-b^3 c^5-5 b^2 c^6-4 b c^7+5 c^8) + a^2 (b-c)^2 (5 b^7+11 b^6 c+10 b^5 c^2+11 b^4 c^3+11 b^3 c^4+10 b^2 c^5+11 b c^6+5 c^7) - a (b^2-c^2)^4 (b^2-b c+c^2) - (b-c)^4 (b+c)^5 (b^2-b c+c^2)) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 27614.
Let ABC be a triangle with incenter I.
The reflection of Hatzipolakis axis of triangle IBC in line BC is
da.
Similarly, we have db and dc.
The lines da,db,dc bound triangle A'B'C'.
Circumcenter of triangle A'B'C' lies on OI line of ABC.
The circumcenter of triangle A'B'C' lies on OI line of ABC and
is:
X(18280) = R (3 R^2-4 s^2)*X(1) + 2 (r R^2+2 R^3+4 r s^2)*X(3)
-
X(18535) = HOMOTHETIC CENTER OF THESE TRIANGLES: EHRMANN MID AND 3rd ANTIPEDAL OF X(3)
Barycentrics a^2((a^2 - b^2 - c^2)^2 - 16b^2c^2)/(b^2 + c^2 - a^2) : :
Given a triangle ABC and a point P, let c(P) be the circumconic having perspector P, and let A' be the center of the conic that passes through P and is tangent to c(P) at B and C. Define points B' and C' cyclically. The triangles ABC and A'B'C' are orthologic if and only P is on the sextic (passing through X(2), X(6)) having this barycentric equation:
Cyclic sum [ y z(17(b^2-c^2) x^4- ((15a^2+31b^2-19c^2) y-(15a^2-19b^2+31c ^2) z)x^3+ a^2(y+z)(y-z)^3) ]= 0.
If P is the centroid then the orthologic center of A'B'C' with respect to ABC is X(15692). The reciprocal orthologic center is X(4). If P is the symmedian then the orthologic center of ABC with respect to A'B'C' is X(18535). The reciprocal orthologic center is X(3). (Angel Montesdeoca, December 12, 2022)
X(15692) y X(18535) centros ortológicos (10/12/2022)
-
X(18866) = (name pending)
Barycentrics a^16-2 a^14 (b^2+c^2)-3 a^12 (b^4-4 b^2 c^2+c^4)-(b^2-c^2)^4 (b^2+c^2)^2 (2 b^4-3 b^2 c^2+2 c^4)+2 a^10 (4 b^6-5 b^4 c^2-5 b^2 c^4+4 c^6)-2 a^6 (b^2-c^2)^2 (5 b^6-2 b^4 c^2-2 b^2 c^4+5 c^6)+a^8 (b^8-15 b^6 c^2+29 b^4 c^4-15 b^2 c^6+c^8)+a^4 (b^2-c^2)^2 (3 b^8+2 b^6 c^2-15 b^4 c^4+2 b^2 c^6+3 c^8)+4 a^2 (b^2-c^2)^2 (b^10-b^8 c^2+2 b^6 c^4+2 b^4 c^6-b^2 c^8+c^10) : :
ADGEOM #4604 (Tran Quang Hung, May 27, 2018)
Let ABC be a triangle with circumcenter O.
P is on its Euler line.
Oa, Ob, Oc are isogonal conjugate of O wrt triangles PBC, PCA, PAB.
Then centroid of OaObOc lies on Euler line of ABC.
ADGEOM #4608 (Angel Montesdeoca, May 28, 2018)
If P is on its Euler line such that OP:PH=t , then centroid Q of
OaObOc ( lies on Euler line of ABC) is:
Q = (a^2-b^2) (a^2-c^2) (a^4-(b^2-c^2)^2) t (a^16 t^2-(b^2-c^2)^6
(b^2+c^2)^2 t^2-a^14 (b^2+c^2) t (1+3 t)+a^2 (b^2-c^2)^4 (b^2+c^2) t (-2
b^2 c^2 (-2+t)+b^4 (1+3 t)+c^4 (1+3 t))-a^6 (b^2-c^2)^2 (b^2+c^2) (b^4
(-5+t) t+c^4 (-5+t) t+b^2 c^2 (-5+7 t-4 t^2))-a^8 (b^4 c^4 (-7+14 t-12
t^2)+b^6 c^2 (3-9 t+4 t^2)+b^2 c^6 (3-9 t+4 t^2))-a^4 (b^2-c^2)^2 (2 b^8
t (2+t)+2 c^8 t (2+t)+b^6 c^2 (2+5 t-3 t^2)+b^2 c^6 (2+5 t-3 t^2)+b^4
c^4 (5-6 t+6 t^2))+a^10 (b^2+c^2) (b^4 (-5+t) t+c^4 (-5+t) t-b^2 c^2
(1-5 t+8 t^2))+a^12 (2 b^4 t (2+t)+2 c^4 t (2+t)+b^2 c^2 (1+9
t^2)))-(-a^2+b^2+c^2) (a^8 t-2 a^6 (b^2+c^2) t+a^4 b^2 c^2 (-2+3
t)-(b^2-c^2)^2 (b^2 c^2 (-1+t)+b^4 t+c^4 t)+a^2 (b^2+c^2) (b^2 c^2 (1-4
t)+2 b^4 t+2 c^4 t)) ((b^2-c^2) (-a^2 c^2-a^4 t+(b^2-c^2)^2 t) (a^4 (-2
b^4+b^2 c^2 (1-2 t))-a^8 t-(b^2-c^2)^3 (b^2+c^2) t+a^6 (2 c^2 t+b^2
(1+t))+a^2 (b^2-c^2) (-b^2 c^2 (-2+t)+2 c^4 t+b^4 (1+t)))+(-b^2+c^2)
(-a^2 b^2-a^4 t+(b^2-c^2)^2 t) (a^4 (-2 c^4+b^2 c^2 (1-2 t))-a^8
t+(b^2-c^2)^3 (b^2+c^2) t+a^6 (2 b^2 t+c^2 (1+t))-a^2 (b^2-c^2) (-b^2
c^2 (-2+t)+2 b^4 t+c^4 (1+t)))) : ... : ...
If P=X(2)
[X(18866) = ] Q = a^16-2 a^14 (b^2+c^2)-3 a^12 (b^4-4 b^2 c^2+c^4)-(b^2-c^2)^4
(b^2+c^2)^2 (2 b^4-3 b^2 c^2+2 c^4)+2 a^10 (4 b^6-5 b^4 c^2-5 b^2 c^4+4
c^6)-2 a^6 (b^2-c^2)^2 (5 b^6-2 b^4 c^2-2 b^2 c^4+5 c^6)+a^8 (b^8-15 b^6
c^2+29 b^4 c^4-15 b^2 c^6+c^8)+a^4 (b^2-c^2)^2 (3 b^8+2 b^6 c^2-15 b^4
c^4+2 b^2 c^6+3 c^8)+4 a^2 (b^2-c^2)^2 (b^10-b^8 c^2+2 b^6 c^4+2 b^4
c^6-b^2 c^8+c^10) : ... : ...
-
X(19210) = X(3) OF 1st ANTI-SHARYGIN TRIANGLE
Barycentrics a^4 (-a^2+b^2+c^2)^2 (-a^4-b^4+b^2 c^2+a^2 (2 b^2+c^2)) (a^4-b^2 c^2+c^4-a^2 (b^2+2 c^2)) : :
Let L be the line through X(3) parallel to BC. Let Ab = L∩AB, and Ac = L∩AC, and let D = midpoint of AX(4). Let A' be the point, other than A, in which the circles {{B,D,Ab}} and {{C, D,Ac}} meet. Define B' and C' cyclically. The finite fixed point of the affine transformation that carries ABC onto A'B'C' is X(19210). (Angel Montesdeoca, April 13, 2021)
See El centro X(19210) como punto fijo de una transformación afín
-
X(19657) = (name pending)
Barycentrics a^2 (a-b) (a-c) (a^10+2 a^9 b-3 a^8 b^2-8 a^7 b^3+2 a^6 b^4+12 a^5 b^5+2 a^4 b^6-8 a^3 b^7-3 a^2 b^8+2 a b^9+b^10+a^9 c+4 a^8 b c+5 a^7 b^2 c-a^6 b^3 c-9 a^5 b^4 c-9 a^4 b^5 c-a^3 b^6 c+5 a^2 b^7 c+4 a b^8 c+b^9 c-4 a^8 c^2-6 a^7 b c^2+3 a^6 b^2 c^2+6 a^5 b^3 c^2+2 a^4 b^4 c^2+6 a^3 b^5 c^2+3 a^2 b^6 c^2-6 a b^7 c^2-4 b^8 c^2-4 a^7 c^3-11 a^6 b c^3-6 a^5 b^2 c^3+6 a^4 b^3 c^3+6 a^3 b^4 c^3-6 a^2 b^5 c^3-11 a b^6 c^3-4 b^7 c^3+6 a^6 c^4+4 a^5 b c^4-5 a^4 b^2 c^4-10 a^3 b^3 c^4-5 a^2 b^4 c^4+4 a b^5 c^4+6 b^6 c^4+6 a^5 c^5+11 a^4 b c^5+6 a^3 b^2 c^5+6 a^2 b^3 c^5+11 a b^4 c^5+6 b^5 c^5-4 a^4 c^6+2 a^3 b c^6+4 a^2 b^2 c^6+2 a b^3 c^6-4 b^4 c^6-4 a^3 c^7-5 a^2 b c^7-5 a b^2 c^7-4 b^3 c^7+a^2 c^8-2 a b c^8+b^2 c^8+a c^9+b c^9) (a^10+a^9 b-4 a^8 b^2-4 a^7 b^3+6 a^6 b^4+6 a^5 b^5-4 a^4 b^6-4 a^3 b^7+a^2 b^8+a b^9+2 a^9 c+4 a^8 b c-6 a^7 b^2 c-11 a^6 b^3 c+4 a^5 b^4 c+11 a^4 b^5 c+2 a^3 b^6 c-5 a^2 b^7 c-2 a b^8 c+b^9 c-3 a^8 c^2+5 a^7 b c^2+3 a^6 b^2 c^2-6 a^5 b^3 c^2-5 a^4 b^4 c^2+6 a^3 b^5 c^2+4 a^2 b^6 c^2-5 a b^7 c^2+b^8 c^2-8 a^7 c^3-a^6 b c^3+6 a^5 b^2 c^3+6 a^4 b^3 c^3-10 a^3 b^4 c^3+6 a^2 b^5 c^3+2 a b^6 c^3-4 b^7 c^3+2 a^6 c^4-9 a^5 b c^4+2 a^4 b^2 c^4+6 a^3 b^3 c^4-5 a^2 b^4 c^4+11 a b^5 c^4-4 b^6 c^4+12 a^5 c^5-9 a^4 b c^5+6 a^3 b^2 c^5-6 a^2 b^3 c^5+4 a b^4 c^5+6 b^5 c^5+2 a^4 c^6-a^3 b c^6+3 a^2 b^2 c^6-11 a b^3 c^6+6 b^4 c^6-8 a^3 c^7+5 a^2 b c^7-6 a b^2 c^7-4 b^3 c^7-3 a^2 c^8+4 a b c^8-4 b^2 c^8+2 a c^9+b c^9+c^10) : :
See Alexandr Skutin, Peter Moses, and Angel Montesdeoca, Hyacinthos 27780 and Hyacinthos 27781.
-
X(19658) = ANTIGONAL IMAGE OF X(484)
Barycentrics (a^2+a b+b^2-c^2) (a^2-b^2+a c+c^2) (a^3-a^2 b-a b^2+b^3+a^2 c-a b c+b^2 c-a c^2-b c^2-c^3) (a^3+a^2 b-a b^2-b^3+a^2 c-a b c+b^2 c-a c^2+b c^2-c^3) (a^3+a^2 b-a b^2-b^3-a^2 c-a b c-b^2 c-a c^2+b c^2+c^3) : :
See Alexandr Skutin, Peter Moses, and Angel Montesdeoca, Hyacinthos 27780 and Hyacinthos 27781.
-
X(19659) = X(2)X(3)∩X(32)X(6178)
Barycentrics (-a^2 - b^2 - c^2) (a^2 b^2 - b^4 + a^2 c^2 + 2 b^2 c^2 - c^4) - 2 a^2 (a^2 - b^2 - c^2) sqrt(a^4 + b^4 + c^4- b^2 c^2 - a^2 b^2 - a^2c^2) : :
See Angel Montesdeoca, HG180618.
-
X(19660) = X(2)X(3)∩X(32)X(6177)
Barycentrics (-a^2 - b^2 - c^2) (a^2 b^2 - b^4 + a^2 c^2 + 2 b^2 c^2 - c^4) + 2 a^2 (a^2 - b^2 - c^2) sqrt(a^4 + b^4 + c^4- b^2 c^2 - a^2 b^2 - a^2c^2) : :
See Angel Montesdeoca, HG180618.
-
X(19661) = X(2)X(1285)∩X(5)X(598)
Barycentrics 16 a^4 - a^2 (b^2 + c^2) + (b^2 + c^2)^2 : :
See Angel Montesdeoca, HG180618.
-
X(19662) = MIDPOINT OF X(115) AND X(599)
Barycentrics 2a^6-6a^4(b^2+c^2)+ 3a^2(b^4+4b^2c^2+c^4)-7b^6+3b^4c^2+3b^2c^4-7c^6 : :
See Angel Montesdeoca, HG180618.
-
X(19663) = X(39)X(597)∩X(384)X(11638)
Barycentrics a^8(b^2+c^2)+ a^6(6b^4-20b^2c^2+6c^4)+ 3a^4(b^6+2b^4c^2+2b^2c^4+c^6)- a^2(b^2+c^2)^2(2b^4+b^2c^2+2c^4)+b^2c^2(b^2+c^2)^3 : :
See Angel Montesdeoca, HG180618.
-
X(20031) = X(98)X(6530)∩X(107)X(685)
Barycentrics (a^2-c^2)(a^4-(b^2-c^2)^2)^2 (a^10 -a^8(2b^2+c^2) +a^6(2b^4+c^4) -a^4(2b^6-2b^4c^2+c^6) +a^2b^4(b^2-c^2)^2 +b^4c^2(b^2-c^2)^2 ) : :
See Angel Montesdeoca, HG260618.
-
X(20115) = (name pending)
Barycentrics a^2 (a^2 b^2-b^4+a^2 c^2+2 b^2 c^2-c^4)/(2 a^8-6 a^6 b^2+7 a^4 b^4-4 a^2 b^6+b^8-6 a^6 c^2+4 a^2 b^4 c^2-4 b^6 c^2+7 a^4 c^4+4 a^2 b^2 c^4+6 b^4 c^4-4 a^2 c^6-4 b^2 c^6+c^8) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 27820.
-
X(20116) = X(1)X(1170)∩X(7)X(79)
Barycentrics a (-a^4 (b+c)+5 a^2 b c (b+c)+2 a^3 (b^2+c^2)-2 a (b-c)^2 (b^2+3 b c+c^2)+(b-c)^2 (b^3+c^3)) : :
See Kadir Altintas and Angel Montesdeoca, ADGEOM 4766.
-
X(20117) = X(1)X(6920)∩X(2)X(5693)
Barycentrics a (a^5 (b+c)-a^4 (b+c)^2-(b^2-c^2)^2 (b^2+b c+c^2)+a^3 (-2 b^3+b^2 c+b c^2-2 c^3)+a (b-c)^2 (b^3+c^3)+a^2 (2 b^4+3 b^3 c-2 b^2 c^2+3 b c^3+2 c^4)) : :
See Kadir Altintas and Angel Montesdeoca, ADGEOM 4766.
-
X(20118) = X(1)X(12619)∩X(2)X(12739)
Barycentrics (a+b-c) (a-b+c) (a^4 (b+c)+a^2 b c (b+c)+2 a (b^2-c^2)^2-2 a^3 (b^2+c^2)-(b-c)^2 (b+c)^3) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 27840.
-
X(20121) = X(1)X(7)∩X(948)X(4031)
Barycentrics (a+b-c) (a-b+c) (a^2-5 a (b+c)+4 (b-c)^2) : :
See Kadir Altintas and Angel Montesdeoca, ADGEOM 4791.
-
X(20123) = X(30)X(146)∩X(74)X(18317)
Barycentrics (a^2-b^2-c^2) (2 a^4-a^2 (b^2+c^2)-(b^2-c^2)^2)/(a^8-4 a^6 (b^2+c^2)+a^4 (6 b^4+b^2 c^2+6 c^4)+a^2 (-4 b^6+b^4 c^2+b^2 c^4-4 c^6)+(b^2-c^2)^2 (b^4+4 b^2 c^2+c^4)) : :
See Angel Montesdeoca, ADGEOM 4801.
-
X(20124) = EULER LINE INTERCEPT OF X(3258)X(18285)
Barycentrics 4 a^16 - 17 a^14 (b^2 + c^2) - (b^2 - c^2)^6 (11 b^4 + 14 b^2 c^2 +
11 c^4) + a^12 (43 b^4 + 10 b^2 c^2 + 43 c^4) +
a^10 (-89 b^6 + 27 b^4 c^2 + 27 b^2 c^4 - 89 c^6) +
a^2 (b^2 - c^2)^4 (37 b^6 + 17 b^4 c^2 + 17 b^2 c^4 + 37 c^6) -
a^4 (b^2 - c^2)^2 (23 b^8 - 80 b^6 c^2 - 75 b^4 c^4 - 80 b^2 c^6 +
23 c^8) +
a^8 (115 b^8 + 4 b^6 c^2 - 162 b^4 c^4 + 4 b^2 c^6 + 115 c^8) -
a^6 (59 b^10 + 71 b^8 c^2 - 121 b^6 c^4 - 121 b^4 c^6 + 71 b^2 c^8 +
59 c^10) : :
See Antreas Hatzipolakis, César Lozada and Angel Montesdeoca Hyacinthos 27871 and Hyacinthos 27872.
-
X(20183) = X(9)X(362)∩X(10)X(164)
Barycentrics a (a^5 - a^4 (b + c) - 2 a^3 (b^2 + 10 b c + c^2) + 2 a^2 (b^3 + 7 b^2 c + 7 b c^2 + c^3) + a (b - c)^2 (b^2 + 6 b c + c^2) - (b - c)^4 (b + c) + 2 Sqrt[ b c (a + b - c) (a - b + c)] (-5 a^2 (b + c) + (b - c)^2 (b + c) + 4 a (b^2 + b c + c^2)) - 2 Sqrt[-a c (a - b - c) (a + b - c) ] (a^3 + a^2 (4 b + c) + c (b^2 - c^2) - a (5 b^2 + 4 b c + c^2)) - 2 Sqrt[ a b (a - b + c) (-a + b + c)] (a^3 - b^3 + b c^2 + a^2 (b + 4 c) - a (b^2 + 4 b c + 5 c^2))) : :
See Angel Montesdeoca, HG110718.
-
X(20477) = X(2)X(53)∩X(3)X(95)
Barycentrics a^8-3*(b^2+c^2)*a^6+3*(b^4+c^4)*a^4-(b^4-c^4)*(b^2-c^2)*a^2+2*b^2*c^2*(b^2-c^2)^2 : :
Let A'B'C' be the tangential triangle. Let La be the reflection of line B'C' in the perpedicular bisector of BC, and define Lb and Lc cyclically. Let A" = Lb∩Lc, and define B" and C" cyclically. Triangle A"B"C" is also the tangential triangle of the dual-of-orthic triangle, and X(20477) = X(7)-of-A"B"C". (Randy Hutson, August 29, 2018)
See Angel Montesdeoca, HG220718.
-
X(20478) = EULER LINE INTERCEPT OF X(578)X(14374)
Barycentrics a*(2*a*(a^8+8*a^4*b^2*c^2-2*(b^2+c^2)*a^6+2*(b^4-3*b^2*c^2+c^4)*(b^2+c^2)*a^2-(b^4+4*b^2*c^2+c^4)*(b^2-c^2)^2)*S*OH-(3*a^10-5*(b^2+c^2)*a^8-2*(b^4-8*b^2*c^2+c^4)*a^6+2*(b^2+c^2)*(3*b^4-7*b^2*c^2+3*c^4)*a^4-(b^2-c^2)^2*(b^4+8*b^2*c^2+c^4)*a^2-(b^4-c^4)*(b^2-c^2)^3)*b*c) : :
See Angel Montesdeoca, HG220718.
-
X(20479) = EULER LINE INTERCEPT OF X(578)X(14375)
Barycentrics a*(-2*a*(a^8+8*a^4*b^2*c^2-2*(b^2+c^2)*a^6+2*(b^4-3*b^2*c^2+c^4)*(b^2+c^2)*a^2-(b^4+4*b^2*c^2+c^4)*(b^2-c^2)^2)*S*OH-(3*a^10-5*(b^2+c^2)*a^8-2*(b^4-8*b^2*c^2+c^4)*a^6+2*(b^2+c^2)*(3*b^4-7*b^2*c^2+3*c^4)*a^4-(b^2-c^2)^2*(b^4+8*b^2*c^2+c^4)*a^2-(b^4-c^4)*(b^2-c^2)^3)*b*c) : :
See Angel Montesdeoca, HG220718.
-
X(20480) = X(110)X(382)∩X(476)X(15646)
Barycentrics 4 a^16 - 10 a^14 (b^2 + c^2) + a^12 (-6 b^4 + 49 b^2 c^2 - 6 c^4) + 5 a^10 (8 b^6 - 11 b^4 c^2 - 11 b^2 c^4 + 8 c^6) - a^8 (40 b^8 + 23 b^6 c^2 - 135 b^4 c^4 + 23 b^2 c^6 + 40 c^8) + 3 a^6 (b^2 - c^2)^2 (2 b^6 + 25 b^4 c^2 + 25 b^2 c^4 + 2 c^6) + a^4 (b^2 - c^2)^2 (10 b^8 - 6 b^6 c^2 - 57 b^4 c^4 - 6 b^2 c^6 + 10 c^8) - 2 a^2 (b^2 - c^2)^4 (2 b^6 + 5 b^4 c^2 + 5 b^2 c^4 + 2 c^6) - 4 b^2 c^2 (b^2 - c^2)^6 : :
See Angel Montesdeoca, HG220718 and Hyacinthos 27999.
-
X(20481) = X(2)X(6)∩X(3)X(111)
Barycentrics a^2(a^4+2a^2(b^2+c^2)+b^4-16b^2c^2+c^4) : :
See Angel Montesdeoca, HG030818.
-
X(20581) = X(1741)X(8758)∩X(2331)X(7649)
Barycentrics a (b^5 - b^4 c - b c^4 + c^5 + (b^4 - 2 b^2 c^2 + c^4) a + (-2 b^3 + 4 b^2 c + 4 b c^2 - 2 c^3) a^2 + (-2 b^2 - 4 b c - 2 c^2) a^3 + (b + c) a^4 + a^5) (b^5 + b^4 c - 2 b^3 c^2 - 2 b^2 c^3 + b c^4 + c^5 + (b^4 - 4 b^3 c + 6 b^2 c^2 - 4 b c^3 + c^4) a + (-2 b^3 + 2 b^2 c + 2 b c^2 - 2 c^3) a^2 + (-2 b^2 - 2 c^2) a^3 + (b + c) a^4 + a^5) : :
See Angel Montesdeoca, HG040818.
-
X(20587) = (name pending)
Barycentrics (2 a^4 - 2 a^2 b^2 + a^2 b c - b^3 c - 2 a^2 c^2 + 2 b^2 c^2 - b c^3) (2 a^4 - 2 a^2 b^2 - a^2 b c + b^3 c - 2 a^2 c^2 + 2 b^2 c^2 + b c^3) (a^6 + a^2 b^4 - 2 b^6 - 2 a^2 b^2 c^2 + 2 b^4 c^2 + a^2 c^4 + 2 b^2 c^4 - 2 c^6) : :
See Angel Montesdeoca, HG040818.
-
X(20588) = X(1)X(1167)∩X(2)X(15298)
Barycentrics a (a - b - c) (a^4 - 2 a^2 b^2 + b^4 + 2 a b^2 c - 2 b^3 c - 2 a^2 c^2 + 2 a b c^2 + 2 b^2 c^2 - 2 b c^3 + c^4) : :
See Angel Montesdeoca, HG040818.
-
X(20794) = X(3)X(69)∩X(6)X(694)
Barycentrics (a^2 b^2 + a^2 c^2 - b^2 c^2) sin 2A : :
Let T = anticevian triangle of X(3). Then X(20794) is the perspector, with respect to T, of the pivotal conic of the conico-pivotal cubic cK(#3,X394). (Angel Montesdeoca, May 4, 2019)
HG040519
-
X(21230) = COMPLEMENT OF X(195)
Barycentrics (a^2 b^2-b^4+a^2 c^2+2 b^2 c^2-c^4) (a^6-3 a^4 b^2+3 a^2 b^4-b^6-3 a^4 c^2+3 a^2 b^2 c^2+b^4 c^2+3 a^2 c^4+b^2 c^4-c^6) : :
Let U be the circle with center X(5) and pass-through point A, and let meets the perpendicular bisector of segment BC in two points: one of them is the U-antipode of A and the other we denote by A'. Define B' and C' cyclically. Then X(21230) is the circumcenter of triangle A'B'C'. (Angel Montesdeoca, March 27, 2019)
Hyacinthos #28933
-
X(21265) = (name pending)
Barycentrics a^20 (b^2+c^2)-(b^2-c^2)^10 (b^2+c^2)-a^18 (7 b^4+10 b^2 c^2+7 c^4)+10 a^16 (2 b^6+3 b^4 c^2+3 b^2 c^4+2 c^6)+11 a^6 (b^2-c^2)^4 (5 b^8+10 b^6 c^2+12 b^4 c^4+10 b^2 c^6+5 c^8)+a^2 (b^2-c^2)^6 (8 b^8-3 b^6 c^2-11 b^4 c^4-3 b^2 c^6+8 c^8)-a^14 (27 b^8+28 b^6 c^2+26 b^4 c^4+28 b^2 c^6+27 c^8)+a^12 (7 b^10-24 b^8 c^2-34 b^6 c^4-34 b^4 c^6-24 b^2 c^8+7 c^10)-a^4 (b^2-c^2)^4 (28 b^10-b^8 c^2-28 b^6 c^4-28 b^4 c^6-b^2 c^8+28 c^10)-a^8 (b^2-c^2)^2 (63 b^10+111 b^8 c^2+128 b^6 c^4+128 b^4 c^6+111 b^2 c^8+63 c^10)+a^10 (35 b^12+55 b^10 c^2+36 b^8 c^4+36 b^6 c^6+36 b^4 c^8+55 b^2 c^10+35 c^12) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28059.
-
X(21267) = COMPLEMENT OF X(15519)
Barycentrics a^3-2 a^2 (b+c)+a (9 b^2-14 b c+9 c^2)-4 (b-c)^2 (b+c) : :
Recalling that triangle centers are functions, at (a,b,c) = (6,9,13), the values of X(21267) and X(4691) are equal.
See Tran Quang Hung, Angel Montesdeoca, and César Lozada, ADGEOM 4851 and ADGEOM 4855.
-
X(21268) = MIDPOINT ON X(4) AND X(5962)
Barycentrics 2 a^16 -7 a^14 (b^2+c^2) +4 a^12 (2 b^4+5 b^2 c^2+2 c^4) -a^10 (3 b^6+17 b^4 c^2+17 b^2 c^4+3 c^6) -2 a^8 b^2 c^2 (b^4-10 b^2 c^2+c^4) +3 a^6 (b^2-c^2)^2 (b^2+c^2)^3 -4 a^4 (b^2-c^2)^2 (2 b^8-b^6 c^2+2 b^4 c^4-b^2 c^6+2 c^8) +a^2 (b^2-c^2)^4 (7 b^6+b^4 c^2+b^2 c^4+7 c^6) -2 (b^2-c^2)^6 (b^4+b^2 c^2+c^4) : :
See Tran Quang Hung and Angel Montesdeoca, ADGEOM 4859.
-
X(21269) = MIDPOINT ON X(265) AND X(14989)
Barycentrics 4 a^16 -9 a^14 (b^2+c^2) +a^12 (-6 b^4+44 b^2 c^2-6 c^4) +14 a^10 (2 b^6-3 b^4 c^2-3 b^2 c^4+2 c^6) -3 a^8 (5 b^8+15 b^6 c^2-44 b^4 c^4+15 b^2 c^6+5 c^8) -a^6 (9 b^10-71 b^8 c^2+63 b^6 c^4+63 b^4 c^6-71 b^2 c^8+9 c^10) +a^4 (b^2-c^2)^2 (4 b^8+14 b^6 c^2-63 b^4 c^4+14 b^2 c^6+4 c^8) +6 a^2 (b^2-c^2)^4 (b^6-2 b^4 c^2-2 b^2 c^4+c^6) -(b^2-c^2)^6 (3 b^4+7 b^2 c^2+3 c^4) : :
See Tran Quang Hung and Angel Montesdeoca, ADGEOM 4867.
-
X(21664) = X(118)X(133)∩X(119)X(2804)
Barycentrics (2 a b c - a^2 (b + c) + (b - c)^2 (b + c))^2 (a^4 - (b^2 - c^2)^2) : :
See Angel Montesdeoca, HG210618.
-
X(21665) = X(4)X(150)∩X(25)X(917)
Barycentrics b^2c^2(-2a^3+a^2(b+c)+(b-c)^2(b+c))^2(a^4-(b^2-c^2)^2) : :
See Angel Montesdeoca, HG210618.
-
X(21666) = X(4)X(151)∩X(25)X(1311)
Barycentrics b^2c^2(b-c)^2(-a+b+c)^2(a^2+b^2-c^2)(a^2-b^2+c^2) : :
See Angel Montesdeoca, HG210618.
-
X(21667) = X(3)X(8754)∩X(5)X(131)
Barycentrics 2 a^14 (b^2 + c^2) - a^12 (11 b^4 + 2 b^2 c^2 + 11 c^4) + 2 a^10 (12 b^6 + b^4 c^2 + b^2 c^4 + 12 c^6) - a^8 (25 b^8 + 8 b^6 c^2 - 18 b^4 c^4 + 8 b^2 c^6 + 25 c^8) + 2 a^6 (5 b^10 + 5 b^8 c^2 - 6 b^6 c^4 - 6 b^4 c^6 + 5 b^2 c^8 + 5 c^10) + a^4 (b^2 - c^2)^2 (3 b^8 - 8 b^6 c^2 - 14 b^4 c^4 - 8 b^2 c^6 + 3 c^8) - 2 a^2 (b^2 - c^2)^4 (2 b^6 - b^4 c^2 - b^2 c^4 + 2 c^6) + (b^2 - c^2)^8 : :
See Angel Montesdeoca, HG250618.
-
X(21668) = X(6)X(1511)∩X(1297)X(13398)
Barycentrics a^2 (a^14 b^2-5 a^12 b^4+9 a^10 b^6-5 a^8 b^8-5 a^6 b^10+9 a^4 b^12-5 a^2 b^14+b^16+a^14 c^2-6 a^12 b^2 c^2+20 a^10 b^4 c^2-29 a^8 b^6 c^2+17 a^6 b^8 c^2-8 a^4 b^10 c^2+10 a^2 b^12 c^2-5 b^14 c^2-5 a^12 c^4+20 a^10 b^2 c^4-40 a^8 b^4 c^4+36 a^6 b^6 c^4-13 a^4 b^8 c^4-8 a^2 b^10 c^4+10 b^12 c^4+9 a^10 c^6-29 a^8 b^2 c^6+36 a^6 b^4 c^6-8 a^4 b^6 c^6+3 a^2 b^8 c^6-11 b^10 c^6-5 a^8 c^8+17 a^6 b^2 c^8-13 a^4 b^4 c^8+3 a^2 b^6 c^8+10 b^8 c^8-5 a^6 c^10-8 a^4 b^2 c^10-8 a^2 b^4 c^10-11 b^6 c^10+9 a^4 c^12+10 a^2 b^2 c^12+10 b^4 c^12-5 a^2 c^14-5 b^2 c^14+c^16) : :
See Angel Montesdeoca, HG250618.
-
X(21975) = COMPLEMENT OF X(3459)
Barycentrics (a^4-a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4) (a^4-2 a^2 b^2+b^4-a^2 c^2-2 b^2 c^2+c^4) (a^8-4 a^6 b^2+6 a^4 b^4-4 a^2 b^6+b^8-4 a^6 c^2+5 a^4 b^2 c^2+a^2 b^4 c^2-2 b^6 c^2+6 a^4 c^4+a^2 b^2 c^4+2 b^4 c^4-4 a^2 c^6-2 b^2 c^6+c^8) : :
Let Q be the pedal curve (a limaçon of Pascal) of the circle with center X(7728) and radius |OH|, with respect to X(265). Let A'B'C' be the triangle formed by the tangents at A,B,C to Q. Then the triangles ABC and A'B'C' are perspective, and their perspector is X(2963). Moreover, X(21975) is the only finite fixed point of the affine transformation that maps a triangle ABC onto A'B'C'. See X(21975). (Angel Montesdeoca, September 10, 2019). See HG080919.
-
X(22100) = X(5)X(524)∩X(7812)X(9487)
Barycentrics 5 a^10-21 a^8 (b^2+c^2) +a^6 (34 b^4+28 b^2 c^2+34 c^4)+a^4 (-31 b^6+15 b^4 c^2+15 b^2 c^4-31 c^6) +15 a^2 (b^2-c^2)^2 (b^4-b^2 c^2+c^4) - (b^2-c^2)^2 (2 b^6-3 b^4 c^2-3 b^2 c^4+2 c^6) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 28146.
-
X(22101) = X(2)X(195)∩X(6)X(3459)
Barycentrics a^2 (a^20-10 a^18 (b^2+c^2)+(b^2-c^2)^8 (b^4-b^2 c^2+c^4)+a^16 (45 b^4+69 b^2 c^2+45 c^4)-2 a^2 (b^2-c^2)^6 (5 b^6-b^4 c^2-b^2 c^4+5 c^6)-4 a^14 (30 b^6+49 b^4 c^2+49 b^2 c^4+30 c^6)+a^12 (210 b^8+278 b^6 c^2+303 b^4 c^4+278 b^2 c^6+210 c^8)-6 a^10 (42 b^10+26 b^8 c^2+27 b^6 c^4+27 b^4 c^6+26 b^2 c^8+42 c^10)-2 a^6 (b^2-c^2)^2 (60 b^10+2 b^8 c^2-3 b^6 c^4-3 b^4 c^6+2 b^2 c^8+60 c^10)+a^4 (b^2-c^2)^2 (45 b^12-84 b^10 c^2+24 b^8 c^4+29 b^6 c^6+24 b^4 c^8-84 b^2 c^10+45 c^12)+a^8 (210 b^12-100 b^10 c^2+2 b^8 c^4+b^6 c^6+2 b^4 c^8-100 b^2 c^10+210 c^12)) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 28146.
-
X(22270) = X(3)X(6748)∩X(97)X(631)
Barycentrics 1/(a^8-4a^6(b^2+c^2)+6a^4(b^4+b^2c^2+c^4) -4a^2(b^2-c^2)^2(b^2+c^2)+(b^2-c^2)^2(b^4-4b^2c^2+c^4)) : :
See Antreas Hatzipolakis and Angel Montesdeoca Hyacinthos Hyacinthos 28174 and HG060918.
-
X(22277) = (A,B,C,X(2); A',B',C',X(10)) COLLINEATION IMAGE OF X(8), WHERE A'B'C' = ANTICEVIAN TRIANGLE OF X(37)
Barycentrics a^2 (b + c) (a b - b^2 + a c + b c - c^2) : :
In the plane of a triangle ABC, let
I = incenter;
DEF = intouch triangle;
(O) = circumcircle;
P = perpendicular bisector of segment ID;
Ai = points of intersection of P and (O), and define Bi and Ci cyclically, for i = 1, 2;
Di = reflection of D in IAi, for i = 1, 2;
A' = E1E2∩F1F2, and define B' and C' cyclically;
The lines DA', EB', FC' concur in X(22277). See X(22277). (Angel Montesdeoca, August 6, 2022) and HG060822.
-
X(23050) = X(1)X(475)∩X(9)X(8750)
Barycentrics a (a^2+b^2-c^2) (a^2-b^2+c^2) (a^3-a^2 b+a b^2-b^3-a^2 c+2 a b c-b^2 c+a c^2-b c^2-c^3) : :
See Angel Montesdeoca, HG300818.
-
X(23051) = X(10)X(400)∩X(19)X(38)
Barycentrics a/(3a^2+b^2+c^2) : :
See Angel Montesdeoca, HG300818.
-
X(23052) = X(1)X(19)∩X(4)X(3663)
Barycentrics a(a^4-(b^2-c^2)^2)(a^4+ 2a^2(b^2+c^2)-3b^4-2b^2c^2-3c^4) : :
See Angel Montesdeoca, HG300818.
-
X(23053) = X(2)X(6)∩X(671)X(3524)
Barycentrics 17a^4-20a^2(b^2+c^2)+11b^4-26b^2c^2+11c^4 : :
See Angel Montesdeoca, HG300818.
-
X(23054) = X(1992)X(16509)∩X(4232)X(8860)
Barycentrics 1/(19a^4-40a^2b^2+13b^4-40a^2c^2-10b^2c^2+13c^4) : :
See Angel Montesdeoca, HG300818.
-
X(23055) = X(2)X(6)∩X(98)X(11172)
Barycentrics 11a^4-8a^2(b^2+c^2)+5b^4-14b^2c^2+5c^4 : :
See Angel Montesdeoca, HG300818.
-
X(23056) = = X(926)X(2170)∩X(2246)X(4845)
Barycentrics a(b-c)^2(b+c-a)^2(5a^2-4a(b+c)-(b-c)^2) : :
Let ABC be a triangle of incenter I, the perpendicular by I to AI intersects AC and AB in Ab and Ac, respectively.
The points Bc, Ba, Ca and Cb are defined cyclically.
The circles (AbBaBc), (BcCbCa) and (CaAcAb) concur in P.
The circles (AbBaAc), (BcCbBa) and (CaAcCb) cuncur in U.
Points P and U form a bicentric pair,
P = f(a,b,c) : f(b,c,a) : f(c,a,b) and Q = f(a,c,b) : f(b,a,c) : f(c,b,a)
with
f(a,b,c) = a (a-b-c) (b-c) (2 a^2-2 a b-a c+b c-c^2) (a^2+a b-2 b^2-2 a c+b c+c^2).
The bicentric difference of P and U is X(23056).
See Emmanuel José García and Angel Montesdeoca, AdGeom4943 and
HG100918.
-
X(23057) = X(1)X(22254)∩X(145)X(3716)
Barycentrics a(b-c)(4a^2-5a(b+c)+b^2+4bc+c^2) : :
Let ABC be a triangle of incenter I, the perpendicular by I to AI intersects AC and AB in Ab and Ac, respectively.
The points Bc, Ba, Ca and Cb are defined cyclically.
The circles (AbBaBc), (BcCbCa) and (CaAcAb) concur in P.
The circles (AbBaAc), (BcCbBa) and (CaAcCb) cuncur in U.
Points P and U form a bicentric pair,
P = f(a,b,c) : f(b,c,a) : f(c,a,b) and Q = f(a,c,b) : f(b,a,c) : f(c,b,a)
with
f(a,b,c) = a (a-b-c) (b-c) (2 a^2-2 a b-a c+b c-c^2) (a^2+a b-2 b^2-2 a c+b c+c^2).
The bicentric sum of P and U is X(23057).
See Emmanuel José García and Angel Montesdeoca, AdGeom4943 and
HG100918.
-
X(23058) = X(1)X(1146)∩X(4)X(9)
Barycentrics (b+c-a)(a^3+a(b-c)^2-2(b-c)(b^2-c^2)) : :
Let DEF be the medial triangle of ABC. Let Ha be the hyperbola with foci E and F that passes through A, and define Hb and Hc cyclically. The three hyperbolas have in common two points, and their midpoint is X(23058).
See Kadir Altintas and Angel Montesdeoca,
HG110918.
-
X(23244) = ALTINTAS-MONTESDEOCA MIDPOINT
Barycentrics a(a-b-c)^3(a^6-3a^4(b-c)^2+3a^2(b-c)^2(b^2+6b c+c^2)-16a b(b-c)^2c(b+c)-(b-c)^4(b^2+6b c+c^2)) : :
Let DEF be the exdtouch triangle of ABC. Let Ha be the hyperbola with foci E and F that passes through A, and define Hb and Hc cyclically. The three hyperbolas have in common two points, and their midpoint is X(23244).
See Kadir Altintas and Angel Montesdeoca,
HG150918 (Sep 17, 2018).
-
X(23286) = X(125)-CROSS CONJUGATE OF X(3)
Barycentrics a^2 (b^2-c^2) (a^2-b^2-c^2) (a^4-2 a^2 b^2+b^4-a^2 c^2-b^2 c^2) (a^4-a^2 b^2-2 a^2 c^2-b^2 c^2+c^4) : :
Let L be the line through X(3) parallel to BC, and let A' = L∩AX(100). Define B' and C' cyclically. The triangle A'B'C' is parallelogic to ABC (by construction), at X(3) and X(14380), and X(23286) is the unique fixed point of the affine transformation that maps ABC onto A'B'C'. (Angel Monesdeoca, June 27, 2020)
HG270620
-
X(23358) = MIDPOINT OF X(3) AND X(2917)
Barycentrics a^2 (a^14-3 a^12 b^2+a^10 b^4+5 a^8 b^6-5 a^6 b^8-a^4 b^10+3 a^2 b^12-b^14-3 a^12 c^2+5 a^10 b^2 c^2+a^8 b^4 c^2-5 a^6 b^6 c^2+4 a^4 b^8 c^2-4 a^2 b^10 c^2+2 b^12 c^2+a^10 c^4+a^8 b^2 c^4+2 a^6 b^4 c^4-3 a^4 b^6 c^4-a^2 b^8 c^4+5 a^8 c^6-5 a^6 b^2 c^6-3 a^4 b^4 c^6+4 a^2 b^6 c^6-b^8 c^6-5 a^6 c^8+4 a^4 b^2 c^8-a^2 b^4 c^8-b^6 c^8-a^4 c^10-4 a^2 b^2 c^10+3 a^2 c^12+2 b^2 c^12-c^14) : :
See Antreas Hatzipolakis, Peter Moses and Angel Montesdeoca, Hyacinthos 28295 and Hyacinthos 28296.
-
X(23408) = (name pending)
Barycentrics 2 a^16-7 a^14 (b^2+c^2)-(b^2-c^2)^6 (b^4-3 b^2 c^2+c^4)+4 a^12 (b^4+3 b^2 c^2+c^4)+2 a^2 (b^2-c^2)^4 (3 b^6-b^4 c^2-b^2 c^4+3 c^6)+2 a^10 (8 b^6-b^4 c^2-b^2 c^4+8 c^6)+a^8 (-35 b^8+3 b^6 c^2-6 b^4 c^4+3 b^2 c^6-35 c^8)-a^4 (b^2-c^2)^2 (18 b^8+4 b^6 c^2-b^4 c^4+4 b^2 c^6+18 c^8)+a^6 (33 b^10-21 b^8 c^2+5 b^6 c^4+5 b^4 c^6-21 b^2 c^8+33 c^10) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28297.
-
X(23409) = MIDPOINT OF X(5) AND X(13163)
Barycentrics 2 a^10+15 a^2 b^2 c^2 (b^2-c^2)^2-3 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)-2 a^6 (b^4-b^2 c^2+c^4)-a^4 (-4 b^6+17 b^4 c^2+17 b^2 c^4-4 c^6) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28297.
-
X(23410) = MIDPOINT OF X(2) AND X(13490)
Barycentrics 2 a^10-2 a^6 (b^2-c^2)^2+10 a^2 b^2 c^2 (b^2-c^2)^2-3 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)+2 a^4 (2 b^6-7 b^4 c^2-7 b^2 c^4+2 c^6) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28297.
-
X(23411) = MIDPOINT OF X(546) AND X(9825)
Barycentrics 2 a^10+16 a^2 b^2 c^2 (b^2-c^2)^2-3 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)-2 a^6 (b^4+c^4)+4 a^4 (b^6-4 b^4 c^2-4 b^2 c^4+c^6) : :
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28297.
-
X(23617) = CEVAPOINT OF X(6) AND X(9)
Barycentrics a/((b-c)^2+a(b+c)) : :
Let P = X(23617). Let Pa be the isotomic conjugate of P with respect to AX(6)X(9), and define Pb and Pc cyclically. Then ABC and PaPbPc are perspective in X(13622). (Angel Montesdeoca, September 23, 2018)
-
X(23618) = CEVAPOINT OF X(7) AND X(9)
Barycentrics 1/((b+c-a)(a^2(b+c)-2a(b-c)^2+(b-c)^2(b+c))) : :
Let P = X(23618). Let Pa be the isotomic conjugate of P with respect to AX(7)X(9), and define Pb and Pc cyclically. Then ABC and PaPbPc are perspective in X(3255). (Angel Montesdeoca, September 23, 2018)
-
X(23709) = X(3)X(95)∩X(1154)X(10606)
Barycentrics a^2 (-(b^2-c^2)^2+a^2 (b^2+c^2)) (a^16-5 a^14 (b^2+c^2)+b^2 c^2 (b^2-c^2)^4 (b^4+4 b^2 c^2+c^4)+3 a^12 (3 b^4+7 b^2 c^2+3 c^4)-a^10 (5 b^6+33 b^4 c^2+33 b^2 c^4+5 c^6)+a^8 (-5 b^8+23 b^6 c^2+38 b^4 c^4+23 b^2 c^6-5 c^8)-a^4 (b^2-c^2)^2 (5 b^8+7 b^6 c^2+8 b^4 c^4+7 b^2 c^6+5 c^8)+a^2 (b^2-c^2)^2 (b^10-b^8 c^2-4 b^6 c^4-4 b^4 c^6-b^2 c^8+c^10)+a^6 (9 b^10-7 b^8 c^2-14 b^6 c^4-14 b^4 c^6-7 b^2 c^8+9 c^10)) : :
See Tran Quang Hung, Angel Montesdeoca, and Ercole Suppa, Hyacinthos 28317 and Hyacinthos 28318.
-
X(23869) = MIDPOINT OF X(1) AND X(6788)
Barycentrics a^3 (b+c)-a^2 (-3 b^2+10 b c-3 c^2)+a (b^3+c^3)-(b^2-c^2)^2 : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 28355 and HG270918.
Let ABC be a triangle.
Denote:
Na, Nb, Nc = the NPC centers of IBC, ICA, IAB, resp.
A1, B1, C1 = points on IA, IB, IC such that:
AA1/AI = BB1/BI = CC1/CI = t
The perpendicular to AI at A1 intersects NbNc at A*
The perpendicular to BI at B1 intersects NcNa at B*
The perpendicular to CI at C1 intersects NaNb at C*
The points A*, B*, C* are collinear.
The envelope of the lines A*B*C* as t varies is the parabola of focus X(23869).
-
X(25466) = (A,B,C,X(2); A',B',C',X(2)) COLLINEATION IMAGE OF X(12), WHERE A'B'C' = GEMINI TRIANGLE 21
Barycentrics -a^2 b^2 + b^4 - 4 a^2 b c - 2 a b^2 c - a^2 c^2 - 2 a b c^2 - 2 b^2 c^2 + c^4 : :
Let DEF be the medial triangle. The circle that touches all three incircles of the triangles AEF, BFD, CDE and encompasses them touches in points that we denote by them in A', B', C', respectively. The lines DA', EB' , FC' concur in X(25466). See X(25466). (Angel Montesdeoca, November 29, 2019)
(HG291119)
-
X(28443) = EULER LINE INTERCEPT OF X(36)X(4870)
Barycentrics a (3 a^6-3 a^5 (b+c)+a^4 (-6 b^2+b c-6 c^2)-2 b c (b^2-c^2)^2+6 a^3 (b^3+c^3)+a^2 (3 b^4+b^3 c+6 b^2 c^2+b c^3+3 c^4)-3 a (b^5-b^4 c-b c^4+c^5)) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 28681.
-
X(30332) = ENDO-HOMOTHETIC CENTER OF THESE TRIANGLES: ANTI-HUTSON INTOUCH AND 2nd EHRMANN
Barycentrics 7*a^3-5*(b+c)*a^2+(b-c)^2*a-3*(b^2-c^2)*(b-c) : :
Let Γa be the circle passing through X(7) tangent to AB and AC such that the touchpoints do not lie on the Adams circle. Define Γb and Γc cyclically. Then X(30332) is the center of the circle tangent to the circles Γa, Γb Γc .and encompassing (Angel Montesdeoca, June 2, 2023)
HG010623
-
X(30443) = X(30)X(21651)∩X(51)X(5895)
Barycentrics a^2 ( a^12 (b^2+c^2)-4 a^10 (b^2-c^2)^2+5 a^8 (b^2-c^2)^2 (b^2+c^2) -40 a^6 b^2 c^2 (b^2-c^2)^2-5 a^4 (b^2-c^2)^2 (b^6-9 b^4 c^2-9 b^2 c^4+c^6) +4 a^2 (b^2-c^2)^2 (b^8-2 b^6 c^2-14 b^4 c^4-2 b^2 c^6+c^8) -(b^2-c^2)^4 (b^6+7 b^4 c^2+7 b^2 c^4+c^6)) : :
Let ABC be a triangle with de Longchamps point L. A'B'C' is pedal triangle of L. L'=X(30443) is de Longchamps point of triangle A'B'C'.
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28754.
-
X(31383) = MARTA POINT
Barycentrics 3a^6-a^4(b^2+c^2)-a^2(b^2-c^2)^2-(b^2-c^2)^2(b^2+c^2) : :
Let ABC be a triangle with centroid G and orthocenter H.
The line parallel to BC for the point Pa, such that APa:PaH= t, intersects the sides AC and AB respectively at Ab and Ac.
Let Da be the point of intersection of the lines BAb and CAc.
Let La be the line joining the orthocenters of the triangles BDaAc and CDaAb.
Lb and Lb are defined similarly.
Let G' be the centroid of A'B'C', the triangle bound by La,Lb,Lc.
Let F be the fixed point (not on the line at infinity) of the affine transformation that applies ABC in A'B'C'.
Then, as t varies, the line G'F passes through a fixed point Q=X(31383).
See Angel Montesdeoca, Hyacinthos 28832 and Centro ortológico y punto fijo de una afinidad.
-
X(31392) = REFLECTION OF X(5) IN X(14051)
Barycentrics (a^4+(b^2-c^2)^2-a^2 (b^2+2 c^2)) (a^12-(b^2-c^2)^6-a^10 (4 b^2+3 c^2)+a^8 (5 b^4+5 b^2 c^2+3 c^4)-a^6 (3 b^4 c^2+2 b^2 c^4)+a^2 (b^2-c^2)^2 (4 b^6-6 b^4 c^2-3 b^2 c^4+3 c^6)+a^4 (-5 b^8+9 b^6 c^2+b^4 c^4+4 b^2 c^6-3 c^8)) : :
Let ABC be a triangle.
Denote:
(O1) ,(O2), (O3) = the circumcircles of NBC, NCA, NAB, resp.
(Oa) ,(Ob), (Ob) = the reflections of (O1) ,(O2), (O3) in BC, CA, AB, resp.
They concurr at D = antigonal conjugate of N = X(1263).
The circumcircles of DAOa, DBOb, DCOc are coaxial.
2nd (other than D=X(1263)) intersection is X(31392) = REFLECTION OF X(5) IN X(14051).
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 28850.
Let A' be the reflection of A in BC. Let Ab be the intersection of AC and the perpendicular bisector of A'B, and let Ac be the intersection of AB and the perpendicular bisector of A'C. Let A'' be the orthogonal projection of A' on AbAc, and define B'' and C'' cyclically. The lines AA'', BB'', CC'' concur in X(31392). (Angel Montesdeoca, July 16, 2020)
(El centro del triángulo X(31392))
-
X(31510) = MIDPOINT OF X(107) AND X(1304)
Barycentrics (a^2-b^2) (a^2-c^2) (2 a^14-2 a^12 (b^2+c^2)+9 a^8 (b^2-c^2)^2 (b^2+c^2)-8 a^4 (b^2-c^2)^4 (b^2+c^2)+(b^2-c^2)^6 (b^2+c^2)+a^10 (-7 b^4+16 b^2 c^2-7 c^4)+4 a^6 (b^2-c^2)^2 (b^4-5 b^2 c^2+c^4)+a^2 (b^2-c^2)^4 (b^4+8 b^2 c^2+c^4)) : :
Let ABC be a triangle.
Euler line meets BC, CA, AB at A', B', C', resp.
Perpendiculars from A', B', C' to BC, CA, AB resp. bound a triangle A"B"C".
Then X(1552) of A"B"C" lies on the Euler line of ABC: X(31510) = MIDPOINT OF X(107) AND X(1304)
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28858.
-
X(31511) = X(1)X(3)∩X(109)X(13138)
Barycentrics a (a-b) (a^2-(b-c)^2) (a-c) (2 a^7-a^6 (b+c)+a^4 (b-c)^2 (b+c)-(b-c)^2 (b+c)^5-6 a^3 (b^2-c^2)^2+4 a (b^2-c^2)^2 (b^2+c^2)+a^2 (b-c)^2 (b^3+7 b^2 c+7 b c^2+c^3)) : :
Let ABC be a triangle.
X(1)X(4) line of ABC meets BC, CA, AB at A', B', C'.
Perpendicular lines from A', B', C' to BC, CA, AB bound triangle A"B"C".
Then X(84) of A"B"C" lies on OI line of ABC: X(31511) = X(1)X(3)∩X(109)X(13138)
See Tran Quang Hung and Angel Montesdeoca, ADGEOM 5142.
-
X(31512) = X(4)X(8)∩X(11)X(901)
Barycentrics a^6+6 a^4 b c-2 a^5 (b+c)-2 a^3 b c (b+c)-(b-c)^4 (b+c)^2+a^2 b c (3 b^2-5 b c+3 c^2)+a (b-c)^2 (2 b^3-3 b^2 c-3 b c^2+2 c^3) : :
See Tran Quang Hung and Angel Montesdeoca, ADGEOM 5144.
-
X(31513) = X(4)X(8)∩X(11)X(901)
Barycentrics a^2 (a^8 b^2 c^2-2 a^2 b^4 c^4 (b^2+c^2)-a^6 (b^6+b^4 c^2+b^2 c^4+c^6)+a^4 (b^8+4 b^4 c^4+c^8)-b^2 c^2 (b^8-3 b^6 c^2+3 b^4 c^4-3 b^2 c^6+c^8)) : :
See Tran Quang Hung and Angel Montesdeoca, ADGEOM 5144.
-
X(31668) = (name pending)
Barycentrics a (a+b) (a+c) ((b-c)^6 (b+c)^7+(b^2-c^2)^4 (b^4-b^3 c+8 b^2 c^2-b c^3+c^4) a-(b-c)^2 (b+c)^3 (4 b^6-2 b^5 c+11 b^4 c^2-14 b^3 c^3+11 b^2 c^4-2 b c^5+4 c^6) a^2-(b^2-c^2)^2 (4 b^6-7 b^5 c-3 b^4 c^2+7 b^3 c^3-3 b^2 c^4-7 b c^5+4 c^6) a^3+(5 b^9-3 b^8 c+15 b^7 c^2+31 b^6 c^3-18 b^5 c^4-18 b^4 c^5+31 b^3 c^6+15 b^2 c^7-3 b c^8+5 c^9) a^4+(5 b^8-18 b^7 c-43 b^6 c^2-16 b^5 c^3+14 b^4 c^4-16 b^3 c^5-43 b^2 c^6-18 b c^7+5 c^8) a^5+b c (12 b^5+3 b^4 c-19 b^3 c^2-19 b^2 c^3+3 b c^4+12 c^5) a^6+b c (22 b^4+41 b^3 c+47 b^2 c^2+41 b c^3+22 c^4) a^7+(-5 b^5-13 b^4 c-17 b^3 c^2-17 b^2 c^3-13 b c^4-5 c^5) a^8+(-5 b^4-13 b^3 c-17 b^2 c^2-13 b c^3-5 c^4) a^9+2 (2 b^3+3 b^2 c+3 b c^2+2 c^3) a^10+(4 b^2+3 b c+4 c^2) a^11+(-b-c) a^12-a^13) : :
I call Kosnita line the line conneting NPC center X(5) and Kosnita point X(54) of a triangle.
Let ABC be a triangle with excenters Ia, Ib, Ic.Then refections L'a, L'b, L'c of Kosnita lines La, Lb, Lc of triangles IaBC, IbCA, and IcAB in lines BC, CA, and AB respectively are concurrent at X(110) = focus of Kiepert parabola.
If Aa=Lb ∩ Lc, Ab=L'a ∩ Lc, Ac=L'a∩ Lb, then the line AAa, BAb, CAc concur in a point Wa, and define Wb and Wc cyclically. WaWbWc is perspective to ABC at X(1290) and WaWbWc is perspective to AaBbCc at X(1290).
Then the three perspectrix of ABC and WaWbWc, ABC and AaBaBc, AaBbBc and WaWbWc concur in X(31668).
See Tran Quang Hung and Angel Montesdeoca, Hyacinthos 28896.
-
X(31676) = X(3)X(125)∩X(25)X(6344)
Barycentrics a^2SA (SA^2 + 5S^2)/(4SA^2-b^2c^2) : :
Let ABC be a triangle of circumcenter O and a point D variable on the circumcircle. Let Ha, Hb, Hc be the orthocenters of the triangles DBC, DCA, DAB, respectively.
The circle of diameter OHa cuts again the lines BHa and CHa in Hab and Hac, respectively.
The perpendicular bisector of HabHac passes through a fixed point Fa, on the perpendicular bisector of BC, when D varies over the circumcircle.
Let p_a be the polar of Fa with respect to the circumcircle. The polar p_b and p_c are defined cyclically.
The triangle A'B'C' formed by the lines p_a, p_b and p_c is perspective with ABC, with perspector X(31676)
See Nguyên Danh Lân and Angel Montesdeoca, Hyacinthos 28906, HG080319, AoPS.
-
X(31846) = X(324)X(547)∩X(343)X(15699)
Barycentrics 1/(5 a^8-17 a^6 (b^2+c^2)+a^4 (21 b^4+17 b^2 c^2+21 c^4)-11 a^2 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^2 (2 b^4-7 b^2 c^2+2 c^4)) : :
See Ioannis Panakis, Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 28926.
-
X(31868) = X(5)X(27684)∩X(2883)X(3845)
Barycentrics 4 a^16-22 a^14 b^2+45 a^12 b^4-31 a^10 b^6-30 a^8 b^8+76 a^6 b^10-63 a^4 b^12+25 a^2 b^14-4 b^16-22 a^14 c^2+58 a^12 b^2 c^2-27 a^10 b^4 c^2-21 a^8 b^6 c^2-56 a^6 b^8 c^2+156 a^4 b^10 c^2-119 a^2 b^12 c^2+31 b^14 c^2+45 a^12 c^4-27 a^10 b^2 c^4-18 a^8 b^4 c^4-20 a^6 b^6 c^4-81 a^4 b^8 c^4+207 a^2 b^10 c^4-106 b^12 c^4-31 a^10 c^6-21 a^8 b^2 c^6-20 a^6 b^4 c^6-24 a^4 b^6 c^6-113 a^2 b^8 c^6+209 b^10 c^6-30 a^8 c^8-56 a^6 b^2 c^8-81 a^4 b^4 c^8-113 a^2 b^6 c^8-260 b^8 c^8+76 a^6 c^10+156 a^4 b^2 c^10+207 a^2 b^4 c^10+209 b^6 c^10-63 a^4 c^12-119 a^2 b^2 c^12-106 b^4 c^12+25 a^2 c^14+31 b^2 c^14-4 c^16 : :
Let DEF be the cevian triangle of X(5). Let ℓb be the perpendicular to BE at E, and let ℓc be the perpendicular to CF at F. Let A' = ℓb∩ℓc, and define B' and C' cyclically. The triangles ABC and A'B'C' are orthologic (by construction), and the orthologic center of A'B'C' respect to ABC is X(31868). (Angel Montesdeoca, March 13, 2021)
-
X(31873) = X(125)X(546)∩X(133)X(1594)
Barycentrics 2 a^14 (b^2+c^2) +a^12 (-6 b^4+8 b^2 c^2-6 c^4) +a^10 (b^6-3 b^4 c^2-3 b^2 c^4+c^6) +a^8 (15 b^8-44 b^6 c^2+62 b^4 c^4-44 b^2 c^6+15 c^8) -a^6 (b^2-c^2)^2 (20 b^6+b^4 c^2+b^2 c^4+20 c^6) +a^4 (b^2-c^2)^2 (8 b^8+31 b^6 c^2-42 b^4 c^4+31 b^2 c^6+8 c^8) +a^2 (b^2-c^2)^4 (b^6-14 b^4 c^2-14 b^2 c^4+c^6) -(b^2-c^2)^6 (b^4+5 b^2 c^2+c^4) : :
See Vu Thanh Tung and Angel Montesdeoca, Hyacinthos 28942.
Let DEF be the pedal triangle of a point P wrt a triangle ABC.
Oa and Ha are the circumcenter and the orthocenter of AEF, resp.
Let α be a real number and A1 be the point such that: OaA1 = α OaHa. Define B1 and C1 cyclically.
(1) The triangle A1B1C1 are orthologic to both triangles ABC and DEF, with orthologic centers V and V', resp.
(2) When P fixed and α varies the orthologic centers move in fixed lines, L and L'.
When the point P traverses the Euler line of ABC the line L envelope the parabola tangent to Euler line at X(5), tangent to line X(4)X(51) at X(185), and tangent to line X(389)X(546) at X(10095).
X(31873) is the focus.
-
X(32006) = POINT II-CAPH OF X(69)
Barycentrics 3*a^4 - 3*b^4 + 2*b^2*c^2 - 3*c^4 : :
Let A'B'C' be the anticevian triangle of X(69). Let A" be the orthogonal projection of A' on the line through X(69) parallel to line BC, and define B" and C" cyclically. The lines AA", BB", CC" concur in X(32006) = Point II-Caph of X(69). See X(33006).png (Angel Montesdeoca, December 6, 2022)
See X(32006) y triángulo anticeviano del retrocentro.
-
X(32319) = X(4)X(19209)∩X(20)X(2979)
Barycentrics a^2 (b^2 c^2 (b^2 - c^2)^6 - 10 a^10 (b^2 - c^2)^2 (b^2 + c^2) - 2 a^2 (b^2 - c^2)^4 (b^2 + c^2)^3 + a^12 (2 b^4 - 5 b^2 c^2 + 2 c^4) + 5 a^8 (b^2 - c^2)^2 (4 b^4 + 7 b^2 c^2 + 4 c^4) - 4 a^6 (b^2 - c^2)^2 (5 b^6 + 9 b^4 c^2 + 9 b^2 c^4 + 5 c^6) + a^4 (b^2 - c^2)^2 (10 b^8 + 13 b^6 c^2 + 18 b^4 c^4 + 13 b^2 c^6 + 10 c^8)) : :
See Angel Montesdeoca, Hyacinthos 29000 and HG020519.
-
X(32320) = REFLECTION OF X(17434) IN X(647)
Barycentrics a^4 (a^2 - b^2 - c^2)^3 (b^2 - c^2) : :
See Angel Montesdeoca, Hyacinthos 29000 and HG020519.
-
X(32446) = X(2)X(2124)∩X(10)X(971)
Barycentrics (b+c-a)(a^5 (b+c)-3 a^4 (b-c)^2+2 a^3 (b-c)^2 (b+c)+2 a^2 (b-c)^2 (b^2+6 b c+c^2)-a (b-c)^2 (3 b^3+13 b^2 c+13 b c^2+3 c^3)+(b-c)^6) : :
See Angel Montesdeoca, Hyacinthos 29006, Hyacinthos 29006 and HG070519.
-
X(32486) = MIDPOINT OF X(1) AND X(5400)
Barycentrics a(a^5(b+c)-4a^4b c+a^3(-2b^3+3b^2c+3b c^2-2c^3)+5a^2b c(b-c)^2+a(b-c)^2(b^3-2b^2c-2b c^2+c^3)- b c(b^2-c^2)^2) : :
See Angel Montesdeoca, Hyacinthos 29011 and HG130519.
-
X(32487) = X(2292)X(3754)∩X(4535)X(18697)
Barycentrics a(b+c)^2/(2a^2-(b+c)^2) : :
See Angel Montesdeoca, Hyacinthos 29011 and HG130519.
-
X(33568) = X(2)X(824)∩X(4809)X(14402)
Barycentrics (b^3 - c^3) (-2 a^3 + b^3 + c^3)^2 : :
See Angel Montesdeoca, Hyacinthos 29181 and HG100719.
-
X(33569) = X(2)X(647)∩X(684)X(2491)
Barycentrics a^4(b^2-c^2)(b^4+c^4-a^2(b^2+c^2))^2(-a^4+2b^2c^2+a^2(b^2+c^2)) : :
See Angel Montesdeoca, Hyacinthos 29181 and HG100719.
-
X(33570) = X(2)X(650)∩X(647)X(1962)
Barycentrics a^2 (b - c) (b^2 + c^2 - a (b + c))^2 (-a^2 + 2 b c + a (b + c)) : :
See Angel Montesdeoca, Hyacinthos 29181 and HG100719.
-
X(33571) = X(2)X(216)∩X(1636)X(2972)
Barycentrics a^4 (b^2 - c^2)^2 (-a^2 + b^2 + c^2)^4 (-2 b^2 c^2 (b^2 - c^2)^2 + a^6 (b^2 + c^2) + a^2 (b^2 - c^2)^2 (b^2 + c^2) - 2 a^4 (b^4 - b^2 c^2 + c^4)) : :
See Angel Montesdeoca, Hyacinthos 29181 and HG100719.
-
X(33572) = X(2)X(92)∩X(7004)X(7117)
Barycentrics a^2 (b - c)^2 (a^3 + b^3 + b^2 c + b c^2 + c^3 - a^2 (b + c) - a (b^2 + c^2))^2 (a^4 (b + c) - a^2 (b - c)^2 (b + c) - 2 b (b - c)^2 c (b + c) + a (b^2 - c^2)^2 - a^3 (b^2 + c^2)) : :
See Angel Montesdeoca, Hyacinthos 29181 and HG100719.
-
X(33573) = REFLECTION OF X(14477) IN X(2)
Barycentrics (b - c)^2 (-a + b + c)^2 (2 a^2 - (b - c)^2 - a (b + c)) : :
See Angel Montesdeoca, Hyacinthos 29181 and HG100719.
-
X(33591) = EULER LINE INTERCEPT OF X(524)X(10282)
Barycentrics -10 a^10+21 a^8 (b^2+c^2)-2 a^6 (b^4+4 b^2 c^2+c^4)-4 a^4 (5 b^6-b^4 c^2-b^2 c^4+5 c^6)+4 a^2 (b^2-c^2)^2 (3 b^4+b^2 c^2+3 c^4)-(b^2-c^2)^4 (b^2+c^2) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 29196.
-
X(34199) = (name pending)
Barycentrics 2 a^10 - 9 a^8 (b^2 + c^2) + 2 a^6 (5 b^4 + 9 b^2 c^2 + 5 c^4) + a^4 (4 b^6 - 9 b^4 c^2 - 9 b^2 c^4 + 4 c^6) - 3 a^2 (b^2 - c^2)^2 (4 b^4 + 3 b^2 c^2 + 4 c^4) + 5 (b^2 - c^2)^4 (b^2 + c^2) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 29455 and HG270819.
-
X(34285) = isogonal conjugate of X(33586)
Barycentrics 1/(a^4+2a^2(b^2+c^2)-3b^4+2b^2c^2-3c^4) : :
Let A'B'C' and A"B"C" be the cevian and circumcevian triangles of the orthocenter. Let La be the radical axis of circles with segments BC and A'A" as diameters, and define Lb and Lc cyclically. The triangle formed by lines La, Lb, Lc is perspective to ABC, and the perspector is X(34285). (Angel Montesdeoca, September 5, 2019)
See
HGT
-
X(34355) = X(1)X(12619)∩X(106)X(18976)
Barycentrics (a-b+c) (a+b-c) (a^7 (b+c)+(b^2-c^2)^4+a^6 (b^2-12 b c+c^2)-a^2 (b^2-c^2)^2 (b^2-b c+c^2)-a (b-c)^2 (b+c)^3 (3 b^2-5 b c+3 c^2)+a^5 (-5 b^3+13 b^2 c+13 b c^2-5 c^3)-a^4 (b^4-11 b^3 c+30 b^2 c^2-11 b c^3+c^4)+a^3 (7 b^5-16 b^4 c+10 b^3 c^2+10 b^2 c^3-16 b c^4+7 c^5)) : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 29575 and HG031019.
Let Na, Nb, Nc denote the nine-point centers of the triangles IBC, ICA, IAB, and let A"B"C" be the reflection of intouch triangle in the line X(1)X(3). Then NaNbNc is similar to A''B''C'', and the center of similitude is X(34355). (Angel Montesdeoca, October 7, 2019)
-
X(34578) = CYCLOLOGIC CENTER S(X(1),X(2))
Barycentrics (a^2 + a*b + b^2 - 2*a*c - 2*b*c + c^2)*(a^2 - 2*a*b + b^2 + a*c - 2*b*c + c^2) : :
Let DEF be the intouch triangle and IaIbIc the excentral-triangle. Let D' be the trisector nearest D of segment DIa. Let La be the radical axis of (DEF) and (BCD'), and define Lb and Lc cyclically. The triangle A'B'C' formed by the lines La, Lb, Lc is perspective to ABC, and the perspector is X(34578). (Angel Montesdeoca, December 31, 2020)
In general, if D' is a point such that DD' / D'Ia = t (a constant real number) then the perspector of ABC and A'B'C', given by barycentrics
a/(a^3-a^2 (b+c) (1+2 t)-a (b^2 (1-4 t)+c^2 (1-4 t)-2 b c (1-2 t+2 t^2))-(b-c)^2 (b+c) (-1+2 t)) : : ,
lies on the circumhyperbola that is the isogonal conjugate of line X(1)X(6). See also X(39980). (Angel Montesdeoca, December 31, 2020)
See HGT301220
-
X(34815) = CENTER OF PERSPECONIC OF ABC AND CIRCUMCEVIAN TRIANGLE OF X(64)
Barycentrics a^2*(a^2 - b^2 - c^2)*(3*a^8 - 2*a^4*b^4 - 8*a^2*b^6 + 7*b^8 + 4*a^4*b^2*c^2 + 8*a^2*b^4*c^2 - 12*b^6*c^2 - 2*a^4*c^4 + 8*a^2*b^2*c^4 + 10*b^4*c^4 - 8*a^2*c^6 - 12*b^2*c^6 + 7*c^8) : :
Let A'B'C' be the circumcevian triangle of X(64). Let A"=AO∩B'C', and define B" and C" cyclically. The points A'A", B'B", C'C" concur in X(34815). More generally, suppose that a point P lies on the Darboux cubic, and let A'B'C' be the circumcevian triangle of P. Define B'' and C'' cyclically. The points A'A", B'B", C'C" concur in a point, Q(P). The appearance of (i,j) in the following list means that X(i) is on the Darboux cubic and Q(X(i)) = X(j): (1,991), (,3), (4,5890), (64,34815). (Angel Montesdeoca, August 3, 2021).
La cúbica de Darboux y triángulos circuncevianos
-
X(35015) = X(1)X(4)∩X(11)X(244)
Barycentrics (a - b - c)*(b - c)^2*(a^2*b - b^3 + a^2*c - 2*a*b*c + b^2*c + b*c^2 - c^3) : :
In the plane of a triangle ABC, let
DEF = orthic triangle;
F' = X(11) = Feuerbach point;
D' = reflection of D in AF;
Da = EF∩D'F';
Oa = circumcenter of ADDa, and define Ob and Oc cyclically;
The finite fixed point of the affine transformation that maps ABC onto OaOObOc is X(35015). (Angel Montesdeoca, May 26, 2022)
See HG250522
-
X(35445) = X(1)X(3) ∩ (line at infinity)
Barycentrics a*(5*a^2 - 4*a*b - b^2 - 4*a*c + 2*b*c - c^2) : :
Let Bc be the reflection of B in the internal angle bisector of angle C, and let Cb be the reflection of C in the internal angle bisector of angle B. Let Γa be the circle that passes through A, Bc, Cb. Let A' be the pole of BC, with respect to Γa and define B 'and C' cyclically. Then X(1156) is the perspector of A'B'C' and ABC, and X(35445) is the perspector of A'B'C' and the excentral triangle. (Angel Montesdeoca, January 13, 2021)
See HG120121.
-
X(36809) = (name pending)
Barycentrics (S^2+SB SC)/(SA(3S^2+5 SB SC)) : :
Barycentrics (a^2 (b^2+c^2)-(b^2-c^2)^2)/((b^2+c^2-a^2) (a^4+3 a^2 (b^2+c^2)-4 (b^2-c^2)^2)) : :
Let H be the orthocenter and M be the midpoint of AH. Let Ba and Ca be the orthogonal projections of B and C on CM and BM, respectively. Define Cb and Ac cyclically, and define Ab and Bc cyclically. Let A'B'C' be the triangle having sidelines BaCa, CbAb, AcBc. Then A'B'C' is perspective to ABC, and the perspector is X(36809).
See Angel Montesdeoca, Euclid 641 .
-
X(36922) = X(1)X(5791)∩X(2)X(14563)
Barycentrics (a - 2*b - 2*c)*(3*a^3 - a^2*b - 3*a*b^2 + b^3 - a^2*c + 2*a*b*c - b^2*c - 3*a*c^2 - b*c^2 + c^3) : :
In the plane of a triangle ABC, let
Ia = A-excenter = -a : b : c, and define Ib and Ic cyclically
Ta = AaBaCa = pedal triangle of Ia, and define Tb and Tc cyclically
T'a = A'aB'aC'a = Ta-cevian triangle of Ia, and define T'b and T'c cyclically
A' = radical center of A-excircle and the circles having diameters BB'a and CC'a, and define B' and C' cyclically.
The lines A'Aa, B'Bb, C'Cc concur in X(36922). (Angel Montesdeoca, January 24, 2023)
-
X(37084) = MIDPOINT OF X(3) AND X(14152)
Barycentrics a^4 (b^2-c^2) (b^2+c^2-a^2)^2 (a^4-2 a^2 (b^2+c^2)+b^4-b^2 c^2+c^4) : :
Dados un triángulo ABC y un punto P, sean PaPbPc y PaPbPc los triángulos
ceviano y pedal de P, respectivamente.
Sean Qa, Qb, Qc los puntos que dividen a los segmentos PaPa, PbPb, PcPc, resp., en la misma razón t.
Las perpendiculares por Qa, Qb, Qc a BC, CA, AB, respectivamente, forman un triángulo A'B'C', directamente semejante a ABC.
El lugar geométrico de los centros de semejanza, cuando t varía, es una circunferencia que pasa por P.
Cuando P es el circuncentro, el centro de esta circunferencia es X(37084).
See Tran Quang Hung and Angel Montesdeoca, Euclid 703. and HG120320
-
X(37085) = X(6)X(826)∩X(512)X(1692)
Barycentrics a^4 (b^6 - c^6 + a^4 (-b^2 + c^2)) : :
Dados un triángulo ABC y un punto P, sean PaPbPc y PaPbPc los triángulos
ceviano y pedal de P, respectivamente.
Sean Qa, Qb, Qc los puntos que dividen a los segmentos PaPa, PbPb, PcPc, resp., en la misma razón t.
Las perpendiculares por Qa, Qb, Qc a BC, CA, AB, respectivamente, forman un triángulo A'B'C', directamente semejante a ABC.
El lugar geométrico de los centros de semejanza, cuando t varía, es una circunferencia que pasa por P.
Cuando P es el simediano, el centro de esta circunferencia es X(37085).
See Tran Quang Hung and Angel Montesdeoca, Euclid 703. and HG120320
-
X(37283) = MIDPOINT OF X(12039) AND X(14810)
Barycentrics 2 a^8-7 a^2 b^2 c^2 (b^2+c^2)-2 a^4 (b^4+b^2 c^2+c^4) : :
Let ABC and A'B'C' be two orthologic triangles such that their orthologic centers coincide at symmedian point, X(6). Then ABC and A'B'C' are perspective, and their perspector P lies on the Jerabek hyperbola. Let P* be the isogonal conjugate of P, and O' the circumcenter of A'B'C'. If ABC remains fixed while A'B'C' varies, then the line P*O' envelopes a hyperbola passing through X(6), X(23), with center X(37283), and asymptotes X(37283)X(5004) and X(37283)X(5005). (Angel Montesdeoca, March 17, 2020)
See Angel Montesdeoca, Euclid 714.
Triángulos con centro ortológico común. HG150320
-
X(37518) = X(3)X(1392)∩X(4)X(1388)
Barycentrics a (9 a^6 - 15 a^5 (b + c) - a^4 (12 b^2 - 49 b c + 12 c^2) + 30 a^3 (b - c)^2 (b + c) - 15 a (b - c)^4 (b + c) - 3 a^2 (b - c)^2 (b^2 + 14 b c + c^2) + (b^2 - c^2)^2 (6 b^2 - 13 b c + 6 c^2) ) : :
See Angel Montesdeoca, Euclid 721.
El centro de la circunferencia de Hatzipolakis-Lozada como centro ortológico.
-
X(37593) = X(1)X(3)∩X(37)X(42)
Barycentrics a*(b + c)*(3*a + b + c) : :
Let DEF be intouch triangle. Let (Ob) be the circle centered at B that passes through D and F. Let (Oc) be the circle centered at C that passes through D and E. Let E' be the point of intersection, other than E, of the circles (AEF) and (Oc). Let F' be the point of intersection, other than F, of the circles (AEF) and (Ob). Let A' be the center of circle DE'F', and define B' and C' cyclically. The finite fixed point of the affine transformation that carries ABC onto A'B'C' is X(37593). (Angel Montesdeoca, September 24, 2020).
Una propiedad del centro del triángulo X(37593)
-
X(37754) = X(1)X(1956)∩X(48)X(163)
Barycentrics a^3 (a^2-b^2-c^2)^3 (b^2-c^2)^2 : :
See Angel Montesdeoca, Euclid 778 and HG030420.
-
X(37755) = ISOGONAL CONJUGATE OF X(2326)
Barycentrics a (b+c)^2 (a^2-b^2-c^2)/(b+c-a)^2 : :
See Angel Montesdeoca, Euclid 778 and HG030420.
-
X(37836) = MIDPOINT OF X(73) AND X(23361)
Barycentrics a^2 (2 a^2+a (b+c)-(b-c)^2) (a^2 (b+c)-a b c-b^3-c^3) : :
Dado un triángulo ABC, sean DEF el triángulo medial y A'B'C' el segundo triángulo circumperpendicular. Se consideran los trapecios isósceles AA'AbE y AA'AcF con AA' paralelo a AbE y a AcF. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
El triángulo UVW formado por las rectas AbAc, BcBa y CaCb es perspectivo al triángulo medial. El centro de perspectividad es X(37836).
See Angel Montesdeoca, Euclid 796 and HG070420.
-
X(37837) = X(1)X(227)∩X(3)X(960)
Barycentrics a( -(b^2-c^2)^2 (b^2+c^2)+(b-c)^2 (3 b^3+b^2 c+b c^2+3 c^3) a+4 b (b-c)^2 c a^2+(-6 b^3+2 b^2 c+2 b c^2-6 c^3)a^3+(3 b^2-4 b c+3 c^2) a^4+3 (b+c) a^5-2 a^6) : :
Dado un triángulo ABC, sean DEF el triángulo medial y A'B'C' el segundo triángulo circumperpendicular. Se consideran los trapecios isósceles AA'AbE y AA'AcF con AA' paralelo a AbE y a AcF. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
El triángulo UVW formado por las rectas AbAc, BcBa y CaCb y ABC son ortológicos . El centro de ortología de ABC respecto a UVW es el circuncentro y el centro de ortología de UVW respecto a ABC es X(378379).
See Angel Montesdeoca, Euclid 799 and HG070420.
-
X(37865) = PERSPECTOR OF THESE TRIANGLES: ABC AND JENKINS TANGENTIAL
Barycentrics (b+c)/(a^3 (b+c)+a^2 b c-a (b-c)^2 (b+c)-b c (b+c)^2) : :
The triangle bounded by the tangents at contact points between each Jenkins circles and its internally tangent excircles is here named the Jenkins Tangential Triangle.
-
See Angel Montesdeoca Euclid 808.
-
X(37874) = PERSPECTOR OF THE PARALLELS-TANGENTIAL-CONIC-OF-X(4)
Barycentrics b^2*c^2*(a^4+2*(3*b^2-c^2)*a^2+(b^2-c^2)^2)*(a^4-2*(b^2-3*c^2)*a^2+(b^2-c^2)^2) : :
There are two parabolas having focus A and axis AB and passing through C; these parabolas also meet AC in two more points, denoted by Ac1 and Ac2. Likewise there are two parabolas having focus A, axis AC, and passing through B. They also meet in two other points on AB, denoted by Ab1 and Ab2. The diagonal points of the complete quadrangle Ab1Ab2Ac1Ac2 are A, the infinity point of BC, and a third point, denoted by A'. Define B' and C' cyclically. The parallels through A',B',C' to BC, CA, AB, respectively, form a triangle A"B"C" that is homothetic to ABC. The homothetic center is X(37874). (Angel Montesdeoca, February 23, 2022)
HG220222.
-
X(37998) = INFINITY POINT OF X(11)X(3835)
Barycentrics a (b-c) (-b^2 c^2+a^3 (b+c)-a^2 (2 b^2+b c+2 c^2)+a (b^3+b^2 c+b c^2+c^3)) : :
Let σ be the similarity transformation between the 1st & 2nd Montesdeoca bisector triangles (see P(160))
When P traverses the line X(1)X(6) (radical axis of the circumcircles of the 1st & 2nd Montesdeoca bisector triangles), then the lines σ(P)σ-1(P) are parallel, with point at infinity at X(37998).
See Angel Montesdeoca Euclid 844 and HGT2017.
-
X(39530) = CENTER OF ((POLAR CIRCLE, LEMOINE AXIS))
Barycentrics (a^2 + b^2 - c^2)*(a^2 - b^2 + c^2)*(a^4 - a^2*b^2 - a^2*c^2 - 2*b^2*c^2)*(a^2*b^2 - b^4 + a^2*c^2 + 2*b^2*c^2 - c^4) : :
In the plane of a triangle ABC, let
N=X(5), DEF = orthic triangle, A'B'C' = Euler triangle, A"=ND∩B'C', and define B" and C" cyclically. The lines A'A", B'B", C'C" concur in X(39530). (Angel Montesdeoca, August 2, 2021)
El centro del triángulo X(39530)
-
X(39704) = ISOTOMIC CONJUGATE OF X(3679)
Barycentrics (2*a + 2*b - c)*(2*a - b + 2*c) : :
In the plane of a tiangle ABC, let (BC) be the half-plane determined by the line BC that does not include A. Let Ab be the point in (BC) that satisfies |BAb| = |AC|, and let Ac be the point in (BC) that satisfies |BAc| = |AB|. Let La be the line of the diagonal points, other than A, of the complete quadrangle BCAbAc. Define Lb and Lc cyclically. Let A' = Lb∩Lc, and define B' and C' cyclically. Then A'B'C' is perspective to ABC, and the perspector is X(39704). (Angerl Montesdeoca, March 20, 2023)
See Angel Montesdeoca, Una propiedad del centro del triángulo X(39704).
-
X(39980) = ISOGONAL CONJUGATE OF X(3731)
Barycentrics a*(3*a + 3*b - c)*(3*a - b + 3*c) : :
Let DEF be the intouch triangle and IaIbIc the excentral-triangle. Let D' be the trisector nearest Ia of segment DIa. Let La be the radical axis of (DEF) and (BCD'), and define Lb and Lc cyclically. The triangle A'B'C' formed by the lines La, Lb, Lc is perspective to ABC, and the perspector is X(39980). See also X(34578). (Angel Montesdeoca, December 31, 2020)
See HG301220
-
X(40257) = TETRAHEDRAL PROJECTION OF ABC TO 2nd CIRCUMPERP TRIANGLE
Barycentrics a*(a^6-2*(b+c)*a^5-(b^2-4*b*c+c^2)*a^4+(b+c)*(4*b^2-7*b*c+4*c^2)*a^3-(b^2+5*b*c+c^2)*(b-c)^2*a^2-(b^2-c^2)*(b-c)*(2*b^2-3*b*c+2*c^2)*a+(b^2-c^2)*(b-c)*(b^3+c^3)) : :
In the plane of a triangle ABC, let
O = circumcenter;
A' = reflection of A in O, and define B'; and C' cyclically;
H = orthocenter;
A''B''C'' = circumcevian triangle of H wrt A''B''C'';
Ab = AC∩B'A'', and define Bc and Ca cyclically;
Ac = AB∩C'A'', and define Ba and Cb cyclically;
Ao = circumcenter of AAbAc, and define Bo and Cocyclically;
σ = the affine transformation that maps ABC onto AoBoCocyclically;
I = incenter;
Then σ(I) = X(40257). Moreover, if X = x : y : z, then
σ(X) = (-a+b+c)^2 (a^4-2 a^2 (b-c)^2+(b-c)^2 (b^2-b c+c^2)) x-a^2 (a-c) c (a-b+c)^2 y-a^2 (a-b) b (a+b-c)^2 z : : .
See X(40257). (Angel Montesdeoca, June 28, 2022)
See Angel Montesdeoca, HG270622.
-
X(41005) = CROSSPOINT OF X(69) AND X(264)
Barycentrics (a^2 - b^2 - c^2)*(a^4*b^2 - 2*a^2*b^4 + b^6 + a^4*c^2 + 4*a^2*b^2*c^2 - b^4*c^2 - 2*a^2*c^4 - b^2*c^4 + c^6) : :
In the plane of a triangle ABC, let
DEF = anticevian triangle of X(3);
Ab = orthogonal projection of D on AB;
Ac = orthogonal projection of D on AC;
Db = BD∩AbAc;
Dc = CD∩AbAc;
A'=BDc∩CDb, and define B' and C' cyclically.
The lines AA', BB', CC' concur in X(41005). See figure
(Angel Montesdeoca, January 2, 2022) and general case in HG291221.
-
X(41300) = MONTESDEOCA HOMOTHETIC CENTER
Barycentrics (b^2-c^2)(3 a^4 - 3 a^2 (b^2 + c^2)- 2 b^2 c^2 ) : :
X(41300) is the homothetic center of the triangles AbBcCa and AcBaCb defined at PU(196) in Bicentric Pairs of Points.
(See Un par bicéntrico sobre la tripolar de X(290))
-
X(41679) = TRILINEAR POLE OF THE BPC-LINE OF X(26)
Barycentrics a^2*(a^4-2*(b^2+c^2)*a^2+b^4+c^4)*(a^2-c^2)*(a^2-b^2+c^2)*(a^2-b^2)*(a^2+b^2-c^2) : :
In the plane of a triangle ABC, let
MaMbMc = medial triangle
DEF = orthic triangle
H = X(4) = orthocenter
Hb = line through H perpendicular to BH
Hab = Hb∩BC
Hc = line through H perpendicular to CH
Hac = Hc∩BC
Pb = line through Hac parallel to DMb
Pc = line through Hab parallel to DMc
Ab = Pb∩AC; define Bc and Ca cyclically
Ac = Pc∩AB; define Ba and Cb cyclically
A'B'C' = triangle with edges AbAc, BcBa, CaCb
Then X(41679) is the unique finite fixed point of the affine transformation that maps ABC onto A'B'C'. The triangles ABC and A'B'C' are perspective, and their perspector is X(51776). The perspector of the perspeconic of ABC and A'B'C' is X(51777), and the center of that conic is X(51778). (Angel Montesdeoca, September 12, 2022)
See HG090922
-
X(42789) = 1ST MONTESDEOCA-EULER POINT
Barycentrics a*(b*c*SB*SC + Sqrt[2]*a*SA*Sqrt[SA*SB*SC]) : :
The mapping X(3) + t X(4) ↦ 8 t SA SB SC X(3) + a^2 b^2 c^2 X(4) is an involution of the Euler line. The mapping includes {X(3), X(4)} and {X(1113), X(1114)} as involutory pairs. The fixed points of the mapping are
(a (b c SBSC + Sqrt[2] a SA Sqrt[SA SB SC]) : : and (a (b c SB SC - Sqrt[2] a SA Sqrt[SA SB SC]) : : ,
These points are real if and only if the reference triangle ABC is acute. (Angel Montesdeoca, April 26, 2021.) The points are here named the 1st Montesdeoca-Euler point and 2nd Montesdeoca-Euler point, respectively.
X(42789) lies on the curves K114 and Q023 and this line: {2, 3}
For a figure showing X(42789) and X(42790) on the curves K114 and Q023, see Euler line, points, and curves. (Angel Montesdeoca, April 27, 2021).
Una involución sobre la recta de Euler
-
X(42790) = 2nd MONTESDEOCA-EULER POINT
Barycentrics a*(b*c*SB*SC - Sqrt[2]*a*SA*Sqrt[SA*SB*SC]) : :
Una involución sobre la recta de Euler
-
X(43448) = X(2)X(99)∩X(4)X(6)
Barycentrics a^4 - 2*a^2*b^2 - 3*b^4 - 2*a^2*c^2 + 6*b^2*c^2 - 3*c^4 : :
In the plane of a triangle ABC, let
G = X(2) = centroid
H = X(4) = orthocenter
Ab = point of intersection, other than B, of BH and circle (G,B,C), and define Bc and Ca cyclically
Ac point of intersection, other than C, of CH and circle (G,B,C), and define Ba and Cb cyclically
A' = BcBa∩CaCb, and define B' and C' cyclically
Then A'B'C' is homothetic to the orthic triangle of ABC, and X(43448) is the homothetic center. (Angel Montesdeoca, January 21, 2023)
X(43448) como centro de homotecia
-
X(43919) = REFLECTION OF X(3) IN X(1624)
Barycentrics a^2*(a^12*b^2 - 5*a^10*b^4 + 10*a^8*b^6 - 10*a^6*b^8 + 5*a^4*b^10 - a^2*b^12 + a^12*c^2 - 6*a^10*b^2*c^2 + 3*a^8*b^4*c^2 + 14*a^6*b^6*c^2 - 15*a^4*b^8*c^2 + 3*b^12*c^2 - 5*a^10*c^4 + 3*a^8*b^2*c^4 - 20*a^6*b^4*c^4 + 10*a^4*b^6*c^4 + 21*a^2*b^8*c^4 - 9*b^10*c^4 + 10*a^8*c^6 + 14*a^6*b^2*c^6 + 10*a^4*b^4*c^6 - 40*a^2*b^6*c^6 + 6*b^8*c^6 - 10*a^6*c^8 - 15*a^4*b^2*c^8 + 21*a^2*b^4*c^8 + 6*b^6*c^8 + 5*a^4*c^10 - 9*b^4*c^10 - a^2*c^12 + 3*b^2*c^12) : :
In the plane of a triangle ABC, let
TaTbTc = tangential triangle;
Oa = line through X(3) parallel to BC, which cuts TbTc at Ua ;
La = line through Ua perpendicular to BC, and define Lb and Lc cyclically;
A' = Lb∩Lc, and define B' and C' cyclically.
Then A'B'C' is perspective to TaTbTc, and the perspector is X(43919).
See X(43919). (Angel Montesedeoca, March 15, 2022)
-
X(44860) = (name pending)
Barycentrics 2 a^18 (b^2-c^2)^2+b^4 c^4 (b^2-c^2)^6 (b^2+c^2)+a^16 (-9 b^6+13 b^4 c^2+13 b^2 c^4-9 c^6)-a^2 b^2 c^2 (b^2-c^2)^4 (2 b^8+3 b^6 c^2-6 b^4 c^4+3 b^2 c^6+2 c^8)+a^14 (14 b^8-5 b^6 c^2-44 b^4 c^4-5 b^2 c^6+14 c^8)+a^4 (b^2-c^2)^4 (b^10+12 b^8 c^2+9 b^6 c^4+9 b^4 c^6+12 b^2 c^8+c^10)-a^12 (5 b^10+30 b^8 c^2-47 b^6 c^4-47 b^4 c^6+30 b^2 c^8+5 c^10)+a^8 (b^2-c^2)^2 (13 b^10+3 b^8 c^2-19 b^6 c^4-19 b^4 c^6+3 b^2 c^8+13 c^10)-a^6 (b^2-c^2)^2 (6 b^12+17 b^10 c^2-18 b^8 c^4+14 b^6 c^6-18 b^4 c^8+17 b^2 c^10+6 c^12)-a^10 (10 b^12-48 b^10 c^2+25 b^8 c^4+30 b^6 c^6+25 b^4 c^8-48 b^2 c^10+10 c^12) : :
In a triangle ABC, let
La = perpendicular bisector of side BC, and define Lb and LCc cyclically;
Ab = La∩AC, Ac = La∩AB, Bc = Lb∩BA, Ba = Lb∩BC, Ca = Lc∩CB, Cb = Lc∩CA,
Then the circumcircles of ABC, T1 = AbBcCa and T2 = AcBaCb are coaxial
The radical axis common to these circles is the trlinear polar of X(44828).
Let Q be a point on the Euler line of ABC and Q1, Q2 same to Q points of T1, T2, resp.-
Let Mq be the midpoint of Q1Q2 (it is a center of ABC).
Which point is its intersection with the Euler line of ABC?
See Antreas Hatzipolakis and Angel Montesdeoca, Euclid 2416 .
Figure in: https://amontes.webs.ull.es/imagenes/euclid2401.png
-
X(44915) = X(2)X(6)∩X(67)X(42007)
Barycentrics (2 a^2-b^2-c^2)(2 a^6-2 a^4 (b^2+c^2)-a^2 (b^4-4 b^2 c^2+c^4)+3 (b^2-c^2)^2 (b^2+c^2)) : :
Un centro del triángulo sobre GK
Given a triangle ABC, with centroid G = X(2), circumcenter O = X(3) and symmedian K = X(6), let A'B'C 'and A"B"C" be the cevian and anticevian triangles of X(524) (on the infinity line), isogonal conjugate of Parry's point (A", B", C" are the midpoints of the segments AA ', BB', CC ', respectively). Let DEF be the pedal triangle of O with respect to A"B"C".
Let AaAbAc, BbBcBa, and CcCaCb be the cevian triangles of D, E, and F, respectively. AaBbCc is the trilinear polar of X(524).
The lines AbAc, BcBa, CaCb concur in X(8030) - 2 X(599) (on the line GK), reflection of the centroid of the triangle A'B'C', X(8030), in the isotomic conjugate, X(599), of the perspector, X(598), of the inscribed ellipse of Lemoine.
-
X(44935) = X(4)X(18853)∩X(30)X(568)
Barycentrics 2 a^10-7 a^8 (b^2+c^2)+2 a^6 (5 b^4+18 b^2 c^2+5 c^4)-8 a^4 (b^6+b^4 c^2+b^2 c^4+c^6)+4 a^2 (b^2-c^2)^2 (b^4-4 b^2 c^2+c^4)-(b^2-c^2)^4 (b^2+c^2) : :
Reflexión de X(7667) en X(16657) como centro ortológico
See Angel Montesdeoca, Euclid 2601 .
Let ABC be a triangle and DEF the orthic triangle of ABC. The circle through the midpoints of EF, EC, FB, cuts again AC and AB in Ab and Ac, respectively, and points Bc, Ca, Ba, Cb are defined similarly. ABC and the triangle A'B'C' bounded by AbAc, BcBa, CaCb are orthologic. The orthology center of ABC and A'B'C' is the centroid and the orthology center of A'B'C' and ABC is the reflection of X(7667) in X(16657) ( i.e. , X(44935)=X(7667) - 2 X(16657)).
-
X(45131) = X(1)X(318)∩X(72)X(519)
Barycentrics a^6 (b+c)-2 a^5 b c-a^4 (b+c) (2 b^2-3 b c+2 c^2)+a^2 (b-c)^2 (b+c) (b^2+c^2)+2 a b c (b^2-c^2)^2-b c(b-c)^2 (b+c)^3 : :
See Antreas Hatzipolakis and Angel Montesdeoca, Hyacinthos 2662.
La is the line joining the midpoints of AH and BC.
The reflections of La, Lb, Lc in AI, BI, CI, resp. bound a triangle A*B*C*.
ABC and A*B*C* are parallelogic.
Parallelogic center (ABC, A*B*C*) = H.
Parallelogic center (A*B*C*, ABC) = X(45131).
-
X(45801) = X(6)X(523)∩X(141)X(525)
Barycentrics (b^2 - c^2)*(-a^6 + a^4*b^2 - a^2*b^4 + b^6 + a^4*c^2 + a^2*b^2*c^2 - b^4*c^2 - a^2*c^4 - b^2*c^4 + c^6) : :
In the plane of a triangle ABC, let
M = X(115), the center of the Kiepert hyperbola;
DEF = tangential triangle of the Kiepert hyperbola;
D' = reflection of D in BC, and define B' and F' cyclically;
A' = AM∩E'F', and define B' and C' cyclically.
The lines A'D', B'E', C'F' concur in X(45801) . (Angel Montesdeoca, August 17, 2022)
See Angel Montesdeoca, HG170822.
-
X(45976) = EULER LINE INTERCEPT OF X(1)X(6797)
Barycentrics a (a^6-a^5 (b+c)+a^4 (-2 b^2+3 b c-2 c^2)+2 a^3 (b^3+c^3)+a^2 (b^4-5 b^3 c+2 b^2 c^2-5 b c^3+c^4)-a (b^5-b^4 c-b c^4+c^5)+2 b c (b^2-c^2)^2) : :
Consider a point Q on the Neuberg cubic and La, Lb, Lc the concurrent Euler lines of QBC, QCA, QAB, resp.
Is there a point P on the Euler line of ABC such that the perpendiculars to same to P points Pa, Pb, Pc of La, Lb, Lc, resp. are concurrent?
For examp;e Q = I
Is there a point P on the Euler line of ABC such that the perpendiculars to Pa, Pb, Pc = same to P points on the Euler lines of IBC, ICA, IAB, resp., are concurrent?
If Q = I, then there is a point P= EULER LINE INTERCEPT OF X(1)X(6797) on the Euler line of ABC such that the perpendiculars to Pa, Pb, Pc = same to P points on the Euler lines of IBC, ICA, IAB, resp., are concurrent at Z= X(1)X(1389)∩X(4)X(496)=X(45977).
See Antreas Hatzipolakis and Angel Montesdeoca, Euclid 3114.
Figure
-
X(45977) = X(1)X(1389)∩X(4)X(496)
Barycentrics a*(a^6-(b+c)*a^5-(2*b-c)*(b-2*c)*a^4+2*(b+c)*(b^2-3*b*c+c^2)*a^3+(b-c)^2*(b^2-4*b*c+c^2)*a^2-(b^2-c^2)*(b-c)*(b^2-4*b*c+c^2)*a+(b^2-c^2)^2*b*c) : :
Consider a point Q on the Neuberg cubic and La, Lb, Lc the concurrent Euler lines of QBC, QCA, QAB, resp.
Is there a point P on the Euler line of ABC such that the perpendiculars to same to P points Pa, Pb, Pc of La, Lb, Lc, resp. are concurrent?
For examp;e Q = I
Is there a point P on the Euler line of ABC such that the perpendiculars to Pa, Pb, Pc = same to P points on the Euler lines of IBC, ICA, IAB, resp., are concurrent?
If Q = I, then there is a point P= EULER LINE INTERCEPT OF X(1)X(6797)=X(45976) on the Euler line of ABC such that the perpendiculars to Pa, Pb, Pc = same to P points on the Euler lines of IBC, ICA, IAB, resp., are concurrent at Z= X(1)X(1389)∩X(4)X(496).
See Antreas Hatzipolakis and Angel Montesdeoca, Euclid 3114.
Figure
-
X(46034) = X(4)X(6)∩X(20)X(1078)
Barycentrics a^8+8 a^6 (b^2+c^2)-2 a^4 (b^2+c^2)^2-8 a^2 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^2 (b^4-10 b^2 c^2+c^4) : :
See Angel Montesdeoca, euclid 3223.
Let GA be the antipode of X(2) in the A-McCay circle, and define GB and GC cyclically; then GAGBGC is homothetic to the McCay triangle at X(2). Let LA be the line tangent to the A-McCay circle at GA, and define LB and LC cyclically. Let A" = LB∩LC, and define B" and C" cyclically. Then A"B"C" is the antipedal triangle of X(2) with respect to GAGBGC, and A"B"C" is inversely similar to ABC and homothetic to the 1st Brocard triangle. Also, X(7620) = X(2)-of-A"B"C" = X(376)-of GAGBGC. (Randy Hutson, May 27, 2015)
Then ABC and A"B"C" are orthologic (Theorem 26 (Mihai Miculiţa)).
The orthologic center of ABC and A"B"C" (on the circumcircle) is X(98).
The orthologic center of A"B"C" and ABC (on the circumcircle of A"B"C") is :
X(4)X(6)∩X(20)X(1078)
-
X(46354) = X(3)X(15474∩X(942)X(39267)
Barycentrics (a - b - c)*(a^3 + a^2*b + a*b^2 + b^3 - a^2*c - 2*a*b*c - b^2*c - a*c^2 - b*c^2 + c^3)^2*(a^3 - a^2*b - a*b^2 + b^3 + a^2*c - 2*a*b*c - b^2*c + a*c^2 - b*c^2 + c^3)^2 : :
See Angel Montesdeoca, HG121221.
Dado un triángulo ABC, sean DEF el triángulo de contacto interior y P un punto no situado sobre la circunferencia inscrita, Γ. Sean A', B', C' las proyecciones de D, E,F desde P sobre Γ.
Las rectas AA', BB', CC' son concurrentes.
Para P=X(3), el punto de concurrencia es X(46354).
-
X(46355) = X(1)X(280)∩X(4)X(189)
Barycentrics (-a+b+c)*(a^3+(b-c)*a^2-(b-c)^2*a-(b+c)*(b^2-c^2))^2*(a^3-(b-c)*a^2-(b-c)^2*a+(b+c)*(b^2-c^2))^2 : :
See Angel Montesdeoca, HG121221.
Dado un triángulo ABC, sean DEF el triángulo de contacto interior y P un punto no situado sobre la circunferencia inscrita, Γ. Sean A', B', C' las proyecciones de D, E,F desde P sobre Γ.
Las rectas AA', BB', CC' son concurrentes.
Para P=X(4), el punto de concurrencia es X(46355).
-
X(46356) = X(1)X(44301)∩X(8)X(8051)
Barycentrics (a + b - c)*(a - b + c)*(a^2 + 2*a*b + b^2 - 6*a*c + 2*b*c + c^2)^2*(a^2 - 6*a*b + b^2 + 2*a*c + 2*b*c + c^2)^2 : :
See Angel Montesdeoca, HG121221.
Dado un triángulo ABC, sean DEF el triángulo de contacto interior y P un punto no situado sobre la circunferencia inscrita, Γ. Sean A', B', C' las proyecciones de D, E,F desde P sobre Γ.
Las rectas AA', BB', CC' son concurrentes.
Para P=X(8), el punto de concurrencia es X(46356).
-
X(46362) = X(1)X(4014)∩X(40)X(550)
Barycentrics a (a ^ 5 (b + c) +5 a ^ 3 bc (b + c) +5 bc (b ^ 2-c ^ 2) ^ 2 + 2 a ^ 4 (b ^ 2-8 b c + c ^ 2) + a ^ 2 (-2 b ^ 4 + 11 b ^ 3 c-10 b ^ 2 c ^ 2 + 11 bc ^ 3-2 c ^ 4) -a (b ^ 5 + 6 b ^ 4 c-3 b ^ 3 c ^ 2-3 b ^ 2 c ^ 3 + 6 bc ^ 4 + c ^ 5)) : :
Given a triangle ABC with the length of its sides a = |BC|, b = |CA|, c = |AB|, let Γa, Γb, Γc be the circles centered in the incenter, X(1), of radii a, b, c, respectively.
A1 is the pole of BC with respect to Γa and A2 is the point of intersection of the polar of B with respect to Γc with the polar of C with respect to Γb. Points B1, B2 and C1, C2 are defined cyclically.
The six points A1, A2, B1, B2, C1, C2 lie on a same conic, which passes through the centers of the triangle X(1), X(3), X(20), X(10454) and whose tangent at X(1) is X(1)X(256).
The center of this conic is X(46362).
See Angel Montesdeoca, Euclid 3557.
-
X(46363) = X(3)X(6)∩X(51)X(3089)
Barycentrics a^2 (-a^12 (b^2+c^2)-2 a^2 (b^2-c^2)^4 (2 b^4+b^2 c^2+2 c^4)+a^10 (4 b^4+6 b^2 c^2+4 c^4)+(b^2-c^2)^4 (b^6+b^4 c^2+b^2 c^4+c^6)+a^4 (b^2-c^2)^2 (5 b^6-17 b^4 c^2-17 b^2 c^4+5 c^6)-a^8 (5 b^6+17 b^4 c^2+17 b^2 c^4+5 c^6)+4 a^6 (7 b^6 c^2+2 b^4 c^4+7 b^2 c^6)) : :
Let ABC be a triangle and A'B'C' the pedal triangle of H
Denote
Ab,Ac = the orthogonal projections of A' on AB, AC resp.
M1 = the midpoint of AbAc
Ma = the midpoint of AA'
Similarly Mb, Mc and M2, M3.
MaMbMc, M1M2M3 are perspective at the center of the Taylor circle X(389) of ABC
Which point is the perspector X(389) wrt triangles MaMbMc, M1M2M3?
The perspector X(389) wrt triangle M1M2M3 is X(46363).
See Antreas Hatzipolakis and Angel Montesdeoca, Euclid 3570.
-
X(46364) = (name pending)
Barycentrics 4 a^34-25 a^32 (b^2+c^2)-(b^2-c^2)^12 (b^2+c^2)^3 (2 b^4+5 b^2 c^2+2 c^4)+a^30 (50 b^4+204 b^2 c^2+50 c^4)-a^28 (b^6+508 b^4 c^2+508 b^2 c^4+c^6)+a^26 (-116 b^8+82 b^6 c^2+2092 b^4 c^4+82 b^2 c^6-116 c^8)+2 a^2 (b^2-c^2)^10 (b^2+c^2)^2 (6 b^8-19 b^6 c^2-70 b^4 c^4-19 b^2 c^6+6 c^8)-2 a^18 (b^2-c^2)^4 (44 b^8-2315 b^6 c^2-7550 b^4 c^4-2315 b^2 c^6+44 c^8)+a^24 (65 b^10+1410 b^8 c^2-2691 b^6 c^4-2691 b^4 c^6+1410 b^2 c^8+65 c^10)+2 a^22 (111 b^12-564 b^10 c^2-2075 b^8 c^4+5888 b^6 c^6-2075 b^4 c^8-564 b^2 c^10+111 c^12)-a^4 (b^2-c^2)^8 (27 b^14-168 b^12 c^2+42 b^10 c^4+1507 b^8 c^6+1507 b^6 c^8+42 b^4 c^10-168 b^2 c^12+27 c^14)-a^20 (297 b^14+2824 b^12 c^2-13546 b^10 c^4+10681 b^8 c^6+10681 b^6 c^8-13546 b^4 c^10+2824 b^2 c^12+297 c^14)+a^16 (b^2-c^2)^2 (407 b^14+226 b^12 c^2-21124 b^10 c^4+17291 b^8 c^6+17291 b^6 c^8-21124 b^4 c^10+226 b^2 c^12+407 c^14)+2 a^6 (b^2-c^2)^6 (17 b^16+30 b^14 c^2+1076 b^12 c^4-430 b^10 c^6-3434 b^8 c^8-430 b^6 c^10+1076 b^4 c^12+30 b^2 c^14+17 c^16)+2 a^10 (b^2-c^2)^4 (62 b^16+439 b^14 c^2-5030 b^12 c^4-1079 b^10 c^6+15312 b^8 c^8-1079 b^6 c^10-5030 b^4 c^12+439 b^2 c^14+62 c^16)-2 a^14 (b^2-c^2)^2 (121 b^16+2364 b^14 c^2-7492 b^12 c^4-9756 b^10 c^6+26454 b^8 c^8-9756 b^6 c^10-7492 b^4 c^12+2364 b^2 c^14+121 c^16)-a^12 (b^2-c^2)^2 (59 b^18-2894 b^16 c^2-5351 b^14 c^4+42427 b^12 c^6-33217 b^10 c^8-33217 b^8 c^10+42427 b^6 c^12-5351 b^4 c^14-2894 b^2 c^16+59 c^18)-a^8 (b^2-c^2)^4 (61 b^18+1118 b^16 c^2-1185 b^14 c^4-12083 b^12 c^6+13113 b^10 c^8+13113 b^8 c^10-12083 b^6 c^12-1185 b^4 c^14+1118 b^2 c^16+61 c^18) : :
Let ABC be a triangle and A'B'C' the pedal triangle of H
Denote
Ab,Ac = the orthogonal projections of A' on AB, AC resp.
M1 = the midpoint of AbAc
Ma = the midpoint of AA'
Similarly Mb, Mc and M2, M3.
MaMbMc, M1M2M3 are perspective at the center of the Taylor circle X(389) of ABC
Which point is the perspector X(389) wrt triangles MaMbMc, M1M2M3?
The perspector X(389) wrt triangle M1M2M3 is X(46364).
See Antreas Hatzipolakis and Angel Montesdeoca, Euclid 3560.
-
X(46365) = (name pending)
Barycentrics a/(3*a^10*b^2 - 2*a^9*b^3 - 14*a^8*b^4 + 6*a^7*b^5 + 24*a^6*b^6 - 6*a^5*b^7 - 18*a^4*b^8 + 2*a^3*b^9 + 5*a^2*b^10 + 10*a^10*b*c + 2*a^9*b^2*c - 10*a^8*b^3*c + 2*a^7*b^4*c - 10*a^6*b^5*c + 10*a^5*b^6*c + 26*a^4*b^7*c - 18*a^3*b^8*c - 16*a^2*b^9*c + 4*a*b^10*c + 3*a^10*c^2 + 2*a^9*b*c^2 + 16*a^8*b^2*c^2 - 8*a^7*b^3*c^2 - 21*a^6*b^4*c^2 + 20*a^5*b^5*c^2 + 5*a^4*b^6*c^2 - 2*a^2*b^8*c^2 - 14*a*b^9*c^2 - b^10*c^2 - 2*a^9*c^3 - 10*a^8*b*c^3 - 8*a^7*b^2*c^3 + 30*a^6*b^3*c^3 - 24*a^5*b^4*c^3 - 26*a^4*b^5*c^3 + 40*a^3*b^6*c^3 + 10*a^2*b^7*c^3 - 6*a*b^8*c^3 - 4*b^9*c^3 - 14*a^8*c^4 + 2*a^7*b*c^4 - 21*a^6*b^2*c^4 - 24*a^5*b^3*c^4 + 26*a^4*b^4*c^4 - 24*a^3*b^5*c^4 - 3*a^2*b^6*c^4 + 30*a*b^7*c^4 - 4*b^8*c^4 + 6*a^7*c^5 - 10*a^6*b*c^5 + 20*a^5*b^2*c^5 - 26*a^4*b^3*c^5 - 24*a^3*b^4*c^5 + 12*a^2*b^5*c^5 - 14*a*b^6*c^5 + 4*b^7*c^5 + 24*a^6*c^6 + 10*a^5*b*c^6 + 5*a^4*b^2*c^6 + 40*a^3*b^3*c^6 - 3*a^2*b^4*c^6 - 14*a*b^5*c^6 + 10*b^6*c^6 - 6*a^5*c^7 + 26*a^4*b*c^7 + 10*a^2*b^3*c^7 + 30*a*b^4*c^7 + 4*b^5*c^7 - 18*a^4*c^8 - 18*a^3*b*c^8 - 2*a^2*b^2*c^8 - 6*a*b^3*c^8 - 4*b^4*c^8 + 2*a^3*c^9 - 16*a^2*b*c^9 - 14*a*b^2*c^9 - 4*b^3*c^9 + 5*a^2*c^10 + 4*a*b*c^10 - b^2*c^10) : :
See Angel Montesdeoca and Peter Moses, Euclid 3563.
-
X(46432) = X(3)X(6)∩X(115)X(393)
Barycentrics a^2 (a^6-3 a^2 b^4+2 b^6+6 a^2 b^2 c^2-2 b^4 c^2-3 a^2 c^4-2 b^2 c^4+2 c^6) : :
In the plane of a triangle ABC, let
I = X(1) = incenter
Ia, Ib, Ic = excenters
DEF = anticomplementary triangle
A1B1C1 = 1st circumperp triangle of DEF
A2B2C2 = 2nd circumperp triangle of DEF
A' = point of intersection, other than X(147), of the circles {{A1,Ib, IC}} and {{A2, X1,Ia}}, and define B' and C' cyclically.
The finite fixed point of the affine transformation from ABC to A'B'C' is X(46432). (Angel Montesdeoca, October 15, 2023).
See:
El centro del triángulo X(46432) punto fijo de una afinidad
-
X(46864) = (name pending)
Barycentrics 1/(3 a^8-9 a^6 (b^2+c^2)+a^4 (9 b^4+b^2 c^2+9 c^4)+a^2 (-3 b^6+17 b^4 c^2+17 b^2 c^4-3 c^6)-9 b^2 c^2 (b^2-c^2)^2) : :
See Angel Montesdeoca, Euclid 4208 and
HG010222.
-
X(46921) = (name pending)
Barycentrics 1/(5 a^8-24 a^6 (b^2+c^2)+a^4 (42 b^4+34 b^2 c^2+42 c^4)-32 a^2 (b^2-c^2)^2 (b^2+c^2)+3 (b^2-c^2)^2 (3 b^4-8 b^2 c^2+3 c^4)) : :
See Antreas Hatzipolakis and Angel Montesdeoca, euclid 4304..
Let ABC be a triangle and A'B'C' the pedal triangle of O
Denote
Ha = the orthocenter of AB'C'
Hab, Hac = the reflections of Ha in A'B', A'C', resp.
Similarly
Hbc, Hba and Hca, Hcb
The six points lie on a conic centered at O
[Angel Montesdeoca]:
Addendum:
Denote:
H'ab = HabA' /\ HacC, H'ac = HacA' /\ HabB
Similarly
H'bc, H'ba and H'ca, H'cb.
The six points H'ab, H'ac, H'bc, H'ba , H'ca, H'cb lie on a conic centered at X(5054).
Barycentric equation:
(3 a^8-20 a^6 (b^2+c^2)-44 a^2 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^2 (15 b^4-26 b^2 c^2+15 c^4)+a^4 (46 b^4+32 b^2 c^2+46 c^4)) x^2+(-6 a^8+44 a^6 (b^2+c^2)+68 a^2 (b^2-c^2)^2 (b^2+c^2)-2 (b^2-c^2)^2 (9 b^4-22 b^2 c^2+9 c^4)-8 a^4 (11 b^4+7 b^2 c^2+11 c^4)) y z + ... = 0.
Perspector P = (name pending) =
= 1/(5 a^8-24 a^6 (b^2+c^2)+a^4 (42 b^4+34 b^2 c^2+42 c^4)-32 a^2 (b^2-c^2)^2 (b^2+c^2)+3 (b^2-c^2)^2 (3 b^4-8 b^2 c^2+3 c^4)) : :
= lies on this line: {5054, 6748}
(6 - 9 - 13) - search numbers [2.76798777984726, 3.51561751656797, -0.0707573894921845]
-
X(46929) = X(4)X(3917)∩X(53)X(39662)
Barycentrics ((a^2 - b^2 - c^2)^2 - 16 b^2 c^2) /((a^2 - b^2 - c^2) (a^4 - 2 a^2 b^2 + b^4 - 2 a^2 c^2 - 6 b^2 c^2 + c^4)) : :
See Angel Montesdeoca, euclid 4323 and HG120222 .
-
X(47032) = EULER LINE INTERCEPT OF X(79)X(517)
Barycentrics a^7-a^6 (b+c)-a^5 (b^2-5 b c+c^2) +a^4 (b-c)^2 (b+c)-a^3 (b^2-b c+c^2) (b^2+4 b c+c^2) +a^2 (b-c)^2 (b+c)^3+a (b-c)^4 (b+c)^2 -(b-c)^4 (b+c)^3 : :
Let ABC be a triangle. Take Ba and Ca on AB and AC, respectively, on the negative side of BC (the region that does not contain A) such that BBa=CCa=BC.
Let Cab and Bac be the points where the circle (ABaCA) cuts again BCa and CBa, respectively.
The points Abc, Cba and Bca, Acb are defined cyclically.
The lines CabBac, AbcCba and BcaAcb form a triangle DEF. ABC and DEF are bilogic.
This perspector is X(5559).
The orthologic center of ABC wrt DEF is X(79) and the orthologic center of DEF wrt ABC is X(47032).
See Angel Montesdeoca, euclid 4468 and HG250222.
-
X(47033) = X(8)X(79)∩X(10)X(21)
Barycentrics a^4-a^3 (b+c)-(b^2-c^2)^2+a^2 b c+a (b^3+b^2 c+b c^2+c^3) : :
See Angel Montesdeoca, euclid 4482 and HG250222.
-
X(47034) = X(65)X(79)∩X(119)X(191)
Barycentrics a^10-a^9 (b+c)+a^8 (-3 b^2+4 b c-3 c^2)+2 a^7 (b-c)^2 (b+c)+a^6 (4 b^4-5 b^3 c+7 b^2 c^2-5 b c^3+4 c^4)+a^5 b c (3 b^3-2 b^2 c-2 b c^2+3 c^3)-a^4 (4 b^6+b^4 c^2-6 b^3 c^3+b^2 c^4+4 c^6)-a^3 (b-c)^2 (2 b^5-5 b^3 c^2-5 b^2 c^3+2 c^5)+a^2 (b^2-c^2)^2 (3 b^4-b^3 c-b c^3+3 c^4)+a (b-c)^4 (b+c)^3 (b^2-3 b c+c^2)-(b-c)^6 (b+c)^4 : :
See Angel Montesdeoca, euclid 4482 and HG250222.
-
X(47074) = X(2)X(187)∩X(30)X(14866)
Barycentrics 20 a^6-3 a^4 (b^2+c^2)-3 a^2 (7 b^4+2 b^2 c^2+7 c^4)+2 (b^6-6 b^4 c^2-6 b^2 c^4+c^6) : :
See Kadir Altintas and Angel Montesdeoca, euclid 4510 and HGT070322
-
X(47075) = X(2)X(187)∩X(22)X(2930)
Barycentrics 16 a^6+3 a^4 (b^2+c^2)-3 a^2 (5 b^4+b^2 c^2+5 c^4)-2 (b^2+c^2)^3 : :
Let G=X(2)-Centroid of ABC. A1B1C1-Circumcevian triangle of G.
Gamma_A:Circle with diameter GA1. Define Gamma_B, Gamma_C cyclically.
Tangent to Gamma_A at G intersects the Gamma_B and Gamma_C at Ab, Ac resp. Define Ba, Bc, Ca, Cb cyclically.
Then Ab, Ac, Ba, Bc, Ca, Cb lie on same circle Gamma.
Barycentric equation of Gamma:
(-a^8+26 a^6 (b^2+c^2)-6 a^4 (7 b^4+20 b^2 c^2+7 c^4)+(b^2+c^2)^2 (11 b^4-14 b^2 c^2+11 c^4)+a^2 (-58 b^6+78 b^4 c^2+78 b^2 c^4-58 c^6)) x^2+2 (-61 a^8+83 a^6 (b^2+c^2)+(b^2+c^2)^2 (5 b^4-26 b^2 c^2+5 c^4)+12 a^4 (7 b^4+11 b^2 c^2+7 c^4)+a^2 (-55 b^6+87 b^4 c^2+87 b^2 c^4-55 c^6)) y z+ ....
The center of Gamma is the midpoint of X(2) and circumcevian-isogonal conjugate of X(2), X(47075).
See Kadir Altintas and Angel Montesdeoca, Euclid 4511.
-
X(47101) = X(2)X(187)∩X(3)X(754)
Barycentrics 5 a^4-3 a^2 (b^2+c^2) -b^4-c^4 : :
Let G=X(2)-Centroid of ABC. O_A, O_B, O_C-Circumcenters of GBC, GCA, GAB resp.
Gamma_A:Circle through points G, O_B, O_C. Define Gamma_B, Gamma_C cyclically.
Tangent to Gamma_A at G intersects the Gamma_B and Gamma_C at Ab, Ac.
Define Ba, Bc, Ca, Cb cyclically.
* Ab, Ac, Ba, Bc, Ca, Cb lie on same circle Gamma.
Barycentric equation of Gamma:
(a^2-2 (b^2+c^2)) (a^4-2 b^4+7 b^2 c^2-2 c^4+a^2 (b^2+c^2)) x^2+(17 a^6-32 a^4 (b^2+c^2)+5 (b^2-c^2)^2 (b^2+c^2)-2 a^2 (b^4+6 b^2 c^2+c^4)) y z+ ....
The center of Gamma is X(47101).
See Kadir Altintas and Angel Montesdeoca, Euclid 4525.
-
X(47102) = X(6)X(8354)∩X(20)X(538)
Barycentrics 9 a^4-4 a^2 (b^2+c^2)-3 b^4+2 b^2 c^2-3 c^4 : :
Let G=X(2)-Centroid of ABC. O_A, O_B, O_C-Circumcenters of GBC, GCA, GAB resp.
Gamma_A:Circle through points G, O_B, O_C. Define Gamma_B, Gamma_C cyclically.
Tangent to Gamma_A at G intersects the Gamma_B and Gamma_C at Ab, Ac.
Define Ba, Bc, Ca, Cb cyclically.
* Ab, Ac, Ba, Bc, Ca, Cb lie on same circle Gamma.
A2=CaAc ∩ AbBa, B2=AbBa ∩ BcCb, C2=BcCb ∩ CaAc.
A3=CbAb ∩ AcBc, B3=AcBc ∩ BaCa, C3=BaCa ∩ CbAb.
The triangles A2B2C2 and A3B3C3 are bilogic, with Sondat line the line that passes through the centroid and the Schoute center.
** The perspector of A2B2C2 and A3B3C3 is X(2)
** The orthologic center of A3B3C3 wrt A2B2C2 is the center of circle (Ab, Ac, Ba, Bc, Ca, Cb): X(47101)
** The orthologic center of A2B2C2 wrt A3B3C3 is X(47102).
See Kadir Altintas See Kadir Altintas and Angel Montesdeoca, Euclid 4525.
-
X(47441) = MIDPOINT OF X(4) AND X(3345)
Barycentrics a^9*b + 3*a^8*b^2 - 8*a^6*b^4 - 6*a^5*b^5 + 6*a^4*b^6 + 8*a^3*b^7 - 3*a*b^9 - b^10 + a^9*c - 6*a^8*b*c + 4*a^6*b^3*c - 6*a^5*b^4*c + 8*a^4*b^5*c + 8*a^3*b^6*c - 4*a^2*b^7*c - 3*a*b^8*c - 2*b^9*c + 3*a^8*c^2 + 8*a^6*b^2*c^2 + 12*a^5*b^3*c^2 - 6*a^4*b^4*c^2 - 8*a^3*b^5*c^2 - 8*a^2*b^6*c^2 - 4*a*b^7*c^2 + 3*b^8*c^2 + 4*a^6*b*c^3 + 12*a^5*b^2*c^3 - 16*a^4*b^3*c^3 - 8*a^3*b^4*c^3 + 4*a^2*b^5*c^3 - 4*a*b^6*c^3 + 8*b^7*c^3 - 8*a^6*c^4 - 6*a^5*b*c^4 - 6*a^4*b^2*c^4 - 8*a^3*b^3*c^4 + 16*a^2*b^4*c^4 + 14*a*b^5*c^4 - 2*b^6*c^4 - 6*a^5*c^5 + 8*a^4*b*c^5 - 8*a^3*b^2*c^5 + 4*a^2*b^3*c^5 + 14*a*b^4*c^5 - 12*b^5*c^5 + 6*a^4*c^6 + 8*a^3*b*c^6 - 8*a^2*b^2*c^6 - 4*a*b^3*c^6 - 2*b^4*c^6 + 8*a^3*c^7 - 4*a^2*b*c^7 - 4*a*b^2*c^7 + 8*b^3*c^7 - 3*a*b*c^8 + 3*b^2*c^8 - 3*a*c^9 - 2*b*c^9 - c^10 : :
Dado un triángulo ABC y un punto P, no situado sobre sus lados; sean DEF el triángulo ceviano
de P y D', E', F' los puntos en los que la tripolar de P cortan a los lados BC, CA, AB, respectivamente.
Sea A' la imagen de un punto mediante la transformación afín que aplica ABC en D'E'F'. Los puntos B' y C' se definen cíclicamente.
El centro ortológico de A'B'C' respecto a ABC, cuando P=X(34404) es X(47441).
See Angel Montesdeoca, HG260322.
-
X(47442) = MIDPOINT OF X(23) AND X(647)
Barycentrics a^2*(b - c)*(b + c)*(3*a^8 - 4*a^6*b^2 - 2*a^4*b^4 + 4*a^2*b^6 - b^8 - 4*a^6*c^2 + 9*a^4*b^2*c^2 - 3*a^2*b^4*c^2 - 2*b^6*c^2 - 2*a^4*c^4 - 3*a^2*b^2*c^4 + 4*b^4*c^4 + 4*a^2*c^6 - 2*b^2*c^6 - c^8) : :
Dados un triángulo ABC y un punto P. Sea DEF el triángulo cevianoSi ABC es un triángulo y P un punto, las rectas AP, BP y CP cortan a los lados opuestos del triángulo en A', B', C'. Al triángulo A'B'C' se le denomina triángulo ceviano de P.
Si (u:v:w) son las coordenadas baricéntricas de P, A'=(0:v:w). de P.
La circunferencia (ABD) vuelve a cortar a AC en Db y la circunferencia (ACD) vuelve a cortar a AB en Dc.
Sea dB la tangente en B a la circunferencia que pasa por B, el punto medio de AD y el punto medio de CDc. Así mismo, sea dC la tangente en C a la circunferencia que pasa por C, el punto medio de AD y el punto medio de BDb.
Consideremos los puntos Ab=AC ∩ dB y
Ac= AB ∩ dC. Se definen cíclicamente, B1, C1;
Bc, Ba y Ca, Cb.
Si P está sobre la hipérbola de Jerabek, los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están sobre una misma cónica, con centro Po en el eje órtico.
La recta P*Po envuelve una cónica, tangente a la recta de Euler en X(7482) y al eje órtico en X(2489).
Su centro es X(47442),
See Angel Montesdeoca, HG230322.
-
X(47443) = X(2)X(18020)∩X(25)X(250)
Barycentrics a^2*(a - b)^3*(a + b)^3*(a - c)^3*(a + c)^3*(a^2 + b^2 - c^2)*(a^2 - b^2 + c^2) : :
Dados un triángulo ABC y un punto P. Sea DEF el triángulo cevianoSi ABC es un triángulo y P un punto, las rectas AP, BP y CP cortan a los lados opuestos del triángulo en A', B', C'. Al triángulo A'B'C' se le denomina triángulo ceviano de P.
Si (u:v:w) son las coordenadas baricéntricas de P, A'=(0:v:w). de P.
La circunferencia (ABD) vuelve a cortar a AC en Db y la circunferencia (ACD) vuelve a cortar a AB en Dc.
Sea dB la tangente en B a la circunferencia que pasa por B, el punto medio de AD y el punto medio de CDc. Así mismo, sea dC la tangente en C a la circunferencia que pasa por C, el punto medio de AD y el punto medio de BDb.
Consideremos los puntos Ab=AC ∩ dB y
Ac= AB ∩ dC. Se definen cíclicamente, B1, C1;
Bc, Ba y Ca, Cb.
Si P está sobre la hipérbola de Jerabek, los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están sobre una misma cónica, con centro Po en el eje órtico.
La recta P*Po envuelve una cónica, tangente a la recta de Euler en X(7482) y al eje órtico en X(2489).
Su perspector es X(47443),
See Angel Montesdeoca, HG230322.
-
X(49304) = X(109)X(42552)∩X(1411)X(10703)
Barycentrics a (a-b) (a-c) (a^13-3 a^12 (b+c)+a^11 (b^2+13 b c+c^2)+a^10 (7 b^3-17 b^2 c-17 b c^2+7 c^3) -a^9 (11 b^4+5 b^3 c-47 b^2 c^2+5 b c^3+11 c^4) +a^8 (b^5+39 b^4 c-43 b^3 c^2-43 b^2 c^3+39 b c^4+c^5) +a^7 (14 b^6-44 b^5 c-16 b^4 c^2+93 b^3 c^3-16 b^2 c^4-44 b c^5+14 c^6) -a^6 (b-c)^2 (14 b^5+23 b^4 c-45 b^3 c^2-45 b^2 c^3+23 b c^4+14 c^5) -a^5 (b-c)^2 (b^6-36 b^5 c+3 b^4 c^2+56 b^3 c^3+3 b^2 c^4-36 b c^5+c^6) +a^4 (b-c)^2 (11 b^7-18 b^6 c-27 b^5 c^2+32 b^4 c^3+32 b^3 c^4-27 b^2 c^5-18 b c^6+11 c^7) -a^3 (b-c)^4 (7 b^6+17 b^5 c+b^4 c^2-13 b^3 c^3+b^2 c^4+17 b c^5+7 c^6) -a^2 (b-c)^4 (b^7-8 b^6 c-6 b^5 c^2+3 b^4 c^3+3 b^3 c^4-6 b^2 c^5-8 b c^6+c^7) +a (b-c)^6 (b+c)^2 (3 b^4-b^3 c+3 b^2 c^2-b c^3+3 c^4) -(b-c)^6 (b+c)^3 (b^4-b^3 c+2 b^2 c^2-b c^3+c^4)) : :
Let I be the incenter of a triangle ABC and DEF the intouch triangle. The circle centered at I passing through A intersects the ray DB in Ab and the ray DC in Ac. The circumcircles of ABAc and ACAb intersect in A', other than A. Define B' and C' cyclically.
The triangles ABC and A'B'C' are cyclologic (i.e. the circles (AB'C'), (BC'A'), and (CA'B) are concurrent in a common point). The cyclologic center of A'B'C' with respect to ABC is X(80), reflection of incenter in feuerbach point, and the cyclologic center of ABC with respect to A'B'C' is X(49304).
See Angel Montesdeoca, Euclid 5089 and HG180522
-
X(50443) = X(1)X(5)∩X(40)X(499)
Barycentrics (a-b-c) (a^3-3 a (b-c)^2-2 (b-c)^2 (b+c)) : :
The tangent to the incircle at a variable point T cuts the Euler circle at points T1 and T2.
** The locus of the point of intersection of the tangents from T1 and T2 (other than the tangent at T) to the incircle is a conic (C) tangent at the Feuberbach point to the incircle. Its center is X(50443).
See Angel Montesdeoca, Euclid 5183 and HGT060622
-
X(50444) = X(1)X(5)∩X(165)X(499)
Barycentrics (a-b-c) (a^3-5 a (b-c)^2-4 (b-c)^2 (b+c)) ::
The tangent to the incircle at a variable point T cuts the Euler circle at points T1 and T2.
** The locus of the point of intersection of the tangents from T1 and T2 (other than the tangent at T) to the incircle is a conic (C) tangent at the Feuberbach point to the incircle.
** The center of the reciprocal polar of I(r) with respect to (C) is X(50444).
See Angel Montesdeoca, Euclid 5183 and HGT060622
-
X(50574) = X(1)X(523)∩X(11)X(7137)
Barycentrics (b^2-c^2) (a^5-a^2 ((a+b-c) c^2+b^2 (a-b+c))-b^5-c^5+b^2 c^2 (a+b+c)) : :
In the affine homology, with center X(523) (isogonal conjugate of the focus of the Kiepert parabola), axis the line that passes through the centers of the Kiepert and Jerabek hyperbolas y ratio -3, the homologue of the incenter is X(50574) = (2r+R) X(12)-2(r+R)X(9276).
See Angel Montesdeoca, euclid 5222 and HG310521
-
X(50729) = X(2)X(11166)∩X(51)X(17430)
Barycentrics (a^2-2 (b^2+c^2)) (20 a^4+a^2 (b^2+c^2)-(b^2+c^2)^2) : :
Let ABC be a triangle and G, K the centroid, symmedian point, resp.
Let Gb, Kb be the orthogonal projections of B to AG and AK respectively, and Gc, Kc be the orthogonal projections of C to AG and AK respectively. Let A1 (on BC) be the intersection of GbKc and GcKb, and define B1 and C1 cyclically. Let A2 (on AH) be the intersection of GbKb and GcKc, and define B2 and C2 cyclically. The triangles A1B1C1 and A2B2C2 are orthologic; the orthologic center of A1B1C1 wrt A2B2C2 is X(50729).
See Angel Montesdeoca, Euclid 5247 and HG120622
-
X(50730) = X(2)X(47859)∩X(3)X(47591)
Barycentrics 20 a^10-19 a^8 (b^2+c^2)+a^6 (-145 b^4+122 b^2 c^2-145 c^4) +a^4 (149 b^6-153 b^4 c^2-153 b^2 c^4+149 c^6)+a^2 (17 b^8-100 b^6 c^2+198 b^4 c^4-100 b^2 c^6+17 c^8) -2 (b^2-c^2)^2 (11 b^6-21 b^4 c^2-21 b^2 c^4+11 c^6) : :
Let ABC be a triangle and G, K the centroid, symmedian point, resp.
Let Gb, Kb be the orthogonal projections of B to AG and AK respectively, and Gc, Kc be the orthogonal projections of C to AG and AK respectively. Let A1 (on BC) be the intersection of GbKc and GcKb, and define B1 and C1 cyclically. Let A2 (on AH) be the intersection of GbKb and GcKc, and define B2 and C2 cyclically. The triangles A1B1C1 and A2B2C2 are orthologic; the orthologic center of A2B2C2 wrt A1B1C1 is X(50730) .
See Angel Montesdeoca, Euclid 5247 and HG120622
-
X(51121) = X(514)X(3158)∩X(519)X(42050)
Barycentrics 3 a^4-4 b (b-c)^2 c-a^3 (b+c)+a^2 (-7 b^2+2 b c-7 c^2)+a (5 b^3-b^2 c-b c^2+5 c^3) : :
Let ABC be a triangle and P, Q two points. The perpendicular through P to BC intersects the parallel through Q to BC at A', and similarly B' and C'.
ABC and A'B'C' have the same symmedian point if Q=f(P), where f is the affine transformation with fixed points the symmedian and the points at infinity of the Kiepert hyperbola, which maps the orthocenter to the centroid.
f[X(1)] = X(51121).
See Angel Montesdeoca, Euclid 5290 and HG140319.
-
X(51122) = X(2)X(2418)∩X(3)X(538)
Barycentrics 3 a^4-7 a^2 (b^2+c^2)+8 b^2 c^2 : :
Let ABC be a triangle and P, Q two points. The perpendicular through P to BC intersects the parallel through Q to BC at A', and similarly B' and C'.
ABC and A'B'C' have the same symmedian point if Q=f(P), where f is the affine transformation with fixed points the symmedian and the points at infinity of the Kiepert hyperbola, which maps the orthocenter to the centroid.
f[X(3)] = X(51122).
See Angel Montesdeoca, Euclid 5290 and HG140319.
-
X(51123) = X(2)X(2418)∩X(5)X(7781)
Barycentrics 4 a^4-9 a^2 (b^2+c^2)+b^4+6 b^2 c^2+c^4 : :
Let ABC be a triangle and P, Q two points. The perpendicular through P to BC intersects the parallel through Q to BC at A', and similarly B' and C'.
ABC and A'B'C' have the same symmedian point if Q=f(P), where f is the affine transformation with fixed points the symmedian and the points at infinity of the Kiepert hyperbola, which maps the orthocenter to the centroid.
f[X(5)] = X(51123).
See Angel Montesdeoca, Euclid 5290 and HG140319.
-
X(51316) = ISOGONAL CONJUGATE OF X(37672)
Barycentrics 1/(3 a^4 - 6 a^2 b^2 + 3 b^4 - 6 a^2 c^2 + 2 b^2 c^2 + 3 c^4) : :
Given a triangle with orthocenter H=X(4), let DEF and D'E'F' be the cevian and precevian triangles of H, and D" be the symmetry of D with respect to D'. Let La be the radical axis of the circumference of diameter DD" and circumference (BCD"). The radical axes Lb and Lc are defined cyclically.
The lines La,Lb,Lc form a perspective triangle with ABC with perspector W (= X(31316) ), the isogonal conjugate of X(37672) and the isotomic conjugate of X(32831).
See Angel Montesdeoca, Euclid 5336 and HG020722.
-
X(51341) = X(1)X(1696)∩X(6)X(7091)
Barycentrics a (a - b - c)/(a^3+a^2 (b+c)-a (b^2-6 b c+c^2)-(b+c)^3) : :
Let A' be the point in which the A-excircle is tangent to the circle that passes through vertices B and C, and define B' and C' cyclically. The lines AA', BB', CC' concur in X(5423). (Peter Moses, December 10, 2015). The tangents at A', B', C' to the corresponding excircle form a perspective triangle with ABC and the perspector is Z= X(51341)
See Angel Montesdeoca, Euclid 5356 and HG030722.
-
X(51342) = X(3)X(133)∩X(4)X(64)
Barycentrics (a^4-(b^2-c^2)^2) (a^12+a^10 (b^2+c^2)+18 a^6 (b^2-c^2)^2 (b^2+c^2)+2 (b^2-c^2)^4 (b^4+4 b^2 c^2+c^4)-7 a^4 (b^2-c^2)^2 (b^4+6 b^2 c^2+c^4)-4 a^8 (3 b^4-5 b^2 c^2+3 c^4)-a^2 (b^2-c^2)^2 (3 b^6-19 b^4 c^2-19 b^2 c^4+3 c^6)) : :
Let DEF be the Euler triangle of ABC. Let La be the perpendicular to OD through D, and define Lb, Lc, cyclically. Let A'B'C' be the triangle formed by the lines La, Lb, Lc. The center of the elipse, imagen of circumcircle for the affine transformation that maps the reference triangle ABC onto A'B'C', is X(51342).
See Angel Montesdeoca, Euclid 5364 and HG040722.
-
X(51513) = X(378)X(1116)∩X(460)X(512)
Barycentrics (b^2-c^2) (a^6 (b^2+c^2)-a^4 (b^2-c^2)^2-a^2 (b^2-c ^2)^2(b^2+c^2)+(b^2-c^2)^4) : :
F1 and F2 are a bicentric pair given by f(a,b,c)= b^2 (b^2-c^2) (a^2+b^2-c^2) (a^2-b^2+c^2)^2.
Bicentric sum F1⊕F2 is X(115).
X(115) is on the line F1F2. Therefore, the harmonic conjugate W of X(115), with respect to F1 and F2 is X(51513) (C.Kimberling, Triangle Centers and Central Triangles, Congressus Numerantium, 129 (1998). Exercise no6, p.46):
See Angel Montesdeoca, Euclid 5464 and HG070822.
-
X(51684) = (name pending)
Barycentrics 6 a+Sqrt(6) Sqrt(a^2+b^2+c^2) : :
See Angel Montesdeoca, Euclid 5486.
HG300822
-
X(51685) = X(3624)X(4657)∩X(3966)X(4034)
Barycentrics (a-b-c)/(a^2+2 a b-b^2+2 a c-b c-c^2) : :
See Angel Montesdeoca, Euclid 5486.
HG300822
-
X(51686) = X(1)X(25)∩X(28)X(86)
Barycentrics a^2/((-a^2+b^2+c^2) (a^2+b^2+2 b c+c^2)) : :
See Angel Montesdeoca, Euclid 5386.
HG300822
-
X(51776) = X(2)X(11610)∩X(69)X(248)
Barycentrics a^2*(a^2 - b^2 - c^2)*(a^4 + b^4 - a^2*c^2 - b^2*c^2)*(a^4 - 2*a^2*b^2 + b^4 - 2*a^2*c^2 + c^4)*(a^4 - a^2*b^2 - b^2*c^2 + c^4)::
X(51776) is the perspector of ABC and the triangle A'B'C' constructed at X(41679).
See HG090922.
-
X(51777) = (name pending)
Barycentrics a^2 (a^4+b^4+c^4-2 a^2 (b^2+c^2)) /(a^16-5 a^14 (b^2+c^2)-(b^2-c^2)^4 (b^4+c^4)^2-a^4 (b^4-c^4)^2 (2 b^4-b^2 c^2+2 c^4)+a^12 (10 b^4+13 b^2 c^2+10 c^4)-a^10 (11 b^6+13 b^4 c^2+13 b^2 c^4+11 c^6)+a^8 (8 b^8+6 b^6 c^2+4 b^4 c^4+6 b^2 c^6+8 c^8)+a^6 (-3 b^10+b^8 c^2-2 b^6 c^4-2 b^4 c^6+b^2 c^8-3 c^10)+a^2 (b^2-c^2)^2 (3 b^10-b^8 c^2+2 b^6 c^4+2 b^4 c^6-b^2 c^8+3 c^10))
X(51777) is the perspector of ABC and the triangle A'B'C' constructed at X(41679).
See HG090922.
-
X(51778) = (name pending)
Barycentrics a^2 (a^22-7 a^20 (b^2+c^2)+a^18 (23 b^4+38 b^2 c^2+23 c^4)-(b^2-c^2)^4 (b^4+c^4)^2 (b^6+c^6)-a^16 (49 b^6+92 b^4 c^2+92 b^2 c^4+49 c^6)+a^14 (78 b^8+136 b^6 c^2+155 b^4 c^4+136 b^2 c^6+78 c^8)-2 a^12 (49 b^10+69 b^8 c^2+76 b^6 c^4+76 b^4 c^6+69 b^2 c^8+49 c^10)+a^10 (98 b^12+92 b^10 c^2+99 b^8 c^4+94 b^6 c^6+99 b^4 c^8+92 b^2 c^10+98 c^12)-2 a^8 (39 b^14+12 b^12 c^2+22 b^10 c^4+19 b^8 c^6+19 b^6 c^8+22 b^4 c^10+12 b^2 c^12+39 c^14)+a^2 (b^2-c^2)^2 (7 b^16-4 b^14 c^2+7 b^12 c^4+7 b^4 c^12-4 b^2 c^14+7 c^16)+a^6 (49 b^16-24 b^14 c^2+21 b^12 c^4+4 b^10 c^6+16 b^8 c^8+4 b^6 c^10+21 b^4 c^12-24 b^2 c^14+49 c^16)-a^4 (23 b^18-33 b^16 c^2+24 b^14 c^4-12 b^12 c^6+6 b^10 c^8+6 b^8 c^10-12 b^6 c^12+24 b^4 c^14-33 b^2 c^16+23 c^18)) : :
X(51778) is the perspector of ABC and the triangle A'B'C' constructed at X(41679).
See HG090922.
-
X(52014) = X(3)X(51)∩X(4)X(1609)
Barycentrics a^2 (a^6-3 a^4 (b^2+c^2)+3 a^2 (b^2-c^2)^2-(b^2-c^2)^2 (b^2+c^2)) (a^8-4 a^6 (b^2+c^2)+a^4 (6 b^4+8 b^2 c^2+6 c^4)-4 a^2 (b^6+c^6)+(b^2-c^2)^4) : :
See Angel Montesdeoca, Euclid 5508 and
X(1609) punto fijo de una transformación afín.
-
X(52457) = X(2)X(7)∩X(3)X(1633)
Barycentrics (b+c-a) (a^4+(b-c)^4-2 a^2 (b^2+c^2)) : :
See Angel Montesdeoca, Euclid 5554.
See HG1122
-
X(52470) = X(3)X(6524)∩X(25)X(6526)
Barycentrics a^2 (a^8-4 a^6 (b^2+c^2)+a^4 (6 b^4+11 b^2 c^2+6 c^4)-2 a^2 (2 b^6+5 b^4 c^2+5 b^2 c^4+2 c^6)+b^8+3 b^6 c^2+8 b^4 c^4+3 b^2 c^6+c^8)/(b^2+c^2-a^2)^3 : :
See Angel Montesdeoca, Euclid 5559.
See HG181122.
-
X(52495) = X(1)X(210)∩X(58)X(1100)
Barycentrics a (4 a^3+13 a^2 (b+c)+2 a (6 b^2+11 b c+6 c^2)+3 (b+c)^3) : :
See Angel Montesdeoca, Euclid 5560.
See HG211122.
-
X(52521) = X(191)X(1050)∩X(21061)X(21936)
Barycentrics a^3 (b+c) (a^6 b c+a^4 (b^4-2 b^3 c+4 b^2 c^2-2 b c^3+c^4)+a^3 (3 b^5-b^4 c-b c^4+3 c^5)+a^2 (3 b^6-b^5 c-5 b^4 c^2+7 b^3 c^3-5 b^2 c^4-b c^5+3 c^6)+a (b^7-b^6 c-b^5 c^2+3 b^4 c^3+3 b^3 c^4-b^2 c^5-b c^6+c^7)+b^3 c^3 (b+c)^2) : :
See Angel Montesdeoca, Euclid 5567.
See La elipse de Hutson y el ortocentro del triángulo incentral.
-
X(52725) = X(2)X(3)∩X(8182)X(33900)
Barycentrics a^2 (a^8-24 a^4 b^2 c^2-4 a^6 (b^2+c^2)+a^2 (4 b^6+21 b^4 c^2+21 b^2 c^4+4 c^6)-b^8+11 b^6 c^2-12 b^4 c^4+11 b^2 c^6-c^8) : :
[Kadir Altintas]:
Let G=X(2) centroid of ABC. Circle (GBC) intersects the AB, AC at Ac, Ab resp. Define Ba, Bc, Ca, Cb cyclically.
O'A: inverse of circumcenter of ABcCb respect to circumcircle of ABC.
Define O'B, O'C cyclically.
* Symmedian point of O'AO'BO'C lies on Euler line of ABC.
[Angel Montesdeoca]:
The symmedian point of O'AO'BO'C is the reflection of X(10204) in X(3).
See Kadir Altintas and Angel Montesdeoca, Euclid 5598.
-
X(52792) = ISOGONAL CONJUGATE OF X(52792)
Barycentrics a^2*(a^4+4*b^4-2*a*b^2*c-5*b^2*c^2+c^4-a^2*(5*b^2+2*c^2))*(a^4+b^4-2*a*b*c^2-5*b^2*c^2+4*c^4-a^2*(2*b^2+5*c^2)) : :
See Angel Montesdeoca and Ivan Pavlov, Euclid 5622.
-
X(52793) = X(3)X(12)∩X(11)X(35)
Barycentrics 4*a^4+(b^2-c^2)^2-a^2*(5*b^2+2*b*c+5*c^2) : :
See Angel Montesdeoca and Ivan Pavlov, Euclid 5622.
-
X(52794) = X(8)X(44149)∩X(319)X(1232)
Barycentrics b^2*c^2*(4*a^4+(b^2-c^2)^2-a^2*(5*b^2+2*b*c+5*c^2)) : :
See Angel Montesdeoca and Ivan Pavlov, Euclid 5622.
-
X(52795) = X(5)X(993)∩X(10)X(547)
Barycentrics 2*a^4-7*a^2*b^2+5*b^4-2*a*b^2*c-7*a^2*c^2-2*a*b*c^2-10*b^2*c^2+5*c^4 : :
See Angel Montesdeoca and Ivan Pavlov, Euclid 5622.
-
X(52796) = X(389)X(3634)∩X(515)X(3819)
Barycentrics a^2*(2*a^3*b^2*c^2*(b+c)-2*a*b^2*(b-c)^2*c^2*(b+c)-a^6*(b^2+c^2)+(b^2-c^2)^2*(b^4+6*b^2*c^2+c^4)+a^4*(3*b^4+4*b^2*c^2+3*c^4)-a^2*(3*b^6+7*b^4*c^2+4*b^3*c^3+7*b^2*c^4+3*c^6)) : :
See Angel Montesdeoca and Ivan Pavlov, Euclid 5622.
-
X(52942) = EULER LINE INTERCEPT OF X(148)X(1992)
Barycentrics 11 a^4-2 a^2 (b^2+c^2)+16 b^2 c^2-7 (c^4 +b^4) : :
See Abdilkadir Altintaşand Angel Montesdeoca, Euclid 5683.
Simedianos de triángulos círculo cevianos sobre la recta de Euler
-
X(52943) = EULER LINE INTERCEPT OF X(315)X(15300)
Barycentrics 25 a^4-16 a^2 (b^2+c^2)+20 b^2 c^2-11 (c^4+b^4) : :
See Abdilkadir Altintaşand Angel Montesdeoca, Euclid 5683.
Simedianos de triángulos círculo cevianos sobre la recta de Euler
-
X(52944) = EULER LINE INTERCEPT OF X(9830)X(35369)
Barycentrics 47 a^4-20 a^2 (b^2+c^2)+52 b^2 c^2-25 (c^4+b^4) : :
See Abdilkadir Altintaşand Angel Montesdeoca, Euclid 5683.
Simedianos de triángulos círculo cevianos sobre la recta de Euler
-
X(52998) = X(98)X(9381) ∩X(110)X(6328)
Barycentrics 1/((b^2-c^2)(a^2-b^2-c^2) (a^8+a^4 b^2 c^2-2 a^6 (b^2+c^2)-(b^2-c^2)^2 (b^4+c^4)+a^2 (2 b^6-b^4 c^2-b^2 c^4+2 c^6))) ::
See Abdilkadir Altintaşand Angel Montesdeoca, Euclid 5705.
Una parábola con foco la reflexión de X(933) en la recta de Euler
-
X(53033) = X(2)X(39)∩X(20)X(636)
Barycentrics 3 a^4-2 a^2 (b^2+c^2)+3 b^4+2 b^2 c^2+3 c^4 : :
Sea ABC un triángulo con incentro I=X1, ortocentro H=X4 y triangulo medial MaMbMc, la bisectriz interior en A corta la altura por C en D y la bisectriz exterior en A corta a la altura por B en E.
Las circunferencias (BDH) y (CEH) se vuelven a cortar en Abc.
Sea ℓbc la recta MaAbc.
Permutando B y C, en la construcción anterior, se define la recta ℓcb.
Procediendo cíclicamente sobre los vértices de ABC, se definen las rectas ℓca, ℓac, ℓab, ℓba.
Las seis rectas ℓbc, ℓcb, ℓca, ℓac, ℓab, ℓba son tangentes a una misma cónica con centro W = (r^2+4 r R-s^2)^2 X141- 5 r^2 s^2 X631= X(53033).
See Angel Montesdeoca, Euclid 5727 and
Seis rectas tangentes a una cónica.
-
X(53841) = (name pending)
Barycentrics (a*(b+c))/(a*b*c*(b+c)+a*Sqrt[-a^2+2*(b+c)^2]*S+2*S^2) : :
See Angel Montesdeoca, Euclid 5796, and HG120323
-
X(53842) = (name pending)
Barycentrics (a*(b+c))/(a*b*c*(b+c)-a*Sqrt[-a^2+2*(b+c)^2]*S+2*S^2) : :
See Angel Montesdeoca, Euclid 5796, and HG120323
- al menos, de colaboraciones
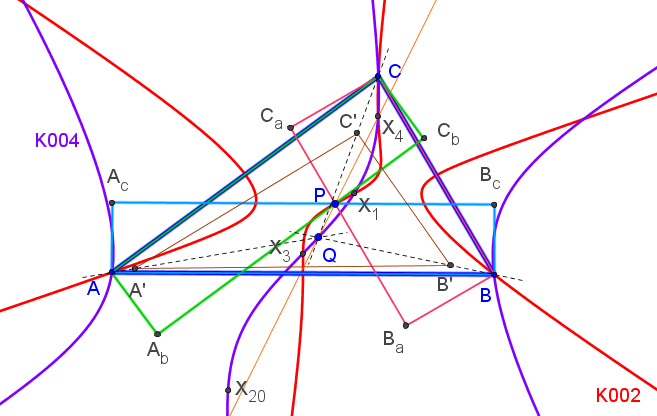
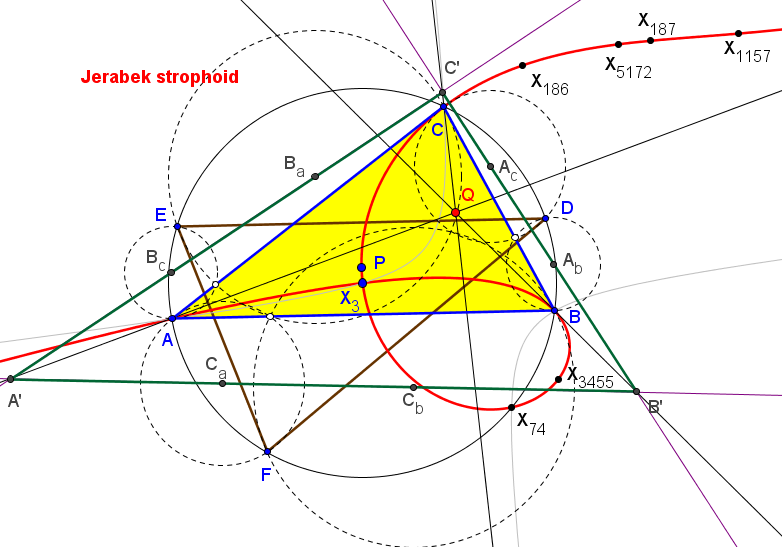
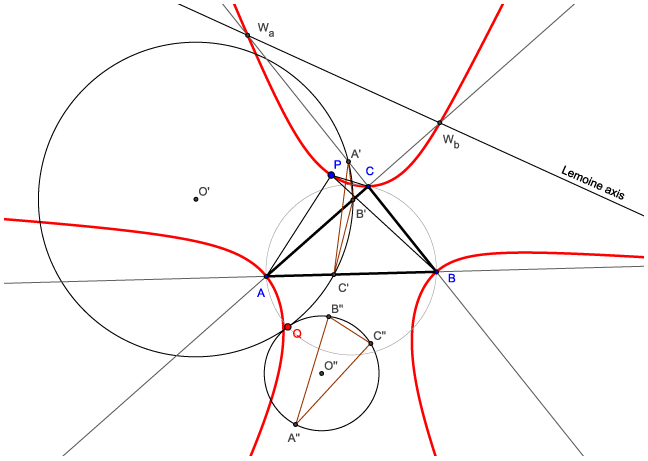
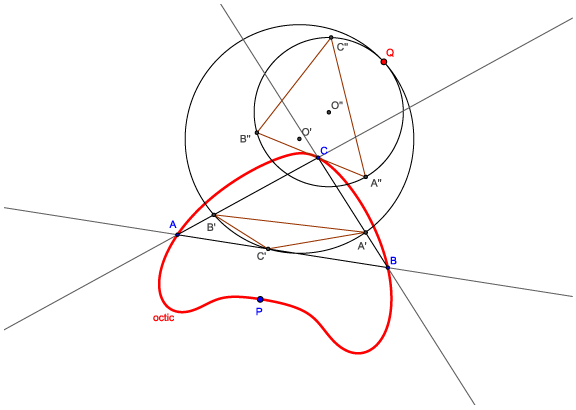
-circle.png)
.png)