Desde 05/12/2019
Hechos Geométricos en el Triángulo de:
(2013)
(2014)
(2015)
(2016)
(2017)
(2018)
(2019)
(2020)
(2021)
(2022)
|
Cómo es el enlace a un Hecho Geométrico correspondiente a un día concreto: http://amontes.webs.ull.es/otrashtm/HGT2023.htm#HGddmmaa EJEMPLO: 1 de enero del 2023 http://amontes.webs.ull.es/otrashtm/HGT2023.htm#HG010123 |
El 26 septiembre de 2008 falleció Paul Newman, a los 83 años de edad, actor estadounidense de renombre mundial, reconocido por su talento en la interpretación y su carisma en la pantalla. Su carrera cinematográfica abarcó más de cinco décadas. Tiene tres Óscars: el premio Humanitario de 1994, el Honorífico en 1985 y el de Mejor Actor en 1986 por el filme "El color del dinero" de Martin Scorsese. No recogió ninguno de ellos porque pensó que "le llegaban tarde". Y es que antes estuvo nominado siete veces por películas como El buscavidas (1961) o La leyenda del indomable (1967) o La gata sobre el tejado de zinc (1958).
Fa = (a^2 (-a^12+b^4 c^4 (b^2-c^2)^2+2 a^10 (b^2+c^2)-2 a^8 (b^4+b^2 c^2+c^4)+2 a^6 (b^6+c^6)-a^4 (b^8-b^4 c^4+c^8)):
b^2 (a^2-c^2)^2 (a^4-a^2 b^2-b^2 c^2+c^4)^2 : (a^2-b^2)^2 c^2 (a^4+b^4-a^2 c^2-b^2 c^2)^2).
Z = ( a^2 (b^2-c^2)^2 (b^4+c^4-a^2 (b^2+c^2))^2 : ... : ...),
que tiene números de búsqueda en (3.05957624678130, 2.69799090588066, 0.360712510091020).El 14 de septiembre de 1769, nació Alexander von Humbolt, fue un naturalista, arqueólogo, explorador y geógrafo alemán que realizó dos importantes expediciones a América Latina (1799-1804) y a Asia (1829). . Durante el primero, equipado con los mejores instrumentos científicos, examinó y recolectó especímenes geológicos, zoológicos, botánicos y etnográficos, incluidas más de 60.000 plantas tropicales nuevas o raras. Trazó e hizo observaciones sobre una corriente oceánica fría a lo largo de la costa peruana, ahora llamada Corriente de Humboldt.
A' = (a^2 (a^2+2 (b^2+c^2)): 2 b^2 (a^2+2 b^2+c^2) : 2 c^2 (a^2+b^2+2 c^2)).
Procediendo cíclicamente, se definen las hipérbolas ℋb y ℋc, con centros B' y C', respectivamente.W = ( a^4 -13 a^2 (b^2+c^2) : ... : ...),
que tiene números de búsqueda en (1.64894680412929, 1.98858674947266, 1.50289820728979).El 12 de septiembre de 1859, Urbain Le Verrier, matemático francés que se especializó en mecánica celeste, presentó un trabajo ante la Academia de Ciencias en el que atribuía el avance del perihelio de Mercurio a un planeta no descubierto, al que llamó Vulcano, más cercano al Sol que Mercurio o a un segundo cinturón de asteroides. tan cerca del Sol que resulta invisible. Se realizaron muchas búsquedas de Vulcano durante las décadas siguientes y no se pudo confirmar su existencia. La necesidad del planeta como explicación de las peculiaridades orbitales de Mercurio se volvió innecesaria cuando la teoría de la relatividad general de Einstein de 1915 demostró que la salida de Mercurio de una órbita predicha por la física newtoniana se explicaba por efectos derivados de la curvatura del espacio-tiempo causada por la masa del Sol
A1 = (a^4-(b^2-c^2)^2,2 b^2 (-a^2+b^2-c^2),2 c^2 (-a^2-b^2+c^2)).
Sea Γa
A' = (b^8-b^6 c^2-b^2 c^6+c^8-a^6 (b^2+c^2)-3 a^2 (b^2-c^2)^2 (b^2+c^2)-a^4 (-3 b^4+b^2 c^2-3 c^4):
-b^2 (-a^2+b^2+c^2) (a^4+b^4+b^2 c^2-2 c^4+a^2 (-2 b^2+c^2)):
-c^2 (-a^2+b^2+c^2) (a^4-2 b^4+b^2 c^2+c^4+a^2 (b^2-2 c^2))
(x:y:z) ↦ a^2 (a^6 b^2-3 a^4 b^4+3 a^2 b^6-b^8+a^6 c^2+a^4 b^2 c^2-3 a^2 b^4 c^2+b^6 c^2-3 a^4 c^4-3 a^2 b^2 c^4+3 a^2 c^6+b^2 c^6-c^8) x+a^2 b^2 (a^2-b^2+c^2) (a^4-2 a^2 b^2+b^4+a^2 c^2+b^2 c^2-2 c^4) y+a^2 c^2 (a^2+b^2-c^2) (a^4+a^2 b^2-2 b^4-2 a^2 c^2+b^2 c^2+c^4) z : ... : ...,
tiene punto fijo el ortocentro y sus restas dobles (aparte de la recta del intinito) son las rectas por el ortocentro paralelas a la síntotas de la .El 29 de agosto de 1973 falleció, a los 34 años, Hermann Hankel, matemático alemán. Sus trabajos versaron sobre geometría proyectiva y sobre la teoría de funciones de variable compleja. Estableció una representación de la función gamma por medio de una integral compleja y obtuvo soluciones a la ecuación diferencial de Friedrich Bessel. De sus obras cabe destacar Lecciones sobre los números complejos (1867), que continúa el análisis de los principios fundamentales del álgebra emprendido por matemáticos como William Rowan Hamilton, Hermann Grassmann, August De Morgan y George Boole, y su Historia de las matemáticas desde la Antigüedad hasta la Edad Media (1874), que es en realidad un recopilación de artículos sobre la materia publicada póstumamente por su padre.
A" = (a^2 v w (c^2 v^2 + b^2 (u + v) w) (b^2 w^2 +
c^2 v (u + w)) :
b^2 u w (-c v + b w) (c v + b w) (c^2 v^2 +
b^2 (u + v) w) :
c^2 u v (c v - b w) (c v + b w) (b^2 w^2 +
c^2 v (u + w)).
ℓa: c^2 v ((-b^2+c^2) u+a^2 (u+2 w))y+b^2w ((b^2-c^2) u+a^2 (u+2 v))z=0,
A1 = (-a^2 v ((a^2-c^2) v+b^2 (2 u+v)) w ((a^2-b^2) w+c^2 (2 u+w)):
b^2 u ((a^2-c^2) v+b^2 (2 u+v)) w ((-a^2+b^2) w+c^2 (2 v+w)):
c^2 u v ((a^2-b^2) w+c^2 (2 u+w)) (-a^2 v+c^2 v+b^2 (v+2 w)).
El 24 de agosto de 1572, La Noche de San Bartolomé, puso de manifiestobel fanatismo y la brutalidad homicida que una comunidad puede desplegar contra una minoría religiosa. Tras cerrar las puertas de la ciudad y convocar a la milicia municipal, a las tres de la madrugada tocaron a rebato las campanas de una iglesia de París, señal del inicio de la matanza. Para el papado, en cambio, el suceso fue un triunfo espectacular, una nueva muestra del favor de Dios a la Iglesia católica, Los católicos parisinos se ensañaban con los cadáveres de los hugonotes, a los que se destripaba para mostrar sus entrañas, clavadas en picas, como símbolo de su pecado.
D' = (-a^2 v w:a^2 v w-c^2 v (v+w):a^2 v w-b^2 w (v+w)),
Db = (a^2 v:0:-a^2 v+b^2 (v+w)), Dc = (a^2 w:-a^2 w+c^2 (v+w):0),
Oa = (2 a^2 (c^2 v+b^2 w):-a^4 v+a^2 (c^2 v+b^2 (2 v-w))-b^2 (b^2-c^2) (v+w):-a^4 w+c^2 (b^2-c^2) (v+w)+a^2 (-c^2 (v-2 w)+b^2 w)).
W = ( a^2(a^6-3 a^4 (b^2+c^2)+a^2 (3 b^4-2 b^2 c^2+3 c^4)-(b^2-c^2)^2 (b^2+c^2))/((-a^2+b^2+c^2)(3 a^8-6 a^6 (b^2+c^2)-2 a^2 (b^2-c^2)^2 (b^2+c^2)+4 a^4 (b^4+c^4)+(b^2-c^2)^4) ) : ... : ...),
que tiene números de búsqueda en (0.0625494032567161, -6.29388785392024, 7.96910250234914).Yo estoy tan firmemente convencido de que las religiones hacen daño, como lo estoy de que son falsas. Bertrand Russell
F = ((a^4-(b^2-c^2)^2) u (u+v) (u+w) (a^2 v w-c^2 v (v+w)-b^2 w (v+w)) : ... : ...).
x:y:z ↦ σP(x:y:z)= (-c^2 u v+b^2 u (u+v)+a^2 v (u+v)) (b^2 u w-c^2 u (u+w)-a^2 w (u+w)) (-(b-c) (b+c) (v-w) (v+w)+a^2 (v^2+w^2)) x+
(a^2-b^2+c^2) u (u+w)(-c^2 u v+b^2 u (u+v)+a^2 v (u+v)) (a^2 v w-c^2 v (v+w)-b^2 w (v+w)) y+
(a^2+b^2-c^2) u (u+v) (-b^2 u w+c^2 u (u+w)+a^2 w (u+w)) (a^2 v w-c^2 v (v+w)-b^2 w (v+w)) z : ... : ...
Let A0B0C0 be the orthic triangle of ABC. Let A15 = X(15)-of-AB0C0, and define B15 and C15 cyclically, so that A15B15C15 is the 3rd isodynamic-Dao equilateral triangle of ABC (see preamble of X(31683))
Let A'15 be the point, other than A, in which the line AA15 meets the circle {{A,B0,C0}}, and define B'15 and C'15 cyclically. The triangle A'15B'15C'15 is the Vu-Dao-X(15)-isodynamic equilateral triangle.
If X(15) is replaced by X(16) in the above construction, the resulting triangle, A'16B'16C'16, is the Vu-Dao-X(16)-isodynamic equilateral triangle.
A Clara por su cumple
x:y:z ↦ σ(x:y:z)=b^2 c^2 (a^2+b^2-c^2)^2 (a^2-b^2+c^2)^2 x-a^4 c^2 (a^2-b^2-c^2)^2 (a^2+b^2-c^2) y-a^4 b^2 (a^2-b^2-c^2)^2 (a^2-b^2+c^2) z: :,
es X577.El 15 de agosto de 1921 falleció Tomás Morales Castellano, médico, político y poeta español, nacido en Moya, Gran Canaria (10 de octubre de 1884). Puede considerarse el máximo representante del movimiento modernista en Canarias y uno de los más importantes poetas de la literatura hispánica. Fue el propulsor de la poesía canaria moderna. Dos de sus obras más importantes son las conocidas como Oda al Atlántico o Las Rosas de Hércules
Ta= (-4 a^2 (a+b-c) (a-b+c) : (a-b-c) (a+b-c)^3 : (a-b-c) (a-b+c)^3).
Γa vuelve a corta a AB, AC en B1, C1, respectivamente.
Aa = (2 a^2 : a^2-b^2+c^2-2 a (b+c) : a^2+b^2-c^2-2 a (b+c)), (A-vértice del triángulo Ascella — axila de Sagitario),
Ab = (-a (3 a+b-c) (a-b+c) : (3 a+b-c) (a^2+c (-b+c)-a (b+2 c)) : c (a-b+c)^2),
Ac = (a (-3 a+b-c) (a+b-c) : b (a+b-c)^2 : (3 a-b+c) (a^2+b (b-c)-a (2 b+c))).
A' = AbBa∩AcCa, B' = BcCb∩BaAb, C' = CaAc∩CbBc.
𝔖abc xyz (a-b-3 c) (a-3 b-c) (3 a-b-c)(a-b-c) x^2+2 (3 a^4+a^2 (-6 b^2+32 b c-6 c^2)+(b-3 c) (b-c)^2 (3 b-c)) y z = 0,
es:W = ( a (a^3 (b+c)-a^2 (b^2+c^2)+a (b^3-2 b^2 c-2 b c^2+c^3)-(b-c)^2 (b^2-3 b c+c^2)) : ... : ...),
que tiene números de búsqueda en (8.40850228431288, 3.31410024886599, -2.53455982160571).Un 50 aniverario de gran significado personal
Ab = ((a^2+b^2-c^2) (a^4+b^4-c^4+a^2 (-2 b^2+c^2)) : (a^2-b^2) (a^2-b^2-c^2) (a^2+b^2-c^2) : c^2 (-b^2+c^2) (-a^2+b^2+c^2)),
Ac = ((a^2-b^2+c^2) (a^4-b^4+c^4+a^2 (b^2-2 c^2)) : b^2 (b^2-c^2) (-a^2+b^2+c^2) : (a^2-c^2) (a^2-b^2-c^2) (a^2-b^2+c^2)).
Ao = (-2 a^10+5 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)-2 a^6 (b^4+4 b^2 c^2+c^4)+2 a^2 (b^2-c^2)^2 (2 b^4+b^2 c^2+2 c^4)+a^4 (-4 b^6+6 b^4 c^2+6 b^2 c^4-4 c^6) :
-b^2 (a^2+b^2-c^2) (-a^2+b^2+c^2) (a^4+(b^2-c^2)^2+a^2 (-2 b^2+c^2)) :
-c^2 (a^2-b^2+c^2) (-a^2+b^2+c^2) (a^4+a^2 (b^2-2 c^2)+(b^2-c^2)^2).
A' = (0 : a^6+b^6-2 b^2 c^4+c^6-a^4 (b^2+c^2)-a^2 (b^4-3 b^2 c^2+c^4) : a^6+b^6-2 b^4 c^2+c^6-a^4 (b^2+c^2)-a^2 (b^4-3 b^2 c^2+c^4).
Cíclicamente, se definen los puntos B' y C'.W = (a^6 (b^4+c^4)+a^4 (-3 b^6+2 b^4 c^2+2 b^2 c^4-3 c^6)+a^2 (b^2-c^2)^2 (3 b^4+b^2 c^2+3 c^4)-(b^2-c^2)^4 (b^2+c^2) : ... : ...),
que tiene números de búsqueda en (1.85095013300357, 1.44474139167132, 1.78617422628720).El 24 de julio de 1982 nació Alexandre Dumas, escritor francés fue muy influyente en la literatura mundial y entre su obra se destaca ‘Los tres mosqueteros’ y ‘El conde de Montecristo’. Fue parte del romanticismo y sus escritos le valieron la distinción de Caballero de la Legión de Honor.
Ao = (-2 a^2 v w : c^2 v^2+b^2 w (2 v+w) : b^2 w^2+c^2 v (v+2 w)).
El de 𝒞a, respecto al triángulo APQ es:Pa = (a^2 u v w : (b^2 u^2+a^2 v^2) w : v (c^2 u^2+a^2 w^2)).
Procediendo cíclicamente, sobre los vértices de ABC, de obienen la cónicas 𝒞a, 𝒞a, sus centros Bo, Co y los puntos Pb, Pc.El 17 de julio de 1912 falleció Henri Poincaré, matemático, físico, científico teórico y filósofo de la ciencia. Hizo importantes descubrimientos en las ecuaciones diferenciales, la topología, la probabilidad y a la teoría de las funciones. Destacó por su desarrollo de las llamadas funciones fuchsianas, y por sus contribuciones a la mecánica analítica. Sus estudios engloban investigaciones sobre la teoría electromagnética de la luz y sobre la electricidad, mecánica de fluidos, transferencia de calor y termodinámica. Además se anticipó a la teoría del caos.
El escritor checo Milan Kundera ha fallecido este miércoles (11/07/2023) en París a los 94 años. Junto con Kafka y Havel, fue uno de los autores de la República Checa con más fama fuera de su país. Eterno candidato al premio Nobel, la literatura de Kundera estaba impregnada de historia, filosofía y política y logró llegar al gran público gracias al éxito de La insoportable levedad del ser, su novela más conocida, publicada en 1984.
Ao = (a^4 (-a^2+b^2+c^2) : ^2 (a^4+2 c^2 (b^2-c^2)+a^2 (-b^2+c^2)) : c^2 (a^4-2 b^4+2 b^2 c^2+a^2 (b^2-c^2))).
Cíclicamente, se obtienen los centros Bo y Co de las hipérbolas ℋb y ℋc.La = (a^8+2 b^2 c^2 (b^2-c^2)^2-2 a^6 (b^2+c^2)+a^4 (b^4+c^4) : -a^2 b^2 (-a^2+b^2+c^2)^2 : -a^2 c^2 (-a^2+b^2+c^2)^2).
Se obtienen cíclicamente los puntos Lb y Lc.W = ( (a^2 (a^2-b^2-c^2)^2)/(a^8+b^2 c^2 (b^2-c^2)^2-2 a^6 (b^2+c^2)+a^4 (b^4+b^2 c^2+c^4)) : ... : ...),
que tiene números de búsqueda en (-0.0291009433224696, -0.0128332361965662, 3.66298023465391). Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {69,1972}, {343,6331}, {394,6638}, {40802,40804}.El 9 de julio de 2011 falleció Facundo Cabral, cantautor, poeta, escritor y filósofo argentino. Su propuesta artística resulta difícil de encasillar. Aunque compuso canciones y algunas de estas trascendieron a nivel hispanoamericano como «No soy de aquí ni soy de allá», su obra también consistía en contar historias con una estética que entremezclaba la crítica social, sátira, misticismo, cristianismo, anarquismo, optimismo, hedonismo y libertad. Facundo Cabral fue asesinado en Ciudad de Guatemala por sicarios que lo confundieron con un empresario vinculado al narcotráfico.
Ao = (a^2 (a^2-b^2-c^2) (a^4 (-1+t)+2 a^2 (b^2+c^2) (1+t)-(b^2-c^2)^2 (1+3 t)):
-(a^2-b^2+c^2) (a^6 t-a^4 (b^2+3 c^2 t)+a^2 (2 b^2 c^2+3 c^4 t+b^4 (2+t))-(b^2-c^2)^2 (c^2 t+b^2 (1+2 t))):
-(a^2+b^2-c^2) (a^6 t-a^4 (c^2+3 b^2 t)+a^2 (2 b^2 c^2+3 b^4 t+c^4 (2+t))-(b^2-c^2)^2 (b^2 t+c^2 (1+2 t)))).
Pa = (2 (b^2-c^2)^2-2 a^2 (b^2+c^2) : -a^4+b^4+2 a^2 c^2-c^4 : -a^4+2 a^2 b^2-b^4+c^4).
Los puntos Pb y Pc se obtienen cíclicamente.U = (1/((a^2-b^2-c^2)^2 (a^4+2 a^2 (b^2+c^2)-3 (b^2-c^2)^2) ) : ... : ...),
que tiene números de búsqueda en (9.77385696235929, 5.74503897845594, -4.84768110118941).El 5 de julio de 1989, en Sudáfrica, Nelson Mandela — quien desde 1962 era preso político y a quien el Gobierno de Estados Unidos tuvo en la lista de terroristas hasta 2012 —, es retirado de su celda e invitado a tomar té en la mansión del racista presidente blanco Pieter Willem Botha.
Ab = ((b+c) (-a^2+b^2-c^2) : -2 b c (b+c) : -c (a^2-b^2+c^2)),
Ac = ((b+c) (a^2+b^2-c^2) : b (a^2+b^2-c^2) : 2 b c (b+c)),
A' = (a^4-(b^2-c^2)^2 : 2 b c (a^2+b^2-c^2) : 2 b c (a^2-b^2+c^2)).
U = ( a^4+2 a^2 b c-(b+c)^2 (b^2+c^2) : ... : ...),
que tiene números de búsqueda en (6.02876701706342, 1.97953907663079, -0.512293502096978).El 2 de julio de 1977 muere el escritor ruso Vladimir Nabokov, nacionalizado estadounidense y posteriormente suizo. Es considerado uno de los grandes autores en lengua inglesa del siglo XX gracias a obras tan conocidas como Lolita (1955), Ada o el ardor, Pálido fuego o Una belleza rusa. El gran éxito de Lolita, polémica novela que ha sido adaptada al cine en varias ocasiones, permitió a Nabokov dedicarse por completo a la literatura, retirándose a la localidad suiza de Montreux.
Ab = (b^4 t+(a^2-c^2)^2 t-b^2 (2 a^2 t+c^2 (4+3 t)):0:-(a^2-b^2-b c-c^2) (a^2-b^2+b c-c^2) t),
Ac = (b^4 t + (a^2 - c^2)^2 t - b^2 (2 a^2 t + c^2 (4 + 3 t)): -(a^2 - b^2 - b c - c^2) (a^2 - b^2 +
b c - c^2) t:0).
𝔖abc xyz t ((a^2-b^2-c^2)^2-b^2 c^2)(a^4 t+(b^2-c^2)^2 t-a^2 (2 c^2 t+b^2 (4+3 t))) (a^4 t+(b^2-c^2)^2 t-a^2 (2 b^2 t+c^2 (4+3 t)))x^2+ 2 (b^4 t+(a^2-c^2)^2 t-b^2 (2 a^2 t+c^2 (4+3 t))) (a^8 t^2+(b^2-c^2)^4 t^2-a^6 (b^2+c^2) t (2+3 t)-a^2 (b^2-c^2)^2 (b^2+c^2) t (2+3 t)+a^4 (4 b^4 t (1+t)+4 c^4 t (1+t)+b^2 c^2 (8+t (12+5 t))))y z = 0.
Ht = (a^2 (b^4 t+(a^2-c^2)^2 t-b^2 (2 a^2 t+c^2 (4+3 t))) : b^2 (a^4 t+(b^2-c^2)^2 t-a^2 (2 b^2 t+c^2 (4+3 t))) : c^2 (a^4 t+(b^2-c^2)^2 t-a^2 (2 c^2 t+b^2 (4+3 t)))),
cuando t varía, es la recta GK (G=X2 baricentro y K=X6 ).
Ao = (-2 a^10+7 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)-8 a^6 (b^4+c^4)+2 a^2 (b^2-c^2)^2 (b^4+3 b^2 c^2+c^4)+2 a^4 (b^6-6 b^4 c^2-6 b^2 c^4+c^6):
-b^2 (a^8+(b^2-c^2)^4+a^6 (-4 b^2+5 c^2)+2 a^4 (3 b^4-4 b^2 c^2-6 c^4)+a^2 (-4 b^6+7 b^4 c^2-8 b^2 c^4+5 c^6)) :
-c^2 (a^8+a^6 (5 b^2-4 c^2)+(b^2-c^2)^4-2 a^4 (6 b^4+4 b^2 c^2-3 c^4)+a^2 (5 b^6-8 b^4 c^2+7 b^2 c^4-4 c^6))).
W = ( a^2 (a^8-4 a^6 (b^2+c^2)+(b^2-c^2)^2 (b^4+7 b^2 c^2+c^4)+a^4 (6 b^4+7 b^2 c^2+6 c^4)-4 a^2 (b^6+2 b^4 c^2+2 b^2 c^4+c^6)) : ... : ...),
que tiene números de búsqueda en (1.59086269744012, 0.266727724506469, 2.72176250458446).Oa = (0 : (a^2-b^2) c^2 (a^4+a^2 (b^2-2 c^2)+(b^2-c^2)^2) : b^2 (-a^2+c^2) (a^4+(b^2-c^2)^2+a^2 (-2 b^2+c^2))).
Los puntos Ob y Oc se obtienen procediendo cíclicamente.La mañana del 30 de junio de 1908, ocurrió una devastadora explosión conocida como el evento de Tunguska. Una enorme bola de fuego atravesó el cielo de la meseta de Siberia central. En cuestión de segundos, un calor abrasador hizo arder el cielo y una explosión ensordecedora sepultó más de 80 millones de árboles en un área de 2100 kilómetros cuadrados de bosque.
Oa = (2 a^6+(b-c)^2 (b+c)^4-a^4 (b^2-4 b c+c^2)-2 a^2 (b^4+b^3 c+b c^3+c^4):
b (-a^4 b-2 a^2 c (2 b^2+3 b c+c^2)+(b+c)^3 (b^2-3 b c+2 c^2)):
c (-a^4 c+(b+c)^3 (2 b^2-3 b c+c^2)-2 a^2 b (b^2+3 b c+2 c^2))).
U = ( (a^2+(b+c)^2)/(a^4+2 a^2 b c-(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en (3.67363387582156, 2.72777871698934, 0.0566789659202675).El 28 de junio de 1577 nació Pedro Pablo Rubens, pintor flamenco genio del Barroco. A sus temas religiosos añade paulatinamente el género mitológico, así como el paisaje y el género costumbrista. Mitológicas son, de hecho, algunas de sus obras más conocidas, como Las tres Gracias, el Rapto de las hijas de Leucipo o Diana y las ninfas, en las que resulta evidente la inclinación del artista hacia las musculaturas poderosas, las carnes sonrosadas y exuberantes y las tonalidades claras y alegres.
A' =((b^2-c^2) (v-w) (b^2 (2 u+v) (u+w)-c^2 (u+v) (2 u+w))-a^4 (v-w) (2 v w+u (v+w))+a^2 (c^2 (-u v (v-5 w)+2 u^2 w+v w (v+w))-b^2 (2 u^2 v+u (5 v-w) w+v w (v+w))):
a^4 (u+2 v) (v-w) (u+w)+c^4 (u+v) (2 v-w) (u+w)+b^4 (u+w) (-u v+2 u w+v w)-b^2 c^2 (2 v^2 w+u (5 v-w) w+u^2 (v+w))+a^2 (b^2 (u^2 w+v w^2-u (2 v^2-5 v w+w^2))+c^2 (u^2 (-3 v+2 w)+v w (-4 v+3 w)+u (-4 v^2+2 w^2))):
b^4 (u+v) (v-2 w) (u+w)+a^4 (u+v) (v-w) (u+2 w)-c^4 (u+v) (2 u v-u w+v w)+b^2 c^2 (-u v (v-5 w)+2 v w^2+u^2 (v+w))-a^2 (b^2 (u^2 (2 v-3 w)+v (3 v-4 w) w+2 u (v^2-2 w^2))+c^2 (u^2 v+v^2 w-u (v^2-5 v w+2 w^2)))),
U = ((a^2-b^2) (a^2-c^2) u (v^2-w^2): ... : ...).
A un punto P y a su , P•, les corresponde el mismo U. Si P está sobre la , entonces U=P. La conjugada isotómica de la hipérbola de Wallace es la cuártica Q124.
V = ((b^2-c^2) (v+w) (b^2 (2 u+v) (u+w)-c^2 (u+v) (2 u+w))-a^4 (v+w) (2 v w+u (v+w))-a^2 (c^2 (2 u^2 w+v w (-v+w)+u v (v+w))+b^2 (2 u^2 v+v (v-w) w+u w (v+w))):
a^4 (u+2 v) (u+w) (v+w)+c^4 (u+v) (u+w) (2 v+w)-b^2 c^2 (u^2 (v-w)+2 v^2 w+u w (v+w))-b^4 (u+w) (v w+u (v+2 w))-a^2 (b^2 (u^2 w+v w^2+u (2 v^2+v w-w^2))+c^2 (u^2 (3 v+2 w)+v w (4 v+3 w)+2 u (2 v^2+3 v w+w^2))):
a^4 (u+v) (v+w) (u+2 w)+b^4 (u+v) (u+w) (v+2 w)+b^2 c^2 (u^2 (v-w)-2 v w^2-u v (v+w))-c^4 (u+v) (v w+u (2 v+w))-a^2 (c^2 (u^2 v+v^2 w+u (-v^2+v w+2 w^2))+b^2 (u^2 (2 v+3 w)+v w (3 v+4 w)+2 u (v^2+3 v w+2 w^2)))).
El 25 de junio de 1852 nació el arquitecto español Antoni Gaudí, considerado el máximo exponente del modernismo catalán Las obras de Gaudí en Barcelona más importantes son la Sagrada Familia, la Casa Vicens, el Palacio Güell, la Casa Batlló, el Park Güell y La Pedrera.
A' = (2 a (a + b - c) (a - b + c) (b + c) : a^4 - b^4 - 4 a b^2 c - 2 a^2 c^2 + c^4 : a^4 - 2 a^2 b^2 + b^4 - 4 a b c^2 - c^4).
(x:y:z) ↦ σ(x:y:z)=(-2 a b (a+b-c) c (a-b+c) (b+c) (-a^4+(b^2-c^2)^2)x + a c(a+b-c) (a-b+c) (a^2-b^2-c^2) (a^2+b^2-c^2) (a^2+(b+c)^2)y+a b (a+b-c) (a-b+c) (a^2-b^2-c^2) (a^2-b^2+c^2) (a^2+(b+c)^2)z : :).
Pares {Xi, Xj=σ(Xi)} para {i, j}: {1, 21147}, {2, 11214}, {3, 10}, {6, 5930}, {63, 5252}, {69, 65}, {72, 10106}, {78, 56}, {518, 515}, {520, 3907}, {521, 514}, {524, 44661}, {525, 4160}, {656, 7178}, {810, 7180}, {905, 3676}, {1038, 1038}, {1350, 39130}, {1459, 3669}, {1818, 241}, {2820, 28172}, {3564, 758}, {3811, 9798}, {3940, 4315}, {4855, 24914}, {4971, 2385}, {5227, 388}, {5440, 3911}, {5622, 6739}, {5847, 44662}, {6510, 1323}, {6776, 72}, {7289, 8}, {8681, 740}, {8766, 43045}, {9007, 35057}, {9028, 518}, {9031, 513}, {9051, 522}, {9242, 34146}, {10519, 3753}, {11898, 4084}, {14414, 1638}, {18446, 956}, {22090, 43051}, {22350, 1465}, {23187, 50337}, {23224, 17072}, {23874, 8678}, {24018, 17094}, {25406, 210}, {29309, 28874}, {33750, 3921}, {34378, 28216}, {34381, 519}, {37700, 8666}, {39471, 2812}, {39472, 2832}, {39899, 4067}, {41014, 35650}, {46974, 34050}, {48876, 3754}, {48906, 3678}.El 22 de junio de 1633 Galileo Galilei, arrodillado ante el tribunal de la inquisición en una sala del romano convento de Santa María sopra Minerva, abjura de sus teorías astronómicas consideradas heréticas. Será condenado a arresto domiciliario, evitando así la pena de muerte. El 12 de abril de 1633 cuando el científico italiano Galileo Galilei (1564-1642) compareció, a la edad de 69 años, ante el Santo Oficio, la Inquisición romana, para dar cuenta de un libro que había publicado un año atrás, el Diálogo sobre los dos máximos sistemas del mundo, en el que defendía el modelo heliocéntrico propuesto por Copérnico. En él planteaba que la Tierra y los planetas giraban alrededor del Sol, y ridiculizaba el geocentrismo, que colocaba a la Tierra en el centro fijo del universo y que está basado en la física aristotélica y, sobre todo, en el modelo ptolemaico, el que mejor encajaba con las Sagradas Escrituras. Ahora ya nadie niega el modelo heliocéntrico, pero en su día refutar las teorías de la Iglesia era poco menos que ir en contra de la voluntad de Dios, lo que conllevaba duros castigos. En 1616, el cardenal Belarmino, inquisidor del Santo Oficio, el mismo que había dirigido el proceso contra el filósofo Giordano Bruno, que fue quemado vivo en la hoguera, ya había amonestado a Galileo por tratar de defender el copernicanismo y por poner en duda la representación tradicional del mundo. El 22 de junio de 1633, Galileo fue obligado a pronunciar de rodillas la abjuración de su doctrina ante la comisión de inquisidores, bajo las órdenes del papa Urbano VIII, que había sido su amigo. El dramático episodio de la abjuración de Galileo, un enfrentamiento entre la ciencia y la religión, se produjo en una sala del convento dominico de Santa Maria sopra Minerva, en Roma. La Inquisición quería que Galileo se retractara y considerara su modelo una simple hipótesis matemática. La pena fue conmutada y fue condenado a vivir bajo arresto domiciliario, pero Galileo permaneció fiel a su método hasta su muerte, en 1642. (National Geographic)
A' = (-2 a (a^2-(b-c)^2) (b+c) : a^4-b^4+2 a^2 (2 b-c) c+4 a b c^2+c^4 : a^4+b^4-2 a^2 b (b-2 c)+4 a b^2 c-c^4).
pa: (a^3+b^3+b^2 c+b c^2+c^3-a^2 (b+c)-a (b^2+c^2))x-2 a c(a+b-c) y-2 a b (a-b+c)z=0,
A" = (-a^6-8 a^3 b c (b+c)+a^4 (b+c)^2-(b-c)^4 (b+c)^2+a^2 (b+c)^4:
-2 b c (a^4+2 a^2 b (3 b-c)-2 a^3 c+(b-c)^3 (b+c)+a (-2 b^2 c+2 c^3):
2 b c (-a^4+2 a^3 b+2 a^2 (b-3 c) c+(b-c)^3 (b+c)-2 a (b^3-b c^2))).
W = ( 1/(a^4-2 a^3 (b+c)+2 a (b^3+b^2 c+b c^2+c^3)-b^4-6 b^2 c^2-c^4) : ... : ...),
que tiene números de búsqueda en (0.998219840076092, 2.27530452967973, 1.60473680440176).El 16 de junio de 1963 la rusa Valentina Tershkova se convirtió en la primera mujer en volar al espacio. A bordo del Vostok 6, tras 48 órbitas y 71 horas, volvió a la Tierra, batiendo el récord de permanencia en el espacio.
Ab = (c^2 (a^2+b^2-c^2):-b^2 (-a^2+b^2+c^2):c^2 (-a^2+b^2+c^2)),
Ac = (b^2 (a^2-b^2+c^2):b^2 (-a^2+b^2+c^2:,-c^2 (-a^2+b^2+c^2)).
Γa: c^2 x y+b^2 x z+a^2 y z+(a^2 (a^2-b^2-c^2)^2 x (x+y+z))/(a^4-b^4+2 b^2 c^2-c^4)=0,
Oa = (a^2 (a^2-b^2-c^2):-(a^2-b^2) (a^2+b^2-c^2):-(a^2-c^2) (a^2-b^2+c^2)).
Γ'a: c^2 x y+b^2 x z+a^2 y z+(x+y+z) ((c^2 (a^4 b^2-2 a^2 b^4+b^6-2 a^2 b^2 c^2-2 b^4 c^2+b^2 c^4) x)/(a^2 (a^2-b^2-c^2)^2)-(c^2 (a^2 b^2-b^4+b^2 c^2) y)/(-a^2+b^2+c^2)^2-((a^2 b^2 c^2+b^4 c^2-b^2 c^4) z)/(a^2-b^2-c^2)^2)=0,
O'a = (a^4 (-a^2+b^2+c^2):b^2 (a^4-b^2 c^2+c^4-a^2 (b^2+c^2)):c^2 (a^4+b^4-b^2 c^2-a^2 (b^2+c^2))):
Las rectas AO'a, BO'b, CO'c concurren en X3060.
El matemático ruso Grigori Perelman, nacido el 13 de junio de 1966 en Leningrado, URSS, es conocido por haber encontrado y publicado en internet en 2003 una prueba de la célebre conjetura de Poincaré, problema topológico propuesto en 1904 por Poincaré, conjeturó es que la esfera es el único espacio tridimensional sin agujeros. La conjetura fue enunciada en 1904, y se probó para todas las dimensiones, excepto en la dimensión 3. El trabajo de Hamilton, usando el llamado flujo de Ricci, no fue capaz de superar una serie de problemas ligados a la aparición de singularidades. La demostración de Perelman fue validada en 2006 pero rehusó el premio (de un millón de dólares), al igual que la medalla Field, descontento por la falta de integridad de la comunidad matemática.
Ab= ((a-b) (a+b):0:-c^2), Ac = ((a-c) (a+c):-b^2:0), A1 = ((a^2-b^2) (a^2-c^2):-a^2 b^2+b^4:-a^2 c^2+c^4), A2 = (0:b^2 (a^2-b^2):-a^2 c^2+c^4).
Los puntos B1, B2 y C1, C2 son definidos cíclicamente.Las circunferencias (AB1C1), (BC1A1), (CA1B1) concurren en X10420.
Las circunferencias (A1BC), (B1CA), (C1AB) concurren en X186, inverso del ortocentro en la circunferencia circunscrita.
W = ( a^2(a^8-a^6 (b^2+c^2)+a^4 (-2 b^4+5 b^2 c^2-2 c^4)+3 a^2 (b^2-c^2)^2 (b^2+c^2)-(b^2-c^2)^2 (b^4+3 b^2 c^2+c^4))/((-a^2+b^2+c^2)(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en (0.133002336306015, 0.0873640660987166, 3.51879597323634).El 7 de junio de 1954 falleció el matemático británico Alan Mathison Turing, lógico especialista en criptografía, está considerado como uno de los padres fundadores de la informática moderna. En 1936 publicó un ensayo titulado On Computable Numbers (Sobre números calculables), con el que contribuyó a la lógica matemática al introducir el concepto teórico de un dispositivo de cálculo que hoy se conoce como la máquina de Turing. Durante la Segunda Guerra Mundial dirige las investigaciones sobre los códigos secretos generados por la máquina Enigma utilizada por los nazis. En 1954 tras ser condenado por homosexualidad, indecencia grave y perversión sexual, a la castración química, considerados delitos graves en el Reino Unido por entonces, se suicidó tomando una manzana envenenada con cianuro.
A' = (-(a^4-(b^2-c^2)^2) (-b^2+c^2+a^2 (-1+2 t)) : (a^2+b^2-c^2) (c^2 (b^2-c^2)+a^2 (-c^2 (-2+t)-b^2 (-1+t))+a^4 (-1+t)) :
(a^2-b^2+c^2) (b^4-b^2 c^2+a^4 t-a^2 (c^2 t+b^2 (1+t)))),
B' = ((a^2+b^2-c^2) (-(b^2-c^2) (b^2 (-1+t)-c^2 t)+a^2 (b^2 (-1+t)+c^2 t)) :
-(a^4-b^4-2 a^2 c^2+c^4) (b^2 (-2+t)+(a^2-c^2) t) :
-(a^2-b^2-c^2) (b^4-b^2 c^2+a^4 t-a^2 (c^2 t+b^2 (1+t)))),
C' = ((a^2-b^2+c^2) (-(b^2-c^2) (b^2 (-1+t)-c^2 t)+a^2 (b^2 (-1+t)+c^2 t)) :
-(a^2-b^2-c^2) (c^2 (b^2-c^2)+a^2 (-c^2 (-2+t)-b^2 (-1+t))+a^4 (-1+t)) :
-(a^4-2 a^2 b^2+b^4-c^4) (a^2 (-1+t)-b^2 (-1+t)+c^2 (1+t))).
El 1 de junio de 2018, Pedro Sánchez se convierte en el séptimo presidente del Gobierno de España, tras aprobar el Congreso de los Diputados la moción de censura al Gobierno de Mariano Rajoy, siendo la primera vez en la democracia que un presidente lo hace en estas circunstancias.
Ab = ((a+b-c) (a^2+b^2+b c-2 c^2+a (-2 b+c)):0:-(a-b-c) (a^2-2 (b-c)^2+a (b+c))),
Ac = ((a-b+c) (a^2-2 b^2+a (b-2 c)+b c+c^2):-(a-b-c) (a^2-2 (b-c)^2+a (b+c)):0).
𝔖abc xyz
((-a+b+c)^2 (2 a^2-(b-c)^2-a (b+c)) (a^2-2 (b-c)^2+a (b+c)) x^2)/(a^2+(b-c)^2-2 a (b+c))^2+
((a+b-c) (a-b+c) (5 a^4-11 a^3 (b+c)+7 a (b-c)^2 (b+c)-2 (b-c)^2 (2 b+c) (b+2 c)+a^2 (3 b^2+20 b c+3 c^2)) y z)/(a^2+(b-c)^2-2 a (b+c))^2 = 0.
𝔖abc xyz
(a (a-b-c)^3 (a^2+2 (b-c)^2-3 a (b+c)) x^2)/(3 (a^2+(b-c)^2-2 a (b+c))^2)
-((a+b-c) (a-b+c) (3 a^4-10 a^3 (b+c)-6 a (b-c)^2 (b+c)+(b-c)^2 (b^2-4 b c+c^2)+2 a^2 (6 b^2+5 b c+6 c^2)) y z)/(3 (a^2+(b-c)^2-2 a (b+c))^2) = 0.
𝔖abc xyz
((-a+b+c)^2 (5 a^2-4 (b-c)^2-a (b+c)) (a^2-2 (b-c)^2+a (b+c)) x^2)/(a^2+(b-c)^2-2 a (b+c))^2+
((a+b-c) (a-b+c) (17 a^4-38 a^3 (b+c)+22 a (b-c)^2 (b+c)+2 a^2 (6 b^2+31 b c+6 c^2)-(b-c)^2 (13 b^2+28 b c+13 c^2)) y z)/(a^2+(b-c)^2-2 a (b+c))^2= 0.
El 30 de mayo de 1994 falleció Marcel Bich, quién popularizó los famosos bolígrafos Bic en el año 1953. El inventor del bolígrafo fue el húngaro Ladislao José Biro. En 1950 Marcel Bich, viajó a la Argentina para comprar a los Biró su patente del bolígrafo para Europa. Bich consiguió su objetivo e introdujo mejoras. Diseñó una punta cónica rematada por una bolita de carburo de tungsteno que tenía por objeto regular el flujo de la tinta, para de una vez por todas acabar con los engorrosos manchones. En la actualidad, Bic vende más de cien billones de bolígrafos al año en todo el mundo.
Ab = ((b-c) c (a^2+b^2-c^2) : b^2 (a^2-b^2+c^2) : c^2 (a^2+b^2-c^2)),
Ac = ((c-b) b (a^2+c^2-b^2) : b^2 (a^2+c^2-b^2) : c^2 (a^2-c^2+b^2)),
A' = ((b-c)^2 (b+c):-a^2 b:-a^2 c).
(x:y:z) ↦ σ((x:y:z))=((a+b) (b-c)^2 (a+c) (b+c) (-a+b+c) x+a b^2 (a+b) (-a+b-c) (b+c) y-a (a+b-c) c^2 (a+c) (b+c) z:...:...).
Pares {Xi, Xj=σ(Xi)}, para {i,j}: {7, 18698}, {10, 5}, {12, 25639}, {65, 10}, {72, 946}, {181, 3846}, {210, 3817}, {226, 2886}, {307, 41007}, {522, 523}, {758, 517}, {1441, 1441}, {3671, 31419}, {3678, 9955}, {3753, 10175}, {3754, 9956}, {3919, 38042}, {3952, 4939}, {3962, 4301}, {4004, 31399}, {4018, 11362}, {4067, 22791}, {4084, 5690}, {4134, 38034}, {4744, 38112}, {4848, 1329}, {12432, 5044}, {15556, 960}, {16609, 20544}, {21060, 7956}, {21075, 7681}, {22275, 2051}, {40663, 3814}, {41538, 21616}, {41539, 3452}, {41804, 3007}, {44301, 9711}, {52385, 3668}."No se es ateo. El hombre es un ser que inventa a los dioses, eso no es ser ateo. A mí me parece que eso está muy bien: no necesitamos ninguna salvación, nuestra salvación está aquí. Estoy completamente convencido de que aquí nos salvamos o nos condenamos. Ésta es nuestra vida, no tenemos otra, no conocemos otra. Una vida que se desconoce es como si no existiese." Antonio Gala
(BDbD'b)
c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-((b^2 c^2 d x)/((c+d) (a^2+c d)))-(a^2 b^2 d z)/((c+d) (a^2+c d)))=0,
(CDcD'c)
c^2 x y+b^2 x z+a^2 y z+ (x+y+z)(-((b^2 c^2 d x)/((b+d) (a^2+b d)))-(a^2 c^2 d y)/((b+d) (a^2+b d)))=0,
(Oa)
c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-((a^2 c^2 y)/(b+c)^2)-(a^2 b^2 z)/(b+c)^2)=0.
D1 = (a^4 (b+c+2 d)+a^2 d (c d+b (-2 c+d)) : b^2 (a^2 (b-c)+d (2 b^2-c d+b (2 c+d))) : c^2 (a^2 (-b+c)+b (2 c-d) d+c d (2 c+d))).
Y el lugar geométrico que describe, cuando D se mueve en AI, es:ℓa: b^2 c^2 (b-c)(b+c)^2x-a^2 c^2 (a^2 (b-c)+ c^2(3 b+c))y-a^2 b^2 (a^2 (b-c)-b^2(b+3c))=0.
Procediendo cíclicamente, se obtienen las rectas ℓb y ℓc.Cuando vinieron los misioneros a África tenían la Biblia y nosotros la tierra. Nos dijeron: vamos a rezar. Cerramos los ojos. Cuando los abrimos, teníamos la Biblia y ellos la tierra. Desmond Tutu
𝔖abc xyz (b^2-2 (a-c)^2)^2 (a^2-2 (b-c)^2)^2 (-2 (a-b)^2+c^2)^2x^2-2 (b^2-2 (a-c)^2)^2 (a^4+4 a^2 (b-c)^2-4 (b-c)^4) (-2 (a-b)^2+c^2)^2y z = 0.
A1 = (0 : a (2 a^3+4 a^2 (b-c)-a (b-c)^2-4 (b-c)^3)-2 (a^3+2 a^2 (b-c)-(b-c)^3)Sqrt[a^2-(b-c)^2] :
a (2 a^3-a (b-c)^2+4 (b-c)^3+4 a^2 (-b+c))-2 (a^3+(b-c)^3+2 a^2 (-b+c)) Sqrt[a^2-(b-c)^2]),
A2 = (0 : a (2 a^3+4 a^2 (b-c)-a (b-c)^2-4 (b-c)^3)+2 (a^3+2 a^2 (b-c)-(b-c)^3)Sqrt[a^2-(b-c)^2] :
a (2 a^3-a (b-c)^2+4 (b-c)^3+4 a^2 (-b+c))+2 (a^3+(b-c)^3+2 a^2 (-b+c))Sqrt[a^2-(b-c)^2]).
El 20 de mayo de 2010 falleció Walter Rudin, matemático estadounidense, la mayor parte de su carrera fue profesor de matemáticas en la Universidad de Wisconsin-Madison, es conocido por tres de sus libros sobre análisis matemático: Principios de Análisis Matemático, Análisis Real y Complejo, Análisis Funcional . El primero fue escrito cuando Rudin era instructor de Moore en el MIT para el curso de análisis de licenciatura y es ampliamente utilizado como libro de texto para los cursos de pregrado en análisis.
U = (a^2 (u+v) w (b^2 (-u^2+v^2) w^2+c^2 v^2 (u^2-w^2)):
a^2 b^2 (u-v) (u+v)^2 w^3+c^4 u v^2 (u+w) (v^2-w^2)+c^2 (u+v) w (v+w) (b^2 u (u-v) (v-w)+a^2 v^2 (u+w)):
c^2 v (u+w) (a^2 (u+v)^2 w^2+c^2 u^2 (v^2-w^2))),
U' = (a^2 v (u+w) (b^2 (-u^2+v^2) w^2+c^2 v^2 (u^2-w^2)):
-b^2 (u+v) w (a^2 v^2 (u+w)^2+b^2 u^2 (-v^2+w^2)):
b^2 u (v^2-w^2) (b^2 (u+v) w^2+c^2 v (u^2-w^2))-a^2 v (u+w) (b^2 (u+v) w^2 (v+w)+c^2 v^2 (u^2-w^2))).
Z = (a^2 (a^2 c^4 v^3 (u-w) (u+w)^2-b^2 c^2 v (u+v) (u+w) (-a^2 (u-v) (u-w) w+c^2 u^2 (v+w))-b^4 (u+v) w (a^2 (-u^2+v^2) w^2+c^2 u^2 (u+w) (v+w))):
-b^2 (-b^2 c^4 u^3 (v-w) (v+w)^2+a^2 c^2 u (u+v) (v+w) (b^2 (u-v) (v-w) w+c^2 v^2 (u+w))+a^4 (u+v) w (b^2 (u^2-v^2) w^2+c^2 v^2 (u+w) (v+w))):
-c^2 (b^4 c^2 u^3 (v-w) (v+w)^2+a^2 b^2 u (u+w) (v+w) (b^2 (u+v) w^2+c^2 v (u-w) (-v+w))+a^4 v (u+w) (b^2 (u+v) w^2 (v+w)+c^2 v^2 (u^2-w^2)))).
El 18 de mayo de 1895 nació Augusto César Sandino, líder guerrillero nicaragüense que luchó contra la ocupación y la intervención norteamericana hasta obligar a los Estados Unidos a retirar sus tropas de Nicaragua. Tras su asesinato a manos del entonces jefe de la Guardia Nacional, Anastasio Somoza, Sandino se convirtió en el referente ideológico del Frente Sandinista de Liberación Nacional (FSLN) y de la revolución promovida por este movimiento que, años más tarde, acabaría con la dictadura somocista.
VT(P) = (a^2(u^2 + u v + u w - v w) : b^2(v^2 + v w + v u - w u) : c^2(w^2 + w u + w v - u v)).
b^2 c^2 u (v^2-w^2)x+a^2 c^2 v (-u^2+w^2)y+a^2 b^2 w(u^2-v^2)z=0.
P está sobre la recta p si y solo si P està sobre la cuártica de Stammler, Q066.
𝔖abc xyz b^2 c^2 (a^6-2 a^4 (b^2+c^2)+4 (b^2-c^2)^2 (b^2+c^2)+a^2 (b^2+c^2)^2) x^2+2 a^2 (-2 a^8+2 a^6 (b^2+c^2)+b^2 c^2 (b^2+c^2)^2+a^4 (2 b^4-7 b^2 c^2+2 c^4)-2 a^2 (b^6+c^6)) y z = 0.
Su centro es X206 y su es X9292y pasa por X15647 (cuando ℓ es la ) y X6593 (cuando ℓ es la perpendicular a la recta de Euler por el baricentro.c^4 x^2 y^2-2 b^2 c^2 x^2 y z-2 a^2 c^2 x y^2 z+b^4 x^2 z^2-2 a^2 b^2 x y z^2+a^4 y^2 z^2=0,
conjugada isogonal de la .El 15 de Mayo de 1989 comenzó la retirada de las tropas soviéticas de Afganistán, que invadió el país en 1979, para apoyar al golpe militar que en 1978 llevó al poder a un grupo de jóvenes oficiales izquierdistas. Poco después de que la Unión Soviética interviniera en Afganistán, Bin Laden comenzó a reclutar guerrilleros y estableció sus primeros campamentos. Entrenado por la CIA, aprendió cómo mover dinero a través de sociedades fantasmas y paraísos fiscales; a preparar explosivos; a utilizar códigos cifrados para comunicarse; y a ocultarse. Por esa época, los Estados Unidos colaboraban incondicionalmente con los grupos afganos, debido a su participación en la guerra contra la URSS (entre 1979 y 1989 los estadounidenses entregaron cerca de tres mil millones de dólares a la resistencia afgana, que favoreció a Bin Laden)
(4 a^4-6 a^2 b^2-b^4-6 a^2 c^2+2 b^2 c^2-c^4+6 a^4 t-8 a^2 b^2 t-4 b^4 t-8 a^2 c^2 t+8 b^2 c^2 t-4 c^4 t+a^4 t^2-4 b^4 t^2+8 b^2 c^2 t^2-4 c^4 t^2) x^2+(4 a^4-12 a^2 b^2+2 b^4+4 a^2 c^2-4 b^2 c^2+2 c^4+8 a^4 t-24 a^2 b^2 t+4 b^4 t+8 a^2 c^2 t-8 b^2 c^2 t+4 c^4 t+2 a^4 t^2-8 a^2 b^2 t^2+8 a^2 c^2 t^2) x y+(-4 a^4+2 a^2 b^2-b^4+2 a^2 c^2+2 b^2 c^2-c^4-6 a^4 t-3 a^4 t^2) y^2+(4 a^4+4 a^2 b^2+2 b^4-12 a^2 c^2-4 b^2 c^2+2 c^4+8 a^4 t+8 a^2 b^2 t+4 b^4 t-24 a^2 c^2 t-8 b^2 c^2 t+4 c^4 t+2 a^4 t^2+8 a^2 b^2 t^2-8 a^2 c^2 t^2) x z+(8 a^4+4 a^2 b^2-2 b^4+4 a^2 c^2+4 b^2 c^2-2 c^4+20 a^4 t+10 a^4 t^2) y z+(-4 a^4+2 a^2 b^2-b^4+2 a^2 c^2+2 b^2 c^2-c^4-6 a^4 t-3 a^4 t^2) z^2=0.
2( x +a^2 y) (SB x + a^2 z)± Sqrt[3] a^2 S x (x+y+z) =0.
Los focos de estas parábolas (simétricos respecto BC) son:F±a = (-a^2 : SC±4Sqrt[3] S : SB±4 Sqrt[3]S ).
Procediendo cíclicamente, sobre los lados de ABC, se definen los focos F±b y F±c.Las rectas AF-a, BF-b, CF-c concurren en Gibert(-24,49,96)=X43444.
El 12 de mayo de 1977 nació Maryam Mirzakhani, fue una matemática iraní y profesora de matemáticas en la Universidad de Stanford. En 2014 fue galardonada con la Medalla Fields, siendo la primera mujer en recibir este premio equivalente al Nobel de las matemáticas. Se doctoró en matemáticas en la Universidad de Harvard con una tesis de geometría hiperbólica titulada «Simple Geodesics on Hyperbolic Surfaces and Volume of the Moduli Space of Curves». Ralph Cohen, profesor de matemáticas de la Universidad de Stanford dijo: «A menudo, la investigación en estas áreas consideradas más teóricas tiene aplicaciones inesperadas, pero perseguirlas no es lo que motiva a matemáticos como Maryam. Más bien, la motivación es entender, lo más profundamente posible, estas estructuras matemáticas básicas»
Ta = (a (a^2 - (b - c)^2) : -2 b^2 (a + b - c) : -2 c^2 (a - b + c)).
La recta DTa corta a la bisectriz AI en A'=(a (a-b-c):-2 b (b+c):-2 c (b+c)). Los puntos B', C' se definen cíclicamente. Entonces, el triángulo A'B'C' es a DEF, con centro de ortología el incentro.(x:y:z) ↦ (a (a-b-c) (2 a+2 b-c) (2 a-b+2 c) x+2 a (a-2 b-2 c) (2 a+2 b-c) (a+c) y+2 a (a+b) (a-2 b-2 c) (2 a-b+2 c) z:..:..).
Pares {Xi, Xj=σ(Xi)}, para los índices {i,j}: {2099,55}, {3679,1}, {3940,999}, {4653,4653}, {4693,238}, {4720,81}, {4770,48328}, {4774,4879}, {4775,667}, {4777,513}, {4791,48294}, {4800,25569}, {4814,4449}, {4833,3733}, {4844,29350}, {4867,36}, {4870,2646}, {4908,1279}, {4930,3}, {4937,1149}, {4948,4367}, {4956,4511}, {5219,13384}, {13391,2828}, {16236,9819}, {17461,30116}, {23884,3887}, {27741,2320}, {28849,541}, {29073,33921}, {29287,28877}, {30605,14419}, {36589,3100}, {36595,7675}, {36911,38316}, {36920,5048}, {36922,11529}, {40587,6767}, {43052,4162}, {47683,1019}, {49280,905}, {51362,25405}.El 11 de mayo de 1924 nació Eugene Borisovich Dynkin, matemático ruso. Hizo contribuciones a los campos de la probabilidad (procesos de Markoc, campos aleatorios) y el álgebra, especialmente a los grupos de Lie semisimples, álgebras de Lie y procesos de Markov. El diagrama de Dynkin, el sistema de Dynkin y el lema de Dynkin llevan su nombre.
A' =AH ∩DKa, B' BH∩EKb, C'=CH∩/\FKc.
A' = (a^2 (-a^2 + b^2 + c^2) : b c (a^2 + b^2 - c^2) : b c (a^2 - b^2 + c^2)).
U = ( a^2/(a^4-a^2 (b^2-b c+c^2)-b c(b-c)^2) : ... : ...),
que tiene números de búsqueda en (6.83480920147454, 7.28575448265290, -4.55784671445588).El 10 de mayo de 1847 nació el matemático alemán Wilhelm Killing, quién hizo importantes contribuciones a la teoría de álgebras de Lie, grupos de Lie y geometría no euclidea. El término "forma de Killing" de un álgebra de Lie es llamada así en su honor.
Oa=(6 a^3-4 a (b-c)^2+2 a^2 (b+c)-4 (b-c)^2 (b+c):-(a-b-c) (a^2+b^2-c^2):-(a-b-c) (a^2-b^2+c^2)).
Cíclicamente se definen los puntos Ob y Oc.U = (1/(5 a^2-2 a (b+c)-3 b^2+2 b c-3 c^2) : ... : ...),
que tiene números de búsqueda en (-25.0386534558771, -25.2915691473506, 32.7065139481704).El sistema ha organizado un casino para que ganen siempre los mismos. José Luis Sampedro
Ab = (0:((b^2-c^2) u+a^2 (u-2 v)) v (a^2 (u-w)+c^2 (-u+w)-b^2 (u+w)):-((a^2-c^2) v+b^2 (-2 u+v)) ((-b^2+c^2) u+a^2 (u-2 w)) w),
Ac = (0:((b^2-c^2) u+a^2 (u-2 v)) v ((a^2-b^2) w+c^2 (-2 u+w)):-(a^2 (u-v)+b^2 (-u+v)-c^2 (u+v)) ((-b^2+c^2) u+a^2 (u-2 w)) w).
¿Estás realmente seguro de que un suelo no puede ser también un techo? (Maurits Cornelis Escher)
A' = (a^2 (a+b-c) (a-b+c):b (b-c) (a+b-c) (-a+b+c):-(b-c) c (a-b+c) (-a+b+c)),
D' = (4 a^4 (a+b-c) (a-b+c):-(a-b-c) (a+b-c) (a^2+b^2-c^2)^2:-(a-b-c) (a-b+c) (a^2-b^2+c^2)^2),
ℓa: (-a^2+a (b+c)-2 (b+c)^2) x+a (-3 a+b+c) y+a (-3 a+b+c) z =0, (contiene a (0:1:-1), punto en el infinito de BC),
A" = (-2 a^3-4 a b c-a^2 (b+c)-(b-c)^2 (b+c):b (-a^2+2 a b+3 b^2-4 b c+c^2):c (-a^2+b^2+2 a c-4 b c+3 c^2)).
Ao = (a (a^5-2 a^3 (b-c)^2+a^4 (b+c)+2 a^2 (b-c)^2 (b+c)+(b-c)^2 (b+c)^3-3 a (b^2-c^2)^2):b (-a+b+c) (a^2+b^2-c^2)^2:-(a-b-c) c (a^2-b^2+c^2)^2).
La Revolución de los Claveles es el nombre dado al levantamiento militar del 25 de abril de 1974 que provocó la caída en Portugal de la dictadura de António de Oliveira Salazar que dominaba el país desde 1926. El fin de este régimen, conocido como Estado Novo, permitió que las últimas colonias portuguesas lograran su independencia tras una larga guerra colonial contra la metrópoli.
A' = ((b-c)^2-a (b+c):-b (-a+b+c):(a-b-c) c).
El 20 de abril de 1893 nació Joan Miró, pintor barcelonés, uno de los pioneros del surrealismo, Además de por la pintura, el artista catalán se interesó por diversas disciplinas artísticas como la escultura, la cerámica y el arte textil.
A' = (-(a^2-b^2) (a^2-c^2) : b^2 (a^2-b^2) : c^2 (a^2-c^2)),
A" = (a^2 (a^2-b^2-b c-c^2) (a^2-b^2+b c-c^2):-b^2 (a^4+b^4-b^2 c^2-a^2 (2 b^2+c^2)):-c^2 (a^4-b^2 c^2+c^4-a^2 (b^2+2 c^2))).
El 18 April 1913 falleció Pieter Hendrik Schoute, ingeniero y matemático holandés. Estudió varios temas en geometría como cuádricas, curvas algebraicas, geometría euclidiana de más de 3 dimensiones, como Sobre las secciones de un bloque de ocho celdas por un espacio que gira alrededor de un plano. En 1909, Schoute publicó "Sobre los ángulos de los politopos regulares del espacio tetradimensional" y, cuatro años más tarde, la continuación, "Sobre los ángulos tetradimensionales de los politopos semirregulares de S4".
W(P) = u (u2 - uv - uw - 2vr) : v (v2 - vw - vu - 2wu) : w (w2 - wu - wv - 2uv)
.png)
Q = u (u^4+3 u^3 (v+w)+u^2 (v+w)^2-u (v^3-7 v^2 w-7 v w^2+w^3)+2 v w (v^2+w^2)) : ... : ...
El 14 de abril de 1986 falleció Simone de Beauvoir, una de las figuras intelectuales francesas más importantes y comprometidas de mediados del siglo XX como novelista, filósofa existencialista y feminista.
X(355) is the homothetic center of the triangles formed by internal and external tangents of circumcircles of BCX(4), CAX(4), ABX(4). Equivalently, the incenter of the trianglar hull of circumcircles of BCX(4), CAX(4), ABX(4). (Randy Hutson, December 2, 2017)
Let Na = X(5)-of-BCX(1), Nb = X(5)-of-CAX(1), Nc = X(5)- of-ABX(1). Then X(355) = X(20)-of-NaNbNc. (Randy Hutson, December 2, 2017)
Let A'B'C' be the anticomplementary triangle. Then X(355) is the radical center of the incircles of A'BC, B'CA, C'AB. (Randy Hutson, December 2, 2017)
Let A'B'C' be the outer Garcia triangle and A"B"C" the inner Garcia triangle. Let A* be the isogonal conjugate, wrt A'B'C', of A", and define B* and C* cyclically. The lines A'A*, B'B*, C'C* concur in X(355); see also X(952). (Randy Hutson, December 2, 2017)
Let OA be the circle centered at the A-vertex of the Yff contact triangle and passing through A; define OB and OC cyclically. X(355) is the radical center of OA, OB, OC. (Randy Hutson, August 30, 2020)
X(355) is the midpoint of orthocenter and Nagel point.
Ab = (c (b+c)^2-a^2 (2 b+c):2 b^2 (b+c):c (a^2+b^2-c^2)), Ac = (b (b+c)^2-a^2 (b+2 c):b (a^2-b^2+c^2):2 c^2 (b+c)).
Se consideran los puntosA1 = AbBa∩AcCa, A2 = BaBc∩CaCb.
Los puntos B1, B2 y C1, C2 se definen cíclicamente.
A1 = (a (2 a+b+c):-b^2+c (a+c):a b+b^2-c^2),
A2 = (a^2 (-2 a^2+(b-c)^2-a (b+c)):b (-a^3+a^2 (b-c)+c (b^2-c^2)+a (2 b^2-b c-c^2)):
c (-a^3-b^3+b c^2+a^2 (-b+c)-a (b^2+b c-2 c^2))).
W = ( a(a^3-a (b-c)^2+(b-c)^2 (b+c)) : ... : ...),
que es el del incentro y X(29662) y que tiene números de búsqueda en (0.524417044485285, 1.35437368056687, 2.46098252867565).A'= B1B2∩C1C2, B'= C1C2∩A1A2, C'= A1A2∩B1B2.
A' = (2 a^2 (a^3+b^3+c^3-a^2 (b+c)-a (b^2+c^2)):El 13 de abril de 1906 nació Samuel Beckett, dramaturgo, novelista, crítico, poeta irlandés y premio Nobel de Literatura en 1969, uno de los más importantes representantes del experimentalismo literario del siglo XX, dentro del modernismo anglosajón. Es el autor de "Esperando a Godott", entre otras grandes obras suyas. Con “Esperando a Godot” el escritor irlandés se convirtió, junto al rumano Eugene Ionesco, como puntal del teatro del absurdo, reflejando la alienación y angustia del individuo, el pesimismo vital y la soledad existencial con una disposición ilógica y grotesca que rompía los cánones previos de la escena tradicional.
ℓa: ((b^2 (-1+t)-c^2 t)^2-a^2 (b^2 (-1+t)^2+c^2 t^2)) x-a^2 c^2 t^2 y-a^2 b^2 (-1+t)^2 z=0,
ℓb: b^2 c^2 x+(c^2 (b^2-c^2)+a^2 (-2 c^2+b^2 (-1+t)) (-1+t)-a^4 (-1+t)^2) y+a^2 b^2 (-1+t)^2 z=0,
ℓc: b^2 c^2 x+a^2 c^2 t^2 y+(-b^4-a^2 (a^2-c^2) t^2+b^2 (c^2+2 a^2 t)) z=0.
P' = (-a^2 t (b^2 c^2 (b^2-c^2)^2 (-1+t)+a^8 (-1+t)^2 t-a^2 (b^4-c^4) (-1+t) (b^2 (-1+t)+c^2 t)-a^6 (-1+t) (c^2 t (-3+2 t)+b^2 (-1-t+2 t^2))+a^4 (c^4 t (3-4 t+t^2)+b^4 (2-3 t+t^3)+b^2 c^2 (1+t-4 t^2+2 t^3))):
b^2 (-(b^3-b c^2)^2 (-1+t) (b^2 (-1+t)-c^2 t)+a^6 (-1+t) t (b^2 (-1+t)+c^2 t)-a^4 (-1+t) (b^2 c^2 t+2 c^4 t^2+b^4 (-1+t) (1+2 t))+a^2 (b^2-c^2) (-b^2 c^2 (-1+t) t-c^4 (-1+t) t^2+b^4 (2-3 t+t^3))):
-c^2 t ((-b^2 c+c^3)^2 (-b^2 (-1+t)+c^2 t)+a^6 (-1+t) (b^2 (-1+t)+c^2 t)+a^4 (b^2 c^2 (-1+t)-2 b^4 (-1+t)^2+c^4 (3-2 t) t)+a^2 (b^2-c^2) (-b^2 c^2 (-1+t)+b^4 (-1+t)^2-c^4 (-3+t) t)).
Q = (-a^2 (a^2-b^2-c^2) (-1+t) t (-b^2+c^2+a^2 (-1+2 t)) :
b^2 (a^2-b^2+c^2) (-1+t) (b^2 (-2+t)+(a^2-c^2) t):
-c^2 (a^2+b^2-c^2) t (a^2 (-1+t)-b^2 (-1+t)+c^2 (1+t))).
𝔖abc SASBSC xyz
a^4 SA^2 y z (c^2 SC^2 y+b^2 SB^2 z)
- a^2 b^2 c^2 (a^2+b^2+c^2) x y z =0.
El 11 de abril de 1894 nació el matemático alemán Paul Finsler. Se le debe una generalización de la geometría distinta de la riemanniana. Comenzó en 1916 un estudio detallado de la geometría que lleva su nombre, y la expuso en su tesis de 1918 en Gotinga. En esta geometría, la métrica ds2 del espacio de Riemann, se sustituye por una función más general F(x,dx) de las coordenadas y sus diferenciales, sobre la que se imponen restricciones que aseguren la posibilidad de minimizar la integral ∫F[x,(dx/dt)]dt, obteniendo así las geodésicas
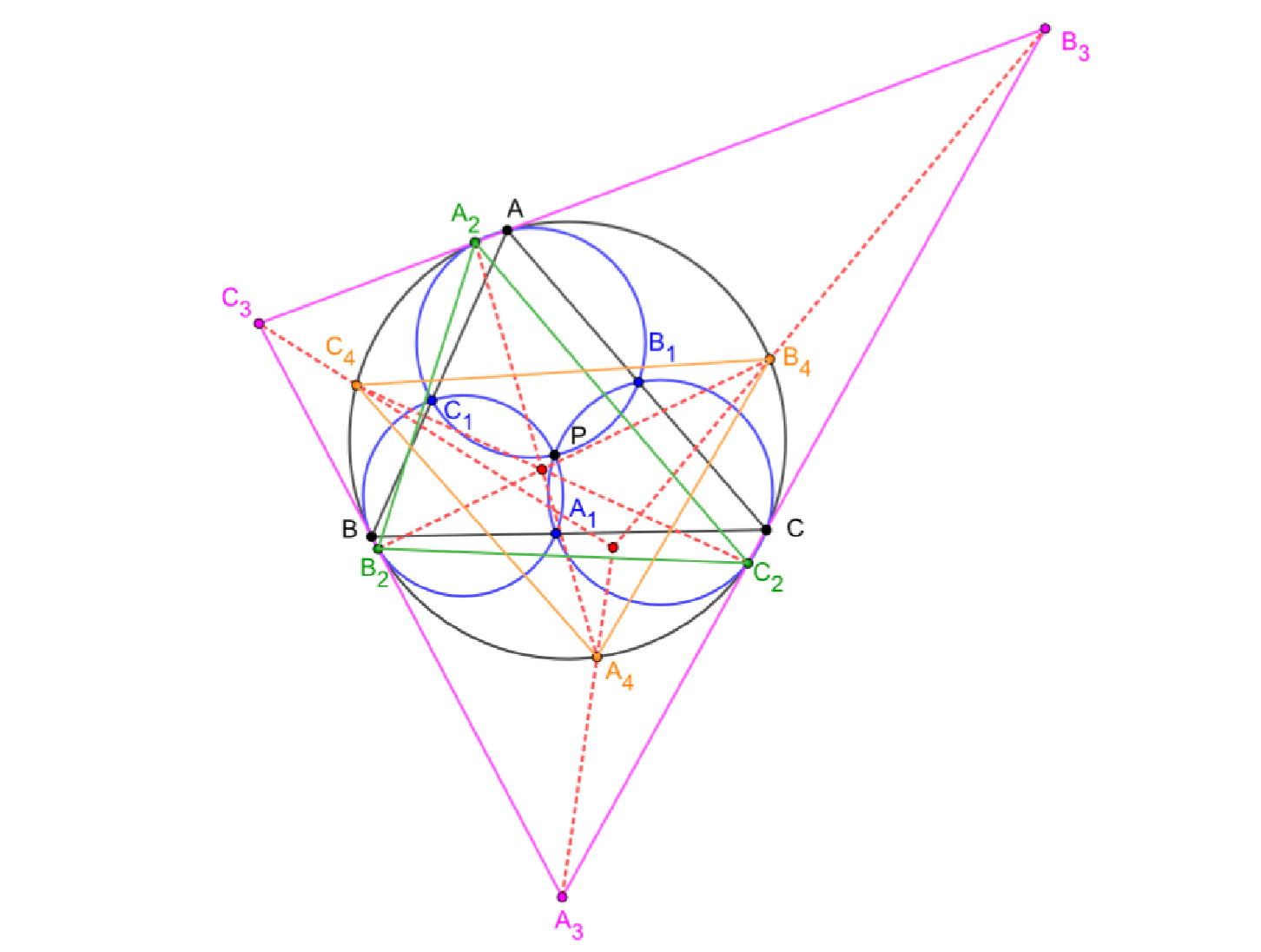
Q=V(P)= PA(P) = a^2(v w a^4+(c^2 v (u-w)+b^2 (u-v) w)a^2-u (c^4 v+b^4 w-b^2 c^2 (2 u+v+w))):...;...
La razón en la que Q divide al segmento OP (O=X3, el circuncentro) es:-2R^2 (u + v + w)^2)/(c^2 u v + b^2 u w + a^2 v w)), R es el radio de la circunferencia circunscrita.
En la lista siguiente {{i,j}, k} significa que V(Xi)=V(Xj) = Xk.W = (b^2-c^2)^2 u^2 (c^2 v+b^2 w)+a^6 v w (3 u+2 (v+w))-a^2 u (c^4 v (4 u+2 v+w)+b^4 w (4 u+v+2 w)-2 b^2 c^2 (2 u^2+v^2+v w+w^2+2 u (v+w)))+a^4 (b^2 w (3 u^2-2 u (v-w)-2 v (v+w))+c^2 v (3 u^2+2 u (v-w)-2 w (v+w))) : ... : ...
El 8 de abril de 1929 nació el cantante franco belga Jacques Brel, cuyas canciones serán conocidas por su bella poesía, pero sobre todo por la honestidad de sus letras en las que tratará de las preocupaciones de todos los tiempos, mencionando en sus temas el amor, la sociedad actual y la espiritualidad. Probablemente, su canción más conocida sea "Ne me quitte pas", del año 1959.
V (u U + w W) +λ W (u U + v V)=0.
La cónica (parábola) de este haz que contiene la recta del infinito, x+y+z=0, se obtiene par λ=-(u+w)/(u + v), y su ecuación puntual (con matriz asociada la matriz adjunta de la asociada a su ecuación tangencial) es:𝒫a: v^2 x^2-2 v w x^2+w^2 x^2-2 u v x y+2 u w x y-2 v w x y+2 w^2 x y+u^2 y^2+2 u w y^2+w^2 y^2+2 u v x z+2 v^2 x z-2 u w x z-2 v w x z+2 u^2 y z+2 u v y z+2 u w y z+2 v w y z+u^2 z^2+2 u v z^2+v^2 z^2=0.
El punto de contacto de esta párabola con B1C1 y su foco son, respectivamente:A'=(u^2 (v-w):v^2 (u+w):-(u+v) w^2), Fa=(a^2 (u+v) (u+w):b^2 (u+v) (v-w):-c^2 (v-w) (u+w)).
El diámetro conjugado de 𝒫a de la tangente en A' (-v w x+u w y + u v z=0) es da: (-v - w) x + (u - w) y + (u - v) z =0.El 5 de abril de 1622 nació el matemático y físico italiano Vincenzo Viviani, fue discípulo de Galileo. Fue autor de un importante trabajo sobre cónicas basado en las secciones cónicas de Apolonio. Tradujo también la física de Arquímedes y los Elementos de Euclides. Propuso un problema (1692) llamado “enigma florentino”, consistente en construir en una bóveda esférica dos ventanas iguales de manera que la porción restante de la semiesfera fuera cuadrable. Dio como solución las ventanas cuya proyección sobre el plano de la bóveda fueran circunferencias de diámetro igual al radio de la esfera, en cuyo caso la porción restante del hemisferio es equivalente al cuadrado construido sobre el diámetro de la esfera. Se le debe también la ventana de Viviani curva obtenida como intersección de una esfera y un cilindro circular de radio la mitad que el de la esfera, y pasando por el centro de la esfera.
U = ( a/((a-b-c) (b-c) (a^7-4 a^6 (b+c)+2 a^5 (b^2+11 b c+c^2)+a^4 (7 b^3-29 b^2 c-29 b c^2+7 c^3)-a^3 (7 b^4+8 b^3 c-71 b^2 c^2+8 b c^3+7 c^4)-2 a^2 (b^5-16 b^4 c+20 b^3 c^2+20 b^2 c^3-16 b c^4+c^5)+a (4 b^6-14 b^5 c-11 b^4 c^2+46 b^3 c^3-11 b^2 c^4-14 b c^5+4 c^6)-(b-c)^2 (b^5+b^4 c-6 b^3 c^2-6 b^2 c^3+b c^4+c^5))) : ... : ...),
que tiene números de búsqueda en (-0.106450824301765, 0.170699447174970, 3.57161909123329).V = ( (b-c)^2/(a^4-2 a^3 (b+c)+a^2 (-2 b^2+9 b c-2 c^2)+a (2 b^3-3 b^2 c-3 b c^2+2 c^3)+(b-c)^4): ... : ...),
que tiene números de búsqueda en ETC (7.68077258572784, 1.38521854762606, -0.863304936784975).
A' = (a (b-c)^2 (a+b-c) (a-b+c) :
(a+b-c) (a^4+a^2 (8 b-3 c) c-a^3 (3 b+c)-2 (b-c)^2 (b^2+2 b c-c^2)+a (4 b^3-10 b^2 c+3 b c^2+c^3)) :
(a-b+c) (a^4-a^3 (b+3 c)+a^2 b (-3 b+8 c)+2 (b-c)^2 (b^2-2 b c-c^2)+a (b^3+3 b^2 c-10 b c^2+4 c^3))).
El 31 de marzo de 1990 el cantautor cubano Silvio Rodríguez ofreció un concierto ante 75 000 personas en el Estadio Nacional de Santiago de Chile, después de haber estado prohibido su ingreso al país durante la dictadura de Augusto Pinochet por 17 años. Silvio Rodríguez Domínguez es un cantautor, guitarrista y poeta cubano, exponente característico de la música de su país surgida con la Revolución cubana, conocida como la Nueva Trova, que comparte con otros reconocidos cantautores tales como Pablo Milanés, Noel Nicola y Vicente Feliú.
Pa =(a^2 (u+v) (u+w)-u (b^2 (u+v)+c^2 (u+w)):-b^2 (u+v) (u+v+w):-c^2 (u+w) (u+v+w)),
(ADaPa): c^2 x y+b^2 x z+a^2 y z+(x+y+z) ((c^2 w y)/(v-w)-(b^2 v z)/(v-w))=0,
Oa = (a^2 (c^2 (v-2 w)+b^2 (2 v-w))+a^4 (-v+w)-(b^2-c^2) (b^2 v+c^2 w):b^2 ((-a^2+b^2) w+c^2 (2 v+w)):-c^2 (-a^2 v+c^2 v+b^2 (v+2 w))).
𝔖abc xyz (b^2-c^2) (b^2+c^2-a^2) x^3+y z ((5 a^4-b^2 c^2+c^4+a^2 (-3 b^2-2 c^2)) y+(-5 a^4-b^4+b^2 c^2+a^2 (2 b^2+3 c^2)) z)= 0.
Pares {P=Xi, Q=Xj}, para los índices {i, j}: {4, 468}, {10, 5205}, {13, 6108}, {14, 6109}, {17, 48441}, {18, 48442}, {76, 48439}, {83, 48440}, {98, 125}, {262, 47638}, {671, 9172}, {1916, 48444}, {5466, 46980}, {11599, 48443}.S = ( (a^6 (b^2+c^2)+a^2 b^2 c^2 (b^2+c^2)-a^4 (b^2+c^2)^2-b^2 c^2 (b^2-c^2)^2) (a^10 (b^2+c^2)-2 a^8 (b^4+3 b^2 c^2+c^4)+a^6 (2 b^6+7 b^4 c^2+7 b^2 c^4+2 c^6)-a^4 (2 b^8+7 b^6 c^2-4 b^4 c^4+7 b^2 c^6+2 c^8)+a^2 (b^10+2 b^8 c^2-b^6 c^4-b^4 c^6+2 b^2 c^8+c^10)-b^2 c^2 (b^2-c^2)^4) : ... : ...),
que tiene números de búsqueda en (5.45157446026838, 5.84334154494646, -2.92083710779473).El 29 de Marzo de 1912 el explorador británico Robert Falcon Scott muere cuando regresaba tras alcanzar el Polo Sur. Le ganó la competición el noruego Roald Amundsen que llegó antes. A principios del siglo XX, el objetivo de alcanzar el polo sur se convirtió en una empresa competitiva, en la que coincidieron los intereses científicos y económicos de las naciones europeas y las ambiciones personales de algunos exploradores. Roald Amundsen y Robert Falcon Scott fueron los protagonistas paradigmáticos de esta pugna de aventura y prestigio.
A'=ℓb∩ℓc=(4 a^2+3 b c+4 a (b+c):a (-2 a-2 b+c):a (-2 a+b-2 c)).
Las rectas AA', BB', CC? concurren en:X(39704) = (1/(a-2 b-2 c):1/(b-2 c-2 a):1/(c-2 a-2 b).
El 27 de marzo de 1973, por interpretar al jefe de una familia mafiosa en El Padrino, Marlon Brando consiguió su segundo Óscar. En esta ocasión Brando rechazó el Óscar. En lugar de recoger el premio, Brando envió a la ceremonia a una actriz estadounidense de origen indio llamada Sacheen Littlefeather, que se manifestó en contra del tratamiento que recibía su pueblo en las películas de Hollywood y por los acontecimientos que ocurrían por aquel entonces en Wounded Knee, ocupado por lakotas oglala integrados en el Movimiento Indígena Americano, por su carácter emblemático, ya que allí se había producido una cruenta batalla más de un siglo antes que supuso el final definitivo de la resistencia indígena.
Ab=(p:q + r:0), Ac=(p:0:q + r),
Uab=(p u:p v + q (u + v + w) + r (u + v + w): p w),
Uac=(p u:p v:p w + q (u + v + w) + r (u + v + w)),
A'=(r (u + v) + q (u + w) + p (u + v + w):q v,:r w).
Q = (p u (-r^2 (u+v) w-q^2 v (u+w)+p^2 u (u+v+w)-q r (v+w) (u+v+w)+p q (u^2+u (-v+w)-v (v+w))+p r (u^2+u (v-w)-w (v+w))) : ... : ...).
(p u+2 q u+2 r u+2 p v+q v+2 r v+2 p w+2 q w+r w) (p u^2 v-q u v^2-p u^2 w+q v^2 w+r u w^2-r v w^2)=0.
• Sean A109={1,2,2}, B109={2,1,2}, C109={2,2,1} los vértices del y U' la imagen de U mediante la homografía que aplica {A,B,C,G=X2} en {A109,B109,C109,G}.((v - w) (u + 2 v + 2 w):(w-u) (2 u + v + 2 w):(u - v) (2 u + 2 v + w)).
La , Ψ1*, de esta parábola es la hipérbola circunscrita a ABC que pasa por G, U'; su es el punto del infinito de Ψ1.(1/(u^2 (v-w)^2) : 1/(v^2 (u-w)^2) : 1/(w^2(u-v)^2)).
La cónica dual Ψ2* es la parábola circunscrita con punto en el infinito (u(v-w):(w-u):w(u-v)), el perspector de la hipérbola circunscrita que pasa por el baricentro y por U.W = ( (b - c)^2 (a + 2 (b + c))^2 : ... : ...),
que tiene números de búsqueda en (1.91363675294238, 3.45223259625394, 0.367440336989010).a^2*c^2*x*y - 2*a*b*c^2*x*y + b^2*c^2*x*y + a^2*b^2*x*z - 2*a*b^2*c*x*z + b^2*c^2*x*z + a^2*b^2*y*z - 2*a^2*b*c*y*z + a^2*c^2*y*z = 0,
which passes through the points X(i) for these i: 513, 649, 660, 889, 901, 3572, 3733, 4581, 7192, 15635, 17929, 17940, 23345, 23836, 32735, 35365, 38242, 43920, 43921, 43922, 43923, 43924, 43925, 43926, 43927, 43928, 43929, 43930, 43931, 43932, 43933, 50344, 50520. (Peter Moses, April 28, 2020)
This circumparabola is the isogonal conjugate of line X(100)X(190) (the tangent to the circumcircle at X(100)), and the isotomic conjugate of line X(668)X(891) (the tangent to the Steiner circumellipse at X(668)). (Randy Hutson, April, 28, 2020)
X(38018) lies on the nine-point circle of the cevian triangle of X(513), and on the curve Q077 (locus of foci of circum-parabolas), and on these lines: {100, 8027}, {513, 3035}, {3271, 6164}, {4083, 5083}, {14474, 31272}
El 24 de marzo de 1826 murió Georg Nikolaus von Nissen, diplomático y escritor danés. Se casó en 1809 con la viuda de Mozart, Constanze. Es conocido sobre todo como biógrafo de Wolfgang Amadeus Mozart.
K281 is a nodal cubic with node K, the nodal tangents being parallel to the asymptotes of the circum-conic through G and K. It has three real asymptotes parallel to those of the Thomson cubic.
Locus properties :
Q = (a^2 (-1+t) t (-2 b^2 c^2+a^2 (b^2 (-1+t)-c^2 t)) : -b^2 (-1+t) (b^2 c^2+a^2 (b^2 (-1+t)+2 c^2 t)) : b^2 c^4 t-a^2 c^2 t (2 b^2 (-1+t)+c^2 t)).
Elimindo t, obtenemos la ecuación d K281:𝔖abc xyz a^2 y z ((a^2 + 2 c^2) y - (a^2 + 2 b^2) z) = 0.
En memoria de Marta
Let P = p : q : r and U = u : v : w be distinct points, neither lying on a sideline of reference triangle ABC. The cevapoint of P and U is the point
(pv + qu)(pw + ru) : (qw + rv)(qu + pv) : (ru + pw)(rv + qw).
Let A"B"C" be the anticevian triangle of U. Let A' =PA"∩BC, and define B' and C' cyclically. The cevapoint of P and U is the perspector, X, of triangles ABC and A'B'C'.
Floor Van Lamoen contributed the following two constructions of cevapoint(P,U). Let ApBpCp be the cevian triangle of P, and let AuBuCu be the cevian triangle of U. Define
| Apu = CpAu∩ApBu | Aup = CuAp∩AuBp | |
| Bpu = ApBu∩BpCu | Bup = AuBp∩BuCp | |
| Cpu = BpCu∩CpAu | Cup = BuCp∩CuAp |
Then triangle ABC is perspective to both triangles ApuBpuCpu and AupBupCup, and the perspector in both cases is the cevapoint of P and U. (Received 10/17/2003)
𝒯1 = ABC (triángulo de referencia) 𝒯2 = A'B'C' 𝒯3 = ApuBpuCpu 𝒯4 = AupBupCup.
Añadimos un triángulo más a esta lista, 𝒯5 = DEF, cuyos vértices son:D =PAu∩UAp, E =PBu∩UBp, F =PCu∩UCp.
P★U = ((pv + qu)(pw + ru) : (qw + rv)(qu + pv) : (ru + pw)(rv + qw)).
Los puntos de intersección de ternas de ejes de perspetividad que se obtienen, considerando las diez ternas posibles de triángulos, son:Q134 = (q r u^2-p^2 v w : p r v^2-q^2 u w : -r^2 u v+p q w^2),
que es P-Hirst inverso de U, la imagen de U en la , respecto a P y a la cónica circunscrita a ABC de P, pyz+qzx+rxy=0.Q135 =(q^3 r^2 u^4 w-p^4 q v^2 w^3:p^2 r^3 u v^4-q^4 r u^3 w^2:-p r^4 u^2 v^3+p^3 q^2 v w^4),
que no es un .Q145 =(-q^2 r^3 u^4 v+p^4 r v^3 w^2:-p^3 r^2 v^4 w+p q^4 u^2 w^3:q r^4 u^3 v^2-p^2 q^3 u w^4),
que no es un centro del triángulo.Q125 =((-r v+q w) (q r u^2-p^2 v w) (q r u^2+p^2 v w):(r u-p w) (p r v^2-q^2 u w) (p r v^2+q^2 u w):-(q u-p v) (-r^2 u v+p q w^2) (r^2 u v+p q w^2)).
Q345 =(p u (q r u^2-p^2 v w) (r^2 v^2-q r v w+q^2 w^2):q v (p r v^2-q^2 u w) (r^2 u^2-p r u w+p^2 w^2):r (q^2 u^2-p q u v+p^2 v^2) w (-r^2 u v+p q w^2)).
Q = ((r v+q w) (q r u^2-p^2 v w) (q r u^2+p^2 v w):(r u+p w) (p r v^2-q^2 u w) (p r v^2+q^2 u w):(q u+p v) (-r^2 u v+p q w^2) (r^2 u v+p q w^2)).
En particular, cuando P es el baricentro y U es el ortocentro, entonces Q=X15143 el X(3)-Hirst inverso de X(25).El 17 de marzo de 2007 falleció John Backus, científico de la computación estadounidense. Comenzó a trabajar para la compañía IBM como programador, donde desarrolló FORTRAN, el primer lenguaje de programación de alto nivel, en 1957. Dos años más tarde desarrolló la notación normalizada que lleva su nombre (BNF, siglas de Backus Normal Form), que describe la sintaxis de los lenguajes de alto nivel. También desarrolló un lenguaje de programación funcional de aplicaciones científicas llamado FP.
A' = (a^2 ((a^2-b^2) w-c^2 (2 v+w)) (a^2 v-c^2 v-b^2 (v+2 w)) : -(a^2 v-c^2 v-b^2 (v+2 w)) (a^2 (-c^2 v+b^2 w)-(b^2-c^2) (c^2 v+b^2 w)) : -((-a^2+b^2) w+c^2 (2 v+w)) (a^2 (-c^2 v+b^2 w)-(b^2-c^2) (c^2 v+b^2 w))),
A" = (0:a^2 v-c^2 v-b^2 (v+2 w):(-a^2+b^2) w+c^2 (2 v+w)).
da: (a^2 (c^2 v-b^2 w)+(b^2-c^2) (c^2 v+b^2 w)) x+a^2 c^2 v y-a^2 b^2 w z = 0.
La tangente desde A" (distinta de BC) a 𝒫a es
ta: (a^4 v w (c^2 v-b^2 w)-(b^2-c^2) (v+w) (c^2 v+b^2 w)^2+a^2 (b^2 c^2 v (v-w) w+b^4 w^2 (2 v+w)-c^4 v^2 (v+2 w))) x
-a^2 (c^2 v^2-b^2 w^2) ((-a^2+b^2) w+c^2 (2 v+w)) y+a^2 (c^2 v^2-b^2 w^2) (a^2 v-c^2 v-b^2 (v+2 w)) z = 0.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
𝔖abc SASBSC xyz a^4 (4 SA^2-b^2 c^2) y z (c^2 SC y - b^2 SBz) = 0,
Cuando P recorre K073, el punto Q queda sobre la cúbica de Neuberg, K001.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Ta = (0:-b^2 ((-a^2+b^2) w+c^2 (2 v+w)):c^2 (-a^2 v+c^2 v+b^2 (v+2 w))).
Similarmente, se definen los puntos de tangencia Tbb y Tcc de las otras parábolas con CA y AB.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
𝔖abc xyz y z (b^2 c^2 (b^2-c^2) (2 a^6+b^6+8 a^2 b^2 c^2-b^4 c^2-b^2 c^4+c^6+a^4 (-3 b^2-3 c^2)) x^3 y z+a^4 (b^2-c^2) (a^6-b^6-3 b^4 c^2-3 b^2 c^4-c^6+a^4 (-3 b^2-3 c^2)+a^2 (3 b^4+6 b^2 c^2+3 c^4)) x y^2 z^2+b^2 c^2 x^4 (-c^2 (2 a^6-3 a^4 c^2+(b-c)^2 c^2 (b+c)^2-2 a^2 b^2 (b^2-3 c^2)) y+b^2 (2 a^6-3 a^4 b^2+b^2 (b-c)^2 (b+c)^2+2 a^2 c^2 (3 b^2-c^2)) z)-a^6 y^2 z^2 (c^2 (a^4+2 a^2 (b^2-c^2)-(b^2-c^2) (3 b^2+c^2)) y-b^2 (a^4-2 a^2 (b^2-c^2)+(b^2-c^2) (b^2+3 c^2)) z)) = 0.
El 12 marzo de 1834 falleció Karl Wilhelm Feuerbach, matemático alemán que trabajó esencialmente en geometría euclidea y proyectiva. Demostró que el centro de la circunferencia de los nueve puntos está situado sobre la recta de Euler del triángulo, coincidiendo con el punto medio del segmento que une el ortocentro y el circuncentro. Además demostró que dicha circunferencia es tangente interior a la circunferencia inscrita, y tangente exterior a las tres circunferencias exinscritas.
Oae=(0:a^4-2 a^2 c (b+c)-(b-c) (b+c)^3-2a S Sqrt[2(b+c)^2-a^2] : a^4-2 a^2 b (b+c)+(b-c) (b+c)^3-2a S Sqrt[2(b+c)^2-a^2]),
donde S es el doble del área del triángulo ABC.We = (a(b+c)/( a b c(b+c)+2S^2 +a S Sqrt[2(b+c)^2-a^2]) : ... : ...),
que tiene números de búsqueda en (1.99041879806885, 1.71845084355469, 1.53231291418397).Oai=(0:a^4-2 a^2 c (b+c)-(b-c) (b+c)^3+2a S Sqrt[2(b+c)^2-a^2] : a^4-2 a^2 b (b+c)+(b-c) (b+c)^3+2a S Sqrt[2(b+c)^2-a^2])
sobre BC, tangente interiormente a Γb y a Γc, en puntos Abi y Aci, respectivamente. Los puntos Bci, Bai y Cai, Cbi, se definen cíclicamente.Wi = (a(b+c)/( a b c(b+c)+2S^2 -a S Sqrt[2(b+c)^2-a^2]) : ... : ...),
que tiene números de búsqueda en ETC (1.19276357190063, 1.64831980103529, 1.94901374031350).Ao = (2 a^2 (a^2-2 (b+c)^2) : (b+c)^2 (a^2+b^2-c^2) : (b+c)^2 (a^2-b^2+c^2)).
Cíclicamente, se definen los puntos Bo y Co. El , U, de ABC respecto a es el de X5432.U = ( a^2/((b+c-a)(2 a^2-(b-c)^2)) : ... : ...),
que tiene números de búsqueda en ETC (0.859598039012814, 1.02238917206480, 2.53611903708745).En Ginebra, el 11 de marzo de 2020, la Organización Mundial de la Salud (OMS), presidida por Tedros Adhanom Ghebreyesus, declara que el coronavirus (covid-19) ya es oficialmente una pandemia. En pocos días, la mitad de la población mundial se verá confinada en sus casas y el destrozo del tejido económico será bestial con decenas de millones de trabajadores engrosando las listas del paro.
p: (c^2 v+b^2 w) x+(c^2 u+a^2 w) y+(b^2 u+a^2 v) z=0,
e: (a^2-b^2-c^2) (a^2 (v-w)-(b^2-c^2) (v+w))x+... =0,
Q = (
a^6 (2 v w+u (v+w))
+a^4 u (c^2 (u+v-2 w)+b^2 (u-2 v+w))
-a^2 (-4 b^2 c^2 v w+c^4 (2 u^2+u v-u w+2 v w)+b^4 (2 u^2-u v+u w+2 v w))+(b^2-c^2)^2 u (c^2 (u-v)+b^2 (u-w))
: ... : ...).
𝔖abc xyz
(a^8 (b^2-c^2)^2+(b^2-c^2)^4 (b^2+c^2)^2+a^6 (-4 b^6+5 b^4 c^2+5 b^2 c^4-4 c^6)-a^2 (b^2-c^2)^2 (4 b^6+3 b^4 c^2+3 b^2 c^4+4 c^6)+a^4 (6 b^8-6 b^6 c^2-4 b^4 c^4-6 b^2 c^6+6 c^8)) x^2+
(-2 a^12+2 b^2 c^2 (b^2-c^2)^4+6 a^10 (b^2+c^2)-4 a^8 (b^2+c^2)^2+2 a^4 (b^2-c^2)^2 (3 b^4+2 b^2 c^2+3 c^4)+a^6 (-4 b^6+5 b^4 c^2+5 b^2 c^4-4 c^6)-a^2 (b^2-c^2)^2 (2 b^6+b^4 c^2+b^2 c^4+2 c^6)) y z = 0.
Fo = ( a^2 (8 a^8-16 a^6 (b^2+c^2) +22 a^4 b^2 c^2 +a^2 (16 b^6-15 b^4 c^2-15 b^2 c^4+16 c^6)-(b^2-c^2)^2 (8 b^4+7 b^2 c^2+8 c^4)) : ... : ...),
que tiene números de búsqueda en (3.09388936466935, 2.21620768350804, 0.678417917323730).W = ( 4 a^10-4 a^8 (b^2+c^2) -2 a^6 (4 b^4-9 b^2 c^2+4 c^4)-a^4 (-8 b^6+7 b^4 c^2+7 b^2 c^4-8 c^6) +a^2 (b^2-c^2)^2 (4 b^4-11 b^2 c^2+4 c^4)-4 (b^2-c^2)^4 (b^2+c^2) : ... : ...),
que tiene números de búsqueda en ETC (-4.85695862658720, -5.71366576999129, 9.83795245801860).El 7 de marzo de 1870 nació Ernst Leonard Lindelöf, matemático finlandés que hizo contribuciones en el análisis real, el análisis complejo y la topología . Los espacios de Lindelöf llevan su nombre, espacio topológico que satisface la siguiente propiedad: cada recubrimiento abierto contiene un subrecubrimiento numerable. Esa definición es una generalización del concepto de compacidad.
D'=(u (v+w)^2:v w^2:v^2 w),
A1=(0:v (u (v-w)+v w):-w (v w+u (-v+w))),
A'=(2 u v^2 w^2:2 u v^3 w+v^3 w^2+u^2 v (v^2+w^2):2 u v w^3+v^2 w^3+u^2 w (v^2+w^2)).
Q1 = ( a (b^2 c^2+a^2 (b+c)^2) : ... : ...),
que tiene números de búsqueda en ETC (1.42022067359990, 1.61248659065074, 1.86884114671853).El 5 de marzo de1512 nació Gérard Mercator, matemático y cartógrafo flamenco, famoso por idear la llamada Proyección de Mercator, en la que se respetan las formas de los continentes pero no los tamaños, está bien adaptada para cartas marítimas, su gran exageración de áreas terrestres en latitudes altas la hace inadecuada para la mayoría de los demás propósitos. En la proyección de Mercator se conservan los ángulos de intersección entre los paralelos y meridianos.
W = ( (3 a^2 + (b + c)^2)/(a^4 + a^2 b c - b^4 - b c (b^2 + c^2) - c^4) : ... : ...),
que tiene números de búsqueda en (-28.7937074071772, -34.9686389470800, 41.1391256331984).
A"= (a^2 (a^5+2 a^4 (b+c)+2 a^3 (b+c)^2+a (b+c)^2 (b^2+c^2)+b c (b^3+b^2 c+b c^2+c^3)+a^2 (2 b^3+3 b^2 c+3 b c^2+2 c^3)):
-b (a^5 b+a^4 (2 b^2+2 b c+c^2)+2 a^3 (b^3+2 b^2 c+b c^2+c^3)+a^2 (2 b^4+3 b^3 c+3 b^2 c^2+2 b c^3+2 c^4)+c (b^5+b^3 c^2+b^2 c^3+c^5)+a (b^5+2 b^4 c+2 b^3 c^2+2 b^2 c^3+b c^4+2 c^5)):
-c (a^5 c+a^4 (b^2+2 b c+2 c^2)+2 a^3 (b^3+b^2 c+2 b c^2+c^3)+a^2 (2 b^4+2 b^3 c+3 b^2 c^2+3 b c^3+2 c^4)+b (b^5+b^3 c^2+b^2 c^3+c^5)+a (2 b^5+b^4 c+2 b^3 c^2+2 b^2 c^3+2 b c^4+c^5))).
Z = ( a(a^4-(b+c)^2 (b^2+c^2))(a^5+2 a^4 (b+c)+2 a^3 (b+c)^2+a^2 (2 b^3+3 b^2 c+3 b c^2+2 c^3)+a (b+c)^2 (b^2+c^2)+b c (b^3+b^2 c+b c^2+c^3)) : ... : ...),
que tiene números de búsqueda en ETC (4.04769586869950, 2.73360813039173, -0.120000778532741).El 3 de marzo de 1996 falleció (a los 82 años) Marguerite Duras, escribió varias novelas (El amante, La amante inglesa, El amor , El dolor, ..), relatos (Cuadernos de la guerra, Un dique contra el Pacífico,.. ), guiones cinematográficos (Hiroshima mon amour, La Ladrona, ...) y dirigió varias películas (La música, Jaune le soleil, India song,...). Su obra más conocida es sin duda El amante, novela semi-autobiográfica que se llevó al cine de la mano de Claude Berri en 1992.
𝔖abc xyz
v^2 w^2 (3 u^8-8 u^6 v^2+6 u^4 v^4-v^8+4 u^6 v w-4 u^5 v^2 w-8 u^4 v^3 w+8 u^3 v^4 w+4 u^2 v^5 w-4 u v^6 w-8 u^6 w^2-4 u^5 v w^2+4 u^4 v^2 w^2-8 u^3 v^3 w^2-4 u^2 v^4 w^2+4 u v^5 w^2-8 u^4 v w^3-8 u^3 v^2 w^3+6 u^4 w^4+8 u^3 v w^4-4 u^2 v^2 w^4+2 v^4 w^4+4 u^2 v w^5+4 u v^2 w^5-4 u v w^6-w^8) x^2+
2 u^2 v w (u+v+w) (u^3-u^2 v-u v^2+v^3-u^2 w-v^2 w-u w^2-v w^2+w^3) (u^4-v^4+2 u^2 v w-2 u v^2 w-2 u v w^2+2 v^2 w^2-w^4) y z = 0.
W = (u (v+w) (u^4-2 u^3 (v+w)-2 u^2 (v^2+v w+w^2)+2 u (v^3-2 v^2 w-2 v w^2+w^3)+(v^2-w^2)^2) : ... : ... ).
Cuando P está en la recta del infinito, W es el de P (baricentro de DEF) y está sobre la cúbica acnodal Bataille (K656 del catálogo de Bernard Gibert). El de 𝒞P, en esta caso, queda indefinido, ya que ABC es , con respecto a esta cónica.
𝔖abc xyz
b^2 c^2 3 a^8-4 a^5 b c (b+c)+8 a^3 b (b-c)^2 c (b+c)+a^6 (-8 b^2+4 b c-8 c^2)+4 a^2 b (b-c)^2 c (b^2+b c+c^2)+2 a^4 (b-c)^2 (3 b^2+2 b c+3 c^2)-(b^4-c^4)^2-4 a b c (b^5-b^4 c-b c^4+c^5) x^2+
2 a^2 b c (a+b+c) (a^4+2 a^2 b c-2 a b c (b+c)-(b^2-c^2)^2) (a^3-a^2 (b+c)+(b-c)^2 (b+c)-a (b^2+c^2)) y z= 0.
W1 = ( a (b+c) (a^4-2 a^3 (b+c)+(b^2-c^2)^2-2 a^2 (b^2+b c+c^2)+2 a (b^3-2 b^2 c-2 b c^2+c^3)) : ... : ...),
que tiene números de búsqueda en (1.43800756346841, 1.37326851529912, 2.02624432663803).El 25 de febrero de 1841 nació Pierre Auguste Renoir, trabajó en sus inicios como pintor de porcelanas y abanicos. Se inscribió en la academia de Charles Gleyre donde conoció a Monet, Bazille y Sisley. . Su obra giró entonces hacia un mayor academicismo inspirado en los grandes maestros clásicos. Las escenas urbanas, los retratos y la representación del cuerpo femenino son algunos de los temas más recurrentes de su obra entre la que destacan cuadros como Baile en el Moulin de la Galette, El palco, Almuerzo de remeros o Retrato de Mme. Monet.
Ab = (a^2 (a+b-c) (a+c) (a-b+c) : b (a+b-c) (a+c) (a^2+b^2-c^2) : -c^2 (a-b+c) (a^2+b^2-c^2)),
Ac = (a^2 (a+b) (a+b-c) (a-b+c) : -b^2 (a+b-c) (a^2-b^2+c^2) : (a+b) c (a-b+c) (a^2-b^2+c^2)),
A' = (a^7-a^5 (b-c)^2+a (b^2-c^2)^2 (b^2-b c+c^2)-a^3 (b-c)^2 (b^2+3 b c+c^2) :
b^2 (-a^5+b^5-b^3 c^2+b^2 c^3-c^5+a^4 (b+2 c)+a^3 (2 b^2-b c-c^2)-a^2 (2 b^3+2 b^2 c-b c^2+c^3)-a (b^4-b^3 c+b^2 c^2+b c^3-2 c^4)) :
c^2 (-a^5-b^5+b^3 c^2-b^2 c^3+c^5+a^4 (2 b+c)-a^3 (b^2+b c-2 c^2)-a^2 (b^3-b^2 c+2 b c^2+2 c^3)+a (2 b^4-b^3 c-b^2 c^2+b c^3-c^4))),
W = ( a^2/(a^4+a^2 b c-a^3 (b+c)+a (b^3+c^3)-(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en (0.652453330579329, 3.38438815325377, 0.996494223233619).
A" = (a (a^3 b c (b+c)-a b (b-c)^2 c (b+c)+(b-c)^4 (b+c)^2+a^4 (b^2+b c+c^2)-a^2 (b-c)^2 (2 b^2+3 b c+2 c^2)):
b^3 (a^4-2 a^3 c-2 a^2 (b^2-c^2)+2 a c (b^2-c^2)+(b^2-c^2)^2) : c^3 (a^4-2 a^3 b+2 a^2 (b^2-c^2)+(b^2-c^2)^2-2 a (b^3-b c^2))).
El 21 de febrero de 1591 nació Gérard Desargues, matemático e ingeniero francés, considerado como el fundador de la geometría proyectiva. El teorema de Desargues establece que los puntos de intersección de una recta con una cónica y con los lados opuestos de cualquier cuadrivértice inscrito en ella son homólogos en una misma involución. En su principal obra, el Tratado sobre las secciones cónicas (1639), desarrolla la idea de que las distintas secciones cónicas (tales como el círculo, la elipse, la parábola y la hipérbola, o, en fin, todo sistema de dos rectas) no son mas que los distintos aspectos de una curva única.
A' = (u (b^2 u (u+2 v) w+a^2 v (v-w) w-c^2 u v (u+2 w)):
-v (c^2 u^2 v+b^2 u^2 w+a^2 v w (2 u+v+w)):w (c^2 u^2 v+b^2 u^2 w+a^2 v w (2 u+v+w))).
Q = (u/(c^2 u^2 v + b^2 u^2 w + a^2 v w (2 u + v + w)): ... : ... ).
Pares {P=Xi, Q=Xj}, para {i, j}: {1, 2}, {2, 10302}, {3, 97}, {4, 275}, {6, 39389}, {13, 11119}, {14, 11120}, {15, 38403}, {16, 38404}, {39162, 39162}, {39163, 39163}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
El 20 de febrero de 1931 nació John Milnor (hoy cumple 92 años), matemático estadounidense conocido por sus trabajos en la topología diferencial y los sistemas dinámicos. Fue galardonado con el premio Abel 2011, la Medalla Fields en 1962 (por sus estudios relacionado con la estructura de ciertas esferas 7-dimensionales). El nombre de Milnor aparece entre otros en: número de Milnor, fibración de Milnor, bola de Milnor, esferas exóticas de Milnor, invariante de Kervaire-Milnor y torsión de Milnor. Entre sus publicaciones figuran: Differential Topology (1958), Morse Theory (1963).
Abc = ((a^2 - b^2 - c^2) (a^4 + 2 b c (b^2 - c^2) - a^2 (b^2 + c^2)) :
-a^6 + b^6 - b^5 c + 5 b^4 c^2 + b^2 c^4 +
b c^5 + c^6 + a^4 (3 b^2 + b c + 3 c^2) - a^2 (3 b^4 + 4 b^2 c^2 + 2 b c^3 + 3 c^4) :
-a^6 + b^6 - b^5 c + b^4 c^2 + 5 b^2 c^4 + b c^5 + c^6 - a^4 (-3 b^2 + b c - 3 c^2) -
a^2 (3 b^4 - 2 b^3 c + 4 b^2 c^2 + 3 c^4)),
ℓbc: 2 b c x+(-a^2+b^2+c^2)+(a^2-b^2-c^2)z=0, ℓcb: 2 b c x +(a^2-b^2-c^2)y+(-a^2+b^2+c^2)z=0.
𝔖abc xyz (a^4+b^2 c^2) (b^4-b^2 c^2+c^4) x^2-(a^2 (b^2+c^2)-b^2 c^2) (a^4+b^4+c^4) y z = 0.
W = ( 3 a^4-2 a^2 (b^2+c^2)+3 b^4+2 b^2 c^2+3 c^4 : ... : ...),
que tiene números de búsqueda en (3.31386281011518, 1.64274094795041, 0.973907144042471).El 17 de febrero de 1949, el gobernador civil de Barcelona, el falangista Eduardo Baeza y Alegría, ordenó la ejecución de los militantes del PSUC (Partido Socialista Unificado de Cataluña) Joaquim Puig, Ángel Carrero, Pere Valverde y Numen Mestre. Los 4 habían sido combatientes del Ejército de la República durante la guerra de España. A su conclusión se habían exiliado en Francia y habían combatido con la resistencia francesa contra la ocupación nazi (1939-1945) y al fin de la II Guerra Mundial (1945) se habían introducido en Catalunya para reorganizar el PSUC en la clandestinidad. Fueron detenidos en una batida policial en agosto de 1948, y juzgados y condenados a muerte el 14 de octubre de 1948. Fueron fusilados juntos en el Campo de la Bota
A' = (a^2 (a^2-b^2-c^2):-a^2 b^2+b^4:-a^2 c^2+c^4),
Ab = (a^2 (-a^2+b^2+c^2):a^4+2 b^2 c^2+c^4-a^2 (b^2+2 c^2):c^2 (a^2-c^2)),
Ac = (a^2 (a^2-b^2-c^2):-a^2 b^2+b^4:-a^4+a^2 (2 b^2+c^2)-b^2 (b^2+2 c^2)).
A" = ((a^2-b^2-c^2) (b^2-c^2)^2 : b^4 (-a^2+b^2-c^2) : c^4 (-a^2-b^2+c^2)).
Como los puntos A', B', C' están sobre las mediatrices de BC, Ca, AB, los triángulos ABC y A'B'C' son . El centro de ortología de ABC respecto a A'B'C' es X24.W = ( a^2 (a^2-b^2-c^2)(a^10 (b^2+c^2)-3 a^2 (b^2-c^2)^4 (b^2+c^2)+(b^2-c^2)^4 (b^4+c^4)+2 a^4 (b^2-c^2)^2 (b^4-b^2 c^2+c^4)-a^8 (3 b^4+2 b^2 c^2+3 c^4)+2 a^6 (b^6+b^4 c^2+b^2 c^4+c^6)) : ... : ...),
que tiene números de búsqueda en (4.44733024465701, 5.34523524561456, -2.11249695489817).El 14 de febrero de 1943 falleció David Hilbert (a los 80 años), matemático alemán. Presentó en 1900 de sus famosos veintitres problemas de Hilbert, que han marcado la investigación matemática durante este siglo. Hibert tambien trabajó en los fundamentos de análisis funcional con los espacios de Hilbert. También elaboró una fundamentación de la geometría con los axiomas de Hilbert. En 1920 propuso un programa de investigación en metamatemáticas conocido como programa de Hilbert.
Ab=((b^2-c^2) u+a^2 (u+2 v):0:a^2 (-v+w)+(b^2-c^2) (v+w)), Ac=(-b^2+c^2) u+a^2 (u+2 w):a^2 (v-w)-(b^2-c^2) (v+w):0),
siendo (u:v.w) las coordenadas baricéntricas de P. Los puntos Bc, Ba y Ab, Ac, se definen cíclicamente.
Pa = (a^2 (a^8-b^2 c^2 (b^2-c^2)^2-3 a^6 (b^2+c^2)-a^2 (b^2-c^2)^2 (b^2+c^2)+3 a^4 (b^4+b^2 c^2+c^4)) u:
a^10 v-3 a^8 (b^2+c^2) v+(b^2-c^2)^3 (2 b^2 c^2 u-c^4 v+b^4 (u+v))-a^2 (b^2-c^2) (4 b^4 c^2 u+5 b^2 c^4 u-3 c^6 v+3 b^6 (u+v))+a^4 (b^2-c^2) (4 b^2 c^2 u-2 c^4 v+b^4 (3 u+2 v))+a^6 (-b^4 (u-2 v)+2 c^4 v+b^2 c^2 (u+5 v)):
a^10 w-3 a^8 (b^2+c^2) w+(b^2-c^2)^3 (-2 b^2 c^2 u+b^4 w-c^4 (u+w))-a^2 (b^2-c^2) (-5 b^4 c^2 u-4 b^2 c^4 u+3 b^6 w-3 c^6 (u+w))+a^4 (b^2-c^2) (-4 b^2 c^2 u+2 b^4 w-c^4 (3 u+2 w))+a^6 (-c^4 (u-2 w)+2 b^4 w+b^2 c^2 (u+5 w))).
Q = a^2 (-(a^2-b^2)^5 (a^2+b^2)^2+(a^2-b^2)^3 (3 a^6+4 a^4 b^2+2 a^2 b^4+2 b^6) c^2-a^2 (a-b) (a+b) (a^6+2 a^4 b^2+4 a^2 b^4+b^6) c^4-(a-b) (a+b) (5 a^6-3 a^2 b^4+b^6) c^6+(5 a^6-4 a^4 b^2+a^2 b^4+b^6) c^8+a^2 (a^2+4 b^2) c^10-(3 a^2+2 b^2) c^12+c^14)+
(a^2-b^2-c^2) (a^2+b^2-c^2) (a^2-b^2+c^2) (a^10-2 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)+a^6 (b^4+3 b^2 c^2+c^4)-a^4 (b^6+2 b^4 c^2+2 b^2 c^4+c^6)+2 a^2 (b^8-b^6 c^2-b^2 c^6+c^8))t : ... : ...
(b^2-c^2) (a^8-2 a^6 (b^2+c^2)+a^4 b^2 c^2+2 a^2 (b^6+c^6) -b^8+b^6 c^2+b^2 c^6-c^8) x+... = 0.
La correspondencia P ↦ Q, entre las rectas de Euler y X3X161 es una proyectividad, en la que se corresponde sus puntos en la recta del infinito X30 y X18400. En consecuencia, la recta PQ envuelve una parábola. Se trata de la parábola de directriz do: X110X933 y foco la reflexión de X933 en la recta de Euler:Fo = 1/((b^2-c^2)(a^2-b^2-c^2) (a^8+a^4 b^2 c^2-2 a^6 (b^2+c^2)-(b^2-c^2)^2 (b^4+c^4)+a^2 (2 b^6-b^4 c^2-b^2 c^4+2 c^6))) : ... : ....
Incorporado a ETC con el número X(52998).
𝔖abc xyz
b^2 c^2 (-b^4+c^4+a^2 (b^2-c^2))^2 (4 a^20+b^2 c^2 (b^2-c^2)^8-16 a^18 (b^2+c^2)-4 a^2 b^2 c^2 (b^2-c^2)^6 (b^2+c^2)+8 a^16 (2 b^4+5 b^2 c^2+2 c^4)+8 a^14 (2 b^6-3 b^4 c^2-3 b^2 c^4+2 c^6)-20 a^12 (2 b^8-b^4 c^4+2 c^8)+2 a^4 (b^2-c^2)^4 (2 b^8+3 b^6 c^2+8 b^4 c^4+3 b^2 c^6+2 c^8)+8 a^10 (2 b^10-b^6 c^4-b^4 c^6+2 c^10)-4 a^6 (b^2-c^2)^2 (4 b^10-b^8 c^2+3 b^6 c^4+3 b^4 c^6-b^2 c^8+4 c^10)+a^8 (16 b^12-23 b^10 c^2+4 b^8 c^4+22 b^6 c^6+4 b^4 c^8-23 b^2 c^10+16 c^12))x^2
-2 a^2 b^2 (a^2-b^2) c^2 (a^2-c^2) (a^22-4 a^20 (b^2+c^2)-2 (b^2-c^2)^8 (b^2+c^2)^3+6 a^8 (b^2-c^2)^2 (b^2+c^2)^3 (b^4+c^4)+2 a^18 (2 b^4+7 b^2 c^2+2 c^4)+4 a^16 (b^6-4 b^4 c^2-4 b^2 c^4+c^6)+2 a^12 (b^2-c^2)^2 (7 b^6+19 b^4 c^2+19 b^2 c^4+7 c^6)+a^14 (-12 b^8+2 b^6 c^2+29 b^4 c^4+2 b^2 c^6-12 c^8)+a^2 (b^2-c^2)^6 (10 b^8+20 b^6 c^2+19 b^4 c^4+20 b^2 c^6+10 c^8)+a^6 (b^2-c^2)^4 (11 b^8+10 b^6 c^2+17 b^4 c^4+10 b^2 c^6+11 c^8)-a^10 (b^2-c^2)^2 (14 b^8+34 b^6 c^2+51 b^4 c^4+34 b^2 c^6+14 c^8)-2 a^4 (b^2-c^2)^4 (9 b^10+7 b^8 c^2+8 b^6 c^4+8 b^4 c^6+7 b^2 c^8+9 c^10))y z = 0.
El 13 de febrero de 1678 fue publicado, post mortem, el "Sistema Tychonico" del astrónomo danés Tycho Brahe (1546-1601), a mitad de camino entre la teoría geocéntrica de Ptolomeo (S II), y la heliocéntrica de Copérnico (1473-1543). Esta, si bien demostró ser cierta, tuvo varios errores de medición que fueron corregidos por el propio Brahe cuando todavía no existía el telescopio.
2 λa^2 b^2 c^2 x^2 -λc^2 (-a^4+2 a^2 b^2+(b^2-c^2)^2) y^2 -λb^2 (-a^4+2 a^2 c^2+(b^2-c^2)^2) z^2 + (λa^4 (b^2+c^2) -(λb^2-c^2)^2 (b^2+c^2)+a^2 (1-4λ b^2 c^2 ))y z +b^2 (1+λa^4-λb^4 +2λ b^2 c^2 -λc^4 ) z x +c^2 (1+a^4 λ-λb^4 +2λb^2 c^2 -λc^4 )x y =0.
La circunferencia de este haz que pase por E, F se obtiene para λ= -1/(2 (a^4-b^4+2 b^2 c^2-c^4)). Con lo que la ecuación de Γa es:2 a^2 b^2 c^2 x^2-a^4 c^2 x y+b^4 c^2 x y-2 b^2 c^4 x y+c^6 x y+a^4 c^2 y^2-2 a^2 b^2 c^2 y^2-b^4 c^2 y^2+2 b^2 c^4 y^2-c^6 y^2-a^4 b^2 x z+b^6 x z-2 b^4 c^2 x z+b^2 c^4 x z-2 a^6 y z+a^4 b^2 y z+2 a^2 b^4 y z-b^6 y z+a^4 c^2 y z-8 a^2 b^2 c^2 y z+b^4 c^2 y z+2 a^2 c^4 y z+b^2 c^4 y z-c^6 y z+a^4 b^2 z^2-b^6 z^2-2 a^2 b^2 c^2 z^2+2 b^4 c^2 z^2-b^2 c^4 z^2=0.
Cuyo centro es:
A' = (2 a^8-(b^2-c^2)^4-3 a^6 (b^2+c^2)+3 a^2 (b^2-c^2)^2 (b^2+c^2)-a^4 (b^4-10 b^2 c^2+c^4):
-b^2 (a^2+b^2-c^2) (a^4-2 a^2 (b^2-3 c^2)+(b^2-c^2)^2),-c^2 (a^2-b^2+c^2) (a^4+a^2 (6 b^2-2 c^2)+(b^2-c^2)^2).
W = ( a/(a^9-a^8 (b+c)-(b-c)^4 (b+c)^5+6 a^5 (b-c)^2 (b^2+c^2)-4 a^7 (b^2-b c+c^2)+4 a^6 (b^3+b^2 c+b c^2+c^3)+a (b^2-c^2)^2 (b^4-4 b^3 c-2 b^2 c^2-4 b c^3+c^4)-4 a^3 (b-c)^2 (b^4-b^3 c-2 b^2 c^2-b c^3+c^4)+4 a^2 (b-c)^2 (b^5+3 b^4 c+2 b^3 c^2+2 b^2 c^3+3 b c^4+c^5)-2 a^4 (3 b^5+3 b^4 c-2 b^3 c^2-2 b^2 c^3+3 b c^4+3 c^5)) : ... : ...),
que tiene números de búsqueda en (22.2839493957673, 20.3290174201994, -20.7181703762770).El 11 de febrero de 1650 fallece en Estocolmo (Suecia) René Descartes, filósofo, matemático y naturalista francés, padre de la geometría analítica y de la filosofía moderna y uno de los nombres más destacados de la Revolución Científica.
{-3 a^2:(b^2-c^2):-b^2+c^2}, {(a^2-c^2):-3 b^2:-a^2+c^2}, {(a^2-b^2):-a^2+b^2:-3 c^2},
y su es K2=X35955, el del simediano de DEF, X3363.11 a^4-2 a^2 (b^2+c^2)+16 b^2 c^2-7 (c^4 +b^4).
Es el anticomplemento de K2; ha sido incorporado a con el número X(52942).
K4:
47 a^4-196 b^2 c^2+380 a^2 (b^2+c^2)-25 (b^4+c^4)
K5:
97 a^4-380 b^2 c^2+772 a^2 (b^2+c^2)-47 (b^4+c^4)
K6: 191 a^4-772 b^2 c^2+1532 a^2 (b^2+c^2)-97 (b^4+c^4)
K7: 385 a^4-1532 b^2 c^2+3076 a^2 (b^2+c^2)-191 (b^4+c^4)
K8: 767 a^4-3076 b^2 c^2+6140 a^2 (b^2+c^2)-385 (b^4+c^4)
K9: 1537 a^4-6140 b^2 c^2+12292 a^2 (b^2+c^2)-767 (b^4+c^4)
K10: 3071 a^4-12292 b^2 c^2+24572 a^2 (b^2+c^2)-1537 (b^4+c^4)
f[0] = 2, f[1] = 7, f[n] = f[n - 1] + 2 f[n - 2]; g[3] = 2, g[4] = 16, g[n] = g[n - 1]+2 g[n - 2].
Así:Kn = f[n-1]a^4 -a^2 (b^2+c^2) g[n]+b^2 c^2 g[n+1] -(b^4+c^4) f[n-2].
A Suki por su cumple
A1 = (2 a^8-3 a^6 (b^2+c^2)+a^2 (b^2-c^2)^2 (b^2+c^2):
-(b^2-c^2)^3 (b^2+c^2)-a^6 (2 b^2+c^2)+a^2 c^2 (b^4+2 b^2 c^2-3 c^4)+a^4 (3 b^4+2 b^2 c^2+3 c^4):
(b^2-c^2)^3 (b^2+c^2)-a^6 (b^2+2 c^2)+a^4 (3 b^4+2 b^2 c^2+3 c^4)-a^2 (3 b^6-2 b^4 c^2-b^2 c^4)),
A2 = (a^2 (2 a^6+8 a^2 b^2 c^2-3 a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)):
-(b^2-c^2)^3 (b^2+c^2)-a^6 (2 b^2+c^2)-3 a^2 (-b^2 c+c^3)^2-a^4 (-3 b^4+2 b^2 c^2-3 c^4):
(b^2-c^2)^3 (b^2+c^2)-a^6 (b^2+2 c^2)-3 a^2 (b^3-b c^2)^2-a^4 (-3 b^4+2 b^2 c^2-3 c^4)).
A1B1∩B2C2 = (a^6+a^4 (b^2-3 c^2)-(-b^2 c+c^3)^2-a^2 (2 b^4+b^2 c^2-3 c^4):
b^2 (-a^4+2 b^4-b^2 c^2-c^4-a^2 (b^2-2 c^2)): -a^6-2 b^4 c^2+b^2 c^4+c^6+a^4 (2 b^2+3 c^2)-a^2 (b^4+5 b^2 c^2+3 c^4))
A1C1∩B2C2 = (-a^6+a^4 (3 b^2-c^2)+(b^3-b c^2)^2+a^2 (-3 b^4+b^2 c^2+2 c^4):
a^6-a^4 (3 b^2+2 c^2)-b^2 (b^4+b^2 c^2-2 c^4)+a^2 (3 b^4+5 b^2 c^2+c^4) : c^2 (a^4+b^4+b^2 c^2-2 c^4+a^2 (-2 b^2+c^2))).
𝒞:
𝔖abc xyz
(3 a^10 (b^2+c^2)-5 a^2 (b^2-c^2)^4 (b^2+c^2)+(b^2-c^2)^4 (2 b^4+5 b^2 c^2+2 c^4)-a^8 (10 b^4+7 b^2 c^2+10 c^4)+2 a^6 (5 b^6+7 b^4 c^2+7 b^2 c^4+5 c^6)-2 a^4 (11 b^6 c^2-6 b^4 c^4+11 b^2 c^6)) x^2+
2 (4 a^12-12 a^10 (b^2+c^2)+4 a^2 b^2 c^2 (b^2-c^2)^2 (b^2+c^2)-6 a^4 (b^2-c^2)^2 (b^4+3 b^2 c^2+c^4)+(b^2-c^2)^4 (b^4+3 b^2 c^2+c^4)+a^8 (9 b^4+23 b^2 c^2+9 c^4)+4 a^6 (b^6-2 b^4 c^2-2 b^2 c^4+c^6)) y z = 0.
El 6 de febrero de 1918 las mujeres votan por primera vez en una elecciones. Se permitió que las mujeres británicas mayores de 30 años pudieran votar. En 1920 se rebajaría la edad a 21 años. En América, fue a fines de 1922, cuando todas las provincias canadienses, excepto Quebec, habían otorgado el sufragio completo a las mujeres blancas y negras, pero las mujeres asiáticas e indígenas aún no podían votar. En España, en 1931 la Constitución de la Segunda República estableció el derecho de sufragio para los mayores de 23 años contemplando la igualdad para ambos sexos.
Da = (a^2 (-a^2+b^2+c^2)^2:-a^4 (b^2+c^2)-(b^2-c^2)^2 (b^2+c^2)+2 a^2 (b^4+b^2 c^2+c^4):
-a^4 (b^2+c^2)-(b^2-c^2)^2 (b^2+c^2)+2 a^2 (b^4+b^2 c^2+c^4)),
Γa: c^2 x y+b^2 x z+a^2 y z+
(x+y+z)
(-(((a^4 b^2-2 a^2 b^4+b^6+a^4 c^2-2 a^2 b^2 c^2-b^4 c^2-2 a^2 c^4-b^2 c^4+c^6) x)/(2 (a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)))-
(a^2 (a^4 b^2-2 a^2 b^4+b^6-2 b^4 c^2+b^2 c^4) y)/(2 (b^2-c^2) (a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4))+
(a^2 (a^4 c^2+b^4 c^2-2 a^2 c^4-2 b^2 c^4+c^6) z)/(2 (b^2-c^2) (a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)))=0,
ta: (a^2-b^2-c^2) (b^2-c^2) (a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)-2 a^2 (b^4+b^2 c^2+c^4)) x-
a^2 b^2 (-a^6+b^6+3 b^4 c^2-5 b^2 c^4+c^6+a^4 (3 b^2+5 c^2)-a^2 (3 b^4+8 b^2 c^2+5 c^4)) y+
a^2 c^2 (-a^6+b^6-5 b^4 c^2+3 b^2 c^4+c^6+a^4 (5 b^2+3 c^2)-a^2 (5 b^4+8 b^2 c^2+3 c^4)) z=0.
((b^2-c^2)^3 (b^2+c^2)+a^4 (b^4-c^4)-2 a^2 (b^6-c^6)) x+a^2 b^2 (a^4-2 a^2 b^2+(b^2-c^2)^2) y-a^2 c^2 (a^4-2 a^2 c^2+(b^2-c^2)^2) z=0.
Las circunferencias Γa, Γb, Γc son , con eje radical común la . El otro punto común es X2072.
Las tres tangentes ta, tb, tc concurren en X7514.
El 5 de febrero de 1937 falleció (a los 75 años de edad) Lou Andreas-Salomé, nacida en Rusia, psicoanalista distinguida y la única mujer que Freud aceptó en él "círculo interno" de la Sociedad Psicoanalítica de Viena. Salome tuvo como pretendientes a las más grandes inteligencias de su tiempo. Fue una gran seductora que no se comprometía con nadie y que quería sentirse siempre libre. Salome solía decir "Mi obligación es estar libre de obligaciones". Andreas-Salomé adquirió una notable popularidad tras la publicación, en 1951, de la primera edición alemana de su autobiografía: "Mirada retrospectiva", que sirvió a Liliana Cavani para hacer su película "Más allá del bien y del mal".
(V - W) ((b - c )U - b V + c W)=0, (b V + c W) (2 a^2 U+(-a^2 - b^2+ c^2) V+(-a^2+ b^2- c^2) W) =0.
Con lo que las rectas tangentes comunes son x=0 (BC), x+y+z=0 (recta del infinito) y la recta paralela a IbIc por por el pie D(0:b:c) de la bisectriz interior en A:ta: 2 b c x-c (-b+c) y-b (b-c) z =0.
Procediendo cíclicamente, se obtienen las tangentes tb y tc. Sea el triángulo formado por estas tres rectas. Como las bisectrices interiores son perpendiculares a ta, tb, tc, entonces los triángulos ABC y son .W = ( a (a^5 (b+c)-4 a^4 b c-a^3 (2 b^3+b^2 c+b c^2+2 c^3)+a^2 b (b-c)^2 c+a (b^5-b^3 c^2-b^2 c^3+c^5)+3 b c (b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en (-1.09954972920206, -1.09219001272548, 4.90428051957989).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
(-2 a^2:a^2+b^2-c^2:a^2-b^2+c^2) [en la recta del infinito],
A'=(0:-a-b+c:-a+b-c),
A"=(0:-a+b-c:-a-b+c),
A1=(-a (a-b-c) (b-c)^2:b (2 a^2 b-(b-c)^2 (b+c)+a (-b^2+c^2)):c (2 a^2 c-(b-c)^2 (b+c)+a (b^2-c^2))),
A2=(a (b-c)^2 (a+b+c):b (-2 a^2 b+(b-c)^2 (b+c)+a (-b^2+c^2)):c (-2 a^2 c+(b-c)^2 (b+c)+a (b^2-c^2))).
𝒞a: 4 a^4 x^2-5 a^2 b^2 x^2+b^4 x^2+10 a^2 b c x^2-5 a^2 c^2 x^2-2 b^2 c^2 x^2+c^4 x^2+4 a^4 x y-4 a^2 b^2 x y+12 a^2 b c x y-8 a^2 c^2 x y+a^4 y^2-a^2 b^2 y^2+2 a^2 b c y^2-a^2 c^2 y^2+4 a^4 x z-8 a^2 b^2 x z+12 a^2 b c x z-4 a^2 c^2 x z-2 a^4 y z-2 a^2 b^2 y z+4 a^2 b c=0.
La directriz de esta parábola (paralela a BC) es:da: (8 a^4+5 (b^2-c^2)^2-a^2 (13 b^2-10 b c+13 c^2)) x+(4 a^4-5 a^2 (b-c)^2+(b^2-c^2)^2) y+(4 a^4-5 a^2 (b-c)^2+(b^2-c^2)^2) z = 0.
Si db y dc son las correspondientes directrices, obtenidas cíclicamente, el centro de homotecia de ABC y el triángulo formado por da, db y dc esZ = ( 4 a^4-5 a^2 (b-c)^2+(b^2-c^2)^2 : ... : ...),
que tiene números de búsqueda en ETC (0.555039866111904, 0.887062121477146, 2.77037230575625).En memoria de mi hija Marta
Ab=(a^2 - c^2:0:-a^2 + b^2 + c^2),
Ac=(a^2-b^2:-a^2+b^2+c^2:0).
A'=AbBa∩AcCa =
(-a^4 (a^2-b^2) (a^2-c^2):-(b^2-c^2) (a^6+(b^2-c^2)^2 (b^2+c^2)-a^4 (2 b^2+c^2)+a^2 (3 b^2 c^2-c^4):
(b^2-c^2) (a^6+(b^2-c^2)^2 (b^2+c^2)-a^4 (b^2+2 c^2)-a^2 (b^4-3 b^2 c^2))),
A"=BcBa∩CaCb =
(a^4:-a^4+b^4-c^4-a^2 (b^2-2 c^2):-a^4-b^4+c^4+a^2 (2 b^2-c^2)).
V = ( a^2 (a^12 (b^2+c^2)-a^10 (4 b^4+3 b^2 c^2+4 c^4) +a^8 (5 b^6+4 b^4 c^2+4 b^2 c^4+5 c^6)-a^6 (6 b^6 c^2-b^4 c^4+6 b^2 c^6) -a^4 (5 b^10-9 b^8 c^2+3 b^6 c^4+3 b^4 c^6-9 b^2 c^8+5 c^10) +a^2 (b^2-c^2)^2 (4 b^8+b^6 c^2+b^2 c^6+4 c^8)-(b^2-c^2)^4 (b^6+2 b^4 c^2+2 b^2 c^4+c^6) ) : ... : ...),
que tiene números de búsqueda en (-1.68591397946276, 0.0709396984503623, 4.36966652734771).W = ( a^2 (a^2-b^2-c^2) (a^10 (b^2+c^2) -a^8 (3 b^4+b^2 c^2+3 c^4)+2 a^6 (b^6+b^4 c^2+b^2 c^4+c^6)+a^4 (2 b^8-8 b^6 c^2+9 b^4 c^4-8 b^2 c^6+2 c^8) -3 a^2 (b^2-c^2)^4 (b^2+c^2) +(b^2-c^2)^4 (b^4+b^2 c^2+c^4) ) : ... : ...),
que tiene números de búsqueda en ETC (10.0636858607265, 13.6623199365962, -10.4626427945330).Este es el artículo nº 1000 de Hechos Geométricos en el Triángulo
A1 =(2a^2(a+b-c)(a-b+c) :
-((a-b+c)(a+b+c)
(a^2-(b-c)(-b+c+Sqrt[a^2+(b-c)^2+
2a(b+c)])+
a(2c+Sqrt[a^2+(b-c)^2+2a(b+c)]))) :
-((a+b-c)(a+b+c)
(a^2-a(-2b+Sqrt[a^2+(b-c)^2+
2a(b+c)])-(b-c)(-b+c+
Sqrt[a^2+(b-c)^2+2a(b+c)])))),
A2 = (2a^2(a+b-c)(a-b+c) :
-((a-b+c)(a+b+c)
(a^2-a(-2c+Sqrt[a^2+(b-c)^2+
2a(b+c)])+(b-c)
(b-c+Sqrt[a^2+(b-c)^2+2a(b+c)]))) :
-((a+b-c)(a+b+c)
(a^2+a(2b+Sqrt[a^2+(b-c)^2+
2a(b+c)])+(b-c)
(b-c+Sqrt[a^2+(b-c)^2+2a(b+c)])))).
W = ( a^2/(3 a^4+2 a^3 (b+c)-2 a^2 (b-c)^2-2 a (b-c)^2 (b+c)-(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en (6.97242915216055, 0.568950218816301, 0.0287316448066879).El 29 de enero de 1860 nació el médico, escritor y dramaturgo ruso Antón Chéjov. Encuadrado en la corriente naturalista, se convertirá en un maestro del relato corto que será magníficamente acogido por escritores y crítica. Entre sus obras dramáticas más conocidas tal vez se encuentren "Tío Vania" y "La gaviota".
Ab=BI∩AA3 = (a:a - c:c), Ac=CI∩AA2 = (a:b:a - b). (coordenadas baricéntricas)
Los puntos Bc, Ba y Ca, Cb, se definen cíclicamente.P1 = (a ((a-c)^2-b^2) (a^3 b (b-c)-a^2 (b^3-4 b c^2+c^3)+a c (b^3-2 b^2 c+c^3)-b^2 (b-c)^2 c) : ... : ...).
P2 = (a ((a-b)^2-c^2) (a^3 c (-b+c)-a^2 (b^3-4 b^2 c+c^3)+a b (b^3-2 b c^2+c^3)-b c^2 (b-c)^2) : ... : ...).
a (a-b-c) (b-c) (a^2+2 b c-a (b+c)) x+b (a-c) (a-b+c) (-a b+b^2+2 a c-b c) y-(a-b) (a+b-c) c (2 a b-(a+b) c+c^2) z=0,
que pasa por los centros del triángulo Xi, para i∈{982, 3663, 4941, 9436, 9950, 11019, 21629, 24210, 24216, 24217, 24241, 30545, 31627, 32023, 33154, 39126, 40593, 44735}.El 25 de enero de 1843 nació Hermann Amandus Schwarz, matemático alemán. Llevó a cabo numerosos trabajos sobre análisis matemático, geometría diferencial y teoría de funciones y transformaciones conformes. Dió una solución geométrica al problema de Fagnano: El , con vértices en los pies de las alturas de un triángulo dado, tiene el perímetro más pequeño de todos los triángulos inscritos en un triángulo agudo.
D2 = (0:b^2+c^2-a^2:2c^2), D3 = (0:2b^2:b^2 + c^2-a^2 ).
Procediendo cíclicamente, se definen los puntos E3, E1 sobre CA y F1, F2 sobre AB.𝒞:
𝔖abc xyz
2 b^2 c^2 (-a^2+b^2-c^2) (a^2+b^2-c^2) (-a^2+b^2+c^2) x^2+
a^2 (a^2+b^2-c^2) (a^2-b^2+c^2) (a^4-2 a^2 (b^2+c^2)+b^4+6 b^2 c^2+c^4) y z = 0.
Z = ( a^2 (a^4-(b^2-c^2)^2) (a^6-b^6-7 b^4 c^2-7 b^2 c^4-c^6+a^4 (b^2+c^2)-a^2 (b^4-6 b^2 c^2+c^4)) : ... : ...),
que tiene números de búsqueda en (1.06061605378784, 1.12734716230681, 2.37067826779297).Po = ( a^2 (a^2-b^2-3 c^2) (a^2-3 b^2-c^2)/ (b^2+c^2-a^2) : ... : ...),
que tiene números de búsqueda en ETC (3.16874807990465, 3.57883919483449, -0.299492536010877).
σ: (x:y:z) ↦
(3 a^2+b^2-c^2) (a^2+3 b^2-c^2) (3 a^2-b^2+c^2) (a^2-b^2+3 c^2) (a^4+b^4+6 b^2 c^2+c^4-2 a^2 (b^2+c^2)) x+
2 a^2 (a^2-b^2-3 c^2) (a^2-3 b^2-c^2) (3 a^2+b^2-c^2) (a^2+3 b^2-c^2) (a^2-b^2+c^2) y+
2 a^2 (a^2-b^2-3 c^2) (a^2-3 b^2-c^2) (a^2+b^2-c^2) (3 a^2-b^2+c^2) (a^2-b^2+3 c^2) z : ... : ...
𝔖abc xyz
4 b^4 c^4 (a^2+b^2-c^2)^2 (a^2-b^2+c^2)^2 (-a^2+b^2+c^2)^2 x^2+
a^4 ((a^2-b^2)^4-4 (a^2-b^2)^3 c^2+2 (3 a^4-6 a^2 b^2+11 b^4) c^4+4 (-a^2+b^2) c^6+c^8) (a^4-(b^2-c^2)^2)^2 y z = 0.
El 24 de enero de1984 sale a la venta la primera computadora Apple Macintosh. Llegando dos elementos claves para el futuro: el GUI (Graphical User Interface) y el ratón.
((a-b-c) (a-b+c)^2 (6 a^2+8 a b+2 b^2+3 a c+3 b c-c^2)-(a-b-c) (a+b-c) (a-b+c) (13 a^2+12 a b+3 b^2+12 a c+12 b c+3 c^2) t+(a-b-c) (a+b-c)^2 (6 a^2+3 a b-b^2+8 a c+3 b c+2 c^2) t^2)x+
((a-b+c)^3 (2 a^2-2 b^2+3 a c+3 b c+3 c^2)-(a+b-c) (a-b+c)^2 (a^2-4 a b-b^2+6 a c+6 b c+5 c^2) t-(a+b-c)^2 (a-b+c) (2 a^2+a b+b^2-4 a c-b c-2 c^2) t^2)y+
(-(a+b-c) (a-b+c)^2 (2 a^2-4 a b-2 b^2+a c-b c+c^2)-(a+b-c)^2 (a-b+c) (a^2+6 a b+5 b^2-4 a c+6 b c-c^2) t+(a+b-c)^3 (2 a^2+3 a b+3 b^2+3 b c-2 c^2) t^2)z=0.
(a-b-c)^2 (25 a^4+48 a^3 b+102 a^2 b^2+80 a b^3+17 b^4+48 a^3 c+164 a^2 b c+176 a b^2 c+60 b^3 c+102 a^2 c^2+176 a b c^2+106 b^2 c^2+80 a c^3+60 b c^3+17 c^4) x^2+2 (a-b-c) (a-b+c) (13 a^4-8 a^3 b+6 a^2 b^2+8 a b^3-3 b^4-14 a^3 c-10 a^2 b c+30 a b^2 c+26 b^3 c-4 a^2 c^2+44 a b c^2+64 b^2 c^2+14 a c^3+38 b c^3+7 c^4) x y+(a-b+c)^2 (17 a^4+6 a^2 b^2-7 b^4+4 a^3 c-8 a^2 b c-4 a b^2 c+8 b^3 c+6 a^2 c^2-16 a b c^2+42 b^2 c^2-12 a c^3+24 b c^3+c^4) y^2+2 (a-b-c) (a+b-c) (13 a^4-14 a^3 b-4 a^2 b^2+14 a b^3+7 b^4-8 a^3 c-10 a^2 b c+44 a b^2 c+38 b^3 c+6 a^2 c^2+30 a b c^2+64 b^2 c^2+8 a c^3+26 b c^3-3 c^4) x z-2 (a+b-c) (a-b+c) (15 a^4-2 a^3 b+12 a^2 b^2+2 a b^3-11 b^4-2 a^3 c+4 a^2 b c+14 a b^2 c-16 b^3 c+12 a^2 c^2+14 a b c^2-6 b^2 c^2+2 a c^3-16 b c^3-11 c^4) y z+(a+b-c)^2 (17 a^4+4 a^3 b+6 a^2 b^2-12 a b^3+b^4-8 a^2 b c-16 a b^2 c+24 b^3 c+6 a^2 c^2-4 a b c^2+42 b^2 c^2+8 b c^3-7 c^4) z^2=0.
El polo de BC respecto a Γ es:
Aa = (2 (a-b-c) (a+b-c) (a-b+c) (a+2 (b+c))^2:
-(a+b-c) (13 a^4+5 b^4+36 b^3 c+62 b^2 c^2+28 b c^3+c^4-2 a^3 (5 b+6 c)+2 a^2 (b^2-6 b c+c^2)+6 a (b^3+6 b^2 c+7 b c^2+2 c^3)):
-(a-b+c) (13 a^4+b^4+28 b^3 c+62 b^2 c^2+36 b c^3+5 c^4-2 a^3 (6 b+5 c)+2 a^2 (b^2-6 b c+c^2)+6 a (2 b^3+7 b^2 c+6 b c^2+c^3))).
Z = ( 5 a^4+17 a^3 (b+c)+a^2 (25 b^2+22 b c+25 c^2)+a (15 b^3+17 b^2 c+17 b c^2+15 c^3) +2 (b^2-c^2)^2 : ... : ...),
que tiene números de búsqueda en (1.81088299248862, 1.79916642684445, 1.55929557448194).(a-b-c) (3 a-b-c) x+(a-3 b+c) (a-b+c) y+(a+b-3 c) (a+b-c) z=0.
W = ( 2 a^3+3 a^2 (b+c)-2 a (5 b^2-6 b c+5 c^2)-3 (b-c)^2 (b+c) : ... : ...),
que tiene números de búsqueda en ETC (5.62902739125691, 5.24629086879998, -2.58939568476495).T = ( (b+c) (a^6+4 a^5 (b+c)+a^4 (5 b^2+6 b c+5 c^2) -a^2 (b-c)^2 (5 b^2+14 b c+5 c^2)-4 a (b-c)^2 (b+c)^3-(b-c)^2 (b+c)^4) : ... : ...),
que tiene números de búsqueda en ETC (-2.94069643343172, -3.27589360843290, 7.26583533394487).El 22 de enero de 1788 nació George Gordon Byron, «Lord Byron», poeta británico y gran exponente del Romanticismo que se involucró en la guerra de independencia de Grecia del imperio otomano. Byron encarnó para sus coetáneos el ideal del héroe romántico, tanto en su obra como en su vida, y como tal fue considerado y admirado por no pocos escritores.
Ab = (a (a^2 - b^2 + c^2) : c (a^2 + b^2 - c^2) : c (a^2 - b^2 + c^2)),
Ac = (a (a^2+b^2-c^2) : b (a^2+b^2-c^2) : b (a^2-b^2+c^2)).
A' = (a^3-3 a (b-c)^2+2 (b-c)^2 (b+c) : b (a^2-2 a b+b^2+2 a c+2 b c-3 c^2) : c (a^2-3 b^2+2 a (b-c)+2 b c+c^2)).
Z = ( (b-c) (-a+b+c)^2 (-2 a^5+8 a^3 (b-c)^2+a^4 (b+c)-10 a^2 (b-c)^2 (b+c)+(b-c)^4 (b+c)+2 a (b-c)^2 (b^2+6 b c+c^2)) (-9 a^6+a^2 (b-c)^4+14 a^5 (b+c)+(b-c)^4 (3 b^2+10 b c+3 c^2)+a^4 (5 b^2-58 b c+5 c^2)-2 a (b-c)^2 (b^3-9 b^2 c-9 b c^2+c^3)-4 a^3 (3 b^3-7 b^2 c-7 b c^2+3 c^3)) : ... : ...),
que tiene números de búsqueda en (-12.1613797032153, 13.7912948075130, -0.294210521809865).El 20 de enero de 1971 falleció, a los 87 años de edad, Jan Arnoldus Schouten, matemático holandés y profesor en la Universidad Tecnológica de Delft . Fue un importante contribuyente al desarrollo del cálculo tensorial y el cálculo de Ricci. Estuvo estimulado por la teoría de la relatividad general de Albert Einstein.
Ab = ((a^2+b^2-c^2) (4 a^4+b^4-3 b^2 c^2+2 c^4-a^2 (b^2+6 c^2) :
b^2 (a^2+b^2-c^2) (-5 a^2+b^2+c^2) :
-(a^2-b^2-c^2) (4 a^4+b^4-3 b^2 c^2+2 c^4-a^2 (b^2+6 c^2))),
Ac = ((a^2-b^2+c^2) (4 a^4+2 b^4-3 b^2 c^2+c^4-a^2 (6 b^2+c^2)):
-(a^2-b^2-c^2) (4 a^4+2 b^4-3 b^2 c^2+c^4-a^2 (6 b^2+c^2)):
c^2 (a^2-b^2+c^2) (-5 a^2+b^2+c^2)).
W = ((b^2+c^2-a^2) (a^6-7 a^4 (b^2+c^2)+a^2 (3 b^4-2 b^2 c^2+3 c^4)-(b^2-c^2)^2 (b^2+c^2)) : ... : ...),
que tiene números de búsqueda en 9.46043181410876, 16.8952312946362, -12.4223872516601).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
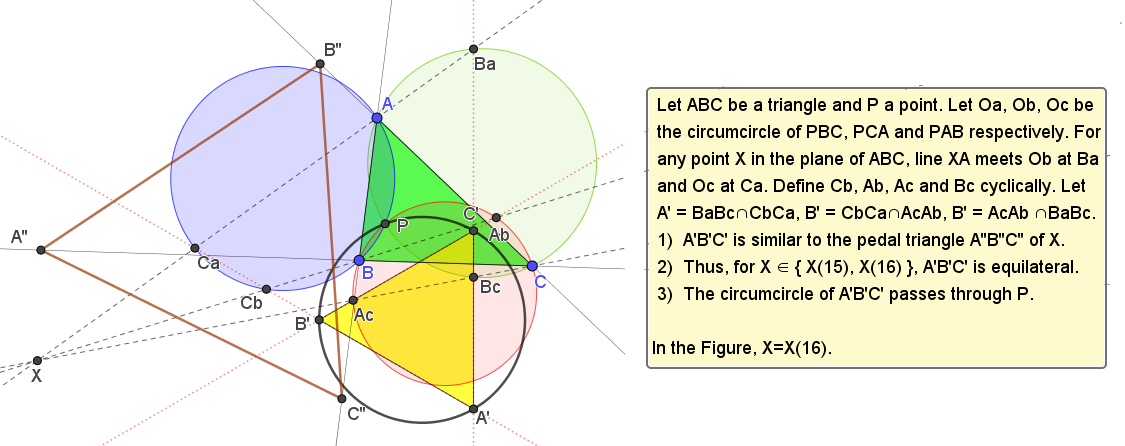
{1, 4, 1837}, {2, 4, 43448}, {3, 1, 7335}, {4, 1, 56}, {4, 3, 26917}.
La expresión de la primera coordenada baricéntrica del centro de semejanza de los triángulos DEF y A'B'C' , en el caso general, si P(p:q:r) y U(u:v:w), es:((a^2-c^2) v+b^2 (2 u+v)) ((-a^2+b^2) w-c^2 (2 u+w)) (-c^4 p q r u^2 v (u+w)+r w^2 (b^4 p q u^2-a^4 p q v (u+w)-a^2 b^2 (q r u^2+p u (q u-q v-r v)+p^2 v w))+c^2 (-a^2 q v (u+w) (r^2 u^2+p^2 w^2)+b^2 p u^2 (-r^2 u v-p q w^2+r w (p v+q v-q w)))) (b^4 p q r u^2 (u+v) w+q v^2 (-c^4 p r u^2+a^4 p r (u+v) w+a^2 c^2 (q r u^2+p^2 v w+p u (r u-q w-r w)))+b^2 (a^2 r (u+v) (q^2 u^2+p^2 v^2) w+c^2 p u^2 (p v (r v-q w)+q (r v (v-w)+q u w))))+(b^6 p q (p+q) u^2 (u+v) w^2+b^4 (-a^2 (u+v) (q^2 r u^2+p q u (q (u-2 v)-2 r v)+p^2 (q u (u-2 v)+r v^2)) w^2+c^2 p u^2 (q^2 v (u+v-2 w) w-q r u v (2 u+2 v+w)+p r v^2 (2 u+2 v+w)+p q w (v (v-w)+u (v+w))))-q v^2 (a^6 p (p+q) (u+v) w^2+c^6 p u^2 (-q (2 u+w)+p (2 v+w))+a^4 c^2 (p u (p (u+v-2 w) w-r v (2 u+2 v+w))+q (r u^2 (2 u+2 v+w)+p w (u^2+u v-u w+v w)))+a^2 c^4 (-q r u^2 (2 u+w)+p u (r v (2 u+w)+q (2 u^2+2 u v+v w))-p^2 (v w^2+2 u^2 (v+w)+u (2 v^2+v w-w^2))))+b^2 (a^4 (u+v) (p^2 r v^2+p q v (-2 r u+p (-2 u+v))+q^2 (r u^2+p v (-2 u+v))) w^2+c^4 p u^2 (-p r v^2 (2 v+w)+q v (2 p v^2+p u (2 v+w)+r u (2 v+w))-q^2 (2 u^2 v+v (2 v-w) w+u (2 v^2+v w+w^2)))+a^2 c^2 (-p q v w (r u (u-v) (u+v-2 w)+p (u^3-u v (v-3 w)-2 u^2 w+v^2 w))+p^2 r v^2 (v w^2+u^2 (2 v+w)+u (2 v^2+2 v w-w^2))-q^2 u (-p w (v^2 (v-2 w)+3 u v w+u^2 (-v+w))+r u (2 u^2 v+v (v-w) w+u (2 v^2+2 v w+w^2)))))) (a^6 p r (p+r) v^2 w^2 (u+w)+a^4 (-c^2 v^2 (u+w) (-p r (p+r) (2 u-w) w+q (r u-p w)^2)+b^2 r w^2 (q u (2 u+v+2 w) (r u-p w)+p v (p u (u-2 v+w)+r (u^2-u v+u w+v w))))-p u^2 (c^6 r (p+r) v^2 (u+w)+b^6 r w^2 (r (2 u+v)-p (v+2 w))+b^4 c^2 (-p q w^2 (v+2 w)+r w (2 p w^2+p u (v+2 w)+q u (v+2 w))-r^2 (2 u^2 w-v (v-2 w) w+u (v^2+v w+2 w^2)))+b^2 c^4 (r w (r v (u-2 v+w)-q u (2 u+v+2 w))+p (q w^2 (2 u+v+2 w)+r v (w (-v+w)+u (v+w)))))+a^2 (c^4 v^2 (u+w) (q r^2 u^2+p r u (r (u-2 w)-2 q w)+p^2 (r u (u-2 w)+q w^2))+b^4 r w^2 (-q r u^2 (2 u+v)+p u (q (2 u+v) w+r (2 u^2+2 u w+v w))-p^2 (v^2 w+2 u^2 (v+w)+u (-v^2+v w+2 w^2)))+b^2 c^2 (q r^2 u^2 (2 u^2 w+v w (-v+w)+u (v^2+2 v w+2 w^2))-p r u v (-q (u-w) w (u-2 v+w)+r (u^2 (v-w)+3 u v w+w^2 (-2 v+w)))+p^2 w (r v (u^3-2 u^2 v+u (3 v-w) w+v w^2)-q w (v^2 w+u^2 (v+2 w)+u (-v^2+2 v w+2 w^2)))))).
El 18 de Enero de 1867 nació Ruben Darío, poeta nicaragüense que jugó un papel decisivo en el movimiento literario hispanoamericano conocido como Modernismo, por su obra "Azul...". Considerado uno de los poetas en lengua española más importantes de finales del siglo XIX y principios del XX.
Pab=((a+b-c) (a-b+c) (a+b+c)^2:4 b^2 (a+b-c) (-a+b+c):-(a-b-c) (a-b+c)^3),
Pac=((-a+b-c) (a+b-c)^3:-(a+b-c) (-a+b+c) (a+b+c)^2:-4 c^2 (a-b+c) (-a+b+c)).
A1 = (a^6+2 a^5 (b+c)+4 a^3 b c (b+c)-(b-c)^4 (b+c)^2-a^2 (b^2-c^2)^2+a^4 (b^2+6 b c+c^2)-2 a (b^5-b^4 c-b c^4+c^5):
2 b^2 (-a^4+b^4-2 a^3 (b-c)+4 a^2 (b-c) c+2 b^2 c^2-3 c^4+2 a (b^3+b^2 c-b c^2+3 c^3)):
2 c^2 (-a^4-3 b^4+2 a^3 (b-c)-4 a^2 b (b-c)+2 b^2 c^2+c^4+2 a (3 b^3-b^2 c+b c^2+c^3))).
Z = ( a^2/((b + c-a) (3 a^2 + b^2 + 2 b c + c^2)) : ... : ...),
que tiene números de búsqueda en (0.226011977654606, 0.531652016310703, 3.16828448092869).Z = 2R(2r^2+4r R-s^2) X1 - r(4r R-s^2) X1350.
Las rectas AP'a, BP'b, CP'c concurren en X57.
El de Pa P'b Pc P'a Pb P'c es
W = (a (a + b - c) (a - b + c) (3 a^4 (b + c) + a^3 (6 b^2 + 8 b c + 6 c^2) + 4 a^2 (b^3 + 4 b^2 c + 4 b c^2 + c^3) + 2 a (b^4 + 6 b^3 c + 2 b^2 c^2 + 6 b c^3 + c^4)+ (b - c)^2 (b + c)^3 ) : ... : ...),
que tiene números de búsqueda en ETC (0.271168450005640, 0.567383057640635, 3.12270615738441).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
D' = (a^2 (a+b-c) (a-b+c):b(b-c) (a+b-c) (-a+b+c):c(a-b-c) (b-c)(a-b+c)).
Ab=((a+b-c) (b+c) (a^3-b^2 c+c^3-a^2 (b+c)-a c (b+c)):b^2 (a+b-c) (b+c) (-a+b+c):-(a-b-c) c (a^3-b^2 c+c^3-a^2 (b+c)-a c (b+c))),
Ac=((a-b+c) (b+c) (a^3+b^3-b c^2-a^2 (b+c)-a b (b+c)):b (-a+b+c) (a^3+b^3-b c^2-a^2 (b+c)-a b (b+c)):-(a-b-c) c^2 (a-b+c) (b+c)).
A2 = (a^10-2 a^9 (b+c)-b (b-c)^4 c (b+c)^2 (b^2+b c+c^2)-a^8 (2 b^2+b c+2 c^2)+a^6 b c (4 b^2+13 b c+4 c^2)+6 a^7 (b^3+b^2 c+b c^2+c^3)+a b^2 (b-c)^2 c^2 (b^3+7 b^2 c+7 b c^2+c^3)-a^2 (b^2-c^2)^2 (b^4-4 b^3 c-3 b^2 c^2-4 b c^3+c^4)-3 a^5 (2 b^5+2 b^4 c+3 b^3 c^2+3 b^2 c^3+2 b c^4+2 c^5)+a^4 (2 b^6-6 b^5 c-17 b^4 c^2-14 b^3 c^3-17 b^2 c^4-6 b c^5+2 c^6)+2 a^3 (b^7+b^6 c+b^5 c^2-7 b^4 c^3-7 b^3 c^4+b^2 c^5+b c^6+c^7):
b^2 (-a^8+2 a^6 b^2+2 a^7 (b+c)-2 a^2 b^3 (b-2 c) (b+c)^2+(b^2-c^2)^3 (b^2+c^2)-a^5 (6 b^3+6 b^2 c+3 b c^2+2 c^3)+a^4 (-4 b^2 c^2+2 c^4)+a^3 (6 b^5+6 b^4 c+4 b^3 c^2+6 b^2 c^3-2 c^5)+a (-2 b^7-2 b^6 c-b^5 c^2+2 b^3 c^4+b c^6+2 c^7)):
c^2 (-a^8+2 a^6 c^2+2 a^7 (b+c)+2 a^2 (2 b-c) c^3 (b+c)^2-(b^2-c^2)^3 (b^2+c^2)+2 a^4 (b^4-2 b^2 c^2)-a^5 (2 b^3+3 b^2 c+6 b c^2+6 c^3)+a^3 (-2 b^5+6 b^3 c^2+4 b^2 c^3+6 b c^4+6 c^5)+a (2 b^7+b^6 c+2 b^4 c^3-b^2 c^5-2 b c^6-2 c^7))).
W = ( a^2/(a^7-a^6 (b+c)-a^5 (b^2+b c+c^2)+a^4 (b^3+c^3)-a^3 (b^4+b^3 c+b c^3+c^4)+a^2 (b+c)^3 (b^2-3 b c+c^2)+a (b-c)^2 (b+c)^4-(b-c)^4 (b+c)^3) : ... : ...),
que tiene números de búsqueda en ETC (1.04239292068923, 3.46873354492885, 0.758129141253992).El 17 de enero dee1944 nació Françoise Hardy, cantante francesa, una de las figuras más icónicas de los años sesenta en Francia. En abril de 1962, su primer disco Oh Oh Chéri lleva en la cara B la composición Tous les garcons et les filles, escrita por ella y que se convirtió en un enorme éxito europeo grabándose también en italiano (Quelli Della Mia Etá).
Ua = (2 (a (b^2-c^2) (q u+r u-p (v+w))+a^3 (r (u+2 v)+p (v-w)-q (u+2 w)))^2:
-(b^2-c^2)^3 ((q+r) u+p (2 u+v+w))^2-a^6 (r^2 (u+2 v)^2+q^2 (9 u^2+8 u v+12 u w+4 w^2)+2 q r (3 u^2-4 v w+2 u (v+w))+p^2 (4 u^2+(v-w)^2+4 u (v+w))+2 p (r (2 u^2+2 v (v-w)+u (3 v+w))+q (6 u^2+2 w (-v+w)+u (5 v+7 w))))+a^4 (c^2 (r^2 (3 u^2+8 u v+4 v^2)+p^2 (12 u^2-v^2-2 v w+3 w^2+12 u (v+w))+q^2 (15 u^2+4 w^2+16 u (v+w))+2 q r (7 u^2-4 v w+4 u (2 v+w))+2 p (r (6 u^2+7 u v+3 u w-4 v w)+q (14 u^2+4 w^2+15 u (v+w))))+b^2 (-r^2 (3 u^2+8 u v+4 v^2)+2 q r (9 u^2+8 u v+12 u w+4 v w)+p^2 (4 u^2+v^2+2 v w-3 w^2+4 u (v+w))+q^2 (17 u^2-4 w^2+16 u (v+w))+2 p (q (10 u^2-4 w^2+9 u (v+w))+r (2 u^2+4 v w+u (v+5 w)))))+a^2 (b^2-c^2) (b^2 (-(q+r) u (7 q u+3 r u+8 q v+4 r v+4 q w)+p^2 (4 u^2+v^2-2 v w-3 w^2+4 u (v+w))-2 p q (2 u^2+2 w (v+w)+u (3 v+w))+2 p r (2 u^2+2 v (v+w)+u (3 v+5 w)))+c^2 ((q+r) u (7 q u+3 r u+8 q v+4 r v+4 q w)+p^2 (12 u^2-v^2+2 v w+3 w^2+12 u (v+w))+2 p (r (6 u^2-2 v (v+w)+u (5 v+3 w))+q (10 u^2+2 w (v+w)+u (11 v+9 w))))):
(b^2-c^2)^3 ((q+r) u+p (2 u+v+w))^2-a^6 (q^2 (u+2 w)^2+r^2 (9 u^2+12 u v+4 v^2+8 u w)+2 q r (3 u^2-4 v w+2 u (v+w))+p^2 (4 u^2+(v-w)^2+4 u (v+w))+2 p (q (2 u^2+2 w (-v+w)+u (v+3 w))+r (6 u^2+2 v (v-w)+u (7 v+5 w))))+a^4 (b^2 (q^2 (3 u^2+8 u w+4 w^2)+p^2 (12 u^2+3 v^2-2 v w-w^2+12 u (v+w))+r^2 (15 u^2+4 v^2+16 u (v+w))+2 q r (7 u^2-4 v w+4 u (v+2 w))+2 p (q (6 u^2+3 u v+7 u w-4 v w)+r (14 u^2+4 v^2+15 u (v+w))))+c^2 (2 q r (9 u^2+12 u v+8 u w+4 v w)-q^2 (3 u^2+8 u w+4 w^2)+p^2 (4 u^2-3 v^2+2 v w+w^2+4 u (v+w))+r^2 (17 u^2-4 v^2+16 u (v+w))+2 p (r (10 u^2-4 v^2+9 u (v+w))+q (2 u^2+4 v w+u (5 v+w)))))-a^2 (b^2-c^2) (c^2 (-(q+r) u (3 q u+7 r u+4 r v+4 q w+8 r w)+p^2 (4 u^2-3 v^2-2 v w+w^2+4 u (v+w))+2 p (-r (2 u^2+2 v (v+w)+u (v+3 w))+q (2 u^2+2 w (v+w)+u (5 v+3 w))))+b^2 ((q+r) u (3 q u+7 r u+4 r v+4 q w+8 r w)+p^2 (12 u^2+3 v^2+2 v w-w^2+12 u (v+w))+2 p (q (6 u^2-2 w (v+w)+u (3 v+5 w))+r (10 u^2+2 v (v+w)+u (9 v+11 w)))))).
(P, U) ↦ Up=Φ(P,U) =
=(a^2 u)/((b^2-c^2)^2 ((q+r) u+p (2 u+v+w))^2+a^4 (p^2 (4 u^2+(v-w)^2+4 u (v+w))+(r (u+2 v)-q (u+2 w))^2+2 p (r (2 u^2+2 v (v-w)+u (3 v+w))+q (2 u^2+2 w (-v+w)+u (v+3 w))))-2 a^2 (c^2 (p^2 (4 u^2-v^2+w^2+4 u (v+w))-(q+r) u (-r (u+2 v)+q (u+2 w))+2 p (r (2 u^2-v (v+w)+u (2 v+w))+q (2 u^2+w (v+w)+u (3 v+2 w))))+b^2 (p^2 (4 u^2+v^2-w^2+4 u (v+w))+(q+r) u (-r (u+2 v)+q (u+2 w))+2 p (q (2 u^2-w (v+w)+u (v+2 w))+r (2 u^2+v (v+w)+u (2 v+3 w)))))): :
A Aye por su cumple
Pa = (2 a^2 (a^4 (u^2-(v-w)^2)+(b^2-c^2)^2 (u^2-(v+w)^2)-2 a^2 (c^2 (u^2+v^2-w^2)+b^2 (u^2-v^2+w^2))):
(a^2+b^2-c^2) ((b^2-c^2)^2 (u+v+w)^2+a^4 (u^2+(v-w)^2+2 u (v+w))-2 a^2 (b^2 (u^2+v^2-w^2+2 u (v+w))+c^2 (u^2-v^2+w^2+2 u (v+w)))):
(a^2-b^2+c^2) ((b^2-c^2)^2 (u+v+w)^2+a^4 (u^2+(v-w)^2+2 u (v+w))-2 a^2 (b^2 (u^2+v^2-w^2+2 u (v+w))+c^2 (u^2-v^2+w^2+2 u (v+w))))).
P' = (a^2 u)/(a^4 (-3 u^2+(v-w)^2-2 u (v+w))+2 a^2 (c^2 (u^2+v^2-w^2)+b^2 (u^2-v^2+w^2))+(b^2-c^2)^2 (u+v+w)^2) : :
(b-c) (a^5-b^5+b^4 c+b c^4-c^5-a^4 (b+c)+a^3 (-2 b^2+b c-2 c^2)+2 a^2 (b^3+b^2 c+b c^2+c^3)+a (b^4-3 b^3 c-3 b c^3+c^4))x + ... =0,
que pasa por los centros del triángulo Xi, para i∈{484, 516, 1737, 2957, 2958, 3583, 6840, 34529, 37718, 37787, 45043, 51768}.El 12 de enero de 1628 nació Charles Perrault, escritor y abogado francés autor de cuentos infantiles como: "Barba Azul", "La Bella durmiente", "Cenicienta", "El Gato con Botas", "Piel de Asno", "Caperucita Roja" y "Pulgarcito".
A1 = (2 a^6 (b + c)^5 :
-(a^4 (b + c)^3 (2 a^4 -
2 a^3 Sqrt[(b - s) (c - s)] +
2 a Sqrt[(b - s) (c - s)] (b + c)^2 -
(b - c) (b + c)^3 + a^2 (b^2 - 2 b c - 3 c^2))) :
-(a^4 (b + c)^3 (2 a^4 -
2 a^3 Sqrt[(b - s) (c - s)] +
2 a Sqrt[(b - s) (c - s)] (b + c)^2 +
(b - c) (b + c)^3 + a^2 (-3 b^2 - 2 b c + c^2)))),
A2 = (2 a^6 (b + c)^5:
a^4 (b + c)^3 (-2 a^4 -
2 a^3 Sqrt[(b - s) (c - s)] +
2 a Sqrt[(b - s) (c - s)] (b + c)^2 +
(b - c) (b + c)^3 + a^2 (-b^2 + 2 b c + 3 c^2)):
-(a^4 (b + c)^3 (2 a^4 +
2 a^3 Sqrt[(b - s) (c - s)] -
2 a Sqrt[(b - s) (c - s)] (b + c)^2 +
(b - c) (b + c)^3 + a^2 (-3 b^2 - 2 b c + c^2)))).
Oa=(2 a^2 (2 a^2-3 (b+c)^2):(b+c)^2 (a^2+b^2-c^2):-(b+c)^2 (-a^2+b^2-c^2)).
Procediendo cíclicamente, se definen Ob y Oc.U = ( a^2 (a^8-7 a^6 (b^2+c^2) -2 a^5 b c (b+c) +a^4 (15 b^4+19 b^2 c^2+15 c^4) +2 a^3 b c (2 b^3+5 b^2 c+5 b c^2+2 c^3) +a^2 (-13 b^6+13 b^4 c^2+4 b^3 c^3+13 b^2 c^4-13 c^6) -2 a b c(b-c)^2 (b^3+6 b^2 c+6 b c^2+c^3) +(b^2-c^2)^2 (4 b^4-17 b^2 c^2+4 c^4)) : ... : ...),
que tiene números de búsqueda en (0.0347580475793658, 0.0408162473353115, 3.59636490410023).Si tu experimento necesita estadística, deberías haber hecho uno mejor. Ernest Rutherford (Premio Nobel de Química de 1908)
Las rectas AbAc, BcBa, CaCb son concurrentes (en el baricentro) si y solo si P está sobre la no pivotal nK0(X32,X6).
dab: a^2 b^2 v w^2 x+v (c^2 u+a^2 w) (c^2 v+b^2 w) y-b^2 u w (c^2 v+b^2 w) z=0,
dac: a^2 c^2 v^2 w x-c^2 u v (c^2 v+b^2 w) y+(b^2 u+a^2 v) w (c^2 v+b^2 w) z=0.
Parábola 𝒫a, inscrita en el triángulo medial y con punto en el infinito D*:
-b^2 c^2 v w x^2+c^2 v (c^2 v+b^2 w) y^2+b^2 w (c^2 v+b^2 w) z^2=0.
Ab = ((c^2 v+b^2 w) (c^4 u^2 v+c^2 u (b^2 u+2 a^2 v) w+a^4 v w^2):b^2 w (c^4 u^2 v+b^2 c^2 u^2 w-a^4 v w^2):
c^2 v (c^4 u^2 v+c^2 u (b^2 u+2 a^2 v) w+a^2 (2 b^2 u+a^2 v) w^2)),
Ac = ((c^2 v+b^2 w) (b^4 u^2 w+a^4 v^2 w+b^2 u v (c^2 u+2 a^2 w)):b^2 w (b^4 u^2 w+a^2 v^2 (2 c^2 u+a^2 w)+b^2 u v (c^2 u+2 a^2 w)):
c^2 v (b^2 c^2 u^2 v+b^4 u^2 w-a^4 v^2 w)).
A' = (a^2 (c^6 u v^3+c^4 v^2 (-b^2 u+a^2 v) w+b^2 c^2 v (-b^2 u+a^2 v) w^2+b^4 (b^2 u+a^2 v) w^3):
-b^2 (c^6 u^2 v^2+3 c^4 u v (b^2 u+a^2 v) w+2 c^2 (b^4 u^2+a^2 b^2 u v+a^4 v^2) w^2+a^2 b^2 (b^2 u+a^2 v) w^3):
-c^2 (b^6 u^2 w^2+a^2 c^2 v^3 (c^2 u+a^2 w)+3 b^4 u v w (c^2 u+a^2 w)+2 b^2 v^2 (c^4 u^2+a^2 c^2 u w+a^4 w^2)).
a^2 x (c^4 y^2+b^4 z^2)+b^2 y (c^4 x^2+a^4 z^2)+c^2 z(b^4 x^2+a^4 y^2) = 0.
Q = a^2/(b^4 u^2 w (c^2 u+2 a^2 w)+a^2 v^2 (2 c^4 u^2+3 a^2 c^2 u w+a^4 w^2)+b^2 u v (c^4 u^2+2 a^2 c^2 u w+3 a^4 w^2)) : ... : ...
• Si P es el simediano, Q es el baricentro.W = ( 1/(a^8-6 a^4 (b^2-c^2)^2-(b^2-c^2)^2 (3 b^4+2 b^2 c^2+3 c^4)+8 a^2 (b^6-2 b^4 c^2-2 b^2 c^4+c^6)) : ... : ...),
que tiene números de búsqueda en (-2.64298225182020, -2.92819464433429, 6.88771412113283).Q1 = ( a/(a^3 + 3 a^2 (b + c) + b c (b + c) + 2 a (b^2 + b c + c^2)) : ... : ...),
que tiene números de búsqueda en ETC (2.20271384366679, 1.76815731285784, 1.39991841439043).Q2 = ( a^2/(a^6 + 3 a^4 (b^2 + c^2) + b^2 c^2 (b^2 + c^2) + 2 a^2 (b^4 + b^2 c^2 + c^4)) : ... : ...),
que tiene números de búsqueda en ETC (1.74471854891119, 1.78922506406983, 1.59671549190010).El 1 de enero de 1972, se adoptó la hora universal coordinada (UTC) en todo el mundo. UTC se determina a partir de una media ponderada de las señales de los relojes atómicos, localizados en cerca de 70 laboratorios nacionales de todo el mundo que son coordinados por la Oficina Internacional de Pesas y Medidas ubicada en Francia (https://dayspedia.com/time/zones/utc-about/?lang=es)
ℓ'a: (a^2 v w-(b+c) (v+w) (c v+b w)) x-a^2 w^2 y-a^2 v^2 z=0,
ℓ"a: (a^2 v w-c^2 v (v+w)-b^2 w (v+w)-b c (v+w)^2) x-a^2 w^2 y-a^2 v^2 z=0,
A1 = (a^4 v (u+v) w (u+w)-a^3 (u+v) (u+w) (b (u+v) w+c v (u+w))-(b^2-c^2) u^2 (b^2 (u+v) w-c^2 v (u+w))-a u (-b^3 (u+v)^2 w+b c^2 (u+v)^2 (u+w)-c^3 v (u+w)^2+b^2 c (u+v) (u+w)^2)+a^2 (c^2 u v (u+v-w) (u+w)+b c (u+v)^2 (u+w)^2+b^2 u (u+v) w (u-v+w)):
b^2 (-(a-b) (u+v) (-b u+a v) w^2+c^2 u v (u v+w^2)):
c^2 (-c^2 u v^2 (u+w)-a^2 v^2 w (u+w)+a c v^2 (u+w)^2+b^2 u w (v^2+u w)),
A2 = (a^4 v (u+v) w (u+w)+a^3 (u+v) (u+w) (b (u+v) w+c v (u+w))-(b^2-c^2) u^2 (b^2 (u+v) w-c^2 v (u+w))+a u (-b^3 (u+v)^2 w+b c^2 (u+v)^2 (u+w)-c^3 v (u+w)^2+b^2 c (u+v) (u+w)^2)+a^2 (c^2 u v (u+v-w) (u+w)+b c (u+v)^2 (u+w)^2+b^2 u (u+v) w (u-v+w)):
-b^2 ((a+b) (u+v) (b u+a v) w^2-c^2 u v (u v+w^2)):
-c^2 (c^2 u v^2 (u+w)+a^2 v^2 w (u+w)+a c v^2 (u+w)^2-b^2 u w (v^2+u w))).
P1 =a^2/(a^2 v w (u^2+v w)+(b-c) u^2 (v+w) (c v-b w)) : ... : ....
Las rectas AA2, BB2, CC2 concurren en:P2 = a^2/(a^2 v w (u^2+v w)-(b+c) u^2 (v+w) (c v+b w)) : ... : ....
W = ( a (2 a^2+3 a b+2 b^2-c^2) (2 a^2-b^2+3 a c+2 c^2) : ... : ...),
que tiene números de búsqueda en (0.720348390617527, 1.04277786563638, 2.58627285618187).
.png)
-ISODYNAMIC.png)
.png)
c.png)
b.png)
d.png)
.png)
.png)
b.png)
.png)
X(406)-X(319)X(3718).png)
.png)
.png)
.png)
.png)
p.png)
h.png)
t.png)
6.png)
.png)
.png)
.png)
.png)
.png)
.png)
c.png)
e.png)
b.png)
.png)
.png)
b.png)
.png)
.png)
b.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
X3.png)
