- Miércoles, 30 de diciembre del 2020
Generalización de la construcción de los centros X(479) y X(5423)
El 30 de diciembre de 1896, en Manila (Filipinas), se procede a la ejecución, por las autoridades españolas, de José Rizal. Por instigación de las órdenes religiosas de dominicos y franciscanos, Rizal fue acusado de asociación ilícita. Fue un médico, escritor, pintor, lingüista y político filipino.
Let A' be the point in which the incircle is tangent to a circle that passes through vertices B and C, and define B' and C' cyclically. The lines AA', BB', CC' concur in
X(479). For an excircle version, see X(5423).
Clark Kimberling and Peter Yff, Problem 10678, American Mathematical Monthly 105 (1998) 666.
Let A' be the point in which the A-excircle is tangent to the circle OA that passes through vertices B and C, and define B' and C' cyclically. The lines AA', BB', CC' concur in
X(5423); for the incircle version, see X(479). (Peter Moses, December 10, 2015)
Dado un triángulo ABC con incentro I=X1 y Ia, Ib, Ic, sean D y D' las proyecciones ortogonales de I y Ia sobre el lado BC, respectivamente.
Se concidera la circunferencia Γa que pasa por B, C y el punto Dt, que divide al segmento DIa en la razón t (DDt:DtIa=t, t número real).
Si Oa es el centro de Γa, sea Pa=DIa∩IOa; Pa es el , respecto a la a ABC, del de ésta y Γa. Los puntos Pb y Pc, se definen cíclicamente.
Utilizando coordenadas baricéntricas, la ecuación del eje radical, eA, de las circunferencias inscrita y Γa es:
eA: ((b - c)^2 (b + c) (-1 + 2 t) + a (b - c)^2 (1 - 3 t + t^2) +
a^3 (-1 + t + t^2) - a^2 (b + c) (-1 + 2 t^2)) x +
a (a - b + c)^2 t (1 + t) y + a (a + b - c)^2 t (1 + t) z = 0.
Pa =(-2 a^2 (a + b - c) (a - b + c) t (1 + t) :
(a + b -
c) (a^3 - (b - c)^2 (b + c) (-1 + 2 t) -
a^2 (b + c + 2 c t - 2 b t^2) -
a (c^2 (1 - 4 t) - 2 b c (1 - 3 t + t^2) +
b^2 (1 - 2 t + 2 t^2))) :
(a - b +
c) (a^3 - (b - c)^2 (b + c) (-1 + 2 t) -
a^2 (b + c + 2 b t - 2 c t^2) +
a (b^2 (-1 + 4 t) + c^2 (-1 + 2 t - 2 t^2) +
2 b c (1 - 3 t + t^2)))).
Los triángulos
ABC y
PaPbPc son perspectivos si y solo si
t = -1, t = 0, t =1/2, t = 1, t = - r/(2R).
Para t = -1 , t = 0, la circunferencia Γa degenera en la recta BC, y el centro de perspectividad es el .
Para t = 1/2, el centro el perspectividad P½ es X21314
AoPS (brokendiamond, Aug 20, 2018)
Let
ABC be the triangle with incircle (I). (I) touch
BC,CA,AB at
D,E,F, respectively .
Ge is the Gergone point of
ABC.
AD cuts (I) at
M,D . Similarly for
N,P. Prove that the radical center of (
ANP), (
BMP), (
CMN) lies on
IGe (Soddy Line).
Hyacinthos 28065 (César Lozada, Sunday, October 27, 2019)
The radical center of the three circles is
X(21314):= X(1)X(7) ∩ X(57)X(1358); (a^2+(b+c)a-2(b-c)^2)(a+b-c)(a-b+c) : ... : ...
Cuando t = 1, es decir cuando se toma el punto medio del segmento DIa, la circunferencia Γa es tangente a la circunferencia inscrita y el centro de perspectividad de ABC y PaPbPc es X479.
Cuando t = -r/(2R), r y R son los radios de las circunferencias inscrita y circunscrita, el centro de perspectividad W=P-r/(2R) es:
W = ( a/( (b + c-a) (3 a^3 - 5 a^2 (b + c) +
a (b + c)^2 + (b - c)^2 (b + c)) ) : ... : ...),
que tiene números de búsqueda en
(5.54644081156577, 0.374217693310462, 0.821694935046781).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,15728}, {7,24389}, {269,3660}.
El triángulo formado por los ejes radicales
eA,
eB y
eC es perspectivo con
ABC. El lugar geométrico del centro de perspectividad,
Zt (cuando t varía), es la
circun-hipérbola
( (a c - b c) x y + (-a b + b c) x z + (a b - a c) y z = 0)
de centro X(1015) [centro de homotecia exterior de la y la circunferencia inscrita]. Es la conjugada isogonal de la recta que pasa por el incentro y simediano.
Zt = (a/(a^3-a^2 (b+c) (1+2 t)-a (b^2 (1-4 t)+c^2 (1-4 t)-2 b c (1-2 t+2 t^2))-(b-c)^2 (b+c) (-1+2 t)) : ... : ...)=
=(a/(4 a b c t^2 -2 (a^2 (b + c) + (b - c)^2 (b + c) -
2 a (b^2 - b c + c^2))t + a^3 - a (b - c)^2 -
a^2 (b + c) + (b - c)^2 (b + c)) : ... : ...).
Casos particulares:
Cuando t=1/2, Z½ = X(34578) .
Cuando t= 2, Z2 = X(39980) .
Cuando t=-r/(2R), Zt es X57= DIa∩EIb∩FIc. En este punto concurren las tres circunferencias Γa, Γb, Γc.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
VERSIÓN CIRCUNFERENCIAS EXINSCRITAS
Se concidera la circunferencia Γ'a que pasa por B, C y el punto D't, que divide al segmento IIaa en la razón t (ID't:D'tIaa=t, t número real). Sea P'a el polo, respecto a la a ABC, del eje radical de ésta y Γ'a. Los puntos P'b y P'c, se definen cíclicamente.
En coordenadas baricéntricas, la ecuación del eje radical, e'A, de las circunferencias A-exinscrita y Γ'a es:
e'A: ((b-c)^2 (b+c) (-2+t) t+a^3 (1+t-t^2)-a^2 (b+c) (-2+t^2)+a (b-c)^2 (1-3 t+t^2)) x+a (a+b-c)^2 (1+t) y+a (a-b+c)^2 (1+t) z = 0.
P'a =(-2 a^2 (a+b-c) (a-b+c) (1+t) :
(a-b+c) (-(b-c)^2 (b+c) (-2+t) t+a^3 t^2+a^2 (c t (2+t)+b (-2+t^2))-a (c^2 (-4+t) t-2 b c (1-3 t+t^2)+b^2 (2-2 t+t^2))) :
(a+b-c) (-(b-c)^2 (b+c) (-2+t) t+a^3 t^2+a^2 (b t (2+t)+c (-2+t^2))-a (b^2 (-4+t) t-2 b c (1-3 t+t^2)+c^2 (2-2 t+t^2)))).
Los triángulos
ABC y
P'aP'bP'c son perspectivos si y solo si
t = -1, t = 0, t = 1, t = (r±Sqrt[r (r+2 R)])/r.
Para t = -1 la circunferencia Γa degenera en la recta BC, y el centro de perspectividad es el .
Para t = 0, los puntos P'a, P'b, P'c coinciden con el incentro.
Cuando t = 1, es decir cuando se toma el punto medio del segmento IIaa, la circunferencia Γ'a es tangente a la circunferencia A-exinscrita y el centro de perspectividad de ABC y P'aP'bP'c es X5423.
Cuando t = (r±Sqrt[r (r+2 R)])/r, las coordenadas de P't son muy complicadas.
- Viernes, 25 de diciembre del 2020
La cúbica de Grebe del triángulo anticomplementario
El 25 de diciembre de 1758, el cometa Halley avistado por primera vez después de que él predijo su regreso. Después de que Newton explicó el movimiento planetario, sugirió que los cometas podrían tener órbitas elípticas alargadas. El cometa Halley tiene una excentricidad de 0,9675
Dados un triángulo ABC y un punto P en su plano, sean DEF el de P y D∘E∘F∘ el triángulo ceviano de P∘, de P.
Las circunferencias (AEF), (BFD), (CDE), vuelven a cortar a la circunferecnia circunscrita a ABC, en los puntos D', E', F', respectivamente.
Los triángulos D'E'F' y D∘E∘F∘ son directamente semejantes.
Si (u:v:w) son las coordenadas baricéntricas de P, entonces:
D' = (a^2 (u + v) (u + w) : b^2 (u + v) (v - w) : -c^2 (v - w) (u + w)).
El centro de la semejanza que aplica D'E'F' en D∘E∘F∘ es:
Z = (a^2 (u + v) (u + w)
(a^4 (u^2 - v^2) (u^2 - w^2) +
2 a^2 (b^2 (u^2 - v^2) (u v + v^2 + v w + w^2) + c^2 (u^2 - w^2) (v^2 + v w + w (u + w))) +
(v + w)^2 (b^4 (-u^2 + v^2) + c^4 (-u^2 + w^2) +
2 b^2 c^2 (u^2 + v^2 + v w + w^2 + u (v + w)))) : ... : ...).
Casos particulares:
• Si P es el baricentro las circunferencias (ABC), (AEF) son tangentes y D•E•F• es el triángulo medial, luego Z es el baricentro.
• Si P es el , Z=X55, centro interior de homotecia de las circunferencias inscrita y circunscrita.
• Si P es el , Z es el baricentros.
En estos tres casos, los triángulos D'E'F' y D∘E∘F∘ son homotéticos.
Más en general:
Los triángulos
D'E'F' y
D∘E∘F∘ son perspectivos si y solo si
P está sobre la cúbica de la
cúbica de Grebe, pK(X6, X6), o sobre la cúbica, 𝒦, anticomplmento de una
nK(X6, X2, ?),
((b^2 x^2+a^2 y^2) z+y (c^2 x^2+a^2 z^2)+x (c^2 y^2+b^2 z^2) - (a^2+b^2+c^2) x y z= 0)
de raíz el baricentro.
La cúbica anticomplemento de la cúbica de Grebe pasa por los centros X2, X8, X69, X10453, X20081, X32548.
El centro de homotecia de los triángulos D'E'F' y D∘E∘F∘ para los puntos X20081, X32548, coincide y es:
W = ( (2 a^4 - a^2 (b^2 + c^2)+ b^2 c^2 )/(b^2 c^2 - a^2 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en
(-11.3091918666326, 1.20036368031517, 8.02927048782741).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,699}, {6,15965}, {25,385}, {194,32543}, {1968,16985}, {3224,7793}.
Cuando P está sobre la cúbica 𝒦 los centros de semejanza y de perspectividad están sobre la circunferencia circunscrita a ABC.
- Miércoles, 16 de diciembre del 2020
gagP, tagP y la segunda circunferencia de Steiner
El 16 de diciembre
de 1965, en las Naciones Unidas (Nueva York), se vota la Resolución 2017, en la que se insta al Gobierno de España como país invasor, a descolonizar los territorios de Ifni y Sáhara Occidental.
Dados un triángulo ABC y un punto P en su plano, establecemos las siguientes notaciones:
gP, de P,
tP, de P,
cP y aP, y anticomplemento de P, respectivamente.
Se pueden combinar entre ellos como en:
gagP, conjugado isogonal del anticomplemento del conjugado isogonal de P,
tagP, conjugado isotómico del anticomplemento del conjugado isogonal de P.
Se da a continuación una construcción que involucra estos dos puntos recién mencionados.
Sea DEF el de P y A', B', C' los puntos donde la circunferencia circunscrita a ABC vuelve a cortar a las rectas EF, FD, DE, respectivamente.
A", B", C" son los puntos donde la circunferencia circunscrita a ABC vuelve a cortar a las rectas A'P, B'P, C'P, respectivamente.
Las rectas AA", BB", CC" concurren en gagP.
Las dos circunferencias que pasan por A" y tales que una es tangente a AB en B y la otra es tangente a AC en C, se vuelven a cortar en A1, sobre BC. Los puntos B1 y C1, se construyen cíclicamente.
Las rectas AA1, BB1, CC1 concurren en tagP.
Si (u:v:w) son las coordenadas baricéntricas de P, entonces
gagP=(a^2/(c^2 u v+b^2 u w-a^2 v w):...:...),
tagP=(1/(c^2 u v+b^2 u w-a^2 v w):...:...).
Cuando P está sobre la circunferencia circunscrita a ABC, gagP=P. Otros casos {P=Xi, gagP=Xj}, para centros que actualmente figuran en , para los
índices {i, j}.
( {1, 56}, {2, 25}, {3, 64}, {4, 3}, {5, 3432}, {6, 6}, {7, 3433}, {8,
3435}, {9, 1436}, {10, 3437}, {11, 36902}, {12, 36903}, {13, 3438},
{14, 3439}, {15, 3440}, {16, 3441}, {17, 3442}, {18, 3443}, {19,
2164}, {20, 34426}, {21, 2217}, {22, 34427}, {23, 22258}, {24,
34428}, {25, 8770}, {27, 34429}, {28, 2218}, {30, 34178}, {31, 2162},
{32, 3224}, {34, 34430}, {36, 34431}, {37, 3444}, {39, 14370}, {40,
34432}, {42, 2248}, {48, 8761}, {53, 34433}, {54, 4}, {55, 11051},
{56, 3445}, {57, 55}, {58, 1}, {60, 34434}, {61, 3489}, {62, 3490},
{63, 7169}, {64, 3532}, {65, 34435}, {66, 34436}, {67, 34437}, {68,
34438}, {69, 34207}, {70, 34439}, {71, 34440}, {75, 7087}, {76,
2353}, {79, 34441}, {80, 34442}, {81, 31}, {82, 34443}, {83, 32},
{84, 963}, {86, 34444}, {87, 34445}, {88, 6187}, {89, 34446}, {90,
34447}, {94, 34448}, {95, 2980}, {96, 34449}, {97, 32319}, {163,
4559}, {184, 1988}, {186, 35372}, {193, 15369}, {194, 32543}, {219,
7152}, {222, 2192}, {223, 7037}, {248, 1987}, {251, 2}, {252, 11816},
{256, 34250}, {262, 3425}, {264, 1485}, {275, 184}, {282, 198}, {284,
19}, {288, 51}, {291, 8852}, {292, 17962}, {294, 911}, {371, 8948},
{372, 8946}, {511, 34130}, {512, 9217}, {513, 3446}, {514, 34179},
{515, 34180}, {516, 34181}, {517, 34182}, {518, 34183}, {519, 34184},
{520, 34185}, {521, 34187}, {522, 34189}, {523, 3447}, {524, 22259},
{525, 34190}, {526, 34191}, {588, 8577}, {589, 8576}, {605, 37882},
{644, 34080}, {648, 1576}, {651, 692}, {662, 4557}, {666, 34067},
{667, 9265}, {671, 3455}, {672, 9500}, {677, 32735}, {749, 7246},
{751, 7236}, {765, 3733}, {801, 33581}, {847, 24}, {895, 1177}, {909,
2161}, {937, 939}, {943, 28}, {947, 84}, {959, 1036}, {961, 21},
{994, 3422}, {1000, 3420}, {1002, 3423}, {1016, 667}, {1073, 154},
{1126, 58}, {1166, 5}, {1167, 34}, {1168, 36}, {1169, 37}, {1170,
41}, {1171, 42}, {1172, 48}, {1173, 54}, {1174, 57}, {1175, 65},
{1176, 66}, {1177, 67}, {1178, 82}, {1179, 96}, {1249, 28783}, {1252,
649}, {1255, 6186}, {1257, 8615}, {1258, 904}, {1262, 663}, {1342,
1677}, {1343, 1676}, {1383, 21448}, {1389, 3417}, {1390, 3415},
{1391, 10428}, {1433, 221}, {1438, 292}, {1461, 8750}, {1487, 3518},
{1783, 1415}, {1914, 2109}, {1945, 17963}, {1976, 694}, {1988,
36617}, {1989, 14579}, {1993, 39109}, {2052, 2351}, {2067, 30336},
{2141, 14377}, {2149, 7252}, {2161, 19302}, {2162, 36614}, {2214,
34819}, {2221, 7050}, {2226, 902}, {2259, 2160}, {2287, 2155}, {2298,
1333}, {2311, 1910}, {2316, 909}, {2341, 2159}, {2981, 3457}, {2982,
2194}, {2983, 1474}, {2984, 3199}, {2985, 1397}, {2987, 1976}, {2990,
34858}, {3108, 251}, {3194, 19614}, {3224, 36615}, {3225, 9468},
{3341, 34167}, {3342, 1035}, {3343, 28781}, {3344, 1033}, {3349,
28785}, {3352, 28784}, {3356, 28782}, {3417, 945}, {3431, 3426},
{3433, 38269}, {3435, 38273}, {3449, 7}, {3450, 8}, {3451, 9}, {3453,
10}, {3527, 14528}, {4558, 32734}, {4577, 1634}, {4590, 18105},
{4629, 35327}, {4630, 35325}, {4638, 23344}, {5378, 23355}, {5381,
23349}, {5383, 1919}, {5481, 3424}, {5504, 11744}, {5627, 186},
{5663, 34192}, {6151, 3458}, {6185, 2223}, {6502, 30335}, {6531,
32654}, {7021, 359}, {7115, 650}, {7121, 2176}, {7123, 1407}, {7128,
21789}, {7132, 2053}, {7133, 34125}, {8269, 1633}, {8749, 14910},
{8770, 36616}, {8882, 2165}, {8884, 22261}, {9190, 9192}, {9262,
9259}, {9268, 23345}, {9309, 1037}, {9469, 5989}, {9472, 8301},
{9506, 17735}, {10159, 3456}, {10308, 10623}, {10415, 23}, {10422,
468}, {10426, 1155}, {10428, 1319}, {10630, 187}, {11071, 11063},
{11075, 19297}, {11082, 11142}, {11087, 11141}, {11610, 34129},
{13136, 32719}, {13472, 3527}, {13492, 38533}, {13603, 20421},
{14248, 3053}, {14371, 6759}, {14483, 3431}, {14528, 22334}, {14534,
1402}, {14586, 1625}, {14910, 1989}, {15905, 31956}, {16459, 15},
{16460, 16}, {16835, 11270}, {17708, 32729}, {18018, 22}, {18315,
32737}, {18532, 34801}, {18771, 59}, {18772, 60}, {19118, 39128},
{19607, 3185}, {19613, 20993}, {20332, 1911}, {21353, 1030}, {21355,
10329}, {23357, 2623}, {23586, 8641}, {23592, 8648}, {23617, 604},
{23963, 36198}, {23964, 647}, {23984, 1946}, {24479, 17798}, {25148,
34418}, {27644, 34248}, {30535, 263}, {32544, 32540}, {32641, 32675},
{32674, 32653}, {32708, 32662}, {32714, 32652}, {34071, 190}, {34238,
1691}, {34260, 1460}, {34277, 197}, {34536, 237}, {34537, 669},
{34538, 39201}, {34539, 351}, {34567, 1173}, {34568, 23347}, {34570,
8749}, {34572, 3108}, {34574, 5467}, {34756, 155}, {36049, 32674},
{36052, 1411}, {38534, 265}, {38809, 3271}, {38810, 560}, {38811,
1334}, {38812, 1917}, {38813, 75}, {38825, 1412}, {38826, 76},
{38827, 561}, {38828, 3939}, {38829, 1502}, {38830, 1501}, {38831,
38813}, {38936, 14264}, {39267, 37579}, {39389, 1383}.)
Pares {P=Xi, tagP=Xj} para los
índices {i, j}.
( {1, 7}, {2, 4}, {3, 253}, {4, 69}, {6, 2}, {7, 13577}, {8, 8048}, {9,
189}, {10, 8044}, {13, 2992}, {14, 2993}, {15, 19776}, {16, 19777},
{19, 2994}, {21, 2995}, {23, 14364}, {25, 2996}, {28, 2997}, {31,
330}, {32, 2998}, {36, 36917}, {37, 1029}, {39, 1031}, {42, 6625},
{44, 8046}, {48, 7361}, {54, 264}, {55, 10405}, {56, 4373}, {57, 8},
{58, 75}, {59, 693}, {61, 19712}, {62, 19713}, {63, 7219}, {64,
35510}, {69, 13575}, {74, 1494}, {75, 7357}, {76, 66}, {81, 1}, {83,
6}, {86, 8049}, {88, 80}, {89, 1000}, {94, 33565}, {97, 15318}, {98,
290}, {99, 670}, {100, 668}, {101, 190}, {102, 34393}, {103, 18025},
{104, 18816}, {105, 2481}, {106, 903}, {107, 6528}, {108, 18026},
{109, 664}, {110, 99}, {111, 671}, {112, 648}, {158, 7331}, {162,
4566}, {163, 4552}, {190, 8050}, {222, 280}, {223, 1034}, {239,
2113}, {248, 1972}, {249, 523}, {250, 850}, {251, 76}, {256, 7224},
{266, 7048}, {275, 3}, {279, 6601}, {282, 329}, {284, 92}, {287,
1297}, {288, 5}, {289, 7057}, {291, 7261}, {292, 6650}, {294, 36101},
{323, 1138}, {346, 34546}, {371, 24244}, {372, 24243}, {393, 6504},
{394, 3346}, {395, 13484}, {396, 13483}, {459, 15077}, {476, 35139},
{493, 1131}, {494, 1132}, {511, 9473}, {512, 35511}, {513, 8047},
{523, 13485}, {524, 13574}, {525, 13573}, {577, 34287}, {588, 485},
{589, 486}, {593, 596}, {598, 5486}, {605, 37883}, {644, 27834},
{647, 15351}, {648, 110}, {649, 6630}, {651, 100}, {662, 3952}, {666,
660}, {667, 9295}, {671, 67}, {677, 927}, {691, 892}, {694, 11606},
{697, 18824}, {699, 3225}, {713, 18825}, {715, 18826}, {727, 3226},
{729, 3228}, {733, 14970}, {739, 3227}, {741, 18827}, {757, 27807},
{759, 14616}, {765, 7192}, {783, 18828}, {801, 64}, {805, 18829},
{813, 4562}, {825, 4586}, {827, 4577}, {829, 255}, {840, 18821},
{842, 5641}, {843, 18823}, {847, 317}, {895, 2373}, {898, 889}, {901,
4555}, {909, 18359}, {919, 666}, {932, 18830}, {933, 18831}, {934,
4569}, {943, 286}, {947, 309}, {959, 30479}, {961, 314}, {1016, 513},
{1073, 20}, {1101, 7372}, {1113, 15164}, {1114, 15165}, {1126, 86},
{1166, 311}, {1167, 273}, {1168, 320}, {1169, 321}, {1170, 9}, {1171,
10}, {1172, 63}, {1173, 95}, {1174, 85}, {1175, 1441}, {1176, 18018},
{1177, 18019}, {1178, 3112}, {1179, 34385}, {1220, 20028}, {1249,
1032}, {1252, 514}, {1255, 79}, {1257, 15314}, {1258, 256}, {1262,
522}, {1290, 35156}, {1296, 35179}, {1297, 35140}, {1304, 16077},
{1308, 35171}, {1331, 1305}, {1332, 13397}, {1333, 35058}, {1379,
6190}, {1380, 6189}, {1383, 5485}, {1407, 6553}, {1412, 34860},
{1427, 13583}, {1433, 347}, {1438, 335}, {1461, 1897}, {1462, 1280},
{1477, 35160}, {1487, 32002}, {1509, 13476}, {1576, 11794}, {1743,
8051}, {1783, 651}, {1797, 2370}, {1814, 26703}, {1945, 17947},
{1967, 30669}, {1976, 1916}, {1988, 38256}, {1989, 13582}, {1993,
254}, {1994, 3459}, {2006, 11604}, {2052, 68}, {2065, 325}, {2149,
4560}, {2161, 21739}, {2162, 38247}, {2163, 36588}, {2165, 13579},
{2207, 6339}, {2214, 25417}, {2221, 1219}, {2222, 35174}, {2226,
519}, {2238, 9510}, {2249, 35145}, {2259, 30690}, {2287, 2184},
{2291, 1121}, {2298, 81}, {2311, 1821}, {2316, 34234}, {2334, 30712},
{2341, 2349}, {2380, 11117}, {2381, 11118}, {2382, 18822}, {2384,
35168}, {2433, 12066}, {2699, 35151}, {2700, 35150}, {2701, 35154},
{2702, 35148}, {2703, 35147}, {2708, 35149}, {2711, 35152}, {2712,
35153}, {2715, 2966}, {2717, 35164}, {2718, 35175}, {2963, 13585},
{2981, 13}, {2982, 21}, {2983, 27}, {2984, 53}, {2985, 56}, {2986,
74}, {2987, 98}, {2988, 102}, {2989, 103}, {2990, 104}, {2991, 105},
{2996, 16774}, {3108, 83}, {3114, 263}, {3194, 19611}, {3224, 38262},
{3225, 694}, {3342, 5932}, {3343, 14365}, {3344, 14361}, {3349,
14362}, {3352, 34162}, {3407, 19222}, {3431, 36889}, {3445, 36606},
{3449, 6063}, {3450, 3596}, {3451, 312}, {3453, 313}, {3457, 11121},
{3458, 11122}, {3563, 35142}, {3565, 35136}, {3939, 37206}, {3978,
34214}, {4558, 925}, {4563, 3565}, {4567, 4581}, {4570, 4608}, {4573,
3903}, {4577, 4576}, {4588, 4597}, {4629, 4427}, {4638, 17780},
{5376, 23836}, {5383, 649}, {5392, 70}, {5395, 17040}, {5627, 340},
{5970, 35146}, {5994, 23896}, {5995, 23895}, {6151, 14}, {6185, 518},
{6531, 2987}, {6551, 6635}, {7115, 4391}, {7121, 192}, {7123, 279},
{7128, 7253}, {7132, 7155}, {7133, 13386}, {7160, 30501}, {7578,
3431}, {7953, 35137}, {8056, 7319}, {8105, 13580}, {8106, 13581},
{8115, 1113}, {8116, 1114}, {8652, 32042}, {8687, 6648}, {8691,
35181}, {8693, 32041}, {8701, 6540}, {8749, 2986}, {8751, 2991},
{8770, 38259}, {8882, 5392}, {9111, 35172}, {9139, 9141}, {9150,
886}, {9190, 9080}, {9262, 4440}, {9268, 6548}, {9307, 34405}, {9309,
8817}, {9472, 20345}, {9506, 6542}, {9516, 1383}, {10159, 15321},
{10415, 316}, {10419, 3260}, {10420, 18878}, {10426, 30806}, {11051,
36605}, {11071, 37779}, {11075, 17484}, {11082, 16770}, {11085,
19779}, {11087, 16771}, {11538, 13418}, {11636, 35138}, {13136, 901},
{13138, 934}, {13404, 21453}, {13472, 8797}, {13582, 5900}, {14248,
193}, {14371, 20477}, {14534, 65}, {14586, 14570}, {14621, 1002},
{14642, 35061}, {14733, 35157}, {14910, 94}, {14919, 1294}, {14970,
20021}, {15378, 3261}, {15379, 35516}, {15380, 35517}, {15381, 3262},
{15382, 3263}, {15383, 3264}, {15384, 3265}, {15385, 35518}, {15386,
35519}, {15387, 3266}, {15388, 3267}, {15396, 35520}, {15397, 3006},
{15401, 1273}, {15407, 30737}, {15460, 22340}, {15461, 22339},
{16039, 933}, {16080, 265}, {16081, 35098}, {16082, 35097}, {16460,
299}, {16606, 13584}, {16806, 32036}, {16807, 32037}, {16813, 35360},
{17708, 691}, {17743, 9309}, {18018, 315}, {18268, 27809}, {18315,
930}, {18771, 4998}, {18772, 261}, {18879, 18808}, {19607, 3869},
{19613, 5596}, {19619, 6224}, {20251, 18575}, {20332, 291}, {20998,
31373}, {21353, 2895}, {21355, 2896}, {21907, 24298}, {23357, 15412},
{23592, 3738}, {23617, 57}, {23964, 525}, {23984, 521}, {24479,
4645}, {24624, 38955}, {25417, 3296}, {25430, 5556}, {26716, 32040},
{27644, 3223}, {28317, 35170}, {28471, 35141}, {28482, 35162},
{30535, 262}, {31626, 15319}, {32014, 15320}, {32641, 655}, {32693,
32038}, {32714, 13138}, {34051, 1320}, {34056, 3254}, {34071, 1978},
{34079, 4080}, {34238, 385}, {34258, 20029}, {34260, 388}, {34277,
3436}, {34533, 5487}, {34534, 5488}, {34536, 511}, {34537, 512},
{34538, 520}, {34568, 4240}, {34570, 16080}, {34572, 10159}, {34574,
5468}, {35105, 35143}, {35106, 35144}, {35107, 35155}, {35108,
35159}, {36049, 653}, {36052, 18815}, {36296, 19774}, {36297, 19775},
{36897, 20022}, {37128, 13576}, {37135, 4589}, {37874, 14457},
{38253, 15749}, {38534, 328}, {38809, 11}, {38810, 31}, {38811,
2321}, {38812, 560}, {38813, 561}, {38825, 1434}, {38826, 1502},
{38827, 1928}, {38828, 3699}, {38830, 32}, {38847, 38845}, {39284,
3519}, {39295, 15328}, {39389, 598}, {39391, 18810}, {39392, 18811},
{39394, 18812}, {39402, 7026}, {39403, 7043}.)
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Cuando el punto
P recorre una recta ℓ, la envolvente de las rectas gag
Ptag
P es una cónica 𝒞
ℓ, con el . Esta cónica es parábola si la recta ℓ pasa por X
249, conjugado isogonal del centro de la .
Cuando ℓ gira alrededor de X249, el foco de la parábola 𝒞ℓ está sobre la .
(b^2-c^2) (a^2 (f-g) (f-h) (f g+t) (f h+t)+b^2 (f-g) (g-h) (f g+t) (g h+t)+c^2 (g-h) (-f+h) (f h+t) (g h+t))x+...=0.
Cuando t varía, la envolvente de esta recta es la cónica 𝒞ℓ, de ecuación:
𝔖abc xyz
(b-c)^2 (b+c)^2 (a^4 f^2+(b^2 g-c^2 h)^2+2 a^2 f (b^2 g+c^2 h)) x^2-2 (a-b) (a+b) (a-c) (a+c) (a^2 f-b^2 g-c^2 h) (a^2 f+b^2 g+c^2 h) y z= 0.
El centro de esta cónica es:
Lo = ((a^2 - b^2) (a^2 - c^2) (2 a^6 f - 2 a^4 (b^2 + c^2) f +
a^2 (b^4 + c^4) f + (b^2 - c^2)^2 (b^2 g + c^2 h)) : ... : ...).
Si L es el de ℓ, se tienen los siguientes pares {L=Xi, Lo=Xj}, para {i,j}: {99, 110}, {101, 4610}, {110, 99}, {112, 4563}, {249, 11123}, {476,
10411}, {691, 5468}, {805, 17941}, {827, 4576}, {2709, 34245}, {2715,
2396}, {4558, 1632}, {6578, 4427}, {7953, 10330}, {9150, 5118},
{10409, 35314}, {10410, 35315}, {10411, 14611}, {10425, 4226},
{11636, 9146}, {12074, 35356}, {18315, 1634}, {36066, 3573}.
El perspector de esta cónica, respecto al triángulo ceviano del punto de Steiner, es:
So = (a^2 (a^2 - b^2) (a^2 - c^2) f (b^2 g + c^2 h) : ... : ...).
Si L es el de ℓ, se tienen los siguientes pares {L=Xi, So=Xj}, para {i,j}
ver aquí
( {1, 100}, {2, 1634}, {3, 110}, {4, 23181}, {6, 99}, {15, 35314}, {16,
35315}, {19, 6516}, {20, 1624}, {22, 1576}, {23, 5467}, {25, 4558},
{30, 15329}, {31, 190}, {32, 4576}, {39, 10330}, {48, 664}, {55,
662}, {56, 643}, {58, 4427}, {63, 1633}, {74, 3233}, {81, 4436}, {99,
669}, {100, 3733}, {101, 7192}, {109, 7253}, {112, 3265}, {154, 648},
{155, 925}, {157, 32661}, {159, 112}, {160, 1625}, {163, 4467}, {184,
14570}, {187, 5468}, {190, 16695}, {195, 930}, {197, 4565}, {198,
1414}, {199, 4556}, {221, 36797}, {237, 2421}, {249, 11123}, {284,
17136}, {333, 23363}, {381, 36829}, {394, 1632}, {399, 476}, {511,
4226}, {512, 2}, {513, 21}, {514, 4184}, {515, 7450}, {516, 4243},
{517, 3658}, {518, 4236}, {520, 20}, {521, 16049}, {522, 4225}, {523,
3}, {524, 11634}, {525, 22}, {542, 7468}, {560, 33946}, {574, 35356},
{595, 3952}, {610, 934}, {647, 69}, {648, 22089}(recta de Euler), {649, 86}, {650,
1444}, {652, 8822}, {654, 17139}, {659, 3286}, {662, 4367}, {663,
333}, {664, 23864}, {665, 30941}, {667, 81}, {669, 6}, {670, 9491},
{674, 4237}, {688, 384}, {690, 23}, {691, 1649}, {692, 4560}, {758,
13589}, {778, 33728}, {792, 33725}, {798, 17103}, {804, 237}, {814,
4215}, {826, 6636}, {827, 2528}, {832, 17521}, {834, 1010}, {838,
17587}, {850, 160}, {875, 4366}, {876, 8299}, {878, 36790}, {882,
8290}, {884, 16728}, {887, 3231}, {888, 13586}, {900, 859}, {918,
16876}, {924, 4}, {926, 14953}, {928, 14956}, {1019, 1621}, {1350,
35278}, {1379, 30509}, {1380, 30508}, {1384, 9146}, {1444, 16680},
{1459, 1043}, {1486, 5546}, {1495, 2407}, {1498, 107}, {1499, 1995},
{1503, 4230}, {1510, 5}, {1511, 14611}, {1613, 670}, {1615, 4616},
{1616, 7256}, {1619, 32713}, {1621, 4557}, {1625, 850}, {1630, 4566},
{1631, 163}, {1632, 39201}, {1633, 21789}, {1649, 2930}, {1691,
2396}, {1740, 932}, {1919, 33296}, {1938, 35981}, {1946, 1812},
{1960, 16704}, {1964, 18047}, {1971, 877}, {1979, 4601}, {1995,
9145}, {2071, 5502}, {2076, 17941}, {2110, 4584}, {2162, 36860},
{2176, 799}, {2178, 4592}, {2328, 14543}, {2352, 1332}, {2360,
14544}, {2393, 4235}, {2420, 3268}, {2422, 5976}, {2433, 6148},
{2441, 17195}, {2483, 16705}, {2485, 3926}, {2488, 16713}, {2489,
6337}, {2491, 12215}, {2492, 6390}, {2501, 9723}, {2502, 9182},
{2514, 7789}, {2528, 2916}, {2531, 10328}, {2574, 1114}, {2575,
1113}, {2605, 8}, {2623, 311}, {2771, 7477}, {2772, 7479}, {2773,
7424}, {2774, 5196}, {2775, 7469}, {2776, 7478}, {2777, 7480}, {2778,
37966}, {2780, 7426}, {2781, 7473}, {2793, 35298}, {2799, 37183},
{2836, 7475}, {2854, 7472}, {2872, 35297}, {2878, 448}, {2881, 441},
{2916, 827}, {2917, 933}, {2930, 691}, {2931, 10420}, {2934, 14586},
{2935, 1304}, {2936, 32729}, {2948, 1290}, {2975, 23845}, {2978,
27164}, {3005, 141}, {3049, 1975}, {3050, 76}, {3052, 645}, {3053,
4563}, {3124, 14588}, {3129, 17402}, {3130, 17403}, {3145, 4636},
{3185, 651}, {3196, 4622}, {3207, 4573}, {3216, 34594}, {3221, 3552},
{3231, 23342}, {3250, 30966}, {3265, 159}, {3267, 15270}, {3286,
3573}, {3288, 183}, {3309, 4228}, {3360, 3222}, {3447, 14366}, {3499,
689}, {3511, 805}, {3556, 162}, {3566, 25}, {3569, 325}, {3573, 659},
{3667, 7419}, {3724, 4585}, {3733, 1}, {3737, 2975}, {3747, 3570},
{3800, 7485}, {3804, 3618}, {3827, 4238}, {3887, 33325}, {3900,
1817}, {3903, 24533}, {3904, 23369}, {3906, 7492}, {3915, 3699},
{3941, 644}, {4057, 58}, {4068, 35342}, {4079, 6626}, {4083, 13588},
{4132, 404}, {4139, 4188}, {4145, 13587}, {4151, 4210}, {4155,
19308}, {4184, 35327}, {4230, 684}, {4367, 55}, {4394, 1014}, {4427,
4057}, {4436, 667}, {4455, 1931}, {4467, 1631}, {4557, 1019}, {4559,
18155}, {4560, 16678}, {4576, 21006}, {4590, 14824}, {4775, 5235},
{4784, 1001}, {4833, 993}, {4834, 5333}, {4840, 5248}, {4843, 11350},
{4879, 1376}, {4897, 1486}, {4977, 17524}, {5027, 385}, {5029,
17731}, {5040, 19623}, {5078, 17944}, {5104, 34245}, {5106, 14607},
{5113, 7779}, {5118, 9147}, {5191, 14999}, {5201, 5118}, {5301,
4561}, {5546, 4897}, {5611, 14185}, {5615, 14187}, {5638, 6189},
{5639, 6190}, {5652, 9149}, {5663, 7471}, {5898, 1291}, {5989,
17938}, {6000, 4240}, {6001, 4246}, {6003, 11101}, {6088, 27088},
{6089, 27086}, {6129, 1792}, {6137, 298}, {6138, 299}, {6140, 37779},
{6363, 17539}, {6368, 7488}, {6370, 37311}, {6371, 11115}, {6562,
1609}, {6563, 157}, {6586, 17206}, {6587, 3964}, {6589, 332}, {6626,
23390}, {6759, 35360}, {7192, 8053}, {7234, 38814}, {7252, 75},
{7253, 23361}, {7254, 32929}, {7468, 34291}, {7492, 35357}, {7669,
249}, {7927, 15246}, {8053, 101}, {8057, 11413}, {8632, 33295},
{8639, 940}, {8640, 27644}, {8641, 2287}, {8644, 1992}, {8646, 2303},
{8651, 193}, {8653, 391}, {8663, 1213}, {8664, 3589}, {8665, 3763},
{8672, 4189}, {8673, 1370}, {8674, 1325}, {8675, 376}, {8676, 27},
{8678, 27174}, {8679, 7462}, {8702, 37294}, {8711, 35929}, {8750,
15411}, {8925, 6037}, {8939, 1306}, {8943, 1307}, {8999, 7415},
{9000, 4229}, {9001, 4221}, {9002, 4234}, {9003, 7464}, {9007,
21312}, {9009, 1003}, {9010, 16046}, {9012, 8356}, {9013, 17512},
{9023, 8598}, {9029, 35935}, {9030, 35924}, {9033, 2071}, {9044,
35955}, {9135, 22329}, {9147, 5201}, {9178, 2482}, {9181, 9168},
{9208, 7840}, {9210, 7788}, {9217, 31632}, {9218, 10190}, {9259,
4600}, {9313, 16050}, {9402, 17693}, {9409, 11064}, {9426, 194},
{9431, 34537}, {9479, 6660}, {9489, 9463}, {9491, 1613}, {9494,
3051}, {9509, 36066}, {9517, 858}, {9937, 13398}, {10097, 7664},
{10117, 250}, {10282, 35311}, {10329, 4577}, {10330, 18105}, {10537,
653}, {11063, 10411}, {11123, 7669}, {11186, 11163}, {11450, 34845},
{11634, 351}, {11641, 36830}, {12073, 7496}, {13152, 13621}, {13754,
30512}, {14077, 35997}, {14270, 323}, {14273, 5866}, {14318, 3329},
{14329, 2883}, {14380, 16163}, {14424, 19596}, {14480, 14809},
{14529, 1897}, {14560, 5664}, {14809, 32609}, {14824, 20998}, {15034,
30221}, {15047, 20189}, {15107, 35345}, {15141, 935}, {15270, 35325},
{15313, 28}, {15411, 23359}, {15451, 343}, {15470, 14264}, {15959,
14587}, {16678, 692}, {16679, 1018}, {16680, 650}, {16681, 32739},
{16685, 668}, {16686, 4567}, {16687, 4553}, {16692, 213}, {16693,
2284}, {16694, 1023}, {16695, 31}, {16872, 4559}, {16874, 37},
{17104, 6758}, {17136, 23865}, {17221, 14723}, {17414, 599}, {17415,
4048}, {17847, 30716}, {18105, 39}, {18155, 16872}, {18311, 2936},
{18610, 906}, {18611, 1783}, {18613, 3939}, {18614, 21859}, {18755,
4610}, {18859, 30510}, {19504, 39193}, {19588, 3565}, {20184, 3518},
{20186, 4232}, {20188, 140}, {20474, 2702}, {20580, 1619}, {20677,
37135}, {20718, 7437}, {20986, 4552}, {20987, 4611}, {20994, 4599},
{20995, 4625}, {20998, 4590}, {20999, 4570}, {21002, 7259}, {21004,
24041}, {21005, 1333}, {21006, 32}, {21007, 274}, {21009, 23889},
{21123, 33954}, {21731, 3580}, {21767, 811}, {21769, 7257}, {21776,
4602}, {21777, 4593}, {21779, 4623}, {21781, 4615}, {21783, 24037},
{21784, 1577}, {21786, 30939}, {21789, 63}, {21791, 310}, {21905,
7665}, {22089, 154}, {23090, 17134}, {23189, 3869}, {23283, 14368},
{23284, 14369}, {23285, 23208}, {23286, 5562}, {23339, 32656},
{23342, 887}, {23359, 8750}, {23361, 109}, {23363, 663}, {23381,
1415}, {23383, 1331}, {23386, 32665}, {23387, 34073}, {23388, 1110},
{23389, 23990}, {23390, 4079}, {23392, 1252}, {23394, 902}, {23399,
2200}, {23400, 41}, {23401, 2210}, {23403, 560}, {23404, 765},
{23843, 4575}, {23844, 2617}, {23845, 3737}, {23846, 4551}, {23858,
4591}, {23860, 1101}, {23861, 661}, {23864, 48}, {23865, 284},
{23866, 5009}, {23867, 2206}, {23870, 34008}, {23871, 34009}, {23878,
37184}, {24303, 36839}, {24304, 36840}, {25423, 11328}, {27550,
38432}, {27551, 38431}, {29328, 36015}, {29350, 35983}, {30202, 453},
{30209, 7493}, {30211, 30552}, {30230, 26255}, {31296, 8266}, {31299,
35222}, {31521, 907}, {32320, 20477}, {32445, 6331}, {32472, 37465},
{32473, 37335}, {32478, 13595}, {32609, 14480}, {32661, 6563},
{32713, 20580}, {32729, 18311}, {32737, 20577}, {33704, 31614},
{33786, 4609}, {33801, 14574}, {33803, 8029}, {33946, 23403}, {34008,
35329}, {34009, 35330}, {34146, 2409}, {34948, 3193}, {34952, 1993},
{35057, 37405}, {35193, 14985}, {35237, 1302}, {35325, 3267}, {35326,
7199}, {35364, 114}, {36201, 37937}, {38348, 8301}, {38401, 12168},
{38402, 12074}, {38861, 5489}, {39199, 283}, {39201, 394}, {39232,
316})
.
• La cónica 𝒞ℓ es parábola si su centro está en la , o sea si:
a^2 (a^2-b^2)^2 (a^2-c^2)^2f+b^2 (a^2-b^2)^2 (b^2-c^2)^2g+c^2 (a^2-c^2)^2 (b^2-c^2)^2h=0.
Es decir, si la recta ℓ pasa por X249.
Cuando ℓ gira alrededor de X249, el lugar geométrico del foco Fℓ de la parábola 𝒞ℓ es la , de ecuación:
c^2 x y+b^2 x z+a^2 y z+
(x+y+z) (-(((a^6-a^4 b^2+a^2 b^4-b^6-a^4 c^2-a^2 b^2 c^2+b^4 c^2+a^2 c^4+b^2 c^4-c^6) x)/(2 (a^2-b^2) (a^2-c^2)))
-((a^6-a^4 b^2+a^2 b^4-b^6-a^4 c^2+a^2 b^2 c^2+b^4 c^2-a^2 c^4-b^2 c^4+c^6) y)/(2 (a^2-b^2) (b^2-c^2))
+((-a^6+a^4 b^2+a^2 b^4-b^6+a^4 c^2-a^2 b^2 c^2+b^4 c^2-a^2 c^4-b^2 c^4+c^6) z)/(2 (a^2-c^2) (-b^2+c^2)))=0.
Cuando ℓ gira alrededor de X249, el lugar geométrico de los puntos de intersección Dℓ, de ℓ con la directriz dℓ, de la parábola 𝒞ℓ, es la cónica que pasa por X3, X249, X2076 (inverso en la circunferencia circunscrita del punto medio de los ), X35296, de ecuación:
𝔖abc xyz
(a^2 (b^2 + c^2) - b^4 - c^4) (
b^2 c^2 (b^2 - c^2)^4 x^2 + (
a^2) (a^2 - b^2) (a^2 - c^2) (a^6 - a^4 (b^2 + c^2) -
a^2 (b^4 - 3 b^2 c^2 + c^4) + (b^2 - c^2)^2 (b^2 + c^2)) y = 0.
• La cónica 𝒞ℓ es si los coeficientes de la recta ℓ satisfacen a:
𝔖abc fgh
a^4 (a^6 - b^6 - b^4 c^2 - b^2 c^4 - c^6 - 3 a^4 (b^2 + c^2) +
3 a^2 (b^4 + b^2 c^2 + c^4))f^2 -2 a^2 b^2 (a^2 - b^2) c^2 (a^2 -
c^2)g h = 0.
Ésta es la ecuación tangencial de una cónica, 𝒞eq, cuya ecuación puntual es:
𝔖abc xyz
b^4 c^4 (b^2 - c^2)^4 (a^4 + (b^2 - c^2)^2 -
2 a^2 (b^2 + c^2))x^2 -2 a^4 b^2 c^2 (a^2 - b^2)(a^2 - c^2) (a^8 -
b^2 c^2 (b^2 - c^2)^2 - 3 a^6 (b^2 + c^2) +
3 a^4 (b^4 + b^2 c^2 + c^4) - a^2 (b^6 + b^4 c^2 + b^2 c^4 + c^6))y z = 0.
Pasa por X3 y X1993 ( de X(3)). Su centro es X39X54∩X110X115, es decir el punto de intersección de la recta que pasa por el punto medio de los puntos de Brocard y el , con la recta que une el foco de la y el centro de la .
A cada recta tangente ℓ a 𝒞eq, le corresponde una hipérbola rectangular 𝒞ℓ, tangente a los lados del triángulo ceviano del punto de Steiner y cuyo centro queda sobre la circunferencia circunscrita a ABC.
La tangente a 𝒞eq en X(3) es el , a la que corresponde la hipérbola de Kiepert del triángulo anticomplemetario, cuyo centro es el punto de Steiner.
La tangente a 𝒞eq en X(1993) es la recta la del punto de Steiner, que pasa por el baricentro y el simediano, a la que corresponde la , cuyo centro es el foco de la parábola de Kiepert.
• Cuando ℓ es la recta de Euler, la cónica 𝒞ℓ tiene por ecuación:
𝔖abc xyz
a^2 (b^2 - c^2) (a^2 (b^4 - b^2 c^2 + c^4)-(b^2 - c^2)^2 (b^2 + c^2))x^2+ 2 b^2c^2 (a^2 - b^2) (a^2 -
c^2) (b^2 - c^2)y z = 0.
Pasa por los centros X22, X9723, X17134, X20477, X22339, X22340. Su centro es:
W = ( (a^2 - b^2) (a^2 - c^2) (a^4 + (b^2 - c^2)^2 - a^2 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en
(0.0195648763671119, -1.64943185773662, 4.77354890201722).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,34981}, {3,338}, {4,23702}, {5,14669}, {67,550}, {99,670}, {110,930}, {290,8266}, {401,3001}, {523,4558}, {599,34510}, {648,5467}, {925,23181}, {935,1296}, {1316,34990}, {1576,4226}, {2453,33813}, {2782,7669}, {6368,34968}, {7668,14060}, {7816,29959}, {9142,25051}, {15526,38738}, {23290,30450}.
La recta de Euler es tangente a 𝒞ℓ en el .
La recta ℓ es tangente a 𝒞ℓ si y solo si ℓ pasa por el punto de Steiner o es tangente a la hipérbola de Stammler.
La condición de tangencia es:
(a^4 f - a^2 b^2 f - a^2 c^2 f + b^2 c^2 f - a^2 b^2 g + b^4 g +
a^2 c^2 g - b^2 c^2 g + a^2 b^2 h - a^2 c^2 h - b^2 c^2 h +
c^4 h)
(a^6 f^2 - a^4 b^2 f^2 - a^4 c^2 f^2 + a^2 b^2 c^2 f^2 -
a^2 b^4 g^2 + b^6 g^2 + a^2 b^2 c^2 g^2 - b^4 c^2 g^2 +
a^2 b^2 c^2 h^2 - a^2 c^4 h^2 - b^2 c^4 h^2 + c^6 h^2)=0.
El primer factor expresa que la recta ℓ para por el punto de Steiner, y el segundo factor indica que es tangente a la hipérbola de Stammler.
- Lunes, 14 de diciembre del 2020
Recta de Euler y puntos de Tixier en un círculo
El 14 de diciembre de 1546 nació, en Suecia, Tycho Brahe.
Las observaciones de Tycho de una nueva estrella en 1572 y un cometa 1577, así como la publicación de estos fenómenos, fueron fundamentales para establecer el hecho de que estos astros se encuentran por encima de la Luna, y que por tanto, el cielo no es inmutable como Aristóteles.
Al morir dejó a Kepler las observaciones realizadas a lo largo de años y años de estudio, con la esperanza de que éste pudiera demostrar su teoría del Universo.
Kepler se sirvió de los trabajos de Tycho para formular sus famosas leyes sobre los movimientos planetarios.
HYACINTHOS 27613
[Tran Quang Hung]: (Oct 26, 2019)
Let ABC be a triangle.
N is the NPC center.
A'B'C' is the pedal triangle of N.
The of the triangles AB'C', BC'A' and CA'B' bound a triangle
A''B''C''.
Then the circumcenter of the triangle A''B''C'' lies on the Euler line of ABC.
[Angel Montesdeoca]:
Is the triangle center W (=
X(18279)), with first barycentric coordinate:
2 a^10-5 a^8 (b^2+c^2)+2 a^6 (b^4+b^2 c^2+c^4)-a^4 (-4 b^6+b^4 c^2+b^2
c^4-4 c^6)-a^2 (b^2-c^2)^2 (4 b^4+b^2 c^2+4 c^4)+(b^2-c^2)^4 (b^2+c^2).
Euclid 1269
[Kadir Altintaş]: (Dec 13, 2020)
Let Euler line of ABC intersects the sidelines BC, CA, AB at P,Q,R resp.
X(476)-Tixier point of ABC, X(476) of ARQ, X(476) of BPR, X(476) of CPQ lie on same circle.
La de un triángulo ABC intersecta a sus lados
BC, CA, AB en P, Q, R , respectivamente.
Sea
Ta el de ARQ. Se definen Tb y Tc cíclicamente.
El punto de Tixier de ABC, Ta, Tb y Tc están sobre una misma circunferencia.
Para obtener las coordenadas baricéntricas del punto de Tiexer respecto al triángulo AQR, en función de las longitudes de los lados de ABC, sustituimos en sus coordenadas respecto a ABC:
((a^2-b^2) (a^2-c^2) (-a^2 b^2+(a^2+b^2-c^2)^2) (-a^2 c^2+(a^2-b^2+c^2)^2):
(-a^2+b^2) (b^2-c^2) (-a^2 b^2+(a^2+b^2-c^2)^2) (-b^2 c^2+(-a^2+b^2+c^2)^2):
(-a^2+c^2) (-b^2+c^2) (-a^2 c^2+(a^2-b^2+c^2)^2) (-b^2 c^2+(-a^2+b^2+c^2)^2)),
a2, b2 y c2 por QR2, AR2,
AQ2, respectivamente, y se obtiene:
T'a = (x':y':z')=
(((-b^4+c^4+a^2 (b^2-c^2))^12 (a^12-(b^2-c^2)^6-a^10 (b^2+c^2)+a^2 (b^2-c^2)^4 (b^2+c^2)-a^8 (b^4-3 b^2 c^2+c^4)+a^4 (b^2-c^2)^2 (b^4-3 b^2 c^2+c^4)))/((b^2-c^2)^12 (-a^2+b^2+c^2)^12):
-(b^2-c^2) (a^4-2 b^4+b^2 c^2+c^4+a^2 (b^2-2 c^2)) (a^6-a^4 b^2+(b^2-c^2)^3+a^2 (-b^4+b^2 c^2)) :
(b^2-c^2) (a^6-a^4 c^2+a^2 c^2 (b^2-c^2)-(b^2-c^2)^3) (a^4+b^4+b^2 c^2-2 c^4+a^2 (-2 b^2+c^2))).
Si las coordenadas baricéntricas de un punto, respecto a ABC son (x:y:z) y queremos obtener su relación con las coordenadas baricéntricas (x':y':z'), respecto a otro triángulo A'B'C', del que se conocen las coordenadas baricéntricas de sus vértices respecto a ABC, debemos dar una determinación fija a éstos para que la suma de los tres sea el baricentro G' de A'B'C'. Esto puede lograrse haciendo que las sumas de las coordenadas de cada uno de ellos sean las mismas.
Por tanto, las coordenadas (x:y:z) de T'a, respecto ABC, vienen dadas por la expresión matricial {x,y,z} = {x',y', z'}*M, donde M=(aij), siendo:
a11 = 1, a12 = 0, a13 = 0
a21 = ((-a^2+b^2) (a^2+b^2-c^2))/((-a^2+b^2) (a^2+b^2-c^2)+(b^2-c^2) (-a^2+b^2+c^2)),
a22 = 0,
a23 = ((b^2-c^2) (-a^2+b^2+c^2))/((-a^2+b^2) (a^2+b^2-c^2)+(b^2-c^2) (-a^2+b^2+c^2)),
a31 = ((-a^2+c^2) (a^2-b^2+c^2))/((-a^2+c^2) (a^2-b^2+c^2)+(-b^2+c^2) (-a^2+b^2+c^2)),
a32 = ((-b^2+c^2) (-a^2+b^2+c^2))/((-a^2+c^2) (a^2-b^2+c^2)+(-b^2+c^2) (-a^2+b^2+c^2)).
a33 = 0.
Se obtiene:
Ta =
(a^2 (a^10-a^8 (b^2+c^2)+2 a^4 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^4 (b^2+c^2)-a^6 (b^4-3 b^2 c^2+c^4)-a^2 (b^2-c^2)^2 (2 b^4+b^2 c^2+2 c^4)) :
-(b-c)^2 (b+c)^2 (-a^2+b^2-c^2) (a^2-a b+b^2-c^2) (a^2+a b+b^2-c^2) (-a^2+b^2+c^2):
(b-c)^2 (b+c)^2 (a^2+b^2-c^2) (-a^2+b^2-a c-c^2) (-a^2+b^2+a c-c^2) (-a^2+b^2+c^2)).
La circunferencia circunscrita a TaTbTc, contiene a X476 (punto de Tixier) y pasa por X265, X1304, X10745, su ecuación baricéntrica es:
𝔖abc xyz
(b-c)^2 (b+c)^2 (-a^2+b^2+c^2) (-a^2+b^2-b c+c^2) (-a^2+b^2+b c+c^2) (-2 a^4+b^4-2 b^2 c^2+c^4+a^2 (b^2+c^2)) x^2-(-b^14+2 b^12 c^2-b^8 c^6-b^6 c^8+2 b^2 c^12-c^14+a^12 (b^2+c^2)+a^10 (-4 b^4+2 b^2 c^2-4 c^4)+a^8 (5 b^6-2 b^4 c^2-2 b^2 c^4+5 c^6)+a^6 (-9 b^6 c^2+16 b^4 c^4-9 b^2 c^6)+a^4 (-5 b^10+13 b^8 c^2-8 b^6 c^4-8 b^4 c^6+13 b^2 c^8-5 c^10)+a^2 (4 b^12-7 b^10 c^2-2 b^8 c^4+10 b^6 c^6-2 b^4 c^8-7 b^2 c^10+4 c^12)) y z = 0.
- Sábado, 12 de diciembre del 2020
Una propiedad de la cúbica de Darboux
a Pablo, por su "cumple"
Dados un triángulo
ABC y un punto
P (que no está sobre la circunferencia circunscrita ni sobre la recta del infinito), sean
DEF el de
P y
D'E'F' el triángulo pedal, respecto a
D'E'F', del
P* de
P. Los triángulos
DEF y
D'E'F' son perspectivos si y solo si
P está sobre la
cúbica de Darboux.
Si (u:v:w) son las coordenadas baricéntricas de P,
D' = (-b^6 w^2 (v+2 w)-c^2 (a^2-c^2) v^2 (a^2 w-c^2 (2 v+w))+b^2 v (-4 a^2 c^2 u w-a^4 w^2+c^4 (2 v^2+w^2+4 u (v+w)))+b^4 w (2 a^2 w (v+w)+c^2 (v^2+2 w^2+4 u (v+w))) :
b^2 w ((-a^2+b^2) w+c^2 (2 v+w)) (-a^2 v+c^2 v+b^2 (v+2 w)) :
c^2 v ((-a^2+b^2) w+c^2 (2 v+w)) (-a^2 v+c^2 v+b^2 (v+2 w))).
Si P está sobre la cúbica de Darboux, el centro de perspectividad de DEF y D'E'F' es:
Q = a^2(a^6 v w (b^2 (u+2 v) w+c^2 v (u+2 w))
-a^4 (-b^2 c^2 u v w (4 u+3 (v+w))+c^4 v^2 (2 u^2+4 (v+w)^2+u (8 v+3 w))+b^4 w^2 (2 u^2+4 (v+w)^2+u (3 v+8 w)))
+a^2 (c^6 v^2 (4 u^2+8 u v+4 v^2+3 u w+8 v w+2 w^2)+b^6 w^2 (4 u^2+3 u v+2 v^2+8 u w+8 v w+4 w^2)-b^2 c^4 v (4 u^3+4 u^2 (5 v+2 w)+2 v (2 v^2+4 v w+w^2)+u (16 v^2+22 v w+5 w^2))-b^4 c^2 w (4 u^3+4 u^2 (2 v+5 w)+2 w (v^2+4 v w+2 w^2)+u (5 v^2+22 v w+16 w^2)))
-(b^2-c^2) u (-c^2 v+b^2 (2 u+v)) (-c^2 v+b^2 w) (b^2 w-c^2 (2 u+w))) : ... : ...).
Algunos pares {P=Xi, Q=Xj}, para {i, j}: {1, 354}, {3, 6}, {4, 185}.
Cuando P=X20, , Q es:
Q20 = ( a^2 (a^2-b^2-c^2) (a^6 (b^2+c^2)-a^4 (b^2-c^2)^2+-a^2 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^2 (b^4+6 b^2 c^2+c^4)) : ... : ...),
que tiene números de búsqueda en
(4.77687090857033, 4.31527007260811, -1.55153983385369).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,185}, {4,18920}, {22,21663}, {25,64}, {51,125}, {69,305}, {184,5085}, {389,8889}, {468,36982}, {511,7396}, {612,1425}, {614,3270}, {858,14531}, {1181,16419}, {1196,3269}, {1216,26944}, {1368,5562}, {1495,1619}, {1843,1853}, {2063,3292}, {3580,12058}, {3819,6776}, {5020,10605}, {5133,27355}, {5622,34986}, {6000,6353}, {6146,10691}, {6241,38282}, {6619,34854}, {6677,12162}, {6995,32062}, {7391,13851}, {7398,11469}, {7485,13367}, {7667,21659}, {7714,13474}, {7734,18914}, {7735,17830}, {9140,27365}, {10154,10575}, {11793,18909}, {13348,18945}, {13754,30771}, {14915,20850}, {18396,36987}, {26958,34146}.
El conjugado isogonal U de P*, respecto a DEF, es el de DEF respecto a D'E'F'. Cuando P está sobre la cúbica de Darboux los puntos P*, U, W están alineados ().
- Lunes, 30 de noviembre del 2020
La cúbica pK(X274, X314) y una generalización de la cónica de Yiu
Si después de morirme quisieran escribir mi biografía
no hay nada más sencillo.
Tiene sólo dos fechas
la de mi nacimiento y la de mi muerte.
Entre una y otra todos los días son míos.
Fernando Pessoa (Lisboa, 13 de junio de 1888- Lisboa, 30 de noviembre de 1935)
Dado un triángulo ABC, sean P un punto y DEF su .
Se consideran los paralelogramos ABDDb y ACDDc y los puntos Ab y Ac (sobre AC y AB, respectivamente) tales que los triángulos AbDbA y AcDcA son isósceles con cúspide A. Por construcción, se verifica DB=AAb y DC=AAc.
Los puntos Bc, Ba y Ca, Cb, se definen cíclicamente.
Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están sobre una misma cónica 𝒞p, si solo si P está sobre la recta que pasa por los puntos de y de , o sobre la .
Si (u:v:w) son las coordenadas baricéntricas de P,
Ab=(a w - b (v + w) : 0 : -a w) y Ac=(a v - c (v + w) : -a v : 0).
Si P está sobre la elipse circunscrita de Steiner, el centro Q de la cónica 𝒞p es la proyección sobre la elipse circunscrita de el incentro, desde X190 (perspector de la ).
Cuando P es el punto de Nagel, la cónica 𝒞X(8) es la cónica inscrita de perspector X8.
El punto de Nagel es el único punto del plano del triángulo ABC, con triángulo ceviano DEF, verificando que BD=AE, CD=AF, CE=BF, AE=BD, AF=CD, DF=CE.
Cuando P recorre la cónica circunscrita de Steiner, el triángulo A'B'C' formado por las rectas AbAc, BcBa, CaCb es perspectivo con ABC (𝒞p es la de ABC y A'B'C') y el centro de perspecividad P' queda sobre una
cuártica
( -c x^2 y^2+(-a-b-c) x^2 y z+(-a-b-c) x y^2 z-b x^2 z^2+(-a-b-c) x y z^2-a y^2 z^2 = 0)
que pasa por X6630, X8046, X8047, X9510.
También son perspectivos los triángulos ABC y A'B'C' cuando P está sobre la recta X7X8, teniéndose los casos particulares de pares {P=Xi, P'=Xj}, para los índices {i, j}:
{8, 8}, {69, 63}, {75, 333}, {190, 8047}, {668, 6630}, {903, 8046}, {18827, 9510}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Sean A'b y A'c los simétricos de Ab y Ac, respecto a A;
B'c y B'a los simétricos de Bc y Ba, respecto a B;
C'a y C'b los simétricos de Ca y Cb, respecto a C.
Los seis puntos
A'b,
A'c,
B'c,
B'a,
C'a,
C'b están sobre una misma cónica 𝒞'
p, si solo si
P está sobre la
pK(X274, X314).
( a^2 b x^2 y-a b^2 x^2 y+a^2 c x^2 y+a c^2 x^2 y+a^2 b x y^2-a b^2 x y^2-b^2 c x y^2-b c^2 x y^2-a^2 b x^2 z-a b^2 x^2 z-a^2 c x^2 z+a c^2 x^2 z+a^2 b y^2 z+a b^2 y^2 z+b^2 c y^2 z-b c^2 y^2 z-a^2 c x z^2+b^2 c x z^2+a c^2 x z^2+b c^2 x z^2-a^2 c y z^2+b^2 c y z^2-a c^2 y z^2-b c^2 y z^2 = 0)
Cuando P es el punto de Gergonne, la cónica 𝒞'X(7) es la , con centro X478.
Cuando P recorre la cúbica 𝒦, el triángulo A"B"C" formado por las rectas A'bA'c, B'cB'a, C'aC'b es perspectivo con ABC. Si P" es el centro de perspectividad, se tienen los siguientes casos particulares de pares {P=Xi, P"=Xj}, para los índices {i, j}: {7, 4}, {69, 63}, {75, 86}.
- Domingo, 29 de noviembre del 2020
Parábolas con eje paralelos y puntos sobre la circunferencia de Euler
a Lolilla, por su cumpleaños
Dados un triángulo ABC y una recta ℓ, que pasa por su circuncentro O=X3, sean N=X5 el centro de la , el y A'B'C' el .
Ab es el punto sobre B'C', por donde pasa la mediatriz del segmento de extremos B y el punto donde la paralela a ℓ por B corta a B'C'. Se considera la parábola 𝒫ab con foco Fab, el simétrico de B respecto a B'C', y directriz dab, la perpendicular por B a BAb. 𝒫ab es tangente a B'C' en Ab.
Ac es el punto sobre B'C', por donde pasa la mediatriz del segmento de extremos C y el punto donde la paralela a ℓ por C corta a B'C'. Se considera la parábola 𝒫ac con foco Fac, el simétrico de C respecto a B'C', y directriz dac, la perpendicular por C a CAc. 𝒫ac es tangente a B'C' en Ac.
Las parábolas 𝒫ab, 𝒫ac (de ejes paralelos) se corta en Ao y son las usadas en la construcción de un triángulo propuesto por Luís Lopes en Euclid#1203, (ver https://amontes.webs.ull.es/geogebra/euclid1203.html).
Los puntos Bo y Co se definen cíclicamente.
El triángulo es pespectivo al triángulo medial. El centro de perspectividad L' es el simétrico, respecto a la paralela a ℓ por N, del punto de intersección L de las de los extremos del diámetro ℓ.
Si se parte del diámetro ℓ', perpendicular a ℓ, se obtiene el mismo triángulo .
Si la recta ℓ es paralela a la recta de ecuación baricéntrica px+qy+rz=0,
L' = (q - r) (b^2 (p - q)^2 - c^2 (p - r)^2)((b^2 - c^2) (q - r) +
a^2 (q + r-2 p)) : ... : ...).
Cuando se toma una recta ℓ': (q - r)x+ SB (r - p)y+ SC (p - q)z=0, perpendicular a ℓ, se obtiene el mismo punto L'.
Algunos casos particulares:
• Si ℓ es paralela a los ejes de la , L' = X(115), centro de la .
• Si ℓ es paralela al eje mayor de la elipse centrada en el circuncentro y que pasa por el de X(125), L'=X(125), centro de la .
• Si ℓ es paralela a la , L'= X(1566), "Stevanovic-circle-inverse" del
(Milorad R. Stevanovic http://forumgeom.fau.edu/FG2003volume3/FG200320.pdf, Theorem 8.)
• Si ℓ paralela al , L'= X(2679), centro de la rectangular circun-hipérbola que pasa por X(32), del .
• Si ℓ es la , o paralela al , L' = X(3258), reflexión de X(125) en la recta de Euler.
• Si ℓ paralela al eje anti-órtico (tripolar del incentro), L'= X(3259), centro de la rectangular circun-hipérbola que pasa por X(56), centro exterior de homotecia de las circunferencias inscrita y circunscrita.
• Si ℓ es paralela a la , L'= X(5516), centro de la rectangular circun-hipérbola que pasa por X(145), anticomplemento del
• Si ℓ es parelela a la recta IK (que pasa por el incentro y simediano), L'= X(5519), centro de la rectangular circun-hipérbola que pasa por X(218), del y el centro interior de homotecia de las circunferencias inscrita y circunscrita.
Estos y otros casos se reflejan en la tabla siguiente, en cuya primera columna figuran los de rectas paralelas o perpendiculares a ℓ, y en la segunda columna aparece el correspondiente índice de del punto L'
| Tripolos de rectas paralelas o perpendiculares a ℓ |
L' = X(k) |
| 6189, 6190, 30508, 30509 |
115 |
| 1113, 1114, 8115, 8116, 16070, 16071, 39298, 39299 |
125 |
| 7, 27,
75, 86, 234, 272, 273, 310, 335, 554, 658, 673, 675, 871, 903, 1081,
1088, 1223, 1240, 1246, 1268, 1440, 1659, 1897, 2296, 2398, 2400,
2989, 4241, 4373, 5936, 6384, 6548, 6650, 7249, 7318, 8049, 9057,
13390, 14621, 15467, 16078, 16099, 18815, 18884, 19975, 20028,
20527, 21453, 24015, 24154, 24155, 27447, 27475, 27483, 27494,
27498, 28626, 28650, 30598, 30712, 31002, 32011, 32040, 34402,
35096, 36588, 36606, 36620, 36807, 38254, 39293 |
1566 |
| 6, 25,
37, 42, 110, 111, 251, 263, 308, 393, 493, 494, 588, 589, 694, 941,
967, 1169, 1171, 1218, 1239, 1241, 1383, 1400, 1427, 1880, 1976,
1989, 2054, 2165, 2248, 2350, 2395, 2396, 2421, 2433, 2963, 2981,
2987, 2998, 3108, 3228, 3444, 3457, 3458, 3572, 4230, 5638, 5639,
5649, 5968, 6094, 6096, 6151, 6331, 6339, 8105, 8106, 8576, 8577,
8749, 8770, 8791, 8794, 8882, 9178, 9281, 9403, 9462, 9513, 10103,
11166, 11175, 11794, 13854, 14553, 14579, 14606, 14624, 14840,
14842, 14910, 14948, 14998, 16081, 16098, 16606, 18372, 18818,
18898, 21448, 21461, 21462, 24861, 27809, 28625, 28658, 30530,
30535, 30537, 33631, 34079, 34204, 34212, 34288, 34533, 34534,
34570, 34572, 34816, 34818, 34898, 35910, 36616, 36886, 37128,
37137, 37876, 38262, 38278, 38280, 39291, 39292, 39389, 39410,
39411 |
2679 |
| 4, 10, 13, 14, 17, 18, 76, 83, 94, 96, 98, 226,
262, 275, 321, 459, 485, 486, 598, 648, 671, 801, 1029, 1131, 1132,
1139, 1140, 1302, 1327, 1328, 1446, 1676, 1677, 1751, 1916, 2009,
2010, 2051, 2052, 2394, 2407, 2592, 2593, 2671, 2672, 2986, 2996,
3316, 3317, 3366, 3367, 3370, 3373, 3374, 3381, 3382, 3387, 3388,
3391, 3392, 3397, 3399, 3406, 3407, 3413, 3414, 3424, 3429, 3590,
3591, 3597, 4049, 4052, 4080, 4240, 4444, 5392, 5395, 5397, 5401,
5402, 5403, 5404, 5466, 5485, 5487, 5488, 5490, 5491, 5503, 6035,
6177, 6178, 6504, 6539, 6568, 6569, 6625, 7578, 7607, 7608, 7612,
8587, 8781, 8796, 8808, 9180, 9211, 9214, 9221, 9290, 9302, 9381,
10153, 10155, 10159, 10185, 10187, 10188, 10194, 10195, 10290,
10302, 10484, 10511, 11121, 11122, 11140, 11167, 11170, 11172,
11538, 11599, 11602, 11603, 11606, 11608, 11611, 11668, 11669,
12066, 12067, 12816, 12817, 12818, 12819, 12820, 12821, 12822,
12823, 13380, 13478, 13576, 13579, 13580, 13581, 13582, 13583,
13584, 13585, 13599, 14223, 14226, 14228, 14229, 14231, 14232,
14234, 14236, 14237, 14238, 14240, 14241, 14243, 14244, 14245,
14458, 14484, 14485, 14488, 14492, 14494, 14534, 14554, 14632,
14633, 16075, 16080, 16277, 17503, 17758, 18316, 18366, 18840,
18841, 18842, 18843, 18844, 18845, 21845, 21846, 22235, 22237,
22244, 22245, 24007, 24008, 24624, 27797, 30505, 30527, 30528,
30588, 31363, 31630, 31943, 32014, 32022, 32130, 32532, 33602,
33603, 33604, 33605, 33606, 33607, 33698, 34087, 34089, 34091,
34258, 34289, 34475, 34899, 35005, 35098, 35353, 36316, 36317,
36840, 36907, 37865, 37874, 37892, 38253, 38259, 38309, 39284,
39290, 39295 |
3258 |
| 1, 28, 57, 81, 88, 89, 105, 274, 277, 278,
279, 291, 330, 367, 651, 955, 957, 959, 961, 985, 1002, 1022, 1123,
1170, 1219, 1224, 1255, 1257, 1258, 1280, 1336, 1390, 1422, 1432,
1929, 2006, 2224, 2282, 2306, 2362, 2397, 2401, 2982, 2990, 3227,
3300, 3302, 4246, 5376, 6335, 6553, 7052, 7132, 7167, 7313, 8056,
9058, 9401, 9445, 10490, 14596, 15474, 16015, 16082, 16100, 16232,
17946, 19296, 21907, 23834, 24029, 24857, 24858, 25417, 25430,
26745, 27789, 30571, 30602, 30701, 30710, 32009, 32017, 32019,
32020, 33654, 33655, 34018, 34051, 34056, 34084, 34578, 34892,
34914, 35058, 35348, 35577, 36122, 36603, 36805, 36871, 37626,
37870, 37887, 38247 |
3259 |
| 145, 190, 1222, 2403, 2415, 4248,
5435, 6336, 6632, 7320, 8051, 9059, 9083, 9311, 17780, 17783, 18743,
24004, 27496, 27818, 31227, 36872 |
5516 |
| 100, 344, 1025, 1026,
1445, 2346, 2402, 2414, 2991, 3870, 4233, 4238, 4554, 9061, 14947,
17093, 27819, 30610, 31615, 31628, 32041, 39272, 39273 |
5519 |
| 8,
29, 85, 92, 178, 189, 257, 312, 333, 653, 1121, 1220, 1311, 1952,
2090, 2399, 2406, 2988, 2994, 4102, 4181, 4518, 4997, 6557, 7020,
7026, 7043, 7090, 7452, 8777, 9056, 10405, 14121, 14218, 14942,
17743, 17947, 18031, 18359, 19607, 21739, 24035, 27424, 28660,
30608, 30690, 30711, 31359, 32008, 32015, 34234, 34527, 36596,
36605, 38255, 39294 |
10017 |
| 99, 1992, 2408, 2418, 4232, 4235,
5468, 9084, 9170, 9227, 11059, 11169, 14608, 17983, 23054, 31614,
36890, 37210, 37860, 37880, 39296 |
31654 |
| 69, 95, 107, 253, 264,
287, 305, 306, 307, 328, 1441, 1494, 1799, 1972, 2373, 2409, 2419,
6330, 6340, 8797, 9229, 10603, 11090, 11091, 13575, 14977, 18018,
18019, 18024, 19774, 19775, 20336, 20563, 20564, 22339, 22340,
30786, 31360, 34211, 34407, 34767, 35510, 36889, 36948, 37202,
39297 |
33504 |
| 3, 97, 276, 394, 1073, 1214, 1217, 1297, 2404,
2416, 3346, 3682, 3926, 3998, 5481, 8813, 9064, 14376, 14489, 14919,
14938, 15352, 15421, 17974, 18317, 18876, 22268, 22270, 26922,
28724, 30441, 31626, 32132, 34129, 34225, 34287, 34427, 34568,
34579, 34897, 35061, 35911, 36609, 37872, 38256 |
Ver preámbulo
35579
(César Eliud Lozada, December 22, 2019) |
| 21, 63,
78, 280, 345, 348, 1791, 1812, 2339, 2405, 2417, 6513, 7131, 7361,
7435, 9107, 26703, 30556, 30557, 30679, 30680, 31623, 34259, 34277,
36100, 36795, 37141 |
35580 |
| 15, 16, 186, 249, 323, 842, 1138,
2410, 2411, 3431, 7480, 7799, 9060, 9213, 10419, 14165, 14355,
14565, 14838, 15412, 16577, 18333, 18593, 36210, 37802,
39149 |
35581 |
| 468, 476, 523, 524, 2770, 2966, 3266, 4062, 4590,
5486, 5967, 7473, 9164, 9516, 10415, 13574, 14999, 15464, 16092,
16103, 17708, 18361, 18823, 31068, 34761, 34763, 35511, 36885,
36953, 37778 |
35582 |
| 662, 4242, 4552, 4585, 9070, 13739, 15455,
33116, 34772 |
35583 |
| 66, 141, 427, 1031, 1502, 3613, 8024, 8801,
9076, 9483, 14617, 15523, 16102, 17949, 20021, 23297, 31125, 34285,
35366 |
35584 |
| 666, 24002, 26015, 30379, 37143,
37788}, 35585}, {{892, 8599, 9080, 9154, 9182, 9187, 9198, 9199,
9487, 17948, 17952, 22329, 34760 |
35586 |
| v514, 519, 655, 996,
1000, 1016, 2726, 2985, 3911, 4358, 6630, 8046, 13136, 14358, 14359,
14628, 16704, 20569, 31011, 32013, 34523, 34764, 35168, 36592,
36915, 36954, 37168, 37222, 37790 |
35587 |
| 24, 54, 254, 371, 372,
1993, 3425, 3563, 4558, 7763, 11547, 13429, 13440, 15329, 16237,
18879, 18883, 30450 |
35588 |
| 55, 241, 650, 672, 677, 949, 1252,
2115, 2340, 3693, 5089, 7123, 37908 |
35589 |
| 59 |
35590 |
| 61,
62, 288, 1166, 1994, 2413, 2984, 3459, 3518, 5966, 7769, 13472,
14570, 14590, 18315, 22101, 30526, 30529, 38342 |
35591 |
| 5, 68,
324, 343, 13157, 14592, 16039, 16813, 18027, 18855, 28706, 31610,
31617, 31846, 34580, 36952 |
35592 |
| 9, 200, 281, 282, 346, 2184,
2287, 2297, 4183, 6605, 7097, 7110, 13138, 13149, 14943, 15889,
15890, 15891, 15892, 16016, 19605, 21446, 23617, 28071, 28132,
30705, 31618, 34525, 36101, 36627, 36629, 36796, 36910,
36916 |
35593 |
| 23, 250, 1304, 4580, 15398, 22151, 37765, 37801,
37804, 37937 |
35594 |
Si (u:v.w) son las coordenadas del de una recta paralela a ℓ, entonces:
L' = (u (v-w) (c^2 v^2 (u-w)^2-b^2 (u-v)^2 w^2) (-(b^2-c^2) u (v-w)+a^2 (-2 v w+u (v+w))) : ... : ...).
- Jueves, 26 de noviembre del 2020
X(10990) centro de una hipérbola rectangular
El 26 de noviembre de 1922, Howard Carter y Lord Carnarvon, después de haber encontrado las escaleras que conducían a la tumba del joven faraón Tutankhamon, y tras tres semanas de intensos trabajos con su equipo, entraron en ella observando que no había sido saqueada. El sucesor de Tutankhamon fue Ay, progenitor de la reina Nefertiti.
Sea DEF el de un triángulo ABC y el de un punto P. Se denota por Ab el antipodal de Pa en la circunferencia (BFPa), y por Ac el antipodal de Pa en la circunferencia (CEPa).
Los puntos Bc, Ba y Ca, Cb, se definen cíclicamente.
Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb, están en una misma cónica, 𝒞pe(P), si y solo si P está sobre la hipérbola (rectangular) ℋ, que pasa por el circuncentro, el y su , y cuyas asíntotas tienen la dirección de los conjugados isogonales de los puntos de intersección de la con la circunferencia circunscrita.
Con estos datos la hipérbola ℋ puede ser construida: (IIPPP) o §2.3. (5P20T).
En coordenadas baricéntricas, si P=(u:v:w),
Ab = (2 a^2 (a^2 - b^2 + c^2) ((b^2 - c^2) u + a^2 (u + 2 v)) :
(b^2 - c^2)^3 u - a^2 (b^2 - c^2)^2 (u + 2 w) -
a^6 (3 u + 4 v + 2 w) + a^4 (b^2 (3 u + 4 (v + w)) + c^2 (5 u + 4 (v + w))) :
-(a^2 - b^2 + c^2)^2 ((b^2 - c^2) u + a^2 (u + 2 v))),
Ac = (2 a^2 (a^2 + b^2 - c^2) ((-b^2 + c^2) u + a^2 (u + 2 w)) :
-(a^2 + b^2 - c^2)^2 ((-b^2 + c^2) u + a^2 (u + 2 w)) :
-(b^2 - c^2)^3 u - a^2 (b^2 - c^2)^2 (u + 2 v) -
a^6 (3 u + 2 v + 4 w) + a^4 (c^2 (3 u + 4 (v + w)) + b^2 (5 u + 4 (v + w)))),
ℋ: 2 b^2 c^2 (b^2 - c^2) (-3 a^4 + (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2))x^2
-a^2 (b^2 - c^2) (-a^6 + b^6 + 7 b^4 c^2 +
7 b^2 c^4 + c^6 + 3 a^4 (b^2 + c^2) -
a^2 (3 b^4 + 10 b^2 c^2 + 3 c^4))y z + ... = 0.
La hipérbola ℋ, que pasa por los centros Xi, para i∈{3, 20, 64, 2574, 2575, 7957, 11469, 12250, 15054, 15062, 16936, 22528, 35253}, tiene su centro en X10990, reflexión del centro de la en el conjugado isogonal del punto del infinito de la recta de Euler.
• Si P es el circuncentro, la cónica
𝒞pe(X3)
( 5 a^6 x^2-17 a^4 b^2 x^2+19 a^2 b^4 x^2-7 b^6 x^2-17 a^4 c^2 x^2+26 a^2 b^2 c^2 x^2-9 b^4 c^2 x^2+19 a^2 c^4 x^2-9 b^2 c^4 x^2-7 c^6 x^2+2 a^6 x y-2 a^4 b^2 x y-2 a^2 b^4 x y+2 b^6 x y+2 a^4 c^2 x y-4 a^2 b^2 c^2 x y+2 b^4 c^2 x y-26 a^2 c^4 x y-26 b^2 c^4 x y+22 c^6 x y-7 a^6 y^2+19 a^4 b^2 y^2-17 a^2 b^4 y^2+5 b^6 y^2-9 a^4 c^2 y^2+26 a^2 b^2 c^2 y^2-17 b^4 c^2 y^2-9 a^2 c^4 y^2+19 b^2 c^4 y^2-7 c^6 y^2+2 a^6 x z+2 a^4 b^2 x z-26 a^2 b^4 x z+22 b^6 x z-2 a^4 c^2 x z-4 a^2 b^2 c^2 x z-26 b^4 c^2 x z-2 a^2 c^4 x z+2 b^2 c^4 x z+2 c^6 x z+22 a^6 y z-26 a^4 b^2 y z+2 a^2 b^4 y z+2 b^6 y z-26 a^4 c^2 y z-4 a^2 b^2 c^2 y z-2 b^4 c^2 y z+2 a^2 c^4 y z-2 b^2 c^4 y z+2 c^6 y z-7 a^6 z^2-9 a^4 b^2 z^2-9 a^2 b^4 z^2-7 b^6 z^2+19 a^4 c^2 z^2+26 a^2 b^2 c^2 z^2+19 b^4 c^2 z^2-17 a^2 c^4 z^2-17 b^2 c^4 z^2+5 c^6 z^2 = 0)
es la descrita en X13881, donde los puntos Ab, Ac de allí son los puntos Cb, Bc de aquí, respectivamente. (El punto X(13881) como centro de una cónica)
Let DEF be the orthic triangle. Let Ab be the point in which the line through B perpendicular to AB meets the perpendicular bisector of segment BD . Let Ac be the point in which the line through C perpendicular to AC meets the perpendicular bisector of segment CD. Define Bc, Ba, Ca, Cb cyclically. The six ponts Ab, Ac, Bc, Ba, Ca, Cb lie on a conic with center X(13881). (Angel Montesdeoca, Decemberr 23, 2018).
• Si P es el conjugado isogonal del punto De Longchamps, el centro de la cónica
𝒞pe(X64)
( a^8 x^2-6 a^4 b^4 x^2+8 a^2 b^6 x^2-3 b^8 x^2+12 a^4 b^2 c^2 x^2-8 a^2 b^4 c^2 x^2-4 b^6 c^2 x^2-6 a^4 c^4 x^2-8 a^2 b^2 c^4 x^2+14 b^4 c^4 x^2+8 a^2 c^6 x^2-4 b^2 c^6 x^2-3 c^8 x^2+2 a^8 x y-8 a^6 b^2 x y+12 a^4 b^4 x y-8 a^2 b^6 x y+2 b^8 x y+12 a^6 c^2 x y-12 a^4 b^2 c^2 x y-12 a^2 b^4 c^2 x y+12 b^6 c^2 x y-16 a^4 c^4 x y+32 a^2 b^2 c^4 x y-16 b^4 c^4 x y-12 a^2 c^6 x y-12 b^2 c^6 x y+14 c^8 x y-3 a^8 y^2+8 a^6 b^2 y^2-6 a^4 b^4 y^2+b^8 y^2-4 a^6 c^2 y^2-8 a^4 b^2 c^2 y^2+12 a^2 b^4 c^2 y^2+14 a^4 c^4 y^2-8 a^2 b^2 c^4 y^2-6 b^4 c^4 y^2-4 a^2 c^6 y^2+8 b^2 c^6 y^2-3 c^8 y^2+2 a^8 x z+12 a^6 b^2 x z-16 a^4 b^4 x z-12 a^2 b^6 x z+14 b^8 x z-8 a^6 c^2 x z-12 a^4 b^2 c^2 x z+32 a^2 b^4 c^2 x z-12 b^6 c^2 x z+12 a^4 c^4 x z-12 a^2 b^2 c^4 x z-16 b^4 c^4 x z-8 a^2 c^6 x z+12 b^2 c^6 x z+2 c^8 x z+14 a^8 y z-12 a^6 b^2 y z-16 a^4 b^4 y z+12 a^2 b^6 y z+2 b^8 y z-12 a^6 c^2 y z+32 a^4 b^2 c^2 y z-12 a^2 b^4 c^2 y z-8 b^6 c^2 y z-16 a^4 c^4 y z-12 a^2 b^2 c^4 y z+12 b^4 c^4 y z+12 a^2 c^6 y z-8 b^2 c^6 y z+2 c^8 y z-3 a^8 z^2-4 a^6 b^2 z^2+14 a^4 b^4 z^2-4 a^2 b^6 z^2-3 b^8 z^2+8 a^6 c^2 z^2-8 a^4 b^2 c^2 z^2-8 a^2 b^4 c^2 z^2+8 b^6 c^2 z^2-6 a^4 c^4 z^2+12 a^2 b^2 c^4 z^2-6 b^4 c^4 z^2+c^8 z^2 = 0)
es el circuncentro.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Cuando se parte del de P, en vez de su triángulo pedal, el lugar geométrico de P tal que los seis puntos Ab, Ac, Bc, Ba, Ca, Cb, están en una misma cónica, 𝒞ce(P), es la hipérbola descrita en X15526. Pasa por los centros Xi, para i∈{
2, 69, 95, 253, 264, 287, 305, 306, 307, 328, 1441, 1494, 1799, 1972, 2373, 2419, 6330, 6340, 8797, 9229, 10603, 11090, 11091, 13575, 14977, 18018, 18019, 18024, 19774, 19775, 20336, 20563, 20564, 22339, 22340, 30786, 31360, 34407, 34767, 35510, 36889, 36948, 37202, 39297}.
X(15526) is the center of hyperbola {{A,B,C,X(2),X(69)}}. This hyperbola is the isotomic conjugate of the Euler line and the isogonal conjugate of line X(6)X(25). It is also the locus of cevapoints of X(2) and a point P as P moves along the Euler line, and also the locus of trilinear poles of lines passing through X(525). (Randy Hutson, January 29, 2018)
• Si P es el baricentro, la cónica 𝒞ce(X2) es la 𝒞pe(X3).
- Martes, 24 de noviembre del 2020
Transformación afín entre triángulos cevianos
El 24 de noviembre de 1927 nació, en Las Palmas de Gran Canaria, Alfredo Kraus. Fue un tenor y profesor de canto español, que será considerado como uno de los mejores tenores líricos ligeros de la segunda mitad del siglo XX.
Dados un triángulo ABC y un punto P, sea Q su , y , sus , respectivamente.
Si (u:v:w) son las coordenadas baricéntricas de P, la matriz ℳ asociada de la transformación afín σP, que aplica en , tiene las entradas (las demás se deducen cíclicamente):
M[1,1] = v w (v + w),
M[1,2] = w u (v - w),
M[1,3] = u v (w-v).
Su punto fijo, correspondiente al valor propio λ=2 u v w, es:
Fo = (u(v - w)^2 : v(u - w)^2 : w(u - v)^2).
Caso particulares {{P=Xi, Q=Xj}, Fo=Xk}, para {{i,j},k}: {{1, 75}, 244}, {{3, 264}, 2972}, {{4, 69}, 125}, {{5, 95}, 35442}, {{6, 76}, 3124},
{{7, 8}, 11}, {{9, 85}, 3119}, {{10, 86}, 3120}, {{13, 298}, 30465}, {{14, 299}, 30468}, {{20, 253}, 122}, {{25, 305}, 20975}, {{27, 306}, 4466}, {{28, 20336}, 18210}, {{30, 1494}, 1650}, {{37, 274}, 3121},
{{42, 310}, 3122}, {{43, 6384}, 3123}, {{57, 312}, 2170}, {{63, 92}, 34591}, {{78, 273}, 7004},
{{81, 321}, 3125}, {{88, 4358}, 2087}, {{94, 323}, 2088}, {{98, 325}, 868}, {{99, 523}, 1649},
{{100, 693}, 3126}, {{105, 3263}, 3675}, {{111, 3266}, 21906}, {{144, 10405}, 13609}, {{145, 4373}, 3756}, {{186, 328}, 16186}, {{189, 329}, 5514}, {{190, 514}, 6544}, {{192, 330}, 6377}, {{193, 2996}, 6388}, {{200, 1088}, 2310}, {{226, 333}, 21044}, {{239, 335}, 27918}, {{263, 20023}, 6784}, {{278, 345}, 7117}, {{279, 346}, 14936}, {{291, 350}, 27846}, {{394, 2052}, 3269}, {{459, 37669}, 1562}, {{513, 668}, 14434}, {{519, 903}, 1647}, {{524, 671}, 1648}, {{525, 648}, 14401}, {{527, 1121}, 33573}, {{536, 3227}, 1646}, {{538, 3228}, 1645}, {{598, 599}, 8288}, {{694, 3978}, 2086}, {{824, 4586}, 33568}, {{899, 31002}, 19945}, {{985, 33931}, 4475}, {{1022, 24004}, 1635}, {{1026}, 2254}, {{1032, 14361}, 13613}, {{1034, 5932}, 3612}, {{1119, 1265}, 38351}, {{1143, 1274}, 21623}, {{1440, 7080}, 38357}, {{1445}, 38375}, {{1446, 2287}, 36197}, {{1447, 4518}, 4124}, {{1647}, 24188}, {{1654, 6625}, 6627}, {{1992, 5485}, 6791}, {{2089}, 6732}, {{2394, 2407}, 1637}, {{2395, 2396}, 2491}, {{2397, 2401}, 3310}, {{2398, 2400}, 676}, {{2403, 2415}, 14425}, {{2408, 2418}, 9125}, {{2421}, 3569}, {{2433}, 14398}, {{2994, 5905}, 6506}, {{3146, 35510}, 13611}, {{3210, *}, 16614}, {{3214, *}, 21963}, {{3413, 6190}, 13722}, {{3414, 6189}, 13636}, {{3911, 4997}, 4530}, {{4049, *}, 4120}, {{4052, *}, 21950}, {{4230, *}, 684}, {{4235, 14977}, 14417}, {{4240, 34767}, 9033},
{{4452, 6553}, 17071}, {{4585}, 2610}, {{4651, *}, 2486}, {{4762, 32041}, 33570}, {{5435, 6557}, 4534}, {{5466, 5468}, 690}, {{5968, *}, 9155}, {{6545, 6632}, 14442}, {{6548, 17780}, 900}, {{6633, *}, 14475}, {{6735, *}, 35015}, {{7081, 7249}, 4459}, {{8027, *}, 14441}, {{8029, 31614}, 14443}, {{8030, *}, 14444}, {{9178, *}, 351}, {{9180, 9182}, 8371}, {{9214, 36890}, 5642}, {{11251, *}, 13212}, {{13386, 13387},26932}, {{13582, 37779}, 10413}, {{14223, 14999}, 1640}, {{14607, *}, 11182}, {{14998, *}, 6041}, {{15774, *}, 34601},
{{16075, 16076}, 1651}, {{16084, 16098}, 865}, {{16085, 16100}, 866}, {{16086, 16099}, 867},
{{16606, 31008}, 21835}, {{17948, *}, 1641}, {{20806, *}, 38356}, {{22016, *},22215}, {{23342, *}, 9148}, {{23354, *}, 3837}, {{23878, *}, 33569}, {{23891, *},4728}, {{27846, *}, 24193}, {{30508, 30509}, 523}, {{30695, *}, 17426}, {{34760, 34763}, 33921}, {{34762, 34764}, 33920}, {{35348, *}, 14413},
{{35353, *}, 14431}, {{36887, *}, 6174}, {{38940, *}, 15357}.
Fo está en la si y solo si P está sobre la cúbica:
K015, "Tucker nodal cubic": x(y-z)^2+y(z-x)^2+z(x-y)^2=0.
En este caso los tres puntos fijos de σP coinciden. Se trata del caso IV de la clasificación de homogafías.
Para puntos sobre K015, se tienen los siguientes casos particulares, {{P=Xi, Q=Xj}, Fo=Xk}, para {{i,j},k}: {{30508, 30509}, 523}, {{5466, 5468}, 690}, {{6548, 17780}, 900}, {{4240, 34767}, 9033}, {{34762, 34764}, 33920}, {{34760, 34763}, 33921}.
Cuando P recorre la el lugar geometrico del punto fijo Fo es la recta que pasa por el centro de la y paralela a la asíntota (que no es la recta de Euler) de la hipérbola circunscrita de centro X1650.
En estas circunstancias, la recta PFo envuelve una
hipérbola,
( (-b^4+c^4+a^2 (b^2-c^2))^4 (-2 a^4+(b^2-c^2)^2+a^2 (b^2+c^2))^2x^2-2 (a^2-b^2)^2 (a^2-c^2)^2 (a^4-(b^2-c^2)^2)^2 (a^8-a^6 (b^2+c^2)+5 a^2 (b^2-c^2)^2 (b^2+c^2)+a^4 (-3 b^4+7 b^2 c^2-3 c^4)-(b^2-c^2)^2 (2 b^4+5 b^2 c^2+2 c^4))y z + ... = 0)
ℋ, con una asíntota e (la recta de Euler), la tangente t en T = X1494 (conjugado isotómico del punto del infinito de la recta de Euler) pasa por el baricentro, y su centro es D = X402 ("Zeeman-Gossard Perspector").
Con estos datos se puede construir (hOt_P) la hipérbola ℋ.
- Miércoles, 18 de noviembre del 2020
Conjugado isogonal como centro ortológico
El 18 de noviembre de 1922 falleció (a los 51 años) Marcel Proust, novelista, ensayista y crítico francés cuya obra maestra, la novela "En busca del tiempo perdido" está compuesta de siete partes publicadas entre 1913 y 1927.
Dados un triángulo ABC y un punto (no situado sobre la circunferencia circunscrita, ni en la recta del infinito), la
circunferencia
( Si P=(u:v:w), en baricéntricas,
c^2 x y + b^2 x z +
a^2 y z + (x + y + z) (-(((c^2 u - c^2 v + a^2 w - b^2 w) y)/(
u + v + w)) - ((b^2 u + a^2 v - c^2 v - b^2 w) z)/(u + v + w)) = 0)
con centro en P y que pasa por A vuelve a cortar a la lados AC y AB en Ab y Ac, respectivamente. Los puntos Bc, Ba y Ca, Cb, se definen cíclicamente. Sea A'B'C' el triángulo formado por las rectas AbAc, BcBa y CaCb.
Los triángulos ABC y A'B'C' son .
El centro de ortología de ABC, respecto a A'B'C', es el P* de P.
Si (u:v:w) son las coordenadas baricéntricas de P, el centro de ortología de A'B'C', respecto a ABC, es:
Q = (a^6 v w (-u+v+w)-2 (b^2-c^2)^2 u^2 (c^2 v+b^2 w)+2 a^4 u (b^2 w (3 v+w)+c^2 v (v+3 w))-a^2 (b^4 w (-2 u^2+v (v+w)+u (5 v+2 w))+c^4 v (-2 u^2+w (v+w)+u (2 v+5 w))-2 b^2 c^2 (u^2 (v+w)+v w (v+w)-u (v^2-v w+w^2))) : ... : ...).
Q es la reflexión, en P, de la reflexión de P* en el circuncentro.
Los puntos P, P*, Q están alineados si P está sobre la cúbica McCay. La recta que los contienen pasa por el circuncentro (propiedad 1).
Algunos pares {P=Xi, Q=Qi=Xj}, para {i, j}: {1, 7982}, {3, 4}, {4, 382}, {5, 15800}, {20, 5925}, {64, 12250}, {84, 7992}.
Cuando P es el baricentro (G=X2), Q2 es la reflexión, en el baricentro, de la reflexión del simediano en el circuncentro:
Q2 = (a^6+8 a^4 (b^2+c^2)+a^2 (-7 b^4+6 b^2 c^2-7 c^4)-2 (b^2-c^2)^2 (b^2+c^2) : ... : ...),
que tiene números de búsqueda en
(-7.31307970834958, -6.79471405421268, 11.7199648463699).
Es el punto medio de Xi y Xj para los índices {i,j}: {1351,3830}, {1353,33699}, {1992,3543}, {6776,15682}, {8593,10723}, {12294,21969}, {14927,15640}, {15534,36990}, {20423,31670}.
Es la reflexión de Xi en Xj para los índices {i,j}: {2,5480}, {3,5476}, {6,20423}, {376,597}, {599,381}, {1350,2}, {1352,3845}, {1853,23049}, {2930,5655}, {3242,3656}, {3534,182}, {5085,14853}, {5648,113}, {5655,32271}, {6776,8584}, {8703,18583}, {10606,23327}, {11646,9880}, {12117,5026}, {12584,25566}, {13169,32274}, {15533,1352}, {15534,1351}, {19161,21849}, {20423,21850}, {31884,14561}, {32233,15303}, {33706,24256}, {36990,3830}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,1350}, {3,5476}, {4,524}, {5,21358}, {6,30}, {25,5642}, {51,31152}, {69,3839}, {113,5648}, {115,11173}, {141,3545}, {182,3534}, {376,597}, {381,511}, {382,576}, {383,9763}, {428,37672}, {518,31162}, {541,16010}, {542,1351}, {547,38136}, {549,14561}, {550,10541}, {551,38035}, {575,1657}, {578,34726}, {1080,9761}, {1181,34613}, {1352,3845}, {1353,33699}, {1469,11238}, {1503,1992}, {1513,11184}, {1853,2781}, {1993,9143}, {2777,23048}, {2810,10710}, {2854,10706}, {2930,5655}, {3056,11237}, {3091,21356}, {3098,5054}, {3146,5032}, {3242,3656}, {3524,3589}, {3564,15687}, {3580,31105}, {3618,10304}, {3654,38087}, {3655,38315}, {3679,38144}, {3763,5055}, {3818,14269}, {3828,38146}, {3843,34507}, {5017,6034}, {5026,12117}, {5028,14537}, {5050,15681}, {5052,11648}, {5064,12294}, {5071,10519}, {5073,11482}, {5092,15688}, {5093,15684}, {5094,32225}, {5104,37637}, {5201,32444}, {5446,37473}, {5846,34627}, {5847,34648}, {5864,37333}, {5865,37332}, {5894,15741}, {5895,8549}, {5965,35403}, {5969,6054}, {6144,18440}, {6173,38143}, {6776,8584}, {6800,37901}, {7464,37827}, {7500,17809}, {7530,19596}, {7540,36747}, {7610,13860}, {7745,10542}, {7778,9993}, {7788,18906}, {7841,22486}, {8537,35490}, {8540,12943}, {8546,37946}, {8593,10723}, {8703,18583}, {9024,10711}, {9053,34631}, {9745,13192}, {9756,22329}, {9830,10753}, {9880,11646}, {9969,16072}, {9974,35821}, {9975,35820}, {9976,38790}, {10056,10387}, {10606,23327}, {10989,11002}, {11064,26255}, {11177,14614}, {11216,36201}, {11470,12173}, {12007,14927}, {12017,15689}, {12100,38079}, {12233,34621}, {12584,25566}, {12953,19369}, {13169,32274}, {13352,18374}, {13857,34417}, {14093,17508}, {14492,24256}, {14787,37486}, {14810,15693}, {14831,34146}, {14893,34380}, {14912,20583}, {15033,19127}, {15274,37200}, {15303,32233}, {15360,37638}, {15520,29323}, {15683,25406}, {15694,38317}, {15696,20190}, {15702,21167}, {15703,25565}, {15811,31802}, {16475,34628}, {17702,34319}, {17845,34117}, {18358,23046}, {19149,34603}, {19161,21849}, {19709,24206}, {25154,33517}, {25164,33518}, {25335,32273}, {30270,33237}, {34200,38110}, {35228,37940}, {35266,37645}, {35707,37925}, {35822,36719}, {35823,36733}.
- Martes, 10 de noviembre del 2020
Un caso del problema de Apolonio: PPC
El 10 de noviembre de 1938 falleció Ataturk, fundador en el 29 de octubre de 1923 de la República Turca, rompiendo definitivamente con el sultanato y suponiendo el fin del Imperio Otomano, y patrocinador de la secularización de la sociedad islámica. Tras la creación de la República, Atatürk introdujo una serie de reformas sociales entre las más destacadas se encuentran la separación de Estado y religión, mayores derechos para las mujeres o la sustitución de la grafía árabe por la latina.
Dado un triángulo ABC con incentro I=X1, y DEF. Sean Db la proyección ortogonal de D sobre AC y Dc la proyección ortogonal de D sobre AB.
Se designan por A' el punto de intersección de la mediatriz de DbDc con la perpendicular por Ma a AI, y por Γa1 la
circunferencia
( Ecuación baricéntrica:
a^6 b^2 x^2-3 a^4 b^4 x^2+3 a^2 b^6 x^2-b^8 x^2-2 a^6 b c x^2+4 a^4 b^3 c x^2-2 a^2 b^5 c x^2+a^6 c^2 x^2-2 a^4 b^2 c^2 x^2-3 a^2 b^4 c^2 x^2+4 b^6 c^2 x^2+4 a^4 b c^3 x^2+4 a^2 b^3 c^3 x^2-3 a^4 c^4 x^2-3 a^2 b^2 c^4 x^2-6 b^4 c^4 x^2-2 a^2 b c^5 x^2+3 a^2 c^6 x^2+4 b^2 c^6 x^2-c^8 x^2+a^8 x y-2 a^6 b^2 x y+2 a^2 b^6 x y-b^8 x y-2 a^6 c^2 x y+4 a^4 b^2 c^2 x y-6 a^2 b^4 c^2 x y+4 b^6 c^2 x y-8 a^4 b c^3 x y+4 a^4 c^4 x y+6 a^2 b^2 c^4 x y-6 b^4 c^4 x y-2 a^2 c^6 x y+4 b^2 c^6 x y-c^8 x y+a^8 y^2-3 a^6 b^2 y^2+3 a^4 b^4 y^2-a^2 b^6 y^2+2 a^6 b c y^2-4 a^4 b^3 c y^2+2 a^2 b^5 c y^2+a^6 c^2 y^2-2 a^4 b^2 c^2 y^2+a^2 b^4 c^2 y^2+4 a^4 b c^3 y^2-4 a^2 b^3 c^3 y^2-a^4 c^4 y^2+a^2 b^2 c^4 y^2+2 a^2 b c^5 y^2-a^2 c^6 y^2+a^8 x z-2 a^6 b^2 x z+4 a^4 b^4 x z-2 a^2 b^6 x z-b^8 x z-8 a^4 b^3 c x z-2 a^6 c^2 x z+4 a^4 b^2 c^2 x z+6 a^2 b^4 c^2 x z+4 b^6 c^2 x z-6 a^2 b^2 c^4 x z-6 b^4 c^4 x z+2 a^2 c^6 x z+4 b^2 c^6 x z-c^8 x z-2 a^8 y z+6 a^6 b^2 y z-2 a^4 b^4 y z-2 a^2 b^6 y z-12 a^6 b c y z+4 a^2 b^5 c y z+6 a^6 c^2 y z+4 a^4 b^2 c^2 y z+2 a^2 b^4 c^2 y z-8 a^2 b^3 c^3 y z-2 a^4 c^4 y z+2 a^2 b^2 c^4 y z+4 a^2 b c^5 y z-2 a^2 c^6 y z+a^8 z^2+a^6 b^2 z^2-a^4 b^4 z^2-a^2 b^6 z^2+2 a^6 b c z^2+4 a^4 b^3 c z^2+2 a^2 b^5 c z^2-3 a^6 c^2 z^2-2 a^4 b^2 c^2 z^2+a^2 b^4 c^2 z^2-4 a^4 b c^3 z^2-4 a^2 b^3 c^3 z^2+3 a^4 c^4 z^2+a^2 b^2 c^4 z^2+2 a^2 b c^5 z^2-a^2 c^6 z^2 = 0)
(A'DbDc), que es tangente a la circunferencia circunscrita en (baricéntricas):
A1 = (-a^2 (a^4 - (b^2 - c^2)^2) : -b (b - c) (-a^4 +
2 a^2 c (b + c) + (b - c) (b + c)^3) : -(b - c) c (a^4 -
2 a^2 b (b + c) + (b - c) (b + c)^3)).
La circunferencia Γa1 también es tangente a la circunferencia inscrita en:
Ai = (4 a^4 (b - c)^2 (a + b - c) (a - b + c) : -(a - b - c) (a + b -
c) (a^3 - a (b - c)^2 +
a^2 (-b + c) - (b - c)^2 (b + c))^2 : -(a - b - c) (a - b +
c) (a^3 + a^2 (b - c) - a (b - c)^2 - (b - c)^2 (b + c))^2),
y a la circunferencia en:
Ae =(4 a^4 (b - c)^2 (a + b - c) (a - b + c) : -(a - b + c) (a + b +
c) (a^3 + a^2 (b - c) - a (b - c)^2 + (b - c)^2 (b + c))^2 : -(a + b - c) (a + b + c) (a^3 -
a (b - c)^2 + a^2 (-b + c) + (b - c)^2 (b + c))^2).
Cíclicamente, se definen los puntos B1, C1, Bi, Ci, Be, Ce.
Los triángulos y son perspectivos, con centro de perspectividad X
56, centro de homotecia externo de las circunferencias inscrita y circunscrita.
El Ta1Tb1Tc1 de es perspectivo con ABC, con centro de perspectividad X2178.
-b^2 (a^5 + b^5 + a^4 (b - c) +
b^4 c - b c^4 - c^5 - 2 a^3 (b^2 + c^2) + a (b^2 + c^2)^2 -
2 a^2 (b^3 - c^3)) :
-c^2 (a^5 - b^5 - b^4 c + b c^4 + c^5 +
a^4 (-b + c) - 2 a^3 (b^2 + c^2) + a (b^2 + c^2)^2 +
2 a^2 (b^3 - c^3))
Se designan por A" el punto de intersección de la mediatriz de DbDc con la paralela por Ma a AI, y por Γa2 la
circunferencia
( Ecuación baricéntrica:
a^6 b^2 x^2-3 a^4 b^4 x^2+3 a^2 b^6 x^2-b^8 x^2+2 a^6 b c x^2-4 a^4 b^3 c x^2+2 a^2 b^5 c x^2+a^6 c^2 x^2-2 a^4 b^2 c^2 x^2-3 a^2 b^4 c^2 x^2+4 b^6 c^2 x^2-4 a^4 b c^3 x^2-4 a^2 b^3 c^3 x^2-3 a^4 c^4 x^2-3 a^2 b^2 c^4 x^2-6 b^4 c^4 x^2+2 a^2 b c^5 x^2+3 a^2 c^6 x^2+4 b^2 c^6 x^2-c^8 x^2+a^8 x y-2 a^6 b^2 x y+2 a^2 b^6 x y-b^8 x y-2 a^6 c^2 x y+4 a^4 b^2 c^2 x y-6 a^2 b^4 c^2 x y+4 b^6 c^2 x y+8 a^4 b c^3 x y+4 a^4 c^4 x y+6 a^2 b^2 c^4 x y-6 b^4 c^4 x y-2 a^2 c^6 x y+4 b^2 c^6 x y-c^8 x y+a^8 y^2-3 a^6 b^2 y^2+3 a^4 b^4 y^2-a^2 b^6 y^2-2 a^6 b c y^2+4 a^4 b^3 c y^2-2 a^2 b^5 c y^2+a^6 c^2 y^2-2 a^4 b^2 c^2 y^2+a^2 b^4 c^2 y^2-4 a^4 b c^3 y^2+4 a^2 b^3 c^3 y^2-a^4 c^4 y^2+a^2 b^2 c^4 y^2-2 a^2 b c^5 y^2-a^2 c^6 y^2+a^8 x z-2 a^6 b^2 x z+4 a^4 b^4 x z-2 a^2 b^6 x z-b^8 x z+8 a^4 b^3 c x z-2 a^6 c^2 x z+4 a^4 b^2 c^2 x z+6 a^2 b^4 c^2 x z+4 b^6 c^2 x z-6 a^2 b^2 c^4 x z-6 b^4 c^4 x z+2 a^2 c^6 x z+4 b^2 c^6 x z-c^8 x z-2 a^8 y z+6 a^6 b^2 y z-2 a^4 b^4 y z-2 a^2 b^6 y z+12 a^6 b c y z-4 a^2 b^5 c y z+6 a^6 c^2 y z+4 a^4 b^2 c^2 y z+2 a^2 b^4 c^2 y z+8 a^2 b^3 c^3 y z-2 a^4 c^4 y z+2 a^2 b^2 c^4 y z-4 a^2 b c^5 y z-2 a^2 c^6 y z+a^8 z^2+a^6 b^2 z^2-a^4 b^4 z^2-a^2 b^6 z^2-2 a^6 b c z^2-4 a^4 b^3 c z^2-2 a^2 b^5 c z^2-3 a^6 c^2 z^2-2 a^4 b^2 c^2 z^2+a^2 b^4 c^2 z^2+4 a^4 b c^3 z^2+4 a^2 b^3 c^3 z^2+3 a^4 c^4 z^2+a^2 b^2 c^4 z^2-2 a^2 b c^5 z^2-a^2 c^6 z^2 = 0)
(A"DbDc), que es tangente a la circunferencia circunscrita en (baricéntricas):
A2 = (a^2 (a^2+b^2-c^2) (a^2-b^2+c^2) : b (b+c) (-a+b-c) (a+b-c) (a^2+b^2-c^2) : c (b+c) (-a-b+c) (a-b+c) (a^2-b^2+c^2)).
es el del .
El triángulo tangencial Ta2Tb2Tc2 de es perspectivo con ABC, con centro de perspectividad X2164.
Los triángulos y son perspectivos, con centro de perspectividad X1609, de punto de Clawson. X1609 también es el centro de perspectividad de los triángulos Ta1Tb1Tc1 y Ta2Tb2Tc2.
Ta2 = (a (a^6 - a^5 (b + c) - 2 b c (b^2 - c^2)^2 + a^2 (b^2 + c^2)^2 -
2 a^4 (b^2 - b c + c^2) + 2 a^3 (b^3 + c^3) -
a (b^5 - b^4 c - b c^4 + c^5)) :
b^2 (-a^5 + b^5 + a^4 (b - c) +
b^4 c - b c^4 - c^5 + 2 a^3 (b^2 + c^2) - a (b^2 + c^2)^2 -
2 a^2 (b^3 - c^3)) :
c^2 (-a^5 - b^5 - b^4 c + b c^4 + c^5 +
a^4 (-b + c) + 2 a^3 (b^2 + c^2) - a (b^2 + c^2)^2 +
2 a^2 (b^3 - c^3))).
Los centros del triángulo Xi, i∈{19, 1609, 2164, 2178, 7120}, estudiados aquí, están sobre una recta, de la
cónica circunscrita
( -a^7 c x y+a^6 b c x y+a^5 b^2 c x y-a^4 b^3 c x y+a^3 b^4 c x y-a^2 b^5 c x y-a b^6 c x y+b^7 c x y-2 a^5 b c^2 x y+2 a b^5 c^2 x y+3 a^5 c^3 x y-a^4 b c^3 x y+a b^4 c^3 x y-3 b^5 c^3 x y+2 a^3 b c^4 x y-2 a b^3 c^4 x y-3 a^3 c^5 x y+a^2 b c^5 x y-a b^2 c^5 x y+3 b^3 c^5 x y+a c^7 x y-b c^7 x y+a^7 b x z-3 a^5 b^3 x z+3 a^3 b^5 x z-a b^7 x z-a^6 b c x z+2 a^5 b^2 c x z+a^4 b^3 c x z-2 a^3 b^4 c x z-a^2 b^5 c x z+b^7 c x z-a^5 b c^2 x z+a b^5 c^2 x z+a^4 b c^3 x z+2 a b^4 c^3 x z-3 b^5 c^3 x z-a^3 b c^4 x z-a b^3 c^4 x z+a^2 b c^5 x z-2 a b^2 c^5 x z+3 b^3 c^5 x z+a b c^6 x z-b c^7 x z+a^7 b y z-3 a^5 b^3 y z+3 a^3 b^5 y z-a b^7 y z-a^7 c y z+a^5 b^2 c y z+2 a^4 b^3 c y z-a^3 b^4 c y z-2 a^2 b^5 c y z+a b^6 c y z-a^5 b c^2 y z+a b^5 c^2 y z+3 a^5 c^3 y z-2 a^4 b c^3 y z-a b^4 c^3 y z+a^3 b c^4 y z+a b^3 c^4 y z-3 a^3 c^5 y z+2 a^2 b c^5 y z-a b^2 c^5 y z-a b c^6 y z+a c^7 y z = 0)
con centro en X6506, punto que se obtiene haciendo las sustituciones a → cosA, b → cosB, c → cosC, en las cordenadas baricéntricas del .
- Viernes, 6 de noviembre del 2020
X(3091) como centro de una homotecia
“Nunca pensé que en la felicidad hubiera tanta tristeza”. Mario Benedetti
Dado un triángulo ABC con ortocentro H=X4 y centro de la N=X5, sean el , DEF es el y el .
La circunferencia de los nueve puntos vuelve a corta a la circunferencia de diámetro HD en A2 y sea A3=AH∩NA2.
A' es el centro de la cónica 𝒞a, que pasa por H, tangente a la recta MaA1 en Ma y tangente a la recta NA2 en A3. Los puntos B' y C' se definen cíclicamente. A'B'C' es el triángulo medial del triángulo de Euler.
Los triángulo ABC y A'B'C' son homoteticos en una homotecia de razón -1/4 y centro X3091, del baricentro respecto a H y N.
En coordenadas baricéntricas:
A1 = (2 (b^2-c^2)^2-2 a^2 (b^2+c^2) : a^4-b^4-2 a^2 c^2+c^4 : a^4-2 a^2 b^2+b^4-c^4),
A2 = (2 (b-c)^2 (b+c)^2 (a^2+b^2-c^2) (a^2-b^2+c^2) : (a^2-b^2-c^2) (a^2+b^2-c^2) (a^4-2 a^2 b^2-(b^2-c^2)^2) : (a^2-b^2-c^2) (a^2-b^2+c^2) (a^4-2 a^2 c^2-(b^2-c^2)^2)),
A3 = (2 (a^2+b^2-c^2) (a^2-b^2+c^2) ((b^2-c^2)^4+a^6 (b^2+c^2)-a^2 (b^2-c^2)^2 (b^2+c^2)-a^4 (b^2+c^2)^2) : -(a^2-b^2-c^2) (a^2+b^2-c^2) (a^8+(b^2-c^2)^4-2 a^4 (b^2+c^2)^2) : -(a^2-b^2-c^2) (a^2-b^2+c^2) (a^8+(b^2-c^2)^4-2 a^4 (b^2+c^2)^2)).
Para determinar la
ecuación
( (b^2-c^2) (-a^2+b^2+c^2)^2 (a^8+(b^2-c^2)^4-2 a^4 (b^2+c^2)^2)x^2+
b^2 (a^4-(b^2-c^2)^2)^2 (a^4-2 a^2 b^2+(b^2-c^2)^2)y^2
-c^2 (a^4-(b^2-c^2)^2)^2 (a^4-2 a^2 c^2+(b^2-c^2)^2)z^2
-(b^2-c^2) (a^4-(b^2-c^2)^2)^2 (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))y z
-a^12 (b^2+2 c^2)-(b^2-c^2)^5 (b^4-b^2 c^2-2 c^4)+2 a^2 (b^2-c^2)^4 (b^4+2 c^4)+2 a^10 (b^4+4 b^2 c^2+2 c^4)+a^8 (b^6-6 b^4 c^2-13 b^2 c^4+2 c^6)+a^4 (b^2-c^2)^2 (b^6+4 b^4 c^2+9 b^2 c^4+2 c^6)-4 a^6 (b^8-b^4 c^4-2 b^2 c^6+2 c^8)z x +
a^12 (2 b^2+c^2)+(b^2-c^2)^5 (2 b^4+b^2 c^2-c^4)-2 a^2 (b^2-c^2)^4 (2 b^4+c^4)-2 a^10 (2 b^4+4 b^2 c^2+c^4)-a^8 (2 b^6-13 b^4 c^2-6 b^2 c^4+c^6)-a^4 (b^2-c^2)^2 (2 b^6+9 b^4 c^2+4 b^2 c^4+c^6)+4 a^6 (2 b^8-2 b^6 c^2-b^4 c^4+c^8)z y = 0)
cónica 𝒞a, podemos partir del haz bitangente de cónicas
MaA32 + λ MaA1 · NA2 = 0,
y determinar la cónica de este haz que pasa por H,
λ = (a^2 - b^2 + c^2)^2 (a^2 + b^2 - c^2)^2.
El centro de la cónica 𝒞a es:
A' = (2 (a^4 - (b^2 - c^2)^2) : -3 a^4 + b^4 + 2 b^2 c^2 - 3 c^4 +
2 a^2 (b^2 + 3 c^2) : -3 a^4 - 3 b^4 + 2 b^2 c^2 + c^4 +
2 a^2 (3 b^2 + c^2)).
Las tangentes en H a las cónicas 𝒞a, 𝒞b, 𝒞c cortan a BC, CA, AB en Ta, Tb, Tc, respectivamente.
es el del del circuncentro,
X264.
La cónica 𝒞a vuelve a cortar a la recta BC en:
Na = (0 : -c^2 (a^4 - 2 a^2 c^2 + (b^2 - c^2)^2) : b^2 (a^4 -
2 a^2 b^2 + (b^2 - c^2)^2)).
Los puntos Nb, sobre CA, y Nc, sobre AB, se definen cíclicamente.
Los tres puntos
Na,
Nb,
Nc están sobre la de
X5392, recta que pasa por X
2072 (inverso en la circunferencia circunscrita del circuncentro del ) y tiene la dirección del del foco de la .
Las tangentes en Na, Nb, Nc a las cónicas 𝒞a, 𝒞b, 𝒞c, respectivamente, forman un triángulo perspectivo con ABC, con centro de perspectividad:
W = ( (
a^2 (b^2 + c^2)-(b^2 - c^2)^2)/((a^2 - b^2 - c^2) (a^8 (b^2 + c^2) +
4 a^4 b^2 c^2 (b^2 + c^2) - (b^2 - c^2)^4 (b^2 + c^2) +
2 a^2 (b^2 - c^2)^2 (b^4 - b^2 c^2 + c^4) -
2 a^6 (b^4 + b^2 c^2 + c^4)) : ... : ...),
que tiene números de búsqueda en
(-0.402824571918432, 0.576070701089292, 3.42776533742338n).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {5,23709}, {1593,3613}, {1968,2165}, {3541,16837}, {6815,8797}.
- Miércoles, 4 de noviembre del 2020
Cónicas asociadas a la recta de De Longschamps
El 4 de noviembre de 1652 falleció Jean-Charles della Faille, jesuita y matemático de los Países Bajos. Su libro más famoso es "Theoremata de centro gravitatis partium circuli et elipsis" (1632) en el que determinaba por vez primera el centro de gravedad del sector de un círculo.
Dado un triángulo ABC con ℓ, sea DEF el de un punto P. Los de D, E, F (sobre ℓ) se denotan por D', E', F', respectivamente.
Se considera la cónica
𝒞a
( P=(u:v:w), u x ((b^2 u + a^2 v) y + (c^2 u + a^2 w) z)-a^2 v w y z = 0)
, circunscrita a ABC y que pasa por E' y F' (isotómica conjugada de la recta EF). Las cónicas 𝒞b y 𝒞c, se definen cíclicamente.
La tangentes en A, B, C a las cónicas 𝒞a, 𝒞b, 𝒞c, respectivamente, forma un triángulo que se denota por .
Las rectas ATa, BTb, CTc son concurrentes. El punto de concurrencia T es el conjugado isotómico del de P y el .
Si A', B' C' son los polos de la recta de De Longschamps respecto a las cónicas 𝒞a, 𝒞b, 𝒞c, respectivamente. Las rectas AA', BB', CC' son concurrentes en un punto Q.
Si (u:v:w) son las coordenadas baricéntricas de P, entonces:
T = ( c^2 v + b^2 w : ... : ... ),
Q = ((c^2 v + b^2 w)/ (c^2 u v + b^2 u w - a^2 v w) : ... : ... ).
Cuando P está sobre la circunferencia circunscrita, el triángulo DEF degenera en P y las cónicas 𝒞a, 𝒞b, 𝒞c coinciden con la cónica circunscrita tangente al recta de De Longschams en el conjugado isotómico de P.
Pares {P=Xi, Q=Xj}, para los índices {i, j}: {1, 1441}, {2, 427}, {3, 253}, {6, 76}, {22, 34427}, {25, 6340}, {81, 21020}, {648, 22089}.
- Lunes, 2 de noviembre del 2020
Un trebol equilátero, K723
El 2 de noviembre de 1789, en París, la Asamblea Nacional Constituyente francesa aprueba (por 568 votos contra 364 con 40 abstenciones) la confiscación de todos los bienes de la Iglesia, que el Estado dividide en lotes para venderlos. El Estado se hace cargo de los hospitales y escuelas.
Trèfle Équilatère
Courbe étudiée par G. de Longchamps en 1884.
The inverse of the regular trifolium with respect to its centre.
Dado un triángulo ABC, sea P un punto sobre su circunferencia circunscrita, Γ, y 𝓈P la de P, que corta los lados BC, CA, AB en los puntos D, E, F, respectivamente.
Si Bf es la reflexión de B en F, la circunferencia de diámetro ABf vuelve a cortar a la recta AC en Ab y si Ce es la reflexión de C en E, la circunferencia de diámetro ACe vuelve a cortar a la recta AB en Ac. Los puntos Bc, Ba, Ca, Cb, se definen cíclicamente.
Las rectas AbAc, BcBa y CaCb son paralelas. Sean P' (sobre Γ) el de su punto común en la recta del infinito, Q el punto medio de la cuerda PP' y Q' el inverso de Q respecto de Γ.
El lugar geométrico de
Q', cuando
P se mueve sobre Γ, es la cúbica
K723, del catálogo de Bernard Gibert.
En coordenadas baricéntricas, si P=(a^2 (-1 + t) t : -b^2 (-1 + t) : c^2 t), entonces:
Ab = (-a^4 t^2 - b^2 (b^2 - c^2) (-1 + 2 t) +
a^2 (c^2 t^2 + b^2 (1 - 2 t + 3 t^2)) : 0 : -(-a^2 + b^2 + c^2) (-b^2 +
a^2 t^2)),
Ac = (-a^4 (-1+t)^2+c^2 (-b^2+c^2) (-1+2 t)+a^2 (b^2 (-1+t)^2+c^2 (2-4 t+3 t^2)) : -(-a^2+b^2+c^2) (-c^2+a^2 (-1+t)^2) : 0),
P' = ((-c^2+a^2 (-1+t)^2) (b^2-a^2 t^2) : -(b^2-a^2 t^2) (b^2 (-1+t)^2-c^2 t^2) : (-c^2+a^2 (-1+t)^2) (-b^2 (-1+t)^2+c^2 t^2)),
Q = (-b^2 c^2 - 2 a^4 (-1 + t)^2 t^2 +
a^2 (-c^2 (-2 + t) t^2 + b^2 (-1 + t)^2 (1 + t)) : -2 b^4 (-1 + t)^2 -
a^2 c^2 t^4 +
b^2 t (a^2 (-1 + t)^2 (1 + t) + c^2 (-1 + 2 t)) : -2 c^4 t^2 +
b^2 c^2 (1 - 3 t + 2 t^2) -
a^2 (-1 + t) (b^2 (-1 + t)^3 - c^2 (-2 + t) t^2)).
El lugar geométrico de Q, cuando P se mueve sobre Γ, es el trifolio regular de centro en el circuncentro:
𝔖abc xyz
b^2 (b-c)^2 c^2 (b+c)^2 x^4-b^2 c^2 (8 a^4+4 b^4-8 b^2 c^2+4 c^4+a^2 (-3 b^2-3 c^2)) x^2 y z-a^2 (2 a^6-3 b^4 c^2-3 b^2 c^4+a^4 (-4 b^2-4 c^2)+a^2 (2 b^4+4 b^2 c^2+2 c^4)) y^2 z^2+a^2 y z (c^2 (a^4-2 a^2 (2 b^2+c^2)+c^2 (3 b^2+c^2)) y^2+b^2 (a^4-2 a^2 (b^2+2 c^2)+b^2 (b^2+3 c^2)) z^2) = 0.
El inverso de Q respecto a Γ es:
Q' = (a^2 b^2 c^2 (1-2 t)+a^4 (b^2 (-1+t)^3+c^2 t^3) : b^4 c^2+a^2 (-b^4 (-1+t)^3+b^2 c^2 (-2+t) t^2): -c^2 (b^2 c^2+a^2 (c^2 t^3-b^2 (-1+t)^2 (1+t)))),
y el lugar geométrico que describe es la cúbica
K723.
( (b^6 c^2-2 b^4 c^4+b^2 c^6) x^3+(3 a^2 b^4 c^2-2 a^2 b^2 c^4) x^2 y+(3 a^4 b^2 c^2-2 a^2 b^2 c^4) x y^2+(a^6 c^2-2 a^4 c^4+a^2 c^6) y^3+(-2 a^2 b^4 c^2+3 a^2 b^2 c^4) x^2 z+(-2 a^4 b^2 c^2-2 a^2 b^4 c^2-2 a^2 b^2 c^4) x y z+(-2 a^4 b^2 c^2+3 a^2 b^2 c^4) y^2 z+(3 a^4 b^2 c^2-2 a^2 b^4 c^2) x z^2+(-2 a^4 b^2 c^2+3 a^2 b^4 c^2) y z^2+(a^6 b^2-2 a^4 b^4+a^2 b^6) z^3 = 0)
- Viernes, 30 de octubre del 2020
Construcciones de X(1617)
El 30 de octubre de 1840 nació Joseph Jean Baptiste Neuberg, matemático luxemburgués que trabajó principalmente en la geometría, sobre todo la geometría del triángulo. Junto Henri Brocard y Émile Lemoine, es conciderado como el creador de la geometría del triángulo y del tetraedro. Lleva su nombre la cúbica de Neuberg, una curva que Neuberg descubrió y publicó en 1885.
Neuberg también se implicó en varias revistas matemáticas. Fundó junto con Eugène Catalan y Paul Mansion la revista Nouvelle correspondance mathématique, que perduró hasta 1880. Catalan aconsejó a Mansion y Neuberg que publicaran una nueva revista. Ellos siguieron su consejo y crearon Mathesis en 1881.
Dado un triángulo ABC, sean I=X1 su incentro, DEF su y A1 la proyección ortogonal de A sobre EF. La circunferencia circunscrita vuelve a corta a la circunferencia (AEF) en A' y a la circunferencia (A'IA1) en A". Los puntos B" y C" se definen cíclicamente.
Las rectas
AA", BB", CC" se cortan en
X1617, centro de perpspectividad de los triángulos y del de .
Las rectas A'A", B'B", C'C" concurren en W=(r^2+2rR-4R^2) I + 4rR O.
W = ( a (a^5 - 3 a^4 (b + c) + 2 a^3 (b^2 + c^2)+
2 a^2 (b - c)^2 (b + c) + (b - c)^4 (b + c) -
a (b - c)^2 (3 b^2 - 2 b c + 3 c^2)) : ... : ...),
que tiene números de búsqueda en
(-0.108673475212006, 0.204842057385918, 3.54900773843044).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1, 3}, {7, 4666}, {9, 17625}, {11, 1750}, {48, 38849}, {63, 7677}, {77, 3598}, {78, 5265}, {103, 30239}, {105, 1422}, {108, 1435}, {200, 3911}, {222, 7290}, {223, 614}, {226, 4321}, {269, 2191}, {479, 4350}, {497, 5732}, {553, 12560}, {672, 2324}, {910, 3554}, {936, 7288}, {954, 10569}, {1042, 28011}, {1279, 1407}, {1412, 17194}, {1423, 28364}, {1445, 3873}, {1453, 34046}, {1455, 16485}, {1465, 5573}, {1490, 3086}, {1708, 5083}, {1788, 6765}, {1836, 38036}, {2003, 16469}, {2057, 6921}, {2360, 5324}, {2951, 9580}, {3174, 8732}, {3434, 30379}, {3476, 9623}, {3681, 30318}, {3720, 4327}, {3870, 5435}, {3924, 34039}, {4308, 19860}, {4320, 28082}, {4334, 29820}, {4423, 8581}, {4551, 23511}, {4654, 38024}, {5273, 19861}, {5274, 18450}, {5284, 8545}, {5436, 7091}, {5517, 35804}, {5720, 15325}, {6049, 36846}, {6174, 37736}, {7190, 29814}, {7580, 17626}, {7675, 10580}, {7965, 11376}, {8544, 9812}, {8580, 31231}, {8583, 30478}, {9533, 38459}, {10382, 11019}, {10396, 12675}, {10884, 14986}, {12053, 12565}, {16487, 34033}, {16572, 22153}, {21454, 29817}, {27414, 33765}, {30223, 30304}.
Otras propiedades de X1617
☆
En un triángulo ABC, A1 y A2 son los puntos de contacto de su circunferencia circunscrita con el y el . Se denota lor ℓa la recta pasa por A1 y A2, y se definen ℓa y ℓa cíclicamente. Sea A'B'C' el triángulo formado por las rectas ℓa, ℓb, ℓc.
La transformación afín σ que aplica ABC en A'B'C' tiene punto fijo finito X1617.
☆
Sea ABC un triángulo con incentro I, circuncentro O y circunferencia inscrita Γ.
Ωb y Ωc son las circunferencias circunscritas a los triángulos AOC y AOB, respectivamente.
Γb es la circunferencia tangente a Γ que pasa por A y C y Γc es la circunferencia tangente a Γ que pasa por A y B.
Existe una circunferencia Λa, tangente a las cuatro circunferencias Γb, Γc, Ωb y Ωc.
Se denota por
Gab, Gac, Oab y Oac
los puntos de contacto de la circunferencia Λa con las circunferencias
Γb, Γc, Ωb y Ωc, respectivamente.
Se considera el punto Ma = GabOac ∩ GacOab.
Se definen cíclicamente los puntos Mb y Mc.
Las rectas AMa, BMb y CMc concurren en
X1617 = 2R^2 I - r(r+2R) O.
☆
Sea ABC un triángulo con incentro I y DEF. Sean Ea la reflexión de E en C y Fa la reflexión de F en B. La circunferencia AEF vuelve a cortara a la circunferencia ircunscita en A1, Las cirunferencias (AEFa) y (AFEa) se vuelven a cortar en A2, sobre la circunferencia circunscrita. Los puntos B1, B2, C1 y C2 se definen cíclicamente.
Las rectas A1A2, A1A2, A1A2 concurren en X1617.
- Miércoles, 28 de octubre del 2020
Compendio de propiedades del cuadrado baricéntrico del ortocentro
El 28 de octubre de 1999 murió (en el Puerto de Santa María, Cádiz) Rafael Alberti, poeta español de la "Generación del 27". Entre sus obras más conocidas caben destacar "Marinero en tierra" por el que recibió el Premio Nacional de Literatura en 1925, y "Cal y canto".
En 1939, al terminar la Guerra Civil española, emigra a la República Argentina, desde donde se traslada a Roma en 1962. A su vuelta a España es elegido diputado por el Partido Comunista de España, pero renuncia a su escaño para proseguir su tarea literaria y dar recitales por toda España.
El del ortocentro es el centro X(393) en .
★
Sea DEF el de un triángulo ABC, cuyo ortorcentro es X4.
La recta que pasa por las proyecciones ortogonales de D sobre BX4 y CX4 corta a BC en el punto A'. Los puntos B' y C' se definen cíclicamente, entonces los puntos A', B' C' están en una misma recta, cuyo es X393.
★
Sean 𝒫a, 𝒫b, 𝒫c, las parábolas circunscritas a ABC tales que sus ejes son perpendiculares a los lados BC, CA, AB, respectivamente.
A1 es el punto de interscción de la tangente a 𝒫b en B con la tangente a 𝒫c en C. Los puntos B1 y C1 se definen cíclicamente.
Las rectas AA1, BB1, CC1 se cortan en X393.
★
Sean DEF su y c(AD) la circunferencia de diámetro AD.
Ab y Ac son los puntos (distintos de A) donde c(AD) corta a AC y AB, respectivamente. Es decir, las proyecciones ortogonales de D sobre AC y AB.
Ta es el punto de intersección de las tangente en Ab y Ac a c(AD). Es decir, el de AbAc respecto a a c(AD).
Si A" es el punto de intersección de las rectas DTa y AbAc, y se definen B" y C" cíclicamente, se tiene:
La rectas AA", BB" y CC" concurren en X393.
★
Sean y los triángulos y de X25, centro de homotecia del los triángulos y .
Se denotan por Γab y Γac las circunferencias circunscritas a los triángulos AB1C2, AB2C1 y por d1 su eje radical. Similarmente, se definen los ejes radicales d2 y d3.
Los ejes radicales d1, d2 y d3 concurren en X393.
★
K406=cK(#X4,X2) has three real asymptotes parallel to the sidelines of ABC forming a triangle homothetic of ABC under the homothety with center X(393) and ratio 2 cotA cotB cotC cotω, where ω is the Brocard angle.
★ Dado un triángulo ABC con circuncentro X3 y ortocentro X4, sea DEF el y A1 la proyeccion ortogonal de A sobre EF. La circunferencia Γa = (AEF) vuelve a cortar a la circunferencia Γ, circunscrita a ABC, en A' y la circunferencia (A'X3A1) en A". Se definen B" y C" cíclicamente.
Las rectas AA", BB", CC" concurren en X393.
En coordenadas baricéntricas:
A' = (a^2 (a^2 + b^2 - c^2) (a^2 - b^2 + c^2) : -(a^2 + b^2 - c^2) (-b^4 +
c^4 + a^2 (b^2 - c^2)) : (a^2 - b^2 + c^2) (-b^4 + c^4 +
a^2 (b^2 - c^2))),
A" = (a^2 (a^4 - (b^2 - c^2)^2)^2 : -(a^2 + b^2 -
c^2)^2 (-2 a^2 (b^2 - c^2)^2 +
a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2)) : -(a^2 - b^2 +
c^2)^2 (-2 a^2 (b^2 - c^2)^2 +
a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2))).
- Domingo, 25 de octubre del 2020
Algunas propiedades asociadas con el Teorema de Napoleón
El 25 de octubre de 1881, en Málaga, nació Pablo Picasso, pintor y escultor español, creador, junto con Georges Braque, del cubismo. Abordó géneros como el dibujo, el grabado, la ilustración de libros, la escultura, la cerámica y el diseño de escenografía y vestuario para montajes teatrales. También tiene una breve obra literaria. En lo político, Picasso se declaraba pacifista y comunista. Fue miembro del Partido Comunista de España y del Partido Comunista Francés hasta su muerte, a los 91 años.
Dado un triángulo ABC, sea A'B'C' el . Se definen los puntos Ba = A'C ∩ C'B, Ca = A'B ∩ B'C, y cíclicamente, Cb, Ab, Ac y Bc.
A" es el baricentro de A'BaCa, y se define cíclicamente B" y C" .
En coordenadas baricéntricas:
A" = (8 a^6+8 a^2 (b^2-c^2)^2-2 a^4 (8 b^2+8 c^2+S) :
-4 a^6+a^4 (7 b^2+9 c^2-2 S)-(b^2-c^2)^2 (b^2-c^2+3 S)+a^2 (-2 b^4-6 c^4+5 c^2 S+b^2 (8 c^2+7 S)) :
-4 a^6+(b^2-c^2)^2 (b^2-c^2-3 S)+a^4 (9 b^2+7 c^2-2 S)+a^2 (-6 b^4-2 c^4+7 c^2 S+b^2 (8 c^2+5 S))).
El triángulo A"B"C" es equilátero, siendo el cuadrado de la longitud de sus lados:
((a^2+b^2+c^2) (29 (a^2 b^2+a^2 c^2+b^2 c^2)-13 (a^4+b^4+c^4))+Sqrt[3] (19 (a^2 b^2+a^2 c^2+b^2 c^2)-3 (a^4+b^4+c^4))S)/(216S^2).
El centro del triángulo A"B"C" es el simétrico de X13083 respecto a X5054:
Oe = ( 3S ( 2SA- a^2)+ Sqrt[3] ( 13 S^2-3 SB SC) : ... : ...),
que tiene números de búsqueda en
(4.74887264160323, 2.67312320190409, -0.401746646304562).
Es el punto medio de Xi y Xj para los índices {i,j}: {5054,9761}, {10304,22491}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,17}, {18,11299}, {30,9736}, {140,33459}, {299,33416}, {302,3642}, {524,11539}, {530,5055}, {531,3524}, {533,5054}, {549,34508}, {616,16967}, {618,6772}, {635,11302}, {3180,33417}, {3525,5862}, {3526,5859}, {3643,23303}, {5858,15694}, {6669,11486}, {6671,37641}, {10124,33458}, {10304,22491}, {16773,37352}, {16962,37785}, {33464,36836}.
Si O=X3 es el circuncentro de ABC, entonces los triángulos OAcAb, OBaBc, OCbCa son equiláteros. El cuadrado de la longitud de el lado de OAcAb es ((b^2 c^2 (a^2+b^2+c^2+Sqrt[3] S))/(8 S^2)).
Sean A0, B0, C0 son los centros de los triángulos OAcAb, OBaBc, OCbCa, respectivamente.
Los triángulos ABC y son homotéticos, de razón de homotecia (12S +Sqrt[3] (a^2+b^2+c^2) )^2/(24 S^2) y centro X16 ().
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Si en vez del triángulo exterior de Napoleón, A'B'C' es el triángulo interior de Napoleón, el centro de homotecia de los triángulos ABC y es X15 (primer punto isodinámico).
El centro del triángulo A"B"C" es el simétrico de X13084 respecto a X5054:
Oi = ( 3S ( 2SA- a^2)- Sqrt[3] ( 13 S^2-3 SB SC) : ... : ...),
que tiene números de búsqueda en ETC
(1.89419631061008, 2.21338132088273, 1.23407911639938).
Es el punto medio de Xi y Xj para los índices {i,j}: {5054, 9763}, {10304, 22492}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,18}, {17,11300}, {30,9735}, {140,33458}, {298,33417}, {303,3643}, {524,11539}, {530,3524}, {531,5055}, {532,5054}, {549,34509}, {617,16966}, {619,6775}, {636,11301}, {3181,33416}, {3525,5863}, {3526,5858}, {3642,23302}, {5459,36763}, {5859,15694}, {6670,11485}, {6672,37640}, {10124,33459}, {10304,22492}, {16772,37351}, {16963,37786}, {33465,36843}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
El punto medio de Oo y Oi es X11539.
La recta OoOi interseca a la recta del infinito en
X524, conjugado isogonal del , y pasa por X38110, baricentro del triángulo con vértices en el circuncentro, centro de la circunferencia de los nueve puntos y simediano.
- Viernes, 23 de octubre del 2020
Rectángulos levantados sobre los lados de un triángulo
El 23 de octubre de 1780, en Zaragoza, falleció a los 60 años de edad, María Andresa Casamayor, matemática, escritora y maestra de niñas española que destacó en el manejo de los números y en la aritmética. Es la única científica española del siglo XVIII de la cual se conserva su obra.
Dado un triángulo ABC, la paralela por un punto P al lado BC corta a las perpendiculares a BC por B y C en Ba y en Bc, respectivamente. Sea A' el punto medio de segmento BaBc. Los puntos Cb, Ca, Ac, Ab, B' y C' se definen cíclicamente.
Las rectas
AA', BB', CC' son concurrentes (en un punto
Q) si y solo si
P está sobre la cúbica de Thomson (
K002). El punto de concurrencia está sobre la cúbica de Darboux (
K004).
Ba = (a^2u : (v+w)+SB(u+v+w) : -SBu),
Ca = (a^2u : -SCu : SB(v+w)+SC(u+v+w)),
A' = (2SA^2(u+v+w)+SBSC(2u+v+w)+SASB(2u+2v+w)+
SASC(2u+v+2w) :
b^2(SBv+SA(v-w)) : -c^2(SA(v-w)-SCw)).
Si P está sobre
K002,
( c^2 x^2 y - c^2 x y^2 - b^2 x^2 z + a^2 y^2 z + b^2 x z^2 - a^2 y z^2 = 0)
las rectas AA', BB', CC' concurren en:
Q = (a^2(v wa^4+2(v-w)(c^2v-b^2w)a^2+b^4(v-2w)w+
2b^2c^2(-2u^2+v^2-v w+w^2)+c^4v(-2v+w)) : ... : ...).
Q está sobre la cúbica K004 y la recta PQ pasa por el ortocentro.
Pares {P=X(i), Q=X(j)}, para {i,j}: {1, 1}, {2, 3}, {3, 20}, {4, 64}, {6, 4}, {9, 40}, {57, 84}, {223, 1490}, {282, 3345}, {1073, 3346}, {1249, 1498}, {3341, 3182}, {3342, 3347}, {3343, 3183}, {3344, 3348}, {3349, 2131}, {3350, 2130}, {3351, 3353}, {3352, 3354}, {3356, 3637}, {14481, 3355}.
Los seis puntos Ba, Bc, Cb, Ca, Ac, Ab están sobre una misma cónica si y solo si está sobre una quíntica 𝒬, circular, circunscrita a ABC, que pasa por el circuncentro y simétrica respecto a éste.
Su ecuación baricéntrica de 𝒬 es:
𝔖abc xyz
a^2 y z (-8 b^2 c^2 (b^2-c^2) (a^4+b^4+2 b^2 c^2+c^4+a^2 (-2 b^2-2 c^2)) x^3+(b^2-c^2) (-5 a^8+b^8-4 b^6 c^2+6 b^4 c^4-4 b^2 c^6+c^8+a^6 (14 b^2+14 c^2)+a^4 (-12 b^4-32 b^2 c^2-12 c^4)+a^2 (2 b^6+22 b^4 c^2+22 b^2 c^4+2 c^6)) x y z-a^2 y z ((a^8-b^8-6 b^6 c^2-8 b^4 c^4+14 b^2 c^6+c^8+a^6 (-2 b^2-4 c^2)+a^4 (2 b^2 c^2+6 c^4)+a^2 (2 b^6+8 b^4 c^2-14 b^2 c^4-4 c^6)) y+(-a^8-b^8-14 b^6 c^2+8 b^4 c^4+6 b^2 c^6+c^8+a^6 (4 b^2+2 c^2)+a^4 (-6 b^4-2 b^2 c^2)+a^2 (4 b^6+14 b^4 c^2-8 b^2 c^4-2 c^6)) z)-2 a^2 (a^4+b^4+2 b^2 c^2+c^4+a^2 (-2 b^2-2 c^2)) (-c^2 (a^2+b^2-c^2) y^3+b^2 (a^2-b^2+c^2) z^3)) = 0.
Sus tres asíntotas reales son las mediatrices de los lados de ABC y las dos imaginarias también se cortan en el circuncentro.
La configuración que estamos estudiando es un caso particular del planteaminto siguiente:
Dao Thanh Oai, (August 11, 2017)
Let ABC be a triangle, let L be the line through B orthogonal to BC, let BA be any point on L, and let BC be the point such that BBABCC is a rectangle. Likewise, let CCBCAA be a rectangle with base CA and let AACABB be a rectangle with base AB. Let A' be the midpoint of BACA, and define B' and C' cyclically.
Let LA be the line through A' perpendicular to BC, and define LB and LC cyclically. Then the lines LA, LB, LC concur.
Las perpendiculares por A', B', C' a BC, CA, AB, respectivamente, son concurrentes en ( de A'B'C' respecto a ABC):
σ(P) = (a^2 (a^6 (c^2 v+b^2 w)+a^2 (3 c^6 v+b^4 c^2 (4 u-v-2 w)+b^2 c^4 (4 u-2 v-w)+3 b^6 w)-(b^2-c^2)^2 (c^4 v+b^4 w+3 b^2 c^2 (2 u+v+w))+a^4 (-3 c^4 v-3 b^4 w+b^2 c^2 (2 u+3 (v+w)))) : ... : ...).
σ es una transformación afín, con punto fijo propio X64 ( del ) y puntos fijos en la recta del infinito X2574 y X2575 (conjugados isogonales de los puntos donde la corta a la circunferencia circunscrita).
Algunos pares {P=X(i), σ(P)=X(j)}, para {i, j}: {1, 9856}, {3, 5}, {4, 13474}, {6, 4}, {30, 14915}, {36, 1538}, {40,
31788}, {64, 64}, {67, 15738}, {69, 5907}, {74, 20417}, {110,
38791}, {159, 2883}, {182, 546}, {185, 13568}, {193, 13598}, {206,
5893}, {371, 36658}, {372, 36657}, {376, 16836}, {511, 30}, {512,
1499}, {513, 3309}, {518, 517}, {520, 525}, {523, 512}, {524,
511}, {525, 30209}, {526, 690}, {542, 5663}, {575, 3861}, {576,
3853}, {578, 16198}, {599, 15030}, {674, 516}, {690, 2780}, {834,
28478}, {900, 2821}, {924, 3566}, {1151, 36656}, {1152,
36655}, {1192, 3089}, {1350, 3}, {1351, 3627}, {1498, 5878}, {1499,
30230}, {1503, 6000}, {1510, 32478}, {1620, 6622}, {1843,
16621}, {2076, 1513}, {2393, 1503}, {2574, 2574}, {2575,
2575}, {2781, 2777}, {2791, 515}, {2810, 952}, {2836, 2771}, {2839,
2391}, {2854, 542}, {2871, 2794}, {2929, 22970}, {2930,
15063}, {3098, 140}, {3221, 30217}, {3242, 12672}, {3313,
12362}, {3564, 13754}, {3566, 20186}, {3581, 16619}, {3818,
32137}, {3827, 6001}, {4259, 20420}, {4265, 6831}, {5050,
3845}, {5085, 381}, {5092, 3850}, {5093, 15687}, {5096,
1532}, {5097, 12102}, {5102, 3830}, {5621, 125}, {5622,
7687}, {5663, 541}, {5844, 28521}, {5845, 2808}, {5848,
2807}, {5965, 1154}, {6003, 30231}, {6371, 28481}, {6403,
13419}, {6467, 12241}, {6776, 389}, {7289, 942}, {7691,
32348}, {7716, 15811}, {8057, 8673}, {8547, 575}, {8549,
18381}, {8550, 10110}, {8674, 2775}, {8675, 523}, {8679,
515}, {8681, 3564}, {8705, 11645}, {8999, 522}, {9000, 514}, {9001,
513}, {9002, 3667}, {9003, 526}, {9004, 518}, {9007, 520}, {9009,
32472}, {9010, 28475}, {9011, 28468}, {9012, 32473}, {9013,
6003}, {9016, 28850}, {9017, 29010}, {9018, 28845}, {9019,
29012}, {9023, 2793}, {9024, 29349}, {9025, 15310}, {9026,
519}, {9027, 524}, {9028, 916}, {9029, 28292}, {9031, 32475}, {9032,
28294}, {9033, 9517}, {9037, 28160}, {9038, 29311}, {9039,
28234}, {9044, 8704}, {9047, 28146}, {9048, 30198}, {9049,
28194}, {9051, 521}, {9052, 28174}, {9054, 29309}, {9142,
11623}, {9145, 38745}, {9786, 1598}, {9924, 1498}, {9969,
16656}, {9971, 16654}, {9973, 16655}, {10249, 23325}, {10387,
12705}, {10516, 16194}, {10541, 3832}, {10605, 11438}, {11477,
382}, {11579, 36253}, {11898, 5876}, {12017, 3858}, {12041,
20397}, {12163, 7689}, {12329, 10}, {13622, 15739}, {14810,
3628}, {14984, 17702}, {15069, 12162}, {15073, 13403}, {15316,
22661}, {15520, 12101}, {15533, 11459}, {15578, 32767}, {15748,
15751}, {16010, 16003}, {16936, 15740}, {17430, 9830}, {17508,
5066}, {17813, 18405}, {17834, 7387}, {18374, 1514}, {19149,
22802}, {19161, 6756}, {19459, 12233}, {19596, 32111}, {20190,
3856}, {21358, 16261}, {22089, 30476}, {22549, 22834}, {22769,
946}, {23885, 29116}, {25406, 5943}, {29291, 6084}, {31884,
2}, {32233, 25711}, {32305, 20379}, {32621, 5480}, {33878,
550}, {34146, 15311}, {34371, 971}, {34372, 5840}, {34381,
912}, {34383, 2782}, {34778, 3357}, {34787, 6759}, {34817,
33537}, {35383, 37459}, {36740, 8727}, {36990, 11381}, {37473,
3575}, {37474, 36663}, {37478, 16618}, {37483, 14791}, {37485,
6823}, {37489, 7530}, {37498, 14790}, {37511, 31833}}.
La imagen del baricentro mediante σ es:
σ(G) = ( a^2 (a^6 (b^2+c^2)+a^4 (-3 b^4+8 b^2 c^2-3 c^4)+a^2 (3 b^6+b^4 c^2+b^2 c^4+3 c^6)-(b^2-c^2)^2 (b^4+12 b^2 c^2+c^4)) : ... : ...),
que tiene números de búsqueda en
(-4.42224780603593, -5.57662790978330, 9.54244432992786).
Es el punto medio de Xi y Xj para los índices {i,j}: {2, 32062}, {4, 15030}, {51, 15305}, {381, 16194}, {568, 12162}, {3543, 3917}, {3627, 15067}, {3830, 5891}, {11188, 12294}, {11381, 15072}, {13363, 32137}, {13474, 16836}, {15060, 15687}, {15682, 36987}, {16654, 34664}.
Es la reflexión de Xi en Xj para los índices {i,j}: {51,13570}, {568,10110}, {5892,5066}, {5907,15030}, {5943,381}, {13363,3850}, {13364,3860}, {15072,9729}, {15644,15067}, {16836,5}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,32062}, {3,5646}, {4,69}, {5,13474}, {20,5650}, {30,3819}, {51,3839}, {185,3832}, {373,3091}, {381,1853}, {382,11793}, {389,546}, {542,16657}, {548,11017}, {568,3843}, {575,11456}, {1154,14893}, {1216,3853}, {1495,7527}, {1498,5050}, {1593,35259}, {1594,36518}, {1596,21243}, {1597,9306}, {2842,31871}, {2883,23300}, {3090,12045}, {3146,7998}, {3292,15052}, {3357,7529}, {3426,37475}, {3522,33879}, {3543,3917}, {3545,6688}, {3581,18551}, {3627,15067}, {3628,14641}, {3830,5891}, {3845,13754}, {3850,13363}, {3851,10575}, {3854,10574}, {3855,12290}, {3856,13630}, {3857,13491}, {3858,5462}, {3859,12006}, {3860,13364}, {3861,5446}, {4550,7530}, {5055,14855}, {5066,5892}, {5068,12279}, {5071,10219}, {5076,10625}, {5085,11479}, {5102,12164}, {5656,14561}, {5946,23046}, {6090,11403}, {6225,9815}, {6241,15012}, {6759,37506}, {6800,26883}, {7387,32620}, {7395,17508}, {7503,35268}, {7528,22802}, {7545,32110}, {9050,14872}, {9976,14094}, {10282,39242}, {10982,15520}, {11002,12111}, {11430,31861}, {11438,11472}, {11454,14002}, {11591,12102}, {11645,16658}, {12082,14810}, {12101,13391}, {12233,38136}, {12362,16656}, {13367,35265}, {13382,18439}, {13402,15102}, {13487,31978}, {13595,21663}, {14269,18435}, {14531,16981}, {14865,15035}, {15032,15516}, {15041,18369}, {15056,17578}, {15060,15687}, {15682,36987}, {16654,29012}, {16776,34146}, {18451,34986}, {18488,23515}, {18492,23841}, {23039,38335}, {23306,33332}, {31884,33537}, {32139,37505}.
El centro de ortológico de ABC respecto a A'B'C es el conjugado isogonal de la imagen de P mediante la homotecia hX3,-1/3, de centro el circuncentro y razón -1/3.
(hX3,-1/3(P))* = (a^2/((b^2 - c^2)^2 u + 2 a^2 (b^2 + c^2) (u + 2 (v + w)) -
a^4 (3 u + 4 (v + w))) : ... : ...).
Pares {P=X(i), (hX3,-1/3(P))*=X(j)}, para {i, j}: {{1, 3062}, {2, 14490}, {3, 4}, {4, 3426}, {5, 13603}, {20, 6}, {23,
11744}, {40, 3577}, {64, 253}, {72, 14493}, {185, 32085}, {376,
3531}, {382, 11738}, {548, 14487}, {550, 14483}, {576,
14458}, {1350, 14484}, {1498, 16251}, {1657, 3431}, {3091,
22334}, {3098, 14488}, {3146, 64}, {3303, 10429}, {3428,
38306}, {3430, 38309}, {3529, 3}, {3534, 14491}, {3579,
14496}, {3627, 16835}, {5188, 14485}, {5537, 80}, {5889,
2980}, {6282, 38308}, {6762, 19604}, {6776, 14486}, {7464,
265}, {7527, 15321}, {7556, 18550}, {7691, 38305}, {7957,
2346}, {7982, 84}, {7991, 1}, {9821, 11170}, {10222, 10308}, {10310,
38307}, {10990, 9139}, {10991, 10630}, {11477, 3424}, {12082,
4846}, {12086, 6145}, {12088, 3521}, {12103, 1173}, {12680,
1014}, {12702, 14497}, {15704, 54}, {15801, 15619}, {17538,
3527}, {17800, 20421}, {22333, 17578}, {31388, 39286}, {33524,
14542}, {33557, 65}, {33795, 1389}, {33878, 14494}, {34147,
10152}, {34795, 13377}, {35001, 33565}, {37946, 10293}.
- Martes, 20 de octubre del 2020
Baricentro de triángulos tangenciales
El 20 de octubre de 1917, en Berlín, nace Stéphane Frédéric Hessel, diplomático, escritor francés. Sus libros "¡Indignaos!" y "¡Comprometeos!" influirán en las protestas ciudadanas de 2011.
Fue uno de los redactores de la Declaración Universal de Derechos Humanos de 1948 y autor del libro ¡Indignaos!, en él se plantea un alzamiento «contra la indiferencia y a favor de la insurrección pacífica».
En su conclusión figura: "Convoquemos una verdadera insurrección pacífica contra los medios de comunicación de masas que no propongan como horizonte para nuestra juventud otras cosas que no sean el consumo en masa, el desprecio hacia los más débiles y hacia la cultura, la amnesia generalizada y la competición excesiva de todos contra todos."
Dado un triángulo ABC con circuncentro O=X3, K=X6 y .
Sea A' el centro de la cónica 𝒞a, que pasa por O y es tangente a TaTb en Tb y a TaTc en Tc. Las cónicas 𝒞b y 𝒞c, se definen cíclicamente; sean B' y C' sus respectivos centros.
Las rectas
A'Ta,
B'Tb,
C'Tc concurren en el baricentro de ,
X154.
La
cónica
( b^4 c^4 x^2+a^2 b^2 c^4 x y-a^4 c^4 y^2+a^2 b^2 c^4 y^2+a^2 c^6 y^2-b^2 c^6 y^2+a^2 b^4 c^2 x z-a^4 b^2 c^2 y z+2 a^2 b^4 c^2 y z+2 a^2 b^2 c^4 y z-2 b^4 c^4 y z-a^4 b^4 z^2+a^2 b^6 z^2+a^2 b^4 c^2 z^2-b^6 c^2 z^2 = 0)
𝒞a es el lugar geométrico del polo P, respecto a la circunferencia circunscrita Γ, de la recta p=MN, siendo M y N puntos variables sobre las rectas AB y AC, tales que AM:MB=CN:NA.
Γ y 𝒞a se intersecan en cuatro puntos (reales o imaginarios). La mediatriz ℓa de la bisectriz en A, pasa por dos puntos (reales) de intersección de Γ y 𝒞a. Cosiderando, cíclicamente, las rectas ℓb y ℓc, el triángulo formado por estas tres rectas es perspectivo con ABC, con centro de perspectividad el primer punto de Sharygin, X256.
Darij Grinberg, Sharygin Points Report,
Hyacinthos #6293 (1/8/03) and
#6315 (1/10/03)
The first of ten sections is an Introduction quoted, in part,
here:
We will treat two remarkable triangles: the triangle bounded by the
perpendicular bisectors of the internal angle bisectors of a
triangle ABC, and the triangle bounded by the perpendicular
bisectors of the external angle bisectors of triangle ABC. These
two triangles and the triangle ABC are three perspective triangles,
having a common perspectrix: the Lemoine axis of ABC. The mutual
perspectors of the three triangles will be called the first, second
and third Sharygin points of ABC (after a problem of Igor Sharygin
- see Section 10).
The report introduces fifteen Sharygin points, of which
the
1st, 2nd, 4th, and 6th are
X(256), X(291), X(846),
and X(1054), respectively. X(1281) is the 3rd Sharygin point
UNA SITUACIÓN MÁS GENERAL
Dados un triángulo, de baricentro G=X2, y un punto P, se considera la cónica circunscrita C(P) a ABC con P y su (de P). Sea A' el centro de la cónica 𝒞a que pasa por el centro Z de C(P) (Z=) y es tangente a TaTb en Tb y a TaTc en Tc. Los puntos B', C' se definen cíclicamente.
Las rectas A'Ta, B'Tb, C'Tc con concurren en Q=(G/P)/P, baricentro de .
Pares {P=X(i), Q=X(j)}, para {i, j}: {1, 165}, {2, 2}, {3, 3167}, {6, 154}, {7, 32079}, {9, 3158}, {10,
3971}, {30, 34582}, {37, 210}, {39, 3917}, {57, 34499}, {115,
8029}, {216, 51}, {233, 32078}, {395, 15769}, {396, 15768}, {512,
38237}, {513, 38238}, {514, 21204}, {523, 10278}, {524,
38239}, {525, 38240}, {650, 11193}, {1015, 8027}, {1084,
23610}, {1086, 6545}, {1146, 23615}, {1212, 354}, {1213,
1962}, {2482, 8030}, {3163, 3081}, {4370, 8028}, {6184,
23612}, {6292, 11205}, {6547, 6546}, {11672, 23611}, {13466,
8031}, {15526, 23616}, {16589, 21020}, {23991, 11123}, {34832,
24165}, {35071, 23613}, {35072, 23614}.
- Lunes, 19 de octubre del 2020
Cuadrado baricéntrico de la cúbica de Lucas
A Kake en su 50 aniversario
Dado un triángulo ABC, sea DEF el de un punto P.
Se considera la hipérbola ℋa, con asíntotas paralelas a los lados AB y AC, que pasa por A y es tangente al lado BC en el punto D.
Si (u:v:w) son las coordenadas baricéntricas de P, la ecuación de ℋa es:
((-b^2+c^2) u+a^2 (u+2 w))^2y^2+((b^2-c^2) u+a^2 (u+2 v))^2z^2-2 ((b^2-c^2) u+a^2 (u+2 v)) ((-b^2+c^2) u+a^2 (u+2 w))y z+((b^2-c^2) u+a^2 (u+2 v))^2z x +((-b^2+c^2) u+a^2 (u+2 w))^2 x y = 0.
Esta ecuacíon se obtiene tomando el haz de cónica determinado por la cónica degenerada del haz producto de la rectas BC (x=0) y la , y la cónica producto de las rectas paralelas por D a los lados AB y AC:
((-2 a^2+b^2+a (b-c)-c^2) x+(-2 a^2+b^2+a (b-c)-c^2) y+(2 a^2+b^2+a (b-c)-c^2) z) ((2 a^2+b^2+a (b-c)-c^2) x+(-2 a^2+b^2+a (b-c)-c^2) y+(2 a^2+b^2+a (b-c)-c^2) z) + λ x (x+y+z)= 0,
y determinando la cónica del haz que pasa por A, que se obtiene para
λ = (2 a^2+a b+b^2-a c-c^2) (2 a^2-a b-b^2+a c+c^2).
La tangente en A a ℋa es:
tA: ((-b^2+c^2) u+a^2 (u+2 w))^2y+((b^2-c^2) u+a^2 (u+2 v))^2z=0.
Procediendo cíclicamente sobre los lados de ABC, se definen las hipérbolas ℋb y ℋc y sus correspondientes tangentes tB y tC.
Las rectas
tA,
tB y
tC no son concurrentes y el triángulo
A'B'C' formado por ellas es perspectivo con
ABC si y solo si
P está sobre la circunferencia circunscrita o sobre la
cúbica de Darboux.
Si
P está sobre la cúbica de Darboux, el centro de perspectividad
P' es el del centro de perspectividad
Q (sobre la
cúbica de Lucas) de
ABC y el triángulo pedal de
P.
Algunas ternas {P=X(i), P'=X(j)=Q^2, Q=X(k)}, para los índices {i,j,k}: {1, 279, 7}, {3, 2, 2}, {4, 393, 4}, {20, 3926, 69}, {40, 346, 8}, {64, *, 253}, {84, *, 189}, {1490, *, 329}, {1498, 36413, 20}, {2130, *, 14362}, {3182, *, 5932}, {3183, *, 14361}, {3345, *, 1034}, {3346, *, 1032}, {3348, *, 14365}, {3353, *, 34162}.
Q^2 indica el cuadrado baricéntrico de Q y el * indica que P' no figura actualmente en .
Cuando DEF es el de P, en vez de su triángulo pedal, el triángulo A'B'C' siempre es perspectivo con ABC y el centro de perspectividad es el cuadrado baricéntrico de P.
- Domingo, 18 de octubre del 2020
Dos propiedades geométricas de K243
El 18 de octubre de 1850 nació en El Ferrol (La Coruña), Pablo Iglesias Posse, líder del movimiento obrero español, fue el cofundador del Partido Socialista Obrero Español (PSOE) en 1879 y de la Unión General de Trabajadores (UGT) en 1888.
•
A Construction For X(21454) (Euclid #1151, Kadir Altintaş, Oct 18, 2020)
Let I be incenter of ABC.
Ka, orthogonal projection of symmedian point of IBC on BC. Define Kb, Kc cyclically.
KaKbKc is cevian triangle of X(21454) respect to ABC.
•
K243.
Locus property
𝔖abc xyz
a^2 y z (a^4 (y - z) +
a^2 (2 c^2 (2 y + z) - 2 b^2 (y + 2 z)) + (b^2 -
c^2) (c^2 (5 y + z) + b^2 (y + 5 z))) = 0.
Points on the curve: excenters, X(1), X(3), X(4), X(376), X(3426), X(5119), X(7284), X(35237)
Let PaPbPc be the circumcevian triangle of P and denote by Ka, Kb, Kc the Lemoine points of triangles BCPa, CAPb, ABPc respectively. Let Qa, Qb, Qc be the orthogonal projections of Ka, Kb, Kc on BC, CA, AB respectively. ABC and QaQbQc are perspective (at Q) if and only if P lies on K243 (Kadir Altintaş, 2020-09-17).
Dado un triángulo y un punto propio P, sean D, E, F las proyecciones ortogonales de los de los triángulos PBC, PCA, PAB, sobre BC, CA, AB, respectivamente.
Las rectas AD, BE, CF son concurrentes si y solo si P está cobre la K243=pK(X6,X276), del catálogo de Bernard Gibert.
Si (u:v:w) son las coordenadas baricéntricas de P (u+v+w≠0), el simediano de PBC es:
Sa = (a^2 u (u + v + w) :
b^2 u^2 + 2 a^2 u v + b^2 u v - c^2 u v + 2 a^2 v^2 + a^2 v w :
c^2 u^2 + 2 a^2 u w - b^2 u w + c^2 u w + a^2 v w + 2 a^2 w^2),
y su proyección ortogonal sobre BC es:
D = (0 : u (c^2 (u + 3 v + w) - b^2 (3 u + 3 v + w)) -
a^2 (u^2 + 2 v (2 v + w) + u (5 v + w)) :
u (b^2 (u + v + 3 w) - c^2 (3 u + v + 3 w)) -
a^2 (u^2 + 2 w (v + 2 w) + u (v + 5 w))).
Las AD, BE, CF son concurren en W, cuando P está sobre K243,
W = (2 b^2 c^2 (20 u^4 + 34 u^3 (v + w) + v w (v + w)^2 +
u^2 (16 v^2 + 53 v w + 16 w^2) +
2 u (v^3 + 8 v^2 w + 8 v w^2 + w^3)) -
c^4 (4 u^4 + v w (v + w)^2 + u^3 (35 v + 9 w) +
u^2 (22 v^2 + 49 v w + 6 w^2) +
u (3 v^3 + 17 v^2 w + 15 v w^2 + w^3)) +
a^4 (3 u^3 (v + w) + u^2 (6 v^2 + 41 v w + 6 w^2) +
v w (13 v^2 + 38 v w + 13 w^2) +
3 u (v^3 + 17 v^2 w + 17 v w^2 + w^3)) -
b^4 (4 u^4 + v w (v + w)^2 + u^3 (9 v + 35 w) +
u^2 (6 v^2 + 49 v w + 22 w^2) +
u (v^3 + 15 v^2 w + 17 v w^2 + 3 w^3)) +
2 a^2 (b^2 (2 u^4 - 2 v^3 w + 2 v w^3 + 2 u^2 w (8 v + 13 w) +
u^3 (3 v + 20 w) - u (v^3 + 6 v^2 w - 19 v w^2 - 8 w^3)) +
c^2 (2 u^4 + u^3 (20 v + 3 w) + 2 u^2 v (13 v + 8 w) +
2 v w (v^2 - w^2) + u (8 v^3 + 19 v^2 w - 6 v w^2 - w^3))) : ... : ...)
Se tienen los siguientes pares {P=X(i), W=X(j)}, para {i, j}: {1, 21454}, {3, 2}, {4, 8796}.
Sean el del punto P, Ka, Kb, Kc los simedianos de los triángulos BCPa, CAPb, ABPc respectivamente, y Qa, Qb, Qc las proyecciones ortogonales de Ka, Kb, Kc sobre BC, CA, AB respectivamente.
ABC y son perspectivos (en
Q) si y solo si
P está sobre K243 (
CTC, Kadir Altintaş).
El centro de perspectividad es:
Q = (u (b^4 w (v + 4 w) + (a^2 - c^2) v (a^2 w - c^2 (4 v + w)) -
2 b^2 (a^2 w (v + 2 w) +
c^2 (8 u^2 + 2 v^2 + v w + 2 w^2 + 12 u (v + w)))) : ... : ...).
La recta QW pasa por el baricentro, para todo P sobre K243.
- Sábado, 17 de octubre del 2020
Asíntotas de una cúbica concurrentes en el Tercer Punto de Stevanovic
El 17 de octubre de 1937 falleció (a la edad de 77 años) Frank Morley, profesor americano de origen inglés que publicó numerosos problemas de la geometría del triángulo. Teorema de Morley (1899): "Si se trazan las trisectrices de los tres ángulos de un triángulo, las trisectrices adyacentes se cortan en los vértices de un triángulo equilátero".
Hyacinthos #7185 (Milorad R. Stevanovic. May 21, 2003)
• 1. If J1,J2,J3 are incenters of triangles IaBC,IbCA,IcAB (where Ia,Ib,Ic are excenters of triangle ABC), and BJ3∩CJ2=K1, CJ1∩AJ3=K2, AJ2∩BJ1=K3 then AK1,BK2,CK3 are concurent in point Q=X(1130) (
1st Stevanovic Point) given in barycentrics by
Q(a(2sinA/2+1):b(2sinB/2+1):c(2sinC/2+1)).
• 2.If I is incenter of ABC and IJ1∩BC=A1, IJ2∩CA=B1, IJ3∩AB=C1 then
AA1,BB1,CC1 are concurent in point S (
X(1488) = 2nd Stevanovic Point),
given in barycentrics by
S(a/(1+sinA/2):b/(1+sinB/2):c/(1+sinC/2)).
• 3.If I1,I2,I3 are incenters of triangles IBC,ICA,IAB and J1I1∩BC=V1, J2I2∩CA=V2, J3I3∩AB=V3 then AV1,BV2,CV3 are concurent in point V (
X(1489) = 3rd Stevanovic Point), given in barycentrics by
V(cosA/2+sinA/2-1:cosB/2+sinB/2-1:
:cosC/2+sinC/2-1).
Euclid #1146 (Kadir Altintaş. Oct 17, 2020)
Let P be point and DEF pedal triangle of P.
Ha, orthogonal projection of midpoint of EF on BC.
Define Hb, Hc cyclically.
HaHbHc is a cevian triangle iff P lies on a cubic curve.
Dado un triángulo ABC, sea DEF el de un punto P, de coordenadas baricéntricas (u:v:w). La proyección ortogonal del punto medio de EF sobe BC es:
Ha = (0 : a^4 (-c^2 v+b^2 w)+(b^2-c^2) (c^4 v+b^4 w-b^2 c^2 (4 u+v+w))-2 a^2 (-c^4 v+b^4 w+b^2 c^2 (2 u+3 v+w)) : a^4 (c^2 v-b^2 w)-(b^2-c^2) (c^4 v+b^4 w-b^2 c^2 (4 u+v+w))+2 a^2 (-c^4 v+b^4 w-b^2 c^2 (2 u+v+3 w))).
Los puntos Hb y Hc se definen cíclicamente.
Las rectas
AHa,
BHb,
CHc son concurrentes si y sólo si el punto
P está sobre la cúbica de ecuación:
𝔖abc xyz
4 b^4 (-a+b-c) (a+b-c) c^4 (-a+b+c) (a+b+c) (b^2-c^2) (-3 a^4+b^4-2 b^2 c^2+c^4+a^2 (2 b^2+2 c^2)) x^3+a^4 y z (c^2 (a^12+2 a^10 (b^2-3 c^2)+a^8 (-17 b^4+22 b^2 c^2+15 c^4)+4 a^6 (7 b^6+13 b^4 c^2-19 b^2 c^4-5 c^6)+(b-c)^3 (b+c)^3 (b^6+17 b^4 c^2-b^2 c^4-c^6)-a^4 (b^2-c^2) (17 b^6+149 b^4 c^2+91 b^2 c^4+15 c^6)+2 a^2 (b^2-c^2) (b^8+26 b^6 c^2+52 b^4 c^4+14 b^2 c^6+3 c^8)) y-b^2 (a^12-2 a^10 (3 b^2-c^2)+a^8 (15 b^4+22 b^2 c^2-17 c^4)-4 a^6 (5 b^6+19 b^4 c^2-13 b^2 c^4-7 c^6)+(b-c)^3 (b+c)^3 (b^6+b^4 c^2-17 b^2 c^4-c^6)+a^4 (b^2-c^2) (15 b^6+91 b^4 c^2+149 b^2 c^4+17 c^6)-2 a^2 (b^2-c^2) (3 b^8+14 b^6 c^2+52 b^4 c^4+26 b^2 c^6+c^8)) z) = 0.
Si Q es el punto de concurrencia de las rectas AHa, BHb, CHc, se tienen los siguientes pares {P=X(i), Q=X(j)}, para {i,j}: {64, 4}, {221, 7}, {1498, 2}, {7959, 8}.
Las ecuaciones de las asíntotas de la cúbica son:
b^2 (a^2 - b^2 + c^2)^2x -a^2 (-a^2 + b^2 + c^2)^2y + 4 a^2 b^2 (a^2 -
b^2)z = 0,
-c^2 (a^2 + b^2 - c^2)^2x + (-4 a^4 c^2 +
4 a^2 c^4)y + a^2 (-a^2 + b^2 + c^2)^2 z = 0,
4 b^2 c^2 (b^2 - c^2)x + c^2 (a^2 + b^2 - c^2)^2 y -b^2 (a^2 - b^2 +
c^2)^2z = 0.
Estas tres rectas concurren en el Tercer Punto de Stevanovic, X1498.
- Lunes, 12 de octubre del 2020
Los centros del triángulo X(950) y X(1214)
Edwin Abbott (20 de diciembre de 1838, 12 de octubre de 1926) fue un maestro de escuela inglés que escribió el popular libro "Planilandia, una novela de muchas dimensiones" (1884), como una introducción a las dimensiones superiores.
En "Planilandia", cuantos más lados tenga, mayor será su clase. Los trabajadores son triángulos equiláteros, el autor mismo es A Cuadrado, una persona de clase media, mientras que las clases más altas son los círculos que son sacerdotes. El mundo de Planilandia es visitado por una esfera que A Cuadrado ve al principio como un punto que crece hasta convertirse en un disco, luego se encoge de nuevo hasta convertirse en un punto y desaparece.
The M-Configuration of a Triangle
Given a triangle
ABC, we consider points
Aa on the line
BC,
Ba on the half line
CA, and
Ca on the half line
BA such that
BCa =
CaAa =
AaBa =
BaC. We shall refer to
BCaAaBaC as M
a, because it looks like the letter M when triangle
ABC is acute-angled. Similarly, we also have M
b and M
c. The three figures M
a, M
b, M
c constitute the M-configuration of triangle
ABC.
Proposition.- The lines
AAa,
BBb,
CCc concur at the point
X92.
Dado un triángulo ABC con incentro I=X1, circuncentro O=X3 y Ia, Ib, Ic, la hipérbola ℋa tangente en A a la , que pasa por O y por los ortocentros de los de I e Ia, vuelve a cortar a los lados de AC y AB en Ab y Ac, respectivamente. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
Las rectas
AbAc,
BcBa,
CaCb concurren en
X1214, de X
92.
El ortocentro del triángulo pedal del incentro () es X65, del . Las coordenadas baricéntricas del ortocentro del triángulo pedal del A-excentro son:
Ha = (-a (a + b - c) (a - b + c) (b + c) : -b (a - c) (-a + b - c) (a + b +
c) : (a - b) (a + b - c) c (a + b + c)).
La ecuación de la cónica tangente en A a la simediana AX6 y que pasa por X3, X65 y Ha es:
ℋa:
(a^2 b c^2-b^3 c^2-a^2 c^3-b^2 c^3+b c^4+c^5) x y+(-a^2 b c^2+b^3 c^2-a^2 c^3-b^2 c^3-b c^4+c^5) y^2+(-a^2 b^3+b^5+a^2 b^2 c+b^4 c-b^3 c^2-b^2 c^3) x z+(-a^2 b^3+b^5+3 a^2 b^2 c-b^4 c+3 a^2 b c^2-a^2 c^3-b c^4+c^5) y z+(-a^2 b^3+b^5-a^2 b^2 c-b^4 c-b^3 c^2+b^2 c^3) z^2=0.
La cónica ℋa (hipérbola de asíntotas paralelas a la mediatriz de BC y a la bisectriz en A) puede ser descrita como lugar geómetrico como sigue:
Sea P un punto sobre la bisectriz del ángulo en A y DEF su triángulo pedal, la de P vuelve a cortar a BC en D'. El lugar geométrico del ortocentro H' de D'EF es la hipérbola ℋa.
La hipérbola ℋ corta, respectivamente, a AC y AB en:
Ab = (-(-a^2 + (b - c)^2) (b + c) : 0 : (b - c) (-a^2 + (b + c)^2)),
Ac = ((-a^2 + (b - c)^2) (b + c) : (b - c) (-a^2 + (b + c)^2) : 0).
Sean A1 y A2 los puntos de intersección de la hipérbola ℋa con el lado BC. Las hipérbolas ℋb y ℋc (definidas cíclicamente) cortan, respectivamente, a los lados CA y AB en los puntos B1, B2 y C1 y C2. Entonces, los seis puntos A1 y A2, B1, B2, C1, C2 están sobre una misma
cónica,
( a^3 b^2 c^2 x^2-a^2 b^3 c^2 x^2-a b^4 c^2 x^2+b^5 c^2 x^2-a^2 b^2 c^3 x^2+2 a b^3 c^3 x^2-b^4 c^3 x^2-a b^2 c^4 x^2-b^3 c^4 x^2+b^2 c^5 x^2+a^5 c^2 x y-a^4 b c^2 x y-a b^4 c^2 x y+b^5 c^2 x y-a^4 c^3 x y+2 a^3 b c^3 x y-2 a^2 b^2 c^3 x y+2 a b^3 c^3 x y-b^4 c^3 x y-a^3 c^4 x y+3 a^2 b c^4 x y+3 a b^2 c^4 x y-b^3 c^4 x y+a^2 c^5 x y-4 a b c^5 x y+b^2 c^5 x y+a^5 c^2 y^2-a^4 b c^2 y^2-a^3 b^2 c^2 y^2+a^2 b^3 c^2 y^2-a^4 c^3 y^2+2 a^3 b c^3 y^2-a^2 b^2 c^3 y^2-a^3 c^4 y^2-a^2 b c^4 y^2+a^2 c^5 y^2+a^5 b^2 x z-a^4 b^3 x z-a^3 b^4 x z+a^2 b^5 x z-a^4 b^2 c x z+2 a^3 b^3 c x z+3 a^2 b^4 c x z-4 a b^5 c x z-2 a^2 b^3 c^2 x z+3 a b^4 c^2 x z+b^5 c^2 x z+2 a b^3 c^3 x z-b^4 c^3 x z-a b^2 c^4 x z-b^3 c^4 x z+b^2 c^5 x z+a^5 b^2 y z-a^4 b^3 y z-a^3 b^4 y z+a^2 b^5 y z-4 a^5 b c y z+3 a^4 b^2 c y z+2 a^3 b^3 c y z-a^2 b^4 c y z+a^5 c^2 y z+3 a^4 b c^2 y z-2 a^3 b^2 c^2 y z-a^4 c^3 y z+2 a^3 b c^3 y z-a^3 c^4 y z-a^2 b c^4 y z+a^2 c^5 y z+a^5 b^2 z^2-a^4 b^3 z^2-a^3 b^4 z^2+a^2 b^5 z^2-a^4 b^2 c z^2+2 a^3 b^3 c z^2-a^2 b^4 c z^2-a^3 b^2 c^2 z^2-a^2 b^3 c^2 z^2+a^2 b^2 c^3 z^2 = 0)
que pasa por los centros X3270, X3271 y su centro está sobre la recta X31X21746:
W = ( a^2 (a^7 (b^2-4 b c+c^2)
-2 a^6 (b^3-3 b^2 c-3 b c^2+c^3)
-10 a^5 b^2 c^2
+3 a^4 (b-c)^2 (b^3+c^3)
+a^3 (-3 b^6+8 b^5 c+3 b^4 c^2-8 b^3 c^3+3 b^2 c^4+8 b c^5-3 c^6)
-2 a^2 b (b-c)^2 c (b^3+5 b^2 c+5 b c^2+c^3)
+2 a (b^4-b^3 c+b c^3-c^4)^2
-(b-c)^4 (b+c)^3 (b^2-b c+c^2)
) : ... : ...),
que tiene números de búsqueda en
(2.90354122421281, 0.575828812010040, 1.90191781626382).
Las dos hipérbolas ℋb y ℋc tienen en común los puntos X3 y X65. La ecuación de la recta da que pasa por el otro par de puntos comunes es:
(a^4 - a^3 (b + c) -
a^2 (b^2 - 3 b c + c^2) + a (b^3 + b^2 c + b c^2 + c^3) + b c (-3 b^2 + 2 b c - 3 c^2))x + (a + b) (a - c) (a - b - c) (a - b + c) y + (a - b) (a - b - c) (a + b - c) (a + c)z = 0.
Las rectas db y dc se definen cíclicamente.
Las rectas da, db, dc concurren en X950.
X(950)
(2 a^4 - a^3 (b + c) -
a^2 (b + c)^2 + a (b - c)^2 (b + c)- (b^2 - c^2)^2 : ... : ...)
A' is the insimilicenter of the circles having as diameters segments CA and AB; and cyclically for B' and C'. A'B'C' is also the complement of the cevian triangle of isotomic conjugate of incenter. Let La be the reflection of line BC in line B'C', and define Lb and Lc cyclically. Let A" = Lb ∩ Lc, and define B" and C" cyclically. The lines AA", BB", CC" concur in X(950). (Randy Hutson, January 29, 2018)
- Viernes, 9 de octubre del 2020
Una propiedad de la cúbica K108
El 9 de octubre de 1911 nació Luis A. Santaló, matemático español que se exilió en la Argentina en 1939 al iniciarse la Segunda Guerra Mundial y ser partidario del derrotado bando republicano en España. Publicó más de cien trabajos de investigación fundamental y de divulgación; y varios libros, en especial Geometría integral (1951, en colaboración con Julio Rey Pastor). Geometría Proyectiva (1966). Vectores y Tensores con sus aplicaciones (1968).
Dado un triángulo ABC y un punto P, no situado sobre su circunferencia circunscrita, la circunferencia (PBC) vuelve a cortar a las tangentes en B y C a la circunferencia circunscrita en Ab y Ac, respectivamente. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
Si las coordenadas baricéntricas de P son (u:v:w), se tiene que:
Ab = (a^2 (c^2 u v+b^2 u w+a^2 v w) : -(a^2-c^2) v (c^2 u+a^2 w)-b^2 u (c^2 (u+v)+a^2 w) : -c^2 (c^2 u v+b^2 u w+a^2 v w),
Ac = (a^2 (c^2 u v+b^2 u w+a^2 v w) : -b^2 (c^2 u v+b^2 u w+a^2 v w) : b^4 u w-a^2 v (c^2 u+a^2 w)-b^2 (a^2 (u-v) w+c^2 u (u+w)).
El triángulo A'B'C' formado por las rectas AbAc, BcBa, CaCb, es homotético a ABC y el centro de homotecia es:
Q = (a^4/u : b^4/v : c^4/w),
es decir, el de P. (X(32) es el la elipse que es el del , Randy Hutson, October 15, 2018).
Los seis puntos
Ab,
Ac,
Bc,
Ba,
Ca,
Cb están en una misma cónica si y solo si
P está sobre la cúbica
K108=pK(X32, X23), del catálogo de Bernard Gibert.
K108 contiene a los centros Xi, para i∈{3, 6, 23, 25, 111, 187, 1177, 2393, 2930, 3455, 8428, 10355, 13493, 22258, 22259, 38532, 38533}.
El tercer punto X de intersección de K108 con la recta X(3)X(8428) es su punto de intersección con su asintota.
X = ( a^2 (a^4 - b^4 + 4 b^2 c^2 - c^4)/(a^12 - 2 a^10 (b^2 + c^2)
- a^8 (b^4 - 9 b^2 c^2 + c^4)
+ 4 a^6 (b^2 - c^2)^2 (b^2 + c^2)
- a^4 (b^8 + 6 b^6 c^2 - 10 b^4 c^4 + 6 b^2 c^6 + c^8)
- 2 a^2 (b^2 - c^2)^4 (b^2 + c^2)
+ (b^4 - c^4)^2 (b^4 - 3 b^2 c^2 + c^4) ) : ... : ...),
que tiene números de búsqueda en
(-1.77616500557179, -0.185194723983688, 4.58864467800622).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,1560}, {2373,37778}.
Las rectas
AbAc,
BcBa,
CaCb son concurrentes si y solo si
P está en la cuártica conjugada isogonal de la circunferencia circunscrita al .
Hyacinthos #29444
Aug 31, 2019
[Randy Hutson]:
The locus of the P-vertex conjugate of P, as P varies on the line at infinity is a curve that is the isogonal conjugate of the anticomplementary circle. The curve passes through the vertices of ABC and X(3446), X(3447), X(9217), and X(22259) (for P = X(513), X(523), X(512) and X(524), resp.). If ABC is acute, the curve is closed. If ABC is obtuse, it has as asymptotes the isogonal conjugates of the anticomplements of PU(4) (the circumcircle intercepts of the anticomplementary circle). Is this curve a cubic or higher degree curve? I could not find a match on Bernard's site.
[Peter Moses]:
c^6 x^2 y^2+b^2 c^2 (a^2+b^2+c^2) x^2 y z+a^2 c^2 (a^2+b^2+c^2) x y^2 z+b^6 x^2 z^2+a^2 b^2 (a^2+b^2+c^2) x y z^2+a^6 y^2 z^2 = 0
passes through
ABC, tangential tiangle, X{3446,3447,9217,22259,34130}, circular points at infinity.
The quartic is not in Bernard's CTC.
[Randy Hutson]
Thank you, Peter!
I wonder if the triangle formed by the tangents to the quartic at the vertices of the tangential triangle has any interesting properties.
[Peter Moses]:
Hi Antreas & Randy,
The tangents form the Ara triangle / excentral of tangential triangle, see ETC
X(5594).
- Miércoles, 7 de octubre del 2020
Otra propiedad del centro del triángulo X(184)
Referencias de
X(184) en ETC
• Inverse of the center of in the
• of of the circumcenter.
• HomothetIc center of and .
• Homothetic center of triangles ABC and A'B'C', the
latter defined as follows: let B
1 and C
1 be the
points where the perpendicular bisector BC meets sidelines CA and AB,
and cyclically define C
2, A
2; A
3,
B
3. Then A'B'C' is formed by the perpendicular bisectors of
segments B
1C
1, C
2A
2,
A
3B
3. (Fred Lang,
Hyacinthos #1190, Aug 13, 2000).
• Homothety center of the orthic triangle and the medial triangle of the (Nikos Dergiades,
Hyacinthos #5437, May 10, 2002).
• Common vertex
of three triangles inside ABC, mutually congruent and similar to ABC.
The triangles can be labeled XB
CC
B,
XC
AA
C, XA
BB
A, with
B
C and C
B on side BC, C
A and
A
C on side CA, and A
B and B
A on side
AB.(Alexei Myakishev,
On the Procircumcenter and Related Points,
Forum Geometricorum 3 (2003) 29-34.)
• Exsimilicenter of the circumcircle and . (Randy Hutson, December 14, 2014)
• Perspector of the tirangles A'B'C' and A"B"C". Being A'B'C' the intersections, other than X(3), of the X(3)-cevians and the Brocard circle, and A"B"C" the intersections, other than X(6), of the X(6)-cevians and the Brocard circle. (Randy Hutson, June 1, 2015)
• p∩q, where p is the isotomic conjugate of polar conjugate of Brocard axis (i.e., line X(3)X(49)), and q is the polar conjugate of isotomic conjugate of Brocard axis (i.e., line X(6)X(25)). (Randy Hutson, June 1, 2015)
Let DEF be the orthic triangle. Let D' be the isotomic conjugate of X(4) wrt AEF, and define E' and F' cyclically; then the lines AD', BE', CF' concur in X(184). (Randy Hutson, June 1, 2015)
• Let DEF be the orthic triangle. Let D' be the isotomic conjugate of X(4) wrt AEF, and define E' and F' cyclically; then the lines AD', BE', CF' concur in X(184). (Randy Hutson, June 1, 2015)
Dado un triángulo ABC con circuncentro O=X3, ortocentro H=X4, radio de su circunferencia circunscrita R y DEF, la circunferencia (BCH) vuelve a cortar a las tangentes en B y C a la circunferencia circunscrita en Ab y Ac, respectivamente. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente. Sea A'B'C' el triángulo formado por las rectas AbAc, BcBa, CaCb.
Los triángulos ABC y A'B'C' son homotéticos, con centro de homotecia X184 y razón de homotecia (4R^2-OH^2)/R^2.
En coordenadas baricéntricas:
Ab = (a^2 (-a^2 + b^2 + c^2) : a^4 + c^4 -
a^2 (b^2 + 2 c^2) : -c^2 (-a^2 + b^2 + c^2)),
Ac = (a^2 (-a^2 + b^2 + c^2) : -b^2 (-a^2 + b^2 + c^2) : a^4 + b^4 -
a^2 (2 b^2 + c^2)),
A' = ((b^2 - c^2)^2 (b^2 + c^2) -
a^2 (b^4 + b^2 c^2 + c^4) : b^4 (a^2 - b^2 + c^2) : c^4 (a^2 + b^2 -
c^2)).
X184 = (a^4 (a^2 - b^2 - c^2) : b^4 (-a^2 + b^2 - c^2) : c^4 (-a^2 - b^2 + c^2)).
- Lunes, 5 de octubre del 2020
Centro de una circunferencia de Apolonio sobre la recta de Euler
El 5 de octubre de 1781 nació Bernard Bolzano, matemático, lógico, filósofo y teólogo checo. Se le conoce por el teorema de Bolzano, así como por el teorema de Bolzano-Weierstrass, que esbozó como lema de otro trabajo en 1817, y décadas después desarrolló Karl Weierstrass.
Dado un triángulo ABC, sean su y A'B'C' el de X25 (centro de homotecia de los triángulos y ).
Las circunferencias Γa=
(A'MbMc),
(
Ecuación baricéntrica:
c^2 x y + b^2 x z +
a^2 y z + (x + y +
z) (-((2 a^2 b^2 c^2 x)/(
a^4 + 2 a^2 b^2 + b^4 + 2 a^2 c^2 - 2 b^2 c^2 + c^4)) - (
c^2 (a^4 - 2 a^2 b^2 + b^4 + 2 a^2 c^2 - 2 b^2 c^2 + c^4) y)/(
2 (a^4 + 2 a^2 b^2 + b^4 + 2 a^2 c^2 - 2 b^2 c^2 + c^4)) - (
b^2 (a^4 + 2 a^2 b^2 + b^4 - 2 a^2 c^2 - 2 b^2 c^2 + c^4) z)/(
2 (a^4 + 2 a^2 b^2 + b^4 + 2 a^2 c^2 - 2 b^2 c^2 + c^4))) = 0)
Γb=(B'McMa), Γc=(C'MaMb), son tangentes a la circunferencia circunscrita a ABC y su es X5020, centro de homotecia del triángulo medial y el tercer del circuncentro.
La recta A'X5020 vuelve a cortar a la circunferencia Γa en:
Ta = (-a^8 - 2 (b^2 - c^2)^4 - 3 a^6 (b^2 + c^2) +
3 a^2 (b^2 - c^2)^2 (b^2 + c^2) +
a^4 (3 b^4 - 14 b^2 c^2 + 3 c^4) : b^2 (-a^6 + a^4 (3 b^2 - 7 c^2) -
3 (b^2 - c^2)^3 + a^2 (b^4 + 2 b^2 c^2 - 3 c^4)) : -c^2 (a^6 +
a^4 (7 b^2 - 3 c^2) - 3 (b^2 - c^2)^3 +
a^2 (3 b^4 - 2 b^2 c^2 - c^4))).
Los puntos Tb y Tc se definen cíclicamente.
La circunferencia Γ=
(TaTbTc)
( 3 a^4 b^2 c^2 x^2 - 5 a^2 b^4 c^2 x^2 - 5 a^2 b^2 c^4 x^2 -
a^6 c^2 x y - a^4 b^2 c^2 x y - a^2 b^4 c^2 x y - b^6 c^2 x y +
a^4 c^4 x y + 12 a^2 b^2 c^4 x y + b^4 c^4 x y + a^2 c^6 x y +
b^2 c^6 x y - c^8 x y - 5 a^4 b^2 c^2 y^2 + 3 a^2 b^4 c^2 y^2 -
5 a^2 b^2 c^4 y^2 - a^6 b^2 x z + a^4 b^4 x z + a^2 b^6 x z -
b^8 x z - a^4 b^2 c^2 x z + 12 a^2 b^4 c^2 x z + b^6 c^2 x z -
a^2 b^2 c^4 x z + b^4 c^4 x z - b^2 c^6 x z - a^8 y z + a^6 b^2 y z +
a^4 b^4 y z - a^2 b^6 y z + a^6 c^2 y z + 12 a^4 b^2 c^2 y z -
a^2 b^4 c^2 y z + a^4 c^4 y z - a^2 b^2 c^4 y z - a^2 c^6 y z -
5 a^4 b^2 c^2 z^2 - 5 a^2 b^4 c^2 z^2 + 3 a^2 b^2 c^4 z^2 = 0)
es una circunferencia de Apolonio de las tres circunferencias Γ
a, Γ
b, Γ
c. Su radio es 2R(r^2+4rR+2R^2-s^2)/(8R^2-r^2-4rR+s^2) y su centro es
W = 12R^2 X2 - ((r+2R)^2-s^2) X3 =
( a^2(a^8 -
2 a^6 (b^2 + c^2)- 4 a^4 b^2 c^2 +
2 a^2 (b^6 + 7 b^4 c^2 + 7 b^2 c^4 + c^6)- (b^2 - c^2)^2 (b^4 + 10 b^2 c^2 + c^4)) : ... : ...),
que tiene números de búsqueda en
(2.08085077722376, 1.20584151743502, 1.84545845727225).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {6,11793}, {54,6090}, {64,16836}, {68,19588}, {155,5050}, {182,17814}, {185,22112}, {389,17825}, {394,11426}, {498,16541}, {511,3527}, {569,3167}, {578,17811}, {1154,5644}, {1216,1351}, {1350,10110}, {1498,37515}, {1503,31521}, {2548,8573}, {3199,36751}, {3564,11487}, {3614,18954}, {3796,14530}, {3817,9911}, {3819,37498}, {3917,10982}, {3964,32828}, {5085,6759}, {5093,15067}, {5422,11444}, {5446,33878}, {5544,37489}, {5562,10601}, {5646,37480}, {5650,11424}, {5651,19357}, {5709,26938}, {5818,8192}, {5886,12410}, {5891,12164}, {5892,12163}, {5907,37514}, {5943,17834}, {6000,33537}, {7173,10833}, {7330,26928}, {7689,32620}, {7746,34809}, {7988,37557}, {8193,8227}, {9306,37476}, {9695,23275}, {9723,19418}, {9777,11412}, {9786,11695}, {9798,10175}, {9861,36519}, {9919,36518}, {10516,18381}, {10576,13889}, {10577,13943}, {10984,32063}, {11477,15606}, {11820,13474}, {11898,13292}, {12161,26206}, {12168,15059}, {12174,15058}, {12309,14852}, {12310,23515}, {12315,15030}, {12329,13374}, {13175,23514}, {13222,23513}, {13336,18451}, {13434,15066}, {13754,15805}, {14561,37491}, {14673,36520}, {14826,31804}, {15082,37497}, {16252,31267}, {18920,18925}, {23039,37493}, {32205,33533}, {37488,38317}, {37505,37672}.
- Domingo, 4 de octubre del 2020
Una circunferencia de Apolonio
El 4 de octubre de 1917 nació Violeta Parra, cantante, poetisa, compositora, pintora, escultora y ceramista chilena. Fue la más importante folclorista de su país y es considerada fundadora de la música popular chilena. "Gracias a la vida"
Dado un triángulo ABC de incentro I=X1 y circuncentro O=X3, sea DEF el y el de éste. Una de las dos circunferencias tangentes a la circunferencia inscrita, que pasan por Mb y Mc tiene diámetro ID; el punto de tangencia D' de la otra, que se designa por Γa, es el segundo punto de intersección de la circunferencia inscrita y la recta D
X57.
( Ejes radicales concurrentes en el conjugado isogonal del punto intermedio
Antipodales del punto de Bevan y el centro X(57)
)
Cíclicamente, se consideran las circunferencias Γb, Γc y sus puntos de tangencia E', F'.
La recta que une D' con el centro radical X10980, de las circunferencias Γa, Γb, Γc, vuelve a cortar a Γa en Ta. Los puntos Tb y Tc se definen cíclicamente.
La
circunferencia
(
Ecuación baricéntrica:
a^5 x^2-3 a^4 b x^2+2 a^3 b^2 x^2+2 a^2 b^3 x^2-3 a b^4 x^2+b^5 x^2-3 a^4 c x^2+3 a^3 b c x^2+5 a^2 b^2 c x^2-7 a b^3 c x^2+2 b^4 c x^2+2 a^3 c^2 x^2+5 a^2 b c^2 x^2-4 a b^2 c^2 x^2-3 b^3 c^2 x^2+2 a^2 c^3 x^2-7 a b c^3 x^2-3 b^2 c^3 x^2-3 a c^4 x^2+2 b c^4 x^2+c^5 x^2+2 a^5 x y-6 a^4 b x y+4 a^3 b^2 x y+4 a^2 b^3 x y-6 a b^4 x y+2 b^5 x y-a^4 c x y-4 a^3 b c x y+10 a^2 b^2 c x y-4 a b^3 c x y-b^4 c x y-2 a^3 c^2 x y+2 a^2 b c^2 x y+2 a b^2 c^2 x y-2 b^3 c^2 x y+8 a b c^3 x y+c^5 x y+a^5 y^2-3 a^4 b y^2+2 a^3 b^2 y^2+2 a^2 b^3 y^2-3 a b^4 y^2+b^5 y^2+2 a^4 c y^2-7 a^3 b c y^2+5 a^2 b^2 c y^2+3 a b^3 c y^2-3 b^4 c y^2-3 a^3 c^2 y^2-4 a^2 b c^2 y^2+5 a b^2 c^2 y^2+2 b^3 c^2 y^2-3 a^2 c^3 y^2-7 a b c^3 y^2+2 b^2 c^3 y^2+2 a c^4 y^2-3 b c^4 y^2+c^5 y^2+2 a^5 x z-a^4 b x z-2 a^3 b^2 x z+b^5 x z-6 a^4 c x z-4 a^3 b c x z+2 a^2 b^2 c x z+8 a b^3 c x z+4 a^3 c^2 x z+10 a^2 b c^2 x z+2 a b^2 c^2 x z+4 a^2 c^3 x z-4 a b c^3 x z-2 b^2 c^3 x z-6 a c^4 x z-b c^4 x z+2 c^5 x z+a^5 y z-2 a^2 b^3 y z-a b^4 y z+2 b^5 y z+8 a^3 b c y z+2 a^2 b^2 c y z-4 a b^3 c y z-6 b^4 c y z+2 a^2 b c^2 y z+10 a b^2 c^2 y z+4 b^3 c^2 y z-2 a^2 c^3 y z-4 a b c^3 y z+4 b^2 c^3 y z-a c^4 y z-6 b c^4 y z+2 c^5 y z+a^5 z^2+2 a^4 b z^2-3 a^3 b^2 z^2-3 a^2 b^3 z^2+2 a b^4 z^2+b^5 z^2-3 a^4 c z^2-7 a^3 b c z^2-4 a^2 b^2 c z^2-7 a b^3 c z^2-3 b^4 c z^2+2 a^3 c^2 z^2+5 a^2 b c^2 z^2+5 a b^2 c^2 z^2+2 b^3 c^2 z^2+2 a^2 c^3 z^2+3 a b c^3 z^2+2 b^2 c^3 z^2-3 a c^4 z^2-3 b c^4 z^2+c^5 z^2 = 0)
() toca a las tres circunferencias Γ
a, Γ
b, Γ
c, permaneciendo en el interior de ellas. Su radio es (2r(r+2R))/(r+12R) y su centro es
W = (5r+12R) I - 4r O.
W = ( a (a^3 - 5 a^2 (b + c) - a (b^2 + 14 b c + c^2) + 5 (b - c)^2 (b + c)) : ... : ...),
que tiene números de búsqueda en
(1.31065860192754, 1.37682165635177, 2.08256090354352).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,3}, {5,30291}, {7,6744}, {10,11038}, {84,24645}, {145,4900}, {169,16667}, {515,3296}, {516,5586}, {518,4866}, {519,11024}, {553,18217}, {938,5290}, {950,4355}, {1056,17706}, {1071,3062}, {1125,31446}, {1698,3475}, {1699,9799}, {3243,3812}, {3616,18249}, {3671,9800}, {3730,16673}, {3742,11523}, {3868,10582}, {3874,5223}, {3881,9623}, {3889,4853}, {3892,12629}, {3894,5506}, {3945,10521}, {3982,5225}, {4208,38054}, {4293,11034}, {4297,15933}, {4314,21454}, {4334,15658}, {4539,16856}, {4666,12526}, {4864,9340}, {4902,24851}, {4915,34791}, {5129,5850}, {5439,8580}, {5493,8236}, {5587,38041}, {5603,9948}, {5726,5818}, {5787,38036}, {5883,6765}, {5904,30393}, {6738,11037}, {7989,13407}, {7992,24644}, {8583,11520}, {9614,11551}, {9624,16137}, {9851,12675}, {10122,18219}, {10399,30326}, {10404,37723}, {11019,11036}, {11025,12560}, {11522,21628}, {12563,14986}, {17151,35633}, {17728,34595}, {20116,30330}, {24391,38053}, {24473,31435}, {31145,37717}.
- Sábado, 3 de octubre del 2020
El centro X(10980) como centro radical
A Silvia en su 50 aniversario
Dado un triángulo ABC sean, respectivamente, DEF, y los triángulos de , , y de DEF.
La recta DHa vuelve a cortar a la circunferencia inscrita en D'. La circunferencia
Γa,
(
Ecuación baricéntrica de Γa:
2 a^6 x^2-7 a^5 b x^2+9 a^4 b^2 x^2-6 a^3 b^3 x^2+4 a^2 b^4 x^2-3 a b^5 x^2+b^6 x^2-7 a^5 c x^2+14 a^4 b c x^2-6 a^3 b^2 c x^2-4 a^2 b^3 c x^2+5 a b^4 c x^2-2 b^5 c x^2+9 a^4 c^2 x^2-6 a^3 b c^2 x^2-2 a b^3 c^2 x^2-b^4 c^2 x^2-6 a^3 c^3 x^2-4 a^2 b c^3 x^2-2 a b^2 c^3 x^2+4 b^3 c^3 x^2+4 a^2 c^4 x^2+5 a b c^4 x^2-b^2 c^4 x^2-3 a c^5 x^2-2 b c^5 x^2+c^6 x^2+5 a^6 x y-18 a^5 b x y+23 a^4 b^2 x y-12 a^3 b^3 x y+3 a^2 b^4 x y-2 a b^5 x y+b^6 x y-6 a^5 c x y+6 a^4 b c x y+4 a^3 b^2 c x y-4 a^2 b^3 c x y+2 a b^4 c x y-2 b^5 c x y-a^4 c^2 x y+4 a^3 b c^2 x y-6 a^2 b^2 c^2 x y+4 a b^3 c^2 x y-b^4 c^2 x y+4 a^3 c^3 x y+12 a^2 b c^3 x y-4 a b^2 c^3 x y+4 b^3 c^3 x y-5 a^2 c^4 x y-2 a b c^4 x y-b^2 c^4 x y+2 a c^5 x y-2 b c^5 x y+c^6 x y+3 a^6 y^2-11 a^5 b y^2+14 a^4 b^2 y^2-6 a^3 b^3 y^2-a^2 b^4 y^2+a b^5 y^2+a^5 c y^2-8 a^4 b c y^2+10 a^3 b^2 c y^2-3 a b^4 c y^2-6 a^4 c^2 y^2-2 a^3 b c^2 y^2+6 a^2 b^2 c^2 y^2+2 a b^3 c^2 y^2-2 a^3 c^3 y^2-8 a^2 b c^3 y^2+2 a b^2 c^3 y^2+3 a^2 c^4 y^2-3 a b c^4 y^2+a c^5 y^2+5 a^6 x z-6 a^5 b x z-a^4 b^2 x z+4 a^3 b^3 x z-5 a^2 b^4 x z+2 a b^5 x z+b^6 x z-18 a^5 c x z+6 a^4 b c x z+4 a^3 b^2 c x z+12 a^2 b^3 c x z-2 a b^4 c x z-2 b^5 c x z+23 a^4 c^2 x z+4 a^3 b c^2 x z-6 a^2 b^2 c^2 x z-4 a b^3 c^2 x z-b^4 c^2 x z-12 a^3 c^3 x z-4 a^2 b c^3 x z+4 a b^2 c^3 x z+4 b^3 c^3 x z+3 a^2 c^4 x z+2 a b c^4 x z-b^2 c^4 x z-2 a c^5 x z-2 b c^5 x z+c^6 x z+2 a^6 y z+2 a^5 b y z-4 a^4 b^2 y z-4 a^3 b^3 y z+2 a^2 b^4 y z+2 a b^5 y z+2 a^5 c y z+8 a^4 b c y z+4 a^3 b^2 c y z-8 a^2 b^3 c y z-6 a b^4 c y z-4 a^4 c^2 y z+4 a^3 b c^2 y z+12 a^2 b^2 c^2 y z+4 a b^3 c^2 y z-4 a^3 c^3 y z-8 a^2 b c^3 y z+4 a b^2 c^3 y z+2 a^2 c^4 y z-6 a b c^4 y z+2 a c^5 y z+3 a^6 z^2+a^5 b z^2-6 a^4 b^2 z^2-2 a^3 b^3 z^2+3 a^2 b^4 z^2+a b^5 z^2-11 a^5 c z^2-8 a^4 b c z^2-2 a^3 b^2 c z^2-8 a^2 b^3 c z^2-3 a b^4 c z^2+14 a^4 c^2 z^2+10 a^3 b c^2 z^2+6 a^2 b^2 c^2 z^2+2 a b^3 c^2 z^2-6 a^3 c^3 z^2+2 a b^2 c^3 z^2-a^2 c^4 z^2-3 a b c^4 z^2+a c^5 z^2 = 0)
que pasa por D', Mb, Mc, es tangente a la circunferencia inscrita en D'. Las circunferencias Γb y Γc son construidas cíclicamente.
El de las circunferencias Γ
a, Γ
b, Γ
c es
X(10980).
D' = (-4 a^2 (a + b - c) (a - b + c) : (a - b - c) (a + b - c)^3 : (a - b -
c) (a - b + c)^3).
- Miércoles, 30 de septiembre del 2020
Dos triángulos ortológicos
El 30 de septiembre de 1894 nació Dirk J. Struik, matemático, historiador de las matemáticas y teórico marxista holandés, que pasó la mayor parte de su vida en los Estados Unidos. Su tesis doctoral versó sobre "La aplicación de los métodos tensoriales a las variedades de Riemann". En 1950 publicó "Geometría Diferencial Clásica, que ha sido un libro utilizado por los estudiantes de Matemáticas.
Otra obra importante de Struik es "Una historia sucinta de las Matemáticas".
Dado un triángulo ABC con circuncentro O=X3, ortocentro H=X4 y DEF, la recta paralela a BC por A vuelve a cortar a la circunferencia circunscrita en A' y la recta A'D la corta en A". Sea D' el punto de intersección de las rectas AD y OA".
La circunferencia de centro D' y que pasa por A" es tangente (Nguyen Dang Khoa) a las circunferencias (ABH) y (ACH) en Ab y Ac, respectivamente. Los puntos Bc, Ba, Ca y Cb son definidos cíclicamente.
Las tangentes comunes en Ab y Ac a las tangentes consideradas, se cortan sobre AH, en A1. Los puntos B1 y C1 son definidos cíclicamente.
Los triángulos ABC y son . El centro ortológico de ABC respecto a es U = (32 r^2 R^2 s^2) X3 + (r^2+4 r R-s^2)^3 .
U = ( (b^2+c^2-a^2)^2 (a^6+a^4 (b^2+c^2)-a^2 (b^4-10 b^2 c^2+c^4)-(b^2-c^2)^2 (b^2+c^2)) : ... : ...),
que tiene números de búsqueda en
(5.45484899922424, 0.442131946456559, 0.816950519334037).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,69}, {4,305}, {76,6803}, {325,3088}, {631,34254}, {1007,7404}, {1204,4175}, {1595,32816}, {1975,7487}, {3266,6816}, {3525,37804}, {4121,26937}, {4176,5562}, {6340,11585}, {6515,32973}, {6643,19583}, {6756,32815}, {6815,8024}, {7401,28706}, {7738,28728}, {7819,18928}, {11413,13575}, {11433,14001}, {14786,34803}, {16043,36212}, {28406,37669}, {32006,34938}, {32820,37460}, {32824,37458}.
En coordenadas baricéntricas:
Ab = (a^4-(b^2-c^2)^2 : 2 (a^2+b^2-c^2) (a^2+c^2) : 2 c^2 (a^2-b^2+c^2)),
Ac = (-a^4+(b^2-c^2)^2 : -2 b^2 (a^2+b^2-c^2) : -2 (a^2+b^2) (a^2-b^2+c^2)),
A1 = (a^6 - a^2 (b^2 - c^2)^2 +
a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2) : 4 b^2 c^2 (a^2 + b^2 -
c^2) : 4 b^2 c^2 (a^2 - b^2 + c^2)).
- Domingo, 27 de septiembre del 2020
El centro del triángulo X(24929) como centro radical
El 27 de septiembre de 1972 murió Ramamrita Ranganathan, matemático y bibliotecario indio. Fue el creador de una de las más destacadas clasificaciones bibliotecarias, la clasificación "colonada".
Dado un triángulo ABC, sea DEF el . Consideremos el triángulo A'B'C' formado por la recta que unen los puntos medios Ab de AE y Ac de AF, la recta que unen los puntos medios Bc de BF y Ba de BD, y la recta que unen los puntos medios Ca de CD y Cb de CE.
El triángulo A'B'C' es el triángulo medio del y el , y se conoce como triángulo Ascella (Referencia: Preámbulo antes de X(8726)).
El centro radical de las circunferencias (
A'BaCa), (
B'CbAb), (
C'AcBc) es
X(24929).
𝔖abc xyz
(a^3-a (5 b^2+6 b c+5 c^2)+4 (b-c)^2 (b+c))x^2 + 2 a (5 a^2-(b-c)^2)y z = 0.
X24929 = (a (2 a^3-a^2 (b+c)-2 a (b^2+b c+c^2)+(b-c)^2 (b+c)) : ... :...).
El punto fijo finito de la transformación afín que aplica ABC en A'B'C' es X38399.
- Viernes, 25 de septiembre del 2020
El centro del triángulo X(6340) como centro de perspectividad
El 25 de septiembre de 1819 nació George Salmon, matemático y teólogo irlandés.
Descubrió, junto con Cayley, las 27 líneas de la superficie cúbica. Salmon realizó, entre otros, trabajos sobre la geometría del triángulo, sobre el método de las polares recíprocas y sobre las transformaciones cuadráticas. Trató de asegurarse de que el Trinity College fuera una institución inaccesible para las mujeres. Cuenta la leyenda que Salmon murió de un infarto cuando vio a la primera mujer entrar en su adorada universidad. Se dice que todas las mujeres que se gradúan en el Trinity College, restriegan (literalmente) su título por la cara de dicha estatua.
Dado un triángulo ABC con ortocentro H=X4, sean y DEF sus triángulos y , respectivamente.
La circunferencia que pasa por E, F, H (su centro es A) vuelve a cortar a las rectas EMa y FMa en Ab y Ac, respectivamente. Sea A' el punto de intersección de las rectas EAc y FAb. Los puntos B' y C' se definen cíclicamente.
Las rectas
A'D, B'E, C'F concurren en
X6240, del triángulo circunórtico respecto al .
En coordenadas baricéntricas,
Ab = ( (a^2 + b^2 - c^2) (3 a^6 - a^2 (b^2 - c^2)^2 - 4 a^4 (b^2 + c^2) +
2 (b^2 - c^2)^2 (b^2 + c^2)) (a^4 - b^2 c^2 + c^4 -
a^2 (b^2 + 2 c^2)) :
-(a^2 - b^2 - c^2) (a^2 + b^2 - c^2) (a^8 +
a^6 (b^2 - 4 c^2) -
2 a^4 (2 b^4 + b^2 c^2 - 3 c^4) + (b^4 - c^4)^2 +
a^2 (b^6 + 2 b^4 c^2 + b^2 c^4 - 4 c^6)) :
-(a^2 - b^2 -
c^2) (4 a^10 - (b^2 - c^2)^3 (b^2 + c^2)^2 -
a^8 (8 b^2 + 15 c^2) - a^2 (b^2 + 3 c^2) (b^3 - b c^2)^2 +
a^6 (b^4 + 11 b^2 c^2 + 20 c^4) +
a^4 (5 b^6 + 4 b^4 c^2 + b^2 c^4 - 10 c^6))),
Ac = ({(a^2 - b^2 + c^2) (3 a^6 - a^2 (b^2 - c^2)^2 - 4 a^4 (b^2 + c^2) +
2 (b^2 - c^2)^2 (b^2 + c^2)) (a^4 + b^4 - b^2 c^2 -
a^2 (2 b^2 + c^2)) :
-(a^2 - b^2 -
c^2) (4 a^10 + (b^2 - c^2)^3 (b^2 + c^2)^2 -
a^8 (15 b^2 + 8 c^2) - a^2 (3 b^2 + c^2) (-b^2 c + c^3)^2 +
a^6 (20 b^4 + 11 b^2 c^2 + c^4) +
a^4 (-10 b^6 + b^4 c^2 + 4 b^2 c^4 + 5 c^6)) :
-(a^2 - b^2 -
c^2) (a^2 - b^2 + c^2) (a^8 + a^6 (-4 b^2 + c^2) +
a^4 (6 b^4 - 2 b^2 c^2 - 4 c^4) + (b^4 - c^4)^2 +
a^2 (-4 b^6 + b^4 c^2 + 2 b^2 c^4 + c^6))),
A' = (-3 a^10 + 4 a^6 (b^2 - c^2)^2 - a^2 (b^2 - c^2)^4 +
4 a^8 (b^2 + c^2) - 6 a^4 (b^2 - c^2)^2 (b^2 + c^2) +
2 (b^2 - c^2)^4 (b^2 + c^2) :
2 a^10 + 2 a^2 (b^2 - c^2)^3 (2 b^2 + c^2) -
a^8 (b^2 + 7 c^2) - (b^2 - c^2)^3 (3 b^4 + 4 b^2 c^2 + c^4) +
a^6 (-6 b^4 + 6 b^2 c^2 + 8 c^4) +
a^4 (4 b^6 + 6 b^4 c^2 - 8 b^2 c^4 - 2 c^6) :
2 a^10 - a^8 (7 b^2 + c^2) - 2 a^2 (b^2 - c^2)^3 (b^2 + 2 c^2) +
a^6 (8 b^4 + 6 b^2 c^2 - 6 c^4) + (b^2 - c^2)^3 (b^4 + 4 b^2 c^2 +
3 c^4) - 2 a^4 (b^6 + 4 b^4 c^2 - 3 b^2 c^4 - 2 c^6)).
Las rectas A'D, B'E, C'F concurren en:
X6240 = ((2 a^6 - 3 a^4 (b^2 + c^2) +
2 a^2 b^2 c^2 + (b^2 - c^2)^2 (b^2 + c^2))/(a^2 - b^2 - c^2) : ... : ...).
- Jueves, 24 de septiembre del 2020
Una propiedad del centro del triángulo X(37593)
El 24 de septiembre de 1905 nació Severo Ochoa de Albornoz, médico y científico español, nacionalizado estadounidense en 1956, renunciando a la nacionalidad española, que no quiso recuperar ni siquiera tras el final de la dictadura franquista. En 1959 fue galardonado con el Premio Nobel de Fisiología o Medicina, junto al estadounidense Arthur Kornberg.
Dado un triángulo ABC, sea DEF el . La circunferencia (AEF) vuelve a cortar en Ac a la circunferencia centrada en C, que pasa por D y E,
y en Ab a la circunferencia centrada en B y que pasa por D y F. Sea A' el centro de la circunferencia (DAbAc). Se definen los puntos B' y C' cíclicamente.
El punto fijo finito de la transformación afín que aplica ABC en A'B'C' es X37593.
En coordenadas baricéntricas,
Ab = ((a + b - c) (3 a + b + c) : (a + b - c) (a + 3 b - c) : 2 (a + 3 b -
c) c),
Ac = ((a - b + c) (3 a + b + c) : -2 b (-a + b - 3 c) : (a - b + c) (a - b +
3 c)),
A' = (a : a + 2 b - c : a - b + 2 c).
La matriz M asociada de la transformación afín σ, que aplica ABC en A'B'C', tiene las entradas (las demás se deducen cíclicamente)
M[1,1] = a (a + 3 b + c) (a + b + 3 c),
M[1,2] = (a+b+ 3 c) (6 a^2 + 5 a b + b^2 - a c - c^2),
M[1,3] = (a + 3 b + c) (6 a^2 - a b - b^2 + 5 a c + c^2).
Su punto fijo propio, correspondiente al valor propio λ=-(3 a + b + c) (a + 3 b + c) (a + b + 3 c), es:
X37593 = (a (b + c) (3 a + b + c) : b (a + c) (a + 3 b + c) : c (a + b) (a + b +
3 c)).
Como la circunferencia (DAbAc) es tangente a BC, los triángulos ABC y A'B'C' son ortológicos, con centro de ortologia de A'B'C' respecto a ABC el incentro. El centro de ortología de ABC respecto a A'B'C' es X3616, centro de perspectividad de ABC y el triángulo homotético al triángulo medial, mediante la homotecia de centro el incentro y razón 1/2.
- Viernes, 18 de septiembre del 2020
La cuártica conjugada isogonal de la elipse inscrita de Steiner
El 18 de septiembre de 2012 fallece en Madrid, a los 97 años, el que fuera secretario general del Partido Comunista de España (PCE) desde 1960 hasta 1982, Santago Carrillo, sucediendo en el cargo a Dolores Ibárruri, la "Pasionaria".
Dados un triángulo ABC y dos puntos P y U, sean DEF, y los triángulos de U y de P respecto a ABC y respecto a , respectivamente.
Las rectas BA2 y CA2 vuelven a cortar a la circunferencia circunscrita a ABC en Ba y Ca, respectivamente.
Sea ℓa la recta que pasa por los puntos Db=DBa∩CA2 y Dc=DCa∩BA2. Se definen cíclicamente las rectas ℓb y ℓc. A'B'C' es el triángulo formado por las rectas ℓa, ℓb y ℓc.
Los triángulos ABC y A'B'C' son perspectivos.
Si, en coordenadas baricéntricas, P=(p:q:r) y U=(u:v:w),
Ba = ( 2 p (2 c^2 p + a^2 r) : -2 b^2 p r : r (2 c^2 p + a^2 r)),
Ca = (2 p (2 b^2 p + a^2 q) : q (2 b^2 p + a^2 q) : -2 c^2 p q)
y el punto de concurrencia de las rectas AA', BB', CC' es:
W(P,U) = (p^2/(a^2 v w (q r u^2 + 4 p^2 v w) +
2 p u^2 (c^2 v + b^2 w) (r v + q w)) : ... : ...).
UN CASO PARTICULAR (AoPS)
Si P=H=X4 es el ortocentro y U=K=X6 es el ,
W(H,K) = ( 1/((b^2 + c^2 - a^2) (a^8 - 6 a^6 (b^2 + c^2) +
a^4 (9 b^4 + 6 b^2 c^2 + 9 c^4) -
4 a^2 (b^2 - c^2)^2 (b^2 + c^2) - 4 b^2 c^2 (b^2 - c^2)^2)) : ... : ...),
que tiene números de búsqueda en
(-5.78265796589107, -7.94747086050246, 11.8116787542050).
Está sobre la circun-hipérbola rectangular que pasa por el centro de la . No existen rectas determinadas por puntos de ETC que lo contengan.
CUANDO P=U,
W(U,U) = (u/(4u(c^2v+b^2w)+5a^2v w ) : ... : ...).
Pares {U=Xi, W(U,U)=Xj}, para {i,j} : {6, 6}, {98, 34536}, {99, 34537}, {100, 1016}, {101, 1252}, {105, 6185}, {106, 2226}, {107, 34538}, {108, 23984}, {109, 1262}, {110, 249}, {111, 10630}, {112, 23964}, {691, 34539}, {934, 23586}, {2222, 23592}.
El lugar geométrico de W(U,U), cuando U se mueve sobre la circunferencia circunscrita, es la cuártica conjugada isogonal de la .
En comunicación personal, Bernard Gibert, observa que W(U,U) es el de U y h1/13,X2(U*).
- Domingo, 6 de septiembre del 2020
Un punto sobre la recta de Euler con una propiedad de unicidad
El 6 de septiembre de 1492, partió Cristóbal Colón de la isla de La Gomera (islas Canarias) hacia las Indias, llegando el 12 de octubre a tierra firme.
Dados un triángulo ABC, de circuncentro O=X3, sean A', B', C' las reflexiones de A, B, C en O, respectivamente. Si DEF el de un punto P, sean A" es la reflexion de A' en D, B" es la reflexion de B' en E y C" es la reflexion de C' en F. Entonces: ABC y A"B"C" son inversamente semejantes.
Cuando P=O, los puntos A", B" y C" coinciden con el ortocentro H=X4.
Sea A'''B'''C''' el triángulo reflexión de A"B"C" en la ; ABC y A'''B'''C''' son directamente semejantes.
Si (u:v:w) son las coordenadas baricéntricas de P en la referencia ABC,
A' = (-a^4 + (b^2 - c^2)^2 : -2 b^2 (-a^2 + b^2 - c^2) : -2 c^2 (-a^2 - b^2 +
c^2)),
A" = (a^2 (a^2 + b^2 - c^2) (a^2 - b^2 + c^2) (u + v +
w) : -(b^2 - c^2)^3 u - a^6 (u + 2 v) +
a^2 (b^2 - c^2) (c^2 (3 u + 2 v) + b^2 (3 u + 2 w)) +
a^4 (c^2 (3 u + 4 v) - b^2 (u - 2 v + 2 w)) : (b^2 - c^2)^3 u -
a^6 (u + 2 w) - a^2 (b^2 - c^2) (c^2 (3 u + 2 v) + b^2 (3 u + 2 w)) +
a^4 (-c^2 (u + 2 v - 2 w) + b^2 (3 u + 4 w))),
A''' =((b^2 - c^2)^6 u + a^12 (u + v + w) -
2 a^2 (b^2 - c^2)^4 (c^2 (u + v) + b^2 (u + w)) -
a^10 (b^2 (u + 3 v - w) + c^2 (u - v + 3 w)) +
a^6 (b^2 - c^2) (c^4 (-7 u - 5 v + w) + 2 b^2 c^2 (-v + w) +
b^4 (7 u - v + 5 w)) -
a^4 (b^2 - c^2)^2 (2 c^4 (u - v) + 2 b^4 (u - w) +
b^2 c^2 (5 u + 3 (v + w))) +
a^8 (b^4 (-4 u + 3 v - 7 w) + c^4 (-4 u - 7 v + 3 w) +
b^2 c^2 (9 u + 5 (v + w))) :
-b^2 (b^2 - c^2)^5 u -
a^12 (u + 2 w) +
a^2 (b^2 - c^2)^3 (c^4 (2 u + v + w) + b^2 c^2 (4 u + 3 v + w) +
b^4 (3 u + 2 w)) -
a^4 (b^2 - c^2) (-4 b^4 c^2 (u + v + w) + c^6 (7 u + 4 v + 2 w) +
b^6 (2 u - v + 3 w) - b^2 c^4 (3 u + v + 3 w)) +
a^10 (b^2 (2 u - v + 3 w) + c^2 (2 u - v + 7 w)) +
a^8 (2 c^4 (u + 2 v - 4 w) + b^4 (3 v + w) -
b^2 c^2 (7 u + 3 v + 7 w)) -
a^6 (2 c^6 (4 u + 3 v - w) + b^6 (u + 3 v + w) -
b^2 c^4 (12 u + 9 v + 7 w) + b^4 c^2 (u + 2 (v + w))) :
c^2 (b^2 - c^2)^5 u - a^12 (u + 2 v) +
a^10 (c^2 (2 u + 3 v - w) + b^2 (2 u + 7 v - w)) -
a^2 (b^2 - c^2)^3 (c^4 (3 u + 2 v) + b^4 (2 u + v + w) +
b^2 c^2 (4 u + v + 3 w)) +
a^8 (2 b^4 (u - 4 v + 2 w) + c^4 (v + 3 w) -
b^2 c^2 (7 u + 7 v + 3 w)) +
a^4 (b^2 - c^2) (c^6 (2 u + 3 v - w) - 4 b^2 c^4 (u + v + w) -
b^4 c^2 (3 u + 3 v + w) + b^6 (7 u + 2 v + 4 w)) -
a^6 (c^6 (u + v + 3 w) + b^6 (8 u - 2 v + 6 w) -
b^4 c^2 (12 u + 7 v + 9 w) + b^2 c^4 (u + 2 (v + w)))).
El único punto sobre la recta de Euler para el cual los triángulos ABC y A'''B'''C''' son semejantes y perspectivos es:
W = ( (b^2+c^2-a^2)(
4 a^14
- 8 a^12 (b^2 + c^2)
- 2 a^10 (b^4 - 14 b^2 c^2 + c^4)
+ a^8 (9 b^6 - 17 b^4 c^2 - 17 b^2 c^4 + 9 c^6)
+ 4 a^6 (b^8 - 7 b^6 c^2 + 13 b^4 c^4 - 7 b^2 c^6 + c^8)
- 10 a^4 (b^2 - c^2)^4 (b^2 + c^2)
+ 2 a^2 (b^2 - c^2)^4 (b^4 + 4 b^2 c^2 + c^4)
+ (b^2 - c^2)^6 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en
(16.1313116550609, 15.2192369247069, -14.3409510759947).
Es el punto de intersección de la recta de Euler con la recta que pasa por
X16163 (punto medio del y del foco de la ) y
X16186.
Los triángulos ABC y A'''B'''C''' son perspectivos y no homotéticos si y solo si P está sobre la recta ℓ de ecuación:
ℓ: (a^12 - a^10 (b^2 + c^2) +
a^8 (-4 b^4 + 5 b^2 c^2 - 4 c^4)+ a^6 (6 b^6 - 2 b^4 c^2 - 2 b^2 c^4 + 6 c^6)
+
a^4 (b^8 - 12 b^6 c^2 + 18 b^4 c^4 - 12 b^2 c^6 + c^8)
- 5 a^2 (b^2 - c^2)^4 (b^2 + c^2) + (b^2 - c^2)^4 (2 b^4 +
3 b^2 c^2 + 2 c^4) )x + ... = 0,
que pasa por X16111 (punto medio del punto de De Longchamps y X74, conjugaado isogonal del punto del infinito de la recta de Euler) y corta a la recta de Euler en W.
Cuando P está sobre la recta de Euler, el centro de semejanza de ABC y A'''B'''C''' es X32710 (punto donde la recta que pasa por el ortocentro y el vuelve a cortar a la circunferencia circunscrita: "circumcircle-X(4)-antipode of X(476)"). X32710 queda sobre las circunferencias circunscritas a ABC y a A'''B'''C''', y sobre la circunferencia (X3X4X110), lugar geométrico del centro de semejanza de ABC y A'''B'''C''', cuando P se mueve sobre la recta de Euler.
Cuando P=W, los triángulos ABC y A'''B'''C''' son además perspectivos y el centro de perspectividad es X1300, punto donde la recta que pasa por el ortocentro y el foco de la parábola de Kierpet, vuelve a cortar a la circunferencia circunscrita a ABC.
Cuando P=X16111, el centro de perspectividad de los triángulos ABC y A'''B'''C''' es X477, antipodal del punto de Tixier en la circunferencia circunscrita a ABC.
- Viernes, 4 de septiembre del 2020
Punto de tangencia de dos circunferencias de Apolonio
El 4 de septiembre de 1870 el político Léon Gambetta, líder de la oposición republicana en la Asamblea Nacional francesa, proclamó la Tercera República en París, al quedar el país sin jefe de Estado al aceptar Napoleón III la capitulación ante los jefes militares prusianos el 2 de septiembre de 1870, y quedando prisionero de guerra junto con varios miles de sus soldados. Léon Gambetta había concurrido, en 1869, a las elecciones generales y elaboró un programa radical, conocido como el «Programa de Belleville»: defendía el sufragio universal, la supresión de los títulos nobiliarios, la elección de los funcionarios, la supresión de los ejércitos permanentes, la separación Iglesia-Estado, la abolición de los monopolios, y numerosas reformas económicas y sociales.
X(8951) = 1st Moses-Apollonian Point
Let A' be the point in which the A-excircle Γ
a is tangent to the circle (O
a) that passes through vertices B and C, and define B' and C', (O
b) and (O
c) cyclically. The lines AA', BB', CC' concur in X(5423). Let Γ be the outer Apollonian circle of (O
a), (O
b), (O
c), and let A'' be the touch-point of (O
a) and Γ. Define B'' and C'' cyclically. The center of the circumcircle of A''B''C'' is X(8951). The circumcircle of A''B''C'' tangent to the Apollonius circle γ of the excircles at X(3030). (Peter Moses, December 10, 2015).
Sea ta la tangente común a las circunferencias Γa y (Oa) y se definen cíclicamente las tangentes tb y tc; UVW es el triángulo formado por las rectas ta, tb y tc.
En coordenadas baricéntricas:
A' = (-4 a^2 (a + b - c) (a - b + c) : (a - b + c)^3 (a + b +
c) : (a + b - c)^3 (a + b + c)),
A" = (4 a^2 (a^2-6 a b+b^2-c^2) (a^2-b^2-6 a c+c^2) : (-a-b-c) (a^2-6 a b+b^2-c^2) (a^3-9 a^2 b-a b^2+b^3+3 a^2 c-2 a b c-b^2 c+3 a c^2-b c^2+c^3) : (-a-b-c) (a^2-b^2-6 a c+c^2) (a^3+3 a^2 b+3 a b^2+b^3-9 a^2 c-2 a b c-b^2 c-a c^2-b c^2+c^3)),
U = ( a^5 + a^4 (b + c) - 2 a^3 (b + c)^2 + (b + c)^5 +
a (b + c)^2 (b^2 - 14 b c + c^2) -
2 a^2 (b^3 - 5 b^2 c - 5 b c^2 + c^3) : -2 b (-a^4 + 4 a^2 b c -
2 a^3 (b + c) + (b^2 - c^2)^2 +
2 a (b^3 - 5 b^2 c + 3 b c^2 + c^3)) : -2 c (-a^4 + 4 a^2 b c -
2 a^3 (b + c) + (b^2 - c^2)^2 +
2 a (b^3 + 3 b^2 c - 5 b c^2 + c^3)))
ta: (a + b - c) (a - b + c) (a + b + c) x + 2 a (a + b - c)^2 y +
2 a (a - b + c)^2 z =0.
Los triángulos ABC y UVW son perspectivos, con centro de perspectividad:
Z = ( a (b + c - a)/(a^3 + a^2 (b + c) - a (b^2 - 6 b c + c^2) - (b + c)^3) : ... : ...),
que tiene números de búsqueda en
(2.28184884981979, 4.44262838116892, -0.488162328049391).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1, 1696}, {6, 7091}, {7, 2999}, {44, 7285}, {84, 1743}, {90, 3973}, {2324, 3680}, {3731, 7160}, {5962, 11459}, {6204, 22380}, {7070, 33590}, {7655, 35355}, {8809, 14557}, {9372, 18594}, {15257, 33405}.
- Miércoles, 2 de septiembre del 2020
Conjugado isogonal del punto Bevan-Schröder
El 2 de septiembre de 1865 falleció, a los 60 años de edad, William Rowan Hamilton, matemático, físico, y astrónomo irlandés. Su descubrimiento del cuaternión y sus trabajos en dinámica son los hechos más conocidos
Los cuaterniones (también llamados cuaternios) son una extensión de los números reales, similar a la de los números complejos. Vocablo fue propuesto por su creador William Rowan Hamilton.
La mecánica hamiltoniana fue formulada en 1833 por William R. Hamilton. Como la mecánica lagrangiana, es una reformulación de la mecánica clásica. La mecánica hamiltoniana puede ser formulada por sí misma, usando los espacios simplécticos
Bevan point and center X(1319)
X(1320) = isogonal conjugate of X(1319)
Let X'Y'Z' be the pedal triangle of the Bevan point, W = X(40); then X(1319) is the point, other than W, in which the circles AWX', BWY', CWZ' concur. (Floor van Lamoen, Hyacinthos #6321,
6352).
(
Mostrar/Ocultar figura )
X(1320) =
Kirikami concurrent circles image of X(1)
Let P be a point in the plane of triangle ABC. Let H
a be
the orthocenter of triangle PBC, and define H
b and
H
c cyclically. Let (O
a) be the circle of the points
A, H
b, H
c, and define (O
b) and
(O
c) cyclically. The circles (O
A, O
B,
O
C concur in a point Q, the
Kirikami concurrent circles
image of P.
Dado un triángulo ABC de incentro I=X1, sea DEF el y Ha el ortocentro del triángulo IBC. La circunferencia de diámetro AI vuelve a cortar a la circunferencia circunscrita a ABC en A1.
Sea ta la tangente a la circunferencia (DHaA1) en Ha. Se definen cíclicamente las tangentes tb y tc
Las rectas
ta,
tb,
tc concuren en
X1320.
En coordenadas baricéntricas en la referencia ABC:
Ha = (a : c-a : b-a),
A1 = (a^2 (a + b - c) (a - b + c) : b (b - c) (a + b - c) (-a + b + c) : (a -
b - c) (b - c) c (a - b + c)),
ta: (b - c) (-2 a + b + c) x + a (a - 2 b + c) y - a (a + b - 2 c) z = 0.
ta∩tb∩tc = X1320 = (a (b + c - a)/ (b + c - 2a):..:...).
- Lunes, 31 de agosto del 2020
Isocúbica no pivotal y 'perspeconic'
El 31 de agosto de 1879 nació Alma Mahler-Werfel, compositora y editora musical austríaca. Alma tuvo una serie de flirteos, entre ellos uno con Klimt, que motivó a éste la creación de su cuadro "El beso". Alma estuvo casada con el compositor Gustav Mahler, su adagietto de la Sinfonía nº 5, su segundo tema de la Sexta, se dice que son retratos musicales de Alma.
Preamble just before
X(15254) (César Eliud Lozada, November 14, 2017)
Let ABC and A'B'C' be two perspective triangles such that neither is inscribed in the other. Let A
b = BC∩A'B', A
c = BC∩A'C', and likewise for B
c, B
a, C
a, and C
b. As ABC and A'B'C' are perspective, the pairs of lines {BC, B'C'}, {CA, C'A'} and {AB, A'B'} concur at three collinear points, and the lines A
bA
c, B
cB
a, C
aC
b join opposite vertices of an hexagon. By Pascal's theorem, the six points lie on a conic, here named the
perspeconic of ABC and A'B'C'.
Preamble just before
X(34807) (Contributed by Clark Kimberling and Peter Moses, November 18, 2019)
The perspeconic of ABC and the circumcevian triangle of a point P = u : v : w (barycentrics) is given by
a^2 v^2 w^2 (c^2 v+b^2 w) x^2-u v w (2 b^2 c^2 u^2+a^2 c^2 u v+a^2 b^2 u w+a^4 v w) y z + (cyclic) = 0,
center = u (2 b^2 c^2 u v+2 a^2 c^2 v^2+2 b^2 c^2 u w-a^4 v w+a^2 b^2 v w+a^2 c^2 v w+2 a^2 b^2 w^2) : :
perspector = u (2 b^2 c^2 u+2 a^2 c^2 v+a^2 b^2 w) (2 b^2 c^2 u+a^2 c^2 v+2 a^2 b^2 w) : :
If P lies inside ABC, the conic is an ellipse; otherwise, a hyperbola. As a degenerate case, if P lies on the circumcircle, then the conic is the line tangent to the circumcircle at P. If P is on the line X(187)X(237), the conic consists of two lines that pass through X(6).
Dado un triángulo ABC, sean DEF el de un punto P, no situado sobre la circunferencia circunscrita, y
C(P)
( Si (u:v:w) son las coordenadas baricéntricas de P:
-a^2 c^2 v^3 w^2 x^2-a^2 b^2 v^2 w^3 x^2+c^4 u^2 v^2 w x y+b^2 c^2 u^2 v w^2 x y+a^2 c^2 u v^2 w^2 x y+2 a^2 b^2 u v w^3 x y-b^2 c^2 u^3 w^2 y^2-a^2 b^2 u^2 w^3 y^2+b^2 c^2 u^2 v^2 w x z+2 a^2 c^2 u v^3 w x z+b^4 u^2 v w^2 x z+a^2 b^2 u v^2 w^2 x z+2 b^2 c^2 u^3 v w y z+a^2 c^2 u^2 v^2 w y z+a^2 b^2 u^2 v w^2 y z+a^4 u v^2 w^2 y z-b^2 c^2 u^3 v^2 z^2-a^2 c^2 u^2 v^3 z^2 = 0)
la de ABC y DEF.
Los
P' y
Q' de C(
P), respecto a
ABC y a
DEF, coinciden si
P está sobre la nK(X6,X32,?) de ecuación baricéntrica:
3(a^4x(c^2y^2+b^2z^2)+b^4y(a^2z^2+c^2x^2)+c^4z(b^2x^2+a^2y^2)) + 7a^2b^2c^2 x y z = 0.
P' = (u/(b^2 c^2 u + 2 a^2 c^2 v + 2 a^2 b^2 w): ... : ... ),
Q' = (u (4 a^4 c^4 v^3 (c^2 u + a^2 w) +
2 b^6 u w (c^4 u^2 + 3 a^2 c^2 u w + 2 a^4 w^2) +
a^2 b^2 c^2 v^2 (6 c^4 u^2 + 13 a^2 c^2 u w + 7 a^4 w^2) +
b^4 v (2 c^6 u^3 + 10 a^2 c^4 u^2 w + 13 a^4 c^2 u w^2 +
4 a^6 w^3)):...:...).
- Sábado, 29 de agosto del 2020
El centro X(29) como punto fijo de una transformación afín
El 29 de agosto de 1915 nació en Estocolmo (Suecia) Ingrid Bergman. Según la lista elaborada por el American Film Institute, es la cuarta estrella femenina más importante en la historia del cine. Entre las películas que intervino están Casablanca, Por quién doblan las campanas, Luz que agoniza, Recuerda y Encadenados. Curiosamente, falleció de cáncer el mismo día y mes de su nacimiento, el 29 de agosto de 1982 en Londres.
X(29)
En un triángulo, el X(29) es el de la recta que pasa por el incentro y ortoncentro , respecto a la hipérbola rectangular circunscrita a su que pasa por el ortocentro.
Dado un triángulo ABC, sea DEF el del incentro. La circunferencia de diámetro BC vuelve a cortar a los lados AC y AB en los puntos Ab y Ac, respectivante. Sea A' el segundo punto de intersección de las circunferencias BDAc y CDAb (está sobre la bisectriz por A). Los puntos B' y C' se definen cíclicamente.
El punto fijo propio de la transformación afín que aplica ABC sobre A'B'C' es X29.
La matriz M asociada de la transformación afín σ, que aplica ABC en A'B'C', tiene las entradas (las demás se deducen cíclicamente)
M[1,1] = a (a + b - c) (a - b + c) (a^2 (b^2 + c^2)-(b^2 - c^2)^2),
M[1,2] = -a b (a^5 - a^4 c - 2 a^3 b^2 + a (b^4 - c^4)+ c (b^2 - c^2)^2),
M[1,3] = -a c (a^5 - a^4 b - 2 a^3 c^2 + a (-b^4 + c^4)+ b (b^2 - c^2)^2 ).
Su punto fijo propio, correspondiente al valor propio λ= 2 a b (b+ c-a) (a + b - c) c (a - b + c) (a + b + c), es:
X29 = ((b + c - a)/((b + c) (b^2 + c^2 - a^2)) : ... : ...).
Pares {X=Xi, X'=σ(X)=Xj}, {i, j}: {1, 946}, {8, 65}, {10, 31870}, {21, 18180}, {29, 29}, {72, 389}, {78, 1210}, {100, 31849}, {145, 12672}, {663, 3716}, {1043, 58}, {1807, 5}, {1897, 4}, {2968, 942}, {3100, 26932}, {3685, 3271}, {3699, 6788}, {3811, 12616}, {4086, 21180}, {4391, 10015}, {4511, 11}, {5081, 1845}, {5904, 31728}, {6735, 12736}, {6740, 3109}, {10538, 1364}, {15252, 5806}, {15500, 25640}, {34772, 6831}, {38460, 1537}, {38554, 5908}.
Las polares de A', B', C' respecto a la de ABC y A'B'C', forman un triángulo perspectivo con ABC con centro de perspectividad:
W = ( (a (a^2 b^2 - b^4 + a^2 c^2 + 2 b^2 c^2 - c^4))/(-a^2 b + b^3 -
a^2 c + 2 a b c - b^2 c - b c^2 + c^3) : ... : ...),
que tiene números de búsqueda en
(-0.261192091126329, 0.273000618755428, 3.57221424944277).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {6,2250}, {104,112}, {909,1319}, {3666,34234}, {14570,16697}, {15352,16082}, {32734,34858}.
- Jueves, 27 de agosto del 2020
Dos cónicas asociadas a la recta de Euler
El 27 de agosto de 2003 ocurrió el mayor acercamiento de Marte a la Tierra en aproximadamente 60 000 años, a tan solo 55,76 millones de km. La próxima vez que Marte esté más cerca que lo que estuvo en el año 2003 será el 28 de agosto de 2287.
A Property of Euler line (Kadir Altintaş - Francisco Javier García Capitán)
Let P be point on Euler line of ABC. DEF anticevian triangle of X(6). A'B'C' is pedal triangle of P respect to DEF.
ABC is orthologic to A'B'C'.
The locus of the orthologic center of ABC with respect to A'B'C' is Jerabek hyperbola.
The locus of the orthologic center of A'B'C' with respect to ABC is line X(4)X(54).
Dados un triángulo ABC y un punto P, sobre su , sea A'B'C' el de P, respecto al DEF.
Siendo O=X3 el circuncentro, H=X4 el ortocentro, X54 el y R el radio de la circunferencia de ABC,
si X3P : PX4 = t y X4V : VX54 = t', siendo V el de A'B'C' respecto a ABC, entonces:
t' = ( OH - 4 R^2 ) t/(2 R^2 + (6 R^2 - OH) t).
Así, la correspondencia P ↦ V es una proyectividad entre las rectas X3X4 y X4X54 y, en consecuencia, la recta PV envuelve una cónica, cuando P varía sobre la recta de Euler. Como los puntos del infinito de ambas rectas se corresponde (t=-1, t'=-1), tal cónica es una parábola 𝒫, de ecuación baricéntrica:
𝔖abc xyz
(b - c)^2 (b + c)^2 (a^16 + b^16 - 2 b^14 c^2 + b^12 c^4 -
2 b^10 c^6 + 4 b^8 c^8 - 2 b^6 c^10 + b^4 c^12 - 2 b^2 c^14 +
c^16 + a^14 (-4 b^2 - 4 c^2) + a^12 (4 b^4 + 6 b^2 c^2 + 4 c^4) +
a^10 (4 b^6 + 16 b^4 c^2 + 16 b^2 c^4 + 4 c^6) +
a^8 (-10 b^8 - 46 b^6 c^2 - 47 b^4 c^4 - 46 b^2 c^6 - 10 c^8) +
a^6 (4 b^10 + 44 b^8 c^2 + 40 b^6 c^4 + 40 b^4 c^6 + 44 b^2 c^8 +
4 c^10) +
a^4 (4 b^12 - 22 b^10 c^2 - 22 b^8 c^4 + 16 b^6 c^6 -
22 b^4 c^8 - 22 b^2 c^10 + 4 c^12) +
a^2 (-4 b^14 + 8 b^12 c^2 + 8 b^10 c^4 - 12 b^8 c^6 -
12 b^6 c^8 + 8 b^4 c^10 + 8 b^2 c^12 - 4 c^14)) x^2 +
2 (a - b) (a + b) (a - c) (a + c) (-a^2 + b^2 + c^2) (a^14 + b^14 +
5 a^10 b^2 c^2 - 5 b^12 c^2 + 9 b^10 c^4 - 5 b^8 c^6 -
5 b^6 c^8 + 9 b^4 c^10 - 5 b^2 c^12 + c^14 +
a^12 (-2 b^2 - 2 c^2) + a^8 (b^6 - 2 b^4 c^2 - 2 b^2 c^4 + c^6) +
a^6 (b^8 - 9 b^6 c^2 + 16 b^4 c^4 - 9 b^2 c^6 + c^8) +
a^4 (9 b^8 c^2 - 9 b^6 c^4 - 9 b^4 c^6 + 9 b^2 c^8) +
a^2 (-2 b^12 + 4 b^10 c^2 + 2 b^8 c^4 - 8 b^6 c^6 + 2 b^4 c^8 +
4 b^2 c^10 - 2 c^12)) y z = 0.
Esta parábala es tangente a la recta de Euler en el circuncentro, su eje tiene la dirección de X17702 y pasa por X9908. Con estos datos la parábola puede ser construida, ver IPt_PC_p, IPt_PCp2 o (3P12T1)1 §10.2
El foco de la parábola 𝒫 es:
Fo = ( a^2 (a^16-3 a^14 (b^2+c^2)+2 a^12 (b^4+5 b^2 c^2+c^4)+a^10 (b^6-9 b^4 c^2-9 b^2 c^4+c^6)+a^8 (-4 b^6 c^2+17 b^4 c^4-4 b^2 c^6)-(b^2-c^2)^4 (b^8+b^6 c^2+2 b^4 c^4+b^2 c^6+c^8)-a^4 (b^2-c^2)^2 (2 b^8+b^6 c^2+7 b^4 c^4+b^2 c^6+2 c^8)-a^6 (b^10-8 b^8 c^2+8 b^6 c^4+8 b^4 c^6-8 b^2 c^8+c^10)+a^2 (b^2-c^2)^2 (3 b^10-2 b^8 c^2+2 b^6 c^4+2 b^4 c^6-2 b^2 c^8+3 c^10)) : ... : ...),
que tiene números de búsqueda en
(-5.34927089818235, -8.21524837266903, 11.7970383852240).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,3258}, {22,842}, {23,147}, {24,1304}, {25,16221}, {186,5667}, {232,8428}, {399,1495}, {468,34131}, {476,15928}, {523,13558}, {647,2079}, {924,3447}, {1614,14979}, {6644,14685}, {14165,37970}, {15959,30715}, {16316,37969}, {19165,21284}, {26883,38595}.
La directriz de 𝒫:
(b^8 - b^6 c^2 - b^2 c^6 + c^8 + a^6 (b^2 + c^2) - a^4 (b^2 + c^2)^2 -
a^2 (b^6 - 2 b^4 c^2 - 2 b^2 c^4 + c^6))x + ... = 0,
pasa por los centros Xi, para i∈{7669, 10117, 13558, 32119}.
El punto de tangencia de 𝒫 con la recta X4X54 es:
T = ( 2 a^10 - 4 a^8 (b^2 + c^2) +
a^4 (b^2 - c^2)^2 (b^2 + c^2) - (b^2 - c^2)^4 (b^2 + c^2) +
a^6 (b^2 + c^2)^2 + a^2 (b^4 - c^4)^2 : ... : ...),
que tiene números de búsqueda en ETC
(-5.62551623372265, -8.25935299608749, 11.9550702024554).
Es el punto medio de Xi y Xj para los índices {i,j}: {3146, 12278}, {6240, 16659}, {12290, 34797}.
Es la reflexión de Xi en Xj para los índices {i,j}: {4, 13419}, {52, 11819}, {125, 12140}, {185, 3575}, {1885, 16621}, {3574, 32332}, {5562, 12134}, {6146, 6756}, {11381, 16655}, {11750, 5}, {12225, 5907}, {12289, 13403}, {18560, 13474}, {21659, 4}, {34224, 389}, {34799, 10112}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,2918}, {4,54}, {5,1495}, {20,1352}, {24,125}, {26,18474}, {30,5562}, {51,6146}, {52,11819}, {64,67}, {113,18377}, {154,7507}, {155,382}, {159,1593}, {182,7544}, {185,1503}, {186,20299}, {235,13851}, {265,18378}, {378,34785}, {389,7576}, {403,18383}, {427,13367}, {428,12241}, {511,14516}, {539,6243}, {542,5889}, {568,10116}, {569,11818}, {1092,14790}, {1141,11816}, {1147,31723}, {1181,18494}, {1204,13399}, {1209,7502}, {1498,12173}, {1514,3853}, {1568,10539}, {1594,10282}, {1598,18396}, {1658,34514}, {1853,3515}, {1885,16621}, {1899,7487}, {2070,5449}, {2777,12281}, {2937,6288}, {2980,22261}, {3060,10112}, {3146,12278}, {3331,7747}, {3357,35471}, {3410,7691}, {3426,17800}, {3518,25739}, {3547,35268}, {3564,14531}, {3627,30522}, {3818,7503}, {3830,12897}, {5064,11425}, {5094,17821}, {5446,7540}, {5448,10540}, {5576,18475}, {5651,6643}, {5907,12225}, {6000,6240}, {6143,10182}, {6241,18559}, {6247,21663}, {6293,9973}, {6696,37931}, {6995,18945}, {7391,13346}, {7399,22352}, {7488,21243}, {7505,23325}, {7517,9927}, {7574,18350}, {7575,13561}, {7577,26882}, {7687,18394}, {7731,13423}, {8779,27376}, {9306,37444}, {9714,14852}, {9730,31830}, {9908,12293}, {10018,32767}, {10110,12022}, {10117,32357}, {10193,17506}, {10263,13417}, {10301,15873}, {10312,15340}, {10594,18390}, {10605,34780}, {10984,18420}, {10996,14927}, {11202,37119}, {11204,35503}, {11245,11745}, {11430,15559}, {11432,34564}, {11438,11457}, {11442,31304}, {11449,31074}, {11563,18379}, {11565,13364}, {11645,38323}, {12084,16163}, {12107,34826}, {12429,33586}, {12605,15030}, {13366,31804}, {13434,19130}, {13474,16658}, {13488,16654}, {13598,34603}, {13630,38322}, {14049,19504}, {14585,27371}, {16195,37638}, {16252,23047}, {17701,23315}, {18128,37481}, {18376,35488}, {18405,37197}, {18488,18570}, {19124,36989}, {21844,25563}, {22802,35480}, {23329,32534}, {24206,37126}, {26937,32064}, {32345,37954}, {34417,37122}, {34609,35602}.
El de 𝒫, respecto a sus tres tangentes X3X4, X4X54
y la recta del infinito, es:
Z = ( 2 a^10-4 a^8 (b^2+c^2)+a^6 (b^4+6 b^2 c^2+c^4)+a^4 (b^6-3 b^4 c^2-3 b^2 c^4+c^6)
+a^2 (b^2-c^2)^2 (b^4+c^4)-(b^2-c^2)^4 (b^2+c^2)
: ... : ...),
que tiene números de búsqueda en ETC
(6.83346607140023, 4.16676219912929, -2.39792445813600).
Es el punto medio de Xi y Xj para los índices {i,j}: {4, 12278}, {6240, 14516}, {12111, 34797}, {18439, 18565}.
Es la reflexión de Xi en Xj para los índices {i,j}: {52, 3575}, {382, 13419}, {6146, 31833}, {11750, 3}, {12162, 12134}, {12225, 1216}, {12295, 12140}, {12370, 31830}, {18563, 5907}, {21659, 5}, {34799, 10116}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,12289}, {3,161}, {4,110}, {5,13367}, {20,3410}, {24,9927}, {25,12293}, {30,5562}, {49,18388}, {51,12370}, {52,3575}, {68,18533}, {125,37814}, {128,23702}, {143,25711}, {155,12173}, {186,5449}, {235,20302}, {378,8907}, {381,11425}, {382,13419}, {389,38321}, {539,5889}, {542,34783}, {549,13470}, {568,10112}, {569,18420}, {578,18428}, {1092,18569}, {1204,16003}, {1216,12225}, {1350,1657}, {1495,15761}, {1503,10575}, {1511,10224}, {1568,18377}, {1594,12038}, {1614,34007}, {1625,7747}, {1885,16194}, {2072,18383}, {2777,18439}, {2889,5059}, {3292,3627}, {3357,16111}, {3515,14852}, {3522,17712}, {3843,8780}, {3858,15807}, {5012,12254}, {5446,7576}, {5462,12022}, {5576,11430}, {5890,10116}, {5891,12605}, {5907,18563}, {5972,10255}, {6102,11562}, {6146,9730}, {6240,11660}, {6639,11202}, {6640,23325}, {6642,18396}, {6699,23294}, {6815,13336}, {7399,37513}, {7506,18390}, {7540,13598}, {7577,11449}, {7592,7706}, {7689,11442}, {9306,18404}, {9820,23047}, {9938,18385}, {10024,10282}, {10113,20771}, {10564,23335}, {10574,18128}, {10619,32046}, {11250,16163}, {11424,11818}, {11438,25738}, {11440,13619}, {11441,35480}, {11550,12084}, {11572,13371}, {12111,34797}, {12160,13431}, {12163,37196}, {12234,15087}, {12359,32110}, {12429,37489}, {12902,13621}, {13160,18475}, {13346,31723}, {13561,15646}, {14831,32358}, {14855,31829}, {14915,16659}, {15102,32339}, {15331,34826}, {15760,34782}, {16266,32332}, {16868,18392}, {18350,18403}, {18435,18562}, {18494,36747}, {19131,36989}, {19361,36752}, {20191,21844}, {20427,32275}, {22115,31724}, {22467,25739}, {23410,27355}, {24206,34864}, {26917,36253}, {32136,36966}, {34224,38323}, {35264,35488}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Sea U el centro de ortología de ABC respecto a A'B'C', que está sobre la , y sea U* su , que está sobre la recta de Euler.
Si X4V : VX54 = t' y X3U* : U*X4 = t'', se obtiene que:
t'' = (R^2 t')/(4 R^2 - OH + 3 R^2 t').
Así, la correspondencia V ↦ U* es una proyectividad entre las rectas X4X54 y X3X4 y, en consecuencia, la recta VU* envuelve una cónica, cuando P varía sobre la recta de Euler. Tal cónica es una hipérbola ℋ, de ecuación baricéntrica:
𝔖abc xyz
b^2 c^2 ((b-c)^2 (b+c)^2 (b^6 c^2-2 b^4 c^4+b^2 c^6+a^6 (-4 b^2-4 c^2)+a^4 (8 b^4+9 b^2 c^2+8 c^4)+a^2 (-4 b^6-6 b^4 c^2-6 b^2 c^4-4 c^6)) x^2+2 a^2 (a-b) (a+b) (a-c) (a+c) (3 a^6-2 b^6+2 b^4 c^2+2 b^2 c^4-2 c^6+a^2 (-b^4+2 b^2 c^2-c^4)) y z) = 0.
Esta hipérbola pasa por X182 (punto medio del ), es tangente a la recta de Euler en el circuncentro y a la recta X4X54 en X6759 (conjugado isogonal del centro de perspectividad de ABC y el triángulo reflexión del del circuncentro, respecto a la de éste). Con estos datos la hiperbola ℋ puede ser construida, ver Pt_Pt_P, Pt_Pt_P2 o (3P2T)2 §10.1
El centro de ℋ se X1495 (conjugado isogonal del del punto del infinito de la recta de Euler, X30 ). Sus asíntotas pasan por los puntos X1113 y X1114, donde la recta de Euler corta a la circunferencia circunscrita, y por los X1113 y X1114 del .
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
La correspondencia P↦U* es una proyectividad sobre la recta de Euler, dada por
t'' = (R^2 t)/((OH - 3 R^2 ) t-2 R^2),
siendo X3P : PX4 = t y X3U* : U*X4 = t''.
Los puntos fijos de esta proyectividad son el circuncentro y X23, inverso del baricentro en la circunferencia circunscrita. Para estos dos puntos las tangentes a 𝒫 y a ℋ coinciden, en la recta de Euler y en la paralela por X23 al , respectivamente.
- Martes, 25 de agosto del 2020
La cúbica de McCay y el centro X(32561) como punto fijo de una afinidad
El 25 de agosto de 1806 nació James Booth clérigo irlandés, matemático y pedagogo. Publicó un tratado relacionado con las coordenadas tangenciales y con la recta polar, se publicó en 1873. Booth inventó independientemente las coordenadas tangenciales que se conocieron como "coordenadas Boothianas", que, sin embargo, fueron introducidas previamente por Julius Plücker en 1830. La lemniscata de Booth, una curva en forma de ocho, y el óvalo de Booth, otra curva con una ecuación de definición similar, llevan el nombre de Booth, que estudió ambas.
Dados un triángulo ABC, un punto P, no situado sobre su circunferencia circunscrita ni en la recta del infinito, sea Q su ; sean y los de P y Q; y son los de P y Q.
Los puntos U=PaP1∩QaQ1, V=PbP2∩QbQ2,
W=PcP2∩QcQ3 están sobre la recta PQ.
Si (u:v:w) son las coordenadas baricéntricas de P respecto a ABC,
U = (a^2 v w (a^4 v (v-w) w+(b^2-c^2) u^2 (c^2 v+b^2 w)+a^2 (-b^2 w (u^2+2 u w+v (v+w))+c^2 v (u^2+2 u v+w (v+w)))) :
w (-b^2 (b^2-c^2) u^2 (v+w) (c^2 v+b^2 w)+a^4 (c^2 v^3 (u+v+w)-b^2 v w (v^2+u w+v w))+a^2 (-c^4 v^3 (u+v+w)+b^4 w (u^2 (v-w)-u v w+v^2 (v+w))+b^2 c^2 v (v^3+u^2 (v-w)-v w^2+u (v^2+w^2)))) :
v (c^2 (-b^2+c^2) u^2 (v+w) (c^2 v+b^2 w)+a^4 (-b^2 w^3 (u+v+w)+c^2 v w (u v+w (v+w)))+a^2 (b^4 w^3 (u+v+w)+c^4 v (u^2 (v-w)+u v w-w^2 (v+w))-b^2 c^2 w (-v^2 w+w^3+u^2 (-v+w)+u (v^2+w^2))))).
U = a^2 v w (u+v+w)^2 (a^2 (c^2 v-b^2 w)+(b^2-c^2) (c^2 v+b^2 w)) P
-(c^2 u v+b^2 u w+a^2 v w)^2 (a^2 (-v+w)+(b^2-c^2) (v+w)) Q.
Los puntos
U, V, W coinciden si y solo si
P está sobre la cúbica de McCay (
K003 en el catálogo de Bernard Gibert).
Pares {P=Xi, U=Xj}, cuando P está sobre K003, para los índices {i,j}: {1,56}, {3,4}, {4,4}. Cuando P=X1 es el incentro, los puntos U, V, W no están definidos, pero cuando P tiende a X1 sobre K003, los puntos U, V, W coinciden con X56, centro de homotecia exterior de las circunferencias inscrita y circunscrita a ABC.
Cuando P tiende, sobre K003, al A-exincentro Ia, los puntos U, V, W coinciden con:
Za = (a^2 (a^2-(b-c)^2) : b^2 (-a^2+b^2-2 a c-c^2) : c^2 (-a^2-2 a b-b^2+c^2)).
Similarmente, cuando P tiende a Ib y a Ic, obtienen los puntos:
Zb = (a^2 (a^2-b^2-2 b c-c^2) : b^2 (b^2-(-a+c)^2) : c^2 (-a^2-2 a b-b^2+c^2)),
Zc = (a^2 (a^2-b^2-2 b c-c^2) : b^2 (-a^2+b^2-2 a c-c^2) : c^2 (-(a-b)^2+c^2)).
Las rectas AZa, BZb, CZc concurren en X75, del incentro.
El punto fijo finito de la trasformación afín que aplica ABC en es X32561, centro de la
cónica
( a^4 b^4 c^3 x^2-2 a^2 b^6 c^3 x^2+b^8 c^3 x^2+a^4 b^3 c^4 x^2+2 a^2 b^5 c^4 x^2-3 b^7 c^4 x^2+2 a^2 b^4 c^5 x^2+2 b^6 c^5 x^2-2 a^2 b^3 c^6 x^2+2 b^5 c^6 x^2-3 b^4 c^7 x^2+b^3 c^8 x^2+2 a^6 b^2 c^3 x y-4 a^4 b^4 c^3 x y+2 a^2 b^6 c^3 x y-4 a^4 b^2 c^5 x y-4 a^2 b^4 c^5 x y+2 a^2 b^2 c^7 x y+a^8 c^3 y^2-2 a^6 b^2 c^3 y^2+a^4 b^4 c^3 y^2-3 a^7 c^4 y^2+2 a^5 b^2 c^4 y^2+a^3 b^4 c^4 y^2+2 a^6 c^5 y^2+2 a^4 b^2 c^5 y^2+2 a^5 c^6 y^2-2 a^3 b^2 c^6 y^2-3 a^4 c^7 y^2+a^3 c^8 y^2+2 a^6 b^3 c^2 x z-4 a^4 b^5 c^2 x z+2 a^2 b^7 c^2 x z-4 a^4 b^3 c^4 x z-4 a^2 b^5 c^4 x z+2 a^2 b^3 c^6 x z+2 a^7 b^2 c^2 y z-4 a^5 b^4 c^2 y z+2 a^3 b^6 c^2 y z-4 a^5 b^2 c^4 y z-4 a^3 b^4 c^4 y z+2 a^3 b^2 c^6 y z+a^8 b^3 z^2-3 a^7 b^4 z^2+2 a^6 b^5 z^2+2 a^5 b^6 z^2-3 a^4 b^7 z^2+a^3 b^8 z^2-2 a^6 b^3 c^2 z^2+2 a^5 b^4 c^2 z^2+2 a^4 b^5 c^2 z^2-2 a^3 b^6 c^2 z^2+a^4 b^3 c^4 z^2+a^3 b^4 c^4 z^2 = 0)
mutualmente polar de los triángulos ABC y Apus.
Apus triangle
Let A' be the insimilicenter of the circumcircle and A-excircle, and define B' and C' cyclically. The triangle with vertices A,' B, C' is introduced here as the Apus triangle. A'B'C' is a central triangle of type 2. The following properties were communicated by Peter Moses, November 12, 2013:
Barycentric coordinates for vertices:
A' = a^2(a - b + c)(a + b - c) : b^2(b - c - a)(a + b + c) : c^2(c - b - a)(a + b + c)
B' = a^2(a - c - b)(a + b + c) : b^2(b - c + a)(b + c - a) : c^2(c - a - b)(a + b + c)
C' = a^2(a - b - c)(a + b + c) : b^2(b - a - c)(a + b + c) : c^2(c - a + b)(c + a - b)
Los puntos U, V, W son distintos y las rectas AU, BV, CW son concurrentes si y solo si P está sobre la séxtica isogonal, con puntos dobles en el incentro y en los exincentros, de
ecuación
( 2 a^4 b^2 c^4 x^4 y^2-2 a^2 b^4 c^4 x^4 y^2+2 b^4 c^6 x^4 y^2-2 b^2 c^8 x^4 y^2+a^6 c^4 x^3 y^3+a^4 b^2 c^4 x^3 y^3-a^2 b^4 c^4 x^3 y^3-b^6 c^4 x^3 y^3-2 a^4 c^6 x^3 y^3+2 b^4 c^6 x^3 y^3+a^2 c^8 x^3 y^3-b^2 c^8 x^3 y^3+2 a^4 b^2 c^4 x^2 y^4-2 a^2 b^4 c^4 x^2 y^4-2 a^4 c^6 x^2 y^4+2 a^2 c^8 x^2 y^4+a^4 b^4 c^2 x^4 y z-2 a^2 b^6 c^2 x^4 y z+b^8 c^2 x^4 y z-a^4 b^2 c^4 x^4 y z+b^6 c^4 x^4 y z+2 a^2 b^2 c^6 x^4 y z-b^4 c^6 x^4 y z-b^2 c^8 x^4 y z+a^6 b^2 c^2 x^3 y^2 z-2 a^4 b^4 c^2 x^3 y^2 z+a^2 b^6 c^2 x^3 y^2 z+a^4 b^2 c^4 x^3 y^2 z-b^6 c^4 x^3 y^2 z-a^2 b^2 c^6 x^3 y^2 z+2 b^4 c^6 x^3 y^2 z-b^2 c^8 x^3 y^2 z-a^6 b^2 c^2 x^2 y^3 z+2 a^4 b^4 c^2 x^2 y^3 z-a^2 b^6 c^2 x^2 y^3 z+a^6 c^4 x^2 y^3 z-a^2 b^4 c^4 x^2 y^3 z-2 a^4 c^6 x^2 y^3 z+a^2 b^2 c^6 x^2 y^3 z+a^2 c^8 x^2 y^3 z-a^8 c^2 x y^4 z+2 a^6 b^2 c^2 x y^4 z-a^4 b^4 c^2 x y^4 z-a^6 c^4 x y^4 z+a^2 b^4 c^4 x y^4 z+a^4 c^6 x y^4 z-2 a^2 b^2 c^6 x y^4 z+a^2 c^8 x y^4 z-2 a^4 b^4 c^2 x^4 z^2+2 b^8 c^2 x^4 z^2+2 a^2 b^4 c^4 x^4 z^2-2 b^6 c^4 x^4 z^2-a^6 b^2 c^2 x^3 y z^2-a^4 b^4 c^2 x^3 y z^2+a^2 b^6 c^2 x^3 y z^2+b^8 c^2 x^3 y z^2+2 a^4 b^2 c^4 x^3 y z^2-2 b^6 c^4 x^3 y z^2-a^2 b^2 c^6 x^3 y z^2+b^4 c^6 x^3 y z^2-a^8 c^2 x y^3 z^2-a^6 b^2 c^2 x y^3 z^2+a^4 b^4 c^2 x y^3 z^2+a^2 b^6 c^2 x y^3 z^2+2 a^6 c^4 x y^3 z^2-2 a^2 b^4 c^4 x y^3 z^2-a^4 c^6 x y^3 z^2+a^2 b^2 c^6 x y^3 z^2-2 a^8 c^2 y^4 z^2+2 a^4 b^4 c^2 y^4 z^2+2 a^6 c^4 y^4 z^2-2 a^4 b^2 c^4 y^4 z^2-a^6 b^4 x^3 z^3+2 a^4 b^6 x^3 z^3-a^2 b^8 x^3 z^3-a^4 b^4 c^2 x^3 z^3+b^8 c^2 x^3 z^3+a^2 b^4 c^4 x^3 z^3-2 b^6 c^4 x^3 z^3+b^4 c^6 x^3 z^3-a^6 b^4 x^2 y z^3+2 a^4 b^6 x^2 y z^3-a^2 b^8 x^2 y z^3+a^6 b^2 c^2 x^2 y z^3-a^2 b^6 c^2 x^2 y z^3-2 a^4 b^2 c^4 x^2 y z^3+a^2 b^4 c^4 x^2 y z^3+a^2 b^2 c^6 x^2 y z^3+a^8 b^2 x y^2 z^3-2 a^6 b^4 x y^2 z^3+a^4 b^6 x y^2 z^3+a^6 b^2 c^2 x y^2 z^3-a^2 b^6 c^2 x y^2 z^3-a^4 b^2 c^4 x y^2 z^3+2 a^2 b^4 c^4 x y^2 z^3-a^2 b^2 c^6 x y^2 z^3+a^8 b^2 y^3 z^3-2 a^6 b^4 y^3 z^3+a^4 b^6 y^3 z^3-a^8 c^2 y^3 z^3+a^4 b^4 c^2 y^3 z^3+2 a^6 c^4 y^3 z^3-a^4 b^2 c^4 y^3 z^3-a^4 c^6 y^3 z^3+2 a^4 b^6 x^2 z^4-2 a^2 b^8 x^2 z^4-2 a^4 b^4 c^2 x^2 z^4+2 a^2 b^4 c^4 x^2 z^4+a^8 b^2 x y z^4+a^6 b^4 x y z^4-a^4 b^6 x y z^4-a^2 b^8 x y z^4-2 a^6 b^2 c^2 x y z^4+2 a^2 b^6 c^2 x y z^4+a^4 b^2 c^4 x y z^4-a^2 b^4 c^4 x y z^4+2 a^8 b^2 y^2 z^4-2 a^6 b^4 y^2 z^4+2 a^4 b^4 c^2 y^2 z^4-2 a^4 b^2 c^4 y^2 z^4 = 0)
:
𝔖abc xyz
y z (b^2 c^2 (b^2-c^2) (a^4+b^4+2 b^2 c^2+c^4+a^2 (-2 b^2-2 c^2)) x^4+a^4 (b^2-c^2) (a^4+b^4+2 b^2 c^2+c^4+a^2 (-2 b^2-2 c^2)) y^2 z^2+b^2 c^2 x^3 ((a^2-c^2) (a^4+(b^2-c^2)^2 -2 a^2 (b^2-c^2)) y-(a^2-b^2) (a^4+(b-c)^2 (b+c)^2+2 a^2 (b^2-c^2)) z)-2 a^4 y z ((a^2-b^2) c^2 (a^2+b^2-c^2) y^2-b^2 (a^2-c^2) (a^2-b^2+c^2) z^2)) = 0.
- Domingo, 23 de agosto del 2020
Circunferencia de diámetro un punto y el baricentro de su triángulo antipedal
Las matemáticas no mienten, lo que hay son muchos matemáticos mentirosos. Henry David Thoreau.
Dados un triángulo ABC y un punto P. Su p corta a los lados BC, CA, AB en D, E, F, respectivamente.
La circunferencia que pasa por B, C y P, vuelve a cortar a la recta PD en Pa; la circunferencia que pasa por C, A y P, vuelve a cortar a la recta PE en Pb; y la circunferencia que pasa por A, B y P, vuelve a cortar a la recta PF en Pc.
La circunferencia Γ(P), circunscrita a , pasa por P. El punto diametralmente opuesto a P es el baricentro del de P.
Pares {P=Xi, M=Xj} de , siendo M el centro de la circunferencia Γ(P), para los índices {i, j}: {1, 3576}, {2, 3}, {3, 11202}, {4, 381}, {6, 182}, {10, 38430}, {13, 2}, {14, 2}, {15, 14170}, {16, 14169}, {67, 11178}, {80, 5587}, {249, 32609}, {265, 23325}, {671, 381}, {1138, 32609}, {3062, 11372},
{5627, 38724}, {6094, 182}, {11599, 38330}, {13377, 11178}, {34578, 3576}, {34579, 11202}.
Cuando P=X5, es el centro de la , el centro de Γ(X5) es:
M5 = ( 2 a^16 - 12 a^14 (b^2 + c^2) + a^12 (33 b^4 + 46 b^2 c^2 + 33 c^4) - 6 a^10 (9 b^6 + 11 b^4 c^2 + 11 b^2 c^4 + 9 c^6)+ a^8 (55 b^8 + 29 b^6 c^2 + 30 b^4 c^4 + 29 b^2 c^6 + 55 c^8)
- a^6 (b^2 - c^2)^2 (32 b^6 + 39 b^4 c^2 + 39 b^2 c^4 + 32 c^6) +
a^4 (b^2 - c^2)^2 (7 b^8 - 13 b^6 c^2 - 18 b^4 c^4 - 13 b^2 c^6 +
7 c^8) + a^2 (b^2 - c^2)^4 (2 b^6 + 9 b^4 c^2 + 9 b^2 c^4 + 2 c^6)
- (b^2 - c^2)^6 (b^2 + c^2)^2
: ... : ...),
que tiene números de búsqueda en
(6.74812988412115, 7.05263045588886, -4.35644731868690).
Es el punto medio de X5 y X35885.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,161}, {4,32904}, {5,27684}, {140,30484}, {549,23237}, {632,33545}, {1656,20414}, {10126,14143}, {13856,35888}, {15712,35728}.
- Martes, 18 de agosto del 2020
La reflexión del punto de Exeter en el circuncentro
El 18 de agosto de 1936, durante el periodo de Guerra Civil, muere asesinado por el franquismo, el poeta granadino Federico García Lorca.
Punto de Exeter
Es uno de los "centros" de un triángulo, designado como centro
X(22) en la Enciclopedia Clark Kimberling. Fue descubierto en un taller de matemáticas por ordenador en la Academia Phillips Exeter en 1986 (la ciudad de Exeter, sede de la academia, pertenece al estado de New Hampshire).
Dado un triángulo ABC, sean DEF el y A' el otro punto de intersección de la circunferencia circunscrita a ABC con la perpendicular por A a la mediana por A. Los puntos B' y C' se define cíclicamnete.
Los triángulos
A'B'C' y
DEF son perspectivos, con centro de perspectividad
X378, reflexión del en el circuncentro.
Las coordenadas baricéntricas de A' son:
(a^2 (a^2 - b^2 - 3 c^2) (a^2 - 3 b^2 -
c^2) : -(a^2 - 3 b^2 - c^2) (a^2 - b^2 - c^2) (b^2 - c^2) : (a^2 -
b^2 - 3 c^2) (a^2 - b^2 - c^2) (b^2 - c^2)).
- Lunes, 17 de agosto del 2020
Una caracterización de la quíntica Q037
a Clara, por su "cumple"
Q037 is an inversible bicircular quintic with a real asymptote parallel to the Euler line.
Q037 is the locus of P such that the Euler line of the circumcevian triangle of P contains P (and obviously O).
Dados un triángulo ABC y un punto P (no situado sobre su circunferencia circunscrita ni en la recta del infinito), sea el de P.
La circunferencia circunscrita a APbPc vuelve a corta a recta PaPb en Pab y a la recta PaPc en Pac. Sea Ha el ortocentro de APabPac. Los puntos Hb y Hc se definen cíclicamente.
Q037 es el lugar geométrico del punto P tal que las rectas AHa, BHb y CHc son concurrentes.
Si (u:v:w) son las coordenadas baricéntricas de P,
Ha = (a^2 u (-b^4 u w (u^2 + 3 u (v + w) + 2 v (v + w)) +
v (a^4 w (v^2 + w^2 + u (v + w)) -
c^4 u (u^2 + 3 u (v + w) + 2 w (v + w)) +
a^2 c^2 (u^3 + 3 u^2 (v + w) + w (v^2 - w^2) +
u (2 v^2 + v w + w^2))) +
b^2 (c^2 u (2 u^3 + 5 u^2 (v + w) + 4 v w (v + w) +
3 u (v + w)^2) +
a^2 w (u^3 - v^3 + v w^2 + 3 u^2 (v + w) +
u (v^2 + v w + 2 w^2)))) :
(a^4 v (u + v) w + (b^2 -
c^2) u^2 (c^2 v + b^2 w) +
a^2 u (c^2 v (u + v - w) + b^2 (v - w) w)) (-u (b^2 (u + v - w) +
c^2 (u - v + w)) +
a^2 (u^2 + 2 v w + u (v + w))) :
(-b^4 u^2 w +
v (c^4 u^2 + a^4 w (u + w) + a^2 c^2 u (-v + w)) +
b^2 u (c^2 u (-v + w) + a^2 w (u - v + w))) (-u (b^2 (u + v - w) +
c^2 (u - v + w)) + a^2 (u^2 + 2 v w + u (v + w))))
y la ecuación de la recta AHa es:
(b^4 u^2 w+v (-c^4 u^2+a^2 c^2 u (v-w)-a^4 w (u+w))+b^2 u (c^2 u (v-w)-a^2 w (u-v+w))) y +
(a^4 v (u+v) w+(b^2-c^2) u^2 (c^2 v+b^2 w)+a^2 u (c^2 v (u+v-w)+b^2 (v-w) w)) z = 0.
Pares {P=Xi, Q=Xj}, si P (i∈{1, 3, 15, 16, 30, 36, 5000, 5001, 32622, 32623, 39162, 39163, 39164, 39165}) está sobre Q037 y Q es el centro de perspectividad de ABC y , para {i, j}: {1, 4}, {3, 3}, {15, 13}, {16, 14}, {30, 265}, {36, 104}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Los triángulos ABC y son , para todo punto P del plano.
Pares {P=Xi, U=Xj},
U = (b^6 u^2 w^2 (v+w) (3 u^2+2 v (v+w)+u (5 v+w))-v^2 (a^4 c^2 u w (u^3-v^3+u v (v-w)-v w^2-2 w^3+3 u^2 (v+w))+a^6 w^2 (2 u^3+5 u^2 (v+w)+2 v w (v+w)+3 u (v+w)^2)-c^6 u^2 (v+w) (3 u^2+2 w (v+w)+u (v+5 w))+a^2 c^4 u (u^2 v (v-w)+(v-w) w (v+w)^2+u^3 (v+2 w)+3 u w (v^2-w^2)))-b^2 u v (a^4 w^2 (u^3-2 v^3-v^2 w-w^3+u w (-v+w)+3 u^2 (v+w))+a^2 c^2 w (u^2 (v-w)^2+3 u^3 (v+w)-3 u (v-w)^2 (v+w)-(v^2-w^2)^2)+c^4 u (v+w) (2 u^3+3 u^2 v+u (v^2+9 v w-4 w^2)+2 w (2 v^2+v w-w^2)))-b^4 u w (c^2 u (v+w) (2 u^3+3 u^2 w+u (-4 v^2+9 v w+w^2)+2 v (-v^2+v w+2 w^2))+a^2 w (u^2 w (-v+w)-v (v-w) (v+w)^2+u^3 (2 v+w)-3 u (v^3-v w^2))) : ... : ...)
es el centro de ortología de ABC respecto a , para {i, j}: {1, 4}, {3, 12162}, {4, 11381}, {74, 13202}, {100, 38389}, {101, 1146}, {109, 38357}, {110, 125}, {112, 1562}, {934, 38388}.
El centro de ortología de ABC respecto a , cuando P es el baricentro, es
U2 = ( 28 a^6-26 b^6+30 b^4 c^2+30 b^2 c^4-26 c^6+3 a^4 (b^2+c^2)+3 a^2 (b^2+c^2)^2 : ... : ...),
que tiene números de búsqueda en
(-3.65928669547773, -5.31440354233865, 9.00876848605470).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,1495}, {381,31748}, {3845,14856}.
Pares {P=Xi, V=Xj},
V = (a^2/(b^6 u^3 (u+v-w) w^2 (v+w)+b^2 u v (c^2 u+a^2 w) (a^2 w (-u^3+2 v^3+v^2 w+u (v-w) w+w^3-3 u^2 (v+w))+c^2 u (v+w) (v^2-3 v w+2 w^2+u (v+2 w)))+b^4 u^2 w (c^2 u (v+w) (2 v^2-3 v w+w^2+u (2 v+w))+a^2 w (3 v^3+2 v^2 w+w^3+u (3 v^2+5 v w+w^2)))+v^2 (c^2 u+a^2 w) (c^4 u^2 (u-v+w) (v+w)-a^4 w (u^3+3 u^2 (v+w)+v w (v+w)+u (2 v^2+3 v w+2 w^2))+a^2 c^2 u (v^3+v^2 w+2 v w^2+2 w^3+u (v^2+4 v w+2 w^2))) : ... : ...)
es el centro de ortología de respecto a ABC, para {i, j}: {1, 84}, {3, 64}.
El centro de ortología de respecto a ABC, cuando P es el baricentro, es:
V2 = ( a^2/(16 a^6+3 a^4 (b^2+c^2)-3 a^2 (5 b^4+b^2 c^2+5 c^4)-2 (b^2+c^2)^3) : ... : ...),
que tiene números de búsqueda en ETC (-82.7042020117640, -146.060616426579, 142.930722936507).
No hay rectas determinadas por pares de puntos que están actualmente en ETC que pasen por este punto.
- Viernes, 14 de agosto del 2020
El centro del triángulo X(3057) con centro radical
El 14 de agosto de 1842 nació Jean Gaston Darboux, matemático francés. Hizo muchas contribuciones importantes a la geometría diferencial y al análisis matemático.
En la geometría diferencial de superficies, la referencia de Darboux es una referencia móvil construida sobre una superficie; es la análoga a referencia Frenet-Serret aplicada a una superficie.
La cúbica de Darboux (Z(X20) o K004=pK(X6, X20)) de un triángulo ABC es el lugar geométrico de todos los puntos cuyo triángulo pedal es perspectivo con ABC.
El vector Darboux asociado a una curva se define como la suma de las velocidades areolares de los vectores del triedro de Frenet.
X(3057)
Let Oa be the circle centered at the A-excenter and passing trough the A-intouch point. Define Ob and Oc cyclically. The radical center of Oa, Ob, Oc is X(3057). (Randy Hutson, February 10, 2016)
X(3057) is the radical center of circles {Oa}, {Ob}, {Oc} used in the construction of the Ursa-minor and Ursa-major triangles; see preamble before X(17603). (Randy Hutson, June 27, 2018)
Dado un triángulo ABC, sean DEF el , el del Na=X8 y A(X8A8) la circunferencia de centro A y radio X8A8 (corta a la cirunferencia inscrita en puntos sobre las cevianas de X8 y de su , X56). Se consideran, procediendo cíclicamente, las circunferencias B(X8B8) y C(X8C8).
El de las circunferencias A(X8A8), B(X8B8), C(X8C8) es X3057.
En coordenadas baricéntricas,
A(X8A8):
𝔖abc xyz
(b+c-a)^2(a^2-a(b+c)-2(b-c)^2)x^2
- 2(a^4+5a^3(b+c)-a^2(3b^2+10b c+3c^2)-5a(b-c)^2(b+c)+2(b^2-c^2)^2)y z = 0.
Γa, Γb y Γc son las circunferencias de centros los y pasan por D, E y F, respectivamente. Sea ℓa el de las circunferencias Γa y A(X8A8). ℓb y ℓc se definen similarmente.
El triánguloa A'B'C' formado por las rectas ℓa, ℓb, ℓc es perspectivo con DEF y el centro de perspectividad es W = 4 (a^2 + b^2 + c^2)X69 - 3 (a + b + c)^2 X210.
W = ( a( a^3 (b + c) + a^2 (b^2 - 6 b c + c^2)- a (b + c)^3 -(b - c)^4) : ... : ...),
que tiene números de búsqueda en
(2.11144252329413, 1.99758804170394, 1.28320698074590).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,1122}, {7,3057}, {37,3942}, {55,269}, {65,3664}, {69,210}, {75,3893}, {77,2646}, {86,9432}, {354,3056}, {374,17245}, {517,4888}, {960,21296}, {1358,3663}, {1364,1439}, {1418,2269}, {1697,7271}, {2098,4328}, {2262,4675}, {2268,6610}, {2348,25878}, {3599,34855}, {3698,10436}, {3869,32093}, {3880,31995}, {4059,10446}, {4648,34371}, {4689,24802}, {4862,9957}, {5048,7190}, {6666,25731}, {7053,22768}, {7223,10444}, {7269,33176}, {7274,7962}, {10401,17170}, {11997,31391}, {14828,20359}, {16859,19604}, {17272,25917}, {17365,21871}, {24179,24805}, {24213,37722}, {31188,31792}.
- Miercoles, 12 de agosto del 2020
Propiedades del cuadrado baricéntrico del ortocentro
El 12 de agosto de 1982 muere (a los 77 años) Henry Fonda, actor de cine y teatro estadounidense, ganador de los premios Óscar, Globo de Oro, ... En 1999, Henry Fonda fue nombrado por el American Film Institute como la sexta mayor estrella masculina en la historia de Hollywood. Algunas de sus numerosas películas:
Doce hombres sin piedad (1957), El destino también juega (1966), En el estanque dorado
(1981).
X(393) (Randy Hutson)
• Let Ha be the foot of the A-altitude of ABC. Let Pa be the foot of the altitude from Ha to AB, and Qa the foot of the altitude from Ha to CA. Define Hb, Hc, Pb, Pc, Qb, Qc cyclically. Let A' be the trilinear pole of line PaQa, and define B' and C' cyclically. The lines AA', BB', CC' concur in X(393). Lines PaQa, PbQb, PcQc are the antiparallels in the construction of the Taylor circle. (Randy Hutson, January 29, 2018)
•
Let A'B'C' and A"B"C" be the Euler and anti-Euler triangles, resp. Let A* be the barycentric product A'*A'', and define B* and C* cyclically. The lines AA*, BB*, CC* concur in X(393). (Randy Hutson, January 29, 2018)
•
Let A'B'C' be the orthic triangle. Let A" be the cevapoint of the (real or imaginary) circumcircle intercepts of line B'C'. Define B" and C" cyclically. The lines AA", BB", CC" concur in X(393). (Randy Hutson, July 31 2018)
•
X(393) is the Brianchon point (perspector) of the inellipse that is the barycentric square of the orthic axis. The center of this inellipse is X(3767). (Randy Hutson, October 15, 2018)
Dados un triángulo ABC y un punto P, sea DEF el de P.
La recta que pasa por las proyecciones ortogonales de D sobre BP y CP corta a BC en el punto A'. Los puntos B' y C' se definen cíclicamente.
En coordenadas baricéntricas, si P=(u:v:w),
A'=(0 : -((b^2 - c^2) u + a^2 (u + 2 v))^2 : ((-b^2 + c^2) u +
a^2 (u + 2 w))^2).
El lugar geométrico del punto
P (con triángulo pedal no degenerado) tal que los puntos
A', B', C' están alineados es la
cúbica de Darboux.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Sean 𝒫a, 𝒫b, 𝒫c, las parábolas circunscritas a ABC tales que sus ejes son perpendiculares a los lados BC, CA, AB, respectivamente.
A1 es el punto de interscción de la tangente a 𝒫b en B con la tangente a 𝒫c en C. Los puntos B1 y C1 se definen cíclicamente.
Las rectas AA1, BB1, CC1 se cortan en X393, del ortocentro.
𝒫a: 4 a^4 y z+ (a^2 + b^2 - c^2)^2 + x z (a^2 - b^2 + c^2)^2 x y = 0,
A1 =(-(a^4 - (b^2 - c^2)^2)^2 : (a^4 - b^4 - 2 a^2 c^2 + c^4)^2 : (a^4 -
2 a^2 b^2 + b^4 - c^4)^2).
- Jueves, 6 de agosto del 2020
Otra propiedad del conjugado isogonal del punto de De Longchamps
El 6 de agosto de 1945 a las 8:15 h, hora local, Hiroshima (Japón) se convierte en la primera ciudad del mundo en ser pasto de una bomba nuclear. El bombardero americano B-29 "Enola Gay" deja caer su única bomba, "Little Boy" sobre el centro de la ciudad. 120.000 de los 450.000 habitantes mueren en el acto, otros 70.000 sufren graves heridas. A consecuencia de la radiación otras decenas de miles irán muriendo en terrible goteo con el paso de los años.
La guerra en Europa contra el nazismo había terminado con el suicidio de Hitler y había un arma nueva que el nuevo presidente de EEUU tras la muerte de Roosevelt, Harry S. Truman, quería mostrar al mundo: la bomba atómica, un artefacto que apuntalaba la supremacía militar de EEUU. Si ya no había tiempo de lanzarla sobre Berlín, el escenario japonés se abría como el escenario ideal para los halcones de EEUU.
Dados un triángulo ABC, de circuncentro O=X3, y un punto P, sean A', B', C' las reflexiones de A, B, C en O, respectivamente, y DEF el de P. A" es la reflexion de A' en D, B" es la reflexion de B' en E y C" es la reflexion de C' en F. Entonces: ABC y A"B"C" son inversamente semejantes.
Denotamos por Sa, Sb y Sc los centros de las semejanzas entre ABC y los triángulos , y , reflexiones de A"B"C" en BC, CA y AB, respectivamente.
Si el punto P recorre una recta ℓ, los lugares geométricos de los puntos Sa, Sb y Sc son circunferencias, Γa, Γb y Γc, que se cortan en un punto f(ℓ), sobre la circunferencia circunscrita a ABC.
Si (u:v.w) son las coordenadas baricéntricas de P,
Sa = (a^2 (b^4 w (v+2 w)+(a^2-c^2) v (a^2 w-c^2 (2 v+w))-2 b^2 (a^2 w (v+w)+c^2 (-v w+u (v+w)))) : -b^2 (a^4 (v-w) w+b^4 w (v+w)+c^4 (2 u+w) (v+w)-2 a^2 c^2 (v^2+u w)-2 b^2 (a^2 v w+c^2 (u+w) (v+w))) : -c^2 (a^4 v (-v+w)+(b^2-c^2) (-c^2 v+b^2 (2 u+v)) (v+w)-2 a^2 (c^2 v w+b^2 (u v+w^2)))),
Si la ecuación de ℓ es px+qy+rz=0, la ecuación de Γa es:
c^2 x y+b^2 x z+a^2 y z+
(x+y+z) (-((2 (2 a^4 b^4 c^2 p-2 a^2 b^6 c^2 p+2 a^4 b^2 c^4 p+4 a^2 b^4 c^4 p-2 a^2 b^2 c^6 p-a^4 b^4 c^2 q+b^8 c^2 q-a^4 b^2 c^4 q-2 a^2 b^4 c^4 q-3 b^6 c^4 q+2 a^2 b^2 c^6 q+3 b^4 c^6 q-b^2 c^8 q-a^4 b^4 c^2 r+2 a^2 b^6 c^2 r-b^8 c^2 r-a^4 b^2 c^4 r-2 a^2 b^4 c^4 r+3 b^6 c^4 r-3 b^4 c^6 r+b^2 c^8 r) x)/((a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)^2 p))-(2 (a^6 b^2 c^2 p-a^2 b^6 c^2 p+2 a^2 b^4 c^4 p-a^2 b^2 c^6 p-2 a^4 b^4 c^2 q+2 a^2 b^6 c^2 q-2 a^2 b^4 c^4 q-a^6 b^2 c^2 r+2 a^4 b^4 c^2 r-a^2 b^6 c^2 r+a^2 b^2 c^6 r) y)/((a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)^2 p)-(2 (a^6 b^2 c^2 p-a^2 b^6 c^2 p+2 a^2 b^4 c^4 p-a^2 b^2 c^6 p-a^6 b^2 c^2 q+a^2 b^6 c^2 q+2 a^4 b^2 c^4 q-a^2 b^2 c^6 q-2 a^4 b^2 c^4 r-2 a^2 b^4 c^4 r+2 a^2 b^2 c^6 r) z)/((a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)^2 p))=0.
f(ℓ) = (a^2 (a^4 (p - q) (p - r) -
2 a^2 (q - r) (b^2 (p - q) + c^2 (-p + r)) -
b^4 (p - q) (p - 2 q + r) -
2 b^2 c^2 (-p^2 + q^2 - 3 q r + r^2 + p (q + r)) -
c^4 (p + q - 2 r) (p - r)) : ... : ...).
Si m es la de un punto M, sobre una hipérbola circunscrita ℋ, que pasa por el baricentro, f(m) es el mismo para todo M.
Si L es el
de intersección de Γ y ℋ, la envolvente de la recta Lf(m) es la
elipse
( a^4 b^4 x^2-2 a^2 b^6 x^2+b^8 x^2-2 a^4 b^2 c^2 x^2+2 a^2 b^4 c^2 x^2+a^4 c^4 x^2+2 a^2 b^2 c^4 x^2-2 b^4 c^4 x^2-2 a^2 c^6 x^2+c^8 x^2+2 a^6 b^2 x y-4 a^4 b^4 x y+2 a^2 b^6 x y+2 a^6 c^2 x y-2 a^4 b^2 c^2 x y-2 a^2 b^4 c^2 x y+2 b^6 c^2 x y-2 a^4 c^4 x y-30 a^2 b^2 c^4 x y-2 b^4 c^4 x y-2 a^2 c^6 x y-2 b^2 c^6 x y+2 c^8 x y+a^8 y^2-2 a^6 b^2 y^2+a^4 b^4 y^2+2 a^4 b^2 c^2 y^2-2 a^2 b^4 c^2 y^2-2 a^4 c^4 y^2+2 a^2 b^2 c^4 y^2+b^4 c^4 y^2-2 b^2 c^6 y^2+c^8 y^2+2 a^6 b^2 x z-2 a^4 b^4 x z-2 a^2 b^6 x z+2 b^8 x z+2 a^6 c^2 x z-2 a^4 b^2 c^2 x z-30 a^2 b^4 c^2 x z-2 b^6 c^2 x z-4 a^4 c^4 x z-2 a^2 b^2 c^4 x z-2 b^4 c^4 x z+2 a^2 c^6 x z+2 b^2 c^6 x z+2 a^8 y z-2 a^6 b^2 y z-2 a^4 b^4 y z+2 a^2 b^6 y z-2 a^6 c^2 y z-30 a^4 b^2 c^2 y z-2 a^2 b^4 c^2 y z+2 b^6 c^2 y z-2 a^4 c^4 y z-2 a^2 b^2 c^4 y z-4 b^4 c^4 y z+2 a^2 c^6 y z+2 b^2 c^6 y z+a^8 z^2-2 a^4 b^4 z^2+b^8 z^2-2 a^6 c^2 z^2+2 a^4 b^2 c^2 z^2+2 a^2 b^4 c^2 z^2-2 b^6 c^2 z^2+a^4 c^4 z^2-2 a^2 b^2 c^4 z^2+b^4 c^4 z^2 = 0)
con centro O, eje mayor el diametro de Γ determinado por la recta de Euler y cuadrado de la longitud del eje menor .
Parallel trilinear polars (Paris Pamfilos)
[1] Every conic 𝒞 passing through the vertices of the triangle of reference ABC and the centroid G of this triangle is a hyperbola.
[2] All trilinear polars tr(M) of points M lying on 𝒞 are parallel to each other and define a point at infinity P0.
[3] P0 is the perspector of the hyperbola 𝒞 with respect to the triangle ABC.
En los pares de la siguiente lista, el primer elemento es un punto de la hipérbola ℋ, que pasa además por A, B,C, G (si está entre {}, es el cuarto punto L de Γ y ℋ) y el segundo elemento es el punto (sobre Γ) correspondiente a las tripolares (que son paralelas) de los puntos de ℋ.
{{98}, 74}, {{111}, 98}, {{110}, 99}, {{9058}, 100}, {{9057}, 101},
{{1311}, 102}, {{675}, 103}, {{105}, 104}, {{9061}, 105}, {{9083},
106}, {{9064}, 107}, {{9107}, 108}, {{9056}, 109}, {{1302}, 110},
{{9084}, 111}, {{107}, 112}, {{9060}, 476}, {{842}, 477}, {2412,
675}, {{476}, 691}, {14614, 729}, {1999, 741}, {13739, 759}, {34085,
813}, {36098, 831}, {24002, 840}, {{477}, 841}, {{2770}, 842}, {8599,
843}, {655, 901}, {{15344}, 915}, {{9085}, 917}, {4558, 925}, {677,
927}, {14570, 930}, {16039, 933}, {13138, 934}, {{1304}, 935},
{{2726}, 953}, {9, 972}, {{1113}, 1113}, {{1114}, 1114}, {{5966},
1141}, {{16166}, 1287}, {{1301}, 1289}, {37966, 1290}, {{100}, 1292},
{{9059}, 1293}, {{1297}, 1294}, {{26703}, 1295}, {{99}, 1296},
{{2373}, 1297}, {436, 1298}, {847, 1299}, {{3563}, 1300}, {35360,
1303}, {15459, 1304}, {1331, 1305}, {36037, 1308}, {28978, 1311},
{6190, 1379}, {6189, 1380}, {8732, 1477}, {37136, 2222}, {12848,
2291}, {1797, 2370}, {895, 2373}, {21466, 2378}, {21467, 2379},
{1487, 2383}, {{2752}, 2687}, {2073, 2688}, {{1290}, 2691}, {4591,
2692}, {{2697}, 2693}, {1325, 2694}, {2075, 2695}, {{691}, 2696},
{23, 2697}, {385, 2698}, {422, 2699}, {423, 2700}, {4615, 2705},
{450, 2706}, {425, 2707}, {415, 2708}, {{9080}, 2709}, {{2857},
2710}, {17951, 2712}, {685, 2715}, {2167, 2716}, {765, 2717}, {5382,
2718}, {59, 2723}, {55, 2724}, {9503, 2725}, {36146, 2730}, {7128,
2733}, {222, 2734}, {36086, 2736}, {{901}, 2737}, {7012, 2739}, {666,
2742}, {3257, 2743}, {908, 2745}, {5380, 2746}, {5379, 2747}, {37963,
2752}, {{10102}, 2770}, {{2374}, 3563}, {{925}, 3565}, {3146, 5896},
{{34168}, 5897}, {3467, 5951}, {3629, 5966}, {36309, 5994}, {799,
6010}, {{9070}, 6011}, {{9136}, 6093}, {{9100}, 6233}, {{11636},
6236}, {11163, 6323}, {174, 7597}, {1997, 8686}, {11056, 9076},
{9190, 9080}, {17092, 9105}, {3477, 9108}, {15328, 9161}, {23895,
9202}, {23896, 9203}, {{935}, 10098}, {{2766}, 10101}, {{16167},
10420}, {{22239}, 10423}, {21468, 11612}, {21469, 11613}, {{9073},
12032}, {1332, 13397}, {30512, 13398}, {11004, 13530}, {14146,
13594}, {34484, 13597}, {{6325}, 14388}, {37779, 14979}, {22836,
14987}, {{9082}, 15323}, {1249, 15324}, {1998, 15728}, {1156, 15731},
{5, 18401}, {{3565}, 20187}, {16868, 22751}, {230, 23700}, {11185,
23701}, {1814, 26703}, {{108}, 26706}, {{26711}, 26712}, {37070,
26717}, {{9103}, 28145}, {5556, 28149}, {5561, 28153}, {{9093},
28159}, {3617, 28163}, {5560, 28167}, {{9108}, 28173}, {3634, 28177},
{3828, 28181}, {3626, 28185}, {4691, 28189}, {{9105}, 28193}, {3624,
28197}, {3632, 28203}, {4668, 28207}, {551, 28211}, {4114, 28215},
{3244, 28219}, {3625, 28223}, {3622, 28227}, {5550, 28231}, {{9095},
28233}, {3621, 28235}, {{9086}, 28291}, {{9089}, 28293}, {6540,
28305}, {4597, 28318}, {32042, 28327}, {{9068}, 28467}, {1978,
28469}, {28974, 28471}, {{9067}, 28474}, {{835}, 28477}, {{8707},
28480}, {4610, 28483}, {29840, 28485}, {4562, 28520}, {35180, 28560},
{4621, 28575}, {{2862}, 28838}, {16826, 28842}, {{9075}, 28844},
{7233, 28848}, {17244, 28853}, {29569, 28857}, {17397, 28861},
{17292, 28865}, {17389, 28869}, {29575, 28873}, {17310, 28876},
{5308, 28880}, {17367, 28884}, {17266, 28892}, {17308, 28896},
{17294, 28900}, {3008, 28914}, {{9074}, 29009}, {{9076}, 29011},
{3187, 29015}, {32778, 29019}, {29667, 29023}, {4812, 29027}, {29631,
29031}, {20565, 29042}, {20566, 29045}, {29679, 29049}, {3757,
29053}, {894, 29056}, {26227, 29068}, {32914, 29072}, {3771, 29084},
{29846, 29096}, {29850, 29100}, {29632, 29104}, {3618, 29180}, {261,
29206}, {37213, 29214}, {20017, 29218}, {1278, 29228}, {3011, 29242},
{{9110}, 29308}, {{9094}, 29310}, {428, 29316}, {3763, 29322},
{29649, 29326}, {17982, 29330}, {{9081}, 29348}, {751, 29352},
{29687, 29356}, {16825, 29364}, {29670, 29368}, {{9104}, 30236},
{644, 30237}, {4612, 30238}, {{112}, 30247}, {{3222}, 30254},
{{1296}, 30256}, {{6011}, 30257}, {5664, 32418}, {21464, 32420},
{21463, 32422}, {{9088}, 32704}, {1167, 32706}, {403, 32710}, {35178,
33638}, {22, 34168}, {811, 36516}
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
La tripolar de un punto Q=(f:g:h) corta a los lados de ABC en:
A1=(0:-g:h),
B1=(f:0:-h),
C1=(-f:g:0).
El centro de semejanza Sa, cuando P=B1 es:
Sab = (-2 a^2 (-c^2 f+(a^2-b^2) h) : (a^2+b^2-c^2) ((a^2-b^2) h+c^2 (-2 f+h)) : 2 c^2 (b^2 f-c^2 f+a^2 h)).
Y el centro de semejanza Sa, cuando P=C1 es:
Sac = (-2 a^2 (-b^2 f+(a^2-c^2) g) : -2 b^2 (b^2 f-c^2 f-a^2 g) : (a^2-b^2+c^2) ((a^2-c^2) g+b^2 (-2 f+g))).
La ecuación de la recta ℓa=SabSac es:
a^8 g h + 2 a^2 (b^4 - c^4) f (-c^2 g + b^2 h) -
2 a^6 f (c^2 g + b^2 h) +
2 a^4 (c^4 g (f - h) + b^2 c^2 f (2 f - g - h) +
b^4 (f - g) h) - (b^2 - c^2)^3 (b^2 (2 f - g) h +
c^2 g (-2 f + h))x+
2 (a^8 g h -
a^2 (b^2 - c^2) (-c^4 f g + b^4 (2 f - g) h + b^2 c^2 g (-f + h)) -
a^6 (b^2 (2 f + g) h + c^2 g (f + 2 h)) +
a^4 (b^4 (4 f - g) h + c^4 g (2 f + h) +
2 b^2 c^2 (f^2 - f g + g h)))y *
2 (a^8 g h -
a^2 (b^2 - c^2) (b^4 f h + b^2 c^2 (f - g) h + c^4 g (-2 f + h)) -
a^6 (b^2 (f + 2 g) h + c^2 g (2 f + h)) +
a^4 (c^4 g (4 f - h) + b^4 (2 f + g) h +
2 b^2 c^2 (f^2 - f h + g h)))z = 0.
Las rectas ℓb y ℓc se definen cíclicamente.
El triángulo
UVW formado por las rectas ℓ
a, ℓ
b y ℓ
c es perspectivo con
ABC si y solo si
Q está sobre la recta
GK, la , una
isocúbica
( 1/(2 a^2 b^2 c^2) (a^8-4 a^6 (b^2+c^2)+6 a^4 (b^4+c^4)-4 a^2 (b^6+c^6)+(b^2-c^2)^4) x y z+(a^2+b^2-c^2) (x^2+y^2) z+(a^2-b^2+c^2) y (x^2+z^2)+(-a^2+b^2+c^2) x (y^2+z^2) = 0)
no pivotal de polo
G y raíz el o una
séxtica.
( 8 a^10 b^2 c^4 x^4 y^2-16 a^8 b^4 c^4 x^4 y^2+8 a^6 b^6 c^4 x^4 y^2-8 a^8 b^2 c^6 x^4 y^2+16 a^6 b^4 c^6 x^4 y^2+8 a^4 b^6 c^6 x^4 y^2-8 a^6 b^2 c^8 x^4 y^2-16 a^4 b^4 c^8 x^4 y^2+8 a^4 b^2 c^10 x^4 y^2-4 a^12 c^4 x^3 y^3+4 a^10 b^2 c^4 x^3 y^3+4 a^8 b^4 c^4 x^3 y^3-8 a^6 b^6 c^4 x^3 y^3+4 a^4 b^8 c^4 x^3 y^3+4 a^2 b^10 c^4 x^3 y^3-4 b^12 c^4 x^3 y^3+16 a^10 c^6 x^3 y^3-16 a^8 b^2 c^6 x^3 y^3-16 a^6 b^4 c^6 x^3 y^3-16 a^4 b^6 c^6 x^3 y^3-16 a^2 b^8 c^6 x^3 y^3+16 b^10 c^6 x^3 y^3-20 a^8 c^8 x^3 y^3+40 a^6 b^2 c^8 x^3 y^3+56 a^4 b^4 c^8 x^3 y^3+40 a^2 b^6 c^8 x^3 y^3-20 b^8 c^8 x^3 y^3-64 a^4 b^2 c^10 x^3 y^3-64 a^2 b^4 c^10 x^3 y^3+20 a^4 c^12 x^3 y^3+52 a^2 b^2 c^12 x^3 y^3+20 b^4 c^12 x^3 y^3-16 a^2 c^14 x^3 y^3-16 b^2 c^14 x^3 y^3+4 c^16 x^3 y^3+8 a^6 b^6 c^4 x^2 y^4-16 a^4 b^8 c^4 x^2 y^4+8 a^2 b^10 c^4 x^2 y^4+8 a^6 b^4 c^6 x^2 y^4+16 a^4 b^6 c^6 x^2 y^4-8 a^2 b^8 c^6 x^2 y^4-16 a^4 b^4 c^8 x^2 y^4-8 a^2 b^6 c^8 x^2 y^4+8 a^2 b^4 c^10 x^2 y^4+4 a^12 b^2 c^2 x^4 y z-8 a^10 b^4 c^2 x^4 y z+8 a^6 b^8 c^2 x^4 y z-4 a^4 b^10 c^2 x^4 y z-8 a^10 b^2 c^4 x^4 y z+32 a^8 b^4 c^4 x^4 y z-24 a^6 b^6 c^4 x^4 y z-24 a^6 b^4 c^6 x^4 y z+8 a^4 b^6 c^6 x^4 y z+8 a^6 b^2 c^8 x^4 y z-4 a^4 b^2 c^10 x^4 y z-2 a^14 c^2 x^3 y^2 z-10 a^12 b^2 c^2 x^3 y^2 z+46 a^10 b^4 c^2 x^3 y^2 z-62 a^8 b^6 c^2 x^3 y^2 z+34 a^6 b^8 c^2 x^3 y^2 z+2 a^4 b^10 c^2 x^3 y^2 z-14 a^2 b^12 c^2 x^3 y^2 z+6 b^14 c^2 x^3 y^2 z+10 a^12 c^4 x^3 y^2 z-24 a^10 b^2 c^4 x^3 y^2 z-10 a^8 b^4 c^4 x^3 y^2 z+16 a^6 b^6 c^4 x^3 y^2 z-18 a^4 b^8 c^4 x^3 y^2 z+40 a^2 b^10 c^4 x^3 y^2 z-14 b^12 c^4 x^3 y^2 z-18 a^10 c^6 x^3 y^2 z+94 a^8 b^2 c^6 x^3 y^2 z+20 a^6 b^4 c^6 x^3 y^2 z-4 a^4 b^6 c^6 x^3 y^2 z-58 a^2 b^8 c^6 x^3 y^2 z-18 b^10 c^6 x^3 y^2 z+10 a^8 c^8 x^3 y^2 z-96 a^6 b^2 c^8 x^3 y^2 z-12 a^4 b^4 c^8 x^3 y^2 z+64 a^2 b^6 c^8 x^3 y^2 z+90 b^8 c^8 x^3 y^2 z+10 a^6 c^10 x^3 y^2 z+50 a^4 b^2 c^10 x^3 y^2 z-34 a^2 b^4 c^10 x^3 y^2 z-110 b^6 c^10 x^3 y^2 z-18 a^4 c^12 x^3 y^2 z-8 a^2 b^2 c^12 x^3 y^2 z+54 b^4 c^12 x^3 y^2 z+10 a^2 c^14 x^3 y^2 z-6 b^2 c^14 x^3 y^2 z-2 c^16 x^3 y^2 z+6 a^14 c^2 x^2 y^3 z-14 a^12 b^2 c^2 x^2 y^3 z+2 a^10 b^4 c^2 x^2 y^3 z+34 a^8 b^6 c^2 x^2 y^3 z-62 a^6 b^8 c^2 x^2 y^3 z+46 a^4 b^10 c^2 x^2 y^3 z-10 a^2 b^12 c^2 x^2 y^3 z-2 b^14 c^2 x^2 y^3 z-14 a^12 c^4 x^2 y^3 z+40 a^10 b^2 c^4 x^2 y^3 z-18 a^8 b^4 c^4 x^2 y^3 z+16 a^6 b^6 c^4 x^2 y^3 z-10 a^4 b^8 c^4 x^2 y^3 z-24 a^2 b^10 c^4 x^2 y^3 z+10 b^12 c^4 x^2 y^3 z-18 a^10 c^6 x^2 y^3 z-58 a^8 b^2 c^6 x^2 y^3 z-4 a^6 b^4 c^6 x^2 y^3 z+20 a^4 b^6 c^6 x^2 y^3 z+94 a^2 b^8 c^6 x^2 y^3 z-18 b^10 c^6 x^2 y^3 z+90 a^8 c^8 x^2 y^3 z+64 a^6 b^2 c^8 x^2 y^3 z-12 a^4 b^4 c^8 x^2 y^3 z-96 a^2 b^6 c^8 x^2 y^3 z+10 b^8 c^8 x^2 y^3 z-110 a^6 c^10 x^2 y^3 z-34 a^4 b^2 c^10 x^2 y^3 z+50 a^2 b^4 c^10 x^2 y^3 z+10 b^6 c^10 x^2 y^3 z+54 a^4 c^12 x^2 y^3 z-8 a^2 b^2 c^12 x^2 y^3 z-18 b^4 c^12 x^2 y^3 z-6 a^2 c^14 x^2 y^3 z+10 b^2 c^14 x^2 y^3 z-2 c^16 x^2 y^3 z-4 a^10 b^4 c^2 x y^4 z+8 a^8 b^6 c^2 x y^4 z-8 a^4 b^10 c^2 x y^4 z+4 a^2 b^12 c^2 x y^4 z-24 a^6 b^6 c^4 x y^4 z+32 a^4 b^8 c^4 x y^4 z-8 a^2 b^10 c^4 x y^4 z+8 a^6 b^4 c^6 x y^4 z-24 a^4 b^6 c^6 x y^4 z+8 a^2 b^6 c^8 x y^4 z-4 a^2 b^4 c^10 x y^4 z+8 a^10 b^4 c^2 x^4 z^2-8 a^8 b^6 c^2 x^4 z^2-8 a^6 b^8 c^2 x^4 z^2+8 a^4 b^10 c^2 x^4 z^2-16 a^8 b^4 c^4 x^4 z^2+16 a^6 b^6 c^4 x^4 z^2-16 a^4 b^8 c^4 x^4 z^2+8 a^6 b^4 c^6 x^4 z^2+8 a^4 b^6 c^6 x^4 z^2-2 a^14 b^2 x^3 y z^2+10 a^12 b^4 x^3 y z^2-18 a^10 b^6 x^3 y z^2+10 a^8 b^8 x^3 y z^2+10 a^6 b^10 x^3 y z^2-18 a^4 b^12 x^3 y z^2+10 a^2 b^14 x^3 y z^2-2 b^16 x^3 y z^2-10 a^12 b^2 c^2 x^3 y z^2-24 a^10 b^4 c^2 x^3 y z^2+94 a^8 b^6 c^2 x^3 y z^2-96 a^6 b^8 c^2 x^3 y z^2+50 a^4 b^10 c^2 x^3 y z^2-8 a^2 b^12 c^2 x^3 y z^2-6 b^14 c^2 x^3 y z^2+46 a^10 b^2 c^4 x^3 y z^2-10 a^8 b^4 c^4 x^3 y z^2+20 a^6 b^6 c^4 x^3 y z^2-12 a^4 b^8 c^4 x^3 y z^2-34 a^2 b^10 c^4 x^3 y z^2+54 b^12 c^4 x^3 y z^2-62 a^8 b^2 c^6 x^3 y z^2+16 a^6 b^4 c^6 x^3 y z^2-4 a^4 b^6 c^6 x^3 y z^2+64 a^2 b^8 c^6 x^3 y z^2-110 b^10 c^6 x^3 y z^2+34 a^6 b^2 c^8 x^3 y z^2-18 a^4 b^4 c^8 x^3 y z^2-58 a^2 b^6 c^8 x^3 y z^2+90 b^8 c^8 x^3 y z^2+2 a^4 b^2 c^10 x^3 y z^2+40 a^2 b^4 c^10 x^3 y z^2-18 b^6 c^10 x^3 y z^2-14 a^2 b^2 c^12 x^3 y z^2-14 b^4 c^12 x^3 y z^2+6 b^2 c^14 x^3 y z^2+a^16 x^2 y^2 z^2-20 a^12 b^4 x^2 y^2 z^2+64 a^10 b^6 x^2 y^2 z^2-90 a^8 b^8 x^2 y^2 z^2+64 a^6 b^10 x^2 y^2 z^2-20 a^4 b^12 x^2 y^2 z^2+b^16 x^2 y^2 z^2+48 a^12 b^2 c^2 x^2 y^2 z^2-96 a^10 b^4 c^2 x^2 y^2 z^2+48 a^8 b^6 c^2 x^2 y^2 z^2+48 a^6 b^8 c^2 x^2 y^2 z^2-96 a^4 b^10 c^2 x^2 y^2 z^2+48 a^2 b^12 c^2 x^2 y^2 z^2-20 a^12 c^4 x^2 y^2 z^2-96 a^10 b^2 c^4 x^2 y^2 z^2+84 a^8 b^4 c^4 x^2 y^2 z^2-32 a^6 b^6 c^4 x^2 y^2 z^2+84 a^4 b^8 c^4 x^2 y^2 z^2-96 a^2 b^10 c^4 x^2 y^2 z^2-20 b^12 c^4 x^2 y^2 z^2+64 a^10 c^6 x^2 y^2 z^2+48 a^8 b^2 c^6 x^2 y^2 z^2-32 a^6 b^4 c^6 x^2 y^2 z^2-32 a^4 b^6 c^6 x^2 y^2 z^2+48 a^2 b^8 c^6 x^2 y^2 z^2+64 b^10 c^6 x^2 y^2 z^2-90 a^8 c^8 x^2 y^2 z^2+48 a^6 b^2 c^8 x^2 y^2 z^2+84 a^4 b^4 c^8 x^2 y^2 z^2+48 a^2 b^6 c^8 x^2 y^2 z^2-90 b^8 c^8 x^2 y^2 z^2+64 a^6 c^10 x^2 y^2 z^2-96 a^4 b^2 c^10 x^2 y^2 z^2-96 a^2 b^4 c^10 x^2 y^2 z^2+64 b^6 c^10 x^2 y^2 z^2-20 a^4 c^12 x^2 y^2 z^2+48 a^2 b^2 c^12 x^2 y^2 z^2-20 b^4 c^12 x^2 y^2 z^2+c^16 x^2 y^2 z^2-2 a^16 x y^3 z^2+10 a^14 b^2 x y^3 z^2-18 a^12 b^4 x y^3 z^2+10 a^10 b^6 x y^3 z^2+10 a^8 b^8 x y^3 z^2-18 a^6 b^10 x y^3 z^2+10 a^4 b^12 x y^3 z^2-2 a^2 b^14 x y^3 z^2-6 a^14 c^2 x y^3 z^2-8 a^12 b^2 c^2 x y^3 z^2+50 a^10 b^4 c^2 x y^3 z^2-96 a^8 b^6 c^2 x y^3 z^2+94 a^6 b^8 c^2 x y^3 z^2-24 a^4 b^10 c^2 x y^3 z^2-10 a^2 b^12 c^2 x y^3 z^2+54 a^12 c^4 x y^3 z^2-34 a^10 b^2 c^4 x y^3 z^2-12 a^8 b^4 c^4 x y^3 z^2+20 a^6 b^6 c^4 x y^3 z^2-10 a^4 b^8 c^4 x y^3 z^2+46 a^2 b^10 c^4 x y^3 z^2-110 a^10 c^6 x y^3 z^2+64 a^8 b^2 c^6 x y^3 z^2-4 a^6 b^4 c^6 x y^3 z^2+16 a^4 b^6 c^6 x y^3 z^2-62 a^2 b^8 c^6 x y^3 z^2+90 a^8 c^8 x y^3 z^2-58 a^6 b^2 c^8 x y^3 z^2-18 a^4 b^4 c^8 x y^3 z^2+34 a^2 b^6 c^8 x y^3 z^2-18 a^6 c^10 x y^3 z^2+40 a^4 b^2 c^10 x y^3 z^2+2 a^2 b^4 c^10 x y^3 z^2-14 a^4 c^12 x y^3 z^2-14 a^2 b^2 c^12 x y^3 z^2+6 a^2 c^14 x y^3 z^2+8 a^10 b^4 c^2 y^4 z^2-8 a^8 b^6 c^2 y^4 z^2-8 a^6 b^8 c^2 y^4 z^2+8 a^4 b^10 c^2 y^4 z^2-16 a^8 b^4 c^4 y^4 z^2+16 a^6 b^6 c^4 y^4 z^2-16 a^4 b^8 c^4 y^4 z^2+8 a^6 b^4 c^6 y^4 z^2+8 a^4 b^6 c^6 y^4 z^2-4 a^12 b^4 x^3 z^3+16 a^10 b^6 x^3 z^3-20 a^8 b^8 x^3 z^3+20 a^4 b^12 x^3 z^3-16 a^2 b^14 x^3 z^3+4 b^16 x^3 z^3+4 a^10 b^4 c^2 x^3 z^3-16 a^8 b^6 c^2 x^3 z^3+40 a^6 b^8 c^2 x^3 z^3-64 a^4 b^10 c^2 x^3 z^3+52 a^2 b^12 c^2 x^3 z^3-16 b^14 c^2 x^3 z^3+4 a^8 b^4 c^4 x^3 z^3-16 a^6 b^6 c^4 x^3 z^3+56 a^4 b^8 c^4 x^3 z^3-64 a^2 b^10 c^4 x^3 z^3+20 b^12 c^4 x^3 z^3-8 a^6 b^4 c^6 x^3 z^3-16 a^4 b^6 c^6 x^3 z^3+40 a^2 b^8 c^6 x^3 z^3+4 a^4 b^4 c^8 x^3 z^3-16 a^2 b^6 c^8 x^3 z^3-20 b^8 c^8 x^3 z^3+4 a^2 b^4 c^10 x^3 z^3+16 b^6 c^10 x^3 z^3-4 b^4 c^12 x^3 z^3+6 a^14 b^2 x^2 y z^3-14 a^12 b^4 x^2 y z^3-18 a^10 b^6 x^2 y z^3+90 a^8 b^8 x^2 y z^3-110 a^6 b^10 x^2 y z^3+54 a^4 b^12 x^2 y z^3-6 a^2 b^14 x^2 y z^3-2 b^16 x^2 y z^3-14 a^12 b^2 c^2 x^2 y z^3+40 a^10 b^4 c^2 x^2 y z^3-58 a^8 b^6 c^2 x^2 y z^3+64 a^6 b^8 c^2 x^2 y z^3-34 a^4 b^10 c^2 x^2 y z^3-8 a^2 b^12 c^2 x^2 y z^3+10 b^14 c^2 x^2 y z^3+2 a^10 b^2 c^4 x^2 y z^3-18 a^8 b^4 c^4 x^2 y z^3-4 a^6 b^6 c^4 x^2 y z^3-12 a^4 b^8 c^4 x^2 y z^3+50 a^2 b^10 c^4 x^2 y z^3-18 b^12 c^4 x^2 y z^3+34 a^8 b^2 c^6 x^2 y z^3+16 a^6 b^4 c^6 x^2 y z^3+20 a^4 b^6 c^6 x^2 y z^3-96 a^2 b^8 c^6 x^2 y z^3+10 b^10 c^6 x^2 y z^3-62 a^6 b^2 c^8 x^2 y z^3-10 a^4 b^4 c^8 x^2 y z^3+94 a^2 b^6 c^8 x^2 y z^3+10 b^8 c^8 x^2 y z^3+46 a^4 b^2 c^10 x^2 y z^3-24 a^2 b^4 c^10 x^2 y z^3-18 b^6 c^10 x^2 y z^3-10 a^2 b^2 c^12 x^2 y z^3+10 b^4 c^12 x^2 y z^3-2 b^2 c^14 x^2 y z^3-2 a^16 x y^2 z^3-6 a^14 b^2 x y^2 z^3+54 a^12 b^4 x y^2 z^3-110 a^10 b^6 x y^2 z^3+90 a^8 b^8 x y^2 z^3-18 a^6 b^10 x y^2 z^3-14 a^4 b^12 x y^2 z^3+6 a^2 b^14 x y^2 z^3+10 a^14 c^2 x y^2 z^3-8 a^12 b^2 c^2 x y^2 z^3-34 a^10 b^4 c^2 x y^2 z^3+64 a^8 b^6 c^2 x y^2 z^3-58 a^6 b^8 c^2 x y^2 z^3+40 a^4 b^10 c^2 x y^2 z^3-14 a^2 b^12 c^2 x y^2 z^3-18 a^12 c^4 x y^2 z^3+50 a^10 b^2 c^4 x y^2 z^3-12 a^8 b^4 c^4 x y^2 z^3-4 a^6 b^6 c^4 x y^2 z^3-18 a^4 b^8 c^4 x y^2 z^3+2 a^2 b^10 c^4 x y^2 z^3+10 a^10 c^6 x y^2 z^3-96 a^8 b^2 c^6 x y^2 z^3+20 a^6 b^4 c^6 x y^2 z^3+16 a^4 b^6 c^6 x y^2 z^3+34 a^2 b^8 c^6 x y^2 z^3+10 a^8 c^8 x y^2 z^3+94 a^6 b^2 c^8 x y^2 z^3-10 a^4 b^4 c^8 x y^2 z^3-62 a^2 b^6 c^8 x y^2 z^3-18 a^6 c^10 x y^2 z^3-24 a^4 b^2 c^10 x y^2 z^3+46 a^2 b^4 c^10 x y^2 z^3+10 a^4 c^12 x y^2 z^3-10 a^2 b^2 c^12 x y^2 z^3-2 a^2 c^14 x y^2 z^3+4 a^16 y^3 z^3-16 a^14 b^2 y^3 z^3+20 a^12 b^4 y^3 z^3-20 a^8 b^8 y^3 z^3+16 a^6 b^10 y^3 z^3-4 a^4 b^12 y^3 z^3-16 a^14 c^2 y^3 z^3+52 a^12 b^2 c^2 y^3 z^3-64 a^10 b^4 c^2 y^3 z^3+40 a^8 b^6 c^2 y^3 z^3-16 a^6 b^8 c^2 y^3 z^3+4 a^4 b^10 c^2 y^3 z^3+20 a^12 c^4 y^3 z^3-64 a^10 b^2 c^4 y^3 z^3+56 a^8 b^4 c^4 y^3 z^3-16 a^6 b^6 c^4 y^3 z^3+4 a^4 b^8 c^4 y^3 z^3+40 a^8 b^2 c^6 y^3 z^3-16 a^6 b^4 c^6 y^3 z^3-8 a^4 b^6 c^6 y^3 z^3-20 a^8 c^8 y^3 z^3-16 a^6 b^2 c^8 y^3 z^3+4 a^4 b^4 c^8 y^3 z^3+16 a^6 c^10 y^3 z^3+4 a^4 b^2 c^10 y^3 z^3-4 a^4 c^12 y^3 z^3+8 a^6 b^6 c^4 x^2 z^4-16 a^4 b^8 c^4 x^2 z^4+8 a^2 b^10 c^4 x^2 z^4+8 a^6 b^4 c^6 x^2 z^4+16 a^4 b^6 c^6 x^2 z^4-8 a^2 b^8 c^6 x^2 z^4-16 a^4 b^4 c^8 x^2 z^4-8 a^2 b^6 c^8 x^2 z^4+8 a^2 b^4 c^10 x^2 z^4-4 a^10 b^2 c^4 x y z^4+8 a^6 b^6 c^4 x y z^4-4 a^2 b^10 c^4 x y z^4+8 a^8 b^2 c^6 x y z^4-24 a^6 b^4 c^6 x y z^4-24 a^4 b^6 c^6 x y z^4+8 a^2 b^8 c^6 x y z^4+32 a^4 b^4 c^8 x y z^4-8 a^4 b^2 c^10 x y z^4-8 a^2 b^4 c^10 x y z^4+4 a^2 b^2 c^12 x y z^4+8 a^10 b^2 c^4 y^2 z^4-16 a^8 b^4 c^4 y^2 z^4+8 a^6 b^6 c^4 y^2 z^4-8 a^8 b^2 c^6 y^2 z^4+16 a^6 b^4 c^6 y^2 z^4+8 a^4 b^6 c^6 y^2 z^4-8 a^6 b^2 c^8 y^2 z^4-16 a^4 b^4 c^8 y^2 z^4+8 a^4 b^2 c^10 y^2 z^4 = 0)
En particular, {Q=Xi, Q'=Xj}, para {i,j}: {110, 2710}, {287, 2710}, {648, 2693}, {651, 2745}, {895, 23701}, {2986, 32710}, {2987, 23700}, {8115, 74}, {8116, 74}, {14919, 2693}.
Los siguientes casos corresponden a puntos Q sobre la recta GK:
Φ(G)= O.
Φ(K) = ( a^2 (a^8 + 4 a^2 (b^2 - c^2)^2 (b^2 + c^2) -
4 a^4 (b^4 - 3 b^2 c^2 + c^4)- b^8 + 6 b^4 c^4 - c^8) : ... : ...),
que tiene números de búsqueda en
(0.713061416586531, 0.589773744171168, 2.90325431290286).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {182,378}, {187,15066}, {287,3972}, {458,37648}, {512,1995}, {524,1003}, {3003,30541}, {5422,19220}, {5663,11653}.
Φ(X1993)= X64, del .
Une construction de X(64)
Emile Lemoine, "Quelques questions se rapportant à l'étude des antiparallèles des côtes d'un triangle", Bulletin de la S. M. F., tome 14 (1886), p. 107-128, specifically, on page 110.
A
1, B
1, C
1 les pôles de BC, AC, AB par rapport au cercle circonscrit.
ℓ
a est la antiparallèle à BC que passe par A
1.
De même ℓ
b et ℓ
c, respectivement antiparallèles à A C que passe par B
1. et à AB que passe par C
1.
Nous appellerons La, Lb, Lc les sommets du triangle formé par les droites ℓ
a, ℓ
b, ℓ
c, ℓ
a étant l'intersection des droites ℓ
b, ℓ
c,....
Les deux triangles ABC, L
aL
bL
c sont homologiques ; le centre d'homologie a pour coordonnées
1/(cosA-cosBcosC), 1/(cosB-cosCcosA), 1/(cosC-cosAcosB).
- Domingo, 2 de agosto del 2020
Las circunferencias de Mannheim y el segundo punto de Sharygin
Un aniversario personal especial
Darij Grinberg, Sharygin Points Report, Hyacinthos
#6293 (Jan 8, 2003)
Let ABC be a triangle. The internal angle bisectors from A, B, C meet
BC, CA, AB at A', B', C'. The external angle bisectors from A, B, C
meet BC, CA, AB at A", B", C". Let X, X', Y, Y', Z, Z' be the
midpoints and x, x', y, y', z, z' the perpendicular bisectors of the
segments AA', AA", BB', BB", CC', CC" respectively.
Now define the points
D = y ∩ z, E = z ∩ x and F = x ∩ y;
D' = y' ∩ z', E' = z' ∩ x' and F' = x' ∩ y'.
The triangles DEF and D'E'F' are the triangles enclosed by the
perpendicular bisectors of the internal and external angle bisectors
of ABC, respectively.
The triangles ABC, DEF and D'E'F' are mutually perspective, having a
common perspectrix - this is the Lemoine axis of triangle ABC.
The perspector of ABC and DEF is the
1ST SHARYGIN POINT of ABC.
The perspector of ABC and D'E'F' is the
2nd SHARYGIN POINT of ABC.
La Γa es tangente a la circunferencia Γ, circunscrita a un triángulo ABC, en el punto Ta y es tangente a los lados AB y AC en los puntos Ac y Ab. respectivamente.
Las rectas BC y AbAc se cortan en U. La tangente en Ta a Γ interseca a AbAc en X.
Sea ℓa la mediatriz del segmento UX, y se definen cíclicamente las rectas ℓb y ℓc. Las rectas ℓa, ℓb, ℓc forman un triángulo .
En coordenadas baricéntricas, respecto a ABC:
Ab = (-a - b + c : 0 : -2 c),
Ac = (a - b + c : 2 b, 0),
Ta = (a (-a^2 + (b - c)^2) : 2 b^2 (a + b - c) : 2 c^2 (a - b + c)),
U = (0 : -b (a + b - c) : c (a - b + c)),
Y = (-a^2 + (b - c)^2) (b - c) : -2 b^2 (a + b - c) : 2 c^2 (a - b + c)),
ℓa: b c (a^2 + (b - c)^2 + 2 a (b + c))x + c^2 (a - b + c) (a + 3 b + c)y +
b^2 (a + b - c) (a + b + 3 c)z = 0,
A2 = (-a (a^4 + 2 a^3 (b + c) + 2 a b c (b + c) - b c (b + c)^2 +
a^2 (-3 b^2 + b c - 3 c^2)) :
b (-3 a^3 b - c^2 (b + c)^2 + a^2 (2 b^2 + 2 b c + 3 c^2) +
a (b^3 + 2 b^2 c - b c^2 - 2 c^3)) :
c (-3 a^3 c - b^2 (b + c)^2 + a^2 (3 b^2 + 2 b c + 2 c^2) +
a (-2 b^3 - b^2 c + 2 b c^2 + c^3))).
X291 = ( a/(a^2 - bc) : b/(b^2 - ca) : c/(c^2 - ab).
NOTA. Una propiedad del pimer y segundo punto de Sharygin aparecen en http://amontes.webs.ull.es/pdf/ejtr2475.pdf
Como la recta AbAc es perpendicular a la bisectriz interior en A, los triángulos ABC y son , con centro de paralelogía de ABC respecto a el incentro.
El centro de paralelogía de recpaecto a ABC es
Z =(r^2-4 r R+s^2)X659 + 8 r R X875 (r y R son los radios de las circunferencias inscrita y circunscrita y s el semiperímetro de ABC).
Z = ( a (b-c) (a^4+2 a^3 (b+c)+a^2 (-3 b^2+b c-3 c^2)+2 a b c (b+c)-b c (b+c)^2) : ... : ...),
que tiene números de búsqueda en
(-3.87341833362457, 1.92531313640961, 4.09548692606599).
- Martes, 28 de julio del 2020
La elipse lugar geométrico de los ortopolos de la rectas que pasan por el incentro
El 28 de julio de 1818 falleció (a los 72 años) el matemático francés Gaspard Monge, considerado el padre de la geometría diferencial debido a su trabajo "Application de l'analyse à la géométrie", donde introdujo el concepto de líneas de curvatura de una superficie en un espacio tridimensional. Desarrolló un método general para aplicar geometría a problemas de construcción. También introdujo dos planos de proyección en ángulo recto entre sí para la descripción gráfica de objetos sólidos. Estas técnicas se generalizaron en un sistema llamado géométrie descriptiva. Estudió las superficies minimales de manera puramente teórica.
Una superficie regular M se dice que es de Monge si M={(u,v,f(u,v))∈R3: (u,v)∈U}, donde f es una función diferenciable definida en un abierto U de R2. Una superficie de Monge es minimal si y solo si
fuu(1 +f2v)-2fufvfuv+fvv(1 +f2u) = 0.
Dados un triángulo ABC, un punto P y una recta ℓ que pasa por P, el lugar geométrico del L de ℓ, cuando ésta gira alrededor de P, es una
cónica,
( Si (u:v:w) son las coordenadas baricéntricas de P:
𝔖abc uvw xyz
((a^2-b^2 -c^2 )v-2 b^2 w) ((a^2 -b^2 -c^2) w-2 c^2 v)((a^4 -(b^2-c^2)^2) u-2 a^2 (b^2+c^2-a^2) (v+w))x^2+ 2 (a^8 v w (u+v+w)+(b^2-c^2)^2 u (c^4 v^2+b^4 w^2-b^2 c^2 (4 u^2+v^2+w^2+4 u (v+w)))+a^6 (c^2 v (2 u^2+(v-w) w+u (3 v+w))+b^2 w (2 u^2+v (-v+w)+u (v+3 w)))+a^2 (b^2-c^2) (b^2 c^2 (v-w) (-6 u^2+2 v w-3 u (v+w))-c^4 v (2 u^2+w (3 v+w)+u (v+3 w))+b^4 w (2 u^2+u (3 v+w)+v (v+3 w)))-a^4 (c^4 v (u+w) (4 u+5 v+w)+b^4 (u+v) w (4 u+v+5 w)-b^2 c^2 (4 u^3+8 u^2 (v+w)+6 v w (v+w)+u (v^2+18 v w+w^2))))y z = 0.
)
𝒸(P).
Su centro es el punto medio de P y el ortocentro.
En particular, cuando P es el incentro la ecuación de la cónica 𝒞(I) es:
𝔖abc xyz
(b+c-a)^2 (a^3+a^2 (b+c)-a (b+c)^2-(b-c)^2 (b+c))x^2+2 a (a^2-(b-c)^2)^2y z = 0.
Su centro es X946 ("center of conic that is the locus of orthopoles of lines passing through X(1)") y pasa por los centros del triángulo Xi, para i∈{11, 1537, 1565, 21618, 38357, 38384, 38385, 38386} y está circunscrita a la , DEF.
Si es el , sea A'B'C' el triángulo formado por las perpendiculares por Ma, Mb y Mc a las bisectrices en A, B y C, respectivamente.
La cónica 𝒞(I) es la imagen de la circunferencia inscrita a ABC, mediante la transformación afín σ, que aplica ABC en A'B'C'.
El punto fijo finito de σ es el y las rectas dobles pasan por los extremos, X2446 y X2447, del diámetro de la circunferencia inscrita que pasa por el circuncentro.
El triángulo , cuya imagen por σ es DEF, es perspectivo con ABC, con centro de perspectividad X55, centro de homotecia interior de las circunferencias inscrita y circunscrita a ABC.
- Martes, 21 de julio del 2020
La elipse circunscrita de centro el simediano, como lugar geométrico
El 21 de julio de 1873 falleció (a los 49 años) Delfino Codazzi matemático italiano que hizo importante contribuciobes a la geometría diferencial de superficies, tales como sus famosas fórmulas que se han demostrado ser de capital importancia en la teoría de superficies. Hoy día, dichas fórmulas son conocidas como las ecuaciones de Mainardi-Codazzi, que son dos relaciones entre la primera y segunda forma fundamental de una superficie que junto con la ecuación de Gauss, dan condiciones necesarias y suficientes para la existencia de una superficie, con esa primera y segunda forma fundamental, en R3.
Dados un triángulo ABC y un punto P, sea DEF el de P.
La circunferencia que pasa por A, E y el circuncentro O=X3, vuelve a cortar a la recta AB en E' y a la circunferencia circunscrita en E1, sea Ab la reflexión de E1 en EE' (queda sobre BC).
La circunferencia que pasa por A, F y O, vuelve a cortar a la recta AC en F' y a la circunferencia circunscrita en F1, sea Ac la reflexión de F1 en FF' (queda sobre BC).
Los puntos Bc, Ba, Ca y Cb se definen cíclicamente.
Los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están sobre una misma cónica, 𝒞(P), si y solo si P está sobre la recta de Euler o sobre la circunferencia circunscrita, Γ, a ABC.
Si P=(a^2 t(t-1) : -b^2 (t-1) : c^2 t) son las coordenadas baricéntricas de un punto sobre Γ, el lugar geométrico del centro
Wt = ( (c^2 + a^2 (-1 + t)) (b^2 - a^2 t) :
(b^2 - a^2 t) (b^2 (-1 + t) -
c^2 t) :
-(c^2 + a^2 (-1 + t)) (-b^2 (-1 + t) + c^2 t)),
de la
cónica
( (a^2-b^2-c^2) (-b^2+a^2 t) (-a^2+c^2+a^2 t) (-b^2+b^2 t-c^2 t) x^2+(a^2-b^2+c^2) t (-b^2+a^2 t) (-a^2+c^2+a^2 t) (-b^2+b^2 t-c^2 t) y^2+2 a^2 t (a^4 b^2+b^6 t+a^4 c^2 t+c^6 t) x z+2 b^2 t^2 (a^6+b^4 c^2+c^6+a^2 b^4 t) y z-(a^2+b^2-c^2) (-1+t) (-b^2+a^2 t) (-a^2+c^2+a^2 t) (-b^2+b^2 t-c^2 t) z^2 = 0)
𝒞(P), cuando P varía sobre Γ, es:
(-a^4 + a^2 b^2 + a^2 c^2) y z
+ (a^2 b^2 - b^4 + b^2 c^2) z x +
(a^2 c^2 + b^2 c^2 - c^4) x y = 0,
que es la ecuación de la elipse de centro el . Pasa por los Xi, para i∈{110, 287, 648, 651, 677, 895, 1331, 1332, 1797, 1813, 1814, 1815, 2986, 2987, 2988, 2989, 2990, 2991, 4558, 4563, 8115, 8116, 8759, 9190, 13136, 13138, 14919, 16039, 17708, 18315, 38413, 38414}.
El centro de la cónica 𝒞() es X110, foco de la .
- Sábado, 18 de julio del 2020
Centro de homotecia externo de las circunferencias inscrita y circunscrita
El 18 de julio de 1918 nació el líder nacionalista negro Nelson Mandela, cuya larga prisión (1962-1990) y su ascensión a la Presidencia de Sudáfrica (1994-1999) simbolizará las aspiraciones de su pueblo.
Sean ABC un triángulo A'B'C' y su imagen mediante la homotecia que transforma la circunferencia circunscrita en la inscrita (su razón es r/R y su centro es X56, del ).
El de la circunferencia inscrita respecto a
A'B'C' es
X1469.
El A"B"C", de la circunferencia inscrita a ABC respecto a A'B'C', es perspectivo con ABC, con centro de perspectividad X65 (ortocentro del ).
El centro de la (bc(a+b)(a+c)(a-b-c)^2x^2- a(b+c)(a+b-c)(a-b+c)(a^2+a(b+c)+2bc)yz+ ... = 0) de ABC y A"B"C" es:
W = ( a^2(b+c)(a^2-(b-c)^2) (a^2 (b+c)-a (b^2+c^2)-b c (b+c)) : ... : ...),
que tiene números de búsqueda en
(7.15669680131694, 8.08134630993316, -5.25720456403870).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,9551}, {7,8049}, {42,181}, {55,34429}, {65,1418}, {73,3649}, {145,37558}, {256,13265}, {1064,1537}, {1071,3931}, {1214,15185}, {1284,2594}, {1404,2309}, {1409,2293}, {1818,3696}, {1827,1880}, {2171,2667}, {3747,21741}, {4068,4559}, {4334,5586}, {4343,14100}, {4424,11570}, {4551,29822}, {4552,25295}, {10052,24248}, {17077,17135}, {21035,21794}, {21859,22279}.
Los de ABC y A"B"C" (b c (-a + b + c)x+...=0) y el de A'B'C' y A"B"C", (b c (-a + b + c) (-a^2 + a b + a c + 2 b c)x+ ...=0), son paralelos y tinen la direccióm de X3669=(a(b-c)(a^2-(b-c)^2) :...:..), con respecto a la circunferencia inscrita de la recta que pasa por los puntos de y Nagel.
- Jueves, 16 de julio del 2020
El centro del triángulo X(31392)
El 16 de julio de 1801 nació Julius Plücker, matemático y físico alemán especialista en curvas algebraicas. Plücker generaliza el concepto de coordenadas homogéneas de Möebius, que aplica a la recta y al plano y a las curvas algebraicas construyendo una teoría analítica de la geometría proyectiva.
X31392 (Antreas Hatzipolakis and Angel Montesdeoca,
Hyacinthos 28850)
Let ABC be a triangle.
Denote:
(
O1) ,(
O1), (
O3) = the circumcircles of NBC, NCA, NAB, resp.
(
Oa) ,(
Ob), (
Oc) = the reflections of (
O1) ,(
O1), (
O3) in BC, CA, AB, resp.
They concurr at D = antigonal conjugate of N = X(1263).
The circumcircles of DAO
a, DBO
b, DCO
c are coaxial.
2nd (other than D=X(1263)) intersection is X(31392) = REFLECTION OF X(5) IN X(14051).
Barycentrics (a^4+(b^2-c^2)^2-a^2 (b^2+2 c^2)) (a^12-(b^2-c^2)^6-a^10 (4 b^2+3 c^2)+a^8 (5 b^4+5 b^2 c^2+3 c^4)-a^6 (3 b^4 c^2+2 b^2 c^4)+a^2 (b^2-c^2)^2 (4 b^6-6 b^4 c^2-3 b^2 c^4+3 c^6)+a^4 (-5 b^8+9 b^6 c^2+b^4 c^4+4 b^2 c^6-3 c^8)) : :
Dado un triángulo ABC, A' es el simétrico de A respecto a BC. La mediatriz de BA' corta a AC en Ab y la mediatriz de CA' corta a AB en Ac. Sea A" la proyección ortogonal de A' sobre la recta AbAc. Se definen B" y C" cíclicamente.
En coordenadas baricéntricas:
Ab = (a^2 (a^2 - b^2) : 0 : -a^4 - (b^2 - c^2)^2 + a^2 (2 b^2 + c^2)),
Ac = ( a^2(a^2- c^2) : -a^4 - (b^2 - c^2)^2 + a^2 (b^2 + 2 c^2) : 0),
A" = (2 a^12 - 7 a^10 (b^2 + c^2) - a^2 (b^2 - c^2)^4 (b^2 + c^2) +
10 a^8 (b^4 + b^2 c^2 + c^4) +
a^4 (b^2 - c^2)^2 (4 b^4 + 3 b^2 c^2 + 4 c^4) -
a^6 (8 b^6 + b^4 c^2 + b^2 c^4 + 8 c^6):
-(a^4 + (b^2 - c^2)^2 -
a^2 (b^2 + 2 c^2)) (a^8 - (b^2 - c^2)^3 (b^2 + c^2) -
2 a^6 (b^2 + 2 c^2) + 3 a^4 c^2 (b^2 + 2 c^2) +
a^2 (2 b^6 - b^4 c^2 + 3 b^2 c^4 - 4 c^6)):
-(a^4 + (b^2 - c^2)^2 -
a^2 (2 b^2 + c^2)) (a^8 + (b^2 - c^2)^3 (b^2 + c^2) -
2 a^6 (2 b^2 + c^2) + 3 a^4 b^2 (2 b^2 + c^2) +
a^2 (-4 b^6 + 3 b^4 c^2 - b^2 c^4 + 2 c^6))).
Las rectas AA", BB", CC" con concurren en X31392.
- Viernes, 10 de julio del 2020
Triángulos bilógicos y el centro X(34147)
El 10 de julio de 2007 falleció (a los 87 años) Paulette Libermann matemática francesa, que obtuvo importantes resultados en Geometría Diferencial: variedades simplécticas, cosimplécticas, de contacto, Poisson,... Su libro "Symplectic geometry and analytical mechanics", escrito en colaboración con Charles-Michel, es hoy en día un clásico en el tema y consulta imprescindible para geómetras e investigadores de la mecánica simpléctica.
Dado un triángulo ABC, una perpendicular, d, a BC corta a AC en Ab y a AB en Ac. El lugar geométrico del , D, de la recta d respecto a la circunferencia (AAbAc), cuando d varía, es una recta ℓa que pasa por A.
Procediendo cíclicamente, se obtienen las rectas ℓb y ℓc.
ABC y el triángulo A'B'C' formado por las rectas ℓa, ℓb y ℓc son .
La ecuación baricéntrica de la recta ℓa es:
(a^2 c^2 + b^2 c^2 - c^4) y + (a^2 b^2 - b^4 + b^2 c^2) z = 0.
A'=ℓb∩ℓc = (a^2 (a^2 - b^2 - c^2) : b^2 (a^2 - b^2 + c^2) : c^2 (a^2 + b^2 - c^2)).
El centro de perspectividad de ABC y A'B'C' es el circuncnetro, X3.
El centro de ortología de ABC respecto a A'B'C' es X64, del .
El centro de ortología de A'B'C' respecto a ABC es X1498, reflexión de X64 en el circuncentro.
El punto de intersección de la de los triangulos ABC y A'B'C' y su es X34147
En la
aplicación afín,
( σ(x:y:z) = (a^2 (-a^2 + b^2 + c^2)^2 x + a^2 (a^4 - 2 a^2 b^2 + b^4 - c^4) y + a^2 (a^4 - b^4 - 2 a^2 c^2 + c^4) z :
b^2 (a^4 - 2 a^2 b^2 + b^4 - c^4) x + b^2 (a^2 - b^2 + c^2)^2 y +
b^2 (-a^4 + (b^2 - c^2)^2) z :
c^2 (a^4 - b^4 - 2 a^2 c^2 + c^4) x + c^2 (-a^4 + (b^2 - c^2)^2) y +
c^2 (a^2 + b^2 - c^2)^2 z))
σ, que transforma ABC en A'B'C' los centros ortológicos se corresponden, σ(X64)=X1498. Sus punto fijos son el y los puntos del infinito de la , X2574 y X2575.
Otros pares {Xi, Xj=σ(Xi)} para {i, j} : {1, 3157}, {2, 3167}, {3, 155}, {4, 3}, {5, 1147}, {6, 6}, {9, 3211},
{11, 36059}, {15, 10661}, {16, 10662}, {19, 219}, {20, 12164}, {25,
394}, {27, 22139}, {28, 22136}, {30, 13754}, {31, 22130}, {32,
23128}, {33, 222}, {34, 7078}, {46, 1069}, {51, 2}, {52, 68}, {53,
577}, {54, 195}, {55, 3173}, {64, 1498}, {65, 1}, {66, 159}, {67,
2930}, {68, 9937}, {69, 19588}, {74, 399}, {75, 23075}, {76, 19597},
{92, 20760}, {112, 22146}, {113, 5504}, {115, 32661}, {125, 110},
{130, 18831}, {132, 17974}, {137, 15958}, {143, 5449}, {154, 37672},
{155, 15316}, {158, 20764}, {162, 22156}, {182, 19139}, {184, 1993},
{185, 4}, {193, 6391}, {196, 38288}, {208, 1433}, {225, 255}, {232,
3289}, {235, 1092}, {242, 17976}, {243, 17975}, {264, 20794}, {265,
2931}, {273, 20793}, {278, 22117}, {281, 20818}, {286, 23079}, {290,
3511}, {318, 20805}, {324, 23158}, {331, 23078}, {338, 1634}, {371,
10665}, {372, 10666}, {378, 18445}, {382, 12163}, {389, 5}, {393,
15905}, {397, 61}, {398, 62}, {403, 22115}, {407, 283}, {423, 20766},
{427, 184}, {428, 3917}, {429, 1437}, {430, 1790}, {460, 36212},
{468, 3292}, {485, 8909}, {511, 3564}, {512, 525}, {513, 521}, {515,
29211}, {516, 916}, {517, 912}, {518, 34381}, {520, 8057}, {523,
520}, {524, 8681}, {525, 8673}, {526, 9033}, {542, 14984}, {546,
12038}, {550, 15083}, {568, 14852}, {576, 8548}, {578, 12161}, {607,
22131}, {608, 22132}, {647, 32320}, {648, 22143}, {650, 36054}, {661,
23090}, {674, 9028}, {690, 9517}, {695, 3499}, {798, 23145}, {811,
23083}, {834, 23874}, {900, 8677}, {905, 34975}, {924, 523}, {973,
1209}, {974, 113}, {1075, 38281}, {1096, 22119}, {1112, 125}, {1131,
8912}, {1146, 101}, {1148, 38284}, {1154, 539}, {1173, 15047}, {1177,
15141}, {1181, 36747}, {1194, 3051}, {1199, 14627}, {1204, 11441},
{1205, 11061}, {1249, 38292}, {1395, 23129}, {1425, 3562}, {1474,
22133}, {1495, 323}, {1498, 37498}, {1499, 30209}, {1503, 511},
{1510, 6368}, {1514, 10564}, {1539, 12901}, {1562, 112}, {1587,
3311}, {1588, 3312}, {1593, 1181}, {1594, 49}, {1637, 1636}, {1770,
6238}, {1783, 22144}, {1824, 63}, {1826, 48}, {1827, 77}, {1828, 78},
{1829, 72}, {1830, 7004}, {1831, 201}, {1834, 58}, {1836, 55}, {1837,
56}, {1839, 71}, {1840, 4020}, {1841, 3990}, {1842, 3682}, {1843,
69}, {1844, 7100}, {1845, 1807}, {1846, 1795}, {1848, 3955}, {1851,
1260}, {1852, 7066}, {1853, 154}, {1854, 221}, {1856, 7125}, {1857,
7011}, {1858, 65}, {1859, 1214}, {1860, 4055}, {1861, 7193}, {1862,
3937}, {1863, 7053}, {1864, 57}, {1865, 2193}, {1870, 23071}, {1871,
26921}, {1872, 24467}, {1877, 22350}, {1878, 5440}, {1880, 22134},
{1881, 4100}, {1885, 185}, {1887, 17102}, {1890, 3781}, {1897,
22148}, {1898, 46}, {1899, 25}, {1900, 3916}, {1901, 284}, {1902,
1071}, {1903, 610}, {1905, 1060}, {1907, 10984}, {1969, 23076},
{1973, 20739}, {1974, 20806}, {1986, 265}, {1990, 3284}, {2052,
6638}, {2082, 218}, {2181, 23112}, {2182, 2323}, {2201, 20741},
{2203, 23130}, {2207, 23115}, {2211, 14965}, {2212, 22125}, {2262,
9}, {2331, 22124}, {2333, 22126}, {2356, 20744}, {2362, 1124}, {2390,
519}, {2393, 524}, {2489, 3049}, {2501, 647}, {2574, 2574}, {2575,
2575}, {2679, 17932}, {2777, 5663}, {2778, 2771}, {2781, 542}, {2818,
952}, {2883, 13346}, {2904, 15317}, {2935, 17838}, {2969, 1331},
{2970, 23181}, {3064, 652}, {3070, 371}, {3071, 372}, {3088, 19347},
{3168, 38283}, {3176, 38290}, {3186, 22152}, {3195, 23122}, {3269,
1625}, {3270, 651}, {3357, 32139}, {3426, 35237}, {3448, 12310},
{3527, 15805}, {3564, 34382}, {3566, 512}, {3567, 1656}, {3574, 54},
{3575, 5562}, {3627, 7689}, {3667, 32475}, {3827, 518}, {3852, 732},
{3867, 19126}, {3914, 31}, {3959, 2176}, {3981, 1613}, {4295, 3295},
{5064, 3796}, {5089, 20752}, {5095, 895}, {5101, 1473}, {5140, 6390},
{5151, 36058}, {5185, 1565}, {5254, 32}, {5286, 30435}, {5318, 15},
{5321, 16}, {5334, 11486}, {5335, 11485}, {5339, 22238}, {5340,
22236}, {5349, 5237}, {5350, 5238}, {5446, 12359}, {5452, 34960},
{5462, 9820}, {5480, 182}, {5523, 10317}, {5562, 6193}, {5663,
17702}, {5706, 36742}, {5721, 5398}, {5799, 13323}, {5800, 37492},
{5868, 5864}, {5869, 5865}, {5870, 1160}, {5871, 1161}, {5878,
12085}, {5887, 9928}, {5889, 12429}, {5890, 381}, {5895, 64}, {5928,
37581}, {6000, 30}, {6001, 517}, {6003, 30212}, {6102, 9927}, {6145,
2917}, {6146, 52}, {6152, 3519}, {6198, 23070}, {6201, 26348}, {6202,
26341}, {6240, 18436}, {6241, 382}, {6247, 6759}, {6291, 488}, {6331,
23180}, {6335, 22158}, {6336, 23081}, {6403, 11898}, {6406, 487},
{6467, 193}, {6524, 6617}, {6525, 1073}, {6591, 22383}, {6747,
23606}, {6748, 216}, {6749, 5158}, {6750, 19210}, {6751, 317}, {6752,
264}, {6753, 30451}, {6756, 1216}, {6759, 16266}, {6776, 1351},
{7009, 22161}, {7017, 23159}, {7046, 23089}, {7071, 23144}, {7079,
22153}, {7101, 23185}, {7119, 23150}, {7297, 17796}, {7507, 19357},
{7576, 23039}, {7577, 9703}, {7581, 6417}, {7582, 6418}, {7592,
36749}, {7649, 1459}, {7686, 1385}, {7687, 1511}, {7699, 11935},
{7722, 12902}, {7728, 12302}, {7745, 39}, {7952, 23072}, {8057,
30211}, {8550, 576}, {8674, 2850}, {8675, 9007}, {8676, 514}, {8735,
906}, {8736, 22118}, {8743, 22120}, {8744, 22121}, {8750, 22145},
{8751, 20740}, {8752, 23135}, {8754, 4558}, {8756, 22356}, {9001,
9051}, {9002, 9031}, {9134, 351}, {9306, 34966}, {9719, 6139}, {9730,
5654}, {9777, 10601}, {9781, 3526}, {9786, 17814}, {9927, 9932},
{9969, 141}, {9971, 599}, {10110, 140}, {10113, 12893}, {10117,
17847}, {10214, 34900}, {10374, 7070}, {10564, 12364}, {10572, 7352},
{10605, 18451}, {10619, 15801}, {10625, 9936}, {10628, 32423},
{10693, 2948}, {10721, 10620}, {10783, 11916}, {10784, 11917},
{10982, 36752}, {10990, 14094}, {11245, 51}, {11381, 20}, {11411,
12309}, {11424, 7592}, {11433, 5020}, {11435, 37543}, {11436, 34048},
{11438, 15068}, {11455, 3534}, {11457, 7517}, {11550, 22}, {11557,
23306}, {11572, 7488}, {11577, 13431}, {11743, 32348}, {11744, 2935},
{11745, 11793}, {11746, 5972}, {11799, 15136}, {11807, 10264},
{11808, 21230}, {11817, 34483}, {12007, 5097}, {12022, 568}, {12077,
17434}, {12099, 5642}, {12112, 37496}, {12133, 16163}, {12135,
23154}, {12143, 4173}, {12162, 12118}, {12233, 578}, {12239, 485},
{12240, 486}, {12241, 389}, {12242, 1493}, {12244, 12308}, {12250,
12315}, {12254, 12316}, {12290, 1657}, {12291, 13432}, {12292,
12121}, {12294, 6776}, {12298, 12257}, {12299, 12256}, {12664, 5709},
{12679, 10310}, {12688, 40}, {12902, 15085}, {13152, 30210}, {13198,
19504}, {13202, 74}, {13292, 12235}, {13366, 1994}, {13382, 546},
{13399, 14157}, {13403, 6102}, {13417, 3448}, {13419, 6101}, {13473,
21663}, {13474, 550}, {13567, 9306}, {13568, 5907}, {13630, 5448},
{13748, 9733}, {13749, 9732}, {13851, 186}, {13854, 22135}, {14053,
28786}, {14054, 28787}, {14055, 28788}, {14216, 7387}, {14230, 9738},
{14233, 9739}, {14248, 6461}, {14417, 13303}, {14593, 6503}, {14644,
32609}, {14645, 29130}, {14715, 22391}, {14717, 36949}, {14790,
9908}, {14853, 5050}, {14864, 17714}, {14912, 5093}, {14975, 23119},
{15004, 5422}, {15033, 15087}, {15118, 6593}, {15151, 6053}, {15232,
23361}, {15311, 6000}, {15313, 513}, {15320, 8053}, {15321, 2916},
{15353, 1651}, {15472, 19456}, {15473, 12358}, {15738, 30714},
{15752, 15748}, {15938, 15937}, {15946, 15945}, {16105, 16003},
{16228, 23224}, {16230, 684}, {16232, 1335}, {16240, 14919}, {16270,
16534}, {16318, 8779}, {16616, 13624}, {16621, 15644}, {16655,
10625}, {16656, 13348}, {16657, 9730}, {16658, 13340}, {16659,
37484}, {16879, 15077}, {17442, 22164}, {17634, 1697}, {17810,
17811}, {17840, 17842}, {17843, 17839}, {17853, 10706}, {17854,
7728}, {17856, 10721}, {17907, 23163}, {17923, 23166}, {17924,
22160}, {18022, 23173}, {18130, 37867}, {18344, 905}, {18376, 18324},
{18381, 26}, {18383, 1658}, {18390, 6644}, {18391, 999}, {18396,
37489}, {18400, 1154}, {18560, 34783}, {18569, 19908}, {18909, 1598},
{18912, 7506}, {18914, 5446}, {18916, 7529}, {19041, 6416}, {19042,
6415}, {19161, 1352}, {19463, 19462}, {19464, 19461}, {19467, 12160},
{20184, 1510}, {20186, 1499}, {20299, 156}, {20303, 34116}, {20410,
34897}, {20414, 15345}, {20417, 5609}, {20883, 23167}, {21045,
35327}, {21639, 37784}, {21645, 17496}, {21646, 31296}, {21650,
12383}, {21655, 12222}, {21656, 12221}, {21659, 5889}, {21660,
11271}, {22334, 16936}, {22336, 38402}, {22466, 2929}, {22533,
22550}, {22802, 12084}, {22829, 32455}, {22833, 22962}, {22948,
3521}, {22967, 5893}, {22968, 22966}, {23047, 13367}, {23249, 6221},
{23251, 1151}, {23253, 6449}, {23259, 6398}, {23261, 1152}, {23263,
6450}, {23267, 6199}, {23273, 6395}, {23290, 23286}, {23291, 8780},
{23292, 34986}, {23300, 206}, {23324, 11202}, {23327, 19153}, {24006,
23189}, {24862, 18315}, {25739, 2070}, {26869, 35259}, {26879,
18350}, {26926, 1843}, {27358, 36433}, {27370, 36952}, {27373,
14376}, {27376, 10316}, {28154, 790}, {30443, 6225}, {30496, 3360},
{31364, 31353}, {31978, 2883}, {32062, 376}, {32064, 9909}, {32085,
22138}, {32111, 37477}, {32140, 32048}, {32191, 24206}, {32246,
5181}, {32247, 32254}, {32274, 12584}, {32317, 32299}, {32337, 9920},
{32340, 7691}, {32345, 17824}, {32351, 10274}, {32352, 2888}, {32366,
3629}, {32369, 23358}, {32377, 6152}, {32393, 32391}, {32587, 10133},
{32588, 10132}, {32676, 23138}, {33565, 5898}, {33630, 33636},
{34146, 1503}, {34224, 6243}, {34417, 15066}, {34507, 9925}, {34563,
15062}, {34564, 1173}, {34565, 34545}, {34783, 12293}, {34854, 441},
{34944, 1619}, {34980, 648}, {35709, 3164}, {35884, 32078}, {36124,
20761}, {36125, 22141}, {36201, 2781}, {36747, 19458}, {36851,
37491}, {36990, 1350}, {37197, 35602}, {37473, 15069}, {37498,
17836}, {37765, 23164}, {38336, 8614}, {38345, 4559}, {38356, 35325},
{38357, 109}, {38358, 35326}, {38359, 35364}, {38360, 35365}, {38361,
35357}, {38362, 35350}, {38388, 934}, {38389, 100}, {38462, 23169}.
Imagen del :
σ(X7) = r ((r+4 R)^2-s^2) X3 + 4 R (R(r+4 R)-s^2) X77 =
(
a^2 (a^6
-2 a^5 (b+c)
+a^4 (b-c)^2
+4 a^3 b c (b+c)
-a^2 (b^4-4 b^3 c+10 b^2 c^2-4 b c^3+c^4)
+2 a (b^5-b^4 c-b c^4+c^5)
-(b-c)^2 (b^4+4 b^3 c+2 b^2 c^2+4 b c^3+c^4)) : ... : ...),
que tiene números de búsqueda en
(1.79318790747633, 1.44589782743362, 1.81203310561818).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,7083}, {3,77}, {6,29957}, {55,15374}, {521,3126}, {651,7071}, {912,6767}, {916,2293}, {954,3564}, {1069,3477}, {1200,2280}, {3270,23144}, {3781,7078}, {5942,28044}, {13754,15937}, {17262,23874}, {18621,34371}, {20760,38288}, {22117,22132}, {23078,23079}, {36059,37541}.
Imagen del :
σ(X8) = (r^2-s^2) X3 + 4R(r+R) X63 =
( a^2 (a^5 + a^4 (b + c) - 4 a^2 b c (b + c) - a (b^2 + c^2)^2- b^5 + 3 b^4 c + 2 b^3 c^2 + 2 b^2 c^3 + 3 b c^4 - c^5 ) : ... : ...),
que tiene números de búsqueda en ETC
(3.59872134271497, -2.84350964207725, 3.94829976824633).
Es la reflexión de X12410 en X3556.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,7083}, {3,63}, {6,29958}, {25,3868}, {38,1036}, {56,4641}, {64,2808}, {65,1773}, {101,4306}, {144,37399}, {145,28029}, {155,10680}, {159,9021}, {218,1400}, {219,23620}, {329,37415}, {394,23154}, {404,26866}, {405,17257}, {518,3556}, {521,6161}, {651,1398}, {758,9798}, {942,5020}, {956,3564}, {958,4643}, {960,22769}, {999,1201}, {1046,1460}, {1069,3478}, {1147,16203}, {1245,6391}, {1423,5247}, {1425,23144}, {1482,12309}, {1593,12528}, {1598,24474}, {1633,3189}, {1722,28039}, {1724,21362}, {1858,16541}, {2178,21874}, {2286,20818}, {2292,3295}, {2800,9910}, {3191,19782}, {3193,11401}, {3218,37257}, {3219,37246}, {3220,11523}, {3487,25514}, {3732,7754}, {3869,8192}, {3874,11365}, {3876,7484}, {3901,8185}, {3913,4952}, {4185,5905}, {4186,12649}, {4223,11036}, {4701,28040}, {5044,16419}, {5777,11479}, {5904,8193}, {6147,7535}, {6642,24475}, {6743,24309}, {7011,23159}, {7078,7193}, {7289,37613}, {7393,31835}, {7532,20256}, {9909,37547}, {10529,28034}, {10822,34931}, {12109,17810}, {12164,22770}, {12635,22654}, {15934,28787}, {16049,20078}, {20007,37328}, {20013,35998}, {22120,22144}, {22148,23072}, {23168,38290}.
- Lunes, 6 de julio del 2020
Triángulos homólogos y la cúbica de Darboux
El 6 de julio de 1907 nace Frida Kahlo, pintora mexicana que destacará por su sentido de la independencia y la rebeldía contra los hábitos sociales impuestos.
Su obra pictórica gira temáticamente en torno a su biografía y a su propio sufrimiento.
Dados un triángulo ABC y un punto P, sea el de P.
El punto Pc divide al segmento AB en la razón:
kab = APc : PcB.
El punto Pb divide al segmento AC en la razón:
kac = APb : PbC.
Ab y Ac son los puntos sobre BC tales que BAb : AbC = kab y CAc : AcB = kac. En coordenadas baricéntricas:
Ab = (0 : (a^2 - b^2) w + c^2 (2 u + w) : (-a^2 + b^2) w + c^2 (2 v + w)),
Ac = (0 : -a^2 v + c^2 v + b^2 (v + 2 w) : (a^2 - c^2) v + b^2 (2 u + v)).
Los puntos Bc, Ba, Ca, Cb son construidos cíclicamente.
Las rectas
BcCb,
CaAc,
AbBa no son concurrentes y el triángulo
A'B'C' formado por ellas
es perspectivo con
ABC si y solo si
P está sobre la circunferencia circunscrita o sobre la cúbica de Darboux (
K004).
Las rectas BcCb, CaAc, AbBa son concurrentes si solo si P está sobre la
cuártica 𝒬 de ecuación:
𝔖abc xyz
(b^2 c^2 (-a^2+b^2-c^2) (a^2+b^2-c^2) (-5 a^4+b^4+6 b^2 c^2+c^4) x^2+4 a^4 (-3 b^6 c^2-2 b^4 c^4-3 b^2 c^6+a^6 (b^2+c^2)+a^4 (-2 b^4-b^2 c^2-2 c^4)+a^2 (b^6+3 b^4 c^2+3 b^2 c^4+c^6)) y z-2 a^4 (c^2 (a^6-b^6+5 b^4 c^2+b^2 c^4+3 c^6+a^4 (b^2+c^2)+a^2 (-b^4-2 b^2 c^2-5 c^4)) y^2+b^2 (a^6+3 b^6+b^4 c^2+5 b^2 c^4-c^6+a^4 (b^2+c^2)+a^2 (-5 b^4-2 b^2 c^2-c^4)) z^2))y z = 0.
{i, j}:
{3, 2}, {4, 9289}, {20, 9307}, {40, 9311},
{110, 14223}, {111, 37860}.
Cuando P está sobre la , Γ, o sobre la
cúbica de Darboux,
( a^4 c^2 x^2 y+2 a^2 b^2 c^2 x^2 y-3 b^4 c^2 x^2 y-2 a^2 c^4 x^2 y+2 b^2 c^4 x^2 y+c^6 x^2 y+3 a^4 c^2 x y^2-2 a^2 b^2 c^2 x y^2-b^4 c^2 x y^2-2 a^2 c^4 x y^2+2 b^2 c^4 x y^2-c^6 x y^2-a^4 b^2 x^2 z+2 a^2 b^4 x^2 z-b^6 x^2 z-2 a^2 b^2 c^2 x^2 z-2 b^4 c^2 x^2 z+3 b^2 c^4 x^2 z+a^6 y^2 z-2 a^4 b^2 y^2 z+a^2 b^4 y^2 z+2 a^4 c^2 y^2 z+2 a^2 b^2 c^2 y^2 z-3 a^2 c^4 y^2 z-3 a^4 b^2 x z^2+2 a^2 b^4 x z^2+b^6 x z^2+2 a^2 b^2 c^2 x z^2-2 b^4 c^2 x z^2+b^2 c^4 x z^2-a^6 y z^2-2 a^4 b^2 y z^2+3 a^2 b^4 y z^2+2 a^4 c^2 y z^2-2 a^2 b^2 c^2 y z^2-a^2 c^4 y z^2 = 0)
como consecuencia de que ABC y A'B'C' son perspectivos, los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están sobre una misma cónica c(P) (llamada
de ABC y A'B'C').
Cuando P se mueve sobre la circunferencia circunscrita, la cónica c(P) degenera en dos rectas y el lugar geométrico de su punto de intersección, D, es un
trifollium
𝔖abc xyz
(2 (-a^2+b^2+c^2) x^2-2 (b^2+c^2) y z+(-a^2+b^2+c^2) (y^2+z^2))y z = 0
𝒯, con punto triple el baricentro y pasa por X14999, que corresponde al del punto del infinito de la . D es el baricentro cuando P coincide con los tres punto reales (a parte de A, B, C) de intersección Γ y 𝒬. En estos tres casos, las rectas BcCb, CaAc, AbBa son paralelas y sus direcciones son las de los conjugados isogonales de los antipodales de A, B,C.
Otra construcción de 𝒯, como lugar geométrico, es descrita en HG120620.
Si P es el foco de la , el punto singular de c(X110) es:
D110 = ( (2 a^6-2 a^4 (b^2+c^2)+a^2 (b^4+c^4)-(b^2-c^2)^2 (b^2+c^2))/(2 a^4-a^2 (b^2+c^2)-(b^2-c^2)^2)) : ... : ...),
que tiene números de búsqueda en
(2.03716448710585, 2.09865854235775, 1.24751726622631).
Es la reflexión de X14999 en X23967.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,525}, {30,74}, {287,524}, {297,671}, {441,14919}, {468,22265}, {542,7473}, {1304,35266}, {7799,11064}, {9214,18808}, {14999,23967}, {16280,36166}, {20423,35908}.
Si P es el , el punto singular de c(X111) es:
D111 = ( (2 a^6-6 a^4 (b^2+c^2)-(b^2+c^2)^3+9 a^2 (b^4+c^4))/((b^2-c^2) (5 a^2-b^2-c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(10.3090414049871, -1.60392550040776, -0.00694466626583736).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,2418}, {523,35179}, {1296,1499}, {2396,17937}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Si tomamos los puntos A'b y A'c, sobre BC, tales que CAb : AbB = kab y BAc : AcC = kac, entonces A'b y A'c son simétricos, respecto al punto medio de BC, de Ab y Ac, respectivamente.
Los puntos B'c, B'a, C'a, C'b son construidos cíclicamente.
Las rectas B'cC'b, C'aA'c, A'bB'a no son concurrentes y el triángulo A"B"C" formado por ellas
es perspectivo con ABC si y solo si P está sobre la circunferencia circunscrita o sobre la cúbica de Darboux.
Los triángulos A'B'C' y A"B"C" son obtenidos tomando puntos, sobre Γ o K004, simétricos respecto al circuncentro.
Si P está sobre Γ, el punto singular D' de la cónica c'(P), intersección de las rectas A'bB'cC'a y A'cB'aC'b es el punto singular de la cónica c(P'), siendo P' la reflexión de P en el circuncentro.
El punto D' es el punto M de HG120610.
- Viernes, 3 de julio del 2020
Los centros del triángulo X(9289) y X(9307)
El 3 de julio de 1897 nació Jesse Douglas, matemático estadounidense. Fue uno de los ganadores de la primera entrega de la Medalla Fields, otorgada en 1936. Se le premió por la resolución del problema de Plateau en 1930, que versa sobre si existe una superficie minimal acotada para una curva de Jordan.
Dado un triángulo ABC, con .
Ab el punto sobre BC tal que
AHc : HcB = BAb : AbC.
Ac el punto sobre BC tal que
AHb : HbC = CAc : AcB.
Se definen cíclicamente los puntos Bc, Ba, Ca, Cb.
El triángulo A'B'C' formado por las rectas BcCb, CaAc, AbBa es perspectivo con ABC, con centro de perspectividad X9289, de PU(37).
En consecuencia, los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están sobre una misma cónica 𝒞 (llamada de ABC y A'B'C') de ecuación baricéntrica
𝔖SASBSC xyz
SB SC x^2 - () y z = 0.
El centro de 𝒞 es:
W = ( a^4 (b^4-4 b^2 c^2+c^4)-a^2 (b^6-4 b^4 c^2-4 b^2 c^4+c^6)+b^2 c^2 (b^4-4 b^2 c^2+c^4) : ... : ...),
que tiene números de búsqueda en
(0.458329276111154, 4.24985124903085, 0.486923182065568).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {69,698}, {75,7209}, {183,2998}, {264,10010}, {325,1368}, {6375,6719}, {6379,37671}, {14913,32819}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
A'b el punto sobre BC tal que
AHc : HcB = CA'b : A'bB.
A'c el punto sobre BC tal que
AHb : HbC = BA'c : A'cC.
Se definen cíclicamente los puntos B'c, B'a, C'a, C'b.
El triángulo
A"B"C" formado por las rectas
B'cC'b,
C'aA'c,
A'bB'a es perspectivo con
ABC, con centro de perspectividad
X9307, de
PU(45).
En consecuencia, los seis puntos A'b, A'c, B'c, B'a, C'a y C'b están sobre una misma cónica 𝒞', de ecuación baricéntrica
𝔖abc xyz
SB SC ( SA^2 x^2 - (SA^2 + SB SC) y z) = 0.
El centro de 𝒞' es:
W' = ( (a^4
+ b^2 c^2 (b^2 - c^2)^2 (b^4 + 4 b^2 c^2 + c^4)
+ a^6 (-3 b^6 + 4 b^4 c^2 + 4 b^2 c^4 - 3 c^6)
+ a^4 (3 b^8 + 5 b^6 c^2 - 14 b^4 c^4 + 5 b^2 c^6 + 3 c^8)
- a^2 (b^2 - c^2)^2 (b^6 + 8 b^4 c^2 + 8 b^2 c^4 + c^6)
- (b^2 - c^2)^2) (a^8 (b^4 - 4 b^2 c^2 + c^4) ) : ... : ...),
que tiene números de búsqueda en ETC
(2.75688487453397, -1.60868256730172, 3.48195939410066).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {297,3981}, {458,1073}.
Los triángulos ABC y A"B"C" son . El centro de ortología de ABC respecto a A"B"C" es el y el centro de ortología de A"B"C" respecto a ABC es X185 (centro de ortología los triángulos órtico y
).
El punto fijo propio de la
transformación afín
( (x:y:z) ↦
(-a^4 (a^4+b^4+2 b^2 c^2-3 c^4-2 a^2 (b^2-c^2)) (a^4-3 b^4+2 b^2 c^2+c^4+2 a^2 (b^2-c^2)) (a^6 (b^2+c^2)-a^2 (b^2-c^2)^2 (b^2+c^2)-a^4 (b^4+c^4)+(b^2-c^2)^2 (b^4+c^4)) x-a^2 b^2 (a^2-b^2+c^2)^2 (a^4+b^4+2 b^2 c^2-3 c^4-2 a^2 (b^2-c^2)) (a^6 (6 b^2-3 c^2)+c^2 (b^2-c^2)^3+a^4 (-4 b^4-5 b^2 c^2+5 c^4)-a^2 (2 b^6-7 b^4 c^2+4 b^2 c^4+c^6)) y+a^2 c^2 (a^2+b^2-c^2)^2 (a^4-3 b^4+2 b^2 c^2+c^4+2 a^2 (b^2-c^2)) (3 a^6 (b^2-2 c^2)+b^2 (b^2-c^2)^3+a^4 (-5 b^4+5 b^2 c^2+4 c^4)+a^2 (b^6+4 b^4 c^2-7 b^2 c^4+2 c^6)) z:
a^4 (-a^2+b^2+c^2)^2 (a^4+b^4+2 b^2 c^2-3 c^4-2 a^2 (b^2-c^2)) (a^4-3 b^4+2 b^2 c^2+c^4+2 a^2 (b^2-c^2)) (-b^2 c^2+c^4+a^2 (2 b^2-c^2)) x-a^2 b^2 (a^4+b^4+2 b^2 c^2-3 c^4-2 a^2 (b^2-c^2)) (-3 a^12+c^2 (b^2-c^2)^4 (b^2+c^2)+a^10 (5 b^2+8 c^2)+a^8 (2 b^4-11 b^2 c^2-9 c^4)+a^6 (-6 b^6+6 b^2 c^4+8 c^6)+a^4 (b^8+2 b^6 c^2+4 b^4 c^4-2 b^2 c^6-5 c^8)+a^2 (b^10+2 b^6 c^4-8 b^4 c^6+5 b^2 c^8)) y-a^2 c^2 (a^2+b^2-c^2)^2 (a^4-3 b^4+2 b^2 c^2+c^4+2 a^2 (b^2-c^2)) (3 a^8-2 b^2 c^2 (b^2-c^2)^2-5 a^6 (b^2+c^2)+a^4 (b^4+12 b^2 c^2+c^4)+a^2 (b^6-5 b^4 c^2-5 b^2 c^4+c^6)) z:
-a^4 (-a^2+b^2+c^2)^2 (-b^4+b^2 c^2+a^2 (b^2-2 c^2)) (a^4+b^4+2 b^2 c^2-3 c^4-2 a^2 (b^2-c^2)) (a^4-3 b^4+2 b^2 c^2+c^4+2 a^2 (b^2-c^2)) x-a^2 b^2 (a^2-b^2+c^2)^2 (a^4+b^4+2 b^2 c^2-3 c^4-2 a^2 (b^2-c^2)) (3 a^8-2 b^2 c^2 (b^2-c^2)^2-5 a^6 (b^2+c^2)+a^4 (b^4+12 b^2 c^2+c^4)+a^2 (b^6-5 b^4 c^2-5 b^2 c^4+c^6)) y-a^2 c^2 (a^4-3 b^4+2 b^2 c^2+c^4+2 a^2 (b^2-c^2)) (-3 a^12+b^2 (b^2-c^2)^4 (b^2+c^2)+a^10 (8 b^2+5 c^2)+a^8 (-9 b^4-11 b^2 c^2+2 c^4)+a^6 (8 b^6+6 b^4 c^2-6 c^6)+a^4 (-5 b^8-2 b^6 c^2+4 b^4 c^4+2 b^2 c^6+c^8)+a^2 (5 b^8 c^2-8 b^6 c^4+2 b^4 c^6+c^10)) z)
)
σ, que aplica ABC en A"B"C" es X14249:
((3 a^4- 2 a^2 (b^2 + c^2) - (b^2 - c^2)^2 )/(a^2 (b^2 + c^2 - a^2)^2) : ... : ...).
- Miércoles, 1 de julio del 2020
Centros de homotecia que son pares bicéntricos
El 1 de julio de 1788 nació Jean-Victor Poncelet, matemático e ingeniero francés.
En la famosa polémica que enfrentó a los geómetras sintéticos con los analíticos, Poncelet se alineó claramente con los primeros. Reconoció en alguna ocasión que los resultados de la geometría sintética son más una consecuencia de la casualidad y la perspicacia del investigador que de la aplicación de un procedimiento general, y que en este sentido era superior la geometría analítica.
Dado un triángulo ABC, sean el y DEF el .
A1=DE∩MaMc, A2=DF∩MaMb. Se definen los puntos B1, B2 y C1, B2 cíclicamente.
La paralela por B a A1C1 interseca a la paralela por C a A1B1 en A'1.
La paralela por B a A2C2 interseca a la paralela por C a A2B2 en A'2.
Se definen B'1, B'2 y C'1, C'2 cíclicamente.
En coordenandas baricéntricas:
A1 = (b - c : b : c),
A'1 = (a c (a b + c (-b + c)) : -a^2 b c :
a^2 b (b - c) + b^2 (b - c) c - a (b^3 + b^2 c - 2 b c^2 + c^3)),
A2 = (b - c : -b : -c),
A'2 = (a b (b^2 + a c - b c) :
a^2 c (-b + c) + b c^2 (-b + c) -
a (b^3 - 2 b^2 c + b c^2 + c^3) : -a^2 b c).
Los triángulos y A'1B'1C'1 son homotéticos (por construcción) y el centro de homotecia es:
P1=(a^2 b+a c (c-b)+b c(b-c) : b^2 c+b a(a-c)+c a(c-a) : c^2 a+c b (b-a)+a b(a-b)).
Los triángulos y A'2B'2C'2 son homotéticos (por construcción) y el centro de homotecia es:
P2=(a^2 c+a b (b-c)+b c(b-c) : c^2 c+c a(a-b)+b a(b-a) : b^2 a+c b (c-a)+a c(a-c)).
P1 y P2 es un .
Su suma bicéntrica es X4885 ( del centro de homotecia externo de las circunferencias inscrita y circunscrita y el del )
y su diferencia bicéntrica es X3752 ( del y el punto intermedio).
La paralela por B1 a AC interseca a la paralela por C1 a AB en A''1.
La paralela por B2 a AC interseca a la paralela por C2 a AB en A''2.
Se definen B''1, B''2 y C''1, C''2 cíclicamente.
A"1 = (a^2 + b c : a (-a + c) : c(a - b)),
A"2 = (a^2 + b c : b (a - c) : a (-a + b)).
Los triángulos ABC y A''1B''1C''1 son homotéticos (por construcción) y el centro de homotecia es:
Q1=(a c(c-b) : a b(a - c) : b c(b-a)).
Los triángulos ABC y A''2B''2C''2 son homotéticos (por construcción) y el centro de homotecia es:
Q2=(a b(b - c) : b c(c-a ) : a c(a - b)).
Q1 y
Q2 es un par bicéntrico.
Su suma bicéntrica es X
244 (diferencia bicéntrica de
PU(34))
y su diferencia bicéntrica es X
661 ( del baricentro y X
244).
El de Q1 y Q2 es X244 y el producto trilineal de Q1 y Q2 es X1086, centro de la hipérbola circunscrita que pasa por el baricentro y por el .
La de Q1 y Q2 es X4579, de la recta que pasa por la 'crosssum' de PU(6) y la 'crosssum' de PU(10).
La de Q1 y Q2 es X3573, 'crossdifference' de todo par de puntos sobre la recta X244X661.
El tripolo de la recta Q1Q2 es X876, tripolo de la recta X244X661 (que pasa por Xi, para i∈{244, 661, 3124, 5098, 16592, 24197, 35505}).
La de Q1 y Q2 es X4369=3 X2 - X661.
- Lunes, 29 de junio del 2020
El centro del triángulo X(34224) como centro ortológico
-Una de las cosas más impresionantes sobre las matemáticas es que la gente que la practica no están normalmente interesadas en su aplicación, porque las matemáticas en si mismas son una forma de hermoso arte.-Danica McKellar.
Dado un triángulo ABC con circuncentro O=X3, ortocentro H=X4 y K=X6, la paralela por A a BC corta a las alturas BH y CH en Ab y Ac, respectivamente.
La paralela por Ab a AB corta a CH en A3 y la paralela por Ac a AC corta a BH en A2. Sea A' la proyección ortogonal de A sobre la recta A2A3.
Los puntos B' y C' se construyen procediendo cíclicamente sobre los lados de ABC.
Los triángulos
ABC y
A'B'C' son .
Su centro de perspectividad es el circuncentro. El de ABC respecto a A'B'C' es X70, del circuncentro del .
El centro de ortología de A'B'C' respecto a ABC es X34224 = X3X70∩X4X6.
Hyacinthos #29470
(Antreas Hatzipolakis and César Lozada)
Let ABC be a triangle and DEF the pedal triangle of H (orthic triangle).
Denote:
La = the reflection of HD in EF.
Lb = the reflection of HE in FD.
Lc = the reflection of HF in DE.
Ma = the reflection of La in OA.
Mb = the reflection of Lb in OB.
Mc = the reflection of Lb in OC.
The lines Ma,Mb,Mc concur at a point Q=
X(34224).
Denote:
A" = BC ∩ Ma.
B" = CA ∩ Mb.
C" = AB ∩ Mc.
The triangles ABC, A"B"C" are orthologic, with orthologic centers Q,S=
X(34225) = isogonal conjugate of X(34224).
Por el , X3, X70 y X34224 están alineados.
En coordenadas baricéntricas:
A' = (a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2) -
2 a^2 (b^4 - b^2 c^2 + c^4) : -b^2 (a^4 - 2 a^2 b^2 + b^4 -
c^4) : -c^2 (a^4 - b^4 - 2 a^2 c^2 + c^4).
La matriz M asociada de la transformación afín σ, que aplica ABC en A'B'C', tiene las entradas (las demás se deducen cíclicamente)
M[1,1] = -a^2 (a^2 - b^2) (a^2 - c^2) (b^2 - c^2) (a^2 + b^2 - c^2) (a^2 -
-a^4 b^2 + 2 a^2 b^4 - b^6 - a^4 c^2 - 2 a^2 b^2 c^2 + b^4 c^2 +
2 a^2 c^4 + b^2 c^4 - c^6,
M[1,2] = a^6 - 2 a^4 b^2 + a^2 b^4 - a^2 c^4,
M[1,3] = a^6 - a^2 b^4 - 2 a^4 c^2 + a^2 c^4.
Su punto fijo propio, correspondiente al valor propio λ=-2 a^2 b^2 c^2, es el simediano.
La imagen mediante σ de la recta de Sondat de los triánguls ABC y A'B'C' es la paralela a la por X34224=σ(X70).
Pares {X=Xi, X'=Xj=σ(X)}, para {i, j} : {3, 34783}, {4, 18560}, {5, 12370}, {6, 6}, {70, 34224}, {155, 12293}, {195, 6288}, {1993, 11442}, {1994, 5133}, {2904, 4}, {5095, 32239}, {8907, 5889}, {15317, 3}, {20303, 6146}, {34114, 6102}, {34116, 52}, {34438, 6293}, {38534, 1986}.
σ(X1) = ( a (a^5 (b + c) - a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2) -
2 a^3 (b^3 + c^3) + 2 a^2 (b^4 - b^2 c^2 + c^4) +
a (b^5 - b^4 c - b c^4 + c^5)) : ... : ...),
que tiene números de búsqueda en
(2.19824758168143, 3.08449987246549, 0.490665686347610).
Es la reflexión de Xi en Xj para los índices {i,j}: {1, 1858}, {1770, 15556}, {3901, 14054}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,90}, {11,24475}, {35,72}, {36,1071}, {46,1490}, {65,79}, {73,1725}, {201,4337}, {354,37735}, {392,24926}, {484,16143}, {517,6243}, {518,3633}, {758,10572}, {920,18446}, {942,7741}, {960,37525}, {971,10483}, {1046,3465}, {1210,11570}, {1399,1807}, {1478,12528}, {1479,3868}, {1737,5884}, {1770,15556}, {1864,37702}, {1898,3583}, {2099,18761}, {2646,5694}, {3057,6286}, {3244,12758}, {3586,3901}, {3612,5692}, {3746,12711}, {3754,16120}, {3874,30384}, {3894,9614}, {3962,5441}, {4067,4304}, {4324,16113}, {5010,31837}, {5119,5904}, {5425,12709}, {5432,31835}, {5444,25917}, {5570,37720}, {5691,5903}, {5720,17700}, {5777,7951}, {5885,17606}, {5902,5927}, {5930,11809}, {6256,10573}, {7082,37615}, {7280,13369}, {8614,18447}, {9627,23071}, {9943,37572}, {10058,12532}, {10090,26877}, {10222,17638}, {10391,37571}, {10950,14988}, {11009,12672}, {12047,18389}, {12560,18412}, {12616,12691}, {12675,21842}, {12680,36975}, {12739,16141}, {14793,24467}, {14872,37710}, {16193,31821}, {17637,22936}, {17660,24928}, {18254,27385}, {18393,31937}, {18395,34339}, {18398,23708}, {20612,21077}, {26201,37605}, {30274,37692}.
La imagen del baricentro es la reflexión del baricentro de ABC en el baricentro del :
σ(X2) = ( 2 a^6 - 3 a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2) +
2 a^2 (b^4 - b^2 c^2 + c^4) : ... : ...),
que tiene números de búsqueda en ETC
(3.39209297415901, 4.88583408212526, -1.30741740917573).
Es la reflexión de Xi en Xj para los índices {i,j}: {2, 11245}, {51, 11225}, {7576, 568}, {15305, 16657}, {34603, 3060}, {38323, 5890}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3167}, {3,32358}, {4,13292}, {5,1199}, {6,5133}, {20,18914}, {22,6515}, {24,18951}, {25,37644}, {30,34796}, {49,10018}, {51,542}, {52,10116}, {54,12359}, {68,7592}, {69,7485}, {97,26905}, {110,13567}, {125,34986}, {140,9545}, {154,7426}, {155,18912}, {182,37636}, {184,3580}, {185,10112}, {193,1370}, {195,13371}, {323,1368}, {343,5012}, {373,32068}, {378,18917}, {389,14516}, {394,18911}, {403,18445}, {427,1353}, {428,11002}, {468,9544}, {524,2979}, {539,9730}, {550,32608}, {568,7576}, {576,11550}, {858,1899}, {1147,26879}, {1351,7391}, {1352,5422}, {1493,13561}, {1503,3060}, {1591,5874}, {1592,5875}, {1594,12161}, {1986,10111}, {1992,11216}, {1995,11433}, {2888,7399}, {2895,7465}, {3090,31831}, {3146,13142}, {3519,37471}, {3567,12134}, {3575,34799}, {3618,7571}, {3681,5849}, {3818,15004}, {3845,38789}, {3873,5848}, {3917,5965}, {5064,5093}, {5159,9716}, {5446,16659}, {5576,18356}, {5889,6146}, {5890,38323}, {5921,6997}, {6102,6240}, {6193,12421}, {6636,37779}, {6676,11003}, {7378,11405}, {7394,9777}, {7484,11898}, {7488,31804}, {7496,15108}, {7503,11411}, {7544,11432}, {7667,34380}, {7762,14957}, {9140,15131}, {9637,26956}, {9704,10020}, {9820,26917}, {10114,21649}, {10169,25320}, {10601,15069}, {10605,16386}, {10625,18128}, {10691,33884}, {11004,31074}, {11064,26913}, {11232,12022}, {11413,18909}, {11422,23292}, {11427,31236}, {11457,36747}, {12007,37649}, {12111,12241}, {12160,37444}, {12163,34005}, {12278,13568}, {12317,13596}, {12370,18560}, {12429,22663}, {13321,13490}, {13366,14389}, {13595,14683}, {14788,36753}, {14831,18400}, {15018,37439}, {15032,15760}, {15140,25328}, {15305,16657}, {15331,36966}, {15559,32140}, {17809,37638}, {18583,37353}, {18925,38444}, {19130,34565}, {19161,27365}, {19481,21650}, {21969,29012}, {22467,32334}, {23291,30744}, {26881,32269}, {32136,34826}, {32423,38321}, {33586,37900}.
- Sábado, 27 de junio del 2020
Los centros del triángulo X(14380) y X(23286)
El 27 de junio de 1806 nació Augustus De Morgan, matemático y lógico británico nacido en la India. Conocido por formular las llamadas leyes de De Morgan, que consisten en dos equivalencias lógicas entre dos formas proposicionales: La negación de la disyunción de dos proposiciones es equivalente a la conjunción de las negaciones de ambas proposiciones.
La negación de la conjunción de dos proposiciones es equivalente a la disyunción de las negaciones de ambas proposiciones.
Dado un triángulo ABC, sea A' el punto de intersección de la paralela por el circuncentro a BC, con la recta que une A con el foco de la . Se definen B' y C' cíclicamente.
Las coordenadas baicéntricas de A' son:
(a^2 (b^2 - c^2) (-a^2 + b^2 +
c^2)^2 :
-b^2 (a^4 (b^2 + c^2) + (b^3 - b c^2)^2 -
a^2 (2 b^4 - b^2 c^2 + c^4)) :
c^2 (a^4 (b^2 + c^2) + (-b^2 c + c^3)^2 -
a^2 (b^4 - b^2 c^2 + 2 c^4))).
Los triángulos
ABC y
A'B'C' son , por construcción, y el centro paralelógico de
ABC respecto a
A'B'C' es
X14380.
El punto fijo finito de la aplicación afín σ, que transforma a ABC en A'B'C' es X23286.
La matriz M asociada de la transformación afín σ tiene las entradas (las demás se deducen cíclicamente)
M[1,1] = -a^2 (a^2 - b^2) (a^2 - c^2) (b^2 - c^2) (a^2 + b^2 - c^2) (a^2 -
b^2 + c^2) (-a^2 + b^2 + c^2)^2,
M[1,2] = a^2 (a^2 - b^2) (b^2 - c^2) (a^2 + b^2 - c^2) (-a^8 +
3 a^6 (b^2 + c^2) + b^2 c^2 (b^4 - c^4) -
a^4 (3 b^4 + 5 b^2 c^2 + 3 c^4) +
a^2 (b^6 + b^4 c^2 + 3 b^2 c^4 + c^6)),
M[1,3] =-(b^2 - c^2) (a^2 - b^2 +
c^2) (a^3 - a c^2)^2 (a^6 - b^6 + b^2 c^4 - a^4 (3 b^2 + 2 c^2) +
a^2 (3 b^4 + 2 b^2 c^2 + c^4)).
Su punto fijo propio, correspondientee al valor propio
λ=
-(a^2-b^2)(a^2-c^2)(b^2-c^2)(b+c-a)(a-b+c)(a+b-c)(a+b+c)(b^2+c^2-a^2)(a^2-b^2+c^2)(a^2+b^2-c^2),
es
X23286 = (a^2 (b^2 - c^2) (b^2 + c^2 - a^2) /((b^2 - c^2)^2 - a^2 (b^2 + c^2)):...:...).
OTRA PROPIEDAD GEOMÉTRICA DEL PUNTO A':
Si H=X4 es el ortocentro y P es un punto variable sobre la circunferencia circunscrita, la mediatriz de PH corta a BC, CA, AB en D, E,F, respectivamente.
El lugar geométrico del circuncentro Oa del triángulo AEF, cuando P varía, es una hipérbola ℋa, con asíntotas paralelas a las alturas BH y CH. El de la respecto a ℋa es el punto A'.
Si P = (a^2(t-1)t : -b^2(t-1) : c^2t),
Oa = (a^8 (-1 + t) t -
3 a^6 (b^2 + c^2) (-1 + t) t + (b^2 - c^2)^2 (b^2 (-1 + t) -
c^2 t)^2 -
a^2 (b^2 - c^2) (c^4 (1 - 3 t) t + b^4 (2 - 5 t + 3 t^2)) +
a^4 (4 b^2 c^2 (-1 + t) t + c^4 t (-3 + 4 t) +
b^4 (1 - 5 t + 4 t^2)) :
b^2 (b^2 c^4 (1 - 3 t) + b^6 (-1 + t) +
2 c^6 t + a^2 c^4 (-3 + t) t - a^6 (-1 + t) t - a^2 b^4 (-2 + t + t^2) +
a^4 b^2 (-1 - t + 2 t^2)) :
-c^2 (b^4 c^2 (2 - 3 t) + 2 b^6 (-1 + t) + c^6 t + a^4 c^2 (3 - 2 t) t + a^2 c^4 (-3 + t) t +
a^6 (-1 + t) t - a^2 b^4 (-2 + t + t^2)).
El lugar geométrico de Oa es la hipérbola ℋa, de ecuación:
(-a^4 b^2 c^2 + a^2 b^4 c^2 + a^2 b^2 c^4) x^2 + (-a^6 c^2 +
2 a^4 b^2 c^2 - 3 a^2 b^4 c^2 + 2 b^6 c^2 + 3 a^4 c^4 -
2 a^2 b^2 c^4 - 3 b^4 c^4 - 3 a^2 c^6 + c^8) x y + (a^6 c^2 -
3 a^4 b^2 c^2 + 2 a^2 b^4 c^2 - 3 a^4 c^4 + a^2 b^2 c^4 -
b^4 c^4 + 3 a^2 c^6 + 2 b^2 c^6 - c^8) y^2 + (-a^6 b^2 +
3 a^4 b^4 - 3 a^2 b^6 + b^8 + 2 a^4 b^2 c^2 - 2 a^2 b^4 c^2 -
3 a^2 b^2 c^4 - 3 b^4 c^4 + 2 b^2 c^6) x z + (-a^8 + 3 a^6 b^2 -
3 a^4 b^4 + a^2 b^6 + 3 a^6 c^2 - 6 a^4 b^2 c^2 + 5 a^2 b^4 c^2 -
2 b^6 c^2 - 3 a^4 c^4 + 5 a^2 b^2 c^4 + 4 b^4 c^4 + a^2 c^6 -
2 b^2 c^6) y z + (a^6 b^2 - 3 a^4 b^4 + 3 a^2 b^6 - b^8 -
3 a^4 b^2 c^2 + a^2 b^4 c^2 + 2 b^6 c^2 + 2 a^2 b^2 c^4 -
b^4 c^4) z^2=0.
- Lunes, 22 de junio del 2020
Los centros 2X3+X648 y 4X3-X648
El 22 de junio de 1925 falleció, a la edad de 76 años, Felix Christian Klein, matemático alemán que demostró que las geometrías métricas, euclidianas o no euclidianas, constituyen casos particulares de la geometría proyectiva. En 1872 presentó una notable clasificación de la geometría, el "programa de Erlangen", que reduce el estudio de las diferentes geometrías al de sus grupos de simetrías respectivos.
Describió por primera vez en 1882 lo que se conoce hoy como botella de Klein.
Dados un triángulo ABC y un punto P, las circunferencias de diámetros AP, BP, CP, vuelven a corta a la circunferencia circunscrita en A', B', C', respectivamente.
Si P' es el simétrico de P respecto al circuncentro, O=X3, sean Ba, Ca los puntos de intersección de la recta A'P con las rectas BP', CP', respectivamente.
Cíclicamente, se definen los puntos Cb, Ab, Ac, Bc.
Los segmentos AbBa, BcCb y CaAc son diámetros de una misma cónica 𝒞(P), con centro el circuncentro.
Cuando P recorre una recta d, que pasa O, las p y p' de P y de P', respecto a
𝒞(P),
pasan por sendos puntos fijos, simétricos respecto a O, Wd=2X3+D y W'd=4X3-D (siendo D el de la recta d).
El lugar geométrico de Wd, cuando d gira alrededor de O, es una
cónica,
( (4 a^6 b^4 c^2-4 a^4 b^6 c^2-4 a^2 b^8 c^2+4 b^10 c^2+4 a^6 b^2 c^4+8 a^4 b^4 c^4+4 a^2 b^6 c^4-16 b^8 c^4-4 a^4 b^2 c^6+4 a^2 b^4 c^6+24 b^6 c^6-4 a^2 b^2 c^8-16 b^4 c^8+4 b^2 c^10) x^2+(a^10 c^2+5 a^8 b^2 c^2-6 a^6 b^4 c^2-6 a^4 b^6 c^2+5 a^2 b^8 c^2+b^10 c^2-a^8 c^4-4 a^6 b^2 c^4+10 a^4 b^4 c^4-4 a^2 b^6 c^4-b^8 c^4-6 a^6 c^6-18 a^4 b^2 c^6-18 a^2 b^4 c^6-6 b^6 c^6+14 a^4 c^8+28 a^2 b^2 c^8+14 b^4 c^8-11 a^2 c^10-11 b^2 c^10+3 c^12) x y+(4 a^10 c^2-4 a^8 b^2 c^2-4 a^6 b^4 c^2+4 a^4 b^6 c^2-16 a^8 c^4+4 a^6 b^2 c^4+8 a^4 b^4 c^4+4 a^2 b^6 c^4+24 a^6 c^6+4 a^4 b^2 c^6-4 a^2 b^4 c^6-16 a^4 c^8-4 a^2 b^2 c^8+4 a^2 c^10) y^2+(a^10 b^2-a^8 b^4-6 a^6 b^6+14 a^4 b^8-11 a^2 b^10+3 b^12+5 a^8 b^2 c^2-4 a^6 b^4 c^2-18 a^4 b^6 c^2+28 a^2 b^8 c^2-11 b^10 c^2-6 a^6 b^2 c^4+10 a^4 b^4 c^4-18 a^2 b^6 c^4+14 b^8 c^4-6 a^4 b^2 c^6-4 a^2 b^4 c^6-6 b^6 c^6+5 a^2 b^2 c^8-b^4 c^8+b^2 c^10) x z+(3 a^12-11 a^10 b^2+14 a^8 b^4-6 a^6 b^6-a^4 b^8+a^2 b^10-11 a^10 c^2+28 a^8 b^2 c^2-18 a^6 b^4 c^2-4 a^4 b^6 c^2+5 a^2 b^8 c^2+14 a^8 c^4-18 a^6 b^2 c^4+10 a^4 b^4 c^4-6 a^2 b^6 c^4-6 a^6 c^6-4 a^4 b^2 c^6-6 a^2 b^4 c^6-a^4 c^8+5 a^2 b^2 c^8+a^2 c^10) y z+(4 a^10 b^2-16 a^8 b^4+24 a^6 b^6-16 a^4 b^8+4 a^2 b^10-4 a^8 b^2 c^2+4 a^6 b^4 c^2+4 a^4 b^6 c^2-4 a^2 b^8 c^2-4 a^6 b^2 c^4+8 a^4 b^4 c^4-4 a^2 b^6 c^4+4 a^4 b^2 c^6+4 a^2 b^4 c^6) z^2 = 0)
con centro X5085 = 2X3 + X6 y pasa por X5622=2X3+X895, X15035=2X3+X110
En particular, si P recorre la , las p y p' de P y de P', respecto a
𝒞(P),
( Ecuación baricéntrica:
𝔖abc xyz
(b^2-c^2) (a^2-b^2-c^2) ((a^2+b^2-c^2) (a^2-b^2+c^2) (b^2+(-a^2+b^2+c^2) t) (c^2+(-a^2+b^2+c^2) t)x^2+2 (b^2 c^2 (b^2-c^2)^2 t+a^2 (b^2-c^2)^2 (b^2+c^2) t^2+a^8 (1+3 t (1+t))-a^6 (b^2+c^2) (2+t (6+5 t))+a^4 (b^4 (1+t (3+t))+c^4 (1+t (3+t))+b^2 c^2 (2+t (5+6 t))))y z) = 0.
)
pasan por sendos puntos fijos, We=2X3+X648 y W'e=4X3-X648 (X648 es el de la recta de Euler):
We = ( 3 a^12-7 a^10 (b^2+c^2)+a^8 (4 b^4+11 b^2 c^2+4 c^4)-4 a^6 b^2 c^2 (b^2+c^2)-a^2 (b^2-c^2)^2 (b^2+c^2)^3+a^4 (b^2-c^2)^2 (b^4+4 b^2 c^2+c^4)-b^2 c^2 (b^2-c^2)^4 : ... : ...),
que tiene números de búsqueda en
(4.20051922069914, 4.17437375974015, -1.18798776131225).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,98}, {3,648}, {4,23583}, {30,250}, {95,549}, {107,37926}, {112,376}, {381,36794}, {631,15526}, {868,20774}, {2790,35278}, {2799,21166}, {3284,35474}, {5050,20792}, {9033,11845}, {9307,15078}, {16075,30528}, {19179,37471}, {33695,38323}, {36898,37930}.
W'e = ( 3 a^12
-5 a^10 (b^2+c^2)
+a^8 (2 b^4+7 b^2 c^2+2 c^4)
+a^6 (-6 b^6+4 b^4 c^2+4 b^2 c^4-6 c^6)
+a^4 (b^2-c^2)^2 (11 b^4+14 b^2 c^2+11 c^4)
-a^2 (b^2-c^2)^2 (5 b^6+9 b^4 c^2+9 b^2 c^4+5 c^6)
+b^2 c^2 (b^2-c^2)^4 : ... : ...),
que tiene números de búsqueda en ETC
(9.36420656769355, 7.61552809372266, -5.95356569114371).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,107}, {3,648}, {20,15526}, {30,30716}, {69,74}, {287,1350}, {2781,35278}, {2799,34473}, {2972,37926}, {3163,10979}, {3523,23583}, {5622,13479}, {9033,15055}.
Las polares de P y de P', respecto a
𝒞(P')
( Ecuación baricéntrica:
𝔖abc xyz
(b^2-c^2) (a^2-b^2-c^2) ((a^2+b^2-c^2) (a^2-b^2+c^2) ((a-c) (a+c) t+b^2 (1+t)) ((a-b) (a+b) t+c^2 (1+t))x^2+2 (a^2 (b^2-c^2)^2 (b^2+c^2) t^2-b^2 c^2 (b^2-c^2)^2 t (1+2 t)+a^8 (1+t+t^2)-a^6 (b^2+c^2) (2+t (2+t))+a^4 (b^4 (1+t-t^2)+c^4 (1+t-t^2)+b^2 c^2 (2+t (3+4 t))))y z) = 0.
)
pasan por W'e y We, respectivamente.
Cuando P se mueve sobre el los puntos fijos son X15035=2X3+X110 y X15055=4X3-X110
Cuando P se mueve sobre la recta X3X647 los puntos fijos son X5622=2X3+X895 y 4X3-X895
4X3-X895 = ( a^2 (a^2-b^2-c^2) (a^8+a^6 (b^2+c^2)-a^4 (3 b^4+b^2 c^2+3 c^4)-a^2 (b^6-3 b^4 c^2-3 b^2 c^4+c^6)+(b^2-c^2)^2 (2 b^4+b^2 c^2+2 c^4)) : ... : ...),
que tiene números de búsqueda en ETC
(8.68373252025191, 6.56677967646236, -4.91344414960583).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,895}, {6,15051}, {20,1632}, {22,110}, {25,35904}, {69,74}, {113,28419}, {125,7386}, {141,10733}, {159,12825}, {182,15036}, {186,249}, {265,28725}, {343,9140}, {378,11188}, {858,15142}, {1092,7556}, {1176,5504}, {1177,7488}, {1204,27082}, {1205,13348}, {1352,35481}, {1370,12827}, {1503,13445}, {1511,10752}, {1568,19924}, {1992,11438}, {1994,19161}, {2063,9909}, {2071,2393}, {2777,35513}, {2854,5621}, {2882,15915}, {2930,15054}, {3260,35474}, {3289,5104}, {3523,15118}, {3564,38723}, {3619,7687}, {5562,8718}, {5642,37669}, {5663,35243}, {5889,32245}, {5972,6353}, {6194,9769}, {6593,15020}, {6699,28438}, {6776,38726}, {7426,11064}, {7484,12099}, {7503,32246}, {7527,29959}, {7691,32233}, {8681,21663}, {9924,11598}, {9967,12893}, {10296,19510}, {10519,17702}, {10545,38072}, {10627,15132}, {10766,32661}, {11413,34787}, {11440,15069}, {11449,34117}, {11579,14810}, {11744,15585}, {11746,17825}, {12117,14833}, {12278,34118}, {12279,15581}, {12310,13416}, {12596,19129}, {13198,22352}, {14643,37971}, {14853,38793}, {14909,30209}, {15021,16010}, {15057,25328}, {15116,37444}, {15128,16196}, {15920,35387}, {18438,19138}, {19121,35228}, {20417,32255}, {21850,38794}, {23049,30744}, {23296,31829}, {25320,38727}, {25711,37486}, {28408,31670}, {30714,32247}, {34148,37473}, {37784,37941}.
- Sábado, 20 de junio del 2020
La isocúbica circular pK(X6,X523)
El 20 de junio de 1838 nació el matemático alemán Karl Theodor Reye.
Investigó en geometría proyectiva siguiendo los trabajos de Steiner y Standt. Escribió Geometría sintética (1879), Geometría de la posición (1899). La configuración de Reye de 12 puntos, 12 planos y 16 líneas lleva su nombre. En la notación de configuraciones, la configuración de Reye se escribe como 124163. Si la configuración de Reye se forma a partir de un cubo en un espacio tridimensional, entonces hay 12 planos que contienen cuatro líneas cada uno: los seis planos de la cara del cubo y los seis planos a través de pares de bordes opuestos del cubo. La intersección de estos 12 planos y 16 líneas con otro plano en posición general produce una configuración 163124, la dual de la configuración Reye.
Dados un triángulo ABC y un punto P, sean D, E, F las reflexiones de P en BC, CA, AB, respectivamente.
Las circunferencias de diámetros
AD, BE, CF son concurrentes si y solo si
P esta sobre la isocúbica isogonal circular con pivote el conjugado isogonal del foco de la parábola de Kiepert,
pK(X6, X523).
a^2 y z+b^2 z x+c^2 x y+
(x+y+z) (-(((a^4 u-2 a^2 b^2 u+b^4 u-2 b^2 c^2 u+c^4 u+a^4 w-a^2 b^2 w+a^2 c^2 w) y)/(2 a^2 (u+v+w)))-((a^4 u+b^4 u-2 a^2 c^2 u-2 b^2 c^2 u+c^4 u+a^4 v+a^2 b^2 v-a^2 c^2 v) z)/(2 a^2 (u+v+w)))
=0.
Las ecuaciones de las circunferencias Γb y Γc, de diámetros BE y CF, respectivamente, se obtienen por permutación cíclica.
El de esta tres circunferencias es:
W = (a^6 v w-a^4 (b^2+c^2) v w-(b^2-c^2)^2 u (c^2 v+b^2 w)-a^2 u (b^2 c^2 u-c^4 v-b^4 w) : ... : ...).
La aplicación P ↦ W coincide con "QF mapping and related curves" (Another description added on 2020-06-21 in Table 74. Bernard Gibert).
El punto W está sobre las tres circunferencias si y sólo si P satisface a la ecuación:
𝔖abc xyz
(b^2-c^2) x (c^2 y^2-b^2 z^2) = 0.
Se trata de la pivotal, isogonal y , de pivote X523, del foco, X110, de la . Pasa por los centros X1 (incentro), X110, X523, X21381. Su singular es X74. conjugado isogonal del punto del infinito de la . Su asíntota real pasa por X110 y X476 ().
Puntos W, de intersección de las circunferencias Γa, Γb y Γc, para P=Xi:
W1=X80 (reflexión del incentro en el ), W110=X476, W523=X265 (reflexión del circuncentro en el centro de la ), W21381 es la reflexión de X80 en X34172.
W21381 = ( (b-c)^4 (b+c)^3 (b^2-b c+c^2)-(b^2-c^2)^2 (b^4-3 b^3 c+3 b^2 c^2-3 b c^3+c^4) a+(-b^7+4 b^5 c^2-3 b^4 c^3-3 b^3 c^4+4 b^2 c^5-c^7) a^2+(b^6-3 b^5 c-b^4 c^2+5 b^3 c^3-b^2 c^4-3 b c^5+c^6) a^3+b c (2 b^3-b^2 c-b c^2+2 c^3) a^4+b c (b^2-b c+c^2) a^5+(-b^3-b^2 c-b c^2-c^3) a^6+(b^2-b c+c^2) a^7+(b+c) a^8-a^9 : ... : ...),
que tiene números de búsqueda en
(-13.5004939878839, -1.94682349191960, 11.2194625861059).
Es la reflexión de X80 en X34172.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {79,476}, {80,758}, {226,2222}, {1836,36815}, {2607,5520}, {2651,5057}, {6003,34789}, {17768,34311}.
La tangente en el incentro a pK(X6, X523) es paralela a su asíntota real, por lo que X523 es su .
El punto tangencial de X110 es:
Z = ( a^2 (a^2-b^2) (a^2-c^2) (a^10-2 a^8 (b^2+c^2)+a^6 (b^4+4 b^2 c^2+c^4)-(b^2-c^2)^2 (b^6+c^6)-a^4 (b^6+b^4 c^2+b^2 c^4+c^6)+a^2 (2 b^8-4 b^6 c^2+5 b^4 c^4-4 b^2 c^6+2 c^8)) : ... : ...),
que tiene números de búsqueda en ETC
(-0.910529457728449, 0.905192850044087, 3.43423687390545).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,2612}, {3,9218}, {5,34365}, {20,31990}, {32,6792}, {512,14366}, {2613,2617}, {4226,14884}, {6328,36163}, {7785,9514}, {13434,18114}.
El punto tangencial de X21381 es:
T = ( (b^2-c^2)/(a^10-2 a^8 (b^2+c^2)+a^6 (b^4+4 b^2 c^2+c^4)-a^4 (b^6+b^4 c^2+b^2 c^4+c^6)+a^2 (2 b^8-4 b^6 c^2+5 b^4 c^4-4 b^2 c^6+2 c^8)-(b^2-c^2)^2 (b^6+c^6)) : ... : ...),
que tiene números de búsqueda en ETC
(-7.28156569882929, 7.32449451721387, 1.93058321560368).
El centro radical W de las circunferencias Γa, Γb y Γc está sobre la circunferencia circunscrita, Γ, si y solo sí P está sobre la cónica 𝒞 circunscrita que pasa por el foco de la y por el .
El centro de la
cónica
( a^4 c^4 x y+a^2 b^2 c^4 x y+b^4 c^4 x y-2 a^2 c^6 x y-2 b^2 c^6 x y+c^8 x y+a^4 b^4 x z-2 a^2 b^6 x z+b^8 x z+a^2 b^4 c^2 x z-2 b^6 c^2 x z+b^4 c^4 x z+a^8 y z-2 a^6 b^2 y z+a^4 b^4 y z-2 a^6 c^2 y z+a^4 b^2 c^2 y z+a^4 c^4 y z = 0)
𝒞 es X11597, punto medio de X54X110, su es X50, pasa además por los centros X10411, X14355, X14385, X14591, X17104, X34210 y por
los conjugados isogonales del par bicéntrico PU(5).
P(5) and U(5) lie on the central line X(5)X(523).
The points PU(5) lie on the orthocentroidal circle. (Randy Hutson, September 10, 2012)
- Martes, 16 de junio del 2020
Triángulos pedales de los conjugados isogonales de los puntos de Napoleón
Julius Weingarten fue un matemático alemán, que falleció el 16 de junio de 1910, a los 74 años de edad. Contribuyó en geometría diferencial de las superficies, como en las Ecuaciones de Weingarten.
Se conocen como superficies de Weigarten aquellas para las que existe un relación entre sus curvaturas principales. Por ejemplo: superficies mínimas (k1+k2=0), superficies de curvatura gaussiana constante (k1k2=cte.), paraboloide de revolución (k2-a2k13=0, parábola x2=2az, y=0 que gira alrededor de OZ).
Dado un triángulo ABC, sea el triángulo homotético a ABC tal que los triángulos equiláteros B1C1A', C1A1B', A1B1C' levantados exteriormente sobre los lados de verifiquen que A', B', C' estén sobre los lados BC, CA, AB, respectivamente.
El triángulo es homotético a ABC en una homotecia con centro en punto P (con coordenadas baricéntricas (u:v:w)) y razón k. Imponiendo que el punto imagen de B1 en el giro de centro C1 y amplitud π/3,
(√3a2k(u+v+w)+2(k-1)u :
√3a2k(u+v+w)+2(k-1)uS:
√3a2k(u+v+w)+2(k-1)uS),
esté sobre BC, se obtiene la relación:
2 (k-1) S u + √3 a2 k (u + v + w) = 0.
Procediendo cíclicamente, se obtiene otras dos relaciones. Al resolver el sistema forma por estas tres ecuaciones se obtiene que P es el y
k = S/(S + √3 Sω).
A'B'C' es el de
X61, del .
X61 = (
a^2 (2 S (a^2 + 2 (b^2 + c^2)) -
√3 (a^4 - a^2 (b^2 + c^2) - 2 b^2 c^2)): ... : ...).
Las circunferencias circunscritas a los triángulos B1C1A', C1A1B', A1B1C' concurren en el punto W1, intersección del con la recta X32X616 (que pasa por el del simediano, X32, y el , X616, del ). W1 también es la reflexión de X11128 (cuadrado baricéntrico del , X299, del segundo punto de Fermat) en X620 (punto medio de los complementos de los puntos de Fermat).
W1 tiene números de búsqueda en
(0.845800443410649, 1.26263942093842, 2.37616006276056).
Si Oa, Ob, Oc son los circuncentros de los triángulos B1C1A', C1A1B', A1B1C', entonces y son perspectivos, con centro de perspectividad Z1, punto de intersección de la recta que pasa por los con la recta X396X629 (X396 es
el punto medio de los primeros puntos de Fermat e y X629 es complemento del primer punto de Napoleón).
Z1 tiene números de búsqueda en ETC
(1.05607701256880, 1.44508560964729, 2.15280043865835).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Si el triángulo homotético a ABC tal que los triángulos equiláteros B2C2A", C2A2B", A2B2C" levantados interiormente sobre los lados de verifiquen que A", B", C" estén sobre los lados BC, CA, AB, respectivamente, entonces:
A"B"C" es el triángulo homtético a
ABC, mediante la homotecia de centro el simediano y razón S/(S - √
3 S
ω).
A"B"C" es el triángulo pedal de
X62, conjugado isogonal del segundo punto de Napoleón.
X62 = (
a^2 (2 S (a^2 + 2 (b^2 + c^2)) +
√3 (a^4 - a^2 (b^2 + c^2) - 2 b^2 c^2)): ... : ...).
Las circunferencias circunscritas a los triángulos B2C2A", C2A2B", A2B2C" concurren en el punto W2, sobre el , reflexión de X11129 (cuadrado baricéntrico de X298, conjugado isotómico del segundo punto de Fermat) en X620 (punto medio de los complementos de los puntos de Fermat).
W2 tiene números de búsqueda en ETC
(0.1943466373, 0.2586170771, 3.3719234421).
es perspectivo al tiángulo formado por los circuncentros de los triángulos B1C1A", C1A1B", A1B1C". El centro de perspectividad Z2 es la intersección de la recta que pasa por los puntos de Napoleón con la recta X395X630 (X395 es el punto medio de los segundos puntos de Fermat e isodinámico y X630 es complemento del segundo punto de Napoleón).
Z2 tiene números de búsqueda en ETC
(5.0733490054, -1.3707678117, 2.2481118875).
- Viernes, 12 de junio del 2020
La cúbica de Darboux y un trifolium
El 12 de junio de 1929 nació, Ana Frank, joven judía alemana, cuyo diario sobre la vida clandestina de su familia en una buhardilla de unos almacenes de Ámsterdam durante dos años, en la cruel ocupación alemana de los Países Bajos, se convertirá en un símbolo contra la barbarie nazi. Morirá en un campo de exterminio en 1945.
Dados un triángulo ABC y un punto P, sea DEF su . La paralela por D a AB corta a AC en Ab y la paralela por D a AC corta a AB en Ac. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
Los seis puntos
Ab,
Ac,
Bc,
Ba,
Ca,
Cb están sobre una misma cónica 𝒞, si
P está sobre la circunferencia circunscrita o sobre la cúbica de Darboux (
K004, en el catálogo de Bernard Gibert).
( (a^2+b^2-c^2) x^3 y+(-2 a^2-2 b^2) x^2 y^2+(a^2+b^2-c^2) x y^3+(a^2-b^2+c^2) x^3 z+(-2 a^2+2 b^2+2 c^2) x^2 y z+(2 a^2-2 b^2+2 c^2) x y^2 z+(-a^2+b^2+c^2) y^3 z+(-2 a^2-2 c^2) x^2 z^2+(2 a^2+2 b^2-2 c^2) x y z^2+(-2 b^2-2 c^2) y^2 z^2+(a^2-b^2+c^2) x z^3+(-a^2+b^2+c^2) y z^3 = 0)
𝒯, con punto triple en el baricentro y pasa por X14999.
Otra construcción de 𝒯, como lugar geométrico, es descrita en HG120620.
Si P=(u:v:w), entonces:
M = (u(a^2 (b^2 + c^2 ) v^2 w^2- u^2 (c^4 v^2+b^4 w^2)) : ... : ...).
El punto M es la intersección de la de P con la recta (pasa por el baricentro) cuyos coeficientes de su ecuación baricéntrica son las coordenadas de P* ( de P).
Toda recta que pasa por el baricentro vuelve a corta al trifoliun en un solo punto. Si la recta pasa por el tal punto es X14999.
Si queremos obtener las coordenadas del punto W de intersección de la con 𝒯, podemos resolver el sistema formado por las ecuaciones de ambas curvas, obteniéndose una solución triple, correspondiente al baricentro, y las coordenadas de W; o bien intersecando la recta de Euler con la recta antipedal del punto X112, conjugado isogonal del punto cuyas coordenadas son los coeficientes de la ecuación de la recta de Euler.
W = ( (2 a^10-2 a^8 b^2-a^6 b^4-a^4 b^6+3 a^2 b^8-b^10-2 a^8 c^2+4 a^6 b^2 c^2+a^4 b^4 c^2-2 a^2 b^6 c^2-b^8 c^2-a^6 c^4+a^4 b^2 c^4-2 a^2 b^4 c^4+2 b^6 c^4-a^4 c^6-2 a^2 b^2 c^6+2 b^4 c^6+3 a^2 c^8-b^2 c^8-c^10)/((b^2-c^2) (a^2-b^2-c^2)) : ... : ...),
que tiene números de búsqueda en
(0.693048908475606, -0.178299294941835, 3.44423372833999).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {99,20580}, {112,525}, {2799,35907}, {3265,23964}, {3566,32696}.
Los seis puntos comunes de 𝒯 con los lados de ABC (aparte de sus vértices) están en una
cónica
( a^6 x^2-a^4 b^2 x^2-a^2 b^4 x^2+b^6 x^2-a^4 c^2 x^2+2 a^2 b^2 c^2 x^2-b^4 c^2 x^2-a^2 c^4 x^2-b^2 c^4 x^2+c^6 x^2-2 a^6 x y+2 a^4 b^2 x y+2 a^2 b^4 x y-2 b^6 x y+2 a^2 c^4 x y+2 b^2 c^4 x y+a^6 y^2-a^4 b^2 y^2-a^2 b^4 y^2+b^6 y^2-a^4 c^2 y^2+2 a^2 b^2 c^2 y^2-b^4 c^2 y^2-a^2 c^4 y^2-b^2 c^4 y^2+c^6 y^2-2 a^6 x z+2 a^2 b^4 x z+2 a^4 c^2 x z+2 b^4 c^2 x z+2 a^2 c^4 x z-2 c^6 x z+2 a^4 b^2 y z-2 b^6 y z+2 a^4 c^2 y z+2 b^4 c^2 y z+2 b^2 c^4 y z-2 c^6 y z+a^6 z^2-a^4 b^2 z^2-a^2 b^4 z^2+b^6 z^2-a^4 c^2 z^2+2 a^2 b^2 c^2 z^2-b^4 c^2 z^2-a^2 c^4 z^2-b^2 c^4 z^2+c^6 z^2 = 0)
cuyo centro es:
U = ( (a^4-(b^2-c^2)^2) (3 a^8-7 a^6 (b^2+c^2)-2 (b^4-c^4)^2-a^4 (b^4-6 b^2 c^2+c^4)+a^2 (7 b^6+b^4 c^2+b^2 c^4+7 c^6)) : ... : ...),
que tiene números de búsqueda en ETC
(0.944594446628652, 1.74768601715249, 1.99476134081943).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,5523}, {3,1560}, {6,468}, {25,5475}, {186,9745}, {216,14580}, {233,11284}, {574,5094}, {1196,37453}, {2501,18311}, {3162,6676}, {6032,35480}, {7746,8791}, {8541,30516}, {15595,37638}, {37752,37753}.
Su es:
V = ( 1/(a^6+b^6-2 b^4 c^2-2 b^2 c^4+c^6-a^4 (b^2+c^2)-a^2 (b^4+b^2 c^2+c^4)) : ... : ...),
que tiene números de búsqueda en ETC
(0.678649189557374, 1.18365893874178, 2.50798559067513).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {5,111}, {6,16511}, {25,5475}, {39,8791}, {251,6676}, {468,8882}, {1383,7493}, {2963,3291}, {2987,14389}, {3580,30535}, {3815,14910}, {7514,9745}, {7539,8770}, {9178,12077}, {10418,14579}, {11548,16317}.
- Miércoles, 10 de junio del 2020
La cúbica de Thomson y la recta del infinito
-Las matemáticas son un lugar donde puedes hacer cosas que no puedes hacer en el mundo real.-Marcus du Sautoy.
Dados un triángulo ABC y un punto P en su plano, sea P* su . Sea Z el punto cuyas coordenadas baricéntricas son proporcionales a las áreas de los triángulos APP*, BPP*, CPP*. Si (u:v:w) son las coordenadas de P, entonces:
Z = (u (c^2 v^2 - b^2 w^2) : v (a^2 w^2 - c^2 u^2) : w (b^2 u^2 - a^2 v^2)).
El punto
Z está en la si y solo si
P está sobre la la cúbica de Thomson
(
K002, en el catálogo de Bernard Gibert).
El lugar geométrico del punto P tal que Z está sobre la es la isogonal circular con pivote X(525), pK(X2, X525).
X(525) = isogonal conjugate of X(112)
Some properties of the triangle center
X(112):
If the line that passes through orthocenter and symmedian, X(4)X(6), is reflected in every side of triangle ABC, then the reflections concur in
X(112). (Randy Hutson, 9/23/2011)
Let P be a point on the other than orthocenter. Let A' be the reflection of P in BC, and define B' and C' cyclically. The circumcircles of AA'B', BC'A', and CA'B' concur at
X(112). (Randy Hutson, December 26, 2015)
Let Q be a point on the other than centroid, X(2). Let A'B'C' be the of Q. Let A" be the {B,C}- of A' (or equivalently, A" = BC∩B'C'), and define B" and C" cyclically. The circumcircles of AB"C", BC"A", CA"B" concur in
X(112). (Randy Hutson, December 26, 2015)
Let A', B', C' be the intersections of the and lines BC, CA, AB, respectively. The circumcircles of AB'C', BC'A', CA'B' concur in
X(112). (Randy Hutson, December 26, 2015)
Let A' be the reflection of X(6) in BC, and define B' and C' cyclically. The circumcircles of AB'C', BC'A', CA'B' concur in
X(112). (Randy Hutson, December 26, 2015)
Let A'B'C' be the . Let A" be the pole, wrt the , of line B'C', and define B" and C" cyclically. The lines A'A", B'B", C'C" concur in
X(112). (Randy Hutson, December 26, 2015)
Let L
1 be the line that is the of the Euler line and
P(4). Let L
2 be the line that is the barycentric product of the Euler line and U(4). Then X(112) = L
1∩L
2. (Randy Hutson, July 11, 2019)
La
cúbica
( a^4 c^2 x^2 y-a^2 b^2 c^2 x^2 y+b^2 c^4 x^2 y-c^6 x^2 y-a^2 b^2 c^2 x y^2+b^4 c^2 x y^2+a^2 c^4 x y^2-c^6 x y^2+a^4 b^2 x^2 z-b^6 x^2 z-a^2 b^2 c^2 x^2 z+b^4 c^2 x^2 z-a^6 y^2 z+a^2 b^4 y^2 z+a^4 c^2 y^2 z-a^2 b^2 c^2 y^2 z+a^2 b^4 x z^2-b^6 x z^2-a^2 b^2 c^2 x z^2+b^2 c^4 x z^2-a^6 y z^2+a^4 b^2 y z^2-a^2 b^2 c^2 y z^2+a^2 c^4 y z^2 = 0)
pK(X2, X525) pasa por X1 (incentro), X112, X525. Su asíntota es la de X112. X112 es el de A, B, C.
Cuando P está sobre la circunferencia circunscrita, Z está sobre la cúbica de Simson del triángulo medial.
Aunque los triángulos APP*, BPP*, CPP* no están definidos, cuando P está sobre la circunferencia circunscrita, por continuidad podemos contemplar esta situación.
- Sábados, 6 de junio del 2020
Cónica centrada en el incentro
El 6 de junio de 1928, murió a los 72 años Luigi Bianchi, matemático italiano. Publico, en 1902, las que hoy se concocen com identidades de Bianchi.
Tensor curvatura de Riemann R(X,Y)Z=∇X∇YZ - ∇Y∇XZ-∇[X,Y]Z. (∇ conexión de Levi-Civita)
Primera identidad de Bianchi R(X,Y)Z+R(Y,Z)X+R(Z,X)Y=0.
En coordenadas, la segunda identidad es Rijkl;m+Rijmk;l+Rijlm;k=0, donde ";" indica derivada covariante.
Sea DEF el de un triángulo dado ABC. Si E' y F' son los simétricos de E y F respecto al incentro I=X1, la recta
E'F' corta a BC en A'.
La perpendicular por B a IC corta a IA' en Ab, y la perpendicular por C a IB corta a IA' en Ac.
Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
Los pares de puntos (Ac, Ab), (Bc, Ba) y (Ca, Cb) son diametralmente opuestos en una misma
cónica
( Ecuación baricéntrica:
𝔖abc xyz
(-a+b+c)^2 (a^7-a^6 (b+c)+a^5 (-4 b^2+5 b c-4 c^2)+b c (b+c)^3 (3 b^2-10 b c+3 c^2)+a^4 (-2 b^3+b^2 c+b c^2-2 c^3)+a^3 (-7 b^4+14 b^3 c+26 b^2 c^2+14 b c^3-7 c^4)-a^2 (13 b^5-53 b^4 c+80 b^3 c^2+80 b^2 c^3-53 b c^4+13 c^5)+a (-6 b^6+37 b^5 c-102 b^4 c^2+222 b^3 c^3-102 b^2 c^4+37 b c^5-6 c^6)) x^2+(a^9-4 a^8 (b+c)+2 a^7 (9 b^2+b c+9 c^2)+6 a^6 (7 b^3-18 b^2 c-18 b c^2+7 c^3)+2 (b-c)^2 (b+c)^3 (b^4-3 b^3 c+8 b^2 c^2-3 b c^3+c^4)-a (b^2-c^2)^2 (5 b^4-10 b^3 c+66 b^2 c^2-10 b c^3+5 c^4)-2 a^5 (6 b^4+29 b^3 c-214 b^2 c^2+29 b c^3+6 c^4)-2 a^4 (19 b^5-96 b^4 c+165 b^3 c^2+165 b^2 c^3-96 b c^4+19 c^5)-2 a^3 (b^6-55 b^5 c+307 b^4 c^2-618 b^3 c^3+307 b^2 c^4-55 b c^5+c^6)-2 a^2 (b^7+6 b^6 c-104 b^5 c^2+113 b^4 c^3+113 b^3 c^4-104 b^2 c^5+6 b c^6+c^7)) y z = 0.
= 0)
con centro en I.
Las rectas AcAb, BcBa y CaCb forman un triángulo A"B"C" perspectivo con DEF, con centro de perspectividad:
W = ( (5 a^3-5 a^2 b-9 a b^2+b^3-5 a^2 c+14 a b c+3 b^2 c-9 a c^2+3 b c^2+c^3) (a^4-3 a^3 b+5 a^2 b^2+7 a b^3-2 b^4-3 a^3 c+2 a^2 b c-11 a b^2 c+5 a^2 c^2-11 a b c^2+4 b^2 c^2+7 a c^3-2 c^4) : ... : ...),
que tiene números de búsqueda en
(2.96761021883621, 2.66315699023225, 0.427274156899187).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,3524}, {8,4373}, {388,4694}, {497,3976}, {3057,4661}, {5558,17723}.
Los triángulos DEF y A"B"C" son con el centro ortológico común.
- Miércoles, 3 de junio del 2020
Propiedades del centro del triángulo X(15740)
El 3 de Junio de 1924
muere, a los 41 años, en el sanatorio de Kierling, en Austria, el escritor Franz Kafka autor de "La metamorfosis", entre otras obras. Su obra es una de las pioneras en la fusión de elementos realistas con fantásticos, y tiene como principales temas los conflictos paternofiliales, la ansiedad, el existencialismo, la brutalidad física y psicológica, la culpa, la filosofía del absurdo, la burocracia y las transformaciones espirituales.
Dado un triángulo
ABC, se consideran las seis rectas perpendiculares a los lados
AB y
AC en
A, a los lados
BC y
BA en
B, y a los lados
CA y
CB en
C. Estas rectas son tangentes a una misma
cónica,
( Ecuación baricéntrica:
a^8 x^2-2 a^4 b^4 x^2+b^8 x^2+4 a^4 b^2 c^2 x^2-4 b^6 c^2 x^2-2 a^4 c^4 x^2+6 b^4 c^4 x^2-4 b^2 c^6 x^2+c^8 x^2+2 a^8 x y-4 a^4 b^4 x y+2 b^8 x y+4 a^6 c^2 x y-4 a^4 b^2 c^2 x y-4 a^2 b^4 c^2 x y+4 b^6 c^2 x y-8 a^4 c^4 x y+8 a^2 b^2 c^4 x y-8 b^4 c^4 x y-4 a^2 c^6 x y-4 b^2 c^6 x y+6 c^8 x y+a^8 y^2-2 a^4 b^4 y^2+b^8 y^2-4 a^6 c^2 y^2+4 a^2 b^4 c^2 y^2+6 a^4 c^4 y^2-2 b^4 c^4 y^2-4 a^2 c^6 y^2+c^8 y^2+2 a^8 x z+4 a^6 b^2 x z-8 a^4 b^4 x z-4 a^2 b^6 x z+6 b^8 x z-4 a^4 b^2 c^2 x z+8 a^2 b^4 c^2 x z-4 b^6 c^2 x z-4 a^4 c^4 x z-4 a^2 b^2 c^4 x z-8 b^4 c^4 x z+4 b^2 c^6 x z+2 c^8 x z+6 a^8 y z-4 a^6 b^2 y z-8 a^4 b^4 y z+4 a^2 b^6 y z+2 b^8 y z-4 a^6 c^2 y z+8 a^4 b^2 c^2 y z-4 a^2 b^4 c^2 y z-8 a^4 c^4 y z-4 a^2 b^2 c^4 y z-4 b^4 c^4 y z+4 a^2 c^6 y z+2 c^8 y z+a^8 z^2-4 a^6 b^2 z^2+6 a^4 b^4 z^2-4 a^2 b^6 z^2+b^8 z^2-2 a^4 c^4 z^2+4 a^2 b^2 c^4 z^2-2 b^4 c^4 z^2+c^8 z^2 = 0)
𝒞, con centro el circuncentro y
X15740.
X(15740)=perspector of the X(4)-orthoparallelogic tangential-conic, 𝒞 of ABC.
(See preamble of X(31353), by César Eliud Lozada, January 27, 2019).
Hyacinthos 26987 (Dec 29, 2017)
[Antreas Hatzipolakis]:
Let ABC be a triangle and A'B'C' the cevian triangle of H.
Denote:
A"B"C" = the midheight triangle
(ie A", B", C" = the midpoints of AA', BB', CC', resp.)
A*, B*, C* = the reflections of A", B", C" in H, resp.
Ab, Ac = the orthogonal projections of A* on AB, AC, resp.
Bc, Ba = the orthogonal projections of B* on BC, BA, resp.
Ca, Cb = the orthogonal projections of C* on CA, ab, resp.
A*B*C* = the triangle bounded by AbAc, BcBa, CaCb
M1, M2, M3 = the midpoints of AbAc, BcBa, CaCb, resp.
1. A'B'C', A*B*C* are homothetic.
2. The perpendicular bisectors of AbAc, BcBa, CaCb are concurrent
3. ABC, M1M2M3 are orthologic
4. A'B'C', M1M2M3 are orthologic
5. A*B*C*, M1M2M3 are orthologic.
[Angel Montesdeoca]:
1. A'B'C', A*B*C* are homothetic with homothetic center X(51).
2. The perpendicular bisectors of AbAc, BcBa, CaCb are concurrent at X(5907).
3. ABC, M1M2M3 are orthologic
The orthology center of ABC with respect to M1M2M3 is
Z
3 [=
X(15740)] with first barycentric coordinate:
a^10+3 a^8 (b^2+c^2)-14 a^6 (b^2-c^2)^2+2 a^4 (7 b^6-15 b^4 c^2-15 b^2 c^4+7 c^6)-a^2 (b^2-c^2)^2 (3 b^4+10 b^2 c^2+3 c^4)-(b^2-c^2)^4 (b^2+c^2) ::
The orthology center of M1M2M3 with respect to ABC is X(13568).
4. A'B'C', M1M2M3 are orthologic
The orthology center of A'B'C' with respect to M1M2M3 is
Z
4 with first barycentric coordinate:
5 a^10 + a^8(b^2+c^2)-2 a^6 (15 b^4+2 b^2 c^2+15 c^4)+2 a^4 (17 b^6-9 b^4 c^2-9 b^2 c^4+17 c^6) -a^2 (b^2-c^2)^2 (7 b^4+2 b^2 c^2+7 c^4) -3 (b^2-c^2)^4 (b^2+c^2) ::
The orthology center of M1M2M3 with respect to A'B'C' is X(5907)
5. A*B*C*, M1M2M3 are orthologic.
The orthology center of A*B*C* with respect to M1M2M3 is
Z
5 with first barycentric coordinate:
a^2 (-a^12 (b^2+c^2)
+a^10 (4 b^4-46 b^2 c^2+4 c^4)
+a^8 (-5 b^6+11 b^4 c^2+11 b^2 c^4-5 c^6)
+5 a^4 (b^10-55 b^8 c^2+22 b^6 c^4+22 b^4 c^6-55 b^2 c^8+c^10)
+4 a^6 (57 b^6 c^2-2 b^4 c^4+57 b^2 c^6)
-2 a^2 (b^2-c^2)^2 (2 b^8-25 b^6 c^2-34 b^4 c^4-25 b^2 c^6+2 c^8)
+(b^2-c^2)^4 (b^6+29 b^4 c^2+29 b^2 c^4+c^6))
The orthology center of M1M2M3 with respect to A*B*C* is X(5907).
-----------------------------------------------
Let A'B'C' be the orthic triangle and L the de Longchamps point, X(20). Let A", B", C" be the midpoints of LA', LB', LC'. Then A"B"C" is perspective to ABC, and the perspector is
X(15740). See also X(6776). (Hyacinthos #20428, Bui Quang Tuan, 11/26/2011)
Hyacinthos 20428
(Nov 26, 2011)
[Bui Quang Tuan]
O, H, K, L are circumcenter, orthocenter, symmedian and de
Longchamps points of reference triangle ABC. Suppose A'B'C' is orthic triangle
of ABC.
Denote A'', B'', C'' as midpoints of LA', LB', LC'
respectively.
Results:
1). A''B''C'' and ABC are perspective at perspector P [=
X(15740)] with
barycentrics:
SA/(SA^2 + b^2*c^2) : :
2). A''B''C'' and circumcevian triangle of O are perspective
at perspector Q [=X(6776)] with barycentrics:
SA*(a^4 - SB*SC) : :
Q is reflection of orthocenter H in symmedian point K.
P and Q are not in current ETC.
------------------------------------------
Let A'B'C' be the medial triangle and L the de Longchamps point, X(20). Let A" = midpoint of AL, and define B" and C" cyclically. Let A1=A'A''∩B''C'', and define B1 and C1 cyclically. The triangle A1B1C1 is perspective to ABC, and the perspector is
X(15740). (Angel Montesdeoca, December 4, 2018)
- Viernes, 29 de mayo del 2020
Dos cónicas bitangentes asociadas a la recta de Euler
Si un teorema lleva el nombre de una matemático, es seguro que este matemático no es su inventor. Félix Klein
En el plano de un triángulo ABC se considera un punto P y su A'B'C'. Sean A', B', C' los inversos de A', B', C', respecto a la circunferencia circunscrita Γ a A"B"C".
Los triángulos
ABC y
A"B"C" son perspectivos si y solo si
P está sobre Γ o sobre la .
El lugar geométrico del centro de perspectividad Q es:
La cuártica Q120, de la , si P se mueve sobre Γ.
Una
cónica
( (-a^2 b^12 c^4+b^14 c^4+4 a^2 b^10 c^6-3 b^12 c^6-6 a^2 b^8 c^8+2 b^10 c^8+4 a^2 b^6 c^10+2 b^8 c^10-a^2 b^4 c^12-3 b^6 c^12+b^4 c^14) x^2+(-2 a^6 b^6 c^6+4 a^6 b^4 c^8+4 a^4 b^6 c^8-2 a^6 b^2 c^10-8 a^4 b^4 c^10-2 a^2 b^6 c^10+4 a^4 b^2 c^12+4 a^2 b^4 c^12-2 a^2 b^2 c^14) x y+(a^14 c^4-a^12 b^2 c^4-3 a^12 c^6+4 a^10 b^2 c^6+2 a^10 c^8-6 a^8 b^2 c^8+2 a^8 c^10+4 a^6 b^2 c^10-3 a^6 c^12-a^4 b^2 c^12+a^4 c^14) y^2+(-2 a^6 b^10 c^2+4 a^4 b^12 c^2-2 a^2 b^14 c^2+4 a^6 b^8 c^4-8 a^4 b^10 c^4+4 a^2 b^12 c^4-2 a^6 b^6 c^6+4 a^4 b^8 c^6-2 a^2 b^10 c^6) x z+(-2 a^14 b^2 c^2+4 a^12 b^4 c^2-2 a^10 b^6 c^2+4 a^12 b^2 c^4-8 a^10 b^4 c^4+4 a^8 b^6 c^4-2 a^10 b^2 c^6+4 a^8 b^4 c^6-2 a^6 b^6 c^6) y z+(a^14 b^4-3 a^12 b^6+2 a^10 b^8+2 a^8 b^10-3 a^6 b^12+a^4 b^14-a^12 b^4 c^2+4 a^10 b^6 c^2-6 a^8 b^8 c^2+4 a^6 b^10 c^2-a^4 b^12 c^2) z^2 = 0)
𝒞, cuando P se mueve sobre la recta de Euler.
Hyacinthos 28625 (Nov 12, 2018)
[Alexandr Skutin]:
Let ABC be a triangle and P a point on the Euler line.
Denote:
Ka, Kb, Kc = the symmedian points of PBC, PCA, PAB, resp.
The reflections of PKa,, PKb, PKc in BC, CA, AB, resp. are concurrent.
The point of concurrence, as P moves on the Euler line, is a conic.
[Ercole Suppa]
The locus of the point of conurrence is the conic 𝒞:
b^4 (b-c)^4 c^4 (b+c)^4 (a^2-b^2-c^2) x^2+2 a^6 (a-b)^2 b^2 (a+b)^2 (a-c)^2 c^2 (a+c)^2 y z + ... = 0
Center of 𝒞: X(2)X(98) ∩ X(3)X(7731).
The perspector of 𝒞: X(110)X(9514) ∩ X(5012)X(5661).
--------------
(Randy Hutson, August 19, 2019)
Another construction of the conic 𝒞 described in Hyacinthos 28625: Let P be a point on the Euler line. Let A'B'C' be the cevian triangle of P. Let A", B", C" be the circumcircle-inverses of A', B', C', resp. Triangle A"B"C" is perspective to ABC, and the locus of the perspector, as P moves on the Euler line, is the conic with center
X(27866) and perspector X(27867). This conic passes through X(3), X(6), X(24), X(60), X(143), X(1511) and X(1986). Update: The conic passes through X(i), for i∈ {3, 6, 24, 60, 143, 1511, 1986, 6593,
15460, 15461, 19118, 20806, 35602, 35603, 36153}.
------------------
X15460 X15461
Hyacinthos 26876 (Antreas Hatzipolakis. Dec 4, 2017)
[APH]:
In K932 we read that the cubic passes through the points:
X(3), X(4), X(110), X(523), X(7471), X(14264), X(7471)*, X(14264)*
The two last ones X(7471)*, X(14264)* are isogonal conjugates of X(7471), X(14264), resp.
In K934 we read that the cubic passes through the points
X(4), X(30), X(143), X(1147), X(1992), X(2574), X(2575), isogonal conjugates of X(1312), X(1313).
Which are these isogonal conjugates of X(7471), X(14264) and X(1312), X(1313) ? (properties)
[Peter Moses]:
gX1312:
a^2 (a^4-2 a^2 b^2+b^4+a^2 c^2+b^2 c^2-2 c^4+(a^4-2 a^2 b^2+b^4-a^2 c^2-b^2 c^2) J) (a^4+a^2 b^2-2 b^4-2 a^2 c^2+b^2 c^2+c^4+(a^4-a^2 b^2-2 a^2 c^2-b^2 c^2+c^4) J)::
on lines {{4,13414}, {69,13415}, {110,1114}, {186,249}, {248,15166}, {265,1313}, {2574,5622}, {13434,14374}}.
on quartic Q120.
on cubic K934.
on Jerabek hyperbola.
isogonal conjugate of X(1312).
isogonal of the complement X(1114).
X(i)-cross conjugate of X(j) for these (i,j): {{3, 1114}, {6, 8116}, {2574, 110}}.
X(i)-isoconjugate of X(j) for these (i,j): {{1, 1312}, {92, 15167}, {2575, 2589}, {2579, 2593}, {2583, 8106}}.
cevapoint of X(1114) and X(14709).
barycentric product X(i)X(j) for these {i,j}: {{249, 1313}, {1114, 8116}, {1823, 2581}}.
barycentric quotient X(i)/X(j) for these {i,j}: {{6, 1312}, {184, 15167}, {1114, 2593}, {1313, 338}, {1823, 2583}, {2577, 2589}, {3284, 14500}, {15166, 125}}.
gX1313:
a^2 (a^4-2 a^2 b^2+b^4+a^2 c^2+b^2 c^2-2 c^4-(a^4-2 a^2 b^2+b^4-a^2 c^2-b^2 c^2) J) (a^4+a^2 b^2-2 b^4-2 a^2 c^2+b^2 c^2+c^4-(a^4-a^2 b^2-2 a^2 c^2-b^2 c^2+c^4) J)::
on lines {{4,13415}, {69,13414}, {110,1113}, {186,249}, {248,15167}, {265,1312}, {2575,5622}, {13434,14375}}.
on quartic Q120.
on cubic K934.
on Jerabek hyperbola.
isogonal conjugate of X(1313).
isogonal of the complement X(1113).
X(i)-cross conjugate of X(j) for these (i,j): {{3, 1113}, {6, 8115}, {2575, 110}}.
X(i)-isoconjugate of X(j) for these (i,j): {{1, 1313}, {92, 15166}, {2574, 2588}, {2578, 2592}, {2582, 8105}}.
cevapoint of X(1113) and X(14710).
barycentric product X(i)X(j) for these {i,j}: {{249, 1312}, {1113, 8115}, {1822, 2580}}.
barycentric quotient X(i)/X(j) for these {i,j}: {{6, 1313}, {184, 15166}, {1113, 2592}, {1312, 338}, {1822, 2582}, {2576, 2588}, {3284, 14499}, {15167, 125}}.
Cuando P se mueve sobre la recta de Euler la recta t=PQ (tangente a la circunhipérbola rectangular que pasa por P) envuelve una
conica
( a^4 b^8 x^2-2 a^2 b^10 x^2+b^12 x^2-4 a^4 b^6 c^2 x^2+6 a^2 b^8 c^2 x^2-2 b^10 c^2 x^2+6 a^4 b^4 c^4 x^2-4 a^2 b^6 c^4 x^2-b^8 c^4 x^2-4 a^4 b^2 c^6 x^2-4 a^2 b^4 c^6 x^2+4 b^6 c^6 x^2+a^4 c^8 x^2+6 a^2 b^2 c^8 x^2-b^4 c^8 x^2-2 a^2 c^10 x^2-2 b^2 c^10 x^2+c^12 x^2+2 a^8 b^4 x y-4 a^6 b^6 x y+2 a^4 b^8 x y-4 a^8 b^2 c^2 x y+4 a^6 b^4 c^2 x y+4 a^4 b^6 c^2 x y-4 a^2 b^8 c^2 x y+2 a^8 c^4 x y+4 a^6 b^2 c^4 x y-14 a^4 b^4 c^4 x y+4 a^2 b^6 c^4 x y+2 b^8 c^4 x y-4 a^6 c^6 x y+8 a^4 b^2 c^6 x y+8 a^2 b^4 c^6 x y-4 b^6 c^6 x y-12 a^2 b^2 c^8 x y+4 a^2 c^10 x y+4 b^2 c^10 x y-2 c^12 x y+a^12 y^2-2 a^10 b^2 y^2+a^8 b^4 y^2-2 a^10 c^2 y^2+6 a^8 b^2 c^2 y^2-4 a^6 b^4 c^2 y^2-a^8 c^4 y^2-4 a^6 b^2 c^4 y^2+6 a^4 b^4 c^4 y^2+4 a^6 c^6 y^2-4 a^4 b^2 c^6 y^2-4 a^2 b^4 c^6 y^2-a^4 c^8 y^2+6 a^2 b^2 c^8 y^2+b^4 c^8 y^2-2 a^2 c^10 y^2-2 b^2 c^10 y^2+c^12 y^2+2 a^8 b^4 x z-4 a^6 b^6 x z+4 a^2 b^10 x z-2 b^12 x z-4 a^8 b^2 c^2 x z+4 a^6 b^4 c^2 x z+8 a^4 b^6 c^2 x z-12 a^2 b^8 c^2 x z+4 b^10 c^2 x z+2 a^8 c^4 x z+4 a^6 b^2 c^4 x z-14 a^4 b^4 c^4 x z+8 a^2 b^6 c^4 x z-4 a^6 c^6 x z+4 a^4 b^2 c^6 x z+4 a^2 b^4 c^6 x z-4 b^6 c^6 x z+2 a^4 c^8 x z-4 a^2 b^2 c^8 x z+2 b^4 c^8 x z-2 a^12 y z+4 a^10 b^2 y z-4 a^6 b^6 y z+2 a^4 b^8 y z+4 a^10 c^2 y z-12 a^8 b^2 c^2 y z+8 a^6 b^4 c^2 y z+4 a^4 b^6 c^2 y z-4 a^2 b^8 c^2 y z+8 a^6 b^2 c^4 y z-14 a^4 b^4 c^4 y z+4 a^2 b^6 c^4 y z+2 b^8 c^4 y z-4 a^6 c^6 y z+4 a^4 b^2 c^6 y z+4 a^2 b^4 c^6 y z-4 b^6 c^6 y z+2 a^4 c^8 y z-4 a^2 b^2 c^8 y z+2 b^4 c^8 y z+a^12 z^2-2 a^10 b^2 z^2-a^8 b^4 z^2+4 a^6 b^6 z^2-a^4 b^8 z^2-2 a^2 b^10 z^2+b^12 z^2-2 a^10 c^2 z^2+6 a^8 b^2 c^2 z^2-4 a^6 b^4 c^2 z^2-4 a^4 b^6 c^2 z^2+6 a^2 b^8 c^2 z^2-2 b^10 c^2 z^2+a^8 c^4 z^2-4 a^6 b^2 c^4 z^2+6 a^4 b^4 c^4 z^2-4 a^2 b^6 c^4 z^2+b^8 c^4 z^2 = 0)
ℰ, inscrita en ABC y bitangente a la cónica 𝒞 en los centros X15460 y X15461. Las tangentes comunes son X1113X15461 y X1114X15460, que se cortan en el foco de la
El de la cónica ℰ, X18020, es el T de la recta lugar geométrcio del tripolo de la recta t tangente en P a la hipérbola ℋP que pasa por A, B, C, X(4), P, cuando P se mueve sobre la recta de Euler. (Randy Hutson, June 27, 2018).
El perspector () de la cónica ℰ respecto al triángulo X110X1113X1114 es X15472.
El foco de la
parábola
( a^10 b^8 x^2-3 a^8 b^10 x^2+2 a^6 b^12 x^2+2 a^4 b^14 x^2-3 a^2 b^16 x^2+b^18 x^2-4 a^10 b^6 c^2 x^2+9 a^8 b^8 c^2 x^2-7 a^6 b^10 c^2 x^2+5 a^2 b^14 c^2 x^2-3 b^16 c^2 x^2+6 a^10 b^4 c^4 x^2-6 a^8 b^6 c^4 x^2+10 a^6 b^8 c^4 x^2-12 a^4 b^10 c^4 x^2-6 a^2 b^12 c^4 x^2+8 b^14 c^4 x^2-4 a^10 b^2 c^6 x^2-6 a^8 b^4 c^6 x^2-10 a^6 b^6 c^6 x^2+10 a^4 b^8 c^6 x^2+27 a^2 b^10 c^6 x^2-16 b^12 c^6 x^2+a^10 c^8 x^2+9 a^8 b^2 c^8 x^2+10 a^6 b^4 c^8 x^2+10 a^4 b^6 c^8 x^2-46 a^2 b^8 c^8 x^2+10 b^10 c^8 x^2-3 a^8 c^10 x^2-7 a^6 b^2 c^10 x^2-12 a^4 b^4 c^10 x^2+27 a^2 b^6 c^10 x^2+10 b^8 c^10 x^2+2 a^6 c^12 x^2-6 a^2 b^4 c^12 x^2-16 b^6 c^12 x^2+2 a^4 c^14 x^2+5 a^2 b^2 c^14 x^2+8 b^4 c^14 x^2-3 a^2 c^16 x^2-3 b^2 c^16 x^2+c^18 x^2+2 a^14 b^4 x y-6 a^12 b^6 x y+4 a^10 b^8 x y+4 a^8 b^10 x y-6 a^6 b^12 x y+2 a^4 b^14 x y-4 a^14 b^2 c^2 x y+6 a^12 b^4 c^2 x y-2 a^10 b^6 c^2 x y-2 a^6 b^10 c^2 x y+6 a^4 b^12 c^2 x y-4 a^2 b^14 c^2 x y+2 a^14 c^4 x y+6 a^12 b^2 c^4 x y-6 a^10 b^4 c^4 x y-2 a^8 b^6 c^4 x y-2 a^6 b^8 c^4 x y-6 a^4 b^10 c^4 x y+6 a^2 b^12 c^4 x y+2 b^14 c^4 x y-6 a^12 c^6 x y+2 a^10 b^2 c^6 x y-2 a^8 b^4 c^6 x y+10 a^6 b^6 c^6 x y-2 a^4 b^8 c^6 x y+2 a^2 b^10 c^6 x y-6 b^12 c^6 x y+2 a^10 c^8 x y-10 a^8 b^2 c^8 x y+14 a^6 b^4 c^8 x y+14 a^4 b^6 c^8 x y-10 a^2 b^8 c^8 x y+2 b^10 c^8 x y+10 a^8 c^10 x y-4 a^6 b^2 c^10 x y-42 a^4 b^4 c^10 x y-4 a^2 b^6 c^10 x y+10 b^8 c^10 x y-10 a^6 c^12 x y+30 a^4 b^2 c^12 x y+30 a^2 b^4 c^12 x y-10 b^6 c^12 x y-2 a^4 c^14 x y-26 a^2 b^2 c^14 x y-2 b^4 c^14 x y+6 a^2 c^16 x y+6 b^2 c^16 x y-2 c^18 x y+a^18 y^2-3 a^16 b^2 y^2+2 a^14 b^4 y^2+2 a^12 b^6 y^2-3 a^10 b^8 y^2+a^8 b^10 y^2-3 a^16 c^2 y^2+5 a^14 b^2 c^2 y^2-7 a^10 b^6 c^2 y^2+9 a^8 b^8 c^2 y^2-4 a^6 b^10 c^2 y^2+8 a^14 c^4 y^2-6 a^12 b^2 c^4 y^2-12 a^10 b^4 c^4 y^2+10 a^8 b^6 c^4 y^2-6 a^6 b^8 c^4 y^2+6 a^4 b^10 c^4 y^2-16 a^12 c^6 y^2+27 a^10 b^2 c^6 y^2+10 a^8 b^4 c^6 y^2-10 a^6 b^6 c^6 y^2-6 a^4 b^8 c^6 y^2-4 a^2 b^10 c^6 y^2+10 a^10 c^8 y^2-46 a^8 b^2 c^8 y^2+10 a^6 b^4 c^8 y^2+10 a^4 b^6 c^8 y^2+9 a^2 b^8 c^8 y^2+b^10 c^8 y^2+10 a^8 c^10 y^2+27 a^6 b^2 c^10 y^2-12 a^4 b^4 c^10 y^2-7 a^2 b^6 c^10 y^2-3 b^8 c^10 y^2-16 a^6 c^12 y^2-6 a^4 b^2 c^12 y^2+2 b^6 c^12 y^2+8 a^4 c^14 y^2+5 a^2 b^2 c^14 y^2+2 b^4 c^14 y^2-3 a^2 c^16 y^2-3 b^2 c^16 y^2+c^18 y^2+2 a^14 b^4 x z-6 a^12 b^6 x z+2 a^10 b^8 x z+10 a^8 b^10 x z-10 a^6 b^12 x z-2 a^4 b^14 x z+6 a^2 b^16 x z-2 b^18 x z-4 a^14 b^2 c^2 x z+6 a^12 b^4 c^2 x z+2 a^10 b^6 c^2 x z-10 a^8 b^8 c^2 x z-4 a^6 b^10 c^2 x z+30 a^4 b^12 c^2 x z-26 a^2 b^14 c^2 x z+6 b^16 c^2 x z+2 a^14 c^4 x z+6 a^12 b^2 c^4 x z-6 a^10 b^4 c^4 x z-2 a^8 b^6 c^4 x z+14 a^6 b^8 c^4 x z-42 a^4 b^10 c^4 x z+30 a^2 b^12 c^4 x z-2 b^14 c^4 x z-6 a^12 c^6 x z-2 a^10 b^2 c^6 x z-2 a^8 b^4 c^6 x z+10 a^6 b^6 c^6 x z+14 a^4 b^8 c^6 x z-4 a^2 b^10 c^6 x z-10 b^12 c^6 x z+4 a^10 c^8 x z-2 a^6 b^4 c^8 x z-2 a^4 b^6 c^8 x z-10 a^2 b^8 c^8 x z+10 b^10 c^8 x z+4 a^8 c^10 x z-2 a^6 b^2 c^10 x z-6 a^4 b^4 c^10 x z+2 a^2 b^6 c^10 x z+2 b^8 c^10 x z-6 a^6 c^12 x z+6 a^4 b^2 c^12 x z+6 a^2 b^4 c^12 x z-6 b^6 c^12 x z+2 a^4 c^14 x z-4 a^2 b^2 c^14 x z+2 b^4 c^14 x z-2 a^18 y z+6 a^16 b^2 y z-2 a^14 b^4 y z-10 a^12 b^6 y z+10 a^10 b^8 y z+2 a^8 b^10 y z-6 a^6 b^12 y z+2 a^4 b^14 y z+6 a^16 c^2 y z-26 a^14 b^2 c^2 y z+30 a^12 b^4 c^2 y z-4 a^10 b^6 c^2 y z-10 a^8 b^8 c^2 y z+2 a^6 b^10 c^2 y z+6 a^4 b^12 c^2 y z-4 a^2 b^14 c^2 y z-2 a^14 c^4 y z+30 a^12 b^2 c^4 y z-42 a^10 b^4 c^4 y z+14 a^8 b^6 c^4 y z-2 a^6 b^8 c^4 y z-6 a^4 b^10 c^4 y z+6 a^2 b^12 c^4 y z+2 b^14 c^4 y z-10 a^12 c^6 y z-4 a^10 b^2 c^6 y z+14 a^8 b^4 c^6 y z+10 a^6 b^6 c^6 y z-2 a^4 b^8 c^6 y z-2 a^2 b^10 c^6 y z-6 b^12 c^6 y z+10 a^10 c^8 y z-10 a^8 b^2 c^8 y z-2 a^6 b^4 c^8 y z-2 a^4 b^6 c^8 y z+4 b^10 c^8 y z+2 a^8 c^10 y z+2 a^6 b^2 c^10 y z-6 a^4 b^4 c^10 y z-2 a^2 b^6 c^10 y z+4 b^8 c^10 y z-6 a^6 c^12 y z+6 a^4 b^2 c^12 y z+6 a^2 b^4 c^12 y z-6 b^6 c^12 y z+2 a^4 c^14 y z-4 a^2 b^2 c^14 y z+2 b^4 c^14 y z+a^18 z^2-3 a^16 b^2 z^2+8 a^14 b^4 z^2-16 a^12 b^6 z^2+10 a^10 b^8 z^2+10 a^8 b^10 z^2-16 a^6 b^12 z^2+8 a^4 b^14 z^2-3 a^2 b^16 z^2+b^18 z^2-3 a^16 c^2 z^2+5 a^14 b^2 c^2 z^2-6 a^12 b^4 c^2 z^2+27 a^10 b^6 c^2 z^2-46 a^8 b^8 c^2 z^2+27 a^6 b^10 c^2 z^2-6 a^4 b^12 c^2 z^2+5 a^2 b^14 c^2 z^2-3 b^16 c^2 z^2+2 a^14 c^4 z^2-12 a^10 b^4 c^4 z^2+10 a^8 b^6 c^4 z^2+10 a^6 b^8 c^4 z^2-12 a^4 b^10 c^4 z^2+2 b^14 c^4 z^2+2 a^12 c^6 z^2-7 a^10 b^2 c^6 z^2+10 a^8 b^4 c^6 z^2-10 a^6 b^6 c^6 z^2+10 a^4 b^8 c^6 z^2-7 a^2 b^10 c^6 z^2+2 b^12 c^6 z^2-3 a^10 c^8 z^2+9 a^8 b^2 c^8 z^2-6 a^6 b^4 c^8 z^2-6 a^4 b^6 c^8 z^2+9 a^2 b^8 c^8 z^2-3 b^10 c^8 z^2+a^8 c^10 z^2-4 a^6 b^2 c^10 z^2+6 a^4 b^4 c^10 z^2-4 a^2 b^6 c^10 z^2+b^8 c^10 z^2 = 0)
𝒫 del haz de cónicas formado por 𝒞 y ℰ es el conjugado isogonal, X249, del centro de la
Ternas {P, Q, Z}, con P, Q, Z sobre la recta de Euler, y sobre las cónicas 𝒞 y ℰ, respectivamente:
{X4,X24,Indefinido}
{X2,X6,X69},
{X3,X3,X1092},
{X5,X143,Z5},
{X20,X35602,Z20},
{X21,X60,Z21},
{X22,X20806,Z22},
{X23,X6593,Z23},
{X24,X35603,Z24},
{X25,X19118,X1974},
{X28,X60,Z28},
{X30,X1511,X16163},
{X186,X1986,X3043},
{X468,Q468,X5095},
{X1113,X15461,X15461},
{X1114,X15460,X15460},
{X3518,X143,Z3518},
{X3542,X35603,Z3542},
{X34484,X34484,Z34484}.
Q468 = ( a^2 (2 a^2-b^2-c^2) (a^2+b^2-c^2) (a^8-2 a^6 b^2-b^8+3 b^6 c^2-3 b^2 c^6+c^8+a^4 (5 b^2 c^2-2 c^4)+2 a^2 (b^6-4 b^4 c^2+2 b^2 c^4)) : ... : ...),
que tiene números de búsqueda en
(-0.0725429577890322, 0.129594607442996, 3.58442650342647).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,19388}, {6,1112}, {24,14984}, {25,895}, {110,19118}, {143,8537}, {235,542}, {427,15118}, {468,524}, {1204,2781}, {1511,19128}, {1593,5622}, {1885,34563}, {1899,32264}, {1974,2854}, {2892,15128}, {5050,15472}, {5609,32234}, {6467,15647}, {9970,13148}, {11579,12133}, {12099,32251}, {12164,35603}, {13416,26206}, {13567,32285}, {15462,35602}, {18947,25321}, {19136,32246}, {19153,32245}, {19504,20806}, {20771,34382}, {25328,32239}, {30739,32300}.
Z5 = ( (a^2-b^2-c^2) ((b^2-c^2)^2-a^2 (b^2+c^2))^2 : ... : ...),
que tiene números de búsqueda en ETC
(-0.167521631040232, -0.0482021967567318, 3.75135290937299).
Es la reflexión de Xi en Xj para los índices {i,j}: {3043, 5972}, {5944, 34577}, {13367, 7542}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,578}, {3,125}, {4,14860}, {5,51}, {20,11204}, {22,18381}, {23,13419}, {26,18474}, {30,11572}, {49,539}, {54,10112}, {68,184}, {69,576}, {110,2888}, {113,5876}, {115,22416}, {140,12370}, {141,23308}, {156,24981}, {182,7558}, {185,12359}, {195,11536}, {235,15030}, {311,13450}, {324,6750}, {373,7405}, {376,23294}, {389,3580}, {394,1656}, {403,5907}, {418,10600}, {467,8887}, {511,1594}, {542,1614}, {546,1531}, {550,13561}, {567,6689}, {631,26917}, {648,3462}, {847,8754}, {858,15644}, {1147,6639}, {1199,11225}, {1216,2072}, {1350,6697}, {1352,1974}, {1495,12134}, {1506,3289}, {1511,10125}, {1533,11381}, {1853,11414}, {1899,3547}, {1994,12242}, {2070,6288}, {2071,25563}, {2777,11440}, {2904,5095}, {3043,5972}, {3153,7691}, {3292,9820}, {3313,20300}, {3518,32223}, {3523,26913}, {3526,35602}, {3564,21637}, {3627,18488}, {3628,11064}, {3818,10594}, {3917,11585}, {5067,37669}, {5094,37498}, {5133,10110}, {5446,5576}, {5447,37452}, {5448,10254}, {5462,37347}, {5480,16254}, {5622,22533}, {5889,18388}, {5943,14788}, {5944,32423}, {6101,10224}, {6146,6676}, {6641,16391}, {6756,32269}, {6759,11442}, {6803,37643}, {7387,11550}, {7399,13567}, {7400,23291}, {7488,18400}, {7493,9833}, {7502,11750}, {7503,18390}, {7505,9306}, {7507,17834}, {7512,25739}, {7528,34417}, {7542,13367}, {7565,15360}, {7568,37513}, {7577,11412}, {7706,37490}, {7794,23098}, {7999,11704}, {9729,26879}, {9781,19130}, {9967,20303}, {10024,13754}, {10182,11449}, {10201,10539}, {10203,33565}, {10255,23039}, {10272,12010}, {10282,14516}, {10298,12278}, {10564,23336}, {10575,13399}, {10619,18475}, {10625,13371}, {10990,32138}, {11273,25150}, {11413,23329}, {11459,16868}, {11592,20396}, {11793,37636}, {12088,29012}, {12111,12827}, {12162,15761}, {12225,18383}, {12233,14831}, {12429,19357}, {12605,13851}, {12897,14130}, {13292,13366}, {13336,18952}, {13346,37119}, {13394,31804}, {13403,14118}, {13413,14449}, {13491,16003}, {13598,15559}, {14389,37505}, {14789,15024}, {15067,23515}, {15069,19153}, {15780,33664}, {15908,21252}, {16111,32210}, {17714,34514}, {18563,24572}, {18569,37478}, {18911,37515}, {20304,32142}, {22151,25555}, {22352,34002}, {23325,37444}, {23332,36987}, {26869,37514}, {30714,32171}, {32348,35921}, {33523,37353}, {34520,36412}, {35717,37127}.
Z20 = ( (a^2-b^2-c^2) (3 a^4-2 a^2 (b^2+c^2)-(b^2-c^2)^2)^2 : ... : ...),
que tiene números de búsqueda en ETC
(6.61655506442307, 5.21388831436237, -3.02274515007714).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,69}, {4,18418}, {20,154}, {99,15324}, {110,6225}, {125,15077}, {184,15740}, {193,1192}, {343,15717}, {376,1092}, {394,3522}, {524,1620}, {631,26917}, {648,3183}, {1097,6060}, {1105,6618}, {1498,2063}, {1531,11541}, {1568,33703}, {1974,13346}, {1992,9786}, {2060,14365}, {2071,12324}, {3043,35503}, {3060,15887}, {3088,28408}, {3146,11064}, {3147,15035}, {3516,14826}, {3528,5562}, {3529,10721}, {3548,18918}, {3618,11425}, {5921,6696}, {6803,11430}, {6908,28754}, {7396,17845}, {7487,28708}, {9833,25712}, {10282,35513}, {10564,34938}, {10996,13367}, {11008,37487}, {11206,11413}, {11433,22467}, {11449,35260}, {11487,18570}, {12429,16976}, {14927,28419}, {15131,37444}, {16051,21659}, {16196,18945}, {17928,18928}, {22151,37460}, {22555,22951}, {37752,37753}.
Z21 = ( a^2 (a+b)^2 (a+c)^2 (b+c-a)^2 (a^2-b^2-c^2) : ... : ...),
que tiene números de búsqueda en ETC
(4.79679965554001, 2.18347862747365, -0.0848821012081496).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {21,60}, {69,261}, {78,1793}, {110,3869}, {125,18123}, {184,1798}, {255,4558}, {283,6514}, {394,593}, {411,662}, {849,1780}, {1092,6875}, {1437,1444}, {1935,23695}, {2651,7098}, {12514,17104}, {22126,32661}.
Z22 = ( a^4 (a^2-b^2-c^2) (b^4+c^4-a^4)^2 : ... : ...),
que tiene números de búsqueda en ETC
(20.4787370417051, 18.9953055859872, -18.9616564814861).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,28708}, {22,206}, {69,184}, {110,2892}, {125,18124}, {182,7558}, {1092,3098}, {1147,37511}, {1974,22151}, {5157,7495}, {9306,28408}, {19149,35602}, {34397,37491}, {37752,37753}.
Z23 = ( a^4 (a^2-b^2-c^2) (b^4-b^2 c^2+c^4-a^4)^2 : ... : ...),
que tiene números de búsqueda en ETC
(-1.86721996852158, -2.66778180887472, 6.34938418121530).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,15462}, {22,15141}, {23,6593}, {49,14984}, {67,19127}, {69,110}, {125,1176}, {182,14644}, {184,895}, {511,3043}, {542,1614}, {1092,7556}, {1992,32245}, {2781,7488}, {2854,3047}, {5012,15118}, {5157,15059}, {5622,36253}, {5972,32239}, {6776,19138}, {12228,14853}, {12310,19125}, {13198,18935}, {15132,32247}, {16163,29317}, {18933,25406}, {19140,22109}, {25335,37638}, {37752,37753}.
Z24 = ( a^4 (a^2+b^2-c^2) (a^2-b^2+c^2) (a^4-2 a^2 (b^2+c^2)+b^4+c^4)^2 : ... : ...),
que tiene números de búsqueda en ETC
(-5.83923691985503, -1.03182428185952, 7.05003679389714).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,18532}, {4,54}, {24,52}, {25,49}, {69,3147}, {70,125}, {110,3542}, {156,235}, {182,37119}, {186,1092}, {206,9707}, {215,11398}, {378,10575}, {403,9927}, {421,847}, {427,32046}, {567,7507}, {569,1594}, {576,1974}, {1112,20773}, {1598,9704}, {1986,12893}, {2477,11399}, {3043,15034}, {3088,11003}, {3089,9544}, {3135,19210}, {3146,15472}, {3515,22115}, {3517,9703}, {3520,10984}, {3541,5012}, {5094,13353}, {5651,14940}, {6240,13352}, {6243,11597}, {7487,9545}, {7502,12363}, {7505,9306}, {7713,9622}, {8745,34756}, {8901,34449}, {9677,11473}, {9706,37122}, {10018,37636}, {10540,37197}, {11456,36982}, {12173,37472}, {12228,18569}, {13198,14216}, {13336,37118}, {13346,15463}, {13371,34114}, {15575,21397}, {16266,21213}, {18374,34787}, {18533,34148}, {21284,37484}, {35503,37480}, {37196,37495}.
Z28 = ( a^2 (a + b)^2 (a + c)^2 (a^2 + b^2 - c^2) (a^2 - b^2 + c^2) : ... : ...),
que tiene números de búsqueda en ETC
(-0.223129350056969, -0.774422936785160, 4.27978621509271).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,14015}, {3,7054}, {4,1798}, {19,9275}, {25,1171}, {27,29833}, {28,60}, {58,1474}, {69,7521}, {110,3868}, {112,741}, {162,4222}, {163,580}, {184,1175}, {186,35203}, {849,1412}, {1092,7501}, {1098,30733}, {1396,1408}, {1509,31900}, {1576,23383}, {1974,17562}, {2074,11363}, {2183,15796}, {2185,4227}, {3437,20975}, {23606,28348}, {28838,36071}.
Z140 = ( (a^2-b^2-c^2) (2 a^4-3 a^2 (b^2+c^2)+(b^2-c^2)^2)^2 : ... : ...),
que tiene números de búsqueda en ETC
(4.49830869760274, 2.25994275283347, -0.0000537458708245153).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,26861}, {69,3533}, {110,2889}, {125,3519}, {140,1493}, {323,12242}, {394,1656}, {550,5562}, {1092,3523}, {1216,10619}, {1568,3850}, {3292,34002}, {5095,10018}, {5642,18282}.
Z3518 = ( a^4 (a^2+b^2-c^2) (a^2-b^2+c^2)
(a^4-2 a^2 (b^2+c^2)+b^4-b^2 c^2+c^4)^2 : ... : ...),
que tiene números de búsqueda en ETC
(-0.0548111433108069, -0.118079325015693, 3.74770915767715).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,569}, {24,3043}, {49,143}, {54,22454}, {110,11271}, {184,1173}, {186,10627}, {1974,8537}, {2070,12226}, {6143,19128}, {10594,15038}, {34397,34484}.
Z3542 = ( (a^2+b^2-c^2) (a^2-b^2+c^2) (a^6-3 a^4 (b^2+c^2)-(b^2-c^2)^2 (b^2+c^2)+a^2 (3 b^4-2 b^2 c^2+3 c^4))^2 : ... : ...),
que tiene números de búsqueda en ETC
(-0.000984771058288283, -0.289890349215837, 3.84181231031455).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,51}, {25,13292}, {69,7505}, {155,3542}, {235,18951}, {403,11411}, {1092,3147}, {1112,14790}, {3089,37644}, {6622,18947}, {8754,36612}, {11441,18934}, {11456,18910}, {11470,14561}, {15081,18920}, {18917,37197}, {18928,37119}.
Z34484 = ( a^4 (a^2+b^2-c^2) (a^2-b^2+c^2) (a^4+b^4-3 b^2 c^2+c^4-2 a^2 (b^2+c^2))^2 : ... : ...),
que tiene números de búsqueda en ETC
(-0.392814037766889, -1.00944218663557, 4.52080785931680).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,13336}, {184,34567}, {1112,3043}, {1974,22234}, {5095,13420}, {10095,11817}.
- Miércoles, 25 de mayo del 2020
Circunferencias coaxiales pasando por el ortocentro. Estrofoide de Ehrmann
El 25 de Mayo de 1828 nació Karl Mikhailovich Peterson, matemático ruso, conocido por una formulación anterior de las ecuaciones de Gauss-Codazzi.
Peterson escribió una tesis inédita en 1853 sobre geometría diferencial. Esta disertación fue escrita en alemán, pero aunque se conservó en los archivos de la Universidad de Dorpat, permaneció prácticamente desconocida hasta que se publicó en traducción rusa cien años después, en 1952. La disertación contiene una derivación de dos ecuaciones equivalentes a las de Mainardi y Codazzi, y en él Peterson esbozó una prueba del teorema fundamental de la teoría de la superficie (§11.3). La tesis también contiene lo que se conoce como el teorema de Bonnet, publicado por Pierre Bonnet quince años después, en 1867. En [*], Esther Phillips presenta un fuerte argumento no solo por la prioridad de Peterson sobre Mainardi, Codazzi y Bonnet, sino también por la mayor elegancia. y la simplicidad de su enfoque.
[*] E R Phillips, Karl M Peterson: la primera derivación de las ecuaciones de Mainardi-Codazzi y el teorema fundamental de la teoría de la superficie.
Algunas propiedades más relacionadas con al mensaje Hyacinthos#26814 (Antreas Hatzipolakis, Angel Montesdeoca, César Lozada)
Hyacinthos#26814 (Nov 19, 2017)
[APH]:
Let ABC be a triangle and L a line.
Denote:
A', B', C' = the intersections of L and BC, CA, AB, resp.
Ma, Mb, Mc = the midpoints of AA', BB', CC', resp.
A", B", C" = the reflections of O in Ma, Mb, Mc, resp.
The circles (A", A"A), (B", B"B), (C", C"C) are coaxial.
One of the intersection points is the orthocenter H.
The other one?
[Angel Montesdeoca]:
If L is the of P(u:v:w) the other point of intersection of circles (A", A"A), (B", B"B), (C", C"C) is:
Q(P) = ((b^2-c^2) u (v-w)+a^2 (-u^2+v w):a^2 v (u-w)+c^2 v (-u+w)+b^2 (-v^2+u w):(a^2-b^2) (u-v) w+c^2 (u v-w^2)).
** The locus of the other point of intersection of the circles (A", A"A), (B", B"B), (C", C"C) when L turn around the centroid is a
quartic
( (-a^4+2 a^2 b^2-b^4+2 a^2 c^2-2 b^2 c^2-c^4) x^3 y+(-2 a^4+4 a^2 b^2-2 b^4+c^4) x^2 y^2+(-a^4+2 a^2 b^2-b^4-2 a^2 c^2+2 b^2 c^2-c^4) x y^3+(-a^4+2 a^2 b^2-b^4+2 a^2 c^2-2 b^2 c^2-c^4) x^3 z+(-a^4+2 a^2 b^2-b^4+2 a^2 c^2-c^4) x^2 y z+(-a^4+2 a^2 b^2-b^4+2 b^2 c^2-c^4) x y^2 z+(-a^4+2 a^2 b^2-b^4-2 a^2 c^2+2 b^2 c^2-c^4) y^3 z+(-2 a^4+b^4+4 a^2 c^2-2 c^4) x^2 z^2+(-a^4-b^4+2 a^2 c^2+2 b^2 c^2-c^4) x y z^2+(a^4-2 b^4+4 b^2 c^2-2 c^4) y^2 z^2+(-a^4-2 a^2 b^2-b^4+2 a^2 c^2+2 b^2 c^2-c^4) x z^3+(-a^4-2 a^2 b^2-b^4+2 a^2 c^2+2 b^2 c^2-c^4) y z^3 = 0)
(Figure and more information in
http://amontes.webs.ull.es/otrashtm/HGT2017.htm#HG141117)
[César Lozada]:
Hi Antreas and Angel,
Please allow me to add a pair of notes about the locus of the 2nd point of intersection Q(P):
Let L be the polar trilinear of P=u:v:w (trilinears), as Angel said.
If P moves on a line, for example the polar trilinear of P0=u0:v0:w0 (trilinears), then Q(P) moves on a circle C0 through H satisfying:
if P0 = X(264) then C0 has radius=0 . In this case the given circles are tangent at H.
ETC centers on this line: 297, 525, 850, 2501, 2592, 2593, 3569, 3580, 4391, 5523, 9979, 10015, 13302, 14316, 14618, 14918
if P0 lies on the then C0 has radius=infinite, ie, C0 is a line which coincides with the radical axis of the circles.
otherwise, C0 has center O*= u0*(b*v0+c*w0)*(S^2+SB*SC)-SA* a*b*c*v0*w0 : : (trilinears)
If P moves on the then Q(P) lies on the circumcircle of ABC
pairs (P,Q(P)), updated:
{1, 5011}, {3, 13509}, {4, 5523}, {5, 15340}, {6, 23}, {8, 5179},
{10, 5134}, {20, 15341}, {22, 34137}, {23, 6}, {30, 6794}, {69, 858},
{75, 5057}, {76, 316}, {81, 1325}, {86, 5196}, {88, 1320}, {94, 265},
{97, 3484}, {99, 15342}, {110, 112}, {111, 895}, {141, 5189}, {144,
16870}, {145, 8074}, {148, 16278}, {190, 15343}, {193, 468}, {194,
5167}, {230, 36181}, {249, 14366}, {287, 98}, {297, 4}, {298, 36186},
{299, 36185}, {312, 5176}, {321, 5080}, {323, 3}, {324, 6761}, {325,
36163}, {333, 7424}, {338, 3448}, {343, 3153}, {346, 17615}, {385,
1316}, {394, 2071}, {401, 18338}, {511, 34235}, {512, 14700}, {514,
6788}, {523, 6792}, {524, 2}, {525, 4}, {538, 6787}, {543, 9144},
{599, 10989}, {648, 107}, {651, 108}, {671, 671}, {693, 18343}, {694,
1916}, {850, 4}, {858, 35902}, {895, 111}, {908, 18340}, {918,
10773}, {1016, 11607}, {1086, 149}, {1111, 10770}, {1230, 20558},
{1252, 14887}, {1331, 101}, {1332, 100}, {1648, 36174}, {1654,
33329}, {1797, 106}, {1813, 109}, {1814, 105}, {1815, 103}, {1976,
11610}, {1992, 7426}, {1993, 186}, {1994, 2070}, {2006, 34242},
{2340, 3730}, {2394, 34150}, {2395, 13137}, {2396, 12833}, {2397,
34151}, {2398, 34805}, {2407, 7471}, {2408, 34806}, {2421, 7468},
{2501, 4}, {2574, 8426}, {2575, 8427}, {2592, 4}, {2593, 4}, {2799,
11005}, {2895, 30447}, {2981, 1337}, {2986, 1300}, {2987, 3563},
{2988, 32706}, {2989, 917}, {2990, 915}, {2991, 15344}, {2996, 5203},
{3124, 148}, {3125, 10769}, {3180, 32461}, {3181, 32460}, {3187,
242}, {3218, 1}, {3219, 3465}, {3231, 36182}, {3239, 18328}, {3265,
18337}, {3266, 69}, {3268, 18331}, {3413, 31862}, {3414, 31863},
{3448, 115}, {3506, 13195}, {3569, 4}, {3580, 4}, {3589, 20063},
{3621, 5199}, {3762, 10774}, {3904, 18341}, {3935, 9}, {3936, 36154},
{3978, 76}, {4240, 35907}, {4358, 8}, {4359, 5180}, {4391, 4}, {4437,
20344}, {4558, 110}, {4563, 99}, {4585, 36167}, {4858, 10777}, {5392,
5962}, {5466, 34169}, {5468, 7472}, {5483, 5535}, {5523, 4}, {5638,
3558}, {5639, 3557}, {5905, 1785}, {6151, 1338}, {6332, 18339},
{6392, 5140}, {6504, 16172}, {6515, 403}, {6542, 10}, {6563, 18347},
{6650, 11599}, {7664, 11061}, {7665, 5095}, {7774, 5112}, {7779,
11007}, {7840, 36194}, {8024, 5207}, {8105, 24651}, {8106, 24650},
{8115, 1113}, {8116, 1114}, {8759, 20624}, {9486, 31962}, {9716,
187}, {9979, 4}, {10015, 4}, {11004, 7575}, {11064, 20}, {11078, 13},
{11092, 14}, {11126, 15}, {11127, 16}, {11130, 5668}, {11131, 5669},
{11140, 19552}, {13136, 1309}, {13302, 4}, {13485, 6328}, {13492,
14262}, {13582, 1263}, {14223, 34174}, {14262, 13492}, {14316, 4},
{14463, 7876}, {14618, 4}, {14918, 4}, {14919, 74}, {14920, 5667},
{14922, 616}, {14999, 4226}, {15066, 7464}, {16039, 20626}, {16080,
10152}, {16704, 3109}, {16732, 10778}, {17264, 3681}, {17434, 4},
{17496, 31849}, {17708, 935}, {17773, 4}, {17778, 36195}, {17790,
321}, {17896, 4}, {17924, 4}, {17946, 11611}, {17947, 11608}, {17948,
5466}, {17949, 11606}, {17950, 226}, {17951, 4052}, {17952, 5485},
{17953, 4049}, {18018, 34237}, {18019, 67}, {18314, 4}, {18315, 933},
{18359, 80}, {19577, 1843}, {20013, 31896}, {20017, 31897}, {20078,
16869}, {20080, 5159}, {20859, 32528}, {21438, 4}, {22151, 22},
{23878, 6785}, {23978, 33650}, {23983, 34188}, {23989, 150}, {24978,
4}, {25257, 31865}, {25259, 4}, {26545, 4}, {26546, 4}, {26611, 153},
{26932, 10776}, {30690, 34301}, {30699, 1878}, {31296, 31850},
{32849, 72}, {32851, 3869}, {33294, 4}, {34211, 7473}, {34545, 5899},
{34767, 17986}, {35466, 36171}, {36213, 13236}, {36789, 146}, {36790,
147}, {36791, 21290}, {36792, 14360}, {36793, 13219}, {37638, 10296},
{37644, 11799}, {37645, 10295}, {37669, 16386}, {37691, 20085}
NOTA: La circunferencia (C", C"C) de Hyacinthos#26814 es la circunferencia circunscrita al triángulo EFC, en AoPS.
Dado un triángulo ABC y un punto P, sean D, E, F los puntos donde la tripolar de P corta a BC, CA, AB, respectivamente. Ab es el punto sobre AC tal que DAb=DC y Ac es el punto sobre AB tal que DAc=DB, entonces la circunferencia (Oa) circunscrita a AAbAc pasa por el ortocentro de ABC.
Las circunferencia (Ob) y (Oc) son construidas cíclicamente.
Las circunferencias (Oa), (Ob), (Oc) son coaxiales.
Si (u:v:w) son las coordenadas baricéntricas de P, el otro punto de intersección de estas tres circunferencias es:
Q = (((b^2-c^2) u (v-w)+a^2 (-u^2+v w): ... : ...).
Cuando P está sobre la circuncónica de MacBeath, P, Q, están alineados.
El punto
P es diferente del ortocentro y los puntos
H, P, Q están alineados si y solo si
P está en la . El lugar geométrico de
Q es la de Ehrmann (
K025)
Si P=X671 (sexto punto de intersección de la hipérbola de Kiepert y la estrofoide de Ehrmann y también el cuarto punto de intersección de la hipérbola de Kiepert y elipse circunscrita de Steiner) entonces P=Q.
- Miércoles, 20 de mayo del 2020
Reflexión de X(11270) en el circuncentro
El 20 de mayo de 1943 nació Al Bano, cantante italiano aclamado internacionalmente, que ha ganado muchos premios y distinciones a lo largo de sus 30 años de carrera. Ha utilizado su fama para dirigir la atención a la lucha contra las drogas. El 16 de octubre de 2001, Al Bano fue nombrado Embajador de Buena Voluntad de la Organización de las Naciones Unidas para la Agricultura y la Alimentación (FAO).
Dado un triángulo ABC, sea A'B'C' el triángulo obtenido reflejando A, B, C en el circuncentro O=X3 (A'B'C' es el de O).
Ab es la reflexión de B' en AC y Ac es la reflexión de C' en AB. El circuncentro Oa del triángulo OAbAc está sobre la altura por A y tiene coordenadas baricéntricas
(4(a^6-3a^4(b^2+c^2)-(b^2-c^2)^2(b^2+c^2)+3a^2(b^4+c^4)) : 4b^2c^2(a^2+b^2-c^2) : 4b^2c^2(a^2-b^2+c^2)).
Los puntos Ob y Oc se definen cíclicamente.
Los triángulos A'B'C' y OaObOc son perspectivos y el centro de perspectividad es la reflexión en el circuncentro del conjugado isogonal de la reflexión del circuncentro en el ortocentro:
W = ( a^2(4a^8-10a^6(b^2+c^2)+a^4(6b^4+17b^2c^2+6c^4)+2a^2(b^6-4b^4c^2-4b^2c^4+c^6)-(b^2-c^2)^2(2b^4+3b^2c^2+2c^4)) : ... : ...),
que tiene números de búsqueda en
(4.51548892994527, 3.13289197959206, -0.612332548554094).
Es la reflexión de X11270 en X3.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {{2,9927}, {3,9544}, {4,1511}, {20,10282}, {110,3357}, {140,3431}, {186,2904}, {195,15040}, {323,32534}, {376,18442}, {550,7712}, {576,15020}, {578,12834}, {631,2888}, {1071,5694}, {1092,7691}, {1147,15035}, {1204,15051}, {1350,7488}, {1498,2071}, {3516,15052}, {3522,4549}, {3523,3620}, {3528,5944}, {3533,14805}, {3543,15751}, {5050,17928}, {5056,11430}, {5059,10564}, {5876,23040}, {6102,9716}, {6640,12383}, {7592,9545}, {8546,10541}, {8567,11441}, {10255,34153}, {10257,34799}, {10304,11821}, {10539,15034}, {11250,32609}, {11413,11820}, {12085,35265}, {12111,35493}, {12162,35494}, {12289,14156}, {13620,37486}, {14118,32620}, {15043,15516}, {15717,18475}, {17818,19357}, {18281,18432}, {18350,35475}, {21844,22115}, {22555,22951}, {23294,30714}, {32233,34118}, {32330,37444}.
Una situación más general:
Circumcenter of reflection (AoPS)
In the ABC, P is an arbitrary point. A'B'C' is the circumcevian triangle of P. F is the reflection of C' in AB and E is the reflection of B' in AC. ω is circumcircle of PEF. Call H the orthocenter of ABC. Prove circumcenter of ω is on AH.
Dado un triángulo ABC y un punto P no situado sobre su circunferencia circunscrita, sea A'B'C' el de P.
Ab es la reflexión de B' en AC y Ac es la reflexión de C' en AB. El circuncentro Pa del triángulo PAbAc está sobre la altura por A y tiene coordenadas baricéntricas, si P=(u:v:w),
(-(b^2-c^2)^2 u (u+v+w)+2 a^2 u (b^2 (u+v)+c^2 (u+w))-a^4 (u^2+2 v w+u (v+w)) :
(a^2+b^2-c^2) (c^2 u v+b^2 u w+a^2 v w) :
(a^2-b^2+c^2) (c^2 u v+b^2 u w+a^2 v w)).
Los puntos Pb y Pc se definen cíclicamente.
Los triángulos
A'B'C' y
PaPbPc son perspectivos
si y solo si está sobre la séptica de ecuación:
𝔖abc xyz
y z ((b^2-c^2) (-2 a^8+b^8+b^6 c^2-4 b^4 c^4+b^2 c^6+c^8+a^6 (5 b^2+5 c^2)+a^4 (-3 b^4-6 b^2 c^2-3 c^4)+a^2 (-b^6-c^6)) x^3 y z-2 a^2 (b^2-c^2) (b^6-b^4 c^2-b^2 c^4+c^6+a^4 (b^2+c^2)+a^2 (-2 b^4+2 b^2 c^2-2 c^4)) x y^2 z^2-a^6 y^2 z^2 ((a^4+b^4+b^2 c^2-2 c^4+a^2 (-2 b^2+c^2)) y+(-a^4+2 b^4-b^2 c^2-c^4+a^2 (-b^2+2 c^2)) z)-x^4 (c^2 (a^6 (2 b^2-c^2)-3 a^4 (2 b^4-c^4)+a^2 (6 b^6+b^4 c^2-5 b^2 c^4-3 c^6)-(b^2-c^2) (2 b^6+2 b^4 c^2+4 b^2 c^4+c^6)) y+b^2 (a^6 (b^2-2 c^2)-3 a^4 (b^4-2 c^4)+a^2 (3 b^6+5 b^4 c^2-b^2 c^4-6 c^6)-(b^2-c^2) (b^6+4 b^4 c^2+2 b^2 c^4+2 c^6)) z) = 0.
Esta curva tiene puntos triples en los vértices de ABC, pasa por los puntos donde las paralelas a la por ellos cortan a sus lados opuestos, por el circuncentro, por el ortocentro y por el punto del infinito X30 de la recta de Euler.
El centro de perspectividad Q de ABC y A'B'C', cuando P es X3, X4 y X30, es W (obtenido arriba), X3 y X110 (foco de la ), respectivamente.
- Martes, 19 de mayo del 2020
Complemento de la X-parábola
El 19 de mayo de 1895, José Martí, poeta cubano y combatiente, general mayor del ejército de liberación, resulta muerto a los 42 años en una emboscada por soldados españoles en Dos Ríos (Cuba).
Junto a Simón Bolívar y José de San Martín, José Martí es considerado uno de los principales protagonistas del proceso de emancipación de Hispanoamérica.
Cultivo Una Rosa Blanca (por José Martí)
Cultivo una rosa blanca
en junio como enero
para el amigo sincero
que me da su mano franca.
Y para el cruel que me arranca
el corazón con que vivo,
cardo ni ortiga cultivo;
cultivo la rosa blanca.
X-parabola of ABC
Let A*B*C* be the of the and triangles of ABC, and let A'B'C' be the medial triangle of A*B*C*. Then A, B, C, A', B', C' lie on a parabola here named the
X-parabola of ABC.
(César Eliud Lozada, February 27, 2017.)
It has barycentric equation: (b^2-c^2)^2*y*z+(c^2-a^2)^2*z*x+(a^2-b^2)^2*x*y=0.
Sea P un punto sobre una recta ℓ que pasa por el baricentro G de un triángulo dado ABC, Se denota por gtP el del de P.
En la referencia baricéntrica dada por el triángulo ABC, la ecuación tangencial (Definición 4.17) de la cónica 𝒞, lugar geométrico de la recta PgtP, cuando ℓ gira alrededor de G, puede ser dada por:
(b^2 - c^2)(1-t) V W + (c^2 -a^2)t W U + (b^2-a^2) U V= 0,
y su ecuación puntual es:
(b^2 - c^2)^2 (t-1)^2x^2 + (a^2 - c^2)^2 t^2 y^2 + (a^2 -
b^2)^2z^2
- 2(a^2-b^2)(a^2-c^2)t y z -2(a^2-b^2)(b^2-c^2)(t-1)z x - 2(a^2-c^2)(b^-c^2)(t-1)t x y = 0.
La ecuación puntual de la cónica 𝒞# con la misma matriz asociada (§ 10.6 The dual conic) que la de la ecuación tangencial anterior, tiene por ecuación:
(b^2 - c^2)(1-t) y z + (c^2 -a^2)t z x + (b^2-a^2) x y = 0.
El centro de esta cónica es:
L = ((c^2-b^2) (t-1) (c^2+b^2 t-a^2 (1+t)):
(c^2-a^2) (-c^2-b^2 (-2+t)+a^2 (t-1)) t :
(a^2-b^2) (c^2 (1-2 t)+a^2 (t-1)+b^2 t).
El lugar geométrico de L, cuando ℓ gira al rededor de G, es una
parábola
( (a^4-a^2 b^2-a^2 c^2+b^2 c^2) x^2+(-a^4+2 a^2 b^2-b^4) x y+(-a^2 b^2+b^4+a^2 c^2-b^2 c^2) y^2+(-a^4+2 a^2 c^2-c^4) x z+(-b^4+2 b^2 c^2-c^4) y z+(a^2 b^2-a^2 c^2-b^2 c^2+c^4) z^2 = 0)
𝒫 circunscrita al triángulo medial y su , punto de Briachon, respecto a este triángulo es X(620), centro de la elipse inscrita en ABC de la recta que pasa por el baricentro y .
El de la parábola 𝒫 es la X-parábola.
- Lunes, 18 de mayo del 2020
Inversión respecto a la circunferencia polar
El 18 de mayo de 1872 nació Bertrand Russell, matemático, lógico, pacifista y escritor británico, premio Nobel de Literatura en 1950 por su pensamiento e ideales humanitarios.
El inverso de un punto P, respecto a la de un triángulo ABC, puede ser construido (independientemente de que tal circunferencia sea real o imaginaria) por el procedimento siguiente:
Las perpendiculares por el ortocentro a las rectas AP, BP, CP cortan a los lados BC, CA, AB en los puntos D, E, F, respectivamente, que están en una misma recta: de P, respecto a la circunferencia polar de ABC.
La proyección ortogonal de P en esta recta es el inverso P' de P, respecto a la circunferencia polar.
Si (u:v:w) son las coordenadas baricéntricas de P, la primera coordenadas de P' es:
(-a^2-b^2+c^2)(a^2-b^2+c^2)(a^2(v^2+w^2+u(v+w))-(v+w)(b^2(u+v-w)+c^2(u-v+w))).
- Sábado, 16 de mayo del 2020
Una recta con la dirección del punto del infinito X(9033)
El 13 de mayo de 1718 nació María Gaetana Agnesi, que fue una importante figura matemática por su influencia en la divulgación del cálculo. Su obra "Instituzioni analítiche" es la obra matemática de autoría femenina más antigua que se conserva.
Su nombre está asociado a la curva llamada indebidamente "bruja de Agnesi". Los dos sustantivos son inciertos: Agnesi no descubrió esa curva (Fermat la había estudiado en 1630 y Guido Grandi, en 1703, había dado un método de construcción) y el nombre de "bruja" surgió de una mala traducción al inglés.
Dado un triángulo ABC, sea DEF el de su ortocentro H=X(4). La recta EF corta a AB y a AC en Ac y Ab, respectivamente y las paralelas a AB y a AC por el circuncentro cortan a BC en a A2 y A3, respectivamente.
Sea A'=AbA3∩AcA2 y se definen cíclicamente los puntos B' y C'.
En coordenadas baricéntricas:
A' = (a^4-(b^2-c^2)^2 : a^2 (-a^2+b^2+c^2) : a^2 (-a^2+b^2+c^2)).
Los triángulos
ABC y
A'B'C' son perspectivos, con centro de perspectividad el baricentro.
Su eje de perspectividad es paralelo a la otra asíntota (dirección de
X9033) de la hipérbola circunscrita a
ABC con una asíntota la recta de Euler.
- Miércoles, 13 de mayo del 2020
Porismo de Poncelet y triángulos circuncevianos
El 13 de mayo de 1753 nació Lazare Carnot, político y matemático francés.
El teorema de Carnot, válido para todas las secciones cónicas no degeneradas, establece que
si los lados AB, BC y CD del triángulo ABC cortan a una cónica en los puntos P,P', Q,Q' y R,R', respectivamente. Entonces, AP * AP'* BQ * BQ' * CR * CR' = AR' * AR * CQ'* CQ * BP' * BP.
Esta relación también es suficiente, es decir, si se satisface, entonces hay una cónica que pasa por los seis puntos P, P', Q, Q', R, R'.
Un triángulo ABC tiene circunferencia circunscrita O(R) y circunferencia inscrita I(r). El es el problema de encontrar todos los triángulos que tiene las mismas circunferencias circunscrita e inscrita que ABC, y es conocido que hay una familia infinita de tales triángulos.
En el mensaje "Construction - Poncelet Porism and concurrency" de AoPS, se plantea la siguiente cuestión:
Triangle ABC with circumcircle (O) and incircle (I). Contruct triangle XYZ such that (O) and (I) are also the circumcircle and the incircle of XYZ, respectively; moreover, AX, BY, CZ are concurrent at a point on IO.
Para resolver este problema, tomemos un punto P sobre la recta IO tal que IP:PO=t, y sea XYZ su . Las coordenadas baricéntricas de X (las de Y y Z, se deducen por permutación cíclica) son:
(a^2 b c ((-a+b-c) (a+b-c) (-a+b+c)+b (-a^2+b^2-c^2) t) ((-a-b+c) (a-b+c) (-a+b+c)+c (-a^2-b^2+c^2) t) :
-b ((-a+b-c) (a+b-c) (-a+b+c)+b (-a^2+b^2-c^2) t) (b c^2 ((-a+b-c) (a+b-c) (-a+b+c)+b (-a^2+b^2-c^2) t)+b^2 c ((-a-b+c) (a-b+c) (-a+b+c)+c (-a^2-b^2+c^2) t)):
-c ((-a-b+c) (a-b+c) (-a+b+c)+c (-a^2-b^2+c^2) t) (b c^2 ((-a+b-c) (a+b-c) (-a+b+c)+b (-a^2+b^2-c^2) t)+b^2 c ((-a-b+c) (a-b+c) (-a+b+c)+c (-a^2-b^2+c^2) t))).
Tratamos de encontrar los puntos P sobre IO para que los lados de XYZ sean tangentes a la de ABC.
Si imponemos que de la recta XY respecto a la circunferencia inscrita esté sobre ésta, el polinomio de cuatro grado en la variable t, que resulta, tiene dos de sus soluciones:
t=((a - b - c)(a + b - c)(a - b + c)
(-a^3 + a^2(b + c) - (b - c)^2
(b + c) + a(b + c)^2 ±
Sqrt[(a - b - c)(a + b - c)
(a - b + c)(a + b + c)
(a^2 + (b - c)^2 - 2a(b + c))]))/
(8a^2b^2c^2)
Los puntos que dividen al segmento IO en las razones dadas por estos valores de t, tienen primera coordenada baricéntrica:
a((a + b - c)(a - b + c)(a + b + c)
(b^3 - b^2c - bc^2 + c^3 +
a^2(b + c) - 2a(b^2 - bc +
c^2)) - 2S(a^2b - b^3 + a^2c -
2abc + b^2c + bc^2 - c^3)
Sqrt[-a^2 - (b - c)^2 + 2a(b + c)]),
a^2((a + b - c)(a - b + c)
(a + b + c)(a^2 + b^2 + c^2 -
2a(b + c)) + 2S(-a^2 + b^2 + c^2)
Sqrt[-a^2 - b^2 - c^2 +
2(ab + ac + bc)]).
Que son, respectivamente, los centros del triángulo X(3513) y X(3514).
X(3513) and X(3514) are the limiting points (point-circles) of the coaxal system that includes the circumcircle and incircle. Their midpoint, X(3660), is the radical trace of the incircle and circumcircle. (Peter Moses, November 15, 2011)
Si se repiten los cálculos anteriores exigiendo que los lados YZ y ZX sean tangentes a la circunferencia inscrita, cada polinomio que resulta, tiene dos raíces que dan lugar a los puntos anteriormente obtenidos.
- Viernes, 8 de mayo del 2020
Pares bicéntricos asociados a brocardianos
El 8 de mayo de 2016 falleció (a los 93 años) Tom M. Apostol, matemático especializado en teoría analítica de los números. Sus padres eran inmigrantes griegos. Es conocido por su dedicación a la docencia y por la multitud de libros de texto que ha escrito, utilizados por estudiantes de todo el mundo (Linear Algebra, Cálculo, Calculus II, Análisis matemático, ...).
Para un punto P sobre la de un triángulo ABC, consideramos sus P1 y P2. Si OP:PH=t (O=X3 el circuncentro, H=X4 el ortocentro y t un número real), las coordenadas baricéntricas de P1 y P2 son:
P1 = (1/(a^4 t + c^4 t - a^2 (b^2 + 2 c^2 t) - b^2 (c^2 + b^2 (t - 1))) : ... : ...),
P2 = (1/(a^4 t + b^4 t - a^2 (c^2 + 2 b^2 t) - c^2 (b^2 + c^2 (t - 1))) : ... : ...).
Se definen los puntos
A'=BP1∩CP2,
B'=AP2∩CP1,
C'=AP1∩BP2.
El triángulo A'B'C' tiene el mismo baricentro, G=X2 que ABC, para todo valor de t.
Los puntos A', B' y C' están en las rectas que pasan por el baricentro y por los puntos donde la tangente a la en X15526, corta a los lados BC, CA y AB, respectivamente.
X(15526) is the center of hyperbola ℋ through A,B,C,X(2),. This hyperbola is the isotomic conjugate of the Euler line and
the of line X(6)X(25), i.e. lines through and the pole of the with respect to the circumcircle. . It is also the locus of of X(2) and a point P as P moves along the Euler line, and also the locus of trilinear poles of lines passing through X(525), of the hyperbola ℋ. (Randy Hutson, January 29, 2018)
El triángulo ABC es perspectivo con los triángulos A'B'C', C'A'B' y B'C'A'.
El centro de perspectividad de ABC y C'A'B' es P1, de ABC y B'C'A' es P2, y de ABC y A'B'C' es:
Po = (1/(a^4 (t-1) + a^2 (b^2 + c^2) - (b^2 - c^2)^2 t) : ... : ...).
El lugar geométrico de Po, cuando P recorre la recta de Euler, es la
hipérbola ℋ,
( (a^4-b^4-a^2 c^2+b^2 c^2) x y+(-a^4+a^2 b^2-b^2 c^2+c^4) x z+(-a^2 b^2+b^4+a^2 c^2-c^4) y z = 0)
circunscrita a ABC con centro X15526. Esta hipérbola es tangente a la recta de Euler en el baricentro y pasa por los centros del triángulo Xi. para i∈{2, 69, 95, 253, 264, 287, 305, 306, 307, 328, 1441, 1494, 1799, 1972, 2373, 2419, 6330, 6340, 8797, 9229, 10603, 11090, 11091, 13575, 14977, 18018, 18019, 18024, 19774, 19775, 20336, 20563, 20564, 22339, 22340, 30786, 31360, 34407, 34767, 35510, 36889, 36948, 37202}.
El lugar geométrico de P1, cuando P recorre la recta de Euler, es la hipérbola
ℋ1,
( (a^2 b^2-b^4-a^2 c^2+c^4) x y+(-a^4+b^4+a^2 c^2-b^2 c^2) x z+(a^4-a^2 b^2+b^2 c^2-c^4) y z = 0)
circunscrita a ABC, que pasa por el baricentro, con centro y perspector (en la recta del infinito), respectivamente:
W1 = ((a^2 - c^2)^2 (a^2 - b^2 + c^2)^2 : ... : ...),
Z1 = ((a^2 - c^2)(a^2 - b^2 + c^2) : ... : ...).
El lugar geométrico de P2, cuando P recorre la recta de Euler, es la hipérbola
ℋ2,
( (-a^4+a^2 b^2-b^2 c^2+c^4) x y+(-a^2 b^2+b^4+a^2 c^2-c^4) x z+(a^4-b^4-a^2 c^2+b^2 c^2) y z = 0)
circunscrita a ABC, que pasa por el baricentro, con centro y perspector (en la recta del infinito), respectivamente:
W2 = ((a^2 - b^2)^2 (a^2 + b^2 - c^2)^2 : ... : ...),
Z2 = ((a^2 - b^2)(a^2 + b^2 - c^2) : ... : ...).
Los de las tangentes en el baricentro a las hipérbolas ℋ1 y ℋ2 son, respectivamente:
Q1 = ((a^2-b^2)(b^2-c^2)(a^2-b^2-c^2)(a^2+b^2-c^2) : ... : ...),
Q2 = ((a^2-c^2)(b^2-c^2)(a^2-b^2-c^2)(a^2-b^2+c^2) : ... : ...).
Sean
po,
( (-a^6 b^2+2 a^4 b^4-a^2 b^6-a^4 c^4-a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8+a^8 t-2 a^6 b^2 t+2 a^4 b^4 t-2 a^2 b^6 t+b^8 t-a^6 c^2 t+a^4 b^2 c^2 t+a^2 b^4 c^2 t-b^6 c^2 t-a^4 c^4 t-b^4 c^4 t+a^2 c^6 t+b^2 c^6 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) x+(a^6 b^2-2 a^4 b^4+a^2 b^6+a^4 c^4+a^2 b^2 c^4+b^4 c^4-2 a^2 c^6-2 b^2 c^6+c^8-a^8 t+2 a^6 b^2 t-2 a^4 b^4 t+2 a^2 b^6 t-b^8 t+a^6 c^2 t-a^4 b^2 c^2 t-a^2 b^4 c^2 t+b^6 c^2 t+a^4 c^4 t+b^4 c^4 t-a^2 c^6 t-b^2 c^6 t) (a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t) y+(-a^8+2 a^6 b^2-a^4 b^4+2 a^6 c^2-a^4 b^2 c^2-b^6 c^2-a^4 c^4+2 b^4 c^4-b^2 c^6+a^6 b^2 t-a^4 b^4 t-a^2 b^6 t+b^8 t+a^6 c^2 t+a^2 b^4 c^2 t-2 b^6 c^2 t-a^4 c^4 t+a^2 b^2 c^4 t+2 b^4 c^4 t-a^2 c^6 t-2 b^2 c^6 t+c^8 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) z = 0)
p1
( (-a^6 b^2+2 a^4 b^4-a^2 b^6-a^4 c^4-a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8+a^8 t-2 a^6 b^2 t+2 a^4 b^4 t-2 a^2 b^6 t+b^8 t-a^6 c^2 t+a^4 b^2 c^2 t+a^2 b^4 c^2 t-b^6 c^2 t-a^4 c^4 t-b^4 c^4 t+a^2 c^6 t+b^2 c^6 t) (a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t) x+(a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) y+(a^6 b^2-2 a^4 b^4+a^2 b^6+a^4 c^4+a^2 b^2 c^4+b^4 c^4-2 a^2 c^6-2 b^2 c^6+c^8-a^8 t+2 a^6 b^2 t-2 a^4 b^4 t+2 a^2 b^6 t-b^8 t+a^6 c^2 t-a^4 b^2 c^2 t-a^2 b^4 c^2 t+b^6 c^2 t+a^4 c^4 t+b^4 c^4 t-a^2 c^6 t-b^2 c^6 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) z = 0)
y
p2
( (a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) x+(a^6 b^2-2 a^4 b^4+a^2 b^6+a^4 c^4+a^2 b^2 c^4+b^4 c^4-2 a^2 c^6-2 b^2 c^6+c^8-a^8 t+2 a^6 b^2 t-2 a^4 b^4 t+2 a^2 b^6 t-b^8 t+a^6 c^2 t-a^4 b^2 c^2 t-a^2 b^4 c^2 t+b^6 c^2 t+a^4 c^4 t+b^4 c^4 t-a^2 c^6 t-b^2 c^6 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) y+(-a^6 b^2+2 a^4 b^4-a^2 b^6-a^4 c^4-a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8+a^8 t-2 a^6 b^2 t+2 a^4 b^4 t-2 a^2 b^6 t+b^8 t-a^6 c^2 t+a^4 b^2 c^2 t+a^2 b^4 c^2 t-b^6 c^2 t-a^4 c^4 t-b^4 c^4 t+a^2 c^6 t+b^2 c^6 t) (a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t) z = 0)
los ejes de perspectividad de ABC y los triángulos A'B'C', C'A'B' y B'C'A', respectivamente.
La envolvente de po es la parábola
𝒫o,
( a^4 b^4 x^2-2 a^2 b^6 x^2+b^8 x^2-2 a^4 b^2 c^2 x^2+2 a^2 b^4 c^2 x^2+a^4 c^4 x^2+2 a^2 b^2 c^4 x^2-2 b^4 c^4 x^2-2 a^2 c^6 x^2+c^8 x^2-2 a^6 b^2 x y+4 a^4 b^4 x y-2 a^2 b^6 x y+2 a^6 c^2 x y-2 a^4 b^2 c^2 x y-2 a^2 b^4 c^2 x y+2 b^6 c^2 x y-2 a^4 c^4 x y+6 a^2 b^2 c^4 x y-2 b^4 c^4 x y-2 a^2 c^6 x y-2 b^2 c^6 x y+2 c^8 x y+a^8 y^2-2 a^6 b^2 y^2+a^4 b^4 y^2+2 a^4 b^2 c^2 y^2-2 a^2 b^4 c^2 y^2-2 a^4 c^4 y^2+2 a^2 b^2 c^4 y^2+b^4 c^4 y^2-2 b^2 c^6 y^2+c^8 y^2+2 a^6 b^2 x z-2 a^4 b^4 x z-2 a^2 b^6 x z+2 b^8 x z-2 a^6 c^2 x z-2 a^4 b^2 c^2 x z+6 a^2 b^4 c^2 x z-2 b^6 c^2 x z+4 a^4 c^4 x z-2 a^2 b^2 c^4 x z-2 b^4 c^4 x z-2 a^2 c^6 x z+2 b^2 c^6 x z+2 a^8 y z-2 a^6 b^2 y z-2 a^4 b^4 y z+2 a^2 b^6 y z-2 a^6 c^2 y z+6 a^4 b^2 c^2 y z-2 a^2 b^4 c^2 y z-2 b^6 c^2 y z-2 a^4 c^4 y z-2 a^2 b^2 c^4 y z+4 b^4 c^4 y z+2 a^2 c^6 y z-2 b^2 c^6 y z+a^8 z^2-2 a^4 b^4 z^2+b^8 z^2-2 a^6 c^2 z^2+2 a^4 b^2 c^2 z^2+2 a^2 b^4 c^2 z^2-2 b^6 c^2 z^2+a^4 c^4 z^2-2 a^2 b^2 c^4 z^2+b^4 c^4 z^2 = 0)
inscrita en ABC, con foco (sobre la circunferencia circunscrita) X112 y directriz la recta que pasa por el ortocentro y simediano. Esta parábola contiene a los centros Xi, para i∈{525 (dirección del eje), 2501, 14401, 15639, 17925, 17926, 23090, 32320}.
La envolvente de p1 es la parábola
𝒫1,
( a^8 x^2-2 a^6 b^2 x^2+a^4 b^4 x^2+2 a^4 b^2 c^2 x^2-2 a^2 b^4 c^2 x^2-2 a^4 c^4 x^2+2 a^2 b^2 c^4 x^2+b^4 c^4 x^2-2 b^2 c^6 x^2+c^8 x^2+2 a^8 x y-2 a^6 b^2 x y-2 a^4 b^4 x y+2 a^2 b^6 x y-2 a^6 c^2 x y+6 a^4 b^2 c^2 x y-2 a^2 b^4 c^2 x y-2 b^6 c^2 x y-2 a^4 c^4 x y-2 a^2 b^2 c^4 x y+4 b^4 c^4 x y+2 a^2 c^6 x y-2 b^2 c^6 x y+a^8 y^2-2 a^4 b^4 y^2+b^8 y^2-2 a^6 c^2 y^2+2 a^4 b^2 c^2 y^2+2 a^2 b^4 c^2 y^2-2 b^6 c^2 y^2+a^4 c^4 y^2-2 a^2 b^2 c^4 y^2+b^4 c^4 y^2-2 a^6 b^2 x z+4 a^4 b^4 x z-2 a^2 b^6 x z+2 a^6 c^2 x z-2 a^4 b^2 c^2 x z-2 a^2 b^4 c^2 x z+2 b^6 c^2 x z-2 a^4 c^4 x z+6 a^2 b^2 c^4 x z-2 b^4 c^4 x z-2 a^2 c^6 x z-2 b^2 c^6 x z+2 c^8 x z+2 a^6 b^2 y z-2 a^4 b^4 y z-2 a^2 b^6 y z+2 b^8 y z-2 a^6 c^2 y z-2 a^4 b^2 c^2 y z+6 a^2 b^4 c^2 y z-2 b^6 c^2 y z+4 a^4 c^4 y z-2 a^2 b^2 c^4 y z-2 b^4 c^4 y z-2 a^2 c^6 y z+2 b^2 c^6 y z+a^4 b^4 z^2-2 a^2 b^6 z^2+b^8 z^2-2 a^4 b^2 c^2 z^2+2 a^2 b^4 c^2 z^2+a^4 c^4 z^2+2 a^2 b^2 c^4 z^2-2 b^4 c^4 z^2-2 a^2 c^6 z^2+c^8 z^2 = 0)
inscrita en ABC, con punto de tangencia:
T1 = ((a^2-c^2) (a^2-b^2+c^2) (a^8 t-(b^2-c^2)^2 (b^4-b^2 c^2 t-c^4 t)+a^4 (b^2 c^2 t-b^4 (1+t)+2 c^4 (1+t))-a^6 (b^2 t+c^2 (1+2 t))+a^2 (-b^4 c^2+b^2 c^4 t+b^6 (2+t)-c^6 (1+2 t)))^2 : ... : ...),
foco (sobre la circunferencia circunscrita):
F1 = (a^2(a^2-b^2)(b^2-c^2)(b^2+c^2-a^2)(a^2+b^2-c^2) :...:...),
directriz (pasa por el ortocentro)
d1: (a^2-c^2) (a^2-b^2-c^2) (a^2-b^2+c^2) x+(a^2-b^2) (a^2+b^2-c^2) (a^2-b^2+c^2) y+(b^2-c^2) (a^2+b^2-c^2) (-a^2+b^2+c^2) z =0,
vértice:
V1 =((a^2-b^2) (a^2-b^2-c^2) (b^2-c^2) (a^2+b^2-c^2)^3 (a^4-a^2 b^2-b^2 c^2+c^4)^2:...:...),
punto en infinito de su eje:
I1 = ((a^2-c^2) (a^2-b^2+c^2):...:...),
punto en infinito de su directriz:
I'1 = (a^6-a^4 c^2+a^2 (-b^4+c^4)-(-b^2 c+c^3)^2:...:...),
punto de intersección de eje y directriz:
D1 = ((a^2-b^2)(b^2-c^2)(a^2-b^2-c^2) (a^2+b^2-c^2) (a^12-2 a^2 c^6 (b^2-c^2)^2-2 a^10 (b^2+c^2)+(-b^2 c+c^3)^4+a^8 (2 b^4+2 b^2 c^2+c^4)-2 a^6 (b^6+b^4 c^2-b^2 c^4)+a^4 (b^8+2 b^6 c^2-2 b^4 c^4-2 b^2 c^6+c^8)):...:...),
perspector (coincide con el tripolo de la tangente en el baricentro a la hipérbola ℋ1):
Q1 = ((a^2 - b^2)(b^2-c^2)(a^2 - b^2 - c^2) (a^2 + b^2 - c^2) : ... : ...).
La envolvente de p2 es la parábola
𝒫2,
( a^8 x^2-2 a^4 b^4 x^2+b^8 x^2-2 a^6 c^2 x^2+2 a^4 b^2 c^2 x^2+2 a^2 b^4 c^2 x^2-2 b^6 c^2 x^2+a^4 c^4 x^2-2 a^2 b^2 c^4 x^2+b^4 c^4 x^2+2 a^6 b^2 x y-2 a^4 b^4 x y-2 a^2 b^6 x y+2 b^8 x y-2 a^6 c^2 x y-2 a^4 b^2 c^2 x y+6 a^2 b^4 c^2 x y-2 b^6 c^2 x y+4 a^4 c^4 x y-2 a^2 b^2 c^4 x y-2 b^4 c^4 x y-2 a^2 c^6 x y+2 b^2 c^6 x y+a^4 b^4 y^2-2 a^2 b^6 y^2+b^8 y^2-2 a^4 b^2 c^2 y^2+2 a^2 b^4 c^2 y^2+a^4 c^4 y^2+2 a^2 b^2 c^4 y^2-2 b^4 c^4 y^2-2 a^2 c^6 y^2+c^8 y^2+2 a^8 x z-2 a^6 b^2 x z-2 a^4 b^4 x z+2 a^2 b^6 x z-2 a^6 c^2 x z+6 a^4 b^2 c^2 x z-2 a^2 b^4 c^2 x z-2 b^6 c^2 x z-2 a^4 c^4 x z-2 a^2 b^2 c^4 x z+4 b^4 c^4 x z+2 a^2 c^6 x z-2 b^2 c^6 x z-2 a^6 b^2 y z+4 a^4 b^4 y z-2 a^2 b^6 y z+2 a^6 c^2 y z-2 a^4 b^2 c^2 y z-2 a^2 b^4 c^2 y z+2 b^6 c^2 y z-2 a^4 c^4 y z+6 a^2 b^2 c^4 y z-2 b^4 c^4 y z-2 a^2 c^6 y z-2 b^2 c^6 y z+2 c^8 y z+a^8 z^2-2 a^6 b^2 z^2+a^4 b^4 z^2+2 a^4 b^2 c^2 z^2-2 a^2 b^4 c^2 z^2-2 a^4 c^4 z^2+2 a^2 b^2 c^4 z^2+b^4 c^4 z^2-2 b^2 c^6 z^2+c^8 z^2 = 0)
inscrita en ABC, con punto de tangencia:
T2 = ((a^2-b^2) (a^2+b^2-c^2) (a^8 t+(b^2-c^2)^2 (-c^4+b^4 t+b^2 c^2 t)+a^4 (b^2 c^2 t+2 b^4 (1+t)-c^4 (1+t))-a^6 (c^2 t+b^2 (1+2 t))+a^2 (-b^2 c^4+b^4 c^2 t+c^6 (2+t)-b^6 (1+2 t)))^2 : ... : ...),
foco (sobre la circunferencia circunscrita):
F2 = (a^2 (a^2 - c^2) (a^2 - b^2 - c^2) (-b^2 + c^2) (a^2 - b^2 + c^2) :...:...),
directriz (pasa por el ortocentro)
d2: (a^2-b^2) (a^2-b^2-c^2) (a^2+b^2-c^2) x+(a^2-b^2-c^2) (b^2-c^2) (a^2-b^2+c^2) y+(a^2-c^2) (a^2+b^2-c^2) (a^2-b^2+c^2) z =0,
vértice:
V2 =((a^2-c^2) (a^2-b^2-c^2) (-b^2+c^2) (a^2-b^2+c^2)^3 (a^4+b^4-a^2 c^2-b^2 c^2)^2 :...:...),
punto en infinito de su eje:
I2 = ((a^2-b^2) (a^2+b^2-c^2) :...:...),
punto en infinito de su directriz:
I'2 = (a^6-a^4 b^2-a^2 (-b^4+c^4)-(b^3-b c^2)^2:...:...),
punto de intersección de eje y directriz:
D2 = ((a^2-c^2)(b^2-c^2)(a^2-b^2-c^2) (a^2-b^2+c^2) (a^12-2 a^2 b^6 (b^2-c^2)^2-2 a^10 (b^2+c^2)+(b^3-b c^2)^4-2 a^6 c^2 (-b^4+b^2 c^2+c^4)+a^8 (b^4+2 b^2 c^2+2 c^4)+a^4 (b^8-2 b^6 c^2-2 b^4 c^4+2 b^2 c^6+c^8)) :...:...),
perspector (coincide con el tripolo de la tangente en el baricentro a la hipérbola ℋ2):
Q2 = ((a^2-c^2)(b^2-c^2)(a^2 - b^2 - c^2) (a^2 - b^2 + c^2) : ... : ...).
Las parejas de puntos {W1, W2}, {Z1, Z2}, {Q1, Q2}, {F1, F2}, {I1, I2}, {I'1, I'2}, {V1, V2}, {D1, D2} son
El par {F1, F2} es P(109).
El resto de pares no figuran actualmente en la lista "BICENTRIC PAIRS OF POINTS", de Clark Kimberling.
En la tabla siguiente el número 23999 (por ejemplo) en la primera fila significa que es el centro del triángulo X23999 (punto de Brianchon o perspector de la cónica inscrita cuadrado trilineal de la recta de Euler) que es el producto trilineal del par bicentrico W1W2.
| Pares bicéntricos |
|
|
suma
bicéntrica |
diferencia
bicéntrica |
|
|
|
punto del infinto |
punto medio |
|
|---|
| W1,W2 |
23999 |
23582 |
23583 |
9033 |
- |
- |
15351 |
9033 |
23583 |
- |
| Z1,Z2 |
811 |
648 |
525 |
30 |
- |
6 |
2 |
recta infinito |
- |
15351 |
| Q1,Q2 | 14208 | 525 | 15526 | 9033 | - | 112 | 525 | 9033 | 15526 | - |
| F1,F2 P(109) | 810 |
3049 |
3269 |
9409 |
refl. 648 en 23582 |
648 |
647 |
- |
- |
- |
| I1,I2 |
811 |
648 |
525 |
30 |
refl. 1971 en 187 |
6 |
2 |
recta infinito |
- |
- |
| I'1,I'2 |
36120 |
6531 |
523 |
1503 |
- |
6 |
2 |
recta infinito |
- |
- |
| V1,V2 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
| D1,D2 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Obsérvese que cosssum(F1,F2) es la reflexión del producto baricéntrico de Z1 y Z2 en el producto baricéntrico de W1 y W2.
Puntos sobre la recta F1F2: {3269, 9409, 20975, 34980, 35236}
Puntos sobre la recta W1W2: {402, 5972, 6130, 6716, 9033, 16073, 16074, 23583, 24930}
Puntos sobre la recta Q1Q2: {122, 125, 684, 1650, 2972, 4466, 9033, 12037, 13212, 13611, 14417, 14429, 15526, 16186, 18210, 20975, 34601, 35442}
También son un par bicéntrico los puntos de tangencia, T1 y T2, de los ejes de perspectividad p1 y p2 con las parábolas 𝒫1 y 𝒫1.
El lugar geométrico del punto medio de T1 y T2, cuando P recorre la recta de Euler, es la parábola a𝒫o, de la parábola 𝒫o, envolvente del eje de perspectividad p0 de ABC y A'B'C'.
El lugar geométrico de la diferencia baricéntrica de T1 y T2, cuando P recorre la recta de Euler, es la hipérbola cℋ, complemento de la hipérbola ℋ lugar del centro de perspectividad Po de ABC y A'B'C'.
El conjugado isogonal Q de Po está sobre la recta X6X25 (recta que pasa por el y el del respecto a la circunferencia circunscrita).
La correspondencia P ↦ Q es una proyectividad entre las rectas que los contienen, X2X3 y X6X25. X4↦X25 y X25↦X1954 (conjugado isogonal del de X25).
La envolvente de la recta PQ es la cónica inscrita ℰ, tangente a los lados de ABC en los pies de las cevianas de X18020, conjugado isotómico del centro de la . ℰ pasa por los centros del triángulo Xi, para i∈{4, 69, 1092, 1974, 3043, 5095, 15460, 15461, 16163}, su centro es X5972 ( de las circunferencias centradas en los vértices de ABC y tangentes a la recta de Euler. Randy Hutson, August 20, 2014).
El lugar geométrico de
Uo = p1∩ p2,
( ((-a^4+a^2 b^2+a^2 c^2+a^4 t-b^4 t+2 b^2 c^2 t-c^4 t) (-a^6 b^2+2 a^4 b^4-a^2 b^6-a^4 c^4-a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8+a^8 t-2 a^6 b^2 t+2 a^4 b^4 t-2 a^2 b^6 t+b^8 t-a^6 c^2 t+a^4 b^2 c^2 t+a^2 b^4 c^2 t-b^6 c^2 t-a^4 c^4 t-b^4 c^4 t+a^2 c^6 t+b^2 c^6 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t) :
(-a^2 b^2+b^4-b^2 c^2+a^4 t-b^4 t-2 a^2 c^2 t+c^4 t) (-a^6 b^2+2 a^4 b^4-a^2 b^6-a^4 c^4-a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8+a^8 t-2 a^6 b^2 t+2 a^4 b^4 t-2 a^2 b^6 t+b^8 t-a^6 c^2 t+a^4 b^2 c^2 t+a^2 b^4 c^2 t-b^6 c^2 t-a^4 c^4 t-b^4 c^4 t+a^2 c^6 t+b^2 c^6 t) (a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t):
(-a^2 c^2-b^2 c^2+c^4+a^4 t-2 a^2 b^2 t+b^4 t-c^4 t) (a^8-2 a^6 b^2+a^4 b^4-2 a^6 c^2+a^4 b^2 c^2+b^6 c^2+a^4 c^4-2 b^4 c^4+b^2 c^6-a^6 b^2 t+a^4 b^4 t+a^2 b^6 t-b^8 t-a^6 c^2 t-a^2 b^4 c^2 t+2 b^6 c^2 t+a^4 c^4 t-a^2 b^2 c^4 t-2 b^4 c^4 t+a^2 c^6 t+2 b^2 c^6 t-c^8 t) (-a^4 b^4+2 a^2 b^6-b^8-a^6 c^2-a^2 b^4 c^2+2 b^6 c^2+2 a^4 c^4-b^4 c^4-a^2 c^6+a^8 t-a^6 b^2 t-a^4 b^4 t+a^2 b^6 t-2 a^6 c^2 t+a^4 b^2 c^2 t+b^6 c^2 t+2 a^4 c^4 t+a^2 b^2 c^4 t-b^4 c^4 t-2 a^2 c^6 t-b^2 c^6 t+c^8 t)))
cuando
P varía sobre la recta de Euler, es
K953=cK0(#X2, X525) (Catálogo de Bernard Gibert).
- Miércoles, 6 de mayo del 2020
Los centros del triángulo X(1319) y X(1420)
El 6 Mayo de 1928 falleció (a la edad de 66 años) el matemático escocés Robert Edgar Allardice, sus trabajos publicados versan sobre todo en geometría.
Propiedades relativas a K219=Allardice cubic A1(G).
X(1319) = Bevan-Schröder Point
Let X'Y'Z' be the of the , W = X(40); then X(1319) is the point, other than W, in which the circles AWX', BWY', CWZ' concur at X(1319) (Floor van Lamoen, Hyacinthos #6321, 6352).
X(1420) = X(145)-Beth conjugate of X(145)
Let Ja, Jb, Jc be the excenters and I the incenter. Let A' be the centroid of JbJcI, and define B' and C' cyclically. The triangle A'B'C' is homothetic to the at X(1420). (Randy Hutson, July 31 2018).
Sean I=X1 el incentro y DEF el de un triángulo dado ABC.
La es tangente a AC en Ab. a AB en Ac y a la circunferencia circunscrita en Ta y ésta vuelve a cortar a la
circunferencia (IDTa)
( c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-(((-a b c+b^2 c+b c^2) x)/(a+b+c))+(a c (a-b+c)^2 y)/(2 (b-c) (a+b+c))-((a^3 b+2 a^2 b^2+a b^3-2 a^2 b c-2 a b^2 c+a b c^2) z)/(2 (b-c) (a+b+c))) = 0)
en T'a. Se denota por A' la proyección ortogonal de Ta sobre la recta AbAc.
Los puntos Tb, T'b, Tc, T'c y B', C' se definen de manera similar, procediendo cíclicamente sobre los vértices de ABC.
X1420 es el punto de concurrencia de las rectas TaT'a, TbT'a, TcT'c, AA', BB', CC'.
- Martes, 5 de mayo del 2020
Punto medio de los centros ortológicos de el triangulo de McCay y los triángulos de Vecten
El 5 de mayo de 1821 , muere Napoleón I, ex emperador de Francia. al que se le atribuye
el teorema de Napoleón (si bien no hay pruebas de que sea el verdadero autor). Teorema de Napoleón:
Si sobre los lados de un triángulo arbitrario ABC, en el exterior de éste, se construyen los triángulos equiláteros ABZ, BCX y ACY entonces los centros de estos triángulos son también vértices de un triángulo equilátero.
X(6177) and X(6178) are the of the real and imaginary foci of the
(Contributed by Bernard Gibert, January 4, 2015.)
X(13087) and X(13088) are the of w.r.t. inner and outer
X(13881)
Let DEF be the orthic triangle. Let Ab be the point in which the line through B perpendicular to AB meets the perpendicular bisector of segment BD . Let Ac be the point in which the line through C perpendicular to AC meets the perpendicular bisector of segment CD. Define Bc, Ba, Ca, Cb cyclically. The six ponts Ab, Ac, Bc, Ba, Ca, Cb lie on a conic with center X(13881).
(See
El punto X(13881) como centro de una cónica.)
Dado un triángulo ABC, sean DEF el y D' la proyección ortogonal de D sobre EF.
Se denotan por Ab y Ac los centros de las circunferencias (BFD') y (CED'), con coordenadas baricéntricas:
Ab = (3 a^4-4 a^2 b^2+(b^2-c^2)^2 : a^4+3 (b^2-c^2)^2-4 a^2 (b^2+c^2) : -4 a^2 c^2),
Ac = (3 a^4-4 a^2 c^2+(b^2-c^2)^2 : -4 a^2 b^2 ; a^4+3 (b^2-c^2)^2-4 a^2 (b^2+c^2)).
Procediendo cíclicamente, se definen los puntos Bc, Ba y Ca, Cb.
Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están cobre una misma cónica, 𝒞.
La
ecuación
( 5 a^6 x^2-25 a^4 b^2 x^2+39 a^2 b^4 x^2-27 b^6 x^2-25 a^4 c^2 x^2+78 a^2 b^2 c^2 x^2-9 b^4 c^2 x^2+39 a^2 c^4 x^2-9 b^2 c^4 x^2-27 c^6 x^2-6 a^6 x y-2 a^4 b^2 x y-2 a^2 b^4 x y-6 b^6 x y+78 a^4 c^2 x y-68 a^2 b^2 c^2 x y+78 b^4 c^2 x y-114 a^2 c^4 x y-114 b^2 c^4 x y+90 c^6 x y-27 a^6 y^2+39 a^4 b^2 y^2-25 a^2 b^4 y^2+5 b^6 y^2-9 a^4 c^2 y^2+78 a^2 b^2 c^2 y^2-25 b^4 c^2 y^2-9 a^2 c^4 y^2+39 b^2 c^4 y^2-27 c^6 y^2-6 a^6 x z+78 a^4 b^2 x z-114 a^2 b^4 x z+90 b^6 x z-2 a^4 c^2 x z-68 a^2 b^2 c^2 x z-114 b^4 c^2 x z-2 a^2 c^4 x z+78 b^2 c^4 x z-6 c^6 x z+90 a^6 y z-114 a^4 b^2 y z+78 a^2 b^4 y z-6 b^6 y z-114 a^4 c^2 y z-68 a^2 b^2 c^2 y z-2 b^4 c^2 y z+78 a^2 c^4 y z-2 b^2 c^4 y z-6 c^6 y z-27 a^6 z^2-9 a^4 b^2 z^2-9 a^2 b^4 z^2-27 b^6 z^2+39 a^4 c^2 z^2+78 a^2 b^2 c^2 z^2+39 b^4 c^2 z^2-25 a^2 c^4 z^2-25 b^2 c^4 z^2+5 c^6 z^2 = 0)
de 𝒞 es:
𝔖abc xyz
(5 a^6-25 a^4 (b^2+c^2)+39 a^2 (b^2+c^2)^2-9 (3 b^6+b^2 c^2(b^2+c^2)+3 c^6))x^2+
2 (45 a^6-57 a^4 (b^2+c^2)+a^2 (39 b^4-34 b^2 c^2+39 c^4) -3 b^6-b^2c^2(b^2+c^2)-3 c^6)y z = 0.
Y su centro W es el punto medio del circuncentro y X13881, de X6177 y X6178, X13087 y X13088:
W = ( 3 a^8-7 a^6 (b^2+c^2)+2 a^4 (4 b^4+b^2 c^2+4 c^4)-a^2 (5 b^6-3 b^4 c^2-3 b^2 c^4+5 c^6)+(b^2-c^2)^4 : ... : ...),
que tiene números de búsqueda en
(4.05922283497132, 4.39695820748854, -1.27687097018676).
Es el punto medio de Xi y Xj para los índices {i,j}: {3, 13881}, {6177, 6178}, {13087, 13088}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,13335}, {3,115}, {20,9754}, {76,631}, {98,7907}, {114,33233}, {140,141}, {230,9737}, {575,31401}, {632,7914}, {1078,3406}, {1352,32970}, {2996,3523}, {3398,31455}, {3525,7940}, {3526,6292}, {3818,37466}, {3933,10256}, {5054,7801}, {5206,15980}, {5254,9734}, {5346,32447}, {5476,20576}, {5569,26614}, {6248,16925}, {6249,13860}, {6289,11316}, {6290,11315}, {6680,35424}, {6683,11261}, {7752,21445}, {7782,14651}, {7836,10303}, {7857,37334}, {7870,15702}, {7886,37242}, {7887,32152}, {9744,33000}, {11257,33259}, {12221,26516}, {12222,26521}, {13087,13088}, {13449,32961}, {14693,35375}, {18281,22463}, {24206,32954}, {34473,37446}, {37752,37753}.
- Lunes, 4 de mayo del 2020
Los centros del triángulo X(5221) y X(32635)
El 4 de mayo de 1859 murió, a la edad de 88 años, Joseph Diaz Gergonne matemático francés, fundador y editor de la primera revista dedicada por completo a las matemáticas, los "Annales de mathématiques pures et appliquées". Descubrió el principio de dualidad en Geometría proyectiva, cuando notó que cada teorema en el plano conectando puntos y líneas tenía un correspondiente con puntos y líneas intercambiados, siempre que el teorema no hiciera intervenir nociones métricas. En 1816, encontró una solución elegante al problema de Apolonio. A él se debe el descubrimiento del punto de Gergonne: punto en que se cortan los tres segmentos que unen cada vértice de un triángulo con el punto de contacto de la circunferencia inscrita con el lado opuesto.
X(32635) = X(1)X(748)∩X(2)X(3296)
(Antreas Hatzipolakis and Peter Moses,
Hyacinthos 29070)
Let ABC be a triangle.
Denote:
Na, Nb, Nc = the NPC centers of IBC, ICA, IAB, resp.
Oa, Ob, Oc = the circumcenters of IBC, ICA, IAB, resp.
O1, O2, O3 = the reflections of Oa, Ob, Oc in BC, CA, AB, resp.
Ma, Mb, Mc = the midpoints of NaO1, NbO2, NcO3, resp.
MaMbMc is perspective to
Garcia reflection triangle at X(1)X(748)∩X(2)X(3296)
The
Garcia-reflection triangle has vertices the reflections of the excenters on the midpoints of their corresponding sides.
Se consideran los triángulos DEF y UVW del incentro I=X1 de un triángulo dado ABC.
La bisectriz en A corta VW en U'. Ab es el punto donde la recta CU' y la circunferencia (ABU') se vuelven a cortar, y Ac es el punto donde la recta BU' y la circunferencia (ACU') se vuelven a cortar.
El punto A' (sobre la bisectriz AI) es la intersección de las rectas BAb y CAc. Los puntos B' y C' se definen cíclicamente.
Las rectas
A'D, B'E, C'F se cortan en
X5221.
En coordenadas baricéntricas:
U' = (2 a : b : c),
Ab = (2 a (a+2 (b+c)) : b (a+2 (b+c)) : -2 c (2 a+b+c)),
Ac = (2 a (a+2 (b+c)) : -2 b (2 a+b+c) : c (a+2 (b+c))),
A' = (a (a+2 (b+c)) : -b (2 a+b+c) : -c (2 a+b+c)),
X5221 = ((a+2(b+c))/(b+c-a) : (b+2(c+a))/(c+a-b) : (c+2(a+b))/(a+b-c)).
El punto fijo finito de la transformación afín σ, que aplica
ABC en
A'B'C', es
X(32635):
(a(b+c-a)/(2a+b+c) : b(c+a-b)/(2b+c+a) , c(a+b-c)/(2c+a+b)).
(a (a + b - c) (a - b + c) (a + 2 (b + c)) x + a (a + b - c)
(a^2 + a b - 2 b^2 - 3 b c - c^2) y + a (a - b + c) (a^2 - b^2 +
a c - 3 b c - 2 c^2) z :
-(b (a + b - c) (a - b + c)
(2 a + b + c) x) + b (a + b - c)
(-2 a^2 + a b + b^2 + 3 b c +
2 c^2) y + b (a - b + c)
(a^2 - b^2 + a c - 3 b c - 2 c^2)
z :
-((a + b - c) c (a - b + c)
(2 a + b + c) x) + (a + b - c) c
(a^2 + a b - 2 b^2 - 3 b c - c^2)
y + c (a - b + c) (-2 a^2 + 2 b^2 +
a c + 3 b c + c^2) z).
Pares {Xi, Xj=σ(Xi)}, para los índices {i,j}:
{1, 12702}, {2, 40}, {8, 1}, {9, 5220}, {10, 3579}, {21, 11684}, {72,
31673}, {78, 37567}, {80, 12738}, {200, 36279}, {210, 10}, {354,
5493}, {392, 11362}, {551, 33795}, {960, 3626}, {2321, 4663}, {3057,
3625}, {3059, 30424}, {3241, 7991}, {3582, 35460}, {3617,
35242}, {3625, 11278}, {3626, 13624}, {3632, 8148}, {3678,
18357}, {3679, 3}, {3681, 4}, {3701, 3214}, {3717, 44}, {3753,
31730}, {3873, 6361}, {3876, 3617}, {3877, 8}, {3878, 37705}, {3885,
3621}, {3899, 18525}, {4041, 4784}, {4102, 1126}, {4134,
18480}, {4147, 4782}, {4391, 4724}, {4511, 3245}, {4512,
3927}, {4525, 33697}, {4543, 764}, {4662, 3634}, {4669,
1385}, {4677, 1482}, {4711, 1125}, {4723, 899}, {4745,
31663}, {4882, 5708}, {5587, 11500}, {5657, 1158}, {5686, 9}, {5692,
355}, {5790, 6796}, {6175, 33557}, {6734, 37568}, {6735,
1155}, {6736, 37582}, {6743, 31794}, {7080, 5128}, {9778,
7992}, {10005, 15601}, {10056, 37584}, {10176, 5690}, {11114,
12528}, {11684, 10308}, {14430, 659}, {14432, 4730}, {14740,
12019}, {15104, 5787}, {17579, 9961}, {18908, 6260}, {21020,
37425}, {21677, 3647}, {24392, 3913}, {24393, 15254}, {31145,
7982}, {31156, 3951}, {32635, 32635}, {34606, 31803}, {34619,
5709}, {34641, 10222}, {34790, 18483}, {36590, 14513}, {36926,
5524}, {37718, 12331}.
- Sábado, 2 de mayo del 2020
Una construcción de X(1799)
El 2 de mayo de 1949, Arthur Miller (1915-2005), escritor y dramaturgo estadounidense, recibe el Premio Pulitzer por la obra “La muerte de un viajante”. Es vista como un ataque al sueño americano de progresar en la vida sin considerar los principios éticos. Su obra tiene una demoledora capacidad para inquietar a una sociedad maquillada de bienestar, confort, éxito y consumismo. Arthur Miller ha sabido reflejar las frustraciones y desengaños de la sociedad estadounidense.
X(1799) = inverse Mimosa transform of X(75)
Let A'B'C' be the circummedial triangle (the circumcevian triangle of X(2)). Let A" be the of B' and C', and define B" and C" cyclically. AA", BB", and CC" concur in X(1799). (Randy Hutson, December 10, 2016)
Se consideran los triángulos DEF y D'E'F' de un triángulo dado ABC.
Las rectas E'F y F'E vuelven a cortar a la circunferencia circunscrita en Ab y Ac
Sea 𝒞a la cónica tangente a las cinco rectas BC, AE', AF', BAb y CAc, y denotamos por Oa su centro. Las cónicas 𝒞b y 𝒞c y sus centros Ob y Oc son definidos cíclicamente.
Las rectas AOa, BOb y COc concurren en X1799.
Si M es un punto sobre la circunferencia circunscrita a ABC y las rectas ME y MF vuelven a cortarla en Mb y Mc, la recta MbMc, cuando M varía, envuelve a la cónica 𝒞a. Su punto de tangencia con BC es D.
La ecuación baricéntrica de 𝒞 es:
a^2(x^2+y^2+z^2) -2 a^2y z -2 (a^2 + 2 b^2)z x -2 (a^2 + 2 c^2)x y = 0.
Oa = (a^2 (a^2 + b^2 + c^2) : (a^2 + b^2) (a^2 - b^2 + c^2) : (a^2 + b^2 -
c^2) (a^2 + c^2)).
El punto fijo finito de la transformación afín, σ, que aplica
ABC en es
X7494,
(b^2 + c^2 - a^2)(3a^4 - b^4 - c^4 + 2a^2b^2 + 2a^2c^2 + 2b^2c^2) : :
σ(x:y:z) = (a^2 (a^2+b^2+c^2) (a^4+b^4-2 b^2 c^2-3 c^4-2 a^2 (b^2+c^2)) (a^4-3 b^4-2 b^2 c^2+c^4-2 a^2 (b^2+c^2)) x+
(a^2+b^2) (a^4+b^4-2 b^2 c^2-3 c^4-2 a^2 (b^2+c^2)) (3 a^6-a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)-a^2 (3 b^4+2 b^2 c^2+3 c^4)) y+
(a^2+c^2) (a^4-3 b^4-2 b^2 c^2+c^4-2 a^2 (b^2+c^2)) (3 a^6-a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)-a^2 (3 b^4+2 b^2 c^2+3 c^4)) z : ... : ...).
Sea La la recta que pasa por los puntos de tangencia de las rectas BAb y CAc con 𝒞a y se definen Lb y Lc cíclicamente.
Las rectas
La,
Lb y
Lc forman un triángulo perspectivo con
ABC, con centro de perspectividad X
39, punto medio de los ,
a^2 (b^2 + c^2) : b^2 (a^2 + c^2) : c^2(a^2 + b^2)
- Viernes, 1 de mayo del 2020
Una construcción del conjugado isogonal del complemento del conjugado isogonal de un punto
El 1 de mayo de 1870 murió, a la edad de 75 años, el matemático francés Gabriel Lamé.
En geometría diferencial crea nuevas herramientas para el estudio de superficies, en particular las coordenadas curvilíneas definidas mediante tres cuádricas homofocales.
Se consideran los triángulos DEF y D'E'C' de un punto P, respecto a un triángulo dado ABC.
Las rectas E'F y F'E vuelven a cortar a la circunferencia circunscrita a ABC en Ab y Ac, respectivamente. Sea A'=BAb∩CAc, y se definen B' y C', cíclicamente.
Si (u:v.w) son las coordenadas baricéntricas de P en la referencia ABC, se tiene que:
Ab = (a^2 u w (c^2 u v+b^2 u w+a^2 v w) : v (c^2 u+a^2 w) (c^2 u v+b^2 u w+a^2 v w) : -c^2 u v w (c^2 u+a^2 w)),
Ac = (a^2 u v (c^2 u v+b^2 u w+a^2 v w) : -b^2 u v (b^2 u+a^2 v) w : (b^2 u+a^2 v) w (c^2 u v+b^2 u w+a^2 v w)),
A' = (a^2 (c^2 u v+b^2 u w+a^2 v w) : -b^2 (b^2 u+a^2 v) w : -c^2 v (c^2 u+a^2 w) ).
Usamos las siguientes notaciones: gP es de P y cP es el de P.
La rectas AA', BB', CC' concurren en gcgP.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Los triángulos ABC y A'B'C' son si y solo si P está sobre la
séxtica
( a^4 c^4 x^3 y^3-b^4 c^4 x^3 y^3-a^2 c^6 x^3 y^3+b^2 c^6 x^3 y^3+2 a^4 b^2 c^2 x^3 y^2 z+a^2 b^4 c^2 x^3 y^2 z-3 b^6 c^2 x^3 y^2 z+5 b^4 c^4 x^3 y^2 z-2 a^2 c^6 x^3 y^2 z-4 b^2 c^6 x^3 y^2 z+2 c^8 x^3 y^2 z+3 a^6 c^2 x^2 y^3 z-a^4 b^2 c^2 x^2 y^3 z-2 a^2 b^4 c^2 x^2 y^3 z-5 a^4 c^4 x^2 y^3 z+4 a^2 c^6 x^2 y^3 z+2 b^2 c^6 x^2 y^3 z-2 c^8 x^2 y^3 z+2 a^2 b^6 x^3 y z^2-2 b^8 x^3 y z^2-2 a^4 b^2 c^2 x^3 y z^2+4 b^6 c^2 x^3 y z^2-a^2 b^2 c^4 x^3 y z^2-5 b^4 c^4 x^3 y z^2+3 b^2 c^6 x^3 y z^2+2 a^6 b^2 x^2 y^2 z^2-2 a^2 b^6 x^2 y^2 z^2-2 a^6 c^2 x^2 y^2 z^2+2 b^6 c^2 x^2 y^2 z^2+2 a^2 c^6 x^2 y^2 z^2-2 b^2 c^6 x^2 y^2 z^2+2 a^8 x y^3 z^2-2 a^6 b^2 x y^3 z^2-4 a^6 c^2 x y^3 z^2+2 a^2 b^4 c^2 x y^3 z^2+5 a^4 c^4 x y^3 z^2+a^2 b^2 c^4 x y^3 z^2-3 a^2 c^6 x y^3 z^2-a^4 b^4 x^3 z^3+a^2 b^6 x^3 z^3-b^6 c^2 x^3 z^3+b^4 c^4 x^3 z^3-3 a^6 b^2 x^2 y z^3+5 a^4 b^4 x^2 y z^3-4 a^2 b^6 x^2 y z^3+2 b^8 x^2 y z^3+a^4 b^2 c^2 x^2 y z^3-2 b^6 c^2 x^2 y z^3+2 a^2 b^2 c^4 x^2 y z^3-2 a^8 x y^2 z^3+4 a^6 b^2 x y^2 z^3-5 a^4 b^4 x y^2 z^3+3 a^2 b^6 x y^2 z^3+2 a^6 c^2 x y^2 z^3-a^2 b^4 c^2 x y^2 z^3-2 a^2 b^2 c^4 x y^2 z^3-a^6 b^2 y^3 z^3+a^4 b^4 y^3 z^3+a^6 c^2 y^3 z^3-a^4 c^4 y^3 z^3 = 0)
con puntos triples en los vértice de ABC, pasa por el baricentro, circuncentro, y por X11270, conjugado isogonal de la reflexión del circuncentro en el ortocentro, de ecuación:
2 (a^2-b^2) (a^2-c^2) (b^2-c^2) (a^2+b^2+c^2) x^2 y^2 z^2 +
𝔖abc xyz
y z (a^4 (b^2-c^2) (-a^2+b^2+c^2) y^2 z^2+x^3 (c^2 (2 a^4 b^2+a^2 (b^4-2 c^4)-(b^2-c^2) (3 b^4-2 b^2 c^2+2 c^4)) y-b^2 (2 a^4 c^2+a^2 (-2 b^4+c^4)+(b^2-c^2) (2 b^4-2 b^2 c^2+3 c^4)) z)) = 0.
Cuando P está sobre esta séxtica, se denota por U el centro de ortologia de ABC respecto a A'B'C' y por V el centro de ortologia de A'B'C' respecto a ABC.
Ternas {P, U, V}: {X2,U2, X3}, {X3,U3,X4},
{X69, U69,X24},
{X11270,X3,V11270}.
U2 = ( a^2 (a^4-b^4-c^4) (a^4+4 a^2 (b^2+c^2)+3 b^4+10 b^2 c^2+3 c^4) : ... : ...),
que tiene números de búsqueda en
(13.3744666451673, 11.0408740791004, -10.1758483321624).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,251}, {4,141}, {20,13575}, {907,1297}, {990,23051}, {3313,8743}, {3425,10323}, {5188,7509}, {32956,33586}.
V11720 = ( a^2 (a^8-4 a^6 (b^2+c^2)+6 a^4 (b^4-b^2 c^2+c^4)-4 a^2 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^2 (b^4+8 b^2 c^2+c^4)) : ... : ...),
V11720 = 5R^2 X4 + (r^2+4r R-s^2) X6,
(r y R son los radios de las circunferencias inscrita y circunscrita y s el semiperímetro de ABC)
que tiene números de búsqueda en ETC
(-12.9018191297064, -15.2199216021018, 20.1322190355348).
Es la reflexión de Xi en Xj para los índices {i,j}: {24, 26883}, {11413, 10539}, {11457, 235}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,6030}, {4,6}, {20,18451}, {22,12162}, {23,12163}, {24,1204}, {25,6241}, {26,18439}, {30,11441}, {54,1597}, {64,186}, {74,3515}, {110,12085}, {154,3520}, {155,3146}, {184,13474}, {185,10594}, {235,11457}, {376,17814}, {378,6759}, {382,1993}, {394,3529}, {399,5073}, {403,14216}, {546,5422}, {550,15066}, {578,32062}, {1216,33524}, {1495,3357}, {1593,1614}, {1596,18912}, {1598,5890}, {1657,15068}, {1853,16868}, {1906,18914}, {2904,34786}, {3089,26879}, {3426,3516}, {3518,10605}, {3522,15052}, {3528,17811}, {3542,12324}, {3543,36747}, {3544,17825}, {3545,37514}, {3567,5198}, {3627,18445}, {3796,35500}, {3830,12161}, {3832,36752}, {3845,36753}, {3853,36749}, {3855,10601}, {5059,37483}, {5068,15805}, {5562,12082}, {5663,7517}, {5876,12083}, {5878,6240}, {5889,18534}, {5894,35503}, {5895,34797}, {5907,10323}, {5925,13619}, {6225,18533}, {6247,7505}, {6642,15072}, {6696,15152}, {6800,7526}, {6834,37687}, {7387,12111}, {7391,22660}, {7464,35602}, {7506,13491}, {7509,15030}, {7529,10574}, {7530,34783}, {7547,11550}, {7550,33537}, {7731,12308}, {7999,37198}, {8567,17506}, {9781,18535}, {9786,34484}, {9818,11439}, {9833,18560}, {9919,12281}, {9934,12292}, {10282,35477}, {10295,20427}, {10539,11413}, {10540,12084}, {10575,17928}, {10606,21844}, {10706,34725}, {10984,20190}, {11160,34621}, {11403,15033}, {11414,11459}, {11425,13596}, {11440,14070}, {11444,35243}, {11468,15750}, {11472,14118}, {11479,16261}, {11799,32140}, {12087,37486}, {12164,12271}, {12234,32340}, {12244,17812}, {13382,34417}, {14865,19357}, {15311,35471}, {16252,37119}, {17810,26863}, {17821,35473}, {18381,35488}, {18394,19361}, {18400,35490}, {18488,31236}, {20806,29012}, {21663,35479}, {22802,35480}, {25739,34780}, {33703,37498}, {34782,35481}.
- Martes, 28 de abril del 2020
Un problema de construcción y el punto de Kosnita
El 28 Abril 1843 falleció (a la edad de 74 años) el matemático británico William Wallace. El trabajo de Wallace fue sobre geometría y la (¡que definitivamente no se debe a Simson!) aparece primero en un artículo de Wallace en 1799. Uno de los teoremas de Wallace:
Teorema (Wallace 1804). Cada tres lados extendidos de un cuadrilátero general determinan un triángulo y, por lo tanto, determinan un círculo circunscrito al triángulo. Por lo tanto, 4 círculos están determinados por un cuadrilátero. Estos cuatro círculos se encuentran en un punto.
Se considera el siguiente problema de construcción:
En los lados AB, AC, prolongados si es necesario, de un triángulo ABC encontrar dos puntos D, E de manera que los segmentos AD, DE y CE sean iguales.
Para construir tales puntos, se traza la circunferencia B(c), de centro B y radio AB, que vuelve a cortar a la recta AC en F. La circunferencia F(c) corta a AC en dos puntos L y L'. La paralela por C a BL corta a AB en el punto D buscado, y la paralela por D a BF corta a AC el segundo punto E buscado.
Tomando el punto L', y repitiendo la misma construcción, se obtiene otra solución.
Pensando en la geometría del triángulo, por permutación cíclica sobre sus vértices, tomando las dos rectas que parten de ellos, se obienen seis de tales construcciones. Para adaptar la notación, con el fin de deducir cuál es el nombre de los extremos de los segmentos a construir, designamos por AAcb, AcbAbcb, AbcbC los tres segmentos iguales, partiendo del vértice A, continuando sobre la recta AB y terminado sobre la recta AC.
Si, partiendo de A, tomamos el primer segmento sobre la recta AC, se denotan los tres segmentos iguales por: AAbc = AbcAcbc = AcbcB.
Partiendo de B, los extremos de los segmento obtenidos se denotan por Bac, Bcac, Bca y Baca.
Finalmente, partiendo de C, Cba, Caba, Cab y Ccac.
Los cuatro puntos Acb, Abcb, Abc y Acbc son , y denotamos el centro de la
circunferencia
( c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-(((-a^2 b^2 c^2+b^4 c^2+b^2 c^4) x)/(a^2-b^2-b c-c^2)^2)-(b c^3 (-a^2+b c+c^2) y)/(-a^2+b^2+b c+c^2)^2-(b^3 c (-a^2+b^2+b c) z)/(-a^2+b^2+b c+c^2)^2) = 0)
que los contiene por Oa. Cíclicamente, definimos Ob y Oc.
Oa = (-a^6+b c (b^2-c^2)^2+a^4 (2 b^2+b c+2 c^2)-a^2 (b^4+2 b^3 c+2 b c^3+c^4) : b^2 (a^4+b^4-b^2 c^2-a^2 (2 b^2+c^2)) : c^2 (a^4-b^2 c^2+c^4-a^2 (b^2+2 c^2))).
Las rectas AOa, BOb y COc concurren en el .
Si se considera la segunda solución del problema planteado, correspondiente a cada vértice y cada uno de los dos lados que parten de él, se obtienen tres cuaternas de puntos sobre circunferencias de centros O'a, O'b y O'c, que están sobre las rectas AOa, BOb y COc, respectivamente.
O'a = ({-a^6-b c (b^2-c^2)^2+a^4 (2 b^2-b c+2 c^2)-a^2 (b^4-2 b^3 c-2 b c^3+c^4) : b^2 (a^4+b^4-b^2 c^2-a^2 (2 b^2+c^2)) : c^2 (a^4-b^2 c^2+c^4-a^2 (b^2+2 c^2))).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Los seis puntos Abcb, Acbc, Bcac, Baca, Caba, Cbab están sobre una misma cónica
cónica,
( a^4 b c x^2-a^2 b^3 c x^2-a^2 b c^3 x^2+a^5 b x y-2 a^3 b^3 x y+a b^5 x y-a^2 b^2 c^2 x y-a b c^4 x y-a^3 b^2 c y^2+a b^4 c y^2-a b^2 c^3 y^2+a^5 c x z-a b^4 c x z-a^2 b^2 c^2 x z-2 a^3 c^3 x z+a c^5 x z-a^4 b c y z+b^5 c y z-a^2 b^2 c^2 y z-2 b^3 c^3 y z+b c^5 y z-a^3 b c^2 z^2-a b^3 c^2 z^2+a b c^4 z^2 = 0)
𝒞, de ecuación baricéntrica:
𝔖abc xyz
a^2 b c (b^2+c^2-a^2)x^2+b c (a^4+a^2 b c-(b^2-c^2)^2)y z = 0.
Así mismo, los seis puntos A'bcb, A'cbc, B'cac, B'aca, C'aba, C'bab (de las segundas construcciones en cada vértice) están sobre una misma cónica
cónica,
( a^4 b c x^2-a^2 b^3 c x^2-a^2 b c^3 x^2-a^5 b x y+2 a^3 b^3 x y-a b^5 x y+a^2 b^2 c^2 x y+a b c^4 x y-a^3 b^2 c y^2+a b^4 c y^2-a b^2 c^3 y^2-a^5 c x z+a b^4 c x z+a^2 b^2 c^2 x z+2 a^3 c^3 x z-a c^5 x z+a^4 b c y z-b^5 c y z+a^2 b^2 c^2 y z+2 b^3 c^3 y z-b c^5 y z-a^3 b c^2 z^2-a b^3 c^2 z^2+a b c^4 z^2 = 0)
𝒞', de ecucación baricéntrica:
𝔖abc xyz
a^2 b c (b^2+c^2-a^2)x^2-b c (a^4+a^2 b c-(b^2-c^2)^2)y z = 0.
Se denota por UVW y U'V'W' los triángulos formados por las de los vértices de ABC respecto a las cónicas 𝒞 y 𝒞', y por P y P' sus , respectivamente.
Los triángulos UVW y U'V'W' son perspectivos, su centro de perspectividad Q está alineado con P y P'.
En consecuencia, los tres ejes de perspectividad de los pares de triángulos (ABC, UVW), (ABC, U'V'W'), (UVW, U'V'W'), coinciden (ver Theorem 19) en una misma recta. Es la del de los centros del triángulo X75 y X3585:
Z = ( (a^4+a^2 b c-(b^2-c^2)^2)/a : ... : ...),
Z = 3R^2 X(2) - (4R^2-r^2-s^2) X(92),
(r y R son los radios de las circunferencias inscrita y circunscrita y s el semiperímetro de ABC)
que tiene números de búsqueda en
(-1.60100366934300, -1.53067534278271, 5.43928756660764).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,92}, {9,14212}, {23,7009}, {35,6757}, {75,5361}, {81,14616}, {94,226}, {171,1109}, {242,13595}, {304,30637}, {312,17791}, {319,321}, {323,1943}, {858,7140}, {1087,3075}, {1851,7394}, {1920,20944}, {2003,24149}, {2064,28654}, {2345,20915}, {2969,5133}, {2994,37644}, {3218,14213}, {3219,6358}, {3262,33168}, {3580,6354}, {4008,30652}, {4358,20919}, {4454,14552}, {4671,20928}, {4858,27003}, {4957,37634}, {7102,7391}, {7544,31387}, {13746,18447}, {14008,21318}, {14211,27065}, {14829,20886}, {16732,33133}, {17126,17871}, {17862,26842}, {20883,27059}, {20887,32939}, {20942,26739}, {23661,37256}, {23690,33142}, {26165,26789}, {26792,30807}.
Sea Pa y P'a los polos de las rectas AbcbAcbc y A'bcbA'cbc respecto a las cónicas 𝒞 y 𝒞', respectivamente. Se definen similarmente los puntos Pb, Pc y P'b, P'c.
Las rectas PaP'a, PbP'b y PcP'c son concurrentes en el producto baricéntrico de X75 y X3583:
T = ( (a^4-a^2 b c-(b^2-c^2)^2)/a : ... : ...),
T = 3R^2 X(2) + (4R^2-r^2-s^2) X(92),
que tiene números de búsqueda en ETC
(5.89867065985038, 4.29052359106732, -2.05216138568548).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,92}, {23,242}, {57,14212}, {190,20887}, {238,1109}, {304,30638}, {320,21739}, {321,4886}, {323,1944}, {333,20886}, {391,28605}, {858,2969}, {908,18359}, {1087,3074}, {1146,3580}, {1851,7391}, {1921,20944}, {2323,24148}, {3218,4858}, {3219,14213}, {3262,32849}, {4000,20915}, {4008,30653}, {4358,18151}, {4462,26546}, {4671,20927}, {4957,35466}, {5133,7140}, {5180,23580}, {5249,30690}, {5259,6757}, {5905,37644}, {6358,27065}, {7009,13595}, {7102,7394}, {7112,23989}, {14211,27003}, {15065,31160}, {15680,23661}, {16732,33129}, {17127,17871}, {17483,17862}, {17484,30807}, {17586,18455}, {20432,32028}, {20643,35543}, {20883,26998}, {23690,33139}, {26165,26837}, {31387,37444}.
- Domingo, 26 de abril del 2020
Los triángulo pedales de los puntos de Brocard. Un par bicéntrico
El bombardeo de Guernica fue un ataque aéreo realizado sobre población civil de esta población vasca el 26 de abril de 1937, por parte de la Legión Cóndor alemana y la Aviación Legionaria italiana, que combatían en favor del bando sublevado contra el gobierno de la Segunda República Española.
Dado ABC un triángulo, sean y los de los , Ω1 y Ω2.
La transformación afín σ1, que aplica el triángulo ABC en tiene un único punto fijo finito con coordenadas baricéntricas:
F1 =
(a^6b^2+4a^4(b^2+c^2)^2-a^2b^2(b^4-4b^2c^2-7c^4)-2b^4c^2(b^2-c^2): ... : ... ).
Así mismo, el punto fijo propio de la transformación afín σ2, que aplica el triángulo ABC en es:
F2 =
(a^6c^2+4a^4(c^2+b^2)^2-a^2c^2(c^4-4c^2b^2-7b^4)-2c^4b^2(c^2-b^2): ... : ... ).
Los puntos
F1 y
F2 forman un , que no figura en la
lista confeccionada por Clark Kimberling. La recta que pasa por estos puntos solamente contiene un centro de : su punto del infinito,
X23878.
La matriz M1 asociada de la transformación afín σ1 tiene las entradas (las demás se deducen cíclicamente)
M1[1,1] = 0,
M1[1,2] = a^2 (a^2+b^2+c^2),
M1[1,3] =-b^4+b^2 c^2+a^2 (b^2+2 c^2).
Su punto fijo propio, corresponde al valor propio λ1=2 (a^2 b^2+a^2 c^2+b^2 c^2).
La matriz M2 asociada de la transformación afín σ2 tiene las entradas:
M2[1,1] = 0,
M2[1,2] = c^2 (b^2-c^2)+a^2 (2 b^2+c^2),
M2[1,3] =a^2 (a^2+b^2+c^2).
Su punto fijo propio, corresponde al valor propio λ2=2 (a^2 b^2+a^2 c^2+b^2 c^2).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Si se toman de los puntos de Brocard, en vez de triángulo pedales, y procediendo análogamente, se obtiene otro par bicéntrico con función:
f(a,b,c) = a^6 (2 b^2+c^2)-2 a^4 (b^4+2 b^2 c^2+2 c^4)-a^2 c^2 (7 b^4 +8 b^2 c^2+c^4)- 4 b^4 c^4
- Jueves, 23 de abril del 2020
La tripolar de X(6630) como lugar geométrico de centros de cónicas inscritas
El 23 de abril de 1858 nació Max Planck, físico y matemático alemán considerado como el fundador de la teoría cuántica y galardonado con el Premio Nobel de Física en 1918. En 1900, descubrió una constante fundamental, la denominada constante de Planck, usada para calcular la energía de un fotón. Esto significa que la radiación no puede ser emitida ni absorbida de forma continua, sino solo en determinados momentos y pequeñas cantidades denominadas cuantos o fotones.
ABC es un triángulo, de incentro I=X(1) y baricentro G=X(2). P es un punto sobre una recta variable ℓ que pasa por G. W es el de I y P.
Cuando ℓ gira alrededor de
G, el lugar geométrico del centro de la cónica 𝒞
ℓ, inscrita en
ABC y tangente a
IW y a
PW es la de
X6630
(b-c)^2 (-1+t)^2x^2+(a-c)^2 t^2y^2+(a-b)^2z^2-2 (a-b) (a-c) t y z-2 (a-b) (b-c) (-1+t)z x-2 (a-c) (b-c) (-1+t) t x y =0.
Su centro es:
(a-b+a t-c t : a+c+b (-2+t)-c t : c+b (-1+t)+a t-2 c t),
que está sobre la recta:
(a^2-a (b+c)-b^2+3 b c-c^2)x + (b^2-b (c+a)-c^2+3 c a-a^2)y + (c^2-c (a+b)-a^2+3 a b-b^2)z=0,
tripolar de X6630 y que pasa por los centros Xi, para i∈{900, 3035, 3716, 4422, 4763, 4925, 6164, 9508, 24003, 28601}.
El lugar geométrico del ((a-b) (a-c) t:(a-b) (b-c) (-1+t):-(a-c) (-b+c) (-1+t) t) de 𝒞ℓ es la cóncia circunscrita, que pasa pot Xi, para i∈{1016, 4555, 4589, 4600, 4607, 4998, 7035, 8709}, de ecuación:
(a - b) (a - c)y z + (b - c) (b - a)z x + (c - a) (c - b)x y = 0.
Su centro es X6631 y su perspector es el perspector de la .
- Lunes, 20 de abril del 2020
El centro X(7971) y una circunferencia de Apolonio
El 20 de abril 1923, en Italia, Benito Mussolini suprime el recuerdo del Primero de Mayo (la masacre contra los obreros de Chicago). En España, la celebración del primero de mayo, sepultada con la guerra civil, reaparece en los años cincuenta transformada en Fiesta de San José Obrero, patrón de los trabajadores católicos, sugerida por la introducción (en 1955 por Pío XII) en el calendario oficial la festividad de San José Obrero, como patrón de los trabajadores, el día 1 de mayo.
Dado un triángulo ABC, se considera su reflexión A'B'C' en el incentro I=X1. A" es la proyección ortogonal de A' en BC, Γa la circunferencia que pasa por I, A', A" y ta la tangente en A' a Γa.
Los puntos B", C", las circunferencias Γb, Γc y las tangentes tb, tc se definen cíclicamente.
La rectas
ta,
ta,
ta concurren en X
7971:
(a (a^6-4 a^5 (b+c)+a^4 (b^2+6 b c+c^2)+8 a^3 (b-c)^2 (b+c)-a^2 (b-c)^2 (5 b^2+14 b c+5 c^2-4 a (b-c)^4 (b+c)+(b^2-c^2)^2 (3 b^2-2 b c+3 c^2))) : ... : ...),
reflexión de
del en el incentro.
La ecuación baricéntrica de Γa es:
c^2 x y+b^2 x z+a^2 y z+(x+y+z) ((2 (a b c-b^2 c-b c^2) x)/(a+b+c)-((-a^3 c+3 a^2 b c-3 a b^2 c+b^3 c-3 a^2 c^2+4 a b c^2-b^2 c^2-a c^3-b c^3+c^4) y)/(2 (b-c) (a+b+c))-((a b+b^2-b c) (a^2+2 a b-b^2-2 a c+c^2) z)/(2 (b-c) (a+b+c)))=0.
Y la tangente ta en A' es:
4 b (b-c) c (-a+b+c) x+c (a^3+3 b^3+a^2 (b-c)-b^2 c-3 b c^2+c^3-a (5 b^2-6 b c+c^2)) y-b (a^3+b^3-3 b^2 c-b c^2+3 c^3+a^2 (-b+c)-a (b^2-6 b c+5 c^2)) z = 0
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Sean Oa, Ob y Oc los centros de las circunferencias Γa, Γb y Γc, respectivamente.
Oa =((b-c) (-a+b+c) : -b (a+3 b-3 c) : c (a-3 b+3 c)).
El centro W de la circunferencia tangente exteriormente a las circunferencias Γa, Γb, Γc es el punto de intersección (distinto de I) de las hipérbolas Φa, Φb, Φc, que pasan por el incentro y con focos, respectivamente Ob y Oc, Oc y Oa, Oa y Ob.
Los números de búsqueda de W en son
(5.4862651337, 10.0041462335, -5.8174052799).
La hipérbola Φa pasa por los puntos de intersección de las circunferencias Γb y Γc y por sus simétricos respecto a su centro, además si DEF es el triángulo antipodal de ABC, su tangente en el incentro es la bisectriz del ángulo ∠EIF. En consecuencia, con estos cinco datos, su ecuación se puede determinar (ver §4.6, Tipos de haces de cónicas. Caso II).
- Sábado, 18 de abril del 2020
X(554), X(1081) y X(5441) como centros de homotecia
El 18 de abril 1955 falleció, a los 76 años, Albert Einstein, físico alemán de origen judío, nacionalizado después suizo, austriaco y estadounidense. Uno de los intelectuales más creativos en la historia de la humanidad, cuyas avanzadas teorías de la relatividad y la gravitación revolucionaron la ciencia y la filosofía. Fallece en Princeton a causa una hemorragia interna, rechazó la cirugía, diciendo: "Quiero irme cuando quiero. Es de mal gusto prolongar artificialmente la vida. He hecho mi parte, es hora de irse. Yo lo haré con elegancia".
En un triángulo ABC, se considera el punto Ab simétrico de B respecto del punto de intersección de AC y la perpendicular por B a la bisectriz interior en A.
Sea Hab el de Ab respecto a los puntos de corte con AB y AC de la perpendicular por Ab a AB.
Las proyecciones desde Ab sobre AB de los puntos de intersección de AC con la circunferencia de diámetro AbHab, los designamos por Bab y Cab.
NOTA: El triángulo AbBabCab es la solución al problema de construcción de un triángulo del que se conocen un vértice Ab, la recta que contiene su lado opuesto BC, y la recta AC, que contiene a los pies de las alturas que no pasan por el vértice dado.
Se considera ahora el punto
Ac, simétrico de C respecto del punto sobre AB y en la perpendicular por C a la bisectriz interior en A.
Sea Hac el conjugado armónico de Ac respecto a los puntos de corte con AB y AC de la perpendicular por Ac a AC.
Las proyecciones desde Ac sobre AC de los puntos de intersección de AB con la circunferencia de diámetro AcHac, los designamos por Bac y Cac.
Se tiene que las rectas ℓab≔BabBac y ℓac≔CabCac son paralelas a BC.
Procediendo cíclicamente se obtienen las rectas ℓbc, ℓba, ℓca y ℓcb.
En coordenadas baricéntricas, se tienen las ecuaciones de las rectas:
ℓab: 3 (b c-2SA)x +
(3 a^2-3 (b-c)^2 + 2√3S) y +
(3 a^2-3 (b-c)^2 + 2√3S)z = 0.
ℓac: 3 (b c-2SA)x +
(3 a^2-3 (b-c)^2 - 2√3S) y +
(3 a^2-3 (b-c)^2 - 2√3S)z = 0.
Las rectas ℓ
ab, ℓ
bc, ℓ
ca forma un triángulo
A'B'C', homotético con
ABC, con centro de homotecia
X554:
(√3 (a+b-c)(a+b+c) +
2 S)( √3 (a-b+c)(a+b+c) + 2 S) : ... : ...).
Las rectas ℓac, ℓba, ℓcb forma un triángulo A"B"C", homotético con ABC, con centro de homotecia X1081:
(√3 (a+b-c)(a+b+c) -
2 S)( √3 (a-b+c)(a+b+c) - 2 S) : ... : ...).
Mab=(3 (a^4+a^2 (-2 b^2+3 b c-2 c^2)+(b-c)^2 (b^2-b c+c^2)):0:9 b c (-a^2+b^2-b c+c^2)) es el punto medio de BabCab y Mac=(3 (a^4+a^2 (-2 b^2+3 b c-2 c^2)+(b-c)^2 (b^2-b c+c^2)):9 b c (-a^2+b^2-b c+c^2):0) es el punto medio de BacCac.
Se definen cíclicamente los puntos Mbc, Mba y Mca, Mcb.
Las rectas MabMac, MbcMba y McaMcb forman un triángulo MaMbMc, homotético con ABC, con centro de homotecia
W = ( (a + b - c) (a - b + c) /(a^2 - b^2 - b c - c^2) : ... : ...),
que tiene números de búsqueda en
(0.00594153130308257, 0.0103849339211635, 3.63073266705292).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,30}, {2,7110}, {7,25417}, {57,2160}, {81,553}, {88,26723}, {105,5322}, {226,1255}, {274,17078}, {278,18688}, {1022,30726}, {1280,6742}, {1358,7313}, {1427,1989}, {2003,2982}, {2688,36064}, {3175,34892}, {3227,19796}, {3676,21141}, {8056,35466}, {8818,17056}, {14844,30571}, {15455,36805}, {20565,30710}, {27789,37635}.
El punto W está sobre la recta que pasa por el incentro y es paralela a la , donde también están X554 y X1081. En dicha recta deben estar los centros de homotecia de los pares de triángulos (A'B'C', A"B"C"), (A'B'C', MaMbMc) y (A"B"C", MaMbMc), que en este caso, coinciden los tres en X5441:
(3 a^4-a^3 (b+c)-a^2 (2 b^2+b c+2 c^2)+a (b-c)^2 (b+c)-(b^2-c^2)^2 : ... : ...).
- Martes, 14 de abril del 2020
Un problema de construcción de triángulos y el centro X(222)
El 14 de abril de 1629 nació Christiaan Huygens, científico neerlandés de vastos conocimientos: obtuvo resultados notables en la matemática, la mecánica aplicada y la óptica. A Huygens pertenece el honor de haber inventado el reloj de péndulo. Elaboró la teoría y construyó los primeros relojes de este tipo. Teorema de Huygens: La evoluta de una cicloide es una cicloide igual a ella, pero desplazada.
Una tautócrona o curva isócrona es la curva para la cual el tiempo tomado por un objeto que desliza sin rozamento en gravedad uniforme hasta su punto más bajo es independiente de su punto de partida.
La identificación de la tautócrona fue resuelto por Christiaan Huygens en 1659. Demostró geométricamente que la curva es un cicloide.
Vamos a utilizar la construcción de un triángulo del que se conocen un vértice, la recta que contiene su lado opuesto y la recta que contiene a los pies de las alturas que no pasan por el vértice dado, para obtener una construcción del X222.
Dado un triángulo ABC, sea DEF el y D', E', F' los puntos antipodales de D, E, F en la circunferencia inscrita en ABC.
F'FabFac es el triángulo tal que FabFac está sobre la recta BC y los pies F'ab y F'ac de sus alturas desde Fab y Fac están sobre la recta AC.
E'EabEac es el triángulo tal que EabEac está sobre la recta AC y los pies E'ab y E'ac de sus alturas desde Eab y Eac están sobre la recta AB.
Los cuatro puntos F'ab, F'ac, E'ab y E'ac están sobre una circunferencia Γa, cuyo centro Oa está sobre la bisectriz interior en A.
Utilizando coordenadas baricéntricas en la referencia ABC:
E'ab, E'ac = (
(a-b-c) (a^4-2 a^2 b^2+b^4-a^3 c+7 a^2 b c+a b^2 c-7 b^3 c-a^2 c^2-6 a b c^2+7 b^2 c^2+a c^3-b c^3± Sqrt[(a^2-(b-c)^2)^3(a^2-b^2+6 b c-c^2)]) : 0 : -c (-a+b+c)^2 (-a^2+b^2-6 b c+c^2)).
El centro de la circunferencia Γa es:
Oa = (6 a^3 b c-a^4 (b+c)-(b-c)^2 (b+c)^3-2 a b c (3 b^2-2 b c+3 c^2)+2 a^2 (b^3+b^2 c+b c^2+c^3) :
b (-a^2+b^2+c^2) (-a^2+b^2-6 b c+c^2) :
c (-a^2+b^2+c^2) (-a^2+b^2-6 b c+c^2)).
La ecuación de la polar pa de A respecto a la circunferencia Γa es:
b c (-a + b + c) x - c (-a + c) (a - b + c) y -
b c (-a+b+c) x-c (-a+c) (a-b+c) y-b (-a+b) (a+b-c) z = 0.
Procediendo cíclicamente, se definen las circunferencia Γb y Γc, se obtienen las coordenadas de sus centros Ob y Oc, y las ecuaciones de sus polares pb y pc.
El triángulo
A'B'C' formado por las rectas
pa,
pb y
pc es perspectivo con
DEF y el centro de perspectividad es X
222:
((a^2 /(b+c-a) : (b^2 SB)/(a-b+c) : (c^2 SC)/(a+b-c)).
Como los centros Oa, Ob, Oc de las circunferencias Γa, Γb, Γc están sobre las bisectrices interiores de ABC, los triángulos A'B'C' y OaObOc son y un centro ortológico es el incentro.
El centro órtologico de A'B'C' respecto a OaObOc es:
Z = ( a(a+b-c)(a-b+c)(3 a^5
-5 a^4 (b+c)+2 a^3 (4 b^2-b c+4 c^2)-8 a^2 (b-c)^2 (b+c)
+a (5 b^4+2 b^3 c-22 b^2 c^2+2 b c^3+5 c^4)-3 (b-c)^2 (b+c)^3) : ... : ...),
que tiene números de búsqueda en
(-1.43398497003681, -1.67417150730665, 5.46154551159828).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {516,21147}, {4488,8270}, {4862,34036}.
La matriz M asociada de la transformación afín que aplica ABC en A'B'C' tiene las entradas:
M[1,1] = -a^2 (-a^2 + (b - c)^2) (-a^2 + b^2 + c^2)
M[1,2] = -a (a - c) (a^4 - 2 a^2 b (b - c) + (b - c)^3 (b + c))
M[1,3] = -(a - b) (a^5 + 2 a^3 (b - c) c - a (b - c)^3 (b + c))
Su punto fijo propio, correspondiente al valor propio λ=(b^2+c^2-a^2) (a^2+b^2-c^2) (a^2-b^2+c^2), es:
U = ( a (a^3+a^2 (b+c)-a (b+c)^2-(b-c)^2 (b+c))/((a-b-c) (b-c) (a^2-b^2-c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(0.113126903796815, -0.151820879914510, 3.69355882778820).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,34040}, {33,11372}, {34,1830}, {100,7012}, {108,109}, {196,3195}, {221,7952}, {222,36996}, {651,1897}, {1455,15500}, {1457,37305}, {1783,4559}, {1785,34789}, {1870,10698}, {1877,12751}, {2800,36121}, {4551,31511}, {6198,21669}, {7046,34048}, {10702,21147}, {10731,18340}, {36044,36059}.
La matriz M asociada de la transformación afín que aplica ABC en tiene las entradas:
M[1,1] =-a (3 a^2-2 a b+3 b^2-3 c^2) (3 a^2-3 b^2-2 a c+3 c^2) (-6 a^3 b c+a^4 (b+c)+(b-c)^2 (b+c)^3+2 a b c (3 b^2-2 b c+3 c^2)-2 a^2 (b^3+b^2 c+b c^2+c^3))
M[1,2] = ,-a b (3 a^2-2 a b+3 b^2-3 c^2) (3 a^6-18 a^5 c+12 a^3 b (3 b-c) c-(b^2-c^2)^2 (3 b^2-2 b c+3 c^2)+a^4 (-9 b^2+2 b c+3 c^2)+a^2 (9 b^4-4 b^3 c-6 b^2 c^2+4 b c^3-3 c^4)+6 a c (-3 b^4+2 b^3 c-2 b c^3+3 c^4))
M[1,3] = -a c (3 a^2-3 b^2-2 a c+3 c^2) (3 a^6-18 a^5 b-12 a^3 b (b-3 c) c+a^4 (3 b^2+2 b c-9 c^2)-(b^2-c^2)^2 (3 b^2-2 b c+3 c^2)+6 a b (3 b^4-2 b^3 c+2 b c^3-3 c^4)+a^2 (-3 b^4+4 b^3 c-6 b^2 c^2-4 b c^3+9 c^4))
Su punto fijo propio, correspondiente al valor propio
λ=a b c (a+b+c) (3 a^2-2 a b+3 b^2-3 c^2) (3 a^2-3 b^2+2 b c-3 c^2) (3 a^2-3 b^2-2 a c+3 c^2),
es:
V = ( ( 3 SA - b c )/( SA ( SA - 3 b c )) : ... : ...),
que tiene números de búsqueda en ETC
(1.37131407442394, 1.18493009537510, 2.18741407383672).
Este punto está en la recta X4X7320.
V = r(2r^2-16r R+32R^2+s^2) X4 + 4(r+12R)((r+2R)^2-s^2) X7320,
Donde r y R son los radios de la circunferencias inscrita y circunscrita, y s es el semiperímetro de ABC.
- Domingo, 12 de abril del 2020
Tres formas diferentes de construir un punto de una cierta cónica
El 12 de abril de 1852 nació Carl Louis Ferdinand von Lindemann, matemático alemán. Es conocido por la demostración en 1882 de que el número π es un número trascendente, es decir, no es cero de algún polinomio con coeficientes racionales.
Partiendo de un punto P sobre la de un triángulo ABC, vamos a exponer la construcción, siguiendo tres métodos distintos, un mismo punto Q de la
cónica
(
𝔖abc xyz
b^2 c^2 ( b^2 c^2 (b^2-c^2)^4 (a^2-b^2-c^2)x^2+2 (a^6) ((a^2-b^2)^2) ((a^2-c^2)^2) y z) = 0.
)
𝒞, que pasa los Xi, para i ∈ {3, 6, 24, 60, 143, 1511, 1986, 6593, 15460, 15461, 19118, 20806, 35602, 35603, 36153}. Su centro es X27866 y su es X27867.
PRIMER MÉTODO (Alexandr Skutin and Ercole Suppa, Hyacinthos 28625)
Sean Ka, Kb, Kc los de los triángulos PBC, PCA, PAB, respectivamente.
Las reflexiones de PKa, PKb, PKc en BC, CA, AB, respectivamente, concurren en el punto Q, sobre la cónica 𝒞.
SEGUNDO MÉTODO (Randy Hutson, August 19, 2019, X27866)
Sea DEF el de P y D', E', F', respectivamente, los inversos de D, E, F en la circunferecia circunscrita a ABC.
Las rectas AD', BE', CF' concurren en el punto Q, sobre la cónica 𝒞.
TERCER MÉTODO
Sea P' el de P, que está sobre la , y A'B'C' su triángulo ceviano.
La circunferencia que pasa por A, B, A' corta de nuevo a AC en Ab y la circunferencia que pasa por A, C, A' corta de nuevo a AB en Ac. La perpendicular por A' a BC corta a AbAc en A". Los puntos B", C" se definen cíclicamente.
Las rectas AA", BB", CC" concurren en un punto Q', conjugado isogonal de Q.
El lugar geomñetrico de Q', cuando P varía en la recta de Euler, es la
cuártica
( (-a^10+3 a^8 b^2-2 a^6 b^4-2 a^4 b^6+3 a^2 b^8-b^10+a^8 c^2-4 a^6 b^2 c^2+6 a^4 b^4 c^2-4 a^2 b^6 c^2+b^8 c^2) x^2 y^2+(2 a^10-4 a^8 b^2+2 a^6 b^4-4 a^8 c^2+8 a^6 b^2 c^2-4 a^4 b^4 c^2+2 a^6 c^4-4 a^4 b^2 c^4+2 a^2 b^4 c^4) x^2 y z+(2 a^4 b^6-4 a^2 b^8+2 b^10-4 a^4 b^4 c^2+8 a^2 b^6 c^2-4 b^8 c^2+2 a^4 b^2 c^4-4 a^2 b^4 c^4+2 b^6 c^4) x y^2 z+(-a^10+a^8 b^2+3 a^8 c^2-4 a^6 b^2 c^2-2 a^6 c^4+6 a^4 b^2 c^4-2 a^4 c^6-4 a^2 b^2 c^6+3 a^2 c^8+b^2 c^8-c^10) x^2 z^2+(2 a^4 b^4 c^2-4 a^4 b^2 c^4-4 a^2 b^4 c^4+2 a^4 c^6+8 a^2 b^2 c^6+2 b^4 c^6-4 a^2 c^8-4 b^2 c^8+2 c^10) x y z^2+(a^2 b^8-b^10-4 a^2 b^6 c^2+3 b^8 c^2+6 a^2 b^4 c^4-2 b^6 c^4-4 a^2 b^2 c^6-2 b^4 c^6+a^2 c^8+3 b^2 c^8-c^10) y^2 z^2 = 0)
𝒬 (conjugada isogonal de la cónica 𝒞) de ecuación baricéntrica:
𝔖abc xyz
a^2 (a^2-b^2)^2 (a^2-c^2)^2 x^2 y z =
𝔖abc xyz SASBSC
(b^2-c^2)^4 SA y^2 z^2.
La cuártica 𝒬 pasa por los vértices A, B, C (dobles) y por los centros Xi, para i∈{2, 4, 12, 68, 252, 1312, 1313, 5627, 6340, 6526, 10415, 12028, 13853, 13854, 32132, 32133, 34110}.
- Sábado, 11 de abril del 2020
Centro de perspectividad de los triangulos de referencia y tangencial de Jenkins
El 11 de abril de 1986
el cometa Halley alcanza su perigeo, o punto más cercano a la Tierra, en su último periodo orbital de 76 años. Su siguiente aparición ocurrirá a mediados de 2061 y su próximo afelio está previsto para finales de 2023.
Las circunferencias de Jenkins de un triángulo ABC son las tres circunferencias tangentes interiormente a una circunferencia exinscrita y exteriormente a las otras dos.
La
A-circunferencia de Jenkins
( a^2 b x^2+2 a b^2 x^2+b^3 x^2+a^2 c x^2+2 a b c x^2+b^2 c x^2+2 a c^2 x^2+b c^2 x^2+c^3 x^2+2 a^2 b x y+2 a b^2 x y+2 a^2 c x y-2 b c^2 x y-2 c^3 x y+a^2 b y^2-b^3 y^2+a^2 c y^2-2 a b c y^2-b^2 c y^2-2 a c^2 y^2+b c^2 y^2+c^3 y^2+2 a^2 b x z-2 b^3 x z+2 a^2 c x z-2 b^2 c x z+2 a c^2 x z-2 a^2 b y z-2 a b^2 y z-2 a^2 c y z-4 a b c y z-2 a c^2 y z+a^2 b z^2-2 a b^2 z^2+b^3 z^2+a^2 c z^2-2 a b c z^2+b^2 c z^2-b c^2 z^2-c^3 z^2 = 0)
y la
A-circunferencia exinscrita
( c^2 x y+b^2 x z+a^2 y z-1/4 (x+y+z) ((a+b+c)^2 x+(a+b-c)^2 y+(a-b+c)^2 z) = 0)
son tangentes en el punto de coordenadas baricéntricas:
Ta = (-(a+b-c) (a-b+c) (b+c)^2 : c^2 (a-b+c) (a+b+c) : b^2 (a+b-c) (a+b+c)).
El centro de la A-circunferencia de Jenkins es:
Ja = (2 a^4 (b+c)+(b-c)^2 (b+c)^3-a (b^2-c^2)^2+a^3 (3 b^2+4 b c+3 c^2)-a^2 (b^3+b^2 c+b c^2+c^3):
-(b-c) c^2 (b+c)^2-a^3 (2 b^2+2 b c+c^2)-a^2 (2 b^3+2 b^2 c+b c^2+c^3)+a c (-2 b^3-b^2 c+2 b c^2+c^3):
b^2 (b-c) (b+c)^2-a^3 (b^2+2 b c+2 c^2)+a b (b^3+2 b^2 c-b c^2-2 c^3)-a^2 (b^3+b^2 c+2 b c^2+2 c^3)).
Las coordenadas de los puntos Tb, Tc y Jb, Jc se deducen por permutación cíclica.
Las rectas ATa, BTb
y CTc concurren en X(3596) = 1st Odehnal Point:
((b+c-a)/a^2 : (a-b+c)/b^2 : (a+b-c)/c^2).
Las rectas AJa, BJb
y CJc concurren en X(3597) = 2nd Odehnal Point:
(1/(a^5+a^4 b-a^3 b^2-a^2 b^3+a^4 c+2 a^3 b c-a^2 b^2 c-2 a b^3 c-a^3 c^2-a^2 b c^2-2 a b^2 c^2-2 b^3 c^2-a^2 c^3-2 a b c^3-2 b^2 c^3) :...:...).
Las circunferencias B-circunferencia de Jenkins y la C-circunferencia de Jenkins se cortan, además de en el , en:
U = (b^3+b^2 c+b c^2+c^3+a^2 (b+c)+2 a (b^2+b c+c^2) : (-a^2+(b-c)^2) (a+c) : -(a+b) (a^2-(b-c)^2)).
Cíclicamente se definen los puntos V y W. Sea DEF el del .
Los triángulos DEF y UVW son perspectivos y el centro de perspectividad es X(3687):
((b+c-a) (a b+b^2+a c+c^2) : (a-b+c) (a^2+a b+b c+c^2) : (a+b-c) (a^2+b^2+a c+b c)).
Las tangentes en los puntos Ta, Tb y Tc a las correspondientes circunferencia exinscritas forman un triángulo A'B'C', que podemos llamar tiángulo tangencial de Jenkins, perspectivo con ABC, con centro de perspectividad:
J = ( (b+c)/(a^3 (b+c)+a^2 b c-a (b-c)^2 (b+c)-b c (b+c)^2) : ... : ...),
que tiene números de búsqueda en
(3.25704532583740, 5.70279605927079, -1.81067678643574).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,43}, {76,3687}, {226,2092}, {284,14534}, {321,21033}, {946,3597}, {3452,34258}, {4052,22020}, {5929,8808}, {6685,11358}, {9565,12053}, {14923,24996}.
A' = (b c (-3 a^3 (b+c)+b c (b+c)^2-a^2 (2 b^2+3 b c+2 c^2)+a (b^3+b^2 c+b c^2+c^3)):
a (a+c) (a^2 b (2 b-c)+a^3 (b+c)+b c (b^2-c^2)+a (b^3-b^2 c-b c^2-c^3)):
a (a+b) (-b^3 c+b c^3+a^3 (b+c)+a^2 c (-b+2 c)-a (b^3+b^2 c+b c^2-c^3))).
El centro J es la intersección de la recta que pasa por el ortocentro y el del simediano y el incentro, con la recta que pasa por el del simediano y
X(3687) (centro de perspectividad de DEF y UVW).
El punto J ha sido incorporado a ETC con el número X(37865).
Sean Tab y Tac los puntos de tangencia de la A-circunferencia de Jenkins con las circunferencias B-exinscrita y C-exinscrita, respectivamente. Los puntos Tbc, Tba y Tca, Tcb, se definen cíclicamente.
Según una observación (en comunicación personal) de César Lozada, se tiene:
El triángulo A"B"C" formado por las rectas TabTac, TbcTba, TcaTcb es perspectivo con ABC y el centro de perspectividad es:
Z = ( (b+c) (-a+b+c)/(a^2 b^2+a b^3+3 a^2 b c+a b^2 c+b^3 c+a^2 c^2+a b c^2+2 b^2 c^2+a c^3+b c^3) : ... : ...),
que tiene números de búsqueda en ETC (4.57674437778157,1.85522742814725,0.243932703444792).
Es el punto está sobre la recta X14624X17751.
A'' = (2 a^5 (b+c)+b^2 c^2 (b+c)^2+a^4 (5 b^2+8 b c+5 c^2)+a b c (3 b^3+7 b^2 c+7 b c^2+3 c^3)+a^3 (4 b^3+13 b^2 c+13 b c^2+4 c^3)+a^2 (b^4+10 b^3 c+15 b^2 c^2+10 b c^3+c^4):
(a+c) (-b^4 c+b^2 c^3+a^4 (b+c)+a^3 (b^2+b c+2 c^2)-a b (b^3-b^2 c+b c^2-3 c^3)+a^2 (-b^3+2 b^2 c+3 b c^2+c^3)):
a^5 (b+c)+b^2 c^2 (b^2-c^2)+a^4 (3 b^2+2 b c+c^2)+a b c (3 b^3+b c^2-2 c^3)+a^3 (3 b^3+4 b^2 c+3 b c^2-c^3)+a^2 (b^4+6 b^3 c+b^2 c^2-c^4)).
- Miércoles, 8 de abril del 2020
Triángulos ortológicos con el mismo centro ortológico. Imagen Kirikami-Euler
El 8 de abril de 2013 falleció, a la edal de 95 años, José Luis Sampedro escritor, humanista y economista español que abogó por una economía «más humana, más solidaria, capaz de contribuir a desarrollar la dignidad de los pueblos». Algunas de sus novelas: El río que nos lleva (1961), La sonrisa etrusca (1985), La vieja sirena (1990).
Kirikami-Euler image
Let P be a point in the plane of triangle ABC. Let H
a be
the orthocenter of triangle PBC, and define H
b and
H
c cyclically. The Euler lines of the triangles
AH
bH
c, BH
cH
a,
CH
aH
b concur in the
Kirikami-Euler image of P.
Let P be given by barycentrics p : q : r. Then Q is given by
Q = g(a,b,c,p,q,r) : g(b,c,a,q,r,p) : g(c,a,b,r,p,q), where
g(a,b,c,p,q,r) = p/[(a2 - b2 -
c2)p2 + (a2 - b2 +
c2)pq + (a2 + b2 - c2)pr +
2a2qr]
If P = X(2), then Q = X(5485). (Seichii Kirikami, May
20, 2013)
The Kirikami-Euler image K(P) of a point P is related to the mapping
H(P) called "pedal antipodal perspector", defined in Hyacinthos #20403
and #20405, November 2011, by Randy Hutson, with general coordinates
given in #20404 by Francisco Javier. X(5485) = H(X(i)) for i = 6 and i
= 187. In general, K(P) = H(P*) = H(P*), where P* denotes the isogonal
conjugate of P, and Pn= (inverse-in-circumcircle of P*)=(); for example,
K(X(1)) = X(8), K(X(3)) = X(68), and K(X(6)) = X(5486).
(Randy Hutson, May 22, 2013)
Dados un triángulo ABC, un punto P y un triángulo A'B'C', con ABC, tal que sus dos centros ortológicos coincidan en P. Las rectas AA', BB', CC' concurren en un punto P' sobre la circun-hipérbola c(P) que pasa por P. Sea H' es el ortocentro de A'B'C' (está sobre la tangente a c(P) en P).
La recta H'P' pasa por un punto fijo Po sobre c(P), cuando el triángulo A'B'C' varía.
Usamos coordenadas baricéntricas respecto a ABC. Tomemos un punto arbitrario A' sobre la perpendicular a BC por P=(u:v:w):
A' = (-2 a^2 u : (-b^2+c^2) t u-a^2 (2 v+t (u+2 v)) : (b^2-c^2) t u-a^2 (2 w+t (u+2 w))),
los otros dos vértices del triángulo A'B'C' ortológico con ABC, tal que sus centros ortológicos coincidan em P, son:
B' = (u ((b^2-c^2) t u+a^2 (2 v+t (u+2 v))) : -2 b^2 t u^2+2 a^2 (1+t) v^2 : (b^2+c^2) t u^2+a^2 (-t u^2+2 v w+2 t v w)),
C' = (u ((-b^2+c^2) t u+a^2 (2 w+t (u+2 w))) : (b^2+c^2) t u^2+a^2 (-t u^2+2 v w+2 t v w) : -2 c^2 t u^2+2 a^2 (1+t) w^2).
Las rectas AA', BB', CC' concurren en:
P' = (u (a^2 t u+b^2 t u-c^2 t u+2 a^2 v+2 a^2 t v) (-a^2 t u+b^2 t u-c^2 t u-2 a^2 w-2 a^2 t w):
-(a^2 t u+b^2 t u-c^2 t u+2 a^2 v+2 a^2 t v) (-a^2 t u^2+b^2 t u^2+c^2 t u^2+2 a^2 v w+2 a^2 t v w):
(-a^2 t u+b^2 t u-c^2 t u-2 a^2 w-2 a^2 t w) (-a^2 t u^2+b^2 t u^2+c^2 t u^2+2 a^2 v w+2 a^2 t v w)).
El lugar geométrico que describe P', cuando el triángulos A'B'C' varía, es la hipérbola rectangular circunscrita a ABC y que pasa por P:
c(P):
u (a^2 (-v+w)+(b^2-c^2) (v+w))y z + v (b^2 (u-w)-a^2 (u+w)+c^2 (u+w))z x + w(c^2 (-u+v)+a^2 (u+v)-b^2 (u+v)) x y = 0.
Si H' es el ortocentro de A'B'C', cuando t varía, la recta H'P' pasa por un punto fijo Po (Kirikami-Euler imagen K(P) de P), sobre c(P):
Po = (
u/(u^2-(SBv+SCw)u-a^2v w) :
v/(SBv^2-(SCw+SAu)v-b^2w u) :
w/(SCw^2-(SAu+SBv)w-c^2u v)).
En particular, si P=X11 es el , entonces P11 ≔ Po=X4X513∩X8X885, es decir el punto de intersección de la recta que pasa por el ortocentro y el del del punto de Feuerbach, con la recta que pasa por el y por el de la recta que pasa por el punto de Feuerbach y el de la . "Kirikami-Euler image of X(11)":
P11 = ( b c(b-c)^3 (b+c-a)^2 : ... : ...),
que tiene números de búsqueda en
(-20.0905239981179,18.6931687590995,-0.0282105060300865).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,33528}, {4,513}, {8,885}, {10,522}, {85,693}, {158,17924}, {341,4397}, {442,1577}, {499,905}, {514,946}, {521,6238}, {667,2217}, {900,14304}, {1212,28143}, {1734,18395}, {2401,3086}, {2517,11024}, {3667,9948}, {3704,4086}, {3762,6366}, {4462,20220}, {6554,28132}, {14505,23100}, {16732,21134}, {21132,23615}, {30591,31936}.
Cuando P está sobre la circunferencia circunscrita, el punto fijo Po es el ortocentro.
Otros puntos fijos {P∈{Xi, Xj}, Po=Xk}, para los índices {{i,j},k}:
{{1, 80}, 8}, {{2, 671}, 5485}, {{3, 265}, 68}, {{5, 1263}, 25043}, {{6, 67}, 5486}, {{7, 1156}, 34919}, {{13, 14}, 2}, {{15, 11600}, 19778}, {{16, 11601}, 19779}, {{17, 11602}, 5487}, {{18, 11603}, 5488}, {{20, 10152}, 33893}, {{54, 33565}, 13418}, {{79, 3065}, 10266}, {{84}, 10309}, {{113}, 34104}, {{115, 6328}, 23105}, {{125}, 5489}, {{186, 5962}, 562}, {{485}, 5490}, {{486}, 5491}, {{502, 5620}, 6757}, {{2009, 2010}, 76}, {{3479}, 36304}, {{3480}, 36305}, {{10215}, 7057}, {{34221, 34222}, 6}.
O bien, ordenados por el punto fijo:
{{13, 14}, 2}, {{34221, 34222}, 6}, {{1, 80}, 8}, {{3, 265}, 68}, {{2009, 2010}, 76}, {{186, 5962}, 562}, {{2, 671}, 5485}, {{6, 67}, 5486}, {{17, 11602}, 5487}, {{18, 11603}, 5488}, {{125}, 5489}, {{485}, 5490}, {{486}, 5491}, {{502, 5620}, 6757}, {{10215}, 7057}, {{79, 3065}, 10266}, {{84}, 10309}, {{54, 33565}, 13418}, {{15, 11600}, 19778}, {{16, 11601}, 19779}, {{115, 6328}, 23105}, {{5, 1263}, 25043}, {{20, 10152}, 33893}, {{113}, 34104}, {{7, 1156}, 34919}, {{3479}, 36304}, {{3480}, 36305}.
- Martes, 7 de abril del 2020
Trapecios isósceles construidos sobre las bisectrices de un triángulo
El 7 de abril de 1761 fallece, a la edad de 59 años, Thomas Bayes matemático británico y ministro presbiteriano. Su obra más conocida es el Teorema de Bayes, utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso.
Dado un triángulo ABC, sean DEF el y A'B'C' el . Se consideran los trapecios isósceles AA'AbE y AA'AcF con AA' paralelo a AbE y a AcF. Los puntos Bc, Ba y Ca, Cb se definen cíclicamente.
En coordenadas baricéntricas:
Ab = (b (b+c)^2-a^2 (b+2 c) : b (a^2-b^2+c^2) : 2 c^2 (b+c)),
Ac = (-c (b+c)^2+a^2 (2 b+c),-2 b^2 (b+c),c (-a^2-b^2+c^2)).
El triángulo UVW formado por las rectas AbAc, BcBa y CaCb es perspectivo al triángulo medial. El centro de perspectividad es el punto medio de X73 y X23361:
Z = ( a^2 (2 a^2+a (b+c)-(b-c)^2) (a^2 (b+c)-a b c-b^3-c^3) : ... : ...),
que tiene números de búsqueda en
(-6.52905418576988, -8.22151795123758, 12.3458942261965).
Es el punto medio de X73 y X23361.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,15232}, {3,14529}, {5,515}, {6,41}, {36,1437}, {407,2646}, {942,4719}, {1064,23383}, {1147,26286}, {1457,23846}, {1464,22345}, {1511,2779}, {3185,10571}, {3720,34471}, {4337,7428}, {4999,34831}, {11281,17045}, {15622,33537}, {22076,35069}.
El punto Z ha sido incorporado a ETC con el número X(37836).
Las cordenadas de U son:
(a^2 (2 a^2-(b-c)^2+a (b+c)) : b (a^3-b^2 c+c^3+a^2 (-b+c)+a (-2 b^2+b c+c^2)) :c (a^3+b^3+a^2 (b-c)-b c^2+a (b^2+b c-2 c^2))).
Los triángulos ABC y UVW son . El centro de ortología de ABC respecto a UVW es el circuncentro y el centro de ortología de UVW respecto a ABC es:
Q = ( a( -(b^2-c^2)^2 (b^2+c^2)+(b-c)^2 (3 b^3+b^2 c+b c^2+3 c^3) a+4 b (b-c)^2 c a^2+(-6 b^3+2 b^2 c+2 b c^2-6 c^3)a^3+(3 b^2-4 b c+3 c^2) a^4+3 (b+c) a^5-2 a^6) : ... : ...),
que tiene números de búsqueda en ETC
(20.3975338271681, 21.8284856247054, -20.8856104092739).
Es el punto medio de Xi y Xj para los índices {i,j}: {1,11500}, {3,6261}, {960,9942}, {1490,12114}, {3811,22770}, {4297,6260}, {5534,12513}, {5709,12635}, {6256,18481}, {6326,22775}, {12119,12761}.
Es la reflexión de Xi en Xj para los índices {i,j}: 5450,13624}, {12616,140}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,227}, {3,960}, {4,2646}, {5,515}, {8,6962}, {20,5057}, {21,12671}, {30,12608}, {35,12672}, {36,1071}, {40,5440}, {56,12675}, {65,6905}, {72,2949}, {78,3428}, {84,7987}, {104,12680}, {140,12616}, {165,7971}, {214,2829}, {355,6863}, {392,10902}, {405,1490}, {411,4511}, {517,6796}, {518,11249}, {549,33899}, {908,11827}, {912,26286}, {944,1319}, {946,4314}, {950,7681}, {952,10916}, {956,17857}, {958,5720}, {971,5450}, {993,5777}, {1006,12664}, {1012,3612}, {1155,6942}, {1455,1745}, {1479,22835}, {1512,10950}, {1519,6284}, {1532,10572}, {1836,6934}, {2095,12559}, {2478,5731}, {2800,3579}, {2975,14872}, {3057,11491}, {3486,6848}, {3523,14647}, {3586,10893}, {3601,11496}, {3616,6835}, {3655,24927}, {3683,6875}, {3689,12245}, {3748,10595}, {3811,22770}, {3812,6911}, {3817,35016}, {3838,6917}, {3897,6933}, {3916,5693}, {4018,5535}, {4192,30986}, {4324,34789}, {4679,5658}, {4855,10310}, {4881,18239}, {5086,6960}, {5087,6256}, {5219,10894}, {5231,5881}, {5252,10786}, {5253,18444}, {5258,18908}, {5267,31803}, {5288,5531}, {5428,17502}, {5438,30503}, {5534,12513}, {5660,12762}, {5709,12635}, {5768,7288}, {5787,6861}, {5790,31494}, {5794,6825}, {5836,11499}, {5880,6885}, {5882,11019}, {5886,24299}, {6245,6675}, {6253,15950}, {6684,12447}, {6744,13607}, {6826,28628}, {6827,25681}, {6868,24703}, {6880,24914}, {6906,12688}, {6907,17647}, {6914,31937}, {6924,34339}, {6927,18391}, {6938,12679}, {6947,24954}, {6949,17606}, {6954,26066}, {7280,15071}, {7680,13411}, {7967,20323}, {8261,10202}, {9615,19068}, {9945,31777}, {10167,16132}, {10179,16202}, {10268,15829}, {10391,22766}, {10395,20418}, {10532,17718}, {10582,12650}, {10680,34791}, {10826,21842}, {10884,18238}, {10914,11014}, {11220,12666}, {11344,19861}, {11374,26332}, {11376,12116}, {11715,12019}, {12119,12761}, {12332,15015}, {12699,33596}, {12705,30282}, {13369,32612}, {13464,22991}, {13600,25439}, {14646,21735}, {15481,31835}, {16616,19541}, {18443,25524}, {20117,31445}, {25440,31788}, {26287,28160}, {30144,31786}, {31162,33595}, {32153,32159}.
- Lunes, 6 de abril del 2020
La cúbica K088
El 6 de abril de 1992
falleció, a los 72 años, Isaac Asimov, bioquímico nacido en Rusia pero nacionalizado estadounidense. Prolífico y existoso escritor de ciencia ficción y de obras de divulgación científica, entre estas "Alpha Centauri. La estrella más próxima".
Dado un triángulo ABC con baricentro G, K y S, sean M un punto sobre la recta GK, ΓM la circunferencia que pasa por G,M,S, y 𝒞M la que pasa por G y M. ΓM y 𝒞M son tangentes en G y se vuelven a corta en un punto P.
El lugar geométrico de
P, cuando
M se mueve sobre
GK, es la cúbica
K088, del catálogo de Bernard Gibert.
M=(b^2+c^2+a^2 (1+3 t) : a^2+c^2+b^2 (1+3 t) : a^2+b^2+c^2 (1+3 t)),
entonces:
P = (( b^2 -c^2 )(a^2+b^2+c^2+3 a^2 t) / ((a^2+b^2+c^2) (2 a^6-6 a^4 b^2+9 a^2 b^4-b^6-6 a^4 c^2-3 b^4 c^2+9 a^2 c^4-3 b^2 c^4-c^6)+3 (a^6 b^2+2 a^4 b^4+a^2 b^6+a^6 c^2-16 a^4 b^2 c^2+8 a^2 b^4 c^2-2 b^6 c^2+2 a^4 c^4+8 a^2 b^2 c^4-4 b^4 c^4+a^2 c^6-2 b^2 c^6)t) : ... : ...).
La ecuación implícita del lugar descrito por el punto P es K088:
𝔖abc xyz
y z ((a^4+(b^2+c^2)^2) (y+z)+a^2 (c^2 (2 y-7 z)+b^2 (2 z-7 y))) =
(6 a^4-6 a^2 b^2+6 b^4-6 a^2 c^2-6 b^2 c^2+6 c^4) x y z.
Una construcción del punto P:
El de ΓM y la circunferencia circunscrita a ABC corta la cónica circuncscrita que pasa por G y S en el punto D. La recta GD pasa por P.
- Sábado, 4 de abril del 2020
Centro ortológico del triángulo órtico respecto al triángulo media-altura
Hoy 4 de abril de 2020 ha fallecido, a los 76 años de edad, Luis Eduardo Aute, uno de los principales referentes de la canción de autor en España. Poeta, pintor, escultor y director de cine, destacó sobre todo como cantautor, con la publicación de más de una veintena de discos de estudio y temas como "Al alba" (inspirada en los últimos fusilamientos del franquismo, una canción que mucha gente creyó de amor, e incluso algo dulzona, pero que es un grito de angustia y de reproche contra la pena de muerte), "Rosas en el mar" o "La belleza".
Dado un triángulo ABC de circuncentro O=X3 y ortocentro H=X4, sus lados AB y AC cortan a una recta variable perpendicular a AO, en los puntos Ab y Ac, respectivamente. La envolvente de la recta que pasa por las proyecciones ortogonales de Ab y Ac sobre BO y CO es una
parábola
( a^12 b^4 x^2-6 a^10 b^6 x^2+15 a^8 b^8 x^2-20 a^6 b^10 x^2+15 a^4 b^12 x^2-6 a^2 b^14 x^2+b^16 x^2-2 a^12 b^2 c^2 x^2+6 a^10 b^4 c^2 x^2-4 a^8 b^6 c^2 x^2-4 a^6 b^8 c^2 x^2+6 a^4 b^10 c^2 x^2-2 a^2 b^12 c^2 x^2+a^12 c^4 x^2+6 a^10 b^2 c^4 x^2-22 a^8 b^4 c^4 x^2+24 a^6 b^6 c^4 x^2-11 a^4 b^8 c^4 x^2+2 a^2 b^10 c^4 x^2-6 a^10 c^6 x^2-4 a^8 b^2 c^6 x^2+24 a^6 b^4 c^6 x^2-4 a^4 b^6 c^6 x^2+6 a^2 b^8 c^6 x^2-16 b^10 c^6 x^2+15 a^8 c^8 x^2-4 a^6 b^2 c^8 x^2-11 a^4 b^4 c^8 x^2+6 a^2 b^6 c^8 x^2+30 b^8 c^8 x^2-20 a^6 c^10 x^2+6 a^4 b^2 c^10 x^2+2 a^2 b^4 c^10 x^2-16 b^6 c^10 x^2+15 a^4 c^12 x^2-2 a^2 b^2 c^12 x^2-6 a^2 c^14 x^2+c^16 x^2+2 a^12 b^4 x y-12 a^10 b^6 x y+30 a^8 b^8 x y-40 a^6 b^10 x y+30 a^4 b^12 x y-12 a^2 b^14 x y+2 b^16 x y-4 a^12 b^2 c^2 x y+16 a^10 b^4 c^2 x y-28 a^8 b^6 c^2 x y+32 a^6 b^8 c^2 x y-28 a^4 b^10 c^2 x y+16 a^2 b^12 c^2 x y-4 b^14 c^2 x y+2 a^12 c^4 x y+8 a^10 b^2 c^4 x y-36 a^8 b^4 c^4 x y+48 a^6 b^6 c^4 x y-30 a^4 b^8 c^4 x y+8 a^2 b^10 c^4 x y-12 a^10 c^6 x y+4 a^8 b^2 c^6 x y+32 a^6 b^4 c^6 x y-8 a^4 b^6 c^6 x y-20 a^2 b^8 c^6 x y+4 b^10 c^6 x y+30 a^8 c^8 x y-16 a^6 b^2 c^8 x y-30 a^4 b^4 c^8 x y-4 a^2 b^6 c^8 x y-4 b^8 c^8 x y-40 a^6 c^10 x y+4 a^4 b^2 c^10 x y+16 a^2 b^4 c^10 x y+4 b^6 c^10 x y+30 a^4 c^12 x y+8 a^2 b^2 c^12 x y-12 a^2 c^14 x y-4 b^2 c^14 x y+2 c^16 x y+a^12 b^4 y^2-6 a^10 b^6 y^2+15 a^8 b^8 y^2-20 a^6 b^10 y^2+15 a^4 b^12 y^2-6 a^2 b^14 y^2+b^16 y^2-2 a^12 b^2 c^2 y^2+10 a^10 b^4 c^2 y^2-24 a^8 b^6 c^2 y^2+36 a^6 b^8 c^2 y^2-34 a^4 b^10 c^2 y^2+18 a^2 b^12 c^2 y^2-4 b^14 c^2 y^2+a^12 c^4 y^2+2 a^10 b^2 c^4 y^2-10 a^8 b^4 c^4 y^2+8 a^6 b^6 c^4 y^2+5 a^4 b^8 c^4 y^2-10 a^2 b^10 c^4 y^2+4 b^12 c^4 y^2-6 a^10 c^6 y^2+8 a^8 b^2 c^6 y^2-8 a^6 b^4 c^6 y^2+12 a^4 b^6 c^6 y^2-10 a^2 b^8 c^6 y^2+4 b^10 c^6 y^2+15 a^8 c^8 y^2-12 a^6 b^2 c^8 y^2+5 a^4 b^4 c^8 y^2+6 a^2 b^6 c^8 y^2-10 b^8 c^8 y^2-20 a^6 c^10 y^2-2 a^4 b^2 c^10 y^2-2 a^2 b^4 c^10 y^2+4 b^6 c^10 y^2+15 a^4 c^12 y^2+10 a^2 b^2 c^12 y^2+4 b^4 c^12 y^2-6 a^2 c^14 y^2-4 b^2 c^14 y^2+c^16 y^2+2 a^12 b^4 x z-12 a^10 b^6 x z+30 a^8 b^8 x z-40 a^6 b^10 x z+30 a^4 b^12 x z-12 a^2 b^14 x z+2 b^16 x z-4 a^12 b^2 c^2 x z+8 a^10 b^4 c^2 x z+4 a^8 b^6 c^2 x z-16 a^6 b^8 c^2 x z+4 a^4 b^10 c^2 x z+8 a^2 b^12 c^2 x z-4 b^14 c^2 x z+2 a^12 c^4 x z+16 a^10 b^2 c^4 x z-36 a^8 b^4 c^4 x z+32 a^6 b^6 c^4 x z-30 a^4 b^8 c^4 x z+16 a^2 b^10 c^4 x z-12 a^10 c^6 x z-28 a^8 b^2 c^6 x z+48 a^6 b^4 c^6 x z-8 a^4 b^6 c^6 x z-4 a^2 b^8 c^6 x z+4 b^10 c^6 x z+30 a^8 c^8 x z+32 a^6 b^2 c^8 x z-30 a^4 b^4 c^8 x z-20 a^2 b^6 c^8 x z-4 b^8 c^8 x z-40 a^6 c^10 x z-28 a^4 b^2 c^10 x z+8 a^2 b^4 c^10 x z+4 b^6 c^10 x z+30 a^4 c^12 x z+16 a^2 b^2 c^12 x z-12 a^2 c^14 x z-4 b^2 c^14 x z+2 c^16 x z+2 a^12 b^4 y z-12 a^10 b^6 y z+30 a^8 b^8 y z-40 a^6 b^10 y z+30 a^4 b^12 y z-12 a^2 b^14 y z+2 b^16 y z-4 a^12 b^2 c^2 y z+12 a^10 b^4 c^2 y z-16 a^8 b^6 c^2 y z+24 a^6 b^8 c^2 y z-36 a^4 b^10 c^2 y z+28 a^2 b^12 c^2 y z-8 b^14 c^2 y z+2 a^12 c^4 y z+12 a^10 b^2 c^4 y z-20 a^8 b^4 c^4 y z+10 a^4 b^8 c^4 y z-12 a^2 b^10 c^4 y z+8 b^12 c^4 y z-12 a^10 c^6 y z-16 a^8 b^2 c^6 y z+24 a^4 b^6 c^6 y z-4 a^2 b^8 c^6 y z+8 b^10 c^6 y z+30 a^8 c^8 y z+24 a^6 b^2 c^8 y z+10 a^4 b^4 c^8 y z-4 a^2 b^6 c^8 y z-20 b^8 c^8 y z-40 a^6 c^10 y z-36 a^4 b^2 c^10 y z-12 a^2 b^4 c^10 y z+8 b^6 c^10 y z+30 a^4 c^12 y z+28 a^2 b^2 c^12 y z+8 b^4 c^12 y z-12 a^2 c^14 y z-8 b^2 c^14 y z+2 c^16 y z+a^12 b^4 z^2-6 a^10 b^6 z^2+15 a^8 b^8 z^2-20 a^6 b^10 z^2+15 a^4 b^12 z^2-6 a^2 b^14 z^2+b^16 z^2-2 a^12 b^2 c^2 z^2+2 a^10 b^4 c^2 z^2+8 a^8 b^6 c^2 z^2-12 a^6 b^8 c^2 z^2-2 a^4 b^10 c^2 z^2+10 a^2 b^12 c^2 z^2-4 b^14 c^2 z^2+a^12 c^4 z^2+10 a^10 b^2 c^4 z^2-10 a^8 b^4 c^4 z^2-8 a^6 b^6 c^4 z^2+5 a^4 b^8 c^4 z^2-2 a^2 b^10 c^4 z^2+4 b^12 c^4 z^2-6 a^10 c^6 z^2-24 a^8 b^2 c^6 z^2+8 a^6 b^4 c^6 z^2+12 a^4 b^6 c^6 z^2+6 a^2 b^8 c^6 z^2+4 b^10 c^6 z^2+15 a^8 c^8 z^2+36 a^6 b^2 c^8 z^2+5 a^4 b^4 c^8 z^2-10 a^2 b^6 c^8 z^2-10 b^8 c^8 z^2-20 a^6 c^10 z^2-34 a^4 b^2 c^10 z^2-10 a^2 b^4 c^10 z^2+4 b^6 c^10 z^2+15 a^4 c^12 z^2+18 a^2 b^2 c^12 z^2+4 b^4 c^12 z^2-6 a^2 c^14 z^2-4 b^2 c^14 z^2+c^16 z^2 = 0)
𝒫a, cuyo eje es la paralela a BC por O, y su foco está sobre la altura AH. Se denota por da su directriz, su ecuación baricéntrica es:
(b^2-c^2) (-a^2+b^2+c^2)^2 x+(b^6-b^4 c^2+b^2 c^4-c^6+a^4 (b^2-c^2)+2 a^2 (-b^4+b^2 c^2+c^4)) y+(b^6-b^4 c^2+b^2 c^4-c^6+a^4 (b^2-c^2)-2 a^2 (b^4+b^2 c^2-c^4)) z=0.
Las parábolas 𝒫b y 𝒫c y sus directrices db y dc, se definen cíclicamente.
Las directrices da, da, da concurren en X185, del respecto al .
Las tangentes a las parábolas 𝒫a, 𝒫b, 𝒫c en sus vértices concurren en X389, centro de la .
- Viernes, 3 de abril del 2020
Puntos sobre la cónica inscrita de perspector X(92)
El 3 de abril de 1924, nació Marlon Brando, actor estadounidense de cine y teatro. Se hizo mundialmente conocido en la década de 1950 por sus intervenciones en películas como Un tranvía llamado deseo (1951), Viva Zapata! (1952), Julio César y On the Waterfront (1954). Otros filmes míticos en los que intervino son El padrino, El último tango en París (1972) y Apocalypse Now (1979).
Dados un triángulo ABC y un punto P, sean el y DEF el de X92 (Proposition 1).
Sean Ab y Ac las interseciones de la altura por A con PaPc y PaPb, respectivamente. Los puntos Bc, Ba y Ca, Cb, se definen cíclicamente.
Se denota por l, m, n los las distancias entre los pares de puntos (Ab, Ac), (Bc, Ba), (Ca, Cb), respectivamente.
Se considera el punto Qo determinado por sus coordenadas baricéntricas (l:m:n), respecto a ABC, y sea el de Qo. El punto Qo está sobre la de X92 y Q1, Q2, Q3 están, respectivamente, sobre los lados EF. FD, DE de DEF.
Las rectas DQ1, EQ2 y FQ3 concurren en un punto Q', sobre la cónica inscrita de de X92.
Si P=(u:v:w), entonces:
Qo = (b c u (a^2 (v-w)-(b^2-c^2) (v+w)) : ... : ...),
Q' = (b c (-a^2+b^2+c^2) u^2 (-a^2 v+b^2 v-c^2 v+a^2 w+b^2 w-c^2 w)^2 : ... : ...).
El punto Q' están sobre la de perpector X92=(:...:..), con ecuación:
a^2 SA^2 x^2+b^2 SB^2 y^2+c^2 SC^2 z^2-2 b c SBSC y z-2 a c SASC x z-2 a b SASB x y = 0.
Esta cónica pasa por los centros del triángulo X20902, X34591.
Pares {P ∈{Xi, Xj,...}, f(P)=Q'=Xk}, para los índices {{i,j,...}, k}:
{{2, 10, 13, 14, 17, 18, 76, 83, 94, 96, 98, 226, 262, 275, 321, 459, 485, 486, 598, 671, 801, 1029, 1131, 1132, 1139, 1140, 1327, 1328, 1446, 1676, 1677, 1751, 1916, 2009, 2010, 2051, 2052, 2394, 2592, 2593, 2671, 2672, 2986, 2996, 3316, 3317, 3366, 3367, 3370, 3373, 3374, 3381, 3382, 3387, 3388, 3391, 3392, 3397, 3399, 3406, 3407, 3413, 3414, 3424, 3429, 3590, 3591, 3597, 4049, 4052, 4080, 4444, 5392, 5395, 5397, 5401, 5402, 5403, 5404, 5466, 5485, 5487, 5488, 5490, 5491, 5503, 6177, 6178, 6504, 6539, 6568, 6569, 6625, 7578, 7607, 7608, 7612, 8587, 8781, 8796, 8808, 9180, 9221, 9290, 9302, 9381, 10153, 10155, 10159, 10185, 10187, 10188, 10194, 10195, 10290, 10302, 10484, 10511, 11121, 11122, 11140, 11167, 11170, 11172, 11538, 11599, 11602, 11603, 11606, 11608, 11611, 11668, 11669, 12066, 12816, 12817, 12818, 12819, 12820, 12821, 12822, 12823, 13380, 13478, 13576, 13579, 13580, 13581, 13582, 13583, 13584, 13585, 13599, 14223, 14226, 14228, 14229, 14231, 14232, 14234, 14236, 14237, 14238, 14240, 14241, 14243, 14244, 14245, 14458, 14484, 14485, 14488, 14492, 14494, 14534, 14554, 14632, 14633, 16080, 16277, 17503, 17758, 18316, 18366, 18840, 18841, 18842, 18843, 18844, 18845, 21845, 21846, 22235, 22237, 22244, 22245, 24007, 24008, 24624, 27797, 30505, 30588, 31363, 31630, 31943, 32014, 32022, 32130, 32532, 33602, 33603, 33604, 33605, 33606, 33607, 33698, 34087, 34089, 34091, 34258, 34289, 34475, 34899, 35005, 35098, 35353, 36316, 36317}, 20902},
{{1, 7, 8, 9, 21, 79, 80, 84, 90, 104, 177, 256, 294, 314, 885, 941, 943, 981, 983, 987, 989, 1000, 1039, 1041, 1061, 1063, 1156, 1172, 1251, 1320, 1389, 1392, 1476, 1896, 1937, 2298, 2320, 2335, 2344, 2346, 2481, 2648, 2997, 3062, 3065, 3254, 3255, 3296, 3307, 3308, 3427, 3467, 3495, 3551, 3577, 3680, 4180, 4866, 4876, 4900, 5377, 5424, 5551, 5553, 5555, 5556, 5557, 5558, 5559, 5560, 5561, 5665, 6595, 6596, 6597, 6598, 6599, 6601, 7003, 7049, 7091, 7126, 7133, 7149, 7155, 7160, 7161, 7162, 7261, 7284, 7285, 7317, 7319, 7320, 7595, 7707, 8372, 8759, 8809, 9365, 9372, 9442, 10266, 10305, 10307, 10308, 10309, 10390, 10429, 10435, 11279, 11604, 11609, 12641, 12867, 12868, 13143, 13426, 13454, 13602, 13606, 14224, 14496, 14497, 14947, 15173, 15175, 15176, 15179, 15180, 15314, 15315, 15446, 15909, 15910, 15997, 15998, 16005, 16615, 17097, 17098, 17501, 18299, 18490, 19551, 21398, 23836, 23838, 23893, 23959, 24297, 24298, 24300, 24302, 26722, 30479, 30494, 30500, 30513, 31316, 31507, 31509, 32635, 33576, 33653, 33696, 34215, 34216, 34256, 34485, 34894, 34917, 34918, 34919, 35097, 35355, 36121, 36599}, 34591}.
{{X3, X6,...}, f(X3)=f(X6)=...=W},
W = ( a^3 (a^2-b^2-c^2)^3 (b^2-c^2)^2 : ... : ...),
que tiene números de búsqueda en
(3.20440116974460, 3.20398941608048, -0.0564364229534639).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,1956}, {48,163}, {520,35072}, {820,4020}, {1973,19614}, {2631,2632}, {7065,34980}, {17438,35201}, {17879,24018}, {17881,20902}, {34589,34591}.
Los puntos I'a=f(Ia), I'b=f(Ib), I'c=f(Ic), que corresponden a los Ia, Ib, Ic, forman un triángulo perspectivo con ABC, con centro de perspectividad:
Z = ( a (b+c)^2 (a^2-b^2-c^2)/(-a+b+c)^2 : ... : ...),
que tiene números de búsqueda en ETC
(-0.606578189344412, -0.671114323140515, 4.38524125454831).
{1,951}, {2,1952}, {12,13853}, {19,223}, {42,65}, {48,57}, {55,6611}, {71,1214}, {77,2359}, {171,8766}, {196,18676}, {201,1425}, {222,3942}, {226,1826}, {278,1953}, {306,1231}, {307,8896}, {651,1762}, {756,2632}, {1020,16577}, {1407,2286}, {1782,34043}, {1796,7177}, {1859,2635}, {1869,5930}, {1876,14547}, {1888,2654}, {2171,6046}, {2184,7079}, {3611,18210}, {3668,18674}, {3752,22063}, {3949,6356}, {4466,26957}, {4605,6358}, {6505,6507}, {7146,7365}, {11529,18446}, {17080,24310}, {18161,18623}.
NOTA:
Cuando P es uno de los cuatro puntos I, Ia, Ib, Ic, una de las longitudes l, m, n es la suma de las otras dos.
(Problema 945, Solución de Saturnino Campo Ruiz).
- Domingo, 29 de marzo del 2020
X(1000) como centro de perspectividad
El 29 de marzo de 1873 nació Tullio Levi-Civita, matemático italiano, famoso por su trabajo sobre cálculo tensorial, Levi-Civita personalmente ayudó a Albert Einstein a aprender el cálculo tensorial, en el cual Einstein basaría su relatividad general.El término Conexión de Levi-Civita es adoptado en su honor.
Sean ABC un triángulo de incentro I=X1 y el , las rectas BI y CI cortan a BbCc en Ba y Ca, respectivamente.
El incentro del triángulo coincide con I.
Sea el triángulo de contacto interior de . Se definen, cíclicamente, los triángulos y .
Si
Oa,
Ob y
Oc son los centros de las circunferencias (), () y (), las rectas
AOa,
AOb,
COc concurren en
X1000, del de los .
En coordenadas baricéntricas:
A1 = ((b - c)^2 - a (b + c) : -b (-a + b + c) : (a - b - c) c),
A2 = (-a^2 (a-b-c):-b (b-c)^2+a b (b+c):a^3-a b (b-3 c)+b (b-c)^2-a^2 (b+c)),
A3 = (-a^2 (a-b-c):a^3+(b-c)^2 c+a (3 b-c) c-a^2 (b+c):c (-(b-c)^2+a (b+c))).
El radio de la circunferencia
()
( a^5 x^2-3 a^4 b x^2+2 a^3 b^2 x^2+2 a^2 b^3 x^2-3 a b^4 x^2+b^5 x^2-3 a^4 c x^2+12 a^3 b c x^2-14 a^2 b^2 c x^2+4 a b^3 c x^2+b^4 c x^2+2 a^3 c^2 x^2-14 a^2 b c^2 x^2+14 a b^2 c^2 x^2-2 b^3 c^2 x^2+2 a^2 c^3 x^2+4 a b c^3 x^2-2 b^2 c^3 x^2-3 a c^4 x^2+b c^4 x^2+c^5 x^2+2 a^5 x y-6 a^4 b x y+4 a^3 b^2 x y+4 a^2 b^3 x y-6 a b^4 x y+2 b^5 x y-6 a^4 c x y+20 a^3 b c x y-24 a^2 b^2 c x y+12 a b^3 c x y-2 b^4 c x y+4 a^3 c^2 x y-8 a^2 b c^2 x y+4 a b^2 c^2 x y+4 a^2 c^3 x y-4 a b c^3 x y-6 a c^4 x y-2 b c^4 x y+2 c^5 x y+a^5 y^2-3 a^4 b y^2+2 a^3 b^2 y^2+2 a^2 b^3 y^2-3 a b^4 y^2+b^5 y^2-3 a^4 c y^2+8 a^3 b c y^2-10 a^2 b^2 c y^2+8 a b^3 c y^2-3 b^4 c y^2+2 a^3 c^2 y^2+6 a^2 b c^2 y^2-10 a b^2 c^2 y^2+2 b^3 c^2 y^2+2 a^2 c^3 y^2+8 a b c^3 y^2+2 b^2 c^3 y^2-3 a c^4 y^2-3 b c^4 y^2+c^5 y^2+2 a^5 x z-6 a^4 b x z+4 a^3 b^2 x z+4 a^2 b^3 x z-6 a b^4 x z+2 b^5 x z-6 a^4 c x z+20 a^3 b c x z-8 a^2 b^2 c x z-4 a b^3 c x z-2 b^4 c x z+4 a^3 c^2 x z-24 a^2 b c^2 x z+4 a b^2 c^2 x z+4 a^2 c^3 x z+12 a b c^3 x z-6 a c^4 x z-2 b c^4 x z+2 c^5 x z+2 a^5 y z-6 a^4 b y z+4 a^3 b^2 y z+4 a^2 b^3 y z-6 a b^4 y z+2 b^5 y z-6 a^4 c y z-4 a^2 b^2 c y z+16 a b^3 c y z-6 b^4 c y z+4 a^3 c^2 y z-4 a^2 b c^2 y z-20 a b^2 c^2 y z+4 b^3 c^2 y z+4 a^2 c^3 y z+16 a b c^3 y z+4 b^2 c^3 y z-6 a c^4 y z-6 b c^4 y z+2 c^5 y z+a^5 z^2-3 a^4 b z^2+2 a^3 b^2 z^2+2 a^2 b^3 z^2-3 a b^4 z^2+b^5 z^2-3 a^4 c z^2+8 a^3 b c z^2+6 a^2 b^2 c z^2+8 a b^3 c z^2-3 b^4 c z^2+2 a^3 c^2 z^2-10 a^2 b c^2 z^2-10 a b^2 c^2 z^2+2 b^3 c^2 z^2+2 a^2 c^3 z^2+8 a b c^3 z^2+2 b^2 c^3 z^2-3 a c^4 z^2-3 b c^4 z^2+c^5 z^2 = 0)
es r√(R-2r)/R/2 y su centro es:
Oa = (-6 a^2:a^2-4 a b+b^2-c^2:a^2-b^2-4 a c+c^2).
Las rectas AOa, AOb, COc concurren en:
X1000 = (1/(a^2-b^2+4 b c-c^2):1/(-a^2+b^2+4 a c-c^2):1/(-a^2+4 a b-b^2+c^2)).
Clic aquí para otra construcción de X1000.
Si Γ y Γa las circunferencias inscritas a los triángulos ABC y , se denosta por da y ea los ejes radicales de () y Γa, y () y Γ, respectivamente. Los ejes radicales db, dc y eb, ec, se definen cíclicamente.
Los triángulos A'B'C' y A"B"C" formados por las rectas da, db, dc y ea, eb, ec, respectivamente, son homotéticos a ABC.
A'= (a (-b^2-c^2+a (b+c)):b (-a^2+(b-c) c+a (b+2 c)):c (-a^2+b (-b+c)+a (2 b+c))),
A" = (a^2 (b+c)+(b-c)^2 (b+c)-2 a (b^2+c^2):-b (a^2+(b-c)^2-2 a (b+c)):-c (a^2+(b-c)^2-2 a (b+c))).
El centro de la homotecia que transforma ABC en A'B'C' es el y su razón es -1/2.
El centro de la homotecia que transforma ABC en A"B"C" es el incentro y su razón es
-(r+2R)/(2R). Siendo r y R los radios de las circunferencias inscrita y circunscrita de ABC.
Conocidos los centros y razones de las homotecias anteriores se puede determina el centro, X, y razón, k, de la homotecia que transforma A'B'C' en A"B"C", mediante las fórmulas:
k=k1k2,
X = X354 + (1-k1)/(1-k1k2) X254X1,
donde k1=-2 y k2=-(r+2R)/(2R).
Así, el centro de la homotecia que transforma A'B'C' en A"B"C" es X5173, inverso en la circunferencia inscrita del inverso en la circunferencia circunscrita del conjugado isogonal del .
- Viernes, 28 de marzo del 2020
X(3160) como centro de una circunferencia de Apolonio
El 28 de marzo de 1942 fallece Miguel Hernández (a los 31 años) poeta y dramaturgo español, a consecuencia de una bronquitis que degenera en tuberculosis, en la enfermería de la prisión de Alicante, donde fue recluido represaliado por el franquismo a causa de sus ideas republicanas. Entre sus obras más conocidas están "Perito en lunas", "El rayo que no cesa", "Cancionero y romancero de ausencias", "Vientos del pueblo. Poesía en la guerra", "Nanas de la cebolla" y varias obras de teatro.
Sean DEF el , Γa la circunferencia que pasa por A y es tangente a BC en D, Γb la circunferencia que pasa por B y es tangente a CA en E, Γc la circunferencia que pasa por C y es tangente a AB en F.
El centro de la
circunferencia
(
𝔖abc xyz
(a-b-c)^4 (b-c)^2x^2-(a+b-c)^2 (a-b+c)^2 (3 a^2-2 a b-b^2-2 a c-c^2)y z = 0.
)
Γ, tangente exteriormente a las circunferencias Γ
a, Γ
b, Γ
c, es X
3160 y es tangente a la circunferencia circunscrita a
ABC en X
934.
Las coordenadas baricéntricas del punto de tangencia, Ta, de Γ y Γa es:
Ta = ((a+b-c)^2 (a-b+c)^2 (a^2-2 (b-c)^2+a (b+c)) :
(b-c) (a+b-c)^2 (-a+b+c)^2 (a-b+3 c) :
-(b-c) (a+3 b-c) (a-b+c)^2 (-a+b+c)^2).
Las rectas DTa, ETb, FTc concurren en X279, del .
Let P be a point on line X(4)X(7) other than X(4). Let A' be the reflection of P in BC, and define B' and C' cyclically. The circumcircles of AA'B', BC'A', and CA'B' concur at
X(934). (Randy Hutson, July 20, 2016)
X(3160) = of X(2) and X(7).
X(3160) = perspector of triangle ABC and the tangential triangle of the conic that passes through A, B, C and has center X(7).
- Miércoles, 25 de marzo del 2020
X(13160) como centro de una circunferencia de Apolonio
El 25 de marzo de 1818 murió (a los 73 años) Caspar Wessel, matemático noruego-danés. Desarrolló métodos matemáticos de topografía cada vez más sofisticados y los explicó en un informe que escribió en 1787. La fama de Wessel como matemático se basa únicamente en este documento, que se publicó en 1799, dando por primera vez una interpretación geométrica de números complejos. Hoy se denomina a esta interpretación geométrica el diagrama de Argand, pero el trabajo de Wessel fue lo primero. Fue redescubierto por Argand en 1806 y nuevamente por Gauss en 1831.
Sean DEF y , respectivamente, los triángulo y de un triágulo dado ABC.
Las circunferencias Γa, Γb y Γc, circunscritas a los triángulos EFHa, FEHb, DEHc (cuyos centros se desigman por Oa, Ob y Oc) son tangentes exteriormente a la .
El centro de la circunferencia Γ, tangente exteriormente a las circunferencias Γa, Γb, Γc, ha de ser el otro punto común (distinto de X5) de las tres hipérbolas ℋa, ℋb y ℋc con focos Ob y Oc, Oc y Oa, Oa y Ob y pasan respectivamnete por D, E y F.
La ecuación baricéntrica de la hipérbola ℋa es:
a^8 b^8 x^2-4 a^6 b^10 x^2+6 a^4 b^12 x^2-4 a^2 b^14 x^2+b^16 x^2-2 a^8 b^4 c^4 x^2+4 a^6 b^6 c^4 x^2-6 a^4 b^8 c^4 x^2+8 a^2 b^10 c^4 x^2-4 b^12 c^4 x^2+4 a^6 b^4 c^6 x^2-4 a^2 b^8 c^6 x^2+a^8 c^8 x^2-6 a^4 b^4 c^8 x^2-4 a^2 b^6 c^8 x^2+6 b^8 c^8 x^2-4 a^6 c^10 x^2+8 a^2 b^4 c^10 x^2+6 a^4 c^12 x^2-4 b^4 c^12 x^2-4 a^2 c^14 x^2+c^16 x^2-2 a^12 b^4 x y+10 a^10 b^6 x y-18 a^8 b^8 x y+12 a^6 b^10 x y+2 a^4 b^12 x y-6 a^2 b^14 x y+2 b^16 x y+6 a^10 b^4 c^2 x y-12 a^8 b^6 c^2 x y+4 a^6 b^8 c^2 x y+6 a^2 b^12 c^2 x y-4 b^14 c^2 x y+2 a^12 c^4 x y-8 a^10 b^2 c^4 x y+4 a^8 b^4 c^4 x y-8 a^6 b^6 c^4 x y+6 a^4 b^8 c^4 x y+8 a^2 b^10 c^4 x y-4 b^12 c^4 x y-8 a^10 c^6 x y+16 a^8 b^2 c^6 x y-4 a^6 b^4 c^6 x y+4 a^4 b^6 c^6 x y-4 a^2 b^8 c^6 x y+12 b^10 c^6 x y+10 a^8 c^8 x y-4 a^6 b^2 c^8 x y+2 a^4 b^4 c^8 x y+2 a^2 b^6 c^8 x y-4 a^4 b^2 c^10 x y-10 a^2 b^4 c^10 x y-12 b^6 c^10 x y-10 a^4 c^12 x y-4 a^2 b^2 c^12 x y+4 b^4 c^12 x y+8 a^2 c^14 x y+4 b^2 c^14 x y-2 c^16 x y+a^16 y^2-6 a^14 b^2 y^2+13 a^12 b^4 y^2-10 a^10 b^6 y^2-4 a^8 b^8 y^2+10 a^6 b^10 y^2-3 a^4 b^12 y^2-2 a^2 b^14 y^2+b^16 y^2-4 a^14 c^2 y^2+12 a^12 b^2 c^2 y^2-6 a^10 b^4 c^2 y^2-4 a^8 b^6 c^2 y^2-8 a^6 b^8 c^2 y^2+12 a^4 b^10 c^2 y^2+2 a^2 b^12 c^2 y^2-4 b^14 c^2 y^2+4 a^12 c^4 y^2+4 a^10 b^2 c^4 y^2-10 a^8 b^4 c^4 y^2-8 a^6 b^6 c^4 y^2-2 a^4 b^8 c^4 y^2+8 a^2 b^10 c^4 y^2+4 b^12 c^4 y^2+4 a^10 c^6 y^2-16 a^8 b^2 c^6 y^2-12 a^6 b^4 c^6 y^2-20 a^4 b^6 c^6 y^2-8 a^2 b^8 c^6 y^2+4 b^10 c^6 y^2-10 a^8 c^8 y^2-2 a^6 b^2 c^8 y^2+a^4 b^4 c^8 y^2-10 a^2 b^6 c^8 y^2-10 b^8 c^8 y^2+4 a^6 c^10 y^2+8 a^4 b^2 c^10 y^2+10 a^2 b^4 c^10 y^2+4 b^6 c^10 y^2+4 a^4 c^12 y^2+4 a^2 b^2 c^12 y^2+4 b^4 c^12 y^2-4 a^2 c^14 y^2-4 b^2 c^14 y^2+c^16 y^2+2 a^12 b^4 x z-8 a^10 b^6 x z+10 a^8 b^8 x z-10 a^4 b^12 x z+8 a^2 b^14 x z-2 b^16 x z-8 a^10 b^4 c^2 x z+16 a^8 b^6 c^2 x z-4 a^6 b^8 c^2 x z-4 a^4 b^10 c^2 x z-4 a^2 b^12 c^2 x z+4 b^14 c^2 x z-2 a^12 c^4 x z+6 a^10 b^2 c^4 x z+4 a^8 b^4 c^4 x z-4 a^6 b^6 c^4 x z+2 a^4 b^8 c^4 x z-10 a^2 b^10 c^4 x z+4 b^12 c^4 x z+10 a^10 c^6 x z-12 a^8 b^2 c^6 x z-8 a^6 b^4 c^6 x z+4 a^4 b^6 c^6 x z+2 a^2 b^8 c^6 x z-12 b^10 c^6 x z-18 a^8 c^8 x z+4 a^6 b^2 c^8 x z+6 a^4 b^4 c^8 x z-4 a^2 b^6 c^8 x z+12 a^6 c^10 x z+8 a^2 b^4 c^10 x z+12 b^6 c^10 x z+2 a^4 c^12 x z+6 a^2 b^2 c^12 x z-4 b^4 c^12 x z-6 a^2 c^14 x z-4 b^2 c^14 x z+2 c^16 x z-2 a^16 y z+10 a^14 b^2 y z-16 a^12 b^4 y z+2 a^10 b^6 y z+20 a^8 b^8 y z-18 a^6 b^10 y z+6 a^2 b^14 y z-2 b^16 y z+10 a^14 c^2 y z-26 a^12 b^2 c^2 y z+6 a^10 b^4 c^2 y z+20 a^8 b^6 c^2 y z+6 a^6 b^8 c^2 y z-18 a^4 b^10 c^2 y z-6 a^2 b^12 c^2 y z+8 b^14 c^2 y z-16 a^12 c^4 y z+6 a^10 b^2 c^4 y z+8 a^8 b^4 c^4 y z+28 a^6 b^6 c^4 y z-18 a^2 b^10 c^4 y z-8 b^12 c^4 y z+2 a^10 c^6 y z+20 a^8 b^2 c^6 y z+28 a^6 b^4 c^6 y z+36 a^4 b^6 c^6 y z+18 a^2 b^8 c^6 y z-8 b^10 c^6 y z+20 a^8 c^8 y z+6 a^6 b^2 c^8 y z+18 a^2 b^6 c^8 y z+20 b^8 c^8 y z-18 a^6 c^10 y z-18 a^4 b^2 c^10 y z-18 a^2 b^4 c^10 y z-8 b^6 c^10 y z-6 a^2 b^2 c^12 y z-8 b^4 c^12 y z+6 a^2 c^14 y z+8 b^2 c^14 y z-2 c^16 y z+a^16 z^2-4 a^14 b^2 z^2+4 a^12 b^4 z^2+4 a^10 b^6 z^2-10 a^8 b^8 z^2+4 a^6 b^10 z^2+4 a^4 b^12 z^2-4 a^2 b^14 z^2+b^16 z^2-6 a^14 c^2 z^2+12 a^12 b^2 c^2 z^2+4 a^10 b^4 c^2 z^2-16 a^8 b^6 c^2 z^2-2 a^6 b^8 c^2 z^2+8 a^4 b^10 c^2 z^2+4 a^2 b^12 c^2 z^2-4 b^14 c^2 z^2+13 a^12 c^4 z^2-6 a^10 b^2 c^4 z^2-10 a^8 b^4 c^4 z^2-12 a^6 b^6 c^4 z^2+a^4 b^8 c^4 z^2+10 a^2 b^10 c^4 z^2+4 b^12 c^4 z^2-10 a^10 c^6 z^2-4 a^8 b^2 c^6 z^2-8 a^6 b^4 c^6 z^2-20 a^4 b^6 c^6 z^2-10 a^2 b^8 c^6 z^2+4 b^10 c^6 z^2-4 a^8 c^8 z^2-8 a^6 b^2 c^8 z^2-2 a^4 b^4 c^8 z^2-8 a^2 b^6 c^8 z^2-10 b^8 c^8 z^2+10 a^6 c^10 z^2+12 a^4 b^2 c^10 z^2+8 a^2 b^4 c^10 z^2+4 b^6 c^10 z^2-3 a^4 c^12 z^2+2 a^2 b^2 c^12 z^2+4 b^4 c^12 z^2-2 a^2 c^14 z^2-4 b^2 c^14 z^2+c^16 z^2=0.
El centro de Γ es:
X13160 = (a^8 (b^2+c^2)-4 a^4 b^2 c^2 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)-2 a^6 (b^4-b^2 c^2+c^4)+2 a^2 (b^8-b^6 c^2-b^2 c^6+c^8) : ... : ...)
X(13160) = Point Beid 42
Hyacinthos 25728
Apr 5, 2017
[Tran Quang Hung]:
Let ABC be a triangle.
A'B'C' is cevian triangle of circumcenter O.
A'',B'',C'' are midpoints of AA',BB',CC', resp..
The isogonal conjugate of O wrt triangle A''B''C'' lies on Euler line.
Which is this point?
[César Lozada]:
Z = 2*(3*R^2-Sω)*S^2-(4*R^2- : : (barycentrics)
= 5*X(3091)-3*X(7565)
= nine-points circle-inverse-of-X(3153)
El radio de Γ (r, R y s son los radios de las circunferencias inscrita y circunscrita, y semiperímetro de ABC) es:
4 R^2 (r^2+4 r R+2 R^2-s^2)^2 / (2 r^2+8 r R+5 R^2-2 s^2)^2.
El punto de tangencia de Γ y Γa es:
Ta= (-3 a^8 (b^2+c^2)-(b^2-c^2)^4 (b^2+c^2)+2 a^2 (b^2-c^2)^2 (b^4+3 b^2 c^2+c^4)-2 a^6 (b^4+5 b^2 c^2+c^4)+4 a^4 (b^6-2 b^4 c^2-2 b^2 c^4+c^6) :
a^10+a^8 c^2+2 a^6 c^2 (b^2-c^2)-(b^2-c^2)^3 (2 b^4+3 b^2 c^2+c^4)+2 a^4 (b^6+2 b^4 c^2-2 b^2 c^4-c^6)+a^2 (-b^8+6 b^6 c^2-6 b^2 c^6+c^8) :
b^8-6 b^6 c^2+6 b^2 c^6-c^8).
El de las circunferencias Γa, Γb y Γc es X5133 (el inverso de X23 en la circunferencia de los nueve puntos), este punto es el centro de perspectividad de los triángulos órtico y .
- Lunes, 23 de marzo del 2020
Reflexión de X(11270) en el circuncentro
Aniversario del nacimiento de mi hija Marta
Sean A', B', C', las reflexiones de los vértices de un triángulo ABC en su circuncentro O=X3, y D, E, F las reflexiones de A', B', C' en sus lados BC, CA, AB, respectivamente. Se denota por Oa, Ob, Oc los circuncentros de los triángulos OEF, OFD, ODE.
Los triángulos A'B'C' y son perspectivos y el centro de perspectividad es la reflexión de X11270 en X3:
W = ( a^2 (4 a^8-10 a^6 (b^2+c^2)
+a^4 (6 b^4+17 b^2 c^2+6 c^4)+2 a^2 (b^6-4 b^4 c^2-4 b^2 c^4+c^6)-(b^2-c^2)^2 (2 b^4+3 b^2 c^2+2 c^4)) : ... : ...),
que tiene números de búsqueda en
(4.51548892994527, 3.13289197959206, -0.612332548554094).
Es la reflexión de X11270 en X3.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,9927}, {3,9544}, {4,1511}, {20,10282}, {110,3357}, {140,3431}, {186,2904}, {195,15040}, {323,32534}, {376,18442}, {550,7712}, {576,15020}, {578,12834}, {631,2888}, {1071,5694}, {1092,7691}, {1147,15035}, {1204,15051}, {1350,7488}, {1498,2071}, {3516,15052}, {3522,4549}, {3523,3620}, {3528,5944}, {3533,14805}, {3543,15751}, {5050,17928}, {5056,11430}, {5059,10564}, {5876,23040}, {6102,9716}, {6640,12383}, {7592,9545}, {8546,10541}, {8567,11441}, {10255,34153}, {10257,34799}, {10304,11821}, {10539,15034}, {11250,32609}, {11413,11820}, {12085,35265}, {12111,35493}, {12162,35494}, {12289,14156}, {14118,32620}, {15043,15516}, {15717,18475}, {17818,19357}, {18281,18432}, {18350,35475}, {21844,22115}, {22555,22951}, {23294,30714}, {32233,34118}.
X(11270)=Isogonal conjugate of X(382).
Hyacinthos 24872 (Antreas Hatzipolakis and César Lozada)
[APH]:
Let ABC be a triangle, P a point and A'B'C' the pedal triangle of P.
Denote:
Ma, Mb, Mc = the midpoints of AA',BB',CC', resp.
A",B",C"= the reflections of Ma,Mb,Mc in PA', PB', PC', resp.
ABC, A"B"C" are orthologic.
If P lies on the Euler line the orthologic center (MaMbMc, ABC) llies on the Euler line.
Which is the locus of the other orthologic center (ABC, MaMbMc) as P moves on the Euler line?
[César Lozada]:
Asked locus = Jerabek hyperbola
ETC-pairs (P, Za(P)=orthologic center (ABC,MaMbMc) ):
(2,3), (4,64), (5,54), (376,3532), (381,4), (403,1177), (3091,3527), (3545,6), (3839,3426), (5055,3431), (5066,1173)
Za(O) = a/(3*a^4-(b^2+c^2)*a^2-2*(b^2- c^2)^2) : : (trilinears)
= isogonal conjugate of X(382),
On Jerabek hyperbola.
En coordenadas baricéntricas, respecto a ABC,
D = (a^2 (a^2+b^2-c^2) (a^2-b^2+c^2):-a^6+(b^2-c^2)^3+a^4 (b^2+c^2)+a^2 (-b^4+c^4) : -a^6-(b^2-c^2)^3+a^4 (b^2+c^2)+a^2 (b^4-c^4)),
Oa = (4 (a^6-3 a^4 (b^2+c^2)-(b^2-c^2)^2 (b^2+c^2)+3 a^2 (b^4+c^4)) : 4 b^2 c^2 (a^2+b^2-c^2) : 4 b^2 c^2 (a^2-b^2+c^2)).
Los puntos Oa, Ob, Oc están sobre las alturas, en consecuencia, los triángulos ABC y son . El centro de ortología de ABC respecto a es X265, punto diametralmente opuesto de X3 en la .
Los triángulos DEF y son perspectivos, con centro de perspectividad X2888, del .
- Viernes, 20 de marzo del 2020
La cúbica K407
Hoy a la 3:49 UTC entra la primavera de manera oficial en el hemisferio norte. No puede existir una fecha exacta porque nuestro calendario de 365 días no coincide con el tiempo que tarda la Tierra en darle la vuelta al Sol (365,2425 días). Este desfase se ajusta en el calendario gracias a los años bisiestos (cada 4 años) y a quitar un bisiesto (cada 400). Así el equinoccio puede darse entre los días 19 al 21 de marzo.
K407 = is an isogonal nonpivotal cubic with singularity I=X(1) and root X(57), isogonal conjugate of .
Let ℋ be a circum-conic through I = X(1) and (N) its normal at I. (N) meets ℋ at I and another point M which lies on K407.
The pivotal conic is the of the . Its center is O=X(3), its real foci are I=X(1) and . Its principal circle is the circumcircle. Its excentricity is OI/R.
La tangente ℓ en un punto L de la circunferencia inscrita a un triángulo ABC corta a las perpendiculares por el incentro I=X1 a AI, BI, CI en A', B', C', respectivamente. Las rectas AA',BB', CC' concurren en un punto W.
El lugar geométrico de W, cuando L varía sobre la circunferencia inscrita, es K407.
Podemos tomar el punto L sobre la circunferencia inscrita como el segundo punto de intersección con una recta variable que pasa por el :
L = ((a-b-c) (-2 a (3 b^2+3 c^2+2 b c (-3+t))+a^2 (b+c) (-3+t)+2 a^3 (3+t)+(b-c)^2 (b+c) (3+t))^2 :
-(a-b+c) (a^3 (3+t)-a^2 (6 b+c (3+t))+a (b^2 (-3+t)-4 b c (-3+t)-c^2 (3+t))+(b+c) (2 b^2 (3+t)+c^2 (3+t)-b c (9+t)))^2:
-(a+b-c) (a^3 (3+t)-a^2 (6 c+b (3+t))-a (4 b c (-3+t)-c^2 (-3+t)+b^2 (3+t))+(b+c) (b^2 (3+t)+2 c^2 (3+t)-b c (9+t)))^2).
La tangente ℓ en L a la circunferencia inscrita corta a la perpendicular por I a AI en:
A' = ((b-c) (-2 a (3 b^2+3 c^2+2 b c (-3+t))+a^2 (b+c) (-3+t)+2 a^3 (3+t)+(b-c)^2 (b+c) (3+t)) (a^3 (3+t)-a^2 (b+c) (3+t)+(b+c) (-6 b c+b^2 (3+t)+c^2 (3+t))-a (b^2 (3+t)+c^2 (3+t)+2 b c (-3+2 t))) :
-(a-b) b (a-b+c) (c (-3+t)+a (3+t)+b (3+t)) (a^3 (3+t)-a^2 (6 b+c (3+t))+a (b^2 (-3+t)-4 b c (-3+t)-c^2 (3+t))+(b+c) (2 b^2 (3+t)+c^2 (3+t)-b c (9+t))) :
(a-c) (a+b-c) c (b (-3+t)+a (3+t)+c (3+t)) (a^3 (3+t)-a^2 (6 c+b (3+t))-a (4 b c (-3+t)-c^2 (-3+t)+b^2 (3+t))+(b+c) (b^2 (3+t)+2 c^2 (3+t)-b c (9+t)))),
La perpendicular por I a BI corta a ℓ en:
B' = (a (a-b) (a-b-c) (c (-3+t)+a (3+t)+b (3+t)) (-2 a (3 b^2+3 c^2+2 b c (-3+t))+a^2 (b+c) (-3+t)+2 a^3 (3+t)+(b-c)^2 (b+c) (3+t)) :
-(a-c) (a^2 c (-3+t)+a c^2 (-3+t)+a^3 (3+t)-a^2 b (3+t)-a b^2 (3+t)+(b-c)^2 (b+c) (3+t)-2 a b c (-3+2 t)) (a^3 (3+t)-a^2 (6 b+c (3+t))+a (b^2 (-3+t)-4 b c (-3+t)-c^2 (3+t))+(b+c) (2 b^2 (3+t)+c^2 (3+t)-b c (9+t))) :
-(b-c) (a+b-c) c (a (-3+t)+(b+c) (3+t)) (a^3 (3+t)-a^2 (6 c+b (3+t))-a (4 b c (-3+t)-c^2 (-3+t)+b^2 (3+t))+(b+c) (b^2 (3+t)+2 c^2 (3+t)-b c (9+t)))),
La perpendicular por I a CI corta a ℓ en:
C' = (a (a-c) (a-b-c) (b (-3+t)+a (3+t)+c (3+t)) (-2 a (3 b^2+3 c^2+2 b c (-3+t))+a^2 (b+c) (-3+t)+2 a^3 (3+t)+(b-c)^2 (b+c) (3+t)) :
-b (b-c) (-a+b-c) (a (-3+t)+(b+c) (3+t)) (a^3 (3+t)-a^2 (6 b+c (3+t))+a (b^2 (-3+t)-4 b c (-3+t)-c^2 (3+t))+(b+c) (2 b^2 (3+t)+c^2 (3+t)-b c (9+t))) :
-(a-b) (a^3 (3+t)+(b-c)^2 (b+c) (3+t)+a^2 (b (-3+t)-c (3+t))+a (b c (6-4 t)+b^2 (-3+t)-c^2 (3+t))) (a^3 (3+t)-a^2 (6 c+b (3+t))-a (4 b c (-3+t)-c^2 (-3+t)+b^2 (3+t))+(b+c) (b^2 (3+t)+2 c^2 (3+t)-b c (9+t)))).
La rectas AA', BB', CC' concurren en:
W = (a (a-b) (a-c) (a-b-c) (-2 a (3 b^2+3 c^2+2 b c (-3+t))+a^2 (b+c) (-3+t)+2 a^3 (3+t)+(b-c)^2 (b+c) (3+t)) (2 a (b+c) t (3+t)+a^2 (3+t)^2+b^2 (-9+t^2)+c^2 (-9+t^2)+2 b c (9+t^2)) : ... : ...).
El lugar geométrico que describe W, cuando L varía sobre la circunferencia inscrita, es
la cúbica K407:
(-a^2 b c^2+b^3 c^2+2 a b c^3-b c^4) x^2 y+(a^3 c^2-a b^2 c^2+2 a b c^3-a c^4) x y^2+(-a^2 b^2 c+2 a b^3 c-b^4 c+b^2 c^3) x^2 z+(2 a^3 b c-4 a^2 b^2 c+2 a b^3 c-4 a^2 b c^2-4 a b^2 c^2+2 a b c^3) x y z+(-a^4 c+2 a^3 b c-a^2 b^2 c+a^2 c^3) y^2 z+(a^3 b^2-a b^4+2 a b^3 c-a b^2 c^2) x z^2+(-a^4 b+a^2 b^3+2 a^3 b c-a^2 b c^2) y z^2=0.
La normal en I a la hipérbola ℋW que pasa por I y W y circunscrita a ABC, pasa por W. El sexto punto Z de intersección de K407 y la hipérbola ℋZ circunscrita, tangente a IW en I, está sobre su normal en I.
Los puntos W y Z son conjugados isogonales y la recta que los une envuelve la cónica de MacBeath del triángulo excentral (pivotal cónica de K407).
El lugar geométrico de los centros de las hipérbolas, circunscritas a ABC que pasan por I, es la elipse del I y G=X2; su centro es X1125, complemento del .
La recta que une los centros Wo y Zo de las hipérbolas ℋW y ℋZ, para todo punto L sobre la circunferencia inscrita, pasa por X2646, del ortocentro, X65, del , respecto al incentro y circuncentro.
- Jueves, 19 de marzo del 2020
El centro de la circunferencia de Hatzipolakis-Lozada como centro ortológico
El 19 de marzo de 1978 falleció, a los 85 años, Gaston Maurice Julia, matemático francés (nacido en Argelia, sus padres eran de origen catalán). Fue un precursor en lo que hoy se conoce como fractales. Todas las propiedades de los fractales las estableció Julia a fuerza de cálculos y deducciones con papel y lápiz, en desventaja con el segundo padre de éstos, el matemático polaco Benoit Mandelbrot, quien pudo aprovechar la invención del ordenador.
Dado un triángulo ABC, sean DEF y los triángulios de y .
ΓM es una circunferencia variable que pasa por B y C (su centro M esta sobre la mediatriz de BC), ΓM' es la circunferencia que pasa por D y Ma, tal que el de ambas es la recta EF (su centro M' es la intersección de la mediatriz de DMa con la perpendicular por M a EF).
Sea Mo la proyección ortogonal de M' sobre el eje radical de ΓM y la circunferencia inscrita a ABC. El lugar geométrico de Mo, cuando ΓM varía, es una
circunferencia
( En coordenadas baricéntricas:
c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-(((3 a^3-8 a^2 b+7 a b^2-2 b^3-8 a^2 c+2 a b c+2 b^2 c+7 a c^2+2 b c^2-2 c^3) x)/(16 a))-((2 a^3-7 a^2 b+8 a b^2-3 b^3+7 a^2 c-16 a b c+9 b^2 c+8 a c^2-9 b c^2+3 c^3) y)/(16 (-b+c))-((-2 a^3-7 a^2 b-8 a b^2-3 b^3+7 a^2 c+16 a b c+9 b^2 c-8 a c^2-9 b c^2+3 c^3) z)/(16 (-b+c))) = 0)
Γa que pasa por el punto A1=(0:-(a+b-c)^2:(a-b+c)^2) (sobre BC), donde pasan los ejes radicales de la circunferencias inscrita y ΓM.
A2=(0:2 a+3 b-3 c:2 a-3 b+3 c) es el segundo punto de intersección de BC y Γa. Los puntos B2 y C2 se definen cíclicamente.
Los triángulos
ABC y son y el centro de ortología de respecto a
ABC es
X10222, centro de la circunferencia de Hatzipolakis-Lozada,
(a(2a^3-3a^2(b+c)+3(b-c)^2(b+c)-2a(b^2-3b c+c^2)+3(b-c)^2(b+c)): ... : ... ).
El centro ortológico de ABC respecto a es el conjugado isogoanal de X10222:
W = ( a/ (2a^3-3a^2(b+c)+3(b-c)^2(b+c)-2a(b^2-3b c+c^2)+3(b-c)^2(b+c)) : ... : ...),
que tiene números de búsqueda en
(2.13985008209120, 4.44430401665096, -0.423784490585299).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,1392}, {4,1388}, {8,140}, {9,17438}, {21,15178}, {35,24302}, {56,14497}, {79,13464}, {80,5882}, {515,17501}, {944,7319}, {1000,34471}, {1156,21740}, {1319,1389}, {1320,1385}, {1476,25405}, {3065,11715}, {3579,28082}, {3680,6940}, {5556,5603}, {5559,24926}, {5561,11522}, {5884,11279}, {6595,33858}, {7317,31520}, {15698,17765}, {17097,24928}, {18446,33576}, {21398,21842}.
El punto W ha sido incorporado a ETC con el número X(37518).
- Miércoles, 18 de marzo del 2020
La cúbica de Thomson y la quíntica de Darboux
El 18 de marzo de 1965 el cosmonauta soviético Alexei Leonov se convierte en el primer ser humano que pasea, durante 12 minutos, por el espacio.
Dados un triángulo ABC y punto P, se denota por p su y por Po la proyección ortogonal de P sobre p.
El lugar geométrico del punto
P tal que la perpendicular a
p por
P pasa por el circuncentro es la cúbica de Thomson (
K002) y el lugar de
Po, cuando
P se mueve sobre K002, es la quíntica de Darboux (
Q071).
Po = (u (a^2 v w (2 u^2 - 4 v w + u (v + w)) -
u (v - w) (b^2 (2 u + v) w - c^2 v (2 u + w))) : ... : ...).
Los puntos O, P, Po están alineados si y solo si
u(c^2v^2-b^2w^2)+v(a^2w^2-c^2u^2)+w(b^2u^2-a^2v^2)=0.
Es decir, P debe estar sobre K002. Entonces, Po está sobre la quíntica Q071, de ecuación:
𝔖abc xyz
y z (-2 b^2 c^2 (b^2 - c^2) (-5 a^2 + 3 b^2 + 3 c^2) x^3 +
a^2 (b^2 - c^2) (10 a^4 + b^4 + 14 b^2 c^2 + c^4 +
a^2 (-11 b^2 - 11 c^2)) x y z +
a^4 y z ((4 a^4 + b^4 + 5 b^2 c^2 - 2 c^4 +
a^2 (-5 b^2 - 2 c^2)) y + (-4 a^4 + 2 b^4 - 5 b^2 c^2 - c^4 +
a^2 (2 b^2 + 5 c^2)) z) -
a^4 (c^2 (3 a^2 - b^2 - 3 c^2) y^3 -
b^2 (3 a^2 - 3 b^2 - c^2) z^3)) = 0.
Sean D, E, F los puntos de intersección de p con las rectas BC, CA, AB, respectivamente, las circunferencias (ADPo), (BEPo), (CFPo) se vuelven a concurrir en:
Q = (
u v^4 w^2 + u^2 v^2 w^3 + 8 v^4 w^3 - u v^2 w^4 - 8 v^3 w^4 +
c^4 u v^2 (u - v - w) (2 u + w) (2 v^2 - v w - w^2) -
w^2 (-b^4 u (2 u + v) (u - v - w) (v^2 + v w - 2 w^2) -
a^4 v^2 (v - w) (-u^2 + 8 v w + u (v + w)) -
2 a^2 b^2 v (u - w) (-u^2 (v + w) + 2 v w (v + w) +
u (v^2 - 4 v w + w^2))) +
2 c^2 u^2 v^4 w^3 (a^2 (u - v) v (u^2 (v + w) - 2 v w (v + w) -
u (v^2 - 4 v w + w^2)) +
b^2 u (v - w) (v^3 + 2 v^2 w + 2 v w^2 + w^3 - 3 u^2 (v + w) +
u (2 v^2 + 5 v w + 2 w^2)))a^4
+ 2 v w (c^2 (u - v) v + b^2 w (-u + w)) (u^2 (v + w) - 2 v w (v + w) -
u (v^2 - 4 v w + w^2))a^2
+ u (u - v - w) (v - w) (-b^2 (2 u + v) w +
c^2 v (2 u + w)) (c^2 v (2 v + w) - b^2 w (v + 2 w))) : ... : ... ).
Cuando P está sobre K002, Q está sobre la cúbica de Darboux (K004) y es el punto de intersección de las normales, en los vértices de ABC, a la cónica circunscrita c(P) de P.
Ternas {P=Xi,Po=Xj,Q=Xk}, para {i,j,k}:
{1,1155,1}, {3,34147,64}, {4,468,20}, {6,187,3}, {9,*,84}, {57,1319,40}, {223,*,3345}, {282,*,1490}, {1073,11589,1498}, {1249,*,3346}, {3341,*,3347}, {3342,*,3182}, {3343,*,3348}, {3344,*,3183}, {3349,*,2130}, {3350,*,2131}, {3351,*,3354}, {3352,*,3353}, {3356,*,3355}, {14481,*,3637}.
- Lunes, 16 de marzo del 2020
La reflexión del circuncentro en el ortocentro como centro radical
"No hay rama de la matemática, por lo abstracta que sea, que no pueda aplicarse algún día a los fenómenos del mundo real".
Nikolai Ivanovich Lobachevski
Dado un triángulo ABC, se denota, como es habitual, las longitudes de los lados BC, CA, AB por a, b, c, respectivamente, y por el .
El centro radical de las circunferencias de centros en Ma, Mb, Mc y radios √3a/2, √3b/2, √3c/2 es X382, reflexión del circuncentro en el ortocentro.
La ecuación baricéntica de la circunferencia de centro Ma y radio √3a/2 es
a^2 y z + b^2 z x + c^2 x y + (x + y + z) (1/2 (2 a^2 - b^2 - c^2) x + (a^2 y)/2 + (
a^2 z)/2) = 0.
Por permutación cíclica se obtienen las ecuaciones de las otras dos circunferencias. El de las tres es:
X382 = ( a^4 - a^2 (b^2 + c^2)- 2 (b^2 - c^2)^2 : ... : ...).
La circunferencia de centro Ma y radio √3a/2 es el lugar geométrico que describe un punto A' tal que el área del
del punto simediano Ka del triángulo A'BC coincida con el área de dicho triángulo.
- Domingo, 15 de marzo del 2020
Triángulos con centro ortológico común
"La esencia de las matemáticas reside en su libertad".-Georg Cantor
Si los centros ortológicos de dos triángulois ortológicos coinciden, entondes los triángulos son perspectivos.
Dados un triángulo ABC un punto P, para construir un triángulo A'B'C' a ABC, tal que sus centros de ortología coincidan, tomamos un puno D sobre la recta AP, verificando que AD : DP = k. Sean E el punto sobre BP y F sobre CP, tales que las perpendiculares por D, E, F a AP, BP, CP, forman un triángulo A'B'C' ortológico a ABC y que sus centros ortológicos coinciden en P.
Si (u:v:w) son las coordenadas baricéntricas de P, entonces:
D=(u+k u+v+w : k v : k w).
E=(u (c^2 u^2+c^2 k u^2-c^2 v^2+a^2 u w-b^2 u w+c^2 u w+a^2 k u w-b^2 k u w+c^2 k u w+a^2 v w-b^2 v w-c^2 v w+a^2 w^2-b^2 w^2+a^2 k w^2) : c^2 u^2 v+c^2 k u^2 v+c^2 u v^2+2 c^2 u v w+a^2 k u v w-b^2 k u v w+c^2 k u v w+c^2 v^2 w+b^2 u w^2+b^2 v w^2+c^2 v w^2+a^2 k v w^2+b^2 w^3 : w (c^2 u^2+c^2 k u^2-c^2 v^2+a^2 u w-b^2 u w+c^2 u w+a^2 k u w-b^2 k u w+c^2 k u w+a^2 v w-b^2 v w-c^2 v w+a^2 w^2-b^2 w^2+a^2 k w^2)),
F=(u (b^2 u^2+b^2 k u^2+a^2 u v+b^2 u v-c^2 u v+a^2 k u v+b^2 k u v-c^2 k u v+a^2 v^2-c^2 v^2+a^2 k v^2+a^2 v w-b^2 v w-c^2 v w-b^2 w^2) : v (b^2 u^2+b^2 k u^2+a^2 u v+b^2 u v-c^2 u v+a^2 k u v+b^2 k u v-c^2 k u v+a^2 v^2-c^2 v^2+a^2 k v^2+a^2 v w-b^2 v w-c^2 v w-b^2 w^2) : c^2 u v^2+c^2 v^3+b^2 u^2 w+b^2 k u^2 w+2 b^2 u v w+a^2 k u v w+b^2 k u v w-c^2 k u v w+b^2 v^2 w+c^2 v^2 w+a^2 k v^2 w+b^2 u w^2+b^2 v w^2).
Se concluye que:
A'=((b^2-c^2)^2 (1+k) u^2+a^4 ((1+k) u^2-4 v w)-2 a^2 (c^2 ((1+k) u^2-2 v (v+w))+b^2 ((1+k) u^2-2 w (v+w))) : a^4 v (u+k u+2 w)-2 a^2 (c^2 v (u+k u+v+2 w)+b^2 ((1+k) u v+w^2))+(b^2-c^2) (-c^2 v ((1+k) u+2 (v+w))+b^2 ((1+k) u v-2 w (v+w))) : a^4 (u+k u+2 v) w-2 a^2 (b^2 w (u+k u+2 v+w)+c^2 (v^2+(1+k) u w))+(b^2-c^2) (c^2 (2 v^2-(1+k) u w+2 v w)+b^2 w ((1+k) u+2 (v+w)))),
B'=(a^4 v (u+k u+2 w)-2 a^2 (c^2 v (u+k u+v+2 w)+b^2 ((1+k) u v+w^2))+(b^2-c^2) (-c^2 v ((1+k) u+2 (v+w))+b^2 ((1+k) u v-2 w (v+w))) :
a^4 (1+k) v^2+c^4 (1+k) v^2+2 b^2 c^2 v (v-k v+2 w)+b^4 ((1+k) v^2+4 v w+4 w^2)-2 a^2 v (c^2 (1+k) v+b^2 (v+k v+2 w)) :
a^4 (-1+k) v w+b^4 ((-1+k) v-2 w) w-c^4 v (2 v+w-k w)-2 b^2 c^2 (v^2+(3+k) v w+w^2)+2 a^2 (b^2 w (v-k v+w)+c^2 v (v+w-k w))),
C'=(-a^4 (u+k u+2 v) w+2 a^2 (b^2 w (u+k u+2 v+w)+c^2 (v^2+(1+k) u w))-(b^2-c^2) (c^2 (2 v^2-(1+k) u w+2 v w)+b^2 w ((1+k) u+2 (v+w))) :
-a^4 (-1+k) v w+b^4 w (v-k v+2 w)+c^4 v (2 v+w-k w)+2 b^2 c^2 (v^2+(3+k) v w+w^2)-2 a^2 (b^2 w (v-k v+w)+c^2 v (v+w-k w)):
-(a^2-b^2)^2 (1+k) w^2-c^4 (4 v^2+4 v w+(1+k) w^2)+2 c^2 w (-b^2 (2 v+w-k w)+a^2 (2 v+w+k w))).
Los triángulos ABC y A'B'C' son y su centro de perspectividad Q está sobre la circunhipérbola que pasa por P.
Q= ((-2 a^2 c^2 v^2+2 b^2 c^2 v^2-2 c^4 v^2+a^4 u w-2 a^2 b^2 u w+b^4 u w-2 a^2 c^2 u w-2 b^2 c^2 u w+c^4 u w+a^4 k u w-2 a^2 b^2 k u w+b^4 k u w-2 a^2 c^2 k u w-2 b^2 c^2 k u w+c^4 k u w+2 a^4 v w-4 a^2 b^2 v w+2 b^4 v w-2 c^4 v w-2 a^2 b^2 w^2+2 b^4 w^2-2 b^2 c^2 w^2) (a^4 u v-2 a^2 b^2 u v+b^4 u v-2 a^2 c^2 u v-2 b^2 c^2 u v+c^4 u v+a^4 k u v-2 a^2 b^2 k u v+b^4 k u v-2 a^2 c^2 k u v-2 b^2 c^2 k u v+c^4 k u v-2 a^2 c^2 v^2-2 b^2 c^2 v^2+2 c^4 v^2+2 a^4 v w-2 b^4 v w-4 a^2 c^2 v w+2 c^4 v w-2 a^2 b^2 w^2-2 b^4 w^2+2 b^2 c^2 w^2):
(2 a^2 c^2 v^2-2 b^2 c^2 v^2-2 c^4 v^2-a^4 v w+2 a^2 b^2 v w-b^4 v w+2 a^2 c^2 v w-6 b^2 c^2 v w-c^4 v w+a^4 k v w-2 a^2 b^2 k v w+b^4 k v w-2 a^2 c^2 k v w-2 b^2 c^2 k v w+c^4 k v w+2 a^2 b^2 w^2-2 b^4 w^2-2 b^2 c^2 w^2) (a^4 u v-2 a^2 b^2 u v+b^4 u v-2 a^2 c^2 u v-2 b^2 c^2 u v+c^4 u v+a^4 k u v-2 a^2 b^2 k u v+b^4 k u v-2 a^2 c^2 k u v-2 b^2 c^2 k u v+c^4 k u v-2 a^2 c^2 v^2-2 b^2 c^2 v^2+2 c^4 v^2+2 a^4 v w-2 b^4 v w-4 a^2 c^2 v w+2 c^4 v w-2 a^2 b^2 w^2-2 b^4 w^2+2 b^2 c^2 w^2):
(2 a^2 c^2 v^2-2 b^2 c^2 v^2-2 c^4 v^2-a^4 v w+2 a^2 b^2 v w-b^4 v w+2 a^2 c^2 v w-6 b^2 c^2 v w-c^4 v w+a^4 k v w-2 a^2 b^2 k v w+b^4 k v w-2 a^2 c^2 k v w-2 b^2 c^2 k v w+c^4 k v w+2 a^2 b^2 w^2-2 b^4 w^2-2 b^2 c^2 w^2) (-2 a^2 c^2 v^2+2 b^2 c^2 v^2-2 c^4 v^2+a^4 u w-2 a^2 b^2 u w+b^4 u w-2 a^2 c^2 u w-2 b^2 c^2 u w+c^4 u w+a^4 k u w-2 a^2 b^2 k u w+b^4 k u w-2 a^2 c^2 k u w-2 b^2 c^2 k u w+c^4 k u w+2 a^4 v w-4 a^2 b^2 v w+2 b^4 v w-2 c^4 v w-2 a^2 b^2 w^2+2 b^4 w^2-2 b^2 c^2 w^2)),
y la equación de la hipérbola es:
a^2 u (v - w) - (b^2 - c^2) u (v + w) y z + ... = 0.
El lugar geométrico del circuncentro O' de A'B'C', cuando k varía, es la recta PP* (siendo P* el de P).
La envolvente de la recta O'Q* es la cónica co(P) con ecuación:
u^2 (4 b^2 c^2 v w (w^2 (a^2 (u+w)+b^2 (v+w))+c^2 (u^2 v-w^2 (v+w)+u (v^2-w^2))) (a^2 v^2 (u+v)+c^2 v^2 (v+w)+b^2 (u^2 w-v^2 (v+w)+u (-v^2+w^2)))-(-c^4 v^2 (u+w) (v+w)+b^2 (u+v) w^2 (a^2 v-b^2 (v+w))+c^2 v w (a^2 v (u+w)+b^2 (2 u^2+2 u (v+w)+(v+w)^2)))^2)x^2+
2 v w ((c^4 u^2 (u+w) (v+w)+a^2 (u+v) w^2 (-b^2 u+a^2 (u+w))-c^2 u w (b^2 u (v+w)+a^2 (u^2+2 v^2+2 v w+w^2+2 u (v+w)))) (a^4 v^2 (u+v) (u+w)+b^2 u^2 (-c^2 v+b^2 (u+v)) (v+w)-a^2 u v (c^2 v (u+w)+b^2 (u^2+v^2+2 v w+2 w^2+2 u (v+w))))-2 a^2 u (-u^2 (b^2 (u+v)+c^2 (u+w))+a^2 (u^3+u^2 (v+w)-v w (v+w))) (c^4 v^2 (u+w) (v+w)-b^2 (u+v) w^2 (a^2 v-b^2 (v+w))-c^2 v w (a^2 v (u+w)+b^2 (2 u^2+2 u (v+w)+(v+w)^2))))y z+ .... = 0.
Su centro es:
Wp = (c^4 u^2 v (u + w) (v + w) -
c^2 u v w (2 b^2 u (v + w) +
a^2 (3 u^2 + 3 u v + 2 v^2 + 4 u w + 3 v w + w^2)) +
w (b^4 u^2 (u + v) (v + w) -
a^2 b^2 u v (3 u^2 + 4 u v + v^2 + 3 u w + 3 v w + 2 w^2) +
a^4 v (2 u^3 + 3 u^2 (v + w) - v w (v + w) + u (v + w)^2)) : ... : ... ).
Algunos pares {P=Xi, Wp=Xj}, para {i,j}: {2, 7622}, {74, 12041}, {98, 12042}, {99, 33813}, {100, 33814}, {110, 1511}, {111, 14650}, {1113, 35231}, {1114, 35232}, ...
CASOS PARTICULARES
• Cuando P es el incentro, co(X1) degenera en la recta doble X1X3, que es la tangente en X1.
• Cuando P es el baricentro, co(X2) es la cónica de ecuación:
a^4 b^4 x^2-4 a^2 b^6 x^2+4 b^8 x^2-2 a^4 b^2 c^2 x^2+4 a^2 b^4 c^2 x^2-18 b^6 c^2 x^2+a^4 c^4 x^2+4 a^2 b^2 c^4 x^2+28 b^4 c^4 x^2-4 a^2 c^6 x^2-18 b^2 c^6 x^2+4 c^8 x^2+4 a^6 b^2 x y-10 a^4 b^4 x y+4 a^2 b^6 x y-4 a^6 c^2 x y+20 a^4 b^2 c^2 x y+20 a^2 b^4 c^2 x y-4 b^6 c^2 x y-10 a^4 c^4 x y-46 a^2 b^2 c^4 x y-10 b^4 c^4 x y+22 a^2 c^6 x y+22 b^2 c^6 x y-8 c^8 x y+4 a^8 y^2-4 a^6 b^2 y^2+a^4 b^4 y^2-18 a^6 c^2 y^2+4 a^4 b^2 c^2 y^2-2 a^2 b^4 c^2 y^2+28 a^4 c^4 y^2+4 a^2 b^2 c^4 y^2+b^4 c^4 y^2-18 a^2 c^6 y^2-4 b^2 c^6 y^2+4 c^8 y^2-4 a^6 b^2 x z-10 a^4 b^4 x z+22 a^2 b^6 x z-8 b^8 x z+4 a^6 c^2 x z+20 a^4 b^2 c^2 x z-46 a^2 b^4 c^2 x z+22 b^6 c^2 x z-10 a^4 c^4 x z+20 a^2 b^2 c^4 x z-10 b^4 c^4 x z+4 a^2 c^6 x z-4 b^2 c^6 x z-8 a^8 y z+22 a^6 b^2 y z-10 a^4 b^4 y z-4 a^2 b^6 y z+22 a^6 c^2 y z-46 a^4 b^2 c^2 y z+20 a^2 b^4 c^2 y z+4 b^6 c^2 y z-10 a^4 c^4 y z+20 a^2 b^2 c^4 y z-10 b^4 c^4 y z-4 a^2 c^6 y z+4 b^2 c^6 y z+4 a^8 z^2-18 a^6 b^2 z^2+28 a^4 b^4 z^2-18 a^2 b^6 z^2+4 b^8 z^2-4 a^6 c^2 z^2+4 a^4 b^2 c^2 z^2+4 a^2 b^4 c^2 z^2-4 b^6 c^2 z^2+a^4 c^4 z^2-2 a^2 b^2 c^4 z^2+b^4 c^4 z^2= 0,
que pasa por X2, X187, X7618; su centro es X7622.
• Cuando P es el circuncentro, co(X3) degenera en la (doble), que es tangente en X3.
• Cuando P es el ortocentro, co(X4) no está definida.
• Cuando P es el , co(X6) es la hipérbola de ecuación:
-4 a^8 b^6 c^2 x^2-4 a^6 b^8 c^2 x^2+4 a^4 b^10 c^2 x^2+4 a^2 b^12 c^2 x^2+8 a^8 b^4 c^4 x^2+4 a^6 b^6 c^4 x^2+a^4 b^8 c^4 x^2+4 b^12 c^4 x^2-4 a^8 b^2 c^6 x^2+4 a^6 b^4 c^6 x^2-10 a^4 b^6 c^6 x^2-4 a^2 b^8 c^6 x^2-4 a^6 b^2 c^8 x^2+a^4 b^4 c^8 x^2-4 a^2 b^6 c^8 x^2-8 b^8 c^8 x^2+4 a^4 b^2 c^10 x^2+4 a^2 b^2 c^12 x^2+4 b^4 c^12 x^2-4 a^8 b^4 c^4 x y-26 a^6 b^6 c^4 x y-4 a^4 b^8 c^4 x y+4 a^8 b^2 c^6 x y+10 a^6 b^4 c^6 x y+10 a^4 b^6 c^6 x y+4 a^2 b^8 c^6 x y+16 a^6 b^2 c^8 x y-2 a^4 b^4 c^8 x y+16 a^2 b^6 c^8 x y-4 a^4 b^2 c^10 x y-4 a^2 b^4 c^10 x y-16 a^2 b^2 c^12 x y+4 a^12 b^2 c^2 y^2+4 a^10 b^4 c^2 y^2-4 a^8 b^6 c^2 y^2-4 a^6 b^8 c^2 y^2+4 a^12 c^4 y^2+a^8 b^4 c^4 y^2+4 a^6 b^6 c^4 y^2+8 a^4 b^8 c^4 y^2-4 a^8 b^2 c^6 y^2-10 a^6 b^4 c^6 y^2+4 a^4 b^6 c^6 y^2-4 a^2 b^8 c^6 y^2-8 a^8 c^8 y^2-4 a^6 b^2 c^8 y^2+a^4 b^4 c^8 y^2-4 a^2 b^6 c^8 y^2+4 a^2 b^4 c^10 y^2+4 a^4 c^12 y^2+4 a^2 b^2 c^12 y^2+4 a^8 b^6 c^2 x z+16 a^6 b^8 c^2 x z-4 a^4 b^10 c^2 x z-16 a^2 b^12 c^2 x z-4 a^8 b^4 c^4 x z+10 a^6 b^6 c^4 x z-2 a^4 b^8 c^4 x z-4 a^2 b^10 c^4 x z-26 a^6 b^4 c^6 x z+10 a^4 b^6 c^6 x z+16 a^2 b^8 c^6 x z-4 a^4 b^4 c^8 x z+4 a^2 b^6 c^8 x z-16 a^12 b^2 c^2 y z-4 a^10 b^4 c^2 y z+16 a^8 b^6 c^2 y z+4 a^6 b^8 c^2 y z-4 a^10 b^2 c^4 y z-2 a^8 b^4 c^4 y z+10 a^6 b^6 c^4 y z-4 a^4 b^8 c^4 y z+16 a^8 b^2 c^6 y z+10 a^6 b^4 c^6 y z-26 a^4 b^6 c^6 y z+4 a^6 b^2 c^8 y z-4 a^4 b^4 c^8 y z+4 a^12 b^4 z^2-8 a^8 b^8 z^2+4 a^4 b^12 z^2+4 a^12 b^2 c^2 z^2-4 a^8 b^6 c^2 z^2-4 a^6 b^8 c^2 z^2+4 a^2 b^12 c^2 z^2+4 a^10 b^2 c^4 z^2+a^8 b^4 c^4 z^2-10 a^6 b^6 c^4 z^2+a^4 b^8 c^4 z^2+4 a^2 b^10 c^4 z^2-4 a^8 b^2 c^6 z^2+4 a^6 b^4 c^6 z^2+4 a^4 b^6 c^6 z^2-4 a^2 b^8 c^6 z^2-4 a^6 b^2 c^8 z^2+8 a^4 b^4 c^8 z^2-4 a^2 b^6 c^8 z^2=0,
que pasa por X6, X23; su centro es el punto medio de X12039 y X14810:
W6 = (2 a^8-7 a^2 b^2 c^2 (b^2+c^2)-2 a^4 (b^4+b^2 c^2+c^4) : ... : ...),
que tiene números de búsqueda en
(5.30381475457525, 3.92023061585448, -1.52125583118037).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,32217}, {3,8705}, {6,7496}, {67,110}, {182,524}, {511,32154}, {599,11003}, {1350,35921}, {2076,30489}, {2854,5092}, {3431,5085}, {3589,22112}, {3631,5157}, {5012,22165}, {5467,14096}, {5650,6593}, {5651,19127}, {8542,17508}, {8550,13339}, {9019,12039}, {9027,20190}, {10354,28662}, {16187,19126}, {25488,29181}
Las asíntotas de co(X6) son W6X5004 y W6X5005.
El punto W ha sido incorporado a ETC con el número X(37283).
• Cuando P recorre la circunferencia circunscrita el centro Wp de co(P) es el punto medio de P y X3.
• Cuando P recorre la cúbica de McCay
(K003 del catálogo de Bernard Gibert), la cónica co(P) degenera en la recta doble que pasa por el circuncentro y contiene a P, P*, Q*, O'.
- Viernes, 13 de marzo del 2020
Una elipse con circunferencia secundaria el incírculo
El 13 de marzo de 1781
con un telescopio reflector de 152 milímetros construido por él mismo, el astrónomo inglés William Herschel observa por primera vez a Urano, séptimo planeta desde el Sol, y le da el nombre del padre del dios Saturno.
Su distancia media del Sol es de 19,19 unidades astronómicas, orbita el Sol cada 84,01 años y tiene un priodo de rotación de 17,24 horas. Su diámetro es de 51.118 kilómetros --cuatro veces el de la Tierra-- y tiene más de 20 satélites observados.
Dados un triángulo ABC, de incentro I=X1, y un punto P sobre su circunferencia circunscrita, sean D el punto de intersección de BC con la reflexión de AP en AI, E el punto de intersección de CA con la reflexión de BP en BI y F el punto de intersección de AB con la reflexión de CP en CI.
Los puntos D, E, F están alineados sobre una recta ℓP, Sea 𝓈P la
de P y Q = ℓP, ∩ 𝓈P.
El lugar geométrico de
Q, cuando
P varía sobre la circunferencia circunscrita, es la
elipse
( (-a^5+3 a^4 b-2 a^3 b^2-2 a^2 b^3+3 a b^4-b^5+3 a^4 c-12 a^3 b c+14 a^2 b^2 c-4 a b^3 c-b^4 c-2 a^3 c^2+14 a^2 b c^2-18 a b^2 c^2+6 b^3 c^2-2 a^2 c^3-4 a b c^3+6 b^2 c^3+3 a c^4-b c^4-c^5) x^2+(-2 a^5+6 a^4 b-4 a^3 b^2-4 a^2 b^3+6 a b^4-2 b^5+2 a^4 c-16 a^3 b c+28 a^2 b^2 c-16 a b^3 c+2 b^4 c+4 a^3 c^2-4 a^2 b c^2-4 a b^2 c^2+4 b^3 c^2-4 a^2 c^3+8 a b c^3-4 b^2 c^3-2 a c^4-2 b c^4+2 c^5) x y+(-a^5+3 a^4 b-2 a^3 b^2-2 a^2 b^3+3 a b^4-b^5-a^4 c-4 a^3 b c+14 a^2 b^2 c-12 a b^3 c+3 b^4 c+6 a^3 c^2-18 a^2 b c^2+14 a b^2 c^2-2 b^3 c^2+6 a^2 c^3-4 a b c^3-2 b^2 c^3-a c^4+3 b c^4-c^5) y^2+(-2 a^5+2 a^4 b+4 a^3 b^2-4 a^2 b^3-2 a b^4+2 b^5+6 a^4 c-16 a^3 b c-4 a^2 b^2 c+8 a b^3 c-2 b^4 c-4 a^3 c^2+28 a^2 b c^2-4 a b^2 c^2-4 b^3 c^2-4 a^2 c^3-16 a b c^3+4 b^2 c^3+6 a c^4+2 b c^4-2 c^5) x z+(2 a^5-2 a^4 b-4 a^3 b^2+4 a^2 b^3+2 a b^4-2 b^5-2 a^4 c+8 a^3 b c-4 a^2 b^2 c-16 a b^3 c+6 b^4 c-4 a^3 c^2-4 a^2 b c^2+28 a b^2 c^2-4 b^3 c^2+4 a^2 c^3-16 a b c^3-4 b^2 c^3+2 a c^4+6 b c^4-2 c^5) y z+(-a^5-a^4 b+6 a^3 b^2+6 a^2 b^3-a b^4-b^5+3 a^4 c-4 a^3 b c-18 a^2 b^2 c-4 a b^3 c+3 b^4 c-2 a^3 c^2+14 a^2 b c^2+14 a b^2 c^2-2 b^3 c^2-2 a^2 c^3-12 a b c^3-2 b^2 c^3+3 a c^4+3 b c^4-c^5) z^2 = 0)
que pasa por los centros X
2446, X
2447 (estos son los puntos de intersección del incírculo con la recta que pasa pòr el incentro y circuncentro), X
3259, X
3756, X
3937.
Ercole Suppa hace notar (comunicación personal) que el semieje mayor de la elipse es R-r, diferencia entre los radios de las circunferencia circunscrita e inscrita a ABC.
- Jueves, 12 de marzo del 2020
Circunferencia lugar de centros de semejanza
El 12 de marzo de 1919 nació Miguel Gila, humorista madrileño, al que se le recordará pegado al teléfono.
Dados un triángulo ABC y un punto P, sean y PaPbPc los triángulos
y de P, respectivamente.
Sean Qa, Qb, Qc los puntos que dividen a los segmentos PaPa, PbPb, PcPc, resp., en la misma razón t.
Las perpendiculares por Qa, Qb, Qc a BC, CA, AB, respectivamente, forman un triángulo A'B'C', directamente semejante a ABC.
Si (u:v:w) son las coordenadas baricéntris de P, el centro de semejanza es:
Sp = ((u+v)(u+w) (
(a^4+(b^2-c^2)^2-2a^2(b^2+c^2))u(u+v)(u+w)(v+w)^2t^2
+2(v+w)((b^2-c^2)u^2(v+w)(b^2(u+v)-c^2(u+w))+
a^4(u+v)(u+w)(2v w+u(v+w))-a^2u(v+w)(c^2(2u+3v)(u+w)+
b^2(u+v)(2u+3w)))t
-4a^2(u+v+w)(c^2u v(u+w)(v+w)-(u+v)w(a^2v(u+w)-b^2u(v+w)))) : ... : ...).
El lugar geométrico de Sp, cuando t varía, es la
circunferencia
( (a^2 c^2 u v^3-b^2 c^2 u v^3-c^4 u v^3+a^2 c^2 u v^2 w-b^2 c^2 u v^2 w-c^4 u v^2 w+a^2 c^2 v^3 w+b^2 c^2 v^3 w-c^4 v^3 w-a^2 b^2 u v w^2+b^4 u v w^2+b^2 c^2 u v w^2-a^2 b^2 v^2 w^2+b^4 v^2 w^2+a^2 c^2 v^2 w^2-c^4 v^2 w^2-a^2 b^2 u w^3+b^4 u w^3+b^2 c^2 u w^3-a^2 b^2 v w^3+b^4 v w^3-b^2 c^2 v w^3) x^2+(-2 a^2 c^2 u^2 v^2+2 b^2 c^2 u^2 v^2+a^2 c^2 u^2 v w+b^2 c^2 u^2 v w-c^4 u^2 v w-a^2 c^2 u v^2 w-b^2 c^2 u v^2 w+c^4 u v^2 w-a^4 u^2 w^2+a^2 b^2 u^2 w^2+2 a^2 c^2 u^2 w^2-b^2 c^2 u^2 w^2-c^4 u^2 w^2-a^4 u v w^2+b^4 u v w^2+a^2 c^2 u v w^2-b^2 c^2 u v w^2-a^2 b^2 v^2 w^2+b^4 v^2 w^2+a^2 c^2 v^2 w^2-2 b^2 c^2 v^2 w^2+c^4 v^2 w^2-a^4 u w^3+b^4 u w^3+2 a^2 c^2 u w^3-c^4 u w^3-a^4 v w^3+b^4 v w^3-2 b^2 c^2 v w^3+c^4 v w^3) x y+(a^2 c^2 u^3 v-b^2 c^2 u^3 v+c^4 u^3 v-a^2 c^2 u^3 w-b^2 c^2 u^3 w+c^4 u^3 w+a^2 c^2 u^2 v w-b^2 c^2 u^2 v w+c^4 u^2 v w-a^4 u^2 w^2+a^2 b^2 u^2 w^2-b^2 c^2 u^2 w^2+c^4 u^2 w^2-a^4 u v w^2+a^2 b^2 u v w^2-a^2 c^2 u v w^2-a^4 u w^3+a^2 b^2 u w^3+a^2 c^2 u w^3-a^4 v w^3+a^2 b^2 v w^3-a^2 c^2 v w^3) y^2+(a^4 u^2 v^2-2 a^2 b^2 u^2 v^2+b^4 u^2 v^2-a^2 c^2 u^2 v^2+b^2 c^2 u^2 v^2+a^4 u v^3-2 a^2 b^2 u v^3+b^4 u v^3-c^4 u v^3-a^2 b^2 u^2 v w+b^4 u^2 v w-b^2 c^2 u^2 v w+a^4 u v^2 w-a^2 b^2 u v^2 w+b^2 c^2 u v^2 w-c^4 u v^2 w+a^4 v^3 w-b^4 v^3 w+2 b^2 c^2 v^3 w-c^4 v^3 w+2 a^2 b^2 u^2 w^2-2 b^2 c^2 u^2 w^2+a^2 b^2 u v w^2-b^4 u v w^2+b^2 c^2 u v w^2-a^2 b^2 v^2 w^2-b^4 v^2 w^2+a^2 c^2 v^2 w^2+2 b^2 c^2 v^2 w^2-c^4 v^2 w^2) x z+(-a^4 u^3 v+2 a^2 b^2 u^3 v-b^4 u^3 v+c^4 u^3 v-a^4 u^2 v^2+2 a^2 b^2 u^2 v^2-b^4 u^2 v^2-a^2 c^2 u^2 v^2+b^2 c^2 u^2 v^2+a^4 u^3 w-b^4 u^3 w-2 a^2 c^2 u^3 w+c^4 u^3 w+a^2 b^2 u^2 v w-b^4 u^2 v w-a^2 c^2 u^2 v w+c^4 u^2 v w-a^4 u v^2 w+a^2 b^2 u v^2 w+a^2 c^2 u v^2 w+a^4 u^2 w^2+a^2 b^2 u^2 w^2-2 a^2 c^2 u^2 w^2-b^2 c^2 u^2 w^2+c^4 u^2 w^2+a^4 u v w^2-a^2 b^2 u v w^2-a^2 c^2 u v w^2-2 a^2 b^2 v^2 w^2+2 a^2 c^2 v^2 w^2) y z+(a^2 b^2 u^3 v-b^4 u^3 v+b^2 c^2 u^3 v+a^4 u^2 v^2-b^4 u^2 v^2-a^2 c^2 u^2 v^2+b^2 c^2 u^2 v^2+a^4 u v^3-a^2 b^2 u v^3-a^2 c^2 u v^3-a^2 b^2 u^3 w-b^4 u^3 w+b^2 c^2 u^3 w-a^2 b^2 u^2 v w-b^4 u^2 v w+b^2 c^2 u^2 v w+a^4 u v^2 w+a^2 b^2 u v^2 w-a^2 c^2 u v^2 w+a^4 v^3 w+a^2 b^2 v^3 w-a^2 c^2 v^3 w) z^2 = 0)
Γp, que pasa por P,
de ecuación:
(v+w)(b^4(u+v)w^2-c^4v^2(u+w)+a^2(-b^2(u+v)w^2+c^2v^2(u+w))+b^2c^2(v-w)(v w-u(v+w)))x^2
-(a^4u(u+v)(v-w)(u+w)-a^2(-c^2(u+w)(2u^2w-2v^2w+u v(v+w))+
b^2(2u^3v+u v w(v-w)-2v^2w^2+u^2(2v^2+v w+w^2)))
+(b^2-c^2)u^2(v+w)(b^2(u+v)+c^2(u+w))y z + ⋯ = 0,
y su centro es:
W = (u (a^2 (u + v) (v - w) (u + w) - u (v + w) (b^2 (u + v) - c^2 (u + w))) : ⋯ : ⋯).
Ternas {P=Xi, W=Xj, Z=Xk}, siendo W el de P y Z, para {i, j , k}:
{1, 2605, 14838}, {30, *, 14566}, {67, *, 18310}, {80, *, 21198}, {265, *, 14566}, {315, *, 30476}, {512, *, 11052}, {514, *, 24980}, {523, *, 24975}, {858, *, 18310}, {1670, *, 647}, {1671, *, 647}, {2394, *, 22104}, {2996, *, 14341}, {3869, *, 14838}, {5176, *, 21198}, {17732, *, 3239}.
El antipodal de P en la circunferncia Γp es:
P' = (u (u + v) (u + w) (a^2 (v - w) - (b^2 - c^2) (v + w)) : ⋯ : ⋯).
Pares {P=Xi, P'=Xj}, para {i,j}: {1, 3737}, {3, 23286}, {10, 31010}, {877, 23582}, {2394, 5627}, {4240, 32230}, {15328, 12028}.
CASOS PARTICULARES
• Si P=X1 es el incentro, la circunferencia
Γ1
( a b^4 c^2 x^2-b^5 c^2 x^2-b^4 c^3 x^2-a b^2 c^4 x^2+b^3 c^4 x^2+b^2 c^5 x^2+a^5 c^2 x y+a^3 b^2 c^2 x y-a^2 b^3 c^2 x y-b^5 c^2 x y-2 a^3 c^4 x y+a^2 b c^4 x y-a b^2 c^4 x y+2 b^3 c^4 x y+a c^6 x y-b c^6 x y+a^5 c^2 y^2-a^4 b c^2 y^2+a^4 c^3 y^2-a^3 c^4 y^2+a^2 b c^4 y^2-a^2 c^5 y^2-a^5 b^2 x z+2 a^3 b^4 x z-a b^6 x z-a^2 b^4 c x z+b^6 c x z-a^3 b^2 c^2 x z+a b^4 c^2 x z+a^2 b^2 c^3 x z-2 b^4 c^3 x z+b^2 c^5 x z+a^6 b y z-2 a^4 b^3 y z+a^2 b^5 y z-a^6 c y z+a^4 b^2 c y z-a^4 b c^2 y z+a^2 b^3 c^2 y z+2 a^4 c^3 y z-a^2 b^2 c^3 y z-a^2 c^5 y z-a^5 b^2 z^2-a^4 b^3 z^2+a^3 b^4 z^2+a^2 b^5 z^2+a^4 b^2 c z^2-a^2 b^4 c z^2 = 0)
pasa por los centros X1, X36, X501, X3737, X5127.
• Si P=X2 es el baricentro, el lugar geométrico de los centros de semejanza S2 constan de la y la .
• Si P=X3 es el circuncentro, la circunferencia
Γ3
( c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-(((a^8 b^4 c^2-3 a^6 b^6 c^2+3 a^4 b^8 c^2-a^2 b^10 c^2+a^8 b^2 c^4-2 a^6 b^4 c^4+a^4 b^6 c^4-3 a^6 b^2 c^6+a^4 b^4 c^6+2 a^2 b^6 c^6+3 a^4 b^2 c^8-a^2 b^2 c^10) x)/((a^2-b^2) (a^2-c^2) (a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)^2))+((-a^10 b^2 c^2+3 a^8 b^4 c^2-3 a^6 b^6 c^2+a^4 b^8 c^2+a^6 b^4 c^4-2 a^4 b^6 c^4+a^2 b^8 c^4+2 a^6 b^2 c^6+a^4 b^4 c^6-3 a^2 b^6 c^6+3 a^2 b^4 c^8-a^2 b^2 c^10) y)/((-a^2+b^2) (-b^2+c^2) (a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)^2)+((-a^10 b^2 c^2+2 a^6 b^6 c^2-a^2 b^10 c^2+3 a^8 b^2 c^4+a^6 b^4 c^4+a^4 b^6 c^4+3 a^2 b^8 c^4-3 a^6 b^2 c^6-2 a^4 b^4 c^6-3 a^2 b^6 c^6+a^4 b^2 c^8+a^2 b^4 c^8) z)/((b^2-c^2) (-a^2+c^2) (a^4-2 a^2 b^2+b^4-2 a^2 c^2-2 b^2 c^2+c^4)^2)) = 0)
pasa por los centros X3, X186, X1157, X6760, X23286. Su centro es el punto medio de X3 y X23286:
W3 = ( a^4 (b^2-c^2) (-a^2+b^2+c^2)^2 (a^4+b^4-b^2 c^2+c^4-2 a^2 (b^2+c^2)) : ... : ...),
que tiene números de búsqueda en
(4.60780876953818, 4.79924127781350, -1.80856814251951).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,6368}, {418,34987}, {520,4091}, {523,15646}, {924,14270}, {1510,6150}, {14380,16665}, {15451,30210}, {22347,23226}.
• Si P=X4 es el ortocentro, los triángulos y PaPbPc coinciden.
• Si P=X6 es el , la circunferencia
Γ6
( a^4 b^6 c^2 x^2-a^2 b^8 c^2 x^2-a^2 b^6 c^4 x^2+2 b^8 c^4 x^2-a^4 b^2 c^6 x^2+a^2 b^4 c^6 x^2+a^2 b^2 c^8 x^2-2 b^4 c^8 x^2-2 a^6 b^4 c^2 x y+2 a^4 b^6 c^2 x y-a^8 c^4 x y+a^6 b^2 c^4 x y-a^2 b^6 c^4 x y+b^8 c^4 x y+a^6 c^6 x y-2 a^4 b^2 c^6 x y+2 a^2 b^4 c^6 x y-b^6 c^6 x y+a^4 c^8 x y-b^4 c^8 x y-a^2 c^10 x y+b^2 c^10 x y+a^8 b^2 c^2 y^2-a^6 b^4 c^2 y^2-2 a^8 c^4 y^2+a^6 b^2 c^4 y^2-a^4 b^2 c^6 y^2+a^2 b^4 c^6 y^2+2 a^4 c^8 y^2-a^2 b^2 c^8 y^2+a^8 b^4 x z-a^6 b^6 x z-a^4 b^8 x z+a^2 b^10 x z-a^6 b^4 c^2 x z+2 a^4 b^6 c^2 x z-b^10 c^2 x z+2 a^6 b^2 c^4 x z-2 a^2 b^6 c^4 x z+b^8 c^4 x z-2 a^4 b^2 c^6 x z+a^2 b^4 c^6 x z+b^6 c^6 x z-b^4 c^8 x z-a^10 b^2 y z+a^8 b^4 y z+a^6 b^6 y z-a^4 b^8 y z+a^10 c^2 y z-2 a^6 b^4 c^2 y z+a^4 b^6 c^2 y z-a^8 c^4 y z+2 a^6 b^2 c^4 y z-2 a^2 b^6 c^4 y z-a^6 c^6 y z-a^4 b^2 c^6 y z+2 a^2 b^4 c^6 y z+a^4 c^8 y z+2 a^8 b^4 z^2-2 a^4 b^8 z^2-a^8 b^2 c^2 z^2-a^6 b^4 c^2 z^2+a^4 b^6 c^2 z^2+a^2 b^8 c^2 z^2+a^6 b^2 c^4 z^2-a^2 b^6 c^4 z^2 = 0)
pasa por los centros X6, X1691, X14885, X34137. Su centro es:
W6 = ( a^4 (b^6 - c^6 + a^4 (-b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(-0.992229815301442, 3.12950807690636, 1.93203418957295).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {6,826}, {512,1692}, {525,13196}, {690,22159}, {2451,7950}, {3050,7927}, {8574,15451}, {9427,24973}.
El antipodal de X6 en Γ6 es la reflexión de X22159 en X3049:
P'6 = ( a^2 (a^2 + b^2) (a^2 + c^2) (b^2 - c^2) ) (a^2 - b^2 - c^2) : ... : ...),
que tiene números de búsqueda en ETC
(-2.97736812566855, 4.76965341121422, 1.71276663983694).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {6,826}, {83,2422}, {251,2433}, {419,2501}, {512,1691}, {525,3049}, {647,8673}, {733,2698}, {810,22061}, {827,1625}, {878,10547}, {1176,10097}, {2623,3569}, {3566,22105}, {4630,35325}, {7254,34055}, {9217,9431}, {10548,15412}.
- Miércoles, 11 de marzo del 2020
Otra construcción del punto de Longuet-Higgins
El 11 de marzo de 2004, entre las 07:36 y las 07:40 se produjeron diez explosiones casi simultáneas en cuatro trenes de Madrid. Los atentados fueron provocados por una célula terrorista de tipo yihadista, tal como reveló la posterior investigación policial, sentenció la Audiencia Nacional y reiteró el Tribunal Supremo. Fallecieron 193 personas y alrededor de dos mil resultaron heridas. Una comunicación manipulada por parte del Gobierno del PP provocará un cambio radical en intención de voto, otorgando el triunfo al PSOE tres días después. (Quien siembra vientos recoge tempestades)
X(962) = LONGUET-HIGGINS POINT
X(962) is shown in Michael S. Longuet-Higgins, "On the principal centers of a triangle," Elemente der Mathematik 56 (2001) 122-129,
Notations:
O is the circumcenter, I is the incenter, M is the centroid, H is the orthocente, L is the Longchamps point, N is the Nagel point, J (=X(40)) is the
Yff point or countercenter (meet of the perpendiculars from the three excenters IA , IB , IC to the corresponding sides of ABC), I' is the Spieker point (incenter of the median triangle ), J' is the countercenter of median triangle.
Longuet-Higgins.png)
X(962) is the radical center of the circles centered at A, B, C, with respective
radii |CA| + |AB|, |AB| + |BC|, |BC| + |CA|. See
Floor van Lamoen, Problem 10734, American Mathematical Monthly 107 (2000) 658-659.

X(40) = BEVAN POINT
Hyacinthos #6771
Date : Thu Mar 20, 2003 3 : 32 am
Subject : excentral triangle
Dear hyacintos
Is the circumcenter of excentral triangle a well know point?
If so, which is it?
Michel
-----------------------------------------------------------------------------------
Hyacinthos #6772
Date : Thu Mar 20, 2003 6 : 16 am
Subject : Re : excentral triangle
Dear Michel,
The circumcenter of the excentral triangle is the reflection of the
incenter in the circumcenter, the point X(40) in ETC.
Best regards
Sincerely
Paul
------------------------------------------------------------------------------------------
Hyacinthos #6773
Date : Thu Mar 20, 2003 9 : 26 am
Subject : Bevan point X(40) (was : [EMHL] Re : excentral triangle)
Dear Michel,
Now you have provoked me to expound the theory of one of my favorite
points, the Bevan point X(40).
I call X(40) the BEVAN POINT of triangle ABC;
former names were Yff
center, countercenter and Hadamard point.
Let IaIbIc be the excentral triangle of ABC.
-- X(40) is defined as the circumcenter of the excentral triangle
IaIbIc.
-- X(40) is the reflection of the incenter of ABC in the circumcenter
of ABC.
-- The perpendiculars from Ia to BC, from Ib to CA, from Ic to AB
concur at X(40).
-- X(40) is the incenter of the extangents triangle of ABC.
-- X(40) is the midpoint between the Nagel point X (8) and the
Longchamps point X (20).
-- X(40) is the reflection of the orthocenter X (4) in the Spieker
point X (10).
-- Let the b - excircle touch BC at Ab and the c - excircle touch BC at
Ac. The circle with diameter AbAc, and two other similarly defined
circles, have radical center X(40).
-- The actual trilinears of X(40) are
[ 2 R - ra, 2 R - rb, 2 R - rc ].
-- The homogeneous trilinears of X(40) are
( cos B + cos C - cos A - 1 : cos C + cos A - cos B - 1 : cos A + cos B - cos C - 1 ).
-- The perpendiculars from Ib to AB and from Ic to CA meet at a point
X. Analogously define points Y and Z. Then the lines AX, BY and CZ
concur at the point X (84), which I call HEXYL POINT of triangle ABC.
This Hexyl point X (84) is the isogonal conjugate of the Bevan point X
(40).
Sincerely,
Darij Grinberg
-----------------------------------------------------------------------------------------------
Constructions received from Randy Hutson, January 29, 2015 :VConstructions received from Randy Hutson, January 29, 2015:
(1) Let A' B' C' be the extangents triangle.Let A " be the reflection of A' in BC, and define B", C " cyclically. A'A", B' B ", C'C" concur in X(40).
(2) Let A' B' C' be the extangents triangle.Let A " be the cevapoint of B' and C', and define B", C " cyclically. The lines AA", BB ", CC" concur in X(40).
(3) Let A' B' C' be the hexyl triangle and A "B" C " be the side-triangle of ABC and hexyl triangle. Let A* be the {B,C}-harmonic conjugate of A", and define B*, C*cyclically.The lines A' A*, B' B*, C' C*concur in X(40).
(4) Let Ia be the reflection of X (1) in the perpendicular bisector of BC, and define Ib, Ic cyclically.X(40) = X (104) - of - IaIbIc.
(5) Let A' B' C' be the cevian triangle of X (189).Let A " be the orthocenter of AB'C', and define B", C " cyclically. The lines AA", BB ", CC" concur in X(40).
(6) Let A' B' C' be the mixtilinear incentral triangle.Let A " be the trilinear product B'*C', and define B", C " cyclically. The lines AA", BB ", CC" concur in X(40).
Let A' B' C' be the intouch triangle of the extangents triangle, if ABC is acute.Then A' B' C' is homothetic to the Aquila triangle at X(40).(Randy Hutson, December 2, 2017)
Let A' B' C' be the excentral triangle.Let A " be the isogonal conjugate, wrt A'BC, of A. Define B" and C " cyclically. (A" is also the reflection of A' in BC, and cyclically for B " and C").The lines A' A ", B'B", C' C " concur in X(40). (Randy Hutson, December 2, 2017)
Dado un triángulo ABC, de incentro I =X1 y circuncentro H=X4, la perpendicular a la bisectriz BI en i corta a AH en Ab y la perpendicular a la bisectriz CI en I corta a AH en Ac.
Sea ℓa la recta que pasa por los puntos donde la circunferencia Γa=() –tangente a AI– vuelve a cortar a BI y CI. Se definen cíclicamente la rectas ℓb y ℓc.
Las rectas ℓa, ℓb, ℓc concurren en X962, reflexión del punto de De Longschamps en el incentro.
En coordenadas baricéntricas:
Ab = (a (a^2 + 2 a (b - c) + b^2 - c^2) : c (a^2 + b^2 - c^2) : c (a^2 -
b^2 + c^2)),
Ac = (a (a^2 - 2 a b - b^2 + 2 a c + c^2) : b (a^2 + b^2 - c^2), b (a^2-
b^2+ c^2)).
La
circunferencia
( c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-((((c (a^2-b^2+c^2) (a^2 b c+a b^2 c+a b c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))+c (a+b+c) (a c^3 (a^2+b^2-c^2) (a^2+b^2+2 a (b-c)-c^2)+a^2 c^2 (a^2+b^2-c^2) (a^2-b^2+c^2)+a b^2 c (a^2+b^2+2 a (b-c)-c^2) (a^2-b^2+c^2))) (-b^2 (a+b+c) (-a^2+b^2-c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2))-b c (a+b+c) (a^2+b^2-c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2)))-(-c^2 (a+b+c) (a^2+b^2-c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))+b c (a+b+c) (a^2-b^2+c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))) (-b (-a^2+b^2-c^2) (a^2 b c+a b^2 c+a b c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2))+c (a+b+c) (-a^2 b^2 (-a^2+b^2-c^2) (a^2+b^2-c^2)-a b^3 (-a^2+b^2-c^2) (a^2-2 a b-b^2+2 a c+c^2)+a b c^2 (a^2+b^2-c^2) (a^2-2 a b-b^2+2 a c+c^2)))) x)/((-a c (a+b+c) (a^2+b^2+2 a (b-c)-c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))+a c (a+b+c) (a^2-b^2+c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))) (-b^2 (a+b+c) (-a^2+b^2-c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2))-b c (a+b+c) (a^2+b^2-c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2)))-(-c^2 (a+b+c) (a^2+b^2-c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))+b c (a+b+c) (a^2-b^2+c^2) (-c (a^2+b^2-c^2)-a (a^2+b^2+2 a (b-c)-c^2)-c (a^2-b^2+c^2))) (-a b (a+b+c) (-a^2+b^2-c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2))-a c (a+b+c) (a^2-2 a b-b^2+2 a c+c^2) (b (-a^2+b^2-c^2)-b (a^2+b^2-c^2)-a (a^2-2 a b-b^2+2 a c+c^2)))))-((a^2 c-2 a b c-b^2 c+2 a c^2+c^3) y)/(a+b+c)-((a^2 b+2 a b^2+b^3-2 a b c-b c^2) z)/(a+b+c)) = 0)
(), cuyo centro es
Oa =(a^3 - 2 a (b - c)^2 - (b - c)^2 (b + c) : b (a^2 + a (b - c) +
2 (b - c) c) : c (a^2 + a (-b + c) + 2 b (-b + c))),
vuelve a cortar a BI y CI en los puntos antipodales de Ab y Ac. La ecuación de la recta ℓa que pasa por ellos –paralela a AH– es:
2 a (-b + c) x + (a^2 - 2 a b - b^2 + 2 a c + c^2) y + (-a^2 - 2 a b -
b^2 + 2 a c + c^2) z = 0.
Esta recta y las que se obienen cíclicamnete, ℓb y ℓc, concurren en:
X962 = (a^4 + 2 a^3 (b + c) - 4 a^2 b c - 2 a (b - c)^2 (b + c) - (b^2 - c^2)^2 : ... : ...).
El triángulo
Las circunferencias Γa, Γb y Γc se cortan dos a dos, a parte de en I, en las reflexiones Ia, Ib, Ic de I en los lados de . Como I está en la circunferencia circunscrita a (que también pasa por X7982, del ), los puntos Ia, Ib, Ic están sobre una recta, que pasa por su ortocentro (que coincide con el ortocentro de ABC).
Reflections in Triangle Geometry
Antreas P. Hatzipolakis and Paul Yiu
On the 10th Anniversary of Hyacinthos
Forum GeometricorumVolume 9 (2009) 301‐348.

Los triángulos ABC y son
El centro ortológico de ABC respecto a es X80, reflexión del incentro en el .
El centro ortológico de respecto a ABC es X12699, punto de Bevan del .
- Sábado, 7 de marzo del 2020
Triángulos asociado a triangulos circuncevianos
El 7 de marzo de 1966, en la costa de Almería (España), el ministro de Información y Turismo, Manuel Fraga, acompañado del embajador de Estados Unidos se bañan supuestamente en la playa de Palomares para hacer creer que no existe riesgo de contaminación radioactiva, ante el temor popular a la radiactividad de una bomba H estadounidense perdida en el mar tras un accidente aéreo. Años después se descubriría que la playa donde se bañó Manuel Fraga no era la de Palomares.
Dados un triángulo ABC y un punto P, sea DEF el de P.
La cónica 𝒞a que pasa por A y que, respecto a ella, DF y DE son las polares de B y C, respectivamente, vuelve a corta a AC y a AB en Ab y Ac, respectivamente.
Los puntos Bc, Ba, Ca, Cb se definen cíclicamente.
Sean los puntos A'=AcBa∩AbCa, B'=AbCa∩CbBc, C'=CbBc∩AcBa.
Las rectas AA', BB' y CC' son concurrentes en un punto Q, las rectas DA', EB' y FC' son concurrentes en un punto Z y los puntos P, Q y Z están alineados.
En concecuencia, los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están en una cónica: de ABC y A'B'C'.
Si (u:v:w) son las coordenadas baricéntricas de P, la ecuación de 𝒞a es:
b^2 u w^2 (c^2 u + a^2 w)y^2 +
c^2 u v^2 (b^2 u + a^2 v)z^2 -2 v (b^2 u + a^2 v) w (c^2 u +
a^2 w)y z -2 v (b^2 u + a^2 v) w (c^2 v + b^2 w)z x -2 v w (c^2 u +
a^2 w) (c^2 v + b^2 w)x y = 0.
Y vuelve a corta a AC y a AB, respectivamente, en:
Ab = (c^2 u v : 0 : 2 w (c^2 v + b^2 w)),
Ac = (b^2 u w : 2 v (c^2 v + b^2 w) : 0).
A'=AcBa∩AbCa =
(-v w (4 a^2 v (c^2 u + a^2 w) +
b^2 u (3 c^2 u + 4 a^2 w)) : 2 v (c^2 v + b^2 w) (c^2 u v +
2 (b^2 u + a^2 v) w) : 2 w (c^2 v + b^2 w) (2 c^2 u v + b^2 u w +
2 a^2 v w)).
Q=(u/(a^2 v w + 2 u (b^2 w + c^2 v)):...:...),
Z=(4 v^2 w^2a^6 -u^2 (4 c^4 v^2 + 9 b^2 c^2 v w +
4 b^4 w^2)a^2 -6 b^2 c^2 u^3 (c^2 v + b^2 w) : ... : ...).
Como los centros de perspectividad P, Q, Z de las pares de triángulos {ABC, DEF}, {ABC, A'B'C'}, {DEF, A'B'C'} están alineados, los tres ejes de perspectividad coinciden (Theorem 19. The Geometry of Homological Triangles (Florentin Smarandache and Ion Pătraşcu)) en la del de P y el simediano.
El la lista siguiente las ternas {i, j, k} indican que P=Xi, Q=Xj y T= Xk, siendo Q el de P y el de T.
{1, 25417, 1698}, {2, *, 3763}, {3, *, 631}, {4, *, 1656}, {6, 6, 2}, {7, *, 31245}, {8, *, 31246}, {9, *, 20196}, {19, *, 31266}, {21, *, 25917}, {22, *, 31267}, {25, *, 3618}, {28, *, 5439}, {31, *, 4687}, {32, *, 7786}, {37, *, 31247}, {39, *, 31268}, {41, *, 31269}, {42, *, 31248}, {43, *, 31270}, {44, *, 31271}, {54, *, 632}, {55, *, 18230}, {56, *, 3616}, {57, *, 20195}, {58, *, 19862}, {59, *,
31235}, {60, *, 31260}, {63, *, 31261}, {64, *, 3091}, {65, *, 31254}, {66, *, 31236}, {67, *, 30745}, {68, *, 31282}, {69, *, 31255}, {70, *, 31283}, {71, *, 31256}, {72, *, 31257}, {73, *, 31258}, {75, *, 31237}, {76, *, 7867}, {79, *, 31262}, {80, *, 31263}, {81, *, 31238}, {82, *, 31264}, {83, *, 31239}, {84, *, 8227}, {85, *, 31240}, {86, *, 31241}, {87, *, 31242}, {88, *, 31243}, {89, *, 31244}, {92, *, 31265},
{98, 34536, *}, {99, 34537, *}, {100, 1016, *}, {101, 1252, *}, {105, 6185, *}, {106, 2226, *}, {107, 34538, *}, {108, 23984, *}, {109, 262, *}, {110, 249, *}, {111, 10630, *}, {112, 23964, *} ,
{190, *, 30835}, {223, *, 20198}, {249, *, 31274}, {269, *, 31249}, {282, *, 20197}, {291, *, 31252}, {292, *, 17266}, {512, *, 14061}, {513, *, 31272}, {514, *, 31273}, {523, *, 15059}, {648, *, 31277}, {649, *, 27191}, {651, *, 31250}, {660, *, 30795}, {661, *, 31278}, {662, *, 24924}, {663, *, 31640}, {667, *, 27195}, {668, *, 4162}, {669, *, 31639}, {670, *, 31279}, {671, *, 31275},
{691, *, 34539},
{692, *, 31209}, {694, *, 7925}, {695, *, 7948}, {893, *, 17326}, {897, *, 31280}, {945, *, 5818}, {1073, *, 20200}, {1126, *, 31253}, {1249, *, 20199}, {1476, *, 3698}, {1743, *, 4052}, {2162, *, 4699}, {2218, *, 3876}, {2980, *, 11451}, {3224, *, 31276}, {3426, *, 5071}, {3431, *, 15694}, {3445, *, 3617}, {3532, *, 3522}, {5237, *, 33386}, {5238, *, 33387}, {8770, *, 3620}, {9292, *, 7851}, {9315, *, 17304}, {11270, *, 3}, {11738, *, 19709}, {11816, *, 15026}, {13452, *, 3843}, {14810, *, 9751}, {16835, *, 5}, {17962, *, 29590}, {20421, *, 15693}, {22261, *, 11444}, {29374, *, 15017},
{33895, 33895, *},
{34435, *, 15674}, {34449, *, 3567},
{35258, 35258, *}, {35372, *, 15081}, {36614, *, 4704},
Aunque, geométricamente, el punto Q no está definido cuando P está sobre la circunferencia circunscrita (su triángulo circunceviano no está definido), por continuidad sí está definido, a partir de su expresión algebraica (son los pares en "bold" de la lista anterior).
TRES CASOS PARTICULARES:
• , P el baricentro.
Q es el conjugado isotómico de X3763.
Q2 = ( 1/(a^2 + 2 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en
(2.30533510949353, 1.67774557866739, 1.41514749229456).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,5007}, {3,14492}, {4,5092}, {5,14458}, {6,10159}, {10,17352}, {13,11290}, {14,11289}, {76,3589}, {83,7784}, {98,1656}, {140,262}, {275,11331}, {315,18841}, {316,5395}, {321,17367}, {550,14488}, {598,6656}, {620,1916}, {671,7770}, {1327,7388}, {1328,7389}, {2996,7803}, {3329,7869}, {3399,25555}, {3407,7808}, {3424,5056}, {3523,14484}, {3533,14494}, {3618,7894}, {3851,7919}, {3972,33021}, {4045,14034}, {5485,7827}, {5503,32954}, {6539,16816}, {6704,7755}, {7375,14241}, {7376,14226}, {7757,16895}, {7760,10302}, {7772,16896}, {7782,14037}, {7822,13571}, {7834,11606}, {7847,14031}, {7870,19694}, {7876,11057}, {7877,34573}, {7913,14045}, {7914,7926}, {7930,11174}, {7936,16897}, {8370,17503}, {10484,16923}, {11172,32975}, {11303,12817}, {11304,12816}, {14762,33010}, {14789,18316}, {14971,16921}, {17381,17758}, {18842,32956}, {21156,33423}, {21157,33422}, {30435,31268}, {31455,35005}.
• Triángulo antipodal de ABC, P el circuncentro.
Q=X(2)X(53)∩X(3)X(51) es el producto baricéntrico del circuncentro y el conjugado isotómico de X631.
Q3 = ( (a^2) (a^2 - b^2 - c^2) /(3 a^4 + (b^2 - c^2)^2 - 4 a^2 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(1.48276440225193, 1.08112266475115, 2.20784214373269).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,53}, {3,51}, {5,22270}, {6,97}, {20,11282}, {22,5481}, {216,394}, {276,2052}, {343,3926}, {418,3066}, {631,1217}, {1214,3306}, {1297,7485}, {1656,22268}, {1995,26909}, {2351,19357}, {3346,3523}, {3526,14938}, {3796,6641}, {5013,11433}, {5020,26907}, {5407,26922}, {5422,36748}, {5943,26865}, {6720,34579}, {7516,34225}, {7542,32132}, {14489,16419}, {14919,17811}, {15421,35361}, {15693,18317}, {17810,26874}, {17825,31626}, {26898,35259}.
• , P el ortocentro.
Q es el producto baricéntrico del ortocentro y el conjugado isotómico de X1656 (centro de homotecia del triángulo antipodal de ABC y el triángulo medial).
Q4 = ( (2 a^4 + 2 b^4 - 3 b^2 c^2 + c^4 -
a^2 (4 b^2 + 3 c^2)) (2 a^8 - (b^2 - 2 c^2) (b^2 - c^2)^3 -
a^6 (3 b^2 + 4 c^2) + a^2 (b^2 - c^2)^2 (3 b^2 + 4 c^2) +
a^4 (-b^4 + b^2 c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(4.73934200803839, 7.07284362059621, -3.44330818221533).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,10985}, {4,11423}, {17,472}, {18,473}, {25,7608}, {30,13599}, {98,5064}, {262,428}, {264,11140}, {427,7607}, {458,10159}, {470,10187}, {471,10188}, {1585,10194}, {1586,10195}, {2052,6748}, {3087,8796}, {3543,31363}, {5094,10185}, {7714,14494}, {9221,18559}.
- Miércoles, 4 de marzo del 2020
Haz elíptico de circunferencias
El 4 de marzo de 1678 nació Antonio Vivaldi, compositor barroco y violinista italiano, famoso por "Las Cuatro Estaciones". Su maestría se refleja en haber cimentado el género del concierto. "Apri le luci, e mira"
Un tipo de haces de circunferencias es el formado por las de un segmento. Las circunferencias no tienen puntos comunes y al haz se dice que es "elíptico".
Polars and poles w.r. to members of a pencil (Paris Pamfilos)
Considering the poles of a fixed line ε w.r. to the circle-members {κ} of a pencil we find them defining certain hyperbolas and in some cases parabolas and degenerate conics.
Theorem 6.
The poles of a fixed line w.r. to the circle-members of a pencil lie on a conic, which is a hyperbola or parabola or a degenerate conic.
Dado un triángulo ABC, sean ℓ una recta que pasa por A y 𝒜k el haz de circunferencias de Apolonio del segmento BC. El lugar geométrico de los de ℓ respecto a las circunferencias del haz 𝒜k es un cónica 𝒞ℓ.
La cónica 𝒞ℓ pasa por cuatro puntos, a saber, B, C, A' (antipodal de A en la circunferencia circunscrita) y el punto del infinito Ai de la dirección perpendicular a la de la recta BC; por consiguiente, cuando ℓ gira alrededor de A, las cónicas 𝒞ℓ forman un haz de cónicas. Si M es el otro punto en el que la recta ℓ corta a la circunferencia circunscrita, su antipodal M' también está en la cónica. Por tanto, dado la recta ℓ, la cónica 𝒞ℓ puede ser construida, ver (IPPPP) o bien (5P10T), §2.2.
El lugar geométrico de los centros de las cónicas 𝒞ℓ es una cónica 𝒫a, y como el haz de cónicas posee una parábola (pasa por B, C, A' y su eje es perpendicular a BC; es la cónica del haz que corresponde a la recta paralala a BC por A) y tres cónicas degeneradas, que son los tres pares de rectas {BA', CAi}, {CA', BAi}, {BC', A'Ai}, 𝒫a contiene a los tres puntos de intersección de estos tres pares de rectas (puntos diagonales del BCA'Ai) y Ai es su único punto en el infinito. Así,
𝒫a es una parábola. El foco Fa puede ser determinado construyendo las tangentes en dos de sus puntos y trazando sus reflexiones en las paralelas en sus puntos de contacto a la dirección del eje. Conocido el foco y una tangente se puede obtener la directriz da.
Descripción analítica en coordenadas baricéntricas:
La ecuación de una recta ℓ por A se puede poner en la forma ty-z=0; una circunferencia de Apolonio del segmento BC:
𝒜ℓ: a^2y z + b^2z x +c^2x y - (x+y+z)((-c^2+b^2k^2)x/(k^2-1)) +
a^2k^2y/(k^2-1) - a^2z/(k^2-1)) = 0.
El polo de ℓ respecto a 𝒜ℓ es:
L = (2a^2k^2(a^2(-1+t)+(b^2-c^2)(1+t)) :
2a^2(c^2+b^2(1-2k^2))t-a^4(-k^2+t)-(b^2-c^2)^2(k^2+t) :
k^2(-2a^2(b^2k^2+c^2(-2+k^2))+a^4(k^2-t)+(b^2-c^2)^2(k^2+t))).
El lugar geométrico de este punto, cuando k varía, es la cónica:
𝒞ℓ: (2b^2x+a^2y+b^2y-c^2y)(a^2x-b^2x+c^2x+2a^2z)t -
(a^2x+b^2x-c^2x+2a^2y)(2c^2x+a^2z-b^2z+c^2z) = 0.
La intersección de de cada recta cuya ecuación forma parte del coeficiente de t con cada recta que aparece en el término independendiente, dan los cuatro puntos base de este haz de cónicas. estos son:
B=(0:1:0), C=(0:0:1),
A'=(a^4-(b^2-c^2)^2 : 2b^2(-a^2+b^2-c^2) :
2c^2(-a^2-b^2+ c^2)) (antipodal de A),
Ai=(-2a^2 : a^2+b^2-c^2 : a^2-b^2+c^2) (punto en el infinito de la dirección perpendicular a la de la recta BC).
La expresión de las coordenadas del centro de la cónica 𝒞ℓ es:
Lo = (-2 a^2 (-1 + t) (a^2 (-1 + t) + (b^2 - c^2) (1 + t)) :
a^4 (1 - 3 t) - (b^2 - c^2)^2 (1 + t) + 4 a^2 t (c^2 + b^2 t) :
a^4 (-3 + t) t - (b^2 - c^2)^2 t (1 + t) + 4 a^2 (c^2 + b^2 t)).
Y su ecuación implícita:
𝒫a: (a^4 - 2 a^2 b^2 - 3 b^4 - 2 a^2 c^2 + 6 b^2 c^2 - 3 c^4) x^2
+ (-2 a^4 - 2 a^2 b^2 + 2 a^2 c^2) y^2
4 a^4 y z + (-2 a^4 + 2 a^2 b^2 - 2 a^2 c^2) z^2
+ (a^4 - 8 a^2 b^2 - b^4 + 4 a^2 c^2 + 2 b^2 c^2 - c^4) x y
+ (a^4 + 4 a^2 b^2 - b^4 - 8 a^2 c^2 + 2 b^2 c^2 - c^4) x z = 0.
Se trata de una parábola de foco:
Fa = (-2 a^2 (a^4 + 5 (b^2 - c^2)^2 - 2 a^2 (b^2 + c^2)) :
9 a^6 + (b^2 - c^2)^3 - 3 a^4 (7 b^2 + 5 c^2) +
a^2 (19 b^4 - 26 b^2 c^2 + 7 c^4) :
9 a^6 - (b^2 - c^2)^3 - 3 a^4 (5 b^2 + 7 c^2) +
a^2 (7 b^4 - 26 b^2 c^2 + 19 c^4)),
y directriz:
da: (7 a^4 + 11 (b^2 - c^2)^2 - 14 a^2 (b^2 + c^2)) x + (-a^4 +
3 (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)) y + (-a^4 +
3 (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2)) z = 0.
Procediendo cíclicamente, se obtienen las parábolas 𝒫b y 𝒫c, sus focos Fb y Fc y sus directrices db y dc.
Los ejes de las parábolas 𝒫a, 𝒫b, 𝒫c concurren en X550, punto medio del circuncentro y el .
El centro de homotecia de ABC y el triángulo formado por las directrices da, db y dc de las parábolas 𝒫a, 𝒫b y 𝒫c es:
Z = ( a^4 - 2 a^2 (b^2 + c^2)- 3 (b^2 - c^2)^2 : ... : ...),
que tiene números de búsqueda en
(2.30425578069583, 3.06634037483221, 0.454310785164003).
Es la reflexión de X32817 en X7778.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,99}, {4,6}, {5,5024}, {20,187}, {30,1384}, {32,3146}, {39,3091}, {69,7841}, {76,2996}, {83,32979}, {141,33190}, {183,32986}, {193,316}, {194,14063}, {230,376}, {232,6623}, {297,30227}, {315,6392}, {325,16041}, {346,34542}, {381,7736}, {382,5305}, {384,32826}, {385,33017}, {390,9664}, {439,7857}, {460,26864}, {546,9605}, {550,15655}, {599,5485}, {625,34511}, {626,32830}, {631,3054}, {966,17677}, {1007,31859}, {1015,5274}, {1078,33023}, {1107,31418}, {1131,31411}, {1194,7378}, {1196,7396}, {1285,5306}, {1383,7519}, {1478,16785}, {1479,16784}, {1495,6620}, {1500,5261}, {1506,5068}, {1562,1899}, {1571,9780}, {1572,9812}, {1574,8165}, {1609,12082}, {1975,14064}, {1992,8352}, {2023,7709}, {2275,10591}, {2276,10590}, {2548,3832}, {3053,3529}, {3055,3090}, {3085,9598}, {3086,9597}, {3247,13161}, {3269,3981}, {3314,32836}, {3329,33016}, {3421,21956}, {3520,21397}, {3522,7756}, {3523,7746}, {3525,15815}, {3528,5585}, {3543,5008}, {3544,22332}, {3545,3815}, {3546,15075}, {3600,9651}, {3618,8370}, {3619,6656}, {3627,30435}, {3631,7784}, {3634,31421}, {3763,33230}, {3785,6655}, {3788,15301}, {3817,9592}, {3830,18907}, {3839,5475}, {3843,22246}, {3845,15484}, {3851,31406}, {3855,9607}, {3926,5025}, {3934,33202}, {3944,24247}, {4208,16589}, {4294,10987}, {5023,11742}, {5028,5921}, {5030,36670}, {5033,12203}, {5056,31401}, {5059,7755}, {5071,31489}, {5140,6467}, {5177,5283}, {5225,16502}, {5319,7747}, {5354,7391}, {5355,14075}, {5395,7878}, {6034,10485}, {6200,12123}, {6321,26316}, {6337,7887}, {6390,11318}, {6396,12124}, {6411,36703}, {6412,36701}, {6422,31412}, {6459,8375}, {6460,8376}, {6531,18850}, {6564,31403}, {6680,33201}, {6781,15683}, {6973,34460}, {7375,32790}, {7376,32789}, {7383,14806}, {7388,13934}, {7389,9600}, {7400,10979}, {7486,31455}, {7487,10985}, {7749,15717}, {7750,33238}, {7752,32980}, {7753,14930}, {7754,11008}, {7758,7825}, {7761,15589}, {7763,32972}, {7769,32988}, {7774,14041}, {7777,33006}, {7778,32817}, {7781,32831}, {7782,32989}, {7783,32829}, {7785,32996}, {7786,32987}, {7787,14068}, {7789,32822}, {7791,32828}, {7792,14033}, {7793,32997}, {7795,7861}, {7797,14035}, {7800,7872}, {7803,32971}, {7806,33007}, {7816,33181}, {7818,10513}, {7823,33279}, {7824,32838}, {7828,32973}, {7833,17008}, {7834,33198}, {7836,32824}, {7839,14062}, {7842,14023}, {7847,32832}, {7850,11054}, {7851,14001}, {7862,32835}, {7864,16924}, {7865,32874}, {7868,33223}, {7886,33203}, {7888,32841}, {7891,33248}, {7898,19570}, {7906,14045}, {7912,32825}, {7920,14042}, {7921,14044}, {7923,16898}, {7924,16990}, {7925,32837}, {7928,32868}, {7932,14037}, {7934,32833}, {7989,31396}, {8164,31477}, {8355,11165}, {8356,34229}, {9214,34169}, {9300,14482}, {9463,14957}, {9465,31099}, {9574,10175}, {9575,18483}, {9593,19925}, {9608,34484}, {9609,35921}, {9721,18347}, {9734,20398}, {9741,22110}, {9744,14639}, {9752,11676}, {9880,11179}, {10304,21843}, {10583,14031}, {10588,31448}, {10592,31461}, {10653,31710}, {10654,31709}, {10895,31402}, {10986,18533}, {11174,32983}, {11180,11646}, {11303,11488}, {11304,11489}, {11361,16989}, {11541,22331}, {11580,16063}, {13492,34165}, {13637,13832}, {13757,13831}, {14484,22682}, {14568,14907}, {14712,33192}, {15031,32991}, {15433,15437}, {15603,15696}, {16051,24855}, {16317,32216}, {16984,33255}, {17000,33032}, {17004,33008}, {18404,22121}, {18581,36252}, {18582,36251}, {18840,33232}, {18842,32532}, {19053,33456}, {19054,33457}, {20065,33019}, {20081,32452}, {21312,34809}, {21448,30739}, {23055,35955}, {27318,33057}, {32818,33292}, {32839,32967}, {32867,33001}, {32883,33015}, {32956,34573}, {34866,35473}, {35060,35687}.
La razón de homotecia entre estos triángulos es:
(18(a^2b^2+a^2c^2+b^2c^2)-13(a^4+b^4+c^4))/(8(b+c-a)(a-b+c)(a+b-c)(a+b+c)).
- Lunes, 2 de marzo del 2020
Polares del incentro respecto a tres circunferencias
El 2 de marzo de 1943, bajo el Régimen de Franco, se promulga en España la Ley de Rebelión Militar, por la que serán juzgados por procedimiento sumarísimo, todos los delitos políticos en Consejo de guerra.
LEY DE 2 DE MARZO DE 1943 por la que se equiparan al delito de rebelión militar las transgresiones de orden jurídico que tengan una manifiesta repercusión en la vida pública.
Dado un triángulo ABC, sean I=X1 su incentro, su y Γa, Γb, Γc las circunferencias inscritas en los triángulos TaBC, TbCA, TcAB.
Las paralelas por el incentro a los lados AB y AC son tangentes a Γa en Ab y Ac, respectivamente.
Las paralelas por el incentro a los lados BC y BA son tangentes a Γb en Bc y Ba, respectivamente.
Las paralelas por el incentro a los lados CA y CB son tangentes a Γc en Ca y Cb, respectivamente.
La rectas AbAc, BcBa y CaCb forman un triángulo .
En coordenadas baricéntricas:
Bc = (b(b+c)+a(b+2c) : -b(a+b-c) : 2c^2),
Cb = (c(b+c)+a(2b+c) : 2b^2 : -c(a-b+c)),
Aa = (a(-2a^2+3a(b+c)+(b+c)^2) :
a b(b+c)-(b-c)(b+c)^2 -a^2(2b+c) :
a c(b+c)+(b-c)(b+c)^2-a^2(b+2c)).
Sea A'B'C' el triángulo formado por las polares del incentro respecto a las circunferencias circunscritas a los triángulos , y .
Las ecuaciones de la circunferencia circunscrita a y de la polar del incentro respecto a ella son:
b c (-3 a + b + c)x^2 -b (-4 a^2 - 2 b^2 - b c + c^2 +
a (-6 b + c))y^2+ ( -4 a^3 - a (-6 b^2 + 2 b c - 6 c^2) +
2 (b^3 + c^3))y z +( -2 b (-2 a^2 - a (b - 2 c) +
b (b + c)))z x +( -2 c (-2 a^2 + a (2 b - c) + c (b + c))) x y = 0,
b c (-a + b + c) x - c (c (b + c) + a (2 b + c)) y -
b (b (b + c) + a (b + 2 c)) z = 0.
A' = ( -a (a^3 + 3 a b c + a^2 (b + c) + b c (b + c)) :
b (a^2 (b + 2 c) + c (2 b^2 + b c - c^2) + a (b^2 + 3 b c + c^2)) :
c (a^2 (2 b + c) + a (b^2 + 3 b c + c^2) + b (-b^2 + b c + 2 c^2))).
Las rectas AA', BB', CC' concurren en el punto
W = ( a/(a^3 - a^2 (b + c) - a (2 b^2 + 3 b c + 2 c^2) - b c (b + c)) : ... : ...),
que tiene números de búsqueda en
(1.46828505689763, 1.49878355956316, 1.92537506825713).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,33097}, {7,24851}, {8,2650}, {9,1046}, {21,3720}, {171,943}, {256,942}, {314,3664}, {940,987}, {941,986}, {983,5711}, {1042,17097}, {2346,5255}, {4888,10435}, {15315,18398}}.
Las rectas IBc y ICb vuelven a cortar a la circunferencia circunscrita a en:
B'c = (3 a + b + c : -a + b - c : 2 c) y
C'b = (3 a + b + c : 2 b : -a - b + c).
Los puntos C'a, A'c, A'b y B'a, se define cíclicamente.
Los seis puntos
B'c,
C'b,
C'a,
A'c,
A'b y
B'a están en una misma
cónica
( -a^2 x^2-2 a b x^2+3 b^2 x^2-2 a c x^2+2 b c x^2+3 c^2 x^2-2 a^2 x y-12 a b x y-2 b^2 x y-8 a c x y-8 b c x y+2 c^2 x y+3 a^2 y^2-2 a b y^2-b^2 y^2+2 a c y^2-2 b c y^2+3 c^2 y^2-2 a^2 x z-8 a b x z+2 b^2 x z-12 a c x z-8 b c x z-2 c^2 x z+2 a^2 y z-8 a b y z-2 b^2 y z-8 a c y z-12 b c y z-2 c^2 y z+3 a^2 z^2+2 a b z^2+3 b^2 z^2-2 a c z^2-2 b c z^2-c^2 z^2 = 0)
con centro en
I y
P = ( 1/(a^2 + 2 a (b + c) + b^2 + 8 b c + c^2) : ... : ...),
que tiene números de búsqueda en ETC
(2.23582220511136, 1.76913301213817, 1.38396214806810).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,3707}, {2,3902}, {57,551}, {81,16483}, {88,3616}, {89,3622}, {277,17382}, {392,1002}, {519,25430}, {957,10179}, {1022,4778}, {1219,6051}, {1255,3241}, {8056,25055}.
- Viernes, 28 de febrero del 2020
Elipses con diámetros los lados de un triángulo
El 28 de febrero de 1789 una Real Cédula del rey de España Carlos IV, permite el tráfico de esclavos africanos en Cuba.
Cuba fue una de las primeras colonias a las que llegaron los esclavos africanos, motivado por la temprana extinción de la población indígena a manos de los colonizadores españoles y la creciente necesidad de explotar las nuevas tierras conquistadas.
Entre los últimos países en abolir la esclavitud se encuentran Cuba, bajo dominio español, en 1888.
Dados un triángulo ABC y un punto P, sean A1, A2 y A4 tres puntos tales que P es el incentro de A1BC, el baricentro de A2BC y el ortocentro de A4BC.
Los puntos A1, A2, A4 están alineados si y solo si P está sobre la elipse con eje principal el segmento BC y eje secundario de longitud a/√3.
Siendo (u:v:w) las coordenadas baricéntricas de P respecto a ABC,
A1 = (-u ((b^2 - c^2) u + a^2 (u + 2 v)) ((-b^2 + c^2) u +
a^2 (u + 2 w)) : -(b u - a v) (b u + a v) ((b^2 - c^2) u -
a^2 (u + 2 w)) : ((b^2 - c^2) u + a^2 (u + 2 v)) (c u - a w) (c u +
a w)),
A2 = (3 u : -u + 2 v - w : -u - v + 2 w),
A4 = (-((b^2 - c^2) u + a^2 (u + 2 v)) ((-b^2 + c^2) u +
a^2 (u + 2 w)) : ((b^2 - c^2) u + a^2 (u + 2 v)) (b^2 (-u + w) +
a^2 (u + w) - c^2 (u + w)) : (c^2 (-u + v) + a^2 (u + v) -
b^2 (u + v)) ((-b^2 + c^2) u + a^2 (u + 2 w))).
Los puntos A1, A2, A4 están alineados (en una recta paralela a BC y A1 es el punto medio del segmento A2A4) si y sólo si P está sobre la cónica de ecuación:
(2a^4-3a^2(b^2+c^2)+(b^2-c^2)^2)x^2+ 2a^4y z +
a^2(a^2+b^2-c^2)z x + a^2(a^2-b^2+c^2)x y = 0.
Se trata de una elipse ℰa cuyo vértices del eje principal son B y C, y la longitud del eje secundario es a/√3.
La de A respecto a ℰa es:
pa: 2 (2 a^4 - 3 a^2 (b^2 + c^2)+ (b^2 - c^2)^2)x + a^2 (a^2 - b^2 +
c^2)y + a^2 (a^2 + b^2 - c^2)z = 0.
Procediendo cíclicamente se definen las elipses ℰb y ℰc, y las polares pb y pc.
El triángulo formado por las rectas
pa,
pb,
pc es pespectivo con
ABC, con centro de perspectividad
X14491
(a^2/(5 a^4 + 2 (b^2 - c^2)^2 - 7 a^2 (b^2 + c^2)):...:...).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Consideremos otras elipses con diámetros BC, CA, AB:
Sean A'B'C' el , correspondiente a un ángulo θ, ℰ'a la elipse con vértices los puntos B, C, A' y ℓa la polar de A, respecto a ℰ'a. Cíclicamente, se definen la elipses ℰ'b y ℰ'c, y las polares ℓb y ℓc.
Si t=Cot(θ):
ℰ'a:
(a^4 (1 + t^2)-2 a^2 (b^2 + c^2) t^2 + (b^2 - c^2)^2 (-1 + t^2))x^2 + 4 a^4y z + 2 a^2 (a^2 + b^2 - c^2)z x + 2 a^2 (a^2 - b^2 + c^2)x y = 0.
ℓa:
(a^4 (1 + t^2)-2 a^2 (b^2 + c^2) t^2 + (b^2 - c^2)^2 (-1 + t^2)) x + a^2 (a^2 - b^2 + c^2) y +
a^2 (a^2 + b^2 - c^2) z = 0.
El triángulo
UVW formado por las rectas ℓ
a, ℓ
b, ℓ
c es perspectivo con
ABC, con centro de perspectividad
T = T(θ) = (a^2/((a^4+(b^2-c^2)^2-2a^2(b^2+c^2))t^2+
2a^4-a^2(b^2+c^2)-(b^2-c^2)^2): ... : ...).
• T(π/6)=X14491.
• Cuando θ=π/4, las elipses son circunferencias y las tres polares pasan por el ortocentro.
• T(π/3) = X11738 (conjugado isogonal de X3534).
X11738
[Antreas Hatzipolakis]:
Let ABC be a triangle and A'B'C', A"B"C" the cevian triangles of H, G, resp.
Denote:
Ma, Mb, Mc = the midpoints of AA', BB', CC', resp.
M1, M2, M3 = the midpoints of AA", BB", CC", resp.
Na, Nb, Nc = the NPC centers of GMaM1, GMbM2, GMcM3, resp.
N1, N2, N3 = the NPC centers of HMaM1, HMbM2, HMcM3, resp.
1. ABC, NaNbNc are orthologic.
The orthologic center (NaNbNc, ABC) lies on the Euler line.
2. ABC, N1N2N3 are orthologic.
The orthologic center (N1N2N3, ABC) lies on the Euler line.
Orthologic centers?
[Peter Moses and César Lozada]:
The orthologic center (ABC,N1N2N3) is
a^2 (2 a^4-4 a^2 b^2+2 b^4+5 a^2 c^2+5 b^2 c^2-7 c^4) (2 a^4+5 a^2 b^2-7 b^4-4 a^2 c^2+5 b^2 c^2+2 c^4)::
isogonal conjugate of X(3534)
• T(ArcTan[2]) = X64.
X(64) isogonal conjugate of .
Una construcción de X
64 aparece en Emile Lemoine, "Quelques questions se rapportant à l'étude des antiparallèles des côtes d'un triangle", Bulletin de la S. M. F., tome 14 (1886), p. 107-128, concretamente, en la página 111. Este artículo está disponible en
Numdam
(dans page 110)
ABC est un triangle. En B je mène une perpendiculaire à AB
qui coupe AC en i
a; en C une perpendiculaire à AC qui coupe AB en i
c.
La droite i
bi
c se denota por (I
a). De même, les droite (I
b) et (I
c) sont définies.
Nous appellerons I
a, I
b, I
c les sommets du triangle formé par les droites
(I
a), (I
b), (I
c), Ia étant l'intersection des droites (I
b), (I
c),...
Le deux triangles ABC, I
aI
bI
c sont homologiques; le centre d'homologie
a pour coordonnées
1/(cosA-cosB cosC), 1/(cosB-cosC cosA), 1/(cosC-cosA cosB)
(
Mostrar/Ocultar figura )
• T(ω) es el conjugado isogonal de X11287 (ω es el ).
T(ω) = (a^2/((a^4 - 3 a^2 (b^2 + c^2) - 2 (b^4 + c^4))) : ... : ...),
que tiene números de búsqueda en
(0.616790984512116, 0.862110481634613, 2.75914600177021).
Es el punto de intersección de las rectas X69X1285 y X895X5039.
- Miércoles, 26 de febrero del 2020
Homotecia directa entre las circunferencia inscrita y circunscrita
El 26 de febrero de 2001, fallece el cuentista, poeta, intelectual, ensayista, novelista y político venezolano Arturo Uslar Pietri, cuyo interés por su país quedó claramente reflejado en su obra narrativa y en su actividad política. Su novela "Las lanzas coloradas", de 1931, contribuyó a moldear el género hispanoamericano del llamado "realismo mágico" (mostrar lo irreal como algo cotidiano y común).
Dado un triángulo ABC con incentro I=X1, la recta ta que corta a los lados en los puntos AC y AB en Ab y Ac, respectivamente, tal que ∠IBC=∠AIAc y ∠ICB=∠AIAb, es tangente a la circunferencia inscrita, en un punto A'.
Procediendo cíclicamente sobre los vértices de ABC, se definen las rectas tb y tc, los puntos Bc, Ba, Ca, Cb, B' y C'. Sean D=tb∩tc, E=tc∩ta y F=ta∩tb.
Los triángulos ABC y A'B'C' son homotéticos en la homotecia directa de las circunferencias inscrita y circunscrita a ABC; el centro de homotecia es X56.
DEF es la imagen, mediante esta homotecia, del , .
Los triángulos A'B'C' y DEF son perspectivos con centro de perspectividad es X1469, producto trilineal de X56 y X984 (reflexión en el incentro del complemento del conjugado isotómico del incentro).
En coordenadas baricéntricas, se tiene que:
Ab=(-(a + b - c) (b + c) : 0 : c (a - b - c)),
Ac=((a - b + c) (b + c) : b (-a + b + c) : 0).
A'=((a + b - c) (a - b + c) (b + c)^2 : b^2 (a + b - c) (-a + b +
c) : -(a - b - c) c^2 (a - b + c)),
D = (a^2 (-a^2 + (b - c)^2) : b (a + c) (-a^2 + b^2 + 2 a c -
c^2) : -(a + b) c (a^2 - 2 a b + b^2 - c^2)).
El centro de la de ABC y DEF (
cónica
( a^4 b c x^2-a^3 b^2 c x^2-a^2 b^3 c x^2+a b^4 c x^2-a^3 b c^2 x^2-a^2 b^2 c^2 x^2+a b^3 c^2 x^2+b^4 c^2 x^2-a^2 b c^3 x^2+a b^2 c^3 x^2+2 b^3 c^3 x^2+a b c^4 x^2+b^2 c^4 x^2+2 a^4 b c x y-2 a^3 b^2 c x y-2 a^2 b^3 c x y+2 a b^4 c x y+a^4 c^2 x y-2 a^2 b^2 c^2 x y+b^4 c^2 x y+a^3 c^3 x y-3 a^2 b c^3 x y-3 a b^2 c^3 x y+b^3 c^3 x y-a^2 c^4 x y-2 a b c^4 x y-b^2 c^4 x y-a c^5 x y-b c^5 x y+a^4 b c y^2-a^3 b^2 c y^2-a^2 b^3 c y^2+a b^4 c y^2+a^4 c^2 y^2+a^3 b c^2 y^2-a^2 b^2 c^2 y^2-a b^3 c^2 y^2+2 a^3 c^3 y^2+a^2 b c^3 y^2-a b^2 c^3 y^2+a^2 c^4 y^2+a b c^4 y^2+a^4 b^2 x z+a^3 b^3 x z-a^2 b^4 x z-a b^5 x z+2 a^4 b c x z-3 a^2 b^3 c x z-2 a b^4 c x z-b^5 c x z-2 a^3 b c^2 x z-2 a^2 b^2 c^2 x z-3 a b^3 c^2 x z-b^4 c^2 x z-2 a^2 b c^3 x z+b^3 c^3 x z+2 a b c^4 x z+b^2 c^4 x z-a^5 b y z-a^4 b^2 y z+a^3 b^3 y z+a^2 b^4 y z-a^5 c y z-2 a^4 b c y z-3 a^3 b^2 c y z+2 a b^4 c y z-a^4 c^2 y z-3 a^3 b c^2 y z-2 a^2 b^2 c^2 y z-2 a b^3 c^2 y z+a^3 c^3 y z-2 a b^2 c^3 y z+a^2 c^4 y z+2 a b c^4 y z+a^4 b^2 z^2+2 a^3 b^3 z^2+a^2 b^4 z^2+a^4 b c z^2+a^3 b^2 c z^2+a^2 b^3 c z^2+a b^4 c z^2-a^3 b c^2 z^2-a^2 b^2 c^2 z^2-a b^3 c^2 z^2-a^2 b c^3 z^2-a b^2 c^3 z^2+a b c^4 z^2 = 0)
que pasa por Ab, Ac, Bc, Ba, Ca, Cb) es:
U = ( a^2 (a^2 - (b - c)^2) (b + c) (a^2 (b + c) -
a (b^2 + c^2) - b c (b + c)) : ... : ...),
que tiene números de búsqueda en
(7.15669680131694, 8.08134630993316, -5.25720456403870).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,9551}, {7,8049}, {42,181}, {55,34429}, {65,1418}, {73,3649}, {256,13265}, {1064,1537}, {1071,3931}, {1214,15185}, {1284,2594}, {1404,2309}, {1409,2293}, {1818,3696}, {1827,1880}, {2171,2667}, {3747,21741}, {4068,4559}, {4334,5586}, {4343,14100}, {4424,11570}, {4551,29822}, {4552,25295}, {10052,24248}, {17077,17135}, {21035,21794}, {21859,22279}.
El es esta cónica es:
V = ( a (b + c)/((b + c - a) (2 a ( b + c) + b c)) : ... : ...),
que tiene números de búsqueda en ETC
(0.605773815052770, 0.759341410764849, 2.83537866750744).
<
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {7, 7243}, {56, 7225}, {65, 22271}, {959, 3671}, {29883, 32013}.
Los triángulos ABC y DEF están inscritos en una misma
cónica
( a^2 (a + b - c) (a - b + c) (b + c)y z +b^2 (b + c-a) (a + b - c) (a +
c) z x + (a + b) (b + c-a) c^2 (a - b + c) = 0)
de perspector (respecto a ABC) X1400, y que pasa por los centros X109, X664, X1411, X1945, X4551, X4559, X32674, X36127. El perspector de esta cónica respecto a DEF es la reflexión de X2293 en el incentro:
W = ( a (a + b - c) (a - b + c) (b + c) (a^2 - a b - a c - 2 b c) : ... : ...),
que tiene números de búsqueda en ETC
(1.07408533580664, 1.10639666326397, 2.37896586773703).
Es la reflexión de X2293 en X1.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,7}, {8,26125}, {10,21931}, {12,3214}, {34,1839}, {37,65}, {38,5173}, {42,226}, {43,5226}, {56,7225}, {57,968}, {72,21039}, {73,3649}, {181,28387}, {238,8543}, {241,15569}, {256,17097}, {354,7004}, {651,4649}, {674,1469}, {740,1441}, {774,942}, {899,5219}, {916,7352}, {934,28842}, {940,9316}, {941,5665}, {954,1253}, {976,28081}, {984,7672}, {1001,1471}, {1066,6147}, {1100,1456}, {1125,17077}, {1193,3485}, {1201,30097}, {1214,1962}, {1245,28786}, {1254,3931}, {1386,34253}, {1411,32259}, {1423,3340}, {1450,15950}, {1457,17301}, {1463,4864}, {1736,30329}, {1738,21617}, {1757,29007}, {1818,5880}, {1834,21955}, {1836,14547}, {1854,2654}, {1892,2356}, {1953,3827}, {2310,5728}, {2318,3925}, {2340,2550}, {2647,17016}, {2650,12709}, {2772,5425}, {3293,3947}, {3660,17450}, {3682,12609}, {3751,8545}, {3812,25067}, {3869,24554}, {3870,30699}, {3883,17152}, {3886,4441}, {3911,30950}, {3993,4552}, {4038,17074}, {4365,6358}, {4658,34043}, {4848,21803}, {4854,6354}, {5249,25941}, {5263,10030}, {5311,8270}, {5435,26102}, {7073,10118}, {7237,15556}, {7613,30275}, {7677,16484}, {7986,15934}, {9791,17950}, {11246,22053}, {11375,17278}, {11518,18216}, {11526,16496}, {11529,33536}, {14942,21453}, {17017,34036}, {17080,17592}, {17257,19860}, {21454,29814}, {24789,28253}, {25453,28776}, {28082,28089}, {28774,29635}, {28780,29633}.
La cónica circunscrita a los triángulos ABC y DEF, vuelve a cortar a los lados del triángulo tangencial en puntos que unidos con los vértices opuestos forman tres rectas concurrentes en X21767.
GENERALIZACIÓN de este último resultado.
X21767 es la imagen del ortocentro en la homografía σ, que aplica {A, B, C,, X1} en {Ta, Tb, Tc, X6}.
σ(u:v:w) = (a^2 b c u - a^3 c v - a^3 b w : -b^3 c u + a b^2 c v -
a b^3 w : -b c^3 u - a c^3 v + a b c^2 w).
Si se toma una cónica circunscrita a ABC con perspector P=(u:v:w), ésta vuelve a cortar a los lados del triángulo tangencial en puntos que unidos con los vértices opuestos forman tres rectas concurrentes en:
Q = f(P) = (3 a^2 b^4 c^4 u^2 - a^6 (c^2 v - b^2 w)^2 -
2 a^4 b^2 c^2 u (c^2 v + b^2 w) :
3 a^4 b^2 c^4 v^2 - b^6 (c^2 u - a^2 w)^2 -
2 a^2 b^4 c^2 v (c^2 u + a^2 w) : -a^4 c^6 v^2 -
2 a^2 b^2 c^4 v (-c^2 u + a^2 w) -
b^4 (c^6 u^2 + 2 a^2 c^4 u w - 3 a^4 c^2 w^2)).
Lista {{Xi, Xj}, Xk=σ(Xi)=f(Xj)}, para los índices {{í,j},k}:
{{42, 21753}, 1}, {{31, 3051}, 3}, {{1, 6}, 6}, {{48, 217}, 25}, {{37,
20970}, 31}, {{38, 11205}, 32}, {{6, 213}, 55}, {{55,
20229}, 56}, {{204, 20232}, 64}, {{19, 32}, 154}, {{56,
20228}, 198}, {{17442, 31390}, 206}, {{1755, 9419}, 237}, {{656,
3269}, 647}, {{513, 1015}, 649}, {{650, 14936}, 663}, {{2254,
35505}, 665}, {{649, 1977}, 667}, {{798, 9427}, 669}, {{44,
1017}, 902}, {{58, 2300}, 1030}, {{19614, 20233}, 1033}, {{2192,
20230}, 1035}, {{221, 20231}, 1436}, {{41, 9449}, 1486}, {{2173,
9408}, 1495}, {{75, 39}, 1613}, {{269, 16502}, 1615}, {{200,
30706}, 1616}, {{32, 21751}, 1631}, {{23493, 23551}, 1740}, {{518,
20662}, 1914}, {{240, 9475}, 1971}, {{190, 667}, 1979}, {{1580,
36213}, 2076}, {{4575, 30451}, 2079}, {{292, 21760}, 2110}, {{192,
20971}, 2162}, {{2, 42}, 2176}, {{3, 1409}, 2178}, {{21,
21748}, 2305}, {{1575, 20671}, 3009}, {{1577, 20975}, 3050}, {{9,
41}, 3052}, {{63, 184}, 3053}, {{57, 31}, 3207}, {{3223,
2}, 3360}, {{3112, 20965}, 3499}, {{1967, 32748}, 3511}, {{25,
21750}, 3556}, {{512, 21755}, 3733}, {{667, 21762}, 4057}, {{1707,
3167}, 5023}, {{905, 3270}, 6586}, {{523, 20982}, 7252}, {{163,
3049}, 7669}, {{100, 649}, 9259}, {{2349, 1495}, 9412}, {{799,
669}, 9431}, {{17957, 9482}, 9480}, {{82, 5007}, 10329}, {{10,
2092}, 16685}, {{101, 3063}, 16686}, {{350, 20457}, 18278}, {{81,
2308}, 18755}, {{2053, 23522}, 20676}, {{39, 21752}, 20990}, {{40,
2199}, 20991}, {{2156, 1501}, 20993}, {{7, 1475}, 20995}, {{2162,
21757}, 20996}, {{662, 512}, 20998}, {{1740, 194}, 21001}, {{514,
3271}, 21007}, {{4, 1400}, 21767}, {{8, 2347}, 21769}, {{22,
21749}, 21771}, {{66, 21744}, 21774}, {{69, 23620}, 21775}, {{76,
3778}, 21776}, {{83, 20964}, 21777}, {{85, 21746}, 21778}, {{86,
20963}, 21779}, {{87, 1}, 21780}, {{88, 902}, 21781}, {{89,
21747}, 21782}, {{99, 20981}, 21783}, {{239, 20663}, 21788}, {{668,
20979}, 21790}, {{693, 20974}, 21791}, {{7121, 23546}, 23857}, {{92,
51}, 32445}, {{24041, 20976}, 33704}, {{561, 20859}, 33786}.
- Martes, 25 de febrero del 2020
Conjugado isogonal respecto al triángulo de contacto interior
El 25 de Febrero de 1983 muere el dramaturgo estadounidense Tennessee Williams, ganador del Premio Pulitzer de teatro en 1948 por "Un tranvía llamado Deseo", y en 1955 por "La gata sobre el tejado de zinc caliente".
Dados un triángulo ABC y un punto P, sean Q el de P respecto al DEF de P y T el de la recta PQ.
Utilizando coordenadas baricéntricas, respecto a ABC, si P=(u:v:w),
Q = (u (v w (u^2 - v w) a^2 - u^2 (v + w) (v c^2 + w b^2) ): ... : ...),
T = (u/ (a^2 (v - w) - (b^2 - c^2) (v + w)) : ... : ...).
Pares de {P=Xi, Ti=Xj}, para los índices: {1, 651}, {2, 99}, {3, 4558}, {5, 14570}, {6, 112}, {8, 646}, {9, 44}, {10, 3952}, {11, 2401}, {19, 1783}, {21, 4612}, {22, 4611}, {25, 112}, {30, 2407}, {33, 1783}, {34, 32714}, {46, 651}, {52, 14570}, {71, 4574}, {74, 34568}, {76, 4609}, {110, 18879}, {113, 2407}, {114, 2396}, {115, 2395}, {116, 2400}, {117, 2406}, {118, 2398}, {119, 2397}, {120, 2414}, {121, 2415}, {122, 2416}, {123, 2417}, {124, 2399}, {125, 2394}, {126, 2418}, {127, 2419}, {132, 2409}, {133, 2404}, {137, 2413}, {155, 4558}, {184, 14586}, {186, 14590}, {193, 99}, {208, 32714}, {226, 4566}, {237, 14966}, {243, 1981}, {278, 36118}, {297, 877}, {321, 27808}, {371, 110}, {372, 110}, {393, 6529}, {403, 16237}, {468, 4235}, {487, 4563}, {488, 4563}, {497, 3732}, {511, 2396}, {512, 2395}, {513, 2401}, {514, 2400}, {515, 2406}, {516, 2398}, {517, 2397}, {518, 2414}, {519, 2415}, {520, 2416}, {521, 2417}, {522, 2399}, {523, 2394}, {524, 2418}, {525, 2419}, {526, 2411}, {571, 14586}, {950, 14543}, {1499, 2408}, {1503, 2409}, {1510, 2413}, {1828, 17906}, {1986, 16237}, {2039, 30509}, {2040, 30508}, {2183, 2427}, {2211, 34859}, {2362, 108}, {2899, 646}, {2900, 644}, {2901, 3952}, {2914, 14590}, {3258, 2411}, {3309, 2402}, {3413, 30509}, {3414, 30508}, {3667, 2403}, {5095, 4235}, {5510, 2403}, {5511, 2402}, {5512, 2408}, {5663, 2410}, {6000, 2404}, {6001, 2405}, {6110, 4240}, {6111, 4240}, {6525, 6529}, {6776, 35278}, {7133, 6135}, {9752, 35278}, {16232, 108}, {25640, 2405}, {25641, 2410}, {25642, 2412}, {35015, 10015}
Entre los once primeros centros , falta el par {X7, T7}.
El tripolo de la recta que pasa por el y por su conjugado isogonal respecto al es:
T7 = ( 1/(a (b - c) (b + c - a)^3) : ... : ...),
que tiene números de búsqueda en
(0.0250801001568389, -0.0260896737123586, 3.64715113286670).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {7,3022}, {85,23058}, {279,34018}, {658,3732}, {664,4569}, {927,934}, {1088,1111}, {4573,4617}, {7056,7215}, {9442,10481}, {17079,30682}, {24002,24011}.
César Lozada en Euclid#659, expone otras propiedades de T7, entre las que están:
• Es el de X(4130).
• Tripolo de la tangente, X7X354, a la del punto de Gergonne.
X(354) = .
Let A', B', C' be the intersections of line X(7)X(8) and lines BC, CA, AB, resp. The circumcircles of AB'C', BC'A', CA'B' concur in
X(927). (Randy Hutson, March 25, 2016)
Let P be a point on line X(4)X(7) other than X(4). Let A' be the reflection of P in BC, and define B' and C' cyclically. The circumcircles of AA'B', BC'A', and CA'B' concur at
X(934). (Randy Hutson, July 20, 2016)
X(3022) = Steiner point of intouch triangle.
La envolvente de la recta
PQ, cuando
P recorre una recta ℓ que pasa por el ortocentro
H, es la cónica 𝒞
ℓ inscrita a
ABC, tangente a ℓ en
H. (
ttttP)
El lugar geométrico del
L de 𝒞
ℓ, cuando ℓ gira alrededor de
H es la cuártica 𝒬, conjugada isogonal de la cónica inscrita de perspector el circuncentro.
La
cuártica
( (-a^8+4 a^6 b^2-6 a^4 b^4+4 a^2 b^6-b^8+2 a^4 c^4-4 a^2 b^2 c^4+2 b^4 c^4-c^8) x^2 y^2+(2 a^8-4 a^6 b^2+4 a^2 b^6-2 b^8-4 a^6 c^2+8 a^4 b^2 c^2-4 a^2 b^4 c^2-4 a^2 b^2 c^4+4 b^4 c^4+4 a^2 c^6-2 c^8) x^2 y z+(-2 a^8+4 a^6 b^2-4 a^2 b^6+2 b^8-4 a^4 b^2 c^2+8 a^2 b^4 c^2-4 b^6 c^2+4 a^4 c^4-4 a^2 b^2 c^4+4 b^2 c^6-2 c^8) x y^2 z+(-a^8+2 a^4 b^4-b^8+4 a^6 c^2-4 a^2 b^4 c^2-6 a^4 c^4+2 b^4 c^4+4 a^2 c^6-c^8) x^2 z^2+(-2 a^8+4 a^4 b^4-2 b^8+4 a^6 c^2-4 a^4 b^2 c^2-4 a^2 b^4 c^2+4 b^6 c^2+8 a^2 b^2 c^4-4 a^2 c^6-4 b^2 c^6+2 c^8) x y z^2+(-a^8+2 a^4 b^4-b^8-4 a^4 b^2 c^2+4 b^6 c^2+2 a^4 c^4-6 b^4 c^4+4 b^2 c^6-c^8) y^2 z^2 = 0)
𝒬 pasa por los centros X15742, X18020, X32230 y los vértices de ABC son cúspides con tangentes las alturas.
- Viernes, 21 de febrero del 2020
Varias propiedades geométricas de X(468)
El 21 de febrero de 1924, Miguel de Unamuno es destituido por la dictadura de Primo de Rivera como rector de la Universidad de Salamanca y desterrado a la isla canaria de Fuerteventura.
Dado un triángulo ABC, sea A'B'C' su . El incentro I' y el circuncentro O' de A'B'C' son, respectivamente, X3 y X26= ( - 3) X3 + 2X4, por lo tanto I'O' es la de ABC.
AoPS
(TelvCohl)
Given a ABC and a point P. Let P
aP
bP
c be the pedal triangle of P WRT ABC and let H
a, H
b, H
c be the orthocenter of AP
bP
c, BP
cP
a, C
aP
b, respectively. Then H
aH
bH
c and the medial triangle M
aM
bM
c of ABC are perspective if and only if P lies on the Stammler hyperbola of ABC. If that's the case, the perspector P' lies on the Euler line of ABC.
Con las notaciones de esta referencia, si P un punto sobre la , sean Q el de P respecto a A'B'C' y P' el centro de perspectividad de y .
La correspondencia
Q ↦ P' es una proyectividad sobre la recta de Euler y su punto central (punto medio de sus puntos dobles) es
X468.
En coordenadas baricéntricas,
Ha = (c^2(a^2-c^2)v-b^4w+b^2(a^2w+c^2(2u+v+w)) : b^2(-a^2+b^2+c^2)w : c^2(-a^2+b^2+c^2)v).
Si Q = X3 + t X4 y P' = X3 + t' X4, se tiene:
t ↦ t' = (2a^2b^2c^2-(a^6-a^4(b^2+c^2)+(b^2-c^2)^2(b^2+c^2)-a^2(b^4+c^4))t) / (2a^2b^2c^2+(b^2+c^2-a^2)(a^2+b^2-c^2)(a^2-b^2+c^2)t).
Los puntos dobles de esta proyectividad corresponden a los valores de t:
t = (1/2) (1 ± Sqrt[(b+c-a)(a+b-c)(a-b+c)(a+b+c)(b^2+c^2-
a^2)(a^2+b^2-c^2)(a^2-b^2+c^2)(a^2+b^2+c^2)] / ((b^2+c^2-a^2)(a^2+b^2-c^2)(a^2-b^2+c^2)),
que son imaginarios conjugados si el triángulo ABC es obtusángulo.
OTRAS PROPIEDADES DE X648
• HG290114: Dado un triángulo ABC y un punto variable P sobre la recta de Euler, el lugar geométrico de los centros de la hipérbola equilátera circunscrita al triángulo pedal de P y que pasa por P es una recta, que corta a la recta de Euler en X468.
• HG311216:
Dados un triángulo ABC y un punto P, sean
y
los triángulos y de P.
Se denotan por Γab y Γac las circunferencias circunscritas a los triángulos AB1C2, AB2C1 y por d1 su eje radical. Similarmente, se definen los ejes radicales d2 y d3.
Si P=X(2930) (conjugado isogonal respecto al triángulo tangencial de X23), los ejes radicales d1, d2 y d3 concurren en X468.
• HG250118:
Dados un triángulo ABC y un punto P, sean DEF el de P, el de ABC y LMN el triángulo medial de DEF.
Denotamos por A' el punto de intersección (distinto de A) de las circunferencias Γ y Γa, circunscritas a ABC y AEF, respectivamente.
A1 es el punto medio de la cuerda en Γa determinada por la tangente en A a Γ y A2 es el punto medio de la cuerda en Γ determinada por la tangente en A a Γa.
Las rectas PA', A1Ma, A2L son concurrentes, en un punto Pa. Se definen, de forma análoga, los puntos Pb y Pc.
El centro de perspectividad de los triángulos ABC y , cuando P es X671 o X2373 es X468.
• HG290318:
Dado un triángulo ABC, sean A'B'C' el .
Se denota por Ba y Ca las proyecciones de B' y C' sobre AA', respectivamente; por B1 y C1 las reflexiones de Ba y Ca en BB' y CC', respectivamente; y por Oa, Ob y Oc los circuncentros de los triángulos A'B1C1, B'C1A1 y C'A1B1, respectivamente.
Los triángulos ABC y son homotéticos, mediante una homotecia de centro X3091 = 2 O + 3 H = 2 H + 3 G y razón -1/4.
X468 es la imagen de X10296 (reflexión del en la ), mediante esta homotecia.
• HG140918:
Dado un triángulo ABC de
, las circunferencias (BMaMb) y (CMaMc) se vuelven a cortar en A'. Los puntos B' y C' se definen cíclicamente.
Los triángulos ABC y A'B'C' son perspectivos con centro de perspectividad X468, intersección de la y el
• HG191018:
Si una recta p corta a los lados BC, CA, AB de un triángulo ABC en los puntos D, E, F, respectivamente, sea D' el punto medio de las reflexiones Dc y Db de D en las rectas AB y AC. Los puntos E' y F' se definen de forma análoga, procediendo cíclicamente sobre los lados de ABC. Entonces, los puntos D', E', F' están alineados, sobre una recta p'.
Cuando la recta p gira alrededor de un punto P, la recta p' gira alrededor de P', del circuncentro y P.
La correspondencia p ↦ p' es una proyectividad entre los haces de rectas de puntos base P y P'; por lo que, el punto de intersección Q de las rectas p y p' describe una hipérbola rectangular que pasa por el , P, P' y sus asíntotas son paralelas a las de .
Si Po es su centro, la correspondencia σ: P ↦ Po es una transformación afín. X468 es la imagen mediante σ de X110 (centro de la .
• HG150519:
Dado un triángulo ABC, sean el , el y A'B'C' el triángulo obtenido reflejando A, B, C en el circuncentro O. Las rectas A'Ma, B'Mb y C'Mc intersecan de nuevo a la circunferencia circunscrita en A", B" y C", respectivamente.
Los puntos
D=BC∩HbHc,
E=CA∩HcHa,
F=AB∩HaHb,
D'=B"C"∩MbMc,
E'=C"A"∩McMa,
F'=A"B"∩MaMb quedan sobre el (eje de perspectividad común de los pares de triángulos ABC y , y A"B"C").
En la proyectividad σ, sobre el eje órtico, que aplica D, E, F en D', E', F', X468 es la imagen de X14580 ( de X111= y X25=centro de homotecia de los triángulos órtico y tangencial).
• HG151219:
Si ABC es un triángulo, de
DEF, entonces el
X468 (inverso en la circunferencia circunscrita del centro de homotecia de los triángulos órtico y ) es el único punto cuyos triángulos pedales (no degenerados) y ,
respecto a ABC y DEF, tienen la misma área y son .
• HG190220:
Dado un triángulo ABC, sean DEF el , Ba and Ca los pies de las perpendiculares desde D a CA y AB, respectivamente. Se denota por Ga el baricentro del triángulos DBaCa, y se definen Gb y Gc cíclicamente. Las rectas AGa, BGb, CGc concurren en X(3527). (Randy Hutson, June 7, 2019)
X468 es la imagen de X323 (inverso en del baricentro) mediante la transformación afín que aplica ABC en .
- Miércoles, 19 de febrero del 2020
X(428) centro de una cónica lugar de intersección de rayos homólogos
El 19 de febrero de 1473 nació Nicolás Copérnico, astrónomo polaco considerado el primero en sugerir que la Tierra y los demás planetas orbitan alrededor del Sol. Su libro "Sobre las revoluciones de las esferas celestes" será considerado libro herético por la Iglesia Católica en 1616.
Dado un triángulo ABC, sean DEF el , Ba and Ca los pies de las perpendiculares desde D a CA y AB, respectivamente. Se denota por Ga el baricentro del triángulos DBaCa, y se definen Gb y Gc cíclicamente. Las rectas AGa, BGb, CGc concurren en X(3527). (Randy Hutson, June 7, 2019)
La
transformación afín
( σ(x:y:z) =
((-2 a^2 (b^2-c^2)^2+a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)) x-a^2 (a^4+b^4-4 b^2 c^2+3 c^4-2 a^2 (b^2+2 c^2)) y-a^2 (a^4+3 b^4-4 b^2 c^2+c^4-2 a^2 (2 b^2+c^2)) z :
-b^2 (a^4+b^4-4 b^2 c^2+3 c^4-2 a^2 (b^2+2 c^2)) x+(a^6-a^4 (2 b^2+c^2)+(-b^2 c+c^3)^2+a^2 (b^4+4 b^2 c^2-c^4)) y-b^2 (3 a^4+(b^2-c^2)^2-4 a^2 (b^2+c^2)) z :
-c^2 (a^4+3 b^4-4 b^2 c^2+c^4-2 a^2 (2 b^2+c^2)) x-c^2 (3 a^4+(b^2-c^2)^2-4 a^2 (b^2+c^2)) y+(a^6-a^4 (b^2+2 c^2)+(b^3-b c^2)^2+a^2 (-b^4+4 b^2 c^2+c^4)) z)
)
σ, que aplica ABC en , tiene punto fijo propio el . Los puntos fijos en la recta del infinito son las direcciones de las asíntotas de la .
Pares {P=Xi, P'=σ(P)=Xj}, para {i, j}: {3,51}, {4,11245}, {6,6}, {20,428}, {74,1112}, {110,12099}, {155,2}, {323,468}, {399,125}, {1147,5943}, {1350,9971}, {1480,65}, {1498,1853}, {1511,11746}, {3098,9969}, {3157,354}, {3167,373}, {3173,17718}, {3211,374}, {3288,2501}, {3426,185}, {4550,389}, {4846,16657}, {5448,32068}, {6126,15904}, {7689,21849}, {8548,8584}, {9927,11225}, {10661,396}, {10662,395}, {10665,32787}, {10666,32788}, {11456,427}, {11472,5890}, {11820,32062}, {12163,3060}, {12164,3917}, {12302,12824}, {12364,11064}, {13509,16318}, {14627,34566}, {15037,34565}, {15068,13567}, {15083,3819}, {15106,12828}, {15316,3167}, {16266,10192}, {17834,34751}, {17838,15131}, {18451,26869}, {19139,597}, {19140,15118}, {19149,23327}, {22146,6793}, {23128,5306}, {32139,23332}, {32320,9209}, {33533,32191}, {33878,1843}, {34117,10169}, {34801,568}, {35237,4}, {36747,11402}.
σ induce una proyectividad entre las rectas que pasan un punto P y las que pasan por P'=σ(P).
En particular, cuando P=X11472 (reflexión de X4846 en el centro de la ) y P'=X5890 (baricentro del ), la cónica lugar de los puntos de intersección de rectas homólogas (Charles–Steiner) es una
hipérbola
( 4 a^6 b^4 c^2 x^2-7 a^4 b^6 c^2 x^2+2 a^2 b^8 c^2 x^2+b^10 c^2 x^2-4 a^6 b^2 c^4 x^2+6 a^2 b^6 c^4 x^2-2 b^8 c^4 x^2+7 a^4 b^2 c^6 x^2-6 a^2 b^4 c^6 x^2-2 a^2 b^2 c^8 x^2+2 b^4 c^8 x^2-b^2 c^10 x^2-a^10 c^2 x y-2 a^8 b^2 c^2 x y+11 a^6 b^4 c^2 x y-11 a^4 b^6 c^2 x y+2 a^2 b^8 c^2 x y+b^10 c^2 x y+2 a^8 c^4 x y-4 a^6 b^2 c^4 x y+4 a^2 b^6 c^4 x y-2 b^8 c^4 x y+7 a^4 b^2 c^6 x y-7 a^2 b^4 c^6 x y-2 a^4 c^8 x y+2 b^4 c^8 x y+a^2 c^10 x y-b^2 c^10 x y-a^10 c^2 y^2-2 a^8 b^2 c^2 y^2+7 a^6 b^4 c^2 y^2-4 a^4 b^6 c^2 y^2+2 a^8 c^4 y^2-6 a^6 b^2 c^4 y^2+4 a^2 b^6 c^4 y^2+6 a^4 b^2 c^6 y^2-7 a^2 b^4 c^6 y^2-2 a^4 c^8 y^2+2 a^2 b^2 c^8 y^2+a^2 c^10 y^2+a^10 b^2 x z-2 a^8 b^4 x z+2 a^4 b^8 x z-a^2 b^10 x z+2 a^8 b^2 c^2 x z+4 a^6 b^4 c^2 x z-7 a^4 b^6 c^2 x z+b^10 c^2 x z-11 a^6 b^2 c^4 x z+7 a^2 b^6 c^4 x z-2 b^8 c^4 x z+11 a^4 b^2 c^6 x z-4 a^2 b^4 c^6 x z-2 a^2 b^2 c^8 x z+2 b^4 c^8 x z-b^2 c^10 x z+a^10 b^2 y z-2 a^8 b^4 y z+2 a^4 b^8 y z-a^2 b^10 y z-a^10 c^2 y z+7 a^6 b^4 c^2 y z-4 a^4 b^6 c^2 y z-2 a^2 b^8 c^2 y z+2 a^8 c^4 y z-7 a^6 b^2 c^4 y z+11 a^2 b^6 c^4 y z+4 a^4 b^2 c^6 y z-11 a^2 b^4 c^6 y z-2 a^4 c^8 y z+2 a^2 b^2 c^8 y z+a^2 c^10 y z+a^10 b^2 z^2-2 a^8 b^4 z^2+2 a^4 b^8 z^2-a^2 b^10 z^2+2 a^8 b^2 c^2 z^2+6 a^6 b^4 c^2 z^2-6 a^4 b^6 c^2 z^2-2 a^2 b^8 c^2 z^2-7 a^6 b^2 c^4 z^2+7 a^2 b^6 c^4 z^2+4 a^4 b^2 c^6 z^2-4 a^2 b^4 c^6 z^2 = 0)
con centro X428 (baricentro del tercer triangulo pedal del ortocentro), asíntotas paralelas a las de la hipérbola de Jerabek y pasa por los centros Xi, para i: 6, 52, 2574, 2575 (estos últimos en la recta del infinito), 5890, 11381, 11472, 12272, 15305, 15801, 16658, 16835, 32616, 32617.
- Martes, 18 de febrero del 2020
Puntos simétricos respecto a los puntos medios de los lados de un triángulo
El 18 de febrero de 1883 nació Nikos Kazantzakis, escritor griego, el que será considerado en su país como el escritor y filósofo más importante del siglo XX. Autor de "Alexis Zorbas", escrita en 1946, que será llevada a la gran pantalla con el nombre de "Zorba el griego". Otra obra suya, "La última tentación de Cristo", también se llevará al cine.
AoPS (Arne)
Let ABC be a triangle, and M the midpoint of its side BC. Let γ be the incircle of triangle ABC. The median AM of triangle ABC intersects the incircle γ at two points K and L. Let the lines passing through K and L, parallel to BC, intersect the incircle γ again in two points X and Y. Let the lines AX and AY intersect BC again at the points P and Q. Then BP = CQ.
Las coordenadas baricéntricas de los puntos P y Q, en la referencia anterior, son:
(0 : -a^3+2 a Sqrt[a^2-(b-c)^2] (b-c)+2 (b-c)^3+a^2 (-2 b+Sqrt[a^2-(b-c)^2]+2 c) : -a^3+a^2 (2 b+Sqrt[a^2-(b-c)^2]-2 c)-2 (b-c)^3+2 a Sqrt[a^2-(b-c)^2] (-b+c)),
(0 : -a^3-a^2 (2 b+Sqrt[a^2-(b-c)^2]-2 c)+2 (b-c)^3+2 a Sqrt[a^2-(b-c)^2] (-b+c) : -a^3+2 a Sqrt[a^2-(b-c)^2] (b-c)-2 (b-c)^3-a^2 (-2 b+Sqrt[a^2-(b-c)^2]+2 c)).
Procediendo cíclicamente, se obtienen pares de puntos en los lados CA y AB, simétricos respecto a sus puntos medios.
Estos seis puntos están en una misma
cónica,
(
𝔖abc xyz
(2 a^2 - 4 a b + 2 b^2 - c^2)^2 (2 a^2 - b^2 - 4 a c +
2 c^2)^2 ((a^2 - 2 (b - c)^2)^2 x^2 -
2 (a^4 + 4 a^2 (b - c)^2 - 4 (b - c)^4) y z) = 0.
)
su centro es:
W = ( a^4 (16 a^12 - 64 a^11 (b + c) - 352 a^9 b c (b + c) +
16 a^10 (5 b^2 + 16 b c + 5 c^2) -
16 a^8 (5 b^4 - 8 b^3 c - 35 b^2 c^2 - 8 b c^3 + 5 c^4) -
32 a^6 b c (5 b^4 - b^3 c - 10 b^2 c^2 - b c^3 + 5 c^4) +
32 a^7 (2 b^5 + 4 b^4 c - 11 b^3 c^2 - 11 b^2 c^3 + 4 b c^4 +
2 c^5) -
32 a^3 b (b - c)^2 c (4 b^5 - 3 b^4 c - 3 b c^4 + 4 c^5) +
32 a (b - c)^4 (2 b^7 - b^5 c^2 - b^2 c^5 + 2 c^7) -
32 a^5 (2 b^7 - 5 b^6 c + 3 b^4 c^3 + 3 b^3 c^4 - 5 b c^6 +
2 c^7) -
8 (b - c)^4 (2 b^8 - 2 b^6 c^2 + b^4 c^4 - 2 b^2 c^6 + 2 c^8) -
8 a^2 (b - c)^2 (10 b^8 - 24 b^7 c + 12 b^6 c^2 + 4 b^5 c^3 -
5 b^4 c^4 + 4 b^3 c^5 + 12 b^2 c^6 - 24 b c^7 + 10 c^8) +
a^4 (80 b^8 - 128 b^7 c - 32 b^6 c^2 + 96 b^5 c^3 - 33 b^4 c^4 +
96 b^3 c^5 - 32 b^2 c^6 - 128 b c^7 + 80 c^8))/(a^2 - 2 (b - c)^2)^2 : ... : ...),
que tiene números de búsqueda en
(11.6062851978057, -2.26388888802463, -0.148774840755044).
- Lunes, 17 de febrero del 2020
El centro del triángulo X(3527)
El 17 de febrero de 1600 fue asesinado por la Inquisición , quemándolo vivo, Giordano Bruno, astrónomo, filósofo, teólogo, matemático y poeta italiano.
Sus teorías cosmológicas superaron el modelo copernicano, pues propuso que el Sol era simplemente una estrella; que el universo debía contener un infinito número de mundos habitados por animales y seres inteligentes. Propuso en el campo teológico una forma particular de panteísmo, lo cual difería considerablemente de la visión cosmológica sostenida por la Iglesia católica.
X(3527) = Isogonal conjugate of X(631), 3/5*OG.
Let H
A be the foot of the A-altitude. Let B
A and C
A be the feet of perpendiculars from H
A to CA and AB, resp. Let G
A be the centroid of H
AB
AC
A. Define G
B and G
C cyclically. The lines AG
A, BG
B, CG
C concur in X(3527). (Randy Hutson, June 7, 2019)
AoPS (Pindp)
Let ABC be an acute triangle, altitudes AD, BE, CF. Line passes though B and perpendicular to AB cuts AD at A
b, line passes though C and perpendicular to AC cuts AD at A
c. FA
b cuts EA
c at X. Define B
a, B
c, C
a, C
b, Y and Z similarly. Prove that XD, YE, ZF are concurrent.
Con las notaciones de las anteriores referencias, los triángulos ABC, , XYZ forman una tripleta de triángulos , con centro de perspectividad común:
X3527 = (a^2/(3 a^4 - 4 a^2 b^2 + b^4 - 4 a^2 c^2 - 2 b^2 c^2 + c^4) : ... : ...).
Sean d1, d2, d3 los ejes de perspectividad de los pares de triángulos (ABC, ), (ABC, XYZ), (, XYZ), respectivamente.
Los tres ejes de perspectividad, d1, d2, d3, concurren (Theorem 17. The Geometry of Homological Triangles (Florentin Smarandache and Ion Pătraşcu) ) en:
W = ( (b^2-c^2)
(5 a^6-15 a^4 (b^2+c^2)+11 a^2 (b^2-c^2)^2-(b^2-c^2)^2 (b^2+c^2))
(a^6-3 a^4 (b^2+c^2)+a^2 (3 b^4+14 b^2 c^2+3 c^4)-(b^2-c^2)^2 (b^2+c^2))
(5 a^12-18 a^10 (b^2+c^2)+a^8 (19 b^4-50 b^2 c^2+19 c^4)+4 a^6 (b^6+43 b^4 c^2+43 b^2 c^4+c^6)-a^4 (21 b^8+100 b^6 c^2+142 b^4 c^4+100 b^2 c^6+21 c^8)+2 a^2 (b^2-c^2)^2 (7 b^6+b^4 c^2+b^2 c^4+7 c^6)-(b^2-c^2)^4 (3 b^4-10 b^2 c^2+3 c^4)) : ... : ...),
que tiene números de búsqueda en
(-14.8362178539846, 15.2549181686618, -0.0729475484039892).
Ninguna recta, determinada por centros de ETC, pasa por W.
- Lunes, 10 de febrero del 2020
El centro X(14683) como foco de una parábola
El 10 de febrero de 1943, el Mahatma Gandhi inicia una huelga de hambre contra su detención.
Dado un triángulo ABC con baricentro G=X2, sean ℰ la y C(U) la cónica circunscrita de un punto U, Q el de intersección de ℰ y C(U) y DEF de Q.
El lugar geométrico de los puntos de intersección de las polares de una recta δ, que pasa por el baricentro, respecto a ℰ y a C(U) es una hipérbola ℋ(δ), circunscrita a DEF (salvo cuando δ es la recta GU, que es una parábola tangente a los lados de ABC en los vértices de DEF).
Una asíntota de ℋ(δ) tiene la dirección del polo de la recta GU, respecto a ℰ.
Cuando δ gira alrededor de G, la envolvente de la otra asíntota de ℋ(δ) es una parábola 𝒫(U), cuyo eje tiene la dirección del polo del la recta GU respecto a ℰ.
Si, en coordenadas baricéntricas, U(u:v:w) el foco de 𝒫(U) es:
U0 = (3 a^2 (u-v) (u-w)+(v-w) (b^2 (u-v)+c^2 (-u+w)): ...:...).
En los siguientes pares {Xi, Xj}, Xj es el foco de la parábola 𝒫(U), para cualquier U sobre la recta GXi. Para {i,j}:
{1,20096}, {6,14683}, {37,20095}, {39,20094}, {514,20098}, {523,20099},
{647,5984}, {650,20097}.
Así, cuando U está sobre la recta X2X6, el foco de la
parábola 𝒫(X6)
( 4 a^4 x^2-4 a^2 b^2 x^2+9 b^4 x^2-4 a^2 c^2 x^2-14 b^2 c^2 x^2+9 c^4 x^2+12 a^4 x y-6 a^2 b^2 x y+12 b^4 x y-18 a^2 c^2 x y-18 b^2 c^2 x y+18 c^4 x y+9 a^4 y^2-4 a^2 b^2 y^2+4 b^4 y^2-14 a^2 c^2 y^2-4 b^2 c^2 y^2+9 c^4 y^2+12 a^4 x z-18 a^2 b^2 x z+18 b^4 x z-6 a^2 c^2 x z-18 b^2 c^2 x z+12 c^4 x z+18 a^4 y z-18 a^2 b^2 y z+12 b^4 y z-18 a^2 c^2 y z-6 b^2 c^2 y z+12 c^4 y z+9 a^4 z^2-14 a^2 b^2 z^2+9 b^4 z^2-4 a^2 c^2 z^2-4 b^2 c^2 z^2+4 c^4 z^2 = 0)
es K0=X14683, su directriz es la recta de Euler y pasa por los centros X523 (dirección del eje, conjugado isogonal del foco de la ), X6562, X31299 y es tangente a los lados del triángulo de Steiner, ceviano del .
Cuando U está sobre la recta de Euler, el foco de la
parábola 𝒫(X3),
( eq = 0)
cuyo eje tiene la dirección de X525, es:
O0 = ( 3 a^10 - b^10 + b^8 c^2 + b^2 c^8 - c^10 - 3 a^8 (b^2 + c^2) +
4 a^4 (b^2 - c^2)^2 (b^2 + c^2) + a^6 (-4 b^4 + 11 b^2 c^2 - 4 c^4) +
a^2 (b^2 - c^2)^2 (b^4 - 3 b^2 c^2 + c^4) : ... : ...),
que tiene números de búsqueda en
(-8.68995726341834, -3.88530296053060, 10.3412391146217).
Es la reflexión de Xi en Xj para los índices {i,j}: {4, 13310}, {8, 13221}, {20, 13200}, {1297, 14900}, {3146, 12384}, {13219, 112}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,112}, {4,13310}, {8,13221}, {20,12253}, {23,11641}, {132,3832}, {148,2794}, {193,2781}, {376,13115}, {390,6020}, {1297,3522}, {1587,35880}, {1588,35881}, {2799,20094}, {2806,20095}, {2825,20077}, {2838,20097}, {2844,20098}, {2853,20100}, {3091,10749}, {3172,26170}, {3320,3600}, {3543,12918}, {3617,13280}, {3622,11722}, {3623,10705}, {3839,19163}, {5261,13296}, {5274,13297}, {6995,13166}, {7500,20099}, {7665,9157}, {7762,12086}, {7793,14676}, {9517,14683}, {9518,20096}, {9530,15683}, {9541,35828}, {9778,12408}, {10735,17578}, {12087,12413} ,{13312,14986}.
El perspector de 𝒫(U), respecto al triángulo ceviano de Q, es:
PU = ((v - w)^3 (3 u^2 + v^2 + v w + w^2 - 3 u (v + w)) : ... : ...).
Para todo punto U sobre la recta X1X2 el perspector PU es X24129.
Si U se mueve sobre la recta de Euler, el perspector PU es:
PO = ( (-b^4+c^4+a^2 (b^2-c^2))^3 (3 a^8-3 a^6 (b^2+c^2)+a^2 (b^2-c^2)^2 (b^2+c^2)+a^4 (-2 b^4+7 b^2 c^2-2 c^4)+(b^2-c^2)^2 (b^4-b^2 c^2+c^4)) : ... : ...),
que tiene números de búsqueda en ETC
(26.568252714286, 66.51164605626, -54.66813019440).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {75,100}, {85,17718}, {312,18037}, {3119,30854}, {3673,17725}, {4872,20947}, {6745,7112}, {14594,31637}, {18057,18743}, {18149,18156}}.
- Domingo, 9 de febrero del 2020
Dos triángulos bilógicos
El 9 de febrero de 1946 la Asamblea General de la ONU, en su Resolución número 32, condena el régimen fascista de Franco y le prohíbe su ingreso en la organización.
Dado un triángulo ABC con circuncentro O=X3, ortocentro H=X4 y centro de la N=X5, sea DEF el de O. La perpendicular por D a BC corta en Ab y Ac a las rectas BH y CH, respectivamente.
Sea Oa el circuncentro del triángulo HAbAc, y se definen cíclicamente los puntos Ob y Oc.
Los triángulos ABC y son .
El centro de ortología de ABC respecto a es el circuncentro y centro de ortología de respecto a ABC es la reflexión de X23181 en X5:
U = ( a^14 (b^2+c^2)-4 a^12 (b^4+b^2 c^2+c^4)+a^10 (5 b^6+8 b^4 c^2+8 b^2 c^4+5 c^6)-a^8 (11 b^6 c^2+2 b^4 c^4+11 b^2 c^6)-a^6 (5 b^10-11 b^8 c^2+2 b^6 c^4+2 b^4 c^6-11 b^2 c^8+5 c^10)+4 a^4 (b^2-c^2)^2 (b^8-b^4 c^4+c^8)-a^2 (b^2-c^2)^4 (b^6+c^6)-b^2 c^2 (b^2-c^2)^6 : ... : ...),
que tiene números de búsqueda en
(1.37065148455076, -0.504731759795997, 3.35748578428126).
Es la reflexión de X23181 en X5.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,110}, {5,23181}, {52,13450}, {53,1625}, {94,12219}, {115,577}, {265,526}, {311,5891}, {317,6528}, {327,11185}, {338,12358}, {381,3613}, {382,17703}, {1141,3153}, {1624,36160}, {2797,6321}, {2980,31723}, {3091,16837}, {5961,30512}, {8797,18537}, {10419,14989}, {11591,25043}, {13556,21731}, {15470,36184}, {15619,31724}, {18404,22261}, {18569,34449}, {23306,35235}.
El centro de perspectividad de ABC y es el punto medio del ortocentro y X31381:
W = (
1/(a^8-3a^6(b^2+c^2)+
a^4(3b^4+5b^2c^2+3c^4)-
a^2(b^6+b^4c^2+b^2c^4+c^6)-b^2c^2(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en ETC (-6.02156715848267, -9.24648646248150, 12.8212630290790).
Es el punto medio de X4 y X31381.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4, 19172}, {5, 389}, {53, 235}, {184, 22261}, {311, 13160}, {403, 13450}, {971, 8064}, {1141, 1614}, {2888, 5877}, {2980, 26883}, {3091, 17500}, {3574, 3613}, {6663, 13406}, {6759, 34449}, {7399, 27356}, {7507, 34845}, {8800, 15760}, {8901, 21659}, {9512, 17824}, {11816, 14157}, {13881, 32445}, {14264, 16868}, {15761, 27361}, {21011, 21670}.
- Viernes, 7 de febrero del 2020
El centro X(13419) como centro radical
El 7 de febrero de 1816 nació Jean Frédéric Frenet, matemático francés. Un fragmento de su tesis doctotal alberga la teoría de curvas en el espacio, incluyendo las fórmulas que actualmente son conocidas como ‘fórmulas de Frenet – Serret’. Frenet aportó seis de dichas fórmulas, mientras que Serret proporcionó las nueve restantes.
X(13419) : Antreas Hatzipolakis and Peter Moses, Hyacinthos 26047.
[Antreas Hatzipolakis]:
Let ABC be a triangle and A'B'C' the pedal triangle of H (orthic triangle).
Denote: A"B"C" = the reflection triangle
(ie A", B", C" = the reflections of A,B,C in BC, CA, AB, resp.)
Ab, Ac = the orthogonal projections of A" on BB', CC', resp.
Na = the NPC center of A"AbAc. Similarly Nb, Nc.
ABC, NaNbNc are orthologic.
[Peter Moses]:
X(13419) is the orthologic center of NaNbNc wrt ABC.
Dado un triángulo ABC, sean A'B'C' su reflexión en el centro de la y DEF el . Sean Ab y Ac las reflexiones de A en C y B, respectivamente, y
la circunferencia Γa
( Ecuación baricéntrica:
a^6 x^2-2 a^4 b^2 x^2+a^2 b^4 x^2-2 a^4 c^2 x^2-2 a^2 b^2 c^2 x^2+4 b^4 c^2 x^2+a^2 c^4 x^2+4 b^2 c^4 x^2+2 a^6 x y-4 a^4 b^2 x y+2 a^2 b^4 x y-4 a^4 c^2 x y+4 b^4 c^2 x y+2 a^2 c^4 x y+a^6 y^2-2 a^4 b^2 y^2+a^2 b^4 y^2-2 a^4 c^2 y^2+2 a^2 b^2 c^2 y^2+a^2 c^4 y^2+2 a^6 x z-4 a^4 b^2 x z+2 a^2 b^4 x z-4 a^4 c^2 x z+2 a^2 c^4 x z+4 b^2 c^4 x z+2 a^6 y z-4 a^4 b^2 y z+2 a^2 b^4 y z-4 a^4 c^2 y z+2 a^2 c^4 y z+a^6 z^2-2 a^4 b^2 z^2+a^2 b^4 z^2-2 a^4 c^2 z^2+2 a^2 b^2 c^2 z^2+a^2 c^4 z^2 = 0)
de centro A' y tangente a AbAc. Las circunferencias Γa y Γa, se definen cíclicamente.
El de las circunferencias Γa, Γb, Γc es X13419.
Sea un punto P sobre su circunferencia circunscrita Γ y D un punto sobre la recta BC, sean Db y Dc las reflexiones de D
en PB y PC, respectivamente.
La envolvente de la recta DbDc, cuando D varía en BC, es una parábola de foco P y directriz da.
La envolvente de da, cuando P se mueve sobre Γ, es una circunferencia Γa.
(ver Euclid #611).
- Miércoles, 5 de febrero del 2020
El centro X(243) como punto fijo finito de una transformación afín
Kirk Douglas, actor y productor de cine estadounidense, uno de los últimos supervivientes de la era dorada de Hollywood, protagonista de joyas del cine como Espartaco o Senderos de Gloria, falleció este miércoles en Los Ángeles a los 103 años de edad.
Dado un triángulo ABC, sean H su ortocentro, DEF y los triángulos y del L. La paralela por L a la recta DH corta a LbLc en A', entonces AA' es la mediana por A.
Los puntos B' y C' se definen cíclicamente.
El punto fijo finito de la transformación afín σ, que aplica ABC en A'B'C' es X343, del de la de H, respecto a la circunferencia circunscrita a ABC; es decir, el punto cuyas coordenadas son los coeficientes de la ecuación de la polar de H, respecto a la circunferencia circunscrita a ABC.
Las coordenadas baricéntricas de A' son:
(2 a^2 (-a^2 + b^2 + c^2) : a^4 - (b^2 - c^2)^2 ; a^4 - (b^2 - c^2)^2).
La matriz M asociada de la transformación afín σ que aplica ABC en A'B'C' tiene las entradas:
M[1,1] = -2 a^2 (a^2 - b^2 - c^2) (a^4 + b^4 - b^2 c^2 -
a^2 (2 b^2 + c^2)) (a^4 - b^2 c^2 + c^4 - a^2 (b^2 + 2 c^2)),
M[1,2] = (a^4 + b^4 - b^2 c^2 -
a^2 (2 b^2 + c^2)) (a^6 (b^2 + c^2) + (b^2 - c^2)^3 (b^2 + c^2) -
a^4 (b^4 + 3 c^4) + a^2 (-b^6 + b^4 c^2 - 3 b^2 c^4 + 3 c^6)),
M[1,3] = (a^2 - b^2 + c^2) (a^4 - b^2 c^2 + c^4 -
a^2 (b^2 + 2 c^2)) (a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2) -
2 a^2 (b^4 + c^4)).
El punto fijo finito de σ, que corresponde la valor propio
λ = 2 (a^4 - 2 a^2 b^2 + b^4 - a^2 c^2 - b^2 c^2) (a^2 b^2 - b^4 +
a^2 c^2 + 2 b^2 c^2 - c^4) (a^4 - a^2 b^2 - 2 a^2 c^2 - b^2 c^2 +
c^4),
es
X343 = ((a^2 - b^2 - c^2) (a^2 b^2 - b^4 + a^2 c^2 + 2 b^2 c^2 - c^4) : ... : ...).
Pares de centros {Xi, Xj = σ(Xi)}, para los índices {i, j}: {5, 3}, {52, 6146}, {343, 343}, {1953, 18650}, {6663, 5447}, {12077, 3265}, {13157, 2}, {14213, 18607}, {15912, 1216}, {31802, 19467}.
- Martes, 4 de febrero del 2020
Puntos de Dixit y puntos de Steiner
El 4 de febrero de 1928 falleció (a los 75 años) Antoon Lorentz, físico neerlandés galardonado con el Premio Nobel de Física del año 1902.
Formuló conjuntamente con George Francis FitzGerald una teoría sobre el cambio de forma de un cuerpo como resultado de su movimiento. En la teoría de la relatividad especial, las transformaciones de Lorentz son un conjunto de relaciones que dan cuenta de cómo se relacionan las medidas de una magnitud física obtenidas por dos observadores diferentes. Matemáticamente el conjunto de todas las transformaciones de Lorentz forman el grupo de Lorentz.
X(3590) = 1st DIXIT POINT
Atul Dixit. Hyacinthoos #2183 (Dec 22, 2000)
Let ABC be a triangle with AD,BE and CF as the medians and with
centroid G. Construct semi-circles with diameters BD,DC and BC all
outwardly.(shoemaker's knife).Let T1 be circle touching the three
semi-circles BD,DC and BC and let A' be the centre of this circle .(It is
easy to prove that the radius of T1 is one-sixth of BC).Similarly define B'
and C' .It seems that AA',BB' and CC' are concurrent.
Paul Yiu. Hyacinthoos #2184 (Dec 22, 2000)
Yes, they are. According to what you have calculated, this perspector is clearly on the , corresponding to the angle θ satisfying tan θ = 2/3. It therefore has homogeneous barycentric coordinates
(1/() : 1/(2SB + 3S) : 1/(2SC+3S)).
Dado un triángulo ABC, en el cuadrado BCDE, levantado externamente sobre le lado BC, se considera el punto medio, Ae, de DE. Sea Sab y Sac los de los triángulos BEAe y CDAe, respectivamente. El centro de la circunferencia Γa, que pasa por Ae, Sab y Sac se denota por A'.
Análogamente, procediendo cíclicamente, se definen los puntos B', C' y las circunferencias Γb y Γc.
Los puntos
A', B', C' son los centros de las circunferencias
consideradas por Atul Dixit.
La circunferencia Γa tiene radio 2a/4 y su ecuación baricéntrica es:
c^2 x y + b^2 x z +
a^2 y z + (x + y + z) ((7 a^2 - 6 b^2 - 6 c^2 - 8 S) x + a^2 y + a^2 z)/12 = 0.
Las coordenadas de Sab y Sac son:
Sab =
(8 a^2 (49 a^4+73 (b^2-c^2)^2-98 a^2 (b^2+c^2)) (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))^2 S+384 a^2 (4 a^8+9 (b^2-c^2)^4-16 a^6 (b^2+c^2)-26 a^2 (b^2-c^2)^2 (b^2+c^2)+a^4 (29 b^4+6 b^2 c^2+29 c^4)) S^3+4608 a^2 (b^2-c^2)^2 S^5 :
29 (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))^4-4 (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))^2 (49 a^6+64 (b^2-c^2)^3-2 a^4 (29 b^2+69 c^2)+a^2 (-7 b^4-146 b^2 c^2+153 c^4)) S-48 (16 a^10+33 (b^2-c^2)^5-8 a^2 (b^2-c^2)^3 (7 b^2+16 c^2)-a^8 (51 b^2+77 c^2)+8 a^6 (8 b^4+3 b^2 c^2+21 c^4)-2 a^4 (3 b^6-9 b^4 c^2-95 b^2 c^4+101 c^6)) S^3-2304 (b^2-c^2)^2 (a^2+b^2-c^2) S^5 :
-3 (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))^4-4 (a^4+(b^2-c^2)^2-2 a^2 (b^2+c^2))^2 (49 a^6-82 (b^2-c^2)^3-4 a^4 (39 b^2+10 c^2)+a^2 (189 b^4-146 b^2 c^2-43 c^4)) S-48 (16 a^10-39 (b^2-c^2)^5+8 a^2 (b^2-c^2)^3 (19 b^2+10 c^2)-a^8 (83 b^2+45 c^2)+8 a^6 (24 b^4+3 b^2 c^2+5 c^4)+a^4 (-238 b^6+202 b^4 c^2+6 b^2 c^4+30 c^6)) S^3-2304 (b^2-c^2)^2 (a^2-b^2+c^2) S^5),
Sac =
(8 a^2 (49 a^4+73 (-b^2+c^2)^2-98 a^2 (b^2+c^2)) (a^4+(-b^2+c^2)^2-2 a^2 (b^2+c^2))^2 S+384 a^2 (4 a^8+9 (-b^2+c^2)^4-16 a^6 (b^2+c^2)-26 a^2 (-b^2+c^2)^2 (b^2+c^2)+a^4 (29 b^4+6 b^2 c^2+29 c^4)) S^3+4608 a^2 (-b^2+c^2)^2 S^5 :
-3 (a^4+(-b^2+c^2)^2-2 a^2 (b^2+c^2))^4-4 (a^4+(-b^2+c^2)^2-2 a^2 (b^2+c^2))^2 (49 a^6-82 (-b^2+c^2)^3-4 a^4 (10 b^2+39 c^2)+a^2 (-43 b^4-146 b^2 c^2+189 c^4)) S-48 (16 a^10-39 (-b^2+c^2)^5+8 a^2 (-b^2+c^2)^3 (10 b^2+19 c^2)-a^8 (45 b^2+83 c^2)+8 a^6 (5 b^4+3 b^2 c^2+24 c^4)+a^4 (30 b^6+6 b^4 c^2+202 b^2 c^4-238 c^6)) S^3-2304 (a^2+b^2-c^2) (-b^2+c^2)^2 S^5 :
29 (a^4+(-b^2+c^2)^2-2 a^2 (b^2+c^2))^4-4 (a^4+(-b^2+c^2)^2-2 a^2 (b^2+c^2))^2 (49 a^6+64 (-b^2+c^2)^3-2 a^4 (69 b^2+29 c^2)+a^2 (153 b^4-146 b^2 c^2-7 c^4)) S-48 (16 a^10+33 (-b^2+c^2)^5-8 a^2 (-b^2+c^2)^3 (16 b^2+7 c^2)-a^8 (77 b^2+51 c^2)+8 a^6 (21 b^4+3 b^2 c^2+8 c^4)-2 a^4 (101 b^6-95 b^4 c^2-9 b^2 c^4+3 c^6)) S^3-2304 (-b^2+c^2)^2 (a^2-b^2+c^2) S^5).
El de las circunferencias Γa, Γb, Γc es:
U = ( 16 a^4 + 13 a^2 (b^2 + c^2) - 29 (b^2 - c^2)^2 +
4 (14 a^2 - b^2 - c^2) S : ... : ...),
que tiene números de búsqueda en
(-0.297935989725528, -0.0833711154923310, 3.83589186481393).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,6398}, {3818,20583}, {14235,15687}.
Si los cuadrados son construidos hacia el interior del triángulo ABC, el centro radical de las circunferencias Γ'a, Γ'b , Γ'c, que se obtienen, es:
V = ( 16 a^4 + 13 a^2 (b^2 + c^2) - 29 (b^2 - c^2)^2 -
4 (14 a^2 - b^2 - c^2) S : ... : ...),
que tiene números de búsqueda en ETC
(3.89275950744947, 7.07838894098036, -3.05641686528640).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,6221}, {3818,20583}, {14239,15687}.
- Sábado, 1 de febrero del 2020
Circunferencias mixtilíneas y cuadriláteros armónicos
En memoria de mi hija Marta
Dado un triángulo ABC, la circunferencia inscrita en el triángulo mixtilineo formado por los dos segmentos AB y AC y el arco BC de la circunferencia circunscrita, que no contiene al vértice A () es tangente en Ac, Ab y Ta, respectivamente.
Si I es el incentro de ABC, los cuadriláteros ITaBAc e ITaCAb son . Entonces, la diagonal IB y las tangentes en Ta y Ac a la circunferencia circunscrita a ITaBAc, son concurrentes en un punto Pab y, así mismo, la diagonal IC y las tangentes en Ta y Ab a la circunferencia circunscrita a ITaCAb, son concurrentes en un punto Pac.
Pab = (-a c (a - b + c), b (a^2 + 2 a b + b^2 - a c + b c - 2 c^2), -c^2 (a -
b + c)),
Pac = (-a b (a + b - c), -b^2 (a + b - c), c (a^2 - a b - 2 b^2 + 2 a c +
b c + c^2)).
Los puntos Pbc, Pba, Pca y Pcb, se definen cíclicamente.
Las rectas PabPac, PbcPba, PcaPcb forman un triángulo perspectivo con ABC. El centro de perspectividad es:
W = ( a/(a^3-a^2 b-2 a b^2-a^2 c+7 a b c-b^2 c-2 a c^2-b c^2) : ... : ...),
que tiene números de búsqueda en
(-8.19169066752207, -9.48027122196374, 13.9847094821233).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {8,17460}, {9,20972}, {256,5919}, {314,17195}, {1149,1320}, {2320,17715}, {3680,13541}, {4866,33795}, {4900,16569}, {4947,6018}, {5255,15179}, {6085,23838}.
Las coordenadas de A1 son:
(a(3a^4+2a^3(b+c)+(b+c)^2(2b^2-5b c+2c^2)-a^2(5b^2+9b c+5c^2)-2a(b^3-5b^2c-5b c^2+c^3)) :
b(-(2b-c)c(b+c)^2-a^2c(10b+c)+a^3(b+2c)-a(b^3-8b^2c-7b c^2+2c^3)) :
c(b(b-2c)(b+c)^2+a^3(2b+c)-a^2b(b+10c)-a(2b^3-7b^2c-8b c^2+c^3))).
La matriz M asociada de la transformación afín σ que aplica ABC en tiene las entradas:
M[1,1] = -a (a + b - 3 c) (b - c) (a - 3 b + c) (3 a^4 +
2 a^3 (b + c) + (b + c)^2 (2 b^2 - 5 b c + 2 c^2) -
a^2 (5 b^2 + 9 b c + 5 c^2) - 2 a (b^3 - 5 b^2 c - 5 b c^2 + c^3)),
M[1,2] = a (a + b - 3 c) (a - c) (3 a^4 (b + 2 c) -
a^3 (b^2 + 27 b c - 7 c^2) + c (b + c)^2 (2 b^2 - 3 b c + c^2) -
a^2 (3 b^3 - 38 b^2 c + 16 b c^2 + 3 c^3) +
a (b^4 - 15 b^3 c + 13 b c^3 - 3 c^4)),
M[1,3] = -a (a - b) (a - 3 b + c) (3 a^4 (2 b + c) +
a^3 (7 b^2 - 27 b c - c^2) + b (b + c)^2 (b^2 - 3 b c + 2 c^2) -
a^2 (3 b^3 + 16 b^2 c - 38 b c^2 + 3 c^3) +
a (-3 b^4 + 13 b^3 c - 15 b c^3 + c^4)).
El punto fijo finito de σ, que corresponde la valor propio
λ = (a - b) (b - c) (c - a) (a + b - 3 c)(3 a - b - c) (a - 3 b + c) (a + b + c)^2,
es:
F = ( a (a - b) (a - c) (3 a - b - c) (a + b - c) (a - b + c) : ... : ...),
que tiene números de búsqueda en ETC
(-0.0584634128350354, -0.106904526326922, 3.74165842144226).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {7,17724}, {40,10696}, {55,17074}, {57,3315}, {78,13539}, {81,3256}, {88,1421}, {100,109}, {108,901}, {165,17080}, {603,3871}, {643,4565}, {644,1415}, {750,8543}, {902,7677}, {934,1293}, {1155,4318}, {1442,4689}, {1457,13587}, {2222,8697}, {2283,8638}, {3052,3756}, {3100,17613}, {3550,4334}, {3562,11248}, {3579,4296}, {3722,14151}, {4188,34040}, {4427,14594}, {4617,7045}, {4848,16948}, {9352,34036}, {11717,13462}, {12515,33649}, {17549,24806}, {24465,33148}, {34474,34586}.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
CASO DE LAS EXCIRCUNFERENCIAS MIXTILÍNEAS
La es tangente a AB y AC, respectivamente, en
A'c = (-a - b + c : 2 b : 0) y
A'b = (a - b + c : 0 : -2 c),
y a la circunferencia circunscrita, exteriormente, en
T'a = (a (a^2 - (b - c)^2) : -2 b^2 (a - b + c) : -2 (a + b - c) c^2).
Si Ia es el de ABC, los cuadriláteros IaT'aBA'c e IaT'aCA'b son armónicos. Entonces, la diagonal IaB y las tangentes en T'a y A'c a la circunferencia circunscrita a IaT'aBA'c, son concurrentes en un punto P'ab y, así mismo, la diagonal IaC y las tangentes en T'a y A'b a la circunferencia circunscrita a IaT'aCA'b, son concurrentes en un punto P'ac.
P'ab = (a (a + b - c) c : -b (a^2 + b^2 + b c - 2 c^2 +
a (-2 b + c)) : -(a + b - c) c^2),
P'ac = (a b (a - b + c) : b^2 (-a + b - c) : -c (a^2 - 2 b^2 + a (b - 2 c) +
b c + c^2)).
Los puntos P'bc, P'ba, P'ca y P'cb, se definen cíclicamente.
Los seis puntos
P'ab,
P'ac,
P'bc,
P'ba,
P'ca y
P'cb están en una misma
cónica,
( a^4 b^3 c^3 x^2-2 a^2 b^5 c^3 x^2+b^7 c^3 x^2+4 a^2 b^4 c^4 x^2-4 b^6 c^4 x^2-2 a^2 b^3 c^5 x^2+6 b^5 c^5 x^2-4 b^4 c^6 x^2+b^3 c^7 x^2+2 a^7 b c^2 x y-3 a^6 b^2 c^2 x y-6 a^5 b^3 c^2 x y+14 a^4 b^4 c^2 x y-6 a^3 b^5 c^2 x y-3 a^2 b^6 c^2 x y+2 a b^7 c^2 x y-4 a^6 b c^3 x y+16 a^5 b^2 c^3 x y-12 a^4 b^3 c^3 x y-12 a^3 b^4 c^3 x y+16 a^2 b^5 c^3 x y-4 a b^6 c^3 x y-3 a^5 b c^4 x y-14 a^4 b^2 c^4 x y+34 a^3 b^3 c^4 x y-14 a^2 b^4 c^4 x y-3 a b^5 c^4 x y+12 a^4 b c^5 x y-8 a^3 b^2 c^5 x y-8 a^2 b^3 c^5 x y+12 a b^4 c^5 x y-8 a^3 b c^6 x y+9 a^2 b^2 c^6 x y-8 a b^3 c^6 x y+a b c^8 x y+a^7 c^3 y^2-2 a^5 b^2 c^3 y^2+a^3 b^4 c^3 y^2-4 a^6 c^4 y^2+4 a^4 b^2 c^4 y^2+6 a^5 c^5 y^2-2 a^3 b^2 c^5 y^2-4 a^4 c^6 y^2+a^3 c^7 y^2+2 a^7 b^2 c x z-4 a^6 b^3 c x z-3 a^5 b^4 c x z+12 a^4 b^5 c x z-8 a^3 b^6 c x z+a b^8 c x z-3 a^6 b^2 c^2 x z+16 a^5 b^3 c^2 x z-14 a^4 b^4 c^2 x z-8 a^3 b^5 c^2 x z+9 a^2 b^6 c^2 x z-6 a^5 b^2 c^3 x z-12 a^4 b^3 c^3 x z+34 a^3 b^4 c^3 x z-8 a^2 b^5 c^3 x z-8 a b^6 c^3 x z+14 a^4 b^2 c^4 x z-12 a^3 b^3 c^4 x z-14 a^2 b^4 c^4 x z+12 a b^5 c^4 x z-6 a^3 b^2 c^5 x z+16 a^2 b^3 c^5 x z-3 a b^4 c^5 x z-3 a^2 b^2 c^6 x z-4 a b^3 c^6 x z+2 a b^2 c^7 x z+a^8 b c y z-8 a^6 b^3 c y z+12 a^5 b^4 c y z-3 a^4 b^5 c y z-4 a^3 b^6 c y z+2 a^2 b^7 c y z+9 a^6 b^2 c^2 y z-8 a^5 b^3 c^2 y z-14 a^4 b^4 c^2 y z+16 a^3 b^5 c^2 y z-3 a^2 b^6 c^2 y z-8 a^6 b c^3 y z-8 a^5 b^2 c^3 y z+34 a^4 b^3 c^3 y z-12 a^3 b^4 c^3 y z-6 a^2 b^5 c^3 y z+12 a^5 b c^4 y z-14 a^4 b^2 c^4 y z-12 a^3 b^3 c^4 y z+14 a^2 b^4 c^4 y z-3 a^4 b c^5 y z+16 a^3 b^2 c^5 y z-6 a^2 b^3 c^5 y z-4 a^3 b c^6 y z-3 a^2 b^2 c^6 y z+2 a^2 b c^7 y z+a^7 b^3 z^2-4 a^6 b^4 z^2+6 a^5 b^5 z^2-4 a^4 b^6 z^2+a^3 b^7 z^2-2 a^5 b^3 c^2 z^2+4 a^4 b^4 c^2 z^2-2 a^3 b^5 c^2 z^2+a^3 b^3 c^4 z^2 = 0)
𝒞.
De las 60 posibles de los hexágonos formados por los seis puntos considerados, la del hexágono P'abP'acP'bcP'baP'caP'cb, inscrito en 𝒞, es la recta que pasa por X(15599) y tiene la dirección de X513, del del .
Los puntos donde los lados opuestos del hexágono P'abP'acP'bcP'baP'caP'cb se cortan son:
U = (-a (b - c) (a^2 + (b - c)^2 - 2 a (b + c)) : -b (a^3 - 3 a (b - c)^2 +
2 (b - c)^2 (b + c)) : c (a^3 - 3 a (b - c)^2 + 2 (b - c)^2 (b + c))),
V = (a (b^3 - 3 b (-a + c)^2 + 2 (-a + c)^2 (a + c)) : -b (-a +
c) (b^2 + (-a + c)^2 - 2 b (a + c)) : -c (b^3 - 3 b (-a + c)^2 +
2 (-a + c)^2 (a + c))),
W = (-a (2 (a - b)^2 (a + b) - 3 (a - b)^2 c +
c^3) : b (2 (a - b)^2 (a + b) - 3 (a - b)^2 c +
c^3) : -(a - b) c ((a - b)^2 - 2 (a + b) c + c^2)).
Hay otras dos rectas de Pascal paralelas a la anteriormente considerada, que pasan por X648 y X5537, y que son, respectivamente, las que corresponden a los hexágonos P'abP'cbP'bcP'acP'caP'ba y P'abP'baP'bcP'cbP'caP'ac. El punto de Steiner correspondiente a estas tres rectas de Pascal es el X513.
X(648) = Of .
X(5537) = Gibert-Burek-Moses concurrent circles image of isogonal conjugate of .
Let P be a point in the plane of a triangle ABC with orthocenter H. Let DEF be the excentral triangle of ABC. The circumcircles of APD, BPE, CPF concur in two points, P and Q. The point Q = Q(P) is the
Gibert-Burek-Moses concurrent circles image of P.
X(15599) = Center of the perspeconic of these triangles: 1st circumperp and yff contact
The perpendicular bisector of BC meets the circumcircle in two points A' and A" (A' in the same side of BC as A). Define B', B", C', C" cyclically. The triangle A'B'C' is the
1st circumperp triangle.
The
Yff contact triangle is the cevian triangle of X(190).
Yff has studied the parabola tangent to sidelines BC, CA, AB and having focus X(101). If A',B',C' are the respective points of tangency, then the lines AA', BB', CC' concur in X(190).
- Jueves, 30 de enero del 2020
Polares respecto a dos cónicas circunscritas
El 30 de enero de 1948, en Nueva Delhi (capital de India), el fanático hinduista Nathuram Godse, aparentemente relacionado con grupos ultraderechistas de la India, asesina al pacifista Mahatma Gandhi, líder de la independencia de India.
En este día, los colegios y centros se convierten en instrumentos de paz y entendimiento entre personas de distinta formación, raza, cultura y religión.
Dados un triángulo ABC, tres puntos L, P y U, una recta δ que pasa por U y las cónicas circunscritas 𝒞(L) y 𝒞(P) a ABC, de L y P, sea
𝒞(δ)
( Si, en coordenadas baricéntricas, L=(l:m:n), P=(p:q:r), U=(u:v:w) y δ: (t v - w)x -t uy+uz =0
𝒞(δ):
(n q t v-m r t v-n q w+m r w) x^2+(n p t u-l r t u) y^2+(m p u-l q u) z^2
+(n q t u-m r t u+n p t v-l r t v-n p w+l r w) x y+(-n q u+m r u-m p t v+l q t v+m p w-l q w) x z+(n p u-l r u+m p t u-l q t u) y z= 0)
la cónica lugar geométrico de los puntos de intersección de las , ℓ y p, de los puntos de δ, respecto a 𝒞(L) y 𝒞(P).
La cónica 𝒞(δ) pasa por los polos, Lδ y Pδ, de la recta δ respecto a las cónicas 𝒞(L) y 𝒞(P), respectivamente.
Cuando δ gira alrededor de
U, la polar
u, de
U respecto 𝒞(δ) pasa por un punto fijo,
Q.
Si U está sobre la recta LP, entonces Q es el , D, de intersección de 𝒞(L) y 𝒞(P).
Si, en coordenadas baricéntricas, L=(l:m:n), P=(p:q:r) y U=(u:v:w), entonces
Q = (u/(3 (n q-m r) u+(n p-l r) v-(m p-l q) w):...:...).
EN PARTICULAR, P=X6, Q=X2, U=X2:
Las polares de los puntos de una recta δ, respecto a la circunferencia circunscrita y a la de un triánguo ABC, se intersecan en puntos sobre una hipérbola ℋ(δ), de entre las cuales solo hay una rectangular (cuando la recta δ tiene la dirección del . X525, del punto de intersección, X112, de las reflexiones, en los lados del triángulo, de la recta que pasa por el ortocentro y simediano).
Esta hipérbola rectangular, de ecuación
𝔖abc xyz
(b^2-c^2)((2a^4-(b^2-c^2)^2-a^2(b^2+c^2))x^2 +
2((b^2+c^2-a^2)^2-b^2c^2)y z) = 0,
tiene centro en X(14731) y pasa por los centros del triángulo X3, X8, X30 (punto del infinito de la recta de Euler), X298, X299, X523, X14264 y por los vértices de los triángulos de y .
Cuando la recta δ gira alrededor del baricentro, el lugar geométrico del centro D de la hipérbola ℋ(δ) es una
parábola
( (-b^4+2 b^2 c^2-c^4) x^2+(-2 a^4+2 a^2 b^2-2 b^4+2 a^2 c^2+2 b^2 c^2-2 c^4) x y+(-a^4+2 a^2 c^2-c^4) y^2+(-2 a^4+2 a^2 b^2-2 b^4+2 a^2 c^2+2 b^2 c^2-2 c^4) x z+(-2 a^4+2 a^2 b^2-2 b^4+2 a^2 c^2+2 b^2 c^2-2 c^4) y z+(-a^4+2 a^2 b^2-b^4) z^2 = 0)
𝒫, que pasa por los centros X523 (dirección de su eje, conjugado isogonal del foco de la ), X6563, X14611, X14721, X14731, X14779, X17161, X30508, X30509, X31296.
La directriz d de 𝒫 es la paralela a la recta de Euler por el circuncentro, X8151, del triángulo de Steiner.
Su foco de 𝒫 es la reflexión de X1511 (punto de intersección de la normal a la circunferencia circunscrita en , con la de X110) en X32204 (centro de la del triángulo de Steiner):
F = ( (b^2 - c^2) (a^10 + b^10 + 6 a^6 b^2 c^2 - b^8 c^2 - b^2 c^8 + c^10 -
2 a^8 (b^2 + c^2) + a^4 (3 b^6 - 5 b^4 c^2 - 5 b^2 c^4 + 3 c^6) +
a^2 (-3 b^8 + 3 b^6 c^2 + b^4 c^4 + 3 b^2 c^6 - 3 c^8)) : ... : ...),
que tiene números de búsqueda en
(12.5375409127293, -6.03607074065305, 2.03292534263837).
Es el punto medio de X15357 y X15357.
Es la reflexión de X1511 en X32204.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,12064}, {110,11123}, {125,523}, {1511,32204}, {5663,8151}, {5972,10190}, {6723,10278}, {8029,15059}, {9168,13291}, {10279,34128}, {15357,19598}.
El punto F ha sido incorporado a ETC con el número X(36739).
Las polares de los puntos de una recta δ , respecto a la circunferencia circunscrita y a la circunelipse de Steiner de un triángulo, se intersecan en puntos sobre una hipérbola ℋ(δ).
Cuando la recta δ gira alrededor de un punto
U, el lugar geométrico del centro
D de la hipérbola ℋ(δ) es una parábola 𝒫(
U) si y solo si
U está sobre la
( b^2 x^2-c^2 x^2+a^2 x y-b^2 x y-a^2 y^2+c^2 y^2-a^2 x z+c^2 x z+b^2 y z-c^2 y z+a^2 z^2-b^2 z^2 = 0
Pasa por los centros X(i), para i: {2, 3, 39, 114, 618, 619, 629, 630, 641, 642, 1125, 1649, 2482, 3413, 3414, 3666, 5664, 5745, 5976, 6292, 6337, 6503, 6509, 6626, 7710, 8290, 8299, 8786, 10291, 10335, 11147, 11165, 13701, 13821, 13882, 13934, 14713, 15349, 15810, 15814, 15819, 15850, 22848, 22892, 27929, 30471, 30472, 33364, 33365, 33614, 33615, 33616, 33617, 33618, 33619, 33620, 33621, 34452, 34834, 34835})
del .
Cuando U=G (baricentro), el foco de 𝒫(G) es X(36739).
Ya que los perspectores de la circunferencia circunscrita y de la elipse circunscrita de Steiner (el simediano y el baricentro) son conjugados isogonales, se puede generalizar el caso particular considerado, tomando las cónicas circunscritas C(P) y C(P*), de perspectores un punto P y su conjugado isogonal P*.
Las polares de los puntos de una recta δ, respecto a C(P) y C(P*) es una cónica
𝒞(δ).
( Si P(p:q:r) y δ: (-r + q t) x - p t y + p z=0,
-c^2 p q^2 r x^2+b^2 p r^3 x^2+c^2 p q^3 t x^2-b^2 p q r^2 t x^2-c^2 p^2 q r x y+a^2 q r^3 x y+2 c^2 p^2 q^2 t x y-b^2 p^2 r^2 t x y-a^2 q^2 r^2 t x y+c^2 p^3 q t y^2-a^2 p q r^2 t y^2-c^2 p^2 q^2 x z+2 b^2 p^2 r^2 x z-a^2 q^2 r^2 x z-b^2 p^2 q r t x z+a^2 q^3 r t x z+c^2 p^3 q y z-a^2 p q r^2 y z+b^2 p^3 r t y z-a^2 p q^2 r t y z+b^2 p^3 r z^2-a^2 p q^2 r z^2 = 0)
Cuando la recta δ gira alrededor de
P, el lugar del centro
D de 𝒞(δ) es una parábola 𝒫(
P) si y solo si
P está sobre la quíntica
Q042 del catálogo de Bernard Gibert.
Cuando P=G (baricentro), el foco de la parábola 𝒫(G) es X(36739).
Como, cuando P está sobre Q042, se conoce la dirección del eje de la parábola 𝒫(P), que tiene punto en el infinito el polo de la recta PP* respecto a C(P), para construirla sólo necesitamos conocer tres puntos sobre ella (IPPPCp(2)). Es decir, tomar los centros de tres hipérbolas del haz; por ejemplo, las que pasan por los vértices de ABC (IPPPP).
- Martes, 28 de enero del 2020
Polo del eje de Brocard respecto a la elipse circunscrita de Steiner
El 28 de enero de 1701 nació Charles-Marie de La Condamine, naturalista, matemático y geógrafo francés, famoso por su expedición de la Académie Royale des Sciences de París a Sudamérica para la medición del meridiano terrestre en la zona del Ecuador, colonia española. Felipe V, primo el rey Luis XV de Francia, quiso participar en la empresa y ordenó elegir a dos oficiales (Jorge Juan y Antonio de Ulloa), para que acompañasen y ayudaran a los científicos franceses en todas las operaciones de la medición (considerados como colaboradores administrativos por La Condamine).
El objetivo era comparar esta medida con una equivalente realizada por otra expedición enviada a Laponia y así determinar si la Tierra está aplanada por los polos o por el ecuador. En sus trabajos contó con colaboración de ilustrados locales.
Ejercicio nº41
Dada una recta r en el plano proyectivo, demostrar que las
rectas polares de los puntos de r respecto de dos cónicas
dadas se intersecan sobre una tercera cónica.
Si
R1 y
R2 son los polos de la recta
r, respecto a dos cónicas dadas, 𝒞
1 y 𝒞
2. A cada punto de
r le corresponde una polar por
R1 y otra por
R2; estas correspondencias son proyectividades. Se tiene así, una correspondecia entre rectas que pasan por
R1 y que pasan por
R2 que es una proyectividad. Por tanto, sus puntos de intersección están sobre una tercera cónica. Esta cónica pasa por
R1 y
R2.
Si
P1 es el polo de
R1R2, respecto a 𝒞
1, la polar de
P1 respecto a 𝒞
2 es la tangente en
R2 a 𝒞
2. Y, análogamente, si
P2 es el polo de
R1R2, respecto a 𝒞
2, la polar de
P2 respecto a 𝒞
1 es la tangente en
R1 a 𝒞
1.
X(31296) is the pole of wrt .
Dado un triángulo ABC, sean Γ la circunferencia circunscrita y ℰ la elipse circunscrita de Steiner.
X31296 es el centro de la hipérbola, ℋ, lugar geométrico del punto de intersección de las polares, con respecto a Γ y ℰ, de un punto que recorre la .
La ecuación de ℋ es:
𝔖abc xyz
(a^2-b^2-c^2) (b^2-c^2)^2x^2-2 a^2 (a^2-b^2) (a^2-c^2)y z = 0.
Sus asíntotas son la rectas X23X385 (polar de X2 respecto a Γ) y X323X401 (polar de X3 respecto a ℰ).
Pasa por los centros X523, X525 (sus puntos del infinito), X4560, X5664, X18311, X20577, X20580.
- Lunes, 27 de enero del 2020
Conjugada isogonal de la circunferencia circunscrita al triángulo antimedial
El 27 de enero de 1945, en Polonia, el Ejército Soviético libera el campo de concentración nazi de Auschwitz.
Preamble of
X(34178):
Let P be a point on the line at infinity. The locus of the , as P varies, is a
quartic which is the
isogonal conjugate of the anticomplementary circle.
This quartic passes through the vertices of ABC and the tangential triangle, the circular points at infinity, and centers X(3446), X(3447), X(9217), X(22259), X(34130), X(34178), X(34179), X(34180), X(34181), X(34182), X(34183), X(34184), X(34185), X(34187), X(34189), X(34190), X(34191) and X(34192). If ABC is acute, the quartic is a closed curve. If ABC is obtuse, it meets the line at infinity at the isogonal conjugates of the anticomplements of PU(4) (the circumcircle intercepts of the anticomplementary circle).
Peter Moses gives the equation for the quartic as:
c^6 x^2 y^2 + b^2 c^2 (a^2 + b^2 + c^2) x^2 y z + a^2 c^2 (a^2 + b^2 + c^2) x y^2 z + b^6 x^2 z^2 + a^2 b^2 (a^2 + b^2 + c^2) x y z^2 + a^6 y^2 z^2 = 0.
Dado un punto P sobre la circunferencia circunscrita a un triángulo ABC, sea Q=P* su (en la recta del infinito), el de Q y el de Q.
Los triángulos ABC y son perspectivos y, cuando P varía sobre la circunferencia circunscrita al triángulo ABC, el lugar geométrico de su centro de perspectividad, Z, es la cuártica , conjugada isogonal de la circunferencia circunscrita al .
El punto Z es el "P*-vertex conjugate of P*" y el conjugado isogonal de la imagen de P en la homotecia de centro el baricentro y razón -2.
Otra construcción del punto Z:
Sea PaPbPc el de P (sobre la circunferencia circunscrita al triángulo ABC) y se denota por ℓa el de las circunferencias circunscritas a ABPb y ACPc. Los ejes radicales ℓb y ℓc se definen cíclicamente.
Las rectas ℓa, ℓb, ℓc concurren en el punto Z.
Más en general, si A'B'C' es un triángulo perspectivo con ABC, con centro de perspectividad P=(u:v:w), (coordenadas baricéntricas) se puede poner:
A'=(u + ξ u + v + w : ξ v : ξ w),
B'=(η u : u + v + η v + w : η w),
B'=(ζ u : ζ v : u + v + w + ζ w).
Entonces, el eje radical de (ABB') y (ACC') es:
ℓa: (1 + η) w (b^2 u^2 + a^2 u v + b^2 u v + c^2 ζ u v + a^2 v^2 +
b^2 u w + b^2 ζ u w + a^2 v w + a^2 ζ v w)y
-(1 + ζ) v (c^2 u^2 +
c^2 u v + c^2 η u v + a^2 u w + c^2 u w + b^2 η u w + a^2 v w +
a^2 η v w + a^2 w^2)z=0.
Las ecuaciones de ℓb y ℓc se deducen por permutación cíclica.
El punto de intersección de estos tres ejes radicales es:
((1 + η) (1 + ζ) u (a^2 ξ v w + c^2 v (u + ξ u + v + w) + b^2 w (u + ξ u + v + w)) :
(1 +ξ) (1 + ζ) v (b^2 η u w + c^2 u (u + v + η v + w) + a^2 w (u + v + η v + w)):
(1 + ξ) (1 +η) w (c^2 ζ u v + b^2 u (u + v + w + ζ w) + a^2 v (u + v + w +ζ w)).
Si ABC = PaPbPc,
Z = ( u (u + v - w) (u - v + w) (c^2 u v + b^2 u w - a^2 v w) :
v (u + v - w) (-u + v + w) (c^2 u v - b^2 u w + a^2 v w) : (u - v -
w) w (u - v + w) (c^2 u v - (b^2 u + a^2 v) w)).
Si P(a^2 (-1 + t) t : -b^2 (-1 + t) : c^2 t), está sobre la circunferencia circunscrita:
Z = ( -b^2 (-1 + t) + (c^2 - a^2 (-1 + t)) t :
b^2 (-1 + t) + (c^2 + a^2 (-1 + t)) t : -b^2 (-1 + t) - c^2 t +
a^2 (-1 + t) t),
que está sobre la cuártica de ecuación
c^6 x^2 y^2 + b^2 c^2 (a^2 + b^2 + c^2) x^2 y z + a^2 c^2 (a^2 + b^2 + c^2) x y^2 z + b^6 x^2 z^2 + a^2 b^2 (a^2 + b^2 + c^2) x y z^2 + a^6 y^2 z^2 = 0.
- Jueves, 23 de enero del 2020
El punto X(15647) como centro de una cónica bitangente a la hipérbola de Jerabek
El 23 de enero de 1862 nació David Hilbert, matemático alemán, desarrolló la teoría de invariantes, la axiomatización de la geometría y la noción de espacio de Hilbert, uno de los fundamentos del análisis funcional.
Suppose that P = p : q : r (barycentyrics) is a point in the plane of a triangle ABC, and let A'B'C' be the cevian triangle of P. Let A'' be the point, other than P, of the interserction of the circumcircles of PBC' and PCB', and define B'' and C'' cyclically. Then A''B''C'' is perspective to ABC, and the perspector is the point
(See
X(18771))
f(P) = a^2(p + q)(p + r) : b^2(q + r)(q + p) : c^2(r + p)(r + q).
El lugar geométrico de f(P), cuando P varía sobre la , es la y si P* es el conjugado isogonal de P, la envolvente de la recta P*f(P) es la cónica, 𝒞, bitangente a la hipérbola de Jerabek en el simediano
(X6) y en el conjugado isogonal del punto del infinito de la recta de Euler (X74), y tangente a la recta de Euler en X24, centro de homotecia de los triángulos y .
La
cónica
( 4 a^12 b^8 c^4 x^2-12 a^10 b^10 c^4 x^2+9 a^8 b^12 c^4 x^2+4 a^6 b^14 c^4 x^2-6 a^4 b^16 c^4 x^2+b^20 c^4 x^2-8 a^12 b^6 c^6 x^2+12 a^10 b^8 c^6 x^2+16 a^8 b^10 c^6 x^2-36 a^6 b^12 c^6 x^2+12 a^4 b^14 c^6 x^2+8 a^2 b^16 c^6 x^2-4 b^18 c^6 x^2+4 a^12 b^4 c^8 x^2+12 a^10 b^6 c^8 x^2-50 a^8 b^8 c^8 x^2+32 a^6 b^10 c^8 x^2+22 a^4 b^12 c^8 x^2-24 a^2 b^14 c^8 x^2+4 b^16 c^8 x^2-12 a^10 b^4 c^10 x^2+16 a^8 b^6 c^10 x^2+32 a^6 b^8 c^10 x^2-56 a^4 b^10 c^10 x^2+16 a^2 b^12 c^10 x^2+4 b^14 c^10 x^2+9 a^8 b^4 c^12 x^2-36 a^6 b^6 c^12 x^2+22 a^4 b^8 c^12 x^2+16 a^2 b^10 c^12 x^2-10 b^12 c^12 x^2+4 a^6 b^4 c^14 x^2+12 a^4 b^6 c^14 x^2-24 a^2 b^8 c^14 x^2+4 b^10 c^14 x^2-6 a^4 b^4 c^16 x^2+8 a^2 b^6 c^16 x^2+4 b^8 c^16 x^2-4 b^6 c^18 x^2+b^4 c^20 x^2+4 a^16 b^4 c^4 x y-10 a^14 b^6 c^4 x y+4 a^12 b^8 c^4 x y+4 a^10 b^10 c^4 x y+4 a^8 b^12 c^4 x y-10 a^6 b^14 c^4 x y+4 a^4 b^16 c^4 x y-4 a^16 b^2 c^6 x y+24 a^12 b^6 c^6 x y-20 a^10 b^8 c^6 x y-20 a^8 b^10 c^6 x y+24 a^6 b^12 c^6 x y-4 a^2 b^16 c^6 x y+10 a^14 b^2 c^8 x y-24 a^12 b^4 c^8 x y-6 a^10 b^6 c^8 x y+40 a^8 b^8 c^8 x y-6 a^6 b^10 c^8 x y-24 a^4 b^12 c^8 x y+10 a^2 b^14 c^8 x y-4 a^12 b^2 c^10 x y+28 a^10 b^4 c^10 x y-24 a^8 b^6 c^10 x y-24 a^6 b^8 c^10 x y+28 a^4 b^10 c^10 x y-4 a^2 b^12 c^10 x y-6 a^10 b^2 c^12 x y-4 a^8 b^4 c^12 x y+18 a^6 b^6 c^12 x y-4 a^4 b^8 c^12 x y-6 a^2 b^10 c^12 x y+4 a^8 b^2 c^14 x y+4 a^2 b^8 c^14 x y-2 a^6 b^2 c^16 x y-8 a^4 b^4 c^16 x y-2 a^2 b^6 c^16 x y+4 a^4 b^2 c^18 x y+4 a^2 b^4 c^18 x y-2 a^2 b^2 c^20 x y+a^20 c^4 y^2-6 a^16 b^4 c^4 y^2+4 a^14 b^6 c^4 y^2+9 a^12 b^8 c^4 y^2-12 a^10 b^10 c^4 y^2+4 a^8 b^12 c^4 y^2-4 a^18 c^6 y^2+8 a^16 b^2 c^6 y^2+12 a^14 b^4 c^6 y^2-36 a^12 b^6 c^6 y^2+16 a^10 b^8 c^6 y^2+12 a^8 b^10 c^6 y^2-8 a^6 b^12 c^6 y^2+4 a^16 c^8 y^2-24 a^14 b^2 c^8 y^2+22 a^12 b^4 c^8 y^2+32 a^10 b^6 c^8 y^2-50 a^8 b^8 c^8 y^2+12 a^6 b^10 c^8 y^2+4 a^4 b^12 c^8 y^2+4 a^14 c^10 y^2+16 a^12 b^2 c^10 y^2-56 a^10 b^4 c^10 y^2+32 a^8 b^6 c^10 y^2+16 a^6 b^8 c^10 y^2-12 a^4 b^10 c^10 y^2-10 a^12 c^12 y^2+16 a^10 b^2 c^12 y^2+22 a^8 b^4 c^12 y^2-36 a^6 b^6 c^12 y^2+9 a^4 b^8 c^12 y^2+4 a^10 c^14 y^2-24 a^8 b^2 c^14 y^2+12 a^6 b^4 c^14 y^2+4 a^4 b^6 c^14 y^2+4 a^8 c^16 y^2+8 a^6 b^2 c^16 y^2-6 a^4 b^4 c^16 y^2-4 a^6 c^18 y^2+a^4 c^20 y^2-4 a^16 b^6 c^2 x z+10 a^14 b^8 c^2 x z-4 a^12 b^10 c^2 x z-6 a^10 b^12 c^2 x z+4 a^8 b^14 c^2 x z-2 a^6 b^16 c^2 x z+4 a^4 b^18 c^2 x z-2 a^2 b^20 c^2 x z+4 a^16 b^4 c^4 x z-24 a^12 b^8 c^4 x z+28 a^10 b^10 c^4 x z-4 a^8 b^12 c^4 x z-8 a^4 b^16 c^4 x z+4 a^2 b^18 c^4 x z-10 a^14 b^4 c^6 x z+24 a^12 b^6 c^6 x z-6 a^10 b^8 c^6 x z-24 a^8 b^10 c^6 x z+18 a^6 b^12 c^6 x z-2 a^2 b^16 c^6 x z+4 a^12 b^4 c^8 x z-20 a^10 b^6 c^8 x z+40 a^8 b^8 c^8 x z-24 a^6 b^10 c^8 x z-4 a^4 b^12 c^8 x z+4 a^2 b^14 c^8 x z+4 a^10 b^4 c^10 x z-20 a^8 b^6 c^10 x z-6 a^6 b^8 c^10 x z+28 a^4 b^10 c^10 x z-6 a^2 b^12 c^10 x z+4 a^8 b^4 c^12 x z+24 a^6 b^6 c^12 x z-24 a^4 b^8 c^12 x z-4 a^2 b^10 c^12 x z-10 a^6 b^4 c^14 x z+10 a^2 b^8 c^14 x z+4 a^4 b^4 c^16 x z-4 a^2 b^6 c^16 x z-2 a^20 b^2 c^2 y z+4 a^18 b^4 c^2 y z-2 a^16 b^6 c^2 y z+4 a^14 b^8 c^2 y z-6 a^12 b^10 c^2 y z-4 a^10 b^12 c^2 y z+10 a^8 b^14 c^2 y z-4 a^6 b^16 c^2 y z+4 a^18 b^2 c^4 y z-8 a^16 b^4 c^4 y z-4 a^12 b^8 c^4 y z+28 a^10 b^10 c^4 y z-24 a^8 b^12 c^4 y z+4 a^4 b^16 c^4 y z-2 a^16 b^2 c^6 y z+18 a^12 b^6 c^6 y z-24 a^10 b^8 c^6 y z-6 a^8 b^10 c^6 y z+24 a^6 b^12 c^6 y z-10 a^4 b^14 c^6 y z+4 a^14 b^2 c^8 y z-4 a^12 b^4 c^8 y z-24 a^10 b^6 c^8 y z+40 a^8 b^8 c^8 y z-20 a^6 b^10 c^8 y z+4 a^4 b^12 c^8 y z-6 a^12 b^2 c^10 y z+28 a^10 b^4 c^10 y z-6 a^8 b^6 c^10 y z-20 a^6 b^8 c^10 y z+4 a^4 b^10 c^10 y z-4 a^10 b^2 c^12 y z-24 a^8 b^4 c^12 y z+24 a^6 b^6 c^12 y z+4 a^4 b^8 c^12 y z+10 a^8 b^2 c^14 y z-10 a^4 b^6 c^14 y z-4 a^6 b^2 c^16 y z+4 a^4 b^4 c^16 y z+a^20 b^4 z^2-4 a^18 b^6 z^2+4 a^16 b^8 z^2+4 a^14 b^10 z^2-10 a^12 b^12 z^2+4 a^10 b^14 z^2+4 a^8 b^16 z^2-4 a^6 b^18 z^2+a^4 b^20 z^2+8 a^16 b^6 c^2 z^2-24 a^14 b^8 c^2 z^2+16 a^12 b^10 c^2 z^2+16 a^10 b^12 c^2 z^2-24 a^8 b^14 c^2 z^2+8 a^6 b^16 c^2 z^2-6 a^16 b^4 c^4 z^2+12 a^14 b^6 c^4 z^2+22 a^12 b^8 c^4 z^2-56 a^10 b^10 c^4 z^2+22 a^8 b^12 c^4 z^2+12 a^6 b^14 c^4 z^2-6 a^4 b^16 c^4 z^2+4 a^14 b^4 c^6 z^2-36 a^12 b^6 c^6 z^2+32 a^10 b^8 c^6 z^2+32 a^8 b^10 c^6 z^2-36 a^6 b^12 c^6 z^2+4 a^4 b^14 c^6 z^2+9 a^12 b^4 c^8 z^2+16 a^10 b^6 c^8 z^2-50 a^8 b^8 c^8 z^2+16 a^6 b^10 c^8 z^2+9 a^4 b^12 c^8 z^2-12 a^10 b^4 c^10 z^2+12 a^8 b^6 c^10 z^2+12 a^6 b^8 c^10 z^2-12 a^4 b^10 c^10 z^2+4 a^8 b^4 c^12 z^2-8 a^6 b^6 c^12 z^2+4 a^4 b^8 c^12 z^2 = 0)
𝒞 pasa por los centros del triángulo X(6), X(24), X(74), X(1498), X(1614), X(1620) y su centro es X(15647) (HG211217):
(a^2(2a^10 -3a^8(b^2+c^2) -2a^6(b^4-5b^2c^2+c^4) +a^4(4b^6-5b^4c^2-5b^2c^4+4c^6) -4a^2b^2c^2(b^2-c^2)^2 -(b^2-c^2)^2(b^6+c^6)) : ... : ...).
- Sábado, 18 de enero del 2020
Una propiedad geométrica del centro X(6353)
El 18 de enero de 1904 nació Cary Grant, actor de origen británico. Según la lista del American Film Institute, está considerado la segunda estrella masculina más importante, trás Humphrey Bogart, de los primeros cien años del cine.
X(6353) = X(393)- OF X(4)
X(393) is the Brianchon point (perspector) of the inellipse that is the barycentric square of the orthic axis. (Randy Hutson, October 15, 2018)
Dado un triángulo ABC con ortocentro H=X4, centro de la N=X5 y DEF, sea D' la reflexión de D en N.
Las recta D'H, vuelve a corta a la circunferencia de los nueve puntos, γ, en A' y pasa por el punto A", en el que la paralela a BC por A vuelve a cortar a la circunferencia circunscrita, Γ, a ABC.
La tangente a γ en A' y el eje radical de de Γ y γ se cortan en Pa. Los puntos de contacto de las tangentes por Pa a Γ son A" y Ta. Las dos circunferencias tangentes a γ en A' y que son tangentes a Γ pasan por A" y Ta.
Los puntos Tb y Tc se definen cíclicamente.
es el de X
6353.
- Viernes, 17 de enero del 2020
Triángulo medial y excircunferencias mixtilíneas
El 17 de enero del 1966, cerca de las costas de España colisionan dos aeronaves de la Fuerza Aérea de los Estados Unidos. Caen cuatro bombas atómicas, tres en las cercanías de Palomares y otra en las proximidades de Almería.
Dado un triángulo ABC con circuncentro O y DEF, sean Γa la circunferencia circunscrita al triángulo AEF, (Oa) el de AEF y Ta el punto de tangencia de ambas.
La circunferencia que pasa por B, C y O es tangente a (Oa) en A1. Existe otra circunferencia tangente a (Oa) y que pasa por B y C; sea A2 su punto de tangencia.
Los puntos de tangencia, Tb, B1, B2, Tc, C1, C2, se definen cíclicamente.
Las rectas
ATa,
BTb y
CTc concurren en X
55 (centro de homotecia interior de las circunferencias inscrita y circunscrita a ABC).
Las rectas AA1, BB1 y CC1 concurren en X59 (conjugado isogonal de ).
Las rectas AA2, BB2 y CC2 concurren en X6065 (perspector de ABC y la reflexión del en la recta que pasa por el incentro y simediano).
El del triángulo AEF tiene coordenadas baricéntricas:
I'a = (-2 a + b + c : b : c).
La perpendicular en I'a a la bisectriz interior en A, corta a los lados AB y AC en los puntos de tangencia de la A-excircunferencia mixtilínea de AEF, cuya ecuación es:
(Oa):
a^2 y z + b^2 x z + c^2 x y
- (x + y + z) ((b^2 c^2 x)/(-a + b + c)^2 + (c^2 (a^2 - 2 a c + c^2) y)/(-a + b + c)^2 + (
b^2 (a^2 - 2 a b + b^2) z)/(-a + b + c)^2) = 0.
Esta circunferencia y la circunscrita a AEF,
Γa: a^2 y z + b^2 x z+c^2 x y + (x + y + z) (-((c^2 y)/2) - (b^2 z)/2) = 0,
son tangentes en el punto:
Ta = (-a^3 - (b - c)^2 (b + c) +
2 a (b^2 - b c + c^2) : b^2 (a - b + c) : (a + b - c) c^2).
La circunferencia que pasa por B, C, O, de ecuación
a^2 y z+ b^2 x z +c^2 x y - (
b^2 c^2 x (x + y + z))/(-a^2 + b^2 + c^2) = 0,
es tangente a (Oa) en:
A1 = (a (a - b) (a - c) (a^2 - b^2 - c^2) : -(a - b)^2 b^2 (a + b -
c) : -(a - c)^2 c^2 (a - b + c)).
Los puntos de tangencia A1 y A2 de las dos circunferencias que pasan por B y C y son tangentes a (Oa) están en la polar, respecto a (Oa), del punto P(0 : (a - b)^2 b^2 : -(a - c)^2 c^2), de intersección de BC y el , -b^2 c^2 x + (-a^2 c^2 + 2 a c^3 - c^4) y + (-a^2 b^2 + 2 a b^3 - b^4) z=0, de (Oa) y la circunferencia circunscrita a ABC.
A2 = (-a (a - b) (a - c) (a^2 + b^2 + c^2 - 2 a (b + c)) : -(a - b)^2 b^2 (a - b + c) : -(a - c)^2 (a + b - c) c^2).
Las rectas ATa, BTb y CTc concurren en:
X55 = (a^2 (a b+ c-a) : b^2 (a - b + c) : c^2 (a + b - c)).
Las rectas AA1, BB1 y CC1 concurren en:
X59 = (a^2 (a - b)^2 (a - c)^2 (a + b - c) (a - b + c) : ... : ...).
Las rectas AA2, BB2 y CC2 concurren en:
X6065 = (a^2 (a - b)^2 (a - c)^2 (a - b - c) : ... : ...).
- Jueves, 16 de enero del 2020
Pares de puntos conjugados isotómicos y punto de Miquel
a Aye, por su "cumple"
Dados un triángulo ABC, S su , ℰ la y una recta ℓ (distinta de la ), sea 𝒞ℓ la cónica circunscrita, lugar geométrico de los de los puntos de ℓ. Además de en los vértices de ABC, 𝒞ℓ y ℰ se cortan en un Q (conjugado isotómico del punto del infinito de la recta ℓ).
Sean U, V dos puntos sobre la recta ℓ y U', V' sus conjugados isotómicos, el del cuadrilátero completo formado por las rectas UV, UV', U'V, U'V' está sobre la circunferencia del haz de cónicas generado por ℰ y la cónica degenerada producto de las rectas ℓ y SQ.
Si px+qy+rz=0 es la ecuación de la recta ℓ, la ecuación del haz
SQ · ℓ + λ ℰ es:
((b^2-c^2)(q-r)x+(a^2-c^2)(p-r)y+(a^2-b^2)(p-q)z)(p x+q y+r z) + λ (x y + x z + y z) = 0
La circunferencia Γℓ de este haz de cónicas se obtiene para
λ = -a^2 (p - q) (p - r) + (q - r) (b^2 (p - q) + c^2 (-p + r)),
y su ecuación es:
a^2 y z + b^2 x z+ c^2 x y -
(x + y + z) (
(b^2 p q - c^2 p q - b^2 p r + c^2 p r) x /(p^2 - p q + q^2 - p r - q r +r^2) +
(a^2 p q - c^2 p q - a^2 q r + c^2 q r) y /(p^2 - p q + q^2 - p r - q r + r^2) +
(a^2 p r - b^2 p r - a^2 q r + b^2 q r) z /(p^2 - p q + q^2 - p r - q r + r^2)) = 0.
El centro de esta circunferencia es:
Z = ( a^4 (p^2 + q^2 + q r + r^2 - 2 p (q + r)) -
a^2 (b^2 (p^2 + q^2 + r^2 - p (2 q + r)) +
c^2 (p^2 + q^2 + r^2 - p (q + 2 r)))-(b^2 - c^2) (b^2 (p - q) r + c^2 q (-p + r)) : ... : ...).
Pares {L=Xi, Z=Xj} (siendo L el de ℓ), para los índices {i, j}: {76, 99}, {83, 9862}, {99, 2}, {671, 376}, {1916, 3098}, {8781, 69}. El primer caso corresponde a ℓ=GK, que pasa por el baricentro y simediano, para cuyos puntos, el punto de Miquel es fijo, M=X99.
Cuando la recta ℓ gira alrededor de un punto P(u:v:w), el lugar geométrico de Z es una
elipse,
( (a^4 b^4 u^3-2 a^4 b^2 c^2 u^3+a^4 c^4 u^3-a^6 b^2 u^2 v+2 a^4 b^4 u^2 v+a^6 c^2 u^2 v-3 a^4 b^2 c^2 u^2 v+a^4 c^4 u^2 v-a^4 b^4 u v^2+2 a^2 b^6 u v^2+a^6 c^2 u v^2-a^4 b^2 c^2 u v^2-3 a^2 b^4 c^2 u v^2+3 a^2 b^2 c^4 u v^2-a^2 c^6 u v^2+b^8 v^3-2 a^2 b^4 c^2 v^3-2 b^6 c^2 v^3+a^4 c^4 v^3+2 a^2 b^2 c^4 v^3+3 b^4 c^4 v^3-2 a^2 c^6 v^3-2 b^2 c^6 v^3+c^8 v^3+a^6 b^2 u^2 w+a^4 b^4 u^2 w-a^6 c^2 u^2 w-3 a^4 b^2 c^2 u^2 w+2 a^4 c^4 u^2 w-a^8 u v w+2 a^6 b^2 u v w-2 a^4 b^4 u v w+a^2 b^6 u v w+2 a^6 c^2 u v w-a^4 b^2 c^2 u v w-2 a^4 c^4 u v w+a^2 c^6 u v w+a^4 b^4 v^2 w-2 a^2 b^6 v^2 w+3 b^8 v^2 w-a^6 c^2 v^2 w+a^4 b^2 c^2 v^2 w-3 a^2 b^4 c^2 v^2 w-6 b^6 c^2 v^2 w+3 a^4 c^4 v^2 w+3 a^2 b^2 c^4 v^2 w+9 b^4 c^4 v^2 w-5 a^2 c^6 v^2 w-6 b^2 c^6 v^2 w+3 c^8 v^2 w+a^6 b^2 u w^2-a^2 b^6 u w^2-a^4 b^2 c^2 u w^2+3 a^2 b^4 c^2 u w^2-a^4 c^4 u w^2-3 a^2 b^2 c^4 u w^2+2 a^2 c^6 u w^2-a^6 b^2 v w^2+3 a^4 b^4 v w^2-5 a^2 b^6 v w^2+3 b^8 v w^2+a^4 b^2 c^2 v w^2+3 a^2 b^4 c^2 v w^2-6 b^6 c^2 v w^2+a^4 c^4 v w^2-3 a^2 b^2 c^4 v w^2+9 b^4 c^4 v w^2-2 a^2 c^6 v w^2-6 b^2 c^6 v w^2+3 c^8 v w^2+a^4 b^4 w^3-2 a^2 b^6 w^3+b^8 w^3+2 a^2 b^4 c^2 w^3-2 b^6 c^2 w^3-2 a^2 b^2 c^4 w^3+3 b^4 c^4 w^3-2 b^2 c^6 w^3+c^8 w^3) x^2+(2 a^6 b^2 u^3-2 a^6 c^2 u^3-2 a^4 b^2 c^2 u^3-2 a^2 b^4 c^2 u^3+2 a^4 c^4 u^3+4 a^2 b^2 c^4 u^3-2 a^2 c^6 u^3-a^8 u^2 v+2 a^6 b^2 u^2 v+2 a^4 b^4 u^2 v-a^2 b^6 u^2 v-3 a^4 b^2 c^2 u^2 v-2 a^2 b^4 c^2 u^2 v+4 a^2 b^2 c^4 u^2 v-a^2 c^6 u^2 v-a^6 b^2 u v^2+2 a^4 b^4 u v^2+2 a^2 b^6 u v^2-b^8 u v^2-2 a^4 b^2 c^2 u v^2-3 a^2 b^4 c^2 u v^2+4 a^2 b^2 c^4 u v^2-b^2 c^6 u v^2+2 a^2 b^6 v^3-2 a^4 b^2 c^2 v^3-2 a^2 b^4 c^2 v^3-2 b^6 c^2 v^3+4 a^2 b^2 c^4 v^3+2 b^4 c^4 v^3-2 b^2 c^6 v^3+a^8 u^2 w+4 a^6 b^2 u^2 w-2 a^4 b^4 u^2 w+a^2 b^6 u^2 w-6 a^6 c^2 u^2 w-3 a^4 b^2 c^2 u^2 w-4 a^2 b^4 c^2 u^2 w+6 a^4 c^4 u^2 w+8 a^2 b^2 c^4 u^2 w-5 a^2 c^6 u^2 w-2 a^8 u v w+6 a^6 b^2 u v w-8 a^4 b^4 u v w+6 a^2 b^6 u v w-2 b^8 u v w+3 a^6 c^2 u v w-2 a^4 b^2 c^2 u v w-2 a^2 b^4 c^2 u v w+3 b^6 c^2 u v w-6 a^4 c^4 u v w+5 a^2 b^2 c^4 u v w-6 b^4 c^4 u v w+4 a^2 c^6 u v w+4 b^2 c^6 u v w-3 c^8 u v w+a^6 b^2 v^2 w-2 a^4 b^4 v^2 w+4 a^2 b^6 v^2 w+b^8 v^2 w-4 a^4 b^2 c^2 v^2 w-3 a^2 b^4 c^2 v^2 w-6 b^6 c^2 v^2 w+8 a^2 b^2 c^4 v^2 w+6 b^4 c^4 v^2 w-5 b^2 c^6 v^2 w+a^8 u w^2+3 a^6 b^2 u w^2-6 a^4 b^4 u w^2+3 a^2 b^6 u w^2-b^8 u w^2-3 a^6 c^2 u w^2+a^4 b^2 c^2 u w^2-a^2 b^4 c^2 u w^2+3 b^6 c^2 u w^2+3 a^2 b^2 c^4 u w^2-6 b^4 c^4 u w^2+a^2 c^6 u w^2+5 b^2 c^6 u w^2-3 c^8 u w^2-a^8 v w^2+3 a^6 b^2 v w^2-6 a^4 b^4 v w^2+3 a^2 b^6 v w^2+b^8 v w^2+3 a^6 c^2 v w^2-a^4 b^2 c^2 v w^2+a^2 b^4 c^2 v w^2-3 b^6 c^2 v w^2-6 a^4 c^4 v w^2+3 a^2 b^2 c^4 v w^2+5 a^2 c^6 v w^2+b^2 c^6 v w^2-3 c^8 v w^2+2 a^6 b^2 w^3-4 a^4 b^4 w^3+2 a^2 b^6 w^3-2 a^4 c^4 w^3+2 a^2 b^2 c^4 w^3-2 b^4 c^4 w^3+2 a^2 c^6 w^3+2 b^2 c^6 w^3-2 c^8 w^3) x y+(a^8 u^3-2 a^6 c^2 u^3-2 a^4 b^2 c^2 u^3+3 a^4 c^4 u^3+2 a^2 b^2 c^4 u^3+b^4 c^4 u^3-2 a^2 c^6 u^3-2 b^2 c^6 u^3+c^8 u^3+2 a^6 b^2 u^2 v-a^4 b^4 u^2 v-3 a^4 b^2 c^2 u^2 v-a^2 b^4 c^2 u^2 v+b^6 c^2 u^2 v+3 a^2 b^2 c^4 u^2 v-b^2 c^6 u^2 v+2 a^4 b^4 u v^2-a^2 b^6 u v^2-3 a^2 b^4 c^2 u v^2+b^6 c^2 u v^2+b^4 c^4 u v^2+a^4 b^4 v^3-2 a^2 b^4 c^2 v^3+b^4 c^4 v^3+3 a^8 u^2 w-2 a^6 b^2 u^2 w+a^4 b^4 u^2 w-6 a^6 c^2 u^2 w-3 a^4 b^2 c^2 u^2 w+a^2 b^4 c^2 u^2 w-b^6 c^2 u^2 w+9 a^4 c^4 u^2 w+3 a^2 b^2 c^4 u^2 w+3 b^4 c^4 u^2 w-6 a^2 c^6 u^2 w-5 b^2 c^6 u^2 w+3 c^8 u^2 w+a^6 b^2 u v w-2 a^4 b^4 u v w+2 a^2 b^6 u v w-b^8 u v w-a^2 b^4 c^2 u v w+2 b^6 c^2 u v w-2 b^4 c^4 u v w+b^2 c^6 u v w+a^4 b^4 v^2 w+a^2 b^6 v^2 w-3 a^2 b^4 c^2 v^2 w-b^6 c^2 v^2 w+2 b^4 c^4 v^2 w+3 a^8 u w^2-5 a^6 b^2 u w^2+3 a^4 b^4 u w^2-a^2 b^6 u w^2-6 a^6 c^2 u w^2+3 a^4 b^2 c^2 u w^2+a^2 b^4 c^2 u w^2+9 a^4 c^4 u w^2-3 a^2 b^2 c^4 u w^2+b^4 c^4 u w^2-6 a^2 c^6 u w^2-2 b^2 c^6 u w^2+3 c^8 u w^2-a^6 b^2 v w^2+a^2 b^6 v w^2+3 a^4 b^2 c^2 v w^2-a^2 b^4 c^2 v w^2-3 a^2 b^2 c^4 v w^2-b^4 c^4 v w^2+2 b^2 c^6 v w^2+a^8 w^3-2 a^6 b^2 w^3+a^4 b^4 w^3-2 a^6 c^2 w^3+2 a^4 b^2 c^2 w^3+3 a^4 c^4 w^3-2 a^2 b^2 c^4 w^3-2 a^2 c^6 w^3+c^8 w^3) y^2+(-2 a^6 b^2 u^3+2 a^4 b^4 u^3-2 a^2 b^6 u^3+2 a^6 c^2 u^3-2 a^4 b^2 c^2 u^3+4 a^2 b^4 c^2 u^3-2 a^2 b^2 c^4 u^3+a^8 u^2 v-6 a^6 b^2 u^2 v+6 a^4 b^4 u^2 v-5 a^2 b^6 u^2 v+4 a^6 c^2 u^2 v-3 a^4 b^2 c^2 u^2 v+8 a^2 b^4 c^2 u^2 v-2 a^4 c^4 u^2 v-4 a^2 b^2 c^4 u^2 v+a^2 c^6 u^2 v+a^8 u v^2-3 a^6 b^2 u v^2+a^2 b^6 u v^2-3 b^8 u v^2+3 a^6 c^2 u v^2+a^4 b^2 c^2 u v^2+3 a^2 b^4 c^2 u v^2+5 b^6 c^2 u v^2-6 a^4 c^4 u v^2-a^2 b^2 c^4 u v^2-6 b^4 c^4 u v^2+3 a^2 c^6 u v^2+3 b^2 c^6 u v^2-c^8 u v^2-2 a^4 b^4 v^3+2 a^2 b^6 v^3-2 b^8 v^3+2 a^6 c^2 v^3+2 a^2 b^4 c^2 v^3+2 b^6 c^2 v^3-4 a^4 c^4 v^3-2 b^4 c^4 v^3+2 a^2 c^6 v^3-a^8 u^2 w-a^2 b^6 u^2 w+2 a^6 c^2 u^2 w-3 a^4 b^2 c^2 u^2 w+4 a^2 b^4 c^2 u^2 w+2 a^4 c^4 u^2 w-2 a^2 b^2 c^4 u^2 w-a^2 c^6 u^2 w-2 a^8 u v w+3 a^6 b^2 u v w-6 a^4 b^4 u v w+4 a^2 b^6 u v w-3 b^8 u v w+6 a^6 c^2 u v w-2 a^4 b^2 c^2 u v w+5 a^2 b^4 c^2 u v w+4 b^6 c^2 u v w-8 a^4 c^4 u v w-2 a^2 b^2 c^4 u v w-6 b^4 c^4 u v w+6 a^2 c^6 u v w+3 b^2 c^6 u v w-2 c^8 u v w-a^8 v^2 w+3 a^6 b^2 v^2 w-6 a^4 b^4 v^2 w+5 a^2 b^6 v^2 w-3 b^8 v^2 w+3 a^6 c^2 v^2 w-a^4 b^2 c^2 v^2 w+3 a^2 b^4 c^2 v^2 w+b^6 c^2 v^2 w-6 a^4 c^4 v^2 w+a^2 b^2 c^4 v^2 w+3 a^2 c^6 v^2 w-3 b^2 c^6 v^2 w+c^8 v^2 w-a^6 c^2 u w^2-2 a^4 b^2 c^2 u w^2+4 a^2 b^4 c^2 u w^2-b^6 c^2 u w^2+2 a^4 c^4 u w^2-3 a^2 b^2 c^4 u w^2+2 a^2 c^6 u w^2-c^8 u w^2+a^6 c^2 v w^2-4 a^4 b^2 c^2 v w^2+8 a^2 b^4 c^2 v w^2-5 b^6 c^2 v w^2-2 a^4 c^4 v w^2-3 a^2 b^2 c^4 v w^2+6 b^4 c^4 v w^2+4 a^2 c^6 v w^2-6 b^2 c^6 v w^2+c^8 v w^2-2 a^4 b^2 c^2 w^3+4 a^2 b^4 c^2 w^3-2 b^6 c^2 w^3-2 a^2 b^2 c^4 w^3+2 b^4 c^4 w^3+2 a^2 c^6 w^3-2 b^2 c^6 w^3) x z+(-2 a^8 u^3+2 a^6 b^2 u^3-2 a^4 b^4 u^3+2 a^6 c^2 u^3+2 a^4 b^2 c^2 u^3+2 b^6 c^2 u^3-2 a^4 c^4 u^3-4 b^4 c^4 u^3+2 b^2 c^6 u^3-3 a^8 u^2 v+a^6 b^2 u^2 v-3 a^2 b^6 u^2 v+b^8 u^2 v+5 a^6 c^2 u^2 v+3 a^4 b^2 c^2 u^2 v+a^2 b^4 c^2 u^2 v+3 b^6 c^2 u^2 v-6 a^4 c^4 u^2 v-a^2 b^2 c^4 u^2 v-6 b^4 c^4 u^2 v+3 a^2 c^6 u^2 v+3 b^2 c^6 u^2 v-c^8 u^2 v-5 a^6 b^2 u v^2+6 a^4 b^4 u v^2-6 a^2 b^6 u v^2+b^8 u v^2+8 a^4 b^2 c^2 u v^2-3 a^2 b^4 c^2 u v^2+4 b^6 c^2 u v^2-4 a^2 b^2 c^4 u v^2-2 b^4 c^4 u v^2+b^2 c^6 u v^2-2 a^6 b^2 v^3+2 a^4 b^4 v^3-2 a^2 b^6 v^3+4 a^4 b^2 c^2 v^3-2 a^2 b^4 c^2 v^3+2 b^6 c^2 v^3-2 a^2 b^2 c^4 v^3-3 a^8 u^2 w+5 a^6 b^2 u^2 w-6 a^4 b^4 u^2 w+3 a^2 b^6 u^2 w-b^8 u^2 w+a^6 c^2 u^2 w+3 a^4 b^2 c^2 u^2 w-a^2 b^4 c^2 u^2 w+3 b^6 c^2 u^2 w+a^2 b^2 c^4 u^2 w-6 b^4 c^4 u^2 w-3 a^2 c^6 u^2 w+3 b^2 c^6 u^2 w+c^8 u^2 w-3 a^8 u v w+4 a^6 b^2 u v w-6 a^4 b^4 u v w+3 a^2 b^6 u v w-2 b^8 u v w+4 a^6 c^2 u v w+5 a^4 b^2 c^2 u v w-2 a^2 b^4 c^2 u v w+6 b^6 c^2 u v w-6 a^4 c^4 u v w-2 a^2 b^2 c^4 u v w-8 b^4 c^4 u v w+3 a^2 c^6 u v w+6 b^2 c^6 u v w-2 c^8 u v w-a^6 b^2 v^2 w-b^8 v^2 w+4 a^4 b^2 c^2 v^2 w-3 a^2 b^4 c^2 v^2 w+2 b^6 c^2 v^2 w-2 a^2 b^2 c^4 v^2 w+2 b^4 c^4 v^2 w-b^2 c^6 v^2 w-5 a^6 c^2 u w^2+8 a^4 b^2 c^2 u w^2-4 a^2 b^4 c^2 u w^2+b^6 c^2 u w^2+6 a^4 c^4 u w^2-3 a^2 b^2 c^4 u w^2-2 b^4 c^4 u w^2-6 a^2 c^6 u w^2+4 b^2 c^6 u w^2+c^8 u w^2-a^6 c^2 v w^2+4 a^4 b^2 c^2 v w^2-2 a^2 b^4 c^2 v w^2-b^6 c^2 v w^2-3 a^2 b^2 c^4 v w^2+2 b^4 c^4 v w^2+2 b^2 c^6 v w^2-c^8 v w^2-2 a^6 c^2 w^3+4 a^4 b^2 c^2 w^3-2 a^2 b^4 c^2 w^3+2 a^4 c^4 w^3-2 a^2 b^2 c^4 w^3-2 a^2 c^6 w^3+2 b^2 c^6 w^3) y z+(a^8 u^3-2 a^6 b^2 u^3+3 a^4 b^4 u^3-2 a^2 b^6 u^3+b^8 u^3-2 a^4 b^2 c^2 u^3+2 a^2 b^4 c^2 u^3-2 b^6 c^2 u^3+b^4 c^4 u^3+3 a^8 u^2 v-6 a^6 b^2 u^2 v+9 a^4 b^4 u^2 v-6 a^2 b^6 u^2 v+3 b^8 u^2 v-2 a^6 c^2 u^2 v-3 a^4 b^2 c^2 u^2 v+3 a^2 b^4 c^2 u^2 v-5 b^6 c^2 u^2 v+a^4 c^4 u^2 v+a^2 b^2 c^4 u^2 v+3 b^4 c^4 u^2 v-b^2 c^6 u^2 v+3 a^8 u v^2-6 a^6 b^2 u v^2+9 a^4 b^4 u v^2-6 a^2 b^6 u v^2+3 b^8 u v^2-5 a^6 c^2 u v^2+3 a^4 b^2 c^2 u v^2-3 a^2 b^4 c^2 u v^2-2 b^6 c^2 u v^2+3 a^4 c^4 u v^2+a^2 b^2 c^4 u v^2+b^4 c^4 u v^2-a^2 c^6 u v^2+a^8 v^3-2 a^6 b^2 v^3+3 a^4 b^4 v^3-2 a^2 b^6 v^3+b^8 v^3-2 a^6 c^2 v^3+2 a^4 b^2 c^2 v^3-2 a^2 b^4 c^2 v^3+a^4 c^4 v^3+2 a^6 c^2 u^2 w-3 a^4 b^2 c^2 u^2 w+3 a^2 b^4 c^2 u^2 w-b^6 c^2 u^2 w-a^4 c^4 u^2 w-a^2 b^2 c^4 u^2 w+b^2 c^6 u^2 w+a^6 c^2 u v w+b^6 c^2 u v w-2 a^4 c^4 u v w-a^2 b^2 c^4 u v w-2 b^4 c^4 u v w+2 a^2 c^6 u v w+2 b^2 c^6 u v w-c^8 u v w-a^6 c^2 v^2 w+3 a^4 b^2 c^2 v^2 w-3 a^2 b^4 c^2 v^2 w+2 b^6 c^2 v^2 w-a^2 b^2 c^4 v^2 w-b^4 c^4 v^2 w+a^2 c^6 v^2 w+2 a^4 c^4 u w^2-3 a^2 b^2 c^4 u w^2+b^4 c^4 u w^2-a^2 c^6 u w^2+b^2 c^6 u w^2+a^4 c^4 v w^2-3 a^2 b^2 c^4 v w^2+2 b^4 c^4 v w^2+a^2 c^6 v w^2-b^2 c^6 v w^2+a^4 c^4 w^3-2 a^2 b^2 c^4 w^3+b^4 c^4 w^3) z^2 = 0)
Ψ.
Sus puntos de intersección con la recta del infinito se determinan sustituyendo en su ecuación las coordenadas (1:-t:t-1) de un punto genérico de dicha recta. La ecuación de segundo grado que resulta tiene discriminate -3(a-b-c)^2(a+b-c)^2(a-b+c)^2(a+b+c)^2(a^4-
a^2b^2+b^4-a^2c^2-b^2c^2+c^4)^2(uv+uw+vw)^2, por lo que esta ecuación no tiene soluciones reales; es decir, se trata en efecto de una elipse, que degenera cuando P está sobre ℰ.
El centro de Ψ es:
D = ((b^2 - c^2) (b^2 (u - v) + c^2 (-u + w)) + a^4 (5 u + 2 (v + w)) -
a^2 (b^2 (4 u + 3 v + 2 w) + c^2 (4 u + 2 v + 3 w)) : .. : ...).
Pares {P=Xi, D=Xj}, para los índices {i, j}: {2, 3}, {69, 599}, {76, 22712}, {99, 376}, {115, 549}, {148,
381}, {298, 5463}, {299, 5464}, {316, 6054}, {325, 2482}, {385,
14830}, {598, 9774}, {620, 34200}, {671, 2}, {1916, 11171}, {2482,
8703}, {5077, 7761}, {5461, 12100}, {5485, 7610}, {5503,
7618}, {6034, 17508}, {6722, 14891}, {7788, 7801}, {7799,
21166}, {7840, 8724}, {8352, 114}, {8353, 32152}, {8354,
7830}, {8591, 3534}, {8596, 3830}, {8597, 6033}, {9166,
3524}, {9870, 14666}, {10754, 11179}, {11054, 98}, {11055,
11257}, {11161, 1352}, {11646, 11178}, {12156, 12252}, {12243,
9756}, {14041, 15561}, {14061, 15692}, {14568, 34473}, {14971,
17504}, {15300, 550}, {15533, 34507}, {20094, 15681}, {22247,
15759}, {31274, 15714}.
Cuando P es el incentro, el centro de la elipse Ψ es:
D1 = ( 5 a^5 + 2 a^4 (b + c) - 4 a^3 (b^2 + c^2) - a^2 (3 b^3 + 2 b^2 c + 2 b c^2 + 3 c^3)
+ a (b^2 - c^2)^2 - b^5 + b^3 c^2 + b^2 c^3 - c^5 : ... : ...),
que tiene números de búsqueda en
(7.37992384394338, 6.87478766669592, -4.52492259993282).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,28862}, {3,2784}, {165,28870}, {516,3534}, {1385,28897}, {3576,28845}, {4655,11711}, {5731,28850}, {10186,28866}, {17502,28901}.
- Miercoles, 8 de enero del 2020
La cuártica Q120 estrechamente relacionada con las cúbicas K257 y K258
El 8 de enero de 1888 nació Richard Courant, matemático alemán.
Con Herbert Robbins escribió la obra divulgativa ¿Qué es la Matemática?, que todavía se reimprime.
El "Instituto Courant" de la Universidad de Nueva York lleva su nombre, del que fue uno de los fundadores.
Dado un triángulo ABC con circuncentro O y centro de la N, sean ℓ una recta que pasa por O y L su .
El centro, D, de la cónica 𝒞ℓ, a ABC tal que uno de sus ejes es ℓ, es la intersección de las rectas ℓ y NL.
El lugar geométrico de D, cuando ℓ gira alrededor de O, es la cúbica K258.
El lugar geométrico del de 𝒞ℓ, P ( del de D), es la cúbica K257.
Sean A", B" y C" los puntos de contacto de 𝒞ℓ con los lados B'C', C'A' y A'B', del triángulo A'B'C', reflexión de ABC en ℓ.
Las rectas
AA", BB", CC" son concurrentes y el lugar del punto de concurrencia,
W, cuando ℓ gira alrededor de
O, es la cuártica
Q120, conjugada isogonal de la circunferencia de los nueve puntos.
NOTA: La recta AA" pasa por el punto en el que ℓ vuelve a corta a la circunferencia (OBC). Análogamente, para BB" y CC".
La ecuación baricéntrica de una recta ℓ que pasa por O se puede poner de la forma:
(a^2 (-c^2 + b^2 t) - (b^2 - c^2) (c^2 + b^2 t)) x +
a^2 (a^2 - b^2 - c^2) t y + a^2 (-a^2 + b^2 + c^2) z = 0.
Su ortopolo es:
L = ((-1 + t) (a^2 (-c^2 + b^2 t) - (b^2 - c^2) (c^2 + b^2 t)) : (a^2 -
b^2 - c^2) t (a^2 - c^2 - b^2 t) : (a^2 - b^2 - c^2) (-c^2 + (a^2 - b^2) t)),
y las coordenadas de D son:
D = (-a^2 (a^2 - b^2 - c^2) (-1 + t) (-(c^2 + b^2 t)^2 +
a^2 (c^2 + b^2 t^2)) : (b^2 - c^2) (c^2 + b^2 t)^3 +
a^6 (c^2 - b^2 t^2) +
a^4 (-3 c^4 + b^2 c^2 (-1 + t) + b^4 t^2 (2 + t)) +
a^2 (3 c^6 + b^2 c^4 t (2 + t) - b^6 t^2 (1 + 2 t) +
b^4 c^2 t (-1 - 3 t + t^2)) : (b^2 - c^2) (c^2 + b^2 t)^3 +
a^6 t (c^2 - b^2 t^2) -
a^4 (-b^2 c^2 (-1 + t) t^2 - 3 b^4 t^3 + c^4 (1 + 2 t)) +
a^2 (-3 b^6 t^3 + c^6 (2 + t) - b^4 c^2 t (1 + 2 t) +
b^2 c^4 (-1 + 3 t + t^2))).
El lugar geométrico de D, cuando ℓ gira alrededor de O es la cúbica K258:
𝔖abc xyz
b^2 c^2 (b^2 - c^2) x^3 +
a^2 y z (c^2 (a^2 + 2 b^2 - c^2) y - b^2 (a^2 - b^2 + 2 c^2) z) = 0.
El perspector de la
cónica
( a^8 c^8 x^2+2 a^6 b^2 c^8 x^2+a^4 b^4 c^8 x^2-4 a^6 c^10 x^2-6 a^4 b^2 c^10 x^2-2 a^2 b^4 c^10 x^2+6 a^4 c^12 x^2+6 a^2 b^2 c^12 x^2+b^4 c^12 x^2-4 a^2 c^14 x^2-2 b^2 c^14 x^2+c^16 x^2-2 a^10 c^6 t x^2-4 a^8 b^2 c^6 t x^2+2 a^6 b^4 c^6 t x^2+4 a^4 b^6 c^6 t x^2+8 a^8 c^8 t x^2+6 a^6 b^2 c^8 t x^2-16 a^4 b^4 c^8 t x^2-10 a^2 b^6 c^8 t x^2-12 a^6 c^10 t x^2+6 a^4 b^2 c^10 t x^2+26 a^2 b^4 c^10 t x^2+6 b^6 c^10 t x^2+8 a^4 c^12 t x^2-14 a^2 b^2 c^12 t x^2-12 b^4 c^12 t x^2-2 a^2 c^14 t x^2+6 b^2 c^14 t x^2+a^12 c^4 t^2 x^2+4 a^10 b^2 c^4 t^2 x^2-5 a^8 b^4 c^4 t^2 x^2-6 a^6 b^6 c^4 t^2 x^2+6 a^4 b^8 c^4 t^2 x^2-4 a^10 c^6 t^2 x^2-2 a^8 b^2 c^6 t^2 x^2+30 a^6 b^4 c^6 t^2 x^2-4 a^4 b^6 c^6 t^2 x^2-20 a^2 b^8 c^6 t^2 x^2+6 a^8 c^8 t^2 x^2-18 a^6 b^2 c^8 t^2 x^2-30 a^4 b^4 c^8 t^2 x^2+40 a^2 b^6 c^8 t^2 x^2+15 b^8 c^8 t^2 x^2-4 a^6 c^10 t^2 x^2+26 a^4 b^2 c^10 t^2 x^2-10 a^2 b^4 c^10 t^2 x^2-30 b^6 c^10 t^2 x^2+a^4 c^12 t^2 x^2-10 a^2 b^2 c^12 t^2 x^2+15 b^4 c^12 t^2 x^2-2 a^12 b^2 c^2 t^3 x^2+2 a^10 b^4 c^2 t^3 x^2+6 a^8 b^6 c^2 t^3 x^2-10 a^6 b^8 c^2 t^3 x^2+4 a^4 b^10 c^2 t^3 x^2+2 a^10 b^2 c^4 t^3 x^2-20 a^8 b^4 c^4 t^3 x^2+14 a^6 b^6 c^4 t^3 x^2+24 a^4 b^8 c^4 t^3 x^2-20 a^2 b^10 c^4 t^3 x^2+6 a^8 b^2 c^6 t^3 x^2+14 a^6 b^4 c^6 t^3 x^2-60 a^4 b^6 c^6 t^3 x^2+20 a^2 b^8 c^6 t^3 x^2+20 b^10 c^6 t^3 x^2-10 a^6 b^2 c^8 t^3 x^2+24 a^4 b^4 c^8 t^3 x^2+20 a^2 b^6 c^8 t^3 x^2-40 b^8 c^8 t^3 x^2+4 a^4 b^2 c^10 t^3 x^2-20 a^2 b^4 c^10 t^3 x^2+20 b^6 c^10 t^3 x^2+a^12 b^4 t^4 x^2-4 a^10 b^6 t^4 x^2+6 a^8 b^8 t^4 x^2-4 a^6 b^10 t^4 x^2+a^4 b^12 t^4 x^2+4 a^10 b^4 c^2 t^4 x^2-2 a^8 b^6 c^2 t^4 x^2-18 a^6 b^8 c^2 t^4 x^2+26 a^4 b^10 c^2 t^4 x^2-10 a^2 b^12 c^2 t^4 x^2-5 a^8 b^4 c^4 t^4 x^2+30 a^6 b^6 c^4 t^4 x^2-30 a^4 b^8 c^4 t^4 x^2-10 a^2 b^10 c^4 t^4 x^2+15 b^12 c^4 t^4 x^2-6 a^6 b^4 c^6 t^4 x^2-4 a^4 b^6 c^6 t^4 x^2+40 a^2 b^8 c^6 t^4 x^2-30 b^10 c^6 t^4 x^2+6 a^4 b^4 c^8 t^4 x^2-20 a^2 b^6 c^8 t^4 x^2+15 b^8 c^8 t^4 x^2-2 a^10 b^6 t^5 x^2+8 a^8 b^8 t^5 x^2-12 a^6 b^10 t^5 x^2+8 a^4 b^12 t^5 x^2-2 a^2 b^14 t^5 x^2-4 a^8 b^6 c^2 t^5 x^2+6 a^6 b^8 c^2 t^5 x^2+6 a^4 b^10 c^2 t^5 x^2-14 a^2 b^12 c^2 t^5 x^2+6 b^14 c^2 t^5 x^2+2 a^6 b^6 c^4 t^5 x^2-16 a^4 b^8 c^4 t^5 x^2+26 a^2 b^10 c^4 t^5 x^2-12 b^12 c^4 t^5 x^2+4 a^4 b^6 c^6 t^5 x^2-10 a^2 b^8 c^6 t^5 x^2+6 b^10 c^6 t^5 x^2+a^8 b^8 t^6 x^2-4 a^6 b^10 t^6 x^2+6 a^4 b^12 t^6 x^2-4 a^2 b^14 t^6 x^2+b^16 t^6 x^2+2 a^6 b^8 c^2 t^6 x^2-6 a^4 b^10 c^2 t^6 x^2+6 a^2 b^12 c^2 t^6 x^2-2 b^14 c^2 t^6 x^2+a^4 b^8 c^4 t^6 x^2-2 a^2 b^10 c^4 t^6 x^2+b^12 c^4 t^6 x^2-2 a^8 b^2 c^6 t x y+2 a^4 b^6 c^6 t x y+6 a^6 b^2 c^8 t x y-2 a^2 b^6 c^8 t x y-6 a^4 b^2 c^10 t x y+2 a^2 b^2 c^12 t x y+4 a^10 b^2 c^4 t^2 x y-2 a^8 b^4 c^4 t^2 x y-8 a^6 b^6 c^4 t^2 x y+6 a^4 b^8 c^4 t^2 x y-10 a^8 b^2 c^6 t^2 x y+12 a^6 b^4 c^6 t^2 x y+6 a^4 b^6 c^6 t^2 x y-8 a^2 b^8 c^6 t^2 x y+6 a^6 b^2 c^8 t^2 x y-18 a^4 b^4 c^8 t^2 x y+2 a^2 b^6 c^8 t^2 x y+2 a^4 b^2 c^10 t^2 x y+8 a^2 b^4 c^10 t^2 x y-2 a^2 b^2 c^12 t^2 x y-2 a^12 b^2 c^2 t^3 x y+12 a^8 b^6 c^2 t^3 x y-16 a^6 b^8 c^2 t^3 x y+6 a^4 b^10 c^2 t^3 x y+2 a^10 b^2 c^4 t^3 x y-10 a^8 b^4 c^4 t^3 x y+2 a^6 b^6 c^4 t^3 x y+18 a^4 b^8 c^4 t^3 x y-12 a^2 b^10 c^4 t^3 x y+6 a^8 b^2 c^6 t^3 x y+12 a^6 b^4 c^6 t^3 x y-26 a^4 b^6 c^6 t^3 x y+8 a^2 b^8 c^6 t^3 x y-10 a^6 b^2 c^8 t^3 x y+6 a^4 b^4 c^8 t^3 x y+12 a^2 b^6 c^8 t^3 x y+4 a^4 b^2 c^10 t^3 x y-8 a^2 b^4 c^10 t^3 x y+2 a^12 b^4 t^4 x y-8 a^10 b^6 t^4 x y+12 a^8 b^8 t^4 x y-8 a^6 b^10 t^4 x y+2 a^4 b^12 t^4 x y+2 a^12 b^2 c^2 t^4 x y-4 a^8 b^6 c^2 t^4 x y-8 a^6 b^8 c^2 t^4 x y+18 a^4 b^10 c^2 t^4 x y-8 a^2 b^12 c^2 t^4 x y-6 a^10 b^2 c^4 t^4 x y+6 a^8 b^4 c^4 t^4 x y+18 a^6 b^6 c^4 t^4 x y-30 a^4 b^8 c^4 t^4 x y+12 a^2 b^10 c^4 t^4 x y+6 a^8 b^2 c^6 t^4 x y-20 a^6 b^4 c^6 t^4 x y+6 a^4 b^6 c^6 t^4 x y+8 a^2 b^8 c^6 t^4 x y-2 a^6 b^2 c^8 t^4 x y+12 a^4 b^4 c^8 t^4 x y-12 a^2 b^6 c^8 t^4 x y-2 a^12 b^4 t^5 x y+6 a^10 b^6 t^5 x y-4 a^8 b^8 t^5 x y-4 a^6 b^10 t^5 x y+6 a^4 b^12 t^5 x y-2 a^2 b^14 t^5 x y-8 a^8 b^6 c^2 t^5 x y+24 a^6 b^8 c^2 t^5 x y-24 a^4 b^10 c^2 t^5 x y+8 a^2 b^12 c^2 t^5 x y+6 a^8 b^4 c^4 t^5 x y-10 a^6 b^6 c^4 t^5 x y+2 a^4 b^8 c^4 t^5 x y+2 a^2 b^10 c^4 t^5 x y-4 a^6 b^4 c^6 t^5 x y+12 a^4 b^6 c^6 t^5 x y-8 a^2 b^8 c^6 t^5 x y+2 a^10 b^6 t^6 x y-8 a^8 b^8 t^6 x y+12 a^6 b^10 t^6 x y-8 a^4 b^12 t^6 x y+2 a^2 b^14 t^6 x y-2 a^6 b^6 c^4 t^6 x y+4 a^4 b^8 c^4 t^6 x y-2 a^2 b^10 c^4 t^6 x y+a^8 b^4 c^4 t^2 y^2-2 a^6 b^6 c^4 t^2 y^2+a^4 b^8 c^4 t^2 y^2-2 a^6 b^4 c^6 t^2 y^2+2 a^4 b^6 c^6 t^2 y^2+a^4 b^4 c^8 t^2 y^2-2 a^10 b^4 c^2 t^3 y^2+6 a^8 b^6 c^2 t^3 y^2-6 a^6 b^8 c^2 t^3 y^2+2 a^4 b^10 c^2 t^3 y^2+2 a^8 b^4 c^4 t^3 y^2-4 a^6 b^6 c^4 t^3 y^2+2 a^4 b^8 c^4 t^3 y^2+2 a^6 b^4 c^6 t^3 y^2-2 a^4 b^6 c^6 t^3 y^2-2 a^4 b^4 c^8 t^3 y^2+a^12 b^4 t^4 y^2-4 a^10 b^6 t^4 y^2+6 a^8 b^8 t^4 y^2-4 a^6 b^10 t^4 y^2+a^4 b^12 t^4 y^2+2 a^10 b^4 c^2 t^4 y^2-6 a^8 b^6 c^2 t^4 y^2+6 a^6 b^8 c^2 t^4 y^2-2 a^4 b^10 c^2 t^4 y^2-6 a^8 b^4 c^4 t^4 y^2+12 a^6 b^6 c^4 t^4 y^2-6 a^4 b^8 c^4 t^4 y^2+2 a^6 b^4 c^6 t^4 y^2-2 a^4 b^6 c^6 t^4 y^2+a^4 b^4 c^8 t^4 y^2-2 a^12 b^4 t^5 y^2+8 a^10 b^6 t^5 y^2-12 a^8 b^8 t^5 y^2+8 a^6 b^10 t^5 y^2-2 a^4 b^12 t^5 y^2+2 a^10 b^4 c^2 t^5 y^2-6 a^8 b^6 c^2 t^5 y^2+6 a^6 b^8 c^2 t^5 y^2-2 a^4 b^10 c^2 t^5 y^2+2 a^8 b^4 c^4 t^5 y^2-4 a^6 b^6 c^4 t^5 y^2+2 a^4 b^8 c^4 t^5 y^2-2 a^6 b^4 c^6 t^5 y^2+2 a^4 b^6 c^6 t^5 y^2+a^12 b^4 t^6 y^2-4 a^10 b^6 t^6 y^2+6 a^8 b^8 t^6 y^2-4 a^6 b^10 t^6 y^2+a^4 b^12 t^6 y^2-2 a^10 b^4 c^2 t^6 y^2+6 a^8 b^6 c^2 t^6 y^2-6 a^6 b^8 c^2 t^6 y^2+2 a^4 b^10 c^2 t^6 y^2+a^8 b^4 c^4 t^6 y^2-2 a^6 b^6 c^4 t^6 y^2+a^4 b^8 c^4 t^6 y^2+2 a^10 c^6 x z-2 a^6 b^4 c^6 x z-8 a^8 c^8 x z+4 a^4 b^4 c^8 x z+12 a^6 c^10 x z-2 a^2 b^4 c^10 x z-8 a^4 c^12 x z+2 a^2 c^14 x z-2 a^12 c^4 t x z+6 a^8 b^4 c^4 t x z-4 a^6 b^6 c^4 t x z+6 a^10 c^6 t x z-8 a^8 b^2 c^6 t x z-10 a^6 b^4 c^6 t x z+12 a^4 b^6 c^6 t x z-4 a^8 c^8 t x z+24 a^6 b^2 c^8 t x z+2 a^4 b^4 c^8 t x z-8 a^2 b^6 c^8 t x z-4 a^6 c^10 t x z-24 a^4 b^2 c^10 t x z+2 a^2 b^4 c^10 t x z+6 a^4 c^12 t x z+8 a^2 b^2 c^12 t x z-2 a^2 c^14 t x z+2 a^12 b^2 c^2 t^2 x z-6 a^10 b^4 c^2 t^2 x z+6 a^8 b^6 c^2 t^2 x z-2 a^6 b^8 c^2 t^2 x z+2 a^12 c^4 t^2 x z+6 a^8 b^4 c^4 t^2 x z-20 a^6 b^6 c^4 t^2 x z+12 a^4 b^8 c^4 t^2 x z-8 a^10 c^6 t^2 x z-4 a^8 b^2 c^6 t^2 x z+18 a^6 b^4 c^6 t^2 x z+6 a^4 b^6 c^6 t^2 x z-12 a^2 b^8 c^6 t^2 x z+12 a^8 c^8 t^2 x z-8 a^6 b^2 c^8 t^2 x z-30 a^4 b^4 c^8 t^2 x z+8 a^2 b^6 c^8 t^2 x z-8 a^6 c^10 t^2 x z+18 a^4 b^2 c^10 t^2 x z+12 a^2 b^4 c^10 t^2 x z+2 a^4 c^12 t^2 x z-8 a^2 b^2 c^12 t^2 x z-2 a^12 b^2 c^2 t^3 x z+2 a^10 b^4 c^2 t^3 x z+6 a^8 b^6 c^2 t^3 x z-10 a^6 b^8 c^2 t^3 x z+4 a^4 b^10 c^2 t^3 x z-10 a^8 b^4 c^4 t^3 x z+12 a^6 b^6 c^4 t^3 x z+6 a^4 b^8 c^4 t^3 x z-8 a^2 b^10 c^4 t^3 x z+12 a^8 b^2 c^6 t^3 x z+2 a^6 b^4 c^6 t^3 x z-26 a^4 b^6 c^6 t^3 x z+12 a^2 b^8 c^6 t^3 x z-16 a^6 b^2 c^8 t^3 x z+18 a^4 b^4 c^8 t^3 x z+8 a^2 b^6 c^8 t^3 x z+6 a^4 b^2 c^10 t^3 x z-12 a^2 b^4 c^10 t^3 x z+4 a^10 b^4 c^2 t^4 x z-10 a^8 b^6 c^2 t^4 x z+6 a^6 b^8 c^2 t^4 x z+2 a^4 b^10 c^2 t^4 x z-2 a^2 b^12 c^2 t^4 x z-2 a^8 b^4 c^4 t^4 x z+12 a^6 b^6 c^4 t^4 x z-18 a^4 b^8 c^4 t^4 x z+8 a^2 b^10 c^4 t^4 x z-8 a^6 b^4 c^6 t^4 x z+6 a^4 b^6 c^6 t^4 x z+2 a^2 b^8 c^6 t^4 x z+6 a^4 b^4 c^8 t^4 x z-8 a^2 b^6 c^8 t^4 x z-2 a^8 b^6 c^2 t^5 x z+6 a^6 b^8 c^2 t^5 x z-6 a^4 b^10 c^2 t^5 x z+2 a^2 b^12 c^2 t^5 x z+2 a^4 b^6 c^6 t^5 x z-2 a^2 b^8 c^6 t^5 x z+2 a^10 b^2 c^4 t y z-4 a^8 b^4 c^4 t y z+2 a^6 b^6 c^4 t y z-6 a^8 b^2 c^6 t y z+8 a^6 b^4 c^6 t y z-2 a^4 b^6 c^6 t y z+6 a^6 b^2 c^8 t y z-4 a^4 b^4 c^8 t y z-2 a^4 b^2 c^10 t y z-2 a^12 b^2 c^2 t^2 y z+6 a^10 b^4 c^2 t^2 y z-6 a^8 b^6 c^2 t^2 y z+2 a^6 b^8 c^2 t^2 y z+2 a^10 b^2 c^4 t^2 y z-8 a^8 b^4 c^4 t^2 y z+10 a^6 b^6 c^4 t^2 y z-4 a^4 b^8 c^4 t^2 y z+6 a^8 b^2 c^6 t^2 y z-2 a^6 b^4 c^6 t^2 y z-4 a^4 b^6 c^6 t^2 y z-10 a^6 b^2 c^8 t^2 y z+4 a^4 b^4 c^8 t^2 y z+4 a^4 b^2 c^10 t^2 y z+4 a^12 b^2 c^2 t^3 y z-10 a^10 b^4 c^2 t^3 y z+6 a^8 b^6 c^2 t^3 y z+2 a^6 b^8 c^2 t^3 y z-2 a^4 b^10 c^2 t^3 y z-10 a^10 b^2 c^4 t^3 y z+24 a^8 b^4 c^4 t^3 y z-18 a^6 b^6 c^4 t^3 y z+4 a^4 b^8 c^4 t^3 y z+6 a^8 b^2 c^6 t^3 y z-18 a^6 b^4 c^6 t^3 y z+12 a^4 b^6 c^6 t^3 y z+2 a^6 b^2 c^8 t^3 y z+4 a^4 b^4 c^8 t^3 y z-2 a^4 b^2 c^10 t^3 y z-2 a^12 b^2 c^2 t^4 y z+2 a^10 b^4 c^2 t^4 y z+6 a^8 b^6 c^2 t^4 y z-10 a^6 b^8 c^2 t^4 y z+4 a^4 b^10 c^2 t^4 y z+6 a^10 b^2 c^4 t^4 y z-8 a^8 b^4 c^4 t^4 y z-2 a^6 b^6 c^4 t^4 y z+4 a^4 b^8 c^4 t^4 y z-6 a^8 b^2 c^6 t^4 y z+10 a^6 b^4 c^6 t^4 y z-4 a^4 b^6 c^6 t^4 y z+2 a^6 b^2 c^8 t^4 y z-4 a^4 b^4 c^8 t^4 y z+2 a^10 b^4 c^2 t^5 y z-6 a^8 b^6 c^2 t^5 y z+6 a^6 b^8 c^2 t^5 y z-2 a^4 b^10 c^2 t^5 y z-4 a^8 b^4 c^4 t^5 y z+8 a^6 b^6 c^4 t^5 y z-4 a^4 b^8 c^4 t^5 y z+2 a^6 b^4 c^6 t^5 y z-2 a^4 b^6 c^6 t^5 y z+a^12 c^4 z^2-2 a^10 b^2 c^4 z^2+a^8 b^4 c^4 z^2-4 a^10 c^6 z^2+6 a^8 b^2 c^6 z^2-2 a^6 b^4 c^6 z^2+6 a^8 c^8 z^2-6 a^6 b^2 c^8 z^2+a^4 b^4 c^8 z^2-4 a^6 c^10 z^2+2 a^4 b^2 c^10 z^2+a^4 c^12 z^2-2 a^12 c^4 t z^2+2 a^10 b^2 c^4 t z^2+2 a^8 b^4 c^4 t z^2-2 a^6 b^6 c^4 t z^2+8 a^10 c^6 t z^2-6 a^8 b^2 c^6 t z^2-4 a^6 b^4 c^6 t z^2+2 a^4 b^6 c^6 t z^2-12 a^8 c^8 t z^2+6 a^6 b^2 c^8 t z^2+2 a^4 b^4 c^8 t z^2+8 a^6 c^10 t z^2-2 a^4 b^2 c^10 t z^2-2 a^4 c^12 t z^2+a^12 c^4 t^2 z^2+2 a^10 b^2 c^4 t^2 z^2-6 a^8 b^4 c^4 t^2 z^2+2 a^6 b^6 c^4 t^2 z^2+a^4 b^8 c^4 t^2 z^2-4 a^10 c^6 t^2 z^2-6 a^8 b^2 c^6 t^2 z^2+12 a^6 b^4 c^6 t^2 z^2-2 a^4 b^6 c^6 t^2 z^2+6 a^8 c^8 t^2 z^2+6 a^6 b^2 c^8 t^2 z^2-6 a^4 b^4 c^8 t^2 z^2-4 a^6 c^10 t^2 z^2-2 a^4 b^2 c^10 t^2 z^2+a^4 c^12 t^2 z^2-2 a^10 b^2 c^4 t^3 z^2+2 a^8 b^4 c^4 t^3 z^2+2 a^6 b^6 c^4 t^3 z^2-2 a^4 b^8 c^4 t^3 z^2+6 a^8 b^2 c^6 t^3 z^2-4 a^6 b^4 c^6 t^3 z^2-2 a^4 b^6 c^6 t^3 z^2-6 a^6 b^2 c^8 t^3 z^2+2 a^4 b^4 c^8 t^3 z^2+2 a^4 b^2 c^10 t^3 z^2+a^8 b^4 c^4 t^4 z^2-2 a^6 b^6 c^4 t^4 z^2+a^4 b^8 c^4 t^4 z^2-2 a^6 b^4 c^6 t^4 z^2+2 a^4 b^6 c^6 t^4 z^2+a^4 b^4 c^8 t^4 z^2 = 0)
𝒞ℓ es:
P = (-a^2 b^2 c^2 (a^2 - b^2 - c^2) (-1 + t) t : c^2 (-a^2 + c^2 +
b^2 t) (a^2 (-c^2 + b^2 t) - (b^2 - c^2) (c^2 +
b^2 t)) : -b^2 t (c^2 + (-a^2 + b^2) t) (a^2 (c^2 -
b^2 t) + (b^2 - c^2) (c^2 + b^2 t))).
El lugar geométrico de P, cuando t varía, es la cúbica K257::
2(a^2-b^2)(a^2-c^2)(b^2-c^2) +
𝔖abc xyz
b^2c^2x((a^2+b^2-c^2)y^2-(a^2-b^2+c^2)z^2) = 0.
Las coordenadas de los puntos A", B" y C" de contacto de 𝒞ℓ con los lados B'C', C'A' y A'B', del triángulo A'B'C' son:
A" =(-a^2 (a^2 - b^2 - c^2) (-1 +
t) t (a^2 (-c^2 + b^2 t) - (b^2 - c^2) (c^2 + b^2 t)) : b^2 (-a^2 +
c^2 + b^2 t) (c^2 + (-a^2 + b^2) t)^2 : c^2 t (-a^2 + c^2 +
b^2 t)^2 (c^2 + (-a^2 + b^2) t)),
B" = (a^2 b^2 (a^2 - b^2 - c^2) (-1 + t) (c^2 + (-a^2 + b^2) t)^2 : (-a^2 +
b^2 + c^2)^2 t (a^2 - c^2 -
b^2 t) (a^2 (-c^2 + b^2 t) - (b^2 - c^2) (c^2 +
b^2 t)) : b^2 c^2 (-1 +
t)^2 (c^2 + (-a^2 + b^2) t) (a^2 (c^2 - b^2 t) + (b^2 - c^2) (c^2 +
b^2 t))),
C" = (-a^2 c^2 (a^2 - b^2 - c^2) (-1 + t) t (-a^2 + c^2 +
b^2 t)^2 : -b^2 c^2 (-1 + t)^2 (-a^2 + c^2 +
b^2 t) (a^2 (c^2 - b^2 t) + (b^2 - c^2) (c^2 + b^2 t)) : -(-a^2 +
b^2 + c^2)^2 t (-c^2 + (a^2 - b^2) t) (a^2 (-c^2 + b^2 t) - (b^2 -
c^2) (c^2 + b^2 t))).
Las rectas AA", BB", CC" concurren en:
W = (a^2 (a^2 - b^2 - c^2) t (a^2 - c^2 - b^2 t) (-c^2 + a^2 t -
b^2 t) : b^2 (-1 + t) (c^2 - a^2 t + b^2 t) (a^2 c^2 + b^2 c^2 -
c^4 - a^2 b^2 t + b^4 t - b^2 c^2 t) : -c^2 (-1 + t) t (-a^2 + c^2 +
b^2 t) (-a^2 c^2 - b^2 c^2 + c^4 + a^2 b^2 t - b^4 t + b^2 c^2 t)).
El lugar geométrico de W, cuando ℓ gira alrededor de O, es la cuártica Q120:
𝔖abc xyz
a^2 y z (-2 b^2 c^2 x^2 + a^2 (-a^2 + b^2 + c^2) y z) = 0.
- Domingo, 5 de enero del 2020
Circunferencia osculatriz y cónicas circunscritas
El 5 de enero de 2020 se ha dado el máximo acercamiento (perihelio) entre la Tierra y el Sol. Desde el último perihelio han transcurrido 367 días; el próximo será dentro de 363 días, el 2 de enero de 2021.
Dado un triángulo ABC y un punto P, sean K el , Γ y co(P) la circunferencia y la cónica , de K y P, respectivamente.
Sean Q el de intersección de Γ y co(P), ci(Q) la de co(P) en Q.
Si (u:v:w) son las coordenadas baricéntricas de P:
Q = (1/(-c^2 v + b^2 w) : 1/(c^2 u - a^2 w) : 1/(-b^2 u + a^2 v)),
Γ: a^2 y z + b^2 z x + c^2 x y = 0,
co(P): u y z+ v z x + w x y = 0,
ci(Q): u (c^2 v - b^2 w)^3 (c^4 u^2 v - 2 a^2 c^2 u v w +
w (-b^4 u^2 + 2 a^2 b^2 u v + a^4 v (-v + w)))x^2 +
(c^10 u^4 v^3 -
2 c^8 u^3 v^2 (b^2 u + a^2 v) w + (b^2 u - a^2 v) w^3 (b^8 u^3 -
a^2 b^6 u^2 v + a^6 b^2 u v (u + 4 v - w) - a^8 v^2 (u + v + w) +
a^4 b^4 u v (-3 u + 2 w)) +
c^6 u^2 v w (b^4 u^2 (-u + w) + a^4 v^2 (-3 u + 2 v + w) +
2 a^2 b^2 u v (2 u - v + 2 w)) +
c^2 u v w^2 (-2 b^8 u^3 + 2 a^2 b^6 u^2 (2 u + 2 v - w) +
4 a^6 b^2 v (u + v) (u + w) - a^8 v^2 (2 u + 5 w) +
a^4 b^4 u (-2 u^2 - 2 v^2 - 2 v w + w^2 + u (-8 v + w))) +
c^4 u v w (b^6 u^3 (-u + v) + a^6 v^2 (u^2 - u v + 7 u w - 2 v w) +
a^4 b^2 u v (-2 u^2 + v^2 + u (v - 8 w) - 2 v w - 2 w^2) +
a^2 b^4 u^2 (u^2 - 2 (v - w)^2 + u (v + w)))) y z + .... = 0.
Para obtener la ecuación de la circunferencia osculatriz ci(Q) podemos utilizar la ecuación de las cónicas del haz osculatriz determinado por co(P) y la cónica degenerada producto de la tangente t en Q a co(P) y una recta variable ℓ que pase por Q:
t ℓ + λ co(P) = f x^2+g y^2 + h z^2 + 2p y z + 2q z x + 2r x y = 0,
ℓ: (c^2 v - b^2 w) (c^2 u + b^2 μ u - a^2 (μ v + w)) x +
μ (b^2 u - a^2 v) (c^2 u - a^2 w) y - (b^2 u - a^2 v) (c^2 u -
a^2 w) z = 0,
t: u (c^2 v - b^2 w)^2 x + v (c^2 u - a^2 w)^2 y + (b^2 u - a^2 v)^2 w z = 0.
La circunferencia de este haz de cónicas se obtiene imponiendo:
(g + h - 2 p)/a^2 = (h + f - 2 q)/b^2 = (f + g - 2 r)/c^2.
Lo que permite obtener los valores de
λ y μ,
(λ = -(((b^2 c^2 u^2-a^2 c^2 u v-b^2 c^2 u v+c^4 u v+a^2 c^2 v^2-a^2 b^2 u w+b^4 u w-b^2 c^2 u w+a^4 v w-a^2 b^2 v w-a^2 c^2 v w+a^2 b^2 w^2) (c^8 u^3 v^2+a^2 b^2 c^4 u^3 v w-b^4 c^4 u^3 v w-b^2 c^6 u^3 v w-a^4 c^4 u^2 v^2 w+a^2 b^2 c^4 u^2 v^2 w-2 a^2 c^6 u^2 v^2 w+b^6 c^2 u^3 w^2-2 a^4 b^2 c^2 u^2 v w^2+2 a^2 b^2 c^4 u^2 v w^2+2 a^6 c^2 u v^2 w^2-a^4 b^2 c^2 u v^2 w^2+a^4 c^4 u v^2 w^2-a^2 b^6 u^2 w^3+a^6 b^2 u v w^3+a^4 b^4 u v w^3-a^4 b^2 c^2 u v w^3-a^8 v^2 w^3))/(-c^4 u^2 v+c^4 u v^2+2 a^2 c^2 u v w-2 b^2 c^2 u v w+b^4 u w^2-a^4 v w^2)),
μ -((c^6 u^2 v^2-b^4 c^2 u^3 w+2 a^2 b^2 c^2 u^2 v w-2 b^2 c^4 u^2 v w-a^4 c^2 u v^2 w-a^2 c^4 u v^2 w+a^2 b^4 u^2 w^2+b^4 c^2 u^2 w^2-2 a^4 b^2 u v w^2+2 a^2 b^2 c^2 u v w^2+a^6 v^2 w^2-a^2 b^4 u w^3)/((b^2 u-a^2 v) (-c^4 u^2 v+c^4 u v^2+2 a^2 c^2 u v w-2 b^2 c^2 u v w+b^4 u w^2-a^4 v w^2))))
que sustituidos en la ecuación del haz de cónicas nos la ecuación de la circunferencia osculatriz ci(Q).
La circunferencia osculatriz, ci(Q), vuelve cortar a la circunferencia circunscrita, Γ, en el punto UP, de primera coordenada baricéntrica:
UP = (a^2 / (u (c^2v-b^2w)^2(2(b^2-c^2)u v w a^2 + u^2(c^4v-b^4w))) : ... : ...).
Los únicos pares encontrados son {P=Xi, UP=Xj}, para {i,j}: {44, 6551}, {9456, 6551}.
La circunferencia osculatriz, ci(Q), y la cónica circunscrita, co(P), tienen tres puntos comunes confundidos en Q y se vuelven cortar en el punto VP:
VP = (u / (v w(v-w)a^4 -2u v w(b^2-c^2)a^2 - u^2(c^4v-b^4w)) : ... : ...).
Pares {P:{Xi, Xj,...}, VP=Xk}, para {{i,j,...}. k}:
{{6189, 6190}, 99}, {{1989}, 476}, {{9468}, 805}, {{232, 325}, 877}, {{385}, 880}, {{111}, 892}, {{9456}, 901}, {{1990, 3284}, 4240}, {{187, 524}, 5468}, {{34581}, 6082}, {{3, 67}, 17708}, {{44}, 17780}, {{81, 17961}, 17929}, {{86, 17962}, 17930}, {{333, 17963}, 17931}, {{69, 248, 4558}, 17932}, {{17966}, 17933}, {{17731, 17735}, 17934}, {{5291, 19623}, 17935}, {{17967}, 17936}, {{17968, 22329}, 17937}, {{2501}, 18808}, {{16318}, 23977}, {{8755}, 23987}, {{32, 32740}, 32729}, {{9182, 17964}, 34760}, {{34369}, 34761}.
CASOS PARTICULARES.
• . P=X2, Q=X99, U2:=UX2 es el conjugado isogonal de X33919 y V2:=VX2=X892.
U2 = ( a^2/((b^2 - c^2)^3 (-2 a^2 + b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en
(-0.263163227091243, 0.473326808260612, 3.43443664253838).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {98,30786}, {99,11123}, {111,34539}, {249,843}, {476,892}, {805,32729}, {2770,4590}, {2868,34537}, {5466,14734}, {5468,20404}, {5970,23357}, {19610,20976}, {32583,32694}.
• . P=X2501, Q=X1300, V2501:=VX2501= X18808.
U2501 = ( a^2/((b^2 - c^2) (a^2 - b^2 - c^2) (2 a^4 - (b^2 - c^2)^2 -
a^2 (b^2 + c^2)) (a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2) -
2 a^2 (b^4 - b^2 c^2 + c^4))^2 ) : ... : ...),
que tiene números de búsqueda en ETC
(3.24370963525445, -1.52118733575515, 3.19669742115897).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {476,687}, {10419,32710}, {32681,32708}.
• . P=X647, Q=X74,
U647 = ( a^2/((b^2 - c^2) (a^2 - b^2 - c^2) (-2 a^4 + (b^2 - c^2)^2 +
a^2 (b^2 + c^2))^2 (a^6 (b^2 + c^2) +
3 a^2 (b^2 - c^2)^2 (b^2 + c^2) +
a^4 (-3 b^4 + 4 b^2 c^2 - 3 c^4) - (b^2 - c^2)^2 (b^4 +
4 b^2 c^2 + c^4))) : ... : ...),
que tiene números de búsqueda en ETC
({0.774973070608706, -0.808994008857256, 3.84305737852769).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1294,34601}, {2693,2972}, {5897,14919}, {9064,34568}.
V647 = ( (b^2 - c^2) (a^2 - b^2 - c^2) /(a^6 (b^2 + c^2) +
3 a^2 (b^2 - c^2)^2 (b^2 + c^2) +
a^4 (-3 b^4 + 4 b^2 c^2 - 3 c^4) - (b^2 - c^2)^2 (b^4 +
4 b^2 c^2 + c^4)) : ... : ...),
que tiene números de búsqueda en ETC
(308.157816395030, -245.409435159552, 31.3128197177373).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,2416}, {4,520}, {6,2430}, {64,523}, {66,8675}, {68,30211}, {74,1294}, {525,3426}, {526,11744}, {684,1942}, {1177,9003}, {1650,14380}, {4846,8673}, {6368,16835}, {9517,10293}, {23977,32646}.
• . P=X523, Q=X98,
U523 = ( a^2/((b^2 - c^2) (b^4 + c^4 - a^2 (b^2 + c^2))^2 (2 a^6 -
a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2)) ) : ... : ...),
que tiene números de búsqueda en ETC
(-0.439663817772149, 0.939926603598172, 3.19286782608048).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {248,1297}, {2710,3269}, {2857,9476}, {32687,32696}.
V523 = ( (b^2 - c^2)/ (2 a^6 - a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(-389.796844571481, 217.729341018539, 32.8112028097563).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,2419}, {4,525}, {98,1297}, {459,2501}, {514,3429}, {523,3424}, {850,2052}, {877,17932}, {2867,23977}, {4240,17708}, {6330,9979}, {9476,34765}, {14458,23878}.
• . P=X3, Q=X110, V3:=VX3=X17708,
U3 = ( a^2 (a^4 - (b^2 - c^2)^2)^2/((b^2 - c^2)^3 (-a^4 + b^4 - b^2 c^2 +
c^4)) : ... : ...),
que tiene números de búsqueda en ETC
(-0.0155222527416984, 0.0235010200063900, 3.63155866162997).
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {98,8791}, {842,23964}, {2697,23357}, {2867,17708}.
- Miércoles, 1 de enero del 2020
Un punto sobre el eje de Lemoine
El 1 de enero de 1959, Fidel Castro llegó a Santiago de Cuba, declarándola capital provisional de Cuba y proclamando al magistrado Manuel Urrutia Lleó como presidente de la nación. Por el momento, el gobierno de Estados Unidos reconoció al gobierno revolucionario como legítimo, poniendo fin, tanto de jure como de facto a la dictadura de Batista.
Dado un triángulo ABC con , la tangente en A a la circunferencia circunscrita corta a los lados MaMb y MaMc, del , en los puntos Ac y Ab, respectivamente.
Las rectas BAb, BAc, CAb, CAc vuelven a cortar a la circunferecia circunscrita en los puntos Bab, Bac, Cab, Cac, respectivamente.
Sea A' el punto de intersección de las rectas BabCab, BacCac. Los puntos B' y C' se obtienen cíclicmente.
Las coordenadas baricéntricas de A' son:
(2 (b^2 + c^2)^2 : -a^2 b^2 : -a^2 c^2).
Los triángulos ABC, A'B'C' y forma una terna de triángulos con centro de perspectividad común (el ) y los tres ejes de perspectividad concurren en
T = ( a^2 (b^2 - c^2) (a^6 (b^2 + c^2) + 2 a^2 (b^2 + c^2)^3 +
a^4 (b^4 + c^4) + 2 (b^2 + c^2)^2 (b^4 + c^4)) : ... : ...),
que tiene números de búsqueda en
(-8.73259709580097, 14.9567656389673, -2.68358999316176).
T está sobre el , el cual pasa los 131 centros Xi, para i= 187, 237, 351, 512, 647, 649, 663, 665, 667, 669, 887, 890, 902, 1055, 1495, 1946, 1960, 2223, 2488, 2502, 2978, 3005, 3009, 3010, 3016, 3229, 3230, 3231, 3250, 3288, 3331, 3569, 3724, 3747, 3804, 4775, 4834, 5027, 5029, 5040, 5075, 5098, 5106, 5113, 5147, 5163, 5167, 5168, 5191, 5202, 5638, 5639, 6137, 6138, 6139, 6140, 7660, 8618, 8619, 8620, 8621, 8622, 8623, 8624, 8625, 8626, 8627, 8628, 8629, 8630, 8631, 8632, 8633, 8634, 8635, 8636, 8637, 8638, 8639, 8640, 8641, 8642, 8643, 8644, 8645, 8646, 8647, 8648, 8649, 8650, 8651, 8653, 8654, 8655, 8656, 8657, 8658, 8659, 8660, 8661, 8662, 8663, 8664, 8665, 9135, 9208, 9210, 9264, 9409, 9420, 9486, 9489, 9491, 9494, 11186, 14270, 14318, 15451, 17414, 17428, 18117, 18773, 18774, 21444, 21645, 21646, 21731, 22388, 23220, 32442, 32518.
El punto fijo finito de la
transformación afín.
( matriz asociada:
{{2 (a^2+b^2) (2 a^2+2 b^2-c^2) (a^2+c^2) (b^2+c^2)^2 (2 a^2-b^2+2 c^2),a^2 b^2 (a^2+b^2) (2 a^2+2 b^2-c^2) (b^2+c^2) (a^2-2 (b^2+c^2)),a^2 c^2 (a^2+c^2) (b^2+c^2) (2 a^2-b^2+2 c^2) (a^2-2 (b^2+c^2))}, {-a^2 b^2 (a^2+b^2) (2 a^2+2 b^2-c^2) (a^2+c^2) (2 a^2-b^2+2 c^2),-2 (a^2+b^2) (2 a^2+2 b^2-c^2) (a^2+c^2)^2 (b^2+c^2) (a^2-2 (b^2+c^2)),b^2 c^2 (a^2+c^2) (b^2+c^2) (2 a^2-b^2+2 c^2) (a^2-2 (b^2+c^2))}, {-a^2 (a^2+b^2) c^2 (2 a^2+2 b^2-c^2) (a^2+c^2) (2 a^2-b^2+2 c^2),b^2 (a^2+b^2) c^2 (2 a^2+2 b^2-c^2) (b^2+c^2) (a^2-2 (b^2+c^2)),-2 (a^2+b^2)^2 (a^2+c^2) (b^2+c^2) (2 a^2-b^2+2 c^2) (a^2-2 (b^2+c^2))}})
σ, que aplica ABC en A'B'C' es:
F = ((b^2 + c^2) (a^2 - 2 (b^2 + c^2)) : ... : ...),
que tiene números de búsqueda en ETC
(4.78942863012863, 1.85645410321279, 0.144921504239237).
Es la reflexión de Xi en Xj para los índices {i,j}: {5008, 7820}, {7853, 3314}.
Es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {32,33242}, {37,4668}, {39,141}, {69,187}, {76,625}, {99,7848}, {115,14711}, {183,7908}, {193,5007}, {194,7849}, {315,33280}, {325,7603}, {384,7882}, {385,7880}, {524,5008}, {538,3314}, {574,599}, {1384,15533}, {1975,7873}, {2482,22165}, {3096,32450}, {3618,5041}, {3620,34511}, {3630,8369}, {3631,6390}, {3734,7788}, {3788,17008}, {3793,7789}, {3849,7850}, {3926,7854}, {3934,7777}, {4403,34542}, {5368,33185}, {6144,33237}, {6329,7889}, {6683,7906}, {6781,14929}, {7737,10513}, {7738,30776}, {7746,32958}, {7748,32830}, {7751,7874}, {7754,7852}, {7760,7915}, {7761,32833}, {7763,33188}, {7764,31239}, {7767,7863}, {7768,7816}, {7770,7916}, {7776,17130}, {7778,17131}, {7779,7804}, {7780,7836}, {7781,7879}, {7783,32027}, {7798,7868}, {7800,31652}, {7805,7832}, {7811,32456}, {7815,32821}, {7817,7931}, {7819,7890}, {7830,32820}, {7833,15301}, {7842,7939}, {7843,7917}, {7861,7922}, {7865,31859}, {7871,31276}, {7886,7909}, {7913,22253}, {7918,20105}, {7934,32457}, {7947,17006}, {8024,31125}, {8356,14148}, {8368,15480}, {11185,31173}, {13468,31274}, {14075,15534}, {14077,26932}, {18440,30270}, {18860,34507}, {23297,31078}, {31455,32818}, {32875,33023}, {32877,32982}, {32878,32980}.
El único par de centros del triángulo (X,X'=σ(X)) que figuran actualmente en ETC es:
(X141, X34512).
Esto es, la imagen del del simediano es el baricentro del () en el triángulo de vértices los centros de curvatura de la en los vértices de ABC.
GENERALIZACIÓN
Sea un punto P, Q su y c(Q) la cónica circunscrita de Q.
La tangente en A a c(Q) corta a los lados PaPb y PaPc, del de P, en los puntos Ac y Ab, respectivamente.
Las rectas BAb, BAc, CAb, CAc vuelven a cortar a c(Q) en los puntos Bab, Bac, Cab, Cac, respectivamente.
Sea A' el punto de intersección de las rectas BabCab, BacCac. Los puntos B' y C' se obtienen cíclicmente.
Los triángulos ABC, A'B'C' y el de c(Q) forma una , con centro de perspectividad común, Q. Los tres ejes de perspectividad concurren en el punto de coordenadas baricéntricas:
(a^2 u^3 (c^2 v^2 - b^2 w^2) (2 c^8 u^6 v^8 +
2 c^6 u^4 v^6 (2 b^2 u^2 + a^2 v^2) w^2 +
c^4 u^2 v^4 (4 b^4 u^4 + 6 a^2 b^2 u^2 v^2 + a^4 v^4) w^4 +
c^2 v^2 (4 b^6 u^6 + 6 a^2 b^4 u^4 v^2 + a^6 v^6) w^6 +
b^2 (2 b^6 u^6 + 2 a^2 b^4 u^4 v^2 + a^4 b^2 u^2 v^4 +
a^6 v^6) w^8):...: ...).
Cuando P es el baricentro se obtiene el punto T.
Página Personal

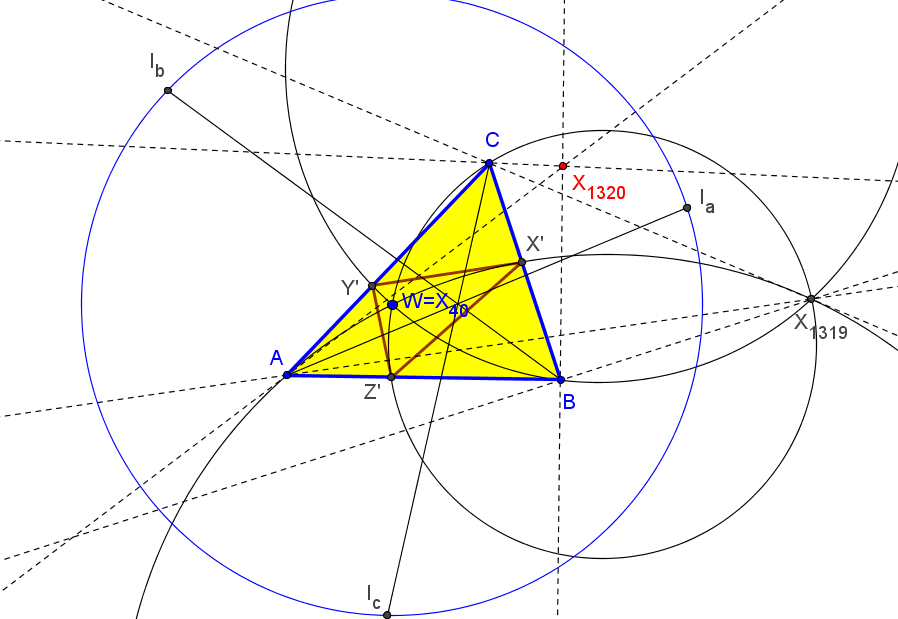
Longuet-Higgins.png)


.png)