- Viernes, 28 de diciembre del 2018
Cúbica nopivotal, isogonal y circular asociada a un punto
Dado un triángulo ABC, sean DEF el y A'B'C' el de un punto M.
Si D', E', F' son los simétricos de D, E, F respecto a A', B', C', respectivamente, entonces la circunferencia circunscrita Γ(M) al triángulo D'E'F' pasa por el ortocentro, X4, de ABC.
Para un punto Q, el lugar geométrico del punto M tal que Q está sobre la circunferencia Γ(M) es una cúbica 𝒞(Q)=(X6,P,Fo) (focal).
El foco Fo de esta cúbica es el del punto del infinito en la dirección perpendicular a la recta X4Q.
Si T es el punto de intersección de la parábola 𝒫(Q) (inscrita en ABC), de foco Fo y directriz X4Q, con la perpendicular por Q a X4Q, entonces la raíz P de la cúbica es el de la tangente t a 𝒫(Q) en T.
Si (p:q:r) son las coordenadas baricéntricas de Q, la ecuación de nK(X6,P,Fo) es:
Σ abc xyz
(a^2(p+q)(p+r)-p(b^2(p+q)+c^2(p+r)))x(c^2y^2+b^2z^2+(b^2+c^2-a^2)y z) = 0.
De raíz P = ((a^2(p+q)(p+r)-p(b^2(p+q)+c^2(p+r))):...:...).
Y foco Fo = (a^2/(a^2(q-r)-(b^2-c^2)(q+r)):...:...).
El parámetro de esta cúbica es cero si y solo si Q está sobre la circunferencia de centro X1351 que pasa por el ortocentro (y por X193, X6792, X24650, X24651), de ecuación (b^2+c^2-a^2)^2x^2+(a^4-a^2(b^2+c^2)+2(b^2-c^2)^2)y z+ ...=0. Es decir, cuando la raíz P está sobre el .
Cuando Q=X6792 (el otro punto de intersección de la recta X2X6 y la ), la cúbica es K018=Brocard (second) cubic, nK0(X6,X523).
Cuando Q=X193 ( del ortocentro y el baricentro), la cúbica tiene foco X3565 (2nd Moses circumcircle point) y punto en el infinito X3566 (2nd Moses infinity point) y raíz
W = ( 2a^6- 3a^4(b^2+c^2)-
4a^2(b^4-3b^2c^2+c^4) + (b^2-c^2)^2(b^2+c^2) : ... : ...),
que tiene números de búsqueda en
(-20.8303977512017, 22.5419217176057, -2.35125159126491) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,1975}, {23,2079}, {25,15591}, {111,858}, {115,5159}, {230,231}, {524,9225}, {546,15820}, {1196,5305}, {1368,7748}, {1503,20998}, {1611,2207}, {1691,15448}, {1995,7745}, {2165,3054}, {2548,5020}, {3053,4232}, {3055,8585}, {3124,11064}, {3292,6791}, {3564,6388}, {3815,11284}, {3851,15880}, {6387,19588}, {6390,6719},{6676,7749}, {7756,10300},{9172,22110}, {13468,19221}.
OTROS EJEMPLOS:
La cúbica es K019=Brocard (third) cubic, nK0(X6, X647) de foco el , es la cúbica 𝒞(Q19)
Q19 = ( a^2(a^8(b^4-b^2c^2+c^4) +
a^6(-3b^6+2b^4c^2+2b^2c^4-3c^6)+
a^4(3b^8-3b^6c^2+b^4c^4-3b^2c^6+3c^8) -
a^2(b^2-c^2)^2(b^6+c^6) -b^4c^4(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en ETC
(-7.62194199760569, -2.12102954072978, 8.62688893207685), reflexión de Xi en Xj para los índices {i,j}: {11674, 187}, {18321, 5}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,2421}, {4,512}, {5,6787}, {20,185}, {32,2698}, {187,11464}, {249,1147}, {631,3111}, {691,13352}, {805,9737}, {842,2713}, {1968,2065}, {2387,11676}, {2699,2714}, {2882,10753}, {3567,15544}, {3767,14113}, {6337,15631}, {7763,12833}, {8870,12110}, {9517,11005}, {10762,11596}, {11554,15043}, {12006,15536}.
La cúbica es K040=Pelletier strophoid, nK0(X6, X650) de foco X105, es la cúbica 𝒞(Q40)
Q40 = ( a^2 (-a^2 b c (b^2 - 3 b c + c^2) + a^4 (b^2 - b c + c^2) +
a^3 (-2 b^3 + b^2 c + b c^2 - 2 c^3) - (b^3 - c^3)^2 +
a (b - c)^2 (2 b^3 + 5 b^2 c + 5 b c^2 + 2 c^3)) : ... : ...),
que tiene números de búsqueda en ETC
(-4.06306796646790, 0.656473984103104, 5.06144463128280) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,885}, {21,1083}, {35,41}, {56,840}, {105,2808}, {144,145}, {1156,3271}, {2711,9090}, {2714,2752}, {2742,11248}, {3270,10763}, {3560,14661}, {5057,20358}, {6841,18345}.
- Viernes, 21 de diciembre del 2018
El punto X(13881) como centro de una cónica
Dado un triángulo ABC y un punto P, sean DEF el de P, Ab es el centro de la circunferencia que pasa por D y es tangente en B al lado AB y Ac es el centro de la circunferencia que pasa por D y es tangente en C al lado AC.
Si (u:v.w) son las coordenadas baricéntricas del punto P, entoces:
Ab = (-a^2(a^2-b^2+c^2)w : -a^4v-(b^2-c^2)^2(v+w)+
a^2(b^2+c^2)(2v+w) : 2a^2c^2w),
Ac = (a^2(a^2+b^2-c^2)v : -2a^2b^2v :
a^4w+(b^2-c^2)^2(v+w)-a^2(b^2+c^2)(v+2w)).
Los puntos Bc, Ba, Ca, Cb se definen procediendo cíclicamente sobre los lados de ABC.
Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están sobre una misma cónica 𝒞(P) si y sólo si P queda sobre una curva algebraica de grado 12. Esta curva pasa por los vértices (triples) de ABC y por los centros del triángulo: X4 (ortocentro), X67 ( del inverso del baricentro en la circunferencia circunscrita), X69 (), X523 (isogonal conjugado del foco de la ), X671 (punto de intersección, distinto de A, B y C, de la con la ).
Cuando
P es el ortocentro, el centro de la
cónica
( 5 a^6 x^2-17 a^4 b^2 x^2+19 a^2 b^4 x^2-7 b^6 x^2-17 a^4 c^2 x^2+26 a^2 b^2 c^2 x^2-9 b^4 c^2 x^2+19 a^2 c^4 x^2-9 b^2 c^4 x^2-7 c^6 x^2+2 a^6 x y-2 a^4 b^2 x y-2 a^2 b^4 x y+2 b^6 x y+2 a^4 c^2 x y-4 a^2 b^2 c^2 x y+2 b^4 c^2 x y-26 a^2 c^4 x y-26 b^2 c^4 x y+22 c^6 x y-7 a^6 y^2+19 a^4 b^2 y^2-17 a^2 b^4 y^2+5 b^6 y^2-9 a^4 c^2 y^2+26 a^2 b^2 c^2 y^2-17 b^4 c^2 y^2-9 a^2 c^4 y^2+19 b^2 c^4 y^2-7 c^6 y^2+2 a^6 x z+2 a^4 b^2 x z-26 a^2 b^4 x z+22 b^6 x z-2 a^4 c^2 x z-4 a^2 b^2 c^2 x z-26 b^4 c^2 x z-2 a^2 c^4 x z+2 b^2 c^4 x z+2 c^6 x z+22 a^6 y z-26 a^4 b^2 y z+2 a^2 b^4 y z+2 b^6 y z-26 a^4 c^2 y z-4 a^2 b^2 c^2 y z-2 b^4 c^2 y z+2 a^2 c^4 y z-2 b^2 c^4 y z+2 c^6 y z-7 a^6 z^2-9 a^4 b^2 z^2-9 a^2 b^4 z^2-7 b^6 z^2+19 a^4 c^2 z^2+26 a^2 b^2 c^2 z^2+19 b^4 c^2 z^2-17 a^2 c^4 z^2-17 b^2 c^4 z^2+5 c^6 z^2 = 0)
𝒞(X
4) es
X13881.
Σ abc xyz
(b^2+c^2-a^2)(5 a^4-12 a^2 (b^2+c^2)+7 b^4+2 b^2 c^2+7 c^4)x^2
-2 (11a^6-13 a^4 (b^2+c^2)+a^2 (b^2-c^2)^2+(b^2-c^2)^2 (b^2+c^2))y z = 0.
X13881 = ( a^4 - a^2(b^2+c^2) + 2(b^2-c^2)^2 : ... : ...).
Si P=X67, el centro de la cónica
𝒞(X67)
( 2 a^14 x^2-9 a^12 b^2 x^2+8 a^10 b^4 x^2+14 a^8 b^6 x^2-22 a^6 b^8 x^2-a^4 b^10 x^2+12 a^2 b^12 x^2-4 b^14 x^2-9 a^12 c^2 x^2+16 a^10 b^2 c^2 x^2-12 a^8 b^4 c^2 x^2+11 a^6 b^6 c^2 x^2+13 a^4 b^8 c^2 x^2-27 a^2 b^10 c^2 x^2+8 b^12 c^2 x^2+8 a^10 c^4 x^2-12 a^8 b^2 c^4 x^2-24 a^6 b^4 c^4 x^2-a^4 b^6 c^4 x^2+45 a^2 b^8 c^4 x^2-12 b^10 c^4 x^2+14 a^8 c^6 x^2+11 a^6 b^2 c^6 x^2-a^4 b^4 c^6 x^2-48 a^2 b^6 c^6 x^2+4 b^8 c^6 x^2-22 a^6 c^8 x^2+13 a^4 b^2 c^8 x^2+45 a^2 b^4 c^8 x^2+4 b^6 c^8 x^2-a^4 c^10 x^2-27 a^2 b^2 c^10 x^2-12 b^4 c^10 x^2+12 a^2 c^12 x^2+8 b^2 c^12 x^2-4 c^14 x^2+2 a^14 x y-21 a^12 b^2 x y+56 a^10 b^4 x y-37 a^8 b^6 x y-37 a^6 b^8 x y+56 a^4 b^10 x y-21 a^2 b^12 x y+2 b^14 x y-11 a^12 c^2 x y+41 a^10 b^2 c^2 x y-70 a^8 b^4 c^2 x y+80 a^6 b^6 c^2 x y-70 a^4 b^8 c^2 x y+41 a^2 b^10 c^2 x y-11 b^12 c^2 x y+15 a^10 c^4 x y-56 a^8 b^2 c^4 x y+36 a^6 b^4 c^4 x y+36 a^4 b^6 c^4 x y-56 a^2 b^8 c^4 x y+15 b^10 c^4 x y-5 a^8 c^6 x y+53 a^6 b^2 c^6 x y-55 a^4 b^4 c^6 x y+53 a^2 b^6 c^6 x y-5 b^8 c^6 x y-10 a^6 c^8 x y-22 a^4 b^2 c^8 x y-22 a^2 b^4 c^8 x y-10 b^6 c^8 x y+15 a^4 c^10 x y+16 a^2 b^2 c^10 x y+15 b^4 c^10 x y-7 a^2 c^12 x y-7 b^2 c^12 x y+c^14 x y-4 a^14 y^2+12 a^12 b^2 y^2-a^10 b^4 y^2-22 a^8 b^6 y^2+14 a^6 b^8 y^2+8 a^4 b^10 y^2-9 a^2 b^12 y^2+2 b^14 y^2+8 a^12 c^2 y^2-27 a^10 b^2 c^2 y^2+13 a^8 b^4 c^2 y^2+11 a^6 b^6 c^2 y^2-12 a^4 b^8 c^2 y^2+16 a^2 b^10 c^2 y^2-9 b^12 c^2 y^2-12 a^10 c^4 y^2+45 a^8 b^2 c^4 y^2-a^6 b^4 c^4 y^2-24 a^4 b^6 c^4 y^2-12 a^2 b^8 c^4 y^2+8 b^10 c^4 y^2+4 a^8 c^6 y^2-48 a^6 b^2 c^6 y^2-a^4 b^4 c^6 y^2+11 a^2 b^6 c^6 y^2+14 b^8 c^6 y^2+4 a^6 c^8 y^2+45 a^4 b^2 c^8 y^2+13 a^2 b^4 c^8 y^2-22 b^6 c^8 y^2-12 a^4 c^10 y^2-27 a^2 b^2 c^10 y^2-b^4 c^10 y^2+8 a^2 c^12 y^2+12 b^2 c^12 y^2-4 c^14 y^2+2 a^14 x z-11 a^12 b^2 x z+15 a^10 b^4 x z-5 a^8 b^6 x z-10 a^6 b^8 x z+15 a^4 b^10 x z-7 a^2 b^12 x z+b^14 x z-21 a^12 c^2 x z+41 a^10 b^2 c^2 x z-56 a^8 b^4 c^2 x z+53 a^6 b^6 c^2 x z-22 a^4 b^8 c^2 x z+16 a^2 b^10 c^2 x z-7 b^12 c^2 x z+56 a^10 c^4 x z-70 a^8 b^2 c^4 x z+36 a^6 b^4 c^4 x z-55 a^4 b^6 c^4 x z-22 a^2 b^8 c^4 x z+15 b^10 c^4 x z-37 a^8 c^6 x z+80 a^6 b^2 c^6 x z+36 a^4 b^4 c^6 x z+53 a^2 b^6 c^6 x z-10 b^8 c^6 x z-37 a^6 c^8 x z-70 a^4 b^2 c^8 x z-56 a^2 b^4 c^8 x z-5 b^6 c^8 x z+56 a^4 c^10 x z+41 a^2 b^2 c^10 x z+15 b^4 c^10 x z-21 a^2 c^12 x z-11 b^2 c^12 x z+2 c^14 x z+a^14 y z-7 a^12 b^2 y z+15 a^10 b^4 y z-10 a^8 b^6 y z-5 a^6 b^8 y z+15 a^4 b^10 y z-11 a^2 b^12 y z+2 b^14 y z-7 a^12 c^2 y z+16 a^10 b^2 c^2 y z-22 a^8 b^4 c^2 y z+53 a^6 b^6 c^2 y z-56 a^4 b^8 c^2 y z+41 a^2 b^10 c^2 y z-21 b^12 c^2 y z+15 a^10 c^4 y z-22 a^8 b^2 c^4 y z-55 a^6 b^4 c^4 y z+36 a^4 b^6 c^4 y z-70 a^2 b^8 c^4 y z+56 b^10 c^4 y z-10 a^8 c^6 y z+53 a^6 b^2 c^6 y z+36 a^4 b^4 c^6 y z+80 a^2 b^6 c^6 y z-37 b^8 c^6 y z-5 a^6 c^8 y z-56 a^4 b^2 c^8 y z-70 a^2 b^4 c^8 y z-37 b^6 c^8 y z+15 a^4 c^10 y z+41 a^2 b^2 c^10 y z+56 b^4 c^10 y z-11 a^2 c^12 y z-21 b^2 c^12 y z+2 c^14 y z-4 a^14 z^2+8 a^12 b^2 z^2-12 a^10 b^4 z^2+4 a^8 b^6 z^2+4 a^6 b^8 z^2-12 a^4 b^10 z^2+8 a^2 b^12 z^2-4 b^14 z^2+12 a^12 c^2 z^2-27 a^10 b^2 c^2 z^2+45 a^8 b^4 c^2 z^2-48 a^6 b^6 c^2 z^2+45 a^4 b^8 c^2 z^2-27 a^2 b^10 c^2 z^2+12 b^12 c^2 z^2-a^10 c^4 z^2+13 a^8 b^2 c^4 z^2-a^6 b^4 c^4 z^2-a^4 b^6 c^4 z^2+13 a^2 b^8 c^4 z^2-b^10 c^4 z^2-22 a^8 c^6 z^2+11 a^6 b^2 c^6 z^2-24 a^4 b^4 c^6 z^2+11 a^2 b^6 c^6 z^2-22 b^8 c^6 z^2+14 a^6 c^8 z^2-12 a^4 b^2 c^8 z^2-12 a^2 b^4 c^8 z^2+14 b^6 c^8 z^2+8 a^4 c^10 z^2+16 a^2 b^2 c^10 z^2+8 b^4 c^10 z^2-9 a^2 c^12 z^2-9 b^2 c^12 z^2+2 c^14 z^2 = 0)
es:
W76 = ( (b^2+c^2-a^2) (11 a^10 - 12 a^8 (b^2 + c^2) - 5 a^6 (b^4 - 5 b^2 c^2 + c^4) + a^4 (15 b^6 - 16 b^4 c^2 - 16 b^2 c^4 + 15 c^6)- a^2 (b^2 - c^2)^2 (4 b^4 + 5 b^2 c^2 + 4 c^4) - (b^2 - c^2)^2 (b^6
c^6) )/(b^2+c^2-2a^2) : ... : ...),
que tiene números de búsqueda en
(-41.1584725065074, -19.0341418604642, 35.8143653883091), y no está sobre ninguna recta determinada por centros de ETC.
Si P=X69, el centro de la cónica
𝒞(X69)
( a^8 x^2-4 a^6 b^2 x^2+2 a^4 b^4 x^2+4 a^2 b^6 x^2-3 b^8 x^2-4 a^6 c^2 x^2-4 a^2 b^4 c^2 x^2+8 b^6 c^2 x^2+2 a^4 c^4 x^2-4 a^2 b^2 c^4 x^2-10 b^4 c^4 x^2+4 a^2 c^6 x^2+8 b^2 c^6 x^2-3 c^8 x^2+2 a^8 x y-16 a^6 b^2 x y+28 a^4 b^4 x y-16 a^2 b^6 x y+2 b^8 x y-12 a^6 c^2 x y+12 a^4 b^2 c^2 x y+12 a^2 b^4 c^2 x y-12 b^6 c^2 x y+16 a^4 c^4 x y+8 a^2 b^2 c^4 x y+16 b^4 c^4 x y-4 a^2 c^6 x y-4 b^2 c^6 x y-2 c^8 x y-3 a^8 y^2+4 a^6 b^2 y^2+2 a^4 b^4 y^2-4 a^2 b^6 y^2+b^8 y^2+8 a^6 c^2 y^2-4 a^4 b^2 c^2 y^2-4 b^6 c^2 y^2-10 a^4 c^4 y^2-4 a^2 b^2 c^4 y^2+2 b^4 c^4 y^2+8 a^2 c^6 y^2+4 b^2 c^6 y^2-3 c^8 y^2+2 a^8 x z-12 a^6 b^2 x z+16 a^4 b^4 x z-4 a^2 b^6 x z-2 b^8 x z-16 a^6 c^2 x z+12 a^4 b^2 c^2 x z+8 a^2 b^4 c^2 x z-4 b^6 c^2 x z+28 a^4 c^4 x z+12 a^2 b^2 c^4 x z+16 b^4 c^4 x z-16 a^2 c^6 x z-12 b^2 c^6 x z+2 c^8 x z-2 a^8 y z-4 a^6 b^2 y z+16 a^4 b^4 y z-12 a^2 b^6 y z+2 b^8 y z-4 a^6 c^2 y z+8 a^4 b^2 c^2 y z+12 a^2 b^4 c^2 y z-16 b^6 c^2 y z+16 a^4 c^4 y z+12 a^2 b^2 c^4 y z+28 b^4 c^4 y z-12 a^2 c^6 y z-16 b^2 c^6 y z+2 c^8 y z-3 a^8 z^2+8 a^6 b^2 z^2-10 a^4 b^4 z^2+8 a^2 b^6 z^2-3 b^8 z^2+4 a^6 c^2 z^2-4 a^4 b^2 c^2 z^2-4 a^2 b^4 c^2 z^2+4 b^6 c^2 z^2+2 a^4 c^4 z^2+2 b^4 c^4 z^2-4 a^2 c^6 z^2-4 b^2 c^6 z^2+c^8 z^2 = 0)
es el circuncentro.
Si P=X523, el centro de la cónica
𝒞(X523)
( 2 a^18 b^2 c^2 x^2-7 a^16 b^4 c^2 x^2+8 a^14 b^6 c^2 x^2-9 a^10 b^10 c^2 x^2+9 a^8 b^12 c^2 x^2-2 a^6 b^14 c^2 x^2-2 a^4 b^16 c^2 x^2+a^2 b^18 c^2 x^2-7 a^16 b^2 c^4 x^2+24 a^14 b^4 c^4 x^2-30 a^12 b^6 c^4 x^2+14 a^10 b^8 c^4 x^2+9 a^8 b^10 c^4 x^2-23 a^6 b^12 c^4 x^2+17 a^4 b^14 c^4 x^2-3 a^2 b^16 c^4 x^2-b^18 c^4 x^2+8 a^14 b^2 c^6 x^2-30 a^12 b^4 c^6 x^2+40 a^10 b^6 c^6 x^2-29 a^8 b^8 c^6 x^2+26 a^6 b^10 c^6 x^2-14 a^4 b^12 c^6 x^2-6 a^2 b^14 c^6 x^2+5 b^16 c^6 x^2+14 a^10 b^4 c^8 x^2-29 a^8 b^6 c^8 x^2+2 a^6 b^8 c^8 x^2-a^4 b^10 c^8 x^2+23 a^2 b^12 c^8 x^2-9 b^14 c^8 x^2-9 a^10 b^2 c^10 x^2+9 a^8 b^4 c^10 x^2+26 a^6 b^6 c^10 x^2-a^4 b^8 c^10 x^2-30 a^2 b^10 c^10 x^2+5 b^12 c^10 x^2+9 a^8 b^2 c^12 x^2-23 a^6 b^4 c^12 x^2-14 a^4 b^6 c^12 x^2+23 a^2 b^8 c^12 x^2+5 b^10 c^12 x^2-2 a^6 b^2 c^14 x^2+17 a^4 b^4 c^14 x^2-6 a^2 b^6 c^14 x^2-9 b^8 c^14 x^2-2 a^4 b^2 c^16 x^2-3 a^2 b^4 c^16 x^2+5 b^6 c^16 x^2+a^2 b^2 c^18 x^2-b^4 c^18 x^2+2 a^20 c^2 x y-7 a^18 b^2 c^2 x y+12 a^16 b^4 c^2 x y-17 a^14 b^6 c^2 x y+22 a^12 b^8 c^2 x y-24 a^10 b^10 c^2 x y+22 a^8 b^12 c^2 x y-17 a^6 b^14 c^2 x y+12 a^4 b^16 c^2 x y-7 a^2 b^18 c^2 x y+2 b^20 c^2 x y-11 a^18 c^4 x y+32 a^16 b^2 c^4 x y-33 a^14 b^4 c^4 x y+17 a^12 b^6 c^4 x y-5 a^10 b^8 c^4 x y-5 a^8 b^10 c^4 x y+17 a^6 b^12 c^4 x y-33 a^4 b^14 c^4 x y+32 a^2 b^16 c^4 x y-11 b^18 c^4 x y+24 a^16 c^6 x y-67 a^14 b^2 c^6 x y+45 a^12 b^4 c^6 x y+5 a^10 b^6 c^6 x y-14 a^8 b^8 c^6 x y+5 a^6 b^10 c^6 x y+45 a^4 b^12 c^6 x y-67 a^2 b^14 c^6 x y+24 b^16 c^6 x y-23 a^14 c^8 x y+87 a^12 b^2 c^8 x y-49 a^10 b^4 c^8 x y-15 a^8 b^6 c^8 x y-15 a^6 b^8 c^8 x y-49 a^4 b^10 c^8 x y+87 a^2 b^12 c^8 x y-23 b^14 c^8 x y-a^12 c^10 x y-76 a^10 b^2 c^10 x y+53 a^8 b^4 c^10 x y+51 a^6 b^6 c^10 x y+53 a^4 b^8 c^10 x y-76 a^2 b^10 c^10 x y-b^12 c^10 x y+27 a^10 c^12 x y+36 a^8 b^2 c^12 x y-71 a^6 b^4 c^12 x y-71 a^4 b^6 c^12 x y+36 a^2 b^8 c^12 x y+27 b^10 c^12 x y-29 a^8 c^14 x y+11 a^6 b^2 c^14 x y+71 a^4 b^4 c^14 x y+11 a^2 b^6 c^14 x y-29 b^8 c^14 x y+11 a^6 c^16 x y-31 a^4 b^2 c^16 x y-31 a^2 b^4 c^16 x y+11 b^6 c^16 x y+3 a^4 c^18 x y+19 a^2 b^2 c^18 x y+3 b^4 c^18 x y-4 a^2 c^20 x y-4 b^2 c^20 x y+c^22 x y+a^18 b^2 c^2 y^2-2 a^16 b^4 c^2 y^2-2 a^14 b^6 c^2 y^2+9 a^12 b^8 c^2 y^2-9 a^10 b^10 c^2 y^2+8 a^6 b^14 c^2 y^2-7 a^4 b^16 c^2 y^2+2 a^2 b^18 c^2 y^2-a^18 c^4 y^2-3 a^16 b^2 c^4 y^2+17 a^14 b^4 c^4 y^2-23 a^12 b^6 c^4 y^2+9 a^10 b^8 c^4 y^2+14 a^8 b^10 c^4 y^2-30 a^6 b^12 c^4 y^2+24 a^4 b^14 c^4 y^2-7 a^2 b^16 c^4 y^2+5 a^16 c^6 y^2-6 a^14 b^2 c^6 y^2-14 a^12 b^4 c^6 y^2+26 a^10 b^6 c^6 y^2-29 a^8 b^8 c^6 y^2+40 a^6 b^10 c^6 y^2-30 a^4 b^12 c^6 y^2+8 a^2 b^14 c^6 y^2-9 a^14 c^8 y^2+23 a^12 b^2 c^8 y^2-a^10 b^4 c^8 y^2+2 a^8 b^6 c^8 y^2-29 a^6 b^8 c^8 y^2+14 a^4 b^10 c^8 y^2+5 a^12 c^10 y^2-30 a^10 b^2 c^10 y^2-a^8 b^4 c^10 y^2+26 a^6 b^6 c^10 y^2+9 a^4 b^8 c^10 y^2-9 a^2 b^10 c^10 y^2+5 a^10 c^12 y^2+23 a^8 b^2 c^12 y^2-14 a^6 b^4 c^12 y^2-23 a^4 b^6 c^12 y^2+9 a^2 b^8 c^12 y^2-9 a^8 c^14 y^2-6 a^6 b^2 c^14 y^2+17 a^4 b^4 c^14 y^2-2 a^2 b^6 c^14 y^2+5 a^6 c^16 y^2-3 a^4 b^2 c^16 y^2-2 a^2 b^4 c^16 y^2-a^4 c^18 y^2+a^2 b^2 c^18 y^2+2 a^20 b^2 x z-11 a^18 b^4 x z+24 a^16 b^6 x z-23 a^14 b^8 x z-a^12 b^10 x z+27 a^10 b^12 x z-29 a^8 b^14 x z+11 a^6 b^16 x z+3 a^4 b^18 x z-4 a^2 b^20 x z+b^22 x z-7 a^18 b^2 c^2 x z+32 a^16 b^4 c^2 x z-67 a^14 b^6 c^2 x z+87 a^12 b^8 c^2 x z-76 a^10 b^10 c^2 x z+36 a^8 b^12 c^2 x z+11 a^6 b^14 c^2 x z-31 a^4 b^16 c^2 x z+19 a^2 b^18 c^2 x z-4 b^20 c^2 x z+12 a^16 b^2 c^4 x z-33 a^14 b^4 c^4 x z+45 a^12 b^6 c^4 x z-49 a^10 b^8 c^4 x z+53 a^8 b^10 c^4 x z-71 a^6 b^12 c^4 x z+71 a^4 b^14 c^4 x z-31 a^2 b^16 c^4 x z+3 b^18 c^4 x z-17 a^14 b^2 c^6 x z+17 a^12 b^4 c^6 x z+5 a^10 b^6 c^6 x z-15 a^8 b^8 c^6 x z+51 a^6 b^10 c^6 x z-71 a^4 b^12 c^6 x z+11 a^2 b^14 c^6 x z+11 b^16 c^6 x z+22 a^12 b^2 c^8 x z-5 a^10 b^4 c^8 x z-14 a^8 b^6 c^8 x z-15 a^6 b^8 c^8 x z+53 a^4 b^10 c^8 x z+36 a^2 b^12 c^8 x z-29 b^14 c^8 x z-24 a^10 b^2 c^10 x z-5 a^8 b^4 c^10 x z+5 a^6 b^6 c^10 x z-49 a^4 b^8 c^10 x z-76 a^2 b^10 c^10 x z+27 b^12 c^10 x z+22 a^8 b^2 c^12 x z+17 a^6 b^4 c^12 x z+45 a^4 b^6 c^12 x z+87 a^2 b^8 c^12 x z-b^10 c^12 x z-17 a^6 b^2 c^14 x z-33 a^4 b^4 c^14 x z-67 a^2 b^6 c^14 x z-23 b^8 c^14 x z+12 a^4 b^2 c^16 x z+32 a^2 b^4 c^16 x z+24 b^6 c^16 x z-7 a^2 b^2 c^18 x z-11 b^4 c^18 x z+2 b^2 c^20 x z+a^22 y z-4 a^20 b^2 y z+3 a^18 b^4 y z+11 a^16 b^6 y z-29 a^14 b^8 y z+27 a^12 b^10 y z-a^10 b^12 y z-23 a^8 b^14 y z+24 a^6 b^16 y z-11 a^4 b^18 y z+2 a^2 b^20 y z-4 a^20 c^2 y z+19 a^18 b^2 c^2 y z-31 a^16 b^4 c^2 y z+11 a^14 b^6 c^2 y z+36 a^12 b^8 c^2 y z-76 a^10 b^10 c^2 y z+87 a^8 b^12 c^2 y z-67 a^6 b^14 c^2 y z+32 a^4 b^16 c^2 y z-7 a^2 b^18 c^2 y z+3 a^18 c^4 y z-31 a^16 b^2 c^4 y z+71 a^14 b^4 c^4 y z-71 a^12 b^6 c^4 y z+53 a^10 b^8 c^4 y z-49 a^8 b^10 c^4 y z+45 a^6 b^12 c^4 y z-33 a^4 b^14 c^4 y z+12 a^2 b^16 c^4 y z+11 a^16 c^6 y z+11 a^14 b^2 c^6 y z-71 a^12 b^4 c^6 y z+51 a^10 b^6 c^6 y z-15 a^8 b^8 c^6 y z+5 a^6 b^10 c^6 y z+17 a^4 b^12 c^6 y z-17 a^2 b^14 c^6 y z-29 a^14 c^8 y z+36 a^12 b^2 c^8 y z+53 a^10 b^4 c^8 y z-15 a^8 b^6 c^8 y z-14 a^6 b^8 c^8 y z-5 a^4 b^10 c^8 y z+22 a^2 b^12 c^8 y z+27 a^12 c^10 y z-76 a^10 b^2 c^10 y z-49 a^8 b^4 c^10 y z+5 a^6 b^6 c^10 y z-5 a^4 b^8 c^10 y z-24 a^2 b^10 c^10 y z-a^10 c^12 y z+87 a^8 b^2 c^12 y z+45 a^6 b^4 c^12 y z+17 a^4 b^6 c^12 y z+22 a^2 b^8 c^12 y z-23 a^8 c^14 y z-67 a^6 b^2 c^14 y z-33 a^4 b^4 c^14 y z-17 a^2 b^6 c^14 y z+24 a^6 c^16 y z+32 a^4 b^2 c^16 y z+12 a^2 b^4 c^16 y z-11 a^4 c^18 y z-7 a^2 b^2 c^18 y z+2 a^2 c^20 y z-a^18 b^4 z^2+5 a^16 b^6 z^2-9 a^14 b^8 z^2+5 a^12 b^10 z^2+5 a^10 b^12 z^2-9 a^8 b^14 z^2+5 a^6 b^16 z^2-a^4 b^18 z^2+a^18 b^2 c^2 z^2-3 a^16 b^4 c^2 z^2-6 a^14 b^6 c^2 z^2+23 a^12 b^8 c^2 z^2-30 a^10 b^10 c^2 z^2+23 a^8 b^12 c^2 z^2-6 a^6 b^14 c^2 z^2-3 a^4 b^16 c^2 z^2+a^2 b^18 c^2 z^2-2 a^16 b^2 c^4 z^2+17 a^14 b^4 c^4 z^2-14 a^12 b^6 c^4 z^2-a^10 b^8 c^4 z^2-a^8 b^10 c^4 z^2-14 a^6 b^12 c^4 z^2+17 a^4 b^14 c^4 z^2-2 a^2 b^16 c^4 z^2-2 a^14 b^2 c^6 z^2-23 a^12 b^4 c^6 z^2+26 a^10 b^6 c^6 z^2+2 a^8 b^8 c^6 z^2+26 a^6 b^10 c^6 z^2-23 a^4 b^12 c^6 z^2-2 a^2 b^14 c^6 z^2+9 a^12 b^2 c^8 z^2+9 a^10 b^4 c^8 z^2-29 a^8 b^6 c^8 z^2-29 a^6 b^8 c^8 z^2+9 a^4 b^10 c^8 z^2+9 a^2 b^12 c^8 z^2-9 a^10 b^2 c^10 z^2+14 a^8 b^4 c^10 z^2+40 a^6 b^6 c^10 z^2+14 a^4 b^8 c^10 z^2-9 a^2 b^10 c^10 z^2-30 a^6 b^4 c^12 z^2-30 a^4 b^6 c^12 z^2+8 a^6 b^2 c^14 z^2+24 a^4 b^4 c^14 z^2+8 a^2 b^6 c^14 z^2-7 a^4 b^2 c^16 z^2-7 a^2 b^4 c^16 z^2+2 a^2 b^2 c^18 z^2 = 0)
es
W523 = ( a^2 (a^30-6 a^28 (b^2+c^2)+a^26 (9 b^4+46 b^2 c^2+9 c^4)+2 a^24 (9 b^6-59 b^4 c^2-59 b^2 c^4+9 c^6)+a^22 (-75 b^8+49 b^6 c^2+454 b^4 c^4+49 b^2 c^6-75 c^8)+a^20 (66 b^10+344 b^8 c^2-678 b^6 c^4-678 b^4 c^6+344 b^2 c^8+66 c^10)+a^18 (77 b^12-724 b^10 c^2-5 b^8 c^4+1776 b^6 c^6-5 b^4 c^8-724 b^2 c^10+77 c^12)+a^16 (-198 b^14+411 b^12 c^2+1471 b^10 c^4-1816 b^8 c^6-1816 b^6 c^8+1471 b^4 c^10+411 b^2 c^12-198 c^14)-(b^2-c^2)^8 (2 b^14+9 b^12 c^2+8 b^10 c^4-b^8 c^6-b^6 c^8+8 b^4 c^10+9 b^2 c^12+2 c^14)+a^2 (b^2-c^2)^6 (15 b^16+22 b^14 c^2-43 b^12 c^4-19 b^10 c^6+41 b^8 c^8-19 b^6 c^10-43 b^4 c^12+22 b^2 c^14+15 c^16)+a^6 (b^2-c^2)^4 (39 b^16-251 b^14 c^2-13 b^12 c^4+362 b^10 c^6+57 b^8 c^8+362 b^6 c^10-13 b^4 c^12-251 b^2 c^14+39 c^16)+a^14 (99 b^16+510 b^14 c^2-2263 b^12 c^4+215 b^10 c^6+2963 b^8 c^8+215 b^6 c^10-2263 b^4 c^12+510 b^2 c^14+99 c^16)-a^10 (b^2-c^2)^2 (165 b^16-264 b^14 c^2-1063 b^12 c^4+863 b^10 c^6+1117 b^8 c^8+863 b^6 c^10-1063 b^4 c^12-264 b^2 c^14+165 c^16)-a^4 (b^2-c^2)^4 (42 b^18-80 b^16 c^2-113 b^14 c^4+231 b^12 c^6-62 b^10 c^8-62 b^8 c^10+231 b^6 c^12-113 b^4 c^14-80 b^2 c^16+42 c^18)+a^8 (b^2-c^2)^2 (54 b^18+248 b^16 c^2-1023 b^14 c^4+339 b^12 c^6+422 b^10 c^8+422 b^8 c^10+339 b^6 c^12-1023 b^4 c^14+248 b^2 c^16+54 c^18)+a^12 (110 b^18-1026 b^16 c^2+1401 b^14 c^4+1617 b^12 c^6-2108 b^10 c^8-2108 b^8 c^10+1617 b^6 c^12+1401 b^4 c^14-1026 b^2 c^16+110 c^18)) : ... : ...),
que tiene números de búsqueda en
(-1.90404616180515, 14.1607332293532, -5.28412952527316), y no está sobre ninguna recta determinada por centros de ETC.
Si P=X671, el centro de la cónica
𝒞(X671)
( 2 a^14 b^2 c^2 x^2-11 a^12 b^4 c^2 x^2+15 a^10 b^6 c^2 x^2-5 a^8 b^8 c^2 x^2-10 a^6 b^10 c^2 x^2+15 a^4 b^12 c^2 x^2-7 a^2 b^14 c^2 x^2+b^16 c^2 x^2-11 a^12 b^2 c^4 x^2+86 a^10 b^4 c^4 x^2-137 a^8 b^6 c^4 x^2+97 a^6 b^8 c^4 x^2-40 a^4 b^10 c^4 x^2+7 a^2 b^12 c^4 x^2+15 a^10 b^2 c^6 x^2-137 a^8 b^4 c^6 x^2+172 a^6 b^6 c^6 x^2-78 a^4 b^8 c^6 x^2+19 a^2 b^10 c^6 x^2-2 b^12 c^6 x^2-5 a^8 b^2 c^8 x^2+97 a^6 b^4 c^8 x^2-78 a^4 b^6 c^8 x^2+10 a^2 b^8 c^8 x^2+b^10 c^8 x^2-10 a^6 b^2 c^10 x^2-40 a^4 b^4 c^10 x^2+19 a^2 b^6 c^10 x^2+b^8 c^10 x^2+15 a^4 b^2 c^12 x^2+7 a^2 b^4 c^12 x^2-2 b^6 c^12 x^2-7 a^2 b^2 c^14 x^2+b^2 c^16 x^2+a^16 c^2 x y-2 a^14 b^2 c^2 x y-8 a^12 b^4 c^2 x y+2 a^10 b^6 c^2 x y+14 a^8 b^8 c^2 x y+2 a^6 b^10 c^2 x y-8 a^4 b^12 c^2 x y-2 a^2 b^14 c^2 x y+b^16 c^2 x y-5 a^14 c^4 x y+26 a^12 b^2 c^4 x y-4 a^10 b^4 c^4 x y-15 a^8 b^6 c^4 x y-15 a^6 b^8 c^4 x y-4 a^4 b^10 c^4 x y+26 a^2 b^12 c^4 x y-5 b^14 c^4 x y+4 a^12 c^6 x y-25 a^10 b^2 c^6 x y-46 a^8 b^4 c^6 x y+128 a^6 b^6 c^6 x y-46 a^4 b^8 c^6 x y-25 a^2 b^10 c^6 x y+4 b^12 c^6 x y+5 a^10 c^8 x y+30 a^8 b^2 c^8 x y-46 a^6 b^4 c^8 x y-46 a^4 b^6 c^8 x y+30 a^2 b^8 c^8 x y+5 b^10 c^8 x y-10 a^8 c^10 x y+3 a^6 b^2 c^10 x y+83 a^4 b^4 c^10 x y+3 a^2 b^6 c^10 x y-10 b^8 c^10 x y+5 a^6 c^12 x y-43 a^4 b^2 c^12 x y-43 a^2 b^4 c^12 x y+5 b^6 c^12 x y+4 a^4 c^14 x y+32 a^2 b^2 c^14 x y+4 b^4 c^14 x y-5 a^2 c^16 x y-5 b^2 c^16 x y+c^18 x y+a^16 c^2 y^2-7 a^14 b^2 c^2 y^2+15 a^12 b^4 c^2 y^2-10 a^10 b^6 c^2 y^2-5 a^8 b^8 c^2 y^2+15 a^6 b^10 c^2 y^2-11 a^4 b^12 c^2 y^2+2 a^2 b^14 c^2 y^2+7 a^12 b^2 c^4 y^2-40 a^10 b^4 c^4 y^2+97 a^8 b^6 c^4 y^2-137 a^6 b^8 c^4 y^2+86 a^4 b^10 c^4 y^2-11 a^2 b^12 c^4 y^2-2 a^12 c^6 y^2+19 a^10 b^2 c^6 y^2-78 a^8 b^4 c^6 y^2+172 a^6 b^6 c^6 y^2-137 a^4 b^8 c^6 y^2+15 a^2 b^10 c^6 y^2+a^10 c^8 y^2+10 a^8 b^2 c^8 y^2-78 a^6 b^4 c^8 y^2+97 a^4 b^6 c^8 y^2-5 a^2 b^8 c^8 y^2+a^8 c^10 y^2+19 a^6 b^2 c^10 y^2-40 a^4 b^4 c^10 y^2-10 a^2 b^6 c^10 y^2-2 a^6 c^12 y^2+7 a^4 b^2 c^12 y^2+15 a^2 b^4 c^12 y^2-7 a^2 b^2 c^14 y^2+a^2 c^16 y^2+a^16 b^2 x z-5 a^14 b^4 x z+4 a^12 b^6 x z+5 a^10 b^8 x z-10 a^8 b^10 x z+5 a^6 b^12 x z+4 a^4 b^14 x z-5 a^2 b^16 x z+b^18 x z-2 a^14 b^2 c^2 x z+26 a^12 b^4 c^2 x z-25 a^10 b^6 c^2 x z+30 a^8 b^8 c^2 x z+3 a^6 b^10 c^2 x z-43 a^4 b^12 c^2 x z+32 a^2 b^14 c^2 x z-5 b^16 c^2 x z-8 a^12 b^2 c^4 x z-4 a^10 b^4 c^4 x z-46 a^8 b^6 c^4 x z-46 a^6 b^8 c^4 x z+83 a^4 b^10 c^4 x z-43 a^2 b^12 c^4 x z+4 b^14 c^4 x z+2 a^10 b^2 c^6 x z-15 a^8 b^4 c^6 x z+128 a^6 b^6 c^6 x z-46 a^4 b^8 c^6 x z+3 a^2 b^10 c^6 x z+5 b^12 c^6 x z+14 a^8 b^2 c^8 x z-15 a^6 b^4 c^8 x z-46 a^4 b^6 c^8 x z+30 a^2 b^8 c^8 x z-10 b^10 c^8 x z+2 a^6 b^2 c^10 x z-4 a^4 b^4 c^10 x z-25 a^2 b^6 c^10 x z+5 b^8 c^10 x z-8 a^4 b^2 c^12 x z+26 a^2 b^4 c^12 x z+4 b^6 c^12 x z-2 a^2 b^2 c^14 x z-5 b^4 c^14 x z+b^2 c^16 x z+a^18 y z-5 a^16 b^2 y z+4 a^14 b^4 y z+5 a^12 b^6 y z-10 a^10 b^8 y z+5 a^8 b^10 y z+4 a^6 b^12 y z-5 a^4 b^14 y z+a^2 b^16 y z-5 a^16 c^2 y z+32 a^14 b^2 c^2 y z-43 a^12 b^4 c^2 y z+3 a^10 b^6 c^2 y z+30 a^8 b^8 c^2 y z-25 a^6 b^10 c^2 y z+26 a^4 b^12 c^2 y z-2 a^2 b^14 c^2 y z+4 a^14 c^4 y z-43 a^12 b^2 c^4 y z+83 a^10 b^4 c^4 y z-46 a^8 b^6 c^4 y z-46 a^6 b^8 c^4 y z-4 a^4 b^10 c^4 y z-8 a^2 b^12 c^4 y z+5 a^12 c^6 y z+3 a^10 b^2 c^6 y z-46 a^8 b^4 c^6 y z+128 a^6 b^6 c^6 y z-15 a^4 b^8 c^6 y z+2 a^2 b^10 c^6 y z-10 a^10 c^8 y z+30 a^8 b^2 c^8 y z-46 a^6 b^4 c^8 y z-15 a^4 b^6 c^8 y z+14 a^2 b^8 c^8 y z+5 a^8 c^10 y z-25 a^6 b^2 c^10 y z-4 a^4 b^4 c^10 y z+2 a^2 b^6 c^10 y z+4 a^6 c^12 y z+26 a^4 b^2 c^12 y z-8 a^2 b^4 c^12 y z-5 a^4 c^14 y z-2 a^2 b^2 c^14 y z+a^2 c^16 y z+a^16 b^2 z^2-2 a^12 b^6 z^2+a^10 b^8 z^2+a^8 b^10 z^2-2 a^6 b^12 z^2+a^2 b^16 z^2-7 a^14 b^2 c^2 z^2+7 a^12 b^4 c^2 z^2+19 a^10 b^6 c^2 z^2+10 a^8 b^8 c^2 z^2+19 a^6 b^10 c^2 z^2+7 a^4 b^12 c^2 z^2-7 a^2 b^14 c^2 z^2+15 a^12 b^2 c^4 z^2-40 a^10 b^4 c^4 z^2-78 a^8 b^6 c^4 z^2-78 a^6 b^8 c^4 z^2-40 a^4 b^10 c^4 z^2+15 a^2 b^12 c^4 z^2-10 a^10 b^2 c^6 z^2+97 a^8 b^4 c^6 z^2+172 a^6 b^6 c^6 z^2+97 a^4 b^8 c^6 z^2-10 a^2 b^10 c^6 z^2-5 a^8 b^2 c^8 z^2-137 a^6 b^4 c^8 z^2-137 a^4 b^6 c^8 z^2-5 a^2 b^8 c^8 z^2+15 a^6 b^2 c^10 z^2+86 a^4 b^4 c^10 z^2+15 a^2 b^6 c^10 z^2-11 a^4 b^2 c^12 z^2-11 a^2 b^4 c^12 z^2+2 a^2 b^2 c^14 z^2 = 0)
es
W671 = ( a^2 (a^14+7 a^10 b^2 c^2-2 a^12 (b^2+c^2)+a^4 b^2 c^2 (b^2+c^2)^3+a^8 (3 b^6-2 b^4 c^2-2 b^2 c^4+3 c^6)+a^6 (-3 b^8+7 b^6 c^2-22 b^4 c^4+7 b^2 c^6-3 c^8)+2 a^2 (b^2-c^2)^2 (b^8-5 b^6 c^2+6 b^4 c^4-5 b^2 c^6+c^8)-(b^2-c^2)^2 (b^10-b^8 c^2+10 b^6 c^4+10 b^4 c^6-b^2 c^8+c^10)) : ... : ...),
que tiene números de búsqueda en
(8.16155876871533, 8.70551551348148, -6.15310415144833), y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,126}, {7530,18381}, {23720,25328}.
- Miércoles, 12 de diciembre del 2018
Circunferencias de Mannheim y de Thébault
a Pablo, en su "cumple"
Dado un triángulo ABC de incentro I,
existen dos circunferencias, Γae y Γai, tangentes interiormente a la circunferencia Γ, circunscrita a ABC, y exteriormente a las dos relativa a la bisectriz AI (situadas en el interior de Γ y en el mismo semiplano que A, respecto a la recta BC).
Se denota por Oae y Oai, Tae y Tai los centros de Γae y Γai y sus puntos de tangencia con Γ, respectivamente.
Procediendo cíclicamente se definen las circunferencias Γbe, Γbi, Γce y Γci, sus centros Obe, Obi, Oce y Oci, y sus puntos de tangencia con Γ, Tbe, Tbi, Tce y Tci.
Las rectas
TaeTai,
TbeTbi,
TceTci concurren en el centro de homotecia externo de las circunferencias inscrita y circunscrita, X
56.
Las rectas ATae, BTbe y CTce concurren en X266, raíz trilineal de X56 ( de las raíces baricéntricas de I y X56).
El triángulo formado por las rectas OaeOai, ObeObi y OceOci es perspectivo con ABC con centro de perspectividad el de las , X999.
Construcción de las A-circunferencias de Thébault:
La construcción de las circunferencias de Thébault de la bisectriz interior del ángulo en A puede hacerse siguiendo los dos procedimientos, para el caso más general de una ceviana por A, descritos en (Patrice Debart.- Le théorème de Thébault-Sawayama, Construction des bissectrices, Construction de Viète).
Por el vértice A del triángulos ABC, se traza la ceviana por un punto P (bisectriz interior, en el caso que nos ocupa) que corta al lado BC en D.
Se trazan las bisectrices de los ángulos ∠ADB y ∠ADC, y las paralelas por I; éstas intersecan a los segementos AD, DB, DC en los puntos de contacto de las A-circunferencias de Thébault.
Basta con trazar las perpendiculares a BC por estos puntos de contacto, que cortan a las biesectrices en los centros de las circunferencias tangentes. Por el teorema de Thébault-Sawayama, estos centros están alineados con I.
Se sigue que
las circunferencias de Thébault de la bisectriz interior del ángulo en A son bitangentes en I.
Construcción de las circunferencias Γae y Γai:
Sean Ae y Ai los puntos de intersección de AI y la A-circunferencia de Mannheim y A' el antipodal de A en Γ. La recta A'Ae vuelve a cortar a Γ en Tae y la recta A'Ai vuelve a cortar a Γ en Tai.
La circunferencia Γae es tangente a Γ en Tae y pasa por Ae.
La circunferencia Γai es tangente a Γ en Tai y pasa por Ai.
En coordenadas baricéntricas, respecto a ABC,
Ae = ( 2 a c-Sqrt[((a^2-(b-c)^2) c)/b] (a+b+c) : 2 b c : 2 c^2 ),
Ai = ( 2 a c+Sqrt[((a^2-(b-c)^2) c)/b] (a+b+c) : 2 b c : 2 c^2 ),
Tae, Tai = (a^2 (a + b - c) (-b (a - b + c) ± Sqrt[b (a + b - c) c (a - b + c)]) :
b^2 (c-b) (a + b - c) (-a + b + c) :
±(c-b) c Sqrt[ b (a + b - c) c (a - b + c)] (-a + b + c)).
- Martes, 4 de diciembre del 2018
Los centros del triángulo X(3218) y X(5537)
Dado un triángulo ABC, sean M un punto variable sobre su circunferencia circunscrita, M* su (en la recta del infinito) y A'B'C' el .
Las rectas A'M*, B'M*, C'M* cortan a BC, CA, AB en A1, B1, C1, respectivamente.
Cuando M se mueve sobre la circunferencia circunscrita a ABC, los lugares geometricos de los puntos U=BB1∩CC1, V=CC1∩AA1 y W=AA1∩BB1, son tres conicas cA, cB y cC.
Si (a^2t(t-1):-b^2 (t-1):c^2t) son las coordenadas baricéntricas de M:
A1 = (0 : b^2-b c-a^2t : c(c-b)+a^2(t-1)),
cA : -a b c x^2 + (-a^2 c - b c^2 + c^3) x y + (-a^2 b + b^3 -
b^2 c) x z + (-a^3 + a b^2 - a b c + a c^2) y z=0.
El único punto común a las tres cónicas
cA, cB, cC es
X3218.
El punto X3218 corresponde a M=X104, antipodal en la circunferencia circunscrita del del , para
t = (b (a^3 - a^2 c- a (b - c)^2 - b^2 c + c^3))/(a (a^2 (b + c) -2 a b c - (b - c)^2 (b + c))).
Las rectas AM*, BM*, CM* cortan a BC, CA, AB en A2, B2, C2, respectivamente.
Cuando M se mueve sobre la circunferencia circunscrita a ABC, los lugares geometricos de los puntos D=B'B2∩C'C2, E=C'C2∩A'A2 y F=A'A2∩B'B2, son tres conicas cA, cB y cC.
Si (a^2t(t-1):-b^2 (t-1):c^2t) son las coordenadas baricéntricas de M:
A2 = (0 : t :1-t),
ccA : -b^2 c^2 x^2 + (-a^2 c^2 - b^2 c^2 + 2 a c^3 - c^4) x y + (-a^2 c^2 +
a c^3) y^2 + (-a^2 b^2 + 2 a b^3 - b^4 - b^2 c^2) x z + (-a^4 +
2 a^3 b - a^2 b^2 + 2 a^3 c - 3 a^2 b c + a b^2 c - a^2 c^2 +
a b c^2) y z + (-a^2 b^2 + a b^3) z^2=0.
El único punto común a las tres cónicas
ccA, ccB, ccC es
X5537.
El punto X5537 corresponde a M=X2291, para
t = (a^2 + a b - 2 b^2 - 2 a c + b c + c^2)/(
2 a^2 - a b - b^2 - a c + 2 b c - c^2).
X(5537) = Gibert-Burek-Moses concurrent circles image of X(57)
Let P be a point in the plane of a triangle ABC with orthocenter H. Let IaIbIc be the excentral triangle of ABC. The circumcircles of APIa, BIbE, IcPF concur in two points, P and Q. The point Q = Q(P) is the
Gibert-Burek-Moses concurrent circles image of P. The points X(1), P, Q(P) are collinear, and circumcenters of APD, BPE, CPF are collinear. Let L denote the line of the circumcenters; then Q is the reflection of P in L.
Examples: Q(X(3)) = X(484), Q(X(4)) = X(3465), Q(X(15)) = X(1276), Q(X(16)) = X(1277), Q(X(20)) = X(5018). (Peter Moses, June 16, 2013)
- Lunes, 3 de diciembre del 2018
El primer triangulo circumperpendicular y tres cónicas concurrentes
Dado un triángulo ABC, sean M un punto variable sobre su circunferencia circunscrita y A'B'C' el .
Las paralelas a MA, MB y MC por A', B' y C', cortan a BC, CA y AB, respectivamente, A1, B1 y C1.
Cuando M se mueve sobre la circunferencia circunscrita a ABC, los lugares geometricos de los puntos U=BB1∩CC1, V=CC1∩AA1 y W=AA1∩BB1, son tres conicas cA, cB y cC.
Si (a^2t(t-1):-b^2 (t-1):c^2t) son las coordenadas baricéntricas de M:
A1 = (0 : b(a^2(b-b t)+(b-c)(b^2(-1+t)-c^2t)) : c(-b^3(-1+
t)+b^2c(-1+t)+b c^2t+c(a^2-c^2)t),
cA : (-a^3 b c + a b^3 c - a b^2 c^2 + a b c^3) x^2 + (-a^4 c + a^2 b^2 c -
a^2 b c^2 + 2 a^2 c^3 + b c^4 - c^5) x y + (-a^4 b + 2 a^2 b^3 -
b^5 - a^2 b^2 c + b^4 c + a^2 b c^2) x z + (-a^5 + 2 a^3 b^2 -
a b^4 - a^3 b c + a b^3 c + 2 a^3 c^2 - a b^2 c^2 + a b c^3 -
a c^4) y z=0.
Existe un único punto común a las tres cónicas cA, cB, cC:
Z = ( a(a^2-a b+b^2-c^2)(a^2-a c-b^2+c^2)(a^4-a^2(2b^2-b c+2c^2)+b^4-b^3c+b^2c^2-b c^3+c^4) : ... : ...),
que tiene números de búsqueda en
(77.4520144678110, -8.77954957433101, -26.0282694133146) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {63,18359}, {1807,4189}, {2006,3218}, {2161,4440}.
El punto Z corresponde a M=X14987, el otro punto de intersección de la circunferencia circunscrita a ABC con la recta que pasa por X100 ( del ) y por X355 (centro de la
M=X14987 = (a^2t0(t0-1):-b^2 (t0-1):c^2t0), para:
t0 = -((b (-a^6 + a^5 (b + c) + (b - c)^3 c (b + c)^2 +
a^4 (2 b^2 - 3 b c + c^2) +
a^3 (-2 b^3 + b^2 c + 2 b c^2 - 2 c^3) +
a^2 (-b^4 + 2 b^3 c - 4 b^2 c^2 + 2 b c^3 + c^4) +
a (b^5 - 2 b^4 c + 2 b^3 c^2 + b^2 c^3 - 3 b c^4 +
c^5)))/(a (a^5 (b + c) - 2 a^3 (b - c)^2 (b + c) +
a (b - c)^4 (b + c) -
a^4 (b + c)^2 - (b^2 - c^2)^2 (b^2 - b c + c^2) +
a^2 (2 b^4 + b^3 c - 4 b^2 c^2 + b c^3 + 2 c^4)))).
- Domingo, 2 de diciembre del 2018
El centro del triángulo X(12515)
Dado un triángulo ABC, sean M un punto variable sobre su circunferencia circunscrita y A'B'C' el .
Las paralelas a MB y a MC por B' y C', respectivamente, se cortan en el punto D. El lugar geométrico de D, cuando M varía, es una circunferencia Γa que pasa por B' y C'.
Si (a^2t(t-1):-b^2 (t-1):c^2t) son las coordenadas baricéntricas de M:
D = (a^2(-a^4(-1+t)t+
a b c(b-b t+c t)-(b-c)(b^3(-1+t)+c^3t)+
a^2(c^2(-2+t)t+b^2(-1+t^2))) :
b(bc^2(b^2-c^2)+a^5(-1+t)t-a^4c(-1+t)t-
a^2c^2(b(-1+t)+c t)+
a b(b-c)(b^2(-1+t)-c^2(1+t))+
a^3(c^2t-b^2(-1+t^2)+b c(-1+t^2))):
c(-b^4c+b^2c^3+a^5(-1+t)t-a^4b(-1+t)t+
a^2b^2(b(-1+t)+c t)-a c(b-c)(b^2(-2+t)-c^2t)+
a^3(-b^2(-1+t)+b c(-2+t)t-c^2(-2+t)t))),
Γa: a^2y z+b^2z x+c^2x y - (x+y+z)(a b c(a^2-b^2+b c-c^2)x + a c(a-c)(a^2-b^2+b c-c^2)y + a b(a-b)(a^2-b^2+b c-c^2)z) / ((b+c-a)(a+b-c)(a-b+c)).
Análogamente, se definen las circunferencias Γb y Γc.
Las tres circunferencias Γ
a, Γ
b y Γ
c concurren en
X12515 (reflexión del circuncentro en el centro de la de
A'B'C').
El punto X12515, corresponde al punto M=X140 (t=(b(a^3-a^2c-a(b-c)^2-b^2c+c^3))/(a(a^2(b+c)-2a b c-(b-c)^2(b+c)))).
- Jueves, 29 de noviembre del 2018
El centro del triángulo X(2334)
a Lolilla, por su "cumple"
Dado un triángulo ABC, sean A'B'C' el de su incentro y Γa la A- con centro Aa y punto de tangencia Ta con la circunferencia circunscrita.
Sea A1 el centro de la circunferencia Ωa circunscrita al triángulo A'AaTa. Los puntos B1 y C1 se definen análogamente, procediendo cíclicamente sobre los vértices de ABC.
Las rectas
AA1,
BB1 y
CC1 concurren en
X2334.
A' = (-a^2 b c : b (b^2 c + b c^2) : c (b^2 c + b c^2)),
Aa = (a^3 + a^2 (b + c) - (b - c)^2 (b + c) -
a (b + c)^2 : -4 b^2 c : -4 b c^2),
Ta = (a (-a^2 + (b - c)^2) : 2 b^2 (a + b - c) : 2 c^2 (a - b + c)),
A1 = (-a (a^2 - 2 b c + a (b + c)) : b^2 (a + b + 3 c) : c^2 (a + 3 b + c)),
Γa: a^2 y z + b^2 z x+ c^2 x y + (x + y +
z) (-((4 b^2 c^2 x)/(a + b + c)^2) + (-c^2 + (
4 b c^2 (a + c))/(a + b + c)^2) y + (-b^2 + (
4 b^2 (a + b) c)/(a + b + c)^2) z)=0,
Ωa: a^2 y z + b^2 z x+ c^2 x y + (x + y + z) ((4 b^2 c^2 (b + c) x)/((a - b - c) (a + b + c)^2) + (
2 b c^2 (-a^2 + a b - a c) y)/((-a + b + c) (a + b + c)^2) - (
2 b^2 c (a^2 + a b - a c) z)/((-a + b + c) (a + b + c)^2))=0.
X2334 = (a^2/(3a + b + c) : b^2/(3b + c + a) : c^2/(3c + a + b)).
Algunas otras consideraciones sobre esta configuración:
• Si Ωb y Ωc son definidas similarmente a la circunferencia Ωa, el de las tres es X3576.
Let 𝒫
a be the parabola with focus A and directrix BC, and define 𝒫
b and 𝒫
c cyclically.
X3576 is the centroid of the six points of tangency of lines from X(1) to 𝒫
a, 𝒫
b, and 𝒫
c. (Randy Hutson, December 2, 2017) .
• Los de los pares de circunferencias (Γa, Ωa), (Γb, Ωb) y (Γc, Ωc) forman un triángulo perspectivo con ABC, con centro de perspectividad X945, de X944.
Let ℋ
a be the hyperbola passing through A, and with foci at B and C. This is called the
A-Soddy hyperbola in (Paul Yiu,
Introduction to the Geometry of the Triangle, 2001 (with corrections 2013); §12.4 The Soddy hyperbolas). Let L
a be the polar of X(3) with respect to ℋ
a. Define L
b and L
c cyclically. Let A' = L
b ∩ L
c, B' = L
c ∩ L
a, C' = L
a ∩ L
b. Triangle A'B'C' is homothetic to ABC, and its orthocenter is
X(944), Hofstadter Trapezoid Point. (Randy Hutson, January 29, 2018)
• La
transformación afín σ
( σ(x,y,z) = (-(a*(a + b - c)*(a - b + c)*
(a^2 - 2*b*c + a*(b + c))*x) -
a^2*(a + b - c)*(a^2 - b^2 + 2*a*c -
4*b*c - 3*c^2)*y - a^2*(a - b + c)*
(a^2 + 2*a*b - 3*b^2 - 4*b*c - c^2)*
z, b^2*(a + b - c)*(a - b + c)*
(a + b + 3*c)*x - b*(a + b - c)*
(-a + b + c)*(a*(b - 2*c) +
b*(b + c))*y + b^2*(a - b + c)*
(-3*a^2 + 2*a*(b + c) + (b + c)^2)*
z, (a + b - c)*c^2*(a - b + c)*
(a + 3*b + c)*x + (a + b - c)*c^2*
(-3*a^2 + 2*a*(b + c) + (b + c)^2)*
y - c*(a - b + c)*(a^2*(2*b - c) -
2*a*b*(b + c) + c*(b + c)^2)*z))
que aplica el triángulo ABC en tiene punto fijo propio el centro X55, centro interior de homotecia de las circunferencias inscrita y circunscrita a ABC.
Algunos pares {Xi, Xj=σ(Xi)}, para {i, j}: {9, 6767}, {55, 55}, {200, 999}, {210, 1}, {650, 667}, {663, 4057}, {1639, 25569}, {1864, 7962}, {2318, 18613}, {2340, 20470}, {3057, 7174}, {3059, 11529}, {3158, 3}, {3689, 36}, {3700, 4879}, {3715, 8162}, {4041, 3733}, {4046, 81}, {4433, 3286}, {4435, 21003}, {4512, 3295}, {4895, 4491}, {8611, 21789}, {11193, 3251}, {11934, 4162}, {14100, 9819}.
• La
transformación afín τ
( τ(x,y,z) = (a*(a + b + c)^16*(a + 3*b + c)^11*
(a + b + 3*c)^6*(a^3 - a*(b - c)^2 -
a^2*(b + c) + (b - c)^2*(b + c))^2*
(a^7 + a^6*(3*b + c) +
2*a^5*(b^2 - 2*b*c - 3*c^2) -
2*a^4*(3*b^3 + 13*b^2*c +
15*b*c^2 + 9*c^3) -
a^3*(7*b^4 + 28*b^3*c +
38*b^2*c^2 + 12*b*c^3 + 7*c^4) -
4*b*c*(2*b^5 - 3*b^4*c -
9*b^3*c^2 - 3*b^2*c^3 + 7*b*c^4 +
6*c^5) + a^2*(3*b^5 + b^4*c +
6*b^3*c^2 + 34*b^2*c^3 +
51*b*c^4 + 17*c^5) +
4*a*(b^6 - 4*b^4*c^2 - 2*b^3*c^3 -
2*b^2*c^4 + 4*b*c^5 + 3*c^6))*x +
a*(a + b + c)^16*(a + 3*b + c)^11*
(a + b + 3*c)^6*(a^2 + 2*c^2 +
a*(-b + c))*(a^3 - a*(b - c)^2 -
a^2*(b + c) + (b - c)^2*(b + c))^2*
(a^5 - 2*a^4*c + 2*a^2*c^2*
(3*b + c) - 2*a^3*(b^2 + 2*b*c +
2*c^2) - 2*b*c*(b^3 - 3*b^2*c -
b*c^2 + 3*c^3) +
a*(b^4 - 8*b^2*c^2 + 4*b*c^3 +
3*c^4))*y + a*(a^2 + 2*b^2 +
a*(b - c))*(a + b + c)^16*
(a + 3*b + c)^11*(a + b + 3*c)^6*
(a^3 - a*(b - c)^2 - a^2*(b + c) +
(b - c)^2*(b + c))^2*
(a^5 - 2*a^4*c + 2*a^2*c^2*
(3*b + c) - 2*a^3*(b^2 + 2*b*c +
2*c^2) - 2*b*c*(b^3 - 3*b^2*c -
b*c^2 + 3*c^3) +
a*(b^4 - 8*b^2*c^2 + 4*b*c^3 +
3*c^4))*z,
b*(a + b + c)^16*(a + 3*b + c)^11*
(a + b + 3*c)^6*(-(a*b) + b^2 +
b*c + 2*c^2)*(a^3 - a*(b - c)^2 -
a^2*(b + c) + (b - c)^2*(b + c))^2*
(a^5 - 2*a^4*c + 2*a^2*c^2*
(3*b + c) - 2*a^3*(b^2 + 2*b*c +
2*c^2) - 2*b*c*(b^3 - 3*b^2*c -
b*c^2 + 3*c^3) +
a*(b^4 - 8*b^2*c^2 + 4*b*c^3 +
3*c^4))*x + b*(a + b + c)^16*
(a + 3*b + c)^11*(a + b + 3*c)^6*
(a^3 - a*(b - c)^2 - a^2*(b + c) +
(b - c)^2*(b + c))^2*
(4*a^2 + b^2 + 3*b*c + 4*c^2 +
3*a*(b + 2*c))*(a^5 - 2*a^4*c +
2*a^2*c^2*(3*b + c) -
2*a^3*(b^2 + 2*b*c + 2*c^2) -
2*b*c*(b^3 - 3*b^2*c - b*c^2 +
3*c^3) + a*(b^4 - 8*b^2*c^2 +
4*b*c^3 + 3*c^4))*y +
b*(2*a^2 + a*b + b*(b - c))*
(a + b + c)^16*(a + 3*b + c)^11*
(a + b + 3*c)^6*(a^3 - a*(b - c)^2 -
a^2*(b + c) + (b - c)^2*(b + c))^2*
(a^5 - 2*a^4*c + 2*a^2*c^2*
(3*b + c) - 2*a^3*(b^2 + 2*b*c +
2*c^2) - 2*b*c*(b^3 - 3*b^2*c -
b*c^2 + 3*c^3) +
a*(b^4 - 8*b^2*c^2 + 4*b*c^3 +
3*c^4))*z,
c*(a + b + c)^16*(a + 3*b + c)^11*
(a + b + 3*c)^6*(2*b^2 + b*c +
c*(-a + c))*(a^3 - a*(b - c)^2 -
a^2*(b + c) + (b - c)^2*(b + c))^2*
(a^5 - 2*a^4*c + 2*a^2*c^2*
(3*b + c) - 2*a^3*(b^2 + 2*b*c +
2*c^2) - 2*b*c*(b^3 - 3*b^2*c -
b*c^2 + 3*c^3) +
a*(b^4 - 8*b^2*c^2 + 4*b*c^3 +
3*c^4))*x + c*(a + b + c)^16*
(a + 3*b + c)^11*(a + b + 3*c)^6*
(2*a^2 + a*c + c*(-b + c))*
(a^3 - a*(b - c)^2 - a^2*(b + c) +
(b - c)^2*(b + c))^2*
(a^5 - 2*a^4*c + 2*a^2*c^2*
(3*b + c) - 2*a^3*(b^2 + 2*b*c +
2*c^2) - 2*b*c*(b^3 - 3*b^2*c -
b*c^2 + 3*c^3) +
a*(b^4 - 8*b^2*c^2 + 4*b*c^3 +
3*c^4))*y + c*(a + b + c)^16*
(a + 3*b + c)^11*(a + b + 3*c)^6*
(a^3 - a*(b - c)^2 - a^2*(b + c) +
(b - c)^2*(b + c))^2*
(4*a^2 + 4*b^2 + 3*b*c + c^2 +
3*a*(2*b + c))*(a^5 - 2*a^4*c +
2*a^2*c^2*(3*b + c) -
2*a^3*(b^2 + 2*b*c + 2*c^2) -
2*b*c*(b^3 - 3*b^2*c - b*c^2 +
3*c^3) + a*(b^4 - 8*b^2*c^2 +
4*b*c^3 + 3*c^4))*z))
que aplica el triángulo A'B'C' en tiene punto fijo propio el centro X999, centro radical de las circunferencias inscritas mixtilineales.
Algunos pares {Xi, Xj=τ(Xi)}, para {i, j}: {10, 7174}, {551, 1}, {659, 4491}, {667, 4057}, {993, 55}, {999, 999}, {1001, 6767}, {3892, 1002}, {4367, 3733}, {5542, 11529}, {11194, 3}, {16418, 3295}, {20517, 21189}.
- Miércoles, 21 de noviembre del 2018
El centro del triángulo X(19861)
Dado un triángulo ABC, la del incentro (X1) y el baricentro (X2) es la cónica biceviana del del incentro de los centros de ABC, X1 y X995 (punto medio de X1 y el del y X1).
Esta cónica pasa por los centros Xi, para i ∈ {11, 214, 244, 1015, 8054, 8299, 10494, 14714, 17417, 17419, 17421, 17761, 17793}.
Si D'E'F' el de X995 respecto al triángulo circunceviano DEF del incentro, sean los puntos A'= BF'∩CE', B'= CD'∩AF' y C'= AE'∩BD'.
Las rectas A'D', B'E' y C'F' concurren en X19861.
En coordenadas baricéntricas:
D' = (a (b^2 + c^2 + a (b + c)) : b^2 (a + b - c) : c^2 (a - b + c)),
A' = (a^2 (a^2 - (b - c)^2) : b (a^3 + a^2 c - b^2 c + c^3 +
a (-b^2 + 2 b c + c^2)) : c (a^3 + a^2 b + b^3 - b c^2 +
a (b^2 + 2 b c - c^2))).
En , el centro X19861 es definido como la imagen de X499=X1X2∩X3X11 mediante la homografía σ, que transforma los puntos P(10) (ortocentro del ), U(10) (ortocentro del 2º triángulo bisector de Montesdeoca), X1, X2 en P(10), U(10), X2, X1, respectivamente.
La entradas de la matriz (aij), asociada a σ son:
a11 = a^3 - b^3 + a b c - b^2 c - b c^2 - c^3 + a^2 (b + c)
a12 = -2 a^2 c + b^2 (b + c) + a (2 b^2 - b c - c^2)
a13 = -2 a^2 b + c^2 (b + c) - a (b^2 + b c - 2 c^2)
a21 = a^3 - a b c + a^2 (2 b + c) - b c (2 b + c)
a22 = -a^3 + b^3 - a^2 c + b^2 c - c^3 + a (b^2 + b c - c^2)
a23 = -a^2 b + c^2 (2 b + c) + a (-2 b^2 - b c + c^2)
a31 = a^3 - a b c + a^2 (b + 2 c) - b c (b + 2 c)
a32 = -a^2 c + b^2 (b + 2 c) + a (b^2 - b c - 2 c^2)
a33 = -a^3 - a^2 b - b^3 + b c^2 + c^3 + a (-b^2 + b c + c^2)
Esta homografía, por su propia definición, transforma las rectas P(10)U(10) y X1X2 en si mismas, por tanto X10=P(10)U(10)∩X1X2 es un punto doble. En consecuencia, P(10)U(10) es una recta de puntos dobles (contiene a los centros Xi, para i∈{10, 514, 764, 876, 1491, 2530, 2533, 3126, 3777, 4147, 4444, 4490, 4705, 4824, 16720, 17072, 21146, 22116, 23596, 23765, 23789, 23814, 24097, 24318, 24720, 25381}).
Así, σ es una homología. El punto doble (centro de homología) de σ, fuera de la recta P(10)U(10), es X1125 (baricentro de {A, B, C, X1} y conjugado armónico de X10, respecto a X1 y X2).
Como σ2(X)=X, se trata de una homología armónica (la razón de homología, razón doble del centro, un punto del eje
y un par de puntos homólogos de la recta (doble) determinada por aquellos, es -1).
Pares {Xi, Xj=σ(Xi)}, para {i, j}:
{1, 2}, {3, 19884}, {4, 19885}, {6, 19886}, {7, 19887}, {8,
1698}, {9, 19888}, {10, 10}, {11, 19889}, {12, 19890}, {31,
19891}, {32, 19892}, {35, 19893}, {36, 19894}, {37, 19895}, {38,
19896}, {39, 19897}, {42, 16828}, {43, 19853}, {44, 19898}, {45,
19899}, {55, 19900}, {56, 19927}, {57, 19928}, {58, 19929}, {63,
19930}, {65, 19931}, {69, 19932}, {75, 19933}, {76, 19934}, {78,
19854}, {86, 19935}, {99, 19936}, {100, 19937}, {101, 19941}, {141,
19942}, {190, 19943}, {192, 19944}, {200, 19855}, {210,
19946}, {239, 19856}, {306, 19857}, {386, 19858}, {387,
19859}, {498, 19860}, {499, 19861}, {513, 19947}, {519, 3634}, {551,
19862}, {612, 19784}, {614, 19836}, {649, 19949}, {656,
19948}, {764, 764}, {876, 876}, {936, 19843}, {976, 19846}, {997,
26363}, {1125, 1125}, {1149, 19847}, {1193, 19863}, {1201,
19864}, {1491, 1491}, {1737, 24987}, {1961, 19865}, {2530,
2530}, {2533, 2533}, {2999, 19866}, {3006, 19867}, {3008,
19868}, {3011, 19869}, {3086, 8583}, {3126, 3126}, {3214,
19870}, {3240, 19871}, {3241, 19872}, {3242, 19873}, {3293,
19874}, {3616, 3624}, {3617, 19875}, {3621, 19876}, {3626,
3828}, {3632, 19877}, {3636, 19878}, {3720, 25512}, {3777,
3777}, {3783, 16819}, {4147, 4147}, {4444, 4444}, {4490,
4490}, {4705, 4705}, {4824, 4824}, {5550, 25055}, {5592,
21204}, {6550, 24099}, {7081, 19879}, {7172, 19880}, {7191,
19881}, {7192, 19882}, {10039, 24982}, {15808, 19883}, {16720,
16720}, {17072, 17072}, {21146, 21146}, {22116, 22116}, {23596,
23596}, {23765, 23765}, {23789, 23789}, {23814, 23814}, {24318,
24318}, {24720, 24720}, {25381, 25381}.
La recta límite
(-3a^2-a b+b^2-a c+3b c+c^2)x + (a^2-a b-3b^2+
3a c-b c+c^2)y + (a^2+3a b+b^2-a c-b c-3c^2)z=0,
contiene a los centros Xi, para i ∈ {514, 3634, 19947, 24099}.
Como la recta límite pasa por X3634(2a + 3b + 3c : 2b + 3c + 3a : 2c + 3a + 3b), en el interior de ABC, corta a la circunferencia circunscrita en dos puntos, por consiguiente, la imagen de esta circunferencia mediante σ es una
hipérbola,
( (-a^7 - 2 a^6 b - a^5 b^2 - a^4 b^3 + a^2 b^5 - 2 a^6 c + a^5 b c +
3 a^4 b^2 c - a^3 b^3 c + 3 a^2 b^4 c - b^6 c - a^5 c^2 +
3 a^4 b c^2 - a^3 b^2 c^2 + 2 a^2 b^3 c^2 + 2 a b^4 c^2 -
2 b^5 c^2 - a^4 c^3 - a^3 b c^3 + 2 a^2 b^2 c^3 + a b^3 c^3 -
3 b^4 c^3 + 3 a^2 b c^4 + 2 a b^2 c^4 - 3 b^3 c^4 + a^2 c^5 -
2 b^2 c^5 - b c^6) x^2 + (a^7 - 2 a^5 b^2 - 3 a^4 b^3 -
3 a^3 b^4 - 2 a^2 b^5 + b^7 + 3 a^6 c - a^5 b c + 2 a^3 b^3 c -
a b^5 c + 3 b^6 c + 4 a^5 c^2 - 2 a^4 b c^2 - 2 a b^4 c^2 +
4 b^5 c^2 + 5 a^4 c^3 - 2 a^3 b c^3 - 3 a^2 b^2 c^3 -
2 a b^3 c^3 + 5 b^4 c^3 + 2 a^3 c^4 - 4 a^2 b c^4 - 4 a b^2 c^4 +
2 b^3 c^4 - c^7) x y + (a^5 b^2 - a^3 b^4 - a^2 b^5 - 2 a b^6 -
b^7 - a^6 c + 3 a^4 b^2 c - a^3 b^3 c + 3 a^2 b^4 c + a b^5 c -
2 b^6 c - 2 a^5 c^2 + 2 a^4 b c^2 + 2 a^3 b^2 c^2 - a^2 b^3 c^2 +
3 a b^4 c^2 - b^5 c^2 - 3 a^4 c^3 + a^3 b c^3 + 2 a^2 b^2 c^3 -
a b^3 c^3 - b^4 c^3 - 3 a^3 c^4 + 2 a^2 b c^4 + 3 a b^2 c^4 -
2 a^2 c^5 + b^2 c^5 - a c^6) y^2 + (a^7 + 3 a^6 b + 4 a^5 b^2 +
5 a^4 b^3 + 2 a^3 b^4 - b^7 - a^5 b c - 2 a^4 b^2 c -
2 a^3 b^3 c - 4 a^2 b^4 c - 2 a^5 c^2 - 3 a^2 b^3 c^2 -
4 a b^4 c^2 - 3 a^4 c^3 + 2 a^3 b c^3 - 2 a b^3 c^3 + 2 b^4 c^3 -
3 a^3 c^4 - 2 a b^2 c^4 + 5 b^3 c^4 - 2 a^2 c^5 - a b c^5 +
4 b^2 c^5 + 3 b c^6 + c^7) x z + (-a^7 + 2 a^4 b^3 + 5 a^3 b^4 +
4 a^2 b^5 + 3 a b^6 + b^7 - 4 a^4 b^2 c - 2 a^3 b^3 c -
2 a^2 b^4 c - a b^5 c - 4 a^4 b c^2 - 3 a^3 b^2 c^2 - 2 b^5 c^2 +
2 a^4 c^3 - 2 a^3 b c^3 + 2 a b^3 c^3 - 3 b^4 c^3 + 5 a^3 c^4 -
2 a^2 b c^4 - 3 b^3 c^4 + 4 a^2 c^5 - a b c^5 - 2 b^2 c^5 +
3 a c^6 + c^7) y z + (-a^6 b - 2 a^5 b^2 - 3 a^4 b^3 -
3 a^3 b^4 - 2 a^2 b^5 - a b^6 + 2 a^4 b^2 c + a^3 b^3 c +
2 a^2 b^4 c + a^5 c^2 + 3 a^4 b c^2 + 2 a^3 b^2 c^2 +
2 a^2 b^3 c^2 + 3 a b^4 c^2 + b^5 c^2 - a^3 b c^3 - a^2 b^2 c^3 -
a b^3 c^3 - a^3 c^4 + 3 a^2 b c^4 + 3 a b^2 c^4 - b^3 c^4 -
a^2 c^5 + a b c^5 - b^2 c^5 - 2 a c^6 - 2 b c^6 - c^7) z^2 = 0)
que pasa por σ(X99)=X19936, σ(X100)=X19937 y σ(X101)=X19941 (la imágenes de otros centros en la circunferencia circunscrita no figuran actualmente en ETC).
El centro de esta hipérbola está sobre la recta X3X142:
W = ( -3 a^8 - a^7 (b + c) +
4 a^5 (b - c)^2 (b + c) - (b^2 - c^2)^2 (3 b^4 + b^3 c + 6 b^2 c^2 +
b c^3 + 3 c^4) +
a^4 (7 b^4 - 4 b^3 c - 5 b^2 c^2 - 4 b c^3 + 7 c^4) +
a^3 (b^5 + 3 b^4 c + 9 b^3 c^2 + 9 b^2 c^3 + 3 b c^4 + c^5) -
a (b - c)^2 (4 b^5 + 3 b^3 c^2 + 3 b^2 c^3 + 4 c^5) -
a^2 (b^6 + b^5 c + 12 b^4 c^2 - 6 b^3 c^3 + 12 b^2 c^4 + b c^5 + c^6) : ... : ...),
que tiene números de búsqueda en
(2.59307539278399, 1.92532644037438, 1.11094214959412).
- Martes, 13 de noviembre del 2018
Cociente baricéntrico de un punto y su anticomplemento
Dados un triángulo ABC de baricentro G y un punto P, una recta que pasa por P corta en Ab y Ac a AC y AB, respectivamente, tal que P es el punto medio de AbAc.
Sea Pa el punto de intersección de las rectas BAb y CAc. Los puntos Pb y Pb se definen similarmente.
Las rectas APa, BPb y CPc concurren en Q, de P y su .
Si las coordenadas baricéntricas de P son (u:v:w), entonces:
Ab = (u+v-w : 0 : 2w), Ac = (u-v+w : 2v : 0),
Pa = (u^2-(v-w)^2 : 2v(u+v-w) : 2w(u-v+w)).
El punto de intersección de las rectas APa, BPb y CPc es:
Q = (u/(v+w-u) : v/(w+u-v) : w/(u+v-w)).
Pares {P=Xi, Qj}, para {i, j}: {1, 57}, {2, 2}, {3, 394}, {4, 459}, {5, 324}, {6, 25}, {8, 6557}, {9, 200}, {10, 321}, {37, 42}, {39, 3051}, {57, 1422}, {63, 6513}, {69, 6340}, {75, 6384}, {115, 8029}, {141, 8024}, {145, 5219}, {174, 16664}, {188, 7028}, {216, 418}, {233, 3078}, {244, 8042}, {395, 8015}, {396, 8014}, {590, 8035}, {615, 8036}, {626, 8039}, {647, 184}, {650, 55}, {661, 756}, {905, 222}, {1015, 8027}, {1084, 23610}, {1086, 6545}, {1125, 8025}, {1146, 23615}, {1196, 3080}, {1212, 8012}, {1213, 8013}, {1249, 3079}, {1577, 6358}, {1637, 14583}, {1645, 23610}, {1646, 8027}, {1647, 6545}, {1648, 8029}, {1649, 8030}, {1650, 23616}, {2482, 8030}, {2485, 17409}, {2501, 14593}, {3005, 8041}, {3068, 8037}, {3069, 8038}, {3161, 3635}, {3162, 455}, {3163, 3081}, {3239, 7046}, {3633, 3617}, {3739, 16748}, {3835, 6382}, {4222, 13804}, {4369, 8033}, {4370, 8028}, {4521, 6555}, {4668, 4859}, {4988, 8040}, {5218, 5947}, {5412, 221}, {6129, 6611}, {6184, 23612}, {6376, 8026}, {6544, 8028}, {6587, 6525}, {6588, 17408}, {7658, 9533}, {8105, 25}, {8106, 25}, {8265, 8023}, {10492, 258}, {11672, 23611}, {13466, 8031}, {14401, 3081}, {14434, 8031}, {14837, 196}, {15223, 3623}, {15526, 23616}, {16583, 8020}, {16584, 8022}, {16589, 21820}, {21752, 1319}, {23302, 8018}, {23303, 8019}, {25139, 11184}.
Si P es el , el punto Q es:
Q7 = (r+4R)((r+4R)^2-4s^2) X7 + 12r s^2 X1699.
Q7 = ( 1/((b+c-a)(3a^2-2a(b+c)-(b-c)^2)) : ... : ...),
que tiene números de búsqueda en
(-0.798287808323914, -0.989589211039375, 4.69420523185345) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3160}, {7,1699}, {11,479}, {347,5936}, {497,3599}, {658,9812}, {673,2898}, {934,19541}, {1223,18230}, {1659,16662}, {1996,5543}, {2400,3676}, {3817,10004}, {4373,9436}, {7056,9779}, {8727,14256}, {13390,16663}.
Cuando el punto P se mueve sobre un recta dμ, que pasa por el circuncentro, de coordenadas:
P = (a^2 (a^2 - b^2 - c^2) (1 + μ) :
a^4 t + (b^2 - c^2) (-c^2 t + b^2 (1 + t + μ)) -
a^2 (2 c^2 t + b^2 (1 + 2 t + μ)) :
a^4 t μ + (b^2 - c^2) (b^2 t μ - c^2 (1 + μ + t μ)) -
a^2 (2 b^2 t μ + c^2 (1 + μ + 2 t μ)),
el lugar geométrico del punto Q es una cúbica nodal Φμ, que pasa por A, B, C, G (posición límite, cuando P tiende al punto del infinito de dμ), X394 (que corresponde al circuncentro).
Las tangentes en los vértices de ABC a la cúbica Φμ concurren en el punto
Z = (a^4(b^2+c^2-a^2)^2(μ-1)^2 : (a^2-b^2+c^2)^2(-a^2+c^2+b^2μ)^2 : (a^2+b^2-c^2)^2(c^2+(-a^2+b^2)μ)^2).
El lugar geométrico del punto Z, cuando la recta dμ gira alrededor del circuncentro, es la
cónica inscrita
( (-a^16+4 a^12 b^4-6 a^8 b^8+4 a^4 b^12-b^16-8 a^12 b^2 c^2+24 a^8 b^6 c^2-24 a^4 b^10 c^2+8 b^14 c^2+4 a^12 c^4-36 a^8 b^4 c^4+60 a^4 b^8 c^4-28 b^12 c^4+24 a^8 b^2 c^6-80 a^4 b^6 c^6+56 b^10 c^6-6 a^8 c^8+60 a^4 b^4 c^8-70 b^8 c^8-24 a^4 b^2 c^10+56 b^6 c^10+4 a^4 c^12-28 b^4 c^12+8 b^2 c^14-c^16) x^2+(2 a^16-8 a^12 b^4+12 a^8 b^8-8 a^4 b^12+2 b^16-8 a^14 c^2+8 a^12 b^2 c^2+24 a^10 b^4 c^2-24 a^8 b^6 c^2-24 a^6 b^8 c^2+24 a^4 b^10 c^2+8 a^2 b^12 c^2-8 b^14 c^2+8 a^12 c^4-32 a^10 b^2 c^4-8 a^8 b^4 c^4+64 a^6 b^6 c^4-8 a^4 b^8 c^4-32 a^2 b^10 c^4+8 b^12 c^4+8 a^10 c^6+40 a^8 b^2 c^6-48 a^6 b^4 c^6-48 a^4 b^6 c^6+40 a^2 b^8 c^6+8 b^10 c^6-20 a^8 c^8+72 a^4 b^4 c^8-20 b^8 c^8+8 a^6 c^10-40 a^4 b^2 c^10-40 a^2 b^4 c^10+8 b^6 c^10+8 a^4 c^12+32 a^2 b^2 c^12+8 b^4 c^12-8 a^2 c^14-8 b^2 c^14+2 c^16) x y+(-a^16+4 a^12 b^4-6 a^8 b^8+4 a^4 b^12-b^16+8 a^14 c^2-24 a^10 b^4 c^2+24 a^6 b^8 c^2-8 a^2 b^12 c^2-28 a^12 c^4+60 a^8 b^4 c^4-36 a^4 b^8 c^4+4 b^12 c^4+56 a^10 c^6-80 a^6 b^4 c^6+24 a^2 b^8 c^6-70 a^8 c^8+60 a^4 b^4 c^8-6 b^8 c^8+56 a^6 c^10-24 a^2 b^4 c^10-28 a^4 c^12+4 b^4 c^12+8 a^2 c^14-c^16) y^2+(2 a^16-8 a^14 b^2+8 a^12 b^4+8 a^10 b^6-20 a^8 b^8+8 a^6 b^10+8 a^4 b^12-8 a^2 b^14+2 b^16+8 a^12 b^2 c^2-32 a^10 b^4 c^2+40 a^8 b^6 c^2-40 a^4 b^10 c^2+32 a^2 b^12 c^2-8 b^14 c^2-8 a^12 c^4+24 a^10 b^2 c^4-8 a^8 b^4 c^4-48 a^6 b^6 c^4+72 a^4 b^8 c^4-40 a^2 b^10 c^4+8 b^12 c^4-24 a^8 b^2 c^6+64 a^6 b^4 c^6-48 a^4 b^6 c^6+8 b^10 c^6+12 a^8 c^8-24 a^6 b^2 c^8-8 a^4 b^4 c^8+40 a^2 b^6 c^8-20 b^8 c^8+24 a^4 b^2 c^10-32 a^2 b^4 c^10+8 b^6 c^10-8 a^4 c^12+8 a^2 b^2 c^12+8 b^4 c^12-8 b^2 c^14+2 c^16) x z+(2 a^16-8 a^14 b^2+8 a^12 b^4+8 a^10 b^6-20 a^8 b^8+8 a^6 b^10+8 a^4 b^12-8 a^2 b^14+2 b^16-8 a^14 c^2+32 a^12 b^2 c^2-40 a^10 b^4 c^2+40 a^6 b^8 c^2-32 a^4 b^10 c^2+8 a^2 b^12 c^2+8 a^12 c^4-40 a^10 b^2 c^4+72 a^8 b^4 c^4-48 a^6 b^6 c^4-8 a^4 b^8 c^4+24 a^2 b^10 c^4-8 b^12 c^4+8 a^10 c^6-48 a^6 b^4 c^6+64 a^4 b^6 c^6-24 a^2 b^8 c^6-20 a^8 c^8+40 a^6 b^2 c^8-8 a^4 b^4 c^8-24 a^2 b^6 c^8+12 b^8 c^8+8 a^6 c^10-32 a^4 b^2 c^10+24 a^2 b^4 c^10+8 a^4 c^12+8 a^2 b^2 c^12-8 b^4 c^12-8 a^2 c^14+2 c^16) y z+(-a^16+8 a^14 b^2-28 a^12 b^4+56 a^10 b^6-70 a^8 b^8+56 a^6 b^10-28 a^4 b^12+8 a^2 b^14-b^16+4 a^12 c^4-24 a^10 b^2 c^4+60 a^8 b^4 c^4-80 a^6 b^6 c^4+60 a^4 b^8 c^4-24 a^2 b^10 c^4+4 b^12 c^4-6 a^8 c^8+24 a^6 b^2 c^8-36 a^4 b^4 c^8+24 a^2 b^6 c^8-6 b^8 c^8+4 a^4 c^12-8 a^2 b^2 c^12+4 b^4 c^12-c^16) z^2 = 0)
de perspector X3926 ( del ), que pasa por X15526 (cuando dμ es la ), X23974 (cuando dμ es la recta X3X66), X23983 (cuando dμ es la recta X3X10) y su centro es X6389.
Otros puntos sobre esta cónica:
• Si dμ es la recta X1X3, Z = X6X911 ∩ X77X216, cuadrado baricéntrico de X905.
• Si dμ es el , Z = X6X1624 ∩ X110X248, cuadrado baricéntrico de X647 ( de la ).
El punto doble de Φμ es:
Dμ = (a^4(-a^2+b^2+c^2)^2(μ-1)μ :
-(a^2-b^2+c^2)(a^4(b^2μ-c^2)+(b^2-c^2)(c^2+b^2μ)^2-a^2(-2c^4-b^2c^2(μ-1)+b^4μ(1+μ))) :
-(a^2+b^2-c^2)μ(a^4μ(b^2μ-c^2)+(b^2-c^2)(c^2+b^2μ)^2+a^2(b^2c^2(μ-1)μ-2b^4μ^2+c^4(1+μ)))).
El lugar geométrico de Dμ, cuando dμ gira alrededor del circuncentro, es una
cúbica nodal
( (a^8 c^4+2 a^6 b^2 c^4-2 a^2 b^6 c^4-b^8 c^4-2 a^6 c^6+6 a^2 b^4 c^6+4 b^6 c^6-6 a^2 b^2 c^8-6 b^4 c^8+2 a^2 c^10+4 b^2 c^10-c^12) x^2 y+(a^8 c^4+2 a^6 b^2 c^4-2 a^2 b^6 c^4-b^8 c^4-4 a^6 c^6-6 a^4 b^2 c^6+2 b^6 c^6+6 a^4 c^8+6 a^2 b^2 c^8-4 a^2 c^10-2 b^2 c^10+c^12) x y^2+(-a^8 b^4+2 a^6 b^6-2 a^2 b^10+b^12-2 a^6 b^4 c^2+6 a^2 b^8 c^2-4 b^10 c^2-6 a^2 b^6 c^4+6 b^8 c^4+2 a^2 b^4 c^6-4 b^6 c^6+b^4 c^8) x^2 z+(2 a^10 b^2-4 a^8 b^4+4 a^4 b^8-2 a^2 b^10-2 a^10 c^2+10 a^6 b^4 c^2-10 a^4 b^6 c^2+2 b^10 c^2+4 a^8 c^4-10 a^6 b^2 c^4+10 a^2 b^6 c^4-4 b^8 c^4+10 a^4 b^2 c^6-10 a^2 b^4 c^6-4 a^4 c^8+4 b^4 c^8+2 a^2 c^10-2 b^2 c^10) x y z+(-a^12+2 a^10 b^2-2 a^6 b^6+a^4 b^8+4 a^10 c^2-6 a^8 b^2 c^2+2 a^4 b^6 c^2-6 a^8 c^4+6 a^6 b^2 c^4+4 a^6 c^6-2 a^4 b^2 c^6-a^4 c^8) y^2 z+(-a^8 b^4+4 a^6 b^6-6 a^4 b^8+4 a^2 b^10-b^12-2 a^6 b^4 c^2+6 a^4 b^6 c^2-6 a^2 b^8 c^2+2 b^10 c^2+2 a^2 b^4 c^6-2 b^6 c^6+b^4 c^8) x z^2+(a^12-4 a^10 b^2+6 a^8 b^4-4 a^6 b^6+a^4 b^8-2 a^10 c^2+6 a^8 b^2 c^2-6 a^6 b^4 c^2+2 a^4 b^6 c^2+2 a^6 c^6-2 a^4 b^2 c^6-a^4 c^8) y z^2 = 0)
𝒬, circunscrita a ABC que pasa por los vértices del del y por los centros X2, X184, X222, X394 (punto doble).
La tangente en el baricentro es X2X648 y su es:
T = ( a^4 (-a^2+b^2+c^2)^2 (a^4+b^4+b^2 c^2-2 c^4+a^2 (-2 b^2+c^2)) (a^10 (b^2+c^2)+a^8 (-2 b^4+3 b^2 c^2-5 c^4)-a^2 (b^2-c^2)^2 (7 b^6+5 b^4 c^2-13 b^2 c^4-5 c^6)-2 a^6 (b^6-3 b^4 c^2+6 b^2 c^4-5 c^6)+(b^2-c^2)^3 (2 b^6+9 b^4 c^2+6 b^2 c^4+c^6)+2 a^4 (4 b^8-11 b^6 c^2+8 b^4 c^4+4 b^2 c^6-5 c^8)) : ... : ...),
que tiene números de búsqueda en
(3.70831011658517, 2.05915545668779, 0.503567573468907).
- Lunes, 5 de noviembre del 2018
Parábolas dado la directriz, un punto y una tangente
Dado un triángulo ABC, las perpendiculares pac y pab por A a los lados AB y AC cortan a BC en los puntos Pac y Pab, respectivamente.
Sea 𝒫ab la única parábola de directriz AB, que pasa por Pab y es tangente a AC (dPtCp). Y sea 𝒫ac la única parábola de directriz AC, que pasa por Pac y es tangente a AB.
La parábola 𝒫ab es tangente a AC en Ba y la parábola 𝒫ac es tangente a AB en Ca. Los puntos Cb, Ab, Ac y Bc se definen de forma análoga, procediendo cíclicamente.
Los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están sobre una misma cónica 𝒞.
Para determinar el foco de la parábola 𝒫ac (dPtCp), hay que intersecar la reflexión sac de su directriz AC en la tangente AB, con la circunferencia de centro Pac y tangente a AC, que es un solo punto, Fac, pues pac es la bisectriz de AC y sac.
En coordenadas baricéntricas:
Pac = (0 : b^2+c^2-a^2 : -2c^2), Pab = (0 : -2b^2 : b^2+c^2-a^2).
Al proyectar el punto Pac sobre sac, se obtiene el foco de la parábola 𝒫ac:
Fac =
((a^2-b^2-c^2)(a^4+b^4-b^2c^2-a^2(2b^2+c^2)) : (b+c-a)(a-b+c)(a+b-c)(a+b+c)(a^2-b^2-c^2) : c^2(b+c-a)(a-b+c)(a+b-c)(a+b+c)).
La
parábola
( a^8 c^2 x^2-4 a^6 b^2 c^2 x^2+6 a^4 b^4 c^2 x^2-4 a^2 b^6 c^2 x^2+b^8 c^2 x^2-4 a^6 c^4 x^2+4 a^4 b^2 c^4 x^2+4 a^2 b^4 c^4 x^2-4 b^6 c^4 x^2+6 a^4 c^6 x^2+4 a^2 b^2 c^6 x^2+6 b^4 c^6 x^2-4 a^2 c^8 x^2-4 b^2 c^8 x^2+c^10 x^2+4 a^8 c^2 x y-16 a^6 b^2 c^2 x y+24 a^4 b^4 c^2 x y-16 a^2 b^6 c^2 x y+4 b^8 c^2 x y-12 a^6 c^4 x y+12 a^4 b^2 c^4 x y+12 a^2 b^4 c^4 x y-12 b^6 c^4 x y+12 a^4 c^6 x y+8 a^2 b^2 c^6 x y+12 b^4 c^6 x y-4 a^2 c^8 x y-4 b^2 c^8 x y+4 a^8 c^2 y^2-16 a^6 b^2 c^2 y^2+24 a^4 b^4 c^2 y^2-16 a^2 b^6 c^2 y^2+4 b^8 c^2 y^2-8 a^6 c^4 y^2+8 a^4 b^2 c^4 y^2+8 a^2 b^4 c^4 y^2-8 b^6 c^4 y^2+4 a^4 c^6 y^2+8 a^2 b^2 c^6 y^2+4 b^4 c^6 y^2-2 a^10 x z+10 a^8 b^2 x z-20 a^6 b^4 x z+20 a^4 b^6 x z-10 a^2 b^8 x z+2 b^10 x z+8 a^8 c^2 x z-20 a^6 b^2 c^2 x z+12 a^4 b^4 c^2 x z+4 a^2 b^6 c^2 x z-4 b^8 c^2 x z-12 a^6 c^4 x z+8 a^4 b^2 c^4 x z+4 a^2 b^4 c^4 x z+8 a^4 c^6 x z+4 a^2 b^2 c^6 x z+4 b^4 c^6 x z-2 a^2 c^8 x z-2 b^2 c^8 x z-2 a^10 y z+10 a^8 b^2 y z-20 a^6 b^4 y z+20 a^4 b^6 y z-10 a^2 b^8 y z+2 b^10 y z+10 a^8 c^2 y z-32 a^6 b^2 c^2 y z+36 a^4 b^4 c^2 y z-16 a^2 b^6 c^2 y z+2 b^8 c^2 y z-16 a^6 c^4 y z+8 a^4 b^2 c^4 y z+16 a^2 b^4 c^4 y z-8 b^6 c^4 y z+8 a^4 c^6 y z+8 a^2 b^2 c^6 y z+2 a^2 c^8 y z+6 b^2 c^8 y z-2 c^10 y z-2 a^10 z^2+10 a^8 b^2 z^2-20 a^6 b^4 z^2+20 a^4 b^6 z^2-10 a^2 b^8 z^2+2 b^10 z^2+7 a^8 c^2 z^2-16 a^6 b^2 c^2 z^2+10 a^4 b^4 c^2 z^2-b^8 c^2 z^2-8 a^6 c^4 z^2+4 a^4 b^2 c^4 z^2+8 a^2 b^4 c^4 z^2-4 b^6 c^4 z^2+2 a^4 c^6 z^2+2 b^4 c^6 z^2+2 a^2 c^8 z^2+2 b^2 c^8 z^2-c^10 z^2 = 0)
𝒫ac, de foco Fac y directriz AC, es tangente a AB en:
Ca =
(2(a^4+b^4-b^2c^2-a^2(2b^2+c^2)) : -a^4-(b^2-c^2)^2+2a^2(b^2+c^2) : 0).
Al proyectar el punto Pab sobre sab, se obtiene el foco de la parábola 𝒫ab:
Fab =
((a^2-b^2-c^2)(a^4-b^2c^2+c^4-a^2(b^2+2c^2)) : b^2(b+c-a)(a-b+c)(a+b-c)(a+b+c) : (b+c-a)(a-b+c)(a+b-c)(a+b+c)(a^2-b^2-c^2)).
La
parábola
( a^8 b^2 x^2-4 a^6 b^4 x^2+6 a^4 b^6 x^2-4 a^2 b^8 x^2+b^10 x^2-4 a^6 b^2 c^2 x^2+4 a^4 b^4 c^2 x^2+4 a^2 b^6 c^2 x^2-4 b^8 c^2 x^2+6 a^4 b^2 c^4 x^2+4 a^2 b^4 c^4 x^2+6 b^6 c^4 x^2-4 a^2 b^2 c^6 x^2-4 b^4 c^6 x^2+b^2 c^8 x^2-2 a^10 x y+8 a^8 b^2 x y-12 a^6 b^4 x y+8 a^4 b^6 x y-2 a^2 b^8 x y+10 a^8 c^2 x y-20 a^6 b^2 c^2 x y+8 a^4 b^4 c^2 x y+4 a^2 b^6 c^2 x y-2 b^8 c^2 x y-20 a^6 c^4 x y+12 a^4 b^2 c^4 x y+4 a^2 b^4 c^4 x y+4 b^6 c^4 x y+20 a^4 c^6 x y+4 a^2 b^2 c^6 x y-10 a^2 c^8 x y-4 b^2 c^8 x y+2 c^10 x y-2 a^10 y^2+7 a^8 b^2 y^2-8 a^6 b^4 y^2+2 a^4 b^6 y^2+2 a^2 b^8 y^2-b^10 y^2+10 a^8 c^2 y^2-16 a^6 b^2 c^2 y^2+4 a^4 b^4 c^2 y^2+2 b^8 c^2 y^2-20 a^6 c^4 y^2+10 a^4 b^2 c^4 y^2+8 a^2 b^4 c^4 y^2+2 b^6 c^4 y^2+20 a^4 c^6 y^2-4 b^4 c^6 y^2-10 a^2 c^8 y^2-b^2 c^8 y^2+2 c^10 y^2+4 a^8 b^2 x z-12 a^6 b^4 x z+12 a^4 b^6 x z-4 a^2 b^8 x z-16 a^6 b^2 c^2 x z+12 a^4 b^4 c^2 x z+8 a^2 b^6 c^2 x z-4 b^8 c^2 x z+24 a^4 b^2 c^4 x z+12 a^2 b^4 c^4 x z+12 b^6 c^4 x z-16 a^2 b^2 c^6 x z-12 b^4 c^6 x z+4 b^2 c^8 x z-2 a^10 y z+10 a^8 b^2 y z-16 a^6 b^4 y z+8 a^4 b^6 y z+2 a^2 b^8 y z-2 b^10 y z+10 a^8 c^2 y z-32 a^6 b^2 c^2 y z+8 a^4 b^4 c^2 y z+8 a^2 b^6 c^2 y z+6 b^8 c^2 y z-20 a^6 c^4 y z+36 a^4 b^2 c^4 y z+16 a^2 b^4 c^4 y z+20 a^4 c^6 y z-16 a^2 b^2 c^6 y z-8 b^4 c^6 y z-10 a^2 c^8 y z+2 b^2 c^8 y z+2 c^10 y z+4 a^8 b^2 z^2-8 a^6 b^4 z^2+4 a^4 b^6 z^2-16 a^6 b^2 c^2 z^2+8 a^4 b^4 c^2 z^2+8 a^2 b^6 c^2 z^2+24 a^4 b^2 c^4 z^2+8 a^2 b^4 c^4 z^2+4 b^6 c^4 z^2-16 a^2 b^2 c^6 z^2-8 b^4 c^6 z^2+4 b^2 c^8 z^2 = 0)
𝒫ab, de foco Fab y directriz AB, es tangente a AC en:
Ba =
(2(a^4-b^2c^2+c^4-a^2(b^2+2c^2)) : 0 : -a^4-(b^2-c^2)^2+2a^2(b^2+c^2)).
La cónica 𝒞 que pasa por los puntos Ab, Ac, Bc, Ba, Ca, Cb,
𝒞: 2 (b^2 c^2 (b^2-c^2)^6+a^14 (b^2+c^2)-2 a^12 (3 b^4+4 b^2 c^2+3 c^4)+a^2 (b^2-c^2)^4 (b^6-4 b^4 c^2-4 b^2 c^4+c^6)+3 a^10 (5 b^6+6 b^4 c^2+6 b^2 c^4+5 c^6)+a^6 (b^2-c^2)^2 (15 b^6+19 b^4 c^2+19 b^2 c^4+15 c^6)-2 a^4 (b^2-c^2)^2 (3 b^8-3 b^6 c^2-4 b^4 c^4-3 b^2 c^6+3 c^8)-a^8 (20 b^8+11 b^6 c^2+10 b^4 c^4+11 b^2 c^6+20 c^8))x^2
(-a^16+5 b^2 c^2 (b^2-c^2)^6+7 a^14 (b^2+c^2)-a^12 (25 b^4+39 b^2 c^2+25 c^4)+a^2 (b^2-c^2)^4 (5 b^6-17 b^4 c^2-17 b^2 c^4+5 c^6)+11 a^10 (5 b^6+7 b^4 c^2+7 b^2 c^4+5 c^6)+a^6 (b^2-c^2)^2 (61 b^6+75 b^4 c^2+75 b^2 c^4+61 c^6)-3 a^8 (25 b^8+15 b^6 c^2+16 b^4 c^4+15 b^2 c^6+25 c^8)-a^4 (b^2-c^2)^2 (27 b^8-25 b^6 c^2-36 b^4 c^4-25 b^2 c^6+27 c^8))y z + ... = 0,
tiene el centro:
.
U = ( (a^4-(b^2-c^2)^2)^2 (a^8-b^2 c^2 (b^2-c^2)^2-3 a^6 (b^2+c^2)-a^2 (b^2-c^2)^2 (b^2+c^2)+3 a^4 (b^4+b^2 c^2+c^4)) (a^16-a^14 (b^2+c^2)-(b^2-c^2)^6 (b^4+3 b^2 c^2+c^4)-a^12 (8 b^4+3 b^2 c^2+8 c^4)+3 a^6 (b^2-c^2)^2 (3 b^6+5 b^4 c^2+5 b^2 c^4+3 c^6)+a^2 (b^2-c^2)^4 (3 b^6+5 b^4 c^2+5 b^2 c^4+3 c^6)+a^10 (21 b^6+11 b^4 c^2+11 b^2 c^4+21 c^6)-a^4 (b^2-c^2)^2 (4 b^8+b^6 c^2+6 b^4 c^4+b^2 c^6+4 c^8)-a^8 (20 b^8+7 b^6 c^2-6 b^4 c^4+7 b^2 c^6+20 c^8)) : ... : ...),
que tiene números de búsqueda en
(0.945886389646165, 3.78005856699763, 0.587137909533942).
El de 𝒞 es:
V = ( 1/(4 a^20-11 a^18 (b^2+c^2)-5 a^16 (5 b^4+2 b^2 c^2+5 c^4)+152 a^14 (b^6+b^4 c^2+b^2 c^4+c^6)-(b^2-c^2)^6 (5 b^8+8 b^6 c^2-10 b^4 c^4+8 b^2 c^6+5 c^8)-4 a^4 (b^2-c^2)^4 (13 b^8+20 b^6 c^2+22 b^4 c^4+20 b^2 c^6+13 c^8)-8 a^12 (35 b^8+32 b^6 c^2+26 b^4 c^4+32 b^2 c^6+35 c^8)-2 a^8 (b^2-c^2)^2 (77 b^8+96 b^6 c^2+110 b^4 c^4+96 b^2 c^6+77 c^8)+16 a^6 (b^2-c^2)^2 (5 b^10+b^6 c^4+b^4 c^6+5 c^10)+a^2 (b^2-c^2)^4 (25 b^10+21 b^8 c^2-30 b^6 c^4-30 b^4 c^6+21 b^2 c^8+25 c^10)+a^10 (266 b^10+98 b^8 c^2+36 b^6 c^4+36 b^4 c^6+98 b^2 c^8+266 c^10)) : ... : ...),
que tiene números de búsqueda en ETC
(7.98640315220058, -5.57340914230166, 3.81314627940834).
El triángulo formado por las rectas
CaBa,
AbCb y
BcAc es perspectivo con
ABC y el centro de perspectividad es
X15319.
Las rectas AbCa, BaAc, BcCb forman un triángulo perspectivo con ABC, con centro de perspectividad:
Wa = (2 (a - b - c) (a + b - c) (a - b + c) (a + b +
c) (a^8 - (b^2 - c^2)^3 (2 b^2 + c^2) - a^6 (b^2 + 2 c^2) +
a^4 (-3 b^4 + b^2 c^2 + 2 c^4) +
a^2 (5 b^6 - 4 b^4 c^2 + b^2 c^4 - 2 c^6)) (a^8 -
a^6 (2 b^2 + c^2) + (b^2 - c^2)^3 (b^2 + 2 c^2) +
a^4 (2 b^4 + b^2 c^2 - 3 c^4) +
a^2 (-2 b^6 + b^4 c^2 - 4 b^2 c^4 +
5 c^6)) :
-(a^8 - (b^2 - c^2)^3 (2 b^2 + c^2) -
a^6 (b^2 + 2 c^2) + a^4 (-3 b^4 + b^2 c^2 + 2 c^4) +
a^2 (5 b^6 - 4 b^4 c^2 + b^2 c^4 - 2 c^6)) (a^12 +
2 a^10 (b^2 + c^2) + (b^2 - c^2)^4 (b^4 + 6 b^2 c^2 + c^4) -
a^8 (17 b^4 + 14 b^2 c^2 + 17 c^4) -
a^4 (b^2 - c^2)^2 (17 b^4 + 22 b^2 c^2 + 17 c^4) +
2 a^2 (b^2 - c^2)^2 (b^6 - 5 b^4 c^2 - 5 b^2 c^4 + c^6) +
4 a^6 (7 b^6 + 3 b^4 c^2 + 3 b^2 c^4 + 7 c^6)) :
-(a^8 -
a^6 (2 b^2 + c^2) + (b^2 - c^2)^3 (b^2 + 2 c^2) +
a^4 (2 b^4 + b^2 c^2 - 3 c^4) +
a^2 (-2 b^6 + b^4 c^2 - 4 b^2 c^4 + 5 c^6)) (a^12 +
2 a^10 (b^2 + c^2) + (b^2 - c^2)^4 (b^4 + 6 b^2 c^2 + c^4) -
a^8 (17 b^4 + 14 b^2 c^2 + 17 c^4) -
a^4 (b^2 - c^2)^2 (17 b^4 + 22 b^2 c^2 + 17 c^4) +
2 a^2 (b^2 - c^2)^2 (b^6 - 5 b^4 c^2 - 5 b^2 c^4 + c^6) +
4 a^6 (7 b^6 + 3 b^4 c^2 + 3 b^2 c^4 + 7 c^6)))
Las rectas BcAb, CbBa, CaAc forman un triángulo perspectivo con ABC, con centro de perspectividad Wb.
Las rectas CaBc, AcCb, AbBa forman un triángulo perspectivo con ABC, con centro de perspectividad Wc.
Los triángulos ABC y son perspectivos con centro de perspectividad
W = 2 X2 - 3 X6748.
W = ( 2a^8-5a^6(b^2+c^2)+
a^4(3b^4+4b^2c^2+3c^4)+a^2(b^2-c^2)^2(b^2+c^2)-(b^2-c^2)^2(b^4+c^4) : ... : ...),
que tiene números de búsqueda en ETC
(2.49576617004953, -1.81654643678009, 3.74638147504004), punto medio de Xi y Xj para los índices {i,j}: {2,6748}, {3,317}, {5,95}, {20,64}, {22,160}, {30,264}, {97,467}, {99,18401}, {141,401}, {183,1370}, {276,13322}, {297,577}, {302,19773}, {303,19772}, {311,12225}, {315,3964}, {319,10538}, {340,550}, {343,8613}, {491,5407}, {492,5406}, {511,6752}, {524,3164}, {1007,10565}, {1494,15686}, {3151,14829}, {3432,7488}, {3832,8797}, {4417,7560}, {5651,14461}, {7763,9715}, {7792,10313}, {7802,14615}, {8795,9291}, {12022,19166}, {14907,21312}, {15905,17907}.
- Domingo, 28 de octubre del 2018
Los centros X(1123) y X(1336) de ETC
Punto de Paasche
Sean D y E circunferencias congruentes tangentes entre sí y a la recta BC, con D además tangente a la recta AB y E además tangente a CA, y con un punto común A' exterior al triángulo ABC. Definimos B' y C' de cíclicamente. Entonces A'B'C' es perspectivo con ABC, y al centro de perspectiva se le llama punto de Paasche, el punto
X(1123).
Ver Ivan Paasche, Aufgabe P 933, Praxis der Mathematik 1 (1990), pág. 40.
Dado un triángulo ABC, vamos a determinar el punto de tangencia de dos circunferencias tangentes a BC, con el mismo radio, tangente una de ellas a AB y la otra tangente a AC.
Sea Bt un punto sobre la bisectriz en B de coordenadas baricéntricas:
Bt = (a t : a + b + c + b t : c t),
y su proyección ortogonal sobre BC:
Bat = (0 : (-b + c) t - a (2 + t) : -(a - b + c) t).
La circunferencia de centro Bt que pasa por Bat es tangente a AB y a BC. El centro Ct de la circunferencia con el mismo radio que la anterior, tangente a AC y a BC, es el punto de intersección de la bisectriz en C con la paralela a BC por Bt:
Ct = (-a t : -b t : -a - b - c (1 + t)).
Cuando t varía, el punto medio Mt de Bt y Ct recorre la recta que pasa por el incentro y el punto medio de B y C, MaX1.
Para resolver el problema deberemos encontrar el valor de t, tal que el punto que resulta de girar Bat un ángulo π/2, alrededor de Bt,
( a^2 t : a (a + b + c + b t)- t : ( S + a c ) t),
esté sobre la recta MaX1. Es decir, cuando t = -2a S/((b+c-a)(c+a-b)(z+b-c)).
Para este valor de t, el punto de contacto de las circunferencias buscadas es:
Aa = (a^2 : S + a b : S + a c)
Procediendo cíclicamente, se obtienen los puntos
Bb = (S + b a : b^2 : S + B c) y Cc = (S + c a : S + c b : c^2).
Las rectas AAa, BBb y CCc concurren en
X1123 = (1/(S + b c) : 1/(S + c a) : 1/(S + a b)).
Si en vez de girar Bat un ángulo π/2, alrededor de Bt, se gira Bat un ángulo -π/2, alrededor de Bt, los puntos de tangencia de los pares de las circunferencias que se obtienen, unidos con los vértices de ABC dan rectas concurrentes en X1336.:
X1336 = (1/(S - b c) : 1/(S - c a) : 1/(S - a b)).
- Sábado, 27 de octubre del 2018
Una configuración de Tran Quang Hung
Dado un triángulo ABC, con circunferencias inscrita (I) y tres (Ia), (Ib), (Ic).
(Ka) es la circunferencia tangente a (Ib), (Ic) y (I) externamente.
Se definen similarmente las circunferencias (Kb) y (Kc).
(K) es la circunferencia tangente a (Ka), (Kb) and (Kc) internamente.
En coordenadas baricéntricas:
(Ka): a^2y z+b^2x z+c^2x y+
(x+y+
z) (-((b^2(a-b-c)^2(a+b-c)(a-b+c)(a+b+
c)(a b-b^2+a c-c^2)(a b^3-b^4+a^2b c +
2b^2c^2+a c^3-
c^4)^2x)/((a-b-c)^2(a+b-c)(a-b+c)(a+b+
c)(a b-b^2+a c-c^2)(a b^3-b^4+a^2b c+
2b^2c^2+ac^3-c^4)^2-
2(a-b-c)(a+b-c)(a-b+c)(a+b+c)(a^2b-
b^3+a^2c-b^2c-a c^2)(a b^3-b^4+a^2b c+
2b^2c^2+a c^3-c^4)^2+(-a+b-c)(a+b-
c)^2(b+c)(-a+b+c)(a+b+c)^2(-a b^3+b^4-
a^2b c-2b^2c^2-a c^3+c^4)^2))+
1/4(-a^2+b^2-2a c-c^2)y+
1/4(-a^2-2a b-b^2+c^2)z) = 0,
(K): a^2y z+b^2x z+c^2x y + (1/4)(x+y+z) ((a^2+a(b+c)-b^2-b c-c^2)x +
(b^2+b(c+a)-c^2-c a-a^2)y + (c^2+c(a+b)-a^2-a b-b^2)z) = 0.
Sus centros son:
Ka = (2a^4(b+c)+(b-c)^2(b+c)^3+a(b^2-c^2)^2-
a^3(3b^2+4b c+3c^2)-
a^2(b^3+b^2c+b c^2+c^3) : -(b-c)c^2(b+c)^2+
a^3(2b^2+2b c+c^2)+a c(2b^3+b^2c-2b c^2-c^3)-
a^2(2b^3+2b^2c+b c^2+c^3) :
b^2(b-c)(b+c)^2+a^3(b^2+2b c+2c^2)+
a b(-b^3-2b^2c+b c^2+2c^3)-
a^2(b^3+b^2c+2b c^2+2c^3)),
y X946, punto medio de incentro y ortocentro.
• (I) toca a (Ka), (Kb), (Kc) en A1, B1, C1, respectivamente.
Sea el triángulo formado por los de (K) y las circunferencias exinscritas (Ia), (Ib), (Ic).
Los triángulos y son perspectivos y el centro de perspectividad es:
V = ( (b+c)(b c (b+c)+a (b^2+3 b c+c^2))/(b+c-a) : ... : ...),
que tiene números de búsqueda en
(1.28660543445332, 1.04197249530107, 2.32548101541288) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {10,12}, {495,24210}, {4061,21926}, {5226,10453}, {10592,20256}.
A1 = ((a+b-c)(a-b+c)(b+c)^2 : c^2(b+c-a)(a+b-c) : b^2(a-b+c)(b+c-a)),
R1 = (b^3+4b^2c+4b c^2+c^3 : -2a b c - a^2(b+c)+c^2(2b+c) : -2a b c-a^2(b+c)+b^2(b+2c)).
• Sea da la recta que pasa por los puntos de tangencia de (Ka) y (Ib), (Ic).
Se definen similarmente las rectas db y dc.
Las rectas da, db y dc forman un triángulo perspectivo con ABC y .
El centro de perspectividad de ABC y es:
W = ( (b+c)/((b+c-a)(a(b^2+3b c+c^2)+b c(b+c))) : ... : ...),
que tiene números de búsqueda en
(0.775695219630953, 0.812829634291599, 2.71992309526052) y está sobre la recta X4059X6063.
El centro de perspectividad de y es:
Z = ( a^7 (3 b^3 + 11 b^2 c + 11 b c^2 + 3 c^3) -
a b^2 (b - c)^2 c^2 (8 b^3 + 25 b^2 c + 25 b c^2 + 8 c^3) +
a^6 (3 b^4 + 21 b^3 c + 38 b^2 c^2 + 21 b c^3 + 3 c^4) -
a^5 (b^5 - 4 b^4 c - 20 b^3 c^2 - 20 b^2 c^3 - 4 b c^4 + c^5) +
a^2 b c (-8 b^6 - 27 b^5 c + 7 b^4 c^2 + 48 b^3 c^3 + 7 b^2 c^4 -
27 b c^5 - 8 c^6) -
a^4 (3 b^6 + 11 b^5 c + 8 b^4 c^2 + 13 b^3 c^3 + 8 b^2 c^4 +
11 b c^5 + 3 c^6) -
a^3 (2 b^7 + 17 b^6 c + 20 b^5 c^2 - 16 b^4 c^3 - 16 b^3 c^4 +
20 b^2 c^5 + 17 b c^6 + 2 c^7) -2 b^3 c^3 (b^2 - c^2)^2 : ... : ...),
que tiene números de búsqueda en
(-20.9791719178215, -20.0587633739133, 27.2101953951497).
NOTA. Como los triángulos ABC, , son perspectivos dos a dos y los centros de perspectividad I, W, Z están alineados, sus ejes de perspectividad coinciden (Theorem 19); es la del incentro.
Sean T1, T2, T3 los puntos de contacto de (K) con (Ka), (Kb), (Kc).
El y son perspectivos, con centro de perspectividad X226.
T1=(b + c : -a + c : -a + b), T2=(-b + c : a + c : a - b), T3=(b - c : a - c : a + b).
- Lunes, 22 de octubre del 2018
Triángulo perspectivos y Transformación de Collings
Dado un triángulo ABC y un punto P, sean A'B'C' el de P y D el de los puntos A, B,C, P.
Sean Da, Db, Dc las reflexiones de D en los centros Na, Nb, Nc de las de los triángulos PBC, PCA, PAB, respectivamente.
Para un punto M, se denota, como es usual, por M*, cM, aM el , el y el anticomplemento de M, respectivamente.
Los triángulos A'B'C' y son perspectivos.
El centro de perspectividad es el punto medio del simétrico de aP* en P y el de cP.
Si (x:y:z) son las coordenadas baricéntricas de P, el centro de perspectividad de A'B'C' y es:
Q = ((a^2y z(2x+y+z)-x(y+z)(c^2y+b^2z))
(2a^4y z(x+y)(x+z)+a^2x(c^2y(x+y-3z)(x+z)+b^2z(x+y)(x-3y+z))
- x((x-y-z)(b^4z(x+y)+c^4y(x+z))+b^2c^2(x^2(y+z)+2y z(y+z)+x(y^2+z^2)))) : ... : ...).
Cuando P está sobre la circunferencia circunscrita, Q=P* y cuando P está en la recta del infinito, Q=P.
Otros pares {P=Xi, Q=Xj}, para los índices {i,j}: {1,1317}, {2,18800}, {3,113}, {5,14071}, {6,15303}, {7,18801}, {8,18802}, {13,9117}, {14,9115}, {15,18803}, {16,18804}, {54,11702}, {671,22329}, {1263,24147}.
Unos pocos pares {P, Q}, en los que Q no figura actualmente es ETC.
• P=X9
Q9 = ( (2 a^2 - (b - c)^2 - a (b + c)) (2 a^6 - 5 a^5 (b + c) - a (b - c)^4 (b + c) + (b - c)^4 (b + c)^2 + a^4 (b^2 + 14 b c + c^2) + 2 a^3 (3 b^3 - 7 b^2 c - 7 b c^2 + 3 c^3) - 4 a^2 (b^4 - b^3 c - 2 b^2 c^2 - b c^3 + c^4)) : ... : ...),
que tiene números de búsqueda en
(1.30929286950241, -0.531539141891952, 3.40436410190846), punto medio de X100 y X12848 ; reflexión de X11 en X8257 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {9, 119}, {11, 8257}, {57, 5856}, {100, 12848}, {527, 1155}, {528, 18391}, {1317, 15185}, {1376, 5851}.
• P=X10
Q10 = ( (2 a^3 - b^3 - c^3 + a^2 (b + c) - a (b^2 + c^2)) (a^5 + a^4 (b + c) - b^2 c^2 (b + c) - a^3 (b^2 + c^2) + a (b^4 - b^2 c^2 + c^4)) : ... : ...),
que tiene números de búsqueda en
(1.62614271745754, -0.297583191784076, 3.09615620662372), punto medio de X99 y X1046; reflexión de X115 en X8258 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {99, 1046}, {114, 124}, {115, 8258}, {758, 11711}, {896, 1281}, {4697, 5988}, {5429, 7983}, {10026, 17770}.
• P=X17
Q17 = ( (6S (2 a^2-b^2-c^2)+Sqrt[3](6 a^4-a^2 (b^2+c^2)+b^4-6 b^2 c^2+c^4))(6S (2 a^2-b^2-c^2)+Sqrt[3](2 a^4-a^2 (b^2+c^2)+(b^2-c^2)^2)) : ... : ...),
que tiene números de búsqueda en
(1.08367436902034, 0.0217358051488212, 3.12545921571811), reflexión de X115 en X8259 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {114, 6109}, {115, 8259}.
• P=X18
Q18 = ( (6S (2 a^2-b^2-c^2)-Sqrt[3](6 a^4-a^2 (b^2+c^2)+b^4-6 b^2 c^2+c^4))(6S (2 a^2-b^2-c^2)-Sqrt[3](2 a^4-a^2 (b^2+c^2)+(b^2-c^2)^2)) : ... : ...),
que tiene números de búsqueda en
(-18.8800639710005, 10.6579211538638, 4.97597936200199), reflexión de X115 en X8260 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {114, 6108}, {115, 8260}.
- Sábado, 20 de octubre del 2018
El centro X(5627) y rectas de Wallace-Simson
X(5627) = YIU REFLECTION POINT
Paul Yiu introduced this point on New Year's Day, January 1, 2014. He noted that X(74) is the unique point whose reflections in the sidelines of triangle ABC are collinear and perspective to ABC. The perspector is X(5627).
(Paul Yiu,
ADGEOM #1022, "An easy new year puzzle", January 1, 2014)
Simson lines of diametral points (Paris Pamfilos)
Consider triangle t=ABC and a point D on its circumcircle (c) and its antipodal point E on (c). Project D, E on the sides of (t) and define the S(D), S(E). Then the angle of the two Simson lines S(D) and S(E) is a right one and their intersection point is on the of t.
Dado un punto P en el plano de un triángulo ABC, sean A1A2, B1B2, C1C2 los diámetros de la circunferencia circunscrita, paralelos a AP, BP, CP, respectivamente.
Las rectas de de los puntos A1 y A2 se intersecan ortogonalmente en Pa, sobre la . Análogamente se definen los puntos Pb y Pc.
Vamos a excluir en este estudio los casos para los cuales se tienen situaciones singulares para los puntos Pa, Pb y Pc, que corresponden a P sobre la (Pa = Pb = Pc) o que coincide con los vértices de ABC o con sus puntos antipodales ( son los ).
El lugar geométrico del punto
P tal que el triángulo es no degenerado y perspectivo con
ABC es la
quíntica
( 2 a^8 b^2 c^4 x^3 y^2-4 a^6 b^4 c^4 x^3 y^2+4 a^2 b^8 c^4 x^3 y^2-2 b^10 c^4 x^3 y^2-2 a^6 b^2 c^6 x^3 y^2+2 a^4 b^4 c^6 x^3 y^2-6 a^2 b^6 c^6 x^3 y^2+6 b^8 c^6 x^3 y^2-2 a^4 b^2 c^8 x^3 y^2-6 b^6 c^8 x^3 y^2+2 a^2 b^2 c^10 x^3 y^2+2 b^4 c^10 x^3 y^2+2 a^10 c^4 x^2 y^3-4 a^8 b^2 c^4 x^2 y^3+4 a^4 b^6 c^4 x^2 y^3-2 a^2 b^8 c^4 x^2 y^3-6 a^8 c^6 x^2 y^3+6 a^6 b^2 c^6 x^2 y^3-2 a^4 b^4 c^6 x^2 y^3+2 a^2 b^6 c^6 x^2 y^3+6 a^6 c^8 x^2 y^3+2 a^2 b^4 c^8 x^2 y^3-2 a^4 c^10 x^2 y^3-2 a^2 b^2 c^10 x^2 y^3+4 a^4 b^6 c^4 x^3 y z-4 b^10 c^4 x^3 y z-4 a^4 b^4 c^6 x^3 y z+12 b^8 c^6 x^3 y z-12 b^6 c^8 x^3 y z+4 b^4 c^10 x^3 y z-a^12 c^2 x^2 y^2 z+4 a^10 b^2 c^2 x^2 y^2 z-5 a^8 b^4 c^2 x^2 y^2 z+5 a^4 b^8 c^2 x^2 y^2 z-4 a^2 b^10 c^2 x^2 y^2 z+b^12 c^2 x^2 y^2 z+5 a^10 c^4 x^2 y^2 z-5 a^8 b^2 c^4 x^2 y^2 z+6 a^6 b^4 c^4 x^2 y^2 z-6 a^4 b^6 c^4 x^2 y^2 z+5 a^2 b^8 c^4 x^2 y^2 z-5 b^10 c^4 x^2 y^2 z-10 a^8 c^6 x^2 y^2 z-4 a^6 b^2 c^6 x^2 y^2 z+4 a^2 b^6 c^6 x^2 y^2 z+10 b^8 c^6 x^2 y^2 z+10 a^6 c^8 x^2 y^2 z+6 a^4 b^2 c^8 x^2 y^2 z-6 a^2 b^4 c^8 x^2 y^2 z-10 b^6 c^8 x^2 y^2 z-5 a^4 c^10 x^2 y^2 z+5 b^4 c^10 x^2 y^2 z+a^2 c^12 x^2 y^2 z-b^2 c^12 x^2 y^2 z+4 a^10 c^4 x y^3 z-4 a^6 b^4 c^4 x y^3 z-12 a^8 c^6 x y^3 z+4 a^4 b^4 c^6 x y^3 z+12 a^6 c^8 x y^3 z-4 a^4 c^10 x y^3 z-2 a^8 b^4 c^2 x^3 z^2+2 a^6 b^6 c^2 x^3 z^2+2 a^4 b^8 c^2 x^3 z^2-2 a^2 b^10 c^2 x^3 z^2+4 a^6 b^4 c^4 x^3 z^2-2 a^4 b^6 c^4 x^3 z^2-2 b^10 c^4 x^3 z^2+6 a^2 b^6 c^6 x^3 z^2+6 b^8 c^6 x^3 z^2-4 a^2 b^4 c^8 x^3 z^2-6 b^6 c^8 x^3 z^2+2 b^4 c^10 x^3 z^2+a^12 b^2 x^2 y z^2-5 a^10 b^4 x^2 y z^2+10 a^8 b^6 x^2 y z^2-10 a^6 b^8 x^2 y z^2+5 a^4 b^10 x^2 y z^2-a^2 b^12 x^2 y z^2-4 a^10 b^2 c^2 x^2 y z^2+5 a^8 b^4 c^2 x^2 y z^2+4 a^6 b^6 c^2 x^2 y z^2-6 a^4 b^8 c^2 x^2 y z^2+b^12 c^2 x^2 y z^2+5 a^8 b^2 c^4 x^2 y z^2-6 a^6 b^4 c^4 x^2 y z^2+6 a^2 b^8 c^4 x^2 y z^2-5 b^10 c^4 x^2 y z^2+6 a^4 b^4 c^6 x^2 y z^2-4 a^2 b^6 c^6 x^2 y z^2+10 b^8 c^6 x^2 y z^2-5 a^4 b^2 c^8 x^2 y z^2-5 a^2 b^4 c^8 x^2 y z^2-10 b^6 c^8 x^2 y z^2+4 a^2 b^2 c^10 x^2 y z^2+5 b^4 c^10 x^2 y z^2-b^2 c^12 x^2 y z^2+a^12 b^2 x y^2 z^2-5 a^10 b^4 x y^2 z^2+10 a^8 b^6 x y^2 z^2-10 a^6 b^8 x y^2 z^2+5 a^4 b^10 x y^2 z^2-a^2 b^12 x y^2 z^2-a^12 c^2 x y^2 z^2+6 a^8 b^4 c^2 x y^2 z^2-4 a^6 b^6 c^2 x y^2 z^2-5 a^4 b^8 c^2 x y^2 z^2+4 a^2 b^10 c^2 x y^2 z^2+5 a^10 c^4 x y^2 z^2-6 a^8 b^2 c^4 x y^2 z^2+6 a^4 b^6 c^4 x y^2 z^2-5 a^2 b^8 c^4 x y^2 z^2-10 a^8 c^6 x y^2 z^2+4 a^6 b^2 c^6 x y^2 z^2-6 a^4 b^4 c^6 x y^2 z^2+10 a^6 c^8 x y^2 z^2+5 a^4 b^2 c^8 x y^2 z^2+5 a^2 b^4 c^8 x y^2 z^2-5 a^4 c^10 x y^2 z^2-4 a^2 b^2 c^10 x y^2 z^2+a^2 c^12 x y^2 z^2+2 a^10 b^2 c^2 y^3 z^2-2 a^8 b^4 c^2 y^3 z^2-2 a^6 b^6 c^2 y^3 z^2+2 a^4 b^8 c^2 y^3 z^2+2 a^10 c^4 y^3 z^2+2 a^6 b^4 c^4 y^3 z^2-4 a^4 b^6 c^4 y^3 z^2-6 a^8 c^6 y^3 z^2-6 a^6 b^2 c^6 y^3 z^2+6 a^6 c^8 y^3 z^2+4 a^4 b^2 c^8 y^3 z^2-2 a^4 c^10 y^3 z^2-2 a^10 b^4 x^2 z^3+6 a^8 b^6 x^2 z^3-6 a^6 b^8 x^2 z^3+2 a^4 b^10 x^2 z^3+4 a^8 b^4 c^2 x^2 z^3-6 a^6 b^6 c^2 x^2 z^3+2 a^2 b^10 c^2 x^2 z^3+2 a^4 b^6 c^4 x^2 z^3-2 a^2 b^8 c^4 x^2 z^3-4 a^4 b^4 c^6 x^2 z^3-2 a^2 b^6 c^6 x^2 z^3+2 a^2 b^4 c^8 x^2 z^3-4 a^10 b^4 x y z^3+12 a^8 b^6 x y z^3-12 a^6 b^8 x y z^3+4 a^4 b^10 x y z^3+4 a^6 b^4 c^4 x y z^3-4 a^4 b^6 c^4 x y z^3-2 a^10 b^4 y^2 z^3+6 a^8 b^6 y^2 z^3-6 a^6 b^8 y^2 z^3+2 a^4 b^10 y^2 z^3-2 a^10 b^2 c^2 y^2 z^3+6 a^6 b^6 c^2 y^2 z^3-4 a^4 b^8 c^2 y^2 z^3+2 a^8 b^2 c^4 y^2 z^3-2 a^6 b^4 c^4 y^2 z^3+2 a^6 b^2 c^6 y^2 z^3+4 a^4 b^4 c^6 y^2 z^3-2 a^4 b^2 c^8 y^2 z^3 = 0)
𝒬 de ecuación baricéntrica:
Σ abc xyz
(4b^4c^4(b^2-c^2)(a^2-b^2+c^2)(a^2+b^2-c^2) x^3
+ 2a^4(-a^2+b^2+c^2)(a^2(b^2+c^2)-b^4+2b^2c^2-c^4) (-c^2(a^2+b^2-c^2)y +
b^2(a^2-b^2+c^2)z)y z
- a^2(b^2-c^2)(-a^2+b^2+c^2)(a^8 + a^6(-4b^2-4c^2) +
a^4(6b^4+8b^2c^2+6c^4) + a^2(-4b^6-4c^6)+ b^8-4b^6c^2+6b^4c^4-4b^2c^6+c^8 )x y z)y z = 0.
Puntos sobre la quíntica 𝒬: el circuncentro (X3), el ortocentro (X4), el foco de la (X110), los vértices de ABC, sus antipodales A', B', C', y los vértices del del circuncentro.
Otra propiedad de esta quíntica es que las tangentes en los puntos A', B', C' concurren en X110.
Excluyendo los puntos A, B, C, A', B', C', para los que son los :
X4 y X110 son los únicos centros del triángulo, para los que los triángulos ABC y son semejantes y perspectivos.
• Cuando P=X4, es el .
• Cuando P=X110, el centro de perspectividad de ABC y es X5627, el centro de semejanza (inversa) es X4 y las rectas fijas son la recta de Euler y su perpendicular por X4 (DEF, ). Ocurre, además, que los puntos Pa, Pb y Pc son los puntos medios de AD, BE y CF, respectivamente.
La semejanza (inversa) que transforma ABC en , en este caso, es la composición de la homotecia de centro X4 y razón 1/2 con la simetría axial respecto a la recta de Euler.
- Viernes, 19 de octubre del 2018
"Crosssum" e hipérbolas rectangulares
a Kaque, por su "cumple"
Simson lines of diametral points (Paris Pamfilos)
Consider triangle t=ABC and a point D on its circumcircle (c) and its antipodal point E on (c). Project D, E on the sides of (t) and define the Simson lines S(D), S(E) (
see Simson.html ). Then the angle of the two Simson lines S(D) and S(E) is a right one and their intersection point is on the Euler circle of t.
Si una recta p corta a los lados BC, CA, AB de un triángulo ABC en los puntos D, E, F, respectivamente, sea D' el punto medio de las reflexiones Dc y Db de D en las rectas AB y AC. Los puntos E' y F' se definen de forma análoga, procediendo cíclicamente sobre los lados de ABC. Entonces, los puntos D', E', F' están alineados, sobre una recta p'.
Cuando la recta p gira alrededor de un punto P, la recta p' gira alrededor de P', del circuncentro y P.
La correspondencia p ↦ p' pude ser descrita analíticamente como sigue:
Si las coordenadas baricéntricas del punto del infinito de la recta p son (1:-t:t-1), entonces las coordenadas del punto del infinito de la recta p' son (1:-t':t'-1), siendo
t' = (b^2((a^2-c^2)+a^2SA t))/(a^2(b^2SB+(b^2-c^2)SA t)).
Se tiene, así, una proyectividad entre los haces de rectas de puntos base P y P'; por lo que, el punto de intersección Q de las rectas p y p' describe una cónica ℋ(P), cuando p gira alrededor de P.
Si P(u:v:w), la ecuación de ℋ(P) es:
Σ abc xyz
(a^2-b^2-c^2)(a^2(c^2v-b^2w)+(b^2-c^2)(c^2v+b^2w))x^2 +
(a^6(w-v)+a^4(b^2(u+2v)-c^2(u+2w))-a^2(b^4-c^4)(2u+v+w)+
((b^2-c^2)^3u)y z = 0.
Se trata de una que pasa por el , P, P' y sus asíntotas son paralelas a las de .
Las coordenadas de su centro Po son:
(a^2 b^2 c^2 (-2 a^6+4 a^2 (b^2-c^2)^2+a^4 (b^2+c^2)-3 (b^2-c^2)^2 (b^2+c^2))u+
a^2 c^2 (-a^8-2 a^4 b^2 c^2-(b^2-c^2)^3 (b^2+c^2)+a^6 (b^2+2 c^2)+a^2 (b^6-2 b^4 c^2+3 b^2 c^4-2 c^6))v+
a^2 b^2 (-a^8-2 a^4 b^2 c^2+(b^2-c^2)^3 (b^2+c^2)+a^6 (2 b^2+c^2)+a^2 (-2 b^6+3 b^4 c^2-2 b^2 c^4+c^6))w : ... : ...).
Por tanto, la correspondencia σ: P ↦ Po es una transformación afín. Sus puntos fijos son el simediano y los de los puntos en los que la corta a la circunferencia circunscrita, X2574 y X2575.
Pares {Xi, Xj=σ(Xi)}, para los índices {i, j}:
{1, 15904}, {2, 12099}, {3, 125}, {4, 1112}, {5, 11746}, {6, 6}, {25, 12828},
{30, 2781},
{110, 468}, {112, 16318}, {155, 110}, {182, 15118}, {378, 427}, {381, 51}, {382, 13417}, {399, 1495},
{520, 9003}, {525, 526}, {541, 6000}, {542, 2393}, {690, 924}, {912, 2836},
{1147, 5972}, {1181, 13198}, {1350, 67}, {1351, 5095}, {1498, 10117}, {1625, 232}, {1636, 9209}, {2420, 6103},
{2574, 2574}, {2575, 2575}, {2771, 3827}, {2775, 15313}, {2780, 3566}, {2850, 9001},
{2931, 3580}, {3167, 5642}, {3426, 13202},
{3564, 2854}, {5663, 1503},
{3569, 2501}, {3818, 9969}, {4549, 15738}, {4550, 7687}, {4846, 974}, {5504, 11064}, {5609, 15448}, {5890, 11245}, {6644, 13567}, {7706, 389}, {7986, 65}, {8549, 13248},
{8673, 9033},
{8717, 20417}, {8909, 8998},
{9033, 8675}, {9517, 523},
{9927, 11800}, {10249, 23327}, {10605, 1899}, {10606, 1853}, {10675, 10681}, {10676, 10682}, {11472, 4}, {11820, 10990}, {12038, 6723}, {12084, 23315}, {12163, 3448}, {12302, 858}, {12964, 13287}, {12970, 13288}, {13293, 15126},
{13754, 542}, {14915, 2777}, {14984, 524},
{15087, 13366}, {15305, 428},
{17702, 511},
{17847, 15139}, {18440, 1843}, {18445, 184}, {18451, 25}, {19139, 6593}, {19149, 1177}, {21733, 9134}, {22146, 8779}.
En particular, cuando el punto P recorre la recta de Euler, las hipérbolas ℋ(P) forman un haz de cónicas, que pasan por el ortocentro. El lugar geométrico del de la recta X4X6, respecto a ℋ(P), es la recta X51X132.
La transformación afín σ induce sobre la recta de Euler y su imagen la recta X51X132 una proyectividad. Luego, las rectas PPo envuelven una cónica 𝒫, que se trata de una
parábola
( 8 a^24 b^6 c^2 x^2-48 a^22 b^8 c^2 x^2+104 a^20 b^10 c^2 x^2-64 a^18 b^12 c^2 x^2-112 a^16 b^14 c^2 x^2+224 a^14 b^16 c^2 x^2-112 a^12 b^18 c^2 x^2-64 a^10 b^20 c^2 x^2+104 a^8 b^22 c^2 x^2-48 a^6 b^24 c^2 x^2+8 a^4 b^26 c^2 x^2-16 a^24 b^4 c^4 x^2+48 a^22 b^6 c^4 x^2+52 a^20 b^8 c^4 x^2-404 a^18 b^10 c^4 x^2+649 a^16 b^12 c^4 x^2-336 a^14 b^14 c^4 x^2-244 a^12 b^16 c^4 x^2+472 a^10 b^18 c^4 x^2-306 a^8 b^20 c^4 x^2+96 a^6 b^22 c^4 x^2-8 a^4 b^24 c^4 x^2-4 a^2 b^26 c^4 x^2+b^28 c^4 x^2+8 a^24 b^2 c^6 x^2+48 a^22 b^4 c^6 x^2-312 a^20 b^6 c^6 x^2+468 a^18 b^8 c^6 x^2+120 a^16 b^10 c^6 x^2-1040 a^14 b^12 c^6 x^2+1144 a^12 b^14 c^6 x^2-480 a^10 b^16 c^6 x^2-8 a^8 b^18 c^6 x^2+80 a^6 b^20 c^6 x^2-48 a^4 b^22 c^6 x^2+28 a^2 b^24 c^6 x^2-8 b^26 c^6 x^2-48 a^22 b^2 c^8 x^2+52 a^20 b^4 c^8 x^2+468 a^18 b^6 c^8 x^2-1314 a^16 b^8 c^8 x^2+1152 a^14 b^10 c^8 x^2+116 a^12 b^12 c^8 x^2-880 a^10 b^14 c^8 x^2+600 a^8 b^16 c^8 x^2-192 a^6 b^18 c^8 x^2+104 a^4 b^20 c^8 x^2-84 a^2 b^22 c^8 x^2+26 b^24 c^8 x^2+104 a^20 b^2 c^10 x^2-404 a^18 b^4 c^10 x^2+120 a^16 b^6 c^10 x^2+1152 a^14 b^8 c^10 x^2-1808 a^12 b^10 c^10 x^2+952 a^10 b^12 c^10 x^2+32 a^8 b^14 c^10 x^2-144 a^6 b^16 c^10 x^2-104 a^4 b^18 c^10 x^2+140 a^2 b^20 c^10 x^2-40 b^22 c^10 x^2-64 a^18 b^2 c^12 x^2+649 a^16 b^4 c^12 x^2-1040 a^14 b^6 c^12 x^2+116 a^12 b^8 c^12 x^2+952 a^10 b^10 c^12 x^2-844 a^8 b^12 c^12 x^2+208 a^6 b^14 c^12 x^2+160 a^4 b^16 c^12 x^2-136 a^2 b^18 c^12 x^2+15 b^20 c^12 x^2-112 a^16 b^2 c^14 x^2-336 a^14 b^4 c^14 x^2+1144 a^12 b^6 c^14 x^2-880 a^10 b^8 c^14 x^2+32 a^8 b^10 c^14 x^2+208 a^6 b^12 c^14 x^2-224 a^4 b^14 c^14 x^2+56 a^2 b^16 c^14 x^2+48 b^18 c^14 x^2+224 a^14 b^2 c^16 x^2-244 a^12 b^4 c^16 x^2-480 a^10 b^6 c^16 x^2+600 a^8 b^8 c^16 x^2-144 a^6 b^10 c^16 x^2+160 a^4 b^12 c^16 x^2+56 a^2 b^14 c^16 x^2-84 b^16 c^16 x^2-112 a^12 b^2 c^18 x^2+472 a^10 b^4 c^18 x^2-8 a^8 b^6 c^18 x^2-192 a^6 b^8 c^18 x^2-104 a^4 b^10 c^18 x^2-136 a^2 b^12 c^18 x^2+48 b^14 c^18 x^2-64 a^10 b^2 c^20 x^2-306 a^8 b^4 c^20 x^2+80 a^6 b^6 c^20 x^2+104 a^4 b^8 c^20 x^2+140 a^2 b^10 c^20 x^2+15 b^12 c^20 x^2+104 a^8 b^2 c^22 x^2+96 a^6 b^4 c^22 x^2-48 a^4 b^6 c^22 x^2-84 a^2 b^8 c^22 x^2-40 b^10 c^22 x^2-48 a^6 b^2 c^24 x^2-8 a^4 b^4 c^24 x^2+28 a^2 b^6 c^24 x^2+26 b^8 c^24 x^2+8 a^4 b^2 c^26 x^2-4 a^2 b^4 c^26 x^2-8 b^6 c^26 x^2+b^4 c^28 x^2+8 a^26 b^4 c^2 x y-40 a^24 b^6 c^2 x y+56 a^22 b^8 c^2 x y+40 a^20 b^10 c^2 x y-176 a^18 b^12 c^2 x y+112 a^16 b^14 c^2 x y+112 a^14 b^16 c^2 x y-176 a^12 b^18 c^2 x y+40 a^10 b^20 c^2 x y+56 a^8 b^22 c^2 x y-40 a^6 b^24 c^2 x y+8 a^4 b^26 c^2 x y-8 a^26 b^2 c^4 x y-4 a^24 b^4 c^4 x y+174 a^22 b^6 c^4 x y-452 a^20 b^8 c^4 x y+272 a^18 b^10 c^4 x y+584 a^16 b^12 c^4 x y-1132 a^14 b^14 c^4 x y+584 a^12 b^16 c^4 x y+272 a^10 b^18 c^4 x y-452 a^8 b^20 c^4 x y+174 a^6 b^22 c^4 x y-4 a^4 b^24 c^4 x y-8 a^2 b^26 c^4 x y+44 a^24 b^2 c^6 x y-144 a^22 b^4 c^6 x y-64 a^20 b^6 c^6 x y+940 a^18 b^8 c^6 x y-1656 a^16 b^10 c^6 x y+880 a^14 b^12 c^6 x y+880 a^12 b^14 c^6 x y-1656 a^10 b^16 c^6 x y+940 a^8 b^18 c^6 x y-64 a^6 b^20 c^6 x y-144 a^4 b^22 c^6 x y+44 a^2 b^24 c^6 x y-86 a^22 b^2 c^8 x y+424 a^20 b^4 c^8 x y-702 a^18 b^6 c^8 x y-16 a^16 b^8 c^8 x y+1780 a^14 b^10 c^8 x y-2800 a^12 b^12 c^8 x y+1780 a^10 b^14 c^8 x y-16 a^8 b^16 c^8 x y-702 a^6 b^18 c^8 x y+424 a^4 b^20 c^8 x y-86 a^2 b^22 c^8 x y+52 a^20 b^2 c^10 x y-372 a^18 b^4 c^10 x y+1144 a^16 b^6 c^10 x y-1784 a^14 b^8 c^10 x y+960 a^12 b^10 c^10 x y+960 a^10 b^12 c^10 x y-1784 a^8 b^14 c^10 x y+1144 a^6 b^16 c^10 x y-372 a^4 b^18 c^10 x y+52 a^2 b^20 c^10 x y+38 a^18 b^2 c^12 x y-128 a^16 b^4 c^12 x y-124 a^14 b^6 c^12 x y+1360 a^12 b^8 c^12 x y-2324 a^10 b^10 c^12 x y+1360 a^8 b^12 c^12 x y-124 a^6 b^14 c^12 x y-128 a^4 b^16 c^12 x y+38 a^2 b^18 c^12 x y-40 a^16 b^2 c^14 x y+296 a^14 b^4 c^14 x y-936 a^12 b^6 c^14 x y+744 a^10 b^8 c^14 x y+744 a^8 b^10 c^14 x y-936 a^6 b^12 c^14 x y+296 a^4 b^14 c^14 x y-40 a^2 b^16 c^14 x y-28 a^14 b^2 c^16 x y+120 a^12 b^4 c^16 x y+460 a^10 b^6 c^16 x y-1280 a^8 b^8 c^16 x y+460 a^6 b^10 c^16 x y+120 a^4 b^12 c^16 x y-28 a^2 b^14 c^16 x y+8 a^12 b^2 c^18 x y-344 a^10 b^4 c^18 x y+368 a^8 b^6 c^18 x y+368 a^6 b^8 c^18 x y-344 a^4 b^10 c^18 x y+8 a^2 b^12 c^18 x y+68 a^10 b^2 c^20 x y+132 a^8 b^4 c^20 x y-338 a^6 b^6 c^20 x y+132 a^4 b^8 c^20 x y+68 a^2 b^10 c^20 x y-68 a^8 b^2 c^22 x y+40 a^6 b^4 c^22 x y+40 a^4 b^6 c^22 x y-68 a^2 b^8 c^22 x y+18 a^6 b^2 c^24 x y-32 a^4 b^4 c^24 x y+18 a^2 b^6 c^24 x y+4 a^4 b^2 c^26 x y+4 a^2 b^4 c^26 x y-2 a^2 b^2 c^28 x y+8 a^26 b^4 c^2 y^2-48 a^24 b^6 c^2 y^2+104 a^22 b^8 c^2 y^2-64 a^20 b^10 c^2 y^2-112 a^18 b^12 c^2 y^2+224 a^16 b^14 c^2 y^2-112 a^14 b^16 c^2 y^2-64 a^12 b^18 c^2 y^2+104 a^10 b^20 c^2 y^2-48 a^8 b^22 c^2 y^2+8 a^6 b^24 c^2 y^2+a^28 c^4 y^2-4 a^26 b^2 c^4 y^2-8 a^24 b^4 c^4 y^2+96 a^22 b^6 c^4 y^2-306 a^20 b^8 c^4 y^2+472 a^18 b^10 c^4 y^2-244 a^16 b^12 c^4 y^2-336 a^14 b^14 c^4 y^2+649 a^12 b^16 c^4 y^2-404 a^10 b^18 c^4 y^2+52 a^8 b^20 c^4 y^2+48 a^6 b^22 c^4 y^2-16 a^4 b^24 c^4 y^2-8 a^26 c^6 y^2+28 a^24 b^2 c^6 y^2-48 a^22 b^4 c^6 y^2+80 a^20 b^6 c^6 y^2-8 a^18 b^8 c^6 y^2-480 a^16 b^10 c^6 y^2+1144 a^14 b^12 c^6 y^2-1040 a^12 b^14 c^6 y^2+120 a^10 b^16 c^6 y^2+468 a^8 b^18 c^6 y^2-312 a^6 b^20 c^6 y^2+48 a^4 b^22 c^6 y^2+8 a^2 b^24 c^6 y^2+26 a^24 c^8 y^2-84 a^22 b^2 c^8 y^2+104 a^20 b^4 c^8 y^2-192 a^18 b^6 c^8 y^2+600 a^16 b^8 c^8 y^2-880 a^14 b^10 c^8 y^2+116 a^12 b^12 c^8 y^2+1152 a^10 b^14 c^8 y^2-1314 a^8 b^16 c^8 y^2+468 a^6 b^18 c^8 y^2+52 a^4 b^20 c^8 y^2-48 a^2 b^22 c^8 y^2-40 a^22 c^10 y^2+140 a^20 b^2 c^10 y^2-104 a^18 b^4 c^10 y^2-144 a^16 b^6 c^10 y^2+32 a^14 b^8 c^10 y^2+952 a^12 b^10 c^10 y^2-1808 a^10 b^12 c^10 y^2+1152 a^8 b^14 c^10 y^2+120 a^6 b^16 c^10 y^2-404 a^4 b^18 c^10 y^2+104 a^2 b^20 c^10 y^2+15 a^20 c^12 y^2-136 a^18 b^2 c^12 y^2+160 a^16 b^4 c^12 y^2+208 a^14 b^6 c^12 y^2-844 a^12 b^8 c^12 y^2+952 a^10 b^10 c^12 y^2+116 a^8 b^12 c^12 y^2-1040 a^6 b^14 c^12 y^2+649 a^4 b^16 c^12 y^2-64 a^2 b^18 c^12 y^2+48 a^18 c^14 y^2+56 a^16 b^2 c^14 y^2-224 a^14 b^4 c^14 y^2+208 a^12 b^6 c^14 y^2+32 a^10 b^8 c^14 y^2-880 a^8 b^10 c^14 y^2+1144 a^6 b^12 c^14 y^2-336 a^4 b^14 c^14 y^2-112 a^2 b^16 c^14 y^2-84 a^16 c^16 y^2+56 a^14 b^2 c^16 y^2+160 a^12 b^4 c^16 y^2-144 a^10 b^6 c^16 y^2+600 a^8 b^8 c^16 y^2-480 a^6 b^10 c^16 y^2-244 a^4 b^12 c^16 y^2+224 a^2 b^14 c^16 y^2+48 a^14 c^18 y^2-136 a^12 b^2 c^18 y^2-104 a^10 b^4 c^18 y^2-192 a^8 b^6 c^18 y^2-8 a^6 b^8 c^18 y^2+472 a^4 b^10 c^18 y^2-112 a^2 b^12 c^18 y^2+15 a^12 c^20 y^2+140 a^10 b^2 c^20 y^2+104 a^8 b^4 c^20 y^2+80 a^6 b^6 c^20 y^2-306 a^4 b^8 c^20 y^2-64 a^2 b^10 c^20 y^2-40 a^10 c^22 y^2-84 a^8 b^2 c^22 y^2-48 a^6 b^4 c^22 y^2+96 a^4 b^6 c^22 y^2+104 a^2 b^8 c^22 y^2+26 a^8 c^24 y^2+28 a^6 b^2 c^24 y^2-8 a^4 b^4 c^24 y^2-48 a^2 b^6 c^24 y^2-8 a^6 c^26 y^2-4 a^4 b^2 c^26 y^2+8 a^2 b^4 c^26 y^2+a^4 c^28 y^2-8 a^26 b^4 c^2 x z+44 a^24 b^6 c^2 x z-86 a^22 b^8 c^2 x z+52 a^20 b^10 c^2 x z+38 a^18 b^12 c^2 x z-40 a^16 b^14 c^2 x z-28 a^14 b^16 c^2 x z+8 a^12 b^18 c^2 x z+68 a^10 b^20 c^2 x z-68 a^8 b^22 c^2 x z+18 a^6 b^24 c^2 x z+4 a^4 b^26 c^2 x z-2 a^2 b^28 c^2 x z+8 a^26 b^2 c^4 x z-4 a^24 b^4 c^4 x z-144 a^22 b^6 c^4 x z+424 a^20 b^8 c^4 x z-372 a^18 b^10 c^4 x z-128 a^16 b^12 c^4 x z+296 a^14 b^14 c^4 x z+120 a^12 b^16 c^4 x z-344 a^10 b^18 c^4 x z+132 a^8 b^20 c^4 x z+40 a^6 b^22 c^4 x z-32 a^4 b^24 c^4 x z+4 a^2 b^26 c^4 x z-40 a^24 b^2 c^6 x z+174 a^22 b^4 c^6 x z-64 a^20 b^6 c^6 x z-702 a^18 b^8 c^6 x z+1144 a^16 b^10 c^6 x z-124 a^14 b^12 c^6 x z-936 a^12 b^14 c^6 x z+460 a^10 b^16 c^6 x z+368 a^8 b^18 c^6 x z-338 a^6 b^20 c^6 x z+40 a^4 b^22 c^6 x z+18 a^2 b^24 c^6 x z+56 a^22 b^2 c^8 x z-452 a^20 b^4 c^8 x z+940 a^18 b^6 c^8 x z-16 a^16 b^8 c^8 x z-1784 a^14 b^10 c^8 x z+1360 a^12 b^12 c^8 x z+744 a^10 b^14 c^8 x z-1280 a^8 b^16 c^8 x z+368 a^6 b^18 c^8 x z+132 a^4 b^20 c^8 x z-68 a^2 b^22 c^8 x z+40 a^20 b^2 c^10 x z+272 a^18 b^4 c^10 x z-1656 a^16 b^6 c^10 x z+1780 a^14 b^8 c^10 x z+960 a^12 b^10 c^10 x z-2324 a^10 b^12 c^10 x z+744 a^8 b^14 c^10 x z+460 a^6 b^16 c^10 x z-344 a^4 b^18 c^10 x z+68 a^2 b^20 c^10 x z-176 a^18 b^2 c^12 x z+584 a^16 b^4 c^12 x z+880 a^14 b^6 c^12 x z-2800 a^12 b^8 c^12 x z+960 a^10 b^10 c^12 x z+1360 a^8 b^12 c^12 x z-936 a^6 b^14 c^12 x z+120 a^4 b^16 c^12 x z+8 a^2 b^18 c^12 x z+112 a^16 b^2 c^14 x z-1132 a^14 b^4 c^14 x z+880 a^12 b^6 c^14 x z+1780 a^10 b^8 c^14 x z-1784 a^8 b^10 c^14 x z-124 a^6 b^12 c^14 x z+296 a^4 b^14 c^14 x z-28 a^2 b^16 c^14 x z+112 a^14 b^2 c^16 x z+584 a^12 b^4 c^16 x z-1656 a^10 b^6 c^16 x z-16 a^8 b^8 c^16 x z+1144 a^6 b^10 c^16 x z-128 a^4 b^12 c^16 x z-40 a^2 b^14 c^16 x z-176 a^12 b^2 c^18 x z+272 a^10 b^4 c^18 x z+940 a^8 b^6 c^18 x z-702 a^6 b^8 c^18 x z-372 a^4 b^10 c^18 x z+38 a^2 b^12 c^18 x z+40 a^10 b^2 c^20 x z-452 a^8 b^4 c^20 x z-64 a^6 b^6 c^20 x z+424 a^4 b^8 c^20 x z+52 a^2 b^10 c^20 x z+56 a^8 b^2 c^22 x z+174 a^6 b^4 c^22 x z-144 a^4 b^6 c^22 x z-86 a^2 b^8 c^22 x z-40 a^6 b^2 c^24 x z-4 a^4 b^4 c^24 x z+44 a^2 b^6 c^24 x z+8 a^4 b^2 c^26 x z-8 a^2 b^4 c^26 x z-2 a^28 b^2 c^2 y z+4 a^26 b^4 c^2 y z+18 a^24 b^6 c^2 y z-68 a^22 b^8 c^2 y z+68 a^20 b^10 c^2 y z+8 a^18 b^12 c^2 y z-28 a^16 b^14 c^2 y z-40 a^14 b^16 c^2 y z+38 a^12 b^18 c^2 y z+52 a^10 b^20 c^2 y z-86 a^8 b^22 c^2 y z+44 a^6 b^24 c^2 y z-8 a^4 b^26 c^2 y z+4 a^26 b^2 c^4 y z-32 a^24 b^4 c^4 y z+40 a^22 b^6 c^4 y z+132 a^20 b^8 c^4 y z-344 a^18 b^10 c^4 y z+120 a^16 b^12 c^4 y z+296 a^14 b^14 c^4 y z-128 a^12 b^16 c^4 y z-372 a^10 b^18 c^4 y z+424 a^8 b^20 c^4 y z-144 a^6 b^22 c^4 y z-4 a^4 b^24 c^4 y z+8 a^2 b^26 c^4 y z+18 a^24 b^2 c^6 y z+40 a^22 b^4 c^6 y z-338 a^20 b^6 c^6 y z+368 a^18 b^8 c^6 y z+460 a^16 b^10 c^6 y z-936 a^14 b^12 c^6 y z-124 a^12 b^14 c^6 y z+1144 a^10 b^16 c^6 y z-702 a^8 b^18 c^6 y z-64 a^6 b^20 c^6 y z+174 a^4 b^22 c^6 y z-40 a^2 b^24 c^6 y z-68 a^22 b^2 c^8 y z+132 a^20 b^4 c^8 y z+368 a^18 b^6 c^8 y z-1280 a^16 b^8 c^8 y z+744 a^14 b^10 c^8 y z+1360 a^12 b^12 c^8 y z-1784 a^10 b^14 c^8 y z-16 a^8 b^16 c^8 y z+940 a^6 b^18 c^8 y z-452 a^4 b^20 c^8 y z+56 a^2 b^22 c^8 y z+68 a^20 b^2 c^10 y z-344 a^18 b^4 c^10 y z+460 a^16 b^6 c^10 y z+744 a^14 b^8 c^10 y z-2324 a^12 b^10 c^10 y z+960 a^10 b^12 c^10 y z+1780 a^8 b^14 c^10 y z-1656 a^6 b^16 c^10 y z+272 a^4 b^18 c^10 y z+40 a^2 b^20 c^10 y z+8 a^18 b^2 c^12 y z+120 a^16 b^4 c^12 y z-936 a^14 b^6 c^12 y z+1360 a^12 b^8 c^12 y z+960 a^10 b^10 c^12 y z-2800 a^8 b^12 c^12 y z+880 a^6 b^14 c^12 y z+584 a^4 b^16 c^12 y z-176 a^2 b^18 c^12 y z-28 a^16 b^2 c^14 y z+296 a^14 b^4 c^14 y z-124 a^12 b^6 c^14 y z-1784 a^10 b^8 c^14 y z+1780 a^8 b^10 c^14 y z+880 a^6 b^12 c^14 y z-1132 a^4 b^14 c^14 y z+112 a^2 b^16 c^14 y z-40 a^14 b^2 c^16 y z-128 a^12 b^4 c^16 y z+1144 a^10 b^6 c^16 y z-16 a^8 b^8 c^16 y z-1656 a^6 b^10 c^16 y z+584 a^4 b^12 c^16 y z+112 a^2 b^14 c^16 y z+38 a^12 b^2 c^18 y z-372 a^10 b^4 c^18 y z-702 a^8 b^6 c^18 y z+940 a^6 b^8 c^18 y z+272 a^4 b^10 c^18 y z-176 a^2 b^12 c^18 y z+52 a^10 b^2 c^20 y z+424 a^8 b^4 c^20 y z-64 a^6 b^6 c^20 y z-452 a^4 b^8 c^20 y z+40 a^2 b^10 c^20 y z-86 a^8 b^2 c^22 y z-144 a^6 b^4 c^22 y z+174 a^4 b^6 c^22 y z+56 a^2 b^8 c^22 y z+44 a^6 b^2 c^24 y z-4 a^4 b^4 c^24 y z-40 a^2 b^6 c^24 y z-8 a^4 b^2 c^26 y z+8 a^2 b^4 c^26 y z+a^28 b^4 z^2-8 a^26 b^6 z^2+26 a^24 b^8 z^2-40 a^22 b^10 z^2+15 a^20 b^12 z^2+48 a^18 b^14 z^2-84 a^16 b^16 z^2+48 a^14 b^18 z^2+15 a^12 b^20 z^2-40 a^10 b^22 z^2+26 a^8 b^24 z^2-8 a^6 b^26 z^2+a^4 b^28 z^2-4 a^26 b^4 c^2 z^2+28 a^24 b^6 c^2 z^2-84 a^22 b^8 c^2 z^2+140 a^20 b^10 c^2 z^2-136 a^18 b^12 c^2 z^2+56 a^16 b^14 c^2 z^2+56 a^14 b^16 c^2 z^2-136 a^12 b^18 c^2 z^2+140 a^10 b^20 c^2 z^2-84 a^8 b^22 c^2 z^2+28 a^6 b^24 c^2 z^2-4 a^4 b^26 c^2 z^2+8 a^26 b^2 c^4 z^2-8 a^24 b^4 c^4 z^2-48 a^22 b^6 c^4 z^2+104 a^20 b^8 c^4 z^2-104 a^18 b^10 c^4 z^2+160 a^16 b^12 c^4 z^2-224 a^14 b^14 c^4 z^2+160 a^12 b^16 c^4 z^2-104 a^10 b^18 c^4 z^2+104 a^8 b^20 c^4 z^2-48 a^6 b^22 c^4 z^2-8 a^4 b^24 c^4 z^2+8 a^2 b^26 c^4 z^2-48 a^24 b^2 c^6 z^2+96 a^22 b^4 c^6 z^2+80 a^20 b^6 c^6 z^2-192 a^18 b^8 c^6 z^2-144 a^16 b^10 c^6 z^2+208 a^14 b^12 c^6 z^2+208 a^12 b^14 c^6 z^2-144 a^10 b^16 c^6 z^2-192 a^8 b^18 c^6 z^2+80 a^6 b^20 c^6 z^2+96 a^4 b^22 c^6 z^2-48 a^2 b^24 c^6 z^2+104 a^22 b^2 c^8 z^2-306 a^20 b^4 c^8 z^2-8 a^18 b^6 c^8 z^2+600 a^16 b^8 c^8 z^2+32 a^14 b^10 c^8 z^2-844 a^12 b^12 c^8 z^2+32 a^10 b^14 c^8 z^2+600 a^8 b^16 c^8 z^2-8 a^6 b^18 c^8 z^2-306 a^4 b^20 c^8 z^2+104 a^2 b^22 c^8 z^2-64 a^20 b^2 c^10 z^2+472 a^18 b^4 c^10 z^2-480 a^16 b^6 c^10 z^2-880 a^14 b^8 c^10 z^2+952 a^12 b^10 c^10 z^2+952 a^10 b^12 c^10 z^2-880 a^8 b^14 c^10 z^2-480 a^6 b^16 c^10 z^2+472 a^4 b^18 c^10 z^2-64 a^2 b^20 c^10 z^2-112 a^18 b^2 c^12 z^2-244 a^16 b^4 c^12 z^2+1144 a^14 b^6 c^12 z^2+116 a^12 b^8 c^12 z^2-1808 a^10 b^10 c^12 z^2+116 a^8 b^12 c^12 z^2+1144 a^6 b^14 c^12 z^2-244 a^4 b^16 c^12 z^2-112 a^2 b^18 c^12 z^2+224 a^16 b^2 c^14 z^2-336 a^14 b^4 c^14 z^2-1040 a^12 b^6 c^14 z^2+1152 a^10 b^8 c^14 z^2+1152 a^8 b^10 c^14 z^2-1040 a^6 b^12 c^14 z^2-336 a^4 b^14 c^14 z^2+224 a^2 b^16 c^14 z^2-112 a^14 b^2 c^16 z^2+649 a^12 b^4 c^16 z^2+120 a^10 b^6 c^16 z^2-1314 a^8 b^8 c^16 z^2+120 a^6 b^10 c^16 z^2+649 a^4 b^12 c^16 z^2-112 a^2 b^14 c^16 z^2-64 a^12 b^2 c^18 z^2-404 a^10 b^4 c^18 z^2+468 a^8 b^6 c^18 z^2+468 a^6 b^8 c^18 z^2-404 a^4 b^10 c^18 z^2-64 a^2 b^12 c^18 z^2+104 a^10 b^2 c^20 z^2+52 a^8 b^4 c^20 z^2-312 a^6 b^6 c^20 z^2+52 a^4 b^8 c^20 z^2+104 a^2 b^10 c^20 z^2-48 a^8 b^2 c^22 z^2+48 a^6 b^4 c^22 z^2+48 a^4 b^6 c^22 z^2-48 a^2 b^8 c^22 z^2+8 a^6 b^2 c^24 z^2-16 a^4 b^4 c^24 z^2+8 a^2 b^6 c^24 z^22 = 0)
(pues sus puntos en el infinito se corresponden).
Esta parábola pasa por X378 (punto de contacto con la recta de Euler), X1986, X2931 y su directriz es:
(b^2+c^2-a^2)(a^4(b^2+c^2)-2a^2(b^4-b^2c^2+c^4)+(b^2-c^2)^2(b^2+c^2))x +
(c^2+a^2-b^2)(b^4(c^2+a^2)-2b^2(c^4-c^2a^2+a^4)+(c^2-a^2)^2(c^2+a^2))y +
(a^2+b^2-c^2)(c^4(a^2+b^2)-2c^2(a^4-a^2b^2+b^4)+(a^2-b^2)^2(a^2+b^2))z = 0,
es la de X1300 y contiene a los centros X6, X2501, X15328.
El foco de 𝒫 es:
W = ( a^2 (a^16-2 a^14 (b^2+c^2)+a^12 (-4 b^4+9 b^2 c^2-4 c^4)+a^4 (b^2-c^2)^4 (12 b^4+25 b^2 c^2+12 c^4)+7 a^10 (2 b^6-b^4 c^2-b^2 c^4+2 c^6)-10 a^8 (b^8+2 b^6 c^2-4 b^4 c^4+2 b^2 c^6+c^8)+(b^2-c^2)^4 (b^8+6 b^6 c^2+6 b^4 c^4+6 b^2 c^6+c^8)-2 a^6 (3 b^10-20 b^8 c^2+15 b^6 c^4+15 b^4 c^6-20 b^2 c^8+3 c^10)-a^2 (b^2-c^2)^2 (6 b^10+11 b^8 c^2-13 b^6 c^4-13 b^4 c^6+11 b^2 c^8+6 c^10)) : ... : ...),
que tiene números de búsqueda en
(2.16743755707507, 0.387678692751454, 2.37191574519873) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {6,686}, {25,14687}, {110,378}, {114,5094}, {136,381}, {1995,3563}, {7577,14769}, {12145,19165}.
- Domingo, 14 de octubre del 2018
Una haz de isocúbicas cK(#X4,W)=nK(X393,W,X4)
Sea P es un punto sobre la recta del infinito del plano del triángulo ABC y P* su conjugado isogonal (sobre la circunferencia circunscrita Γ al triángulo ABC).
ℋ(P) es la circunscrita a ABC que pasa por P*.
Si H es el ortocentro de ABC y U es un punto sobre ℋ(P), las circunferencias circunscritas a los triángulos AHU, BHU, CHU vuelven a cortar a Γ en A', B', C'.
El lugar geométrico del punto
V de concurrencia de las rectas
AA', BB', CC' es la cK(#X4,
W), siendo
W la intersección de la de
X264 y la tangente desde
P a la parábola de foco
X107 y directriz
d la tripolar de
X276.
Si P(1:-t:t-1) son las coordenadas baricéntricas de un punto en la recta del infinito, la ecuación de cK(#X4,W) es:
(2 a^8 b^2 c^2-6 a^6 b^4 c^2+6 a^4 b^6 c^2-2 a^2 b^8 c^2-2 a^6 b^2 c^4+4 a^4 b^4 c^4-2 a^2 b^6 c^4-2 a^4 b^2 c^6+2 a^2 b^4 c^6+2 a^2 b^2 c^8-a^10 c^2 t+2 a^8 b^2 c^2 t-2 a^4 b^6 c^2 t+a^2 b^8 c^2 t+2 a^8 c^4 t-4 a^6 b^2 c^4 t+2 a^4 b^4 c^4 t+2 a^4 b^2 c^6 t-2 a^2 b^4 c^6 t-2 a^4 c^8 t+a^2 c^10 t) x^2 y+(a^8 b^2 c^2-2 a^6 b^4 c^2+2 a^2 b^8 c^2-b^10 c^2+2 a^4 b^4 c^4-4 a^2 b^6 c^4+2 b^8 c^4-2 a^4 b^2 c^6+2 a^2 b^4 c^6-2 b^4 c^8+b^2 c^10-2 a^8 b^2 c^2 t+6 a^6 b^4 c^2 t-6 a^4 b^6 c^2 t+2 a^2 b^8 c^2 t-2 a^6 b^2 c^4 t+4 a^4 b^4 c^4 t-2 a^2 b^6 c^4 t+2 a^4 b^2 c^6 t-2 a^2 b^4 c^6 t+2 a^2 b^2 c^8 t) x y^2+(a^10 b^2-2 a^8 b^4+2 a^4 b^8-a^2 b^10-4 a^8 b^2 c^2+6 a^6 b^4 c^2-2 a^2 b^8 c^2+6 a^6 b^2 c^4-6 a^4 b^4 c^4-4 a^4 b^2 c^6+2 a^2 b^4 c^6+a^2 b^2 c^8-a^10 b^2 t+2 a^8 b^4 t-2 a^4 b^8 t+a^2 b^10 t+2 a^8 b^2 c^2 t-4 a^6 b^4 c^2 t+2 a^4 b^6 c^2 t+2 a^4 b^4 c^4 t-2 a^2 b^6 c^4 t-2 a^4 b^2 c^6 t+a^2 b^2 c^8 t) x^2 z+(2 a^10 b^2-4 a^8 b^4+4 a^4 b^8-2 a^2 b^10-2 a^8 b^2 c^2+4 a^6 b^4 c^2-4 a^4 b^6 c^2+4 a^2 b^8 c^2-2 b^10 c^2-4 a^2 b^6 c^4+4 b^8 c^4+4 a^2 b^4 c^6-2 a^2 b^2 c^8-4 b^4 c^8+2 b^2 c^10-2 a^10 b^2 t+4 a^8 b^4 t-4 a^4 b^8 t+2 a^2 b^10 t-2 a^10 c^2 t+4 a^8 b^2 c^2 t-4 a^6 b^4 c^2 t+4 a^4 b^6 c^2 t-2 a^2 b^8 c^2 t+4 a^8 c^4 t-4 a^6 b^2 c^4 t+4 a^4 b^2 c^6 t-4 a^4 c^8 t-2 a^2 b^2 c^8 t+2 a^2 c^10 t) x y z+(a^10 b^2-2 a^8 b^4+2 a^4 b^8-a^2 b^10+2 a^6 b^4 c^2-4 a^4 b^6 c^2+2 a^2 b^8 c^2-2 a^6 b^2 c^4+2 a^4 b^4 c^4-2 a^2 b^4 c^6+a^2 b^2 c^8-a^10 b^2 t+2 a^8 b^4 t-2 a^4 b^8 t+a^2 b^10 t-2 a^8 b^2 c^2 t+6 a^4 b^6 c^2 t-4 a^2 b^8 c^2 t-6 a^4 b^4 c^4 t+6 a^2 b^6 c^4 t+2 a^4 b^2 c^6 t-4 a^2 b^4 c^6 t+a^2 b^2 c^8 t) y^2 z+(a^8 b^2 c^2+2 a^6 b^4 c^2-2 a^2 b^8 c^2-b^10 c^2-4 a^6 b^2 c^4-6 a^4 b^4 c^4+2 b^8 c^4+6 a^4 b^2 c^6+6 a^2 b^4 c^6-4 a^2 b^2 c^8-2 b^4 c^8+b^2 c^10-2 a^8 b^2 c^2 t-2 a^6 b^4 c^2 t+2 a^4 b^6 c^2 t+2 a^2 b^8 c^2 t+6 a^6 b^2 c^4 t+4 a^4 b^4 c^4 t-2 a^2 b^6 c^4 t-6 a^4 b^2 c^6 t-2 a^2 b^4 c^6 t+2 a^2 b^2 c^8 t) x z^2+(2 a^8 b^2 c^2+2 a^6 b^4 c^2-2 a^4 b^6 c^2-2 a^2 b^8 c^2-2 a^6 b^2 c^4+4 a^4 b^4 c^4+6 a^2 b^6 c^4-2 a^4 b^2 c^6-6 a^2 b^4 c^6+2 a^2 b^2 c^8-a^10 c^2 t-2 a^8 b^2 c^2 t+2 a^4 b^6 c^2 t+a^2 b^8 c^2 t+2 a^8 c^4 t-6 a^4 b^4 c^4 t-4 a^2 b^6 c^4 t+6 a^4 b^2 c^6 t+6 a^2 b^4 c^6 t-2 a^4 c^8 t-4 a^2 b^2 c^8 t+a^2 c^10 t) y z^2 = 0.
Su polo es X393 ( del ortocentro) y su es:
W = (b^2 c^2 (-a^2+b^2-c^2) (a^2+b^2-c^2) (b^2-c^2+a^2 (1-2 t)):
a^2 c^2 (a^2-b^2-c^2) (a^2+b^2-c^2) (b^2 (-2+t)+(a^2-c^2) t):
a^2 b^2 (a^2-b^2-c^2) (a^2-b^2+c^2) (a^2 (-1+t)-b^2 (-1+t)+c^2 (1+t))).
Cuando P varía en la recta del infinito, W queda sobre la tripolar w de X264, que pasa por los centros Xi para los índices i = 297, 525, 850, 2501, 2592, 2593, 3569, 3580, 4391, 5523, 9979, 10015, 13302, 14316, 14618, 14918, 17434, 17773, 17896, 17924, 18314, 21438.
La envolvente de la tripolares de los puntos de la recta w es la .
El haz de cúbicas cK(#X4,W) tiene los nueve puntos base: A, B, C, H (contado cuatro veces) y los puntos imaginarios conjugados (intersección de la circunferencia circunscrita a ABC con la tripolar de X2052):
((-a^2 - b^2 + c^2) (a^2 - b^2 + c^2) (a^4 +
a^2 (-2 b^2 ± 2 i S) - (b^2 - c^2) (-b^2 + c^2 ±
2 i S)) (a^4 c^2 +
a^2 (b^4 + b^2 c^2 - c^2 (2 c^2 ± 2 i S)) + (b^2 - c^2)^2 (-b^2 +
c^2 ± 2 i S)):
2 a^2 b^2 (a^2 - b^2 - c^2) (a^2 + b^2 - c^2) (a^6 +
a^4 (-3 b^2 ± 2 i S) + (b^2 - c^2)^2 (-b^2 + c^2 ± 2 i S) +
a^2 (3 b^4 - b^2 (3 c^2 ± 4 i S) ± 2 i c^2 S)):
2 a^2 c^2 (a^2 - b^2 - c^2) (a^2 - b^2 + c^2) (a^4 c^2 +
a^2 (b^4 + b^2 c^2 - c^2 (2 c^2 ± 2 i S)) + (b^2 - c^2)^2 (-b^2 +
c^2 ± 2 i S)))
donde S es el doble del área de ABC.
La correspondencia P ↦ W está dada por
(u:v:w) ↦
((3a^2(v-w)-b^2(v+w-2u)+c^2(v+w-2u))/(a^2(b^2+c^2-a^2)) : ... : ...).
Pares {P=Xi, W=Xj}, para los índices {i, j}:
{30, 14618}, {511, 2501}, {512, 297}, {517, 17924}, {924, 3580}, {1503, 850}, {1510, 14918}, {2574, 2593}, {2575, 2592}, {2781, 9979}, {2818, 10015}, {6000, 525}, {6001, 4391}, {18400, 18314}.
CASOS PARTICULARES
• P = X511, t= (b^2(-a^4+a^2b^2+b^2c^2-c^4))/(
a^2(-a^2b^2+b^4-a^2c^2+c^4)), ℋ(P): .
K954 =
cK0(#X4,X2501)
( a^8 x^2 y-3 a^6 b^2 x^2 y+3 a^4 b^4 x^2 y-a^2 b^6 x^2 y-2 a^6 c^2 x^2 y+5 a^4 b^2 c^2 x^2 y-4 a^2 b^4 c^2 x^2 y+b^6 c^2 x^2 y-a^2 b^2 c^4 x^2 y+b^4 c^4 x^2 y+2 a^2 c^6 x^2 y-b^2 c^6 x^2 y-c^8 x^2 y+a^6 b^2 x y^2-3 a^4 b^4 x y^2+3 a^2 b^6 x y^2-b^8 x y^2-a^6 c^2 x y^2+4 a^4 b^2 c^2 x y^2-5 a^2 b^4 c^2 x y^2+2 b^6 c^2 x y^2-a^4 c^4 x y^2+a^2 b^2 c^4 x y^2+a^2 c^6 x y^2-2 b^2 c^6 x y^2+c^8 x y^2-a^8 x^2 z+2 a^6 b^2 x^2 z-2 a^2 b^6 x^2 z+b^8 x^2 z+3 a^6 c^2 x^2 z-5 a^4 b^2 c^2 x^2 z+a^2 b^4 c^2 x^2 z+b^6 c^2 x^2 z-3 a^4 c^4 x^2 z+4 a^2 b^2 c^4 x^2 z-b^4 c^4 x^2 z+a^2 c^6 x^2 z-b^2 c^6 x^2 z-a^8 y^2 z+2 a^6 b^2 y^2 z-2 a^2 b^6 y^2 z+b^8 y^2 z-a^6 c^2 y^2 z-a^4 b^2 c^2 y^2 z+5 a^2 b^4 c^2 y^2 z-3 b^6 c^2 y^2 z+a^4 c^4 y^2 z-4 a^2 b^2 c^4 y^2 z+3 b^4 c^4 y^2 z+a^2 c^6 y^2 z-b^2 c^6 y^2 z+a^6 b^2 x z^2+a^4 b^4 x z^2-a^2 b^6 x z^2-b^8 x z^2-a^6 c^2 x z^2-4 a^4 b^2 c^2 x z^2-a^2 b^4 c^2 x z^2+2 b^6 c^2 x z^2+3 a^4 c^4 x z^2+5 a^2 b^2 c^4 x z^2-3 a^2 c^6 x z^2-2 b^2 c^6 x z^2+c^8 x z^2+a^8 y z^2+a^6 b^2 y z^2-a^4 b^4 y z^2-a^2 b^6 y z^2-2 a^6 c^2 y z^2+a^4 b^2 c^2 y z^2+4 a^2 b^4 c^2 y z^2+b^6 c^2 y z^2-5 a^2 b^2 c^4 y z^2-3 b^4 c^4 y z^2+2 a^2 c^6 y z^2+3 b^2 c^6 y z^2-c^8 y z^2 = 0)
= nK(X393,X2501,X4), que pasa por los centros Xi, para i = 4, P*=98, 468, 1942, 6530, 16070, 16071, 17927, 17980, 17981, 17982, 17983, 17984, 17985, 17986, 17987, 17988.
• P = X30, t = (a^4+a^2 b^2-2 b^4-2 a^2 c^2+b^2 c^2+c^4)/(2 a^4-a^2 b^2-b^4-a^2 c^2+2 b^2 c^2-c^4), ℋ(P): .
cK(#X4,X14618),
( -a^10 c^2 x^2 y+3 a^8 b^2 c^2 x^2 y-3 a^6 b^4 c^2 x^2 y+a^4 b^6 c^2 x^2 y+2 a^8 c^4 x^2 y-5 a^6 b^2 c^4 x^2 y+4 a^4 b^4 c^4 x^2 y-a^2 b^6 c^4 x^2 y+a^4 b^2 c^6 x^2 y-a^2 b^4 c^6 x^2 y-2 a^4 c^8 x^2 y+a^2 b^2 c^8 x^2 y+a^2 c^10 x^2 y-a^6 b^4 c^2 x y^2+3 a^4 b^6 c^2 x y^2-3 a^2 b^8 c^2 x y^2+b^10 c^2 x y^2+a^6 b^2 c^4 x y^2-4 a^4 b^4 c^4 x y^2+5 a^2 b^6 c^4 x y^2-2 b^8 c^4 x y^2+a^4 b^2 c^6 x y^2-a^2 b^4 c^6 x y^2-a^2 b^2 c^8 x y^2+2 b^4 c^8 x y^2-b^2 c^10 x y^2+a^10 b^2 x^2 z-2 a^8 b^4 x^2 z+2 a^4 b^8 x^2 z-a^2 b^10 x^2 z-3 a^8 b^2 c^2 x^2 z+5 a^6 b^4 c^2 x^2 z-a^4 b^6 c^2 x^2 z-a^2 b^8 c^2 x^2 z+3 a^6 b^2 c^4 x^2 z-4 a^4 b^4 c^4 x^2 z+a^2 b^6 c^4 x^2 z-a^4 b^2 c^6 x^2 z+a^2 b^4 c^6 x^2 z+2 a^10 b^2 x y z-4 a^8 b^4 x y z+4 a^4 b^8 x y z-2 a^2 b^10 x y z-2 a^10 c^2 x y z+10 a^6 b^4 c^2 x y z-10 a^4 b^6 c^2 x y z+2 b^10 c^2 x y z+4 a^8 c^4 x y z-10 a^6 b^2 c^4 x y z+10 a^2 b^6 c^4 x y z-4 b^8 c^4 x y z+10 a^4 b^2 c^6 x y z-10 a^2 b^4 c^6 x y z-4 a^4 c^8 x y z+4 b^4 c^8 x y z+2 a^2 c^10 x y z-2 b^2 c^10 x y z+a^10 b^2 y^2 z-2 a^8 b^4 y^2 z+2 a^4 b^8 y^2 z-a^2 b^10 y^2 z+a^8 b^2 c^2 y^2 z+a^6 b^4 c^2 y^2 z-5 a^4 b^6 c^2 y^2 z+3 a^2 b^8 c^2 y^2 z-a^6 b^2 c^4 y^2 z+4 a^4 b^4 c^4 y^2 z-3 a^2 b^6 c^4 y^2 z-a^4 b^2 c^6 y^2 z+a^2 b^4 c^6 y^2 z-a^6 b^4 c^2 x z^2-a^4 b^6 c^2 x z^2+a^2 b^8 c^2 x z^2+b^10 c^2 x z^2+a^6 b^2 c^4 x z^2+4 a^4 b^4 c^4 x z^2+a^2 b^6 c^4 x z^2-2 b^8 c^4 x z^2-3 a^4 b^2 c^6 x z^2-5 a^2 b^4 c^6 x z^2+3 a^2 b^2 c^8 x z^2+2 b^4 c^8 x z^2-b^2 c^10 x z^2-a^10 c^2 y z^2-a^8 b^2 c^2 y z^2+a^6 b^4 c^2 y z^2+a^4 b^6 c^2 y z^2+2 a^8 c^4 y z^2-a^6 b^2 c^4 y z^2-4 a^4 b^4 c^4 y z^2-a^2 b^6 c^4 y z^2+5 a^4 b^2 c^6 y z^2+3 a^2 b^4 c^6 y z^2-2 a^4 c^8 y z^2-3 a^2 b^2 c^8 y z^2+a^2 c^10 y z^2 = 0)
que pasa por los centros Xi, para i = 4, P*=74, 186, 6344, 8744, 8753.
• P = X517, t= (b (-a^3+a b^2+a^2 c-2 a b c+b^2 c+a c^2-c^3))/(a (-a^2 b+b^3-a^2 c+2 a b c-b^2 c-b c^2+c^3)), ℋ(P): .
cK(#X4,X17924),
(-a^8 c x^2 y+3 a^6 b^2 c x^2 y-3 a^4 b^4 c x^2 y+a^2 b^6 c x^2 y+a^7 c^2 x^2 y-3 a^5 b^2 c^2 x^2 y+3 a^3 b^4 c^2 x^2 y-a b^6 c^2 x^2 y+a^6 c^3 x^2 y-2 a^4 b^2 c^3 x^2 y+a^2 b^4 c^3 x^2 y-a^5 c^4 x^2 y+2 a^3 b^2 c^4 x^2 y-a b^4 c^4 x^2 y+a^4 c^5 x^2 y-a^2 b^2 c^5 x^2 y-a^3 c^6 x^2 y+a b^2 c^6 x^2 y-a^2 c^7 x^2 y+a c^8 x^2 y-a^6 b^2 c x y^2+3 a^4 b^4 c x y^2-3 a^2 b^6 c x y^2+b^8 c x y^2+a^6 b c^2 x y^2-3 a^4 b^3 c^2 x y^2+3 a^2 b^5 c^2 x y^2-b^7 c^2 x y^2-a^4 b^2 c^3 x y^2+2 a^2 b^4 c^3 x y^2-b^6 c^3 x y^2+a^4 b c^4 x y^2-2 a^2 b^3 c^4 x y^2+b^5 c^4 x y^2+a^2 b^2 c^5 x y^2-b^4 c^5 x y^2-a^2 b c^6 x y^2+b^3 c^6 x y^2+b^2 c^7 x y^2-b c^8 x y^2+a^8 b x^2 z-a^7 b^2 x^2 z-a^6 b^3 x^2 z+a^5 b^4 x^2 z-a^4 b^5 x^2 z+a^3 b^6 x^2 z+a^2 b^7 x^2 z-a b^8 x^2 z-3 a^6 b c^2 x^2 z+3 a^5 b^2 c^2 x^2 z+2 a^4 b^3 c^2 x^2 z-2 a^3 b^4 c^2 x^2 z+a^2 b^5 c^2 x^2 z-a b^6 c^2 x^2 z+3 a^4 b c^4 x^2 z-3 a^3 b^2 c^4 x^2 z-a^2 b^3 c^4 x^2 z+a b^4 c^4 x^2 z-a^2 b c^6 x^2 z+a b^2 c^6 x^2 z+2 a^8 b x y z-2 a^7 b^2 x y z-2 a^6 b^3 x y z+2 a^5 b^4 x y z-2 a^4 b^5 x y z+2 a^3 b^6 x y z+2 a^2 b^7 x y z-2 a b^8 x y z-2 a^8 c x y z+4 a^6 b^2 c x y z-4 a^2 b^6 c x y z+2 b^8 c x y z+2 a^7 c^2 x y z-4 a^6 b c^2 x y z+6 a^4 b^3 c^2 x y z-6 a^3 b^4 c^2 x y z+4 a b^6 c^2 x y z-2 b^7 c^2 x y z+2 a^6 c^3 x y z-6 a^4 b^2 c^3 x y z+6 a^2 b^4 c^3 x y z-2 b^6 c^3 x y z-2 a^5 c^4 x y z+6 a^3 b^2 c^4 x y z-6 a^2 b^3 c^4 x y z+2 b^5 c^4 x y z+2 a^4 c^5 x y z-2 b^4 c^5 x y z-2 a^3 c^6 x y z+4 a^2 b c^6 x y z-4 a b^2 c^6 x y z+2 b^3 c^6 x y z-2 a^2 c^7 x y z+2 b^2 c^7 x y z+2 a c^8 x y z-2 b c^8 x y z+a^8 b y^2 z-a^7 b^2 y^2 z-a^6 b^3 y^2 z+a^5 b^4 y^2 z-a^4 b^5 y^2 z+a^3 b^6 y^2 z+a^2 b^7 y^2 z-a b^8 y^2 z+a^6 b c^2 y^2 z-a^5 b^2 c^2 y^2 z+2 a^4 b^3 c^2 y^2 z-2 a^3 b^4 c^2 y^2 z-3 a^2 b^5 c^2 y^2 z+3 a b^6 c^2 y^2 z-a^4 b c^4 y^2 z+a^3 b^2 c^4 y^2 z+3 a^2 b^3 c^4 y^2 z-3 a b^4 c^4 y^2 z-a^2 b c^6 y^2 z+a b^2 c^6 y^2 z-a^6 b^2 c x z^2-a^4 b^4 c x z^2+a^2 b^6 c x z^2+b^8 c x z^2+a^6 b c^2 x z^2+a^4 b^3 c^2 x z^2-a^2 b^5 c^2 x z^2-b^7 c^2 x z^2+3 a^4 b^2 c^3 x z^2+2 a^2 b^4 c^3 x z^2-b^6 c^3 x z^2-3 a^4 b c^4 x z^2-2 a^2 b^3 c^4 x z^2+b^5 c^4 x z^2-3 a^2 b^2 c^5 x z^2-b^4 c^5 x z^2+3 a^2 b c^6 x z^2+b^3 c^6 x z^2+b^2 c^7 x z^2-b c^8 x z^2-a^8 c y z^2-a^6 b^2 c y z^2+a^4 b^4 c y z^2+a^2 b^6 c y z^2+a^7 c^2 y z^2+a^5 b^2 c^2 y z^2-a^3 b^4 c^2 y z^2-a b^6 c^2 y z^2+a^6 c^3 y z^2-2 a^4 b^2 c^3 y z^2-3 a^2 b^4 c^3 y z^2-a^5 c^4 y z^2+2 a^3 b^2 c^4 y z^2+3 a b^4 c^4 y z^2+a^4 c^5 y z^2+3 a^2 b^2 c^5 y z^2-a^3 c^6 y z^2-3 a b^2 c^6 y z^2-a^2 c^7 y z^2+a c^8 y z^2 = 0)
que pasa por los centros Xi, para i = 4, P*=104, 1870, 2074.
• P = X525, t = (a^4-a^2b^2+b^2c^2-c^4)/((b^2+c^2-a^2)(b^2-c^2)), ℋ(P): hipérbola que pasa por Xi, para i = 4, 112, 877, 4230, 6528.
cK(#X4,Z),
( a^14 c^2 x^2 y-3 a^12 b^2 c^2 x^2 y+4 a^10 b^4 c^2 x^2 y-6 a^8 b^6 c^2 x^2 y+9 a^6 b^8 c^2 x^2 y-7 a^4 b^10 c^2 x^2 y+2 a^2 b^12 c^2 x^2 y-2 a^12 c^4 x^2 y+5 a^10 b^2 c^4 x^2 y-4 a^8 b^4 c^4 x^2 y+2 a^6 b^6 c^4 x^2 y-2 a^4 b^8 c^4 x^2 y+a^2 b^10 c^4 x^2 y-a^10 c^6 x^2 y+2 a^8 b^2 c^6 x^2 y-4 a^6 b^4 c^6 x^2 y+6 a^4 b^6 c^6 x^2 y-3 a^2 b^8 c^6 x^2 y+4 a^8 c^8 x^2 y-6 a^6 b^2 c^8 x^2 y+4 a^4 b^4 c^8 x^2 y-2 a^2 b^6 c^8 x^2 y-a^6 c^10 x^2 y+a^4 b^2 c^10 x^2 y-2 a^4 c^12 x^2 y+a^2 b^2 c^12 x^2 y+a^2 c^14 x^2 y+2 a^12 b^2 c^2 x y^2-7 a^10 b^4 c^2 x y^2+9 a^8 b^6 c^2 x y^2-6 a^6 b^8 c^2 x y^2+4 a^4 b^10 c^2 x y^2-3 a^2 b^12 c^2 x y^2+b^14 c^2 x y^2+a^10 b^2 c^4 x y^2-2 a^8 b^4 c^4 x y^2+2 a^6 b^6 c^4 x y^2-4 a^4 b^8 c^4 x y^2+5 a^2 b^10 c^4 x y^2-2 b^12 c^4 x y^2-3 a^8 b^2 c^6 x y^2+6 a^6 b^4 c^6 x y^2-4 a^4 b^6 c^6 x y^2+2 a^2 b^8 c^6 x y^2-b^10 c^6 x y^2-2 a^6 b^2 c^8 x y^2+4 a^4 b^4 c^8 x y^2-6 a^2 b^6 c^8 x y^2+4 b^8 c^8 x y^2+a^2 b^4 c^10 x y^2-b^6 c^10 x y^2+a^2 b^2 c^12 x y^2-2 b^4 c^12 x y^2+b^2 c^14 x y^2+a^14 b^2 x^2 z-2 a^12 b^4 x^2 z-a^10 b^6 x^2 z+4 a^8 b^8 x^2 z-a^6 b^10 x^2 z-2 a^4 b^12 x^2 z+a^2 b^14 x^2 z-3 a^12 b^2 c^2 x^2 z+5 a^10 b^4 c^2 x^2 z+2 a^8 b^6 c^2 x^2 z-6 a^6 b^8 c^2 x^2 z+a^4 b^10 c^2 x^2 z+a^2 b^12 c^2 x^2 z+4 a^10 b^2 c^4 x^2 z-4 a^8 b^4 c^4 x^2 z-4 a^6 b^6 c^4 x^2 z+4 a^4 b^8 c^4 x^2 z-6 a^8 b^2 c^6 x^2 z+2 a^6 b^4 c^6 x^2 z+6 a^4 b^6 c^6 x^2 z-2 a^2 b^8 c^6 x^2 z+9 a^6 b^2 c^8 x^2 z-2 a^4 b^4 c^8 x^2 z-3 a^2 b^6 c^8 x^2 z-7 a^4 b^2 c^10 x^2 z+a^2 b^4 c^10 x^2 z+2 a^2 b^2 c^12 x^2 z+2 a^14 b^2 x y z-4 a^12 b^4 x y z-2 a^10 b^6 x y z+8 a^8 b^8 x y z-2 a^6 b^10 x y z-4 a^4 b^12 x y z+2 a^2 b^14 x y z+2 a^14 c^2 x y z-8 a^12 b^2 c^2 x y z+12 a^10 b^4 c^2 x y z-6 a^8 b^6 c^2 x y z-6 a^6 b^8 c^2 x y z+12 a^4 b^10 c^2 x y z-8 a^2 b^12 c^2 x y z+2 b^14 c^2 x y z-4 a^12 c^4 x y z+12 a^10 b^2 c^4 x y z-12 a^8 b^4 c^4 x y z+8 a^6 b^6 c^4 x y z-12 a^4 b^8 c^4 x y z+12 a^2 b^10 c^4 x y z-4 b^12 c^4 x y z-2 a^10 c^6 x y z-6 a^8 b^2 c^6 x y z+8 a^6 b^4 c^6 x y z+8 a^4 b^6 c^6 x y z-6 a^2 b^8 c^6 x y z-2 b^10 c^6 x y z+8 a^8 c^8 x y z-6 a^6 b^2 c^8 x y z-12 a^4 b^4 c^8 x y z-6 a^2 b^6 c^8 x y z+8 b^8 c^8 x y z-2 a^6 c^10 x y z+12 a^4 b^2 c^10 x y z+12 a^2 b^4 c^10 x y z-2 b^6 c^10 x y z-4 a^4 c^12 x y z-8 a^2 b^2 c^12 x y z-4 b^4 c^12 x y z+2 a^2 c^14 x y z+2 b^2 c^14 x y z+a^14 b^2 y^2 z-2 a^12 b^4 y^2 z-a^10 b^6 y^2 z+4 a^8 b^8 y^2 z-a^6 b^10 y^2 z-2 a^4 b^12 y^2 z+a^2 b^14 y^2 z+a^12 b^2 c^2 y^2 z+a^10 b^4 c^2 y^2 z-6 a^8 b^6 c^2 y^2 z+2 a^6 b^8 c^2 y^2 z+5 a^4 b^10 c^2 y^2 z-3 a^2 b^12 c^2 y^2 z+4 a^8 b^4 c^4 y^2 z-4 a^6 b^6 c^4 y^2 z-4 a^4 b^8 c^4 y^2 z+4 a^2 b^10 c^4 y^2 z-2 a^8 b^2 c^6 y^2 z+6 a^6 b^4 c^6 y^2 z+2 a^4 b^6 c^6 y^2 z-6 a^2 b^8 c^6 y^2 z-3 a^6 b^2 c^8 y^2 z-2 a^4 b^4 c^8 y^2 z+9 a^2 b^6 c^8 y^2 z+a^4 b^2 c^10 y^2 z-7 a^2 b^4 c^10 y^2 z+2 a^2 b^2 c^12 y^2 z+2 a^12 b^2 c^2 x z^2+a^10 b^4 c^2 x z^2-3 a^8 b^6 c^2 x z^2-2 a^6 b^8 c^2 x z^2+a^2 b^12 c^2 x z^2+b^14 c^2 x z^2-7 a^10 b^2 c^4 x z^2-2 a^8 b^4 c^4 x z^2+6 a^6 b^6 c^4 x z^2+4 a^4 b^8 c^4 x z^2+a^2 b^10 c^4 x z^2-2 b^12 c^4 x z^2+9 a^8 b^2 c^6 x z^2+2 a^6 b^4 c^6 x z^2-4 a^4 b^6 c^6 x z^2-6 a^2 b^8 c^6 x z^2-b^10 c^6 x z^2-6 a^6 b^2 c^8 x z^2-4 a^4 b^4 c^8 x z^2+2 a^2 b^6 c^8 x z^2+4 b^8 c^8 x z^2+4 a^4 b^2 c^10 x z^2+5 a^2 b^4 c^10 x z^2-b^6 c^10 x z^2-3 a^2 b^2 c^12 x z^2-2 b^4 c^12 x z^2+b^2 c^14 x z^2+a^14 c^2 y z^2+a^12 b^2 c^2 y z^2-2 a^8 b^6 c^2 y z^2-3 a^6 b^8 c^2 y z^2+a^4 b^10 c^2 y z^2+2 a^2 b^12 c^2 y z^2-2 a^12 c^4 y z^2+a^10 b^2 c^4 y z^2+4 a^8 b^4 c^4 y z^2+6 a^6 b^6 c^4 y z^2-2 a^4 b^8 c^4 y z^2-7 a^2 b^10 c^4 y z^2-a^10 c^6 y z^2-6 a^8 b^2 c^6 y z^2-4 a^6 b^4 c^6 y z^2+2 a^4 b^6 c^6 y z^2+9 a^2 b^8 c^6 y z^2+4 a^8 c^8 y z^2+2 a^6 b^2 c^8 y z^2-4 a^4 b^4 c^8 y z^2-6 a^2 b^6 c^8 y z^2-a^6 c^10 y z^2+5 a^4 b^2 c^10 y z^2+4 a^2 b^4 c^10 y z^2-2 a^4 c^12 y z^2-3 a^2 b^2 c^12 y z^2+a^2 c^14 y z^2 = 0)
que pasa por los centros Xi, para i = 4, P*=112, 14618 (raíz de la isocúbica cónico pivotal correspondiente a la hipérbola de Jerabek).
Z el punto de tangencia de la recta w con la parábola 𝒫.
Z = ( (2a^6-a^4(b^2+c^2)-(b^2-c^2)^2(b^2+c^2))/(a^2(b^2+c^2-a^2)) : ... : ...),
que tiene números de búsqueda en
(1.62924082862474, 1.50280512246861, 1.84830363006392) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,1235}, {4,51}, {76,459}, {112,401}, {264,1249}, {290,9476}, {297,525}, {311,17907}, {324,458}, {338,1990}, {419,685}, {441,9475}, {460,2970}, {648,3260}, {2782,15143}, {2967,21531}.
- Viernes, 12 de octubre del 2018
La isocúbica cónico pivotal cK(#X3,X2) y la cúbica de Lemoine K009
Dado un triángulo ABC de baricentro G, circuncentro O, ortocentro H y simediano K, sean ℓt=OT una recta que pasa por O y P un punto sobre ella; P* es el de P.
Cuando
P se mueve sobre ℓ
t, la envolvente de la paralela
p por
P a la recta
P*H es una
parábola 𝒫
t, con foco
Ft sobre la circunferencia circunscrita a
ABC.
• Recta OI, t=0, 𝒫0 es la parábola de foco X2720, directriz la recta X100X108, y que pasa por los centros X56, X944, X2829 (en la recta del infinito), X18861.
• Recta OG, t=∞, 𝒫∞ es la parábola de foco X1304, directriz la recta X107X110, y que pasa por los centros X4, X2777 (en la recta del infinito), X6225, X6759.
• Recta OK, t=- 3a b c/((a+b)(a+c)(b+c)), 𝒫t es la parábola de foco X2715, directriz la recta X99X112, y que pasa por los centros X32, X2549, X2794 (en la recta del infinito), X8721, X8982.
La envolvente de la directriz dt de la parábola 𝒫t, cuando la recta ℓt gira alrededor del circuncentro, es la cónica 𝒞 de focos el ortocentro y el , y bitangente a la circunferencia circunscrita en los puntos de intercción con la .
Para ℓt: (3b^3c-3a b c(b-c)-3b c^3+b^4t-c^4t-a^2(b^2-c^2)t)x +
(-3a^3c-3a(b-c)c^2-a^4t-c^2(b^2-c^2)t+a^2b(3c+b t)) y
+ (3a^3b-3a b^2(b-c)+a^4t-b^2(b^2-c^2)t-a^2c(3b+c t)) z = 0, la directriz es:
dt:
(b-c)^2(-a^2+b^2+c^2)(3a+(b+c)t)(-3a b c - a^2(b+c)t+(b+c)(3b c+b^2t+c^2t)) x
+ (a-c)^2(a^2-b^2+c^2)(3b+(a+c)t)(a^3t+c(-b^2+c^2)t+a^2c(3+t)-a(b-c)(b t+c(3+t))) y
+ (a-b)^2(a^2+b^2-c^2)(3c+(a+b)t)(a^3t+b(b^2-c^2)t+a^2b(3+t)+a(b-c)(c t+b(3+t))) z = 0.
La
cónica
( a^4 b^4 x^2-2 a^2 b^6 x^2+b^8 x^2-2 a^4 b^2 c^2 x^2+2 a^2 b^4 c^2 x^2+a^4 c^4 x^2+2 a^2 b^2 c^4 x^2-2 b^4 c^4 x^2-2 a^2 c^6 x^2+c^8 x^2+2 a^6 b^2 x y-4 a^4 b^4 x y+2 a^2 b^6 x y+2 a^6 c^2 x y-2 a^4 b^2 c^2 x y-2 a^2 b^4 c^2 x y+2 b^6 c^2 x y-2 a^4 c^4 x y+2 a^2 b^2 c^4 x y-2 b^4 c^4 x y-2 a^2 c^6 x y-2 b^2 c^6 x y+2 c^8 x y+a^8 y^2-2 a^6 b^2 y^2+a^4 b^4 y^2+2 a^4 b^2 c^2 y^2-2 a^2 b^4 c^2 y^2-2 a^4 c^4 y^2+2 a^2 b^2 c^4 y^2+b^4 c^4 y^2-2 b^2 c^6 y^2+c^8 y^2+2 a^6 b^2 x z-2 a^4 b^4 x z-2 a^2 b^6 x z+2 b^8 x z+2 a^6 c^2 x z-2 a^4 b^2 c^2 x z+2 a^2 b^4 c^2 x z-2 b^6 c^2 x z-4 a^4 c^4 x z-2 a^2 b^2 c^4 x z-2 b^4 c^4 x z+2 a^2 c^6 x z+2 b^2 c^6 x z+2 a^8 y z-2 a^6 b^2 y z-2 a^4 b^4 y z+2 a^2 b^6 y z-2 a^6 c^2 y z+2 a^4 b^2 c^2 y z-2 a^2 b^4 c^2 y z+2 b^6 c^2 y z-2 a^4 c^4 y z-2 a^2 b^2 c^4 y z-4 b^4 c^4 y z+2 a^2 c^6 y z+2 b^2 c^6 y z+a^8 z^2-2 a^4 b^4 z^2+b^8 z^2-2 a^6 c^2 z^2+2 a^4 b^2 c^2 z^2+2 a^2 b^4 c^2 z^2-2 b^6 c^2 z^2+a^4 c^4 z^2-2 a^2 b^2 c^4 z^2+b^4 c^4 z^2 = 0)
𝒞 pasa por X1897 y su es X246.
El lugar geométrico del punto
Lt((3a+b t+
c t)(3a b(a+b-c)+(a+b)(a^2+b^2-c^2)t)(3a c(a-b+c)+(a+c)(a^2-b^2+c^2)t):...:...) de contacto de ℓ
t y la parábola 𝒫
t, cuando la recta ℓ
t gira alrededor del circuncentro, es la cúbica de Lemoine (
K009 del catálogo de Bernard Gibert).
El lugar geométrico del punto M de intersección de ℓt y la directriz dt de la parábola 𝒫t, cuando la recta ℓt gira alrededor del circuncentro, es la cK(#X3,X2) = nK(X577,X2,X3).
M = (27 a^3b c(a-b)(a-c)(-2 a^3 b c+2 a b (b-c)^2 c+a^4 (b+c)-2 a^2 (b-c)^2 (b+c)+(b-c)^4 (b+c))+
9 a^2 (a-b) (a-c) (a^5 (b-c)^2 (b+c)+3 b (b-c)^4 c (b+c)^2+a^6 (b^2+4 b c+c^2)+a (b+c) (b^3-b^2 c+b c^2-c^3)^2+a^2 (b-c)^2 (b^4-4 b^2 c^2+c^4)-a^4 (2 b^4+5 b^3 c-8 b^2 c^2+5 b c^3+2 c^4)-2 a^3 (b^5-b^4 c-b c^4+c^5))t +
3 a (a-b) (a-c) (3 a^8 (b+c)+3 b (b-c)^4 c (b+c)^3+3 a^7 (b^2+c^2)-a^3 (b^2-c^2)^2 (b^2+c^2)+a^6 (-4 b^3+b^2 c+b c^2-4 c^3)-a^4 (b-c)^2 (b^3+10 b^2 c+10 b c^2+c^3)+a^5 (-4 b^4+2 b^2 c^2-4 c^4)+2 a (b^2-c^2)^2 (b^4-b^2 c^2+c^4)+a^2 (b-c)^2 (2 b^5+5 b^4 c+b^3 c^2+b^2 c^3+5 b c^4+2 c^5))t^2+
(a^2-b^2) (a^2-c^2) (2 a^8-3 a^4 (b^2-c^2)^2+(b^2-c^2)^4-a^6 (b^2+c^2)+a^2 (b^2-c^2)^2 (b^2+c^2))t^3 : ... : ...).
El cuarto punto de intersección de las cónicas pivotal y de contacto con
cK(#X3,X2),
( (-a^4 c^4-2 a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8) x^2 y+(-a^4 c^4-2 a^2 b^2 c^4-b^4 c^4+2 a^2 c^6+2 b^2 c^6-c^8) x y^2+(-a^4 b^4+2 a^2 b^6-b^8-2 a^2 b^4 c^2+2 b^6 c^2-b^4 c^4) x^2 z+(-2 a^6 b^2+4 a^4 b^4-2 a^2 b^6-2 a^6 c^2+2 a^4 b^2 c^2+2 a^2 b^4 c^2-2 b^6 c^2+4 a^4 c^4+2 a^2 b^2 c^4+4 b^4 c^4-2 a^2 c^6-2 b^2 c^6) x y z+(-a^8+2 a^6 b^2-a^4 b^4+2 a^6 c^2-2 a^4 b^2 c^2-a^4 c^4) y^2 z+(-a^4 b^4+2 a^2 b^6-b^8-2 a^2 b^4 c^2+2 b^6 c^2-b^4 c^4) x z^2+(-a^8+2 a^6 b^2-a^4 b^4+2 a^6 c^2-2 a^4 b^2 c^2-a^4 c^4) y z^2 = 0)
aparte de sus puntos de tangencia con la cúbica, es:
W = ( (a^2-b^2)(a^2-c^2) (3S^2 - SBSC) : ... : ...),
que tiene números de búsqueda en
(-20.4725926879376, 17.7733982039299, 0.784893119773357) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,195}, {107,110}, {125,14920}, {250,14480}, {264,11422}, {394,15576}, {877,10330}, {930,933}, {1493,14978}, {1993,19174}, {2407,23181}, {2888,3462}, {5468,6331}, {5965,14918}, {7480,14611}, {8884,15801}, {11562,15454}, {15958,18831}.
NOTA: A pesar de que la cónica 𝒞 está inscrita en el triángulo antimedial (anticeviano del circuncentro) y es tritangente a la isocúbica cónico pivotal cK(#X3,X2), no se trata de su
- Miércoles, 10 de octubre del 2018
Una perspectividad entre las rectas IN y IO
Dados un triángulo ABC, de incentro I, circuncentro O y N, y un punto P, sean Na, Nb y Nc los centros de las circunferencias de los nueve puntos de los triángulos IBC, ICA y IAB, respectivamente.
El lugar geométrico de P tal que las reflexiones ℓ1, ℓ2, ℓ3 de PNa, PNb, PNc en AI, BI, CI, respectivamente, son concurrentes es la recta IN ( de ) y la circunferencia de centro N y que pasa por el .
En coordenadas baricéntricas,
Na = (-a(b+c) : a^2+a b-(b+c)^2 : a^2+a c-(b+c)^2).
La ecuación de la reflexión ℓ1 de la recta PNa en AI es:
ℓ1: b c(a^2(v-w)-(b+c)^2(v-w)+a(c v-b w))x
+ c(a^2(b(v-w)+c(u-v+w))-(b+c)^2(b(v-w)+c(u-v+w))+a b(-bw+c(u+2v+w)))y
+ b(-a^2(b(u+v-w)+c(-v+w))+(b+c)^2(b(u+v-w)+c(-v+w))-a c(-c v+b(u+v+2w)))z = 0.
Cuando P está sobre la recta IN (IP:PN=t), las rectas ℓ1, ℓ2, ℓ3 concurren en el punto Q (IQ:QO=t'), sobre la recta IO, siendo
t' = (b+c-a)(a+b-c)(c+a-b)t /
(a^3-a^2(b+c)+(b-c)^2(b+c)-a(b^2+c^2)t - 2(a^3-a^2(b+c)+(b-c)^2(b+c)-a(b^2-3b c+c^2))).
Así, P ∈ IN ↦ Q ∈ IO es una proyectividad, y como I=IN ∩ IO se corresponde en esta proyectividad (t=0 ↦ t'=0), se trata de una perspectividad. Es decir, las rectas PQ (para todo P) pasan por un punto fijo (centro de perspectividad), que es X946 (punto medio del incentro y ortocentro).
Las rectas ℓ1, ℓ2, ℓ3 son también concurrentes si el punto P está sobre la
circunferencia
( a^2y z+b^2x z+c^2x y +
(x+y+z)(
(a^3+a^2(b+c)-a(b^2+b c+c^2)-b^3-b^2c-b c^2-c^3)x +
(b^3+b^2(c+a)-b(c^2+c a+a^2)-c^3-c^2a-c a^2-a^3)y +
(c^3+c^2(a+b)-c(a^2+a b+b^2)-a^3-a^2b-a b^2-b^3)z )/(4(a+b+c)) = 0)
Γ de centro N y que pasa por los centros X10, X502, X946, X11798, X13604, X15529, X23477, X23517, X23869. El lugar geométrico del punto de concurrencia Q es la
circunferencia
( a^2y z+b^2x z+c^2x y -
(x+y+z)(
(a^3-a^2(b+c)-a(b^2+5b c+c^2)+b^3+5b^2c+5b c^2+c^3)x +
(b^3-b^2(c+a)-b(c^2+5c a+a^2)+c^3+5c^2a+5c a^2+a^3)y +
(c^3-c^2(a+b)-c(a^2+5a b+b^2)+a^3+5a^2b+5a b^2+b^3)z )/(4(a+b+c)) = 0)
Γ′ de centro X10222 y que pasa por X946, X3244, X23341, X23869 (foco de la parábola descrita en HG270918).
La transformación P ∈ Γ ↦ Q ∈ Γ′ es una proyectividad, ya que el punto Q se obtiene intersecando la circunferencia Γ′ con la recta que pasa por X946 y por el simétrico de P, respecto a la recta IN.
- Domingo, 7 de octubre del 2018
La cúbica K003 y la quíntica Q050
Generalization of
Q050
Let P be a point. The locus of point M such that P, M and the isogonal conjugate M' of M with respect to the circumcevian triangle of M are collinear is in general a circular circum-quintic Q(P) passing through H, P, the vertices of the cevian triangle of P, the infinite points of pK(X6, P), the foci of the P ≠ O (when P = O, Q(P) splits into the circumcircle and the McCay cubic). A, B, C are three nodes on Q(P). For example, Q050 = Q(X2) and Q094 = Q(X6).
Dado un triángulo ABC con G y O el baricentro y el circuncentro de ABC, sean un punto M, Na, Nb, Nc los centros de las de los triángulos MBC, MCA, MAB, respectivamente, y O' es circuncentro de .
Las reflexiones de las rectas O'Na, O'Na, O'Na en las rectas AM, BM, CM, son paralelas. Se designa por Mi su punto del infinito.
Si (u:v:w) son las coordenadas baricéntricas de M,
Mi = (v w(u+v)(u+w) (v+w)a^4 +u v w(u-v-w) ((b^2 +c^2 )u+b^2 v+c^2 w)a^2 -u^2 (v+w) (u(c^4 v+b^4 w)+ v w (b^2 -c^2)^2 ) : ... : ... ).
El lugar geométrico del punto M, tal que Mi es el punto del infinito de la recta OM, es la cúbica de McCay, junto con la recta del infinito y la circunferencia circunscrita.
Esta caracterización es equivalente a:
Locus properties of
K003
30. Locus of point M such that O, M and the isogonal conjugate M' of M with respect to the circumcevian triangle DEF of M are collinear (together with the circumcircle)
El lugar geométrico del punto
P, tal que
Q es el punto del infinito de la recta
GP, es la quíntica
Q050.
Esta caracterización es equivalente a:
Geometric properties of
Q050
Q050 is the locus of point M such that G, M and the isogonal conjugate of M with respect to the circumcevian triangle DEF of M (or the inverse in (O) of the isogonal conjugate of M) are collinear.
- Viernes, 5 de octubre del 2018
Simetría central respecto a X(942)
Dado un triángulo ABC y un punto P, sean el y A'B'C' el de P.
R1, R2 y R3 son las rectas PA', PB' y PC', respectivamente.
Ra, Rb y Rc son las reflexiones de R1, R2 y R3 en B1C1, C1A1 y A1B1, respectivamente.
R'1, R'2 y R'3 son las reflexiones de Ra, Rb y Rc en AI, BI y CI, respectivamente.
Las rectas R'1, R'2, R'3 concurren en el simétrico P' de P respecto a X942 (inverso, respecto a la circunferencia inscrita, del inverso del incentro, respecto a la circunferencia circunscrita).
Usando coordenadas baricéntricas, se pueden obtener las coordenadas de P', en función de las de P=(x:y:z), que son la imagen mediante la colineación de matriz asociada M=(Aij):
A11 = a(b+c)(-a^2+b^2+c^2)
A12 = -a(2abc+a^2(b+c)-(b-c)^2(b+c))
A13 = -a(2abc+a^2(b+c)-(b-c)^2(b+c))
A21 = -b(-a^3+a^2c+a(b+c)^2+c(b^2-c^2))
A22 = b(a+c)(a^2-b^2+c^2)
A23 = -b(-a^3+a^2c+a(b+c)^2+c(b^2-c^2))
A31 = -c(-a^3+a^2b-b^3+bc^2+a(b+c)^2)
A32 = -c(-a^3+a^2b-b^3+bc^2+a(b+c)^2)
A33 = c(a+b)(a^2+b^2-c^2)
Para averiguar de que colineación se trata, se hallan las raíces del polinomio característico p(λ)=|M-λI|=-(2abc(a+b+c) - λ)^2 (2abc(a+b+c) + λ)=0,
λ1 = -2abc(a+b+c), simple;
λ2 = 2abc(a+b+c), doble.
Y como el rango de (M-λ2) es 1, se trata de una homología.
El centro, punto doble correspondiente a la raíz simple, es:
X942 = (a^2(b+c)+a(2abc-(b-c)^2(b+c)): ... : ...).
La recta de puntos dobles (eje de homología), correspondiente a la raíz doble, es la recta del infinito x+y+z=0.
La razón de homología es λ1/λ2=-1, por lo que es una homología armónica (involutiva). Por tanto, P y P' son simétricos respecto a su centro: se trata de una simetría central.
Pares {P=X(i), P'=X(j)}, para 1≤i,j≤23838: {1, 65}, {4, 1071}, {7, 5728}, {8, 3555}, {10, 3874}, {11, 11570}, {72, 3868}, {79, 17637}, {80, 17660}, {145, 10914}, {210, 3894}, {222, 1905}, {226, 18389}, {354, 5902}, {942, 942}, {946, 5884}, {950, 4292}, {1362, 18413}, {1364, 1845}, {1770, 6284}, {1829, 18732}, {2093, 17642}, {2550, 15185}, {3057, 5903}, {3419, 16465}, {3633, 3893}, {3753, 3873}, {3754, 3881}, {3869, 4018}, {3878, 4084}, {3884, 4757}, {3889, 4004}, {3892, 3919}, {3898, 4744}, {3901, 3962}, {3937, 15906}, {4295, 12711}, {4298, 6738}, {4312, 14100}, {5083, 12736}, {5570, 18838}, {5691, 12680}, {5885, 6583}, {6915, 16594}, {7354, 10572}, {7686, 12675}, {7727, 11670}, {7972, 17636}, {8581, 18412}, {10247, 10273}, {10698, 17654}, {11571, 17638}, {12688, 15071}, {17154, 22306}, {17625, 18391}, {17626, 18419}.
- Jueves, 4 de octubre del 2018
El centro X(1897) y una tangente a la elipse inscrita de Steiner
Dado un triángulo ABC, sea Γa la circunferencia que pasa por el incentro y por los puntos donde la altura desde el vértice A corta a las bisectrices interiores en B y C (Γa es tangente a la bisectriz en A).
Similarmente, se definen las circunferencias Γb y Γc.
El ea de las circunferencias Γb y Γc interseca a los lados BC, CA y AB en Aa, Ab y Ac, respectivamente.
El eje radical eb de las circunferencias Γc y Γa interseca a los lados BC, CA y AB en Ba, Bb y Bc, respectivamente.
El eje radical ec de las circunferencias Γa y Γb interseca a los lados BC, CA y AB en Ca, Cb y Cc, respectivamente.
En coordenadas baricéntricas:
ea: (b-c)(-a^2+b^2+c^2)x + a(a-b)(a+b-c)y - a(a-c)(a-b+c)z = 0,
Aa = (0 : (a-c)(a-b+c) : (a-b)(a+b-c)),
Ab = (a(a-c)(a-b+c) : 0 : (b-c)(-a^2+b^2+c^2)),
Ac = (-a(a-b)(a+b-c) : (b-c)(-a^2+b^2+c^2) : 0).
Los puntos
Aa,
Bb y
Cc están alineados, sobre la tangente en
X1146 a la .
Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están en una misma cónica:
𝒞: b c(a-b)(a-c)(b-c)^2(a^5
-a^4(b+c)+a(b-c)^2(b^2+c^2)
-2a^3(b^2-b c+c^2)+
2a^2(b^3+c^3)
-b^5+b^4c+b c^4-c^5)x^2
-a(a-b)(a-c)(a^8-a^7(b+c)
- a^6(b^2-3b c+c^2)
+ a^5(b-c)^2(b+c)
-a^4(b-c)^2(b^2+4b c+c^2)
+ a^3(b-c)^2(b^3+5b^2c+5b c^2+c^3)
+ a^2(b-c)^2(b^4-b^3c-8b^2c^2-b c^3+c^4)
- a(b-c)^4(b^3+5b^2c+5b c^2+c^3)
+ 2 b c(b-c)^4(b+c)^2) y z + ... = 0.
El centro de la cónica 𝒞 está sobre la recta X37X109:
W = ( a(a-b)(a-c)(a^2-(b-c)^2)(a^7-a^6(b+c)-a^5(b^2-3b c+c^2)
+a^3(b-c)^2(b^2+c^2)
+a^2(b-c)^2(b^3+5b^2c+5b c^2+c^3)
-a(b^2-c^2)^2(b^2+5b c+c^2)
+2b c(b-c)^2(b+c)^3) : ... : ...),
que tiene números de búsqueda en
(0.359412341523550, -0.0122864110068921, 3.48328783959367).
Y su (ninguna recta determinada por pares de centros, que figuren actualmente en ETC, pasa por él):
Z = ( a/((b-c)(2a^3-a(2b^2+b c+2c^2)+b c(b+c)) : ... : ...),
que tiene números de búsqueda en
(-10.0098958384950, 2.74178965115800, 6.36245434118036).
Con las rectas que pasan por los seis puntos Ab, Ac, Bc, Ba, Ca, Cb se forman tres triángulos perspectivos con ABC, a saber:
• Las rectas BcCb, AcBa, CaAb forman un triángulo perspectivo con ABC, con centro de perspectividad:
Pa = (2a : (a-b)(b-c)(a+b+c)SC : (a-c)(c-b)(a+b+c)SB).
• Las rectas AbBc, CaAc, BaCb forman un triángulo perspectivo con ABC, con centro de perspectividad:
Pb = ( (b-a)(a-c)(a+b+c)SC : 2b SCSA : (b-c)(c-a)(a+b+c)SA).
• Las rectas CbAc, BcCa, AbBa forman un triángulo perspectivo con ABC, con centro de perspectividad:
Pc = ( (c-a)(a-b)(a+b+c)SB : (c-b)(b-a)(a+b+c)SA : 2c SASB ).
Los triángulos
ABC y son perspectivos, con centro de perspectividad
X1897:
(1/((b-c)SA) : 1/((c-a)SB) : 1/((c-a)SC)).
- Miércoles, 3 de octubre del 2018
Un triángulo ceviano respecto al triángulo órtico
a Silvia, por su "cumple"
Dados un triángulo ABC, sean DEF el , Ab = DF ∩ BE, Ac = DE ∩ CF y d la tangente en D a la circunferencia circunscrita al triángulo DAbAc.
Se definen, cíclicamente, los puntos Bc, Ba, Ca, Cb y las tangentes e, f, en E, F.
Las rectas d, e, f forman un triángulo A'B'C' y las rectas AA', BB', CC' forman un triángulo A"B"C".
A"B"C" es el , respecto de DEF, del punto
W = ( (b^2-c^2)^2 (a^2-b^2-c^2)(a^2(b^2+c^2) - (b^2-c^2)^2)^2 : ... : ...),
que tiene números de búsqueda en
(-0.737109343836377, -0.484468776518512, 4.31627025511398) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4, 16813}, {115, 130}, {125, 137}, {184, 11082}, {338, 23290}, {1879, 6752}, {3574, 5095}, {7687, 18402}, {13851, 16337}, {15451, 20975}.
- Martes, 2 de octubre del 2018
Circunferencias exinscritas y hexágono circunscrito
Circumscribed hexagon problem (
AoPS, Mosquitall)
Consider any triangle ABC. Let A-excircle ω
A of ABC is tangent to BC at A'. Similarly define ω
B, ω
C, B', C'. Consider two tangent lines ℓ
a, ℓ
a' from A' to ω
B, ω
C which are different from BC. Similarly define ℓ
b, ℓ
b', ℓ
c, ℓ
c'. Then ℓ
a, ℓ
a', ℓ
b, ℓ
b', ℓ
c, ℓ
c' form a hexagon which has an incircle.
En coordenadas baricéntricas:
ℓa: (a + b - c)^2 (a - b + c) x + 4 a (a + b - c) c y -
4 a c (a - b + c) z = 0,
ℓa': (a + b - c) (a - b + c)^2 x - 4 a b (a + b - c) y +
4 a b (a - b + c) z = 0.
La cónica tangente a las seis rectas ℓa, ℓa', ℓb, ℓb', ℓc, ℓc' es la circunferencia de ecuación:
a^2 y z + b^2 z x +c^2 x y - (x + y + z)/(4 (a^3+ b^3+ c^3 - (a^2 (b+c) + b^2 (c+a) + c^2(a+b)) + 10 a b c)^2) (
(a^8 - 4 a^7 b + 4 a^6 b^2 + 4 a^5 b^3 - 10 a^4 b^4 + 4 a^3 b^5 +
4 a^2 b^6 - 4 a b^7 + b^8 - 4 a^7 c + 16 a^6 b c -
52 a^5 b^2 c + 64 a^4 b^3 c + 20 a^3 b^4 c - 80 a^2 b^5 c +
36 a b^6 c + 4 a^6 c^2 - 52 a^5 b c^2 + 36 a^4 b^2 c^2 -
24 a^3 b^3 c^2 + 380 a^2 b^4 c^2 - 84 a b^5 c^2 - 4 b^6 c^2 +
4 a^5 c^3 + 64 a^4 b c^3 - 24 a^3 b^2 c^3 - 608 a^2 b^3 c^3 +
52 a b^4 c^3 - 10 a^4 c^4 + 20 a^3 b c^4 + 380 a^2 b^2 c^4 +
52 a b^3 c^4 + 6 b^4 c^4 + 4 a^3 c^5 - 80 a^2 b c^5 -
84 a b^2 c^5 + 4 a^2 c^6 + 36 a b c^6 - 4 b^2 c^6 - 4 a c^7 +
c^8) x +
(a^8 - 4 a^7 b + 4 a^6 b^2 + 4 a^5 b^3 - 10 a^4 b^4 +
4 a^3 b^5 + 4 a^2 b^6 - 4 a b^7 + b^8 + 36 a^6 b c -
80 a^5 b^2 c + 20 a^4 b^3 c + 64 a^3 b^4 c - 52 a^2 b^5 c +
16 a b^6 c - 4 b^7 c - 4 a^6 c^2 - 84 a^5 b c^2 +
380 a^4 b^2 c^2 - 24 a^3 b^3 c^2 + 36 a^2 b^4 c^2 -
52 a b^5 c^2 + 4 b^6 c^2 + 52 a^4 b c^3 - 608 a^3 b^2 c^3 -
24 a^2 b^3 c^3 + 64 a b^4 c^3 + 4 b^5 c^3 + 6 a^4 c^4 +
52 a^3 b c^4 + 380 a^2 b^2 c^4 + 20 a b^3 c^4 - 10 b^4 c^4 -
84 a^2 b c^5 - 80 a b^2 c^5 + 4 b^3 c^5 - 4 a^2 c^6 +
36 a b c^6 + 4 b^2 c^6 - 4 b c^7 + c^8) y +
(a^8 - 4 a^6 b^2 +
6 a^4 b^4 - 4 a^2 b^6 + b^8 - 4 a^7 c + 36 a^6 b c -
84 a^5 b^2 c + 52 a^4 b^3 c + 52 a^3 b^4 c - 84 a^2 b^5 c +
36 a b^6 c - 4 b^7 c + 4 a^6 c^2 - 80 a^5 b c^2 +
380 a^4 b^2 c^2 - 608 a^3 b^3 c^2 + 380 a^2 b^4 c^2 -
80 a b^5 c^2 + 4 b^6 c^2 + 4 a^5 c^3 + 20 a^4 b c^3 -
24 a^3 b^2 c^3 - 24 a^2 b^3 c^3 + 20 a b^4 c^3 + 4 b^5 c^3 -
10 a^4 c^4 + 64 a^3 b c^4 + 36 a^2 b^2 c^4 + 64 a b^3 c^4 -
10 b^4 c^4 + 4 a^3 c^5 - 52 a^2 b c^5 - 52 a b^2 c^5 +
4 b^3 c^5 + 4 a^2 c^6 + 16 a b c^6 + 4 b^2 c^6 - 4 a c^7 -
4 b c^7 + c^8) z ) = 0.
Esta circunferencia no pasa por ningún centro del triángulo de ETC (1-23110) y su centro es X4882 = (r+8R) X1 - 12R X2:
(a(b+c-a)(3b c + ) : b(a-b+c)(3a c + SB) : c(a+b-c)(3a b + SC),
(a (r + 8 R) - 8 R s : b (r + 8 R) - 8 R s : c (r + 8 R) - 8 R s),
donde r y R son los radios de las circunferencias inscrita y circunscrita, y s el semiperímetro de ABC.
El de esta circunferencia es
W = 4(r-2R)(r^3+4r^2R-16rR^2-64R^3-2Rs^2) X200 - 3r(r^2-16R^2) X8236.
W = ( (b+c-a)/(a^5-3a^4(b+c)+
2a^3(b^2+4b c+c^2)+
2a^2(b^3-11b^2c-11b c^2+c^3)-a(b-c)^2(3b^2-10b c+3c^2)+(b-c)^2(b+c)^3) : ... : ...),
que tiene números de búsqueda en
(4.64000640465217, 1.90924761124290, 0.177336256592140) y está sobre la recta X200X8236.
- Domingo, 30 de septiembre del 2018
El centro del triángulo X(1384) como centro radical
X(1384) = 2nd GRINBERG HOMOTHETIC CENTER
Let G
a be the circumcenter of triangle BCG, where G -
centroid(ABC). Define G
b and G
c cyclically.
Triangle G
aG
bG
c is homothetic to the
pedal triangle of X(6), and X(1384) is the center of the homothety.
Dados un triángulo ABC de circuncentro O, ortocentro H y K, sea DEF el y Γa la circunferencia tangente en D a la circunferencia circunscrita a ABC y centro sobre la altura por A; su centro es Oa=AH∩OD.
Las circunferencias Γb y Γc, con centros Ob y Oc, respectivamente, se definen cíclicamente.
El de las circunferencias Γa, Γb y Γc es 2º Centro de Homotecia de Grinberg.
La ecuación baricéntrica de la circunferencia Γa:
4b^2c^2x^2 + a^2c^2y^2 + a^2b^2z^2 + a^2(-a^2+b^2+c^2)y z + 4b^2c^2z x + 4b^2c^2x y = 0,
y su centro es:
Oa = (-a^2(a^4+b^4+6b^2c^2+c^4-2a^2(b^2+c^2)) :
4b^2c^2(a^2+b^2-c^2) : 4b^2c^2(a^2-b^2+c^2)).
Las circunferencias Γa, Γb, Γc como envolventes:
Si M(0:1:t) es un punto sobre la recta BC, sea M' el punto de intersección de BC con la recta que resulta de girar la recta AD alrededor de A un ángulo α=∠BAC,
la envolvente de la circunferencia circunscrita a AMM', cuando M varía sobre BC, es la circunferencia Γa.
Giro contrario a las agujas del reloj:
(AMM'): c^2 x y + b^2 x z +
a^2 y z + (x + y +
z) (-(((a^2 c^2 t - a^4 t^2 + a^2 b^2 t^2 + a^2 c^2 t^2) y)/((1 +
t) (c^2 - a^2 t + c^2 t))) - (
a^2 b^2 t z)/((1 + t) (-c^2 + a^2 t - c^2 t))) = 0.
Giro en el sentido de las agujas del reloj:
(AMM''): c^2 x y + b^2 x z +
a^2 y z + (x + y + z) ((
a^2 c^2 t y)/((1 + t) (-a^2 + b^2 + b^2 t)) + (
a^2 (a^2 - b^2 - c^2 - b^2 t) z)/((1 + t) (-a^2 + b^2 + b^2 t))) = 0.
El de los triángulos ABC y es la de X5651.
Let u be the tangent to the
Thomson-Gibert-Moses hyperbola at X(3), and let v be the tangent at X(6); then X(5651) = u∩v. Also, X(5651) is the inverse-in-Thomson-Gibert-Moses hyperbola of X(182). (Randy Hutson, June 16, 2014)
or equivalently:
X(5651) = pole of the Brocard axis line with respect to the Thomson-Gibert-Moses hyperbola. (Peter Moses, June 17, 2014)
- Sábado, 29 de septiembre del 2018
Angulo de Brocard y envolvente de circunferencias
Dado un triángulo ABC y un punto D sobre la recta BC, sea D' el punto de intersección de BC con la recta que resulta de girar la recta AD, alrededor de A, un ángulo igual al .
La envolvente de la circunferencia circunscrita a ADD', cuando D varía sobre BC, es una circunferencia Γa con centro Oa, sobre la altura por A.
Si se hace el giro en el sentido contrario a las agujas del reloj:
(ADD'): a^2 c^2 x y + c^4 x y + 2 c^4 t x y - a^2 b^2 t^2 x y -
a^2 c^2 t^2 x y + c^4 t^2 x y - a^2 c^2 t y^2 - a^2 b^2 t^2 y^2 -
a^2 c^2 t^2 y^2 - a^4 x z + a^2 b^2 x z + b^2 c^2 x z +
2 a^2 b^2 t x z + 2 b^2 c^2 t x z + b^2 c^2 t^2 x z + a^2 c^2 y z +
a^4 t y z + a^2 b^2 t y z + a^2 c^2 t y z - a^2 b^2 t^2 y z -
a^4 z^2 + a^2 b^2 t z^2 = 0.
Girando en el sentido de las agujas del reloj:
(ADD''): b^2 c^2 x y + 2 a^2 c^2 t x y + 2 b^2 c^2 t x y - a^4 t^2 x y +
a^2 c^2 t^2 x y + b^2 c^2 t^2 x y + a^2 c^2 t y^2 - a^4 t^2 y^2 -
a^2 b^2 x z + b^4 x z - a^2 c^2 x z + 2 b^4 t x z + a^2 b^2 t^2 x z +
b^4 t^2 x z - a^2 c^2 y z + a^4 t y z + a^2 b^2 t y z +
a^2 c^2 t y z + a^2 b^2 t^2 y z - a^2 b^2 z^2 - a^2 c^2 z^2 -
a^2 b^2 t z^2 = 0.
La ecuación baricéntrica de la circunferencia Γa es:
a^2yz+b^2zx+c^2xy +
(x+y+z)(-((4(a^2b^2+a^2c^2+b^2c^2)x)/a^2)-c^2y-b^2z) = 0,
y las coordenadas de su centro son:
Oa = (a^2(a^4+b^4+6b^2c^2+c^4+6a^2(b^2+c^2)) : -4(a^2+b^2-
c^2)(b^2c^2+a^2(b^2+c^2)) : -4(a^2-b^2+c^2)(b^2c^2+a^2(b^2+c^2))).
Las circunferencias Γb y Γc se definen cíclicamente.
Los ejes radicales de la circunferencia circunscrita a ABC y las circunferencias Γa, Γb y Γc, forman un triángulo A'B'C', perspectivo a ABC con centro de perspectividad el de 9 X2 + 2 X39:
W = ( 1/(4a^2(b^2+c^2)+3b^2c^2 ) : ... : ...),
que tiene números de búsqueda en
(2.82977396933974, 1.71707444015421, 1.14587111441312) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {251,15271}, {263,3763}.
- Viernes, 28 de septiembre del 2018
La cúbica isogonal de pivote el punto medio del circuncentro y el punto de De Longchamps
X(5506) = Wolk Perspector
Let I be the incenter of a triangle ABC. Let N
a be the nine-point center of IBC, and define N
b and N
c cyclically. The triangle N
aN
bN
c is similar and perspective to the excentral triangle of ABC. The perspector is X(5506). (Barry Wolk, June 1, 2013) .
Dados un triángulo ABC y un punto P (que no está en la recta del infinito ni sobre la circunferencia circunscrita), sea A'B'C' el de P.
Se denota por Na, Nb, Nc los centros de las de los triángulos PBC, PCA, PAB, respectivamente.
Los triángulos A'B'C' y son perspectivos si y solo si el punto P queda sobre la pK(X6, X550).
Si (u:v:w) son las coordenadas baricéntricas de P,
Na=((b^2-c^2)^2u^2-a^2u(c^2(u+v-w)+b^2(u-v+w))-
a^4(2v w+u(v+w)) :
(b^2-c^2)u(b^2(v+w)-
c^2(u+v+w))+a^4(u^2+v w+u(2v+w))-
a^2(b^2(u^2+3u v-v w) +
c^2(2u^2+3u v+2u w+v w)) :
(b^2-c^2)u(-c^2(v+w)+
b^2(u+v+w))+a^4(u^2+v w+u(v+2w))-
a^2(c^2(u^2+3u w-v w)+b^2(2u^2+2u v+3u w+v w))).
Las rectas A'Na, B'Nb, C'Nc
son concurrentes si y sólo si las coordenadas de P satisfacen a la ecuación:
Σ abc xyz
a^2y z((a^4+b^4+3b^2c^2-4c^4+a^2(-2b^2+3c^2))y -(a^4-4b^4+3b^2c^2+c^4+a^2(3b^2-2c^2))z) = 0,
de la cubica isogonal pK(X6,X550).
pK(X6, X550) contiene a los centros X1 (incentro), X3 (circuncentro), X4 (ortocentro), X550 (punto medio del circuncentro y el ), X11010 (reflexión del incentro en el conjugado armónico, respecto al incentro y circuncentro, del inverso del incentro en la circunferencia circunscrita), X16835 (conjugado isogonal se X550).
Centros de perspectividad, Q, de A'B'C' y :
• Si P = X1, Q1 = X5506 (Wolk Perspector, Barry Wolk, June 1, 2013).
• Si P = X3, Q3 = X3.
• Si P = X4, Q4 = X5.
• Si P = X550,
Q550 = ( 12a^16-
73a^14(b^2+c^2)+(b^2-c^2)^6(b^4-16b^2c^2+c^4)+
a^12(177b^4-58b^2c^2+177c^4)+
a^10(-211b^6+453b^4c^2+453b^2c^4-211c^6)+
a^2(b^2-c^2)^4(3b^6+11b^4c^2+11b^2c^4+3c^6)-
a^4(b^2-c^2)^2(17b^8-260b^6c^2-87b^4c^4-260b^2c^6+
17c^8)+
a^8(115b^8-214b^6c^2-366b^4c^4-214b^2c^6+115c^8)-
a^6(7b^10+379b^8c^2-89b^6c^4-89b^4c^6+379b^2c^8+
7c^10) : ... : ...),
que tiene números de búsqueda en
(0.229677805688296, -0.664578981093136, 3.99475248157734).
• Si P = X11010,
Q11010 = ( a (a^3 + a^2 b - a b^2 - b^3 + a^2 c - 3 a b c + b^2 c - a c^2 +
b c^2 - c^3) (a^12 - 2 a^11 b - 4 a^10 b^2 + 10 a^9 b^3 +
5 a^8 b^4 - 20 a^7 b^5 + 20 a^5 b^7 - 5 a^4 b^8 - 10 a^3 b^9 +
4 a^2 b^10 + 2 a b^11 - b^12 - 2 a^11 c + 4 a^10 b c +
6 a^9 b^2 c - 26 a^8 b^3 c + 12 a^7 b^4 c + 48 a^6 b^5 c -
52 a^5 b^6 c - 28 a^4 b^7 c + 54 a^3 b^8 c - 4 a^2 b^9 c -
18 a b^10 c + 6 b^11 c - 4 a^10 c^2 + 6 a^9 b c^2 -
4 a^8 b^2 c^2 + 40 a^7 b^3 c^2 - 52 a^6 b^4 c^2 - 58 a^5 b^5 c^2 +
126 a^4 b^6 c^2 - 28 a^3 b^7 c^2 - 60 a^2 b^8 c^2 + 40 a b^9 c^2 -
6 b^10 c^2 + 10 a^9 c^3 - 26 a^8 b c^3 + 40 a^7 b^2 c^3 -
68 a^6 b^3 c^3 + 98 a^5 b^4 c^3 - 2 a^4 b^5 c^3 -
156 a^3 b^6 c^3 + 114 a^2 b^7 c^3 + 8 a b^8 c^3 - 18 b^9 c^3 +
5 a^8 c^4 + 12 a^7 b c^4 - 52 a^6 b^2 c^4 + 98 a^5 b^3 c^4 -
217 a^4 b^4 c^4 + 134 a^3 b^5 c^4 + 56 a^2 b^6 c^4 -
114 a b^7 c^4 + 33 b^8 c^4 - 20 a^7 c^5 + 48 a^6 b c^5 -
58 a^5 b^2 c^5 - 2 a^4 b^3 c^5 + 134 a^3 b^4 c^5 -
220 a^2 b^5 c^5 + 82 a b^6 c^5 + 12 b^7 c^5 - 52 a^5 b c^6 +
126 a^4 b^2 c^6 - 156 a^3 b^3 c^6 + 56 a^2 b^4 c^6 +
82 a b^5 c^6 - 52 b^6 c^6 + 20 a^5 c^7 - 28 a^4 b c^7 -
28 a^3 b^2 c^7 + 114 a^2 b^3 c^7 - 114 a b^4 c^7 + 12 b^5 c^7 -
5 a^4 c^8 + 54 a^3 b c^8 - 60 a^2 b^2 c^8 + 8 a b^3 c^8 +
33 b^4 c^8 - 10 a^3 c^9 - 4 a^2 b c^9 + 40 a b^2 c^9 -
18 b^3 c^9 + 4 a^2 c^10 - 18 a b c^10 - 6 b^2 c^10 + 2 a c^11 +
6 b c^11 - c^12) : ... : ...),
que tiene números de búsqueda en
(4.73611093113494, 3.68606698030115, -1.09712539574793) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {5,11014}.
• Si P = X16835,
Q16835 = ( a^2(a^14-6a^12(b^2+c^2)+
a^10(13b^4+4b^2c^2+13c^4)+(b^2-c^2)^4(2b^6-
21b^4c^2-21b^2c^4+2c^6)-
2a^8(5b^6-3b^4c^2-3b^2c^4+5c^6)+
a^6(-5b^8+47b^6c^2-243b^4c^4+47b^2c^6-5c^8)-
3a^2(b^2-c^2)^2(3b^8-29b^6c^2-91b^4c^4-
29b^2c^6+3c^8)+
a^4(14b^10-127b^8c^2+59b^6c^4+59b^4c^6-
127b^2c^8+14c^10)) : ... : ...),
que tiene números de búsqueda en
(-139.600337380830, -150.565994233006, 172.309585434371) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {10095,10620}, {12006,16835}.
- Jueves, 27 de septiembre del 2018
Envolvente de rectas y lugar de sus tripolos
Dado un triángulo ABC de incentro I, sean Na, Nb, Nc los centros de las de los triángulos IBC, ICA, IAB, respectivamente.
Se consideran loa puntos A1, B1, C1
sobre las rectas IA, IB, IC, respectivamente, tales que:
AA1/A1I =
BB1/B1I =
CC1/C1I = t.
La perpendicular a AI por A1 interseca a NbNc en A'.
La perpendicular a BI por B1 interseca a NcNa en B'.
La perpendicular a CI por C1 interseca a NaNb en C'.
Los puntos A', B', C' están alineados.
La ecuación de la recta que los contienen es:
ℓ:
((a^6+16a^3b c(b+c)-(b^2-c^2)^2(b^2-6b c+c^2)-
a^4(3b^2+8b c+3c^2)-
4a b c(4b^3-5b^2c-5b c^2+4c^3)+
a^2(3b^4+2b^3c-37b^2c^2+2b c^3+3c^4))t^2 +
2 (a^6-4ab^2c^2(b+c)-(b-c)^4(b+c)^2-
3a^4(b^2+c^2)+
a^2(3b^4-2b^3c+11b^2c^2-2b c^3+3c^4))t +
a^6-12a b^2c^2(b+c)-(b-c)^2(b+c)^4-
a^4(3b^2+8b c+3c^2)+
a^2(3b^4+10b^3c+11b^2c^2+10b c^3+3c^4)) x + ... = 0.
La ecuación de la envolvente de la recta ℓ, cuando t varía, puede ser obtenida por el método descrito por Paul Yiu en §10.4 Conics parametrized by quadratic functions, §11.4 Envelopes (Introduction to the Geometry of the Triangle, 2001 (with corrections 2013)).
Se trata de la parábola:
b c ((a^10 + a^9 (-b - c) + b^9 c - 4 b^7 c^3 + 6 b^5 c^5 -
4 b^3 c^7 + b c^9 + a^8 (-4 b^2 - b c - 4 c^2) +
a^7 (4 b^3 + 10 b^2 c + 10 b c^2 + 4 c^3) +
a^6 (6 b^4 - 3 b^3 c - 7 b^2 c^2 - 3 b c^3 + 6 c^4) +
a^5 (-6 b^5 - 18 b^4 c - 17 b^3 c^2 - 17 b^2 c^3 - 18 b c^4 -
6 c^5) +
a^4 (-4 b^6 + 10 b^5 c + 29 b^4 c^2 + 51 b^3 c^3 + 29 b^2 c^4 +
10 b c^5 - 4 c^6) +
a^3 (4 b^7 + 10 b^6 c - b^5 c^2 - 49 b^4 c^3 - 49 b^3 c^4 -
b^2 c^5 + 10 b c^6 + 4 c^7) +
a^2 (b^8 - 7 b^7 c - 18 b^6 c^2 + 11 b^5 c^3 + 42 b^4 c^4 +
11 b^3 c^5 - 18 b^2 c^6 - 7 b c^7 + c^8) +
a (-b^9 - b^8 c + 8 b^7 c^2 + 8 b^6 c^3 - 14 b^5 c^4 -
14 b^4 c^5 + 8 b^3 c^6 + 8 b^2 c^7 - b c^8 - c^9)) x^2 -
2 a^2 (-b^8 + 3 b^7 c - b^6 c^2 - 3 b^5 c^3 + 4 b^4 c^4 -
3 b^3 c^5 - b^2 c^6 + 3 b c^7 - c^8 + a^6 (b^2 - 3 b c + c^2) +
a^5 (2 b^2 c + 2 b c^2) +
a^4 (-3 b^4 + 11 b^3 c - 22 b^2 c^2 + 11 b c^3 - 3 c^4) +
a^3 (-2 b^4 c + 4 b^3 c^2 + 4 b^2 c^3 - 2 b c^4) +
a (-4 b^5 c^2 + 4 b^4 c^3 + 4 b^3 c^4 - 4 b^2 c^5) +
a^2 (3 b^6 - 11 b^5 c + 24 b^4 c^2 - 33 b^3 c^3 + 24 b^2 c^4 -
11 b c^5 + 3 c^6)) y z) + ... = 0.
Su foco es F = (r^2+13rR-s^2) I - 3r(2r-R) G (donde I es el incentro, G el baricentro, r, R son los radios de las circunferencias inscrita y circunscrita, y s el semiperímetro del triángulo ABC).
F = ( a^3(b+c)-a^2(-3b^2+10b c-3c^2)+
a(b^3+c^3)-(b^2-c^2)^2 : ... : ...),
que tiene números de búsqueda en
(-0.287932454429568, 1.55842577853126, 2.69464622958408), punto medio de X1 y X6788; reflexión de Xi en Xj para los índices {i,j}: {6789, 1125}, {21087, 11814}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,2}, {65,13756}, {244,21630}, {764,21201}, {946,3667}, {952,11717}, {1015,21090}, {1290,2718}, {2802,3756}, {3315,16173}, {4694,11813}, {11814,21087}, {12016,18240}, {18326,18493}.
El punto F ha sido incorporado a ETC con el número X(23869).
La directriz d de la parábola es la recta X1X88 y la dirección de su eje es la del punto en el infinito X2827.
El lugar geométrico del de ℓ es la cuártica:
(-a^5 c + a^4 b c + 2 a^3 b^2 c - 2 a^2 b^3 c - a b^4 c + b^5 c +
a^3 b c^2 - a b^3 c^2 + 2 a^3 c^3 - 7 a^2 b c^3 + 7 a b^2 c^3 -
2 b^3 c^3 - a c^5 + b c^5) x^2 y^2 + (2 a^3 b^2 c - 2 a b^4 c -
2 a^3 b c^2 + 4 a b^3 c^2 - 4 a b^2 c^3 +
2 a b c^4) x^2 y z + (2 a^4 b c - 2 a^2 b^3 c - 4 a^3 b c^2 +
2 a b^3 c^2 + 4 a^2 b c^3 - 2 a b c^4) x y^2 z + (a^5 b -
2 a^3 b^3 + a b^5 - a^4 b c - a^3 b^2 c + 7 a^2 b^3 c - b^5 c -
2 a^3 b c^2 - 7 a b^3 c^2 + 2 a^2 b c^3 + a b^2 c^3 + 2 b^3 c^3 +
a b c^4 - b c^5) x^2 z^2 + (-2 a^4 b c + 4 a^3 b^2 c -
4 a^2 b^3 c + 2 a b^4 c + 2 a^2 b c^3 -
2 a b^2 c^3) x y z^2 + (-a^5 b + 2 a^3 b^3 - a b^5 + a^5 c -
7 a^3 b^2 c + a^2 b^3 c + a b^4 c + 7 a^3 b c^2 + 2 a b^3 c^2 -
2 a^3 c^3 - a^2 b c^3 - 2 a b^2 c^3 - a b c^4 + a c^5) y^2 z^2 = 0.
Tiene puntos dobles en los vértices de ABC y pasa por los centros del triángulo X2 (tripolo de la recta del infinito, t=-1), X8046 (tripolo de la recta X900X1387, t=3), X21907 (tripolo de la recta X513X942, t = (2r+3R)/(R-2r)).
- Sábado, 22 de septiembre del 2018
Producto ceviano y triángulos perspectivos
Dados un triángulo ABC y dos puntos P y U, sea Q el de P y U.
Qa, Qb y Qc son los de Q respecto a los triángulos APU, BPU y CPU.
Los triángulos ABC y son perspectivos.
Si (p:q:r) y (u:v.w) son las coordenadas baricéntricas de P y U, respectivamente, el centro de perspectividad es W=Φ(P,U):
(1/(q r u^2+p^2 v w+4 q r v w+2 p (q+r) v w+2 q r u (v+w)+q v (r v+q w)+r w (r v+q w)) : ... : ...).
El punto W queda sobre la cónica circunscrita a ABC que pasa por P y U:
𝒞PU: p u (r v - q w)yz + q v (p w - r u)zx + r v (q u - p v)xy = 0.
Algunos casos particulares:
Φ(X1,X8)=X5559,
Φ(X3,X4)=X3521,
Φ(X6,X69)=X13622,
Φ(X7,X9)=X3255.
Alexander Skutin.- Creative Geometry
Theorem 6.1.(3):
W = Φ(X1,X2)= ( 1/(a^2+2a(b+c)+b^2+11b c+c^2) : ... : ...),
que tiene números de búsqueda en
(2.14195816594921, 1.76526565762615, 1.42996141157433) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {81,16489}, {88,551}.
ALEXANDER SKUTIN.- Creative Geometry
6. Fun with triangle centers

X = I I
• ∩ G G* = X(1)X(75) ∩ X(2)X(6) = X(86) = cevapoint of incenter and centroid.
El de W respecto al incentro y baricentro, sobre la cónica circunscrita que pasa por estos últimos puntos, es:
W' = ( a^4-5a^3(b+c)-
3a^2(4b^2-19b c+4c^2)-5a(b+c)^3+(b+c)^4 : ... : ...),
que tiene números de búsqueda en
(-2.47806447906720, 5.41950686885428, 1.03242025534705); reflexión de X4767 en X551 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,4370}, {2,4738}, {57,1317}, {81,16490}, {88,519}, {89,3241}, {106,8028}, {551,4767}, {900,1022}, {4677,8056}.
En una situación general, el conjugado armónico de W respecto a P y U, sobre la cónica 𝒞PU, es W' = Ψ(P,U):
W' = Ψ(P,U) = (1/(2 p q v w + q^2 v w + (p + r)^2 v w -
q r (u^2 + v^2 + w^2 + 2 u (v + w))) : ... : ...).
Algunos casos particulares, para P o U entre los 10 primeros centros de ETC:
Ψ(X1,X8) = X80,
Ψ(X1,X40) = X1295,
Ψ(X1,X764) = X244,
Ψ(X1,X984) = X335,
Ψ(X1,X3679) = X903,
Ψ(X1,X3751) = X2991,
Ψ(X1,X14421) = X1635,
Ψ(X1,X21132) = X1111.
Ψ(X2,X3) = X18317,
Ψ(X2,X376) = X1294,
Ψ(X2,X381) = X265,
Ψ(X2,X599) = X67,
Ψ(X2,X3081) = X3163,
Ψ(X2,X3241) = X1120,
Ψ(X2,X3679) = X80,
Ψ(X2,X4240) = X16075,
Ψ(X2,X5466) = X9180,
Ψ(X2,X6173) = X3254, ,
Ψ(X2,X6545) = X1086, ,
Ψ(X2,X8027) = X1015,
Ψ(X2,X8028) = X4370,
Ψ(X2,X8029) = X115,
Ψ(X2,X8030) = X2482,
Ψ(X2,X8031) = X13466,
Ψ(X2,X10278) = X9293,
Ψ(X2,X14995) = X14559.
Ψ(X3,X2) = X18317,
Ψ(X3,X4) = X265,
Ψ(X3,X381) = X1494,
Ψ(X3,X1351) = X2987,
Ψ(X3,X1482) = X1320,
Ψ(X3,X3095) = X1916,
Ψ(X3,X5489) = X339,
Ψ(X3,X23109) = X1313,
Ψ(X3,X23110) = X1312.
Ψ(X4,X3) = X265,
Ψ(X4,X20) = X1294,
Ψ(X4,X376) = X1494,
Ψ(X4,X3534) = X18317,
Ψ(X4,X5489) = X125,
Ψ(X4,X6776) = X287.
Ψ(X5,X549) = X1494,
Ψ(X5,X550) = X1294,
Ψ(X5,X8703) = X18317,
Ψ(X5,X15774) = X20123,
Ψ(X5,X23105) = X8901.
Ψ(X6,X69) = X67,
Ψ(X6,X599) = X671,
Ψ(X6,X1350) = X1297,
Ψ(X6,X2321) = X14554,
Ψ(X6,X3094) = X1916,
Ψ(X6,X3242) = X1280,
Ψ(X6,X8030) = X20380,
Ψ(X6,X9171) = X351,
Ψ(X6,X22260) = X3124.
Ψ(X7,X9) = X3254,
Ψ(X7,X390) = X14942,
Ψ(X7,X6172) = X1121.
Ψ(X8,X1) = X80,
Ψ(X8,X145) = X1120,
Ψ(X8,X390) = X673,
Ψ(X8,X944) = X2734,
Ψ(X8,X1469) = X7077,
Ψ(X8,X2098) = X17101,
Ψ(X8,X3241) = X903,
Ψ(X8,X21132) = X11.
Ψ(X9,X7) = X3254,
Ψ(X9,X3243) = X1280,
Ψ(X9,X6173) = X1121.
Ψ(X10,X551) = X903,
Ψ(X10,X764) = X17205,
Ψ(X10,X3244) = X1120,
Ψ(X10,X11263) = X11604.
- Miércoles, 19 de septiembre del 2018
Cónicas con focos en los vértices de un triángulo ceviano y la cúbica Soddy-Gergonne-Nagel
Sea ABC el triángulo de referencia, P un punto y DEF su .
Fa es la reflexión de F en la bisectriz interior en A. Ma el punto medio de E y Fa.
La circunferencia de centro en Oa (= punto medio de E y F) y radio EMa, corta a la recta EF en A1 y A2.
Sea 𝒞a la cónica de focos E y F, vértices A1 y A2 (pasa por A, ver (FFP)).
Nota: Si en vez de tomar la reflexión de F en la bisectriz en A, se toma la reflexión de E y, si se procede análogamente, se obtiene la misma cónica 𝒞a.
Las cónicas 𝒞b y 𝒞c se determinan cíclicamente.
Si (u:v:w) son las coordenadas baricéntricas de P,
Fa (cv-b(u+v) : 0 : -cv),
Ma (cv(u+w)-b(u+v)(2u+w) : 0 : -b(u+v)w-cv(u+w)),
EMa² =
(cv(u+w)-b(u+v)w)^2/(4(u+v)^2(u+w)^2).
La ecuación de la circunferencia de centro en Oa y radio EMa es:
a^2y z + b^2z x + c^2x y
- (1/(4(u+v)(u+w)))(x+y+z)
((-a^2+(b+c)^2)v w x +
(2b c v w + (a^2-b^2)(2u+v)w + c^2(4u^2+2u w - v w)) y +
(2b c v w + (a^2-c^2)v(2u+w)+b^2(4u^2+2u v - v w)) z) =0,
y corta a la recta EF en los puntos:
A1,2 = (u*(-2*b*c*v*(v-w)*w*(u+w)+
a^2*v*w*(u+w)*(2*u+v+w)+
b^2*(v-w)*w*(-2*u^2-u*v+v*w)+
c^2*v*(v-w)*(2*u^2+3*u*w+
w^2)-2*(b*(u+v)*w ±
c*v*(u+w))*Sqrt[c^2*u*v*(v-w)*(u+w)+(u+v)*w*(a^2*v*(u+w)+b^2*u*(-v+w))]):
(a^2-(b-c)^2)*v^2*w*(u+w)^2:
w*(-2*b*c*v*(u+v)*w*(u+w)+
c^2*v*(u+w)*(2*u*v-u*w+v*w)+
(u+v)*w*(a^2*v*(u+w)+
b^2*(-(u*v)+2*u*w+v*w)) ±
2*(b*(u+v)*w-c*v*(u+w))*Sqrt[c^2*u*v*(v-w)*(u+w)+(u+v)*w*(a^2*v*(u+w)+b^2*u*(-v+w))])).
La cónica que pasa por A, de vértices A1 y A2, pasa también por las reflexiones de A en el eje EF,
(c^2u^2v(v-w)+b^2u^2w(-v+w)+a^2vw(u^2-vw) :
vw(a^2v(u+w)-c^2v(u+w)+b^2(-uv+2uw+v w)) :
vw((a^2-b^2)(u+v)w+c^2(2uv-uw+vw))),
y en el centro Oa, (u^2-vw : v(u+w) : w(u+v)), respectivamente.
Con estos cinco puntos la cónica queda determinada y tiene ecuación:
𝒞a : w(-(a^2-b^2)(u+v)^2w+2b c(u^2-v^2)w+
c^2(-2u v w+v^2w+u^2(-4v+w)))y^2 +
v(-a^2v(u+w)^2+c^2v(u+w)^2+2b c v(u^2-w^2)+
b^2(u^2(v-4w)-2u v w+v w^2))z^2 +
2v w(a^2(u+v)(u+w)-(b-c)(b(u+v)(u-w)-c(u-v)(u+w)))y z +
4b v w(b(u+v)w-c v(u+w))z x +
4c v w(-b(u+v)w+c v(u+w))x y = 0.
Permutando cíclicamente esta ecuación, se deducen las ecuaciones de cónicas 𝒞b y 𝒞c, de focos F, D y D, E y que pasan, respectivamente, por B y C.
Las cónicas 𝒞
a, 𝒞
b y 𝒞
c tienen dos puntos comunes si y solo si
P está sobre la cúbica Soddy-Gergonne-Nagel (
K200, del Catálogo de Bernard Gibert).
Una de las rectas que forman la cónica degenerada (siempre real) del haz 𝒞b + λ 𝒞c, correspondiente al valor de λ:
λa = -(((a-b+c)(a(u+v)w-cu(v+w))^2)/((a+b-c)(av(u+w)-bu(v+w))^2)),
tiene por ecuación:
ℓa : (2a^3v w(u+v)(v-w)(u+w) -
a^2u(v+w)(b(u+v)(3v-w)w+c v(v-3w)(u+w))+(b-
c)u(v+w)^2(2b c v w+b^2(u+v)w+c^2v(u+w)-
b c u(v+w))+
2a(v+w)(b^2(u^2-v^2)w^2+b c u^2(v^2-w^2)+
c^2v^2(-u^2+w^2)) x +
(-a(u+v)w+
c u(v+w))(-(b^2-c^2)u(v+w)^2+2a b u(v^2-w^2)-
a^2(u(v-w)^2-4v w^2)) y
-(a v(u+w)-
b u(v+w))(-(b^2-c^2)u(v+w)^2+
a^2(u(v-w)^2 -4v^2w)+2a c u(v^2-w^2))) z = 0.
Análogamente, para los haces de cónicas 𝒞c + λ 𝒞a y 𝒞a + λ 𝒞b, resultan las rectas ℓb y ℓc.
Las rectas ℓa, ℓb, ℓc coinciden (y, por tanto, las tres cónicas 𝒞a, 𝒞b, 𝒞c, tienen dos puntos comunes) si y solo si las coordenadas de P satisfacen a la ecuación
Σ abc xyz
y z ((a + b - c) y - (a - b + c) z) = 0,
de la cúbica Soddy-Gergonne-Nagel (K200, del Catálogo de Bernard Gibert), que pasa por los centros del triángulo X2, , , X144, , X1143, X1274, X10405, X13386, X13387, X20534.
Punto medio de los dos puntos comunes a las cónicas 𝒞a, 𝒞b, 𝒞c. Tres casos particulares:
• Si P es el baricentro, el punto medio es X(23058).
(Ver HG110918).
• Si P es el , el punto medio es X(23244).
(Ver HG150918).
• Si P=X10405, el del del , el punto medio es X(23058). (Como hace notar Antreas Hatzipolakis, Anopolis #8236, 21/09/2018).
En este caso, los Pa, Pb y Pc de la recta UV con respecto a las hipérbolas ℋa, ℋb y ℋc, forman un triángulo perspectivo con DEF, con centro de perspectividad W=X7X10405∩X281X1886. De hecho, DEF es el triángulo ceviano de W respecto a .
W = ( a^8
- a^7(b+c)
- 5a^6(b-c)^2
+ 11a^5(b-c)^2(b+c)
- 5a^4(b-c)^2(3b^2+2b c+3c^2)
+ a^3(b-c)^2(29b^3-13b^2c-13b c^2+29c^3)
- a^2(b-c)^4(39b^2+82b c+39c^2)
+ a(b-c)^4(25b^3+87b^2c+87b c^2+25c^3)
- 2(b-c)^4(b+c)^2(3b^2+10b c+3c^2) : ... : ...),
que tiene números de búsqueda en
(2.37574846683558, 2.03084124434523, 1.13819817420588) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {7,10405}, {281,1886}.
- Sábado, 15 de septiembre del 2018
Hipérbolas con focos en los vértices del triángulo de contacto exterior
Dado un triángulo ABC de DEF, se consideran las hipérbolas:
ℋa
( (4 a^2 b^2 c^2 x y-4 b^4 c^2 x y-4 a^2 b c^3 x y+12 b^3 c^3 x y-12 b^2 c^4 x y+4 b c^5 x y+a^4 c^2 y^2+2 a^3 b c^2 y^2+4 a^2 b^2 c^2 y^2-2 a b^3 c^2 y^2-5 b^4 c^2 y^2-2 a^3 c^3 y^2-4 a^2 b c^3 y^2-2 a b^2 c^3 y^2+8 b^3 c^3 y^2+2 a b c^4 y^2-2 b^2 c^4 y^2+2 a c^5 y^2-c^6 y^2-4 a^2 b^3 c x z+4 b^5 c x z+4 a^2 b^2 c^2 x z-12 b^4 c^2 x z+12 b^3 c^3 x z-4 b^2 c^4 x z-2 a^4 b c y z+2 b^5 c y z-8 b^4 c^2 y z+12 b^3 c^3 y z-8 b^2 c^4 y z+2 b c^5 y z+a^4 b^2 z^2-2 a^3 b^3 z^2+2 a b^5 z^2-b^6 z^2+2 a^3 b^2 c z^2-4 a^2 b^3 c z^2+2 a b^4 c z^2+4 a^2 b^2 c^2 z^2-2 a b^3 c^2 z^2-2 b^4 c^2 z^2-2 a b^2 c^3 z^2+8 b^3 c^3 z^2-5 b^2 c^4 z^2) = 0)
de focos E y F y que pasa por A,
ℋb de focos F y D y que pasa por B,
ℋc de focos D y E y que pasa por C.
Para construir estas hipérbolas y, de paso, obtener sus ecuaciones baricéntricas utilizamos (FFP)
Existe solo una cónica degenerada real, para cualquier triángulo, en los tres haces de cónicas formados por tres pares de estas hipérbolas. Tales cónicas degeneradas tienen en común la recta que pasa por el y por X971 ( del cuarto punto de intersección de la circunferencia circunscrita con la hipérbola rectangular que pasa por el punto de Bevan).
En el haz ℋb + λ ℋc, los valores de λ que corresponden a las cónicas degeneradas son:
((a-c)^2c^2(a^2-b^2-2a c+c^2))/(b^2(a-b)^2(a-b+c)^2),
((a-b-c)(a+b-c)^3(-a^4-b^4+4b^3c+2b^2c^2+4b c^3-c^4-8a b c(b+c)+2a^2(b+c)^2 ± (b+c-a)(a+b-c)(a-b+c)Sqrt[(a+b+c)^2-8b c]))/(8(a-b)^2b^2(a-b+c)^4).
Al intersecar la recta X40X971 con cualquiera de las tres hipérbolas, se obtienen los puntos U y V comunes a las tres, de coordenadas baricéntricas:
(a(a^4+5b^4+2a^2b(b-c)-2a^3c+2b^3c-4b^2c^2-2b c^3-c^4+2a(-4b^3+b^2c+2b c^2+c^3))((b-c)(a^2-b^2-2a c+c^2)^2 ± 4(a-c)(a-b+c)|b-c| ) :
b(b-c)(5a^4-2a(b-c)^2c+(b-c)^3(b+c)+a^3(-8b+2c)+2a^2(b^2+b c-2c^2))((a^2-(b-c)^2)^2 ± 4(-a+b+c)|b-c|S) :
(b-c)(a+b-c)^2c(5a^6+2a^5(b-4c)+2a b(b-c)^4+a^4(11b^2-8b c-3c^2)+(b-c)^3(5b^3+7b^2c+3b c^2+c^3)+4a^3(-9b^3+4b^2c+3b c^2+2c^3)+a^2(11b^4+16b^3c-18b^2c^2-8b c^3-c^4))).
El punto medio de U y V es:
M = ( a(a-b-c)^3(a^6
-3a^4(b-c)^2
+3a^2(b-c)^2(b^2+6b c+c^2)
-16a b(b-c)^2c(b+c)
-(b-c)^4(b^2+6b c+c^2)) : ... : ...),
que tiene números de búsqueda en
(4.82972221662700, 2.06288484562882, -0.0165891265864994) y está sobre la recta que contiene a los centros del triángulo: X40, X971, X2951, X3059, X3927, X4882, X5223, X5696, X7992, X14872.
El punto M ha sido incorporado a ETC con el número X(23244).
Los Pa, Pb y Pc de la recta UV con respecto a las hipérbolas ℋa, ℋb y ℋc, forman un triángulo perspectivo con DEF con centro de perspectividad X4012. De hecho, DEF es el triángulo ceviano de X4012 respecto a .
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Si se consideran las elipses:
ℰa ( c^2(-a+b+c)^2y^2+b^2(-a+b+c)^2z^2+
2bc(-a^2-2a(b+c)+(b+c)^2)yz-4ab^2czx = 0) de focos E y F y que pasa por A,
ℰb de focos F y D y que pasa por B,
y ℰc de focos D y E y que pasa por C,
una de las rectas de la cónica degenerada siempre real, para cualquier triángulo, del haz ℰb + λ ℰc, correspondiente a λ = -1, es:
ℓa: ((b - c)^2 + a (b + c))x + a (a + b - c)y + a (a - b + c)z = 0,
la otra es la recta que pasa por el A-exincentro y por el .
Cíclicamente, se obtienen las rectas ℓb y ℓc.
El triángulo A'B'C' formado por las rectas ℓa, ℓb y ℓc es perspectivo con ABC, con centro de perspectividad X84, conjugado isogonal del punto de Bevan.
- Viernes, 14 de septiembre del 2018
El centro del triángulo X(468)
Dado un triángulo ABC de , las circunferencias (BMaMb) y (CMaMc) se vuelven a cortar en A', punto de coordenadas baricéntricas:
A' = (a^2(a^2+b^2+c^2) : -a^4+a^2b^2+2b^4-3b^2c^2+
c^4 : -a^4+b^4+a^2c^2-3b^2c^2+2c^4).
Los puntos B' y C' se definen cíclicamente.
Los triángulos ABC y A'B'C' son perspectivos con centro de perspectividad X468, intersección de la y el
El de los triángulos ABC y A'B'C' es la de X7493 ( del ortocentro respecto al baricentro y X23.
X(23), FAR-OUT POINT
Let A
1B
1C
1 be the antipedal triangle of X(3) (the tangential triangle). The circumcircles of AA
1X(3), BB
1X(3), CC
1X(3) concur in two points: X(3) and X(23). (Randy Hutson, October 13, 2015)
La matriz (aij) asociada a la aplicación afín σ, que transforma ABC en A'B'C', tiene entradas:
a11 = a^2(a^2+b^2+c^2)(3a^4-b^4+2b^2c^2+3c^4+
2a^2(b^2-3c^2))(3a^4+3b^4+2b^2c^2-c^4+
a^2(-6b^2+2c^2)),
a12 = (3a^4+3b^4+2b^2c^2-c^4+
a^2(-6b^2+2c^2))(-2a^8-3(b^2-c^2)^3(b^2+c^2)+
a^6(3b^2+7c^2)+a^4(9b^4-16b^2c^2-c^4)+
a^2(b^6-17b^4c^2+23b^2c^4-7c^6)),
a13 = -(3a^4-b^4+
2b^2c^2+3c^4+2a^2(b^2-3c^2))(2a^8-
3(b^2-c^2)^3(b^2+c^2)-a^6(7b^2+3c^2)+
a^4(b^4+16b^2c^2-9c^4)+
a^2(7b^6-23b^4c^2+17b^2c^4-c^6)),
a21 = -(a^4-
a^2b^2-2b^4+3b^2c^2-c^4)(3a^4-b^4+2b^2c^2+
3c^4+2a^2(b^2-3c^2))(3a^4+3b^4+2b^2c^2-c^4+
a^2(-6b^2+2c^2)),
a22 =
b^2(3a^4+3b^4+2b^2c^2-c^4+a^2(-6b^2+2c^2))(-a^6+
a^4(b^2+c^2)+3(b^2-c^2)^2(b^2+c^2)+
a^2(5b^4-2b^2c^2+5c^4)),
a23 = -(3a^4-b^4+2b^2c^2+
3c^4+2a^2(b^2-3c^2))(a^8-a^6(5b^2+2c^2)+
a^4(5b^4+13b^2c^2-4c^4)-
3(b^2-c^2)^2(2b^4+b^2c^2-c^4)+
a^2(5b^6-24b^4c^2+9b^2c^4+2c^6)),
a31 = -(a^4-b^4-
a^2c^2+3b^2c^2-2c^4)(3a^4-b^4+2b^2c^2+3c^4+
2a^2(b^2-3c^2))(3a^4+3b^4+2b^2c^2-c^4+
a^2(-6b^2+2c^2)),
a32 = (3a^4+3b^4+2b^2c^2-c^4+
a^2(-6b^2+2c^2))(-a^8+a^6(2b^2+5c^2)+
a^4(4b^4-13b^2c^2-5c^4)-
3(b^2-c^2)^2(b^4-b^2c^2-2c^4)-
a^2(2b^6+9b^4c^2-24b^2c^4+5c^6)),
a33 = c^2(3a^4-b^4+2b^2c^2+3c^4+2a^2(b^2-3c^2))(-a^6+
a^4(b^2+c^2)+3(b^2-c^2)^2(b^2+c^2)+
a^2(5b^4-2b^2c^2+5c^4)).
El único punto fijo finito F (correspondiente al valor propio
λ = (3a^4+2a^2(b^2-3c^2)-b^4+2b^2c^2+3c^4)(-a^4+2a^2(b^2+c^2)+
3(b^2-c^2)^2)(3a^4+a^2(-6b^2+2c^2)+3b^4+2b^2c^2-c^4)
es:
F = ( (2a^2-b^2-c^2)(a^4-2a^2(b^2+c^2)-3(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en
(8.28736757577840, 2.66412581552228, -2.02866919458261 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,6}, {5,8585}, {30,10418}, {111,858}, {113,9193}, {115,16317}, {126,6390}, {187,468}, {427,18424}, {625,6719}, {690,9209}, {1503,2502}, {1513,1514}, {2030,5972}, {3291,5159}, {5107,6388}, {5210,7493}, {5915,10564}, {6791,13857}, {9759,14982}.
- Jueves, 13 de septiembre del 2018
La cúbica K033 como lugar geométrico
Dado un triángulo ABC de circunferencias A- (Ia), B-exinscritas (Ib) y C-exinscritas (Ic), se denota por el de un punto P.
Sean Ab y Ac los puntos de contacto de las tangentes (distintas de BC) desde Pa a (Ib) y (Ic), respectivamente. Los puntos Bc, Ba, Ca y Cb, se definen cíclicamente.
Si (u:v:w) son las coordenadas baricéntricas del punto P, respecto a ABC,
Ab = (-(a(v-w)+(b+c)(v+w))^2 : (a^2+2a b+b^2-
c^2)v^2 : (a^2-b^2-2a c+c^2)w^2),
Ac = (-(a(v-w)-(b+c)(v+w))^2 : (a^2-2a b+b^2-
c^2)v^2 : (a^2-b^2+2a c+c^2)w^2).
Si A'B'C' el triángulo formado por la rectas BaCa, CbAb, AcBc y si el punto P no está sobre las rectas determinadas por los lados de ABC:
Los triángulos
ABC y
A'B'C' son perspectivos si y solo si
P está sobre la cúbica
K033, del catálogo de Bernard Gibert, o sobre la
séxtica:
Φ :
Σ abc xyz
[ y z(-(a+b-c)(a-b+c)(a+b+c) (a^3+b^3+a^2(-b-c)+3b^2c+3b c^2+c^3+a(-b^2+2b c-c^2))x^4 -
4a(a+b-c)(a-b+c)(b+c)(a^2+b^2+2b c+c^2)y^2z^2 - x^3((a^6-b^6-2a^5c-4b^5c+3b^4c^2-3b^2c^4+
4b c^5+c^6+a^4(-3b^2-c^2) + a^3(8b^2c+12b c^2+4c^3) + a^2(3b^4+4b^3c+22b^2c^2+12b c^3-c^4) +
a(-6b^4c+12b^3c^2+40b^2c^3+4b c^4-2c^5))y + (a^6-2a^5b+b^6+4b^5c-3b^4c^2+3b^2c^4-4bc^5-c^6+a^4(-b^2-3c^2)+
a^3(4b^3+12b^2c+8bc^2) + a^2(-b^4+12b^3c+22b^2c^2+4bc^3+3c^4) + a(-2b^5+4b^4c+40b^3c^2+12b^2c^3-
6b c^4))z) - 2a(a+b-c)(a-b+c)(b+c)(-a+b+c)(a+b+c)y z(y^2+z^2))]
-2(a^6+12a^3b c(b+c)+4a b c(b+c)^3+(b^2-c^2)^2(b^2+c^2)-a^4(b^2-4b c+c^2)-
a^2(b^4-12b^3c-34b^2c^2-12b c^3+c^4))x^2y^2z^2 = 0.
La séxtica Φ pasa por los vértices (puntos dobles) de ABC y por los puntos, en el exterior de la circunferencia circunscrita, en los que los las circunferencia exinscritas son tangentes a los lados de ABC (estos seis puntos están sobre la cónica de Yiu, con centro en X478).
Bernard Gibert (comunicación personal, 19-09-2018) hace notar que la séxtica Φ es el lugar geométrico del punto P tal que las rectas BaCa, CbAb, AcBc son concurrentes.
La cúbica K033 pasa por los centros del triángulo X(1), X(4), X(8), X(10), X(40), X(65), X(72), X(3176), X(5930). Para P=X(8), punto de Nagel, el punto de concurrencia de las rectas AA', BB', CC' es X(11578). Ver Hyacinthos #25070.
Si P es el incentro, el punto de concurrencia es:
W = ( a^2 (a^8-4 a^7 (b+c)
-8 a^6 (b^2-3 b c+c^2)
+4 a^5 (3 b^3+b^2 c+b c^2+3 c^3)
+2 a^4 (9 b^4-32 b^3 c+54 b^2 c^2-32 b c^3+9 c^4)
-4 a^3 (b-c)^2 (3 b^3+5 b^2 c+5 b c^2+3 c^3)
-8 a^2 (b-c)^2 (2 b^4-3 b^3 c-2 b^2 c^2-3 b c^3+2 c^4)
+4 a (b-c)^4 (b+c)^3
+(b-c)^2 (b+c)^4 (5 b^2-26 b c+5 c^2)) : ... : ...),
que tiene números de búsqueda en
(-8.15286524513444, -9.89008622291298, 14.2505081339862) y está sobre la recta que pasa por los centros X(1709), X(4915), X(7991), X(10914).
- Martes, 11 de septiembre del 2018
Hipérbolas con focos en los vértices del triángulo medial
Dado un triángulo ABC de DEF, se consideran las hipérbolas:
ℋa de focos E y F y que pasa por A,
ℋb de focos F y D y que pasa por B,
ℋc de focos D y E y que pasa por C.
Para construir estas hipérbolas y, de paso, obtener sus ecuaciones baricéntricas utilizamos (FFP)
ℋa: (a^2-b^2+c^2)y^2+(a^2+b^2-c^2)z^2-2a^2y z+ 2b(c-b)z x +
2c (b - c) x y = 0.
Existe solo una cónica degenerada real, para cualquier triángulo, en los tres haces de cónicas formados por tres pares de estas hipérbolas. Tales cónicas degeneradas tienen en común la recta que pasa por el ortocentro y el .
De hecho, estas cónicas degeneradas reales de los haces formados por las hipérbolas (ℋb, ℋc), (ℋc, ℋa) y (ℋa, ℋb) son, respetivamente, la unión de la rectas:
X4X10∪X1X3854,
X4X10∪X1X14078,
X4X10∪X1X14087.
En el haz ℋb + λ ℋc, los valores de λ que corresponden a las cónicas degeneradas son:
-(a-c)^2(a-b+c)/((a-b)^2(a+b-c)),
(-(a-b)^2+(2a-c)c ± Sqrt[(3a-b-c)(-a+b+c)(a+b-c)(a-b+c)])/(2(a-b)^2)
Al intersecar la recta X4X10 con cualquiera de las tres hipérbolas, se obtienen los puntos U y V comunes a las tres:
(2(c(b-c)SC-(b-c)(abc ± (b-a)S)) : 2(c-b)(a-b+c)SA SC : (c-b)SA(a(a+b-c)(a-b+c)±2(b-c)S)).
El punto medio de U y V es M = (r+4R)^2 X9- 4s^2 X10:
M = ( (-a+b+c)(a^3+a(b-c)^2-2(b-c)(b^2-c^2)) : ... : ...),
que tiene números de búsqueda en
(5.43433690679566, 3.99719508875701, -1.63477992113771), punto medio de Xi y Xj para los índices {i,j}: {3160, 10405}, {7090, 14121}; reflexión de Xi en Xj para los índices {i,j}: {10004, 142}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,1146}, {2,3160}, {4,9}, {5,5514}, {41,5727}, {101,5881}, {142,10004}, {219,4034}, {220,3679}, {282,7100}, {610,5787}, {728,6735}, {910,5691}, {938,1449}, {1212,1698}, {1375,16832}, {1419,5942}, {1446,18634}, {1737,16572}, {2082,9581}, {2262,5806}, {2324,4007}, {2886,5574}, {3061,17284}, {3119,5219}, {3632,6603}, {3673,4858}, {3684,12625}, {4136,4901}, {4515,4873}, {4534,11376}, {4875,5231}, {5437,20205}, {5540,10826}, {5880,15725}, {6506,7741}, {6706,20195}, {6913,7367}, {7988,13609}, {7991,17747}, {8558,9579}, {9367,16975}, {17435,20271}.
El punto M ha sido incorporado a ETC con el número X(23058).
Si se consideran las elipses:
ℰa ((a^2-b^2+c^2)y^2+(a^2+b^2-c^2)z^2-2a^2y z-2b(b+c)z x = 0) de focos E y F y que pasa por A,
ℰb de focos F y E y que pasa por B,
y ℰc de focos D y E y que pasa por C,
una de las rectas de la cónica degenerada siempre real, para cualquier triángulo, del haz ℰb + λ ℰc, correspondiente a λ = -(a+b-c)(a+c)^2)/((a+b)^2(a-b+c)), es:
ℓa: (b^2+c^2+a(b+c))x + (a+b-c)(a+c)y + (a+b)(a-b+c)z = 0.
Cíclicamente, se obtienen las rectas ℓb y ℓc.
El triángulo A'B'C' formado por las rectas ℓa, ℓb y ℓc es perspectivo con ABC, con centro de perspectividad X13478.
X(13478) = perspector of the excentral-hexyl ellipse
The excentral-hexyl ellipse is the ellipse passing through vertices of the and triangles. It has center at the circumcenter.
The only Kimberling center the ellipse passes through is X(1768).
- Lunes, 10 de septiembre del 2018
Dos pares bicéntricos
Dado un triángulo ABC de incentro I, la perpendicular a AI en I interseca a AC, AB en Ab, Ac, respectivamente. Los puntos Bc, Ba, Ca, Cb, se definen cíclicamente.
Las circunferencias circunscritas a los triángulos , y concurren en
U.
Las circunferencias circunscritas a los triángulos , y concurren en
V.
Los puntos U y V forman un con
f(a,b,c) = a(a-b-c)(b-c)(2a^2-2a b-ac+b c-c^2)(a^2+a b-2b^2-2a c+b c+c^2)
( a(b-c)^2(b+c-a)^2(5a^2-4a(b+c)-(b-c)^2) : ... : ...),
que tiene números de búsqueda en
(3.01760078443673, 3.25289748021838, -0.00408028952222515) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {926,2170}, {2246,4845}, {3119,3900}, {4162,7004}.
La diferencia bicéntrica de P y U es:
( a(b-c)(4a^2-5a(b+c)+b^2+4b c+c^2) : ... : ...),
que tiene números de búsqueda en
(5.41971934778287, 0.657342198122180, 0.684172491923085), punto medio de Xi y Xj para los índices {i,j}: {1,2254}, {145,3716}, {513,4162}, {519,14430}, {663,14077}, {891,3251}, {905,4959}, {1635,3722}, {2814,16200}, {2832,10699}, {3244,3762}, {3295,8648}, {3900,14414}, {8572,20315}; reflexión de Xi en Xj para los índices {i,j}: {2254,14413}, {14413,1}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,2254}, {145,3716}, {513,4162}, {519,14430}, {663,14077}, {891,3251}, {905,4959}, {1635,3722}, {2814,16200}, {2832,10699}, {3244,3762}, {3295,8648}, {3900,14414}, {8572,20315}.
Los circuncentros O1, O2 de los triángulos y forman un con
f(a,b,c) = a(a^3-2a^2b + a(b^2-6b c-3c^2) + 2c(-2b^2+b c+c^2))
El punto medio de O1 y O2 es el incentro.
La de O1 y O2 es el .
El de la recta O1O2 es X1156, del punto de Schröder.
El punto en el infinito de la recta O1O2 es X14077, conjugado isogonal de X14074.
ADGEOM #2800
Given triangle ABC and a point P.
PA,PB,PC intersect the circle (PBC),(PCA),(PAB) at D,E,F.
Euler lines of DBC,ECA,FAB are concurrent (at a point on the circumcircle of ABC) if only if P lies on Euler-Morley quintic (
Q003 in related curves of Bernard Gibert).
Writing Q as Q(P)=Intersection of the three lines of Euler , the occurrence of {i,j} in the following list means that Q(X(i)) = X(j): {1, 100}, {2, 1296}, {4, 110}, {1113, 1114}, {1114, 1113}.
X(14074) = Q(X(1156))=(a/((b - c) (a^2 + b^2 + 4 b c + c^2 - 2 a (b + c))):...:...)
- Domingo, 9 de septiembre del 2018
Triángulo circunceviano, porismo de Poncelet y la cúbica K024
Kjp = K024
Shuzo TAKAMATSU and Shusaku OGINO.-
On Some Cubics connected with Simson lines. Tohoku Math. J. 43, p 102 (1937)
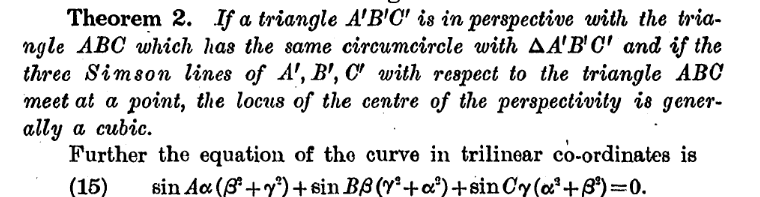
Dados un triángulo ABC y un punto P, sea DEF el de P, entonces existe una cónica inscrita C(P) a estos dos triángulos ().
La cónica C(P) puede ser construida, al conocer cinco tangentes (ttttt). O bien, construyendo su centro, como se describe a continuación. Esto permite determinar su ( del de su centro), y así, determinar los puntos de tangencia de C(P) con los lados de ABC.
Sean Ea = BC ∩ DF, Fa = BC ∩ DE, Ab y Ac los puntos medios de EEa y FFa, respectivamente.
Se definen Bc, Ba, Ca, Cb, cíclicamente.
Las rectas AbAc, BcBa y CaCb son concurrentes en Q, centro de C(P).
Si P(u:v:w), las coordenadas baricéntricas del punto Q son:
(u(a^2 (c^2 v^2+b^2 w^2)+b^2 c^2 u (v+w)) : ... : ...).
La cónica C(P) es parábola si y sólo si P está sobre la cúbica K024.
C(P) es parábola si su centro Q está en la recta del infinito, x+y+z=0. Es decir, si
las coordenadas de P satisfacen a la ecuación:
b^2 c^2 x^2 y + b^2 c^2 x^2 z+ a^2 c^2 x y^2 + a^2 c^2 y^2 z +
a^2 b^2 x z^2 + a^2 b^2 y z^2 = 0.
OTRAS CONSIDERACIONES:
• Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están sobre una misma cónica, para todo punto P. En particular si P es el ortocentro su centro es el de la .
• Cúbicas descritas por centros de C(P).
El lugar geométrico de Q, cuando P se mueve sobre la circunferencia circunscrita, es la
cúbica
( ((a^6 - 3 a^4 b^2 + 3 a^2 b^4 - b^6 - 3 a^4 c^2 - 21 a^2 b^2 c^2 -
3 b^4 c^2 + 3 a^2 c^4 - 3 b^2 c^4 - c^6) x^3 + (-3 a^6 +
9 a^4 b^2 - 9 a^2 b^4 + 3 b^6 + 3 a^4 c^2 + 21 a^2 b^2 c^2 +
3 b^4 c^2 + 3 a^2 c^4 - 3 b^2 c^4 - 3 c^6) x^2 y + (3 a^6 -
9 a^4 b^2 + 9 a^2 b^4 - 3 b^6 + 3 a^4 c^2 + 21 a^2 b^2 c^2 +
3 b^4 c^2 - 3 a^2 c^4 + 3 b^2 c^4 - 3 c^6) x y^2 + (-a^6 +
3 a^4 b^2 - 3 a^2 b^4 + b^6 - 3 a^4 c^2 - 21 a^2 b^2 c^2 -
3 b^4 c^2 - 3 a^2 c^4 + 3 b^2 c^4 - c^6) y^3 + (-3 a^6 +
3 a^4 b^2 + 3 a^2 b^4 - 3 b^6 + 9 a^4 c^2 + 21 a^2 b^2 c^2 -
3 b^4 c^2 - 9 a^2 c^4 + 3 b^2 c^4 + 3 c^6) x^2 z + (6 a^6 -
6 a^4 b^2 - 6 a^2 b^4 + 6 b^6 - 6 a^4 c^2 - 42 a^2 b^2 c^2 -
6 b^4 c^2 - 6 a^2 c^4 - 6 b^2 c^4 + 6 c^6) x y z + (-3 a^6 +
3 a^4 b^2 + 3 a^2 b^4 - 3 b^6 - 3 a^4 c^2 + 21 a^2 b^2 c^2 +
9 b^4 c^2 + 3 a^2 c^4 - 9 b^2 c^4 + 3 c^6) y^2 z + (3 a^6 +
3 a^4 b^2 - 3 a^2 b^4 - 3 b^6 - 9 a^4 c^2 + 21 a^2 b^2 c^2 +
3 b^4 c^2 + 9 a^2 c^4 + 3 b^2 c^4 - 3 c^6) x z^2 + (-3 a^6 -
3 a^4 b^2 + 3 a^2 b^4 + 3 b^6 + 3 a^4 c^2 + 21 a^2 b^2 c^2 -
9 b^4 c^2 + 3 a^2 c^4 + 9 b^2 c^4 - 3 c^6) y z^2 + (-a^6 -
3 a^4 b^2 - 3 a^2 b^4 - b^6 + 3 a^4 c^2 - 21 a^2 b^2 c^2 +
3 b^4 c^2 - 3 a^2 c^4 - 3 b^2 c^4 + c^6) z^3 = 0)
complemento de K244.
Si P recorre la , Q queda sobre la
cúbica
( (a^8 b^4 - 3 a^6 b^6 + 3 a^4 b^8 - a^2 b^10 - 2 a^8 b^2 c^2 +
3 a^6 b^4 c^2 - a^4 b^6 c^2 + a^2 b^8 c^2 - b^10 c^2 + a^8 c^4 +
3 a^6 b^2 c^4 - 4 a^4 b^4 c^4 + 2 b^8 c^4 - 3 a^6 c^6 -
a^4 b^2 c^6 - 2 b^6 c^6 + 3 a^4 c^8 + a^2 b^2 c^8 + 2 b^4 c^8 -
a^2 c^10 - b^2 c^10) x^3 + (a^10 b^2 - 3 a^8 b^4 + 3 a^6 b^6 -
a^4 b^8 - a^10 c^2 + a^8 b^2 c^2 + 5 a^6 b^4 c^2 -
7 a^4 b^6 c^2 + 2 b^10 c^2 + 2 a^8 c^4 - 8 a^6 b^2 c^4 +
4 a^4 b^4 c^4 + 5 a^2 b^6 c^4 - 5 b^8 c^4 + 6 a^4 b^2 c^6 -
5 a^2 b^4 c^6 + 5 b^6 c^6 - 2 a^4 c^8 - a^2 b^2 c^8 - 3 b^4 c^8 +
a^2 c^10 + b^2 c^10) x^2 y + (-a^8 b^4 + 3 a^6 b^6 - 3 a^4 b^8 +
a^2 b^10 + 2 a^10 c^2 - 7 a^6 b^4 c^2 + 5 a^4 b^6 c^2 +
a^2 b^8 c^2 - b^10 c^2 - 5 a^8 c^4 + 5 a^6 b^2 c^4 +
4 a^4 b^4 c^4 - 8 a^2 b^6 c^4 + 2 b^8 c^4 + 5 a^6 c^6 -
5 a^4 b^2 c^6 + 6 a^2 b^4 c^6 - 3 a^4 c^8 - a^2 b^2 c^8 -
2 b^4 c^8 + a^2 c^10 + b^2 c^10) x y^2 + (-a^10 b^2 + 3 a^8 b^4 -
3 a^6 b^6 + a^4 b^8 - a^10 c^2 + a^8 b^2 c^2 - a^6 b^4 c^2 +
3 a^4 b^6 c^2 - 2 a^2 b^8 c^2 + 2 a^8 c^4 - 4 a^4 b^4 c^4 +
3 a^2 b^6 c^4 + b^8 c^4 - 2 a^6 c^6 - a^2 b^4 c^6 - 3 b^6 c^6 +
2 a^4 c^8 + a^2 b^2 c^8 + 3 b^4 c^8 - a^2 c^10 -
b^2 c^10) y^3 + (-a^10 b^2 + 2 a^8 b^4 - 2 a^4 b^8 + a^2 b^10 +
a^10 c^2 + a^8 b^2 c^2 - 8 a^6 b^4 c^2 + 6 a^4 b^6 c^2 -
a^2 b^8 c^2 + b^10 c^2 - 3 a^8 c^4 + 5 a^6 b^2 c^4 +
4 a^4 b^4 c^4 - 5 a^2 b^6 c^4 - 3 b^8 c^4 + 3 a^6 c^6 -
7 a^4 b^2 c^6 + 5 a^2 b^4 c^6 + 5 b^6 c^6 - a^4 c^8 - 5 b^4 c^8 +
2 b^2 c^10) x^2 z + (-2 a^10 b^2 + 8 a^8 b^4 - 12 a^6 b^6 +
8 a^4 b^8 - 2 a^2 b^10 - 2 a^10 c^2 - 4 a^8 b^2 c^2 +
6 a^6 b^4 c^2 + 6 a^4 b^6 c^2 - 4 a^2 b^8 c^2 - 2 b^10 c^2 +
8 a^8 c^4 + 6 a^6 b^2 c^4 - 24 a^4 b^4 c^4 + 6 a^2 b^6 c^4 +
8 b^8 c^4 - 12 a^6 c^6 + 6 a^4 b^2 c^6 + 6 a^2 b^4 c^6 -
12 b^6 c^6 + 8 a^4 c^8 - 4 a^2 b^2 c^8 + 8 b^4 c^8 - 2 a^2 c^10 -
2 b^2 c^10) x y z + (a^10 b^2 - 2 a^8 b^4 + 2 a^4 b^8 - a^2 b^10 +
a^10 c^2 - a^8 b^2 c^2 + 6 a^6 b^4 c^2 - 8 a^4 b^6 c^2 +
a^2 b^8 c^2 + b^10 c^2 - 3 a^8 c^4 - 5 a^6 b^2 c^4 +
4 a^4 b^4 c^4 + 5 a^2 b^6 c^4 - 3 b^8 c^4 + 5 a^6 c^6 +
5 a^4 b^2 c^6 - 7 a^2 b^4 c^6 + 3 b^6 c^6 - 5 a^4 c^8 - b^4 c^8 +
2 a^2 c^10) y^2 z + (2 a^10 b^2 - 5 a^8 b^4 + 5 a^6 b^6 -
3 a^4 b^8 + a^2 b^10 + 5 a^6 b^4 c^2 - 5 a^4 b^6 c^2 -
a^2 b^8 c^2 + b^10 c^2 - a^8 c^4 - 7 a^6 b^2 c^4 +
4 a^4 b^4 c^4 + 6 a^2 b^6 c^4 - 2 b^8 c^4 + 3 a^6 c^6 +
5 a^4 b^2 c^6 - 8 a^2 b^4 c^6 - 3 a^4 c^8 + a^2 b^2 c^8 +
2 b^4 c^8 + a^2 c^10 - b^2 c^10) x z^2 + (a^10 b^2 - 3 a^8 b^4 +
5 a^6 b^6 - 5 a^4 b^8 + 2 a^2 b^10 + a^10 c^2 - a^8 b^2 c^2 -
5 a^6 b^4 c^2 + 5 a^4 b^6 c^2 - 2 a^8 c^4 + 6 a^6 b^2 c^4 +
4 a^4 b^4 c^4 - 7 a^2 b^6 c^4 - b^8 c^4 - 8 a^4 b^2 c^6 +
5 a^2 b^4 c^6 + 3 b^6 c^6 + 2 a^4 c^8 + a^2 b^2 c^8 - 3 b^4 c^8 -
a^2 c^10 + b^2 c^10) y z^2 + (-a^10 b^2 + 2 a^8 b^4 - 2 a^6 b^6 +
2 a^4 b^8 - a^2 b^10 - a^10 c^2 + a^8 b^2 c^2 + a^2 b^8 c^2 -
b^10 c^2 + 3 a^8 c^4 - a^6 b^2 c^4 - 4 a^4 b^4 c^4 -
a^2 b^6 c^4 + 3 b^8 c^4 - 3 a^6 c^6 + 3 a^4 b^2 c^6 +
3 a^2 b^4 c^6 - 3 b^6 c^6 + a^4 c^8 - 2 a^2 b^2 c^8 + b^4 c^8) z^3 = 0)
complemento de K1065.
Si P está en la recta X1X3, Q queda sobre la
cúbica
( (-a^2 b^3 c + 2 a b^4 c - b^5 c + 2 a^2 b^2 c^2 - 2 a b^3 c^2 +
b^4 c^2 - a^2 b c^3 - 2 a b^2 c^3 + 2 a b c^4 + b^2 c^4 -
b c^5) x^3 + (-a^4 b c + 3 a^3 b^2 c - 2 a^2 b^3 c - a b^4 c +
b^5 c + a^4 c^2 - 2 a^3 b c^2 - 2 a^2 b^2 c^2 + 4 a b^3 c^2 -
2 b^4 c^2 - a^3 c^3 + 5 a^2 b c^3 - 2 a b^2 c^3 + b^3 c^3 -
a^2 c^4 - 2 a b c^4 + a c^5) x^2 y + (a^5 c - a^4 b c -
2 a^3 b^2 c + 3 a^2 b^3 c - a b^4 c - 2 a^4 c^2 + 4 a^3 b c^2 -
2 a^2 b^2 c^2 - 2 a b^3 c^2 + b^4 c^2 + a^3 c^3 - 2 a^2 b c^3 +
5 a b^2 c^3 - b^3 c^3 - 2 a b c^4 - b^2 c^4 +
b c^5) x y^2 + (-a^5 c + 2 a^4 b c - a^3 b^2 c + a^4 c^2 -
2 a^3 b c^2 + 2 a^2 b^2 c^2 - 2 a^2 b c^3 - a b^2 c^3 + a^2 c^4 +
2 a b c^4 - a c^5) y^3 + (a^4 b^2 - a^3 b^3 - a^2 b^4 + a b^5 -
a^4 b c - 2 a^3 b^2 c + 5 a^2 b^3 c - 2 a b^4 c + 3 a^3 b c^2 -
2 a^2 b^2 c^2 - 2 a b^3 c^2 - 2 a^2 b c^3 + 4 a b^2 c^3 +
b^3 c^3 - a b c^4 - 2 b^2 c^4 + b c^5) x^2 z + (-a^5 b +
2 a^3 b^3 - a b^5 - a^5 c + 6 a^4 b c - 5 a^3 b^2 c -
5 a^2 b^3 c + 6 a b^4 c - b^5 c - 5 a^3 b c^2 + 12 a^2 b^2 c^2 -
5 a b^3 c^2 + 2 a^3 c^3 - 5 a^2 b c^3 - 5 a b^2 c^3 + 2 b^3 c^3 +
6 a b c^4 - a c^5 - b c^5) x y z + (a^5 b - a^4 b^2 - a^3 b^3 +
a^2 b^4 - 2 a^4 b c + 5 a^3 b^2 c - 2 a^2 b^3 c - a b^4 c -
2 a^3 b c^2 - 2 a^2 b^2 c^2 + 3 a b^3 c^2 + a^3 c^3 +
4 a^2 b c^3 - 2 a b^2 c^3 - 2 a^2 c^4 - a b c^4 +
a c^5) y^2 z + (a^5 b - 2 a^4 b^2 + a^3 b^3 - a^4 b c +
4 a^3 b^2 c - 2 a^2 b^3 c - 2 a b^4 c + b^5 c - 2 a^3 b c^2 -
2 a^2 b^2 c^2 + 5 a b^3 c^2 - b^4 c^2 + 3 a^2 b c^3 -
2 a b^2 c^3 - b^3 c^3 - a b c^4 + b^2 c^4) x z^2 + (a^3 b^3 -
2 a^2 b^4 + a b^5 + a^5 c - 2 a^4 b c - 2 a^3 b^2 c +
4 a^2 b^3 c - a b^4 c - a^4 c^2 + 5 a^3 b c^2 - 2 a^2 b^2 c^2 -
2 a b^3 c^2 - a^3 c^3 - 2 a^2 b c^3 + 3 a b^2 c^3 + a^2 c^4 -
a b c^4) y z^2 + (-a^5 b + a^4 b^2 + a^2 b^4 - a b^5 +
2 a^4 b c - 2 a^3 b^2 c - 2 a^2 b^3 c + 2 a b^4 c - a^3 b c^2 +
2 a^2 b^2 c^2 - a b^3 c^2) z^3 = 0)
complemento de K1066.
Si P está en la recta del infinito, Q queda sobre K258 complemento de K028.
Para todo punto P sobre el , Q = X39, punto medio de los .
Otros pares {P=Xi, Q=Xj} son para {i,j} = {1, 1125}, {2, 3934}, {3, 3}, {4, 389}, {6, 39}, {25, 3767}, {55, 1212}, {513, 1}, {514, 2140}, {523, 5}, {1510, 15345}, {2574, 3}, {2575, 3}, {2590, 1212}, {2591, 1212}, {3513, 1}, {3514, 1}, {4057, 4075}, {4083, 14823}, {8105, 3767}, {8106, 3767}, {18105, 7829}.
- Jueves, 6 de septiembre del 2018
Envolvente de elipses con centros en la recta de Euler
Dado un triángulo ABC de circuncentro O=X3, ortocentro H=X4, centro de la N=X5 y A'B'C'.
Sea Oa el centro de la circunferencia Γa de diámetro AO (pasa por B' y C'); en consecuencia, los triángulos AOB' y AOC' tienen circuncentro común, Oa, y ortocentros B' y C', respectivamente.
Se toma un punto P, sobre la de ABC, tal que OP:PH=t. Sean Pab y Pac los puntos sobre las rectas de Euler de AOB' y AOC', tales que OaPab:PabB' = OaPac:PacC' = t, respectivamente.
Los puntos Pbc, Pba, Pca y Pcb, se definen cíclicamente.
Los seis puntos
Pab,
Pac,
Pbc,
Pba,
Pca y
Pcb están sobre una misma elipse ℰ
t con centro
Q, sobre la recta de Euler, tal que
OQ:QH = 8+16t : 8(5+4t).
La envolvente de las elipses ℰt es una cónica 𝒞 de centro el punto medio de O y N.
En coordenadas baricéntricas:
Pab = ((a^4-2a^2(b^2+c^2)+(b^2-c^2)^2) t+2a^4-3a^2(b^2+c^2)+(b^2-c^2)^2 :
-b^2(a^2-b^2+c^2) : (a^4-2a^2(b^2+c^2)+(b^2-c^2)^2) t-c^2(a^2+b^2-c^2) ),
Pac = ((a^4+(b^2-c^2)^2-2a^2(b^2+c^2)) t+2a^4+(b^2-c^2)^2-3a^2(b^2+c^2) :
(a^4-2a^2(b^2+c^2)+(b^2-c^2)^2) t-b^2(a^2-b^2+c^2) : -c^2(a^2+b^2-c^2) ).
La ecuación de la elipse ℰt es:
(((a^4+(b^2-c^2)^2-2a^2(b^2+c^2))^2) t^2 +
(a^8+3(b^2-c^2)^4-6a^6(b^2+c^2)-10a^2(b^2-c^2)^2(b^2+c^2)+4a^4(3b^4+2b^2c^2+3c^4)) t
- a^6(b^2+c^2)-5a^2(b^2-c^2)^2(b^2+c^2)+(b^2-c^2)^2(2b^4-
3b^2c^2+2c^4)+a^4(4b^4+3b^2c^2+4c^4)) x^2 +
((-2(a^4+(b^2-c^2)^2-2a^2(b^2+c^2))^2) t ^2 +
(-2(a^8+2(b^2-c^2)^4-5a^6(b^2+c^2)-7a^2(b^2-c^2)^2(b^2+c^2)+
a^4(9b^4+6b^2c^2+9c^4))) t +
4a^6(b^2+c^2)+8a^2(b^2-c^2)^2(b^2+c^2)-2(b^2-c^2)^2(b^4-3b^2c^2+c^4)-2a^4(5b^4+3b^2c^2+5c^4)) y z + ⋯ = 0.
Algunos pares {P=Xi), Q=Xj}, para {i,j}:
{2,5054}, {3,549}, {4,2}, {5,140}, {20,3}, {30,30}, {140,11812}, {376,3524}, {381,11539}, {382,5}, {546,10124}, {547,14890}, {548,3530}, {550,12100}, {631,631}, {858,10257}, {1656,15713}, {1657,8703}, {2041,18585}, {2042,15765}, {3090,15702}, {3091,15694}, {3146,381}, {3149,17564}, {3522,15693}, {3523,15701}, {3524,15708}, {3525,15721}, {3526,14869}, {3528,3523}, {3529,376}, {3530,12108}, {3534,17504}, {3543,5055}, {3545,15709}, {3627,547}, {3830,15699}, {3832,3526}, {3843,632}, {3850,11540}, {3853,3628}, {3855,3525}, {3861,16239}, {5059,3534}, {5067,10303}, {5073,3845}, {5899,16532}, {6845,7483}, {6930,6883}, {6934,16371}, {6938,16370}, {6999,13633}, {7553,10127}, {10296,2072}, {10304,15707}, {11001,10304}, {11541,3543}, {12103,14891}, {12362,7734}, {14494,20}, {14790,18281}, {15640,14269}, {15682,3545}, {15683,15688}, {15696,15712}, {15717,15720}, {17538,15692}, {17578,1656}, {17714,15330}, {17800,550}, {20063,2070}.
La envolvente de las elipses ℰt es la cónica
𝒞 : (a^8-4a^6(b^2+c^2)+a^4(6b^4+8b^2c^2+6c^4)-4a^2(b^2-c^2)^2(b^2+c^2)+(b^2-c^2)^2(b^4-6b^2c^2+c^4)) x^2 +
2(a^8+2a^6(b^2+c^2)-8a^4(b^4+c^4)+6a^2(b^2-c^2)^2(b^2+c^2)-(b^2-c^2)^4) y z + ⋯ = 0.
El centro de 𝒞 es X140 (punto medio de O y N). Su es:
T = ( 1/(a^8-4a^6(b^2+c^2)+6a^4(b^4+b^2c^2+c^4)
-4a^2(b^2-c^2)^2(b^2+c^2)+(b^2-c^2)^2(b^4-4b^2c^2+c^4) ) : ... : ...),
que tiene números de búsqueda en
(3.37591225079395, 3.92978264299378, -0.638067617454672) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,6748}, {97,631}, {140,394}, {1073,3526}, {1214,6958}, {1232,3926}, {3525,14919}, {3682,21012}, {13336,17974}.
Cada elipse ℰt es bitangente a la cónica 𝒞.
Caso particular, P=N (Kadir Altintas):
ℰ1 y 𝒞 son tangentes en los extremos del diámetro conjugado, respecto a ambas cónicas, de la recta de Euler.
TRIÁNGULOS HOMOTÉTICOS
Se definen los puntos:
A1 = PbaPbc ∩ PcaPcb
B1 = PcbPca ∩ PabPac
C1 = PacPab ∩ PbcPba
A2 = PabPba ∩ PacPca
B2 = PbcPcb ∩ PbaPab
C2 = PcaPac ∩ PcbPbc
Los triángulos y son homotéticos a
ABC y los centros de homotecia están sobre la recta de Euler y son, respectivamente,
Z1 = (3+2t) O + (1+t) H
Z2 = (1+2t) O + t H.
El punto P = O + t H coincide con Z1 para t= 1/2 (-1 ± √3). Es decir, cuando P es X2041, X2042 (primer y segundo punto Euler-Vecten-Gibert).
Si P = X2041, el centro de la correspondiente elipse ℰt es X18585 = √3X2 - X3, y para P = X2042, el centro es X15765 = √3X2 + X3.
El punto P = O + t H coincide con Z2 solo cuando t= 0.
- Sábado, 1 de septiembre del 2018
Una propiedad del centro del triángulo X(262)
Let A'B'C' be the orthic triangle.
X(262) is the radical center of the Brocard circles of AB'C', BC'A', CA'B'. (Randy Hutson, February 10, 2016)
Let Pa be the parabola with focus A and directrix BC. Let La be the polar of X(3) wrt Pa and define Lb and Lc cyclically. Let A' = Lb∩Lc, B' = Lc∩La, C' = La∩Lb. The lines AA', BB', CC' concur in X(262). Also, X(262) is also the isotomic conjugate, wrt A'B'C', of X(3).
Let A' be the apex of the isosceles triangle BA'C constructed outward on BC such that ∠A'BC = ∠A'CB = ω. Define B', C' cyclically. Let Ha be the orthocenter of BA'C, and define Hb, Hc cyclically. The lines AHa, BHb, CHc concur in X(262). (Randy Hutson, July 20, 2016)
Let A' be the apex of the isosceles triangle BA'C constructed intward on BC such that ∠A'BC = ∠A'CB = ω/2. Define B', C' cyclically. Let Oa be the circumcenter of BA'C, and define Ob, Oc cyclically. The lines AOa, BOb, COc concur in X(262). (Randy Hutson, July 20, 2016)
Dado un triángulo ABC sea su .
Existe un único punto Ac, sobre la recta AB, tal que los cuatro puntos A, Mb, Ac y BMb ∩ CAc son distintos y cocíclicos. Sea Oac el centro de la circunferencia que los contiene.
Así mismo, existe un único punto Ab, sobre la recta AC, tal que los cuatro puntos A, Mc, Ac y CMc ∩ BAb son distintos y cocíclicos. Sea Oab el centro de la circunferencia que los contiene.
Se definen los puntos Obc, Oba, Oca y Ocb cíclicamente.
El triángulo A'B'C' formado por las rectas OabOac, ObcOba y OcaOcb es el
.
Los triángulos ABC y A'B'C' son perspectivos con centro de perspectividad X262, el conjugado isogonal de punto medio del .
La circunferencia que pasa por A, Mb y por un punto de coordenadas baricéntricas Ac(1:t:0) sobre AC (t ≠ 0,-1), que tiene ecuación
a^2y z+b^2z x + c^2x y - (x+y+z)(c^2y/(1+t)+b^2z/2) = 0,
pasa por BMb ∩ CAc si t = (b^2+2c^2-2a^2)/(2a^2-b^2).
Su centro es:
Oab = (2b^2(-2a^2+b^2-c^2) : -b^2(-3a^2+b^2+3c^2) :
2a^4-a^2(3b^2+4c^2)+b^4+b^2c^2+2c^4).
La circunferencia que pasa por A, Mc y por un punto de coordenadas baricéntricas Ab(1:0:t) sobre AB (t ≠ 0,-1), que tiene ecuación
a^2y z + b^2z x + c^2x y - (x+y+z)(c^2y/2+b^2z/(1+t)) = 0,
pasa por BMc ∩ CAb si t = (2b^2+c^2-2a^2)/(2a^2-c^2).
Su centro es:
Oac = (2c^2(-2a^2-b^2+c^2) :
2a^4-a^2(4b^2+3c^2)+2b^4+b^2c^2+c^4 : -c^2(-3a^2+3b^2+c^2)).
La ecuación de la recta OabOac es (b^2+c^2-a^2) x - 2c^2y - 2b^2z = 0,
directriz de la A-parábola de Artzt.
El centro de la de ABC y A'B'C' es X15265
(César Eliud Lozada, November 14, 2017).
- Jueves, 30 de agosto del 2018
Una propiedad de la quíntica de Euler-Morley
Dados un triángulo ABC y un punto P (no situado en la recta del infinito), la perpendicular por P a AP corta a BC en Pa. Sea Ma el punto medio de A y Pa; la recta PMa corta a BC, CA, AB en los puntos Paa, Pab, Pac, respectivamente.
Los puntos Pbb, Pbc, Pba y Pcc, Pca, Pcb, se definen cíclicamente.
El punto
P queda sobre quíntica de Euler-Morley (
Q003) si y solo si los puntos
Paa,
Pbb y
Pcc están alineados, si y solo si los puntos
Pab,
Pac,
Pbc,
Pba,
Pca y
Pcb están sobre una misma cónica.
Si (u:v:w) son las coordenadas baricéntricas del punto P, respecto al triángulo ABC,
Pa = (0 : v^2-SC(u+v)w-SAu(v+w) : -SCw^2+SBv(u+w)+SAu(v+w)),
Paa = (0 : SAu^2(v+w)+SBv^2(v+w)+
SCw(u^2-v(v+w)) : -SAu^2(v+w)-SCw^2(v+w)-
SBv(u^2-w(v+w)) ),
Pab = (-SAu^2(v+w)-SBv^2(v+w)+
SCw(-u^2+v(v+w)) : 0 :-u(SBv^2+SCw^2+SA(v+w)^2)),
Pac = (SAu^2(v+w)+SCw^2(v+w)+
SBv(u^2-w(v+w)) : u(SBv^2+SCw^2+SA(v+w)^2) : 0).
La condición para que los puntos Paa, Pbb y Pcc estén alineados, y para que los puntos Pab, Pac, Pbc, Pba, Pca y Pcb están sobre una misma cónica es:
-a^2 c^2 u^3 v^2+b^2 c^2 u^3 v^2+c^4 u^3 v^2-a^2 c^2 u^2 v^3+b^2 c^2 u^2 v^3-c^4 u^2 v^3+a^2 b^2 u^3 w^2-b^4 u^3 w^2-b^2 c^2 u^3 w^2+a^4 v^3 w^2-a^2 b^2 v^3 w^2+a^2 c^2 v^3 w^2+a^2 b^2 u^2 w^3+b^4 u^2 w^3-b^2 c^2 u^2 w^3-a^4 v^2 w^3-a^2 b^2 v^2 w^3+a^2 c^2 v^2 w^3 = 0,
es decir, que P quede sobre la quíntica Q003, que pasa por los centros del triángulo Xi, para los índices i = 1, 2, 4, 13, 14, 357, 1113, 1114, 1134, 1136, 1156.
Para P sobre Q003, se desina por r(P) la recta que pasa por Paa, Pbb y Pcc, y por c(P) la cónica que contiene a los seis puntos Pab, Pac, Pbc, Pba, Pca y Pcb.
• Si P=X1 (el incentro), r(X1) es la de X63, el del .
El centro de la cónica
c(X1)
( 2 a^7 b c x^2-2 a^5 b^3 c x^2-2 a^3 b^5 c x^2+2 a b^7 c x^2-2 a^5 b c^3 x^2+4 a^3 b^3 c^3 x^2-2 a b^5 c^3 x^2-2 a^3 b c^5 x^2-2 a b^3 c^5 x^2+2 a b c^7 x^2-a^8 c x y-4 a^6 b^2 c x y+10 a^4 b^4 c x y-4 a^2 b^6 c x y-b^8 c x y+2 a^6 c^3 x y-2 a^4 b^2 c^3 x y-2 a^2 b^4 c^3 x y+2 b^6 c^3 x y+8 a^2 b^2 c^5 x y-2 a^2 c^7 x y-2 b^2 c^7 x y+c^9 x y+2 a^7 b c y^2-2 a^5 b^3 c y^2-2 a^3 b^5 c y^2+2 a b^7 c y^2-2 a^5 b c^3 y^2+4 a^3 b^3 c^3 y^2-2 a b^5 c^3 y^2-2 a^3 b c^5 y^2-2 a b^3 c^5 y^2+2 a b c^7 y^2-a^8 b x z+2 a^6 b^3 x z-2 a^2 b^7 x z+b^9 x z-4 a^6 b c^2 x z-2 a^4 b^3 c^2 x z+8 a^2 b^5 c^2 x z-2 b^7 c^2 x z+10 a^4 b c^4 x z-2 a^2 b^3 c^4 x z-4 a^2 b c^6 x z+2 b^3 c^6 x z-b c^8 x z+a^9 y z-2 a^7 b^2 y z+2 a^3 b^6 y z-a b^8 y z-2 a^7 c^2 y z+8 a^5 b^2 c^2 y z-2 a^3 b^4 c^2 y z-4 a b^6 c^2 y z-2 a^3 b^2 c^4 y z+10 a b^4 c^4 y z+2 a^3 c^6 y z-4 a b^2 c^6 y z-a c^8 y z+2 a^7 b c z^2-2 a^5 b^3 c z^2-2 a^3 b^5 c z^2+2 a b^7 c z^2-2 a^5 b c^3 z^2+4 a^3 b^3 c^3 z^2-2 a b^5 c^3 z^2-2 a^3 b c^5 z^2-2 a b^3 c^5 z^2+2 a b c^7 z^2 = 0)
es:
W1 = ( a(a^3-a^2(b+c)+
a(b+c)^2)(a^4-(b^2-c^2)^2-b^3-b^2c-bc^2-c^3) : ... : ...),
que tiene números de búsqueda en
(1.74243545983045, 1.38031111519091, 1.88086349762278) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,475}, {9,8750}, {19,25}, {34,1883}, {75,1897}, {200,3192}, {210,3195}, {318,5263}, {474,17102}, {594,2331}, {975,6198}, {1041,5236}, {1249,2345}, {1876,3242}, {2207,7079}, {2550,7952}, {8270,11677}, {12329,20613}.
El de la cónica c(X1) es:
P1 = ( a/(3a^2+b^2+c^2) : ... : ...),
que tiene números de búsqueda en
(2.29191070937116, 1.83148221864927, 1.31491031082512) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {10,4000}, {19,38}, {37,614}, {63,82}, {65,3242}, {75,16750}, {158,20883}, {225,8801}, {759,907}, {969,3873}, {1910,17467}, {2186,17445}, {2345,3677}, {3668,11677}, {8769,17446}, {16517,18785}.
El de recta r(X1) respecto a la cónica c(X1) es:
Q1 = ( a(a^4-(b^2-c^2)^2)(a^4+
2a^2(b^2+c^2)-3b^4-2b^2c^2-3c^4) : ... : ...),
que tiene números de búsqueda en
(1.44575902949956, 1.36288319713096, 2.02985656258622) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,19}, {4,3663}, {33,3666}, {34,6180}, {38,1096}, {63,162}, {75,1895}, {158,20883}, {278,3677}, {281,7174}, {474,17102}, {518,2331}, {811,3403}, {982,1435}, {984,7079}, {986,11471}, {1040,19649}, {1210,1861}, {1767,8270}, {1783,5223}, {1859,17599}, {3242,14571}, {4310,5236}, {4847,17903}, {5573,17917}.
• Si P=X2 (el baricentro), r(X2) es la tripolar de X5485, del del baricentro.
El centro de la cónica
c(X2)
( 10 a^4 x^2-22 a^2 b^2 x^2+4 b^4 x^2-22 a^2 c^2 x^2+8 b^2 c^2 x^2+4 c^4 x^2-13 a^4 x y+46 a^2 b^2 x y-13 b^4 x y+4 a^2 c^2 x y+4 b^2 c^2 x y+17 c^4 x y+4 a^4 y^2-22 a^2 b^2 y^2+10 b^4 y^2+8 a^2 c^2 y^2-22 b^2 c^2 y^2+4 c^4 y^2-13 a^4 x z+4 a^2 b^2 x z+17 b^4 x z+46 a^2 c^2 x z+4 b^2 c^2 x z-13 c^4 x z+17 a^4 y z+4 a^2 b^2 y z-13 b^4 y z+4 a^2 c^2 y z+46 b^2 c^2 y z-13 c^4 y z+4 a^4 z^2+8 a^2 b^2 z^2+4 b^4 z^2-22 a^2 c^2 z^2-22 b^2 c^2 z^2+10 c^4 z^2 = 0)
es:
W2 = ( 17a^4-20a^2(b^2+c^2)+11b^4-26b^2c^2+11c^4 : ... : ...),
que tiene números de búsqueda en
(13.0364521767226, 3.42895966511254, -4.75005475242702) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,6}, {671,3524}, {1153,2549}, {3545,13449}, {5067,7812}, {5210,20112}, {7607,11172}, {7612,11179}, {11147,16509}, {14568,15709}.
El perspector de la cónica c(X2) es:
P2 = ( 1/(19a^4-40a^2b^2+13b^4-40a^2c^2-10b^2c^2+13c^4) : ... : ...),
que tiene números de búsqueda en
(6.78059459026019, 0.333960683425304, 0.279955736339079) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1992,16509}, {4232,8860}.
El polo de r(X2) respecto a c(X2) es la reflexión de X1007 en el baricentro:
Q2 = (11a^4-8a^2(b^2+c^2)+5b^4-14b^2c^2+5c^4 : ... : ...),
que tiene números de búsqueda en
(-6.91949028070401, 0.215081291819118, 6.68537294789607); reflexión de X1007 en X2 para los índices {i,j}: {6697, 3589}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,6}, {98,11172}, {99,5485}, {115,8182}, {187,7615}, {376,671}, {381,9752}, {598,1285}, {1384,3363}, {2549,5569}, {3090,7812}, {3524,14568}, {3533,7760}, {3543,9756}, {3545,10788}, {3785,11318}, {5067,6179}, {5461,16041}, {6054,9754}, {7617,7737}, {7619,7798}, {7620,8598}, {7710,11177}, {7757,15702}, {7810,14064}, {7817,16043}, {9166,14907}, {9167,17131}, {9209,14977}, {9741,11054}, {9759,11061}, {11159,16509}, {12150,18842}.
• Si P=X4 (el ortocentro), r(X4) es la recta del infinito y la cónica
c(X4)
( 2 a^12 x^2-6 a^10 b^2 x^2+4 a^8 b^4 x^2+4 a^6 b^6 x^2-6 a^4 b^8 x^2+2 a^2 b^10 x^2-6 a^10 c^2 x^2+16 a^8 b^2 c^2 x^2-12 a^6 b^4 c^2 x^2+2 a^2 b^8 c^2 x^2+4 a^8 c^4 x^2-12 a^6 b^2 c^4 x^2+12 a^4 b^4 c^4 x^2-4 a^2 b^6 c^4 x^2+4 a^6 c^6 x^2-4 a^2 b^4 c^6 x^2-6 a^4 c^8 x^2+2 a^2 b^2 c^8 x^2+2 a^2 c^10 x^2+a^12 x y+2 a^10 b^2 x y-17 a^8 b^4 x y+28 a^6 b^6 x y-17 a^4 b^8 x y+2 a^2 b^10 x y+b^12 x y-2 a^10 c^2 x y+6 a^8 b^2 c^2 x y-4 a^6 b^4 c^2 x y-4 a^4 b^6 c^2 x y+6 a^2 b^8 c^2 x y-2 b^10 c^2 x y-a^8 c^4 x y-12 a^6 b^2 c^4 x y+26 a^4 b^4 c^4 x y-12 a^2 b^6 c^4 x y-b^8 c^4 x y+4 a^6 c^6 x y-4 a^4 b^2 c^6 x y-4 a^2 b^4 c^6 x y+4 b^6 c^6 x y-a^4 c^8 x y+10 a^2 b^2 c^8 x y-b^4 c^8 x y-2 a^2 c^10 x y-2 b^2 c^10 x y+c^12 x y+2 a^10 b^2 y^2-6 a^8 b^4 y^2+4 a^6 b^6 y^2+4 a^4 b^8 y^2-6 a^2 b^10 y^2+2 b^12 y^2+2 a^8 b^2 c^2 y^2-12 a^4 b^6 c^2 y^2+16 a^2 b^8 c^2 y^2-6 b^10 c^2 y^2-4 a^6 b^2 c^4 y^2+12 a^4 b^4 c^4 y^2-12 a^2 b^6 c^4 y^2+4 b^8 c^4 y^2-4 a^4 b^2 c^6 y^2+4 b^6 c^6 y^2+2 a^2 b^2 c^8 y^2-6 b^4 c^8 y^2+2 b^2 c^10 y^2+a^12 x z-2 a^10 b^2 x z-a^8 b^4 x z+4 a^6 b^6 x z-a^4 b^8 x z-2 a^2 b^10 x z+b^12 x z+2 a^10 c^2 x z+6 a^8 b^2 c^2 x z-12 a^6 b^4 c^2 x z-4 a^4 b^6 c^2 x z+10 a^2 b^8 c^2 x z-2 b^10 c^2 x z-17 a^8 c^4 x z-4 a^6 b^2 c^4 x z+26 a^4 b^4 c^4 x z-4 a^2 b^6 c^4 x z-b^8 c^4 x z+28 a^6 c^6 x z-4 a^4 b^2 c^6 x z-12 a^2 b^4 c^6 x z+4 b^6 c^6 x z-17 a^4 c^8 x z+6 a^2 b^2 c^8 x z-b^4 c^8 x z+2 a^2 c^10 x z-2 b^2 c^10 x z+c^12 x z+a^12 y z-2 a^10 b^2 y z-a^8 b^4 y z+4 a^6 b^6 y z-a^4 b^8 y z-2 a^2 b^10 y z+b^12 y z-2 a^10 c^2 y z+10 a^8 b^2 c^2 y z-4 a^6 b^4 c^2 y z-12 a^4 b^6 c^2 y z+6 a^2 b^8 c^2 y z+2 b^10 c^2 y z-a^8 c^4 y z-4 a^6 b^2 c^4 y z+26 a^4 b^4 c^4 y z-4 a^2 b^6 c^4 y z-17 b^8 c^4 y z+4 a^6 c^6 y z-12 a^4 b^2 c^6 y z-4 a^2 b^4 c^6 y z+28 b^6 c^6 y z-a^4 c^8 y z+6 a^2 b^2 c^8 y z-17 b^4 c^8 y z-2 a^2 c^10 y z+2 b^2 c^10 y z+c^12 y z+2 a^10 c^2 z^2+2 a^8 b^2 c^2 z^2-4 a^6 b^4 c^2 z^2-4 a^4 b^6 c^2 z^2+2 a^2 b^8 c^2 z^2+2 b^10 c^2 z^2-6 a^8 c^4 z^2+12 a^4 b^4 c^4 z^2-6 b^8 c^4 z^2+4 a^6 c^6 z^2-12 a^4 b^2 c^6 z^2-12 a^2 b^4 c^6 z^2+4 b^6 c^6 z^2+4 a^4 c^8 z^2+16 a^2 b^2 c^8 z^2+4 b^4 c^8 z^2-6 a^2 c^10 z^2-6 b^2 c^10 z^2+2 c^12 z^2 = 0)
es "the parallels-conic of X4", de centro X10002 (punto medio de X4 y X1249).
El perspector de c(X4) es X8801.
The parallels-conic of P
Let d be the line through a point P parallel to line BC. Let Ab =d∩AB and Ac = d∩AC. Define Bc and Ca cyclically, and define Ba and Cb cyclically. The six points Ab, Bc, Ca, Ab, Bc, Ca lie on a conic, here called the parallels-conic of P.
(Preamble of
X(10001). Peter Moses, May 2, 2016.)
Let Ab and Ac be the intersections of lines CA and AB, respectlivey, with the parallel to BC through X(4). Define Bc and Ca cyclically, and define and Ba, Cb cyclically. The points Ab, Ac, Bc, Ba, Ca, Cb lie on a conic centered at the midpoint of X(4) and X(1249). The perspector of the conic is X(8801) (Randy Hutson, December 26, 2015)
- Martes, 28 de agosto del 2018
Rectas de Euler y cónicas asociadas
En un triángulo ABC, sean Γ la circunferencia circunscrita, O=X3 el circuncentro, H=X4 el ortocentro y A', B', C' las reflexiones de O en BC, CA, AB, respectivamente.
La circunferencia Γa de centro A' y que pasa por A interseca de nuevo a Γ en A".
La circunferencia Γb de centro B' y que pasa por B interseca de nuevo a Γ en B".
La circunferencia Γc de centro C' y que pasa por C interseca de nuevo a Γ en C".
Sea P un punto sobre la de ABC (tal que OP:PH= t) y Pa, Pb, Pc el mismo punto que P de los triángulos A"BC, B"CA, C"AB, respectivamente.
Los triángulos ABC y son perspectivos. El lugar geométrico del centro de perspectividad es la hipérbola de Jerabek, cuando P varía sobre la recta de Euler.
En coordenadas baricéntricas:
A' =(a^2(a^2-b^2-c^2) : -a^4+c^2(b^2-c^2)+
a^2(b^2+2c^2) : -a^4-b^4+b^2c^2+a^2(2b^2+c^2)),
A'' = (-a^2 : b^2-c^2 : -b^2+c^2).
Un punto P sobre la recta de Euler tal que OP:PH= t es:
P = (a^2(b^2+c^2)+a^4(-1+t)-(b^2-c^2)^2t :
b^2c^2+b^4(-1+t)-a^4t-c^4t+a^2(b^2+2c^2t) :
b^2c^2+c^4(-1+t)-a^4t-b^4t+a^2(c^2+2b^2t)).
El mismo punto sobre la recta de Euler de A"BC tiene coordenadas:
Pa = (
a^4(b^2+c^2)+a^6(-1+t)-a^2(b^2-c^2)^2t :
-(a^2-b^2+c^2)(a^4t+(b^2-c^2)^2t-a^2(b^2+2c^2t)) :
-(a^2+b^2-c^2)(a^4t+(b^2-c^2)^2t-a^2(c^2+2b^2t))).
El punto de intersección de las rectas APa, BPb, CPc es
Q = ( (b^2+c^2-a^2)((a^8 + (b^2 - c^2)^4 - 2 a^6 (b^2 + c^2) -
2 a^2 (b^2 - c^2)^2 (b^2 + c^2) +
2 a^4 (b^4 +
c^4))t^2 -a^2 (a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2) -
2 a^2 (b^4 + c^4))t + a^4 b^2 c^2) : ... : ...),
que es un punto de la ( de la recta de Euler), de ecuación implícita:
a^2(a^2 (b^2 - c^2)-b^4 + c^4)y z + b^2(b^2 (c^2 - a^2)-c^4 + a^4)z x + c^2(c^2 (a^2 - b^2)-a^4 + b^4)x y = 0.
Para cada punto P, sobre la recta de Euler, sea P* su conjugado isogonal (sobre la hipérbola de Jerabek).
La envolvente de la recta P*Q, cuando P se mueve sobre la recta de Euler, es una hipérbola ℋ.
Si ABC es acutángulo, ℋ es la imagen de la hipérbola de Jerabek, mediante la homotecia de centro X125 y razón abc/√8 .
Si ABC es obtusángulo, ℋ es la imagen de la hipérbola de Jerabek, mediante el producto de la homotecia de centro X125 y razón abc/√-8 SASBSC, y la rotación de centro X125 y amplitud 90º.
La
hipérbola
( a^4 b^2 x^2 - a^2 b^4 x^2 - a^4 c^2 x^2 + b^4 c^2 x^2 + a^2 c^4 x^2 -
b^2 c^4 x^2 + 2 a^4 b^2 x y - 2 a^2 b^4 x y + 2 a^4 c^2 x y -
2 b^4 c^2 x y - 2 a^2 c^4 x y + 2 b^2 c^4 x y + a^4 b^2 y^2 -
a^2 b^4 y^2 - a^4 c^2 y^2 + b^4 c^2 y^2 + a^2 c^4 y^2 -
b^2 c^4 y^2 - 2 a^4 b^2 x z + 2 a^2 b^4 x z - 2 a^4 c^2 x z -
2 b^4 c^2 x z + 2 a^2 c^4 x z + 2 b^2 c^4 x z - 2 a^4 b^2 y z +
2 a^2 b^4 y z + 2 a^4 c^2 y z + 2 b^4 c^2 y z - 2 a^2 c^4 y z -
2 b^2 c^4 y z + a^4 b^2 z^2 - a^2 b^4 z^2 - a^4 c^2 z^2 +
b^4 c^2 z^2 + a^2 c^4 z^2 - b^2 c^4 z^2 = 0)
ℋ (con las misma asíntotas que la hipérbola de Jerabek) es tangente a la recta de Euler en el centro de la y pasa por los centros X10, X141, X2574, X2575, X6247, X10264, X12359, X13605.
Los triángulos ABC y son inversamente semejantes, para todo t. Con el circuncentro como centro de semejanza.
Para P (OP:PH=t) se designa por σt la semejanza inversa que transforma ABC en . σt(P) queda sobre la recta X3X74.
La envolvente de la recta Pσ(P), cuando P se mueve sobre la recta de Euler, es la parábola 𝒫, de foco el y directriz la recta que pasa por el foco de la y por el centro de la .
La
parábola
( 4 a^12 b^6 c^2 x^2-16 a^10 b^8 c^2 x^2+24 a^8 b^10 c^2 x^2-16 a^6 b^12 c^2 x^2+4 a^4 b^14 c^2 x^2-8 a^12 b^4 c^4 x^2+16 a^10 b^6 c^4 x^2-8 a^8 b^8 c^4 x^2+a^4 b^12 c^4 x^2-2 a^2 b^14 c^4 x^2+b^16 c^4 x^2+4 a^12 b^2 c^6 x^2+16 a^10 b^4 c^6 x^2-32 a^8 b^6 c^6 x^2+16 a^6 b^8 c^6 x^2-4 a^4 b^10 c^6 x^2+6 a^2 b^12 c^6 x^2-6 b^14 c^6 x^2-16 a^10 b^2 c^8 x^2-8 a^8 b^4 c^8 x^2+16 a^6 b^6 c^8 x^2-2 a^4 b^8 c^8 x^2-4 a^2 b^10 c^8 x^2+15 b^12 c^8 x^2+24 a^8 b^2 c^10 x^2-4 a^4 b^6 c^10 x^2-4 a^2 b^8 c^10 x^2-20 b^10 c^10 x^2-16 a^6 b^2 c^12 x^2+a^4 b^4 c^12 x^2+6 a^2 b^6 c^12 x^2+15 b^8 c^12 x^2+4 a^4 b^2 c^14 x^2-2 a^2 b^4 c^14 x^2-6 b^6 c^14 x^2+b^4 c^16 x^2+4 a^14 b^4 c^2 x y-12 a^12 b^6 c^2 x y+8 a^10 b^8 c^2 x y+8 a^8 b^10 c^2 x y-12 a^6 b^12 c^2 x y+4 a^4 b^14 c^2 x y-4 a^14 b^2 c^4 x y+22 a^10 b^6 c^4 x y-36 a^8 b^8 c^4 x y+22 a^6 b^10 c^4 x y-4 a^2 b^14 c^4 x y+12 a^12 b^2 c^6 x y-20 a^10 b^4 c^6 x y+8 a^8 b^6 c^6 x y+8 a^6 b^8 c^6 x y-20 a^4 b^10 c^6 x y+12 a^2 b^12 c^6 x y-10 a^10 b^2 c^8 x y+20 a^8 b^4 c^8 x y-22 a^6 b^6 c^8 x y+20 a^4 b^8 c^8 x y-10 a^2 b^10 c^8 x y+4 a^6 b^4 c^10 x y+4 a^4 b^6 c^10 x y-12 a^4 b^4 c^12 x y+4 a^4 b^2 c^14 x y+4 a^2 b^4 c^14 x y-2 a^2 b^2 c^16 x y+4 a^14 b^4 c^2 y^2-16 a^12 b^6 c^2 y^2+24 a^10 b^8 c^2 y^2-16 a^8 b^10 c^2 y^2+4 a^6 b^12 c^2 y^2+a^16 c^4 y^2-2 a^14 b^2 c^4 y^2+a^12 b^4 c^4 y^2-8 a^8 b^8 c^4 y^2+16 a^6 b^10 c^4 y^2-8 a^4 b^12 c^4 y^2-6 a^14 c^6 y^2+6 a^12 b^2 c^6 y^2-4 a^10 b^4 c^6 y^2+16 a^8 b^6 c^6 y^2-32 a^6 b^8 c^6 y^2+16 a^4 b^10 c^6 y^2+4 a^2 b^12 c^6 y^2+15 a^12 c^8 y^2-4 a^10 b^2 c^8 y^2-2 a^8 b^4 c^8 y^2+16 a^6 b^6 c^8 y^2-8 a^4 b^8 c^8 y^2-16 a^2 b^10 c^8 y^2-20 a^10 c^10 y^2-4 a^8 b^2 c^10 y^2-4 a^6 b^4 c^10 y^2+24 a^2 b^8 c^10 y^2+15 a^8 c^12 y^2+6 a^6 b^2 c^12 y^2+a^4 b^4 c^12 y^2-16 a^2 b^6 c^12 y^2-6 a^6 c^14 y^2-2 a^4 b^2 c^14 y^2+4 a^2 b^4 c^14 y^2+a^4 c^16 y^2-4 a^14 b^4 c^2 x z+12 a^12 b^6 c^2 x z-10 a^10 b^8 c^2 x z+4 a^4 b^14 c^2 x z-2 a^2 b^16 c^2 x z+4 a^14 b^2 c^4 x z-20 a^10 b^6 c^4 x z+20 a^8 b^8 c^4 x z+4 a^6 b^10 c^4 x z-12 a^4 b^12 c^4 x z+4 a^2 b^14 c^4 x z-12 a^12 b^2 c^6 x z+22 a^10 b^4 c^6 x z+8 a^8 b^6 c^6 x z-22 a^6 b^8 c^6 x z+4 a^4 b^10 c^6 x z+8 a^10 b^2 c^8 x z-36 a^8 b^4 c^8 x z+8 a^6 b^6 c^8 x z+20 a^4 b^8 c^8 x z+8 a^8 b^2 c^10 x z+22 a^6 b^4 c^10 x z-20 a^4 b^6 c^10 x z-10 a^2 b^8 c^10 x z-12 a^6 b^2 c^12 x z+12 a^2 b^6 c^12 x z+4 a^4 b^2 c^14 x z-4 a^2 b^4 c^14 x z-2 a^16 b^2 c^2 y z+4 a^14 b^4 c^2 y z-10 a^8 b^10 c^2 y z+12 a^6 b^12 c^2 y z-4 a^4 b^14 c^2 y z+4 a^14 b^2 c^4 y z-12 a^12 b^4 c^4 y z+4 a^10 b^6 c^4 y z+20 a^8 b^8 c^4 y z-20 a^6 b^10 c^4 y z+4 a^2 b^14 c^4 y z+4 a^10 b^4 c^6 y z-22 a^8 b^6 c^6 y z+8 a^6 b^8 c^6 y z+22 a^4 b^10 c^6 y z-12 a^2 b^12 c^6 y z+20 a^8 b^4 c^8 y z+8 a^6 b^6 c^8 y z-36 a^4 b^8 c^8 y z+8 a^2 b^10 c^8 y z-10 a^8 b^2 c^10 y z-20 a^6 b^4 c^10 y z+22 a^4 b^6 c^10 y z+8 a^2 b^8 c^10 y z+12 a^6 b^2 c^12 y z-12 a^2 b^6 c^12 y z-4 a^4 b^2 c^14 y z+4 a^2 b^4 c^14 y z+a^16 b^4 z^2-6 a^14 b^6 z^2+15 a^12 b^8 z^2-20 a^10 b^10 z^2+15 a^8 b^12 z^2-6 a^6 b^14 z^2+a^4 b^16 z^2-2 a^14 b^4 c^2 z^2+6 a^12 b^6 c^2 z^2-4 a^10 b^8 c^2 z^2-4 a^8 b^10 c^2 z^2+6 a^6 b^12 c^2 z^2-2 a^4 b^14 c^2 z^2+4 a^14 b^2 c^4 z^2+a^12 b^4 c^4 z^2-4 a^10 b^6 c^4 z^2-2 a^8 b^8 c^4 z^2-4 a^6 b^10 c^4 z^2+a^4 b^12 c^4 z^2+4 a^2 b^14 c^4 z^2-16 a^12 b^2 c^6 z^2+16 a^8 b^6 c^6 z^2+16 a^6 b^8 c^6 z^2-16 a^2 b^12 c^6 z^2+24 a^10 b^2 c^8 z^2-8 a^8 b^4 c^8 z^2-32 a^6 b^6 c^8 z^2-8 a^4 b^8 c^8 z^2+24 a^2 b^10 c^8 z^2-16 a^8 b^2 c^10 z^2+16 a^6 b^4 c^10 z^2+16 a^4 b^6 c^10 z^2-16 a^2 b^8 c^10 z^2+4 a^6 b^2 c^12 z^2-8 a^4 b^4 c^12 z^2+4 a^2 b^6 c^12 z^2 = 0)
𝒫 es tangente a la recta de Euler en el circuncentro y pasa por los centros
X143 (centro de la circunferencia de los nueve puntos del ),
X5640 (baricentro del ),
X5663 (su punto en la recta del infinito, conjugado isogonal del antipodal del punto de Tixier),
X5889 (ortocentro del del ortocentro),
X12279 ( del anti-tercer Euler triángulo respecto al triángulo cuyos vértices son los puntos medios de las alturas).
- Sábado, 25 de agosto del 2018
Un centro del triángulo sobre la circunferencia de Steiner
En un triángulo ABC, los X3, X115, X131, X187, X399, X11799, X14981, X15478 están sobre una
circunferencia
( c^2 x y + b^2 x z +
a^2 y z + (x + y +
z) (-((b^2 c^2 (a^4 b^2 - 2 a^2 b^4 + b^6 + a^4 c^2 +
2 a^2 b^2 c^2 - b^4 c^2 - 2 a^2 c^4 - b^2 c^4 + c^6) x)/(
2 (-a^2 + b^2) (-a + b - c) (a + b - c) (-a + b + c) (a + b +
c) (-a^2 + c^2))) + (
a^2 c^2 (a^6 - 2 a^4 b^2 + a^2 b^4 - a^4 c^2 + 2 a^2 b^2 c^2 +
b^4 c^2 - a^2 c^4 - 2 b^2 c^4 + c^6) y)/(
2 (a^2 - b^2) (a - b - c) (b - c) (a + b - c) (a - b + c) (b +
c) (a + b + c)) - (
a^2 b^2 (a^6 - a^4 b^2 - a^2 b^4 + b^6 - 2 a^4 c^2 +
2 a^2 b^2 c^2 - 2 b^4 c^2 + a^2 c^4 + b^2 c^4) z)/(
2 (a - b - c) (b - c) (a + b - c) (a - b + c) (b + c) (a + b +
c) (a^2 - c^2))) = 0)
Γ. Su centro es X6132.
Uno de los puntos de intersección de la circunferencia Γ con la es X14981 y el otro es
W = 4 X5 - 3 X131 = X131 - 2 X136:
W = (
2 a^14 (b^2 + c^2)
- a^12 (11 b^4 + 2 b^2 c^2 + 11 c^4)
+ 2 a^10 (12 b^6 + b^4 c^2 + b^2 c^4 + 12 c^6)
- a^8 (25 b^8 + 8 b^6 c^2 - 18 b^4 c^4 + 8 b^2 c^6 + 25 c^8)
+ 2 a^6 (5 b^10 + 5 b^8 c^2 - 6 b^6 c^4 - 6 b^4 c^6 + 5 b^2 c^8 + 5 c^10)
+ a^4 (b^2 - c^2)^2 (3 b^8 - 8 b^6 c^2 - 14 b^4 c^4 - 8 b^2 c^6 + 3 c^8)
- 2 a^2 (b^2 - c^2)^4 (2 b^6 - b^4 c^2 - b^2 c^4 + 2 c^6)
+ (b^2 - c^2)^8 : ... : ...),
que tiene números de búsqueda en
(11.5530734415503, 6.43081754055810, -6.14362771150214); reflexión de X131 en X136 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,8754}, {5,131}, {20,254}, {155,382}, {187,16310}, {631,925}, {9714,13558}.
El del de la circunferencia Γ y la circunscrita a ABC es X10420, y queda sobre esta última.
El de la circunferencia de Steiner, circunferencia circunscrita a ABC y Γ es
Z = X6X1511 ∩ X1297X13398.
Z = ( a^2 (a^14 (b^2 + c^2)
- a^12 (5 b^4 + 6 b^2 c^2 + 5 c^4) +
a^10 (9 b^6 + 20 b^4 c^2 + 20 b^2 c^4 + 9 c^6) -
a^8 (5 b^8 + 29 b^6 c^2 + 40 b^4 c^4 + 29 b^2 c^6 + 5 c^8) +
a^6 (-5 b^10 + 17 b^8 c^2 + 36 b^6 c^4 + 36 b^4 c^6 + 17 b^2 c^8 - 5 c^10)
+ a^4 (9 b^12 - 8 b^10 c^2 - 13 b^8 c^4 - 8 b^6 c^6 - 13 b^4 c^8 -
8 b^2 c^10 + 9 c^12))
- a^2 (b^2 - c^2)^2 (5 b^10 + 3 b^6 c^4 + 3 b^4 c^6 + 5 c^10)
+ (b^2 - c^2)^6 (b^4 + b^2 c^2 + c^4) : ... : ...),
que tiene números de búsqueda en
(9.96545576051735, 4.65971695918266, -4.18473453315009).
- Martes, 21 de agosto del 2018
La cónica inscrita de MacBeath y las cúbicas K004 y K647
Dados un triángulo ABC y un punto P, sea DEF el de P.
Se denota por:
Bc y Bd las proyecciones ortogonales de B sobre AC y AD, respectivamente.
Cb y Cd las proyecciones ortogonales de C sobre AB y AD, respectivamente.
Db y Dc las proyecciones ortogonales de D sobre AB y AC, respectivamente.
Si (p:q:r) son las coordenadas baricéntricas de P, respecto a ABC, entonces:
Bc = (-a^2-b^2+c^2 : 0 : a^2-b^2-c^2),
Bd = ( -r(a^2(-q+r)+(b^2-c^2)(q+r)) : -q r((-a^2+b^2)+
c^2(2q+r)) : -r((-a^2+b^2)r+c^2(2q+r))),
Cd = (a^2q(-q+r)+q(b^2-c^2)(q+r) :
q(a^2q-c^2q-b^2(q+2r)) : -r(-a^2q+c^2q+
b^2(q+2r))),
Cb = (-a^2+b^2-c^2 : a^2-b^2-c^2 : 0),
Db = (-(a^2-b^2+c^2)r : (a^2-b^2)r-c^2(2q+r) : 0),
Dc = (-(a^2+b^2-c^2)q : 0 : a^2q-c^2q-b^2(q+2r)).
Los triángulos , y (directamente semejantes) es una tripleta de triángulos perspectivos. Los tres pares de triángulos tienen centro de semejanza común (Ha, pie de la altura desde A) y centro de perspectividad común (A, por construcción). En consecuencia, los tres ejes de perspectividad de pares de triángulos son concurrentes (ver Ion Pătraşcu, Florentin Smarandache.- The geometry of homological triangles. Theorem 17). Su punto de concurrencia A' está sobre BC.
Procediendo cíclicamente, se obtienen los puntos B' y C'.
Los puntos A', B', C' están alineados si y sólo si P está sobre la circunferencia circunscrita a ABC. La envolvente de la recta tP, que los contiene, es la .
La ecuación del eje de perspectividad de los triángulos y es:
(a^2-b^2-c^2)(a^2(q-r)-(b^2-c^2)(q+r))x
+ (a^2-b^2+c^2)(a^2q-c^2q-b^2(q+2r))y
-(a^2+b^2-c^2)((a^2-b^2)r-c^2(2q+r))z = 0.
De los triángulos y es:
-(a^2+b^2-c^2)((a^2-b^2)r-c^2(2q+r))x
+ (a^2-b^2+c^2)(a^2q-c^2q-b^2(q+2r))y
-(a^2+b^2-c^2)((a^2-b^2)r-c^2(2q+r))z = 0.
De los triángulos y es:
(a^2-b^2+c^2)(a^2q-c^2q-b^2(q+2r))x
+ (a^2-b^2+c^2)(a^2q-c^2q-b^2(q+2r))y
-(a^2+b^2-c^2)((a^2-b^2)r-c^2(2q+r))z = 0.
Estas tres rectas y la BC concurren en:
A' = (0 : (a^2+b^2-c^2)((a^2-b^2)r-c^2(2q+r)) : (a^2-b^2+
c^2)(a^2q-c^2q-b^2(q+2r))).
La correspondencia Φ que transforma un punto P de la circunferencia circunscrita en el punto de tangencia Q, de la recta tP y la cónica inscrita de MacBeath,
(x:y:z) ↦ Φ(x:y:z) = ((a^4-(b^2-c^2)^2)(a^4(c^2y+b^2z)+(b^2-c^2)^2(c^2y+b^2z)+
a^2(-2c^4y-2b^4z+2b^2c^2(2x+y+z))) : ⋯ : ⋯),
que tiene actualmente los siguientes pares correspondientes {P=Xi, Q = Φ(P)=Xj} de (1-20770), para los índices {i, j}: {74, 2970}, {98, 2971}, {99, 2967}, {103, 2973}, {104, 2969}, {1113, 1312}, {1114, 1313}, {1294, 2972}, {1295, 2968}, {1297, 339}, {3565, 2974}, permite dar las coordenadas de otros centros sobre la cónica inscrita de MacBeath; por ejemplo:
Φ(X100) = ( (2 a b c - a^2 (b + c) + (b - c)^2 (b + c))^2 (a^4 - (b^2 - c^2)^2) : ... : ...),
que tiene números de búsqueda en
(-3.55890127594422, -2.79182915088501, 7.21603909834056), punto medio de Xi y Xj para los índices {i,j}: {4, 1897}, {10696, 18340}; reflexión de Xi en Xj para los índices {i,j}: {3, 15252}, {2968, 5}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {118,133}, {119,2804}, {225,1830}, {342,6356}, {429,2970}, {442,2972}, {517,1361}, {1068,1398}, {1118,10306}, {1119,2095}, {1565,18026}, {1895,6922}, {5081,5844}, {5690,17555}, {5761,7524}, {5790,7046}, {5901,11109}, {7071,10679}, {7412,11849}, {7649,20619}, {10696,18340}.
Φ(X101) = ( b^2c^2(-2a^3+a^2(b+c)+(b-c)^2(b+c))^2(a^4-(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en
(-3.04540395159970, -3.14604011274419, 7.22426330685330) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,150}, {25,917}, {118,20622}, {430,2970}, {2968,8226}, {2972,3136}.
Φ(X102) = ( b^2c^2(b-c)^2(-a+b+c)^2(a^2+b^2-c^2)(a^2-b^2+c^2) : ... : ...),
que tiene números de búsqueda en
(4.13016072150051, 2.52651217410898, -0.0146873562451495)y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,151}, {25,1311}, {124,20620}, {318,7141}, {1109,14618}, {2968,14010}, {2972,3137}, {7017,7046}, {14936,17926}.
Las rectas
AA', BB', CC' son concurrentes si y sólo si
P está sobre la cúbica de Darboux (
K004 (Catalogue of Triangle Cubics. Bernard Gibert)). El lugar geométrico de los puntos de concurrencia es la cúbica
K647.
La transformación P ↦ Q (P sobre K004 y Q sobre K647) es:
(x:y:z) ↦ ((a^4-(b^2-c^2)^2)(a^4y z+c^4y(2y+z)+b^4z(y+2z)-
2a^2(y+z)(c^2y+b^2z)-2b^2c^2(2x^2+y^2+y z+z^2+4x(y+z))) : ⋯ : ⋯ ).
Pares {P=Xi, Q=Xj}, para {i, j}: {1, 92}, {3, 264}, {4, 4}, {20, 2}, {40, 318}, {64, 2052}, {84, 273}, {1490, 342}, {1498, 14249}, {3345, 7020}, {3346, 253}.
- Viernes, 17 de agosto del 2018
Triángulo pedal y transformación afín
a Clara, por su "cumple"
Dados un triángulo ABC y un punto P (que no está sobre la circunferencia circunscrita ni en la recta del infinito), sea A'B'C' el de P.
La matriz (aij) asociada a la transformación afín X ↦ X' = F(X), que aplica A ↦ A', B ↦ B', C ↦ C' , si (u:v:w) son las coordenadas baricéntricas de P, tiene las entradas:
a11 = 0
a12 = a^2c^2((a^2-c^2)v + b^2(2u+v))
a13 = a^2b^2((a^2-b^2)w + c^2(2u+w))
a21 = b^2c^2((b^2-c^2)u + a^2(u+2v))
a22 = 0
a23 = a^2b^2((-a^2+b^2)w + c^2(2v+w))
a31 = -b^2c^2((b^2-c^2)u - a^2(u+2w))
a32 = a^2c^2(-a^2v + c^2v + b^2(v+2w))
a33 = 0
El único punto fijo finito Q (correspondiente al valor propio λ = 2a^2b^2c^2(u+v+w)), tiene primera coordenada:
a^2(a^4v w-2a^2(v+w)(c^2v+b^2w)+b^4w(v+2w) -
2b^2c^2(2u^2+4u(v+w)+v^2+v w+w^2)+
c^4v(2v+w))
En el siguiente listado, {i,j} son los índices correspondientes a centros del triángulo, tales que P=Xi y Q=Xj:
{1, 1}, {2, 5544}, {3, 2}, {4, 6}, {5, 5643}, {6, 14482}, {20,
3}, {40, 9}, {64, 4}, {84, 57}, {164, 363}, {376, 5646}, {381,
5645}, {382, 9716}, {550, 5888}, {576, 7757}, {631, 14924}, {944,
55}, {1490, 223}, {1498, 1249}, {1657, 7712}, {2130, 3350}, {2131,
3349}, {3091, 5644}, {3146, 3167}, {3182, 3341}, {3183,
3343}, {3345, 282}, {3346, 1073}, {3347, 3342}, {3348, 3344}, {3353,
3351}, {3354, 3352}, {3355, 14481}, {3529, 154}, {3637,
3356}, {5537, 5660}, {6361, 198}, {6762, 40}, {7464, 15131}, {7957,
3651}, {7982, 3158}, {7991, 165}, {8915, 3731}, {9837, 259}, {11257,
574}, {11469, 5020}, {11477, 9741}, {12246, 56}, {12250,
25}, {15062, 5}, {15704, 6030}, {16936, 631}.
La transformación cuadrática que esta construcción proporciona:
(x:y:z) ↦ Φ(x:y:z) =
(a^2(a^4y z-2a^2(y+z)(c^2y+b^2z)+b^4z(y+2z)-2b^2c^2(2x^2+4x(y+z)+y^2+y z+z^2)+c^4y(2y+z)) :
b^2(b^4x z+c^4x(2x+z)+a^4z(x+2z)-2b^2(x+z)(c^2x+a^2z)-2a^2c^2(x^2+2y^2+x z+z^2+4y(x+z))) :
c^2(c^4x y+b^4x(2x+y)+a^4y(x+2y)-2c^2(x+y)(b^2x+a^2y)-2a^2b^2(x^2+x y+y^2+4(x+y)z+2z^2)),
tiene como puntos fijos el incentro y los exincentros.
Si X está sobre la recta del infinito (x+y+z=0), Φ(X) es el antipodal. en la circunferencia circunscrita, del de X.
El lugar geométrico de Φ(X), cuando X recorre la recta de Euler, es la hipérbola de Thomson-Gibert-Moses.
Si X es un punto sobre la , tal que OX:XH=t,
Φ(X) = (a^2(t^2a^4-(b^2+c^2)t(1+2t)a^2 +
b^4t(1+t)+c^4t(1+t)-b^2c^2(3+6t+2t^2)) : ⋯ : ⋯ ).
La eliminación del parámetro t, nos lleva a la
ecuación implícita
( 2 b^2 c^2 (b^2 - c^2), -2 a^4 c^2 +
2 a^2 c^4, 2 a^2 b^2 (a^2 - b^2), a^2 (b^2 - c^2) (-a^2 + b^2 +
c^2), -b^2 (a^2 - c^2) (a^2 - b^2 + c^2), (a^2 - b^2) c^2 (a^2 +
b^2 - c^2) = 0)
de la
Si P se mueve sobre la recta de Euler (OP:PH=t), el punto Q=Φ(P) y el conjugado isogonal P* de P, respecto al (baricentro del del conjugado isogonal de P, ver X(5642)),
P* = (a^2(3t^2a^4-(b^2+c^2)t(-1+2t)a^2-b^4t(1+t)-
c^4t(1+t)+b^2c^2(-1-2t+2t^2)) : ⋯ : ⋯ ),
quedan sobre la hipérbola de Thomson-Gibert-Moses,
y la envolvente de la recta QP*,
b^2c^2(b^2-c^2)(
a^6(-1-2t+t^2)-a^4(b^2+c^2)(-1+3t^2)+
a^2(2b^2c^2(1+t)^2+b^4t(2+3t)+c^4t(2+3t)) (b^2-c^2)^2(b^2+c^2)t^2) x + ⋯ = 0,
es la
elipse
( -2 a^10 b^6 c^2 x^2+4 a^8 b^8 c^2 x^2-4 a^6 b^10 c^2 x^2+4 a^4 b^12 c^2 x^2-2 a^2 b^14 c^2 x^2+4 a^10 b^4 c^4 x^2-4 a^8 b^6 c^4 x^2+6 a^6 b^8 c^4 x^2-10 a^4 b^10 c^4 x^2+6 a^2 b^12 c^4 x^2-2 b^14 c^4 x^2-2 a^10 b^2 c^6 x^2-4 a^8 b^4 c^6 x^2-4 a^6 b^6 c^6 x^2+6 a^4 b^8 c^6 x^2-6 a^2 b^10 c^6 x^2+6 b^12 c^6 x^2+4 a^8 b^2 c^8 x^2+6 a^6 b^4 c^8 x^2+6 a^4 b^6 c^8 x^2+4 a^2 b^8 c^8 x^2-4 b^10 c^8 x^2-4 a^6 b^2 c^10 x^2-10 a^4 b^4 c^10 x^2-6 a^2 b^6 c^10 x^2-4 b^8 c^10 x^2+4 a^4 b^2 c^12 x^2+6 a^2 b^4 c^12 x^2+6 b^6 c^12 x^2-2 a^2 b^2 c^14 x^2-2 b^4 c^14 x^2-a^14 b^2 c^2 x y+2 a^12 b^4 c^2 x y-7 a^10 b^6 c^2 x y+12 a^8 b^8 c^2 x y-7 a^6 b^10 c^2 x y+2 a^4 b^12 c^2 x y-a^2 b^14 c^2 x y+a^14 c^4 x y+a^12 b^2 c^4 x y-a^10 b^4 c^4 x y-a^8 b^6 c^4 x y-a^6 b^8 c^4 x y-a^4 b^10 c^4 x y+a^2 b^12 c^4 x y+b^14 c^4 x y-3 a^12 c^6 x y+6 a^10 b^2 c^6 x y-a^8 b^4 c^6 x y+4 a^6 b^6 c^6 x y-a^4 b^8 c^6 x y+6 a^2 b^10 c^6 x y-3 b^12 c^6 x y+2 a^10 c^8 x y-12 a^8 b^2 c^8 x y-6 a^6 b^4 c^8 x y-6 a^4 b^6 c^8 x y-12 a^2 b^8 c^8 x y+2 b^10 c^8 x y+2 a^8 c^10 x y+13 a^6 b^2 c^10 x y+18 a^4 b^4 c^10 x y+13 a^2 b^6 c^10 x y+2 b^8 c^10 x y-3 a^6 c^12 x y-13 a^4 b^2 c^12 x y-13 a^2 b^4 c^12 x y-3 b^6 c^12 x y+a^4 c^14 x y+6 a^2 b^2 c^14 x y+b^4 c^14 x y-2 a^14 b^2 c^2 y^2+4 a^12 b^4 c^2 y^2-4 a^10 b^6 c^2 y^2+4 a^8 b^8 c^2 y^2-2 a^6 b^10 c^2 y^2-2 a^14 c^4 y^2+6 a^12 b^2 c^4 y^2-10 a^10 b^4 c^4 y^2+6 a^8 b^6 c^4 y^2-4 a^6 b^8 c^4 y^2+4 a^4 b^10 c^4 y^2+6 a^12 c^6 y^2-6 a^10 b^2 c^6 y^2+6 a^8 b^4 c^6 y^2-4 a^6 b^6 c^6 y^2-4 a^4 b^8 c^6 y^2-2 a^2 b^10 c^6 y^2-4 a^10 c^8 y^2+4 a^8 b^2 c^8 y^2+6 a^6 b^4 c^8 y^2+6 a^4 b^6 c^8 y^2+4 a^2 b^8 c^8 y^2-4 a^8 c^10 y^2-6 a^6 b^2 c^10 y^2-10 a^4 b^4 c^10 y^2-4 a^2 b^6 c^10 y^2+6 a^6 c^12 y^2+6 a^4 b^2 c^12 y^2+4 a^2 b^4 c^12 y^2-2 a^4 c^14 y^2-2 a^2 b^2 c^14 y^2+a^14 b^4 x z-3 a^12 b^6 x z+2 a^10 b^8 x z+2 a^8 b^10 x z-3 a^6 b^12 x z+a^4 b^14 x z-a^14 b^2 c^2 x z+a^12 b^4 c^2 x z+6 a^10 b^6 c^2 x z-12 a^8 b^8 c^2 x z+13 a^6 b^10 c^2 x z-13 a^4 b^12 c^2 x z+6 a^2 b^14 c^2 x z+2 a^12 b^2 c^4 x z-a^10 b^4 c^4 x z-a^8 b^6 c^4 x z-6 a^6 b^8 c^4 x z+18 a^4 b^10 c^4 x z-13 a^2 b^12 c^4 x z+b^14 c^4 x z-7 a^10 b^2 c^6 x z-a^8 b^4 c^6 x z+4 a^6 b^6 c^6 x z-6 a^4 b^8 c^6 x z+13 a^2 b^10 c^6 x z-3 b^12 c^6 x z+12 a^8 b^2 c^8 x z-a^6 b^4 c^8 x z-a^4 b^6 c^8 x z-12 a^2 b^8 c^8 x z+2 b^10 c^8 x z-7 a^6 b^2 c^10 x z-a^4 b^4 c^10 x z+6 a^2 b^6 c^10 x z+2 b^8 c^10 x z+2 a^4 b^2 c^12 x z+a^2 b^4 c^12 x z-3 b^6 c^12 x z-a^2 b^2 c^14 x z+b^4 c^14 x z+a^14 b^4 y z-3 a^12 b^6 y z+2 a^10 b^8 y z+2 a^8 b^10 y z-3 a^6 b^12 y z+a^4 b^14 y z+6 a^14 b^2 c^2 y z-13 a^12 b^4 c^2 y z+13 a^10 b^6 c^2 y z-12 a^8 b^8 c^2 y z+6 a^6 b^10 c^2 y z+a^4 b^12 c^2 y z-a^2 b^14 c^2 y z+a^14 c^4 y z-13 a^12 b^2 c^4 y z+18 a^10 b^4 c^4 y z-6 a^8 b^6 c^4 y z-a^6 b^8 c^4 y z-a^4 b^10 c^4 y z+2 a^2 b^12 c^4 y z-3 a^12 c^6 y z+13 a^10 b^2 c^6 y z-6 a^8 b^4 c^6 y z+4 a^6 b^6 c^6 y z-a^4 b^8 c^6 y z-7 a^2 b^10 c^6 y z+2 a^10 c^8 y z-12 a^8 b^2 c^8 y z-a^6 b^4 c^8 y z-a^4 b^6 c^8 y z+12 a^2 b^8 c^8 y z+2 a^8 c^10 y z+6 a^6 b^2 c^10 y z-a^4 b^4 c^10 y z-7 a^2 b^6 c^10 y z-3 a^6 c^12 y z+a^4 b^2 c^12 y z+2 a^2 b^4 c^12 y z+a^4 c^14 y z-a^2 b^2 c^14 y z-2 a^14 b^4 z^2+6 a^12 b^6 z^2-4 a^10 b^8 z^2-4 a^8 b^10 z^2+6 a^6 b^12 z^2-2 a^4 b^14 z^2-2 a^14 b^2 c^2 z^2+6 a^12 b^4 c^2 z^2-6 a^10 b^6 c^2 z^2+4 a^8 b^8 c^2 z^2-6 a^6 b^10 c^2 z^2+6 a^4 b^12 c^2 z^2-2 a^2 b^14 c^2 z^2+4 a^12 b^2 c^4 z^2-10 a^10 b^4 c^4 z^2+6 a^8 b^6 c^4 z^2+6 a^6 b^8 c^4 z^2-10 a^4 b^10 c^4 z^2+4 a^2 b^12 c^4 z^2-4 a^10 b^2 c^6 z^2+6 a^8 b^4 c^6 z^2-4 a^6 b^6 c^6 z^2+6 a^4 b^8 c^6 z^2-4 a^2 b^10 c^6 z^2+4 a^8 b^2 c^8 z^2-4 a^6 b^4 c^8 z^2-4 a^4 b^6 c^8 z^2+4 a^2 b^8 c^8 z^2-2 a^6 b^2 c^10 z^2+4 a^4 b^4 c^10 z^2-2 a^2 b^6 c^10 z^2 = 0)
ℰ, bitangente a esta hipérbola, en el baricentro y en el foco de , con su mismo centro, X5642, y que pasa además por X25 (polo del respecto a la circunferencia circunscrita), X394 (raíz baricéntrica del conjugado isogonal del ), X3066 (punto donde la recta X6X110 vuelve a corta a la elipse ℰ).
El polo de la recta de Euler respecto a la elipse ℰ es el baricentro del , X51.
El polo de la recta de Euler respecto a la hipérbola de Thomson-Gibert-Moses es el X5650 (Peter Moses, June 17, 2014).
La transformación Φ coincide con la transformación T descrita en R. Deaux.-"Cercles polaires dans les cubiques autoisogonales à pivot". Mathesis, 1959.
K609 (Catalogue of Triangle Cubics. Bernard Gibert)
The following construction of M = T(P) is given in the 1959 Mathesis paper "Cercles polaires dans les cubiques autoisogonales à pivot" by Deaux.
Let A1B1C1 be the pedal triangle of P and let C1b, B1c be the reflections of C1, B1 about B, C respectively.
The parallels through B, C to CC1b, BB1c meet AC, AB at Ba, Ca respectively. Let La be the line BaCa and let Lb, Lc the two other lines defined similarly.
These three lines La, Lb, Lc concur at the requested point M.
- Martes, 14 de agosto del 2018
Reflexión de rectas de Euler en las alturas
Dado un triángulo ABC con ortocentro H y foco de la P= X110.
da es la reflexión de la del triángulo PBC en AH. Se definen similarmente, las rectas db y dc.
Las rectas da, db y dc concurren en W, punto medio de X(265) y X(14989).
La ecuación de la recta da es:
(b^2 - c^2) (-a^8 - 7 a^4 b^2 c^2 +
2 a^6 (b^2 + c^2) + (b^2 - c^2)^2 (b^4 + 3 b^2 c^2 + c^4) -
2 a^2 (b^6 - 2 b^4 c^2 - 2 b^2 c^4 + c^6))x +
(a^10 - 3 a^8 b^2 +
a^6 (6 b^2 c^2 - 3 c^4) + (b^2 - c^2)^3 (3 b^4 + 7 b^2 c^2 + 3 c^4) +
a^4 (8 b^6 - 18 b^4 c^2 + 10 b^2 c^4 - c^6) +
a^2 (-9 b^8 + 14 b^6 c^2 + 4 b^4 c^4 - 15 b^2 c^6 + 6 c^8))y +
(-a^10 +
3 a^8 c^2 +
3 a^6 (b^4 - 2 b^2 c^2) + (b^2 - c^2)^3 (3 b^4 + 7 b^2 c^2 + 3 c^4) +
a^4 (b^6 - 10 b^4 c^2 + 18 b^2 c^4 - 8 c^6) +
a^2 (-6 b^8 + 15 b^6 c^2 - 4 b^4 c^4 - 14 b^2 c^6 + 9 c^8))z = 0.
W = ( 4 a^16
-9 a^14 (b^2+c^2)
+a^12 (-6 b^4+44 b^2 c^2-6 c^4)
+14 a^10 (2 b^6-3 b^4 c^2-3 b^2 c^4+2 c^6)
-3 a^8 (5 b^8+15 b^6 c^2-44 b^4 c^4+15 b^2 c^6+5 c^8)
-a^6 (9 b^10-71 b^8 c^2+63 b^6 c^4+63 b^4 c^6-71 b^2 c^8+9 c^10)
+a^4 (b^2-c^2)^2 (4 b^8+14 b^6 c^2-63 b^4 c^4+14 b^2 c^6+4 c^8)
+6 a^2 (b^2-c^2)^4 (b^6-2 b^4 c^2-2 b^2 c^4+c^6)
-(b^2-c^2)^6 (3 b^4+7 b^2 c^2+3 c^4) : ... : ...),
que tiene números de búsqueda en
(-12.3731515365849, -12.2736427038067, 17.8484870629667), punto medio de X265 y X14989; reflexión de Xi en Xj para los índices {i,j}: {14677,12079}, {14934,546}, {16340,10113}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {30,74}, {523,3627}, {546,14934}, {10113,16340}, {12295,16168}.
- Lunes, 13 de agosto del 2018
Puntos de Clawson y triángulos perspectivos
ABC es un triángulo,
I su incentro y
A', B', C' los de los triángulos
IBC, ICA, IAB, respectivamente.
Los triángulos ABC y A'B'C' son perspectivos.
Las coordenadas baricéntricas de A', respecto a ABC, son:
(-a^2 √a + b + c :
(b-c) √a b (a + b - c) +
a (-b √a + b + c + √a b (a + b - c)) :
(c-b) √a c (a - b + c) + a (-c √a + b + c + √a c (a - b + c))).
El centro de perspectividad de >ABC y A'B'C' es:
W = ( 1/(b c √a + b + c - (b + c - a) √b c (b + c - a)) : ... : ...),
que tiene números de búsqueda en
(44.9033950249813, -16.4110149685243, -5.72250747449015).
Rectas que pasen por W contienen como máximo otro centro de ETC (1-20113).
Caso del :
Sean A", B", C" los puntos de Clawson de los triángulos , , , entonces las rectas AA", BB", CC" concurren en X845.
Las coordenadas del punto de Clawson del triángulo son:
A" = (-a^2 √b+c-a :
a b √b+c-a + (a-b+c) √a b(a-b+c) :
a c √b+c-a + (a+b-c) √a c(a+b-c)).
- Domingo, 12 de agosto del 2018
El triángulo órtico y la recta X(3)X(49)
Dado un triángulo ABC con A'B'C', sean A3 y A49 los centros de la circunferencias circunscrita y de AB'C'.
Análogamente, se definen los puntos B3, B49 y C3, C49.
Las rectas A3A49, B3B49 y C3C49 concurren en X136, centro de la hipérbola rectangular que pasa por A, B, C y el del centro de la circunferencia seno-triple-ángulo.
Las reflexiones de las rectas A3A49, B3B49 y C3C49 en las alturas AA', BB' y CC', respectivamente, concurren en D, punto medio de los ortocentro de ABC y el inverso en la del ortocentro del triángulo órtico (X4 y X5962).
En coordenadas baricéntricas,
A3 = (-2 (b^2 - c^2)^2 + 2 a^2 (b^2 + c^2) : -a^4 + b^4 +
2 a^2 c^2 - c^4 : -a^4 + 2 a^2 b^2 - b^4 + c^4),
A49 = (-2 a^10 + 7 a^8 (b^2 + c^2) - (b^2 - c^2)^4 (b^2 + c^2) -
8 a^6 (b^4 + b^2 c^2 + c^4) + 2 a^4 (b^6 + c^6) +
2 a^2 (b^8 - b^6 c^2 - b^2 c^6 + c^8) :
c^2 (a^2 + b^2 - c^2) (-a^2 + b^2 + c^2) (a^4 + (b^2 - c^2)^2 - a^2 (b^2 + 2 c^2)) :
-b^2 (-a^2 + b^2 - c^2) (-a^2 + b^2 + c^2) (a^4 + (b^2 - c^2)^2 - a^2 (2 b^2 + c^2))),
La ecuación de la recta A3A49:
(b^2 - c^2) (a^6 - a^2 (b^2 - c^2)^2 -
a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2)) x +
(2 a^8 + (b^2 - c^2)^4 - a^6 (5 b^2 + c^2) +
a^4 (5 b^4 + 2 b^2 c^2 - 3 c^4) +
a^2 (-3 b^6 + 3 b^4 c^2 - b^2 c^4 + c^6)) y +
( -2 a^8 - (b^2 - c^2)^4 +
a^6 (b^2 + 5 c^2) + a^4 (3 b^4 - 2 b^2 c^2 - 5 c^4) +
a^2 (-b^6 + b^4 c^2 - 3 b^2 c^4 + 3 c^6))z = 0,
y su simétrica respecto a AA' es:
a^2 (b^2 - c^2) (a^6 - a^2 (b^2 - c^2)^2 -
a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2))x +
(-2 a^10 +
2 (b^2 - c^2)^5 - a^2 (b^2 - c^2)^3 (3 b^2 + c^2) +
a^8 (5 b^2 + c^2) + a^6 (-3 b^4 - 2 b^2 c^2 + c^4) +
a^4 (b^6 + 3 b^4 c^2 - 5 b^2 c^4 + c^6)) y +
(2 a^10 + 2 (b^2 - c^2)^5 - a^2 (b^2 - c^2)^3 (b^2 + 3 c^2) -
a^8 (b^2 + 5 c^2) + a^6 (-b^4 + 2 b^2 c^2 + 3 c^4) -
a^4 (b^6 - 5 b^4 c^2 + 3 b^2 c^4 + c^6)) z = 0.
D = ( 2 a^16
-7 a^14 (b^2+c^2)
+4 a^12 (2 b^4+5 b^2 c^2+2 c^4)
-a^10 (3 b^6+17 b^4 c^2+17 b^2 c^4+3 c^6)
-2 a^8 b^2 c^2 (b^4-10 b^2 c^2+c^4)
+3 a^6 (b^2-c^2)^2 (b^2+c^2)^3
-4 a^4 (b^2-c^2)^2 (2 b^8-b^6 c^2+2 b^4 c^4-b^2 c^6+2 c^8)
+a^2 (b^2-c^2)^4 (7 b^6+b^4 c^2+b^2 c^4+7 c^6)
-2 (b^2-c^2)^6 (b^4+b^2 c^2+c^4) : ... : ...),
que tiene números de búsqueda en
(-1.77451732881372, -1.23193647064380, 5.31255157488257), punto medio de X4 y X5962; reflexión de X12095 en X5; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,52}, {5,12095}, {30,131}, {381,13557}, {403,14769}, {924,13851}, {5203,9880}, {7547,14889}.
- Sábado, 11 de agosto del 2018
Otro par de puntos con los mismos números de búsqueda en el triángulo de ETC
A triangle center X is a function whose domain is a set of triangles. The value of X at a triangle given by sidelengths (a,b,c) is denoted by X[a,b,c]. For example,
X(15519)[] = X(3635)[6,9,13].
Dado un triángulo ABC de DEF y Na, sean Ka, Kb y Kc los de los triángulos , y .
Los triángulos ABC y son .
El centro de perspectividad es W = (4r^2+16rR-s^2) X1 - 12r^2 X2.
Donde s el semiperímetro, r y R son los radios de las circunferencias inscrita y circunscrita al triángulo ABC.
W = ( a^3-2 a^2 (b+c)+a (9 b^2-14 b c+9 c^2)-4 (b-c)^2 (b+c) : ... : ...),
cuyos números de búsqueda en ,
(3.45104654014144, 1.80769104483599, 0.796395355417256), son los mismos que tiene el centro X4691 = (-2a+5b+5c : 5a-2b+5c : 5a+5b-2c).
La siguiente información sobre el punto W es de César Lozada y Ercole Suppa:
W es el de X15519 y es el punto de intersección de las rectas XiXj, para los índices {i,j}:
{1, 2}, {165, 3021}, {1699, 4902}, {1997, 4929}, {3756, 8056}, {4862, 5274}, {7963, 12625}.
- Martes, 7 de agosto del 2018
Otro enfoque de la excónica coseno
Preamble of
X(17807) contributed by César Eliud Lozada
If the tangents at B and C to the circumcircle of a triangle ABC intersect at A', then the circle with center A' passing through B and C is called A-excosine circle of ABC. This circle cuts AB and AC again at two points which are the extremities of a diameter of it.. (Reference:
Weisstein, Eric W. "Excosine Circle." From MathWorld)
Let Ab, Ac be the points where the A-excosine circle cuts again the sidelines AC and AB, respectively, and build {Bc, Ba}, {Ca, Cb} cyclically.
Points Ab, Ac, Bc, Ba, Ca, Cb lie on a conic, here named the excosine conic, with center X(17807) and perspector X(17808).
Dado un triángulo ABC y un punto D sobre la recta BC, sean Oab y Oac los circuncentros de los triángulos ADB y ADC, respectivamente.
El triángulo es inversamente semejante a ABC. El lugar geométrico del centro de semejanza D', al variar D, es una
hipérbola
( (a^4 - 2 a^2 b^2 + b^4 - 2 a^2 c^2 - 2 b^2 c^2 + c^4) x^2 +
a^2 c^2 y^2 + (-a^4 + a^2 b^2 + a^2 c^2) y z + a^2 b^2 z^2 = 0)
Φa.
Sea el , la circunferencia de centro Ta y que pasa por B y C, vuelve a cortar a las rectas AC y AB en Ab y Ac, respectivamente. Los puntos Bc, Ba y Ca, Cb, se definen cíclicamente.
Los seis puntos Ab, Ac, Bc, Ba, Ca, Cb están sobre una misma
cónica,
(2 a^6 b^2 c^2 x^2-2 a^4 b^4 c^2 x^2-2 a^2 b^6 c^2 x^2+2 b^8 c^2 x^2-2 a^4 b^2 c^4 x^2+4 a^2 b^4 c^4 x^2-2 b^6 c^4 x^2-2 a^2 b^2 c^6 x^2-2 b^4 c^6 x^2+2 b^2 c^8 x^2+a^8 c^2 x y+4 a^6 b^2 c^2 x y-10 a^4 b^4 c^2 x y+4 a^2 b^6 c^2 x y+b^8 c^2 x y-2 a^6 c^4 x y+2 a^4 b^2 c^4 x y+2 a^2 b^4 c^4 x y-2 b^6 c^4 x y-8 a^2 b^2 c^6 x y+2 a^2 c^8 x y+2 b^2 c^8 x y-c^10 x y+2 a^8 c^2 y^2-2 a^6 b^2 c^2 y^2-2 a^4 b^4 c^2 y^2+2 a^2 b^6 c^2 y^2-2 a^6 c^4 y^2+4 a^4 b^2 c^4 y^2-2 a^2 b^4 c^4 y^2-2 a^4 c^6 y^2-2 a^2 b^2 c^6 y^2+2 a^2 c^8 y^2+a^8 b^2 x z-2 a^6 b^4 x z+2 a^2 b^8 x z-b^10 x z+4 a^6 b^2 c^2 x z+2 a^4 b^4 c^2 x z-8 a^2 b^6 c^2 x z+2 b^8 c^2 x z-10 a^4 b^2 c^4 x z+2 a^2 b^4 c^4 x z+4 a^2 b^2 c^6 x z-2 b^4 c^6 x z+b^2 c^8 x z-a^10 y z+2 a^8 b^2 y z-2 a^4 b^6 y z+a^2 b^8 y z+2 a^8 c^2 y z-8 a^6 b^2 c^2 y z+2 a^4 b^4 c^2 y z+4 a^2 b^6 c^2 y z+2 a^4 b^2 c^4 y z-10 a^2 b^4 c^4 y z-2 a^4 c^6 y z+4 a^2 b^2 c^6 y z+a^2 c^8 y z+2 a^8 b^2 z^2-2 a^6 b^4 z^2-2 a^4 b^6 z^2+2 a^2 b^8 z^2-2 a^6 b^2 c^2 z^2+4 a^4 b^4 c^2 z^2-2 a^2 b^6 c^2 z^2-2 a^4 b^2 c^4 z^2-2 a^2 b^4 c^4 z^2+2 a^2 b^2 c^6 z^2 = 0)
denominada excónica coseno.
El de ABC respecto a la hipérbola Φa es .
- Domingo, 5 de agosto del 2018
Las cúbicas K044 y K045 del catálogo de Bernard Gibert
Dados un triángulo ABC de circuncentro O y ortocentro H, y un punto P, sean DEF el de P, pa, pb y pb las paralelas por D, E y F a AO, BO y CO, respectivamente.
Las rectas
pa,
pb y
pb son concurrentes si y solo si
P está sobre la
cúbica
( a^6 c^2 x^2 y-a^2 b^4 c^2 x^2 y-2 a^4 c^4 x^2 y+a^2 c^6 x^2 y+a^4 b^2 c^2 x y^2-b^6 c^2 x y^2+2 b^4 c^4 x y^2-b^2 c^6 x y^2-a^6 b^2 x^2 z+2 a^4 b^4 x^2 z-a^2 b^6 x^2 z+a^2 b^2 c^4 x^2 z+a^6 b^2 y^2 z-2 a^4 b^4 y^2 z+a^2 b^6 y^2 z-a^2 b^2 c^4 y^2 z-a^4 b^2 c^2 x z^2+b^6 c^2 x z^2-2 b^4 c^4 x z^2+b^2 c^6 x z^2-a^6 c^2 y z^2+a^2 b^4 c^2 y z^2+2 a^4 c^4 y z^2-a^2 c^6 y z^2 = 0)
K045. El punto de concurrencia
Q queda sobre la
cúbica
( a^10 c^2 x^2 y-a^8 b^2 c^2 x^2 y-2 a^6 b^4 c^2 x^2 y+2 a^4 b^6 c^2 x^2 y+a^2 b^8 c^2 x^2 y-b^10 c^2 x^2 y-4 a^8 c^4 x^2 y+2 a^6 b^2 c^4 x^2 y+2 a^4 b^4 c^4 x^2 y-2 a^2 b^6 c^4 x^2 y+2 b^8 c^4 x^2 y+6 a^6 c^6 x^2 y+2 a^2 b^4 c^6 x^2 y-4 a^4 c^8 x^2 y-2 a^2 b^2 c^8 x^2 y-2 b^4 c^8 x^2 y+a^2 c^10 x^2 y+b^2 c^10 x^2 y+a^10 c^2 x y^2-a^8 b^2 c^2 x y^2-2 a^6 b^4 c^2 x y^2+2 a^4 b^6 c^2 x y^2+a^2 b^8 c^2 x y^2-b^10 c^2 x y^2-2 a^8 c^4 x y^2+2 a^6 b^2 c^4 x y^2-2 a^4 b^4 c^4 x y^2-2 a^2 b^6 c^4 x y^2+4 b^8 c^4 x y^2-2 a^4 b^2 c^6 x y^2-6 b^6 c^6 x y^2+2 a^4 c^8 x y^2+2 a^2 b^2 c^8 x y^2+4 b^4 c^8 x y^2-a^2 c^10 x y^2-b^2 c^10 x y^2-a^10 b^2 x^2 z+4 a^8 b^4 x^2 z-6 a^6 b^6 x^2 z+4 a^4 b^8 x^2 z-a^2 b^10 x^2 z+a^8 b^2 c^2 x^2 z-2 a^6 b^4 c^2 x^2 z+2 a^2 b^8 c^2 x^2 z-b^10 c^2 x^2 z+2 a^6 b^2 c^4 x^2 z-2 a^4 b^4 c^4 x^2 z-2 a^2 b^6 c^4 x^2 z+2 b^8 c^4 x^2 z-2 a^4 b^2 c^6 x^2 z+2 a^2 b^4 c^6 x^2 z-a^2 b^2 c^8 x^2 z-2 b^4 c^8 x^2 z+b^2 c^10 x^2 z+a^10 b^2 y^2 z-4 a^8 b^4 y^2 z+6 a^6 b^6 y^2 z-4 a^4 b^8 y^2 z+a^2 b^10 y^2 z+a^10 c^2 y^2 z-2 a^8 b^2 c^2 y^2 z+2 a^4 b^6 c^2 y^2 z-a^2 b^8 c^2 y^2 z-2 a^8 c^4 y^2 z+2 a^6 b^2 c^4 y^2 z+2 a^4 b^4 c^4 y^2 z-2 a^2 b^6 c^4 y^2 z-2 a^4 b^2 c^6 y^2 z+2 a^2 b^4 c^6 y^2 z+2 a^4 c^8 y^2 z+a^2 b^2 c^8 y^2 z-a^2 c^10 y^2 z-a^10 b^2 x z^2+2 a^8 b^4 x z^2-2 a^4 b^8 x z^2+a^2 b^10 x z^2+a^8 b^2 c^2 x z^2-2 a^6 b^4 c^2 x z^2+2 a^4 b^6 c^2 x z^2-2 a^2 b^8 c^2 x z^2+b^10 c^2 x z^2+2 a^6 b^2 c^4 x z^2+2 a^4 b^4 c^4 x z^2-4 b^8 c^4 x z^2-2 a^4 b^2 c^6 x z^2+2 a^2 b^4 c^6 x z^2+6 b^6 c^6 x z^2-a^2 b^2 c^8 x z^2-4 b^4 c^8 x z^2+b^2 c^10 x z^2-a^10 b^2 y z^2+2 a^8 b^4 y z^2-2 a^4 b^8 y z^2+a^2 b^10 y z^2-a^10 c^2 y z^2+2 a^8 b^2 c^2 y z^2-2 a^6 b^4 c^2 y z^2+2 a^4 b^6 c^2 y z^2-a^2 b^8 c^2 y z^2+4 a^8 c^4 y z^2-2 a^4 b^4 c^4 y z^2-2 a^2 b^6 c^4 y z^2-6 a^6 c^6 y z^2-2 a^4 b^2 c^6 y z^2+2 a^2 b^4 c^6 y z^2+4 a^4 c^8 y z^2+a^2 b^2 c^8 y z^2-a^2 c^10 y z^2 = 0)
K044
y
P, Q, H están alineados.
Special case of Special Isocubics, §3.1.3.
"Let M be a point on the isotomic pK with pivot tQ, with traces AM, BM and CM. The
lines through AM, BM and CM parallel to AQ, BQ, CQ respectively concur at a point Z.
As M traverses the isotomic pK, Z traverses a central pK."
La ecuación baricéntrica de la recta pa, si P=(u:v:w), es:
(a^2 (c^2 v-b^2 w)+(b^2-c^2) (c^2 v+b^2 w)) x+
((b^2-c^2)^2-a^2 (b^2+c^2)) w y+
(-(b^2-c^2)^2+a^2 (b^2+c^2)) v z = 0.
Correspondencia entre centros sobre K045 y K044, {P=Xi, Q=Xj}, para {i, j}: {2, 5}, {3, 3}, {4, 52}, {69, 5562}, {254, 8800}, {264, 4}, {1993, 155}, {5392, 68}.
Esta correspondencia, que tiene puntos fijos A, B, C y el circuncentro, está dada por:
X = (x:y:z) ↦ X'=f(X) = (a^8(x^2-y z)
-a^6(c^2(3x^2-4y z+x(2y+z))+b^2(3x^2-4y z+x(y+2z)))
+a^4(c^4(3x^2+5x y+3x z-5y z)+b^4(3x^2+3x y+5x z-5y z)+2b^2c^2(x^2-y z+x(y+z)))
-a^2(b^4-c^4)(-c^2(x^2+4x y+3x z-2y z)+b^2(x^2+3x y+4x z-2y z))
+(b^2-c^2)^4x(y+z) : ... : ...).
Otros pares correspondientes, no situados sobre las cúbicas K044 y K045, son: {6, 195}, {140, 14938}, {182,
567}, {2889, 15644}, {5645, 5097}, {7706, 568}, {12325, 10625}, {15047, 14627}, {18381, 6243}.
- Sábado, 4 de agosto del 2018
El centro del triángulo X(1741)X(8758) ∩ X(2331)X(7649)
Dado un triángulo ABC de incentro I y circunferencia circunscrita Γ, la circunferencia Γa de diámetro AI vuelve a cortar a Γ en A'. Sea ta la tangente a Γa en A'. Se definen tb y tc, cíclicamente.
Se consideran el triángulo formado por las rectas ta, tb y tc y DEF el .
Los triángulos DEF y son y el centro de perspectividad es X1741X8758∩X2331X7649.
X(1741) = of the perspector of triangle ABC and the pedal triangle of the isogonal conjugate of .
X(2331) = of incenter and the perspector of the and triangles.
X(7649) = of 3 circles: circumcircle, , .
X(8758) = of every pair of points on line X(3)X(650)
X(650) is the perspector of triangle ABC and the of the .
La ecuación baricéntrica de la tangente ta en
A'(a^2(a+b-c)(a-b+c) : b(b-c)(a+b-c)(-a+b+c) : c(a-b-c)(b-c)(a-b+c))
a Γa es:
2b c(b-c)^2(-a+b+c)x
+ c(a^4-2a^3(b-c)-2a(b-c)^2c+(b-c)^3(b+c))y
- b(-a^4-2a^3(b-c)+2a b(b-c)^2+(b-c)^3(b+c))z = 0.
El centro de perspectividad de los triángulos DEF y es W = X1741X8758∩X2331X7649:
W = ( a (b^5 - b^4 c - b c^4 +
c^5 + (b^4 - 2 b^2 c^2 + c^4) a + (-2 b^3 + 4 b^2 c + 4 b c^2 -
2 c^3) a^2 + (-2 b^2 - 4 b c - 2 c^2) a^3 + (b + c) a^4 +
a^5) (b^5 + b^4 c - 2 b^3 c^2 - 2 b^2 c^3 + b c^4 +
c^5 + (b^4 - 4 b^3 c + 6 b^2 c^2 - 4 b c^3 + c^4) a + (-2 b^3 +
2 b^2 c + 2 b c^2 - 2 c^3) a^2 + (-2 b^2 - 2 c^2) a^3 + (b +
c) a^4 + a^5) : ... : ...),
que tiene números de búsqueda en
(1.02268471887704, 0.995817058291808, 2.47924434053141) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1741,8758}, {2331,7649}.
El punto W ha sido incorporado a ETC con el número X(20581).
Un caso más general:
Si el punto P está sobre la cúbica de Darboux (K004), sea DEF es el de P y ta es la tangente a la circunferencia de diámetro AP en el punto A', donde vuelve a cortar a la circunferencia circunscrita. Las rectas tb y tc se definen cíclicamente. es el triángulo formado por las rectas ta, tb y tc. Entonces, los triángulos DEF y son perspectivos.
El centro de perspectividad, para:
• P=X3 es X3.
• P=X4 es:
W4 = ( (a^2 + b^2 - c^2) (a^2 - b^2 + c^2) (3 a^6 - 2 a^4 b^2 - 5 a^2 b^4 +
4 b^6 - 2 a^4 c^2 + 10 a^2 b^2 c^2 - 4 b^4 c^2 - 5 a^2 c^4 -
4 b^2 c^4 + 4 c^6) (2 a^6 b^2 - 2 a^4 b^4 - 2 a^2 b^6 + 2 b^8 +
2 a^6 c^2 - 5 a^4 b^2 c^2 + 4 a^2 b^4 c^2 - b^6 c^2 - 2 a^4 c^4 +
4 a^2 b^2 c^4 - 2 b^4 c^4 - 2 a^2 c^6 - b^2 c^6 + 2 c^8) : ... : ...),
que tiene números de búsqueda en
(28.1641239786103, 26.4413945892736, -27.6637428392559).
• P=X20 es:
W20 = ( (2 a^4 - 2 a^2 b^2 + a^2 b c - b^3 c - 2 a^2 c^2 + 2 b^2 c^2 -
b c^3) (2 a^4 - 2 a^2 b^2 - a^2 b c + b^3 c - 2 a^2 c^2 +
2 b^2 c^2 + b c^3) (a^6 + a^2 b^4 - 2 b^6 - 2 a^2 b^2 c^2 +
2 b^4 c^2 + a^2 c^4 + 2 b^2 c^4 - 2 c^6) : ... : ...),
que tiene números de búsqueda en
(3.06528631190481, 0.194190602427221, 2.09147730550178) y está sobre la recta X3523X3620.
• P=X40 es:
W40 = ( a (a - b - c) (a^4 - 2 a^2 b^2 + b^4 + 2 a b^2 c - 2 b^3 c -
2 a^2 c^2 + 2 a b c^2 + 2 b^2 c^2 - 2 b c^3 + c^4) : ... : ...),
que tiene números de búsqueda en
(4.68132395321563, 1.62059691407239, 0.358101716834741) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,1167}, {2,15298}, {8,90}, {9,497}, {10,10629}, {36,78}, {40,2123}, {46,7080}, {55,17658}, {57,6745}, {63,100}, {72,3428}, {191,4882}, {210,11502}, {354,8257}, {518,1260}, {944,6737}, {1040,3939}, {1158,5687}, {1259,3811}, {1478,6735}, {1490,12059}, {1709,17784}, {1741,3694}, {3190,3751}, {3305,5231}, {3717,3719}, {3729,17860}, {3870,18412}, {3872,5251}, {3885,4853}, {4430,4511}, {4863,7082}, {5176,5691}, {5552,13407}, {6600,10391}.
- Viernes, 3 de agosto del 2018
Una propiedad de la cuártica Euler-Morley
Sean P y Q dos puntos , respecto a un triángulos ABC, de circunferencia circunscrita Γ. La circunferencia Γa que pasa por A, P, Q, vuelve a cortar a Γ, AB, AC, BQ, CQ en los puntos Aa, Ab, Ac, Qab, Qac. Sea Qa = AbAc ∩ QabQac y la recta ℓa=AaQa.
Las rectas ℓb y ℓc, se definen cíclicamente.
Si P' es el punto de intersección de las rectas ℓa, ℓb y ℓc, cuando P está sobre la cuártica Q002, se tienen los siguientes emparejamientos de centros del triángulo {P=Xi, P'=Xj}, para {i,j}: {3, 3}, {2574, 1113}, {2575, 1114}.
Cuando P es X6 (), P'6 = X2X6∩X3X111 = 108r^2R^2s^2 X2 + (r^2+4rR-s^2)^3 X6:
P'6 = ( a^2(a^4+2a^2(b^2+c^2)+b^4-16b^2c^2+c^4) : ... : ...),
que tiene números de búsqueda en
(14.5267101900984, 3.66896376464497, -5.60402282750755) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,6}, {3,111}, {22,8588}, {23,5210}, {25,15655}, {187,1995}, {353,5085}, {399,9759}, {549,16317}, {574,3291}, {647,9175}, {1350,13192}, {1383,3053}, {1384,11284}, {2030,5651}, {2502,6800}, {5023,14002}, {5024,9465}, {5055,6032}, {5569,9172}, {5585,7492}, {5640,11173}, {7485,8589}, {8716,9870}, {8770,15246}, {9225,10485}.
- Jueves, 2 de agosto del 2018
Una cúbica isogonal no pivotal con raíz el punto de De Longchamps
Recordando un entrañable aniversario
Sean P y Q dos puntos , respecto a un triángulos ABC. Consideremos circunferencias variables Γa, Γb y Γc con cuerdas AP, BP y CP, respectivamente.
Γa vuelve a cortar a las rectas AB y AC en Ab y Ac, respectivamente. Se denota por Aa y da el punto medio y la mediatriz del segmento AbAc. Los puntos Bb, Bc y las rectas db, dc, se definen cíclicamente.
Cuando Γa varía, la recta da envuelve la parábola 𝒫a, de foco P y directriz AQ.
Sean (u:v:w) las coordenadas baricéntricas de P, existe una única circunferencia Γa, tal que el punto Aa (que denotamos por A0) está sobre la
parábola
( 4 b^2 c^6 v^4 x^2-8 a^2 b^2 c^4 v^3 w x^2+8 b^4 c^4 v^3 w x^2+8 b^2 c^6 v^3 w x^2+4 a^4 b^2 c^2 v^2 w^2 x^2-8 a^2 b^4 c^2 v^2 w^2 x^2+4 b^6 c^2 v^2 w^2 x^2-8 a^2 b^2 c^4 v^2 w^2 x^2+16 b^4 c^4 v^2 w^2 x^2+4 b^2 c^6 v^2 w^2 x^2-8 a^2 b^4 c^2 v w^3 x^2+8 b^6 c^2 v w^3 x^2+8 b^4 c^4 v w^3 x^2+4 b^6 c^2 w^4 x^2-8 b^2 c^6 u v^3 x y+12 a^2 b^2 c^4 u v^2 w x y-12 b^4 c^4 u v^2 w x y-12 b^2 c^6 u v^2 w x y-4 a^2 b^2 c^4 v^3 w x y+4 b^4 c^4 v^3 w x y-4 b^2 c^6 v^3 w x y-4 a^4 b^2 c^2 u v w^2 x y+8 a^2 b^4 c^2 u v w^2 x y-4 b^6 c^2 u v w^2 x y+8 a^2 b^2 c^4 u v w^2 x y-16 b^4 c^4 u v w^2 x y-4 b^2 c^6 u v w^2 x y+4 a^4 b^2 c^2 v^2 w^2 x y-8 a^2 b^4 c^2 v^2 w^2 x y+4 b^6 c^2 v^2 w^2 x y+4 a^2 b^2 c^4 v^2 w^2 x y+4 b^4 c^4 v^2 w^2 x y-8 b^2 c^6 v^2 w^2 x y+4 a^2 b^4 c^2 u w^3 x y-4 b^6 c^2 u w^3 x y-4 b^4 c^4 u w^3 x y-4 a^4 b^2 c^2 v w^3 x y-4 a^2 b^4 c^2 v w^3 x y+8 b^6 c^2 v w^3 x y+8 a^2 b^2 c^4 v w^3 x y-4 b^4 c^4 v w^3 x y-4 b^2 c^6 v w^3 x y+4 a^2 b^4 c^2 w^4 x y+4 b^6 c^2 w^4 x y-4 b^4 c^4 w^4 x y+a^4 c^4 u^2 v^2 y^2-2 a^2 b^2 c^4 u^2 v^2 y^2+b^4 c^4 u^2 v^2 y^2-2 a^2 c^6 u^2 v^2 y^2+2 b^2 c^6 u^2 v^2 y^2+c^8 u^2 v^2 y^2+2 a^4 c^4 u v^3 y^2-4 a^2 b^2 c^4 u v^3 y^2+2 b^4 c^4 u v^3 y^2-4 a^2 c^6 u v^3 y^2-4 b^2 c^6 u v^3 y^2+2 c^8 u v^3 y^2+a^4 c^4 v^4 y^2-2 a^2 b^2 c^4 v^4 y^2+b^4 c^4 v^4 y^2-2 a^2 c^6 v^4 y^2-2 b^2 c^6 v^4 y^2+c^8 v^4 y^2-4 a^2 b^2 c^4 u^2 v w y^2+4 b^4 c^4 u^2 v w y^2+4 b^2 c^6 u^2 v w y^2+2 a^4 c^4 u v^2 w y^2-2 b^4 c^4 u v^2 w y^2-4 a^2 c^6 u v^2 w y^2+2 c^8 u v^2 w y^2+2 a^4 c^4 v^3 w y^2-4 a^2 b^2 c^4 v^3 w y^2+2 b^4 c^4 v^3 w y^2-4 a^2 c^6 v^3 w y^2-4 b^2 c^6 v^3 w y^2+2 c^8 v^3 w y^2+4 b^4 c^4 u^2 w^2 y^2-4 a^4 b^2 c^2 u v w^2 y^2+8 a^2 b^4 c^2 u v w^2 y^2-4 b^6 c^2 u v w^2 y^2+4 b^2 c^6 u v w^2 y^2+a^4 c^4 v^2 w^2 y^2+2 a^2 b^2 c^4 v^2 w^2 y^2+b^4 c^4 v^2 w^2 y^2-2 a^2 c^6 v^2 w^2 y^2-2 b^2 c^6 v^2 w^2 y^2+c^8 v^2 w^2 y^2+4 a^2 b^4 c^2 u w^3 y^2-4 b^6 c^2 u w^3 y^2+4 b^4 c^4 u w^3 y^2-4 a^4 b^2 c^2 v w^3 y^2+4 a^2 b^4 c^2 v w^3 y^2+4 a^2 b^2 c^4 v w^3 y^2+4 a^2 b^4 c^2 w^4 y^2+4 a^2 b^2 c^4 u v^3 x z-4 b^4 c^4 u v^3 x z-4 b^2 c^6 u v^3 x z+4 a^2 b^2 c^4 v^4 x z-4 b^4 c^4 v^4 x z+4 b^2 c^6 v^4 x z-4 a^4 b^2 c^2 u v^2 w x z+8 a^2 b^4 c^2 u v^2 w x z-4 b^6 c^2 u v^2 w x z+8 a^2 b^2 c^4 u v^2 w x z-16 b^4 c^4 u v^2 w x z-4 b^2 c^6 u v^2 w x z-4 a^4 b^2 c^2 v^3 w x z+8 a^2 b^4 c^2 v^3 w x z-4 b^6 c^2 v^3 w x z-4 a^2 b^2 c^4 v^3 w x z-4 b^4 c^4 v^3 w x z+8 b^2 c^6 v^3 w x z+12 a^2 b^4 c^2 u v w^2 x z-12 b^6 c^2 u v w^2 x z-12 b^4 c^4 u v w^2 x z+4 a^4 b^2 c^2 v^2 w^2 x z+4 a^2 b^4 c^2 v^2 w^2 x z-8 b^6 c^2 v^2 w^2 x z-8 a^2 b^2 c^4 v^2 w^2 x z+4 b^4 c^4 v^2 w^2 x z+4 b^2 c^6 v^2 w^2 x z-8 b^6 c^2 u w^3 x z-4 a^2 b^4 c^2 v w^3 x z-4 b^6 c^2 v w^3 x z+4 b^4 c^4 v w^3 x z-4 a^2 b^2 c^4 u^2 v^2 y z+4 b^4 c^4 u^2 v^2 y z+4 b^2 c^6 u^2 v^2 y z-4 a^2 b^2 c^4 u v^3 y z+4 b^4 c^4 u v^3 y z-4 b^2 c^6 u v^3 y z+2 a^4 b^2 c^2 u^2 v w y z-4 a^2 b^4 c^2 u^2 v w y z+2 b^6 c^2 u^2 v w y z-4 a^2 b^2 c^4 u^2 v w y z+12 b^4 c^4 u^2 v w y z+2 b^2 c^6 u^2 v w y z+4 a^2 b^2 c^4 u v^2 w y z+4 b^4 c^4 u v^2 w y z-4 b^2 c^6 u v^2 w y z-2 a^4 b^2 c^2 v^3 w y z+4 a^2 b^4 c^2 v^3 w y z-2 b^6 c^2 v^3 w y z-4 a^2 b^2 c^4 v^3 w y z+4 b^4 c^4 v^3 w y z-2 b^2 c^6 v^3 w y z-4 a^2 b^4 c^2 u^2 w^2 y z+4 b^6 c^2 u^2 w^2 y z+4 b^4 c^4 u^2 w^2 y z+4 a^2 b^4 c^2 u v w^2 y z-4 b^6 c^2 u v w^2 y z+4 b^4 c^4 u v w^2 y z+4 a^4 b^2 c^2 v^2 w^2 y z-4 b^6 c^2 v^2 w^2 y z+8 b^4 c^4 v^2 w^2 y z-4 b^2 c^6 v^2 w^2 y z-4 a^2 b^4 c^2 u w^3 y z-4 b^6 c^2 u w^3 y z+4 b^4 c^4 u w^3 y z-2 a^4 b^2 c^2 v w^3 y z-4 a^2 b^4 c^2 v w^3 y z-2 b^6 c^2 v w^3 y z+4 a^2 b^2 c^4 v w^3 y z+4 b^4 c^4 v w^3 y z-2 b^2 c^6 v w^3 y z+4 b^4 c^4 u^2 v^2 z^2+4 a^2 b^2 c^4 u v^3 z^2+4 b^4 c^4 u v^3 z^2-4 b^2 c^6 u v^3 z^2+4 a^2 b^2 c^4 v^4 z^2-4 a^2 b^4 c^2 u^2 v w z^2+4 b^6 c^2 u^2 v w z^2+4 b^4 c^4 u^2 v w z^2-4 a^4 b^2 c^2 u v^2 w z^2+4 b^6 c^2 u v^2 w z^2+8 a^2 b^2 c^4 u v^2 w z^2-4 b^2 c^6 u v^2 w z^2-4 a^4 b^2 c^2 v^3 w z^2+4 a^2 b^4 c^2 v^3 w z^2+4 a^2 b^2 c^4 v^3 w z^2+a^4 b^4 u^2 w^2 z^2-2 a^2 b^6 u^2 w^2 z^2+b^8 u^2 w^2 z^2-2 a^2 b^4 c^2 u^2 w^2 z^2+2 b^6 c^2 u^2 w^2 z^2+b^4 c^4 u^2 w^2 z^2+2 a^4 b^4 u v w^2 z^2-4 a^2 b^6 u v w^2 z^2+2 b^8 u v w^2 z^2-2 b^4 c^4 u v w^2 z^2+a^4 b^4 v^2 w^2 z^2-2 a^2 b^6 v^2 w^2 z^2+b^8 v^2 w^2 z^2+2 a^2 b^4 c^2 v^2 w^2 z^2-2 b^6 c^2 v^2 w^2 z^2+b^4 c^4 v^2 w^2 z^2+2 a^4 b^4 u w^3 z^2-4 a^2 b^6 u w^3 z^2+2 b^8 u w^3 z^2-4 a^2 b^4 c^2 u w^3 z^2-4 b^6 c^2 u w^3 z^2+2 b^4 c^4 u w^3 z^2+2 a^4 b^4 v w^3 z^2-4 a^2 b^6 v w^3 z^2+2 b^8 v w^3 z^2-4 a^2 b^4 c^2 v w^3 z^2-4 b^6 c^2 v w^3 z^2+2 b^4 c^4 v w^3 z^2+a^4 b^4 w^4 z^2-2 a^2 b^6 w^4 z^2+b^8 w^4 z^2-2 a^2 b^4 c^2 w^4 z^2-2 b^6 c^2 w^4 z^2+b^4 c^4 w^4 z^2 = 0)
𝒫a, sus coordenadas son:
A0 = (b^6 w^2 (v+w)-c^2 (a^2-c^2) v^2 (a^2 w-c^2 (v+w))-b^4 w (a^2 w (2 v+w)+c^2 (2 v^2+4 u w+3 v w+w^2))+b^2 v (3 a^2 c^2 (v-w) w+a^4 w^2+c^4 (4 u v+v^2+3 v w+2 w^2)) : -b^2 (c^4 v (-2 v^2-v w+w^2)+(a^2-b^2) w^2 (a^2 v-b^2 (v+w))+c^2 w (a^2 v (v-2 w)+b^2 (-v^2+w^2))) : c^2 (a^4 v^2 w+c^4 v^2 (v+w)+b^4 w (v^2-v w-2 w^2)+b^2 c^2 v (v^2-w^2)-a^2 v (b^2 (2 v-w) w+c^2 v (v+2 w)))).
Similarmente, se tienen las coordenadas de B0 y C0.
Las rectas
AA0,
BB0,
CC0 son concurrentes si y solo si
P está sobre la
cúbica
( a^4 c^2 x^2 y+2 a^2 b^2 c^2 x^2 y-3 b^4 c^2 x^2 y-2 a^2 c^4 x^2 y+2 b^2 c^4 x^2 y+c^6 x^2 y-3 a^4 c^2 x y^2+2 a^2 b^2 c^2 x y^2+b^4 c^2 x y^2+2 a^2 c^4 x y^2-2 b^2 c^4 x y^2+c^6 x y^2+a^4 b^2 x^2 z-2 a^2 b^4 x^2 z+b^6 x^2 z+2 a^2 b^2 c^2 x^2 z+2 b^4 c^2 x^2 z-3 b^2 c^4 x^2 z-a^6 x y z+a^4 b^2 x y z+a^2 b^4 x y z-b^6 x y z+a^4 c^2 x y z-10 a^2 b^2 c^2 x y z+b^4 c^2 x y z+a^2 c^4 x y z+b^2 c^4 x y z-c^6 x y z+a^6 y^2 z-2 a^4 b^2 y^2 z+a^2 b^4 y^2 z+2 a^4 c^2 y^2 z+2 a^2 b^2 c^2 y^2 z-3 a^2 c^4 y^2 z-3 a^4 b^2 x z^2+2 a^2 b^4 x z^2+b^6 x z^2+2 a^2 b^2 c^2 x z^2-2 b^4 c^2 x z^2+b^2 c^4 x z^2+a^6 y z^2+2 a^4 b^2 y z^2-3 a^2 b^4 y z^2-2 a^4 c^2 y z^2+2 a^2 b^2 c^2 y z^2+a^2 c^4 y z^2 = 0)
isogonal nK(X6,X20,?), de raíz el .
El punto de concurrencia queda sobre la misma cúbica.
Esta cúbica no contiene en la actual edición de .
Si P(u:v:w) es un punto de la cúbica, el punto f(P) = P'=AA0∩BB0∩ CC0, de coordenadas:
( a^2(-3v w a^4 + 2(b^2w(2u+v-w)+c^2v(2u-v+w))a^2 + b^4w(-4u+v+2w)+c^4v(-4u+2v+w)-
2b^2c^2(2u^2+v^2+v w+w^2-2u(v+w))), : ... : ...),
también está sobre la cúbica.
La aplicación X ↦ f(X) es involutiva.
Los únicos centros tales que su imagen también es un centro que está en ETC son:
f(X1)=X1743, f(X2)=X3167, f(X4)=X6.
Utilizando la aplicación f, podemos encontrar puntos por donde pasa la curva.
Así, recordando que la de X20 interseca a los lados de ABC en U, V, W (tres puntos sobre la cúbica), entonces
f(U) = (-a^4+(b^2-c^2)^2 : -2b^2(a^2-b^2+c^2) : -2c^2(a^2+b^2-c^2))
es uno de los puntos de intersección de la recta AO con la cúbica. El tercero es:
U'' = ( -3 a^6 (b^2 - c^2)^2 + a^8 (b^2 + c^2) +
3 a^4 (b^2 - c^2)^2 (b^2 + c^2) -
a^2 (b^2 - c^2)^2 (b^4 + 6 b^2 c^2 + c^4) : -b^2 (-a^2 + b^2 -
c^2) (a^6 - 3 a^2 (b^2 - c^2)^2 +
2 (b^2 - c^2)^2 (b^2 + c^2)) : -c^2 (-a^2 - b^2 + c^2) (a^6 -
3 a^2 (b^2 - c^2)^2 + 2 (b^2 - c^2)^2 (b^2 + c^2))).
f(U'')=( -a^6 - a^2 (b^2 - c^2)^2 +
2 (b^2 - c^2)^2 (b^2 + c^2) : -(b^2 - c^2) (a^4 - 3 b^4 + 2 b^2 c^2 +
c^4 + 2 a^2 (b^2 - c^2)) : (b^2 - c^2) (a^4 + b^4 + 2 b^2 c^2 -
3 c^4 - 2 a^2 (b^2 - c^2))).
Análogamente, para puntos sobre las rectas BO y CO.
Los puntos
f(A)=(-2a^2 : -a^2-b^2+c^2 : -a^2+b^2-c^2), f(B) y f(B), están sobre las alturas.
El tercer punto de intersección de la altura por A con la cúbica es:
( -a^10 + 4 a^6 (b^2 - c^2)^2 - 3 a^2 (b^2 - c^2)^4 -
2 a^4 (b^2 - c^2)^2 (b^2 + c^2) +
2 (b^2 - c^2)^4 (b^2 + c^2) : -(a^2 + b^2 -
c^2) (-3 a^4 (b^2 - c^2)^2 + a^6 (b^2 + c^2) +
3 a^2 (b^2 - c^2)^2 (b^2 + c^2) - (b^2 - c^2)^2 (b^4 + 6 b^2 c^2 +
c^4)) : -(a^2 - b^2 + c^2) (-3 a^4 (b^2 - c^2)^2 +
a^6 (b^2 + c^2) +
3 a^2 (b^2 - c^2)^2 (b^2 + c^2) - (b^2 - c^2)^2 (b^4 + 6 b^2 c^2 +
c^4))).
- Domingo, 29 de julio del 2018
Reflexiones de centros de circunferencias
Dado un triángulo ABC de circuncentro O, una circunferencia variable Γa, de centro Oa y que pasa por A y O, vuelve a corta a AB y AC en los puntos Ab y Ac. Sea Aa el punto medio del segmento AbAc y At el punto que divide al segmento OaAa en la razón OaAt : AtAa = t.
La ecuación baricéntrica de una circunferencia que pasa por A y O se puede expresar por:
c^2 x y + b^2 x z +
a^2 y z + (x + y + z) (-c^2 μ y - (
b^2 (a^2 - a^2 μ + b^2 μ - c^2 μ) z)/(a^2 + b^2 - c^2))=0,
con centro en:
Oa = (-a^6 - (b^2 - c^2)^3 μ + a^4 (-b^2 (-1 + μ) + c^2 (2 + μ)) +
a^2 (b^2 - c^2) (2 b^2 μ +
c^2 (1 + 2 μ)) :
b^2 ((b^2 - c^2)^2 (-1 + μ) + a^4 μ -
a^2 (b^2 + c^2) (-1 + 2 μ)) :
-c^2 (a^4 (-1 + μ) + (b^2 -
c^2)^2 (-1 + μ) - 2 a^2 (c^2 (-1 + μ) + b^2 μ)))
El punto medio de AbAc es:
Aa = ( -a^2 + 2 (-b^2 + c^2) μ : (a^2 + b^2 - c^2) (-1 + μ) :
b^2 (-1 + μ) - c^2 (-1 + μ) - a^2 μ).
Cuando Γa varía, el lugar geométrico del punto At es la tangente ℓa, desde At (distinta de OaAa) a la parábola 𝒫a, de foco O y directriz la altura ha, desde A.
Para construir la tangente ℓa a la parábola 𝒫a ver: PARÁBOLA: Tangentes desde un punto exterior (Ester Alonso).
Análogamente, procediendo cíclicamente, se obtienen las recta ℓb y ℓc.
El punto At
(-2 (b^2 - c^2)^3 μ (1 + t) - a^6 (2 + t) +
a^4 (-2 b^2 (-1 + μ) (1 + t) +
2 c^2 (2 + μ + t + μ t)) +
a^2 (b^2 - c^2) (b^2 (-t + 4 μ (1 + t)) +
c^2 (2 + t + 4 μ (1 + t))) :
a^6 (-1 + μ) t + (b^2 - c^2)^2 (-1 + μ) (-c^2 t +
b^2 (2 + t)) + a^4 (-3 c^2 (-1 + μ) t + b^2 (-μ (-2 + t) + t)) +
a^2 (3 c^4 (-1 + μ) t + 2 b^2 c^2 (1 + t - μ (2 + t)) +
b^4 (2 + t - μ (4 + t))) :
-a^6 μ t + (b^2 - c^2)^2 (-1 + μ) (b^2 t - c^2 (2 + t)) +
a^4 (b^2 (-1 + 3 μ) t + c^2 (2 + μ (-2 + t) + t)) +
a^2 (b^4 (2 - 3 μ) t + 2 b^2 c^2 μ (2 + t) + c^4 (-2 (2 + t) + μ (4 + t)))).
Eliminando μ se obtiene la recta ℓa:
x (-4 a^2 b^2 c^2 - 8 a^2 b^2 c^2 t + a^6 t^2 -
2 a^4 b^2 t^2 + a^2 b^4 t^2 - 2 a^4 c^2 t^2 -
2 a^2 b^2 c^2 t^2 + a^2 c^4 t^2) +
y (-4 a^4 c^2 + 4 a^2 b^2 c^2 - 4 b^4 c^2 + 8 a^2 c^4 + 8 b^2 c^4 -
4 c^6 - 2 a^6 t + 6 a^4 b^2 t - 6 a^2 b^4 t +
2 b^6 t - 2 a^4 c^2 t + 4 a^2 b^2 c^2 t -
10 b^4 c^2 t + 10 a^2 c^4 t + 14 b^2 c^4 t -
6 c^6 t - a^6 t^2 + 4 a^4 b^2 t^2 -
5 a^2 b^4 t^2 + 2 b^6 t^2 + 2 a^2 b^2 c^2 t^2 -
6 b^4 c^2 t^2 + 3 a^2 c^4 t^2 + 6 b^2 c^4 t^2 -
2 c^6 t^2) +
z (-4 a^4 b^2 + 8 a^2 b^4 - 4 b^6 + 4 a^2 b^2 c^2 + 8 b^4 c^2 -
4 b^2 c^4 - 2 a^6 t - 2 a^4 b^2 t + 10 a^2 b^4 t -
6 b^6 t + 6 a^4 c^2 t + 4 a^2 b^2 c^2 t +
14 b^4 c^2 t - 6 a^2 c^4 t - 10 b^2 c^4 t +
2 c^6 t - a^6 t^2 + 3 a^2 b^4 t^2 -
2 b^6 t^2 + 4 a^4 c^2 t^2 + 2 a^2 b^2 c^2 t^2 +
6 b^4 c^2 t^2 - 5 a^2 c^4 t^2 - 6 b^2 c^4 t^2 +
2 c^6 t^2)=0.
Cuando t varía, esta recta envuelve la parábola de foco el circuncentro y directriz la altura ha por A:
4 a^4 b^2 c^2 x^2 + 4 a^6 c^2 x y + 4 a^2 b^4 c^2 x y -
8 a^4 c^4 x y - 8 a^2 b^2 c^4 x y + 4 a^2 c^6 x y + a^8 y^2 -
4 a^6 b^2 y^2 + 6 a^4 b^4 y^2 - 4 a^2 b^6 y^2 + b^8 y^2 +
8 a^2 b^4 c^2 y^2 - 4 b^6 c^2 y^2 - 2 a^4 c^4 y^2 -
4 a^2 b^2 c^4 y^2 + 6 b^4 c^4 y^2 - 4 b^2 c^6 y^2 + c^8 y^2 +
4 a^6 b^2 x z - 8 a^4 b^4 x z + 4 a^2 b^6 x z - 8 a^2 b^4 c^2 x z +
4 a^2 b^2 c^4 x z + 2 a^8 y z - 4 a^6 b^2 y z + 4 a^4 b^4 y z -
4 a^2 b^6 y z + 2 b^8 y z - 4 a^6 c^2 y z + 4 a^2 b^4 c^2 y z -
8 b^6 c^2 y z + 4 a^4 c^4 y z + 4 a^2 b^2 c^4 y z + 12 b^4 c^4 y z -
4 a^2 c^6 y z - 8 b^2 c^6 y z + 2 c^8 y z + a^8 z^2 - 2 a^4 b^4 z^2 +
b^8 z^2 - 4 a^6 c^2 z^2 - 4 a^2 b^4 c^2 z^2 - 4 b^6 c^2 z^2 +
6 a^4 c^4 z^2 + 8 a^2 b^2 c^4 z^2 + 6 b^4 c^4 z^2 - 4 a^2 c^6 z^2 -
4 b^2 c^6 z^2 + c^8 z^2 = 0.
Las rectas ℓa, ℓb y ℓc coinciden si y solo si t=-1 (recta del infinito) y t=-2 ().
La condición analítica para que las tres rectas ℓa, ℓb y ℓc coincidan es:
(1 + t) (2 + t) = 0.
Para t=-2, At es la reflexión de Oa en Aa. En este caso, la expresión paramétrica de las coordenadas de At son:
x = -(b^2 - c^2)^3 μ + a^4 (-b^2 (-1 + μ) + c^2 μ) +
a^2 (b^2 c^2 - 2 c^4 μ + b^4 (-1 + 2 μ)),
y = a^4 (b^2 (1 - 2 μ) - 3 c^2 (-1 + μ)) +
a^6 (-1 + μ) - (-b^2 c + c^3)^2 (-1 + μ) +
a^2 (b^2 c^2 + 3 c^4 (-1 + μ) + b^4 μ),
z = (b^3 - b c^2)^2 (-1 + μ) -
a^6 μ - a^2 (c^4 μ + b^4 (-2 + 3 μ)) +
a^4 (2 c^2 μ + b^2 (-1 + 3 μ))).
Eliminado μ resulta:
(a^6 - 2 a^4 b^2 + a^2 b^4 - 2 a^4 c^2 + a^2 b^2 c^2 +
a^2 c^4) x + (a^4 b^2 - 2 a^2 b^4 + b^6 + a^2 b^2 c^2 -
2 b^4 c^2 + b^2 c^4) y + (a^4 c^2 + a^2 b^2 c^2 + b^4 c^2 -
2 a^2 c^4 - 2 b^2 c^4 + c^6) z=0,
que es la ecuación de la recta que pasa por Xi (i = 5, 523, 6757, 8151, 10287, 10288, 10412, 14254, 14356, 14566, 14592, 14670, 15475, 18039, 18114, 18115, 18116, 18117, 18118, 18119, 18120, 18121, 18122, 18279, 18312). Siendo X5 es el centro de la y X523 es el punto que tiene la dirección perpendicular a la recta de Euler. Se trata de la mediatriz de OH,
el eje de Hatzipolakis es la tangente común a las tres parábolas 𝒫a, 𝒫b y 𝒫c, de foco común, el circuncentro, y directrices las tres alturas.
Las rectas ℓa, ℓb y ℓc son concurrentes si y solo si
t = - S^2R(R±OH)/()
R es el radio de la circunferencia circunscrita y OH es la distancia del circuncentro al ortocentro.
La condición analítica para que las tres rectas ℓa, ℓb y ℓc sean concurrentes es:
(1 + t)^2 (2 + t)^2 (-4 a^2 b^2 c^2 - 4 a^2 b^2 c^2 t +
a^6 t^2 - a^4 b^2 t^2 - a^2 b^4 t^2 +
b^6 t^2 - a^4 c^2 t^2 + 2 a^2 b^2 c^2 t^2 -
b^4 c^2 t^2 - a^2 c^4 t^2 - b^2 c^4 t^2 +
c^6 t^2) = 0.
Los puntos de intersección son los puntos imagen U y V, de las intersecciones, X1113 y X1114, de la recta de Euler con la circunferencia circunscrita, mediante la homotecia h[H.k] de centro el ortocentro y razón
k= -OH^2 S^2/(2SASBSC) = -OH^2/(2S cotA cotB cotC) =
-(a^6-a^4b^2-a^2b^4+b^6-a^4c^2+3a^2b^2c^2-b^4c^2-a^2c^4-b^2c^4+c^6) / ((b^2+c^2-a^2)(c^2+a^2-b^2)(a^2+b^2-c^2)).
U = ( a (b c (-2 a^10+3 a^8 (b^2+c^2)+2 a^6 (b^4-5 b^2 c^2+c^4)+a^4 (-4 b^6+5 b^4 c^2+5 b^2 c^4-4 c^6)+5 a^2 b^2 c^2 (b^2-c^2)^2+(b^2-c^2)^4 (b^2+c^2)) + 2OH S (a^9-2 a^7 (b^2+c^2)+6 a^5 b^2 c^2+a^3 (2 b^6-3 b^4 c^2-3 b^2 c^4+2 c^6)-a (b^2-c^2)^2 (b^4+3 b^2 c^2+c^4))) : ... : ...),
que tiene números de búsqueda en
(2.55807648933939, 1.68180829607230, 1.29568497416230) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {578,14374}, {1147,2574}, {2575,3357}, {6102,13414}.
V = ( a (b c (-2 a^10+3 a^8 (b^2+c^2)+2 a^6 (b^4-5 b^2 c^2+c^4)+a^4 (-4 b^6+5 b^4 c^2+5 b^2 c^4-4 c^6)+5 a^2 b^2 c^2 (b^2-c^2)^2+(b^2-c^2)^4 (b^2+c^2))- 2OH S (a^9-2 a^7 (b^2+c^2)+6 a^5 b^2 c^2+a^3 (2 b^6-3 b^4 c^2-3 b^2 c^4+2 c^6)-a (b^2-c^2)^2 (b^4+3 b^2 c^2+c^4))) : ... : ...),
que tiene números de búsqueda en
(19.9057882277275, 18.9837563328706, -18.6892229305695) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {578,14375}, {1147,2575}, {2574,3357}, {6102,13415}.
Las correspondientes rectas ℓa para los valores de t = - S^2R(R ± OH)/(SASBSC), se cortan en Ak = h[H,k](A)
Ak = ((b^2-c^2) (-a^2+b^2+c^2)^4 (a^4-(b^2-c^2)^2)^2 (a^8+2 a^4 b^2 c^2-(b^2-c^2)^4-2 a^6 (b^2+c^2)+2 a^2 (b^2-c^2)^2 (b^2+c^2)) :
-a^2 b^2 c^2 (b^2-c^2) (a^2+b^2-c^2)^3 (a^2-b^2+c^2)^2 (-a^2+b^2+c^2)^4 :
-a^2 b^2 c^2 (b^2-c^2) (a^2+b^2-c^2)^2 (a^2-b^2+c^2)^3 (-a^2+b^2+c^2)^4).
La circunferencia circunscrita a AkBkCk (Bk = h[H,k](B), Ck = h[H,k](C)) tiene como puntos antipedales a X1147 y X3357, su centro es X11250.
X(1147) is the insimilicenter of the circumcircle and the
sine-triple-angle circle. (Randy Hutson, December 14, 2014) .
X(2574) = isogonal conjugate of X(1113).
X(2575) = isogonal conjugate of X(1114).
X(3357) = midpoint of X(3) and X(64) (isogonal conjugate of ).
X(3357) = X(8)-of-Trinh-triangle if ABC is acute
X(11250) = circumcenter of
Trinh triangle. (See Antreas Hatzipolakis and Angel Montesdeoca,
Hyacinthos 25511).
El triángulo DEF formado por las rectas ℓa, ℓb y ℓc es no degenerado y perspectivo con ABC si y solo si t=-4/3.
El centro de perspectividad W está sobre la circunferencia circunscrita:
W = ( 4 a^16
- 10 a^14 (b^2 + c^2)
+ a^12 (-6 b^4 + 49 b^2 c^2 - 6 c^4)
+ 5 a^10 (8 b^6 - 11 b^4 c^2 - 11 b^2 c^4 + 8 c^6)
- a^8 (40 b^8 + 23 b^6 c^2 - 135 b^4 c^4 + 23 b^2 c^6 + 40 c^8)
+ 3 a^6 (b^2 - c^2)^2 (2 b^6 + 25 b^4 c^2 + 25 b^2 c^4 + 2 c^6)
+ a^4 (b^2 - c^2)^2 (10 b^8 - 6 b^6 c^2 - 57 b^4 c^4 - 6 b^2 c^6 +
10 c^8)
- 2 a^2 (b^2 - c^2)^4 (2 b^6 + 5 b^4 c^2 + 5 b^2 c^4 + 2 c^6)
- 4 b^2 c^2 (b^2 - c^2)^6 : ... : ...),
que tiene números de búsqueda en
(13.8170920945170, 11.3399485420684, -10.5871885523785) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {110,382}, {476,15646}.
X(110) = focus of .
X(382) = reflection of circumcenter in orthocenter.
X(476) = .
X(15646) = circumcircle-inverse of X(382)
La condición para que el triángulo DEF formado por las rectas ℓa, ℓb sea perspectivo con ABC es:
t (1 + t) (2 + t) (4 + 3 t) (-4 a^2 b^2 c^2 -
4 a^2 b^2 c^2 t + a^6 t^2 - a^4 b^2 t^2 -
a^2 b^4 t^2 + b^6 t^2 - a^4 c^2 t^2 +
2 a^2 b^2 c^2 t^2 - b^4 c^2 t^2 - a^2 c^4 t^2 -
b^2 c^4 t^2 + c^6 t^2) = 0.
El triángulo DEF es no degenerado para t=0 (formado por la mediatrices de AO, BO, CO y el centro de perspectividad es el ) y para t=-4/3.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
UNA GENERALIZACIÓN
Sean P y Q dos puntos , respecto al triángulos ABC. Consideremos circunferencias variables Γa, Γb y Γc con cuerdas AP, BP y CP, cuyos centros de denotan por Oa, Ob y Oc, respectivamente.
Γa vuelve a cortar a las rectas AB y AC en Ab y Ac, respectivamente, y Aa es el punto medio de estos dos puntos. Los puntos Bb y Bc, se definen cíclicamente.
Para tres números reales λ, μ y ν, se consideran los puntos Aλ, Bμ y Cν, tales que:
OaAλ : AλAa = λ,
OaBμ : BμBb = μ,
OaCν : CνCc = ν.
El lugar geométrico de los puntos Aλ, Bμ y Cν son sendas rectas ℓa, ℓb y ℓc.
Las rectas ℓ
a, ℓ
b y ℓ
c coinciden con la mediatriz de
PQ, tangente común a las tres parábolas 𝒫
a, 𝒫
b y 𝒫
c con focos
P y directrices las cevianas de
Q, si y solo si
λ = 2b^2c^2u(u+v+w)/(b^4u w-(a^2-c^2)v(c^2u+a^2w)-b^2(a^2(u-v)w+c^2u(2u+v+w))),
μ = 2c^2a^2v(u+v+w)/(c^4v u-(b^2-a^2)w(a^2v+b^2u)-c^2(b^2(v-w)u+a^2v(u+2v+w))),
ν = 2a^2b^2w(u+v+w)/(a^4w v-(c^2-b^2)v(b^2w+c^2v)-a^2(c^2(w-u)v+b^2w(u+v+2w))).
Para λ=μ=ν=-2, las rectas ℓa, ℓb y ℓc son concurrentes si solo si P=O o P está sobre la cónica conjugada isogonal del eje de Hatzipolakis.
Cuando P se mueve sobre la cónica conjugada isogonal del eje de Hatzipolakis y λ=μ=ν=-2, el punto de concurrencia de las rectas ℓa, ℓb y ℓc queda sobre la cónica
(a^8 b^2 c^2 - 2 a^6 b^4 c^2 + a^4 b^6 c^2 - 2 a^6 b^2 c^4 +
a^4 b^4 c^4 + a^4 b^2 c^6) x^2 + (a^8 b^2 c^2 - a^6 b^4 c^2 -
a^4 b^6 c^2 + a^2 b^8 c^2 - a^8 c^4 - a^6 b^2 c^4 +
2 a^4 b^4 c^4 - a^2 b^6 c^4 - b^8 c^4 + 4 a^6 c^6 +
3 a^4 b^2 c^6 + 3 a^2 b^4 c^6 + 4 b^6 c^6 - 6 a^4 c^8 -
7 a^2 b^2 c^8 - 6 b^4 c^8 + 4 a^2 c^10 + 4 b^2 c^10 -
c^12) x y + (a^6 b^4 c^2 - 2 a^4 b^6 c^2 + a^2 b^8 c^2 +
a^4 b^4 c^4 - 2 a^2 b^6 c^4 + a^2 b^4 c^6) y^2 + (-a^8 b^4 +
4 a^6 b^6 - 6 a^4 b^8 + 4 a^2 b^10 - b^12 + a^8 b^2 c^2 -
a^6 b^4 c^2 + 3 a^4 b^6 c^2 - 7 a^2 b^8 c^2 + 4 b^10 c^2 -
a^6 b^2 c^4 + 2 a^4 b^4 c^4 + 3 a^2 b^6 c^4 - 6 b^8 c^4 -
a^4 b^2 c^6 - a^2 b^4 c^6 + 4 b^6 c^6 + a^2 b^2 c^8 -
b^4 c^8) x z + (-a^12 + 4 a^10 b^2 - 6 a^8 b^4 + 4 a^6 b^6 -
a^4 b^8 + 4 a^10 c^2 - 7 a^8 b^2 c^2 + 3 a^6 b^4 c^2 -
a^4 b^6 c^2 + a^2 b^8 c^2 - 6 a^8 c^4 + 3 a^6 b^2 c^4 +
2 a^4 b^4 c^4 - a^2 b^6 c^4 + 4 a^6 c^6 - a^4 b^2 c^6 -
a^2 b^4 c^6 - a^4 c^8 + a^2 b^2 c^8) y z + (a^6 b^2 c^4 +
a^4 b^4 c^4 + a^2 b^6 c^4 - 2 a^4 b^2 c^6 - 2 a^2 b^4 c^6 +
a^2 b^2 c^8) z^2=0.
Su centro es el . El circuncentro y X195 son extremos de un diámetro.
- Domingo, 22 de julio del 2018
Un triángulo formado por ejes radicales
Dado un triángulo ABC de circunferencia circunscrita Γ, la mediatriz de BC corta a AB y AC en Ab y Ac, respectivamente.
Sea Γa la circunferencia circunscrita al triángulo y Oa su centro. Los puntos Ob y Oc se definen análogamente. Γ′ es la circunferencia circunscrita a . es el del .
El eje radical ℓa de Γ′ y Γa es tangente a Γ. Las rectas ℓb y ℓc se definen análogamente.
El del triángulo formado por las rectas ℓa, ℓb y ℓc, respecto a Γ, es
W = 3 X2 - 2 X53.
X2 es el baricentro de ABC y X53 es el de su .
La ecuación baricéntrica de la circunferencia Γa es:
c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-a^2c^2 y/(2 )-a^2b^2 z/(2 SC)) = 0
y su centro es:
Oa (a^4 : b^2(c^2-c^2) : c^2(b^2-c^2)).
La circunferencia
( c^2 x y+b^2 x z+a^2 y z+(x+y+z) (-((((-(-a^2 b^2+b^4) (-a^2 b^2+b^4+a^2 (a-b) (a+b)-c^4) (-b^2 c^2+c^4) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c))+b^2 (b-c) (b+c) (-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c))) (-c^2 (-a+c) (a+c) (a^2 (a-b) (a+b) (-a^2 b^2+b^4) c^2-a^2 (a-b) b^2 (a+b) c^4-a^2 (-a^2 b^2+b^4) c^4) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))+(-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (-a^2 b^4 c^2 (-a+c) (a+c)-b^4 c^2 (a^4-a^2 c^2)+b^2 c^2 (-a+c) (a+c) (a^4-a^2 c^2)))-(-(-a^2 b^2+b^4) c^2 (-a+c) (a+c) (-a^2 b^2+b^4+a^2 (a-b) (a+b)-c^4) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))-b^4 (-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))) (-(-b^2 c^2+c^4) (a^2 (a-b) (a+b) (-a^2 b^2+b^4) c^2-a^2 (a-b) b^2 (a+b) c^4-a^2 (-a^2 b^2+b^4) c^4) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c))+(-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (-a^4 b^2 (b-c) c^2 (b+c)-a^4 b^2 (-b^2 c^2+c^4)+a^2 b^2 (b-c) (b+c) (-b^2 c^2+c^4)))) x)/(-(-(-a^2 b^2+b^4) c^2 (-a+c) (a+c) (-a^2 b^2+b^4+a^2 (a-b) (a+b)-c^4) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))-b^4 (-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))) (-a^2 (a-b) (a+b) (-a^2 b^2+b^4+a^2 (a-b) (a+b)-c^4) (-b^2 c^2+c^4) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c))-a^4 (-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c)))+(-a^2 (a-b) (a+b) c^2 (-a+c) (a+c) (-a^2 b^2+b^4+a^2 (a-b) (a+b)-c^4) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))+(a^4-a^2 c^2) (-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (a^4-b^4-a^2 c^2+c^2 (-a+c) (a+c))) (-(-a^2 b^2+b^4) (-a^2 b^2+b^4+a^2 (a-b) (a+b)-c^4) (-b^2 c^2+c^4) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c))+b^2 (b-c) (b+c) (-a^4 c^4+2 a^2 b^2 c^4-b^4 c^4+c^8) (-a^4-b^2 c^2+c^4+b^2 (b-c) (b+c)))))-(c^2 (a^6-2 a^4 c^2+a^2 c^4) y)/((-a^2-b^2+c^2) (a^2-b^2+c^2) (-a^2+b^2+c^2))-((a^6 b^2-2 a^4 b^4+a^2 b^6) z)/((a^2-b^2-c^2) (a^2+b^2-c^2) (a^2-b^2+c^2))) = 0)
Γ′ ( del triángulo tangencial) es tangente a Γ en el foco de la .
El eje radical de Γ′ y Γa es:
ℓa: (b - c)^2 (b + c)^2x + a^2 b^2y + a^2 c^2z = 0,
que es tangente a Γ en A' (a^2 : -b^2 + c^2 : b^2 - c^2).
El punto de Brianchon del triángulo formado por las rectas ℓa, ℓb y ℓc, respecto a Γ, es:
W = ( a^8 - 3 a^6 (b^2 + c^2) + 3 a^4 (b^4 + c^4)-
a^2 (b^2 - c^2)^2 (b^2 + c^2) + 2 b^2 c^2 (b^2 - c^2)^2 : ... : ...),
que tiene números de búsqueda en
(8.15713122786573, 4.99160130708427, -3.57988929739660), reflexión de X9308 en X577 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,53}, {3,95}, {6,401}, {20,64}, {22,157}, {30,317}, {75,10538}, {76,11414}, {97,19212}, {99,1294}, {159,1632}, {216,458}, {286,1012}, {297,6389}, {302,19772}, {303,19773}, {325,1370}, {338,8553}, {339,12083}, {340,1657}, {394,8613}, {441,17907}, {511,6751}, {577,9308}, {648,15905}, {925,2373}, {940,18667}, {1007,7396}, {1078,9715}, {1235,10323}, {1238,7788}, {1272,13219}, {1305,2370}, {1494,15681}, {1993,19180}, {2871,12220}, {3151,4417}, {3153,18380}, {3186,11676}, {3260,9723}, {6515,18953}, {6617,15466}, {6638,16089}, {7560,14829}, {9307,10602}, {10313,14614}, {10979,14767}, {11257,19459}, {11412,19206}, {19121,19156}.
El punto W ha sido incorporado a ETC con el número X(20477).
- Lunes, 16 de julio del 2018
Focos de parábolas sobre la recta paralela por el incentro a su tripolar
Dado un triángulo ABC de circuncentro O, incentro I y , sea (Oa) la circunferencia que pasa por B y C y cuyo centro Oa es tal que OOa : OaMa = t (número real).
La rectas AB, AC, IB, IC vuelven a corta a la circunferencia (Oa) en los puntos Ab, Ac, Iab, Iac, respectivamente.
Se denotan los puntos diagonales del por:
Ua= BaIac∩CaIab,
Va= BaCa∩IabIac,
Wa= BaIab∩CaIac,
Cuando t varía, Ua recorre la bisectriz AI (cy-bz=0, en coordenadas baricéntricas), Va se mueve sobre la recta (bcx-acy-abz=0) que pasa por los pies de las bisectrices por B y C, y el lugar geométrico que describe Wa es una
cúbica
( (a b^2 c^3-a b c^4+b^2 c^4-b c^5) x^2 y+(-2 a^2 b c^3+a b^2 c^3+a^2 c^4-2 a b c^4+a c^5) x y^2+(a^3 c^3-a^2 b c^3+a^2 c^4) y^3+(-a b^4 c-b^5 c+a b^3 c^2+b^4 c^2) x^2 z+(a^2 b^3 c-a b^4 c-2 b^5 c+a b^3 c^2+a^2 b c^3+a b^2 c^3+4 b^3 c^3-a b c^4-2 b c^5) x y z+(a^2 b^3 c-b^5 c+2 a b^3 c^2+b^4 c^2-a^3 c^3-a^2 b c^3-2 a b^2 c^3+2 b^3 c^3-2 a b c^4-2 b^2 c^4+2 a c^5-b c^5+c^6) y^2 z+(a^2 b^4+a b^5-2 a^2 b^3 c-2 a b^4 c+a b^3 c^2) x z^2+(-a^3 b^3+2 a b^5+b^6-a^2 b^3 c-2 a b^4 c-b^5 c-2 a b^3 c^2-2 b^4 c^2+a^2 b c^3+2 a b^2 c^3+2 b^3 c^3+b^2 c^4-b c^5) y z^2+(a^3 b^3+a^2 b^4-a^2 b^3 c) z^3 = 0)
Ψau.
La envolvente de la recta
VaWa, cuando t varía, es una
parábola
( 4 a^2 b^2 c^2 x^2+4 a b^3 c^2 x^2+b^4 c^2 x^2+4 a b^2 c^3 x^2+2 b^3 c^3 x^2+b^2 c^4 x^2-4 a^3 b c^2 x y+2 a^2 b^2 c^2 x y+6 a b^3 c^2 x y+2 b^4 c^2 x y-2 a^2 b c^3 x y+6 a b^2 c^3 x y+2 b^3 c^3 x y-2 b^2 c^4 x y-2 b c^5 x y+a^4 c^2 y^2-2 a^3 b c^2 y^2-a^2 b^2 c^2 y^2+2 a b^3 c^2 y^2+b^4 c^2 y^2-4 a^2 b c^3 y^2-2 a^2 c^4 y^2-2 a b c^4 y^2-2 b^2 c^4 y^2+c^6 y^2-4 a^3 b^2 c x z-2 a^2 b^3 c x z-2 b^5 c x z+2 a^2 b^2 c^2 x z+6 a b^3 c^2 x z-2 b^4 c^2 x z+6 a b^2 c^3 x z+2 b^3 c^3 x z+2 b^2 c^4 x z+2 a^4 b c y z-2 a^3 b^2 c y z-4 a^2 b^3 c y z-2 a b^4 c y z-2 b^5 c y z-2 a^3 b c^2 y z-6 a^2 b^2 c^2 y z+2 a b^3 c^2 y z-4 a^2 b c^3 y z+2 a b^2 c^3 y z+4 b^3 c^3 y z-2 a b c^4 y z-2 b c^5 y z+a^4 b^2 z^2-2 a^2 b^4 z^2+b^6 z^2-2 a^3 b^2 c z^2-4 a^2 b^3 c z^2-2 a b^4 c z^2-a^2 b^2 c^2 z^2-2 b^4 c^2 z^2+2 a b^2 c^3 z^2+b^2 c^4 z^2 = 0)
𝒫
au.
El foco Fau=( a (b-c) (a^3-2 a^2 (b+c)+2 (b-c)^2 (b+c)-a (b^2-3 b c+c^2)) : b^2 (2 a^3-a^2 (b+c)+(b-c)^2 (b+c)+a (-2 b^2+5 b c-3 c^2)) : c^2 (-2 a^3+a^2 (b+c)-(b-c)^2 (b+c)+a (3 b^2-5 b c+2 c^2)) ) de la parábola 𝒫au está en la recta que pasa por el incentro y es paralela a su . 𝒫au es tangente en el incentro a la perpendicular a la bisectriz AI, y también a la recta que pasa por los pies de las bisectrices por B y C. Con estos datos, podemos determinar la dirección de su eje y, así, puede ser construida (ver §12.3. (2P13T1)1. Paris Pamfilos.- A Gallery of Conics by Five Elements. Forum Geometricorum Volume 14 (2014) 295–348).
Procediendo cíclicamente sobre los vértices de ABC, se deducen los puntos diagonales Ub, Vb, Wb y Uc, Vc, Wc, las parábolas 𝒫bu, 𝒫cu y las cúbicas Ψbu, Ψcu.
Los focos Fau, Fbu y Fcu de las parábolas 𝒫au, 𝒫bu y 𝒫cu están sobre la recta por X1 paralela a su tripolar.
Las tangentes a las cubicas Ψau, Ψbu y Ψcu en A, B y C, respectivamente, concurren en X58.
X58 is the point of concurrence of the Brocard axes of triangles BIC, CIA, AIB, ABC, (where I denotes the incenter, X
1), as proved in Antreas P. Hatzipolakis, Floor van Lamoen, Barry Wolk, and Paul Yiu,
Concurrency of Four Euler Lines, Forum Geometricorum 1 (2001) 59-68.
Las paralelas por A, B y C a las directrices de la parábolas 𝒫au, 𝒫bu y 𝒫cu concurren en X104 (antipodal del ortocentro en la ).
Las paralelas por A, B y C a los ejes de las parábolas 𝒫au, 𝒫bu y 𝒫cu, concurren en X100 ( del ).
La envolvente de la recta
WaUa, cuando t varía, es una
parábola
( b^4 c^2 x^2-2 b^3 c^3 x^2+b^2 c^4 x^2-2 a^2 b^2 c^2 x y-2 a b^3 c^2 x y+2 b^4 c^2 x y+2 a^2 b c^3 x y-2 a b^2 c^3 x y-2 b^3 c^3 x y+4 a b c^4 x y-2 b^2 c^4 x y+2 b c^5 x y+a^4 c^2 y^2+2 a^3 b c^2 y^2-a^2 b^2 c^2 y^2-2 a b^3 c^2 y^2+b^4 c^2 y^2+4 a^2 b c^3 y^2-2 a^2 c^4 y^2+2 a b c^4 y^2-2 b^2 c^4 y^2+c^6 y^2+2 a^2 b^3 c x z+4 a b^4 c x z+2 b^5 c x z-2 a^2 b^2 c^2 x z-2 a b^3 c^2 x z-2 b^4 c^2 x z-2 a b^2 c^3 x z-2 b^3 c^3 x z+2 b^2 c^4 x z-2 a^4 b c y z-2 a^3 b^2 c y z+4 a^2 b^3 c y z+6 a b^4 c y z+2 b^5 c y z-2 a^3 b c^2 y z-10 a^2 b^2 c^2 y z-6 a b^3 c^2 y z+4 a^2 b c^3 y z-6 a b^2 c^3 y z-4 b^3 c^3 y z+6 a b c^4 y z+2 b c^5 y z+a^4 b^2 z^2-2 a^2 b^4 z^2+b^6 z^2+2 a^3 b^2 c z^2+4 a^2 b^3 c z^2+2 a b^4 c z^2-a^2 b^2 c^2 z^2-2 b^4 c^2 z^2-2 a b^2 c^3 z^2+b^2 c^4 z^2 = 0)
𝒫
av.
Las paralelas por A, B y C a los ejes de las parábolas 𝒫av, 𝒫bv y 𝒫cv, concurren en el .
La envolvente de la recta
UaVa, cuando t varía, es una
parábola
( 4 a^2 b^2 c^2 x^2+4 a b^3 c^2 x^2+b^4 c^2 x^2+4 a b^2 c^3 x^2+2 b^3 c^3 x^2+b^2 b^4 c^2 x^2+2 b^3 c^3 x^2+b^2 c^4 x^2+2 a^2 b^2 c^2 x y+2 a b^3 c^2 x y+2 b^4 c^2 x y-6 a^2 b c^3 x y-6 a b^2 c^3 x y+2 b^3 c^3 x y-8 a b c^4 x y-2 b^2 c^4 x y-2 b c^5 x y+a^4 c^2 y^2+2 a^3 b c^2 y^2+3 a^2 b^2 c^2 y^2+2 a b^3 c^2 y^2+b^4 c^2 y^2+4 a^3 c^3 y^2-4 a b^2 c^3 y^2+6 a^2 c^4 y^2-2 a b c^4 y^2-2 b^2 c^4 y^2+4 a c^5 y^2+c^6 y^2-6 a^2 b^3 c x z-8 a b^4 c x z-2 b^5 c x z+2 a^2 b^2 c^2 x z-6 a b^3 c^2 x z-2 b^4 c^2 x z+2 a b^2 c^3 x z+2 b^3 c^3 x z+2 b^2 c^4 x z+2 a^4 b c y z+6 a^3 b^2 c y z-6 a b^4 c y z-2 b^5 c y z+6 a^3 b c^2 y z+18 a^2 b^2 c^2 y z+6 a b^3 c^2 y z+6 a b^2 c^3 y z+4 b^3 c^3 y z-6 a b c^4 y z-2 b c^5 y z+a^4 b^2 z^2+4 a^3 b^3 z^2+6 a^2 b^4 z^2+4 a b^5 z^2+b^6 z^2+2 a^3 b^2 c z^2-2 a b^4 c z^2+3 a^2 b^2 c^2 z^2-4 a b^3 c^2 z^2-2 b^4 c^2 z^2+2 a b^2 c^3 z^2+b^2 c^4 z^2 = 0)
𝒫
aw.
Los focos Faw, Fbw y Fcw de las parábolas 𝒫aw, 𝒫bw y 𝒫cw forman un triángulo con ABC, con centro de perspectividad X35 ( de X79).
Let A' be the reflection of X(1) in sideline BC, and define B' and C' cyclically. Then the lines AA', BB', CC' concur in X(79). (Eric Danneels, Hyacinthos
7892, 9/13/03)
Faw = (a (a^3+2 a^2 (b+c)-2 (b-c)^2 (b+c)-a (b^2-5 b c+c^2)) : -b^2 (-a^2+b^2-a c-c^2) : c^2 (a^2+a b+b^2-c^2)).
- Sábado, 14 de julio del 2018
Una propiedad del centro X(7319)
Dado un triángulo ABC, sea DEF el . Las rectas AD, BE, CF intersecan de nuevo a los A-excírculo, B-excírculo, C-excírculo en los puntos D', E', F', respectivamente. Se denota por A'B'C' el triángulo delimitado por las tangentes en D', E', F' a los A-excírculo, B-excírculo, C-excírculo, respectivamente.
A'B'C' es con ABC. El centro de perspectividad es X(7319).
En coordenadas baricéntricas,
D' (4(a^2-(b-c)^2) : -(a-b+c)(a+b+c) : -(a+b-c)(a+b+c)),
y la tangente en D' a el A-excírculo es:
(a+b+c)x + 2(a+b-c)y + 2(a-b+c)z = 0.
Las tangentes en E', F' a los B-excírculo, C-excírculo se cortan en:
A' (3a^2-10a(b+c)+3(b+c)^2 : 6a^2-4a b+6b^2-6c^2 : 6a^2-6b^2-4a c+6c^2).
El centro de perspectividad de ABC y A'B'C' es:
X7319 = (1/(3 - b c) : 1/(3SB - c a) : 1/(3SC - a b)).
- Miércoles, 11 de julio del 2018
Triangulo excentral y circunferencias inscritas
Dado un triángulo ABC, sea el . Se denota por I1, I2 e I3 los centros de las circunferencias inscritas a los triángulos , y , respectivamente. Los puntos de contacto de estas circunferencias con los lados BC, CA y AB son, respectivamente, D, E y F.
Las coordenadas baricéntricas de I1 y D (ver §16.4.19) son:
I1 (-a^2 :
a b + √a b(-a^2 + 2a b - b^2 + c^2) :
a c + √a c(-a^2 + b^2 + 2a c - c^2) ).
D (0 : -a^2+2a b-b^2+c^2+
2√a b(-a^2+2a b-b^2+c^2) :
-a^2+b^2+2 a c-c^2+
2 √-a c(a^2-b^2-2a c+c^2)).
Los triángulos ABC y DEF son
El centro de perspectividad es X7048
( tan (B+C)/4 : ... : ...) = (1/(2 b c - 2 + 2 √b c (2 b c - 2 SA) ) : ... : ...).
Los triángulos ABC y son perspectivos.
El centro de perspectividad es el segundo punto de De Villiers (X1128)
(sen A/(1 + 2 sin(A/2)) : ... : ...) =
(1/(bc+√2bc(bc-SA) ).
Los triángulos DEF y son perspectivos.
El centro de perspectividad es:
Z = ( a (a^5 - a^4 (b + c) - 2 a^3 (b^2 + 10 b c + c^2) +
2 a^2 (b^3 + 7 b^2 c + 7 b c^2 + c^3) +
a (b - c)^2 (b^2 + 6 b c + c^2) - (b - c)^4 (b + c) +
2 Sqrt[
b c (a + b - c) (a - b +
c)] (-5 a^2 (b + c) + (b - c)^2 (b + c) +
4 a (b^2 + b c + c^2)) -
2 Sqrt[-a c (a - b - c) (a + b - c) ] (a^3 + a^2 (4 b + c) +
c (b^2 - c^2) - a (5 b^2 + 4 b c + c^2)) -
2 Sqrt[
a b (a - b + c) (-a + b + c)] (a^3 - b^3 + b c^2 + a^2 (b + 4 c) -
a (b^2 + 4 b c + 5 c^2))) : ... : ...),
que tiene números de búsqueda en
(7.35374739906161, 5.91710429249933, -3.84982959708205) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {9,362}, {40,164}, {57,173}, {63,16017}, {165,3659}, {168,7028}, {504,3928}, {1489,3645}, {1697,8078}.
- Martes, 10 de julio del 2018
Una quíntica bicircular
Dado un triángulo ABC, sea su y P un punto de su plano.
Las perpendiculares por Ma, Mb y Mc a AP, BP y CP, respectivamente, forman un triángulo A'B'C'. Se denota por N' el centro de su .
El lugar geométrico de P tal que N' queda sobre la de ABC es una quíntica.
Si (u:v:w) son las coordenadas baricéntricas de P, respecto a ABC, la ecuación de la perpendicular por Ma(0:1:1) a la recta AP se puede determinar usando (12.43), dando:
(a^2(v+w)-c^2(3v+w)-b^2(v+3w))x +
(a^2(v-w)-(b^2-c^2)(v+w))y + (a^2(w-v)+(b^2-c^2)(v+w))z = 0.
Por permutación cíclica, se deducen las ecuaciones de las otras dos perpendiculares; éstas se cortan en:
A' ((b^2-c^2)^2u(2u+v+w)-a^4(4v w+u(v+w))-2a^2u(c^2(u+2v)+b^2(u+2w)) :
((b^2-c^2)u+a^2(u+2v))(b^2(w-u)+a^2(u+w)-c^2(u+w)) :
(c^2(-u+v)+a^2(u+v)-b^2(u+v))((-b^2+c^2)u+a^2(u+2w))).
El centro de la circunferencia de los nueve puntos de ABC es:
N' (a^4v^2w^2(2u+v+w) +
a^2u(b^2w(u^2(v-w)+v^2(v+w)+u(2v^2+2v w-w^2)) +
c^2v(u^2(-v+w)+w^2(v+w)+u(-v^2+2v w+2w^2))) -
u(b^4w(u^2v+v(v+w)^2+u(2v^2+3v w+w^2)) +
c^4v(u^2w+w(v+w)^2+u(v^2+3v w+2w^2)) -
b^2c^2(2v w(v+w)^2+u^2(v^2+4v w+w^2)+
u(v^3+5v^2w+5v w^2+w^3))) : ... : ...).
N' está sobre sobre la recta de Euler de ABC si y sólo si P está sobre la quíntica , circunscrita a ABC, de ecuación:
a^6 c^2 x^3 y^2 - 3 a^4 b^2 c^2 x^3 y^2 + 3 a^2 b^4 c^2 x^3 y^2 -
b^6 c^2 x^3 y^2 - a^4 c^4 x^3 y^2 + a^2 b^2 c^4 x^3 y^2 -
a^2 c^6 x^3 y^2 + c^8 x^3 y^2 + a^6 c^2 x^2 y^3 -
3 a^4 b^2 c^2 x^2 y^3 + 3 a^2 b^4 c^2 x^2 y^3 - b^6 c^2 x^2 y^3 -
a^2 b^2 c^4 x^2 y^3 + b^4 c^4 x^2 y^3 + b^2 c^6 x^2 y^3 -
c^8 x^2 y^3 + 3 a^2 b^4 c^2 x^3 y z - 3 b^6 c^2 x^3 y z -
3 a^2 b^2 c^4 x^3 y z + 3 b^2 c^6 x^3 y z + 2 a^6 c^2 x^2 y^2 z -
2 b^6 c^2 x^2 y^2 z - 4 a^4 c^4 x^2 y^2 z + 4 b^4 c^4 x^2 y^2 z +
2 a^2 c^6 x^2 y^2 z - 2 b^2 c^6 x^2 y^2 z + 3 a^6 c^2 x y^3 z -
3 a^4 b^2 c^2 x y^3 z + 3 a^2 b^2 c^4 x y^3 z - 3 a^2 c^6 x y^3 z -
a^6 b^2 x^3 z^2 + a^4 b^4 x^3 z^2 + a^2 b^6 x^3 z^2 - b^8 x^3 z^2 +
3 a^4 b^2 c^2 x^3 z^2 - a^2 b^4 c^2 x^3 z^2 - 3 a^2 b^2 c^4 x^3 z^2 +
b^2 c^6 x^3 z^2 - 2 a^6 b^2 x^2 y z^2 + 4 a^4 b^4 x^2 y z^2 -
2 a^2 b^6 x^2 y z^2 + 2 b^6 c^2 x^2 y z^2 - 4 b^4 c^4 x^2 y z^2 +
2 b^2 c^6 x^2 y z^2 + 2 a^6 b^2 x y^2 z^2 - 4 a^4 b^4 x y^2 z^2 +
2 a^2 b^6 x y^2 z^2 - 2 a^6 c^2 x y^2 z^2 + 4 a^4 c^4 x y^2 z^2 -
2 a^2 c^6 x y^2 z^2 + a^8 y^3 z^2 - a^6 b^2 y^3 z^2 -
a^4 b^4 y^3 z^2 + a^2 b^6 y^3 z^2 + a^4 b^2 c^2 y^3 z^2 -
3 a^2 b^4 c^2 y^3 z^2 + 3 a^2 b^2 c^4 y^3 z^2 - a^2 c^6 y^3 z^2 -
a^6 b^2 x^2 z^3 + b^8 x^2 z^3 + 3 a^4 b^2 c^2 x^2 z^3 +
a^2 b^4 c^2 x^2 z^3 - b^6 c^2 x^2 z^3 - 3 a^2 b^2 c^4 x^2 z^3 -
b^4 c^4 x^2 z^3 + b^2 c^6 x^2 z^3 - 3 a^6 b^2 x y z^3 +
3 a^2 b^6 x y z^3 + 3 a^4 b^2 c^2 x y z^3 - 3 a^2 b^4 c^2 x y z^3 -
a^8 y^2 z^3 + a^2 b^6 y^2 z^3 + a^6 c^2 y^2 z^3 -
a^4 b^2 c^2 y^2 z^3 - 3 a^2 b^4 c^2 y^2 z^3 + a^4 c^4 y^2 z^3 +
3 a^2 b^2 c^4 y^2 z^3 - a^2 c^6 y^2 z^3=0.
Esta quíntica pasa por los vértices del de X265 (reflexión del circuncentro en el centro de la ) y por los centros: X1 (incentro), X4 (ortocentro), X5 (centro de la circunferencia de los nueve puntos), X30 (punto del infinito de la recta de Euler), X1113, X1114 (puntos de intersección de la recta de Euler con la circunferencia circunscrita), X1138 (uno de los puntos de intersección de la quíntica con su asíntota real: la paralela a la recta de Euler que pasa por los centros Xi, para i = 30, 146, 323, 399, 1138, 9143, 11749, 12112, 12383, 14451, 14611, 14731, 18285, 18781); la asíntota también contiene al punto W (9 de julio del 2018).
Pares {P=Xi, N'=Xj}, con P sobre la quíntica y N' sobre la recta de Euler, para los índices {i,j}: {1, 5}, {4, 5}, {5, 5501}, {30, 30}, {1113, 1312}, {1114, 1313}.
X1312 y X1313 son los puntos de intersección de la recta de Euler con la circunferencia de los nueve puntos. X5501 (9th Hatzipolakis-Montesdeoca Point).
Si P=X1138, entonces
N' = ( 4 a^16-17 a^14 (b^2+c^2)-(b^2-c^2)^6 (11 b^4+14 b^2 c^2+11 c^4)+a^12 (43 b^4+10 b^2 c^2+43 c^4)+a^10 (-89 b^6+27 b^4 c^2+27 b^2 c^4-89 c^6)+a^2 (b^2-c^2)^4 (37 b^6+17 b^4 c^2+17 b^2 c^4+37 c^6)-a^4 (b^2-c^2)^2 (23 b^8-80 b^6 c^2-75 b^4 c^4-80 b^2 c^6+23 c^8)+a^8 (115 b^8+4 b^6 c^2-162 b^4 c^4+4 b^2 c^6+115 c^8)-a^6 (59 b^10+71 b^8 c^2-121 b^6 c^4-121 b^4 c^6+71 b^2 c^8+59 c^10) : ... : ...),
que tiene números de búsqueda en
(4.80573227945818, 3.92353471346419, -1.29365906408691)
y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {3258,18285}, {5627,11749}..
- Lunes, 9 de julio del 2018
Rectas de Euler relativas a los centros X(74) y X(1138)
X(74) is the of the point in which the meets the line at infinity, lies on the circumcircle.
X(1138) is the isogonal conjugate of X(399).
There are only two points X such that the pedal triangle of X is similar to the cevian triangle of X. They are X(4) and
X(1138). (Jean-Pierre Ehrmann, January 4, 2003)
X(399) is the Parry reflection point. X(399) is the reflection of circumcenter in the focus of
Let L, M, and N be lines through A, B, C, respectively, parallel to the Euler line. Let L' be the reflection of L in sideline BC, let M' be the reflection of M in sideline CA, and let N' be the reflection of N in sideline AB. The lines L', M', and N' then concur in a point known as the
Parry reflection point, which is Kimberling center X(399).
Cyril Parry, "Problem 10637", American Mathematical Monthly 105 (1998) 68.
X(146) is the reflection of in the focus of .
X(18317) is the of Ehrmann conic.
(For the definition of Ehrmann conic, see preamble just before
X(18300)).
Dado un triángulo ABC sea A' el punto de intersección de las rectas de Euler de los triángulos X74BC y X1138BC. Los puntos B', C' se definen cíclicamente.
Los triángulos ABC y A'B'C' son
La ecuación baricéntrica de la recta de Euler de X74BC es:
(b-c)(b+c)(-a^2+b^2-c^2)(a^2+b^2-c^2)x-a^2(a-
b)(a+b)(a^2+b^2-c^2)y+a^2(a-c)(a+c)(a^2-b^2+c^2)z = 0,
y la de X1138BC es:
2(b-c)(b+c)(a^4-2b^4+b^2c^2+c^4+a^2(b^2-2c^2))(a^4+b^4+b^2c^2-2c^4+a^2(-2b^2+c^2))x +
(a^4+b^4+b^2c^2-2c^4+
a^2(-2b^2+c^2))(3a^6-(b^2-c^2)^3-a^4(b^2+5c^2)+a^2(-b^4+3b^2c^2+c^4))y -
(a^4-2b^4+b^2c^2+c^4+a^2(b^2-2c^2))(3a^6+(b^2-c^2)^3-a^4(5b^2+c^2)+a^2(b^4+3b^2c^2-c^4))z = 0.
El punto de intersección de esta rectas es:
A' = (-2a^2(a^4+b^4+b^2c^2+c^4-2a^2(b^2+c^2))(-2a^4+(b^2-c^2)^2+a^2(b^2+c^2))^2 :
a^14+a^12(2b^2-5c^2)+(b^2-c^2)^6(2b^2+c^2)+a^10(-9b^4+3b^2c^2+9c^4)-
3a^4(b^2-c^2)^2(6b^6+4b^4c^2-2b^2c^4-3c^6)+a^2(b^2-c^2)^3(b^6+15b^4c^2+6b^2c^4+5c^6)-
a^8(2b^6-24b^4c^2+18b^2c^4+5c^6)+a^6(23b^8-47b^6c^2+9b^4c^4+20b^2c^6-5c^8) :
a^14+a^12(-5b^2+2c^2)+(b^2-c^2)^6(b^2+2c^2)+3a^10(3b^4+b^2c^2-3c^4)+3a^4(b^2-c^2)^2(3b^6+2b^4c^2-4b^2c^4-6c^6)-
a^2(b^2-c^2)^3(5b^6+6b^4c^2+15b^2c^4+c^6)-a^8(5b^6+18b^4c^2-24b^2c^4+2c^6)+
a^6(-5b^8+20b^6c^2+9b^4c^4-47b^2c^6+23c^8)).
El centro de perspectividad de los triángulos ABC y A'B'C' es
W = ( (a^2-b^2-c^2)(2a^4-a^2(b^2+c^2)-(b^2-c^2)^2)/(a^8-
4a^6(b^2+c^2)+a^4(6b^4+b^2c^2+6c^4)+a^2(-4b^6+b^4c^2+b^2c^4-4c^6)+(b^2-c^2)^2(b^4+4b^2c^2+c^4)) : ... : ...),
que tiene números de búsqueda en
(6.26250855866268, 3.50369184105253, -1.67535689666554) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {30,146}, {74,18317}, {265,14919}, {1294,14677}, {1494,10264}, {1511,3163}, {6699,8552}, {10272,14920}, {16163,19223}.
El punto W está sobre la asíntota de la quíntica estudiada el 10 de julio del 2018.
- Viernes, 6 de julio del 2018
Las cúbicas K007 y K758
Dado un triángulo ABC y un punto P, sean el triángulo de P.
A12 es el punto medio de C1B, A13 es el punto medio de B1C y A' es el centro de la circunferencia que pasa por A, A12 y A13. Se definen los puntos B' y C', análogamente.
El triángulo
A'B'C' es perspectivo a
ABC si y sólo si
P está sobre la recta del infinito, la o la cúbica de Lucas (
K007).
Cuando P está sobre K007, ABC y A'B'C' son homotéticos y el centro de homotecia U, queda sobre la cúbica K758, imagen de la cúbica de Darboux
(K004) mediante la homotecia h(X3,1/3), de centro el circuncentro y razón 1/3.
Pares {P=Xi, U=Xj} con P en K007 y U en K758, para {i, j}:
{2, 3}, {4, 2}, {7, 3576}, {8, 165}, {20, 154}, {69, 376}, {253, 10606}.
Si P está sobre K007, A'B'C' es la imagen de ABC, mediante la homotecia h(U,1/4).
Cuando P está en la , ABC y A'B'C' son directamente semejantes y el centro de perspectividad U es el antipodal, en la circunferencia circunscrita, del de P.
El centro de semejanza F es el otro punto de intersección de las circunferencias circunscritas a ambos triángulos.
Pares {P=Xi, U=Xj} con P en la recta del infinito y U en la circunferencia circunscrita, para {i, j}: {30, 110}, {511, 99}, {512, 98}, {513, 104}, {514, 103}, {515, 109}, {516, 101}, {517, 100}, {518, 1292}, {519, 1293}, {520, 1294}, {521, 1295}, {522, 102}, {523, 74}, {524, 1296}, {525, 1297}, {526, 477}, {528, 2742}, {530, 9202}, {531, 9203}, {541, 9060}, {542, 691}, {543, 2709}, {690, 842}, {740, 6010}, {758, 6011}, {804, 2698}, {812, 12032}, {900, 953}, {912, 13397}, {916, 1305}, {924, 1300}, {926, 2724}, {928, 2723}, {952, 901}, {971, 934}, {1154, 930}, {1499, 111}, {1503, 112}, {1510, 1141}, {2574, 1114}, {2575, 1113}, {2771, 1290}, {2772, 2690}, {2773, 2695}, {2774, 2688}, {2775, 2752}, {2776, 2758}, {2777, 1304}, {2778, 2766}, {2779, 2689}, {2780, 2770}, {2781, 935}, {2782, 805}, {2783, 2703}, {2784, 2702}, {2785, 2708}, {2786, 2700}, {2787, 2699}, {2788, 2711}, {2789, 2712}, {2790, 2713}, {2791, 2714}, {2792, 2701}, {2793, 843}, {2794, 2715}, {2795, 2704}, {2796, 2705}, {2797, 2706}, {2798, 2707}, {2799, 2710}, {2800, 2222}, {2801, 1308}, {2802, 2743}, {2803, 2744}, {2804, 2745}, {2805, 2746}, {2806, 2747}, {2807, 929}, {2808, 927}, {2809, 2736}, {2810, 2737}, {2811, 2738}, {2812, 2739}, {2813, 2740}, {2814, 2751}, {2815, 2757}, {2816, 2762}, {2817, 2765}, {2818, 1309}, {2819, 2768}, {2820, 2725}, {2821, 2726}, {2822, 2727}, {2823, 2728}, {2824, 2729}, {2826, 840}, {2827, 2718}, {2828, 2719}, {2829, 2720}, {2830, 2721}, {2831, 2722}, {2835, 2730}, {2836, 2691}, {2841, 2731}, {2842, 2692}, {2846, 2732}, {2849, 2733}, {2850, 2694}, {2852, 2735}, {2854, 2696}, {3307, 1382}, {3308, 1381}, {3309, 105}, {3413, 1380}, {3414, 1379}, {3564, 3565}, {3566, 3563}, {3667, 106}, {3738, 2716}, {3849, 6233}, {3887, 2717}, {3900, 972}, {3906, 14388}, {4083, 15323}, {5663, 476}, {5840, 6099}, {5842, 15439}, {5854, 15168}, {6000, 107}, {6001, 108}, {6002, 741}, {6003, 759}, {6088, 6093}, {6368, 18401}, {8057, 5897}, {8674, 2687}, {8676, 917}, {8677, 2734}, {8702, 5951}, {8704, 6323}, {8705, 6236}, {9003, 841}, {9033, 2693}, {9517, 2697}, {9518, 2741}, {9519, 2748}, {9520, 2749}, {9521, 2750}, {9522, 2753}, {9523, 2754}, {9524, 2755}, {9525, 2756}, {9526, 2759}, {9527, 2760}, {9528, 2761}, {9529, 2763}, {9530, 2764}, {9531, 2767}, {9532, 2769}, {9830, 13241}, {11645, 11636}, {13754, 925}, {14077, 15731}, {14915, 1302}, {15310, 932}, {15311, 1301}, {15313, 915}, {15726, 14074}, {16168, 16170}, {16171, 16169}, {17702, 10420}, {18400, 933}.
Cuando P está en la , ABC y A'B'C' son directamente semejantes y el centro de perspectividad U queda sobre la circunferencia circunscrita.
A puntos antipodales en la elipse circunscrita de Steiner les corresponde el mismo punto U.
Pares {P=Xi, U=Xj} con P en la elipse circunscrita de Steiner y U en la circunferencia circunscrita, para {i, j}: {99, 842}, {190, 953}, {648, 2693}, {671, 842}, {903, 953}, {1494, 2693}, {2479, 1297}, {2480, 1297}, {6189, 74}, {6190, 74}.
Sea ahora el triángulo de P.
A22 es el punto medio de C2B, A23 es el punto medio de B2C y A" es el centro de la circunferencia que pasa por A, A22 y A23. Se definen los puntos B" y C", análogamente.
El triángulo A"B"C" es homotético a ABC, para todo punto P del plano. El centro de homotecia V es la imagen de P mediante la homotecia h(X3,1/3). A"B"C" es la imagen de ABC, mediante la homotecia h(V,1/4).
Para todo punto P sobre la cúbica K007, la recta UV pasa por X376 (reflexión del baricentro en el circuncentro). Además, las rectas A'A", B'B" y B'B", pasan por sendos puntos fijos, Fa Fb y Fc, respectivamente.
El triángulo es homotético a ABC, mediante la homotecia h(X376,1/4).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Generalización:
En vez de tomar puntos medios, se toman los puntos A1i y A2i (i=1,2), tales que,
CiAi2 : Ai2B = t y
BiAi3 : Ai3C = t.
A' es el centro de la circunferencia (AA12A13) y A" es el centro de la circunferencia (AA22A23). Análogamente se definen B', C', B", C".
El triángulo
A'B'C' es perspectivo a
ABC si y sólo si
P está sobre la cúbica de Lucas (
K007)
o sobre la cúbica 𝒦
t de ecuación baricéntrica:
2 x y z + (x + y) (x + z) (y + z) t (1 + t) = 0.
Cuando P se mueve sobre la cúbica de Lucas, los triángulos son homotéticos y el centro de homotecia U está sobre la cúbica imagen de la cúbica de Darboux, mediante la homotecia h(X3,1/(1+2t)).
Cuando P se mueve sobre la cúbica 𝒦t, el centro de perspectividad U de ABC y A'B'C' está sobre las circunferencias circunscritas a ambos triángulos.
- Sábado, 30 de junio del 2018
Centros de semejanzas inversas y las cúbicas K006 y K028
Dado un triángulo ABC y un punto P, sean A', B', C' las reflexiones de A, B, C en el circuncentro y DEF el de P.
A", B", C" son las reflexiones de A', B', C' en D, E, F, respectivamente.
Los triángulos ABC y A"B"C" son inversamente semejantes.
Si (u:v:w) son las coordenadas baricéntricas de P,
A" = ( a^2(a^2+b^2-c^2)(a^2-b^2+c^2)(u+v+w) :
-(b^2-c^2)^3u-a^6(u+2v)+a^2(b^2-c^2)(c^2(3u+2v)+b^2(3u+2w))+a^4(c^2(3u+4v)-b^2(u-2v+2w)):
(b^2-c^2)^3u-a^6(u+2w)-a^2(b^2-c^2)(c^2(3u+2v)+b^2(3u+2w))+a^4(-c^2(u+2v-2w)+b^2(3u+4w))).
La matriz asociada a la transformación afín σP que aplica ABC en A"B"C" es (aij):
a11 = a^2b^2c^2(a^2+b^2-c^2)(a^2-b^2+c^2)(u+v+w),
a12 = -a^2c^2(a^6v+(b^2-c^2)^2(-c^2v+b^2(2u+v))+
a^2(3c^4v+2b^2c^2(-u+w)+b^4(-2u+v+2w))-
a^4(3c^2v+b^2(3v+2w))),
a13 = -a^2b^2(a^6w-(b^2-c^2)^2(b^2w-c^2(2u+w))+
a^2(2b^2c^2(-u+v)+3b^4w+c^4(-2u+2v+w))-
a^4(3b^2w+c^2(2v+3w))),
a21 = -b^2c^2((b^2-c^2)^3u+a^6(u+2v)-
a^2(b^2-c^2)(c^2(3u+2v)+b^2(3u+2w))+a^4(-c^2(3u+4v)+b^2(u-2v+2w))),
a22 = -a^2b^2c^2(a^2-b^2-c^2)(a^2+b^2-c^2)(u+v+w),
a23 = a^2b^2(a^6w-(b^2-c^2)(b^4w-2b^2c^2(u+w)-c^4(2v+w))-a^4(3b^2w+c^2(2v+3w))+
a^2(2b^2c^2(-u+v)+3b^4w+c^4(4v+3w))),
a31 = -b^2c^2(-(b^2-c^2)^3u+a^6(u+2w)+
a^2(b^2-c^2)(c^2(3u+2v)+b^2(3u+2w))+
a^4(c^2(u+2v-2w)-b^2(3u+4w))),
a32 = -a^2c^2(-a^6v+(b^2-c^2)(-c^4v+2b^2c^2(u+v)+
b^4(v+2w))+a^4(3c^2v+b^2(3v+2w))-
a^2(3c^4v+2b^2c^2(-u+w)+b^4(3v+4w))),
a33 = -a^2b^2c^2(a^2-b^2-c^2)(a^2-b^2+c^2)(u+v+w).
A la raíz λ = a^2b^2c^2(-a+b+c)(a+b-c)(a-b+c)(a+b+c)(u+v+w), del polinomio característico |σ-λ I|=0, le corresponde el punto fijo, centro de semejanza inversa:
Q = (a^2(v wa^4-2(v+w)(c^2v+b^2w)a^2+
c^4v(2v+w)+b^4w(v+2w)-2b^2c^2(u(v+w)-v w)) : ... : ... ).
Pares de centros del triángulo {P=Xi, Q=Xj} (P no en la recta del infinito), para los índices {i,j}: {1, 3811}, {2, 1351}, {3, 4}, {4, 155}, {5, 15801}, {20, 3}, {22, 1352}, {40, 1158}, {154, 10002}, {376, 11472}, {858, 9970}, {944, 11248}, {1158, 46}, {1370, 19149}, {1498, 6523}, {2071, 7728}, {2360, 946}, {5171, 76}, {5210, 7620}, {6261, 1}, {6759, 14249}, {7488, 6288}, {7710, 6}, {7712, 381}, {8718, 5}, {8721, 8743}, {9732, 487}, {9733, 488}, {9934, 403}, {10131, 3095}, {11249, 8}, {11257, 9737}, {11413, 5878}, {11414, 11487}, {12163, 20}, {12256, 9733}, {12257, 9732}, {16049, 5887}.
Si P está sobre la circunferencia circunscrita, Q=P* ( de P, en la recta del infinito).
Cuando P se mueve sobre una recta m, que pasa por el circuncentro, el lugar geométrico de Q es una hipérbola rectangular hM, que pertenece al haz de hipérbolas que pasa por el ortocentro y por los tres puntos U', V', W', en los que la circuncúbica K006 vuelve a cortar a la circunferencia circunscrita.
Las asíntotas de la hipérbola hM son paralelas a las de la hipérbola m*, conjugada isogonal de la recta m.
Los puntos U', V', W' son las reflexiones, respecto al circuncentro, de los tres puntos U, V, W (a parte de X79), en los que la circunferencia circunscrita corta a la hipérbola traslada de la hipérbola de Jerabek, mediante la traslación de vector X4X3.
Algunas hipérbolas de este haz son:
• hE:
( (2 a^4 b^4 c^2 - 2 a^2 b^6 c^2 - 2 a^4 b^2 c^4 +
2 a^2 b^2 c^6) x^2 + (a^8 c^2 - b^8 c^2 - 3 a^6 c^4 -
a^4 b^2 c^4 + a^2 b^4 c^4 + 3 b^6 c^4 + 3 a^4 c^6 - 3 b^4 c^6 -
a^2 c^8 + b^2 c^8) x y + (2 a^6 b^2 c^2 - 2 a^4 b^4 c^2 +
2 a^2 b^4 c^4 - 2 a^2 b^2 c^6) y^2 + (-a^8 b^2 + 3 a^6 b^4 -
3 a^4 b^6 + a^2 b^8 + a^4 b^4 c^2 - b^8 c^2 - a^2 b^4 c^4 +
3 b^6 c^4 - 3 b^4 c^6 + b^2 c^8) x z + (-a^8 b^2 + 3 a^6 b^4 -
3 a^4 b^6 + a^2 b^8 + a^8 c^2 - a^4 b^4 c^2 - 3 a^6 c^4 +
a^4 b^2 c^4 + 3 a^4 c^6 - a^2 c^8) y z + (-2 a^6 b^2 c^2 +
2 a^2 b^6 c^2 + 2 a^4 b^2 c^4 - 2 a^2 b^4 c^4) z^2 = 0)
Lugar geométrico de Q, cuando P recorre la . El centro de hE es X113 (antipodo del centro de la en la ) y pasa por los centros Xi, para i: 3, 4, 110, 155, 1351, 1352, 2574, 2575, 5878, 5887, 6288, 7728, 9970, 11472, 11487, 15062, 15801, 16543, 19149.
X3 y X155 son los otros dos puntos sobre K006, los cuales son X4- (X3 = X4/X155, X155 = X4/X3).
• hB:
( (-2 a^4 b^2 + 2 a^2 b^4 + 2 a^4 c^2 - 2 a^2 c^4) x^2 + (-a^6 -
a^4 b^2 + a^2 b^4 + b^6 + 4 a^4 c^2 - 4 b^4 c^2 - 3 a^2 c^4 +
3 b^2 c^4) x y + (-2 a^4 b^2 + 2 a^2 b^4 - 2 b^4 c^2 +
2 b^2 c^4) y^2 + (a^6 - 4 a^4 b^2 + 3 a^2 b^4 + a^4 c^2 -
3 b^4 c^2 - a^2 c^4 + 4 b^2 c^4 - c^6) x z + (-3 a^4 b^2 +
4 a^2 b^4 - b^6 + 3 a^4 c^2 - b^4 c^2 - 4 a^2 c^4 + b^2 c^4 +
c^6) y z + (2 a^4 c^2 - 2 b^4 c^2 - 2 a^2 c^4 + 2 b^2 c^4) z^2 = 0)
Lugar geométrico de Q, cuando P recorre el . El centro de hB es X114 (antipodo del centro de la en la circunferencia de los nueve puntos) y pasa por los centros Xi, para i: 4, 76, 99, 376,487, 488, 3413, 3414, 7620.
X487 y X488 son los otros dos puntos sobre K006, los cuales son X4-Ceva conjugados (X487 = X4/X488, X488 = X4/X487).
• cónica
( (-2 a^6 b^4 c^2 + 4 a^4 b^6 c^2 - 2 a^2 b^8 c^2 + 2 a^6 b^2 c^4 -
2 a^2 b^6 c^4 - 4 a^4 b^2 c^6 + 2 a^2 b^4 c^6 +
2 a^2 b^2 c^8) x^2 + (a^10 c^2 - a^8 b^2 c^2 - 2 a^6 b^4 c^2 +
2 a^4 b^6 c^2 + a^2 b^8 c^2 - b^10 c^2 - 2 a^8 c^4 +
4 a^6 b^2 c^4 - 4 a^2 b^6 c^4 + 2 b^8 c^4 - 4 a^4 b^2 c^6 +
4 a^2 b^4 c^6 + 2 a^4 c^8 - 2 b^4 c^8 - a^2 c^10 +
b^2 c^10) x y + (2 a^8 b^2 c^2 - 4 a^6 b^4 c^2 + 2 a^4 b^6 c^2 +
2 a^6 b^2 c^4 - 2 a^2 b^6 c^4 - 2 a^4 b^2 c^6 + 4 a^2 b^4 c^6 -
2 a^2 b^2 c^8) y^2 + (-a^10 b^2 + 2 a^8 b^4 - 2 a^4 b^8 +
a^2 b^10 + a^8 b^2 c^2 - 4 a^6 b^4 c^2 + 4 a^4 b^6 c^2 -
b^10 c^2 + 2 a^6 b^2 c^4 - 4 a^2 b^6 c^4 + 2 b^8 c^4 -
2 a^4 b^2 c^6 + 4 a^2 b^4 c^6 - a^2 b^2 c^8 - 2 b^4 c^8 +
b^2 c^10) x z + (-a^10 b^2 + 2 a^8 b^4 - 2 a^4 b^8 + a^2 b^10 +
a^10 c^2 - 4 a^6 b^4 c^2 + 4 a^4 b^6 c^2 - a^2 b^8 c^2 -
2 a^8 c^4 + 4 a^6 b^2 c^4 - 2 a^2 b^6 c^4 - 4 a^4 b^2 c^6 +
2 a^2 b^4 c^6 + 2 a^4 c^8 + a^2 b^2 c^8 -
a^2 c^10) y z + (-2 a^8 b^2 c^2 - 2 a^6 b^4 c^2 + 2 a^4 b^6 c^2 +
2 a^2 b^8 c^2 + 4 a^6 b^2 c^4 - 4 a^2 b^6 c^4 - 2 a^4 b^2 c^6 +
2 a^2 b^4 c^6) z^2 = 0)
de X25 (polo del respecto a la circunferencia circunscrita) respecto a la cúbica K006: Lugar geométrico de Q, cuando P recorre la recta X3X66. El centro de esta cónica es X132 (punto medio de X4X112) y pasa por los centros Xi, para i: 4, 112, 371, 372, 378, 1064, 8743, 14983.
X371 y X362 son los otros dos puntos sobre K006, los cuales son X4-Ceva conjugados (X371 = X4/X372, X372 = X4/X371).
• hX1:
( (-2 a^4 b^2 c + 2 a^2 b^4 c + 2 a^4 b c^2 - 2 a^2 b^3 c^2 +
2 a^2 b^2 c^3 - 2 a^2 b c^4) x^2 + (-a^6 c - a^4 b^2 c +
a^2 b^4 c + b^6 c + a^5 c^2 + a^4 b c^2 - a b^4 c^2 - b^5 c^2 +
2 a^4 c^3 - 2 b^4 c^3 - 2 a^3 c^4 + 2 b^3 c^4 - a^2 c^5 +
b^2 c^5 + a c^6 - b c^6) x y + (-2 a^4 b^2 c + 2 a^2 b^4 c +
2 a^3 b^2 c^2 - 2 a b^4 c^2 - 2 a^2 b^2 c^3 +
2 a b^2 c^4) y^2 + (a^6 b - a^5 b^2 - 2 a^4 b^3 + 2 a^3 b^4 +
a^2 b^5 - a b^6 - a^4 b^2 c + b^6 c + a^4 b c^2 - b^5 c^2 -
2 b^4 c^3 - a^2 b c^4 + a b^2 c^4 + 2 b^3 c^4 + b^2 c^5 -
b c^6) x z + (a^6 b - a^5 b^2 - 2 a^4 b^3 + 2 a^3 b^4 + a^2 b^5 -
a b^6 - a^6 c + a^2 b^4 c + a^5 c^2 - a b^4 c^2 + 2 a^4 c^3 -
2 a^3 c^4 - a^2 b c^4 + a b^2 c^4 - a^2 c^5 +
a c^6) y z + (2 a^4 b c^2 - 2 a^3 b^2 c^2 + 2 a^2 b^3 c^2 -
2 a b^4 c^2 - 2 a^2 b c^4 + 2 a b^2 c^4) z^2 = 0)
Lugar geométrico de Q, cuando P recorre la recta X1X3. El centro de hX1 es X119 (antipodo del en la circunferencia de los nueve puntos) y pasa por los centros Xi, para i: 4, 8, 100, 1158, 3307, 3308, 3651, 3811, 6261, 10698.
Intersection of K006 (The Orthocubic ) with the circumcircle (Bernard Gibert)
The points U', V', W' are the intersections (apart A, B, C) of K006 and the circumcircle. These points lie on several remarkable rectangular hyperbolas:
• (H1) passing through X(3), X(4), X(110), X(155), X(1351), X(1352), X(2574), X(2575),
• (H2) passing through X(4), X(76), X(99), X(376), X(487), X(488),
• the polar conic of X(25) passing through X(4), X(112), X(371), X(372), X(378), X(1064).
These form a pencil and each hyperbola meets K006 at H, U', V', W' and two other points which are H-Ceva conjugates.
Si P se mueve sobre una recta m, que pasa por el circuncentro, entonces la recta que une P* con Q, pasa por un punto fijo M'.
El punto M' es cuarto punto de interseción de las hipérbolas hM y m* (a parte del ortocentro y sus puntos del infinito).
El lugar geométrico del punto
M', cuando
m gira alrededor del circuncentro, es la tercera cúbica de Mulsseman,
K028.
- Martes, 26 de junio del 2018
Dos hipérbolas asociadas a la recta de Euler
Dado un triángulo ABC, sean P y Q dos puntos . y son los de P y Q, respectivamente.
Ap = BPb ∩ CPc,
Aq = BQb ∩ CQc.
Bp = CPc ∩ APa,
Bq = CQc ∩ AQa.
Cp = APa ∩ BPb,
Cq = AQa ∩ BQb.
A1 = PCp ∩ QBq,
B1 = PAp ∩ QCq,
C1 = PBp ∩ QAq.
A2 = PBp ∩ QCq,
B2 = PCp ∩ QAq,
C2 = PAp ∩ QBq.
Si (u:v:w) son las coordenadas baricéntricas de P:
Ap = (((a^2 - c^2) v + b^2 (2 u + v)) ((a^2 - b^2) w +
c^2 (2 u + w)) : ((a^2 - c^2) v + b^2 (2 u + v)) ((-a^2 + b^2) w +
c^2 (2 v + w)) : -((a^2 - b^2) w + c^2 (2 u + w)) (a^2 v - c^2 v -
b^2 (v + 2 w)) ),
Aq = (v ((b^2 - c^2) u + a^2 (u + 2 v)) w ((-b^2 + c^2) u +
a^2 (u + 2 w)) : u ((b^2 - c^2) u + a^2 (u + 2 v)) w (-a^2 v +
c^2 v + b^2 (v + 2 w)) : u v ((-a^2 + b^2) w +
c^2 (2 v + w)) ((-b^2 + c^2) u + a^2 (u + 2 w)) ),
A1 = ((b^2 - c^2) u (-c^2 v + b^2 (2 u + v)) - a^4 v (3 u + 2 w) +
a^2 (2 c^2 v (u + w) - 2 b^2 (u^2 - u v + v w)) : (a^2 + b^2 -
c^2) u (a^2 v - c^2 v - b^2 (v + 2 w)) : (a^2 - b^2 +
c^2) u (a^2 v - c^2 v - b^2 (v + 2 w)) ),
A2 = (a^4 (3 u + 2 v) w - (b^2 - c^2) u (b^2 w - c^2 (2 u + w)) +
2 a^2 (-b^2 (u + v) w + c^2 (u^2 - u w + v w)) : -(a^2 + b^2 -
c^2) u ((a^2 - b^2) w -
c^2 (2 v + w)) : -(a^2 - b^2 + c^2) u ((a^2 - b^2) w -
c^2 (2 v + w))).
El triángulo ABC es a los triángulos y .
El centro ortológico de y respecto a ABC es el ortocentro.
El centro ortológico de ABC respecto a es:
U = (1/((a^2 b^2 u - b^4 u + b^2 c^2 u + a^4 v - a^2 b^2 v -
a^2 c^2 v) (-2 c^2 v + a^2 w - b^2 w - c^2 w) (a^2 u - b^2 u -
c^2 u + a^2 w + b^2 w - c^2 w)) : ... : ...).
El centro ortológico de ABC respecto a es:
V = (1/((-a^2 u + b^2 u + c^2 u - a^2 v + b^2 v - c^2 v) (-a^2 v + b^2 v +
c^2 v + 2 b^2 w) (-a^2 c^2 u - b^2 c^2 u + c^4 u - a^4 w +
a^2 b^2 w + a^2 c^2 w)) : ... : ...).
Si el punto P se mueve sobre la (OP : PH = t), los puntos U y V describen sendas
hipérbolas
( (-a^10 + 2 a^8 b^2 - 2 a^4 b^6 + a^2 b^8 + 2 a^8 c^2 - 3 a^6 b^2 c^2 +
a^4 b^4 c^2 - a^2 b^6 c^2 + b^8 c^2 - 2 a^6 c^4 + a^4 b^2 c^4 +
2 a^2 b^4 c^4 - b^6 c^4 + 2 a^4 c^6 - a^2 b^2 c^6 - b^4 c^6 -
a^2 c^8 + b^2 c^8) x y + (a^8 b^2 - a^6 b^4 - a^4 b^6 + a^2 b^8 +
a^8 c^2 - a^6 b^2 c^2 + 2 a^4 b^4 c^2 - a^2 b^6 c^2 - b^8 c^2 -
2 a^6 c^4 + a^4 b^2 c^4 + a^2 b^4 c^4 + 2 b^6 c^4 -
3 a^2 b^2 c^6 - 2 b^4 c^6 + 2 a^2 c^8 + 2 b^2 c^8 -
c^10) x z + (-a^8 b^2 + 2 a^6 b^4 - 2 a^4 b^6 + 2 a^2 b^8 - b^10 +
a^8 c^2 - a^6 b^2 c^2 + a^4 b^4 c^2 - 3 a^2 b^6 c^2 + 2 b^8 c^2 -
a^6 c^4 + 2 a^4 b^2 c^4 + a^2 b^4 c^4 - a^4 c^6 - a^2 b^2 c^6 -
2 b^4 c^6 + a^2 c^8 + b^2 c^8) y z = 0)
( (-a^8 b^2 + 2 a^6 b^4 - 2 a^2 b^8 + b^10 - a^8 c^2 + a^6 b^2 c^2 -
a^4 b^4 c^2 + 3 a^2 b^6 c^2 - 2 b^8 c^2 + a^6 c^4 -
2 a^4 b^2 c^4 - a^2 b^4 c^4 + 2 b^6 c^4 + a^4 c^6 + a^2 b^2 c^6 -
2 b^4 c^6 - a^2 c^8 + b^2 c^8) x y + (a^10 - 2 a^8 b^2 +
2 a^6 b^4 - 2 a^4 b^6 + a^2 b^8 - 2 a^8 c^2 + 3 a^6 b^2 c^2 -
a^4 b^4 c^2 + a^2 b^6 c^2 - b^8 c^2 - a^4 b^2 c^4 -
2 a^2 b^4 c^4 + b^6 c^4 + 2 a^4 c^6 + a^2 b^2 c^6 + b^4 c^6 -
a^2 c^8 - b^2 c^8) x z + (-a^8 b^2 + a^6 b^4 + a^4 b^6 - a^2 b^8 +
a^8 c^2 + a^6 b^2 c^2 - 2 a^4 b^4 c^2 + a^2 b^6 c^2 - b^8 c^2 -
2 a^6 c^4 - a^4 b^2 c^4 - a^2 b^4 c^4 + 2 b^6 c^4 + 2 a^4 c^6 +
3 a^2 b^2 c^6 - 2 a^2 c^8 - 2 b^2 c^8 + c^10) y z = 0)
circunscritas a ABC, con dos de sus asíntotas paralelas, a la dirección dada por X525 (conjugado isogonal de X112).
If the line X(4)X(6) is reflected in every side of triangle ABC, then the reflections concur in X(112). (Randy Hutson, 9/23/2011)
El punto de intersección de las otras dos asíntotas (que no tienen la dirección de X525) es
W = ( (a^2-c^2)(a^4-(b^2-c^2)^2)^2
(a^10
-a^8(2b^2+c^2)
+a^6(2b^4+c^4)
-a^4(2b^6-2b^4c^2+c^6)
+a^2b^4(b^2-c^2)^2
+b^4c^2(b^2-c^2)^2 ) : ... : ...),
que tiene números de búsqueda en
(-0.104492602507159, 0.270604174702043, 3.50155048519396), y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {98,6530}, {107,685}, {112,2966}, {648,17932}, {2422,2442}, {14273,15459}.
NOTA:
El lugar geométrico de los centros de las hipérbolas del haz con puntos base {A, B, C, X525}, es la
parábola
( (a^8 - a^6 b^2 - a^4 b^4 + a^2 b^6 - a^6 c^2 + 3 a^4 b^2 c^2 -
a^2 b^4 c^2 - b^6 c^2 - a^4 c^4 - a^2 b^2 c^4 + 2 b^4 c^4 +
a^2 c^6 - b^2 c^6) x^2 + (-a^8 + 2 a^4 b^4 - b^8 + 2 a^6 c^2 -
2 a^4 b^2 c^2 - 2 a^2 b^4 c^2 + 2 b^6 c^2 - a^4 c^4 +
2 a^2 b^2 c^4 - b^4 c^4) x y + (a^6 b^2 - a^4 b^4 - a^2 b^6 +
b^8 - a^6 c^2 - a^4 b^2 c^2 + 3 a^2 b^4 c^2 - b^6 c^2 +
2 a^4 c^4 - a^2 b^2 c^4 - b^4 c^4 - a^2 c^6 +
b^2 c^6) y^2 + (-a^8 + 2 a^6 b^2 - a^4 b^4 - 2 a^4 b^2 c^2 +
2 a^2 b^4 c^2 + 2 a^4 c^4 - 2 a^2 b^2 c^4 - b^4 c^4 + 2 b^2 c^6 -
c^8) x z + (-a^4 b^4 + 2 a^2 b^6 - b^8 + 2 a^4 b^2 c^2 -
2 a^2 b^4 c^2 - a^4 c^4 - 2 a^2 b^2 c^4 + 2 b^4 c^4 + 2 a^2 c^6 -
c^8) y z + (-a^6 b^2 + 2 a^4 b^4 - a^2 b^6 + a^6 c^2 -
a^4 b^2 c^2 - a^2 b^4 c^2 + b^6 c^2 - a^4 c^4 + 3 a^2 b^2 c^4 -
b^4 c^4 - a^2 c^6 - b^2 c^6 + c^8) z^2 = 0)
que pasa por los centros del triángulo X525, X647, X6587, X14401, X17434.
- Lunes, 18 de junio del 2018
Triángulos con baricentro en la recta de Euler
Dado un triángulo ABC, sean G=X2, O=X3,
H=X4 y K=X6 sus baricentro, circuncentro, ortocentro y , respectivamente.
Pt es un punto sobre la tal que HPt : PtO = t.
Ha es el ortocentro de GBC, Oa el circuncentro de GBC y Pa, tal que HaPa : PaOa.
Hb es el ortocentro de GCA, Ob el circuncentro de GCA y Pb, tal que HbPb : PbOb.
Hc es el ortocentro de GAB, Oc el circuncentro de GAB y Pc, tal que HcPc : PcOc.
Pt es el baricentro de .
En coordenadas baricéntricas:
Pt = ( b((b^2 - c^2)^2 + a^4 (-1 + t) - a^2 (b^2 + c^2) t :
a^4 + c^4 + b^4 (-1 + t) - b^2 c^2 t - a^2 (2 c^2 + b^2 t) :
a^4 + (b^2 - c^2) (b^2 - c^2 (-1 + t)) - a^2 (2 b^2 + c^2 t) ),
Pa = ( (b^2 - c^2)^2 - a^2 (b^2 + c^2) t + a^4 (-9 + 5 t) :
a^2 (-8 c^2 + b^2 (2 - 5 t)) - a^4 (-6 + t) + (b^2 - c^2) (2 b^2 t - c^2 (2 + t))
a^2 (-8 b^2 + c^2 (2 - 5 t)) - a^4 (-6 + t) + (b^2 - c^2) (-2 c^2 t + b^2 (2 + t)) ).
Los puntos
Pa,
Pb y
Pc están alineados si
t = (a^2+b^2+c^2±2√a^4+b^4+c^4-a^2b^2-a^2c^2-b^2c^2)/(a^2+b^2+c^2) =
= (R ± OK)/R.
Las dos rectas que los contienen son las paralelas por X39 a las asíntotas de la .
Los correspondientes baricentros de los puntos {Pa, Pb, Pc} son los puntos W1 y W2 de intersección de la recta de Euler con las rectas que pasan por el del simediano (X141) y los puntos de intersección del con la circunferencia circunscrita (X1379 y X1380). Y también, la intersección de las rectas que pasan por estos puntos y el punto medio del ortocentro y simediano (X5480), con la recta de Euler.
The Brocard axis, OK, is the line of the circumcenter, O [= X(3)], and the symmedian point, K [= X(6)]. This line meets the circumcircle in two points,
X(1379) and X(1380); the closer to X(6) is X(1379).
W1 = ( (-a^2 - b^2 - c^2) (a^2 b^2 - b^4 + a^2 c^2 + 2 b^2 c^2 - c^4)
-
2 a^2 (a^2 - b^2 - c^2) √a^4 + b^4 + c^4- b^2 c^2 - a^2 b^2 - a^2c^2 : ... : ...),
que tiene números de búsqueda en
(-3.77051914860199, -4.63009234678124, 8.58635263672616) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {32,6178}, {39,3414}, {141,1380}, {187,2040}, {524,3558}, {574,1349}, {597,14630}, {1340,3589}, {1341,1503}, {1379,5480}, {3933,6189}, {8550,14631}.
Añadido en ETC (27/06/2018) como el X19659.
W2 = ( (-a^2 - b^2 - c^2) (a^2 b^2 - b^4 + a^2 c^2 + 2 b^2 c^2 - c^4)
+
2 a^2 (a^2 - b^2 - c^2) √a^4 + b^4 + c^4- b^2 c^2 - a^2 b^2 - a^2c^2 : ... : ...),
que tiene números de búsqueda en
(2.36330674918221, 1.48755236340753, 1.52006357684891) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {32,6177}, {39,3413}, {141,1379}, {187,2039}, {524,3557}, {574,1348}, {597,14631}, {1340,1503}, {1341,3589}, {1380,5480}, {3933,6190}, {8550,14630}.
Añadido en ETC (27/06/2018) como el X19660.
Los triángulos ABC y son .
El centro ortológico de ABC respecto a es:
Ut = (-(c^2 (-5 + t) + a^2 (1 + t) + b^2 (1 + t)) (b^2 (-5 + t) +
a^2 (1 + t) +
c^2 (1 + t)) :
-(c^2 (-5 + t) + a^2 (1 + t) +
b^2 (1 + t)) (a^2 (-5 + t) + (b^2 + c^2) (1 +
t)) :
-(b^2 (-5 + t) + a^2 (1 + t) +
c^2 (1 + t)) (a^2 (-5 + t) + (b^2 + c^2) (1 + t))),
que está sobre la .
El centro ortológico de respecto a ABC es:
Vt = (-(b^2 - c^2)^2 - a^4 (1 + 3 t) +
a^2 (b^2 + c^2) (2 + 3 t) :
-a^4 - (b^2 - c^2) (-c^2 +
b^2 (1 + 3 t)) +
a^2 (2 c^2 + b^2 (2 + 3 t)) :
-a^4 - (b^2 - c^2) (b^2 -
c^2 (1 + 3 t)) + a^2 (2 b^2 + c^2 (2 + 3 t))),
que está sobre la .
Los triángulos ABC y son perspectivos si t=2 o t=-2/3, que corresponden a Pt, el baricentro y el del .
Los centros de perspectividad son, respectivamente, el baricentro y el ortocentro. Las correspondientes son la recta de Euler y la recta X4X15533 (X15533 es la reflexión del simediano en el punto medio del baricentro y el ).
Los triángulos ABC y son si los si
t = (5(a^4+b^4+c^4)-2(a^2b^2+a^2c^2+b^2c^2))/(a^2+b^2+c^2)^2 = 4S^2(2-5Sin^2ω)Csc^2ω.
es decir, cuando
Pt = X8369 = (4(a^4+b^4+c^4)-a^2(b^2+c^2) : ... : ....).
El centro paralológico de ABC respecto a es el .
El centro paralológico de respecto a ABC es:
W = ( 16 a^4 - a^2 (b^2 + c^2) + (b^2 + c^2)^2 : ... : ...),
que tiene números de búsqueda en
(0.893302861584896, 1.04606138925610, 2.50417450707559) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,1285}, {5,598}, {6,7618}, {30,9753}, {32,524}, {187,597}, {230,3363}, {315,8365}, {489,7584}, {490,7583}, {543,5306}, {549,2080}, {550,7827}, {599,3793}, {1353,8724}, {1992,6390}, {2482,5008}, {3053,8182}, {3815,7619}, {3845,9166}, {5032,11165}, {5182,16508}, {5215,7753}, {6329,8588}, {7620,7735}, {7622,9300}, {7745,8176}, {7804,11168}, {7806,8352}, {7812,7940}, {7856,15704}, {7878,15712}, {8362,15810}, {8370,8859}, {8598,15048}, {9740,14039}, {9770,11288}, {14537,14971}.
Añadido en ETC (26/06/2018) como el X19661.
El punto fijo (propio) de la transformación afín que aplica el triángulo
ABC en el es:
Ft = (4 a^4 t (1 + t) - a^2 c^2 t (10 + 7 t) - 2 b^4 (-6 - 5 t + t^2) -
2 c^4 (-6 - 5 t + t^2) - b^2 (a^2 t (10 + 7 t) + 4 c^2 (6 + t + t^2)) : ... : ...).
(5a^2b^2-b^4-5a^2c^2+c^4)x^2+(a^4-5a^2b^2+5b^2c^2-c^4)y^2
+(-a^4+b^4+5a^2c^2-5b^2c^2)z^2
+(a^2b^2+7b^4-a^2c^2-7c^4)y z
+(-7a^4-a^2b^2+b^2c^2+7c^4)z x
+(7a^4-7b^4+a^2c^2-b^2c^2)x y = 0,
que pasa por los centros del triángulo X2, X115, X599, X3413, X3414, X5485, X14711, X15810. Con centro en:
D = ( 2a^6-6a^4(b^2+c^2)+
3a^2(b^4+4b^2c^2+c^4)-7b^6+3b^4c^2+3b^2c^4-7c^6 : ... : ...),
que tiene números de búsqueda en
(3.24525877591039, 2.70212381382359, 0.272151637301710), punto medio de Xi y Xj para los índices {i,j}: {115, 599}, {1352, 6055}, {2482, 11646}, {11161, 18800}; reflexión de X597 en X6722; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,98}, {6,14971}, {69,9166}, {115,599}, {141,543}, {524,625}, {597,6722}, {620,9830}, {690,18310}, {1992,14061}, {2482,11646}, {3619,14928}, {3763,9167}, {3818,11159}, {5071,10753}, {6034,15533}, {8360,11623}, {8369,18553}.
Añadido en ETC (27/06/2018) como el X19662.
La envolvente de las rectas de Euler de es la
parábola
( a^8 b^4 x^2-3 a^4 b^8 x^2+2 a^2 b^10 x^2-2 a^8 b^2 c^2 x^2+6 a^4 b^6 c^2 x^2+2 a^2 b^8 c^2 x^2-2 b^10 c^2 x^2+a^8 c^4 x^2-6 a^4 b^4 c^4 x^2-4 a^2 b^6 c^4 x^2+6 a^4 b^2 c^6 x^2-4 a^2 b^4 c^6 x^2+4 b^6 c^6 x^2-3 a^4 c^8 x^2+2 a^2 b^2 c^8 x^2+2 a^2 c^10 x^2-2 b^2 c^10 x^2+2 a^10 b^2 x y+2 a^8 b^4 x y-8 a^6 b^6 x y+2 a^4 b^8 x y+2 a^2 b^10 x y-2 a^10 c^2 x y-4 a^8 b^2 c^2 x y+2 a^6 b^4 c^2 x y+2 a^4 b^6 c^2 x y-4 a^2 b^8 c^2 x y-2 b^10 c^2 x y+2 a^8 c^4 x y+4 a^6 b^2 c^4 x y+6 a^4 b^4 c^4 x y+4 a^2 b^6 c^4 x y+2 b^8 c^4 x y+2 a^6 c^6 x y-8 a^4 b^2 c^6 x y-8 a^2 b^4 c^6 x y+2 b^6 c^6 x y-2 a^4 c^8 x y+6 a^2 b^2 c^8 x y-2 b^4 c^8 x y+2 a^10 b^2 y^2-3 a^8 b^4 y^2+a^4 b^8 y^2-2 a^10 c^2 y^2+2 a^8 b^2 c^2 y^2+6 a^6 b^4 c^2 y^2-2 a^2 b^8 c^2 y^2-4 a^6 b^2 c^4 y^2-6 a^4 b^4 c^4 y^2+b^8 c^4 y^2+4 a^6 c^6 y^2-4 a^4 b^2 c^6 y^2+6 a^2 b^4 c^6 y^2+2 a^2 b^2 c^8 y^2-3 b^4 c^8 y^2-2 a^2 c^10 y^2+2 b^2 c^10 y^2-2 a^10 b^2 x z+2 a^8 b^4 x z+2 a^6 b^6 x z-2 a^4 b^8 x z+2 a^10 c^2 x z-4 a^8 b^2 c^2 x z+4 a^6 b^4 c^2 x z-8 a^4 b^6 c^2 x z+6 a^2 b^8 c^2 x z+2 a^8 c^4 x z+2 a^6 b^2 c^4 x z+6 a^4 b^4 c^4 x z-8 a^2 b^6 c^4 x z-2 b^8 c^4 x z-8 a^6 c^6 x z+2 a^4 b^2 c^6 x z+4 a^2 b^4 c^6 x z+2 b^6 c^6 x z+2 a^4 c^8 x z-4 a^2 b^2 c^8 x z+2 b^4 c^8 x z+2 a^2 c^10 x z-2 b^2 c^10 x z-2 a^8 b^4 y z+2 a^6 b^6 y z+2 a^4 b^8 y z-2 a^2 b^10 y z+6 a^8 b^2 c^2 y z-8 a^6 b^4 c^2 y z+4 a^4 b^6 c^2 y z-4 a^2 b^8 c^2 y z+2 b^10 c^2 y z-2 a^8 c^4 y z-8 a^6 b^2 c^4 y z+6 a^4 b^4 c^4 y z+2 a^2 b^6 c^4 y z+2 b^8 c^4 y z+2 a^6 c^6 y z+4 a^4 b^2 c^6 y z+2 a^2 b^4 c^6 y z-8 b^6 c^6 y z+2 a^4 c^8 y z-4 a^2 b^2 c^8 y z+2 b^4 c^8 y z-2 a^2 c^10 y z+2 b^2 c^10 y z-2 a^10 b^2 z^2+4 a^6 b^6 z^2-2 a^2 b^10 z^2+2 a^10 c^2 z^2+2 a^8 b^2 c^2 z^2-4 a^6 b^4 c^2 z^2-4 a^4 b^6 c^2 z^2+2 a^2 b^8 c^2 z^2+2 b^10 c^2 z^2-3 a^8 c^4 z^2+6 a^6 b^2 c^4 z^2-6 a^4 b^4 c^4 z^2+6 a^2 b^6 c^4 z^2-3 b^8 c^4 z^2+a^4 c^8 z^2-2 a^2 b^2 c^8 z^2+b^4 c^8 z^2 = 0)
tangente a la recta de Euler en el baricentro, cuyo eje tiene la dirección de v=AX+BX+CX, para X=X39, punto medio del . Su foco F es la intersección de las rectas X39X597∩X384X11638.
F = ( a^8(b^2+c^2)+
a^6(6b^4-20b^2c^2+6c^4)+
3a^4(b^6+2b^4c^2+2b^2c^4+c^6)-
a^2(b^2+c^2)^2(2b^4+b^2c^2+2c^4)+b^2c^2(b^2+c^2)^3 : ... : ...),
que tiene números de búsqueda en
(2.84709686365317, 0.347825611987395, 2.08581742884549).
Añadido en ETC (26/06/2018) como el X19663.
Las polares de Pa, Pb y Pc, respecto a esta parábola, son concurrentes para los valores t = (R ± OK)/R.
Uno de los puntos de concurrencia es la intersección de la paralela a la recta de Euler por X5188 (reflexión de X39 en X3), con la paralela a una asíntota (de punto en el infinito X3413) por X39.
El otro punto de concurrencia es la intersección de la paralela a la recta de Euler por X5188 (reflexión de X39 en X3), con la paralela a una asíntota (de punto en el infinito X3414) por X39.
Es decir, estos dos puntos son las intersecciones de las paralelas por X39 a la asíntotas de la hipérbola de Kiepert, con la paralela por X5188 a la recta de Euler.
La primera coordenada de estos puntos de concurrencia es:
Z± = ( ±(a^2 + b^2 + c^2)*
Sqrt[a^4 + b^4 - b^2*c^2 + c^4 -
a^2*(b^2 + c^2)]*(64*a^20 -
344*a^18*(b^2 + c^2) +
12*a^16*(59*b^4 + 130*b^2*c^2 +
59*c^4) - 3*a^14*(217*b^6 +
927*b^4*c^2 + 927*b^2*c^4 +
217*c^6) + 18*a^12*(11*b^8 +
126*b^6*c^2 + 206*b^4*c^4 +
126*b^2*c^6 + 11*c^8) -
6*a^10*(97*b^10 - 238*b^8*c^2 +
457*b^6*c^4 + 457*b^4*c^6 -
238*b^2*c^8 + 97*c^10) +
18*a^8*(52*b^12 - 203*b^10*c^2 +
178*b^8*c^4 - 358*b^6*c^6 +
178*b^4*c^8 - 203*b^2*c^10 +
52*c^12) - 3*a^6*(181*b^14 -
743*b^12*c^2 + 528*b^10*c^4 -
1750*b^8*c^6 - 1750*b^6*c^8 +
528*b^4*c^10 - 743*b^2*c^12 +
181*c^14) + 6*a^4*(b^16 -
49*b^14*c^2 + 244*b^12*c^4 -
1105*b^10*c^6 + 442*b^8*c^8 -
1105*b^6*c^10 + 244*b^4*c^12 -
49*b^2*c^14 + c^16) -
2*(b^2 + c^2)^2*(16*b^16 -
124*b^14*c^2 + 421*b^12*c^4 -
832*b^10*c^6 + 1102*b^8*c^8 -
832*b^6*c^10 + 421*b^4*c^12 -
124*b^2*c^14 + 16*c^16) +
a^2*(112*b^18 - 468*b^16*c^2 +
585*b^14*c^4 + 201*b^12*c^6 +
1170*b^10*c^8 + 1170*b^8*c^10 +
201*b^6*c^12 + 585*b^4*c^14 -
468*b^2*c^16 + 112*c^18)) +
2*(-32*a^24 + 156*a^22*(b^2 + c^2) -
24*a^20*(11*b^4 + 23*b^2*c^2 +
11*c^4) + a^18*(109*b^6 +
519*b^4*c^2 + 519*b^2*c^4 +
109*c^6) + 18*a^16*(11*b^8 +
24*b^6*c^2 + 46*b^4*c^4 +
24*b^2*c^6 + 11*c^8) -
9*a^14*(64*b^10 + 45*b^8*c^2 +
407*b^6*c^4 + 407*b^4*c^6 +
45*b^2*c^8 + 64*c^10) +
3*a^12*(137*b^12 - 33*b^10*c^2 +
1707*b^8*c^4 + 802*b^6*c^6 +
1707*b^4*c^8 - 33*b^2*c^10 +
137*c^12) + 9*a^10*
(b^14 + 71*b^12*c^2 -
416*b^10*c^4 - 12*b^8*c^6 -
12*b^6*c^8 - 416*b^4*c^10 +
71*b^2*c^12 + c^14) -
36*a^8*(10*b^16 - b^14*c^2 -
63*b^12*c^4 + 241*b^10*c^6 -
188*b^8*c^8 + 241*b^6*c^10 -
63*b^4*c^12 - b^2*c^14 +
10*c^16) + a^6*(286*b^18 -
945*b^16*c^2 + 2070*b^14*c^4 +
921*b^12*c^6 + 4284*b^10*c^8 +
4284*b^8*c^10 + 921*b^6*c^12 +
2070*b^4*c^14 - 945*b^2*c^16 +
286*c^18) - 3*a^4*(11*b^20 -
121*b^18*c^2 + 390*b^16*c^4 +
153*b^14*c^6 + 75*b^12*c^8 +
2184*b^10*c^10 + 75*b^8*c^12 +
153*b^6*c^14 + 390*b^4*c^16 -
121*b^2*c^18 + 11*c^20) +
(b^2 + c^2)^2*(16*b^20 -
116*b^18*c^2 + 357*b^16*c^4 -
597*b^14*c^6 + 567*b^12*c^8 -
582*b^10*c^10 + 567*b^8*c^12 -
597*b^6*c^14 + 357*b^4*c^16 -
116*b^2*c^18 + 16*c^20) -
3*a^2*(16*b^22 - 44*b^20*c^2 -
26*b^18*c^4 + 213*b^16*c^6 -
663*b^14*c^8 - 72*b^12*c^10 -
72*b^10*c^12 - 663*b^8*c^14 +
213*b^6*c^16 - 26*b^4*c^18 -
44*b^2*c^20 + 16*c^22)) : ... : ...),
que tienen números de búsqueda en
(3.16213385190149, 1.05079476166564, 1.45374479218440) y (-9.10551794366692, -11.1844946587119, 15.5863229119389), respectivamente.
- Miércoles, 13 de junio del 2018
Triángulos homólogos y semejantes
Dado un triángulo ABC, sean I=X1 su incentro y P, Q dos puntos .
Se denota por Ipa y Iqa los conjugados isogonales de I, respecto a PBC y a QPC, respectivamente.
Si (u:v:w) son las coordenadas baricéntricas de P,
Ipa = (a (-b u + a v) (-c u +
a w) : -(-a b v - (a^2 - c^2) v - b^2 (u + v)) (c u -
a w) : -(b u - a v) ((-a^2 + b^2) w - a c w - c^2 (u + w))),
Iqa = (a^2 (-b u + a v) (-c u + a w) : b (a b u + (b^2 - c^2) u +
a^2 (u + v)) (-c u + a w) : c (-b u + a v) (a c u + (-b^2 + c^2) u +
a^2 (u + w)))
La recta que pasa por ellos,
da: (a b c(-b+c)u^2+a^2(-b^2+c^2)v w+
a^3(b(u+v)w-c v(u+w))-(b^2-c^2)u(c^2v+b^2w-
b c(u+v+w)))x
- a(a-b+c)(-b u+a v)(c u+a w)y + a(a+
b-c)(b u+ av) (-c u+ a w)z = 0,
es perpendicular a BC, pues (ver §12 Perpendicularidad) su punto del infinito es (-a^2 : SC : SB).
Procediendo cíclicamente, se obtienen las rectas db y dc. Se denota por A'B'C' el triángulo formado por las tres rectas da, db y dc.
Los triángulos
ABC y
A'B'C' son perspectivos y semejantes.
Entonces, sus centros de semejanza y perspectividad quedan sobre las circunferencias circunscritas a ambos,
Z = ( a/(u(-(a+b-c) c^2 (a-b+c) (b+c)v^2-b^2 (a+b-c) (a-b+c) (b+c)w^2)+
v(-a^2 b (a-b-c) (a+b-c)w^2-b (a-b-c) (a+b-c) c^2u^2)+
w(-b^2 (a-b-c) c (a-b+c)u^2-a^2 (a-b-c) c (a-b+c)v^2)+
2 b c (2 a^3-a^2 b-b^3-a^2 c+b^2 c+b c^2-c^3)u v w) : .... : .... ).
En el siguiente listado {{i,j,...}, k}, significa que para P=X(i), X(j), ... el centro de perspectividad es el mismo, Z=X(k):
{{484, 758, 759, 3065, 5525, 7313}, 74};
{{740, 741, 5018, 5143, 5524, 7281, 7312, 8481, 8482}, 98};
{{3907}, 99};
{{109, 522}, 100}; {{934, 3900}, 101};
{{104, 517, 1339, 5088}, 102};
{{105, 243, 296, 518, 1155, 1156, 2651, 2652, 5205,
7061, 9432, 12008, 14189, 14190, 14191, 14192, 14193, 14194, 14195,
14196, 14197, 14198, 14199, 14200, 14201, 14202, 14203, 14204}, 103};
{{36, 80, 106, 519, 1323, 1785, 1795, 4845, 5127, 5209, 5526, 5620, 7317, 7343}, 104};
{{1477, 2078, 3254, 5853}, 105};
{{1319, 1320, 3880, 8686}, 106};
{{8058, 8059}, 108};
{{108, 521}, 109};
{{5061, 11609}, 741};
{{5172, 11604}, 759};
{{926, 927}, 813};
{{3910, 8687}, 831};
{{9, 57}, 840};
{{2222, 3738}, 901};
{{2718, 2802}, 953};
{{103, 516, 5537}, 972};
{{101, 514}, 1292};
{{100, 513}, 1293};
{{3465, 3466}, 1294};
{{102, 515, 2077}, 1295};
{{4160, 8691}, 1296};
{{885, 2283, 6366, 14733}, 1308};
{{1381, 3307}, 1381};
{{1382, 3308}, 1382};
{{3660}, 1477};
{{2720, 2804}, 2222};
{{15728, 15733}, 2291};
{{35, 79}, 2687};
{{1442, 7073}, 2688};
{{6198, 7100}, 2695};
{{171, 256}, 2699};
{{7176}, 2700};
{{7009, 7015}, 2708};
{{1432, 2329}, 2711};
{{1431, 7081}, 2712};
{{3, 4, 952, 953, 3109, 6790, 14260, 14887}, 2716};
{{7, 55, 528, 840, 15729}, 2717};
{{8, 56, 5854}, 2718};
{{33, 77}, 2723};
{{12032}, 2724};
{{220, 279}, 2725};
{{200, 269}, 2726};
{{2401, 2427}, 2730};
{{1433, 7952}, 2733};
{{918, 919, 2284}, 2736};
{{1026, 1027}, 2737};
{{347, 2192}, 2739};
{{4296}, 2741};
{{1022, 1023, 1308, 3887}, 2742};
{{900, 901, 17780}, 2743};
{{40, 84, 2716, 2800}, 2745};
{{5285, 15314}, 2747};
{{1422, 2324}, 2750};
{{219, 278}, 2751};
{{1413, 7080}, 2756};
{{34, 78}, 2757};
{{4420}, 2758};
{{13444}, 3659};
{{99, 512}, 6010};
{{110, 523}, 6011};
{{3810, 8685}, 6012};
{{6571, 8710}, 6574};
{{10215, 10231, 13385}, 7597};
{{5193, 12641}, 8686};
{{1083, 3110, 5091, 14665, 14839, 14947}, 12032};
{{18798, 18799}, 14665};
{{4843, 5545}, 15322};
{{726, 727}, 15323};
{{527, 2291}, 15731}.
El lugar geométrico de los focos de la cónica inscrita en ABC de un punto U, sobre una hipérbola ℋM circunscrita a ABC que pasa por el y por un punto M sobre la , es una isogonal 𝒦M, con punto doble en el incentro y F, el foco de la parábola de perspector M.
Los centros de las cónicas inscritas en ABC de perspector U, sobre la hipérbola ℋM, están sobre la recta (que pasa por el incentro) de ℋM.
A todos los puntos P sobre la cúbica 𝒦M (su conjugado isogonal Q, también está sobre ella), les correspondiente el mismo centro de perspectividad Z de ABC y A'B'C'.
Como casos particulares se tienen:
•
K040 = 𝒦X2481 "Pelletier strophoid". Z = X103.
•
K086 = 𝒦X903 "Gergonne strophoid". Z = X104.
•
K165 = 𝒦X•952 "NPC strophoid". Z = X2716.
•
K359 = 𝒦X•14839 "Brocard strophoid". Z = X12032.
Las rectas
da,
db y
dc son concurrentes (en la circunferencia circunscrita) si y solo si
P queda sobre la
séxtica isogonal, que pasa por los exincentros,
X(1), X(36), X(80), X(1381), X(1382), X(3307), X(3308).
El triángulo
A'B'C' es no degenerado y los puntos
P, Q y
Z están alineados si y solo si
P está sobre la cúbica
K407.
K407 es lugar geométrico de los centros de las inversiones que dejan invariante a las cúbicas 𝒦M, los otros dos puntos de intersección de 𝒦M con la perpendicular por su foco F a la recta IF.
- Sábado, 9 de junio del 2018
X(16030) como centro de homotecia
Dado un triángulo ABC, sean Γ su
y el .
La tangente ta a Γ en A corta a BC en D; sean Ta el punto de contacto de la otra tangente t'a desde D a Γ, y T'a el otro extremo de la cuerda de Γ que pasa por Ta y Ma.
La tangente a Γ en T'a corta a ta en D'.
Se denota por da la paralela por D' a BC. Las rectas db y dc se definen cíclicamente.
Las rectas
da, db y
dc forman un triángulo
A'B'C', homotético a
ABC, cuyo centro de homotecia es
X(16030).
NOTA. Si Dab y Dac son los puntos de intersección de da con AB y AC, respectivamente, las dos soluciones del Problema de Apolonio PPC, relativo a los puntos Dab y Dac y a la circunferencia Γ, son las circunferencias (DabDacA) y (DabDacT'a).
UNA SITUACIÓN MÁS GENERAL.
En vez de tomar el triángulo medial , tomemos el de un punto P (distinto del ) de coordenadas baricéntricas (u:v.w). En este caso:
D (0 : -b^2 : c^2), Ta (-a^2 : 2 b^2 : 2 c^2),
T'a (a^2 v w : v (c^2 v - b^2 w) : w (-c^2 v + b^2 w)),
D' (a^2 (c^2 v + b^2 w) : b^2 c^2 v - b^4 w : -c^4 v + b^2 c^2 w).
La paralela por D' a BC es:
(b^2 - c^2) (-c^2 v + b^2 w)x + a^2 (c^2 v + b^2 w)y + a^2 (c^2 v +
b^2 w)z = 0.
El centro de homotecia de ABC y A'B'C' es:
Q (a^2(c^2v + b^2w)/(c^2(a^2+b^2-c^2)v + b^2(a^2+c^2-b^2)w) : ... : ... ).
Pares de puntos {P=X(i), Q=X(j)}, de centros en , de índices {i, j}: {1, 55}, {2, 16030}, {3, 184}, {6, 2}, {31, 7123}, {48, 222}, {63, 1473}, {101, 1407}, {109, 2192}, {110, 25}, {112, 1073}, {155, 14593}, {159, 17409}, {394, 1899}, {399, 14583}, {512, 8770}, {520, 154}, {521, 197}, {523, 2351}, {525, 22}, {610, 6611}, {647, 394}, {652, 7011}, {906, 3173}, {1459, 1260}, {1498, 6525}, {1625, 2052}, {1634, 1501}, {2574, 25}, {2575, 25}, {2605, 7072}, {2623, 5392}, {4558, 3167}, {4559, 13478}, {7252, 1751}, {8673, 3162}.
Cuando P queda en la recta del infinito, el lugar geométrico del centro de homotecia Q es la cúbica unicursal circunscrita a ABC, de ecuación baricéntrica:
a^2 c^4 (a^2 - b^2 + c^2) (a^4 - 2 a^2 b^2 + b^4 + 2 b^2 c^2 - c^4)y^2 x
-a^2 b^4 (a^2 + b^2 - c^2) (a^4 - b^4 - 2 a^2 c^2 + 2 b^2 c^2 + c^4)z^2 x
-a^4 b^2 (a^2 + b^2 - c^2) (a^4 - b^4 - 2 a^2 c^2 + 2 b^2 c^2 - c^4)z^2 y +
b^2 c^4 (a^2 - b^2 - c^2) (a^4 - 2 a^2 b^2 + b^4 + 2 a^2 c^2 - c^4)x^2 y
-b^4 c^2 (a^2 - b^2 - c^2) (a^4 + 2 a^2 b^2 - b^4 - 2 a^2 c^2 + c^4)x^2 z +
a^4 c^2 (a^2 - b^2 + c^2) (a^4 - 2 a^2 b^2 - b^4 + 2 b^2 c^2 - c^4)y^2 z
-4 a^2 (a - b) b^2 (a + b) (a - c) (b - c) c^2 (a + c) (b + c) x y z = 0.
Esta cúbica pasa por los centros X(22), X(25) (punto doble), X(154), X(197), X(2351), X(31629), X(8770).
Cuando P queda sobre la circunferencia circunscrita, el lugar geométrico del centro de homotecia Q es la cúbica unicursal circunscrita a ABC, de ecuación baricéntrica:
-a^2 c^4 (a^2-b^2-c^2) (a^4-2 a^2 b^2+b^4+2 a^2 c^2+2 b^2 c^2-3 c^4)y^2 x +
a^2 b^4 (a^2-b^2-c^2) (a^4+2 a^2 b^2-3 b^4-2 a^2 c^2+2 b^2 c^2+c^4)z^2 x
-a^4 b^2 (a^2-b^2+c^2) (3 a^4-2 a^2 b^2-b^4-2 a^2 c^2+2 b^2 c^2-c^4)z^2 y
-b^2 c^4 (a^2-b^2+c^2) (a^4-2 a^2 b^2+b^4+2 a^2 c^2+2 b^2 c^2-3 c^4)x^2 y+
b^4 c^2 (a^2+b^2-c^2) (a^4+2 a^2 b^2-3 b^4-2 a^2 c^2+2 b^2 c^2+c^4)x^2 z +
a^4 c^2 (a^2+b^2-c^2) (3 a^4-2 a^2 b^2-b^4-2 a^2 c^2+2 b^2 c^2-c^4)y^2 z+
16 a^2 (a-b) b^2 (a+b) (a-c) (b-c) c^2 (a+c) (b+c) x y z = 0.
Esta cúbica pasa por los centros X(25), X(154) (punto doble), X(1073), X(1407), X(2192).
- Martes, 5 de junio del 2018
Cuártica de Stammler deducida de triángulos cevianos y circuncevianos
Dados un triángulo ABC y un punto P (no situado sobre su circunferencia circunscrita), sean A'B'C' y A"B"C" los triángulos y de P, respectivamente.
Se denota por da el de las circunferencias circunscritas a los triángulos AB'B" y AC'C". Las rectas db y dc se definen cíclicamente.
Los ejes radicales da, db y dc son concurrentes (sobre la ) si y solo si P está sobre la cuártica de Stammler.
Las ecuaciones baricéntricas de las circunferencias circunscritas a los triángulos AB'B" y AC'C" son, respectivamente, si P(u:v:w):
a^2 y z + b^2 z x + c^2 x y -
(x + y + z) ((c^2 u + a^2 w) y/(u + w) + b^2 u z /(u + w)) = 0,
a^2 y z + b^2 z x + c^2 x y - (x + y + z) ( c^2 u y /(u + v) + (b^2 u + a^2 v) z /(u + v))= 0.
El eje radical de estas circunferencias es:
da: (-a^2 (u + v) w + c^2 u (-v + w))y + ( a^2 v (u + w) + b^2 u (-v + w))z=0.
La condición para que las rectas da, db y dc sean concurrentes es que las coordenadas de P satisfagan a la ecuación de la (el triángulo circunceviano no está definido) o a:
a^2(b^2 - c^2) y^2z^2 + b^2(c^2-a^2) z^2x^2 + c^2(a^2 - b^2) x^2z^2 = 0.
Se trata de la cuártica de Stammler, de la .
Si P está sobre la cuártica de Stammler y W es el punto de concurrencia de las rectas da, db y dc, se tiene los siguiente pares {P=X(i), W=X(j)}, de centros del triángulo que figuran actualmente en , para los índices {i,j}:
{1, 21}, {2, 2}, {4, 3}, {254, 4}, {1113, 1113}, {1114, 1114}, {1138, 30}, {2184, 1817}, {3223, 13588}, {3346, 20}, {3459, 5}, {8049, 4184}, {13483, 11146}, {13484, 11145}, {13574, 23}, {13575, 22}.
El centro X9510, sobre la cúartica de Stammler, no tiene su correspondiente W en ETC. Se trata de 3R(r^2+4r R+s^2) X2 - 8rs^2 X3 (donde r y R son los radios de las circunferencia inscrita y circunscrita, y s es el semiperímetro del triángulo ABC):
W = ( a (a^4 + a^3 (b + c) - a^2 (b^2 + c^2) - a (b^3 + c^3) + b^2 c^2) : ... : ...),
que tiene números de búsqueda en
(-1.17995416807787, -2.04636134208665, 5.60197041169569 y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,3}, {35,16826}, {36,239}, {56,4393}, {81,18755}, {86,1030}, {99,3948}, {100,4433}, {192,2178}, {198,17350}, {291,18266}, {662,2245}, {757,4272}, {1284,6650}, {1444,1654}, {1931,2238}, {2160,18714}, {2895,17206}, {4384,7280}, {5010,16831}, {5124,17277}, {5204,16816}, {6511,18663}, {8715,17389}, {15586,16568}.
Añadido en ETC como el X19308.
VARIACIÓN
Sea ra el de las circunferencias circunscritas a los triángulos BC'C" y CB'B". Las rectas rb y rc se definen cíclicamente.
Las rectas
ra,
rb y
rc son concurrentes si
P queda sobre la cuártica de ecuación baricéntrica
a^2 c^2 x^3 y + 2 a^2 c^2 x^2 y^2 - 2 b^2 c^2 x^2 y^2 -
b^2 c^2 x y^3 - a^2 b^2 x^3 z - a^2 b^2 x^2 y z + a^2 c^2 x^2 y z +
a^2 b^2 x y^2 z - b^2 c^2 x y^2 z + a^2 b^2 y^3 z -
2 a^2 b^2 x^2 z^2 + 2 b^2 c^2 x^2 z^2 - a^2 c^2 x y z^2 +
b^2 c^2 x y z^2 + 2 a^2 b^2 y^2 z^2 - 2 a^2 c^2 y^2 z^2 +
b^2 c^2 x z^3 - a^2 c^2 y z^3 = 0.
Los centros de las circunferencias circunscritas a los triángulos
AB'B", AC'C", BC'C", BA'A", CA'A", CB'B" están sobre una misma cónica si
P está sobre una
curva
( 6 a^2 b^2 c^4 x^6 y^4-6 b^4 c^4 x^6 y^4+2 a^2 c^6 x^6 y^4-4 b^2 c^6 x^6 y^4-2 c^8 x^6 y^4+6 a^4 c^4 x^5 y^5-6 b^4 c^4 x^5 y^5+6 a^4 c^4 x^4 y^6-6 a^2 b^2 c^4 x^4 y^6+4 a^2 c^6 x^4 y^6-2 b^2 c^6 x^4 y^6+2 c^8 x^4 y^6-5 a^4 b^2 c^2 x^6 y^3 z+12 a^2 b^4 c^2 x^6 y^3 z-7 b^6 c^2 x^6 y^3 z+a^4 c^4 x^6 y^3 z+9 a^2 b^2 c^4 x^6 y^3 z-10 b^4 c^4 x^6 y^3 z-a^2 c^6 x^6 y^3 z-7 b^2 c^6 x^6 y^3 z-5 a^6 c^2 x^5 y^4 z+14 a^4 b^2 c^2 x^5 y^4 z-7 a^2 b^4 c^2 x^5 y^4 z-2 b^6 c^2 x^5 y^4 z+16 a^4 c^4 x^5 y^4 z-3 a^2 b^2 c^4 x^5 y^4 z-13 b^4 c^4 x^5 y^4 z-9 a^2 c^6 x^5 y^4 z-4 b^2 c^6 x^5 y^4 z+c^8 x^5 y^4 z+2 a^6 c^2 x^4 y^5 z+7 a^4 b^2 c^2 x^4 y^5 z-14 a^2 b^4 c^2 x^4 y^5 z+5 b^6 c^2 x^4 y^5 z+13 a^4 c^4 x^4 y^5 z+3 a^2 b^2 c^4 x^4 y^5 z-16 b^4 c^4 x^4 y^5 z+4 a^2 c^6 x^4 y^5 z+9 b^2 c^6 x^4 y^5 z-c^8 x^4 y^5 z+7 a^6 c^2 x^3 y^6 z-12 a^4 b^2 c^2 x^3 y^6 z+5 a^2 b^4 c^2 x^3 y^6 z+10 a^4 c^4 x^3 y^6 z-9 a^2 b^2 c^4 x^3 y^6 z-b^4 c^4 x^3 y^6 z+7 a^2 c^6 x^3 y^6 z+b^2 c^6 x^3 y^6 z+a^6 b^2 x^6 y^2 z^2-4 a^4 b^4 x^6 y^2 z^2+5 a^2 b^6 x^6 y^2 z^2-2 b^8 x^6 y^2 z^2-a^6 c^2 x^6 y^2 z^2+7 a^2 b^4 c^2 x^6 y^2 z^2-4 b^6 c^2 x^6 y^2 z^2+4 a^4 c^4 x^6 y^2 z^2-7 a^2 b^2 c^4 x^6 y^2 z^2-5 a^2 c^6 x^6 y^2 z^2+4 b^2 c^6 x^6 y^2 z^2+2 c^8 x^6 y^2 z^2+a^8 x^5 y^3 z^2-6 a^6 b^2 x^5 y^3 z^2+10 a^4 b^4 x^5 y^3 z^2-6 a^2 b^6 x^5 y^3 z^2+b^8 x^5 y^3 z^2-4 a^6 c^2 x^5 y^3 z^2+12 a^4 b^2 c^2 x^5 y^3 z^2-4 b^6 c^2 x^5 y^3 z^2+6 a^4 c^4 x^5 y^3 z^2-10 a^2 b^2 c^4 x^5 y^3 z^2-7 b^4 c^4 x^5 y^3 z^2-3 a^2 c^6 x^5 y^3 z^2-2 b^2 c^6 x^5 y^3 z^2-2 a^8 x^4 y^4 z^2+4 a^6 b^2 x^4 y^4 z^2-4 a^2 b^6 x^4 y^4 z^2+2 b^8 x^4 y^4 z^2+3 a^6 c^2 x^4 y^4 z^2+a^4 b^2 c^2 x^4 y^4 z^2-a^2 b^4 c^2 x^4 y^4 z^2-3 b^6 c^2 x^4 y^4 z^2+4 a^4 c^4 x^4 y^4 z^2-4 b^4 c^4 x^4 y^4 z^2+a^2 c^6 x^4 y^4 z^2-b^2 c^6 x^4 y^4 z^2-a^8 x^3 y^5 z^2+6 a^6 b^2 x^3 y^5 z^2-10 a^4 b^4 x^3 y^5 z^2+6 a^2 b^6 x^3 y^5 z^2-b^8 x^3 y^5 z^2+4 a^6 c^2 x^3 y^5 z^2-12 a^2 b^4 c^2 x^3 y^5 z^2+4 b^6 c^2 x^3 y^5 z^2+7 a^4 c^4 x^3 y^5 z^2+10 a^2 b^2 c^4 x^3 y^5 z^2-6 b^4 c^4 x^3 y^5 z^2+2 a^2 c^6 x^3 y^5 z^2+3 b^2 c^6 x^3 y^5 z^2+2 a^8 x^2 y^6 z^2-5 a^6 b^2 x^2 y^6 z^2+4 a^4 b^4 x^2 y^6 z^2-a^2 b^6 x^2 y^6 z^2+4 a^6 c^2 x^2 y^6 z^2-7 a^4 b^2 c^2 x^2 y^6 z^2+b^6 c^2 x^2 y^6 z^2+7 a^2 b^2 c^4 x^2 y^6 z^2-4 b^4 c^4 x^2 y^6 z^2-4 a^2 c^6 x^2 y^6 z^2+5 b^2 c^6 x^2 y^6 z^2-2 c^8 x^2 y^6 z^2-a^4 b^4 x^6 y z^3+a^2 b^6 x^6 y z^3+5 a^4 b^2 c^2 x^6 y z^3-9 a^2 b^4 c^2 x^6 y z^3+7 b^6 c^2 x^6 y z^3-12 a^2 b^2 c^4 x^6 y z^3+10 b^4 c^4 x^6 y z^3+7 b^2 c^6 x^6 y z^3-a^8 x^5 y^2 z^3+4 a^6 b^2 x^5 y^2 z^3-6 a^4 b^4 x^5 y^2 z^3+3 a^2 b^6 x^5 y^2 z^3+6 a^6 c^2 x^5 y^2 z^3-12 a^4 b^2 c^2 x^5 y^2 z^3+10 a^2 b^4 c^2 x^5 y^2 z^3+2 b^6 c^2 x^5 y^2 z^3-10 a^4 c^4 x^5 y^2 z^3+7 b^4 c^4 x^5 y^2 z^3+6 a^2 c^6 x^5 y^2 z^3+4 b^2 c^6 x^5 y^2 z^3-c^8 x^5 y^2 z^3+3 a^6 b^2 x^4 y^3 z^3-5 a^4 b^4 x^4 y^3 z^3+3 a^2 b^6 x^4 y^3 z^3-b^8 x^4 y^3 z^3-3 a^6 c^2 x^4 y^3 z^3+2 a^2 b^4 c^2 x^4 y^3 z^3+4 b^6 c^2 x^4 y^3 z^3+5 a^4 c^4 x^4 y^3 z^3-2 a^2 b^2 c^4 x^4 y^3 z^3-3 a^2 c^6 x^4 y^3 z^3-4 b^2 c^6 x^4 y^3 z^3+c^8 x^4 y^3 z^3+a^8 x^3 y^4 z^3-3 a^6 b^2 x^3 y^4 z^3+5 a^4 b^4 x^3 y^4 z^3-3 a^2 b^6 x^3 y^4 z^3-4 a^6 c^2 x^3 y^4 z^3-2 a^4 b^2 c^2 x^3 y^4 z^3+3 b^6 c^2 x^3 y^4 z^3+2 a^2 b^2 c^4 x^3 y^4 z^3-5 b^4 c^4 x^3 y^4 z^3+4 a^2 c^6 x^3 y^4 z^3+3 b^2 c^6 x^3 y^4 z^3-c^8 x^3 y^4 z^3-3 a^6 b^2 x^2 y^5 z^3+6 a^4 b^4 x^2 y^5 z^3-4 a^2 b^6 x^2 y^5 z^3+b^8 x^2 y^5 z^3-2 a^6 c^2 x^2 y^5 z^3-10 a^4 b^2 c^2 x^2 y^5 z^3+12 a^2 b^4 c^2 x^2 y^5 z^3-6 b^6 c^2 x^2 y^5 z^3-7 a^4 c^4 x^2 y^5 z^3+10 b^4 c^4 x^2 y^5 z^3-4 a^2 c^6 x^2 y^5 z^3-6 b^2 c^6 x^2 y^5 z^3+c^8 x^2 y^5 z^3-a^6 b^2 x y^6 z^3+a^4 b^4 x y^6 z^3-7 a^6 c^2 x y^6 z^3+9 a^4 b^2 c^2 x y^6 z^3-5 a^2 b^4 c^2 x y^6 z^3-10 a^4 c^4 x y^6 z^3+12 a^2 b^2 c^4 x y^6 z^3-7 a^2 c^6 x y^6 z^3-2 a^2 b^6 x^6 z^4+2 b^8 x^6 z^4-6 a^2 b^4 c^2 x^6 z^4+4 b^6 c^2 x^6 z^4+6 b^4 c^4 x^6 z^4+5 a^6 b^2 x^5 y z^4-16 a^4 b^4 x^5 y z^4+9 a^2 b^6 x^5 y z^4-b^8 x^5 y z^4-14 a^4 b^2 c^2 x^5 y z^4+3 a^2 b^4 c^2 x^5 y z^4+4 b^6 c^2 x^5 y z^4+7 a^2 b^2 c^4 x^5 y z^4+13 b^4 c^4 x^5 y z^4+2 b^2 c^6 x^5 y z^4+2 a^8 x^4 y^2 z^4-3 a^6 b^2 x^4 y^2 z^4-4 a^4 b^4 x^4 y^2 z^4-a^2 b^6 x^4 y^2 z^4-4 a^6 c^2 x^4 y^2 z^4-a^4 b^2 c^2 x^4 y^2 z^4+b^6 c^2 x^4 y^2 z^4+a^2 b^2 c^4 x^4 y^2 z^4+4 b^4 c^4 x^4 y^2 z^4+4 a^2 c^6 x^4 y^2 z^4+3 b^2 c^6 x^4 y^2 z^4-2 c^8 x^4 y^2 z^4-a^8 x^3 y^3 z^4+4 a^6 b^2 x^3 y^3 z^4-4 a^2 b^6 x^3 y^3 z^4+b^8 x^3 y^3 z^4+3 a^6 c^2 x^3 y^3 z^4+2 a^4 b^2 c^2 x^3 y^3 z^4-2 a^2 b^4 c^2 x^3 y^3 z^4-3 b^6 c^2 x^3 y^3 z^4-5 a^4 c^4 x^3 y^3 z^4+5 b^4 c^4 x^3 y^3 z^4+3 a^2 c^6 x^3 y^3 z^4-3 b^2 c^6 x^3 y^3 z^4+a^6 b^2 x^2 y^4 z^4+4 a^4 b^4 x^2 y^4 z^4+3 a^2 b^6 x^2 y^4 z^4-2 b^8 x^2 y^4 z^4-a^6 c^2 x^2 y^4 z^4+a^2 b^4 c^2 x^2 y^4 z^4+4 b^6 c^2 x^2 y^4 z^4-4 a^4 c^4 x^2 y^4 z^4-a^2 b^2 c^4 x^2 y^4 z^4-3 a^2 c^6 x^2 y^4 z^4-4 b^2 c^6 x^2 y^4 z^4+2 c^8 x^2 y^4 z^4+a^8 x y^5 z^4-9 a^6 b^2 x y^5 z^4+16 a^4 b^4 x y^5 z^4-5 a^2 b^6 x y^5 z^4-4 a^6 c^2 x y^5 z^4-3 a^4 b^2 c^2 x y^5 z^4+14 a^2 b^4 c^2 x y^5 z^4-13 a^4 c^4 x y^5 z^4-7 a^2 b^2 c^4 x y^5 z^4-2 a^2 c^6 x y^5 z^4-2 a^8 y^6 z^4+2 a^6 b^2 y^6 z^4-4 a^6 c^2 y^6 z^4+6 a^4 b^2 c^2 y^6 z^4-6 a^4 c^4 y^6 z^4-6 a^4 b^4 x^5 z^5+6 b^4 c^4 x^5 z^5-2 a^6 b^2 x^4 y z^5-13 a^4 b^4 x^4 y z^5-4 a^2 b^6 x^4 y z^5+b^8 x^4 y z^5-7 a^4 b^2 c^2 x^4 y z^5-3 a^2 b^4 c^2 x^4 y z^5-9 b^6 c^2 x^4 y z^5+14 a^2 b^2 c^4 x^4 y z^5+16 b^4 c^4 x^4 y z^5-5 b^2 c^6 x^4 y z^5+a^8 x^3 y^2 z^5-4 a^6 b^2 x^3 y^2 z^5-7 a^4 b^4 x^3 y^2 z^5-2 a^2 b^6 x^3 y^2 z^5-6 a^6 c^2 x^3 y^2 z^5-10 a^2 b^4 c^2 x^3 y^2 z^5-3 b^6 c^2 x^3 y^2 z^5+10 a^4 c^4 x^3 y^2 z^5+12 a^2 b^2 c^4 x^3 y^2 z^5+6 b^4 c^4 x^3 y^2 z^5-6 a^2 c^6 x^3 y^2 z^5-4 b^2 c^6 x^3 y^2 z^5+c^8 x^3 y^2 z^5+2 a^6 b^2 x^2 y^3 z^5+7 a^4 b^4 x^2 y^3 z^5+4 a^2 b^6 x^2 y^3 z^5-b^8 x^2 y^3 z^5+3 a^6 c^2 x^2 y^3 z^5+10 a^4 b^2 c^2 x^2 y^3 z^5+6 b^6 c^2 x^2 y^3 z^5-6 a^4 c^4 x^2 y^3 z^5-12 a^2 b^2 c^4 x^2 y^3 z^5-10 b^4 c^4 x^2 y^3 z^5+4 a^2 c^6 x^2 y^3 z^5+6 b^2 c^6 x^2 y^3 z^5-c^8 x^2 y^3 z^5-a^8 x y^4 z^5+4 a^6 b^2 x y^4 z^5+13 a^4 b^4 x y^4 z^5+2 a^2 b^6 x y^4 z^5+9 a^6 c^2 x y^4 z^5+3 a^4 b^2 c^2 x y^4 z^5+7 a^2 b^4 c^2 x y^4 z^5-16 a^4 c^4 x y^4 z^5-14 a^2 b^2 c^4 x y^4 z^5+5 a^2 c^6 x y^4 z^5+6 a^4 b^4 y^5 z^5-6 a^4 c^4 y^5 z^5-6 a^4 b^4 x^4 z^6-4 a^2 b^6 x^4 z^6-2 b^8 x^4 z^6+6 a^2 b^4 c^2 x^4 z^6+2 b^6 c^2 x^4 z^6-7 a^6 b^2 x^3 y z^6-10 a^4 b^4 x^3 y z^6-7 a^2 b^6 x^3 y z^6+12 a^4 b^2 c^2 x^3 y z^6+9 a^2 b^4 c^2 x^3 y z^6-b^6 c^2 x^3 y z^6-5 a^2 b^2 c^4 x^3 y z^6+b^4 c^4 x^3 y z^6-2 a^8 x^2 y^2 z^6-4 a^6 b^2 x^2 y^2 z^6+4 a^2 b^6 x^2 y^2 z^6+2 b^8 x^2 y^2 z^6+5 a^6 c^2 x^2 y^2 z^6+7 a^4 b^2 c^2 x^2 y^2 z^6-7 a^2 b^4 c^2 x^2 y^2 z^6-5 b^6 c^2 x^2 y^2 z^6-4 a^4 c^4 x^2 y^2 z^6+4 b^4 c^4 x^2 y^2 z^6+a^2 c^6 x^2 y^2 z^6-b^2 c^6 x^2 y^2 z^6+7 a^6 b^2 x y^3 z^6+10 a^4 b^4 x y^3 z^6+7 a^2 b^6 x y^3 z^6+a^6 c^2 x y^3 z^6-9 a^4 b^2 c^2 x y^3 z^6-12 a^2 b^4 c^2 x y^3 z^6-a^4 c^4 x y^3 z^6+5 a^2 b^2 c^4 x y^3 z^6+2 a^8 y^4 z^6+4 a^6 b^2 y^4 z^6+6 a^4 b^4 y^4 z^6-2 a^6 c^2 y^4 z^6-6 a^4 b^2 c^2 y^4 z^6 = 0)
algebraica de grado 10, circunscrita a
ABC y su que pasa por el baricentro y por el conjugado isogonal del foco de la .
Los vértices de ABC son puntos cuádruples. Tres de sus cuatro asíntotas reales son paralelas a las medianas.
Cuando P=X2, la cónica
( a^6 x^2 - 7 a^4 b^2 x^2 + 5 a^2 b^4 x^2 + b^6 x^2 - 7 a^4 c^2 x^2 +
a^2 b^2 c^2 x^2 + 3 b^4 c^2 x^2 + 5 a^2 c^4 x^2 + 3 b^2 c^4 x^2 +
c^6 x^2 - 2 a^6 x y + 2 a^4 b^2 x y + 2 a^2 b^4 x y - 2 b^6 x y +
4 a^4 c^2 x y - 14 a^2 b^2 c^2 x y + 4 b^4 c^2 x y -
28 a^2 c^4 x y - 28 b^2 c^4 x y + 2 c^6 x y + a^6 y^2 +
5 a^4 b^2 y^2 - 7 a^2 b^4 y^2 + b^6 y^2 + 3 a^4 c^2 y^2 +
a^2 b^2 c^2 y^2 - 7 b^4 c^2 y^2 + 3 a^2 c^4 y^2 + 5 b^2 c^4 y^2 +
c^6 y^2 - 2 a^6 x z + 4 a^4 b^2 x z - 28 a^2 b^4 x z + 2 b^6 x z +
2 a^4 c^2 x z - 14 a^2 b^2 c^2 x z - 28 b^4 c^2 x z +
2 a^2 c^4 x z + 4 b^2 c^4 x z - 2 c^6 x z + 2 a^6 y z -
28 a^4 b^2 y z + 4 a^2 b^4 y z - 2 b^6 y z - 28 a^4 c^2 y z -
14 a^2 b^2 c^2 y z + 2 b^4 c^2 y z + 4 a^2 c^4 y z + 2 b^2 c^4 y z -
2 c^6 y z + a^6 z^2 + 3 a^4 b^2 z^2 + 3 a^2 b^4 z^2 + b^6 z^2 +
5 a^4 c^2 z^2 + a^2 b^2 c^2 z^2 + 5 b^4 c^2 z^2 - 7 a^2 c^4 z^2 -
7 b^2 c^4 z^2 + c^6 z^2 = 0)
tiene centro en X140 y ecuación:
(a^6 - 7 a^4 (b^2 + c^2) +
a^2 (5 b^4 + b^2 c^2 + 5 c^4) + (b^2 + c^2)^3)x^2 + 2 (a^6 -
14 a^4 (b^2 + c^2) +
a^2 (2 b^4 - 7 b^2 c^2 + 2 c^4)- (b^2 - c^2)^2 (b^2 + c^2))y z + ... = 0.
- Lunes, 4 de junio del 2018
El punto X(1138) como centro de semejanza
El único punto del plano de un triángulo
ABC para el cual su y su son distintos y semejantes es
X(1138).
Además, X(1138) es el único punto
P tal que las de los triángulos
ABC, BCP, CAP, ABP son paralelas.
There are only two points X such that the pedal triangle of X is similar to the cevian triangle of X. They are X(4) and X(1138). (Jean-Pierre Ehrmann, January 4, 2003)
Let A'B'C' be the anticomplementary triangle of a triangle ABC, and let E
A be the line through A parallel to the Euler line. Let A" be the point of intersection, other than A, of E
A and the circumcircle. Define E
B and E
C cyclically. The locus of a point P such that the Euler line of PBC is parallel to the Euler line of ABC is a conic ABCA'A'' having the midpoint of segment BC as center. The conics, ABCA'A'', ABCB'B'', ABCC'C'' pass through X(1138). (Francisco Javier García Capitán, April 3, 2015:
ADGEOM #2458)
Locus properties:2.
The Euler lines of triangles PBC, PCA, PAB concur (on the Euler line) if and only if P lies on the
Neuberg cubic (together with C(O,R) and line at infinity).
El centro de semejanza de los triángulos pedal y ceviano de X(1138) es el punto de coordenadas baricéntricas:
F = ( (b^2-c^2)^2 SA (4SA^2-b^2c^2) () / (a^8-4a^6(b^2+c^2) +
a^4(6b^4+b^2c^2+6c^4) - a^2(4b^6-b^2c^2(b^2+c^2)+4c^6) + (b^2-c^2)^2(b^4+4b^2c^2+c^4))
: ... : ...),
que tiene números de búsqueda en
(5.07021033859440, 1.87521451781722, 0.00234196714426759) y está sobre la recta X(477)X(1188).
Añadido en ETC como el X19223.
Las entradas de la matriz (Mij) de la semejanza σ que transforma el triángulo ceviano de X(1138) en su triángulo pedal son:
M11 = -a^2 (a^4 + b^4 + b^2 c^2 + c^4 -
2 a^2 (b^2 + c^2)) (a^10 (b^2 + c^2) +
a^8 (-5 b^4 + 4 b^2 c^2 - 5 c^4) - (b^2 - c^2)^4 (b^4 + c^4) +
a^2 (b^2 - c^2)^2 (5 b^6 + 6 b^4 c^2 + 6 b^2 c^4 + 5 c^6) +
a^6 (10 b^6 - 7 b^4 c^2 - 7 b^2 c^4 + 10 c^6) -
2 a^4 (5 b^8 - b^6 c^2 - 7 b^4 c^4 - b^2 c^6 + 5 c^8)),
M12 = a^2 (a^2 - b^2 - c^2) (b^2 - c^2) (a^4 + b^4 + b^2 c^2 + c^4 -
2 a^2 (b^2 + c^2)) (-a^8 - (b^2 - c^2)^4 + 2 a^6 (2 b^2 - c^2) -
a^4 (6 b^4 + b^2 c^2 - 6 c^4) -
a^2 (-4 b^6 + b^4 c^2 + b^2 c^4 + 2 c^6)),
M13 = -a^2 (a^2 - b^2 - c^2) (b^2 - c^2) (a^4 + b^4 + b^2 c^2 + c^4 -
2 a^2 (b^2 + c^2)) (-a^8 - 2 a^6 (b^2 - 2 c^2) - (b^2 - c^2)^4 +
a^4 (6 b^4 - b^2 c^2 - 6 c^4) -
a^2 (2 b^6 + b^4 c^2 + b^2 c^4 - 4 c^6)),
M21 = -b^2 (a^2 - c^2) (-a^14 - 21 a^10 b^4 +
a^12 (7 b^2 + 2 c^2) + (b^2 - c^2)^5 (b^4 + 4 b^2 c^2 + c^4) +
a^8 (35 b^6 - 21 b^4 c^2 + 6 b^2 c^4 - c^6) -
a^2 (b^2 - c^2)^3 (7 b^6 + 9 b^4 c^2 - 6 b^2 c^4 + 2 c^6) +
3 a^4 b^2 (7 b^8 - 12 b^6 c^2 + 3 b^4 c^4 + 4 b^2 c^6 - 2 c^8) -
a^6 (35 b^8 - 44 b^6 c^2 + 18 b^4 c^4 - 4 b^2 c^6 + c^8)),
M22 = -b^2 (-a^16 + c^2 (b^2 - c^2)^7 + a^14 (7 b^2 + 3 c^2) -
a^12 (21 b^4 + 5 b^2 c^2 + 4 c^4) +
a^2 (b^2 - c^2)^4 (b^6 + 4 b^4 c^2 + 7 b^2 c^4 + 3 c^6) +
a^10 (35 b^6 - 6 b^4 c^2 + 6 b^2 c^4 + 5 c^6) +
a^8 (-35 b^8 + 15 b^6 c^2 + 9 b^4 c^4 - 8 b^2 c^6 - 6 c^8) -
a^4 (b^2 - c^2)^2 (7 b^8 + 17 b^6 c^2 - 9 b^4 c^4 + 2 b^2 c^6 +
4 c^8) +
a^6 (21 b^10 - 5 b^8 c^2 - 37 b^6 c^4 + 30 b^4 c^6 - 8 b^2 c^8 +
5 c^10)),
M23 = b^2 (a^2 - c^2) (-a^6 + a^4 (3 b^2 - 2 c^2) + (b^2 - c^2)^3 +
a^2 (-3 b^4 + 5 b^2 c^2 - 2 c^4)) (a^8 +
2 a^6 (b^2 - 2 c^2) + (b^2 - c^2)^4 +
a^4 (-6 b^4 + b^2 c^2 + 6 c^4) +
a^2 (2 b^6 + b^4 c^2 + b^2 c^4 - 4 c^6)),
M31 = (a^2 - b^2) c^2 (a^14 + 21 a^10 c^4 -
a^12 (2 b^2 + 7 c^2) + (b^2 - c^2)^5 (b^4 + 4 b^2 c^2 + c^4) +
a^8 (b^6 - 6 b^4 c^2 + 21 b^2 c^4 - 35 c^6) -
a^2 (b^2 - c^2)^3 (2 b^6 - 6 b^4 c^2 + 9 b^2 c^4 + 7 c^6) -
3 a^4 c^2 (-2 b^8 + 4 b^6 c^2 + 3 b^4 c^4 - 12 b^2 c^6 + 7 c^8) +
a^6 (b^8 - 4 b^6 c^2 + 18 b^4 c^4 - 44 b^2 c^6 + 35 c^8)),
M32 = (a^2 - b^2) c^2 (a^6 + a^4 (2 b^2 - 3 c^2) + (b^2 - c^2)^3 +
a^2 (2 b^4 - 5 b^2 c^2 + 3 c^4)) (-a^8 - (b^2 - c^2)^4 +
2 a^6 (2 b^2 - c^2) - a^4 (6 b^4 + b^2 c^2 - 6 c^4) -
a^2 (-4 b^6 + b^4 c^2 + b^2 c^4 + 2 c^6)),
M33 = -c^2 (-a^16 - b^2 (b^2 - c^2)^7 + a^14 (3 b^2 + 7 c^2) -
a^12 (4 b^4 + 5 b^2 c^2 + 21 c^4) +
a^2 (b^2 - c^2)^4 (3 b^6 + 7 b^4 c^2 + 4 b^2 c^4 + c^6) +
a^10 (5 b^6 + 6 b^4 c^2 - 6 b^2 c^4 + 35 c^6) +
a^8 (-6 b^8 - 8 b^6 c^2 + 9 b^4 c^4 + 15 b^2 c^6 - 35 c^8) -
a^4 (b^2 - c^2)^2 (4 b^8 + 2 b^6 c^2 - 9 b^4 c^4 + 17 b^2 c^6 +
7 c^8) +
a^6 (5 b^10 - 8 b^8 c^2 + 30 b^6 c^4 - 37 b^4 c^6 - 5 b^2 c^8 +
21 c^10)).
La raíz del polinomio característico p(λ)=|M-λI| = 0,
λ1 = -6 a^2 b^2 c^2 (a^6 - a^4 (b^2 + c^2) + (b^2 - c^2)^2 (b^2 + c^2) -
a^2 (b^4 - 3 b^2 c^2 + c^4))^2,
da lugar al punto fijo (propio) F, del enunciado.
Las rectas fijas (a parte de la del infinito) de σ son las paralelas por F a las asíntotas de la .
- Sábado, 26 de mayo del 2018
La isocúbica no pivotal nK(P^2,GST(P),P)
Sean ABC un triángulo, P y M puntos sobre su circunferencia circunscrita.
c(PM) es la cónica inscrita en ABC, tangente a PM y a la de P (también es tangente a la recta de Simson de M).
El lugar geométrico del punto de contacto T de PM y c(PM), cuando M varía, es la isocúbica no pivotal nK(P^2,GST(P),P) = cK(#P,GST(P)).
El polo de esta cúbica es el de P, la raíz es el transformado de P, mediante la transformación de Gibert-Simson ( de la recta de Simson de P), que queda sobre cúbica de Simson. P es el punto singular de la cúbica, la cual pasa por el ortocentro.
Si P es el del punto (1:-t:t-1) de la , una expresión de la ecuación baricéntrica de nK(P^2,GSF(P),P) es:
x(c^4 t^2 (a^2 t - SC) y^2 + b^4 (t - 1)^2 (a^2 t - SC) z^2)
-
y(a^4 (t - 1)^2 t (b^2 - SC t) z^2 - c^4 t (b^2 - SC t) x^2)
-
z(b^4 (t - 1) (SA + SB t) x^2 - a^4 (t - 1) t^2 (SA + SB t) y^2)
+
2 t(t - 1)( b^2 () + a^2 (SA^2 - SB SC) t) x y z = 0.
El lugar geométrico del punto de contacto Q, de la otra tangente a c(PM) desde M, cuando M varía, es la hipérbola rectangular circunscrita a ABC, que pasa por SR(P,P'), punto simétrico de P respecto a la perpendicular d, a la recta de Simsom de P por el circuncentro (P' es el antipodal de P).
El punto SR(P,P') es el "sexto punto" de intersección de nK(P^2,GST(P),P) y la circunferencia circunscrita.
RS Points and SR Points (See preamble to X(2677))
Suppose that P and U are distinct points on the circumcircle of a triangle ABC. Their Simson lines meet in a point X which is here called the
Rigby-Simson point of P and U, denoted by RS(P,U). That is, RS(P,U) is the orthopole of line PU with respect to triangle ABC.
On the circumcircle, there is a unique point K whose Simson line is perpendicular to line PU, and whose Simson line also passes through RS(P,U). The point K is here called the
Simson-Rigby point of P and U, denoted by SR(P,U).
El punto de contacto T' = P^2×T•, de la otra tangente desde P con c(PM), es el P^2-isoconjugado de T, de P^2 y el de T. Las tangentes PT' y MQ se cortan en M' (sobre la circunferencia circunscrita), reflexión de M en d.
ALGUNOS CASOS PARTICULARES
• P el
La única cúbica de parámetro cero es
nK0(X(98)^2,X(2395),X(98)),
(-a^10 b^4 x^2 y+3 a^8 b^6 x^2 y-3 a^6 b^8 x^2 y+a^4 b^10 x^2 y-2 a^10 b^2 c^2 x^2 y+5 a^8 b^4 c^2 x^2 y-4 a^6 b^6 c^2 x^2 y+a^4 b^8 c^2 x^2 y-a^10 c^4 x^2 y+5 a^8 b^2 c^4 x^2 y-7 a^6 b^4 c^4 x^2 y+3 a^4 b^6 c^4 x^2 y+a^2 b^8 c^4 x^2 y-b^10 c^4 x^2 y+3 a^8 c^6 x^2 y-6 a^6 b^2 c^6 x^2 y+3 a^4 b^4 c^6 x^2 y+b^8 c^6 x^2 y-4 a^6 c^8 x^2 y+4 a^4 b^2 c^8 x^2 y-2 a^2 b^4 c^8 x^2 y-2 b^6 c^8 x^2 y+4 a^4 c^10 x^2 y+2 b^4 c^10 x^2 y-3 a^2 c^12 x^2 y-b^2 c^12 x^2 y+c^14 x^2 y-a^10 b^4 x y^2+3 a^8 b^6 x y^2-3 a^6 b^8 x y^2+a^4 b^10 x y^2-a^8 b^4 c^2 x y^2+4 a^6 b^6 c^2 x y^2-5 a^4 b^8 c^2 x y^2+2 a^2 b^10 c^2 x y^2+a^10 c^4 x y^2-a^8 b^2 c^4 x y^2-3 a^6 b^4 c^4 x y^2+7 a^4 b^6 c^4 x y^2-5 a^2 b^8 c^4 x y^2+b^10 c^4 x y^2-a^8 c^6 x y^2-3 a^4 b^4 c^6 x y^2+6 a^2 b^6 c^6 x y^2-3 b^8 c^6 x y^2+2 a^6 c^8 x y^2+2 a^4 b^2 c^8 x y^2-4 a^2 b^4 c^8 x y^2+4 b^6 c^8 x y^2-2 a^4 c^10 x y^2-4 b^4 c^10 x y^2+a^2 c^12 x y^2+3 b^2 c^12 x y^2-c^14 x y^2+a^10 b^4 x^2 z-3 a^8 b^6 x^2 z+4 a^6 b^8 x^2 z-4 a^4 b^10 x^2 z+3 a^2 b^12 x^2 z-b^14 x^2 z+2 a^10 b^2 c^2 x^2 z-5 a^8 b^4 c^2 x^2 z+6 a^6 b^6 c^2 x^2 z-4 a^4 b^8 c^2 x^2 z+b^12 c^2 x^2 z+a^10 c^4 x^2 z-5 a^8 b^2 c^4 x^2 z+7 a^6 b^4 c^4 x^2 z-3 a^4 b^6 c^4 x^2 z+2 a^2 b^8 c^4 x^2 z-2 b^10 c^4 x^2 z-3 a^8 c^6 x^2 z+4 a^6 b^2 c^6 x^2 z-3 a^4 b^4 c^6 x^2 z+2 b^8 c^6 x^2 z+3 a^6 c^8 x^2 z-a^4 b^2 c^8 x^2 z-a^2 b^4 c^8 x^2 z-b^6 c^8 x^2 z-a^4 c^10 x^2 z+b^4 c^10 x^2 z+a^14 y^2 z-3 a^12 b^2 y^2 z+4 a^10 b^4 y^2 z-4 a^8 b^6 y^2 z+3 a^6 b^8 y^2 z-a^4 b^10 y^2 z-a^12 c^2 y^2 z+4 a^8 b^4 c^2 y^2 z-6 a^6 b^6 c^2 y^2 z+5 a^4 b^8 c^2 y^2 z-2 a^2 b^10 c^2 y^2 z+2 a^10 c^4 y^2 z-2 a^8 b^2 c^4 y^2 z+3 a^6 b^4 c^4 y^2 z-7 a^4 b^6 c^4 y^2 z+5 a^2 b^8 c^4 y^2 z-b^10 c^4 y^2 z-2 a^8 c^6 y^2 z+3 a^4 b^4 c^6 y^2 z-4 a^2 b^6 c^6 y^2 z+3 b^8 c^6 y^2 z+a^6 c^8 y^2 z+a^4 b^2 c^8 y^2 z+a^2 b^4 c^8 y^2 z-3 b^6 c^8 y^2 z-a^4 c^10 y^2 z+b^4 c^10 y^2 z-a^10 b^4 x z^2+a^8 b^6 x z^2-2 a^6 b^8 x z^2+2 a^4 b^10 x z^2-a^2 b^12 x z^2+b^14 x z^2+a^8 b^4 c^2 x z^2-2 a^4 b^8 c^2 x z^2-3 b^12 c^2 x z^2+a^10 c^4 x z^2+a^8 b^2 c^4 x z^2+3 a^6 b^4 c^4 x z^2+3 a^4 b^6 c^4 x z^2+4 a^2 b^8 c^4 x z^2+4 b^10 c^4 x z^2-3 a^8 c^6 x z^2-4 a^6 b^2 c^6 x z^2-7 a^4 b^4 c^6 x z^2-6 a^2 b^6 c^6 x z^2-4 b^8 c^6 x z^2+3 a^6 c^8 x z^2+5 a^4 b^2 c^8 x z^2+5 a^2 b^4 c^8 x z^2+3 b^6 c^8 x z^2-a^4 c^10 x z^2-2 a^2 b^2 c^10 x z^2-b^4 c^10 x z^2-a^14 y z^2+a^12 b^2 y z^2-2 a^10 b^4 y z^2+2 a^8 b^6 y z^2-a^6 b^8 y z^2+a^4 b^10 y z^2+3 a^12 c^2 y z^2+2 a^8 b^4 c^2 y z^2-a^4 b^8 c^2 y z^2-4 a^10 c^4 y z^2-4 a^8 b^2 c^4 y z^2-3 a^6 b^4 c^4 y z^2-3 a^4 b^6 c^4 y z^2-a^2 b^8 c^4 y z^2-b^10 c^4 y z^2+4 a^8 c^6 y z^2+6 a^6 b^2 c^6 y z^2+7 a^4 b^4 c^6 y z^2+4 a^2 b^6 c^6 y z^2+3 b^8 c^6 y z^2-3 a^6 c^8 y z^2-5 a^4 b^2 c^8 y z^2-5 a^2 b^4 c^8 y z^2-3 b^6 c^8 y z^2+a^4 c^10 y z^2+2 a^2 b^2 c^10 y z^2+b^4 c^10 y z^2 = 0)
que corresponde a
t= b^2 ( SB^2 - SA SC) / (a^2 (SA^2 - SB SC)).
en esta cúbica: X(4), X(98) punto doble, X(2698) "sexto punto", X(5967), X(9154), X(14382).
Las tangentes en el punto doble, X(98), son paralelas a las asíntotas de la . Son las rectas que unen X(98) con los puntos de intersección del con la circunferencia circunscrita (X(1379) y X(1380)); estas tangentes pasan también por los puntos (X(6039) y X(6040)) de intersección de la con la circunferencia de centro el baricentro y que pasa por X(98).
Como X(98)^2
no está
( X(98)^2, X(2) y X(6) están alineados si y solo si
(a - b) (a + b) (a - c) (a - b - c) (b - c) (a + b - c) (a + c) (a -
b + c) (b + c) (a + b + c) (a^2 + b^2 + c^2)^2 (a^4 - a^2 b^2 +
b^4 - a^2 c^2 - b^2 c^2 + c^4) = 0.
Es decir, si el triángulo ABC es isósceles o el ángulo de Brocard ω=π/6 (ABC equilátero).
a^4 + b^4 + c^4 = 2S^2(-2 + cosec^2 ω), a^2 b^2 + a^2 c^2 + b^2 c^2 = S^2 cosec^2 ω.
)
en la recta que pasa por el baricentro y , existe una única hipérbola rectangular ℋ en el haz de cónicas que definen la isoconjugación (§1.5.2 Characterization of nK0 isocubics), su ecuación es:
(b^2 - c^2) (b^2 c^2-a^4) (b^4 + c^4 - a^2 (b^2 + c^2))^2 x^2
+(c^2 - a^2) (a^2 c^2-b^4) (c^4 + a^4 - b^2 (c^2 + a^2))^2 y^2
+(a^2 - b^2) (a^2 b^2 - c^4)(a^4 + b^4 - c^2 (a^2 + b^2))^2 z^2 = 0.
Pasa por los centros X(1), X(98), X(3404), X(8861), X(8870); estos dos últimos son los centros de perspectividad del de X(98) y del y triángulos de Brocard, respectivamente.
El centro de la hipérbola ℋ (que está sobre la circunferencia circunscrita a ABC) es:
W = ( 1/((b^2 - c^2) (-a^4 + b^2 c^2) (b^4 + c^4 - a^2 (b^2 + c^2))^2) : ... : ...),
que tiene números de búsqueda en
(0.124707642945284, 5.55316924128348, -0.261394674186625) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {98,446}, {805,2966}, {1297,1916}, {2698,12176}, {6037,17938}.
Añadido en ETC como el X18858.
• P el
La cúbica
nK(X4590,X2396,X99)
( (-a^6 b^4+a^4 b^6+2 a^6 b^2 c^2-a^4 b^4 c^2-a^6 c^4-a^4 b^2 c^4-a^2 b^4 c^4-b^6 c^4+a^4 c^6+2 a^2 b^2 c^6+3 b^4 c^6-a^2 c^8-3 b^2 c^8+c^10) x^2 y+(-a^6 b^4+a^4 b^6+a^4 b^4 c^2-2 a^2 b^6 c^2+a^6 c^4+a^4 b^2 c^4+a^2 b^4 c^4+b^6 c^4-3 a^4 c^6-2 a^2 b^2 c^6-b^4 c^6+3 a^2 c^8+b^2 c^8-c^10) x y^2+(a^6 b^4-a^4 b^6+a^2 b^8-b^10-2 a^6 b^2 c^2+a^4 b^4 c^2-2 a^2 b^6 c^2+3 b^8 c^2+a^6 c^4+a^4 b^2 c^4+a^2 b^4 c^4-3 b^6 c^4-a^4 c^6+b^4 c^6) x^2 z+(4 a^8 b^2-8 a^6 b^4+8 a^4 b^6-4 a^2 b^8-4 a^8 c^2+4 b^8 c^2+8 a^6 c^4-8 b^6 c^4-8 a^4 c^6+8 b^4 c^6+4 a^2 c^8-4 b^2 c^8) x y z+(a^10-a^8 b^2+a^6 b^4-a^4 b^6-3 a^8 c^2+2 a^6 b^2 c^2-a^4 b^4 c^2+2 a^2 b^6 c^2+3 a^6 c^4-a^4 b^2 c^4-a^2 b^4 c^4-b^6 c^4-a^4 c^6+b^4 c^6) y^2 z+(-a^6 b^4+3 a^4 b^6-3 a^2 b^8+b^10-a^4 b^4 c^2+2 a^2 b^6 c^2-b^8 c^2+a^6 c^4-a^4 b^2 c^4-a^2 b^4 c^4+b^6 c^4-a^4 c^6+2 a^2 b^2 c^6-b^4 c^6) x z^2+(-a^10+3 a^8 b^2-3 a^6 b^4+a^4 b^6+a^8 c^2-2 a^6 b^2 c^2+a^4 b^4 c^2-a^6 c^4+a^4 b^2 c^4+a^2 b^4 c^4-b^6 c^4+a^4 c^6-2 a^2 b^2 c^6+b^4 c^6) y z^2 = 0)
que corresponde a
t= (b^2 (a^2 - c^2))/(a^2 (b^2 - c^2)).
Centros del triángulo sobre la cúbica X(4), X(99) punto doble, X(2698) = SR(X(98), X(99)) "sexto punto", X(5641), X(14382)
• P el foco de la
La cúbica
nK(X(110)^2,X(2407),X(110))
( -a^6 b^4 c^4 x^2 y-a^4 b^6 c^4 x^2 y+2 a^2 b^8 c^4 x^2 y+2 a^6 b^2 c^6 x^2 y+5 a^4 b^4 c^6 x^2 y-4 a^2 b^6 c^6 x^2 y-2 b^8 c^6 x^2 y-a^6 c^8 x^2 y-7 a^4 b^2 c^8 x^2 y-a^2 b^4 c^8 x^2 y+5 b^6 c^8 x^2 y+3 a^4 c^10 x^2 y+6 a^2 b^2 c^10 x^2 y-3 b^4 c^10 x^2 y-3 a^2 c^12 x^2 y-b^2 c^12 x^2 y+c^14 x^2 y-2 a^8 b^2 c^4 x y^2+a^6 b^4 c^4 x y^2+a^4 b^6 c^4 x y^2+2 a^8 c^6 x y^2+4 a^6 b^2 c^6 x y^2-5 a^4 b^4 c^6 x y^2-2 a^2 b^6 c^6 x y^2-5 a^6 c^8 x y^2+a^4 b^2 c^8 x y^2+7 a^2 b^4 c^8 x y^2+b^6 c^8 x y^2+3 a^4 c^10 x y^2-6 a^2 b^2 c^10 x y^2-3 b^4 c^10 x y^2+a^2 c^12 x y^2+3 b^2 c^12 x y^2-c^14 x y^2+a^6 b^8 x^2 z-3 a^4 b^10 x^2 z+3 a^2 b^12 x^2 z-b^14 x^2 z-2 a^6 b^6 c^2 x^2 z+7 a^4 b^8 c^2 x^2 z-6 a^2 b^10 c^2 x^2 z+b^12 c^2 x^2 z+a^6 b^4 c^4 x^2 z-5 a^4 b^6 c^4 x^2 z+a^2 b^8 c^4 x^2 z+3 b^10 c^4 x^2 z+a^4 b^4 c^6 x^2 z+4 a^2 b^6 c^6 x^2 z-5 b^8 c^6 x^2 z-2 a^2 b^4 c^8 x^2 z+2 b^6 c^8 x^2 z+2 a^10 b^4 x y z-6 a^8 b^6 x y z+6 a^6 b^8 x y z-2 a^4 b^10 x y z+2 a^8 b^4 c^2 x y z-2 a^4 b^8 c^2 x y z-2 a^10 c^4 x y z-2 a^8 b^2 c^4 x y z+2 a^2 b^8 c^4 x y z+2 b^10 c^4 x y z+6 a^8 c^6 x y z-6 b^8 c^6 x y z-6 a^6 c^8 x y z+2 a^4 b^2 c^8 x y z-2 a^2 b^4 c^8 x y z+6 b^6 c^8 x y z+2 a^4 c^10 x y z-2 b^4 c^10 x y z+a^14 y^2 z-3 a^12 b^2 y^2 z+3 a^10 b^4 y^2 z-a^8 b^6 y^2 z-a^12 c^2 y^2 z+6 a^10 b^2 c^2 y^2 z-7 a^8 b^4 c^2 y^2 z+2 a^6 b^6 c^2 y^2 z-3 a^10 c^4 y^2 z-a^8 b^2 c^4 y^2 z+5 a^6 b^4 c^4 y^2 z-a^4 b^6 c^4 y^2 z+5 a^8 c^6 y^2 z-4 a^6 b^2 c^6 y^2 z-a^4 b^4 c^6 y^2 z-2 a^6 c^8 y^2 z+2 a^4 b^2 c^8 y^2 z-2 a^8 b^6 x z^2+5 a^6 b^8 x z^2-3 a^4 b^10 x z^2-a^2 b^12 x z^2+b^14 x z^2+2 a^8 b^4 c^2 x z^2-4 a^6 b^6 c^2 x z^2-a^4 b^8 c^2 x z^2+6 a^2 b^10 c^2 x z^2-3 b^12 c^2 x z^2-a^6 b^4 c^4 x z^2+5 a^4 b^6 c^4 x z^2-7 a^2 b^8 c^4 x z^2+3 b^10 c^4 x z^2-a^4 b^4 c^6 x z^2+2 a^2 b^6 c^6 x z^2-b^8 c^6 x z^2-a^14 y z^2+a^12 b^2 y z^2+3 a^10 b^4 y z^2-5 a^8 b^6 y z^2+2 a^6 b^8 y z^2+3 a^12 c^2 y z^2-6 a^10 b^2 c^2 y z^2+a^8 b^4 c^2 y z^2+4 a^6 b^6 c^2 y z^2-2 a^4 b^8 c^2 y z^2-3 a^10 c^4 y z^2+7 a^8 b^2 c^4 y z^2-5 a^6 b^4 c^4 y z^2+a^4 b^6 c^4 y z^2+a^8 c^6 y z^2-2 a^6 b^2 c^6 y z^2+a^4 b^4 c^6 y z^2 = 0)
que corresponde a
t= (c^2-a^2)/( c^2-b^2).
Centros del triángulo sobre la cúbica X(4), X(110) punto doble, X(477) = SR(X(110), X(74)) "sexto punto", X(5967), X(14385), X(15460), X(15461).
- Sábado, 19 de mayo del 2018
Una caracterización del punto de Segovia del triángulo circunceviano del circuncentro
Segovia Point
Let ABC be a triangle, A1B1C1 the pedal triangle of H (orthic triangle), A2B2C2 the 2nd Euler triangle (the antipodal triangle of A1B1C1 with respect the circumcircle of A1B1C1 (NPC of ABC)) and A'B'C' the antipodal triangle of ABC (circumcevian triangle of O). Then A2B2C2 and A'B'C' are perspective.
The point of concurrency is
Segovia Point (
4549).
Existen dos puntos
Ai (i=1,2) sobre la circunferencia circunscrita a un triángulos
ABC, tales que las rectas de Euler de
ABAi,
ACAi coinciden. Sea
Ma el punto medio de
A1A2. Se definen
Mb y
Mc análogamente. Entonces, las rectas
AMa,
BMb,
CMc concurren en
X(4846), del del circuncentro.
-c^2(-a^4(-1+t)t+(b^2-c^2)(b^2(-2+t)-c^2t)+a^2(c^2(-2+t)t-b^2(2-4t+t^2)))x
+ c^2((b^2-c^2)(b^2(-1+t)-c^2t)+a^4(t-2t^2)-a^2(-2c^2(-1+t)t+b^2(1-4t+2t^2)))y +
(a^6(-1+t)t+b^2(b^2-c^2)(b^2(-1+t)-c^2t)+a^4(-2+t)(b^2(-1+t)-c^2t)-
a^2(c^4t-2b^2c^2(-1+t^2)+b^4(1-3t+2t^2))z=0,
-b^2(b^4(-1+t)-2b^2c^2t+a^4(-1+t)t+c^4(1+t)+a^2(-b^2(-1+t^2)+c^2(-1+2t+t^2)))x
+(-a^6(-1+t)t+a^4(1+t)(b^2(-1+t)-c^2t)+c^2(-b^2+c^2)(-b^2(-1+t)+c^2t)+a^2(-b^4(-1+t)-2b^2c^2(-2+t)t+
c^4t(-1+2t)))y
+ b^2((b^2-c^2)(b^2(-1+t)-c^2t)+a^4(1-3t+2t^2)+a^2(-2b^2(-1+t)t+c^2(-1+2t^2)))z=0.
La condición necesaria y suficiente para que estas rectas (que tienen en común el circuncentro) coincidan es:
a^2(a^4-2(b^2-c^2)^2+a^2(b^2+c^2))t^2
+ (-a^2+b^2-c^2)(a^4+a^2(4b^2-2c^2)+(b^2-c^2)^2)t + b^2(2a^4-(b^2-c^2)^2-a^2(b^2+c^2)) = 0
Las dos raíces de esta ecuación, sustituidas en las coordenadas de D, dan dos puntos A1 y A2, cuyo punto medio (siempre real) es:
Ma (16a^4b^2c^2(a^4-2(b^2-c^2)^2+
a^2(b^2+c^2))^2(2a^8-(b^2-c^2)^4-5a^6(b^2+c^2)+a^2(b^2-c^2)^2(b^2+c^2)+a^4(3b^4+2b^2c^2+3c^4)) :
8a^2b^2c^2(-a^4+2(b^2-c^2)^2-a^2(b^2+c^2))(a^14+2a^12(b^2-c^2)+
a^2(b^2-7c^2)(b^2-c^2)^5+2(b^2-c^2)^7-6a^4(b^2-c^2)^3(3b^4-c^4)-3a^10(3b^4+c^4)-
2a^8(b^6+3b^4c^2+9b^2c^4-5c^6)+a^6(23b^8-20b^6c^2-18b^4c^4+20b^2c^6-5c^8)) :
8a^2b^2c^2(-a^4+2(b^2-c^2)^2-a^2(b^2+c^2))(a^14-2a^12(b^2-c^2)-2(b^2-c^2)^7+
a^2(b^2-c^2)^5(7b^2-c^2)-6a^4(b^2-c^2)^3(b^4-3c^4)-3a^10(b^4+3c^4)+
2a^8(5b^6-9b^4c^2-3b^2c^4-c^6)+a^6(-5b^8+20b^6c^2-18b^4c^4-20b^2c^6+23c^8)).
La ecuación de la recta AMa es:
(a^6-a^4(b^2-3c^2)+(b^2-c^2)^3-
a^2(b^4-4b^2c^2+3c^4))y + (-a^6+(b^2-c^2)^3+
a^4(-3b^2+c^2)+a^2(3b^4-4b^2c^2+c^4))z = 0.
Procediendo cíclicamente, se obtienen los puntos B1 y B2, C1 y C2, y las ecuaciones de las otras rectas AMb AMc. Las tres concurren en:
X4846 (a^10
+ a^8 (b^2 + c^2)
- 4 a^6 (2 b^4 - 3 b^2 c^2 + 2 c^4) +
4 a^4 (2 b^6 - 3 b^4 c^2 - 3 b^2 c^4 + 2 c^6)
- a^2 (b^2 - c^2)^2 (b^4 + 6 b^2 c^2 + c^4)
- (b^2 - c^2)^4 (b^2 + c^2) : ... : ...).
El triángulo formado por las rectas A1A2, B1B2 y C1C2 es el trasladado de ABC, mediante la traslación de vector HO, con origen en el ortocentro y extremo en el circuncentro. Por lo que podemos enunciar:
Descargar fichero GeoGebra
Los lados del triángulo trasladado de ABC, mediante la traslación de vector X4X5, cortan a la circunferencia circunscrita en pares de puntos (reales o imaginarios), cuyos puntos medios son los vértices de un triángulo MaMbMc, perspectivo con ABC, con perspector X4846.
NOTA.
La determinación del punto medio de los puntos de intersección de una recta y una circunferencia, cuando son imaginarios conjugados, está descrita por Roger Cuppens en "Faire de la géométrie supèrieure en jouant avec Cabri-Géomètre II", Tome I, APMEP nº 124, pp, 14,15. (M. Chasles, Traité de géométrie supérieure, Paris: Bachelier, 1852. p.54).
- Miércoles, 16 de mayo del 2018
Haz de hipérbolas rectangulares asociado a una estrofoide
Dado un triángulo ABC con ortocentro H, sean P un punto y ℓ1, ℓ2 dos rectas perpendiculares por H, que cortan a BC en A1, A2, respectivamente.
Para cada número real μ, se denota por Aμ el punto tal que A1Aμ : AμA2 = μ.
Se definen, de forma análoga, los puntos B1, B2, Bμ; C1, C2, Cμ.
Los puntos Aμ, Bμ, Cμ están alineados. Cuando μ varía, la recta que pasa por ellos envuelve la parábola ℘, tangente a las rectas BC, CA, AB, ℓ1, ℓ2.
Generalization of the Droz-Farny line theorem. Forum Geometricorum Volume 4 (2004) 225–227. (
Wolfram MathWorld Jean-Pierre Ehrmann and Floor van Lamoen)
If two perpendicular lines are drawn through the orthocenter H of any triangle, these lines intercept each side (or its extension) in two points (labeled P
12, P'
12, P
13, P'
13, P
23, P'
23). Then the midpoints M
12, M
12, and M
23 of these three segments are collinear.
The two given lines, the lines connecting the midpoints and the sides of the reference triangle are all tangent to the same (inscribed) parabola. Instead of the midpoints, one may take any other ratio t with
P23M23:M23P'23=P13M13:M13P'13 =P12M12:M12P'12=t
and the points M
23, M
13, and M
12 will still be collinear in addition to being tangent to the same parabola (Ehrmann and van Lamoen 2004).
Consideremos la hipérbola rectangular ℋa que pasa por P, H, A1, A2 y, análogamente, las hipérbolas rectangulares ℋb y ℋc.
Estas hipérbolas forman un haz de cónicas.
Theorem 7.4 (Perpendiculars through the orthocenter).
Creative Geometry (Alexander Skutin)
Consider any triangle with the orthocenter H and let P be any point on the plane. Let ℓ
1, ℓ
2 be two perpendicular lines through H. Consider the intersection points
A1,
B1,
C1 of ℓ
1 with BC, CA, AB, respectively. Similarly define
A2,
B2,
C2. Let ℋ
A be an orthogonal hyperbola through
A1,
A2, H, P. Similarly define ℋ
B, ℋ
C. Then ℋ
A, ℋ
B, ℋ
C intersect at four different points.
Las hipérbolas rectangulares del haz formado por ℋb y ℋc son tangentes en P a una misma recta si y solo si P está sobre la , de la parábola ℘ respecto a H.
Una de las tangentes a la parábola ℘ desde el punto P, de la estrofoide, es la tangente común de todas las hipérbolas del haz, y la otra toca a la parábola en T, tercer punto base del haz. Así, una cónica degenerada del haz está formada por las rectas PH y PT; la otra la forman la recta HT y la tangente común en P.
Los centros de las hipérbolas del haz quedan sobre la circunferencia de los nueve puntos de PHT, la cual pasa por el F de la estrofoide (punto medio del punto singular H y el foco de la parábola).
La estrofoide es la envolvente de la circunferencia de los nueve puntos de PHT, cuando T se mueve sobre la parábola ℘.
Un caso particular:
Si ℓ1, ℓ2 son la y su perpendicular por H, el eje de la
estrofoide,
( -2 a^10 b^2 x^3+7 a^8 b^4 x^3-8 a^6 b^6 x^3+2 a^4 b^8 x^3+2 a^2 b^10 x^3-b^12 x^3+2 a^10 c^2 x^3-12 a^6 b^4 c^2 x^3+16 a^4 b^6 c^2 x^3-6 a^2 b^8 c^2 x^3-7 a^8 c^4 x^3+12 a^6 b^2 c^4 x^3-8 a^2 b^6 c^4 x^3+3 b^8 c^4 x^3+8 a^6 c^6 x^3-16 a^4 b^2 c^6 x^3+8 a^2 b^4 c^6 x^3-2 a^4 c^8 x^3+6 a^2 b^2 c^8 x^3-3 b^4 c^8 x^3-2 a^2 c^10 x^3+c^12 x^3-2 a^10 b^2 x^2 y+7 a^8 b^4 x^2 y-8 a^6 b^6 x^2 y+2 a^4 b^8 x^2 y+2 a^2 b^10 x^2 y-b^12 x^2 y+2 a^10 c^2 x^2 y-4 a^8 b^2 c^2 x^2 y-2 a^6 b^4 c^2 x^2 y+10 a^4 b^6 c^2 x^2 y-8 a^2 b^8 c^2 x^2 y+2 b^10 c^2 x^2 y-3 a^8 c^4 x^2 y+12 a^6 b^2 c^4 x^2 y-14 a^4 b^4 c^4 x^2 y+4 a^2 b^6 c^4 x^2 y+b^8 c^4 x^2 y-2 a^6 c^6 x^2 y-2 a^4 b^2 c^6 x^2 y+8 a^2 b^4 c^6 x^2 y-4 b^6 c^6 x^2 y+4 a^4 c^8 x^2 y-6 a^2 b^2 c^8 x^2 y+b^4 c^8 x^2 y+2 b^2 c^10 x^2 y-c^12 x^2 y+a^12 x y^2-2 a^10 b^2 x y^2-2 a^8 b^4 x y^2+8 a^6 b^6 x y^2-7 a^4 b^8 x y^2+2 a^2 b^10 x y^2-2 a^10 c^2 x y^2+8 a^8 b^2 c^2 x y^2-10 a^6 b^4 c^2 x y^2+2 a^4 b^6 c^2 x y^2+4 a^2 b^8 c^2 x y^2-2 b^10 c^2 x y^2-a^8 c^4 x y^2-4 a^6 b^2 c^4 x y^2+14 a^4 b^4 c^4 x y^2-12 a^2 b^6 c^4 x y^2+3 b^8 c^4 x y^2+4 a^6 c^6 x y^2-8 a^4 b^2 c^6 x y^2+2 a^2 b^4 c^6 x y^2+2 b^6 c^6 x y^2-a^4 c^8 x y^2+6 a^2 b^2 c^8 x y^2-4 b^4 c^8 x y^2-2 a^2 c^10 x y^2+c^12 x y^2+a^12 y^3-2 a^10 b^2 y^3-2 a^8 b^4 y^3+8 a^6 b^6 y^3-7 a^4 b^8 y^3+2 a^2 b^10 y^3+6 a^8 b^2 c^2 y^3-16 a^6 b^4 c^2 y^3+12 a^4 b^6 c^2 y^3-2 b^10 c^2 y^3-3 a^8 c^4 y^3+8 a^6 b^2 c^4 y^3-12 a^2 b^6 c^4 y^3+7 b^8 c^4 y^3-8 a^4 b^2 c^6 y^3+16 a^2 b^4 c^6 y^3-8 b^6 c^6 y^3+3 a^4 c^8 y^3-6 a^2 b^2 c^8 y^3+2 b^4 c^8 y^3+2 b^2 c^10 y^3-c^12 y^3-2 a^10 b^2 x^2 z+3 a^8 b^4 x^2 z+2 a^6 b^6 x^2 z-4 a^4 b^8 x^2 z+b^12 x^2 z+2 a^10 c^2 x^2 z+4 a^8 b^2 c^2 x^2 z-12 a^6 b^4 c^2 x^2 z+2 a^4 b^6 c^2 x^2 z+6 a^2 b^8 c^2 x^2 z-2 b^10 c^2 x^2 z-7 a^8 c^4 x^2 z+2 a^6 b^2 c^4 x^2 z+14 a^4 b^4 c^4 x^2 z-8 a^2 b^6 c^4 x^2 z-b^8 c^4 x^2 z+8 a^6 c^6 x^2 z-10 a^4 b^2 c^6 x^2 z-4 a^2 b^4 c^6 x^2 z+4 b^6 c^6 x^2 z-2 a^4 c^8 x^2 z+8 a^2 b^2 c^8 x^2 z-b^4 c^8 x^2 z-2 a^2 c^10 x^2 z-2 b^2 c^10 x^2 z+c^12 x^2 z-6 a^10 b^2 x y z+12 a^8 b^4 x y z-12 a^4 b^8 x y z+6 a^2 b^10 x y z+6 a^10 c^2 x y z-30 a^6 b^4 c^2 x y z+30 a^4 b^6 c^2 x y z-6 b^10 c^2 x y z-12 a^8 c^4 x y z+30 a^6 b^2 c^4 x y z-30 a^2 b^6 c^4 x y z+12 b^8 c^4 x y z-30 a^4 b^2 c^6 x y z+30 a^2 b^4 c^6 x y z+12 a^4 c^8 x y z-12 b^4 c^8 x y z-6 a^2 c^10 x y z+6 b^2 c^10 x y z-a^12 y^2 z+4 a^8 b^4 y^2 z-2 a^6 b^6 y^2 z-3 a^4 b^8 y^2 z+2 a^2 b^10 y^2 z+2 a^10 c^2 y^2 z-6 a^8 b^2 c^2 y^2 z-2 a^6 b^4 c^2 y^2 z+12 a^4 b^6 c^2 y^2 z-4 a^2 b^8 c^2 y^2 z-2 b^10 c^2 y^2 z+a^8 c^4 y^2 z+8 a^6 b^2 c^4 y^2 z-14 a^4 b^4 c^4 y^2 z-2 a^2 b^6 c^4 y^2 z+7 b^8 c^4 y^2 z-4 a^6 c^6 y^2 z+4 a^4 b^2 c^6 y^2 z+10 a^2 b^4 c^6 y^2 z-8 b^6 c^6 y^2 z+a^4 c^8 y^2 z-8 a^2 b^2 c^8 y^2 z+2 b^4 c^8 y^2 z+2 a^2 c^10 y^2 z+2 b^2 c^10 y^2 z-c^12 y^2 z-a^12 x z^2+2 a^10 b^2 x z^2+a^8 b^4 x z^2-4 a^6 b^6 x z^2+a^4 b^8 x z^2+2 a^2 b^10 x z^2-b^12 x z^2+2 a^10 c^2 x z^2-8 a^8 b^2 c^2 x z^2+4 a^6 b^4 c^2 x z^2+8 a^4 b^6 c^2 x z^2-6 a^2 b^8 c^2 x z^2+2 a^8 c^4 x z^2+10 a^6 b^2 c^4 x z^2-14 a^4 b^4 c^4 x z^2-2 a^2 b^6 c^4 x z^2+4 b^8 c^4 x z^2-8 a^6 c^6 x z^2-2 a^4 b^2 c^6 x z^2+12 a^2 b^4 c^6 x z^2-2 b^6 c^6 x z^2+7 a^4 c^8 x z^2-4 a^2 b^2 c^8 x z^2-3 b^4 c^8 x z^2-2 a^2 c^10 x z^2+2 b^2 c^10 x z^2+a^12 y z^2-2 a^10 b^2 y z^2-a^8 b^4 y z^2+4 a^6 b^6 y z^2-a^4 b^8 y z^2-2 a^2 b^10 y z^2+b^12 y z^2+6 a^8 b^2 c^2 y z^2-8 a^6 b^4 c^2 y z^2-4 a^4 b^6 c^2 y z^2+8 a^2 b^8 c^2 y z^2-2 b^10 c^2 y z^2-4 a^8 c^4 y z^2+2 a^6 b^2 c^4 y z^2+14 a^4 b^4 c^4 y z^2-10 a^2 b^6 c^4 y z^2-2 b^8 c^4 y z^2+2 a^6 c^6 y z^2-12 a^4 b^2 c^6 y z^2+2 a^2 b^4 c^6 y z^2+8 b^6 c^6 y z^2+3 a^4 c^8 y z^2+4 a^2 b^2 c^8 y z^2-7 b^4 c^8 y z^2-2 a^2 c^10 y z^2+2 b^2 c^10 y z^2-a^12 z^3+3 a^8 b^4 z^3-3 a^4 b^8 z^3+b^12 z^3+2 a^10 c^2 z^3-6 a^8 b^2 c^2 z^3-8 a^6 b^4 c^2 z^3+8 a^4 b^6 c^2 z^3+6 a^2 b^8 c^2 z^3-2 b^10 c^2 z^3+2 a^8 c^4 z^3+16 a^6 b^2 c^4 z^3-16 a^2 b^6 c^4 z^3-2 b^8 c^4 z^3-8 a^6 c^6 z^3-12 a^4 b^2 c^6 z^3+12 a^2 b^4 c^6 z^3+8 b^6 c^6 z^3+7 a^4 c^8 z^3-7 b^4 c^8 z^3-2 a^2 c^10 z^3+2 b^2 c^10 z^3 = 0)
ℰ, que se obtiene, pasa por X74, de punto del infinito de la recta de Euler.
La estrofoide ℰ pasa por X2777 (su punto en el infinito) y por X6794. Es inversa en de la
hipérbola
( (b^2 - c^2) (-2 a^4 + (b^2 - c^2)^2 +
a^2 (b^2 + c^2))y z + (c^2-a^2) (a^4 - 2 b^4 + b^2 c^2 + c^4 +
a^2 (b^2 - 2 c^2)) z x + (a^2 - b^2) (a^4 + b^4 + b^2 c^2 - 2 c^4 +
a^2 (-2 b^2 + c^2)) x y= 0)
ℋ rectangular circunscrita a ABC, que pasa por los centros X(4), X(30), X(477), X(523), X(1138), X(1990)=inverso de X6794, X(3260), X(3471), X(5627), X(5641), X(6662), X(9154), X(9214), X(11085), X(11815), X(13489), X(14254), X(14387), X(14536), X(15454), X(16104). Su centro es X(3258) y es X(1637).
La estrofoide ℰ es la podaria, respecto al ortocentro, de la
parábola
( (-4 a^12 b^4+12 a^10 b^6-9 a^8 b^8-4 a^6 b^10+6 a^4 b^12-b^16+8 a^12 b^2 c^2-12 a^10 b^4 c^2-16 a^8 b^6 c^2+36 a^6 b^8 c^2-12 a^4 b^10 c^2-8 a^2 b^12 c^2+4 b^14 c^2-4 a^12 c^4-12 a^10 b^2 c^4+50 a^8 b^4 c^4-32 a^6 b^6 c^4-22 a^4 b^8 c^4+24 a^2 b^10 c^4-4 b^12 c^4+12 a^10 c^6-16 a^8 b^2 c^6-32 a^6 b^4 c^6+56 a^4 b^6 c^6-16 a^2 b^8 c^6-4 b^10 c^6-9 a^8 c^8+36 a^6 b^2 c^8-22 a^4 b^4 c^8-16 a^2 b^6 c^8+10 b^8 c^8-4 a^6 c^10-12 a^4 b^2 c^10+24 a^2 b^4 c^10-4 b^6 c^10+6 a^4 c^12-8 a^2 b^2 c^12-4 b^4 c^12+4 b^2 c^14-c^16) x^2+(-4 a^14 b^2+6 a^12 b^4+12 a^10 b^6-28 a^8 b^8+12 a^6 b^10+6 a^4 b^12-4 a^2 b^14+4 a^14 c^2+8 a^12 b^2 c^2-48 a^10 b^4 c^2+36 a^8 b^6 c^2+36 a^6 b^8 c^2-48 a^4 b^10 c^2+8 a^2 b^12 c^2+4 b^14 c^2-14 a^12 c^4+24 a^10 b^2 c^4+50 a^8 b^4 c^4-120 a^6 b^6 c^4+50 a^4 b^8 c^4+24 a^2 b^10 c^4-14 b^12 c^4+12 a^10 c^6-68 a^8 b^2 c^6+56 a^6 b^4 c^6+56 a^4 b^6 c^6-68 a^2 b^8 c^6+12 b^10 c^6+10 a^8 c^8+36 a^6 b^2 c^8-94 a^4 b^4 c^8+36 a^2 b^6 c^8+10 b^8 c^8-20 a^6 c^10+24 a^4 b^2 c^10+24 a^2 b^4 c^10-20 b^6 c^10+6 a^4 c^12-24 a^2 b^2 c^12+6 b^4 c^12+4 a^2 c^14+4 b^2 c^14-2 c^16) x y+(-a^16+6 a^12 b^4-4 a^10 b^6-9 a^8 b^8+12 a^6 b^10-4 a^4 b^12+4 a^14 c^2-8 a^12 b^2 c^2-12 a^10 b^4 c^2+36 a^8 b^6 c^2-16 a^6 b^8 c^2-12 a^4 b^10 c^2+8 a^2 b^12 c^2-4 a^12 c^4+24 a^10 b^2 c^4-22 a^8 b^4 c^4-32 a^6 b^6 c^4+50 a^4 b^8 c^4-12 a^2 b^10 c^4-4 b^12 c^4-4 a^10 c^6-16 a^8 b^2 c^6+56 a^6 b^4 c^6-32 a^4 b^6 c^6-16 a^2 b^8 c^6+12 b^10 c^6+10 a^8 c^8-16 a^6 b^2 c^8-22 a^4 b^4 c^8+36 a^2 b^6 c^8-9 b^8 c^8-4 a^6 c^10+24 a^4 b^2 c^10-12 a^2 b^4 c^10-4 b^6 c^10-4 a^4 c^12-8 a^2 b^2 c^12+6 b^4 c^12+4 a^2 c^14-c^16) y^2+(4 a^14 b^2-14 a^12 b^4+12 a^10 b^6+10 a^8 b^8-20 a^6 b^10+6 a^4 b^12+4 a^2 b^14-2 b^16-4 a^14 c^2+8 a^12 b^2 c^2+24 a^10 b^4 c^2-68 a^8 b^6 c^2+36 a^6 b^8 c^2+24 a^4 b^10 c^2-24 a^2 b^12 c^2+4 b^14 c^2+6 a^12 c^4-48 a^10 b^2 c^4+50 a^8 b^4 c^4+56 a^6 b^6 c^4-94 a^4 b^8 c^4+24 a^2 b^10 c^4+6 b^12 c^4+12 a^10 c^6+36 a^8 b^2 c^6-120 a^6 b^4 c^6+56 a^4 b^6 c^6+36 a^2 b^8 c^6-20 b^10 c^6-28 a^8 c^8+36 a^6 b^2 c^8+50 a^4 b^4 c^8-68 a^2 b^6 c^8+10 b^8 c^8+12 a^6 c^10-48 a^4 b^2 c^10+24 a^2 b^4 c^10+12 b^6 c^10+6 a^4 c^12+8 a^2 b^2 c^12-14 b^4 c^12-4 a^2 c^14+4 b^2 c^14) x z+(-2 a^16+4 a^14 b^2+6 a^12 b^4-20 a^10 b^6+10 a^8 b^8+12 a^6 b^10-14 a^4 b^12+4 a^2 b^14+4 a^14 c^2-24 a^12 b^2 c^2+24 a^10 b^4 c^2+36 a^8 b^6 c^2-68 a^6 b^8 c^2+24 a^4 b^10 c^2+8 a^2 b^12 c^2-4 b^14 c^2+6 a^12 c^4+24 a^10 b^2 c^4-94 a^8 b^4 c^4+56 a^6 b^6 c^4+50 a^4 b^8 c^4-48 a^2 b^10 c^4+6 b^12 c^4-20 a^10 c^6+36 a^8 b^2 c^6+56 a^6 b^4 c^6-120 a^4 b^6 c^6+36 a^2 b^8 c^6+12 b^10 c^6+10 a^8 c^8-68 a^6 b^2 c^8+50 a^4 b^4 c^8+36 a^2 b^6 c^8-28 b^8 c^8+12 a^6 c^10+24 a^4 b^2 c^10-48 a^2 b^4 c^10+12 b^6 c^10-14 a^4 c^12+8 a^2 b^2 c^12+6 b^4 c^12+4 a^2 c^14-4 b^2 c^14) y z+(-a^16+4 a^14 b^2-4 a^12 b^4-4 a^10 b^6+10 a^8 b^8-4 a^6 b^10-4 a^4 b^12+4 a^2 b^14-b^16-8 a^12 b^2 c^2+24 a^10 b^4 c^2-16 a^8 b^6 c^2-16 a^6 b^8 c^2+24 a^4 b^10 c^2-8 a^2 b^12 c^2+6 a^12 c^4-12 a^10 b^2 c^4-22 a^8 b^4 c^4+56 a^6 b^6 c^4-22 a^4 b^8 c^4-12 a^2 b^10 c^4+6 b^12 c^4-4 a^10 c^6+36 a^8 b^2 c^6-32 a^6 b^4 c^6-32 a^4 b^6 c^6+36 a^2 b^8 c^6-4 b^10 c^6-9 a^8 c^8-16 a^6 b^2 c^8+50 a^4 b^4 c^8-16 a^2 b^6 c^8-9 b^8 c^8+12 a^6 c^10-12 a^4 b^2 c^10-12 a^2 b^4 c^10+12 b^6 c^10-4 a^4 c^12+8 a^2 b^2 c^12-4 b^4 c^12) z^2 = 0)
℘ de foco X1304 y directriz X(4)X(74). El perspector de esta parábola es X(16077), su eje tiene la dirección de X(9033), es tangente a la recta de Euler en X(4240) y a su perpendicular por el ortocentro en:
Z = ( (b^2-c^2)/(2 a^6-3 a^4 (b^2+c^2)+4 a^2 b^2 c^2+(b^2-c^2)^2 (b^2+c^2)) : ... : ...),
que tiene números de búsqueda en
(79.1679455521851, -92.0184910873782, 30.8067219029300)
y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {4,523}, {74,1300}, {93,18039}, {264,850}, {297,14977}, {393,2433}, {476,1304}, {512,16263}, {520,12111}, {525,16253}, {685,879}, {847,11704}, {877,892}, {924,12290}, {1105,6368}, {1826,4024}, {2395,6531}, {5466,16080}, {6344,10412}, {9033,10152}.
Añadido en ETC como el X18808.
Let A
1, B
1, C
1 be the intersections of the Euler line and lines BC, CA, AB, resp. The circumcircles of AB
1C
1, BC
1A
1, CA
1B
1 concur in
X(1304). (Randy Hutson, February 10, 2016)
X(4240) is the only point on the Euler line whose trilinear polar is parallel to the Euler line. (Randy Hutson, January 29, 2015).
Let Ω be the circumconic with center X(1650). One of the asymptotes of W is the Euler line. The other is in the direction of
X(9033). Also, X(9033) is the infinity point of the isotomic line of the Euler line. For a sketch, click
X(9033). (Angel Montesdeoca, April 19, 2016) .
El foco F de la estrofoide ℰ, punto medio de X4 y X1304, es:
F = ( 2 a^20 (b^2+c^2)
-8 a^18 (b^4+c^4)
+a^16 (5 b^6+7 b^4 c^2+7 b^2 c^4+5 c^6)
+a^14 (22 b^8-66 b^6 c^2+72 b^4 c^4-66 b^2 c^6+22 c^8)
-a^12 (42 b^10-87 b^8 c^2+43 b^6 c^4+43 b^4 c^6-87 b^2 c^8+42 c^10)
+2 a^10 (b^2-c^2)^2 (7 b^8+41 b^6 c^2-59 b^4 c^4+41 b^2 c^6+7 c^8)
+a^8 (b^2-c^2)^2 (28 b^10-119 b^8 c^2+79 b^6 c^4+79 b^4 c^6-119 b^2 c^8+28 c^10)
-2 a^6 (b^2-c^2)^4 (15 b^8+11 b^6 c^2-46 b^4 c^4+11 b^2 c^6+15 c^8)
+a^4 (b^2-c^2)^4 (8 b^10+43 b^8 c^2-41 b^6 c^4-41 b^4 c^6+43 b^2 c^8+8 c^10)
+2 a^2 (b^2-c^2)^6 (b^8-5 b^6 c^2-15 b^4 c^4-5 b^2 c^6+c^8)
-(b^2-c^2)^8 (b^6+4 b^4 c^2+4 b^2 c^4+c^6) : ... : ...),
que tiene números de búsqueda en
(-2.56477225506529, -3.57875714976302, 7.30200662638891), punto medio de X4 y X1304; reflexión de X16177 en X5; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2,2693}, {4,477}, {5,16177}, {30,122}, {113,520}, {115,1990}, {125,403}, {127,11799}, {133,523}, {136,10151}, {235,16221}, {1552,2777}, {1553,7480}, {1560,9209}, {1596,5099}, {5520,15763}, {6761,11792}.
Añadido en ETC como el X18809.
- Viernes, 11 de mayo del 2018
Las circunferencias O(R) y N(R/2) inversas respecto a una circunferencia centrada en el baricentro
Dado un triángulo ABC se denota, como es habitual, por G, O, H, N y R el baricentro, circuncentro, ortocentro, centro de la y el radio de la circunferencia circunscrita, respectivamente. Sean O(R) la circunferencia circunscrita y N(R/2) la circunferencia de los nueve puntos. Los centros de homotecia interior y exterior de estas dos circunferencias son, respectivamente, G y H (OG : GN = R : R/2 y OH : HN = R : -R/2).
La circunferencia de inversión de la inversión de polo G, que transforma O(R) en N(R/2) tiene radio
√
/3.
En coordenadas baricéntricas, la expresión analítica del inverso de un punto (x:y:z) en una inversión de polo (p:q:r) y razón k es:
( k^2*(p+q+r)^2*(x+y+z)*(q*x+r*x-p*(y+z))+p*(r*(x+y)-(p+q)*z)*(a^2*((p+r)*y-q*(x+z))+
b^2*(q*x+r*x-p*(y+z)))+c^2*p*(q^2*x*(x+z)+(p+r)*y*(-(r*x)+p*(y+z))+q*(r*x*(x-y+z)-p*(z*(y+z)+x*(2*y+z)))) :
-(k^2*(p+q+r)^2*(x+y+z)*(-((p+r)*y)+q*(x+z)))+q*((r*(x+y)-(p+q)*z)*(a^2*((p+r)*y-q*(x+z))+
b^2*(q*x+r*x-p*(y+z)))+c^2*(q^2*x*(x+z)+(p+r)*y*(-(r*x)+p*(y+z))+q*(r*x*(x-y+z)-p*(z*(y+z)+x*(2*y+z))))) :
-(k^2*(p+q+r)^2*(x+y+z)*(r*(x+y)-(p+q)*z))+r*((r*(x+y)-(p+q)*z)*(a^2*((p+r)*y-q*(x+z))+
b^2*(q*x+r*x-p*(y+z)))+c^2*(q^2*x*(x+z)+(p+r)*y*(-(r*x)+p*(y+z))+q*(r*x*(x-y+z)-p*(z*(y+z)+x*(2*y+z))))) ).
El inverso de un punto (a^2(t-1)t:-b^2(t-1):c^2t), sobre la circunferencia circunscrita, en la inversión de polo G y razón k (potencia de inversión) es:
( b^2*(2*c^2+9*k^2*(-1+t))+b^4*(-1+t)-c^2*(c^2+9*k^2)*t-a^4*(-1+t)*t+2*a^2*(b^2*(-1+t)^2+t*(9*k^2*(-1+t)+c^2*t)) :
2*b^2*(c^2-9*k^2*(-1+t))+ b^4*(-1+t)-c^2*(c^2+9*k^2)*t-a^4*(-1+t)*t+a^2*(2*b^2*(-1+t)^2+t*(-9*k^2*(-1+t)+2*c^2*t)) :
b^2*(2*c^2+9*k^2*(-1+t))+b^4*(-1+t)-c^2*(c^2-18*k^2)*t-a^4*(-1+t)*t+a^2*(2*b^2*(-1+t)^2+t*(-9*k^2*(-1+t)+2*c^2*t)) ).
Este punto está sobre la circunferencia de los nueve puntos si k = √Sω/3.
Este valor coincide con el dado en X(5577), "definition of inverter":
sqrt[uv(1 - (|UV|/(u + v))^2)], donde u=R, v=R/2, U=O y V=N.
El inverso de un punto P(x:y:z), en la inversión de polo G y potencia √a²+b²+c²/3, es:
Q (b^2(2x^2-y^2+x(y-3z)+z^2)+c^2(2x^2+y^2-z^2+x(-3y+z))+a^2(y^2-4y z+z^2+x(y+z)) :
c^2(x^2-3x y+2y^2+y z-z^2)+a^2(-x^2+x y+2y^2-3y z+z^2)+b^2(x^2+x(y-4z)+z(y+z)) :
a^2(-x^2+y^2+x z-3y z+2z^2)+b^2(x^2-y^2-3x z+y z+2z^2)+c^2(x^2+x(-4y+z)+y(y+z)) ).
Este punto Q es el segundo punto de intersección de las circunferencia coaxiales descritas en Hyacinthos #27637:
[Antreas Hatzipolakis]:
Let ABC be a triangle, A'B'C' the cevian triangle of G and P a point..
Denote:
A", B", C" = the second intersections of the NPC and AA', BB', CC',
resp.
(ie A"B"C" is the circumcevian triangle of G wrt A'B'C')
Which is the locus of P such that the circumcircles of APA", BPB",
CPC" are coaxial?
- Viernes, 4 de mayo del 2018
Porismo de Poncelet y triángulos con el mismo ortocentro
Dado un triángulo
ABC con circunferencia inscrita (I) y ortocentro
H. El lugar geométrico
de los vértices de los triángulos circunscritos a (I) y ortocentro
H es la
cónica
( (a^2-b^2+c^2) (-a^2+b^2+c^2) (-a^3+a^2 b+a b^2-b^3-a^2 c-2 a b c-b^2 c+a c^2+b c^2+c^3) ((a^2+b^2-c^2) (-a^2+b^2+c^2) (-a^3-a^2 b+a b^2+b^3+a^2 c-2 a b c+b^2 c+a c^2-b c^2-c^3)+(a^2+b^2-c^2) (a^2-b^2+c^2) (a^3+a^2 b-a b^2-b^3+a^2 c-2 a b c+b^2 c-a c^2+b c^2-c^3)-(a^2-b^2+c^2) (-a^2+b^2+c^2) (-a^3+a^2 b+a b^2-b^3-a^2 c-2 a b c-b^2 c+a c^2+b c^2+c^3)) x y+(a^2+b^2-c^2) (-a^2+b^2+c^2) (-a^3-a^2 b+a b^2+b^3+a^2 c-2 a b c+b^2 c+a c^2-b c^2-c^3) (-(a^2+b^2-c^2) (-a^2+b^2+c^2) (-a^3-a^2 b+a b^2+b^3+a^2 c-2 a b c+b^2 c+a c^2-b c^2-c^3)+(a^2+b^2-c^2) (a^2-b^2+c^2) (a^3+a^2 b-a b^2-b^3+a^2 c-2 a b c+b^2 c-a c^2+b c^2-c^3)+(a^2-b^2+c^2) (-a^2+b^2+c^2) (-a^3+a^2 b+a b^2-b^3-a^2 c-2 a b c-b^2 c+a c^2+b c^2+c^3)) x z+(a^2+b^2-c^2) (a^2-b^2+c^2) (a^3+a^2 b-a b^2-b^3+a^2 c-2 a b c+b^2 c-a c^2+b c^2-c^3) ((a^2+b^2-c^2) (-a^2+b^2+c^2) (-a^3-a^2 b+a b^2+b^3+a^2 c-2 a b c+b^2 c+a c^2-b c^2-c^3)-(a^2+b^2-c^2) (a^2-b^2+c^2) (a^3+a^2 b-a b^2-b^3+a^2 c-2 a b c+b^2 c-a c^2+b c^2-c^3)+(a^2-b^2+c^2) (-a^2+b^2+c^2) (-a^3+a^2 b+a b^2-b^3-a^2 c-2 a b c-b^2 c+a c^2+b c^2+c^3)) y z = 0)
(Co) circunscrita
a
ABC de X
281.
La cónica (Co) es hipérbola si k > 0, es elipse si k < 0, y es parábola si k=0. O equivalentemente, la cónica (Co) es parábola, elipse o hipérbola si el ortocentro está sobre, en el interior o en el exterior de la circunferencia inscrita, respectivamente.
Let Ea be the ellipse passing through A, and with foci at B and C (the A-Soddy ellipse). Let La be the polar of X(3) with respect to Ea. Define Lb and Lc cyclically. Let A' = Lb∩Lc, B' = Lc∩La, C' = La∩Lb. Triangle A'B'C' is homothetic to ABC, and the center of homothety is
X(281). (Randy Hutson, September 14, 2016)
El centro de la cónica (Co) es X7952, y pasa por X1897 y X1309 ( de intersección con la circunferencia circunscrita a ABC). Un foco es el ortocentro y el otro es:
F' = ( (a^2 + b^2 - c^2) (a^2 - b^2 + c^2) (5 a^6 - 2 a^5 (b + c)
+ a^4 (-9 b^2 + 2 b c - 9 c^2)+
4 a^3 (b^3 + b^2 c + b c^2 + c^3)
+ a^2 (b - c)^2 (3 b^2 + 2 b c + 3 c^2)
- 2 a (b - c)^2 (b + c)^3
+ (b - c)^2 (b + c)^4 ) : ... : ...),
que tiene números de búsqueda en
(8.53009774007008, 9.32349585350002, -6.75103160439414), reflexión de Xi en Xj para los índices {i,j}: {4, 7952}, {280, 3}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,4}, {3,280}, {20,1897}, {24,1604}, {104,963}, {108,3176}, {198,7003}, {318,5731}, {451,10786}, {1071,5908}, {3183,3198}.
Añadido en ETC como el X18283.
El lado opuesto al vértice X1897 del triángulo inscrito en (Co) y circunscrito a (I), es tangente en el .
El lado opuesto al vértice X1309 del triángulo inscrito en (Co) y circunscrito a (I), es tangente en el X3326.
Estos dos triángulos son simétricos respecto a la recta IH, eje focal de la cónica (Co).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Breve descripción de los pasos dados para llegar a la ecuación de la cónica (Co), usando Mathematica y coordenadas baricéntricas:
• Se toma un punto genérico Pt sobre una tangente a la circunferencia inscrita a ABC (por ejemplo, sobre la tangente en el punto de Feuerbach: -(a-b)(a-c)x+(a-b)(b-c)y+(a-c)(-b+c)z=0).
Pt (
(b - c)^2 ((-a + b + c) (a^2 (b + c) + b c (b + c) +
a (b^2 - 6 b c + c^2)) +
2 a (a^3 - a^2 (b + c) + (b - c)^2 (b + c) -
a (b^2 - 3 b c + c^2)) t) :
(a -
c)^2 ((a - b + c) (a^2 (b + c) + b c (b + c) +
a (b^2 - 6 b c + c^2)) +
2 b (a^3 - a^2 (b + c) + (b - c)^2 (b + c) -
a (b^2 - 3 b c + c^2)) t):
(a -
b)^2 ((a + b - c) (a^2 (b + c) + b c (b + c) +
a (b^2 - 6 b c + c^2)) +
2 c (a^3 - a^2 (b + c) + (b - c)^2 (b + c) -
a (b^2 - 3 b c + c^2)) t)).
• La otra tangente desde Pt a la circunferencia inscrita, pasa por la reflexión de X11 en la recta IPt:
(a - b) (a - c) (a - b - c) (a^3 (b + c + 2 b t) -
2 a^2 (-c^2 + b^2 t + b c (3 + t)) +
b (b^2 - c^2) (2 b t - c (1 + 2 t)) +
a (c^3 - 2 b c^2 (3 + t) - b^3 (1 + 2 t) +
2 b^2 c (4 + 3 t))) (c (b^2 - c^2) (b + 2 b t - 2 c t) +
a^3 (b + c + 2 c t) + 2 a^2 (b^2 - c^2 t - b c (3 + t)) +
a (b^3 - 2 b^2 c (3 + t) - c^3 (1 + 2 t) +
2 b c^2 (4 + 3 t)))x+
(a - b) (b - c) (a - b +
c) (c (b^2 - c^2) (b + 2 b t - 2 c t) + a^3 (b + c + 2 c t) +
2 a^2 (b^2 - c^2 t - b c (3 + t)) +
a (b^3 - 2 b^2 c (3 + t) - c^3 (1 + 2 t) +
2 b c^2 (4 + 3 t))) (b c (b + c)^2 + 2 a^4 t -
a^3 (b + c) (1 + 2 t) - 2 a^2 (b^2 t + c^2 t - b c (4 + 3 t)) +
a (b + c) (b^2 (1 + 2 t) + c^2 (1 + 2 t) - b c (7 + 4 t)))y+
(a -
c) (a + b - c) (-b + c) (a^3 (b + c + 2 b t) -
2 a^2 (-c^2 + b^2 t + b c (3 + t)) +
b (b^2 - c^2) (2 b t - c (1 + 2 t)) +
a (c^3 - 2 b c^2 (3 + t) - b^3 (1 + 2 t) +
2 b^2 c (4 + 3 t))) (b c (b + c)^2 + 2 a^4 t -
a^3 (b + c) (1 + 2 t) - 2 a^2 (b^2 t + c^2 t - b c (4 + 3 t)) +
a (b + c) (b^2 (1 + 2 t) + c^2 (1 + 2 t) - b c (7 + 4 t)))z=0.
• Estas dos tangentes vuelven a corta a una cónica genérica de haz de cónicas de puntos base A, B, C, Pt (AC˙BPt + λ AB˙CPt = 0)
y ((a - b)^2 (c (b^2 - c^2) (b + 2 b t - 2 c t) +
a^3 (b + c + 2 c t) + 2 a^2 (b^2 - c^2 t - b c (3 + t)) +
a (b^3 - 2 b^2 c (3 + t) - c^3 (1 + 2 t) +
2 b c^2 (4 + 3 t))) x - (b - c)^2 (b c (b + c)^2 + 2 a^4 t -
a^3 (b + c) (1 + 2 t) -
2 a^2 (b^2 t + c^2 t - b c (4 + 3 t)) +
a (b + c) (b^2 (1 + 2 t) + c^2 (1 + 2 t) -
b c (7 + 4 t))) z) + λ(-(a - c)^2 (a^3 (b + c + 2 b t) -
2 a^2 (-c^2 + b^2 t + b c (3 + t)) +
b (b^2 - c^2) (2 b t - c (1 + 2 t)) +
a (c^3 - 2 b c^2 (3 + t) - b^3 (1 + 2 t) +
2 b^2 c (4 + 3 t))) x + (b - c)^2 (b c (b + c)^2 + 2 a^4 t -
a^3 (b + c) (1 + 2 t) -
2 a^2 (b^2 t + c^2 t - b c (4 + 3 t)) +
a (b + c) (b^2 (1 + 2 t) + c^2 (1 + 2 t) -
b c (7 + 4 t))) y) z =0,
en los puntos:
P1 = ( (b-c)(1-λ) : (c-a)λ : b-a),
P2 = (-(b-c)(a+b-c)(a-b+c)(bc(b+c)^2+2a^4t-
a^3(b+c)(1+2t)-2a^2(b^2t+c^2t-bc(4+3t))+
a(b+c)(b^2(1+2t)+c^2(1+2t)-bc(7+4t)))(-1+λ) :
(a-c)(a-b-c)(a+b-c)(a^3(b+c+2bt)-2a^2(-c^2+b^2t+bc(3+t))+
b(b^2-c^2)(2bt-c(1+2t))+a(c^3-2bc^2(3+t)-b^3(1+2t)+ 2b^2c(4+3t))) λ :
(a-b)(a-b-c)(a-b+c)(c(b^2-c^2)(b+2bt-2ct)+a^3(b+c+2ct)+
2a^2(b^2-c^2t-bc(3+t))+a(b^3-2b^2c(3+t)-c^3(1+2t)+2bc^2(4+3t))))
• La recta P1P2 es tangente a la circunferencia inscrita
().
El punto de tangencia es: ((a+b-c)(a-b+c)(λ-1)^2 : -(a-b-c)(a+b-
c)λ^2 : -(a-b-c)(a-b+c)).
• Finalmente, se determina el ortocentro H' del triángulo , que ha de coincidir con el ortocentro H de ABC. Esto permite determinar los valores de λ y t.
λ = (2*a^4*b - 4*a^2*b^3 + 2*b^5 +
2*a^4*c - 8*a^3*b*c +
6*a^2*b^2*c + 8*a*b^3*c -
8*b^4*c + 6*a^2*b*c^2 -
16*a*b^2*c^2 + 6*b^3*c^2 -
4*a^2*c^3 + 8*a*b*c^3 +
6*b^2*c^3 - 8*b*c^4 + 2*c^5 +
Sqrt[(-2*a^4*b + 4*a^2*b^3 -
2*b^5 - 2*a^4*c + 8*a^3*b*c -
6*a^2*b^2*c - 8*a*b^3*c +
8*b^4*c - 6*a^2*b*c^2 +
16*a*b^2*c^2 - 6*b^3*c^2 +
4*a^2*c^3 - 8*a*b*c^3 -
6*b^2*c^3 + 8*b*c^4 - 2*c^5)^
2 - 4*(a^5 - 3*a^4*b +
3*a^3*b^2 + a^2*b^3 -
4*a*b^4 + 2*b^5 + a^4*c -
5*a^2*b^2*c + 8*a*b^3*c -
4*b^4*c - 2*a^3*c^2 +
6*a^2*b*c^2 - 5*a*b^2*c^2 +
b^3*c^2 - 2*a^2*c^3 +
3*b^2*c^3 + a*c^4 - 3*b*c^4 +
c^5)*(a^5 + a^4*b -
2*a^3*b^2 - 2*a^2*b^3 +
a*b^4 + b^5 - 3*a^4*c +
6*a^2*b^2*c - 3*b^4*c +
3*a^3*c^2 - 5*a^2*b*c^2 -
5*a*b^2*c^2 + 3*b^3*c^2 +
a^2*c^3 + 8*a*b*c^3 +
b^2*c^3 - 4*a*c^4 - 4*b*c^4 +
2*c^5)])/(2*(a^5 + a^4*b -
2*a^3*b^2 - 2*a^2*b^3 + a*b^4 +
b^5 - 3*a^4*c + 6*a^2*b^2*c -
3*b^4*c + 3*a^3*c^2 -
5*a^2*b*c^2 - 5*a*b^2*c^2 +
3*b^3*c^2 + a^2*c^3 + 8*a*b*c^3 +
b^2*c^3 - 4*a*c^4 - 4*b*c^4 +
2*c^5)).
t = -((a^3 - a*(b - c)^2 - a^2*(b + c) +
(b - c)^2*(b + c))*
(a^2*(b + c) + b*c*(b + c) +
a*(b^2 - 6*b*c + c^2))^2)/
(2*(b^2*(b - c)^2*c^2*(b + c)^3 -
7*a*b^2*c^2*(b^2 - c^2)^2 +
a^7*(b^2 + c^2) +
a^6*(b^3 - 7*b^2*c - 7*b*c^2 +
c^3) - 2*a^5*(b^4 -
16*b^2*c^2 + c^4) -
2*a^4*(b^5 - 7*b^4*c +
14*b^3*c^2 + 14*b^2*c^3 -
7*b*c^4 + c^5) +
a^3*(b^6 - 28*b^4*c^2 +
72*b^3*c^3 - 28*b^2*c^4 +
c^6) + a^2*(b^7 - 7*b^6*c +
32*b^5*c^2 - 28*b^4*c^3 -
28*b^3*c^4 + 32*b^2*c^5 -
7*b*c^6 + c^7))) +
(Sqrt[-((a^3 - a^2*b - a*b^2 + b^3 -
a^2*c + 3*a*b*c - b^2*c -
a*c^2 - b*c^2 + c^3)^2*
(a^4 - 2*a^2*b^2 + b^4 -
2*a^2*c^2 - 2*b^2*c^2 + c^4))]*
(-(b^2*(b - c)*c^2*(b + c)^2) +
7*a*b^2*c^2*(b^2 - c^2) +
a^5*(-b^2 + c^2) +
a^4*(-b^3 + 7*b^2*c - 7*b*c^2 +
c^3) + a^3*(b^4 - c^4) +
a^2*(b^5 - 7*b^4*c + 7*b*c^4 -
c^5)))/(2*(-8*a^9*b*c*(b + c) +
b^2*c^2*(b^2 - c^2)^4 +
a^10*(b^2 + c^2) -
a*b^2*(b - c)^2*c^2*(b + c)^3*
(8*b^2 - 17*b*c + 8*c^2) +
25*a^7*b*c*(b^3 - 3*b^2*c -
3*b*c^2 + c^3) +
a^8*(-4*b^4 + 9*b^3*c +
44*b^2*c^2 + 9*b*c^3 - 4*c^4) -
2*a^5*b*c*(13*b^5 - 83*b^4*c +
88*b^3*c^2 + 88*b^2*c^3 -
83*b*c^4 + 13*c^5) +
a^2*(b^2 - c^2)^2*(b^6 -
8*b^5*c + 46*b^4*c^2 -
91*b^3*c^3 + 46*b^2*c^4 -
8*b*c^5 + c^6) +
a^6*(6*b^6 - 26*b^5*c -
45*b^4*c^2 + 240*b^3*c^3 -
45*b^2*c^4 - 26*b*c^5 +
6*c^6) + a^3*b*c*(9*b^7 -
75*b^6*c + 240*b^5*c^2 -
176*b^4*c^3 - 176*b^3*c^4 +
240*b^2*c^5 - 75*b*c^6 +
9*c^7) - a^4*(4*b^8 -
25*b^7*c + 45*b^6*c^2 +
176*b^5*c^3 - 426*b^4*c^4 +
176*b^3*c^5 + 45*b^2*c^6 -
25*b*c^7 + 4*c^8))).
• Sustituidos estos valores en la ecuación del haz de cónicas se obtiene la ecuación de (Co):
a^5 x y + a^4 b x y - 2 a^3 b^2 x y - 2 a^2 b^3 x y + a b^4 x y +
b^5 x y - a^4 c x y + 2 a^2 b^2 c x y - b^4 c x y - a c^4 x y -
b c^4 x y + c^5 x y + a^5 x z - a^4 b x z - a b^4 x z + b^5 x z +
a^4 c x z - b^4 c x z - 2 a^3 c^2 x z + 2 a^2 b c^2 x z -
2 a^2 c^3 x z + a c^4 x z - b c^4 x z + c^5 x z + a^5 y z -
a^4 b y z - a b^4 y z + b^5 y z - a^4 c y z + b^4 c y z +
2 a b^2 c^2 y z - 2 b^3 c^2 y z - 2 b^2 c^3 y z - a c^4 y z +
b c^4 y z + c^5 y z=0.
- Viernes, 20 de abril del 2018
Una propiedad de la cúbica de Thomson
Dados un triángulo ABC y un punto P, sea p el de la de P y la . Se denota por co(P) la de centro P (de Q, el del de P).
El lugar geométrico de los puntos
P tales que el eje radical
p es tangente a la cónica inscrita co(
P) consta de la cúbica de Thomson (
K002) y la cúbica
K426 (complemento de la cúbica de Quang Tuan Bui).
Tomemos un punto P(u:v:w), no situado sobre los lados de ABC, ni sobre los lados del , y ni en la recta del infinito. La ecuación baricéntrica del eje radical p es:
a^4v w(2u+v+w)+
u(c^4v(-u+v)+b^4w(-u+w)+ b^2c^2(v^2+4v w+w^2-u(v+w)))+a^2(-b^2w(-u^2+v(v+w)+u(2v+w))-
c^2v(-u^2+w(v+w)+u(v+2w)))x + ... = 0,
que es tangente a la cónica co(P),
(-u + v + w)^2 x^2 + (u - v + w)^2 y^2 + (u + v - w)^2 z^2 -
2 (u + v - w) (u - v + w) y z -
2 (u + v - w) (-u + v + w) x z-
2 (u - v + w) (-u + v + w) x y = 0,
si sólo si satisface a las ecuaciones:
c^2 x^2 y - c^2 x y^2 - b^2 x^2 z + a^2 y^2 z + b^2 x z^2 - a^2 y z^2 =0,
-a^4 c^2 x^2 y + 2 a^2 b^2 c^2 x^2 y - b^4 c^2 x^2 y -
2 a^2 c^4 x^2 y - 2 b^2 c^4 x^2 y + 3 c^6 x^2 y + a^4 c^2 x y^2 -
2 a^2 b^2 c^2 x y^2 + b^4 c^2 x y^2 + 2 a^2 c^4 x y^2 +
2 b^2 c^4 x y^2 - 3 c^6 x y^2 + a^4 b^2 x^2 z + 2 a^2 b^4 x^2 z -
3 b^6 x^2 z - 2 a^2 b^2 c^2 x^2 z + 2 b^4 c^2 x^2 z +
b^2 c^4 x^2 z + 8 a^4 b^2 x y z - 8 a^2 b^4 x y z -
8 a^4 c^2 x y z + 8 b^4 c^2 x y z + 8 a^2 c^4 x y z -
8 b^2 c^4 x y z + 3 a^6 y^2 z - 2 a^4 b^2 y^2 z - a^2 b^4 y^2 z -
2 a^4 c^2 y^2 z + 2 a^2 b^2 c^2 y^2 z - a^2 c^4 y^2 z -
a^4 b^2 x z^2 - 2 a^2 b^4 x z^2 + 3 b^6 x z^2 +
2 a^2 b^2 c^2 x z^2 - 2 b^4 c^2 x z^2 - b^2 c^4 x z^2 -
3 a^6 y z^2 + 2 a^4 b^2 y z^2 + a^2 b^4 y z^2 + 2 a^4 c^2 y z^2 -
2 a^2 b^2 c^2 y z^2 + a^2 c^4 y z^2 = 0.
de las cúbicas del Catálogo de Bernard Gibert, K002 y K426, respectivamente.
Centros sobre K002: 1, 2, 3, 4, 6, 9, 57, 223, 282, 1073, 1249, 3341, 3342, 3343, 3344, 3349, 3350, 3351, 3352, 3356, 14481.
Centros sobre K426: 3, 4, 20, 3532.
Si T el punto de tangencia (que queda sobre la circunferencia de los nueve puntos) del eje radical p y la cónica co(P), cuando P está sobre la cúbica de Thomson, se tienen los siguientes pares {P, T}, de centros del triángulo para los índices {i, j}:
{1, 11}, {2, 115}, {6, 125}, {9, 11}, {57, 5514}, {223, 5514}, {282, 13612}, {1073, 13613}, {1249, 122}, {3341, 13612}, {3343, 13613}.
Las rectas que pasan por simediano (polo) cortan a la cúbica de Thomson en dos puntos a los que les corresponde el mismo punto T. Así:
• 1, 9 ↦ 11
• 2 ↦ 115 (el de X(2) es X(6))
• 6 ↦ 125 (el tangencial de X(6) es X(3); la circunferencia pedal de X(3) coincide con la NPC)
• 57, 223 ↦ 5514
• 282, 3341 ↦ 13612
• 1073, 3343 ↦ 13613
• 1249 ↦ 122 (la recta X(6)X(1249) vuelve a cortar a la cúbica en X(4); la circunferencia pedal de X(4) coincide con la NPC).
• 3342, 3351 ↦ T3342:
T3342 = ( (b-c)^2 (a^3+a^2 (b+c)-(b-c)^2 (b+c)-a (b+c)^2) (a^6-2 a^5 (b+c)-a^4 (b+c)^2+(b-c)^2 (b+c)^4-a^2 (b^2-c^2)^2+4 a^3 (b^3+c^3)-2 a (b^5-b^4 c-b c^4+c^5))^2 (a^10+2 a^9 (b+c)-3 a^8 (b+c)^2+(b-c)^6 (b+c)^4+2 a^6 (b+c)^2 (b^2+c^2)+2 a (b-c)^2 (b+c)^5 (b^2+c^2)+2 a^4 (b^2-c^2)^2 (b^2+4 b c+c^2)-a^2 (b-c)^2 (b+c)^4 (3 b^2-2 b c+3 c^2)+a^7 (-8 b^3+4 b^2 c+4 b c^2-8 c^3)+4 a^5 (b-c)^2 (3 b^3+4 b^2 c+4 b c^2+3 c^3)-4 a^3 (b-c)^2 (2 b^5+5 b^4 c+9 b^3 c^2+9 b^2 c^3+5 b c^4+2 c^5)) : ... : ...),
que tiene números de búsqueda en
(2.29566751695484, 3.38969144283636, 0.234416167503126). No existen pares de centros en ETC (entre 1 y 17511) alineados con T3342.
• 3344, 3350 ↦ T3344:
T3344 = ( (b^2 - c^2)^2 (3 a^4 - (b^2 - c^2)^2 - 2 a^2 (b^2 + c^2)) (a^8 -
4 a^6 (b^2 + c^2) -
4 a^2 (b^2 - c^2)^2 (b^2 + c^2) + (b^2 - c^2)^2 (b^4 + 6 b^2 c^2 +
c^4) + a^4 (6 b^4 - 4 b^2 c^2 + 6 c^4))^2 (5 a^12 + (b^2 -
c^2)^6 - 10 a^10 (b^2 + c^2) + 36 a^6 (b^2 - c^2)^2 (b^2 + c^2) +
a^8 (-9 b^4 + 34 b^2 c^2 - 9 c^4) -
a^4 (b^2 - c^2)^2 (29 b^4 + 54 b^2 c^2 + 29 c^4) +
2 a^2 (b^2 - c^2)^2 (3 b^6 + 13 b^4 c^2 + 13 b^2 c^4 + 3 c^6)) : ... : ...),
que tiene números de búsqueda en
(2.98413908721516, 3.30643249294932, -0.0256991303875278). No existen pares de centros en ETC (entre 1 y 17511) alineados con T3344.
• 3349, 14841 ↦ T3349:
T3349 = ( (b^2-c^2)^2 (a^8-4 a^6 (b^2+c^2)-4 a^2 (b^2-c^2)^2 (b^2+c^2)+(b^2-c^2)^2 (b^4+6 b^2 c^2+c^4)+a^4 (6 b^4-4 b^2 c^2+6 c^4)) (5 a^12+(b^2-c^2)^6-10 a^10 (b^2+c^2)+36 a^6 (b^2-c^2)^2 (b^2+c^2)+a^8 (-9 b^4+34 b^2 c^2-9 c^4)-a^4 (b^2-c^2)^2 (29 b^4+54 b^2 c^2+29 c^4)+2 a^2 (b^2-c^2)^2 (3 b^6+13 b^4 c^2+13 b^2 c^4+3 c^6))^2 (a^18-9 a^16 (b^2+c^2)+12 a^14 (3 b^4-2 b^2 c^2+3 c^4)+3 a^2 (b^2-c^2)^6 (3 b^4+10 b^2 c^2+3 c^4)+2 a^10 (b^2-c^2)^2 (63 b^4+170 b^2 c^2+63 c^4)+a^12 (-84 b^6+68 b^4 c^2+68 b^2 c^4-84 c^6)-(b^2-c^2)^6 (b^6+15 b^4 c^2+15 b^2 c^4+c^6)-6 a^8 (b^2-c^2)^2 (21 b^6+83 b^4 c^2+83 b^2 c^4+21 c^6)+4 a^6 (b^2-c^2)^2 (21 b^8+64 b^6 c^2+150 b^4 c^4+64 b^2 c^6+21 c^8)-4 a^4 (b^2-c^2)^2 (9 b^10+b^8 c^2+54 b^6 c^4+54 b^4 c^6+b^2 c^8+9 c^10)) : ... : ...),
que tiene números de búsqueda en
(3.94161329399262, 2.63301804492801, -0.00140030027006888). No existen pares de centros en ETC (entre 1 y 17511) alineados con T3349.
- Miércoles, 18 de abril del 2018
Triángulo: a b AMa ⊥ BMb
Construir un triángulo ABC conociendo las longitudes de los lados
BC y CA y tal que las medianas realtivas a estos lados son
perpendiculares (AMa ⊥ BMb).
Ver Ejercicio 196
Construcciones de triángulos
- Martes, 17 de abril del 2018
Circunferencias coaxiales y la cuártica de Stammler
Dados un triángulo ABC y un punto P (no situado en la recta del infinito) , sean A'B'C' y DEF los triángulos
y de P.
La circunferencia circunscrita a AB'C' vuelve a cortar a la circunferencia circunscrita a ABC en A". Denotamos por (Oa) la circunferencia circunscrita a A"DP; las circunferencias (Ob) y (Oc) se definen cíclicamente.
Si (u:v:w) son las coordenadas baricéntricas de P (u+v+w ≠ 0), entonces:
A" (a^2 (u + v) (u + w) : b^2 (u + v) (v - w) : -c^2 (v - w) (u + w)).
La ecuación de la circunferencia circunscrita a A"DP es:
c^2 x y + b^2 x z +
a^2 y z + (x + y +
z) (-(((c^2 v + b^2 w) x)/(
u + v + w)) - ((-a^2 u w - a^2 w^2) y)/((v - w) (u + v +
w)) - ((a^2 u v + a^2 v^2) z)/((v - w) (u + v + w)))=0.
Cuyo centro es:
Oa (2a^2(-b^2(u+v)w+c^2v(u+w)) :
-a^4v(u+v)-(b^2-c^2)(-c^2v+b^2(u+v))(v-w)+a^2(c^2v(u+2v-w)+b^2(u+v)(2v+w)) :
a^4w(u+w)-(b^2-c^2)(v-w)(b^2w-c^2(u+w))-a^2(b^2w(u-v+2w)+c^2(u+w)(v+2w))).
La condición analítica para que los puntos Oa, Ob, Oc estén alineados es:
a^2 (b^2 - c^2)v^2w^2 + b^2 (c^2-a^2)w^2u^2 + c^2(a^2 - b^2)u^2v^2=0,
por lo que las coordenadas de P satisfacen a la ecuación de la cuártica de Stammler.
Si P' es el otro punto de intersección de las circunferencias (Oa), (Ob), (Oc), cuando P está sobre la cuártica de Stammler, se tiene la siguiente lista de pares {P, P'} de centros del triángulo:
{1, 5127}, {4, 186}, {254, 16172}, {1113, 15461}, {1114, 15460}, {1138, 1138}, {3459, 11584}.
- Jueves, 12 de abril del 2018
Un haz de cónicas bitangentes
Dados un triángulo ABC y un punto P sobre la , sea A'B'C' el de P, Na, Nb y Nc los centros de las de los triángulos PBC, PCA y PAB, respectivamente.
Los triángulos
A'B'C' y son perspectivos. El centro de perspectividad
Q queda sobre la
hipérbola
( (-3 a^12 b^6 c^2 + 7 a^10 b^8 c^2 - 10 a^6 b^12 c^2 +
5 a^4 b^14 c^2 + 3 a^2 b^16 c^2 - 2 b^18 c^2 + 6 a^12 b^4 c^4 -
7 a^10 b^6 c^4 - 19 a^8 b^8 c^4 + 34 a^6 b^10 c^4 -
4 a^4 b^12 c^4 - 19 a^2 b^14 c^4 + 9 b^16 c^4 - 3 a^12 b^2 c^6 -
7 a^10 b^4 c^6 + 38 a^8 b^6 c^6 - 24 a^6 b^8 c^6 -
29 a^4 b^10 c^6 + 39 a^2 b^12 c^6 - 14 b^14 c^6 +
7 a^10 b^2 c^8 - 19 a^8 b^4 c^8 - 24 a^6 b^6 c^8 +
56 a^4 b^8 c^8 - 23 a^2 b^10 c^8 + 7 b^12 c^8 + 34 a^6 b^4 c^10 -
29 a^4 b^6 c^10 - 23 a^2 b^8 c^10 - 10 a^6 b^2 c^12 -
4 a^4 b^4 c^12 + 39 a^2 b^6 c^12 + 7 b^8 c^12 + 5 a^4 b^2 c^14 -
19 a^2 b^4 c^14 - 14 b^6 c^14 + 3 a^2 b^2 c^16 + 9 b^4 c^16 -
2 b^2 c^18) x^2 + (-a^16 b^2 c^2 - 5 a^14 b^4 c^2 +
21 a^12 b^6 c^2 - 15 a^10 b^8 c^2 - 15 a^8 b^10 c^2 +
21 a^6 b^12 c^2 - 5 a^4 b^14 c^2 - a^2 b^16 c^2 + a^16 c^4 +
9 a^14 b^2 c^4 - 14 a^12 b^4 c^4 - 33 a^10 b^6 c^4 +
74 a^8 b^8 c^4 - 33 a^6 b^10 c^4 - 14 a^4 b^12 c^4 +
9 a^2 b^14 c^4 + b^16 c^4 - 4 a^14 c^6 - 10 a^12 b^2 c^6 +
62 a^10 b^4 c^6 - 48 a^8 b^6 c^6 - 48 a^6 b^8 c^6 +
62 a^4 b^10 c^6 - 10 a^2 b^12 c^6 - 4 b^14 c^6 + 3 a^12 c^8 -
24 a^10 b^2 c^8 - 39 a^8 b^4 c^8 + 112 a^6 b^6 c^8 -
39 a^4 b^8 c^8 - 24 a^2 b^10 c^8 + 3 b^12 c^8 + 10 a^10 c^10 +
53 a^8 b^2 c^10 - 45 a^6 b^4 c^10 - 45 a^4 b^6 c^10 +
53 a^2 b^8 c^10 + 10 b^10 c^10 - 25 a^8 c^12 - 31 a^6 b^2 c^12 +
48 a^4 b^4 c^12 - 31 a^2 b^6 c^12 - 25 b^8 c^12 + 24 a^6 c^14 +
4 a^4 b^2 c^14 + 4 a^2 b^4 c^14 + 24 b^6 c^14 - 11 a^4 c^16 -
2 a^2 b^2 c^16 - 11 b^4 c^16 + 2 a^2 c^18 +
2 b^2 c^18) x y + (-2 a^18 c^2 + 3 a^16 b^2 c^2 +
5 a^14 b^4 c^2 - 10 a^12 b^6 c^2 + 7 a^8 b^10 c^2 -
3 a^6 b^12 c^2 + 9 a^16 c^4 - 19 a^14 b^2 c^4 - 4 a^12 b^4 c^4 +
34 a^10 b^6 c^4 - 19 a^8 b^8 c^4 - 7 a^6 b^10 c^4 +
6 a^4 b^12 c^4 - 14 a^14 c^6 + 39 a^12 b^2 c^6 -
29 a^10 b^4 c^6 - 24 a^8 b^6 c^6 + 38 a^6 b^8 c^6 -
7 a^4 b^10 c^6 - 3 a^2 b^12 c^6 + 7 a^12 c^8 - 23 a^10 b^2 c^8 +
56 a^8 b^4 c^8 - 24 a^6 b^6 c^8 - 19 a^4 b^8 c^8 +
7 a^2 b^10 c^8 - 23 a^8 b^2 c^10 - 29 a^6 b^4 c^10 +
34 a^4 b^6 c^10 + 7 a^8 c^12 + 39 a^6 b^2 c^12 - 4 a^4 b^4 c^12 -
10 a^2 b^6 c^12 - 14 a^6 c^14 - 19 a^4 b^2 c^14 +
5 a^2 b^4 c^14 + 9 a^4 c^16 + 3 a^2 b^2 c^16 -
2 a^2 c^18) y^2 + (a^16 b^4 - 4 a^14 b^6 + 3 a^12 b^8 +
10 a^10 b^10 - 25 a^8 b^12 + 24 a^6 b^14 - 11 a^4 b^16 +
2 a^2 b^18 - a^16 b^2 c^2 + 9 a^14 b^4 c^2 - 10 a^12 b^6 c^2 -
24 a^10 b^8 c^2 + 53 a^8 b^10 c^2 - 31 a^6 b^12 c^2 +
4 a^4 b^14 c^2 - 2 a^2 b^16 c^2 + 2 b^18 c^2 - 5 a^14 b^2 c^4 -
14 a^12 b^4 c^4 + 62 a^10 b^6 c^4 - 39 a^8 b^8 c^4 -
45 a^6 b^10 c^4 + 48 a^4 b^12 c^4 + 4 a^2 b^14 c^4 -
11 b^16 c^4 + 21 a^12 b^2 c^6 - 33 a^10 b^4 c^6 -
48 a^8 b^6 c^6 + 112 a^6 b^8 c^6 - 45 a^4 b^10 c^6 -
31 a^2 b^12 c^6 + 24 b^14 c^6 - 15 a^10 b^2 c^8 +
74 a^8 b^4 c^8 - 48 a^6 b^6 c^8 - 39 a^4 b^8 c^8 +
53 a^2 b^10 c^8 - 25 b^12 c^8 - 15 a^8 b^2 c^10 -
33 a^6 b^4 c^10 + 62 a^4 b^6 c^10 - 24 a^2 b^8 c^10 +
10 b^10 c^10 + 21 a^6 b^2 c^12 - 14 a^4 b^4 c^12 -
10 a^2 b^6 c^12 + 3 b^8 c^12 - 5 a^4 b^2 c^14 + 9 a^2 b^4 c^14 -
4 b^6 c^14 - a^2 b^2 c^16 + b^4 c^16) x z + (2 a^18 b^2 -
11 a^16 b^4 + 24 a^14 b^6 - 25 a^12 b^8 + 10 a^10 b^10 +
3 a^8 b^12 - 4 a^6 b^14 + a^4 b^16 + 2 a^18 c^2 -
2 a^16 b^2 c^2 + 4 a^14 b^4 c^2 - 31 a^12 b^6 c^2 +
53 a^10 b^8 c^2 - 24 a^8 b^10 c^2 - 10 a^6 b^12 c^2 +
9 a^4 b^14 c^2 - a^2 b^16 c^2 - 11 a^16 c^4 + 4 a^14 b^2 c^4 +
48 a^12 b^4 c^4 - 45 a^10 b^6 c^4 - 39 a^8 b^8 c^4 +
62 a^6 b^10 c^4 - 14 a^4 b^12 c^4 - 5 a^2 b^14 c^4 +
24 a^14 c^6 - 31 a^12 b^2 c^6 - 45 a^10 b^4 c^6 +
112 a^8 b^6 c^6 - 48 a^6 b^8 c^6 - 33 a^4 b^10 c^6 +
21 a^2 b^12 c^6 - 25 a^12 c^8 + 53 a^10 b^2 c^8 -
39 a^8 b^4 c^8 - 48 a^6 b^6 c^8 + 74 a^4 b^8 c^8 -
15 a^2 b^10 c^8 + 10 a^10 c^10 - 24 a^8 b^2 c^10 +
62 a^6 b^4 c^10 - 33 a^4 b^6 c^10 - 15 a^2 b^8 c^10 +
3 a^8 c^12 - 10 a^6 b^2 c^12 - 14 a^4 b^4 c^12 +
21 a^2 b^6 c^12 - 4 a^6 c^14 + 9 a^4 b^2 c^14 - 5 a^2 b^4 c^14 +
a^4 c^16 - a^2 b^2 c^16) y z + (-2 a^18 b^2 + 9 a^16 b^4 -
14 a^14 b^6 + 7 a^12 b^8 + 7 a^8 b^12 - 14 a^6 b^14 +
9 a^4 b^16 - 2 a^2 b^18 + 3 a^16 b^2 c^2 - 19 a^14 b^4 c^2 +
39 a^12 b^6 c^2 - 23 a^10 b^8 c^2 - 23 a^8 b^10 c^2 +
39 a^6 b^12 c^2 - 19 a^4 b^14 c^2 + 3 a^2 b^16 c^2 +
5 a^14 b^2 c^4 - 4 a^12 b^4 c^4 - 29 a^10 b^6 c^4 +
56 a^8 b^8 c^4 - 29 a^6 b^10 c^4 - 4 a^4 b^12 c^4 +
5 a^2 b^14 c^4 - 10 a^12 b^2 c^6 + 34 a^10 b^4 c^6 -
24 a^8 b^6 c^6 - 24 a^6 b^8 c^6 + 34 a^4 b^10 c^6 -
10 a^2 b^12 c^6 - 19 a^8 b^4 c^8 + 38 a^6 b^6 c^8 -
19 a^4 b^8 c^8 + 7 a^8 b^2 c^10 - 7 a^6 b^4 c^10 -
7 a^4 b^6 c^10 + 7 a^2 b^8 c^10 - 3 a^6 b^2 c^12 +
6 a^4 b^4 c^12 - 3 a^2 b^6 c^12) z^2 = 0)
ℋ,
que pasa por los centros del triángulo X
3, X
5, X
5663, X
10539, X
13394.
El centro de la hipérbola ℋ es D = 2((r+2R)^2-s^2) X110 + R^2 X185,
donde r y R son los radios de las circunferencias inscrita y circunscrita, y s el semiperímetro del triángulo ABC.
D = ( a^2 (a^2 - b^2 - c^2) (2 a^12 -
5 a^10 (b^2 + c^2)
+ a^8 (b^4 + 12 b^2 c^2 + c^4)
+ a^6 (6 b^6 - 9 b^4 c^2 - 9 b^2 c^4 + 6 c^6)
- 2 a^4 (b^2 - c^2)^2 (2 b^4 + 5 b^2 c^2 + 2 c^4)
- a^2 (b^2 - c^2)^2 (b^6 - 6 b^4 c^2 - 6 b^2 c^4 + c^6)
+ (b^2 - c^2)^4 (b^4 + c^4) ) : ... : ...),
que tiene números de búsqueda en
(3.75162417286593, 2.65042851195987, 0.0742335861509618) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,11559}, {24,13417}, {49,11806}, {51,15463}, {74,10282}, {110,185}, {125,128}, {186,10628}, {265,12038}, {389,3043}, {399,1204}, {1092,2931}, {1192,12165}, {1205,15577}, {1495,2777}, {2072,13851}, {3448,11449}, {3518,11807}, {5562,12893}, {5650,15035}, {5663,15646}, {5972,13160}, {6467,12584}, {6644,16223}, {10990,15647}, {11381,13293}, {11430,14644}, {11597,11802}, {12605,16163}, {13198,15034}.
X5663 es el del simétrico, respecto a la recta de Euler, del conjugado isogonal del punto del infinito de esta recta. Por tanto, es un punto del infinito de la hipérbola ℋ. La correspondiente asíntota pasa por X15646 (inverso en la circunferencia circunscrita del simétrico, X382, del circuncentro en el ortocentro).
La otra asíntota de ℋ pasa por los puntos: X2072 (inverso en la circunferencia circunscrita del circuncentro, X26, del ), X13851 (punto donde la paralela a la recta de Euler por el baricentro, X51, del , corta a la recta que pasa por el ortocentro y por el centro, X125, de la ), X14156 (punto medio del circuncentro y la reflexión de X125 en X2072).
Su punto de tangencia con la hipérbola (en la recta del infinito) es:
W = ( 2 a^10-4 a^8 (b^2+c^2)+a^6 (b^4+8 b^2 c^2+c^4)
+a^4 (b^6-3 b^4 c^2-3 b^2 c^4+c^6)
+a^2 (b^2-c^2)^4
-(b^2-c^2)^4 (b^2+c^2) : ... : ...),
que tiene números de búsqueda en
(1.22023184857025, 1.04347413196238, -1.28558909839099) y está en las rectas XiXj (paralelas) s.e.u.o., para los índices {i,j}: {1,12888}, {2,14644}, {3,125}, {4,110}, {5,1511}, {6,7706}, {15,10663}, {16,10664}, {20,68}, {26,9938}, {30,511}, {40,12407}, {51,16222}, {52,1986}, {55,12903}, {56,12904}, {67,1350}, {69,4549}, {99,11005}, {104,10778}, {140,6723}, {143,11561}, {146,3146}, {155,382}, {182,15118}, {185,10111}, {195,14049}, {323,10296}, {355,12778}, {371,12891}, {372,12892}, {376,9140}, {378,12827}, {381,5642}, {389,11800}, {477,15396}, {485,8998}, {486,10820}, {546,9820}, {548,13470}, {550,10264}, {576,12596}, {578,12228}, {631,15051}, {671,11656}, {858,10564}, {895,4846}, {944,7984}, {946,11720}, {962,7978}, {974,6146}, {1069,12374}, {1112,3575}, {1141,15958}, {1151,8994}, {1152,13969}, {1160,12804}, {1161,12803}, {1209,14118}, {1216,12358}, {1351,5095}, {1352,4550}, {1385,11735}, {1478,10088}, {1479,10091}, {1482,12898}, {1495,11799}, {1498,11744}, {1531,3292}, {1539,3627}, {1550,7472}, {1593,12168}, {1614,3047}, {1656,15040}, {1657,10620}, {1885,12133}, {2072,13851}, {2079,15538}, {2420,6103}, {2930,14982}, {2935,9937}, {2948,5691}, {3024,6284}, {3028,7354}, {3090,15020}, {3091,15034}, {3157,12373}, {3167,3830}, {3258,14934}, {3398,12201}, {3519,11559}, {3523,15036}, {3525,15025}, {3528,15057}, {3529,11411}, {3534,15041}, {3543,9143}, {3545,11693}, {3574,11597}, {3580,10295}, {3628,15088}, {3818,12584}, {3850,13392}, {4297,11709}, {4299,10071}, {4302,10055}, {5066,11694}, {5073,12164}, {5447,12362}, {5462,9826}, {5465,9880}, {5480,6593}, {5512,9129}, {5562,7723}, {5870,7733}, {5871,7732}, {5889,7722}, {5892,12099}, {6036,15359}, {6102,10112}, {6152,11560}, {6237,7724}, {6238,7727}, {6241,12284}, {6243,14448}, {6247,11598}, {6288,14130}, {6321,16278}, {6391,10293}, {6592,10213}, {6689,13160}, {6841,16164}, {7352,10483}, {7387,10117}, {7471,15468}, {7553,16105}, {7574,15136}, {7576,12824}, {7725,9929}, {7726,9930}, {7731,15102}, {7748,14901}, {7749,8571}, {8548,9976}, {8717,11579}, {8981,13915}, {9181,16188}, {9730,12022}, {9818,10516}, {9821,12501}, {9825,15465}, {9833,9934}, {9834,13208}, {9835,13209}, {9838,13215}, {9839,13216}, {9873,13210}, {9896,9904}, {9908,9919}, {9923,9984}, {9932,12084 }, {10024,13367}, {10201,11202}, {10226,13561}, {10282,15761}, {10297,11064}, {10525,12889}, {10526,12890}, {10610,11804}, {10619,15089}, {10625,12225}, {10657,10661}, {10658,10662}, {10665,12375}, {10666,12376}, {10669,12894}, {10673,12895} ,{10679,12905} , {10680,12906}, {10693,14110}, {10723,15342}, {10724,10767}, {10750,14499}, {10751,14500}, {10752,11061}, {11006,12117}, {11248,12334}, {11251,12790}, {11252,12466}, {11253,12467}, {11412,12219}, {11414,13171}, {11449,16868}, {11500,13204}, {11566,12002}, {11807,11819}, {12042,15535}, {12110,13193}, {12111,12273}, {12112,12364}, {12113,13212}, {12114,13213}, {12115,13217}, {12116,13218}, {12160,12165}, {12161,12227}, {12162,12292}, {12192,12193}, {12327,12328}, {12365,12415}, {12366,12416}, {12369,12418}, {12371,12422}, {12372,12423}, {12377,12426}, {12378,12427}, {12381,12430}, {12382,12431}, {13201,15100}, {13292,13568}, {13346,15132}, {13358,13630}, {13394,15760}, {13966,13979}, {14561,15462}, {14677,15704}, {15122,15123}.
El punto W ha sido incorporado a ETC con el número X(17702).
La envolvente de las rectas PQ es la
parábola
( a^12 b^8 x^2 - 6 a^10 b^10 x^2 + 15 a^8 b^12 x^2 - 20 a^6 b^14 x^2 +
15 a^4 b^16 x^2 - 6 a^2 b^18 x^2 + b^20 x^2 + 12 a^12 b^6 c^2 x^2 -
30 a^10 b^8 c^2 x^2 + 2 a^8 b^10 c^2 x^2 + 52 a^6 b^12 c^2 x^2 -
48 a^4 b^14 c^2 x^2 + 10 a^2 b^16 c^2 x^2 + 2 b^18 c^2 x^2 -
26 a^12 b^4 c^4 x^2 + 36 a^10 b^6 c^4 x^2 + 65 a^8 b^8 c^4 x^2 -
132 a^6 b^10 c^4 x^2 + 36 a^4 b^12 c^4 x^2 + 40 a^2 b^14 c^4 x^2 -
19 b^16 c^4 x^2 + 12 a^12 b^2 c^6 x^2 + 36 a^10 b^4 c^6 x^2 -
164 a^8 b^6 c^6 x^2 + 100 a^6 b^8 c^6 x^2 + 112 a^4 b^10 c^6 x^2 -
120 a^2 b^12 c^6 x^2 + 24 b^14 c^6 x^2 + a^12 c^8 x^2 -
30 a^10 b^2 c^8 x^2 + 65 a^8 b^4 c^8 x^2 + 100 a^6 b^6 c^8 x^2 -
230 a^4 b^8 c^8 x^2 + 76 a^2 b^10 c^8 x^2 + 18 b^12 c^8 x^2 -
6 a^10 c^10 x^2 + 2 a^8 b^2 c^10 x^2 - 132 a^6 b^4 c^10 x^2 +
112 a^4 b^6 c^10 x^2 + 76 a^2 b^8 c^10 x^2 - 52 b^10 c^10 x^2 +
15 a^8 c^12 x^2 + 52 a^6 b^2 c^12 x^2 + 36 a^4 b^4 c^12 x^2 -
120 a^2 b^6 c^12 x^2 + 18 b^8 c^12 x^2 - 20 a^6 c^14 x^2 -
48 a^4 b^2 c^14 x^2 + 40 a^2 b^4 c^14 x^2 + 24 b^6 c^14 x^2 +
15 a^4 c^16 x^2 + 10 a^2 b^2 c^16 x^2 - 19 b^4 c^16 x^2 -
6 a^2 c^18 x^2 + 2 b^2 c^18 x^2 + c^20 x^2 + 2 a^16 b^4 x y -
12 a^14 b^6 x y + 30 a^12 b^8 x y - 40 a^10 b^10 x y +
30 a^8 b^12 x y - 12 a^6 b^14 x y + 2 a^4 b^16 x y +
4 a^16 b^2 c^2 x y + 12 a^14 b^4 c^2 x y - 60 a^12 b^6 c^2 x y +
44 a^10 b^8 c^2 x y + 44 a^8 b^10 c^2 x y - 60 a^6 b^12 c^2 x y +
12 a^4 b^14 c^2 x y + 4 a^2 b^16 c^2 x y - 6 a^16 c^4 x y -
28 a^14 b^2 c^4 x y + 58 a^12 b^4 c^4 x y + 116 a^10 b^6 c^4 x y -
280 a^8 b^8 c^4 x y + 116 a^6 b^10 c^4 x y + 58 a^4 b^12 c^4 x y -
28 a^2 b^14 c^4 x y - 6 b^16 c^4 x y + 28 a^14 c^6 x y +
16 a^12 b^2 c^6 x y - 248 a^10 b^4 c^6 x y + 204 a^8 b^6 c^6 x y +
204 a^6 b^8 c^6 x y - 248 a^4 b^10 c^6 x y + 16 a^2 b^12 c^6 x y +
28 b^14 c^6 x y - 44 a^12 c^8 x y + 116 a^10 b^2 c^8 x y +
162 a^8 b^4 c^8 x y - 468 a^6 b^6 c^8 x y + 162 a^4 b^8 c^8 x y +
116 a^2 b^10 c^8 x y - 44 b^12 c^8 x y + 12 a^10 c^10 x y -
200 a^8 b^2 c^10 x y + 188 a^6 b^4 c^10 x y + 188 a^4 b^6 c^10 x y -
200 a^2 b^8 c^10 x y + 12 b^10 c^10 x y + 40 a^8 c^12 x y +
76 a^6 b^2 c^12 x y - 234 a^4 b^4 c^12 x y + 76 a^2 b^6 c^12 x y +
40 b^8 c^12 x y - 44 a^6 c^14 x y + 48 a^4 b^2 c^14 x y +
48 a^2 b^4 c^14 x y - 44 b^6 c^14 x y + 12 a^4 c^16 x y -
36 a^2 b^2 c^16 x y + 12 b^4 c^16 x y + 4 a^2 c^18 x y +
4 b^2 c^18 x y - 2 c^20 x y + a^20 y^2 - 6 a^18 b^2 y^2 +
15 a^16 b^4 y^2 - 20 a^14 b^6 y^2 + 15 a^12 b^8 y^2 -
6 a^10 b^10 y^2 + a^8 b^12 y^2 + 2 a^18 c^2 y^2 +
10 a^16 b^2 c^2 y^2 - 48 a^14 b^4 c^2 y^2 + 52 a^12 b^6 c^2 y^2 +
2 a^10 b^8 c^2 y^2 - 30 a^8 b^10 c^2 y^2 + 12 a^6 b^12 c^2 y^2 -
19 a^16 c^4 y^2 + 40 a^14 b^2 c^4 y^2 + 36 a^12 b^4 c^4 y^2 -
132 a^10 b^6 c^4 y^2 + 65 a^8 b^8 c^4 y^2 + 36 a^6 b^10 c^4 y^2 -
26 a^4 b^12 c^4 y^2 + 24 a^14 c^6 y^2 - 120 a^12 b^2 c^6 y^2 +
112 a^10 b^4 c^6 y^2 + 100 a^8 b^6 c^6 y^2 - 164 a^6 b^8 c^6 y^2 +
36 a^4 b^10 c^6 y^2 + 12 a^2 b^12 c^6 y^2 + 18 a^12 c^8 y^2 +
76 a^10 b^2 c^8 y^2 - 230 a^8 b^4 c^8 y^2 + 100 a^6 b^6 c^8 y^2 +
65 a^4 b^8 c^8 y^2 - 30 a^2 b^10 c^8 y^2 + b^12 c^8 y^2 -
52 a^10 c^10 y^2 + 76 a^8 b^2 c^10 y^2 + 112 a^6 b^4 c^10 y^2 -
132 a^4 b^6 c^10 y^2 + 2 a^2 b^8 c^10 y^2 - 6 b^10 c^10 y^2 +
18 a^8 c^12 y^2 - 120 a^6 b^2 c^12 y^2 + 36 a^4 b^4 c^12 y^2 +
52 a^2 b^6 c^12 y^2 + 15 b^8 c^12 y^2 + 24 a^6 c^14 y^2 +
40 a^4 b^2 c^14 y^2 - 48 a^2 b^4 c^14 y^2 - 20 b^6 c^14 y^2 -
19 a^4 c^16 y^2 + 10 a^2 b^2 c^16 y^2 + 15 b^4 c^16 y^2 +
2 a^2 c^18 y^2 - 6 b^2 c^18 y^2 + c^20 y^2 - 6 a^16 b^4 x z +
28 a^14 b^6 x z - 44 a^12 b^8 x z + 12 a^10 b^10 x z +
40 a^8 b^12 x z - 44 a^6 b^14 x z + 12 a^4 b^16 x z +
4 a^2 b^18 x z - 2 b^20 x z + 4 a^16 b^2 c^2 x z -
28 a^14 b^4 c^2 x z + 16 a^12 b^6 c^2 x z + 116 a^10 b^8 c^2 x z -
200 a^8 b^10 c^2 x z + 76 a^6 b^12 c^2 x z + 48 a^4 b^14 c^2 x z -
36 a^2 b^16 c^2 x z + 4 b^18 c^2 x z + 2 a^16 c^4 x z +
12 a^14 b^2 c^4 x z + 58 a^12 b^4 c^4 x z - 248 a^10 b^6 c^4 x z +
162 a^8 b^8 c^4 x z + 188 a^6 b^10 c^4 x z - 234 a^4 b^12 c^4 x z +
48 a^2 b^14 c^4 x z + 12 b^16 c^4 x z - 12 a^14 c^6 x z -
60 a^12 b^2 c^6 x z + 116 a^10 b^4 c^6 x z + 204 a^8 b^6 c^6 x z -
468 a^6 b^8 c^6 x z + 188 a^4 b^10 c^6 x z + 76 a^2 b^12 c^6 x z -
44 b^14 c^6 x z + 30 a^12 c^8 x z + 44 a^10 b^2 c^8 x z -
280 a^8 b^4 c^8 x z + 204 a^6 b^6 c^8 x z + 162 a^4 b^8 c^8 x z -
200 a^2 b^10 c^8 x z + 40 b^12 c^8 x z - 40 a^10 c^10 x z +
44 a^8 b^2 c^10 x z + 116 a^6 b^4 c^10 x z - 248 a^4 b^6 c^10 x z +
116 a^2 b^8 c^10 x z + 12 b^10 c^10 x z + 30 a^8 c^12 x z -
60 a^6 b^2 c^12 x z + 58 a^4 b^4 c^12 x z + 16 a^2 b^6 c^12 x z -
44 b^8 c^12 x z - 12 a^6 c^14 x z + 12 a^4 b^2 c^14 x z -
28 a^2 b^4 c^14 x z + 28 b^6 c^14 x z + 2 a^4 c^16 x z +
4 a^2 b^2 c^16 x z - 6 b^4 c^16 x z - 2 a^20 y z + 4 a^18 b^2 y z +
12 a^16 b^4 y z - 44 a^14 b^6 y z + 40 a^12 b^8 y z +
12 a^10 b^10 y z - 44 a^8 b^12 y z + 28 a^6 b^14 y z -
6 a^4 b^16 y z + 4 a^18 c^2 y z - 36 a^16 b^2 c^2 y z +
48 a^14 b^4 c^2 y z + 76 a^12 b^6 c^2 y z - 200 a^10 b^8 c^2 y z +
116 a^8 b^10 c^2 y z + 16 a^6 b^12 c^2 y z - 28 a^4 b^14 c^2 y z +
4 a^2 b^16 c^2 y z + 12 a^16 c^4 y z + 48 a^14 b^2 c^4 y z -
234 a^12 b^4 c^4 y z + 188 a^10 b^6 c^4 y z + 162 a^8 b^8 c^4 y z -
248 a^6 b^10 c^4 y z + 58 a^4 b^12 c^4 y z + 12 a^2 b^14 c^4 y z +
2 b^16 c^4 y z - 44 a^14 c^6 y z + 76 a^12 b^2 c^6 y z +
188 a^10 b^4 c^6 y z - 468 a^8 b^6 c^6 y z + 204 a^6 b^8 c^6 y z +
116 a^4 b^10 c^6 y z - 60 a^2 b^12 c^6 y z - 12 b^14 c^6 y z +
40 a^12 c^8 y z - 200 a^10 b^2 c^8 y z + 162 a^8 b^4 c^8 y z +
204 a^6 b^6 c^8 y z - 280 a^4 b^8 c^8 y z + 44 a^2 b^10 c^8 y z +
30 b^12 c^8 y z + 12 a^10 c^10 y z + 116 a^8 b^2 c^10 y z -
248 a^6 b^4 c^10 y z + 116 a^4 b^6 c^10 y z + 44 a^2 b^8 c^10 y z -
40 b^10 c^10 y z - 44 a^8 c^12 y z + 16 a^6 b^2 c^12 y z +
58 a^4 b^4 c^12 y z - 60 a^2 b^6 c^12 y z + 30 b^8 c^12 y z +
28 a^6 c^14 y z - 28 a^4 b^2 c^14 y z + 12 a^2 b^4 c^14 y z -
12 b^6 c^14 y z - 6 a^4 c^16 y z + 4 a^2 b^2 c^16 y z +
2 b^4 c^16 y z + a^20 z^2 + 2 a^18 b^2 z^2 - 19 a^16 b^4 z^2 +
24 a^14 b^6 z^2 + 18 a^12 b^8 z^2 - 52 a^10 b^10 z^2 +
18 a^8 b^12 z^2 + 24 a^6 b^14 z^2 - 19 a^4 b^16 z^2 +
2 a^2 b^18 z^2 + b^20 z^2 - 6 a^18 c^2 z^2 + 10 a^16 b^2 c^2 z^2 +
40 a^14 b^4 c^2 z^2 - 120 a^12 b^6 c^2 z^2 + 76 a^10 b^8 c^2 z^2 +
76 a^8 b^10 c^2 z^2 - 120 a^6 b^12 c^2 z^2 + 40 a^4 b^14 c^2 z^2 +
10 a^2 b^16 c^2 z^2 - 6 b^18 c^2 z^2 + 15 a^16 c^4 z^2 -
48 a^14 b^2 c^4 z^2 + 36 a^12 b^4 c^4 z^2 + 112 a^10 b^6 c^4 z^2 -
230 a^8 b^8 c^4 z^2 + 112 a^6 b^10 c^4 z^2 + 36 a^4 b^12 c^4 z^2 -
48 a^2 b^14 c^4 z^2 + 15 b^16 c^4 z^2 - 20 a^14 c^6 z^2 +
52 a^12 b^2 c^6 z^2 - 132 a^10 b^4 c^6 z^2 + 100 a^8 b^6 c^6 z^2 +
100 a^6 b^8 c^6 z^2 - 132 a^4 b^10 c^6 z^2 + 52 a^2 b^12 c^6 z^2 -
20 b^14 c^6 z^2 + 15 a^12 c^8 z^2 + 2 a^10 b^2 c^8 z^2 +
65 a^8 b^4 c^8 z^2 - 164 a^6 b^6 c^8 z^2 + 65 a^4 b^8 c^8 z^2 +
2 a^2 b^10 c^8 z^2 + 15 b^12 c^8 z^2 - 6 a^10 c^10 z^2 -
30 a^8 b^2 c^10 z^2 + 36 a^6 b^4 c^10 z^2 + 36 a^4 b^6 c^10 z^2 -
30 a^2 b^8 c^10 z^2 - 6 b^10 c^10 z^2 + a^8 c^12 z^2 +
12 a^6 b^2 c^12 z^2 - 26 a^4 b^4 c^12 z^2 + 12 a^2 b^6 c^12 z^2 +
b^8 c^12 z^2 = 0)
𝒫 de foco X1304 y directriz X110X648. Esta parábola pasa por los centros X4, X2777 (dirección de su eje) , X6225, X6759.
Let A
1, B
1, C
1 be the intersections of the Euler line and lines BC, CA, AB, resp. The circumcircles of AB
1C
1, BC
1A
1, CA
1B
1 concur in
X(1304). (Randy Hutson, February 10, 2016)
X(110) = focus of
X(648) = of Euler line.
Las cónicas ℋ y 𝒫 forman un haz bitangente. La recta X2X110 une los puntos de tangencia y las tangentes comunes se cortan en el punto medio X1495 de X23 (inverso del baricentro en la circunferencia circunscrita) y X110.
La polar recíproca de la parábola 𝒫 respecto a la hipérbola ℋ (lugar geométrico de los polos de las tangentes a 𝒫, respecto a ℋ, o equivalentemente, la envolvente de las polares de los puntos de 𝒫 respecto a ℋ) es una cónica del haz bitangente generado por las cónicas ℋ y 𝒫, que pasa por el centro de ℋ y por X185 ( del ) y X13367 ( de X4 y X5).
- Martes, 10 de abril del 2018
Puntos de Brocard y triángulos semejantes
Dado un triángulo ABC, sea A'B'C' el . Las tres rectas que unen los de los triángulos AB'C', BC'A' y CA'B' delimitan un triángulo, que se denota por A"B"C".
Los triángulos ABC y A"B"C" son inversamente semejantes y el centro de semejanza es X8290
X8290 es el del y el triángulo , cuyo es ABC.
Los triángulos A"B"C" y son homotéticos, con centro de homotecia X4027, sobre la recta de Euler de A"B"C".
Los puntos de Brocard de AB'C' son (baricéntricas):
Ωa (a^4-b^4+b^2c^2+a^2(2b^2+c^2) : b^2(-a^2+b^2+c^2) : a^2(-a^2+b^2+c^2)),
Ω'a (a^4+c^2(b^2-c^2)+a^2(b^2+2c^2) : a^2(-a^2+b^2+c^2) : c^2(-a^2+b^2+c^2)).
Las coordenadas del vértice A" de A"B"C" son:
A" (a^6(b^2+c^2)-a^2b^2c^2(b^2+c^2)-a^4(b^4+c^4)+b^2c^2(b^4+c^4) :
a^6b^2+b^8-b^4c^4+b^2c^6-c^8-a^4b^2(b^2+c^2)+a^2(b^6-3b^4c^2+2b^2c^4+c^6) :
-b^8+a^6c^2+b^6c^2-b^4c^4+c^8-a^4c^2(b^2+c^2)+a^2(b^6+2b^4c^2-3b^2c^4+c^6)).
Las ecuaciones de cambios de coordenadas son:
λx" = a^4(b^2+c^2)(x-y-z)-a^6(x+y+z)-b^2c^2(b^2(x+y-z)+c^2(x-y+z))+a^2(2c^4y+2b^4z+b^2c^2(x+y+z)),
λy" = a^4(-c^2(x+y-z)+2b^2z)-b^2(-2c^4x+b^2c^2(x-y+z)+b^4(x+y+z))+
a^2(c^4(x-y-z)-b^4(x-y+z)+b^2c^2(x+y+z)),
λz"=2b^4c^2x-b^2c^4(x+y-z)-c^6(x+y+z)+a^4(2c^2y-b^2(x-y+z))+a^2(b^4(x-y-z)-c^4(x+y-z)+b^2c^2(x+y+z)).
Lista de pares {Xi,X"j} para los índices {i,j}, donde el X"j de A"B"C" es el Xi de ABC:
{2, 13586}, {39, 1691}, {98, 11676}, {99, 12215}, {114, 3}, {115, 2076}, {147, 5999}, {325, 5152}, {1569, 6}, {1916, 385}, {2023, 187}, {4027, 384}, {5026, 5149}, {5976, 99}, {8290, 8290}, {12830, 115}.
La transformación afín σ: X ↦ X'=σ(X), que aplica ABC en A"B"C" tiene a X8290 como punto fijo propio, y las rectas fijas (aparte de la del infinito) son paralelas a las asíntotas de la .
- Lunes, 9 de abril del 2018
Una quíntica circunscrita bicircular
Sean ABC un triángulo, N el centro de la , Γ la circunferencia circunscrita y un punto P. Se denota por Ab y Ac los simétricos de A, respecto a las rectas BP y CP, y por Na el centro de la circunferencia de los nueve puntos del triángulo AAbAc. Se definen análogamente los puntos Nb y Nc.
La de pasa por
N si y solo si
P está sobre Γ o sobre una
quíntica 𝒬.
Ab (u^2-SCw^2+SB(u^2-w^2) : 2w(-SAu+SCw) :2w(SAu+SB(u+w))),
Ac (SAu^2-SBv^2+
SC(u^2-v^2) : 2v(SAu+SC(u+v)) : 2v(-SAu+SBv)).
El centro de la circunferencia de los nueve puntos de AAbAc es:
Na (b^4u^2w(u^2+2u(v+w)+v(v+w))+
v(a^4v w^2(2u+v+w)-
a^2c^2u^2(u^2+v^2+w^2+2u(v+w))+
c^4u^2(u^2+2u(v+w)+w(v+w)))-
b^2u^2(a^2w(u^2+v^2+w^2+2u(v+w))+
2c^2(u^3+2u^2(v+w)+v w(v+w)+u(v+w)^2)):
b^4u w(u^3+3u^2v+v^3-v w^2+u(3v^2+v w-w^2))-
v(u+w)(c^4u(-v^2+w(u+w))-
2a^2c^2w(u^2+u(v+w)+v(v+w))+
a^4w(u^2+u(2v+w)+v(v+2w)))-
b^2(a^2w(u^4+2u^3(v+w)+4u v w(v+w)+2v^2w(v+w)+
u^2(v^2+6v w+w^2))+
c^2u(u^3(v-w)+2v w(v^2-w^2)+2u^2(v^2+v w-w^2)+
u(v^3+3v^2w-v w^2-w^3))):
-a^4v w(u^3+
2u^2(v+w)+v w(2v+w)+u(v^2+4v w+w^2))-
a^2v(-2b^2w(u^3+v w(v+w)+u(v+w)^2+u^2(2v+w))+
c^2(u^4+2u^3(v+w)+4u v w(v+w)+2v w^2(v+w)+
u^2(v^2+6v w+w^2)))+
u(b^4w(-u^2v-v^3+v w^2+u(-2v^2+w^2))+
c^4v(u^3+3u^2w-v^2w+w^3+u(-v^2+v w+3w^2))+
b^2c^2(u^3(v-w)+2v w(v^2-w^2)+
2u^2(v^2-v w-w^2)+u(v^3+v^2w-3v w^2-w^3)))).
La quíntica 𝒬 pasa por los centros del triángulo X1, X5, X13, X14, X30, X80, X399.
La asíntota es la recta de Euler y las tangentes en los vértices de ABC concurren en el circuncentro.
- Domingo, 8 de abril del 2018
Puntos de De Longchamps y baricentro sobre la recta de Euler
Dado un triángulo ABC, sea L el .
Se denota por La, Lb y Lc los puntos de De Longchamps de los triángulos LBC, LCA y LAB, respectivamente.
Y por L'a, L'b y L'c los puntos de De Longchams de los triángulos LLbLc, LLcLa y LLaLb, respectivamente.
El baricentro de L'aL'bL'c queda sobre la de ABC.
En coordenadas baricéntricas:
La (),
L'a
(-SB^5SC^5+SA^5(SB-SC)^4(SB+SC)+9SASB^4SC^4(SB+SC)+
7SA^4SB(SB-SC)^2SC(SB^2+6SBSC+SC^2)-
2SA^2SB^3SC^3(3SB^2+38SBSC+3SC^2)-
2SA^3SB^2SC^2(5SB^3-37SB^2SC-37SBSC^2+
5SC^3) :
-8SASBSC(2SA^4(SB-SC)^3+SB^3SC^4-
SASB^2SC^3(5SB+SC)-
SA^2SBSC^2(3SB^2-12SBSC+SC^2)+
SA^3SC(5SB^3-5SB^2SC-SBSC^2+
SC^3)) :
8SASBSC(2SA^4(SB-SC)^3-SB^4SC^3+
SASB^3SC^2(SB+5SC)+
SA^2SB^2SC(SB^2-12SBSC+3SC^2)+
SA^3SB(-SB^3+SB^2SC+5SBSC^2-5SC^3))).
El baricentro de L'aL'bL'c es:
G' = ( SA^4 (SB^2-SC^2)^2 - 32a^2SA^3 SB^2 SC^2 - 2SA^2 SB^2 SC^2 (SB^2 - 32SB SC+SC^2)+SB^4 SC^4 : ... : ...),
que tiene números de búsqueda en
(-14.1863025175153, -15.0183986161722, 20.5855416088799).
- Martes, 3 de abril del 2018
Relativo a la hipérbola de Feuerbach
Dado un triángulo ABC, sean A'B'C' el del incentro y t un número real positivo.
Los puntos Ao y Ai son las intersecciones de la perpendicular La por A' a la recta BC con la circunferencia Γa de centro A' y radio t AA' sen(A/2) (Ao en el semiplano que divide BC donde no está A).
Similarmente, se definen los puntos Bo, Bi, Co y Ci.
Los triángulos y son perspectivos con ABC y los centros de perspectividad, Po y Pi (que están alineados con el ortocentro del , X65), quedan sobre la .
La ecuación baricéntrica de Γa es:
(-2 b c - SA^2 t^2 +
b^2 c^2 (-2 + t^2)) x^2 - (a^2 c^2 + (-b^2 c^2 +
SA^2) t^2) y^2 - (a^2 b^2 + (-b^2 c^2 + SA^2) t^2) z^2 +
2 (a^2 b c + (b^2 c^2 - SA^2) t^2) y z - (a^2 b^2 - b^4 - 2 b^3 c +
2 b c SA + 2 SA^2 t^2 + b^2 c^2 (1 - 2 t^2)) z x - (a^2 c^2 -
c^4 - 2 b (c^3 - c SA) + 2 SA^2 t^2 + b^2 c^2 (1 - 2 t^2)) x y = 0.
Y la de la rectas La es:
(b - c) ((b + c)^2-a^2)x + 2 a^2 c y -2 a^2 b z = 0.
Los puntos de intersección de ambas son:
Ao (- a^2 t : a b + SC t : a c + SB t),
Ai ( a^2 t : a b - SC t : a c - SB t).
El punto de intersección de las rectas AAo, BBo y CCo es:
Po (1/(b c + t SA) : 1/(c a + t SB) : 1/(a b + t SC)).
El punto de intersección de las rectas AAi, BBi y CCi es:
Pi (1/(b c - t SA) : 1/(c a - t SB) : 1/(a b - t SC)).
Estos dos puntos quedan, para todo t, sobre la hipérbola de Feuerbach:
a(a-b-c)(b-c)y z + b(b-c-a)(c-a)z x + c(c-a-b)(a-b)x y = 0.
ALGUNOS puntos Po , Pi
En el siguiente listado aparecen los centros de perspectividad Po y Pi y el correspondiente valor de t.
t → 0, X1, X1,
t → ∞, X4, X4,
t = 1, X7, X8,
t = 2R/(r+2R), X9, X5665,
t = R/(r+R), X21, r(2r+3R)X21+(4R(r+R))X65,
( a(a^6
- 3a^5(b+c)
+5a^4b c
+(b^2-c^2)^2(2b^2-5b c+2c^2)
+6a^3(b^3+c^3)
+a^2(-3b^4+10b^2c^2-3c^4) -
3a(b^5-b^4c- b c^4+c^5)
+(b^2-c^2)^2(2b^2-5b c+2c^2)) : ... : ...),
que tiene números de búsqueda en
(0.895606123154127, 0.948585640298456, 2.57059467409124), y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,411}, {4,15911}, {7,3486}, {8,12}, {9,1405}, {21,65}, {35,5424}, {56,2320}, {57,5303}, {72,12867}, {79,3671}, {80,7548}, {84,5884}, {90,6912}, {100,6596}, {104,942}, {145,6601}, {226,5086}, {314,1441}, {354,1476}, {517,943}, {651,2647}, {758,15910}, {938,3427}, {987,4332}, {1000,1482}, {1156,1858}, {1159,3560}, {1172,1880}, {1320,11011}, {1937,2654}, {2098,7320}, {2298,4318}, {2346,3057}, {3062,10394}, {3065,11571}, {3243,10865}, {3254,10106}, {3296,3600}, {3577,6261}, {3649,11604}, {3678,4866}, {3680,3870}, {4298,5557}, {4308,5558}, {4853,11526}, {4900,6765}, {5045,15179}, {5559,11009}, {5665,10393}, {5730,6856}, {5902,15446}, {5903,15175}, {6909,13750}, {7091,11518}, {7160,7982}, {12709,16133}.
t = 2, X79, X80,
t = 2R/r, X84, X3577,
t = 2R/(r+R), X90, (4R(r+R))X65 + (r^2+2rR-R^2)X90,
( a (a^6 - 4 a^5 (b + c) +
a^4 (b^2 + 10 b c + c^2) + (b^2 - c^2)^2 (3 b^2 - 10 b c +
3 c^2) + 8 a^3 (b^3 + c^3) +
a^2 (-5 b^4 + 14 b^2 c^2 - 5 c^4) -
4 a (b^5 - b^4 c - b c^4 + c^5)) : ... : ...),
que tiene números de búsqueda en
(0.285536014484069, 0.309787809445305, 3.29441014560652), reflexión de Xi en Xj para los índices {i,j}: {6697, 3589}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,6985}, {7,10572}, {8,6871}, {9,5903}, {21,46}, {40,15175}, {57,15446}, {65,90}, {79,11529}, {80,3340}, {84,5902}, {104,3338}, {517,7162}, {942,7284}, {943,5119}, {1000,3485}, {1159,1898}, {1389,6261}, {1392,3957}, {1478,11520}, {2346,13375}, {3254,9613}, {3255,4312}, {3296,3486}, {3427,5804}, {3601,5424}, {3612,6876}, {3671,5555}, {3680,11009}, {4338,7491}, {5425,5665}, {5531,13143}, {5557,11518}, {5558,15933}, {5559,6842}, {5697,7160}, {5726,11280}, {5734,6838}, {6598,7700}, {6866,10826}, {7962,13606}.
t = R/r, X104, X1389,
t = 1/2, X1000, X3296,
t = 4R^2/((r+2R)^2-s^2), X1039, X1041,
t = 2R^2/((r+2R)^2-s^2), X1061, X1063,
t = R/(R-r), X1320, X1476,
t = 2R/(2R-r), X3680, X7091,
t = 3/4, X5551, X7317,
t = 3, X5556, X7319,
t = 2/3, X5557, X5559,
t = 1/3, X5558, X7320,
t = 4, X5560, X7320,
t = 2R/(2r+3R), X15173, X15175.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
El lugar geométrico del punto medio M de PoPi es la hipérbola ℋ con asíntotas paralelas a las de la hipérbola de Feuerbach, con centro el punto medio, X12736, de X11X65 y que pasa por los centros Xi, para los índices, 1, 4, 11, 65, 442, 2550, 2588, 2589, 3307, 3308, 4312, 5728, 10914, 11041. Su ecuación baricéntrica es:
SA (b SB - c SC)x^2 + (b SB^2 + a b c (SB - SC) - c SC^2)y z + .... = 0.
Si Qo y Qi son los conjugados isogonales de Po y Pi, y M' es el punto medio de QoQi, la envolvente de las rectas MM' es una cónica 𝒞 bitangente a la hipérbola ℋ. Pasa por X35, X3651.
Su centro es W = (2r^2+r R-2R^2) X214 + 2R(r+R) X960 ,
donde r y R son los radios de las circunferencias inscrita y circunscrita a ABC, respectivamente.
W = ( a (-2a^9
+4a^8(b+c)
+2a^7(2b^2-5b c+2c^2)
-3a^6(4b^3-b^2c-b c^2+4c^3)
+2a^5b c(7b^2-8b c+7c^2)
+ a^4(12b^5-17b^4c+10b^3c^2+10b^2c^3-17b c^4+12c^5)
+a^3(-4b^6+2b^5c+9b^4c^2-22b^3c^3+9b^2c^4+2bc^5-4c^6)
-a^2(b-c)^2(4b^5-b^4c+6b^3c^2+6b^2c^3-b c^4+4c^5)
+a(b^2-c^2)^2(2b^4-6b^3c+7b^2c^2-6b c^3+2c^4)
+b c(b-c)^4(b+c)^3 ) : ... : ...),
que tiene números de búsqueda en
(6.92619557553115, 6.84145817591086, -4.29243529012213); y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3,10265}, {21,10165}, {30,6713}, {104,15931}, {214,960}, {758,15528}, {1155,5427}, {1768,6875}, {2829,6675}, {3256,14563}, {3651,10090}, {5426,6950}, {10543,12832}, {14526,14800}.
Una de las cónicas degeneradas del haz de cónicas base ℋ y 𝒞 es la recta (contada dos veces):
(b-c)(2a^6-3a^5(b+c)+a^4(-3b^2+2b c-3c^2)
+3a^3(2b^3+b^2c+b c^2+2c^3)
-a^2b c(b^2-4b c+c^2)
-3a(b^5+b^3c^2+b^2c^3+c^5)
+(b^2-c^2)^2(b^2-b c+c^2) )x + ... = 0,
que pasa por Xk, para k = 80, 226, 5425, 10711, 14563.
El punto de intersección de las dos rectas, tangentes comunes a las dos cónicas ℋ y 𝒞, es el punto medio V de X36 (inverso del incentro en la circunferencia circunscrita) y X10058 = R X1+r X104.
V = ( a(2a^6
-2a^5(b+c)
-4a^4(b^2-b c+c^2)
+a^3(4b^3-b^2c-b c^2+4c^3)
+a^2(b-c)^2(2b^2+b c+2c^2)
-a(b-c)^2(2b^3+b^2c+b c^2+2c^3)
-b c(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en
(0.418075236708187, 1.00450167747170, 2.75228244210020) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1,89}, {3,950}, {21,908}, {36,516}, {56,13464}, {57,6950}, {104,2078}, {226,6914}, {499,4190}, {514,1946}, {515,5172}, {519,10087}, {527,954}, {993,8069}, {1155,5427}, {1319,2800}, {1478,6974}, {1728,4855}, {1776,6326}, {3086,3522}, {3601,6875}, {4292,6906}, {4311,5450}, {4973,5570}, {5193,12775}, {5840,15325}, {6942,9581}, {7288,15866}, {7675,10398}, {8666,11508}, {8758,11700}, {10624,11012}, {11019,14793}, {12047,14804}.
- Jueves, 29 de marzo del 2018
X(3091) como centro de homotecia
Dado un triángulo ABC, sean A'B'C' el . Se denota por Ba y Ca las proyecciones de B' y C' sobre AA', respectivamente; por B1 y C1 las reflexiones de Ba y Ca en BB' y CC', respectivamente; y por Oa, Ob y Oc los circuncentros de los triángulos A'B1C1, B'C1A1 y C'A1B1, respectivamente.
Los triángulos ABC y son homotéticos, mediante una homotecia de centro X3091 = 2 O + 3 H = 2 H + 3 G y razón -1/4.
Las coordenadas baricéntricas de Oa son
Oa (2(a^4-(b^2-c^2)^2) : -3a^4+b^4+2b^2c^2-3c^4+2a^2(b^2+3c^2) :
-3a^4-3b^4+2b^2c^2+c^4+2a^2(3b^2+c^2)).
El centro de homotecia de ABC y es:
X3091 (a^4+2a^2(b^2+c^2)-3(b^2-c^2)^2 : ... : ....).
La ecuación de la homotecia de centro X3091 y razón -1/4 es:
(x:y:z) ↦ (-2a^2(b^2+c^2)(y+z)-a^4(2x+y+z)+(b^2-c^2)^2(2x+3(y+z)) : ... : ...).
En la siguiente lista, {i,j} son los índices de los centros {Xi, Xj}, donde Xj es la imagen de Xi mediante la homotecia considerada.
{2, 381}, {3, 546}, {4, 5}, {5, 3850}, {8, 946}, {10, 12571}, {20, 4}, {23, 10297}, {64, 5893}, {68, 5448}, {69, 5480}, {72, 5806}, {110, 7687}, {140, 3856}, {143, 11017}, {144, 5805}, {145, 355}, {146, 125}, {147, 115}, {148, 114}, {149, 119}, {150, 118}, {151, 124}, {152, 116}, {153, 11}, {193, 1352}, {194, 6248}, {253, 10002}, {329, 7682}, {355, 9955}, {376, 3845}, {381, 5066}, {382, 140}, {399, 11801}, {452, 6849}, {487, 6251}, {488, 6250}, {546, 12811}, {549, 3860}, {550, 3861}, {616, 5478}, {617, 5479}, {621, 7684}, {622, 7685}, {631, 3858}, {938, 9842}, {962, 10}, {1330, 7683}, {1370, 1596}, {1539, 15088}, {1656, 3859}, {1657, 3853}, {1885, 9825}, {2071, 10151}, {2475, 6841}, {2888, 3574}, {2896, 6249}, {3090, 3857}, {3091, 3091} , {3146, 3}, {3151, 15762}, {3153, 403}, {3421, 7956}, {3424, 7694}, {3434, 7680}, {3436, 7681}, {3448, 113}, {3522, 3843}, {3523, 3832}, {3529, 3627}, {3534, 14893}, {3543, 2}, {3547, 7564}, {3555, 9947}, {3621, 1482}, {3627, 3628}, {3648, 16125}, {3830, 547}, {3832, 3851}, {3839, 3545}, {3845, 11737}, {3868, 5777}, {3869, 7686}, {3917, 13570}, {4295, 12617}, {5056, 3855}, {5059, 382}, {5073, 548}, {5076, 12812}, {5177, 6866}, {5189, 11799}, {5562, 10110}, {5691, 1125}, {5876, 10095}, {5881, 13464}, {5889, 5907}, {5895, 6696}, {5921, 6}, {5984, 6033}, {6193, 9927}, {6223, 6245}, {6224, 6246}, {6225, 6247}, {6243, 11591}, {6776, 3818}, {6839, 8226}, {6840, 1532}, {6888, 7548}, {6895, 6842}, {6925, 8727}, {7080, 10893}, {7391, 15760}, {7396, 6623}, {7486, 3854}, {7620, 8176}, {7712, 15432}, {8591, 9880}, {8596, 8724}, {9799, 6260}, {9809, 10265}, {9812, 10175}, {9863, 7745}, {9874, 12599}, {10152, 6716}, {10263, 14128}, {10285, 15335}, {10296, 468}, {10304, 3839}, {10431, 6907}, {10721, 6699}, {10722, 6036}, {10723, 620}, {10724, 3035}, {10725, 6710}, {10726, 6711}, {10727, 6712}, {10728, 6713}, {10729, 6714}, {10730, 6715}, {10731, 6717}, {10732, 6718}, {10733, 5972}, {10734, 6719}, {10735, 6720}, {11001, 15687}, {11148, 7620}, {11180, 5476}, {11282, 11283}, {11381, 9729}, {11412, 5446}, {11414, 16198}, {11455, 5892}, {11469, 9815}, {11531, 3626}, {11541, 15704}, {11671, 128}, {12111, 389}, {12162, 5462}, {12219, 1112}, {12221, 6290}, {12222, 6289}, {12225, 6756}, {12226, 11576}, {12244, 1539}, {12247, 12611}, {12251, 14881}, {12273, 11800}, {12278, 13403}, {12279, 13474}, {12281, 11557}, {12292, 9826}, {12293, 9820}, {12294, 9822}, {12295, 12900}, {12296, 642}, {12297, 641}, {12298, 9823}, {12299, 9824}, {12300, 9827}, {12324, 2883}, {12383, 10113}, {12384, 127}, {12528, 942}, {12688, 3812}, {12699, 9956}, {12751, 16174}, {12825, 11746}, {12849, 12600}, {12902, 10272}, {13019, 13053}, {13020, 13054}, {13201, 11807}, {13202, 6723}, {13219, 132}, {13474, 11695}, {13678, 13687}, {13798, 13807}, {14023, 7843}, {14269, 14892}, {14360, 5512}, {14516, 12241}, {14683, 265}, {14712, 13449}, {14790, 15761}, {14807, 1312}, {14808, 1313}, {14872, 13374}, {15305, 5943}, {15640, 376}, {15681, 12101}, {15682, 549}, {15683, 3830}, {15684, 12100}, {15687, 10109}, {15704, 12102}, {15800, 13565}.
La transformación de coordenadas entre las coordenadas baricéntricas respecto a ABC y son:
x' = 2a^2(b^2+c^2)(3x-y-z)-a^4(5x+y+z)-(b^2-c^2)^2(x-3(y+z))
y' = a^4(3x-y+3z)-2a^2(b^2(x-3y+z)+c^2(3x-y+3z))-(b^2-c^2)(b^2(x+5y+z)+c^2(3x-y+3z))
z' = -2a^2(c^2(x+y-3z)+b^2(3x+3y-z))+a^4(3x+3y-z)+(b^2-c^2)(b^2(3x+3y-z)+c^2(x+y+5z))
En la siguiente lista, {i,j} son los índices de los centros {Xi, Xj}, donde Xj
es el centro Xi de ABC, respecto .
{2, 3543}, {3, 3146}, {4, 20}, {5, 4}, {6, 5921}, {10, 962}, {11, 153}, {113, 3448}, {114, 148}, {115, 147}, {116, 152}, {118, 150}, {119, 149}, {124, 151}, {125, 146}, {127, 12384}, {128, 11671}, {132, 13219}, {140, 382}, {265, 14683}, {355, 145}, {376, 15640}, {381, 2}, {389, 12111}, {403, 3153}, {468, 10296}, {546, 3}, {547, 3830}, {548, 5073}, {549, 15682}, {620, 10723}, {641, 12297}, {642, 12296}, {942, 12528}, {946, 8}, {1112, 12219}, {1125, 5691}, {1312, 14807}, {1313, 14808}, {1352, 193}, {1482, 3621}, {1532, 6840}, {1539, 12244}, {1596, 1370}, {2883, 12324}, {3035, 10724}, {3091, 3091}, {3545, 3839}, {3574, 2888}, {3626, 11531}, {3627, 3529}, {3628, 3627}, {3812, 12688}, {3818, 6776}, {3830, 15683}, {3832, 3523}, {3839, 10304}, {3843, 3522}, {3845, 376}, {3850, 5}, {3851, 3832}, {3853, 1657}, {3854, 7486}, {3855, 5056}, {3856, 140}, {3857, 3090}, {3858, 631}, {3859, 1656}, {3860, 549}, {3861, 550}, {5066, 381}, {5446, 11412}, {5448, 68}, {5462, 12162}, {5476, 11180}, {5478, 616}, {5479, 617}, {5480, 69}, {5512, 14360}, {5777, 3868}, {5805, 144}, {5806, 72}, {5892, 11455}, {5893, 64}, {5907, 5889}, {5943, 15305}, {5972, 10733}, {6033, 5984}, {6036, 10722}, {6246, 6224}, {6247, 6225}, {6248, 194}, {6249, 2896}, {6250, 488}, {6251, 487}, {6289, 12222}, {6290, 12221}, {6623, 7396}, {6696, 5895}, {6699, 10721}, {6710, 10725}, {6711, 10726}, {6712, 10727}, {6713, 10728}, {6714, 10729}, {6715, 10730}, {6716, 10152}, {6717, 10731}, {6718, 10732}, {6719, 10734}, {6720, 10735}, {6723, 13202}, {6756, 12225}, {6841, 2475}, {6842, 6895}, {6849, 452}, {6866, 5177}, {6907, 10431}, {7548, 6888}, {7564, 3547}, {7620, 11148}, {7680, 3434}, {7681, 3436}, {7682, 329}, {7683, 1330}, {7684, 621}, {7685, 622}, {7686, 3869}, {7687, 110}, {7694, 3424}, {7745, 9863}, {7843, 14023}, {7956, 3421}, {8176, 7620}, {8226, 6839}, {8724, 8596}, {8727, 6925}, {9729, 11381}, {9815, 11469}, {9820, 12293}, {9822, 12294}, {9823, 12298}, {9824, 12299}, {9825, 1885}, {9826, 12292}, {9827, 12300}, {9842, 938}, {9880, 8591}, {9927, 6193}, {9947, 3555}, {9955, 355}, {9956, 12699}, {10002, 253}, {10095, 5876}, {10109, 15687}, {10110, 5562}, {10113, 12383}, {10151, 2071}, {10175, 9812}, {10265, 9809}, {10272, 12902}, {10297, 23}, {10893, 7080}, {11017, 143}, {11283, 11282}, {11557, 12281}, {11576, 12226}, {11591, 6243}, {11695, 13474}, {11737, 3845}, {11746, 12825}, {11799, 5189}, {11800, 12273}, {11801, 399}, {11807, 13201}, {12100, 15684}, {12101, 15681}, {12102, 15704}, {12241, 14516}, {12571, 10}, {12599, 9874}, {12600, 12849}, {12611, 12247}, {12617, 4295}, {12811, 546}, {12812, 5076}, {12900, 12295}, {13053, 13019}, {13054, 13020}, {13374, 14872}, {13403, 12278}, {13449, 14712}, {13464, 5881}, {13474, 12279}, {13565, 15800}, {13570, 3917}, {13687, 13678}, {13807, 13798}, {14128, 10263}, {14881, 12251}, {14892, 14269}, {14893, 3534}, {15088, 1539}, {15335, 10285}, {15432, 7712}, {15687, 11001}, {15760, 7391}, {15761, 14790}, {15762, 3151}, {16174, 12751}, {16198, 11414}.
- Viernes, 23 de marzo del 2018
Estrofoide lugar de tripolos de tangentes a una cónica
En recuerdo de Marta en el 42 aniversario de su nacimiento
Dado un triángulo ABC, sean y los triángulos y , respectivamente.
Para un punto At sobre BC, sean Ab y Ac los puntos donde las paralelas por At a AB y a AB cortan a AC y a AB, respectivamente. Se denota por A't la reflexión de At en la recta AbAc.
El lugar geométrico de A't, cuando At varía sobre la recta BC, es la ℰa, que pasa por los , de punto doble A, eje la mediana por A y Fa, el punto de intersección de la por A con la recta que une la punto medio de la mediana AMa con Ha.
Utilizando , At(0:1:t), Ab(1:0:t) y Ac(t:1:0).
A't (t((b^2-c^2)(t-1)+a^2(1+t)) : (c-bt)(c+bt) : t(-c+bt)(c+bt)).
Eliminando t, la ecuación implícita del lugar geométrico descrito por el punto A't es:
ℰa: -c^2x y^2+(-a^2+b^2-c^2)y^2z+b^2x z^2+(a^2+b^2-c^2)y z^2 = 0.
En particular, si el triángulo ABC es isósceles, con cúspide A, esta cúbica es el producto
(y-z) (a^2 y z + b^2 z x + c^2 x y) = 0.
de la mediana por A y la circunferencia circunscrita.
Más información sobre la estrofoide ℰa:
Las coordenadas del foco Fa son (b^2+c^2-a^2 : b^2 : c^2), que es el A-vértices del .
La ecuación de su asíntota es
(b^2-c^2)x + (-a^2+3b^2+c^2)y + (a^2-b^2-3c^2)z = 0, que corta a la estrofoide en:
(-(a^2-b^2-3c^2)(a^2-3b^2-c^2)(b^2+c^2) : b^2(b^2-c^2)(-a^2+b^2+3c^2) : c^2(-b^2+c^2)(-a^2+3b^2+c^2)).
La de A't pasa por At y envuelve una cónica 𝒞a tangente a BC en Ta , punto de intersección con el ; donde está también su centro Wa (-2b^2+2c^2 : -a^2-3b^2+c^2 : a^2-b^2+3c^2).
𝒞a es tangente a las bisectrices interior y exterior en A, que son las tangentes en el punto doble de la estrofoide.
La ecuación tangencial de esta cónica es (-a^2-b^2+c^2)u v - b^2v^2 + (a^2-b^2+c^2)u w + c^2w^2 = 0, y su ecuación puntual:
𝒞a:
4b^2c^2x^2 + (a^2-b^2+c^2)^2y^2 + (a^2+b^2-c^2)^2z^2 +
2(a^4-(b^2-c^2)^2)y z + 4b^2(-a^2+b^2-c^2)z x + 4c^2(-a^2-b^2+c^2)x y = 0.
La del baricentro respecto a esta cónica (que pasa por el simediano) es la tripolar del .
La cónica 𝒞a queda determinada por las tres tangentes mencionadas, el punto de tangencia de una de ellas, y por la polar del baricentro. Así, la estrofoide ℰa puede ser descrita a partir de la cónica 𝒞a, considerando los de sus tangentes.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Procediendo cíclicamente sobre los vértices del triángulo ABC se obtienen las estrofoides ℰb y ℰc, así como las cónicas 𝒞b y 𝒞c.
• ℰa, ℰb y ℰc son las estrofoides de Apolonio (K053, en el catálogo de Bernard Gibert)
• Como los puntos de Fermat (X13, X14) son comunes a las tres estrofoides ℰa, ℰb y ℰc, sus tripolares (que pasan por los puntos medios de X14 y X13X15, respectivamente) son tangentes comunes a las tres cónicas 𝒞a, 𝒞b y 𝒞c. Estas tangentes son paralelas (tienen la dirección del del foco de la ), por lo que los puntos de tangencia en cada cónica son diametralmente opuestos. Los correspondientes diámetros pasan por el baricentro.
• Los puntos de tangencia Ta, Tb, Tc, con los lados BC, CA, AB, de las cónicas 𝒞a, 𝒞b, 𝒞c y sus centros
Wa, Wb, Wc están en el eje órtico.
• Las polares del baricentro respecto a las cónicas 𝒞a, 𝒞b, 𝒞c coinciden en la tripolar del punto de Tarry (recta que pasa por el simediano y tiene la dirección del del foco de la ).
• Las polares pa, pb, pc de un punto P, respecto a las cónicas 𝒞a, 𝒞b, 𝒞c, son concurrentes si y solo si P está sobre la tripolar del punto de Tarry. El punto de concurrencia es el baricentro.
• El lugar geométrico de un punto P cuyas polares pa, pb, pc, respecto a las cónicas 𝒞a, 𝒞b, 𝒞c, forman un triángulo A'B'C' perspectivo con ABC consta del eje órtico y de la hipérbola rectangular ℋ, que pasa por los centros del triángulo de índices 2, 4, 3168, 3924, 6525, 7735, 13636, 13722.
-- Para todo punto P sobre la hipérbola ℋ, el centro de perspectividad de los triángulos ABC y A'B'C' es el ortocentro.
-- Cuando P recorre el eje órtico, los triángulos ABC y A'B'C' son homotéticos y el lugar geométrico del centro de homotecia Q es una cúbica circunscrita a ABC, que pasa por el baricentro y el ortocentro (punto nodal), de ecuación:
x((c^2+SA)SBy^2 - (b^2+SA)SCz^2) +
y((a^2+SB)SCz^2 - (b^2+SB)SAx^2) +
z((b^2+SC)SAx^2 - (b^2+SC)SBy^2) = 0.
Esta cúbica puede ser descrita geométricamente así:
Sean
ABC un triángulo,
P un punto y 𝒞
a la cónica tangente a las cinco rectas:
BC, bisectrices interior y exterior en
A, tripolares de X
13 y X
14.
p
a es la polar de
P respecto a 𝒞
a. Se definen p
b y p
c cíclicamente.
Cuando P recorre el eje órtico, los triángulos ABC y A'B'C', formado por las rectas pa, pb y pc, son homotéticos y el lugar geométrico del centro de homotecia Q es una cúbica circunscrita a ABC, que pasa por el baricentro y el ortocentro (punto nodal).
- Jueves, 15 de marzo del 2018
Reflexiones de rectas de Euler
Dados un triángulo ABC, sean (), () y los del circuncentro, ortocentro y centro de la , respectivamente.
Se denota por:
Hab y Hac los puntos medios de los segmentos HaOb y HaOc, respectivamente; y La la del triángulo .
Hbc y Hba los puntos medios de los segmentos HbOc y HbOa, respectivamente; y Lb la recta de Euler del triángulo .
Hca y Hcb los puntos medios de los segmentos HcOa y HcOb, respectivamente; y Lc la recta de Euler del triángulo .
Sea A'B'C' el triángulo homotético a ABC en la homotecia de centro el baricentro y razón t.
Las reflexiones L'a, L'b y L'c de La, Lb y Lc en B'C', C'A' y A'B', respectivamente, son concurrentes en un punto Wt, sobre la recta L que pasa por el centro de la circunferencia de los nueve puntos y es paralela al .
La ecuación baricéntrica de L es:
(b^2-c^2)(a^4+2b^4+b^2c^2+2c^4-3a^2(b^2+c^2))x +
(c^2-a^2)(b^4+2c^4+c^2a^2+2a^4-3b^2(c^2+a^2))y +
(a^2-b^2)(c^4+2a^4+a^2b^2+2b^4-3c^2(a^2+b^2))z = 0.
Esta recta pasa por los centros del triángulo Xi, para los índices i = 5, 542, 575, 597, 5459, 5460, 5461, 5609, 6593, 7668, 7817, 7829, 8550, 8787, 10116, 11623, 13870, 15118, 15359, 15535.
Casos particulares:
• Para t=1/4, Wt = X5.
• Para t=1 (ABC y A'B'C' coinciden), W1 = X4 + 3 X110.
W1 = (
2a^10
-8a^8(b^2+c^2)
+a^6(11b^4+4b^2c^2+11c^4)-
a^4(5b^6+b^4c^2+b^2c^4+5c^6)
-a^2(b^2-c^2)^2(b^4-6b^2c^2+c^4)
+(b^2-c^2)^4(b^2+c^2)
: ... : ...),
que tiene números de búsqueda en
(-0.738482622155366, -2.30834546137749, 5.57958793462512), punto medio de Xi y Xj para los índices {i,j}: {3, 15063}, {5, 5609}, {110, 113}, {125, 399}, {146, 16111}, {1553, 14934}, {1568, 10540}, {3292, 11799}, {5181, 9970}, {5642, 5655}, {5972, 6053}, {7728, 16163}, {11562, 12825}, {12121, 13202}, {12295, 12383}, {14094, 16003}; reflexión de Xi en Xj para los índices {i,j}: {125, 12900}, {5972, 10272}, {6699, 5972}, {10264, 6723}, {11806, 9826}, {15115, 9820}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2, 14094}, {3, 541}, {4, 110}, {5, 542}, {17, 10658}, {18, 10657}, {20, 10706}, {30, 15152}, {52, 10294}, {74, 3523}, {125, 399}, {140, 5663}, {146, 3522}, {155, 5095}, {265, 3851}, {376, 11693}, {382, 15039}, {403, 539}, {468, 13148}, {548, 11694}, {550, 1511}, {631, 15054}, {690, 6132}, {1216, 2781}, {1498, 15131}, {1553, 14934}, {1568, 7574}, {1625, 6103}, {1657, 7728}, {2771, 11281}, {2836, 13374}, {2914, 13431}, {2931, 3517}, {2948, 11522}, {3090, 9140}, {3091, 9143}, {3292, 11799}, {3448, 5056}, {3515, 12168}, {3516, 12901}, {3524, 15021}, {3525, 15057}, {3542, 12828}, {3545, 15029}, {3564, 15471}, {3628, 13393}, {3635, 15519}, {3850, 7687}, {3855, 15044}, {3858, 10113}, {5055, 15027}, {5068, 14644}, {5071, 15025}, {5181, 9970}, {5189, 14157}, {5446, 14984}, {5449, 11441}, {5621, 7393}, {5648, 11477}, {5882, 11720}, {5891, 7495}, {6000, 14156}, {6622, 9936}, {6689, 15738}, {6723, 10264}, {6759, 14791}, {7530, 12584}, {8254, 11017}, {8960, 12376}, {9306, 15132}, {9820, 15115}, {9826, 11806}, {10018, 11562}, {10299, 15055}, {10619, 11597}, {10620, 15720}, {11064, 14915}, {11598, 15105}, {11723, 13464}, {11803, 11808}, {12041, 15712}, {5073, 12121}, {12244, 15051}, {12308, 15061}, {12317, 15059}, {13382, 14708}, {1657, 7728}.
El punto W1 tiene coordenadas (1,3) en la referencia proyectiva {X4, X110; X113}. Es decir, la razón doble (X4 X110 X113 W1) es 1/3.
En la referencia {X(4), X(110); X(10733)} son: (-1,6). En la referencia {X(4), X(110); X(12295)} son: (-1,9). En la referencia {X(4), X(110); X(12383)} son: (-2,3).
En la referencia {X(4), X(113); X(110)} son: (2,3) (pues se intercambian los puntos medios en la razón doble). En la referencia {X(4), X(113); X(10733)} son: (2,9). En la referencia {X(4), X(113); X(12295)} son: (1,6).
Para la definición de referencia proyectiva ver §1.3 Definición 1.23 aquí y abscisa proyectiva.
• Sean D= La∩L'a, E= Lb∩L'b y F= Fc∩L'c.
Los puntos D, E, F están alineados si solo si
to = (-2a^12+5a^10(b^2+c^2)-
2a^8(b^4+7b^2c^2+c^4)-(b^2-c^2)^4(2b^4+3b^2c^2+
2c^4)+a^6(-2b^6+9b^4c^2+9b^2c^4-2c^6)+
a^2(b^2-c^2)^2(5b^6-4b^4c^2-4b^2c^4+5c^6)+
a^4(-2b^8+9b^6c^2-18b^4c^4+9b^2c^6-
2c^8)) /
(4(b^2c^2(b^2-c^2)^4+a^10(b^2+c^2)+
a^8(-4b^4+2b^2c^2-4c^4)+
a^2(b^2-c^2)^2(b^6+4b^4c^2+4b^2c^4+c^6)+
a^6(6b^6-3b^4c^2-3b^2c^4+6c^6)-
a^4(4b^8+3b^6c^2-12b^4c^4+3b^2c^6+4c^8)))
Wto es el punto de intersección de L con la recta que pasa por el baricentro y X5627 ( de los ).
Wto = ( 2 a^16-8 a^14 (b^2+c^2)+14 a^12 (b^2+c^2)^2-(b^2-c^2)^6 (b^4+5 b^2 c^2+c^4)+a^2 (b^2-c^2)^4 (b^6-4 b^4 c^2-4 b^2 c^4+c^6)-a^10 (19 b^6+27 b^4 c^2+27 b^2 c^4+19 c^6)+a^4 (b^2-c^2)^2 (8 b^8+25 b^6 c^2-6 b^4 c^4+25 b^2 c^6+8 c^8)+a^8 (25 b^8-2 b^6 c^2+24 b^4 c^4-2 b^2 c^6+25 c^8)+a^6 (-22 b^10+7 b^8 c^2+5 b^6 c^4+5 b^4 c^6+7 b^2 c^8-22 c^10) : ... : ...),
que tiene números de búsqueda en
(1.39852320882844, 0.985213626359095, 2.31312125958419) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2, 5627}, {5, 542}, {3635, 15519}, {8675, 10170}.
La ecuación de la recta DEF, cuando t=to es:
(a^8-6a^6(b^2+c^2)+
a^4(10b^4+b^2c^2+10c^4)+
a^2(-6b^6+b^4c^2+b^2c^4-6c^6)+(b^2-c^2)^2(b^4+8b^2c^2+c^4)) x + .... = 0,
con punto del infinito X526.
Una generalización:
Sea P un punto sobre la recta de Euler y el triángulo pedal de P.
Las reflexiones de La, Lb y Lc en PPa, PPb, PPa, respectivamente, son concurrentes. El lugar geométrico del punto de concurrencia es la recta paralela a la recta de Euler por el del centro de la , de ecuación:
(b^2-c^2)(-3a^8+5a^6(b^2+c^2)+
a^4(3b^4-17b^2c^2+3c^4)+(b^2-c^2)^2(4b^4+
9b^2c^2+4c^4)+
a^2(-9b^6+11b^4c^2+11b^2c^4-9c^6)) x+.....= 0,
que pasa por X30, X5972 (complemento de X125), X14156, X15448.
- Jueves, 8 de marzo del 2018
Parábolas inscritas en un triángulo y centros de semejanza
AMM, March 2015, Problem 11830.

Dados un triángulo ABC, un punto P y la parábola 𝒫(P), inscrita en ABC y tangente a la p de P, sean A1, B1 y C1 los puntos de tangencia de 𝒫(P) con los lados BC, CA y AB, respectivamente.
Se denota por A2, B2 y C2 los centros de las circunferencias cA, cB y cC, circunscritas a los triángulos , y , respectivamente.
Los triángulos ABC y son semejantes. El centro de semejanza S es el punto común de las circunferencias cA, cB y cC y queda sobre la de la .
Las ecuaciones tangenciales de los puntos B, C y los puntos del infinito de las rectas AB, AC son, respectivamente:
V=0, W=0, V-U=0, W-U=0.
Las ecuación tangencial del haz de parábolas tangentes a los lados de ABC y la recta del infinito es
V (U - W) + λ(U - V) W = 0.
La parábola 𝒫(P), tangente a la tripolar p de un punto P, de coordenadas baricéntricas (u:v:w), tiene ecuación tangencial
(v-w)V W + (w-u)W U + (u-v)U V = 0,
que se obtiene sustituyendo, en la ecuación del haz de parábolas, las coordenadas (v w : u w : u v) de la tripolar de P, para obtener λ=(u-w)/(v-u).
La ecuación puntual de 𝒫(P) es:
(v-w)^2 x^2 + (w-u)^2 y^2 + (u-v)^2 z^2 - 2 (w-u)(u-v) y z - 2 (u-v)(v-w) z x - 2 (v-w)(w-u) x y = 0.
Su es (1/(v-w):1/(w-u):1/(u-v)), su punto en el infinito es (v-w : w-u : u-v) y su foco (que está sobre la circunferencia circunscrita a ABC y es el de su punto del infinito, como es conocido) es
F = (a^2 (u-v)(u-w) : b^2 (v-w)(v-u) : c^2 (w-u)(w-v)).
Los puntos de contacto con los lados BC, CA, AB son, respectivamente:
A1 = (0 : -u + v : u - w),
B1 = (u - v : 0 : v - w),
C1 = (u - w : -v + w : 0).
El centro de la circunferencia circunscrita
cA: c^2xy+b^2xz+
a^2yz-(x+y+z)(((c^2(u-w)y)/(u-v))+(b^2(u-v)z)/(u-w))=0
al triángulo es:
A2 = ((b^2-c^2)(b^2(u-v)^2-c^2(u-w)^2)+a^4(u-v)(u-w)-a^2(b^2(u-v)+c^2(u-w))(2u-v-w) :
b^2(b^2(u-v)+a^2(-u+v)+c^2(3u-v-2w))(v-w) :
c^2(v-w)(a^2(u-w)+c^2(-u+w)+b^2(-3u+2v+w))).
Las coordenadas de los circuncentros B2 y C2 de los triángulos y , se obtienen por permutación cíclica.
El cuadrado de la distancia de B2 a C2 es:
a2² = a^2(a^4(u-v)^3(u-w)^3
+a^2(u-v)(u-w)(v-w)(b^2(u-v)^3-c^2(u-w)^3)
+(v-w)^3(-b^4(u-v)^3+c^4(u-w)^3+b^2c^2(u-v)(u-w)(v-w))) /
((b+c-a)(a+b-c)(a-b+c)(a+b+c)(u-v)^2(u-w)^2(v-w)^2)
Similarmente se tienen los cuadrados de las longitudes, b2² y c2², de los lados C2A2 y A2B2 del triángulo . Con lo que se deduce que
cos A2 = ( b2² + c2² - a2²)/(2 b2 c2) = (b²+c²-a²)/(2ab) = cos A.
Así, los triángulos ABC y son semejantes.
Si
A'=BC∩B2C2=
(0 : (v-u)(a^2(u-v)^2(u-w)+(v-w)^2(-2b^2(u-v)+c^2(-u+w))) : (u-w)(a^2(u-v)(u-w)^2+(v-w)^2(b^2(-u+v)+
2c^2(-u+w)))),
el centro de semejanza S es el otro punto de intersección de las circunferencias circunscritas a los triángulos A'BB2 y A'CC2:
S = (a^2(u-v)^2(u-w)^2(a^2(u-v)(u-w)+(v-w)(b^2(u-v)+c^2(w-u))):
-b^2(u-v)^2(a^2(u-v)(u-w)+(b^2(u-v)+c^2(u-w))(v-w))(v-w)^2:
-c^2(u-w)^2(v-w)^2(a^2(u-v)(u-w)+(v-w)(b^2(-u+v)+c^2(w-u))))
Este punto está sobre las circunferencias cA, cB y cC y es el conjugado antigonal de
Z = (-a^2(u-v)(u-w)+(b^2(-u+v)+c^2(u-w))(v-w) :
a^2(u-v)(u-w)+(b^2(u-v)+c^2(u-w))(v-w) :
a^2(u-v)(u-w)+(v-w)(b^2(-u+v)+c^2(-u+w))),
que está sobre la circunferencia anticomplementaria, de ecuación:
a^2 x^2+a^2 x y+b^2 x y+c^2 x y+b^2 y^2+a^2 x z+b^2 x z+c^2 x z+a^2 y z+b^2 y z+c^2 y z+c^2 z^2 = 0.
La curva donde están los centros de semejanza pasa los centros del triángulo X11607, X14366, X14887, conjugados antigonales de los centros X149, X249, X3448, respectivamente.
Para todo punto que P sobre una recta que pasa por el baricentro, la parábola 𝒫(P) es fija; por lo que da lugar a mismo centro semejanza S. En particular, para los puntos sobre la recta X2X37, S es X11607, para los puntos sobre la recta X2X6, S es X14366, y para los puntos sobre la recta X1X2, S es X14887.
- Viernes, 2 de marzo del 2018
Unos lugares geométricos
Dados un triángulo ABC, un punto P y un número real t, sea el triángulo A'B'C', tal que AA':A'P = BB':B'P = CC':C'P = t (ABC y A'B'C' son homotéticos, con centro de homotecia P y razón t/(t+1)).
Las perpendiculares pa, pb, pc por A', B', C' a AP, BP, CP intersecan a BC, CA, AB en D, E, F, respectivamente.
En coordenadas baricéntricas, si P (u:v:w) y a, b, c son las longitudes de los lados BC, CA, AB de ABC.
D (0 : a^2v(u+tu+v+tv+w-tw)+
c^2v(-(1+t)u+(-1+t)(v+w))-
b^2((1+t)u(v+2w)+(v+w)(v+tv+2w)) :
c^2((1+t)u(2v+w)+(v+w)(2v+w+tw))-
w(a^2(u+tu+v-tv+w+tw)-
b^2((1+t)u-(-1+t)(v+w)))),
E (u(c^2((-1+t)u-(1+t)v+(-1+t)w)+
b^2(u+tu+v+tv+w-tw))-
a^2((1+t)u^2+2w(v+tv+w)+u((1+t)v+(3+t)w)) : 0 :
c^2(2u^2+(1+t)w(v+w)+u(2(1+t)v+(3+t)w))-
w(a^2((-1+t)u-(1+t)v+(-1+t)w)+
b^2(u-tu+(1+t)(v+w)))),
F (-u(c^2(u+tu+v-tv+w+tw)+
b^2((-1+t)u+(-1+t)v-(1+t)w))+
a^2((1+t)u^2+2v(v+w+tw)+
u((3+t)v+(1+t)w)) : -b^2(2u^2+(1+t)v(v+w)+
u((3+t)v+2(1+t)w))+
v(a^2((-1+t)u+(-1+t)v-(1+t)w)+
c^2(u-tu+(1+t)(v+w))) : 0).
Los puntos D, E, F están alineados si el determinante formado por sus coordenadas es cero, esto es, si
K006(u,v,w) t - K004(u,v,w) = 0,
donde:
K004(x,y,z) = -a^4 c^2 x^2 y - 2 a^2 b^2 c^2 x^2 y +
3 b^4 c^2 x^2 y + 2 a^2 c^4 x^2 y - 2 b^2 c^4 x^2 y - c^6 x^2 y -
3 a^4 c^2 x y^2 + 2 a^2 b^2 c^2 x y^2 + b^4 c^2 x y^2 +
2 a^2 c^4 x y^2 - 2 b^2 c^4 x y^2 + c^6 x y^2 + a^4 b^2 x^2 z -
2 a^2 b^4 x^2 z + b^6 x^2 z + 2 a^2 b^2 c^2 x^2 z +
2 b^4 c^2 x^2 z - 3 b^2 c^4 x^2 z - a^6 y^2 z + 2 a^4 b^2 y^2 z -
a^2 b^4 y^2 z - 2 a^4 c^2 y^2 z - 2 a^2 b^2 c^2 y^2 z +
3 a^2 c^4 y^2 z + 3 a^4 b^2 x z^2 - 2 a^2 b^4 x z^2 - b^6 x z^2 -
2 a^2 b^2 c^2 x z^2 + 2 b^4 c^2 x z^2 - b^2 c^4 x z^2 + a^6 y z^2 +
2 a^4 b^2 y z^2 - 3 a^2 b^4 y z^2 - 2 a^4 c^2 y z^2 +
2 a^2 b^2 c^2 y z^2 + a^2 c^4 y z^2
K006(x,y,z)=
a^4 c^2 x^2 y - b^4 c^2 x^2 y - 2 a^2 c^4 x^2 y + c^6 x^2 y +
a^4 c^2 x y^2 - b^4 c^2 x y^2 + 2 b^2 c^4 x y^2 - c^6 x y^2 -
a^4 b^2 x^2 z + 2 a^2 b^4 x^2 z - b^6 x^2 z + b^2 c^4 x^2 z +
a^6 y^2 z - 2 a^4 b^2 y^2 z + a^2 b^4 y^2 z - a^2 c^4 y^2 z -
a^4 b^2 x z^2 + b^6 x z^2 - 2 b^4 c^2 x z^2 + b^2 c^4 x z^2 -
a^6 y z^2 + a^2 b^4 y z^2 + 2 a^4 c^2 y z^2 - a^2 c^4 y z^2
K004(x,y,z) = 0 es la ecuación baricéntrica de la cúbica de Darboux.
K006(x,y,z) = 0 es la ecuación la ortocúbica.
El lugar geométrico de P tal que los puntos D, E, F están alineados, para todo t, es la intersección de la cúbica de Darboux (K004= pK(X6, X20)) con la ortocúbica (K006=pK(X6, X4)), del catálogo de Bernard Gibert.
• Si P es el incentro las rectas DEF son paralelas a la dirección de X513, del del .
• Si P es el circuncentro, la envolvente de las rectas DEF es la .
• Si P es el ortocentro, DEF es la recta del infinito.
• Otros puntos de intersección de las cúbicas K004 y K006 son los . Las rectas DEF correspondientes a cada uno de ellos, Ia, Ib, Ic, son paralelas entre sí, con puntos del infinito
Ao(a(-b+c) : b(a+c) : -c(a+b)),
Bo(-a(b+c) : b(a-c) : c(a+b)),
Co(a(b+c) : -b(a+c) : c(-a+b)).
El triángulo formado por las rectas AAo, BBo, CCo es perspectivo con ABC, con centro de perspectividad X37 ( del incentro y el baricentro).
Las tres rectas correspondientes a los exincentros, para t = r/(r+2R), donde r y R son los radios de las circunferencias inscrita y circunscrita a ABC, son concurrentes en X55 (centro de homotecia interior de las circunferencias inscrita y circunscrita).
Para todo punto P(u:v:w) existe un único t, tal que los puntos D, E, F están sobre una misma recta dp.
El valor de t es tp=K004(u,v,w)/K006(u,v,w) y la ecuación de la recta dp es:
(a^4vw(v-w)+(b^2-c^2)u^2(c^2v+b^2w)+a^2(-b^2w(u^2+2uw+v(v+w))+c^2v(u^2+2uv+w(v+w))))x / (b^2u-c^2u+a^2(v-w)) + ··· = 0.
Por el , ABC y el triángulo formado por las perpendiculares pa, pb, pc son perspectivos, con centro de perspectividad:
Q ((a^2(-v+w)+(b^2-c^2)(v+w))/(
a^2(c^2v-b^2w)+(b^2-c^2)(c^2v+b^2w)) : ... : ...).
Si P se mueve sobre una recta que pasa por el circuncentro, Q queda sobre esa recta.
Si P se mueve sobre la , el punto Q permanece fijo en el ortocentro.
El lugar geométrico de P tal que las perpendiculares pa, pb, pc son concurrentes es la circunferencia circunscrita. Cuando P se mueve sobre esta circunferencia, el lugar geométrico del punto de concurrencia Q es la Tercera cúbica Musselman (K028 en el catálogo ce Bernard Gibert).
En la siguiente lista los pares {i,j} significa que {Xi, Xj} son centros del triángulo, tales que Xi es un punto finito y Xj es el de dXi.
{2, 5485}, {4, 2}, {5, 13582}, {13, 396}, {14, 395}, {15, 6}, {16, 6}, {20, 4}, {36, 57}, {40, 57}, {64, 3}, {74, 323}, {84, 9}, {98, 3978}, {103, 2340}, {104, 4358}, {111, 13492}, {147, 420}, {371, 8577}, {372, 8576}, {399, 323}, {484, 81}, {616, 3180}, {617, 3181}, {1075, 2}, {1113, 2592}, {1114, 2593}, {1157, 1994}, {1379, 5638}, {1380, 5639}, {1490, 282}, {1498, 1073}, {1745, 2}, {2130, 3349}, {2131, 3350}, {3182, 3342}, {3183, 3344}, {3345, 223}, {3346, 1249}, {3347, 3341}, {3348, 3343}, {3353, 3352}, {3354, 3351}, {3355, 3356}, {3362, 2}, {3479, 3181}, {3480, 3180}, {3637, 14481}, {8172, 396}, {8173, 395}, {13855, 2}.
La recta
dp es la recta del infinito si y solo si
P está en la cúbica de
McCay.
El lugar geométrico del punto
P tal que
dp pasa por
P es una
quíntica
( a^2 b^2 c^4 x^4 y+b^4 c^4 x^4 y-b^2 c^6 x^4 y+a^4 c^4 x^3 y^2+a^2 b^2 c^4 x^3 y^2-2 a^2 c^6 x^3 y^2-b^2 c^6 x^3 y^2+c^8 x^3 y^2-a^2 b^2 c^4 x^2 y^3-b^4 c^4 x^2 y^3+a^2 c^6 x^2 y^3+2 b^2 c^6 x^2 y^3-c^8 x^2 y^3-a^4 c^4 x y^4-a^2 b^2 c^4 x y^4+a^2 c^6 x y^4-a^2 b^4 c^2 x^4 z+b^6 c^2 x^4 z-b^4 c^4 x^4 z+a^2 b^4 c^2 x^3 y z-b^6 c^2 x^3 y z-a^2 b^2 c^4 x^3 y z+b^2 c^6 x^3 y z+a^6 c^2 x^2 y^2 z+a^4 b^2 c^2 x^2 y^2 z-a^2 b^4 c^2 x^2 y^2 z-b^6 c^2 x^2 y^2 z-2 a^4 c^4 x^2 y^2 z+2 b^4 c^4 x^2 y^2 z+a^2 c^6 x^2 y^2 z-b^2 c^6 x^2 y^2 z+a^6 c^2 x y^3 z-a^4 b^2 c^2 x y^3 z+a^2 b^2 c^4 x y^3 z-a^2 c^6 x y^3 z-a^6 c^2 y^4 z+a^4 b^2 c^2 y^4 z+a^4 c^4 y^4 z-a^4 b^4 x^3 z^2+2 a^2 b^6 x^3 z^2-b^8 x^3 z^2-a^2 b^4 c^2 x^3 z^2+b^6 c^2 x^3 z^2-a^6 b^2 x^2 y z^2+2 a^4 b^4 x^2 y z^2-a^2 b^6 x^2 y z^2-a^4 b^2 c^2 x^2 y z^2+b^6 c^2 x^2 y z^2+a^2 b^2 c^4 x^2 y z^2-2 b^4 c^4 x^2 y z^2+b^2 c^6 x^2 y z^2+a^6 b^2 x y^2 z^2-2 a^4 b^4 x y^2 z^2+a^2 b^6 x y^2 z^2-a^6 c^2 x y^2 z^2+a^2 b^4 c^2 x y^2 z^2+2 a^4 c^4 x y^2 z^2-a^2 b^2 c^4 x y^2 z^2-a^2 c^6 x y^2 z^2+a^8 y^3 z^2-2 a^6 b^2 y^3 z^2+a^4 b^4 y^3 z^2-a^6 c^2 y^3 z^2+a^4 b^2 c^2 y^3 z^2-a^2 b^6 x^2 z^3+b^8 x^2 z^3+a^2 b^4 c^2 x^2 z^3-2 b^6 c^2 x^2 z^3+b^4 c^4 x^2 z^3-a^6 b^2 x y z^3+a^2 b^6 x y z^3+a^4 b^2 c^2 x y z^3-a^2 b^4 c^2 x y z^3-a^8 y^2 z^3+a^6 b^2 y^2 z^3+2 a^6 c^2 y^2 z^3-a^4 b^2 c^2 y^2 z^3-a^4 c^4 y^2 z^3+a^4 b^4 x z^4-a^2 b^6 x z^4+a^2 b^4 c^2 x z^4+a^6 b^2 y z^4-a^4 b^4 y z^4-a^4 b^2 c^2 y z^4 = 0)
𝒬 que pasa por los vértices de
ABC y del .
Los vértices de
ABC son puntos de inflexión y las tangentes en ellos concurren en el circuncentro, que es punto doble.
La quíntica 𝒬 pasa por el incentro y los exincentros.
- Jueves, 22 de febrero del 2018
Focos de parábolas y cónicas inscritas
Dados un triángulo ABC y un punto P, sean el de P y el de .
Se denota por ℘a la parábola tangente a AB, a AC y a PbPc en A1 (Paris Pamfilos.- A Gallery of Conics by Five Elements. Forum Geometricorum Volume 14 (2014) 295–348.§13.2. Parabola by 1 tangent-at, 2 tangents (1P4T1)1).
Esta parábola es la envolvente de la recta variable que determina, sobre AB y AC, un segmento cuyo punto medio está sobre PbPc. Así, si M=BC∩PbPc y M' es el punto de intersección de AB con la reflexión de AC en M, la recta MM' es tangente a ℘a. Por tanto, esta parábola puede ser construida a partir de cuatro tangentes: AB, AC, MM' y PbPc.
Si (u:v:w) son las coordenadas baricéntricas de P, la ecuación tangencial del haz de cónicas tangentes a AB, AC, PbPc y a la es:
U (u (2u+v+w)U + v(u+w)V + w(u+v)W) + λ(u U + v V) (u U + w W) = 0.
La parábola ℘a de este haz (tangente a la recta del infinito) se obtiene para λ=-2. Su ecuación puntual es:
4v^2w^2x^2 + w^2(u-v)^2y^2 + v^2(u-w)^2z^2 -2vw(u^2+vw+3u(v+w))yz + 4v^2w(w-u)zx + 4vw^2(v-u)xy = 0.
El foco de ℘a es:
Fa = (c^2uv(u+w)(v+w)-w(u+v)(a^2v(u+w)-
b^2u(v+w)) : 2b^2vw^2(u+v) : 2c^2v^2w(u+w)).
Y la directriz es:
da: 2vw(-a^2+b^2+c^2)x + ((a^2-b^2)(u-v)w-
c^2(vw+u(2v+w)))y + (a^2v(u-w)+c^2v(-u+w)-b^2(uv+2uw+vw))z = 0.
Procediendo cíclicamente, se obtienen las parábolas ℘b y ℘c, sus focos Fb y Fc, y sus directrices db y dc.
Los triángulos ABC y son perspectivos, y el centro de perspectividad F es el del centro Q de la cónica inscrita C(P) de P.
Las coordenadas del centro de perspectividad son:
F = (a^2/(u(v+w)) : b^2/(v(w+u)) : c^2/(w(u+v))).
El triángulo formado por la directrices
da,
db y
dc es perspectivo con
ABC, con centro de perspectividad
D = (1/(a^4 v w (-u^2 + 3 v w + 3 u (v + w)) +
2 a^2 (b^2 w (-2 v^2 w + u^2 (v + w) - u v (3 v + w)) +
c^2 v (-2 v w^2 + u^2 (v + w) - u w (v + 3 w)))-
c^4 v (u (v - 3 w) w - v w^2 + u^2 (2 v + w)) -
b^4 w (-v^2 w + u v (-3 v + w) + u^2 (v + 2 w)) -
2 b^2 c^2 (v^2 w^2 + u v w (v + w) + u^2 (v^2 + 3 v w + w^2))) : ... : ...).
ALGUNAS SITUACIONES PARTICULARES:
• Cuando P está sobre la , C(P) es una parábola (su centro está en la recta del infinito) y, por tanto, F queda sobe la circunferencia circunscrita. En este caso, los triángulos ABC y son simétricos respecto a F, y las directrices da, db y dc son paralelas (perpendiculares al eje de la parábola C(P)).
• Cuando P está sobre la
cuártica
( c^2 x^2 y^2 + a^2 x^2 y z + b^2 x^2 y z + c^2 x^2 y z + a^2 x y^2 z +
b^2 x y^2 z + c^2 x y^2 z + b^2 x^2 z^2 + a^2 x y z^2 + b^2 x y z^2 +
c^2 x y z^2 + a^2 y^2 z^2 = 0
Esta cuártica pasa por los centros del triángulo X8047, X9473, X13485, X13573, X13574.
)
de la elipse circunscrita de Steiner,
los focos Fa, Fb y Fc están sobre una recta tangente a C(P).
- Martes, 20 de febrero del 2018
El centro X(1000) y el triángulo de contacto interior
Theorem 18 (Florentin Smarandache and Ion Pătraşcu.- The Geometry of Homological Triangles.)
Given the triplet of triangles (T
1, T
2, T
3) such that (T
1, T
2)
are homological, (T
2, T
3) are homological, and the two homology having the same homological axis, then:
i) The triplet (T
1, T
2, T
3) is homological(*). The homology axis of triangles (T
1, T
3) coincide with the previous homological axis.
ii) The homological centers of the triangles (T
1, T
2), (T
2,T
3)
and (T
1, T
3) are collinear or coincide.
(*) The triplet (T1, T2, T3) is a triplet of homological triangles if the triangles (T1, T2) are homological, the triangles (T2, T3) are homological and the triangles (T1, T3) are homological.
Dado un triángulo ABC, sean DEF el , D', E' y F', los puntos donde las rectas AD, BE y CF vuelven a cortar a la circunferencia inscrita a ABC.
Se denotan por ea, eb y ec los ejes radicales de la circunferencia inscrita y las circunferencias de diámetros AD, BE y CF, respectivamente. Sea el triángulo formado por estas tres rectas.
Las rectas pa, pb y pc son las perpendiculares por D', E' y F' a AD, BE y CF, respetivamente. Sea el triángulo delimitado por las rectas pa, pb y pc.
En coordenadas baricéntricas, se tienen las ecuaciones de las rectas:
EF: (-a+b+c)x + (-a+b-c)y + (-a-b+c)z = 0.
ea: (a-b-c)(a^2-ab-ac)x +(a-b-c)(-ab+b^2+ac-
2bc+c^2)y + (a-b-c)(ab+b^2-ac-2bc+c^2)z = 0,
pa: a(-a+b+c)x -(2a+b-c)(a-b+c)y -(a+b-c)(2a-b+c)z = 0.
Estas tres rectas concurren en:
A' = (2 (b - c) : a - b - c : -a + b + c).
Similarmente, se deducen las coordenadas de B' y C'. Estos tres puntos están sobre la recta
(3a^2-4a(b+c)+(b+c)^2)x + (a^2-4a b+3b^2+2a c-
4b c+c^2)y + (a^2+b^2+2a(b-2c)-4b c+3c^2)z = 0,
que pasa por los centros del triángulo X3667, X3676, X3999, X4106, X4887, X4897, X4927. Por tanto, los triángulos DEF, y forma una terna perspectiva. El centro de perspectividad de DEF y es el incentro; el centro de perspectividad de y es X1000; y el centro de perspectividad de DEF y es:
W = 3 X1 - 2 X1000 = ( (a-2b-2c)(5a-b-c)/(b+c-a) : ... : ...),
que tiene números de búsqueda en
(0.288552216349359, 0.763397793429532, 2.97898037121808), es la reflexión de Xi en Xj para los índices {i,j}: {1, 11041}, {1000, 14563}, {3632, 11525}, {8275, 1}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1, 631}, {7, 519}, {8, 3947}, {46, 7966}, {57, 1317}, {65, 3633}, {80, 1537}, {145, 3339}, {226, 4677}, {517, 14100}, {952, 4312}, {1071, 5903}, {1405, 4752}, {2099, 3679}, {2802, 7672}, {3241, 13462}, {3243, 5854}, {3244, 3361}, {3340, 3632}, {3476, 4031}, {3485, 4668}, {3621, 3671}, {3622, 4675}, {3624, 11011}, {3626, 4323}, {3635, 15519}, {3880, 15185}, {3885, 12432}, {4304, 7991}, {4355, 10944}, {4669, 5226}, {4701, 5261}, {4816, 9578}, {5561, 9897}, {5586, 10106}, {5722, 5763}, {5804, 10573}, {5844, 11529}, {9589, 10950}, {9613, 10052}, {9614, 11280}, {11009, 15079}.
Se tienen estas otras expresiones:
W = 2(r+4R) X7 - 3r X4900 = 5r X8 - 2(3r+2R) X3947,
donde r y R son los radios de las circunferencias inscrita y circunscrita a ABC, respectivamente.
- Viernes, 16 de febrero del 2018
Una construcción de la cúbica de Neuberg
X(8431) is the perspector of the triangle pairs {T1, T24} and {T3, T11} in
Table 19-1 of Bernard Gibert’s Cubics in the Triangle Plane.
T3 = A'B'C' = .
T9 = = of .
T11 = is the cevian triangle of X(74) wrt T9.
X(8431) = (a^2(b^ 2+c^2-a^ 2)/(3 a^12-7 a^10 (b^2+c^2)-a^8 (b^4-21 b^2 c^2+c^4)+2 a^6 (7 b^6-9 b^4 c^2-9 b^2 c^4+7 c^6)-a^4 (b^2-c^2)^2 (11 b^4+24 b^2 c^2+11 c^4)+a^2 (b^2-c^2)^2 (b^6+11 b^4 c^2+11 b^2 c^4+c^6) +(b^2-c^2)^4 (b^4+b^2 c^2+c^4)) : ... : ...).
T24 = , A6 = X(4) Ao ∩ X(8431) A, ...
Las coordenadas baricéntricas de A6 son:
(a^16 + 3 a^8 b^2 c^2 (b^2 - c^2)^2 - 3 a^14 (b^2 + c^2) -
a^6 (b^2 - c^2)^2 (b^2 + c^2)^3 - (b^2 - c^2)^6 (b^4 + b^2 c^2 +
c^4) + a^12 (2 b^4 + 5 b^2 c^2 + 2 c^4) -
a^4 (b^2 - c^2)^4 (2 b^4 + 5 b^2 c^2 + 2 c^4) +
a^10 (b^6 - 3 b^4 c^2 - 3 b^2 c^4 + c^6) +
3 a^2 (b^2 - c^2)^4 (b^6 + b^4 c^2 + b^2 c^4 + c^6) :
b^2 (a^14 +
a^12 (-4 b^2 + 2 c^2) + a^10 (6 b^4 + 5 b^2 c^2 - 10 c^4) +
a^2 (b^2 - c^2)^4 (4 b^4 + 5 b^2 c^2 - 4 c^4) - (b^2 -
c^2)^5 (b^4 + 5 b^2 c^2 + 3 c^4) +
a^8 (-5 b^6 - 16 b^4 c^2 + 18 b^2 c^4 + 3 c^6) -
2 a^4 (b^2 - c^2)^2 (3 b^6 - 5 b^4 c^2 + 6 b^2 c^4 + 4 c^6) +
a^6 (5 b^8 - 2 b^6 c^2 + 18 b^4 c^4 - 34 b^2 c^6 +
13 c^8)) :
c^2 (a^14 + 2 a^12 (b^2 - 2 c^2) -
a^2 (b^2 - c^2)^4 (4 b^4 - 5 b^2 c^2 - 4 c^4) + (b^2 -
c^2)^5 (3 b^4 + 5 b^2 c^2 + c^4) +
a^10 (-10 b^4 + 5 b^2 c^2 + 6 c^4) +
a^8 (3 b^6 + 18 b^4 c^2 - 16 b^2 c^4 - 5 c^6) -
2 a^4 (b^2 - c^2)^2 (4 b^6 + 6 b^4 c^2 - 5 b^2 c^4 + 3 c^6) +
a^6 (13 b^8 - 34 b^6 c^2 + 18 b^4 c^4 - 2 b^2 c^6 + 5 c^8))).
Se considera un punto M sobre la
cónica
( b^2 c^2 (b^2-c^2) (a^6-a^2 (b^2-c^2)^2-a^4 (b^2+c^2)+(b^2-c^2)^2 (b^2+c^2)) (3 a^12-7 a^10 (b^2+c^2)-a^8 (b^4-21 b^2 c^2+c^4)+(b^2-c^2)^4 (b^4+b^2 c^2+c^4)-a^4 (b^2-c^2)^2 (11 b^4+24 b^2 c^2+11 c^4)+a^2 (b^2-c^2)^2 (b^6+11 b^4 c^2+11 b^2 c^4+c^6)+2 a^6 (7 b^6-9 b^4 c^2-9 b^2 c^4+7 c^6))^2x^2-a^2 (b^2-c^2) (-a^2+b^2+c^2)^2 (2 a^28-13 a^26 (b^2+c^2)-(b^2-c^2)^10 (b^4+b^2 c^2+c^4)^2+a^24 (35 b^4+46 b^2 c^2+35 c^4)-a^22 (53 b^6+69 b^4 c^2+69 b^2 c^4+53 c^6)+a^20 (61 b^8+152 b^6 c^2-160 b^4 c^4+152 b^2 c^6+61 c^8)+a^2 (b^2-c^2)^8 (5 b^10+17 b^8 c^2+41 b^6 c^4+41 b^4 c^6+17 b^2 c^8+5 c^10)-a^6 (b^2-c^2)^6 (5 b^10+91 b^8 c^2+420 b^6 c^4+420 b^4 c^6+91 b^2 c^8+5 c^10)-2 a^14 (b^2-c^2)^2 (39 b^10+33 b^8 c^2+722 b^6 c^4+722 b^4 c^6+33 b^2 c^8+39 c^10)-a^18 (77 b^10+353 b^8 c^2-357 b^6 c^4-357 b^4 c^6+353 b^2 c^8+77 c^10)+8 a^12 (b^2-c^2)^2 (6 b^12-24 b^10 c^2+19 b^8 c^4+250 b^6 c^6+19 b^4 c^8-24 b^2 c^10+6 c^12)-a^4 (b^2-c^2)^6 (7 b^12+18 b^10 c^2-77 b^8 c^4-184 b^6 c^6-77 b^4 c^8+18 b^2 c^10+7 c^12)+a^8 (b^2-c^2)^4 (25 b^12+218 b^10 c^2-95 b^8 c^4-840 b^6 c^6-95 b^4 c^8+218 b^2 c^10+25 c^12)+a^16 (93 b^12+324 b^10 c^2+434 b^8 c^4-1670 b^6 c^6+434 b^4 c^8+324 b^2 c^10+93 c^12)-a^10 (b^2-c^2)^2 (35 b^14+25 b^12 c^2-863 b^10 c^4+1059 b^8 c^6+1059 b^6 c^8-863 b^4 c^10+25 b^2 c^12+35 c^14))yz + ... = 0)
Ψ que pasa por los cinco puntos A6, B6, C6, X4 y X8431.
La cónica circunscrita C(M) a ABC, tangente en X8431 a la recta MX8431, pasa por los otros dos puntos P, P' en los que la recta MX4 vuelve a cortar a la cúbica de Neuberg.
- Lunes, 12 de febrero del 2018
Una caracterización de la cúbica de Neuberg
The
Neuberg cubic is the locus of point M such that the triangles ABC and MaMbMc are in perspective, where Ma, Mb, Mc are the reflections of M about the sidelines of ABC.
Dados un triángulo ABC y un punto P, no situado en la recta del infinito, la recta que pasa por el baricentro y el simediano del triángulo PBC corta a BC en A'. Los puntos B' y C' de definen análogamente.
Si (u:v:w) son las coordenadas baricéntricas de P, el baricentro Ga y el simediano Ka de PBC son, respectivamente:
Ga (u:u+2v+w : u+v+2w),
Ka (a^2u(u+v+w) : b^2u(u+v)+v(-c^2u+a^2(2u+2v+w)) :
c^2u(u+w)+w(-b^2u+a^2(2u+v+2 w)))
y el punto de intersección de BC y GaKa es:
A' (0 : u(-c^2v+b^2(u+v))+a^2(u^2+w(2v+w)+u(v+2w)) : u(-b^2w+c^2(u+w))+a^2(u^2+u(2v+w)+v(v+2w))).
Los triángulos
ABC y
A'B'C' son perspectivos si y solo si
P está sobre la cúbica de Neuberg.
El centro de perspectividad F(P)=Q queda sobre la recta que pasa por el baricentro y simediano de ABC.
{{3,30},2}; {{1276,1277},86}; {{13,5669},298}; {{14,5668},299}; {{15,8174},302}; {{16,8175},303}; {{1,3465},333}; {{4,3484},343}; {{617,1338},395}; {{616,1337},396}; {{74,5667},11064}.
Si Q' es la intersección de PX4 y X2X6, la correspondencia Q ↦ Q' es una involución con puntos dobles X2 y X193 ( del ortocentro y el baricentro).
Si Q = X2 + t X6. entonces Q' = (2+3t) X2 - 2t X6.
El lugar geométrico de la proyección ortogonal
M de
Q sobre
PX
4, cuando
P varía sobre la cúbica de Neuberg, es un
cúbica
( (-2 a^6 b^2+5 a^4 b^4-4 a^2 b^6+b^8+2 a^6 c^2-4 a^2 b^4 c^2+2 b^6 c^2-5 a^4 c^4+4 a^2 b^2 c^4+4 a^2 c^6-2 b^2 c^6-c^8) x^3+(-2 a^6 b^2+5 a^4 b^4-4 a^2 b^6+b^8+2 a^6 c^2-4 a^4 b^2 c^2+2 a^2 b^4 c^2-a^4 c^4+4 a^2 b^2 c^4-2 b^4 c^4-2 a^2 c^6+c^8) x^2 y+(-a^8+4 a^6 b^2-5 a^4 b^4+2 a^2 b^6-2 a^4 b^2 c^2+4 a^2 b^4 c^2-2 b^6 c^2+2 a^4 c^4-4 a^2 b^2 c^4+b^4 c^4+2 b^2 c^6-c^8) x y^2+(-a^8+4 a^6 b^2-5 a^4 b^4+2 a^2 b^6-2 a^6 c^2+4 a^4 b^2 c^2-2 b^6 c^2-4 a^2 b^2 c^4+5 b^4 c^4+2 a^2 c^6-4 b^2 c^6+c^8) y^3+(-2 a^6 b^2+a^4 b^4+2 a^2 b^6-b^8+2 a^6 c^2+4 a^4 b^2 c^2-4 a^2 b^4 c^2-5 a^4 c^4-2 a^2 b^2 c^4+2 b^4 c^4+4 a^2 c^6-c^8) x^2 z+(-2 a^6 b^2+2 a^2 b^6+2 a^6 c^2-2 b^6 c^2-2 a^2 c^6+2 b^2 c^6) x y z+(a^8-2 a^6 b^2-a^4 b^4+2 a^2 b^6+4 a^4 b^2 c^2-4 a^2 b^4 c^2-2 b^6 c^2-2 a^4 c^4+2 a^2 b^2 c^4+5 b^4 c^4-4 b^2 c^6+c^8) y^2 z+(a^8-2 a^4 b^4+b^8-4 a^6 c^2+2 a^4 b^2 c^2+4 a^2 b^4 c^2-2 b^6 c^2+5 a^4 c^4-4 a^2 b^2 c^4-b^4 c^4-2 a^2 c^6+2 b^2 c^6) x z^2+(-a^8+2 a^4 b^4-b^8+2 a^6 c^2-4 a^4 b^2 c^2-2 a^2 b^4 c^2+4 b^6 c^2+a^4 c^4+4 a^2 b^2 c^4-5 b^4 c^4-2 a^2 c^6+2 b^2 c^6) y z^2+(a^8+2 a^6 b^2-2 a^2 b^6-b^8-4 a^6 c^2-4 a^4 b^2 c^2+4 a^2 b^4 c^2+4 b^6 c^2+5 a^4 c^4-5 b^4 c^4-2 a^2 c^6+2 b^2 c^6) z^3 = 0)
Ψ, con punto nodal el ortocentro.
Esta cúbica pasa por X2, X4 (punto nodal), X193, X542 (punto del infinito de la recta de Euler del ,
X6792 (proyección ortogonal de X4 en X2X6).
Ψ es una (Bernard Gibert, comunicación personal), inversa en de la
hipérbola
( a^8 x y-2 a^6 b^2 x y+2 a^2 b^6 x y-b^8 x y-2 a^6 c^2 x y+6 a^4 b^2 c^2 x y-6 a^2 b^4 c^2 x y+2 b^6 c^2 x y-a^4 c^4 x y+b^4 c^4 x y+2 a^2 c^6 x y-2 b^2 c^6 x y-a^8 x z+2 a^6 b^2 x z+a^4 b^4 x z-2 a^2 b^6 x z+2 a^6 c^2 x z-6 a^4 b^2 c^2 x z+2 b^6 c^2 x z+6 a^2 b^2 c^4 x z-b^4 c^4 x z-2 a^2 c^6 x z-2 b^2 c^6 x z+c^8 x z+2 a^6 b^2 y z-a^4 b^4 y z-2 a^2 b^6 y z+b^8 y z-2 a^6 c^2 y z+6 a^2 b^4 c^2 y z-2 b^6 c^2 y z+a^4 c^4 y z-6 a^2 b^2 c^4 y z+2 a^2 c^6 y z+2 b^2 c^6 y z-c^8 y z = 0)
rectangular circunscrita a ABC, que pasa por los centros X(468), X(2501), X(5203), X(10603), X(14052).
El F de Ψ es el punto medio del ortocentro y X691 (reflexión del en la ):
F = ( (2 a^6 - 2 a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2) +
a^2 (b^4 + c^4)) (a^6 (b^2 + c^2) -
a^4 (b^2 + c^2)^2 + (b^2 - c^2)^2 (b^4 - b^2 c^2 + c^4) -
a^2 (b^6 - 2 b^4 c^2 - 2 b^2 c^4 + c^6)) : ... : ...),
que tiene números de búsqueda en
(-3.15241018411752, -1.97512841043429, 6.46301962026235), de X842, punto medio de Xi y Xj para los índices {i,j}: {4, 691}, {1550, 14999}, {2080, 7574}; reflexión de Xi en Xj para los índices {i,j}: {5099, 5}, {7575, 14693}, {13449, 10297}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2, 476}, {4, 691}, {5, 5099}, {11, 6023}, {12, 6027}, {23, 137}, {30, 115}, {113, 512}, {114, 523}, {122, 5159}, {125, 511}, {127, 625}, {136, 468}, {249, 12383}, {403, 5139}, {542, 1550}, {1560, 2501}, {2080, 7574}, {2696, 14659}, {2697, 2715}, {3153, 14712}, {3635, 15519}, {5094, 14687}, {5189, 11792}, {5512, 11799}, {7575, 14693}, {8705, 12494}, {9151, 15820}, {9218, 10733}, {9970, 15899}, {10297, 13449}, {10556, 15398}, {11007, 15819}.
El punto F ha sido incorporado a ETC con el número X(16188).
- Sábado, 10 de febrero del 2018
Una caracterización de la quíntica Q068
Dados un triángulo ABC y un punto P (no situado en la recta del infinito), sean Q es de P y el de P.
Se denota por Φa, Φb y Φc las cónicas que pasan por los respectivos cinco puntos {A,P,Q,Pb,Pc}, {B,P,Q,Pc,Pa} y {C,P,Q,Pa,Pb}.
Las tangentes en
P a las cónicas Φ
a, Φ
b y Φ
c son coincidentes si y sólo si
P está sobre la
quíntica
( a^2 b^2 c^4 x^4 y+b^4 c^4 x^4 y-b^2 c^6 x^4 y+2 a^2 b^2 c^4 x^3 y^2-2 a^2 b^2 c^4 x^2 y^3-a^4 c^4 x y^4-a^2 b^2 c^4 x y^4+a^2 c^6 x y^4-a^2 b^4 c^2 x^4 z+b^6 c^2 x^4 z-b^4 c^4 x^4 z+2 a^4 b^2 c^2 x^2 y^2 z-2 a^2 b^4 c^2 x^2 y^2 z-a^6 c^2 y^4 z+a^4 b^2 c^2 y^4 z+a^4 c^4 y^4 z-2 a^2 b^4 c^2 x^3 z^2-2 a^4 b^2 c^2 x^2 y z^2+2 a^2 b^2 c^4 x^2 y z^2+2 a^2 b^4 c^2 x y^2 z^2-2 a^2 b^2 c^4 x y^2 z^2+2 a^4 b^2 c^2 y^3 z^2+2 a^2 b^4 c^2 x^2 z^3-2 a^4 b^2 c^2 y^2 z^3+a^4 b^4 x z^4-a^2 b^6 x z^4+a^2 b^4 c^2 x z^4+a^6 b^2 y z^4-a^4 b^4 y z^4-a^4 b^2 c^2 y z^4 = 0)
Q068 (catálogo Bernard Gibert).
- Viernes, 9 de febrero del 2018
El centro del triángulo X(2163)
Dado un triángulo ABC, sea su .
La mediatriz de BC interseca a la bisectrices interiores en B y C en los puntos A2 y A3, respectivamente, y a las bisectrices exteriores en B y C en A'2 y A'3, respectivamente.
Se denotan por Oab y Oac los circuncentros de los triángulos IbA2A'3 y IcA3A'2, respectivamente. Se definen Obc, Oba, Oac, Ocb, cíclicamente.
En coordenadas baricéntricas:
Oab (-a^3 : b(a^2+a(b+c)-(b+c)^2) : c(-a^2+a(b+c)+(b+c)^2)),
Oac (-a^3 : b(-a^2+a(b+c)+(b+c)^2) : c(a^2+a(b+c)-(b+c)^2)).
El triángulo A'B'C' formado por las rectas OabOac, ObcOba, OcaOcb
es perspectivo con ABC, con centro de perspectividad X2163.
El centro de la
( 2b^3c^3(b+c)x^2+2a^3c^3(a+c)y^2+2a^3b^3(a+
b)z^2+a^3bc(4a^2+5bc+4a(b+c))yz+ab^3c(4b(b+c)+
a(4b+5c))zx+abc^3(4c(b+c)+a(5b+4c))xy = 0)
de ABC y A'B'C' es:
W = ( a^2(16a^6+32(b+c)a^5+8(2b^2+7bc+2c^2)a^4+4(-4b^3+b^2c+
bc^2-4c^3)a^3+(-32b^4-32b^3c+b^2c^2-32bc^3-
32c^4)a^2+(-16b^5-32b^4c+7b^3c^2+7b^2c^3-32bc^4-
16c^5)a-4bc(b+c)^2(5b^2-9bc+5c^2)) : ... : ...),
que tiene números de búsqueda en
(-2.68855439782344, -3.72735418621320, 7.46201171751203).
- Miércoles, 7 de febrero del 2018
El centro del triángulo X(15262)
Ver PDF
- Lunes, 5 de febrero del 2018
Dos pares bicéntricos y la segunda circunferencia de Lemoine
Dado un triángulo ABC con K,
la a BC, respecto a AB y a AC, corta en Ba y Ca a AC y AB, respectivamente;
la antiparalela a CA, respecto a BC y a BA, corta en Cb y Ab a BA y BC, respectivamente;
la antiparalela a AB, respecto a CA y a CB, corta en Ac y Bc a CB y CA, respectivamente.
Los seis puntos así determinados son cocíclicos estando en la que se conoce como segunda circunferencia de Lemoine.
Ab = (0::c^2),
Bc = (a^2:0:SA),
Ca = (SB:b^2:0).
Ac = (0:b^2:SB),
Ba = (SC:0:c^2),
Cb = (a^2:SA:0).
El ortocentro PH=(SB:SC:SA) de y el ortocentro UH=(SC:SA:SB) de , forman el P(45) de la lista de Clark Kimberling.
El baricentro
PG = (3a^2-b^2+c^2 : a^2+3b^2-c^2 : -a^2+b^2+3c^2)
de y el baricentro
UG = (3a^2+b^2-c^2 : -a^2+3b^2+c^2 : a^2-b^2+3c^2)
de , forman un par bicéntrico.
• El de PG y UG es X1285.
X(1285) is the homothetic center of the of X(2) and the of X(6). (Darij Grinberg,
Hyacinthos #6577, 2/21/03).
• El producto trilineal de PG y UG (producto baricéntrico de X75×X1285 es
W = 4R(3r^2+6rR-s^2) X31 - r(r^2-4R^2+s^2) X92
W = ( (9a^4-(b^2-c^2)^2)/a : ... : ...),
y tiene números de búsqueda en
(0.207252394186685, 0.971877440313071, 2.87217130283532).
• La suma baricéntrica de PG y UG es el simediano.
• La diferencia baricéntrica de PG y UG es el del foco de la .
• La de PG y UG es
Z = ( a^2(a^4-a^2(b^2+c^2)+10b^2c^2) : ... : ...),
que tiene números de búsqueda en
(2.41693613610358, 1.42551075158512, 1.53826343722380) ; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {2, 98}, {3, 5646}, {6, 5544}, {25, 14810}, {373, 576}, {394, 5097}, {511, 3066}, {549, 8717}, {567, 5070}, {575, 6090}, {578, 3628}, {1092, 5067}, {1350, 3819}, {1351, 5943}, {1656, 13352}, {1995, 3098}, {3090, 13346}, {3124, 8585}, {3231, 5039}, {3525, 13347}, {3526, 6759}, {3533, 10984}, {4550, 12041}, {5034, 9225}, {5643, 5645}, {5888, 7492}, {7486, 11424}, {7496, 10546}, {8722, 11328}, {10117, 11204}, {10170, 11438}, {10219, 10601}, {10539, 13339}, {11484, 13598}.
• La de PG y UG es el conjugado isogonal del .
• El de la recta PGUG es el punto de Tarry.
- Jueves, 1 de febrero del 2018
Punto fijo de una afinidad
Recordando a Marta (hace 19)
Dados un triángulo ABC con circuncentro O=X3 y centro de la N=X5. La interseca a la circunferencia circunscrita en X1113 y X1114, y a la circunferencia de los nueve puntos en X1312 y X1313.
Como se vio en: Rectas de Euler concurrentes asociadas a los centros X(1113) y X(1114):
X10287 es la intersección de la perpendicular por N a la recta de Euler con la recta que pasa por O y tiene la dirección del de X1114.
X10288 es intersección de la perpendicular por N a la recta de Euler con la recta que pasa por O y tiene la dirección del conjugado isogonal de X1113
Sean el ,
A' la intersección de la reflexión de AB en TaTc con a la reflexión de AC en TaTb,
B' la intersección de la reflexión de BC en TbTa con a la reflexión de BA en TbTc, y
C' la intersección de la reflexión de CA en TcTb con a la reflexión de CB en TcTa.
A' =(a^2(a^2-b^2)(a^2-c^2) : -2b^2(a^2-c^2) : -2c^2(a^2-b^2)SC)
es la intersección de las rectas 2c^2SCx + a^2(a^2-c^2)z = 0, 2b^2SBx + a^2(a^2-b^2)y = 0
El punto fijo (propio) de la transformación afín σ que aplica ABC en A'B'C' es la intersección de las rectas X1312X10287 y X1313X10288.
La matriz asociada a σ es:

Los valores propios del polinomio característico y puntos fijos asociados son:
-16a^2b^2c^2S^4|OH|^2 → X13764,
-a^2b^2c^2(3SA^2-S^2)(3SB^2-S^2)(3SC^2-S^2) → X526 (conjugado isogonal de X476, ),
a^2b^2c^2(3SA^2-S^2)(3SB^2-S^2)(3SC^2-S^2) →
F = (a^2(b^2-c^2)^2SA(3SA^2-S^2) : ... : ...),
que tiene números de búsqueda en
(4.23219867830010, 2.43171474849666, 0.00384718911740988) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {3, 49}, {4, 15111}, {30, 14670}, {122, 125}, {186, 7740}, {323, 14355}, {402, 11657}, {511, 15329}, {523, 3134}, {868, 6328}, {1312, 10287}, {1313, 10288}, {1495, 5502}, {1624, 13417}, {3001, 13857}, {3470, 14157}, {5651, 14687}, {6000, 14264}, {7669, 15106}.
El puntos F ha sido incorporado a ETC con el número X(16186)
Pares {Xi, Xj=σ(Xi)}, para los índices {i,j}: {50, 7669}, {186, 74}, {323, 110}, {526, 526},
{830, 6088}, {1154, 5663}, {1511, 12041}, {3581, 10620}, {5851, 13754}, {13754, 13754}.
Los números en color rojo corresponden a puntos en la recta del infinito.
- Jueves, 25 de enero del 2018
Una séptica bicircular
Dados un triángulo ABC y un punto P, sean DEF el de P, el de ABC y LMN el triángulo medial de DEF.
Denotamos por A' el punto de intersección (distinto de A) de las circunferencias Γ y Γa, circunscritas a ABC y AEF, respectivamente.
A1 es el punto medio de la cuerda en Γa determinada por la tangent en A a Γ y A2 es el punto medio de la cuerda en Γ determinada por la tangent en A a Γa.
Las rectas PA', A1Ma, A2L son concurrentes, en un punto Pa. Se definen, de forma análoga, los puntos Pb y Pc.
Si (u:v:w) son las coordenadas baricéntricas de P,
Pa = (2 a^4 v (u+v)^2 w (u+w)^2+a^2 u (u+v) (u+w) (-b^2 (u+v) (3 v-w) w+c^2 v (v-3 w) (u+w))+u^2 (v-w) (b^4 (u+v)^2 w-b^2 c^2 (u+v) (v-w) (u+w)-c^4 v (u+w)^2):
-(u+w) (b^2 (u+v) w+c^2 v (u+w)) (-u (-c^2 v+b^2 (u+v)) (v-w)+a^2 v (u+v) (u+2 w)):
-(u+v) (b^2 (u+v) w+c^2 v (u+w)) (c^2 u (v-w) (u+w)+w (a^2 (u+2 v) (u+w)+b^2 u (-v+w)))).
Los triángulos
ABC y son perspectivos si y solo si
P está sobre la circunferencia circunscrita a
ABC o sobre la séptica Φ de ecuación baricéntrica:
Σ abc xyz
y^3z^3(a^2(a^2-2b^2+2c^2)y-a^2(a^2+2b^2-2c^2)z) +
x^3y^2z^2(-b^4+c^4+a^2(b^2-c^2))+
x y z(((b^2-c^2)^2-a^2(b^2-2c^2))y^3z+(a^2(c^2-2b^2)-(b^2-c^2)^2)z^3y+a^2(c^2-b^2)y^2z^2) = 0.
La séptica Φ pasa por los vértices de ABC (puntos triples) y del , por los (dobles), por los centros del triángulo: X2 (baricentro), X4 (ortocentro), X13, X14 (), X671 (antipodal del en la ), X2373 ( del del inverso del baricentro en la circunferencia circunscrita).
Sus asíntotas reales son las medianas de ABC.
Pares {P,Q} = {Xi.Xj}, P sobre Φ y Q el centro de perspectividad de ABC y , para {i,j}: {2, 2}, {4, 2}, {13, 6671}, {14, 6672}, {671, 468}, {2373, 468}.
X468 es el inverso en la circunferencia circunscrita del centro de homotecia, X25, de los triángulos y . X6671 es el baricentro de {A, B, C, } y
X6672 es el baricentro de {A, B, C, X16}.
El lugar geométrico del centro de perspectividad Q de ABC y , cuando P recorre la circunferencia circunscrita, es el .
En este caso, es el triángulo de P y coincide con el triángulo medial del triángulo ceviano de P.
Q es el del del y el conjugado isogonal de P.
Pares {P,Q} = {Xi.Xj}, P sobre la circunferencia circunscrita y Q, el centro de perspectividad de ABC y , sobre el eje órtico, para {i,j}:
{74, 3003}, {98, 230}, {99, 523}, {100, 650}, {101, 6586}, {102, 8607}, {103, 8608}, {104, 8609}, {105, 3290}, {106, 8610}, {107, 6587}, {108, 6588}, {109, 6589}, {110, 647}, {111, 3291}, {112, 2485}, {476, 1637}, {477, 3018}, {675, 3011}, {691, 2492}, {789, 4874}, {805, 2491}, {835, 6590}, {842, 2493}, {901, 3310}, {925, 2501}, {927, 676}, {930, 12077}, {934, 6129}, {1113, 8105}, {1114, 8106}, {1141, 231}, {1294, 1990}, {1295, 14571}, {1297, 232}, {1302, 9209}, {1305, 7649}, {2370, 8756}, {2373, 468}, {2697, 6103}, {2770, 10418}, {3565, 2489}, {6079, 14425}, {6082, 9125}, {8706, 2490}, {9080, 9189}, {9150, 11176}, {10425, 6132}, {13397, 6591}, {13398, 6753}
- Sábado, 20 de enero del 2018
Complemento de un punto respecto a su triángulo ceviano
Dados un triángulo ABC y un punto P, sean DEF el de P y D'E'F' el de DEF.
Denotamos por Ab y Ac los puntos de intersección de la recta E'F' con AC y AB, respectivamente. Los puntos Bc, Ba, Ca y Cb, se definen análogamente.
Los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están en una misma cónica C(P) con centro en el de P, respecto al triángulo ceviano de P.
Cuando el punto P está en la recta del infinito, C(P) es una parábola circunscrita a ABC, cuyo eje tiene la dirección dada por P y sobre la .
Si (u:v:w) son las coordenadas baricéntricas de P:
Ab = (u v : 0 : w (u + v + w)),
Ac = (u w : v (u + v + w) : 0).
La ecuación de la cónica C(P) que pasa por Ab, Ac, Bc, Ba, Ca y Cb es:
v^2 w^2 (u + v + w)x^2 -u v w (2 u^2 + 2 u (v + w) + (v + w)^2)y z + ⋯ = 0.
Con centro en:
W = (u (v + w) (u^2 + 2 u (v + w) + v^2 + v w + w^2 ) : ⋯ : ⋯ ),
que es el complemento de P respecto al triángulo ceviano de P.
Solo existen 8 pares {P, W}, tales que P y W son centros del triángulo que figuren en (entre los 15423 primeros):
{1, 3743}, {2, 2}, {4, 389}, {7, 5572}, {8, 960}, {20, 2883}, {69, 11574}, {145, 12640}, {693, 15280}
Cuando P = X693
( del del )
el triángulo formado por las rectas AbBa, BcCb y CaAc es el , imagen de ABC mediante la homotecia de centro el punto de Feuerbach y razón (R-r)/r (r y R son los radios de las circunferencias inscrita y circunscrita a ABC).
Las asíntotas de la cónica C(X693), con centro en X15280, son X15280X514 y X15280X522.
- Martes, 16 de enero del 2018
Lugar geométrico de centros de circunferencias que pasan por el punto de Feuerbach
a Aye, por su "cumple"
Dado un triángulo ABC, sean r y R los radios de las circunferencias inscrita y circunscrita, y su .
La altura por A corta a A1B1 y a A1C1 en A2 y A3, respectivamente.
Análogamente, procediendo cíclicamente, se definen los puntos B2, B3, C2, C3.
Se toman los mismos puntos A', B' y C' sobre las de los triángulos , y , respectivamente.
La circunferencia circunscrita al triángulo
A'B'C' pasa por el .
En coordenadas baricéntricas:
A1 = (0 : a+b-c : a-b+c),
A2 = (-2a(b-c) : a^2+b^2-c^2 : a^2-b^2+c^2),
A3 = (-2a(b-c) : -a^2-b^2+c^2 : -a^2+b^2-c^2).
El circuncentro y el ortocentro de son, respectivamente:
Oa = (2a(b-c)^2 : -a^3+(b-c)^3+a^2(-b+c)+
a(-b^2+c^2) : -a^3+a^2(b-c)-(b-c)^3+a(b^2-c^2))
Ha = (0 : -a+b-c : -a-b+c).
Sea A' un puntos sobre la recta de Euler de , tal que OaA' : A'Ha = t. Se definen B' y C', análogamente.
La ecuación de la circunferencia circunscrita Γ a A'B'C' (que pasa por
X11(((b-c)^2(b+c-a) : ... : ...)) se puede poner en la forma:
a^2yz+b^2zx+c^2xy + (1/δ) (px+qy+rz)=0,
donde
δ = 4(a^3-a(b-c)^2-a^2(b+c)+(b-c)^2(b+c))^2t^3
- 4(a^6-a^4(b-c)^2-2a^5(b+c)+(b-c)^4(b+c)^2+4a^3(b^3+c^3)-a^2(b^4+6b^2c^2+c^4)-
2a(b^5-b^4c-b c^4+c^5))t^2
-4(a^6-2a^5(b+c)+4a^3(b-c)^2(b+c)-2a(b-c)^4(b+c)+(b-c)^4(b+c)^2-
a^4(b^2-6bc+c^2)-a^2(b^4+4b^3c-6b^2c^2+4b c^3+c^4))t
+ 4(a^6-a^4(b-c)^2-2a^5(b+c)+(b-c)^4(b+c)^2-a^2(b^2+c^2)^2+4a^3(b^3+c^3)-2a(b^5-b^4c-b c^4+c^5))
p = (a^2-(b-c)^2)^2(a^4+4a b c(b+c)-
2a^2(b+c)^2+(b^2-c^2)^2)t^3
(-5a^8+
4a^7(b+c)-(b-c)^4(b+c)^2(b^2-6b c+c^2)+
8a^6(2b^2-b c+2c^2)-12a^5(b^3+b^2c+b c^2+c^3)+
8a^2(b-c)^2(b^4-2b^3c-3b^2c^2-2b c^3+c^4)-
2a^4(9b^4-16b^3c+10b^2c^2-16b c^3+9c^4)-
4a(b-c)^2(b^5+b^4c-4b^3c^2-4b^2c^3+b c^4+c^5)+
4a^3(3b^5+b^4c-2b^3c^2-2b^2c^3+b c^4+3c^5))t^2
+ (7a^8-8a^7(b+c)-(b-c)^4(b+c)^2(b^2+6b c+c^2)-
4a^6(5b^2-2b c+5c^2)+
4a(b-c)^4(2b^3+5b^2c+5b c^2+2c^3)+
4a^5(6b^3+5b^2c+5b c^2+6c^3)+
6a^4(3b^4-6b^3c+4b^2c^2-6b c^3+3c^4)-
8a^3(3b^5+2b^3c^2+2b^2c^3+3c^5)-
4a^2(b^6-8b^5c+2b^4c^2-2b^3c^3+2b^2c^4-8b c^5+
c^6))t
+ (-3a^8+4a^7(b+c)+(b^2-c^2)^4+
8a^6(b^2+c^2)-12a^5(b^3+b^2c+b c^2+c^3)+
a^4(-6b^4+8b^3c-8b^2c^2+8b c^3-6c^4)-
4a^2b c(2b^4+b^3c+2b^2c^2+b c^3+2c^4)-
4a(b-c)^2(b^5+b^4c+b c^4+c^5)+
4a^3(3b^5+b^4c+4b^3c^2+4b^2c^3+b c^4+3c^5)).
El lugar geométrico del baricentro G' de A'B'C' es la recta que pasa por X210 (baricentro del ) y X3817 ( del baricentro X165 del ).
El baricentro de A'B'C' es:
G' = (a((a^2-(b-c)^2) (b+c) (-a+b+c)^2 t
-a^4 (b+c)-2 a^2 b c (b+c)+2 a^3 (b+c)^2-2 a (b-c)^2 (b^2+c^2)+(b-c)^2 (b^3-3 b^2 c-3 b c^2+c^3) : ... : ...),
que está sobre la recta de ecuación:
(b-c) (3 a^5-6 a^4 (b+c)-a^3 b c
+a^2 (6 b^3+b^2 c+b c^2+6 c^3)+a (-3 b^4+9 b^3 c-4 b^2 c^2+9 b c^3-3 c^4)-3 b (b-c)^2 c (b+c)) x + ... = 0.
El lugar geométrico del centro
O' de la circunferencia circunscrita Γ a
A'B'C' es una
cúbica que pasa por X
5 (centro de la ), X
1158 (circuncentro del ), X
3307 y X
3308 (direcciones de dos asíntotas perpendiculares, puntos conjugados isogonales de los puntos en que la recta que pasa por el incentro y circuncentro corta a la circunferencia circunscrita), y por otros dos puntos en la recta de Euler: X
6882 y X
13852.
X6882 es la intersección de la recta de Euler con la perpendicular por X11 a la dirección del conjugado isogonal del X100 de X11.
La recta X11X6882 es tangente a la cúbica en el punto:
T = ( a^5(b-c)^2-a^4 (b^3-3 b^2 c-3 b c^2+c^3)
-2 a^3 (b^4-2 b^3 c+4 b^2 c^2-2 b c^3+c^4) +2 a^2 (b-c)^2 (b^3+c^3)
+a (b-c)^4 (b+c)^2-(b-c)^4 (b+c)^3 : ... : ...),
que tiene números de búsqueda en
(-6.71451455961081, -4.35410541520193, 9.75405187379070).
La recta que pasa por el punto de Feuerbach y por el centro X14526, de la circunferencia circunscrita al de X79 (centro de perspectividad de ABC y el del incentro), corta a la cúbica en X13852 (sobre la recta de Euler) y en su punto doble:
D = (
a^8(b-c)^2-2a^7(b^3+c^3)+a^5(6b^5+5b^4c-b^3c^2-b^2c^3+5bc^4+6c^5)
+2a^4b c(5b^4-4b^3c+8b^2c^2-4b c^3+5c^4)
-2a^3(b-c)^2(3b^5+11b^4c+13b^3c^2+13b^2c^3+11b c^4+3c^5)
+a^2(b^2-c^2)^2(2b^4-9b^3c+6b^2c^2-9b c^3+2c^4)
+a(b-c)^4(b+c)^3(2b^2+7b c+2c^2)
-(b-c)^6(b+c)^4-a^6(b+c)^2(2b^2-3b c+2c^2) : ... : ...),
que tiene números de búsqueda en
(0.434103890295403, -0.794522111411274, 3.99036260967123).
La tercera asíntota tiene la dirección de la recta que une X5 con X191 ( de los incentros de los triángulos medial y de referencia (X10/X1)); su punto del infinito es:
W = ( 2a^7-a^5(5b^2+2b c+5c^2)-a^4(b-c)^2(b+c)-(b-c)^4(b+c)^3
+a^3(4b^4+b^3c+b c^3+4c^4)
+2a^2(b^5-b^4c-b c^4+c^5)
-a(b^2-c^2)^2(b^2-b c+c^2) : ... : ...),
que tiene números de búsqueda en
(1.27907176003337, 1.00378312961141, -1.28526759436176).
Las circunferencias inscrita a ABC y circunscrita Γ a A'B'C' son tangentes (en el punto de Feuerbach) si y solo si t = 1 ó t = (r + R)/r.
Para t=1, el centro de Γ es X5.
Para t = (r + R)/r, el centro de Γ es otro punto de intersección de la cúbica con su tangente, X1X11, en X5:
U = ( a^5(b-c)^2-a^4(b-c)^2(b+c)-2a^3(b^4-b^3c+2b^2c^2-b c^3+c^4)
+2a^2(b^5-b^4c-bc^4+c^5)+a(b^2-c^2)^2(b^2+c^2)-(b-c)^4(b+c)^3 : ... : ...),
que tiene números de búsqueda en
(-0.228420441350550, -1.69766386911033, 4.92139505653025) y es X1X5∩X6882
Los triángulos ABC y A'B'C' son perspectivos si y solo si t = (r+R)/r ó t = (r+2R)/(3r+4R).
Los centros de perspectividad son, respectivamente, X2886 ( del centro X55, de homotecia interior de las circunferencias inscrita y circunscrita) y
Pe = ( a^8 - 3a^7(b+c) + a^6(2b^2+5b c+2c^2) + a^5(b-c)^2(b+c)
- 2a^4b c(b-c)^2 - a^3(b-c)^4(b+c) - a^2(b-c)^2(2b^4+3b^3c+6b^2c^2+3b c^3+2c^4))
+ a(b-c)^4(3b^3+5b^2c+5b c^2+3c^3) - (b-c)^6(b+c)^2 : ... : ...),
que tiene números de búsqueda en
(-3.66898662867361, -4.18791365772457, 8.23336776587383), y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1, 5805}, {8, 6894}, {9, 1699}, {21, 516}, {79, 971}, {84, 4312}, {90, 11372}, {518, 6598}, {528, 6596}, {885, 6003}, {943, 946}, {1172, 1886}, {1476, 12573}, {1836, 3062}, {2346, 11218}, {2801, 11604}, {3254, 15185}, {4295, 10429}, {4866, 5587}, {4900, 5844}, {5536, 6067}, {5665, 5691}, {5715, 15298}, {7162, 7951}, {10398, 12858}.
Los triángulos ABC y A'B'C' son .
El lugar geométrico del centro ortológico de ABC respecto a A'B'C' es la .
El lugar geométrico del centro ortológico de A'B'C' respecto a ABC es la recta que pasa por X5 (centro de la ) y por X40 (punto de ).
Para t = (r+R)/r, los triángulos ABC y A'B'C' son .
El centro ortológico de ABC respecto a A'B'C' es el ortocentro.
El centro ortológico de A'B'C' respecto a ABC es:
V1 = ( a^5(b+c)^2 - a^4(b-c)^2(b+c) - 2a^3(b^2+c^2)^2
+ 2a^2(b^5-b^4c-b c^4+c^5) + a(b-c)^4(b+c)^2-(b-c)^4(b+c)^3 : ... : ...),
que tiene números de búsqueda en
(8.32951065277495, 6.83769118670393, -4.93751125632217).
Por el , X4, V1 y X2886 están alineados: V1 = 2 (r + R)X2886- R X4.
Para t = (r+2R)/(3r+4R), los triángulos ABC y A'B'C' son bilógicos.
El centro ortológico de ABC respecto a A'B'C' es:
U2 = ( a(b+c-a)/(a^4-a^2(2b^2+3b c+2c^2)-a b c(b+c)+(b^2-c^2)^2) : ... : ...),
que tiene números de búsqueda en
(3.83696685731664, 2.15324790911666, 0.379046610680551).
El centro ortológico de A'B'C' respecto a ABC es:
V2 = ( 2a^7-a^5(3b^2+8b c+3c^2)+a^4(-3b^3+b^2c+b c^2-3c^3)
+2a^3b(b-c)^2c+2a^2(b-c)^2(3b^3+4b^2c+4b c^2+3c^3)
+a(b^2-c^2)^2(b^2+6b c+c^2)-3(b-c)^4(b+c)^3 : ... : ...),
que tiene números de búsqueda en
(-3.46987032479265, -4.01969670089715, 8.02501004012517).
Los puntos Pe, U2, V2 están en una recta (), paralela a la recta que pasa por el circuncentro y el . Su punto del infinito es X5762, que es el único centro del triángulo que contiene, entre los 15423 primeros que figuran en .
Los triángulos ABC y A'B'C' son si y solo si t = (r-R)/r.
El centro paralelógico de ABC respecto a A'B'C' es X100 (anticomplemento del punto de Feuerbach).
El centro paralelógico de A'B'C' respecto a ABC es el punto de Feuerbach.
- Sábado, 13 de enero del 2018
Una caracterización de la cúbica K024
Shuzo TAKAMATSU and Shusaku OGINO.-
On Some Cubics connected with Simson lines. Tohoku Math. J. 43, p 102 (1937)
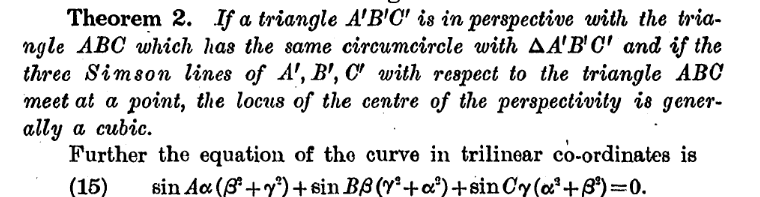
Dados un triángulo ABC y un punto P (no situado sobre sus lados, ni en la recta del infinito), sea el de P.
La mediatriz de PbPc corta a los lados MbMc, McMa, MaMb del , en los puntos Aa, Ab, Ac, respectivamente.
Los puntos Ba, Bb, Bc y Ca, Cb, Cc, se definen cíclicamente.
Four cyclic points AoPS ("Mosquitall"):
Los cuatro puntos
Ba,
Bc Ca,
Cb, están en una circunferencia, Γ
a.
Análogamente:
Los cuatro puntos Ab, Ac. Ca, Cb, están en una circunferencia, Γb.
Los cuatro puntos Ab, Ac, Ba, Bc, están en una circunferencia, Γc.
El lugar geométrico del punto
P tal que los seis puntos
Ab,
Ac,
Ba,
Bc,
Ca,
Cb, están sobre una misma circunferencia es la cúbica
K024 del catálogo de Bernard Gibert.
Si (u:v:w) son las coordenadas baricéntricas de P,
Aa = ((u+v+w)(c^2v+b^2w) : c^2v^2+b^2(u+v)w :
b^2w^2+c^2v(u+w)),
Ab = (-b^2(u+v)w+c^2v(u+w) : -b^2w(u+v+w) : -b^2w^2-c^2v(u+w)),
Ac = (b^2(u+v)w-c^2v(u+w) : -c^2v^2-b^2(u+v)w : -c^2v(u+v+w)).
- Jueves, 11 de enero del 2018
Circunferencias centradas en los vértices de un triángulo y radios los de las exinscritas
Dado un triángulo ABC, sean ra, rb y rc los radios de sus .
La circunferencia B(ra) de centro B y radio ra, corta a BC en Ab y A'b:
BAb : AbC = ra : a - ra,
BA'b : A'bC = -ra : a + ra
Es decir, Ab=(0 : a - ra : ra) y A'b=(0 : a + ra : -ra), en coordenadas baricéntricas.
La circunferencia C(ra) de centro C y radio ra, corta a BC en Ac y A'c:
CAc : AcB = ra : a - ra,
CA'c : A'cB = -ra : a + ra
Es decir, Ac=(0 : ra : a - ra) y A'c=(0 : -ra : a + ra).
Los puntos Bc, B'c, Ca, C'a, Ba, B'a, Cb y C'b se definen cíclicamente.
Se denota por M1, M2 y M3 los puntos medios de los segmentos BcCb, CaAc y AbBa, respectivamente.
Las rectas
AM1,
BM2 y
CM3 concurren en el punto
U de coordenadas baricéntricas:
U = ( a(b+c-a)/(a(b+c-a) - ) : ... : ...),
Se denota por M'1, M'2 y M'3 los puntos medios de los segmentos B'cC'b, C'aA'c y A'bB'a, respectivamente.
Las rectas
AM'1,
BM'2 y
CM'3 concurren en el punto
V de coordenadas baricéntricas:
V = ( a(b+c-a)/(a(b+c-a) + ) : ... : ...),
Se denota por N1, N2 y N3 los puntos medios de los segmentos BaCa, CbAb y AcBc, respectivamente.
Las rectas AN1, BN2 y CN3 concurren en el punto .
Se denota por N'1, N'2 y N'3 los puntos medios de los segmentos B'aC'a, C'bA'b y A'cB'c, respectivamente.
Las rectas AN'1, BN'2 y CN'3 concurren en el punto .
Los triángulos y son perspectivos, con centro de perspectividad
Z = ((r+4R)^2-s(2r+12R-s)) X6666 + (R s) X13359 =
(
2a^6-3a^5(b+c)-3a^4(b+c)^2
+2a^3(3b^3+5b^2c+5b c^2+3c^3)
+8a^2b c(b-c)^2
-a(b-c)^2(3b^3+13b^2c+13b c^2+3c^3)
+(b-c)^4(b+c)^2
+
2S(3a^3(b+c)-2a^2(3b^2+b c+3c^2)
+ 3a(b-c)^2(b+c)+2b c(b-c)^2 ) : ... : ...),
Los triángulos
M'1M'2M'3 y
N'1N'2N'3 son perspectivos, con centro de perspectividad
W = ((r+4R)^2+s(2r+12R+s)) X6666 - (R s) X13359 =
(
2a^6-3a^5(b+c)-3a^4(b+c)^2
+2a^3(3b^3+5b^2c+5b c^2+3c^3)
+8a^2b c(b-c)^2
-a(b-c)^2(3b^3+13b^2c+13b c^2+3c^3)
+(b-c)^4(b+c)^2
-
2S(3a^3(b+c)-2a^2(3b^2+b c+3c^2)
+ 3a(b-c)^2(b+c)+2b c(b-c)^2 ) : ... : ...),
Las coordenadas de los centros X13359 y X13360 son obtenidas en HG090417
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Sean ha, hb y hc las longitudes de las alturas en los vértices A, B y C. Si en vez de tomar las circunferencias B(ra) y C(ra), tomamos las B(ha) y C(ha) con centros en B y C y radio ha, entonces:
El centro de perspectividad de los triángulos
ABC y es
X494, 2º Centro de Homotecia de van Lamoen (
Floor van Lamoen, 4/27/98),
(a^2/(a^2 - ) : b^2/(b^2 - S) : c^2/(c^2 - S)).
El centro de perspectividad de los triángulos ABC y M'1M'2M'3 es X493, 1er Centro de Homotecia de van Lamoen,
(a^2/(a^2 - S) : b^2/(b^2 - S) : c^2/(c^2 - S)).
El centro de perspectividad de ABC y los triángulos y
N'1N'2N'3 es X6, el
El centro de perspectividad de los triángulos y es:
U1 = (
2a^6
-3a^4(b^2+c^2)
-12a^2b^2c^2
+(b^2-c^2)^2(b^2+c^2)
+ 2S(3a^2(b^2+c^2)+2b^2c^2) : ... : ...),
El centro de perspectividad de los triángulos
M'1M'2M'3 y
N'1N'2N'3 es:
U2 = (
2a^6
-3a^4(b^2+c^2)
-12a^2b^2c^2
+(b^2-c^2)^2(b^2+c^2)
- 2S(3a^2(b^2+c^2)+2b^2c^2) : ... : ...),
- Miércoles, 10 de enero del 2018
Circunferencias centradas en los vértices del triángulo medial y radios los de las exinscritas
Dado un triángulo ABC, sean ra, rb y rc los radios de sus y DEF el .
La circunferencia D(ra) de centro D y radio ra, corta a BC en A' y A":
BA' : A'C = a + 2 ra : a - 2 ra,
BA" : A"C = a - 2 ra : a + 2 ra
Es decir, A'=(0 : a - 2 ra : a + 2 ra) y A"=(0 : a + 2 ra : a - 2 ra), en coordenadas baricéntricas.
Los puntos B', B", C', C" de definen cíclicamente.
Se denota por M1, M2 y M3 los puntos medios de los segmentos B'C", C'A" y A'B", respectivamente.
Las rectas
AM1,
BM2 y
CM3 concurren en el punto
U de coordenadas baricéntricas:
U = ( a(b+c-a)/(a(b+c-a)-2) : ... : ...),
Se denota por N1, N2 y N3 los puntos medios de los segmentos B"C', C"A' y A"B', respectivamente.
Las rectas
AN1,
BN2 y
CN3 concurren en el punto
V de coordenadas baricéntricas:
V = ( a(b+c-a)/(a(b+c-a)+2) : ... : ...),
Los triángulos y son perspectivos, con centro de perspectividad X6666, el baricentro de {A,B,C, }.
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Sean ha, hb y hc las longitudes de las alturas en los vértices A, B y C. Si en vez de tomar la circunferencia D(ra), tomamos la D(ha) con centro en D y radio ha, entonces:
El centro de perspectividad de los triángulos
ABC y es
X589, 2º punto de Kenmotu-van Lamoen,
(a^2/(a^2 - 2) : b^2/(b^2 - 2S) : c^2/(c^2 - 2S)).
El centro de perspectividad de los triángulos ABC y M1M2M3 es X588 , 1er punto de Kenmotu-van Lamoen,
(a^2/(a^2 + 2) : b^2/(b^2 + 2S) : c^2/(c^2 + 2S)).
El centro de perspectividad de los triángulos M1M2M3 y N1N2N3 es X3589,
(2 a^2 + b^2 + c^2 : a^2 + 2 b^2 + c^2 : a^2 + b^2 + 2 c^2).
Let A' be the midpoint midpoint of A and X(6) (symmedian), and define B' and C' cyclically. Then A'B'C' is homothetic to the medial triangle, and the homothetic center is X(3589). (Randy Hutson, December 26, 2015)
- Lunes, 8 de enero del 2018
Otras propiedades del centro (r+2R) I - 4r O
Some other properties of this point, W = (r+2R) I - 4r O (Randy Hutson)
Trilinears: 3 cos A - cos B - cos C - 1 : :
W = X(84)-Ceva conjugate of X(1)
W = homothetic center of Ascella triangle and reflection triangle of X(1)
As a point P moves on the circumcircle, the centroid of the 12 excenters of triangles ABC, BCP, CAP, ABP traces a curvilinear triangle, T.
Let A', B', C' be the vertices of T, and (Oa), (Ob), (Oc) the circles whose arcs form the sides of T. A'B'C' is the orthic triangle of the anticomplementary triangle of OaObOc, and OaObOc is the medial triangle of the excentral triangle of A'B'C'.
Let A" be the intersection, other than A', of circles (Ob) and (Oc), and define B", C" cyclically.
A"B"C" is the excentral triangle of A'B'C', and the anticomplementary triangle of OaObOc.
A"B"C" is homothetic to the inverse-in-incircle triangle at W.
Dados un triángulo ABC (con incentro I y circuncentro O) y un punto P, sean , , , los de los triángulos ABC, PBC, CPA, ABP, respectivamente, y GP el baricentro de los doce puntos {Ia, Ib, Ic, Paa, Pab, Pac, Pba, Pbb, Pbc, Pca, Pcb, Pcc}.
Cuando P varía, sobre su circunferencia circunscrita a ABC, el punto GP describe una triángulo curvilíneo de vértices A'B'C'.
En la posición límite P=A, el punto A' = 2A + 2Ia + 2Ib + 2Ic + Ibb + Ibc + Icc + Icb, donde los puntos Ibb, Ibc, Icc, Icb, se obtienen como sigue:
Las tangentes en Ib e Ic a la circunferencia de diámetro IbIb vuelven a cortar a las circunferencias circunscritas a los triángulos IbAC, IbAB, IcAB e IcAC en los puntos Ibb, Ibc, Icc, Icb, respectivamente.
En coordenadas baricéntricas:
Ibb = (-a^2-b^2+c^2 : 2b^2 : -2c(a+c)),
Ibc = (a^2-b^2+c^2 : -2b(a-b) : -2c^2),
Icc = (-a^2+b^2-c^2 : -2b(a+b) : 2c^2),
Icb = (a^2-c^2+b^2 : -2b^2 : -2c(a-c)).
A' = (6a^4+a^3(b+c)-a(b-c)^2(b+c)-(b^2-c^2)^2-a^2(5b^2+2b c+5c^2) :
b(-a^3+7b^3+a(b-c)^2+b^2c-7bc^2-c^3+a^2(-7b+c)) :
c(-a^3-b^3+a^2(b-7c)+a(b-c)^2-7b^2c+b c^2+7c^3)).
Los triángulos
ABC y
A'B'C' son perspectivos, con centro de perspectividad Z = I - 8 O:
Z = X16192 = ( a(7a^3+a^2(b+c)-a(7b^2+2b c+7c^2)-(b-c)^2(b+c)) : ... : ...),
complemento de X
10248.
Las coordenadas del vértice A" del triángulo excentral A"B"C" de A'B'C' son:
A" = (a^2(3a^2-3b^2-2bc-3c^2) : b(3b^3+b^2c-3bc^2-
c^3+a^2(-3b+c)) : c(-b^3+a^2(b-3c)-3b^2c+bc^2+3c^3)).
El triángulo es el que tiene por vértices los inversos de los vértices de ABC, respecto a la circunferencia inscrita.
A1 = ((b-c)^2-a(b+c) : -b(b+c-a) : -c(b+c-a)).
Los triángulos y
A"B"C" son homotéticos, con centro de homotecia
W = X15803 = (r+2R) I - 4r O,
y razón k= 2R/(3r).
- Sábado, 6 de enero del 2018
El centro (r+2R) I - 4r O
Sea ABC un triángulo con incentro I, circuncentro O y circunferencia inscrita Γ.
Ωb y Ωc son las circunferencias circunscritas a los triángulos AOC y AOB, respectivamente.
Γb es la circunferencia tangente a Γ que pasa por A y C y Γc es la circunferencia tangente a Γ que pasa por A y B.
Existe una circunferencia Λa, tangente a las cuatro circunferencias Γb, Γc, Ωb y Ωc.
El punto Ab, de tangencia de las circunferencias Γ y Γb, se determina trazando la tangente a Γ, desde el punto ((a+b-c)^2:0:-(-a+b+c)^2) (en coordenadas baricéntricas), por donde pasan los ejes radicales de Γ y cualquier circunferencia que pasa por A y C. Este punto es la intersección de AC con el eje radical de las circunferencias inscrita y circunscrita a ABC, con lo que:
Ab = ((a+b-c)^3(a-b+c) : -4b^2((a-c)^2-b^2) : -(a-b-c)^3(a-b+c)).
Análogamente, para:
Ac = ((a-b+c)^3(a+b-c) : -(a-b-c)^3(a+b-c) : -4c^2((a-b)^2-c^2)).
La existencia de la circunferencia Λa va emparejada con que el cuadrilátero formado por las rectas inversas (respecto a una circunferencia centrada en A) de las circunferencias Γb, Γc, Ωb y Ωc, sea .
Ecuaciones de las circunferencias:
Γb :
a^2y z +b^2z x+ c^2x y
- ((-a^3+3a^2b-3a b^2+b^3+a^2c+2a b c -
3b^2c+a c^2+3b c^2-c^3)y (x+y+z))/(8 b) = 0,
Γc : a^2y z +b^2z x+ c^2x y - ((-a^3+a^2b+a b^2-b^3+3a^2c+2a b c+
3b^2c-3a c^2-3b c^2+c^3)z(x+y+z))/(8c) = 0,
Ωb : a^2y z +b^2z x+ c^2x y-(a^2c^2y(x+y+z))/(a^2-b^2+c^2) = 0,
Ωc : a^2y z +b^2z x+ c^2x y-(a^2b^2z(x+y+z))/(a^2+b^2-c^2) = 0.
Tomando como circunferencia de inversión la de centro en A y que pasa por O:
a^2y z +b^2z x+ c^2x y - (x+y+z)
(- a^2b^2c^2x /((a+b-c)(a-b+c)(-a+b+c)(a+b+c)) +
(c^2-(a^2b^2c^2)/((a+b-c)(a-b+c)(-a+b+c)(a+b+c)))y +
(b^2-(a^2b^2c^2)/((a+b-c)(a-b+c)(-a+b+c)(a+b+c)))z) = 0.
Los ejes radicales de esta circunferencia y cada una de las circunferencias Γb, Γc, Ωb y Ωc son, respectivamente:
γb : 8a^2b^3c^2x
+ (a^7-a^6(3b+c)+a(b-c)^3(b+c)^2(3b+c)+a^5(b^2-2bc-3c^2)-(b-c)^2(b+c)^3(b^2-4b c-
c^2)+a^4(5b^3+5b^2c+11b c^2+3c^3)+a^3(-5b^4+4b^3c-6b^2c^2+4b c^3+3c^4)-
a^2(b^5+7b^4c-6b^3c^2+6b^2c^3+13b c^4+3c^5))y
+ 8b^3(a^4+(b^2-c^2)^2-a^2(2b^2+c^2))z = 0,
γc : 8a^2b^2c^3x
+ 8c^3(a^4+(b^2-c^2)^2-a^2(b^2+2c^2))y
+ (a^7-a^6(b+3c)-a(b-c)^3(b+c)^2(b+3c)+(b-c)^2(b+c)^3(b^2+4b c-c^2)+a^5(-3b^2-2b c+c^2)+
a^4(3b^3+11b^2c+5b c^2+5c^3)+a^3(3b^4+4b^3c-6b^2c^2+4b c^3-5c^4)-
a^2(3b^5+13b^4c+6b^3c^2-6b^2c^3+7bc^4+c^5))z = 0,
ωb : a^2b^2c^2(a^2-b^2+c^2)x + c^2(a^4c^2-(b^2-c^2)^3+
a^2(b^4+b^2c^2-2c^4))y + b^2(a^6-3a^4b^2-(b^2-c^2)^3+3a^2(b^4-b^2c^2))z = 0,
ωc : a^2b^2c^2(a^2+b^2-c^2)x + c^2(a^6-3a^4c^2+(b^2-c^2)^3+
a^2(-3b^2c^2+3c^4))y + b^2(a^4b^2+(b^2-c^2)^3+a^2(-2b^4+b^2c^2+c^4))z = 0.
El punto de intersección de las rectas ωb y ωb es, evidentemente, el circuncentro O=X3.
γb ∩ γc es:
P = (a^8-4a^4b(b-c)^2c-2a^7(b+c)+2a(b-c)^2(b+c)^5-
2a^6(b^2+c^2)-(b-c)^4(b+c)^2(b^2+6b c+c^2)+
2a^5(3b^3+5b^2c+5bc^2+3c^3)+2a^2(b-c)^2(b^4+6b^3c+6b^2c^2+6b c^3+c^4)-
2a^3(3b^5+7b^4c+2b^3c^2+2b^2c^3+7b c^4+3c^5) :
-8a^2b^3(a+b-c)c^2 : -8a^2b^2c^3(a-b+c)).
γb ∩ ωb ∩ AC es:
Pb = (a^4-a^2(2b^2+c^2)+(b^2-c^2)^2 : 0 : -a^2c^2)
γc ∩ ωc ∩ AB es:
Pc = (a^4-a^2(b^2+2c^2)+(b^2-c^2)^2 : -a^2b^2 : 0)
El centro de la circunferencia inscrita a las rectas γb, γc, ωb y ωc es:
(a^6(b-c)^2-a^7(b+c)+a(b-c)^2(b+c)^5-(b^2-c^2)^4-
3a^3(b+c)^3(b^2-b c+c^2)+
a^2(b^2-c^2)^2(3b^2+b c+3c^2)+
a^5(3b^3+4b^2c+4b c^2+3c^3)+
a^4(-3b^4+b^3c+b c^3-3c^4) :
a^2b^2c(a^3-3b^3+
a^2(3b-c)-b^2c+3b c^2+c^3-
a(b+c)^2) :
a^2bc^2(a^3+b^3-a^2(b-3c)+3b^2c-
b c^2-3c^3-a(b+c)^2)),
intersección de las bisectrices de ∠PbOPc y ∠PbPPc, de ecuaciones respectivas:
a^2b^2(b-c)c^2x -c^2(-b^5+b^4c+2b^3c^2+b^2c(a^2-2c^2)+bc^2(a^2-c^2)+c(a^2-c^2)^2)y + b^2(a^4b+(b-c)^3(b+c)^2+
a^2b(-2b^2+b c+c^2))z = 0,
16a^2b^3(b-c)c^3x
-c(a^8-2a^7(b-c)+
2a(b-c)^3(b+c)^4-2a^6(b^2+2b c+3c^2)+
2a^5(3b^3-b^2c+b c^2-3c^3)-
2a^3(b+c)^2(3b^3-5b^2c+5b c^2-3c^3)+
4a^4c(2b^3-b^2c+4b c^2+3c^3)-(b-c)^3(b+
c)^2(b^3+b^2c+11b c^2+3c^3)+
2a^2(b^6-2b^5c+b^4c^2+4b^3c^3+11b^2c^4-
10b c^5-5c^6))y +
b(a^8+2a^7(b-c)-
2a(b-c)^3(b+c)^4-2a^6(3b^2+2b c+c^2)+
2a^3(b+c)^2(3b^3-5b^2c+5b c^2-3c^3)+(b-
c)^3(b+c)^2(3b^3+11b^2c+b c^2+c^3)+
4a^4b(3b^3+4b^2c-b c^2+2c^3) +
a^5(-6b^3+2b^2c-2b c^2+6c^3) +
2a^2(-5b^6-10b^5c+11b^4c^2+4b^3c^3+b^2c^4-
2b c^5+c^6))z = 0.
Y la inversa de esta circunferencia, respecto a la circunferencia de centro A y radio AO, es la circunferencia
Λa,
( 4 a^2 b^4 c^2 x^2-8 a b^5 c^2 x^2+4 b^6 c^2 x^2+8 a^2 b^3 c^3 x^2+8 a b^4 c^3 x^2-16 b^5 c^3 x^2+4 a^2 b^2 c^4 x^2+8 a b^3 c^4 x^2+24 b^4 c^4 x^2-8 a b^2 c^5 x^2-16 b^3 c^5 x^2+4 b^2 c^6 x^2+4 a^4 b^2 c^2 x y-8 a^3 b^3 c^2 x y+8 a^2 b^4 c^2 x y-8 a b^5 c^2 x y+4 b^6 c^2 x y+4 a^4 b c^3 x y+16 a^3 b^2 c^3 x y-16 a^2 b^3 c^3 x y-4 b^5 c^3 x y+8 a^3 b c^4 x y+24 a^2 b^2 c^4 x y+16 a b^3 c^4 x y-24 b^4 c^4 x y-16 a^2 b c^5 x y+56 b^3 c^5 x y-8 a b c^6 x y-44 b^2 c^6 x y+12 b c^7 x y+a^6 c^2 y^2-2 a^5 b c^2 y^2+3 a^4 b^2 c^2 y^2-4 a^3 b^3 c^2 y^2+3 a^2 b^4 c^2 y^2-2 a b^5 c^2 y^2+b^6 c^2 y^2-2 a^5 c^3 y^2+2 a^4 b c^3 y^2+4 a^3 b^2 c^3 y^2-4 a^2 b^3 c^3 y^2+6 a b^4 c^3 y^2-6 b^5 c^3 y^2-a^4 c^4 y^2-4 a^3 b c^4 y^2-2 a^2 b^2 c^4 y^2-4 a b^3 c^4 y^2+15 b^4 c^4 y^2+4 a^3 c^5 y^2+4 a^2 b c^5 y^2-4 a b^2 c^5 y^2-20 b^3 c^5 y^2-a^2 c^6 y^2+6 a b c^6 y^2+15 b^2 c^6 y^2-2 a c^7 y^2-6 b c^7 y^2+c^8 y^2+4 a^4 b^3 c x z+8 a^3 b^4 c x z-16 a^2 b^5 c x z-8 a b^6 c x z+12 b^7 c x z+4 a^4 b^2 c^2 x z+16 a^3 b^3 c^2 x z+24 a^2 b^4 c^2 x z-44 b^6 c^2 x z-8 a^3 b^2 c^3 x z-16 a^2 b^3 c^3 x z+16 a b^4 c^3 x z+56 b^5 c^3 x z+8 a^2 b^2 c^4 x z-24 b^4 c^4 x z-8 a b^2 c^5 x z-4 b^3 c^5 x z+4 b^2 c^6 x z-a^8 y z+2 a^7 b y z+2 a^6 b^2 y z-6 a^5 b^3 y z+6 a^3 b^5 y z-2 a^2 b^6 y z-2 a b^7 y z+b^8 y z+2 a^7 c y z+2 a^6 b c y z+10 a^5 b^2 c y z-18 a^4 b^3 c y z-18 a^3 b^4 c y z+22 a^2 b^5 c y z+6 a b^6 c y z-6 b^7 c y z+2 a^6 c^2 y z+10 a^5 b c^2 y z+28 a^4 b^2 c^2 y z+12 a^3 b^3 c^2 y z-62 a^2 b^4 c^2 y z-6 a b^5 c^2 y z+16 b^6 c^2 y z-6 a^5 c^3 y z-18 a^4 b c^3 y z+12 a^3 b^2 c^3 y z+84 a^2 b^3 c^3 y z+2 a b^4 c^3 y z-26 b^5 c^3 y z-18 a^3 b c^4 y z-62 a^2 b^2 c^4 y z+2 a b^3 c^4 y z+30 b^4 c^4 y z+6 a^3 c^5 y z+22 a^2 b c^5 y z-6 a b^2 c^5 y z-26 b^3 c^5 y z-2 a^2 c^6 y z+6 a b c^6 y z+16 b^2 c^6 y z-2 a c^7 y z-6 b c^7 y z+c^8 y z+a^6 b^2 z^2-2 a^5 b^3 z^2-a^4 b^4 z^2+4 a^3 b^5 z^2-a^2 b^6 z^2-2 a b^7 z^2+b^8 z^2-2 a^5 b^2 c z^2+2 a^4 b^3 c z^2-4 a^3 b^4 c z^2+4 a^2 b^5 c z^2+6 a b^6 c z^2-6 b^7 c z^2+3 a^4 b^2 c^2 z^2+4 a^3 b^3 c^2 z^2-2 a^2 b^4 c^2 z^2-4 a b^5 c^2 z^2+15 b^6 c^2 z^2-4 a^3 b^2 c^3 z^2-4 a^2 b^3 c^3 z^2-4 a b^4 c^3 z^2-20 b^5 c^3 z^2+3 a^2 b^2 c^4 z^2+6 a b^3 c^4 z^2+15 b^4 c^4 z^2-2 a b^2 c^5 z^2-6 b^3 c^5 z^2+b^2 c^6 z^2 = 0)
tangente a las circunferencias Γb, Γc, Ωb y Ωc es:
Λa : 4 b^2 c^2 ((b - c)^2 - a (b + c))^2 x^2 + (-a^8 + 2 a^7 (b + c) +
6 a^3 (b - c)^4 (b + c) + (b - c)^6 (b^2 + c^2) +
2 a^6 (b^2 + b c + c^2) - 2 a^4 b c (9 b^2 - 14 b c + 9 c^2) -
2 a (b - c)^4 (b^3 + b^2 c + b c^2 + c^3) -
2 a^5 (3 b^3 - 5 b^2 c - 5 b c^2 + 3 c^3) -
2 a^2 (b - c)^2 (b^4 - 9 b^3 c + 12 b^2 c^2 - 9 b c^3 + c^4)) y z + ⋯ = 0,
cuyo centro es:
Oa = (a^8-2a^7(b+c)+6a^5(b-c)^2(b+c)-
2a^6(b+c)^2-(b-c)^6(b+c)^2+2a(b-c)^4(b+c)^3+
4a^4b c(5b^2-6bc+5c^2)+
2a^2(b-c)^2(b^4-8b^3c-2b^2c^2-8b c^3+c^4)-
2a^3(3b^5-5b^4c-6b^3c^2-6b^2c^3-5b c^4+
3c^5) :
4b^2c(a^4(b+c)-2a(b-c)(b+c)^3+
2a^3(b^2+2b c-c^2)+(b-c)^3(3b^2+4b c+c^2)-
4a^2b(b^2-b c+2c^2)) :
4b c^2(a^4(b+c)+
2a(b-c)(b+c)^3-4a^2c(2b^2-b c+c^2)+
a^3(-2b^2+4b c+2c^2)-(b-c)^3(b^2+4b c+3c^2))).
Los puntos Ob y Oc se definen cíclicamente. Los radios de las circunferencias inscrita y circunscrita a ABC se designa por r y R, respectivamente.
Los triángulos
ABC y son perspectivos, con centro de perspectividad
W = (r+2R) I - 4r O.
W = ( a(3a^3+a^2(b+c)+
a(-3b^2+2bc-3c^2)-(b-c)^2(b+c)) : ... : ...),
que tiene números de búsqueda en
(-1.83665556655288, -1.22199792675032, 5.33435023114362), punto medio de X1420 y X5128; reflexión de Xi en Xj para los índices {i,j}: {1, 1420}, {9614, 3086}; y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1, 3}, {2, 4292}, {4, 3911}, {5, 9579}, {7, 3523}, {8, 4311}, {9, 474}, {10, 4293}, {20, 1210}, {21, 3306}, {28, 8056}, {30, 9581}, {34, 7501}, {58, 937}, {63, 404}, {72, 3928}, {78, 3218}, {79, 4679}, {80, 5787}, {84, 1728}, {90, 3062}, {100, 6765}, {104, 12650}, {108, 1753}, {109, 602}, {140, 5219}, {142, 3624}, {169, 5030}, {172, 9593}, {200, 4973}, {223, 580}, {226, 631}, {238, 1777}, {255, 269}, {282, 1741}, {329, 6700}, {376, 950}, {377, 5705}, {380, 2260}, {386, 4303}, {388, 6684}, {405, 5437}, {411, 1445}, {443, 1478}, {452, 9843}, {496, 9580}, {498, 5290}, {499, 1699}, {515, 1788}, {516, 3086}, {549, 4654}, {550, 5722}, {553, 3487}, {579, 610}, {908, 6921}, {910, 5022}, {920, 1768}, {938, 3522}, {944, 4848}, {946, 3474}, {956, 1706}, {962, 5265}, {970, 3784}, {978, 1044}, {997, 12526}, {1054, 1722}, {1103, 1106}, {1124, 9616}, {1125, 4295}, {1158, 7995}, {1323, 14256}, {1376, 4662}, {1394, 1465}, {1407, 7078}, {1436, 2270}, {1439, 14528}, {1453, 3752}, {1490, 1708}, {1571, 2242}, {1702, 6502}, {1703, 2067}, {1724, 3182}, {1732, 2173}, {1737, 4299}, {1795, 3345}, {1836, 5433}, {1837, 15326}, {1838, 7490}, {1876, 3515}, {2066, 9582}, {2096, 6260}, {2178, 2324}, {2362, 9583}, {2948, 10081}, {2951, 10092}, {2975, 9352}, {3085, 4298}, {3146, 5704}, {3158, 3555}, {3476, 11362}, {3485, 10165}, {3488, 3528}, {3525, 5714}, {3530, 6147}, {3583, 4333}, {3585, 6826}, {3633, 12437}, {3634, 10590}, {3646, 3683}, {3651, 10382}, {3731, 7523}, {3868, 4855}, {3901, 11570}, {3929, 5044}, {4031, 10299}, {4190, 6734}, {4224, 5272}, {4257, 7520}, {4294, 11019}, {4305, 6738}, {4313, 10304}, {4316, 6869}, {4317, 9588}, {4325, 6885}, {4338, 6892}, {4355, 13407}, {4853, 8666}, {4866, 7284}, {4915, 5288}, {4999, 5880}, {5084, 6692}, {5223, 6763}, {5226, 10303}, {5229, 10175}, {5248, 10582}, {5249, 6910}, {5250, 5253}, {5252, 5771}, {5270, 5726}, {5281, 11037}, {5298, 11376}, {5432, 10404}, {5436, 5439}, {5440, 11523}, {5442, 7951}, {5445, 5791}, {5506, 9814}, {5531, 12757}, {5541, 10074}, {5586, 11551}, {5587, 7354}, {5657, 10106}, {5687, 6762}, {5715, 6833}, {5720, 6924}, {5735, 6966}, {5768, 10573}, {5836, 11194}, {6261, 7098}, {6361, 12053}, {6824, 7988}, {6876, 10393}, {6911, 7330}, {6985, 7171}, {7082, 7701}, {7293, 11337}, {7580, 9841}, {7741, 8727}, {7972, 9945}, {8583, 12514}, {8703, 12433}, {9654, 11231}, {9655, 9956}, {9778, 10624}, {9860, 10089}, {9904, 10091}, {9942, 15071}, {9946, 11571}, {10069, 13174}, {10391, 10399}, {10461, 13588}, {10483, 10826}, {11246, 11375}, {12119, 12832}, {12408, 13312}, {12699, 15325}, {13117, 13221}.
El centro W ha sido incluido en ETC, X15803.
Se denota por
Gab, Gac, Oab y Oac
los puntos de contacto de la circunferencia Λa con las circunferencias
Γb, Γc, Ωb y Ωc, respectivamente.
Se consideran los puntos diagonales del cuadrivértice GabGacOabOac :
La = GabOab ∩ GacOac,
Ma = GabOac ∩ GacOab,
Na = GabGac ∩ OabOac.
Se definen cíclicamente los puntos Lb, Mb, Nb, Lc, Mc y Nc.
Las rectas
ALa,
BLb y
CLc concurren en
L = 2R^2(r+2R)
I + r(r^2+4rR-4R^2)
O.
Las rectas AMa, BMb y CMc concurren en
X1617 = 2R^2 I - r(r+2R) O.
L = 4R^2(2r-R) X3911 - r(r^2+4rR+6R^2) X13615=
( a^2(a+b-c)(a-b+c)(a^5-
3a^4(b+c)+2a^3(b^2+b c+c^2) +
2a^2(b^3+2b^2c+2b c^2+c^3) -
a(3b^4+2b^3c+14b^2c^2+2b c^3+3c^4)+b^5-b^4c-b c^4+c^5) : ... : ...),
con números de búsqueda en
(0.754029207956068, 0.917198214856652, 2.65766762179620) y es el punto de intersección de las rectas XiXj s.e.u.o., para los índices {i,j}: {1, 3}, {3598, 7485}, {3911, 13615}.
El centro L ha sido incluido en ETC, X15804.
- Jueves, 4 de enero del 2018
La cúbica generalizada de Tucker T(P, -5/4)
Generalized Tucker Cubic (Bernard Gibert)
Let P = u:v:w be a point and k a real number.
The generalized Tucker cubic T(P, k) is the cubic with equation:
For.png)
T(P, k) is a non-pivotal cubic nK(#P, P) with pole the barycentric square Ω of P and root P.
Dado un triángulo ABC y un punto P, no situado sobre sus lados, la de P corta a los lados BC, CA y AB en U, V y W, respectivamente.
Para un punto Q, es su y QaQbQc es su .
Ab = QaV ∩ QbQc
Ac = QaW ∩ QbQc
Se definen Bc, Ba, Cb y Cb, cíclicamente.
Los puntos Ab, Ac, Bc, Ba, Cb y Ca están sobre una misma cónica si y solo si Q está sobre la cúbica generalizada de Tucker T(P, -5/4).
Descargar fichero GeoGebra
Si, en coordenadas baricéntricas, P(u:v:w) y Q(p:q:r), entonces:
Ab(2ru : qw ; -rw), Ac(2qu : -qv : rv), Bc(pu : -2pv : -ru), Ba(pw : 2rv : -rw), Cb(-pu : qu : 2pw) y Ca(pv : -qv : 2qw).
Estos seis puntos están sobre una misma cónica si las coordenadas de Q satisfacen a la ecuación:
4 u x(w^2y^2+v^2 z^2) + 4 v y(u^2z^2+w^2 x^2) +4 w z(v^2x^2+u^2 y^2)+ 17 u v w x y z = 0.
Que es una no pivotal de polo el
de P, raíz P y parámetro 17uvw/4.
Esta ecuación se puede expresar en la forma siguiente:
For.png)
Con lo que se trata de la cúbica generalizada de Tucker T(P, -5/4).
- Lunes, 1 de enero del 2018
Hexágonos regulares sobre los lados de un triángulo
Dado un triángulo ABC se levantan hexágonos regulares sobre cada lado, hacia el exterior, denotados por CBBaA2A3Ca,
ACCbB3B1Ab, BAAcC1C2Bc.
Las mediatrices de los segmentos AbAc, BcBa y CaCb concurren en P1 = 3 X2 - 4 .
El punto 3 X2 - 4 X18 es el ORTOCENTRO del correspondiente al ángulo θ=-π/6 y está sobre la de este triángulo. Esta
hipérbola
( (b - c) (b + c) (-a^10 + 12 a^8 (b^2 + c^2) -
5 a^6 (7 b^4 + 11 b^2 c^2 + 7 c^4) + (b^2 - c^2)^2 (5 b^6 -
8 b^4 c^2 - 8 b^2 c^4 + 5 c^6) +
a^4 (43 b^6 + 47 b^4 c^2 + 47 b^2 c^4 + 43 c^6) +
a^2 (-24 b^8 + 14 b^6 c^2 + 38 b^4 c^4 + 14 b^2 c^6 - 24 c^8) -
Sqrt[3] Sqrt[(b + c - a) (a + b - c) (a - b + c) (a + b +
c)] (3 a^8 -
9 a^6 (b^2 + c^2) - (b^2 - c^2)^2 (b^4 + 7 b^2 c^2 + c^4) +
a^4 (8 b^4 + b^2 c^2 + 8 c^4) -
a^2 (b^6 - 16 b^4 c^2 - 16 b^2 c^4 + c^6))) x^2 - (b - c) (b +
c) (-5 a^10 + 24 a^8 (b^2 + c^2) -
a^6 (43 b^4 + 44 b^2 c^2 + 43 c^4) + (b^2 - c^2)^2 (b^6 -
4 b^4 c^2 - 4 b^2 c^4 + c^6) +
a^4 (35 b^6 + b^4 c^2 + b^2 c^4 + 35 c^6) +
a^2 (-12 b^8 + 25 b^6 c^2 - 8 b^4 c^4 + 25 b^2 c^6 - 12 c^8) -
Sqrt[3] Sqrt[(b + c - a) (a + b - c) (a - b + c) (a + b +
c)] (a^8 + a^6 (b^2 + c^2) -
4 a^4 (2 b^4 + 3 b^2 c^2 + 2 c^4) - (b^2 - c^2)^2 (3 b^4 +
b^2 c^2 + 3 c^4) +
3 a^2 (3 b^6 + b^4 c^2 + b^2 c^4 + 3 c^6))) y z + ... = 0)
pasa por X2 (baricentro), X3 (circuncentro), X14 ( X616 ( del primer punto de Fermat), X3104 (imagen del mediante el giro de centro el primer punto de Brocard y amplitud -60º), X3413, X3414 (estos últimos son puntos del infinito de la hipérbola de Kiepert de ABC) y X5858.
Las coordenadas baricéntricas de los vértices de los hexágonos en cuestión se pueden determinar utilizando giro de rectas. Así, el vértice Ab, es la intersección de las rectas que resultan de girar la recta AC alrededor de A un ángulo 2π/3 y, la otra, alrededor de C un ángulo -π/6; es decir:
Ab = (3(+√3S) : -3b^2 : 3SA -
√3 S) es la intersección de
(3 - √3S)y+ 3b^2z=0, y
b^2x +(SC + √3S)y=0.
Obtenidas las coordenadas de Ab, las de Ac serán
(3(SB+√3S) : 3SA -
√3 S : -3c^2).
La mediatriz del segmento AbAc es:
4(b^2-c^2)√3Sx + (-3a^4+a^2(6b^2+6c^2-2√3S)+
3(b^2-c^2)(-b^2+c^2+2√3 S)) y + (3a^4+
a^2(-6b^2-6c^2+2√3S)+
3(b^2-c^2)(b^2-c^2+2√3 S)) z = 0.
Por permutación cíclica, se deducen las ecuaciones de las mediatrices de los segmentos BcBa y CaCb. Estas tres rectas concurren en:
P1 = ( S^2 - √3 (
a^2 - SA) S + 2 SB SC
: ... : ...),
que divide al segmento de extremos el baricentro y el en la razón X2:X18=-4:3, y tiene números de búsqueda en
(-73.0108023685801, 49.1294658431783, 3.32525076059021).
Si los hexágonos CBBaA2A3Ca,
ACCbB3B1Ab, BAAcC1C2Bc son construidos hacia el interior del triángulo ABC, las mediatrices de los segmentos AbAc, BcBa y CaCb concurren en:
( S^2 + √3 (
a^2 - SA) S + 2 SB SC
: ... : ...),
que está sobre la
hipérbola
( (b - c) (b + c) (-a^10 + 12 a^8 (b^2 + c^2) -
5 a^6 (7 b^4 + 11 b^2 c^2 + 7 c^4) + (b^2 - c^2)^2 (5 b^6 -
8 b^4 c^2 - 8 b^2 c^4 + 5 c^6) +
a^4 (43 b^6 + 47 b^4 c^2 + 47 b^2 c^4 + 43 c^6) +
a^2 (-24 b^8 + 14 b^6 c^2 + 38 b^4 c^4 + 14 b^2 c^6 - 24 c^8) +
Sqrt[3] Sqrt[(b + c - a) (a + b - c) (a - b + c) (a + b +
c)] (3 a^8 -
9 a^6 (b^2 + c^2) - (b^2 - c^2)^2 (b^4 + 7 b^2 c^2 + c^4) +
a^4 (8 b^4 + b^2 c^2 + 8 c^4) -
a^2 (b^6 - 16 b^4 c^2 - 16 b^2 c^4 + c^6))) x^2 - (b - c) (b +
c) (-5 a^10 + 24 a^8 (b^2 + c^2) -
a^6 (43 b^4 + 44 b^2 c^2 + 43 c^4) + (b^2 - c^2)^2 (b^6 -
4 b^4 c^2 - 4 b^2 c^4 + c^6) +
a^4 (35 b^6 + b^4 c^2 + b^2 c^4 + 35 c^6) +
a^2 (-12 b^8 + 25 b^6 c^2 - 8 b^4 c^4 + 25 b^2 c^6 - 12 c^8) +
Sqrt[3] Sqrt[(b + c - a) (a + b - c) (a - b + c) (a + b +
c)] (a^8 + a^6 (b^2 + c^2) -
4 a^4 (2 b^4 + 3 b^2 c^2 + 2 c^4) - (b^2 - c^2)^2 (3 b^4 +
b^2 c^2 + 3 c^4) +
3 a^2 (3 b^6 + b^4 c^2 + b^2 c^4 + 3 c^6))) y z + ... = 0)
de Kiepert del triángulo de Kiepert
correspondiente al ángulo θ=60º y divide al segmento de extremos el baricentro y el en la razón X2:X17=-4:3, y tiene números de búsqueda en
(-2.34148817718688, -0.405250874980819, 5.00190963098043).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Las mediatrices de los segmentos B1C1, C2A2 y A3B3 concurren en X5858.
Utilizando el mismo procedimiento del caso anterior, el punto B1 es la intersección de las rectas:
SAy + b^2z = 0,
3 b^2 x + (3SC +
√3 S) y = 0
B1 = (3 SC+
√3
S : -3 b^2 : 3 SA)
⇒
C1 = (3 SB+
√3
S : 3 SA: -3 c^2).
Las mediatrices de los segmentos B1C1, C2A2 y A3B3 concurren en:
X5858 = (3(a^2-2SA ) - 2√3 S :
3(b^2-2SB) - 2√3 S :
3(c^2-2SC) - 2√3 S).
El punto X5858 es el BARICENTRO del triángulo T(1,3) y está sobre la del correspondiente al ángulo θ=-60º.
Si los hexágonos CBBaA2A3Ca,
ACCbB3B1Ab, BAAcC1C2Bc son construidos hacia el interior del triángulo ABC, las mediatrices de los segmentos B1C1, C2A2 y A3B3 concurren en X5859.
X5859 = (3(a^2-2SA ) + 2√3 S :
3(b^2-2SB) + 2√3 S :
3(c^2-2SC) + 2√3 S).
El punto X5859 es el BARICENTRO del triángulo U(1,3) y está sobre la del correspondiente al ángulo θ=60º.
The triangles T(k,n) and U(k,n) (Peter Moses, June 27, 2014)
On side BC of a triangle ABC, erect a regular
n-sided polygon, externally. Starting at B and going around the polygon
until reaching C, label the vertices v(0), v(1), ..., v(n-1), so that
line v(0)v(n-1) = BC, and if n is even, then the lines L(A,k,n) =
v(k)v(n-k-1), for k = 1, ..., (n-2)/n, are parallel to BC. If n is odd,
let L(A,k,n), for k = (n-1)/2, be the line through v((n-1)/2)) that is
parallel to BC. Define lines L(B,k,n) and L(C,k,n) cyclically.
Then for
each k from 1 to floor((n-1)/2), the lines L(A,k,n), L(B,k,n), L(C,k,n)
form a triangle T(k,n) homothetic to ABC.
T(1,4) and U(1,4) are the
outer and inner , respectively.
Triangle centers defined
from T(k,n) include the following, given by 1st barycentrics:
centroid of T(k,n): -2a2 + b2 + c2
+ S*[cot(kπ/n)) - cot(kπ/n+π/n)]
circumcenter of T(k,n): a2[2S2A -
2SBSC + SSA csc(kπ/n)
csc(π/n+kπ/n) sin(π/n)]
orthocenter of T(k,n): a2SBSC -
SA(S2B + S2C) +
SSBSC[cot(kπ/n)) - cot(kπ/n+π/n)]
nine-point center of T(k,n): 2SA(a2SA
- S2B - S2C) +
S(SBSC + S2)[cot(kπ/n)) -
cot(kπ/n+π/n)]
If the polygons are erected internally instead of externally, the
resulting triangles are denoted by U(k,n), with triangle centers given
by changing S to - S in the above first barycentrics:
centroid of U(k,n): -2a2 + b2 + c2 -
S*[cot(kπ/n)) - cot(kπ/n+π/n)]
circumcenter of U(k,n): a2[2S2A -
2SBSC - SSA csc(kπ/n)
csc(π/n+kπ/n) sin(π/n)]
orthocenter of U(k,n): a2SBSC -
SA(S2B + S2C) -
SSBSC[cot(kπ/n)) - cot(kπ/n+π/n)]
nine-point center of U(k,n): 2SA(a2SA
- S2B - S2C) -
S(SBSC + S2)[cot(kπ/n)) -
cot(kπ/n+π/n)]
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Las mediatrices de los segmentos B3C2, C1A3 y A2B1 concurren en P3 = 6 X2 - 5 .
El punto B3 es la intersección de las rectas:
(3 SA + √3 S)y+ 3 b^2 z= 0,
b^2x + SC y = 0
B3 = (3 SC : -3 b^2 : 3 SA + √3 S)
⇒
C2 = (3 SB : 3 SA + √3 S : -3 c^2).
Las mediatrices de los segmentos B3C2, C1A3 y A2B1 concurren en:
P3 = ( 5 a^2 SA + √3 (4SA-a^2) S : ... : ...),
que está sobre la hipérbola de Kiepert del triángulo de Kiepert
correspondiente al ángulo θ=-60º y divide al segmento de extremos el baricentro y el en la razón X2:X17=-6:5, y tiene números de búsqueda en
(8.84294000458321, 4.45061678245910, -3.52188867729494).
Si los hexágonos CBBaA2A3Ca,
ACCbB3B1Ab, BAAcC1C2Bc son construidos hacia el interior del triángulo ABC, las mediatrices de los segmentos B3C2, C1A3 y A2B1 concurren en:
( 5 a^2 SA - √3 (4SA-a^2) S : ... : ...),
que está sobre la hipérbola de Kiepert del triángulo de Kiepert
correspondiente al ángulo θ=60º y divide al segmento de extremos el baricentro y el en la razón X2:X18=-6:5, y tiene números de búsqueda en
(97.1795827438248, -57.4677791152399, -1.42606508930717).
∗ ∗ ∗ ∗ ∗
∗ ∗ ∗ ∗ ∗
Las mediatrices de los segmentos CbBc, AcCa y BaAb concurren en X616, del .
El punto Cb es la intersección de las rectas:
(SA + √3 S)y + b^2 z = 0,
3 b^2x + (3 SC -√3 S) y = 0
Cb = (3 SC - √3 S : -3 b^2 : 3 (SA + √3 S))
⇒
Bc = (3 SB - √3 S : 3 (SA + √3 S): -3 c^2).
Las mediatrices de los segmentos CbBc, AcCa y BaAb concurren en:
X616 = ( SBSC+SA (2a^2-√3 S) :
SCSA+SB (2a^2-√3 S) :
SASB+SC(2a^2-√3 S)),
que está sobre la hipérbola de Kiepert del triángulo de Kiepert
correspondiente al ángulo θ=-60º
Si los hexágonos CBBaA2A3Ca,
ACCbB3B1Ab, BAAcC1C2Bc son construidos hacia el interior del triángulo ABC, las mediatrices de los segmentos CbBc, AcCa y BaAb concurren en X617 (anticomplemento del segundo punto de Fermat) y está sobre la hipérbola de Kiepert del triángulo de Kiepert
correspondiente al ángulo θ=60º.





For.png)
For.png)