Hechos Geométricos en el Triángulo
(2013)
(2014)
(2015)
(2016)
(2017)
(2018)
(2019)
(2020)
(2021)
(2022)
(2023)
(2024)
|
Cómo es el enlace a un Hecho Geométrico correspondiente a un día concreto: http://amontes.webs.ull.es/otrashtm/HechosGeometricos.htm#HGddmmaa EJEMPLO: Domingo, 3 de noviembre del 2013 http://amontes.webs.ull.es/otrashtm/HechosGeometricos.htm#HG031113 |
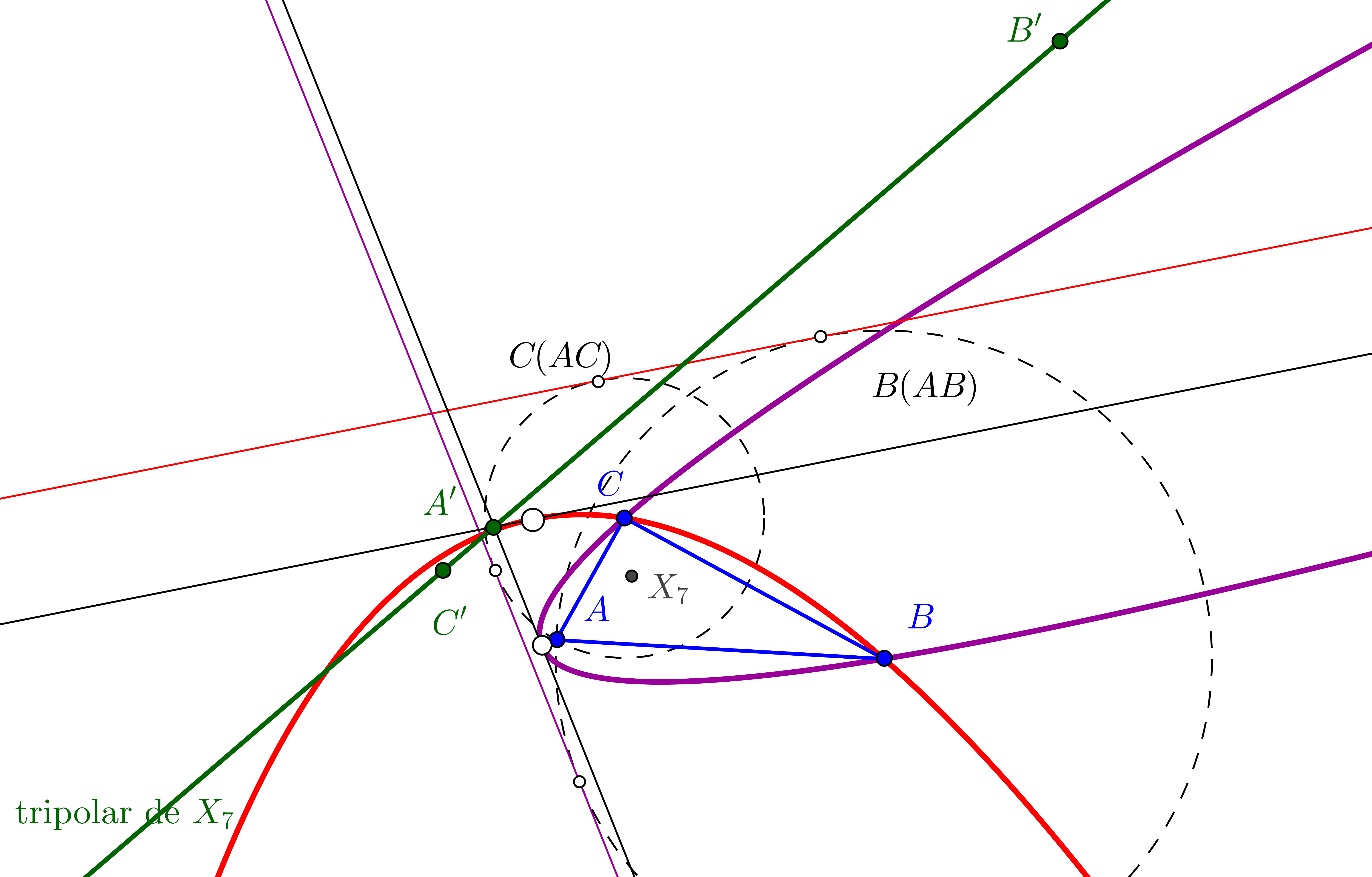
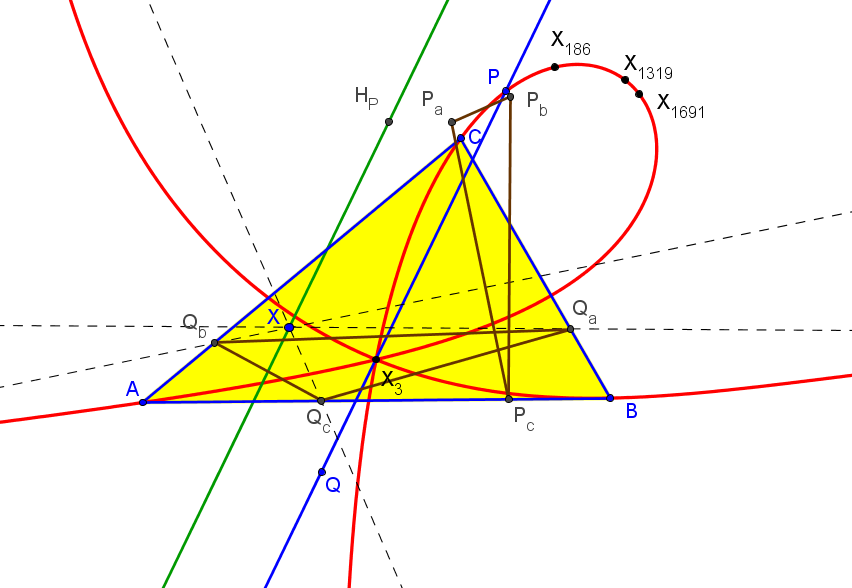
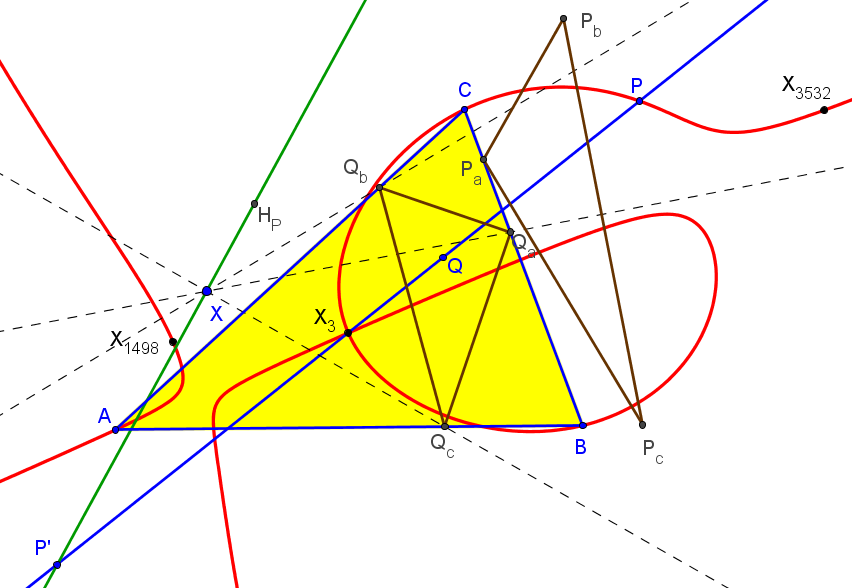
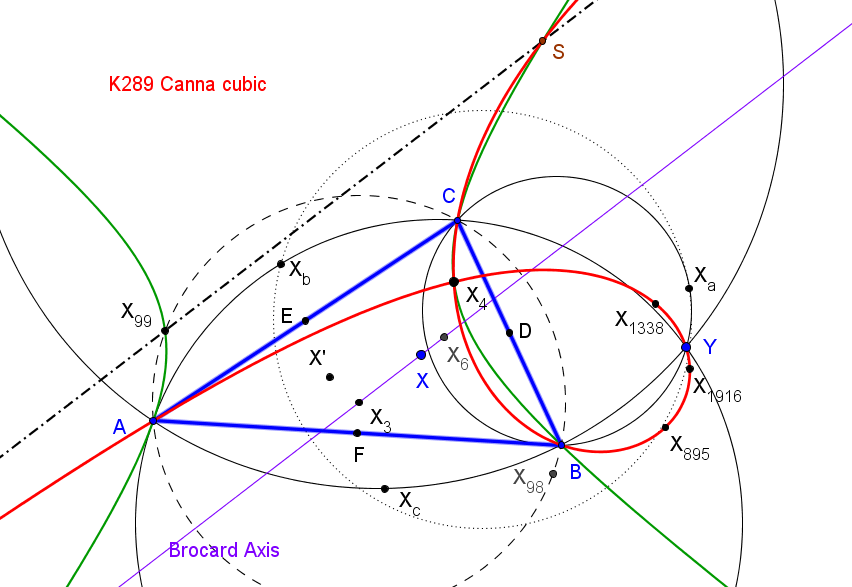
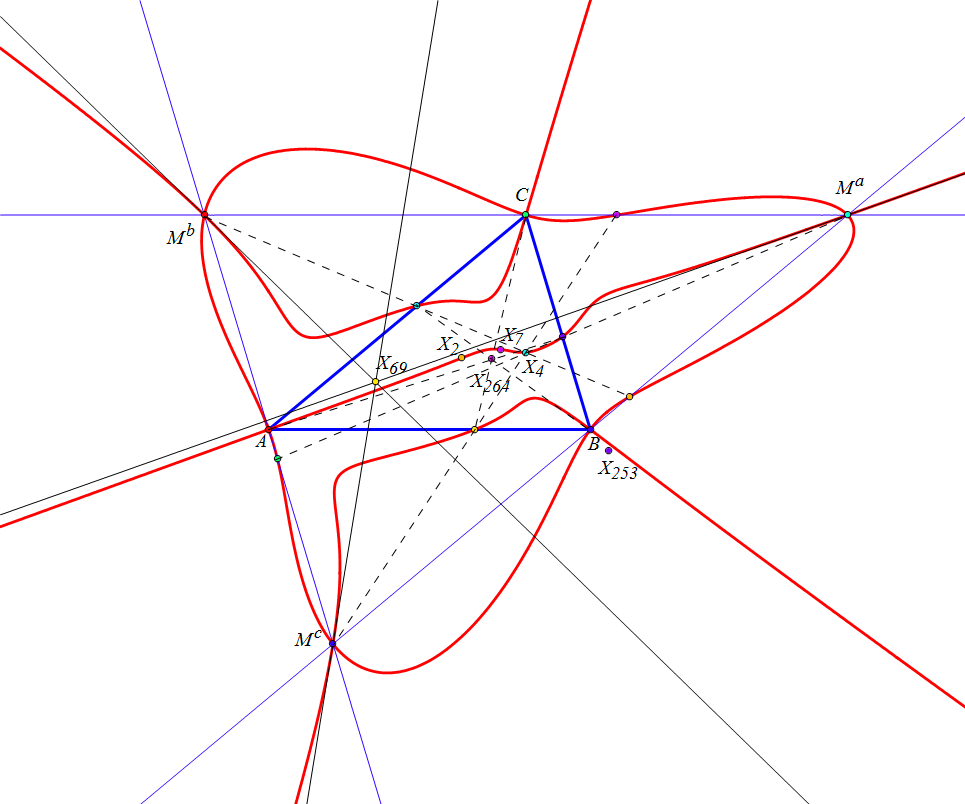
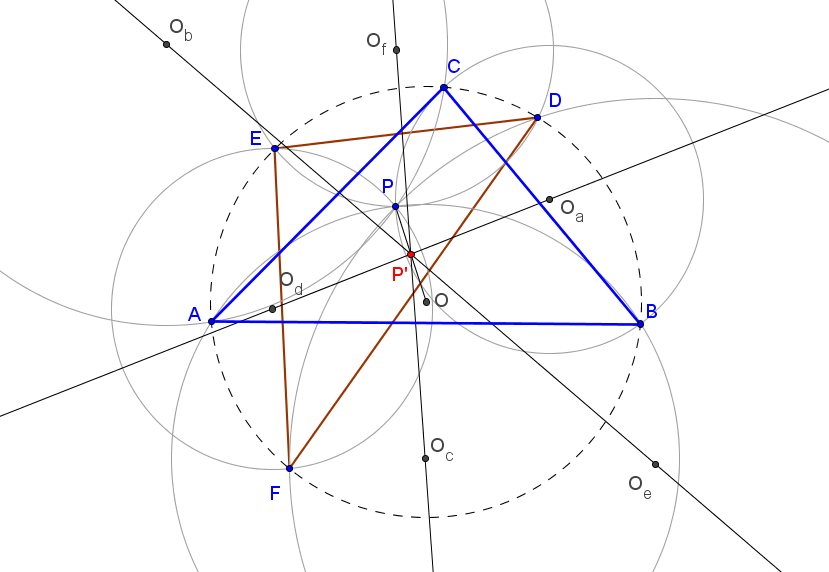
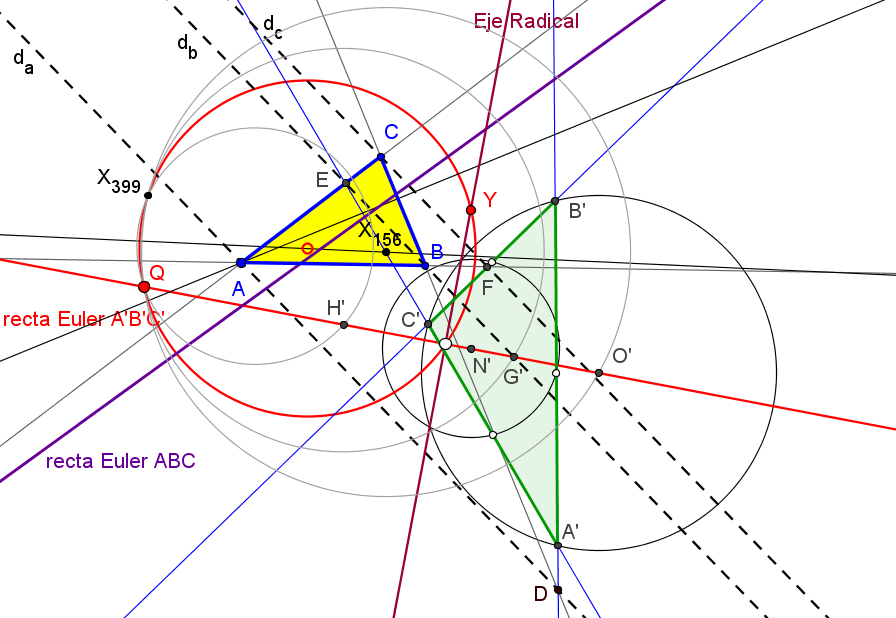
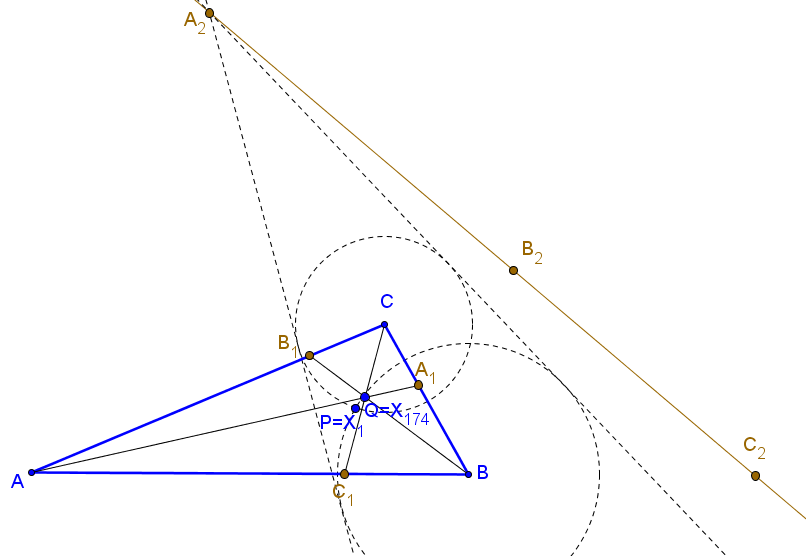
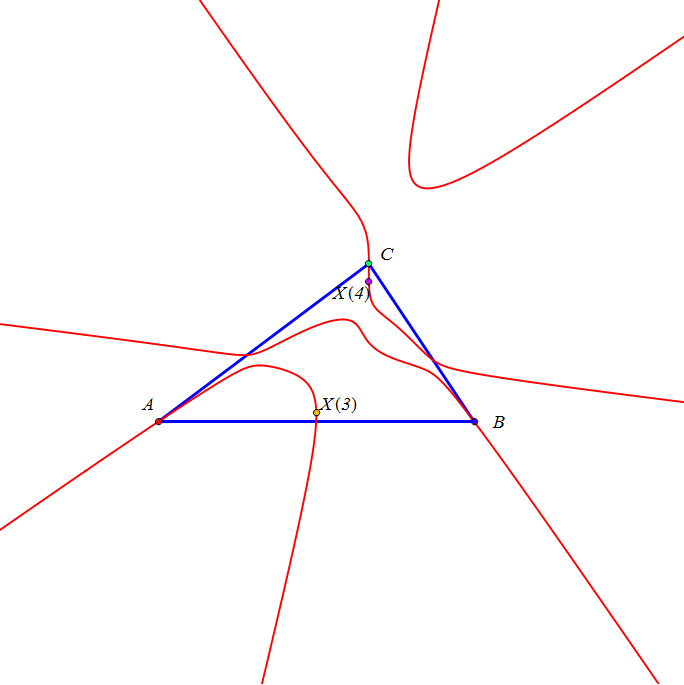
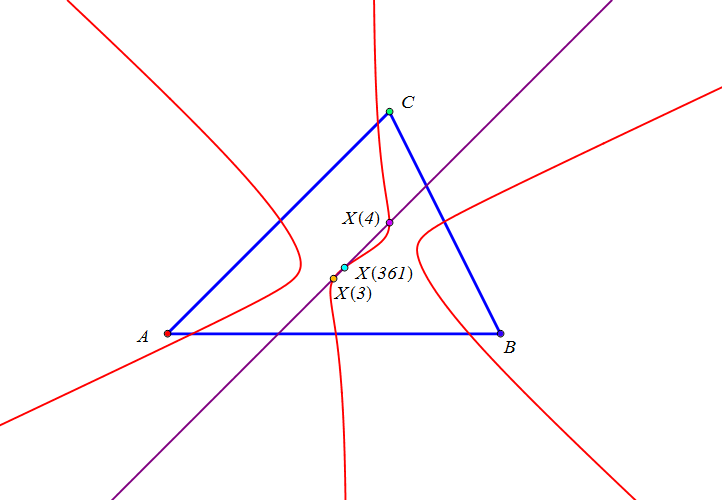
Dado un punto P, el lugar geométrico de los puntos Q tal que los triángulos pedales de P y Q son ortológicos es la recta OP.
(0 : (b^2-c^2)p + a^2(p+2q) : (-b^2+c^2)p + a^2(p+2r)).
La perpendicular por Pa al lado XbXc, si Q(u:v:w), es:
(b^2-c^2)p(c^2v+b^2w)+a^2(c^2(p+2q)v-b^2(p+2r)w)x -
((-b^2+c^2)p+a^2(p+2r))(c^2v+b^2w)y +
((b^2-c^2)p+a^2(p+2q))(c^2v+b^2w)z = 0.
a^2(b^2r-c^2q) - (b^2-c^2)(c^2q+b^2r)u+... =0,
es decir, el punto Q está en la recta OP.
Sean P un punto con triángulo pedal PaPbPc y Q un punto variable sobre la recta OP, con triángulo pedal QaQbQc.
•
El lugar geométrico del centro de ortología X de QaQbQc respecto a PaPbPc es una recta (L) que pasa por el ortocentro HP de PaPbPc.
La recta (L) pasa por O si y solo si P está en la cúbica K389.
La recta (L) pasa por P si y solo si P está en la cuártica Q098.
• El lugar geométrico del centro de ortología Y de PaPbPc respecto a QaQbQc es la hipérbola equilátera (H) circunscrita a PaPbPc que pasa por P.
(L): (b^2SBr-c^2SCq)x ⁄ (c^2q+b^2r)+... = 0.
HP (a^2(c^2q+b^2r) (SA(c^2p q+b^2p r+a^2q r) - b^2c^2p(p+q+r)): ... : ... )
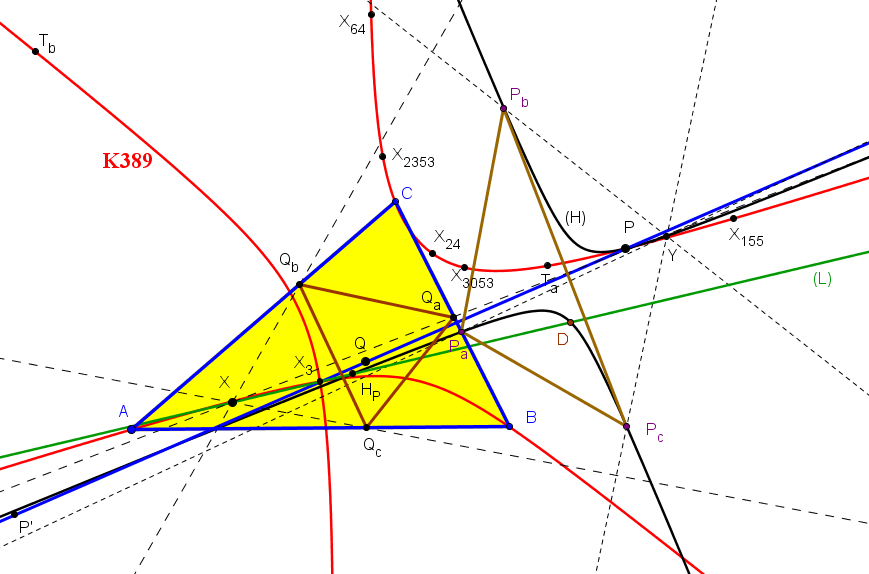
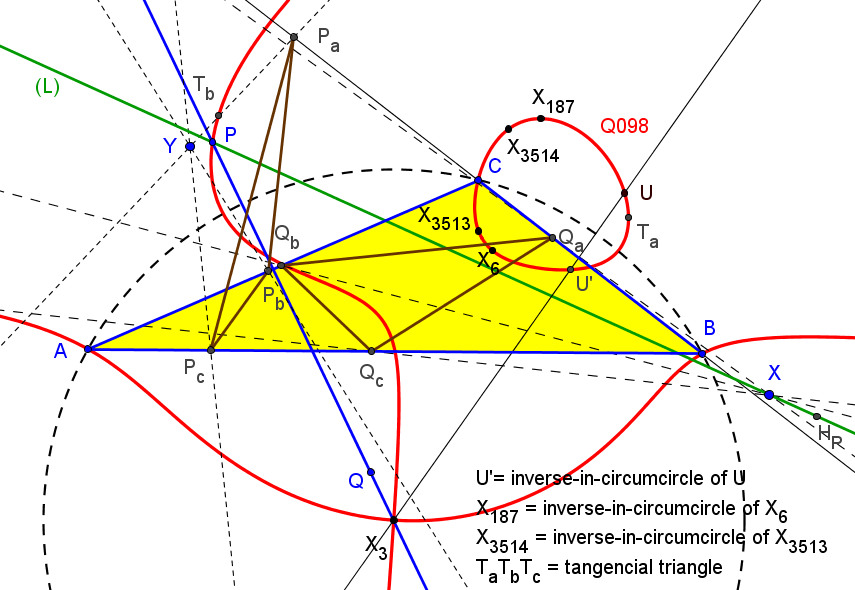
El lugar geométrico de los puntos P tales que la recta (L) pasa por el punto P0, que divide al segmento OP en la razón OP0 : P0P = m : n, es la cuártica
m a^2b^2c^2 Q098 + n R^2 (x+y+z) K389 = 0.
R es el radio de la circunferencia circunscrita a ABC. Todas las cuárticas de este haz están circunscritas a ABC, tiene al circuncentro como punto singular, pasan por los vértices del triángulo tangencial y por los puntos en el infinito de la hipérbola de Jerabek.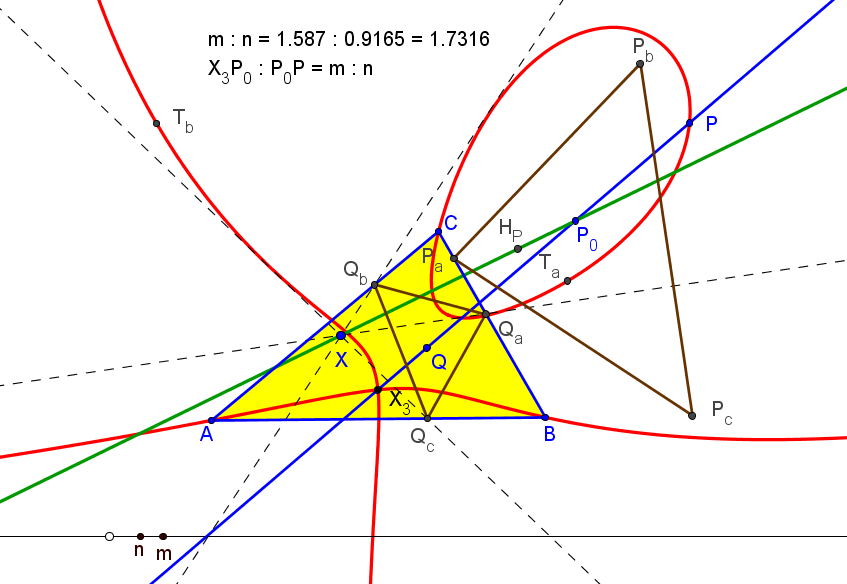
F(X) = Y = ((u-v-w) /(2 a^2 v w+(b^2 w+c^2 v) (u-v-w)) : ... : ...)
Para X el circuncentro, F(X) no está definido. Si X está en el infinito F(X)=X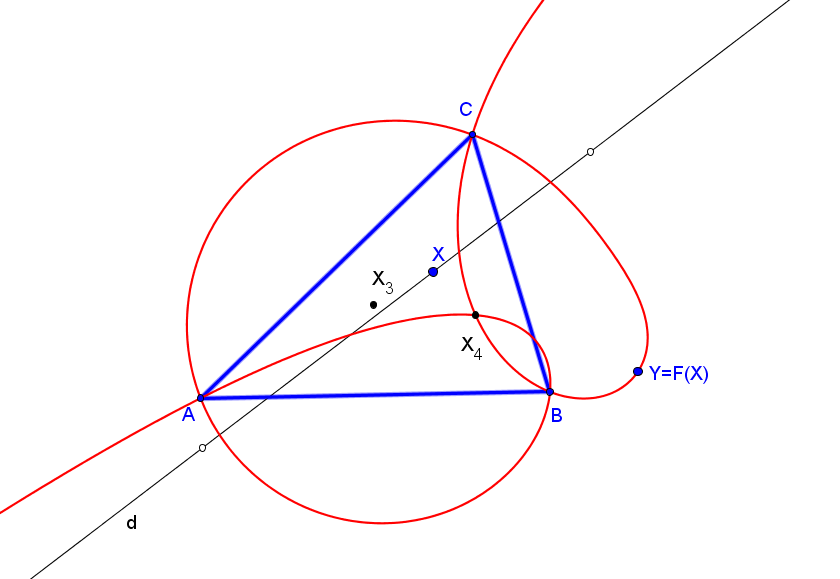
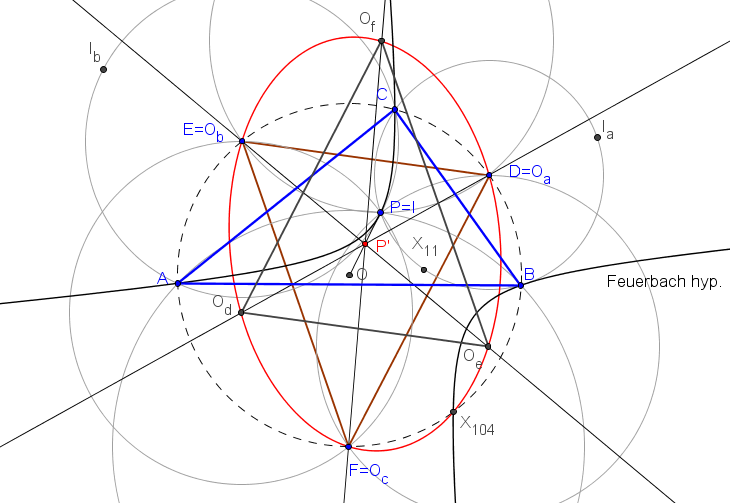
Sea ABC un triángulo, O su circuncentro y P un punto, el lugar geométrico de P tal que el ortocentro de su triángulo pedal queda en la recta OP es la cuártica Q023, del catálogo de Bernard Gibert).
Si (x:y:z) son las coordenadas baricéntricas de P el ortocentro del triángulo pedal A'B'C' es:H' (a^2(c^2y+b^2z) (yza^4 + (b^2z(x-y)+c^2y(x-z))a^2 - x(b^4z+c^4y-b^2c^2(2x+y+z))) : ... : ...)
Los puntos P que están alineados con H' y O (a^2(b^2+c^2-a^2):...:...) satisfacen a la ecuación de la cuártica Q023.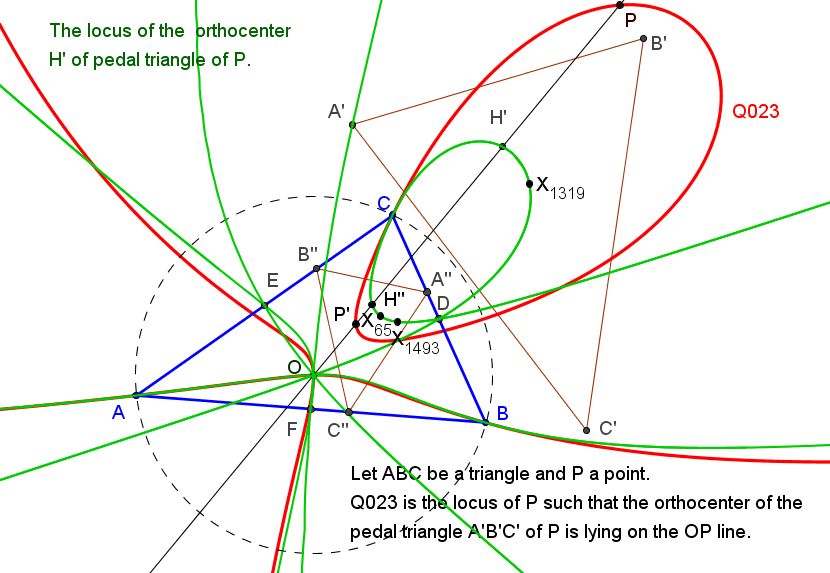
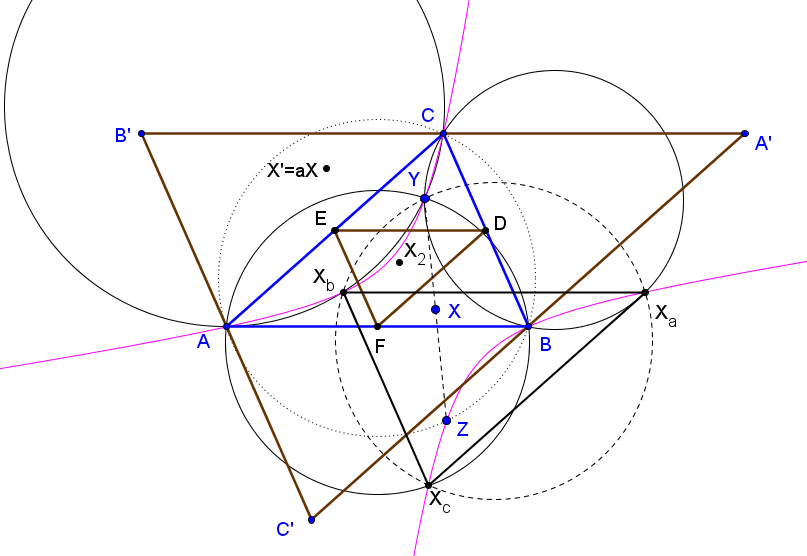
Sean ABC un triángulo y DEF el triángulo ceviano de un punto U. Tomemos los puntos D1=BC∩EF, E1=CA∩FD y F1=AB∩DE y sus reflexiones D2, E2, F2 respecto a los puntos medios D0, E0, F0 de los lados de DEF.
Sea Ka el punto de intersección de la paralela por D1 a AU con la recta AD0.
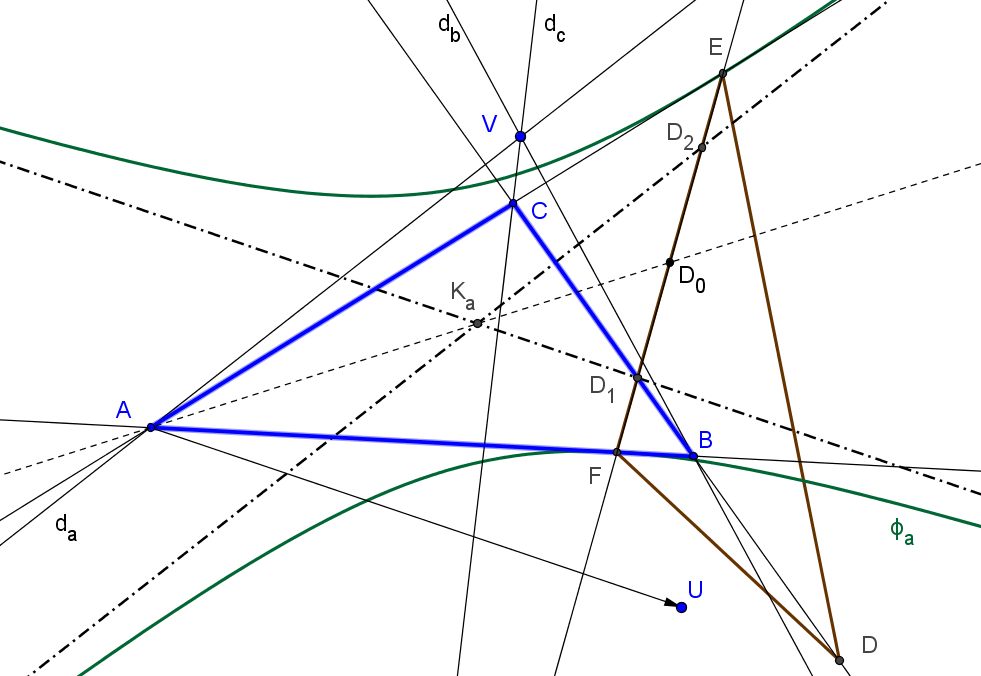
Las tres rectas da, db y dc son concurrentes.
Si U(u:v:w), las coordenadas baricéntricas del punto V, de intersección de las tres rectas da, db, dc, son:F(U) = V = (u(v+w)^2 : v(u+w)^2 : w(u+v)^2)
A un punto U y a su conjugado isotómico U• les corresponde el mismo punto V.
Cuando U recorre la cónica circunscrita de perspector P(p:q:r), pyz+qzx+rxy=0, o la recta px+qy+rz=0, V=F(U) describe la cúbica:
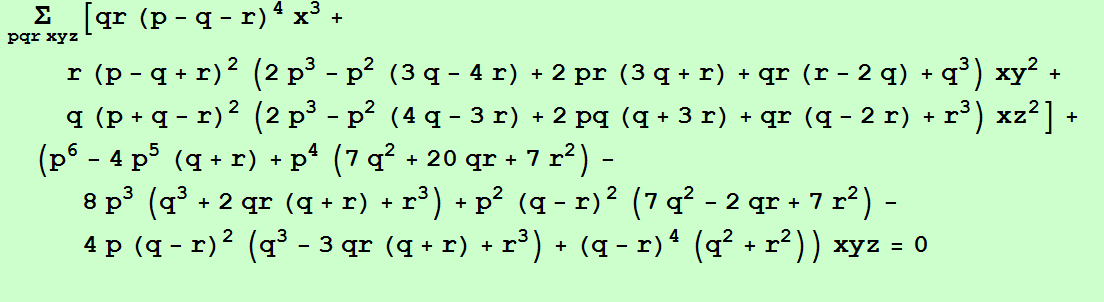
D = (p/(q + r - p) : q/(r + p - q) : r/(p + q - r)).
Es el punto que correponde, mediante la aplicación F, a los puntos de intersección de la cónica circunscrita de perspector P y la tripolar de P.
Si U(u:v:w) se mueve sobre la recta del infinito, x+y+z=0, o sobre la elipse circunscrita de Steiner, yz+zx+xy=0, V (u^3:v^3:w^3) o V (1/u^3:1/v^3:1/w^3) describe la cúbica de Bataille (K656):
x^3 + 3 x^2 y + 3 x y^2 + y^3 + 3 x^2 z - 21 x y z + 3 y^2 z +
3 x z^2 + 3 y z^2 + z^3 =0
ó (x + y + z)^3 = 27 x y z.
a Lolilla, por su "cumple"
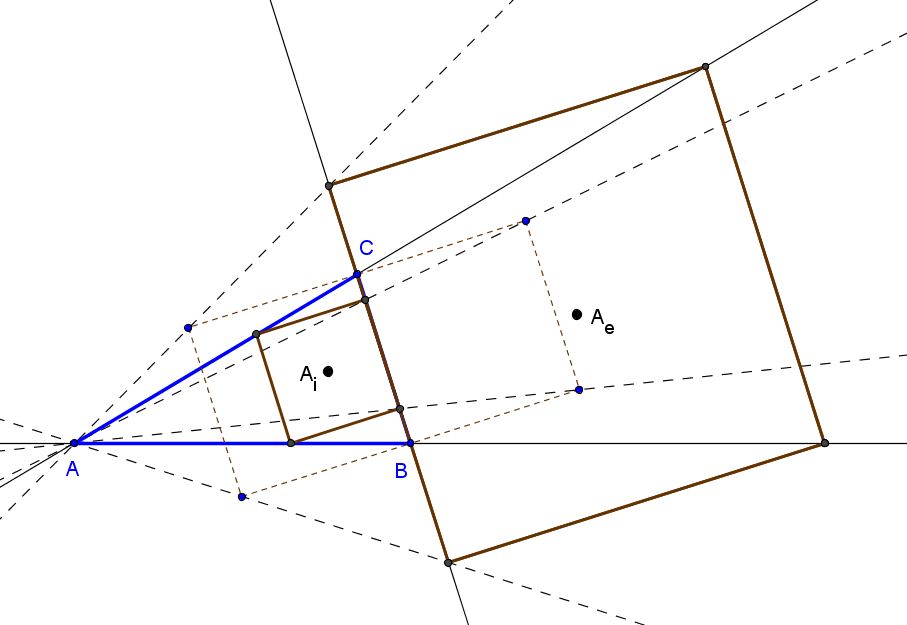
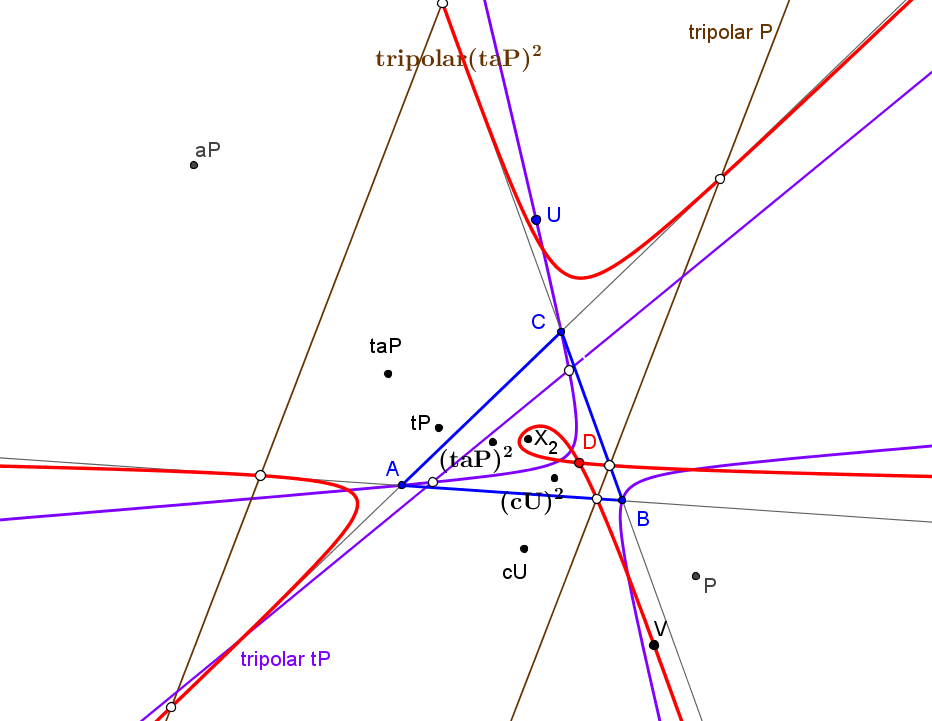
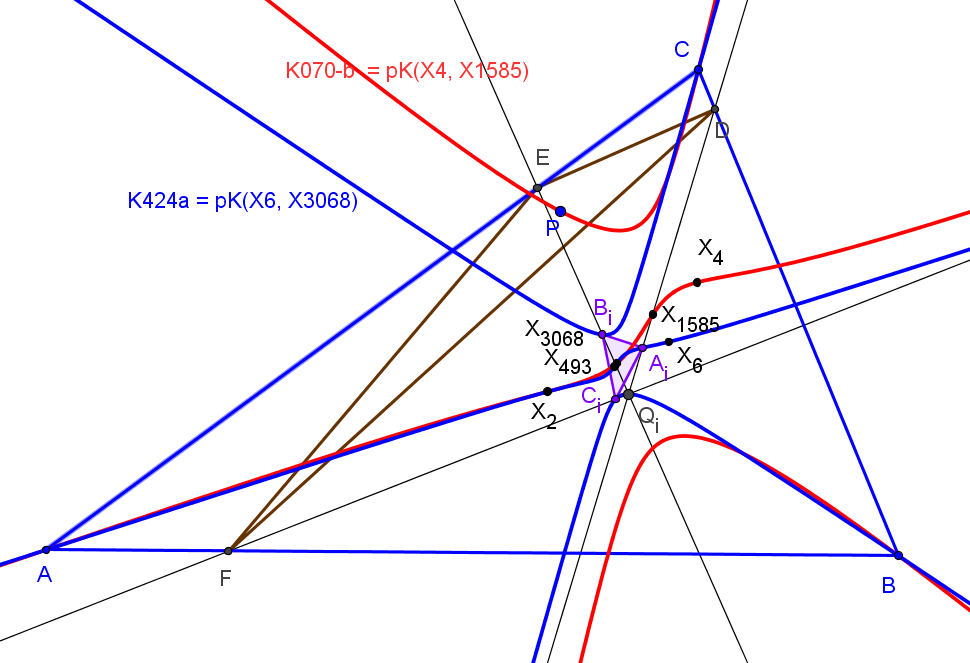
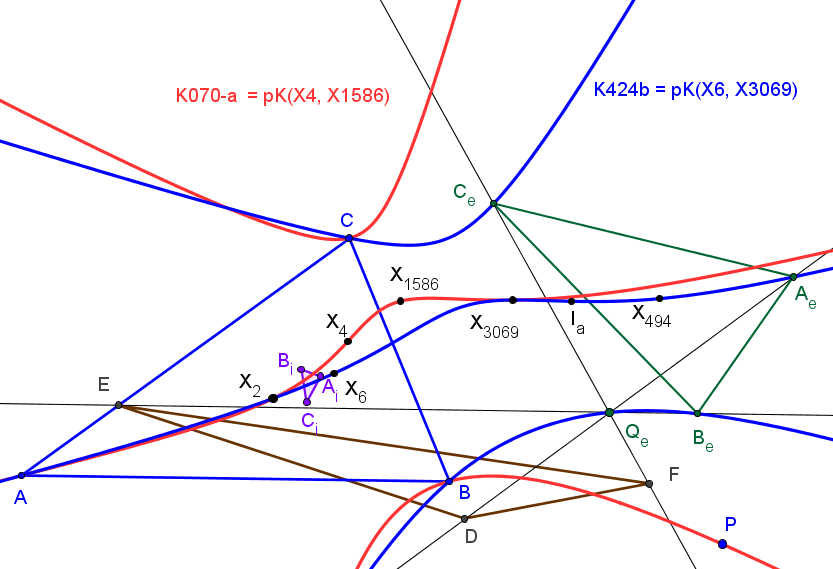
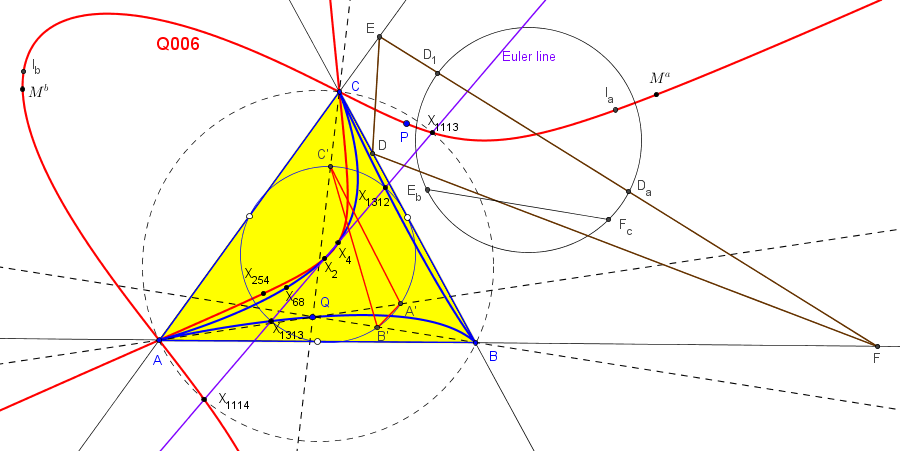
Los triángulos AiBiCi y AeBeCe son perspectivos con centro de perspectividad el simediano.
El lugar geométrico de los puntos P tales que los triángulos DEF y AiBiCi son perspectivos es la cúbica K070-b, "Shoemaker's (inner) cubic" = pK(X4, X1585). El centro de perspectividad Qi queda sobre la cúbica isogonal de pivote X3068 (K424a, del catálogo de cúbicas de Bernard Gibert).
a^4(-p^2+p(q+r)+3q r) + 2a^2(p(c^2(p+q)+b^2(p+r))+2(p-q)(p-r)S) - b^4(p+q)(p-r) - c^4(p-q)(p+r) + 2b^2c^2(p^2-qr) - 4pS(c^2(p-q)+b^2(p-r))-4(p-q)(p-r)S^2
Este punto está, cuando P=(p:q:r) recorre K070-b, en la cúbica K424a que pasa por los centros X(1), X(2), X(6), X(371), X(485), X(493), X(3068), por los excentros Ia, Ib, Ic y por los vértices de AiBiCi.El lugar geométrico de los puntos P tales que los triángulo DEF y AeBeCe son perspectivos es la cúbica K070-a, "Shoemaker's (outer) cubic" = pK(X4, X1586). El centro de perspectividad Qe queda sobre la cúbica isogonal de pivote X3069 (K424b).
∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗
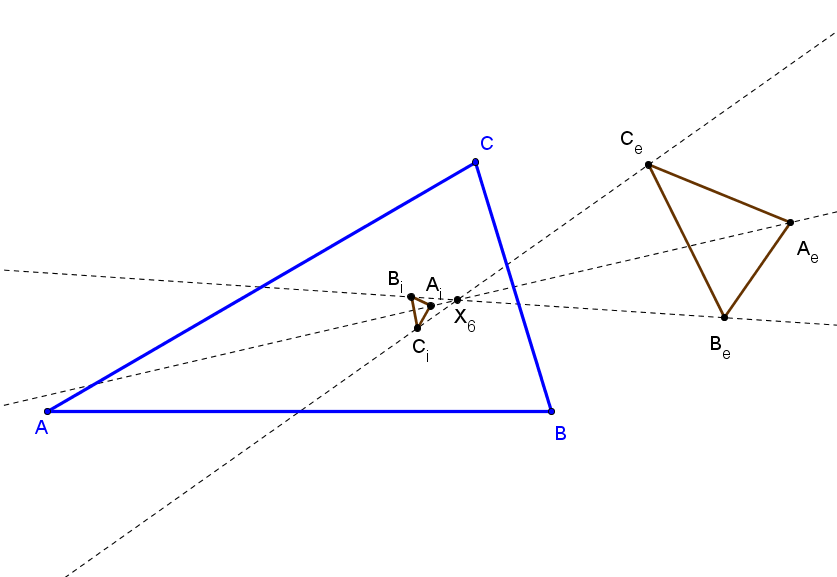
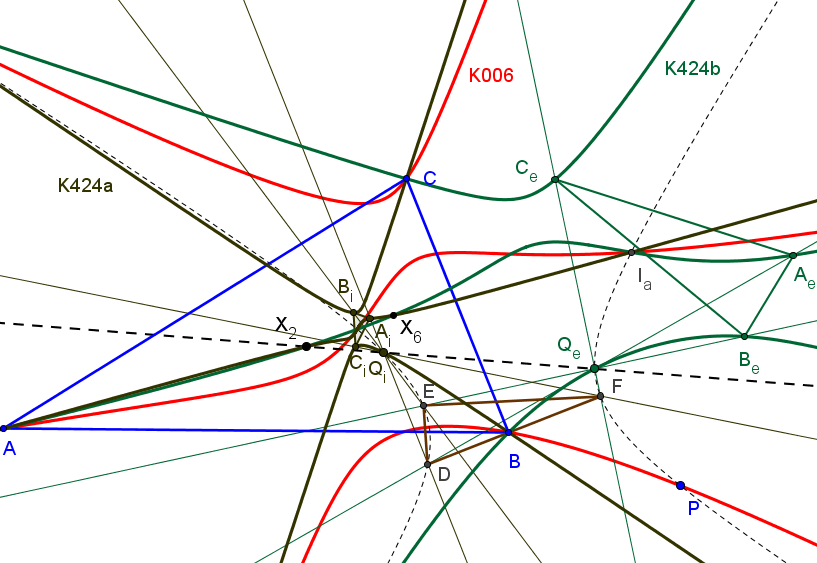
El lugar geométrico de los puntos P tales que su triángulo anticeviano DEF es perspectivo con AiBiCi y con AeBeCe, es la cúbica K006, "Orthocubic" = pK(X6, X4). Los centros de perspectividad Qi y Qe quedan, respectivamente, sobre la cúbicas isogonales K424a y K424b.
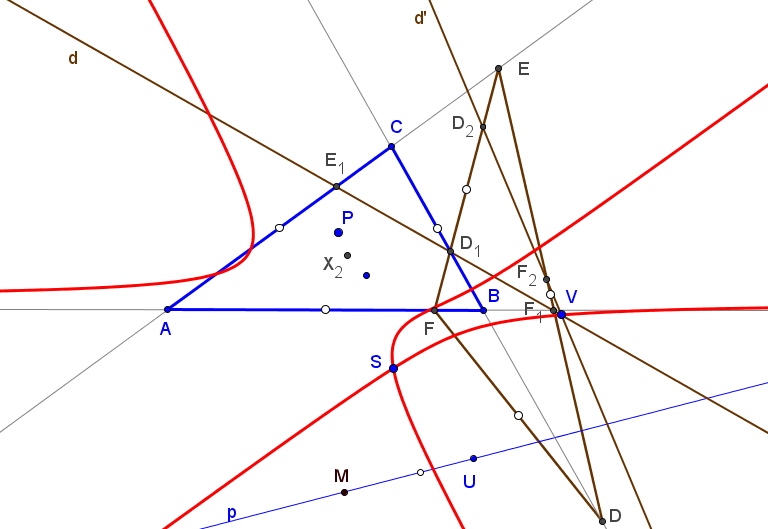
Sean ABC un triángulo, U un punto y DEF su triángulo ceviano. Los puntos D1=BC∩EF, E1=CA∩FD y F1=AB∩DE están en el eje d de perspectividad ("perspectrix") de los triángulos ABC y DEF. Denotamos por d′ la recta que pasa por las reflexiones D2, E2, F2 de D1, E1, F1 respecto a los puntos medios de los lados de DEF
Si U=(u:v:w), las coordenadas baricéntricas de V=d∩d′ son:
V = (u(v-w)(2u+v+w) : v(w-v)(u+2v+w) : w(u-v)(u+v+2w)).
El lugar geométrico del punto de intersección V de las la rectas d y d′, cuando U se mueve sobre una recta p : px+qy+rz=0 es la cúbica:
p(p:q:r) ↦ S(3p-2(q+r) : 3q-2(r+p) :3r-2(p+q))
es una correlación. Si la recta p es tangente a la elipse x^2+y^2+z^2+4xy+4xz+4yz=0, homotética de la elipse inscrita de Steiner en la homotecia h(G,Sqrt[10]), el punto singular S es el punto de tangencia.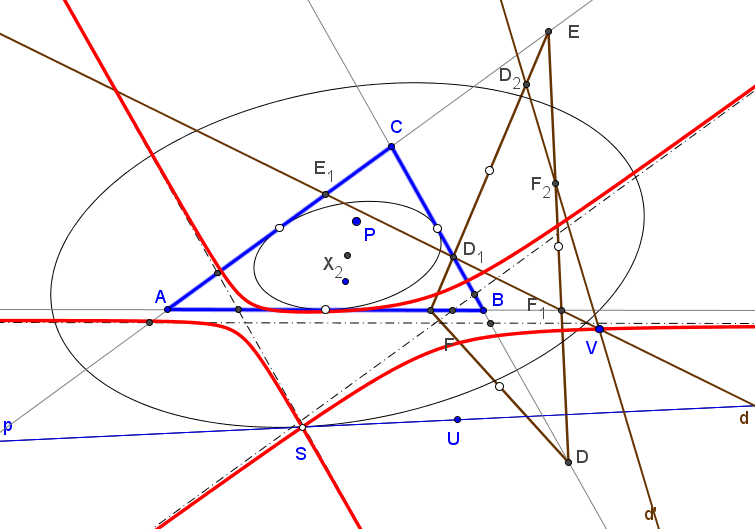
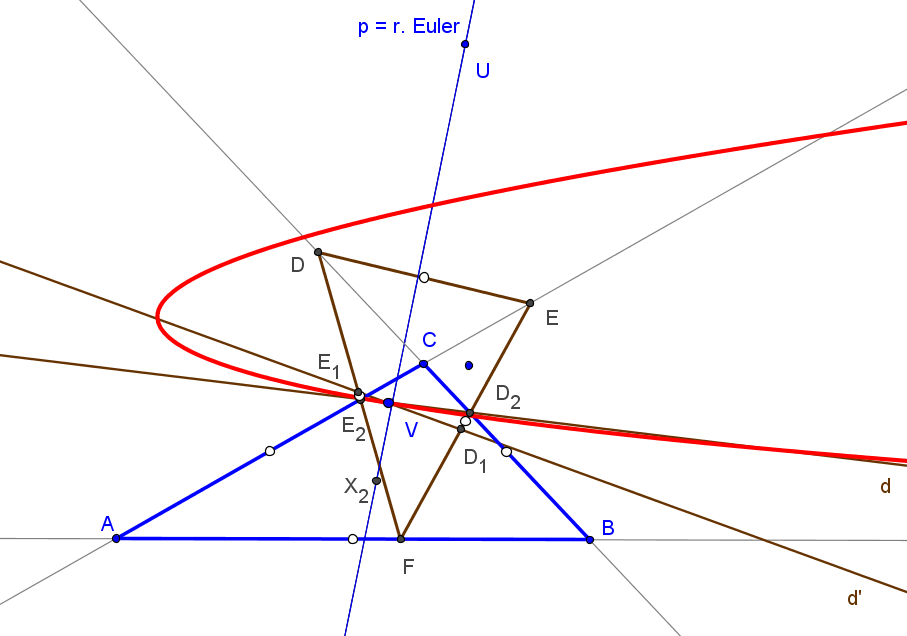

Sean ABC un triángulo, O el circuncentro, P un punto y A'B'C' el triángulo ceviano de P.
El lugar geométrico de P, tal que el centro N' de la circunferencia de los nueve puntos de A'B'C' esté sobre la recta OP, es una séptica
que pasa por los vértices de los triángulos ABC (triples), medial y excentral, y por X1, X2, X3, X370 (y los otros cinco -tres siempre reales- "equilateral cevian points"), X1138.
a^2 c^2 u^3 v^3 - b^2 c^2 u^3 v^3 + c^4 u^3 v^3 - 3 a^4 u^3 v^2 w +
6 a^2 b^2 u^3 v^2 w - 3 b^4 u^3 v^2 w + 5 a^2 c^2 u^3 v^2 w +
5 b^2 c^2 u^3 v^2 w - 2 c^4 u^3 v^2 w - a^4 u^2 v^3 w +
2 a^2 b^2 u^2 v^3 w - b^4 u^2 v^3 w + 4 a^2 c^2 u^2 v^3 w +
2 b^2 c^2 u^2 v^3 w - c^4 u^2 v^3 w - 3 a^4 u^3 v w^2 +
5 a^2 b^2 u^3 v w^2 - 2 b^4 u^3 v w^2 + 6 a^2 c^2 u^3 v w^2 +
5 b^2 c^2 u^3 v w^2 - 3 c^4 u^3 v w^2 - 4 a^4 u^2 v^2 w^2 +
6 a^2 b^2 u^2 v^2 w^2 - 2 b^4 u^2 v^2 w^2 + 6 a^2 c^2 u^2 v^2 w^2 +
4 b^2 c^2 u^2 v^2 w^2 - 2 c^4 u^2 v^2 w^2 - a^4 u v^3 w^2 +
a^2 b^2 u v^3 w^2 - a^2 c^2 u v^3 w^2 + a^2 b^2 u^3 w^3 +
b^4 u^3 w^3 - b^2 c^2 u^3 w^3 - a^4 u^2 v w^3 + 4 a^2 b^2 u^2 v w^3 -
b^4 u^2 v w^3 + 2 a^2 c^2 u^2 v w^3 + 2 b^2 c^2 u^2 v w^3 -
c^4 u^2 v w^3 - a^4 u v^2 w^3 - a^2 b^2 u v^2 w^3 +
a^2 c^2 u v^2 w^3 - 2 a^4 v^3 w^3.
Los triángulos ABC y A'B'C' son ortológicos si sólo si el punto P está en una nónica con puntos cuádruples en los vértices de ABC, puntos dobles los vértices del triángulo antimedial y que pasa por el baricentro, ortocentro y punto de Gergonne.
D' = (u(c^2uv(v-w)+ w(b^2u(-v+w)+a^2v(2u+v+w))) : v(c^2uv(u+w)+ w(-b^2u(u+2v-w)+a^2v(u+w))) : -w(-(u+v)(b^2u+ a^2v)w+c^2uv(u-v+2w))).
La reflexión de D' en la recta EbFc es:A' = (-u(v-w)(-b^2(u+v)w+c^2v(u+w)) : -v(u+ w)(c^2u(v-w)+a^2(u+v)w) : -(u+v)w(a^2v(u+w)+ b^2u(-v+w)).

Los triángulos ABC y A'B'C' son perspectivos si sólo si el punto P está en la circunferencia circunscrita o en la cuártica de Stammler (Q066)
Si (u:v:w) son las coordenadas baricéntricas de P:D' = (u(c^2uv(v-w)+w(b^2u(-v+w)+a^2v(2u+v+w))) : v(c^2uv(u+w)+w(-b^2u(u+2v-w)+a^2v(u+w))) : -w(-(u+v)(b^2u+a^2v)w+c^2uv(u-v+2w))).
El simétrico de este punto respecto a EF es:A' =( u(v-w)(-b^2(u+v)w+c^2v(u+w)) : v(u+w)(c^2u(v-w)+a^2(u+v)w) : (u+v)w(a^2v(u+w)+b^2u(-v+w)) ).
Las rectas AA', BB', CC' son concurrrentes si las coordenadas de P satifacen a una de las ecuaciones:
a^2 yz + b^2 zx + c^2 xy =0,
Q066: a^2(b^2-c^2)y^2z^2 + b^2(c^2-a^2)z^2x^2 + c^2(a^2-b^2)x^2y^2= 0.
Si el punto P recorre la cuártica de Stammler Q066, el lugar geométrico del centro de perspectividad de ABC y A'B'C' es la cuártica (Q) de ecuación:
Pt = (1/(b^2(a^2-c^2)-c^2(a^2-b^2)t^2) :
1/(b^2(c^2- a^2)-2c^2(b^2-a^2)t+c^2(b^2-a^2)t^2) :
1/(b^2(a^2-c^2)-2b^2(a^2-c^2)t+c^2(a^2-b^2)t^2)).
Qt = ((b^2-c^2)^2t(-a^2t+b^2(1+t))(a^2-c^2(1+t)):
(a^2-c^2)^2(1+t)(b^2+c^2t)(a^2t-b^2(1+t)) :
(a^2-b^2)^2t(1+t)(b^2+c^2t)(a^2-c^2(1+t))).
Si el punto P recorre la la circunferencia circunscrita, el lugar geométrico del centro Q de perspectividad de ABC y A'B'C' es la circunferencia de los nueve puntos. El punto Q es la imagen de P en la homotecia de centro el baricentro y razón -1/2.
.png)
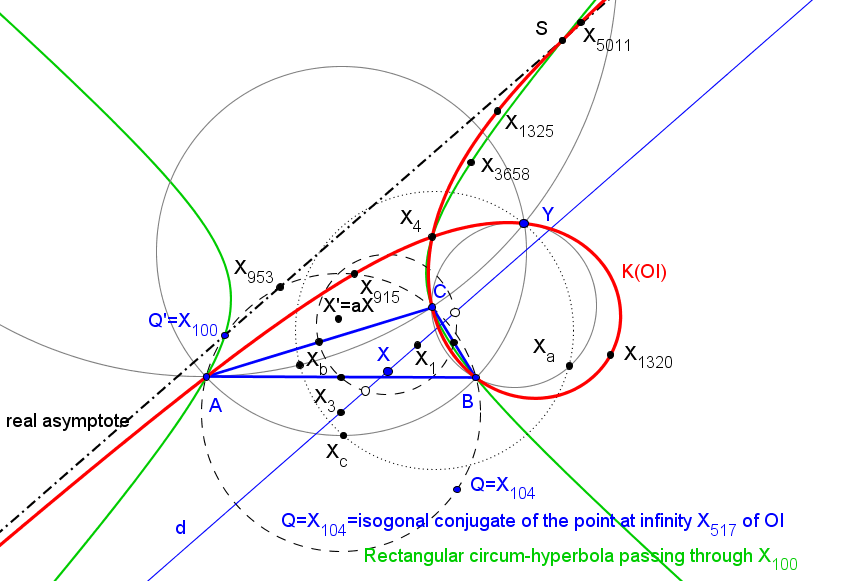
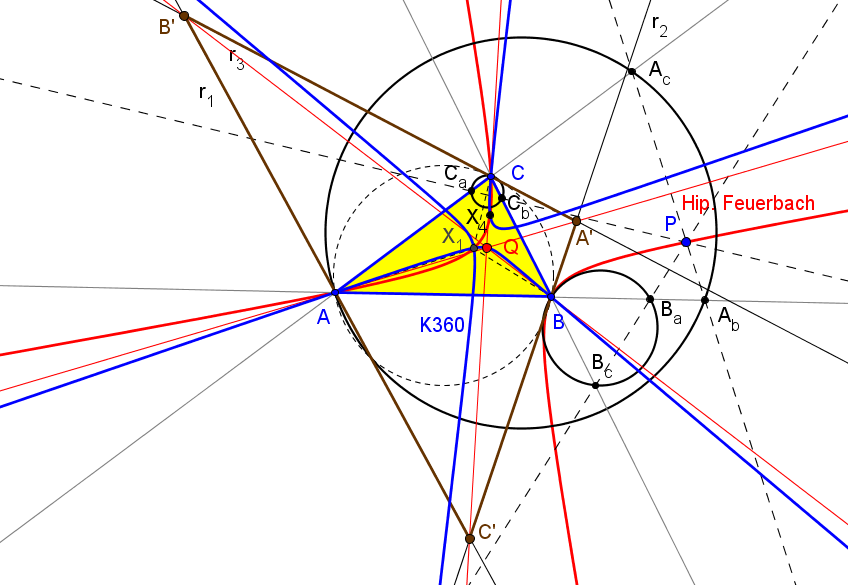
Sean ABC un triángulo y A'B'C' el triángulo ceviano del incentro X1. El conjugado antigonal Q de X1 respecto A'B'C' está en la recta X1O', donde O' es el circuncentro de A'B'C'.
Se verifica que
Q = 3R X1 + 2r X399,
donde R y r son los radios de las circunfencias circunscrita e inscrita a ABC, respectivamente.
a^2 (a^5 + a^4(b+c) - 2a^3(b^2+c^2) - a^2(2b^3-b*c(b+c)+2c^3)+ a(b^4+b^2c^2+c^4) + (b-c)^2(b^3+c^3))
con (6,9,13)-número de búsqueda en ETC: 0.812149174855219822306671631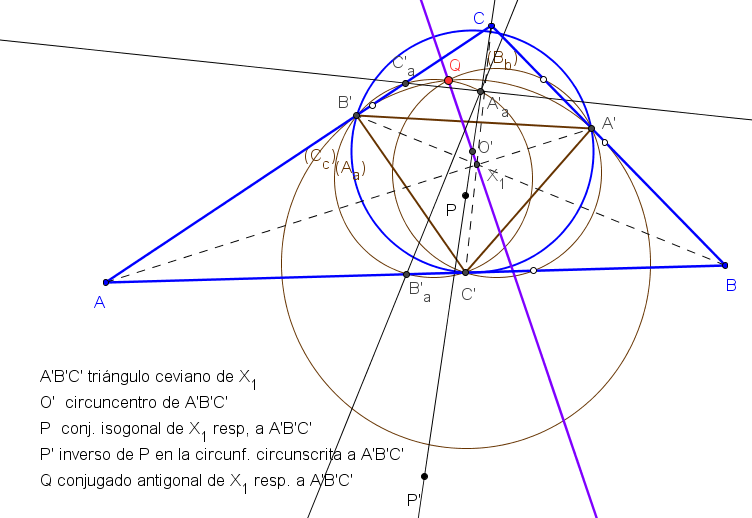
Let ABC be a triangle and A'B'C' the cevian triangle of I. Denote: B'a, C'a = the reflections of B',C' in AA', resp. A'a = (perpendicular to BB' from B'a) /\ (perpendicular to CC' from C'a). C'b, A'b = the reflections of C',A' in BB', resp. B'b = (perpendicular to CC' from C'b) /\ (perpendicular to AA' from A'b). A'c, B'c = the reflections of A',B' in CC', resp. C'c = (perpendicular to AA' from A'c) /\ (perpendicular to BB' from B'c). Are the circumcircles of A'aB'aC'a, B'bC'bA'b, C'cA'cB'c concurrent?. Antreas P. HatzipolakisHyacinthos #21651 (Feb 28, 2013)
The circumcircles are concurrent at non-ETC 0.812149174855220, which is, the antigonal conjugate, wrt incentral triangle, of X(1) Randy Hutson
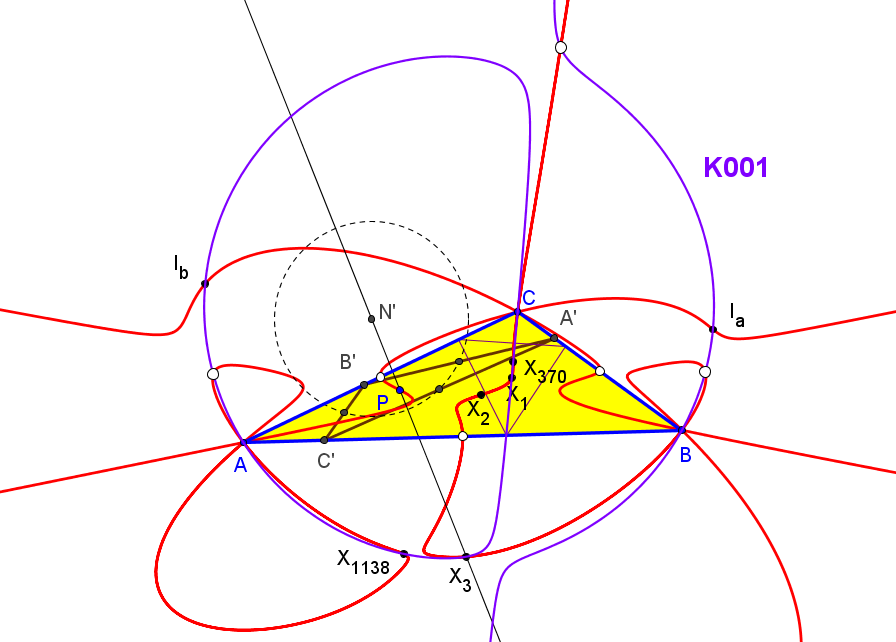
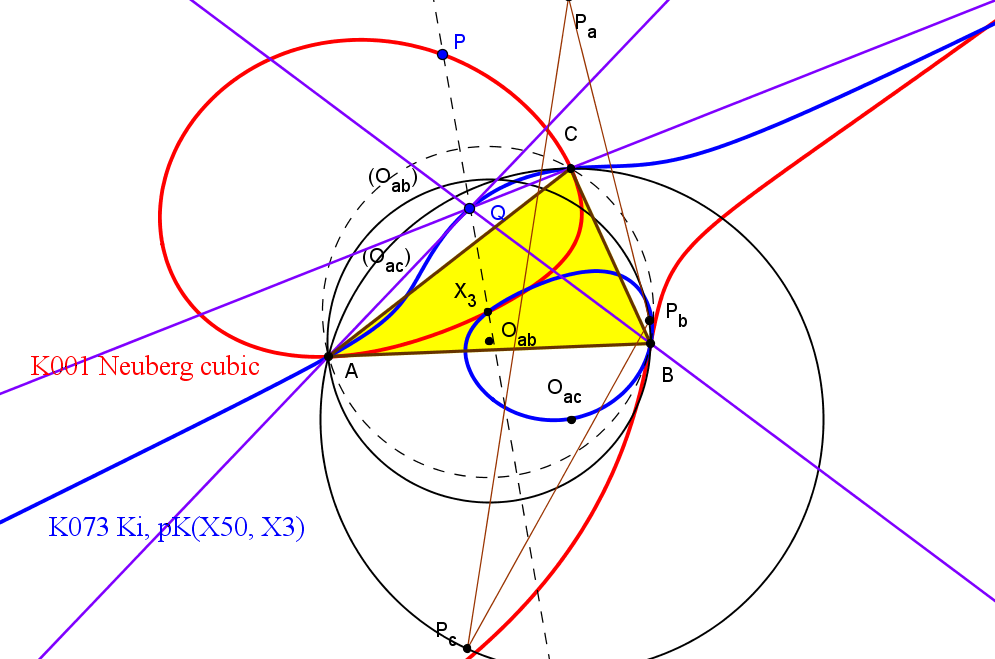
Los ejes radicales ea, eb y ec concurren en un punto Q si y solo si P está en la cúbica de Neuberg (K001, del catálogo de cúbicas de Bernard Gibert).
Los triángulos TaTbTc y PaPbPc son perspectivos si P está sobre el díámetro de ABC que pasa por X110 (foco de la parábola de Kiepert) o en la circunferencia con centro en la reflexión de X110 en X156 (centro de la circunferencia de los nueve puntos de TaTbTc) y que pasa por X155 (ortocentro de TaTbTc).
((b^2-c^2)^3-a^2(b^4-c^4))x - a^2(a^2-c^2)(a^2-b^2+c^2)y + a^2(a^2-b^2)(a^2+b^2-c^2)z=0.
Si P(u:v:w), las coordenadas baricéntricas de la reflexión Pa de P en da son:
(-a^2(a^8u -
a^6(b^2(u+v-w)+c^2(u-v+ w)) -
a^4(b^4(u-v)+c^4(u-w)+b^2c^2(-3u+v+w))
- a^2(b^2-c^2)^2(c^2v+b^2w) + (b^2-c^2)^4u ) :
(b^2-c^2)^5u - a^10w - a^2(b^2-c^2)^3(c^2(u+v)+b^2w) +
a^8(b^2(-v+w)+c^2(v+w)) -
a^4(b^2-c^2)(c^4(u-v-w)+b^4(2u+w)+b^2c^2(-u+2v+w)) +
a^6(-c^4(u+v-w)-4b^2c^2w+b^4(u+v+2 w)) :
-(b^2-c^2)^5u - a^10v+
a^2(b^2-c^2)^3(c^2v+b^2(u+w)) +
a^8(c^2(v-w)+b^2(v+w)) +
a^6(-4b^2c^2v-b^4(u-v+w)+c^4(u+2v+w)) +
a^4(b^2-c^2)(c^4(2u+v)+b^4(u-v-w) +
b^2c^2(-u+v+2w)))
{(-a^2:b^2:c^2), (a^2:-b^2:c^2), (a^2:b^2:-c^2)}
d: b^2c^2(b^2-c^2)(2a^4 - a^2(b^2+c^2) - (b^2-c^2)^2x+...=0
o a la ecuación circunferencia Γ con centro en P0 (reflexión de X110 en X156, dato proporcionado por Peter Moses) y pasa por X155 (ortocentro de TaTbTc).P0 = ( a^2 (a^14 - 4a^12(b^2+c^2) + a^10(5b^4+11b^2c^2+5c^4) - 13a^8b^2c^2(b^2+c^2) + a^6(-5b^8+12b^6c^2+2b^4c^4+12b^2c^6-5c^8) + 2a^4(2b^10-4b^8c^2+b^6c^4+b^4c^6-4b^2c^8+2c^10) - a^2(b^2-c^2)^2(b^8+b^6c^2-6b^4c^4+b^2c^6+c^8) + b^2c^2(b^2-c^2)^4(b^2+c^2)) : ... : ... ).
Cuando el punto P recorre la circunferencia Γ, los triángulos TaTbTc y PaPbPc son perspectivos y SEMEJANTES. Si T1 es uno de los puntos de intersección de la recta d con Γ (el antipodal de X155 en Γ), el centro de semejanza S es el segundo punto de intersersección de la recta PT1 con la circunferencia circunscrita al triángulo tangencial Γ'. El centro de pesrpectividad es el punto Q (distinto de S) de intersección de las circunferencias circunscritas a los triángulos TaTbTc y PaPbPc.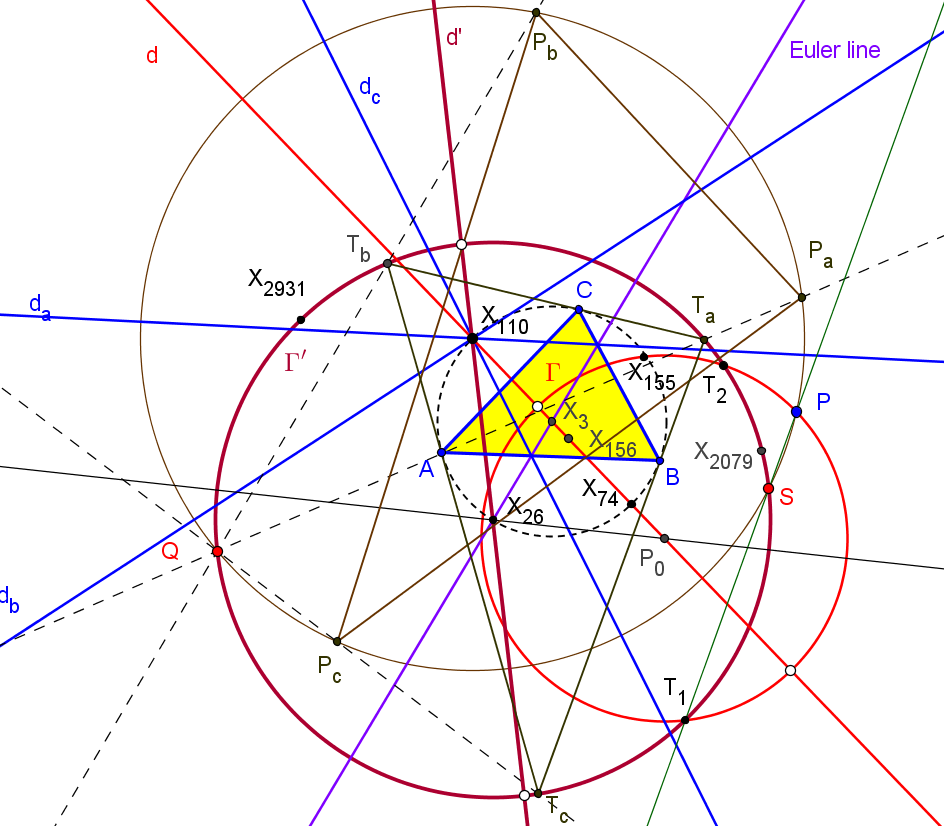
P ∈ d ↦ Q ∈ d'
es una perspectividad con centro en T1, el antipodal de X155 en Γ:T1 = (a^2(a^10 - a^8(b^2+c^2) + a^6(-2b^4+5b^2c^2-2c^4) + 2a^4(b^2-c^2)^2(b^2+c^2) + a^2(b^2-c^2)^2(b^4-b^2c^2+c^4)- b^10+b^2c^2(b^6+c^6)-c^10) : ... : ... ).
con (6,9,13)-número de búsqueda en ETC: -6.312998437457754226552932181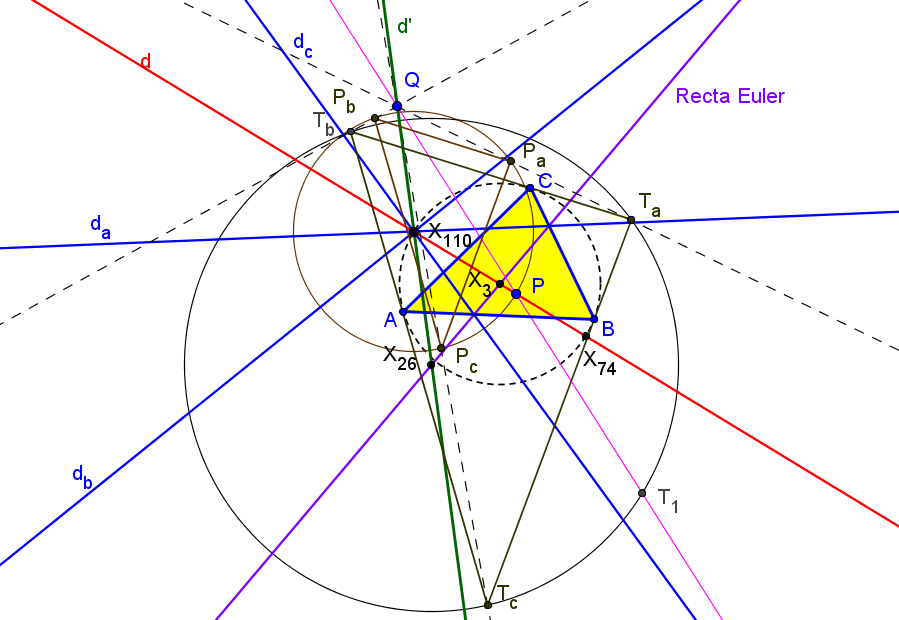
El conjunto d∪Γ se tansforma en d'∪Γ' mediante una semejanza directa de centro en T2, el otro punto de intersección (distinto de T1) de las circunferencia Γ y Γ'.
T2 = (a^2(a^2+b^2-c^2)(a^2-b^2+c^2) (a^12 - 4a^10(b^2+c^2) + a^8(7b^4+11b^2c^2+7c^4) - a^6(8b^6+11b^4c^2+11b^2c^4+8c^6) + a^4(7b^8+3b^6c^2+8b^4c^4+3b^2c^6+7c^8) - a^2(4b^10-3b^8c^2+3b^6c^4+3b^4c^6-3b^2c^8+4c^10) + (b^6-b^4c^2+b^2c^4-c^6)^2): ... : ...).
con (6,9,13)-número de búsqueda en ETC: -1.88300482666727983296569296El lugar geométrico de los puntos P tal que los ejes radicales da, db y dc son concurrentes es una séptica circunscrita a los triángulos ABC y antimedial, y que pasa por el baricentro y ortocentro.
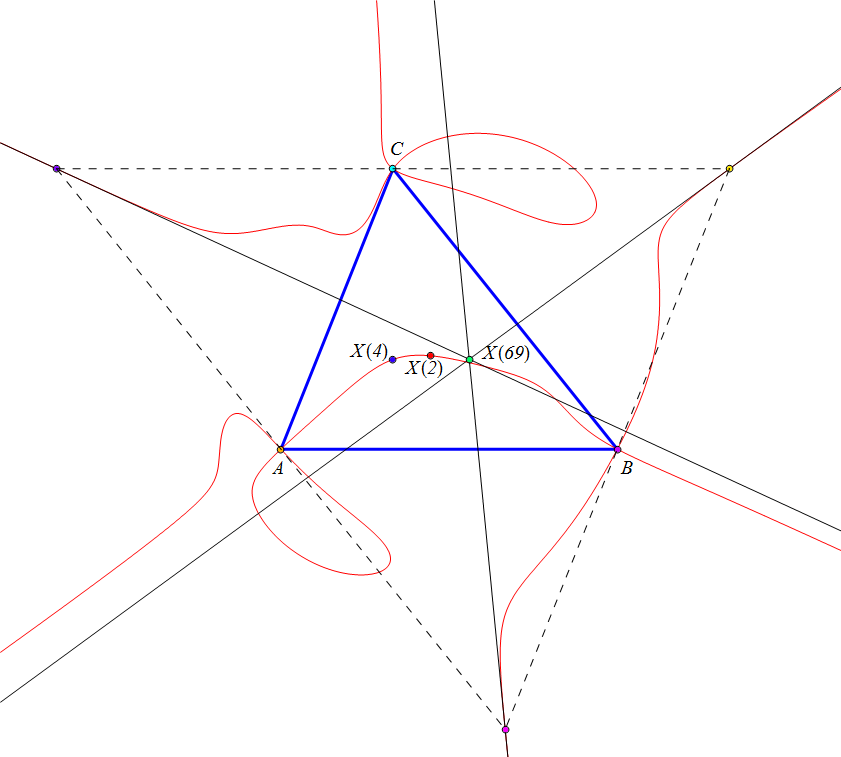
Cuando P es el ortocentro la intersección de los ejes radicales da, db y dc es el centro X3574,
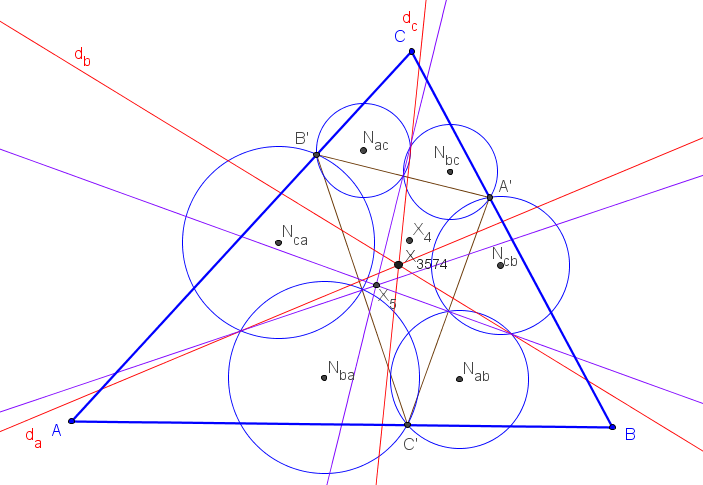
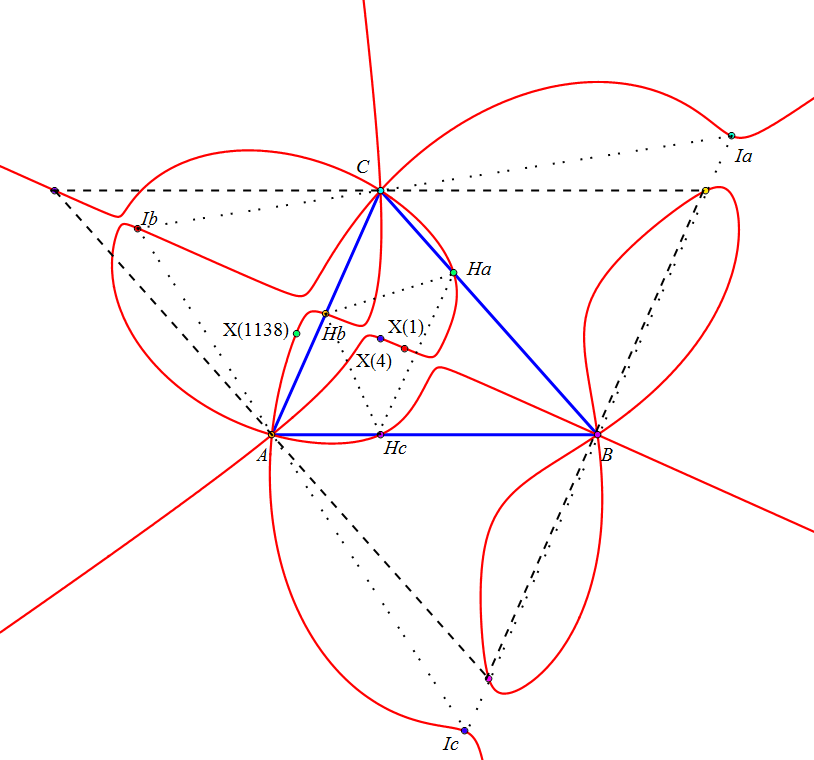
El lugar geométrico de los puntos P tal que los ejes radicales ea, eb y ec son concurrentes es una séptica circunscrita a los triángulos ABC, órtico, antimedial y excentral, y que pasa por el incentro, ortocentro y X1138. Los vértices de ABC son puntos triples.
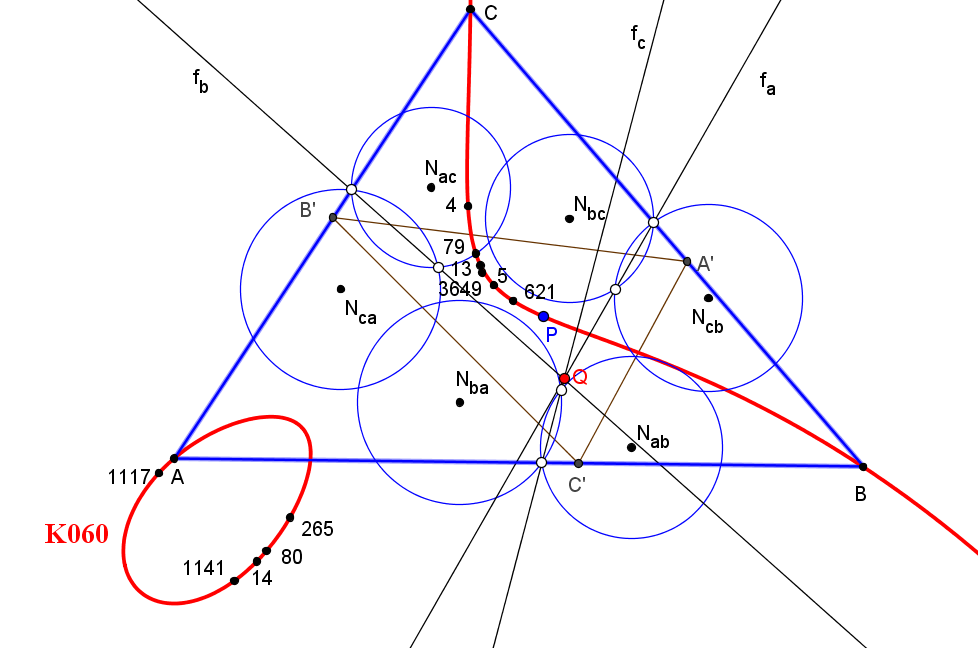
El lugar geométrico de los puntos P tal que los ejes radicales fa, fb y fc son concurrentes es la "O(X5) orthopivotal cubic" (K060, del catálogo de cúbicas de Bernard Gibert).
Dado un triángulo ABC, sea MaMbMc el su triángulo medial.
Lab es la recta que pasa por Ma y por el punto de intersección de la bisectriz interior en B y la altura desde C.
Lac es la recta que pasa por Ma y por el punto de intersección de la bisectriz interior en C y la altura desde B.
Ab es el punto de intersección de AB con Lab y Ac es el punto de intersección de AC con Lac.
Similarmente se definen los puntos Bc, Ba, Ca y Cb.
Las mediatrices de los segmentos BcCb, CaAc y AbBa son concurrentes.
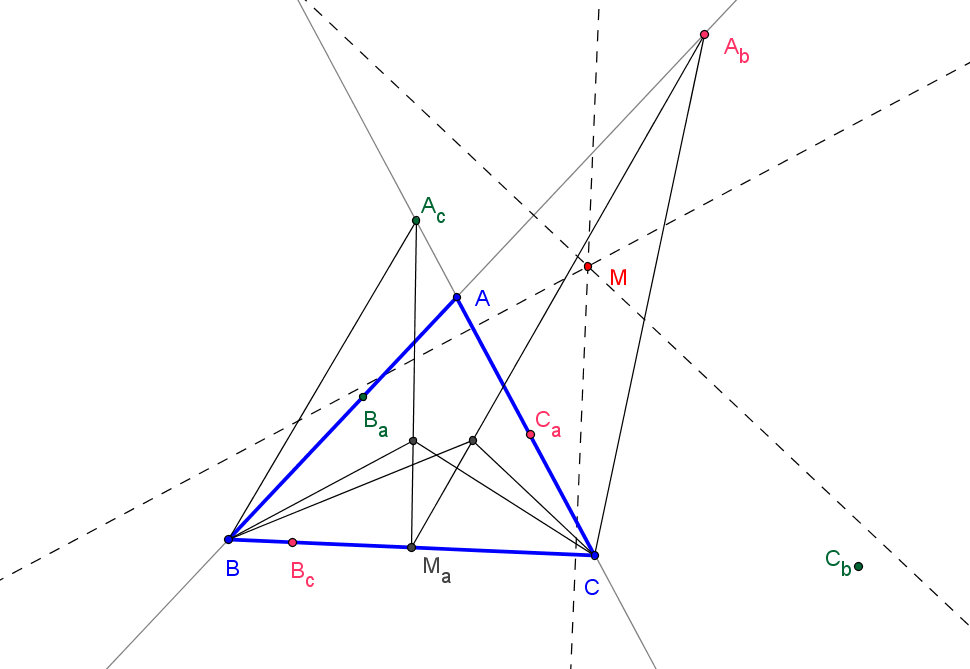
(a(a^6 - a^4(b+c)^2 + 2a^3(b^3+b^2c+bc^2+c^3) - 2a(b^5+b^4c+bc^4+c^5) - (b-c)^4(b+c)^2+a^2(b^2+c^2)^2) : ... : ... )
con (6,9,13)-número de búsqueda en ETC: -88.3239018332220355783645503
Dado un triángulo ABC, sea A'B'C' el triángulo de reflexión que resulta de reflejar cada vértice de ABC en su lado opuestos. Se denota por:
℘ab la parábola de foco C y directriz BC', Dab el polo de CB' respecto a ℘ab.
℘ac la parábola de foco B y directriz CB', Dac el polo de BC' respecto a ℘ac.
Similarmente, se definen las parábolas ℘bc, ℘ba, ℘ca y ℘cb, y los puntos Dbc, Dba, Dca y Dcb.
Las rectas DabDac, DbcDba y DcaDcb delimitan un triángulo perspectivo con ABC.
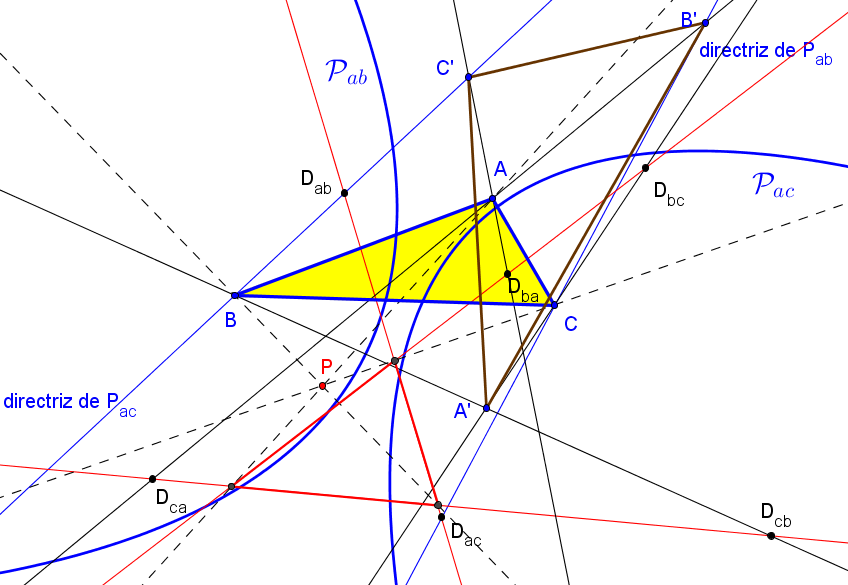
A' (-a^2 : 2SC : 2SB), B' (2SC : -b^2 : 2SA), C' (2SB : 2SA : -c^2).
Ecuaciones de las parábolas (R radio de la circunferencia circunscrita):
℘ab :
b^2R^2SB^2x^2 + a^2c^2SC^2y^2+a^4b^2R^2z^2 +
2a^2b^2R^2SBzx - a^2b^2c^2SCxy= 0,
℘ac :
c^2R^2SC^2x^2 + a^4c^2R^2y^2 + a^2b^2SB^2z^2 - a^2b^2c^2SBzx +
2a^2c^2R^2SCxy = 0.
Dab ((a^2-b^2+c^2)(a^4-2a^2c^2+(b^2-c^2)^2) : b^2(-a^4+(b^2-c^2)^2) : -c^2(a^4-2a^2c^2+(b^2-c^2)^2)).
El polo de la directriz de ℘ac respcto a ℘ab es:Dac (-(a^2+b^2-c^2)(a^4-2a^2b^2+(b^2-c^2)^2) : b^2(a^4-2a^2b^2+(b^2-c^2)^2) : -c^2(-a^4+(b^2-c^2)^2)).
La ecuación de la recta DabDac es:-b^2c^2(a^4(b^2+c^2)+(b^2-c^2)^2(b^2+c^2)-2a^2(b^4-b^2c^2+c^4))x + c^4(-a^6-a^4(b^2-3c^2)-(b^2-c^2)^3-a^2(b^4-4b^2c^2+3c^4))y + b^4(-a^6+(b^2-c^2)^3+a^4(3b^2-c^2)-a^2(3b^4-4b^2c^2+c^4))z = 0.
El centro de perspectividad P de ABC y el triángulo delimitado por las rectas DabDac, DbcDba, DcaDcb tiene primera coordenada:
a^2 / (a^14(b^2+c^2) -
a^12(5b^4+3b^2c^2+5c^4)+
2a^10(5b^6+2b^4c^2+2b^2c^4+5c^6) -
a^8(10b^8+3b^6c^2-2b^4c^4+3b^2c^6+10c^8) +
a^6(5b^10+b^8c^2-2b^6c^4-2b^4c^6+b^2c^8+5c^10)-
a^4(b^4-c^4)^2(b^4+b^2c^2+c^4)+
2a^2b^2c^2(b^2-c^2)^4(b^2+c^2)-b^2c^2(b^2-c^2)^6 )
a Kake, por su "cumple"
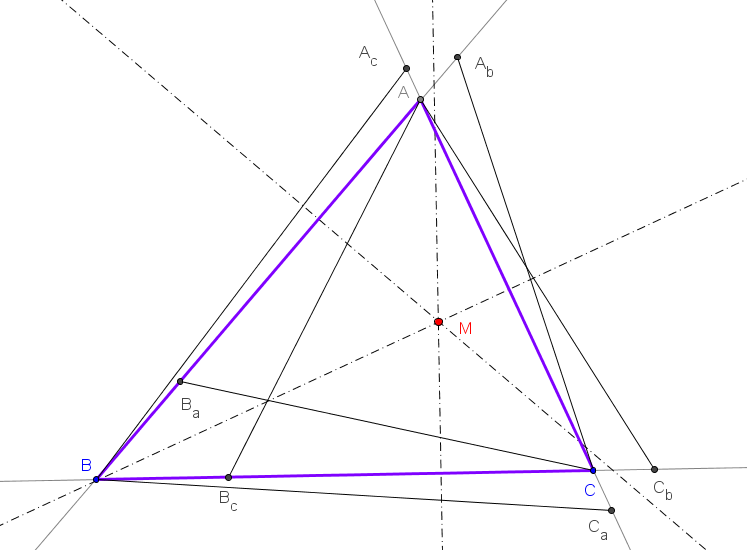
Dado un triángulo ACUTÁNGULO ABC, sean:
Ab es el único punto sobre AB tal que, en el triángulo AbBC, la simediana en Ab, la bisectriz interior en B y la altura en C son concurrentes.
Ac es el único punto sobre AC tal que, en el triángulo AcBC, la simediana en Ac, la bisectriz interior en C y la altura en B son concurrentes.
Similarmente se define los puntos Bc, Ba, Ca y Cb.
Las mediatrices de los segmentos BcCb, CaAc y AbBa son concurrentes.
(a-b-c)(a+b-c)c^2t^2 - (a^2-b^2+c^2)(a^2-b^2-ac+c^2)t + a^2(a^2-b^2+c^2) = 0.
El único valor de 't' que anula esta ecuación que determina un punto Ab sobre AB tal que, en el triángulo AbBC, la simediana en Ab, la bisectriz interior en B y la altura en C son concurrentes es:t = (a^2-b^2+c^2)(a^2-ac+c^2-b^2) - ((a^2-b^2+c^2)f2(a,b,c))½
donde
Ab = ((a^2-b^2+c^2)(a^2-ac+c^2-b^2) - ((a^2-b^2+c^2)f2(a,b,c))½ :
-a^4+a^3c+2a^2b^2-ac(b^2+3c^2)-b^4+c^4 + ((a^2-b^2+c^2)f2(a,b,c))½ :
0).
Ac = (
a^4-a^3b+2a^2(b^2-c^2)+a(-b^3+bc^2)+(b^2-c^2)^2 -((a^2+b^2-c^2)f3(a,b,c))½ : 0 :
-a^4+a^3b+2a^2c^2+b^4-ab(3b^2+c^2)-c^4)-c^2 +f3(a,b,c))½).
f0(a,b,c) - 2a^2(b+c-a)((b^2+c^2-a^2)f1(a,b,c))½ + (a-b+c)(a^2+b^2-c^2)((a^2-b^2+c^2)f2(a,b,c))½ + (a+b-c)(a^2-b^2+c^2)((a^2+b^2-c^2)f3(a,b,c))½
donde
Las circunferencias circunscritas a los triángulos ABC, ANbNc, BNcNc y CNaNb son concurrentes en X930.
Las circunferencias circunscritas a los triángulos NaNbNc, NaBC, NbCA y NcAB son concurrentes en:
Q = (a^2(a^6(b^2+c^2)- a^4(3b^4+4b^2c^2+3c^4)+ a^2(3b^6+2b^4c^2+2b^2c^4+3c^6)-b^8+b^6c^2+b^2c^6-c^8) : ... : ...)
con (6,9,13)-número de búsqueda en ETC: 8.07910137097857081131659206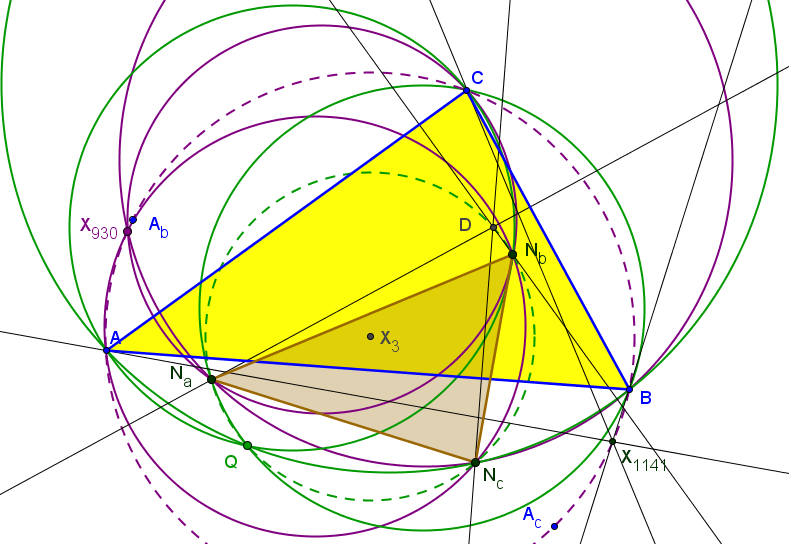
D = (a^2(a^6(b^2+c^2)- 3a^4(b^4+c^4)+a^2(3b^6-2b^4c^2-2b^2c^4+3c^6)-b^8+b^6c^2+b^2c^6-c^8) : ... :...)
con (6,9,13)-número de búsqueda en ETC: 5.485624417414120257712782094
Sean ABC un triángulo, P un punto y PaPbPc el triángulo preceviano de P.
Se denotan por da, db y dc las rectas de Euler de los triángulos PaBC, PbCA y PcAB, respectivamente.
Las rectas de Euler da, db y dc son concurrentes si y solo si P está en una nónica (ver su ecuación baricéntrica), que pasa por los vértices de los triángulos ABC (dobles), medial y excentral, por los centros X1, X2 y X6.
Las rectas da, db y dc son concurrentes cuando los triángulos precevianos son los triángulos excentral, antimedial y tangencial. En el primer caso las rectas concurren en X100, en el segundo son paralelas a la recta de Euler de ABC y en el tercero concurren en el circuncentro.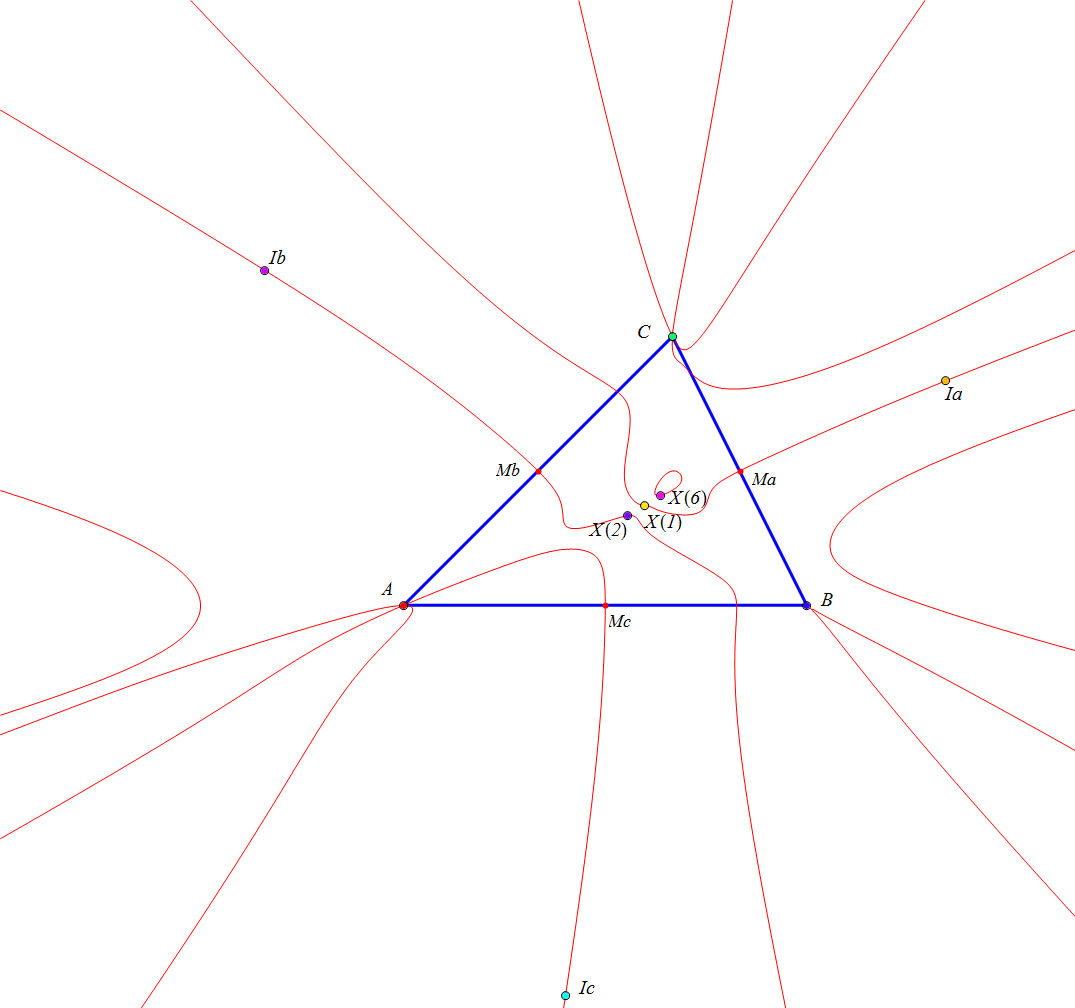
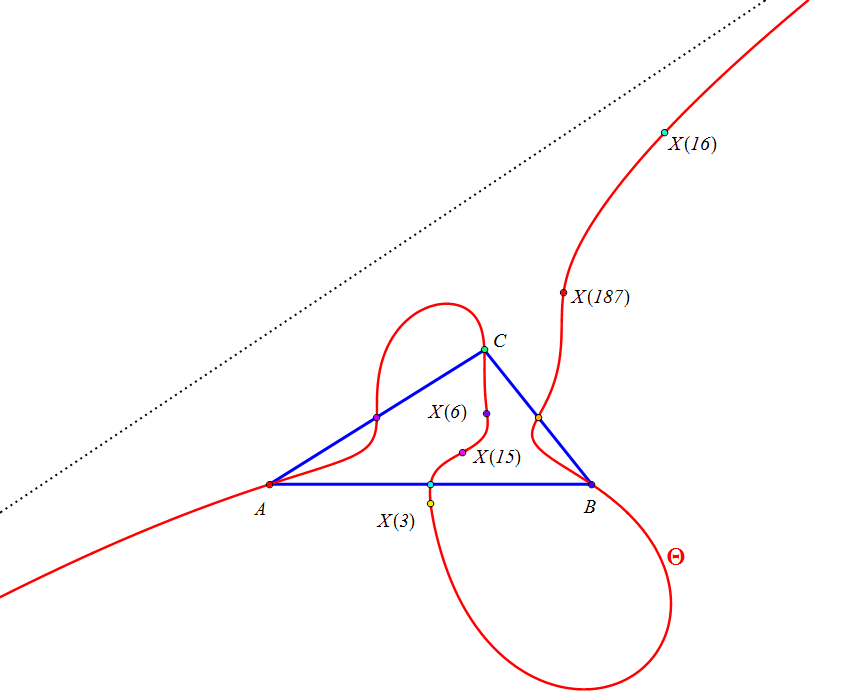
Sean ABC un triángulo, MaMbMc el triángulo medial y P un punto, la recta da que une P con Ma vuelve a cortar a la circunferencia circunscrita a PBC en Pa; sea Fa la reflexión de Pa en la mediatriz de BC. Similarmente, procediendo cíclicamente, se consideran los puntos Fb y Fc.
Los triángulos ABC y FaFbFc son perspectivos si y sólo si el punto P está sobre la quíntica Θ de ecuación baricéntrica:
b^2 c^4 x^4 y + 2 a^2 c^4 x^3 y^2 + b^2 c^4 x^3 y^2 - 2 c^6 x^3 y^2 - a^2 c^4 x^2 y^3 - 2 b^2 c^4 x^2 y^3 + 2 c^6 x^2 y^3 - a^2 c^4 x y^4 - b^4 c^2 x^4 z - b^4 c^2 x^3 y z + b^2 c^4 x^3 y z + 4 a^4 c^2 x^2 y^2 z - 4 b^4 c^2 x^2 y^2 z - 4 a^2 c^4 x^2 y^2 z + 4 b^2 c^4 x^2 y^2 z + a^4 c^2 x y^3 z - a^2 c^4 x y^3 z + a^4 c^2 y^4 z - 2 a^2 b^4 x^3 z^2 + 2 b^6 x^3 z^2 - b^4 c^2 x^3 z^2 - 4 a^4 b^2 x^2 y z^2 + 4 a^2 b^4 x^2 y z^2 - 4 b^4 c^2 x^2 y z^2 + 4 b^2 c^4 x^2 y z^2 - 4 a^4 b^2 x y^2 z^2 + 4 a^2 b^4 x y^2 z^2 + 4 a^4 c^2 x y^2 z^2 - 4 a^2 c^4 x y^2 z^2 - 2 a^6 y^3 z^2 + 2 a^4 b^2 y^3 z^2 + a^4 c^2 y^3 z^2 + a^2 b^4 x^2 z^3 - 2 b^6 x^2 z^3 + 2 b^4 c^2 x^2 z^3 - a^4 b^2 x y z^3 + a^2 b^4 x y z^3 + 2 a^6 y^2 z^3 - a^4 b^2 y^2 z^3 - 2 a^4 c^2 y^2 z^3 + a^2 b^4 x z^4 - a^4 b^2 y z^4=0.
a^2 y z + b^2 z x + c^2 x y - ((c^2 u v + b^2 u w + a^2 v w) x (x + y + z))/( u (u + v + w))=0
en el puntoPa = ( a^2u(u+v+w) : -b^2u(u+v-w)-(u-v+w)(c^2u+a^2w) : -b^2u(u+v-w)-a^2v(u+v-w)-c^2u(u-v+w)).
La reflexión de Pa en la mediatriz de BC esFa = ( a^2u(u+v+w) : -2b^2u(u+v)+v(2c^2u-a^2(u+v-w)) : -2c^2u(u+w)+w(2b^2u-a^2(u-v+w)) ).
Finalmente, la recta AFa tiene por ecuación:(2c^2u(u+w)+ w(-2b^2u+a^2(u-v+w)))y+(-2b^2u(u+v)+ v(2c^2u-a^2(u+v-w)))z=0.
(b^2-c^2)(11a^6 - 6a^4(b^2+c^2) - 3a^2(5b^4-7b^2c^2+5c^4) + 2b^6+3b^4c^2+3b^2c^4+2c^6)x+....=0
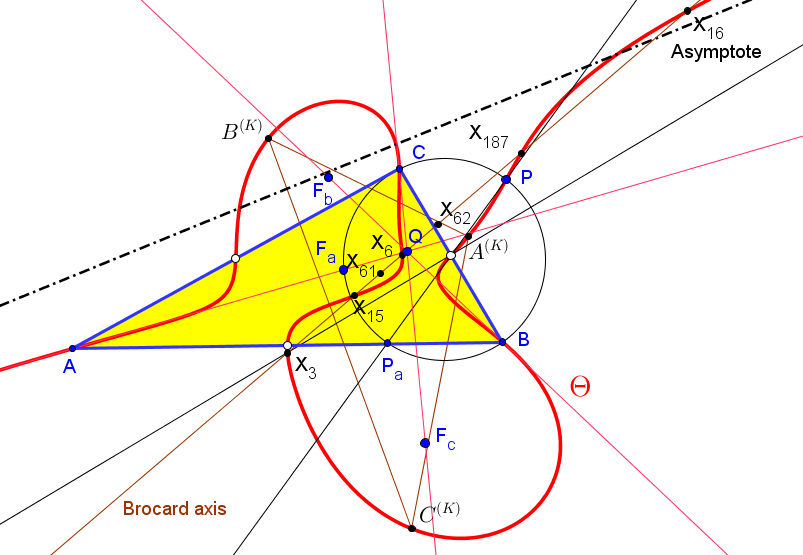
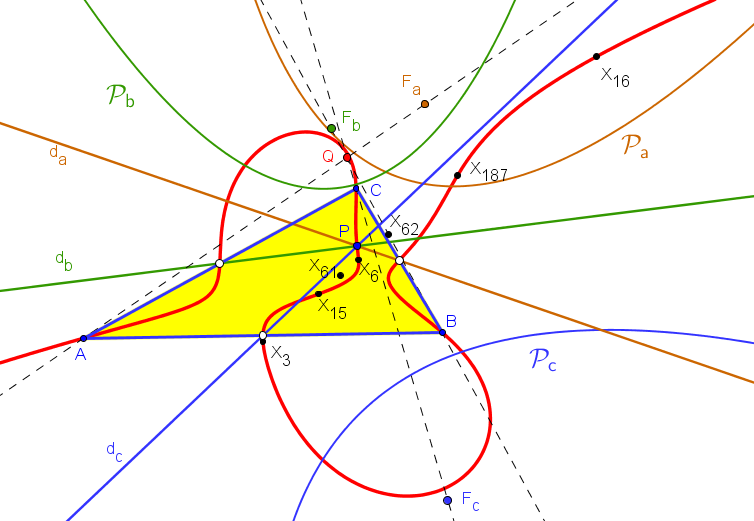
Si concideramos los pares {P,Q}, siendo Q el centro de perspectividad de los triángulos ABC y FaFbFc, cuando son perspectivos, tenemos:{X3, X6}; {X6,X25}; {X15, X62}; {X16, X61}; {X187, X6}; {X524,X2}.
El eje de Brocard interseca a la quíntica en los cinco puntos: X3, X6, X15, X16 y X187.==============================================================
Sea ℘a la parábola envolvente de las polares de P respecto a las cónicas homofocales de focos en los vértices B y C; su foco lo denotamos por Fa. Similarmente, procediendo cíclicamente, se consideran los focos Fb y Fc de las parábolas ℘b y ℘c, respectivamente.
Los triángulos ABC y FaFbFc son perspectivos si y sólo si el punto P está sobre la quíntica Θ.
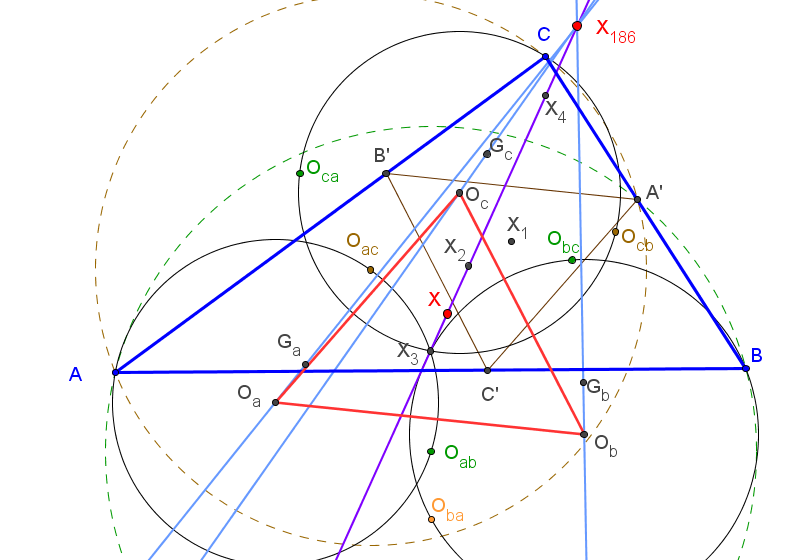
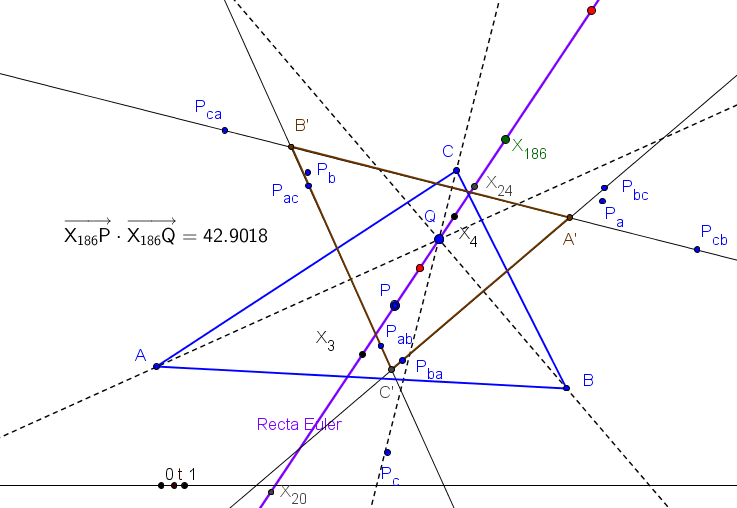
Las recta de Euler de los triángulos ABC, AOabOac, BObcOba, COcaOcb concurren en el inverso del ortocentro en la circunferencia circunscrita, X186.
El ortocentro del triángulo OaObOc es el punto sobre la recta de Euler:
X = (r^2 + 2 r R - R^2 + s^2)*X(3) + R^2*X(4),
R y r, radios de las circunferencias circunscrita e inscrita, y s el semiperímetro.
Oab = (a^2(bc^2+cSA) : b^2cSB + b(S^2+SASB)) : c^2(-bSB+cSC)),
El circuncentro del triángulo ACA' es:Oac = (a^2(cb^2+bSA) : b^2(-cSC+bSB): c^2bSC + c(S^2+SASC)) ),
El circuncentro del triángulo AOabOac es:Oa = (a^2(b(3SA+SB)+c(3SA+SC)) : b^2(2bSB+c(SB-SC)) : -c^2(b(SB-SC)-2cSC) ).
((-2a^2+(b-c)^2)(b+c) : b(-a^2+2b(b-c)) : c(-a^2+2c(-b+c))).
(a^2(a^2-b^2+c^2)(a^2+b^2-c^2)(a^2-b^2-bc-c^2)(a^2-b^2+bc-c^2) : ... : ...).
(a^2(a^2-b^2-bc-c^2)(a^5(b+c)+bc(b^2-c^2)^2 - 2a^3(b^3+c^3) - a^2bc(b^2+c^2) + a(b^5-b^4c-bc^4+c^5)) : ... : ...).
con (6,9,13)-número de búsqueda en ETC: 3.5037197568390148045586626416,
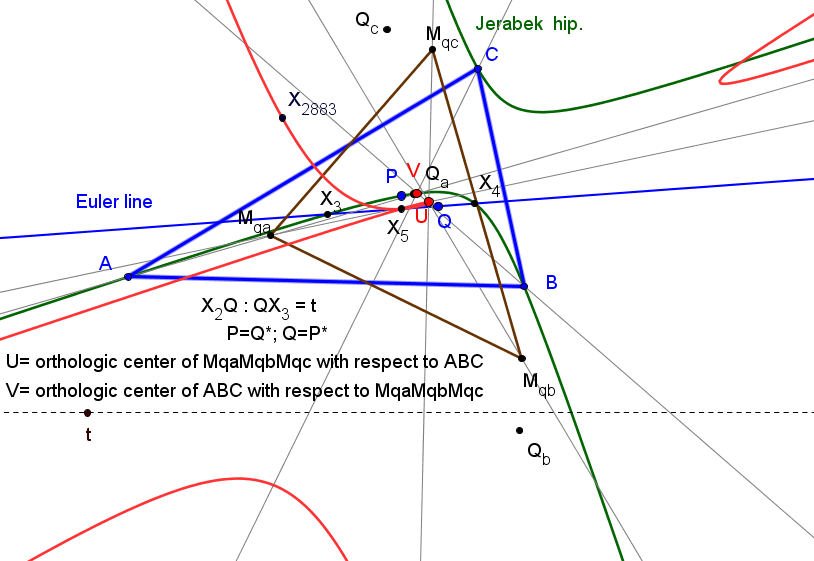
Los triángulos ABC y MqaMqbMqc son ortológicos.
El lugar geométrico de los centros de ortología de ABC con respcto a MqaMqbMqc, cuando Q varía en la recta de Euler, es la hipérbola de Jerabek.
El lugar geométrico de los centros de ortología de MqaMqbMqc con respcto a ABC, cuando Q varía en la recta de Euler, es una cúbica, con punto doble en el centro de la circunferencia de los nueve pountos, X5, con puntos en la recta del infinito los dos de la hipérbola de Jerabek (X2574, X2575) y el conjugado isogonal (X5663) del antipodal del punto de Tixier; esta cúbica también pasa por el conjugado isogonal (X2883) del ortocentro respecto al triángulo medial.
(a^4(3m+n) - a^2(b^2+c^2) (3m+2n)+(b^2-c^2)^2n:...:...)
Para un punto P(u:v:w) arbitrario del plano, el punto Qa respecto al triángulo PBC, que es el mismo que Q respecto al triángulo ABC es:
Qa = (-(b^2-c^2)^2nu^2 +
a^2u(b^2(2nu+3m(u+v-w)) +
c^2(2nu+3m(u-v+w))) -
a^4(nu^2+3m(u^2+2vw+u(v+w))):
-a^4(-3mvw +
nu(u+2v+w)) - (b^2-c^2)u(-c^2(3mv+n(u+2v+w)) +
b^2(3m(u+v)+n(u+2v+w))) +
a^2(c^2(3mv(u-w) + 2nu(u+2v+w)) +
b^2(2nu(u+2v+w) +
3m(u^2+uv+2uw+vw))):
-a^4(-3mvw+nu(u+v+2w)) - (b^2-c^2)u(b^2(3mw+n(u+v+2w)) -
c^2(3m(u+w) + n(u+v+2w))) +
a^2(b^2(3m(u-v)w + 2nu(u+v+2w)) +
c^2(2nu(u+v+2w) + 3m(u^2+2uv+uw+vw)))).
Mqa = (-(b^2-c^2)^2u(3m(u+v+w)+n(4u+3(v+w)))-
a^4(6m(u+v)(u+w)+nu(4u+3(v+w)))+
a^2u(b^2(3m(3u+3v+w)+2n(4u+3(v+w)))+
c^2(3m(3u+v+3w)+
2n(4u+3(v+w)))) :
-a^4(-3mvw+
nu(u+2v+w))-(b^2-
c^2)u(-c^2(3mv+n(u+2v+w))+
b^2(3m(u+v)+n(u+2v+w)))+
a^2(c^2(3mv(u-w)+2nu(u+2v+w))+
b^2(2nu(u+2v+w)+
3m(u^2+uv+2uw+vw))) :
-a^4(-3mvw+
nu(u+v+2w))-(b^2-
c^2)u(b^2(3mw+n(u+v+2w))-
c^2(3m(u+w)+n(u+v+2w)))+
a^2(b^2(3m(u-v)w+2nu(u+v+2w))+
c^2(2nu(u+v+2w)+3m(u^2+2uv+uw+vw))))
( a^4n(v+w) + a^2(b^2+c^2)(3m(u+v+w)+2n(2u+v+w)) - (b^2-c^2)^2(3m(u+v+w)+n(4u+3(v+w))) : ... : ...).
ρ(x:y:z) = ( - a^8(b^2+c^2)(5+6t) + a^6(2b^2c^2(2+3t)^2+3b^4(4+5t)+3c^4(4+5t)) - a^4(b^2+c^2)(3c^4(2+3t)+b^4(6+9t) - a^2(b^2-c^2)^2(3b^2c^2(2+t)(2+3t)^2+b^4(4+3t) +3(b^2-c^2)^4(b^2+c^2)(1+t) -b^2c^2(28+78t+72t^2+27t^3)) + c^4(4+3t)) : ... : ...)
Eliminado ρ y t, resulta la ecuación implícita de una cúbica.(u/(a^2(3m(u+v)(u+w)+2nu(u+v+w))- u(b^2(3m(u+v)+2n(u+v+w))+ c^2(3m(u+w)+2n(u+v+w)))):...:...).
En particular, si P es el conjugado isogonal de Q, poniendo m=tn:ρ(x:y:z) = (1/(2(a-b-c)(a+b-c)(a-b+c)(a+b+c)(a^2+b^2- c^2)(a^2+b^2+c^2) + 3(a^8-3a^6b^2+4a^4b^4-3a^2b^6+b^8-2a^6c^2- 12a^4b^2c^2-12a^2b^4c^2-2b^6c^2+13a^2b^2c^4+ 2a^2c^6+2b^2c^6-c^8)t - 9a^2b^2(a^4-2a^2b^2+b^4+3a^2c^2+3b^2c^2-4c^4)t^2) : ...:...).
Eliminado ρ y t, resulta la ecuación implícita de la hipérbola de Jerabek:a^2(b^2-c^2)(-a^2+b^2+c^2)yz+ b^2(-a^2+c^2)(a^2-b^2+c^2)zx+(a^2-b^2)c^2(a^2+b^2-c^2)xy = 0.
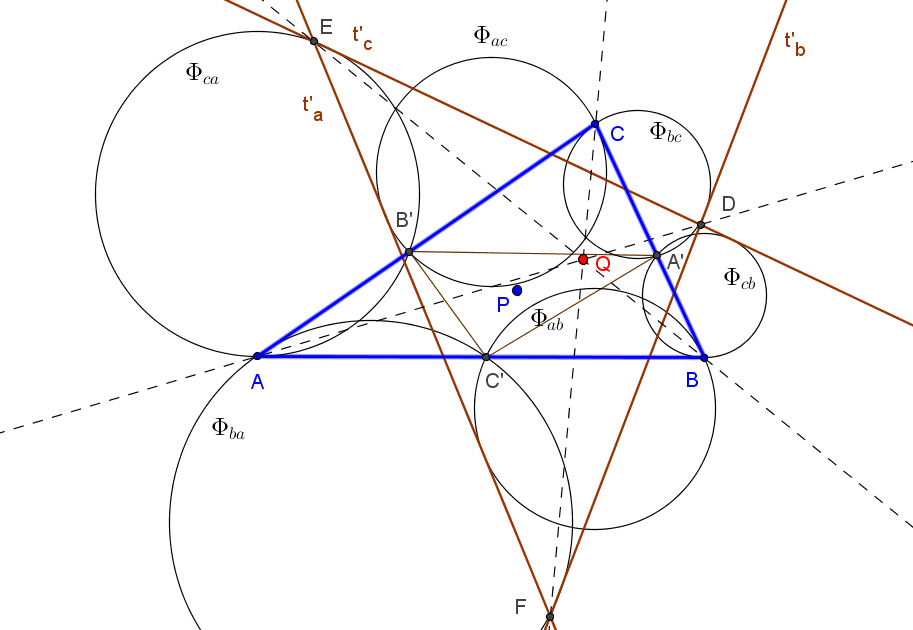
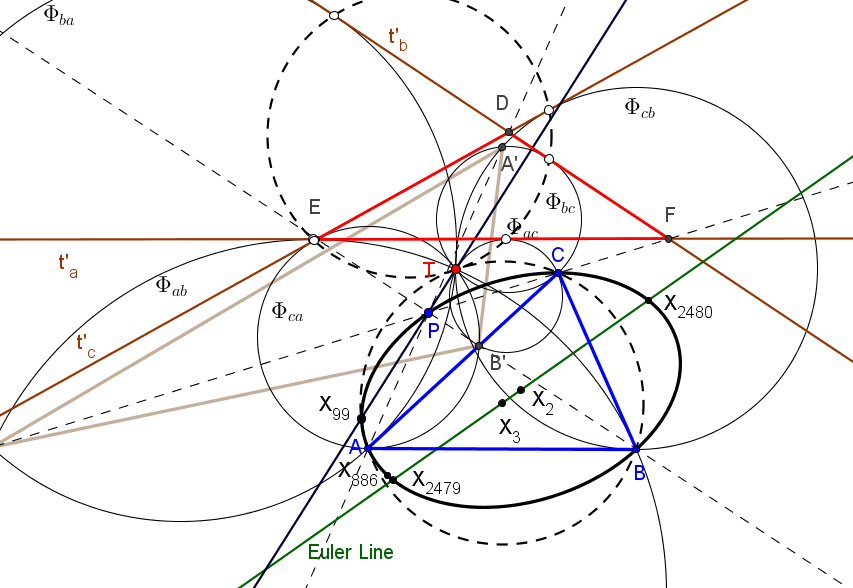
Las tangentes t'a, t'b y t'c delimitan un triángulo DEF perspectivo con ABC.
Φab: a^2yz+b^2zx+c^2xy-(x+y+z)(c^2vx/(u+v)+a^2z)=0
Φac: a^2yz+b^2xz+c^2xy-(x+y+z)(b^2wx/(u+w)+a^2y)=0.
u/((v+w)(b^4(u+v)^2w^2 + c^4v^2(u + w)^2 + a^4(u+v)^2(u+w)^2 - 2a^2(u+v)(u+w)(b^2(u+v)w+c^2v(u+w))- 2b^2c^2(u+v)(u+w)(vw+2u(v+w)))).
El centro de perspectividad Q de los triángulos ABC y DEF coincide con P si P está sobre la elipse circunscrita de Steiner.
Además, en este caso:
• Las seis circunferencias Φab, Φac, Φbc, Φba, Φca, Φcb concurren en el punto T donde la recta X99P vuelve a corta a la circunferencia circunscrita.
• Los puntos de tangencia de las tangentes t'a, t'b y t'c con las circunferencias Φab, Φac, Φbc, Φba, Φca, Φcb están en la circunferencia reflexión de la circunferencia circunscrita en el punto T.
(1/((b^2-c^2)(a^2(b^2+c^2)-2b^2c^2)) : ... : ....),
con (6,9,13)-número de búsqueda en ETC: 6.784805747166842285745353786(a^2 (a^8 - a^6(b^2+c^2) + a^4b^2c^2 - a^2(b^2-c^2)^2(b^2+c^2) + b^8- b^6c^2-b^2c^6+c^8 + (-2a^4+a^2(b^2+c^2)+(b^2-c^2)^2)Λ) : ... : ....),
donde Λ=[a^8 - a^6(b^2+c^2) + a^4b^2c^2 - a^2(b^6-b^4c^2-b^2c^4+c^6) + b^8-b^6c^2-b^2c^6+c^8]½ y con (6,9,13)-número de búsqueda en ETC: 6.770997724920497989820816646(a^2 (a^8 - a^6(b^2+c^2) + a^4b^2c^2 - a^2(b^2-c^2)^2(b^2+c^2) + b^8- b^6c^2-b^2c^6+c^8 - (-2a^4+a^2(b^2+c^2)+(b^2-c^2)^2)Λ) : ... : ....),
donde Λ=[a^8 - a^6(b^2+c^2) + a^4b^2c^2 - a^2(b^6-b^4c^2-b^2c^4+c^6) + b^8-b^6c^2-b^2c^6+c^8]½ y con (6,9,13)-número de búsqueda en ETC: 0.11661014590270525314320708434
El triángulo A'1B'1C'1 es perpectivo con ABC, con centro de perspectividad en el producto baricéntrico Y de P y el simediano.
Tambien los triángulos A'1B'1C'1 y DEF son perspectivos.
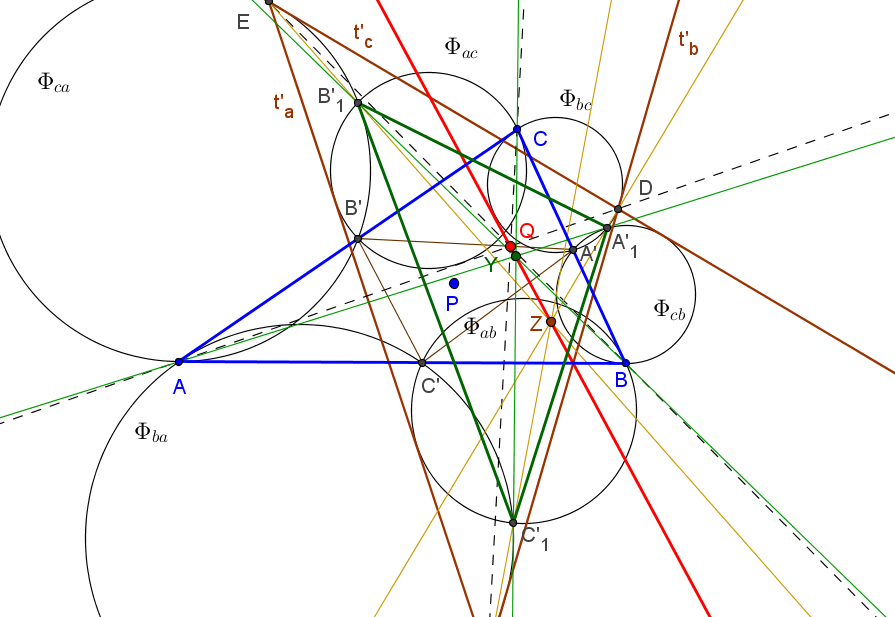
(a^2u : b^2v : c^2w).
El lugar geométrico de los puntos P tales que A*B*C* es el triángulo ceviano de un punto Q es una séxtica con puntos dobles en los vértices de ABC, pasa por los vértices del triángulo excentral IaIbIc y por los pies de las bisectrices interiores y exteriores.
(5a^2-b^2-c^2) (a^4-6a^2b^2+b^4+2a^2c^2+2b^2c^2-3c^4) (a^4+2a^2b^2-3b^4-6a^2c^2+2b^2c^2+c^4),
con (6,9,13)-número de búsqueda en ETC: 0.9249381788103438608692305a^2(a^4-(b^2-c^2)^2)^2 (a^12 - 5a^10(b^2+c^2) + 5a^8(2b^4+3b^2c^2+2c^4) - 2a^6(5b^6+7b^4c^2+7b^2c^4+5c^6) + a^4(5b^8+2b^6c^2+4b^4c^4+2b^2c^6+5c^8) - a^2(b^2-c^2)^4(b^2+c^2) - b^2c^2(b^2-c^2)^2(b^4+c^4) ),
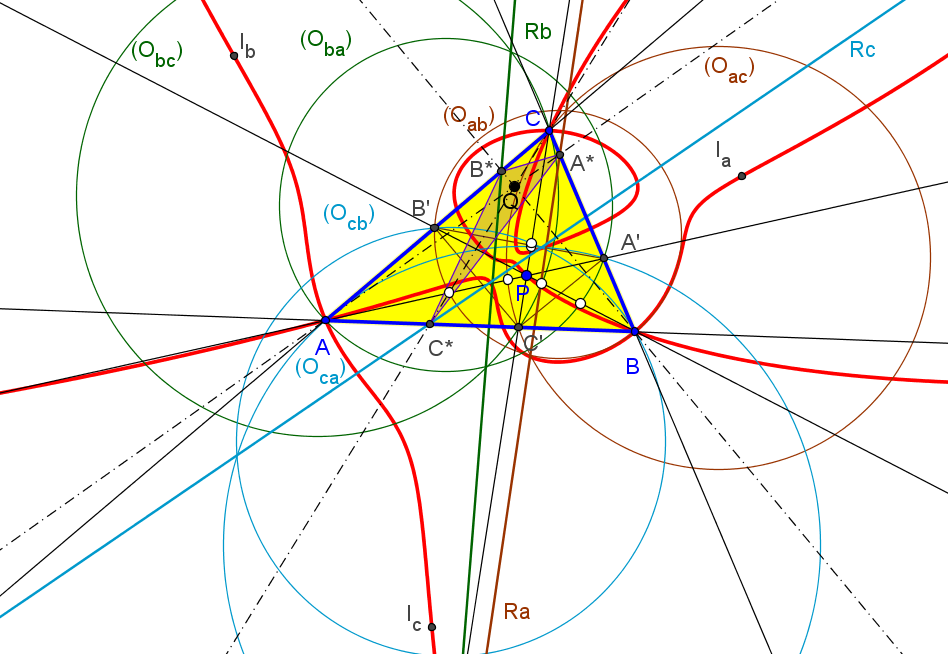
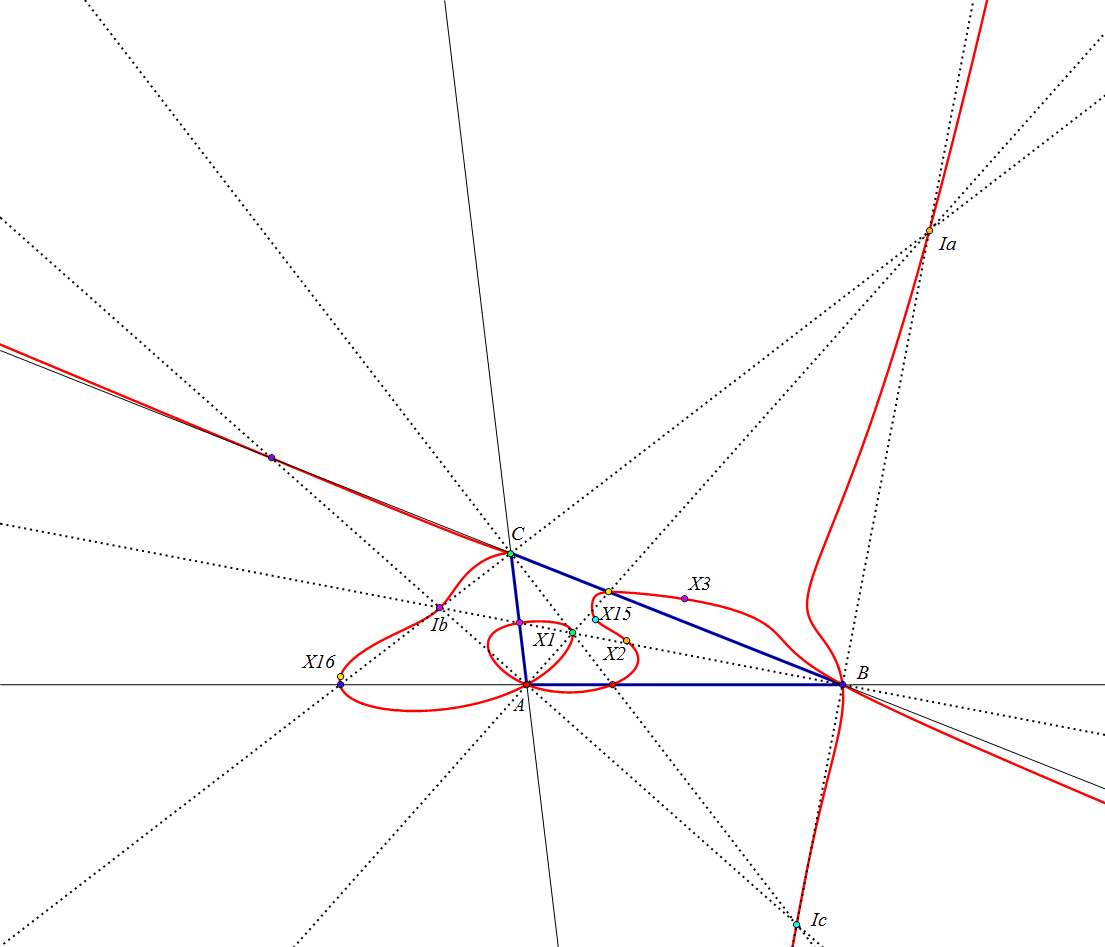
con (6,9,13)-número de búsqueda en ETC: -6.0305312940593606748466345El lugar geométrico de los puntos P tales que los ejes radicales Ra, Rb y Rc son concurrentes es una curva algebraica de grado once con puntos cuádruples en los vértices de ABC, pasa por los vértices del triángulo excentral IaIbIc y por los pies de las alturas.
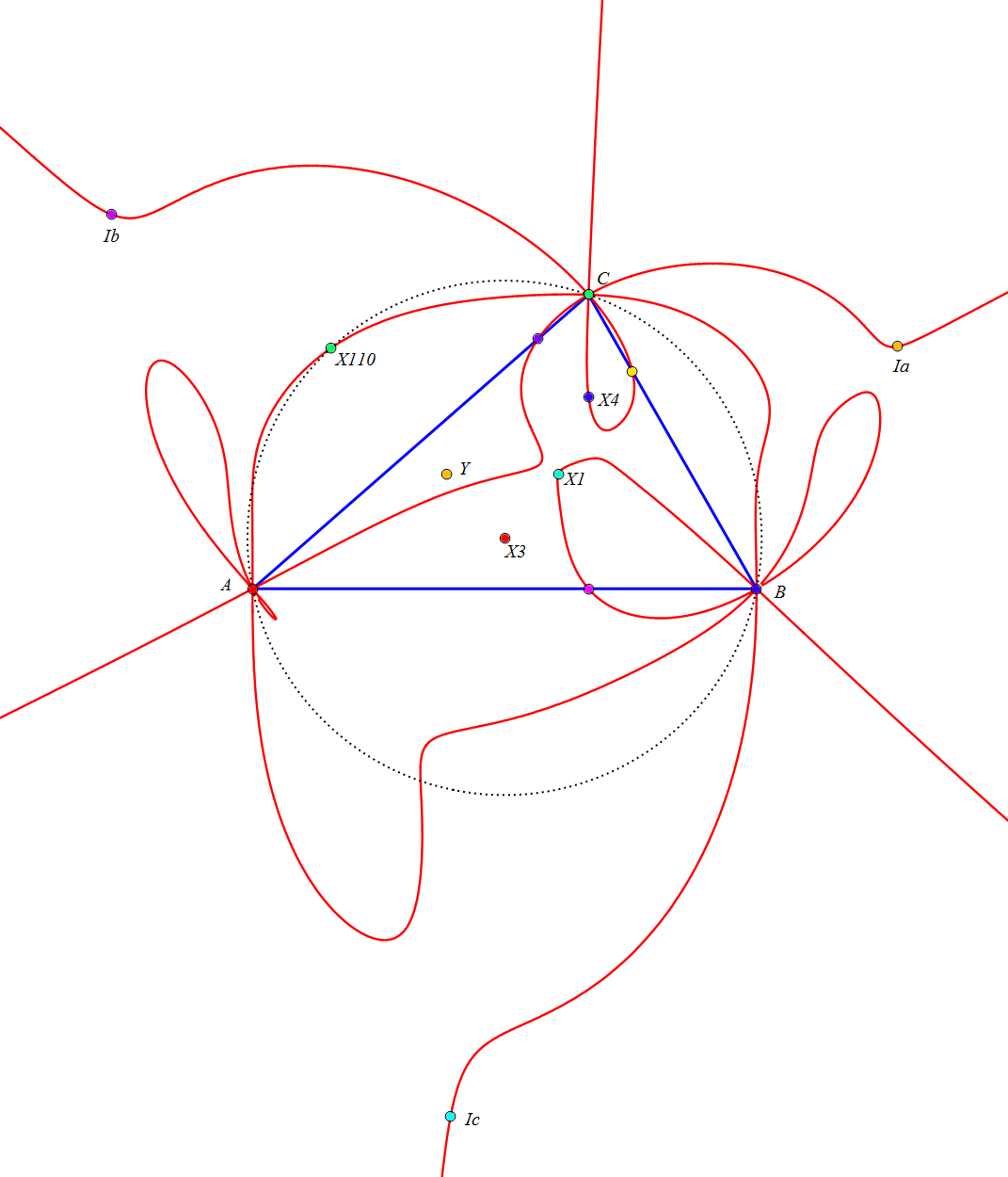
a^2(3a^8 - 7a^6(b^2+c^2) + a^4(3b^4+13b^2c^2+3c^4) + a^2(3b^6-7b^4 c^2-7b^2c^4+3c^6) - (b^2-c^2)^2(2b^4+3b^2c^2+2c^4))
con (6,9,13)-número de búsqueda en ETC: 4.824096254164793916494256409Las rectas DIa, EIb, FIc concurren en X2136.
.png)
Las rectas AOa, BOb y COc son concurrentes, para cualquier punto P.
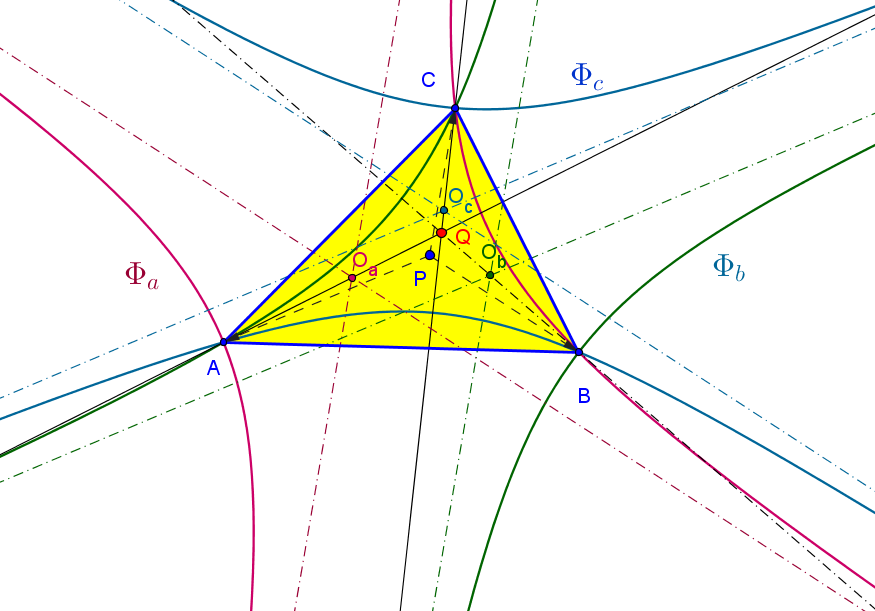
Oa(u(u^2+u(v+w)+2vw) : v(u+w)(u+v-w) : w(v+u)(u-v+w))
El punto Q de intersección de las rectas AOa, BOb y ACc es:(u(v+w)(u^2-(v-w)^2) : v(w+u)(v^2-(w-u)^2 : w(u+v)(w^2-(u-v)^2).
Pares de puntos (P,Q) que son ambos centros del triángulo que figuran actualmente en ETC:(X(1),X(65)) (X(2),X(2)) (X(3),X(5562)) (X(4),X(64)) (X(6),X(1843)) (X(7),X(3062)) (X(8),X(3680)) (X(9),X(3059)) (X(10),X(4647)) (X(37),X(2667))
Los centros Oa, Ob y Oc de las hipérbolas Φa, Φb y Φc están alineados si y solo si P está en la cúbica isotómica no-pivotal de raíz el baricentro y parámetro k=6 del triángulo medial.
La envolvente de las rectas que contienen los centros, cuando P varía en esta cúbica, es la elipse inscrita de Stenier.
La ecuación de la cúbica, en coordenadas baricéntricas respecto al triángilo medial, es x(y^2+z^2)+y(z^2+x^2)+z(x^2+y^2)+6xyz=0.
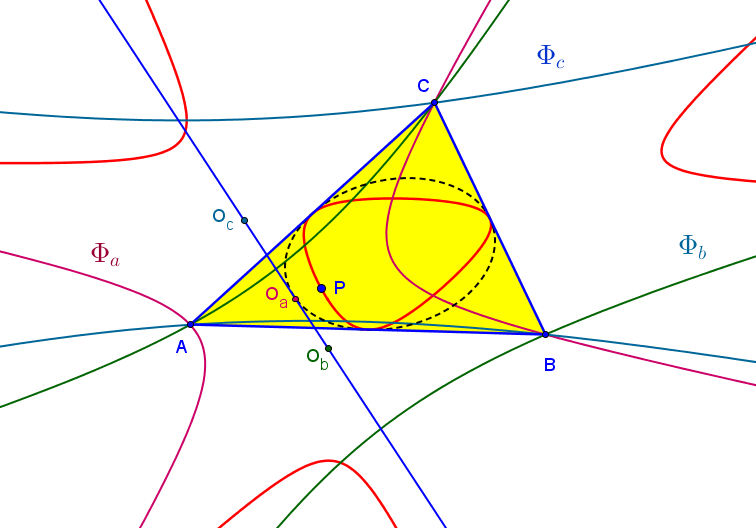
Pa = (1/(b^2(u+v)w-c^2v(u+w)) : -1/(c^2u^2+a^2w(u+v)) : 1/(b^2u^2+a^2v(u+w)).
Si P está sobre la circunferencia circunscrita, las rectas AOa, BOb, COc son paralelas, de dirección perpendicular a la del diámetro que pasa por P.
.png)
Si P está sobre la cúbica isogonal no-pivotal Kjp= K024 = nK0+(X6,X6) , las rectas AOa, BOb, COc concurren en el conjugado isogonal P' de P, sobre dicha cúbica.
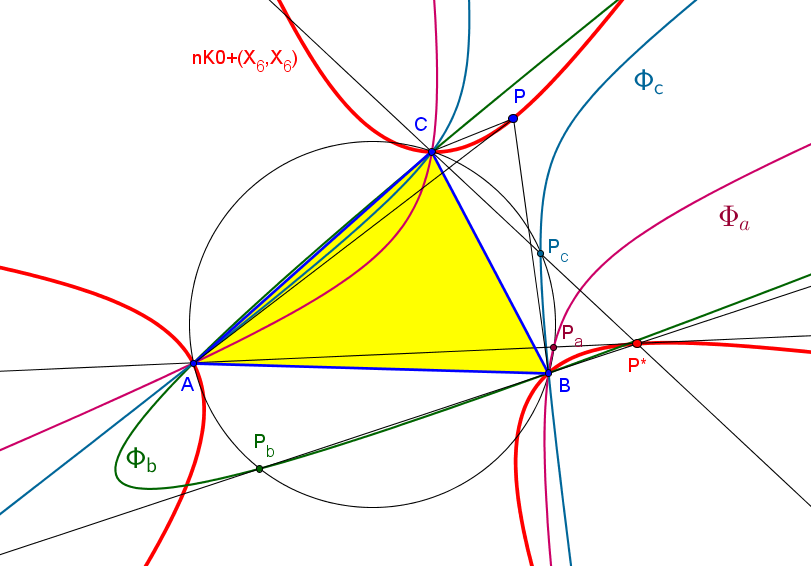
Kjp = K024=nK0+(X6,X6) is the locus of point P such that AP and APa are isogonal lines with respect to the sidelines AB and AC, BP and BPb are isogonal lines with respect to the sidelines BC and BA, and CP and CPc are isogonal lines with respect to the sidelines CA and CB.
A1 = ((q-r) (-p^2q r + p q^2r + p q r^2 - p^2μ + p q μ +
p r μ + q r μ + 2 t μ- t^2) :
(p-r) (p^3r - p^2q r -
p^2r^2 + p^2μ - p q μ - 2 p r μ - 2 t μ+ t^2) :
-(p-q) (p^3q - p^2q^2 - p^2q r + p^2μ - 2 p q μ - p r μ - 2 t μ+ t^2)).
∗ Las rectas DA1, EA1, FA1 concurren en un punto N.
∗ Cuando el punto P queda fijo y M varía sobre la recta δ, el punto N describe la cónica δP, circunscrita a DEF tangente a δ en P.
∗ El lugar geométrico del centro Q de la cónica δP, cuando P se mueve sobre la recta δ es la cuártica Φδ con puntos singulares en los vértices de ABC y tangente a los lados de DEF en los puntos de corte con la recta δ, de ecuación:
El cuarto punto común de la cuártica Φδ y la recta δ es el punto D0 de coordenadas baricéntricas:
D0 = (qr(q-r) : pr(r-p) : pq(p-q)).
Cuando la recta δ gira alrededor del circuncentro, el punto D0 recorre la isocúbica no-pivotal nK(X577,X2,X3).
x (c^4 (a^2 + b^2 - c^2)^2 y^2 + b^4 (a^2 - b^2 + c^2)^2 z^2) + y (a^4 (b^2 + c^2 - a^2)^2 z^2 + c^4 (b^2 - c^2 + a^2)^2 x^2) + z (b^4 (c^2 + a^2 - b^2)^2 x^2 + a^4 (c^2 - a^2 + b^2)^2 y^2) + 2 (b^2 c^2 (b^2 - c^2)^2 + a^6 (b^2 + c^2) + a^2 (b^2 - c^2)^2 (b^2 + c^2) - a^4 (2 b^4 + b^2 c^2 + 2 c^4)) x y z =0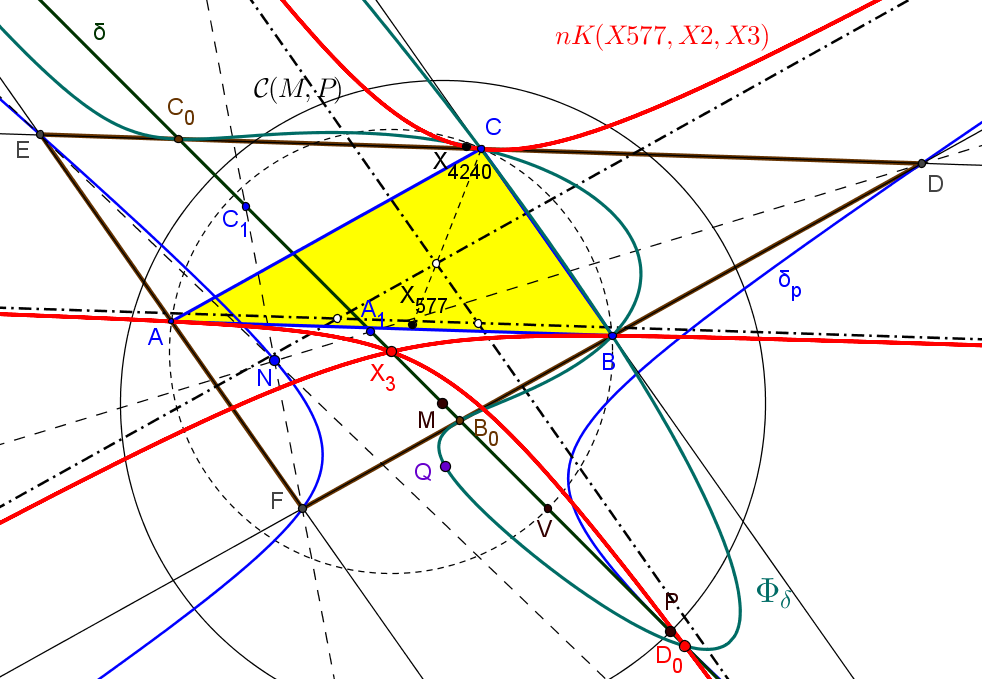
A1 = ((q-r)(qr+t)(qr-t+2μ) : (r-p)(pqr^2-t^2+prμ+qrμ+2tμ) : (p-q)(pq^2r-t^2+pqμ+qrμ+2tμ)).
Los inversos B1, C1 de los puntos B0, C0 se obtienen por permutación cíclica.N = ((q-r)/(p^2qr+p(q+r)μ-t(t-2μ)) : ... : ...).
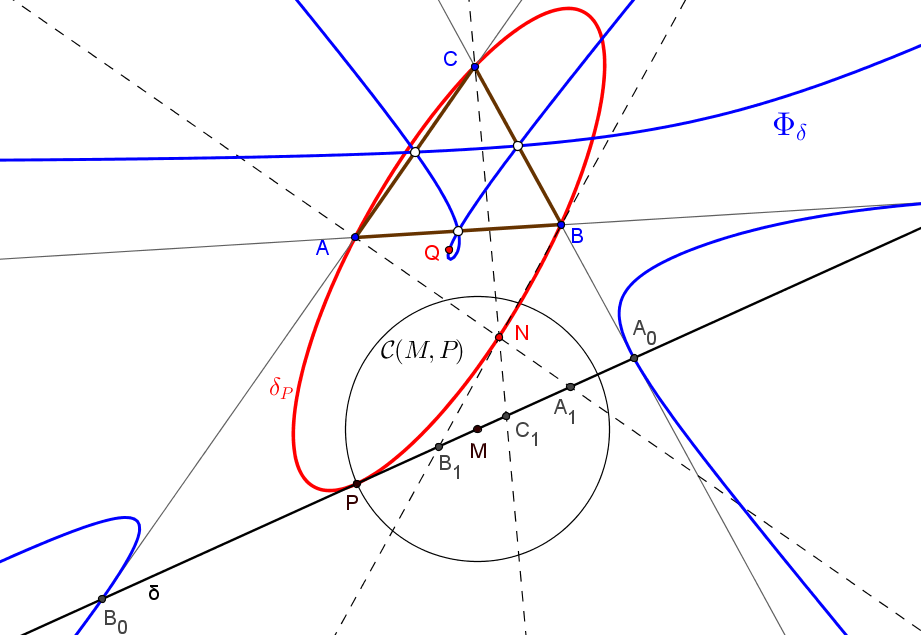
Cuando el punto P queda fijo y M varía sobre la recta δ, el punto N describe la cónica δP, circunscrita a ABC tangente a δ en P:
δP: p(q-r)^2+(qr+t)^2yz + q(r-p)^2+(rp+t)^2zx + r(p-q)^2+(pq+t)^2)xy=0.
El centro de δP es el punto:Q = (p(q-r)(qr+t)^2 (p^2qr(q+r)-pqr(q^2-2qr+r^2-4t)+(q+r)t^2) : ... : ...).
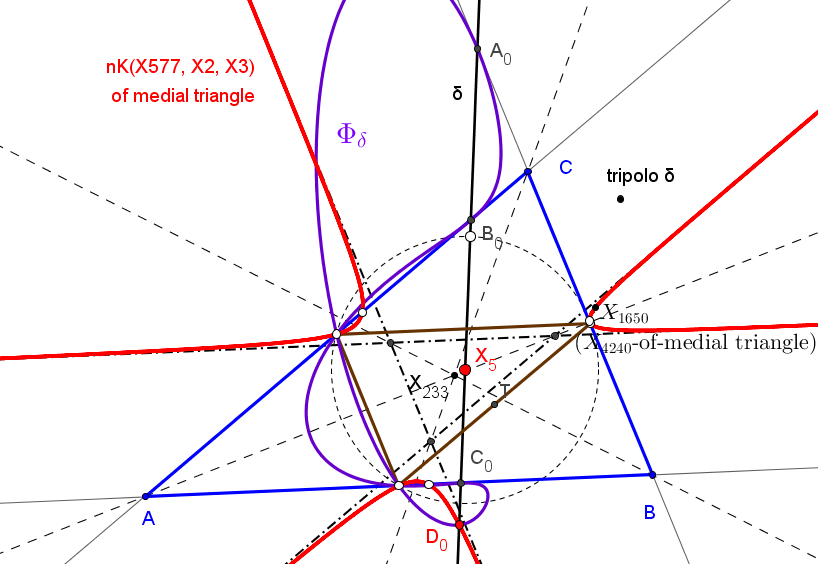
El lugar geométrico del centro de la cónica δP, cuando P se mueve sobre la recta δ es la cuártica Φδ con puntos singulares en los vértices del triángulo medial y tangente a los lados de ABC en los puntos de corte con la recta δ, de ecuación:
p^2x^4 + (-2p^2+2pq)x^3y + (p^2-4pq+q^2)x^2y^2 + (2pq-2q^2)xy^3 + q^2y^4 + (-2p^2+2pr)x^3z + (2p^2-2qr)x^2yz + (2q^2-2pr)xy^2z + (-2q^2+2qr)y^3z + (p^2-4pr+r^2)x^2z^2 + (-2pq+2r^2)xyz^2 + (q^2-4qr+r^2)y^2z^2 + (2pr-2r^2)xz^3 + (2qr-2r^2)yz^3 + r^2z^4=0.
El cuarto punto común de la cuártica Φδ y la recta δ es el punto D0 de coordenadas baricéntricas:
D0 = (p(q^2-r^2) : q(r^2-p^2) : r(p^2-q^2)).
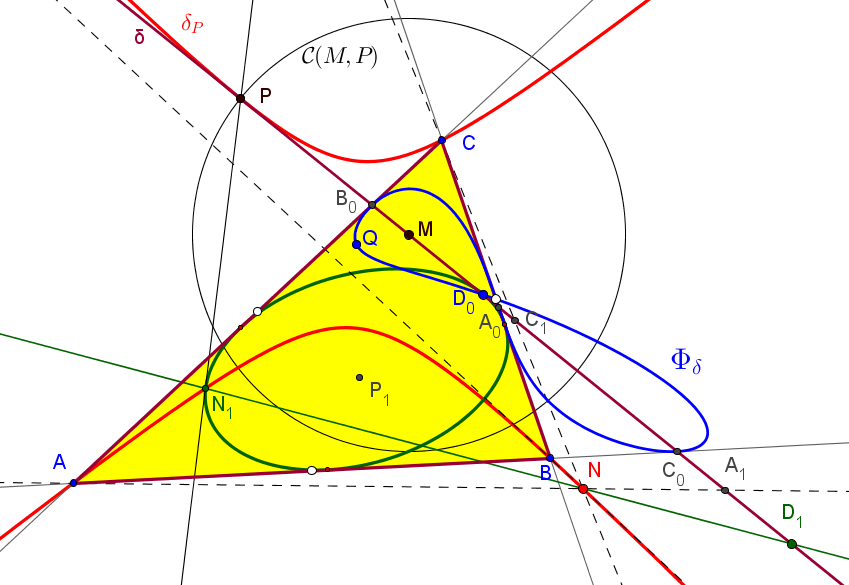
Si D1 es el inverso de D0 respecto a C(M,P) la recta ND1 pasa por un punto fijo N1 sobre la cónica δP, cuando P queda fijo y M varía.
Las coordenadas de D1 y N1 son
D1 = ((q-r)(p(q+r)(qr+μ)+(qr+t)(qr-t+2μ)) : ... : ...),
N1 = (qr(q-r)(qr+μ)/(q+r) : rp(r-p)(rp+μ)/(r+p) :
pq(p-q)(pq+μ)/(p+q)).
El lugar geométrico del punto N1, cuando P, es la cónica inscrita en ABC tangente a δ en D0.
Esta cónica inscrita es la envolvente de las rectas PN1 y su perspector es:P1 = (q^3r^3/(q^2-r^2) : r^3p^3/(r^2-p^2) : p^3q^3/(p^2-q^2)).
(b^2-c^2)yz/SA + (c^2-a^2)zx/SB + (a^2-b^2)xy/SC = 0.
Su perspector es el centro radical de las circunferencias circunscrita, de los nueve puntos y de Taylor, X2501.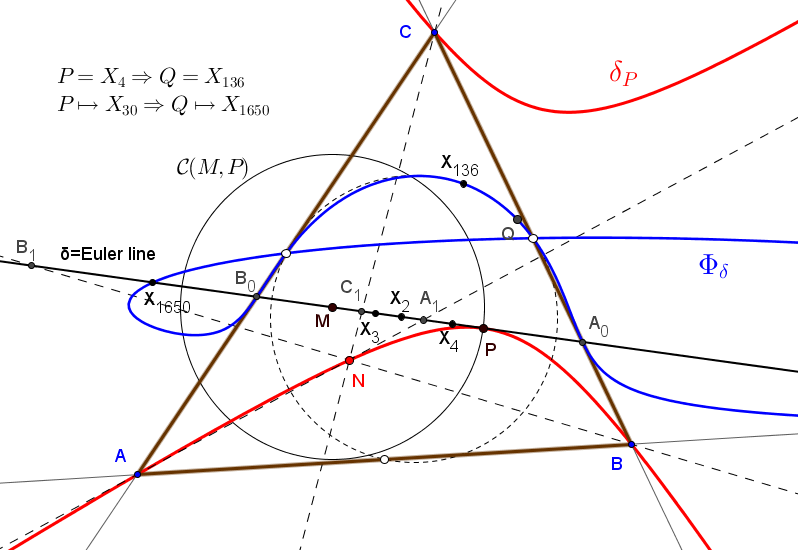
(a^2(b^2-c^2)^2(b^2+c^2-a^2)(a^2(b^2+c^2)-b^4-c^4) : ... : ...)
(con (6,9,13)-número de búsqueda en ETC: 2.9801797228438530320754966389) que es la posición del centro de δP cuando P tiende al punto del infinito del eje de Brocard.a^2(b^2-c^2)yz + b^2(c^2-a^2)zx + c^2(a^2-b^2)xy = 0.
Su perspector es el centro radical de las circunferencias circunscrita, de los nueve puntos y de Taylor, X2501.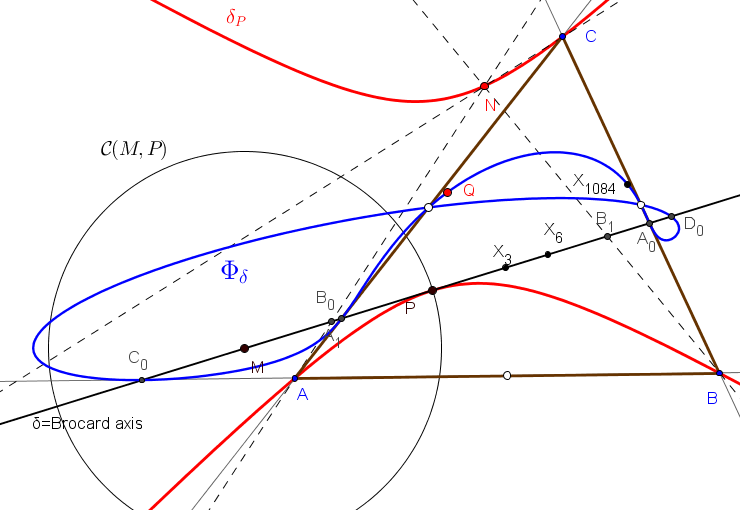
El triángulo delimitado por los ejes radicales ea, eb y ec es perspectivo con ABC con centro de perspectividad el punto de coordenadas baricentricas:
(a/(a^4-2a^2b c-2a^3(b+c)+2a(b^3+c^3)-(b-c)^4) : ... : ...)
con (6,9,13)-número de búsqueda en ETC: 2.2548851539334829652783884
Ab = (w(u+v+w)((-b^2+c^2)u+a^2(u+2w)) :
(u+w)(-w(a^2(u-v+w)+b^2(-u+v+w))+c^2(w(v+w)+u(2 v+w))) :
w(w(a^2(u-v+w)+b^2(-u+v+w))-c^2(w(v+w)+u(2v+w))) )
El lugar geométrico de los puntos P tales que las rectas La, Lb, Lc son paralelas es una séxtica con puntos dobles en los vértices de ABC.
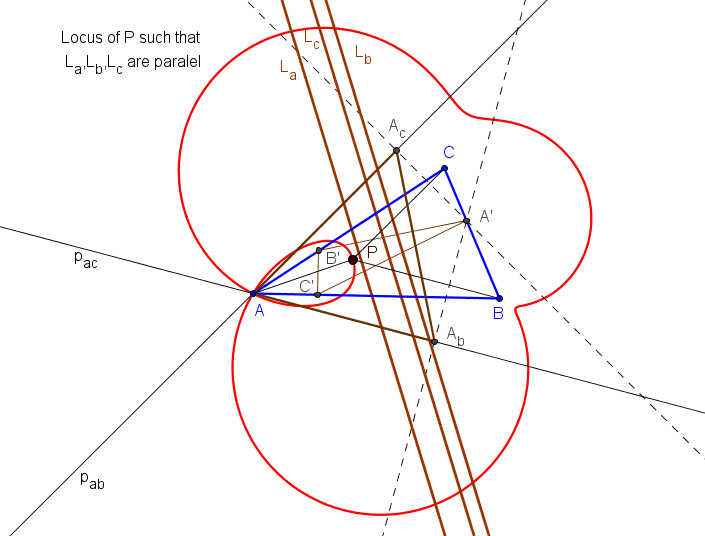
El lugar geométrico de los puntos P tales que las rectas La, Lb, Lc son concurrentes una séptica con puntos dobles en los vértices de ABC y que pasa por los centros X3, X4, X13, X14, X20.
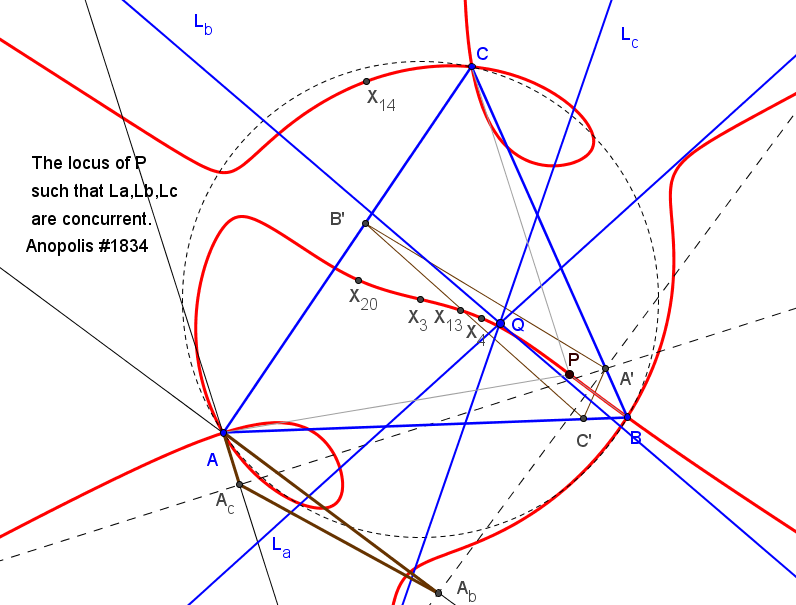
Dear Jean-Pierre, [APH]: So, we have the Theorem: Let AA', BB', CC' be the three altitudes of ABC, and Let Ab, Ac be the orth. proj. of A' on AB, AC resp. Bc, Ba " B' BC, BA Ca, Cb " C' CA, CB Then the Euler lines of A'B'C', A'AbAc, B'BcBa, C'CaCb are concurrent. Which is the point of concurrence [a point lying on the Euler line of the orthic triangle A'B'C' of ABC]? Is it in ETC? [JPE]: X(442) of the orthic triangle (not in ETC, I think) [JPE]: Let's name them temporarily (or not!) as: Triangles A'AbAc, B'BcBa, C'CaCb = Orthiac Triangles [APH]: A PS for Clark Kimberling: Dear Clark, If the above point of concurrence of the Euler lines of the Orthiacs (ie X442 of Orthic) is not already in your list, then you may of course include them, but with these name: 1st Ehrmann Point.
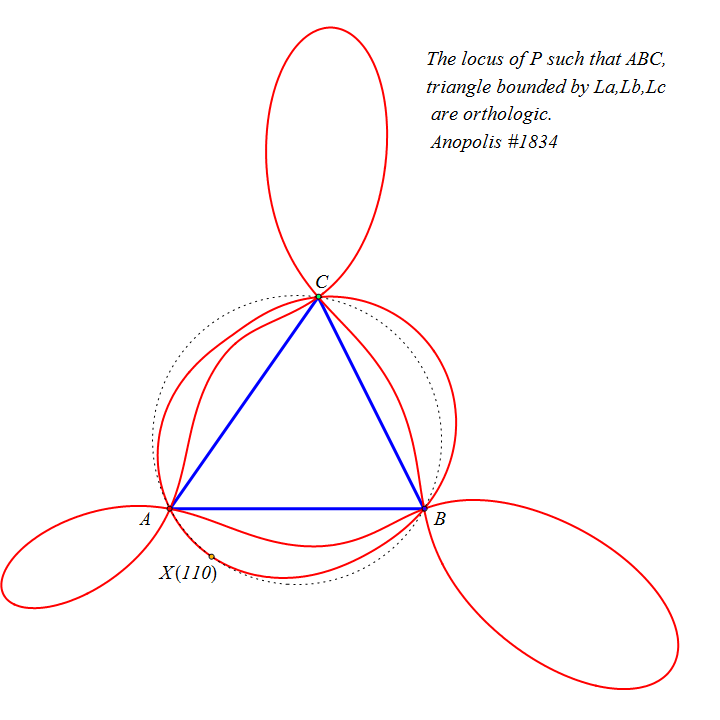
El lugar geométrico de los puntos P tales que los triángulos ABC y el delimitado por las rectas La, Lb, Lc son ortológicos es una curva algebraica de grado ocho, con puntos triples en los vértices de ABC y pasa por el foco de la parábola de Kiepert, X110..
Ab = ((a^2-c^2) SB : 0 : -2(b^2-c^2)SA)
Ac = ((a^2-b^2)SC : -2(c^2-b^2)SA : 0)
2 (b^2-c^2)^2SA^2x + (a^2-b^2)(a^2-c^2)SBSC(y + z) = 0.
Por permutación cíclica resultan las ecuaciones de las rectas de Euler de los triángulos BBcBa y CCaCb.( (2a^4-a^2(b^2+c^2)-(b^2-c^2)^2)/((b^2-c^2)SA) : ... : ...).
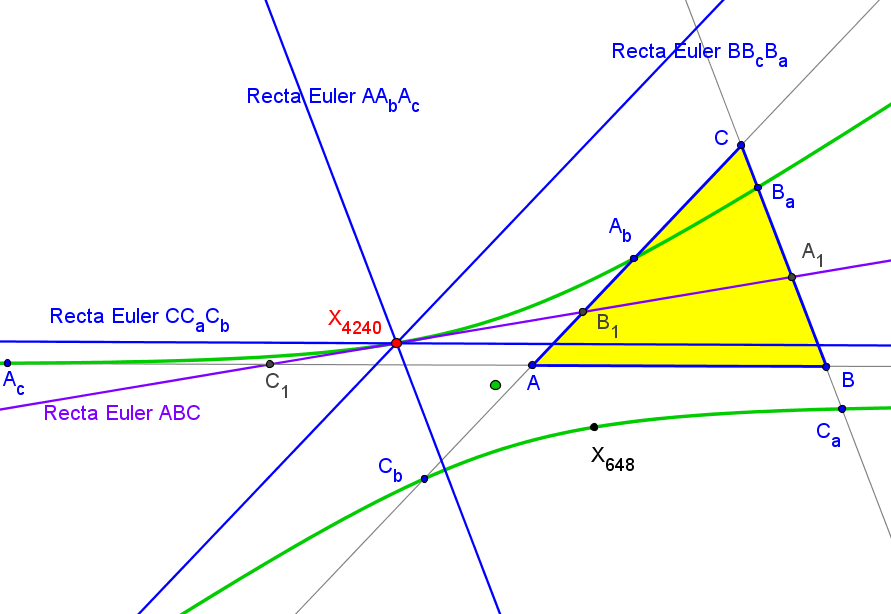
Los seis puntos Ab, Ac, Ba, Bc, Ca, Cb están en una misma cónica, tangente en X4240 a la recta de Euler y que pasa por X648 (tripolo de la recta de Euler). Estos dos puntos son antipodales en esta cónica.
La ecuación de la cónica es:
Los triángulos ABC y A'B'C' son ortológicos si y solo si P está sobre la recta de Euler.
El centro de ortología de A'B'C' con respecto a ABC es P; el centro de ortología de ABC con respecto a A'B'C' es un punto Q sobre la recta de Euler.
La correspondencia P ↦ Q es una involución de centro en el inverso del ortocentro respecto a la circunferencia circunscrita de ABC.
t' = -(a^2b^2c^2)/((a^2+b^2-c^2)(a^4-2a^2b^2+b^4-c^4)t).
P=(a2SA+2SBSC t:...:...) ↦ Q=(a2b2c2SBSC+4a2SA2SBSC t:...:...).
±abc/((-a^2+b^2+c^2)(a^2-b^2+c^2)(a^2+b^2-c^2))½,
que serán reales si el triángulos ABC es acutángulo (involución hiperbólica) e imaginarios conjugados cuando es obtusángulo.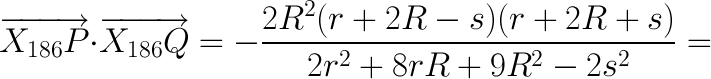
Se cree que fue Isaac Newton el
primero
que resolvió, por medio de la regla y el
compás,
el problema de encontrar la circunferencia tangente
a otras tres circunferencias.
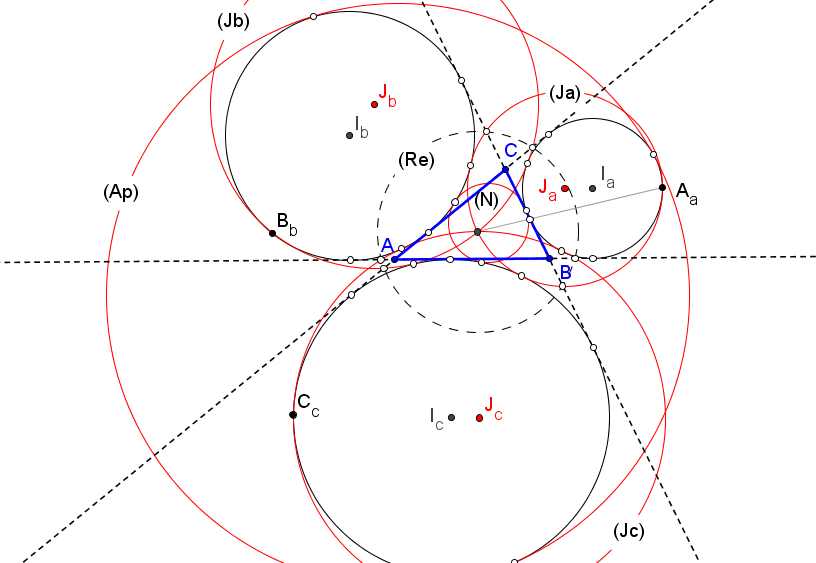
Aa = ((a+b-c)(a-b+c)(b+c)^2 : -c^2(a-b+c)(a+b+c) : -b^2(a+b-c)(a+b+c)).
Permutando cíclicamente estas coordenadas obtenemos las de los puntos de tangencia Bb de (Ib) y (Jb), y Cc de (Ic) y (Jc).
Los triángulos ABC y AaBbCc son perspectivos con centro de perspectividad en X3596 (1st Odehnal Point):
((-a+b+c)/a^2 :
(a-b+c)/b^2 : (a+b-c)/c^2).
Los triángulos ABC y JaJbJc son perspectivos con centro de perspectividad en X3597 (2nd Odehnal Point):
(1/(a^5+a^4(b+c) - a^3(b-c)^2-a^2(b^3+b^2c+bc^2+c^3) -
2abc(b^2+bc+c^2) - 2b^2c^2(b+c)) : .. : .. ).
*************************************
Las tangentes en los puntos de contacto Aa, Bb y Cc de las circunferenicias (Ia), (Ib) y (Ic) con las (Ja), (Jb) y (Jc) delimitan un triángulo T1T2T3 perspectivo con ABC. El centro de perspectividad T tiene coordenadas baricéntricas:
T = ((b+c)/(a^3(b+c) + a^2bc - a(b-c)^2(b+c) - bc(b+c)^2) : ... : ...)
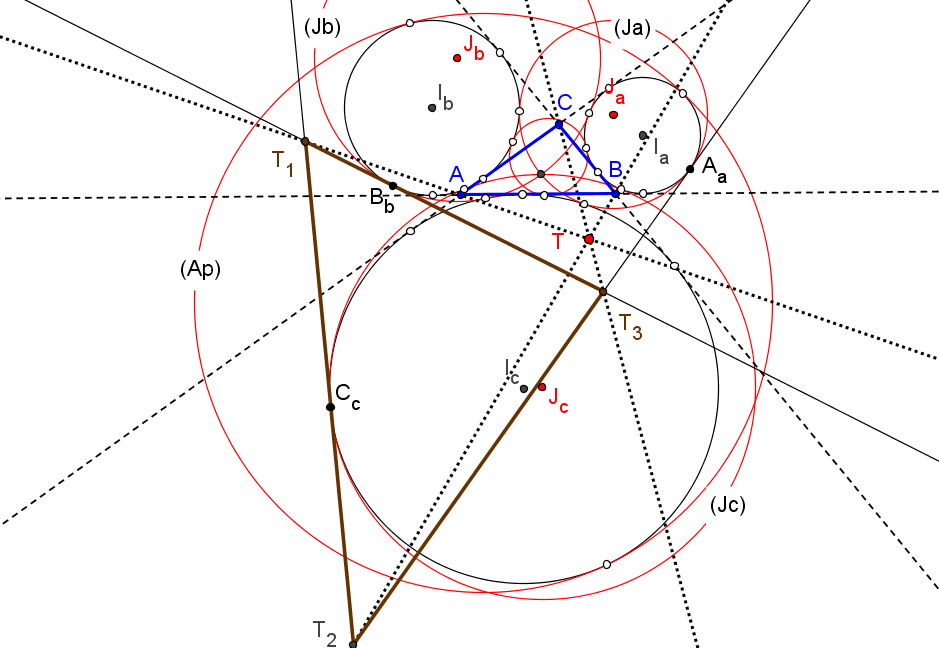
bc(a+b+c)x + b(a+b-c)(b+c)y + c(a-b+c)(b+c)z = 0.
*************************************
Ab = ((-a+b+c)(a+b-c)(b+c)^2 : c^2(a-b-c)(a+b+c) : (b(b+c)+a(b+2c))^2),
Ac = ((a-b-c)(a-b+c)(b+c)^2, : -(c(b+c)+a(2b+c))^2 : b^2(-a+b+c)(a+b+c)).
Las rectas AbAc, BcBa y CaCb delimitan un triángulo P1P2P3 perspectivo con ABC. El centro de perspectividad es:
P = ( (b+c)(b+c-a)/(a^2(b^2+3bc+c^2) +
a(b^3+b^2c+bc^2+c^3) + bc(b+c)^2) : ... : ... )
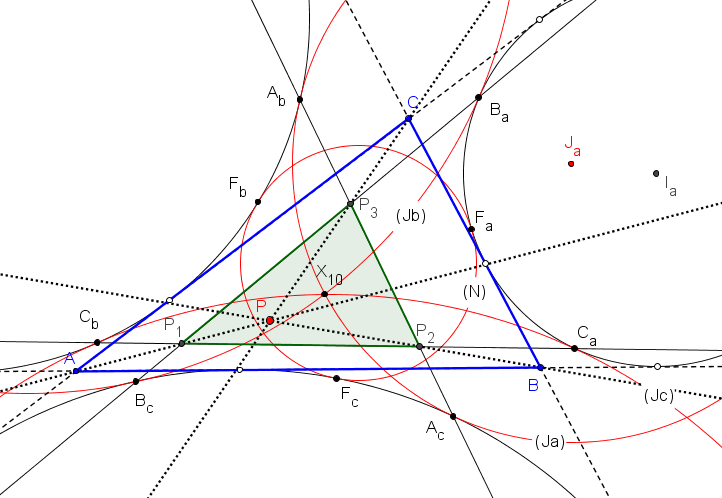
Las rectas BaCa, CbAb y AcBc delimitan un triángulo Q1Q2Q3 perspectivo con JaJbJc. El centro de perspectividad Q tiene primera coordenada baricéntrica:
a^10 (b + c)^3 + a^9 (b + c)^2 (5 b^2 - b c + 5 c^2) -
a^8 (5 b^5 + 28 b^4 c + 42 b^3 c^2 + 42 b^2 c^3 + 28 b c^4 + 5 c^5) -
a^7 (33 b^6 + 101 b^5 c + 182 b^4 c^2 + 243 b^3 c^3 + 182 b^2 c^4 +
101 b c^5 + 33 c^6) -
a^6 (21 b^7 + 86 b^6 c + 257 b^5 c^2 + 411 b^4 c^3 + 411 b^3 c^4 +
257 b^2 c^5 + 86 b c^6 + 21 c^7) -
a^5 (-27 b^8 - 27 b^7 c + 83 b^6 c^2 + 290 b^5 c^3 + 454 b^4 c^4 +
290 b^3 c^5 + 83 b^2 c^6 - 27 b c^7 - 27 c^8) +
a^4 (29 b^9 + 104 b^8 c + 160 b^7 c^2 - 53 b^6 c^3 - 372 b^5 c^4 -
372 b^4 c^5 - 53 b^3 c^6 + 160 b^2 c^7 + 104 b c^8 + 29 c^9) +
a^3 (b^2 - c^2)^2 (b^6 + 73 b^5 c + 182 b^4 c^2 + 239 b^3 c^3 +
182 b^2 c^4 + 73 b c^5 + c^6) -
a^2 (b - c)^2 (b + c)^3 (4 b^6 - 11 b^5 c - 49 b^4 c^2 -
99 b^3 c^3 - 49 b^2 c^4 - 11 b c^5 + 4 c^6) -
a b c (b - c)^2 (b + c)^4 (8 b^4 - 21 b^3 c - 9 b^2 c^2 -
21 b c^3 + 8 c^4) -
b^2 c^2 (b - c)^2 (b + c)^5 (4 b^2 - 11 b c + 4 c^2)
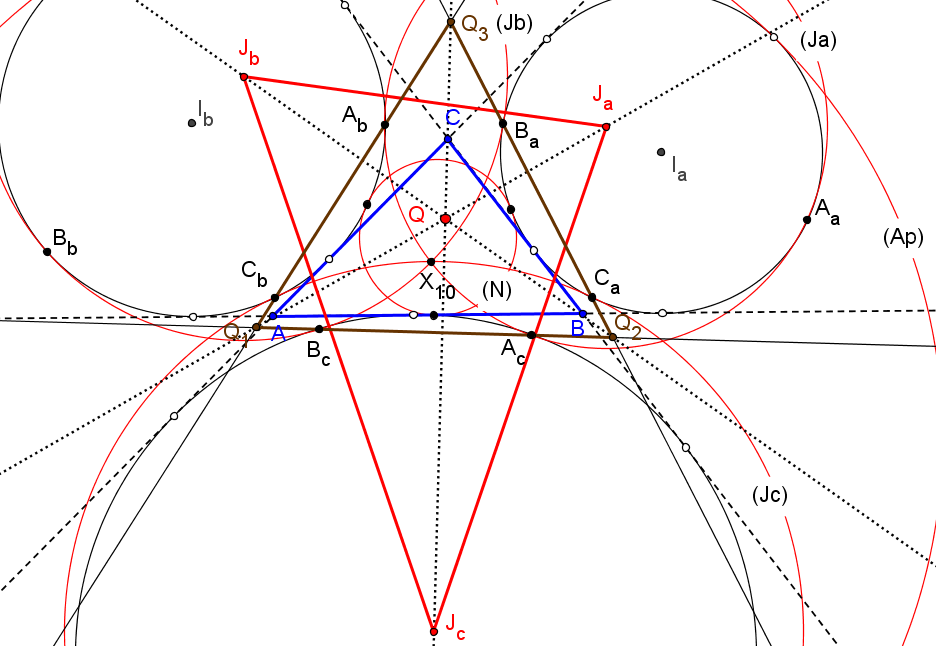
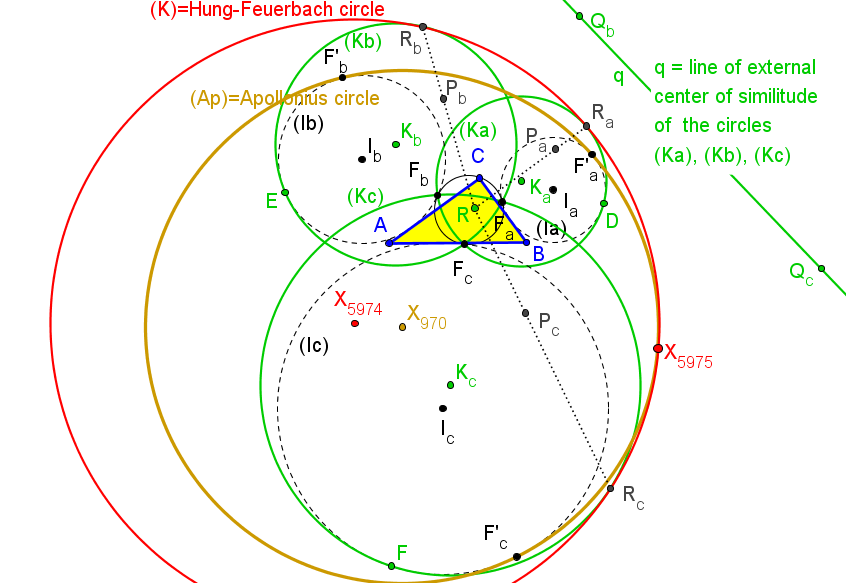
La circunferenica (J) tangente a las (Ja), (Jb) y (Jc), abarcándolas, es tangente a la circunferencia de Apolonio de ABC en el centro del triángulo X3030.
( ADGEOM #1541).png)
k(a,b,c)(a^2yz+b^2zx+c^2xy)-(x+y+z)(f(a,b,c)x+f(b,c,a)y+f(c,a,b)z)=0
dondeJ = (a(a^2(b+c)-3bc(b+c)+a(b^2+bc+c^2)) : ... : .. )
con (6,9,13)-número de búsqueda en ETC: 166.4953881815177657693948105
El triángulo tangencial de SaSbSc es perspectivo con ABC, con centro de perpectividad el punto de Spieker X10.
a Clara, por su 13 "cumple", con 9 días de retraso
Los puntos La, Lb y Lc están en una misma recta y su tripolo L tiene coordenadas baricéntricas:
((b+c)/(a^2+bc) : (a+c)/(b^2+ac) : (a+b)/(ab+c^2))
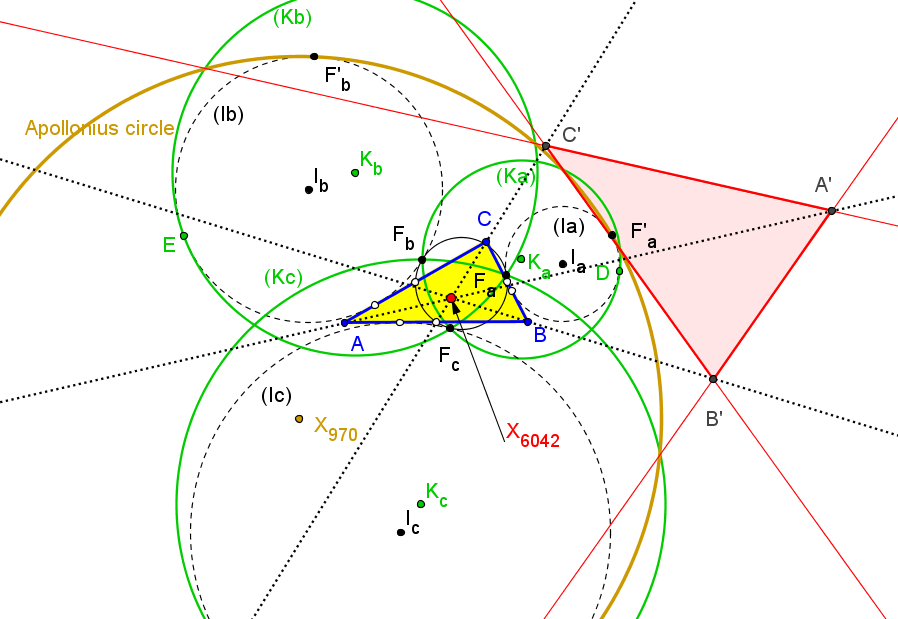
Los ejes radicales de la circunferencia de Apolonio de ABC y cada una de las circunferencias
(Ka), (Kb), (Kc) delimitan un triángulo perspectivo con ABC. El centro de perspectividad es X6042:
(a(b+c)^2(a(b+c)+b^2+c^2)^2 : b(c+a)^2(b(b+a)+c^2+a^2)^2 : c(a+b)^2(c(a+b)+a^2+b^2)^2).
PP'a / PPa = PP'b / PPb = PP'c / PPc = t, (t≠1)
La paralela por P'a a BC interseca a BA, CA en Ba, Ca, respectivamente.El lugar geométrico de los puntos P tales que las mediatrices de BaCa, CbAb, AcBc son concurrentes es la recta que pasa por el baricentro y el simediano.
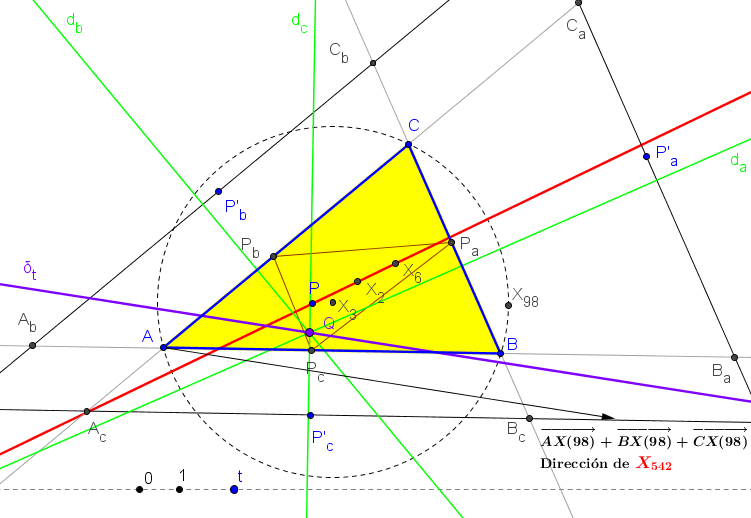
(b^2-c^2)(tu+v+w)x + ((b^2-c^2)(t-1)u+a^2(u+v+w))y + ((b^2-c^2)(t-1)u-a^2(u+v+w))z = 0.
La condición para que las tres mediatrices sean concurrentes es:(b^2-c^2)u + (c^2-a^2)v + (a^2-b^2)w = 0.
Es decir, el lugar geométrico es la recta que pasa por el baricento G(1:1:1) y el simediano K(a^2:b^2:c^2).Si P es el punto Pt de intersección de las rectas GK y δt, el correspondiente punto Qt de intersección de las mediatrices da, db, dc, describe la parábola que contiene al baricentro, circuncentro y simediano y con punto en el infinito X542.
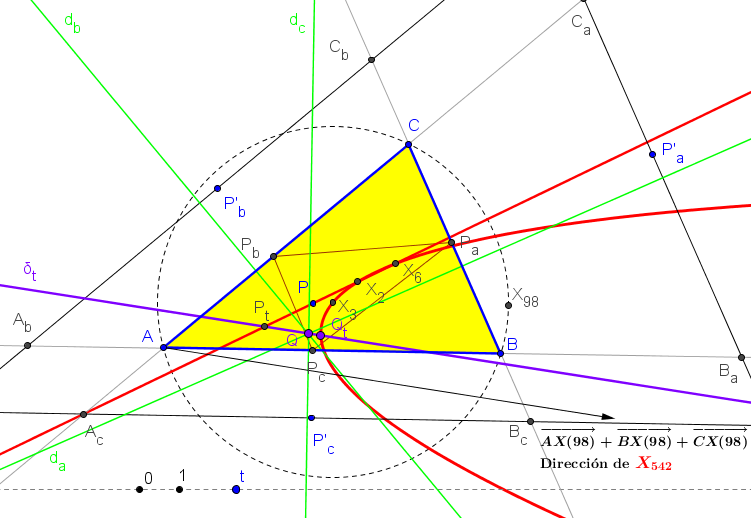
Cuando t varía y P queda fijo en la recta GK , el lugar geométrico que describe el punto Q de intersección de las mediatrices da, db, dc, es una recta δP que pasa por el circuncentro, X3.
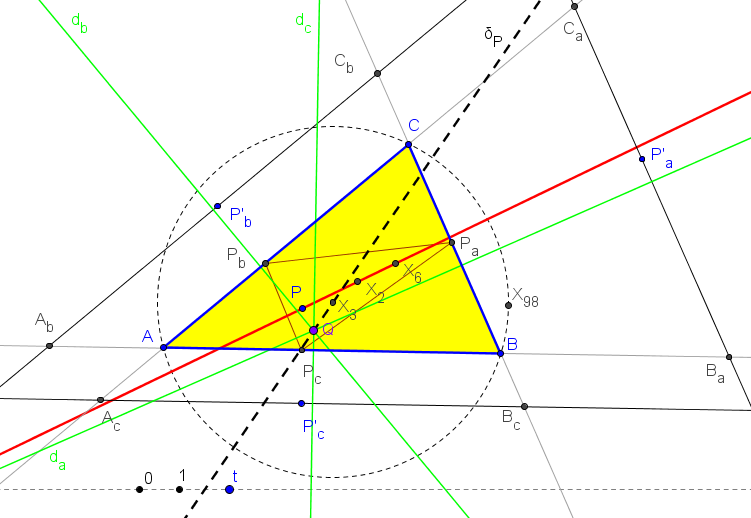
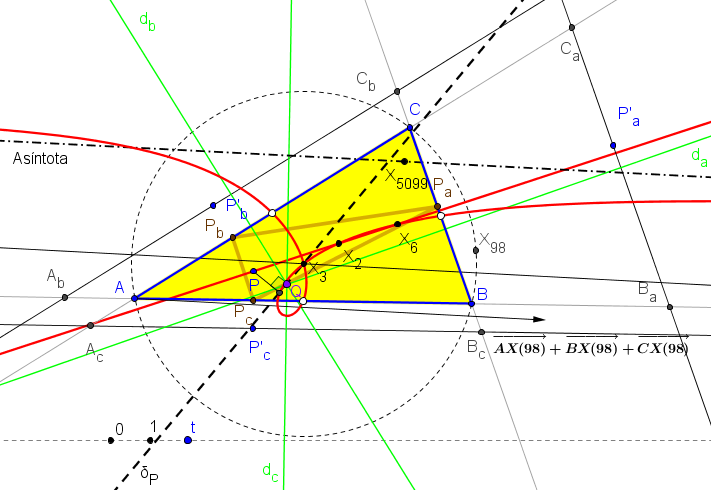
(b^2-c^2)((a^2-b^2-c^2+b^2c^2)ξ-b^2c^2)x + ... = 0.
La recta δP contiene al punto P solamente si éste es el baricentro o el simediano.Cuando P varía en la recta GK, el lugar geométrico que describe el pie de la perpendicular, trazada por él a la recta δP, es una cúbica circunscrita al triángulo medial, que contiene a los centros X2, X3 (doble), X6, X542, X5108 y con asíntota pasando por X5099 (descrito por Seiichi Kirikami en Anopolis #846) y dirección la del punto del infinito X542.
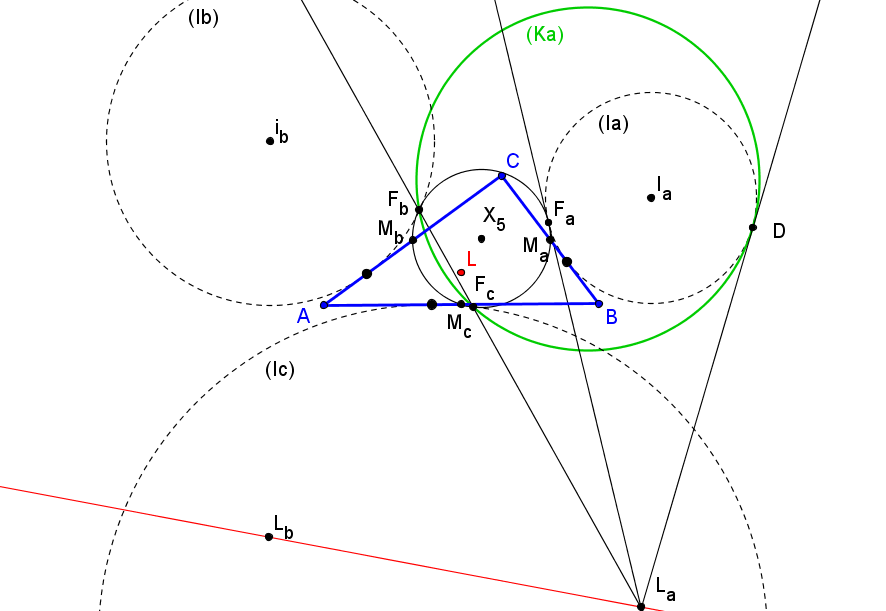
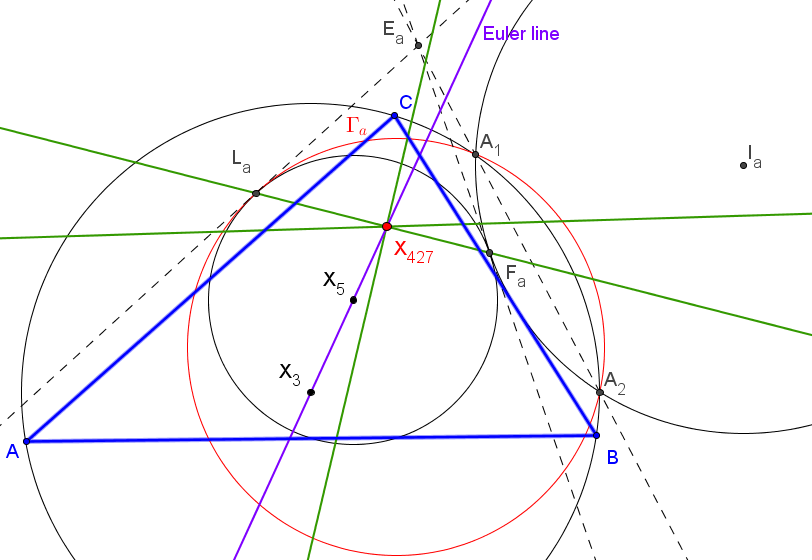
Sean ABC un triángulo, A1 y A2 los puntos de intersección de la circunferencia circunscrita con la circunferencia A-exinscrita, Fa el punto de tangencia de la circunferencia de los nueve puntos y la circunferencia A-exinscrita.
Sea Γa la circunferencia, distinta de la A-exinscrita, que pasa por A1 y A2 es tangente a la circunferencia de los nueve puntos y La el punto de contacto.
Similarmente se definen los puntos Fb, Fc, Lb, Lc.
Las rectas FaLa, FbLb, FcLc concurren en X427, sobre la recta de Euler.
Ea = ((b-c)(2a^3+a^2(b+c)+(b-c)^2(b+c)) : -(a+c)(a^3+2b^3+a^2c-b^2c-c^3+a(b^2-c^2)) : (a+b)(a^3+a^2b-b^3-bc^2+2c^3+a(-b^2+c^2))).
La ecuación de la recta FaLa:
(c-b)(-a^2+b^2+c^2)(a^3+b^3+c^3+a^2(b+c)+a(b^2+bc+c^2))x +
(a+c)(a^2-b^2+c^2)(a^3+a^2b+b^3+ab(b-c)-b^2c+bc^2-c^3)y -
(a+b)(a^2+b^2-c^2)(a^3-b^3+a^2c+b^2c-bc^2+c^3+ac(-b+c))z=0.
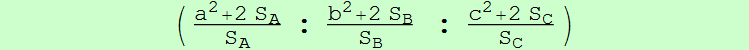
((a^4(b+c) + 2a^3(b^2+c^2) + 2a^2(b^3+b^2c+bc^2+c^3) + 2a(b+c)^2(b^2+c^2) + (b+c)(b^2+c^2)^2)/(b^2+c^2-a^2) : ... : ...)
con (6,9,13)-número de búsqueda en ETC: -23.546702367310941758314
Sea, ABC un triángulo, P un punto y DEF su triángulo circunceviano.
Oa, Ob, Oc son los circuncentros de los triángulos BCP, CAP, ABP, respectivamente.
Od, Oe, Of son los circuncentros de los triángulos EFP, FDP, DEP, respectivamente.
Las rectas OaOd, ObOe, OcOf concurren en el punto P', imagen de P en la homotecia de centro el circuncentro y razón 1/2.
D=(-a^2vw : v(c^2v+b^2w) : w(c^2v+b^2w)),
E=(u(c^2u+a^2w) : -b^2uw : w(c^2u+a^2w)),
F= (u(b^2u+a^2 v) : v(b^2u+a^2v) : -c^2uv).
Oa =(-a^2(-u(b^2(u+v-w)+c^2(u-v+w))+ a^2(u^2+2vw+u(v+w))) : -(b^2-c^2)u(-c^2v+ b^2(u+v))+a^4vw+ a^2(c^2v(u-w)+b^2(u^2+uv+2uw+vw)) : a^4vw-(b^2-c^2)u(b^2w-c^2(u+w))+ a^2(b^2(u-v)w+c^2(u^2+2uv+uw+vw))).
Y el circuncentro de DFP es:P' = ( (3S^2-SBSC)u + a^2SAv + a^2SAw : ... : ... ).
Sean ABC un triángulo, Γa la circunferencia que pasa por B y C y es tangente internamente a la circunferencia inscrita y similarmente, las circunferencias Γb y Γc. Designamos por Pa el punto de contacto de Γa y la circunferencia inscrita; similarmente, sean Pb y Pc. Sea Qa el punto de concurrencia de las tangentes a la circunferencia inscrita en Pb y Pc; y similarmente, Qb y Qc. Finalmente, sea Ta el punto de intersección de las rectas BPc y CPb; similarmente se definen Tb y Tc.
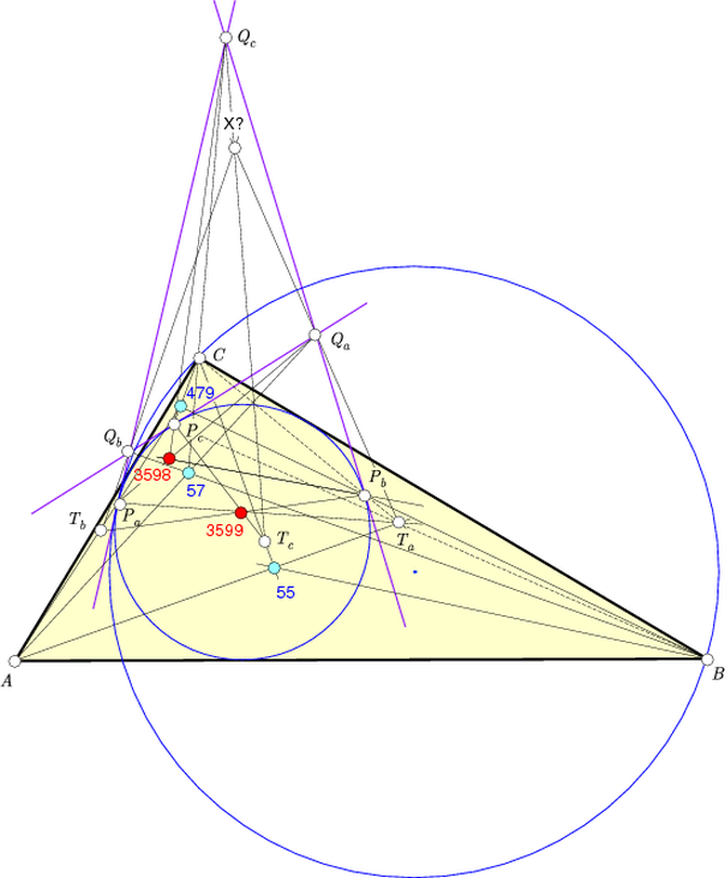
(a(a^4-4a^3(b+c)+2a^2(3b^2-2bc+3c^2)-4a(b-c)^2(b+c)+(b-c)^2(b^2+6bc+c^2))) /(b+c-a)^2: ... : ... ).
Sea ABC un triángulo y Φa la cónica circunscrita con tangentes en B y C perpendiculares a BC. Similarmente se definen las cónicas circunscritas Φb y Φc.
Denotamos por A', B', C' los cuartos puntos de intersección de Φb y Φc, Φc y Φa, Φa y Φb, respectivamete.
La tangente en B a Φb vuelve a cortar a Φa en Ba. La tangente en C a Φc vuelve a cortar a Φa en Ca. Similarmente se definen los puntos Cb, Ab y Ac, Bc.
En coordenadas baricéntricas:
Φa : a²yz+SCzx+SBxy=0,
Φb : SCyz+b²zx+SAxy=0,
Φc : SByz+SAzx+c²xy=0.
Cuarto punto de intersección de la cónicas circunscritas Φb y Φc, tripolo de la recta determinada por sus perspectores E=(SC:b²:SA) y F=(SB:SA:c²):
Las rectas AA', BB', CC' concurren en el punto de De Longchamps, X20.
Ab=(SBSC^2 : -SC(SA(SB-SC)+SBSC) : SB(SA(SB-SC)+SBSC)),
y a Φc enAc=(SB^2SC : -SC(SA(SB-SC)-SBSC) : SB(SA(SB-SC)-SBSC).
Los puntos Ab, Ac, Bc, Ba, Ca y Cb están en una misma cónica, de centro:
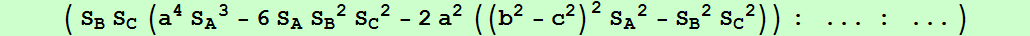
con (6,9,13)-número de búsqueda en ETC: 0.4464942066184852070174993, y está alineado (Peter Moses) con los centros del triángulo:
X112, X376, X577, X1249, X1294, X3163, X3184.
El triángulo delimitado por las rectas BaCa, CbAb, AcBc es perspectivo con ABC con centro de perspectividad el punto de De Longschamps.
El triángulo delimitado por las rectas BcCb, CaAc, AbBa es perspectivo con ABC con centro de perspectividad el punto
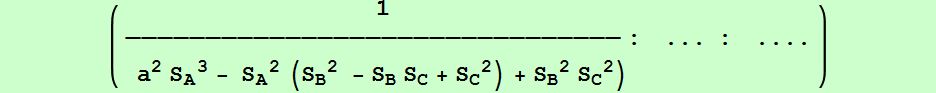
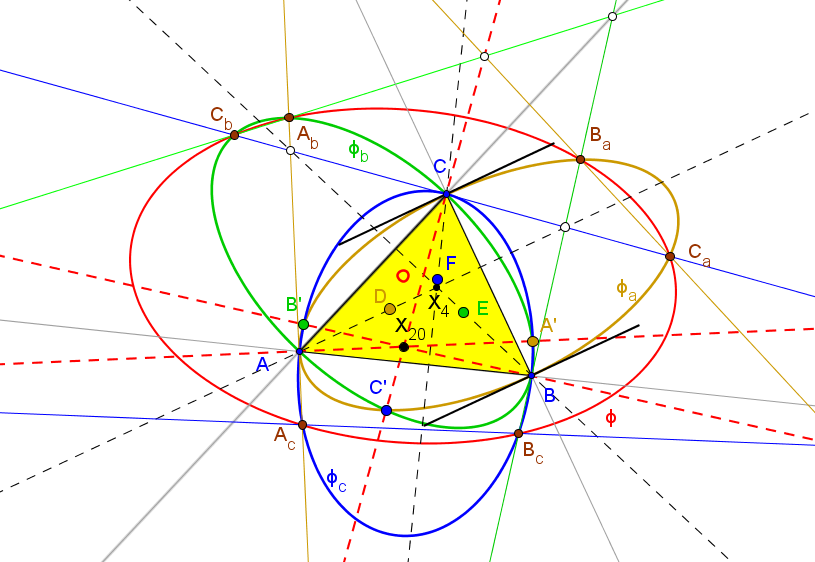
Sea ABC un triángulo y P un punto sobre su circunferencia circunscrita Γ. Se denotan por A', B', C' las reflexiones de P en las mediatrices de BC, CA, AB, respectivamente; A'B'C' está inscrito en Γ.
• Se designa por A+ el centro de la semejanza directa que transforma el segmento BC en
el C'A', por B+ el centro de la semejanza directa que transforma el segmento CA en
el A'B' y por C+ el centro de la semejanza directa que transforma el segmento AB en
el B'C'.
El lugar geométrico de los centros de semejanza A+, B+, C+ son tres circunferencias Γ+a,
Γ+b,
Γ+c, con un punto común B1 (primer punto de Beltrami, inverso del primer punto de Brocard Ω1, respecto a la circunferencia circunscrita, Γ).
La circunferencia Γ+t circunscrita a A+B+C+ pasa por B1 y el circuncentro, O.
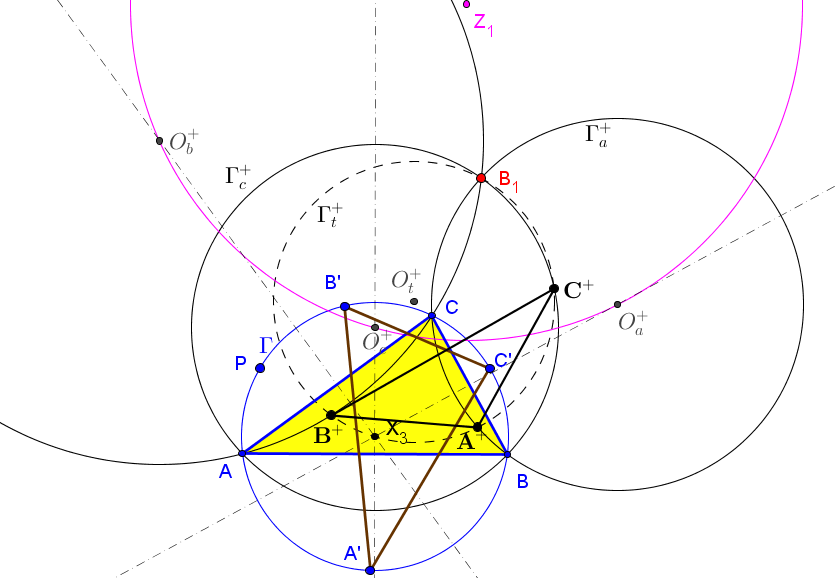

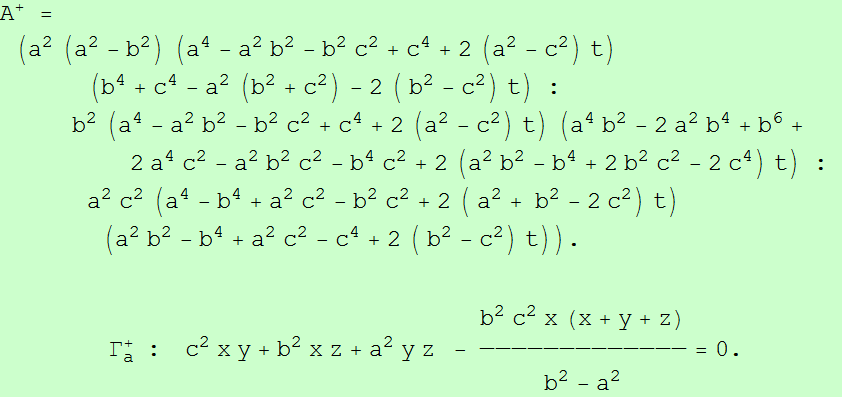
B1 = ( a^2(a^2-b^2) : b^2(b^2-c^2) : c^2(c^2-a^2)).
El lugar geométrico de los centros de semejanza A-, B-, C- son tres circunferencias Γ-a,
Γ-b,
Γ-c, con un punto común B2 (segundo punto de Beltrami, inverso del segundo punto de Brocard Ω2, respecto a la circunferencia circunscrita, Γ).
La circunferencia Γ-t circunscrita a A-B-C- pasa por B2 y el circuncentro O.
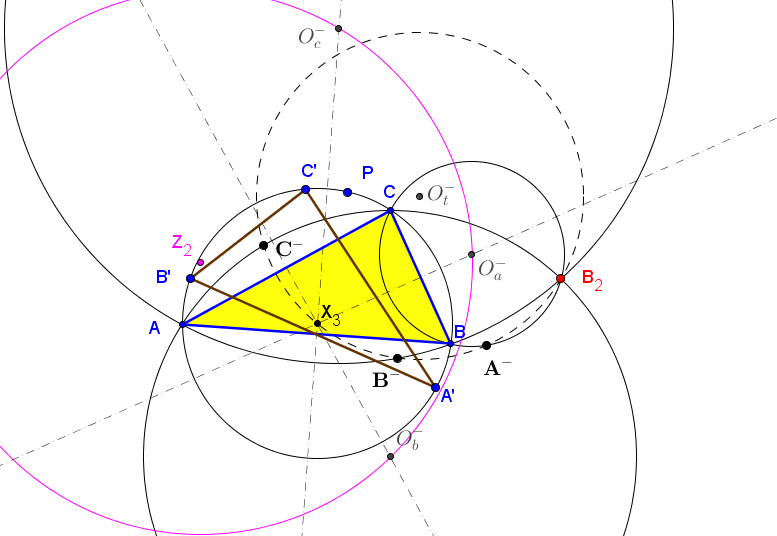
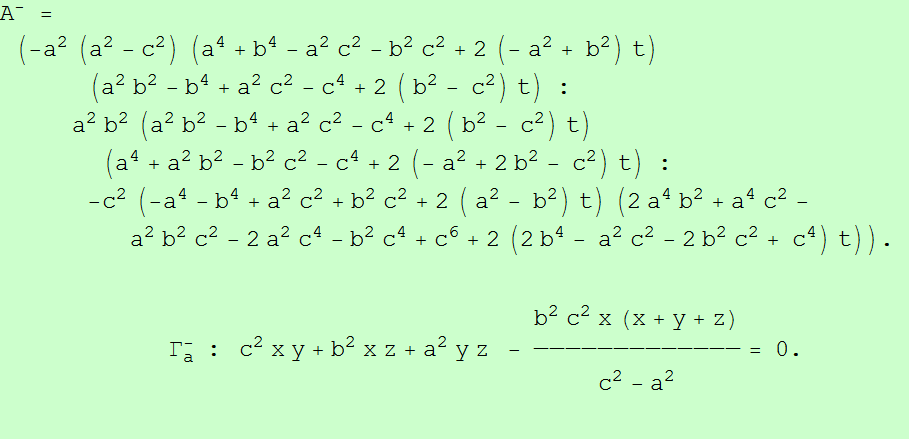
B1 = ( a^2(a^2-c^2) : b^2(b^2-a^2) : c^2(c^2-b^2)).
(a^2(-a^8 + a^6(b^2+c^2) + a^4(b^4+5b^2c^2+c^4) - a^2(2b^6+3b^4c^2+3b^2c^4+2c^6) + b^8 + c^8),
con (6,9,13)-número de búsqueda en ETC: 1.99844087285917963875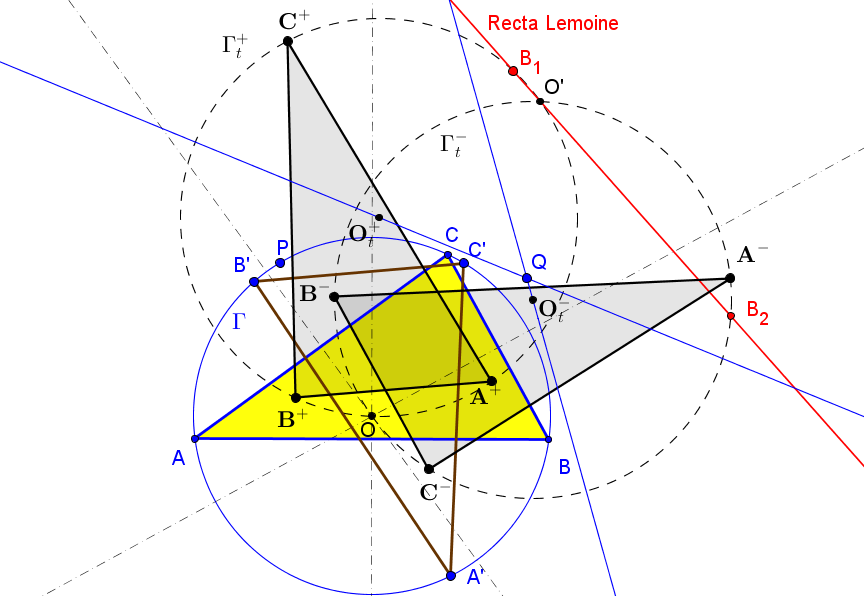
V= (a^2(4a^6 - 9a^4(b^2+c^2) + 2a^2(4b^4+b^2c^2+4c^4) - 3b^6+b^4c^2+ b^2c^4-3c^6 ) : ... : ...),
con (6,9,13)-número de búsqueda en ETC: 2.47073957830213664904597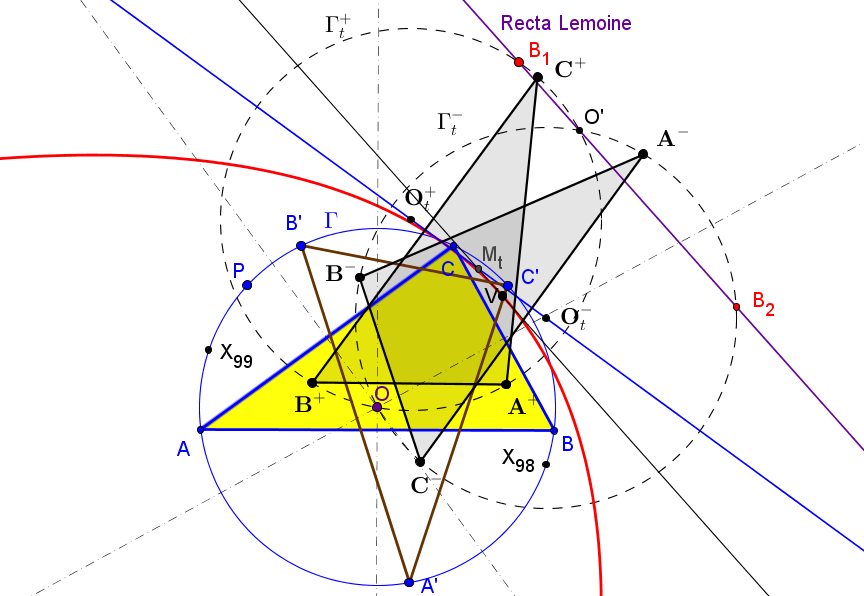
Construir un triángulo ABC, dado A'B'C' el triángulo ceviano de algún punto, tal que A' es el pie de bisectriz en A y B' es el pie de la mediana por B.
4 u w (u + w) (u + v + w)=0
Luego, una condición necesaria para construir el triángulo es que el punto P esté sobre la recta δ: x+z=0, paralela a A'C' por B'.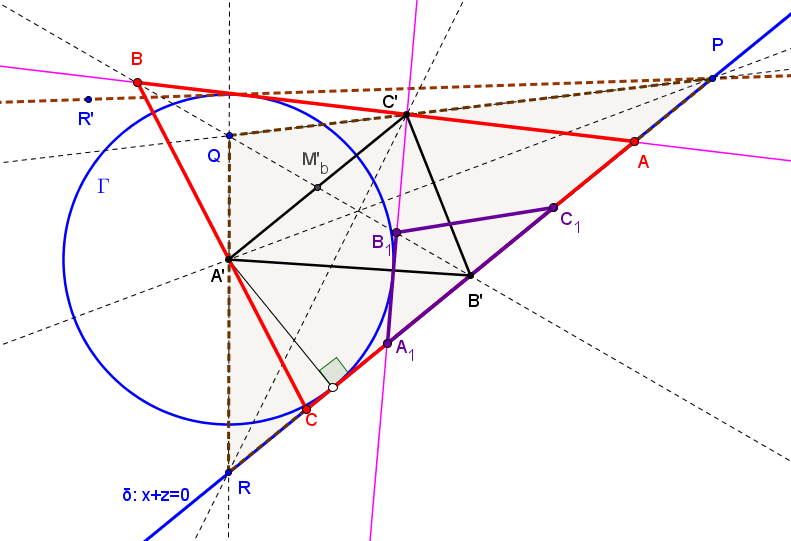
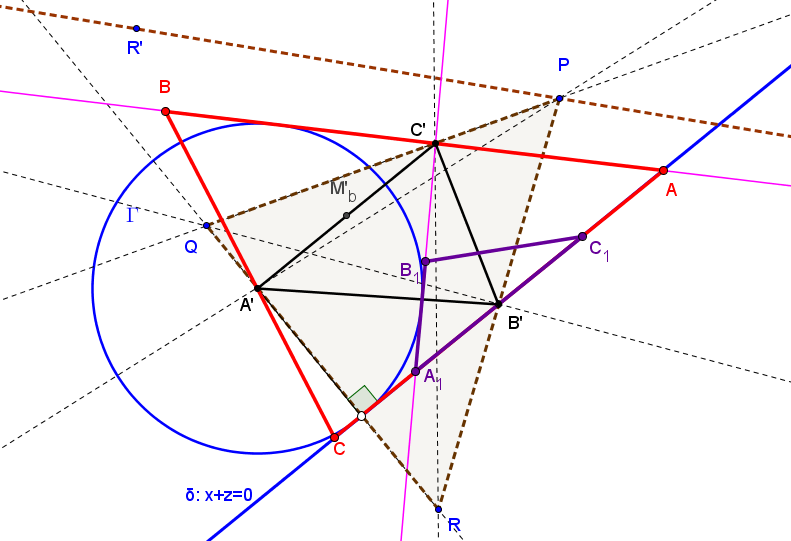
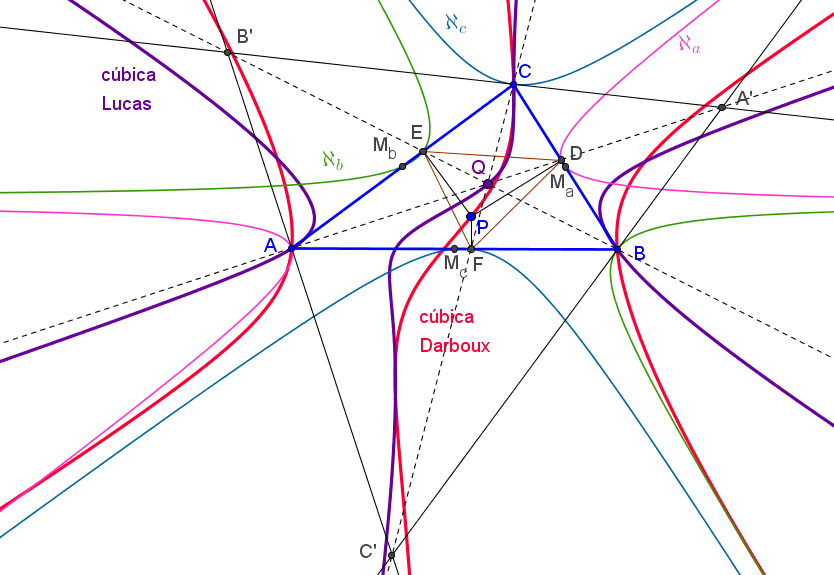
Sean ABC un triángulo, P un punto en su plano y ℵP la hipérbola equilátera circunscrita a ABC y que pasa por P (pasa también por el ortocentro H). Una recta δ que pasa por P, vuelve a cortar a la hipérbola en un punto Q. Denotamos por A1, B1, C1 los puntos en los que las rectas por P y perpendiculares a AQ, BQ, CQ cortan a los lados BC, CA, AB, respectivamente.
Los puntos A1, B1, C1 están alineados sobre una recta δ1 perpendicular a PQ.
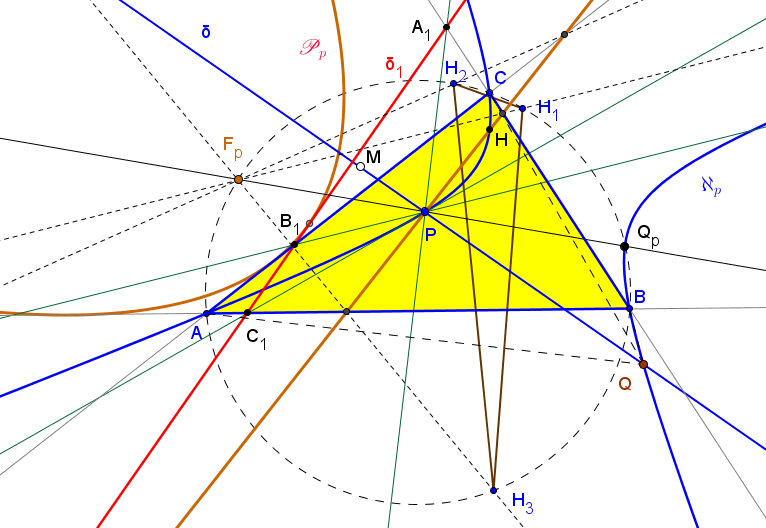
u(SBv-SCw)yz + v(SCw-SAu)xz + w(SAu-SBv)xy = 0.
((1-t)tu(SBv-SCw) : -t(SAu-SCw)((t-1)v+ tw) : (t-1)(SAu-SBv)((t-1)v+tw)) ).
La envolvente de las rectas δ1, cuando δ gira alrededor de P, es una cónica (es fácil ver que la correspondencia B1↦ C1 entre las rectas AC y AB es una proyectividad) tangente a los lados de ABC y a la recta del infinito (párabola inscrita ℘p). Por tanto, su directriz pasa por H (es la recta PH) y su foco Fp está en la circunferencia circunscrita (es el conjugado isogonal del punto del infinito determinado por la dirección perpendicular a la recta PH).El cuarto punto Qp de intersección de la hipérbola ℵp con la circunferencia circunscrita es el segundo punto de intersección de la hipérbola con la recta PFp.
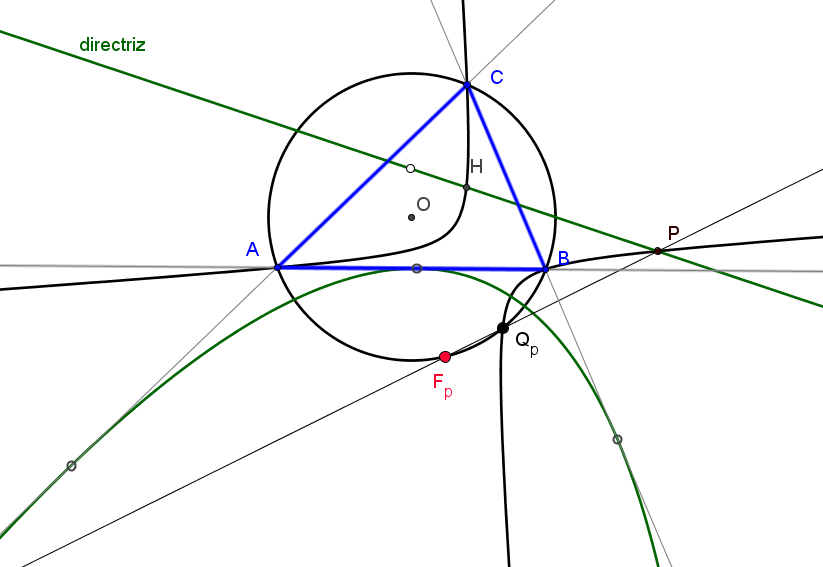
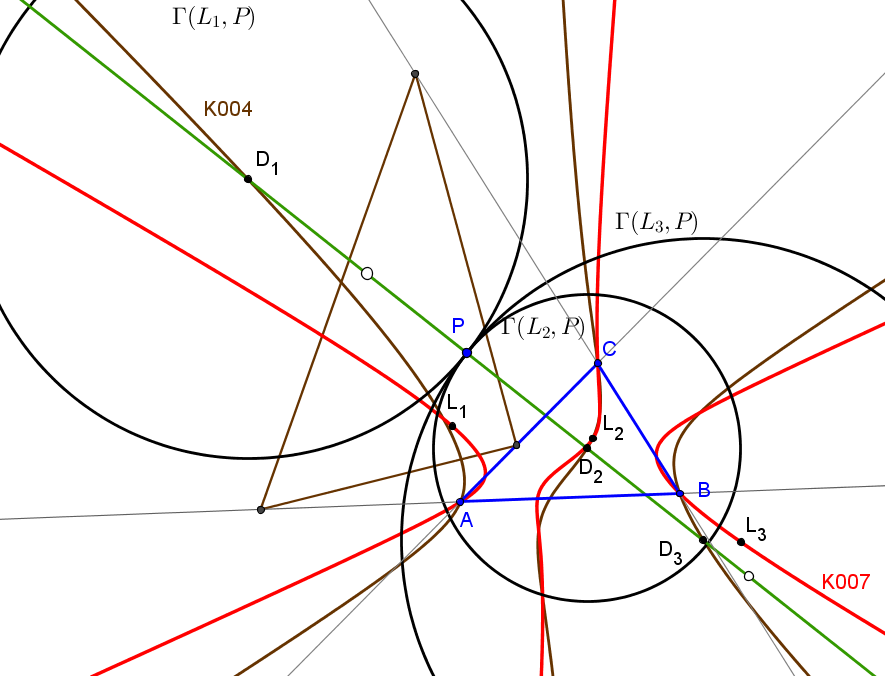
Sean ABC un triángulo y P un punto en su plano. Las reflexiones de P en los vértices del triángulo ceviano XaXbXc de un punto X, forman un triángulo QaQbQc. Los tres puntos que resultan de reflejar este triángulo en los lados de ABC determinan una circunferencia Γ(X,P).
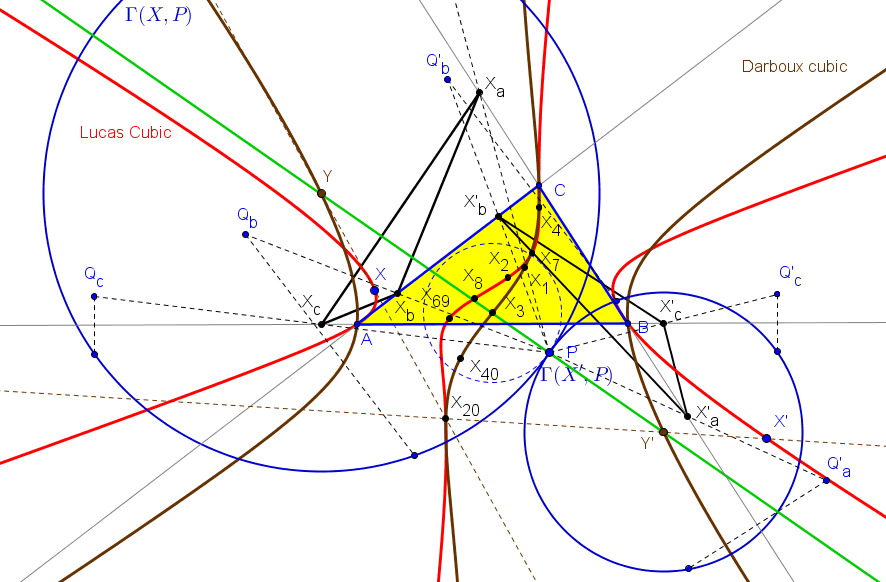
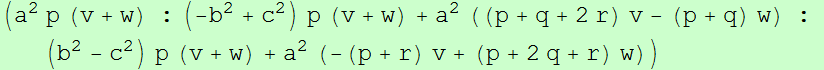
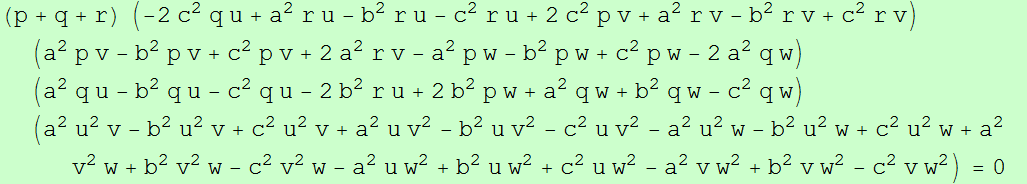
P está sobre la circunferencia Γ(X,P) si y solo si X está sobre la cúbica de Lucas o sobre las rectas perpendiculares a los lados de ABC en los pies de las cevianas del punto X.
Tomemos un punto L1 sobre la curva de Lucas y un punto P arbitrario del plano, entonces P está en la circunferencia Γ(L1,P) cuyo centro es el punto D1 (en la cúbica de Darboux, K004), tal que el triángulo pedal de D1 es el triángulo ceviano de L1.
La recta D1P corta a la cúbica de Darboux en otros dos puntos D2 y D3 (reales o imaginarios). Si L2 y L3 son los puntos (en la cúbica de Lucas) tales que sus triángulos cevianos son los triángulos pedales de D2 y D3, respectivamente, se verifica que las tres circunferencias Γ(L1,P), Γ(L2,P) y Γ(L3,P) son tangentes en P.
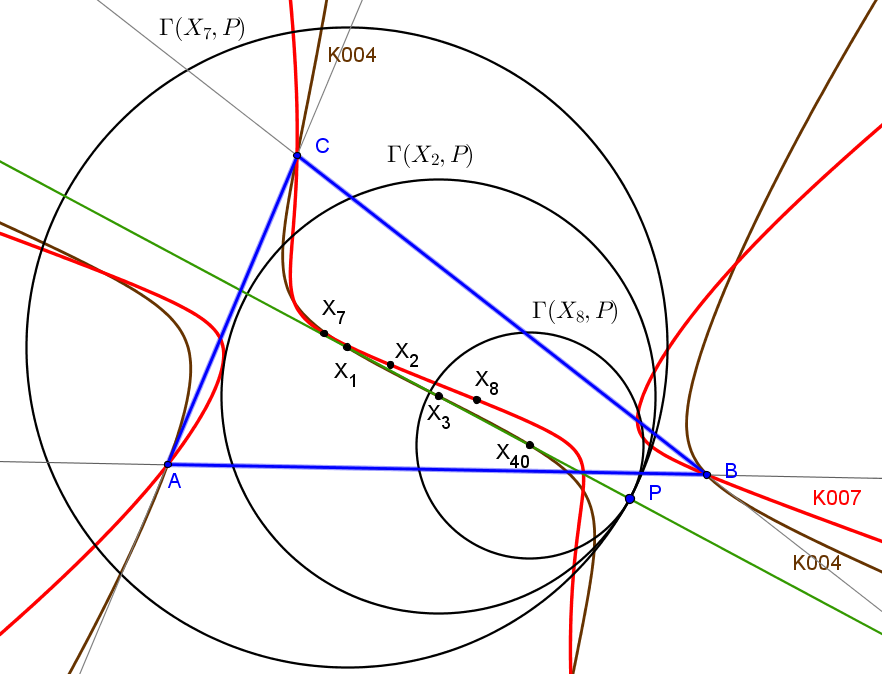
Las circunferencias Γ(X,P) y Γ(X',P) son tangentes en P si y solo si P está en la recta YY'.
En estas circunstancias, si G es el baricentro, también la circunferencia Γ(G,P), con centro en el circuncentro, es tangente en P a las circunferencias Γ(X,P) y Γ(X',P).
En particular (Peter Moses):
Si X=X7 = punto de Gergonne y X'=X8 = punto de Nagel, las circunferencias Γ(X7,P) y Γ(X8,P) son tangentes en P si y solo si P queda en la recta que pasa por O=X3, I=X1 and X40.
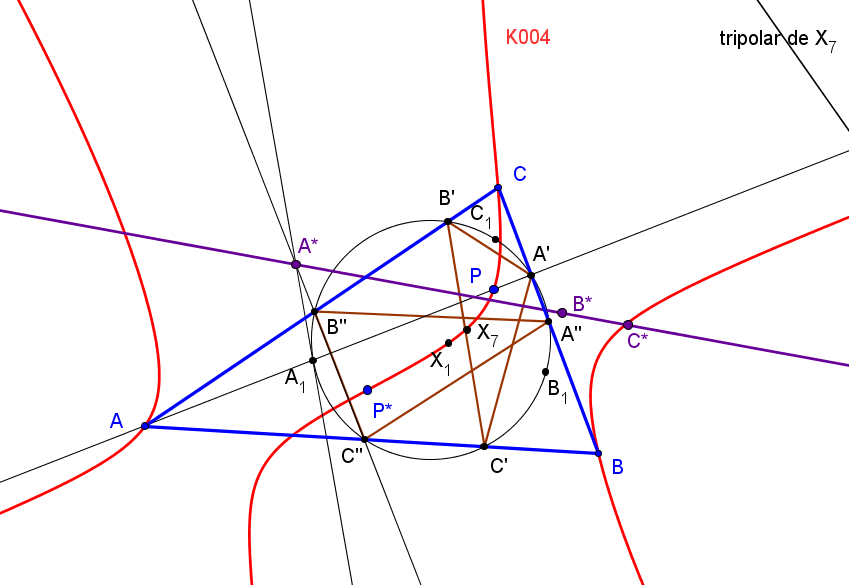
Sean ABC un triángulo y P, Q dos puntos conjugados isogonales.
Ap es el punto de intersección, distinto de P, de la recta AP con la circunferencia circunscrita a BPC; Aq es el punto de intersección, distinto de Q, de la recta AQ con la circunferencia circunscrita a BQC.
Similarmente se definen los puntos Bp, Bq, Cp y Cq.
Denotamos por R el centro radical de las circunferenecias cicunscritas a los triángulos AApAq, BBpBq y CCpCq.
Si las coordenadas baricéntricas de P son (u:v:w),
Rp =(a^2u(c^2v^2+b^2w^2) : b^2v(c^2 u^2+a^2w^2) : c^2(b^2u^2+a^2v^2)w).
El lugar geométrico de los puntos P tales que el circuncentro, P y R están alineados es la cuártica de Euler-Morley.

Sean ABC un triángulo, P, P* dos puntos conjugados isogonales y A'B'C', A"B"C" los triángulos pedales de P, P*, respectivamente.
Se denota por A1 el punto de intersección (distinto de A) de la recta AA' con la circunferencia pedal de P, y por
A* el punto de intersección de la recta B"C" con la tangente a la circunferencia pedal de P en A1.
De forma similar se define los puntos B* y C*.
El lugar geométrico de los puntos P tales que su circunferencia pedal está definida y los puntos A*, B* y C* están alineados es la cúbica de Darboux.
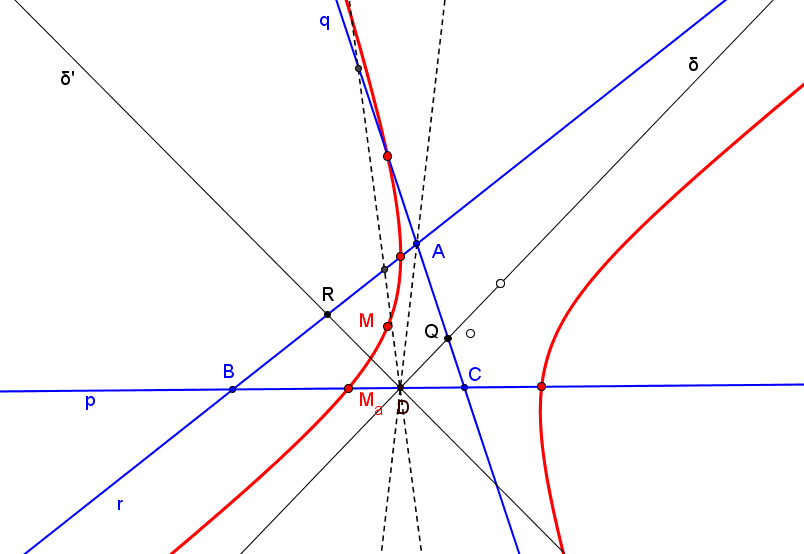
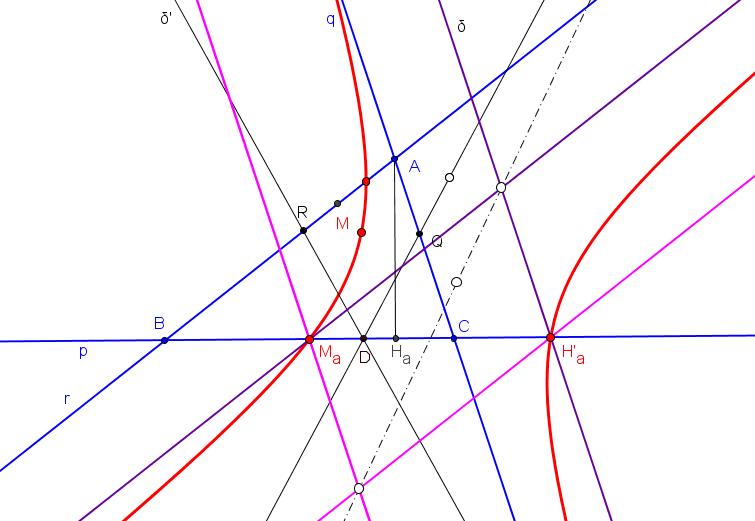
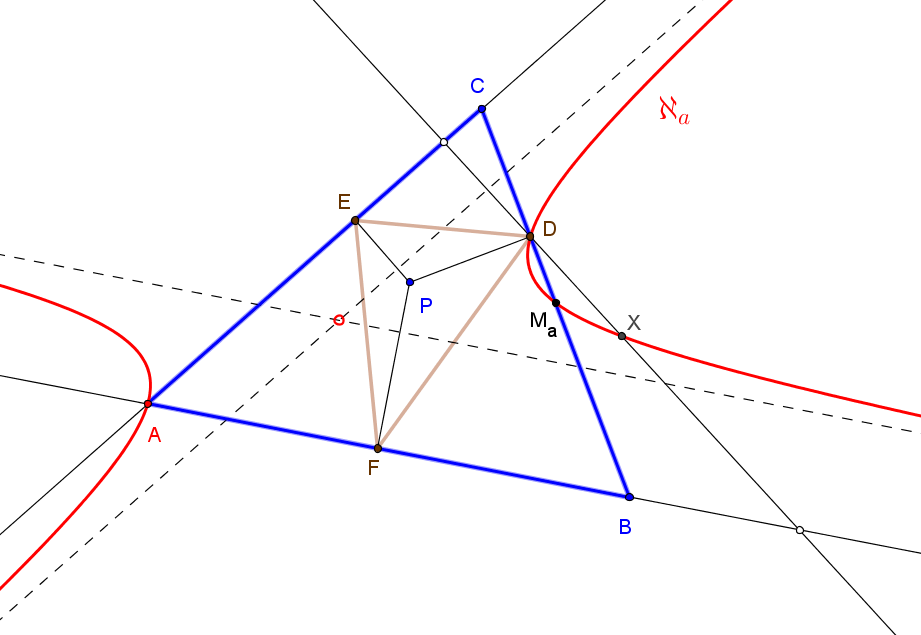
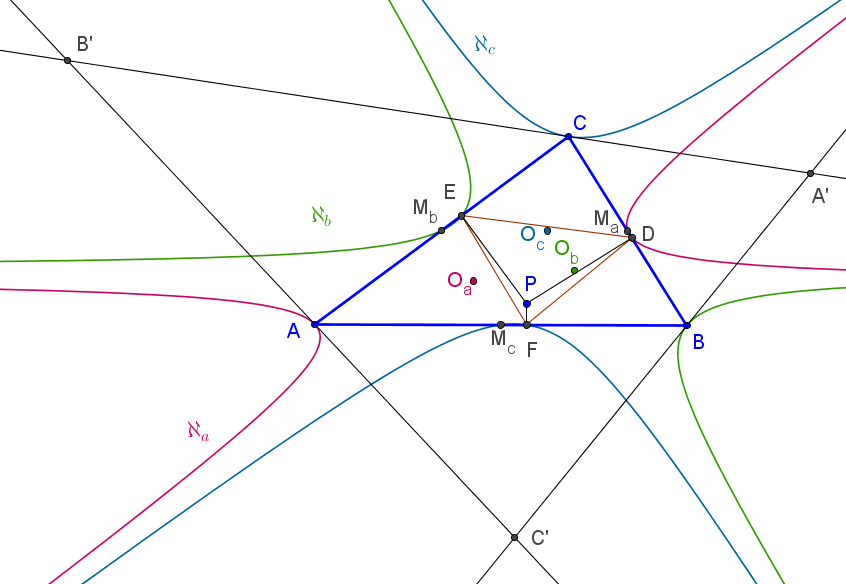
Sean p, q, r tres recta fijas y D un punto fijo sobre p. Una recta variable δ a través de D interseca a q en Q y δ', la reflexión de δ en p, corta a r en R. Sea M el punto medio de QR.
El lugar geométrico de M, cuando δ gira alrededor de D, es una hipérbola de asíntotas paralelas a las rectas q y r, y que pasa por los puntos medios de B=p∩r y C=p∩q (cuando δ=p), de A=q∩r y q∩δ' (cuando δ pasa por A=q∩r) y de A=q∩r y r∩δ' (cuando δ pasa por A=q∩r).

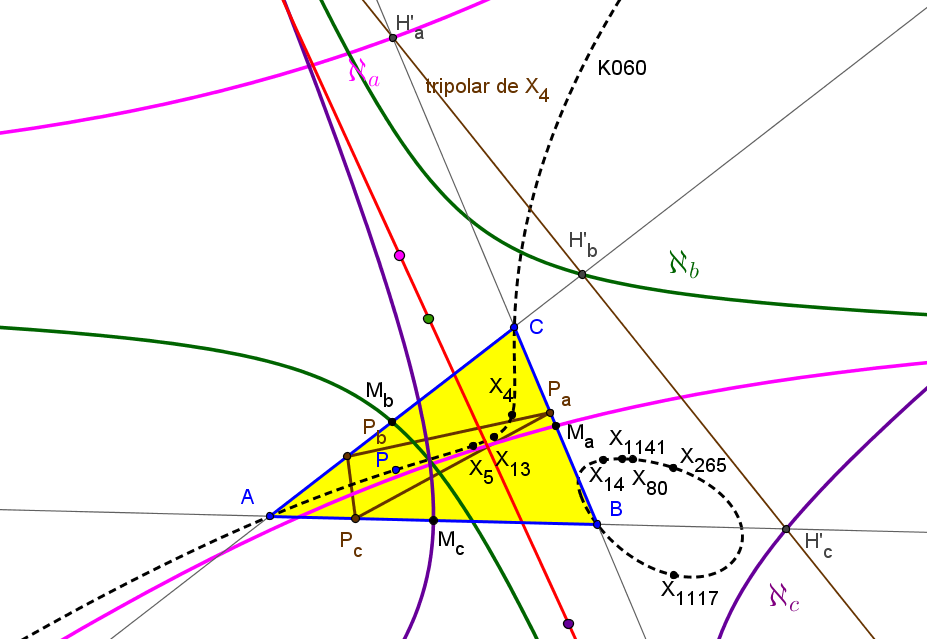
Los centros de las hipérbolas ℵa, ℵb y ℵc están alineados si y sólo si P está sobre la hipérbola de Kiepert.
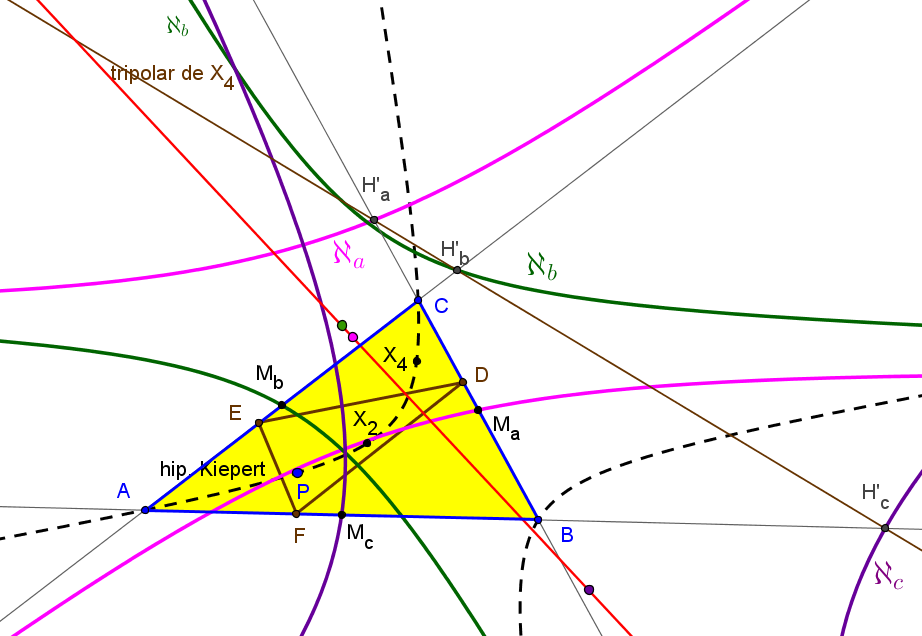
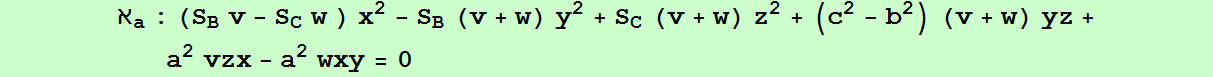
Los centros de las hipérbolas ℵa, ℵb y ℵc están alineados si y sólo si P está sobre la ortopivotal cúbica de ortopivote X5, K060.
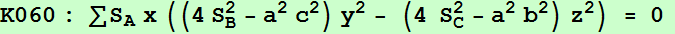
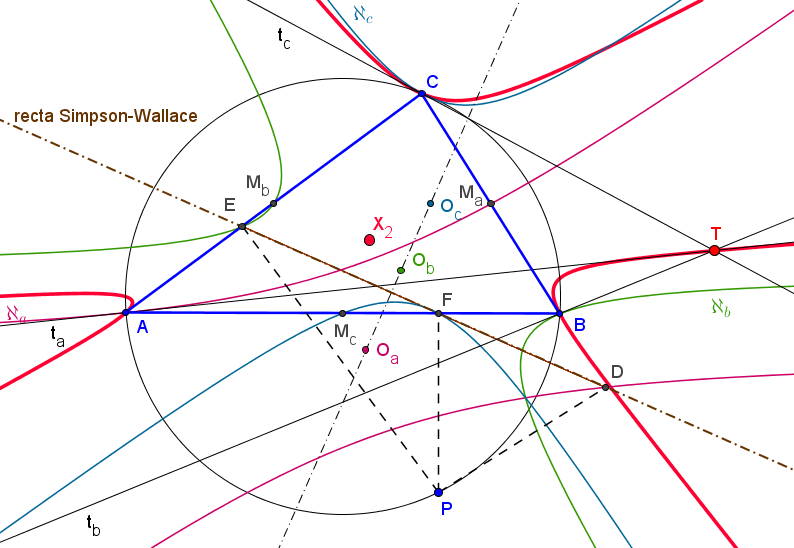
Dados un triángulo ABC y un punto P, sean MaMbMc el triángulo medial y DEF el triángulo pedal de P.
Consideremos el lugar geométrico del punto medio de los puntos en que una recta variable, que pasa por D, corta a las rectas AB y AC.
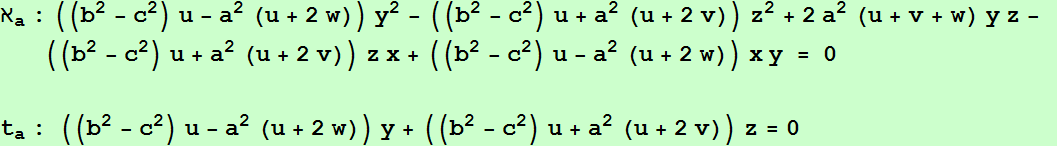
El triángulo A'B'C' delimitado por las tangentes ta, tb y tc es perspectivo con ABC si y solo si P está sobre la circunferencia circunscrita o sobre la cúbica de Darboux.
El centro de perspectividad Q de ABC y A'B'C', cuando P recorre la cúbica de Darboux está sobre la cúbica de Lucas.
Cuando P queda sobre la circunferencia circunscrita a ABC, los vértices de su triángulo pedal quedan sobre la recta de Simson s(P) de P, y las tres tangentes ta, tb y tc concurren en el tripolo de s(P), sobre la cúbica de Simson.
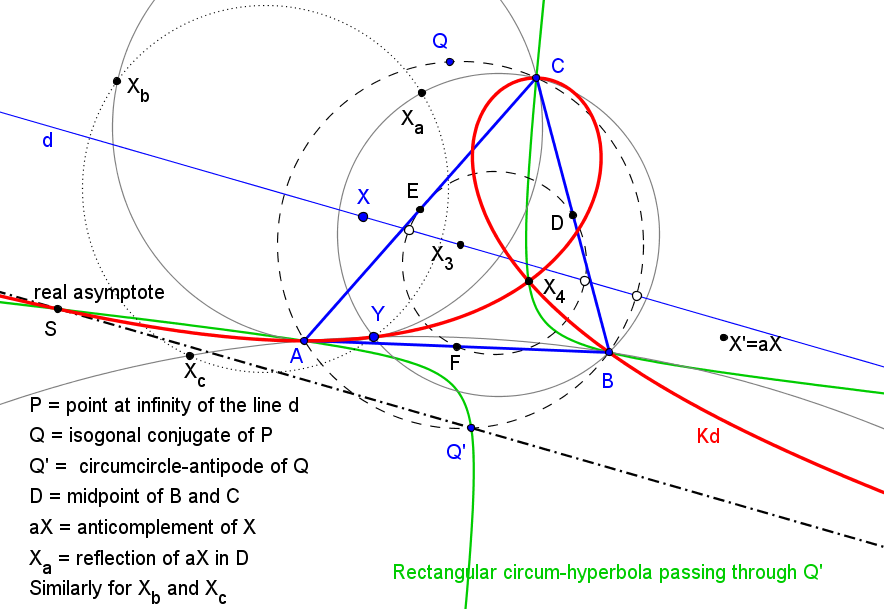
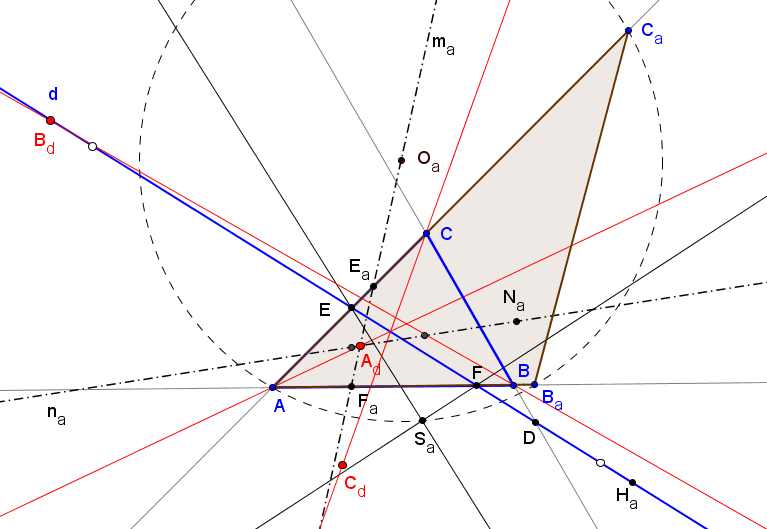
Dado un triángulo ABC y una recta d.
Se consideran los triángulos ABaCa, con Ba en AB, Ca en AC y el ortocentro Ha sobre la recta d.
1.1. El circuncentro Oa de ABaCa recorre la mediatriz ma de ASa. donde Sa es el punto "Anti-Steiner" (denominado así por Darij Grinberg en "Anti-Steiner point with respect to a triangle") de la recta d respecto al triángulo ABaCa.
1.2. El centro de la circunferencia de los nueve puntos Na de ABaCa recorre una recta na.
El punto Sa (en la circunferencia es circunscrita a ABaCa) es la intersección de las refleciones de d en AB y AC.
Dos puntos particulares de la recta na son los puntos medios de EFa y FEa, siendo E y F las intersecciones de d con los lados AB y AC, respectivamente; y Ea y Fa las intersecciones de ma con los lados AB y AC, respectivamente.
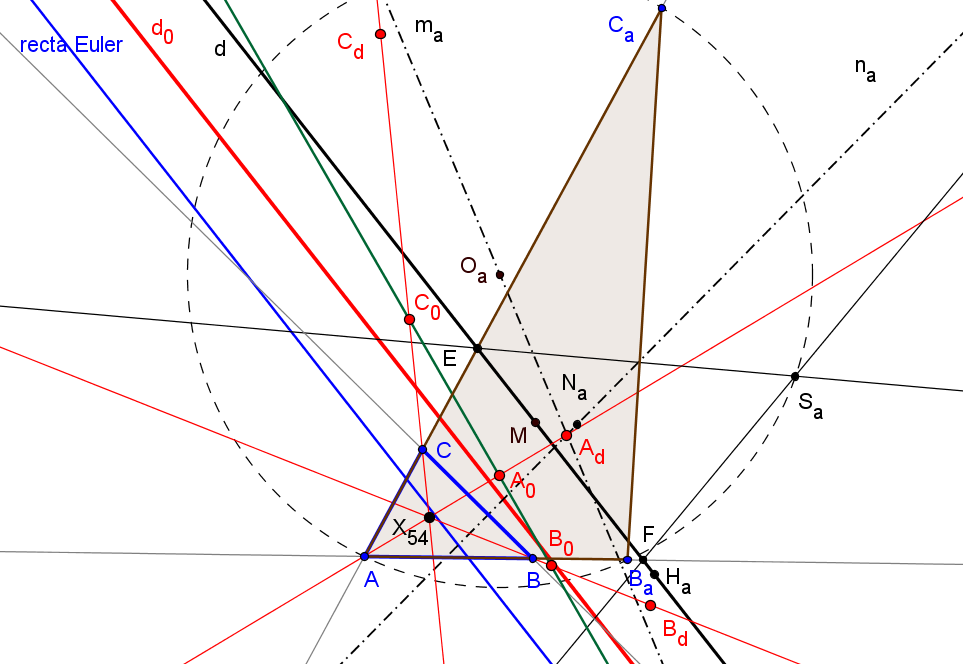
Cuando la recta d es paralela a la recta de Euler de ABC, las rectas AAd, BBd, CCd concurren en el punto de Kosnita, X54.
Existe una única recta d0, paralela a la recta de Euler, para la cual los puntos A0, B0 y C0 están alineados.
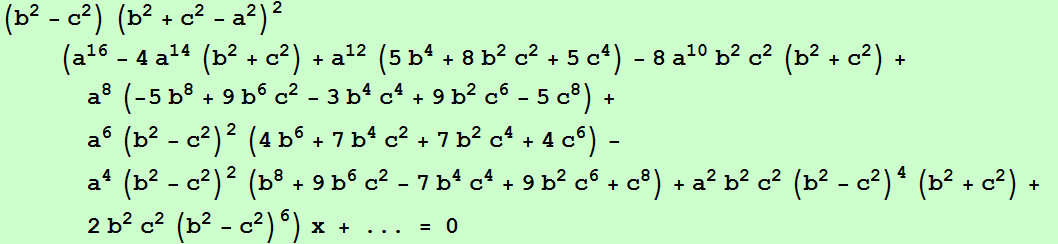
Dado un triángulo ABC, su recta de Euler corta a los lados BC, CA, AB en los puntos D, E, F, respectivamente. La circunferencia de centro en F y que pasa por A vuelve a cortar a AC en Ab. La circunferencia de centro en E y que pasa por A vuelve a cortar a AB en Ac. La recta AbAc (que pasa por el ortocentro) corta a BC en Aa.
Similarmente, se definen los puntos Ba, Bb, Bc, Ca, Cb, Cc.
Los puntos Aa, Bb y Cc están en la recta que corta a la circunferencia de Euler en los centros de las hipérbolas rectangulares de Jerabek y circunscrita que pasa por el centro X93.
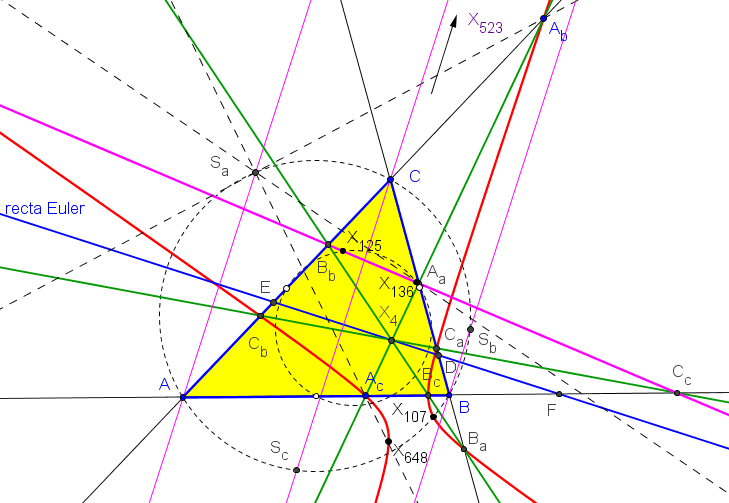
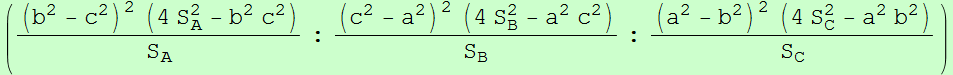
Los seis puntos Ab, Ac, Ba, Bc, Ca y Cb están en una hipérbola que pasa por X107 (en la circunferencia circunscrita), X648 (tripolo de la recta de Euler).
Las rectas ASa, BSb, CSc son parelelas, con punto del infinito X523, conjugado isogonal del foco de la parábola de Kiepert.
Sean ABC un triángulo, P un punto y A'B'C' su triángulo ceviano.
Conideremos los siguentes puntos: Ma el punto medio de AH, M'a el punto medio de A'H, y M1 el punto medio de MaM'a. Similarmente, se definen M2 y M3.
Denotamos por:
Ra el eje radical de las circunferencias M2(M2B') y M3(M3C').
Rb el eje radical de las circunferencias M3(M3C') y M1(M1A').
Rc el eje radical de las circunferencias M1(M1A') y M2(M2B').
Las paralelas La, Lb, Lc a Ra, Rb, Rc a través de A, B, C, respectivamente, son concurrentes si y sólo si P está en la cúbica de Lucas. El punto de concurrencia Q queda sobre la cúbica de Darboux.
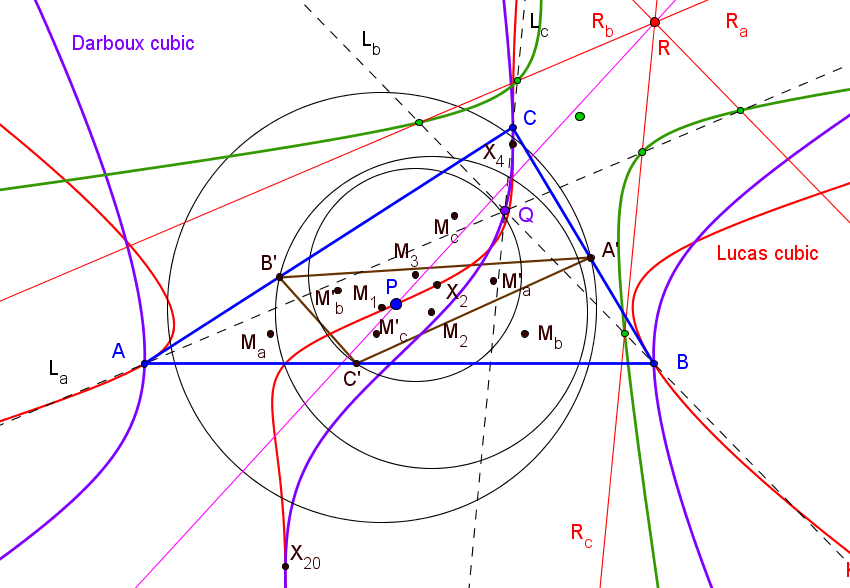
Los puntos P, Q y R están alineados si y sólo si P está en una curva algebraica de grado diez, que pasa por A, B, C, X2, X4, X20, los puntos medios de los lados (donde es tangente a los lados), pies de las cevianas de X69 y por los puntos del infinto de los lados.
Si P es el baricentro, Q es el ortocentro, y R es X3830, que divide al segmento X2X4 en la razón 3:-1.
Los puntos La∩Rb, La∩Rc, Lb∩Rc, Lb∩Ra, Lc∩Ra, Lc∩Rb quedan sobre una misma cónica de centro el punto medio de Q y R.
Construcción de un triángulo conocidas las rectas determinadas por dos de sus lados y la recta que pasa por el incentro y el ortocentro.
Del triángulo ABC a determinar, admitamos que el vértice A sea el punto de intersección de las dos rectas lb y lc dadas, que coinciden con lados del triángulo. El incentro I de ABC ha de estar en una de las dos bisectrices de tales rectas y sobre la recta r dada, que ha de contener también al ortocentro H.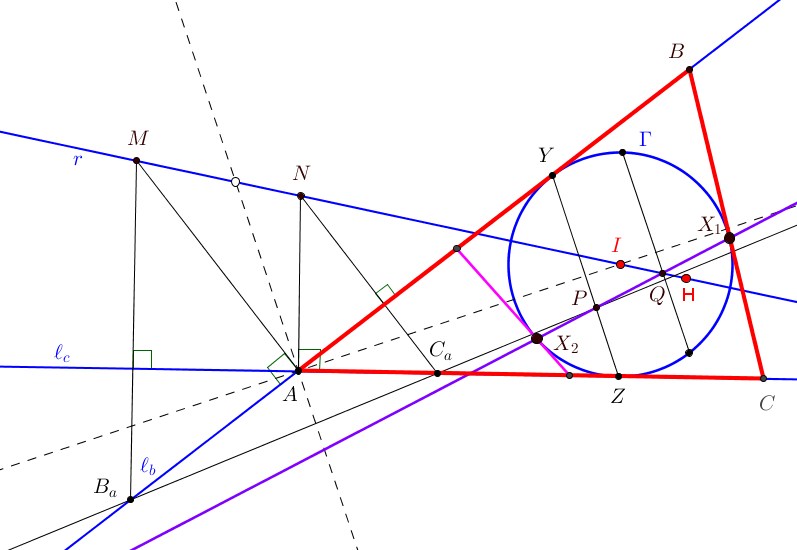
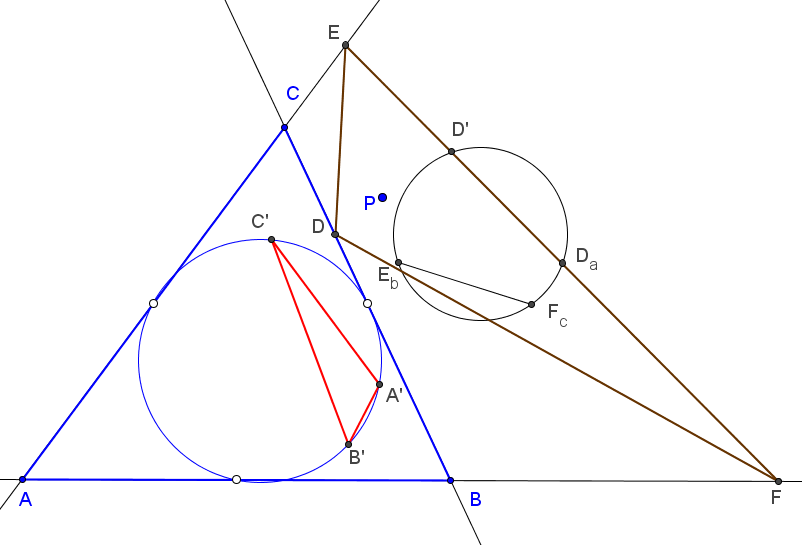
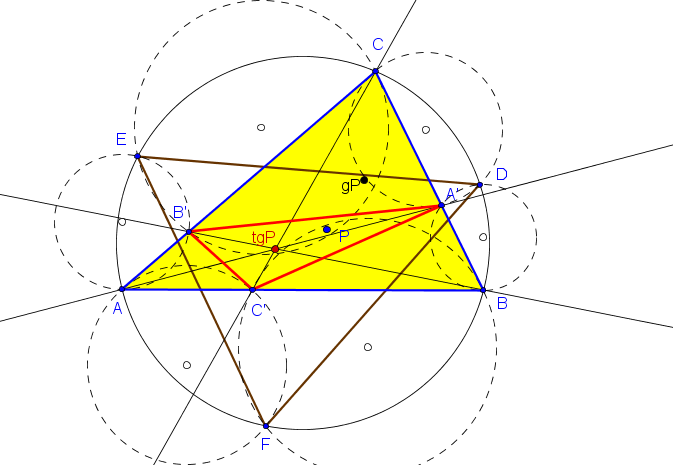
Sean ABC un triángulo, P un punto y DEF su triángulo circunceviano. Denotamos por (Ab) la circunferencia que pasa por D y es tangente a AB en B, y por (Ac) la circunferencia que pasa por D y es tangente a AC en C.
Sea A' el otro punto de intersección de estas circunferencias (está sobre BC).
Similarmente, se definen los puntos B' y C'.
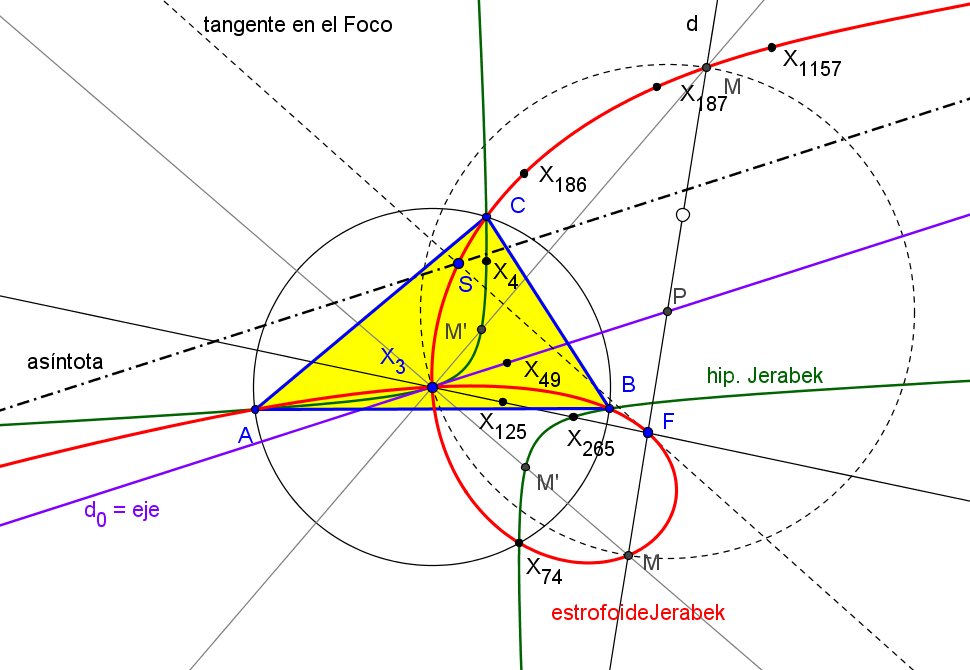
(ver Estrofoide de Jerabek)
A'B'C' es el triángulo ceviano de tgP, conjugado isotómico del conjugado isogonal de P.
Sean ABC un triángulo y P un punto. El triángulo circunceviano de P es perspectivo con el triángulo ceviano del conjugado isotómico del conjugado isogonal de P si y solo si P está en la recta de Euler.
El perspector P' también está en al recta de Euler y la correspondencia P ↦ P' es una proyectividad, con puntos dobles los de intersección de la recta de Euler con la circunferencia circunscrita.
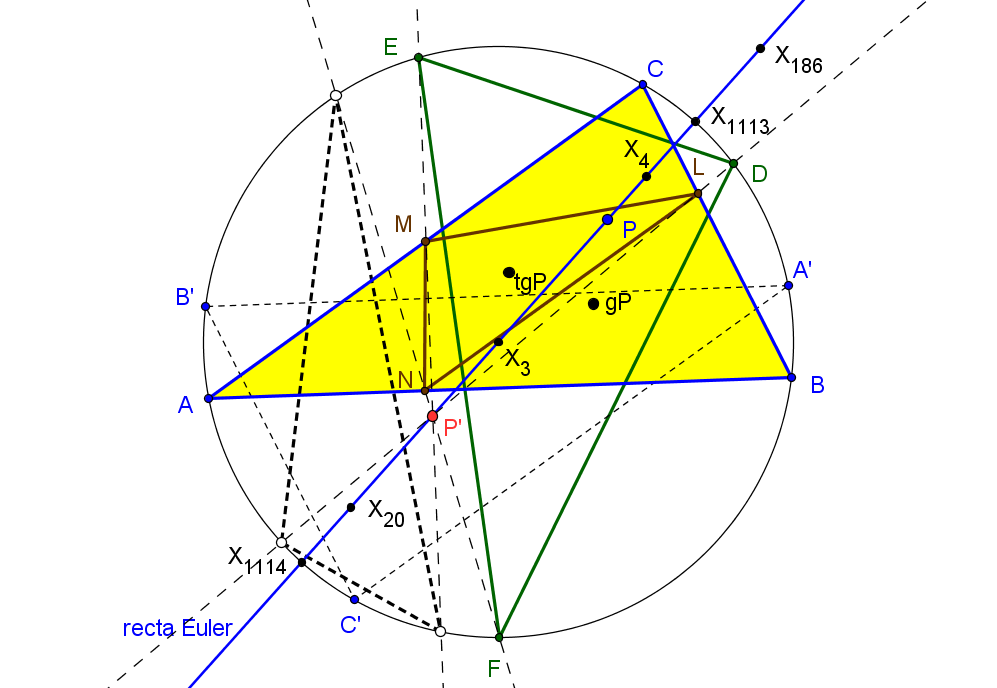
D(-a^2vw : v(c^2v+b^2w) : w(c^2v + b^2w)), E(u(c^2u+a^2w) : -b^2uw : w(c^2u+a^2w)), F(u(b^2u+a^2v) : v(b^2u+a^2v) : -c^2uv).
Y las coordenadas de los vértices del triángulo ceviano de tgP:L(0 : c^2v : b^2w), M(c^2u : 0 : a^2w), N(b^2u : a^2v : 0).
Los triángulos DEF y LMN son perspectivos si y sólo siP' (2b^2c^2SAu^2 + a^2(b^2c^2+a^2(SA-a^2))vw + b^2(b^2c^2+a^2(SA-b^2))wu + c^2(b^2c^2+a^2(SA-c^2))uv : ... : ...)

Cuando P varía en al recta de Euler, las rectas DL, EM, DN pasan por puntos fijos (sobre la circunferencia circunscrita) que son los vértices del triángulo circunceviano del punto de De Longchamps, respecto al triángulo A'B'C', antipodal de ABC.
Sean ABC un triángulo, P un punto y DEF su triángulo circunceviano. Denotamos por Ab el centro de la circunferencia que pasa por D y es tangente a AB en B, y por Ac el centro de la circunferencia que pasa por D y es tangente a AC en C.
Similarmente, se definen los puntos Bc, Ba y Ca, Cb.
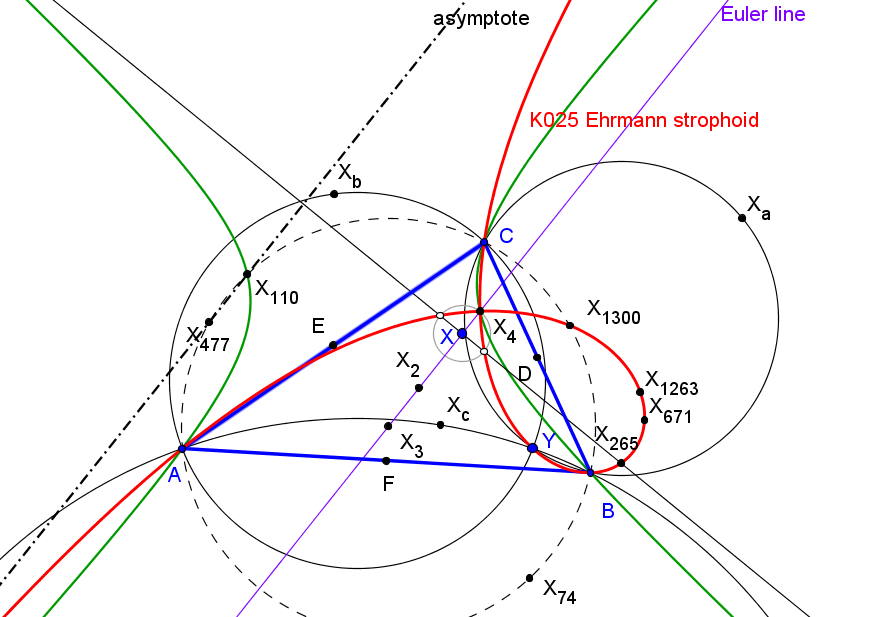
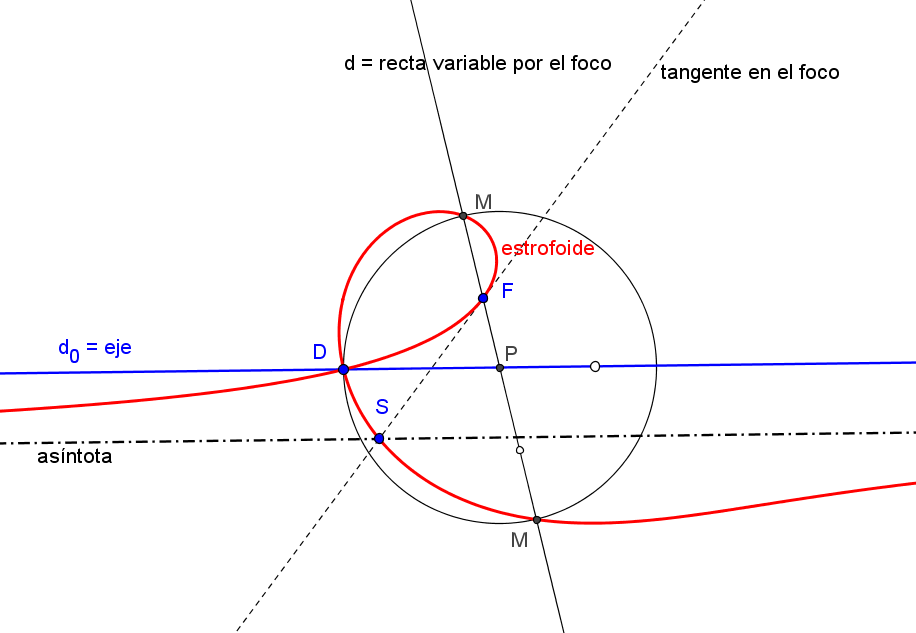
Las rectas AbAc, BcBa y CaCb no son concurrentes y el triángulo A'B'C' delimitado por ellas es perspectivo con ABC si y solo si P queda en la estrofoide de Jerabek (K039).
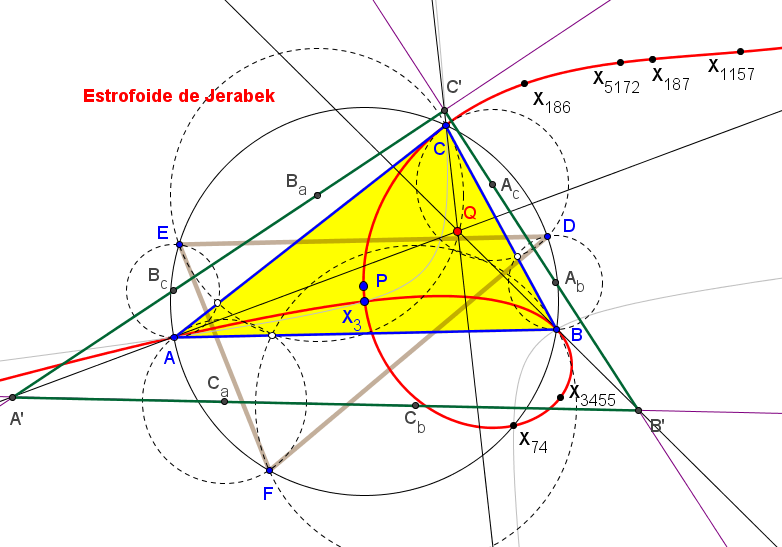
Las rectas AbAc, BcBa y CaCb son concurrentes si y solo si P queda en una séxtica con puntos dobles en los vértices de ABC
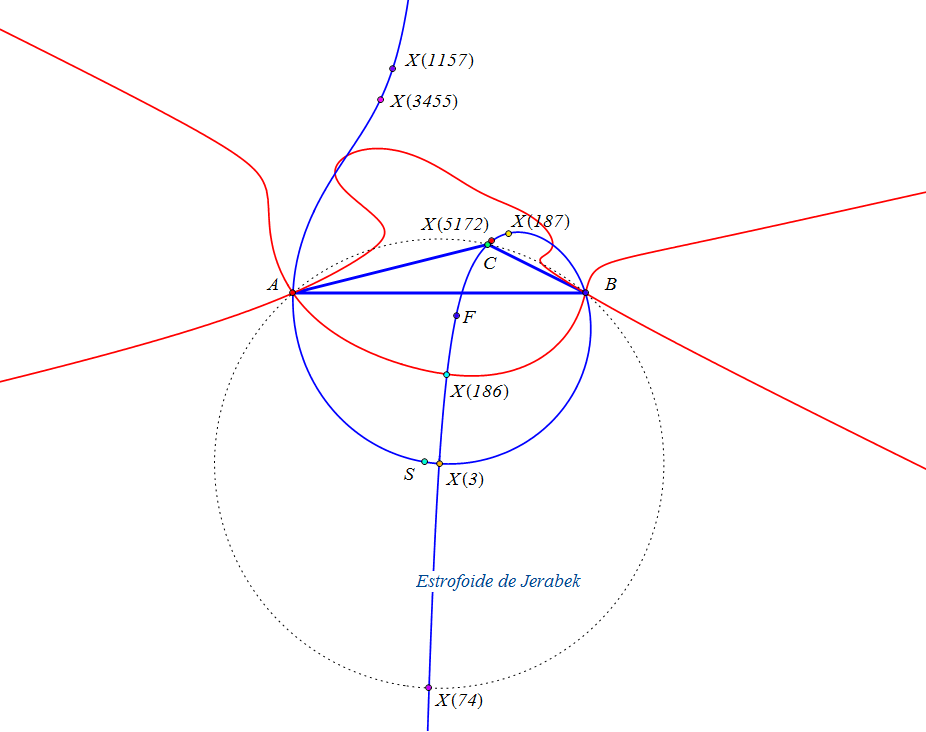
Los triángulos ABC y A'B'C' son ortológicos si y solo si P está sobre la estrofoide de Jerabek. En este caso, el centro de ortología de ABC respecto a A'B'C' describe la estrofoide de Ehrmann (K025).
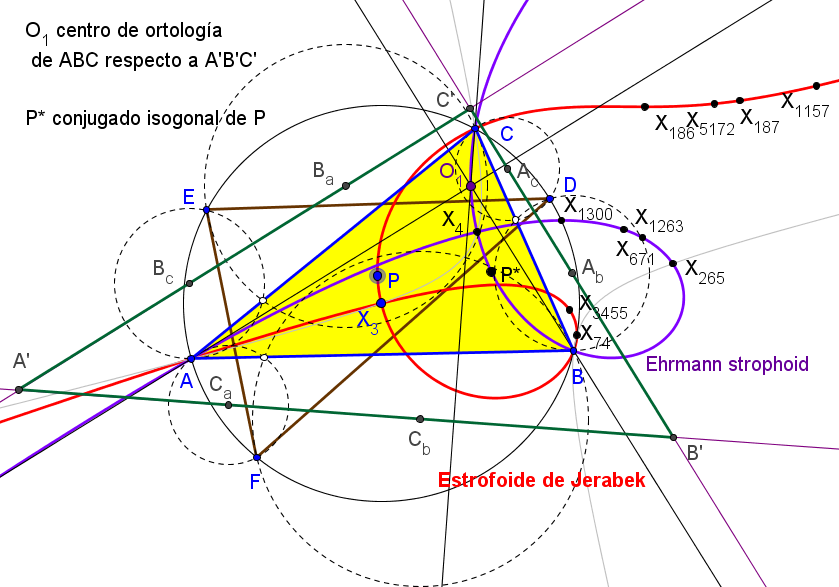
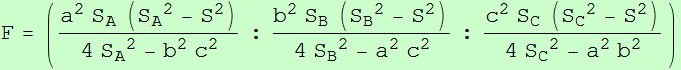
Sean ABC un triángulo, P un punto y A'B'C' su triángulo circunceviano.
Denotamos:
Ab el centro de la circunferencia pasando por C' y tangente a AB en B,
Ac el centro de la circunferencia pasando por B' y tangente a AC en C.
Similarmente se definen los puntos Bc,Ba y Ca,Cb.
Sean además
Ma, Mb, Mc los puntos medios de los segmentos AbAc, BcBa, CaCb.
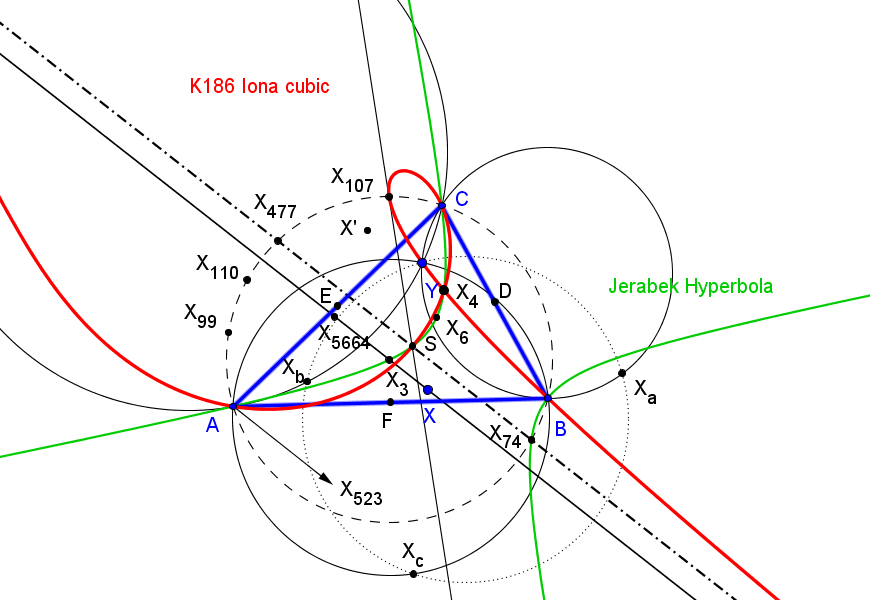
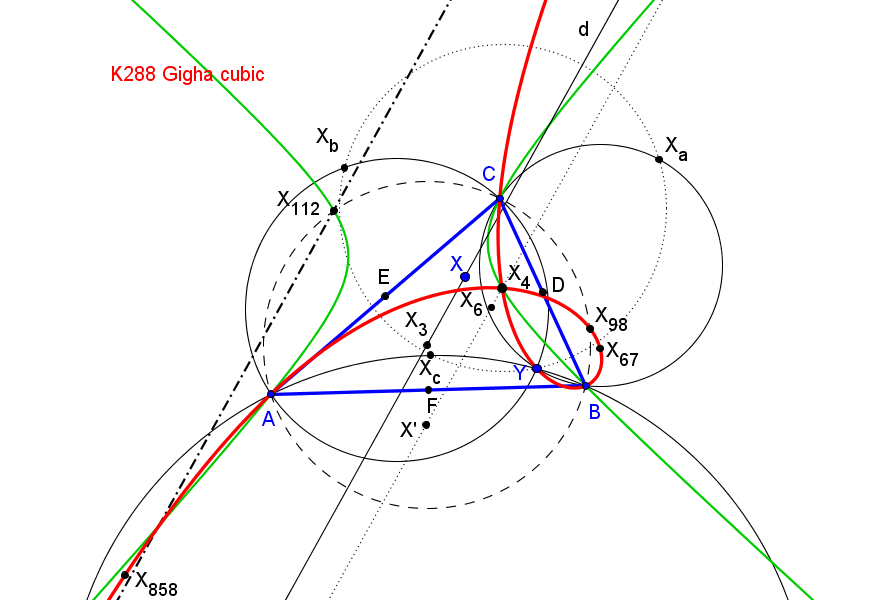
• El lugar geométrico de los puntos P tales que el triángulo delimitado por las rectas AbAc, BcBa, CaCb es nodegenerado y perspectivo con ABC es la cúbica de Neuberg, K001 = pK(X6, X30),
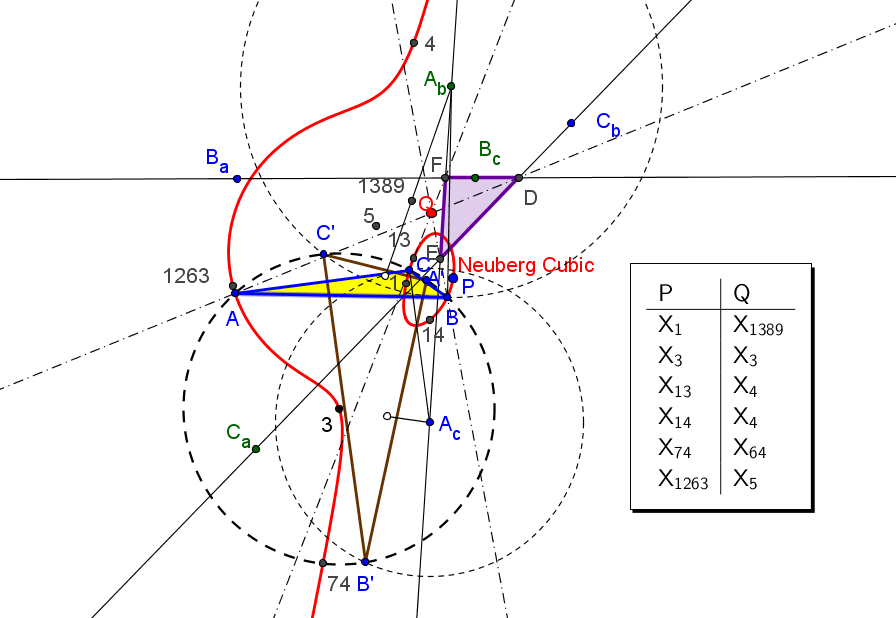
• El lugar geométrico de los puntos P tales que las rectas AbAc, BcBa, CaCb son concurrentes es una séxtica con puntos dobles en los vértices de ABC, pasa por los centros X2, X3 y X1139 y por los puntos, Oa, Ob, Oc, donde las cevianas del circuncentro vuelven a corta a al cúbica de Neuberg.
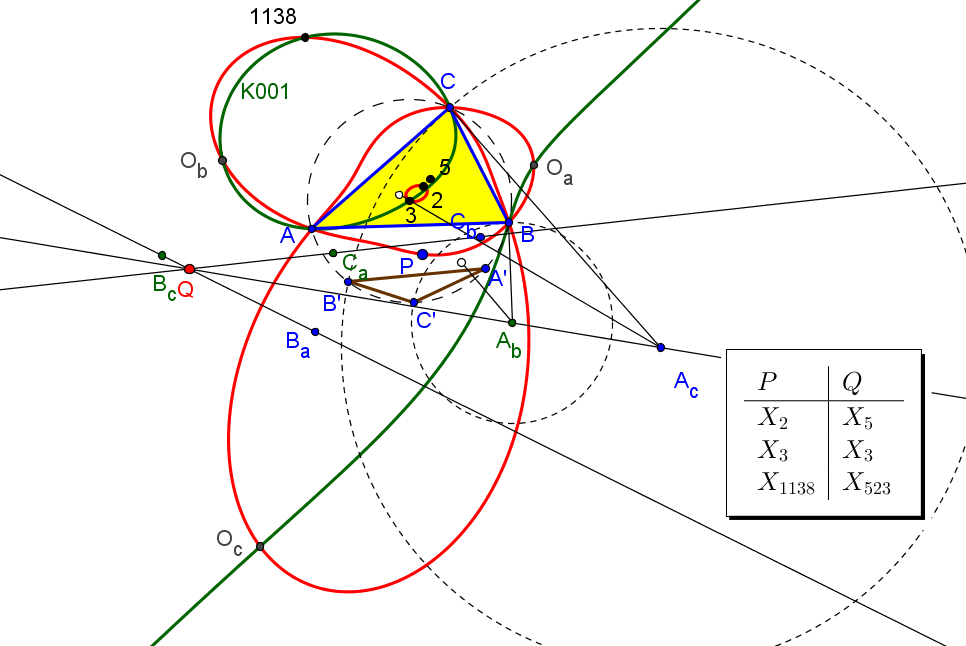
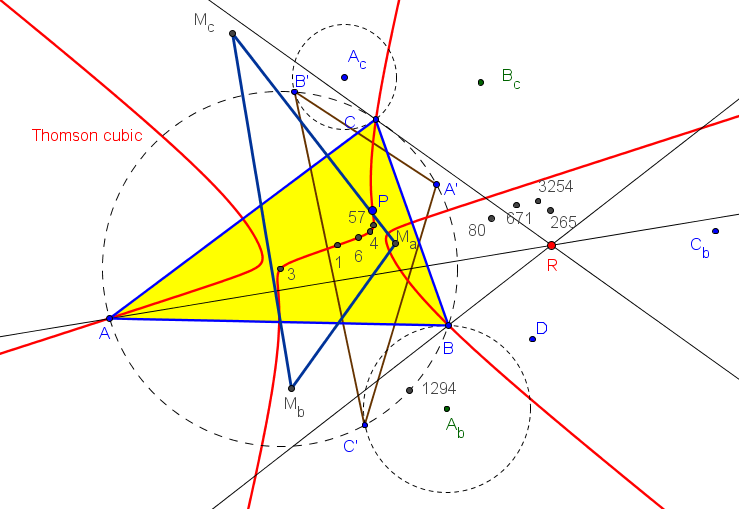
• El lugar geométrico de los puntos P tales que los triángulos ABC y MaMbMc son ortológicos es es la cúbica de Thomson, K002 = pK(X6, X2),
Si P recorre la cúbica de Thomson, el centro ortológico Q de MaMbMc con respecto a ABC recorre la cúbica imagen de la cúbica de Darboux mediente la homotecia de centro el circuncentro y razón 1/2.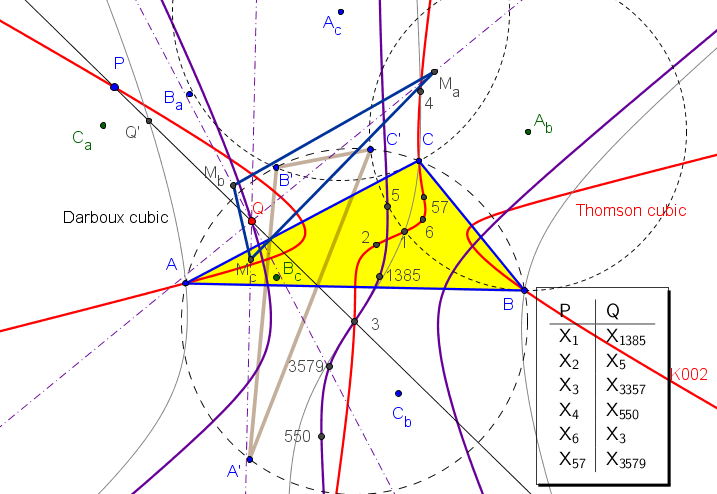
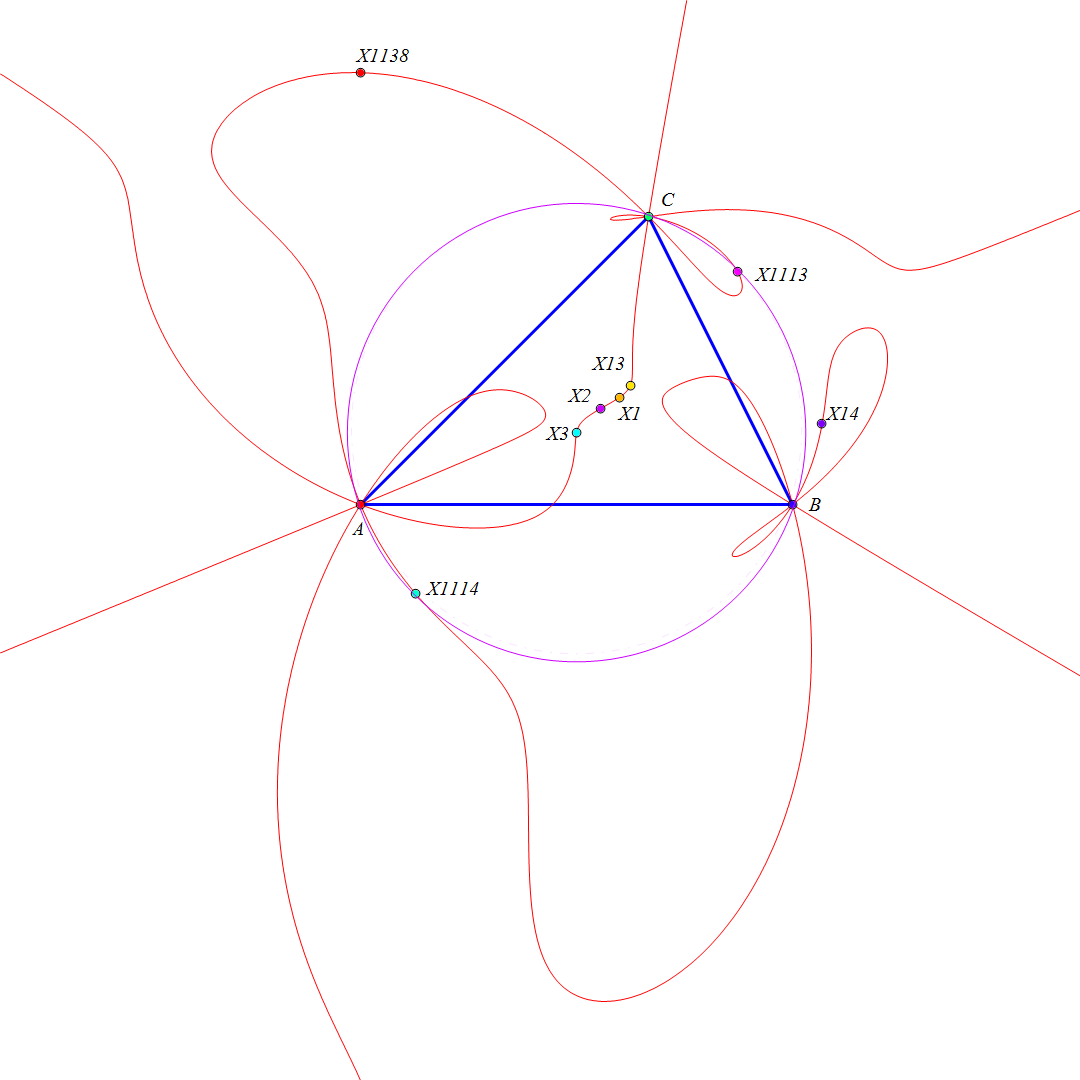
• El lugar geométrico de los puntos P tales que las mediatrices de los segmentos AbAc, BcBa, CaCb son concurrentes es una nónica con puntos cuadruples en los vértices de ABC, pasa por los centros X1, X2, X3, X13, X14, X1113, X1114, y X1138 y por los pies de las cevianas del circuncentro.
Sean ABC un triángulo, da, db, dc
tres rectas paralelas a través de A, B, C, respectivamente, y
d'a, d'b, d'c las reflexiones de
da, db, dc en BC, CA, AB,
respectivamente.
Si las recta da, db, dc son paralelas a la
recta de Euler de ABC, las rectas d'a, d'b,
d'c concurren en X399 (punto de reflexión de Parry)
El eje radical de las circunferencias circunscrita y de Euler de A'B'C' pasa por un punto fijo Y, cuando las rectas da, db, dc giran alrededor de A, B, C, permaneciendo paralelas.
Y = (a^10(b^2+c^2)
-a^8(3b^4+4b^2c^2+3c^4)
+a^6(2b^6+5b^4c^2+5b^2c^4+2c^6)
+2a^4(b^8-3b^6c^2+b^4c^4-3b^2c^6+c^8)
-a^2(b^2-c^2)^2(3b^6-4b^4c^2-4b^2c^4+3c^6)
+(b^2-c^2)^6: ... : ...)
• Sean ABC un triángulo, I su incentro y P un punto. La perpendicular por P a AI corta a AB y AC en Ab y Ac, respectivamente. Se denota por r1 el eje radical de las circunferencias circunscritas a los triángulos ABC y AAbAc.
Los ejes radicales r2 y r3 se definen de forma cíclica.
El lugar geométrico de los puntos P tales que el triángulo ABC es perspectivo con el triángulo A'B'C', delimitado por los ejes radicales r1, r2 y r3, está formado por la hipérbola equilátera que pasa por el incentro (hipérbola de Feuerbach) y por la cúbica circunscrita a ABC de ecuación baricéntrica:
x (c (a - b) (a - b + c) y^2 + b (a - c) (a + b - c) z^2) +
y (a (b - c) (a + b - c) z^2 + c (b - a) (-a + b + c) x^2) +
z (b (c - a) (-a + b + c) x^2 + a (c - b) (a - b + c) y^2 ) - 2 a b c x y z = 0.
El lugar geométrico de los puntos P tales que el triángulo ABC es perspectivo con el triángulo A'B'C', delimitado por los ejes radicales r1, r2 y r3, está formado por la circunferencia circunscrita a ABC y por la cúbica de Darboux K004
Cuando P se mueve sobre la circunferencia circunscrita los ejes radicales r1, r2 y r3 son concurrentes en un punto Q,
que describe la isocúbica no pivotal nK(X(577),X(394),X(3))=cK(#X(3),X(394)) (conico-pivotal isocubic, Jean-Pierre Ehrmann and Bernard Gibert.- Special Isocubics in the Triangle Plane, §8), que tiene al circuncentro como punto aislado y pasa por X878 (que corresponde a P=X98, punto de Tarry).
La "cónica de contacto" de cK(#X(3),X(394)) es la cónica circunscrita de Johnson.
(Otros ejemplos de "conico-pivotal isocubics" )

Dado un triángulo ABC, el lugar geométrico de los puntos P para los cuales su triángulo pedal tiene la misma área que el triángulo órtico es la circunferencia de centro el circuncentro y que pasa por el ortocentro.
Las coordenadas baricentricas de los vértices del triángulo pedal de un punto P=(x:y:z) son: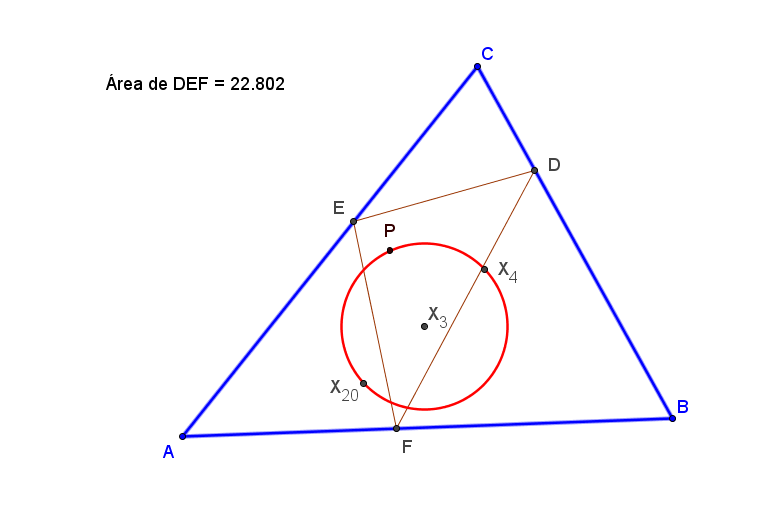
Sean ABC un triángulo y L un punto variable sobre la paralela a BC por A. El lugar geométrico de los ortocentros de los triángulos LBC es una parábola; denotamos por ta la tangente en su vértice. Similarmente y de forma cíclica se consideran la tangentes tb y tc.
El cento de homotecia de los triángulos ABC y el delimitado por ta, tb y tc es el X32.
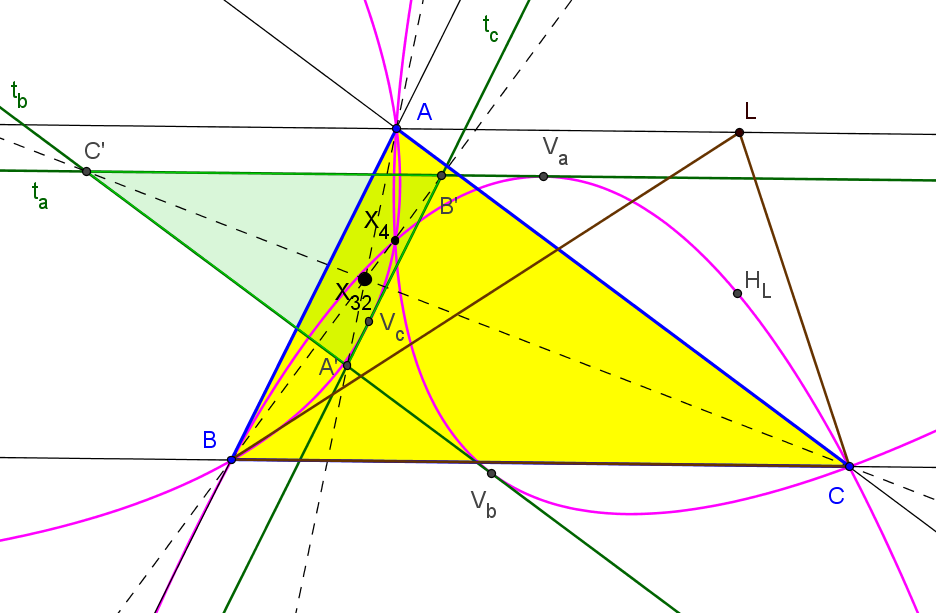
• El centro de homotecia de los triángulos ABC y el delimitado por las directrices de las tres parábolas ℘a, ℘b y ℘c tiene coordenadas baricentricas:
(a^4+S^2 : b^4+S^2 : c^4+S^2)
con número de búsqueda en ETC: 0.64658408249618255603004536878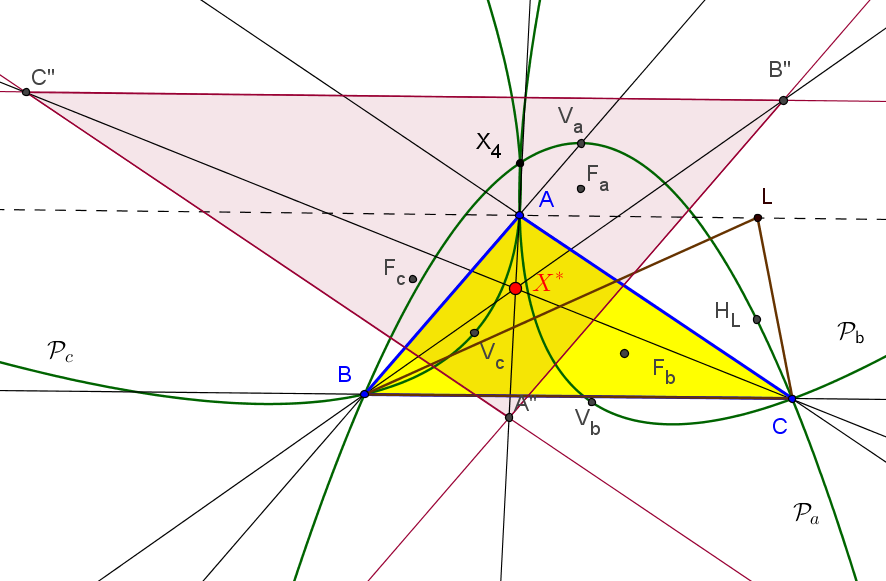
• El centro de homotecia de los triángulos ABC y el delimitado por las perpendiculares por los focos a los ejes de las tres parábolas ℘a, ℘b y ℘c tiene coordenadas baricentricas:
(a^4-S^2 : b^4-S^2 : c^4-S^2)
con número de búsqueda en ETC: -0.2507364947244949174662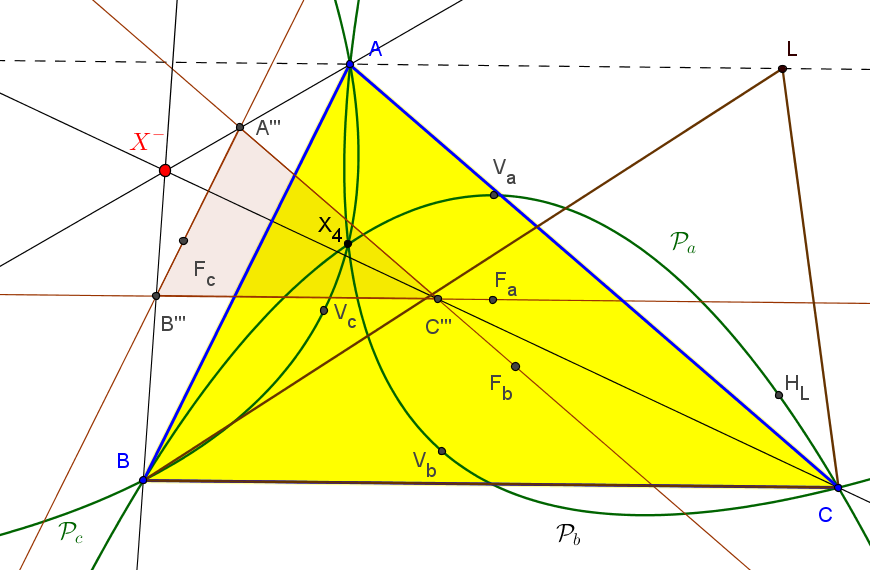
(SASBSC + 2(b^2SB^2+c^2 SC^2) : SASBSC + 2(c^2SC^2+a^2SA^2 ) : SASBSC + 2(a^2SA^2+b^2SB^2)),
con número de búsqueda en ETC: 1.8894135371622742397888827245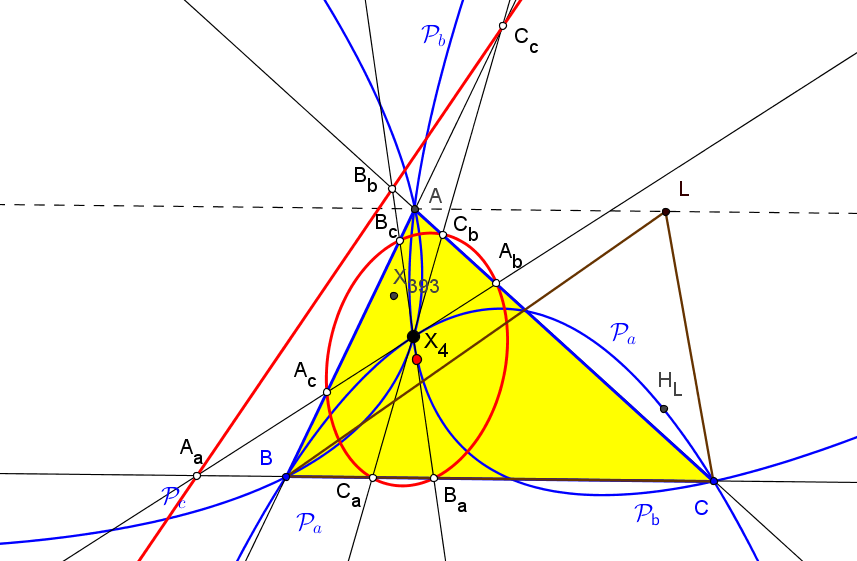
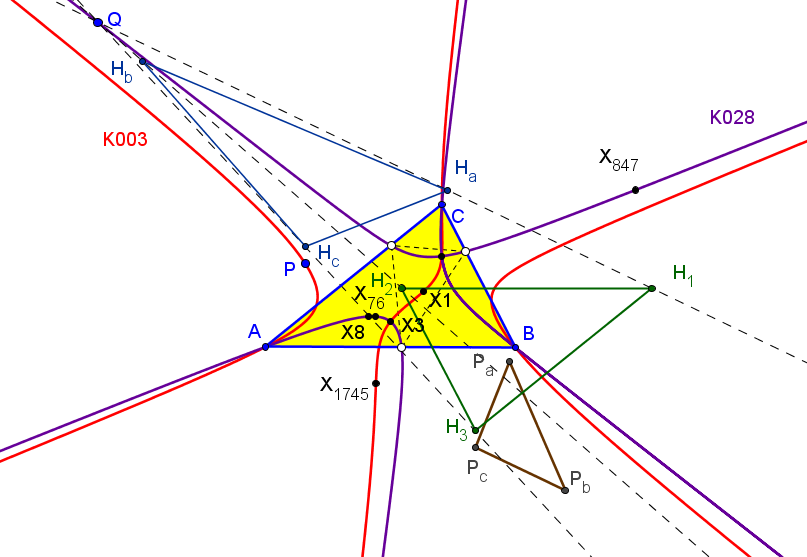
Sean ABC un triángulo, P un punto y A'B'C' el triángulo antipedal de P. El lugar geométrico de los puntos P tales que P, el conjugado isogonal de P respecto a ABC y el conjugado isogonal de P respecto a A'B'C' están alineados es cúbica de McKay, K003 = pK(X6, X3).
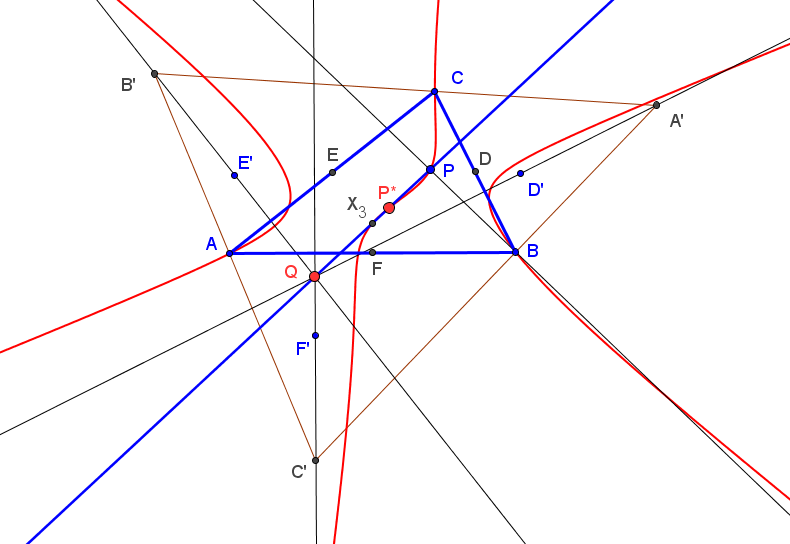
Sean ABC un triángulo, P un punto, A1 y A2 los centros de semejanza interno y externo de las circunferencias con centro en B y C que pasan por P. Similarmente, y de forma cíclica, se definen los puntos B1, B2, C1, A2. Entonces, las rectas AA1, BB2 y CC1 concurren en un punto Q, cuya polar trilineal pasa por A2, B2 y C2.
Esta construcción de los puntos A1 y A2 conincide con la generalización dada por Peter Moses en ETC, ya que PA1 es la bisectriz del ángulo ∠BPC:
"Let ABC be a triangle and P a point. Let D be the point on side BC such that ∠BPD = ∠DPC), and likewise for point E on side CA and point F on side AB. If P = (p : q : r) (trilinears), then the lines AD, BE, CF concur in the point K(P) = f(p,q,r,A) : f(q,r,p,B) : f(r,p,q,C), where f(p,q,r,A) = (q^2 + r^2 + 2qr cos A)-1/2. Moreover, if P* is the inverse of P in the circumcircle, then K(P*) = K(P). [Peter Moses, Feb. 1, 2010, based on Seiichi Kirikami's construction of X(174)]"
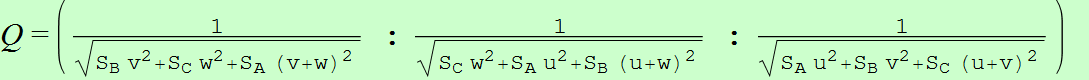
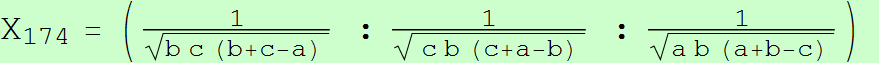
Sean ABC un triángulo y A'B'C' el triángulo medial.
Adoptamos las siguientes notaciones:
Ab y Ac los circuncentros de los triángulos AGB' y AGC', resp.
Bc y Ba los circuncentros de los triángulos BGC' y BGA', resp.
Ca y Cb los circuncentros de los triángulos CGA' y CGB', resp.
Ma, Mb y Mc los puntos medios de AbAc, BcBa, CaCb, resp.
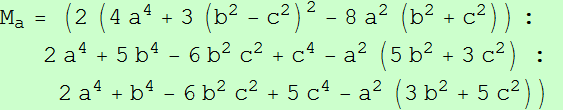
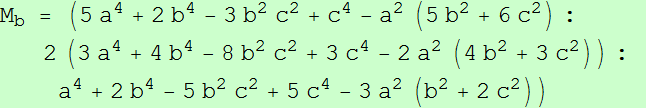
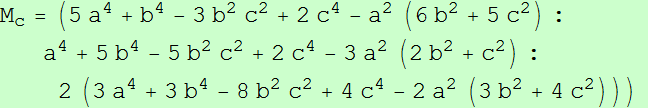
Los triángulos ABC y MaMbMc son ortológicos.
El centro de ortología de MaMbMc con respecto a ABC es el centro de la circunferencia de los nueve puntos, X5.
El centro de ortología de ABC con respecto a MaMbMc es:
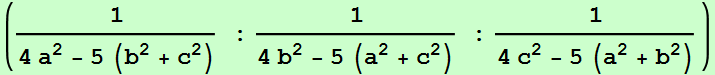
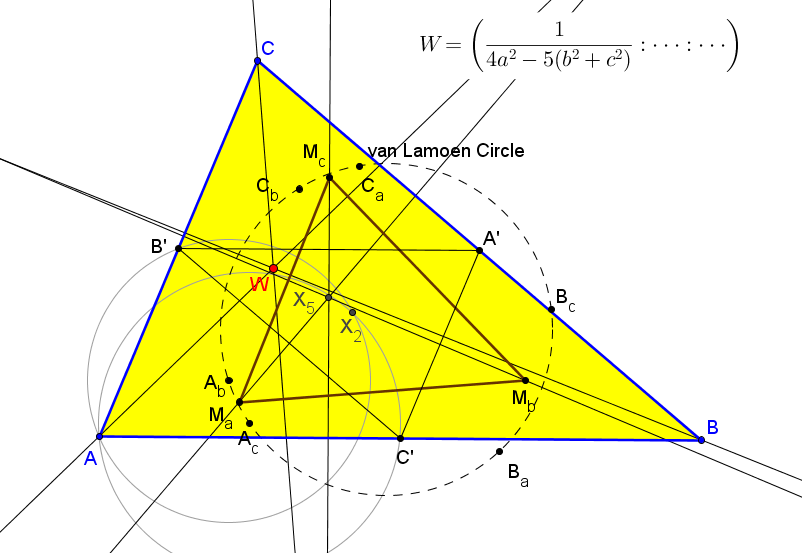
Sean M1, M2 y M3 los simétricos de Ma, Mb y Mc respecto a las medianas AA', BB' y CC'. Los triángulos ABC y M1M2M3 son ortológicos
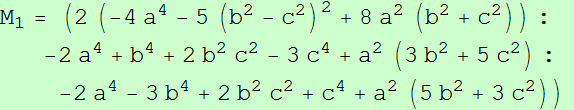
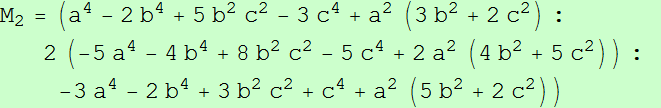
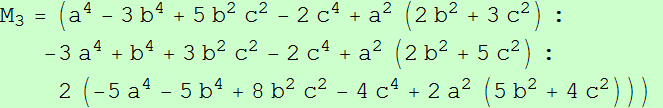
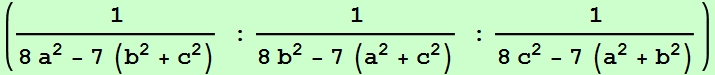
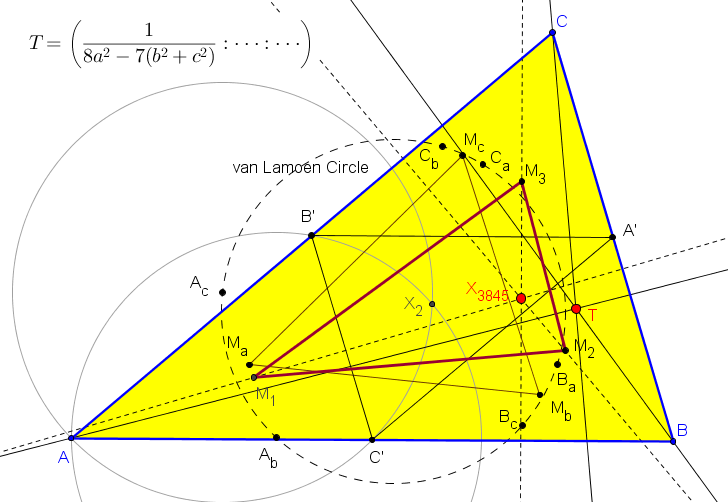
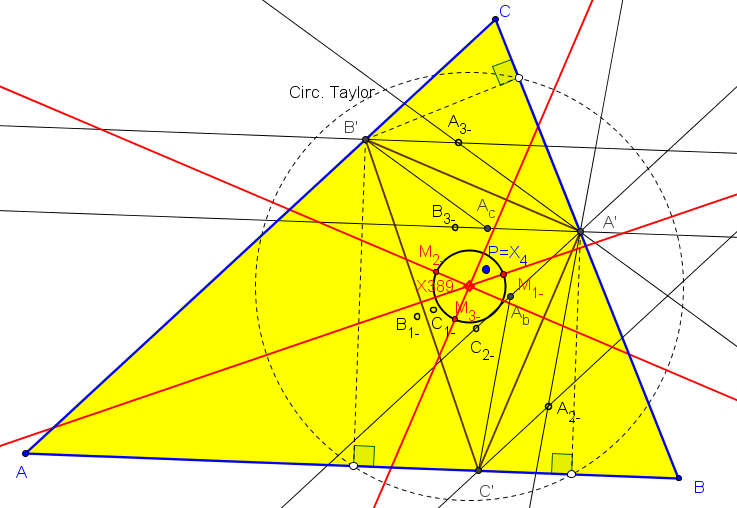
Sean ABC un triángulo, P un punto y A'B'C' el triángulo pedal de P.
Adoptamos las siguientes notaciones:
Ab y Ac son las proyecciones ortogonales de A' sobre PB' y PC', respectivamente.
A3+ es la intersección de la paralela por B' a AC con la paralela por Ac a A'B'.
A3- es la intersección de la paralela por B' a AC con la paralela por A' a B'Ac.
Es decir, la circunferencia de centro en B' y radio A'Ac interseca a la paralela por B' a A'Ac en los dos puntos A3+ y A3-.
A2+ es la intersección de la paralela por C' a AB con la paralela por Ab a A'C'.
A2- es la intersección de la paralela por C' a A'B con la paralela por A' a C'Ab.
M1+ y M1- son los puntos medios de A2+A3+ y A2-A3-, respectivamente.
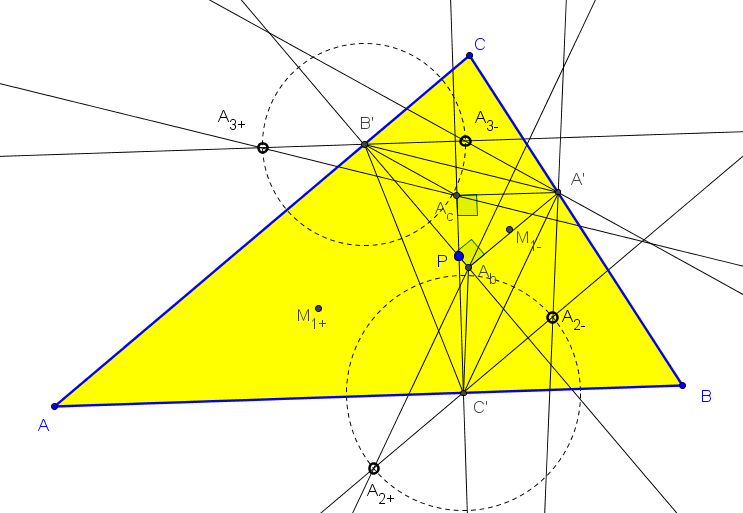
1. El lugar geométrico de los puntos P tales que las mediatrices de los segmentos A2+A3+, B3+B1+, C1+C2+ son concurrentes es una quártica circunscrita a ABC.
a^2(a^6(b^2+c^2) - 3a^4(b^4+c^4) + a^2(3b^6+b^4c^2+b^2c^4+3c^6) - (b^2-c^2)^2(b^4+4b^2c^2+c^4)),
con número de búsqueda en ETC: -1.913504596254703237175078062. El lugar geométrico de los puntos P tales que las mediatrices de los segmentos A2-A3-, B3-B1-, C1-C2- son concurrentes es una quártica circunscrita a ABC.
3. El lugar geométrico de los puntos P tales que los triángulos ABC y M1+M2+M3+ son perspectivos es una cúbica circunscrita a ABC.
Estos triángulos son ortológicos si solo si P está sobre la recta de Euler.
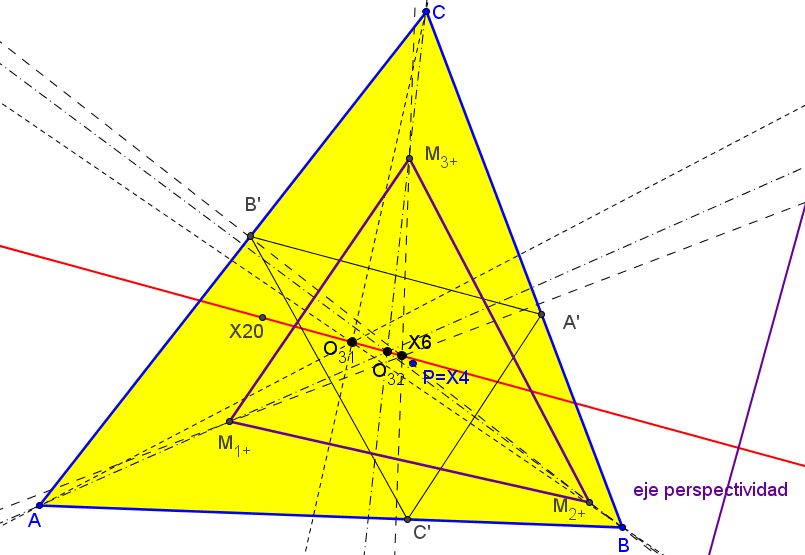
O31 = ( SA/(a^4 - 2a^2(b^2+c^2) + b^4+6b^2c^2+c^4) : ... : ...),
con número de búsqueda en ETC: 10.2893367499920063626210307O32 = ( 2a^10 - a^8(b^2+c^2) - 8a^6(b^4-b^2c^2+c^4) + 10a^4(b^2-c^2)^2(b^2+c^2) - 2a^2(b^4-c^4)^2 - (b^2-c^2)^4(b^2+c^2): ... : ...),
con número de búsqueda en ETC: 7.3799576190510080677803629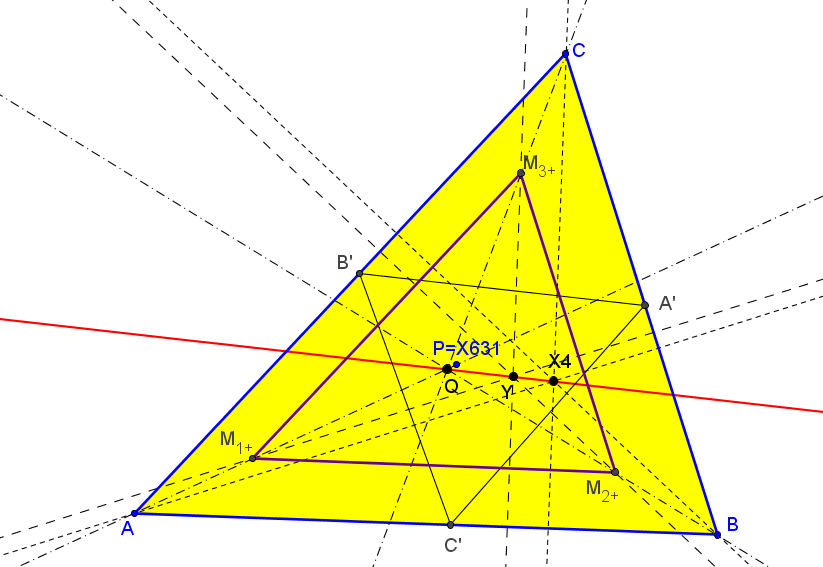
Q = ( a^2(a^4 - 2a^2(b^2+c^2) + b^4+6b^2c^2+c^4 ) : ... : ...),
con número de búsqueda en ETC: 3.08200205691896287503357243Y = ( 2a^10 - 5a^8(b^2+c^2) + 4a^6(b^2-c^2)^2 - 2a^4(b^6+7b^4c^2+7b^2c^4+c^6) + 2a^2(b^2-c^2)^2(b^4+14b^2c^2+c^4) - (b^2-c^2)^4(b^2+c^2): ... : ...),
con número de búsqueda en ETC:-1.5600580790622942195564665
4. El lugar geométrico de los puntos P tales que los triángulos ABC y M1-M2-M3- son perspectivos es una cúbica circunscrita a ABC.
Estos triángulos son ortológicos si solo si P está sobre la recta de Euler.
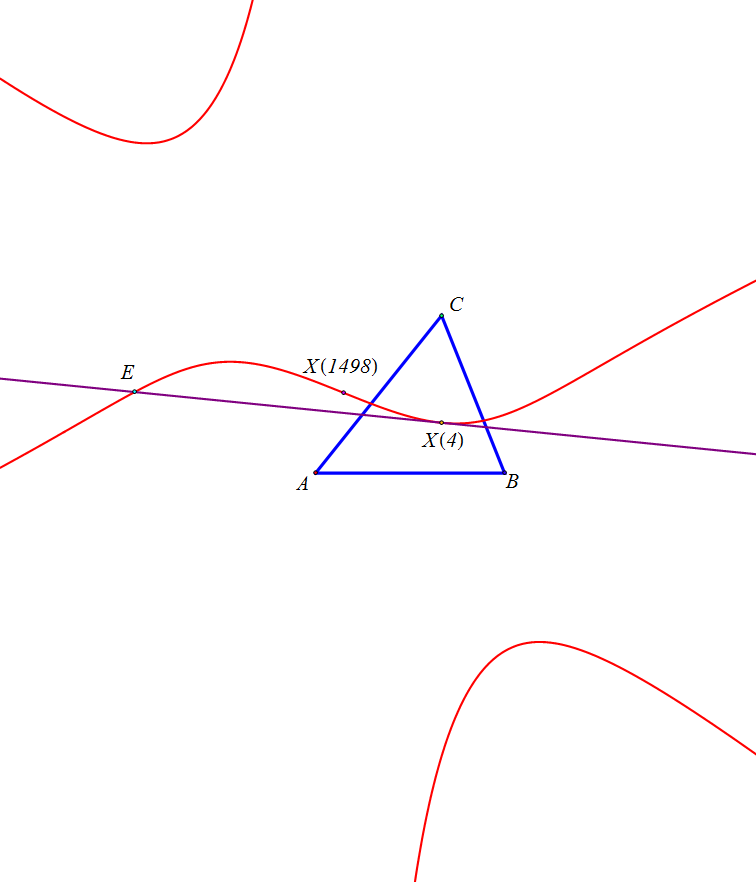
E = ( a^2(a^8 - 2a^6(b^2+c^2) - 12a^4b^2c^2+ 2a^2(b^2+c^2)^3 - (b^2-c^2)^2(b^4-6b^2c^2+c^4)): ... : ...),
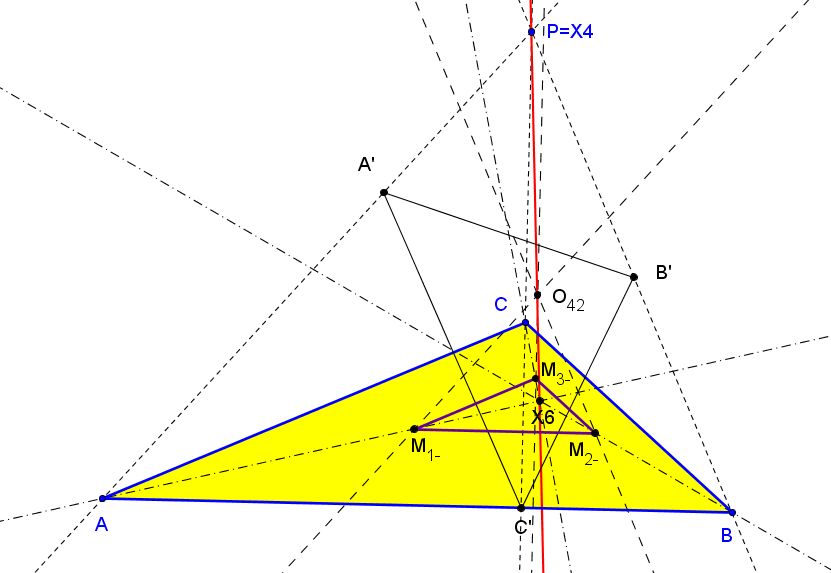
O42 = ( 2a^10 - 5a^8(b^2+c^2) + 4a^6(b^2+c^2)^2 - 2a^4(b^2-c^2)^2(b^2+c^2) + 2a^2(b^2-c^2)^4- (b^2-c^2)^4(b^2+c^2): ... : ...),
con número de búsqueda en ETC:-1.34146146000198321561337218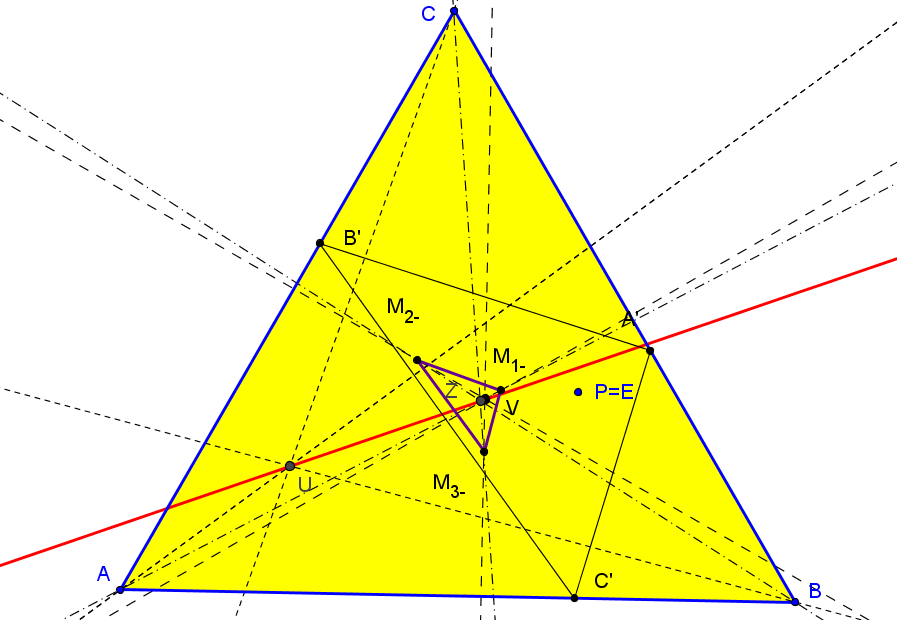
Z = ( a^2SA /(b^2+c^2-3a^2) : b^2SB /(c^2+a^2-3b^2) : c^2SC /(a^2+b^2-3c^2) ),
con número de búsqueda en ETC: -2.28208807333641855014440139U = ( a^2/(5a^10 - 11a^8(b^2+c^2) + 2a^6(b^4+22b^2c^2+c^4) + 2a^4(5b^6-13b^4c^2-13b^2c^4+5c^6) - a^2(b^2-c^2)^2(7b^4+18b^2c^2+7c^4)+ (b^2-c^2)^4(b^2 + c^2)) : ... : ...),
con número de búsqueda en ETC:-16.11015588490167262757688V = ( a^2(a^12(b^2+c^2) - 2a^10(2b^4+7b^2c^2+2c^4) + 5a^8(b^6+5b^4c^2+5b^2c^4+c^6) - 12a^6b^2c^2(b^4+6b^2c^2+c^4) + a^4(-5b^10+11b^8c^2+26b^6c^4+26b^4c^6+11b^2c^8-5c^10) + 2a^2(b^2-c^2)^4(2b^4-3b^2c^2+2c^4) - (b^2-c^2)^4(b^6-7b^4c^2-7b^2c^4+c^6)) : ... : ... ),
con número de búsqueda en ETC: -12.9339740896891882583691075. El lugar geométrico de los puntos P tales que los triángulos M1+M2+M3+ y M1-M2-M3- son perspectivos es la recta de Euler. Estos triángulos son ortológicos para todo punto P del plano.
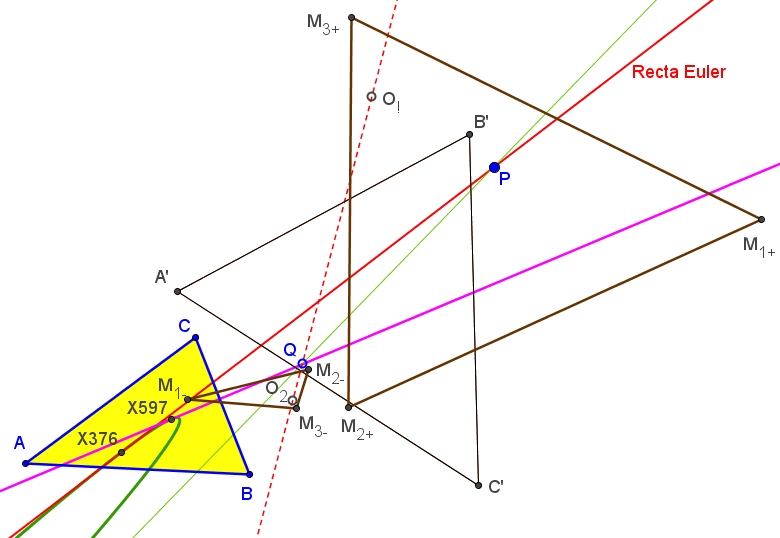
( 10a^6 - a^4(b^2+c^2) - 4a^2(b^4+c^4) - 5(b^2-c^2)^2(b^2+c^2): ... : ... ),
con número de búsqueda en ETC: 1.0956343251291829068665975668Sean ABC un triángulo, P un punto y A'B'C' el triángulo antipedal de P. El lugar geométrico de P tal que la recta de Euler de su triángulo antipedal pasa por el circuncentro es una séptica que pasa por: X(1), X(4), X(6), X(13), X(14), X(74), los excentros, por los pies de las alturas.
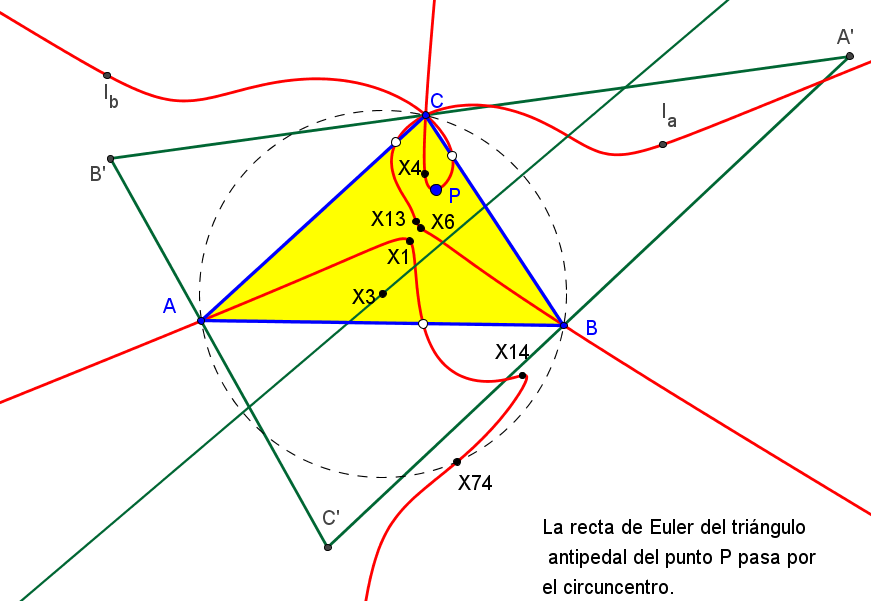
Sean ABC un triángulo, P un punto y A'B'C' el triángulo pedal de P.
Se denota por Ab, Ac las proyecciones ortogonales de A' sobre PB',PC', respectivamente.
l1 es el eje radical de las circunferencias Ab(AbB') y Ac(AcC'), y m1 es el eje radical de las circunferencias Ab(AbC') y Ac(AcB').
l1 y m1 son paralelos, ya que son perpendiculares a AbAc.
Similarmente, se consideran los ejes radicales l2, l3, m2 y m3.
Consideremos el triángulo LaLbLc delimitado por l1, l2 y L3 y el triángulo MaMbMc
delimitado por m1, m2 y m3, ellos son homotéticos.
El lugar geométrico de los puntos P que coinciden con el centro de homotecia de los triángulos LaLbLc y MaMbMc es la cuártica:
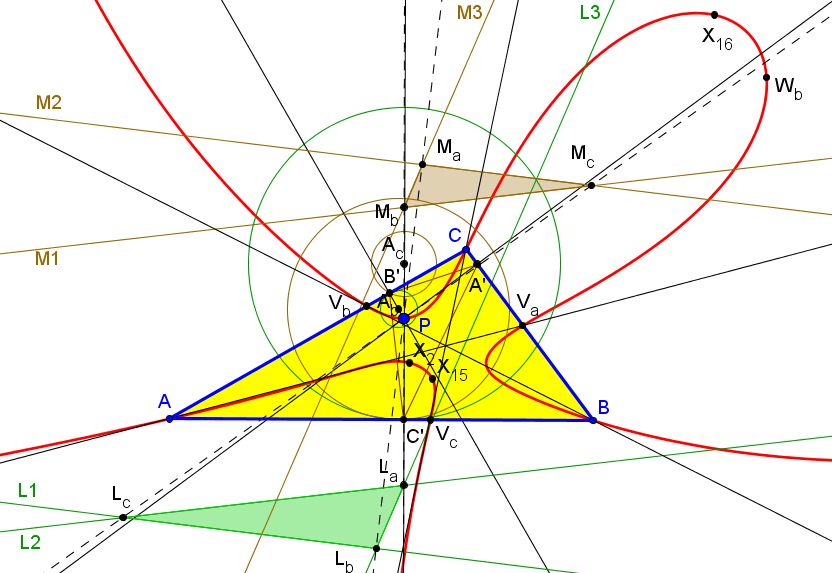
Sean ABC un triángulo, P un punto y PaPbPc el triángulo antipedal de P.
Se denota por Ha, Hb y Hc los ortocentros de los triángulos
PBC, PCA y PAB, respectivamente.
Y por H1, H2 y H3 los ortocentros de los triángulos
PaBC, PbCA y PcAB, respectivamente.
El lugar geométrico de los puntos P tales que los triángulos HaHbHc y H1H2H3 sean perspectivos es la cúbica de McKay,
En ETC, justo antes del centro X2979, se da el concepto de triángulo dual:
Sea UVW un triángulo en plano del triángulo ABC. U' el conjugado isogonal del punto del infinito de la recta VW; se definen V' y W' cíclicamente. Al triángulo U'V'W' se le denomina dual de UVW.
Y se define una aplicación entre puntos del plano (en coordenadas baricéntricas) por:
DC(X13) = X2981, conjugado isogonal de X396 = punto medio de X13 y X15.
DC(X14) (no incluido actualmente en ETC), conjugado isogonal de X395 = punto medio de X14 y X16.
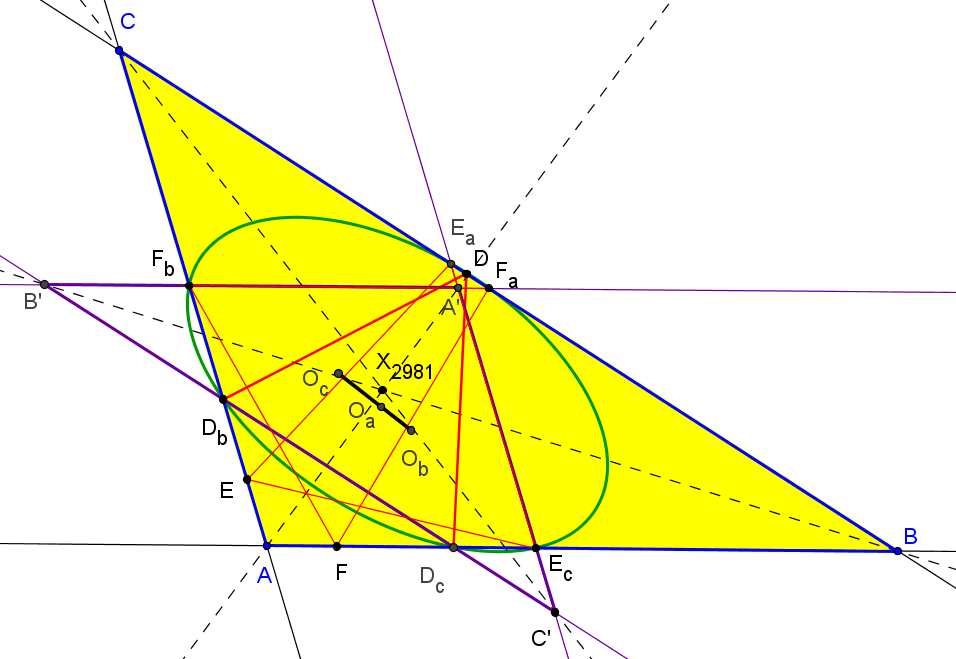
Dado un triángulo ABC, sea DDbDc el triángulo equilátero INSCRITO en ABC, con D, Db y Dc sobre BC, CA y AB, respectivamente, y DbDc paralelo a BC. Cíclicamente se define los triángulos equiláteros inscritos EEcEa y FFaFb.
Las rectas DbDc, EcEa y FaFb delimitan un triángulo A'B'C' homotético a ABC y el centro de homotecia es DC(X13)= X2981:
).png)
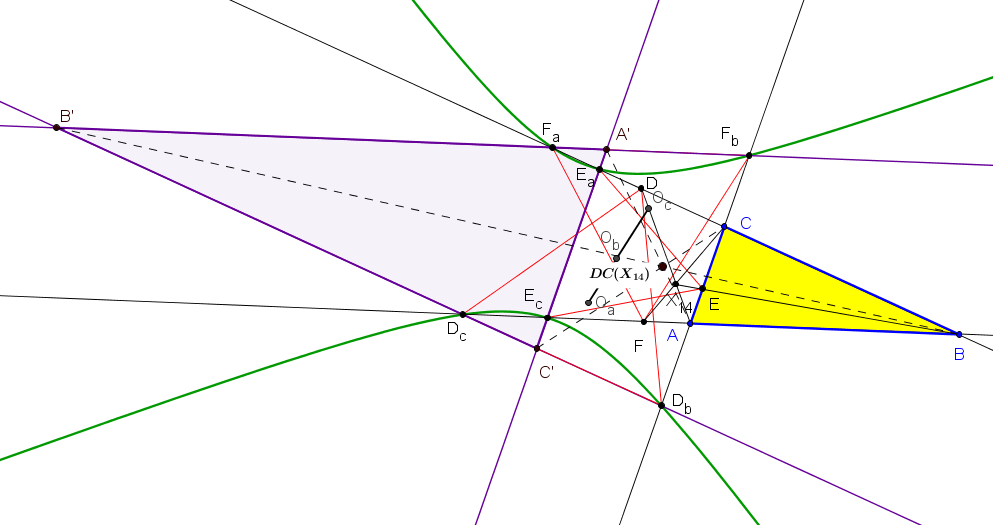
Dado un triángulo ABC, sea DDbDc el triángulo equilátero EXINSCRITO en ABC, con D, Db y Dc sobre BC, CA y AB, respectivamente, y DbDc paralelo a BC. Cíclicamente se define los triángulos equiláteros exinscritos EEcEa y FFaFb.
Las rectas DbDc, EcEa y FaFb delimitan un triángulo A'B'C' homotético a ABC y el centro de homotecia es DC(X14):
).png)
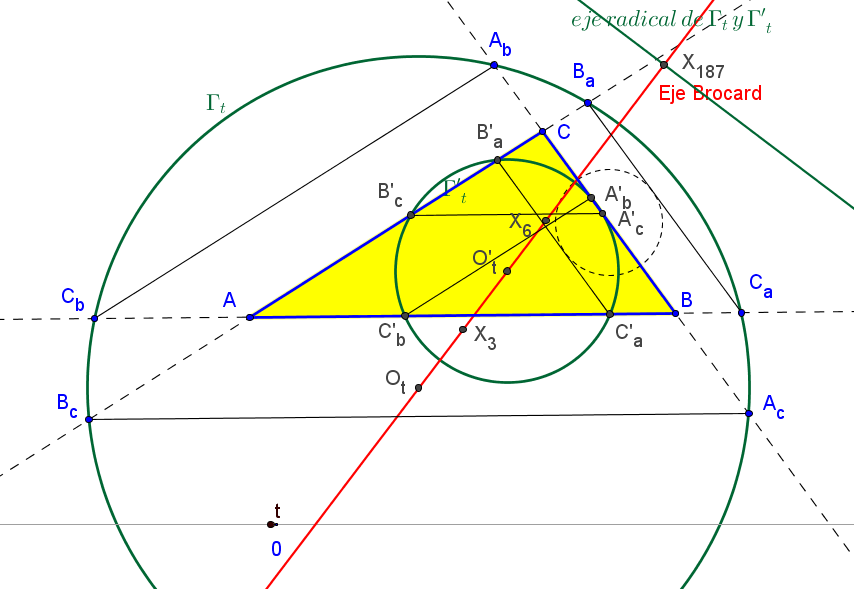
Dados un triángulo ABC y un número real t, las paralelas al lado BC a la distancia |ta| cortan a AB en Cb y C'b (hacia el exterior e interior del triángulo, respectivamente), y al lado AC en Bc y B'c (hacia el exterior e interior del triángulo, respectivamente).
Procediendo cíclicamente, tomando las distancias tb y tc, se definen los puntos Ca, Ac, Ab y Ba, y los puntos C'a, A'c, A'b y B'a.
Los puntos Cb, Bc, Ca, Ac, Ab y Ba están en una misma circunferencia Γt; así mismo,
los puntos C'b, B'c, C'a, A'c, A'b y B'a están en una misma circunferencia Γ′t. Estas son circunferencias de Tucker, cambiando t por (-t), se pasa de una circunferencia a otra.

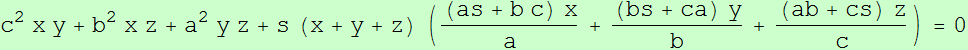
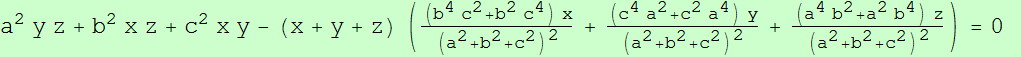
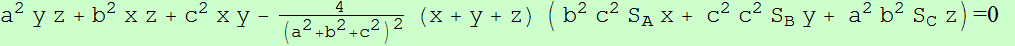
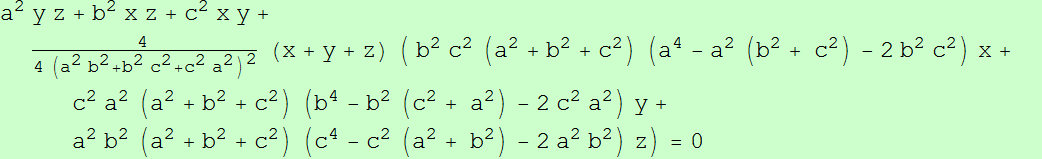
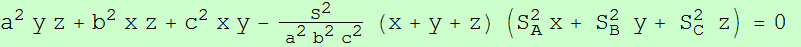
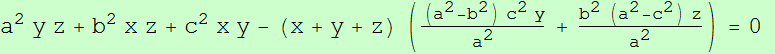
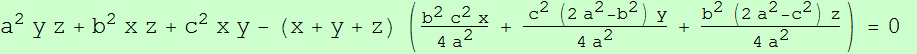
Dados un triángulo ABC y un punto P, se denotan las reflexiones de P en BC, CA y AB por P1, P2 y P3, respectivamente.
Sean P12 y P13 las reflexiones de P1 en CA y AB, respectivamente. Se definen P23, P21 y P31, P32 cíclicamente.
Finalmente, se denotan las reflexiones de P21 y P31 en CA y AB por P212 P213 y P312, P313 respectivamente. Y se definen cíclicamente los puntos P323, P321, P123, P121 y P131, P132, P231, P232.
Los puntos P1, P21, P31, P231 y P321 están en una misma circunferencia Γa, cuyo centro Oa no depende de la posición del punto P y tiene coordenadas baricéntricas (-a^2:2SC:2SB).
De forma similar se consideran las circunferencias Γb y Γc y sus respectivos centros Ob y Oc.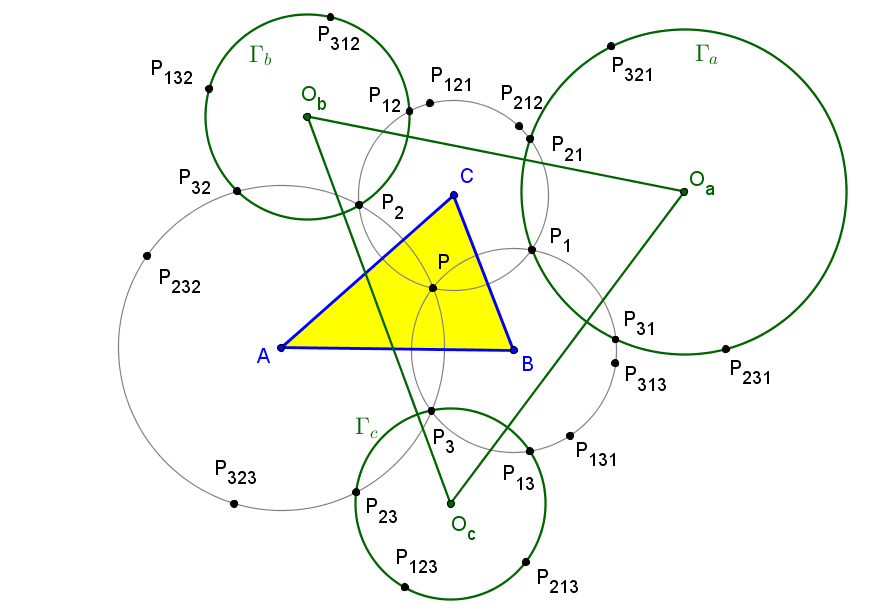
Los triángulos ABC y DEF son perspectivos si y solo si P queda en la
hipérbola
( a^4 b^2 x^2-2 a^2 b^4 x^2+b^6 x^2-a^4 c^2 x^2+b^4 c^2 x^2+2 a^2 c^4 x^2-b^2 c^4 x^2-c^6 x^2-a^6 x y+3 a^4 b^2 x y-3 a^2 b^4 x y+b^6 x y-a^4 c^2 x y+b^4 c^2 x y+2 a^2 c^4 x y-2 b^2 c^4 x y-a^6 y^2+2 a^4 b^2 y^2-a^2 b^4 y^2-a^4 c^2 y^2+b^4 c^2 y^2+a^2 c^4 y^2-2 b^2 c^4 y^2+c^6 y^2+a^6 x z+a^4 b^2 x z-2 a^2 b^4 x z-3 a^4 c^2 x z+2 b^4 c^2 x z+3 a^2 c^4 x z-b^2 c^4 x z-c^6 x z+2 a^4 b^2 y z-a^2 b^4 y z-b^6 y z-2 a^4 c^2 y z+3 b^4 c^2 y z+a^2 c^4 y z-3 b^2 c^4 y z+c^6 y z+a^6 z^2+a^4 b^2 z^2-a^2 b^4 z^2-b^6 z^2-2 a^4 c^2 z^2+2 b^4 c^2 z^2+a^2 c^4 z^2-b^2 c^4 z^2 = 0)
(H) equilátera que pasa por el ortocentro, por el simediano, por la reflexión del circuncentro en el ortocentro (X382), por el punto de reflexión de Parry (X399) y de puntos del infinito X2574 y X2575, conjugados isogonales de los puntos en los que la recta de Euler corta a la circunferencia circunscrita.
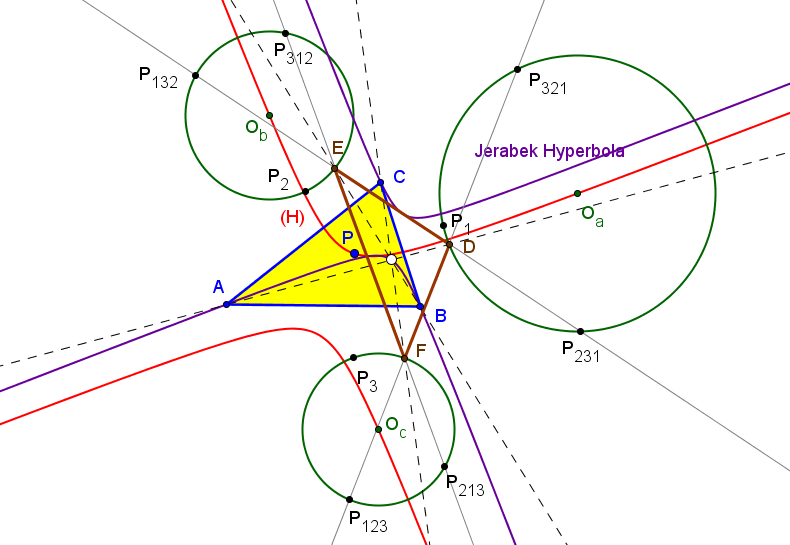
(a^2 (a^8(b^2+c^2) - 2a^6(b^4+c^4) + a^4b^2c^2(b^2+c^2) + a^2(b^2-c^2)^2(2b^4+b^2c^2+2c^4) - b^10 + b^8c^2 + b^2c^8 - c^10) : ... : ...),
que tiene (6-9-13)-número de búsqueda en ETC: -6.618666655241975536408988331.Los triángulos OaObOc y DEF son perspectivos si y solo si P queda en la hipérbola de Jerabek. El centro de perspectividad queda sobre la hipérbola equilátera (H).
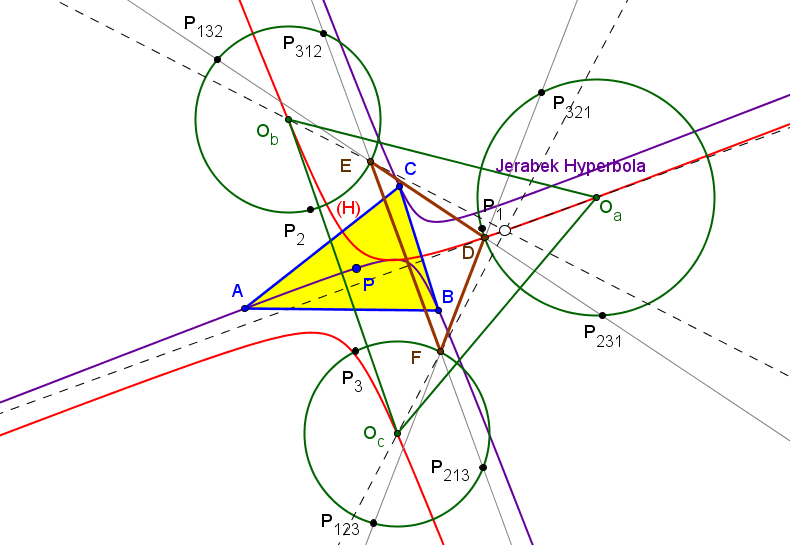
Las tangentes en D, E y F a las circunferencias Γa, Γa y Γc son concurrentes si y solo si P recorre la cónica circunscrita a ABC con centro X5 (centro de la circunferencia de los nueve puntos).
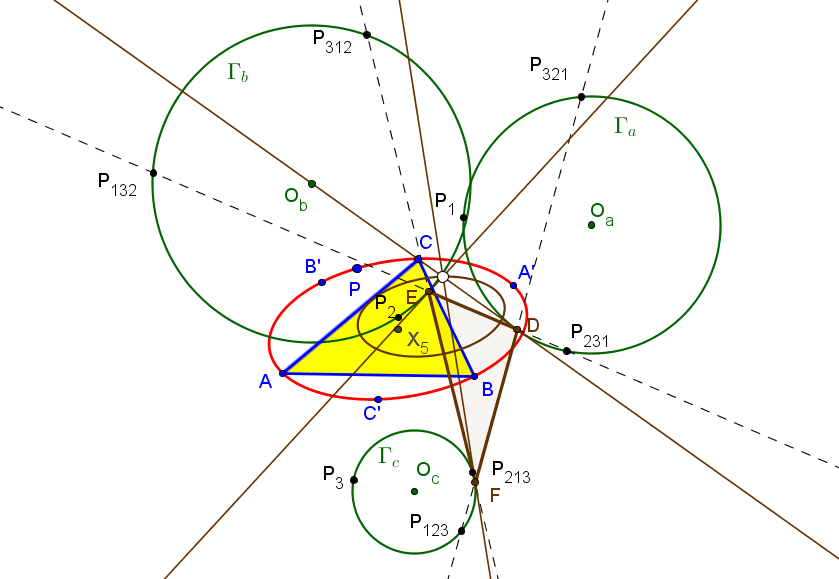
Las tangentes en D, E y F a las circunferencias Γa, Γa y Γc delimitan un triángulo no degenerado perspectivo con DEF si y solo si P recorre la cúbica de Darboux del triángulo órtico, K044 = pK(X216,X4).
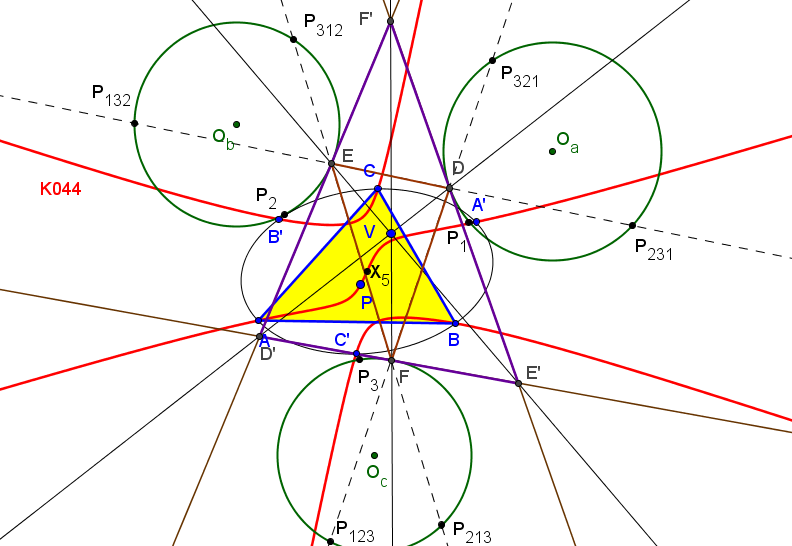
Las tangentes en D, E y F a las circunferencias Γa, Γa y Γc delimitan un triángulo no degenerado perspectivo con ABC si y solo si P recorre una cuártica circunscrita a ABC, que pasa por el ortocentro (doble), por X265 (reflexión del circuncentro en el centro de la hipérbola de Jerabek) y por X1986 (punto de reflexión de Hatzipolakis) y sus dos asíntotas (ortogonales) tienen la dirección de los puntos X2574 y X2575 (conjugados isogonales de los puntos de intersección de la recta de Euler con la circunferencia circunscrita).
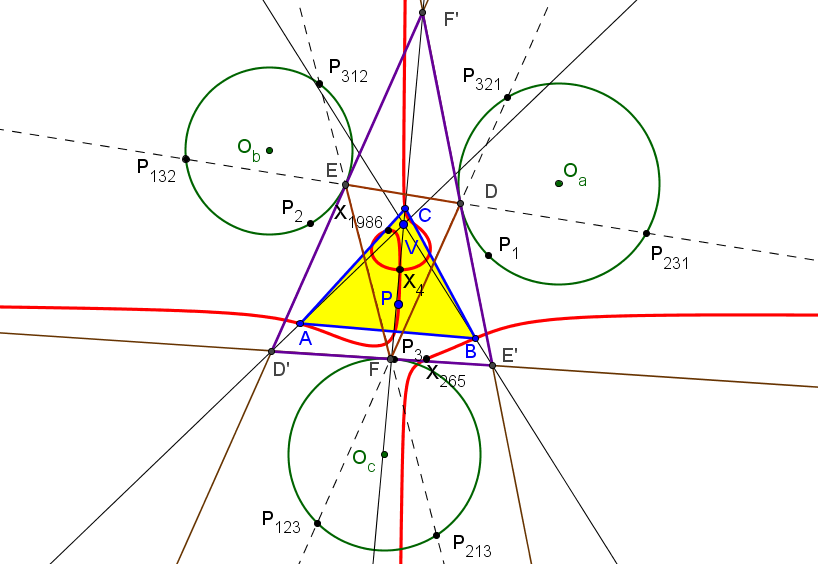
Las tangentes en D, E y F a las circunferencias Γa, Γa y Γc delimitan un triángulo no degenerado perspectivo con OaObOc si y solo si P recorre una cuártica circunscrita a ABC, que pasa por el circuncentro, ortocentro y X54 (punto de Kosnita) y sus dos asíntotas (ortogonales) tienen la dirección de los puntos X2574 y X2575 (conjugados isogonales de los puntos de intersección de la recta de Euler con la circunferencia circunscrita).
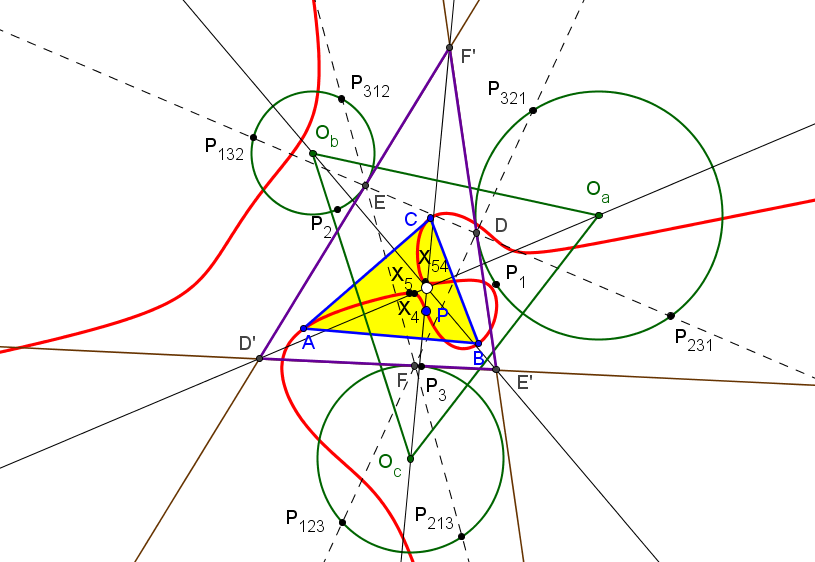
Lugar geométrico de los puntos del plano del triángulo ABC tales que sus triángulos ceviano y pedal tiene la misma área
Si P=(u:v:w) son las coordenadas baricéntricas de un punto del plano, las áreas de sus triángulos ceviano PaPbPc y pedal DEF son, respectivamente: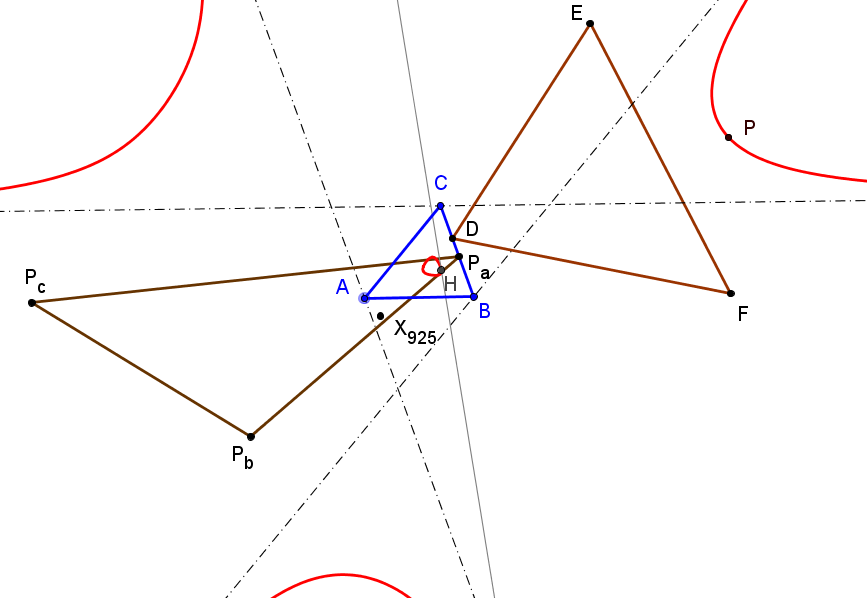
Dados un triángulo ABC y un punto Q, el lugar geométrico de los puntos P tales que los triángulos antipedal de P y ceviano de Q son ortológicos es la cónica circunscrita que pasa por Q y por su complemento.
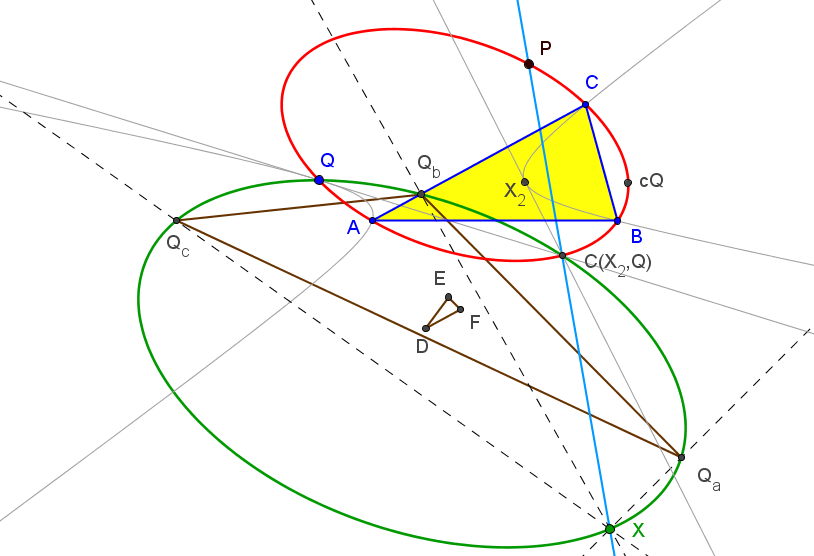
Dados un triángulo ABC y un punto P, el lugar geométrico de los puntos Q tales que los triángulos antipedal de P y ceviano de Q son ortológicos es la isocúbica pivotal pK(G,P•), de polo el baricentro y pivote el conjugado isotómico de P.
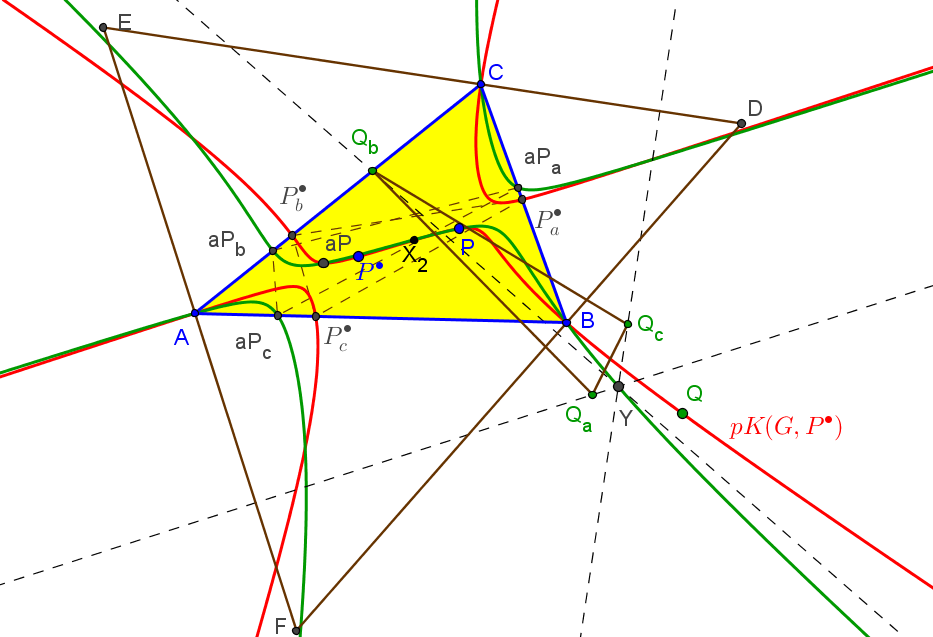
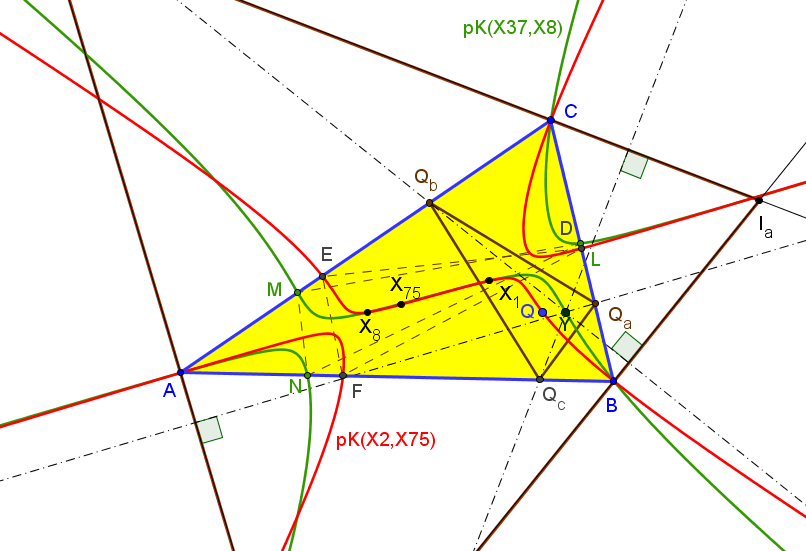
Dados un triángulo ABC, el lugar geométrico de los puntos Q tales que los triángulos antipedal (excentral) del incentro y ceviano de Q son ortológicos es la isocúbica pivotal K034 = pK(X2,X75), de polo el baricentro y pivote el conjugado isotómico del incentro.
Dado un triángulo ABC, sean A' el punto diametralmente opuesto a A, D el punto de intersección de AA' con BC y A" la reflexión de A' en D.
Los puntos Ba y Ca son las proyecciones ortogonales de A" sobre AC y AB, respectivamente. Se definen similarmente los puntos Cb, Ab, Ac y Bc.
El triángulo UVW, delimitado por las rectas BaCa, CbAb y AcBc, es homotético a ABC y su centro de homotecia es X275.
X275 = (1/(SA (SB SC + S^2)) : 1/(SB (SC SA + S^2)) : 1/(SC (SA SB + S^2))).
Y = (SB SC (3 a^4 SA^4 - SA^3 (SB^3 - 3 a^2 SB SC + SC^3) - SA^2 SB SC (7 SB^2 + 16 SB SC + 7 SC^2) - 8 a^2 SA SB^2 SC^2 - 2 SB^3 SC^3):...:...),
con número de búsqueda en ETC: 25.2481990527062715026144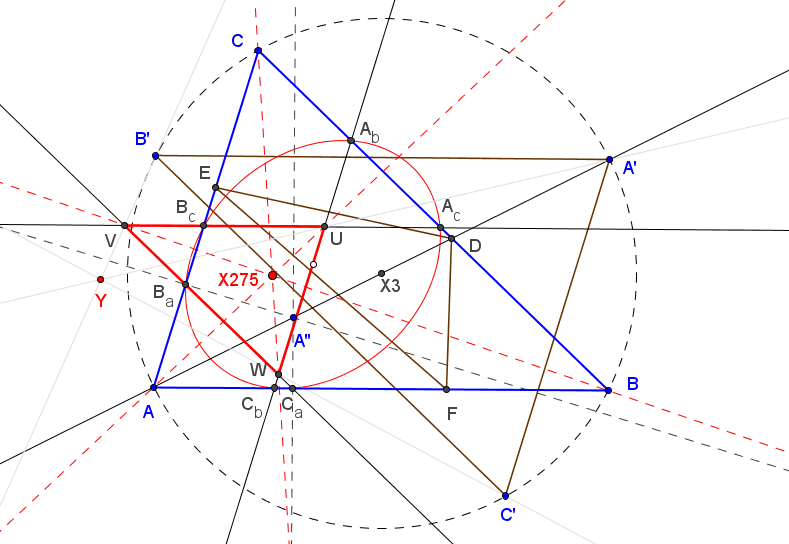
Dado un triángulo ABC, los triángulos A1B1C1 y A2B2C2 tales que
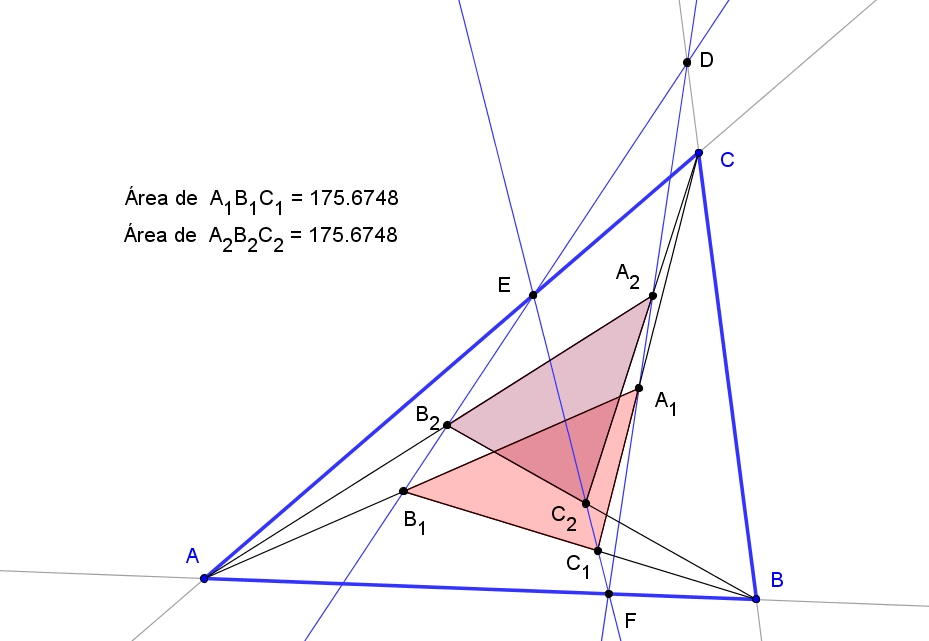
Construir un triángulo conociendo su circuncentro y los pies de la mediana y la altura desde dos vértices distintos.
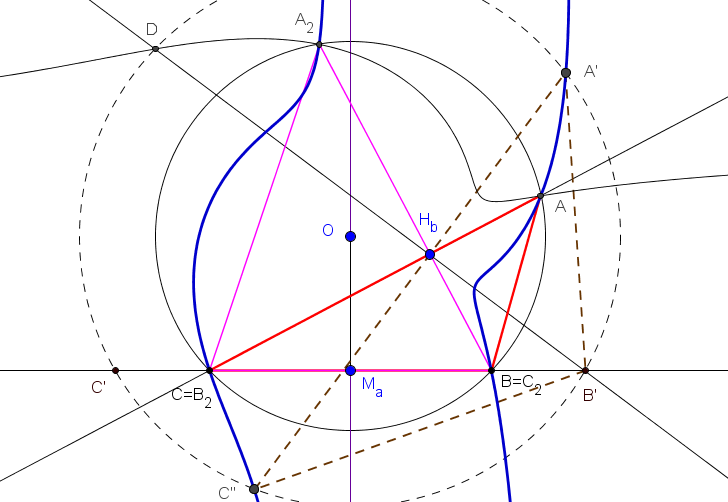
Dado un triángulo ABC, con longitud de lados a=BC, b=CA y c=AB, sean |at|, |bt| y |ct| las distancias de los lados de ABC a los lados del triángulo A'B'C', tal que at=bt=ct (t número real). El circuncentro y el ortocentro son los únicos puntos del plano tales que sus triángulo pedales son perspectivos con A'B'C', para todo número real t.
Relativo al triángulo ABC, sean I el incentro, r el radio de la circunferencia inscrita y LMN el triángulo de contacto interior. La recta pa situada a una distancia |at| del lado BC es la paralela a dicho lado por el punto que resulta de aplicar una homotecia de centro en I y razón (r+at)/r al punto L. Esta recta pa tiene ecuación baricéntrica (similarmente, las rectas pb y pc):
pa: (a+b+c)r+a^2t)x + a^2ty + a^2tz = 0
pa: b^2tx + (a+b+c)r+b^2t)y + b^2tz = 0
pa: c^2tx + c^2ty + (a+b+c)r+c^2t)y = 0.
Los vértices del triángulo A'B'C' delimitado por las rectas pa, pb y pc son:
A' = ((a+b+c)r + (b^2+c^2)t : -b^2t : -c^2t),
B' = (-a^2 t : (a+b+c)r + (c^2+a^2)t : -c^2t},
C' = (-a^2t : -b^2 t : (a+b+c)r + (a^2+b^2)t).
D = (0 : (b^2-c^2)u + a^2(u+2v) : (c^2-b^2)u + a^2(u+2 w)),
E = ((a^2-c^2)v + b^2(v+2u) : 0 : (c^2-a^2)v + b^2(v+2w)),
F = ((a^2-b^2)w + c^2(w+2u), (b^2-a^2)w + c^2(w+2v) : 0).
Los únicos triángulos pedales que son perspectivos a todos los triángulos homotéticos a ABC, mediante las homotecias de centro en el simediano, son los triángulos medial y órtico.
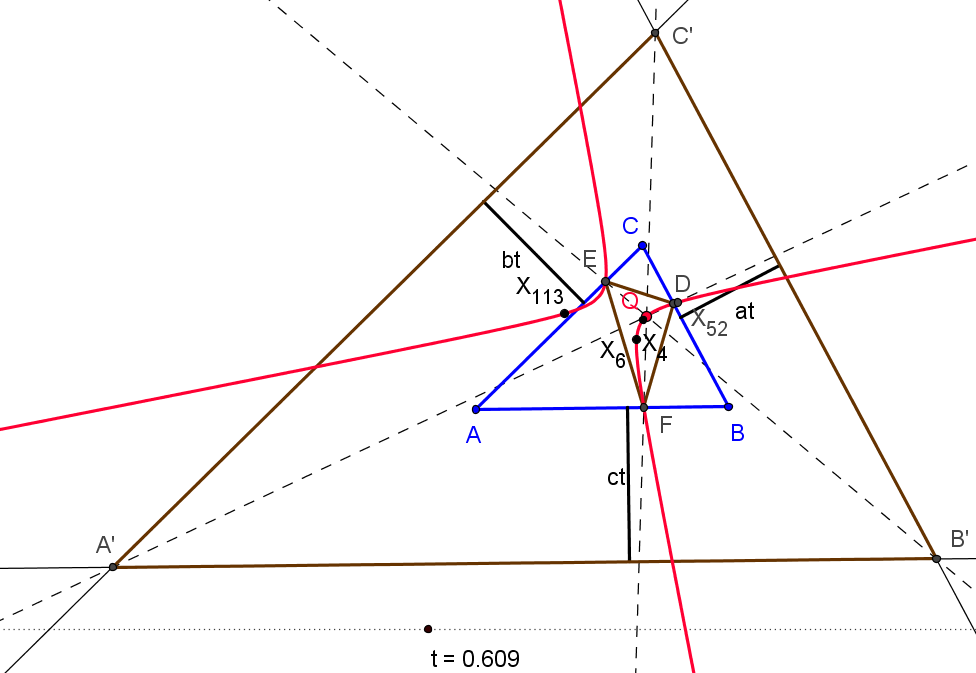
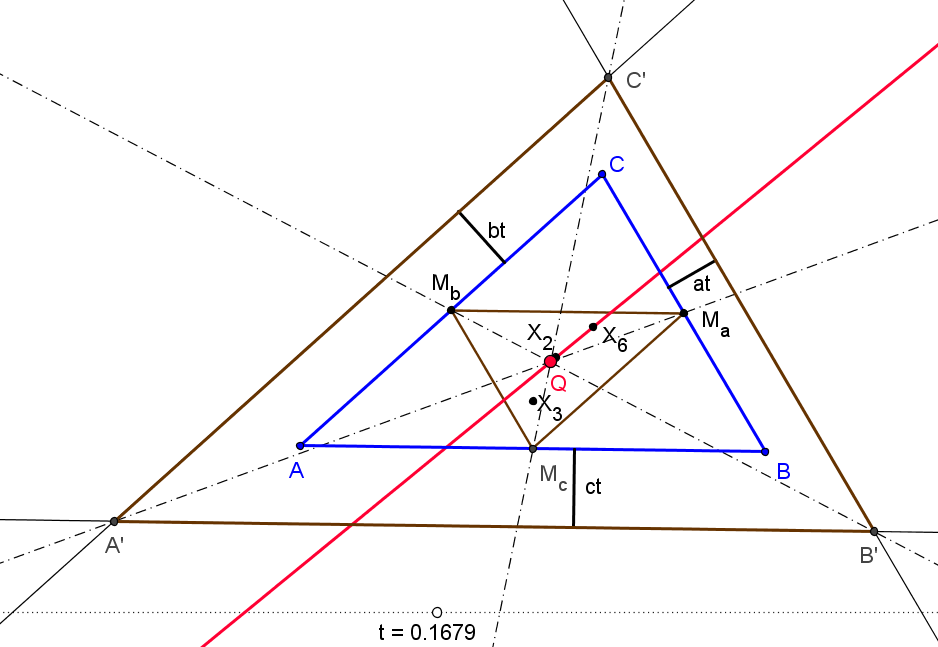
Dado un triángulo ABC y un punto variable P sobre la recta de Euler, el lugar geométrico de los centros de la hipérbola equilátera circunscrita al triángulo pedal de P y que pasa por P es una recta, que corta a la recta de Euler en X468.
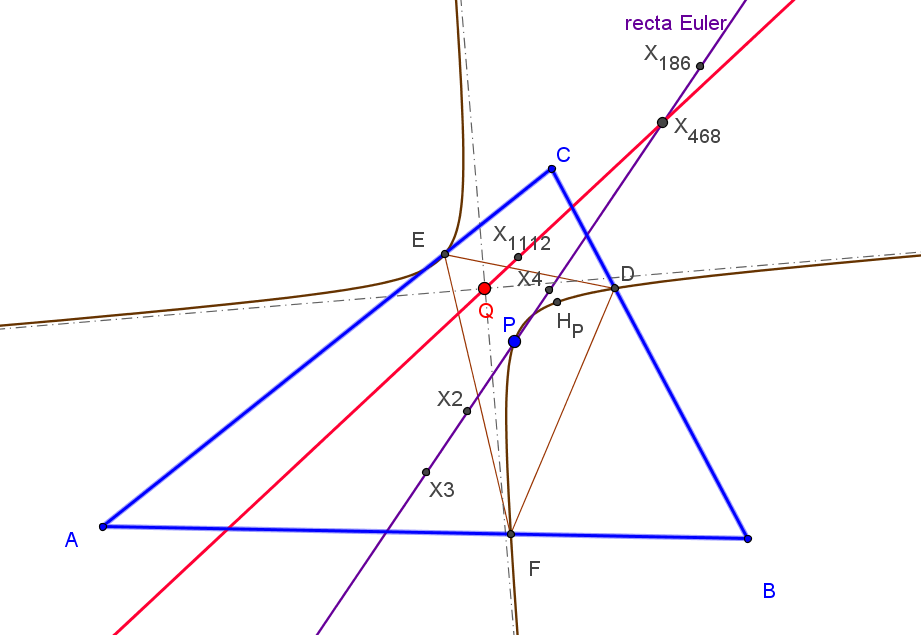
(b^2-c^2)(-a^10 + 2a^8(b^2+c^2) - 5a^6b^2c^2 + a^4(-2b^6+3b^4c^2+3b^2c^4-2c^6) + a^2(b^2-c^2)^2(b^4-b^2c^2+c^4) + 3b^2c^2(b^2-c^2)^2(b^2 + c^2))x+ ... = 0.
Esta recta pasa por los centros X(468) (sobre la recta de Euler), por X(1112) y cuyo punto del infinito es X(511) (conjugado isogonal del punto de Tarry, cuarto punto de intersección de la circunferencia circunscrita y la hipérbola de Kiepert).
X(1112) es el centro de la hipérbola cuando P es el ortocentro.
X(468) es el centro de la hipérbola cuando P es X(186), el inverso del ortocentro en la circunferencia circunscrita
Dado un triángulo ABC, sean TaTbTc su triángulo tangencial y DEF el triángulo circunceviano del ortocentro. La tangente en D a la circunferencia circunscrita corta a TaTb en Db y a TaTc en Dc.
Los puntos Tb, Tc, Db y Dc están en una circunferencia Γa y denotamos por da el eje radical de esta circunferencia y la circunferencia circunscrita.
Similarmente se definen los ejes radicales db y dc.
ABC y el triángulo A'B'C', delimitado por da, db y dc, son perspectivos, con centro de perspectividad en X2165.
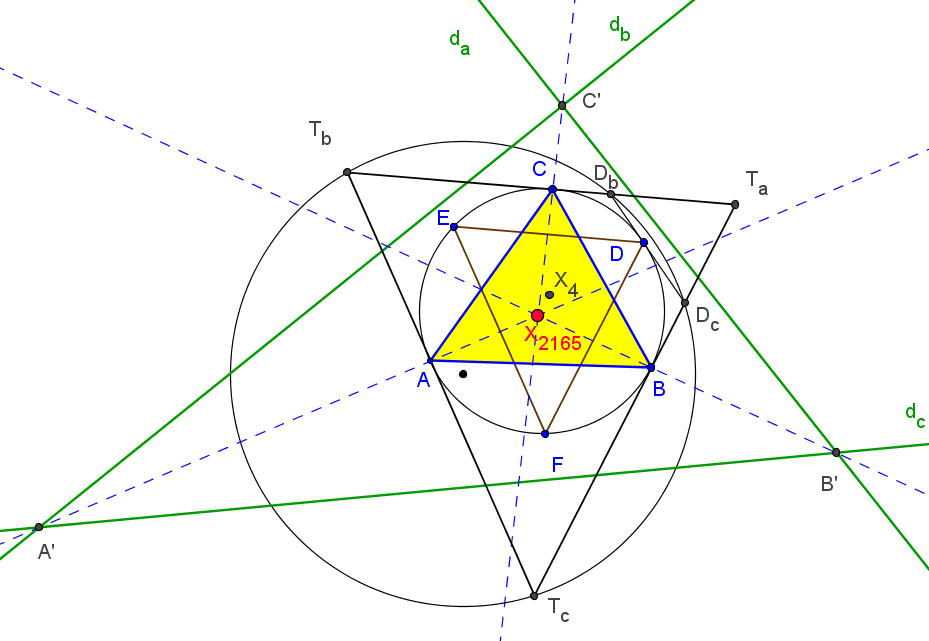
Dado un triángulo ABC y un punto P, sean Pr y Pl sus brocardianos (Paul Yiu.- Introduction to the Geometry of the Triangle, 8.4 pag, 106), PcbPacPba y PbcPcaPab los triángulos cevianos de Pr y Pl, respectivamente.
La isocúbica pivotal pK(X2, X6) es el lugar geométrico de los puntos P tales que las mediatrices de PcbPbc, PacPca y PbaPab son concurrentes.
Esta caracterización geométrica de pK(X2, X6) le ha motivado a Bernard Gibert a asignarle el número K659 es su catálogo de cúbicas asociadas a un triángulo..png)
a^2 x (y^2 - z^2) + b^2 y (z^2 - x^2) + c^2 z (x^2 - y^2) = 0,
pasa por los vértices de ABC y de su triángulo antimedial y por los centros X(2), X(6), X(76), X(194), X(2998).vwx^2 + wuy^2 + uvz^2 -(u^2 + vw)yz -(v^2 + wu)zx -(w^2 + uv)xy = 0.
Una cónica de ecuación baricéntrica f x^2 + g y^2 + h z^2 + 2 p y z + 2 q z x + 2 r x y = 0 es una circunferencia cuando(g + h -2p)/a^2 = (h + f -2q)/b^2 = (f + g -2r)/c^2.
Así, la cónica biceviana que nos ocupa es circunferencia cuando:(u + v)(u + w)/a^2 = (v + w)(v + u)/b^2 = (w + u)(w + v)/c^2.
Resolviendo estas ecuaciones obtenemos que las coordenadas (u:v:u) son proporcionales a (a^2(b^2+c^2)-b^2c^2 : b^2(c^2+a^2)-c^2a^2 : c^2(a^2+b^2)-a^2b^2), que son las el centro X194.(a^2 (a^4 (b^4-4 b^2 c^2+c^4)-a^2 (b^6-4 b^4 c^2-4 b^2 c^4+c^6)+b^2 c^2 (b^4-4 b^2 c^2+c^4)) : ... : ...),
que tiene (6-9-13)-número de búsqueda en ETC: 0.1830166211743119241902625514Steiner.png)
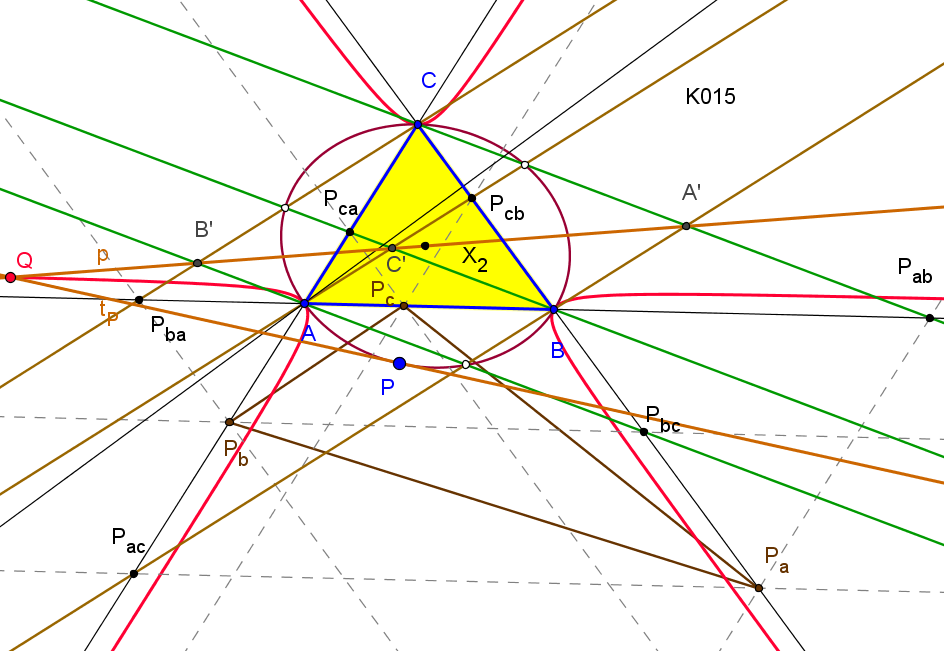
Dado un triángulo ABC y un punto P, existen DOS triángulos isósceles con baricentro A, el ángulo desigual de amplitud la del ángulo en el vértice A, y los vértices iguales sobre las cevianas BP y CP.
Sean A1B1C1 y A2B2C2 tales triángulos, con ∠B1A1C1 = ∠B2A2C2 = ∠BAC, B1 y B2 sobre BP, C1 y C2 sobre CP, y A el baricentro de A1B1C1 y de A2B2C2.
Los triángulos isósceles A1B1C1 y A2B2C2 son inversamente semejantes. Si A'1 es la reflexión de A1 en B1C1, los triángulos A'1B1C1 y A2B2C2 son directamente semejantes; denotamos por A' su centro de semejanza directa. Similarmente se consideran los centros de semejanza B' y C'.
1) Para cualquier P, las circunferencias (BB'∩CC',B,C), (CC'∩AA',C,A) y (AA'∩BB',A,B) son concurrentes en un punto Q.
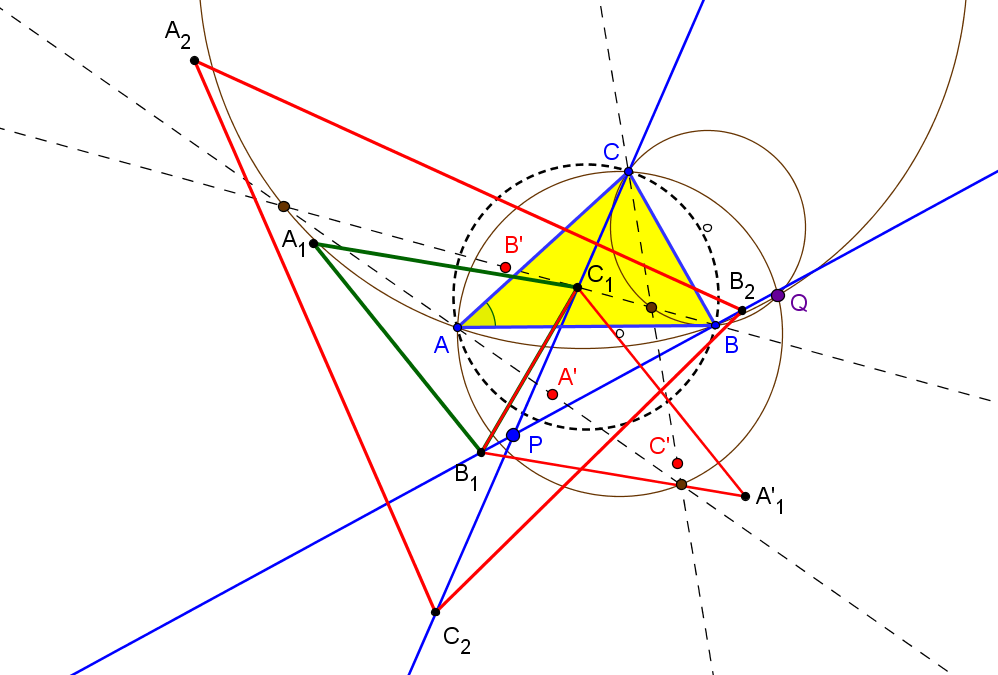
2) Si P recorre la circunferencia circunscrita a ABC, las circunferencias (BB'∩CC',B,C), (CC'∩AA',C,A) y (AA'∩BB',A,B) concurren en un punto fijo Q0, con (6-9-13)-número de búsqueda en ETC: 19.52051544033555
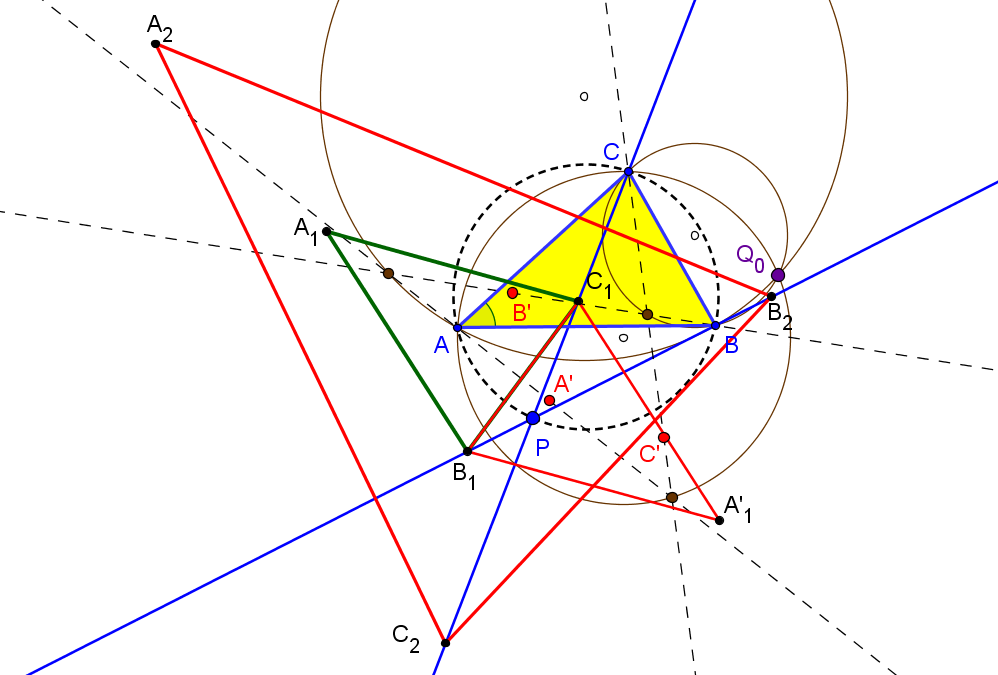
3) Existe un único punto P0 sobre la circunferencia circunscrita tal que AA', BB' y CC' son concurrentes (en el punto Q0).
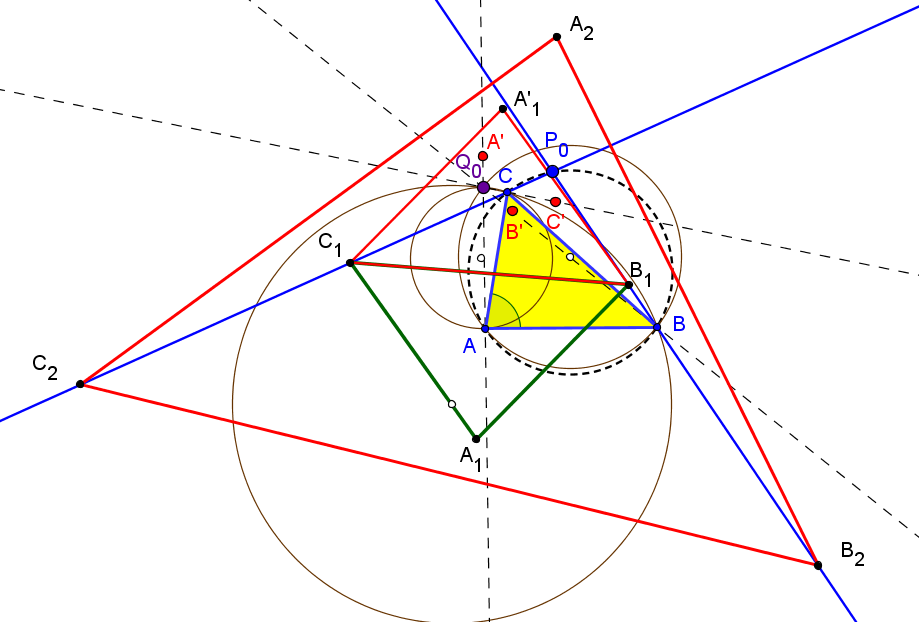
Sean un punto D y dos rectas p y q, entonces la recta que pasa por los puntos medios de los dos segmentos que pares de rectas perpendiculares por D determinan sobre p y q, pasa por un mismo punto al variar las rectas perpendiculares.
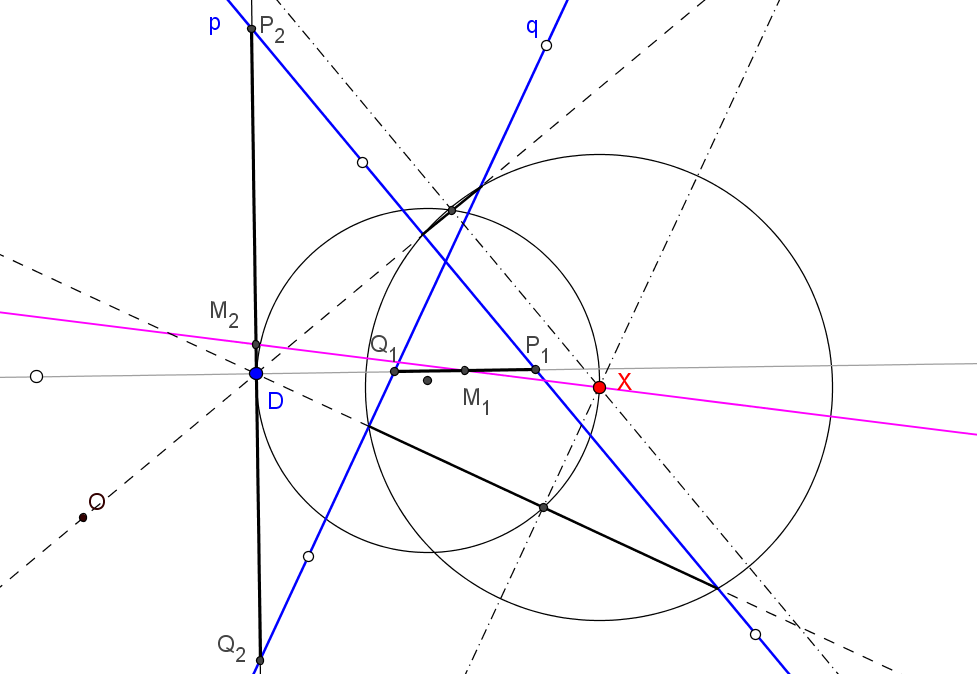
1a) Dado un triángulo ABC y un punto P, los puntos medios de los segmentos que dos rectas perpendiculares variables que pasan por A determinan al cortar cada una a las rectas PB y PC, definen un recta que pasa por un punto fijo Pa.
Pa es el punto de intersección de la mediatriz del segmento que la perpendicular por A a PB determina sobre las rectas PB y PC con la mediatriz del segmento que la perpendicular por A a PC determina sobre las rectas PB y PC.El lugar geométrico de los puntos P tales que ABC y PaPbPc son perspectivos es la hipérbola de Kiepert, y el centro de perspectividad Q es el punto donde la paralela por P a la recta de Euler vuelve a cortar a la hipérbola de Kiepert.
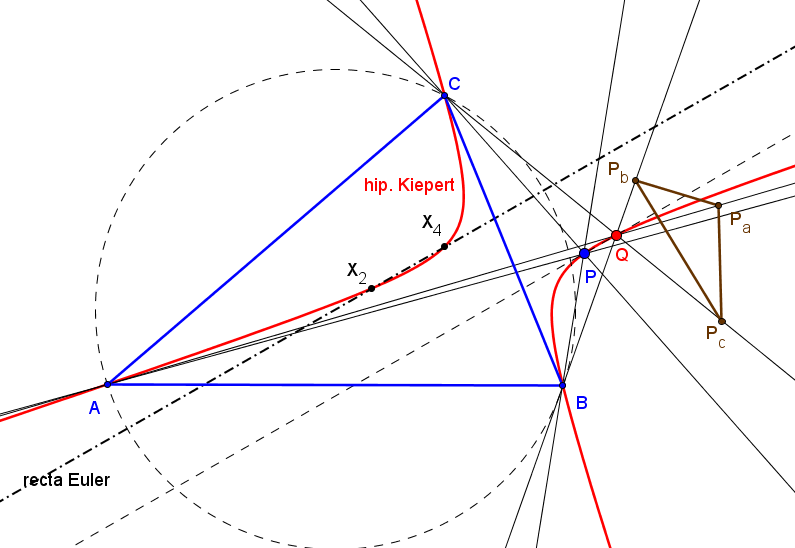
Q=(1/(S²+SAt) : 1/(S²+SBt) : 1/(S²+SCt)).
Pares de centros {P,Q} sobre la hipérbola de Kiepert que figuran actualmente en ETC, expresados por sus correspondientes índices {i,j}, P=Xi, Q=Xj:2a) Dado un triángulo ABC y un punto P, los puntos medios de los segmentos que dos rectas perpendiculares variables que pasan por P determinan al cortar cada una a las rectas AB y AC, definen un recta que pasa por un punto fijo Pa.
Pa es el punto de intersección de la mediatriz del segmento que la perpendicular por P a AB determina sobre las rectas AB y AC con la mediatriz del segmento que la perpendicular por P a AC determina sobre las rectas AB y AC.El lugar geométrico de los puntos P tales que ABC y PaPbPc son perspectivos es la cúbica de Darboux (K004), y el centro de perspectividad Q queda sobre la cúbica de Thomson (K002).
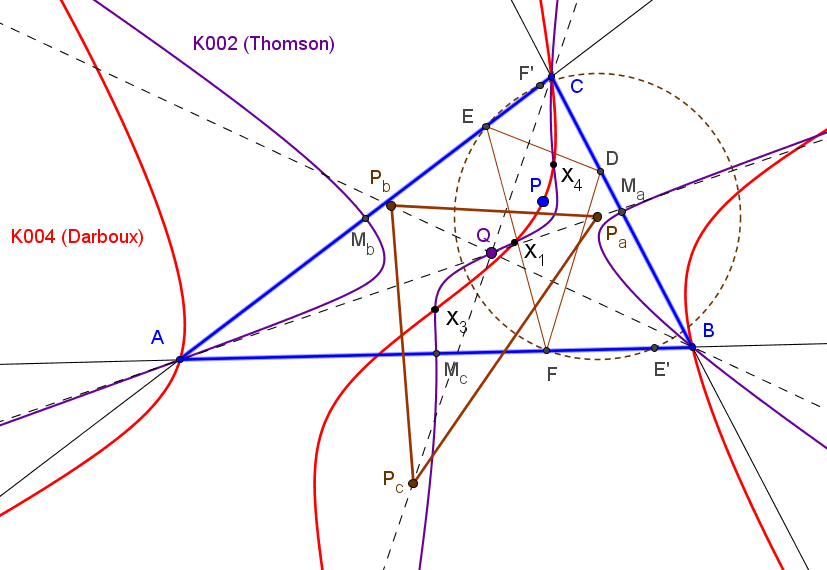
Sean ABC un triángulo, un punto P y DEF su triángulo pedal. La recta PE corta a AB en E' y PF corta a AC en F'. Los puntos E, F, E' y F' están en una circunferencia de centro Pa. Se definen similarmente los puntos Pb y Pc. El lugar geométrico de los puntos P tales que ABC y PaPbPc son perspectivos es la cúbica de Darboux (K004), y el centro de perspectividad Q queda sobre la cúbica de Thomson (K002).
Si P=(p:q:r) es un punto de la cúbica de Darboux, entonces el centro de perspectividad Q, en la cúbica de Thomson, tiene coordenadas baricéntricas
Q=(a^4(p^2-2(q-r)^2+p(q+r)) + 2a^2(b^2(p(3r-q)+(q+r)^2)+c^2(p(3q-r)+(q+r)^2)) - (b^2-c^2)^2p(p-q-r) : ... : ... ).
Pares de centros {P,Q} sobre las cúbicas de Darboux y Thomson que figuran actualmente en ETC, expresados por sus correspondientes índices {i,j}, P=Xi, Q=Xj:Construir un triángulo sabiendo que es isósceles y conociendo la altura y la mediana desde uno de los vértices de ángulos iguales.
Sean ABC un triángulo, Q un punto, y el cuadrivértice ℘ = P1P2P3P4=GPaPbPc, formado por el baricentro y los vértices de triángulo antimedial.
Consideremos las reflexiones de Q respecto de los lados del cuadrivértice ℘:
El lugar geométrico de los puntos Q tales que sus reflexiones Qij, en los lados de ℘, estén en una misma cónica es una séptica que tiene a los vértices de ℘ como puntos singulares aislados, contiene a los vértices del triángulos diagonal y a los vértices(1) del triángulo de Miquel (QA-Tr2 ) de ℘, pasa por X316, Droussent pivot (QA-P4 "Isogonal Center") y tiene como punto del infinito al conjugado isogonal del foco X110 de la parábola de Kiepert: X523 ("Involutory Conjugate" de QA-P2=X99).
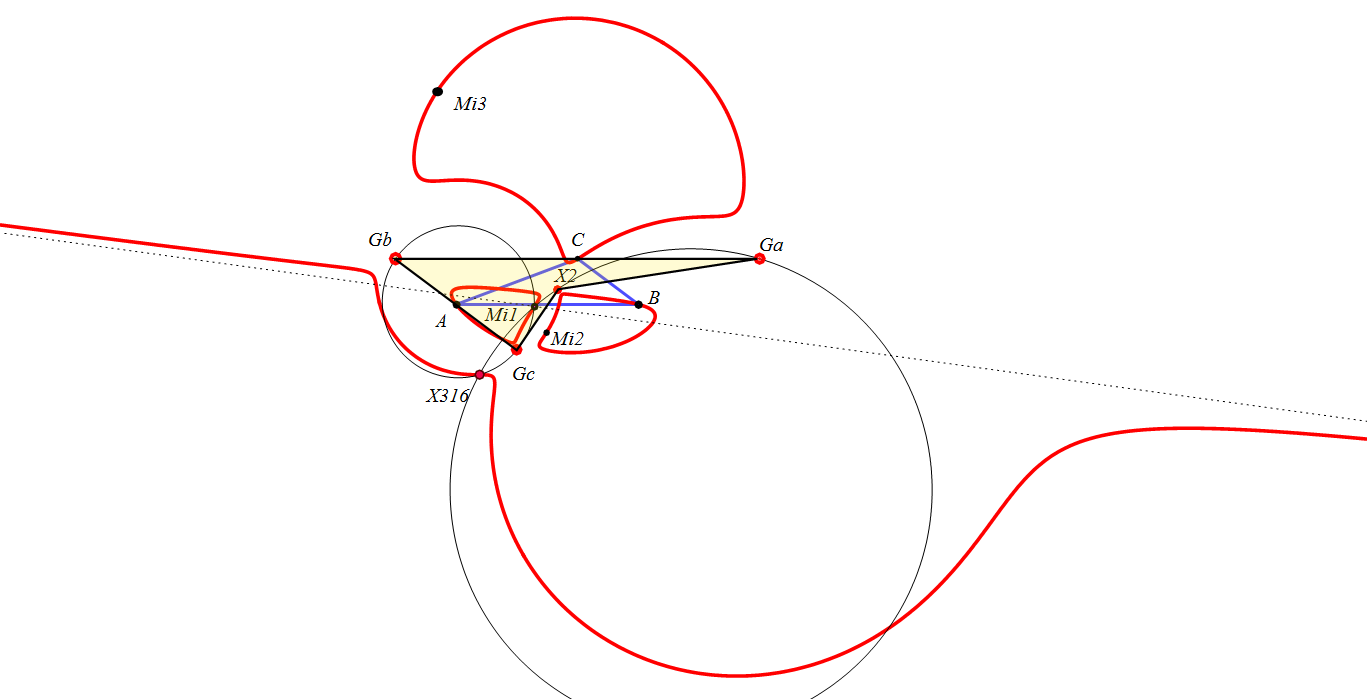
Sean ABC un triángulo y P un punto. Consideremos los dos triángulos equiláteros AAbAc y AA'bA'c tales que Ab y A'b están en la ceviana BP, Ac y A'c están en la ceviana CP (ver HG03113). Denotamos por A' el punto de intersección de AbAc y A'bA'c. Se definen cíclicamente los puntos B' y C'.
Las rectas AA', BB', CC' son paralelas.
Si P varía sobre la circunferencia circunscrita, el lugar geométrico del punto A' es una circunferencia Γa que pasa por A y su centro Oa tiene coordenadas baricéntricas:
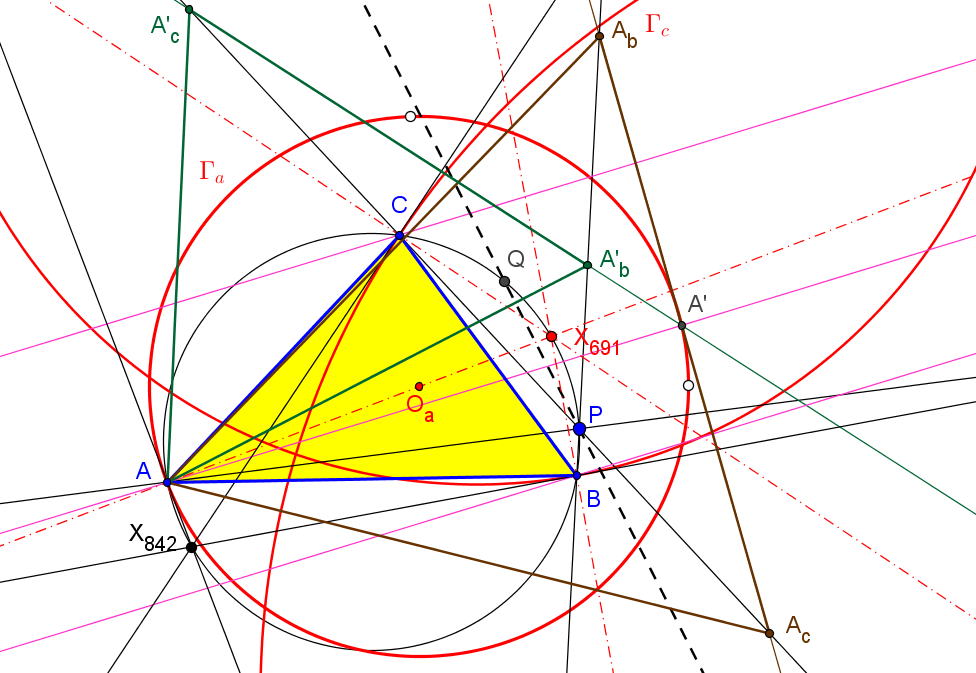
Sean ABC un triángulo, P un punto, P* su conjugado isogonal, A'B'C' y A"B"C" los triángulos pedales de P y P*, respectivamente.
Denotamos por:
Ab la intersección de la paralela a AP* por A' con AB.
Ac la intersección de la paralela a AP* por A' con AC.
A2 la intersección de la paralela a AP por A" con AB.
A3 la intersección de la paralela a AP por A" con AC.
Los puntos Ab, Ac, A2 y A3 están en una circunferencia, por construcción. Sea Oa su centro. Similarmente se definen Ob y Oc.
El lugar geométrico de los puntos P tales que los triángulos ABC y OaObOb son ortológicos es una curva algebraica de grado seis, invariante por isoconjugación, que pasa por el circuncentro, ortocentro, por los puntos X1113 y X1114 (en los que la recta de Euler corta a la circunferencia circunscrita) y por los conjugados de éstos, X2574, X2575, en la recta del infinito, de ecuación baricéntrica:
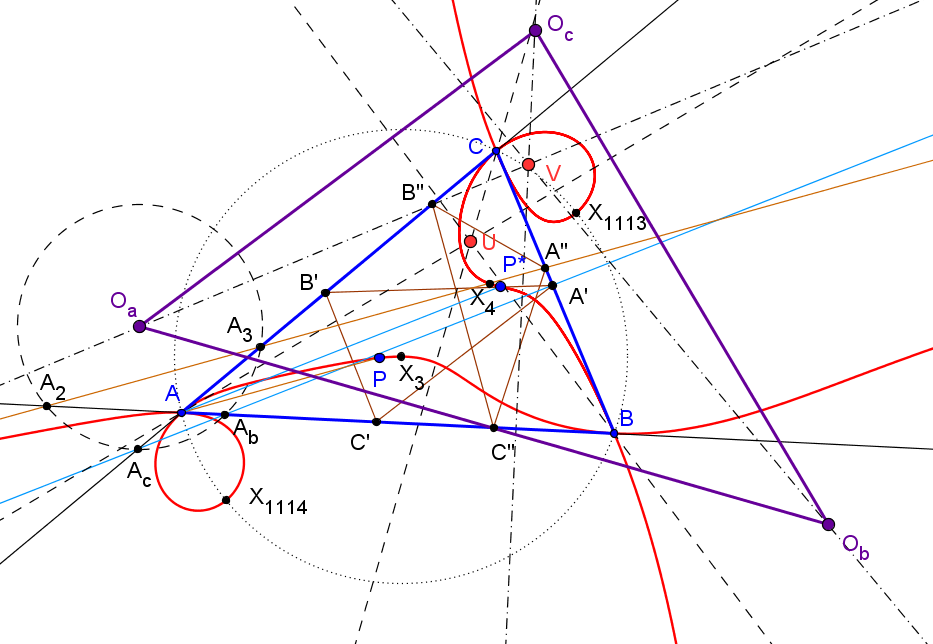
( a^10 - 2 a^8 (b^2 + c^2) + a^6 (b^4 + c^4) - a^4 (b^2 - c^2)^2 (b^2 + c^2) + 2 a^2 (b^8 - b^6 c^2 - b^2 c^6 + c^8) - (b^2 - c^2)^4 (b^2 + c^2) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 6.74586117499516838898883187( a^2/(2 a^10 - 5 a^8 (b^2 + c^2) + 2 a^6 (2 b^4 + b^2 c^2 + 2 c^4)- 2 a^4 (b^2 - c^2)^2 (b^2 + c^2) + 2 a^2 (b^8 - b^6 c^2 - b^2 c^6 + c^8)- (b^2 - c^2)^4 (b^2 + c^2) ) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 146.543260333090931926435953Sean ABC un triángulo y Q un punto. El lugar geométrico de los puntos P tales que la tripolar de P y la recta QP* (P* conjugado isogonal de P) son perpendiculares es una cuártica C(Q) con puntos nodales en los vértices de ABC, que pasa por el baricentro y por los puntos de intersección, X1113 y X1114, de la recta de Euler con la circunferencia circunscrita.
Si Q(p:q:r) (coordenadas baricéntricas) la ecuación de la cuártica C(Q) es:
Q el incentro. El lugar geométrico es la cuártica C(X1) que pasa por los centros X1, X2, X29, X280, X1113, X1114 y X1222, de ecuación:
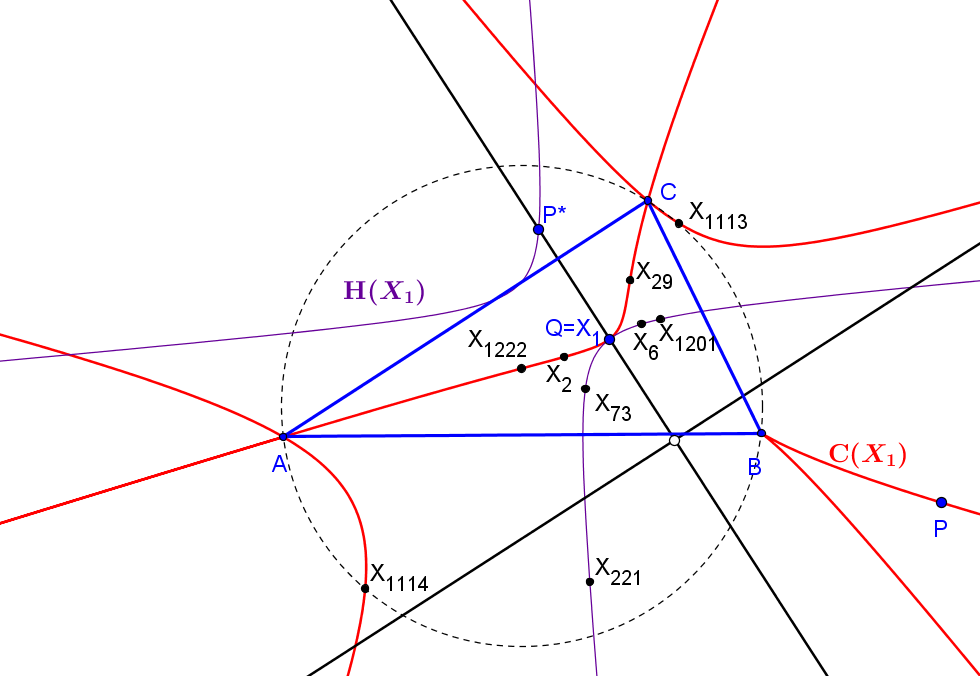
Q el baricentro. El lugar geométrico es la cuártica C(X2) que pasa por los centros X2, X4, X6, X253, X523, X1113, X1114, X1222, X2346, de ecuación:
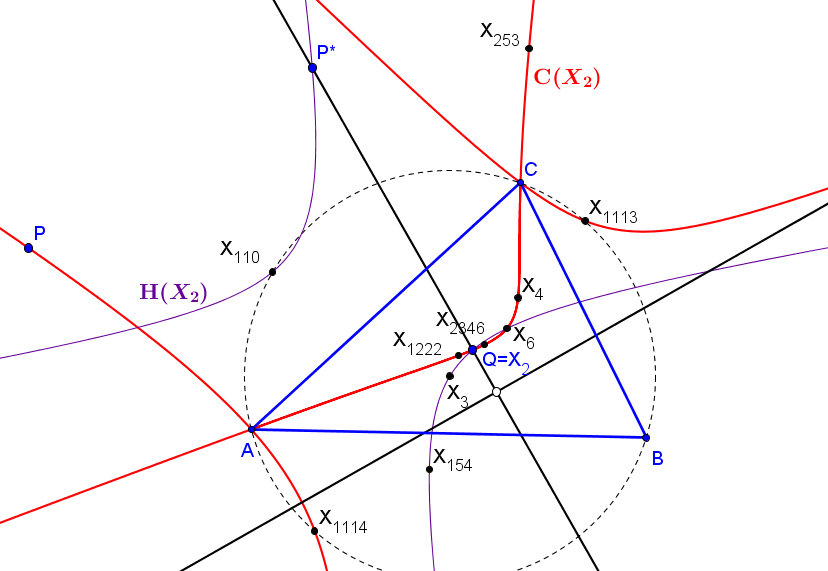
Q el circuncentro. El lugar geométrico es la cuártica de Stammler (Q066), que pasa por los centros X1, X2, X4, X254, X1113, X1114, X1138, X2184, X3223, X3346 y X3459, de ecuación:
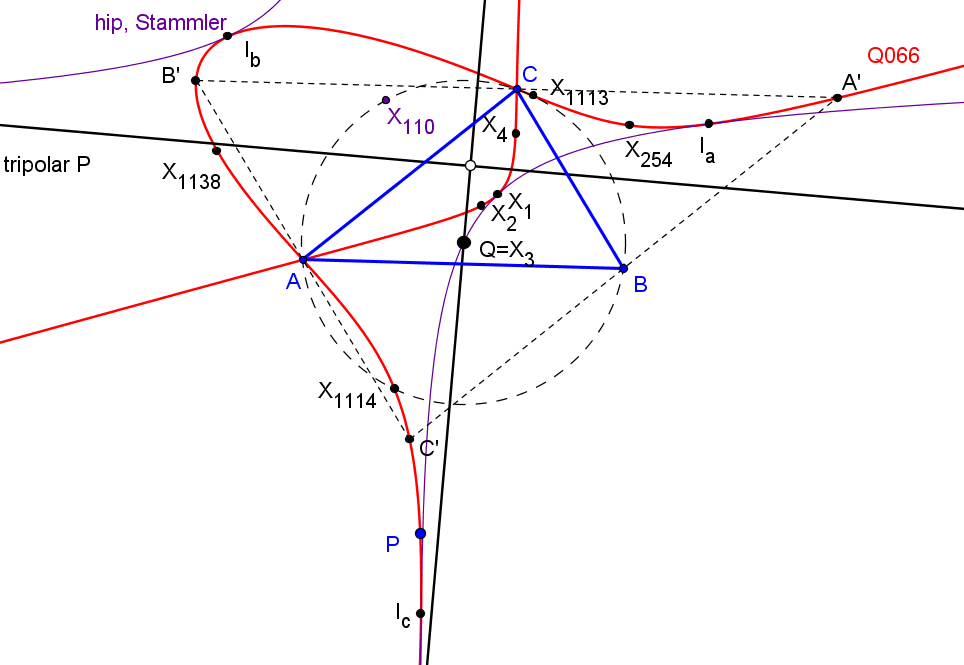
Q el ortocentro. El lugar geométrico es la recta de Euler (junto con los lados de ABC).
"La quíntica de Euler-Morley (Q003, Bernard Gibert) es el lugar geométrico de los puntos Q tales la cuártica C(Q) pasa por Q".
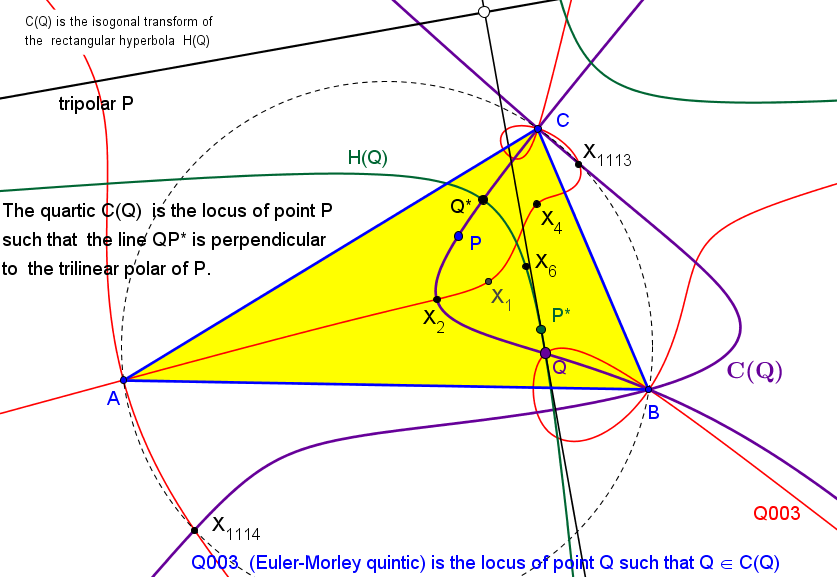
a Lolilla, por su "cumple"
Sean ABC un triángulo, A(Ra), B(Rb), C(Rc) circunferencias centradas en los vértices A, B, C, de radios Ra, Ra, Ra, respectivamente. Si P es el centro radical de estas circunferencias, consideremos la circunferencia P(Rp) centrada en P y de radio Rp y los ejes radicales ea, eb, ec de P(Rp) con las circunferencias A(Ra), B(Rb), C(Rc), respectivamente. Entonces:
El triángulo A1B1C1, delimitado por ea, eb y ec es perspectivo con ABC
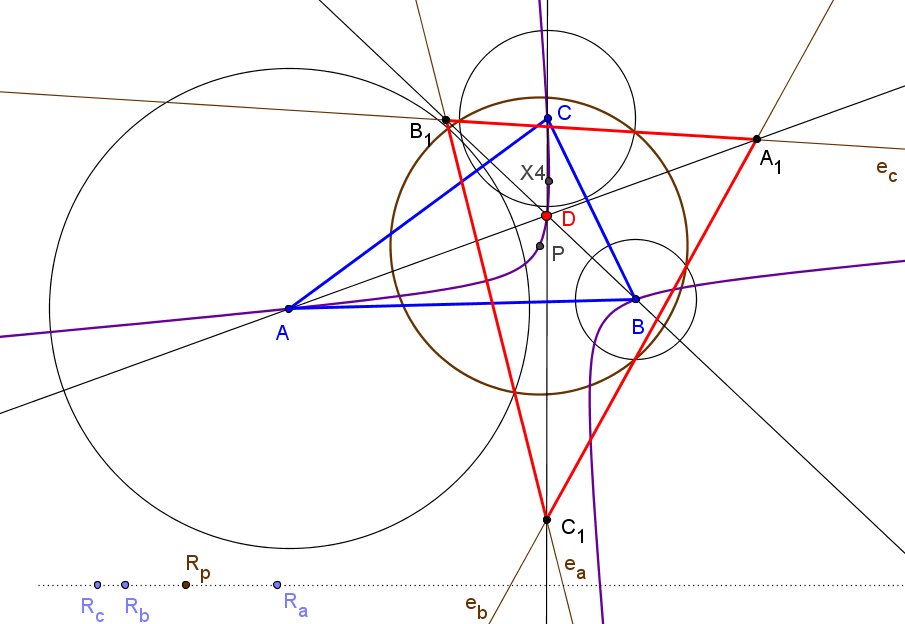
P = ( a4 - a²(b²+c²-2Ra²+Rb²+Rc²) - (b²-c²)(Rb²-Rc²): ... : ... ).
y el centro de perspectividad D de A1B1C1 y ABC es:
D = ( 1/(-a^2 b^4 c^2 + b^6 c^2 - a^2 b^2 c^4 - 2 b^4 c^4 + b^2 c^6 + a^6 Ra^2 - 3 a^4 b^2 Ra^2 + 3 a^2 b^4 Ra^2 - b^6 Ra^2 - 3 a^4 c^2 Ra^2 - 2 a^2 b^2 c^2 Ra^2 + b^4 c^2 Ra^2 + 3 a^2 c^4 Ra^2 + b^2 c^4 Ra^2 - c^6 Ra^2 - a^2 b^2 Ra^4 + b^4 Ra^4 - a^2 c^2 Ra^4 - 2 b^2 c^2 Ra^4 + c^4 Ra^4 + 2 a^2 b^2 c^2 Rb^2 + 2 b^4 c^2 Rb^2 - 2 b^2 c^4 Rb^2 + 2 a^2 b^2 Ra^2 Rb^2 - 2 b^4 Ra^2 Rb^2 + 2 b^2 c^2 Ra^2 Rb^2 - a^2 b^2 Rb^4 + b^4 Rb^4 + b^2 c^2 Rb^4 + 2 a^2 b^2 c^2 Rc^2 - 2 b^4 c^2 Rc^2 + 2 b^2 c^4 Rc^2 + 2 a^2 c^2 Ra^2 Rc^2 + 2 b^2 c^2 Ra^2 Rc^2 - 2 c^4 Ra^2 Rc^2 - 4 b^2 c^2 Rb^2 Rc^2 - a^2 c^2 Rc^4 + b^2 c^2 Rc^4 + c^4 Rc^4 - a^6 Rp^2 + 3 a^4 b^2 Rp^2 - 3 a^2 b^4 Rp^2 + b^6 Rp^2 + 3 a^4 c^2 Rp^2 - 2 a^2 b^2 c^2 Rp^2 - b^4 c^2 Rp^2 - 3 a^2 c^4 Rp^2 - b^2 c^4 Rp^2 + c^6 Rp^2) : ... : ... ).
(b^2 - c^2 + Rb^2 - Rc^2) (a^4 - a^2 b^2 - a^2 c^2 + 2 a^2 Ra^2 - a^2 Rb^2 - b^2 Rb^2 + c^2 Rb^2 - a^2 Rc^2 + b^2 Rc^2 - c^2 Rc^2) y z + ... = 0.
Hipérbola de Feuerbach Ra² = bc(b+c-a)/(a+b+c), Rb² = ca(a -b+c)/(a+b+c), Rc² = ab(a+b-c)/(a+b+c).
Hipérbola de Jerabek Ra=Rb=Rc = R (radio de la circunferencia circunscrita).
Hipérbola de Kiepert Ra² = 1/9 (-a^2+2b^2+2c^2), Rb² = 1/9 (2a^2-b^2+2c^2), Rc² = 1/9 (2a^2+2b^2-c^2).
Estos valores de los radios, tomados para las circunferencias centradas en los vértices, no son los únicos posibles para describir las citadas hipérbolas. Para la hipérbola de Feuerbach, por ejemplo, se ha tomado las distancias de los vértices al incentro, que está en dicha hipérbola; pero podemos tomar la distancia de los vértices a cualquier otro punto que esté en la hipérbola, como radios de tales circunferencias.u((a^2-b^2+c^2)v - (a^2+b^2-c^2)w)yz + v((a^2+b^2-c^2)w - (-a^2+b^2+c^2)w)zx + w((-a^2+b^2+c^2)u - (a^2-b^2+c^2)v)xy = 0.
Circunferencias de radios las longitudes de los lados opuestos. Le corresponde la hipérbola que pasa por los centros X4, P=X20, X253, X1249, X1294, X3346 y X3668, Su ecuación es:
(b^2-c^2) (3 a^4 - 2 a^2 b^2 - b^4 - 2 a^2 c^2 + 2 b^2 c^2 - c^4)yz+ ... = 0.
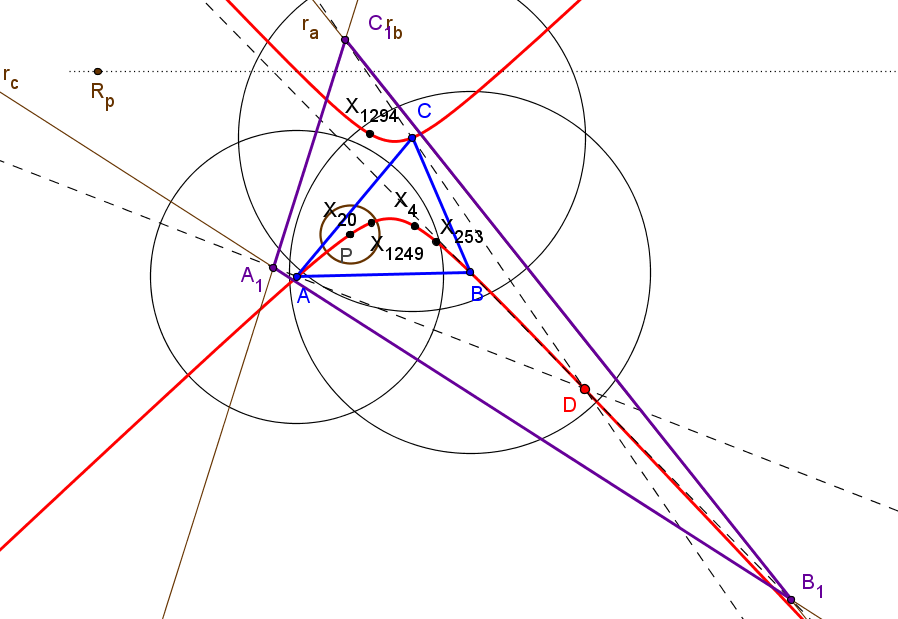
Circunferencias tangentes a los lados opuestos del vértice en el que está centrada. La correspondiente hipérbola rectangular contiene a los centros X4, X389, X577 y tiene por ecuación:
a^4 (b^2 - c^2)(a^2 - b^2 - c^2)^2 (a^6 b^2 - 3 a^4 b^4 +
3 a^2 b^6 - b^8 + a^6 c^2 - 3 a^2 b^4 c^2 + 2 b^6 c^2 -
3 a^4 c^4 - 3 a^2 b^2 c^4 - 2 b^4 c^4 + 3 a^2 c^6 + 2 b^2 c^6 -
c^8)yz+ ... = 0.
Circunferencias de radios los ex-inradios
El centro de perspectividad D está en la hipérbola que contiene a los centros X4, X282, X1034, X1490, X3176, X3341, X3347. Tiene en común con la cúbica de Thomson los seis puntos A, B, C, X4, X282 y X3341. Su ecuación es:
a (a - b - c) (b - c) (a^6 - 2 a^5 b - a^4 b^2 + 4 a^3 b^3 -
a^2 b^4 - 2 a b^5 + b^6 - 2 a^5 c - 2 a^4 b c + 2 a b^4 c +
2 b^5 c - a^4 c^2 + 2 a^2 b^2 c^2 - b^4 c^2 + 4 a^3 c^3 -
4 b^3 c^3 - a^2 c^4 + 2 a b c^4 - b^2 c^4 - 2 a c^5 + 2 b c^5 +
c^6)yz+ ... = 0.
Sean ABC un triángulo, P un punto y A'B'C' el triángulo circunceviano de P. Las rectas BC, CA, AB intersecan a las rectas B'C', C'A', A'B' en 9 puntos, de los cuales 6 no están en la tripolar p del producto ceviano(1) de P y K (simediano); estos seis puntos quedan en una cónica C(P) cuya ecuación baricéntrica, si (u:v:w) son las coordenadas de P, es:
|
|
a^2v^2w^2(c^2v+b^2w)x^2 - uvw(2b^2c^2u^2 + a^2u(c^2v+b^2w) + a^4vw)yz = 0. |
Q = ( u(a^2v(a^2w-c^2(2v+w)) - b^2(2c^2u(v+w)+a^2w(v+2w))) : ... : ... ).
El lugar geométrico de los puntos P tales que P, Q, K son distintos y están alineados es la cúbica de Thomson.
{X1, X1001}, {X3, X3}, {X4, X6}, {X6, X5024}, {X513, X999}, {X523, X381}, {X2574, X3}, {X2575, X3}.
El centro de la cónica C(X2) es:( a^4-3a^2(b^2+c^2)-4b^2c^2 : b^4-3b^2(c^2+a^2)-4c^2a^2 : c^4-3c^2(a^2+b^2)-4a^2b^2 ),
que tiene (6-9-13)-número de búsqueda en ETC: 3.332127762248135206469312965
Sean ABC un triángulo, I el incentro y Ia, Ib, Ic los exincentros. Denotemos por N1, N2, N3, los centros de las circunferencias de los nueve puntos de los triángulos IBC, ICA, IAB y por Na, Nb, Nc, los centros de las circunferencias de los nueve puntos de los triángulos IaBC, IbCA, IcAB.
Las circunferencias circunscritas a los triángulos N1BC, N2CA, N3AB, concurren en X502.
Las circunferencias circunscritas a los triángulos NaBC, NbCA, NcAB, concurren en X5620, de coordenadas baricéntricas:
( (b+c)(a^6 - a^4(b^2+c^2) - a^2(b^4-3b^2c^2+c^4)- 2abc(b-c)^2(b+c) + (b-c)^4(b+c)^2) : ... : ... ).
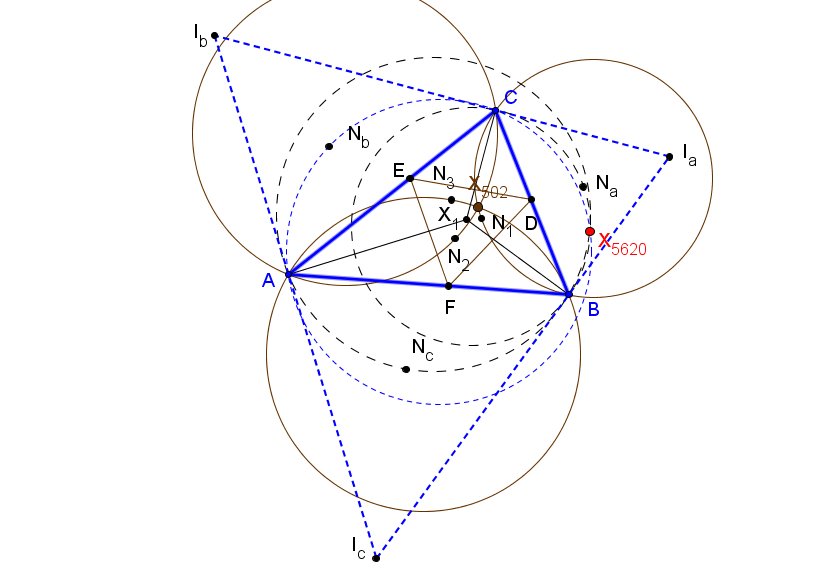
• Información complementaria:
Las rectas IaNa, IbNb y IcNc concurren en X191.
Las rectas IaN1, IbN2 y IcN3 concurren en X5506.
• Randy Hutson da una construcción alternativa del punto X5620 en Anopolis #1132:
Sea DEF el triángulo incentral (triángulo ceviano del incentro), Se considera el triángulo BCA' semejante a DEF, construido hacia el interior de ABC. El punto A' es el segundo puntos de intersección de la recta IaNa con la circunferencia circunscrita al triángulo NaBC.
Se definen B' y C' cíclicamente. Entonces la rectas AA', BB', CC' concurren en X5620.
Las coordenadas baricéntricas de A' son:
A' = (2a^2(a+b)(a+c) :
-(a+c)(a^3+a^2(b-c)+(b-c)^2(b+c)+a(b^2-b c-c^2)) :
-(a+b)(a^3+a^2(c-b)+(b-c)^2(b+c)-a(b^2+b c-c^2)) ).
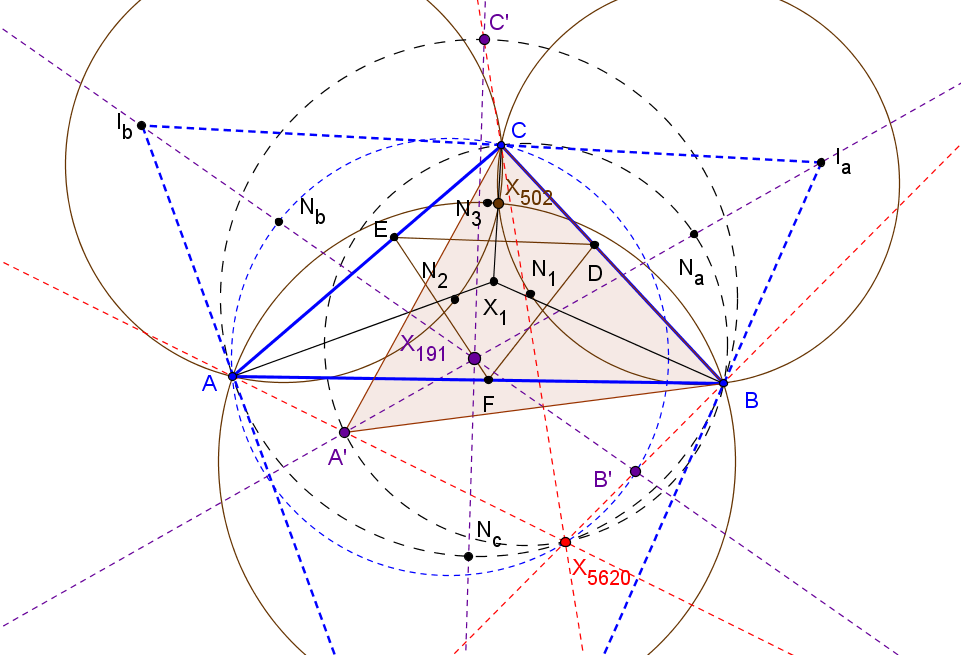
• Caso en que los triángulos semejantes al triángulo incentral son construidos externamente:
Sea DEF el triángulo incentral (triángulo ceviano del incentro), Se considera el triángulo BCA" semejante a DEF, construido hacia el exterior de ABC.
Se definen B" y C" cíclicamente. Entonces la rectas AA", BB", CC" concurren en X502.
(Randy Hutson, 9/23/2011)
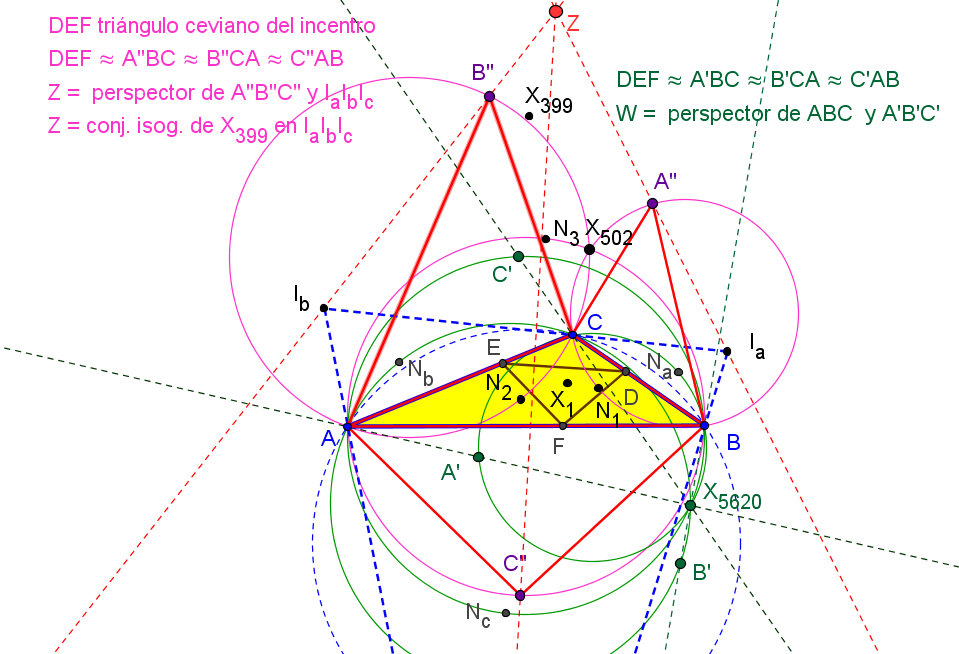
Z = ( a(a^6+2a^5(b+c) + a^4(b^2+4b c+c^2) - a^2(b^4+2b^3c+b^2c^2+2b c^3+c^4) - 2a(b^5+b^4c-b^3c^2-b^2c^3+b c^4+c^5) - (b-c)^2(b+c)^4) : ... : ... )
que tiene (6-9-13)-número de búsqueda en ETC: -10.786517909750622287908
Sean ABC un triángulo, δ una recta, D su tripolo, M un punto en δ, C(M) la cónica biceviana de D y M (que pasa por los vértices de los triángulos cevianos DaDbDc y MaMbMc de D y M) y, finalmente, Mδ el centro de C(M).
El lugar geométrico de Mδ, cuando M varía, es una cuártica que pasa por los puntos de intersección de δ con los lados de ABC.
Si px+qy+rz=0 es la ecuación baricéntrica de la recta δ, su cuarto punto de intersección con la cuártica tiene de coordenadas:
Q(δ) = ( (q - r) (2 q r + p (q + r)) : (r - p) (2 r p + q (r + p)) : (p - q) (2 p q + r (p + q)) )
Este punto es el centro de la cónica C(M∞), donde M∞ es el punto del infinito de la recta δ. La ecuación de la cónica C(M∞) es (Bernard Gibert.- Bicevian Conics § 1.3 (1) ):p(p-q)(r-p)x^2 + q(q-r)(p-q)y^2 + r(r-p)(q-r)z^2 + p(q-r)^2yz + q(r-p)^2zx + r(p-q)^2xy = 0.
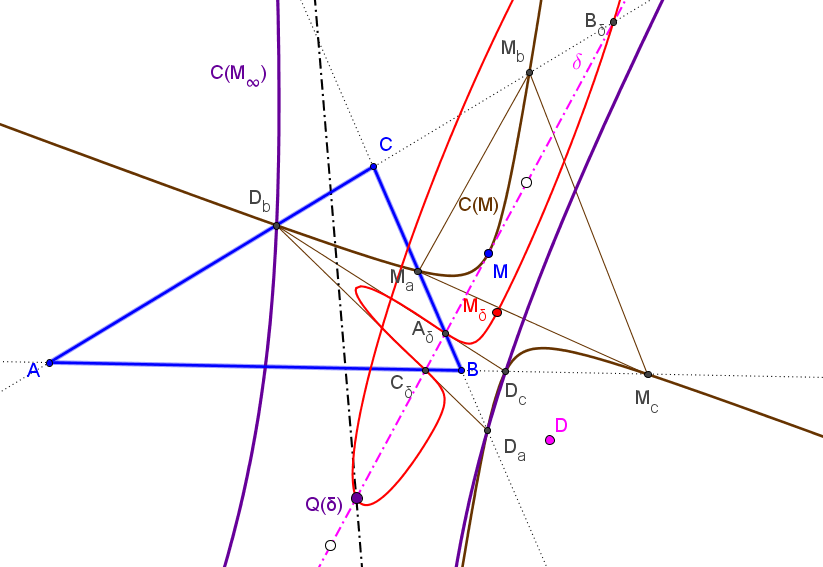
| "central line" δ | ecuación / nombre | centro asociado Q(δ) | nº de búsqueda |
| L1 | ax+by+cz=0 | ( (b-c)(2bc+a(b+c)) :...:... ) | 137.478425435838696608231248 |
| L3 | a^2SAx+...=0 | ( (b^2-c^2)SA(a^6(b^2+c^2)-2a^4(b^4+b^2c^2+c^4)+ a^2(b^2-c^2)^2(b^2+ c^2)+2b^2c^2(b^2-c^2)^2):...:... ) | 34.10580608877537813269670609 |
| L4 | SBSCx+ ... =0 | X2525 | |
| L7 | (a-b+c)(a+b-c)x+ ... =0 | X3700 | |
| L75 | "Antiorthic Axis" | X4979 | |
| L76 | "Lemoine axis" | ( a^2(b^2-c^2)(2a^2+b^2+c^2):..:... ) | 15.27801656267128914852474955 |
| L99 | (c^2-a^2)(a^2-b^2)x+ ... =0 | X1648 | |
| L190 | (c-a)(a-b)x+ ... =0 | X1647 | |
| L514 | "Nagel Line" | ( (2a-b-c) (2a^2-2a(b+c)+b^2+c^2):..:... ) | -41.5918336266397249053218231 |
| L525 | "Euler Line" | ( (2a^4-a^2(b^2+c^2)-(b^2-c^2)^2) (2a^8-2a^6(b^2+c^2))- a^4(b^4-4 b^2c^2+c^4)+(b^2-c^2)^2(b^4+c^4):..:... ) | -2.926469376504842758944837077 |
| L648 | x/((b^2-c^2)SA)+ ... =0 | X1650 | |
| L668 | x/(a(b-c))+ ... =0 | X1646 | |
| L670 | x/(a^2(b^2-c^2))+ ... =0 | X1645 | |
| L671 | x/(2a^2-b^2-c^2)+ ... =0 | X1649 | |
| L850 | "Brocard axis" | ( a^2(a^2(b^2+c^2)-b^4-c^4) (2a^6- 2a^4(b^2+c^2)-a^2(b^4-4b^2c^2+c^4)+(b^2-c^2)^2(b^2+c^2)):..:... ) | -3.75510528847191427972334279 |
| L3239 | "Soddy line" | ( (2a^3-a^2(b+c)-(b-c)^2(b+c)) (-2(a-b)(a-c)(a+b-c)^2(a-b+c)^2 + (b-c)(-a+b+ c)^2((a-b)(a+b-c)^2-(a-c)(a-b+c)^2)):..:... ) | -3.2612053200015515644411874 |
| L3265 | "VanAubel line" | ( (2 a^6 - a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2)) (-2 (a - b) (a + b) (a - c) (a + c) (a^4 - (b^2 - c^2)^2)^2 + (b - c) (b + c) (-a^2 + b^2 + c^2)^2 (3 a^4 (b^2 - c^2) - (b^2 - c^2)^3 - 2 a^2 (b^4 - c^4))):..:... ) | -2.740416687177399065884132982 |
| L3268 | "Fermat axis" | ( (2 a^6 - 2 a^4 (b^2 + c^2) - (b^2 - c^2)^2 (b^2 + c^2) + a^2 (b^4 + c^4)) (-2 (a - b) (a + b) (a - c) (a + c) (a^2 - a b + b^2 - c^2) (a^2 + a b + b^2 - c^2) (a^2 - b^2 - a c + c^2) (a^2 - b^2 + a c + c^2) - (b - c) (b + c) (b^2 - c^2) (-a^2 + b^2 - b c + c^2) (-a^2 + b^2 + b c + c^2) (-2 a^4 + (b^2 - c^2)^2 + a^2 (b^2 + c^2))):..:... ) | -2.39457958479639858720527989 |
| L4373 | x/(b+c-3a)+ ... =0 | X4394 |
Sean un triángulo ABC, I el incentro; Na, Nb , Nc los centros de las circunferencias de los nueve puntos de IBC, ICA, IAB. Las circunferencias {ANbNc}, {BNcNa}, {CNaNb} concurren en un punto de la circunferencia circunscrita.
El centro de la circunferencia de los nueve puntos del triángulo IBC tiene por coordenadas baricéntricas:
Na = (-a (b + c) : a^2 + a b - (b + c)^2 : a^2 + a c - (b + c)^2).
Permutando cíclicamente estas coordenadas se obtienen las de los puntos Nb y Nc.c^2 x y + b^2 x z + a^2 y z + (x + y + z) (-(((a^4 c - a^3 b c - a^2 b^2 c + a b^3 c + 2 a^3 c^2 - b^3 c^2 + b^2 c^3 - 2 a c^4 + b c^4 - c^5) y)/( 2 (a^3 + a^2 b - a b^2 - b^3 + a^2 c - a b c + b^2 c - a c^2 + b c^2 - c^3))) - ((-a^4 b - 2 a^3 b^2 + 2 a b^4 + b^5 + a^3 b c - b^4 c + a^2 b c^2 - b^3 c^2 - a b c^3 + b^2 c^3) z)/( 2 (-a^3 - a^2 b + a b^2 + b^3 - a^2 c + a b c - b^2 c + a c^2 - b c^2 + c^3)))=0.
Por permutación cíclica obtenemos las ecuaciones de las circunferencias circunscritas a los triángulos BNcNa y CNaNb.(a/((b - c) (a^3 - a^2 (b + c) - a (b^2 + b c + c^2) + (b + c)^3)) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 0.2921043592404663185080644011
Sean ABC un triángulo. Se construyen triángulos semejantes variables ABBa, rectángulo en B, y ACCa, rectángulo en C, tales que θ = ∠BABa = - ∠CACa (ángulos orientados). La envolvente de las rectas BaCa es una parábola ℘a.
En efecto, la correspondencia Ba (θ) ↦ Ca (-θ), entre puntos de la recta perpendicular a AB por B y los de la recta perpendicular a AC por C, es una proyectividad; por lo que, las rectas BaCa envuelven un cónica, tangente a estas rectas y también al lado BC en un punto Ta, ya que B ↦ C. Finalmente, como los puntos del infinito de cada recta se corresponden, la recta del infinito es también tangente: se trata de una parábola.4 b²c²x² + SB²y² + SC²z² + 2 SB SC yz + 4 b²SB zx + 4 c² SCxy = 0,
su directriz es la mediana por A y su foco es el punto D donde la simediana por A vuelve a cortar a la circunferencia circunscrita a ABC.Ta = (0 : a^2 + b^2 - c^2 : -a^2 + b^2 - c^2).
Las parábolas ℘a, ℘b y ℘c son tangentes a los lados de ABC en puntos alineados, sobre la tripolar del ortocentro X4.
Gracias a Viktor Kitaysky, por una corrección
Sean ABC un triángulo y Wa el pie de la bisectriz exterior en A. Denotamos por Ωa la única cónica circunscrita que tiene las mismas tangentes desde Wa que la circunferencia circunscrita, su ecuación baricéntrica es:
b c x (y + z) + a^2 y z = 0.
Es tangente en A al lado (y+z=0) del triángulo antimedial y pasa por el punto Ta de intersección de la bisectriz interior en A con la mediatriz de BC (cuarto punto de intersección de Ωa con la circunferencia circunscrita).Para la construcción de la cónica Ωa ver: Cónica: dado tres puntos y dos tangentes (PPPtt) o bien (PPPtP), (PPPtP(1)).
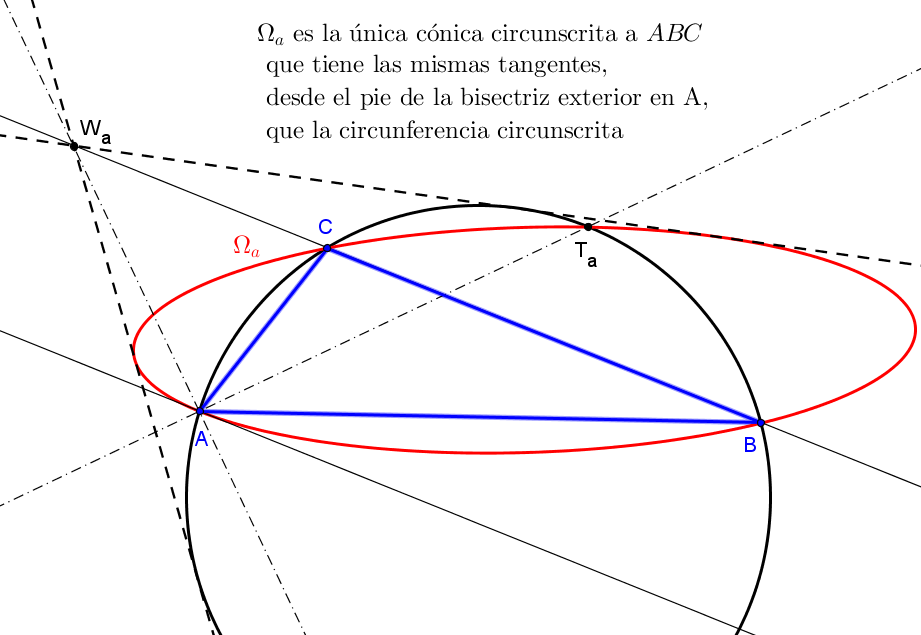
Los triángulos ABC y QaQbQc son perspectivos con centro de perspectividad el punto X238.
(a (a^2 - b c) : b (b^2 - c a) : c (c^2 - a b))
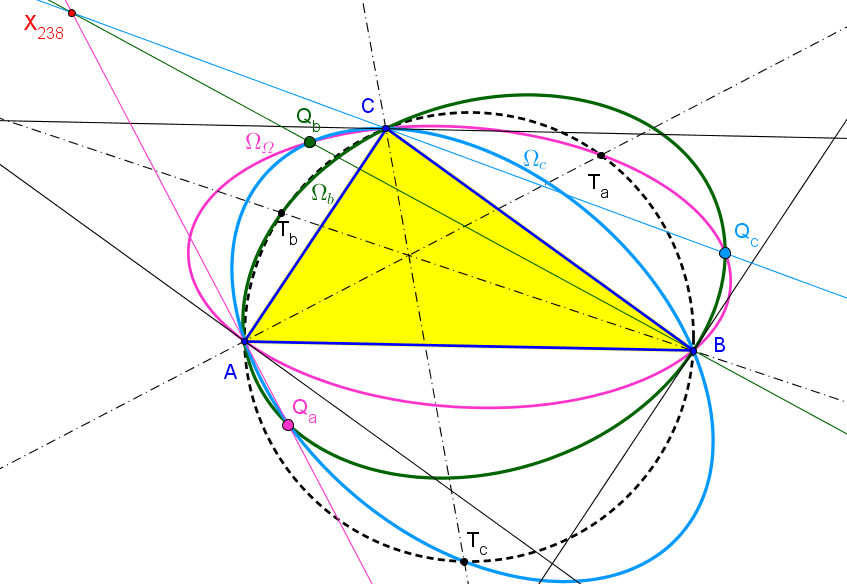
(a/(b^2+b c+c^2) : b/(c^2+c a+a^2) : c/(a^2+a b+b^2))
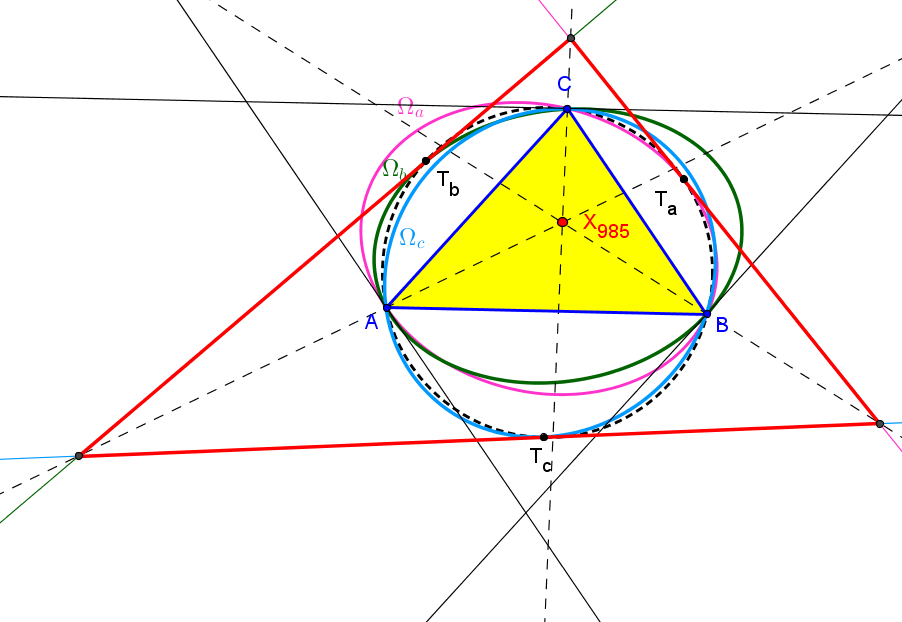
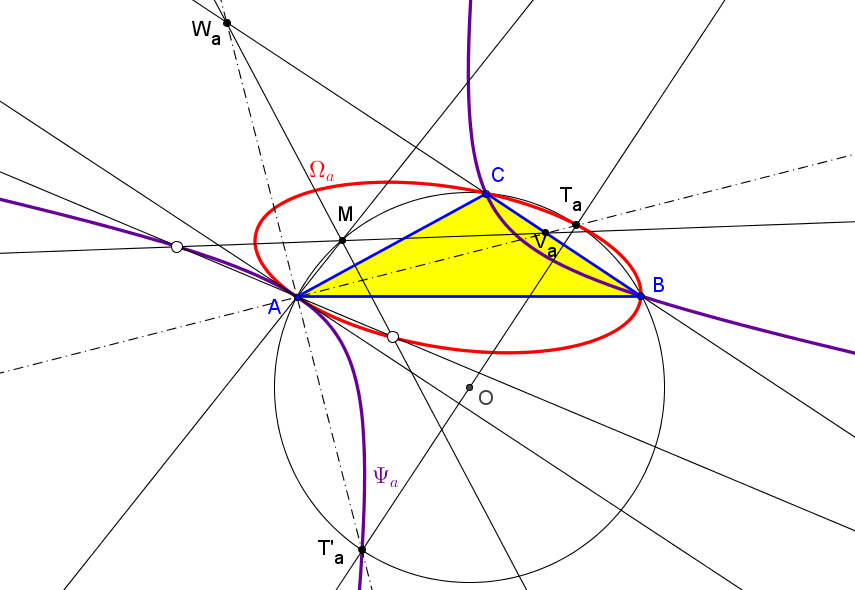
b c x (y + z) - a^2 y z = = 0.
Similarmente, se definen la cónicas Ψb y Ψc.Los triángulos ABC y PaPbPc son perspectivos con centro de perspectividad el punto X171.
(a (a^2 + b c) : b (b^2 + c a) : c (c^2 + a b))
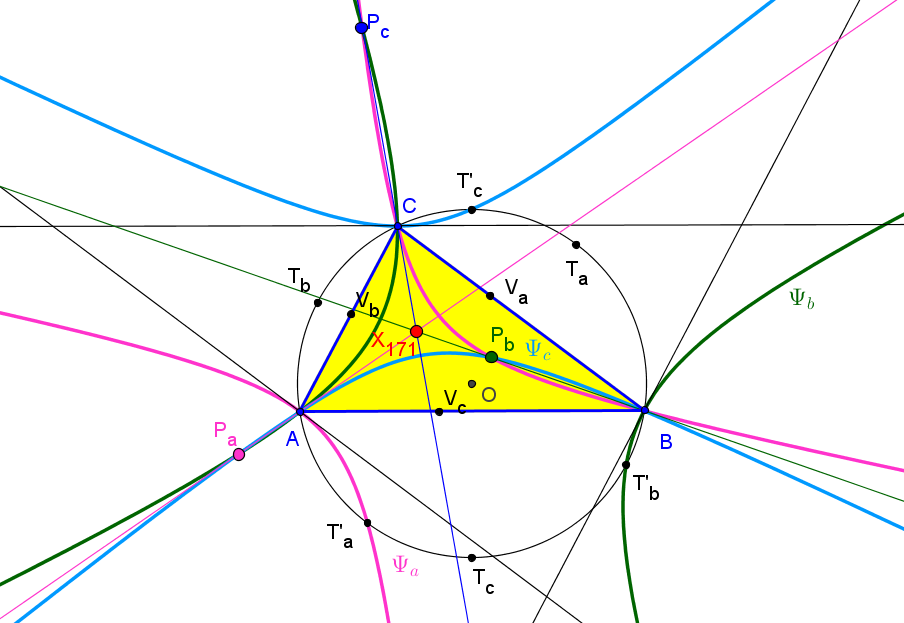
(a/(b^2-b c+c^2) : b/(c^2-c a+a^2) : c/(a^2-a b+b^2))
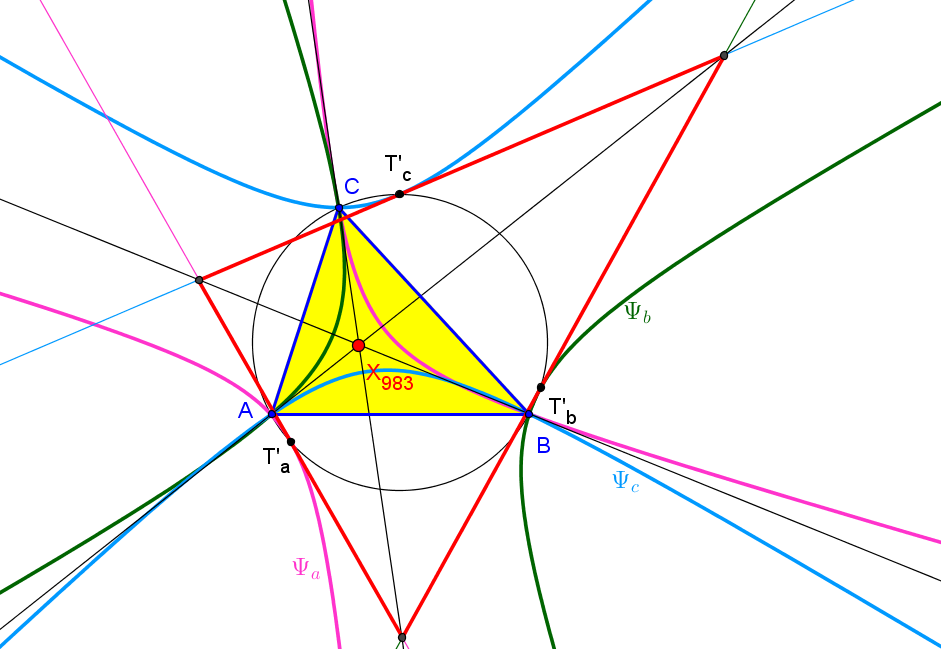
en recuerdo de Ricardo Mariño Caruncho, mi profesor.
1912-2003, La Coruña
Escritor, periodista, Licenciado en ciencias exactas, estudioso y admirador de la obra de Juan Jacobo Durán Loríga.
Era hijo de Pedro Mariño Ortega el gran Arquitecto Municipal entre cuyas obras destaca el Ayuntamiento de
La Coruña.
Otras facetas de su vida además de las matemáticas son sus conocimientos lingüísticos:inglés,francés
en este idioma escribe un libro "Geometrie Euclidianne Abstraite" publicación muy valorada en el campo matemático europeo.
Obras suyas son además: Elementos de la geometría vectorial, Notas sobre Juan Jacobo Durán-Loríga y Estudio genealógico sobre Juan Jacobo Durán Loríga.
Sea ABC un triángulo, para todo punto P situado en una recta d que pasa por el baricentro, el lugar geométrico de los puntos del plano del triángulo igualmente iluminados por tres focos de igual intensidad, colocados en sus vértices, que por otro de intensidad suma, situado en P, tiene una asíntota perpendicular a la recta d.
3/QP² = 1/QA² + 1/QB² + 1/QC².
El lugar geométrico es un curva algebraica de grado cinco, cuya ecuación consta de gran número de sumandos (junto con la recta del infinito).( 3a^2(v-w) + (b^2-c^2)(2u-v-w) : 3b^2(w-u) + (c^2-a^2)(2v-w-u) : 3c^2(u-v) + (a^2-b^2)(2w-u-v) ).
Este punto está en la dirección perpendicular a la de la recta GP.a^2 b^2 c^2 x^4 - 2 b^4 c^2 x^4 - 2 b^2 c^4 x^4 + a^4 c^2 x^3 y - 4 a^2 b^2 c^2 x^3 y + b^4 c^2 x^3 y - 3 a^2 c^4 x^3 y + 9 b^2 c^4 x^3 y + 2 c^6 x^3 y - 2 a^4 c^2 x^2 y^2 + 2 a^2 b^2 c^2 x^2 y^2 - 2 b^4 c^2 x^2 y^2 + 11 a^2 c^4 x^2 y^2 + 11 b^2 c^4 x^2 y^2 - 11 c^6 x^2 y^2 + a^4 c^2 x y^3 - 4 a^2 b^2 c^2 x y^3 + b^4 c^2 x y^3 + 9 a^2 c^4 x y^3 - 3 b^2 c^4 x y^3 + 2 c^6 x y^3 - 2 a^4 c^2 y^4 + a^2 b^2 c^2 y^4 - 2 a^2 c^4 y^4 + a^4 b^2 x^3 z - 3 a^2 b^4 x^3 z + 2 b^6 x^3 z - 4 a^2 b^2 c^2 x^3 z + 9 b^4 c^2 x^3 z + b^2 c^4 x^3 z + a^6 x^2 y z - 6 a^4 b^2 x^2 y z + 8 a^2 b^4 x^2 y z - 3 b^6 x^2 y z - 6 a^4 c^2 x^2 y z + 8 a^2 b^2 c^2 x^2 y z + b^4 c^2 x^2 y z + 8 a^2 c^4 x^2 y z + b^2 c^4 x^2 y z - 3 c^6 x^2 y z - 3 a^6 x y^2 z + 8 a^4 b^2 x y^2 z - 6 a^2 b^4 x y^2 z + b^6 x y^2 z + a^4 c^2 x y^2 z + 8 a^2 b^2 c^2 x y^2 z - 6 b^4 c^2 x y^2 z + a^2 c^4 x y^2 z + 8 b^2 c^4 x y^2 z - 3 c^6 x y^2 z + 2 a^6 y^3 z - 3 a^4 b^2 y^3 z + a^2 b^4 y^3 z + 9 a^4 c^2 y^3 z - 4 a^2 b^2 c^2 y^3 z + a^2 c^4 y^3 z - 2 a^4 b^2 x^2 z^2 + 11 a^2 b^4 x^2 z^2 - 11 b^6 x^2 z^2 + 2 a^2 b^2 c^2 x^2 z^2 + 11 b^4 c^2 x^2 z^2 - 2 b^2 c^4 x^2 z^2 - 3 a^6 x y z^2 + a^4 b^2 x y z^2 + a^2 b^4 x y z^2 - 3 b^6 x y z^2 + 8 a^4 c^2 x y z^2 + 8 a^2 b^2 c^2 x y z^2 + 8 b^4 c^2 x y z^2 - 6 a^2 c^4 x y z^2 - 6 b^2 c^4 x y z^2 + c^6 x y z^2 - 11 a^6 y^2 z^2 + 11 a^4 b^2 y^2 z^2 - 2 a^2 b^4 y^2 z^2 + 11 a^4 c^2 y^2 z^2 + 2 a^2 b^2 c^2 y^2 z^2 - 2 a^2 c^4 y^2 z^2 + a^4 b^2 x z^3 + 9 a^2 b^4 x z^3 + 2 b^6 x z^3 - 4 a^2 b^2 c^2 x z^3 - 3 b^4 c^2 x z^3 + b^2 c^4 x z^3 + 2 a^6 y z^3 + 9 a^4 b^2 y z^3 + a^2 b^4 y z^3 - 3 a^4 c^2 y z^3 - 4 a^2 b^2 c^2 y z^3 + a^2 c^4 y z^3 - 2 a^4 b^2 z^4 - 2 a^2 b^4 z^4 + a^2 b^2 c^2 z^4=0.
SumaCiclica[x^4 - 2 x^3 (y + z) - 3 x^2 y z - 3 y^2 z^2]=0
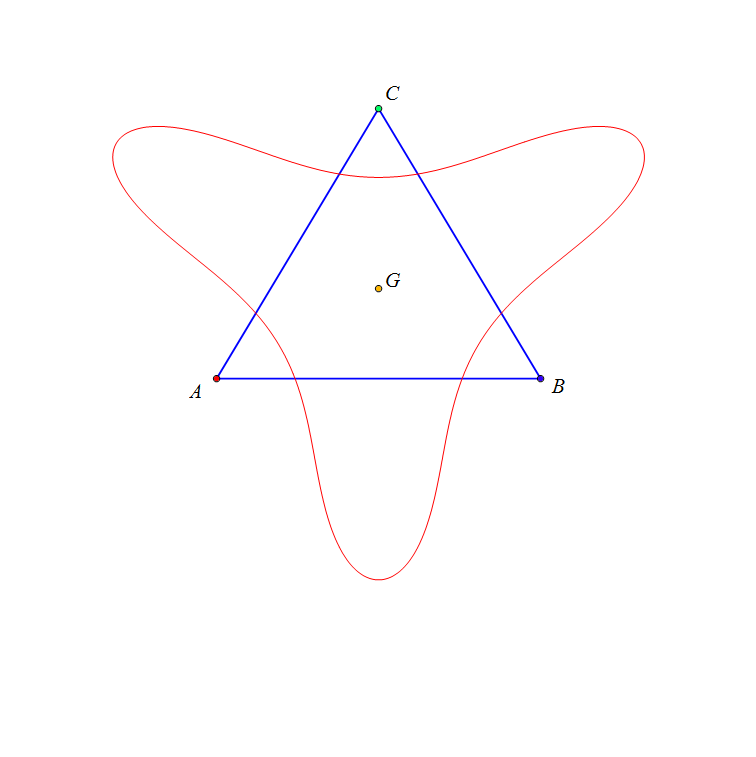
S4 - 6ωS2 + 9Sαβγ + 3 ω2=0,
S = α+β+γ ω = αβ+βγ+γα.

Juan Jacobo Durán Loriga
(Fuente: http://www.culturagalega.org/albumdaciencia/detalle.php?id=246)
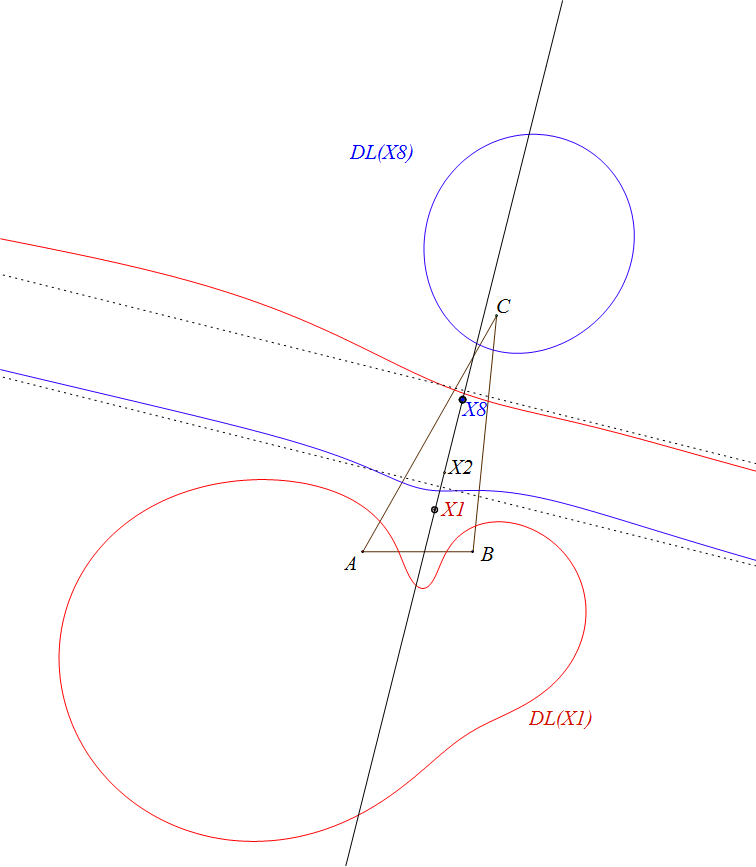
Sean ABC un triángulo, P un punto no situado en sus lados y DEF el triángulo ceviano de P. Las circunferencias de diámetros AE y AF se vuelven a cortar en A'. Los puntos B' y C' se definen cíclicamente. Los triángulos ABC y A'B'C' son perspectivos si y solo si P está en cúbica de Lucas (K007). El centro de perspectividad queda en la cúbica de Darboux.
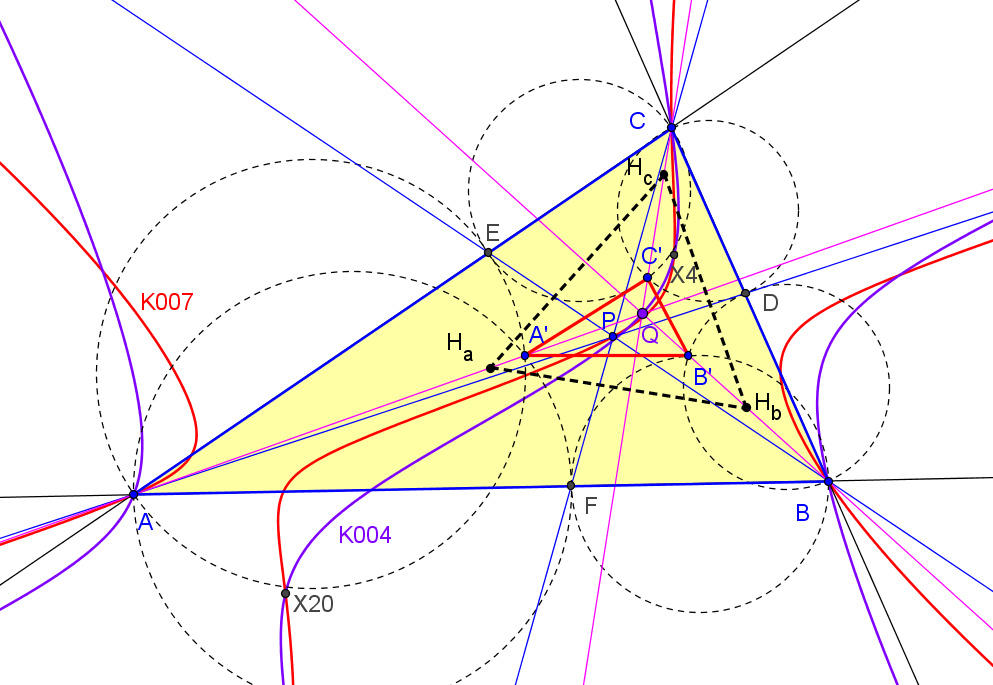
( u(SAu(v-w)² + SC(u+v)w² + SBv²(u+w)) : vw(SC(u+v)w + SAu(-v+w)) : vw(SAu(v-w) + SBv(u+w)) ).
Sean ABC un triángulo y P un punto.
Consideremos los tres triángulos equiláteros AAbAc, BBcBa y CCaCb, tales que Ba y Ca están en la ceviana AP, Cb y Ab están en la ceviana BP, y Ac y Bc están en la ceviana CP.
El punto Ab es la intersección de la recta BP con la recta pac que resulta de girar PC alrededor de A un ángulo de 60° en el sentido antihorario. El punto Ac es la intersección de la recta CP con la recta pab que resulta de girar BP alrededor de A un ángulo de 60° en el sentido horario. Procediendo cíclicamente, se construyen los puntos Bc, Ba, Ca y Cb.
Los centros Oa, Ob y Oc de estos tres triángulos equiláteros están alineados con P
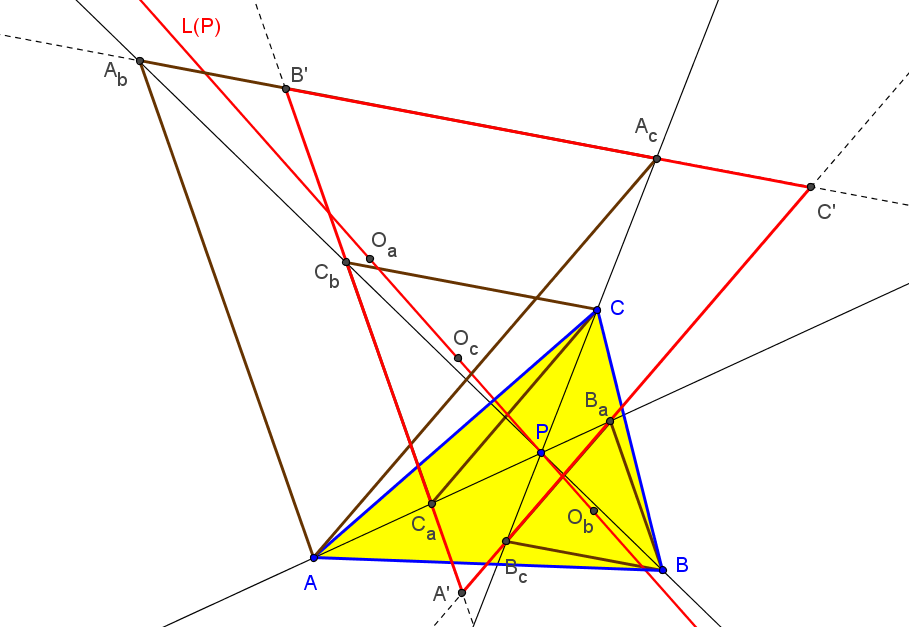
(a^2vw(v-w)-b^2w(v^2+uw+vw)+c^2v(w^2+uv+vw))x + (b^2wu(w-u)-c^2u(w^2+vu+wu)+a^2w(u^2+vw+wu))y + (c^2uv(u-v)-a^2v(u^2+wv+uv)+b^2u(v^2+wu+uv))z = 0
Ocurre además que el triángulo A'B'C' delimitado por las rectas AbAc, BcBa y CaCb es equilátero.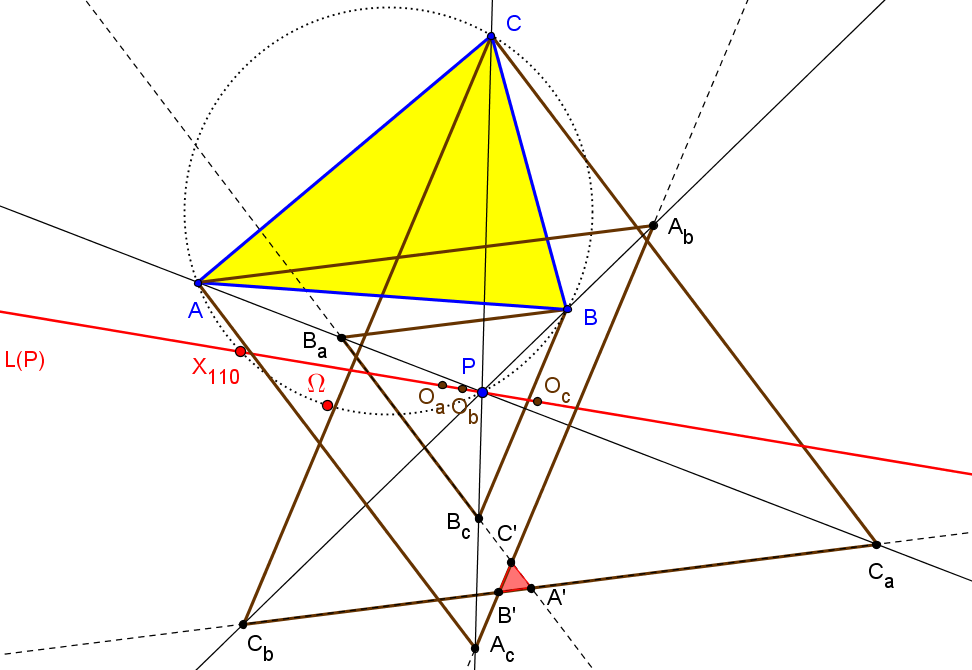
Ω = (1 / ((b²-c²)(3√3 b²c²SA+S(S²+9SA²))) : ... : ... ).
Este centro tiene primera coordenada trilineal exacta en el triángulo de ETC: 0.00000387325998676449736 y ha sido incluido en ETC con el nombre X(5618) = "1st Montesdeoca Equilateral Triangles Point".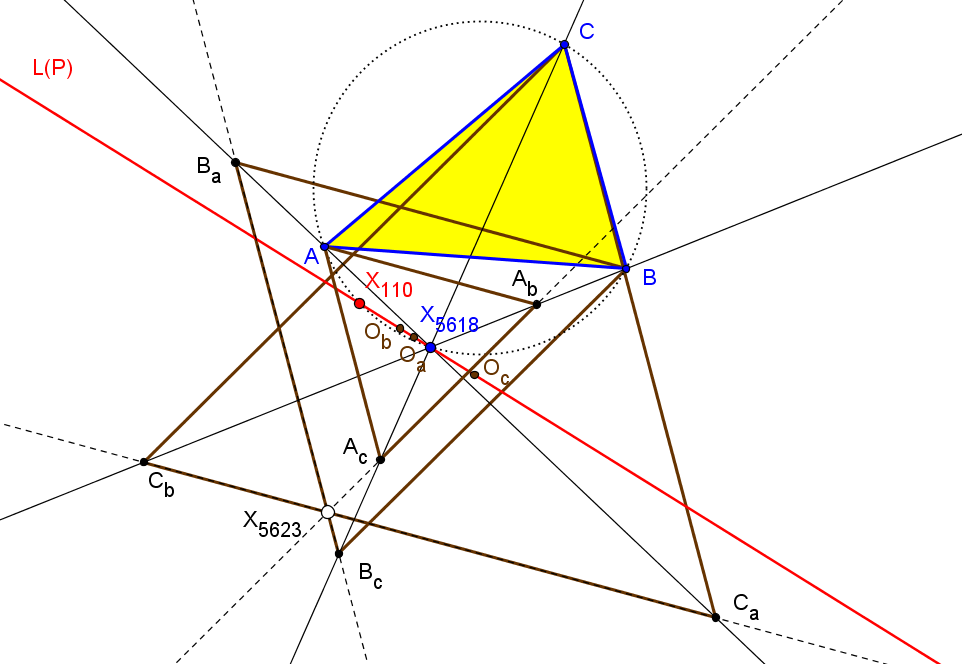
Invirtiendo los sentidos de los giros para construir el triángulo equilátero con un vértice en A y los otros dos vértices en las cevianas que no parten de A (así como para los que tienen uno de sus vértices en B o en C), obtenemos la descripción del punto X5619 = "2nd montesdeoca equilateral triangles point"
X5619 = (1 / ((b²-c²)(3√3 b²c²SA-S(S²+9SA²))) : ... : ... ).
Sea el punto A'b de intersección de BP con la recta qac que resulta de girar CP alrededor de A un ángulo de 60° en el sentido de las agujas del reloj. Y el punto A'c de intersección de CP con la recta qab que resulta de girar BP alrededor de A un ángulo de 60° en el sentido antihorario. El triángulo AA'bA'c resulta ser equilátero.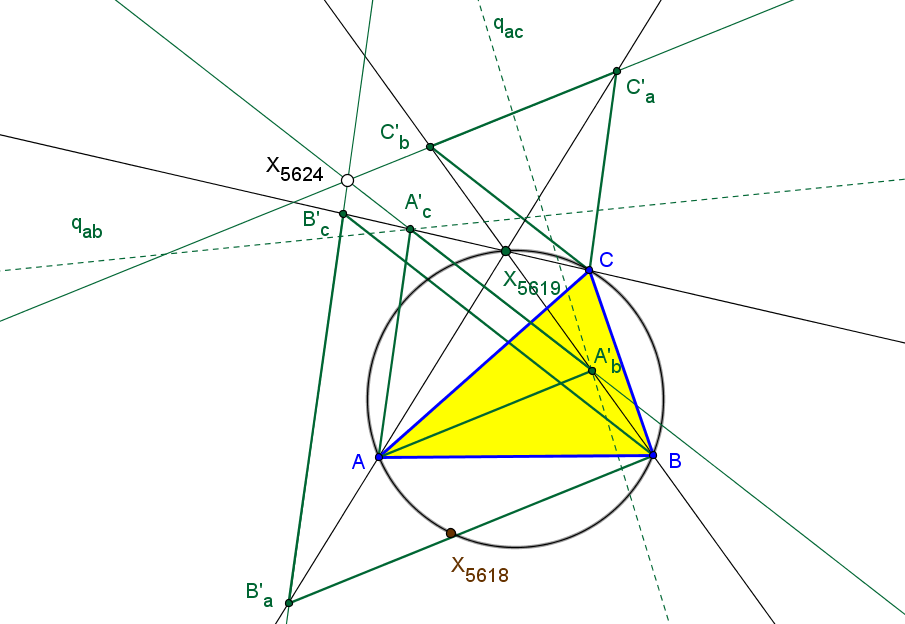
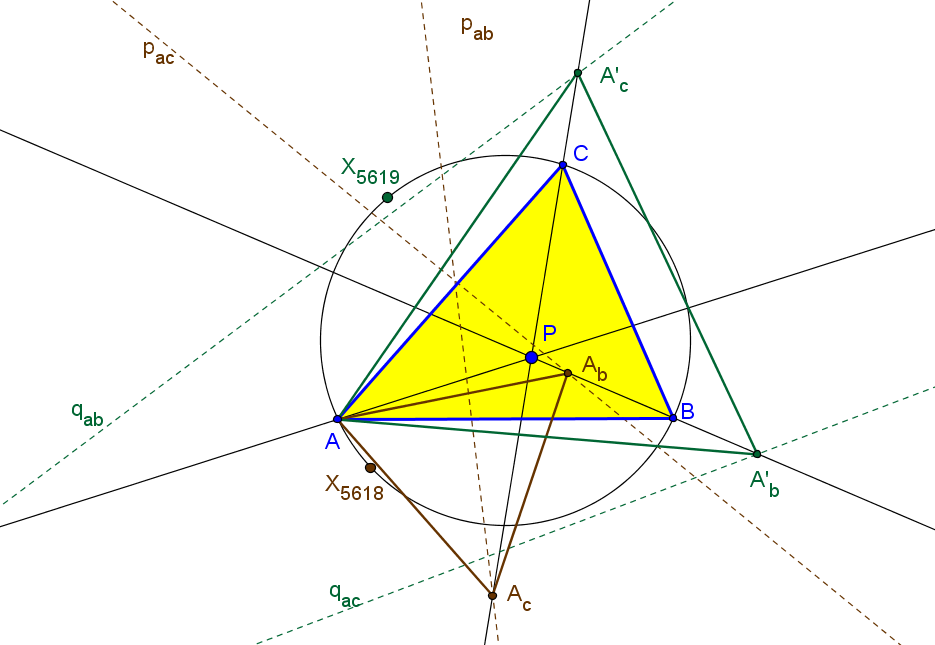
Sean ABC un triángulo y Q un punto. Encontrar los puntos P sobre la ceviana AQ tales que si Pb y Pc son los pies de las cevianas BP y CP, respectivamente, se cumpla que APb=APc.
(b^2 w^2)/(u + w)^2, (c^2 v^2)/(u + v)^2.
Por lo que, APb = APc si P está en una de las dos cónicas circunscritas a ABC con centro en el punto medio de BC y tangentes en A a las bisectrices interior y exterior, de ecuaciones respectivas:cy(x+z) + bz(x+y) = 0, cy(x+z) - bz(x+y) = 0.
Así, las solución del problema planteado son los dos puntos A1 y A2: segundos puntos de intersección de la ceviana AQ con cada una de las cónicas consideradas:
A1 = (-(b+c)qr : q(cq+br) : r(cq+br)), A2 = ((b-c)qr : q(cq-br) : r(cq-br)).
En el caso de que Q=H (ortocentro) :
A1 = (-a^4+(b^2-c^2)^2 : (a+b-c)(a-b+c)(a^2+b^2-c^2) : (a+b-c)(a-b+c)(a^2-b^2+c^2))
A2 = (a^4-(b^2-c^2)^2 : (b+c-a)(a+b+c)(a^2+b^2-c^2) : (b+c-a)(a+b+c)(a^2-b^2+c^2))
(Ver otra solución en el caso de Q el ortocentro de Ercole Suppa)
Sean ABC un triángulo, P un punto y DEF el triángulo ceviano de P.
La transformación afín que lleva los puntos A, B y C en D, E y F, respectivamente, tiene sus rectas fijas (propias) perpendiculares si y solo si P está en la cúbica de Lucas (K007).
Si las coordenadas baricéntricas de P, respecto a ABC, son (u:v:w) la matriz asociada a esta transformación afín es:
| 0 | u(u+v)(v+w) | u(u+w)(v+w) |
| v(u+v)(u+w) | 0 | v(u+w)(v+w) |
| w(u+v)(u+w) | w(u+v)(v+w) | 0 |
λ2,3 = 1/2 ((u+v)(u+w)(v+ w) ± (v+w)½ ((u+v)(u+ w)(u(v^2-w^2)+v(w^2-u^2)+w(u^2-v^2)))½)
La condición necesaria y suficiente para que los puntos fijos (en la recta del infinito) correspondientes a las raíces λ2 y λ3, determinen dos direcciones perpendiculares es:(b^2+c^2-a^2)u(v^2+w^2) + (c^2+a^2-b^2)v(w^2+u^2) + (a^2+b^2-c^2)w(u^2+v^2)=0.
Es decir, el punto P debe de estar en la cúbica de Lucas. En este caso, el punto fijo Q está sobre la cúbica de Thomson (K002).
Comparar esta propiedad de la cúbica de Lucas con la nº 7 en la web de Bernard Gibert:
"Let P be the perspector of an inscribed conic (C) with center Q. The circum-conic (C') passing through P and Q is a rectangular hyperbola if and only if P lies on the Lucas cubic".
Sean ABC un triángulo, P un punto y DEF el triángulo ceviano de P.
Consideremos los puntos U, V y W tales que:
AU : UD = BV : VE = CW : WF = m : n
Si (u:v:w) son las coordenadas baricéntricas de P, existen dos pares (m1,m1) y (m2,m2) reales o imaginarios:( u^2(v+w) + v^2(w+u) + w^2(u+v) + 2uvw ∓ √[(u+v)(v+w)(w+u)] √[u(v-w)^2+v(w-u)^2+w(u-v)^2], 4uvw )
para los cuales los puntos U, V y W están alineados. Las rectas que los contienen se cortan en el "crosspoint" de P y el baricentro.
Se considera la aplicación definida en términos de coordenadas baricéntricas, respecto a un triángulo ABC, por las ecuaciones:
| x' | = | (2SB SC - S²)x + (2SB² + S²)y + (2SC² + S²)z |
| y' | = | (2SA² + S²)x + (2SA SC - S²)y + (2SC² + S²)z |
| z' | = | (2SA² + S²)x + (2SB² + S²)y + (2SA SB - S²)z |
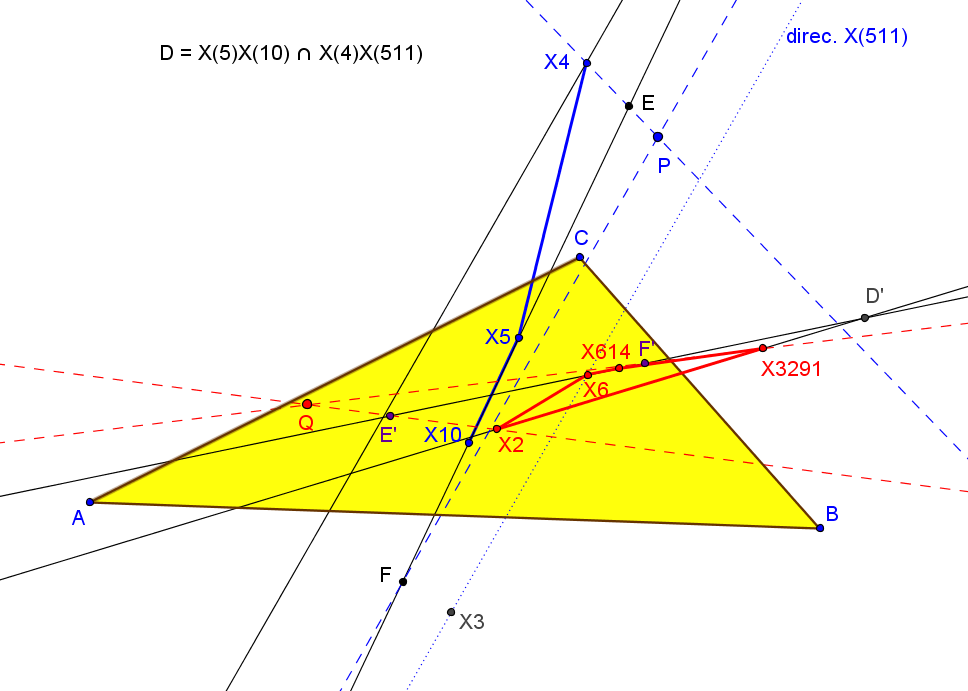
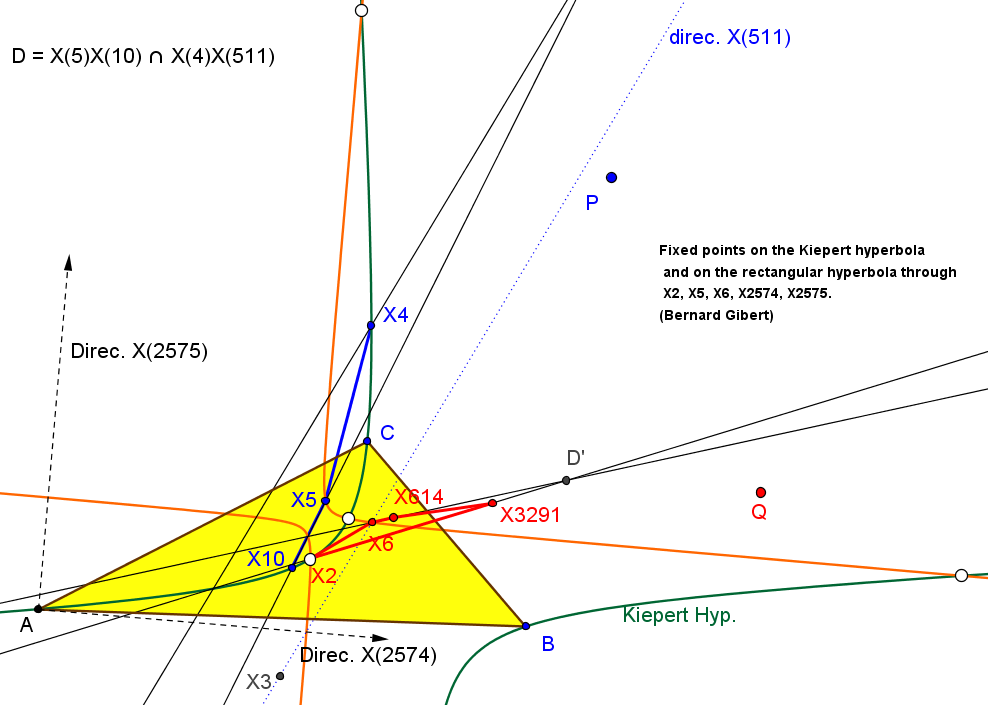
a Kake, por su "cumple"
Sean ABC un triángulo, A'B'C' su triángulo antipodal, P un punto y DEF el triángulo pedal de P.
Designamos por D' el conjugado armónico de D respecto a B y C. Definimos los conjugados armónicos E' y F' similarmente.
El punto A1 es la intersección del lado BC con la perpendicular a AD' por A'. De forma similar se definen B1 y C1.
Los triángulos ABC y A1B1C1 son perspectivos si y solo si P queda en al cúbica de Darboux.
El lugar geométrico de los centros de perspectividad de los triángulos ABC y A1B1C1, cuando P varía sobre la cúbica de Darboux, es la isocúbica pivotal pK(X3926,X3926), de ecuación baricéntrica: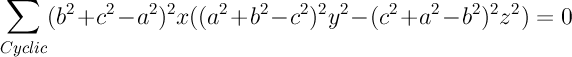
"La cúbica de Darboux es el lugar geométrico de los puntos P, en el plano del triángulo ABC, tal que los conjugados armónicos (respecto a los vértices de ABC) de los vértices de su triángulo pedal están alineados."
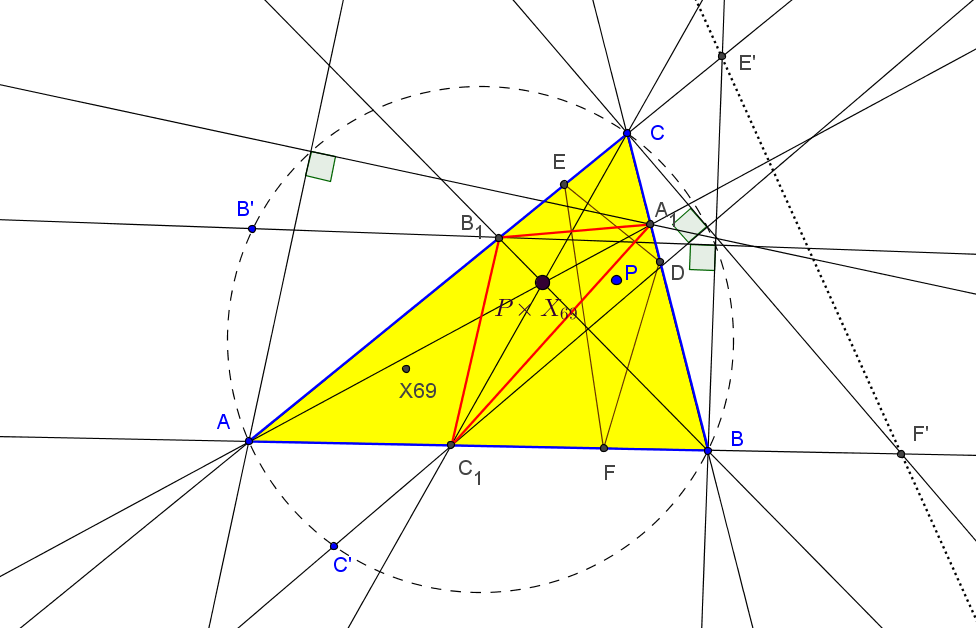
Resultado r1896 (Quim Castellsaguer):
Los baricentros Ga, Gb, Gc de los triángulos antimediales de ABC y el baricentro G de ABC son concíclicos en una circunferencia de centro el mismo de la circunferencia de los nueve puntos.
Otros centros sobre esta circunferencia son los de su intersección con el eje de Fermat: X381 (punto medio de X2X4) y X5465 (proyección ortogonal de X2 sobre el eje de Fermat).
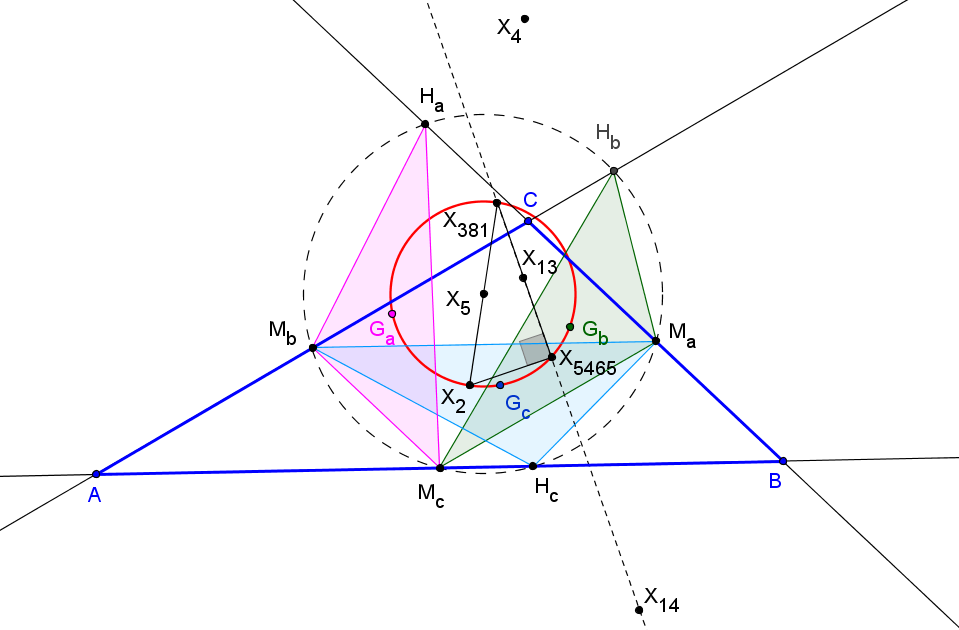
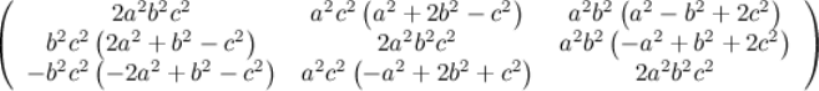
(6a^2b^2c^2 - λ) (a^8b^2c^2 - a^6b^4c^2 - a^4b^6c^2 + a^2b^8c^2 - a^6b^2c^4 + 3a^4b^4c^4 - a^2b^6c^4 - a^4b^2c^6 - a^2b^4c^6 + a^2b^2c^8 - λ^2)=0.
El punto correspondiente a la raíz λ=6a^2b^2c^2 es el centro de la semejanza inversa:S= (a^2(a^4 - 3a^2(b^2 + c^2) + 2b^4 - 11b^2c^2 +2c^4): ... : ... )
Los puntos correspondientes a las otras dos raíces del polinomio característico son los puntos del infinito de la hipérbola equilátera de Jerabek. Por lo que las rectas fijas de la semejanza son las paralelas por S a las asíntotas de esta hipérbola.
Sean ABC un triángulo, P un punto y DEF el triángulo pedal de P, Denotamos por E' el punto sobre BC tal que las circunferencias de los nueve puntos de ABC y A'B'C' son tangentes. Los puntos E' y F' se definen de forma similar, procediendo cíclicamente sobre los lados de ABC.
Los triángulos ABC y D'E'F son perspectivos si y solo si P está sobre la cúbica de Darboux ( K008). El lugar de los centros de perspectividad están sobre la cúbica K172.
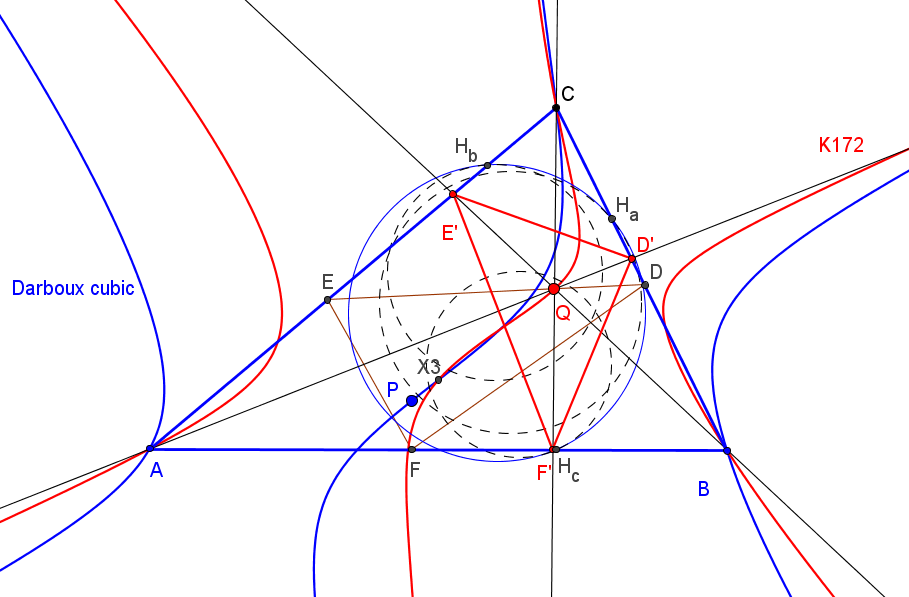
a Silvia, por su "cumple"
Sean ABC un triángulo, Ab el punto de intersección de la altura por B con la perpendicular a AB por A, y Ac el punto de intersección de la altura por C con la perpendicular a AC por A. Similarmente y cíclicamente se define los puntos Bc, Ba, Ca y Cb , entonces las rectas AbAc, BcBa y CaCb determinan un triángulo A'B'C' perspectivo con ABC, con centro de perspectividad en X262, de coordenadas baricéntricas:
( 1/(a^4 - a^2(b^2+c^2) - 2b^2c^2) : 1/(b^4 - b^2(c^2+a^2) - 2c^2a^2) : 1/(c^4 - c^2(a^2+b^2) - 2a^2b^2) ).
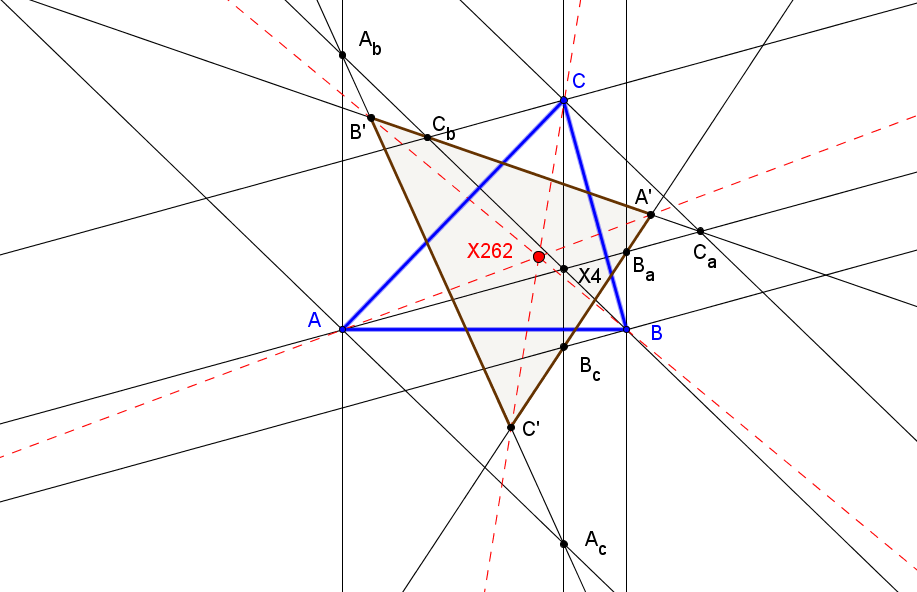
(a^2/(5a^4 - 4a^2(b^2+c^2) - (b^2-c^2)^2) : b^2/(5b^4 - 4b^2(c^2+a^2) - (c^2-a^2)^2) : c^2/(5c^4 - 4c^2(a^2+b^2) - (a^2-b^2)^2) ).
(Otra propiedad de X3426 en "El punto X(3426) como centro ortológico" )
Con las notaciones dadas en "A question from Mathesis and Bicentric Pairs" :
En el plano del triángulo ABC el lugar geométrico de los puntos P tales que las perpendiculares trazadas desde los vértices A, B, C respectivamente a las rectas PC, PA, PB son concurrentes en un punto Q es la cónica Φ1 circunscrita a ABC, que pasa por el punto de Tarry (X98) y por el conjugado isogonal P(40) del primer punto de Beltrami, P(2) (inverso del primer punto de Brocard, Ω1, respecto a la circunferencia circunscrita).
El lugar de los puntos Q, cuando P varía en la cónica Φ1 es la cónica Φ2 circunscrita a ABC, que pasa por el punto de Tarry (X98) y por el conjugado isogonal U(40) del segundo punto de Beltrami, U(2) (inverso del segundo punto de Brocard Ω2, respecto a la circunferencia circunscrita).
Cuando P=A, el punto Q (que denotamos por Ac) es la intersección de la perpendicular por A a AC con la altura por C.
Cuando Q=A, el punto P (que denotamos por Ab) es la intersección de la perpendicular por A a AB con la altura por B.
El lugar geométrico del punto D=PC ∩ QB, cuando P varía sobre la cónica Φ1, es una cónica, Γa, tangente en B y C a las perpendiculares a AB y AC, respectivamente; además pasa por Db=AC∩BAc y por Dc=AB∩CAb. Su ecuación baricéntrica respecto a ABC es:
SA² x² + SBSC yz + b² SB zx + c² SC xy =0.
Procediendo cíclicamente, resultan las cónicas Γb y Γc, lugares geométricos de los puntos E=PA ∩ QC y F=PB ∩ QA. Sus ecuaciones son:SB² y² + a² SA yz + SCSA zx + c² SC xy=0, SC² z² + a² SA yz + b² SB zx + SASB xy =0
( 1/(2a²SA³ - b²c²SBSC) : 1/(2b²SB³ - c²a²SCSA) : 1/(2c²SC³ - a²b²SASB) ).
Este centro tiene primera coordenada trilineal exacta en el triángulo de ETC: -5.73512334607375866920459161
Sean A'B'C' el triángulo antipodal de ABC; A"B"C" el triángulo ceviano del retrocentro R (X69 conjugado isotómico del ortocentro); D, E, F los puntos medios de A'A", B'B", C'C". Los triángulos ABC y DEF son ortológicos, y un centro de ortología es el punto de De Longchamps, X20.
El otro centro de ortología es el centro X3426 = X(3)-VERTEX CONJUGATE OF X(6).
Los triángulos circuncevianos del circuncentro y simediano son, respectivamente, A'B'C' y LMN; entonces las rectas A'L, B'M, C'N delimitan un triángulo A1B1C1 perspectivo con ABC, con centro de perspectividad en X3426.
(Otra propiedad de X3426 en "Los puntos X(74), X(262) y X(3426) como centros de perspectividad de triángulos" )
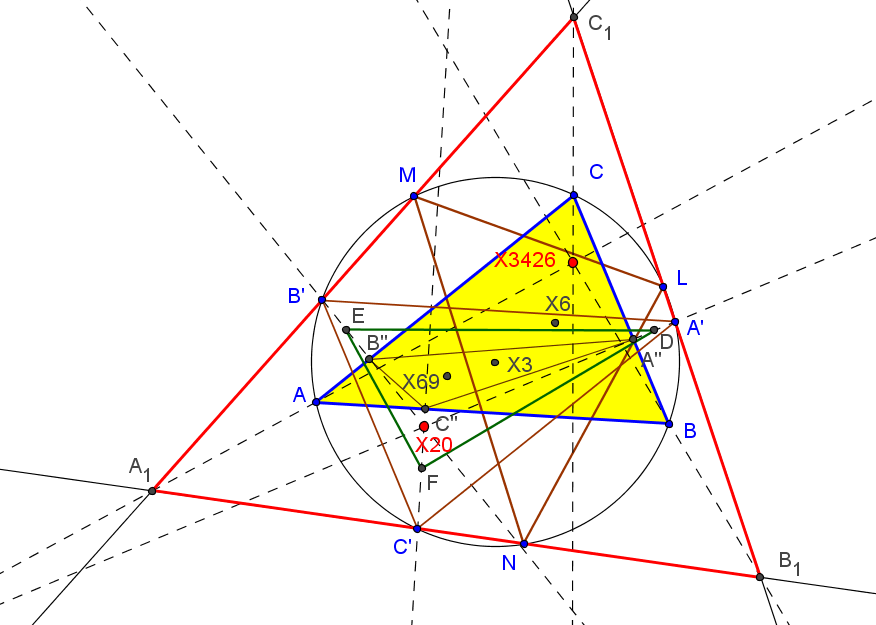
En el plano del triángulo ABC el lugar geométrico de los puntos P tales que las perpendiculares trazadas desde los vértices A, B, C respectivamente a las rectas PC, PA, PB son concurrentes en un punto Q es la cónica Φ1 circunscrita a ABC, que pasa por el punto de Tarry (X98) y por el conjugado isogonal P(40) del primer punto de Beltrami, P(2) (inverso del primer punto de Brocard, Ω1, respecto a la circunferencia circunscrita).
El lugar de los puntos Q, cuando P varía en la cónica Φ1 es la cónica Φ2 circunscrita a ABC, que pasa por el punto de Tarry (X98) y por el conjugado isogonal U(40) del segundo punto de Beltrami, U(2) (inverso del segundo punto de Brocard Ω2, respecto a la circunferencia circunscrita).
El lugar geométrico de los puntos P tales que las perpendiculares trazadas desde los vértices A, B, C respectivamente a las rectas PB, PC, PA son concurrentes en un punto Q es la cónica Φ2 circunscrita a ABC, que pasa por el punto de Tarry (X98) y por el conjugado isogonal del segundo punto de Beltrami (inverso del segundo punto de Brocard respecto a la circunferencia circunscrita). El lugar de los puntos Q, cuando P varía en la cónica Φ2 es la cónica Φ1 circunscrita a ABC, que pasa por el punto de Tarry (X98) y por el conjugado isogonal del primer punto de Beltrami (inverso del primer punto de Brocard respecto a la circunferencia circunscrita).
Las ecuaciones baricéntricas de las cónicas Φ1 y Φ2 son respectivamente:
(a^2+b^2-c^2)y z+ (-a^2+b^2+c^2)z x + (a^2-b^2+c^2)x y =0,
(a^2-b^2+c^2)y z+ (a^2+b^2-c^2)z x + (-a^2+b^2+c^2)x y =0.
(a^4 + 2a^2(b^2-2c^2) + b^4-4b^2c^2+3c^4 : ... : ...) y
(a^4 + 2a^2(c^2-2b^2) + c^4-4b^2c^2+3b^4 : ... : ...)
((a^2-b^2)(b^2-c^2)(a^2+b^2-c^2) : (b^2-c^2)(c^2-a^2)(-a^2+b^2+c^2) : (c^2-a^2)(a^2-b^2)(a^2-b^2+c^2)),
((a^2-c^2)(c^2-b^2)(a^2-b^2+c^2) : (b^2-a^2)(a^2-c^2)(a^2+b^2-c^2) : (c^2-b^2)(b^2-a^2)(-a^2+b^2+c^2)),
(a^8 - a^6(b^2+c^2) + a^4b^2c^2 + a^2(b^2-c^2)^3 - (b^2-c^2)^2(b^4+b^2c^2-c^4) : ... : ...),
(a^8 - a^6(b^2+c^2) + a^4b^2c^2 - a^2(b^2-c^2)^3 - (b^2-c^2)^2(c^4+b^2c^2-b^4) : ... : ...),
Sean ABC un triángulo, P un punto, A'B'C' el triángulo pedal de P y
A", B", C" las reflexiones de P en los lados BC, CA, AB, respectivamente.
El centro radical Rp de las circunferencias de diámetros A'B", B'C", C'A" y el centro radical Sp de las circunferencias de diámetros A'C", B'A", C'B" forman un par bicéntrico
Si (u:v:w) son las coordenadas baricéntricas de P:
Rp = (a^2 (3 b^2 c^2 u^2 (c^2 v + b^2 w) + u (c^4 (a^2 + b^2 - c^2) v^2 + 2 b^4 (a^2 - b^2 + c^2) w^2 + b^2 c^2 (3 a^2 - 2 b^2 + 2 c^2) v w) + a^2 (a^2 - b^2 - c^2)v w (2 c^2 v + b^2 w)) : ... : ... ),
Sp = (a^2 (3 b^2 c^2 u^2 (c^2 v + b^2 w) + u (2 c^4 (a^2 + b^2 - c^2) v^2 + b^2 c^2 (3 a^2 + 2 b^2 - 2 c^2) v w + b^4 (a^2 - b^2 + c^2) w^2) + a^2 (a^2 - b^2 - c^2) v w (c^2 v + 2 b^2 w) ) : ... : ... ).
Sean ABC un triángulo, P un punto, A'B'C' el triángulo pedal de P y
A", B", C" las reflexiones de P en los lados BC, CA, AB, respectivamente.
Los seis puntos medios de los segmentos
A'B", B'C", C'A", A'C", B'A", C'B" están sobre una cónica,
ya que los lados opuestos del hexágono que ellos forman son paralelos.
El lugar geométrico de los puntos P tales que las rectas de Euler de los triángulos ABC y IPP* son paralelas es una séxtica que pasa por A, B, C, (puntos dobles), por I, por los exincentros, por los conjugados isogonales de sus puntos.
Ecuación baricéntrica:
(Mostrar)
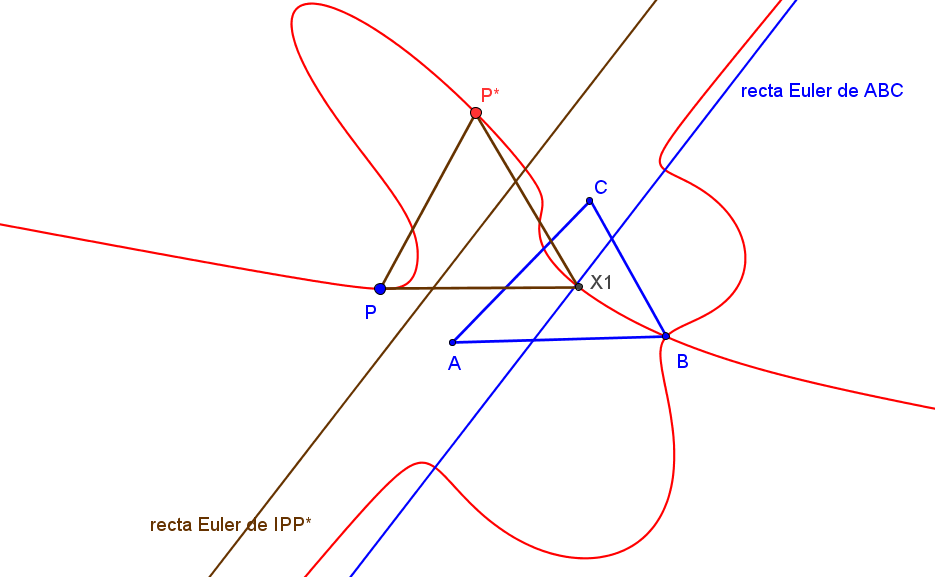
Sean ABC un triángulo, P un punto, A'B'C' el triángulo tangencial, P un punto y L una recta por P.
Consideremos las proyecciones ortogonales A*, B*, C* de los vértices A, B, C sobre la recta L, respectivamente.
Los puntos medios Ma, Mb, Mc de AA*, BB*, CC*, respectivamente.
Los puntos medios M1, M2, M3 de A'Ma, B'Mb, C'Mc, respectivamente.
Entonces, los triángulos ABC y M1M2M3 son ortológicos.
Si (u:v:w) son las coordenadas baricéntricas de P, las perpendiculares por los vértices M1, M2 y M3 a los lados BC, AC y AB, respectivamente, concurren sobre una cónica. cuyo centro tiene coordenadas baricéntricas:
Q = ( a^4(2u+v+w) - 2a^2(b^2+c^2)(3u+2(v+w)) + (b^2-c^2)^2(4u+3(v+w)) : ... : ... ).
(2a^4 - a^3(b+c) - a^2(5b^2-2bc+5c^2) + a(b-c)^2(b+c) + 3(b^2-c^2)^2 :...:...)
que tiene (6-9-13)-número de búsqueda en ETC: 1.473737731682850782032396958a^2yz+b^2zx+c^2xy + (3/64)(x+y+z)((3a^2-5b^2-5c^2)x + (3b^2-5c^2-5a^2)y + (3c^2-5a^2-5b^2)z) = 0.
(2a^4 - 9a^2(b^2+c^2) + 7(b^2-c^2)^2:...:..)
que tiene (6-9-13)-número de búsqueda en ETC: 1.3315581357050847119617684585(2a^6 - 5a^4(b^2+c^2) - 16a^2b^2c^2 + 3(b^2-c^2)^2(b^2+c^2) : ..:...)
que tiene (6-9-13)-número de búsqueda en ETC: 1.3865627298839303658207405225

Sean ABC un triángulo, O el circuncentro, DEF el triángulo medial y A', B', C' los puntos medios de AO, BO, CO, respectivamente.
Los centros radicales:
P, de las circunferencias de diámetros A'E, B'F, C'D, y
U, de las circunferencias de diámetros A'F, B'D, C'E, forman un par bicéntrico (que podría recibir el nombre de una flor: CRESTA DE GALLO).
Sus coordenadas baricéntricas son:
P = (3a^4-a^2(2b^2+7c^2)+b^4-3b^2c^2+2c^4 : ... : ... )
U = (3a^4-a^2(7b^2+2c^2)+2b^4-3b^2c^2+c^4 : ... : ... ).
Sean ABC un triángulo y P un punto. La circunferencia circunscrita al triángulo BCP interseca a las rectas AB y AC en los puntos Ca y Ba. Similarmente, tenemos los puntos Ab, Cb, Bc y Ac. El lugar geométrico de los puntos P tales que Ca, Ba, Ab, Cb, Bc y Ac estén en una cónica es la (segunda) cúbica de Brocard ( K018 del catálogo de Bernard Gibert):
Locus property:
6.
Locus of point M such that the three circles MBC, MCA, MAB meet the sidelines of triangle ABC again at six points lying on a same conic.
Sean ABC un triángulo, O su circuncentro, P un punto y Oa, Ob, Oc los circuncentros de los triángulos PBC, PCA, PAB, respectivamente.
La cúbica de Thomson
es el lugar geométrico de los puntos P tales que el baricentro de OaObOc está sobre la recta OP.
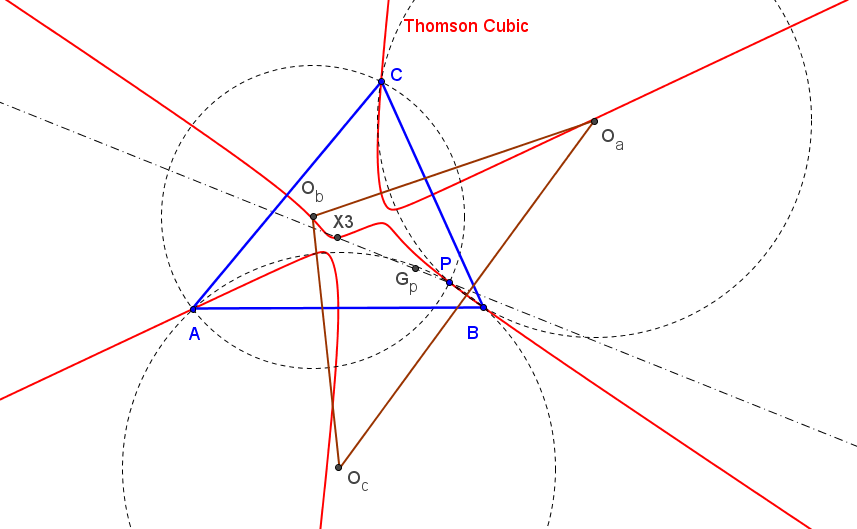
Sea ABC un triángulo y A'B'C' el triángulo homotético a ABC por la homotecia de centro en el baricentro y razón t.
Se denota por:
Ab = B'C' ∩ AC, Ac = B'C' ∩ AB,
Bc = C'A' ∩ BA, Ba = C'A' ∩ BC,
Ca = A'B' ∩ CB, Cb = A'B' ∩ CA.
Rt el centro radical de las circunferencias A(AAb),
B(BBc), C(CCa):
( c^2 (b^2 - c^2) (2 + t)^2 + a^4 (-5 + 4 t + t^2) + a^2 (-3 b^2 (1 + 4 t + t^2) + c^2 (17 + 8 t + 2 t^2)) :
-a^4 (2 + t)^2 + b^2 (b^2 (-5 + 4 t + t^2) - 3 c^2 (1 + 4 t + t^2)) + a^2 (c^2 (2 + t)^2 + b^2 (17 + 8 t + 2 t^2)) : -b^4 (2 + t)^2 + c^4 (-5 + 4 t + t^2) + b^2 c^2 (17 + 8 t + 2 t^2) + a^2 (b^2 (2 + t)^2 - 3 c^2 (1 + 4 t + t^2)) )
St el centro radical de las circunferencias A(AAc),
B(BBa), C(CCb):
( -b^2 (b^2 - c^2) (2 + t)^2 + a^4 (-5 + 4 t + t^2) +
a^2 (-3 c^2 (1 + 4 t + t^2) + b^2 (17 + 8 t + 2 t^2)) :
-c^4 (2 + t)^2 + b^4 (-5 + 4 t + t^2) + b^2 c^2 (17 + 8 t + 2 t^2) +
a^2 (c^2 (2 + t)^2 - 3 b^2 (1 + 4 t + t^2)) :
-a^4 (2 + t)^2 + c^2 (c^2 (-5 + 4 t + t^2) - 3 b^2 (1 + 4 t + t^2)) +
a^2 (b^2 (2 + t)^2 + c^2 (17 + 8 t + 2 t^2)) )
Rt y St forman un par bicéntrico de punto medio sobre la recta de Euler, si t=m/n:
Mt = ( (b^2-c^2)^2(m+2 n)^2 + a^2(b^2+c^2)(m^2+4mn-14n^2) -
2a^4(m^2+ 4mn-5n^2) : ... : .... ).
| t=1,-5 | X(5) | ABC=A'B'C' |
|---|---|---|
| t=-1/2 | X(3530) | A'B'C'= triángulo medial |
| t=-2 | X(3) | A'B'C'= triángulo anticomplementario |
| t=-1 | (16a^4 - 17a^2(b^2+c^2) + (b^2-c^2)^2: ... : ...) | A'B'C'= triángulo reflexión de ABC en el baricentro |
| t↦0 | X(5054) | A'B'C' degenera en el baricentro |
| t= -2 ± Sqrt[6] | X(2) | |
| t= -2 ± 3Sqrt[2] | X(4) |
Sean ABC un triángulo, P un punto y DEF el triángulo ceviano de P.
Las rectas que pasan por E y F, paralelas a AD intersecan a BC en A1 y A2. Similarmente tenemos los puntos B1, B2, C1, C2. Entonces los seis puntos A1, A2, B1, B2, C1, C2 están en una cónica.
Su ecuación baricéntrica, si P(u:v:w), es
Σ v^2w^2(u+v+w)x^2 - uvw(2u^2+(v+w)(2u+v+w))yz=0.
Esta cónica es homotética a la cónica circunscrita de centro en el complemento P' de P (PG=2GP'). ( Francisco Javier García Capitán )
| P | X(1) | X(2) | X(4) | X(8) | X(20) |
| Centro cónica | X(3743) | X(2) | X(389) | X(960) | X(2883) |
|---|
Sea ABC un triángulo. Se denota por:
Ab y Ac las proyecciones ortogonales de A sobre las bisectrices por B y C, respectivamente. Ha es el ortocentro del triángulo AAbAc. Similarmente, se consideran los ortocentros Hb y Hc.
Entonces los triángulos ABC y HaHbHb son ortológicos y sus centros ortológicos son el ortocentro de ABC y el centro del triángulo X84.
Sean ABC un triángulo y O su circuncentro. Se denota por:
Na, Nb, Nc los centros de las circunferencias de los nueve puntos de los triángulos OBC, OCA, OAB, respectivamente, y por
Ma, Mb, Mc los puntos medios de ANa, BNb, CNc, respectivamente.
Entonces, los triángulos ABC y MaMbMc son ortológicos. Los centro ortológicos son X5 y X3521.
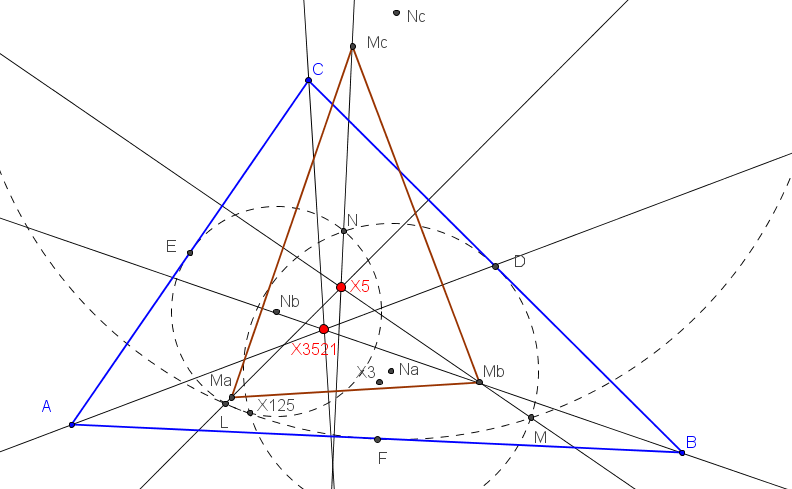
Sean ABC un triángulo, P4 un punto y P1P2P3 su triángulo anticeviano; entonces, P1P2P3P4 es un cuadrivértice con puntos diagonales A, B y C (ABC es el triángulo diagonal del cuadrivértice).
Un sistema de QA-DT-coordenadas relativas al cuadrivértice P1P2P3P4, se define tomando como triángulo de referencia el triángulo diagonal y uno de los vértices del cuadrivértices, por ejemplo P4, con coordenadas (p:q:r); los otros tres vértices forman el triángulo anticeviano de P4:
P1(-p:q:r), P2(p:-q:r), P3(p:q:-r).
Denotamos por Ci el centro de la cónica que pasa por los cinco puntos A, B, C, Pi y QA-P10 (i=1,2,3,4), donde QA-P10 es el baricentro del triángulo diagonal ABC. Se verifica que las rectas PiCi son concurrentes en el punto de DT-coordenadas:
( p^2(q^2+r^2) : q^2(r^2+p^2) : r^2(p^2+q^2 ).
p^2(q^2-r^2)y^2z^2 + q^2(r^2-p^2)z^2x^2 + r^2(p^2-q^2)x^2y^2 = 0.
Esta cuártica es conjugada isogonal de la cónica de ecuación:p^2x^2(q^2-r^2)+q^2y^2(r^2-p^2)+r^2z^2(p^2-q^2)=0.
Esta cónica contiene a las vértices del triángulo anticeviano de sus puntos. Como pasa por los centros QA-P10 y QA-P19 también pasa por los vértices de sus triángulos anticevianos, GaGbGc (triángulo antimedial del triángulo diagonal) y LMN, respectivamente. Así, cónica y cuártica pueden construirse.( 1/(p^2(q^2-r^2)) : 1/(q^2(r^2-p^2)) : 1/(r^2(p^2-q^2)) ).
q^2 r^2 (q^2 - r^2) x^3 + q^2 r^2 (2 p^2 (y - z) - (q^2 - r^2) (y + z)) x^2 + p^2 r^2 (r^2 - p^2) y^3 + p^2 r^2 (2 q^2 (z - x) - (r^2 - p^2) (x + z)) y^2 + p^2 q^2 (p^2 - q^2) z^3 + p^2 q^2 (2 r^2 (x - y) - (p^2 - q^2) (x + y)) z^2=0.

Sean ABC un triángulo y A'B'C' el triángulo ceviano del incentro. Se denota por:
(Oab), (Oac) las circunferencias circunscritas a los triángulos AAbA', AAcA', resp.
(Obc), (Oba) las circunferencias circunscritas a los triángulos BAcB', BBaB', resp.
(Oca), (Ocb) las circunferencias circunscritas a los triángulos CCaC', CCbC', resp.
Las coordenadas baricéntricas del centro radical R de las circunferencias (Obc), (Oca), (Oab) son:
R = (a (a^2(b-2c) - a(b^2+b c-c^2) - (b-c)c^2 ) : ... : ... ).
Las coordenadas baricéntricas del centro radical S de las circunferencias (Oba), (Ocb), (Oac) son:
S = (a (a^2(2b-c) - a(b^2-b c-c^2) - b^2(b-c)) : ... : ... ).
Los puntos R y S forman un par bicéntrico P(110) (que podría recibir el nombre de una flor: MORGALLANA o botón de oro), por tanto el punto del infinito de la recta RS es un centro: X1938, que coincide con el punto del infinito del par bicéntrico PU(15).
La suma de las coordenadas baricéntricas de este par baricéntrico es el centro X942, inverso en la circunferencia inscrita del inverso en la circunferencia circunscrita del incentro.
La diferencia de las coordenadas baricéntricas de este par baricéntrico es el centro de coordenadas baricéntricas:
( a(b-c)(3a^2-2a b-b^2-2a c-c^2): ... : ...),
con número de búsqueda en ETC: -8.16982446237566024925964383. El punto medio de RS es un centro, de coordenadas baricéntricas:M = (a (3a^4(b-c)^2 + a^3(-5b^3+4 b^2c+4b c^2-5c^3) + a^2(b^4+5b^3c-14b^2c^2+5b c^3+c^4) + a(b-c)^2(b^3+c^3) - b c(b-c)^2(b^2+c^2)) : ... : ...),
con número de búsqueda en ETC: 1.2448168635877587605351158452.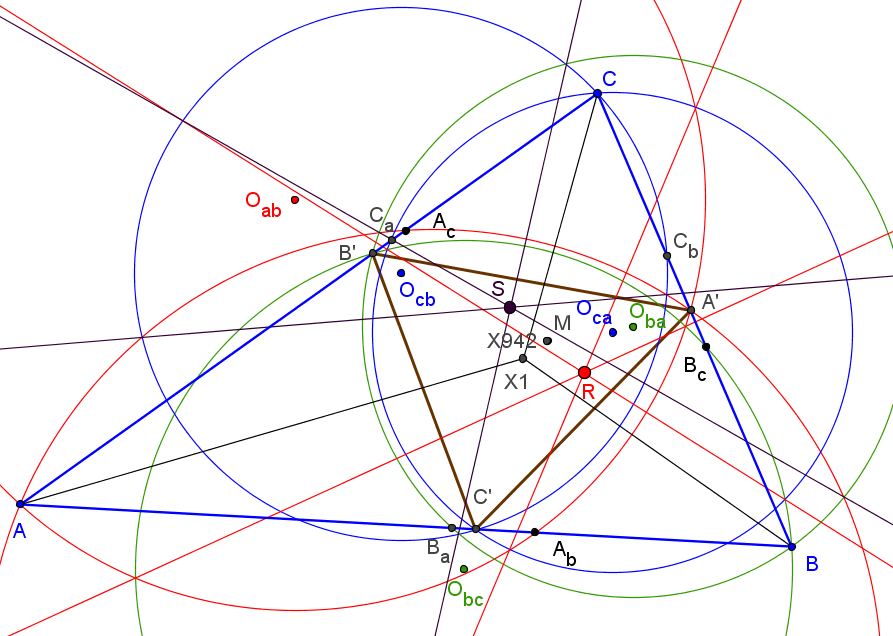
Sean ABC un triángulo y A'B'C' su triángulo medial. Se denota por:
Obc y Ocb los circuncentros de los triángulos BCB' y BCC', respectivamente, y por Ma el punto medio de ObcOcb. Similarmente se definen Mb y Mc.
El baricentro G' de MaMbMc queda en la recta de Euler de ABC y sus coordenadas baricéntricas son:
G' = (2 SB SC + 11 a^2 SA : 2 SC SA + 11 b^2 SB : 2 SA SB + 11 c^2 SC),
es el complemento de X3845 y divide al segmento GO en la razón GG':G'O = 3:1.

Sean ABC un triángulo y A'B'C' el triángulo ceviano del incentro. Se denota por:
(Nab), (Nac) las circunferencias de los nueve puntos de los triángulos AIB', AIC', resp.
(Nbc), (Nba) las circunferencias de los nueve puntos de los triángulos BIC', BIA', resp.
(Nca), (Ncb) las circunferencias de los nueve puntos de los triángulos CIA', CIB', resp.
Las coordenadas baricéntricas del centro radical R de las circunferencias (Nbc), (Nca), (Nab) son:
R = ( a(a + b - c) (a - b + c) (a^3 b - a b^3 + 2 a^3 c - 2 a b^2 c - b^3 c +
a^2 c^2 - 3 a b c^2 - 3 b^2 c^2 - 2 a c^3 - 3 b c^3 - c^4) : ... : ... ).
Las coordenadas baricéntricas del centro radical S de las circunferencias (Nba), (Ncb), (Nac) son:
S = ( a (a + b - c) (a - b + c) (2 a^3 b + a^2 b^2 - 2 a b^3 - b^4 +
a^3 c - 3 a b^2 c - 3 b^3 c - 2 a b c^2 - 3 b^2 c^2 - a c^3 -
b c^3) : ... : ... ).
Los puntos R y S forman un par bicéntrico P(111) (que podría recibir el nombre de una flor: CANARINA o bicácaro), por tanto el punto del infinito de la recta RS es un centro: X513.
También el punto medio de RS es un centro, de coordenadas baricéntricas:
M = (a(3a^5(b+c)+ a^4(b^2+c^2) - 2a^3(3b^3+b^2c+b c^2+3c^3) - 2a^2(b^4+ b^3c+4b^2c^2+b c^3+c^4) + a(b-c)^2(3b^3+5b^2c+5b c^2+3c^3)+ (b-c)^2(b+c)^4) : ... : ...),
con número de búsqueda en ETC: 2.235165076122804495064988816.
Sean ABC un triángulo, P un punto y A'B'C' el triángulo ceviano de P. Denotamos por Ab la reflexión, respecto a C, de la proyección ortogonal de A' sobre AC y por Ac la reflexión, respecto a B, de la proyección ortogonal de A' sobre AB . Sea Oa el circuncentro del triángulo AAbAc; similarmente, se consideran los circuncentros Ob y Oc.
• Los triángulos ABC y OaObOc son perspectivos si y solo si P está en la cúbica pivotal pK(X1073, X253). Esta cúbica pasa por los centros X(2), X(3), X(64), X(69), X(253), X(1073), ...
Ω = ( a^2SA/(a^4 + 2a^2(b^2+c^2) - 3(b^2-c^2)^2) : ... : ...),
con número de búsqueda en ETC: 5.40902452312896952998608493.X = ( 1/(a^4 + 2a^2(b^2+c^2) - 3(b^2-c^2)^2) : ... : ...),
con número de búsqueda en ETC: 6.399682552061115067504709200.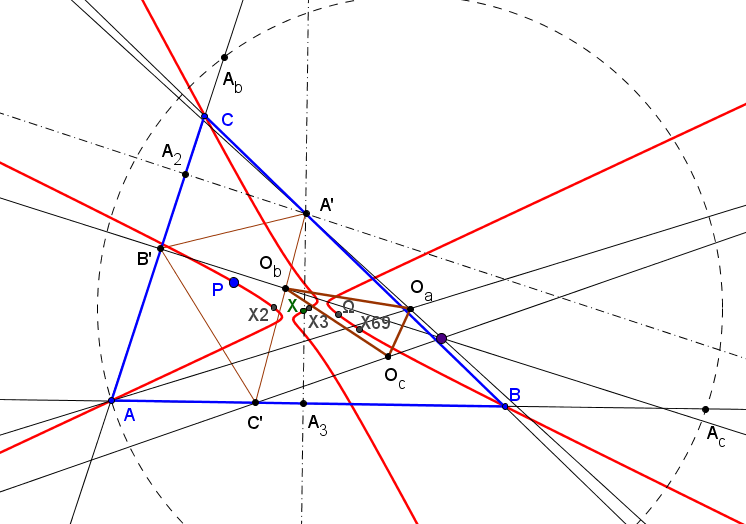
a Clara, por su "cumple"
Sean ABC un triángulo, P un punto y A'B'C' el triángulo ceviano de P. Denotamos por Ab la reflexión de C respecto a la perpendicular por A' a AC y por Ac la reflexión de B respecto a la perpendicular por A' a AB. Sea Oa el circuncentro del triángulo AAbAc; similarmente, se consideran los circuncentros Ob y Oc.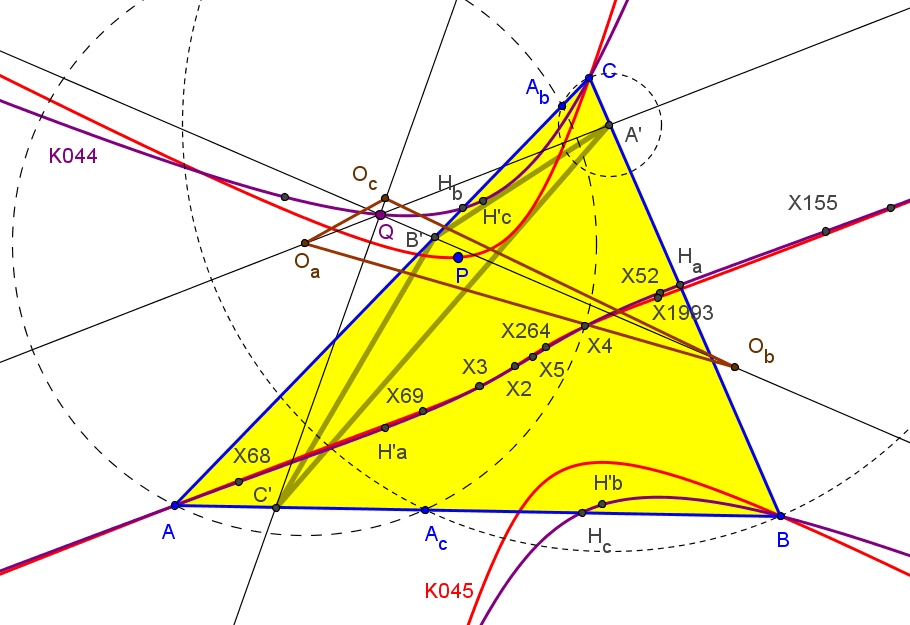
Σ[ x(c^2(a^2+b^2-c^2)(a^4-a^2 b^2-2a^2c^2-b^2c^2+ c^4) y^2 - b^2(a^2-b^2+ c^2)(a^4-2a^2b^2+b^4-a^2c^2-b^2c^2) z^2)] =0.
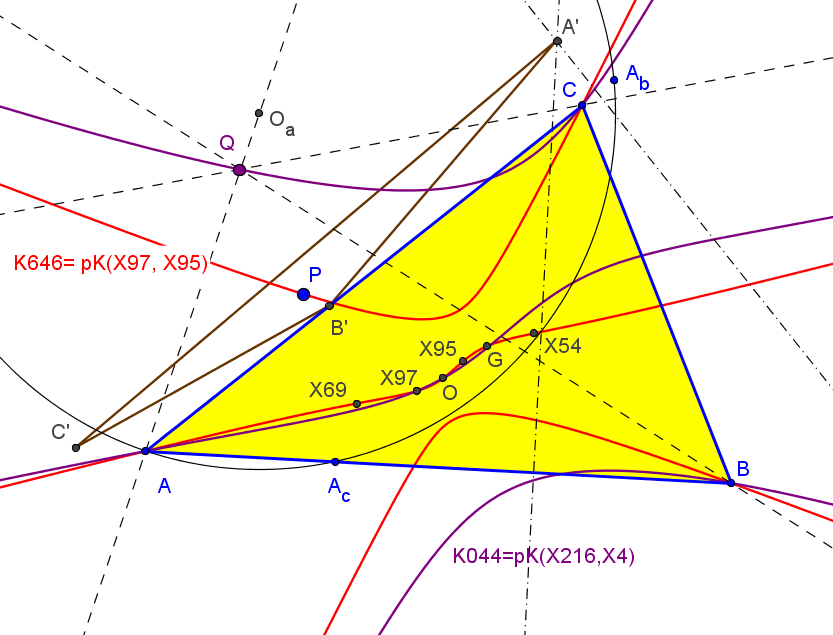
X = ( (a^3+a^2(b+c) - a(b+c)^2 - (b-c)^2(b+c)) (a^3(b+c) - a^2(b-c)^2 - a(b-c)^2(b+c) + (b^2-c^2)^2) : ... : ... ).
que tiene (6-9-13)-número de búsqueda en ETC: 30.3292407999481595887008929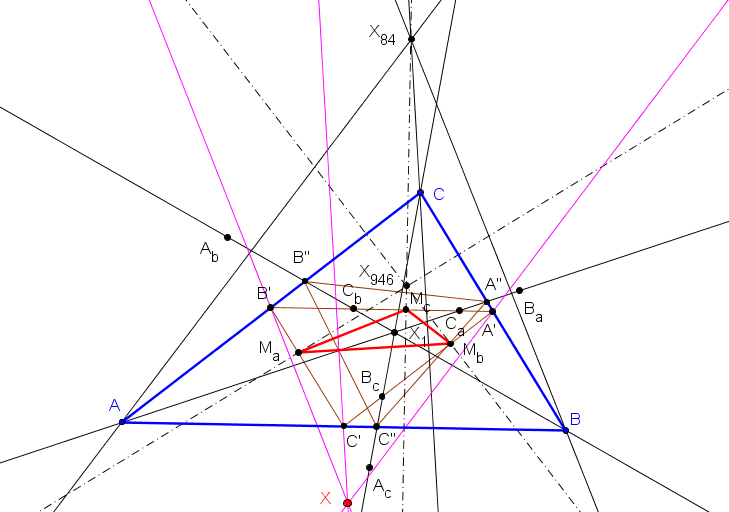
fx^2 + gy^2 + hz^2 + 2pyz + 2qzx + 2rxy = 0,
su centro y perspector (centro de perspectividad de ABC y el triángulo formado por las polares de sus vértices respecto a la cónica) coinciden si y sólo si p=q=r≠0.
(Paul Yiu).
UN EJEMPLO:
(Anopolis #774 Antreas P. Hatzipolakis)
Sean ABC un triángulo, A'B'C' su triángulo antimedial y A"B"C" el triángulo pedal del incentro.
Se denota por Ab = A"B" ∩ B'C' y por Ac = A"C" ∩ B'C'.
Similarmente y de forma cíclica de definen Bc, Ba y Ca, Cb.
Los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están en una misma cónica de ecuación:
(b+c-a)^2(a+b-3c)(a-3b+c)x^2 + (c+a-b)^2(b+c-3a)(b-3c+a)y^2 + (a+b-c)^2(c+a-3b)(c-3a+b)z^2 + 8S^2(yz+zx+xy) =0.
Su centro y perspector coinciden en el centro de coordenadas:
( 1/((b+c-a)(a^3-a^2(b+c) - a(b^2-8b c+c^2) + (b+c)(b^2-4b c+c^2)) : ... : ...),
que tiene (6-9-13)-número de búsqueda en ETC: -1.411602064280868133943591227.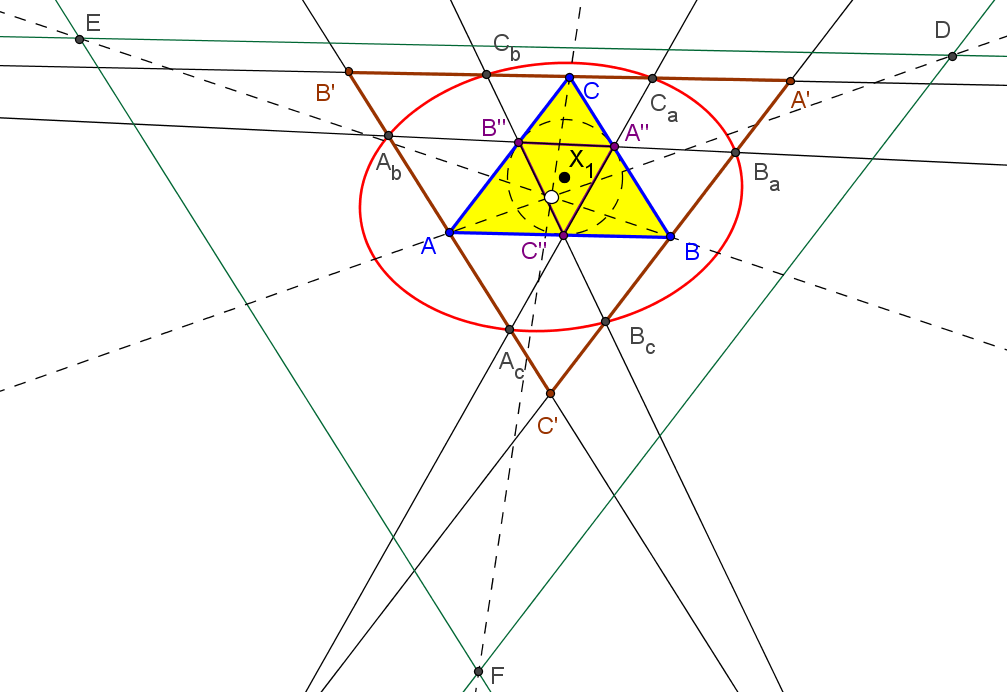
(1/(f-k) : 1/(g-k) : 1/(h-k)),
y la razón de homotecia es:
(k^2(f+g+h-2k)-fgh)/((f-k)(g-k)(h-k)).
El centro de perspectividad del triángulo antimedial A'B'C' y el triángulo DEF formado por las polares de sus vértices respecto a la cónica son homotéticos, con centro de homotecia:
(f g h - 2 g h k - f k^2 + g k^2 + h k^2, f g h - 2 f h k + f k^2 - g k^2 + h k^2, f g h - 2 f g k + f k^2 + g k^2 - h k^2).
Trazamos un segmento BC de longitud a dada.
Sea un punto V sobre el arco capaz de ángulo A sobre el segmento BC.
La circunferencia de centro V y radio VB corta a la recta CV en los punto S y D, tales que CS=VC+VB y SD=VC-CB.
El punto Cv que divide al segmento DS en la relación DCv : CvS = m:n, describe una circunferencia que pasa por B y C.
Deberemos localizar la ubicación del punto V tal que Cv coincida con C.
El punto V solución es la intersección de la tangente en C a tal circunferencia con el arco capaz considerado.
Sean ABC un triángulo, I el incentro y A'B'C' el triángulo medial y A"B"C" el triángulo ceviano del incentro.
Se toman los puntos
Ab=BB" ∩ B'C', Ac=CC" ∩ B'C', Bc=CC" ∩ C'A', Ba=AA" ∩ C'A', Ca=AA" ∩ A'B', Cb=BB" ∩ A'B'.
La tangente en Ab a la cónica que pasa por los puntos Ab, Bc, Ba, Ca, Cb, de ecuación baricéntrica:(-a^3-a(b+c)^2+c(b+c)^2+ a^2(2b+c))x+ (a-c)(a-b+c)^2y + (-a^3+3a^2c-(b-c)^2c+ a(b^2-4b c-c^2))z=0,
y la tangente en Ac a la cónica que pasa por los puntos Ac, Bc, Ba, Ca, Cb, de ecuación baricéntrica:(a^3+a(b+c)^2-b(b+c)^2-a^2(b+2c))x + (a^3-3a^2b+b(b-c)^2+ a(b^2+4b c-c^2))y -(a-b)(a+b-c)^2z=0,
se cortan en el centro X3663:( (b-c)^2+a(b+c) : (c-a)^2+b(c+a) : (a-b)^2+c(a+b) ).
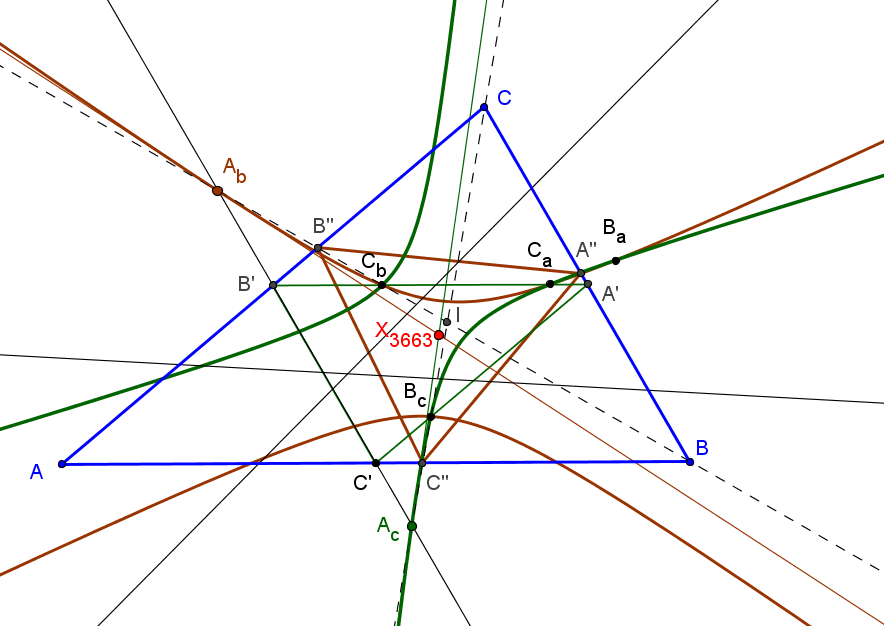
Sean ABC un triángulo, P un punto, O1, O2 y O3 los circuncentros de los triángulos BCP, CAP y ABP. Entonces el triángulo O1O2O3 y el triángulo pedal del conjugado isogonal P* de P, con respecto a ABC, son homotéticos con centro de homotecia, si P(u:v:w), de coordenadas baricéntricas:
Q = ( a^2v w(a^2(u^2+2v w + u(v+w)) - u(b^2(u+v-w) + c^2(u-v+w)): ... : ... )
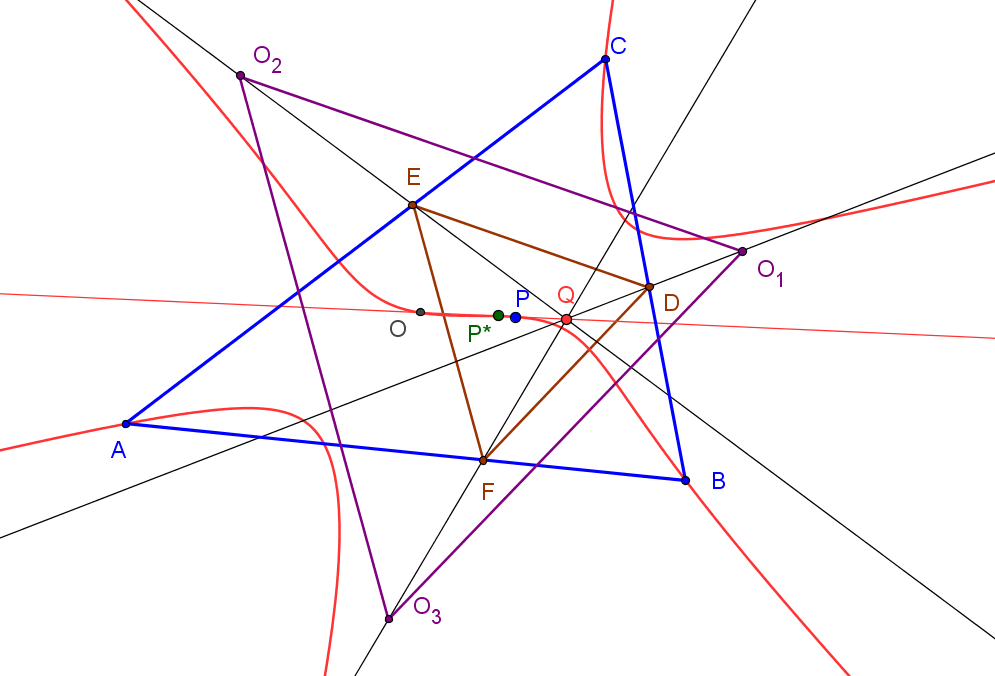
Sean ABC un triángulo, I el incentro y Oa, Ob, Ob los circuncentros de los triángulos IBC, ICA, IAB, respectivamente.
Sean P un punto y Aa, Ab, Ac las proyecciones ortogonales de Oa sobre AP, BP, CP, respectivamente, y O1 el circuncentro del triángulo AaAbAc. Similarmente, se definen O2 y O3.
El circuncentro OP del triángulo O1O2O3 es el punto medio de P y el circuncentro O de ABC.
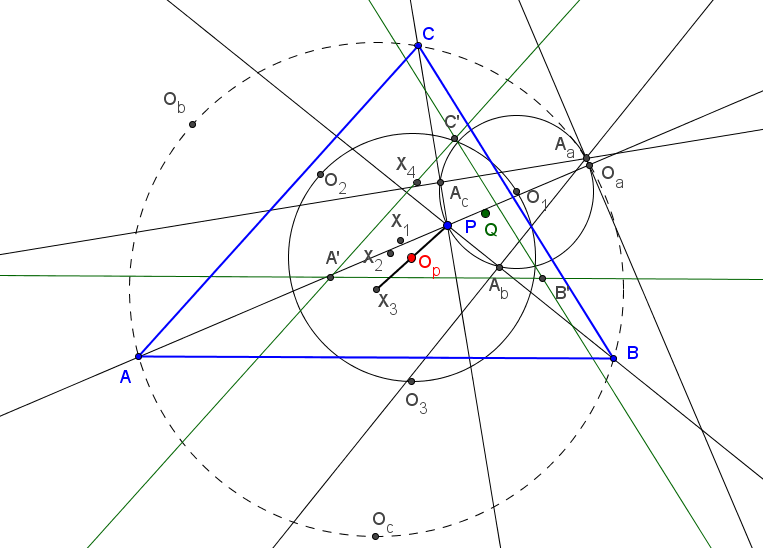
Q = ( a(2b c u^2 - a^2v w- b(b-2c)u w + c(2b-c)u v):
b(2c a v^2 - b^2w u- c(c-2a)v u + a(2c-a)v w):
c(2a b w^2 - c^2u v- a(a-2b)w v + b(2a-b)w u) ).
Sean ABC un triángulo, A'B'C' el triángulo ceviano de un punto P y Oa, Ob, Oc los centros de las circunferencias circunscritas a los triángulos AB'C', BC'A', CA'B', respectivamente, los cuales se cortan en un punto M. Se denota por O* el circuncentro del triángulo OaObOc.
• El lugar geométrico de los puntos P tales que O* está en la recta de Euler es la cúbica (K279 = pK(X2,X3260) del catálogo de Bernard Gibert):
Σ b^2c^2 (2a^4-a^2(b^2+c^2)-(b^2-c^2)^2)x(y^2-z^2)=0.
Sean ABC un triángulo, D, E, F puntos sobre los lados BC, CA, AB, respectivamente. Se denota por Ha, Hb, Hc los ortocentros de los triángulos AEF, BFD, CDE, respectivamente, entonces los puntos D, E, F, Ha, Hb, Hc quedan sobre una cónica.
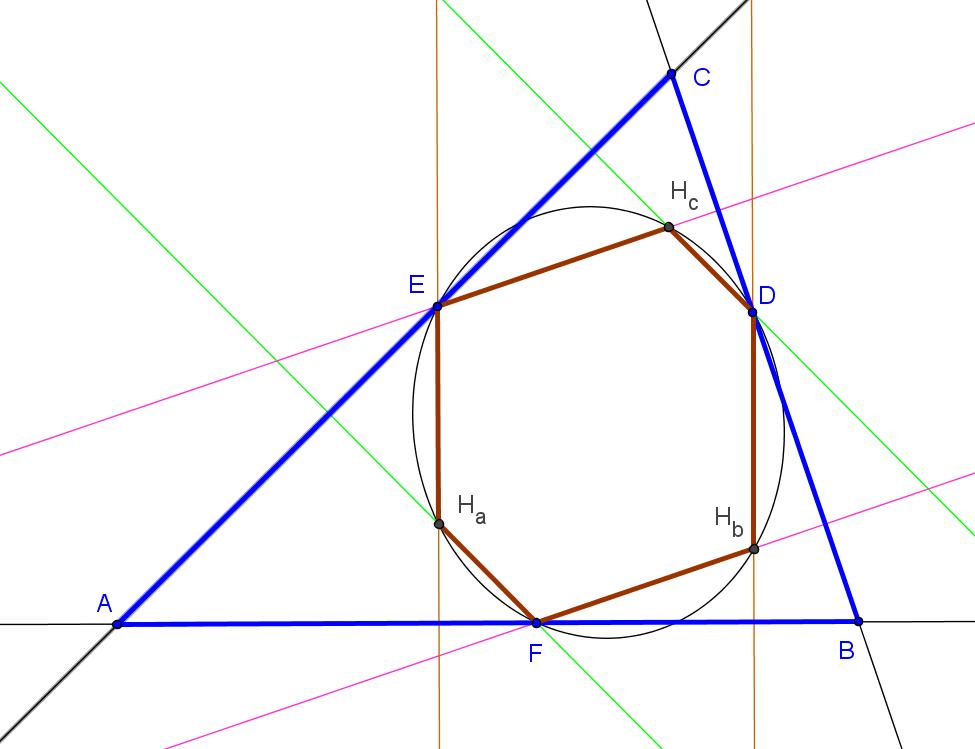
Sean ABC un triángulo, A'B'C' el triángulo ceviano de un punto P y A", B", C" los puntos simétricos de P respecto a A', B', C', respectivamente.
El centro N" de la circunferencia de los nueve puntos de A"B"C" está en la recta OP si P queda en una
séptica
Sean ABC un triángulo, entonces el centro de la circunferencia de los nueve puntos del triángulo medial DEF del triángulo excentral IaIbIc es el centro X3579.
Sean ABC un triángulo, P un punto, DEF el triángulo circunceviano de P y D1, E1, F1 los puntos de intersección de BC, CA, AB con EF, FD, DE, respectivamente. Los puntos D1, E1, F1 están en una recta que denotamos por dP y, si P=(u:v:w), el tripolo de dP (respeto a ABC) es el punto:
U = ( 1/(c^2v+b^2w) : 1/(a^2w+c^2u) : 1/(b^2u+a^2v) ),
que es el "cevapoint" de P y el simediano.
V = ( (c^2uv+b^2uw-a^2vw)/(c^2v+b^2w) : (a^2wu+c^2vu-b^2wu)/(a^2w+c^2u) : (b^2wu+a^2wv-c^2uv)/(b^2u+a^2v) ).
que es el producto baricéntrico de U y el anticomplemento del conjugado isogonal P* de P (ADGEOM #422).Los puntos P, U, V están alineados.
El triángulo A"B"C" determinado por las rectas AA', BB', CC' es perspectivo con ABC y con A'B'C', con centros de perspectividad U y V, respectivamente.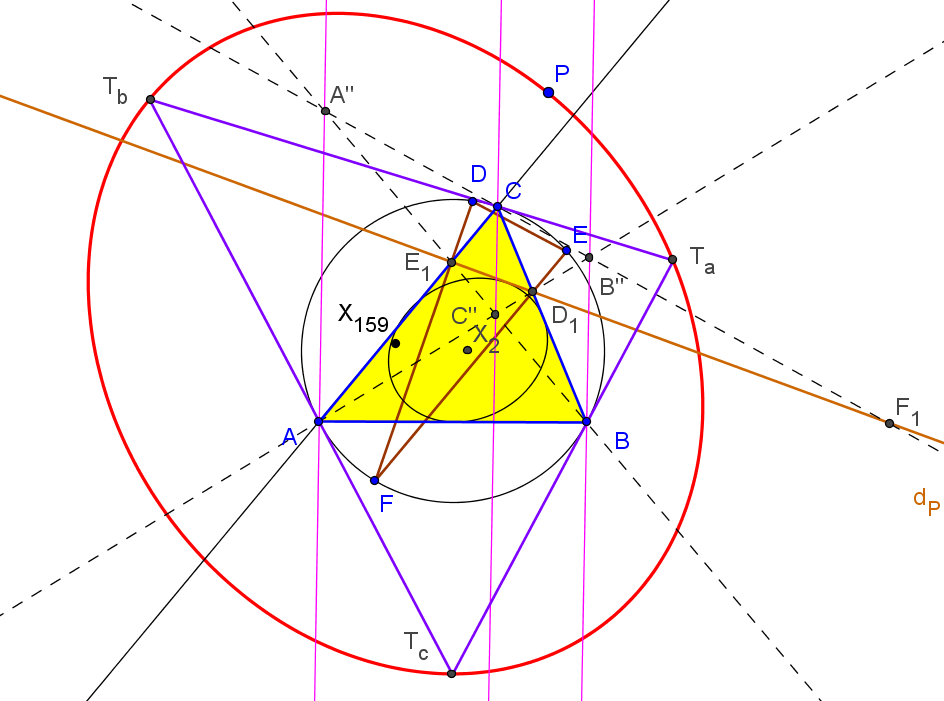
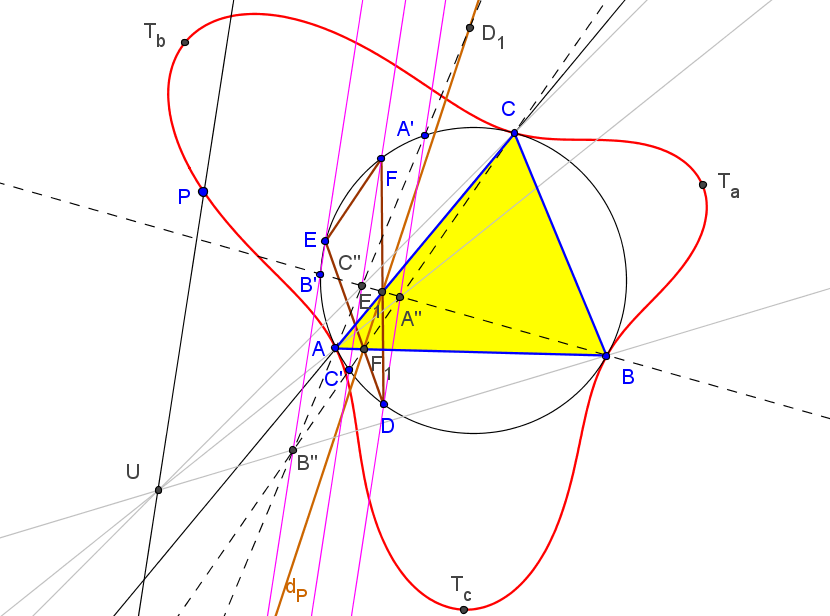
-- X3,
-- (a^2 (a^8 - 8a^4b^2c^2 - 2a^6(b^2+c^2) + 2a^2(b^2+c^2)^3- (b^2-c^2)^4):...:...), está en la recta de Euler.
-- X25,
-- ( a^2 (a+b-c)(a-b+c)(a^6 - a^4(b-c)^2 +
4a^3b c(b+c) - a^2(b^4-4b^3c+22 b^2c^2-4b c^3+c^4) + 4a b c(b+c)^3 + (b-c)^2(b+c)^4 ) : ... : ...),
-- X1180.
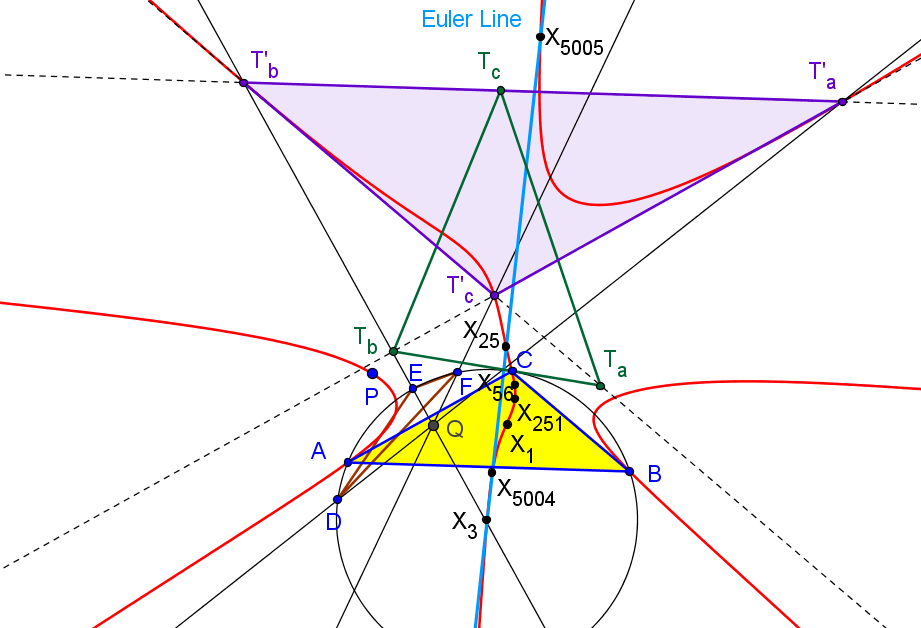
Sean ABC un triángulo, P un punto y Ha, Hb, Hc los ortocentros de los triángulos PBC, PCA, PAB, respectivamente.
Denotamos por Da, Db, Dc los conjugados isogonales de Ha, Hb, Hc, con respecto al triángulo ABC.
• Los puntos Da, Db, Dc están alineados con el circuncentro O en la recta dP de ecuación baricéntrica, si P=(u:v:w),
dP: b^2c^2u(a^2(w-v)+(b^2-c^2)(v+w))x +
a^2c^2v(b^2(u-w)-a^2(u+w)+c^2(u+w))y +
a^2b^2w(c^2(v-u) + a^2(u+v)- b^2(u+v))z =0.

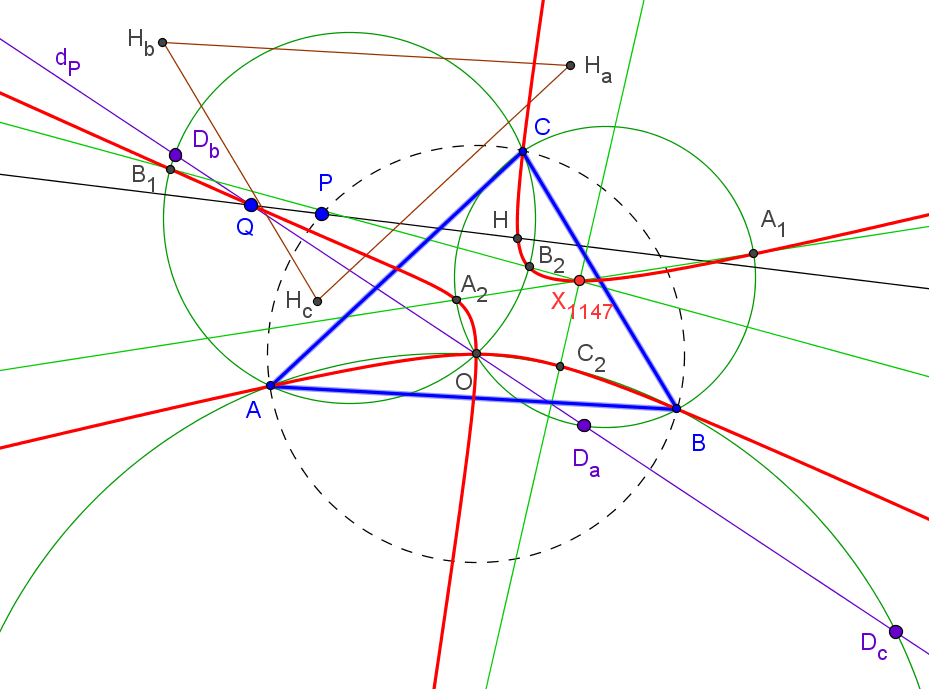
Sean ABC un triángulo, P un punto y A'B'C' el triángulo ceviano de P. Se denota por Pa, Pb, Pc los conjugados isogonales de P con respecto a los triángulos AB'C', BC'A', CA'B', respectivamente.
Entonces:
1. Las circunferencias circunscritas a los triángulos PaB'C', PbC'A', PcA'B' son concurrentes en un punto R1.
2. Las circunferencias circunscritas a los triángulos A'PbPc, B'PcPa, C'PaPb son concurrentes en un punto R2.
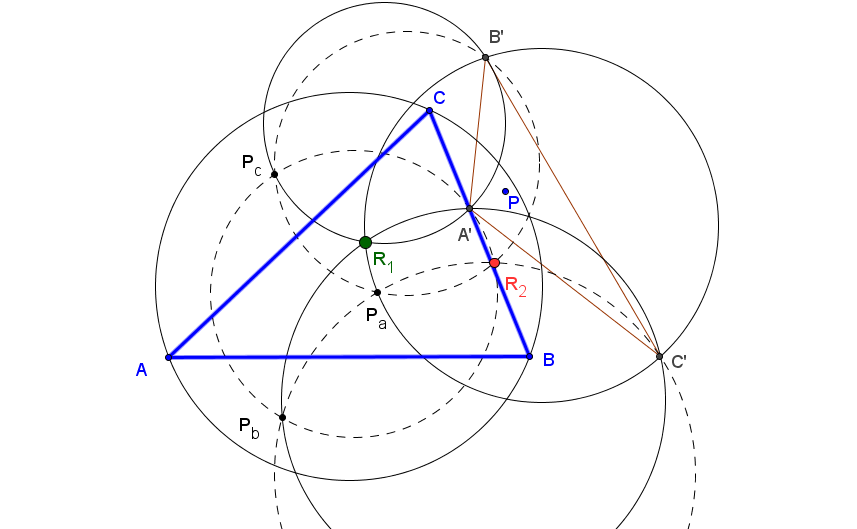
R1 = (a^2(a^2-b^2-b*c-c^2)(a^3+a^2b-a*b^2-b^3+a^2c+a*b*c+b^2c-a*c^2+b*c^2-c^3)
(a^6-2a^4b^2+a^2b^4+a^2b^3c-b^5c-2a^4c^2-a^2b^2c^2+a^2b*c^3+2b^3c^3+a^2c^4-b*c^5)
:...:...),
R2 = ( (a-b-c) (b-c)^2 (a^3+a^2b-a*b^2-b^3+a^2c+a*b*c+b^2c-a*c^2+b*c^2-c^3)
(a^6-a^4b^2-a^2b^4+b^6-2a^2b^3c+2b^5c-a^4c^2-a^2b^2c^2-b^4c^2-2a^2b*c^3
-4b^3c^3-a^2c^4-b^2c^4+2b*c^5+c^6):...:...),
R1 = (a^2(4a^4-7a^2b^2-2b^4-7a^2c^2+14b^2c^2-2c^4) (4a^4-6a^2b^2+2b^4-6a^2c^2+b^2c^2+2c^4):...:...),
con número de búsqueda en ETC: 5.184059393723475028771865549R2 = ((b-c)^2(b+c)^2(-7a^2+2b^2+2c^2)(-2a^4+2b^4-5b^2c^2+2c^4):...:...),
con número de búsqueda en ETC: -0.196430427865079067265962063( (b+c)(2a+b+c)(a-b+c)(a+b-c) : (c+a)(2b+c+a)(b-c+a)(b+c-a) : (a+b)(2c+a+b)(c-a+b)(c+a-b) ).
Las paralelas citadas anteriormente son las rectas DO1, EO2, FO3, siendo O1, O2, O3 los circuncentros de los triángulos AEF, BFD, CDE, respectivamente.
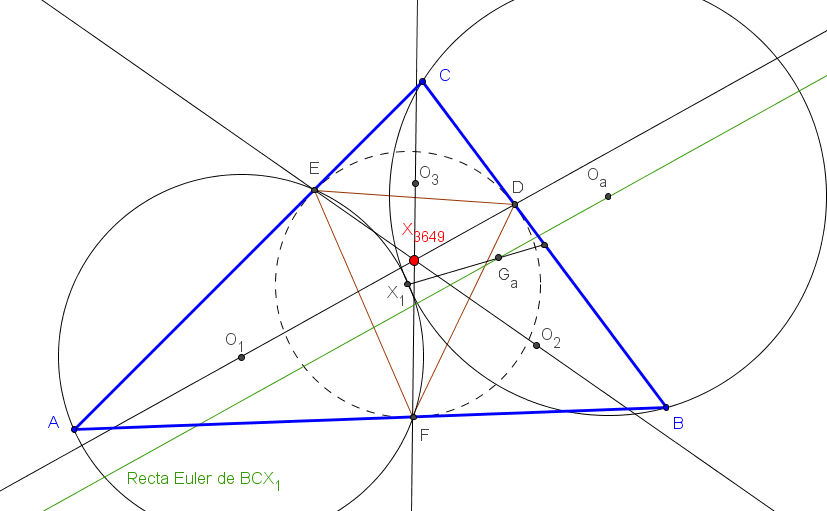
Sea ABC un triángulo, de los rectángulos inscritos en ABC, con uno de sus lados sobre los lados del triángulo, tomemos los tres que tienen diagonal de longitud mínima. Los lados de estos rectángulos paralelos a los de ABC, delimitan un triángulo A'B'C' homotético a ABC, con centro de homotecia en el punto de coordenadas baricéntricas:
U = ( a^4 / (3a^4+ 2a^2(b^2 + c^2) - (b^2 - c^2)^2 ) :
b^4 / (3b^4+ 2b^2(c^2 + a^2) - (c^2 - a^2)^2 ) :
c^4 / (3c^4+ 2c^2(a^2 + b^2) - (a^2 -b^2)^2 ) ) =
= ( a^4/(a^4+S^2) : b^4/(b^4+S^2) : c^4/(c^4+S^2) ),
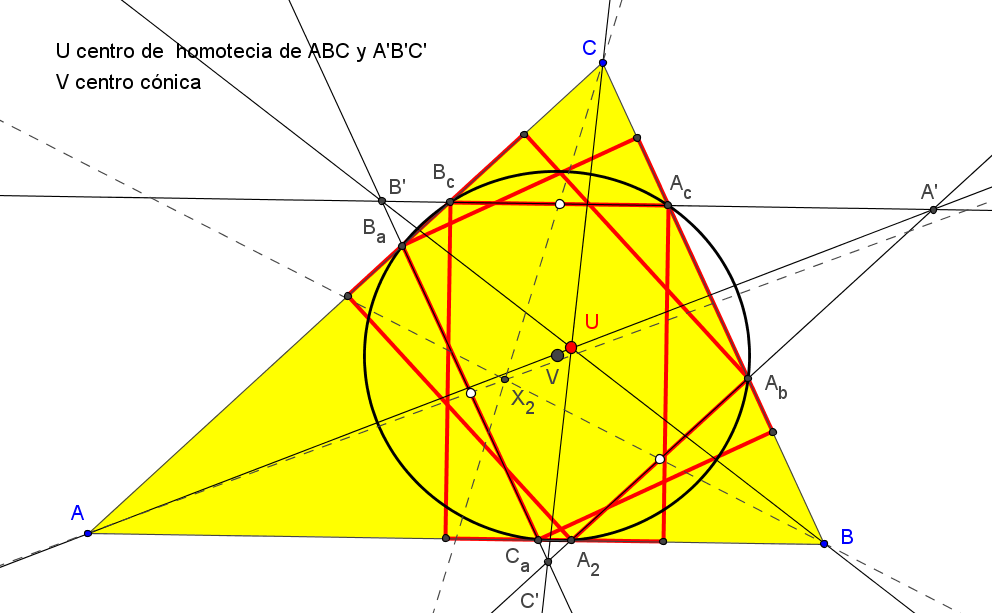
z (SB x + a^2 z) + t (SB y + (-SC + S) z) (-SB y + (SC + S) z)=0,
e imponiendo que pase por A', t= -2 a^2/(4 S^2).
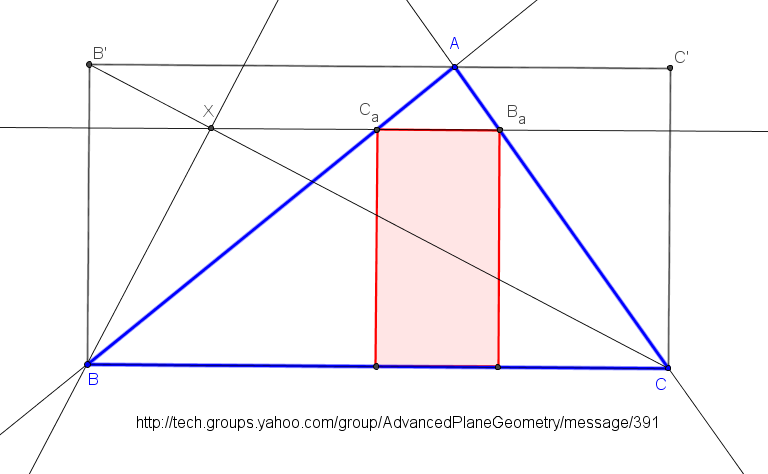
Sean ABC un triángulo, P un punto y A'B'C' el triángulo antipedal de P. Si P está sobre la cúbica de Darboux, las paralelas a IA', IB' y I'C (I el incentro) por A,B y C, concurren en un punto R sobre la cúbica central de Spieker (K033 del catálogo de Bernard Gibert).
Sean ABC un triángulo, A1B1C1 el triángulo órtico y P un punto. Las rectas AP,BP,CP vuelven a cortas a las circunferencias circunscritas a los triángulos PBC,PCA,PAB, resp. en A',B',C', resp.
Las circunferencias circunscritas a los triángulos AA1A', BB1B', CC1C' son coaxiales si P está sobre la cúbica de Darboux (K004 del catálogo de Bernard Gibert).
El eje radical de las circunferencias coaxiales pasa por el ortocentro.
Sean ABC un triángulo, P un punto y P* su conjugado isogonal. Denotamos por A',B',C' los puntos medios de AP, BP, CP, respectivamente, y por A",B",C" los puntos medios de AP*, BP*, CP*, respectivamente.
Sean D,E,F los puntos medios de A'A", B'B", C'C", respectivamente, entonces los triángulos ABC y DEF son ortológicos (las perpendiculares desde los vértices de uno de ellos a los correspondientes lados del otro son concurrentes) y los centros ortológicos son el circuncentro y el punto de coordenadas, P(u:v:w):
(a^2vw(4u+3v+3w)+ b^2uw(3u+2v+2w) +
c^2uv(3u+2v+2w)) /
3b^2c^4u^4v^2 + a^2c^4u^3v^3 + 5b^2c^4u^3v^3 + 3c^6u^3v^3 +
a^2c^4u^2v^4 + 2b^2c^4u^2v^4 +
2c^6u^2v^4 + a^2b^2c^2u^4vw +
3b^4c^2u^4vw + 3b^2c^4u^4vw +
7a^2b^2c^2u^3v^2*w +
5b^4c^2u^3v^2w + 19b^2c^4u^3v^2w + a^4c^2u^2v^3w +
9a^2b^2c^2u^2v^3w +
2b^4c^2u^2v^3w + 9a^2c^4u^2v^3w + 12b^2c^4u^2v^3w +
2c^6u^2v^3w + a^4c^2uv^4w +
3a^2b^2c^2uv^4w +
5a^2c^4uv^4w + 3b^4c^2u^4w^2 +
7a^2b^2c^2u^3vw^2 +
19b^4c^2u^3vw^2 + 5b^2c^4u^3vw^2 + 34a^2b^2c^2u^2v^2w^2 +
12b^4c^2u^2v^2w^2 +
12b^2c^4u^2v^2w^2 +
7a^4c^2uv^3w^2 + 19a^2b^2c^2uv^3w^2 + 5a^2c^4uv^3w^2 +
3a^4c^2v^4w^2 + a^2b^4u^3w^3 +
3b^6u^3w^3 + 5b^4c^2u^3w^3 +
a^4b^2u^2vw^3 + 9a^2b^4u^2vw^3 + 2b^6u^2vw^3 +
9a^2b^2c^2u^2vw^3 +
12b^4c^2u^2vw^3 + 2b^2c^4u^2vw^3 + 7a^4b^2uv^2w^3 +
5a^2b^4uv^2w^3 + 19a^2b^2c^2uv^2w^3 + a^6v^3w^3 +
3a^4b^2v^3w^3 + 3a^4c^2v^3w^3 +
a^2b^4u^2w^4 + 2b^6u^2w^4 +
2b^4c^2u^2w^4 + a^4b^2uvw^4 +
5a^2b^4uvw^4 + 3a^2b^2c^2uvw^4 + 3a^4b^2v^2w^4 : ... : ...).
( (10a^2 + 7(b^2+c^2))/ (a^6+15a^4(b^2+c^2) + 3a^2(7b^4+37b^2c^2+7c^4)+7(b^6+9b^4c^2+9b^2c^4+c^6)) : ... : ...)
( (2a^4 - 5a^2(b^2+c^2)+ 3(b^2-c^2)^2 )/ (a^6+a^4(b^2+c^2) - 5a^2(b^4+b^2c^2+c^4) + 3(b^2-c^2)^2 (b^2+c^2)) : ... : ...)
Sean ABC un triángulo, A'B'C' el triángulo órtico, P un punto y A", B", C" los puntos medios de AP, BP, CP, respectivamente.
Si P está sobre la cúbica de Neuberg (K001 del catálogo de Bernard Gibert) las circunferencias circunscritas a los triángulos AA'A", BB'B", CC'C", son coaxiales, con eje la recta de Euler.
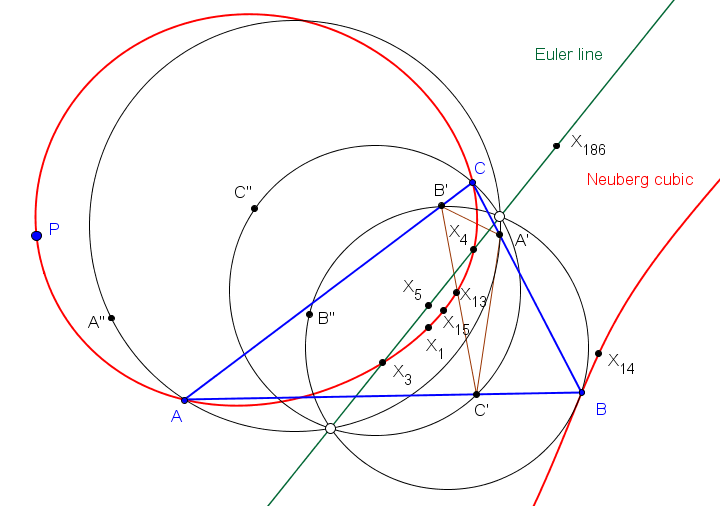
Sean ABC un triángulo, I el incentro y Na, Nb, Nc los centros de las circunferencias de los nueve puntos de los triángulos IBC, ICA, IAB, resp.
Se denota por Ka, Kb, Kc los conjugados isogonales de Na, Nb, Nc con respecto a los triángulos IBC, ICA, IAB, resp. (es decir, Ka, Kb, Kc son los puntos de Kosnita de los triángulos IBC, ICA, IAB).
Las coordenadas baricéntricas del punto de Kosnita de IBC son:
Ka = (a^2(a-b)(a-c) : b(a-b)(a^2- b^2+c^2-a(b+2c)) : c(a-c)(a^2+b^2-c^2-a(2b+c)).
Las circunferencias circunscritas a ABC, AKbKc, BKcKa, CKaKb son concurrentes en el punto X de coordenadas baricéntricas:
X = ( a^2/((b-c)(2a^4-a^3(b+c)-a^2(3b^2+4b*c+3c^2)+a(b+c)(b^2+3b*c+c^2)+(b^2-c^2)^2)) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: -0.4151794812633478152167512428
Sean ABC un triángulo, HaHbHc el triángulo órtico
y MaMbMc triángulo medial.
A'=(2a^4+a^2(b^2+c^2)-(b^2-c^2)^2: b^2(a^2+b^2-c^2):c^2(a^2-b^2+c^2)) es el conjugado isogonal de Ha respecto al triángulo GMbMc,
B' el conjugado isogonal de Hb respecto al triángulo GMcMa y
C' el conjugado isogonal de Hc respecto al triángulo GMaMb.
Entonces, los triángulos ABC y A'B'C' son perspectivos, con centro de perspectividad X25, el centro de homotecia de los triángulo órtico y tangencial.
( a^2( 3a^16(b^2+c^2) -
a^14(9b^4+26b^2c^2+9c^4) +
3a^12(b^6+16b^4c^2+16b^2c^4+c^6) +
a^10(15b^8-24b^6c^2-62b^4c^4-24b^2c^6+15c^8) -
a^8(15b^10+12b^8c^2-11b^6c^4-11b^4c^6+12b^2c^8+15c^10) +
a^6(-3b^12+30b^10c^2+51b^8c^4+116b^6c^6+51b^4c^8+30b^2c^10-3c^12) +
a^4(9b^14-36b^12c^2-26b^10c^4+85b^8c^6+85b^6c^8-26b^4c^10-36b^2c^12+9c^14) -
a^2(b^2-c^2)^2(3b^12-14b^10c^2-3b^8c^4+76b^6c^6-3b^4c^8-14b^2c^10+3c^12)-
3b^2c^2(b^2-c^2)^6(b^2+c^2)) : ... : ... ),
( (a^2+2SA)(a^4+SBSC+S^2) : (b^2+2SB)(b^4+SCSA+S^2) : (c^2+2SC)(c^4+SASB+S^2) ),
que tiene (6-9-13)-número de búsqueda en ETC: 0.6225282852339818799280226572
Sean ABC un triángulo y P un punto, denotamos por A'B'C' el triángulo circunceviano de P.
Ab y Ac son las proyecciones ortogonales de A' sobre BB' y CC', respectivamente y Ha el ortocentro de A'AbAc.
Similarmente se consideran los correspondientes ortocentros Hb y Hc.
Los triángulos ABC y HaHbHc son ortológicos (las perpendiculares desde los vértices de uno de ellos a los correspondientes lados del otro son concurrentes) en los siguientes casos:
1. Cuando P está sobre la circunferencia circunscrita: el triángulo circunceviano degenera en el punto P.
2. Cuando P está sobre la cúbica de Darboux (K004 del catálogo de Bernard Gibert).
Sean ABC un triángulo, P un punto y k un número real. A'B'C' el triángulo homotético a ABC, mediante la homotecia de centro P y razón k.
Sea Ab=BC∩C'A', Ac=BC∩A'B', y se definen Bc, Ba, Ca, Cb cíclicamente.
Esta seis intersecciones están en una cónica, c(P,k).
Cuando k varía los centros Z(P,k) de las cónicas c(P,k) quedan sobre una recta d(P) que pasa por P.
d(P) es un eje de las cónicas c(P,k), para todo k, si y solo si P está en la quíntica Stothers o en la recta del infinito".
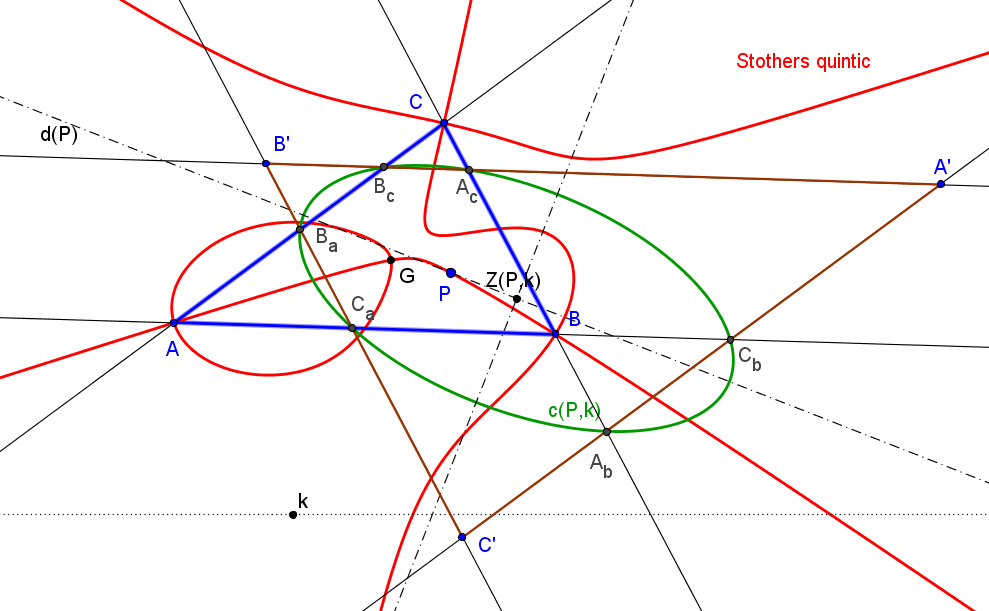
Sean ABC un triángulo, A'B'C' el triángulo excentral, y A",B",C" los puntos medios de las alturas A'A, B'B, C'C del triángulo excentral
Las circunferencias circunscritas a los triángulos A"BC, B"CA, C"AB concurren en el punto (sobre la recta de Euler del triángulo excentral) X1319 = Bevan-Schröder point.
( a (2 a^3 - a^2 (b + c) - 2 a (b^2 - b*c + c^2) + b^3 + b^2 c + c^2 b + c^3): ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 2.763124242396552353038
Sean ABC un triángulo, A'B'C' el triángulo órtico, y A",B",C" los puntos medios de las alturas.
Las circunferencias circunscritas a los triángulos A"B'C', B"C'A', C"A'B' concurren en el punto (sobre la recta de Euler) de coordenadas baricéntricas:
( SB SC(SA(c^2-b^2)^2 - SB SC(2SA-a^2)): ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: -3.381534618985148558065036
Sean ABC un triángulo y una recta h. La hipérbola circunscrita a ABC y con asíntota h, puede ser construida como en el caso (PPPtP), cuando se dan cuatro puntos y la tangente en uno de ellos.
También podemos hacer uso del hecho de que la otra asíntota es la conjugada isotómica de la asíntota dada , y acudir a cualquiera de los casos de construcción de una hipérbola dado un punto y dos asíntotas: (hhP) o (hhP(2)).
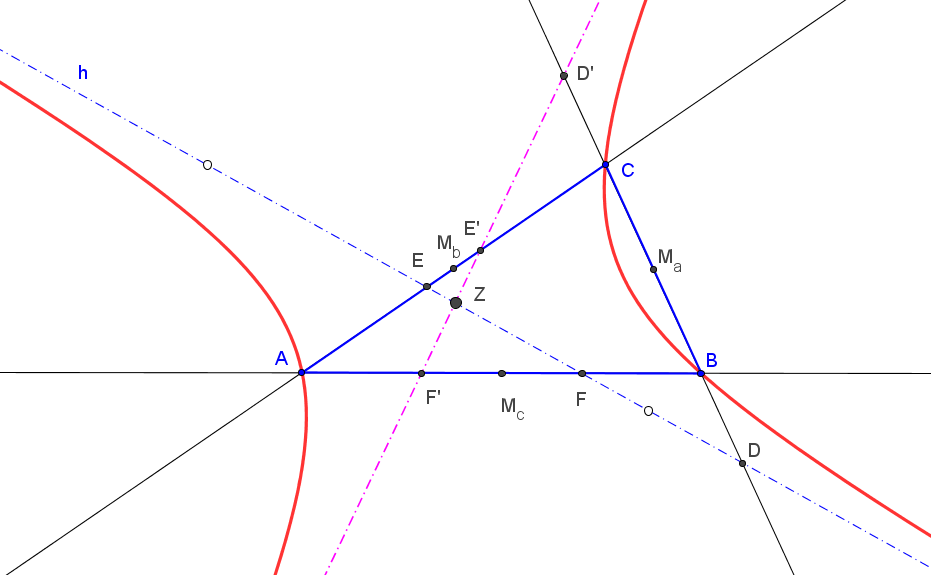
Sean ABC un triángulo, DEF su triángulo medial y t un número real. Denotamos por D', E', F' las imágenes de D, E, F mediante las homotecias de centro en el circuncentro O y razón t. Consideremos los rectángulos BCCaBa, CAAbCb, ABBcAc tales que D', E', F' son, respectivamente, los puntos medios de los lados CaBa, AbCb, BcAc.
Entonces, las mediatrices de AbAc, BcBa, CaCb concurren en el punto, sobre la recta de Euler, P(t)=3(1+t) X(2) - (1+3t) X(3)
Enunciado:
Si ABC es un triángulo con B', C' los puntos medios de AC, AB, respectivamente, H y I el ortocentro e incentro de ABC. Probar que si IH biseca a B'C' entonces ABC es isósceles.
Las coordenadas baricéntricas del punto de intersección de las rectas IH y B'C' son:
(2a^4 - a^2(b-c)^2 - a^3(b+c) + a(b-c)^2(b+c) - (b^2-c^2)^2 :
(a-c)(a^3 + a^2(b-c) - a(b-c)^2 - (b-c)(b+c)^2) :
(a-b)(a^3 - a(b-c)^2 - a^2(b-c) + (b-c)(b+c)^2) ).
Para que este punto coincida con el punto medio de B'C' de coordenadas (2:1:1), ha de ocurrir que b=c (solución trivial) o bien que:
c = a - b + (2*2^(2/3)a(a - b))/
(3^(1/3)(a(a - b)(-9b + Sqrt[-48a^2 + 48a*b + 81b^2]))^(1/3)) +
(2^(1/3)(a(a - b)(-9b + Sqrt[-48a^2 + 48a*b + 81b^2]))^(1/3))/3^(2/3).
Así, existen triángulos NO isósceles para los cuales IH y B'C'.
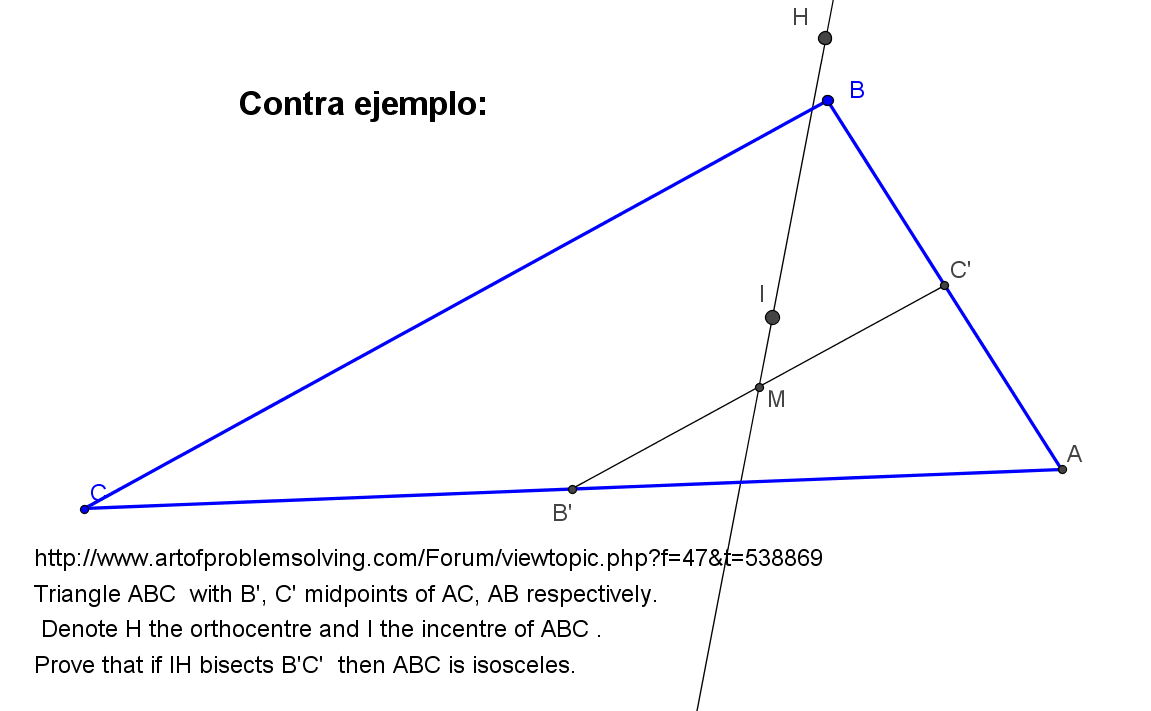
Sean ABC un triángulo y los dos triángulos equiláteros A1A2A3, A'1A'2A'3, con el mismo baricentro G que ABC y tales que los segmentos A2A3, A'2A'3 son iguales y paralelos al segmento BC.
• Las rectas AA1, BB1 y CC1 se cortan en X13, primer punto isogonal (Fermat - Torricelli).
• Las rectas AA'1, BB'1 y CC'1 se cortan en X14, segundo punto isogonal.
• Denotamos por M1, N1 y P1 los puntos medios de A2A3, B2B3 y C2C3, respectivamente. Las rectas AM1, BN1 y CP1 se cortan en el centro de perspectividad de Kiepert K1 (sobre la hipérbola de Kiepert) de coordenadas baricéntricas:
K1 = ( 1 / (SA-2S/√3) : 1 / (SB-2S/√3) : 1 / (SC-2S/√3) ),
que tiene (6-9-13)-número de búsqueda en ETC: 1.05544963972706758475865636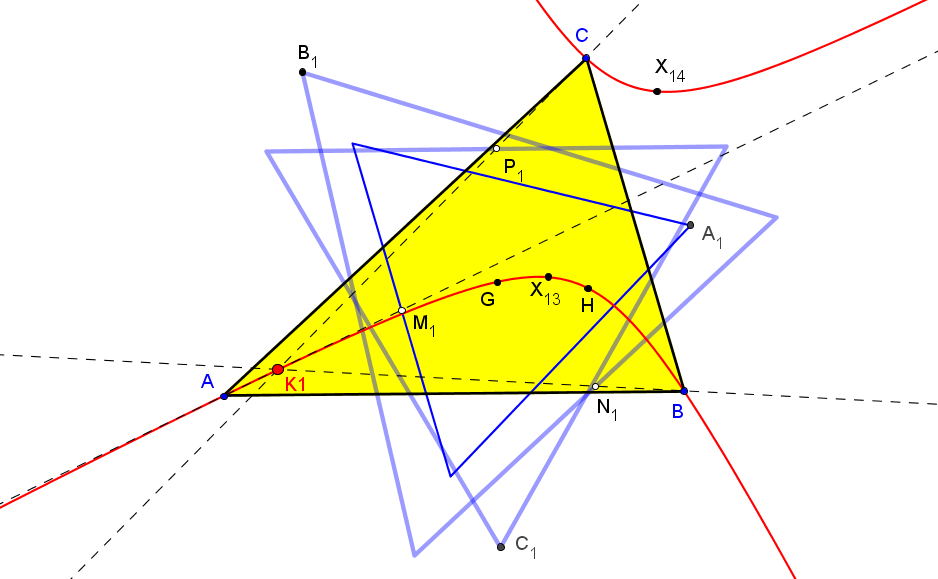
• Denotamos por M'1, N'1 y P'1 los puntos medios de A'2A'3, B'2B'3 y C'2C'3, respectivamente. Las rectas AM'1, BN'1 y CP'1 se cortan en el punto K2 (sobre la hipérbola de Kiepert) de coordenadas baricéntricas:
K2 = ( 1 / (SA+2S/√3) : 1 / (SB+2S/√3) : 1 / (SC+2S/√3) ),
que tiene (6-9-13)-número de búsqueda en ETC: 0.982582066301352428967254767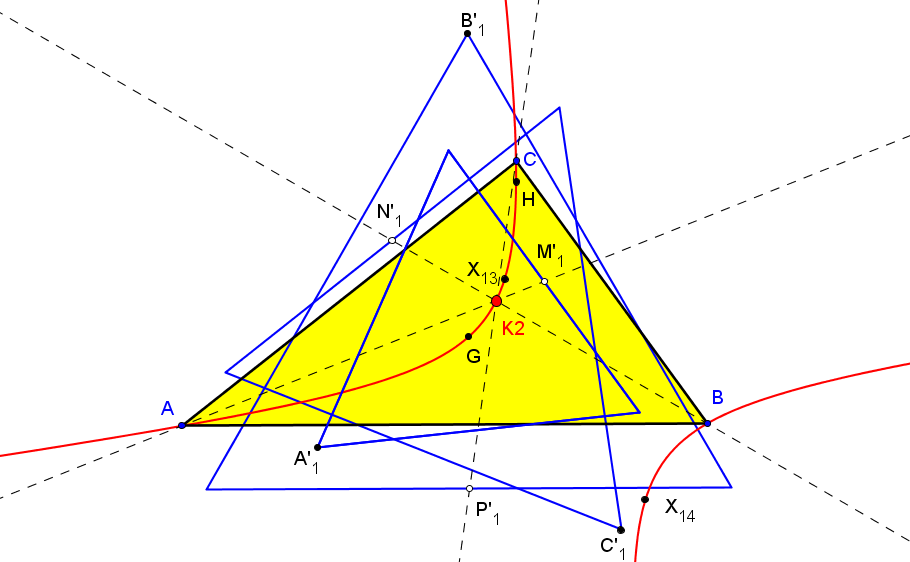
• Denotamos por M el punto medio de M1 y el punto medio Ma de BC, por N el punto medio de N1 y el punto medio Mb de CA y por P el punto medio Mc de P1 y el punto medio de AB. Las rectas AM, BN y CP se cortan en el punto K3 (sobre la hipérbola de Kiepert) de coordenadas baricéntricas:
K3 = ( 1 / (SA-5S/√3) : 1 / (SB-5S/√3) : 1 / (SC -5S/√3) ),
que tiene (6-9-13)-número de búsqueda en ETC: 4.995109899468789806283186502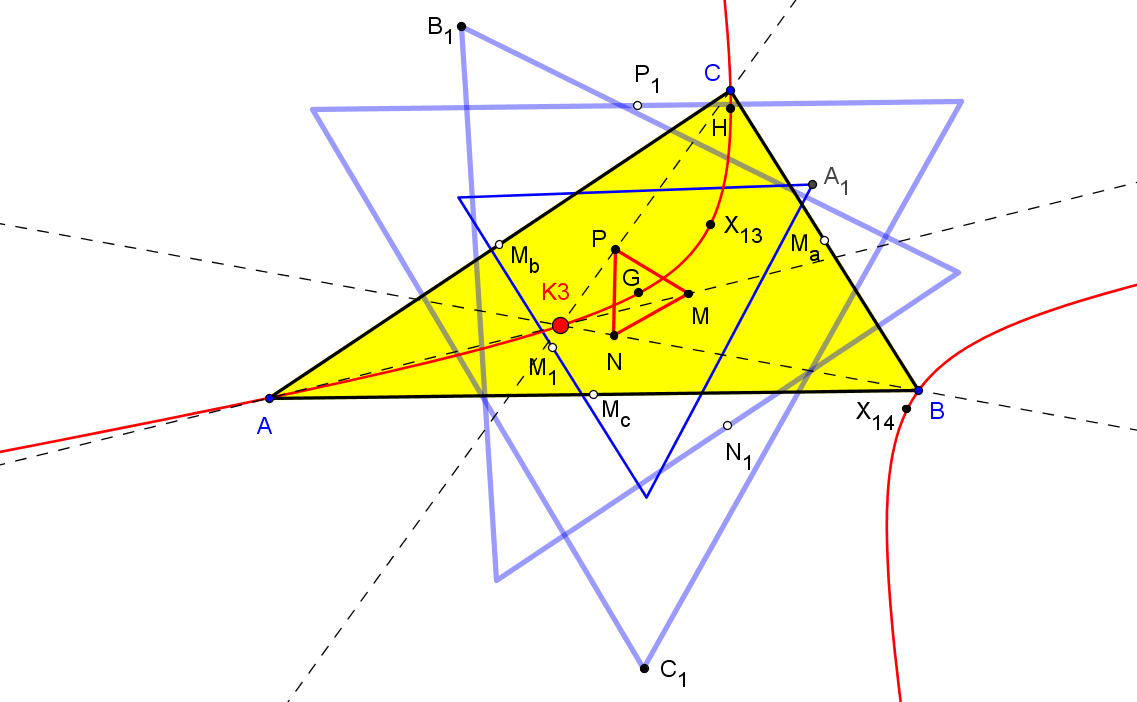
• Denotamos por M' el punto medio de M'1 y el punto medio Ma de BC, por N' el punto medio de N'1 y el punto medio Mb de CA y por P' el punto medio Mc de P'1 y el punto medio de AB. Las rectas AM', BN' y CP' se cortan en el punto K4 (sobre la hipérbola de Kiepert) de coordenadas baricéntricas:
K4 = ( 1 / (SA+5S/√3) : 1 / (SB+5S/√3) : 1 / (SC+5S/√3) ),
que tiene (6-9-13)-número de búsqueda en ETC: 1.781091236364735925107070176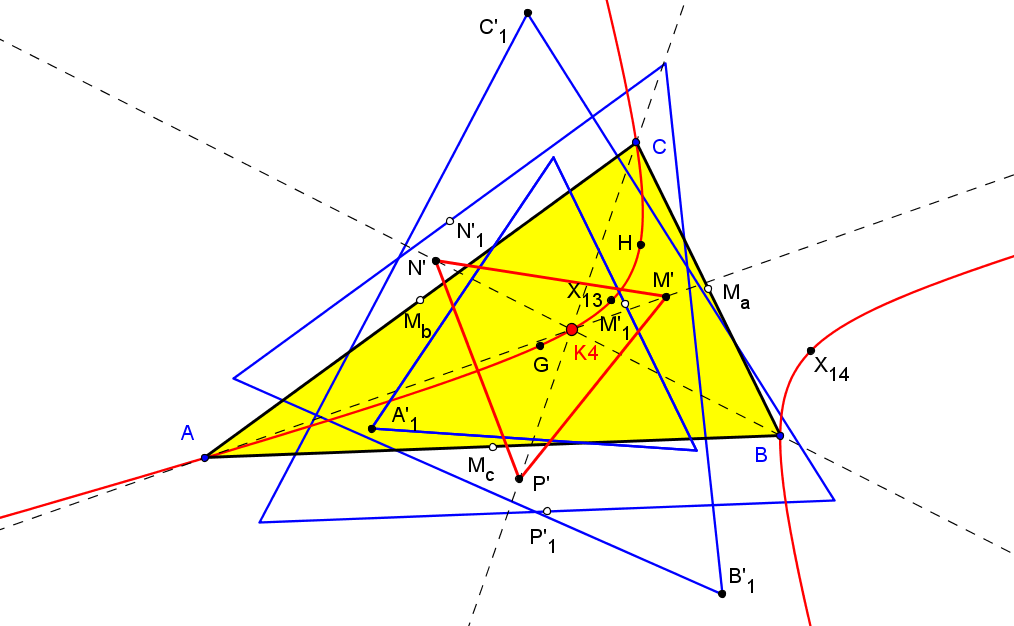
• Denotamos por Ga, Gb y Gb los baricentros de BCA1, CAB1 y ABC1, respectivamente. Las rectas AGa, BGb y CGc se cortan en el punto K5 (sobre la hipérbola de Kiepert) de coordenadas baricéntricas:
K5 = ( 1 / (SA+4S/√3) : 1 / (SB+4S/√3) : 1 / (SC+4S/√3) ),
que tiene (6-9-13)-número de búsqueda en ETC: 1.623294634697676359144692801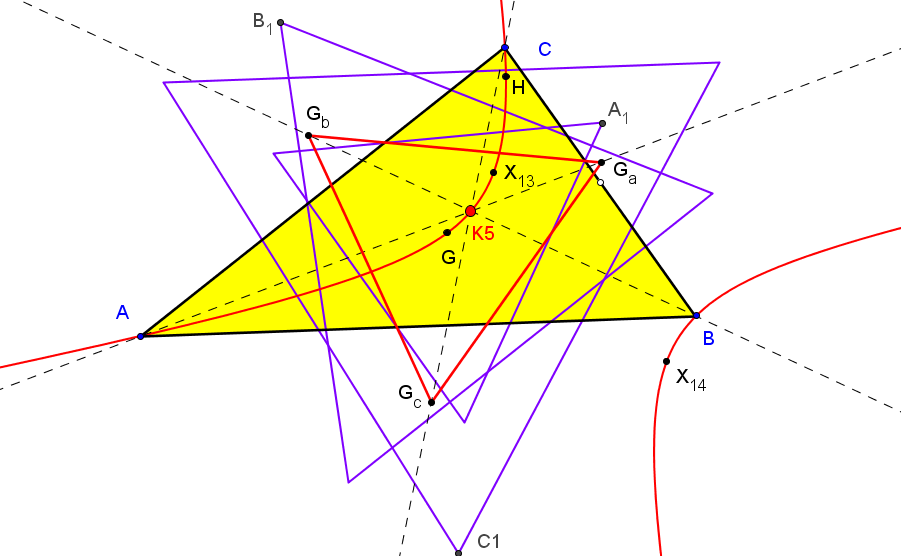
• Denotamos por G'a, G'b y G'b los baricentros de BCA'1, CAB'1 y ABC'1, respectivamente. Las rectas AG'a, BG'b y CG'c se cortan en el punto K6 (sobre la hipérbola de Kiepert) de coordenadas baricéntricas:
K6 = ( 1 / (SA-4S/√3) : 1 / (SB-4S/√3) : 1 / (SC-4S/√3) ),
que tiene (6-9-13)-número de búsqueda en ETC: 7.402174494117207095178203633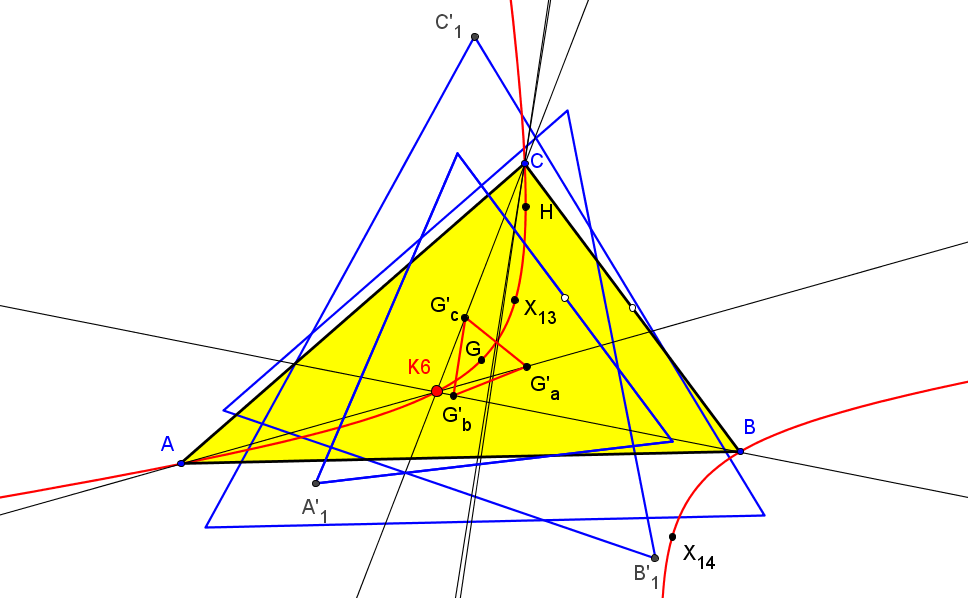
• Las rectas MaM1, MbN1 y McP1 concurren en X618, primer punto isogónico del triángulo medial.
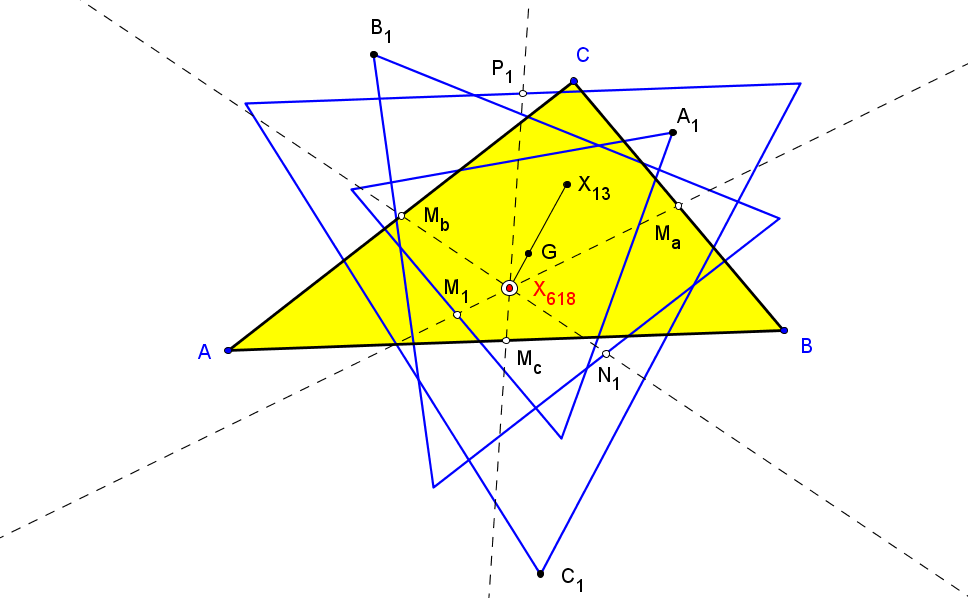
• Las rectas MaM'1, MbN'1 y McP'1 concurren en X619, segundo punto isogónico del triángulo medial.
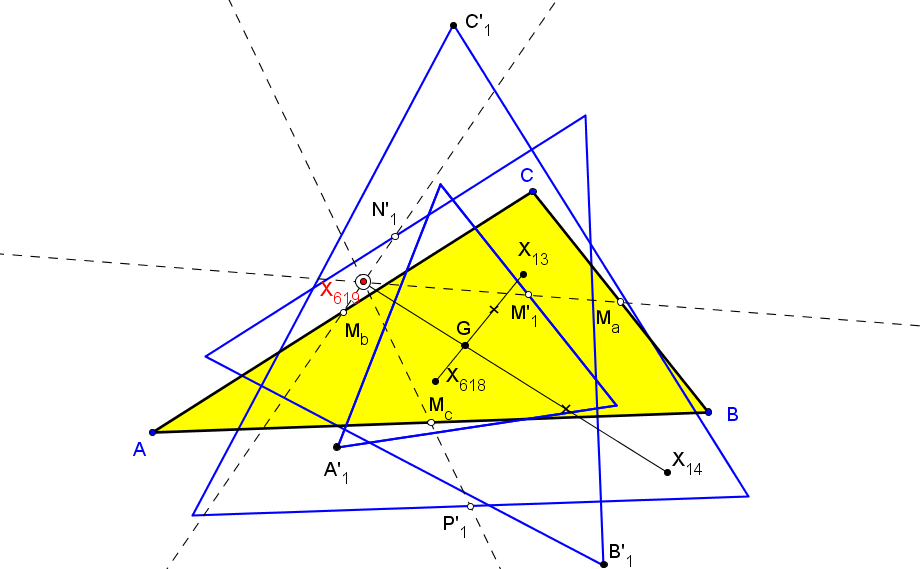
• Las rectas MM', NN' y PP' concurren en X549, punto medio del baricentro y el circuncentro de ABC.
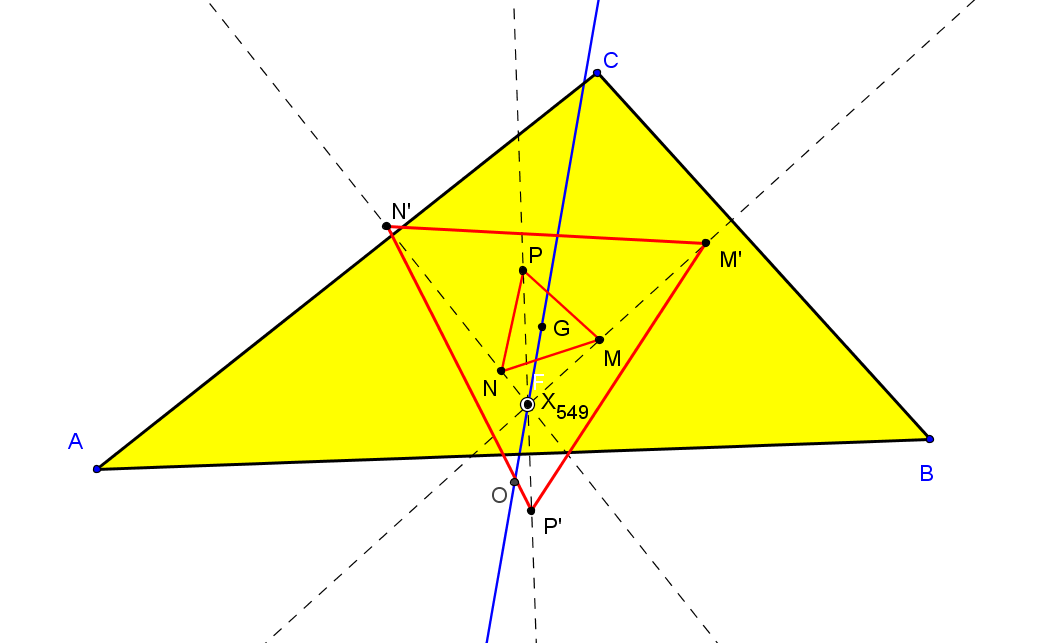
• Las rectas GaG'a, GbG'b y GcG'c concurren en X3524, en la recta de Euler de ABC.
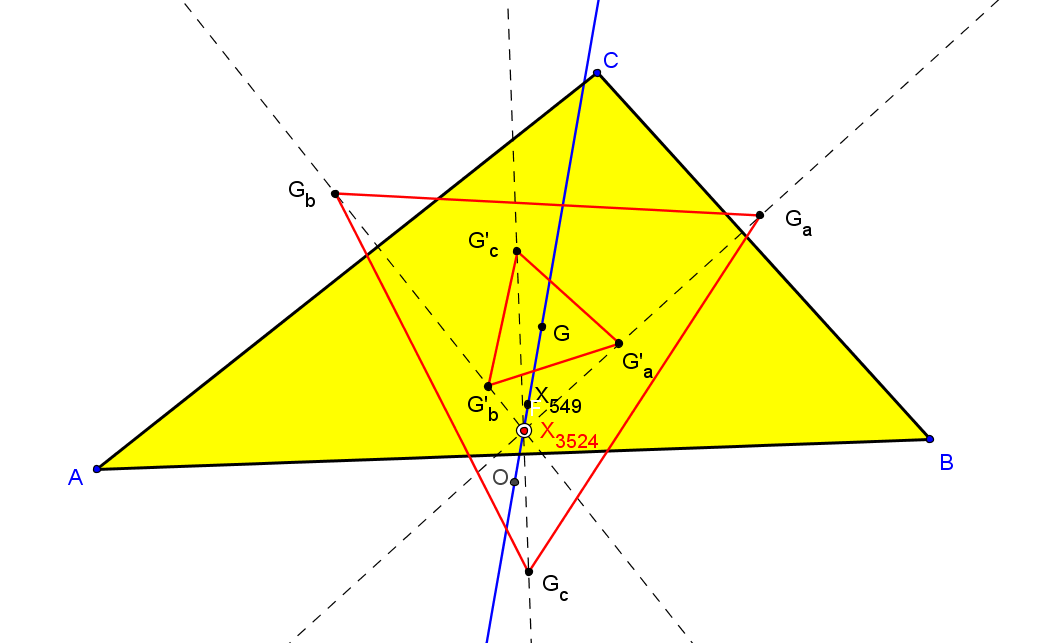
• Las rectas MGa, NGb y PGc concurren en el punto de coordenadas baricéntricas:
( 53a^4 + 11(b^2-c^2)^2 - 64a^2(b^2+c^2) - 2√3(a^2+3b^2+3c^2)S : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 4.3452957082099683645807850740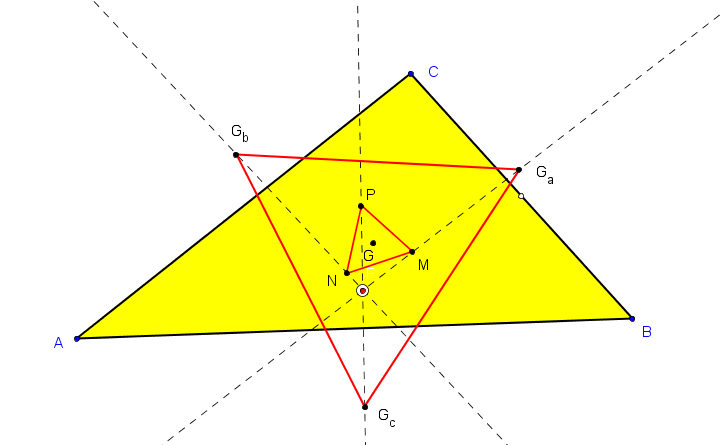
• Las rectas M'G'a, N'G'b y P'G'c concurren en el punto de coordenadas baricéntricas:
( 53a^4 + 11(b^2-c^2)^2 - 64a^2(b^2+c^2) + 2√3(a^2+3b^2+3c^2)S : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 6.729170058363700358702487375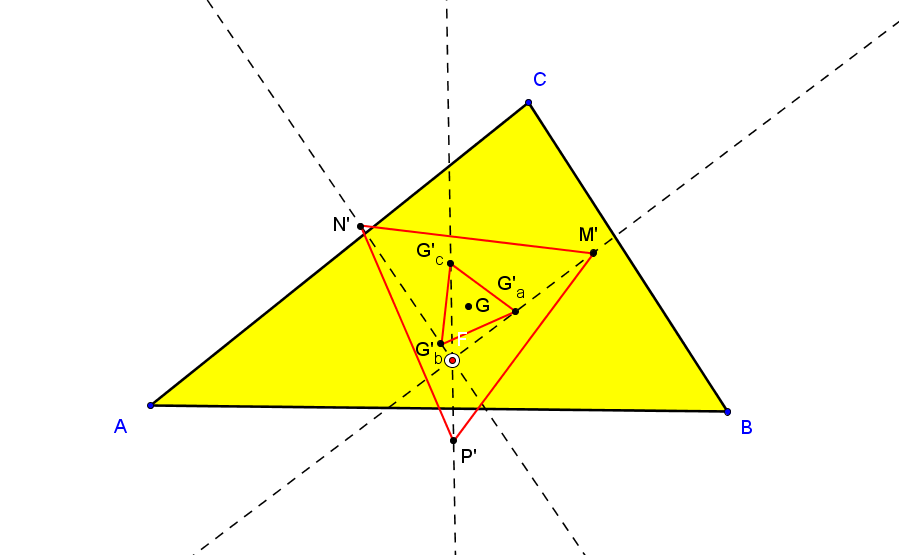
Sean ABC un triángulo, P un punto, D, E y F los pies de las cevianas de P en los lados BC, CA y AB. Denotamos por A', B' y C' los puntos donde las mediatrices de AD, BE y CF cortan a BC, CA y AB, respectivamente. El lugar geométrico de los puntos P tales que A', B' y C' estén alineados es una séxtica ( Mostrar/Ocultar fórmula )
( 1 / (a^6 + a^4(b^2+c^2) - a^2((b^2+c^2)^2-b^2 c^2) - (b^2+c^2)(b^4-b^2c^2+c^4)) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 8.11040473813735146364958223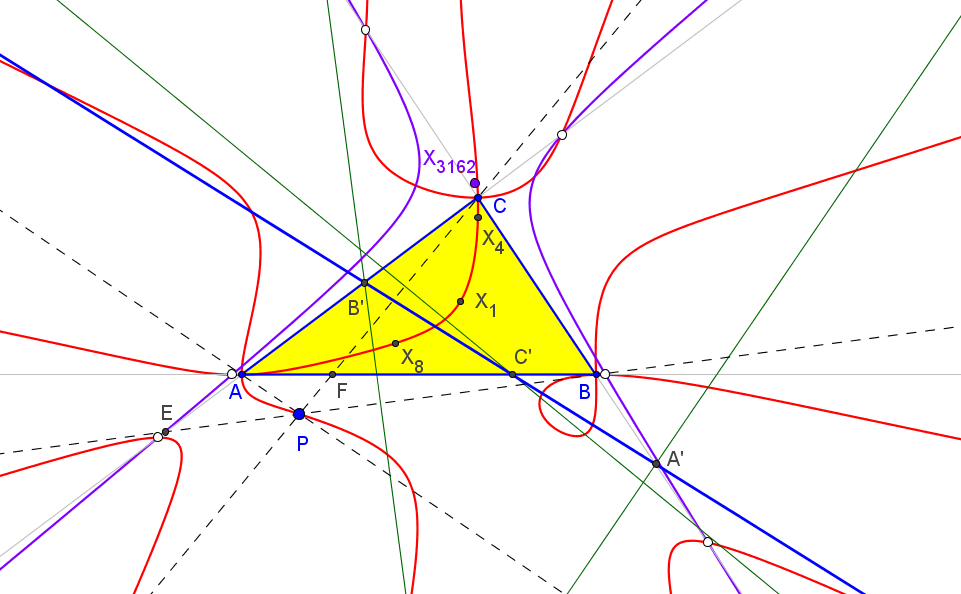
Sean ABC un triángulo y A'B'C' su triángulo de reflexión (ie. A', B' y C' son los simétricos de A, B y C respecto a BC, CA y AB, resp.). Denotamos por:
Ab y Ac las proyecciones ortogonales de A' sobre BB' y CC', resp.
Bc y Ba las proyecciones ortogonales de B' sobre CC' y AA', resp.
Ca y Cb las proyecciones ortogonales de C' sobre AA' y BB', resp.
Entonces, las rectas de Euler La, Lb y Lc de los triángulos A'AbAc, B'BcBa y C'CaCb, respectivamente, son concurrentes en el punto X de coordenadas baricéntricas:
( a^2 (a^8(b^2+c^2) - 2a^6(b^4+c^4) + a^4b^2c^2(b^2+c^2) + a^2(b^2-c^2)^2(2b^4+b^2c^2+2c^4) - b^10+b^8c^2+b^2c^8-c^10) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: -6.61866665524197553640898833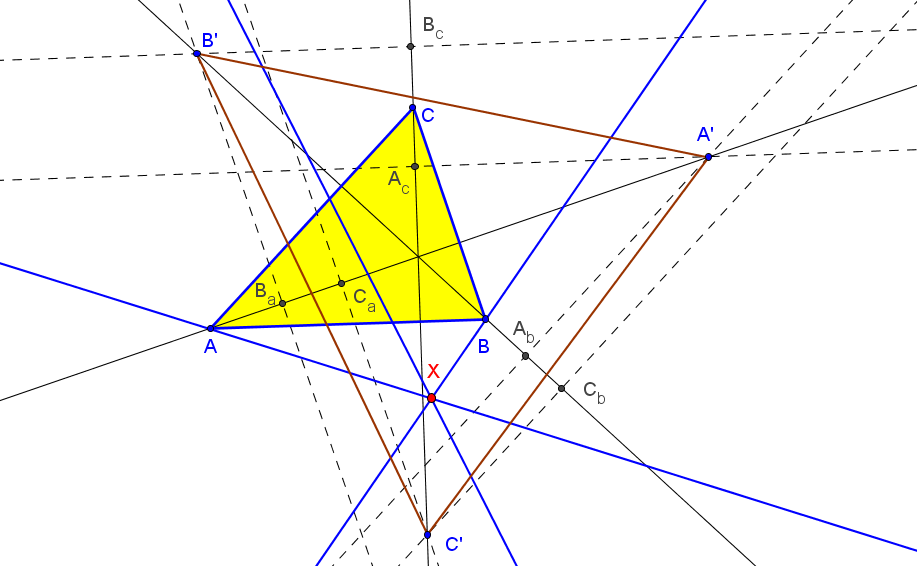
Sean ABC un triángulo, A'B'C' su triángulo de reflexión (ie. A', B' y C' son los simétricos de A, B y C respecto a BC, CA y AB, resp.) y AtBtCt el triángulo antipedal del circuncentro O (triángulo tangencial).
Sean Oa, Ob y Oc los circuncentros de los triángulos AtB'C', BtC'A' y CtA'B', resp. Ellos quedan en las alturas de ABC (sobre las rectas AA', BB' y CC').
Por tanto, ABC y OaObOc son ortológicos con un centro de ortología en el ortocentro H de ABC.
El otro centro de ortología es el punto de intersección de las perpendiculares por A, B y C a las rectas ObOc, OcOa y OaOb, resp., de ecuaciones baricéntricas:
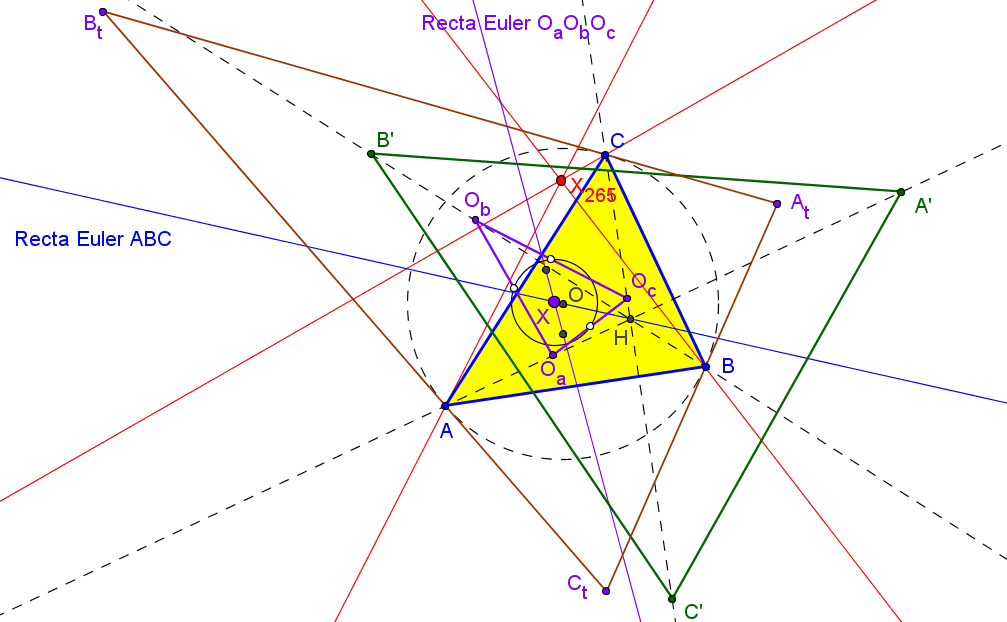
( a^8(b^2+c^2) - 2a^6(b^4-b^2c^2+c^4) - a^4b^2c^2(b^2+c^2) + a^2(b^2-c^2)^2(2b^4-b^2c^2+2c^4) - (b^2-c^2)^4(b^2+c^2) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: -1.67191299053365041718858431
Dado un triángulo ABC, sea DEF el triángulo acotado por las rectas La, Lb y Lc, donde La es la polar del ortocentro H con respecto a la circunferencia centrada en A y pasando por N, centro de la circunferencia de los nueve puntos; Lb y Lc se definen cíclicamente.
El triángulo DEF es homotético a ABC con centro de homotecia X (en la recta de Euler), de coordenadas baricéntricas:
((a^6-3a^4(b^2+c^2)+a^2(3b^4+b^2c^2+3c^4)-(b^2-c^2)^2(b^2+c^2)) /(b^2+c^2-a^2) : ... : ... ),
que tiene (6-9-13)-número de búsqueda en ETC: 1.7457649287207846078851083739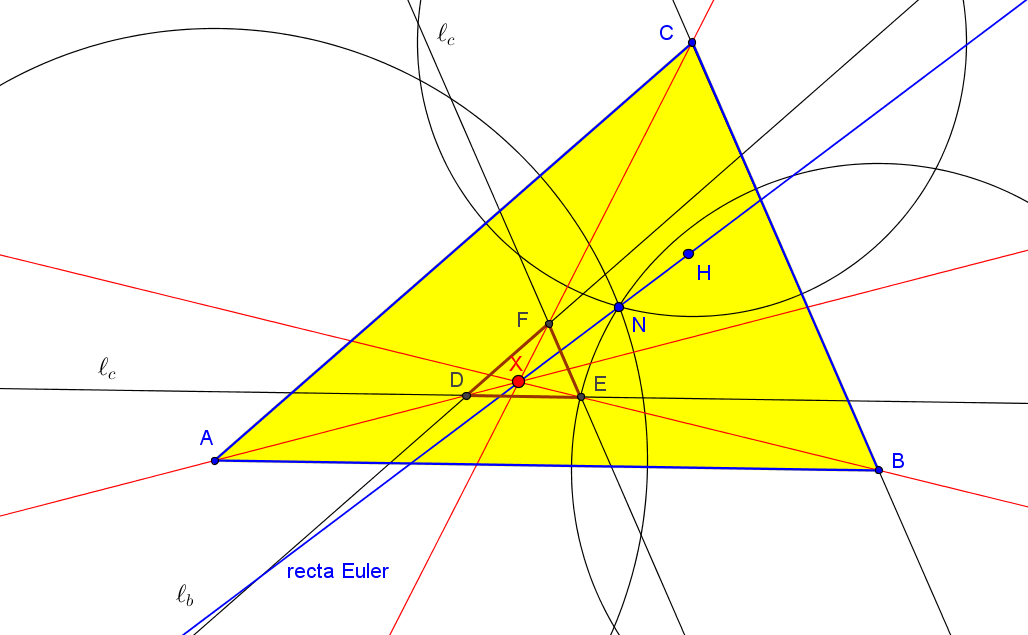
Dado un triángulo ABC, construir:
1. Tres circunferencias de igual radio, tangentes a los lados AB y AC, BC y BA, CA y CB, respectivamente, y que tengan un punto común.
2. Tres circunferencias de igual radio, tangentes a los lados AB y AC, BC y BA, CA y CB, respectivamente, y tangentes exteriormente a otra circunferencia, también de mismo radio.
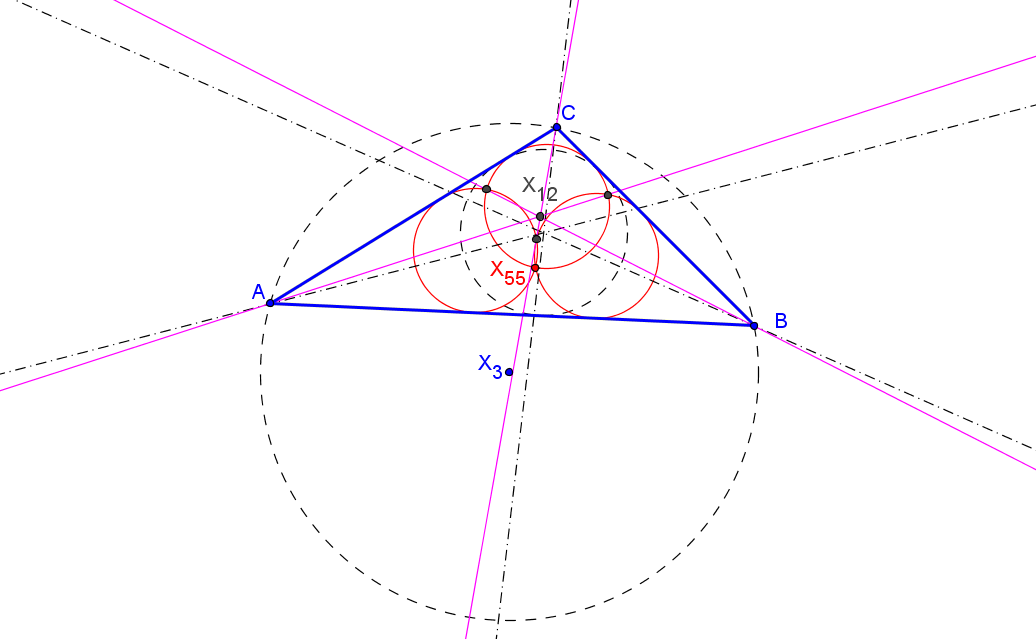
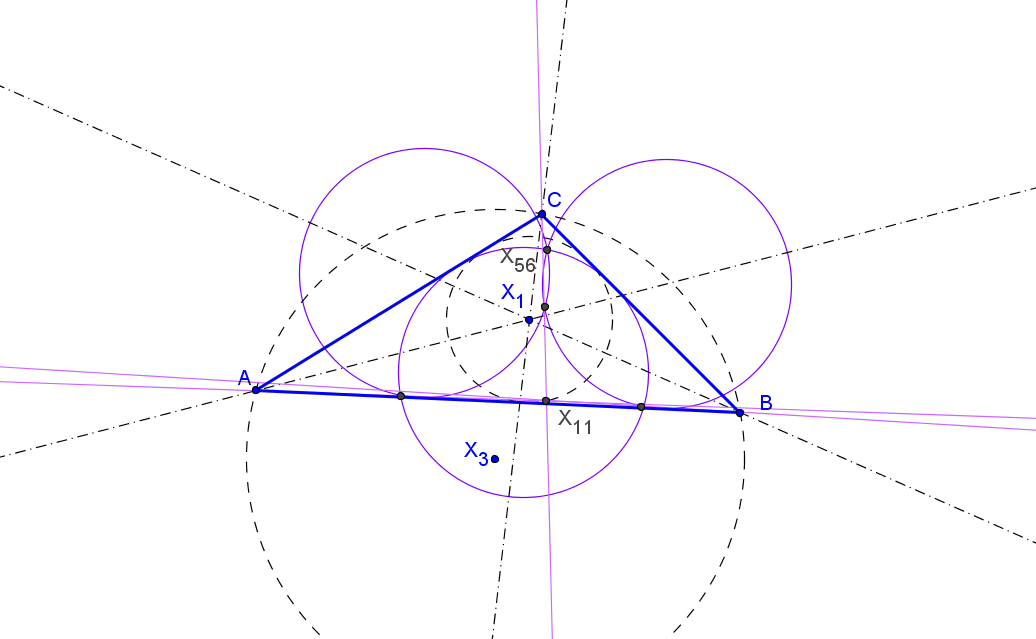
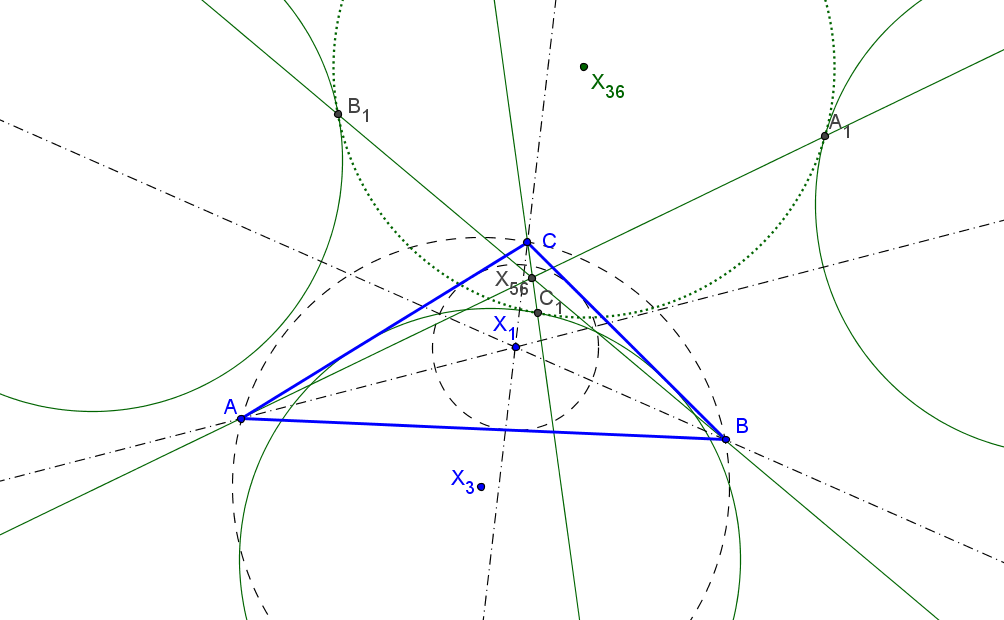
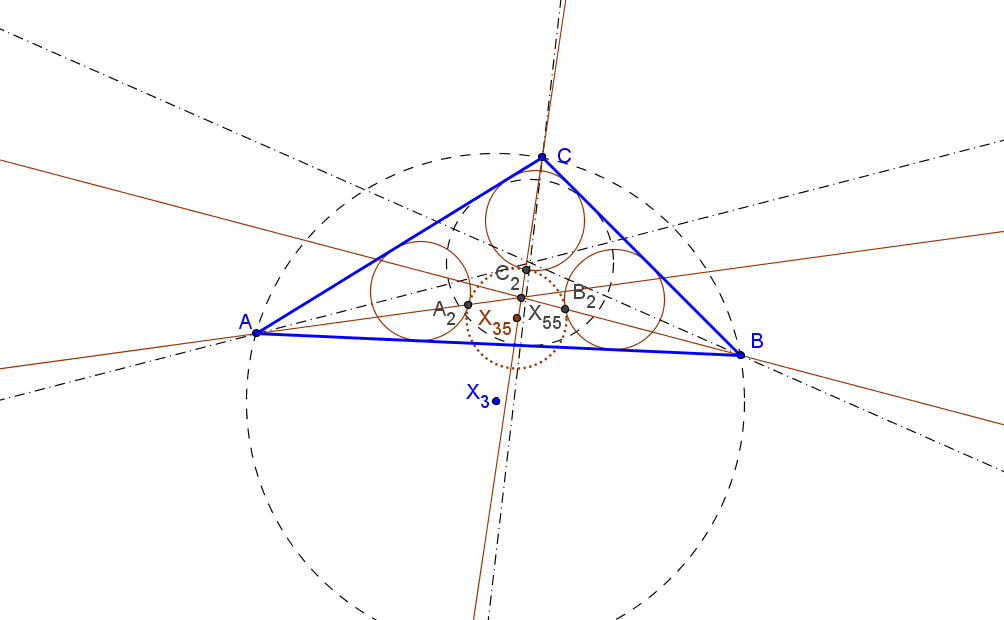
◊ Sean ABC un triángulo, P y P* dos puntos conjugados isogonales y A'B'C' el triángulo antipedal de P.
Las perpendiculares por A', B' y C' a las reflexiones de AP, BP y CP, respectivamente, respecto a PP* son concurrentes, en un punto Q sobre las circunferencia circunscrita a A'B'C'.
En particular, si P=O (A'B'C' es el triángulo tangencial), el punto de concurrencia Q tiene coordenadas baricéntricas (Anopolis #419):
( a^2(a^16 - 2a^14(b^2+c^2)- 2a^12(b^4-5b^2c^2+c^4)+ 2a^10(b^2+c^2)(3b^4-7b^2c^2+3c^4) - a^8b^2c^2(3b^2-4c^2)(4b^2-3c^2)- 6a^6(b-c)^2(b+c)^2(b^2+c^2)(b^4-b^2c^2+c^4)+ a^4(b-c)^2(b+c)^2(2b^8+12b^6c^2-b^4c^4+12b^2c^6+2c^8)+ 2a^2(b-c)^2(b+c)^2(b^2+c^2)(b^8-4b^6c^2+3b^4c^4-4b^2c^6+c^8)- (b-c)^4(b+c)^4(b^8+2b^6c^2+2b^2c^6+c^8)) : ... : ...),
y tiene (6-9-13)-número de búsqueda en ETC: -6.980189770294538.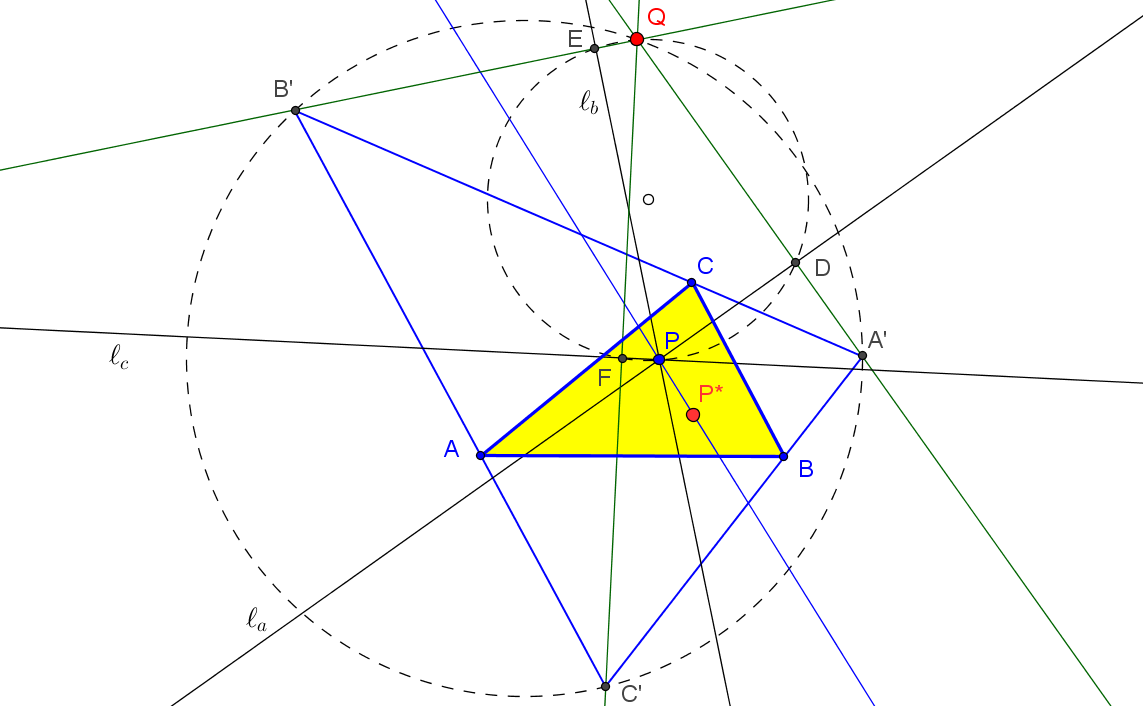
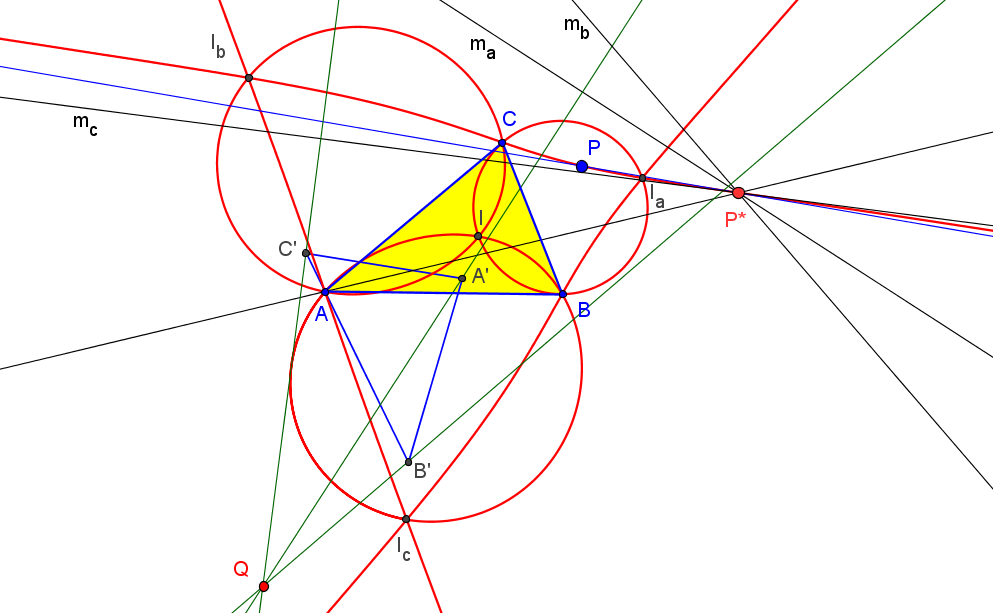
Sean ABC un triángulo, P y P* dos puntos conjugados isogonales y A'B'C' el triángulo pedal de P.
Las perpendiculares por A', B' y C' a las reflexiones de PP*, respecto a AP, BP y CP son concurrentes en un punto Q, si P está sobre la nónica que pasa por los vértices de ABC (puntos triples), por el incentro I, por el ortocentro H y por los exincentros Ia, Ib, Ic.
(
Mostrar/Ocultar fórmula )
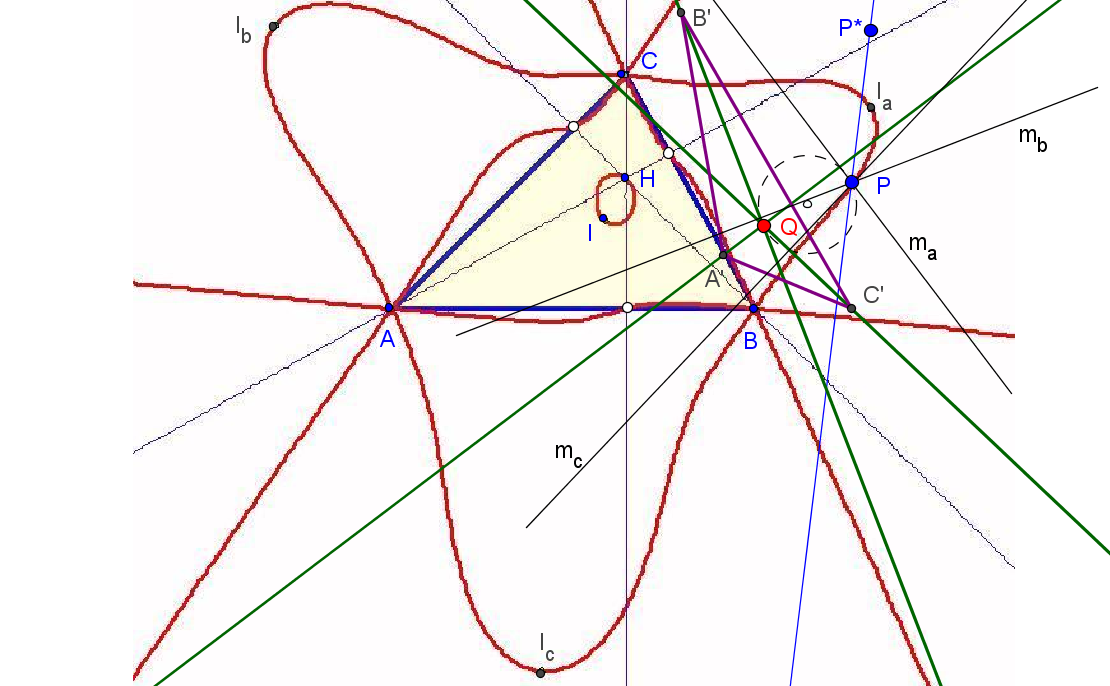
Sean ABC un triángulo, I su incentro, O su circuncentro, IaIbIc el triángulo excentral y La, Lb, Lc las reflexiones de la recta IO en las bisectrices AI, BI y CI, respectivamente.
Las perpendiculares a La, Lb y Lc por Ia, Ib y Ic, respectivamente, concurren en el punto de coordenadas baricéntricas:
( a^9 - 2a^8(b+c) + 6a^7b*c + 2a^6(b-2c)(2b-c)(b+c) - a^5(4b^4+4b^3c-17b^2c^2+4c^3b+4c^4)- 2a^4(b-c)^2(b+c)(b^2-6b*c+c^2)+ a^3(b-c)^2(4b^4+2b^3c-11b^2c^2+2c^3b+4c^4)- 2a^2b*c(b-c)^2(b+c)(3b^2-5b*c+3c^2)- a(b-c)^6(b+c)^2 : ... : ... ),
y tiene (6-9-13)-número de búsqueda en ETC: 26.33820686266028262904684.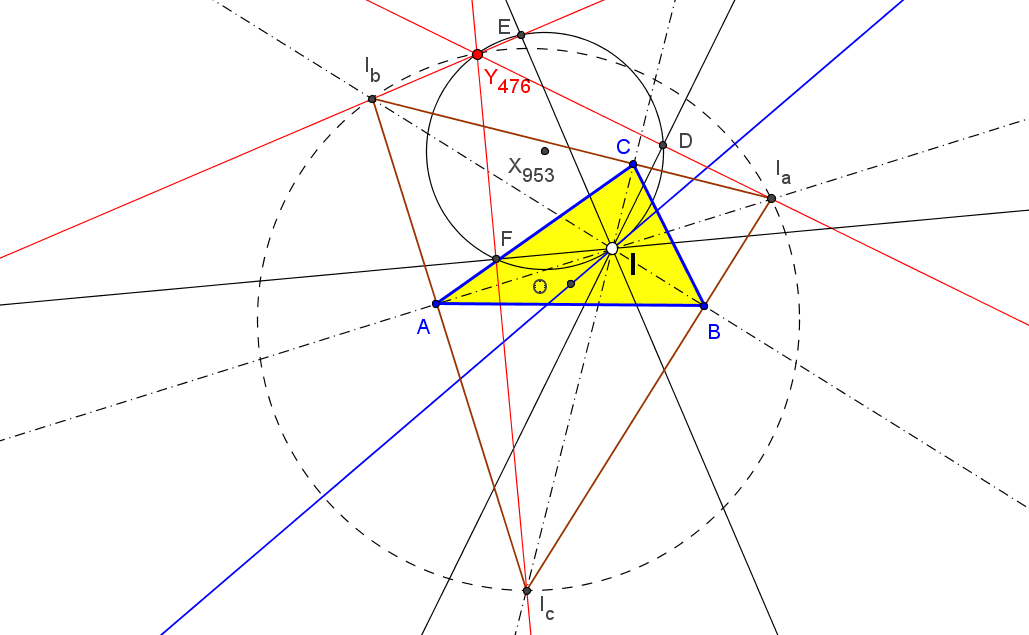
Sean ABC un triángulo, p una recta que pasa por el ortocentro H y P un punto (distinto de H) sobre p. Se denotan por D, E y F los puntos simétricos de H respecto a las perpendiculares por P a los lados BC, CA y AB, respectivamente, y consideramos los puntos:
A'=BE∩CF B'=CF∩AD C'=AD∩BE,
y las tres cónicas, (Ca) que pasa por B, C, H, P, A', (Cb) que pasa por C, A, H, P, B' y (Cc) que pasa por A, B, H, P, C'.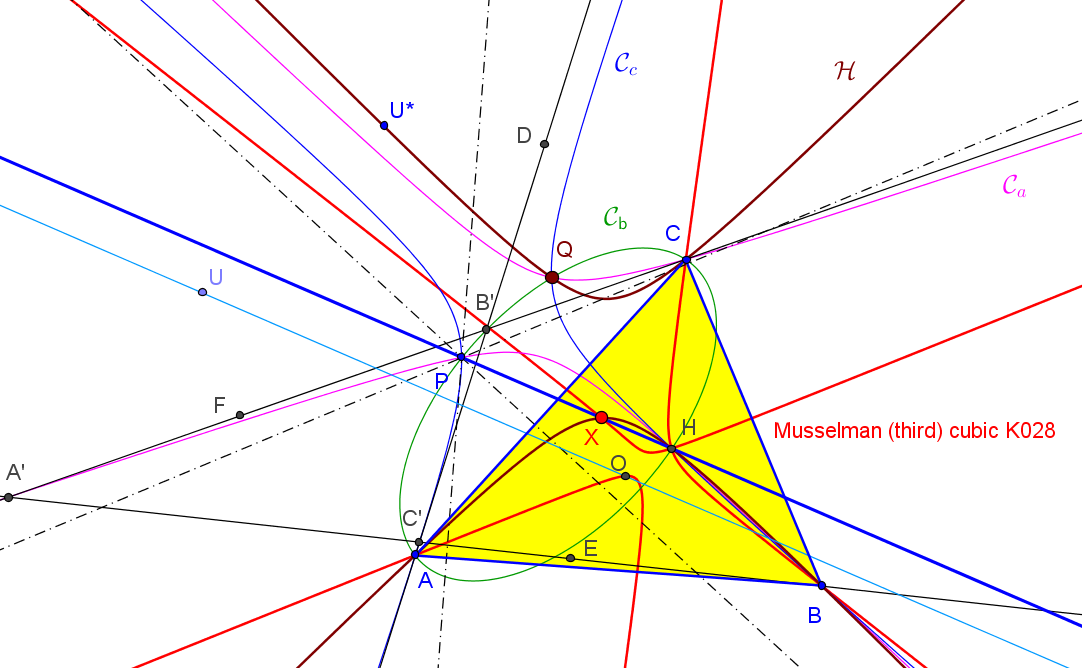
Sean ABC un triángulo y O su circuncentro. Consideramos las circunferencias exinscritas relativas al ángulo en O de los triángulos OBC, OCA y OAB; su centro radical es el punto de coordenadas baricéntricas:
( a(a^2-b^2-c^2)(2a^5(b+c)^2 - 4a^3(b^2+b*c+c^2)^2 + 2a(b-c)^2(b+c)^4 + 2S(b+c)(a^4-a^2(2b^2+5b*c+2c^2) + b^4-b^3c-c^3b+c^4)) : ... : ... ),
donde S es el doble del área de ABC, y tiene (6-9-13)-número de búsqueda en ETC: 5.60319717911870517696190546.
( a(a^2-b^2-c^2)(a^4-2a^2(b+c)^2 - 4a(b+c)S + (b^2-c^2)^2) : ... : ... ).
con (6-9-13)-número de búsqueda en ETC: 6.13472549396753240388995633.
Sean ABC un triángulo, P un punto y A'B'C' su triángulo ceviano. Adoptemos las siguientes notaciones:
Ab y Ac son las proyecciones ortogonales de A sobre BB' y CC',
Bc y Ba son las proyecciones ortogonales de B sobre CC' y AA',
Ca y Cb son las proyecciones ortogonales de C sobre AA' y BB',
A2 y A3 son las proyecciones ortogonales de A' sobre BB' y CC',
B3 y B1 son las proyecciones ortogonales de B' sobre CC' y AA',
C1 y C2 son las proyecciones ortogonales de C' sobre AA' y BB'.
Na, Nb y Nc los centros de las circunferencia de los nueve puntos de los triángulos
AAbAc, BBcBa, CCaCb,
N1, N2 y N3 los centros de las circunferencia de los nueve puntos de los triángulos
A'A2A3, B'B3B1, C'C1C2.
Se verifica:
Las rectas N1Na, N2Nb y N3Nc concurren en el punto P. De hecho, N1N2N3 es el triángulo ceviano de P respecto a NaNbNc.
( a^4 - 3a^3(b+c)+ 9a^2b*c + 3a(b-c)^2(b+c) - (b^2-c^2)^2 : ... : ... ).
( a^2/(4a^4 - (b^2-c^2)^2 - 3a^2(b^2+c^2)) : b^2/(4b^4 - (c^2-a^2)^2 - 3b^2(c^2+a^2)) : c^2/(4c^4 - (a^2-b^2)^2 - 3c^2(a^2+b^2)) ).
Este punto es el conjugado isogonal de X550, es decir, es el punto donde concurren las tangentes en los vértices de ABC a la isocúbica pK(X6,X550) (ver la sección La isocúbica pK(X6,X550))( a^2(a^2+b^2-c^2)(a^2-b^2+c^2) (a^4 - 2a^2(b^2+c^2) + b^4+3b^2c^2+c^4 ) (a^4(b^2+c^2) - 2a^2(b^4-3b^2c^2+c^4) + (b^2-c^2)^2(b^2+c^2)): ... : ... ).
Sean ABC un triángulo, A'B'C' el antipedal de N (centro de la circunferencia de los nueve puntos de ABC) y N1, N2, N3 los centros de la circunferencias de los nueve puntos de los triángulos NB'C', NC'A', NA'B', respectivamente.
El centro de la circunferencia de los nueve puntos del triángulo N1N2N3 es el punto X5500 (8th Hatzipolakis-Montesdeoca Point) que está en la recta de Euler de ABC y sus coordenadas baricéntricas son:
( 2a^22
- 15a^20(b^2+c^2)
+
6a^18(8b^4+13b^2c^2+8c^4)-(b^2-c^2)^8(b^6+b^4c^2+b^2c^4+c^6)
-
a^16(81b^6+152b^4c^2+152b^2c^4+81c^6)
+
a^14(64b^8+111b^6c^2+128b^4c^4+111b^2c^6+64c^8)
+
a^12(14b^10+29b^8c^2+36b^6c^4+36b^4c^6+29b^2c^8+14c^10)
-
a^10(84b^12+67b^10c^2+56b^8c^4+48b^6c^6+56b^4c^8+67b^2c^10+84c^12)
+
a^8(82b^14-23b^12c^2-31b^10c^4-19b^8c^6-19b^6c^8-31b^4c^10-23b^2c^12+82c^14)
-
a^6(b^2-c^2)^2(34b^12+11b^10c^2-30b^8c^4-35b^6c^6-30b^4c^8+11b^2c^10+34c^12)
+
a^4(b^2-c^2)^4(b^10-2b^8c^2-22b^6c^4-22b^4c^6-2b^2c^8+c^10)
+
a^2(b^2-c^2)^6(4b^8+5b^6c^2+8b^4c^4+5b^2c^6+4c^8) : ... : ... ).
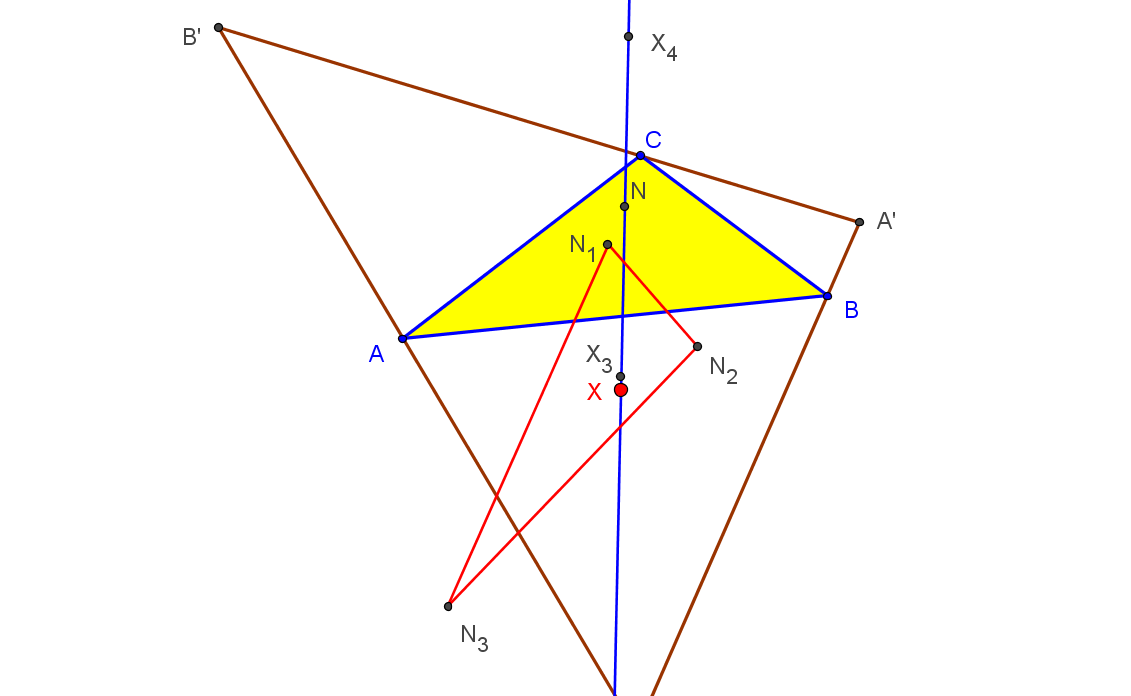
Sean ABC un triángulo y l la recta de Euler, que corta a los lados BC, CA y AB en los puntos A', B' y C', respectivamente. Las circunferencias de diámetros AA', BB' y CC' son coaxiales y el eje d pasa por el ortocentro. Las tres circunferencias concurren en el punto X107 sobre la circunferencia circunscrita y en X125 (centro de la hipérbola de Jerabek: hipérbola equilátera circunscrita a ABC y que pasa por el circuncentro).

Sean ABC un triángulo, para todo punto P las circunferencias de los nueve puntos de los triángulos PBC, PCA y PAB son concurrentes, en un punto sobre la circunferencia de los nueve puntos de ABC.
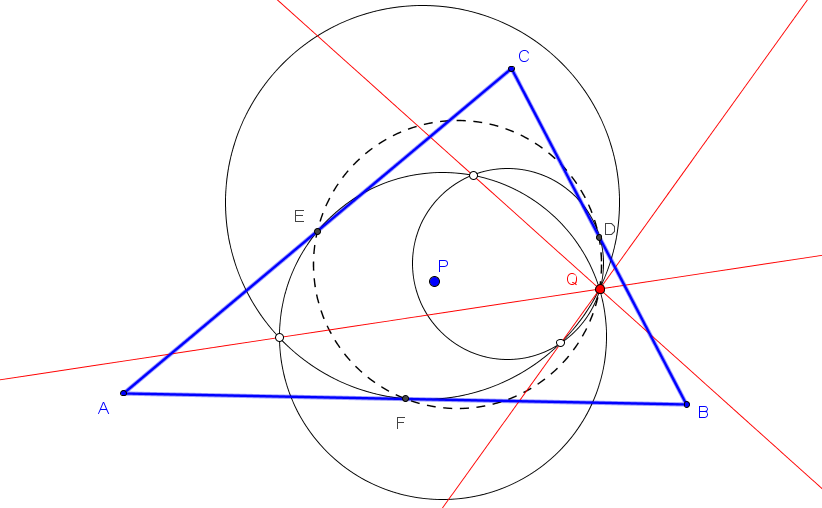
Sean ABC un triángulo, X un punto; N1, N2, N3 los centros de las circunferencias de los nueve puntos de los triángulos XBC, XCA, XAB, resp. and A'B'C' el triángulo antipedal de X. Los triángulos N1N2N3 y A'B'C' son perspectivos si y solo si X queda sobre la cúbica isogonal pK(X6,X550) (junto con la recta del infinito y la circunferencia circunscrita a ABC).
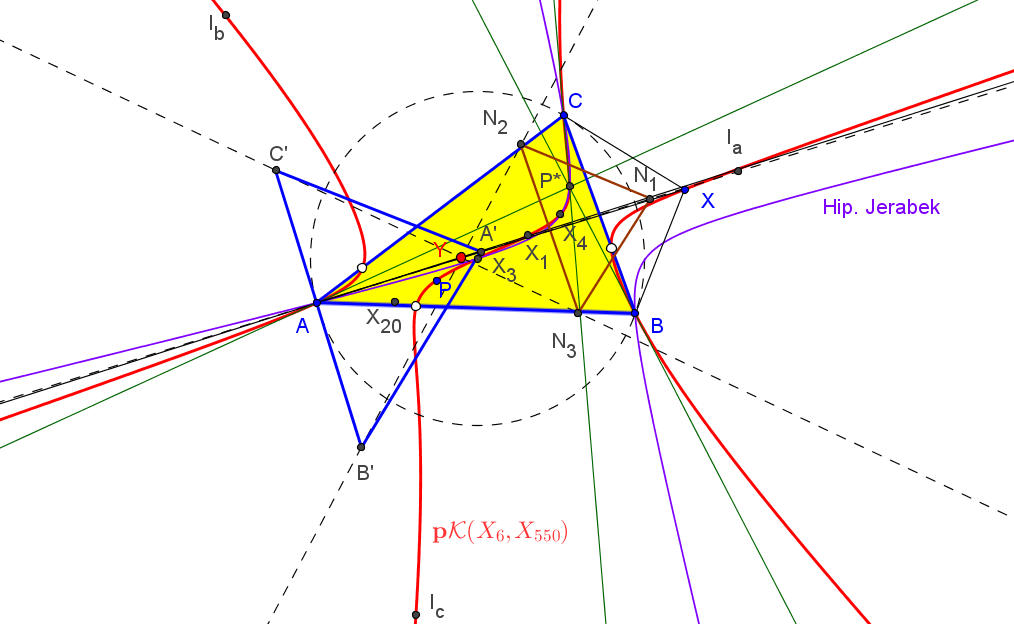
( a^2(a^8 + a^6(b^2+c^2)+ a^4(-9b^4+19b^2c^2-9c^4) + 11a^2(b^2-c^2)^2(b^2+c^2) - (b^2-c^2)^2(4b^4+17b^2c^2+4c^4)): ... : ... ),
que está sobre la cúbica y con (6-9-13)-número de búsqueda en ETC: -702.0040014335101057823010.
Sean ABC un triángulo, P un punto, N1, N2 y N3 los centros de las circunferencias de los nueve puntos de los triángulos PBC, PCA y PAB, respectivamente, O' el circuncentro de N1N2N3 y N' el centro de la circunferencia de los nueve puntos de N1N2N3.
Si P=N (centro de la circunferencia de los nueve puntos de ABC), el punto O', que está en la recta de Euler de ABC, tiene coordenadas baricéntricas:
( -2a^16+ 9a^14(b^2+c^2)-
a^10(b^6+b^4c^2+b^2c^4+c^6)+
a^8(25b^8+10b^6c^2+8b^4c^4+10b^2c^6+25c^8) +
a^6(-33b^10+31b^8c^2+11b^6c^4+11b^4c^6+31b^2c^8-33c^10)+
a^4(b^2-c^2)^2(21b^8-20b^6c^2-25b^4c^4-20b^2c^6+21c^8)-
a^2(b^2-c^2)^4(7b^6-13b^4c^2-13b^2c^4+7c^6)+
(b^2-c^2)^6(b^4-4b^2c^2+c^4)-a^12(13b^4+18b^2c^2+13c^4): ... : ... )
( 2a^10 - 5a^8(b^2+c^2) + 2a^6(b^4+5b^2c^2+c^4) + a^4(4b^6-5b^4c^2-5b^2c^4+4c^6) - a^2(b^2-c^2)^2(4b^4+5b^2c^2+4c^4) + (b^2-c^2)^4(b^2+c^2) : ... : ...)
(con (6-9-13)-número de búsqueda en ETC: 4.7800096839999025703058)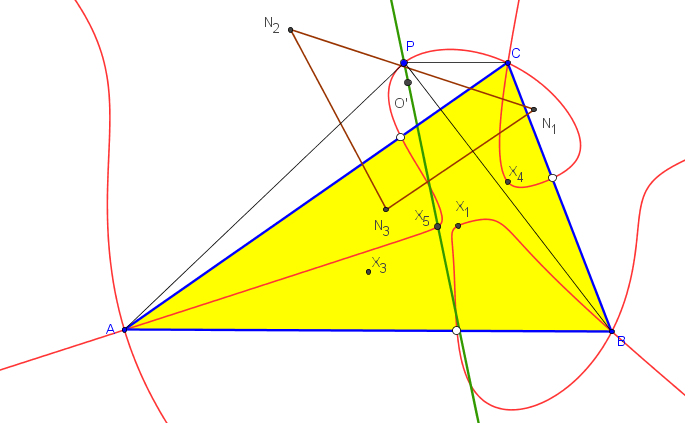
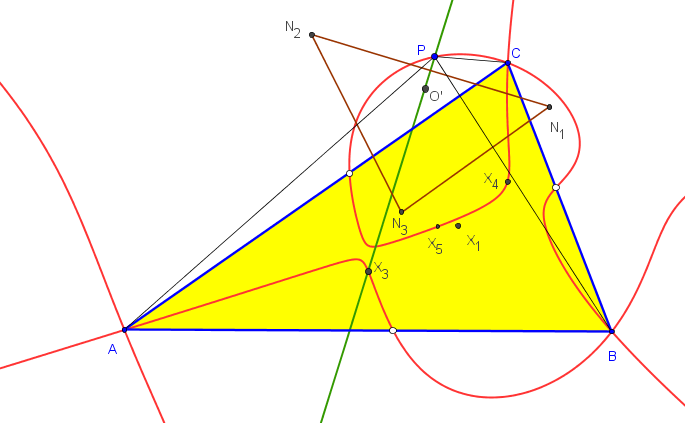
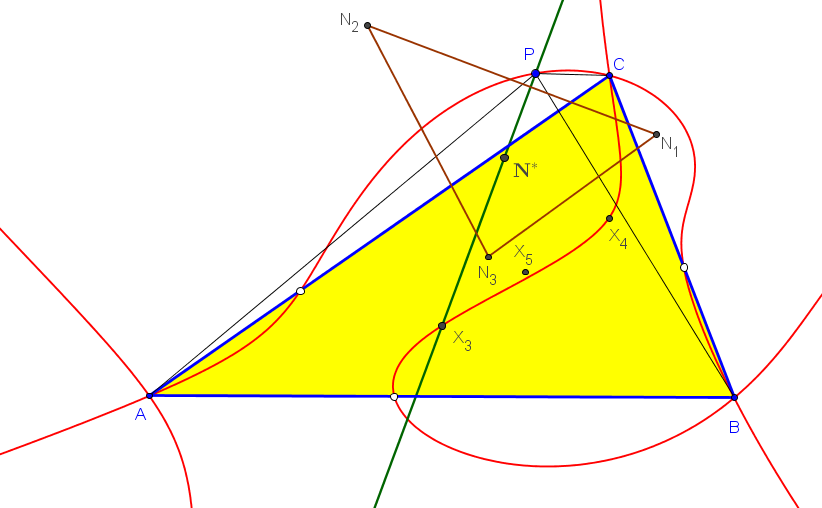
Sean ABC un triángulo y P un punto, P* su conjugado isogonal, A'B'C' y A"b"C" los triángulos cevianos de P y P*, respectivamente.
A* es el punto de intersección de la perpendicular a AA' por A' y de la perpendicular a AA" por A",
B* es el punto de intersección de la perpendicular a BB' por B' y de la perpendicular a BB" por B" y
C* es el punto de intersección de la perpendicular a CC' por C' y de la perpendicular a CC" por C".
Entonces, los triángulos ABC y A*B*C* son perspectivos, para cualquier punto P, y el centro de perspectividad es el circuncentro de ABC.
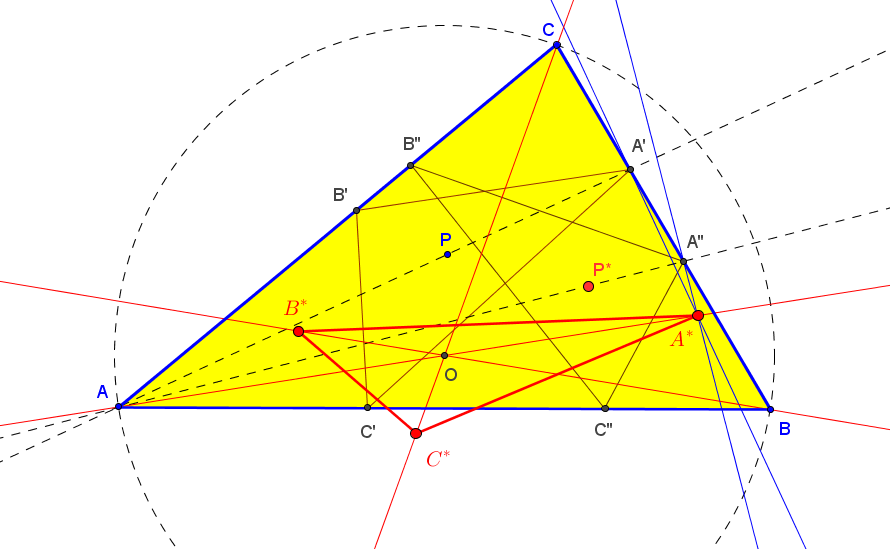
Sean ABC un triángulo, P un punto, N, N1, N2, N3 los centro de las circunferencias de los nueve puntos de los triángulos ABC, PBC, PCA y PAB, respectivamente y N* el centro de la circunferencia de los nueve puntos del triángulo N1N2N3.
Los puntos P, N y N* están alineados si y solo si P está en la circunferencia circunscrita a ABC o en la cúbica de Napoleon-Feuerbach (K005 del catálogo de Bernard Gibert)
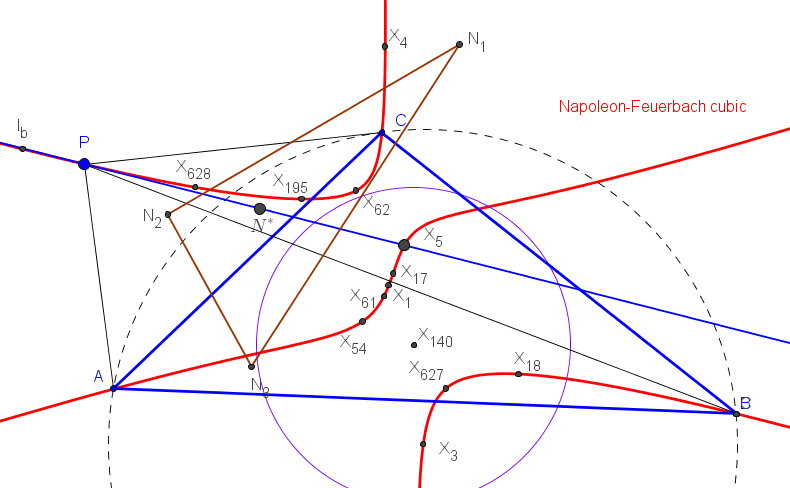
Sea ABC un triángulo y A'B'C' el triángulo ceviano de un punto P. Se denota por
L11 la perpendicular a AA' por A',
L22 la perpendicular a BB' por B',
L33 la perpendicular a CC' por C'.
L12 la simétrica de L11 respecto a BB',
L13 la simétrica de L11 respecto a CC'.
A"=L12∩L13 y similarmente se definen B" y C".
El lugar geométrico de los puntos P tal que los triángulos ABC y A"B"C" son perspectivos es una curva algebraica de grado nueve ( Mostrar/Ocultar ecuacíón )

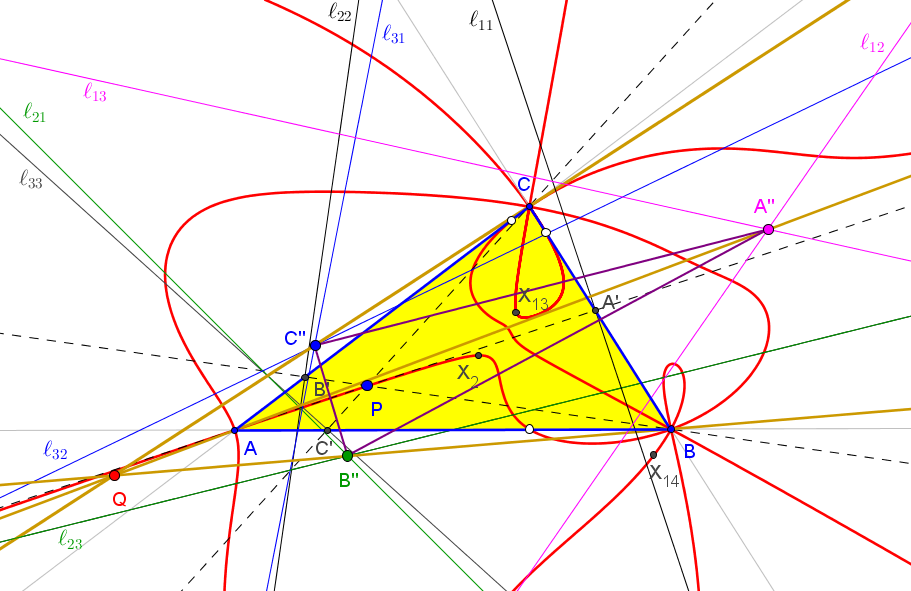
Sea ABC un triángulo y A'B'C' el triángulo ceviano del incentro I. Se denota por
L11 la perpendicular a AA' por A',
L22 la perpendicular a BB' por B',
L33 la perpendicular a CC' por C'.
L12 la simétrica de L11 respecto a BB',
L13 la simétrica de L11 respecto a CC'.
M12 la paralela a L12 por B',
M13 la paralela a L13 por C'.
A"=M12∩M13 y similarmente se definen B" y C".
O1 el circuncentro del triángulo A"B'C',
O2 el circuncentro del triángulo B"C'A',
O3 el circuncentro del triángulo C"A'B'.
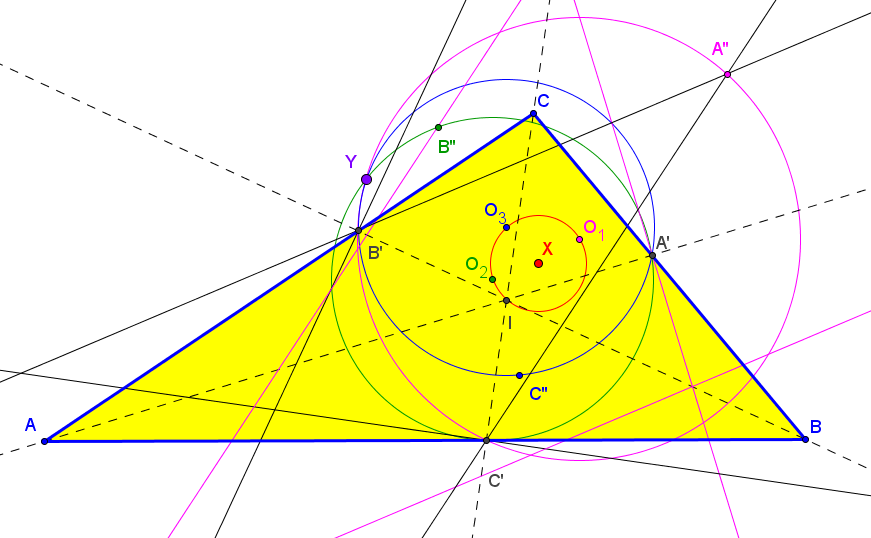
Sea ABC un triángulo y A'B'C' el triángulo ceviano del incentro I. Se denota por
L1 la perpendicular a AA' por A',
L2 la perpendicular a BB' por B',
L3 la perpendicular a CC' por C',
(i.e. las rectas determinan el triángulo antipedal de I con respecto a A'B'C'),
L11 la simétrica de L1 respecto a AA' (coincide con L1),
L12 la simétrica de L1 respecto a BB',
L13 la simétrica de L1 respecto a CC'.
L21 la simétrica de L2 respecto a AA',
L22 la simétrica de L2 respecto a BB' (coincide con L2),
L23 la simétrica de L2 respecto a CC'.
L31 la simétrica de L3 respecto a AA',
L32 la simétrica de L3 respecto a BB',
L33 la simétrica de L3 respecto a CC' (coincide con L3).
O1 el circuncentro del triángulo AaAbAc acotado por las rectas L11, L12 y L13,
O2 el circuncentro del triángulo BaBbBc acotado por las rectas L21, L22 y L23,
O3 el circuncentro del triángulo CaCbCc acotado por las rectas L31, L32 y L33.
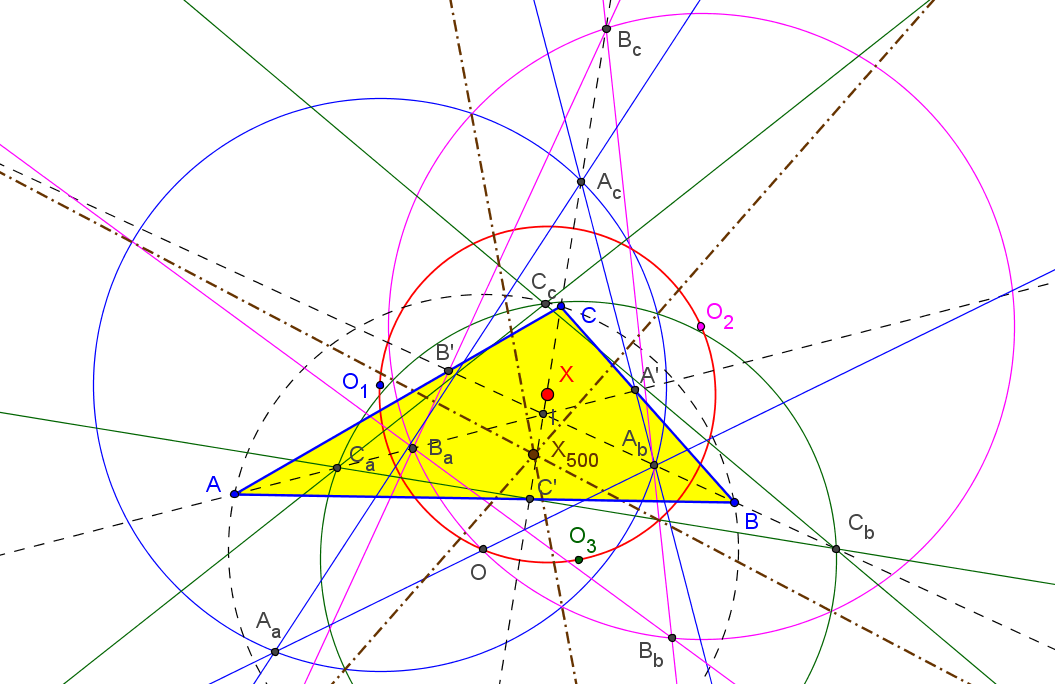
NOTA: Este punto ha sido incluido (28/05/2013) en la "Encyclopedia of Triangle Centers- ETC" con el número X5495="3rd Hatzipolakis-Montesdeoca point".
El centro radical de las circunferencias circunscritas a los triángulos AaAbAc, BaBbBc y CaCbCc es X500, ortocentro del triángulo A'B'C'. (Randy Hutson)
Sea ABC un triángulo y A'B'C' el triángulo ceviano del incentro. Se denota por
Ab, Ac las reflexiones de A' en BB' y CC', resp.
Bc, Ba las reflexiones de B' en CC', AA', resp.
Ca, Cb las reflexiones de C' en AA', BB', resp.
La, Lb y Lc las rectas de Euler de los triángulos A'AbAc, B'BcBa, C'CaCb, resp.
L'a, L'b, L'c las rectas paralelas a La, Lb, Lc por A, B y C, resp.
Entonces, las rectas L'a, L'b, L'c concurren en X80 (simétrico del incentro respecto al punto de Feuerbach).
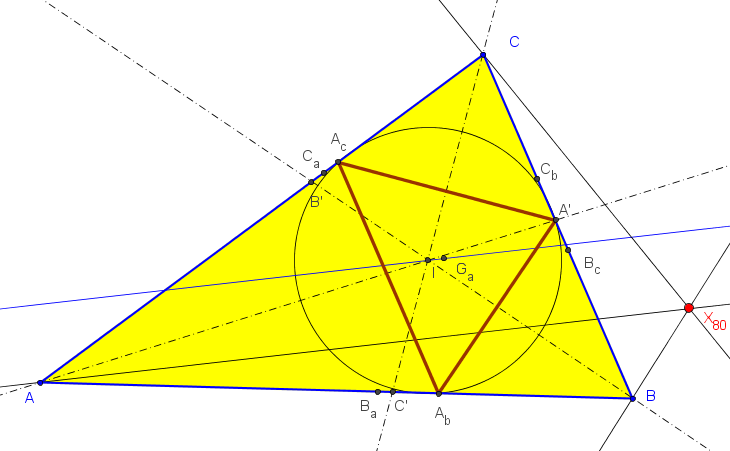
Sea ABC un triángulo y A'B'C' el triángulo ceviano del incentro. Se denota por
Ab, Ac las reflexiones de A' en BB' y CC', resp.
Bc, Ba las reflexiones de B' en CC', AA', resp.
Ca, Cb las reflexiones de C' en AA', BB', resp.
L, La, Lb y Lc las rectas de Euler de los triángulos ABC, AAbAc, BBcBa, CCaCb, resp.
L'a, L'b, L'c las rectas simétricas de La, Lb, Lc respecto a AA', BB', CC', resp.
Entonces, las rectas L,La, Lb, Lc son paralelas y las rectas L'a, L'b, L'c concurren en el punto de coordenadas baricéntricas:
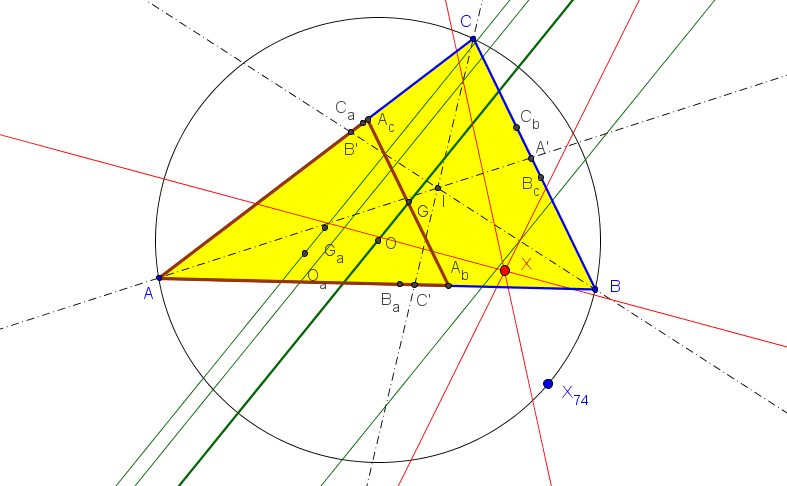
Este punto ha sido incluido (28/05/2013) en la "Encyclopedia of Triangle Centers- ETC" con el número X5494="2nd Hatzipolakis-Montesdeoca point".
Un triángulo ABC es ortológico respecto otro DEF si las perpendiculares por A, B y C a los lados de DEF se cortan en un punto.
En tal caso, se verifica que, recíprocamente, DEF es ortológico respecto ABC: las perpendiculares por D, E y F a los lados de ABC también se cortan en un punto. A estos puntos de concurrencia se les llama centros de ortología.
Sea ABC un triángulo y A'B'C', A"B"C" los triángulo órtico y medial, respectivamente.
Se denota por:
(Ab), (Ac) las circunferencias de los nueve puntos de A'BC", A'B"C, resp.
(Bc), (Ba) las circunferencias de los nueve puntos de B'CA", B'C"A, resp.
(Ca), (Cb) las circunferencias de los nueve puntos de C'AB", C'A"B, resp.
Entonces, los triángulos ABC y DEF, el acotado por las recta (que pasan por los centros de las circunferencias) BcCb, CaAc, AbBa, son ortológicos.
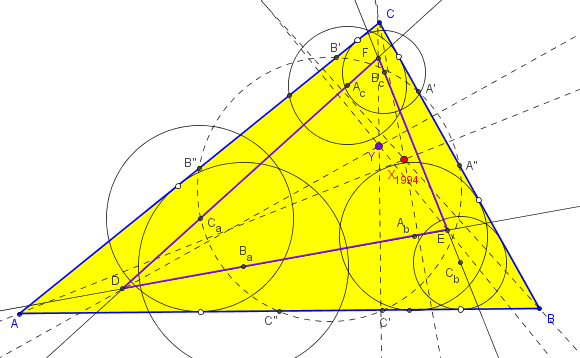
El centro de ortología Y de DEF y ABC tiene coordenadas baricéntricas:
Sea ABC un triángulo y A'B'C', A"B"C" los triángulo órtico y medial, respectivamente.
Se denota por:
(Ab), (Ac) las circunferencias de los nueve puntos de A'BC", A'B"C, resp.
(Bc), (Ba) las circunferencias de los nueve puntos de B'CA", B'C"A, resp.
(Ca), (Cb) las circunferencias de los nueve puntos de C'AB", C'A"B, resp.
r1 el eje radical de (Bc), (Cb);
r2 el eje radical de (Ca), (Ac);
r3 el eje radical de (Ab), (Ba)
Entonces, r1, r2, r3 son concurrentes en el punto de X de coordenadas baricéntricas:
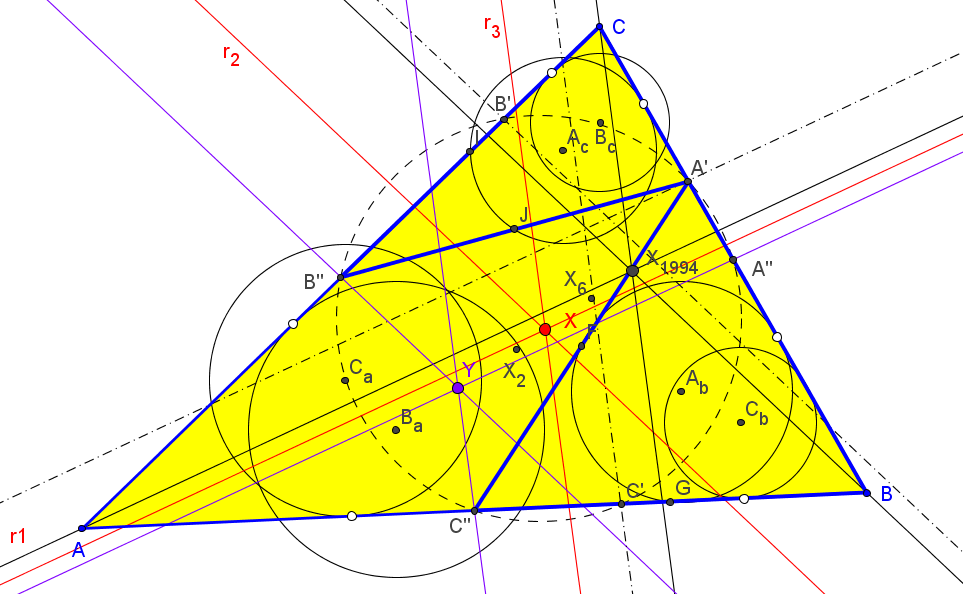
Sea ABC un triángulo y A'B'C', A"B"C" los triángulo órtico y medial, respectivamente.
Se denota por:
(I11) la circunferencia exinscrita a A'B"C" respecto al ángulo B"A'C"
(I22) la circunferencia exinscrita a A"B'C" respecto al ángulo C"B'A"
(I33) la circunferencia exinscrita a A"B"C' respecto al ángulo A"C'B".
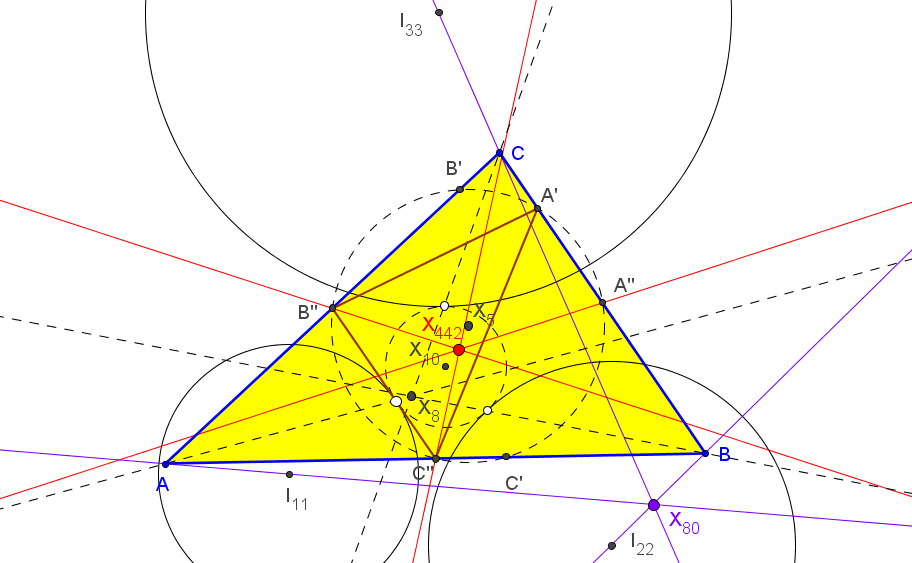
Dados un triángulo ABC y un punto P. sea A'B'C' el triángulo preceviano (anticeviano) de P, entonces el lugar geométrico de los puntos Q tales que ABC es perspectivo con el triángulo A"B"C", simétrico de A'B'C' respecto a Q, es la cónica biceviana C(G,P') del baricentro G y el tripolo P' de la recta pasando por P y por el cociente ceviano G/P, de G y P.
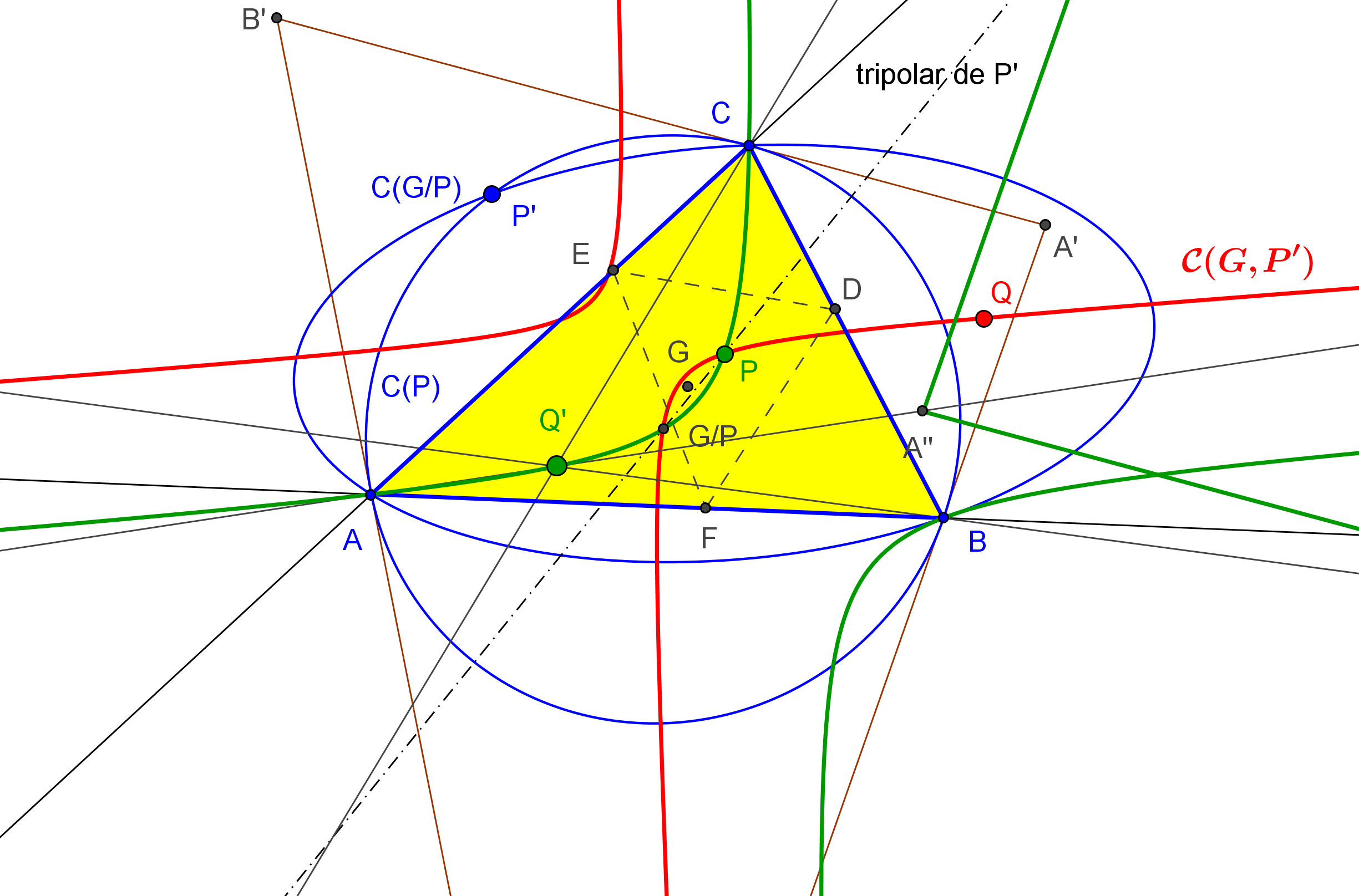
Si P(p:q:r) y Q(x:y:z), en coordenadas baricéntricas, los vértices del triángulo anticeviano de P y los de su triángulo simétrico respecto a Q son:
Las rectas AA", BB" y CC" son concurrentes si Q está en la cónica:
![\newfont{\euii}{eufm10 scaled \magstep4}
{\hbox{\euii S}}_{
\begin{array}
ppqr\\[-3pt]
xyz
\end{array}}
\left[\frac{x^2}{\displaystyle\frac{1}{qr(q-r)}}
-\left(\frac{1}{\displaystyle\frac{1}{pq(p-q)}}+
\frac{1}{\displaystyle\frac{1}{rp(r-p)}}
\right)yz
\right]=0](../imagenes/AdvancedPlaneGeometry33Formula.png)
El lugar geométrico de los centros de perspectividad Q' de ABC y A"B"C", cuando Q varía en la cónica biceviana C(G,P'), es la cónica circunscrita que pasa por P y G/P.
Dado un triángulo ABC, se consideran los puntos A', B' y C', donde las paralelas por A, B y C a sus correspondientes lados opuestos, vuelven a cortar a la circunferencia circunscrita a ABC. Entonces, cada par de triángulos (AA'B, AA'C), (BB'C, BB'A) y (CC'A, CC'B) tienen circunferencias inscritas de mismo radio.
Se tienen las siguientes coordenadas baricéntricas: A'(a^2: c^2-b^2 : b^2-c^2), B'(c^2-a^2 : b^2 : a^2-c^2) y C'(b^2-c^2 : a^2-b^2 : c^2).
Los incentros de los triángulos AA'B y AA'C son, respectivamente:
(a^2 : c(c-b)+a|b-c| : c(b-c)), y (a^2 : b(c-b) : b(b-c)+a|b-c|); éstos determinan las recta de ecuación |b-c|x-ay-az=0.
El valor común del radio de las circunferencias inscritas a AA'B y AA'C es: bc(b^2-c^2)^2 / (2R(ab(b^2-c^2) + (b^2+c(a-c))|b^2-c^2|), con R el radio de la circunferencia circunscrita a ABC.
Similarmente, los triángulos de las rectas que unen los incentros de los pares de triángulos restantes son: bx-|c-a|y+bz=0, cx+cy-|a-b|z=0.
Estas tres rectas determinan un triángulo A1B1C1 homotético a ABC, con centro de homotecia:
Sean ABC un triángulo acutángulo y δ una recta que pasa por el ortocentro H. Denotemos por δa, δb y δc las reflexiones de δ en AH, BH, CH, resp.; δ'a, δ'b y δ'c las paralelas a δa, δb y δc a través de A, B, C, resp., y I' el incentro del triángulo A'B'C' acotado por las rectas δ'a, δ'b y δ'c.
El lugar geométrico de I' cuando δ gira alrededor de H es la circunferencia de centro H y que pasa por X265, su radio es el de la circunferencia circunscrita a ABC.
Ocurre además que los vértices de A'B'C' describen las circunferencias (B,C, X265), (C, A, X265) y (A, B, X265).
Sean ABC un triángulo, H su ortocentro y (u:v:w) las coordenadas baricéntricas de un punto P. Se denota por Ha, Hb, Hc los ortocentros de los triángulos PBC, PCA, PAB, resp.
Las reflexiones de las rectas HHa en los lados de ABC concurren en P1:
Las reflexiones de las rectas HHa en los lados de PBC en P'1:
Procediendo de forma similar, obtenemos:
Las reflexiones de la recta HHb en los lados de ABC concurren en P2 y en los lados de PCA en P'2.
Las reflexiones de la recta HHc en los lados de ABC concurren en P3 y en los lados de PAB en P'3.
El lugar geométrico de los puntos P tales que los triángulos P1P2P3 y P'1P'2P'3 son perspectivos (junto con la recta del infinito) es la hipérbola de Jerabek (conjugada isogonal de la recta de Euler):
• Cuando P se mueve en la hipérbola de Jerabek las rectas P1P'1, P2P'2 y P3P'3 concurren en Q, sobre la recta de Euler.
• También, cuando P se mueve en la hipérbola de Jerabek las rectas paralelas a P1P'1, P2P'2 y P3P'3 a través de los vértices del triángulo de contacto interior, son concurrentes en el punto medio M de H y Q.
Dado un punto P en el plano del triángulo ABC, se traza la paralela por P al lado BC que interseca a AB en Ca y a AC en Ba. Similarmente, se construyen Ab, Cb sobre BC, BA, y Bc, Ac sobre CA, CB, respectivamente.
(1) El punto P para el que BcCb, CaAc, y AbBa son todas tangentes a la circunferencia inscrita es el anticomplemento del punto de Nagel, X145 en ETC
(E. M. H. Lemoine.- Étude sur de nouveaux points remarquables du plan d’un triangle, Journal de Math. Spéciales, ser. 2, 2 (1883) 3--6).
Si P(x:y:z), coordenadas baricéntricas, entonces Ca(x : y+z : 0), Ba(x : 0 : y-z), Ab(0 : y : x+z), Cb(x+z : y : 0), Bc(x+y : 0 : z) y Ac(0 : x+y : z).
Para que la recta BcCb sea tangente al circunferencia inscrita se ha de verificar que debe contener a su polo respecto a ella; por lo que el punto P ha de estar en las cónicas (la misma situación para las otras dos rectas CaAc, y AbBa):
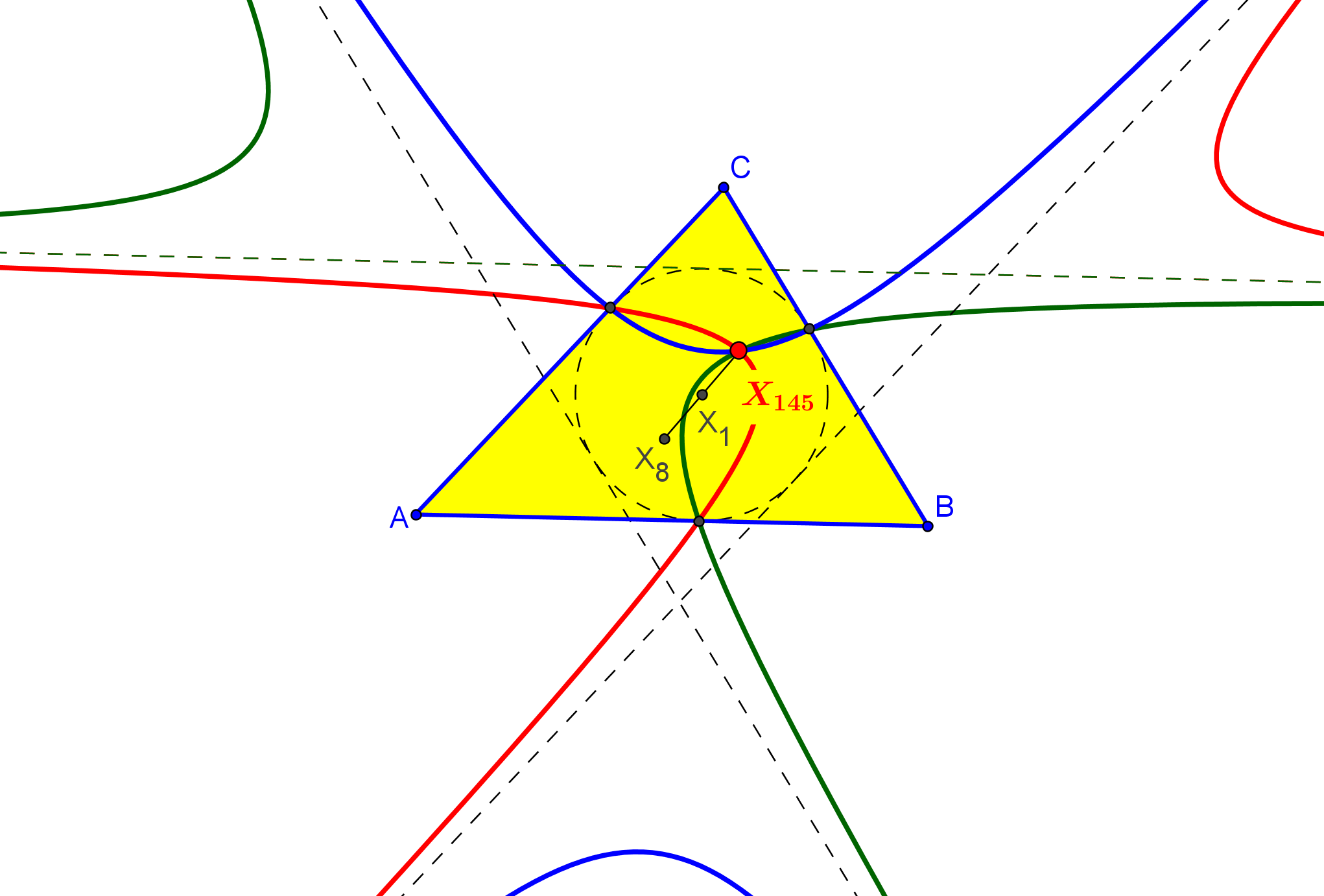
(2) Los puntos de tangencia determinan un triángulo XYZ perspectivo con ABC, con centro de perspectividad el punto de coordenadas baricéntricas:
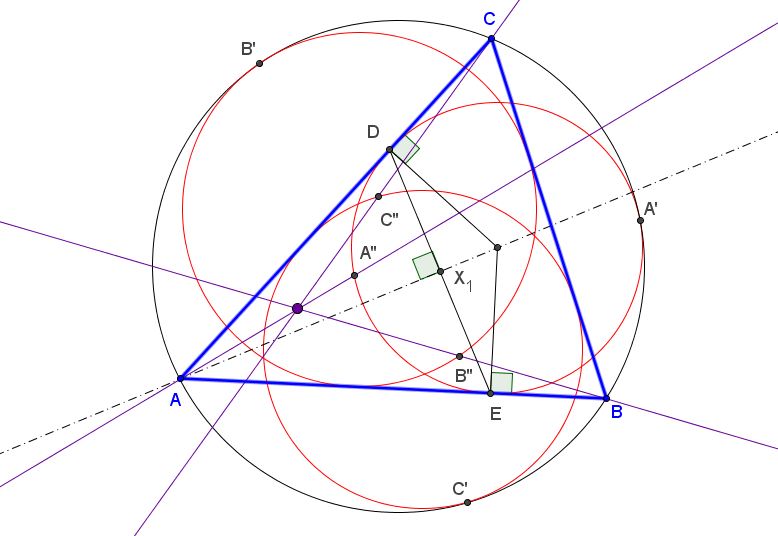
(3) El triángulo XYZ es perspectivo con el triángulo de contacto interior DEF y el centro de perspectividad también es el X145.
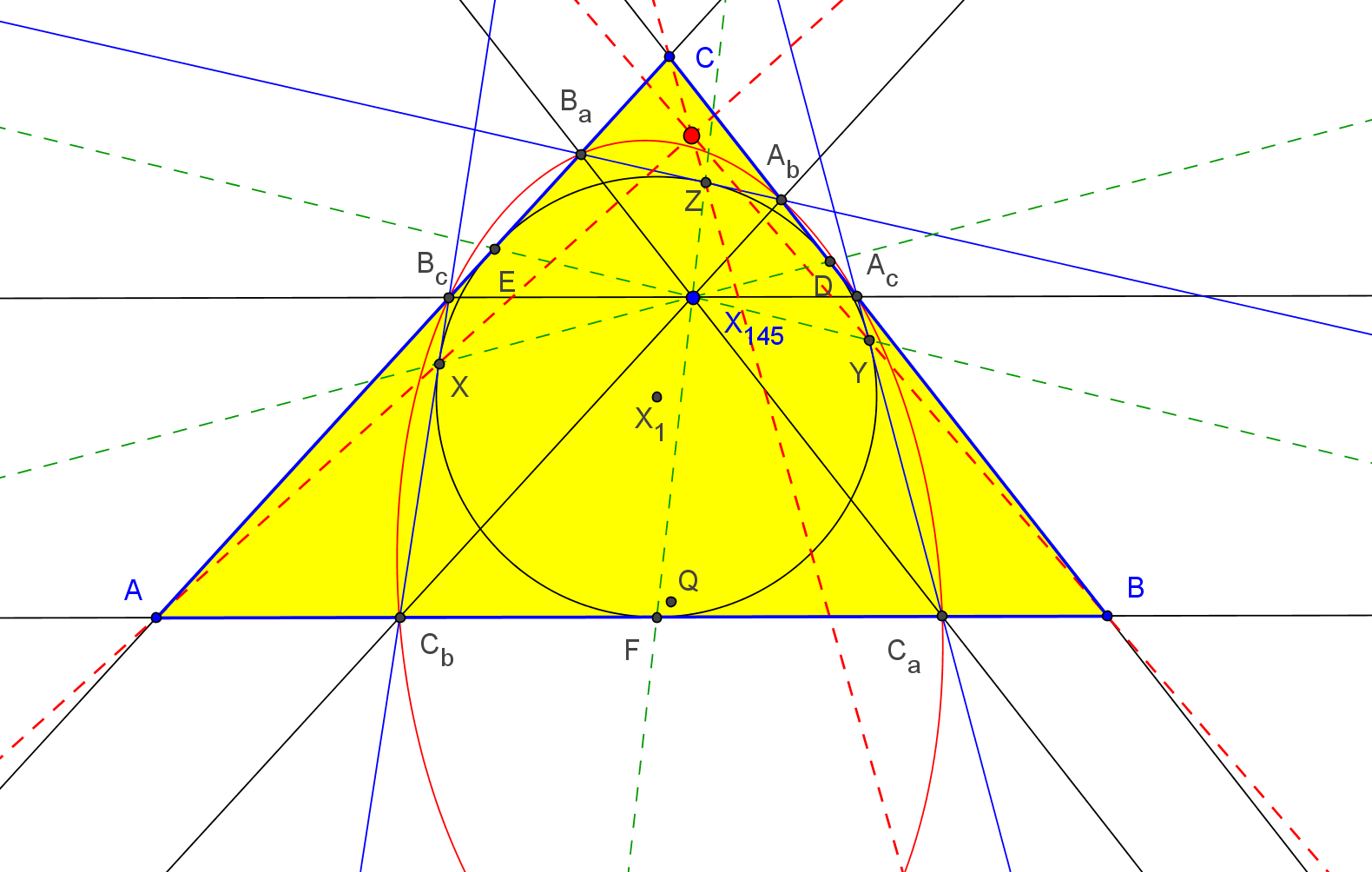
(4) Los seis puntos Ab, Ac, Bc, Ba, Ca y Cb están en una misma cónica:
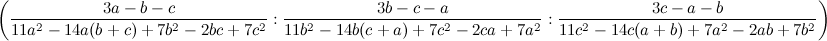
a^6(b^2w(3v*w(v-w) + u^2(v+w) + u(v^2+2v*w-2w^2)) +
c^2v(3v*w(w-v) + u^2(v+w) + u(w^2+2v*w-2v^2))) +
a^4(c^4v(u^3 + 2v*w(v-2w) - u^2(v+w) + u(v^2+v*w-2w^2)) +
b^4w(u^3 + 2v*w(w-2v) - u^2(v+w) + u(w^2+v*w-2v^2)) +
b^2c^2(u^3(v+w)+2u(v-w)^2(v+w)-6u^2(v^2+w^2)-2v*w(v^2-4v*w+w^2))) -
a^2(-c^6v(-2u^3+ u^2(v-w) + u*w(w-4v) + v*w(v+w)) -
b^6w(-2u^3+ u^2(w-v) + u*v(v-4w) + v*w(v+w)) +
b^4c^2(2u^3(2v+w) - u^2(5v^2+v*w-6w^2) +
v*w(-v^2+v*w+2w^2) + u*w(10v^2-v*w+4w^2)) +
b^2*c^4(2u^3(v+2w) + u^2(6v^2-v*w-5w^2) +
v*w(2v^2+ v*w-w^2) + u*v(4v^2-v*w+10w^2))) +
(b^2-c^2)^2u(c^4v(u^2 + u(w-v) + v(v+w)) + b^4w(u^2+u(v-w)+w(v+w)) +
b^2c^2(-4u*v*w+3u^2(v+w)+2v*w(v+w)) ) : ... : ...
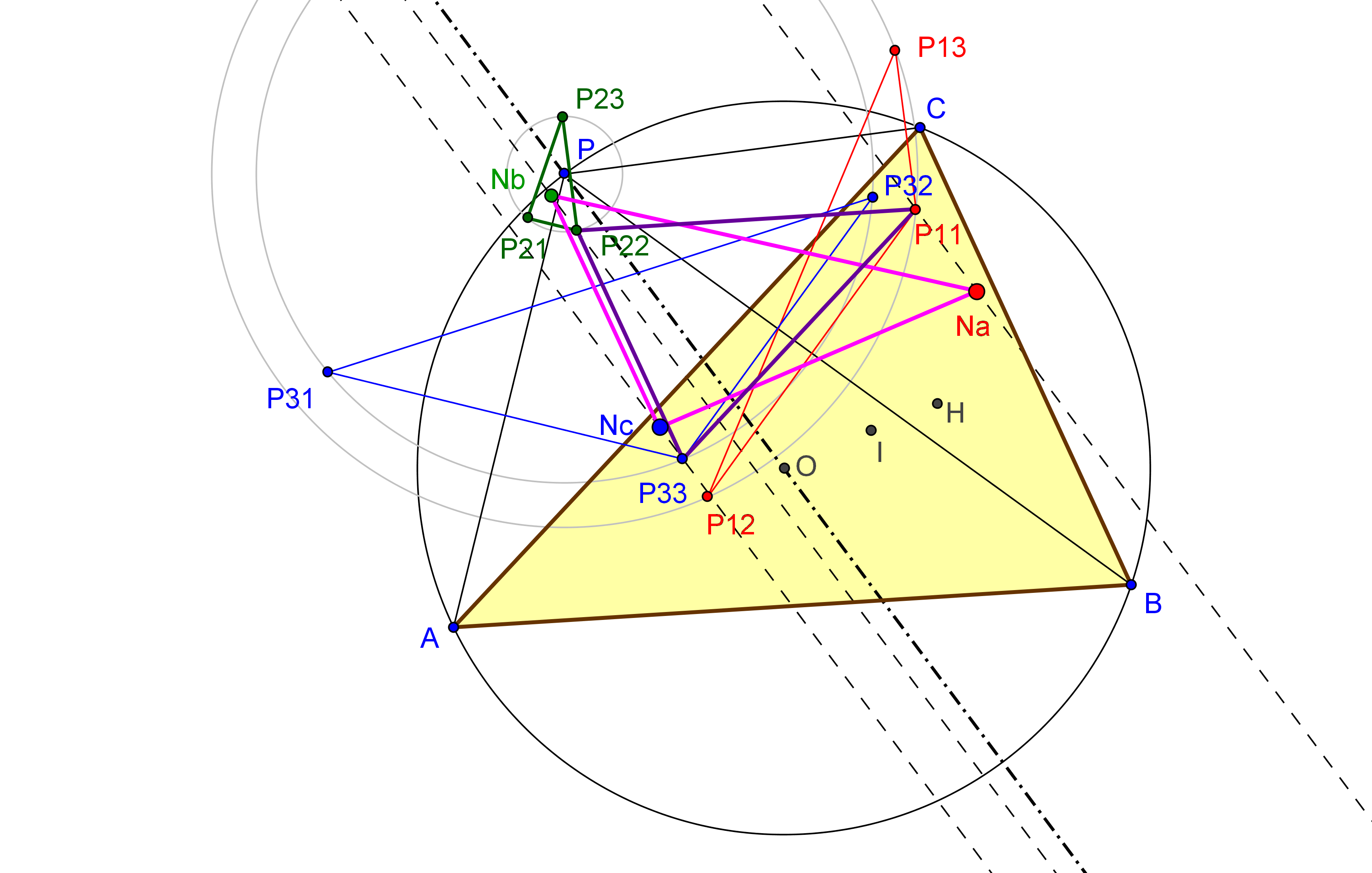
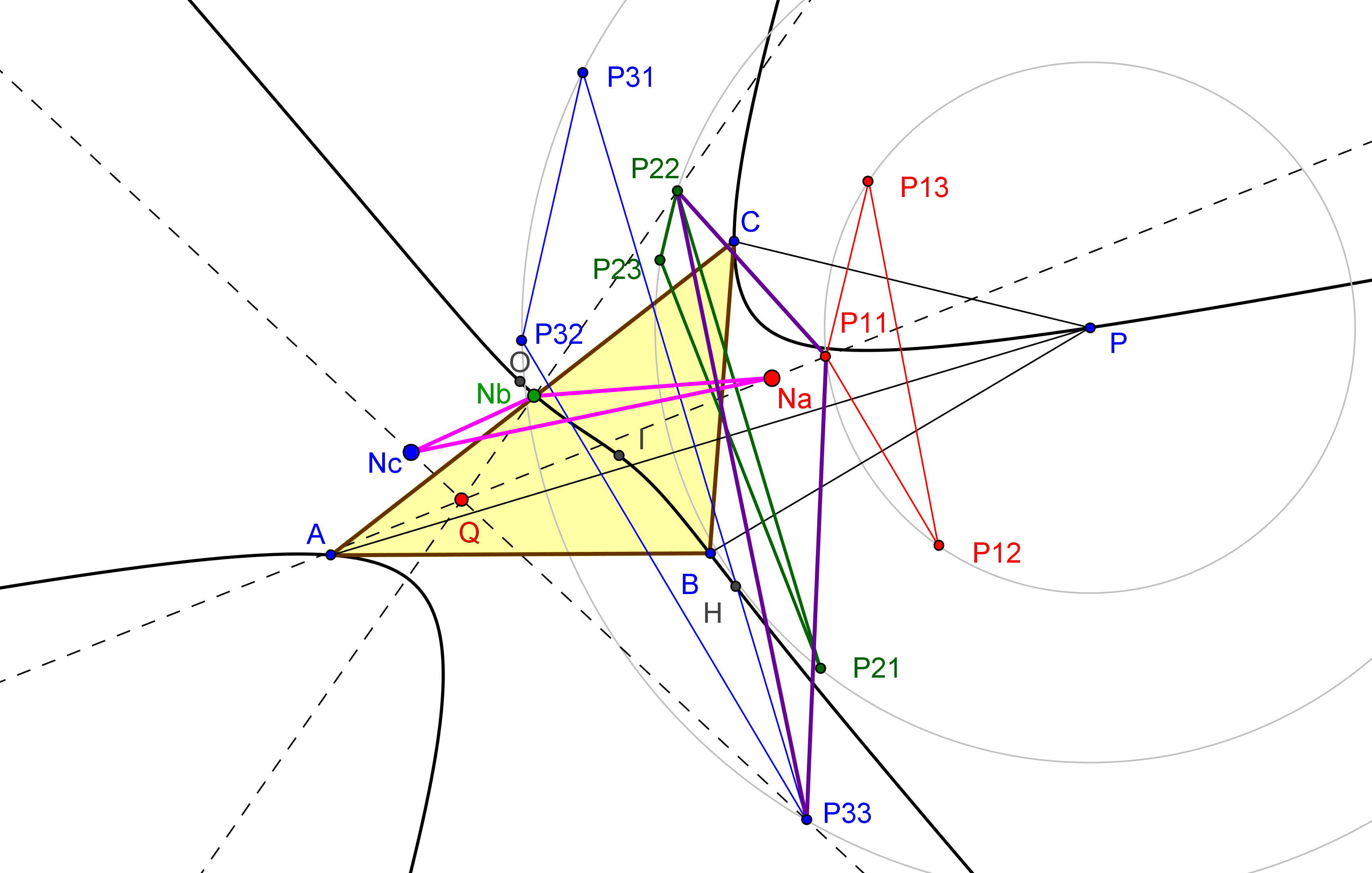
Consideremos un triángulo ABC de incentro I y denotamos por A'B'C' el triángulo ceviano de I.
• Sea W- el centro radical de las circunferencias A'(A'B), C'(C'A) y B'(B'C), y W+ el centro radical de las circunferencias A'(A'C), B'(B'A) y C'(C'B).
Los puntos W+W- forman un par bicéntrico, por lo que el punto medio de W+W- es un centro del triángulo (sobre la recta IO), que tiene (6-9-13)-número de búsqueda en ETC: -4.58771580677070881713647893, y coordenadas baricéntricas:
NOTA: Este punto ha sido incluido en la "Encyclopedia of Triangle Centers- ETC" con el número X5482="1st Hatzipolakis-Montesdeoca point".
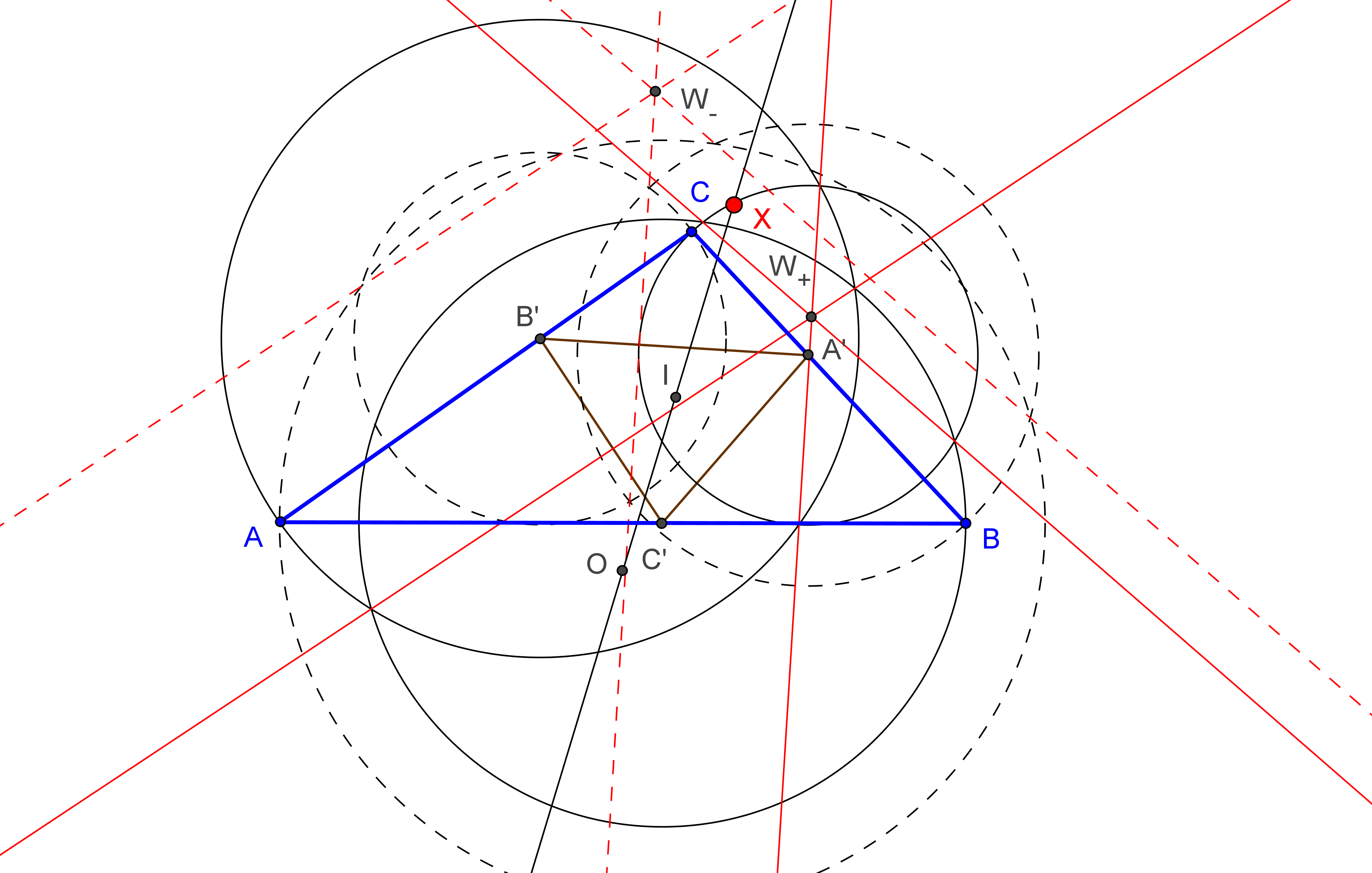
• Otro caso de punto medio de centros radicales: Sea W+ el centro radical de las circunferencias A'(A'B'), B'(B'C') y C'(C'A'), y W- el centro radical de las circunferencias A'(A'C'), B'(B'A') y C'(C'B').
Los puntos W+W- forman un par bicéntrico y el punto medio de W+W-, situado sobre la recta IO, (con (6-9-13)-número de búsqueda en ETC: 2.182865285269536019160224004) es:
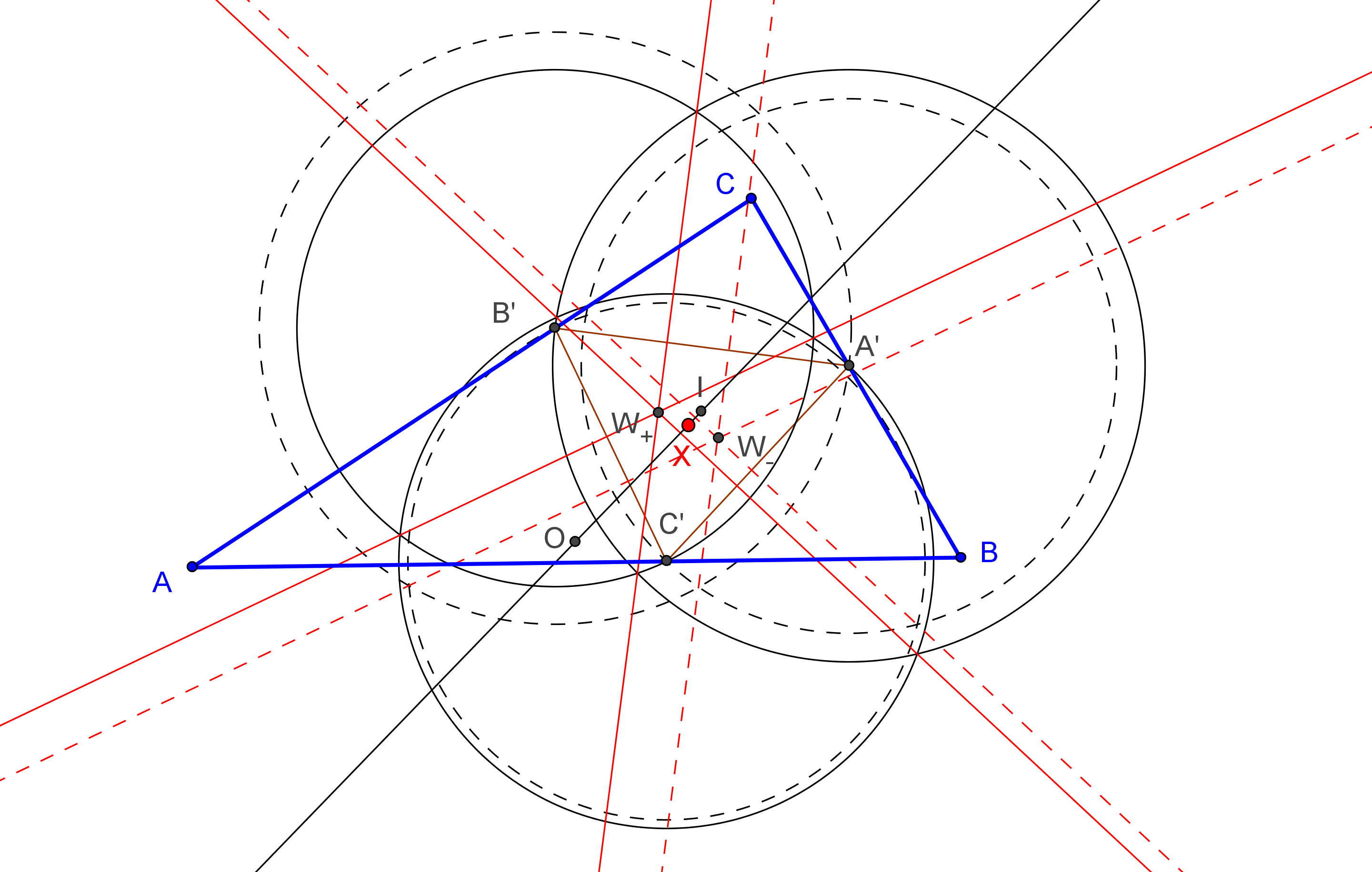
• Consideremos un triángulo ABC de circuncentro O y denotamos por A'B'C' el triángulo ceviano de O. Sea da el eje radical de la circunferencia O(OA'), de centro O y radio OA', y de la circunferencia circunscrita a OBC; de forma similar se consideran los ejes radicales db y dc.
El triángulo ABC y el acotado por las rectas da, db y dc son homotéticos
El centro de homotecia tiene coordenadas baricéntricas:
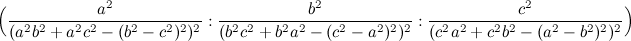
• Consideremos un triángulo ABC de circuncentro O y denotamos por A'B'C' su triángulo medial. Sea A"B"C" el triángulo circunceviano de O respecto a A'B'C', D=BC∩AA", E=CA∩BB" y F=AB∩CC".
Denotamos por da el eje radical de la circunferencia A"(A"D), de centro A" y radio A"D, y de la circunferencia circunscrita a A"BC; de forma similar se consideran los ejes radicales db y dc.
El triángulo ABC y el acotado por las rectas da, db y dc son homotéticos
El centro de homotecia tiene coordenadas baricéntricas:
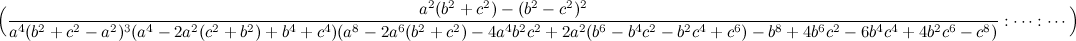
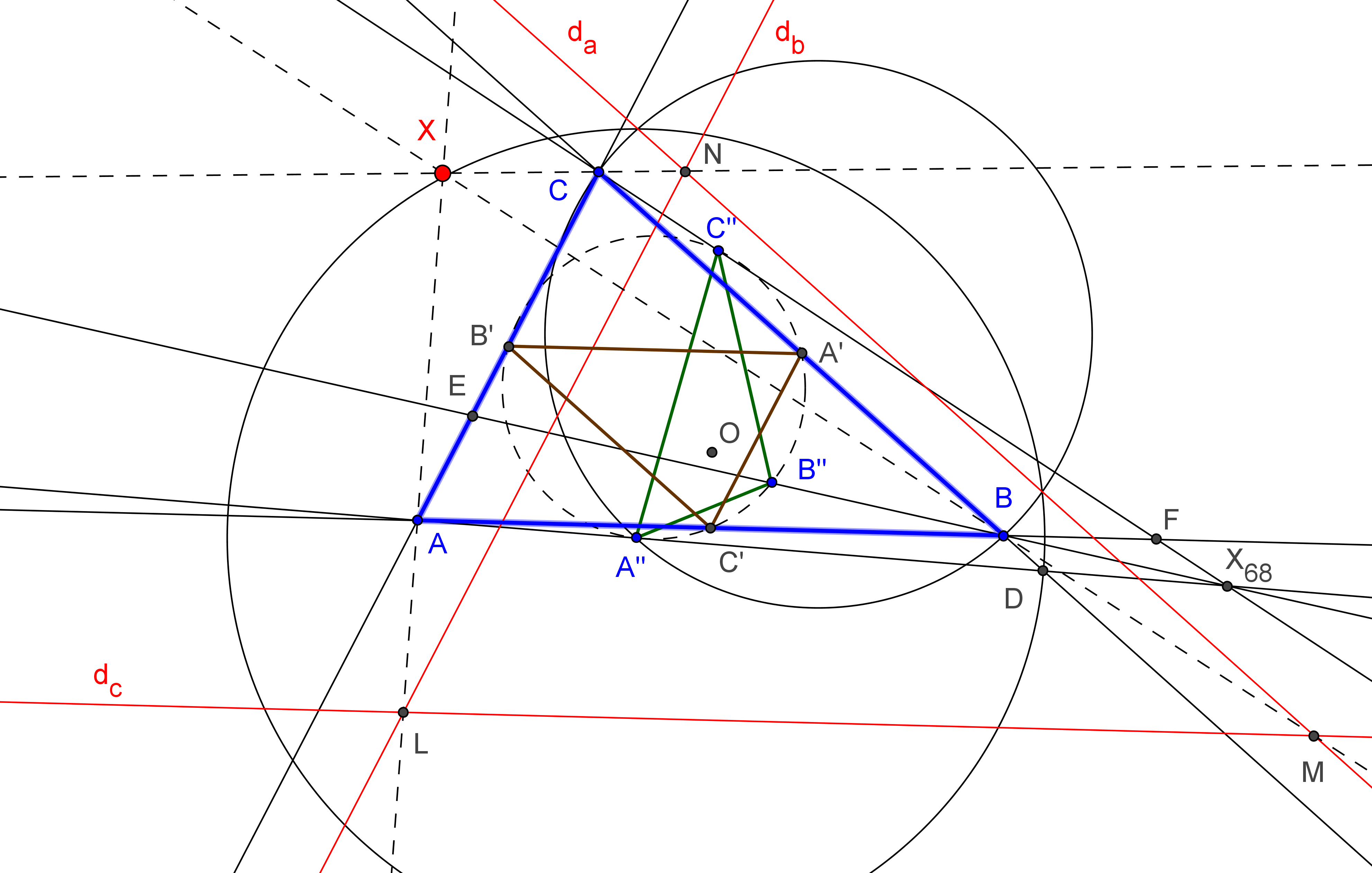
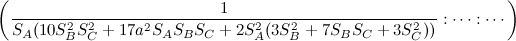
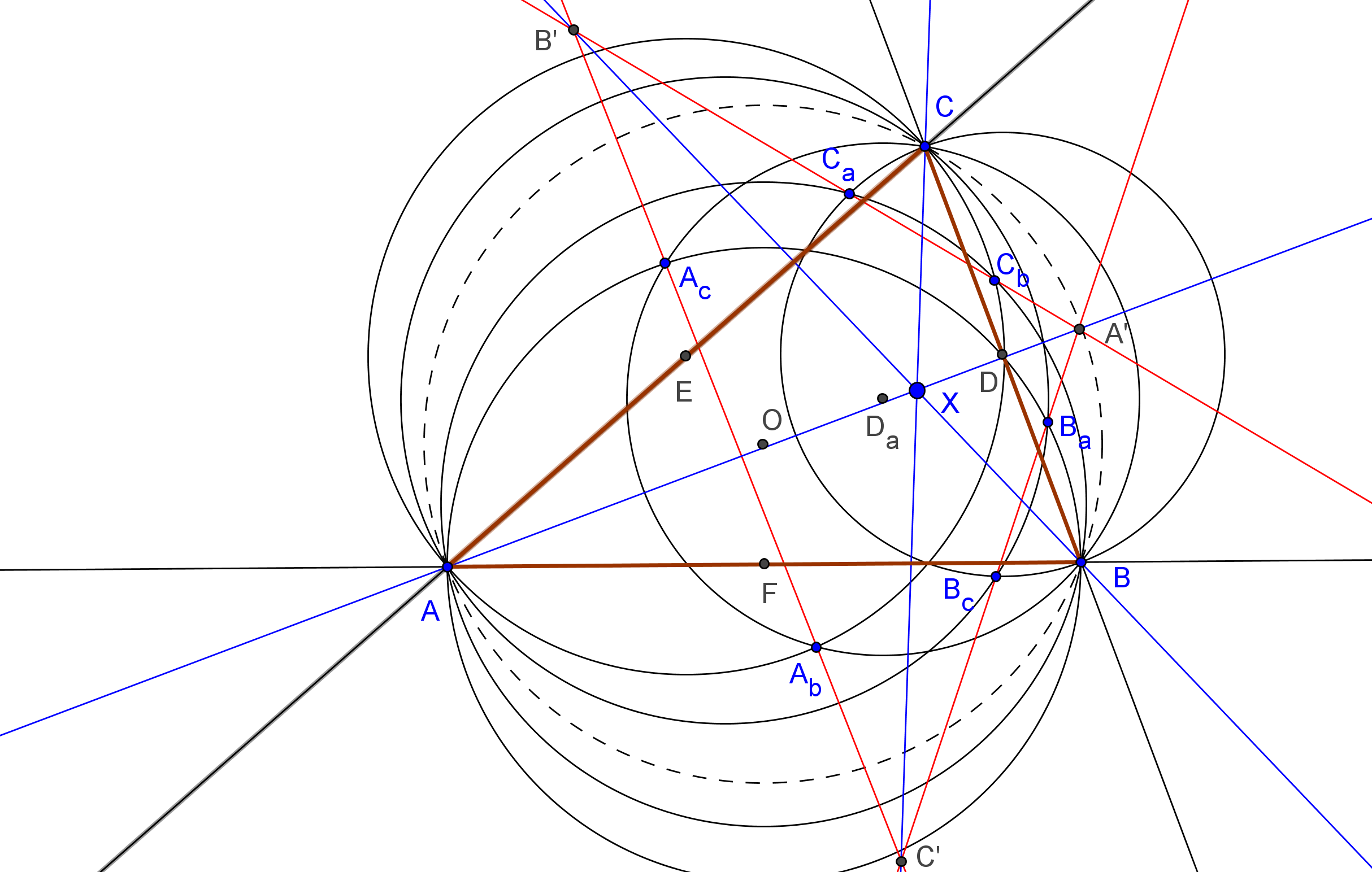
• Cuando U está en la circunferencia circunscrita, el punto de intersección de las rectas A1A2, B1B2 y C1C2 es el propio punto U.
• Cuando U se mueve en la cúbica de Darboux el lugar geométrico (?) de los puntos U' de intersección de las rectas A1A2, B1B2 y C1C2, contiene a los puntos A, B, C, antipodales de A, B, C en la circunferencia circunscrita, X3, X6, X22, X24, X1498, X1604, X1617, ...
Puntos U' como centros de perspectividad de los triángulos tangencial y circunceviano de un punto V:
(Clark Kimberling.- Triangle Centers and Central Triangles, (TCCT) §7.18, p. 201)
| U, en la cúbica de Darboux | U', punto de intersección de las rectas A1A2, B1B2 y C1C2 | V, tal que U' es el centro perspectividad de los triángulos tangencial y circunceviano de V |
| X1 | X1617 | X57 |
| X4 | X24 | X4 |
| X20 | X22 | X2 |
| X40 | X3 | X1 |
| X64 | 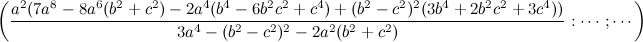 | ? |
| X84 | 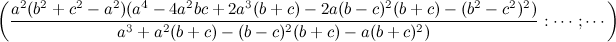 | ? |
| X1490 | X1604 | X9 | X1498 | X1498 | X83 |
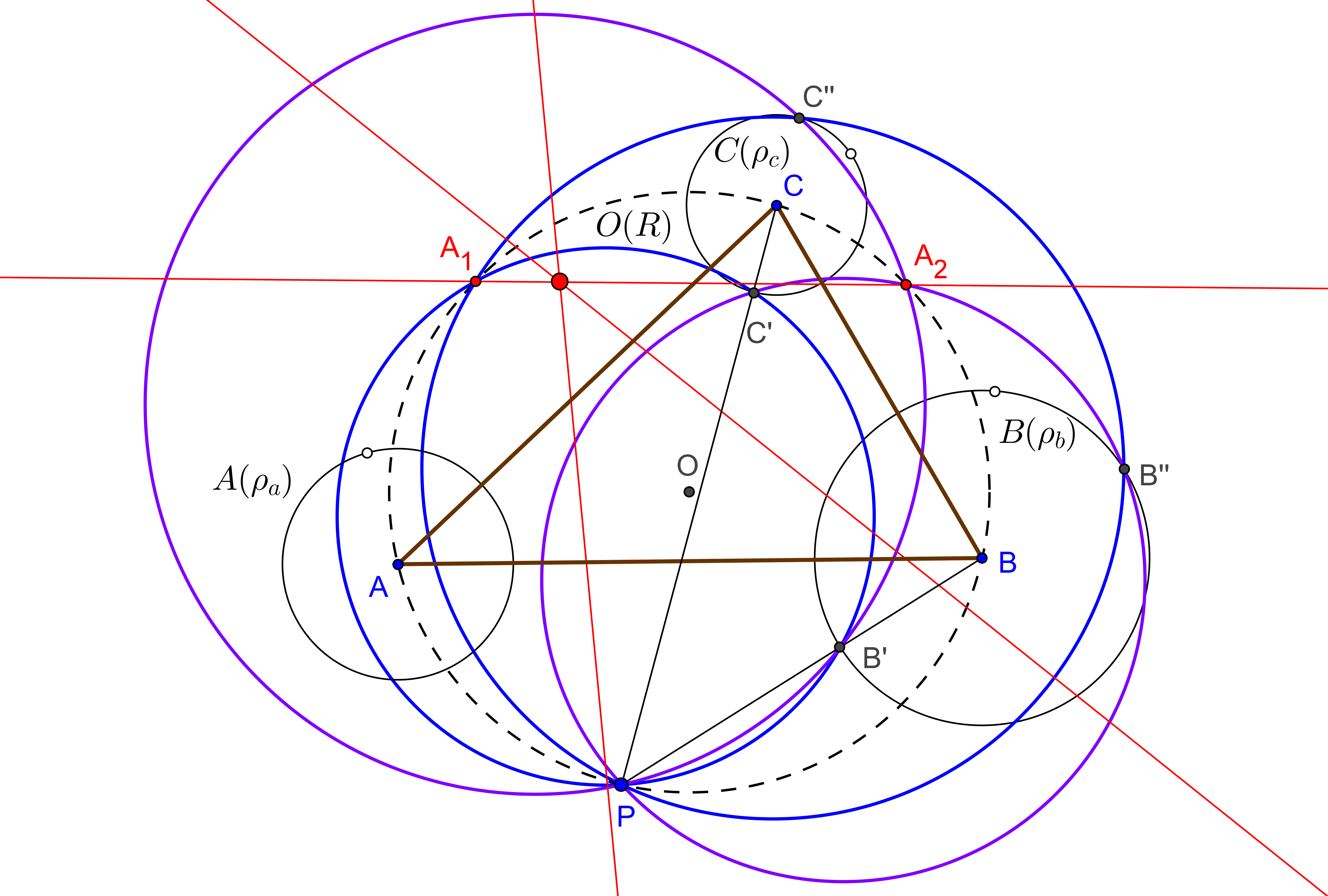
• Para las circunferencias centradas en los vértices del triángulo ABC y mutuamente tangentes, el punto común de las rectas A1A2, B1B2 y C1C2 es el X1617, centro de perspectividad de los triángulos tangencial y circunceviano de X57.
• Para las circunferencias A(a), B(b) y C(c), centradas en los vértices del triángulo ABC y de radios la longitud del lado opuesto, el punto común de las rectas A1A2, B1B2 y C1C2 es el X22, centro de perspectividad de los triángulos tangencial y circunceviano de X2.
• Para las circunferencias A(ma), B(mb) y C(mc), centradas en los vértices del triángulo ABC y de radios la longitud de la mediana correspondiente, el punto común de las rectas A1A2, B1B2 y C1C2 es el X1995 (como en el caso de las circunferencias que pasan por el baricentro).
• Para las circunferencias A(ha), B(hb) y C(hc), centradas en los vértices del triángulo ABC y tangentes al lado opuesto, el punto común de las rectas A1A2, B1B2 y C1C2 es el simediano, X6.
• Para las circunferencias A(AOa), B(BOb) y C(COc), centradas en los vértices del triángulo ABC y que pasan por los pies de las cevianas del circuncentro, el punto común de las rectas A1A2, B1B2 y C1C2 tiene primera coordenada baricéntrica:
• Para las circunferencias A(AI), B(BI) y C(CI), centradas en los vértices del triángulo ABC y que pasan todas por el incentro (I=X1), el punto común de las rectas A1A2, B1B2 y C1C2 es el X56, centro de perspectividad de los triángulos tangencial y circunceviano de X266.
• Para las circunferencias A(AG), B(BG) y C(CG), centradas en los vértices del triángulo ABC y que pasan todas por el baricentro (G=X2), el punto común de las rectas A1A2, B1B2 y C1C2 es el X1995 (como en el caso de radio las medianas), centro de perspectividad de los triángulos tangencial y circunceviano de la raíz baricéntrica de X1383.
• Para las circunferencias A(AO), B(BO) y C(CO), centradas en los vértices del triángulo ABC y que pasan todas por el circuncentro (O=X3), el punto común de las rectas A1A2, B1B2 y C1C2 (mediatrices de ABC) es el X3, centro de perspectividad de los triángulos tangencial y circunceviano de X1.
• Para las circunferencias A(AH), B(BH) y C(CH), centradas en los vértices del triángulo ABC y que pasan todas por el ortocentro (H=X4), el punto común de las rectas A1A2, B1B2 y C1C2 es el X24, centro de perspectividad de los triángulos tangencial y circunceviano de X4.
• Para las circunferencias A(AK), B(BK) y C(CK), centradas en los vértices del triángulo ABC y que pasan todas por el simediano (K=X6), el punto común de las rectas A1A2, B1B2 y C1C2 es el X1384, centro de perspectividad de los triángulos tangencial y circunceviano del punto con coordenadas baricéntricas:
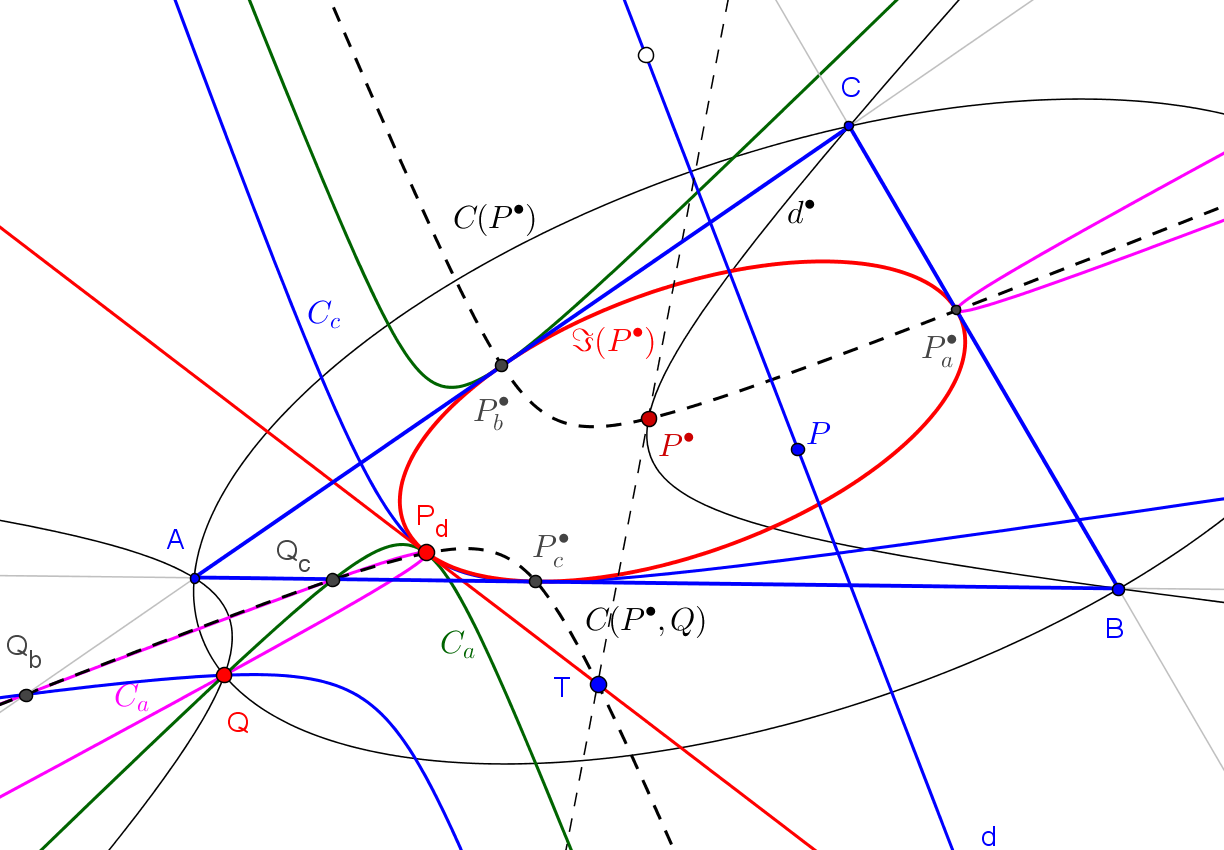
| P | X1 | X3 | X6 | X9 | X10 | X30 | X37 |
| Q | X63 | X1993 | X22 | X3870 | X3995 | X2 | X4651 |

.png)
| Generalización |
|---|
| ¿Se tiene estos mismos resultados en otra cónica biceviana C(P,Q) que pasa por P? |
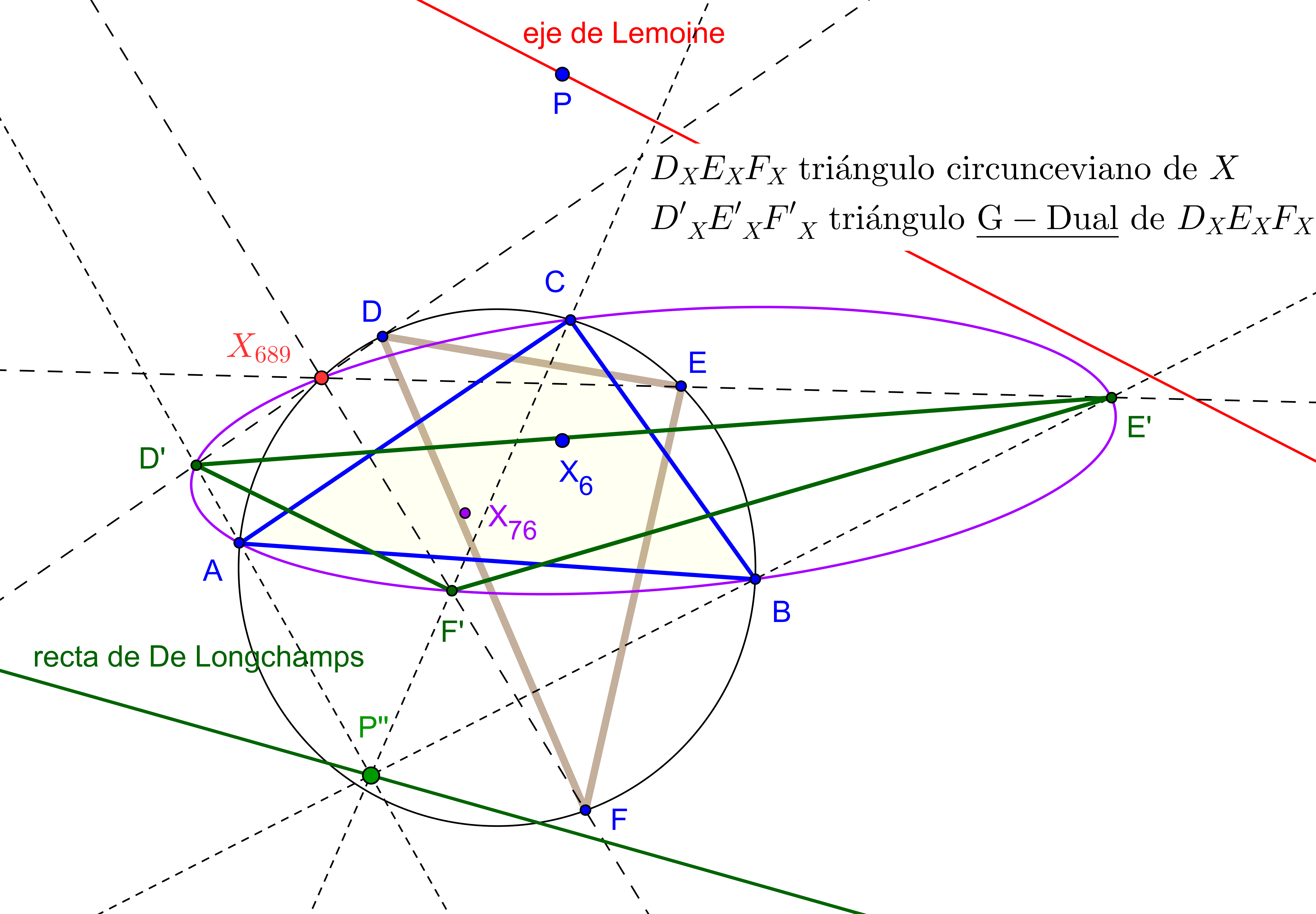
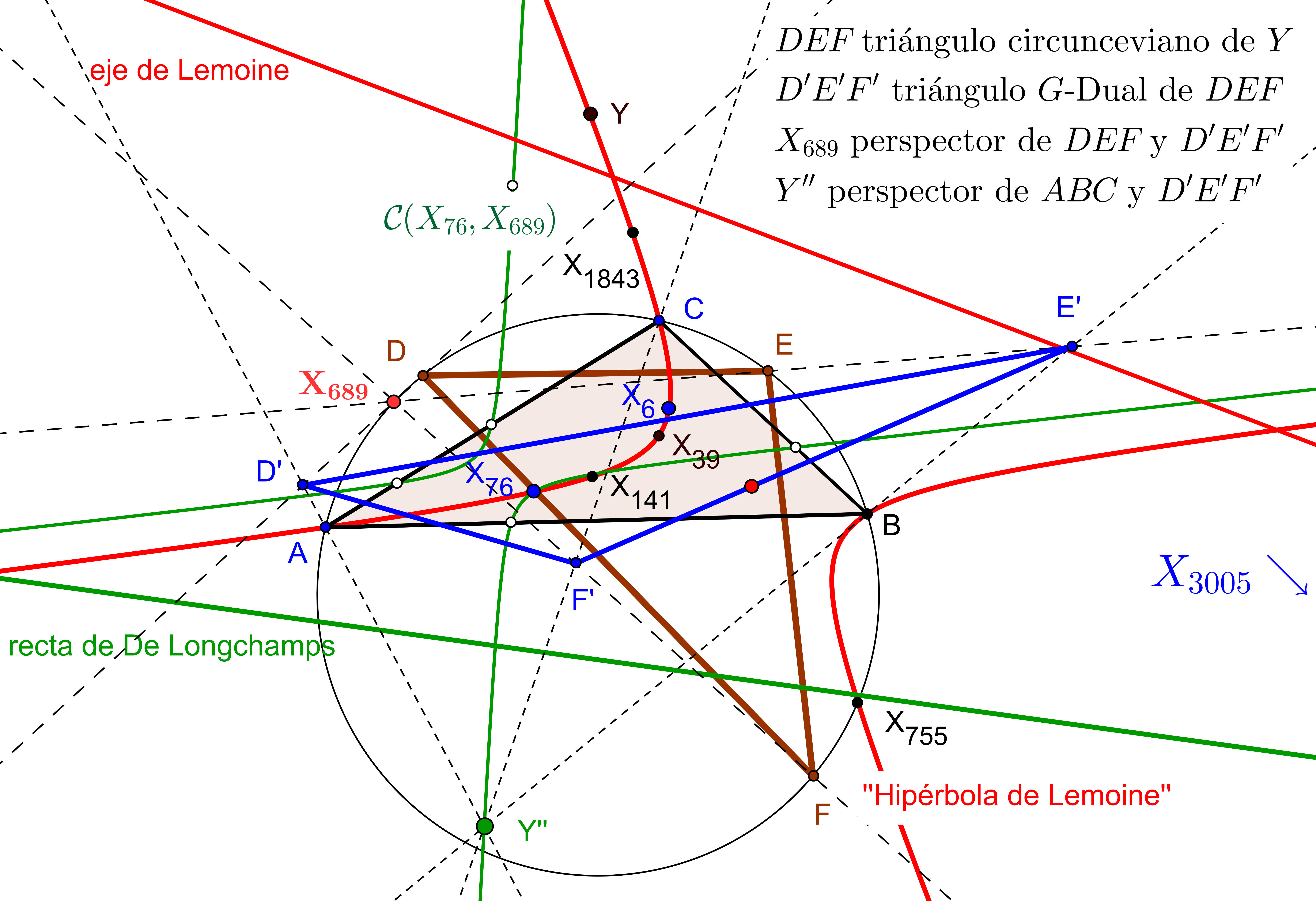
Dado un triángulo DEF, se considera el triángulo D'E'F' de vértices los puntos D'=dE∩dF, E'=dF∩dE y F'=dD∩dE. Diremos que D'E'F' es el triángulo G-Dual de DEF.
Los triángulos DEF y D'E'F' son perspectivos.
Además, si D, E y F están en una cónica circunscrita a ABC, el centro de perspectividad también está en la cónica.
Si ABC y DEF son perspectivos, también son perspectivos ABC y D'E'F'.
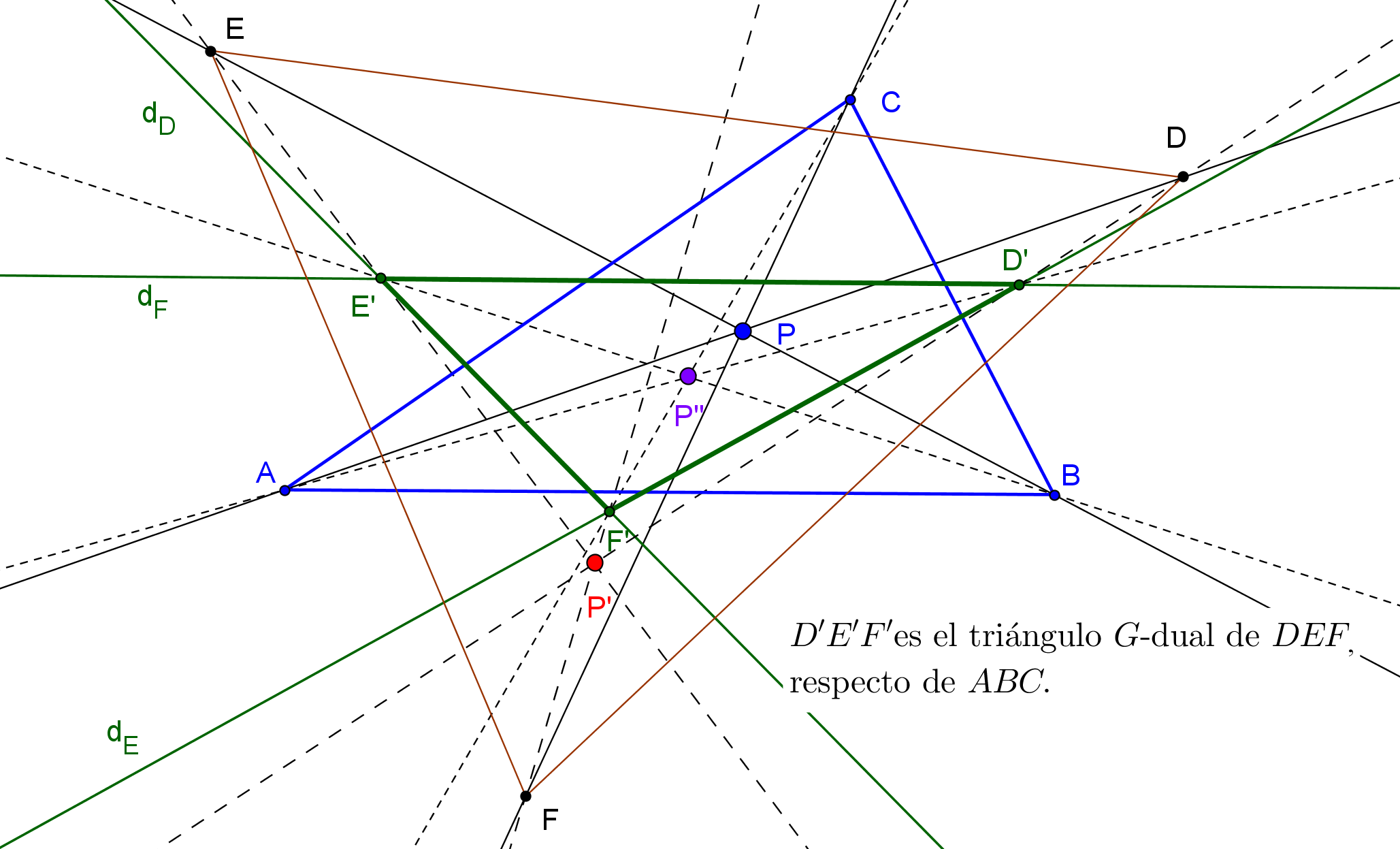
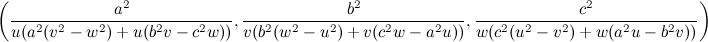
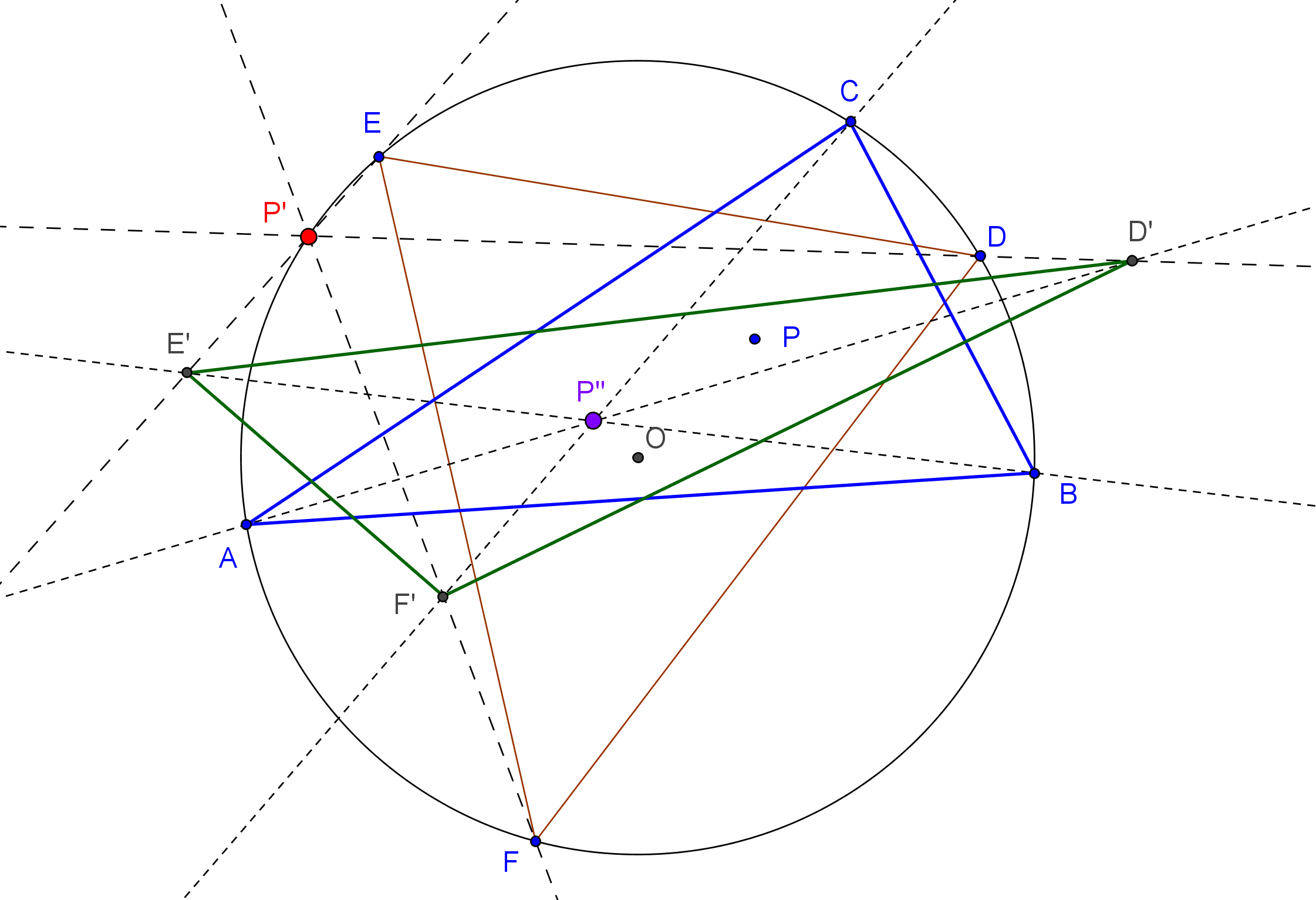

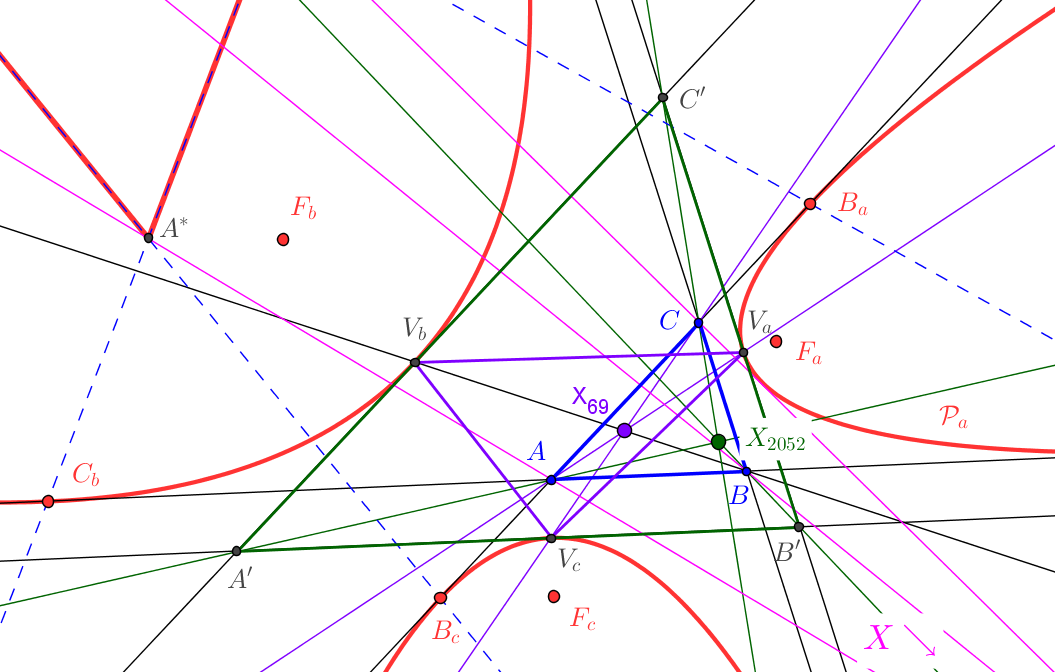
X=(1/(SA2(a4 - SBSC) - SB2SC2): ... : ... )
con (6-9-13)-número de búsqueda en ETC: 7.600894940587217504799796347